【易错题】高中必修二数学下期中第一次模拟试卷含答案(1)

合集下载

【易错题】高中必修二数学下期中试卷带答案(1)

【易错题】高中必修二数学下期中试卷带答案(1)一、选择题1．水平放置的ABC V 的斜二测直观图如图所示，若112A C ＝，111A B C △的面积为22，则AB 的长为（）A ．2B ．217C ．2D ．82．下列命题正确的是（）A ．经过三点确定一个平面B ．经过一条直线和一个点确定一个平面C ．两两相交且不共点的三条直线确定一个平面D ．四边形确定一个平面3．<九章算术>中，将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥P ABC -为鳖臑，PA ⊥平面,2,4ABC PA AB AC ===，三棱锥P ABC -的四个顶点都在球O 的球面上，则球O 的表面积为（）A ．8πB ．12πC ．20πD ．24π 4．已知一个三棱锥的三视图如图所示，其中俯视图是等腰直角三角形，则该三棱锥的外接球表面积为（）A 3πB ．3πC ．43πD ．12π5．四棱锥P ABCD -的底面ABCD 为正方形，PA ⊥底面ABCD ，2AB =，72PA =，若该四棱锥的所有顶点都在同一球面上，则该球的表面积为（） A ．812π B ．814π C ．65π D ．652π 6．已知三棱锥S ABC -的每个顶点都在球O 的表面上，ABC ∆是边长为43角形，SA ⊥平面ABC ，且SB 与平面ABC 所成的角为6π，则球O 的表面积为（） A ．20π B ．40π C ．80π D ．160π7．在三棱锥P ABC -中，PA ⊥平面1202,2ABC BAC AP AB ∠=︒==，，，M 是线段BC 上一动点，线段PM 长度最小值为3，则三棱锥P ABC -的外接球的表面积是（）A ．92πB ．92πC ．18πD ．40π8．在梯形ABCD 中，90ABC ∠=︒，//AD BC ，222BC AD AB ===.将梯形ABCD 绕AD 所在直线旋转一周而形成的曲面所围成的几何体的体积为（）A ．23πB ．43πC ．53πD ．2π9．点A 、B 、C 、D 在同一个球的球面上，AB=BC=2，AC=2，若四面体ABCD 体积的最大值为23，则这个球的表面积为（） A ．1256π B ．8π C ．2516π D ．254π 10．如图1，ABC ∆是以B 为直角顶点的等腰直角三角形，T 为线段AC 的中点，G 是BC 的中点，ABE ∆与BCF ∆分别是以AB 、BC 为底边的等边三角形，现将ABE ∆与BCF ∆分别沿AB 与BC 向上折起（如图2），则在翻折的过程中下列结论可能正确的个数为（）图1 图2（1）直线AE ⊥直线BC ；（2）直线FC ⊥直线AE ；（3）平面//EAB 平面FGT ；（4）直线//BC 直线AE .A ．1个B ．2个C ．3个D ．4个11．已知直三棱柱111ABC A B C -的所有棱长都相等，M 为11A C 的中点，则AM 与1BC 所成角的余弦值为( )A ．153B ．53C ．64D ．10412．若圆的参数方程为12cos ,32sin x y θθ=-+⎧⎨=+⎩（θ为参数），直线的参数方程为21,61x t y t =-⎧⎨=-⎩（t 为参数），则直线与圆的位置关系是（） A ．相交且过圆心 B ．相交但不过圆心C ．相切D ．相离二、填空题13．已知棱长为1的正方体ABCD －A 1B 1C 1D 1中，E ，F ，M 分别是线段AB 、AD 、AA 1的中点，又P 、Q 分别在线段A 1B 1、A 1D 1上，且A 1P ＝A 1Q ＝x (0<x <1).设平面MEF ∩平面MPQ＝l ，现有下列结论：①l ∥平面ABCD ；②l ⊥AC ；③直线l 与平面BCC 1B 1不垂直；④当x 变化时，l 不是定直线.其中不成立的结论是________.(写出所有不成立结论的序号)14．《九章算术》中，将底面为长方形且由一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的三棱锥称之为鳖臑．若三棱锥P ABC -为鳖臑，PA ⊥平面ABC ，2,4PA AB AC ===，三棱锥P ABC -的四个顶点都在球O 的球面上，则球O 的表面积为__________.15．已知在直角梯形ABCD 中，AB AD ⊥，CD AD ⊥，224AB AD CD ===，将直角梯形ABCD 沿AC 折叠，使平面BAC ⊥平面DAC ，则三棱锥D ABC -外接球的体积为__________．16．若过点(8,1)P 的直线与双曲线2244x y -=相交于A ，B 两点，且P 是线段AB 的中点，则直线AB 的方程为________．17．已知三棱锥D ABC -的体积为2，ABC ∆是边长为2的等边三角形，且三棱锥D ABC -的外接球的球心O 恰好是CD 的中点，则球O 的表面积为_______.18．圆台的两个底面面积之比为4：9，母线与底面的夹角是60°，轴截面的面积为1803，则圆台的侧面积为_____．19．已知PA 垂直于平行四边形ABCD 所在平面，若PC BD ⊥，则平行四边形ABCD 一定是___________.20．如图：点P 在正方体1111ABCD A B C D -的面对角线1BC 上运动，则下列四个命题： ①三棱锥1A D PC -的体积不变； ②1A P ∥面1ACD ；③1DP BC ^；④面1PDB ^面1ACD ．其中正确的命题的序号是__________.三、解答题21．已知圆C 过点()1,1A ，()3,1B -，圆心C 在直线250x y --=上，P 是直线34100x y -+=上任意一点．（1）求圆C 的方程；（2）过点P 向圆C 引两条切线，切点分别为M ，N ，求四边形PMCN 的面积的最小值．22．如图四棱锥C ABDE -的侧面ABC ∆是正三角形，BD ⊥面ABC ，//BD AE 且2BD AE =，F 为CD 的中点.（1）求证：//EF 面ABC（2）若6BD AB ==，求BF 与平面BCE 所成角的正弦值23．如图，四棱锥P ABCD -的底面ABCD 是直角梯形，//AB CD ， 33AB CD ==，AB AD ⊥，AB PA ⊥，且2AD PA ==，22PD =，13PE PB =uur uu r（1）证明：//CE 平面PAD ；（2）求点B 到平面ECD 的距离；24．已知以点C （1，﹣2）为圆心的圆与直线x+y ﹣1=0相切．（1）求圆C 的标准方程；（2）求过圆内一点P （2，﹣）的最短弦所在直线的方程．25．已知点(3,4),(9,0)A B -，,C D 分别为线段,OA OB 上的动点，且满足AC BD =（1）若4,AC =求直线CD 的方程；（2）证明：OCD ∆的外接圆恒过定点（异于原点）．26．已知圆22:20M x y x a +-+=（1）若8a =-，过点(4,5)P 作圆M 的切线，求该切线的方程；（2）当圆22:(1)(23)4N x y ++-=与圆M 相外切时，从点(2,8)Q -射出一道光线，经过y 轴反射，照到圆M 上的一点R ，求光线从点Q 经反射后走到点R 所走过路线的最小值.【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【解析】【分析】依题意由111A B C △的面积为22114B C =，所以8BC =，2AC =，根据勾股定理即可求AB ．【详解】依题意，因为111A B C △的面积为2所以11111sin 452AC B C ︒=⨯⋅=111222B C ⨯⨯⨯，解得114B C =，所以8BC =，2AC =，又因为AC BC ⊥，由勾股定理得：AB ====故选B ．【点睛】本题考查直观图还原几何图形，属于简单题. 利用斜二测画法作直观图，主要注意两点：一是与x 轴平行的线段仍然与x '轴平行且相等；二是与y 轴平行的线段仍然与y '轴平行且长度减半. 2．C解析：C【解析】【分析】根据确定一个平面的公理及推论即可选出.【详解】A 选项，根据平面基本性质知，不共线的三点确定一个平面，故错误；B 选项，根据平面基本性质公理一的推论，直线和直线外一点确定一个平面，故错误；C 选项，根据公理一可知，不共线的三点确定一个平面，而两两相交且不共点的三条直线，在三个不共线的交点确定的唯一平面内，所以两两相交且不共点的三条直线确定一个平面，正确；选项D,空间四边形不能确定一个平面，故错误；综上知选C.【点睛】本题主要考查了平面的基本性质公理一及其推论，属于中档题.3．C解析：C【解析】【分析】先作出三棱锥P ABC -的图像，根据P ABC -四个面都为直角三角形和PA ⊥平面ABC ，可知PC 中点即为球心，利用边的关系求出球的半径，再由24S R π=计算即得.【详解】三棱锥P ABC -如图所示，由于P ABC -四个面都为直角三角形，则ABC V 是直角三角形，且2ABC π∠=，BC ∴=PA ⊥平面ABC ，且PAC V 是直角三角形，∴球O 的直径2PC R ===R ∴=，则球O 的表面积2420S R ππ==.故选：C【点睛】本题考查多面体外接球的表面积，是常考题型.4．C解析：C【解析】【分析】 2的等腰直角三角形，与底面垂直的侧面是个等腰三角形，底边长为2，高为2，故三棱锥的外接球与以棱长为2的正方体的外接球相同，由此可得结论【详解】由三视图知几何体是一个侧棱与底面垂直的三棱锥， 2与底面垂直的侧面是个等腰三角形，底边长为2，高为2，故三棱锥的外接球与以棱长为2的正方体的外接球相同，其直径为33∴三棱锥的外接球体积为(343433ππ⨯=故选C【点睛】本题主要考查了三视图，几何体的外接球的体积，考查了空间想象能力，计算能力，属于中档题．5．B解析：B【解析】【分析】根据题意可知，该四棱锥的外接球即为其所在长方体的外接球，根据公式即可求得.【详解】根据题意，为方便说明，在长方体中找出该四棱锥如图所示：由图可知在长方体中的四棱锥P ABCD -完全满足题意，故该四棱锥的外接球即是长方体的外接球，故外接球半径222722294R ⎛⎫++ ⎪⎝⎭==，故该球的表面积为28144S R ππ==. 故选：B .【点睛】本题考查四棱锥外接球的问题，关键的步骤是将问题转化为求长方体的外接球. 6．C解析：C【解析】【分析】根据线面夹角得到4SA =，计算ABC ∆的外接圆半径为42sin a r A==，2222SA R r ⎛⎫=+ ⎪⎝⎭，解得答案. 【详解】 SA ⊥平面ABC ，则SB 与平面ABC 所成的角为6SBA π∠=，故4SA =.ABC ∆的外接圆半径为42sin a r A ==，设球O 的半径为R ，则2222SA R r ⎛⎫=+ ⎪⎝⎭，解得5R =O 的表面积为2480R ππ=. 故选：C .【点睛】本题考查了三棱锥的外接球问题，意在考查学生的计算能力和空间想象能力.7．C解析：C【解析】首先确定三角形ABC 为等腰三角形，进一步确定球的球心，再求出球的半径，最后确定球的表面积．【详解】解：如图所示：三棱锥P ABC -中，PA ⊥平面2,2ABC AP AB ==，，M 是线段BC 上一动点，线段PM 3则：当AM BC ⊥时，线段PM 达到最小值，由于：PA ⊥平面ABC ，所以：222PA AM PM +=，解得：1AM =，所以：3BM =，则：60BAM ∠=︒，由于：120BAC ∠=︒，所以：60MAC ∠=︒则：ABC V 为等腰三角形．所以：23BC =在ABC V 中，设外接圆的直径为324120r sin ==︒，则：2r =，所以：外接球的半径2229222R ⎛⎫=+= ⎪ ⎪⎝⎭，则：94182S ππ=⋅⋅=，故选：C ．【点睛】本题考查的知识要点：三棱锥的外接球的球心的确定及球的表面积公式的应用． 8．C解析：C【分析】【详解】由题意可知旋转后的几何体如图:直角梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体是一个底面半径为1，母线长为2的圆柱挖去一个底面半径同样是1、高为1的圆锥后得到的组合体，所以该组合体的体积为2215121133V V V πππ=-=⨯⨯-⨯⨯⨯=圆柱圆锥故选C.考点：1、空间几何体的结构特征；2、空间几何体的体积. 9．D解析：D【解析】试题分析：根据题意知，ABC V 是一个直角三角形，其面积为1．其所在球的小圆的圆心在斜边AC 的中点上，设小圆的圆心为Q ，若四面体ABCD 的体积的最大值，由于底面积ABC S V 不变，高最大时体积最大，所以，DQ 与面ABC 垂直时体积最大，最大值为12·33ABC S DQ =V ，即12133DQ ⨯⨯=，∴2DQ =，设球心为O ，半径为R ，则在直角AQO V 中，222OA AQ OQ =+，即()22212R R =+-，∴54R =，则这个球的表面积为：2525444S ππ⎛⎫== ⎪⎝⎭；故选Ｄ．考点：球内接多面体，球的表面积． 10．C解析：C【解析】【分析】（1）翻折时使得平面ABE ⊥平面ABC ，由面面垂直的性质定理得出BC ⊥平面ABE ，从而使得（1）有可能；（2）翻折时使得点E 、F 两点重合，利用勾股定理可证得此时AE CE ⊥，即AE FC ⊥；（3）翻折时使得平面ABE 和平面BCF 同时与平面ABC 垂直，利用面面垂直的性质定理、直线与平面平行的判定定理以及面面平行的判定定理可证明出平面//EAB 平面（4）利用反证法，可推出//BC AE 不成立. 【详解】（1）翻折时，若平面ABE ⊥平面ABC ，由于ABC ∆是以B 为直角顶点的等腰直角三角形，则BC AB ⊥，又Q 平面ABE I 平面ABC AB =，BC ⊂平面ABC ，BC ∴⊥平面ABE ，AE ⊂Q 平面ABC ，此时AE BC ⊥；（2）设AB BC a ==，则2AC a =，且有AE CF a ==，翻折时，若点E 、F 重合，则AE CE a ==，222AE CE AC ∴+=，此时，AE CE ⊥，即AE FC ⊥；（3）如下图所示：翻折时，若平面ABE 和平面BCF 同时与平面ABC 垂直，取AB 的中点D ，连接DE 、FG 、GT 、FT .ABE ∆Q 是等边三角形，且D 为AB 的中点，DE AB ⊥∴.Q 平面ABE ⊥平面ABC ，平面ABE I 平面ABC AB =，DE ⊂平面ABE .DE ∴⊥平面ABC ，同理可证FG ⊥平面ABC ，//DE FG ∴， DE ⊄Q 平面FGT ，FG ⊂平面FGT ，//DE ∴平面FGT .G Q 、T 分别为BC 、AC 的中点，//AB GT ∴，AB ⊄Q 平面FGT ，GT ⊂平面FGT ，//AB ∴平面FGT . DE AB D =Q I ，∴平面//EAB 平面FGT ；（4）假设AE 与BC 可能平行，BC AB ⊥Q ，则AE AB ⊥，事实上60BAE ∠=o ，即AE 与AB 不垂直，假设不成立，因此，AE 与BC 不可能平行. 因此，可能正确命题的个数为3. 故选：C. 【点睛】本题考查的是线面位置关系的判定，判断时要熟悉线面、面面平行与垂直的判定、性质定理，考查推理能力，属于中等题.11．D【解析】【分析】取AC 的中点N ，连接1C N ，则1//AM C N ,所以异面直线AM 与1BC 所成角就是直线AM 与1C N 所成角，在1BNC ∆中，利用余弦定理，即可求解．【详解】由题意，取AC 的中点N ，连接1C N ，则1//AM C N , 所以异面直线AM 与1BC 所成角就是直线AM 与1C N 所成角，设正三棱柱的各棱长为2,则115,22,3C N BC BN ===，设直线AM 与1C N 所成角为θ，在1BNC ∆中，由余弦定理可得222(5)(22)(3)10cos 42522θ+-==⨯⨯，即异面直线AM 与1BC 所成角的余弦值为10，故选D ．【点睛】本题主要考查了异面直线所成角的求解，其中解答中把异面直线所成的角转化为相交直线所成的角是解答的关键，着重考查了推理与运算能力，属于基础题．12．B解析：B 【解析】【分析】根据题意，将圆和直线的参数方程变形为普通方程，分析可得圆心不在直线上，再利用点到直线的距离公式计算可得圆心(1,3)-到直线320y x --=的距离2d <，得到直线与圆的位置关系为相交．【详解】根据题意，圆的参数方程为1232x cos y sin θθ=-+⎧⎨=+⎩（θ为参数），则圆的普通方程为22(1)(3)4x y ++-=，其圆心坐标为(1,3)-，半径为2.直线的方程为2161x t y t =-⎧⎨=-⎩（t 为参数），则直线的普通方程为13(1)y x +=+，即320y x --=，圆心不在直线上.∴圆心(1,3)-到直线320y x --=的距离为33(1)2210219d -⨯--==<+，即直线与圆相交. 故选A. 【点睛】本题考查直线、圆的参数方程，涉及直线与圆的位置关系，解答本题的关键是将直线与圆的参数方程变形为普通方程.二、填空题13．④【解析】【详解】连接BDB1D1∵A1P ＝A1Q ＝x ∴PQ ∥B1D1∥BD ∥EF 则P Q ∥平面MEF 又平面MEF∩平面MPQ ＝l ∴PQ ∥ll ∥EF ∴l ∥平面ABCD 故①成立；又EF ⊥AC ∴l ⊥AC 故解析：④ 【解析】【详解】连接BD ，B 1D 1，∵A 1P ＝A 1Q ＝x ，∴PQ ∥B 1D 1∥BD ∥EF ，则PQ ∥平面MEF ，又平面MEF ∩平面MPQ ＝l ，∴PQ ∥l ，l ∥EF ， ∴l ∥平面ABCD ，故①成立；又EF ⊥AC ，∴l ⊥AC ，故②成立；∵l ∥EF ∥BD ，故直线l 与平面BCC 1B 1不垂直，故③成立；当x 变化时，l 是过点M 且与直线EF 平行的定直线，故④不成立．即不成立的结论是④.14．【解析】【分析】由题意得该四面体的四个面都为直角三角形且平面可得因为为直角三角形可得所以因此结合几何关系可求得外接球的半径代入公式即可求球的表面积【详解】本题主要考查空间几何体由题意得该四面体的四个解析：20π【解析】【分析】由题意得该四面体的四个面都为直角三角形，且PA ⊥平面ABC ，可得PC =PB =PBC V 为直角三角形，可得BC =PB BC ⊥，因此AB BC ⊥，结合几何关系，可求得外接球O 的半径R ===O 的表面积．【详解】本题主要考查空间几何体．由题意得该四面体的四个面都为直角三角形，且PA ⊥平面ABC ，2PA AB ==，4AC =，PC =PB =因为PBC V 为直角三角形，因此BC =BC =（舍）．所以只可能是BC = 此时PB BC ⊥，因此AB BC ⊥，所以平面ABC 所在小圆的半径即为22ACr ==，又因为2PA =，所以外接球O 的半径R ===所以球O 的表面积为24π20πS R ==．【点睛】本题考查三棱锥的外接球问题，难点在于确定BC 的长，即得到AB BC ⊥，再结合几何性质即可求解，考查学生空间想象能力，逻辑推理能力，计算能力，属中档题．15．【解析】结合题意画出折叠后得到的三棱锥如图所示由条件可得在底面中取AB 的中点OAC 的中点E 连OCOE 则∵∴∵平面平面∴平面∴又∴∴∴点O 为三棱锥外接球的球心球半径为2∴答案：点睛：（1）本题是一道关解析：323π【解析】结合题意画出折叠后得到的三棱锥D ABC -如图所示，由条件可得在底面ACB ∆中，90,ACB AC BC ∠=︒==AB 的中点O ，AC 的中点E ，连OC,OE 。

【易错题】高中必修二数学下期中试卷附答案

【易错题】高中必修二数学下期中试卷附答案一、选择题1．已知三棱锥A BCD -中，5AB CD ==，2==AC BD ，3AD BC ==，若该三棱锥的四个顶点在同一个球面上，则此球的体积为（） A ．32π B ．24πC ．6πD ．6π2．已知m ，n 表示两条不同直线，α表示平面，下列说法正确的是（） A ．若//,//,m n αα则//m n B ．若m α⊥，n α⊂，则m n ⊥ C ．若m α⊥，m n ⊥，则//n α D ．若//m α，m n ⊥，则n α⊥ 3．圆心在x +y =0上，且与x 轴交于点A （-3，0）和B （1，0）的圆的方程为（）A ．22(1)(1)5x y ++-=B ．22(1)(1)5x y -++=C ．22(1)(1)5x y -++=D ．22(1)(1)5x y ++-=4．已知定义在R 上的函数()21()x m f x m -=-为实数为偶函数,记0.5(log 3),a f =2b (log 5),c (2)f f m ==,则,,a b c ,的大小关系为（）A ．a b c <<B ．c a b <<C ．a c b <<D ．c b a <<5．已知三棱锥S ABC -的所有顶点都在球O 的球面上，SC 为球O 的直径，且SC OA ⊥，SC OB ⊥，OAB V 为等边三角形，三棱锥S ABC -的体积为43，则球O 的半径为( ) A ．3B ．1C ．2D ．46．在我国古代数学名著九章算术中，将四个面都为直角三角形的四面体称为鳖臑，如图，在鳖臑ABCD 中， AB ⊥平面BCD ，且AB BC CD ==，则异面直线AC 与BD 所成角的余弦值为（）A ．12B ．12-C 3D ．3 7．已知圆O ：2224110x y x y ++--=，过点()1,0M 作两条相互垂直的弦AC 和BD ，那么四边形ABCD 的面积最大值为（）A ．42B ．24C ．212D ．68．椭圆22221(0)x y a b a b+=>>的左右焦点分别是1F 、2F ，以2F 为圆心的圆过椭圆的中心，且与椭圆交于点P ，若直线1PF 恰好与圆2F 相切于点P ，则椭圆的离心率为（）A ．312+ B ．31-C ．22D ．512- 9．某锥体的三视图如图所示（单位：cm ），则该锥体的体积（单位：cm 3）是（）A ．13B ．12C ．16D ．110．如图，正四面体ABCD 中，,E F 分别是线段AC 的三等分点，P 是线段AB 的中点，G 是线段BD 的动点，则( )A ．存在点G ，使PG EF ⊥成立B ．存在点G ，使FG EP ⊥成立C ．不存在点G ，使平面EFG ⊥平面ACD 成立D ．不存在点G ，使平面EFG ⊥平面ABD 成立11．某几何体的三视图如图所示（单位：cm ），其俯视图为等边三角形，则该几何体的体积（单位：3cm ）是（）A ．3B 1033C ．23D 83312．α，β是两个不重合的平面，在下列条件中，可判断平面α，β平行的是（） A ．m ，n 是平面α内两条直线，且//m β，//n β B ．α内不共线的三点到β的距离相等 C ．α，β都垂直于平面γD ．m ，n 是两条异面直线，m α⊂，n β⊂，且//m β，//n α二、填空题13．已知圆22:20(0)M x y ay a +-=>截直线0x y +=所得线段的长度是22M 与圆22:(1)(1)1N x y -+-=的位置关系是_________．14．在平面直角坐标xOy 系中,设将椭圆()2222110y x a a a +=>-绕它的左焦点旋转一周所覆盖的区域为D ，P 为区域D 内的任一点，射线()02x y x =≥－上的点为Q ，若PQ 的最小值为a ，则实数a 的取值为_____．15．已知P 是抛物线24y x =上的动点，点Q 是圆22:(3)(3)1C x y ++-=上的动点，点R 是点P 在y 轴上的射影，则PQ PR +的最小值是____________．16．若圆1C ：220x y ax by c ++++=与圆2C ：224x y +=关于直线21y x =-对称，则c =______.17．已知,m n 为直线，,αβ为空间的两个平面，给出下列命题：①,//m n m n αα⊥⎧⇒⎨⊥⎩；②,////m n m n αβαβ⊂⎧⎪⊂⇒⎨⎪⎩；③,//m m ααββ⊥⎧⇒⎨⊥⎩；④,//m m n n ββ⊥⎧⇒⎨⊥⎩．其中的正确命题为_________________．18．已知正方体1111ABCD A B C D -的棱长为1，点E 是棱1BB 的中点，则点1B 到平面ADE 的距离为__________.19．若圆C ：222430x y x y ++-+=，关于直线260ax by ++=对称，则由点(),a b 向圆所作的切线长的最小值为______． 20．在正方体1111ABCD A B C D -中，①BD P 平面11CB D ②直线AD 与1CB 所成角的大小为60︒ ③1AA BD ⊥ ④平面11A BC ∥平面1ACD 请把所有正确命题的序号填在横线上________．三、解答题21．如图，在四棱锥P ABCD -中，底面ABCD 是平行四边形，平面PBD ⊥平面ABCD ，2AD =，25PD =，4AB PB ==，60BAD ∠=︒.（1）求证：AD PB ⊥；（2）E 是侧棱PC 上一点，记PEPCλ=，当PB ⊥平面ADE 时，求实数λ的值 22．如图，在四棱锥P ABCD -中，底面ABCD 为正方形，PA ⊥平面ABCD ，PA AB =，AC 与BD 交于点O ，E ，F 分别为AB ，PC 的中点．（Ⅰ）求证：EF ∥平面PAD ；（Ⅱ）求证：AF ⊥平面POD ．23．如图所示，四棱锥B AEDC -中，平面AEDC ⊥平面ABC ，F 为BC 的中点，P 为BD 的中点，且AE ∥DC ，90ACD BAC ∠=∠=︒，2DC AC AB AE ===．（Ⅰ）证明：平面BDE ⊥平面BCD ；（Ⅱ）若2DC =，求三棱锥E BDF -的体积．24．如图，已知三棱锥A BPC -中，AP PC ⊥，AC BC ⊥，M 为AB 的中点，D 为PB 的中点，且PMB △为正三角形.（1）求证：//DM 平面APC ；（2）求证：BC ⊥平面APC ；（3）若4BC =，10AB =，求三棱锥D BCM -的体积.25．如图，在ABC V 中AC BC ⊥且点O 为AB 的中点，矩形ABEF 所在的平面与平面ABC 互相垂直.（1）设EC 的中点为M ，求证：//OM 平面ACF ；（2）求证：AC ⊥平面CBE26．如图，矩形ABCD 的两条对角线相交于点M(2，0)，AB 边所在直线的方程为x －3y －6＝0，点T(－1，1)在AD 边所在直线上．求：(1) AD 边所在直线的方程； (2) DC 边所在直线的方程．【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【解析】【分析】作出三棱锥A BCD -的外接长方体AEBF GDHC -，计算出该长方体的体对角线长，即可得出其外接球的半径，然后利用球体体积公式可计算出外接球的体积. 【详解】作出三棱锥A BCD -的外接长方体AEBF GDHC -，如下图所示：设DG x =，DH y =，DE z =，则2223AD x z =+=，2224DB y z =+=，2225DC x y =+=，上述三个等式相加得()222222234512AD BD CD x y z++=++=++=，2226x y z ++=62R =，因此，此球的体积为34663ππ⨯=⎝⎭. 故选：C. 【点睛】本题考查三棱锥外接球体积的计算，将三棱锥补成长方体，利用长方体的体对角线作为外接球的直径是解题的关键，考查空间想象能力与计算能力，属于中等题.2．B解析：B 【解析】试题分析：线面垂直，则有该直线和平面内所有的直线都垂直，故B 正确. 考点：空间点线面位置关系．3．A解析：A 【解析】【分析】由题意得：圆心在直线x=-1上，又圆心在直线x+y=0上，故圆心M 的坐标为（-1，1），再由点点距得到半径。

【易错题】高中必修二数学下期中模拟试卷(含答案)(1)

【易错题】高中必修二数学下期中模拟试卷(含答案)(1)一、选择题1．已知三棱锥A BCD -中，5AB CD ==，2==AC BD ，3AD BC ==，若该三棱锥的四个顶点在同一个球面上，则此球的体积为（） A ．32π B ．24πC ．6πD ．6π2．已知m ，n 表示两条不同直线，α表示平面，下列说法正确的是（） A ．若//,//,m n αα则//m n B ．若m α⊥，n α⊂，则m n ⊥ C ．若m α⊥，m n ⊥，则//n α D ．若//m α，m n ⊥，则n α⊥ 3．设l 为直线，,αβ是两个不同的平面，下列命题中正确的是( )A ．若//l α，//l β，则//αβB ．若l α⊥，l β⊥，则//αβC ．若l α⊥，//l β，则//αβD ．若αβ⊥，//l α，则l β⊥4．已知,,,A B C D 是同一球面上的四个点，其中ABC ∆是正三角形，AD ⊥平面ABC ，26AD AB ==，则该球的体积为（）A ．48πB ．24πC ．16πD ．323π5．已知直线m 、n 及平面α，其中m ∥n ，那么在平面α内到两条直线m 、n 距离相等的点的集合可能是：（1）一条直线；（2）一个平面；（3）一个点；（4）空集。

其中正确的是（）A ．（1）（2）（3）B ．（1）（4）C ．（1）（2）（4）D ．（2）（4）6．已知一个三棱锥的三视图如图所示，其中俯视图是等腰直角三角形，则该三棱锥的外接球表面积为（）A 3πB ．3πC ．43πD ．12π7．若直线20ax y +-=和直线()2140x a y +-+=平行，则a 的值为（） A ．1-或2B ．1-C ．2D ．不存在8．若某几何体的三视图（单位：cm ）如图所示，则该几何体的体积等于（）A ．310cmB ．320cmC ．330cmD ．340cm9．椭圆22221(0)x y a b a b+=>>的左右焦点分别是1F 、2F ，以2F 为圆心的圆过椭圆的中心，且与椭圆交于点P ，若直线1PF 恰好与圆2F 相切于点P ，则椭圆的离心率为（） A ．312+ B ．31-C ．22D ．512- 10．在长方体1111ABCD A B C D -中，11111,2AA A D a A B a ===，点P 在线段1AD 上运动，当异面直线CP 与1BA 所成的角最大时，则三棱锥11C PA D -的体积为（）A ．34aB ．33aC ．32aD ．3a 3a11．，为两个不同的平面，，为两条不同的直线，下列命题中正确的是（）①若，，则； ②若，，则； ③若，，，则④若，，，则.A ．①③B ．①④C ．②③D ．②④12．若底面是菱形的棱柱其侧棱垂直于底面，且侧棱长为5，它的对角线的长分别是9和15，则这个棱柱的侧面积是( )． A ．130B ．140C ．150D ．160二、填空题13．已知直线40Ax By A +-=与圆O ：2236x y +=交于M ，N 两点，则线段MN 中点G 的轨迹方程为______．14．过正方体1111ABCD A B C D -的顶点A 作直线l ，使l 与棱AB 、AD 、1AA 所成的角都相等，这样的直线l 可以作_________条.15．已知正方体1111ABCD A B C D -的棱长为1，点E 是棱1BB 的中点，则点1B 到平面ADE 的距离为__________.16．正四棱锥P ABCD -底面的四个顶点,,,A B C D 在球O 的同一个大圆上，点P 在球面上.若163P ABCDV -=，则球O 的体积是______． 17．已知B 与点()1,2,3A 关于点()0,1,2M -对称，则点B 的坐标是______．18．直线10x y --=与直线20x ay --=互相垂直，则a =__________．19．已知双曲线的半焦距为，过右焦点且斜率为1的直线与双曲线的右支交于两点，若抛物线的准线被双曲线截得的弦长是（为双曲线的离心率），则的值为__________．20．已知棱长等于23的正方体1111ABCD A B C D -，它的外接球的球心为O ﹐点E 是AB 的中点，则过点E 的平面截球O 的截面面积的最小值为________.三、解答题21．在平面直角坐标系xOy 中，已知圆C 经过()0,2A ，()0,0O ，(),0D t （0t >）三点，M 是线段AD 上的动点，1l ，2l 是过点()10B ,且互相垂直的两条直线，其中1l 交y 轴于点E ，2l 交圆C 于P 、Q 两点. （1）若6t PQ ==，求直线2l 的方程；（2）若t 是使2AM BM ≤恒成立的最小正整数 ①求t 的值； ②求三角形EPQ 的面积的最小值．22．如图，在三棱锥S ABC -中，SAC ∆为等边三角形，4AC =，43BC=，BC AC ⊥，3cos SCB ∠=-，D 为AB 的中点．（1）求证：AC SD ⊥；（2）求直线SD 与平面SAC 所成角的大小．23．如图1所示，在等腰梯形ABCD 中，4524AB CD BAD AB CD ∠=︒==∥，，，点E 为AB 的中点.将ADE ∆沿DE 折起，使点A 到达P 的位置，得到如图2所示的四棱锥P EBCD -，点M 为棱PB 的中点.（1）求证：PD MCE ∥平面；（2）若PDE EBCD ⊥平面平面，求三棱锥M BCE -的体积.24．如图所示，已知四棱锥P ABCD -中，底面ABCD 为菱形，PA ⊥平面ABCD ，60,,ABC E F ∠=o 分别是,BC PB 的中点．（1）证明：AE ⊥平面PAD ；（2）若H 为PD 上的动点，EH 与平面PAD 所成最大角的正切值为3，求二面角B AFC --的正切值．25．已知圆22C (4)4x y +-=：，直线:(31)(1)40l m x m y ++--=.（1）求直线l 所过定点A 的坐标；（2）求直线l 被圆C 所截得的弦长最短时直线l 的方程及最短弦长；（3）已知点M (-3,4)，在直线MC 上(C 为圆心)，存在定点N (异于点M )，满足：对于圆C 上任一点P ，都有||||PM PN 为一常数，试求所有满足条件的点N 的坐标及该常数. 26．如图，矩形ABCD 的两条对角线相交于点M(2，0)，AB 边所在直线的方程为x －3y －6＝0，点T(－1，1)在AD 边所在直线上．求：(1) AD 边所在直线的方程； (2) DC 边所在直线的方程．【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【解析】【分析】作出三棱锥A BCD -的外接长方体AEBF GDHC -，计算出该长方体的体对角线长，即可得出其外接球的半径，然后利用球体体积公式可计算出外接球的体积. 【详解】作出三棱锥A BCD -的外接长方体AEBF GDHC -，如下图所示：设DG x =，DH y =，DE z =，则2223AD x z =+=，2224DB y z =+=，2225DC x y =+=，上述三个等式相加得()222222234512AD BD CD x y z++=++=++=，2226x y z ++=6R =，因此，此球的体积为34663ππ⨯=⎝⎭. 故选：C.【点睛】本题考查三棱锥外接球体积的计算，将三棱锥补成长方体，利用长方体的体对角线作为外接球的直径是解题的关键，考查空间想象能力与计算能力，属于中等题.2．B解析：B 【解析】试题分析：线面垂直，则有该直线和平面内所有的直线都垂直，故B 正确. 考点：空间点线面位置关系．3．B解析：B 【解析】A 中，,αβ也可能相交；B 中，垂直与同一条直线的两个平面平行，故正确；C 中，,αβ也可能相交；D 中，l 也可能在平面β内. 【考点定位】点线面的位置关系4．D解析：D 【解析】【分析】根据球的性质可知球心O 与ABC ∆外接圆圆心O '连线垂直于平面ABC ；在Rt POE ∆和Rt OO A ∆'中利用勾股定理构造出关于半径R 和OO '的方程组，解方程组求得R ，代入球的体积公式可得结果. 【详解】设O '为ABC ∆的外心，如下图所示：由球的性质可知，球心O 与O '连线垂直于平面ABC ，作OE AD ⊥于E 设球的半径为R ，OO x '=ABC ∆为等边三角形，且3AB = 3AO '∴=OO '⊥Q 平面ABC ，AD ⊥平面ABC ，OE AD ⊥ OO AE x '∴==，3OE AO '==在Rt POE ∆和Rt OO A ∆'中，由勾股定理得：22222OE PE O O O A R ''+=+=，即()222363x x R +-=+= 解得：3x =，23R =∴球的体积为：343233V R ππ==本题正确选项：D 【点睛】本题考查棱锥外接球的体积求解问题，关键是能够确定棱锥外接球球心的位置，从而在直角三角形中利用勾股定理构造方程求得半径.5．C解析：C 【解析】【分析】根据题意，对每一个选项进行逐一判定，不正确的只需举出反例，正确的作出证明，即可得到答案. 【详解】如图（1）所示，在平面内不可能由符合题的点；如图（2），直线,a b 到已知平面的距离相等且所在平面与已知平面垂直，则已知平面为符合题意的点；如图（3），直线,a b 所在平面与已知平面平行，则符合题意的点为一条直线，综上可知（1）（2）（4）是正确的，故选C.【点睛】本题主要考查了空间中直线与平面之间的位置关系，其中熟记空间中点、线、面的位置关系是解答此类问题的关键，着重考查了空间想象能力，以及推理与论证能力，属于基础题.6．C解析：C 【解析】【分析】2的等腰直角三角形，与底面垂直的侧面是个等腰三角形，底边长为2，高为2，故三棱锥的外接球与以棱长为2的正方体的外接球相同，由此可得结论【详解】由三视图知几何体是一个侧棱与底面垂直的三棱锥，底面是斜边上的高为2的等腰直角三角形，与底面垂直的侧面是个等腰三角形，底边长为2，高为2，故三棱锥的外接球与以棱长为2的正方体的外接球相同，其直径为23，半径为3∴三棱锥的外接球体积为()343433ππ⨯=故选C 【点睛】本题主要考查了三视图，几何体的外接球的体积，考查了空间想象能力，计算能力，属于中档题．7．C解析：C 【解析】【分析】直接根据直线平行公式得到答案. 【详解】直线20ax y +-=和直线()2140x a y +-+=平行，则()12a a -=，解得2a =或1a =-.当1a =-时，两直线重合，排除. 故选：C . 【点睛】本题考查了根据直线平行求参数，意在考查学生的计算能力，多解是容易发生的错误.8．B解析：B 【解析】【分析】【详解】试题分析：. 由三视图知几何体为三棱柱削去一个三棱锥如图：棱柱的高为5；底面为直角三角形，直角三角形的直角边长分别为3、4， ∴几何体的体积V ＝×3×4×5﹣××3×4×5＝20（cm 3）．考点：1.三视图读图的能力；2.几何体的体积公式.9．B解析：B 【解析】【分析】根据椭圆的定义可知12||||2PF PF a +=，又1PF 恰好与圆2F 相切于点P ，可知2||PF c =且12PF PF ⊥，即可列出方程求椭圆的离心率. 【详解】由1PF 恰好与圆2F 相切于点P ，可知2||PF c =，且 12PF PF ⊥，又12||||2PF PF a +=，可知1||2PF a c =-，在12Rt PF F ∆中，222(2)4a c c c -+=，即2222a ac c -= 所以2220,(0,1)e e e +-=∈，解得212312e -+==-，故选：B 【点睛】本题主要考查了椭圆的定义，椭圆的简单几何性质，圆的切线的性质，属于中档题.10．B解析：B 【解析】【分析】当P 与A 重合时，异面直线CP 与BA 1所成的角最大，由此能求出当异面直线CP 与BA 1所成的角最大时，三棱锥C ﹣PA 1D 1的体积．【详解】如图，当P 与A 重合时，异面直线CP 与BA 1所成的角最大， ∴当异面直线CP 与BA 1所成的角最大时，三棱锥C ﹣PA 1D 1的体积：11C PA D V -=11C AA D V -=1113AA D S AB ⨯⨯V =1111132AA A D AB ⎛⎫⨯⨯⨯⨯ ⎪⎝⎭=11232a a a ⎛⎫⨯⨯⨯⨯ ⎪⎝⎭=33a ．故选:B ．【点睛】求锥体的体积要充分利用多面体的截面和旋转体的轴截面，将空间问题转化为平面问题求解，注意求体积的一些特殊方法——分割法、补形法、等体积法. ①割补法：求一些不规则几何体的体积时，常用割补法转化成已知体积公式的几何体进行解决．②等积法：等积法包括等面积法和等体积法．等积法的前提是几何图形(或几何体)的面积(或体积)通过已知条件可以得到，利用等积法可以用来求解几何图形的高或几何体的高，特别是在求三角形的高和三棱锥的高时，这一方法回避了通过具体作图得到三角形(或三棱锥)的高，而通过直接计算得到高的数值．11．B解析：B 【解析】【分析】在①中，由面面平行的性质定理得m ∥β；在②中，m 与n 平行或异面；在③中，m 与β相交、平行或m ⊂β；在④中，由n ⊥α，m ⊥α，得m ∥n ，由n ⊥β，得m ⊥β．【详解】由α，β为两个不同的平面，m ，n 为两条不同的直线，知：在①中，若α∥β，m ⊂α，则由面面平行的性质定理得m ∥β，故①正确；在②中，若m ∥α，n ⊂α，则m 与n 平行或异面，故②错误；在③中，若α⊥β，α∩β＝n ，m ⊥n ，则m 与β相交、平行或m ⊂β，故③错误；在④中，若n ⊥α，m ⊥α，则m ∥n ，由n ⊥β，得m ⊥β，故④正确．故选：B ．【点睛】本题考查命题真假的判断，考查空间中线线、线面、面面间的位置关系等基础知识，考查空间想象能力、推理论证能力，考查化归与转化思想，是中档题．12．D解析：D 【解析】设直四棱柱1111ABCD A B C D -中，对角线119,15AC BD ==，因为1A A ⊥平面,ABCD AC Ì,平面ABCD ，所以1A A AC ⊥，在1Rt A AC ∆中，15A A =，可得AC ==同理可得BD ===，因为四边形ABCD 为菱形，可得,AC BD 互相垂直平分，所以2211()()1450822AB AC BD =+=+=，即菱形ABCD 的边长为8，因此，这个棱柱的侧面积为1()485160S AB BC CD DA AA =+++⨯=⨯⨯=，故选D.点睛：本题考查了四棱锥的侧面积的计算问题，解答中通过给出的直四棱柱满足的条件，求得底面菱形的边长，进而得出底面菱形的底面周长，即可代入侧面积公式求得侧面积，着重考查了学生分析问题和解答问题的能力，以及空间想象能力，其中正确认识空间几何体的结构特征和线面位置关系是解答的关键.二、填空题13．【解析】【分析】直线过定点设代入方程利用点差法计算得到答案【详解】直线过定点设则两式相减得到即故整理得到：故答案为：【点睛】本题考查了轨迹方程意在考查学生对于点差法的理解和掌握解析：()2224x y -+=【解析】【分析】直线40Ax By A +-=过定点()4,0，设()()1122,,,M x y N x y ，(),G x y ，代入方程利用点差法计算得到答案. 【详解】直线40Ax By A +-=过定点()4,0，设()()1122,,,M x y N x y ，(),G x y ，则221136x y +=，222236x y +=，两式相减得到()()()()121212120x x x x y y y y +-++-=，即220x ky +=. 故2204y x y x +=-，整理得到：()2224x y -+=. 故答案为：()2224x y -+=. 【点睛】本题考查了轨迹方程，意在考查学生对于点差法的理解和掌握.14．【解析】【分析】将小正方体扩展成4个小正方体根据直线夹角的定义即可判断出符合条件的条数【详解】解：设ABCD ﹣A1B1C1D1边长为1第一条：AC1是满足条件的直线；第二条：延长C1D1到C1且D1 解析：4【解析】【分析】将小正方体扩展成4个小正方体，根据直线夹角的定义即可判断出符合条件的条数．【详解】解：设ABCD ﹣A 1B 1C 1D 1边长为1．第一条：AC 1是满足条件的直线；第二条：延长C 1D 1到C 1且D 1C 2＝1，AC 2是满足条件的直线；第三条：延长C 1B 1到C 3且B 1C 3＝1，AC 3是满足条件的直线；第四条：延长C 1A 1到C 4且C 4A 12=，AC 4是满足条件的直线．故答案为4．【点睛】本题考查满足条件的直线条数的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查空间想象能力，考查分类与整合思想，是基础题．15．【解析】【分析】点到平面的距离等价于点到平面的距离过作交于证得平面利用等面积法求得点到平面的距离也即点到平面的距离【详解】由于是的中点故点到平面的距离等价于点到平面的距离过作交于由于故平面在直角三角 5 【解析】【分析】点1B 到平面ADE 的距离等价于点B 到平面ADE 的距离，过B 作BF AE ⊥，交AE 于F ，证得BF ⊥平面ADE ，利用等面积法求得点B 到平面ADE 的距离，也即点1B 到平面ADE 的距离. 【详解】由于E 是1BB 的中点，故点1B 到平面ADE 的距离等价于点B 到平面ADE 的距离，过B 作BF AE ⊥，交AE 于F ，由于BF AD ⊥，AD AE E ⋂=，故BF ⊥平面ADE .在直角三角形ABE 中，151,,22AB BE AE ===，所以1122AB BE AE BF ⋅⋅=⋅⋅,解得5BF =.【点睛】本小题主要考查点到面的距离，考查等面积法求高，考查线面垂直的证明，属于基础题.16．【解析】【分析】正四棱锥底面的四个顶点在球的同一个大圆上则棱锥的高等于球的半径由此可由棱锥体积求得球的半径从而得球体积【详解】∵正四棱锥底面的四个顶点在球的同一个大圆上∴球心是正方形对角线交点是棱锥解析：323π【解析】【分析】正四棱锥P ABCD -底面的四个顶点,,,A B C D 在球O 的同一个大圆上，则棱锥的高等于球的半径，由此可由棱锥体积求得球的半径，从而得球体积．【详解】∵正四棱锥P ABCD -底面的四个顶点,,,A B C D 在球O 的同一个大圆上，∴球心O 是正方形ABCD 对角线交点，PO 是棱锥的高，设球半径为R ，则2AB R =，22(2)2ABCD S R R ==，211162333P ABCD ABCD V S PO R R -==⨯⨯=，2R =，∴3344322333V R πππ==⨯=球．故答案为：323π．【点睛】本题考查球的体积，考查正四棱锥与半球的截接问题．解题关键是确定球半径与正四棱锥中的线段长之间的关系．17．【解析】【分析】根据空间直角坐标系中点坐标公式求结果【详解】设B 则所以所以的坐标为【点睛】本题考查空间直角坐标系中点坐标公式考查基本分析求解能力属基础题解析：()1,4,1--【解析】【分析】根据空间直角坐标系中点坐标公式求结果. 【详解】设B (),,x y z ,则1230,1,2222x y z+++=-==，所以1,4,1x y z =-=-=，所以B 的坐标为()1,4,1--．【点睛】本题考查空间直角坐标系中点坐标公式，考查基本分析求解能力，属基础题.18．【解析】【分析】根据直线垂直的条件计算即可【详解】因为直线与直线互相垂直所以解得故填【点睛】本题主要考查了两条直线垂直的条件属于中档题解析：1-【解析】【分析】根据直线垂直的条件计算即可. 【详解】因为直线10x y --=与直线20x ay --=互相垂直，所以110a ⨯+= 解得1a =-.故填1-. 【点睛】本题主要考查了两条直线垂直的条件，属于中档题.19．62【解析】试题分析：由题意得抛物线的准线为x=-c 它正好经过双曲线的左焦点所以准线被双曲线截得的弦长为2b2a 所以2b2a=223be2即ba=23e2所以整理得2e4-9e2+1=0解得e=62 解析：【解析】试题分析：由题意，得抛物线的准线为，它正好经过双曲线的左焦点，所以准线被双曲线截得的弦长为，所以，即，所以，整理，得，解得或．又过焦点且斜率为1的直线与双曲线的右支交于两点，所以．考点：1、抛物线与双曲线的几何性质；2、直线与双曲线的位置关系．【方法点睛】关于双曲线的离心率问题，主要是有两类试题：一类是求解离心率的值，一类是求解离心率的范围．基本的解题思路是建立椭圆和双曲线中的关系式，求值问题就是建立关于的等式，求取值范围问题就是建立关于的不等式．20．【解析】【分析】当过球内一点的截面与垂直时截面面积最小可求截面半径即可求出过点的平面截球的截面面积的最小值【详解】解：棱长等于的正方体它的外接球的半径为3当过点的平面与垂直时截面面积最小故答案为：【解析：3π. 【解析】【分析】当过球内一点E 的截面与OE 垂直时，截面面积最小可求截面半径，即可求出过点E 的平面截球O 的截面面积的最小值．【详解】解：棱长等于231111ABCD A B C D -，它的外接球的半径为3，||6OE = 当过点E 的平面与OE 垂直时，截面面积最小，963r -33S ππ=⨯=，故答案为：3π．【点睛】本题考查过点E 的平面截球O 的截面面积的最小值及接体问题，找准量化关系是关键，属于中档题．三、解答题21．（1）4340x y --=；（2）①4，②152. 【解析】【分析】（1）求出圆的标准方程，设直线2l 的方程(1)y k x =-，利用6PQ =，结合圆心到直线的210911k -=+，解可得k 的值，验证直线与y 轴有无交点，即可得答案；（2）①设(,)M x y ，由点M 在线段AD 上，得220x ty t +-=，由2AM BM ≤，得224220()()339x y -++…，结合题意，线段AD 与圆224220()()339x y -++=至多有一个公共88||t -t 的值，②由①的结论，分直线的斜率存在与不存在2种情况讨论，用k 表示三角形EPQ 的面积，结合二次函数的性质分析可得答案．【详解】解：（1）由题意可知，圆C 的直径为AD ，所以圆C 方程为：()()223110x y -+-=，设2l 方程为：()1y k x =-，则()222213101k k -+=+，解得10k =，243k =，当0k =时，直线1l 与y 轴无交点，不合题意，舍去. 所以，43k =时直线2l 的方程为4340x y --=. （2）①设(,)M x y ，由点M 在线段AD 上，则有12x yt +=，即220x ty t +-=．由2AM BM …，则有224220()()339x y -++…依题意知，线段AD 与圆224220()()339x y -++=至多有一个公共点，88||t -t …或t ，因为t 是使2AM BM ≤恒成立的最小正整数，所以4t =； ②由①的结论，圆C 的方程为22(2)(1)5x y -+-=．分2种情况讨论：a 当直线2:1l x =时，直线1l 的方程为0y =，此时，2EPQ S =V ；b 当直线2l 的斜率存在时，设2l 的方程为(1)y k x =-，0k ≠，则1l 的方程为1(1)y x k=--，点1(0,)E k，所以BE =又圆心到2l，所以PQ =故2222221114244244215124221EPQ k k k k S BE PQ k k k k k -+-+==⨯+⨯==-++V g …，又由152<，故求三角形EPQ 的面积的最小值为152．【点睛】本题考查直线与圆的方程的综合应用，涉及三角形面积的最小值的求法，（2）的关键是确定三角形面积的表达式，属于中档题． 22．（1）证明见解析；（2）6π. 【解析】【分析】（1）取AC 的中点O ，连接OS 、OD ，证明出OS AC ⊥，OD AC ⊥，利用直线与平面垂直的判定定理可得出AC ⊥平面SOD ，即可证明出AC SD ⊥；（2）延长SO ，过点D 作SO 延长线的垂线，垂足记为H ，说明直线SD 与平面SAC 所成的角为OSD ∠，求出OSD ∆三边边长，利用余弦定理求出OSD ∠，即可求出直线SD 与平面SAC 所成角的大小．【详解】（1）取AC 的中点O ，连接OS 、OD ，SAC ∆Q 为等边三角形，O 为AC 的中点，SO AC ∴⊥，D Q 、O 分别为AB 、AC 的中点，//OD BC ∴，BC AC ⊥Q ，OD AC ∴⊥， SO OD O =Q I ，AC ∴⊥平面SOD ，SD ⊂Q 平面SOD ，AC SD ∴⊥；（2）延长SO ，过点D 作SO 延长线的垂线，垂足记为H ， AC ⊥Q 平面SOD ，DH ⊂平面SOD ，DH AC ∴⊥，DH SO ⊥Q ，SO AC O =I ，DH ∴⊥平面SAC ，所以，直线SD 与平面SAC 所成的角为OSD ∠，由（2）知，1232OD BC ==AC BC ⊥Q ，228AB AC BC ∴+=. SAC ∆Q 是边长为4的等边三角形，4sin233SO π∴==在SBC ∆中，4SC =，43BC=由余弦定理得2222cos 88SB SC BC SC BC SCB =+-⋅⋅∠=，222SB ∴=.由余弦定理得2221cos 28SA AB SB SAB SA AB +-∠==-⋅，2222cos 36SD SA AD SA AD SAD ∴=+-⋅⋅∠=，6SD ∴=.在SOD ∆中，由余弦定理得2223cos 2SO SD OD OSD SO SD +-∠==⋅. 0OSD π<∠<Q ，6OSD π∴∠=，因此，直线SD 与平面SAC 所成角的大小为6π. 【点睛】本题考查利用线面垂直的性质证明线线垂直，同时也考查了直线与平面所成角的计算，涉及到利用余弦定理解三角形，考查推理能力与计算能力，属于中等题. 23．（1）见解析；（2）26【解析】【分析】（1）连接BD ，交CE 于点O ，连接OM ，易知底面EBCD 是平行四边形，则O 为BD 中点，又M 是BP 中点，可知PD MO P ，则结论可证.（2）先证明ADE V 是等腰直角三角形，由条件中的面面垂直可得PD ⊥平面BCDE ，则由（1）可知MN ⊥平面BCDE ，则MN 为三棱锥M BCE -的高，底面BCE V 的面积容易求得，根据公式求三棱锥M BCE -的体积. 【详解】（1）在平面图中，因为12BE AB CD ==且//BE CD ，所以四边形EBCD 是平行四边形；在立体图中，连接BD ，交CE 于点O ，连接OM ，所以点O 是BD 的中点，又因为点M 为棱PB 的中点，所以//OM PD ，因为PD ⊄平面MCE ，OM ⊂平面MCE ，所以//PD 平面MCE ；（2）在平面图中，因为EBCD 是平行四边形，所以DE BC =，因为四边形ABCD 是等腰梯形，所以AD BC =，所以AD DE =，因为45BAD ∠=︒，所以AD DE ⊥；在立体图中，PD DE ⊥，又平面PDE ⊥平面EBCD ，且平面PDE ⋂平面EBCD DE =，PD ⊂平面PDE 所以PD ⊥平面EBCD ，由（1）知//OM PD ，所以OM ⊥平面EBCD ，在等腰直角三角形ADE 中，因为2AE =，所以2AD DE ==所以11222OM PD AD ===，又1BCE ADE S S ∆∆==，所以1236M BCE BCE V S OM -∆=⋅⋅=. 【点睛】本题考查平面几何与立体几何的关系，线面平行的证明，面面垂直的性质等，有一定的综合性，属中等题.24．(1)见证明；(2) 23【解析】【分析】(1)由PA ⊥面ABCD 可知PA AE ⊥，又可证AE BC ⊥，根据线面垂直的判定即可证明 (2) 取AB 中点M ，作MN AF ⊥于N ，连CN ，可证MNC ∠是二面角B AF C --的平面角，解三角形即可求解. 【详解】（1）PA ⊥Q 面ABCD ，AE ⊂面ABCD ，PA AE ∴⊥；又Q 底面ABCD 为菱形，60ABC ∠=o ，E 为BC 中点，,//,,AE BC AD BC AE AD ∴⊥∴⊥QAE ∴⊥面PAD ；（2）AE ^Q 面PAD ，AHE ∴∠是EH 与面PAD 所成角，tan ,AEAHE AH PO AH∠=⊥时，AH 最小，tan AHE ∠最大，AHE ∠最大，令2AB =，则3,1AE AH ==，在Rt AHD ∆中，2,30AD ADH =∠=o ，在Rt PAD ∆中，233PA =PA ⊥Q 面ABCD ，∴面PAB ⊥面ABCD ，且交线为AB ，取AB 中点M ，正ABC ∆中，,CM AB CM ⊥∴⊥面PAB ，作MN AF ⊥于N ，连CN ，由三垂线定理得CN AF ⊥，MNC ∠是二面角B AF C --的平面角.3CM =.在PAB ∆中，23,2,3BF AF AB ===边AF 上的高11,2BG MN ==， tan 23CMMNC MN∠==【点睛】本题主要考查了线面垂直的判定，线面垂直的性质，二面角的求法，属于难题. 25．（1）A （1，3）；（2）直线l 方程为20x y -+=，最短弦长为23）在直线MC 上存在定点4,43N ⎛⎫- ⎪⎝⎭，使得||||PM PN 为常数32．【解析】【分析】（1）利用直线系方程的特征，直接求解直线l 过定点A 的坐标；（2）当AC ⊥l 时，所截得弦长最短，由题知C （0，4），2r =，求出AC 的斜率，利用点到直线的距离，转化求解即可；（3）由题知，直线MC 的方程为4y =，假设存在定点N （t ，4）满足题意，则设(),P x y ，||||PM PN λ=，得222||||(0)PM PN λλ=>，且()2244y x -=-，求出λ，然后求解比值. 【详解】解：（1）依题意得，(3)(4)0m x y x y -++-=，令30x y -=且40x y +-=，得1,3x y ==，∴直线l 过定点A （1，3）；（2）当AC ⊥l 时，所截得弦长最短，由题知C （0，4），2r =，43101ACk -∴==--，得1111l AC k k --===-， ∴由3111m m +=-得1m =-，此时直线l 方程为20x y -+=，∴圆心到直线的距离为||d AC ==∴最短弦长为==（3）由题知，直线MC 的方程为4y =，假设存在定点N （t ，4）满足题意，则设(),P x y ，||||PM PN λ=，得222||||(0)PM PN λλ=>，且()2244y x -=-， 222222(3)(4)()(4)x y x t y λλ∴++-=-+-，()222222(3)4()4x x x t x λλ∴++-=-+-，整理得，()()2222624130t x t λλλ+-+-=， ∵上式对任意[2,2]x ∈-恒成立，2620t λ∴+=且2224130t λλ+-=，解得 43,32t λ=-=或3,1t λ=-=（舍去，与M 重合），综上可知，在直线MC 上存在定点4,43N ⎛⎫- ⎪⎝⎭，使得||||PM PN 为常数32. 【点睛】本题考查直线与圆的方程的综合应用，考查转化思想以及计算能力，是中档题.26．（1）320x y ++=；（2）320x y -+=【解析】分析：（1）先由AD 与AB 垂直，求得AD 的斜率，再由点斜式求得其直线方程；（2）根据矩形特点可以设DC 的直线方程为()306x y m m -+=≠-，然后由点到直线的=m 的值，即可求出结果. 详解：(1)由题意：ABCD 为矩形，则AB⊥AD，又AB 边所在的直线方程为：x －3y －6＝0，所以AD 所在直线的斜率k AD ＝－3，而点T(－1，1)在直线AD 上．所以AD 边所在直线的方程为：3x ＋y ＋2＝0.(2)方法一：由ABCD 为矩形可得，AB∥DC，所以设直线CD 的方程为x －3y ＋m ＝0.由矩形性质可知点M到AB、CD的距离相等所以＝,解得m＝2或m＝－6(舍)．所以DC边所在的直线方程为x－3y＋2＝0.方法二：方程x－3y－6＝0与方程3x＋y＋2＝0联立得A（0，-2），关于M的对称点C （4，2）因AB∥DC，所以DC边所在的直线方程为x－3y＋2＝0.点睛：本题主要考查直线方程的求法，在求直线方程时，应先选择适当的直线方程的形式，并注意各种形式的适用条件．用斜截式及点斜式时，直线的斜率必须存在，而两点式不能表示与坐标轴垂直的直线，截距式不能表示与坐标轴垂直或经过原点的直线．故在解题时，若采用截距式，应注意分类讨论，判断截距是否为零；若采用点斜式，应先考虑斜率不存在的情况．。

【典型题】高中必修二数学下期中第一次模拟试卷附答案(1)

【典型题】高中必修二数学下期中第一次模拟试卷附答案(1)一、选择题1．圆224470x y x y +--+=上的动点P 到直线0x y +=的最小距离为（） A ．1 B ．221- C ．22 D ．22．已知,,,A B C D 是同一球面上的四个点，其中ABC ∆是正三角形，AD ⊥平面ABC ，26AD AB ==，则该球的体积为（）A ．48πB ．24πC ．16πD ．323π 3．已知定义在R 上的函数()21()x m f x m -=-为实数为偶函数,记0.5(log 3),a f =2b (log 5),c (2)f f m ==,则,,a b c ,的大小关系为（）A ．a b c <<B ．c a b <<C ．a c b <<D ．c b a <<4．若函数6(3)3,7(),7x a x x f x a x ---≤⎧=⎨>⎩单调递增,则实数a 的取值范围是( ) A ．9,34⎛⎫ ⎪⎝⎭ B ．9,34⎡⎫⎪⎢⎣⎭ C ．()1,3 D ．()2,35．已知平面//α平面β，直线m αÜ，直线n βÜ，点A m ∈,点B n ∈，记点A 、B 之间的距离为a ,点A 到直线n 的距离为b ,直线m 和n 的距离为c ,则A ．b a c ≤≤B ．a c b ≤≤C ． c a b ≤≤D ．c b a ≤≤6．如图是某四面体ABCD 水平放置时的三视图（图中网格纸的小正方形的边长为1，则四面体ABCD 外接球的表面积为A ．20πB ．1256πC ．25πD ．100π7．已知m 和n 是两条不同的直线，α和β是两个不重合的平面，那么下面给出的条件中一定能推出m ⊥β的是( )A ．α⊥β，且m ⊂αB ．m ⊥n ，且n ∥βC ．α⊥β，且m ∥αD ．m ∥n ，且n ⊥β8．已知三棱锥S ABC -的每个顶点都在球O 的表面上，ABC ∆是边长为43角形，SA ⊥平面ABC ，且SB 与平面ABC 所成的角为6π，则球O 的表面积为（） A ．20π B ．40π C ．80π D ．160π9．若直线20ax y +-=和直线()2140x a y +-+=平行，则a 的值为（） A ．1-或2 B ．1- C ．2 D ．不存在10．已知三条直线,,m n l ，三个平面,,αβγ，下列四个命题中，正确的是（）A ．||αγαββγ⊥⎫⇒⎬⊥⎭B ．||m l l m ββ⎫⇒⊥⎬⊥⎭C ．||||||m m n n γγ⎫⇒⎬⎭D ．||m m n n γγ⊥⎫⇒⎬⊥⎭ 11．点A 、B 、C 、D 在同一个球的球面上，AB=BC=2，AC=2，若四面体ABCD 体积的最大值为23，则这个球的表面积为（） A ．1256π B ．8π C ．2516π D ．254π 12．已知点()1,2-和3,0⎛⎫ ⎪⎪⎝⎭在直线():100l ax y a --=≠的两侧，则直线l 的倾斜角的取值范围是 ( )A ．,43ππ⎛⎫⎪⎝⎭ B ．2,33ππ⎛⎫ ⎪⎝⎭ C ．25,36ππ⎛⎫ ⎪⎝⎭ D ．30,,34πππ⎛⎫⎛⎫⋃ ⎪ ⎪⎝⎭⎝⎭二、填空题13．如图，在长方形ABCD 中，2AB =，1BC =，E 为DC 的中点，F 为线段EC （端点除外）上一动点，现将AFD V 沿AF 折起，使平面ABD ⊥平面ABC ，在平面ABD 内过点D 作DK AB ⊥，K 为垂足，设AK t =，则t 的取值范围是__________．14．正方体1111ABCD A B C D -的棱长为1，P 为1CC 上的动点，Q 为1BD 上的动点，则线段PQ 的长度的最小值为______.15．三棱锥P ABC -中，5PA PB ==2AC BC ==AC BC ⊥，3PC =，则该三棱锥的外接球面积为________.16．直线10ax y ++=与连接A （4，5），B （-1，2）的线段相交，则a 的取值范围是___．17．底面边长为2的正三棱柱111ABC A B C -被不平行于底面的平面MNP 所截，其中3AM =，4BN =，5PC =，则多面体ABC MNP -体积为________18．在平面直角坐标系内，到点A （1，2），B （1，5），C （3，6），D （7，﹣1）的距离之和最小的点的坐标是．19．已知棱长等于23的正方体1111ABCD A B C D -，它的外接球的球心为O ﹐点E 是AB 的中点，则过点E 的平面截球O 的截面面积的最小值为________.20．如图：点P 在正方体1111ABCD A B C D -的面对角线1BC 上运动，则下列四个命题： ①三棱锥1A D PC -的体积不变； ②1A P ∥面1ACD ；③1DP BC ^；④面1PDB ^面1ACD ．其中正确的命题的序号是__________.三、解答题21．已知圆22:(1)(2)25C x y -+-=，直线:(21)(1)74l m x m y m +++--=0，（m ∈R ）．（1）证明：无论m 取何值，直线l 过定点；（2）求直线l 被圆C 截得的弦长最短时m 的值及最短弦长．22．如图1，有一边长为2的正方形ABCD ，E 是边AD 的中点，将ABE △沿着直线BE 折起至A BE 'V 位置（如图2），此时恰好A E A C ''⊥，点A '在底面上的射影为O .（1）求证：A E BC '⊥；（2）求直线A B '与平面BCDE 所成角的正弦值.23．如图所示，四棱锥S ABCD -中，SA ⊥底面ABCD ，090ABC ∠=，23SA AB ==，1BC =，23AD =060ACD ∠=，E 为CD 的中点.（1）求证：//BC 平面SAE ；（2）求直线SD 与平面SBC 所成角的正弦值.24．如图，在Rt AOB V 中，30OAB ∠=︒，斜边4AB =，Rt AOC V 可以通过Rt AOB V 以直线AO 为轴旋转得到，且平面AOB ⊥平面AOC ．动点D 在斜边AB 上．（1）求证：平面COD ⊥平面AOB ；（2）当D 为AB 的中点时，求异面直线AO 与CD 所成角的正切值．25．如图，正方形ABCD 所在平面与平面四边形ABEF 所在平面互相垂直，ABE ∆是等腰直角三角形，AB AE =，FA FE =，45AEF ∠=︒．（1）设线段CD AE 、的中点分别为P M 、，求证：//PM 平面BCE ；（2）求二面角F BD A --所成角的正弦值．26．已知三角形ABC 的顶点坐标分别为A (4,1)，B (1,5)，C (3,2)-；（1）求直线AB 方程的一般式；（2）证明△ABC 为直角三角形；（3）求△ABC 外接圆方程．【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【解析】【分析】先求出圆心到直线0x y +=的距离，根据距离的最小值为d r -，即可求解.【详解】由圆的一般方程可得22(2)(2)1x y -+-=，圆心到直线的距离222d == 所以圆上的点到直线的距离的最小值为221-.故选B.【点睛】本题主要考查了点到直线的距离，圆的方程，属于中档题.2．D解析：D 【解析】【分析】根据球的性质可知球心O 与ABC ∆外接圆圆心O '连线垂直于平面ABC ；在Rt POE ∆和Rt OO A ∆'中利用勾股定理构造出关于半径R 和OO '的方程组，解方程组求得R ，代入球的体积公式可得结果. 【详解】设O '为ABC ∆的外心，如下图所示：由球的性质可知，球心O 与O '连线垂直于平面ABC ，作OE AD ⊥于E设球的半径为R ，OO x '=ABC ∆为等边三角形，且3AB = 3AO '∴=OO '⊥Q 平面ABC ，AD ⊥平面ABC ，OE AD ⊥OO AE x '∴==，3OE AO '==在Rt POE ∆和Rt OO A ∆'中，由勾股定理得：22222OE PE O O O A R ''+=+=，即()222363x x R +-=+= 解得：3x =，R =∴球的体积为：343V R π== 本题正确选项：D【点睛】本题考查棱锥外接球的体积求解问题，关键是能够确定棱锥外接球球心的位置，从而在直角三角形中利用勾股定理构造方程求得半径.3．B解析：B【解析】由()f x 为偶函数得0m =,所以0,52log 3log 32121312,a =-=-=-=2log 521514b =-=-=,0210c =-=,所以c a b <<,故选B.考点：本题主要考查函数奇偶性及对数运算.4．B解析：B【解析】【分析】利用函数的单调性，判断指数函数底数的取值范围，以及一次函数的单调性，及端点处函数值的大小关系列出不等式求解即可【详解】解：Q 函数6(3)3,7(),7x a x x f x a x ---⎧=⎨>⎩…单调递增， ()301373a a a a ⎧->⎪∴>⎨⎪-⨯-≤⎩解得934a ≤< 所以实数a 的取值范围是9,34⎡⎫⎪⎢⎣⎭．故选：B ．【点睛】本题考查分段函数的应用，指数函数的性质，考查学生的计算能力，属于中档题． 5．D解析：D【解析】【分析】根据平面与平面平行的判断性质,判断c 最小,再根据点到直线距离和点到直线上任意点距离判断a 最大.【详解】由于平面//α平面β,直线m 和n 又分别是两平面的直线,则c 即是平面之间的最短距离. 而由于两直线不一定在同一平面内,则b 一定大于或等于c ,判断a 和b 时,因为B 是上n 任意一点,则a 大于或等于b .故选D.【点睛】本题主要考查面面平行的性质以及空间距离的性质，考查了空间想象能力，意在考查灵活应用所学知识解答问题的能力，属于中档题.6．C解析：C【解析】【分析】【详解】由三视图可知，这是三棱锥的三视图，如下图所示，三角形BCD 为等腰直角三角形，其外心为BD 中点1O ，设O 为AD 中点，则O 为外接球球心，半径长度为1522AD =，所以表面积为25π.7．D解析：D【解析】【分析】根据所给条件，分别进行分析判断，即可得出正确答案.【详解】解：αβ⊥且m α⊂⇒m β⊂或//m β或m 与β相交，故A 不成立；m n ⊥且//n β⇒m β⊂或//m β或m 与β相交，故B 不成立；αβ⊥且//m α⇒m β⊂或//m β或m 与β相交，故C 不成立；//m n 且n β⊥⇒m β⊥，故D 成立；故选：D【点睛】本题考查直线与平面的位置关系，线面垂直判定，属于基础题.8．C解析：C【解析】【分析】根据线面夹角得到4SA =，计算ABC ∆的外接圆半径为42sin a r A==，2222SA R r ⎛⎫=+ ⎪⎝⎭，解得答案. 【详解】SA ⊥平面ABC ，则SB 与平面ABC 所成的角为6SBA π∠=，故4SA =.ABC ∆的外接圆半径为42sin a r A ==，设球O 的半径为R ，则2222SA R r ⎛⎫=+ ⎪⎝⎭，解得R =O 的表面积为2480R ππ=. 故选：C .【点睛】本题考查了三棱锥的外接球问题，意在考查学生的计算能力和空间想象能力.9．C解析：C【解析】【分析】直接根据直线平行公式得到答案.【详解】直线20ax y +-=和直线()2140x a y +-+=平行，则()12a a -=，解得2a =或1a =-.当1a =-时，两直线重合，排除.故选：C .【点睛】本题考查了根据直线平行求参数，意在考查学生的计算能力，多解是容易发生的错误.10．D解析：D【解析】试题分析：A.}r rααββ⊥⇒⊥P 不正确，以墙角为例，,αβ可能相交；B.}m l l m ββ⇒⊥⊥P 不正确，,l β有可能平行；C.}m r m n n r⇒P P P 不正确，m,n 可能平行、相交、异面；故选D 。

【易错题】高中必修二数学下期中试卷(含答案)

【易错题】高中必修二数学下期中试卷(含答案)一、选择题1．一正四面体木块如图所示，点P 是棱VA 的中点，过点P 将木块锯开，使截面平行于棱VB 和AC ，则下列关于截面的说法正确的是（）．A ．满足条件的截面不存在B ．截面是一个梯形C ．截面是一个菱形D ．截面是一个三角形 2．三棱锥P -ABC 中，P A ⊥平面ABC ，AB ⊥BC ，P A =2，AB =BC =1，则其外接球的表面积为（）A ．6πB ．5πC ．4πD ．3π3．已知直线m 、n 及平面α，其中m ∥n ，那么在平面α内到两条直线m 、n 距离相等的点的集合可能是：（1）一条直线；（2）一个平面；（3）一个点；（4）空集。

其中正确的是（）A ．（1）（2）（3）B ．（1）（4）C ．（1）（2）（4）D ．（2）（4）4．已知三棱锥S ABC -的所有顶点都在球O 的球面上，SC 为球O 的直径，且SC OA ⊥，SC OB ⊥，OAB V 为等边三角形，三棱锥S ABC -43，则球O 的半径为( )A ．3B ．1C ．2D ．45．已知点(),P x y 是直线()400kx y k ++=>上一动点，,PA PB 是圆22:20C x y y +-=的两条切线，切点分别为,A B ，若四边形PACB 的面积最小值为2，则k 的值为（）A ．3B ．212C ．22D ．2 6．直线20x y ++=截圆222210x y x y a ++-+-=所得弦的长度为4，则实数a 的值是（）A ．－3B ．－4C ．－6D ．367．如图是某四面体ABCD 水平放置时的三视图（图中网格纸的小正方形的边长为1，则四面体ABCD 外接球的表面积为A ．20πB ．1256πC ．25πD ．100π 8．已知圆截直线所得线段的长度是，则圆与圆的位置关系是（） A ．内切 B ．相交 C ．外切D ．相离 9．在三棱锥P ABC -中，PA ⊥平面1202,2ABC BAC AP AB ∠=︒==，，，M 是线段BC 上一动点，线段PM 长度最小值为3，则三棱锥P ABC -的外接球的表面积是（）A ．92πB ．92πC ．18πD ．40π10．某几何体的三视图如图所示，则该几何体的体积为( )A ．12B ．18C ．24D ．3011．点A 、B 、C 、D 在同一个球的球面上，2，AC=2，若四面体ABCD 体积的最大值为23，则这个球的表面积为（） A ．1256π B ．8π C ．2516π D ．254π 12．一个几何体的三视图如图所示，则该几何体的表面积为（）A ．B ．C ．D ．二、填空题13．光线由点P(2,3)射到直线x+y+1=0上，反射后过点Q(1,1) ，则反射光线方程为__________．14．在学习公理四“平行于同一条直线的两条直线平行”时，有同学进行类比，提出了下列命题：① 平行于同一平面的两个不同平面互相平行；② 平行于同一直线的两个不同平面互相平行；③ 垂直于同一直线的两个不同平面互相平行；④ 垂直于同一平面的两个不同平面互相平行；其中正确的有________15．已知在直角梯形ABCD 中，AB AD ⊥，CD AD ⊥，224AB AD CD ===，将直角梯形ABCD 沿AC 折叠，使平面BAC ⊥平面DAC ，则三棱锥D ABC -外接球的体积为__________．16．若过点(8,1)P 的直线与双曲线2244x y -=相交于A ，B 两点，且P 是线段AB 的中点，则直线AB 的方程为________．17．已知三棱锥D ABC -的体积为2，ABC ∆是边长为2的等边三角形，且三棱锥D ABC -的外接球的球心O 恰好是CD 的中点，则球O 的表面积为_______.18．如上图所示，在正方体1111ABCD A B C D -中，,M N 分别是棱1AB CC 、的中点，1MB P ∆的顶点P 在棱1CC 与棱11C D 上运动，有以下四个命题：A ．平面1MB P 1ND ⊥； B ．平面1MB P ⊥平面11ND A ；C ．∆1MB P 在底面ABCD 上的射影图形的面积为定值；D ．∆1MB P 在侧面11D C CD 上的射影图形是三角形．其中正确命题的序号是__________.19．若圆C ：222430x y x y ++-+=，关于直线260ax by ++=对称，则由点(),a b 向圆所作的切线长的最小值为______．20．已知棱长等于31111ABCD A B C D -，它的外接球的球心为O ﹐点E 是AB 的中点，则过点E 的平面截球O 的截面面积的最小值为________.三、解答题21．如图（1）在等腰直角三角形ABC 中，90B ∠=︒，将ABC ∆沿中位线DE 翻折得到如图（2）所示的空间图形，使二面角A DE C --的大小为02πθθ⎛⎫<< ⎪⎝⎭.（1）求证：平面ABD ⊥平面ABC ；（2）若3πθ=，求直线AE 与平面ABC 所成角的正弦值.22．如图，在四棱锥P ABCD -中，侧面PAD ⊥底面ABCD ，侧棱PA PD ⊥，底面ABCD 是直角梯形，其中//BC AD ，90BAD ∠=︒，3AD BC =，2AO OD =.（1）求证：平面PAB ⊥平面PCD .（2）试问在棱PA 上是否存在点E ，使得面//BOE 面PCD ，若存在，试指出点E 的位置并证明；若不存在，请说明理由.23．如图，四棱锥P ABCD -的底面ABCD 是直角梯形，//AB CD ， 33AB CD ==，AB AD ⊥，AB PA ⊥，且2AD PA ==，22PD =，13PE PB =uur uu r（1）证明：//CE 平面PAD ；（2）求点B 到平面ECD 的距离；24．如图，已知三棱锥A BPC -中，AP PC ⊥，AC BC ⊥，M 为AB 的中点，D 为PB 的中点，且PMB △为正三角形.（1）求证：//DM 平面APC ；（2）求证：BC ⊥平面APC ；（3）若4BC =，10AB =，求三棱锥D BCM -的体积.25．若圆M 的方程为22(2)(5)10x y -+-=，△ABC 中，已知(1,1)A ，(4,2)B ，点C 为圆M 上的动点．（1）求AC 中点D 的轨迹方程；（2）求△ABC 面积的最小值．26．如图所示，直角梯形ABCD 中，//AD BC ，,AD AB ⊥22,AB BC AD ===四边形EDCF 为矩形，2DE =，平面EDCF ⊥ABCD .（1）求证：//DF 平面ABE ；（2）求二面角B EF D --二面角的正弦值；（3）在线段BE 上是否存在点P ，使得直线AP 与平面BEF 所成角的正弦值为66，若存在，求出线段BP 的长，若不存在，请说明理由.【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【解析】【分析】取AB 的中点D ，BC 的中点E ，VC 的中点F ，连接,,,PD PF DE EF ，易得即截面为四边形PDEF ，且四边形PDEF 为菱形即可得到答案.【详解】取AB 的中点D ，BC 的中点E ，VC 的中点F ，连接,,,PD PF DE EF ，易得PD ∥VB 且12PD VB =，EF ∥VB 且12EF VB =，所以PD ∥EF ，PD EF =，所以四边形PDEF 为平行四边形，又VB ⊄平面PDEF ，PD ⊂平面PDEF ,由线面平行的判定定理可知，VB ∥平面PDEF ，AC ∥平面PDEF ，即截面为四边形PDEF ，又1122DE AC VB PD ===，所以四边形PDEF 为菱形，所以选项C 正确. 故选：C【点睛】本题考查线面平行的判定定理的应用，考查学生的逻辑推理能力，是一道中档题.2．A解析：A【解析】分析：将三棱锥的外接球转化为以,,AP AB BC 为长宽高的长方体的外接球，从而可得球半径，进而可得结果.详解：因为PA ⊥平面AB ，,AB BC ⊂平面ABC ，PA BC ∴⊥，,PA AB AB BC ⊥⊥Q ，所以三棱锥的外接球，就是以,,AP AB BC 为长宽高的长方体的外接球，外接球的直径等于长方体的对角线，即24116R =++=246R ππ=，故选A.点睛：本题主要考查三棱锥外接球表面积的求法，属于难题.要求外接球的表面积和体积，关键是求出求的半径，求外接球半径的常见方法有：①若三条棱两垂直则用22224R a b c =++（,,a b c 为三棱的长）；②若SA ⊥面ABC （SA a =），则22244R r a =+（r 为ABC ∆外接圆半径） ③可以转化为长方体的外接球；④特殊几何体可以直接找出球心和半径.3．C解析：C【解析】【分析】根据题意，对每一个选项进行逐一判定，不正确的只需举出反例，正确的作出证明，即可得到答案.【详解】如图（1）所示，在平面内不可能由符合题的点；如图（2），直线,a b 到已知平面的距离相等且所在平面与已知平面垂直，则已知平面为符合题意的点；如图（3），直线,a b 所在平面与已知平面平行，则符合题意的点为一条直线，综上可知（1）（2）（4）是正确的，故选C.【点睛】本题主要考查了空间中直线与平面之间的位置关系，其中熟记空间中点、线、面的位置关系是解答此类问题的关键，着重考查了空间想象能力，以及推理与论证能力，属于基础题. 4．C解析：C【解析】【分析】根据题意作出图形，欲求球的半径r ．利用截面的性质即可得到三棱锥S ABC -的体积可看成是两个小三棱锥S ABO -和C ABO -的体积和，即可计算出三棱锥的体积，从而建立关于r 的方程，即可求出r ，从而解决问题．【详解】解：根据题意作出图形：设球心为O ，球的半径r ．SC OA ⊥Q ，SC OB ⊥，SC ∴⊥平面AOB ，三棱锥S ABC -的体积可看成是两个小三棱锥S ABO -和C ABO -的体积和．2343123S ABC S ABO C ABO V V V r r ---∴=+=⨯⨯=三棱锥三棱锥三棱锥， 2r ∴=．故选：C ．【点睛】本题考查棱锥的体积，考查球内接多面体，解题的关键是确定将三棱锥S ABC -的体积看成是两个小三棱锥S ABO -和C ABO -的体积和，属于中档题．5．D解析：D【解析】【分析】当且仅当PC 垂直于()400kx y k ++=>时，四边形PACB 的面积最小，求出PC 后可得最小面积，从而可求k 的值.【详解】圆C 方程为()2211x y +-=，圆心()0,1C ，半径为1．因为PA ，PB 为切线，221PC PA ∴=+且1=2122PACB S PA PA ⨯⨯⨯==四边形． ∴当PA 最小时，PACB S 四边形最小，此时PC 最小且PC 垂直于()400kx y k ++=>．又min 21PC k =+，222221+1k ⎛⎫∴=+，2k ∴=，故选D. 【点睛】圆中的最值问题，往往可以转化圆心到几何对象的距离的最值来处理，这类问题属于中档题. 6．A解析：A【解析】【分析】求出圆心坐标和半径，根据圆的弦长公式，进行求解即可.【详解】由题意，根据圆的方程222210x y x y a ++-+-=，即22(1)(1)2x y a ++-=-，则圆心坐标为(1,1)-，半径1r a =-，又由圆心到直线的距离为11222d -++==，所以由圆的弦长公式可得222(1)(2)4a --=，解得3a =-，故选A.【点睛】本题主要考查了直线与圆的位置关系的因公，以及弦长公式的应用，其中根据圆的方程，求得圆心坐标和半径，合理利用圆的弦长公式列出方程求解是解答的关键，着重考查了推理与运算能力.7．C解析：C【解析】【分析】【详解】由三视图可知，这是三棱锥的三视图，如下图所示，三角形BCD 为等腰直角三角形，其外心为BD 中点1O ，设O 为AD 中点，则O 为外接球球心，半径长度为1522AD =，所以表面积为25π.8．B解析：B【解析】化简圆到直线的距离，又两圆相交. 选B9．C解析：C【解析】【分析】首先确定三角形ABC 为等腰三角形，进一步确定球的球心，再求出球的半径，最后确定球的表面积．【详解】解：如图所示：三棱锥P ABC -中，PA ⊥平面2,2ABC AP AB ==，，M 是线段BC 上一动点，线段PM 3则：当AM BC ⊥时，线段PM 达到最小值，由于：PA ⊥平面ABC ，所以：222PA AM PM +=，解得：1AM =，所以：3BM =，则：60BAM ∠=︒，由于：120BAC ∠=︒，所以：60MAC ∠=︒则：ABC V 为等腰三角形．所以：23BC =在ABC V 中，设外接圆的直径为2324r ==，则：2r =，所以：外接球的半径2229222R ⎛⎫=+= ⎪ ⎪⎝⎭，则：94182S ππ=⋅⋅=，故选：C ．【点睛】本题考查的知识要点：三棱锥的外接球的球心的确定及球的表面积公式的应用．10．C解析：C 【解析】试题分析：由三视图可知，几何体是三棱柱消去一个同底的三棱锥，如图所示，三棱柱的高为，消去的三棱锥的高为，三棱锥与三棱柱的底面为直角边长分别为和的直角三角形，所以几何体的体积为，故选C ．考点：几何体的三视图及体积的计算．【方法点晴】本题主要考查了几何体的三视图的应用及体积的计算，着重考查了推理和运算能力及空间想象能力，属于中档试题，解答此类问题的关键是根据三视图的规则“长对正、宽相等、高平齐”的原则，还原出原几何体的形状，本题的解答的难点在于根据几何体的三视图还原出原几何体和几何体的度量关系，属于中档试题．11．D解析：D 【解析】试题分析：根据题意知，ABC V 是一个直角三角形，其面积为1．其所在球的小圆的圆心在斜边AC 的中点上，设小圆的圆心为Q ，若四面体ABCD 的体积的最大值，由于底面积ABC S V 不变，高最大时体积最大，所以，DQ 与面ABC 垂直时体积最大，最大值为12·33ABC S DQ =V ，即12133DQ ⨯⨯=，∴2DQ =，设球心为O ，半径为R ，则在直角AQO V 中，222OA AQ OQ =+，即()22212R R =+-，∴54R =，则这个球的表面积为：2525444S ππ⎛⎫== ⎪⎝⎭；故选Ｄ．考点：球内接多面体，球的表面积．12．D解析：D 【解析】该几何体为半圆柱，底面为半径为1的半圆，高为2，因此表面积为,选D.二、填空题13．4x－5y+1=0【解析】【分析】先求P点关于直线x+y+1=0对称点M再根据两点式求MQ方程即得结果【详解】因为P点关于直线x+y+1=0对称点为所以反射光线方程为【点睛】本题考查点关于直线对称问解析：4x－5y+1=0【解析】【分析】先求P点关于直线x+y+1=0对称点M，再根据两点式求 MQ方程，即得结果.【详解】因为P点关于直线x+y+1=0对称点为(4,3)M--，所以反射光线方程为13:1(1),451014MQ y x x y+-=--+=+.【点睛】本题考查点关于直线对称问题，考查基本分析求解能力，属基本题.14．①③【解析】【分析】对4个命题分别进行判断即可得出结论【详解】解：①平行于同一平面的两个不同平面互相平行正确；②平行于同一直线的两个不同平面互相平行或相交不正确；③垂直于同一直线的两个不同平面互相平解析：①③【解析】【分析】对4个命题分别进行判断，即可得出结论．【详解】解：①平行于同一平面的两个不同平面互相平行，正确；②平行于同一直线的两个不同平面互相平行或相交，不正确；③垂直于同一直线的两个不同平面互相平行，正确；④垂直于同一平面的两个不同平面互相平行或相交，不正确．故答案为：①③．【点睛】本题考查类比推理，考查学生分析解决问题的能力，属于基础题．15．【解析】结合题意画出折叠后得到的三棱锥如图所示由条件可得在底面中取AB的中点OAC的中点E连OCOE则∵∴∵平面平面∴平面∴又∴∴∴点O为三棱锥外接球的球心球半径为2∴答案：点睛：（1）本题是一道关解析：32 3π【解析】结合题意画出折叠后得到的三棱锥D ABC -如图所示，由条件可得在底面ACB ∆中，90,22ACB AC BC ∠=︒==。

【常考题】高中必修二数学下期中第一次模拟试题(含答案)

【常考题】高中必修二数学下期中第一次模拟试题(含答案)一、选择题1．圆心在x +y =0上，且与x 轴交于点A （-3，0）和B （1，0）的圆的方程为（） A ．22(1)(1)5x y ++-= B ．22(1)(1)5x y -++= C ．22(1)(1)5x y -++= D ．22(1)(1)5x y ++-=2．若函数6(3)3,7(),7x a x x f x a x ---≤⎧=⎨>⎩单调递增,则实数a 的取值范围是( ) A ．9,34⎛⎫⎪⎝⎭ B ．9,34⎡⎫⎪⎢⎣⎭C ．()1,3D ．()2,33．直线(2)4y k x =-+与曲线2320x y y ++-=有两个不同的交点，则实数k 的取值范围是（） A ．53(,]124B ．51(,]122C ．13(,]24D ．1[,)2+∞4．已知三棱锥S ABC -的所有顶点都在球O 的球面上，SC 为球O 的直径，且SC OA ⊥，SC OB ⊥，OAB 为等边三角形，三棱锥S ABC -的体积为433，则球O 的半径为( ) A ．3 B ．1C ．2D ．45．对于平面、β、γ和直线a 、b 、m 、n ,下列命题中真命题是( )A ．若,,,,a m a n m n αα⊥⊥⊂⊂,则a α⊥B ．若//,a b b α⊂,则//a αC ．若//,,,a b αβαγβγ==则//a bD ．若,,//,//a b a b ββαα⊂⊂,则//βα6．<九章算术>中，将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥P ABC -为鳖臑，PA ⊥平面,2,4ABC PA AB AC ===，三棱锥P ABC -的四个顶点都在球O 的球面上，则球O 的表面积为（） A ．8πB ．12πC ．20πD ．24π7．设α表示平面，a ，b 表示直线，给出下列四个命题：①a α//，a b b α⊥⇒//； ②a b //，a b αα⊥⇒⊥；③a α⊥，a b b α⊥⇒⊂；④a α⊥，b a b α⊥⇒//，其中正确命题的序号是（） A ．①② B ．②④ C ．③④ D ．①③ 8．已知直线20ax y a +-+=在两坐标轴上的截距相等，则实数(a = )A ．1B ．1-C ．2-或1D ．2或19．正方体ABCD ﹣A 1B 1C 1D 1中，E ，F 分别是AD ，DD 1的中点，AB ＝4，则过B ，E ，F 的平面截该正方体所得的截面周长为（） A ．25B ．25C ．25D ．2510．设有两条直线m ，n 和三个平面α，β，γ，给出下面四个命题： ①m αβ=，////n m n α⇒，//n β ②αβ⊥，m β⊥，//m m αα⊄⇒；③//αβ，//m m αβ⊂⇒； ④αβ⊥，//αγβγ⊥⇒ 其中正确命题的个数是（） A ．1B ．2C ．3D ．411．若方程21424x kx k +-=-+有两个相异的实根，则实数k 的取值范围是（）A ．13,34⎛⎤ ⎥⎝⎦B ．13,34⎛⎫ ⎪⎝⎭C ．53,124⎛⎫ ⎪⎝⎭D ．53,12412．已知ABC 的三个顶点在以O 为球心的球面上，且2AB =，4AC =，25BC =,三棱锥O ABC -的体积为43，则球O 的表面积为（） A ．22πB ．743πC ．24πD ．36π二、填空题13．如图，在圆柱O 1 O 2 内有一个球O ，该球与圆柱的上、下底面及母线均相切．记圆柱O 1O 2 的体积为V 1 ,球O 的体积为V 2 ，则12V V 的值是_____14．已知菱形ABCD 中，2AB =，120A ∠=，沿对角线BD 将ABD △折起，使二面角A BD C --为120，则点A 到BCD 所在平面的距离等于． 15．过点(1,2)-且与直线2390x y -+=垂直的直线方程为____________． 16．若直线y x b =+与曲线234y x x =-b 的取值范围是______．17．已知,m n 为直线，,αβ为空间的两个平面，给出下列命题：①,//m n m n αα⊥⎧⇒⎨⊥⎩；②,////m n m n αβαβ⊂⎧⎪⊂⇒⎨⎪⎩；③,//m m ααββ⊥⎧⇒⎨⊥⎩；④,//m m n n ββ⊥⎧⇒⎨⊥⎩．其中的正确命题为_________________．18．已知圆22:(2)1M x y +-=，Q 是x 轴上的动点，QA ，QB 分别切圆M 于A ，B 两点，则动弦AB 的中点P 的轨迹方程为__________.19．若圆C ：222430x y x y ++-+=，关于直线260ax by ++=对称，则由点(),a b 向圆所作的切线长的最小值为______．20．直线10x y --=与直线20x ay --=互相垂直，则a =__________．三、解答题21．在平面直角坐标系xOy 中，已知两直线1:330l x y --=和2:10l x y ++=，定点(1,2)A .（1）若1l 与2l 相交于点P ，求直线AP 的方程；（2）若1l 恰好是△ABC 的角平分线BD 所在的直线，2l 是中线CM 所在的直线，求△ABC 的边BC 所在直线的方程.22．如图，在棱长均为4的三棱柱111ABC A B C -中，1,D D 分别是BC 和11B C 的中点.（1）求证：11//A D 平面1AB D（2）若平面ABC ⊥平面111,60BCC B B BC ∠=︒，求三棱锥1B ABC -的体积. 23．已知平面内两点(8,6),(2,2)A B -. （1）求AB 的中垂线方程；（2）求过点(2,3)P -且与直线AB 平行的直线l 的方程．24．如图，在Rt AOB 中，30OAB ∠=︒，斜边4AB =，Rt AOC 可以通过Rt AOB以直线AO 为轴旋转得到，且平面AOB ⊥平面AOC ．动点D 在斜边AB 上．（1）求证：平面COD ⊥平面AOB ；（2）当D 为AB 的中点时，求异面直线AO 与CD 所成角的正切值．25．如图，已知三棱锥A BPC -中，AP PC ⊥，AC BC ⊥，M 为AB 的中点，D 为PB 的中点，且PMB △为正三角形.（1）求证：//DM 平面APC ；（2）求证：BC ⊥平面APC ；（3）若4BC =，10AB =，求三棱锥D BCM -的体积.26．如图所示，已知四棱锥P ABCD -中，底面ABCD 为菱形，PA ⊥平面ABCD ，60,,ABC E F ∠=分别是,BC PB 的中点．（1）证明：AE ⊥平面PAD ；（2）若H 为PD 上的动点，EH 与平面PAD 3B AF C --的正切值．【参考答案】***试卷处理标记，请不要删除一、选择题1．A 解析：A 【解析】【分析】由题意得：圆心在直线x=-1上，又圆心在直线x+y=0上，故圆心M 的坐标为（-1，1），再由点点距得到半径。

【易错题】高中必修二数学下期中试卷附答案(1)

【易错题】高中必修二数学下期中试卷附答案(1)一、选择题1．设l 为直线，,αβ是两个不同的平面，下列命题中正确的是( )A ．若//l α，//l β，则//αβB ．若l α⊥，l β⊥，则//αβC ．若l α⊥，//l β，则//αβD ．若αβ⊥，//l α，则l β⊥ 2．对于平面、β、γ和直线a 、b 、m 、n ,下列命题中真命题是( )A ．若,,,,a m a n m n αα⊥⊥⊂⊂,则a α⊥B ．若//,a b b α⊂,则//a αC ．若//,,,a b αβαγβγ==I I 则//a bD ．若,,//,//a b a b ββαα⊂⊂,则//βα3．四棱锥P ABCD -的底面ABCD 为正方形，PA ⊥底面ABCD ，2AB =，72PA =，若该四棱锥的所有顶点都在同一球面上，则该球的表面积为（） A ．812π B ．814π C ．65π D ．652π 4．已知三棱锥S ABC -的每个顶点都在球O 的表面上，ABC ∆是边长为43的等边三角形，SA ⊥平面ABC ，且SB 与平面ABC 所成的角为6π，则球O 的表面积为（） A ．20π B ．40π C ．80π D ．160π5．在三棱锥P ABC -中，PA ⊥平面1202,2ABC BAC AP AB ∠=︒==，，，M 是线段BC 上一动点，线段PM 长度最小值为3，则三棱锥P ABC -的外接球的表面积是（）A ．92πB ．92πC ．18πD ．40π6．某几何体的三视图如图所示，则该几何体的体积为( )A ．12B ．18C ．24D ．307．如图所示，在棱长为a 的正方体1111ABCD A B C D -中，E 是棱1DD 的中点，F 是侧面11CDD C 上的动点，且1//B F 面1A BE ，则F 在侧面11CDD C 上的轨迹的长度是( )A ．aB ．2aC ．2aD ．22a 8．已知直三棱柱111ABC A B C -的所有棱长都相等，M 为11A C 的中点，则AM 与1BC 所成角的余弦值为( )A ．15B ．5C ．6D ．104 9．已知直线()()():21110l k x k y k R ++++=∈与圆()()221225x y -+-=交于A ，B 两点，则弦长AB 的取值范围是（）A ．[]4,10B ．[]3,5C ．[]8,10D ．[]6,1010．若底面是菱形的棱柱其侧棱垂直于底面，且侧棱长为5，它的对角线的长分别是9和15，则这个棱柱的侧面积是( )．A ．130B ．140C ．150D ．16011．已知ABC V 的三个顶点在以O 为球心的球面上，且2AB =，4AC =，25BC =,三棱锥O ABC -的体积为43，则球O 的表面积为（） A ．22π B ．743π C ．24π D ．36π12．如图，在正方体1111ABCD A B C D -中，M ，N 分别是1BC ，1CD 的中点，则下列说法错误．．的是( )A ．MN 与1CC 垂直B ．MN 与AC 垂直 C ．MN 与BD 平行 D ．MN 与11A B 平行二、填空题13．已知平面α与正方体的12条棱所成角相等，设所成角为θ，则sin θ=______.14．已知圆22:20(0)M x y ay a +-=>截直线0x y +=所得线段的长度是22，则圆M 与圆22:(1)(1)1N x y -+-=的位置关系是_________．15．直线10ax y ++=与连接A （4，5），B （-1，2）的线段相交，则a 的取值范围是___．16．若圆1C ：220x y ax by c ++++=与圆2C ：224x y +=关于直线21y x =-对称，则c =______.17．若直线l ：-3y kx =与直线23-60x y +=的交点位于第一象限，则直线l 的倾斜角的取值范围是___________.18．在各棱长均为1的正四棱锥P ABCD -中，M 为线段PB 上的一动点，则当AM MC +最小时，cos AMC ∠=_________19．如图所示，二面角l αβ--为60,,A B o是棱l 上的两点，,AC BD 分别在半平面内,αβ，且AC l ⊥，，4,6,8AB AC BD ===，则CD 的长______．20．在正方体1111ABCD A B C D -中，E 是棱1DD 的中点，则直线BE 和平面11ABB A 所成的角的正弦值为_____________.三、解答题21．在平面直角坐标系xOy 中，已知圆C 经过()0,2A ，()0,0O ，(),0D t （0t >）三点，M 是线段AD 上的动点，1l ，2l 是过点()10B ,且互相垂直的两条直线，其中1l 交y 轴于点E ，2l 交圆C 于P 、Q 两点.（1）若6t PQ ==，求直线2l 的方程；（2）若t 是使2AM BM ≤恒成立的最小正整数①求t 的值； ②求三角形EPQ 的面积的最小值．22．已知圆C 的圆心坐标()1,1，直线l ：1x y +=被圆C 2.（1）求圆C 的方程；（2）从圆C 外一点()2,3P 向圆引切线，求切线方程.23．如图，在直三棱柱ABC －A 1B 1C 1中，D ，E 分别为BC ，AC 的中点，AB =BC ．求证：（1）A 1B 1∥平面DEC 1；（2）BE ⊥C 1E ．24．如图，在正三棱柱111ABC A B C -中，点D 、E 、F 分别是BC 、1AC 、1BB 的中点.（1）求证：AD ⊥平面11BCC B ；（2）求证：//EF 平面111A B C .25．如图，在四棱锥P ABCD -中，侧面PAD ⊥底面ABCD ，侧棱PA PD ⊥，底面ABCD 是直角梯形，其中//BC AD ，90BAD ∠=︒，3AD BC =，2AO OD =.（1）求证：平面PAB ⊥平面PCD .（2）试问在棱PA 上是否存在点E ，使得面//BOE 面PCD ，若存在，试指出点E 的位置并证明；若不存在，请说明理由.26．求满足下列条件的直线方程：（1）经过两条直线23100x y -+=和3420x y +-=的交点，且平行于直线10x y -+=；（2）经过两条直线280x y +-=和210x y -+=的交点，且垂直于直线320x y --=.【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【解析】A 中，,αβ也可能相交；B 中，垂直与同一条直线的两个平面平行，故正确；C 中，,αβ也可能相交；D 中，l 也可能在平面β内.【考点定位】点线面的位置关系2．C解析：C【解析】【分析】【详解】若由线面垂直的判定定理知,只有当和为相交线时,才有错误；若此时由线面平行的判定定理可知,只有当在平面外时,才有错误；由面面平行的性质定理:若两平面平行,第三个平面与他们都相交,则交线平行,可判断,若//αβ，a αγ⋂=，b βγ=I ，则//a b 为真命题, 正确；若此时由面面平行的判定定理可知,只有当、为相交线时,才有//,D βα错误.故选C.考点：考查直线与直线，直线与平面，平面与平面的位置关系. 3．B解析：B【解析】【分析】根据题意可知，该四棱锥的外接球即为其所在长方体的外接球，根据公式即可求得.【详解】根据题意，为方便说明，在长方体中找出该四棱锥如图所示：由图可知在长方体中的四棱锥P ABCD -完全满足题意，故该四棱锥的外接球即是长方体的外接球，故外接球半径222722294R ⎛⎫++ ⎪⎝⎭==，故该球的表面积为28144S R ππ==. 故选：B .【点睛】本题考查四棱锥外接球的问题，关键的步骤是将问题转化为求长方体的外接球. 4．C解析：C【解析】【分析】根据线面夹角得到4SA =，计算ABC ∆的外接圆半径为42sin a r A==，2222SA R r ⎛⎫=+ ⎪⎝⎭，解得答案. 【详解】 SA ⊥平面ABC ，则SB 与平面ABC 所成的角为6SBA π∠=，故4SA =.ABC ∆的外接圆半径为42sin a r A ==，设球O 的半径为R ，则2222SA R r ⎛⎫=+ ⎪⎝⎭，解得5R =O 的表面积为2480R ππ=. 故选：C .【点睛】本题考查了三棱锥的外接球问题，意在考查学生的计算能力和空间想象能力.5．C解析：C【解析】首先确定三角形ABC 为等腰三角形，进一步确定球的球心，再求出球的半径，最后确定球的表面积．【详解】解：如图所示：三棱锥P ABC -中，PA ⊥平面2,2ABC AP AB ==，，M 是线段BC 上一动点，线段PM 3则：当AM BC ⊥时，线段PM 达到最小值，由于：PA ⊥平面ABC ，所以：222PA AM PM +=，解得：1AM =，所以：3BM =，则：60BAM ∠=︒，由于：120BAC ∠=︒，所以：60MAC ∠=︒则：ABC V 为等腰三角形．所以：23BC =在ABC V 中，设外接圆的直径为324120r sin ==︒，则：2r =，所以：外接球的半径2229222R ⎛⎫=+= ⎪ ⎪⎝⎭，则：94182S ππ=⋅⋅=，故选：C ．【点睛】本题考查的知识要点：三棱锥的外接球的球心的确定及球的表面积公式的应用． 6．C解析：C试题分析：由三视图可知，几何体是三棱柱消去一个同底的三棱锥，如图所示，三棱柱的高为，消去的三棱锥的高为，三棱锥与三棱柱的底面为直角边长分别为和的直角三角形，所以几何体的体积为，故选C ．考点：几何体的三视图及体积的计算．【方法点晴】本题主要考查了几何体的三视图的应用及体积的计算，着重考查了推理和运算能力及空间想象能力，属于中档试题，解答此类问题的关键是根据三视图的规则“长对正、宽相等、高平齐”的原则，还原出原几何体的形状，本题的解答的难点在于根据几何体的三视图还原出原几何体和几何体的度量关系，属于中档试题．7．D解析：D【解析】【分析】设H ，I 分别为1CC 、11C D 边上的中点，由面面平行的性质可得F 落在线段HI 上，再求HI 的长度即可.【详解】解：设G ，H ，I 分别为CD 、1CC 、11C D 边上的中点，则ABEG 四点共面，且平面1//A BGE 平面1B HI ，又1//B F Q 面1A BE ，F ∴落在线段HI 上，Q 正方体1111ABCD A B C D -中的棱长为a ，1122HI CD ∴==，即F 在侧面11CDD C 上的轨迹的长度是22a ．故选D ．【点睛】本题考查了面面平行的性质及动点的轨迹问题，属中档题.8．D解析：D【解析】【分析】取AC 的中点N ，连接1C N ，则1//AM C N ,所以异面直线AM 与1BC 所成角就是直线AM 与1C N 所成角，在1BNC ∆中，利用余弦定理，即可求解．【详解】由题意，取AC 的中点N ，连接1C N ，则1//AM C N ,所以异面直线AM 与1BC 所成角就是直线AM 与1C N 所成角，设正三棱柱的各棱长为2,则115,22,3C N BC BN ===，设直线AM 与1C N 所成角为θ，在1BNC ∆中，由余弦定理可得222(5)(22)(3)10cos 42522θ+-==⨯⨯，即异面直线AM 与1BC 所成角的余弦值为10，故选D ．【点睛】本题主要考查了异面直线所成角的求解，其中解答中把异面直线所成的角转化为相交直线所成的角是解答的关键，着重考查了推理与运算能力，属于基础题．9．D解析：D【解析】【分析】由直线()()21110k x k y ++++=，得出直线恒过定点()1,2P -，再结合直线与圆的位置关系，即可求解.【详解】由直线()()():21110l k x k y k R ++++=∈，可得()210k x y x y ++++=，又由2010x y x y +=⎧⎨++=⎩，解得12x y =⎧⎨=-⎩，即直线恒过定点()1,2P -，圆心()1,2C ，当CP l ⊥时弦长最短，此时2222AB CP r ⎛⎫+= ⎪⎝⎭，解得min 6AB =，再由l 经过圆心时弦长最长为直径210r =，所以弦长AB 的取值范围是[]6,10.故选：D.【点睛】本题主要考查了直线系方程的应用，以及直线与圆的位置关系的应用，其中解答中熟练利用直线的方程，得出直线恒过定点，再结合直线与圆的位置关系求解是解答的关键，着重考查了分析问题和解答问题的能力，属于中档试题.10．D解析：D【解析】设直四棱柱1111ABCD A B C D -中，对角线119,15AC BD ==，因为1A A ⊥平面,ABCD AC Ì,平面ABCD ，所以1A A AC ⊥，在1Rt A AC ∆中，15A A =，可得AC ==同理可得BD ===，因为四边形ABCD 为菱形，可得,AC BD 互相垂直平分，所以8AB ===，即菱形ABCD 的边长为8，因此，这个棱柱的侧面积为1()485160S AB BC CD DA AA =+++⨯=⨯⨯=，故选D.点睛：本题考查了四棱锥的侧面积的计算问题，解答中通过给出的直四棱柱满足的条件，求得底面菱形的边长，进而得出底面菱形的底面周长，即可代入侧面积公式求得侧面积，着重考查了学生分析问题和解答问题的能力，以及空间想象能力，其中正确认识空间几何体的结构特征和线面位置关系是解答的关键.11．C解析：C 【解析】【分析】由已知可得三角形ABC 为直角三角形，斜边BC 的中点O '就是ABC V 的外接圆圆心，利用三棱锥O ABC -的体积，求出O 到底面的距离，可求出球的半径，然后代入球的表面积公式求解．【详解】在ABC V 中，∵2AB =，4AC =，25BC =得AB AC ⊥，则斜边BC 的中点O '就是ABC V 的外接圆的圆心， ∵三棱锥O ABC -的体积为43， 11424323OO '⨯⨯⨯⨯=，解得1OO '=，221(5)6R =+=，球O 的表面积为2424R ππ=．故选C ．【点睛】本题考查球的表面积的求法，考查锥体体积公式的应用，考查空间想象能力和计算能力，属于基础题.12．D解析：D 【解析】【分析】先利用三角形中位线定理证明//MN BD ，再利用线面垂直的判定定理定义证明MN 与1CC 垂直，由异面直线所成的角的定义证明MN 与AC 垂直，即可得出结论.【详解】如图：连接1C D ，BD ，Q 在三角形1C DB 中，//MN BD ，故C 正确．1CC ⊥Q 平面ABCD ，1CC BD ∴⊥，MN ∴与1CC 垂直，故A 正确；AC BD ^Q ，//MN BD ，MN ∴与AC 垂直，B 正确；∵//MN BD ，MN ∴与11A B 不可能平行，D 错误故选：D ．【点睛】本题主要考查了正方体中的线面关系，线线平行与垂直的证明，异面直线所成的角及其位置关系，熟记正方体的性质是解决本题的关键.二、填空题13．【解析】【分析】棱与平面所成的角相等所以平面就是与正方体的12条棱的夹角均为θ的平面之一设出棱长即可求出【详解】因为棱与平面所成的角相等所以平面就是与正方体的条棱的夹角均为的平面设棱长为：易知故答案 3【解析】【分析】棱11111,,A A A B A D 与平面11AB D 所成的角相等，所以平面11AB D 就是与正方体的12条棱的夹角均为θ的平面之一，设出棱长，即可求出sin θ. 【详解】因为棱11111,,A A A B A D 与平面11AB D 所成的角相等，所以平面11AB D 就是与正方体的12条棱的夹角均为θ的平面，1A AO θ∠=，设棱长为：1，126AO AO ==，易知232sin 36θ==. 故答案为：33【点睛】本题考查了线面所成的角，解题的关键是作出线面角，属于基础题.14．相交【解析】【分析】根据直线与圆相交的弦长公式求出的值结合两圆的位置关系进行判断即可【详解】解：圆的标准方程为则圆心为半径圆心到直线的距离圆截直线所得线段的长度是即则圆心为半径圆的圆心为半径则即两个解析：相交【解析】【分析】根据直线与圆相交的弦长公式，求出a 的值，结合两圆的位置关系进行判断即可．【详解】解：圆的标准方程为222:()(0)M x y a a a +-=>，则圆心为(0,)a ，半径R a =，圆心到直线0x y +=的距离2d =，Q 圆22:20(0)M x y ay a +-=>截直线0x y +=所得线段的长度是22222222a a ∴-即24a =，2a =，则圆心为(0,2)M ，半径2R =，圆22:(1)(1)1N x y -+-=的圆心为(1,1)N ，半径1r =，则2MN =3R r +=Q ，1R r -=， R r MN R r ∴-<<+，即两个圆相交．故答案为：相交．【点睛】本题主要考查直线和圆相交的应用，以及两圆位置关系的判断，根据相交弦长公式求出a 的值是解决本题的关键．15．或【解析】【分析】判断直线恒过定点P （0-1）计算PAPB 的斜率再利用数形结合求a 的取值范围【详解】解：由直线ax+y+1=0的方程判断直线恒过定点P （0-1）如图所示计算且或则或即实数a 的取值范围解析：32a ≤-或3a ≥ 【解析】【分析】判断直线0ax by c ++=恒过定点P （0，-1），计算PA 、PB 的斜率，再利用数形结合求a 的取值范围．【详解】解：由直线ax+y+1=0的方程，判断直线恒过定点P （0，-1），如图所示，计算513402PA k +==-，21310PB k +==--- 且PA k k ≥或PB k k ≤，则PA a k ≤-或PB a k ≥-，即实数a 的取值范围是：32a ≤-或3a ≥．故答案为：32a ≤-或3a ≥．【点睛】本题考查直线的斜率与直线方程的应用问题，是基础题．16．【解析】【分析】两圆关于直线对称即圆心关于直线对称则两圆的圆心的连线与直线垂直且中点在直线上圆的半径也为即可求出参数的值【详解】解：因为圆：即圆心半径由题意得与关于直线对称则解得圆的半径解得故答案为解析：165-【解析】【分析】两圆关于直线对称即圆心关于直线对称，则两圆的圆心的连线与直线21y x =-垂直且中点在直线21y x =-上，圆1C 的半径也为2，即可求出参数,,a b c 的值. 【详解】解：因为圆1C ：220x y ax by c ++++=，即22224224ab a b cx y 骣骣+-琪琪+++=琪琪桫桫，圆心111,22C a b ⎛⎫-- ⎪⎝⎭，半径r =由题意，得111,22C a b ⎛⎫-- ⎪⎝⎭与()20,0C 关于直线21y x =-对称，则112,122112221,22b a ba ⎧-⎪=-⎪⎪-⎨⎪--⎪⎪=⨯-⎩解得85=-a ，45b =，圆1C的半径22r ==，解得165c =-. 故答案为：165-【点睛】本题考查圆关于直线对称求参数的值，属于中档题.17．【解析】若直线与直线的交点位于第一象限如图所示：则两直线的交点应在线段上（不包含点）当交点为时直线的倾斜角为当交点为时斜率直线的倾斜角为∴直线的倾斜角的取值范围是故答案为解析：(,)62ππ 【解析】若直线:l y kx =2360x y +-=的交点位于第一象限，如图所示：则两直线的交点应在线段AB 上（不包含,A B 点）, 当交点为()0,2A 时，直线l 的倾斜角为2π，当交点为()3,0B 时，斜率(03330k -==-l 的倾斜角为6π ∴直线的倾斜角的取值范围是,62ππ⎛⎫⎪⎝⎭．故答案为,62ππ⎛⎫⎪⎝⎭ 18．【解析】【分析】将侧面和侧面平展在一个平面上连即可求出满足最小时点的位置以及长解即可求出结论【详解】将侧面和侧面平展在一个平面上连与交点即为满足最小正四棱锥各棱长均为在平展的平面中四边形为菱形且在正解析：13-【解析】【分析】将侧面PAB 和侧面PBC 平展在一个平面上，连AC ，即可求出满足AM MC +最小时，点M 的位置，以及,AM CM 长，解AMC V ，即可求出结论. 【详解】将侧面PAB 和侧面PBC 平展在一个平面上，连AC 与PB 交点即为满足AM MC +最小，正四棱锥P ABCD -各棱长均为1，在平展的平面中四边形PABC 为菱形，且60PAB ∠=o ，32AM MC ==P ABCD -中，2AC =在ACM V 中，222332144cos 32324AM CM AC AMC AM CM +-+-∠===-⋅⋅. 故答案为:13-.【点睛】本题考查线线角，要注意多面体表面的长度关系转化为共面的长度关系，考查直观想象能力，属于中档题.19．【解析】【分析】推导出两边平方可得的长【详解】二面角为是棱上的两点分别在半平面内且的长故答案为：【点睛】本题考查线段长的求法考查空间中线线线面面面间的位置关系等基础知识考查运算求解能力考查函数与方程解析：217. 【解析】【分析】推导出CD CA AB BD =++u u u r u u u r u u u r u u u r，两边平方可得CD 的长．【详解】Q 二面角l αβ--为60︒，A 、B 是棱l 上的两点，AC 、BD 分别在半平面α、β内，且AC l ⊥，BD l ⊥，4AB =，6AC =，8BD =，∴CD CA AB BD =++u u u r u u u r u u u r u u u r， ∴22()CD CA AB BD =++u u u r u u u r u u u r u u u r2222CA AB BD CA BD =+++u u u r u u u r u u u r u u u r u u u r g361664268cos12068=+++⨯⨯⨯︒=，CD ∴的长||68217CD ==u u u r．故答案为：217．【点睛】本题考查线段长的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，考查函数与方程思想，是中档题．20．【解析】【分析】作出直线和平面所成的角解直角三角形求得线面角的正弦值【详解】设为的中点连接根据正方体的性质可知平面所以是直线和平面所成的角设正方体的边长为在中所以故答案为：【点睛】本小题主要考查线面解析：23【解析】【分析】作出直线BE 和平面11ABB A 所成的角，解直角三角形求得线面角的正弦值. 【详解】设F 为1AA 的中点，连接,,EF EB BF ，根据正方体的性质可知EF ⊥平面11ABB A ，所以EBF ∠是直线BE 和平面11ABB A 所成的角.设正方体的边长为2，在Rt EBF ∆中2EF =，2222213BE =++=，所以2sin 3EF EBF BE ∠==. 故答案为：23【点睛】本小题主要考查线面角的求法，考查空间想象能力，属于基础题.三、解答题21．（1）4340x y --=；（2）①4，②152. 【解析】【分析】（1）求出圆的标准方程，设直线2l 的方程(1)y k x =-，利用6PQ =，结合圆心到直线的210911k -=+，解可得k 的值，验证直线与y 轴有无交点，即可得答案；（2）①设(,)M x y ，由点M 在线段AD 上，得220x ty t +-=，由2AM BM ≤，得224220()()339x y -++…，结合题意，线段AD 与圆224220()()339x y -++=至多有一个公共288||25334t t -+…t 的值，②由①的结论，分直线的斜率存在与不存在2种情况讨论，用k 表示三角形EPQ 的面积，结合二次函数的性质分析可得答案．【详解】解：（1）由题意可知，圆C 的直径为AD ，所以圆C 方程为：()()223110x y -+-=，设2l 方程为：()1y k x =-，则()222213101k k-+=+，解得10k =，243k =，当0k =时，直线1l 与y 轴无交点，不合题意，舍去. 所以，43k =时直线2l 的方程为4340x y --=. （2）①设(,)M x y ，由点M 在线段AD 上，则有12x yt +=，即220x ty t +-=．由2AM BM „，则有224220()()339x y -++…依题意知，线段AD 与圆224220()()339x y -++=至多有一个公共点，88||t -t „或1611t +…，因为t 是使2AM BM ≤恒成立的最小正整数，所以4t =； ②由①的结论，圆C 的方程为22(2)(1)5x y -+-=．分2种情况讨论：a 当直线2:1l x =时，直线1l 的方程为0y =，此时，2EPQ S =V ；b 当直线2l 的斜率存在时，设2l 的方程为(1)y k x =-，0k ≠，则1l 的方程为1(1)y x k=--，点1(0,)E k，所以BE =又圆心到2l，所以PQ =故1122EPQ S BE PQ ===V g2<，故求三角形EPQ．【点睛】本题考查直线与圆的方程的综合应用，涉及三角形面积的最小值的求法，（2）的关键是确定三角形面积的表达式，属于中档题．22．（1）()()22111x y -+-=；（2）2x =和3460x y -+=. 【解析】【分析】()1设圆C 的半径为r ，根据圆心坐标写出圆的标准方程，利用点到直线的距离公式求出圆心到直线l 的距离即为弦心距，然后根据垂径定理得到其垂足为弦的中点，由弦长的一半，圆心距及半径构成的直角三角形，根据勾股定理列出关于r 的方程，求出方程的解即可得到r 的值，从而确定圆C 的方程；()2当切线方程的斜率不存在时，显然得到2x =为圆的切线；当切线方程的斜率存在时，设出切线的斜率为k ，由p 的坐标和k 写出切线方程，利用点到直线的距离公式求出圆心到所设直线的距离d ，根据直线与圆相切，得到d 等于圆的半径，列出关于k 的方程，求出方程的解即可得到k 的值，从而确定出切线的方程，综上，得到所求圆的两条切线方程. 【详解】（1）设圆C 的标准方程为： ()()22211x y r -+-= (0)r > 圆心()1,1C 到直线10x y +-=的距离：d ==则22211122r d =+=+=⎝⎭∴圆C 的标准方程： ()()22111x y -+-=（2）①当切线斜率不存在时，设切线： 2x =，此时满足直线与圆相切. ②当切线斜率存在时，设切线： ()32y k x -=-，即23y kx k =-+ 则圆心()1,1C 到直线230kx y k --+=的距离：1d ==解得： 43k =，即34k =则切线方程为： 3460x y -+=综上，切线方程为： 2x =和3460x y -+= 23．（1）见解析；（2）见解析. 【解析】【分析】(1)由题意结合几何体的空间结构特征和线面平行的判定定理即可证得题中的结论； (2)由题意首先证得线面垂直，然后结合线面垂直证明线线垂直即可. 【详解】（1）因为D ，E 分别为BC ，AC 的中点，所以ED ∥AB .在直三棱柱ABC-A 1B 1C 1中，AB ∥A 1B 1，所以A 1B 1∥ED .又因为ED ⊂平面DEC 1，A 1B 1⊄平面DEC 1，所以A 1B 1∥平面DEC 1.（2）因为AB =BC ，E 为AC 的中点，所以BE ⊥AC .因为三棱柱ABC-A 1B 1C 1是直棱柱，所以CC 1⊥平面ABC .又因为BE ⊂平面ABC ，所以CC 1⊥BE .因为C 1C ⊂平面A 1ACC 1，AC ⊂平面A 1ACC 1，C 1C ∩AC =C ，所以BE ⊥平面A 1ACC 1.因为C 1E ⊂平面A 1ACC 1，所以BE ⊥C 1E .【点睛】本题主要考查直线与直线、直线与平面、平面与平面的位置关系等基础知识，考查空间想象能力和推理论证能力.24．（1）见解析；（2）见解析.【解析】【分析】（1）可证1AD CC ⊥，AD BC ⊥，从而可证AD ⊥平面11BCC B .（2）取11A C 的中点为G ，连接1,EG B G ，可证1//EF B G ，从而可证//EF 平面111A B C .【详解】由正三棱柱111ABC A B C -可得1C C ⊥平面ABC ，而AD ⊂平面ABC ，故1AD CC ⊥.因为ABC ∆为等边三角形，BD DC =，故AD BC ⊥，因为1BC CC C =I ，BC ⊂平面11BCC B ，1C C ⊂平面11BCC B ，所以AD ⊥平面11BCC B .（2）取11A C 的中点为G ，连接1,EG B G .在11A AC ∆，因为111,A G GC AE EC ==，故111//,2EG AA EG AA =.由正三棱柱111ABC A B C -可得四边形11ABB A 为平行四边形，故1111,//AA BB AA BB =，而1112B F BB =，所以11111//,2B F AA B F AA =，故11//,EG B F EG B F =，故四边形1B FEG 为平行四边形，1//EF B G .因为EF ⊄平面111A B C ， 1B G ⊂平面111A B C ，故//EF 平面111A B C .【点睛】本题考查线面垂直与线面平行的证明，前者转化为线线垂直，注意平面中的两条直线需为相交直线，后者转化为线线平行，注意一条线是平面外，另一条线是平面内，本题属于中档题.25．（1）见解析；（2）在棱PA 上存在点E 且E 满足2AE EP=时能使得面//BOE 面PCD ，证明见解析.【解析】【分析】（1）可证PD ⊥平面PAB ，从而得到要证明的面面垂直.（2）在棱PA 上存在点E 且E 满足2AE EP =时能使得面//BOE 面PCD ，利用面面平行的判断定理可证明该结论.【详解】（1）因为90BAD ∠=︒，故BA AD ⊥又因为侧面PAD ⊥底面ABCD ，侧面PAD I 底面ABCD AD =，BA ⊂平面ABCD ，所以BA ⊥平面PAD . 因为PD ⊂平面PAD ，故BA PD ⊥，又因为PA PD ⊥，PA AB A =I ，PA ⊂平面PAB ，AB Ì平面PAB ，所以PD ⊥平面PAB ，而PD ⊂平面PCD ，故平面PAB ⊥平面PCD .（2）在棱PA 上存在点E ，使得面//BOE 面PCD ，E 满足2AE EP =，证明如下：因为2AE EP =，2AO OD =，所以DAE EP AO O =，故//OE PD .因为OE ⊄平面PCD ，PD ⊂平面PCD ，故//OE 平面PCD .因为//BC AD ，13OD AD BC ==，故//,OD BC OD BC =，所以四边形BCDO 为平行四边形，故//BO CD ，因为BO ⊄平面PCD ，CD ⊂平面PCD ，故//BO 平面PCD . 因为BO ⊂平面EOB ，EO ⊂平面EOB ，BO EO O ⋂=，故面//BOE 面PCD .【点睛】本题考查面面垂直的证明和面面平行的探索，前者注意空间中三种垂直关系的转化，后者应根据题设条件得到动点满足的位置特征，然后再根据判定定理来证明，本题属于中档题.26．（1）40x y -+=（2）390x y +-=【解析】【分析】【详解】得23100{3420x y x y -+=+-=⇒2{2x y =-= 即两直线交点坐标为()2,2-.∵所求直线与已知直线平行.∴设直线方程1:0l x y C -+=；将交点坐标代入直线方程，解得4C =.∴直线1:40l x y -+=.（2）联立两直线方程得280{210x y x y +-=-+=⇒32x y =⎧⎨=⎩ 即两直线交点坐标为()3,2.∵所求直线与已知直线垂直.∴设直线方程2:30l x y C ++=；将交点坐标代入直线方程，解得9C =-.∴直线2:390l x y +-=.。

【典型题】高中必修二数学下期中第一次模拟试题(附答案)

【典型题】高中必修二数学下期中第一次模拟试题(附答案)一、选择题1．直线(2)4y k x =-+与曲线2320x y y ++-=有两个不同的交点，则实数k 的取值范围是（） A ．53(,]124B ．51(,]122C ．13(,]24D ．1[,)2+∞2．如图是水平放置的平面图形的斜二测直观图，其原来平面图形面积是（）A ． 22B ． 42C ．4D ．83．已知圆截直线所得线段的长度是，则圆与圆的位置关系是（） A ．内切B ．相交C ．外切D ．相离4．已知三棱锥S ABC -的每个顶点都在球O 的表面上，ABC ∆是边长为43的等边三角形，SA ⊥平面ABC ，且SB 与平面ABC 所成的角为6π，则球O 的表面积为（） A ．20πB ．40πC ．80πD ．160π5．某几何体的三视图如图所示，图中的四边形都是边长为4的正方形，两条虚线互相垂直且相等，则该几何体的体积是（）A ．1763B ．1603C ．1283D ．326．已知三条直线,,m n l ，三个平面,,αβγ，下列四个命题中，正确的是（）A ．||αγαββγ⊥⎫⇒⎬⊥⎭B ．||m l l m ββ⎫⇒⊥⎬⊥⎭C ．||||||m m n n γγ⎫⇒⎬⎭D ．||m m n n γγ⊥⎫⇒⎬⊥⎭7．椭圆22221(0)x y a b a b+=>>的左右焦点分别是1F 、2F ，以2F 为圆心的圆过椭圆的中心，且与椭圆交于点P ，若直线1PF 恰好与圆2F 相切于点P ，则椭圆的离心率为（） A ．312+ B ．31-C ．22D ．512- 8．若圆22240x y x y +--=的圆心到直线0x y a -+=的距离为22，则a 的值为( ) A ．-2或2B ．12或32C ．2或0D ．-2或09．若方程21424x kx k +-=-+ 有两个相异的实根，则实数k 的取值范围是（）A ．13,34⎛⎤ ⎥⎝⎦B ．13,34⎛⎫⎪⎝⎭C ．53,124⎛⎫⎪⎝⎭ D ．53,12410．如图1，ABC ∆是以B 为直角顶点的等腰直角三角形，T 为线段AC 的中点，G 是BC 的中点，ABE ∆与BCF ∆分别是以AB 、BC 为底边的等边三角形，现将ABE ∆与BCF ∆分别沿AB 与BC 向上折起（如图2），则在翻折的过程中下列结论可能正确的个数为（）图1 图2（1）直线AE ⊥直线BC ；（2）直线FC ⊥直线AE ；（3）平面//EAB 平面FGT ；（4）直线//BC 直线AE . A ．1个B ．2个C ．3个D ．4个11．如图，平面四边形ABCD 中，1AB AD CD ===，2BD =，BD CD ⊥，将其沿对角线BD 折成四面体A BCD '-，使平面A BD '⊥平面BCD ，若四面体A BCD '-的顶点在同一个球面上，则该球的表面积为（）A．3πB．32πC．4πD．34π12．如图，在三棱柱111ABC A B C-中，1CC⊥平面ABC，ABC是等腰三角形，BA BC=，123AC CC==，，D是AC的中点，点F在侧棱1A上，若要使1C F⊥平面BDF，则1AFFA的值为( )A．1B．12或2C．2或2D．13或3二、填空题13．如图，正方体ABCD﹣A1B1C1D1的棱长为1，M为B1C1中点，连接A1B，D1M，则异面直线A1B和D1M所成角的余弦值为________________________．14．已知圆22(1)16x y++=，点(1,0),(1,0)E F-，过(1,0)E-的直线1l与过(1,0)F的直线2l垂直且圆相交于,A C和,B D，则四边形ABCD的面积的取值范围是_________. 15．点(5,2)到直线()1(21)5m x m y m-+-=-的距离的最大值为________.16．已知正三棱锥P-ABC，点P，A，B，C3PA，PB，PC两两互相垂直，则球心到截面ABC 的距离为________．17．将正方形ABCD 沿对角线BD 折成直二面角A BD C --，①AB 与平面BCD 所成角的大小为60 ②ACD ∆是等边三角形 ③AB 与CD 所成的角为60 ④AC BD ⊥⑤二面角B AC D --为120︒ 则上面结论正确的为_______．18．已知直线:0l x my m ++=，且与以A (-1,1)、B (2,2)为端点的线段相交，实数m 的取值范围为___________.19．已知球的表面积为20π，球面上有A 、B 、C 三点．如果2AB AC ==，22BC =，则球心到平面ABC 的距离为__________．20．如图，在体积为1V 的圆柱中挖去以圆柱上下底面为底面、共顶点的两个圆锥，剩余部分的体积为2V ，则21V V =__________．三、解答题21．如图，直角梯形BDFE 中，//,,2EF BD BE BD EF ⊥=ABCD 中，//,,24AB CD AC BD AB CD ⊥==，且平面BDFE ⊥平面ABCD ．（1）求证：AC ⊥平面BDFE ；（2）若BF 与平面ABCD 所成角为4π，求二面角B DF C --的余弦值．22．如图，在直三棱柱111ABC A B C -中，D 是BC 的中点．AB AC ⊥，1AB AC ==，12AA =．（Ⅰ）求直线1AC 与平面11BCC B 所成角的正弦值；（Ⅱ）求二面角1A A B C --的余弦值．23．如图，在四棱锥P ABCD -中，侧面PAD ⊥底面ABCD ，侧棱PA PD ⊥，底面ABCD 是直角梯形，其中//BC AD ，90BAD ∠=︒，3AD BC =，2AO OD =.（1）求证：平面PAB ⊥平面PCD .（2）试问在棱PA 上是否存在点E ，使得面//BOE 面PCD ，若存在，试指出点E 的位置并证明；若不存在，请说明理由.24．如图，在Rt AOB 中，30OAB ∠=︒，斜边4AB =，Rt AOC 可以通过Rt AOB 以直线AO 为轴旋转得到，且平面AOB ⊥平面AOC ．动点D 在斜边AB 上．（1）求证：平面COD ⊥平面AOB ；（2）当D 为AB 的中点时，求异面直线AO 与CD 所成角的正切值．25．如图，直三棱柱111ABC A B C -的底面是边长为4的正三角形，M ，N 分别是BC ，1CC 的中点.（1）证明：平面AMN ⊥平面11B BCC ；（2）若直线1A C 与平面11A ABB 所成的角为30，试求三棱锥M ANC -的体积. 26．（1）用符号表示下来语句，并画出同时满足这四个语句的一个几何图形： ①直线l 在平面α内； ②直线m 不在平面α内； ③直线m 与平面α交于点A ； ④直线l 不经过点A .（2）如图，在长方体1111ABCD A B C D -中，E 为棱1BB 的中点，F 为棱1CC 的三等分点，画出由1,,D E F 三点所确定的平面β与平面ABCD 的交线.(保留作图痕迹)【参考答案】***试卷处理标记，请不要删除一、选择题1．B 解析：B 【解析】【分析】利用数形结合，作出图象，计算得直线1l 与直线2l 的斜率，即可得到结论. 【详解】曲线可化简为()22(1)40x y x +-=≤，如图所示：直线()1:24l y k x =-+23221k k -=+，解得512k =，直线()2:24l y k x =-+，此直线与曲线有两个交点，此时有12k =. 所以，过点()2,4的直线与该半圆有两个交点，数形结合，解得51122k <≤. 故选：B. 【点睛】本题考查了直线与圆相交的性质，涉及的知识有：恒过定点的直线方程，点到直线的距离公式，以及直线斜率的求法，利用了数形结合的思想，其中抓住两个关键点是解本题的关键．2．C解析：C 【解析】分析：由三视图还原实物图,再根据三角形面积公式求解.详解：在斜二测直观图中OB=2,OA=2, 所以在平面图形中OB=2,OA=4， OA ⊥OB ，所以面积为12442S =⨯⨯=. 选C.点睛： 1.解答此类题目的关键是由多面体的三视图想象出空间几何体的形状并画出其直观图． 2．三视图中“正侧一样高、正俯一样长、俯侧一样宽”，因此，可以根据三视图的形状及相关数据推断出原几何图形中的点、线、面之间的位置关系及相关数据．3．B解析：B 【解析】化简圆到直线的距离，又两圆相交. 选B4．C解析：C 【解析】【分析】根据线面夹角得到4SA =，计算ABC ∆的外接圆半径为42sin ar A==，2222SA R r ⎛⎫=+ ⎪⎝⎭，解得答案.【详解】SA ⊥平面ABC ，则SB 与平面ABC 所成的角为6SBA π∠=，故4SA =. ABC ∆的外接圆半径为42sin ar A==，设球O 的半径为R ，则2222SA R r ⎛⎫=+ ⎪⎝⎭，解得5R =O 的表面积为2480R ππ=. 故选：C . 【点睛】本题考查了三棱锥的外接球问题，意在考查学生的计算能力和空间想象能力.5．B解析：B 【解析】该几何体为一个正方体去掉一个倒四棱锥，其中正方体棱长为4，倒四棱锥顶点为正方体中心，底面为正方体上底面，因此体积是32116042433-⨯⨯=，选B. 点睛： 1.解答此类题目的关键是由多面体的三视图想象出空间几何体的形状并画出其直观图．2．三视图中“正侧一样高、正俯一样长、俯侧一样宽”，因此，可以根据三视图的形状及相关数据推断出原几何图形中的点、线、面之间的位置关系及相关数据．6．D解析：D 【解析】试题分析：A.}r rααββ⊥⇒⊥不正确，以墙角为例，,αβ可能相交；B.}m l l m ββ⇒⊥⊥不正确，,l β有可能平行；C.}m rm n n r⇒不正确，m,n 可能平行、相交、异面；故选D 。

【典型题】高中必修二数学下期中第一次模拟试题(带答案)

【典型题】高中必修二数学下期中第一次模拟试题(带答案)一、选择题1．已知,,,A B C D 是同一球面上的四个点，其中ABC ∆是正三角形，AD ⊥平面ABC ，26AD AB ==，则该球的体积为（）A ．48πB ．24πC ．16πD ．2．已知两点()A 3,4-，()B 3,2，过点()P 1,0的直线l 与线段AB 有公共点，则直线l 的斜率k 的取值范围是( ) A ．()1,1- B ．()(),11,∞∞--⋃+ C ．[]1,1-D ．][(),11,∞∞--⋃+3．设圆C ：223x y +=，直线l ：360x y +-=，点()00,P x y l ∈，若存在点Q C ∈，使得60OPQ ∠=︒（O 为坐标原点），则0x 的取值范围是( ) A ．1,12⎡⎤-⎢⎥⎣⎦B ．60,5⎡⎤⎢⎥⎣⎦C ．[]0,1D ．16,25⎡⎤-⎢⎥⎣⎦ 4．已知三棱锥S ABC -的所有顶点都在球O 的球面上，SC 为球O 的直径，且SC OA ⊥，SC OB ⊥，OAB V 为等边三角形，三棱锥S ABC -，则球O 的半径为( ) A ．3B ．1C ．2D ．45．直线20x y ++=截圆222210x y x y a ++-+-=所得弦的长度为4，则实数a 的值是（）A ．－3B ．－4C ．－6D ．36．已知m 和n 是两条不同的直线，α和β是两个不重合的平面，那么下面给出的条件中一定能推出m ⊥β的是( ) A ．α⊥β，且m ⊂α B ．m ⊥n ，且n ∥β C ．α⊥β，且m ∥α D ．m ∥n ，且n ⊥β 7．已知直线20ax y a +-+=在两坐标轴上的截距相等，则实数(a = )A ．1B ．1-C ．2-或1D ．2或18．已知三棱锥S ABC -的每个顶点都在球O 的表面上，ABC ∆是边长为角形，SA ⊥平面ABC ，且SB 与平面ABC 所成的角为6π，则球O 的表面积为（） A ．20πB ．40πC ．80πD ．160π9．若方程124kx k =-+ 有两个相异的实根，则实数k 的取值范围是（）A ．13,34⎛⎤ ⎥⎝⎦B ．13,34⎛⎫ ⎪⎝⎭C ．53,124⎛⎫ ⎪⎝⎭D ．53,124纟çúçú棼10．如图，在正方体1111ABCD A B C D -中，M ，N 分别是1BC ，1CD 的中点，则下列说法错误．．的是( )A ．MN 与1CC 垂直B ．MN 与AC 垂直 C ．MN 与BD 平行D ．MN 与11A B 平行11．某几何体的三视图如图所示（单位：cm ），其俯视图为等边三角形，则该几何体的体积（单位：3cm ）是（）A ．43B ．1033C ．23D ．83312．如图，网格纸上小正方形的边长为1，粗实（虚）线画出的是某多面体的三视图，则该多面体的体积为（）A ．64B ．643C ．16D ．163二、填空题13．《九章算术》中，将底面为长方形且由一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的三棱锥称之为鳖臑．若三棱锥P ABC -为鳖臑，PA ⊥平面ABC ，2,4PA AB AC ===，三棱锥P ABC -的四个顶点都在球O 的球面上，则球O的表面积为__________.14．如图，在圆柱O 1 O 2 内有一个球O ，该球与圆柱的上、下底面及母线均相切．记圆柱O 1O 2 的体积为V 1 ,球O 的体积为V 2 ，则12V V 的值是_____15．在三棱锥P ABC -中,PA ⊥平面ABC ，AB BC ⊥，3AB =，4BC =，5PA =，则三棱锥P ABC -的外接球的表面积为__________16．将正方形ABCD沿对角线BD 折成直二面角A BD C --，①AB 与平面BCD 所成角的大小为60o ②ACD ∆是等边三角形 ③AB 与CD 所成的角为60o ④AC BD ⊥⑤二面角B AC D --为120︒ 则上面结论正确的为_______．17．正四棱锥P ABCD -底面的四个顶点,,,A B C D 在球O 的同一个大圆上，点P 在球面上.若163P ABCDV -=，则球O 的体积是______． 18．三棱锥A BCD -中，E 是AC 的中点，F 在AD 上，且2AF FD =，若三棱锥A BEF -的体积是2，则四棱锥B ECDF -的体积为_______________．19．如图所示，二面角l αβ--为60,,A B o是棱l 上的两点，,AC BD 分别在半平面内,αβ，且AC l ⊥，，4,6,8AB AC BD ===，则CD 的长______．20．如图，在体积为1V的圆柱中挖去以圆柱上下底面为底面、共顶点的两个圆锥，剩余部分的体积为2V，则21VV=__________．三、解答题21．如图，在三棱锥S ABC-中，SAC∆为等边三角形，4AC=，43BC=，BC AC⊥，3cos SCB∠=-，D为AB的中点．（1）求证：AC SD⊥；（2）求直线SD与平面SAC所成角的大小．22．如图，在三棱锥A BCD-中，,E F分别为棱,BC CD上的中点.（1）求证：EF P 平面ABD ；（2）若,BD CD AE ⊥⊥平面BCD ，求证：平面AEF ⊥平面ACD .23．如图，已知三棱锥A BPC -中，AP PC ⊥，AC BC ⊥，M 为AB 的中点，D 为PB 的中点，且PMB △为正三角形.（1）求证：//DM 平面APC ；（2）求证：BC ⊥平面APC ；（3）若4BC =，10AB =，求三棱锥D BCM -的体积.24．如图，在四棱锥P ABCD -中，底面ABCD 为直角梯形，//AD BC ，90ADC ∠=︒，12BC AD =，PA PD =，M ，N 分别为AD 和PC 的中点．（1）求证：//PA 平面MNB ；（2）求证：平面PAD ⊥平面PMB ．25．如图，三棱柱111ABC A B C -中，平面11AAC C ⊥平面11AA B B ,平面11AACC ⊥平面ABC ，12AB AC AA ===,点P 、M 分别为棱BC 、1CC 的中点，过点B 、M 的平面交棱1AA 于点N ,使得AP ∥平面BMN .（1）求证：AB ⊥平面11AAC C ; （2）若四棱锥B ACMN -的体积为32，求1A AC ∠的正弦值. 26．如图，1AA 、1BB 为圆柱1OO 的母线（母线与底面垂直），BC 是底面圆O 的直径，D 、E 分别是1AA 、1CB 的中点，DE ⊥平面1CBB ．（1）证明：AC ⊥平面11AA B B ；（2）证明：//DE 平面ABC .【参考答案】***试卷处理标记，请不要删除一、选择题 1．D 解析：D 【解析】【分析】根据球的性质可知球心O 与ABC ∆外接圆圆心O '连线垂直于平面ABC ；在Rt POE ∆和Rt OO A ∆'中利用勾股定理构造出关于半径R 和OO '的方程组，解方程组求得R ，代入球的体积公式可得结果. 【详解】设O '为ABC ∆的外心，如下图所示：由球的性质可知，球心O 与O '连线垂直于平面ABC ，作OE AD ⊥于E 设球的半径为R ，OO x '=ABC ∆为等边三角形，且3AB = 3AO '∴=OO '⊥Q 平面ABC ，AD ⊥平面ABC ，OE AD ⊥OO AE x '∴==，3OE AO '==在Rt POE ∆和Rt OO A ∆'中，由勾股定理得：22222OE PE O O O A R ''+=+=，即()222363x x R +-=+=解得：3x =，3R =∴球的体积为：343233V R ππ==本题正确选项：D 【点睛】本题考查棱锥外接球的体积求解问题，关键是能够确定棱锥外接球球心的位置，从而在直角三角形中利用勾股定理构造方程求得半径.2．D解析：D 【解析】分析：根据两点间的斜率公式，利用数形结合即可求出直线斜率的取值范围．详解：∵点A （﹣3，4），B （3，2），过点P （1，0）的直线L 与线段AB 有公共点， ∴直线l 的斜率k≥k PB 或k≤k PA ，∵PA 的斜率为4031--- =﹣1，PB 的斜率为2031--=1， ∴直线l 的斜率k≥1或k≤﹣1，故选：D ．点睛：本题主要考查直线的斜率的求法，利用数形结合是解决本题的关键，比较基础．直线的倾斜角和斜率的变化是紧密相联的，tana=k,一般在分析角的变化引起斜率变化的过程时，是要画出正切的函数图像，再分析.3．B解析：B 【解析】【分析】圆O 外有一点P ，圆上有一动点Q ，OPQ ∠在PQ 与圆相切时取得最大值．如果OP 变长，那么OPQ ∠可以获得的最大值将变小．因为sin QOOPQ PO∠=，QO 为定值，即半径，PO 变大，则sin OPQ ∠变小，由于(0,)2OPQ π∠∈，所以OPQ ∠也随之变小．可以得知，当60OPQ ∠=︒，且PQ 与圆相切时，2PO =，而当2PO >时，Q 在圆上任意移动，60OPQ ∠<︒恒成立．因此，P 的取值范围就是2PO …，即满足2PO …，就能保证一定存在点Q ，使得60OPQ ∠=︒，否则，这样的点Q 是不存在的．【详解】由分析可得：22200PO x y =+又因为P 在直线l 上，所以00(36)x y =--要使得圆C 上存在点Q ，使得60OPQ ∠=︒，则2PO …故2222000103634PO x y y y ==+-+… 解得0825y 剟，0605x 剟即0x 的取值范围是6[0,]5，故选：B ．【点睛】解题的关键是充分利用几何知识，判断出2PO …，从而得到不等式求出参数的取值范围．4．C解析：C 【解析】【分析】根据题意作出图形，欲求球的半径r ．利用截面的性质即可得到三棱锥S ABC -的体积可看成是两个小三棱锥S ABO -和C ABO -的体积和，即可计算出三棱锥的体积，从而建立关于r 的方程，即可求出r ，从而解决问题．【详解】解：根据题意作出图形：设球心为O ，球的半径r ．SC OA ⊥Q ，SC OB ⊥，SC ∴⊥平面AOB ，三棱锥S ABC -的体积可看成是两个小三棱锥S ABO -和C ABO -的体积和． 2343123S ABC S ABO C ABO V V V r r ---∴=+=⨯⨯⨯⨯=三棱锥三棱锥三棱锥， 2r ∴=．故选：C ．【点睛】本题考查棱锥的体积，考查球内接多面体，解题的关键是确定将三棱锥S ABC -的体积看成是两个小三棱锥S ABO -和C ABO -的体积和，属于中档题．5．A解析：A 【解析】【分析】求出圆心坐标和半径，根据圆的弦长公式，进行求解即可. 【详解】由题意，根据圆的方程222210x y x y a ++-+-=，即22(1)(1)2x y a ++-=-，则圆心坐标为(1,1)-，半径1r a =- 又由圆心到直线的距离为11222d -++==所以由圆的弦长公式可得4=，解得3a =-，故选A. 【点睛】本题主要考查了直线与圆的位置关系的因公，以及弦长公式的应用，其中根据圆的方程，求得圆心坐标和半径，合理利用圆的弦长公式列出方程求解是解答的关键，着重考查了推理与运算能力.6．D解析：D 【解析】【分析】根据所给条件，分别进行分析判断，即可得出正确答案. 【详解】解：αβ⊥且m α⊂⇒m β⊂或//m β或m 与β相交，故A 不成立；m n ⊥且//n β⇒m β⊂或//m β或m 与β相交，故B 不成立；αβ⊥且//m α⇒m β⊂或//m β或m 与β相交，故C 不成立； //m n 且n β⊥⇒m β⊥，故D 成立；故选：D 【点睛】本题考查直线与平面的位置关系，线面垂直判定，属于基础题.7．D解析：D 【解析】【分析】根据题意讨论直线它在两坐标轴上的截距为0和在两坐标轴上的截距不为0时，求出对应a 的值，即可得到答案．【详解】由题意，当2a 0-+=，即a 2=时，直线ax y 2a 0+-+=化为2x y 0+=，此时直线在两坐标轴上的截距都为0，满足题意；当2a 0-+≠，即a 2≠时，直线ax y 2a 0+-+=化为122x y a a a+=--，由直线在两坐标轴上的截距相等，可得2a2a a-=-，解得a 1=；综上所述，实数a 2=或a 1=．故选：D ．【点睛】本题主要考查了直线方程的应用，以及直线在坐标轴上的截距的应用，其中解答中熟记直线在坐标轴上的截距定义，合理分类讨论求解是解答的关键，着重考查了运算与求解能力，属于基础题.8．C解析：C 【解析】【分析】根据线面夹角得到4SA =，计算ABC ∆的外接圆半径为42sin ar A==，2222SA R r ⎛⎫=+ ⎪⎝⎭，解得答案.【详解】SA ⊥平面ABC ，则SB 与平面ABC 所成的角为6SBA π∠=，故4SA =. ABC ∆的外接圆半径为42sin ar A==，设球O 的半径为R ，则2222SA R r ⎛⎫=+ ⎪⎝⎭，解得25R =，故球O 的表面积为2480R ππ=. 故选：C . 【点睛】本题考查了三棱锥的外接球问题，意在考查学生的计算能力和空间想象能力.9．D解析：D 【解析】【分析】由题意可得，曲线22(1)4(1)x y y +-=…与直线4(2)y k x -=-有2个交点，数形结合求得k 的范围. 【详解】如图所示，化简曲线得到22(1)4(1)x y y +-=…，表示以(0,1)为圆心，以2为半径的上半圆，直线化为4(2)y k x -=-，过定点(2,4)A ，设直线与半圆的切线为AD ，半圆的左端点为(2,1)B -，当AD AB k k k <…，直线与半圆有两个交点，AD 与半圆相切时，221k =+，解得512AD k =，4132(2)4AB k -==--，所以53,124k ⎛⎤∈ ⎥⎝⎦.故选：D 【点睛】本题考查直线与圆的位置关系，属于中档题.10．D解析：D 【解析】【分析】先利用三角形中位线定理证明//MN BD ，再利用线面垂直的判定定理定义证明MN 与1CC 垂直，由异面直线所成的角的定义证明MN 与AC 垂直，即可得出结论.【详解】如图：连接1C D ，BD ，Q 在三角形1C DB 中，//MN BD ，故C 正确．1CC ⊥Q 平面ABCD ，1CC BD ∴⊥，MN ∴与1CC 垂直，故A 正确；AC BD ^Q ，//MN BD ，MN ∴与AC 垂直，B 正确；∵//MN BD ，MN ∴与11A B 不可能平行，D 错误故选：D ．【点睛】本题主要考查了正方体中的线面关系，线线平行与垂直的证明，异面直线所成的角及其位置关系，熟记正方体的性质是解决本题的关键.11．B解析：B 【解析】由题意可知该几何体为正三棱柱去掉一个小三棱锥，1104323333V =⋅=. 故选：B.12．D解析：D 【解析】根据三视图知几何体是：三棱锥D ABC -为棱长为4的正方体一部分，直观图如图所示：B 是棱的中点，由正方体的性质得，CD ⊥平面,ABC ABC ∆的面积12442S =⨯⨯=，所以该多面体的体积1164433V =⨯⨯=，故选D.二、填空题13．【解析】【分析】由题意得该四面体的四个面都为直角三角形且平面可得因为为直角三角形可得所以因此结合几何关系可求得外接球的半径代入公式即可求球的表面积【详解】本题主要考查空间几何体由题意得该四面体的四个解析：20π【解析】【分析】由题意得该四面体的四个面都为直角三角形，且PA ⊥平面ABC ，可得25PC =22PB =PBC V 为直角三角形，可得23BC =PB BC ⊥，因此AB BC ⊥，结合几何关系，可求得外接球O 的半径2222152PA R r ⎛⎫=+=+= ⎪⎝⎭O 的表面积．【详解】本题主要考查空间几何体．由题意得该四面体的四个面都为直角三角形，且PA ⊥平面ABC ，2PA AB ==，4AC =，25PC =22PB =因为PBC V 为直角三角形，因此23BC =7BC =（舍）．所以只可能是23BC = 此时PB BC ⊥，因此AB BC ⊥，所以平面ABC 所在小圆的半径即为22ACr ==，又因为2PA =，所以外接球O的半径R ===所以球O 的表面积为24π20πS R ==．【点睛】本题考查三棱锥的外接球问题，难点在于确定BC 的长，即得到AB BC ⊥，再结合几何性质即可求解，考查学生空间想象能力，逻辑推理能力，计算能力，属中档题．14．【解析】设球半径为则故答案为点睛:空间几何体体积问题的常见类型及解题策略：①若给定的几何体是可直接用公式求解的柱体锥体或台体则可直接利用公式进行求解；②若所给定的几何体的体积不能直接利用公式得出则常解析：32【解析】设球半径为r ，则213223423V r r V r π⨯==π．故答案为32．点睛:空间几何体体积问题的常见类型及解题策略：①若给定的几何体是可直接用公式求解的柱体、锥体或台体，则可直接利用公式进行求解；②若所给定的几何体的体积不能直接利用公式得出，则常用转换法、分割法、补形法等方法进行求解．15．【解析】【分析】以为长宽高构建长方体则长方体的外接球是三棱锥的外接球由此能求出三棱锥的外接球的表面积【详解】由题意在三棱锥中平面以为长宽高构建长方体则长方体的外接球是三棱锥的外接球所以三棱锥的外接球解析：50π【解析】【分析】以,,AB BC PA 为长宽高构建长方体，则长方体的外接球是三棱锥P ABC -的外接球，由此能求出三棱锥P ABC -的外接球的表面积. 【详解】由题意，在三棱锥P ABC -中，PA ⊥平面,,3,4,5ABC AB BC AB BC PA ⊥===，以,,AB BC PA 为长宽高构建长方体，则长方体的外接球是三棱锥P ABC -的外接球，所以三棱锥P ABC -的外接球的半径为2R ==，所以三棱锥P ABC -的外接球的表面积为2244()502S R πππ==⨯=. 【点睛】本题主要考查了三棱锥的外接球的表面积的计算问题，其中解答中根据几何体的结构特征，以,,AB BC PA 为长宽高构建长方体，得到长方体的外接球是三棱锥P ABC -的外接球是解答的关键，着重考查了数形结合思想，以及推理与运算能力.16．②③④【解析】【分析】作出此直二面角的图象由图形中所给的位置关系对命题逐一判断即可得出正确结论【详解】作出如图的图象E 是BD 的中点易得∠AED ＝90°即为此直二面角的平面角对于命题①AB 与平面BCD解析：②③④ 【解析】【分析】作出此直二面角的图象，由图形中所给的位置关系对命题逐一判断，即可得出正确结论．【详解】作出如图的图象，E 是BD 的中点，易得∠AED ＝90°即为此直二面角的平面角对于命题①AB 与平面BCD 所成的线面角的平面角是∠ABE ＝45°，故AB 与平面BCD 成60°的角不正确；对于命题②，在等腰直角三角形AEC 中AC 等于正方形的边长，故△ACD 是等边三角形，此命题正确；对于命题③可取AD 中点F ，AC 的中点H ，连接EF ，EH ，FH ，则EF ，FH 是中位线，故∠EFH 或其补角为异面直线AB 与CD 所成角，又EF,FH 其长度为正方形边长的一半，而EH 是直角三角形AEC 的中线，其长度是AC 的一半即正方形边长的一半，故△EFH 是等边三角形，由此AB 与CD 所成的角为60°，此命题正确；对于命题④，BD ⊥面AEC ，故AC ⊥BD ，此命题正确；对于命题⑤，连接BH ，HD,则BH ⊥AC, DH ⊥AC,则∠BHD 为二面角B AC D --的平面角，又32,cos ∠BHD=-1,3故二面角B AC D --不是120︒综上知②③④是正确的故答案为②③④ 【点睛】本题考查与二面角有关立体几何中线线之间的角的求法，线面之间的角的求法，以及线线之间位置关系的证明方法．综合性较强，对空间立体感要求较高．17．【解析】【分析】正四棱锥底面的四个顶点在球的同一个大圆上则棱锥的高等于球的半径由此可由棱锥体积求得球的半径从而得球体积【详解】∵正四棱锥底面的四个顶点在球的同一个大圆上∴球心是正方形对角线交点是棱锥解析：323π【解析】【分析】正四棱锥P ABCD -底面的四个顶点,,,A B C D 在球O 的同一个大圆上，则棱锥的高等于球的半径，由此可由棱锥体积求得球的半径，从而得球体积．【详解】∵正四棱锥P ABCD -底面的四个顶点,,,A B C D 在球O 的同一个大圆上，∴球心O 是正方形ABCD 对角线交点，PO 是棱锥的高，设球半径为R ，则2AB R =，22(2)2ABCD S R R ==，211162333P ABCD ABCD V S PO R R -==⨯⨯=，2R =，∴3344322333V R πππ==⨯=球．故答案为：323π．【点睛】本题考查球的体积，考查正四棱锥与半球的截接问题．解题关键是确定球半径与正四棱锥中的线段长之间的关系．18．【解析】【分析】以B 为顶点三棱锥与四棱锥等高计算体积只需找到三角形AEF 与四边形ECDF 的面积关系即可求解【详解】设B 到平面ACD 的距离为h 三角形ACD 面积为因为是的中点在上且所以所以又=2所以所以解析：【解析】【分析】以B 为顶点，三棱锥B AEF -与四棱锥B ECDF -等高，计算体积只需找到三角形AEF 与四边形ECDF 的面积关系即可求解. 【详解】设B 到平面ACD 的距离为h ，三角形ACD 面积为S ，因为E 是AC 的中点，F 在AD 上，且2AF FD =，所以16AEF ACD S AE AF S AC AD∆∆⋅==⋅,16AEF S S ∆=，所以56ECDF S S =，又A BEF V -=2，所以⨯=11236Sh ，36Sh =，所以153610318B ECDF ECDF V S h -==⋅=. 故答案为10. 【点睛】本题考查空间几何体的体积计算，考查空间想象能力和运算能力，属于基础题.19．【解析】【分析】推导出两边平方可得的长【详解】二面角为是棱上的两点分别在半平面内且的长故答案为：【点睛】本题考查线段长的求法考查空间中线线线面面面间的位置关系等基础知识考查运算求解能力考查函数与方程解析：217. 【解析】【分析】推导出CD CA AB BD =++u u u r u u u r u u u r u u u r，两边平方可得CD 的长．【详解】Q 二面角l αβ--为60︒，A 、B 是棱l 上的两点，AC 、BD 分别在半平面α、β内，且AC l ⊥，BD l ⊥，4AB =，6AC =，8BD =，∴CD CA AB BD =++u u u r u u u r u u u r u u u r， ∴22()CD CA AB BD =++u u u r u u u r u u u r u u u r2222CA AB BD CA BD =+++u u u r u u u r u u u r u u u r u u u r g361664268cos12068=+++⨯⨯⨯︒=，CD ∴的长||68217CD ==u u u r．故答案为：217．【点睛】本题考查线段长的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，考查函数与方程思想，是中档题．20．【解析】分析：设上下圆锥的高分别为圆柱的底面圆的半径为圆柱的高为h 再求详解：设上下圆锥的高分别为圆柱的底面圆的半径为圆柱的高为h 则故答案为：点睛：（1）本题主要考查圆锥圆柱体积的计算意在考查学生对这解析：23【解析】分析：设上下圆锥的高分别为12,,h h 圆柱的底面圆的半径为r ，圆柱的高为h,再求21V V . 详解：设上下圆锥的高分别为12,,h h 圆柱的底面圆的半径为r ，圆柱的高为h, 则222212222111()233.3r h r h h r h r hV V r hr hππππππ-+-===故答案为：23. 点睛：（1）本题主要考查圆锥圆柱体积的计算，意在考查学生对这些知识的掌握水平.(2)圆柱的体积为2V sh r h π==，圆锥的体积为21133V sh r h π==. 三、解答题21．（1）证明见解析；（2）6π. 【解析】【分析】（1）取AC 的中点O ，连接OS 、OD ，证明出OS AC ⊥，OD AC ⊥，利用直线与平面垂直的判定定理可得出AC ⊥平面SOD ，即可证明出AC SD ⊥；（2）延长SO ，过点D 作SO 延长线的垂线，垂足记为H ，说明直线SD 与平面SAC 所成的角为OSD ∠，求出OSD ∆三边边长，利用余弦定理求出OSD ∠，即可求出直线SD 与平面SAC 所成角的大小．【详解】（1）取AC 的中点O ，连接OS 、OD ，SAC ∆Q 为等边三角形，O 为AC 的中点，SO AC ∴⊥，D Q 、O 分别为AB 、AC 的中点，//OD BC ∴，BC AC ⊥Q ，OD AC ∴⊥， SO OD O =Q I ，AC ∴⊥平面SOD ，SD ⊂Q 平面SOD ，AC SD ∴⊥；（2）延长SO ，过点D 作SO 延长线的垂线，垂足记为H ， AC ⊥Q 平面SOD ，DH ⊂平面SOD ，DH AC ∴⊥，DH SO ⊥Q ，SO AC O =I ，DH ∴⊥平面SAC ，所以，直线SD 与平面SAC 所成的角为OSD ∠，由（2）知，1232OD BC ==AC BC ⊥Q ，228AB AC BC ∴+=. SAC ∆Q 是边长为4的等边三角形，4sin233SO π∴==在SBC ∆中，4SC =，43BC=由余弦定理得2222cos 88SB SC BC SC BC SCB =+-⋅⋅∠=，222SB ∴=由余弦定理得2221cos 28SA AB SB SAB SA AB +-∠==-⋅，2222cos 36SD SA AD SA AD SAD ∴=+-⋅⋅∠=，6SD ∴=.在SOD ∆中，由余弦定理得2223cos 2SO SD OD OSD SO SD +-∠==⋅. 0OSD π<∠<Q ，6OSD π∴∠=，因此，直线SD 与平面SAC 所成角的大小为6π. 【点睛】本题考查利用线面垂直的性质证明线线垂直，同时也考查了直线与平面所成角的计算，涉及到利用余弦定理解三角形，考查推理能力与计算能力，属于中等题. 22．（1）证明见解析；（2）证明见解析. 【解析】【分析】（1）根据线面平行的判定定理，在平面ABD 中找EF 的平行线，转化为线线平行的证明；（2）根据面面垂直的判定定理，转化为CD ⊥平面AEF . 【详解】（1）E Q ，F 分别是BC ，CD 的中点，EF ∴P BD ；又Q EF ⊄平面ABD ，BD ⊂平面ABD ，EF ∴P 平面ABD .（2）BD CD ⊥Q ，EF P BD ，EF CD ∴⊥；AE ^Q 平面BCD ，AE CD ∴⊥；又EF ⊂平面AEF ，AE ⊂平面AEF ，CD \^平面AEF ，又CD ⊂平面ACD ， ∴平面AEF ⊥平面ACD .【点睛】本题考查了面面垂直的证明，难点在于转化为线面垂直,方法：结合已知条件，选定其中一个面为垂面，在另外一个面中找垂线，不行再换另外一个面.23．（1）见详解；（2）见详解；（3. 【解析】【分析】(1)先证DM AP ∥，可证//DM 平面APC .(2)先证AP PBC ⊥平面，得⊥AP BC ，结合AC BC ⊥可证得BC ⊥平面APC . (3)等积转换，由D BCM M DBC V V --＝，可求得体积. 【详解】(1)证明：因为M 为AB 的中点，D 为PB 的中点，所以MD 是ABP △的中位线，MD AP P . 又MD APC ⊄平面，AP APC ⊂平面，所以MD APC ∥平面.(2)证明：因为PMB △为正三角形，D 为PB 的中点，所以MD PB ⊥. 又MD AP P ，所以AP PB ⊥.又因为AP PC ⊥，PB PC P I ＝，所以AP PBC ⊥平面. 因为BC PBC ⊂平面，所以⊥AP BC . 又因为BC AC ⊥，AC AP A ⋂＝，所以BC APC ⊥平面.(3)因为AP PBC ⊥平面，MD AP P ，所以MD PBC ⊥平面，即MD 是三棱锥M DBC -的高. 因为10AB =，M 为AB 的中点，PMB △为正三角形，所以5,PB MB MD MB ====. 由BC APC ⊥平面，可得BC PC ⊥，在直角三角形PCB 中，由54PB BC ＝，＝，可得3PC ＝. 于是111433222BCD BCP S S ⨯⨯⨯=△△＝＝.所以1133322D BCM M DBC BCD V V S MD --⨯⨯=g △＝＝＝. 【点睛】本题考查空间线面平行与垂直的证明，体积的计算.空间中的平行与垂直的证明过程就是利用相关定义、判定定理和性质定理实现线线平行(垂直)、线面平行(垂直)、面面平行(垂直)的转换.求三棱锥的体积常采用等积转换的方法，选择易求的底面积和高来求体积. 24．（1）见解析；（2）见解析.【解析】【分析】（1）通过证明//NQ PA ，即可得到本题结论；（2）由题，先证PM AD ⊥和AD MB ⊥，即可得到AD ⊥平面PMB ，由此即可得到本题结论.【详解】（1）连接AC 交MB 于Q ，连接,NQ MC ．因为//AM BC ，12AM AD BC ==，所以四边形ABCM 是平行四边形，所以Q 是AC 的中点．又N 是PC 的中点，所以//NQ PA ，因为NQ ⊂平面MNB ，PA ⊄平面MNB ，所以//PA 平面MNB ；（2）因为PA PD =，AM MD =，所以PM AD ⊥，因为//MD BC ，MD BC =，所以四边形BCDM 是平行四边形，所以//MB DC ，因为=90ADC ∠︒，即AD DC ⊥，所以AD MB ⊥，因为PM MB M ⋂=，,PM MB ⊂平面PMB ，所以AD ⊥平面PMB ，又AD ⊂平面PAD ，所以平面PAD ⊥平面PMB ．【点睛】本题主要考查线面平行的判定与面面垂直的判定，考查学生的空间想象能力和逻辑推理能力.25．（1）见解析；（2）32. 【解析】（1）在平面ABC 中，过点B 作棱AC 的垂线，垂足为D ，Q 平面11AAC C ⊥平面ABC ，∴ BD ⊥平面11AAC C .在平面11AA B B 中，过点B 作棱1AA 的垂线，垂足为E ，Q 平面11AAC C ⊥平面11AA B B ，∴BE ⊥平面11AAC C .Q 过点B 与平面11AAC C 垂直的直线有且只有一条，∴BE 与BD 重合，又∵平面ABC I 平面11AA B B AB =,∴BE 与BD 重合于AB ，所以AB ⊥平面11AAC C .（2）设BM 的中点为Q ，连接PQ ，NQ ，Q 点P 为棱BC 的中点，∴PQ ∥CM 且PQ =12CM ， Q 1AA ∥1CC ，∴PQ ∥AN ，∴P 、Q 、N 、A 四点共面，∵AP ∥平面BMN ，∴AP ∥NQ ，∴四边形PQNA 是平行四边形，∴PQ =AN ，∵M 为1CC 的中点且12AB AC AA ===，∴1CM =，∴PQ =AN =12，设梯形ACMN 的高为h ，Q 2AB =， ∴111132×2322B ACMN h V h -⎛⎫+ ⎪⎝⎭=⨯==，∴3h = ∴13sin 2h A AC AC ∠==,∴1A AC ∠的正弦值为32. 26．（1）证明见解析；（2）证明见解析【解析】【分析】（1）通过证明1A A AC ⊥和AB AC ⊥，即可证得AC ⊥平面11AA B B ；（2）通过证明//DE AO ，即可证得//DE 平面ABC .【详解】（1）由题，得1A A ⊥平面ABC ，所以1A A AC ⊥，又BC 是底面圆O 的直径，所以AB AC ⊥，因为1AB AA A =I ，所以AC ⊥平面11AA B B ；（2）连接,OE OA ，因为,E O 分别为1,B C BC 的中点，所以1//OE BB 且112OE BB =，易得1//AD BB 且112AD BB =，所以//AD OE 且AD OE =，所以四边形OADE 为平行四边形，则//DE AO ，因为AO ⊂平面ABC ，DE ⊄平面ABC ，所以//DE 平面ABC .【点睛】本题主要考查线面垂直和线面平行的判定，考查学生的空间想象能力和推理证明能力，体现了数形结合的数学思想.。

【典型题】高中必修二数学下期中第一次模拟试题(及答案)

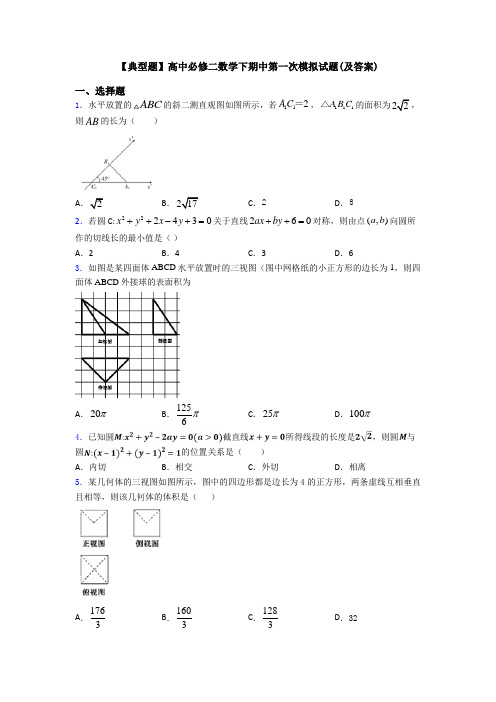
【典型题】高中必修二数学下期中第一次模拟试题(及答案)一、选择题1．水平放置的ABC 的斜二测直观图如图所示，若112A C ＝，111A B C △的面积为22，则AB 的长为（）A ．2B ．217C ．2D ．82．若圆C:222430x y x y ++-+=关于直线260ax by ++=对称，则由点(,)a b 向圆所作的切线长的最小值是（） A ．2B ．4C ．3D ．63．如图是某四面体ABCD 水平放置时的三视图（图中网格纸的小正方形的边长为1，则四面体ABCD 外接球的表面积为A ．20πB ．1256π C ．25π D ．100π4．已知圆截直线所得线段的长度是，则圆与圆的位置关系是（） A ．内切B ．相交C ．外切D ．相离5．某几何体的三视图如图所示，图中的四边形都是边长为4的正方形，两条虚线互相垂直且相等，则该几何体的体积是（）A ．1763B ．1603C ．1283D ．326．在梯形ABCD 中，90ABC ∠=︒，//AD BC ，222BC AD AB ===.将梯形ABCD 绕AD 所在直线旋转一周而形成的曲面所围成的几何体的体积为（）A ．23π B ．43π C ．53π D ．2π7．若a ＞b ＞0，0＜c ＜1，则A ．log a c ＜log b cB ．log c a ＜log c bC ．a c ＜b cD ．c a ＞c b8．若圆22240x y x y +--=的圆心到直线0x y a -+=的距离为22，则a 的值为( ) A ．-2或2B ．12或32C ．2或0D ．-2或09．如图1，ABC ∆是以B 为直角顶点的等腰直角三角形，T 为线段AC 的中点，G 是BC 的中点，ABE ∆与BCF ∆分别是以AB 、BC 为底边的等边三角形，现将ABE ∆与BCF ∆分别沿AB 与BC 向上折起（如图2），则在翻折的过程中下列结论可能正确的个数为（）图1 图2（1）直线AE ⊥直线BC ；（2）直线FC ⊥直线AE ；（3）平面//EAB 平面FGT ；（4）直线//BC 直线AE . A ．1个B ．2个C ．3个D ．4个10．如图，在正方体1111ABCD A B C D -中，M ，N 分别是1BC ，1CD 的中点，则下列说法错误．．的是( )A ．MN 与1CC 垂直B ．MN 与AC 垂直 C ．MN 与BD 平行 D ．MN 与11A B 平行11．已知平面αβ⊥且l αβ=，M 是平面α内一点，m ，n 是异于l 且不重合的两条直线，则下列说法中错误的是（）.A ．若//m α且//m β，则//m lB ．若m α⊥且n β⊥，则m n ⊥C ．若M m ∈且//m l ，则//m βD ．若M m ∈且m l ⊥，则m β⊥12．α，β是两个不重合的平面，在下列条件中，可判断平面α，β平行的是（） A ．m ，n 是平面α内两条直线，且//m β，//n β B ．α内不共线的三点到β的距离相等 C ．α，β都垂直于平面γD ．m ，n 是两条异面直线，m α⊂，n β⊂，且//m β，//n α二、填空题13．给出下面四个命题：①“直线l ⊥平面α内所有直线”的充要条件是“l ⊥平面α”； ②“直线//a 直线b ”的充要条件是“a 平行于b 所在的平面”； ③“直线a ，b 为异面直线”的充分不必要条件是“直线a ，b 不相交”；④“平面//α平面β”的必要不充分条件是“α内存在不共线三点到β的距离相等”. 其中正确命题的序号是____________________14．如图，在正方体1111—ABCD A B C D 中，M N ，分别为棱111C D C C ，的中点，有以下四个结论：①直线AM 与1CC 是相交直线； ②直线AM 与BN 是平行直线； ③直线BN 与1MB 是异面直线； ④直线AM 与1DD 是异面直线．其中正确的结论的序号为________．15．如图，以等腰直角三角形斜边BC 上的高AD 为折痕，把△ABD 与△ACD 折成互相垂直的两个平面后，某学生得出下列四个结论： ①0BD AC ⋅≠； ②∠BAC ＝60°；③三棱锥D ﹣ABC 是正三棱锥；④平面ADC 的法向量和平面ABC 的法向量互相垂直．其中正确结论的序号是．（请把正确结论的序号都填上）16．已知三棱锥P ABC -的四个顶点在球O 的球面上，PA PB PC ==，ABC △是边长为2正三角形，,E F 分别是,PA AB 的中点，90CEF ︒∠=，则球O 的体积为_________________。

新高中必修二数学下期中第一次模拟试卷(带答案)

新高中必修二数学下期中第一次模拟试卷(带答案)
一、选择题 1．在长方体 ABCD A1B1C1D1 中， AB BC 2 ， AC1 与平面 BB1C1C 所成的角为 30 ，则该长方体的体积为（）
A． 8
B． 6 2
C． 8 2
D． 8 3
2．已知 m，n 表示两条不同直线，表示平面，下列说法正确的是（）
（1）求证： AB 平面 AA1C1C ;
（2）若四棱锥 B ACMN 的体积为 3 ，求 A1AC 的正弦值. 2
26．如图， AA1 、 BB1 为圆柱 OO1 的母线（母线与底面垂直），BC 是底面圆 O 的直径， D、E 分别是 AA1 、 CB1 的中点， DE 平面 CBB1 ．
A．若 m / /, n / /, 则 m // n
B．若 m ， n ，则 m n
C．若 m ， m n ，则 n / /
D．若 m / / ， m n ，则 n
3．已知三棱锥 D ABC 的外接球的表面积为128 ， AB BC 4, AC 4 2 ，则三棱
锥 D ABC 体积的最大值为（）
2 时，直线 ax
y
2a
0 化为
2
x
a
2
y
a
1，
a
由直线在两坐标轴上的截距相等，可得 2 a 2 a ，解得 a 1； a
综上所述，实数 a 2 或 a 1．
故选：D．
【点睛】
本题主要考查了直线方程的应用，以及直线在坐标轴上的截距的应用，其中解答中熟记直
线在坐标轴上的截距定义，合理分类讨论求解是解答的关键，着重考查了运算与求解能
所以异面直线 AD1 与 A1C 所成的角的大小是 90 ．

【典型题】高中必修二数学下期中第一次模拟试卷(含答案)

【典型题】高中必修二数学下期中第一次模拟试卷(含答案)一、选择题1．已知a ，b 是两条异面直线，且a b ⊥，直线c 与直线a 成30角，则c 与b 所成的角的大小范围是( )A ．[]60,90︒︒B ．[]30,90︒︒C ．[]30,60︒︒D ．[]45,90︒︒2．<九章算术>中，将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥P ABC -为鳖臑，PA ⊥平面,2,4ABC PA AB AC ===，三棱锥P ABC -的四个顶点都在球O 的球面上，则球O 的表面积为（）A ．8πB ．12πC ．20πD ．24π 3．已知一个三棱锥的三视图如图所示，其中俯视图是等腰直角三角形，则该三棱锥的外接球表面积为（）A 3πB ．3πC ．43πD ．12π4．已知三棱锥S ABC -的每个顶点都在球O 的表面上，ABC ∆是边长为43角形，SA ⊥平面ABC ，且SB 与平面ABC 所成的角为6π，则球O 的表面积为（） A ．20π B ．40πC ．80πD ．160π 5．从点(,3)P m 向圆22(2)(2)1x y +++=引切线，则切线长的最小值( )A ．26B ．5C 26D ．426．正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为（）A ．814πB ．16πC ．9πD ．274π 7．已知AB 是圆22620x y x y +-+=内过点(2,1)E 的最短弦，则||AB 等于（）A 3B ．2C ．23D ．258．若方程21424x kx k -=-+ 有两个相异的实根，则实数k 的取值范围是（）A ．13,34⎛⎤ ⎥⎝⎦ B ．13,34⎛⎫ ⎪⎝⎭ C ．53,124⎛⎫ ⎪⎝⎭ D ．53,1249．若底面是菱形的棱柱其侧棱垂直于底面，且侧棱长为5，它的对角线的长分别是9和15，则这个棱柱的侧面积是( )．A ．130B ．140C ．150D ．16010．如图，在正方体1111ABCD A B C D 中，M ，N 分别是1BC ，1CD 的中点，则下列说法错误．．的是( )A ．MN 与1CC 垂直B ．MN 与AC 垂直 C ．MN 与BD 平行D ．MN 与11A B 平行 11．某几何体的三视图如图所示（单位：cm ），其俯视图为等边三角形，则该几何体的体积（单位：3cm ）是（）A ．43B ．1033C ．23D ．83312．如图，网格纸上小正方形的边长为1，粗实（虚）线画出的是某多面体的三视图，则该多面体的体积为（）A ．64B ．643C ．16D ．163二、填空题13．光线由点P(2,3)射到直线x+y+1=0上，反射后过点Q(1,1) ，则反射光线方程为__________．14．如图，在圆柱O1 O2内有一个球O，该球与圆柱的上、下底面及母线均相切．记圆柱O1O2的体积为V1 ,球O的体积为V2，则12VV的值是_____15．已知三棱锥P ABC-中，侧面PAC⊥底面ABC，90BAC∠=︒，4AB AC==，23PA PC==，则三棱锥P ABC-外接球的半径为______.16．若直线y x b=+与曲线234y x x=+-有公共点，则b的取值范围是______．17．直线10ax y++=与连接A（4，5），B（-1，2）的线段相交，则a的取值范围是___．18．如图所示，二面角lαβ--为60,,A B是棱l上的两点，,AC BD分别在半平面内,αβ，且AC l⊥，，4,6,8AB AC BD===，则CD的长______．19．已知四面体ABCD的外接球球心O在棱CD上，AB=3，CD=2，则A、B两点在四面体ABCD的外接球上的球面距离是________.20．已知球的表面积为20π，球面上有A、B、C三点．如果2AB AC==，22BC=，则球心到平面ABC的距离为__________．三、解答题21．如图，正方形ABCD所在平面与三角形CDE所在平面相交于CD，AE⊥平面CDE，且1AE=,2AB=.(Ⅰ)求证：AB⊥平面ADE；(Ⅱ)求凸多面体ABCDE的体积.22．已知ABC ∆的三个顶点(),A m n 、()2,1B 、()2,3C -.（1）求BC 边所在直线的方程；（2）BC 边上中线AD 的方程为2360x y -+=，且7ABC S ∆=，求点A 的坐标. 23．如图，ABCD 是正方形，O 是该正方体的中心，P 是平面ABCD 外一点，PO ⊥平面ABCD ，E 是PC 的中点.（1）求证：//PA 平面BDE ；（2）求证：BD ⊥平面PAC .24．四棱锥P -ABCD 中，底面ABCD 是直角梯形，//AB CD ，90BCD ∠=︒，22AB AD DC ===.PAD △ 为正三角形，二面角P -AD -C 的大小为23π.（1）线段AD 的中点为M.求证：平面PMB ⊥平面ABCD ；（2）求直线BA 与平面P AD 所成角的正弦值.25．如图，正方形ABCD 所在平面与平面四边形ABEF 所在平面互相垂直，ABE ∆是等腰直角三角形，AB AE =，FA FE =，45AEF ∠=︒．（1）设线段CD AE 、的中点分别为P M 、，求证：//PM 平面BCE ；（2）求二面角F BD A --所成角的正弦值．26．如图，在梯形ABCD 中，AB CD ∥，1AD DC BC ===，60ABC ∠=︒，四边形ACFE 为矩形，平面ACFE ⊥平面ABCD ，1CF =.(1)证明：BC ⊥平面ACFE ；(2)设点M 在线段EF 上运动，平面MAB 与平面FCB 所成锐二面角为θ，求cos θ的取值范围.【参考答案】***试卷处理标记，请不要删除一、选择题1．A解析：A【解析】【分析】将异面直线所成的角转化为平面角，然后由题意，找出与直线a 垂直的直线b 的平行线，与直线c 平行线的夹角.【详解】在直线a 上任取一点O ，过O 做//c c '，则,a c '确定一平面α，过O 点做直线b 的平行线b '，所有平行线b '在过O 与直线a 垂直的平面β内，若存在平行线1b '不在β内，则1b '与b '相交又确定不同于β的平面，这与过一点有且仅有一个平面与一条直线垂直矛盾，所以b '都在平面β内，且,l αβαβ⊥=，在直线c '上任取不同于O 的一点P ，做PP l '⊥于P '，则PP β'⊥，POP '∠为是c '与β所成的角为60︒，若b l '⊥，则,b b c α'''⊥⊥，若b '不垂直l 且不与l 重合，过P '做P A b ''⊥，垂足为A ，连PA ，则b '⊥平面PP A '，所以b PA '⊥，即1,cos 2OA OP OA PA AOP OP OP '⊥∠=<=， 60AOP ∠>︒，综上b '与c '所成角的范围为[60,90]︒︒，所以直线b 与c 所成角的范围为[]60,90︒︒.故选：A.【点睛】本题考查异面直线所成角，空间角转化为平面角是解题的关键，利用垂直关系比较角的大小，属于中档题.2．C解析：C【解析】【分析】先作出三棱锥P ABC -的图像，根据P ABC -四个面都为直角三角形和PA ⊥平面ABC ，可知PC 中点即为球心，利用边的关系求出球的半径，再由24S R π=计算即得.【详解】三棱锥P ABC -如图所示，由于P ABC -四个面都为直角三角形，则ABC 是直角三角形，且2ABC π∠=，2223BC AC AB ∴=-=，又PA ⊥平面ABC ，且PAC 是直角三角形，∴球O 的直径2222PC R PA AB BC ==++2025==，5R ∴=，则球O 的表面积2420S R ππ==.故选：C【点睛】本题考查多面体外接球的表面积，是常考题型.3．C解析：C【解析】【分析】的等腰直角三角形，与底面垂直的侧面是个等腰三角形，底边长为2，高为2，故三棱锥的外接球与以棱长为2的正方体的外接球相同，由此可得结论【详解】由三视图知几何体是一个侧棱与底面垂直的三棱锥，与底面垂直的侧面是个等腰三角形，底边长为2，高为2，故三棱锥的外接球与以棱长为2的正方体的外接球相同，其直径为∴三棱锥的外接球体积为343π⨯=故选C【点睛】本题主要考查了三视图，几何体的外接球的体积，考查了空间想象能力，计算能力，属于中档题．4．C解析：C【解析】【分析】根据线面夹角得到4SA =，计算ABC ∆的外接圆半径为42sin a r A==，2222SA R r ⎛⎫=+ ⎪⎝⎭，解得答案. 【详解】SA ⊥平面ABC ，则SB 与平面ABC 所成的角为6SBA π∠=，故4SA =.ABC ∆的外接圆半径为42sin a r A ==，设球O 的半径为R ，则2222SA R r ⎛⎫=+ ⎪⎝⎭，解得R =O 的表面积为2480R ππ=. 故选：C .【点睛】本题考查了三棱锥的外接球问题，意在考查学生的计算能力和空间想象能力.5．A解析：A【解析】【分析】设切线长为d ,则2222(2)51(2)24d m m =++-=++再利用二次函数的图像和性质求函数的最小值得解.【详解】设切线长为d ,则2222(2)51(2)24d m m =++-=++, min 26d ∴=.故选:A.【点睛】本题主要考查圆的切线问题,考查直线和圆的位置关系,意在考查学生对这些知识的掌握水平和分析推理能力. 6．A解析：A【解析】【分析】【详解】正四棱锥P-ABCD 的外接球的球心在它的高1PO 上，记为O ，PO=AO=R ，14PO =，1OO =4-R ，在Rt △1AOO 中，12AO =，由勾股定理()2224R R =+-得94R =， ∴球的表面积814S π=，故选A.考点：球的体积和表面积7．D解析：D【解析】【分析】求出圆的标准方程，确定最短弦的条件，利用弦长公式进行求解即可．【详解】圆的标准方程为（x ﹣3）2+（y +1）2＝10，则圆心坐标为C （3，﹣1），半径为10 过E 的最短弦满足E 恰好为C 在弦上垂足，则CE 22(32)[11]5=-+--=（），则|AB |222(10)(5)25=-=，故选D ．【点睛】本题主要考查圆的标准方程的求解，以及直线和圆相交的弦长问题,属于中档题．8．D解析：D【解析】【分析】由题意可得，曲线22(1)4(1)x y y +-=与直线4(2)y k x -=-有2个交点，数形结合求得k 的范围.【详解】如图所示，化简曲线得到22(1)4(1)x y y +-=，表示以(0,1)为圆心，以2为半径的上半圆，直线化为4(2)y k x -=-，过定点(2,4)A ，设直线与半圆的切线为AD ，半圆的左端点为(2,1)B -，当AD AB k k k <，直线与半圆有两个交点，AD 221k =+，解得512AD k =， 4132(2)4AB k -==--，所以53,124k ⎛⎤∈ ⎥⎝⎦. 故选：D【点睛】本题考查直线与圆的位置关系，属于中档题.9．D解析：D【解析】设直四棱柱1111ABCD A B C D -中，对角线119,15AC BD ==，因为1A A ⊥平面,ABCD AC ,平面ABCD ，所以1A A AC ⊥，在1Rt A AC ∆中，15A A =，可得221156AC AC A A =-= 同理可得2211200102BD D B D D =-==，因为四边形ABCD 为菱形，可得,AC BD 互相垂直平分，所以2211()()1450822AB AC BD =+=+=，即菱形ABCD 的边长为8，因此，这个棱柱的侧面积为1()485160S AB BC CD DA AA =+++⨯=⨯⨯=，故选D.点睛：本题考查了四棱锥的侧面积的计算问题，解答中通过给出的直四棱柱满足的条件，求得底面菱形的边长，进而得出底面菱形的底面周长，即可代入侧面积公式求得侧面积，着重考查了学生分析问题和解答问题的能力，以及空间想象能力，其中正确认识空间几何体的结构特征和线面位置关系是解答的关键.10．D解析：D【解析】【分析】先利用三角形中位线定理证明//MN BD ，再利用线面垂直的判定定理定义证明MN 与1CC 垂直，由异面直线所成的角的定义证明MN 与AC 垂直，即可得出结论.【详解】如图：连接1C D ，BD ，在三角形1C DB 中，//MN BD ，故C 正确．1CC ⊥平面ABCD ，1CC BD ∴⊥，MN ∴与1CC 垂直，故A 正确；AC BD ，//MN BD ，MN ∴与AC 垂直，B 正确；∵//MN BD ，MN ∴与11A B 不可能平行，D 错误故选：D ．【点睛】本题主要考查了正方体中的线面关系，线线平行与垂直的证明，异面直线所成的角及其位置关系，熟记正方体的性质是解决本题的关键.11．B解析：B【解析】由题意可知该几何体为正三棱柱去掉一个小三棱锥，1104323333V =-⋅⋅=. 故选：B. 12．D解析：D【解析】根据三视图知几何体是：三棱锥D ABC -为棱长为4的正方体一部分，直观图如图所示：B 是棱的中点，由正方体的性质得，CD ⊥平面,ABC ABC ∆的面积12442S =⨯⨯=，所以该多面体的体积1164433V =⨯⨯=，故选D. 二、填空题13．4x －5y+1=0【解析】【分析】先求P 点关于直线x+y+1=0对称点M 再根据两点式求MQ 方程即得结果【详解】因为P 点关于直线x+y+1=0对称点为所以反射光线方程为【点睛】本题考查点关于直线对称问解析：4x －5y +1=0 【解析】【分析】先求P 点关于直线x+y+1=0对称点M ，再根据两点式求 MQ 方程，即得结果.【详解】因为P 点关于直线x+y+1=0对称点为(4,3)M --，所以反射光线方程为13:1(1),451014MQ y x x y +-=--+=+. 【点睛】本题考查点关于直线对称问题，考查基本分析求解能力，属基本题.14．【解析】设球半径为则故答案为点睛:空间几何体体积问题的常见类型及解题策略：①若给定的几何体是可直接用公式求解的柱体锥体或台体则可直接利用公式进行求解；②若所给定的几何体的体积不能直接利用公式得出则常解析：32【解析】设球半径为r ，则213223423V r r V r π⨯==π．故答案为32．点睛:空间几何体体积问题的常见类型及解题策略：①若给定的几何体是可直接用公式求解的柱体、锥体或台体，则可直接利用公式进行求解；②若所给定的几何体的体积不能直接利用公式得出，则常用转换法、分割法、补形法等方法进行求解．15．【解析】【分析】设三棱锥外接球球心为半径为如图所示作辅助线设则解得答案【详解】设三棱锥外接球球心为半径为故在平面的投影为中点为中点故侧面底面故底面连接作于易知为矩形设则解得故答案为：【点睛】本题考查解析：2【解析】【分析】设三棱锥P ABC -外接球球心为O ，半径为R ，如图所示作辅助线，设1OO h =，则()2222221R PD h OH R h CO ⎧=-+⎪⎨=+⎪⎩，解得答案. 【详解】设三棱锥P ABC -外接球球心为O ，半径为R ，90BAC ∠=︒，故O 在平面ABC 的投影为BC 中点1O ，D 为AC 中点，PA PC =，故PD AC ⊥，侧面PAC ⊥底面ABC ，故PD ⊥底面ABC .连接1O D ，作OH PD ⊥于H ，易知1OO DH 为矩形，设1OO h =，则()2222221R PD h OH R h CO ⎧=-+⎪⎨=+⎪⎩，PD =，12OH DO ==，122CO，解得R =故答案为：2.【点睛】本题考查了三棱锥的外接球问题，意在考查学生的计算能力和空间想象能力.16．【解析】【分析】由曲线y=3+得（x ﹣2）2+（y ﹣3）2=40≤x≤4直线y=x+b 与曲线y=3+有公共点圆心（23）到直线y=x+b 的距离d 不大于半径r=2由此结合图象能求出实数b 的取值范围【详解析：122,3⎡⎤-⎣⎦【解析】【分析】由曲线y=3+24x x -，得（x ﹣2）2+（y ﹣3）2=4，0≤x≤4，直线y=x+b 与曲线y=3+24x x -有公共点，圆心（2，3）到直线y=x+b 的距离d 不大于半径r=2，由此结合图象能求出实数b 的取值范围．【详解】由曲线y=3+24x x -，得（x ﹣2）2+（y ﹣3）2=4，0≤x≤4，∵直线y=x+b 与曲线y=3+24x x -有公共点，∴圆心（2，3）到直线y=x+b 的距离d 不大于半径r=2，即232122b 1+222b d -+=≤⇒-≤≤∵0≤x≤4， ∴x=4代入曲线y=3+24x x -，得y=3，把（4，3）代入直线y=x+b ，得b min =3﹣4=﹣1，②联立①②，得-1b 122≤≤+．∴实数b 的取值范围是[﹣1，1+22]．故答案为1,122⎡⎤-+⎣⎦.【点睛】本题考查实数的取值范围的求法，是中档题，解题时要认真审题，注意数形结合思想的合理运用．一般直线和圆的题很多情况下是利用数形结合来解决的，联立的时候较少；在求圆上的点到直线或者定点的距离时，一般是转化为圆心到直线或者圆心到定点的距离，再加减半径，分别得到最大值和最小值；涉及到圆的弦长或者切线长时，经常用到垂径定理．17．或【解析】【分析】判断直线恒过定点P （0-1）计算PAPB 的斜率再利用数形结合求a 的取值范围【详解】解：由直线ax+y+1=0的方程判断直线恒过定点P （0-1）如图所示计算且或则或即实数a 的取值范围解析：32a ≤-或3a ≥ 【解析】【分析】判断直线0ax by c ++=恒过定点P （0，-1），计算PA 、PB 的斜率，再利用数形结合求a 的取值范围．【详解】解：由直线ax+y+1=0的方程，判断直线恒过定点P （0，-1），如图所示，计算513402PA k +==-，21310PB k +==--- 且PA k k ≥或PB k k ≤，则PA a k ≤-或PB a k ≥-，即实数a 的取值范围是：32a ≤-或3a ≥．故答案为：32a ≤-或3a ≥．【点睛】本题考查直线的斜率与直线方程的应用问题，是基础题． 18．【解析】【分析】推导出两边平方可得的长【详解】二面角为是棱上的两点分别在半平面内且的长故答案为：【点睛】本题考查线段长的求法考查空间中线线线面面面间的位置关系等基础知识考查运算求解能力考查函数与方程解析：217.【解析】【分析】推导出CD CA AB BD =++，两边平方可得CD 的长．【详解】二面角l αβ--为60︒，A 、B 是棱l 上的两点，AC 、BD 分别在半平面α、β内，且AC l ⊥，BD l ⊥，4AB =，6AC =，8BD =，∴CD CA AB BD =++，∴22()CD CA AB BD =++2222CA AB BD CA BD =+++361664268cos12068=+++⨯⨯⨯︒=，CD ∴的长||68217CD ==．故答案为：217．【点睛】本题考查线段长的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，考查函数与方程思想，是中档题．19．【解析】【分析】根据球心到四个顶点距离相等可推断出O 为CD 的中点且OA ＝OB ＝OC ＝OD 进而在△A0B 中利用余弦定理求得cos∠AOB 的值则∠AOB 可求进而根据弧长的计算方法求得答案【详解】解：球心解析：23π 【解析】【分析】根据球心到四个顶点距离相等可推断出O 为CD 的中点，且OA ＝OB ＝OC ＝OD ，进而在△A 0B 中，利用余弦定理求得cos ∠AOB 的值，则∠AOB 可求，进而根据弧长的计算方法求得答案．【详解】解：球心到四个顶点距离相等，故球心O 在CD 中点，则OA ＝OB ＝OC ＝OD ＝1，再由AB =A 0B 中，利用余弦定理cos ∠AOB 11312112+-==-⨯⨯，则∠AOB 23π=，则弧AB 23π=•123π=．故答案为：23π．【点睛】本题主要考查了余弦定理的应用、四面体外接球的性质等，考查了学生观察分析和基本的运算能力． 20．【解析】设球的半径为表面积解得∵在中∴从圆心作平面的垂线垂足在斜边的中点处∴球心到平面的距离故答案为点睛：本题考查的知识点是空间点线面之间的距离计算其中根据球心距球半径解三角形我们可以求出所在平面截【解析】设球的半径为r ，表面积24π20πS r ==，解得r =ABC 中，2AB AC ==，BC =222AB AC BC +=，∴90BAC ∠=︒，从圆心作平面ABC 的垂线，垂足在斜边BC 的中点处，∴球心到平面ABC 的距离d == 点睛：本题考查的知识点是空间点、线、面之间的距离计算，其中根据球心距d ，球半径R ，解三角形我们可以求出ABC 所在平面截球所得圆（即ABC 的外接圆半径），构造直角三角形，满足勾股定理，我们即可求出球心到平面ABC 的距离是与球相关的距离问题常用方法.三、解答题21．(Ⅰ)见解析； (Ⅱ) 3ABCDE V =【解析】【分析】（1）推导出AE ⊥CD ，CD ⊥AD ，从而CD ⊥平面ADE ，再由AB ∥CD ，能证明AB ⊥平面ADE ．（2）凸多面体ABCDE 的体积V=V B-CDE +V B-ADE ，由此能求出结果．【详解】（1）证明：,AE CDE CD CDE ⊥⊂平面平面,AE CD ∴⊥又在正方形ABCD 中，CD AD ⊥AE AD A ⋂=CD ADE ∴⊥平面,又在正方形ABCD 中，//AB CD∴ //AB 平面ADE .(2) 连接BD ，设B 到平面CDE 的距离为h ，//,,AB CD CD CDE ⊂平面//AB CDE ∴平面，又AE CDE ⊥平面，∴ h AE = 1=又11222CDE S CD DE ∆=⨯=⨯=113B CDE V -∴==又11112332B ADE ADE V S AB -∆=⨯⨯=⨯⨯=所以ABCDE V =【点睛】本题考查线面垂直的证明，考查多面体的体积的求法，是中档题，注意空间思维能力的培养．22．（1）240x y +-=；（2）点A 坐标为()3,4、()3,0-【解析】【分析】（1）利用两点式求得BC 边所在直线方程；（2）利用点到直线的距离公式求得A 到直线BC 的距离，根据面积7ABC S ∆=以及点A 在直线2360x y -+=上列方程组，解方程组求得A 点的坐标.【详解】（1）由()2,1B 、()2,3C -得BC 边所在直线方程为123122y x --=---，即240x y +-=.（2）BC ==A 到BC 边所在直线240x y +-=的距离为d =A 在直线2360x y -+=上，故1722360ABC S BC d m n ∆⎧=⋅⋅=⎪⎨⎪-+=⎩，即2472360m n m n ⎧+-=⎨-+=⎩，解得()3,4A 或()30A -,. 【点睛】本小题主要考查利用两点式求直线方程，考查点到直线的距离公式，考查三角形面积公式，属于基础题.23．证明见解析．【解析】试题分析：（1）要证PA 与平面EBD 平行，而过PA 的平面PAC 与平面EBD 的交线为EO ，因此只要证//PA EO 即可，这可由中位线定理得证；（2）要证BD 垂直于平面PAC ，就是要证BD 与平面PAC 内两条相交直线垂直，正方形中对角线BD 与AC 是垂直的，因此只要再证BD PO ⊥，这由线面垂直的性质或定义可得．试题解析：证明：（1）连接EO ，∵四边形ABCD 为正方形，∴O 为AC 的中点，∵E 是PC 的中点，∴OE 是APC ∆的中位线.∴//EO PA ，∵EO ⊂平面BDE ，PA ⊄平面BDE ，∴//PA 平面BDE .（2）∵PO ⊥平面ABCD ，BD ⊂平面ABCD ，∴PO BD ⊥，∵四边形ABCD 是正方形，∴AC BD ⊥，∵PO AC O ⋂=，AC ⊂平面PAC ，PO ⊂平面PAC ，∴BD ⊥平面PAC .考点：线面平行与线面垂直的判断．24．（1）证明见解析；（2）34. 【解析】【分析】(1)直角梯形ABCD 中,过D 作DF ⊥AB 于F ,求解三角形可得ABD △为正三角形，又PAD △为正三角形，M 为线段AD 的中点，可得PM ⊥AD ，BM ⊥AD ，再由线面垂直的判定可得AD ⊥平面PBM ，从而得到平面PMB ⊥平面ABCD ；(2)在平面PMB 中，过B 作BO ⊥PM ,垂足为O ,则BO ⊥平面P AD ,连接AO ,则∠BAO 为直线BA 与平面P AD 所成角，然后求解三角形得答案.【详解】（1）证明：过D 作DF ⊥AB 于F在Rt ADE ∆中，2,1AD AE ==, 3BAD π∴∠=∴BAD 和PAD △是正三角形，∵M 是AD 的中点，∴AD MB ⊥，AD MP ⊥，又∵MB MP M ⋂=，∴AD ⊥平面PMB ，又∵AD ⊂平面ABCD∴平面PMB ⊥平面ABCD.（2）由（1）知PMB ∠是二面角P -AD -B 的平面角∴23PMB π∠=. 由（1）知AD ⊥平面PMB∵AD ⊂平面P AD∴平面PAD ⊥平面PBM∴过B 作平面P AD 的垂线，则垂足E 在PM 延长线上,∴3BME π∠=. 连结AE ，则BAE ∠是AB 与平面P AD 所成的角,∴BM =，∴32BE =， ∴3sin 4BAE BE AB ∠== 【点睛】本题主要考查平面与平面垂直的判定，线面角的求法，二面角，考查空间想象能力与思维能力，属于中档题.25．（1）证明见解析；（2. 【解析】【分析】（1）取BE 中点N ，连,MN CN ，得1//,2MN AB MN AB =，可证四边形CPMN 为平行四边形，进而有//MP CN ，即可证明结论；（2）设2AB AE ==，由已知可得AE ⊥平面ABCD ，过F 做//FQ AE ，交AB 于Q ，得FQ ⊥平面ABCD ，过Q 做QO BD ⊥垂足为O ，连FO ，可证BD ⊥平面FOQ ，得到FOQ ∠为二面角F BD A --的平面角，解Rt OFQ ∆即可.【详解】（1）取BE 中点N ，连,MN CN ，又M 为AE 的中点，1//,2MN AB MN AB ∴=，在正方形ABCD 中，P 是CD 中点， //,CP MN CP MN ∴=，∴四边形CPMN 为平行四边形，//MP CN ∴，MP ⊄平面BCE ，CN ⊂平面BCE ，//PM ∴平面BCE ；（2）设2AB AE ==，ABE ∆是等腰直角三角形，AB AE =，AE AB ∴⊥，平面ABCD ⊥平面ABEF ，平面ABCD 平面ABEF AB =，AE ⊂平面ABEF ，AE ∴⊥平面ABCD ，过F 做//FQ AE ，交AB 于Q ，FQ ∴⊥平面ABCD ， FA FE =，45AEF ∠=︒，,45,45EF AF EAF AF FAQ ∴⊥∠=︒∴=∠=︒，在Rt AFQ ∆中，1,3FQ AQ BQ ===，过Q 做QO BD ⊥垂足为O ，连FO ，FQ ⊥平面,ABCD FQ BD ∴⊥，FQ OQ Q =，BD ∴⊥平面,FOQ BD OF ⊥，FOQ ∠为二面角F BD A --的平面角，在Rt BOQ ∆中，323,45,BQ OBQ OQ =∠=︒∴=，在Rt FOQ ∆中，22222OF FQ OQ =+=， 22sin 11FQ FOQ OF ∴∠==， ∴二面角F BD A --所成角的正弦值2211.【点睛】本题考查空间线、面位置关系，证明直线与平面平行以及求二面角，利用垂直关系做出二面角的平面角是解题的难点，要注意空间垂直间的相互转化，属于中档题.26．（1）证明见解析（2）71cos 2θ⎤∈⎥⎣⎦【解析】【分析】(1)先证明BC AC ⊥，结合面面垂直性质定理即可得到BC ⊥平面ACFE ；(2) 建立分别以直线CA ，CB ，CF 为x 轴，y 轴，z 轴的如图所示的空间直角坐标系，求出平面MAB 与平面FCB 的法向量，表示cos θ，求函数的值域即可.【详解】解：（1）证明：在梯形ABCD 中，因为//AB CD ，1===AD DC CB ，60ABC ∠=︒所以2AB =，所以2222cos603AC AB BC AB BC ︒=+-=，所以222AB AC BC =+，所以BC AC ⊥.因为平面ACFE ⊥平面ABCD ，平面ACFE ⋂平面ABCD AC =，因为BC ⊂平面ABCD ，所以BC ⊥平面ACFE .（2）由（1）可建立分别以直线CA ，CB ，CF 为x 轴，y 轴，z 轴的如图所示的空间直角坐标系，令()03FM λλ=≤≤，则()0,0,0C ，()3,0,0A ，()0,1,0B ，(),0,1M λ. ∴()3,1,0AB =-，(),1,1BM λ=-.设()1,,n x y z =为平面MAB 的一个法向量，由11·0·0n AB n BM ⎧=⎪⎨=⎪⎩得300x y x y z λ⎧+=⎪⎨-+=⎪⎩，取1x =，则()11,3,3n λ=， ∵()21,0,0n =是平面FCB 的一个法向量1212cos n n n n θ⋅∴==⋅()21331λ++-⨯()2134λ=-+∵03λ≤≤0λ=时，cos θ有最小值77，当3λ=cos θ有最大值12． ∴71cos 72θ⎤∈⎥⎣⎦. 【点睛】本题考查线面垂直的证明，二面角的度量，考查推理能力、计算能力以及空间想象能力，属于中档题.。

新高中必修二数学下期中第一次模拟试题含答案

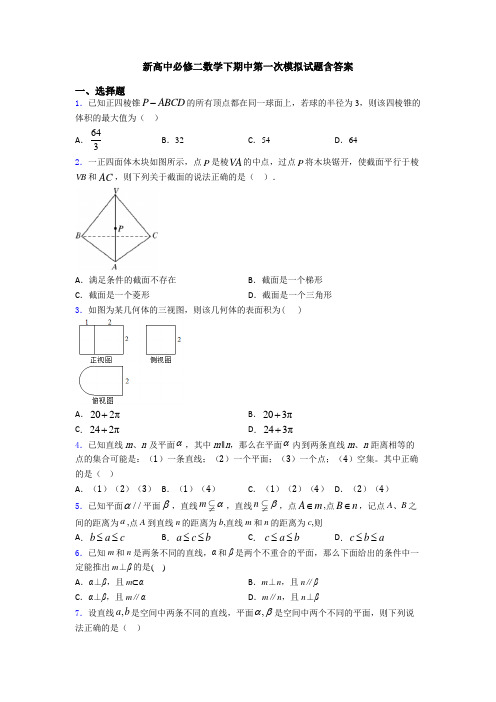
新高中必修二数学下期中第一次模拟试题含答案一、选择题1．已知正四棱锥P ABCD -的所有顶点都在同一球面上，若球的半径为3，则该四棱锥的体积的最大值为（）A ．643B ．32C ．54D ．642．一正四面体木块如图所示，点P 是棱VA 的中点，过点P 将木块锯开，使截面平行于棱VB 和AC ，则下列关于截面的说法正确的是（）．A ．满足条件的截面不存在B ．截面是一个梯形C ．截面是一个菱形D ．截面是一个三角形3．如图为某几何体的三视图，则该几何体的表面积为( )A ．202π+B ．203π+C ．242π+D ．243π+4．已知直线m 、n 及平面α，其中m ∥n ，那么在平面α内到两条直线m 、n 距离相等的点的集合可能是：（1）一条直线；（2）一个平面；（3）一个点；（4）空集。

其中正确的是（）A ．（1）（2）（3）B ．（1）（4）C ．（1）（2）（4）D ．（2）（4） 5．已知平面//α平面β，直线mα，直线n β，点A m ∈,点B n ∈，记点A 、B 之间的距离为a ,点A 到直线n 的距离为b ,直线m 和n 的距离为c ,则 A ．b a c ≤≤ B ．a c b ≤≤ C ． c a b ≤≤D ．c b a ≤≤ 6．已知m 和n 是两条不同的直线，α和β是两个不重合的平面，那么下面给出的条件中一定能推出m ⊥β的是( )A ．α⊥β，且m ⊂αB ．m ⊥n ，且n ∥βC ．α⊥β，且m ∥αD ．m ∥n ，且n ⊥β 7．设直线,a b 是空间中两条不同的直线，平面,αβ是空间中两个不同的平面，则下列说法正确的是（）A ．若a ∥α，b ∥α，则a ∥bB ．若a ∥b ，b ∥α，则a ∥αC ．若a ∥α，α∥β，则a ∥βD ．若α∥β，a α⊂，则a ∥β 8．点A 、B 、C 、D 在同一个球的球面上，AB=BC=2，AC=2，若四面体ABCD 体积的最大值为23，则这个球的表面积为（） A ．1256π B ．8π C ．2516π D ．254π 9．某锥体的三视图如图所示（单位：cm ），则该锥体的体积（单位：cm 3）是（）A ．13 B ．12 C ．16 D ．110．若圆锥的高等于底面直径，则它的底面积与侧面积之比为A ．1∶2B ．1∶3C ．1∶5D ．3∶211．如图是一个几何体的三视图（侧视图中的弧线是半圆），则该几何体的表面积是（）A ．20＋3πB ．24＋3πC ．20＋4πD ．24＋4π12．已知平面αβ⊥且l αβ=，M 是平面α内一点，m ，n 是异于l 且不重合的两条直线，则下列说法中错误的是（）. A ．若//m α且//m β，则//m l B ．若m α⊥且n β⊥，则m n ⊥C ．若M m ∈且//m l ，则//m βD ．若M m ∈且m l ⊥，则m β⊥ 二、填空题13．给出下面四个命题：①“直线l ⊥平面α内所有直线”的充要条件是“l ⊥平面α”；②“直线//a 直线b ”的充要条件是“a 平行于b 所在的平面”；③“直线a ，b 为异面直线”的充分不必要条件是“直线a ，b 不相交”；④“平面//α平面β”的必要不充分条件是“α内存在不共线三点到β的距离相等”. 其中正确命题的序号是____________________14．经过两条直线2310x y ++=和340x y -+=的交点，并且平行于直线3470x y +-=的直线方程是________.15．在平面直角坐标系xOy 中，A 为直线:2l y x =上在第一象限内的点，()5,0B ，以AB 为直径的圆C 与直线l 交于另一点D ．若0AB CD ⋅=，则点A 的横坐标为________．16．若一个圆柱的侧面展开图是边长为2的正方形，则此圆柱的体积为 .17．如图，在ABC ∆中，6AB BC ==，90ABC ∠=，点D 为AC 的中点，将ABD △沿BD 折起到的位置，使PC PD =，连接PC ，得到三棱锥P BCD -，若该三棱锥的所有顶点都在同一球面上，则该球的表面积是__________.18．若直线y x b =+与曲线234y x x =-b 的取值范围是______．19．已知圆O ：224x y +=, 则圆O 在点3)A 处的切线的方程是___________.20．已知直线1:1l y x =-上有两个点11(,)A x y 和22(,)B x y , 且12,x x 为一元二次方程2610x x -+=的两个根, 则过点,A B 且和直线2:1l x =-相切的圆的方程为______________.三、解答题21．已知点(3,3)M ，圆22:(1)(2)4C x y -+-=.（1）求过点M 且与圆C 相切的直线方程；（2）若直线40()ax y a -+=∈R 与圆C 相交于A ，B 两点，且弦AB 的长为23实数a 的值.22．已知ABC ∆的三个顶点(),A m n 、()2,1B 、()2,3C -.（1）求BC 边所在直线的方程；（2）BC 边上中线AD 的方程为2360x y -+=，且7ABC S ∆=，求点A 的坐标.23．如图，直角梯形BDFE 中，//,,2EF BD BE BD EF ⊥=ABCD 中，//,,24AB CD AC BD AB CD ⊥==，且平面BDFE ⊥平面ABCD ．（1）求证：AC ⊥平面BDFE ；（2）若BF 与平面ABCD 所成角为4π，求二面角B DF C --的余弦值．24．如图，在三棱柱111ABC A B C -中，1CC ⊥平面ABC ,1,2AC BC AC BC CC ⊥===，点,,D E F 分别为棱11111,,AC B C BB 的中点．（1）求证：//AB 平面DEF ；（2）求证：平面1ACB ⊥平面DEF ；（3）求三棱锥1E ACB -的体积.25．如图，在直三棱柱ABC -A 1B 1C 1中，∠ACB ＝90°，∠BAC ＝30°，BC ＝1，A 1A ＝6，M 是CC 1的中点．(1)求证：A 1B ⊥AM ；(2)求二面角B --AM--C 的平面角的大小．.26．如图所示，直角梯形ABCD 中，//AD BC ，,AD AB ⊥22,AB BC AD ===四边形EDCF 为矩形，2DE =，平面EDCF ⊥ABCD .（1）求证：//DF 平面ABE ；（2）求二面角B EF D --二面角的正弦值；（3）在线段BE 上是否存在点P ，使得直线AP 与平面BEF 6存在，求出线段BP 的长，若不存在，请说明理由.【参考答案】***试卷处理标记，请不要删除一、选择题1．A解析：A【解析】【分析】设底面ABCD 的边长为a ，四棱锥的高为h ，可得22122a h h =-，得出四棱锥的体积关于h 的函数()V h ，求出V 的极大值点，即可得到四棱锥的体积的最大值.【详解】正四棱锥P ABCD -的所有顶点都在同一球面上，若球的半径为3，设底面ABCD 的边长为a ，四棱锥的高为h ，设正四棱锥的底面ABCD 的中心为1O . 则22a OA =,1PO ⊥ 平面ABCD . 则22211OO O A OA +=,即()2222332a h ⎛⎫+-= ⎪ ⎪⎝⎭，可得22122a h h =-. 则该四棱锥的体积为()221112233V a h h h h =⨯=- 令()()2122f h h h h =-，则()2246f h h h '=-当04h <<时，()0f h '>，f h 单调递增.当4h >时，()0f h '<，f h 单调递减.所以当4h =时，该四棱锥的体积有最大值，最大值为：()216412424433⨯⨯-⨯⨯= .【点睛】本题考查了四棱锥与球的组合体，求椎体的体积，关键是利用了导数求体积的最值．属于中档题．2．C解析：C【解析】【分析】取AB 的中点D ，BC 的中点E ，VC 的中点F ，连接,,,PD PF DE EF ，易得即截面为四边形PDEF ，且四边形PDEF 为菱形即可得到答案.【详解】取AB 的中点D ，BC 的中点E ，VC 的中点F ，连接,,,PD PF DE EF ，易得PD ∥VB 且12PD VB =，EF ∥VB 且12EF VB =，所以PD ∥EF ，PD EF =，所以四边形PDEF 为平行四边形，又VB ⊄平面PDEF ，PD ⊂平面PDEF ,由线面平行的判定定理可知，VB ∥平面PDEF ，AC ∥平面PDEF ，即截面为四边形PDEF ，又1122DE AC VB PD ===，所以四边形PDEF 为菱形，所以选项C 正确. 故选：C【点睛】本题考查线面平行的判定定理的应用，考查学生的逻辑推理能力，是一道中档题.3．B【解析】该几何体是一个正方体与半圆柱的组合体，表面积为2215221122032S πππ=⨯+⨯⨯+⨯⨯=+，故选B ． 4．C解析：C【解析】【分析】根据题意，对每一个选项进行逐一判定，不正确的只需举出反例，正确的作出证明，即可得到答案.【详解】如图（1）所示，在平面内不可能由符合题的点；如图（2），直线,a b 到已知平面的距离相等且所在平面与已知平面垂直，则已知平面为符合题意的点；如图（3），直线,a b 所在平面与已知平面平行，则符合题意的点为一条直线，综上可知（1）（2）（4）是正确的，故选C.【点睛】本题主要考查了空间中直线与平面之间的位置关系，其中熟记空间中点、线、面的位置关系是解答此类问题的关键，着重考查了空间想象能力，以及推理与论证能力，属于基础题. 5．D解析：D【解析】【分析】根据平面与平面平行的判断性质,判断c 最小,再根据点到直线距离和点到直线上任意点距离判断a 最大.【详解】由于平面//α平面β,直线m 和n 又分别是两平面的直线,则c 即是平面之间的最短距离. 而由于两直线不一定在同一平面内,则b 一定大于或等于c ,判断a 和b 时,因为B 是上n 任意一点,则a 大于或等于b .故选D.本题主要考查面面平行的性质以及空间距离的性质，考查了空间想象能力，意在考查灵活应用所学知识解答问题的能力，属于中档题.6．D解析：D【解析】【分析】根据所给条件，分别进行分析判断，即可得出正确答案.【详解】解：αβ⊥且m α⊂⇒m β⊂或//m β或m 与β相交，故A 不成立；m n ⊥且//n β⇒m β⊂或//m β或m 与β相交，故B 不成立；αβ⊥且//m α⇒m β⊂或//m β或m 与β相交，故C 不成立；//m n 且n β⊥⇒m β⊥，故D 成立；故选：D【点睛】本题考查直线与平面的位置关系，线面垂直判定，属于基础题.7．D解析：D【解析】【分析】利用空间直线和平面的位置关系对每一个选项逐一分析判断得解.【详解】A. 若a ∥α，b ∥α，则a 与b 平行或异面或相交，所以该选项不正确；B. 若a ∥b ，b ∥α，则a ∥α或a α⊂，所以该选项不正确；C. 若a ∥α，α∥β，则a ∥β或a β⊂，所以该选项不正确；D. 若α∥β，a α⊂，则a ∥β，所以该选项正确.故选：D【点睛】本题主要考查空间直线平面位置关系的判断，意在考查学生对这些知识的理解掌握水平.8．D解析：D【解析】试题分析：根据题意知，ABC 是一个直角三角形，其面积为1．其所在球的小圆的圆心在斜边AC 的中点上，设小圆的圆心为Q ，若四面体ABCD 的体积的最大值，由于底面积ABC S 不变，高最大时体积最大，所以，DQ 与面ABC 垂直时体积最大，最大值为12·33ABC S DQ =，即12133DQ ⨯⨯=，∴2DQ =，设球心为O ，半径为R ，则在直角AQO 中，222OA AQ OQ =+，即()22212R R =+-，∴54R =，则这个球的表面积为：2525444S ππ⎛⎫== ⎪⎝⎭；故选Ｄ．考点：球内接多面体，球的表面积． 9．A解析：A【解析】【分析】根据三视图知该几何体对应的三棱锥，结合图中数据求得三棱锥的体积．【详解】由题意可知三棱锥的直观图如图：三棱锥的体积为：111211323⨯⨯⨯⨯=．故选：A ．【点睛】本题考查了利用三视图求几何体体积的应用问题，考查了空间想象能力，是基础题．10．C解析：C【解析】【分析】由已知，求出圆锥的母线长，进而求出圆锥的底面面积和侧面积，可得答案【详解】设圆锥底面半径为r ，则高h ＝2r ，∴其母线长l ＝r ．∴S 侧＝πrl ＝πr 2，S 底＝πr 故选C ．【点睛】本题考查的知识点是旋转体，圆锥的表面积公式，属于基础题． 11．A解析：A【解析】【分析】【详解】由几何体的三视图分析可知，该几何体上部为边长为2的正方体，下部为底面半径为1、高为2的半圆柱体，故该几何体的表面积是20＋3π，故选A.考点：1、几何体的三视图；2、几何体的表面积.12．D解析：D【解析】【分析】根据已知条件和线面位置关系一一进行判断即可.【详解】选项A ：一条直线平行于两个相交平面，必平行于两个面交线，故A 正确；选项B ：垂直于两垂直面的两条直线相互垂直，故B 正确；选项C ：M m ∈且//m l 得m α⊂且//m β，故C 正确；选项D ：M m ∈且m l ⊥不一定得到m α⊂，所以,m l 可以异面，不一定得到m β⊥. 故选：D .【点睛】本题主要考查的是空间点、线、面的位置关系的判定，掌握线面、线线之间的判定定理和性质定理是解决本题的关键，是基础题.二、填空题13．①④【解析】【分析】利用直线与直线平面与平面间的位置关系及性质判断前后两个条件的推出关系利用充要条件的定义得结论【详解】解：对于①直线与平面垂直的定义是直线与平面内的所有直线垂直故①正确；对于②平行解析：①④【解析】【分析】利用直线与直线、平面与平面间的位置关系及性质判断前后两个条件的推出关系，利用充要条件的定义得结论．【详解】解：对于①直线与平面垂直的定义是直线与平面内的所有直线垂直，故①正确；对于②，a 平行于b 所在的平面//a b ⇒或a 与b 异面，故②错；对于③，直线a 、b 不相交⇒直线a ，b 异面或平行，故③错；对于④，平面//α平面βα⇒内存在不共线三点到β的距离相等；α内存在不共线三点到β的距离相等⇒平面//α平面β或相交，故④正确故答案为：①④【点睛】本题考查直线与直线间的位置关系及性质；充要条件的判断．命题真假的判断，属于中档题．14．【解析】【分析】先求出两相交直线的交点设出平行于直线的直线方程根据交点在直线上求出直线方程【详解】联立直线的方程得到两直线的交点坐标平行于直线的直线方程设为则所以直线的方程为：故答案为：【点睛】本题解析：1934011x y ++= 【解析】【分析】先求出两相交直线的交点，设出平行于直线3470x y +-=的直线方程，根据交点在直线上，求出直线方程. 【详解】联立直线的方程23103470x y x y ++=⎧⎨+-=⎩，得到两直线的交点坐标135(,)1111-，平行于直线3470x y +-=的直线方程设为340x y c ++=，则1353()4()+01111c ⋅-+⋅= 所以直线的方程为：1934011x y ++= 故答案为：1934011x y ++= 【点睛】本题考查了直线的交点，以及与已知直线平行的直线方程，考查了学生概念理解，转化与划归的能力，属于基础题.15．3【解析】分析：先根据条件确定圆方程再利用方程组解出交点坐标最后根据平面向量的数量积求结果详解：设则由圆心为中点得易得与联立解得点的横坐标所以所以由得或因为所以点睛：以向量为载体求相关变量的取值或范解析：3 【解析】分析：先根据条件确定圆方程，再利用方程组解出交点坐标，最后根据平面向量的数量积求结果.详解：设(),2(0)A a a a >，则由圆心C 为AB 中点得5,,2a C a +⎛⎫⎪⎝⎭易得()()():520C x x a y y a --+-=，与2y x =联立解得点D 的横坐标1,D x =所以()1,2D .所以()55,2,1,22a AB a a CD a +⎛⎫=--=-- ⎪⎝⎭，由0AB CD ⋅=得()()()2551220,230,32a a a a a a a +⎛⎫--+--=--== ⎪⎝⎭或1a =-，因为0a >，所以 3.a =点睛：以向量为载体求相关变量的取值或范围，是向量与函数、不等式、三角函数、曲线方程等相结合的一类综合问题.通过向量的坐标运算，将问题转化为解方程或解不等式或求函数值域，是解决这类问题的一般方法.16．2π【解析】试题分析：设圆柱的底面半径为r高为h底面积为S体积为V则有2πr=2⇒r=1π故底面面积S=πr2=π×(1π)2=1π故圆柱的体积V=Sh=1π×2=2π考点：圆柱的体积解析：【解析】试题分析：设圆柱的底面半径为，高为，底面积为，体积为，则有，故底面面积，故圆柱的体积.考点：圆柱的体积17．【解析】【分析】由题意得该三棱锥的面PCD是边长为的正三角形且BD⊥平面PCD求出三棱锥P﹣BDC的外接球半径R＝由此能求出该球的表面积【详解】由题意得该三棱锥的面PCD是边长为的正三角形且BD⊥平解析：7π【解析】【分析】由题意得该三棱锥的面PCD3的正三角形，且BD⊥平面PCD，求出三棱锥P﹣BDC的外接球半径R＝72，由此能求出该球的表面积．【详解】由题意得该三棱锥的面PCD3的正三角形，且BD⊥平面PCD，设三棱锥P﹣BDC外接球的球心为O，△PCD外接圆圆心为O1，则OO1⊥面PCD，∴四边形OO1DB为直角梯形，由BD3O1D＝1，OB＝OD，得OB7∴三棱锥P﹣BDC的外接球半径R 7，∴该球的表面积S＝4πR2＝474π⨯＝7π．故答案为：7π．【点睛】本题考查三棱锥外接球的表面积的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方思想，是中档题．18．【解析】【分析】由曲线y=3+得（x ﹣2）2+（y ﹣3）2=40≤x≤4直线y=x+b 与曲线y=3+有公共点圆心（23）到直线y=x+b 的距离d 不大于半径r=2由此结合图象能求出实数b 的取值范围【详解析：122,3⎡⎤-⎣⎦【解析】【分析】由曲线y=3+24x x -，得（x ﹣2）2+（y ﹣3）2=4，0≤x≤4，直线y=x+b 与曲线y=3+24x x -有公共点，圆心（2，3）到直线y=x+b 的距离d 不大于半径r=2，由此结合图象能求出实数b 的取值范围．【详解】由曲线y=3+24x x -，得（x ﹣2）2+（y ﹣3）2=4，0≤x≤4，∵直线y=x+b 与曲线y=3+24x x -有公共点，∴圆心（2，3）到直线y=x+b 的距离d 不大于半径r=2，即23212b 1+222bd -+=≤⇒-≤≤∵0≤x≤4，∴x=4代入曲线24x x -y=3，把（4，3）代入直线y=x+b ，得b min =3﹣4=﹣1，② 联立①②，得-1b 122≤≤+ ∴实数b 的取值范围是[﹣1，2]．故答案为1,122⎡-+⎣.【点睛】本题考查实数的取值范围的求法，是中档题，解题时要认真审题，注意数形结合思想的合理运用．一般直线和圆的题很多情况下是利用数形结合来解决的，联立的时候较少；在求圆上的点到直线或者定点的距离时，一般是转化为圆心到直线或者圆心到定点的距离，再加减半径，分别得到最大值和最小值；涉及到圆的弦长或者切线长时，经常用到垂径定理．19．【解析】【分析】先求出kOA=从而圆O 在点处的切线的方程的斜率由此能出圆O 在点处的切线的方程【详解】kOA=∴圆O 在点处的切线的方程的斜率∴圆O 在点A 处的切线的方程整理得即答案为【点睛】本题考查圆的30y +-=【解析】【分析】先求出k OA ，从而圆O 在点(处的切线的方程的斜率k = ，由此能出圆O在点A 处的切线的方程．【详解】k OA =O 在点(处的切线的方程的斜率k =，∴圆O 在点A (处的切线的方程1y x =-），30y +-=．30y +-=. 【点睛】本题考查圆的切线方程的求法，属中档题.20．或【解析】【分析】由题意可知所以中点坐标为圆心在直线的中垂线上故过圆心满足直线设圆心的坐标为由圆与直线相切故由弦长公式可得圆心到直线的距离为由勾股定理可知解得：当时；当时得解【详解】上有两个点和为一解析：223(2)16x y -+-=（）或2211(6)144x y -++=（）【解析】【分析】由题意可知，126x x +=，124y y +=，所以AB 中点坐标为32（，），圆心在直线AB 的中垂线上，故过圆心满足直线5y x =-+，设圆心的坐标为a 5a -（，），由圆与直线2:1l x =-相切故r a 1=+，由弦长公式可得128AB x =-=，圆心到直线AB222221r (a 1)2(3)162d AB a =+↔+=-+解得：当3a =时，r 4=；当11a =时，r 11=得解。

【压轴卷】高中必修二数学下期中第一次模拟试卷(含答案)

【压轴卷】高中必修二数学下期中第一次模拟试卷(含答案)一、选择题1．已知m ，n 表示两条不同直线，α表示平面，下列说法正确的是（）A ．若//,//,m n αα则//m nB ．若m α⊥，n α⊂，则m n ⊥C ．若m α⊥，m n ⊥，则//n αD ．若//m α，m n ⊥，则n α⊥2．圆224470x y x y +--+=上的动点P 到直线0x y +=的最小距离为（）A ．1B ．221-C ．22D ．23．已知三棱锥S ABC -的所有顶点都在球O 的求面上，ABC ∆是边长为1的正三角形，SC 为球O 的直径，且2SC =，则此棱锥的体积为（）A ．2B ．3C ．2D ．2 4．三棱锥P -ABC 中，P A ⊥平面ABC ，AB ⊥BC ，P A =2，AB =BC =1，则其外接球的表面积为（）A ．6πB ．5πC ．4πD ．3π 5．已知直线20ax y a +-+=在两坐标轴上的截距相等，则实数(a = ) A ．1B ．1-C ．2-或1D ．2或1 6．已知圆M ：2220x y y =++与直线l ：350ax y a +-+=，则圆心M 到直线l 的最大距离为（）A ．5B ．6C ．35D ．417．某几何体的三视图如图所示，则该几何体的体积为( )A ．12B ．18C ．24D ．308．椭圆22221(0)x y a b a b+=>>的左右焦点分别是1F 、2F ，以2F 为圆心的圆过椭圆的中心，且与椭圆交于点P ，若直线1PF 恰好与圆2F 相切于点P ，则椭圆的离心率为（） A 31+ B 31 C ．22 D 51- 9．若a ＞b ＞0，0＜c ＜1，则A ．log a c ＜log b cB ．log c a ＜log c bC ．a c ＜b cD ．c a ＞c b10．已知直线()()():21110l k x k y k R ++++=∈与圆()()221225x y -+-=交于A ，B两点，则弦长AB 的取值范围是（）A ．[]4,10B ．[]3,5C ．[]8,10D ．[]6,1011．如图是正方体的平面展开图，则在这个正方体中：①BM 与ED 平行 ②CN 与BE 是异面直线③CN 与BM 成60︒角 ④DM 与BN 是异面直线以上四个命题中，正确命题的个数是（）A ．1B ．2C ．3D ．412．若底面是菱形的棱柱其侧棱垂直于底面，且侧棱长为5，它的对角线的长分别是9和15，则这个棱柱的侧面积是( )．A ．130B ．140C ．150D ．160二、填空题13．经过两条直线2310x y ++=和340x y -+=的交点，并且平行于直线3470x y +-=的直线方程是________.14．已知圆22(1)16x y ++=，点(1,0),(1,0)E F -，过(1,0)E -的直线1l 与过(1,0)F 的直线2l 垂直且圆相交于,A C 和,B D ，则四边形ABCD 的面积的取值范围是_________.15．如图，在圆柱O 1 O 2 内有一个球O ，该球与圆柱的上、下底面及母线均相切．记圆柱O 1 O 2 的体积为V 1 ,球O 的体积为V 2 ，则12V V 的值是_____16．如图，以等腰直角三角形斜边BC 上的高AD 为折痕，把△ABD 与△ACD 折成互相垂直的两个平面后，某学生得出下列四个结论： ①0BD AC ⋅≠u u u r u u u r ；②∠BAC ＝60°；③三棱锥D ﹣ABC 是正三棱锥；④平面ADC 的法向量和平面ABC 的法向量互相垂直．其中正确结论的序号是．（请把正确结论的序号都填上）17．如图，在△ABC 中，AB=BC=2，∠ABC=120°.若平面ABC 外的点P 和线段AC 上的点D ，满足PD=DA ，PB=BA ，则四面体PBCD 的体积的最大值是 .18．在各棱长均为1的正四棱锥P ABCD -中，M 为线段PB 上的一动点，则当AM MC +最小时，cos AMC ∠=_________19．如图，AB 是底面圆O 的直径,点C 是圆O 上异于A 、B 的点，PO 垂直于圆O 所在的平面，且1,2PO OB BC ===，点E 在线段PB 上，则CE OE +的最小值为________.20．已知球的表面积为20π，球面上有A 、B 、C 三点．如果2AB AC ==，22BC =ABC 的距离为__________．三、解答题21．已知点()1,0P ，圆22:6440C x y x y +-++=. （1）若直线l 过点P 且到圆心C 的距离为2，求直线l 的方程；（2）设过点()0,1Q -的直线m 与圆C 交于A 、B 两点（m 的斜率为负），当||4AB =时，求以线段AB 为直径的圆的方程.22．如图，在直三棱柱111ABC A B C -中，D 是BC 的中点．AB AC ⊥，1AB AC ==，12AA =．（Ⅰ）求直线1AC 与平面11BCC B 所成角的正弦值；（Ⅱ）求二面角1A A B C --的余弦值．23．四棱锥P -ABCD 中，底面ABCD 是直角梯形，//AB CD ，90BCD ∠=︒，22AB AD DC ===.PAD △ 为正三角形，二面角P -AD -C 的大小为23π.（1）线段AD 的中点为M.求证：平面PMB ⊥平面ABCD ；（2）求直线BA 与平面P AD 所成角的正弦值.24．如图，正方形ABCD 所在平面与平面四边形ABEF 所在平面互相垂直，ABE ∆是等腰直角三角形，AB AE =，FA FE =，45AEF ∠=︒．（1）设线段CD AE 、的中点分别为P M 、，求证：//PM 平面BCE ；（2）求二面角F BD A --所成角的正弦值．25．如图，正方体1111ABCDA B C D 的棱长为2，E F M 、、分别是1111C B C D ，和AB 的中点．（1）求证：1//MD 平面BEFD ．（2）求M 到平面BEFD 的距离．26．设直线l 的方程为()()1520a x y a a R ++--=∈.(1)求证:不论a 为何值，直线l 必过一定点P ;(2)若直线l 分别与x 轴正半轴，y 轴正半轴交于点(),0A A x ，()0,B B y ，当AOB ∆而积最小时，求AOB ∆的周长;(3)当直线l 在两坐标轴上的截距均为整数时，求直线l 的方程.【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【解析】试题分析：线面垂直，则有该直线和平面内所有的直线都垂直，故B 正确.考点：空间点线面位置关系．2．B解析：B【解析】【分析】先求出圆心到直线0x y +=的距离，根据距离的最小值为d r -，即可求解.【详解】由圆的一般方程可得22(2)(2)1x y -+-=，圆心到直线的距离222d == 所以圆上的点到直线的距离的最小值为221.故选B.【点睛】本题主要考查了点到直线的距离，圆的方程，属于中档题.3．A解析：A【解析】【分析】【详解】根据题意作出图形：设球心为O ，过ABC 三点的小圆的圆心为O 1，则OO 1⊥平面ABC ，延长CO 1交球于点D ，则SD ⊥平面ABC ．∵CO 1=2333⨯=， ∴116133OO =-=， ∴高SD=2OO 1=263，∵△ABC 是边长为1的正三角形，∴S △ABC =3， ∴132623S ABC V -=⨯⨯=三棱锥．考点：棱锥与外接球，体积．【名师点睛】本题考查棱锥与外接球问题，首先我们要熟记一些特殊的几何体与外接球（内切球）的关系，如正方体（长方体）的外接球（内切球）球心是对角线的交点，正棱锥的外接球（内切球）球心在棱锥的高上，对一般棱锥来讲，外接球球心到名顶点距离相等，当问题难以考虑时，可减少点的个数，如先考虑到三个顶点的距离相等的点是三角形的外心，球心一定在过此点与此平面垂直的直线上．如直角三角形斜边中点到三顶点距离相等等等．4．A解析：A【解析】分析：将三棱锥的外接球转化为以,,AP AB BC 为长宽高的长方体的外接球，从而可得球半径，进而可得结果.详解：因为PA ⊥平面AB ，,AB BC ⊂平面ABC ，PA BC ∴⊥，,PA AB AB BC ⊥⊥Q ，所以三棱锥的外接球，就是以,,AP AB BC 为长宽高的长方体的外接球，外接球的直径等于长方体的对角线，即24116R =++=246R ππ=，故选A.点睛：本题主要考查三棱锥外接球表面积的求法，属于难题.要求外接球的表面积和体积，关键是求出求的半径，求外接球半径的常见方法有：①若三条棱两垂直则用22224R a b c =++（,,a b c 为三棱的长）；②若SA ⊥面ABC （SA a =），则22244R r a =+（r 为ABC ∆外接圆半径） ③可以转化为长方体的外接球；④特殊几何体可以直接找出球心和半径.5．D解析：D【解析】【分析】根据题意讨论直线它在两坐标轴上的截距为0和在两坐标轴上的截距不为0时，求出对应a 的值，即可得到答案．【详解】由题意，当2a 0-+=，即a 2=时，直线ax y 2a 0+-+=化为2x y 0+=，此时直线在两坐标轴上的截距都为0，满足题意；当2a 0-+≠，即a 2≠时，直线ax y 2a 0+-+=化为122x y a a a+=--，由直线在两坐标轴上的截距相等，可得2a 2a a-=-，解得a 1=；综上所述，实数a 2=或a 1=．故选：D ．【点睛】本题主要考查了直线方程的应用，以及直线在坐标轴上的截距的应用，其中解答中熟记直线在坐标轴上的截距定义，合理分类讨论求解是解答的关键，着重考查了运算与求解能力，属于基础题. 6．A解析：A【解析】【分析】计算圆心为()0,1M -，350ax y a +-+=过定点()3,5N -，最大距离为MN ，得到答案.【详解】圆M ：2220x y y =++，即()2211x y ++=，圆心为()0,1M -， 350ax y a +-+=过定点()3,5N -，故圆心M 到直线l 的最大距离为5MN =. 故选：A .【点睛】本题考查了点到直线距离的最值问题，确定直线过定点()3,5N -是解题的关键.7．C解析：C【解析】试题分析：由三视图可知，几何体是三棱柱消去一个同底的三棱锥，如图所示，三棱柱的高为，消去的三棱锥的高为，三棱锥与三棱柱的底面为直角边长分别为和的直角三角形，所以几何体的体积为，故选C ．考点：几何体的三视图及体积的计算．【方法点晴】本题主要考查了几何体的三视图的应用及体积的计算，着重考查了推理和运算能力及空间想象能力，属于中档试题，解答此类问题的关键是根据三视图的规则“长对正、宽相等、高平齐”的原则，还原出原几何体的形状，本题的解答的难点在于根据几何体的三视图还原出原几何体和几何体的度量关系，属于中档试题．8．B解析：B【解析】【分析】根据椭圆的定义可知12||||2PF PF a +=，又1PF 恰好与圆2F 相切于点P ，可知2||PF c =且12PF PF ⊥，即可列出方程求椭圆的离心率.【详解】由1PF 恰好与圆2F 相切于点P ，可知2||PF c =，且 12PF PF ⊥，又12||||2PF PF a +=，可知1||2PF a c =-，在12Rt PF F ∆中，222(2)4a c c c -+=，即2222a ac c -=所以2220,(0,1)e e e +-=∈，解得212312e -==，故选：B【点睛】本题主要考查了椭圆的定义，椭圆的简单几何性质，圆的切线的性质，属于中档题. 9．B解析：B【解析】试题分析：对于选项A ，a b 1gc 1gc log c ,log c lg a lg b==，01c <<Q ，10gc ∴<，而0a b >>，所以lg lg a b >，但不能确定lg lg a b 、的正负，所以它们的大小不能确定;对于选项B ，c lg lg log ,log lg lg c a b a b c c ==,lg lg a b >，两边同乘以一个负数1lg c改变不等号方向，所以选项B 正确;对于选项C ，利用c y x =在第一象限内是增函数即可得到c c a b >，所以C 错误;对于选项D ，利用xy c =在R 上为减函数易得a b c c <，所以D 错误.所以本题选B.【考点】指数函数与对数函数的性质【名师点睛】比较幂或对数值的大小,若幂的底数相同或对数的底数相同,通常利用指数函数或对数函数的单调性进行比较；若底数不同,可考虑利用中间量进行比较. 10．D解析：D【解析】【分析】由直线()()21110k x k y ++++=，得出直线恒过定点()1,2P -，再结合直线与圆的位置关系，即可求解.【详解】由直线()()():21110l k x k y k R ++++=∈，可得()210k x y x y ++++=，又由2010x y x y +=⎧⎨++=⎩，解得12x y =⎧⎨=-⎩，即直线恒过定点()1,2P -，圆心()1,2C ，当CP l ⊥时弦长最短，此时2222AB CP r ⎛⎫+= ⎪⎝⎭，解得min 6AB =，再由l 经过圆心时弦长最长为直径210r =，所以弦长AB 的取值范围是[]6,10.故选：D.【点睛】本题主要考查了直线系方程的应用，以及直线与圆的位置关系的应用，其中解答中熟练利用直线的方程，得出直线恒过定点，再结合直线与圆的位置关系求解是解答的关键，着重考查了分析问题和解答问题的能力，属于中档试题.11．B解析：B【解析】【分析】把平面展开图还原原几何体，再由棱柱的结构特征及异面直线定义、异面直线所成角逐一核对四个命题得答案．【详解】把平面展开图还原原几何体如图：由正方体的性质可知，BM 与ED 异面且垂直，故①错误；CN 与BE 平行，故②错误；连接BE ，则BE CN P ，EBM ∠为CN 与BM 所成角，连接EM ，可知BEM ∆为正三角形，则60EBM ∠=︒，故③正确；由异面直线的定义可知，DM 与BN 是异面直线，故④正确．∴正确命题的个数是2个．故选：B ．【点睛】本题考查棱柱的结构特征，考查异面直线定义及异面直线所成角，是中档题．12．D解析：D【解析】设直四棱柱1111ABCD A B C D -中，对角线119,15AC BD ==，因为1A A ⊥平面,ABCD AC Ì,平面ABCD ，所以1A A AC ⊥，在1Rt A AC ∆中，15A A =，可得221156AC AC A A =-= 同理可得2211200102BD D B D D =-==，因为四边形ABCD 为菱形，可得,AC BD 互相垂直平分，所以2211()()1450822AB AC BD =+=+=，即菱形ABCD 的边长为8，因此，这个棱柱的侧面积为1()485160S AB BC CD DA AA =+++⨯=⨯⨯=，故选D.点睛：本题考查了四棱锥的侧面积的计算问题，解答中通过给出的直四棱柱满足的条件，求得底面菱形的边长，进而得出底面菱形的底面周长，即可代入侧面积公式求得侧面积，着重考查了学生分析问题和解答问题的能力，以及空间想象能力，其中正确认识空间几何体的结构特征和线面位置关系是解答的关键.二、填空题13．【解析】【分析】先求出两相交直线的交点设出平行于直线的直线方程根据交点在直线上求出直线方程【详解】联立直线的方程得到两直线的交点坐标平行于直线的直线方程设为则所以直线的方程为：故答案为：【点睛】本题解析：1934011x y ++= 【解析】【分析】先求出两相交直线的交点，设出平行于直线3470x y +-=的直线方程，根据交点在直线上，求出直线方程. 【详解】联立直线的方程23103470x y x y ++=⎧⎨+-=⎩，得到两直线的交点坐标135(,)1111-，平行于直线3470x y +-=的直线方程设为340x y c ++=，则1353()4()+01111c ⋅-+⋅= 所以直线的方程为：1934011x y ++= 故答案为：1934011x y ++= 【点睛】本题考查了直线的交点，以及与已知直线平行的直线方程，考查了学生概念理解，转化与划归的能力，属于基础题.14．【解析】【分析】由题可知而过的弦过圆心时最长与垂直时最短据此则可以确定四边形的面积的取值范围【详解】由题知直线过圆心故设圆心到直线的距离为则所以所以四边形的面积;故答案为:【点睛】本题主要考查直线与解析：⎡⎤⎣⎦【解析】【分析】由题可知8AC =,而过(1,0)F 的弦BD 过圆心时最长,与EF 垂直时最短,据此则可以确定四边形ABCD 的面积的取值范围. 【详解】由题知,直线1l 过圆心(1,0)E -,故8AC =,设圆心(1,0)E -到直线2l 的距离为d ,则02d EF ≤≤=,所以BD ⎡⎤=⎣⎦,所以四边形ABCD的面积12S AB CD ⎡⎤=⋅⋅∈⎣⎦; 故答案为:⎡⎤⎣⎦.【点睛】本题主要考查直线与圆相交时的弦长､面积问题,解题关键是明确:过圆内一点的作弦,弦过圆心时最长,与最长的弦垂直时弦最短.15．【解析】设球半径为则故答案为点睛:空间几何体体积问题的常见类型及解题策略：①若给定的几何体是可直接用公式求解的柱体锥体或台体则可直接利用公式进行求解；②若所给定的几何体的体积不能直接利用公式得出则常解析：32【解析】设球半径为r ，则213223423V r r V r π⨯==π．故答案为32．点睛:空间几何体体积问题的常见类型及解题策略：①若给定的几何体是可直接用公式求解的柱体、锥体或台体，则可直接利用公式进行求解；②若所给定的几何体的体积不能直接利用公式得出，则常用转换法、分割法、补形法等方法进行求解．16．②③【解析】【分析】①由折叠的原理可知BD⊥平面ADC 可推知BD⊥AC 数量积为零②由折叠后AB ＝AC ＝BC 三角形为等边三角形得∠BAC＝60°；③由DA ＝DB ＝DC 根据正三棱锥的定义判断④平面ADC解析：②③ 【解析】【分析】①由折叠的原理，可知BD ⊥平面ADC ，可推知BD ⊥AC ，数量积为零，②由折叠后AB ＝AC ＝BC ，三角形为等边三角形，得∠BAC ＝60°；③由DA ＝DB ＝DC ，根据正三棱锥的定义判断．④平面ADC 和平面ABC 不垂直．【详解】BD ⊥平面ADC ，⇒BD ⊥AC ，①错； AB ＝AC ＝BC ，②对；DA ＝DB ＝DC ，结合②，③对④错．故答案为②③ 【点睛】本题主要考查折叠前后线线，线面，面面关系的不变和改变，解题时要前后对应，仔细论证，属中档题．17．【解析】中因为所以由余弦定理可得所以设则在中由余弦定理可得故在中由余弦定理可得所以过作直线的垂线垂足为设则即解得而的面积设与平面所成角为则点到平面的距离故四面体的体积设因为所以则（1）当时有故此时因解析：12【解析】 ABC ∆中，因为2,120AB BC ABC ==∠=o ，所以30BAD BCA ∠==o .由余弦定理可得2222cos AC AB BC AB BC B =+-⋅2222222cos12012=+-⨯⨯=o ，所以23AC =.设AD x =，则023t <<，23DC x =-.在ABD ∆中，由余弦定理可得2222cos BD AD AB AD AB A =+-⋅22222cos30x x =+-⋅o 2234x x =-+.故2234BD x x =-+.在PBD ∆中，PD AD x ==，2PB BA ==.由余弦定理可得2222222(234)3cos 2PD PB BD x x x BPD PD PB +-+--+∠===⋅，所以30BPD ∠=o .过P 作直线BD 的垂线，垂足为O .设PO d = 则11sin 22PBD S BD d PD PB BPD ∆=⨯=⋅∠， 2112342sin 3022x x d x -+=⋅o ，解得d =.而BCD ∆的面积111sin )2sin 30)222S CD BC BCD x x =⋅∠=⋅=o . 设PO 与平面ABC 所成角为θ，则点P 到平面ABC 的距离sin h d θ=. 故四面体PBCD的体积11111sin )33332BcD BcD BcD V S h S d S d x θ∆∆∆=⨯=≤⋅=⨯=设t ==0x ≤≤12t ≤≤.则x -=（1）当0x ≤≤时，有x x ==故x =此时，V =21414()66t t t t-=⋅=-. 214()(1)6V t t=--'，因为12t ≤≤，所以()0V t '<，函数()V t 在[1,2]上单调递减，故141()(1)(1)612V t V ≤=-=. （2x <≤x x =-=故x =此时，16V t +=21414()66t t t t-=⋅=-. 由（1）可知，函数()V t 在(1,2]单调递减，故141()(1)(1)612V t V <=-=. 综上，四面体PBCD 的体积的最大值为12. 18．【解析】【分析】将侧面和侧面平展在一个平面上连即可求出满足最小时点的位置以及长解即可求出结论【详解】将侧面和侧面平展在一个平面上连与交点即为满足最小正四棱锥各棱长均为在平展的平面中四边形为菱形且在正解析：13-【解析】【分析】将侧面PAB 和侧面PBC 平展在一个平面上，连AC ，即可求出满足AM MC +最小时，点M 的位置，以及,AM CM 长，解AMC V ，即可求出结论. 【详解】将侧面PAB 和侧面PBC 平展在一个平面上，连AC 与PB 交点即为满足AM MC +最小，正四棱锥P ABCD -各棱长均为1，在平展的平面中四边形PABC 为菱形，且60PAB ∠=o ，AM MC ==P ABCD -中，AC =在ACM V 中，222332144cos 32324AM CM AC AMC AM CM +-+-∠===-⋅⋅. 故答案为:13-.【点睛】本题考查线线角，要注意多面体表面的长度关系转化为共面的长度关系，考查直观想象能力，属于中档题.19．【解析】【分析】首先求出即有将三棱锥展开当三点共线时值最小可证为中点从而可求从而得解【详解】在中所以同理所以在三棱锥中将侧面绕旋转至平面使之与平面共面如图所示当共线时取得最小值又因为所以垂直平分即为解析：2【解析】【分析】首先求出PB PC ==，即有PB PC BC ==，将三棱锥展开，当三点共线时，值最小，可证E 为PB 中点，从而可求OC OE EC ''=+，从而得解．【详解】在POB V 中，1PO OB ==，90POB ∠=︒，所以PB ==，同理PC =PB PC BC ==，在三棱锥P ABC -中，将侧面BCP 绕PB 旋转至平面BC P '，使之与平面ABP 共面，如图所示，当O ，E ，C '共线时，CE OE +取得最小值，又因为OP OB =，C P C B '='，所以OC '垂直平分PB ，即E 为PB 中点，从而2626OC OE EC +''=+== 亦即CE OE +的最小值为：262，故答案为262. 【点睛】本题主要考查了空间中线段和最小值问题，考查了空间想象能力、推理论证能力，考查了数形结合思想、化归与转化思想，属于中档题．20．【解析】设球的半径为表面积解得∵在中∴从圆心作平面的垂线垂足在斜边的中点处∴球心到平面的距离故答案为点睛：本题考查的知识点是空间点线面之间的距离计算其中根据球心距球半径解三角形我们可以求出所在平面截 3【解析】设球的半径为r ，表面积24π20πS r ==，解得5r =ABC V 中，2AB AC ==，22BC =222AB AC BC +=，∴90BAC ∠=︒，从圆心作平面ABC 的垂线，垂足在斜边BC 的中点处，∴球心到平面ABC 的距离22132d r BC ⎛⎫=-= ⎪⎝⎭3点睛：本题考查的知识点是空间点、线、面之间的距离计算，其中根据球心距d ，球半径R ，解三角形我们可以求出ABC V 所在平面截球所得圆（即ABC V 的外接圆半径），构造直角三角形，满足勾股定理，我们即可求出球心到平面ABC 的距离是与球相关的距离问题常用方法. 三、解答题21．（1）1x =或0y =；（2）()()22134x y -++=. 【解析】【分析】（1）对直线l 的斜率是否存在进行分类讨论，利用圆心到直线l 的距离等于2可求得直线l 的方程；（2）先通过点到直线的距离及勾股定理可解得直线m 的斜率，然后将直线m 的方程与圆的方程联立，求出线段AB 的中点，作为圆心，并求出所求圆的半径，进而可得出所求圆的方程. 【详解】（1）由题意知，圆C 的标准方程为()()22329x y -++=，∴圆心()3,2C -，半径3r =，①当直线l 的斜率k 存在时，设直线的方程为()01y k x -=-，即kx y k 0--=，则圆心到直线l的距离为2d ==，0k ∴=.∴直线l 的方程为0y =；②当直线l 的斜率不存在时，直线l 的方程为1x =，此时圆心C 到直线l 的距离为2，符合题意. 综上所述，直线l 的方程为1x =或0y =；（2）依题意可设直线m 的方程为1y kx =-，即()100kx y k --=<，则圆心()3,2C -到直线m的距离d ===22320k k ∴+-=，解得12k =或2k =-，又0k <Q ，2k ∴=-，∴直线m 的方程为210x y ---=即210x y ++=，设点()11,A x y 、()22,B x y ，联立直线m 与圆C 的方程得()()22210329x y x y ++=⎧⎪⎨-++=⎪⎩，消去y 得251010x x -+=，122x x ∴+=，则线段AB 的中点的横坐标为1212x x +=，把1x =代入直线m 中得3y =-，所以，线段AB 的中点的坐标为()1,3-，由题意知，所求圆的半径为：122AB =， ∴以线段AB 为直径的圆的方程为：()()22134x y -++=.【点睛】本题考查利用圆心到直线的距离求直线方程，同时也考查了圆的方程的求解，涉及利用直线截圆所得弦长求参数，考查计算能力，属于中等题. 22．23.【解析】【分析】（Ⅰ）由题意结合线面垂直的判定可得AD ⊥平面11BCC B ，则1AC D ∠即为直线1AC 与平面11BCC B所成的角，求得2AD =，1AC =后即可得解；（Ⅱ）作1AE A B ⊥，垂足为E ，连接1A C ，CE，由题意可得BE =，由余弦定理可得295CE =，进而可得90BEC ∠=o ，则AEC ∠即为二面角1A A B C --的平面角，再由余弦定理即可得解. 【详解】（Ⅰ）Q 三棱柱111ABC A B C -是直三棱柱，∴1BB ⊥平面ABC ，∴1BB AD ⊥， Q AB AC =，D 是BC 的中点，∴AD BC ⊥，又1BB BC B =I ，∴AD ⊥平面11BCC B ，∴1AC D ∠即为直线1AC 与平面11BCC B 所成的角， Q 1AB AC ==，12AA =，∴2AD =，1AC =∴11sin AD AC D AC ∠===， ∴直线1AC 与平面11BCC B（Ⅱ）作1AE A B ⊥，垂足为E ，连接1A C ，CE ，Q 1AB AC ==，112AA A C ==，∴11A B AC ==，BC = 由1ABE A BA V V ∽可得BE =，AE = 在1A BC V中，2221111cos 210A B BC AC A BC A B BC +-∠===⋅，∴在EBC V 中，22292cos 5CE BE BC BE BC EBC =+-⋅⋅∠=即5CE =， ∴222CE BE BC +=即90BEC ∠=o ， ∴AEC ∠即为二面角1A A B C --的平面角，在AEC V 中，222491255cos 232535255AE CE AC AEC AE CE +-+-∠===⋅⨯⨯. ∴二面角1A A B C --的余弦值为23.【点睛】本题考查了线面角和面面角的求解，考查了空间思维能力和计算能力，属于中档题. 23．（1）证明见解析；（2）34. 【解析】【分析】(1)直角梯形ABCD 中,过D 作DF ⊥AB 于F ,求解三角形可得ABD △为正三角形，又PAD △为正三角形，M 为线段AD 的中点，可得PM ⊥AD ，BM ⊥AD ，再由线面垂直的判定可得AD ⊥平面PBM ，从而得到平面PMB ⊥平面ABCD ；(2)在平面PMB 中，过B 作BO ⊥PM ,垂足为O ,则BO ⊥平面P AD ,连接AO ,则∠BAO 为直线BA 与平面P AD 所成角，然后求解三角形得答案. 【详解】（1）证明：过D 作DF ⊥AB 于F在Rt ADE ∆中，2,1AD AE ==,3BAD π∴∠=∴BAD V 和PAD △是正三角形， ∵M 是AD 的中点， ∴AD MB ⊥，AD MP ⊥，又∵MB MP M ⋂=， ∴AD ⊥平面PMB ，又∵AD ⊂平面ABCD ∴平面PMB ⊥平面ABCD.（2）由（1）知PMB ∠是二面角P -AD -B 的平面角 ∴23PMB π∠=. 由（1）知AD ⊥平面PMB ∵AD ⊂平面P AD ∴平面PAD ⊥平面PBM∴过B 作平面P AD 的垂线，则垂足E 在PM 延长线上,∴3BME π∠=. 连结AE ，则BAE ∠是AB 与平面P AD 所成的角,∴3BM =，∴32BE =，∴3sin 4BAE BE AB ∠== 【点睛】本题主要考查平面与平面垂直的判定，线面角的求法，二面角，考查空间想象能力与思维能力，属于中档题. 24．（1）证明见解析；（2）2211. 【解析】【分析】（1）取BE 中点N ，连,MN CN ，得1//,2MN AB MN AB =，可证四边形CPMN 为平行四边形，进而有//MP CN ，即可证明结论；（2）设2AB AE ==，由已知可得AE ⊥平面ABCD ，过F 做//FQ AE ，交AB 于Q ，得FQ ⊥平面ABCD ，过Q 做QO BD ⊥垂足为O ，连FO ，可证BD ⊥平面FOQ ，得到FOQ ∠为二面角F BD A --的平面角，解Rt OFQ ∆即可.【详解】（1）取BE 中点N ，连,MN CN ，又M 为AE 的中点，1//,2MN AB MN AB ∴=，在正方形ABCD 中，P 是CD 中点， //,CP MN CP MN ∴=，∴四边形CPMN 为平行四边形，//MP CN ∴，MP ⊄平面BCE ，CN ⊂平面BCE ，//PM ∴平面BCE ；（2）设2AB AE ==，ABE ∆是等腰直角三角形，AB AE =，AE AB ∴⊥，平面ABCD ⊥平面ABEF ，平面ABCD I 平面ABEF AB =，AE ⊂平面ABEF ，AE ∴⊥平面ABCD ，过F 做//FQ AE ，交AB 于Q ，FQ ∴⊥平面ABCD ， FA FE =Q ，45AEF ∠=︒，,45,45EF AF EAF AF FAQ ∴⊥∠=︒∴=∠=︒，在Rt AFQ ∆中，1,3FQ AQ BQ ===，过Q 做QO BD ⊥垂足为O ，连FO ，FQ ⊥Q 平面,ABCD FQ BD ∴⊥，FQ OQ Q =I ，BD ∴⊥平面,FOQ BD OF ⊥，FOQ ∠为二面角F BD A --的平面角，在Rt BOQ ∆中，3,45,2BQ OBQ OQ =∠=︒∴=，在Rt FOQ ∆中，2OF ==，sin 11FQ FOQ OF ∴∠==，∴二面角F BD A --.【点睛】本题考查空间线、面位置关系，证明直线与平面平行以及求二面角，利用垂直关系做出二面角的平面角是解题的难点，要注意空间垂直间的相互转化，属于中档题.25．（1）见解析（2）23 【解析】【分析】（1）连接BF ，证明四边形1BMD F 是平行四边形即可得出1//D M BF ，故1//MD 平面BEFD ；（2）根据M BDE E BDM V V --=求出M 到平面BEFD 的距离．【详解】解：（1）证明：连接BF ， ∵111111111111////22D F A B D F A B BM A B BM A B ==，，，， ∴11//D F BM D F BM =，，∴四边形1BMD F 是平行四边形，∴1//D M BF ，又1D M ⊄平面BEFD ，BF ⊂平面BEFD ，∴1//MD 平面BEFD ．（2）解：连接ED EM DM ，，，则112122323E BDM V -=⨯⨯⨯⨯=，又22221111122253BD BE BB B E DE D C C E ===+==+=，，， ∴22210cos 2BD BE DE DBE BD BE +-∠==⋅，∴310sin DBE ∠=∴1310 2253210BDES=⨯⨯⨯=V，设M到平面BEFD的距离为d，则12333M BDEV d-=⨯⨯=，∴23d=．即M到平面BEFD的距离为23．【点睛】本题考查了线面平行的判定，棱锥的体积计算，属于中档题．26．(1)证明见解析；(2)1013+(3) 330x y--=，10x y-+=，50x y+-=，390x y+-=，320x y-=【解析】【分析】(1)将原式变形为()250a x x y-++-=，由2050xx y-=⎧⎨+-=⎩可得直线l必过一定点()2,3P；(2)由题可得52By a=+，521Aaxa+=+，则()1252521AOBaS aa++⋅=⋅+V，求出最值，并找到最值的条件，进而可得AOB∆的周长；(3) 52a+，521aa++均为整数，变形得523211aa a+=+++，只要31a+是整数即可，另外不要漏掉截距为零的情况，求出a，进而可得直线l的方程.【详解】解：(1)由()1520a x y a++--=得()250a x x y-++-=，则2050xx y-=⎧⎨+-=⎩，解得23xy=⎧⎨=⎩，所以不论a为何值，直线l必过一定点()2,3P；(2)由()1520a x y a++--=得，当0x=时，52By a=+，当0y=时，521Aaxa+=+，又由520521BAy aaxa=+>⎧⎪+⎨=>⎪+⎩，得1a>-，()()119141+121212221252521AOB a a a S a a ⎡⎤⎡⎤∴=⋅++++⋅=≥=⎢⎥⎢⎥+⎣⎦⎣⎦+V ，当且仅当()9411a a +=+，即12a =时，取等号. ()4,0A ∴，()0,6B ，AOB ∴∆的周长为4610OA OB AB ++=+=+(3) 直线l 在两坐标轴上的截距均为整数，即52a +，521a a ++均为整数， 523211a a a +=+++Q ，4,2,0,2a ∴=--，又当52a =-时，直线l 在两坐标轴上的截距均为零，也符合题意，所以直线l 的方程为330x y --=，10x y -+=，50x y +-=，390x y +-=，320x y -=.【点睛】本题考查直线恒过定点问题，考查直线与坐标轴围成的三角形的面积的最值，是中档题.。

【典型题】高中必修二数学下期中第一次模拟试卷(带答案)

【典型题】高中必修二数学下期中第一次模拟试卷(带答案)一、选择题1．一正四面体木块如图所示，点P 是棱VA 的中点，过点P 将木块锯开，使截面平行于棱VB 和AC ，则下列关于截面的说法正确的是（）．A ．满足条件的截面不存在B ．截面是一个梯形C ．截面是一个菱形D ．截面是一个三角形2．已知两点()A 3,4-，()B 3,2，过点()P 1,0的直线l 与线段AB 有公共点，则直线l 的斜率k 的取值范围是( ) A ．()1,1- B ．()(),11,∞∞--⋃+ C ．[]1,1-D ．][(),11,∞∞--⋃+3．设圆C ：223x y +=，直线l ：360x y +-=，点()00,P x y l ∈，若存在点Q C ∈，使得60OPQ ∠=︒（O 为坐标原点），则0x 的取值范围是( ) A ．1,12⎡⎤-⎢⎥⎣⎦B ．60,5⎡⎤⎢⎥⎣⎦C ．[]0,1D ．16,25⎡⎤-⎢⎥⎣⎦ 4．直线(2)4y k x =-+与曲线2320x y y +-=有两个不同的交点，则实数k 的取值范围是（） A ．53(,]124B ．51(,]122C ．13(,]24D ．1[,)2+∞5．已知点(),P x y 是直线()400kx y k ++=>上一动点，,PA PB 是圆22:20C x y y +-=的两条切线，切点分别为,A B ，若四边形PACB 的面积最小值为2，则k 的值为（） A ．3B ．212C ．22D ．26．从点(,3)P m 向圆22(2)(2)1x y +++=引切线，则切线长的最小值( ) A ．26B ．5C 26D ．427．椭圆22221(0)x y a b a b+=>>的左右焦点分别是1F 、2F ，以2F 为圆心的圆过椭圆的中心，且与椭圆交于点P ，若直线1PF 恰好与圆2F 相切于点P ，则椭圆的离心率为（）A ．312+ B ．31-C ．22D ．512- 8．设直线,a b 是空间中两条不同的直线，平面,αβ是空间中两个不同的平面，则下列说法正确的是（）A ．若a ∥α，b ∥α，则a ∥bB ．若a ∥b ，b ∥α，则a ∥αC ．若a ∥α，α∥β，则a ∥βD ．若α∥β，a α⊂，则a ∥β9．正方体ABCD ﹣A 1B 1C 1D 1中，E ，F 分别是AD ，DD 1的中点，AB ＝4，则过B ，E ，F 的平面截该正方体所得的截面周长为（） A ．62+45B ．62+25C ．32+45D ．32+2510．已知点()1,2-和3,03⎛⎫⎪ ⎪⎝⎭在直线():100l ax y a --=≠的两侧，则直线l 的倾斜角的取值范围是 ( ) A ．,43ππ⎛⎫⎪⎝⎭ B ．2,33ππ⎛⎫⎪⎝⎭C ．25,36ππ⎛⎫⎪⎝⎭D ．30,,34πππ⎛⎫⎛⎫⋃ ⎪ ⎪⎝⎭⎝⎭11．一锥体的三视图如图所示,则该棱锥的最长棱的棱长为 ( )A ．B ．C ．D ．12．若圆的参数方程为12cos ,32sin x y θθ=-+⎧⎨=+⎩（θ为参数），直线的参数方程为21,61x t y t =-⎧⎨=-⎩（t 为参数），则直线与圆的位置关系是（） A ．相交且过圆心B ．相交但不过圆心C ．相切D ．相离二、填空题13．已知棱长为1的正方体ABCD －A 1B 1C 1D 1中，E ，F ，M 分别是线段AB 、AD 、AA 1的中点，又P 、Q 分别在线段A 1B 1、A 1D 1上，且A 1P ＝A 1Q ＝x (0<x <1).设平面MEF ∩平面MPQ＝l ，现有下列结论：①l ∥平面ABCD ； ②l ⊥AC ；③直线l 与平面BCC 1B 1不垂直； ④当x 变化时，l 不是定直线.其中不成立的结论是________.(写出所有不成立结论的序号)14．已知正三棱锥P -ABC ，点P ，A ，B ，C 都在半径为3的求面上，若PA ，PB ，PC 两两互相垂直，则球心到截面ABC 的距离为________．15．将正方形ABCD 沿对角线BD 折成直二面角A BD C --，①AB 与平面BCD 所成角的大小为60 ②ACD ∆是等边三角形 ③AB 与CD 所成的角为60 ④AC BD ⊥⑤二面角B AC D --为120︒ 则上面结论正确的为_______．16．已知正方体1111ABCD A B C D -的棱长为1，点E 是棱1BB 的中点，则点1B 到平面ADE 的距离为__________.17．如图，AB 是底面圆O 的直径,点C 是圆O 上异于A 、B 的点，PO 垂直于圆O 所在的平面，且1,2PO OB BC ===，点E 在线段PB 上，则CE OE +的最小值为________.18．函数2291041y x x x =++-+的最小值为_________.19．三棱锥A BCD -中，E 是AC 的中点，F 在AD 上，且2AF FD =，若三棱锥A BEF -的体积是2，则四棱锥B ECDF -的体积为_______________．20．已知圆225x y +=和点()1,2A ，则过点A 的圆的切线方程为______三、解答题21．如图1，有一边长为2的正方形ABCD ，E 是边AD 的中点，将ABE △沿着直线BE 折起至A BE '位置（如图2），此时恰好A E A C ''⊥，点A '在底面上的射影为O .（1）求证：A E BC '⊥；（2）求直线A B '与平面BCDE 所成角的正弦值.22．如图，在三棱锥S ABC -中，SAC ∆为等边三角形，4AC =，43BC=BC AC ⊥，3cos SCB ∠=D 为AB 的中点．（1）求证：AC SD ⊥；（2）求直线SD 与平面SAC 所成角的大小． 23．已知平面内两点(8,6),(2,2)A B -. （1）求AB 的中垂线方程；（2）求过点(2,3)P -且与直线AB 平行的直线l 的方程．24．如图，三棱柱111ABC A B C -中，平面11AAC C ⊥平面11AA B B ,平面11AACC ⊥平面ABC ，12AB AC AA ===,点P 、M 分别为棱BC 、1CC 的中点，过点B 、M 的平面交棱1AA 于点N ,使得AP ∥平面BMN .（1）求证：AB ⊥平面11AAC C ; （2）若四棱锥B ACMN -的体积为32，求1A AC ∠的正弦值. 25．如图，矩形ABCD 的两条对角线相交于点M(2，0)，AB 边所在直线的方程为x －3y －6＝0，点T(－1，1)在AD 边所在直线上．求：(1) AD 边所在直线的方程； (2) DC 边所在直线的方程．26．若圆M 的方程为22(2)(5)10x y -+-=，△ABC 中，已知(1,1)A ，(4,2)B ，点C 为圆M 上的动点．（1）求AC 中点D 的轨迹方程；（2）求△ABC 面积的最小值．【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【解析】【分析】取AB 的中点D ，BC 的中点E ，VC 的中点F ，连接,,,PD PF DE EF ，易得即截面为四边形PDEF ，且四边形PDEF 为菱形即可得到答案. 【详解】取AB 的中点D ，BC 的中点E ，VC 的中点F ，连接,,,PD PF DE EF ，易得PD ∥VB 且12PD VB =，EF ∥VB 且12EF VB =，所以PD ∥EF ，PD EF =，所以四边形PDEF 为平行四边形，又VB ⊄平面PDEF ，PD ⊂平面PDEF ,由线面平行的判定定理可知，VB ∥平面PDEF ，AC ∥平面PDEF ，即截面为四边形PDEF ，又1122DE AC VB PD ===，所以四边形PDEF 为菱形，所以选项C 正确. 故选：C【点睛】本题考查线面平行的判定定理的应用，考查学生的逻辑推理能力，是一道中档题.2．D解析：D 【解析】分析：根据两点间的斜率公式，利用数形结合即可求出直线斜率的取值范围．详解：∵点A （﹣3，4），B （3，2），过点P （1，0）的直线L 与线段AB 有公共点， ∴直线l 的斜率k≥k PB 或k≤k PA ，∵PA 的斜率为4031--- =﹣1，PB 的斜率为2031--=1， ∴直线l 的斜率k≥1或k ≤﹣1，故选：D ．点睛：本题主要考查直线的斜率的求法，利用数形结合是解决本题的关键，比较基础．直线的倾斜角和斜率的变化是紧密相联的，tana=k,一般在分析角的变化引起斜率变化的过程时，是要画出正切的函数图像，再分析.3．B解析：B 【解析】【分析】圆O 外有一点P ，圆上有一动点Q ，OPQ ∠在PQ 与圆相切时取得最大值．如果OP 变长，那么OPQ ∠可以获得的最大值将变小．因为sin QOOPQ PO∠=，QO 为定值，即半径，PO 变大，则sin OPQ ∠变小，由于(0,)2OPQ π∠∈，所以OPQ ∠也随之变小．可以得知，当60OPQ ∠=︒，且PQ 与圆相切时，2PO =，而当2PO >时，Q 在圆上任意移动，60OPQ ∠<︒恒成立．因此，P 的取值范围就是2PO ，即满足2PO ，就能保证一定存在点Q ，使得60OPQ ∠=︒，否则，这样的点Q 是不存在的．【详解】由分析可得：22200PO x y =+又因为P 在直线l 上，所以00(36)x y =--要使得圆C 上存在点Q ，使得60OPQ ∠=︒，则2PO故2222000103634PO x y y y ==+-+解得825y ，0605x 即0x 的取值范围是6[0,]5，故选：B ．【点睛】解题的关键是充分利用几何知识，判断出2PO ，从而得到不等式求出参数的取值范围．4．B解析：B 【解析】【分析】利用数形结合，作出图象，计算得直线1l 与直线2l 的斜率，即可得到结论. 【详解】曲线可化简为()22(1)40x y x +-=≤，如图所示：直线()1:24l y k x =-+23221k k -=+，解得512k =，直线()2:24l y k x =-+，此直线与曲线有两个交点，此时有12k =. 所以，过点()2,4的直线与该半圆有两个交点，数形结合，解得51122k <≤. 故选：B. 【点睛】本题考查了直线与圆相交的性质，涉及的知识有：恒过定点的直线方程，点到直线的距离公式，以及直线斜率的求法，利用了数形结合的思想，其中抓住两个关键点是解本题的关键．5．D解析：D 【解析】【分析】当且仅当PC 垂直于()400kx y k ++=>时，四边形PACB 的面积最小，求出PC 后可得最小面积，从而可求k 的值. 【详解】圆C 方程为()2211x y +-=，圆心()0,1C ，半径为1．因为PA ，PB 为切线，221PC PA ∴=+且1=2122PACB S PA PA ⨯⨯⨯==四边形．∴当PA 最小时，PACB S 四边形最小，此时PC 最小且PC 垂直于()400kx y k ++=>．又min PC =，2222+1⎛⎫∴=，2k ∴=，故选D. 【点睛】圆中的最值问题，往往可以转化圆心到几何对象的距离的最值来处理，这类问题属于中档题.6．A解析：A 【解析】【分析】设切线长为d ,则2222(2)51(2)24d m m =++-=++再利用二次函数的图像和性质求函数的最小值得解. 【详解】设切线长为d ,则2222(2)51(2)24d m m =++-=++, min d ∴= 故选:A. 【点睛】本题主要考查圆的切线问题,考查直线和圆的位置关系,意在考查学生对这些知识的掌握水平和分析推理能力.7．B解析：B 【解析】【分析】根据椭圆的定义可知12||||2PF PF a +=，又1PF 恰好与圆2F 相切于点P ，可知2||PF c =且12PF PF ⊥，即可列出方程求椭圆的离心率. 【详解】由1PF 恰好与圆2F 相切于点P ，可知2||PF c =，且 12PF PF ⊥，又12||||2PF PF a +=，可知1||2PF a c =-，在12Rt PF F ∆中，222(2)4a c c c -+=，即2222a ac c -= 所以2220,(0,1)e e e +-=∈，解得212e -==，故选：B 【点睛】本题主要考查了椭圆的定义，椭圆的简单几何性质，圆的切线的性质，属于中档题.8．D解析：D 【解析】【分析】利用空间直线和平面的位置关系对每一个选项逐一分析判断得解. 【详解】A. 若a ∥α，b ∥α，则a 与b 平行或异面或相交，所以该选项不正确；B. 若a ∥b ，b ∥α，则a ∥α或a α⊂，所以该选项不正确；C. 若a ∥α，α∥β，则a ∥β或a β⊂，所以该选项不正确；D. 若α∥β，a α⊂，则a ∥β，所以该选项正确. 故选：D 【点睛】本题主要考查空间直线平面位置关系的判断，意在考查学生对这些知识的理解掌握水平.9．A解析：A 【解析】【分析】利用线面平行的判定与性质证明直线1BC 为过直线EF 且过点B 的平面与平面11BCC B 的交线,从而证得1,,,B E F C 四点共面,然后在正方体中求等腰梯形1BEFC 的周长即可. 【详解】作图如下:因为,E F 是棱1,AD DD 的中点, 所以11////EF AD BC ,因为EF ⊄平面11BCC B ,1BC ⊂平面11BCC B , 所以//EF 平面11BCC B ，由线面平行的性质定理知,过直线EF 且过点B 的平面与平面11BCC B 的交线l 平行于直线EF , 结合图形知,l 即为直线1BC ,过B ，E ，F 的平面截该正方体所得的截面即为等腰梯形1BEFC , 因为正方体的棱长AB ＝4,所以1122,25,42EF BE C F BC ==== 所以所求截面的周长为2+5 故选:A 【点睛】本题主要考查多面体的截面问题和线面平行的判定定理和性质定理；重点考查学生的空间想象能力;属于中档题.10．D解析：D 【解析】设直线l 的倾斜角为θ∈[0,π).点A (1,−2),B 3 直线l :ax −y −1=0(a ≠0)经过定点P (0,−1).()121, 3.01303PA PB k k ---==-==--∵点(1,−2)和(33,0)在直线l :ax −y −1=0(a ≠0)的两侧， ∴k P A <a <k PB ,∴−1<tanθ3tanθ≠0.解得30,34ππθθπ<<<<.本题选择D 选项.11．C解析：C 【解析】试题分析：该几何体为一个侧面与底面垂直，底面为正方形的四棱锥（如图所示），其中底面边长为，侧面平面，点在底面的射影为，所以,所以,,,,底面边长为，所以最长的棱长为，故选C.考点：简单几何体的三视图．12．B解析：B 【解析】【分析】根据题意，将圆和直线的参数方程变形为普通方程，分析可得圆心不在直线上，再利用点到直线的距离公式计算可得圆心(1,3)-到直线320y x --=的距离2d <，得到直线与圆的位置关系为相交．【详解】根据题意，圆的参数方程为1232x cos y sin θθ=-+⎧⎨=+⎩（θ为参数），则圆的普通方程为22(1)(3)4x y ++-=，其圆心坐标为(1,3)-，半径为2.直线的方程为2161x t y t =-⎧⎨=-⎩（t 为参数），则直线的普通方程为13(1)y x +=+，即320y x --=，圆心不在直线上.∴圆心(1,3)-到直线320y x --=的距离为33(1)22102519d -⨯--==<+，即直线与圆相交. 故选A. 【点睛】本题考查直线、圆的参数方程，涉及直线与圆的位置关系，解答本题的关键是将直线与圆的参数方程变形为普通方程.二、填空题13．④【解析】【详解】连接BDB1D1∵A1P ＝A1Q ＝x ∴PQ ∥B1D1∥BD ∥EF 则P Q ∥平面MEF 又平面MEF∩平面MPQ ＝l ∴PQ ∥ll ∥EF ∴l ∥平面ABCD 故①成立；又EF ⊥AC ∴l ⊥AC 故解析：④ 【解析】【详解】连接BD ，B 1D 1，∵A 1P ＝A 1Q ＝x ，∴PQ ∥B 1D 1∥BD ∥EF ，则PQ ∥平面MEF ，又平面MEF ∩平面MPQ ＝l ，∴PQ ∥l ，l ∥EF ， ∴l ∥平面ABCD ，故①成立；又EF ⊥AC ，∴l ⊥AC ，故②成立；∵l ∥EF ∥BD ，故直线l 与平面BCC 1B 1不垂直，故③成立；当x 变化时，l 是过点M 且与直线EF 平行的定直线，故④不成立．即不成立的结论是④.14．【解析】正三棱锥P-ABC 可看作由正方体PADC-BEFG 截得如图所示PF 为三棱锥P-ABC 的外接球的直径且设正方体棱长为a 则由得所以因为球心到平面ABC 的距离为考点定位：本题考查三棱锥的体积与球的 3【解析】正三棱锥P-ABC 可看作由正方体PADC-BEFG 截得，如图所示，PF 为三棱锥P-ABC 的外接球的直径，且PF ABC ⊥平面,设正方体棱长为a ，则2312,2,2a a AB AC BC =====132232ABC S ∆=⨯=由P ABC B PAC V V --=，得111••222332ABC h S ∆=⨯⨯⨯⨯，所以23h =ABC的距离为3 3.考点定位：本题考查三棱锥的体积与球的几何性质，意在考查考生作图的能力和空间想象能力15．②③④【解析】【分析】作出此直二面角的图象由图形中所给的位置关系对命题逐一判断即可得出正确结论【详解】作出如图的图象E是BD的中点易得∠AED＝90°即为此直二面角的平面角对于命题①AB与平面BCD解析：②③④【解析】【分析】作出此直二面角的图象，由图形中所给的位置关系对命题逐一判断，即可得出正确结论．【详解】作出如图的图象，E是BD的中点，易得∠AED＝90°即为此直二面角的平面角对于命题①AB与平面BCD所成的线面角的平面角是∠ABE＝45°，故AB与平面BCD成60°的角不正确；对于命题②，在等腰直角三角形AEC中AC等于正方形的边长，故△ACD是等边三角形，此命题正确；对于命题③可取AD中点F，AC的中点H，连接EF，EH，FH，则EF，FH是中位线，故∠EFH或其补角为异面直线AB与CD所成角，又EF,FH其长度为正方形边长的一半，而EH是直角三角形AEC的中线，其长度是AC的一半即正方形边长的一半，故△EFH是等边三角形，由此AB与CD所成的角为60°，此命题正确；对于命题④，BD⊥面AEC，故AC⊥BD，此命题正确；对于命题⑤，连接BH，HD,则BH⊥AC, DH⊥AC,则∠BHD为二面角B AC D--的平面角，又32,cos∠BHD=-1,3故二面角B AC D--不是120︒综上知②③④是正确的故答案为②③④ 【点睛】本题考查与二面角有关立体几何中线线之间的角的求法，线面之间的角的求法，以及线线之间位置关系的证明方法．综合性较强，对空间立体感要求较高．16．【解析】【分析】点到平面的距离等价于点到平面的距离过作交于证得平面利用等面积法求得点到平面的距离也即点到平面的距离【详解】由于是的中点故点到平面的距离等价于点到平面的距离过作交于由于故平面在直角三角 5 【解析】【分析】点1B 到平面ADE 的距离等价于点B 到平面ADE 的距离，过B 作BF AE ⊥，交AE 于F ，证得BF ⊥平面ADE ，利用等面积法求得点B 到平面ADE 的距离，也即点1B 到平面ADE 的距离. 【详解】由于E 是1BB 的中点，故点1B 到平面ADE 的距离等价于点B 到平面ADE 的距离，过B 作BF AE ⊥，交AE 于F ，由于BF AD ⊥，AD AE E ⋂=，故BF ⊥平面ADE .在直角三角形ABE 中，151,,22AB BE AE ===，所以1122AB BE AE BF ⋅⋅=⋅⋅,解得55BF =.【点睛】本小题主要考查点到面的距离，考查等面积法求高，考查线面垂直的证明，属于基础题.17．【解析】【分析】首先求出即有将三棱锥展开当三点共线时值最小可证为中点从而可求从而得解【详解】在中所以同理所以在三棱锥中将侧面绕旋转至平面使之与平面共面如图所示当共线时取得最小值又因为所以垂直平分即为解析：26+ 【解析】【分析】首先求出2PB PC ==，即有PB PC BC ==，将三棱锥展开，当三点共线时，值最小，可证E 为PB 中点，从而可求OC OE EC ''=+，从而得解．【详解】在POB 中，1PO OB ==，90POB ∠=︒，所以22112PB =+=，同理2PC =，所以PB PC BC ==，在三棱锥P ABC -中，将侧面BCP 绕PB 旋转至平面BC P '，使之与平面ABP 共面，如图所示，当O ，E ，C '共线时，CE OE +取得最小值，又因为OP OB =，C P C B '='，所以OC '垂直平分PB ，即E 为PB 中点，从而2OC OE EC ''=+==亦即CE OE +的最小值为：2，故答案为2. 【点睛】本题主要考查了空间中线段和最小值问题，考查了空间想象能力、推理论证能力，考查了数形结合思想、化归与转化思想，属于中档题．18．【解析】【分析】将变形为设则即轴上的一动点到的距离之和作点关于轴的对称点即可求出距离和的最小值；【详解】解：设则即轴上的一动点到的距离之和作点关于轴的对称点连接则即为距离和的最小值故答案为：【点睛】【解析】【分析】将y y =()0,3A ，()5,4B ，(),0C x ，则y AC BC =+即x 轴上的一动点C 到()0,3A ，()5,4B 的距离之和，作()0,3A 点关于x 轴的对称点()10,3A -，即可求出距离和的最小值；【详解】解：y ==()0,3A ，()5,4B ，(),0C x ，则y AC BC +，即x 轴上的一动点(),0C x 到()0,3A ，()5,4B 的距离之和，作()0,3A 点关于x 轴的对称点()10,3A -，连接1BA ，则1BA 即为距离和的最小值，1BA ==min y ∴=【点睛】本题考查平面直角坐标系上两点间的距离公式的应用，将军饮马问题，属于中档题.19．【解析】【分析】以B 为顶点三棱锥与四棱锥等高计算体积只需找到三角形AEF 与四边形ECDF 的面积关系即可求解【详解】设B 到平面ACD 的距离为h 三角形ACD 面积为因为是的中点在上且所以所以又=2所以所以解析：【解析】【分析】以B 为顶点，三棱锥B AEF -与四棱锥B ECDF -等高，计算体积只需找到三角形AEF 与四边形ECDF 的面积关系即可求解. 【详解】设B 到平面ACD 的距离为h ，三角形ACD 面积为S ，因为E 是AC 的中点，F 在AD 上，且2AF FD =，所以16AEF ACD S AE AF S AC AD ∆∆⋅==⋅,16AEF S S ∆=，所以56ECDF S S =，又A BEF V -=2，所以⨯=11236Sh ，36Sh =，所以153610318B ECDF ECDF V S h -==⋅=. 故答案为10. 【点睛】本题考查空间几何体的体积计算，考查空间想象能力和运算能力，属于基础题.20．【解析】【分析】先由题得到点A 在圆上再设出切线方程为利用直线和圆相切得到k 的值即得过点A 的圆的切线方程【详解】因为所以点在圆上设切线方程为即kx-y-k+2=0因为直线和圆相切所以所以切线方程为所以解析：25x y +=【解析】【分析】先由题得到点A 在圆上，再设出切线方程为2(1),y k x -=-利用直线和圆相切得到k 的值，即得过点A 的圆的切线方程. 【详解】因为22125+=，所以点()1,2A 在圆上，设切线方程为2(1),y k x -=-即kx-y-k+2=0,12k =∴=-，所以切线方程为112022x y --++=，所以切线方程为25x y +=，故答案为：25x y += 【点睛】（1）本题主要考查圆的切线方程的求法，意在考查学生对该知识的掌握水平和分析推理能力.(2) 点00(,)P x y 到直线:0l Ax By C ++=的距离d =.三、解答题21．（1）证明见解析（2【解析】【分析】（1）利用直线与平面垂直的判定定理证明A E '⊥面A BC '，再根据直线与平面垂直的性质可得A E BC '⊥；（2）依题意得就是直线A B '与面BCDE 所成角，延长EO 交BC 于H ，连接A H '，在直角三角形A EH '中得60A EH '=︒，在直角三角形A EO '中得2A O '=，在直角三角形A OB '中得sin A BO '∠=. 【详解】（1）证明：∵A E A B ''⊥，A E A C ''⊥ 又∵A B A C A '''⋂= ∴A E '⊥面A BC ' ∴A E BC '⊥.（2）∵点A '在底面上的射影为O .∴AO '⊥面BCDE∴A BO '∠就是直线A B '与面BCDE 所成角. 延长EO 交BC 于H ，连接A H ' 如图：∵A E BC '⊥，AO BC '⊥且A O A E A '''⋂= ∴BC ⊥面A EO ' ∴BC EO ⊥ ∵E 为AD 中点 ∴H 为BC 中点 ∵1A E '=，2EH = 由（1）知A E A H ''⊥ ∴60A EH '=︒ ∴3A O '=∴332sin 2A O BO A A B '∠==''=所以直线A B '与平面BCDE 3【点睛】本题考查了直线与平面垂直的判定和性质，考查了直线与平面所成角的计算，属于中档题. 22．（1）证明见解析；（2）6π. 【解析】【分析】（1）取AC 的中点O ，连接OS 、OD ，证明出OS AC ⊥，OD AC ⊥，利用直线与平面垂直的判定定理可得出AC ⊥平面SOD ，即可证明出AC SD ⊥；（2）延长SO ，过点D 作SO 延长线的垂线，垂足记为H ，说明直线SD 与平面SAC 所成的角为OSD ∠，求出OSD ∆三边边长，利用余弦定理求出OSD ∠，即可求出直线SD 与平面SAC 所成角的大小．【详解】（1）取AC 的中点O ，连接OS 、OD ，SAC ∆为等边三角形，O 为AC 的中点，SO AC ∴⊥， D 、O 分别为AB 、AC 的中点，//OD BC ∴，BC AC ⊥，OD AC ∴⊥， SO OD O =，AC ∴⊥平面SOD ，SD ⊂平面SOD ，AC SD ∴⊥；（2）延长SO ，过点D 作SO 延长线的垂线，垂足记为H ，AC ⊥平面SOD ，DH ⊂平面SOD ，DH AC ∴⊥，DH SO ⊥，SO AC O =，DH ∴⊥平面SAC ，所以，直线SD 与平面SAC 所成的角为OSD ∠，由（2）知，1232OD BC ==AC BC ⊥，228AB AC BC ∴+=. SAC ∆是边长为4的等边三角形，4sin233SO π∴== 在SBC ∆中，4SC =，43BC =由余弦定理得2222cos 88SB SC BC SC BC SCB =+-⋅⋅∠=，222SB ∴= 由余弦定理得2221cos 28SA AB SB SAB SA AB +-∠==-⋅， 2222cos 36SD SA AD SA AD SAD ∴=+-⋅⋅∠=，6SD ∴=.在SOD ∆中，由余弦定理得2223cos 2SO SD OD OSD SO SD +-∠==⋅. 0OSD π<∠<，6OSD π∴∠=，因此，直线SD 与平面SAC 所成角的大小为6π. 【点睛】本题考查利用线面垂直的性质证明线线垂直，同时也考查了直线与平面所成角的计算，涉及到利用余弦定理解三角形，考查推理能力与计算能力，属于中等题.23．（1）34230x y --=; （2）4310x y ++=.【解析】试题分析：(1)首先求得中点坐标，然后求得斜率，最后利用点斜式公式即可求得直线方程；(2)利用点斜式可得直线方程为4310x y ++=.试题解析：（1）8252+=，6222-+=- ∴AB 的中点坐标为()5,2-624823AB k --==--，∴AB 的中垂线斜率为34 ∴由点斜式可得()3254y x +=- ∴AB的中垂线方程为34230x y --= （2）由点斜式()4323y x +=-- ∴直线l 的方程4310x y ++= 24．（1）见解析；（2）3. 【解析】（1）在平面ABC 中，过点B 作棱AC 的垂线，垂足为D ，平面11AAC C ⊥平面ABC ，∴ BD ⊥平面11AAC C .在平面11AA B B 中，过点B 作棱1AA 的垂线，垂足为E ，平面11AAC C ⊥平面11AA B B ，∴BE ⊥平面11AAC C .过点B 与平面11AAC C 垂直的直线有且只有一条，∴BE 与BD 重合，又∵平面ABC 平面11AA B B AB =,∴BE 与BD 重合于AB ，所以AB ⊥平面11AAC C .（2）设BM 的中点为Q ，连接PQ ，NQ ，点P 为棱BC 的中点，∴PQ ∥CM 且PQ =12CM ， 1AA ∥1CC ，∴PQ ∥AN ，∴P 、Q 、N 、A 四点共面，∵AP ∥平面BMN ，∴AP ∥NQ ，∴四边形PQNA 是平行四边形，∴PQ =AN ，∵M 为1CC 的中点且12AB AC AA ===，∴1CM =，∴PQ =AN =12，设梯形ACMN 的高为h ，2AB =， ∴111132×2322B ACMN h V h -⎛⎫+ ⎪⎝⎭=⨯==，∴3h = ∴13sin h A AC AC ∠==,∴1A AC ∠3 25．（1）320x y ++=；（2）320x y -+=【解析】分析：（1）先由AD 与AB 垂直，求得AD 的斜率，再由点斜式求得其直线方程；（2）根据矩形特点可以设DC 的直线方程为()306x y m m -+=≠-，然后由点到直线的距离得出2210510m+=，就可以求出m 的值，即可求出结果. 详解：(1)由题意：ABCD 为矩形，则AB⊥AD，又AB 边所在的直线方程为：x －3y －6＝0，所以AD 所在直线的斜率k AD ＝－3，而点T(－1，1)在直线AD 上．所以AD 边所在直线的方程为：3x ＋y ＋2＝0.(2)方法一：由ABCD 为矩形可得，AB∥DC，所以设直线CD 的方程为x －3y ＋m ＝0.由矩形性质可知点M 到AB 、CD 的距离相等所以＝,解得m ＝2或m ＝－6(舍)．所以DC 边所在的直线方程为x －3y ＋2＝0.方法二：方程x －3y －6＝0与方程3x ＋y ＋2＝0联立得A （0，-2），关于M 的对称点C （4，2）因AB ∥DC ，所以DC 边所在的直线方程为x －3y ＋2＝0.点睛：本题主要考查直线方程的求法，在求直线方程时，应先选择适当的直线方程的形式，并注意各种形式的适用条件．用斜截式及点斜式时，直线的斜率必须存在，而两点式不能表示与坐标轴垂直的直线，截距式不能表示与坐标轴垂直或经过原点的直线．故在解题时，若采用截距式，应注意分类讨论，判断截距是否为零；若采用点斜式，应先考虑斜率不存在的情况．26．（1）2235()(3)22x y -+-=（2）12【解析】【分析】（1）利用相关点法求出点D 的轨迹方程；（2）首先求出直线AB 的方程，求出圆心到直线的距离，圆心到直线的距离减去半径即圆上的点到直线的距离的最小值，即可求出ABC ∆面积的最小值。

【好题】高中必修二数学下期中一模试题含答案(1)

【好题】高中必修二数学下期中一模试题含答案(1)一、选择题1．已知m ，n 表示两条不同直线，α表示平面，下列说法正确的是（）A ．若//,//,m n αα则//m nB ．若m α⊥，n α⊂，则m n ⊥C ．若m α⊥，m n ⊥，则//n αD ．若//m α，m n ⊥，则n α⊥2．已知,,,A B C D 是同一球面上的四个点，其中ABC ∆是正三角形，AD ⊥平面ABC ，26AD AB ==，则该球的体积为（）A ．48πB ．24πC ．16πD ．323π 3．对于平面、β、γ和直线a 、b 、m 、n ,下列命题中真命题是( )A ．若,,,,a m a n m n αα⊥⊥⊂⊂,则a α⊥B ．若//,a b b α⊂,则//a αC ．若//,,,a b αβαγβγ==I I 则//a bD ．若,,//,//a b a b ββαα⊂⊂,则//βα4．已知平面//α平面β，直线m αÜ，直线n βÜ，点A m ∈,点B n ∈，记点A 、B 之间的距离为a ,点A 到直线n 的距离为b ,直线m 和n 的距离为c ,则A ．b a c ≤≤B ．a c b ≤≤C ． c a b ≤≤D ．c b a ≤≤5．已知正四面体ABCD 中，M 为棱AD 的中点，设P 是BCM ∆（含边界）内的点，若点P 到平面ABC ，平面ACD ，平面ABD 的距离相等，则符合条件的点P （） A ．仅有一个 B ．有有限多个 C ．有无限多个 D ．不存在6．如图，已知正方体1111ABCD A B C D -中，异面直线1AD 与1A C 所成的角的大小是( )A ．30oB ．60oC ．90oD ．120o7．设直线,a b 是空间中两条不同的直线，平面,αβ是空间中两个不同的平面，则下列说法正确的是（）A ．若a ∥α，b ∥α，则a ∥bB ．若a ∥b ，b ∥α，则a ∥αC ．若a ∥α，α∥β，则a ∥βD ．若α∥β，a α⊂，则a ∥β8．已知点()1,2-和3,0⎛⎫ ⎪ ⎪⎝⎭在直线():100l ax y a --=≠的两侧，则直线l 的倾斜角的取值范围是 ( )A ．,43ππ⎛⎫ ⎪⎝⎭B ．2,33ππ⎛⎫ ⎪⎝⎭C ．25,36ππ⎛⎫ ⎪⎝⎭D ．30,,34πππ⎛⎫⎛⎫⋃ ⎪ ⎪⎝⎭⎝⎭9．一个几何体的三视图如图所示，则该几何体的表面积为（）A ．B ．C ．D ．10．一锥体的三视图如图所示,则该棱锥的最长棱的棱长为 ( )A ．B ．C ．D ．11．如图1，ABC ∆是以B 为直角顶点的等腰直角三角形，T 为线段AC 的中点，G 是BC 的中点，ABE ∆与BCF ∆分别是以AB 、BC 为底边的等边三角形，现将ABE ∆与BCF ∆分别沿AB 与BC 向上折起（如图2），则在翻折的过程中下列结论可能正确的个数为（）图1 图2（1）直线AE ⊥直线BC ；（2）直线FC ⊥直线AE ；（3）平面//EAB 平面FGT ；（4）直线//BC 直线AE .A ．1个B ．2个C ．3个D ．4个12．已知平面αβ⊥且l αβ=I ，M 是平面α内一点，m ，n 是异于l 且不重合的两条直线，则下列说法中错误的是（）.A ．若//m α且//m β，则//m lB ．若m α⊥且n β⊥，则m n ⊥C ．若M m ∈且//m l ，则//m βD ．若M m ∈且m l ⊥，则m β⊥二、填空题13．已知圆22(1)16x y ++=，点(1,0),(1,0)E F -，过(1,0)E -的直线1l 与过(1,0)F 的直线2l 垂直且圆相交于,A C 和,B D ，则四边形ABCD 的面积的取值范围是_________.14．已知菱形ABCD 中，2AB =，120A ∠=o ，沿对角线BD 将ABD △折起，使二面角A BD C --为120o ，则点A 到BCD V 所在平面的距离等于．15．若直线y x b =+与曲线234y x x =+-有公共点，则b 的取值范围是______．16．在平面直角坐标xOy 系中,设将椭圆()2222110y x a a a +=>-绕它的左焦点旋转一周所覆盖的区域为D ，P 为区域D 内的任一点，射线()02x y x =≥－上的点为Q ，若PQ 的最小值为a ，则实数a 的取值为_____．17．直线10ax y ++=与连接A （4，5），B （-1，2）的线段相交，则a 的取值范围是___．18．如图，在ABC V 中，AB BC ⊥，SA ⊥平面ABC ，DE 垂直平分SC ，且分别交AC ，SC 于点D ，E ，又SA AB =，SB BC =，则二面角E BD C --的大小为_______________.19．已知直线:0l x my m ++=，且与以A (-1,1)、B (2,2)为端点的线段相交，实数m 的取值范围为___________.20．已知B 与点()1,2,3A 关于点()0,1,2M -对称，则点B 的坐标是______．三、解答题21．已知圆C 过点()1,1A ，()3,1B -，圆心C 在直线250x y --=上，P 是直线34100x y -+=上任意一点．（1）求圆C 的方程；（2）过点P 向圆C 引两条切线，切点分别为M ，N ，求四边形PMCN 的面积的最小值．22．如图，在直三棱柱111ABC A B C -中，D 是BC 的中点．AB AC ⊥，1AB AC ==，12AA =．（Ⅰ）求直线1AC 与平面11BCC B 所成角的正弦值；（Ⅱ）求二面角1A A B C --的余弦值．23．如图所示，四棱锥B AEDC -中，平面AEDC ⊥平面ABC ，F 为BC 的中点，P 为BD 的中点，且AE ∥DC ，90ACD BAC ∠=∠=︒，2DC AC AB AE ===．（Ⅰ）证明：平面BDE ⊥平面BCD ；（Ⅱ）若2DC =，求三棱锥E BDF -的体积．24．在三棱柱111ABC A B C -中，侧面11AA C C ⊥底面ABC ，112AA AC AC AB BC =====，且点O 为AC 中点.(1)证明：1A O ⊥平面ABC ；(2)求三棱锥1C ABC -的体积.25．已知圆22:20M x y x a +-+=（1）若8a =-，过点(4,5)P 作圆M 的切线，求该切线的方程；（2）当圆22:(1)(23)4N x y ++-=与圆M 相外切时，从点(2,8)Q -射出一道光线，经过y 轴反射，照到圆M 上的一点R ，求光线从点Q 经反射后走到点R 所走过路线的最小值.26．如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，底面ABCD 是菱形．（1）求证：BD PC ⊥；（2）若平面PBC 与平面PAD 的交线为l ，求证：//BC l ．【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【解析】试题分析：线面垂直，则有该直线和平面内所有的直线都垂直，故B 正确.考点：空间点线面位置关系．2．D解析：D【解析】【分析】根据球的性质可知球心O 与ABC ∆外接圆圆心O '连线垂直于平面ABC ；在Rt POE ∆和Rt OO A ∆'中利用勾股定理构造出关于半径R 和OO '的方程组，解方程组求得R ，代入球的体积公式可得结果.【详解】设O '为ABC ∆的外心，如下图所示：由球的性质可知，球心O 与O '连线垂直于平面ABC ，作OE AD ⊥于E设球的半径为R ，OO x '=ABC ∆为等边三角形，且3AB = 3AO '∴=OO '⊥Q 平面ABC ，AD ⊥平面ABC ，OE AD ⊥ OO AE x '∴==，3OE AO '==在Rt POE ∆和Rt OO A ∆'中，由勾股定理得：22222OE PE O O O A R ''+=+=，即()222363x x R +-=+= 解得：3x =，23R =∴球的体积为：343233V R ππ==本题正确选项：D【点睛】本题考查棱锥外接球的体积求解问题，关键是能够确定棱锥外接球球心的位置，从而在直角三角形中利用勾股定理构造方程求得半径. 3．C解析：C【解析】【分析】【详解】若由线面垂直的判定定理知,只有当和为相交线时,才有错误；若此时由线面平行的判定定理可知,只有当在平面外时,才有错误；由面面平行的性质定理:若两平面平行,第三个平面与他们都相交,则交线平行,可判断,若//αβ，a αγ⋂=，b βγ=I ，则//a b 为真命题, 正确；若此时由面面平行的判定定理可知,只有当、为相交线时,才有//,D βα错误.故选C.考点：考查直线与直线，直线与平面，平面与平面的位置关系. 4．D解析：D【解析】【分析】根据平面与平面平行的判断性质,判断c 最小,再根据点到直线距离和点到直线上任意点距离判断a 最大.【详解】由于平面//α平面β,直线m 和n 又分别是两平面的直线,则c 即是平面之间的最短距离. 而由于两直线不一定在同一平面内,则b 一定大于或等于c ,判断a 和b 时,因为B 是上n 任意一点,则a 大于或等于b .故选D.【点睛】本题主要考查面面平行的性质以及空间距离的性质，考查了空间想象能力，意在考查灵活应用所学知识解答问题的能力，属于中档题.5．A解析：A【解析】【分析】根据正四面体的对称性分析到平面ABC ，平面ACD ，平面ABD 的距离相等的点的轨迹，与BCM ∆所在平面的公共部分即符合条件的点P .【详解】在正四面体ABCD 中，取正三角形BCD 中心O ，连接AO ，根据正四面体的对称性，线段AO 上任一点到平面ABC ，平面ACD ，平面ABD 的距离相等，到平面ABC ，平面ACD ，平面ABD 的距离相等的点都在AO 所在直线上，AO 与BCM ∆所在平面相交且交于BCM ∆内部，所以符合题意的点P 只有唯一一个.故选：A【点睛】此题考查正四面体的几何特征，对称性，根据几何特征解决点到平面距离问题，考查空间想象能力.6．C解析：C【解析】【分析】在正方体1111ABCD A B C D -中，利用线面垂直的判定定理，证得1AD ⊥平面1A DC ，由此能求出结果．【详解】如图所示，在正方体1111ABCD A B C D -中，连结1A D ，则1AD DC ⊥，11A D AD ⊥，由线面垂直的判定定理得1AD ⊥平面1A DC ，所以11AD AC ⊥, 所以异面直线1AD 与1A C 所成的角的大小是90o ．故选C ．【点睛】本题主要考查了直线与平面垂直的判定与证明，以及异面直线所成角的求解，其中解答中牢记异面直线所成的求解方法和转化思想的应用是解答的关键，平时注意空间思维能力的培养，着重考查了推理与论证能力，属于基础题．7．D解析：D【解析】【分析】利用空间直线和平面的位置关系对每一个选项逐一分析判断得解.【详解】A. 若a ∥α，b ∥α，则a 与b 平行或异面或相交，所以该选项不正确；B. 若a ∥b ，b ∥α，则a ∥α或a α⊂，所以该选项不正确；C. 若a ∥α，α∥β，则a ∥β或a β⊂，所以该选项不正确；D. 若α∥β，a α⊂，则a ∥β，所以该选项正确.故选：D【点睛】本题主要考查空间直线平面位置关系的判断，意在考查学生对这些知识的理解掌握水平.8．D解析：D【解析】设直线l 的倾斜角为θ∈[0,π).点A (1,−2),B 3 直线l :ax −y −1=0(a ≠0)经过定点P (0,−1). ()121, 3.0130PA PB k k ---==-==-- ∵点(1,−2)和(33,0)在直线l :ax −y −1=0(a ≠0)的两侧， ∴k P A <a <k PB ,∴−1<tanθ3tanθ≠0. 解得30,34ππθθπ<<<<.本题选择D 选项. 9．D解析：D【解析】该几何体为半圆柱，底面为半径为1的半圆，高为2，因此表面积为,选D.10．C解析：C【解析】试题分析：该几何体为一个侧面与底面垂直，底面为正方形的四棱锥（如图所示），其中底面边长为，侧面平面，点在底面的射影为，所以,所以,,,,底面边长为，所以最长的棱长为，故选C.考点：简单几何体的三视图．11．C解析：C【解析】【分析】（1）翻折时使得平面ABE ⊥平面ABC ，由面面垂直的性质定理得出BC ⊥平面ABE ，从而使得（1）有可能；（2）翻折时使得点E 、F 两点重合，利用勾股定理可证得此时AE CE ⊥，即AE FC ⊥；（3）翻折时使得平面ABE 和平面BCF 同时与平面ABC 垂直，利用面面垂直的性质定理、直线与平面平行的判定定理以及面面平行的判定定理可证明出平面//EAB 平面FGT ；（4）利用反证法，可推出//BC AE 不成立.【详解】（1）翻折时，若平面ABE ⊥平面ABC ，由于ABC ∆是以B 为直角顶点的等腰直角三角形，则BC AB ⊥，又Q 平面ABE I 平面ABC AB =，BC ⊂平面ABC ，BC ∴⊥平面ABE ，AE ⊂Q 平面ABC ，此时AE BC ⊥；（2）设AB BC a ==，则2AC a =，且有AE CF a ==，翻折时，若点E 、F 重合，则AE CE a ==，222AE CE AC ∴+=，此时，AE CE ⊥，即AE FC ⊥；（3）如下图所示：翻折时，若平面ABE 和平面BCF 同时与平面ABC 垂直，取AB 的中点D ，连接DE 、FG 、GT 、FT .ABE ∆Q 是等边三角形，且D 为AB 的中点，DE AB ⊥∴.Q 平面ABE ⊥平面ABC ，平面ABE I 平面ABC AB =，DE ⊂平面ABE .DE ∴⊥平面ABC ，同理可证FG ⊥平面ABC ，//DE FG ∴，DE ⊄Q 平面FGT ，FG ⊂平面FGT ，//DE ∴平面FGT .G Q 、T 分别为BC 、AC 的中点，//AB GT ∴，AB ⊄Q 平面FGT ，GT ⊂平面FGT ，//AB ∴平面FGT .DE AB D =Q I ，∴平面//EAB 平面FGT ；（4）假设AE 与BC 可能平行，BC AB ⊥Q ，则AE AB ⊥，事实上60BAE ∠=o ，即AE 与AB 不垂直，假设不成立，因此，AE 与BC 不可能平行.因此，可能正确命题的个数为3.故选：C.【点睛】本题考查的是线面位置关系的判定，判断时要熟悉线面、面面平行与垂直的判定、性质定理，考查推理能力，属于中等题.12．D解析：D【解析】【分析】根据已知条件和线面位置关系一一进行判断即可.【详解】选项A ：一条直线平行于两个相交平面，必平行于两个面交线，故A 正确；选项B ：垂直于两垂直面的两条直线相互垂直，故B 正确；选项C ：M m ∈且//m l 得m α⊂且//m β，故C 正确；选项D ：M m ∈且m l ⊥不一定得到m α⊂，所以,m l 可以异面，不一定得到m β⊥. 故选：D . 【点睛】本题主要考查的是空间点、线、面的位置关系的判定，掌握线面、线线之间的判定定理和性质定理是解决本题的关键，是基础题.二、填空题13．【解析】【分析】由题可知而过的弦过圆心时最长与垂直时最短据此则可以确定四边形的面积的取值范围【详解】由题知直线过圆心故设圆心到直线的距离为则所以所以四边形的面积;故答案为:【点睛】本题主要考查直线与解析：⎡⎤⎣⎦【解析】【分析】由题可知8AC =,而过(1,0)F 的弦BD 过圆心时最长,与EF 垂直时最短,据此则可以确定四边形ABCD 的面积的取值范围. 【详解】由题知,直线1l 过圆心(1,0)E -,故8AC =,设圆心(1,0)E -到直线2l 的距离为d ,则02d EF ≤≤=,所以BD ⎡⎤=⎣⎦,所以四边形ABCD 的面积12S AB CD ⎡⎤=⋅⋅∈⎣⎦;故答案为:⎡⎤⎣⎦.【点睛】本题主要考查直线与圆相交时的弦长､面积问题,解题关键是明确:过圆内一点的作弦,弦过圆心时最长,与最长的弦垂直时弦最短.14．【解析】【分析】【详解】设AC 与BD 交于点O 在三角形ABD 中因为∠A ＝120°AB ＝2可得AO ＝1过A 作面BCD 的垂线垂足E 则AE 即为所求由题得∠AOE ＝180°−∠AOC ＝180°−120°＝60解析：2【解析】【分析】【详解】设AC 与BD 交于点O ．在三角形ABD 中，因为∠A ＝120°，AB ＝2．可得AO ＝1．过A 作面BCD 的垂线，垂足E ，则AE 即为所求．由题得，∠AOE ＝180°−∠AOC ＝180°−120°＝60°．在RT △AOE 中，AE ＝AO•sin ∠AOE ＝32．15．【解析】【分析】由曲线y=3+得（x ﹣2）2+（y ﹣3）2=40≤x≤4直线y=x+b 与曲线y=3+有公共点圆心（23）到直线y=x+b 的距离d 不大于半径r=2由此结合图象能求出实数b 的取值范围【详解析：122,3⎡⎤-⎣⎦【解析】【分析】由曲线y=3+24x x -，得（x ﹣2）2+（y ﹣3）2=4，0≤x≤4，直线y=x+b 与曲线y=3+24x x -有公共点，圆心（2，3）到直线y=x+b 的距离d 不大于半径r=2，由此结合图象能求出实数b 的取值范围．【详解】由曲线y=3+24x x -，得（x ﹣2）2+（y ﹣3）2=4，0≤x≤4，∵直线y=x+b 与曲线y=3+24x x -有公共点，∴圆心（2，3）到直线y=x+b 的距离d 不大于半径r=2，即23212b 1+222bd -+=≤⇒-≤≤∵0≤x≤4，∴x=4代入曲线y=3，把（4，3）代入直线y=x+b ，得b min =3﹣4=﹣1，②联立①②，得-1b 1≤≤+∴实数b 的取值范围是[﹣1，]．故答案为1,1⎡-+⎣.【点睛】本题考查实数的取值范围的求法，是中档题，解题时要认真审题，注意数形结合思想的合理运用．一般直线和圆的题很多情况下是利用数形结合来解决的，联立的时候较少；在求圆上的点到直线或者定点的距离时，一般是转化为圆心到直线或者圆心到定点的距离，再加减半径，分别得到最大值和最小值；涉及到圆的弦长或者切线长时，经常用到垂径定理．16．【解析】【分析】先确定轨迹再根据射线上点与圆的位置关系求最值即得结果【详解】所以为以为圆心为半径的圆及其内部设射线的端点为所以的最小值为故答案为：【点睛】本题考查动点轨迹以及点与圆位置关系考查数形结解析：12-+ 【解析】【分析】先确定D 轨迹，再根据射线上点与圆的位置关系求最值，即得结果. 【详解】2222222(1)1,111,y x c a a c a a =+∴=--=∴=-Q ，所以D 为以(1,0)F -为圆心，1a +为半径的圆及其内部，设射线()02x y x =≥－的端点为(2,2)A ，所以PQ 的最小值为||(1),12,AF a a a a -+===.【点睛】本题考查动点轨迹以及点与圆位置关系，考查数形结合思想以及基本分析求解能力，属中档题.17．或【解析】【分析】判断直线恒过定点P （0-1）计算PAPB 的斜率再利用数形结合求a 的取值范围【详解】解：由直线ax+y+1=0的方程判断直线恒过定点P （0-1）如图所示计算且或则或即实数a 的取值范围解析：32a ≤-或3a ≥ 【解析】【分析】判断直线0ax by c ++=恒过定点P （0，-1），计算PA 、PB 的斜率，再利用数形结合求a 的取值范围．【详解】解：由直线ax+y+1=0的方程，判断直线恒过定点P （0，-1），如图所示，计算513402PA k +==-，21310PB k +==--- 且PA k k ≥或PB k k ≤，则PA a k ≤-或PB a k ≥-，即实数a 的取值范围是：32a ≤-或3a ≥．故答案为：32a ≤-或3a ≥．【点睛】本题考查直线的斜率与直线方程的应用问题，是基础题．18．60°【解析】【分析】首先证得是二面角的平面角解直角三角形求得的大小【详解】由于是的中点所以由于所以平面所以由于平面所以而所以平面所以所以是二面角的平面角设则所以所以在中所以所以故答案为：【点睛】本解析：60° 【解析】【分析】首先证得EDC ∠是二面角E BD C --的平面角，解直角三角形求得EDC ∠的大小. 【详解】由于SB BC =，E 是SC 的中点，所以SC BE ⊥，由于,SC DE DE BE E ⊥⋂=，所以SC ⊥平面BDE ，所以SC BD ⊥.由于SA ⊥平面ABC ，所以SA BD ⊥，而SA SC S ⋂=，所以BD ⊥平面SAC ，所以,BD DC BD DE ⊥⊥，所以EDC ∠是二面角E BD C --的平面角.设1SA AB ==，则2SB BC ==2SC =，所以在Rt SAC ∆中，12SA SC =，所以30SCA ∠=o ，所以60EDC ∠=o . 故答案为：60o 【点睛】本小题主要考查二面角的求法，考查空间想象能力和逻辑推理能力，属于中档题.19．【解析】【分析】由直线系方程求出直线所过定点再由两点求斜率求得定点与线段两端点连线的斜率数形结合求得实数的取值范围【详解】解：由直线可知直线过定点又如图∵∴由图可知直线与线段相交直线的斜率或斜率不存解析：21,32⎡⎤-⎢⎥⎣⎦【解析】【分析】由直线系方程求出直线所过定点，再由两点求斜率求得定点与线段两端点连线的斜率，数形结合求得实数m 的取值范围．【详解】解：由直线:0l x my m ++=可知直线过定点()0,1P -，又()1,1A -，()2,2B ，如图∵()11201PA K --==---，123022PB K --==-，∴由图可知，直线与线段相交，直线l 的斜率(]3,2,2k ⎡⎫∈-∞-+∞⎪⎢⎣⎭U ，或斜率不存在， ∴(]13,2,2m ⎡⎫-∈-∞-+∞⎪⎢⎣⎭U ，或0m =，即203m -≤<或102m <≤，或0m =， ∴21,32m ⎡⎤∈-⎢⎥⎣⎦ 故答案为：21,32⎡⎤-⎢⎥⎣⎦．【点睛】本题主要考查直线系方程的应用，考查了直线的斜率计算公式，考查了数形结合的解题思想方法，属于中档题．20．【解析】【分析】根据空间直角坐标系中点坐标公式求结果【详解】设B 则所以所以的坐标为【点睛】本题考查空间直角坐标系中点坐标公式考查基本分析求解能力属基础题解析：()1,4,1--【解析】【分析】根据空间直角坐标系中点坐标公式求结果. 【详解】设B (),,x y z ,则1230,1,2222x y z+++=-==，所以1,4,1x y z =-=-=，所以B 的坐标为()1,4,1--．【点睛】本题考查空间直角坐标系中点坐标公式，考查基本分析求解能力，属基础题.三、解答题21．（1）()()22314x y -+-=（2）【解析】【分析】（1）首先列出圆的标准方程()()()2220x a y b r r -+-=>，根据条件代入，得到关于,,a b r 的方程求解；（2）根据切线的对称性，可知，12222S PM PM =⨯⨯⨯=，这样求面积的最小值即是求PM 的最小值，当点P 是圆心到直线的距离的垂足时，PM 最小. 【详解】解：（1）设圆C 的方程为()()()2220x a y b r r -+-=>．由题意得()()()()222222250,11,31,a b a b r a b r ⎧--=⎪⎪-+--=⎨⎪-+--=⎪⎩解得3,1,2.a b r =⎧⎪=⎨⎪=⎩故圆C 的方程为()()22314x y -+-=．另解：先求线段AB 的中垂线与直线250x y --=的交点，即2,25,y x y x =-⎧⎨=-⎩解得3,1,x y =⎧⎨=⎩从而得到圆心坐标为()3,1，再求24r =，故圆C 的方程为()()22314x y -+-=．（2）设四边形PMCN 的面积为S ，则2PMC S S =V ．因为PM 是圆C 的切线，所以PM CM ⊥，所以12PMC S PM CM PM =⋅=V ，即22PMC S S PM ==V ．因为PM CM ⊥，所以PM ==因为P 是直线34100x y -+=上的任意一点，所以3PC ≥=，则PM =，即2PMC S S =≥V故四边形PMCN 的面积的最小值为【点睛】本题考查了圆的标准方程，和与圆，切线有关的最值的计算，与圆有关的最值计算，需注意数形结合.22．（Ⅰ）10；（Ⅱ）23.【解析】【分析】（Ⅰ）由题意结合线面垂直的判定可得AD ⊥平面11BCC B ，则1AC D ∠即为直线1AC 与平面11BCC B 所成的角，求得2AD =，1AC =后即可得解；（Ⅱ）作1AE A B ⊥，垂足为E ，连接1A C，CE ，由题意可得BE =，由余弦定理可得295CE =，进而可得90BEC ∠=o ，则AEC ∠即为二面角1A A B C --的平面角，再由余弦定理即可得解. 【详解】（Ⅰ）Q 三棱柱111ABC A B C -是直三棱柱，∴1BB ⊥平面ABC ，∴1BB AD ⊥， Q AB AC =，D 是BC 的中点，∴AD BC ⊥，又1BB BC B =I ，∴AD ⊥平面11BCC B ，∴1AC D ∠即为直线1AC 与平面11BCC B 所成的角， Q 1AB AC ==，12AA=，∴2AD =，1AC =∴11sin AD AC D AC ∠===，∴直线1AC 与平面11BCC B 所成角的正弦值为1010.（Ⅱ）作1AE A B ⊥，垂足为E ，连接1A C ，CE ，Q 1AB AC ==，112AA A C ==，∴115A B AC ==，2BC =，由1ABE A BA V V ∽可得55BE =，255AE = 在1A BC V 中，222111110cos 2210A B BC AC A BC A B BC +-∠===⋅，∴在EBC V 中，22292cos 5CE BE BC BE BC EBC =+-⋅⋅∠=即355CE =， ∴222CE BE BC +=即90BEC ∠=o ， ∴AEC ∠即为二面角1A A B C --的平面角，在AEC V 中，222491255cos 2325352AE CE AC AEC AE CE +-+-∠===⋅⨯⨯. ∴二面角1A A B C --的余弦值为23.【点睛】本题考查了线面角和面面角的求解，考查了空间思维能力和计算能力，属于中档题. 23．（Ⅰ）证明见解析；（Ⅱ）23. 【解析】【分析】（Ⅰ）连接PF ，由题意可得//PE AF ，由面面垂直的性质和等腰三角形的性质可得DC ⊥平面ABC ，AF BC ⊥，进而可得AF ⊥平面BCD 即PE ⊥平面BCD ，由面面垂直的判定即可得证；（Ⅱ）由（1）知PE ⊥平面BDF ，计算出2PE BF ==，进而可得2BDF S =V ，由三棱锥体积公式即可得解. 【详解】（Ⅰ）证明：连接PF ，Q F 为BC 的中点，P 为BD 的中点，∴//PF CD 且12PF CD =， Q //AE CD 且2DC AE =，∴//PF AE 且PF AE =， ∴四边形AEPF 为平行四边形，∴//PE AF ，Q 平面AEDC ⊥平面ABC ，平面AEDC I 平面ABC AC =，90ACD ∠=︒，∴DC ⊥平面ABC ，∴DC AF ⊥，又AC AB =，∴AF BC ⊥，Q BC DC C =I ，∴AF ⊥平面BCD ，∴PE ⊥平面BCD ，又PE ⊂平面BDE ，∴平面BDE ⊥平面BCD .（Ⅱ）由（Ⅰ）得PE ⊥平面BCD 即PE ⊥平面BDF ，Q 22DC AC AB AE ====，90ACD BAC ∠=∠=︒∴221122222PE AF BF BC ====+= ∴122BDF S BF DC =⋅=V ， ∴11332223BDF E BDF S PE V -⋅===V . 【点睛】本题考查了面面垂直的判定和三棱锥体积的求解，考查了空间思维能力，属于中档题. 24．（1）证明见解析；（2）1. 【解析】试题分析：（1）利用等腰三角形的性质可得1A O AC ⊥，利用面面垂直的性质可得1A O ⊥平面ABC ，根据线面垂直的性质可得结论；（2）先证明11||A C 平面ABC ，可得1C 到平面ABC 的距离等于1A 到平面ABC 的距离，利用等积变换及棱锥的体积公式可得11113C ABC A ABC ABC V V S AO --∆==⋅=112132⨯⨯=. 试题解析：（1）∵11AA A C =，且O 为AC 的中点. ∴1A O AC ⊥.又∵平面11AA C C ⊥平面ABC ，平面11AA C C ⋂平面ABC AC =，且1AO ⊂平面11AAC C ，∴1A O ⊥平面ABC . ∵BC ⊂平面ABC ， ∴1A O BC ⊥.（2）∵11||A C AC ，11A C ⊄平面ABC ，AC ⊂平面ABC ， ∴11||A C 平面ABC .即1C 到平面ABC 的距离等于1A 到平面ABC 的距离. 由（1）知1A O ⊥平面ABC且1AO ==∴三棱锥1C ABC -的体积：11113C ABC A ABC ABC V V S AO --∆==⋅=112132⨯⨯=. 25．（1）815430x y -+=或4x =;（22. 【解析】【分析】（1）把8a =-代入圆的方程中，可得圆心坐标和半径，当直线斜率不存在时，可得:4l x =，此时和圆相切符合题意；当直线斜率存在时，由点斜式设出直线方程，由圆心3=，进而可求出815k =，则切线方程可求. （2）由两圆外切可知圆心距为半径之和，即可求出a 的值，从而可得22:(1)4M x y -+=，求出点Q 关于y 轴对称的点为(2,8)Q -'-，求出Q M '的值，即可求出所求路线的最小值. 【详解】解：（1）当8a =-时，圆22:280M x y x +--=，即22(1)9x y -+=，当切线斜率不存在时，直线:4l x =，点()1,0M 到直线l 距离为3，等于半径r ，符合题意.当切线斜率存在时，设直线:5(4)l y k x -=-，即450kx y k --+=，由题意点M 到直线l 距离等于半径r3=，解得815k =.843:1515l y x ∴=+，整理得815430x y -+=. 综上：切线方程为815430x y -+=或4x =.（2）圆22:(1)1M x y a -+=-，则圆心为(1,0)M ，半径)11r a =<.圆22:(1)(4N x y ++-=，则圆心(N -，半径22r =.Q圆M 和圆N 相外切，12MN r r ∴=+2=，3a ∴=-.此时圆22:(1)4M x y -+=，圆心(1,0)M ，半径12r =.由点Q 关于y 轴对称的点为(2,8)Q -'-，Q M '=Q ∴所走路线的最小值为2.【点睛】本题考查了直线与圆位置关系的应用，考查了圆圆的位置关系的应用.由直线和圆相切可得等量关系为，圆心到直线的距离等于半径；由圆圆外切可得等量关系为，圆心距为两圆的半径之和.本题的易错点是，在求第一问的切线方程时，没讨论直线斜率不存在的情况.26．（1）见解析；（2）见解析【解析】【分析】（1）要想证明线线垂直，可以考虑线面垂直.已知底面ABCD 是菱形，显然有BD AC ⊥ ，已知PA ⊥平面ABCD ，可以得到PA BD ⊥，这样就可以根据线面垂直的判定定理，证明出BD ⊥平面APC ，进而可以证明出BD PC ⊥;（2）可以先证明出线面平行，然后利用线面平行的性质定理证明出//BC l .【详解】（1）证明：连接AC ，交BD 于点O ．∵四边形ABCD 为菱形，所以BD AC ⊥又∵PA ⊥平面ABCD ，BD ⊂ 平面ABCD ,∴PA BD ⊥又∵PA AC A ⋂=, PA ⊂平面PAC , AC ⊂平面PAC∴BD ⊥平面APC ，又∵PC ⊂平面APC∴ BD PC ⊥（2）∵四边形ABCD 为菱形，∴//BC AD∵AD ⊂平面PAD ，BC ⊄平面PAD ．∴//BC 平面PAD .又∵BC ⊂平面PBC ，平面PBC ⋂平面PAD l =.∴//BC l ．【点睛】本题考查了线面垂直的判定定理、线面平行的判定定理以及性质定理.关键是考查了转化思想.。

【好题】高中必修二数学下期中一模试题(含答案)(1)

【好题】高中必修二数学下期中一模试题(含答案)(1)一、选择题1．已知m ，n 表示两条不同直线，α表示平面，下列说法正确的是（）A ．若//,//,m n αα则//m nB ．若m α⊥，n α⊂，则m n ⊥C ．若m α⊥，m n ⊥，则//n αD ．若//m α，m n ⊥，则n α⊥2．已知,,,A B C D 是同一球面上的四个点，其中ABC ∆是正三角形，AD ⊥平面ABC ，26AD AB ==，则该球的体积为（）A ．48πB ．24πC ．16πD ．323π 3．设圆C ：223x y +=，直线l ：360x y +-=，点()00,P x y l ∈，若存在点Q C ∈，使得60OPQ ∠=︒（O 为坐标原点），则0x 的取值范围是( )A ．1,12⎡⎤-⎢⎥⎣⎦B ．60,5⎡⎤⎢⎥⎣⎦C ．[]0,1D ．16,25⎡⎤-⎢⎥⎣⎦4．直线(2)4y k x =-+与曲线2320x y y ++-=有两个不同的交点，则实数k 的取值范围是（）A ．53(,]124B ．51(,]122C ．13(,]24D ．1[,)2+∞ 5．已知三棱锥S ABC -的所有顶点都在球O 的球面上，SC 为球O 的直径，且SC OA ⊥，SC OB ⊥，OAB V 为等边三角形，三棱锥S ABC -的体积为433，则球O 的半径为( )A ．3B ．1C ．2D ．46．已知m 和n 是两条不同的直线，α和β是两个不重合的平面，那么下面给出的条件中一定能推出m ⊥β的是( )A ．α⊥β，且m ⊂αB ．m ⊥n ，且n ∥βC ．α⊥β，且m ∥αD ．m ∥n ，且n ⊥β7．如图是水平放置的平面图形的斜二测直观图，其原来平面图形面积是（）A ． 22B ． 42C ．4D ．88．在三棱锥P ABC -中，PA ⊥平面1202,2ABC BAC AP AB ∠=︒==，，，M 是线段BC 上一动点，线段PM 3P ABC -的外接球的表面积是（）A ．92πB ．92πC ．18πD ．40π9．某几何体的三视图如图所示，则该几何体的体积为( )A ．12B ．18C ．24D ．3010．已知点()1,2-和3,0⎛⎫ ⎪ ⎪⎝⎭在直线():100l ax y a --=≠的两侧，则直线l 的倾斜角的取值范围是 ( )A ．,43ππ⎛⎫⎪⎝⎭ B ．2,33ππ⎛⎫ ⎪⎝⎭ C ．25,36ππ⎛⎫ ⎪⎝⎭ D ．30,,34πππ⎛⎫⎛⎫⋃ ⎪ ⎪⎝⎭⎝⎭11．如图1，ABC ∆是以B 为直角顶点的等腰直角三角形，T 为线段AC 的中点，G 是BC 的中点，ABE ∆与BCF ∆分别是以AB 、BC 为底边的等边三角形，现将ABE ∆与BCF ∆分别沿AB 与BC 向上折起（如图2），则在翻折的过程中下列结论可能正确的个数为（）图1 图2（1）直线AE ⊥直线BC ；（2）直线FC ⊥直线AE ；（3）平面//EAB 平面FGT ；（4）直线//BC 直线AE .A ．1个B ．2个C ．3个D ．4个12．某几何体的三视图如图所示（单位：cm ），其俯视图为等边三角形，则该几何体的体积（单位：3cm ）是（）A ．43 B．1033 C ．23 D ．833二、填空题13．设P ，A ，B ，C 是球O 表面上的四个点，PA ，PB ，PC 两两垂直，且1PA PB PC ===，则球O 的表面积为____________.14．已知在直角梯形ABCD 中，AB AD ⊥，CD AD ⊥，224AB AD CD ===，将直角梯形ABCD 沿AC 折叠，使平面BAC ⊥平面DAC ，则三棱锥D ABC -外接球的体积为__________．15．若直线y x b =+与曲线234y x x =+-有公共点，则b 的取值范围是______．16．已知三棱锥P ABC -的四个顶点在球O 的球面上，PA PB PC ==，ABC △是边长为2正三角形，,E F 分别是,PA AB 的中点，90CEF ︒∠=，则球O 的体积为_________________。

【压轴题】高中必修二数学下期中第一次模拟试卷附答案

【压轴题】高中必修二数学下期中第一次模拟试卷附答案一、选择题1．已知m ，n 表示两条不同直线，α表示平面，下列说法正确的是（） A ．若//,//,m n αα则//m n B ．若m α⊥，n α⊂，则m n ⊥ C ．若m α⊥，m n ⊥，则//n αD ．若//m α，m n ⊥，则n α⊥2．已知直线l 过点(1,0)，且倾斜角为直线0l ：220x y --=的倾斜角的2倍，则直线l 的方程为（） A ．4330x y --= B ．3430x y --= C ．3440x y --=D ．4340x y --=3．若函数6(3)3,7(),7x a x x f x a x ---≤⎧=⎨>⎩单调递增,则实数a 的取值范围是( ) A ．9,34⎛⎫⎪⎝⎭B ．9,34⎡⎫⎪⎢⎣⎭C ．()1,3D ．()2,34．直线(2)4y k x =-+与曲线2320x y y ++-=有两个不同的交点，则实数k 的取值范围是（） A ．53(,]124B ．51(,]122C ．13(,]24D ．1[,)2+∞5．在我国古代数学名著九章算术中，将四个面都为直角三角形的四面体称为鳖臑，如图，在鳖臑ABCD 中， AB ⊥平面BCD ，且AB BC CD ==，则异面直线AC 与BD 所成角的余弦值为（）A ．12 B ．12-C ．32D ．3 6．长方体的三个相邻面的面积分别为2，3，6，则该长方体外接球的表面积为( ) A ．72π B ．56πC ．14πD ．64π7．矩形ABCD 中，4AB =，3BC =，沿AC 将矩形ABCD 折成一个直二面角B ACD --，则四面体ABCD 的外接球的体积是（）A ．12512π B ．1259π C ．1256π D ．1253π 8．椭圆22221(0)x y a b a b+=>>的左右焦点分别是1F 、2F ，以2F 为圆心的圆过椭圆的中心，且与椭圆交于点P ，若直线1PF 恰好与圆2F 相切于点P ，则椭圆的离心率为（）A ．312+ B ．31-C ．22D ．512- 9．若方程21424x kx k +-=-+ 有两个相异的实根，则实数k 的取值范围是（）A ．13,34⎛⎤ ⎥⎝⎦B ．13,34⎛⎫ ⎪⎝⎭C ．53,124⎛⎫ ⎪⎝⎭D ．53,124纟çúçú棼10．若底面是菱形的棱柱其侧棱垂直于底面，且侧棱长为5，它的对角线的长分别是9和15，则这个棱柱的侧面积是( )． A ．130B ．140C ．150D ．16011．如图，正四面体ABCD 中，,E F 分别是线段AC 的三等分点，P 是线段AB 的中点，G 是线段BD 的动点，则( )A ．存在点G ，使PG EF ⊥成立B ．存在点G ，使FG EP ⊥成立C ．不存在点G ，使平面EFG ⊥平面ACD 成立D ．不存在点G ，使平面EFG ⊥平面ABD 成立 12．如图在正方体中，点为线段的中点. 设点在线段上，直线与平面所成的角为，则的取值范围是( )A ．B ．C ．D ．二、填空题13．已知圆22:20(0)M x y ay a +-=>截直线0x y +=所得线段的长度是22M 与圆22:(1)(1)1N x y -+-=的位置关系是_________．14．已知三棱锥P ABC -中，侧面PAC ⊥底面ABC ，90BAC ∠=︒，4AB AC ==，23PA PC ==，则三棱锥P ABC -外接球的半径为______.15．已知在直角梯形ABCD 中，AB AD ⊥，CD AD ⊥，224AB AD CD ===，将直角梯形ABCD 沿AC 折叠，使平面BAC ⊥平面DAC ，则三棱锥D ABC -外接球的体积为__________．16．在平面直角坐标xOy 系中,设将椭圆()2222110y x a a a +=>-绕它的左焦点旋转一周所覆盖的区域为D ，P 为区域D 内的任一点，射线()02x y x =≥－上的点为Q ，若PQ 的最小值为a ，则实数a 的取值为_____．17．已知平面α，β，γ是空间中三个不同的平面，直线l ，m 是空间中两条不同的直线，若α⊥γ，γ∩α＝m ，γ∩β＝l ，l⊥m，则 ①m⊥β；②l⊥α；③β⊥γ；④α⊥β.由上述条件可推出的结论有________(请将你认为正确的结论的序号都填上)． 18．圆221x y +=上的点到直线34250x y +-=的距离的最小值是．19．三棱锥A BCD -中，E 是AC 的中点，F 在AD 上，且2AF FD =，若三棱锥A BEF -的体积是2，则四棱锥B ECDF -的体积为_______________．20．已知点(,)P x y 是直线4(0)y kx k =-->上的一个动点，PA ，PB 是圆22:20C x y y +-=的两条切线，A ，B 是切点，若四边形PACB 的面积的最小值为2，则实数k 的值为__________．三、解答题21．如图，正方形ABCD 所在平面与三角形CDE 所在平面相交于CD ，AE ⊥平面CDE ，且1AE =,2AB =.(Ⅰ)求证：AB ⊥平面ADE ； (Ⅱ)求凸多面体ABCDE 的体积.22．如图，四棱锥P ABCD -，底面ABCD 为矩形，PA ⊥平面ABCD ，E 为PD 的中点.（1）证明：//PB 平面AEC ；（2）设二面角D AE C --为60°，1AP =，3AD =，求直线AC 与平面ECD 所成角的正弦值.23．已知平面内两点(8,6),(2,2)A B -. （1）求AB 的中垂线方程；（2）求过点(2,3)P -且与直线AB 平行的直线l 的方程． 24．在三棱柱111ABC A B C -中，侧面11AA C C ⊥底面ABC ，112AA AC AC AB BC =====，且点O 为AC 中点.(1)证明：1A O ⊥平面ABC ； (2)求三棱锥1C ABC -的体积.25．如图，矩形ABCD 的两条对角线相交于点M(2，0)，AB 边所在直线的方程为x －3y －6＝0，点T(－1，1)在AD 边所在直线上．求：(1) AD 边所在直线的方程； (2) DC 边所在直线的方程．26．如图，在三棱柱111ABC A B C -中，1C C ⊥底面ABC ，AC BC ⊥，1AC BC CC ==，M ､N 分别是1A B ､11B C 的中点.（1）求证：MN ⊥平面1A BC ；（2）求直线1BC 和平面1A BC 所成角的大小.【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【解析】试题分析：线面垂直，则有该直线和平面内所有的直线都垂直，故B 正确. 考点：空间点线面位置关系．2．D解析：D 【解析】设直线0l 的倾斜角为α，则斜率01tan 2k α==，所以直线l 的倾斜角为2α，斜率22tan 4tan 21tan 3k ααα===-，又经过点（1,0），所以直线方程为4(1)3y x =-，即4340x y --=，选D.3．B解析：B 【解析】【分析】利用函数的单调性，判断指数函数底数的取值范围，以及一次函数的单调性，及端点处函数值的大小关系列出不等式求解即可【详解】解：Q 函数6(3)3,7(),7x a x x f x a x ---⎧=⎨>⎩…单调递增， ()301373a a a a⎧->⎪∴>⎨⎪-⨯-≤⎩解得934a ≤<所以实数a 的取值范围是9,34⎡⎫⎪⎢⎣⎭．故选：B ．【点睛】本题考查分段函数的应用，指数函数的性质，考查学生的计算能力，属于中档题．4．B解析：B 【解析】【分析】利用数形结合，作出图象，计算得直线1l 与直线2l 的斜率，即可得到结论. 【详解】曲线可化简为()22(1)40x y x +-=≤，如图所示：直线()1:24l y k x =-+，此直线与曲线相切，此时有23221k k -=+，解得512k =，直线()2:24l y k x =-+，此直线与曲线有两个交点，此时有12k =. 所以，过点()2,4的直线与该半圆有两个交点，数形结合，解得51122k <≤. 故选：B. 【点睛】本题考查了直线与圆相交的性质，涉及的知识有：恒过定点的直线方程，点到直线的距离公式，以及直线斜率的求法，利用了数形结合的思想，其中抓住两个关键点是解本题的关键．5．A解析：A 【解析】如图，分别取,,,BC CD AD BD 的中点,,,M N P Q ，连,,,MN NP PM PQ ，则,MN BD NP AC P P ，∴PNM ∠即为异面直线AC 和BD 所成的角（或其补角）．又由题意得PQ MQ ⊥，11,22PQ AB MQ CD ==. 设2AB BC CD ===，则PM =又1122MN BD NP AC ==== ∴PNM ∆为等边三角形， ∴60PNM =︒∠，∴异面直线AC 与BD 所成角为60︒，其余弦值为12．选A ．点睛：用几何法求空间角时遵循“一找、二证、三计算”的步骤，即首先根据题意作出所求的角，并给出证明，然后将所求的角转化为三角形的内角．解题时要注意空间角的范围，并结合解三角形的知识得到所求角的大小或其三角函数值．6．C解析：C 【解析】【分析】由题意首先求得长方体的棱长，然后求解其外接球的表面积即可. 【详解】设长方体的棱长分别为,,a b c ，则236ab bc ac =⎧⎪=⎨⎪=⎩，所以()236abc =，于是213a b c =⎧⎪=⎨⎪=⎩，设球的半径为R ，则2222414R a b c =++=，所以这个球面的表面积为24R π=14π．本题选择C 选项. 【点睛】与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径.7．C解析：C 【解析】【分析】由矩形的对角线互相平分且相等即球心到四个顶点的距离相等推出球心为AC 的中点，即可求出球的半径，代入体积公式即可得解.【详解】因为矩形对角线互相平分且相等，根据外接球性质易知外接球球心到四个顶点的距离相等，所以球心在对角线AC 上，且球的半径为AC 长度的一半，即22115222r AC AB BC ==+=，所以334451253326V r πππ⎛⎫==⋅= ⎪⎝⎭.故选：C 【点睛】本题考查球与几何体的切、接问题，二面角的概念，属于基础题.8．B解析：B 【解析】【分析】根据椭圆的定义可知12||||2PF PF a +=，又1PF 恰好与圆2F 相切于点P ，可知2||PF c =且12PF PF ⊥，即可列出方程求椭圆的离心率. 【详解】由1PF 恰好与圆2F 相切于点P ，可知2||PF c =，且 12PF PF ⊥，又12||||2PF PF a +=，可知1||2PF a c =-，在12Rt PF F ∆中，222(2)4a c c c -+=，即2222a ac c -= 所以2220,(0,1)e e e +-=∈，解得21231e -+==，故选：B 【点睛】本题主要考查了椭圆的定义，椭圆的简单几何性质，圆的切线的性质，属于中档题.9．D解析：D 【解析】【分析】由题意可得，曲线22(1)4(1)x y y +-=…与直线4(2)y k x -=-有2个交点，数形结合求得k 的范围. 【详解】如图所示，化简曲线得到22(1)4(1)x y y +-=…，表示以(0,1)为圆心，以2为半径的上半圆，直线化为4(2)y k x -=-，过定点(2,4)A ，设直线与半圆的切线为AD ，半圆的左端点为(2,1)B -，当AD AB k k k <…，直线与半圆有两个交点， AD 221k =+，解得512AD k =，4132(2)4AB k -==--，所以53,124k ⎛⎤∈ ⎥⎝⎦.故选：D 【点睛】本题考查直线与圆的位置关系，属于中档题.10．D解析：D 【解析】设直四棱柱1111ABCD A B C D -中，对角线119,15AC BD ==，因为1A A ⊥平面,ABCD AC Ì,平面ABCD ，所以1A A AC ⊥，在1Rt A AC ∆中，15A A =，可得221156AC AC A A =-= 同理可得2211200102BD D B D D =-==，因为四边形ABCD 为菱形，可得,AC BD 互相垂直平分，所以2211()()1450822AB AC BD =+=+=，即菱形ABCD 的边长为8，因此，这个棱柱的侧面积为1()485160S AB BC CD DA AA =+++⨯=⨯⨯=，故选D.点睛：本题考查了四棱锥的侧面积的计算问题，解答中通过给出的直四棱柱满足的条件，求得底面菱形的边长，进而得出底面菱形的底面周长，即可代入侧面积公式求得侧面积，着重考查了学生分析问题和解答问题的能力，以及空间想象能力，其中正确认识空间几何体的结构特征和线面位置关系是解答的关键.11．C解析：C【解析】【分析】利用空间中线线、线面、面面间的位置关系对选项进行一一验证，即可得答案．【详解】正四面体ABCD中，,E F分别是线段AC的三等分点，P是线段AB的中点，G是直线BD的动点，⊥成立，故A错误；在A中，不存在点G，使PG EF⊥成立，故B错误；在B中，不存在点G，使FG EP在C中，不存在点G，使平面EFG⊥平面ACD成立，故C正确；在D中，存在点G，使平面EFG⊥平面ABD成立，故D错误.故选：C.【点睛】本题考查命题真假的判断、考查空间中线线、线面、面面间的位置关系，考查转化与化归思想，考查空间想象能力．12．B解析：B【解析】【分析】【详解】设正方体的棱长为，则，所以，. 又直线与平面所成的角小于等于，而为钝角，所以的范围为，选B.【考点定位】空间直线与平面所成的角. 二、填空题13．相交【解析】【分析】根据直线与圆相交的弦长公式求出的值结合两圆的位置关系进行判断即可【详解】解：圆的标准方程为则圆心为半径圆心到直线的距离圆截直线所得线段的长度是即则圆心为半径圆的圆心为半径则即两个解析：相交【解析】【分析】根据直线与圆相交的弦长公式，求出a 的值，结合两圆的位置关系进行判断即可．【详解】解：圆的标准方程为222:()(0)M x y a a a +-=>，则圆心为(0,)a ，半径R a =，圆心到直线0x y +=的距离2d =，Q 圆22:20(0)M x y ay a +-=>截直线0x y +=所得线段的长度是22222222a a ∴-即24a =，2a =，则圆心为(0,2)M ，半径2R =，圆22:(1)(1)1N x y -+-=的圆心为(1,1)N ，半径1r =，则2MN =3R r +=Q ，1R r -=，R r MN R r ∴-<<+，即两个圆相交．故答案为：相交．【点睛】本题主要考查直线和圆相交的应用，以及两圆位置关系的判断，根据相交弦长公式求出a 的值是解决本题的关键．14．【解析】【分析】设三棱锥外接球球心为半径为如图所示作辅助线设则解得答案【详解】设三棱锥外接球球心为半径为故在平面的投影为中点为中点故侧面底面故底面连接作于易知为矩形设则解得故答案为：【点睛】本题考查【解析】【分析】设三棱锥P ABC -外接球球心为O ，半径为R ，如图所示作辅助线，设1OO h =，则()2222221R PD h OH R h CO ⎧=-+⎪⎨=+⎪⎩，解得答案. 【详解】设三棱锥P ABC -外接球球心为O ，半径为R ，90BAC ∠=︒，故O 在平面ABC 的投影为BC 中点1O ，D 为AC 中点，PA PC =，故PD AC ⊥，侧面PAC ⊥底面ABC ，故PD ⊥底面ABC .连接1O D ，作OH PD ⊥于H ，易知1OO DH 为矩形，设1OO h =，则()2222221R PD h OH R h CO ⎧=-+⎪⎨=+⎪⎩，PD =，12OH DO ==，1CO =2R =.故答案为：2.【点睛】本题考查了三棱锥的外接球问题，意在考查学生的计算能力和空间想象能力.15．【解析】结合题意画出折叠后得到的三棱锥如图所示由条件可得在底面中取AB 的中点OAC 的中点E 连OCOE 则∵∴∵平面平面∴平面∴又∴∴∴点O 为三棱锥外接球的球心球半径为2∴答案：点睛：（1）本题是一道关解析：323π 【解析】结合题意画出折叠后得到的三棱锥D ABC -如图所示，由条件可得在底面ACB ∆中，90,22ACB AC BC ∠=︒==。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

【易错题】高中必修二数学下期中第一次模拟试卷含答案(1)一、选择题1．在长方体1111ABCD A B C D -中，2AB BC ==，1AC 与平面11BB C C 所成的角为30o ，则该长方体的体积为（）A ．8B ．C ．D ．2．已知三棱锥A BCD -中，AB CD ==2==AC BD ，AD BC ==三棱锥的四个顶点在同一个球面上，则此球的体积为（）A ．32π B ．24πCD ．6π3．已知三棱锥D ABC -的外接球的表面积为128π，4,AB BC AC ===锥D ABC -体积的最大值为（）A ．2732B C D 4．已知a ，b 是两条异面直线，且a b ⊥r r，直线c 与直线a 成30°角，则c 与b 所成的角的大小范围是( ) A ．[]60,90︒︒B ．[]30,90︒︒C ．[]30,60︒︒D ．[]45,90︒︒5．已知正四棱锥P ABCD -的所有顶点都在同一球面上，若球的半径为3，则该四棱锥的体积的最大值为（） A ．643B ．32C ．54D ．646．已知,,,A B C D 是同一球面上的四个点，其中ABC ∆是正三角形，AD ⊥平面ABC ，26AD AB ==，则该球的体积为（）A ．48πB ．24πC ．16πD ．7．已知直线m 、n 及平面α，其中m ∥n ，那么在平面α内到两条直线m 、n 距离相等的点的集合可能是：（1）一条直线；（2）一个平面；（3）一个点；（4）空集。

其中正确的是（）A ．（1）（2）（3）B ．（1）（4）C ．（1）（2）（4）D ．（2）（4）8．已知定义在R 上的函数()21()x mf x m -=-为实数为偶函数,记0.5(log 3),a f =2b (log 5),c (2)f f m ==,则,,a b c ,的大小关系为（）A ．a b c <<B ．c a b <<C ．a c b <<D ．c b a <<9．椭圆22221(0)x y a b a b+=>>的左右焦点分别是1F 、2F ，以2F 为圆心的圆过椭圆的中心，且与椭圆交于点P ，若直线1PF 恰好与圆2F 相切于点P ，则椭圆的离心率为（）A B 1C ．2D10．已知AB 是圆22620x y x y +-+=内过点(2,1)E 的最短弦，则||AB 等于（）A B ． C ．D ．11．若圆22240x y x y +--=的圆心到直线0x y a -+=，则a 的值为( ) A ．-2或2B ．12或32C ．2或0D ．-2或012．已知直三棱柱111ABC A B C -的所有棱长都相等，M 为11A C 的中点，则AM 与1BC 所成角的余弦值为( )A ．3B ．3C ．4D ．4二、填空题13．经过两条直线2310x y ++=和340x y -+=的交点，并且平行于直线3470x y +-=的直线方程是________.14．已知点1232M N （，），（，），点F 是直线l:3y x =-上的一个动点，当MFN ∠最大时，过点M ，N ，F 的圆的方程是__________.15．在平面直角坐标xOy 系中,设将椭圆()2222110y x a a a +=>-绕它的左焦点旋转一周所覆盖的区域为D ，P 为区域D 内的任一点，射线()02x y x =≥－上的点为Q ，若PQ 的最小值为a ，则实数a 的取值为_____．16．已知平面α，β，γ是空间中三个不同的平面，直线l ，m 是空间中两条不同的直线，若α⊥γ，γ∩α＝m ，γ∩β＝l ，l⊥m，则 ①m⊥β；②l⊥α；③β⊥γ；④α⊥β.由上述条件可推出的结论有________(请将你认为正确的结论的序号都填上)． 17．小明在解题中发现函数()32x f x x -=-，[]0,1x ∈的几何意义是：点(),x x []()0,1x ∈与点()2,3连线的斜率，因此其值域为3,22⎡⎤⎢⎥⎣⎦，类似地，他研究了函数()g x =，[]0,1x ∈，则函数()g x 的值域为_____18．在棱长为1的正方体1111ABCD A B C D -中，M 是1BB 的中点，直线1D M 与平面ABCD 交于点N ，则线段AN 的长度为________19．若圆C ：222430x y x y ++-+=，关于直线260ax by ++=对称，则由点(),a b 向圆所作的切线长的最小值为______．20．已知棱长等于1111ABCD A B C D -，它的外接球的球心为O ﹐点E 是AB 的中点，则过点E 的平面截球O 的截面面积的最小值为________.三、解答题21．如图（1）在等腰直角三角形ABC 中，90B ∠=︒，将ABC ∆沿中位线DE 翻折得到如图（2）所示的空间图形，使二面角A DE C --的大小为02πθθ⎛⎫<<⎪⎝⎭.（1）求证：平面ABD ⊥平面ABC ；（2）若3πθ=，求直线AE 与平面ABC 所成角的正弦值.22．如图所示，四棱锥S ABCD -中，SA ⊥底面ABCD ，090ABC ∠=，23SA AB ==，，1BC =，23AD =，060ACD ∠=，E 为CD 的中点.（1）求证：//BC 平面SAE ；（2）求直线SD 与平面SBC 所成角的正弦值.23．如图，AB 是半圆O 的直径，C 是半圆O 上除A ，B 外的一个动点，DC 垂直于半圆O 所在的平面，DC ∥EB ，DC ＝EB ＝1，AB ＝4.（1）证明：平面ADE ⊥平面ACD ；（2）当C 点为半圆的中点时，求二面角D ﹣AE ﹣B 的余弦值. 24．在三棱柱111ABC A B C -中，侧面11AA C C ⊥底面ABC ，112AA AC AC AB BC =====，且点O 为AC 中点.(1)证明：1A O ⊥平面ABC ； (2)求三棱锥1C ABC -的体积.25．如图，在四棱锥P ABCD -中，底面ABCD 为直角梯形，//AD BC ，90ADC ∠=︒，12BC AD =，PA PD =，M ，N 分别为AD 和PC 的中点．（1）求证：//PA 平面MNB ；（2）求证：平面PAD ⊥平面PMB ．26．如图，在直三棱柱ABC -A 1B 1C 1中，∠ACB ＝90°，∠BAC ＝30°，BC ＝1，A 1A ＝6，M 是CC 1的中点．(1)求证：A 1B ⊥AM ；(2)求二面角B --AM--C 的平面角的大小．.【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【解析】【分析】首先画出长方体1111ABCD A B C D -，利用题中条件，得到130AC B ∠=o，根据2AB =，求得123BC =，可以确定122CC =，之后利用长方体的体积公式求出长方体的体积. 【详解】在长方体1111ABCD A B C D -中，连接1BC ，根据线面角的定义可知130AC B ∠=o，因为2AB =，所以123BC =，从而求得122CC =，所以该长方体的体积为222282V =⨯⨯=，故选C. 【点睛】该题考查的是长方体的体积的求解问题，在解题的过程中，需要明确长方体的体积公式为长宽高的乘积，而题中的条件只有两个值，所以利用题中的条件求解另一条边的长就显得尤为重要，此时就需要明确线面角的定义，从而得到量之间的关系，从而求得结果.2．C解析：C 【解析】【分析】作出三棱锥A BCD -的外接长方体AEBF GDHC -，计算出该长方体的体对角线长，即可得出其外接球的半径，然后利用球体体积公式可计算出外接球的体积. 【详解】作出三棱锥A BCD -的外接长方体AEBF GDHC -，如下图所示：设DG x =，DH y =，DE z =，则2223AD x z =+=，2224DB y z =+=，2225DC x y =+=，上述三个等式相加得()222222234512AD BD CD x y z++=++=++=，所以，该长方体的体对角线长为2226x y z ++=，则其外接球的半径为62R =，因此，此球的体积为34663ππ⎛⎫⨯= ⎪ ⎪⎝⎭. 故选：C. 【点睛】本题考查三棱锥外接球体积的计算，将三棱锥补成长方体，利用长方体的体对角线作为外接球的直径是解题的关键，考查空间想象能力与计算能力，属于中等题.3．D解析：D 【解析】【分析】先求出球心O 到底面距离的最大值，从而可求顶点D 到底面的距离的最大值，利用该最大值可求体积的最大值. 【详解】设外接球的球心为O ，半径为R ，则24128R ππ=，故42R =设球心O 在底面上的投影为E ，因为OA OC OB ==，故E 为ABC ∆的外心. 因为4AB BC ==，42AC =222AC AB BC =+，故ABC ∆为直角三角形，故E 为AC 的中点，所以2226OE OA AE =-=，设D 到底面ABC 的距离为h ，则2642h OE R ≤+= 所以三棱锥D ABC -的体积的最大值为(11322166442642323⨯⨯⨯⨯=. 故选：D. 【点睛】几何体的外接球、内切球问题，关键是球心位置的确定，必要时需把球的半径放置在可解的几何图形中，注意球心在底面上的投影为底面外接圆的圆心．如果球心的位置不易确定，则可以把该几何体补成规则的几何体，便于球心位置和球的半径的确定．4．A解析：A 【解析】【分析】将异面直线所成的角转化为平面角，然后由题意，找出与直线a 垂直的直线b 的平行线，与直线c 平行线的夹角. 【详解】在直线a 上任取一点O ，过O 做//c c '，则,a c '确定一平面α，过O 点做直线b 的平行线b '，所有平行线b '在过O 与直线a 垂直的平面β内，若存在平行线1b '不在β内，则1b '与b '相交又确定不同于β的平面，这与过一点有且仅有一个平面与一条直线垂直矛盾，所以b '都在平面β内，且,l αβαβ⊥=I ，在直线c '上任取不同于O 的一点P ，做PP l '⊥于P '，则PP β'⊥，POP '∠为是c '与β所成的角为60︒，若b l '⊥，则,b b c α'''⊥⊥，若b '不垂直l 且不与l 重合，过P '做P A b ''⊥，垂足为A ，连PA ，则b '⊥平面PP A '，所以b PA '⊥，即1,cos 2OA OP OA PA AOP OP OP '⊥∠=<=， 60AOP ∠>︒，综上b '与c '所成角的范围为[60,90]︒︒，所以直线b 与c 所成角的范围为[]60,90︒︒. 故选：A.【点睛】本题考查异面直线所成角，空间角转化为平面角是解题的关键，利用垂直关系比较角的大小，属于中档题.5．A解析：A 【解析】【分析】设底面ABCD 的边长为a ，四棱锥的高为h ，可得22122a h h =-，得出四棱锥的体积关于h 的函数()V h ，求出V 的极大值点，即可得到四棱锥的体积的最大值. 【详解】正四棱锥P ABCD -的所有顶点都在同一球面上，若球的半径为3，设底面ABCD 的边长为a ，四棱锥的高为h ，设正四棱锥的底面ABCD 的中心为1O . 则22a OA =,1PO ⊥ 平面ABCD . 则22211OO O A OA +=,即()222233a h ⎛⎫+-= ⎪ ⎪⎝⎭，可得22122a h h =-. 则该四棱锥的体积为()221112233V a h h h h =⨯=- 令()()2122f h h hh =-，则()2246f h h h'=-当04h <<时，()0f h '>，()f h 单调递增. 当4h >时，()0f h '<，()f h 单调递减.所以当4h =时，该四棱锥的体积有最大值，最大值为：()216412424433⨯⨯-⨯⨯= . 故选：A【点睛】本题考查了四棱锥与球的组合体，求椎体的体积，关键是利用了导数求体积的最值．属于中档题．6．D解析：D 【解析】【分析】根据球的性质可知球心O 与ABC ∆外接圆圆心O '连线垂直于平面ABC ；在Rt POE ∆和Rt OO A ∆'中利用勾股定理构造出关于半径R 和OO '的方程组，解方程组求得R ，代入球的体积公式可得结果. 【详解】设O '为ABC ∆的外心，如下图所示：由球的性质可知，球心O 与O '连线垂直于平面ABC ，作OE AD ⊥于E 设球的半径为R ，OO x '=ABC ∆为等边三角形，且3AB = 3AO '∴=OO '⊥Q 平面ABC ，AD ⊥平面ABC ，OE AD ⊥OO AE x '∴==，3OE AO '==在Rt POE ∆和Rt OO A ∆'中，由勾股定理得：22222OE PE O O O A R ''+=+=，即()222363x x R +-=+=解得：3x =，3R =∴球的体积为：343233V R ππ==本题正确选项：D 【点睛】本题考查棱锥外接球的体积求解问题，关键是能够确定棱锥外接球球心的位置，从而在直角三角形中利用勾股定理构造方程求得半径.7．C解析：C 【解析】【分析】根据题意，对每一个选项进行逐一判定，不正确的只需举出反例，正确的作出证明，即可得到答案. 【详解】如图（1）所示，在平面内不可能由符合题的点；如图（2），直线,a b 到已知平面的距离相等且所在平面与已知平面垂直，则已知平面为符合题意的点；如图（3），直线,a b 所在平面与已知平面平行，则符合题意的点为一条直线，综上可知（1）（2）（4）是正确的，故选C.【点睛】本题主要考查了空间中直线与平面之间的位置关系，其中熟记空间中点、线、面的位置关系是解答此类问题的关键，着重考查了空间想象能力，以及推理与论证能力，属于基础题.8．B解析：B 【解析】由()f x 为偶函数得0m =,所以0,52log 3log 32121312,a =-=-=-=2log 521514b =-=-=,0210c =-=,所以c a b <<,故选B.考点：本题主要考查函数奇偶性及对数运算.9．B解析：B 【解析】【分析】根据椭圆的定义可知12||||2PF PF a +=，又1PF 恰好与圆2F 相切于点P ，可知2||PF c =且12PF PF ⊥，即可列出方程求椭圆的离心率. 【详解】由1PF 恰好与圆2F 相切于点P ，可知2||PF c =，且 12PF PF ⊥，又12||||2PF PF a +=，可知1||2PF a c =-，在12Rt PF F ∆中，222(2)4a c c c -+=，即2222a ac c -= 所以2220,(0,1)e e e +-=∈，解得212312e -==，故选：B 【点睛】本题主要考查了椭圆的定义，椭圆的简单几何性质，圆的切线的性质，属于中档题.10．D解析：D【解析】【分析】求出圆的标准方程，确定最短弦的条件，利用弦长公式进行求解即可．【详解】圆的标准方程为（x ﹣3）2+（y +1）2＝10，则圆心坐标为C （3，﹣1），半径为过E 的最短弦满足E 恰好为C 在弦上垂足，则CE ==，则|AB |==，故选D ．【点睛】本题主要考查圆的标准方程的求解，以及直线和圆相交的弦长问题,属于中档题．11．C解析：C【解析】【分析】把圆的方程化为标准方程,找出圆心坐标,根据点到直线的距离公式列出关于a 的方程,求出方程的解得到a 的值即可.【详解】把圆的方程化为标准式为:22(1)(2)5x y -+-=,所以圆心坐标为(1,2).则圆心到直线0x y a -+=的距离2d ==, 即11a -=,化简得11a -=或11a -=-,解得:2a =或0a =.所以a 的值为0或2.故选C.【点睛】本题考查学生会将圆的一般式方程化为标准式方程,灵活运用点到直线的距离公式化简求值.12．D解析：D【解析】【分析】取AC 的中点N ，连接1C N ，则1//AM C N ,所以异面直线AM 与1BC 所成角就是直线AM 与1C N 所成角，在1BNC ∆中，利用余弦定理，即可求解．【详解】由题意，取AC 的中点N ，连接1C N ，则1//AM C N ,所以异面直线AM 与1BC 所成角就是直线AM 与1C N 所成角，设正三棱柱的各棱长为2,则11C N BC BN ===设直线AM 与1C N 所成角为θ，在1BNC ∆中，由余弦定理可得222(5)(22)(3)10cos 2522θ+-==⨯⨯，即异面直线AM 与1BC 所成角的余弦值为10，故选D ．【点睛】本题主要考查了异面直线所成角的求解，其中解答中把异面直线所成的角转化为相交直线所成的角是解答的关键，着重考查了推理与运算能力，属于基础题．二、填空题13．【解析】【分析】先求出两相交直线的交点设出平行于直线的直线方程根据交点在直线上求出直线方程【详解】联立直线的方程得到两直线的交点坐标平行于直线的直线方程设为则所以直线的方程为：故答案为：【点睛】本题解析：1934011x y ++= 【解析】【分析】先求出两相交直线的交点，设出平行于直线3470x y +-=的直线方程，根据交点在直线上，求出直线方程.【详解】联立直线的方程23103470x y x y ++=⎧⎨+-=⎩，得到两直线的交点坐标135(,)1111-，平行于直线3470x y +-=的直线方程设为340x y c ++=，则1353()4()+01111c ⋅-+⋅= 所以直线的方程为：1934011x y ++=故答案为：1934011x y ++= 【点睛】本题考查了直线的交点，以及与已知直线平行的直线方程，考查了学生概念理解，转化与划归的能力，属于基础题.14．【解析】【分析】【详解】试题分析：根据题意设圆心坐标为C （2a ）当∠MFN 最大时过点MNF 的圆与直线y=x-3相切∴∴a=1或9a=1时r=∠MCN=90°∠MFN=45°a=9时r=∠MCN ＜90解析：22(2)(1)2x y -+-=【解析】【分析】【详解】试题分析：根据题意，设圆心坐标为C （2，a ），当∠MFN 最大时，过点M ，N ，F 的圆与直线y=x-3相切．=，∴a=1或9，a=1时，，∠MCN=90°，∠MFN=45°，a=9时，r=MCN ＜90°，∠MFN ＜45°，则所求圆的方程为22(2)(1)2x y -+-=考点：圆的标准方程 15．【解析】【分析】先确定轨迹再根据射线上点与圆的位置关系求最值即得结果【详解】所以为以为圆心为半径的圆及其内部设射线的端点为所以的最小值为故答案为：【点睛】本题考查动点轨迹以及点与圆位置关系考查数形结解析：12-+ 【解析】【分析】先确定D 轨迹，再根据射线上点与圆的位置关系求最值，即得结果.【详解】2222222(1)1,111,y x c a a c a a =+∴=--=∴=-Q ，所以D 为以(1,0)F -为圆心，1a +为半径的圆及其内部，设射线()02x y x =≥－的端点为(2,2)A ，所以PQ 的最小值为||(1),12,AF a a a a -+===.故答案为：12-+. 【点睛】本题考查动点轨迹以及点与圆位置关系，考查数形结合思想以及基本分析求解能力，属中档题.16．②④【解析】【分析】对每一个选项分析判断得解【详解】根据已知可得面β和面γ可成任意角度和面α必垂直所以直线m 可以和面β成任意角度①不正确；l ⊂γl ⊥m 所以l ⊥α②正确；③显然不对；④因为l ⊂βl ⊥α解析：②④【解析】【分析】对每一个选项分析判断得解.【详解】根据已知可得面β和面γ可成任意角度，和面α必垂直．所以直线m 可以和面β成任意角度，①不正确；l ⊂γ，l⊥m，所以l⊥α，②正确；③显然不对；④因为l ⊂β，l⊥α，所以α⊥β，④正确．故答案为②④【点睛】本题主要考查空间线面垂直和面面垂直的证明，意在考查学生对这些知识的理解掌握水平，属于基础题.17．【解析】【分析】根据斜率的几何意义表示函数图象上的点与点连线的斜率数形结合即可求解【详解】为点与点连线的斜率点在函数图像上在抛物线图象上的最大值为最小值为过点与图象相切的切线斜率设为切线方程为代入得解析：2] 【解析】【分析】根据斜率的几何意义，()g x =表示函数y =(2,3)连线的斜率，数形结合，即可求解.【详解】()32g x x =-为点(x 与点(2,3)连线的斜率，点([0,1]x x ∈在函数[0,1]y x =∈图像上， (1,1)B 在抛物线图象上，()g x 的最大值为31221AB k -==-，最小值为过A 点与[0,1]y x =∈图象相切的切线斜率，设为k ，切线方程为(2)3y k x =-+，代入,[0,1]y x x =∈得， 320,0,14(32)0kx x k k k k -+-=≠∆=--=，即281210k k -+=，解得37k +=或37k -= 当37k +=时，37[0,1]372x ==-∈+⨯，当374k -=时，37[0,1]372x ==+∉-⨯ 不合题意，舍去， ()g x 值域为37[,2]4+. 故答案为:37[,2]+.【点睛】本题考查函数的值域、斜率的几何意义，考查数形结合思想，属于中档题.18．【解析】【分析】在平面中与的交点即为求出长即可求解【详解】连在正方体中所以四边形为矩形相交其交点为平面的交点是的中点为的中位线为中点正方体各棱长为1故答案为:【点睛】本题考查空间线面位置关系确定直线 5【解析】【分析】在平面11BB D D 中，1D M 与BD 的交点即为N ，求出BN 长，即可求解.【详解】连BD ，在正方体1111ABCD A B C D -中，11111,//,BB DD BB DD DD BD =⊥，所以四边形11BB D D 为矩形，1,BD D M 相交，其交点为1D M 平面ABCD 的交点N ，Q M 是1BB 的中点，111,//2BM DD BM DD ∴=， BM 为1DD N V 的中位线，B 为DN 中点，正方体各棱长为1，2BN BD ∴==，,1,2,135ABN AB BN ABN ==∠=o V ，2222cos AN AB BN AB BN ABN =+-⋅⋅∠232125=+⨯⨯⨯=，5AN ∴=. 故答案为:5.【点睛】本题考查空间线面位置关系，确定直线与平面交点是解题的关键，意在考查直观想象能力，属于中档题.19．4【解析】因为圆=关于直线=对称所以圆心在直线=上所以即又圆的半径为当点(ab)与圆心的距离最小时切线长取得最小值又点(ab)与圆心的距离为=所以切线长的最小值为=故答案为4点睛：本题主要考查直线与解析：4【解析】因为圆22:243C x y x y ++-+=0关于直线26ax by ++=0对称,所以圆心()1,2C -在直线26ax by ++=0上,所以2260a b -++=,即3a b -=,2,当点(a,b )与圆心的距离最小时,切线长取得最小值,又点(a,b )与圆心的距离为()()2212a b ++-()2221832a -+≥所以切线长的最小值为()22(32)2-=4.故答案为4 点睛：本题主要考查直线与圆的位置关系,考查了转化思想.利用勾股关系，切线长取得最小值时即为当点(a,b )与圆心的距离最小时.20．【解析】【分析】当过球内一点的截面与垂直时截面面积最小可求截面半径即可求出过点的平面截球的截面面积的最小值【详解】解：棱长等于的正方体它的外接球的半径为3当过点的平面与垂直时截面面积最小故答案为：【解析：3π.【解析】【分析】当过球内一点E 的截面与OE 垂直时，截面面积最小可求截面半径，即可求出过点E 的平面截球O 的截面面积的最小值．【详解】解：棱长等于1111ABCD A B C D -，它的外接球的半径为3，||OE =当过点E 的平面与OE 垂直时，截面面积最小，r 33S ππ=⨯=，故答案为：3π．【点睛】本题考查过点E 的平面截球O 的截面面积的最小值及接体问题，找准量化关系是关键，属于中档题．三、解答题21．（1）证明见解析；（2）4【解析】【分析】（1）证明DE ∥BC ，DE ⊥平面ABD ，可得BC ⊥平面ABD ，由面面垂直的判定定理即可证出平面ABD ⊥平面ABC ；（2）取BD 的中点O ，所以AO BD ⊥，由（1）可知平面ABD ⊥平面BCDE ，所以AO ⊥平面BCDE ，所以以O 为原点建立如图所示空间直角坐标系，则(00A ,，()1,0,0B ，()1,4,0C ，()1,2,0E -，设平面ABC 的法向量为(),,m x y z =u r ，利用空间向量法求解即可.【详解】（1）由题意可知DE 为ABC V 的中位线，所以//DE BC BC ，因为90B =o ∠，所以BC AB ⊥，所以DE AB ⊥，因为图（2）所示的空间图形是由ABC V 沿中位线DE 翻折得到的，所以DE AD ⊥，DE BD ⊥，又AD BD D =I ，所以DE ⊥平面ABD ，所以BC ⊥平面ABD ，因为BC ⊂平面ABC ，所以平面ABD ⊥平面ABC ；（2）由（1）可知二面角A DE C --的平面角即为ADB ∠，所以3πθ∠==ADB ，因为AD BD =，所以ABD △为等边三角形，如图取BD 的中点O ，所以AO BD ⊥，由（1）可知平面ABD ⊥平面BCDE ，Q 平面ABD ⋂平面BCDE BD =，AO ⊂平面ABD ，所以AO ⊥平面BCDE ，所以以O 为原点建立如图所示空间直角坐标系，设图1等腰直角ABC V 中4AB =，则图2中2AD BD AB ===，则()003A ,,，()1,0,0B，()1,4,0C ，()1,2,0E -，所以()1,0,3AB =-uu u r ，()1,4,3=-u u u r AC ，()1,2,3=--u u u r AE ，设平面ABC 的法向量为(),,m x y z =u r ，所以有00m AB m AC ⎧⋅=⎨⋅=⎩u u u v v u u u v v ，即30430x z x y z ⎧-=⎪⎨+-=⎪⎩，取()3,0,1m =u r ，设直线AE 与平面ABC 所成的角为α，所以6sin cos ,m AE m AE m AEα⋅=<>==⋅u r u u u r u r u u u r u u r u u u u r ，所以直线AE 与平面ABC 所成的角的正弦值为64.【点睛】本题主要考查面面垂直的判定定理以及空间中直线与平面所成角的求法，解题时要会用法向量求线面角.22．（1）见解析；（221. 【解析】【分析】（1）在ACD ∆中，由余弦定理可解得：4CD =所以222AC AD CD +=，所以ACD ∆是直角三角形，又ACE ∆可证为等边三角形，所以060CAE BCA ∠==∠，所以//BC AE ，即可证明//BC 平面SAE ；（2）：由（1）可知090BAE ∠=，以点A 为原点，以AB ,AE ，AS 所在直线分别为x 轴，y 轴，z 轴建立空间直角坐标系，利用空间向量可求直线SD 与平面SBC 所成角的正弦值.（1）证明：因为3AB =，1BC =，090ABC ∠=，所以2AC =，060BCA ∠=，在ACD ∆中，23AD =，2AC =，060ACD ∠=，由余弦定理可得：2222?cos AD AC CD AC CD ACD =+-∠解得：4CD =所以222AC AD CD +=，所以ACD ∆是直角三角形，又E 为CD 的中点，所以12AE CD CE == 又060ACD ∠=，所以ACE ∆为等边三角形，所以060CAE BCA ∠==∠，所以//BC AE ，又AE ⊂平面SAE ，BC ⊄平面SAE ，所以//BC 平面SAE .（2）解：由（1）可知090BAE ∠=，以点A 为原点，以AB ,AE ，AS 所在直线分别为x 轴，y 轴，z 轴建立空间直角坐标系，则()0,0,2S ，()3,0,0B ，()3,1,0C ，()3,3,0D -.所以)3,0,2SB =-u u v ，()3,1,2SC =-u u u v ，()3,3,2SD =--u u u v . 设(),,n x y z =v 为平面SBC 的法向量，则·0·0n SB n SC ⎧=⎨=⎩u u v v u u u v v ，即320320x z x y z ⎧-=⎪⎨+-=⎪⎩ 设1x =，则0y =，32z =，即平面SBC 的一个法向量为31,0,2n ⎛= ⎝⎭v ，所以·2321cos ,77164n SD n SD n SD -===-⨯u u u v v u u u v v u u u v v 所以直线SD 与平面SBC 21.不妨考查线面平行的证明以及利用空间向量求线面角，属中档题.23．（1）证明见解析（2）6-【解析】【分析】（1）由BC ⊥AC ，BC ⊥CD 得BC ⊥平面ACD ，证明四边形DCBE 是平行四边形得DE ∥BC ，故而DE ⊥平面ACD ，从而得证面面垂直；（2）建立空间坐标系，求出两半平面的法向量，计算法向量的夹角得出二面角的大小.【详解】（1）证明：∵AB 是圆O 的直径，∴AC ⊥BC ，∵DC ⊥平面ABC ，BC ⊂平面ABC ，∴DC ⊥BC ，又DC ∩AC ＝C ，∴BC ⊥平面ACD ，∵DC ∥EB ，DC ＝EB ，∴四边形DCBE 是平行四边形，∴DE ∥BC ，∴DE ⊥平面ACD ，又DE ⊂平面ADE ，∴平面ACD ⊥平面ADE.（2）当C 点为半圆的中点时，AC ＝BC ＝，以C 为原点，以CA ，CB ，CD 为坐标轴建立空间坐标系如图所示：则D （0，0，1），E （0，，1），A （，0，0），B （0，，0）， ∴AB =uu u r （﹣，，0），BE =u u u r （0，0，1），DE =uuu r （0，，0），DA =u u u r （0，﹣1），设平面DAE 的法向量为m =r （x 1，y 1，z 1），平面ABE 的法向量为n =r（x 2，y 2，z 2），则00m DA m DE ⎧⋅=⎨⋅=⎩u u u v r u u u v r ，00n AB n BE ⎧⋅=⎨⋅=⎩u u u v r u u u v r，即11100z ⎧-=⎪⎨=⎪⎩，22200z ⎧-+=⎪⎨=⎪⎩，令x 1＝1得m =r （1，0，），令x 2＝1得n =r （1，1，0）.∴cos 6m n m n m n ⋅===r r r r r r <，>. ∵二面角D ﹣AE ﹣B 是钝二面角，∴二面角D ﹣AE ﹣B的余弦值为【点睛】本题考查了面面垂直的判定，空间向量与二面角的计算，属于中档题.24．（1）证明见解析；（2）1.【解析】试题分析：（1）利用等腰三角形的性质可得1A O AC ⊥，利用面面垂直的性质可得1A O ⊥平面ABC ，根据线面垂直的性质可得结论；（2）先证明11||A C 平面ABC ，可得1C 到平面ABC 的距离等于1A 到平面ABC 的距离，利用等积变换及棱锥的体积公式可得11113C ABC A ABC ABC V V S AO --∆==⋅= 11233132⨯⨯=. 试题解析：（1）∵11AA A C =，且O 为AC 的中点.∴1A O AC ⊥.又∵平面11AA C C ⊥平面ABC ，平面11AA C C ⋂平面ABC AC =，且1AO ⊂平面11AAC C ，∴1A O ⊥平面ABC .∵BC ⊂平面ABC ，∴1A O BC ⊥.（2）∵11||A C AC ，11A C ⊄平面ABC ，AC ⊂平面ABC ，∴11||A C 平面ABC .即1C 到平面ABC 的距离等于1A 到平面ABC 的距离.由（1）知1A O ⊥平面ABC 且22113AO AA AO =-=∴三棱锥1C ABC -的体积： 11113C ABC A ABC ABC V V S AO --∆==⋅= 11233132⨯⨯=. 25．（1）见解析；（2）见解析.【解析】【分析】（1）通过证明//NQ PA ，即可得到本题结论；（2）由题，先证PM AD ⊥和AD MB ⊥，即可得到AD ⊥平面PMB ，由此即可得到本题结论.【详解】（1）连接AC 交MB 于Q ，连接,NQ MC ．因为//AM BC ，12AM AD BC ==，所以四边形ABCM 是平行四边形，所以Q 是AC 的中点．又N 是PC 的中点，所以//NQ PA ，因为NQ ⊂平面MNB ，PA ⊄平面MNB ，所以//PA 平面MNB ；（2）因为PA PD =，AM MD =，所以PM AD ⊥，因为//MD BC ，MD BC =，所以四边形BCDM 是平行四边形，所以//MB DC ，因为=90ADC ∠︒，即AD DC ⊥，所以AD MB ⊥，因为PM MB M ⋂=，,PM MB ⊂平面PMB ，所以AD ⊥平面PMB ，又AD ⊂平面PAD ，所以平面PAD ⊥平面PMB ．【点睛】本题主要考查线面平行的判定与面面垂直的判定，考查学生的空间想象能力和逻辑推理能力.26．（1）见解析（2）45°【解析】(1)以点C 为原点，CB 、CA 、CC 1所在直线为x ，y ，z 轴，建立空间直角坐标系C －xyz ，如图所示，则B (1,0,0)，A (03，0)，A 1(036)，M 6⎛ ⎝⎭. 所以1A B u u u r ＝(136)，AM u u u u r ＝60,3,2⎛ ⎝⎭. 因为1A B u u u r ·AM u u u u r ＝1×0＋(33)＋(6)×620，所以A 1B ⊥AM . (2)因为ABC -A 1B 1C 1是直三棱柱，所以CC 1⊥平面ABC ，又BC ⊂平面ABC ，所以CC 1⊥BC . 因为∠ACB ＝90°，即BC ⊥AC ，又AC ∩CC 1＝C ，所以BC ⊥平面ACC 1A 1，即BC ⊥平面AMC . 所以CB u u u r 是平面AMC 的一个法向量，CB u u u r ＝(1,0,0)．设n ＝(x ，y ，z )是平面BAM 的一个法向量，BA u u u r ＝(－130)，BM u u u u r ＝61,0,2⎛⎫- ⎪ ⎪⎝⎭. 由0,{0nBA nBM ==u u u r u u u u r 得30{602x y x z -=-+=，令z ＝2，得x 6，y 2. 所以n ＝62，2)因为|CB u u u r |＝1，|n |＝3cos 〈CB u u u r ，n 〉＝CB n CB n ⋅⋅u u u r u u u r ＝22，因此二面角B -AM -C 的大小为45°。