2016_2018学年高考数学试题分项版解析专题07导数的应用理含解析
三年高考(2016-2018)数学(理)真题分项版解析专题1 集合解析版

三年高考(2016-2018)数学(理)专题01 集合考纲解读明方向1.掌握集合的表示方法,能判断元素与集合的“属于”关系、集合与集合之间的包含关系.2.深刻理解、掌握集合的元素,子、交、并、补集的概念.熟练掌握集合的交、并、补的运算和性质.能用韦恩(Venn)图表示集合的关系及运算.3.本部分内容在高考试题中多以选择题或填空题的形式出现,以函数、不等式等知识为载体,以集合语言和符号语言表示为表现形式,考查数学思想方法.4.本节内容在高考中分值约为5分,属中低档题.命题探究练扩展2018年高考全景展示1.【2018年理北京卷】已知集合A={x||x|<2},B={–2,0,1,2},则A B= A. {0,1} B. {–1,0,1} C. {–2,0,1,2} D. {–1,0,1,2}【答案】A【解析】,因此A B=,选A.点睛:认清元素的属性,解决集合问题时,认清集合中元素的属性(是点集、数集或其他情形)和化简集合是正确求解的两个先决条件.2.【2018年理新课标I卷】已知集合,则A. B.C. D.【答案】B点睛:该题考查的是有关一元二次不等式的解法以及集合的补集的求解问题,在解题的过程中,需要明确一元二次不等式的解集的形式以及补集中元素的特征,从而求得结果.3.【2018年全国卷Ⅲ理】已知集合,,则A. B. C. D.【答案】C【解析】由集合A得,所以,故答案选C.点睛:本题主要考查交集的运算,属于基础题。
4.【2018年理数全国卷II】已知集合,,,,则中元素的个数为A. 9B. 8C. 5D. 4【答案】A【解析】.,当时,;当时,;当时,;所以共有9个,选A.点睛:本题考查集合与元素关系,点与圆位置关系,考查学生对概念理解与识别.5.【2018年理数天津卷】设全集为R,集合,,则A. B. C. D.【答案】B【解析】由题意可得:,结合交集的定义可得:.本题选择B选项.点睛:本题主要考查交集的运算法则,补集的运算法则等知识,意在考查学生的转化能力和计算求解能力.6.【2018年江苏卷】已知集合,,那么________.【答案】{1,8}【解析】由题设和交集的定义可知:.点睛:本题考查交集及其运算,考查基础知识,难度较小.2017年高考全景展示1.【2017课标1,理1】1},则()A .{|0}AB x x =<B .A B =RC .{|1}A B x x =>D .A B =∅【答案】A 【解析】由31x <可得033x <,则0x <,即{|0}B x x =<,所以{|1}{|0}{|0}A B x x x x x x =<<=<,{|1}{|0}{|1}A B x x x x x x =<<=<,故选A.【考点】集合的运算,指数运算性质.【名师点睛】集合的交、并、补运算问题,应先把集合化简再计算,常常借助数轴或韦恩图进行处理.2.【2017课标II ,理】设集合{}1,2,4A =,{}240x x x m B =-+=.若{}1A B =,则B =( )A.{}1,3-B.{}1,0C.{}1,3D.{}1,5【答案】C【考点】 交集运算,元素与集合的关系【名师点睛】集合中元素的三个特性中的互异性对解题影响较大,特别是含有字母的集合,在求出字母的值后,要注意检验集合中的元素是否满足互异性.两个防范:一是不要忽视元素的互异性;二是保证运算的准确性.3.【2017课标3,理1】已知集合A ={}22(,)1x y x y +=│,B ={}(,)x y y x =│,则A B 中元素的个数为( )A .3B .2C .1D .0【答案】B【考点】 交集运算;集合中的表示方法.【名师点睛】求集合的基本运算时,要认清集合元素的属性(是点集、数集或其他情形)和化简集合,这是正确求解集合运算的两个先决条件.集合中元素的三个特性中的互异性对解题影响较大,特别是含有字母的集合,在求出字母的值后,要注意检验集合中的元素是否满足互异性.4.【2017北京,理1】若集合A ={x |–2<x <1},B={x |x <–1或x >3},则AB =( )(A ){x |–2<x <–1} (B ){x |–2<x <3}(C ){x |–1<x <1} (D ){x |1<x <3}【答案】A 【解析】利用数轴可知{}21A B x x =-<<-,故选A.【考点】集合的运算【名师点睛】集合分为有限集合和无限集合,若集合个数比较少时可以用列举法表示,若集合是无限集合就用描述法表示,注意代表元素是什么,集合的交、并、补运算问题,应先把集合化简再计算,常常借助数轴或韦恩图进行处理.5.【2017浙江,1】已知}11|{<<-=x x P ,}20{<<=x Q ,则=Q P ( )A .)2,1(-B .)1,0(C .)0,1(-D .)2,1( 【答案】A【解析】利用数轴,取Q P ,所有元素,得=Q P )2,1(-.【考点】集合运算【名师点睛】对于集合的交、并、补运算问题,应先把集合化简再计算,常常借助数轴或韦恩图处理.6.【2017天津,理1】设集合{1,2,6},{2,4},{|15}A B C x x ===∈-≤≤R ,则()A B C =( )(A ){2} (B ){1,2,4} (C ){1,2,4,6} (D ){|15}x x ∈-≤≤R【答案】B【解析】(){1246}[15]{124}A B C =-=,,,,,, ,选B.【考点】 集合的运算【名师点睛】集合的交、并、补运算问题,应先把集合化简再计算,常常借助数轴或韦恩图进行处理.7.【2017江苏,1】已知集合{1,2}A =,2{,3}B a a =+,若{1}A B =则实数a 的值为 .【答案】1【解析】由题意1B ∈,显然233a +≥,所以1a =,此时234a +=,满足题意,故答案为1.【考点】元素的互异性【名师点睛】(1)认清元素的属性,解决集合问题时,认清集合中元素的属性(是点集、数集或其他情形)和化简集合是正确求解的两个先决条件.(2)注意元素的互异性.在解决含参数的集合问题时,要注意检验集合中元素的互异性,否则很可能会因为不满足“互异性”而导致解题错误.(3)防范空集.在解决有关,A B A B=∅⊆等集合问题时,往往忽略空集的情况,一定先考虑∅是否成立,以防漏解. 2016年高考全景展示1.【2016课标1,理1】设集合2430A x x x =-+< ,{}230x x ->,则A B = ( ) (A )33,2⎛⎫-- ⎪⎝⎭ (B )33,2⎛⎫- ⎪⎝⎭ (C )31,2⎛⎫ ⎪⎝⎭ (D )3,32⎛⎫ ⎪⎝⎭ 【答案】D考点:集合的交集运算【名师点睛】集合是每年中的必考题,一般以基础题形式出现,属得分题.解决此类问题一般要把参与运算的集合化为最简形式再进行运算,如果是不等式解集、函数定义域及值域有关数集之间的运算,常借助数轴进行运算.2.【2016新课标3理数】设集合{}{}|(2)(3)0,|0S x x x T x x =--≥=> ,则S T =( )(A) [2,3] (B)(-∞ ,2]U [3,+∞) (C) [3,+∞) (D)(0,2]U[3,+∞)【答案】D【技巧点拨】研究集合的关系,处理集合的交、并、补的运算问题,常用韦恩图、数轴等几何工具辅助解题.一般地,对离散的数集、抽象的集合间的关系及运算,可借助韦恩图,而对连续的集合间的运算及关系,可借助数轴的直观性,进行合理转化.3.【2016新课标2理数】已知集合{1,}A =2,3,{|(1)(2)0,}B x x x x =+-<∈Z ,则A B =( )(A ){1} (B ){12}, (C ){0123},,, (D ){10123}-,,,, 【答案】C【解析】试题分析:集合B {x |1x 2,x Z}{0,1}=-<<∈=,而A {1,2,3}=,所以A B {0,1,2,3}=,故选C.考点: 集合的运算.【名师点睛】集合的交、并、补运算问题,应先把集合化简在计算,常常借助数轴或韦恩图处理.4. 【2016山东理数】设集合2{|2,},{|10},x A y y x B x x ==∈=-<R 则A B =( )(A )(1,1)-(B )(0,1) (C )(1,)-+∞ (D )(0,)+∞【答案】C【解析】 试题分析:}0|{>=y y A ,}11|{<<-=x x B ,则A B =∞(-1,+),选C. 考点:1.指数函数的性质;2.解不等式;3.及集合的运算.【名师点睛】本题主要考查集合的并集、补集,是一道基础题目.从历年题目看,集合的基本运算,是必考考点,也是考生必定得分的题目之一.本题与求函数值域、解不等式等相结合,增大了考查的覆盖面.5.【2016浙江理数】已知集合{}{}213,4,P x x Q x x =∈≤≤=∈≥R R 则()P Q ⋃=R ð( )A .[2,3]B .( -2,3 ]C .[1,2)D .(,2][1,)-∞-⋃+∞【答案】B【解析】 试题分析:根据补集的运算得{}[](]24(2,2),()(2,2)1,32,3=<=-∴=-=-R R Q x x P Q 痧.故选B .考点:1、一元二次不等式;2、集合的并集、补集.【易错点睛】解一元二次不等式时,2x 的系数一定要保证为正数,若2x 的系数是负数,一定要化为正数,否则很容易出错.6.【2016年北京理数】已知集合{|||2}A x x =<,{1,0,1,2,3}B =-,则A B =( )A.{0,1}B.{0,1,2}C.{1,0,1}-D.{1,0,1,2}-【答案】C【解析】由}22|{<<-=x x A ,得}1,0,1{-=B A ,故选C.考点:集合交集.【名师点睛】1.首先要弄清构成集合的元素是什么(即元素的意义),是数集还是点集,如集合)}|)y=,)},(yx=三者是不同的.yf{(xyf{x|(yfx=,)}|{x(2.集合中的元素具有三性——确定性、互异性、无序性,特别是互异性,在判断集合中元素的个数时,以及在含参的集合运算中,常因忽视互异性,疏于检验而出错.3.数形结合常使集合间的运算更简捷、直观.对离散的数集间的运算或抽象集合间的运算,可借助Venn图实施,对连续的数集间的运算,常利用数轴进行,对点集间的运算,则通过坐标平面内的图形求解,这在本质上是数形结合思想的体现和运用.4.空集是不含任何元素的集合,在未明确说明一个集合非空的情况下,要考虑集合为空集的可能.另外,不可忽视空集是任何元素的子集.7.【2016年四川理数】设集合{|22}=-≤≤,Z为整数集,则A ZA x x中元素的个数是()(A)3 (B)4 (C)5 (D)6【答案】C【解析】由题意,{2,1,0,1,2}A Z=--,故其中的元素个数为5,选C.考点:集合中交集的运算.【名师点睛】集合的概念及运算一直是的热点,几乎是每年必考内容,属于容易题.一般是结合不等式,函数的定义域值域考查,解题的关键是结合韦恩图或数轴解答.8.【2016天津理数】已知集合{1,2,3,4},{|32},,则A B===-∈A B y y x x A=()(A){1}(B){4}(C){1,3}(D){1,4}【答案】D【解析】试题分析:{1,4,7,10},A B{1,4}.B==选D.考点:集合运算【名师点睛】本题重点考查集合的运算,容易出错的地方是审错题意,误求并集,属于基本题,难点系数较小.一要注意培养良好的答题习惯,避免出现粗心错误,二是明确集合交集的考查立足于元素互异性,做到不重不漏.9.【2016江苏卷】已知集合则____________.【答案】{}1,2-【解析】试题分析:{1,2,3,6}{|23}{1,2}A B x x =--<<=-考点:集合运算【名师点睛】本题重点考查集合的运算,容易出错的地方是审错题意,属于基本题,难点系数较小.一要注意培养良好的答题习惯,避免出现粗心错误,二是明确江苏对于集合题的考查立足于列举法,强调对集合运算有关概念及法则的理解{1,2,3,6},{|23},A B x x =-=-<<=A B。
高考(2016-2018)数学(理)真题分项版解析——专题07导数的应用(解析版)
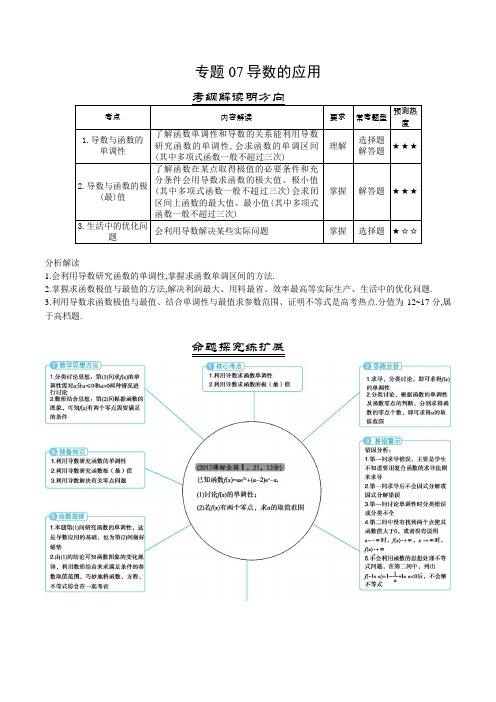
专题07导数的应用考纲解读明方向考点内容解读要求常考题型预测热度1.导数与函数的单调性了解函数单调性和导数的关系能利用导数研究函数的单调性,会求函数的单调区间(其中多项式函数一般不超过三次)理解选择题解答题★★★2.导数与函数的极(最)值了解函数在某点取得极值的必要条件和充分条件会用导数求函数的极大值、极小值(其中多项式函数一般不超过三次)会求闭区间上函数的最大值、最小值(其中多项式函数一般不超过三次)掌握解答题★★★3.生活中的优化问题会利用导数解决某些实际问题掌握选择题★☆☆分析解读1.会利用导数研究函数的单调性,掌握求函数单调区间的方法.2.掌握求函数极值与最值的方法,解决利润最大、用料最省、效率最高等实际生产、生活中的优化问题.3.利用导数求函数极值与最值、结合单调性与最值求参数范围、证明不等式是高考热点.分值为12~17分,属于高档题.命题探究练扩展2018年高考全景展示1.2018年理数天津卷已知函数,,其中a>1.(I)求函数的单调区间;(II)若曲线在点处的切线与曲线在点处的切线平行,证明;(III)证明当时,存在直线l,使l是曲线的切线,也是曲线的切线.答案(Ⅰ)单调递减区间,单调递增区间为;(Ⅱ)证明见解析;(Ⅲ)证明见解析.(III)由题意可得两条切线方程分别为l1:.l2:.则原问题等价于当时,存在,,使得l1和l2重合.转化为当时,关于x1的方程存在实数解,构造函数,令,结合函数的性质可知存在唯一的x0,且x0>0,使得,据此可证得存在实数t,使得,则题中的结论成立.详解:(I)由已知,,有.令,解得x=0.由a>1,可知当x变化时,,的变化情况如下表:x0极小值所以函数的单调递减区间,单调递增区间为.(III)曲线在点处的切线l1:.曲线在点处的切线l2:.要证明当时,存在直线l,使l是曲线的切线,也是曲线的切线,只需证明当时,存在,,使得l1和l2重合.即只需证明当时,方程组有解,由①得,代入②,得. ③因此,只需证明当时,关于x1的方程③存在实数解.设函数,即要证明当时,函数存在零点.,可知时,;时,单调递减,又,,故存在唯一的x0,且x0>0,使得,即.由此可得在上单调递增,在上单调递减.在处取得极大值.因为,故,所以.下面证明存在实数t,使得.由(I)可得,当时,有,所以存在实数t,使得,因此,当时,存在,使得.所以,当时,存在直线l,使l是曲线的切线,也是曲线的切线.点睛:导数是研究函数的单调性、极值(最值)最有效的工具,而函数是高中数学中重要的知识点,所以在历届高考中,对导数的应用的考查都非常突出,本专题在高考中的命题方向及命题角度从高考来看,对导数的应用的考查主要从以下几个角度进行: (1)考查导数的几何意义,往往与解析几何、微积分相联系. (2)利用导数求函数的单调区间,判断单调性;已知单调性,求参数. (3)利用导数求函数的最值(极值),解决生活中的优化问题. (4)考查数形结合思想的应用.2.2018年理北京卷设函数=[].(Ⅰ)若曲线y= f(x)在点(1,)处的切线与轴平行,求a;(Ⅱ)若在x=2处取得极小值,求a的取值范围.答案(1) a的值为1 (2) a的取值范围是(,∞)解析分析:(1)先求导数,再根据得a;(2)先求导数的零点:,2;再分类讨论,根据是否满足在x=2处取得极小值,进行取舍,最后可得a的取值范围.详解:解:(Ⅰ)因为=[],所以f ′(x)=[2ax–(4a1)]e x[ax2–(4a1)x4a3]e x(x∈R)=[ax2–(2a1)x2]e x.f′(1)=(1–a)e.由题设知f′(1)=0,即(1–a)e=0,解得a=1.此时f (1)=3e≠0.所以a的值为1.点睛:利用导数的几何意义解题,主要是利用导数、切点坐标、切线斜率之间的关系来进行转化.以平行、垂直直线斜率间的关系为载体求参数的值,则要求掌握平行、垂直与斜率之间的关系,进而和导数联系起来求解.3.2018年江苏卷记分别为函数的导函数.若存在,满足且,则称为函数与的一个“S点”.(1)证明:函数与不存在“S点”;(2)若函数与存在“S点”,求实数a的值;(3)已知函数,.对任意,判断是否存在,使函数与在区间内存在“S点”,并说明理由.答案(1)证明见解析(2)a的值为(3)对任意a>0,存在b>0,使函数f(x)与g(x)在区间(0,∞)内存在“S点”.解析分析:(1)根据题中“S点”的定义列两个方程,根据方程组无解证得结论;(2)同(1)根据“S点”的定义列两个方程,解方程组可得a的值;(3)通过构造函数以及结合“S点”的定义列两个方程,再判断方程组是否有解即可证得结论.详解:解:(1)函数f(x)=x,g(x)=xx2,则f′(x)=1,g′(x)=2x2.由f(x)=g(x)且f′(x)= g′(x得,此方程组无解,因此,f(x)与g(x)不存在“S”点.(2)函数,,则.设x0为f(x)与g(x)的“S”点,由f(x0)与g(x0)且f′(x0)与g′(x0得,即,(*)得,即,则.当时,满足方程组(*即为f(x)与g(x)的“S”点.因此,a的值为.(3)对任意a>0,设.因为,且h(x)的图象是不间断的,所以存在∈(0,1使得,令,则b>0.函数,则.由f(x)与g(x)且f′(x)与g′(x得,即(**)此时,满足方程组(**即是函数f(x)与g(x)在区间(0,1)内的一个“S点”.因此,对任意a>0,存在b>0,使函数f(x)与g(x)在区间(0,∞)内存在“S点”.点睛:涉及函数的零点问题、方程解的个数问题、函数图象交点个数问题,一般先通过导数研究函数的单调性、最大值、最小值、变化趋势等,再借助函数的大致图象判断零点、方程根、交点的情况,归根到底还是研究函数的性质,如单调性、极值,然后通过数形结合的思想找到解题的思路.4.2018年理新课标I卷已知函数.(1)讨论的单调性;(2)若存在两个极值点,证明:.答案(1)当时,在单调递减.,当时,在单调递减,在单调递增.(2)证明见解析.(i)若,则,当且仅当,时,所以在单调递减.(ii)若,令得,或.当时,;当时,.所以在单调递减,在单调递增.(2)由(1)知,存在两个极值点当且仅当.由于的两个极值点满足,所以,不妨设,则.由于,所以等价于.设函数,由(1)知,在单调递减,又,从而当时,.所以,即.点睛:该题考查的是应用导数研究函数的问题,涉及到的知识点有应用导数研究函数的单调性、应用导数研究函数的极值以及极值所满足的条件,在解题的过程中,需要明确导数的符号对单调性的决定性作用,再者就是要先保证函数的生存权,先确定函数的定义域,要对参数进行讨论,还有就是在做题的时候,要时刻关注第一问对第二问的影响,再者就是通过构造新函数来解决问题的思路要明确.2017年高考全景展示1.2017课标II ,理11若2x =-是函数21()(1)x f x x ax e -=+-的极值点,则()f x 的极小值为( )A.1-B.32e --C.35e -D.1 答案A 解析试题分析:由题可得12121()(2)(1)[(2)1]x x x f x x a e x ax e x a x a e ---'=+++-=+++-因为(2)0f '-=,所以1a =-,21()(1)x f x x x e -=--,故21()(2)x f x x x e -'=+-令()0f x '>,解得2x <-或1x >,所以()f x 在(,2),(1,)-∞-+∞单调递增,在(2,1)-单调递减 所以()f x 极小值为()111(111)1f e -=--=-,故选A 。
三年高考(2016-2018)数学(文)真题分类解析:专题07-导数的应用
考纲解读明方向分析解读1.会利用导数研究函数的单调性,掌握求函数单调区间的方法.2.掌握求函数极值与最值的方法,解决利润最大、用料最省、效率最高等实际生产、生活中的优化问题.3.利用导数求函数极值与最值、结合单调性与最值求参数范围、证明不等式是高考热点.分值为12~17分,属于高档题.命题探究练扩展2018年高考全景展示1.【2018年新课标I卷文】已知函数.(1)设是的极值点.求,并求的单调区间;(2)证明:当时,.【答案】(1) a=;f(x)在(0,2)单调递减,在(2,+∞)单调递增.(2)证明见解析.详解:(1)f(x)的定义域为,f ′(x)=a e x–.由题设知,f ′(2)=0,所以a=.从而f(x)=,f ′(x)=.当0<x<2时,f ′(x)<0;当x>2时,f ′(x)>0.所以f(x)在(0,2)单调递减,在(2,+∞)单调递增.(2)当a ≥时,f (x )≥.设g (x )=,则当0<x <1时,g′(x )<0;当x >1时,g′(x )>0.所以x =1是g (x )的最小值点.故当x >0时,g (x )≥g (1)=0.因此,当时,.点睛:该题考查的是有关导数的应用问题,涉及到的知识点有导数与极值、导数与最值、导数与函数的单调性的关系以及证明不等式问题,在解题的过程中,首先要保证函数的生存权,先确定函数的定义域,之后根据导数与极值的关系求得参数值,之后利用极值的特点,确定出函数的单调区间,第二问在求解的时候构造新函数,应用不等式的传递性证得结果.2017年高考全景展示1.【2016高考四川文科】已知a 函数3()12f x x x =-的极小值点,则a = ( ) (A)-4 (B) -2 (C)4 (D)2 【答案】D 【解析】考点:函数导数与极值.【名师点睛】本题考查函数的极值.在可导函数中函数的极值点0x 是方程'()0f x =的解,但0x 是极大值点还是极小值点,需要通过这点两边的导数的正负性来判断,在0x 附近,如果0x x <时,'()0f x <,0x x >时'()0f x >,则0x 是极小值点,如果0x x <时,'()0f x >,0x x >时,'()0f x <,则0x 是极大值点,2.【2017浙江,7】函数y=f (x )的导函数()y f x '=的图像如图所示,则函数y=f (x )的图像可能是【答案】D【解析】试题分析:原函数先减再增,再减再增,且由增变减时,极值点大于0,因此选D . 【考点】导函数的图象【名师点睛】本题主要考查导数图象与原函数图象的关系:若导函数图象与x 轴的交点为0x ,且图象在0x 两侧附近连续分布于x 轴上下方,则0x 为原函数单调性的拐点,运用导数知识来讨论函数单调性时,由导函数)('x f 的正负,得出原函数)(x f 的单调区间. 3.【2017课标1,文21】已知函数()f x =e x (e x ﹣a )﹣a 2x . (1)讨论()f x 的单调性;(2)若()0f x ≥,求a 的取值范围.【答案】(1)当0a =,)(x f 在(,)-∞+∞单调递增;当0a >,()f x 在(,ln )a -∞单调递减,在(ln ,)a +∞单调递增;当0a <,()f x 在(,ln())2a -∞-单调递减,在(ln(),)2a-+∞单调递增;(2)34[2e ,1]-.【解析】(2)①若0a =,则2()xf x e =,所以()0f x ≥.【考点】导数应用【名师点睛】本题主要考查导数的两大方面的应用:(一)函数单调性的讨论:运用导数知识来讨论函数单调性时,首先考虑函数的定义域,再求出)('x f ,有)('x f 的正负,得出函数)(x f 的单调区间;(二)函数的最值(极值)的求法:由确认的单调区间,结合极值点的定义及自变量的取值范围,得出函数)(x f 极值或最值.4.【2017课标II ,文21】设函数2()(1)x f x x e =-. (1)讨论()f x 的单调性;(2)当0x ≥时,()1f x ax ≤+,求a 的取值范围.【答案】(Ⅰ)在(,1-∞-和(1)-+∞单调递减,在(11--单调递增(Ⅱ)[1,)+∞ 【解析】试题分析:(1)先求函数导数,再求导函数零点,列表分析导函数符号确定单调区间(2)对a 分类讨论,当a ≥1时,()(1)(1)1x f x x x e x a x =-+≤+≤+,满足条件;当0a ≤时,取200000()(1)(1)11x f x x x ax =>-+=>+,当0<a <1时,取0x =,20000()(1)(1)1f x x x ax >-+>+.试题解析:(1)2()(12)x f x x x e '=--令()0f x '=得1x =-当(,1x ∈-∞-时,()0f x '<;当(11x ∈--+时,()0f x '>;当(1)x ∈-+时,()0f x '<所以()f x 在(,1-∞-和(1)-+∞单调递减,在(11--单调递增【考点】利用导数求函数单调区间,利用导数研究不等式恒成立【名师点睛】利用导数研究不等式恒成立或存在型问题,首先要构造函数,利用导数研究函数的单调性,求出最值,进而得出相应的含参不等式,从而求出参数的取值范围;也可分离变量,构造函数,直接把问题转化为函数的最值问题.2016年高考全景展示1.【2016高考山东文数】(本小题满分13分) 设f (x )=x ln x –ax 2+(2a –1)x ,a ∈R . (Ⅰ)令g (x )=f'(x ),求g (x )的单调区间;(Ⅱ)已知f (x )在x =1处取得极大值.求实数a 的取值范围.【答案】 (Ⅰ)当0a ≤时,函数()g x 单调递增区间为()0,+∞; 当0a >时,函数()g x 单调递增区间为10,2a ⎛⎫ ⎪⎝⎭,单调递减区间为1,2a ⎛⎫+∞ ⎪⎝⎭. (Ⅱ)12a >. 【解析】试题分析:(Ⅰ)求导数()'ln 22,f x x ax a =-+ 可得()()ln 22,0,g x x ax a x =-+∈+∞,从而()112'2ax g x a x x-=-=, 讨论当0a ≤时,当0a >时的两种情况下导函数正负号,确定得到函数的单调区间. (Ⅱ)分以下情况讨论:①当0a ≤时,②当102a <<时,③当12a =时,④当12a >时,综合即得.(Ⅱ)由(Ⅰ)知,()'10f =.①当0a ≤时,()'0f x <,()f x 单调递减. 所以当()0,1x ∈时,()'0f x <,()f x 单调递减. 当()1,x ∈+∞时,()'0f x >,()f x 单调递增. 所以()f x 在1x =处取得极小值,不合题意. ②当102a <<时,112a >,由(Ⅰ)知()'f x 在10,2a ⎛⎫⎪⎝⎭内单调递增, 可得当当()0,1x ∈时,()'0f x <,11,2x a ⎛⎫∈ ⎪⎝⎭时,()'0f x >, 所以()f x 在(0,1)内单调递减,在11,2a ⎛⎫⎪⎝⎭内单调递增,所以()f x 在1x =处取得极小值,不合题意.考点:1.应用导数研究函数的单调性、极值;2.分类讨论思想.【名师点睛】本题主要考查导数的计算、应用导数研究函数的单调性与极值、分类讨论思想.本题覆盖面广,对考生计算能力要求较高,是一道难题.解答本题,准确求导数是基础,恰当分类讨论是关键,易错点是分类讨论不全面、不彻底、不恰当.本题能较好的考查考生的逻辑思维能力、基本计算能力、分类讨论思想等.。
三年高考(2016-2018)高考数学试题分项版解析专题04函数性质与应用理(含解析)

A. -50B. 0C. 2D. 50专题04函数性质与应用考纲解读明方向考点 内容解读要求 常考题型 预测热度1.函数的单调性及最 值理解函数的单调性、最大(小)值及 其几何意义出选择题、 填空题、★★★2.函数的奇偶性 了解函数奇偶性的含义,会判断简 单的函数的奇偶性3.函数的周期性了解函数周期性的含义分析解读1.考查函数的单调区间的求法及单调性的应用,如应用单调性求值域、比较大小或证明不等式,运用定义或导数判断或证明函数的单调性等•重视•2018年咼考全景展示1.【2018年理数全国卷II 】已知’ 是定义域为的奇函数,满足厂」…门-:;「:'•〕•若」,2•借助数形结合的思想解题 .函数的单调性、周期性、奇偶性的综合性问题是高考热点,应引起足够的3.本节内容在高考中分值为5分左右,属于中档题.弋龍力荽 ---------------------------- 1 一会求強合瞋敷的单调区崗一 去已知童合确数的单爾区例,求举数 師.命题探究练扩展•❶核心署点:匚对数爾数的单调性,2二次爾数农麻定区向上苗单鬪卄一 玄总合雨数的单斜性,p (?爺露赃〕 ------------------------ 1麻當见的相箭熨型臭介两數 和对豪型复合南数,求复自甬数的臥训 区闭时.先求定里战・然垢站今河堆 异减求解.应注尬葷后騎壤的单闊贰 间用徒用“U"连摸一 丸窪合團数tft 域怕求解也址曲考鬆型, 注慰对函数进行井屁虎#r(2017律拆全国II , £ 5^)声丽預储备. ------------------- 九能#f —元二就不等式一2圮令系数单岡性的求解方社: 恫增舁减”.吐卜叫1)11(4.2)善案1 D也*=-加-iX )可徘叭4威x-Z 所妝曰-叫-打U (4,+*),爭"T-吐_£期菽在± E f- 3 “-芻上单调通减“在 T e (4,+1} 尸怙 u 在uE ((h*呵上单调 谨塔馬恥冃亦[-毎-朋左工E 貿,+ b )上草漏盧增.故选A了复各気址码車谶怦匹闻刹咼■同 丄扑堤对乐禽蔬車调建懵.弓車翎罡甸厦逼乳惫临帕貳.售世申思路分析}先求出苗妣定区换,潘篙对响9(分.W 尸In u v 和用同増井藏求单训毀间,対融齒龜.由最【答案】C【解析】分析:先根据奇函数性质以及对称性确定函数周期,再根据周期以及对应函数值求结果 详解:因为; 是定义域为' V • Q 的奇函数,且;: ,所以小….一 宀-.-:■■:■ ,;—,因此;「m+十儿心.*「.:亠」:门+八:—"+;「:亠「;门,因为/■-」「:!•—:::,所以「江u ,-工—「—,从而 ⑴:• C -……;:,一「17,选 C.点睛:函数的奇偶性与周期性相结合的问题多考查求值问题,常利用奇偶性及周期性进行变换,将所求函 数值的自变量转化到已知解析式的函数定义域内求解.【解析】分析:先根据函数周期将目变量韩化到已知区间,代入对应函数解析式求值』再代入对应函数解 析式求结果- 详解:由f (工+4)=金)得函数f (幻的周期为4,所以4 5) = /(16^1)=/(-l)=|-l + f|= 3•因此AA/(/(15)) = K|) = cos^ = ^点睛:(1)求分段函数的函数值,要先确定要求值的自变量属于哪一段区间,然后代入该段的解析式求值, 当出现’的形式时,应从内到外依次求值.(2)求某条件下自变量的值,先假设所求的值在分段函数定义区间的各段上,然后求出相应自变量的值,切记代入检验,看所求的自变量的值是否满足相应段自变量 的取值范围•3.【2018年理新课标I 卷】已知函数f (对二禹inr + R 曲N ,则f (对的最小值是 _______________________________ .【答案】1f (X )— 4(COSX +--)【解析】分析:首先对函数进行求导,化简求得,从而确定出函数的单调区间,JTjryr[2k?r - — - -](/c e Z)[2kn - -t 2kjr +—](fr E Z),增区间为2 .【2018年江苏卷】函数’ 满足二•: 一广—W ;「匚,且在区间’上,fW = JTXcos —,0 <x <2,|x + \ - 2 < X < 0,,确定出函数的最小值点,从而求得减区间为— %」22代入求得函数的最小值.7 1 1f (兀)二 Icosx + 2cos2x 二 4cos x + 2cosx 「2 = ^{cosx +< -详解:,所以当时函数单调减,点睛:该题考查的是有关应用导数研究函数的最小值问题,在求解的过程中,需要明确相关的函数的求导 公式,需要明白导数的符号与函数的单调性的关系,确定出函数的单调增区间和单调减区间,进而求得函 数的最小值点,从而求得相应的三角函数值,代入求得函数的最小值2017年咼考全景展示1.【2017 天津,理 6】已知奇函数 f (x)在 R 上是增函数,g(x) =xf(x).若 a 二 g(-log 2 5.1), b = g(2°8) , c = g(3),则a , b , c 的大小关系为(【答案】C【解析】因为f(x)是奇函数且在 R 上是增函数,所以在 x 0时,f (x) 0 , 从而g(x)二xf(x)是R 上的偶函数,且在[0,七)上是增函数,a =g( -Iog 25.1) =g(log 25.1),20.8 :2,又 4 :: 5.1 :: 8,则 2 :: log 2 5.^: 3,所以即 0 :: 20.8 ::: log 2 5.1 :: 3 ,g(20.8) ::g(log 25.1) ::g(3),所以b ::: a : c ,故选C.【考点】 指数、对数、函数的单调性【名师点睛】比较大小是高考常见题,指数式、对数式的比较大小要结合指数函数、对数函数,借助指数 函数和对数函数的图象,禾U 用函数的单调性进行比较大小,特别是灵活利用函数的奇偶性和单调性数形结 合不仅能比较大小,还可以解不等式 .x +1 x 兰0 12.【2017课标3,理15】设函数f(x)=< ' '则满足f(x) + f(x ——)>1的x的取值范围是2x , x>0,2bJT ST— — — —] (k E Z~) 33 ,函数的增区间为n 7TJT\)3 ^J3\2krr —,2k?r + —1(^ e Z)x — 2女TT —f k E Zsinx = ------ t sin2x = -------33•,所以当3 时,函数八对取得最小值,此时22^3 琲3筋1COSX > -当时函数单调增,从而得到函数的减区间为7T所以' (A) a ::: b ::: c (B ) c ::: b :::a (C)b :a ::: c(D) b ::【答案】 —1 , +oC 1< 4丿【解析】( 1 试题分析:令g(X )=X--1 -3当.r<OB 寸〉f (.¥)= /(x)+/|-当 0 < .Y < — 0 寸,| -X -------- J = 2* +X ■— JT 1' ' \ I T 1Fg(x\ = /(x) + /2x 3,x^0 2写成分段函数的形式:P 1]I 2丿1 12x x ,0 :: 2 22函数g x 在区间-::,0 1, 0,1 ,丄厂::三段区间内均单调递增,2 ' 2,且:g -J 九2。
三年高考(2016-2018)(文)真题分类解析:专题06-导数的几何意义

考纲解读明方向),y=x,y=,y=x ,y=导数能利用基本初等函数导数公式和导数四则本部分主要是对导数概念及其运算考查,以导数运算公式和运算法则为基础,以导数几何意义为重点.1.导数几何意义最常见是求过曲线上某点切线斜率、方程、斜率与倾斜角关系、切点坐标,或以平行、垂直直线斜率间关系为载体求字母取值等.2.导数运算是每年必考内容,一般不单独考查,而在考查导数应用时与单调性、极值与最值结合出题考查.3.本节内容在高考中分值为5分左右,属于容易题.2018年高考全景展示1.【2018年新课标I 卷文】设函数.若为奇函数,则曲线在点处切线方程为A.B.C.D.【答案】D【解析】分析:利用奇函数偶此项系数为零求得,进而得到解析式,再对求导得出切线斜率,进而求得切线方程.点睛:该题考查是有关曲线在某个点处切线方程问题,在求解过程中,首先需要确定函数解析式,此时利用到结论多项式函数中,奇函数不存在偶次项,偶函数不存在奇次项,从而求得相应参数值,之后利用求导公式求得,借助于导数几何意义,结合直线方程点斜式求得结果.2.【2018年天津卷文】已知函数f(x)=e x ln x,为f(x)导函数,则值为__________.【答案】e【解析】分析:首先求导函数,然后结合导函数运算法则整理计算即可求得最终结果.详解:由函数解析式可得:,则:.即值为e.点睛:本题主要考查导数运算法则,基本初等函数导数公式等知识,意在考查学生转化能力和计算求解能力.3.【2018年全国卷II文】曲线在点处切线方程为__________.【答案】y=2x–2点睛:求曲线在某点处切线方程步骤:①求出函数在该点处导数值即为切线斜率;②写出切线点斜式方程;③化简整理.4.【2018年天津卷文】设函数,其中,且是公差为等差数列.(I)若求曲线在点处切线方程;(II)若,求极值;(III)若曲线与直线有三个互异公共点,求d取值范围.【答案】(Ⅰ)x+y=0;(Ⅱ)极大值为6;极小值为−6;(Ⅲ)【解析】分析:(Ⅰ)由题意可得f(x)=x3−x,=3x2−1,结合f(0)=0,=−1,可得切线方程为x+y=0.(Ⅱ)由已知可得:f(x)=x3−3t2x2+(3t22−9)x− t23+9t2.则= 3x2−6t2x+3t22−9.令=0,解得x= t2−,或x= t2+.据此可得函数f(x)极大值为f(t2−)=6;函数极小值为f(t2+)=−6.(III)原问题等价于关于x方程(x−t2+d) (x−t2) (x−t2−d)+ (x−t2)+ 6=0有三个互异实数解,令u= x−t2,可得u3+(1−d2)u+6=0.设函数g(x)= x3+(1−d2)x+6,则y=g(x)有三个零点.利用导函数研究g(x)性质可得取值范围是详解:(Ⅰ)由已知,可得f(x)=x(x−1)(x+1)=x3−x,故=3x2−1,因此f(0)=0,=−1,又因为曲线y=f(x)在点(0,f(0))处切线方程为y−f(0)=(x−0),故所求切线方程为x+y=0.(Ⅱ)由已知可得f(x)=(x−t2+3)(x−t2)(x−t2−3)=(x−t2)3−9(x−t2)=x3−3t2x2+(3t22−9)x−t23+9t2.故=3x2−6t2x+3t22−9.令=0,解得x=t2−,或x=t2+.当x变化时,,f(x)变化如下表:),++,所以函数f(x)极大值为f(t2−)=(−)3−9×(−)=6;函数f(x)极小值为f(t2+)=()3−9×()=−6.若即,也就是,此时,且,从而由单调性,可知函数在区间内各有一个零点,符合题意.所以,取值范围是.点睛:导数是研究函数单调性、极值(最值)最有效工具,而函数是高中数学中重要知识点,所以在历届高考中,对导数应用考查都非常突出,本专题在高考中命题方向及命题角度从高考来看,对导数应用考查主要从以下几个角度进行:(1)考查导数几何意义,往往与解析几何、微积分相联系.(2)利用导数求函数单调区间,判断单调性;已知单调性,求参数.(3)利用导数求函数最值(极值),解决生活中优化问题.(4)考查数形结合思想应用.5.【2018年文北京卷】设函数.(Ⅰ)若曲线在点处切线斜率为0,求a;(Ⅱ)若在处取得极小值,求a取值范围.【答案】(Ⅰ)(Ⅱ)【解析】分析:(1)求导,构建等量关系,解方程可得参数值;(2)对分及两种情况进行分类讨论,通过研究变化情况可得取得极值可能,进而可求参数取值范围.详解:(1)当a=0时,令得x=1.随x变化情况如下表:∴在x=1处取得极大值,不合题意.(2)当a>0时,令得.①当,即a=1时,,∴在上单调递增,∴无极值,不合题意.②当,即0<a<1时,随x变化情况如下表:∴在x=1处取得极大值,不合题意.③当,即a>1时,随x变化情况如下表:∴在x =1处取得极小值,即a >1满足题意.(3)当a <0时,令得.随x 变化情况如下表:∴在x =1处取得极大值,不合题意.综上所述,a 取值范围为.点睛:导数类问题是高考数学中必考题,也是压轴题,主要考查形式有以下四个:①考查导数几何意义,涉及求曲线切线方程问题;②利用导数证明函数单调性或求单调区间问题;③利用导数求函数极值最值问题;④关于不等式恒成立问题.解题时需要注意有以下两个方面:①在求切线方程问题时,注意区别在某一点和过某一点解题步骤不同;②在研究单调性及极值最值问题时常常会涉及到分类讨论思想,要做到不重不漏;③不等式恒成立问题属于高考中难点,要注意问题转换等价性.2017年高考全景展示1.【2017课标1,文14】曲线21y x x=+在点(1,2)处切线方程为______________. 【答案】1y x =+ 【解析】试题分析:设()y f x = 则21()2f x x x'=-,所以(1)211f '=-= 所以在(1,2)处切线方程为21(1)y x -=⨯-,即1y x =+ 【考点】导数几何意义【名师点睛】求曲线切线方程是导数重要应用之一,用导数求切线方程关键在于求出切点),(00y x P 及斜率,其求法为:设),(00y x P 是曲线)(x f y =上一点,则以P 切点切线方程为:))(('000x x x f y y -=-.若曲线)(x f y =在点))(,(00x f x P 切线平行于y 轴(即导数不存在)时,由切线定义知,切线方程为0x x =.2.【2017天津,文10】已知a ∈R ,设函数()ln f x ax x =-图象在点(1,(1)f )处切线为l ,则l 在y 轴上截距为 . 【答案】1 【解析】【考点】导数几何意义【名师点睛】本题考查了导数几何意义,属于基础题型,函数()f x 在点0x 处导数()0f x '几何意义是曲线()y f x =在点()00,P x y 处切线斜率.相应地,切线方程为()()000y y f x x x '-=-.注意:求曲线切线时,要分清在点P 处切线与过点P 切线不同,谨记,有切点直接带入切点,没切点设切点,建立方程组求切点.3.【2017山东,文20】(本小题满分13分)已知函数()3211,32f x x ax a =-∈R ., (I)当a =2时,求曲线()y f x =在点()()3,3f 处切线方程;(II)设函数()()()cos sin g x f x x a x x =+--,讨论()g x 单调性并判断有无极值,有极值时求出极值.【答案】(I)390x y --=,(2)(II)⑴0a =无极值;⑵0a <极大值为31sin 6a a --,极小值为a -; ⑶0a >极大值为a -,极小值为31sin 6a a --. 【解析】试题分析:(I)根据求出切线斜率,再用点斜式写出切线方程;(II)由()()(sin )g x x a x x '=--,通过讨论确定()g x 单调性,再由单调性确定极值. 试题解析:(I )由题意'2()f x x ax =-,所以,当2a =时,(3)0f =,'2()2f x x x =-, 所以'(3)3f =,因此,曲线()y f x =在点(3,(3))f 处切线方程是3(3)y x =-, 即390x y --=.(1)当0a <时,'()()(sin )g x x a x x =--,当(,)x a ∈-∞时,0x a -<,'()0g x >,()g x 单调递增;当(,0)x a ∈时,0x a ->,'()0g x <,()g x 单调递减;当(0,)x ∈+∞时,0x a ->,'()0g x >,()g x 单调递增.所以,当x a =时,()g x 取到极大值,极大值是31()sin 6g a a a =--, 当0x =时,()g x 取到极小值,极小值是(0)g a =-.(2)当0a =时,'()(sin )g x x x x =-,当(,)x ∈-∞+∞时,'()0g x ≥,()g x 单调递增;所以,()g x 在(,)-∞+∞上单调递增,()g x 无极大值也无极小值.【考点】导数几何意义及导数应用4.【2017北京,文20】已知函数()e cos x f x x x =-. (Ⅰ)求曲线()y f x =在点(0,(0))f 处切线方程; (Ⅱ)求函数()f x 在区间π[0,]2上最大值和最小值. 【答案】(Ⅰ)1y =;(Ⅱ)最大值1;最小值2π-.【解析】试题分析:(Ⅰ)根据导数几何意义,求斜率再代入切线方程公式()()()000y f f x '-=-;(Ⅱ)设()()h x f x '=,求()h x ',根据()0h x '<确定函数()h x 单调性,根据单调减求函数最大值()00h =,可以知道()()0h x f x '=≤恒成立,所以函数()f x 是单调递减函数,根据单调性求最值.试题解析:(Ⅰ)因为()e cos x f x x x =-,所以()e (cos sin )1,(0)0x f x x x f ''=--=. 又因为(0)1f =,所以曲线()y f x =在点(0,(0))f 处切线方程为1y =.【考点】1.导数几何意义;2.利用导数求函数最值.【名师点睛】这道导数题并不难,比一般意义上压轴题要简单很多,第二问比较有特点是需要求二阶导数,因为()f x '不能判断函数单调性,所以需要再求一次导数,设()()h x f x '= ,再求()h x ',一般这时就可求得函数()h x '零点,或是()h x '恒成立,这样就能知道函数()h x 单调性,根据单调性求最值,从而判断()y f x =单调性,求得最值.2016年高考全景展示1.【2016高考四川文科】设直线l 1,l 2分别是函数f (x )= ln ,01,ln ,1,x x x x -<<⎧⎨>⎩图象上点P 1,P 2处切线,l 1与l 2垂直相交于点P ,且l 1,l 2分别与y 轴相交于点A ,B ,则△P AB 面积取值范围是( ) (A)(0,1) (B) (0,2) (C) (0,+∞) (D) (1,+ ∞) 【答案】A 【解析】试题分析:设()()111222,ln ,,ln P x x P x x -(不妨设121,01x x ><<),则由导数几何意义易得切线12,l l 斜率分别为121211,.k k x x ==-由已知得12122111,1,.k k x x x x =-∴=∴=∴切线1l 方程分别为()1111ln y x x x x -=-,切线2l 方程为()2221ln y x x x x +=--,即1111ln y x x x x ⎛⎫-=-- ⎪⎝⎭.分别令0x =得()()110,1ln ,0,1ln .A xB x -++又1l 与2l 交点为221111112222111121121,ln .1,1,0111211PAB A B P PAB x x x x P x x S y y x S x x x x ∆∆⎛⎫-++>∴=-⋅=<=∴<< ⎪++++⎝⎭,故选A. 考点:1.导数几何意义;2.两直线垂直关系;3.直线方程应用;4.三角形面积取值范围.【名师点睛】本题首先考查导数几何意义,其次考查最值问题,解题时可设出切点坐标,利用切线垂直求出这两点关系,同时得出切线方程,从而得点,A B 坐标,由两直线相交得出P 点坐标,从而求得面积,题中把面积用1x 表示后,可得它取值范围.解决本题可以是根据题意按部就班一步一步解得结论.这也是我们解决问题一种基本方法,朴实而基础,简单而实用.2.[2016高考新课标Ⅲ文数]已知()f x 为偶函数,当0x ≤ 时,1()x f x ex --=-,则曲线()y f x =在(1,2)处切线方程式_____________________________.【答案】2y x =【解析】考点:1、函数奇偶性;2、解析式;3、导数几何意义.【知识拓展】本题题型可归纳为“已知当0x >时,函数()y f x =,则当0x <时,求函数解析式”.有如下结论:若函数()f x 为偶函数,则当0x <时,函数解析式为()y f x =-;若()f x 为奇函数,则函数解析式为()y f x =--.3.【2016高考新课标2文数】已知函数()(1)ln (1)f x x x a x =+--.(I )当4a =时,求曲线()y f x =在()1,(1)f 处切线方程;(Ⅱ)若当()1,x ∈+∞时,()0f x >,求a 取值范围.【答案】(Ⅰ)220x y +-=;(Ⅱ)(],2.-∞【解析】试题分析:(Ⅰ)先求函数定义域,再求()f x ',(1)f ',(1)f ,由直线方程得点斜式可求曲线()=y f x 在(1,(1))f 处切线方程为220.x y +-=(Ⅱ)构造新函数(1)()ln 1-=-+a x g x x x ,对实数a 分类讨论,用导数法求解.(i )当2≤a ,(1,)∈+∞x 时,222(1)1210+-+≥-+>x a x x x , 故()0,()'>g x g x 在(1,)∈+∞x 上单调递增,因此()0>g x ;(ii )当2>a 时,令()0'=g x 得1211=-=-x a x a 由21>x 和121=x x 得11<x ,故当2(1,)∈x x 时,()0'<g x ,()g x 在2(1,)∈x x 单调递减,因此()0<g x .综上,a 取值范围是(],2.-∞考点: 导数几何意义,函数单调性.【名师点睛】求函数单调区间方法:(1)确定函数y=f(x)定义域;(2)求导数y′=f′(x);(3)解不等式f′(x)>0,解集在定义域内部分为单调递增区间;(4)解不等式f′(x)<0,解集在定义域内部分为单调递减区间.。
2016-2018三年高考数学(理)真题分类专题汇编解析版

3 1,
2
(D)
3 ,3
2
考点:集合的交集运算
【名师点睛】集合是每年中的必考题 ,一般以基础题形式出现 ,属得分题 .解决此类问题一
般要把参与运算的集合化为最简形式再进行运算 ,如果是不等式解集、函数定义域及值
域有关数集之间的运算 ,常借助数轴进行运算 . 2.【2016新课标 3理数】设集合 S x | (x 2)( x 3) 0 ,T
【解析】由题意 1 B ,显然 a2 3 3,所以 a 1,此时
a2 3 4 ,满足题意,故答案为 1. 【考点】元素的互异性 【名师点睛】 (1)认清元素的属性,解决集合问题时,认清集合中元素的属性 (是点集、 数集或其他情形 )和化简集合是正确求解的两个先决条件 . (2)注意元素的互异性 .在解决含参数的集合问题时,要注意检验集合中元素的互异性, 否则很可能会因为不满足 “互异性 ”而导致解题错误 .
(B){ x|–2<x<3}
( C) { x|–1<x<1}
( D ){ x|1<x<3}
【答案】 A
【解析】利用数轴可知 A B x 2 x 1 ,故选 A.
【考点】集合的运算 【名师点睛】集合分为有限集合和无限集合,若集合个数比较少时可以用列举法表示 ,若集合是无限集合就用描述法表示,注意代表元素是什么,集合的交、并、补运算 问题,应先把集合化简再计算,常常借助数轴或韦恩图进行处理 .
6【. 2017 天津,理 1】设集合 A {1,2,6}, B {2,4}, C { x R | 1 x 5} ,则 ( A B) C
()
( A) {2}
( B) {1,2, 4}
( C) {1,2,4,6}
2018-2016三年高考真题理科数学分类汇编:导数的应用(解析版附后)

三年真题专题07:导数的应用(解析版附后)考纲解读明方向分析解读1.会利用导数研究函数的单调性,掌握求函数单调区间的方法.2.掌握求函数极值与最值的方法,解决利润最大、用料最省、效率最高等实际生产、生活中的优化问题.3.利用导数求函数极值与最值、结合单调性与最值求参数范围、证明不等式是高考热点.分值为12~17分,属于高档题.命题探究练扩展2018年高考全景展示1.【2018a>1.(I(II处的切线与曲线在点处的切线平行,证明(III l,使l.2.【2018(Ⅰ)若曲线y= f(x)在点(1a;x=2处取得极小值,求a的取值范围.3.【2018的导函数.若存在S 点”.(1S 点”;(2S 点”,求实数a 的值;(3S 点”,并说明理由.4.【2018年理新课标I(1(22017年高考全景展示1.【2017课标II ,理11】若2x =-是函数21()(1)x f x x ax e -=+-的极值点,则()f x 的极小值为( )A.1-B.32e --C.35e -D.12.【2017浙江,7】函数y=f (x )的导函数()y f x '=的图像如图所示,则函数y=f (x )的图像可能是3.【2017课标II ,理】已知函数()2ln f x ax ax x x =--,且()0f x ≥。
(1)求a ;(2)证明:()f x 存在唯一的极大值点0x ,且()2202e f x --<<。
4.【2017课标3,理21】已知函数()1ln f x x a x =-- . (1)若()0f x ≥ ,求a 的值;(2)设m 为整数,且对于任意正整数n 2111111222n m ⎛⎫⎛⎫⎛⎫+++< ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭,求m 的最小值.5.【2017浙江,20】(本题满分15分)已知函数f (x )=(x e x -(12x ≥). (Ⅰ)求f (x )的导函数;(Ⅱ)求f (x )在区间1[+)2∞,上的取值范围. 6.【2017江苏,20】 已知函数32()1(0,)f x x ax bx a b =+++>∈R 有极值,且导函数()f x '的极值点是()f x 的零点.(极值点是指函数取极值时对应的自变量的值)(1)求b 关于a 的函数关系式,并写出定义域; (2)证明:23b a >;(3)若()f x ,()f x '这两个函数的所有极值之和不小于72-,求a 的取值范围.2016年高考全景展示1.【2016高考江苏卷】(本小题满分16分)已知函数()(0,0,1,1)x xf x a b a b a b =+>>≠≠.设12,2a b ==. (1)求方程()2f x =的根;(2)若对任意x R ∈,不等式(2)f()6f x m x ≥-恒成立,求实数m 的最大值;(3)若01,1a b <<>,函数()()2g x f x =-有且只有1个零点,求ab 的值。
三年高考(2016-2018)数学(文)真题分类解析:专题07-导数的应用
考纲解读明方向分析解读1.会利用导数研究函数单调性,掌握求函数单调区间方法.2.掌握求函数极值与最值方法,解决利润最大、用料最省、效率最高等实际生产、生活中优化问题.3.利用导数求函数极值与最值、结合单调性与最值求参数范围、证明不等式是高考热点.分值为12~17分,属于高档题.命题探究练扩展2018年高考全景展示1.【2018年新课标I卷文】已知函数.(1)设是极值点.求,并求单调区间;(2)证明:当时,.【答案】(1) a=;f(x)在(0,2)单调递减,在(2,+∞)单调递增.(2)证明见解析.详解:(1)f(x)定义域为,f ′(x)=a e x–.由题设知,f ′(2)=0,所以a =.从而f (x )=,f ′(x )=.当0<x <2时,f ′(x )<0;当x >2时,f ′(x )>0.所以f (x )在(0,2)单调递减,在(2,+∞)单调递增.(2)当a ≥时,f (x )≥.设g (x )=,则 当0<x <1时,g′(x )<0;当x >1时,g′(x )>0.所以x =1是g (x )最小值点.故当x >0时,g (x )≥g (1)=0.因此,当时,.点睛:该题考查是有关导数应用问题,涉及到知识点有导数与极值、导数与最值、导数与函数单调性关系以及证明不等式问题,在解题过程中,首先要保证函数生存权,先确定函数定义域,之后根据导数与极值关系求得参数值,之后利用极值特点,确定出函数单调区间,第二问在求解时候构造新函数,应用不等式传递性证得结果.2017年高考全景展示1.【2016高考四川文科】已知a 函数3()12f x x x =-极小值点,则a = ( ) (A)-4 (B) -2 (C)4 (D)2 【答案】D 【解析】考点:函数导数与极值.【名师点睛】本题考查函数极值.在可导函数中函数极值点0x 是方程'()0f x =解,但0x 是极大值点还是极小值点,需要通过这点两边导数正负性来判断,在0x 附近,如果0x x <时,'()0f x <,0x x >时'()0f x >,则0x 是极小值点,如果0x x <时,'()0f x >,0x x >时,'()0f x <,则0x 是极大值点,2.【2017浙江,7】函数y=f (x )导函数()y f x '=图像如图所示,则函数y=f (x )图像可能是【答案】D【解析】试题分析:原函数先减再增,再减再增,且由增变减时,极值点大于0,因此选D . 【考点】 导函数图象【名师点睛】本题主要考查导数图象与原函数图象关系:若导函数图象与x 轴交点为0x ,且图象在0x 两侧附近连续分布于x 轴上下方,则0x 为原函数单调性拐点,运用导数知识来讨论函数单调性时,由导函数)('x f 正负,得出原函数)(x f 单调区间. 3.【2017课标1,文21】已知函数()f x =e x (e x ﹣a )﹣a 2x . (1)讨论()f x 单调性;(2)若()0f x ≥,求a 取值范围.【答案】(1)当0a =,)(x f 在(,)-∞+∞单调递增;当0a >,()f x 在(,ln )a -∞单调递减,在(ln ,)a +∞单调递增;当0a <,()f x 在(,ln())2a-∞-单调递减,在(ln(),)2a -+∞单调递增;(2)34[2e ,1]-.【解析】(2)①若0a =,则2()xf x e =,所以()0f x ≥.【考点】导数应用【名师点睛】本题主要考查导数两大方面应用:(一)函数单调性讨论:运用导数知识来讨论函数单调性时,首先考虑函数定义域,再求出)('x f ,有)('x f 正负,得出函数)(x f 单调区间;(二)函数最值(极值)求法:由确认单调区间,结合极值点定义及自变量取值范围,得出函数)(x f 极值或最值.4.【2017课标II ,文21】设函数2()(1)x f x x e =-. (1)讨论()f x 单调性;(2)当0x ≥时,()1f x ax ≤+,求a 取值范围.【答案】(Ⅰ)在(,1-∞- 和(1)-+∞单调递减,在(11--单调递增(Ⅱ)[1,)+∞【解析】试题分析:(1)先求函数导数,再求导函数零点,列表分析导函数符号确定单调区间(2)对a 分类讨论,当a ≥1时,()(1)(1)1x f x x x e x a x =-+≤+≤+,满足条件;当0a ≤时,取200000()(1)(1)11x f x x x ax =>-+=>+,当0<a <1时,取0x =,20000()(1)(1)1f x x x ax >-+>+.试题解析:(1)2()(12)x f x x x e '=--令()0f x '=得1x =-当(,1x ∈-∞-时,()0f x '<;当(1x ∈--+时,()0f x '>;当(1)x ∈-+时,()0f x '<所以()f x 在(,1-∞- 和(1)-+∞单调递减,在(11--单调递增【考点】利用导数求函数单调区间,利用导数研究不等式恒成立【名师点睛】利用导数研究不等式恒成立或存在型问题,首先要构造函数,利用导数研究函数单调性,求出最值,进而得出相应含参不等式,从而求出参数取值范围;也可分离变量,构造函数,直接把问题转化为函数最值问题.2016年高考全景展示1. 【2016高考山东文数】(本小题满分13分) 设f (x )=x ln x –ax 2+(2a –1)x ,a ∈R . (Ⅰ)令g (x )=f'(x ),求g (x )单调区间;(Ⅱ)已知f (x )在x =1处取得极大值.求实数a 取值范围.【答案】 (Ⅰ)当0a ≤时,函数()g x 单调递增区间为()0,+∞; 当0a >时,函数()g x 单调递增区间为10,2a ⎛⎫ ⎪⎝⎭,单调递减区间为1,2a ⎛⎫+∞ ⎪⎝⎭. (Ⅱ)12a >.【解析】试题分析:(Ⅰ)求导数()'ln 22,f x x ax a =-+ 可得()()ln 22,0,g x x ax a x =-+∈+∞, 从而()112'2ax g x a x x-=-=, 讨论当0a ≤时,当0a >时两种情况下导函数正负号,确定得到函数单调区间. (Ⅱ)分以下情况讨论:①当0a ≤时,②当102a <<时,③当12a =时,④当12a >时,综合即得.(Ⅱ)由(Ⅰ)知,()'10f =.①当0a ≤时,()'0f x <,()f x 单调递减. 所以当()0,1x ∈时,()'0f x <,()f x 单调递减. 当()1,x ∈+∞时,()'0f x >,()f x 单调递增. 所以()f x 在1x =处取得极小值,不合题意. ②当102a <<时,112a >,由(Ⅰ)知()'f x 在10,2a ⎛⎫⎪⎝⎭内单调递增,可得当当()0,1x ∈时,()'0f x <,11,2x a ⎛⎫∈ ⎪⎝⎭时,()'0f x >, 所以()f x 在(0,1)内单调递减,在11,2a ⎛⎫⎪⎝⎭内单调递增, 所以()f x 在1x =处取得极小值,不合题意.考点:1.应用导数研究函数单调性、极值;2.分类讨论思想.【名师点睛】本题主要考查导数计算、应用导数研究函数单调性与极值、分类讨论思想.本题覆盖面广,对考生计算能力要求较高,是一道难题.解答本题,准确求导数是基础,恰当分类讨论是关键,易错点是分类讨论不全面、不彻底、不恰当.本题能较好考查考生逻辑思维能力、基本计算能力、分类讨论思想等.。
三年高考(2016-2018)数学(文)真题分项版解析专题06导数的几何意义(原卷版)

专业文档珍贵文档考纲解读明方向考点内容解读要求常考题型预测热度1.导数的概念与几何意义1.了解导数概念的实际背景2.理解导数的几何意义Ⅱ选择题、填空题★★2.导数的运算1.能根据导数定义求函数y=C(C 为常数),y=x,y=,y=x 2,y=x 3,y=的导数2.能利用基本初等函数的导数公式和导数的四则运算法则求简单函数的导数Ⅲ]选择题、解答题本部分主要是对导数概念及其运算的考查,以导数的运算公式和运算法则为基础,以导数的几何意义为重点.1.导数的几何意义最常见的是求过曲线上某点的切线的斜率、方程、斜率与倾斜角的关系、切点的坐标,或以平行、垂直直线的斜率间的关系为载体求字母的取值等.2.导数的运算是每年必考的内容,一般不单独考查,而在考查导数的应用时与单调性、极值与最值结合出题考查.3.本节内容在高考中分值为5分左右,属于容易题.2018年高考全景展示1.【2018年新课标I 卷文】设函数.若为奇函数,则曲线在点处的切线方程为A.B.C.D.2.【2018年天津卷文】已知函数f(x)=e xln x ,为f (x)的导函数,则的值为__________.3.【2018年全国卷II 文】曲线在点处的切线方程为__________.4.【2018年天津卷文】设函数,其中,且是公差为的等差数列.(I )若求曲线在点处的切线方程;(II )若,求的极值;(III )若曲线与直线有三个互异的公共点,求d 的取值范围.。
【三年高考】(2016-2018)数学(理科)真题分类解析:专题07-导数的应用(含答案)

专题07导数的应用函数一般不超过三次)分析解读1.会利用导数研究函数的单调性,掌握求函数单调区间的方法.2.掌握求函数极值与最值的方法,解决利润最大、用料最省、效率最高等实际生产、生活中的优化问题.3.利用导数求函数极值与最值、结合单调性与最值求参数范围、证明不等式是高考热点.分值为12~17分,属于高档题.命题探究练扩展2018年高考全景展示1.【2018年理数天津卷】已知函数,,其中a>1.(I)求函数的单调区间;(II)若曲线在点处的切线与曲线在点处的切线平行,证明(III)证明当时,存在直线l,使l是曲线的切线,也是曲线的切线.【答案】(Ⅰ)单调递减区间,单调递增区间为;(Ⅱ)证明见解析;(Ⅲ)证明见解析.(III)由题意可得两条切线方程分别为l1:.l2:.则原问题等价于当时,存在,,使得l1和l2重合.转化为当时,关于x1的方程存在实数解,构造函数,令,结合函数的性质可知存在唯一的x0,且x0>0,使得,据此可证得存在实数t,使得,则题中的结论成立.详解:(I)由已知,,有.令,解得x=0.由a>1,可知当x变化时,,的变化情况如下表:所以函数的单调递减区间,单调递增区间为.(III)曲线在点处的切线l1:.曲线在点处的切线l2:.要证明当时,存在直线l,使l是曲线的切线,也是曲线的切线,只需证明当时,存在,,使得l1和l2重合.即只需证明当时,方程组有解,由①得,代入②,得. ③因此,只需证明当时,关于x1的方程③存在实数解.设函数,即要证明当时,函数存在零点.,可知时,;时,单调递减,又,,故存在唯一的x0,且x0>0,使得,即.由此可得在上单调递增,在上单调递减.在处取得极大值.因为,故,所以.下面证明存在实数t,使得.由(I)可得,当时,有,所以存在实数t,使得,因此,当时,存在,使得.所以,当时,存在直线l,使l是曲线的切线,也是曲线的切线.点睛:导数是研究函数的单调性、极值(最值)最有效的工具,而函数是高中数学中重要的知识点,所以在历届高考中,对导数的应用的考查都非常突出,本专题在高考中的命题方向及命题角度从高考来看,对导数的应用的考查主要从以下几个角度进行:(1)考查导数的几何意义,往往与解析几何、微积分相联系.(2)利用导数求函数的单调区间,判断单调性;已知单调性,求参数.(3)利用导数求函数的最值(极值),解决生活中的优化问题.(4)考查数形结合思想的应用.2.【2018年理北京卷】设函数=[].(Ⅰ)若曲线y= f(x)在点(1,)处的切线与轴平行,求a;(Ⅱ)若在x=2处取得极小值,求a的取值范围.【答案】(1) a的值为1 (2) a的取值范围是(,+∞)【解析】分析:(1)先求导数,再根据得a;(2)先求导数的零点:,2;再分类讨论,根据是否满足在x=2处取得极小值,进行取舍,最后可得a的取值范围.详解:解:(Ⅰ)因为=[],所以f ′(x)=[2ax–(4a+1)]e x+[ax2–(4a+1)x+4a+3]e x(x∈R)=[ax2–(2a+1)x+2]e x.f′(1)=(1–a)e.由题设知f′(1)=0,即(1–a)e=0,解得a=1.此时f (1)=3e≠0.所以a的值为1.点睛:利用导数的几何意义解题,主要是利用导数、切点坐标、切线斜率之间的关系来进行转化.以平行、垂直直线斜率间的关系为载体求参数的值,则要求掌握平行、垂直与斜率之间的关系,进而和导数联系起来求解.3.【2018年江苏卷】记分别为函数的导函数.若存在,满足且,则称为函数与的一个“S点”.(1)证明:函数与不存在“S点”;(2)若函数与存在“S点”,求实数a的值;(3)已知函数,.对任意,判断是否存在,使函数与在区间内存在“S点”,并说明理由.【答案】(1)证明见解析(2)a的值为(3)对任意a>0,存在b>0,使函数f(x)与g(x)在区间(0,+∞)内存在“S点”.【解析】分析:(1)根据题中“S点”的定义列两个方程,根据方程组无解证得结论;(2)同(1)根据“S 点”的定义列两个方程,解方程组可得a的值;(3)通过构造函数以及结合“S点”的定义列两个方程,再判断方程组是否有解即可证得结论.详解:解:(1)函数f(x)=x,g(x)=x2+2x-2,则f′(x)=1,g′(x)=2x+2.由f(x)=g(x)且f′(x)= g′(x),得,此方程组无解,因此,f(x)与g(x)不存在“S”点.(2)函数,,则.设x0为f(x)与g(x)的“S”点,由f(x0)与g(x0)且f′(x0)与g′(x0),得,即,(*)得,即,则.当时,满足方程组(*),即为f(x)与g (x)的“S”点.因此,a的值为.(3)对任意a>0,设.因为,且h(x)的图象是不间断的,所以存在∈(0,1),使得,令,则b>0.函数,则.由f(x)与g(x)且f′(x)与g′(x),得,即(**)此时,满足方程组(**),即是函数f(x)与g(x)在区间(0,1)内的一个“S点”.因此,对任意a>0,存在b>0,使函数f(x)与g(x)在区间(0,+∞)内存在“S点”.点睛:涉及函数的零点问题、方程解的个数问题、函数图象交点个数问题,一般先通过导数研究函数的单调性、最大值、最小值、变化趋势等,再借助函数的大致图象判断零点、方程根、交点的情况,归根到底还是研究函数的性质,如单调性、极值,然后通过数形结合的思想找到解题的思路. 4.【2018年理新课标I卷】已知函数.(1)讨论的单调性;(2)若存在两个极值点,证明:.【答案】(1)当时,在单调递减.,当时,在单调递减,在单调递增.(2)证明见解析.(i)若,则,当且仅当,时,所以在单调递减.(ii)若,令得,或.当时,;当时,.所以在单调递减,在单调递增.(2)由(1)知,存在两个极值点当且仅当.由于的两个极值点满足,所以,不妨设,则.由于,所以等价于.设函数,由(1)知,在单调递减,又,从而当时,.所以,即.点睛:该题考查的是应用导数研究函数的问题,涉及到的知识点有应用导数研究函数的单调性、应用导数研究函数的极值以及极值所满足的条件,在解题的过程中,需要明确导数的符号对单调性的决定性作用,再者就是要先保证函数的生存权,先确定函数的定义域,要对参数进行讨论,还有就是在做题的时候,要时刻关注第一问对第二问的影响,再者就是通过构造新函数来解决问题的思路要明确.2017年高考全景展示1.【2017课标II ,理11】若2x =-是函数21()(1)x f x x ax e -=+-的极值点,则()f x 的极小值为( ) A.1- B.32e -- C.35e - D.1 【答案】A 【解析】试题分析:由题可得12121()(2)(1)[(2)1]x x x f x x a ex ax e x a x a e ---'=+++-=+++-因为(2)0f '-=,所以1a =-,21()(1)x f x x x e -=--,故21()(2)x f x x x e-'=+-令()0f x '>,解得2x <-或1x >,所以()f x 在(,2),(1,)-∞-+∞单调递增,在(2,1)-单调递减 所以()f x 极小值为()111(111)1f e-=--=-,故选A 。
精品三年高考2016_2018高考数学试题分项版解析专题07导数的应用理含解析53

专题07导数的应用
分析解读
1.会利用导数研究函数的单调性,掌握求函数单调区间的方法.
2.掌握求函数极值与最值的方法,解决利润最大、用料最省、效率最高等实际生产、生活中的优化问题.
3.利用导数求函数极值与最值、结合单调性与最值求参数范围、证明不等式是高考热点.分值为12~17分,属于高档题.
命题探究练扩展
2018年高考全景展示
1.【2018年理数天津卷】已知函数,,其中a>1.
(I)求函数的单调区间;
(II)若曲线在点处的切线与曲线在点处的切线平行,证明
;
(III)证明当时,存在直线l,使l是曲线的切线,也是曲线的切线.
【答案】(Ⅰ)单调递减区间,单调递增区间为;(Ⅱ)证明见解析;(Ⅲ)证明见解析.
(III)由题意可得两条切线方程分别为l1:.l2:.则原问题等价于当时,存在,,使得l1和l2重合.转化为当时,关于x1的方程存在实数解,构造函数,令,结合函数的性质可知存在唯一的x0,且x0>0,使得,据此可证得存在实数t,使得,则题中的结论成立.
详解:(I)由已知,,有.
令,解得x=0.
由a>1,可知当x变化时,,的变化情况如下表:。
高考(2016-2018)数学(理)真题分项版解析——专题06导数的几何意义(原卷版)

专题06 导数的几何意义考纲解读明方向考点内容解读要求常考题型预测热度1.导数的概念与几何意义1.了解导数概念的实际背景2.理解导数的几何意义Ⅱ选择题、填空题★★★2.导数的运算1.能根据导数定义求函数y=C(C为常数),y=x, y=,y=x2,y=x3,y=的导数2.能利用基本初等函数的导数公式和导数的四则运算法则求简单函数的导数Ⅲ选择题、解答题.1.导数的几何意义最常见的是求过曲线上某点的切线的斜率、方程、斜率与倾斜角的关系、切点的坐标,或以平行、垂直直线的斜率间的关系为载体求字母的取值等.2.导数的运算是每年必考的内容,一般不单独考查,而在考查导数的应用时与单调性、极值与最值结合出题考查.3.本节内容在高考中分值为5分左右,属于容易题.2018年高考全景展示1.2018年理新课标I卷设函数,若为奇函数,则曲线在点处的切线方程为()A. B. C. D.2.2018年全国卷Ⅲ理曲线在点处的切线的斜率为,则________.3.2018年理数全国卷II曲线在点处的切线方程为__________.4.2018年理数天津卷已知函数,,其中a>1.(I)求函数的单调区间;(II)若曲线在点处的切线与曲线在点处的切线平行,证明;(III)证明当时,存在直线l,使l是曲线的切线,也是曲线的切线.5.2018年理北京卷设函数= [].(Ⅰ)若曲线y= f (x )在点(1,)处的切线与轴平行,求a ; (Ⅱ)若在x =2处取得极小值,求a 的取值范围.2017年高考全景展示1.2017,理20已知函数()22cos f x x x =+,()()cos sin 22x g x e x x x =-+-,其中2.71828e =是自然对数的底数.(Ⅰ)求曲线()y f x =在点()(),f ππ处的切线方程; (Ⅱ)令()()()()h x g x af x a R =-∈,讨论()h x 的单调性并判断有无极值,有极值时求出极值.2.2017北京,理19已知函数()e cos x f x x x =-.(Ⅰ)求曲线()y f x =在点(0,(0))f 处的切线方程;(Ⅱ)求函数()f x 在区间π[0,]2上的最大值和最小值.2016年高考全景展示1. 2016高考理数若函数()y f x =的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称()y f x =具有T 性质.下列函数中具有T 性质的是( )(A )sin y x = (B )ln y x = (C )e x y = (D )3y x =2. 2016年高考四川理数设直线l 1,l 2分别是函数f (x )= ln ,01,ln ,1,x x x x -<<⎧⎨>⎩图象上点P 1,P 2处的切线,l 1与l 2垂直相交于点P ,且l 1,l 2分别与y 轴相交于点A ,B ,则△P AB 的面积的取值范围是( )(A )(0,1) (B )(0,2) (C )(0,∞) (D )(1,∞)3.2016高考新课标3理数已知()f x 为偶函数,当0x <时,()ln()3f x x x =-+,则曲线()y f x = 在点(1,3)-处的切线方程是_______________.4.2016年高考北京理数设函数()a x f x xe bx -=+,曲线()y f x =在点(2,(2))f 处的切线方程为(1)4y e x =-+,(1)求a ,b 的值;(2)求()f x 的单调区间.。
三年高考(2016-2018)数学(文)真题分类解析:专题07-导数的应用
考纲解读明方向分析解读1.会利用导数研究函数的单调性,掌握求函数单调区间的方法.2.掌握求函数极值与最值的方法,解决利润最大、用料最省、效率最高等实际生产、生活中的优化问题.3.利用导数求函数极值与最值、结合单调性与最值求参数范围、证明不等式是高考热点.分值为12~17分,属于高档题.命题探究练扩展2018年高考全景展示1.【2018年新课标I卷文】已知函数.(1)设是的极值点.求,并求的单调区间;(2)证明:当时,.【答案】(1) a=;f(x)在(0,2)单调递减,在(2,+∞)单调递增.(2)证明见解析.详解:(1)f(x)的定义域为,f ′(x)=a e x–.由题设知,f ′(2)=0,所以a =.从而f (x )=,f ′(x )=.当0<x <2时,f ′(x )<0;当x >2时,f ′(x )>0.所以f (x )在(0,2)单调递减,在(2,+∞)单调递增.(2)当a ≥时,f (x )≥.设g (x )=,则 当0<x <1时,g′(x )<0;当x >1时,g′(x )>0.所以x =1是g (x )的最小值点.故当x >0时,g (x )≥g (1)=0.因此,当时,.点睛:该题考查的是有关导数的应用问题,涉及到的知识点有导数与极值、导数与最值、导数与函数的单调性的关系以及证明不等式问题,在解题的过程中,首先要保证函数的生存权,先确定函数的定义域,之后根据导数与极值的关系求得参数值,之后利用极值的特点,确定出函数的单调区间,第二问在求解的时候构造新函数,应用不等式的传递性证得结果.2017年高考全景展示1.【2016高考四川文科】已知a 函数3()12f x x x =-的极小值点,则a = ( ) (A)-4 (B) -2 (C)4 (D)2 【答案】D 【解析】考点:函数导数与极值.【名师点睛】本题考查函数的极值.在可导函数中函数的极值点0x 是方程'()0f x =的解,但0x 是极大值点还是极小值点,需要通过这点两边的导数的正负性来判断,在0x 附近,如果0x x <时,'()0f x <,0x x >时'()0f x >,则0x 是极小值点,如果0x x <时,'()0f x >,0x x >时,'()0f x <,则0x 是极大值点,2.【2017浙江,7】函数y=f (x )的导函数()y f x '=的图像如图所示,则函数y=f (x )的图像可能是【答案】D【解析】试题分析:原函数先减再增,再减再增,且由增变减时,极值点大于0,因此选D . 【考点】 导函数的图象【名师点睛】本题主要考查导数图象与原函数图象的关系:若导函数图象与x 轴的交点为0x ,且图象在0x 两侧附近连续分布于x 轴上下方,则0x 为原函数单调性的拐点,运用导数知识来讨论函数单调性时,由导函数)('x f 的正负,得出原函数)(x f 的单调区间. 3.【2017课标1,文21】已知函数()f x =e x (e x ﹣a )﹣a 2x . (1)讨论()f x 的单调性;(2)若()0f x ≥,求a 的取值范围.【答案】(1)当0a =,)(x f 在(,)-∞+∞单调递增;当0a >,()f x 在(,ln )a -∞单调递减,在(ln ,)a +∞单调递增;当0a <,()f x 在(,ln())2a-∞-单调递减,在(ln(),)2a -+∞单调递增;(2)34[2e ,1]-.【解析】(2)①若0a =,则2()xf x e =,所以()0f x ≥.【考点】导数应用【名师点睛】本题主要考查导数的两大方面的应用:(一)函数单调性的讨论:运用导数知识来讨论函数单调性时,首先考虑函数的定义域,再求出)('x f ,有)('x f 的正负,得出函数)(x f 的单调区间;(二)函数的最值(极值)的求法:由确认的单调区间,结合极值点的定义及自变量的取值范围,得出函数)(x f 极值或最值.4.【2017课标II ,文21】设函数2()(1)x f x x e =-. (1)讨论()f x 的单调性;(2)当0x ≥时,()1f x ax ≤+,求a 的取值范围.【答案】(Ⅰ)在(,1-∞- 和(1)-+∞单调递减,在(11--单调递增(Ⅱ)[1,)+∞【解析】试题分析:(1)先求函数导数,再求导函数零点,列表分析导函数符号确定单调区间(2)对a 分类讨论,当a ≥1时,()(1)(1)1x f x x x e x a x =-+≤+≤+,满足条件;当0a ≤时,取200000()(1)(1)11x f x x x ax =>-+=>+,当0<a <1时,取0x =,20000()(1)(1)1f x x x ax >-+>+.试题解析:(1)2()(12)x f x x x e '=--令()0f x '=得1x =-当(,1x ∈-∞-时,()0f x '<;当(1x ∈--+时,()0f x '>;当(1)x ∈-+时,()0f x '<所以()f x 在(,1-∞- 和(1)-+∞单调递减,在(11--单调递增【考点】利用导数求函数单调区间,利用导数研究不等式恒成立【名师点睛】利用导数研究不等式恒成立或存在型问题,首先要构造函数,利用导数研究函数的单调性,求出最值,进而得出相应的含参不等式,从而求出参数的取值范围;也可分离变量,构造函数,直接把问题转化为函数的最值问题.2016年高考全景展示1. 【2016高考山东文数】(本小题满分13分) 设f (x )=x ln x –ax 2+(2a –1)x ,a ∈R . (Ⅰ)令g (x )=f'(x ),求g (x )的单调区间;(Ⅱ)已知f (x )在x =1处取得极大值.求实数a 的取值范围.【答案】 (Ⅰ)当0a ≤时,函数()g x 单调递增区间为()0,+∞; 当0a >时,函数()g x 单调递增区间为10,2a ⎛⎫ ⎪⎝⎭,单调递减区间为1,2a ⎛⎫+∞ ⎪⎝⎭. (Ⅱ)12a >.【解析】试题分析:(Ⅰ)求导数()'ln 22,f x x ax a =-+ 可得()()ln 22,0,g x x ax a x =-+∈+∞, 从而()112'2ax g x a x x-=-=, 讨论当0a ≤时,当0a >时的两种情况下导函数正负号,确定得到函数的单调区间. (Ⅱ)分以下情况讨论:①当0a ≤时,②当102a <<时,③当12a =时,④当12a >时,综合即得.(Ⅱ)由(Ⅰ)知,()'10f =.①当0a ≤时,()'0f x <,()f x 单调递减. 所以当()0,1x ∈时,()'0f x <,()f x 单调递减. 当()1,x ∈+∞时,()'0f x >,()f x 单调递增. 所以()f x 在1x =处取得极小值,不合题意. ②当102a <<时,112a >,由(Ⅰ)知()'f x 在10,2a ⎛⎫⎪⎝⎭内单调递增,可得当当()0,1x ∈时,()'0f x <,11,2x a ⎛⎫∈ ⎪⎝⎭时,()'0f x >, 所以()f x 在(0,1)内单调递减,在11,2a ⎛⎫⎪⎝⎭内单调递增, 所以()f x 在1x =处取得极小值,不合题意.考点:1.应用导数研究函数的单调性、极值;2.分类讨论思想.【名师点睛】本题主要考查导数的计算、应用导数研究函数的单调性与极值、分类讨论思想.本题覆盖面广,对考生计算能力要求较高,是一道难题.解答本题,准确求导数是基础,恰当分类讨论是关键,易错点是分类讨论不全面、不彻底、不恰当.本题能较好的考查考生的逻辑思维能力、基本计算能力、分类讨论思想等.。
三年高考(2016-2018)高考数学试题分项版解析 专题06 导数的几何意义 理(含解析)

专题06 导数的几何意义纲解读明方向),y=x,y=的导数能利用基本初等函数的导数公式和导数的四则运算法则求简单函数的导数点.1.导数的几何意义最常见的是求过曲线上某点的切线的斜率、方程、斜率与倾斜角的关系、切点的坐标,或以平行、垂直直线的斜率间的关系为载体求字母的取值等.2.导数的运算是每年必考的内容,一般不单独考查,而在考查导数的应用时与单调性、极值与最值结合出题考查.3.本节内容在高考中分值为5分左右,属于容易题.2018年高考全景展示1.【2018年理新课标I卷】设函数,若为奇函数,则曲线在点处的切线方程为A. B. C. D.【答案】D点睛:该题考查的是有关曲线在某个点处的切线方程的问题,在求解的过程中,首先需要确定函数解析式,此时利用到结论多项式函数中,奇函数不存在偶次项,偶函数不存在奇次项,从而求得相应的参数值,之后利用求导公式求得,借助于导数的几何意义,结合直线方程的点斜式求得结果. 2.【2018年全国卷Ⅲ理】曲线在点处的切线的斜率为,则________.【答案】【解析】分析:求导,利用导数的几何意义计算即可。
详解:,则,所以,故答案为-3.点睛:本题主要考查导数的计算和导数的几何意义,属于基础题。
3.【2018年理数全国卷II】曲线在点处的切线方程为__________.【答案】【解析】分析:先求导数,再根据导数几何意义得切线斜率,最后根据点斜式求切线方程.详解:点睛:求曲线的切线要注意“过点P的切线”与“在点P处的切线”的差异,过点P的切线中,点P不一定是切点,点P也不一定在已知曲线上,而在点P处的切线,必以点P为切点.4.【2018年理数天津卷】已知函数,,其中a>1.(I)求函数的单调区间;(II)若曲线在点处的切线与曲线在点处的切线平行,证明;(III)证明当时,存在直线l,使l是曲线的切线,也是曲线的切线.【答案】(Ⅰ)单调递减区间,单调递增区间为;(Ⅱ)证明见解析;(Ⅲ)证明见解析.【解析】分析:(I)由题意可得.令,解得x=0.据此可得函数的单调递减区间,单调递增区间为.(II)曲线在点处的切线斜率为.曲线在点处的切线斜率为.原问题等价于.两边取对数可得.(III)由题意可得两条切线方程分别为l1:.l2:.则原问题等价于当时,存在,,使得l1和l2重合.转化为当时,关于x1的方程存在实数解,构造函数,令,结合函数的性质可知存在唯一的x0,且x0>0,使得,据此可证得存在实数t,使得,则题中的结论成立.详解:(I)由已知,,有.令,解得x=0.由a>1,可知当x变化时,,的变化情况如下表:所以函数的单调递减区间,单调递增区间为.(II)由,可得曲线在点处的切线斜率为.由,可得曲线在点处的切线斜率为.因为这两条切线平行,故有,即.两边取以a为底的对数,得,所以. (III)曲线在点处的切线l1:.曲线在点处的切线l2:.要证明当时,存在直线l,使l是曲线的切线,也是曲线的切线,只需证明当时,存在,,使得l1和l2重合.即只需证明当时,方程组有解,由①得,代入②,得. ③因此,只需证明当时,关于x1的方程③存在实数解.设函数,即要证明当时,函数存在零点.,可知时,;时,单调递减,又,,故存在唯一的x0,且x0>0,使得,即.由此可得在上单调递增,在上单调递减.在处取得极大值.因为,故,所以.下面证明存在实数t,使得.由(I)可得,当时,有,所以存在实数t,使得,因此,当时,存在,使得.所以,当时,存在直线l,使l是曲线的切线,也是曲线的切线.点睛:导数是研究函数的单调性、极值(最值)最有效的工具,而函数是高中数学中重要的知识点,所以在历届高考中,对导数的应用的考查都非常突出,本专题在高考中的命题方向及命题角度从高考来看,对导数的应用的考查主要从以下几个角度进行: (1)考查导数的几何意义,往往与解析几何、微积分相联系. (2)利用导数求函数的单调区间,判断单调性;已知单调性,求参数. (3)利用导数求函数的最值(极值),解决生活中的优化问题. (4)考查数形结合思想的应用.5.【2018年理北京卷】设函数=[].(Ⅰ)若曲线y= f(x)在点(1,)处的切线与轴平行,求a;(Ⅱ)若在x=2处取得极小值,求a的取值范围.【答案】(1) a的值为1 (2) a的取值范围是(,+∞)(Ⅱ)由(Ⅰ)得f ′(x )=[ax 2–(2a +1)x +2]e x =(ax –1)(x –2)e x.若a >,则当x ∈(,2)时,f ′(x )<0;当x ∈(2,+∞)时,f ′(x )>0.所以f (x )<0在x =2处取得极小值.若a ≤,则当x ∈(0,2)时,x –2<0,ax –1≤x –1<0,所以f ′(x )>0.所以2不是f (x )的极小值点. 综上可知,a 的取值范围是(,+∞).点睛:利用导数的几何意义解题,主要是利用导数、切点坐标、切线斜率之间的关系来进行转化.以平行、垂直直线斜率间的关系为载体求参数的值,则要求掌握平行、垂直与斜率之间的关系,进而和导数联系起来求解.2017年高考全景展示1.【2017山东,理20】已知函数()22cos f x x x =+,()()cos sin 22x g x e x x x =-+-,其中2.71828e =是自然对数的底数.(Ⅰ)求曲线()y f x =在点()(),f ππ处的切线方程;(Ⅱ)令()()()()h x g x af x a R =-∈,讨论()h x 的单调性并判断有无极值,有极值时求出极值.【答案】(Ⅰ)222y x ππ=--.(Ⅱ)综上所述:当0a ≤时,()h x 在(),0-∞上单调递减,在()0,+∞上单调递增,函数()h x 有极小值,极小值是()021h a =--;当01a <<时,函数()h x 在(),ln a -∞和()0,ln a 和()0,+∞上单调递增,在()ln ,0a 上单调递减,函数()h x 有极大值,也有极小值,极大值是()()()2ln ln 2ln sin ln cos ln 2h a a a a a a ⎡⎤=--+++⎣⎦极小值是()021h a =--;当1a =时,函数()h x 在(),-∞+∞上单调递增,无极值;当1a >时,函数()h x 在(),0-∞和()ln ,a +∞上单调递增,在()0,ln a 上单调递减,函数()h x 有极大值,也有极小值,极大值是()021h a =--;极小值是()()()2ln ln 2ln sin ln cos ln 2h a a a a a a ⎡⎤=--+++⎣⎦.试题解析:(Ⅰ)由题意()22f ππ=-又()22sin f x x x '=-,所以()2f ππ'=,因此 曲线()y f x =在点()(),f ππ处的切线方程为()()222y x πππ--=-,即 222y x ππ=--.(Ⅱ)由题意得 2()(cos sin 22)(2cos )x h x e x x x a x x =-+--+,因为()()()()cos sin 22sin cos 222sin x x h x e x x x e x x a x x '=-+-+--+--()()2sin 2sin x e x x a x x =---()()2sin x e a x x =--,令()sin m x x x =-则()1cos 0m x x '=-≥所以()m x 在R 上单调递增.因为(0)0,m =所以 当0x >时,()0,m x >当0x <时,()0m x <(1)当0a ≤时,x e a -0>当0x <时,()0h x '<,()h x 单调递减,当0x >时,()0h x '>,()h x 单调递增,所以 当0x =时()h x 取得极小值,极小值是 ()021h a =--;(2)当0a >时,()()()ln 2sin x ah x e e x x '=--由 ()0h x '=得 1ln xa =,2=0x①当01a <<时,ln 0a <,当(),ln x a ∈-∞时,()ln 0,0x a e e h x '-<>,()h x 单调递增;当()ln ,0x a ∈时,()ln 0,0x a e e h x '-><,()h x 单调递减;当()0,x ∈+∞时,()ln 0,0x a e e h x '->>,()h x 单调递增.所以 当ln x a =时()h x 取得极大值.极大值为()()()2ln ln 2ln sin ln cos ln 2h a a a a a a ⎡⎤=--+++⎣⎦,当0x =时()h x 取到极小值,极小值是 ()021h a =--;②当1a =时,ln 0a =,所以 当(),x ∈-∞+∞时,()0h x '≥,函数()h x 在(),-∞+∞上单调递增,无极值;③当1a >时,ln 0a >所以 当(),0x ∈-∞时,ln 0x a e e -<,()()0,h x h x '>单调递增;当()0,ln x a ∈时,ln 0x a e e -<,()()0,h x h x '<单调递减;当()ln ,x a ∈+∞时,ln 0x a e e ->,()()0,h x h x '>单调递增;所以 当0x =时()h x 取得极大值,极大值是()021h a =--;当ln x a =时()h x 取得极小值.极小值是()()()2ln ln 2ln sin ln cos ln 2h a a a a a a ⎡⎤=--+++⎣⎦.综上所述:当0a ≤时,()h x 在(),0-∞上单调递减,在()0,+∞上单调递增,函数()h x 有极小值,极小值是()021h a =--;当01a <<时,函数()h x 在(),ln a -∞和()0,ln a 和()0,+∞上单调递增,在()ln ,0a 上单调递减,函数()h x 有极大值,也有极小值,极大值是()()()2ln ln 2ln sin ln cos ln 2h a a a a a a ⎡⎤=--+++⎣⎦极小值是()021h a =--;当1a =时,函数()h x 在(),-∞+∞上单调递增,无极值;当1a >时,函数()h x 在(),0-∞和()ln ,a +∞上单调递增,在()0,ln a 上单调递减,函数()h x 有极大值,也有极小值,极大值是()021h a =--;极小值是()()()2ln ln 2ln sin ln cos ln 2h a a a a a a ⎡⎤=--+++⎣⎦.【考点】1.导数的几何意义.2.应用导数研究函数的单调性、极值.3.分类讨论思想.【名师点睛】1.函数f (x )在点x 0处的导数f ′(x 0)的几何意义是曲线y =f (x )在点P (x 0,y 0)处的切线的斜率.相应地,切线方程为y −y 0=f ′(x 0)(x −x 0).注意:求曲线切线时,要分清在点P 处的切线与过点P 的切线的不同.2. 本题主要考查导数的几何意义、应用导数研究函数的单调性与极值、分类讨论思想.本题覆盖面广,对考生计算能力要求较高,是一道难题.解答本题,准确求导数是基础,恰当分类讨论是关键,易错点是分类讨论不全面、不彻底、不恰当,或因复杂式子变形能力差,而错漏百出.本题能较好的考查考生的逻辑思维能力、基本计算能力、分类讨论思想等.2.【2017北京,理19】已知函数()e cos x f x x x =-. (Ⅰ)求曲线()y f x =在点(0,(0))f 处的切线方程; (Ⅱ)求函数()f x 在区间π[0,]2上的最大值和最小值. 【答案】(Ⅰ)1y =;(Ⅱ)最大值1;最小值2π-.【解析】(Ⅱ)设()e (cos sin )1x h x x x =--,则()e (cos sin sin cos )2e sin x x h x x x x x x '=---=-. 当π(0,)2x ∈时,()0h x '<, 所以()h x 在区间π[0,]2上单调递减.所以对任意π(0,]2x ∈有()(0)0h x h <=,即()0f x '<. 所以函数()f x 在区间π[0,]2上单调递减.因此()f x 在区间π[0,]2上的最大值为(0)1f =,最小值为ππ()22f =-. 【考点】1.导数的几何意义;2.利用导数求函数的最值.【名师点睛】这道导数题并不难,比一般意义上的压轴题要简单很多,第二问比较有特点是需要求二阶导数,因为()f x '不能判断函数的单调性,所以需要再求一次导数,设()()h x f x '= ,再求()h x ',一般这时就可求得函数()h x '的零点,或是()h x '恒成立,这样就能知道函数()h x 的单调性,根据单调性求最值,从而判断()y f x =的单调性,求得最值.2016年高考全景展示1. 【2016高考山东理数】若函数()y f x =的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称()y f x =具有T 性质.下列函数中具有T 性质的是( )(A )sin y x = (B )ln y x =(C )e x y =(D )3y x =【答案】A 【解析】试题分析:由函数的图象在两点处的切线互相垂直可知,存在两点处的切线斜率的积,即导函数值的乘积为负一.当sin y x =时,cos y x '=,有cos0cos 1π⋅=-,所以在函数sin y x =图象存在两点0,x x π==使条件成立,故A 正确;函数3ln ,,x y x y e y x ===的导数值均非负,不符合题意,故选A. 考点:1.导数的计算;2.导数的几何意义.【名师点睛】本题主要考查导数的计算、导数的几何意义及两直线的位置关系,本题给出常见的三角函数、指数函数、对数函数、幂函数,突出了高考命题注重基础的原则.解答本题,关键在于将直线的位置关系与直线的斜率、切点处的导数值相联系,使问题加以转化,利用特殊化思想解题,降低难度.本题能较好的考查考生分析问题解决问题的能力、基本计算能力及转化与化归思想的应用等. 2. 【2016年高考四川理数】设直线l 1,l 2分别是函数f (x )= ln ,01,ln ,1,x x x x -<<⎧⎨>⎩图象上点P 1,P 2处的切线,l 1与l 2垂直相交于点P ,且l 1,l 2分别与y 轴相交于点A ,B ,则△PAB 的面积的取值范围是( )(A )(0,1) (B )(0,2) (C )(0,+∞) (D )(1,+∞) 【答案】A 【解析】试题分析:设()()111222,ln ,,ln P x x P x x -(不妨设121,01x x ><<),则由导数的几何意义易得切线12,l l 的斜率分别为121211,.k k x x ==-由已知得12122111,1,.k k x x x x =-∴=∴=∴切线1l 的方程分别为()1111ln y x x x x -=-,切线2l 的方程为()2221ln y x x x x +=--,即1111ln y x x x x ⎛⎫-=-- ⎪⎝⎭.分别令0x =得()()110,1ln ,0,1ln .A x B x -++又1l 与2l 的交点为2111221121,ln 11x x P x x x ⎛⎫-+ ⎪++⎝⎭,11x >,21122112111211PABA B P x x S y y x x x ∆+∴=-⋅=<=++,01PAB S ∆∴<<.故选A . 考点:1.导数的几何意义;2.两直线垂直关系;3.直线方程的应用;4.三角形面积取值范围.【名师点睛】本题首先考查导数的几何意义,其次考查最值问题,解题时可设出切点坐标,利用切线垂直求出这两点的关系,同时得出切线方程,从而得点,A B 坐标,由两直线相交得出P 点坐标,从而求得面积,题中把面积用1x 表示后,可得它的取值范围.解决本题可以是根据题意按部就班一步一步解得结论.这也是我们解决问题的一种基本方法,朴实而基础,简单而实用.3.【2016高考新课标3理数】已知()f x 为偶函数,当0x <时,()ln()3f x x x =-+,则曲线()y f x = 在点(1,3)-处的切线方程是_______________.【答案】21y x =--考点:1、函数的奇偶性与解析式;2、导数的几何意义.【知识拓展】本题题型可归纳为“已知当0x >时,函数()y f x =,则当0x <时,求函数的解析式”.有如下结论:若函数()f x 为偶函数,则当0x <时,函数的解析式为()y f x =-;若()f x 为奇函数,则函数的解析式为()y f x =--.4.【2016年高考北京理数】设函数()a x f x xe bx -=+,曲线()y f x =在点(2,(2))f 处的切线方程为(1)4y e x =-+,(1)求a ,b 的值;(2)求()f x 的单调区间.【答案】(Ⅰ)2a =,b e =;(2))(x f 的单调递增区间为(,)-∞+∞.【解析】试题分析:(1)根据题意求出()f x ',根据(2)22f e =+,(2)1f e '=-,求a ,b 的值;(2)由题意知判断)(x f ',即判断11)(-+-=x e x x g 的单调性,知()0g x >,即()0f x '>,由此求得()f x 的单调区间.所以,当)1,(-∞∈x 时,0)(<'x g ,)(x g 在区间)1,(-∞上单调递减;当),1(+∞∈x 时,0)(>'x g ,)(x g 在区间),1(+∞上单调递增.故1)1(=g 是)(x g 在区间),(+∞-∞上的最小值,从而),(,0)(+∞-∞∈>x x g .综上可知,0)(>'x f ,),(+∞-∞∈x ,故)(x f 的单调递增区间为),(+∞-∞.考点:导数的应用.【名师点睛】用导数判断函数的单调性时,首先应确定函数的定义域,然后在函数的定义域内,通过讨论导数的符号,来判断函数的单调区间.在对函数划分单调区间时,除了必须确定使导数等于0的点外,还要注意定义区间内的间断点.。
三年高考2016_2018高考数学试题分项版解析专题07导数的应用理含解析

专题 07 导数的应用考纲解读明方向考点内容解读要求常考题型展望热度认识函数单调性和导数的关系; 能利用导数选择题1. 导数与函数的, 会求函数的单调区间理解★★★研究函数的单调性解答题单调性)( 其中多项式函数一般不高出三次认识函数在某点获取极值的必要条件和充分条件 ; 会用导数求函数的极大值、极小值2. 导数与函数的极); 会求闭掌握解答题★★★( 其中多项式函数一般不高出三次(最)值( 其中多项式区间上函数的最大值、最小值函数一般不高出三次 )3. 生活中的优化问掌握选择题★☆☆会利用导数解决某些实责问题题解析解读1.会利用导数研究函数的单调性 , 掌握求函数单调区间的方法 .2. 掌握求函数极值与最值的方法, 解决利润最大、用料最省、效率最高等实质生产、生活中的优化问题.3. 利用导数求函数极值与最值、结合单调性与最值求参数范围、证明不等式是高考热点. 分值为12~17 分, 属于高档题 .命题研究练扩展2018 年高考全景显现1.【 2018 年理数天津卷】已知函数,,其中a>1.(I )求函数的单调区间;(II )若曲线在点处的切线与曲线在点处的切线平行,证明;(III)证明当时,存在直线l ,使 l 是曲线的切线,也是曲线的切线.【答案】 ( Ⅰ ) 单调递减区间,单调递加区间为;(Ⅱ )证明见解析;(Ⅲ )证明见解析.(III)由题意可得两条切线方程分别为l 1:. l2:. 则原问题等价于当时,存在,,使得l1和l2重合.转变成当时,关于 x1的方程存在实数解,构造函数,令,结合函数的性质可知存在唯一的x0,且 x0>0,使得,据此可证得存在实数t ,使得,则题中的结论成立.详解:( I )由已知,,有.令,解得 x=0.由 a>1,可知当 x 变化时,,的变化情况以下表:x00+极小值所以函数的单调递减区间,单调递加区间为.(III )曲线在点处的切线 l 1. :曲线在点2. 处的切线 l :要证明当时,存在直线l ,使 l 是曲线的切线,也是曲线的切线,只需证明当时,存在,,使得 l 1和 l 2重合.即只需证明当时,方程组有解,由①得,代入②,得. ③所以,只需证明当时,关于 x1的方程③存在实数解.设函数,即要证明当时,函数存在零点 .,可知时,;时,单调递减,又,,故存在唯一的x0,且 x0>0,使得,即.由此可得在上单调递加,在上单调递减.在处获取极大值. 由于,故,所以.下面证明存在实数 t ,使得.由(I)可得,当时,有,所以存在实数 t ,使得,所以,当时,存在,使得.所以,当时,存在直线l ,使 l 是曲线的切线,也是曲线的切线 .点睛:导数是研究函数的单调性、极值( 最值 ) 最有效的工具,而函数是高中数学中重要的知识点,所以在历届高考中,对导数的应用的观察都特别突出,本专题在高考中的命题方向及命题角度从高考来看,对导数的应用的观察主要从以下几个角度进行:(1) 观察导数的几何意义,经常与解析几何、微积分相联系. (2) 利用导数求函数的单调区间,判断单调性;已知单调性,求参数.(3) 利用导数求函数的最值 ( 极值 ) ,解决生活中的优化问题.(4) 观察数形结合思想的应用.2.【 2018 年理北京卷】设函数=[ ] .(Ⅰ)若曲线y= f ( x)在点(1,)处的切线与轴平行,求 a;(Ⅱ)若在 x=2处获取极小值,求 a 的取值范围.【答案】 (1) a 的值为 1 (2) a 的取值范围是(,+∞)【解析】解析:(1)先求导数,再依照得 a;(2)先求导数的零点:,2;再分类谈论,依照是否满足在 x=2处获取极小值,进行弃取,最后可得 a 的取值范围.详解:解:(Ⅰ)由于=[ ] ,x x x 所以 f ′( x)=[2ax–(4a+1)]e +[ ax2–(4a+1)x+4a+3] e ( x∈R)=[ ax2–(2a+1) x+2]e.f′ (1)=(1 –a)e .由题设知f′ (1)=0 ,即 (1 –a)e=0 ,解得a=1.此时 f (1)=3e≠0.所以 a 的值为1.点睛:利用导数的几何意义解题,主若是利用导数、切点坐标、切线斜率之间的关系来进行转变. 以平行、垂直直线斜率间的关系为载体求参数的值,则要求掌握平行、垂直与斜率之间的关系,进而和导数联系起来求解 .3.【 2018 年江苏卷】记分别为函数 的导函数.若存在 ,满足 且,则称为函数与的一个“ S 点”.(1)证明:函数与 不存在“ S 点”;(2)若函数与存在“ S 点”,求实数 a 的值;(3)已知函数, .对任意 ,判断可否存在 ,使函数 与 在区间内存在“ S 点”,并说明原由.【答案】( 1)证明见解析( 2)a 的值为 ( 3)对任意 a >0,存在 b >0,使函数 f ( x )与 g (x )在区间( 0,+∞)内存在“ S 点”.【解析】解析: ( 1)依照题中“ S 点”的定义列两个方程,依照方程组无解证得结论; (2)同( 1)依照“S 点”的定义列两个方程,解方程组可得a 的值;( 3)经过构造函数以及结合“ S 点”的定义列两个方程,再判断方程组可否有解即可证得结论.详解:解:( 1)函数 f ( x ) =x , g ( x )=x 2+2x -2 ,则 f ′( x ) =1, g ′( x )=2x +2.由 f ( x ) =g ( x )且 f ′( x )= g ′( x ),得,此方程组无解,所以, f ( x )与 g (x )不存在“ S ”点.(2)函数, ,则.设 x 0 为 f ( )与 g ( )的“ ”点,由f ( 0)与g ( 0)且 f ′( x 0)与 g ′( 0),得x x S x x x,即,(* )得,即 ,则 .当 时, 满足方程组( * ),即 为 f ( x )与 g( )的“ ”点.所以, a 的值为 .xS(3)对任意 >0,设 .由于,且 ( )的图象是不中止的,所以存在∈( 0, 1),使得,令,则b>0.函数,则.由 f ( x)与 g( x)且 f ′( x)与 g′( x),得,即(** )此时,满足方程组(** ),即是函数f(x)与g(x)在区间(0,1)内的一个“ S点”.所以,对任意a>0,存在 b>0,使函数 f ( x)与 g( x)在区间(0,+∞)内存在“ S 点”.点睛:涉及函数的零点问题、方程解的个数问题、函数图象交点个数问题,一般先经过导数研究函数的单调性、最大值、最小值、变化趋势等,再借助函数的大体图象判断零点、方程根、交点的情况,归根终究还是研究函数的性质,如单调性、极值,尔后经过数形结合的思想找到解题的思路. 4.【 2018 年理新课标 I 卷】已知函数.(1)谈论的单调性;(2)若存在两个极值点,证明:.【答案】( 1)当时,在单调递减.,当时,在单调递减,在单调递加 . ( 2)证明见解析.(i )若,则,当且仅当,时,所以在单调递减.(ii )若,令得,或. 当时,;当时,.所以在单调递减,在单调递加 .(2)由( 1)知,存在两个极值点当且仅当.由于的两个极值点满足,所以,不如设,则. 由于,所以等价于. 设函数,由(1)知,在单调递减,又,进而当时,. 所以,即. 点睛:该题观察的是应用导数研究函数的问题,涉及到的知识点有应用导数研究函数的单调性、应用导数研究函数的极值以及极值所满足的条件,在解题的过程中,需要明确导数的符号对单调性的决定性作用,再者就是要先保证函数的生计权,先确定函数的定义域,要对参数进行谈论,还有就是在做题的时候,要时辰关注第一问对第二问的影响,再者就是经过构造新函数来解决问题的思路要明确.2017 年高考全景显现1.【2017 课标 II ,理 11】若x 2 是函数 f ( x) ( x2 ax 1)e x 1的极值点,则 f ( x) 的极小值为()A. 1B. 2e 3C. 5e 3D.1【答案】 A【解析】试题解析:由题可得 f ( x) (2 x a)e x 1 ( x2 ax 1)e x 1 [ x2 ( a 2) x a 1]e x 1由于 f ( 2) 0 ,所以 a 1 ,f ( x) ( x2 x 1)e x 1,故 f ( x) (x2 x 2)e x 1所以 f (x) 极小值为 f 1 (1 1 1)e1 1 1 ,应选A。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题07导数的应用分析解读1.会利用导数研究函数的单调性,掌握求函数单调区间的方法.2.掌握求函数极值与最值的方法,解决利润最大、用料最省、效率最高等实际生产、生活中的优化问题.3.利用导数求函数极值与最值、结合单调性与最值求参数范围、证明不等式是高考热点.分值为12~17分,属于高档题.命题探究练扩展2018年高考全景展示1.【2018年理数天津卷】已知函数,,其中a>1.(I)求函数的单调区间;(II)若曲线在点处的切线与曲线在点处的切线平行,证明;(III)证明当时,存在直线l,使l是曲线的切线,也是曲线的切线.【答案】(Ⅰ)单调递减区间,单调递增区间为;(Ⅱ)证明见解析;(Ⅲ)证明见解析.(III)由题意可得两条切线方程分别为l1:.l2:.则原问题等价于当时,存在,,使得l1和l2重合.转化为当时,关于x1的方程存在实数解,构造函数,令,结合函数的性质可知存在唯一的x0,且x0>0,使得,据此可证得存在实数t,使得,则题中的结论成立.详解:(I)由已知,,有.令,解得x=0.由a>1,可知当x变化时,,的变化情况如下表:所以函数的单调递减区间,单调递增区间为.(III)曲线在点处的切线l1:.曲线在点处的切线l2:.要证明当时,存在直线l,使l是曲线的切线,也是曲线的切线,只需证明当时,存在,,使得l1和l2重合.即只需证明当时,方程组有解,由①得,代入②,得. ③因此,只需证明当时,关于x1的方程③存在实数解.设函数,即要证明当时,函数存在零点.,可知时,;时,单调递减,又,,故存在唯一的x0,且x0>0,使得,即.由此可得在上单调递增,在上单调递减.在处取得极大值.因为,故,所以.下面证明存在实数t,使得.由(I)可得,当时,有,所以存在实数t,使得,因此,当时,存在,使得.所以,当时,存在直线l,使l是曲线的切线,也是曲线的切线.点睛:导数是研究函数的单调性、极值(最值)最有效的工具,而函数是高中数学中重要的知识点,所以在历届高考中,对导数的应用的考查都非常突出,本专题在高考中的命题方向及命题角度从高考来看,对导数的应用的考查主要从以下几个角度进行: (1)考查导数的几何意义,往往与解析几何、微积分相联系. (2)利用导数求函数的单调区间,判断单调性;已知单调性,求参数. (3)利用导数求函数的最值(极值),解决生活中的优化问题. (4)考查数形结合思想的应用.2.【2018年理北京卷】设函数=[].(Ⅰ)若曲线y= f(x)在点(1,)处的切线与轴平行,求a;(Ⅱ)若在x=2处取得极小值,求a的取值范围.【答案】(1) a的值为1 (2) a的取值范围是(,+∞)【解析】分析:(1)先求导数,再根据得a;(2)先求导数的零点:,2;再分类讨论,根据是否满足在x=2处取得极小值,进行取舍,最后可得a的取值范围.详解:解:(Ⅰ)因为=[],所以f ′(x)=[2ax–(4a+1)]e x+[ax2–(4a+1)x+4a+3]e x(x∈R)=[ax2–(2a+1)x+2]e x.f′(1)=(1–a)e.由题设知f′(1)=0,即(1–a)e=0,解得a=1.此时f (1)=3e≠0.所以a的值为1.点睛:利用导数的几何意义解题,主要是利用导数、切点坐标、切线斜率之间的关系来进行转化.以平行、垂直直线斜率间的关系为载体求参数的值,则要求掌握平行、垂直与斜率之间的关系,进而和导数联系起来求解.3.【2018年江苏卷】记分别为函数的导函数.若存在,满足且,则称为函数与的一个“S点”.(1)证明:函数与不存在“S点”;(2)若函数与存在“S点”,求实数a的值;(3)已知函数,.对任意,判断是否存在,使函数与在区间内存在“S点”,并说明理由.【答案】(1)证明见解析(2)a的值为(3)对任意a>0,存在b>0,使函数f(x)与g(x)在区间(0,+∞)内存在“S点”.【解析】分析:(1)根据题中“S点”的定义列两个方程,根据方程组无解证得结论;(2)同(1)根据“S 点”的定义列两个方程,解方程组可得a的值;(3)通过构造函数以及结合“S点”的定义列两个方程,再判断方程组是否有解即可证得结论.详解:解:(1)函数f(x)=x,g(x)=x2+2x-2,则f′(x)=1,g′(x)=2x+2.由f(x)=g(x)且f′(x)= g′(x),得,此方程组无解,因此,f(x)与g(x)不存在“S”点.(2)函数,,则.设x0为f(x)与g(x)的“S”点,由f(x0)与g(x0)且f′(x0)与g′(x0),得,即,(*)得,即,则.当时,满足方程组(*),即为f(x)与g(x)的“S”点.因此,a的值为.(3)对任意a>0,设.因为,且h(x)的图象是不间断的,所以存在∈(0,1),使得,令,则b>0.函数,则.由f(x)与g(x)且f′(x)与g′(x),得,即(**)此时,满足方程组(**),即是函数f(x)与g(x)在区间(0,1)内的一个“S点”.因此,对任意a>0,存在b>0,使函数f(x)与g(x)在区间(0,+∞)内存在“S点”.点睛:涉及函数的零点问题、方程解的个数问题、函数图象交点个数问题,一般先通过导数研究函数的单调性、最大值、最小值、变化趋势等,再借助函数的大致图象判断零点、方程根、交点的情况,归根到底还是研究函数的性质,如单调性、极值,然后通过数形结合的思想找到解题的思路.4.【2018年理新课标I卷】已知函数.(1)讨论的单调性;(2)若存在两个极值点,证明:.【答案】(1)当时,在单调递减.,当时,在单调递减,在单调递增.(2)证明见解析.(i)若,则,当且仅当,时,所以在单调递减.(ii)若,令得,或.当时,;当时,.所以在单调递减,在单调递增.(2)由(1)知,存在两个极值点当且仅当.由于的两个极值点满足,所以,不妨设,则.由于,所以等价于.设函数,由(1)知,在单调递减,又,从而当时,.所以,即.点睛:该题考查的是应用导数研究函数的问题,涉及到的知识点有应用导数研究函数的单调性、应用导数研究函数的极值以及极值所满足的条件,在解题的过程中,需要明确导数的符号对单调性的决定性作用,再者就是要先保证函数的生存权,先确定函数的定义域,要对参数进行讨论,还有就是在做题的时候,要时刻关注第一问对第二问的影响,再者就是通过构造新函数来解决问题的思路要明确.2017年高考全景展示1.【2017课标II ,理11】若2x =-是函数21()(1)x f x x ax e -=+-的极值点,则()f x 的极小值为( )A.1-B.32e --C.35e -D.1 【答案】A 【解析】试题分析:由题可得12121()(2)(1)[(2)1]x x x f x x a e x ax e x a x a e ---'=+++-=+++-因为(2)0f '-=,所以1a =-,21()(1)x f x x x e -=--,故21()(2)x f x x x e -'=+-令()0f x '>,解得2x <-或1x >,所以()f x 在(,2),(1,)-∞-+∞单调递增,在(2,1)-单调递减 所以()f x 极小值为()111(111)1f e-=--=-,故选A 。
【考点】 函数的极值;函数的单调性【名师点睛】(1)可导函数y =f (x )在点x 0处取得极值的充要条件是f ′(x 0)=0,且在x 0左侧与右侧f ′(x )的符号不同。
(2)若f (x )在(a ,b )内有极值,那么f (x )在(a ,b )内绝不是单调函数,即在某区间上单调增或减的函数没有极值。
2.【2017浙江,7】函数y=f (x )的导函数()y f x '=的图像如图所示,则函数y=f (x )的图像可能是【答案】D 【解析】试题分析:原函数先减再增,再减再增,且由增变减时,极值点大于0,因此选D . 【考点】 导函数的图象【名师点睛】本题主要考查导数图象与原函数图象的关系:若导函数图象与x 轴的交点为0x ,且图象在0x 两侧附近连续分布于x 轴上下方,则0x 为原函数单调性的拐点,运用导数知识来讨论函数单调性时,由导函数)('x f 的正负,得出原函数)(x f 的单调区间.3.【2017课标II ,理】已知函数()2ln f x ax ax x x =--,且()0f x ≥。
(1)求a ;(2)证明:()f x 存在唯一的极大值点0x ,且()2202e f x --<<。
【答案】(1)1a =;(2)证明略。
【解析】试题分析:(1)利用题意结合导函数与原函数的关系可求得1a =,注意验证结果的正确性;(2)结合(1)的结论构造函数()22ln h x x x =--,结合()h x 的单调性和()f x 的解析式即可证得题中的不等式()2202ef x --<<。
试题解析:(1)()f x 的定义域为()0,+∞。
设()ln g x ax a x =--,则()()f x xg x =,()0f x ≥等价于()0g x ≥。
因为()()10,0g g x =≥,因()'10g =,而()()1','11g x a g a x=-=-,得1a =。
若1a =,则()1'1g x x=-。
当01x <<时,()'0g x <,()g x 单调递减; 当1x >时,()'0g x >,()g x 单调递增。
所以1x =是()g x 的极小值点,故()()10g x g ≥= 综上,1a =。
(2)由(1)知 ()2ln f x x x x x =--,()'22ln f x x x =--。
设()22ln h x x x =--,则()1'2h x x=-。
当10,2x ⎛⎫∈ ⎪⎝⎭ 时,()'0h x < ;当1,2x ⎛⎫∈+∞ ⎪⎝⎭时,()'0h x > ,所以()h x 在10,2⎛⎫ ⎪⎝⎭单调递减,在1,2⎛⎫+∞⎪⎝⎭单调递增。
又()20h e ->,102h ⎛⎫<⎪⎝⎭,()10h = , 所以()h x 在10,2⎛⎫ ⎪⎝⎭有唯一零点0x ,在1,2⎡⎫+∞⎪⎢⎣⎭有唯一零点1,且当()00,x x ∈ 时,()0h x > ;当()0,1x x ∈ 时,()0h x < , 当()1,x ∈+∞ 时, ()0h x >。
