高一下月考(文科答案)
河南省洛阳第一高级中学2013-2014学年高一下学期第一次月考试题 文科综合

河南省洛阳第一高级中学2013-2014学年高一下学期第一次月考试题文科综合满分:100分时间:50分钟一、选择题(每题4分,共60分)1、截止到2012年,世界上有196个主权国家被国际普遍承认。
下列关于国家的说法正确的有①国家都是民主与专政的统一体②国家都是阶级统治的工具③任何国家的统治阶级内部都有民主④任何国家都是统治阶级对被统治阶级的专政A.②③B.①③C.①④D.②④2、2013年4月和6月,新疆巴楚和鄯善发生两起暴力恐怖事件。
事件发生后,国家进行了严厉打击,维护了社会的稳定。
这体现了①专政是我国的立国之本②人民的权益得到充分的实现③国家具有专政职能④我国对极少数敌人实行专政A.①④B.③④C.②③D.①②3、民主是衡量一个社会文明程度的重要指标,也是建设社会主义的必要条件。
只有充分发扬民主,才不会出现人亡政息。
这一观点主要强调了A.发扬民主就能维护国家长治久安B.人民民主是社会主义的生命C.发扬人民民主,就能保障公民的权益D.人民民主是我们国家生存发展的政治基石4、党的十八大报告提出,改革征地制度,提高农民在土地增值收益中的分配比例,让失地农民分享到更为合理的土地增值收益。
这体现了A.国家从制度层面消除城乡差别B.社会主义民主政治进一步发展C.国家尊重农民的主人翁地位D.国家保障和实现农民的政治自由5、雅安芦山地震发生后,天全县老场乡大庙村一组组长韩世芳的丈夫失踪了,但她强忍悲痛,依然坚守岗位,化悲痛为力量,打通了救灾生命线。
韩世芳的事迹给我们的启示是A.要抛弃个人利益来实现集体利益B.要实现整体利益与局部利益的统一C.要正确处理个人利益和集体利益的关系D.维护社会稳定是公民根本的行为准则6、某市在基层3个单位开展试点,以公推直选方式从89名候选人中选举产生了9名人大代表。
这种做法A.扩大了选民的选举权利B.为选民行使选举权提供了选择的余地C.限制了候选人之间的竞争D.比较充分地考虑了当选者结构的合理性7、近年来,每当涉及国计民生的重大问题面向社会公开征求意见时,都会受到人们的广泛关注,并纷纷通过各种渠道发表自己的意见和建议。
辽宁省葫芦岛市第一高级中学2013—2014学年高一下学期第一次月考文科数学试题

辽宁省葫芦岛市第一高级中学2013—2014学年高一下学期第一次月考文科数学试题考试时间:120分钟一.选择题(每小题5分,共60分)1.-300°化为弧度是 ( ) A. 34π-B. 35π- C .32π- D .65π- 2.α是第二象限角,(P x为其终边上一点,且cos x α=,则sin α的值为 ( )A .104 B .64 C .24 D .-1043.已知2tan =θ,则=-----+)sin()2sin()cos()2sin(θπθπθπθπ( )A .2B .-2C .0D .32 4.若函数f(sinx)=cos2x,则f(cos150)的值为 ( )A. 12B. -12C. -32D. 32 5.设π20<≤x ,且x 2sin 1-=,cos sin x x -则 ( )A .0≤x ≤B .4π≤x ≤45πC .4π≤x ≤47πD .2π≤x ≤23π6.函数2()12sin ()4--f x xπ=是( )A .最小正周期为π的偶函数B .最小正周期为π的奇函数C .最小正周期为2π的偶函数D .最小正周期为2π的奇函数7.关于函数()sin cos f x x x =+,下列命题正确的是 ( ) A.函数()f x 最大值为2 B.函数()f x 的一条对称轴为4x π=C.函数()f x 的图像向左平移4π个单位后对应的函数是奇函数D.函数()y f x =的周期为2π8.已知函数sin()y A x ωϕ=+,在一个周期内当π12x =时,有最大值2,当7π12x =时,有最小值2-,那么 ( )A.1πsin 223y x ⎛⎫=+ ⎪⎝⎭B.1πsin 226y x ⎛⎫=+ ⎪⎝⎭C.π2sin 26y x ⎛⎫=+ ⎪⎝⎭D.π2sin 23y x ⎛⎫=+ ⎪⎝⎭9.如果函数)0(cos sin >⋅=ωωωx x y 的最小正周期为4π,那么常数ω为 ( )A .41 B .2 C .21D .4 10.函数)42sin(log 21π+=x y 的单调减区间为( )A .)(],4(Z k k k ∈-πππB .)(]8,8(Z k k k ∈+-ππππC .)(]8,83(Z k k k ∈+-ππππD .)(]83,8(Z k k k ∈++ππππ11.已知y x y x sin cos ,21cos sin 则=的取值范围是 ( )A.]21,21[-B.]21,23[-C.]23,21[- D.]1,1[-12.圆(x +21)2+(y +1)2=1681与圆(x -sin θ)2+(y -1)2=161 (θ为锐角)的位置关系是( )A.相离B.外切C.内切D.相交二.填空题(每小题5分,共20分)13.)(x f 为奇函数,=<+=>)(0,cos 2sin )(,0x f x x x x f x 时则时 ____ . 14.设),2(ππα∈,函数322)(sin )(+-=x xx f α的最大值为43,则α=_____________. 15.计算:cot2600+tan350+tan100cot4150=___________. 16.α是第四象限角,53cos =α,则)4cos(πα-=___________________. 三.解答题(共70分)17.(10分)求值: sin80+sin70sin75cos80-sin70cos7518.(12分)已知tanx=-2,(π2<x<π),求下列各式的值:(1)2212sin cos cos sin x x x x -- (2)2221sin cos 34x x +19.(12分)求函数y =x sin +lg (2cos x -1)的定义域.20.(12分)已知α为第三象限角,问是否存在这样的实数m ,使得αsin 、αcos 是关于x 的方程286210x mx m +++=的两个根,若存在,求出实数m ,若不存在,请说明理由.21.(12分)已知f(x)=5sinxcosx-35cos 2x+325(x ∈R )(1)求f(x)的最小正周期;(2)求f(x)单调区间;(3)求f(x)图象的对称轴,对称中心。
山西省运城市闻喜中学2023-2024学年高一下学期6月月考语文试题(含答案)

高一6月份自测性考试语文试题本试卷满分150分,考试时间150分钟。
注意事项:1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号;回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、现代文阅读中国古代小说每每被视为史余、史补而受轻视,大方之家每不屑道及。
“戊戌变法”前后,一些较早接触域外文学文化的知识分子,基于小说可以化民成俗的认识,开始译介欧美及日本的小说,并充分肯定小说的社会价值和教化功用。
梁启超首倡“小说界革命”,他肯定了小说的“载道”功用,以小说为文学之“最上乘”者,适应了晚清维新派改良群治的愿望。
兼之借助日渐兴盛的报纸刊物等快捷面广的传播媒介,动摇和瓦解了以往歧视小说的正统文学观,使得小说的译印和创作风起云涌。
这就改变了中国文学场域的格局,创造了一种新的文化语境......。
在这样的文化语境中,一些有新思想、用新方法的学人开始以空前的热情对古代小说开展了学术研究。
1918年3月15日,胡适首先在北大文科研究所作了《论短篇小说》的演讲,讲稿修改后发于《新青年》。
该文虽只6000余字,却昭示了中国古代短篇小说研究的系统性。
不过让胡适付出更大热情的是中国章回小说的考证研究。
1920年8月,上海亚东图书馆推出汪原放标点版的《水浒传》,胡适撰写的《水浒传考证》置于卷首作为前言。
此后8年中,胡适先后为《儒林外史》《红楼梦》等章回小说撰写了20余篇考证及序跋文章。
在胡适的系列考证中,影响最大的首推1921年5月置于亚东版《红楼梦》卷首的《〈红楼梦〉考证》。
《红楼梦》对中国古代社会文化的影响,可能难以与流播久远的世代累积型经典小说《三国演义》《水浒传》相比,但因其精神内涵丰富,艺术表现高妙,题材与格调更适合文人读者的口味,所以程甲本问世后,它便受到读书人阶层的群体青睐。
山西省大同市第一中学2020届高三下学期3月月考数学(文)试题 Word版含解析

故选: .
【点睛】本题考查了线面夹角,意在考查学生 计算能力和空间想象能力.
10.“勾股定理”在西方被称为“毕达哥拉斯定理”,国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明 如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个大正方形 若直角三角形中较小的锐角 ,现在向该大止方形区域内随机地投掷一枚飞镖,则飞镖落在阴影部分的概率是
18.如图,在四棱锥 中, 为平行四边形, , 平面 ,且 ,点 是 的中点.
(1)求证: 平面 ;
(2)求 到平面 的距离.
【答案】(1)证明见解析;(2)
【解析】
【分析】
(1)连接 交 于 点,连接 ,在 中, ,得到证明.
(2)计算 ,根据等体积法得到 ,计算得到答案.
【详解】(1)连接 交 于 点,连接 ,
【详解】 ,故 ,则 ,
故 .
故选:B.
【点睛】本题考查了回归方程的中心点,意在考查学生的计算能力和应用能力.
5.已知角 的顶点与坐标原点重合,始边与 轴的非负半轴重合.若点 是角 终边上一点,则 ( )
A. -2B. C. D. 2
【答案】B
【解析】
【分析】
由题意利用任意角的三角函数的定义求得 的值,再利用两角差的正切公式,求得 的值.
一、选择题:本大题共12小题,每小題5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设全集 ,集合 ,则 ( )
A. B. C. D.
【答案】A
【解析】
【分析】
计算 , ,再计算交集得到答案.
【详解】 , ,
故 .
故选: .
【点睛】本题考查了交集运算,意在考查学生的计算能力.
安徽省合肥一中高一下学期第一次月考(文科)试卷

安徽省合肥一中高一下学期第一次月考(文科)试卷英语本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至12页。
第Ⅱ卷13至14页。
考试结束,将本试卷和答题卡一并交回。
第Ⅰ卷注意事项:1.答题前,考生在答题卡上务必用黑色签字笔将自己的姓名、准考证号填写清楚,并贴好条形码。
请认真核准条形码上的准考证号、姓名和科目。
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,在试题卷上作答无效。
第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.Where can the city children have their “Classroom Extra”?A. On the Internet.B. At schools.C. In the New York Post.2.What does the man mean?A. The woman should want to buy new clothes.B. The cold weather will probably continue.C. He already has a warm cold.3.What else does the man want at last?A. Fired vegetables and a bowl of rice.B. Coconut (椰子) juice and coke.C. Shrimp salad and coconut juice.4.What does the woman want to know?A. Whether she can make a proposal.B. Whether Bill needs her help.C. Whether she can review Bill’s summary.5.What does the man imply about the man?A. He should do more.B. She’d be glad to help him.C. He should be paid.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话。
四川省内江市第六中学2022-2023学年高三上学期第二次月考《文科》数学(解析版)

内江六中2022—2023学年(上)高2023第二次月考文科数学试题第Ⅰ卷 选择题(满分60分)一、选择题(每题5分,共60分)1. 已知向量()1,2a =r ,()1,1b = ,若c a kb =+ ,且b c ⊥ ,则实数k =( )A. 32B. 53-C. 53D. 32-【答案】D 【解析】【分析】根据平面向量坐标的线性运算得c得坐标,在根据向量垂直的坐标关系,即可得实数k 的值.【详解】解:因为向量()1,2a =r ,()1,1b = ,所以()1,2c a kb k k =+=++ ,又b c ⊥,所以120b c k k ⋅=+++= ,解得32k =-.故选:D.2. 复数13i2iz -=+的虚部为( )A. 75-B. 7i 5-C. 73-D. 7i 3-【答案】A 【解析】【分析】利用复数的除法运算化简,即可得复数的虚部.【详解】解:复数13i (13i)(2i)17i 17i 2i (2i)(2i)555z -----====--++-故z 的虚部为75-.故选:A .3. 若集合{1A =-,0,1},2{|1B y y x ==-,}x A ∈,则A B = ( )A. {0} B. {1}C. {0,1}D. {0,1}-【答案】D 【解析】【分析】把A 中元素代入B 中解析式求出y 的值,确定出B ,找出两集合的交集即可.【详解】解:把A 中=1x -,0,1代入B 中得:0y =,1,即{0B =,1},则{0A B = ,1}-,故选:D .4. 若变量x 、y 满足约束条件211y x x y y ≤⎧⎪+≤⎨⎪≥-⎩,则目标函数2z x y =+取最大值时的最优解是( )A. 5,03⎛⎫ ⎪⎝⎭B. 1,12⎛⎫-- ⎪⎝⎭C. 12,33⎛⎫⎪⎝⎭D. ()2,1-【答案】C 【解析】【分析】作出满足约束条件的可行域,平移直线20x y +=,即可得出结果.【详解】作出满足约束条件的可行域(如图中阴影部分所示).2z x y =+可化为20x y z +-=,平移直线20x y +=,当其经过点C 时,目标函数2z x y =+取得最大值,联立21y x x y =⎧⎨+=⎩,解得13x =,23y =,故最优解是12,33⎛⎫⎪⎝⎭,故选:C.5. 若a ,b 均为实数,则“ln ln a b >”是“e e a b >”的( )A. 充分不必要条件 B. 必要不充分条件C. 充分必要条件D.既不充分也不必要条件【答案】A 【解析】【分析】根据函数ln y x =与e x y =解不等式,即可判断.【详解】解:因为ln ln a b >,由函数ln y x =在()0,+∞上单调递增得:0a b >>又e e a b >,由于函数e x y =在R 上单调递增得:a b >由“0a b >>”是“a b >”的充分不必要条件可得“ln ln a b >”是“e e a b >”的充分不必要条件.故选:A.6. 如图是函数()()sin 0,0,02f x A x A πωϕωϕ⎛⎫=+>><< ⎪⎝⎭的图象的一部分,则函数()f x 的解析式为( )A. ()2sin 26f x x π⎛⎫=+⎪⎝⎭B. ()2sin 23f x x π⎛⎫=+⎪⎝⎭C. ()sin 3f x x π⎛⎫=+ ⎪⎝⎭D. ()2sin 23f x x π⎛⎫=-⎪⎝⎭【答案】B 【解析】【分析】由图象可确定()f x 最小正周期T ,由此可得ω;根据712f A π⎛⎫=- ⎪⎝⎭可求得ϕ;由()0f =可求得A ,由此可得()f x .【详解】由图象可知:()f x 最小正周期23471T πππ⎛⎫-=⎪⎝⎭=⨯,22T πω∴==;又77sin 126f A A ππϕ⎛⎫⎛⎫=+=-⎪ ⎪⎝⎭⎝⎭,()73262k k ππϕπ∴+=+∈Z ,解得:()23k k πϕπ=+∈Z ,又02πϕ<<,3πϕ∴=,()sin 23f x A x π⎛⎫∴=+⎪⎝⎭,()0sin 3f A A π=== ,2A ∴=,()2sin 23f x x π⎛⎫∴=+ ⎪⎝⎭.故选:B.7. 已知向量,a b 的夹角为4π,且1||4,(23)122a a b a b ⎛⎫=+⋅-= ⎪⎝⎭,则向量b 在向量a 方向上的投影是( )A.B. 3C. D. 1【答案】D 【解析】【分析】由题意,根据数量积的运算,化简等式,解得模长,结合投影的计算公式,可得答案.【详解】由()123122a b a b ⎛⎫+⋅-= ⎪⎝⎭,22323122a a b a b b -⋅+⋅-= ,2213122a a b b +⋅-= ,21164cos 31224b b π+⨯⋅-=,230b -= ,(30b += ,解得b = b 在向量a 方向上的投影为cos 14b π= ,故选:D.8. 蒙特卡洛算法是以概率和统计的理论、方法为基础的一种计算方法,将所求解的问题同一定的概率模型相联系.用均匀投点实现统计模拟和抽样,以获得问题的近似解,故又称统计模拟法或统计实验法,现设计一个实验计算圆周率的近似值,向两直角边长分别为6和8的直角三角形中均匀投点40个.落入其内切圆中的点有22个,则圆周率π≈( )A.6320B.3310C.7825D.9429【答案】B 【解析】【分析】根据几何概型的计算公式和题意即可求出结果.【详解】直角三角形内切圆的直径等于两直角边的和与斜边的差,即268104r =+-=,由几何概型得2222140682π⨯≈⨯⨯,从而3310π≈.故选:B.9. 双碳,即碳达峰与碳中和的简称,2020年9月中国明确提出2030年实现“碳达峰”,2060年实现“碳中和”.为了实现这一目标,中国加大了电动汽车的研究与推广,到2060年,纯电动汽车在整体汽车中的渗透率有望超过70%,新型动力电池随之也迎来了蓬勃发展的机遇.Peukert 于1898年提出蓄电池的容量C (单位:A·h ),放电时间t (单位:h )与放电电流I (单位:A )之间关系的经验公式n C I t =⋅,其中32log 2n =为Peukert 常数.在电池容量不变的条件下,当放电电流10A I =时,放电时间57h t =,则当放电电流15A I =,放电时间为( )A. 28h B. 28.5hC. 29hD. 29.5h【答案】B 【解析】【分析】根据题意求出蓄电池的容量C ,再把15A I =代入,结合指数与对数的运算性质即可得解.【详解】解:根据题意可得5710n C =⋅,则当15A I =时,571015n n t ⋅=⋅,所以32231log 2log 222257575728.5h 333nt ⎛⎫⎛⎫⎛⎫=⋅=⋅=⋅= ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭,即当放电电流15A I =,放电时间为28.5h.故选:B .10. 已知函数()32e ,0461,0x x f x x x x ⎧<=⎨-+≥⎩,则函数()()()2232g x f x f x =--⎡⎤⎣⎦的零点个数为( ).A. 2 B. 3 C. 4 D. 5【答案】B 【解析】【分析】首先根据()()22320f x f x --=⎡⎤⎣⎦,得到()2f x =或1()2f x =-,然后利用导数分析0x ≥时函数的单调性,结合单调性画出函数的图象,通过图象即可观察出函数零点的个数.【详解】由()()()22320g x f x f x =--=⎡⎤⎣⎦,得()2f x =或1()2f x =-.当0x ≥时,2()121212(1)f x x x x x '=-=-,所以当(0,1)x ∈,()0,()'<f x f x 单调递减;当()1,x ∈+∞,()0,()'>f x f x 单调递增,所以1x =时,()f x 有极小值(1)4611f =-+=-.又0x <时,()x f x e =,画出函数()f x 的图象如图所示,由图可知:函数()()()2232g x f x f x =--⎡⎤⎣⎦的零点个数为3.故选:B .11. 已知()f x 是定义在R 上的函数满足(4)()f x f x -=-,且满足(31)f x -为奇函数,则下列说法一定正确的是( )A. 函数()f x 图象关于直线=2x 对称B. 函数()f x 的周期为2C. 函数()f x 关于点1,03⎛⎫- ⎪⎝⎭中心对称 D. (2023)0f =【答案】D 【解析】【分析】对于A.令2x x =+代入(4)()f x f x -=-即可判断.对于C.可考虑图像平移或者将3x 换元进行判断.对于BD.通过AB对称轴和对称中心即可判断出函数周期,继而计算出(2023)f 【详解】因为函数()f x 关于直线2x =-对称,不能确定()f x 是否关于直线2x =对称,A 错误;因为(31)f x -为奇函数,所以(31)(31)f x f x -=---,所以(1)(1)f x f x -=---,所以()(2)f x f x =---,所以函数()f x 关于点(1,0)-中心对称,故C 错误;由()(4)f x f x =--与()(2)f x f x =---得(4)(2)f x f x --=---,即(4)(2)f x f x -=--,故(4)()f x f x -=,所以函数()f x 的周期为4,故B 错误;(2023)(50641)(1)0f f f =⨯-=-=,故D 正确.故选:D的的12. 已知关于x 的不等式(e )e ->x x x x m m 有且仅有两个正整数解(其中e 2.71828= 为自然对数的底数),则实数m 的取值范围是( )A. 43169(,]5e 4eB. 3294(,4e 3eC. 43169[,5e 4eD. 3294[,e 3e 4【答案】D 【解析】【分析】问题转化为2(1)e x x m x +<(0x >)有且仅有两个正整数解,讨论0m ≤、0m >并构造()(1)f x m x =+、2()ex x g x =,利用导数研究单调性,进而数形结合列出不等式组求参数范围.【详解】当0x >时,由2e e 0xxx mx m -->,可得2(1)ex x m x +<(0x >),显然当0m ≤时,不等式2(1)ex x m x +<在(0,)+∞恒成立,不合题意;当0m >时,令()(1)f x m x =+,则()f x 在(0,)+∞上单调递增,令2()ex x g x =,则(2)()e xx x g x '-=,故(0,2)上()0g x '>,(2,)+∞上()0g x '<,∴()g x 在(0,2)上递增,在(2,)+∞上递减,又(0)(0)0f m g =>=且x 趋向正无穷时()g x 趋向0,故()240,e g x ⎛⎤∈ ⎥⎝⎦,综上,(),()f x g x 图象如下:由图知:要使()()f x g x <有两个正整数解,则()()()()()()11{2233f g f g f g <<≥,即2312e 43e 94e m m m ⎧<⎪⎪⎪<⎨⎪⎪≥⎪⎩,解得32944e 3e m ≤<.故选:D【点睛】关键点点睛:问题转化为2(1)ex x m x +<(0x >)有且仅有两个正整数解,根据不等式两边的单调性及正整数解个数列不等式组求范围.第Ⅱ卷非选择题(满分90分)二、填空题(每题5分,共20分)13. 1289log 24⎛⎫+= ⎪⎝⎭______ .【答案】116##516【解析】【分析】利用指数幂与对数运算即可求解.【详解】112388893111log 2log 8log 84236⎛⎫+=+=+= ⎪⎝⎭.故答案为:116.14. 曲线123x y x -=+在点()1,2--处的切线方程为________.(用一般式表示)【答案】530x y -+=【解析】【分析】利用导数的几何意义即得.【详解】由123x y x -=+,得22(23)2(1)5(23)(23)x x y x x +--'==++,所以切线的斜率为255(23)k ==-+,所以所求的切线方程为(2)5[(1)]y x --=--,即530x y -+=.故答案为:530x y -+=.15. 已知π4sin 35α⎛⎫+= ⎪⎝⎭,则πsin 26α⎛⎫+= ⎪⎝⎭___________.【答案】725##0.28【解析】分析】利用倍角余弦公式求得2π7cos(2)325α+=-,由诱导公式π2πsin(2cos(263αα+=-+,即可求值.【详解】22ππ167cos(212sin 12332525αα⎛⎫+=-+=-⨯=- ⎪⎝⎭,而πππ2π7sin(2cos(2)cos(2)662325ααα+=-++=-+=.故答案为:72516. 已知函数()sin 3f x x πω⎛⎫=+ ⎪⎝⎭(ω>0),若()f x 在20,3π⎡⎤⎢⎥⎣⎦上恰有两个零点,且在,424ππ⎡⎤-⎢⎥⎣⎦上单调递增,则ω的取值范围是________.【答案】510,23⎡⎤⎢⎥⎣⎦【解析】【分析】由()f x 在20,3π⎡⎤⎢⎥⎣⎦上恰有两个零点,令3x k πωπ+=,Z k ∈,可得52338233ππωππω⎧≤⎪⎪⎨⎪>⎪⎩,令22232k x k ππππωπ-+≤+≤+,Z k ∈,可得f (x )在5,66ππωω⎡⎤-⎢⎥⎣⎦上单调递增,从而有5646240ππωππωω⎧-≤-⎪⎪⎪≥⎨⎪>⎪⎪⎩,联立求解即可得答案.【详解】解:由题意,令3x k πωπ+=,Z k ∈,得x =33k ππω-,Z k ∈,∴f (x )的第2个、第3个正零点分别为53πω,83πω,【∴52338233ππωππω⎧≤⎪⎪⎨⎪>⎪⎩,解得542ω≤<,令22232k x k ππππωπ-+≤+≤+,Z k ∈,∴52266k k x ππππωωωω-+≤≤+,Z k ∈,令k =0,f (x )在5,66ππωω⎡⎤-⎢⎥⎣⎦上单调递增,∴5,,42466ππππωω⎡⎤⎡⎤-⊆-⎢⎥⎢⎥⎣⎦⎣⎦,∴5646240ππωππωω⎧-≤-⎪⎪⎪≥⎨⎪>⎪⎪⎩,解得1003ω<≤,综上,ω的取值范围是51023ω≤≤.故答案为:510,23⎡⎤⎢⎥⎣⎦.三、解答题(共70分)(一)必考题(共60分)17. 在锐角ABC 中,内角,,A B C 所对的边分别为,,a b c,已知sin sin ,2A Ca b A b +==.(1)求角B 的大小;(2)求2a c -的取值范围.【答案】(1)3π(2)()0,6【解析】【分析】(1)结合A C B π+=-,以及诱导公式、二倍角公式、正弦定理化简原式,即得解;(2)利用正弦定理,辅助角公式可化简26a c A π⎛⎫-=-⎪⎝⎭,结合A 的范围即得解【小问1详解】A CB π+=- ,sinsin 2B a b A π-∴=cos sin 2B a b A ∴=sin cos sin sin 2B A B A ∴=cos sin 2sin cos 222B B B B ∴==1sin 22B ∴=,又B 为锐角,263B B ππ∴==【小问2详解】由正弦定理4sin sin sin a b c A B C ====,214sin ,4sin 4sin 4sin 2sin 32a A c C A A A A A π⎫⎛⎫∴===-=+=+⎪ ⎪⎪⎝⎭⎭,128sin 2sin 6sin cos 2a c A A A A A A A ⎫∴-=--=-=-⎪⎪⎭6A π⎛⎫=- ⎪⎝⎭由锐角ABC ,故20,0232A C A πππ<<<=-<故(),sin ,20,6626A A a c πππ⎛⎛⎫<<∴-∈∴-∈ ⎪ ⎝⎭⎝.18. 已知等差数列{}n a 的前n 项和为n S ,2512a a +=,424S S =.(1)求n a 及n S ;(2)若11n n n n a b S S ++=⋅,求数列{}n b 的前n 项和n T .【答案】(1)21n a n =-,2n S n =(2)()2111n T n =-+【解析】【分析】(1)设出等差数列的首项和公差,利用等差数列的通项公式、前n 项和公式得到关于首项和公差的方程组求出1a 和d ,进而求出n a 及n S ;(2)利用(1)求出n b ,再利用裂项抵消法进行求和.【小问1详解】设等差数列{}n a 的公差为d ,则11125124344(2)2a d a d a d +=⎧⎪⎨⨯+=+⎪⎩,解得112a d =⎧⎨=⎩,所以()12121n a n n =+-=-,()21212n n n S n n -⨯=⨯+=.【小问2详解】由(1)得:+121n a n =+,21(1)n S n +=+,则()()122221211111n n n n a n b S S n n n n +++===-⋅++,所以123n nT b b b b =+++⋅⋅⋅+()22222222111111122331114n n =-+-+-+⋅⋅-+⋅+()2111n =-+..19. 已知()2ex x a f x -=.(1)当1a =时,求曲线()y f x =在点()()0,0f 处的切线方程;(2)若()1f x x ≤-对[)1,x ∞∈+恒成立,求a 的取值范围.【答案】(1)10x y --=(2)1a ≥【解析】【分析】(1)利用导数的几何意义以及直线方程的点斜式即可求解.(2)分离参数a ,转化成不等式恒成立问题,利用导数求最值即可.【小问1详解】当1a =时,()21ex x f x -=,()01f =-,()22(1)ex x x f x --'=,(0)1k f '∴==,所以切线方程为:11(0)y x +=⨯-,即10x y --=.【小问2详解】()1f x x ≤-恒成立,即2(1)e x a x x ≥--在[)1,x ∞∈+上恒成立,设2()(1)e x g x x x =--,()(2e )x g x x '=-,令()0g x '=,得120,ln 2x x ==,在[)1,+∞上,()0g x '<,所以函数2()(1)e x g x x x =--在[)1,+∞上单调递减,所以max ()(1)1g x g ==,max ()a g x ∴≥,故有1a ≥.20. 2022年2月4日北京冬奥运会正式开幕,“冰墩墩”作为冬奥会的吉祥物之一,受到各国运动员的“追捧”,成为新晋“网红”,尤其在我国,广大网友纷纷倡导“一户一墩”,为了了解人们对“冰墩墩”需求量,某电商平台采用预售的方式,预售时间段为2022年2月5日至2022年2月20日,该电商平台统计了2月5日至2月9日的相关数据,这5天的第x 天到该电商平台参与预售的人数y (单位:万人)的数据如下表:日期2月5日2月6日2月7日2月8日2月9日第x 天12345人数y (单位:万人)4556646872(1)依据表中的统计数据,请判断该电商平台的第x 天与到该电商平台参与预售的人数y (单位:万人)是否具有较高的线性相关程度?(参考:若0.300.75r <<,则线性相关程度一般,若0.75r ≥,则线性相关程度较高,计算r 时精确度为0.01)(2)求参与预售人数y 与预售的第x 天的线性回归方程;用样本估计总体,请预测2022年2月20日该电商平台的预售人数(单位:万人).参考数据:()()()55211460, 6.78i i i i i y y x x y y ==-=--=≈∑∑,附:相关系数()()()121ˆˆˆ,n i i i n i i x x y y r b ay bx x x ==--===--∑∑【答案】(1)具有较高的线性相关程度(2)ˆ 6.641.2yx =+,146.8万人【解析】【分析】(1)根据已知数据计算出相关系数r 可得;(2)由已知数据求出回归方程的系数得回归方程,然后在回归方程中令16x =代入计算可得估计值.【小问1详解】由表中数据可得1234545566468723,6155x y ++++++++====,所以()52110i i x x =-=∑又()()()55211460,66i i i i i y y x x y y ==-=--=∑∑所以0.970.75nx x y y r --==≈>所以该电商平台的第x 天与到该电商平台参与预售的人数y (单位:万人)具有较高的线性相关程度即可用线性回归模型拟合人数y 与天数x 之间的关系.【小问2详解】由表中数据可得()()()12166ˆ 6.610ni ii n i i x x y y b x x ==--===-∑∑则ˆˆ61 6.6341.2a y bx=-=-⨯=所以ˆ 6.641.2yx =+令16x =,可得ˆ 6.61641.2146.8y=⨯+=(万人)故预测2022年2月20日该电商平台预售人数146.8万人21. 已知()()2e 2ln x f x x a x x =-+(1)当e a =时,求()f x 的单调性;(2)讨论()f x 的零点个数.【答案】(1)()f x 在()0,1上单调递减,在()1,+∞上单调递增; (2)当0e ≤<a ,0个零点;当e a =或a<0,1个零点;e a >,2个零点【解析】【分析】(1)求出函数的导函数()()e 2e x f x x x x ⎛⎫'=+- ⎪⎝⎭,可得()10f '=,令()e e x g x x x =-,利用导数说明()g x 的单调性,即可求出()f x 的单调区间;(2)依题意可得()()2ln e 2ln 0x x f x a x x +=-+=,令2ln t x x =+,则问题转化为e t at =,R t ∈,利用零点存在定理结合单调性可判断方程的解的个数.【小问1详解】解:因为e a =,0x >,()()2e e 2ln x f x x x x =-+所以()()()()()2e 22e 2e e 12e 2e x x x x f x x x x x x x x x x +⎛⎫⎛⎫'=+-+=+-=+- ⎪ ⎪⎝⎭⎝⎭,()10f '=令()e e xg x x x =-,()()2e 1e 0x g x x x '=++>,所以()g x 在()0,+∞单增,且()10g =,当()0,1∈x 时()e e 0x g x x x =-<,当()1,x ∈+∞时()e e 0x g x x x =->,所以当()0,1∈x 时()0f x ¢<,当()1,x ∈+∞时()0f x ¢>,所以()f x 在()0,1单调递减,在()1,+∞单调递增【小问2详解】解:因为()()()2ln 2ln e e 2ln e 2ln 0x x x x f x a x x a x x +=⋅-+=-+=令2ln t x x =+,易知2ln t x x =+在()0,+∞上单调递增,且R t ∈,故()f x 零点转化为()()2ln e 2ln e 0x x t f x a x x at +=-+=-=即e t at =,R t ∈,的设()e t g t at =-,则()e tg t a '=-,当0a =时,()e tg t =无零点;当a<0时,()e 0t g t a '=->,故()g t 为R 上的增函数,而()010g =>,11e 10a g a ⎛⎫=-< ⎪⎝⎭,故()g t 在R 上有且只有一个零点;当0a >时,若(),ln t a ∈-∞,则()0g t '<;()ln ,t a ∈+∞,则()0g t '>;故()()()min ln 1ln g t g a a a ==-,若e a =,则()min 0g t =,故()g t 在R 上有且只有一个零点;若0e a <<,则()min 0g t >,故()g t 在R 上无零点;若e a >,则()min 0g t <,此时ln 1a >,而()010g =>,()()22ln 2ln 2ln g a a a a a a a =-=-,设()2ln h a a a =-,e a >,则()20a h a a-'=>,故()h a 在()e,+∞上为增函数,故()()e e 20h a h >=->即()2ln 0g a >,故此时()g t 在R 上有且只有两个不同的零点;综上:当0e ≤<a 时,0个零点;当e a =或a<0时,1个零点;e a >时,2个零点;【点睛】思路点睛:导数背景下的零点问题,注意利用零点存在定理结合函数单调性来讨论.(二)选考题(10分)请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.选修4-4:坐标系与参数方程22. 已知曲线1C 的参数方程为e e e e t tt t x y --⎧=+⎨=-⎩(t 为参数),以直角坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系.曲线2C 的极坐标方程4cos ρθ=.(1)求1C 的极坐标方程;(2)若曲线π(0)6θρ=>与曲线1C 、曲线2C 分别交于两点A ,B ,点(40)P , ,求△PAB 的面积.【答案】(1)24ππ(cos 244ρθθ=-<<(2)【解析】【分析】(1)将1C 的参数方程化为普通方程,再根据极坐标与直角坐标的转化公式即可得答案;(2)联立方程,分别求得点A ,B 的极坐标,根据三角形面积公式即可求得答案.【小问1详解】由e e e et tt t x y --⎧=+⎨=-⎩消去参数t ,得224x y -=,因为e e 2t t -+≥,所以曲线1C 的直角坐标方程为224(2)x y x -=≥,因为cos sin x y ρθρθ=⎧⎨=⎩,所以曲线1C 的极坐标方程为24ππ()cos 244ρθθ=-<< ;【小问2详解】由2π64cos2θρθ⎧=⎪⎪⎨⎪=⎪⎩得:A ρ=所以曲线π(0)6θρ=>与曲线1C 交于点A π)6,由π64cos θρθ⎧=⎪⎨⎪=⎩,得:B ρ=, 所以曲线π(0)6θρ=>与曲线2C :4cos ρθ=交于点B π6,则PAB S =△PA PBS S -△O △O 1π4()sin 26B A ρρ=⨯⨯-=选修4-5:不等式选讲23. 己知函数()221f x x a x a =+++-.(1)当0a =时,求不等式()2f x ≥的解集;(2)若对于任意x ∈R ,都有()2f x ≥,求实数a 的取值范围.【答案】(1)()1,1,3⎡⎫-∞-⋃+∞⎪⎢⎣⎭(2)32a ≤-或1a ≥.【解析】【分析】(1)分0x ≥,102x -≤<,12x <-三种情况打开绝对值,求解即可;(2)打开绝对值,将函数()f x 写成分段函数,结合单调性求解即可【小问1详解】()21f x x x=++当0x ≥时,()312f x x =+≥,解得13x ≥,当102x -≤<时,()12f x x =+≥,解得x ∈∅,当12x <-时,()312f x x =--≥,解得1x ≤-,所以不等式()2f x >的解集为()1,1,3⎡⎫-∞-⋃+∞⎪⎢⎣⎭.【小问2详解】因为222172()12148(0222a a a a a +++++--==>,故212a a +>-所以()2222231,11,2131,2x a a x a a f x x a a x a a x a a x ⎧⎪++-≥⎪+⎪=+++-≤<⎨⎪+⎪---+<-⎪⎩所以函数()f x 在1,2a +⎛⎤-∞- ⎥⎝⎦上递减,在1,2a +⎡⎫-+∞⎪⎢⎣⎭上递增,所以函数()f x 在R 上的最小值为21122a a f a ++⎛⎫-=+ ⎪⎝⎭.所以2122a a ++≥,即223(23)(1)0a a a a +-=+-≥解得32a ≤-或1a ≥。
【恒心】2015届山东省滕州市第五中学高三第二次月考数学(文科)试题及参考答案【word版】

山东省滕州市第五中学2015届高三第二次月考数学(文)试题一、选择题(10×5分=50分)1.已知全集U=R ,集合A={x||x ﹣2|<1},B={x|y=x 24-},则A∩B=( )A .(1,2)B .(2,3)C .[2,3)D .(1,2]2.已知i 是虚数单位,且复数2121,21,3z z i z bi z 若-=-=是实数,则实数b 的值为 A .6B .6-C .0D .61 3.设n S 为等比数列}{n a 的前n 项和,已知342332,32S a S a =-=-,则公比q =A .3B .4C .5D .64.知函数()f x 的定义域是(0,1),则(2)xf 的定义域是( )A .(0,1)B .(1,2)C .(,0)-∞D .(0,)+∞5.设2(log )2(0)x x f x =>,则(2)f 的值是( )A .128B .16C .8D .2566.若幂函数()322233-+++=m m x m m y 的图像不过原点,且关于原点对称,则m 的取值是( ) A .2-=mB .1-=mC .12-=-=m m 或D .13-≤≤-m7.设c b a ,,均为正数,且a a21log 2=,b b21log 21=⎪⎭⎫⎝⎛,则( )A .c b a <<B .a b c <<C .b a c <<D .c a b <<8.若log 4(3a +4b )=log 2ab ,则a +b 的最小值是( )A .6+2 3B .7+2 3C .7+4 3D .6+4 39.函数2()xf x x a=+的图象不可能是 ( )10.对于函数2()3f x x k =-+,当实数k 属于下列选项中的哪一个区间时,才能确保一定存在实数对,a b (0)a b <<,使得当函数()f x 的定义域为[],a b 时,其值域也恰好是[],a b ( )A .[)2,0-B .1(2,)12--C .1(,0)12-D .1(,)12-+∞ 二、填空题(5×5分=25分)11.“a R ∃∈,使函数2()f x x ax =-是偶函数”的否定是____________________ 12.集合{}220M x x x a =-+=有8个子集,则实数a 的值为 13.若不等式x 2+ax +1>0对于一切x ∈(0,12]成立,则a 的取值范围是14.已知函数xx x f 2ln )(+=, 若2)4(2<-x f , 则实数x 的取值范围为 . 15.函数()f x 对于任意实数x 满足条件()()12f x f x +=,若()15,f =-则()()5f f =______三、解答题16.(12分)已知函数222()2(log )2(log )f x x a x b =-+,当12x =时有最小值-8,(1)求,a b 的值;(2)当1,84x ⎡⎤∈⎢⎥⎣⎦时,求()f x 的最值.17.(12分)已知定义在R 上函数2()1x bf x x ax +=++为奇函数.(1)求a b +的值;(2)求函数()f x 的值域.18.(12分)已知函数()y f x =和()y g x =的图象关于y 轴对称,且2()242f x x x =+-.(1)求函数()y g x =的解析式;(2)当12k <时,解不等式4()()1k f x g x x <+-. 19.(12分)已知p :关于x 的方程210x m +-=有实数解;q :函数()1f x x m =-+在),(2∞-上为减函数.若p 或q 为真,p 且q 为假,求实数m 的取值范围.20.(13分)设二次函数2()(,,)f x ax bx c a b c R =++∈满足下列条件: ①当x ∈R 时,()f x 的最小值为0,且f (x -1)=f (-x -1)成立; ②当x ∈(0,5)时,x ≤()f x ≤21x -+1恒成立。
宁夏银川一中2015届高三第二次月考数学(文科)试卷及答案

银川一中2015届高三年级第二次月考数 学 试 卷(文)第Ⅰ卷一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合2{|10},{|A x x B x y =-<==,则A∩B 等于( )A .{|1}x x >B .{|01}x x <<C . {|1}x x <D .{|01}x x <≤2.已知复数 z 满足(1)1z i =+,则||z =( )A B .21C D . 23.在△ABC 中,“sin A >”是“3πA >”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.O 是ABC ∆所在平面内的一点,且满足()(2)0OB OC OB OC OA -⋅+-=,则ABC ∆的形状一定为( )A .正三角形B .直角三角形C .等腰三角形D .斜三角形5.设向量,+=10-=6,则=⋅( )A .5B .3C .2D .16.函数2sin 2xy x =-的图象大致是( )7.若角α的终边在直线y =2x 上,则ααααcos 2sin cos sin 2+-的值为( )A .0 B. 34 C .1 D. 548.ABC ∆的内角A B C 、、的对边分别是a b c 、、,若2B A =,1a =,b =,则c = ( )A .B .2CD .19.若f(x)=21ln(2)2x b x -++∞在(-1,+)上是减函数,则b 的取值范围是( ) A.[-1,+∞) B.(-1,+∞) C.(-∞,-1] D.(-∞,-1) 10.函数()()xx x f 21ln -+=的零点所在的大致区间是( ) A.(0,1)B.(1,2)C.(2,3)D.(3,4)11.)0)(sin(3)(>+=ωϕωx x f 部分图象如图,若2||=⋅,ω等于( ) A .12π B .4πC .3π D .6π 12.函数()x f 是R 上的偶函数,在区间[)+∞,0上是增函数.令⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=75tan ,75cos ,72sinπππf c f b f a ,则( )A .c b a <<B .a b c <<C .a c b <<D .c a b <<第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须做答.第22题~第24题为选考题,考生根据要求做答. 二、填空题:本大题共4小题,每小题5分,共20分.13.设1232,2()log (1),2x e x f x x x -⎧<⎪=⎨-≥⎪⎩,则((2))f f 的值为 . 14.若sin cos θθ+=tan 3πθ⎛⎫+ ⎪⎝⎭的值是 ___________.15.设奇函数()x f 的定义域为R ,且周期为5,若()1f <—1,(),log 42a f =则实数a 的取值范围是 .16.以下命题:①若||||||a b a b ⋅=⋅,则a ∥b ; ②a =(-1,1)在b =(3,4)方向上的投影为15; ③若△ABC 中,a=5,b =8,c =7,则BC ·CA =20;④若非零向量a 、b 满足||||a b b +=,则|2||2|b a b >+. 所有真命题的标号是______________.三、解答题: 解答应写出文字说明,证明过程或演算步骤. 17、(本小题12分)已知向量⎪⎭⎫ ⎝⎛=23,sin x m ,()02cos 3,cos 3>⎪⎭⎫⎝⎛=A x A x A ,函数()f x m n =⋅的最大值为6.(1)求A ;(2)将函数()y f x =的图象向左平移12π个单位,再将所得图象上各点的横坐标缩短为原来的12倍,纵坐标不变,得到函数()y g x =的图象.求()g x 在⎥⎦⎤⎢⎣⎡40π,上的值域.18.(本小题12分)设函数)0(19)(23<--+=a x ax x x f ,且曲线)(x f y =斜率最小的切线与直线612=+y x 平行.求:(1)a 的值;(2)函数)(x f 的单调区间.19.(本小题12分)a ax e x f x,1)(2+=为正实数(1)当34=a ,求)(x f 极值点; (2)若)(x f 为R 上的单调函数,求a 的范围. 20.(本题满分12分)已知,,a b c 分别为ABC ∆三个内角,,A B C 的对边,cos sin 0a C C b c --=。
精品解析:四川省绵阳南山中学2022-2023学年高三下学期3月月考试题文综政治试题(解析版)

绵阳南山中学2023年春高2020级3月月考文科综合政治试题一、选择题。
1. 2022年中央经济工作会议提出:做好明年经济工作,要全面深化改革开放,把实施扩大内需战略同深化供给侧结构性改革有机结合起来,突出做好稳增长、稳就业、稳物价工作,有效防范化解重大风险,推动经济运行整体好转。
下列关于扩大内需战略措施传导正确的是()①稳就业→增加居民收入→提振消费信心→拉动消费增长②加大金融扶持→企业融资成本降低→企业资金充足→增强企业竞争力③保交楼专项贷款→保障房企资金链→房地产需求增加→房地产市场回暖④供给侧结构性改革→有效供给增加→居民消费欲望增加→刺激消费需求A. ①③B. ①④C. ②③D. ②④【答案】B【解析】【详解】①:突出做好稳就业工作,有利于增加居民收入,从而稳定并提振居民消费信心,扩大内需,进而拉动经济增长,①入选。
①:加大金融扶持,在一定程度上能够降低融资成本,使企业有充足的资金,能够激发企业活力,但企业有充足的资金,不一定能够增强企业的竞争力,①不选。
①:保交楼专项贷款,有利于保障房企资金链,维护住房消费者合法权益,促进房地产市场平稳健康发展,而不是增加房地产需求,①不选。
①:通过供给侧结构性改革,从而增加有效供给,促进居民消费欲望增加,从而刺激消费需求,扩大内需,①入选。
故本题选B。
2. 2022年1月,国务院印发《“十四五”数字经济发展规划》提出,到2035年,数字经济发展水平位居世界前列。
下图为我国数字经济内部结构“数字产业化”和“产业数字化”占比变化图,产生这种变化的原因可能是()①我国数字技术与产业融合发展促进了数字鸿沟有效弥合②数据成为经济发展的关键,在生产力发展中起主导作用③传统产业应用数字技术带来的数字化转型升级深入推进④数字领域关键技术创新能力不足阻碍了数字新业态发展A. ①②B. ①④C. ②③D. ③④【答案】D【解析】【详解】①:材料强调的是数字经济内部结构“数字产业化”和“产业数字化”的占比变化的原因,不涉及数字技术与产业融合,故①不符合题意。
莆田一中高三下学期月考文科综合文综试卷及答案
莆田一中2013届高考第五次月考文综(完卷150分钟满分300分)第I卷选择题 (共144分)本卷共36小题,每小题4分,满分144分。
在每小题给出的四个选项中,只有一项是最符合题目要求的。
请将答案填涂于答题卡中。
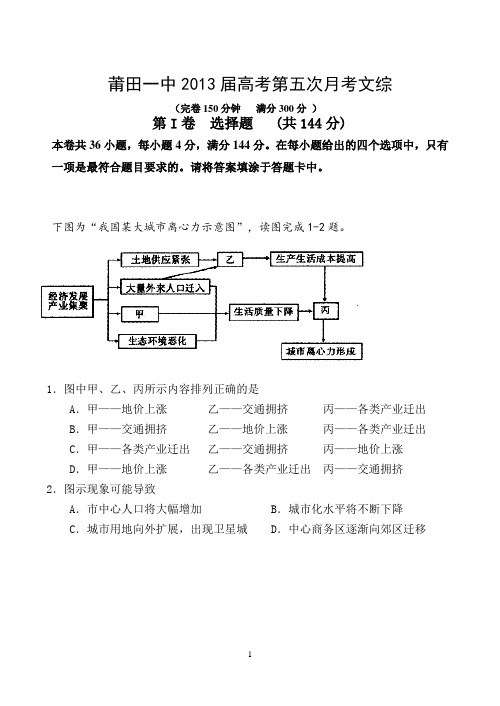
下图为“我国某大城市离心力示意图”,读图完成1-2题。
1.图中甲、乙、丙所示内容排列正确的是A.甲——地价上涨乙——交通拥挤丙——各类产业迁出B.甲——交通拥挤乙——地价上涨丙——各类产业迁出C.甲——各类产业迁出乙——交通拥挤丙——地价上涨D.甲——地价上涨乙——各类产业迁出丙——交通拥挤2.图示现象可能导致A.市中心人口将大幅增加 B.城市化水平将不断下降 C.城市用地向外扩展,出现卫星城 D.中心商务区逐渐向郊区迁移下图为我国目前油库分布图,据此完成3-4题。
3. 根据分布情况可知影响油库分布的主要区位因素是A. 市场B. 交通C. 资源D. 科技4. 随着石油资源的丰富的地区,为新油库的建设提供了充分的保障.如果要新建油库,应优先考虑是A. 东北地区B. 西北地区C. 华南地区D. 青藏地区山地迎风面的气压比背风面高很多,使等压线突然变形或突然密集,可将几根等压线用一条锯齿形线连结起来,称之为地形等压线,应画在山的迎风面或冷空气的一侧,与山脉平行,不能横穿山脉。
读我国某山地某季节地形等压线图,回答5-6题。
5.山地迎风面气压比背风面气压高的原因是A.迎风面气温高 B.迎风面气流下沉C.迎风面降水多 D.迎风面空气堆积6.图示季节最有可能是A.春季 B.夏季 C.冬季 D.秋季图中数码分别示意我国和欧洲的某山地南坡与北坡植被垂直带谱,读图回答7-8题:7. 关于各数码示意的坡向说法正确的是A. ①坡是北坡和迎风坡B. ②坡是南坡和迎风坡C. ③坡是阴坡和背风坡D. ④坡是阳坡和迎风坡8. 下列说法正确的是A.造成①②坡雪线低于③④坡的主导因素是纬度B.影响①②坡与③④坡基带植被差异的主导因素是热量C.②坡植被带上限高于①坡是因为②坡是迎风坡降水多D.④坡上针叶林分布体现了地方性分异规律气溶胶是大气中悬浮的液态或固态微粒的总称,是大气的重要组成部分。
高一第二学期第一次月考化学文科试题

河北平山中学2013-2014学年第二学期 高一年级 文科化学试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分100 分,考试时间90分钟。
第Ⅰ卷(选择题,共 40 分)本卷共20 个小题,每小题 2 分,共 40分。
在每小题给出的答案中,只有一个是最符合题意的一、选择题1.某粒子含有6个电子、7个中子,呈电中性,则它的化学符号可能是( )。
A .13AlB .13AlC .13CD .13C2.下列粒子半径最小的是( )。
A .Na +B .NaC .ClD .Cl -3.下列各组中属于同位素关系的是( )。
A .K 4019与Ca 4020B .T 2O 与H 2OC .K 4019与K 3919D .金刚石与石墨4.在元素周期表中位于金属元素和非金属元素交界处最容易找到的材料是( )。
A .制催化剂的材料 B .耐高温、耐腐蚀的合金材料 C .制农药的材料D .半导体材料5.下列递变规律不正确的是( )。
A .Na 、Mg 、Al 还原性依次减弱 B .I 2、Br 2、Cl 2氧化性依次增强 C .C 、N 、O 原子半径依次增大D .P 、S 、Cl 最高正价依次升高6.下列各组微粒具有相同的质子数和电子数的是( )。
A .OH -、H 2O 、F -B .NH 3、NH +4、NH -2C .H 3O +、NH +4、NH -2 D .HCl 、F 2、H 2S 7.X 元素的阳离子和Y 元素的阴离子具有相同的核外电子结构,下列叙述正确的是( )。
A .原子序数:X <Y B .原子半径:X <YC .离子半径:X >YD .原子最外层电子数:X <Y8.下列各组化合物的性质比较,不正确的是( )。
A .酸性:HClO 4>HBrO 4>HIO 4B .碱性:NaOH >Mg (OH )2>Al (O H )3C .稳定性:PH 3>H 2S >HClD .非金属性:F >O >S9.同周期的X 、Y 、Z 三种元素,已知其最高价氧化物对应的水化物的酸性强弱顺序是:HXO 4>H 2YO 4>H 3ZO 4,则下列各判断中正确的是( )。
四川省广安市邻水二中2014-2021学年高一下学期4月月考数学试卷(文科) Word版含解析

四川省广安市邻水二中2022-2021学年高一下学期4月月考数学试卷(文科)一、选择题:本大题共10小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.cos15°的值为()A.B.C.D .2.在△ABC中,∠B为钝角,则有()A.s inA>cosB B.s inA<cosBC.s inA=cosB D.s inA,cosB大小不确定3.函数y=cos2πx的最小正周期是()A.πB.2πC.1D.24.以下函数在区间(0,)上是减函数的是()A.y=﹣cosx B.y=﹣sinx C.y=tanx D.5.在△ABC中,三个内角A,B,C的对边分别为a,b,c,则下列各式错误的是()A.若sinA+cosA<1,则△ABC为钝角三角形B.若a2+b2<c2,则△ABC为钝角三角形C.若•<0,则△ABC为钝角三角形D.若A、B为锐角且cosA>sinB,则△ABC为钝角三角形6.在锐角△ABC中,设x=sinA•sinB,y=cosA•cosB.则x,y的大小关系为()A.x≤y B.x>y C.x<y D.x≥y7.已知tanα、tanβ是方程x2+x﹣2=0的两个根,且﹣<α<,﹣<β<,则α+β的值是()A.﹣B.﹣C.或﹣D .﹣或8.已知﹣<α<﹣π,则的值为()A.﹣sin B.c os C.s in D.﹣cos9.△ABC中,若A=60°,a=,则等于()A.2B.C.D .10.在△ABC 中,若==,则△ABC是()A.直角三角形B.等边三角形C.钝角三角形D.等腰直角三角形二、填空题(本大题共5小题,每题5分,共25分,请把答案填在答题卡上的相应横线上).11.在数列{a n}中,若a1=1,a n+1=a n+2(n≥1),则该数列的通项a n=.12.化简(tan10°﹣)•=.13.已知α,β均为锐角,cosα=,cos(α+β)=﹣,则cosβ=.14.设{a n}是公差为正数的等差数列,若a1+a2+a3=15,a1a2a3=80,则a11+a12+a13=.15.设f(n)=+++…+(n∈N),那么f(n+1)﹣f(n)等于.三、解答题(本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤).16.设数列{a n}的前n项和为S n,点(n ,)(n∈N*)均在函数y=3x﹣2的图象上,求数列{a n}的通项公式.17.如图所示,我艇在A处发觉一走私船在方位角45°且距离为12海里的B处正以每小时10海里的速度向方位角105°的方向逃跑,我艇马上以14海里/小时的速度追击,求我艇追上走私船所需要的最短时间.18.一个等差数列前4项的和是24,前5项的和与前2项的和的差是27,求这个等差数列的通项公式.19.设函数f(x)=sin(2x+φ)(﹣π<φ<0),y=f(x )图象的一条对称轴是直线.(Ⅰ)求φ;(Ⅱ)求函数y=f(x)的单调增区间.20.已知向量=(cosα,sinα),=(cosβ,sinβ),|﹣|=.(1)求cos(α﹣β)的值;(2)若﹣<β<0<α<,且sinβ=﹣,求sinα的值.21.在△ABC中,内角A,B,C的对边三边分别为a,b,c,已知f(A)=4sinAsin2(+)+cos2A,若满足|f(A)﹣m|<2对任意三角形都成立,求实数m的取值范围.四川省广安市邻水二中2022-2021学年高一下学期4月月考数学试卷(文科)一、选择题:本大题共10小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.cos15°的值为()A.B.C.D .考点:两角和与差的余弦函数.专题:不等式的解法及应用.分析:由条件利用两角差的余弦公式求得cos15°的值.解答:解:cos15°=cos(45°﹣30°)=cos45°cos30°+sin45°sin30°=﹣=,故选:A.点评:本题主要考查两角差的余弦公式的应用,属于基础题.2.在△ABC中,∠B为钝角,则有()A.s inA>cosB B.s inA<cosBC.s inA=cosB D.s inA,cosB大小不确定考点:三角函数值的符号;正弦定理.专题:三角函数的求值.分析:依据三角函数值的符号值进行推断即可.解答:解:在△ABC中,∠B为钝角,则cosB<0,sinA>0,则恒有sinA>cosB,故选:A点评:本题主要考查三角函数取值符号和角的关系,比较基础.3.函数y=cos2πx的最小正周期是()A.πB.2πC.1D.2考点:三角函数的周期性及其求法.专题:三角函数的图像与性质.分析:利用倍角公式可得y=,依据三角函数的周期性及其求法即可得解.解答:解:∵y=cos2πx=,∴最小正周期T==1.故选:C.点评:本题主要考查了倍角公式,三角函数的周期性及其求法的应用,属于基础题.4.以下函数在区间(0,)上是减函数的是()A.y=﹣cosx B.y=﹣sinx C.y=tanx D.考点:正切函数的单调性;函数单调性的推断与证明.专题:函数的性质及应用;三角函数的图像与性质.分析:依据余弦函数、正弦函数,及正切函数的单调性及单调性的定义即可推断每个选项的正误,从而得出正确选项.解答:解:A.y=cosx在(0,)上是减函数,∴y=﹣cosx在[0,]上是增函数;B.y=sinx在(0,)上是增函数,∴y=﹣sinx在(0,)上是减函数,即该选项正确;C.正切函数y=tanx 在上是增函数;D.,∴;而函数y=sinx 在上是增函数;∴函数在(0,)上是增函数.故选B.点评:考查正弦函数,余弦函数,及正切函数的单调性,以及依据单调性的定义推断函数的单调性的方法.5.在△ABC中,三个内角A,B,C的对边分别为a,b,c,则下列各式错误的是()A.若sinA+cosA<1,则△ABC为钝角三角形B.若a2+b2<c2,则△ABC为钝角三角形C.若•<0,则△ABC为钝角三角形D.若A、B为锐角且cosA>sinB,则△ABC为钝角三角形考点:余弦定理.专题:解三角形;平面对量及应用.分析:对A,利用两角和正弦公式及正弦函数的单调性,推断角A是否大于直角即可;对B,利用余弦定理推断角C是否为钝角;对C,利用向量数量积公式,推断角B是否为钝角;对D,先化同名三角函数,再利用单调性分析推断即可.解答:解:A选项∵sinA+cosA=sin(A+)<1,∴sin(A+)<,∵<A+<π+,∴A+>,∴A >,故A正确;B选项,cosC=<0,∴C >,故B正确;C选项,∵•=﹣•,∴•=||||cosB>0,∴B <,故不能确定三角形为钝角三角形,故C错误;D选项,∵cosA=sin (﹣A)>sinB,又∵若A、B为锐角,∴>B⇒A+B <,∴C >,故D正确.故选:C.点评:本题借助考查命题的真假推断,考查三角形外形的推断,以及向量的数量积的定义,属于基础题和易错题.6.在锐角△ABC中,设x=sinA•sinB,y=cosA•cosB.则x,y的大小关系为()A.x≤y B.x>y C.x<y D.x≥y考点:两角和与差的正弦函数.专题:计算题.分析:运用特殊值法,令A=60°,B=45°代入x和y的表达式,可分别求得x和y的值,则二者的大小可知.解答:解:令A=60°,B=45°x=sinA•sinB=×=,y=cosA•cosB=×=,∴x>y.故选:B.点评:考查了两角和与差的余弦函数.对于选择题和填空题来说,用特殊值法有时更便捷.7.已知tanα、tanβ是方程x2+x﹣2=0的两个根,且﹣<α<,﹣<β<,则α+β的值是()A.﹣B.﹣C.或﹣D .﹣或考点:两角和与差的正切函数.专题:三角函数的求值.分析:由条件利用韦达定理求得tanα+tanβ和tanαtanβ的值,可得tan(α+β)的值,从而结合α+β的范围求得α+β的值.解答:解:∵tanα、tanβ是方程x2+x﹣2=0的两个根,∴tanα+tanβ=﹣,tanα•tanβ=﹣2,∴tan(α+β)==.再依据﹣<α<,﹣<β<,可得α+β∈(﹣π,π),∴α+β=或﹣,故选:C.点评:本题主要考查韦达定理,两角和的正切公式,依据三角函数的值求角,属于基础题.8.已知﹣<α<﹣π,则的值为()A.﹣sin B.c os C.s in D.﹣cos考点:三角函数的化简求值.专题:三角函数的求值.分析:由二倍角公式和根式的性质逐步化简可得.解答:解:∵﹣<α<﹣π,∴cosα<0,∴==﹣cosα,∴原式===|sin|,∵﹣<α<﹣π,∴<<,∴sin<0,∴原式=﹣sin故选:A.点评:本题考查三角函数的化简求值,涉及二倍角公式和根式的化简,属基础题.9.△ABC中,若A=60°,a=,则等于()A.2B.C.D .考点:正弦定理的应用.专题:计算题.分析:由正弦定理可得2r==2,故==2r=2.解答:解:由正弦定理可得2r===2,(r为外接圆半径);==2r=2,故选A.点评:本题考查正弦定理的应用,求出2r的值,是解题的关键.10.在△ABC 中,若==,则△ABC是()A.直角三角形B.等边三角形C.钝角三角形D.等腰直角三角形考点:正弦定理的应用.专题:计算题.分析:先依据正弦定理将边的关系变为角的关系,进而再由两角和与差的正弦公式确定B=C得到三角形是等腰三角形.解答:解:由=,得=.又=,∴=.∴=.∴sinAcosB=cosAsinB,sin(A﹣B)=0,A=B.同理B=C.∴△ABC是等边三角形.故选B.点评:本题主要考查正弦定理和两角和与差的正弦公式的应用.三角函数公式比较多,要对公式强化记忆.二、填空题(本大题共5小题,每题5分,共25分,请把答案填在答题卡上的相应横线上).11.在数列{a n}中,若a1=1,a n+1=a n+2(n≥1),则该数列的通项a n =2n ﹣1.考点:等差数列的通项公式.专题:计算题.分析:利用等差数列的定义推断出数列为等差数列,利用等差数列的通项公式求出通项.解答:解:由a n+1=a n +2(n≥1)可得数列{a n}为公差为2的等差数列,又a1=1,所以a n=2n﹣1故答案为2n﹣1点评:本题考查等差数列的定义、等差数列的通项公式.12.化简(tan10°﹣)•=﹣2.考点:两角和与差的正弦函数;同角三角函数间的基本关系.专题:计算题;三角函数的求值.分析:将tan10°﹣切化弦,通分后用帮助角公式合并,化简得tan10°﹣=,代入原式即可得到所求.解答:解:∵tan10°﹣====∴(tan10°﹣)•=•=﹣2故答案为:﹣2点评:本题将一个三角函数式化简后,求式子的值.着重考查了同角三角函数的基本关系、两角差的正弦公式、帮助公式等三角恒等变换公式的学问,属于中档题.13.已知α,β均为锐角,cosα=,cos(α+β)=﹣,则cosβ=.考点:两角和与差的余弦函数.专题:三角函数的求值.分析:先利用同角三角函数的基本关系求得sinα和sin(α+β)的值,然后利用cosβ=cos[(α+β)﹣α],依据两角和公式求得答案.解答:解:∵α,β均为锐角,∴sinα==,sin(α+β)==∴cosβ=cos[(α+β)﹣α]=cos(α+β)cosα+sin(α+β)sinα=.故答案为:点评:本题主要考查了两角和公式的化简求值和同角三角函数的基本关系的应用.娴熟记忆三角函数的基本公式是解题的基础.14.设{a n}是公差为正数的等差数列,若a1+a2+a3=15,a1a2a3=80,则a11+a12+a13=105.考点:等差数列的性质.专题:计算题.分析:由a1+a2+a3=15,利用等差中项的性质,可求得a2,然后利用a1a2a3=80通过解方程得到公差d,即可求出a11+a12+a13的值.解答:解:设数列的公差为d(d>0),∵a1+a2+a3=3a2=15∴a2=5.∵a1a2a3=80∴(5﹣d)•5•(5+d)=5(25﹣d2)=80∴d2=25﹣16=9∴d=3∴a11+a12+a13=(a1+a2+a3)+30d=15+90=105故答案为105.点评:本题考查等差数列的性质,通过对等差数列的争辩,养成细心观看、认真分析、擅长总结的良好思维习惯.是个基础题.15.设f(n)=+++…+(n∈N),那么f(n+1)﹣f(n )等于.考点:函数的值.专题:函数的性质及应用.分析:依据题中所给式子,求出f(n+1)和f(n),再两者相减,即得到f(n+1)﹣f(n)的结果.解答:解:∵f(n)=+++…+,∴f(n+1)=++…+++,∴f(n+1)﹣f(n)=+﹣=﹣=,故答案为:点评:此题主要考查函数的值,依据已知中的函数解析式,直接代入即可.三、解答题(本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤).16.设数列{a n}的前n项和为S n,点(n ,)(n∈N*)均在函数y=3x﹣2的图象上,求数列{a n}的通项公式.考点:数列递推式.专题:等差数列与等比数列.分析:通过将点(n ,)代入函数y=3x﹣2、整理可知S n=3n2﹣2n,利用a n+1=S n+1﹣S n可知当n≥2时a n=6n ﹣5,验证当n=1时是否成马上得结论.解答:解:∵点(n ,)(n∈N*)均在函数y=3x﹣2的图象上,∴=3n﹣2,即S n=3n2﹣2n,∴a n+1=S n+1﹣S n=3(n+1)2﹣2(n+1)﹣(3n2﹣2n)=6(n+1)﹣5,∵a1=S1=3﹣2=1满足上式,∴数列{a n}的通项公式a n=6n﹣5.点评:本题考查数列的通项,留意解题方法的积累,属于中档题.17.如图所示,我艇在A处发觉一走私船在方位角45°且距离为12海里的B处正以每小时10海里的速度向方位角105°的方向逃跑,我艇马上以14海里/小时的速度追击,求我艇追上走私船所需要的最短时间.考点:解三角形的实际应用.专题:应用题;解三角形.分析:设我艇追上走私船所需要的时间为t小时,依据各自的速度表示出BC与AC,由∠ABC=120°,利用余弦定理列出关于t的方程,求出方程的解即可得到t的值.解答:解:设我艇追上走私船所需要的时间为t小时,则BC=10t,AC=14t,在△ABC中,∠ABC=120°,依据余弦定理知:(14t)2=(10t)2+122﹣2•12•10tcos 120°,∴t=2或t=﹣(舍去),故我艇追上走私船所需要的时间为2小时.点评:此题考查了正弦、余弦定理,以及特殊角的三角函数值,娴熟把握正弦、余弦定理是解本题的关键.18.一个等差数列前4项的和是24,前5项的和与前2项的和的差是27,求这个等差数列的通项公式.考点:等差数列的通项公式.专题:等差数列与等比数列.分析:设出等差数列的首项和公差,由题意列方程组求得首项和公差,则答案可求.解答:解:依据题意,得S4=24,S5﹣S2=27.设等差数列首项为a1,公差为d,即,解得:.∴an=3+2(n﹣1)=2n+1.点评:本题考查等差数列的通项公式,考查了等差数列的前n项和,是基础的计算题.19.设函数f(x)=sin(2x+φ)(﹣π<φ<0),y=f(x )图象的一条对称轴是直线.(Ⅰ)求φ;(Ⅱ)求函数y=f(x)的单调增区间.考点:由y=Asin(ωx+φ)的部分图象确定其解析式;复合三角函数的单调性.专题:计算题;三角函数的图像与性质.分析:(I)依据正弦函数图象的对称轴方程,得函数f(x)图象的对称轴方程为2x+ϕ=(k∈Z).再将代入得到关于ϕ的等式,结合﹣π<ϕ<0可得ϕ的值;(II)由(I)得f(x)=sin(2x ﹣),由正弦函数的单调区间公式,建立关于x的不等式,解之即可得到y=f(x)的单调增区间.解答:解:(I)函数f(x)=sin(2x+ϕ)图象的对称轴方程为2x+ϕ=(k∈Z).∵直线是函数图象的一条对称轴,∴2•+ϕ=(k∈Z),结合﹣π<ϕ<0,取k=﹣1得ϕ=﹣;(II)由(I)得函数解析式为f(x)=sin(2x ﹣),令﹣+2mπ≤2x ﹣≤+2mπ(m∈Z),得+mπ≤x ≤+mπ(m∈Z),∴函数y=f(x)的单调增区间是[+mπ,+mπ],(m∈Z).点评:本题给出三角函数图象的一条对称轴,求函数的解析式并求单调增区间.着重考查了三角函数的图象与性质和函数的单调性以图象的对称性等学问,属于中档题.20.已知向量=(cosα,sinα),=(cosβ,sinβ),|﹣|=.(1)求cos(α﹣β)的值;(2)若﹣<β<0<α<,且sinβ=﹣,求sinα的值.考点:两角和与差的余弦函数;向量的模.专题:三角函数的求值.分析:(1)由模长公式和三角函数公式可得|﹣|2=2﹣2co(α﹣β)=,变形可得;(2)结合角的范围分别可得sin(α﹣β)=和cosβ=,而sinα=sin[(α﹣β)+β]=sin(α﹣β)cosβ+cos(α﹣β)sinβ,代入化简可得.解答:解:(1)∵=(cosα,sinα),=(cosβ,sinβ),∴||=||=1,∴|﹣|2==1+1﹣2(cosαcosβ+sinαsinβ)=2﹣2cos(α﹣β),又∵|﹣|=,∴|﹣|2=2﹣2cos(α﹣β)=,∴cos(α﹣β)=;(2)∵﹣<β<0<α<,∴0<α﹣β<π,由cos(α﹣β)=可得sin(α﹣β)=,由sinβ=﹣可得cosβ=,∴sinα=sin[(α﹣β)+β]=sin(α﹣β)cosβ+cos(α﹣β)sinβ==点评:本题考查两角和与差的正余弦函数,涉及向量的模长公式,属基础题.21.在△ABC中,内角A,B,C的对边三边分别为a,b,c,已知f(A)=4sinAsin2(+)+cos2A,若满足|f(A)﹣m|<2对任意三角形都成立,求实数m的取值范围.考点:三角函数中的恒等变换应用.专题:计算题;三角函数的求值.分析:化简f(A),由A的范围可得f(A)的范围,由恒成立可得m<[f(x)+2]min且m>[f(x)﹣2]max,可得答案.解答:解:(1)化简可得f(A)=4sinA •+cos2A=2sinA(1+sinA)+1﹣2sin2A=2sinA+1,∵x∈R,∴sinx∈[﹣1,1],∴f(x)的值域是[﹣1,3];(2)当A∈(0,π)时,sinA∈(0,1],∴f(x)∈(1,3],由|f(x)﹣m|<2可得﹣2<f(x)﹣m<2,∴f(x)﹣2<m<f(x)+2恒成立.∴m<[f(x)+2]min=3,且m>[f(x)﹣2]max=1.故m的取值范围是(1,3).点评:本题考查三角函数的恒等变形,涉及恒成立问题,属中档题.。
河北省邢台一中2013-2014学年下学期高一年级第三次月考数学试卷(文科)

河北省邢台一中2013-2014学年下学期高一年级第三次月考数学试卷(文科)第Ⅰ卷(选择题 共60分)一、选择题:(本大题共12小题,每小题5分,满分60分)1.若集合M={}直线,N={}圆,则集合M ⋂N 中元素的个数为( ) A. 0个 B. 1个 C.0个或1个 D.1个或2个2.直线0x a +=(a 为实常数)的倾斜角的大小是( )A .30B .60C .120D .1503. 若R c b a ∈,,,且b a >,则下列不等式一定成立的是( )A .c b c a -≥+B .bc ac >C .0)(2≥-c b a D .02>-ba c 4.直线5x y +=和圆22: x 40O y y +-=的位置关系是( ) A .相切B .相离C .相交不过圆心D .相交过圆心5.若方程02)2(x 22=++++a ax y a 表示圆,则a 的值为 A.-1 B.2 C.-1或2 D 。
不存在 6.不等式y≥|x|表示的平面区域是( )7、点(0,1)A 和(2,0)B 关于直线l 对称,则l 的方程为 ( ) A.2430x y +-= B. 4230x y -+= C.2430x y -+= D. 4230x y --=8.关于x 的不等式2282a ax x --<0(a >0)的解集为(21,x x ),且1512=-x x ,则a ( ) A .25B .27 C .415 D .2159.已知圆:C x y x y +++-=2212880与圆 :C x y x y +---=2224420相交,则圆C 1 与圆C 2的公共弦所在的直线的方程为( )A .210x y ++=B .210x y +-=C .210x y -+=D .210x y --=10.当a 为任意实数时,直线(a -1)x -y +a +1=0恒过定点C ,则以C 为圆心,的圆的方程为( ).A .x 2+y 2-2x +4y =0B .x 2+y 2+2x +4y =0C .x 2+y 2+2x -4y =0D .x 2+y 2-2x -4y =011.已知数列{}n a 的前n 项之和142+-=n n S n ,则1021a a a +++ 的值为( )A. 61B. 65C. 67D. 6812.若直线1l :y=kx+k+2与直线2l :y=-2x+4的交点在第一象限,则实数k 的取值范围是A.(-32,∞+) B.(-∞,2) C.(-32,2) D.(-∞,-32)⋃(2,∞+) 第Ⅱ卷(共90分)二、填空题:本大题共4小题,每小题5分,满分20分。
2019-2020学年贵州省贵阳一中高三第二学期月考(文科)数学试卷 含解析

2019-2020学年高三第二学期月考(文科)数学试卷一、选择题1.已知集合A={(x,y)|x2+y2≤2,x∈Z,y∈Z},B={(x,y)|x+1>0},则A∩B的元素个数为()A.9B.8C.6D.52.i是虚数单位,x,y是实数,x+i=(2+i)(y+yi),则x=()A.3B.1C.D.3.平面向量,满足||=4,||=2,(+2)=24,则|﹣2|=()A.2B.4C.8D.164.命题p:∀x∈R,e x>x,命题q:∃x0∈R,x02<0,下列给出四个命题①p∨q;②p∧q;③p∧¬q;④¬p∨q所有真命题的编号是()A.①③B.①④C.②③D.②④5.为了研究一种新药的疗效,选100名患者随机分成两组,每组各50名,一组服药,另一组不服药.一段时间后,记录了两组患者的生理指标x和y的数据,并制成如图,其中“*”表示服药者,“+”表示未服药者.下列说法中,错误的是()A.服药组的指标x的均值和方差比未服药组的都低B.未服药组的指标y的均值和方差比服药组的都高C.以统计的频率作为概率,患者服药一段时间后指标x低于100的概率约为0.94 D.这种疾病的患者的生理指标y基本都大于1.56.已知,则sin2α=()A.﹣1B.1C.D.07.直线x=m与椭圆交于A,B两点,△OAB(O为原点)是面积为3的等腰直角三角形,则b等于()A.1B.2C.3D.48.函数f(x)=A sin(ωx+φ)(其中A>0,|φ|<)的部分图象如图所示,为得到的图象,可以将函数f(x)的图象()A.向右平移个单位长度﹣1B.向左平移个单位长度C.向左平移个单位长度D.向右平移个单位长度9.在正方体ABCD﹣A1B1C1D1中,E,F分别在B1B和C1C上(异于端点),则过三点A,F,E的平面被正方体截得的图形(截面)不可能是()A.正方形B.不是正方形的菱形C.不是正方形的矩形D.梯形10.已知数列{a n}满足a1=1,a n+1=2a n+1,如图是计算该数列的前n项和的程序框图,图中①②③应依次填入()A.i<n,a=2a+1,S=S+a B.i<n,S=S+a,a=2a+1C.i≤n,a=2a+1,S=S+a D.i≤n,S=S+a,a=2a+111.过点A(2a,0)作双曲线的一条渐近线的垂线,垂足为B,与另一条渐近线交于点C,B是AC的中点,则双曲线的离心率为()A.B.C.2D.12.x1=1是函数f(x)=+(b﹣3)x+2b﹣a的一个极值点,则ab的取值范围是()A.B.C.D.二、填空题(共4小题)13.函数的零点个数为.14.在四棱锥P﹣ABCD中,PA⊥底面ABCD,PA=AB=AD=1,BC=CD=BD=,则四棱锥的外接球的表面积为.15.在△ABC中,D是AB边上一点,AD=2DB,DC⊥AC,DC=,则AB =.16.奇函数f(x)满足f(1+x)=f(1﹣x),当0<x≤1时,f(x)=log2(4x+a),若,则a+f(a)=.三、解答题(共70分.)17.为抗击“新冠肺炎”,全国各地“停课不停学”,各学校都开展了在线课堂,组织学生在线学习,并自主安排时间完成相应作业为了解学生的学习效率,某在线教育平台统计了部分高三备考学生每天完成数学作业所需的平均时间,绘制了如图所示的频率分布直方图.(1)如果学生在完成在线课程后每天平均自主学习时间(完成各科作业及其他自主学习)为5小时,估计高三备考学生每天完成数学作业的平均时间占自主学习时间的比例(同一组中的数据用该组区间的中点值为代表)(结果精确到0.01);(2)以统计的频率作为概率,估计一个高三备考学生每天完成数学作业的平均时间不超过45分钟的概率.18.S n是等差数列{a n}的前n项和,对任意正整数n,2S n是a n a n+1与1的等差中项.(1)求数列{a n}的通项公式;(2)求数列的最大项与最小项.19.点P是直线y=﹣2上的动点,过点P的直线l1,l2与抛物线y=x2相切,切点分别是A,B.(1)证明:直线AB过定点;(2)以AB为直径的圆过点M(2,1),求点P的坐标及圆的方程.20.如图,在多面体ABCDE中,平面ACD⊥平面ABC,AC⊥BC,BC=2AC=4,DA=DC,CD=3,F是BC的中点,EF⊥平面ABC,.(1)证明:A,B,E,D四点共面;(2)求三棱锥B﹣CDE的体积.21.已知函数;(1)试讨论f(x)的单调性;(2)当函数f(x)有三个不同的零点时,a的取值范围恰好是,求b的值.请考生在第22、23两题中任选一题作答,并用2B铅笔在答题卡上把所选题目的题号涂黑,注意所做题目的题号必须与所涂题目的题号一致,在答题卡选答区域指定位置答题如果多做,则按所做的第一题计分.(本小题满分10分)[选修4-4:坐标系与参数方程]22.在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系.若曲线C的极坐标方程为,P点的极坐标为,在平面直角坐标系中直线l经过点P,且倾斜角为60°.(1)写出曲线C的直角坐标方程以及点P的直角坐标;(2)设直线与曲线C相交于A,B两点,求的值.[选修4-5:不等式选讲](本小题满分0分)23.已知f(x)=|x﹣m|(x+2)+|x|(x﹣m).(1)当m=2时,求不等式f(x)<0的解集;(2)若x>1时,f(x)>0,求m的取值范围.参考答案一、选择题(共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合A={(x,y)|x2+y2≤2,x∈Z,y∈Z},B={(x,y)|x+1>0},则A∩B的元素个数为()A.9B.8C.6D.5【分析】利用交集定义先求出A∩B,由此能求出A∩B的元素个数.解:∵集合A={(x,y)|x2+y2≤2,x∈Z,y∈Z},B={(x,y)|x+1>0},∴A∩B={(x,y)|}={(0,﹣1),(0,0),(0,1),(1,﹣1),(1,0),(1,1)},∴A∩B的元素个数为6.故选:C.2.i是虚数单位,x,y是实数,x+i=(2+i)(y+yi),则x=()A.3B.1C.D.【分析】先利用复数代数形式的乘除运算化简,再利用复数相等的定义计算即可.解:(2+i)(y+yi)=y+3yi,所以3y=1,x=y=,故选:D.3.平面向量,满足||=4,||=2,(+2)=24,则|﹣2|=()A.2B.4C.8D.16【分析】先根据数量积求出•=4,再求模长的平方,进而求得结论.解:因为平面向量,满足||=4,||=2,∵(+2)=24⇒+2•=24⇒•=4,则|﹣2|2=﹣4•+4=42﹣4×4+4×22=16;∴|﹣2|=4;故选:B.4.命题p:∀x∈R,e x>x,命题q:∃x0∈R,x02<0,下列给出四个命题①p∨q;②p∧q;③p∧¬q;④¬p∨q所有真命题的编号是()A.①③B.①④C.②③D.②④【分析】判定出p真q假⇒¬p为假,¬q为真,①③为真命题.解:令f(x)=e x﹣x,利用导数可求得当x=0时,f(x)=e x﹣x=1,1是极小值,也是最小值,从而可判断p为真命题,命题q为假命题.故①p∨q为真;②p∧q为假;③p∧¬q为真;④¬p∨q为假.所有真命题的编号是①③.故选:A.5.为了研究一种新药的疗效,选100名患者随机分成两组,每组各50名,一组服药,另一组不服药.一段时间后,记录了两组患者的生理指标x和y的数据,并制成如图,其中“*”表示服药者,“+”表示未服药者.下列说法中,错误的是()A.服药组的指标x的均值和方差比未服药组的都低B.未服药组的指标y的均值和方差比服药组的都高C.以统计的频率作为概率,患者服药一段时间后指标x低于100的概率约为0.94 D.这种疾病的患者的生理指标y基本都大于1.5【分析】由图可得服药组的指标x的均值和方差比未服药组的都低判断A;未服药组的指标y的取值相对集中,方差较小判断B;再求出患者服药一段时间后指标x低于100的频率判断C;直接由图象判断D.解:由图可知,服药组的指标x的均值和方差比未服药组的都低,∴A说法正确;未服药组的指标y的取值相对集中,方差较小,∴B说法不对;以统计的频率作为概率,患者服药一段时间后指标x低于100的概率约为0.94,∴C说法正确;这种疾病的患者的生理指标y基本都大于1.5,∴D说法正确.故选:B.6.已知,则sin2α=()A.﹣1B.1C.D.0【分析】由题意利用诱导公式求得2α=2kπ﹣,可得sin2α的值.解:由诱导公式及,可得cos(+α)=cos(+α),可得(舍去),或(+α)+(+α)=2kπ,k∈Z,即2α=2kπ﹣,∴sin2α=﹣1,故选:A.7.直线x=m与椭圆交于A,B两点,△OAB(O为原点)是面积为3的等腰直角三角形,则b等于()A.1B.2C.3D.4【分析】利用△OAB(O为原点)是面积为3的等腰直角三角形,求出A的坐标,代入椭圆方程求解即可.解:直线x=m与椭圆交于A,B两点,△OAB是等腰直角三角形,解得m=±,不妨A取,A点在椭圆上,代入椭圆,可得,解得b=2,故选:B.8.函数f(x)=A sin(ωx+φ)(其中A>0,|φ|<)的部分图象如图所示,为得到的图象,可以将函数f(x)的图象()A.向右平移个单位长度﹣1B.向左平移个单位长度C.向左平移个单位长度D.向右平移个单位长度【分析】由函数图象可得A,利用周期公式可求ω,由f()=sin(2×+φ)=﹣1,结合范围|φ|<,可求φ,可求函数解析式f(x)=sin(2x+),进而化简g(x)解析式由函数y=A sin(ωx+φ)的图象变换即可求解.解:由函数f(x)=A sin(ωx+φ)(其中A>0,|φ|<)的图象,可得A=1,=﹣=,即=π求得ω=2,∵f()=sin(2×+φ)=﹣1,即sin(+φ)=1,∴+φ=+2kπ,k∈Z,即φ=+2kπ,k∈Z,∵|φ|<,∴φ=,∴f(x)=2sin(2x+).由图可知,,,所以把f(x)的图象向右平移个单位得到g(x)的图象.故选:D.9.在正方体ABCD﹣A1B1C1D1中,E,F分别在B1B和C1C上(异于端点),则过三点A,F,E的平面被正方体截得的图形(截面)不可能是()A.正方形B.不是正方形的菱形C.不是正方形的矩形D.梯形【分析】画出图形,通过特殊位置判断截面形状即可.解:当BE=CF时,截面是矩形;当2BE=CF时,截面是菱形;当BE>CF时,截面是梯形,故选:A.10.已知数列{a n}满足a1=1,a n+1=2a n+1,如图是计算该数列的前n项和的程序框图,图中①②③应依次填入()A.i<n,a=2a+1,S=S+a B.i<n,S=S+a,a=2a+1C.i≤n,a=2a+1,S=S+a D.i≤n,S=S+a,a=2a+1【分析】模拟程序的运行过程,即可得出程序框图中应填的内容.解:取n=1,有S=a=1,即a1=1,不能进入循环,判断框应是i<n进入循环;进入循环后第一次加上的应该是a2=2a1+1,所以先算a=2a+1.故选:A.11.过点A(2a,0)作双曲线的一条渐近线的垂线,垂足为B,与另一条渐近线交于点C,B是AC的中点,则双曲线的离心率为()A.B.C.2D.【分析】有题意BO垂直平分AC∠AOB=∠BOC,又∠AOB,AOC互为补角,所以∠AOB为60°,求出渐近线的斜率,即得出a,b的关系,再由a,b,c之间的关系进而求出a,c的关系,即求出离心率.解:依题意,一条渐近线是x轴与另一条渐近线的对称轴,OB垂直平分AC,∠AOB=∠BOC,又∠AOB,AOC互为补角,所以渐近线的倾斜角是60°或120°,所以渐近线的斜率为,即=,c2=a2+b2,所以离心率e====2,故选:C.12.x1=1是函数f(x)=+(b﹣3)x+2b﹣a的一个极值点,则ab的取值范围是()A.B.C.D.【分析】先求导,再f'(1)=0得2a+b﹣2=0且△>0,所以a≠﹣1,ab=a(2﹣2a),(a≠﹣1)利用二次函数图象和性质求出答案.解:f'(x)=x2+2ax+b﹣3,f'(1)=0⇒2a+b﹣2=0,若函数f(x)有一个极值点,则△=4a2﹣4(b﹣3)=4a2﹣4(2﹣2a﹣3)=4a2+4(2a+1)=4(a+1)2>0所以a≠﹣1,ab=a(2﹣2a)=,故选:A.二、填空题(共4小题,每小题5分,共20分)13.函数的零点个数为3.【分析】条件等价于函数与y=x2的图象交点个数,数形结合即可.解:令,分别作与y=x2的图象如图,又因为指数函数的增长速度最终会远远超过幂函数的增长速度,所以两函数图象有3个交点,即f(x)有3个零点,故答案为3.14.在四棱锥P﹣ABCD中,PA⊥底面ABCD,PA=AB=AD=1,BC=CD=BD=,则四棱锥的外接球的表面积为5π.【分析】根据已知条件定出球心的位置,然后求出球的半径,代入球的表面积公式可求.解:如图,由已知,在底面ABCD中,AB⊥BC,AD⊥CD,由PA⊥底面ABCD,易得△PAC,△PBC,△PCD都是直角三角形,所以球心是PC的中点,,S=4πR2=5π.故答案为:5π15.在△ABC中,D是AB边上一点,AD=2DB,DC⊥AC,DC=,则AB =3.【分析】设BD=x,由已知结合锐角三角函数定义及余弦定理分别表示cos A,建立关系x的方程,可求.解:如图,设BD=x,则由余弦定理可得,,又由余弦定理可得,7=BC2=9x2,=13x2﹣3,即7=6+x2,解得x=1,∴AB=3.故答案为:116.奇函数f(x)满足f(1+x)=f(1﹣x),当0<x≤1时,f(x)=log2(4x+a),若,则a+f(a)=2.【分析】根据题意,分析可得f(x)是以4为周期的奇函数,结合函数的解析式分析可得,解可得a=2,分析可得f(2)的值,计算可得答案.解:根据题意,函数f(x)满足f(1+x)=f(1﹣x),则f(﹣x)=f(x+2),又由f(x)为奇函数,则f(﹣x)=﹣f(x),则有f(x+2)=﹣f(x),则有f(x+4)=﹣f(x+2)=f(x),即f(x)是以4为周期的奇函数,又由当0<x≤1时,f(x)=log2(4x+a),则,解可得a=2,又由f(x)是以4为周期的奇函数,则f(2)=f(﹣2)且f(2)+f(﹣2)=0,则f (2)=0,故a+f(a)=2+f(2)=2;故答案为:2.三、解答题(共70分.解答题应写出文字说明,证明过程或演算步骤)17.为抗击“新冠肺炎”,全国各地“停课不停学”,各学校都开展了在线课堂,组织学生在线学习,并自主安排时间完成相应作业为了解学生的学习效率,某在线教育平台统计了部分高三备考学生每天完成数学作业所需的平均时间,绘制了如图所示的频率分布直方图.(1)如果学生在完成在线课程后每天平均自主学习时间(完成各科作业及其他自主学习)为5小时,估计高三备考学生每天完成数学作业的平均时间占自主学习时间的比例(同一组中的数据用该组区间的中点值为代表)(结果精确到0.01);(2)以统计的频率作为概率,估计一个高三备考学生每天完成数学作业的平均时间不超过45分钟的概率.【分析】(1)先利用每组的频率×该组区间的中点值再相加求出平均值的估计值,再处于总时间5小时,即可得到所求的结果;(2)由直方图,算出[25,35)和[35,45)这两组的概率,再相加即可得到样本中高三备考学生每天完成数学作业的平均时间不超过45分钟的频率,以样本估算总体,进而得出每个高三备考学生每天完成数学作业的平均时间不超过45分钟的概率.解:(1)高三备考学生每天完成数学作业的平均时间的平均值的估计值为30×0.1+40×0.18+50×0.3+60×0.25+70×0.12+80×0.05=52.6,完成数学作业的平均时间占自主学习时间的比例估计值为;(2)由直方图,样本中高三备考学生每天完成数学作业的平均时间不超过45分钟的频率为0.28,估计每个高三备考学生每天完成数学作业的平均时间不超过45分钟的概率为0.28.18.S n是等差数列{a n}的前n项和,对任意正整数n,2S n是a n a n+1与1的等差中项.(1)求数列{a n}的通项公式;(2)求数列的最大项与最小项.【分析】(1)设{a n}的首项为a1,公差为d,取n=1,2,求出数列的通项公式即可.(2)记,利用函数图象结合函数的单调性推出当n≤4时,递增且都大于﹣1,当n≥5时,递增且都小于﹣1,得到结果即可.解:(1)设{a n}的首项为a1,公差为d,取n=1,2,得,解得或,当a1=1,d=2时,满足条件;当时,不满足条件,舍去,综上,数列{a n}的通项公式为a n=2n﹣1.(2),记,f(x)在(﹣∞,4.5)与(4.5,+∞)上都是增函数(图象如图3),对数列,当n≤4时,递增且都大于﹣1,当n≥5时,递增且都小于﹣1,数列的最大项是第4项,值为9,最小项是第5项,值为﹣11.19.点P是直线y=﹣2上的动点,过点P的直线l1,l2与抛物线y=x2相切,切点分别是A,B.(1)证明:直线AB过定点;(2)以AB为直径的圆过点M(2,1),求点P的坐标及圆的方程.【分析】(1)设A,B,P的坐标,求出直线AP,BP的方程,因为两条直线的交点P,可得直线AB的方程为:,整理可得恒过(0,2)点;(2)因为AB为直径的圆过点M(2,1),所以,由(1)设直线AB的方程,与椭圆联立求出两根之和及两根之积,进而可得直线AB的斜率,即求出P的坐标,即求出直线AB,进而求出圆心坐标.解:(1)证明:设点A(x1,y1),B(x2,y2),P(b,﹣2),过点A,P的直线方程为,同理过点B,P的直线方程为,因为点P是两切线的交点,所以,即y=2bx+2恒过(0,2).(2)解:设直线AB为y=kx+2(k=2b),与抛物线方程联立得x2﹣kx﹣2=0,其中△>0,x1x2=﹣2,x1+x2=k,因为M(2,1)在AB为直径的圆上,所以,即(x1﹣2,y1﹣1)(x2﹣2,y2﹣1)=0⇔(x1﹣2)(x2﹣2)+(y1﹣1)(y2﹣1)=0⇔(x1﹣2)(x2﹣2)+(kx1+1)(kx2+1)=0,整理得(k2+1)x1x2+(k﹣2)(x1+x2)+5=0,即k2+2k﹣3=0,解得k=1或k=﹣3.当k=1时,,圆心为,半径,圆的标准方程为;当k=﹣3时,,圆心为,半径,圆的标准方程为.20.如图,在多面体ABCDE中,平面ACD⊥平面ABC,AC⊥BC,BC=2AC=4,DA=DC,CD=3,F是BC的中点,EF⊥平面ABC,.(1)证明:A,B,E,D四点共面;(2)求三棱锥B﹣CDE的体积.【分析】(1)设M是AC的中点,则DM⊥AC,且,从而DM⊥平面ABC,由EF⊥平面ABC,得DM∥EF,且,四边形DEFM是平行四边形,从而DE∥MF,推导出MF∥AB,DE∥AB,由此能证明A,B,E,D四点共面.(2)D到平面BCE的距离是A到平面BCE距离的,EF⊥平面ABC,从而EF⊥AC,AC⊥BC,进而AC⊥平面BCE,由V B﹣CDE=V D﹣BCE.能求出三棱锥B﹣CDE的体积.解:(1)证明:如图4,设M是AC的中点,因为DA=DC=3,所以DM⊥AC,且,因为平面ACD⊥平面ABC,交线为AC,DM⊂平面ACD,所以DM⊥平面ABC,又EF⊥平面ABC,所以DM∥EF,且,四边形DEFM是平行四边形,从而DE∥MF,在△ABC中,M,F是AC,BC的中点,所以MF∥AB,所以DE∥AB,从而A,B,E,D四点共面.(2)解:由(1),所以D到平面BCE的距离是A到平面BCE距离的,EF⊥平面ABC⇒EF⊥AC,又AC⊥BC⇒AC⊥平面BCE,所以D到平面BCE的距离为,△BCE的面积,故三棱锥B﹣CDE的体积为.21.已知函数;(1)试讨论f(x)的单调性;(2)当函数f(x)有三个不同的零点时,a的取值范围恰好是,求b的值.【分析】(1)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;(2)求出f(x)的极值,函数f(x)有3个零点等价于f(a)•f(1)<0,即(a3﹣3a2﹣6b)(3a﹣1+6b)>0,根据函数的单调性求出b的值即可.解:(1)f'(x)=x2﹣(a+1)x+a=(x﹣1)(x﹣a),当a=1时,f'(x)=(x﹣1)2≥0,f(x)在(﹣∞,+∞)上单调递增;当a<1时,在(a,1)上,f'(x)<0,f(x)单调递减;在(﹣∞,a)和(1,+∞)上,f'(x)>0,f(x)单调递增;当a>1时,在(1,a)上,f'(x)<0,f(x)单调递减;在(﹣∞,1)和(a,+∞)上,f'(x)>0,f(x)单调递增;综上,当a=1时,f(x)在(﹣∞,+∞)上单调递增;当a<1时,f(x)在(a,1)上单调递减;在(﹣∞,a)和(1,+∞)上单调递增;当a>1时,f(x)在(1,a)上单调递减;在(﹣∞,1)和(a,+∞)上单调递增.(2)当a≠1时,函数有两个极值和,若函数f(x)有三个不同的零点⇔f(a)•f(1)<0,即(a3﹣3a2﹣6b)(3a﹣1+6b)>0,又因为a的取值范围恰好是,所以令g(a)=(a3﹣3a2﹣6b)(3a﹣1+6b)恰有三个零点,若a=3时,g(3)=﹣6b(6b+8),b=0或;当b=0时,g(a)=a2(3a﹣1)(a﹣3)>0,解得符合题意;当时,g(a)=(a3﹣3a2+8)(3a﹣9)=0,则a3﹣3a2+8=0不存在这个根,与题意不符,舍去,所以b=0.请考生在第22、23两题中任选一题作答,并用2B铅笔在答题卡上把所选题目的题号涂黑,注意所做题目的题号必须与所涂题目的题号一致,在答题卡选答区域指定位置答题如果多做,则按所做的第一题计分.(本小题满分10分)[选修4-4:坐标系与参数方程]22.在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系.若曲线C的极坐标方程为,P点的极坐标为,在平面直角坐标系中直线l经过点P,且倾斜角为60°.(1)写出曲线C的直角坐标方程以及点P的直角坐标;(2)设直线与曲线C相交于A,B两点,求的值.【分析】(1)运用极坐标和直角坐标的关系:x=ρcosθ,y=ρsinθ,x2+y2=ρ2,代入化简可得所求;(2)由题意可设直线l的参数方程,代入曲线C的直角坐标方程,运用韦达定理和参数的几何意义,化简可得所求值.解:(1)因为,所以ρ﹣ρsinθ=2,则,即=y+2,两边平方整理得x2=4y+4;由P点的极坐标,可得P点的直角坐标x=ρcosθ=0,y=ρsinθ=1,所以P(0,1).(2)由题意设直线l的参数方程为(t为参数),与曲线C的方程x2=4y+4联立,得,设PA,PB对应的参数分别为t1,t2,则,t1t2=﹣32,所以==,而,所以.[选修4-5:不等式选讲](本小题满分0分)23.已知f(x)=|x﹣m|(x+2)+|x|(x﹣m).(1)当m=2时,求不等式f(x)<0的解集;(2)若x>1时,f(x)>0,求m的取值范围.【分析】(1)将f(x)写成分段函数式,讨论x≤0时,0<x<2时,x≥2时,不等式的解,再求并集可得所求解集;(2)由题意可得f(m)=0,且x>m恒成立,求得m的范围,检验可得所求范围.解:(1)当m=2时,f(x)=|x﹣2|(x+2)+|x|(x﹣2)=,当x≤0时,﹣2x2+2x+4<0⇒x<﹣1;当0<x<2时,﹣2x+4<0⇒x>2矛盾;当x≥2时,2x2﹣2x﹣4<0⇒﹣1<x<2矛盾,综上,x<﹣1,则f(x)<0的解集为{x|x<﹣1};(2)对任意的x>1时,因为f(m)=0,f(x)>0=f(m),所以x>m,则m≤1,当m≤1,x>1时,x﹣m>0,则f(x)=(x﹣m)(x+2)+x(x﹣m)>0恒成立,所以m的取值范围是m≤1.。
高一化学月考试题及答案-2015-2016学年河北保定市曲阳一中高一(下)第一次月考化学试卷(文科)

2015-2016学年河北省保定市曲阳一中高一(下)第一次月考化学试卷(文科)一.选择题(本题共20小题,每小题2分,共40分,每题只有一个正确选项,将答案填涂在答题卡上)1.在元素周期表中金属元素与非金属元素的分界线附近的一些元素能用于制()A.合金B.半导体C.催化剂D.农药2.元素的性质呈周期性变化的根本原因是()A.元素的相对原子质量呈周期性变化B.元素的原子半径呈周期性变化C.元素的金属性和非金属性呈周期性变化D.元素原子的核外电子排布呈周期性变化3.188O 可作为示踪原子来证实乙酸乙酯的反应过程.188O的原子核内中子数是()A.8B.10C.18D.264.下列关于F、Cl、Br、I性质的比较,不正确的是()A.它们的原子核外电子层数随核电核数的增加而增多B.被其它卤素单质从其卤化物中置换出来的可能性随核电核数的增加而增大C.它们的氢化物的稳定性随核电核数的增加而增强D.单质的颜色随核电核数的增加而加深5.下列物质中碱性最强的是()A.LiOH B.NaOH C.Mg(OH)2D.Al(OH)36.下列原子中,半径最小的是()A.F B.Cl C.Al D.I7.对于Na+、Mg2+、Al3+三种离子,下列说法不正确的是()A.核外电子层数相同B.半径大小顺序Na+<Mg2+<Al3+C.核外电子数相同D.最外层电子数相同8.下列物质的电子式书写正确的是()A.B.C.D.9.下列物质中,既含离子键又含共价键的是()A.NaCl B.CO2C.NaOH D.N210.下列元素中,属于第三周期的是()A.Li B.F C.P D.Fe11.下列第ⅠA族元素中,金属性最强的是()A.锂B.钠C.钾D.铷12.下列各组物质中,互为同位素的是()A.O2和O3B.C和CC.CH4和C2H6D.和13.下列叙述中,正确的是()A.在多电子的原子里,能量高的电子通常在离核近的区域内运动B.核外电子总是先排在能量低的电子层里,例如一般先排满了L层后才排M层C.两种微粒,若核外电子排布完全相同,则其化学性质一定相同D.微粒的最外层只能是8个电子才稳定14.某元素的原子结构示意图为:,则该元素在元素周期表中的位置()A.第二周期,第ⅠA族B.第二周期,第ⅠA族C.第三周期,第ⅠA族D.第三周期,第ⅠA族15.下图微粒的结构示意图,正确的是()A.Mg2+B.Cl C.Ar D.K16.下列原子中,最容易形成阳离子的是()A.B.C.D.17.元素的化学性质主要决定于()A.主要化合价B.核外电子数C.原子半径D.最外层电子数18.和氖原子有相同的电子层结构的微粒是()A.He B.K+C.Cl﹣D.Na+19.从某微粒的原子结构示意图反映出()A.质子数和中子数B.中子数和电子数C.核电荷数和核外电子层排布的电子数D.质量数和核外电子层排布的电子数20.下列有关原子结构的说法,正确的是()A.稀有气体元素原子的最外层电子数都是8B.非金属元素的最外层电子数都大于3C.金属元素的最外层电子数不都小于4D.所有原子核都是由质子和中子构成的二.选择题(本题共10小题,每小题3分,共30分,每题只有一个正确选项,将答案填涂在答题卡上)21.下列各项中表达正确的是()A.NH3分子的电子式:B.CH4分子的比例模型:C.O原子的结构示意图:D.N2的结构式:N≡N22.若a A n+与b B2﹣两种离子的核外电子层结构相同,则a等于()A.b+n﹣2B.b+n+2C.b﹣n﹣2D.b﹣n+223.下列递变规律不正确的是()A.Na、Mg、Al还原性依次减弱B.I2、Br2、Cl2氧化性依次增强C.F、Cl、Br、I原子半径依次增大D.N、O、F最高正价依次升高24.构成下列四种物质的微粒间,既存在离子键又存在共价键的是()A.K2S B.Na2O2C.MgCl2D.SO325.下列各组物质的性质顺序,不正确的是()A.原子半径:Na<Mg<AlB.热稳定性:HCl>HBr>HIC.酸性强弱:H2SiO3<H2CO3<H2SO4D.熔点:SiO2>NaCl>CO226.下列各组物质各自形成的晶体,均属于分子晶体的化合物是()A.NH3,H2,CH4B.PCl5,CO2,H2SO4C.SO2,SiO2,P2O5D.CCl4,Na2S,H2O227.下列不能说明氯元素的非金属性比硫元素强的事实是()①HCl比H2S稳定;②HClO氧化性比H2SO4强;③HClO4酸性比H2SO4强;④Cl2能与H2S反应生成S;⑤氯原子最外层有7个电子,硫原子最外层有6个电子.A.②⑤B.①②C.①②④D.①③⑤28.短周期元素X、Y、Z、W、Q在元素周期表中的位置如表所示,其中X元素的原子内层电子数是最外层电子数的一半,则下列说法中正确的是()A.钠与W可能形成Na2W2化合物B.由Z与Y组成的物质在熔融时能导电C.W得电子能力比Q强D.X有多种同素异形体,而Y不存在同素异形体29.下列分子的结构中,原子的最外层电子不能都满足8电子稳定结构的是()A.CO2B.PCl3C.CCl4D.NO230.下列物质性质的变化规律与分子间作用力有关的是()A.HF、HCl、HBr、HI的热稳定性依次减弱B.金刚石的硬度大于硅,其熔、沸点也高于硅C.NaF、NaCl、NaBr、NaI的熔点依次降低D.F2、Cl2、Br2、I2的沸点依次升高二、简答题31.用电子式表示下列化合物的形成过程(1)H2S;(2)MgF2.32.下表列出了A~R九种元素在周期表的位置:IA IIA IIIA IV A V A VIA VIIA0主族周期2E R F3A C D H I G4B(1)写出EF2分子的电子式.(2)A、C、D三种元素的最高价氧化物对应的水化物中碱性最强的是(填化学式).(3)H、I、G三种元素的最高价氧化物对应的水化物中酸性由大到小的顺序排列为.(只填写元素符号)(4)写出A的单质与水反应的化学方程式.(5)H在元素周期表中位置:33.氯化铝的物理性质非常特殊,如:氯化铝的熔点为190Ⅰ(2.02×103 Pa),但在180Ⅰ就开始升华,据此判断,氯化铝是(填“共价化合物”或“离子化合物”),可以证明你的判断正确的实验依据是.34.写出NaHSO4溶液的电离方程式.参考答案与试题解析一.选择题(本题共20小题,每小题2分,共40分,每题只有一个正确选项,将答案填涂在答题卡上)1.在元素周期表中金属元素与非金属元素的分界线附近的一些元素能用于制()A.合金B.半导体C.催化剂D.农药【考点】元素周期律的作用.【分析】本题根据元素周期表中的元素分布及元素常见的性质来解题,一般金属延展性较好,可用于做合金,金属元素和非金属元素交界处的元素可以制作半导体材料,一般过度金属可以用来做催化剂,农药分为有机和无机,一般非金属元素可以制作有机农药.【解答】解:A.在元素周期表中,金属元素位于元素周期表的左下方,可以用来做导体,可以用来做合金等,像镁和铝等,故A错误;B.在金属元素和非金属元素交接区域的元素可以用来做良好的半导体材料,像硅等,故B 正确;C.可以用于做催化剂的元素种类较多,一般为过渡金属元素,故C错误;D.非金属元素位于右上方,非金属可以制备有机溶剂,部分有机溶剂可以用来做农药,故D错误.故选B.2.元素的性质呈周期性变化的根本原因是()A.元素的相对原子质量呈周期性变化B.元素的原子半径呈周期性变化C.元素的金属性和非金属性呈周期性变化D.元素原子的核外电子排布呈周期性变化【考点】元素周期律的实质.【分析】根据元素周期律可知,元素的性质随原子序数的递增而呈现周期性的变化,而这种变化是由原子的电子排布的周期性变化引起,而与相对原子质量、元素金属性和非金属性、原子半径等没有必然关系,据此进行判断.【解答】解:A.结构决定性质,相对原子质量的递增与元素性质的变化没有必然的联系,故A错误;B.元素的原子半径的变化属于元素的性质,不能解释元素性质的周期性变化,故B错误;C.元素的金属性和非金属性都是元素的性质,不能解释元素性质的周期性变化,故C错误;D.由原子的电子排布可知,随原子序数的递增,原子结构中电子层数和最外层电子数呈现周期性变化,则元素原子的核外电子排布的周期性变化是元素的性质呈周期性变化的根本原因,故D正确;故选D.3.188O 可作为示踪原子来证实乙酸乙酯的反应过程.188O的原子核内中子数是()A.8B.10C.18D.26【考点】乙酸乙酯的制取.【分析】188O是氧元素的一种核素,它的原子核内质量数是18,其质子数是8,中子数是10.【解答】解:188O、816O都是氧元素的核素,188O原子核内含有8个质子,10个中子,故选B.4.下列关于F、Cl、Br、I性质的比较,不正确的是()A.它们的原子核外电子层数随核电核数的增加而增多B.被其它卤素单质从其卤化物中置换出来的可能性随核电核数的增加而增大C.它们的氢化物的稳定性随核电核数的增加而增强D.单质的颜色随核电核数的增加而加深【考点】卤素原子结构及其性质的比较.【分析】A、同主族,从上到下,元素原子的电子层数依次增多;B、同主族,从上到下,单质的氧化性逐渐减弱;C、同主族,从上到下,元素氢化物的稳定性逐渐减弱;D、卤素单质的颜色从上到下逐渐加深.【解答】解:A、F、Cl、Br、I的原子核外电子层数随核电核数的增加而增多,故A正确;B、F、Cl、Br、I的核电核数逐渐增多,单质的氧化性逐渐减弱,被其它卤素单质从其卤化物中置换出来的可能性越来越大,故B正确;C、按照F、Cl、Br、I的顺序,核电核数逐渐增加,它们的氢化物的稳定性逐渐减弱,故C 错误;D、F2、Cl2、Br2、I2单质的颜色分别是浅黄绿色、黄绿色、深红棕色和紫黑色,即其颜色逐渐加深,故D正确.故选C.5.下列物质中碱性最强的是()A.LiOH B.NaOH C.Mg(OH)2D.Al(OH)3【考点】碱金属的性质.【分析】同周期元素从左向右金属性在减弱,同主族元素从上到下金属性增强;金属性越强,对应的最高价氧化物的水化物的碱性越强;由此分析解答.【解答】解:Na、Mg、Al在同周期,同周期元素从左向右金属性在减弱,则金属性:Na >Mg>Al,所以碱性NaOH>Mg(OH)2>Al(OH)3,而锂与钠同主族,钠的金属性强于锂,所以碱性最强的为NaOH,故选B.6.下列原子中,半径最小的是()A.F B.Cl C.Al D.I【考点】微粒半径大小的比较.【分析】电子层越多,半径越大,电子层一样多,质子数越多,半径小,根据原子半径的比较方法来回答.【解答】解:四种原子中I的电子层最多,半径最大,其次是Cl和Al,三个电子层,电子层最少的是F,两个电子层,所以F半径最小.故选A.7.对于Na+、Mg2+、Al3+三种离子,下列说法不正确的是()A.核外电子层数相同B.半径大小顺序Na+<Mg2+<Al3+C.核外电子数相同D.最外层电子数相同【考点】原子核外电子排布;微粒半径大小的比较.【分析】Na+、Mg2+、Al3+三种离子,核外电子排布相同,都是2,8结构,所以核电荷数越大半径越小,据此分析.【解答】解:因为Na+、Mg2+、Al3+三种离子,核外电子排布相同,所以核外电子层数、核外电子层数、最外层电子数都相同,又核外电子排布相同,核电荷数越大半径越小,所以半径大小顺序Na+>Mg2+>Al3+,故ACD正确,B错误;故选:B.8.下列物质的电子式书写正确的是()A.B.C.D.【考点】电子式.【分析】A.根据阴离子应该用中括号括起来;B.双氧水分子中氧原子和氢原子之间形成1对共用电子对,氧原子与氧原子之间形成1对共用电子对;C.根据共价化合物中没有括号和所带电荷数;D.氯离子电子式书写错误.无论是简单阴离子,还是复杂的阴离子,都应标出电子对等,还应加中括号,并在括号的右上方标出离子所带的电荷.【解答】解:A.氯化钠中,氯离子的电子式应加上括号,电子式为:,故A错误;B.双氧水分子中氧原子和氢原子之间形成1对共用电子对,氧原子与氧原子之间形成1对共用电子对,其电子式为,故B正确;C.硫化氢是共价化合物,在共价化合物中没有括号和所带电荷数,电子式为:,故C错误;D.氯化铵是离子化合物,由铵根离子与氯离子构成,其电子式为,故D 错误.故选B.9.下列物质中,既含离子键又含共价键的是()A.NaCl B.CO2C.NaOH D.N2【考点】共价键的形成及共价键的主要类型;离子化合物的结构特征与性质.【分析】一般来说,活泼金属和活泼非金属元素之间易形成离子键,非金属元素之间易形成共价键,既含离子键、又含共价键的物质应为离子化合物,并且含有由多个原子组成的阴离子,据此分析解答.【解答】解:A.氯化钠只含离子键,故A错误;B,二氧化碳中只含共价键,故B错误;C.氢氧化钠中钠离子和氢氧根离子之间存在离子键,氧原子和氢原子之间存在共价键,故C正确;D.氮气中只含共价键,故D错误;故选C.10.下列元素中,属于第三周期的是()A.Li B.F C.P D.Fe【考点】元素周期表的结构及其应用.【分析】主族元素周期数=原子核外电子层数、主族族序数=最外层电子数,书写各元素原子的核外电子排布式进行判断.【解答】解:A、Li元素原子的核外电子排布式为1s22s1,电子层数为2,故处于第二周期,故A不选;B、F元素原子的核外电子排布式为1s22s22p5,电子层数为2,故处于第二周期,故B不选;C、P元素原子的核外电子排布式为1s22s22p63s23p3,电子层数为3,故处于第三周期,故C 选;D、Fe元素原子的核外电子排布式为1s22s22p63s23p63d64s2,电子层数为4,故处于第四周期,故D不选;故选C.11.下列第ⅠA族元素中,金属性最强的是()A.锂B.钠C.钾D.铷【考点】金属在元素周期表中的位置及其性质递变的规律.【分析】同主族元素自上而下金属性增强,据此判断.【解答】解:同主族自上而下原子半径增大,原子核对最外层电子的吸引减弱,元素的金属性增强,故第ⅠA族元素中铷的金属性最强,故选D.12.下列各组物质中,互为同位素的是()A.O2和O3B.C和CC.CH4和C2H6D.和【考点】同位素及其应用.【分析】具有相同质子数,不同中子数同一元素的不同核素互为同位素A、同位素指的是不同核素间的关系,是同素异形体;B、都是碳原子的不同核素;C、属于同系物,不是同位素;D、互为同分异构体,不是同位素.【解答】解:同位素是指具有相同质子数,不同中子数同一元素的不同核素,即原子间的关系比较A、O2和O3是氧元素的两单质,互为同素异形体,不是同位素,故A错误;B、都是碳原子,中子数不同,它们是碳元素的不同核素,互为同位素,故B正确;C、CH4和C2H6是烷烃的同系物,不是同位素,故C错误;D、二者互为同分异构体,不是同位素,故D错误;故选B.13.下列叙述中,正确的是()A.在多电子的原子里,能量高的电子通常在离核近的区域内运动B.核外电子总是先排在能量低的电子层里,例如一般先排满了L层后才排M层C.两种微粒,若核外电子排布完全相同,则其化学性质一定相同D.微粒的最外层只能是8个电子才稳定【考点】原子核外电子的运动状态;原子核外电子排布.【分析】A.根据原子核外电子能量与距核远近的关系判断;B.根据电子首先进入能量最低、离核最近的轨道判断;C.两种粒子,核外电子排布相同,则最外层电子数相等,它们的化学性质相似;D.根据通常认为最外层有8个电子(最外层是第一电子层时有2个电子)的结构是一种稳定结构.【解答】解:A.在多电子的原子里,能量低的电子通常在离核近的区域内运动,能量高的电子通常在离核远的区域内运动,故A错误;B.核外电子总是先排在能量低的、离核最近的轨道电子层里,例如一般先排满了L层后才排M层,故B正确;C.两种粒子,核外电子排布相同,则最外层电子数相等,它们的化学性质相似,不能说相同,故C错误;D.通常认为最外层有8个电子(最外层是第一电子层时有2个电子)的结构是一种稳定结构,故D错误;故选B.14.某元素的原子结构示意图为:,则该元素在元素周期表中的位置()A.第二周期,第ⅠA族B.第二周期,第ⅠA族C.第三周期,第ⅠA族D.第三周期,第ⅠA族【考点】元素周期表的结构及其应用.【分析】主族元素周期数=电子层数、主族族序数=最外层电子数,据此判断.【解答】解:由3个电子层,处于第三周期,最外层电子数为5,处于ⅠA族,故该元素处于第三周期第ⅠA族,故选D.15.下图微粒的结构示意图,正确的是()A.Mg2+B.Cl C.Ar D.K【考点】原子结构示意图.【分析】核外电子排布规律:K层不超过2个电子;第二层不超过8个电子;最外层不超过8个电子;次外层不超过18个电子,结合当核电荷数=质子数=核外电子数,为原子;当核电荷数=质子数>核外电子数,为阳离子;当核电荷数=质子数<核外电子数,为阴离子分析.各结构示意图表示的微粒:A.为镁离子;B.为氯离子;C.为氩原子,但第二层超过8个电子;D.为钾原子,但最外层不超过8个电子.【解答】解:A.从结构示意图可以看出其核内质子数为12,核外电子数是10,则电子数大于质子数,所以该微粒带负电荷,故表示的是镁离子,故A正确;B.其核内质子数为17,核外电子数是18,为氯离子,故B错误;C.核外电子排布规律:K层不超过2个电子;第二层不超过8个电子,故C错误;D.核外电子排布规律:K层不超过2个电子;第二层不超过8个电子;最外层不超过8个电子,故D错误;故选A.16.下列原子中,最容易形成阳离子的是()A.B.C.D.【考点】原子核外电子排布.【分析】根据原子的最外层电子数判断,当原子的最外层电子数少于4个时,容易失去电子形成阳离子,多于4个时容易获得电子形成阴离子.【解答】解:A、由结构示意图可知,该原子最外层有5个电子,获得电子的能力比较强,不易形成阳离子,故A不符合;B、由结构示意图可知,该原子最外层有4个电子,不易获得电子也不易失去电子,不易形成阳离子,易形成共价化合物,故B不符合;C、由结构示意图可知,原子含有3个电子层,最外层是2个电子,属于金属,容易失去而形成阳离子,故C符合;D、由结构示意图可知,该原子有1个电子层,核外有2个电子,属于稳定结构,化学性质稳定.不能失去电子形成阳离子,故D不符合.故选:C.17.元素的化学性质主要决定于()A.主要化合价B.核外电子数C.原子半径D.最外层电子数【考点】原子核外电子排布.【分析】元素的性质化学性质,与原子的最外层电子数关系非常密切:原子的最外层电子少于4个时,容易失去电子;多于4个少于8个时,容易获得电子;最外层为8个电子时,元素的化学性质最稳定,据此进行解答.【解答】解:元素的化学性质主要决定于粒子的最外层电子数,最外层电子数大于4个小于8个,容易得到电子,具有较强的氧化性;最外层电子数小于4个,一般容易失去电子,具有较强的还原性,而与主要化合价、核外电子总数无关,主要因素不是原子半径,故选D.18.和氖原子有相同的电子层结构的微粒是()A.He B.K+C.Cl﹣D.Na+【考点】质子数、中子数、核外电子数及其相互联系.【分析】氖原子核外有10个电子,有2个电子层,最外层电子数为8.据此结合选项判断.【解答】解:氖原子核外有10个电子,有2个电子层,最外层电子数为8,A、He只有1个电子层,有2个电子,故A错误;B、K+核外有18个电子,有3个电子层,最外层电子数为8,故B错误;C、Cl﹣核外有18个电子,有3个电子层,最外层电子数为8,故C错误;D、Na+核外有10个电子,有2个电子层,最外层电子数为8,故D正确.故选D.19.从某微粒的原子结构示意图反映出()A.质子数和中子数B.中子数和电子数C.核电荷数和核外电子层排布的电子数D.质量数和核外电子层排布的电子数【考点】原子结构示意图.【分析】注意原子结构示意图是表示原子核电荷数和电子层排布的图示形式,中子数和质量数没有体现.【解答】解:A、在微粒的原子结构示意图上,只能体现出原子核电荷数和电子层排布的图示形式,中子数没有体现,故A错误;B、在微粒的原子结构示意图上,只能体现出原子核电荷数和电子层排布的图示形式,中子数没有体现,故B错误;C、原子结构示意图是表示原子核电荷数和电子层排布的图示形式,能反映出核电荷数和核外电子层排布的,股D正确;D、在微粒的原子结构示意图上,只能体现出原子核电荷数和电子层排布的图示形式,质量数数没有体现,故D错误;故选C.20.下列有关原子结构的说法,正确的是()A.稀有气体元素原子的最外层电子数都是8B.非金属元素的最外层电子数都大于3C.金属元素的最外层电子数不都小于4D.所有原子核都是由质子和中子构成的【考点】原子构成.【分析】A.根据氦原子的最外层电子数判断;B.氢元素属于非金属元素,但最外层电子数为1;C.金属元素的最外层电子数大多数小于4,但部分元素的最外层电子数大于或等于4;D.原子核一般是由质子和中子构成,氢原子核除外;【解答】解:A.氦原子最外层是两个电子,氦除外,稀有气体元素的原子最外层电子数都是8,故A错误;B.氢元素属于非金属元素,是主族元素,原子的最外层电子数为1,小于3,故B错误;C.金属元素的最外层电子数大多数小于4,但部分元素的最外层电子数大于或等于4,如铋、钋等,故C正确;D.氢原子核只有质子而没有中子,故D错误;故选C.二.选择题(本题共10小题,每小题3分,共30分,每题只有一个正确选项,将答案填涂在答题卡上)21.下列各项中表达正确的是()A.NH3分子的电子式:B.CH4分子的比例模型:C.O原子的结构示意图:D.N2的结构式:N≡N【考点】电子式、化学式或化学符号及名称的综合;原子结构示意图;球棍模型与比例模型.【分析】A.氨气分子中的N原子上有1对孤对电子;B.图中为甲烷的球棍模型;C.氧原子原子序数为8,核外有2个电子层,最外层有6个电子;D.用短线“﹣”代替共用电子对即为结构式,氮气中存在三对共价键.【解答】解:A.NH3分子的电子式为,故A错误;B.CH4分子的比例模型为,为甲烷的球棍模型,故B错误;C.氧原子原子序数为8,核外有2个电子层,最外层有6个电子,O原子结构示意图为,故C错误;D.N原子之间形成三对共用电子对,结构式只把共用电子对用短线表示,未成键的电子不画出,N2的结构式为N≡N,故D正确,故选D.22.若a A n+与b B2﹣两种离子的核外电子层结构相同,则a等于()A.b+n﹣2B.b+n+2C.b﹣n﹣2D.b﹣n+2【考点】原子核外电子排布.【分析】a A n+与b B2﹣两离子具有相同的电子层结构,说明二者核外电子数相同,阴离子核外电子数=质子数+所带的电荷数,阳离子核外电子数=质子数﹣所带电荷数,据此计算判断.【解答】解:阳离子核外电子数=质子数﹣所带电荷数,所以a A n+的核外电子数为a﹣n;阴离子核外电子数=质子数+所带的电荷数,所以b B2﹣的核外电子数为b+2;a A n+与b B2﹣两离子具有相同的电子层结构,说明二者核外电子数相同,所以a﹣n=b+2,即a=b+n+2.故选:B.23.下列递变规律不正确的是()A.Na、Mg、Al还原性依次减弱B.I2、Br2、Cl2氧化性依次增强C.F、Cl、Br、I原子半径依次增大D.N、O、F最高正价依次升高【考点】同一周期内元素性质的递变规律与原子结构的关系;同一主族内元素性质递变规律与原子结构的关系.【分析】A.元素的金属性越强,对应的单质的还原性越强;B.元素的非金属性越强,对应单质的氧化性越强;C.同主族从上向下元素的原子半径逐渐增大;D.氧和氟的非金属性强,无正价.【解答】解:A.金属性:Na>Mg>Al,元素的金属性越强,对应的单质的还原性越强,所以还原性:Na>Mg>Al,故A正确;B.非金属性:Cl>Br>I,元素的非金属性越强,对应单质的氧化性越强,所以氧化性:Cl2>Br2>I2,故B正确;C.同主族从上向下元素的原子半径逐渐增大,所以半径:F<Cl<Br<I,故C正确;D.氧和氟的非金属性强,只有0价和负价,无正价,故D错误;故选:D.24.构成下列四种物质的微粒间,既存在离子键又存在共价键的是()A.K2S B.Na2O2C.MgCl2D.SO3【考点】化学键;离子键的形成;共价键的形成及共价键的主要类型.【分析】一般,金属元素与非金属元素形成离子键,非金属元素之间形成共价键,以此来解答.【解答】解:A.K2S中只有钾离子、硫离子形成的离子键,故A不选;B.Na2O2中存在钠离子与过氧根离子之间的离子键、氧氧元素之间的非极性共价键,故B 选;C.MgCl2中只有镁离子与氯离子形成的离子键,故C不选;D.SO3中只有S、O元素之间的极性共价键,故D不选;。
重庆市重庆一中2017届高三下学期第一次月段考试数学文科试题含答案 bybao 精品

2017年重庆一中高2017级高三下期第一次月考数学试卷(文科)一选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,有且只有一项符合题目要求.1.已知集合{}{}0,2,4,6|233xA B x N ==∈≤,则集合AB 的子集个数为A. 6B. 7C. 8D. 4 2.设i 是虚数单位,复数21a ii++为实数,则实数a 的值为 A. B. C. D.3.抛物线28y x =的焦点到直线30x y -=的距离是 A.3 B. 23 C. 2 D.14.“p ⌝是真”是“p q ∨为假”的A. 充分不必要条件B.必要不充分条件C. 充要条件D.既不充分也不必要条件 5.已知等比数列的前三项分别是1,1,4a a a -++,则数列{}n a 的通项公式为A. 342n n a ⎛⎫=⨯ ⎪⎝⎭B. 1342n n a -⎛⎫=⨯ ⎪⎝⎭C. 243nn a ⎛⎫=⨯ ⎪⎝⎭ D. 1243n n a -⎛⎫=⨯ ⎪⎝⎭6.变量,x y 之间的一组相关数据如下表所示:若,x y 之间的线性回归方程为ˆˆ12.28ybx =+,则ˆb 的值为 A. 0.96 B. -0.94 C. -0.92 D.-0.987.若n S 是等差数列{}n a 的前n 项和,且8520S S -=,则11S 的值为 A. 66 B. 48 C. 44 D. 128.在如图所示的程序框图中,若输出的值是3,则输入的x 的取值范围是 A. (]2,4 B. ()2,+∞ C. (]4,10 D. ()4,+∞ 9.如图,网格纸的小正方形的边长为1,粗线画出的是一个几何体的三视图,则这个几何体的体积为 A.52 B. 72 C. 324+ D. 333+10.已知圆()22314x y -+=的一条切线y kx =与双曲线()222210,0x y C a b a b-=>>没有公共点,则双曲线C 的离心率的取值范围是 A. ()1,3 B. (]1,2 C.()3,+∞ D.[)2,+∞11.已知点M 的坐标(),x y 满足不等式组2402030x y x y y +-≥⎧⎪--≤⎨⎪-≤⎩,N 为直线23y x =-+上任一点,则MN 的最小值是A.55 B. 255 C. 1 D.17212.已知函数()()ln ln ,1xf x x f x x =-+在0x x =处取得最大值,以下各式中:①()00f x x <;②()00f x x =;③()00f x x =;④()012f x <;⑤()012f x >,正确是序号是A.③⑤B. ②⑤C. ①④D. ②④二、填空题:本大题共4小题,每小题5分,共20分.13. 函数()[]223,4,4fx x x x =--∈-,任取一点[]04,4x ∈-,则()00f x ≤的概率为 .14. 已知平面向量()()1,2,2,a b m ==-,且a b a b +=-,则2a b += . 15. 如图,球面上有A,B,C 三点,90,2ABC BA BC ∠===,球心O 到平面ABC 的距离为2,则球的体积为 .16. 已知函数()()()ln ,0,f x x a b f a f b =>>=,则22a b a b+-的最小值为 .三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明或推理、验算过程. 17.(本题满分12分)(中国好声音(The Voice of China ))是由浙江卫视联合星空传媒旗下灿星制作强力打造的大型励志专业音乐评论节目,于2012年7月13日在浙江卫视播出,每期节目有四位导师参加.导师背对歌手,当每位参赛选手演唱完之前有导师为其转身,则该选手可以选择加入为其转身导师的团队中接受指导训练.已知某期《中国好声音》中,6位选手唱完后,四位导师为其转身的情况如下表所示:现从这6位选手中随机抽取两位参加某节目录制. (1)请回答基本事件总数并列出所有的基本事件;(2)求两人中恰好其中一位为其转身的导师不少于3人,而另一人为其转身的导师不多于2人的概率.18.(本题满分12分)如图,在各棱长均为2的三棱柱111ABC A B C -中,侧面11A ACC ⊥底面.ABC(1)求三棱柱111ABC A B C -的体积;(2)已知点D 是平面ABC 内一点,且四边形ABCD 为平行四边形,在直线1AA 上是否存在点P ,使//DP 平面1ABC ?若存在,请确定点P 的位置,若不存在,请说明理由.19.(本题满分12分)函数()()sin 0,2f x x πωϕωϕ⎛⎫=+<< ⎪⎝⎭的部分图象如图所示,将()y f x =的图象向右平移4π个单位长度后得到函数()y g x =的图象.(1)求函数()y g x =的解析式; (2)在ABC ∆中,内角A,B,C 满足22sin123A B g C π+⎛⎫=++ ⎪⎝⎭,且其外接圆的半径为1,求ABC ∆的面积的最大值.20.(本题满分12分)平面直角坐标系xoy 中,椭圆()22122:10x y C a b a b+=>>的离心率为22,过椭圆右焦点F 作两条相互垂直的弦,当其中一条弦所在直线斜率为0时,两弦长之和为6.(1)求椭圆的方程;(2)A,B 是抛物线22:4C x y =上两点,且A,B 处的切线相互垂直,直线AB 与椭圆1C 相交于C,D 两点,求弦CD 的最大值.21.(本题满分12分) 已知函数()ln a xf x x+=在点()(),e f e 处切线与直线20e x y e -+=垂直.(注:e 为自然对数的底数)(1)求a 的值;(2)若函数()f x 在区间(),1m m +上存在极值,求实数m 的取值范围; (3)求证:当1x >时,()21f x x >+恒成立.请考生在第22、23两题中任选一题作答,如果多做,则按照所做的第一题计分. 22.(本题满分10分)选修4-4:极坐标与参数方程 已知曲线1C 的极坐标方程为()2cos sin a ρθθ-=,曲线2C 的参数方程为sin cos 1sin 2x y θθθ=+⎧⎨=+⎩(θ为参数),且1C 与2C 有两个不同的交点. (1)写出曲线1C 的直角坐标方程和曲线2C 的普通方程; (2)求实数a 的取值范围.23.(本题满分10分)选修4-5:不等式选讲 已知函数()()223,1 2.f x x a x g x x =-++=-+ (1)解不等式()22g x x <-+;(2)若对任意1x R ∈都有2x R ∈,使得()()12f x g x =成立,求实数a 的取值范围.。
2015高一第二次月考文科生

2014—2015学年满城中学高一第二学期第二次月考数学试题(文科生卷)(时间120分钟,满分150分) 命题人:石兰柱一、选择题:本大题共12小题,每小题5分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
请把答案涂在客观题答题卡上。
1、已知(1,2),(1,0),(3,)A B C a -三点在同一条直线上, 则a 的值为( )A 、2-B 、4-C 、4D 、22、设,,l m n 是不同的直线,,,αβγ是不重合的平面,则下列命题不.正确..的是( ) A 、若//,//,m n m n ββ⊄,则//n β B 、若,,l αβγβαγ⊥⊥⋂=,则l β⊥ C 、//,,,l m αβαγβγ⋂=⋂=则//l mD 、若,,,,A C B D ααββ∈∈∈∈,AB CD ‖且AB CD =,则//αβ3、已知,,l m n 是不同的直线,,,αβγ是不重合的平面,下列命题中正确的个数..为( ) ①若,,m m αβ⊥⊥则αβ‖ ②若,,αγβγ⊥⊥则αβ‖③若//,//,m m αβ则αβ‖ ④//,,l m αα⊂则//lm A 、1 B 、2 C 、3 D 、44、若图4T -,直线123,,l l l 的斜率分别为123,,k k k ,则( )A 、321k k k <<B 、123k k k <<C 、312k k k <<D 、213k k k <<5、已知,αβ是不重合的平面,,,l m n 是不同的直线,则下列命题不正确的个数是( )①若//,//l m m n ,则//l n ②若,,m n αα⊥⊥则//m n ③若//,,a l αβαβ⊂⊂,则//a l ④若,m m αβ⊥⊂,则αβ⊥A 、0B 、1C 、2D 、3 6、设,αβ是不重合的平面,,,l m n 是不同的直线,下列命题不能..推导出线面垂直的是( ) A .若//,l αββ⊥,则l α⊥ B .若//,m n m α⊥,则n α⊥ C .若,,,l m m l αβαβα⊥⋂=⊂⊥,则m β⊥ D .若,,,l m l n m n ββ⊥⊥⊂⊂,则l β⊥7、平面α截球O 所得截面的面积为4π,球心O) Aπ B、π C、π D、π8、下列命题正确的是( )①过平面外一点有且只有一条直线和已知平面垂直 ②过直线外一点有且只有一个平面和已知直线垂直 ③过平面外一点有且只有一条直线与已知平面平行 ④过平面外一点有且只有一个平面与已知平面垂直A.①②③B.①②C. ①④D.②③④9、一个几何体的三视图如图9T -所示,则该几何体的体积为( )A .14+πB .134+πC .834+πD .84+π10、直线l 经过点(2,),(3,A y B ,且倾斜角范围是2[,]33ππ, 则y 的范围是( )A 、[-B 、(,0])-∞⋃+∞C 、(,[0,)-∞-⋃+∞D 、11、已知(1,2),(1,0),(2,A B C --若平面ABC 内存在一点D 满足:,CD AB ⊥且//CB AD ,则D 点坐标为( )A 、(2,3)-B 、(2,3)-C 、(2,3)--D 、(2,3)12、如图12T -,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各面中,面积最小的是( )A .4B . 8C .D .12二、填空题:本大题共4个小题,每小题5分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高 2017 届 高 一 下 学 期 月 考 测 试 卷 数 学
( 文 科 参 考 答 案)
一 选择题。
(本题10个小题,每题5分,共50分)
1. 已知数列{a n }的通项公式为a n =4n -3,则a 5的值是(C )
A .9
B .13
C .17
D .21
2. 已知0a b <<,则下列不等式正确的是(C )
A .22a b <
B .11a b
< C .22a b < D . 2ab b < 3.在△ABC 中,P 是BC 上一点,若AP →=mAB →+211
AC →,则实数m 的值为( A ) A.911 B.511 C.411 D.311
4.在△ABC 中,A ,B ,C 为内角,且sin A cos A =sin B cos B ,则△ABC 是( D )
A .等腰三角形
B .直角三角形
C .等腰直角三角形
D .等腰或直角三角形
5.在等差数列{a n }中,若a 3+a 4+a 5+a 6+a 7=450,则a 2+a 8的值等于(D )
A .45
B .75
C .300
D .180
6 设等差数列{a n }的前n 项和为S n . 若a 1=-11,a 4+a 6=-6,则当S n 取最小值时,n 等于( A )
A .6
B .7
C . 8
D .9
7.在△ABC 中,a ,b ,c 分别是三个内角A ,B ,C 的对边,设向量p =(b -c ,a -c ), q =(c +a ,b ),若p ∥q ,则角A 的大小是(C )A .90° B .45° C .60° D .30°
8. 若A 、B 是锐角ABC ∆的两个内角,则点)cos sin ,sin (cos A B A B P --在 ( B )
A. 第一象限
B. 第二象限
C. 第三象限
D.第四象限
9.已知等差数列{}n a 的前n 项和n S 满足65S S <且876S S S >=,则下列结论错误..
的是( D ) A .6S 和7S 均为n S 的最大值. B .07=a ; C .公差0d <; D .59S S >;
10.函数4
tan
)(x x f π=,)6,2(∈x 的图象与x 轴交于A 点,过点A 的直线l 与函数的图象交于,B C 两点,则()OB OC OA +⋅ = ( A ) A.32 B.16 C .8 D. 4
12. 不等式01
x +≤的解集是:__ (12]-, __
13.在△ABC 中,已知a =32,cos C =13
,S △ABC =43,则b =
14. 已知数列{}n a 中,11a =-,11n n n n a a a a ++⋅=-,则数列通项n a =__ 1n -____ 15.下列命题: 在ABC ∆中,内角,,A B C 所对的边分别为,,a b c ,给出下列结论:
①若A B C >>,则C B A sin sin sin >>;②若sin cos cos A B C a b c
==,则ABC ∆为等边三角形;③必存在,,A B C ,使C B A C B A tan tan tan tan tan tan ++<成立;④若︒===25,20,40B b a ,则ABC ∆必有两解.其中,结论正确的编号为 ①④ .(注:把你认为正确的序号都填上)
三.解答题(本题6个大题、共75分.请写出详细的解题步骤否则概不给分!)
16(本题满分12分).已知非零向量a 、b
满足b 1()()4
-=a b a +b ⋅. (Ⅰ)求a ;(Ⅱ)当32
a b =
⋅时,求向量a 与b 的夹角θ的值. 解:(Ⅰ)因为1()()4-=a b a +b ⋅ ,即2214
-=a b ,………2分 所以221192444
=+=+=a b ,故32=a .………6分 (Ⅱ)因为cos θ=a b a b ⋅=22,故45θ= . ……………………12分 17.(本题满分12分)在△ABC 中,已知B =45°,D 是BC 边上
的一点,AD =5,AC =7,DC =3,求AB 的长.
解 在△ACD 中,由余弦定理,得
cos C =AC 2+CD 2-AD 22AC 〃CD =72+32-522×7×3=1114
……..6分 ∴sin C =1-cos 2 C =2)1411(1-=5143……8分 在△ABC 中,由正弦定理,得AB sin C =AC sin B .∴AB =AC 〃sin C sin B =7×5143sin 45°=562
……..12分 18.(本题满分12分)(1)已知等差数列{a n }的公差d > 0,且53,a a 是方程x 2-14x +45=0的两根,求数列{}n a 通项公式(2)设1
2+=n n n a a b ,数列{b n }的前n 项和为S n ,证明1<n S . 解:(1)由题意⎩⎨⎧=⋅=+45145353a a a a 又d>0,)(12235599
5*53N n n a d a a n ∈-=∴=--=∴⎩⎨⎧==∴…….6分 (2)1
21121)12)(12(221+--=+-=⋅=∴+n n n n a a b n n n …….9分 A D C
B
11
211)121121()7151()5131()311(<+-=+--++-+-+-=n n n s n ……..12分 19(12分)设ABC ∆的三个内角分别为,,A B C
.3(1,cos )cos ,)2222
C C C m n ==+
与共线(Ⅰ)求角C 的大小(Ⅱ)设角,,A B C 的对边分别是,,a b c ,且满足2cos 2a C c b +=,试判断∆ABC 的形状 解:(Ⅰ)m 与n 共线∴ )2
cos 2sin 3(2cos 23C C C +
=1π1(1cos )sin()262C C C =++=++。
3分 πsin()16
C += ∴C=3π …6分 (Ⅱ)由已知2a c b += 根据余弦定理可得:222c a b ab =+- …………8分
联立解得:()0b b a -= 0,,b b a >∴=3
C π=
,所以△ABC 为等边三角形, …………12分 20.(本题满分13分)如图,A ,B ,C ,D 为平面四边形ABCD 的四个内角。
(Ⅰ)证明:B B B sin cos 12tan
-=;(Ⅱ)若180A C += ,6AB =,3BC =,4CD =,5AD =, 求2
tan 2tan D B +的值。
分)解(52tan 2
cos 2sin 2cos 2sin 22sin 22cos 2sin 2)2sin 21(1sin cos 1sin )cos 1(sin cos 1)cos 1(sin )cos 1)(cos 1()cos 1(sin cos 1sin 12222 B B B B B B B B B B
B B B B B B B B B B B B B ===--=-=---=-+-=+ (2)D B D B D B
C A cos cos ,sin sin .180,1800
0-==∴=+∴=+ 。
6分 由(1)可知:B
B B B D D B B D B sin 2sin cos 1cos 1sin cos 1sin cos 12tan 2tan =++-=-+-=+……..8分 连接AC,在三角形AB
C 和ADC 中,利用余弦定理可得:
),2.....(cos 2),1(,cos 2222222D DC AD DC AD AC B BC AB BC AB AC ∙-+=⋅-+= 联立(1)
,(2)可得:19
1cos ,4cos 76,cos cos ,cos 3645cos 4041=∴=∴-=-=-B B D B B D ……10分 .19106sin ,191cos =∴=B B 。
12分30
101919
1062sin 22tan 2tan ===+∴B D B ……13分 21(本题满分14分)设数列{}n a 的前n 项和为S n ,且1*1
2(),2n n S n N -=-∈。
(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)设数列n n a n b 2
=求数列{}n b 的前n 项和T n ;
也成立。
此式对时时解1,)2
1(2,11)1(1111n s s a n s a n n n n n ==-=≥===--
分分可得:分分14........22212.......)21(2
11)21(-21)21(-)21()2
1()21(2121)2()1(10)........2()2
1()21()1()21(3)21(2211218).....1()2
1()21(3)21(2211)21(,2)2(11132143232n n n n n n n n n n n n n n n n n
T n n T n n T n T n b a n b --=∴⋅--=⋅++++=-⋅+⋅-++⨯+⨯+⨯=⋅++⨯+⨯+⨯=∴⋅=∴=++++。
