青岛大学824运筹学2016-2017年考研专业课真题试卷
青岛大学818理论力学2016-2017年考研专业课真题试卷

1
青岛大学2017年硕士研究生入学考试试题
科目代码:818科目名称:理论力学
(共
5页)
请考生写明题号,将答案全部答在答题纸上,答在试卷上无效
一.选择题(每题5分,共55分)
1、楔形块、自重不计,并在光滑的mm 和nn 平面相接触,若其上分别作用有两个大小相等,方向相反,作用线相同的力F 和F',如图所示,则、两个刚体是否处于平衡状态?____
A .
、都不平衡B.
、都平衡C .
平衡,不平衡D.不平衡,
平衡2、如图,x 轴和y 轴的夹角为,设一力系在xy 平面内,对y 轴上的点和x 轴上的点有,且但已知OA =l 则点在x 轴的位置为____
A.
B.
C.
D.
3、如图所示若尖劈两侧与槽之间的摩擦角均为
,则欲使尖劈被打入后不致自动滑出,角应为多大?____
A.
B.
C.
D.
青岛大学考研专业课真题试卷
精都考研网(专业课精编资料、一对一辅导、视频网课)。
南京航空航天大学824运筹学(A卷)2016年考研真题
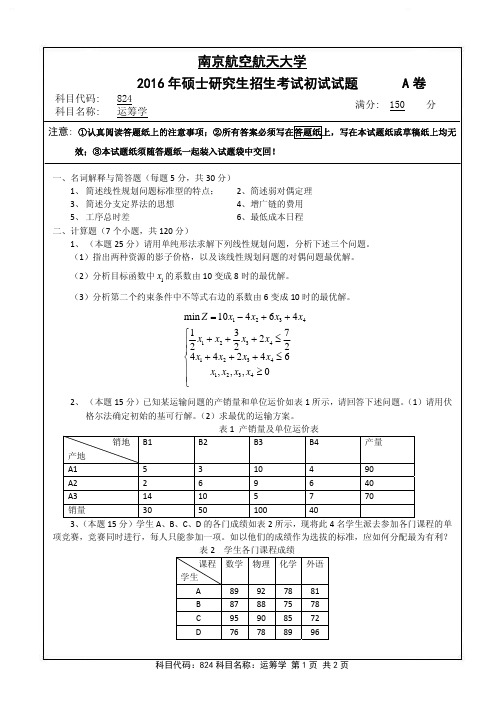
7、(本题15分)已知面对四种自然状态的三种备选方案损益值如表3所示,假设不知道各种自然状 态出现的概率,请用后悔值准则、折中准则(乐观系数取0.3)求最优执行方案。
表3 自然状态及损益值表
S1
S2
S3
S4
A1
16
7
1
‐2
A2
8
13
7
5
A3
4
7
10
12
科目代码:824 科目名称:运筹学 第 2 页 共 2 页
8
V2 5
3
V4 10 V6
3
V3
3
5
V5 图 1 某网络图
5、(本题 15 分)某项目网络图、作业名称及其作业时间如图 2 所示(网络图中字母是作业名,“/” 后是作业时间),请计算:
(1)各作业的最早开始时间、最晚结束时间及总时差; (2)关键路线及项目完工总工期。
a/60
1
2
c/10
b/45
3
B
87 88 75 78
C
95 90 85 72
D
76 78 89 96
科目代码:824 科目名称:运筹学 第 1 页 共 2 页
4、(本题 15 分)已知某网络及其各弧的容量(标于箭线),见图 1,请回答下述问题。(1)列出求 解网络最大流的数学模型。(2)求解该网络的最大流(要求计算过程)。
6 V1
南京航空航天大学
科目代码: 科目名称:
2016 年硕士研究生招生考试初试试题ď A 卷 Đ
824 运筹学
满分: 150 分
注意: ①认真阅读答题纸上的注意事项;②所有答案必须写在答题纸上,写在本试题纸或草稿纸上均无
2017青岛大学自动控制理论(825)真题答案

1
]
+ 1)
0.368 + 0.264
G(Z) =
( − 1)( − 0.368)
G(Z)
0.368 + 0.264
∅(z) =
= 2
1 + G(Z) − + 0.632
G(Z) = (1 − −1 )[
2 (
解:(1)令s = jω带入G(s)中,得
G(jω) =
(10jω + 1)
−2 (jω + 1)(0.1jω + 1)
ω → 0+ 时,G(j0+ ) = ∞ < −1800 ,ω → ∞时,G(j∞) = 0 < −2700
G(jω) =
(10. 92 + 1) + (8.9−3 )
实轴根轨迹区域( − ∞, −1.5),( − 0.5,0)
分离点d = −0.23
虚轴交点:D(s) = ( + 0.5)( + 1.5) + =0
令s = jω带入D(s)中,
−ω3 j − 2ω2 + 0.75 + = 0
得,K = 1.5,ω = ±0.865
系统根轨迹如图所示:
()
1
由R(s) = () = +1得,
1
1
1 1
1
1 1
=
−
+
+ 1 2 + 1 2 + 1 2 2 + 1 2 2 + 1
对C(s)进行反拉氏变换得,
1
1
青岛大学2017年硕士研究生入学考试试题
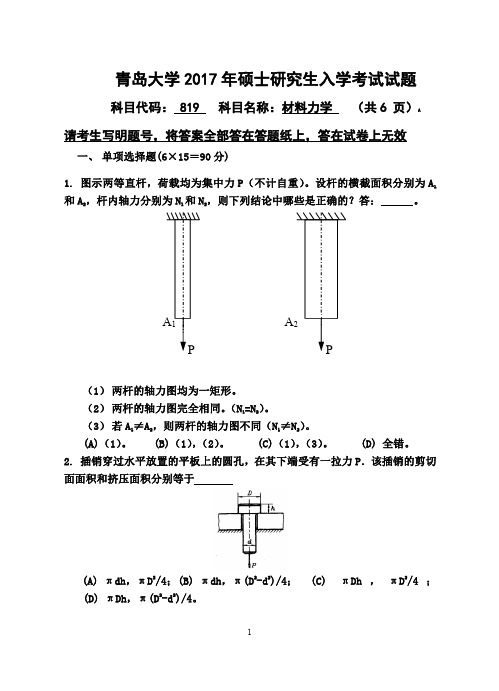
(应力单位:MPa)。答:
。
12. 将沸水倒人玻璃杯中,如杯子破裂,问杯的内外壁是否同时破裂? (A)同时破裂 (B)内壁先裂 (C)外壁先裂 (D)无法判定
4
13. 材料相同的四个直杆如图所示。其中哪一根杆变形能最大?
14.长度因数的物理意义是
。
(A)压杆绝对长度的大小;
(B)对压杆材料弹性模数的修正;
(D)压杆的许可载荷随着 A 的增加呈非线性变化。
二、 已知图示梁的载荷图,试作其剪力图和弯矩图 (14 分)
q=30kN/m A
C 1m
P=20kN
q=30kN/mBiblioteka D1m1m
E
B
1m
5
三、 图示桁架,各杆各截面的拉压刚度均为 EA,试计算节点 A 的水平位移。 ( 本题 15 分)
四、 图示钢杆,横截面面积 A=2500mm2 ,弹性模量 E=210GPa,轴向载荷 F=200kN。未加外载时,间隙δ=0.3 mm。试确定杆端的约束反力。 (本题 15 分)
9.弯曲与扭转组合变形圆轴表面 1、2、3、4 点的应力状态如图所示。其中哪个 是错误的?(图中的阴影面为自由表面)
3
10. 圆轴受扭时,轴表面各点处于
。
(A)单向应力状态。 (B) 各向等应力状态.
(C)三向应力状态. (D) 二向应力状态。
11. 绘出图示应力状态所对应的应力圆并求出图示斜面上的应力值σα和τα。
变为
。
(A) 1.82τ。 (B) 1.59τ。 (C) 1.35τ。 (D) 1.14τ。
4. 等强度梁各个横截面上的 (A) 最大正应力相等; (C) 最大剪应力相等;
。 (B) 最大正应力都等于许用正应力[σ]; (D) 最大剪应力都等于许用剪应力[τ]。
2017年南京航空航天大学考研试题824运筹学
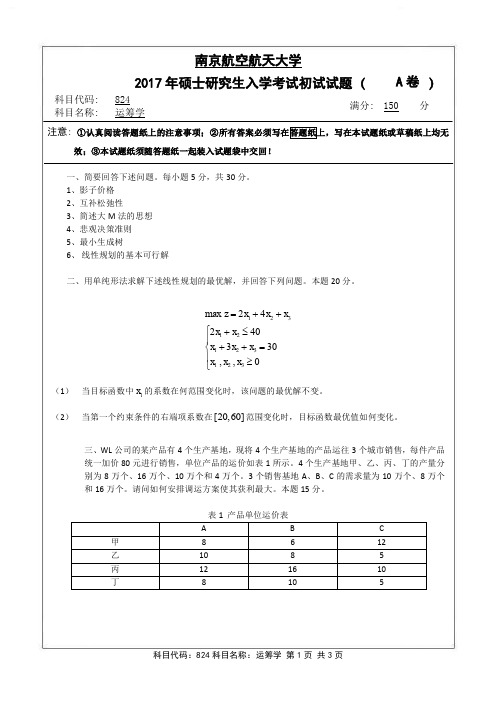
(50,30)
(85,35) I (45,15) H (50,15)
(20,0) G
表 4 前 3 年和后 7 年投资销售ቤተ መጻሕፍቲ ባይዱ态
科目代码:824 科目名称:运筹学 第 2 页 共 3 页
七、 某公司每月需某种化学品 2000 瓶,每瓶成本 150 元,每次订购费为 125 元,每瓶化学品每年 存储费为成本的 16%。试求 1) 若不允许缺货,求最优订货量及最小费用; 2) 若允许缺货,缺货费为每瓶 101 元,求最大库存量及最大缺货量。本题 15 分。 八、已知某项目的各工作正常工时、极限工时及相应直接费用如表 5,网络如图 2。 表5 工作 A→B A→C B→D C→D C→E D→F E→F 正常工作 时间(天) 24 30 22 26 24 18 18 费用(元) 5 000 9 000 4 000 10 000 8 000 5 400 6 400 16 18 18 24 20 18 10 项目工作资料 极限工作 时间(天) 费用(元) 7 000 10 200 4 800 10 300 9 000 5 400 6 800
max z 2 x1 4 x2 x3 2 x1 x2 40 x1 3x2 x3 30 x , x , x 0 1 2 3
(1) 当目标函数中 x1 的系数在何范围变化时,该问题的最优解不变。 (2) 当第一个约束条件的右端项系数在 [20, 60] 范围变化时,目标函数最优值如何变化。
B 24 A 30 C
22
D 18
26 E 24 图 2 项目的工程网络图 18
F
求:1)计算在正常工时下每个工作的最早开始时间、最迟结束时间、总时差; 2)设正常工时下,任务总间接费用为 18000 元,工期每缩短一天,间接费用可节省 330 元, 求最低成本日程。本题 20 分。
青岛大学2016年硕士研究生入学考试试题

青岛大学2016年硕士研究生入学考试试题科目代码: 910 科目名称: 数据结构 (共 5 页) 请考生写明题号,将答案全部答在答题纸上,答在试卷上无效 一、单项选择题(本大题共10道小题,每小题2分,共20分) 1.一个算法具有( )等特点。
A .快速性B .至少有一个输入量C .确定性D .健壮性2.下列函数中渐近时间复杂度T(n)最小的是( )。
A .T(n) = 73128*64*n n + B .T(n) = 2256*64*n n -- C .T(n) = 21024**log n n D .T(n) = 2log 1024*232*n n --3.在计算机的存储器中表示时,物理地址和逻辑地址相同并且是连续的,称之为( )。
A .逻辑结构B .顺序存储结构C .链式存储结构D .以上都对4.若让元素1,2,3,4,5依次进栈,则出栈次序不可能出现在( )种情况。
A .5,4,3,2,1B .2,1,5,4,3C .4,3,1,2,5D .2,3,5,4,15.设栈S 用顺序存储结构表示,则栈S 为空的条件是( )。
A .S.top - S.base != 0B .S.top - S.base == 0C .S.top - S.base != nD .S.top - S.base == n6.一棵完全二叉树上有1001个结点,其中叶子结点的个数是( )。
A .500B . 501C .250D .251 7.任何一棵二叉树的叶子结点在先序、中序和后序遍历中的相对次序( )。
A .不发生改变B .发生改变C.不能确定D.以上都不对8.用邻接表表示图进行广度优先遍历时,通常借助()来实现算法。
A.栈 B. 队列 C. 树D.图9.折半查找法和二叉排序树的时间性能()。
A.与处理数据量有关B.相同C.不相同D.不确定10.对n个不同的关键字由小到大进行冒泡排序,在下列()情况下比较的次数最多。
2016年山东科技大学824工程经济学考研真题试题试卷

目录2016年山东科技大学824工程经济学考研真题试题试卷 (2)2016年山东科技大学考研真题试题试卷一、选择题(单选)(共15题,每题2分,共30分注:答案写在答题纸上)1.资金时间价值是( )。
A.利息 B.资金随时间推移产生的增值(或减值)C.资金随时间推移产生的增值D.利率2.不属于项目现金流入的是( )。
A.营业收入 B.回收固定资产余值 C.营业税金及附加 D.回收流动资金3.单利计息与复利计息的区别在于()。
A.是否考虑资金的时间价值B.采用名义利率还是实际利率C.是否考虑先前计息周期累计利息的时间价值D.是否考虑本金的时间价值4.在资金等值计算中,下列表述正确的是( )。
A.P一定,n相同,i越高,F越大B.P一定,i相同,n越长,F越小C.F一定,i相同,n越长,P越大D.F一定,n相同,i越高,P越大5.已知年名义利率为10%,每季度计息1次,复利计息,则年有效利率为( )。
A.10.47% B.10.38% C.10.25% D. 10.00%6.企业行政管理部门为管理和组织经营活动发生的各项费用是( )。
A.制造费用B.管理费用C.财务费用D.营业费用7.总成本中应不包括( )。
A.折旧费、摊销费B.利息支出C.所得税D.经营成本8.在工程经济分析中,下列各项中不属于经营成本的有( )。
A.外购原材料、燃料费用B.工资及福利费用C.修理D.折旧费用9.净利润是从利润总额中扣除( )的差额。
A.增值税B.营业税C.所得税D.消费税10.某固定资产原值为10000元,净残值为800元,若采用平均年限法按4年计提折旧,第一年应计提的折旧额为()。
A.2600元B.2300元C.2400元D.2500元1。
青岛大学2016年硕士研究生入学考试初试试题考试科目:824运筹学

3
4
2
定由 5 家建筑公司分别承建。 已知建筑公司 Ai( i 1, 的建造费用报价为 cij( i, j 1,
对新商店 B j( j 1, ,5 )
,5 )
。 商业公司应当对 5 家建筑公司怎样分配建造任 ,5 )
务,才能使得总的建造费用最少?请写出模型并求解。
Bj cij
Ai A1
A2
青岛大学 2016 年硕士研究生入学考试试题
科目代码: 824 科目名称: 运筹学 (共 4 页) 请考生写明题号,将答案全部答在答题纸上,答在试卷上无效 第一题(20 分, 每题 5 分) :简答题 (1) 线性规划问题的解有哪几种可能情况? (2) 简述线性规划问题图解法的原理和基本步骤。 (3) 什么是线性规划的基解和基可行解? (4) 何谓线性规划的影子价格?影子价格有何实际意义? 第二题(15 分) :计算题:用单纯形算法求解线性规划问题 min x1 2 x2 x3 s.t. x1 x 2 2 x3 x4 10, 2 x1 x2 4 x3 8,
min 12 x1 8 x2 16 x3 12 x4 , s.t. 2 x1 x2 4 x3 2 2 x1 2 x2 4 x4 3 x1 , x2 , x3 , x4 0.
第五题(15 分)给定线性规划问题
1
min x1 x 2 4 x3 x1 x 2 2 x3 9 x x x 2 2 3 s.t. 1 x1 x 2 x3 4 x1 , x 2 , x3 0
销地 产地 A1 A2 A3 销量(吨) 4 2 8 8 12 10 5 14 4 3 11 12 11 9 6 14 16 10 22 B1 B2 B3 B4 产量(吨)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一题(20 分, 每题 5 分):简答题 (1) 线性规划问题的解有哪几种可能情况? (2) 简述线性规划问题图解法的原理和基本步骤。 (3) 什么是线性规划的基解和基可行解? (4) 何谓线性规划的影子价格?影子价格有何实际意义?
第二题(15 分):计算题:用单纯形算法求解线性规划问题
min
x1 2x2 x3
销地 产地 A1
B1 4
A2
2
A3
8
销量(吨)
8
B2
B3
B4
12
4
11
10
3
9
5
11
6
14
12
14
-2-
产量(吨)
16 10 22
(1) 用最小元素法或西北角法确定初始调运方案;(5 分) (2) 用闭回路法或位势法检验上述初始调运方案是否最优;若不是最优,请用
解的改进方法求出最优解;(10 分) (3) 该运输问题有唯一最优解还是有无穷多个最优解,为什么?(5 分)
s.t. x1 x 2 2x3 x4 10,
2x1 x2 4x3 8,
x1 2x2 4x3 4,
x j 0, j 1, 2,3, 4.
第三题(15 分)计算题:给定线性规划问题
min 2x1 3x2 x3 s.t. 3x1 x2 x3 1,
为 g1(x1) 4x1 , g2 (x2 ) 9x2 和 g3 (x3 ) 2x32 ,问应该如何分配投资数额才能使得 总收益最大?
-3-
青岛大学 201称: 运筹学 (共 4 页)
请考生写明题号,将答案全部答在答题纸上,答在试卷上无效
2x1 x2 x3 x4 1
s.t.
5x1x1x32 x2
6x3 4x4 x4 5
8
x1, x2 , x3, x4 {0,1}
第九题(20 分)利用动态规划原理求解如下问题: 某公司有资金 10 万元,若投资于项目 i(i 1, 2,3) 的投资额为 xi 时,其收益分别
和最小元素法好。
(
)
4. 对于线性规划来说,在互为对偶的一对原问题和对偶问题中,不管原问题
是求极大或极小,原问题可行解的目标函数值一定不超过其对偶问题可行解
的目标函数值。
(
)
第三题(15 分)计算题:用单纯形算法求解线性规划问题
max
2 x1 x2
s.t.
6
x1
5x2 15 2x2 24 x1 x2 5
第七题(10 分)给定标准指派问题的系数为
4 8 7 15 12
7
9
17
14
10
C 6 9 12 8 7
6 7 14 6 10
6 9 12 10 6
用匈牙利算法求最优指派。
第八题(10 分)求解 0-1 整数规划问题
min 3x1 7 x2 x3 x4
x1 2x2 3x3 2, x1, x2 , x3 0.
(1) 写出该问题的对偶问题; (2) 利用图解法求解对偶问题; (3) 利用对偶性质写出原问题的解。
第四题(15 分)计算题:用对偶单纯形算法求解线性规划问题
min 12x1 8x2 16x3 12x4,
s.t.
2x1 x2 4x3 2
2x1 2x2 4x4 3
x1, x2 , x3, x4 0.
第五题(15 分)给定线性规划问题
1
它的最优单纯形表格如下
min x1 x2 4x3
x1 x2 2x3 9
s.t.xx1 1xx2
x3 2 2 x3 4
x1, x2 , x3 0
青岛大学 2017 年硕士研究生入学考试试题
科目代码: 824
科目名称: 运筹学 (共 3 页)
请考生写明题号,将答案全部答在答题纸上,答在试卷上无效
第一题(20 分, 每题 5 分)简答题 (1) 什么是线性规划问题的基解和基可行解? (2) 简述线性规划问题图解法的原理和基本步骤。 (3) 简述用运筹学方法解决实际问题时应遵循的基本步骤。 (4) 线性规划问题的解的个数会有哪几种情况?各自对应的单纯形表格的特点 是什么?
-3
0
-1
-2
0
考虑如下问题:
(1) 把 c1 1改变为 c1' 4 ,求新问题的最优解。
(2) 讨论 c2 在什么范围内变化时原来的最优解也是新问题的最优解(当然,最 优值可以不同)。
第六题(20 分)某公司的产品有 3 个产地和 4 个销地。各产地的产量、各销地 的销量(吨)和各产地到各销地的单位运价(万元/吨)见下表:
x1, x2 0
第四题(15 分)计算题:给定线性规划问题
min 2 x1 3x2 x3
s.t.
3x1 x1
x2 2x2
x3 3x3
1 2
x1, x2 , x3 0
-1-
(1) 写出该问题的对偶问题; (2) 利用图解法求解对偶问题; (3) 利用对偶性质写出原问题的解。
第五题(20 分)给定线性规划问题
max x1 2x2 x3
s.t.
x1 x2 2x1
x3 x2
4
6
x1, x2 , x3 0
它的最优单纯形表格如下
cj
-1
2
1
0
0
CB
基
b Bb x1
x2
x3
x4
x5
2
x2
6
1
1
1
1
0
0
x5
10
3
0
1
1
1
cj zj
第二题(20 分,每题 5 分)判断题,对者在后面括号内填写,错者填写。 1. 动态规划只能处理与时间有关的动态优化问题,而不能处理与时间无关的
静态问题。
()
2. 整数规划的分支定界算法是一种隐枚举方法,如何进行分支和定界是其效
果好坏的关键因素。
(
)
3. 对于运输问题来说,用沃格尔法得到的初始可行解的质量一般较西北角法
x1
x2
x3
x4
x5
x6
x1
1
-1/3
0
1/3
0
-2/3
1/3
x5
0
2
0
0
1
1
6
x3
0
2/3
1
1/3
0
1/3
13/3
0
-4
0
-1
0
-2
-17
其中,x4 ,x5 和 x6 分别是三个约束条件的松弛变量。现将右端 (9,2,4)T 改为 (3,2,3)T , 利用上述表格求新问题的最优解。
第六题(20 分):某公司的产品有 3 个产地和 4 个销地。各产地的产量、各销地的 销量(吨)和各产地到各销地的单位运价(万元/吨)见下表:
