第一章 语音信号的时域及频域特征(幻灯讲义)_554406537
语音信号的时域及频域特征

( 3)
6
3. 语音信号的短时谱特征
3.1. 短时傅立叶谱分析
对于能量受限的时域信号 f (t ) ,它的傅立叶变换可以写成
ˆ f ( )
f (t ) e
j t
dt
( 4)
以上这个傅立叶变换, 在 “宏观上” 给出信号 f (t ) 的频谱信息, 但是却无法确定某个 “局 部”时间段频谱的确切信息。在语音信号中,信息是按照特定的时间序列方式出现的。 如果谱分析不能确定这种时间序列的次序(即位置) ,那么这种信号分析的手段在应用 上就会受到限制。同时我们也希望能够通过观测到的局部时域信号的频谱信息来了解 (构造)整个 f (t ) 的频谱信息。为此我们引入了所谓的短时傅立叶谱分析技术。 有许多技术都可以用来完成信号的短时谱分析。 最典型的就是小波变换和我们现在 常采用的傅立叶短时谱分析技术。
第一章 语音信号的时域及频域特征
1. 语音信号的主要特点
1.1. 语音信号带宽
语音信号的带宽约为 5KHz , 主要能量集中在低频段。 上图为一段语音信号语谱图。
1
1.2. 语音信号是典型的随机信号
1)人的每次发音过程都是一个随机过程。很难得到两次完全相同的发音样本。 2)在信号处理中,通常假设语音信号是短时平稳的。例如,可以认为在语音的浊 音段部分,语音的二阶矩统计量是平稳的(在 5~10mS 内),即二阶矩平稳,或称为宽平 稳。
对于时域离散信号 x (n) ,短时傅立叶变换定义:
X n (e j )
m
x(m) w(n m) e
1, 0 n N 1 n 其它 0,
jm
这里 w( n) 为窗函数。例如,常用的窗函数有 矩形窗: w( n)
语音信号的时域及频域特征

(12)
当短时谱为使用 DFT 计算时,可以证明窗函数和插值函数需要满足一下条件:
r
h(n r ) w(r n pN ) ( p)
(13)
例如,我们可以特别地选择 W ( n) 为窗长为 N 的三角窗,而 h[ n] 为矩形窗,
1 n [0, N 1] h[ n] 0 其它
第一章 语音信号的时域及频域特征
1. 语音信号的主要特点
1.1. 语音信号带宽
语音信号的带宽约为 5KHz , 主要能量集中在低频段。 上图为一段语音信号语谱图。
1
1.2. 语音信号是典型的随机信号
1)人的每次发音过程都是一个随机过程。很难得到两次完全相同的发音样本。 2)在信号处理中,通常假设语音信号是短时平稳的。例如,可以认为在语音的浊 音段部分,语音的二阶矩统计量是平稳的(在 5~10mS 内),即二阶矩平稳,或称为宽平 稳。
2
2. 语音信号的时域波形
图 1.
语音信号的波形(shi4)
3
图 2. 语音信号波形(shi4)的局部细节
4
2.1. 语音时域信号特征
2.1.1. 语音时域信号的特点
1)清音段:能量低,过零率高,波形特点有点像随机的噪声。这部分信号常与语 音的辅音段对应。 2)浊音段:能量高,过零率低,波形具有周期性特点。所谓的短时平稳性质就是 处于这个语音浊音(元音)段中。 3)过渡段:一般是指从辅音段向元音段信号变化之间的部分。信号变化快,是语 音信号处理中最复杂、困难的部分。
r 取值为周期时刻采样分析短时谱,间隔为
h(n)
w( n)
T N 2。
N
h( n )
w(n)
语音信号采集与时频域分析正文
第一章引言语音信号是一种非平稳的时变信号,它携带着各种信息。
在语音编码、语音合成、语音识别和语音增强等语音处理中无一例外需要提取语音中包含的各种信息。
语音信号分析的目的就在与方便有效的提取并表示语音信号所携带的信息。
语音信号分析可以分为时域和频域等处理方法。
语音信号可以认为在短时间内(一般认为在 10~30ms 的短时间内)近似不变,因而可以将其看作是一个准稳态过程, 即语音信号具有短时平稳性。
任何语音信号的分析和处理必须建立在“短时”的基础上, 即进行“短时分析”。
时域分析:直接对语音信号的时域波形进行分析,提取的特征参数有短时能量,短时平均过零率,短时自相关函数等。
频域分析:对语音信号采样,并进行傅里叶变换来进行频域分析。
主要分析的特征参数:短时谱、倒谱、语谱图等。
本文采集作者的声音信号为基本的原始信号。
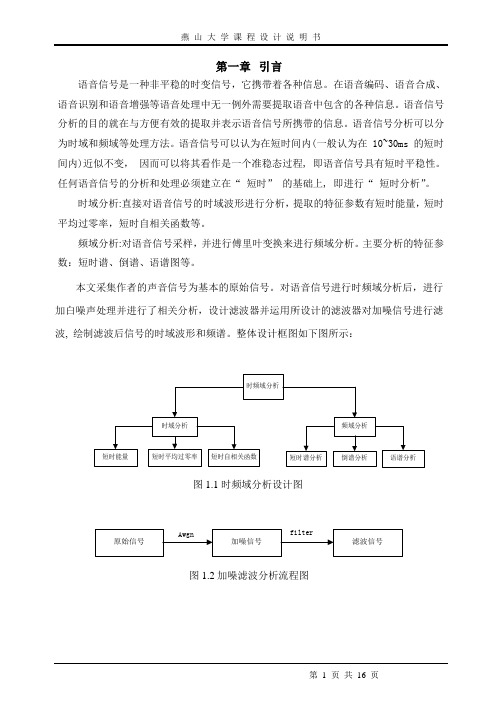
对语音信号进行时频域分析后,进行加白噪声处理并进行了相关分析,设计滤波器并运用所设计的滤波器对加噪信号进行滤波, 绘制滤波后信号的时域波形和频谱。
整体设计框图如下图所示:图1.1时频域分析设计图图1.2加噪滤波分析流程图第二章 语音信号时域分析语音信号的时域分析可直接对语音信号进行时域波形分析,在此只只针对语音信号的短时能量、短时平均过零率、短时自相关函数进行讨论。
2.1窗口选择由人类的发生机理可知,语音信号具有短时平稳性,因此在分析讨论中需要对语音信号进行加窗处理进而保证每个短时语音长度为10~30ms 。
通常选择矩形窗和哈明窗能得到较理想的“短时分析”设计要求。
两种窗函数的时域波形如下图2.1所示:samplew (n )samplew (n )图2.1 矩形窗和Hamming 窗的时域波形矩形窗的定义:一个N 点的矩形窗函数定义为如下{1,00,()n Nw n ≤<=其他(2.1)哈明窗的定义:一个N 点的哈明窗函数定义为如下0.540.46cos(2),010,()n n NN w n π-≤<-⎧⎨⎩其他= (2.2)这两种窗函数都有低通特性,通过分析这两种窗的频率响应幅度特性可以发现(如图2.2):矩形窗的主瓣宽度小(4*pi/N ),具有较高的频率分辨率,旁瓣峰值大(-13.3dB ),会导致泄漏现象;哈明窗的主瓣宽8*pi/N ,旁瓣峰值低(-42.7dB ),可以有效的克服泄漏现象,具有更平滑的低通特性。
语音信号数字处理课件

人工智能在语音信号处理中的应用
语音识别
利用人工智能技术将语音转换为文本,提高语音输入的准确性和 效率。
语音合成
通过人工智能技术将文本转换为语音,实现自然语言交互和语音助 手等功能。
情感分析
利用人工智能技术对语音中的情感进行识别和分析,用于人机交互 和智能客服等领域。
深度学习在语音信号处理中的应用
实时性与低延迟
由于语音数据的分布广泛且复杂,如何有 效利用稀疏数据进行语音信号处理是一个 重要挑战。
随着语音交互的普及,对语音信号处理的 实时性和低延迟要求越来越高,需要进一 步优化算法和硬件实现。
个性化与自适应性
多模态交互
针对不同用户的个性化需求和口音差异, 如何实现自适应的语音信号处理是一个重 要发展方向。
01
语音合成的基本原理是将文本信息转换为语音信号。它通过分析文本的语义和 语法信息,结合语音合成算法和语音库,生成逼真的语音输出。
02
语音合成技术主要依赖于自然语言处理和数字信号处理技术,通过将文本转换 为韵律、音高、音长等参数,再通过数字信号处理器将这些参数转换为模拟信 号,最终输出逼真的语音。
03
语音压缩
将语音信号的动态范围压缩,提高语音的清晰 度。
语音去混响
去除语音信号中的混响效应,提高语音的可懂度。
语音信号的编码与压缩
波形编码
将语音信号转换为数字波 形,以保留原始语音的波 形信息。
参数编码
提取语音信号的特征参数 ,以减少数据量。
混合编码
结合波形编码和参数编码 ,实现高效的语音压缩。
2023
语音信号的数字化
采样
采样是将连续的模拟语音信号转换为离散的数字信号的过程,通过 采样可以得到语音信号的时间序列。
语音信号的时域特征与频域特征

实验报告课程名称____________语音信号处理__________________ 实验项目语音信号的时域特征与频域特征实验仪器__台式计算机、Matlab软件、Cool Edit__系别____信息与通信工程学院_____专业_____电子信息工程专业______班级/学号_____学生姓名___________________实验日期_______2013/4/17________成绩_________________________指导教师_____________________实验一:语音信号的时域特征与频域特征一、实验目的使学生通过本实验观察语音信号在时域和频域的基本特征(语音波形、基音频率、过零数、共振峰),验证教材中关于语音信号在时域和频域的基本特征的概念与论述;通过采集语音数据与在实验中记录每个元音的基音周期、过零数、共振峰等环节熟悉这些语音的基本特征,为今后深入学习语音信号处理奠定基础。
二、实验内容学习音频编辑软件Cool Edit的使用方法及语音文件的建立;采集语音数据;观察语音波形;记录每个元音的基音周期(其倒数为基音频率)、过零数、共振峰;观察语音频域特征;分析不同元音的共振峰模式的特点(频率、相对振幅)。
三、实验原理元音与辅音在发音方法有如下基本区别:发元音时气流顺利通过声腔,声带颤动,形成的声波是周期性的;发辅音时气流暂时被阻不能通过或只能勉强挤出去。
元音具有基音与共振峰结构,辅音则不具有这两者。
基音由声带振动频率产生,决定语音的音高、音调。
在语音波形中表现为准周期峰值。
共振峰是语音频谱上的强频区,表现为频谱上呈峰状。
共振峰由声腔形状的变化决定,不同的声腔形状有不同的固有频率,产生不同的共振峰模式。
每个元音有特定的共振峰模式。
四、实验方法与实验步骤(一)音频编辑软件Cool Edit的使用方法及语音文件的建立①点击桌面上“cool edit”图标,选不同项可激活cool edit菜单中不同功能。
第一章:语音信号的基本理论

声带每开启和闭合一次的时间就是基调周期,其倒数称为基 调频率.
语音信号的产生模型
激励模型 辐射模型 共振峰模型
浊音激励信号
激励模型
AV E (Z ) = 1 z 1
U ( Z ) = E ( Z )G ( Z )
1 G(Z ) = (1 g1 z 1 )(1 g 2 z 1 )
语音信号的产生模型—激励模型
系数的作用是调整浊音信号的幅度或能量清音情况下激励信号是一个随机噪声发生器可以设其均值系数的作用是调节清音信号的幅度或能量声道模型将声道作为一个变截面积的声管来研究大多数情况下是一个全极点函数p为阶数实际应用中取812激励源的修正模型周期脉冲发生器声门脉冲模型随机噪声发生器auav将语音信号截然分为周期脉冲激励和噪声激励两种情况与实际情况不相符将激励源进行修正激励源可以是两种激励按照任意比例进行叠加一种更精确的域音产生模型周期脉冲发生器随机噪声发生器avfnavf1f2f3f4fnaufk1fk2ak鼻音分支口腔分支擦音分支
当气流在声道中受到阻碍时,产生湍流,此时生成清音. 清音在时域类似随机噪声,在频域具有宽带特征;
混合音(Mixed Speech )
浊音的能谱由精细的谐波结构和共振峰结构刻画.
共振峰结构,即谱包络(Spectral Envelope) 共振峰(Formant)就是谱包络的峰值. 共振峰反应了声道的共振特性,一般人的声道有3到5个 低于5kHz的共振峰.
受用语谱图
瀑布 语谱图(SPECTROGRAM)
时间,频率,幅值三维坐标, 频谱帧随时间变化
彩色语谱图
发 "ah."时的单元音 /a/ ah."
发 "eye"时的双元音 /ai/
《时域与频域响应》课件

小波变换
将信号分解成多个短时窗口内的频谱,用 于分析信号的局部特性。
通过变换系数在不同尺度上的变化,实现 对信号的时频分析。
经验模式分解(EMD)
滤波器组
将信号分解成一系列固有模式函数(IMF) ,用于分析非线性和非平稳信号。
通过设计滤波器组,将信号分解成不同频 带,用于分析信号在不同频带内的特性。
通信系统
在通信系统中,傅立叶变换用于 信号调制和解调、频分复用等。
04
系统稳定性分析
系统稳定性的定义
系统稳定性是指在受到外部激励或扰动时,系统能够保持其平衡状态或按预定方式 响应的能力。
系统稳定性是系统的重要性能指标,它决定了系统能否正常工作,以及系统性能的 优劣。
系统稳定性通常可以通过分析系统的响应特性来判断,包括时域和频域两种方法。
傅里叶变换
频谱
频域分析中,将信号在频率轴上的分 布称为频谱,可以反映信号中各频率 分量的强度。
将时间域的信号通过数学运算转换为 频率域的信号,是频域分析的基础。
频域分析的方法
频谱分析
通过分析信号的频谱,了解信号 中各频率分量的强度和分布。
滤波器设计
根据需求设计不同特性的滤波器, 对信号进行滤波处理,提取所需频 率分量或抑制干扰频率。
时频分析在信号处理中的应用
语音信号处理
用于分析语音信号的音调和节 奏,实现语音识别和语音合成
。
音乐信息检索
用于提取音乐信号的特征,实 现音乐分类和检索。
雷达信号处理
用于分析雷达回波信号的频率 和时间延迟,实现目标检测和 跟踪。
地震信号处理
用于分析地震信号的频率和时 间变化,实现地震预警和地震
定位。
通过绘制系统的伯德图来判断系统的稳定性。如果系统的 伯德图在负频率轴上没有穿越虚轴,则系统稳定;否则系 统不稳定。
《信号与系统讲义》课件

信号与系统是理解和分析信号处理的基础。本课件将介绍信号与系统的基本 概念、时域信号与频域信号、连续信号与离散信号、线性时不变系统、卷积 运算、采样与重构,以及系统的频率响应和频率特性。
信号与系统的基本概念
了解信号与系统的基本概念是理解信号处理的关键。本节将介绍信号的定义、 分类以及常见的信号类型,以及系统的定义和特性。
卷积运算
卷积运算是信号处理中常用的操作。本节将介绍卷积运算的定义和性质,并 通过实例演示如何使用卷积运算来处理信号。
采样与重构
采样是将连续信号转换为离散信号的过程,而重构则是将离散信号还原为连续信号的过程。本节将介绍 采样和重构的原理和方法。
பைடு நூலகம்
系统的频率响应和频率特性
系统的频率响应和频率特性描述了系统对不同频率的信号的响应情况。本节 将介绍频率响应和频率特性的概念,以及它们在信号处理中的应用。
时域信号与频域信号
在信号处理中,时域信号和频域信号是两种常见的表示方式。本节将解释时 域和频域的概念,以及如何在两个域中相互转换。
连续信号与离散信号
信号可以是连续的,也可以是离散的。本节将讨论连续信号和离散信号的区别,以及在信号处理中如何 处理这两种类型的信号。
线性时不变系统
线性时不变系统是信号处理中常用的模型。本节将介绍线性时不变系统的基本概念和特性,以及如何利 用系统的响应来分析信号的处理过程。
语音信号时域和频域通俗理解_概述及解释说明

语音信号时域和频域通俗理解概述及解释说明1. 引言1.1 概述语音是人类最基本、也是最常用的沟通方式之一。
人们通过声音来传递信息和表达情感。
对于语音信号的分析和处理,时域和频域是两个重要的角度。
时域分析主要关注声音信号在时间上的变化规律,而频域分析则关注声音信号在频率上的成分组成。
1.2 文章结构本文将以通俗易懂的方式,对语音信号的时域和频域进行解释和说明。
首先,我们将介绍时域和频域分析的基本概念及其重要性,然后详细讨论时域与频域分析中涉及到的关键点和方法。
最后,我们将总结观点并给出读者一些启示和建议。
1.3 目的本文旨在帮助读者理解语音信号时域与频域这两个概念,并且能够清晰明了地认识到它们在语音信号处理中所起到的作用。
通过对时域与频域分析方法的说明,读者可以更好地理解并应用这些知识于实际问题中。
同时,本文也希望能够引发读者对语音信号处理的更深层次的思考和探索。
2. 语音信号时域与频域通俗理解:2.1 语音信号时域分析:语音信号的时域分析是对声音在时间上的变化进行研究和处理。
时域分析主要关注声音的振幅和时间之间的关系。
在时域中,我们可以观察到声音振动的波形图。
当我们录制一段语音时,在录制过程中,麦克风会将声音转换为电信号,并按照一定的采样率记录下来。
这些记录的电信号就是我们所说的波形图。
波形图横坐标表示时间,纵坐标表示振幅。
通过观察波形图,我们可以获得很多有用的信息。
例如,振幅可以告诉我们声音的强度或者说响度,而波形图上不同部分振幅大小和模式的变化可以揭示出不同语音特征(如元音、辅音等)以及语速、语调等信息。
2.2 语音信号频域分析:语音信号的频域分析是对声音中各种频率成分进行研究和处理。
频域分析更注重声音中各个频率成分之间的关系以及它们在声谱上呈现出来的特征。
通过傅里叶变换的方法,我们可以将时域中记录的波形图转换为频谱图。
频谱图显示了声音中不同频率成分在整个录制时间内的存在情况。
横坐标表示频率,纵坐标表示声音强度。
语音信号的短时时域分析ppt课件
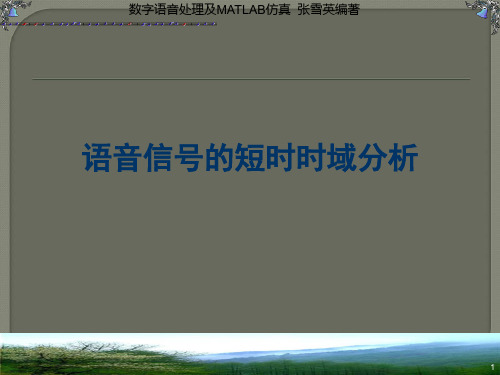
图3-4 语音信号处理系统框图
语音信号的频率范围通常是300~3400Hz,一 般情况下取采样率为8kHz即可。
采样后的信号在进行量化的过程中不可避免
的产生量化误差,一般可用量化信噪比来表示量
化误差的大小:SNRdB
10 lg(
2 e
x2 max
)
6.02 B
4.77
20
log10
(
xm ax
语音信号的分帧实现方法:
采用可移动的有限长度窗口进行加权的方法 来实现的。一般每秒的帧数约为33~100帧。
分帧一般采用交叠分段的方法,这是为了使 帧与帧之间平滑过渡,保持其连续性。前一帧和 后一帧的交叠部分称为帧移,帧移与帧长的比值
一般取为0~1/2。
图3.3给出了帧移与帧长示意图。
加窗常用的两种方法: 矩形窗,窗函数如下:
MATLAB的具体实现如下 : 1、用Cooledit读入语音“我到北京去”。 2、将读入的语音文件wav保存为txt文件,设置采样
率为8kHz,16位,单声道。 3、把保存的文件zqq.txt读入Matlab。
fid=fopen('zqq.txt','rt'); x=fscanf(fid,'%f');
y(n) x(n) x(n 1)
高通滤波器的幅频特性和相频特性如下
预加重前和预加重后的一段语音信号时域波形
预加重前和预加重后的一段语音信号频谱
3.2.2 语音信号的加窗处理
由于发音器官的惯性运动,可以认为在一小 段时间里(一般为10ms~30ms)语音信号近似不 变,即语音信号具有短时平稳性。这样,可以把 语音信号分为一些短段(称为分析帧)来进行处 理。
实验一、语音信号的时域特性和频域特性

实验一、语音信号的时域特性和频域特性实验一、语音信号的时域特性和频域特性学院:信息与通信工程学院专业:通信工程班级:104学号:2010026410姓名:黄余芳指导教师:崔艳秋1.实验名称语音信号的时域特性和频域特性2.实验类型验证性实验3.实验目的观察并验证语音信号的时域特性和频域特性,理解并掌握典型的语音信号时域分析方法和频域分析方法,为深入学习数字语音信号处理的相关理论奠定基础。
4.实验设备安装有MATLAB的计算机5.实验内容1.输入并运行MATLAB代码。
2.观察语音信号的时域特性(1)发一个清音和一个浊音,由麦克风采集语音数据,参考实验内容1中的程序将这些数据分别存成两个“.wav”文件(例如[a]的语音存为“”,要求采样率为8000),存在本人的文件夹中。
(2)读取WA V文件,显示语音波形,观察清音和浊音波形的差异。
(3)读取WA V文件,计算并显示语音的短时能量(要求分帧加窗的帧长为256,帧移为128),观察并分析清音和浊音短时能量的差异。
(4)读取WA V文件,计算并显示语音的短时过零率(要求分帧加窗是的帧长为256,帧移为128),观察并分析清音和浊音短时过零率的差异。
3. 观察语音信号的频域特性(1)读取WA V文件,计算并显示一帧语音的原始信号、加窗信号、短时频谱(要求分帧加窗的窗函数为汉明窗、帧长为256,帧移为128),观察并分析清音和浊音短时频谱的差异。
(2)读取WA V文件,计算并显示不同窗函数情况下一帧语音的加窗信号、短时频谱(要求分帧加窗的窗函数分别为矩形窗和汉明窗、帧长为256,帧移为128),观察并分析不同的窗函数对短时谱分析的影响。
6.相关函数wavread、plot、fft7.MATLAB程序代码1. 输入并运行以下MATLAB代码。
(1) 短时能量clear;close all;Fs=11025;y=wavrecord(5*Fs,Fs,'double'); wavwrite(y,'f:\\a');soundview(y,Fs);x = wavread('f:\\a.wav');x = double(x);x = filter([1 -0.9375], 1, x); % 预加重FrameLen = 256;FrameInc = 128;s = enframe(x, FrameLen, FrameInc); energy = sum(abs(s), 2);figure;subplot(2,1,1);plot(x);title('语音信号时域波形');xlabel('样点数');ylabel('幅度');subplot(2,1,2);plot(energy);title('语音信号的短时能量');xlabel('帧数');ylabel('短时能量');legend('帧长FrameLen = 240'); (2) 短时过零率clear;close all;x = wavread('f:\\a.wav');x = double(x);FrameLen = 256;FrameInc =128;tmp1 = enframe(x(1:end-1), FrameLen, FrameInc);tmp2 = enframe(x(2:end) , FrameLen, FrameInc);signs = (tmp1.*tmp2)<0;diffs = (tmp1 -tmp2)>0.02;zcr = sum(signs.*diffs, 2);figure;subplot(2,1,1);plot(x);title('语音信号时域波形');xlabel('样点数');ylabel('幅度');subplot(2,1,2);plot(zcr);xlabel('帧数');ylabel('短时过零率');title('语音信号的短时过零率');(3) 短时傅里叶变换clear;close all;x = wavread('f:\\a.wav');x = double(x);FrameLen =256;FrameInc =128;s = enframe(x, FrameLen, FrameInc);ss=s(50,:); %选取一帧语音信号(可以通过观察短时能量的分布来判断哪一帧是清音段还是浊音段)f=ss'.*hamming(length(ss));r=fft(f,512);r1=abs(r);r1=r1/max(r1);yuanlai=20*log10(r1);signal(1:256)=yuanlai(1:256);pinlv=(0:1:255)*11025/512;figure;subplot(3,1,1);plot(ss);axis([0,256,-1,1])title('截取的语音段');xlabel('样点数');ylabel('幅度');subplot(3,1,2);plot(f);axis([0,256,-1,1])title('窗选语音信号');xlabel('样点数');ylabel('幅度');subplot(3,1,3);plot(pinlv,signal);xlabel('频率/Hz');ylabel('对数幅度/dB');title ('加Hamming窗时语音频谱');(4) 显示清音短时过零率clear;close all;x = wavread('f:\\k.wav');x = double(x);FrameLen = 256;FrameInc =128;tmp1 = enframe(x(1:end-1), FrameLen, FrameInc); tmp2 = enframe(x(2:end) , FrameLen, FrameInc); signs = (tmp1.*tmp2)<0;diffs = (tmp1 -tmp2)>0.02;zcr = sum(signs.*diffs, 2);figure;subplot(2,1,1);plot(x);title('语音信号时域波形');xlabel('样点数');ylabel('幅度');subplot(2,1,2);plot(zcr);xlabel('帧数');ylabel('短时过零率');title('语音信号的短时过零率');2:语音信号的频域分析1.加汉明窗的浊音clear;close all;x = wavread('f:\\a.wav');x = double(x);FrameLen =256;FrameInc =128;s = enframe(x, FrameLen, FrameInc);ss=s(125,:); %选取一帧语音信号(可以通过观察短时能量的分布来判断哪一帧是清音段还是浊音段)f=ss'.*hamming(length(ss));r=fft(f,512);r1=abs(r);r1=r1/max(r1);yuanlai=20*log10(r1);signal(1:256)=yuanlai(1:256);pinlv=(0:1:255)*11025/512;figure;subplot(3,1,1);plot(ss);axis([0,256,-1,1])title('截取的语音段');xlabel('样点数');ylabel('幅度');subplot(3,1,2);plot(f);axis([0,256,-1,1])title('窗选语音信号');xlabel('样点数');ylabel('幅度');subplot(3,1,3);plot(pinlv,signal);xlabel('频率/Hz');ylabel('对数幅度/dB');title ('加Hamming窗时语音频谱2.加汉明窗的清音clear;close all;x = wavread('f:\\k.wav');x = double(x);FrameLen =256;FrameInc =128;s = enframe(x, FrameLen, FrameInc);ss=s(90,:); %选取一帧语音信号(可以通过观察短时能量的分布来判断哪一帧是清音段还是浊音段)f=ss'.*hamming(length(ss));r=fft(f,512);r1=abs(r);r1=r1/max(r1);yuanlai=20*log10(r1);signal(1:256)=yuanlai(1:256);pinlv=(0:1:255)*11025/512;figure;subplot(3,1,1);plot(ss);axis([0,256,-1,1])title('截取的语音段');xlabel('样点数');ylabel('幅度');subplot(3,1,2);plot(f);axis([0,256,-1,1])title('窗选语音信号');xlabel('样点数');ylabel('幅度');subplot(3,1,3);plot(pinlv,signal);xlabel('频率/Hz');ylabel('对数幅度/dB');title ('加Hamming窗时语音频谱3.加矩形窗的浊音clear;close all;x = wavread('f:\\a.wav');x = double(x);FrameLen =256;FrameInc =128;s = enframe(x, FrameLen, FrameInc);ss=s(125,:); %选取一帧语音信号(可以通过观察短时能量的分布来判断哪一帧是清音段还是浊音段)f=ss'.*rectwin(length(ss));r=fft(f,512);r1=abs(r);r1=r1/max(r1);yuanlai=20*log10(r1);signal(1:256)=yuanlai(1:256);pinlv=(0:1:255)*11025/512;figure;subplot(3,1,1);plot(ss);axis([0,256,-1,1])title('截取的语音段');xlabel('样点数');ylabel('幅度');subplot(3,1,2);plot(f);axis([0,256,-1,1])title('窗选语音信号');xlabel('样点数');ylabel('幅度');subplot(3,1,3);plot(pinlv,signal);xlabel('频率/Hz');ylabel('对数幅度/dB');title ('加矩形窗时语音频谱)8.实验结果及其分析浊音(1) 短时能量00.51 1.52 2.53 3.54x 104-1012语音信号时域波形样点数幅度050100150200250300350050100语音信号的短时能量帧数短时能量帧长FrameLen = 240(2) 短时过零率00.51 1.52 2.53 3.54x 104-1-0.500.51语音信号时域波形样点数幅度0501001502002503003500102030帧数短时过零率语音信号的短时过零率(3) 短时傅里叶变换1截取的语音段样点数幅度0501001502002501窗选语音信号样点数幅度-1000频率/Hz对数幅度/d B 加Hamming 窗时语音频谱清音(1) 短时能量 x 10412语音信号时域波形样点数幅度0204060语音信号的短时能量帧数短时能量帧长FrameLen = 240(2) 短时过零率00.51 1.52 2.53 3.54x 104-1-0.50.51语音信号时域波形样点数幅度05101520帧数短时过零率语音信号的短时过零率 (3) 短时傅里叶变换1截取的语音段样点数幅度1窗选语音信号样点数幅度05001000150020002500300035004000-1000频率/Hz对数幅度/d B 加Hamming 窗时语音频谱(4) 显示清音短时过零率x 1041语音信号时域波形样点数幅度05101520帧数短时过零率语音信号的短时过零率加窗(1)加汉明窗的浊音050100150200250-101截取的语音段样点数幅度050100150200250-101窗选语音信号样点数幅度0100020003000400050006000-100-500频率/Hz 对数幅度/d B 加Hamming 窗时语音频谱(2)加汉明窗的清音050100150200250-101截取的语音段样点数幅度-101窗选语音信号样点数幅度-100-500频率/Hz 对数幅度/d B 加Hamming 窗时语音频谱(3)加矩形窗的浊音-101截取的语音段样点数幅度-101窗选语音信号样点数幅度-100-500频率/Hz 对数幅度/d B 加矩形窗时语音频谱分析:(1)对于浊音与清音,浊音的幅值比较明显,有一个的波动,能清楚的看清楚它的周期;而清音类似于白噪声,没有明显的幅值,很平缓。
语音信号的时域特征与频域特征

实验报告课程名称____________语音信号处理__________________ 实验项目语音信号的时域特征与频域特征实验仪器__台式计算机、Matlab软件、Cool Edit__系别____信息与通信工程学院_____专业_____电子信息工程专业______班级/学号_____学生姓名___________________实验日期_______2013/4/17________成绩_________________________指导教师_____________________实验一:语音信号的时域特征与频域特征一、实验目的使学生通过本实验观察语音信号在时域和频域的基本特征(语音波形、基音频率、过零数、共振峰),验证教材中关于语音信号在时域和频域的基本特征的概念与论述;通过采集语音数据与在实验中记录每个元音的基音周期、过零数、共振峰等环节熟悉这些语音的基本特征,为今后深入学习语音信号处理奠定基础。
二、实验内容学习音频编辑软件Cool Edit的使用方法及语音文件的建立;采集语音数据;观察语音波形;记录每个元音的基音周期(其倒数为基音频率)、过零数、共振峰;观察语音频域特征;分析不同元音的共振峰模式的特点(频率、相对振幅)。
三、实验原理元音与辅音在发音方法有如下基本区别:发元音时气流顺利通过声腔,声带颤动,形成的声波是周期性的;发辅音时气流暂时被阻不能通过或只能勉强挤出去。
元音具有基音与共振峰结构,辅音则不具有这两者。
基音由声带振动频率产生,决定语音的音高、音调。
在语音波形中表现为准周期峰值。
共振峰是语音频谱上的强频区,表现为频谱上呈峰状。
共振峰由声腔形状的变化决定,不同的声腔形状有不同的固有频率,产生不同的共振峰模式。
每个元音有特定的共振峰模式。
四、实验方法与实验步骤(一)音频编辑软件Cool Edit的使用方法及语音文件的建立①点击桌面上“cool edit”图标,选不同项可激活cool edit菜单中不同功能。
语音信号实验讲义

语音信号MATLAB实验总体说明:程序的具体使用方法可察看help或程序本身的说明,希望同学们都能独立完成练习的内容;感觉有余力的同学可以将时域分析中的方法应用于we_be10k语音段,还可以用auread、wavread等命令读入语音段进行处理。
注意:用view-desktoplayout-defaut恢复matlab的默认窗口,左上角为workspace和current directory;将所使用的工作空间程序和语音段拷入matlab的work文件夹后可在窗口中看到并可以使用,双击mat 文件可到如此工作空间,在命令窗输入命令执行即可!注意相关命令,可以发现其它有用命令。
abs、log、fft、conv、xcov、xcorr、plot、figure、sqrt、sign一、 matlab的一般使用见精通matlab6.5(文件夹中的pdf 文档,只需其中一、二章的内容,了解即可)二、 练习题目的:熟悉matlab的界面和一般操作,准确画出语音信号波形及其频谱,加窗和滤波的实现。
1、找到工作空间ex2M1.mat, speech1_10k这段语音取自一段准周期元音,持续时间是25ms,并且采样率为10000点/秒。
A、画出标号为speech1_10k的语音波形(可用plot),根据语音波形,估计准周期信号以秒为单位的周期,听一下感受一下25ms是多长(可用sound )。
B 、 使用1024点FFT,画出信号的傅里叶变换在区间[0, π]上的对数幅度曲线(可用fft )。
C 、 分别使用25ms 和10ms 的汉明窗进行加窗(可用hamming ),窗的位置都应该在信号中心,画出加窗后的对应幅度图。
实验一 显示语音信号的语谱图一、实验目的综合信号频谱分析和滤波器功能,对语音信号的频谱进行分析,并对信号含进行高通、低通滤波,实现信号特定处理功能。
加深信号处理理论在语音信号中的应用;理解语谱图与时频分辨率的关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)AMDF 法: 定义平均幅度差函数
γ (l ) =
N − l −1 n =0
∑S
w
( n + l ) − S w ( n)
在这里 S w(n) 是加窗截取的一段语音信号。 假设 T 为语音信号的基音周期,当 l = n ⋅ T , n = 1,2 ,L 时, γ (l ) 函数接近局部极小值。
1) 基音的周期就是声带振动的周期。 基音周期的倒数就是 基音频率。 2)基音是与人的声带长度、质量等物理量有关。因此与人 的年龄、性别、情绪等生理状态有关。
[注意]:音高(Pitch)与基音的关系。音高是听觉量,基音是物理 量。正如冷热与温度的关系一样。
22
图 4.
基音周期示意图
23
4.2. 基音的检测
jω
)=
m = −∞
∑ x(m) ⋅ w(n − m) ⋅ e
∞
− jω m
对信号 x (n) 进行调制, 将频谱搬移到低端, 然后用 w(n ) 滤 波器进行滤波分析。
x(n)
w(n)
X n (e jω )
e − jωn
15
实现形式二: X n (e
jω
) = e − j ωn
m = −∞
∑ x(n − m) ⋅ w(m) ⋅ e ω
ˆ f w (ω ) |t0 =
∞
−∞
∫ f (t ) ⋅ w(t − t
− t2 4a
0
) ⋅ e − jωt ⋅ dt
例如,如果选择窗的形式为一个高斯函数
w(t ) =
1 2 πa
e
这个窗函数有如下性质:
8
∞
−∞
∫ w(t − t 0 ) ⋅ dt 0 =
∞
∞
−∞
∫ w(t ) ⋅ dt = 1
∞ ∞
所以有
−∞ ∞
∫
ˆ f w (ω ) |t0 ⋅dt0 =
∞
− ∞− ∞
∫ ∫ f (t ) ⋅ w(t − t ) ⋅ e
0
− j ωt
⋅ dt ⋅ dt0
=
−∞
∫
ˆ f (t ) ⋅ e − jωt ∫ w(t − t0 ) ⋅ dt0 ⋅ dt = f (ω )
−∞
ˆ ˆ 这说明 f (ω ) 可以被加窗后的短时谱 f w (ω ) | t0 所精确地分解。
1
2. 语音信号的时域波形
图 1.
语音信号的波形(shi4)
2
图 2. 语音信号波形(shi4)的局部细节
3
2.1. 语音时域信号特征
2.1.1. 语音时域信号的特点
1)清音段:能量低,过零率高,波形特点有点像随机的噪 声。这部分信号常与语音的辅音段对应。 2)浊音段:能量高,过零率低,波形具有周期性特点。所 谓的短时平稳性质就是处于这个语音浊音(元音)段中。 3) 过渡段: 一般是指从辅音段向元音段信号变化之间的部 分。信号变化快,是语音信号处理中最复杂、困难的部分。
N −1 ⎧ 2n ,0 ≤ n ≤ ⎪ N −1 2 w(n) = ⎨ 2n N −1 ⎪2 , < n ≤ N -1 2 ⎩ N −1
11
布莱克曼(Blackman)窗:
w( n) = 0.42 − 0.5 cos(
2πn 4πn ) + 0.08 cos( ) N −1 N −1
0 ≤ n ≤ N −1
4.4. 汉语孤立字的基音调式
汉语的声调起着辨字、辨义的作用。
4.4.1. 汉语孤立字的四声
阴平-------一声 阳平--------二声 上声--------三声 去声--------四声
34
4.4.2. 汉语四声与基音频率的关系
对于孤立字音节的声调轨迹,一般可以分成三段: (1)弯头段:对应于音节发音开始时的过渡段。 (2)调型段:对应于音节的饱满发音过程。 (3)降尾段:对应于音节结束时的过渡段。
4
2.1.2. 语音的短时能量、短时平均幅度和短时过零率
(1)短时能量:
E = ∑ s 2 ( n)
n =0
3)短时过零率:
∑ s (n)
n =0
N −1
⎧ N −1 ⎫ Z = 1 ⎨∑ sgn[ s (n)] − sgn[ s (n − 1)] ⎬ 2 ⎩ n =0 ⎭ ⎧1 x≥0 其中sgn[n] = ⎨ ⎩− 1 x < 0
18
图 3. 浊音信号的傅立叶分析谱 19
3.3.3. 元音三角形图
所谓的元音三角形图就是指不同元音的 F1、F2 共振峰频 率在平面图上的关系。
20
3.4.
清音谱特征
清音的频谱无明显的规律,比较平坦。在语音识别中使用 统计模型的方法加以解决。
21
4. 基音与四声
4.1. 基音周期与基音频率
6
手段在应用上就会受到限制。同时我们也希望能够通过观测到 的局部时域信号的频谱信息来了解(构造)整个 f (t ) 的频谱信 息。为此我们引入了所谓的短时傅立叶谱分析技术。 有许多技术都可以用来完成信号的短时谱分析。最典型的 就是小波变换和我们现在常采用的傅立叶短时谱分析技术。
7
傅立叶短时谱分析与窗的形状和位置有关(与时刻有关) 。 假设窗函数为 w(t ) ,那么信号 f (t ) 的短时傅立叶变换为
37
4.5. 语音信号的端点检测
在实验室较为安静的环境下,利用短时能量和过零率特征 可以得到较为满意的语音端点检测结果。
38
5. 作业与复习内容
(1)复习语音信号在时域和频域上的特点 (2)了解汉语四声与基音周期的关系。 (3)编写语音端点检测算法程序。
39
26
图 5. 语音(浊音)的自相关函数和 AMDF 曲线
27
(3)中心削波法 在计算语音信号的自关函数时, 为了提高效率, 减少干扰, 可以先对语音信号进行中心削波,然后再计算自相关函数。 根据实验观察, 自相关函数 R (l ) 的局部峰值点位置与语音幅度 的峰值点位置重合。根据这个特点,在自关法中只需要计算这 些峰值点位置的自关函数 R (l ) , 然后再搜索比较即可得到信号 的基音周期。
第一章 语音信号的时域及频域特征
1. 语音信号的主要特点
1.1. 语音信号带宽
语音信号的带宽约为 5KHz ,主要能量集中在低频段。
1.2. 语音信号是典型的随机信号
1) 人的每次发音过程都是一个随机过程。 很难得到两次完 全相同的发音样本。 2) 在信号处理中, 通常假设语音信号是短时平稳的。 例如, 可以认为在语音的浊音段部分,语音的二阶矩统计量是平稳的 (在 5~10mS 内),即二阶矩平稳,或称为宽平稳。
谱线结构是与浊音信号中的周期信号密切相关的。具有与 基音及其谐波相对应的谱线。
3.3.2. 浊音谱的共振峰结构
频谱包络中有几个凸起点,与声道的谐振频率相对应。这 些凸起点称为共振峰(Formant) 。其频率称为共振峰频率。按 频率由低到高依次为第一共振峰、第二共振峰…。相应频率用 F1、F2、F3…来表示。
28
29
4.2.2. 频域上的基音检测方法
在频域中,常常是用谐波分析法,即对浊音信号的谱线结 构进行分析来计算得到基音周期。
[注意] 在频域上可能不存在与基频对应的谱线。
30
4.3. 基音的平滑
由于在基音的提取过程中不可避免地要产生误差,主要是 基音周期减半或加倍的现象(根据方法的不同,误差的现象会 有所不同) 。一般情况下 90%左右的基音周期都会被准确提取, 但是总有少部分的基音是提取不准确的。因此需要采取平滑的 方法去掉这些奇异点。 在语音编码和汉语四声识别中,基音平滑直接影响到系统 的性能。
5
3. 语音信号的短时谱特征
3.1. 短时傅立叶谱分析
对于能量受限的时域信号 f (t ) , 它的傅立叶变换可以写成
∞
ˆ f (ω ) =
−∞
∫ f (t ) ⋅ e
− j ωt
⋅ dt
以上这个傅立叶变换, “宏观上” 在 给出信号 f (t ) 的频谱信息, 但是却无法确定某个“局部”时间段频谱的确切信息。在语音 信号中,信息是按照特定的时间序列方式出现的。如果谱分析 不能确定这种时间序列的次序 (即位置) 那么这种信号分析的 ,
这正是我们所希望的性质。
9
对于时域离散信号 x (n) ,短时傅立叶变换定义:
X n ( e jω ) =
m = −∞
∑ x(m) ⋅ w(n − m) ⋅ e
⎧1, 0 < n < N − 1 n = 其它 ⎩0,
∞
− jω m
这里 w(n ) 为窗函数。例如,常用的窗函数有 矩形窗: w(n) = ⎨
25
信号处理器中有专门的硬件指令来快速完成(只要一个周期) 这种乘-累加运算。因此这种算法在 DSP 中得到了普遍的应用。 无论是使用 AMDF 法或是自关法求语音信号的基音周期, 都要在基音周期 T 的范围内 [Tmin , Tmax ] 搜索 γ (l ) 或 R(l) 的极 值点位置。一般取 0.5 ⋅ Tmin < l < 1.5 ⋅ Tmax ,先计算所有的 γ (l ) 或 R(l) 值,然后再搜索得到基音。
31
几种常用基音平滑方法: (1)非线性平滑 例如:采用中值平滑。
5点 中值平滑 3点 中值平滑
(2)线性平滑 例如:采用 FIR 滤波器进行低通滤波平滑
FIR 滤波平滑
32
(3)组合平滑 例如: (1)和(2)方法的组合
中值平滑
线性平滑
中值平滑
线性平滑
−
延迟
+ +
+
延迟
