端口网络参数及等效电路
【推荐】电路原理基础:第二章 二端口网络的方程和参数
D
i1 i2
u2 0, 10
四、H参数方程: 已知i1和 u2求u1和 i2
u1 H11i1 H12u2 i2 H 21i1 H 22u2
1 i1
u1
1' i1
i2 2
N
u2
i2 2'
u1
i2
H11 H 21
H12 H 22
i1 u2
T
0.5 0.75S
0.6
0.5
将其变换为其它参数方程,则可求得其他参数,
注意变换时有些参数可能不存在。
12
六、二端口网络参数的互易性(reciprocal)
若网络中只含有R、 L、 C、 M 等线性元件而不 含有受控源,则网络参数就具有如下性质:
(1) R12 R21 (3) T AD - BC 1
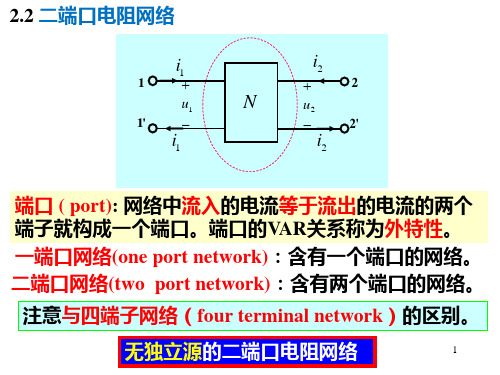
注意与四端子网络(four terminal network)的区别。
无独立源的二端口电阻网络
1
第一节 二端口网络的方程和参数
i1
1
u1
1'
i1
i2
2
N
u2
2'
i2
二端口的外特性决定于网络的本身与外部所接
电路无关,用端口电压、电流(共四个量)间的关 系反映,共六种情况。
2
一、R参数方程:
i1
u1
i2
Rl
u2
R
Rl Rl
Rl
Rl
但G不存在
电路分析基础二端口网络的等效电路

返回
X
3.双端接的二端口网络
端口电压、电流关系: U&1 U&s ZsI& 1 (1)
Z s 1 I1
++
I2 2
+
U&2 ZLI&2
(2)
二端口网络的Z参数方程:
Us
-
U1
-
1'
N
U2
-
2'
ZL
U & 1Z11I& 1Z12I& 2 (3)
U & 2Z21I& 1Z22I& 2 (4)
由方程(2)(3)(4)消去U & 2 和 I& 2得到二端口网络的策动
北京邮电大学电子工程学院退出开始11互易二端口网络的t形等效电路11122212222111121221221212非互易二端口网络的t形等效电路zi122112其中
§12-5 二端口网络的等效电路
北京邮电大学电子工程学院
退出 开始
1.T形等效电路
1.2 非互易二端口网络的T形等效电路
U & 1Z11I& 1Z12I& 2 U & 2Z21I& 1Z22I& 2
i2 R 1 1 R 2 2 R 1 1 R L R R 2 2 1 2 u R ss R L R s R 1 2 R 2 1 0 .1 4 A
输出电压:u 2 R L i2 5 1 0 3 ( 0 .1 4 ) 7 0 0 V
X
解(续)
(2)负载获得的功率:
P L u 2 i2 7 0 0 ( 0 .1 4 ) 9 8 W
点阻抗:
Z DU I & & 1 1Z 2 1Z 2 2 Z Z 2 2 1 1 Z Z L L Z 1 2Z 2 1
二端口网络参数和方程和等效电路相关知识讲解培训

(1) H 参数
UI21
H 11 I1 H 21I1
H12U 2 H 22U 2
矩阵形式:
UI21
H11
H
21
H12 H 22
UI12
(2) H 参数的计算与测定
H11
U 1 I1
U 2 0
H21
I2 I1
U 2 0
UI21
H 11 I1 H 21I1
H12U 2 H 22U 2
Y21
I2 U 1
U 2 0 Yb Y12
Ya Yb Y11 即:Yb Y12 Y21
Yb Yc Y22
解之得
Ya Y11 Y12 Yb Y12 Yc Y22 Y12
注意: (1) 等效只对两个端口的电压,电流关系成立。对端 口间电压则不一定成立。
(2) 适用于互易网络。
I2
Y12U1 Y22U 2
Y21 Y12
U 1
I2
其中
I1 I'2
Y11U 1 Y12U 1
Y12U 2 Y22U 2
相当于一互易二端口,
可求出其等效电路(型):
(计算见前例)
•
I1
+
•
U1
Yb
Ya
Yc
I2
+
•
U2
而I2 I2 Y21 Y12 U1相 当 于 在 端 口2并 入 一 受 控 源.
C
I1 U 2
I2 0
D
I1 I2
U 2 0
U1 AU 2 BI2
I1
CU 2
DI2
(3) 互易二端口 Y12 Y21
T 参数满足: AD BC 1
简单电路分析3二端口网络Circuits_Lec4

i2
+ u2
法1
Gb Gc Gb Ga Gc
u2 0
u1
i1
u1 0
Ga
i2
u2
+
i1 Ga Gb G11 u2 0 u1 i2 G21 u2 0 Gb u1 i1 G12 u1 0 Gb u2 G22 i2 u2
u2 0
Gb Gc
35二端口网络的等效电路等效电路r参数1111iru端口vcr相同rri212221121121iirruu22212122i12rriru二端口吸收的功率pu1i1u2i236g参数22212122121111ugugiugugi37h参数22212122121111uhihiuhihu38t参数没有直接的拓扑结构对应利用参数比较的方法求等效电路111i1ur1r22ir32ur21t21r1t11r3t221t211t21112121222222uitututitiriu111322uriurir12u223212ii1r312132211r1rrrruurrirr321222ii39二端口网络的联接级联串联并联级联将一个二端口的输出端直接与另一个端口的输入端相连的方式特征前一个双口的输出端口电压与后一个双口的输入端口电压相等前一个双口的输出端口电流与后一个双口的输入端口电流大小相等方向相反
G12 G22
(电气)对称二端口:端口互换后对外特性完全一样。
G11=G22 G12=G21
(电气)对称二端口
对称二端口, G中有2个独立参数 激励无论加在那个端口上,相应端口上的响应不变。 电气对称二端口 结构对称二端口(从结构上看拓扑 结构元件参数一致)
18
电路分析基础 网络的VAR和电路的等效

解: 设端口电压u,支路电路i1和i2
有
KCL I i1 3 0
I a
i1 10
+
i2
2A
u
10
i1 2 i2 0 可得 i1 I 3, i2 I 1
-
3A
b
u/V
2A
u 10i1 10i2 20I 40
i/A
-40V
返节目录
电路分析基础
测试题2 求单口网络的VAR,并画出其伏安特性曲线。
uS= uSk 注意参考方向 2、理想电压源并联
+
º
uS1_
+
-
uS _
uS2+
º
uS= uS1- u S2
实电际压电值压相源同可的电压源 才能以并并联联吗?
+
+
uS_ uS _
+ uS_
这种情况下每个电源的电流不确定。
返节目录
电路分析基础
3、理想电流源并联
iS1
iS2
iS
iS= iSk
iS3
注意参考方向
返节目录
电路分析基础
如何找到电路的最简等效电路呢?
+i
首先求出电路外端口的VAR。
u
-
①若VAR为 u K i 则电路等效为R=K的电阻
②若VAR为 u K i A
则电路等效为R=K的电阻 串联一个电压为A的电压源
或者 i K u A 则电路等效为R=1/K'的电阻
并联一个电流为A'的电流源
(1)分压电路:
uk
Rk
n
u
两个电阻串联:
Rk
k 1
u1
电工基础第十一章 二端口网络

式中H11、H22、H12、H21称为H参数。对于任何一个互易二端
; 口网络,H参数中只有三个是独立的, 有H12=-H21 网络对称时,
还有 H11H22-H12H21=1。
第二节 二端口网络的参数方程
2.混合(H)参数
H11
U&1 I&1
U&2 0
H 21
I&2 I&1 U&2 0
H12
由于Y参数在输入或输出端口短路时确定,故也称为短路导纳参数。
第二节 二端口网络的参数方程
3.Y 参数矩阵
导纳(Y) 参数方程可写成矩阵形式
式中
I1
I2
Y11 Y21
Y12
Y22
U1 U 2
Y
U1
U2
第一节 二端口网络的概念
二端口网络内部含有电源时称为含源二端口网络;内 部没有电源时称为无源二端口网络。根据构成网络的 元件是线性还是非线性,二端口网络又可以分为线性 和非线性两种。本章主要讨论无源线性二端口网络.
第二节 二端口网络的参数方程
一.导纳(Y)参数方程
1.导纳(Y) 参数方程
I&1
U&1 U&2
H 22
I&2 U&2
I& 1 0
I& 1 0
式中:H11为输出端口短路时输入端口的入端阻抗。
H21为输出端口短路时对输入端口的转移电流比。
H12为输入端口开路时对输出端口的转移电压比。
第十一章二端口网络解析

第二节 二端口网络的参数方程
一、导纳参数方程
1. 导纳参数方程
I1 I2
Y11U1 Y12U 2 Y21U1 Y22U 2
上式也称为Y参数方程,式中Y11、Y12、Y21、Y22
称为 Y参数,具有导纳的性质,是一组只与网络内
部结构、参数及电源频率有关而与电源大小无关的
参数。
电工基础
3. A参数矩阵
A=
A
A11 A21
A12
A22
线性无源二端口网络即互易二端口网络的A参数中只
有三个是独立的。存在
A11 A22 A12 A21 1
电工基础
第二节 二端口网络的参数方程
四、混合参数方程
1. 混合参数方程
U1 H11I1 H12U 2
I2
H 21I1
H 22U 2
•
•
•
•
图示网络P 满足端口条件 I 1 I1'
;I2
I
' 2
形成两个端口,称之为二端口网络或双口网络。
电工基础
第一节 二端口网络的概念
二端口网络内部含有电源(包括独立电源和受控电源) 时称为含源二端口网络;内部没有电源时称为无源二端口 网络。根据构成网络的元件是线性还是非线性,二端口网 络又可以分为线性和非线性两种。
第十一章 二端口网络
本章重点 二端口网络的参数方程 二端口网络的等效电路
电工基础
第十一章 二端口网络
主要内容 第一节 二端口网络的概念 第二节 二端口网络的参数方程 第三节 二端口网络的特性阻抗 第四节 二端口网络的等效电路 第五节 二端口网络的连接 第六节 理想变压器 本章小结
电工基础
第一节 二端口网络的概念
二端口基础知识讲解

[
Z
]
Za Zb
Zb Z
Zb
Zb
Zc
例2 求Z、Y参数
解
U 1
(jR1MI2jL1
)I1
U
2
jMI1 ( R2 jL2
)
I2
•
I1
+ R1 *
•
U1
jL1
•
jM
I2
* R2 +
N
•
I2
Y12
I1 U 2
U 1 0
转移导纳
Y22
I2 U 2
U 1 0
自导纳
•
I1
N
Y → 短路导纳参数
•
I2
+ • U2
例1 求Y 参数。 • I1
解
+
•
•
U1 0U1
Yb
Ya
Yc
•
I2
+
U 0 U• • 2
2
Y11
I1 U 1
U 2 0 Ya Yb
Y21
I2 U 1
U2 0 Yb
•
例
I1
+
•
U1
R1
•
I2
+
•
βI1
R2
•
U2
UI21
H11I1 H 21I1
H12U 2 H 22U 2
U1 R1I1
I2
I1
1 R2
U 2
H
R1
0
1
/
R2
15.3 二端口的等效电路
实验九 二端口网络参数的测定

4. 实验内容及要求
4.1以下二端口网络参数的测量是建立在如图 2所示的基础上。所用电源为直流电源。
图2
4.2 无源线性二端口网络实验线路:
1. 选择挂箱DG05 2. 绘制电路图。并标出两个端口的电压电流方向。 如图3所示。
图3
4.3 按实验电路,进行Z参数的测量和计算。
4.2.1 将输出开路(I2=0),在输入端加一直流 电源U=10V,测量输入端口的电压U1和电流I1, 输出端口的电压U2,则Z11=U1/I1,Z21=U2/I1;
6. 思考题
1)如何判断所设计的两端口网络是否互易或 对称? 2)网络参数(Z、H)是否与外加电压电流有 关?为什么?
等值电路的电压和电流间的相互关系与原网络对应端
口的电压电流间的关系完全相同,这就是所谓“黑盒
理论”的基本内容。这一理论具有很大的实用价值。
因为对任何一个线性系统,我们所关心的往往只是输 入端口与输出端口的特性,而对系统内部的复杂结构 不需要研究。
复杂二端口网络的端口特性往往很难用计算分
析的方法求取其等效电路。因此,实用上一般都是
4.2.2 输入开路(I1=0),在输出端加一直流电 源U=10V ,测量输出端口的电压U2和电流I2, 输入端口的电压U1,则Z22=U2/I2,Z12=U1/I2。 将以上测量数据填入表1。
表1 二端口网络的Z参数的测量 输出开路(I2=0) U1/V 计算值 测量值 Z11=U1/I1= Z21=U2/I1= 写出Z参数方程 Ω, Ω Z22=U2/I2= Z12=U1/I2= Ω, Ω I1/mA 输入开路(I1=0) I2/mA
1任何一个无源二端口网络如果我们仅对它的两对端口的外部特性感兴趣而对它的内部结构不要求了解时那么不管二端口网络多么复杂总可以找到一个极其简单的等值双端口电路来替代元网络而该等值电路的电压和电流间的相互关系与原网络对应端口的电压电流间的关系完全相同这就是所谓黑盒理论的基本内容
§12-5 二端口网络的等效电路

I 2 Y21U1 Y22U 2
Y12U1 Y22U 2 (Y21 Y12 )U1
其中:
I 1
Yb
I2
U1
Ya
Yc
YU1
U2
Ya Y11 Y12 Yb Y12 Yc =Y22 Y12
Y Y21 Y12
X
U1 Z11 I1 Z12 I 2 U 2 Z 21 I1 Z 22 I 2
I1
+ + I2
U1
Za
Z12 I1 Z 22 I 2 ( Z 21 Z12 ) I1 其中:
Zb
Zc
ZI1
+
U2
-
Z Z 21 Z12 Za Z11 Z12 Zb Z12 Zc Z 22 Z12
2
U2
1' U1 Z11 I1 Z12 I 2 将方程 改写为如下形式: U 2 Z 21 I1 Z 22 I 2 U1 ( Z11 Z12 ) I1 Z12 ( I1 I 2 ) Za I1 Zb I1 I 2 U 2 Z 21 ( I1 I 2 ) ( Z 22 Z 21 ) I 2
1
1 I1 0.2U 2 0.5 I1 U 2 5
X
解(续)
其型等效电路及各元件参数如图所示。 Ya 0.6S I1 I2 Yb Y12 0S U1 0.6S 0.2S Yc 0.2S 0.2U
U2
1
返回
X
I2
Zb
Zc
5 I1
二端口网络介绍

项目五二端口网络基本要求1. 掌握二端口网络的概念;2. 熟悉二端口网络的方程(Z、Y、H、T)及参数;3. 理解二端口网络等效的概念和计算方法;4. 理解二端口网络的输入电阻、输出电阻和特性阻抗的定义重点●二端口网络及其方程●二端口网络的Z、Y、T(A)、H参数矩阵以及参数之间的相互关系●二端口网络的连接方式以及等效难点二端口网络的T形和 形等效电路分析计算任务1 二端口网络方程和参数1..二端口网络一个网络,如果有n个端子可以与外电路连接,则称为n端网络,如图5.1(a)所示。
如果有n对端可以与外电路连接,且满足端口条件,则称为n端口网络,如图5.1(b)所示。
仅有一个端口的网络称为一端口网络或单端口网络,如图5.1(c)所示。
只有两个端口的网络称为二端口网络或双端口网络,如图5.1(d)所示。
图5.1 端口网络框图2.二端口网络Z 方程和Z 参数1)Z 方程图5.2 线性二端口网络图5.3 线性二端口网络二端口的Z 参数方程是一组以二端口网络的电流1I 和2I 表征电压1U 和2U 的方程。
二端口网络以电流1I 和2I 作为独立变量,电压1U 和2U 作为待求量,根据置换定理,二端口网络端口的外部电路总是可以用电流源替代,如图5.2和图5.311111222211222U Z I Z I U Z I Z I ⎫=+⎪⎬=+⎪⎭2)Z 参数Z 参数具有阻抗的性质,是与网络内部结构和参数有关而与外部电路无关的一组参数11Z 为输出端口开路时,输入端口的入端阻抗;22Z 为输入端口开路时,输出端口的入端阻抗;12Z 为输入端口开路时,输入端口电压与输出端口电流构成的转移阻抗; 21Z 为输出端口开路时,输出电压与输入电流构成的转移阻抗。
3)Z 方程矩阵形式[]11121112122222 Z Z U I I Z Z Z U I I ⎛⎫⎛⎫⎛⎫⎛⎫== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭其中 Z []11122122ZZ Z Z Z ⎛⎫== ⎪⎝⎭称为二端口的Z 参数矩阵,也称开路阻抗矩阵。
29二端口网络方程参数及等效电路

29二端口网络方程参数及等效电路
一、二端口网络方程
二端口网络的方程如下:
V1=Z11I1+Z12I2
V2=Z21I1+Z22I2
其中V1和V2代表两端口的电压,I1和I2代表两端口的电流,Z11、Z12、Z21和Z22代表四个参数,每个参数对应一条电阻等效的连续线。
二、网络方程参数
网络方程的参数:
(1)Z11:端口1的电阻或电抗,它代表端口1电流I1通过端口1
电阻时,端口1的电压。
(2)Z12:端口1和端口2的电阻或电抗,它代表端口1电流I1通
过端口1和端口2电阻时,端口2的电压。
(3)Z21:端口2的电阻或电抗,它代表端口2电流I2通过端口2
电阻时,端口1的电压。
(4)Z22:端口2和端口1的电阻或电抗,它代表端口2电流I2通
过端口2和端口1电阻时,端口2的电压。
三、网络方程等效电路
二端口网络方程可以用下图所示的等效电路来表达:
等效电路中的电压源的电压值与实际网络中可以使用的电压值相同,即V1和V2分别代表端口1和端口2的电压。
同时,Z11、Z12、Z21和
Z22分别代表端口1、端口1和端口2、端口2之间的电阻或电抗。
四、总结
二端口网络方程的形式为:V1=Z11I1+Z12I2;V2=Z21I1+Z22I2,其中V1和V2代表两端口的电压,I1和I2代表两端口的电流。
第十六章 二端口网络

放大器
2 、二端口网络
1
i1in
1
i2 in
2
u1
1 i1out
u2
i2out 2
(1)给定一个四端网络,若 i1in i1out , i2 in i2out , 则这个四端网络构成了二端口网络。 (2)二端口网络的对外联接特性由端口电压 u1 , u2 和电流 i1 , i2 确定。端口四个变量的相互关系可 通过二端口的参数和方程来描述,参数只决定于 二端口本身的元件及联接方式。
Z1 Z 2
[Z ]
Z2
Z2 Z2 Z3
例2:若上图中加上一个受控电压源,如图所示, 求二端口网络的Z参数。 Z I I Z1
1
3
2
U1
Z2 U R
3U R
U2
Z1
Z3
Z2 U R
I1
3U R
解: 方法一:
在左边端口加电流为 I1的电流源,右端开路,则: U1 U1 ( Z1 Z 2 ) I1 Z11 Z1 Z 2 I1 U2 U2 Z 2 I1 3 Z 2 I1 Z 21 4 Z 2 I1 在右边端口加电流为 I 2 的电流源,左端开路,则: U1 U1 Z 2 I 2 Z12 Z 2 I2 U2 U2 ( Z 2 Z 3 ) I 2 3 Z 2 I 2 Z 22 4 Z 2 Z 3 I2
直接列方程
1
Yc
2
I1 YaU1 Yb (U1 U2 ) (Ya Yb )U1 YbU2 I 2 YcU2 Yb (U2 U1 ) YbU1 (Yb Yc )U2
电路-第8章 二端口网络

在工程实际中,研究信号及能量的传输和信号变换时,经常碰到如下形式的电路(或网络):放大器A滤波器R C C三极管传输线n:1变压器3. 研究二端口网络的意义①两端口的分析方法易推广应用于n端口网络;②大网络可以分割成许多子网络(两端口)进行分析;③仅研究端口特性时,可以用二端口网络的电路模型进行研究。
4. 分析方法①分析前提:讨论初始条件为零的线性无源二端口网络;②找出两个端口的电压、电流关系的独立网络方程,这些方程通过一些参数来表示。
约定端口物理量4个i 1u 1i 2u 2端口电压电流有六种不同的方程来表示,即可用六套参数描述二端口网络。
线性RLCM 受控源i 1i 2i 2i 1u 1+–u 2+–注意1. Z参数和方程将两个端口各施加一电流源,则端口电压可视为电流源单独作用时产生的电压之和。
即:Z 参数方程①Z 参数方程+-+-N其矩阵形式为:Z参数矩阵+-2∙I +-1∙I N②Z 参数的物理意义及计算和测定Z →开路阻抗参数转移阻抗输入阻抗输入阻抗转移阻抗1)互易双口和互易定理互易双口:满足互易定理的双口网络根据互易定理:互易双口满足:1221Z Z ③互易性和对称性互易二端口四个参数中只有三个是独立的。
特点:只含线性非时变二端元件(R 、L 、C )耦合电感和理想变压器的双口网络注意2)对称双口对称双口:无独立源双口网络,若其两个端口可以互换而不改变外部电路的工作状况,则称该网络为(电气)对称双口网络。
特点:▪对称双口网络的每组参数中只有2个是独立。
▪结构对称的双口网络一定是电气对称的,反之却不一定。
2211Z Z 对称二端口满足:④Z 参数的求解方法1:由定义求得;21U U 、方法2:假定已知,对原电路求解,求出,即得Z 方程。
21I I 、解法1Z bZ aZ c+-+-求图示两端口的Z 参数。
【例8.2.1】解法2列KVL 方程:Z bZ aZ c+-+-求图示两端口的Z参数。
第4章网络的VAR和电路的等效介绍

25
20
u
-
V
i/mA
与二极管伏安特性曲线交于Q
得二极管工作点
Q(0.8V ,5m A)
5 0 0.3 0.8
i + u -
Q(UQ,IQ)
1.0
u/V
返节目录
电路分析基础
§ 4.2 单口网络(二端网络)的等效
端口:指电路中与外电路相连接的一对端钮,其电流由一个端钮流出, 又由另一端钮流入。
2A
i + 0.5 u -
i 2u 2
+
1V
-
画出等效电路如图所示
返节目录
电路分析基础
思考:
(1)N1与N2等效即N1 =N2? (2)若N1与N2对某外电路M效果一样,则N1 与N2等效?
注意:等效是对任意外电路的等效。 若N1和N2只对某一特定电路效果相等,一般不能保证他们对另 一外接电路也如此。就不能说他们是等效的,只能说他们对这一外 接电路是等效的
对网络N2有
u 5i
u 5V
②
N1
N2
联立解得
i 1A
返节目录
电路分析基础
例3 电路如图(a)所示,二极管伏安特性曲线如图(b)所示, 试求其工作点电压、电流。
解:划分电路的线性部分和非线性部分
线性网络VAR:
50mA
2
20
i +
u 20i 20(5 10 i) 1 40i
返节目录
电路分析基础
引言 网络方程法 等效变换法 叠加法 一个复杂的单口网络,若可以用一个简单 的或易于计算的单口网络来代替,将大大简化 对外部响应的求解
y参数等效电路

y参数等效电路
等效电路是指不同的电路具有相同的电学特性,可以用一个简化的电路来代替原始电路。
在电路分析中,我们通常使用等效电路来简化计算,使分析更加容易。
y参数等效电路是将一个复杂的电路转化为一个y参数网络的简化电路。
y参数等效电路可以描述电路的传输特性,包括增益和阻抗。
y参数等效电路通常用于分析单频网络,可以通过多个单频的y参数等效电路来分析多频网络。
y参数等效电路的基本结构是两个端口的电路,其中每个端口都包括一个y参数网络。
y参数网络由四个参数组成:y11,y12,y21和y22。
这些参数描述了电路的端口特性,包括输入电压和输出电流之间的关系。
y11和y22表示电路各自的自阻抗,y12和y21表示电路之间的互阻抗。
y参数等效电路的优点是可以方便地对电路进行串联和并联。
另外,y参数等效电路可以用于分析任意复杂的电路。
但是,y参数等效电路只适用于线性电路,对于非线性电路并不适用。
线性有源一端口网络等效参数测定电路设计

线性有源一端口网络等效参数测定电路设计一、实验目的1、验证戴维南定理和诺顿定理,加深对戴维南定理和诺顿定理的的理解。
2、掌握有源二端口网络等效电路参数的测量方法。
二、实验设备序号名称型号与规格数量备注1 可调直流稳压电源0~30V 或0~12V 12 可调直流恒流源 13 万用表MF500B或其他 14 直流数字毫安表 15 直流数字电压表 16 电位器470Ω 1三、实验原理1、任何一个线性含源网络,如果仅研究其中一条支路的电压和电源,则可将电路的其余部分看作是一个有源二端口网络(或称为有源二端网络)。
戴维南定理指出:任何一个线性有源二端口网络,总可以用一个电压源和一个电阻的串联来等效代替,如图6-1图6-1其电压源的电动势US 等于这个有源二端口网络的开路电压UOC,其等效内阻R等于该网络中所有独立源均置零(理想电压源视为短接,理想电流源视为开路)时的等效电阻。
诺顿定理指出:任何一个线性有源网络,总可以用一个电流源与一个电阻并联组成来等效代替,如图6-2图6-2此电流源的电流IS 等于这个有源二端口网络的短路电流ISC,其等效内阻R定义同戴维南定理。
U OC (US)和R或者ISC(IS)和R称为有源二端口网络的等效参数。
2、有源二端口网络等效参数的测量方法(1)开路电压、短路电流法测R在有源二端口网络输出端开路时,用电压表直接测其输出端的开路电压UOC,然后再将其输出端短路,用电流表测其短路电流ISC ,其等效内阻为R= UOC/ISC。
如果二端网络的内阻很小,若将其输出端口短路则易损坏其内部元件,因此不宜用此法。
(2)伏安法用电压表、电流表测出有源二端网络的外特性如图6-3根据外特性曲线求出斜率tgФ,则内阻为。
用伏安法,主要是测量开路电压及电流为额定值IN 时的输出端电压值UN,则内阻为。
若二端网络的内阻值很低时,则不宜测其短路电流。
图6-3(3)半电压法测R如图6-4所示,当负载RL的电压为被测网络开路电压的一半时,负载电阻(由电阻箱的读数确定)即为被测有源二端口网络的等效内阻值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
+
.U_1
N
1’
. I 2 2 + .U_2 2’
互易二端口网络:满足互易定理的二端口网络
互易二端口满足:Z12 = Z21
一、阻抗方程和Z参数
.1
I1
+
.U_1
N
1’
. I 2 2 + .U_2 2’
对称二端口网络:如果将二端口网络的输入端口(端口11’) 与输出端口(端口22’)对调后,其各端口电流、电压关系均 不改变,这种二端口网络称为对称二端口网络,这种网络 从联接结构看也是对称的
二、导纳方程和Y参数
例:求如图所示二端口的Y参数
. . j4S I1
+
U1
2S
_. .
. . I 2 +
-j1S
U2
.
_.
Y
2 j4
j4
j4
j3
S
二、导纳方程和Y参数
例:求如图所示二端口的Y参数
I 1 1Ω
1
+
U1
_
1'
2Ω I 2 2
+
3Ω
+
U2
4_I 1 _
2'
8 3 Z 7 5
三、混合方程和H参数
互易二端口满足:H12 = -H21 对称二端口满足:H12 = -H21, H11H22 - H12H21=1
三、混合方程和H参数
例:求如图所示二端口的H参数
. I1
+
.U_1
**
n:1
. I 2 + .U_ 2
H
0 n
n 0
三、混合方程和H参数
例:图示为晶体管在小信号条件下的简化等效电路, 求H参数
U1 H11 I 1 H12 U 2 I 2 H21 I 1 H22 U 2
H参数也可用实验法测试得到:
令22’短路得:
| H11
U1 I1
—— 具有电阻的量纲
U 20
| H21
I2 I1
—— 电流比
U 20
三、混合方程和H参数
.1
I1
+
.U_1
N
1’
. I 2 2 + .U_2 2’
H参数也可用实验法测试得到:
(3)
Z21
Z21
将(3)式代入(1)式得:
记 T CA为传DB输参数矩阵
四、传输方程和T参数
. I1
+
.U_1
网络的级连
. I 2
+
N1
.U_2
*
. I1
+*
._U 1
N2
*
. I 2 *+ .U 2_
T T1 T2
四、传输方程和T参数
T参数也可利用实验法测试得到(略)
互易二端口满足:AD - BC = 1
对称二端口满足:AD – BC = 1, A=D
对称二端口满足:Z12 = Z21, Z11 = Z22
一、阻抗方程和Z参数
例:求如图所示二端口的Z参数
-j2Ω
. I1
+
U1
_.
. + 2 I _
4Ω
j1Ω
I.
. I 2 + U2 _.
Z
2
j1
j
2+j 4+j
二、导纳方程和Y参数
导纳方程和Y参数
.1
I1
+
.U_1
N
1’
. I 2 2 + .U_2 2’
二端口是四端网络,但四端网络不一定是二端口网络
一、阻抗方程和Z参数
阻抗方程和Z参数
.1
I1
+
.U_1
N
1’
. I 2 2 + .U_2 2’
取 I 1作, 自I 2变量,取 为因变U量1, U 2
U1 Z11 I 1 Z12 I 2 U 2 Z21 I 1 Z22 I 2
U U
1 2
Z11
选用二端口网络何种参数要看实际需要。 如分析晶体管等效电路常用H参数和Y参数; 分析电力系统级联网络则常用T参数。 选择的原则在于:便于分析和易于实际测量
四、传输方程和T参数
例:已知
U 1
Z11
I 1,Z求12TI参2数
(1)
U 2 Z21 I 1 Z22 I 2 (2)
解:由(2)式:
I 1 1 U 2 Z22 ( I 2 )
取 U1作, U自2变量,取 为因变量I 1, I 2
I
1
Y11U 1 Y12 U
2
I 2 Y21U1 Y22 U 2
I I
1 2
Y11 Y21
Y12 Y22
U U
1 2
记为: I Y U
Y参数:
Y
Y11 Y21
Y12 Y22
S
二、导纳方程和Y参数
可见:Y参数又称为短路导纳参数 互易二端口满足:Y12 = Y21 对称二端口满足:Y12 = Y21, Y11 = Y22
Z
21
Z12 Z 22
I I
1 2
记为: U Z I
Z参数:
Z
Z11 Z21
Z12 Z22
一、阻抗方程和Z参数
.1
I1
+
.U_1
N
1’
. I 2 2 + .U_2 2’
注意:讨论二端网络的网络方程式,其端口上电压、电流 的参考方向必须向内关联!
一、阻抗方程和Z参数
.1
I1
作业
13-3 (a) 13-4 13-10 (c,d) 13-20
13.1 二端口网络概述
二端口网络
如图所示的四端网络,如果满足
,
则称该网络为二端口网络
I1' I1 , I2' I2
.1
I1
+
.U_1 I1'
N
1’
. I 2 2 +
. I2' U_2 2’
其中11’ 端口称为输入端口,22’ 端口称为输出端口。 在输入端口处加上激励,在输出端口处产生响应
取 I 1作, U自2变量,取 为因变U量1, I 2
U 1
H11
I1
H12 U 2
I 2 H21 I 1 H22 U 2
U
1
I2
H11
H
21
记
H
H11 H 21
为混HH合1222参 数矩阵
H12 H 22
I
1
U 2
三、混合方程和H参数
.1
I1
+
.U_1
N
1’
. I 2 2 + .U_2 2’
U1 H11 I 1 H12 U 2 I 2 H21 I 1 H22 U 2
令22’短路得:
| H11
U1 I1
—— 具有电阻的量纲
U 20
令11’开路得:
| H21
I2 I1
—— 电流比
U 20
| H12 U1
U2
—— 电压比
I 10
| H22 I 2
U2
——具有导纳的量纲
I 10
Y
Z 1
8 7
31 1 5 5 19 7
3 0.26
8
0.37
0.16
0.42
S
13.2 二端口网络方程和参数
一、阻抗方程和Z参数 二、导纳方程和Y参数 三、混合方程和H参数 四、传输方程和T参数
三、混合方程和H参数
混合方程和H参数
ห้องสมุดไป่ตู้.1
I1
+
.U_1
N
1’
. I 2 2 + .U_2 2’
I 1 Yb
1
+
U1
R1 R2
_
1'
I2
2
+
β I1
U2
_
2'
R1 0
H
1
R2
四、传输方程和T参数
传输方程和T参数
.1
I1
+
.U_1
N
1’
. I 2 2 + .U_2 2’
取 U 2 , (作自I 2变)量,取 为因变量U 1, I 1
U 1 AU 2 B( I 2 ) I1 C U 2 D( I 2 )
