三因素三水平正交表极差分析表
三水平三因素正交试验设计

LOGO
Three Applications
正交试验设计法探究银镜 反应的反应条件
常用的三个水平三个因素与三水平四因素的正交表一样 都是L9(34)正交表。
LOGO
正交表
简 正介交:表的正代交号表是,一n为整试套验规的则次的数设,计t表为格水,平L数n(,tcc)为用列L数为, 也 表就示是需可作能9次安实排验最,多最的多因可素观个察数4。个例因如素正,交每表个L因9(素34均),为它3 水平。一个正交表中也可以各列的水平数不相等,我们 称 列它为为4水混平合,型4正列交为表2水,平如。L8(4× 24),此表的5列中,有1
Bent-Ca-OH 脱水率X (%)
1
1
1(10.5)
1(10)
1(1.5)
5.872
5.232
10.90
2
1
2(14)
2(12)
2(2.0)
7.747
6.834
11.79
3
1
3(17.5)
3(14)
3(2.5)
7.861
7.022
10.67
4
2
1(10.5)
2(12)
3(2.5)
7.270
6.456
11.20
5
2
2(14)
3(14) 1(1.5)
7.880
7.011
11.03
6
2
3(17.5)
1(10)
常用三水平三因素正交试验设计

正交表
正交表是一整套规则的设计表格,Ln(tc)用 L为正 交表的代号,n为试验的次数,t为水平数,c为列数, 也就是可能安排最多的因素个数。
例如正交表L9(34),它表示需作9次实验,最多可 观察4个因素,每个因素均为3水平。一个正交表中 也可以各列的水平数不相等,我们称它为混合型正交 表,如L8(4×24),此表的5列中,有1列为4水平,4 列为2水平。
9
3 3(17.5) 2(12) 1(1.5) 6.668 5.909 11.38
脱水率X(%) 脱水率X(%)
12.5 12
11.5 11
10.5 10 9.5 9 8.5 8 1.5 2 2.5 3 3.5 4 4.5 5 水土比L/S(ml•g-1)
12.5
12
11.5
11
10.5
10 1.5 1.6 1.7 1.8 1.9 2 2.1 2.2 2.3 2.4 Cao用量(g)
正交试验设计 Orthogonal experimental design
例如作一个三因素三水平的实验,按全面实验要求,须 进行3 × 3 = 27种组合的实验,且尚未考虑每一组合的重 复数。若按L9(34)正交表安排实验,只需作9次,按L16(45) 正交表进行16次实验,显然大大减少了工作量。
水土比L/S对脱水材料脱水率影响
CaO与活性白土配比对脱水材料脱水率影响
正交表数据分析
K1 11.17 11.01 11.10
K2 11.15 11.46 11.57
K3 11.83 11.04 10.83
Rபைடு நூலகம்
0.68 0.45 0.74
正交实验设计的基本方法

示例
在用乙醇溶液提取葛根中有效成分的试验中,为了提 高葛根中有效成分的提取期探索性试验,决定选取3个 相对重要的因素,乙醇浓度、液固比(乙醇溶液与葛 根质量之比)和提取剂回流次数进行正交试验,因素 水平表如下:
试验方案及实验结果
综合平衡分析依据的原则:
1. 对于某个因素,可能对某个指标是主要因素,但对另外的 指标则可能是次要因素,那么在确定该因素的优水平时, 应首先选取作为主要因素时的优水平;
表头设计 列号
试验号
1 2
… n
K1j K2j
…
Kmj K1j2 K2j2
…
Kmj2 SSj
表1 Ln(mk)正交表及计算表格
A
B
…
…
1
2
…
k
试验数据
xi
xi2
1
…
…
1
…
…
…
…
…
m
…
…
K11
K12
…
K21
K22
…
…
…
…
Km1
Km2
…
K112
K122
…
K212
K222
…
…
…
Km12
Km22
…
SS1
SS2
欢迎学习
实验设计与数据 处理
第三节 多因素正交实验设计
一、正交实验设计的基本原理
(一)正交表
正交表,是依据数学原理,从大量 的全面试验点中,为挑选少量具有 代表性的试验点,所制成的排列整 齐的规范化表格 。
正交表符号的含义
(三)正交性原理
正交性原理是设计正交表的科学依据, 主要表现为均衡搭配性。
正交实验设计及结果分析

正交试验设计对于单因素或两因素试验,因其因素少,试验的设计、实施与分析都比较简单。
但在实际工作中,常常需要同时考察3个或3个以上的试验因素,若进行全面试验,则试验的规模将很大,往往因试验条件的限制而难于实施。
正交试验设计就是安排多因素试验、寻求最优水平组合的一种高效率试验设计方法。
1正交试验设计的概念及原理1.1正交试验设计的基本概念正交试验设计是利用正交表来安排与分析多因素试验的一种设计方法。
它是由试验因素的全部水平组合中,挑选部分有代表性的水平组合进行试验的,通过对这部分试验结果的分析了解全面试验的情况,找岀最优的水平组合。
例如:设计一个三因素、3水平的试验A因素,设A、A?> As3个水平;B因素,设B、B2、Bs3个水平;C因素,设G、G、G 3个水平,各因素的水平之间全部可能组合有27种。
全面试验:可以分析各因素的效应,交互作用,也可选岀最优水平组合。
但全面试验包含的水平组合数较多(图示的27个节点),工作量大,在有些情况下无法完成。
若试验的主要目的是寻求最优水平组合,则可利用正交表来设计安排试验。
全面试验法示意图三因素、三水平全面试验方案卫具e8G正交试验设计的基本特点是:用部分试验来代替全面试验,通过对部分试验结果的分析,了解全面试验的情况。
正因为正交试验是用部分试验来代替全面试验的,它不可能像全面试验那样对各因素效应、交互作用一一分析;当交互作用存在时,有可能岀现交互作用的混杂。
虽然正交试验设计有上述不足,但它能通过部分试验找到最优水平组合,因而很受实际工作者青睐。
如对于上述3因素3水平试验,若不考虑交互作用,可利用正交表1_9(34)安排,试验方案仅包含9个水平组合,就能反映试验方案包含27个水平组合的全面试验的情况,找出最佳的生产条件1.2正交试验设计的基本原理正交设计就是从选优区全面试验点(水平组合)中挑选出有代表性的部分试验点(水平组合)来进行试验。
上图中标有试验号的九个“(・)”就是利用正交表L(34)从27个试验点中挑选出来的9个试验点。
正交试验设计的极差分析

正交试验设计的极差分析(共25页)-本页仅作为预览文档封面,使用时请删除本页-第7章 正交试验设计的极差分析正交试验设计和分析方法大致分为二种:一种是极差分析法(又称直观分析法),另一种是方差分析法(又称统计分析法)。
本章介绍极差分析法,它简单易懂,实用性强,在工农业生产中广泛应用。
单指标正交试验设计及其极差分析极差分析法简称R 法。
它包括计算和判断两个步骤,其内容如图7-1所示。
图7-1 R 法示意图图中,K jm 为第j 列因素m 水平所对应的试验指标和,K jm 为K jm 的平均值。
由K jm 的大小可以判断j 因素的优水平和各因素的水平组合,即最优组合。
R j 为第j 列因素的极差,即第j 列因素各水平下平均指标值的最大值与最小值之差:R j =max(jm j j K K K ,,,21 )-min(jm j j K K K ,,,21 )R j反映了第j列因素的水平变动时,试验指标的变动幅度。
R j 越大,说明该因素对试验指标的影响越大,因此也就越重要。
于是依据R j的大小,就可以判断因素的主次。
极差分析法的计算与判断,可直接在试验结果分析表上进行,现以例6-2来说明单指标正交试验结果的极差分析方法。
一、确定因素的优水平和最优水平组合例6-2 为提高山楂原料的利用率,某研究组研究了酶法液化工艺制造山楂精汁。
拟通过正交试验寻找酶法液化工艺的最佳工艺条件。
在例6-2中,不考虑因素间的交互作用(因例6-2是四因素三水平试验,故选用L9(34)正交表),表头设计如表6-5所示,试验方案则示于表6-6中。
试验结果的极差分析过程,如表7-1所示.表6-4 因素水平表酶解温度(C)C表6-6 试验方案及结果试验指标为液化率,用y i表示,列于表6-6和表7-1的最后一列。
表7-1 试验方案及结果分析=计算示例:因素A 的第1水平A 1所对应的试验指标之和及其平均值分别为:K A1=y 1+y 2+y 3=0+17+24=41,=1A K 31K A1=同理,对因素A 的第2水平A 2和第3水平A 3,有K A2=y 4+y 5+y 6=12+47+28=87,=2A K 31K A2=29K A3=y 7+y 8+y 9=1+18+42=61,=3A K 31K A3=由表7-1或表6-6可以看出,考察因素A 进行的三组试验中(A 1,A 2,A 3),B 、C 、D 各水平都只出现了一次,且由于B 、C 、D 间无交互作用,所以B 、C 、D 因素的各水平的不同组合对试验指标无影响,因此,对A 1、A 2和A 3来说,三组试验的试验条件是完全一样的。
正交实验结果如何进行数据分析

正交实验如何数据分析我们把在试验中考察的有关影响试验指标的条件称为因素(也叫因子),把在试验中准备考察的各种因索的不同状态 (或配方 )称为水平。
在研究比较复杂的工程问题中,往往都包含着多个因素,而且每个因素要取多个水平。
对于包含五个因素、五个水平的工程项目,理论计算必须进行55= 3125 次试验。
显然,所需要的试验次数太多了,工作量太大。
实践告诉我们,合理安排试验和科学分析试验,是试验工作成败的关键。
试验方案设计的好,试验次数就少,周期也短,这样不仅节省了大量人力、物力、财力和时间,而且可以得到理想的结果。
相反,如果试验设计安排的不好,即使进行了很多次试验,浪费了大量材料、人力和时间,也不一定能够得到预期的结果。
正交试验法,就是在多因素优化试验中,利用数理统计学与正交性原理,从大量的试验点中挑选有代表性和典型性的试验点,应用“正交表”科学合理地安排试验,从而用尽量少的试验得到最优的试验结果的一种试验设计方法。
正交试验法也叫正交试验设计法,它是用“正交表” 来安排和分析多因素问题试验的一种数理统计方法。
这种方法的优点是试验次数少,效果好,方法筒单,使用方便,效率高。
由于试验次数大大减少,使得试验数据处理非常重要。
我们可以从所有的试验数据中找到最优的一个数据,当然,这个数据肯定不是最佳匹配数据,但是肯定是最接近最佳的了。
用正交表安排的试验具有均衡分散和整齐可比的特点。
均衡分散,是指用正交表挑选出来的各因素和各水平组合在全部水平组合中的分布是均衡的。
整齐可比是说每一因素的各水平间具有可比性。
最简单的正交表 L 4(23) 如表 -1 所示。
表-1水列号1 2 3实平验号1 1 1 12 1 2 23 2 1 24 2 2 1记号 L4(23)的含意如下:“ L”代表正交表;L 下角的数字“ 4”表示有 4 横行 (简称为行 ),即要做四次试验;括号内的指数“ 3”表示有3 纵列 (简称为列 ),即最多允许安排的因素个数是 3 个;括号内的数“ 2”表示表的主要部分只有2 种数字,即因素有两种水平l 与 2,称之为l水平与 2 水平。
三水平三因素正交试验设计

5.872 7.747 7.861 7.270 7.880 6.662 8.053 6.405 6.668
5.232 6.834 7.022 6.456 7.011 5.896 7.134 5.725 5.909
10.90 11.79 10.67 11.20 11.03 11.50 11.41 10.62 11.38 LOGO
K2
11.15
11.46
11.57
K3
11.83
11.04
10.83
R
0.68
0.45
0.74
LOGO
LOGO
Example2正交试验设计优化碱性钙基膨润土
的改性条件
设置三水平三因素正交试验
因素 水平 1 2 3
A水土比 ( ml· g-1) 1.5:1 2:1 2.5:1
B 反应时 间(h) 10 12 14
C CaO/活性白土质量比 (g· g-1) 0.3:1 0.4:1 0.5:1
LOGO
LOGO
kI,k2,k3为其平均值, R为极差
LOGO
结果分析: 直接比较表2可知在这9个实验结果中,以实验5产生的银镜效果最好, 其水平组合为A2,B2,C3,分别是各因素中影响最大的水平。 由图可以看出本实验各因素组合中的最优组合为A2,B2,C3, 而通过R值的大小可以看出本实验因素存在显著性顺序,其主 次关系为C>A>B. 即影响银镜反应的因素最主要的是乙醛的浓度, 其次是温度、硝酸银的浓度。 结果与讨论 通过利用正交试验法得出的用乙醛作为还原剂做银镜反应时, 对实验影响最大的因素是乙醛的浓度。实验的最佳条件是 用水浴加热到80℃ ,2%的硝酸银溶液,使用40%的乙醛溶液。
第七章_极差分析

第一节 单指标正交试验设计及极差分析
本例得出的最优工艺条件, 本例得出的最优工艺条件,只有在试验所 考虑的范围内才有意义,超出了这个范围, 考虑的范围内才有意义 , 超出了这个范围, 情况可能发生变化。欲扩大适用范围, 情况可能发生变化 。欲扩大适用范围 , 必须 再进行扩大范围的试验, 再进行扩大范围的试验 , 能否扩大其适用范 围应有再次试验结果分析决定。 围应有再次试验结果分析决定 。 如试验只使 用了一种果胶酶,如果改用其它果胶酶, 用了一种果胶酶 , 如果改用其它果胶酶 ,本 例所找出的最优条件就不一定是最优条件, 例所找出的最优条件就不一定是最优条件, 就需要再次试验。 就需要再次试验。
1 2 3 4 5 6 7 8 9 K1
K2 K3
K1
K2
优水平 Rj
主次顺序
K3
A 1(10) 1(10) 1(10) 2(50) 2(50) 2(50) 3(90) 3(90) 3(90) 41 87 61 13.7 29.0 20.3 A2 15.3
B C 1(1) 1(20) 2(4) 2(35) 3(7) 3(50) 1(1) 2(35) 2(4) 3(50) 3(7) 1(20) 1(1) 3(50) 2(4) 1(20) 3(7) 2(35) 13 46 82 71 94 72 4.3 15.3 27.3 23.7 31.3 24.0 B3 C3 27.0 8.7 BADC
第七章 正交试验设计的极差分析
极差分析法又称直观分析法, 极差分析法又称直观分析法,它具有计 算简单、直观形象、简单易懂等优点, 算简单、直观形象、简单易懂等优点,是正 交试验结果分析最常用的方法。 交试验结果分析最常用的方法。
第一节 单指标正交试验设计及极差分析
正交试验结果的极差分析法
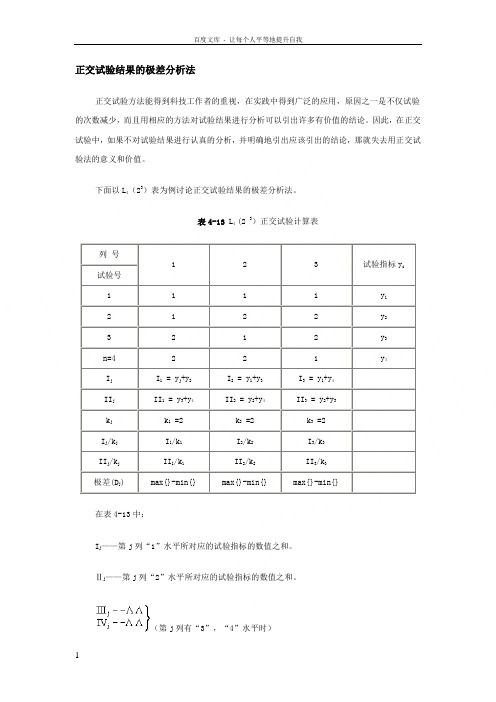
正交试验结果的极差分析法正交试验方法能得到科技工作者的重视,在实践中得到广泛的应用,原因之一是不仅试验的次数减少,而且用相应的方法对试验结果进行分析可以引出许多有价值的结论。
因此,在正交试验中,如果不对试验结果进行认真的分析,并明确地引出应该引出的结论,那就失去用正交试验法的意义和价值。
下面以L4(23)表为例讨论正交试验结果的极差分析法。
表4-13 L4 (2 3)正交试验计算表列号1 2 3 试验指标y i试验号1 1 1 1 y12 1 2 2 y23 2 1 2 y3n=4 2 2 1 y4I j I1 = y j+y2I2 = y1+y3I3 = y1+y4II j II1 = y3+y4II2 = y2+y4II3 = y2+y3k j k1 =2 k2 =2 k3 =2I j/k j I1/k1I2/k2I3/k3II j/k j II1/k1II2/k2II3/k3极差(D j) max{}-min{} max{}-min{} max{}-min{}在表4-13中:I j——第j列“1”水平所对应的试验指标的数值之和。
Ⅱj——第j列“2”水平所对应的试验指标的数值之和。
(第j列有“3”,“4”水平时)k j——第j列同一水平出现的次数。
等于试验的次数(n)除以第j列的水平数。
——第j列“1”水平所对应的试验指标的平均值。
——第j列“2”水平所对应的试验指标的平均值。
D j——第j列的极差。
等于第j列各水平对应的试验指标平均值中的最大值减最小值,即用极差法分析正交试验结果应引出以下几个结论:①在试验范围内,各列对试验指标的影响从大到小的排队。
某列的极差最大,表示该列的数值在试验范围内变化时,使试验指标数值的变化最大。
所以各列对试验指标的影响从大到小的排队,就是各列极差D的数值从大到小的排队。
②试验指标随各因素的变化趋势。
③使试验指标最好的适宜的操作条件(适宜的因素水平搭配)。
④对所得结论和进一步研究方向的讨论。
正交试验法(含案例)

正交试验设计法一、定义:正交试验设计法就是利用正交表来合理安排多因素试验的一种方法。
二、常用术语1、指标:指标就是试验要考察的效果。
常用X、Y、Z……来表示。
▼定量指标:能够用数量来表示的试验指标,如重量、尺寸、温度。
▼定性指标:不能用数量来表示的试验指标,如颜色、味道、外观。
●定性指标量化:可用打分法、分等法。
2、因素:因素是指对试验指标可能产生影响的原因。
因素是在试验中应当加以考察的重点内容。
一般用大写字母A、B、C……来表示。
3、水平(位级):位级是指因素在试验中所处的状态或条件。
常用阿拉伯数字1、2、3……来表示。
如: A1、A2、A3、B1、B2、B3。
三、正交表 (已设计好的标准化表格,是进行正试验法的基本工具)1、日本型正交表:由日本质量管理专家田口玄一博士创立。
该正交试验设计法,除需试验的因素外,还要研究分析因素与因素之间的交互作用,一起上列,对试验结果的分析用方差分析等方法,过程较复杂。
2、中国型正交表是由以我国张千里教授为首的中国专家所创立。
它不考虑因素之间的交互作用,而将其交互作用融于试验之中,对试验结果的分析采用极差分析法,简单的用“看一看”与“算一算”相结合的分析、简单、易行、同样能得到满意的结论,是一种实用的试验方法,很适合现场应用。
四、正交表的特点:1、均衡分散性:每一列中各种字码出现的次数相同,保证试验条件均衡地分散在配合完全的位级组合之中,因而代表性强,容易出现好条件。
2、整齐可比性:任意两列中全部有序数字对出现次数都是相同的。
保证了在各个位级的效果之中,最大限度地排除了其他因素的干扰,能最有效地进行比较,作出展望。
五、用中国型正交表安排试验的步骤 1、明确试验目的 2、确定考察指标 3、挑因素、选位级,制定因素位级表 ①挑因素的原则: ▼分析影响指标的各种因素,排除: 不可控因素 对指标影响不大的因素 已掌握得好的因素(让其固定在适当位置上) ▼选对指标可能影响大,又无把握的因素。
三因素三水平正交表例题

三因素三水平正交表例题例题1:某产品的质量受A、B、C三个因素影响,每个因素有三个水平。
A因素的三个水平为A1 = 10,A2 = 20,A3 = 30;B因素的三个水平为B1 = 5,B2 = 10,B3 = 15;C因素的三个水平为C1 = 2,C2 = 4,C3 = 6。
试用正交表安排试验,找出最佳的因素水平组合以提高产品质量(以产品质量指标越大越好)。
1. 选择正交表。
- 对于三因素三水平的试验,我们可以选用L9(3⁴)正交表。
2. 表头设计。
- 将A、B、C三个因素分别安排在正交表的三列上,例如A安排在第1列,B安排在第2列,C安排在第3列。
3. 确定试验方案。
- 根据正交表L9(3⁴)的安排进行试验。
例如,第1号试验的因素水平组合为A1、B1、C1;第2号试验为A1、B2、C2;第3号试验为A1、B3、C3;第4号试验为A2、B1、C2;第5号试验为A2、B2、C3;第6号试验为A2、B3、C1;第7号试验为A3、B1、C3;第8号试验为A3、B2、C1;第9号试验为A3、B3、C2。
4. 进行试验并记录结果。
- 假设经过试验得到9个试验结果分别为y1,y2,y3,y4,y5,y6,y7,y8,y9。
5. 分析试验结果。
- 计算各因素同一水平下试验结果的平均值。
- 对于A因素:- K1A=(y1 + y2+y3)/3,K2A=(y4 + y5 + y6)/3,K3A=(y7 + y8 + y9)/3。
- 计算极差RA = max(K1A,K2A,K3A)-min(K1A,K2A,K3A)。
- 对于B因素:- K1B=(y1 + y4 + y7)/3,K2B=(y2 + y5 + y8)/3,K3B=(y3 + y6 + y9)/3。
- 计算极差RB = max(K1B,K2B,K3B)-min(K1B,K2B,K3B)。
- 对于C因素:- K1C=(y1 + y6 + y8)/3,K2C=(y2 + y4 + y9)/3,K3C=(y3 + y5 + y7)/3。
正交试验设计(极差分析)

正交试验设计适用于多因素多水平的情况,对于非等水平的情况可能不适用; 同时,正交试验设计要求因素之间相互独立,如果有交互作用则无法准确反映 各因素对试验结果的影响。
ห้องสมุดไป่ตู้
02 极差分析方法
极差的概念与计算
极差的概念
极差是指一组数据中最大值与最 小值之差,用于描述数据的波动 范围。
极差的计算
极差 = 最大值 - 最小值,通过计 算极差可以了解数据的变化范围 。
05 正交试验设计软件介绍
正交试验设计软件的功能与特点
自动化试验设计
软件可以根据用户需求,自动生 成正交试验方案,大大提高了试
验效率。
数据分析与可视化
软件内置强大的数据分析功能,可 以将试验结果进行极差分析、方差 分析等,并生成各种可视化图表。
多因素分析
支持多因素、多水平的试验设计, 能够全面评估各因素对试验结果的 影响。
折线图
通过折线图展示各因素与试验结果的 关系,可以更直观地看出各因素对试 验结果的影响趋势。
03 正交试验设计的应用场景
工业生产优化
01
02
03
生产工艺优化
通过正交试验设计,对生 产工艺参数进行优化,提 高产品质量和生产效率。
设备性能测试
通过正交试验设计,测试 设备的性能参数,找出最 佳工作条件,延长设备使 用寿命。
详细描述
在机械制造过程中,工艺参数如温度、压力、时间等对产品质量和生产效率有重要影响。通过正交试 验设计,可以确定最佳的工艺参数组合,从而提高产品质量和生产效率。
案例三:农业生产中的肥料配比实验
总结词
通过正交试验设计,优化肥料配比,提 高农作物产量和品质。
VS
4.1.7 正交试验结果的极差分析法

4.1.7 正交试验结果的极差分析法正交试验方法能得到科技工作者的重视,在实践中得到广泛的应用,原因之一是不仅试验的次数减少,而且用相应的方法对试验结果进行分析可以引出许多有价值的结论。
因此,在正交试验中,如果不对试验结果进行认真的分析,并明确地引出应该引出的结论,那就失去用正交试验法的意义和价值。
下面以L4(23)表为例讨论正交试验结果的极差分析法。
表4-13 L4(2 3)正交试验计算表列号1 2 3 试验指标yi 试验号1 1 1 1 y12 1 2 2 y23 2 1 2 y3 n=4 2 2 1 y4I j I1= yj+y2I2= y1+y3I3= y1+y4IIj II1= y3+y4II2= y2+y4II3= y2+y3k j k1=2 k2=2 k3=2I j /kjI1/k1I2/k2I3/k3IIj /kjII1/k1II2/k2II3/k3极差(Dj) max{}-min{} max{}-min{} max{}-min{}在表4-13中:Ij——第j列“1”水平所对应的试验指标的数值之和。
Ⅱj——第j列“2”水平所对应的试验指标的数值之和。
(第j列有“3”,“4”水平时)kj——第j列同一水平出现的次数。
等于试验的次数(n)除以第j列的水平数。
——第j列“1”水平所对应的试验指标的平均值。
——第j列“2”水平所对应的试验指标的平均值。
D——第j列的极差。
等于第j列各水平对应的试验指标平均值中的最大值减最j小值,即用极差法分析正交试验结果应引出以下几个结论:①在试验范围内,各列对试验指标的影响从大到小的排队。
某列的极差最大,表示该列的数值在试验范围内变化时,使试验指标数值的变化最大。
所以各列对试验指标的影响从大到小的排队,就是各列极差D的数值从大到小的排队。
②试验指标随各因素的变化趋势。
③使试验指标最好的适宜的操作条件(适宜的因素水平搭配)。
④对所得结论和进一步研究方向的讨论。
4.1.7 正交试验结果的极差分析法

4.1.7 正交试验结果的极差分析法正交试验方法能得到科技工作者的重视,在实践中得到广泛的应用,原因之一是不仅试验的次数减少,而且用相应的方法对试验结果进行分析可以引出许多有价值的结论。
因此,在正交试验中,如果不对试验结果进行认真的分析,并明确地引出应该引出的结论,那就失去用正交试验法的意义和价值。
下面以L4(23)表为例讨论正交试验结果的极差分析法。
表4-13 L4(2 3)正交试验计算表列号1 2 3 试验指标yi 试验号1 1 1 1 y12 1 2 2 y23 2 1 2 y3 n=4 2 2 1 y4I j I1= yj+y2I2= y1+y3I3= y1+y4IIj II1= y3+y4II2= y2+y4II3= y2+y3k j k1=2 k2=2 k3=2I j /kjI1/k1I2/k2I3/k3IIj /kjII1/k1II2/k2II3/k3极差(Dj) max{}-min{} max{}-min{} max{}-min{}在表4-13中:Ij——第j列“1”水平所对应的试验指标的数值之和。
Ⅱj——第j列“2”水平所对应的试验指标的数值之和。
(第j列有“3”,“4”水平时)kj——第j列同一水平出现的次数。
等于试验的次数(n)除以第j列的水平数。
——第j列“1”水平所对应的试验指标的平均值。
——第j列“2”水平所对应的试验指标的平均值。
D——第j列的极差。
等于第j列各水平对应的试验指标平均值中的最大值减最j小值,即用极差法分析正交试验结果应引出以下几个结论:①在试验范围内,各列对试验指标的影响从大到小的排队。
某列的极差最大,表示该列的数值在试验范围内变化时,使试验指标数值的变化最大。
所以各列对试验指标的影响从大到小的排队,就是各列极差D的数值从大到小的排队。
②试验指标随各因素的变化趋势。
③使试验指标最好的适宜的操作条件(适宜的因素水平搭配)。
④对所得结论和进一步研究方向的讨论。
正交试验设计—直观分析法(试验设计与数据处理课件)

(5)计算极差,确定因素的主次顺序
R越大,因素越重要 若空列R较大,可能原因:
➢ 漏掉某重要因素 ➢ 因素之间可能存在不可忽略的交互作用
(6)最优方案的确定
➢ 优方案:在所做的试验范围内,各因素较优的水平组合 ➢ 若指标越大越好 ,应选取使指标大的水平 ➢ 若指标越小越好,应选取使指标小的水平 ➢ 还应考虑:降低消耗、提高效率等
② 例题6-3
水平
(A)乙醇浓度/%
1
80
2
60
3
70
目标:检验三个指标 :
(B)液固比
7 6 8
(C)回流次数
1 2 3
提取物得率
总黄酮含量
葛根素含量
注意:三个指标都是越大越好。
对三个指标分别进行直观分析: ➢ 提取物得率: 因素主次:C A B 优方案:C3A2B2 或C3A2B3 ➢ 总黄酮含量: 因素主次:A C B 优方案:A3C3B3 ➢ 葛根素含量 : 因素主次:C A B 优方案:C3A3B2
110
120 130 温度/℃
2
3
4
时间/h
趋势图
甲
乙
丙
催化剂种类
多指标正交试验设计及其结果 的直观分析
多指标正交试验设计及其结果的直观分析
有两种分析方法: ➢ 综合平衡法 ➢ 综合评分法
(1)综合平衡法
❖ 先对每个指标分别进行单指标的直观分析 ❖ 对各指标的分析结果进行综合比较和分析,得出较优方案
❖ 选 L9(34) 正交表
(2)表头设计
➢ 将试验因素安排到所选正交表相应的列中 ➢ 因不考虑因素间的交互作用,一个因素占有一列(可以随机排列) ➢ 空白列(空列):最好留有至少一个空白列
正交试验结果的极差分析法
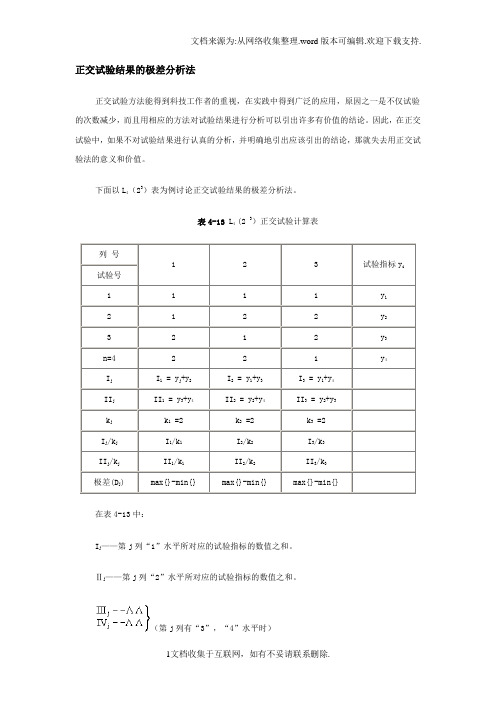
正交试验结果的极差分析法正交试验方法能得到科技工作者的重视,在实践中得到广泛的应用,原因之一是不仅试验的次数减少,而且用相应的方法对试验结果进行分析可以引出许多有价值的结论。
因此,在正交试验中,如果不对试验结果进行认真的分析,并明确地引出应该引出的结论,那就失去用正交试验法的意义和价值。
下面以L4(23)表为例讨论正交试验结果的极差分析法。
表4-13 L4 (2 3)正交试验计算表列号1 2 3 试验指标y i试验号1 1 1 1 y12 1 2 2 y23 2 1 2 y3n=4 2 2 1 y4I j I1 = y j+y2I2 = y1+y3I3 = y1+y4II j II1 = y3+y4II2 = y2+y4II3 = y2+y3k j k1 =2 k2 =2 k3 =2I j/k j I1/k1I2/k2I3/k3II j/k j II1/k1II2/k2II3/k3极差(D j) max{}-min{} max{}-min{} max{}-min{}在表4-13中:I j——第j列“1”水平所对应的试验指标的数值之和。
Ⅱj——第j列“2”水平所对应的试验指标的数值之和。
(第j列有“3”,“4”水平时)k j——第j列同一水平出现的次数。
等于试验的次数(n)除以第j列的水平数。
——第j列“1”水平所对应的试验指标的平均值。
——第j列“2”水平所对应的试验指标的平均值。
D j——第j列的极差。
等于第j列各水平对应的试验指标平均值中的最大值减最小值,即用极差法分析正交试验结果应引出以下几个结论:①在试验范围内,各列对试验指标的影响从大到小的排队。
某列的极差最大,表示该列的数值在试验范围内变化时,使试验指标数值的变化最大。
所以各列对试验指标的影响从大到小的排队,就是各列极差D的数值从大到小的排队。
②试验指标随各因素的变化趋势。
③使试验指标最好的适宜的操作条件(适宜的因素水平搭配)。
④对所得结论和进一步研究方向的讨论。
正交试验设计多指标

9
3
3
2
13.4
20.2
K1
9.3 3.3 20.8
K2
落 K3 下 k1 强 k2 度 k3
17.8 9.8 24.9 25.9 39.9 7.3 3.1 1.1 6.9 5.9 3.3 8.3 8.6 13.3 2.4
极 差 5.5 12.2 5.9
最佳方案 A3B3C2
优方案 A3 B3 C2
R=max{K1 ,K2 ,K3}-min{K1 ,K2 ,K3}, 或 R=max{k1 ,k2 ,k3}-min{k1 ,k2 ,k3}
R越大,因素越重要 若空列R较大,可能原因: 漏掉某重要因素 因素之间可能存在不可忽略的交互作用
(6)优优方方案案:的在确所定做的试验范围内,各因素较优的水平组 合
D
加水量
1:6 1:4 1:2
返回
这是4因素3水平的试验,采用正交表L9(34)安排试验,
结果列于表中。根据实际经验,纯度的重要性比回收率 的重要性大,纯度的权数取4,回收率的权数取1,计算 加权指标得出综合评分。
总分=4纯度+1 回收率
列 号 试验号
1 2 3 4 5 6 7 8 9 K1 K2 K3 k1
从表看出,A、D两个因素的极差都很大,是对试验 影响很大的两个因素,还可以看出,A、D都是取第 1水平为好;B因素的极差比A、D的极差小,对试验 的影响比A、D都小,B因素取第3水平为好;C因素 的极差最小,是影响最小的因素,C取第2水平为好。 综合考虑,最好的试验方案是
A1B3C2D1
历史ⅱ岳麓版第13课交通与通讯 的变化资料
用这类正交表安排试验的话,可以考察因子间的交互作用, 每张正交表都附有一张交互作用列表;由于L4( 23 ) ,L9( 34 ) L16( 45 ) ,L25( 56 ) 中任意两列的交互作用是其它各列,所以 就不再给出交互作用列表了。
