(理数)09届江门市普通高中高三调研测试

合集下载

江门2009年高三调研测试化学科质量分析

江门市2009年高三调研测试化学科质量分析一、试题分析试题有较高的知识覆盖率，题型结构、能力结构比较合理，总体难度则与2008年广东省高考题相近，这是一份能反映考生现状的较好试题。

试题有如下特点：⑴选择题以常见常考的题型为主，重点考查双基，难度适中。

⑵具有一定的阅读量，借助图像、数据、模型、工艺流程创设各种情景题，最大限度地考核学生在审题、联想、分析、评价等方面的能力。

如第5、8、13、19、20、22、23、24、25、27题等。

⑶实验题第20、21题为课题型考题，密切联系实际。

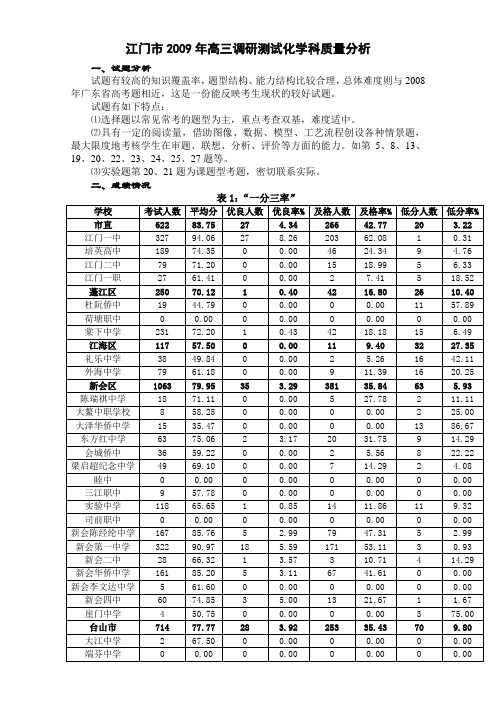
二、成绩情况三、试卷抽样分析（282份）表3：平均分和最高分表4：分段人数统计表5：各小题的平均得分及得分率四、存在的主要问题及其分析（一）选择题在选择题里，不少是常见题、热点题，是复习、训练的重点，反复训练，仍有错误。

1、对化学概念模糊、混淆。

如第1、11题。

2、对化学基本原理的理解不够深入，未能灵活运用。

如：第3题氧化还原规律的应用；第14题盖斯定律的应用；第15题原子结构和周期律的应用；第17题化学平衡的应用。

（二）非选择题1、审题不够细致，审题能力薄弱，特别对陌生度高的新情景题和课题型考题在读题时未能准确理解题意，找不到解题的切入点，导致分析不全面甚至分析错误。

如：新情景题第23、24题，课题型考题第20、21题。

其中第23题失分率极高。

2、基础知识不够扎实。

答选择题的时间过长，影响答非选择题的时间，部分学生没有完成后两道题。

学生花时间在前面题，导致时间分配不好，来不及做，做卷安排不科学。

3、答题表达不够规范、不够准确。

在实验方法或操作的表述、有机物结构简式的表示、化学方程式或离子方程式的书写等方面，部分考生答题不规范导致该得的分得不到。

4、考生获取信息能力和从图表中分析归纳的能力较差，在从这些图表中获取信息进行答题时，明显存在着对信息不理解、信息获取不全面、表述不准确的问题。

24题是无机化工题，要求书写离子反应方程式却写成化学方程式。

广东省江门市2009届高三第一次模拟考试(数学理)Word版

试卷类型：A江门市2009年高考模拟考试数学（理科）本试卷共4页，21小题，满分150分。

考试用时120分钟。

注意事项：⒈答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。

用2B铅笔将试卷类型（A）填涂在答题卡相应位置上。

将条形码横贴在答题卡右上角“条形码粘贴处”。

⒉选择题每小题选出答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

⒊非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

⒋作答选做题时，请先用2B铅笔填涂选做题的题号（或题组号）对应的信息点，再作答。

漏涂、错涂、多涂的，答案无效。

⒌考生必须保持答题卡的整洁。

考试结束后，将试卷和答题卡一并交回。

参考公式：锥体的体积公式Sh V 31=，其中S 是锥体的底面积，h 是锥体的高．用最小二乘法求线性回归方程系数公式2121 xn xy x n yx b ni ini ii --=∑∑==，x b y a-=．一、选择题：本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的． ⒈函数)12lg(231-+-=x x y 的定义域是A.⎪⎭⎫⎢⎣⎡∞+ , 32 B.⎪⎭⎫ ⎝⎛∞+ , 21 C.⎪⎭⎫ ⎝⎛∞+ , 32 D.⎪⎭⎫ ⎝⎛32 , 21⒉i 为虚数单位，复平面内表示复数iiz ++=21的点在 A.第一象限 B.第二象限 C.第三象限 D.第四象限 ⒊在三角形ABC 中，“B A sin sin >”是“B A >”的A.充分不必要条件B.必要不充分条件C.充要条件D.以上都不是⒋某地2008年第二季各月平均气温x （℃）与某户用水量y （吨）如下表，根据表中数据，用最小二乘法求得用水量y 关于月平均气温x 的线性回归方程是 A.5.115ˆ-=x yB.5.115.6ˆ-=x yC.5.112.1ˆ-=x yD.5.113.1ˆ-=x y⒌已知R m ∈，直线1l ：03)1()12(=-++-y m x m ，2l ：022=-+y mx ．则A.2=m 时，21//l lB.2≠m 时，1l 与2l 相交C.2=m 时，21l l ⊥D.对任意R m ∈，1l 不垂直于2l⒍任意a 、R b ∈，定义运算⎩⎨⎧>≤=⊗b a b ba ab a , , ，则函数x x y cos sin ⊗=的值域是A BC D EF1A 1B1C1D 图Q A B C 图D ·PA.[]1 , 1-B.⎥⎦⎤⎢⎣⎡-22 , 1C.⎥⎦⎤⎢⎣⎡-1 , 22D. ⎥⎦⎤⎢⎣⎡-22, 22⒎如图1，棱长为1的正方体1111D C B A ABCD -中，E 、F 是侧面对角线1BC 、1AD 上一点，若F BED 1是菱形，则 F BED 1在底面ABCD 上投影四边形的面积是A.21B.43C.22D.423-⒏如图2，矩形ABCD 中，点P 、Q 同时从A 点出发，分别沿A B C A →→→、A CB A →→→运动，相遇时运动停止。

(物理)09届江门市普通高中高三调研测试

江门市2009届普通高中高三调研测试物理本试卷分选择题和非选择题两部分，满分150分．考试用时120分钟，注意事项：答案必须写在答卷上各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效．第一部分选择题（共48分）一、本题共12小题，每小题4分，共48分。

每小题给出的四个选项中，有一项或一项以上是正确的，全部选对的得4分，选不全的得2分，有错选或不答的得0分1．用比值法定义物理量是物理学中一种常用的方法。

下面四个物理量中用比值法定义的是 A ．加速度mF a =B ．磁感应强度ILF B =C ．电场强度2rQ k E = D ．电阻IU R =2．利用速度传感器与计算机结合，可以自动作出物体运动的图像．某同学在一次实验中得到的运动小车的速度一时间图像如图所示，由此可以知道 A ．小车先做加速运动，后做减速运动 B ．小车运动的最大速度约为0.8m/s C ．小车的最大位移是0.8m D ．小车做曲线运动3．农民在精选谷种时，常用一种叫“风车”的农具进行分选。

在同一风力作用下，谷种和瘪谷（空壳）谷粒都从洞口水平飞出，结果谷种和瘪谷落地点不同，自然分开，如图所示。

对这一现象，下列分析正确的是 A ．M 处是谷种，N 处为瘪谷B. M 处是瘪谷，N 处为谷种C ．谷种质量大，惯性大，飞得远些D ．谷种飞出洞口时的速度比瘪谷飞出洞口时的速度小些4．如甲图所示，小车上固定着三角硬杆，杆的端点固定着一个质量为m 的小球．杆对小球的作用力的变化如乙图所示，则关于小车的运动说法中正确的是（杆对小球的作用力用由F1至F 4变化）A ．小车向右做匀加速运动B ．小车由静止开始向右做变加速运动C ．小车的加速度越来越大D ．小车的加速度越来越小5．如图所示，质量相等的A 、B 两物体在同一水平线上，当A 物体被水平抛出的同时，B 物体开始自由下落（空气阻力忽略不计），曲线AC 为A 物体的运动轨迹，直线BD 为B 物体的运动轨迹，两轨迹相交于O 点，则两物体 A ．经O 点时速率一定相等 B ．在O 点一定相遇C ．在O 点时动能一定相等D ．下落至O 点的过程中重力的功率一定相等6．在2008北京奥运会上，俄罗斯著名撑杆跳高运动员伊辛巴耶娃以5.05m 的成绩第24次打破世界纪录.图为她在比赛中的几个画面．下列说法中正确的是A ．运动员过最高点时的速度为零B ．撑杆恢复原状时，弹性势能完全转化为动能C ．运动员要成功跃过横杆，其重心不一定高于横杆D ．运动员在上升过程中对杆先做正功后做负功7．如图所示，某点O 处固定点电荷+Q ，另一带电-q 的粒子以O 为焦点做椭圆轨道运动，运动过程中经过最近点a 和最远点b ，下述说法不正确的是 A ．粒子在a 点运动速率大于在b 点速率 B ．粒子在a 点运动加速度大于在b 点加速度 C ．粒子在a 点电势能大于在b 点电势能D ．+Q 所产生的电场中，a 点电势高于b 点8．下面图中A 球系在绝缘细线的下端，B 球固定在绝缘平面上，它们带电的种类以及位置已在图中标出，A 球能保持静止的是9．如图是某中学科技小组制作的利用太阳能驱动小车的装置，当太阳光照射到小车上方的光电板，光电板中产生的电流经电动机带动小车前进。

2009年高考试题数学理(广东卷)Word版

绝密★启用前试卷类型：B2009年普通高等学校招生全国统一考试（广东卷）数学（理科）本试卷共4页，21小题，满分150分。

考试用时120分钟。

参考公式：锥体的体积公式13V sh=，其中S 是锥体的底面积，h 是锥体的高选择题：本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的．１．巳知全集U R =，集合{212}M x x =-≤-≤和{21,1,2,}N x x k k ==-=的关系的韦恩（Ｖenn ）图如图1所示，则阴影部分所示的集合的元素共有 A ．３个Ｂ．２个Ｃ．１个Ｄ．无穷个２．设z 是复数，()a z 表示满足1nz =的最小正整数n ，则对虚数单位i ，()a i =Ａ．８Ｂ．６Ｃ．４Ｄ．２３．若函数()y f x =是函数(0,1)xy a a a =>≠且的反函数，其图像经过点)a ，则()f x =Ａ．2log x Ｂ．12log xＣ．12xＤ．2x４．已知等比数列{}n a 满足0,1,2,n a n >=，且25252(3)nn a a n -⋅=≥，则当1n ≥时，2123221log log log n a a a -+++=Ａ．(21)n n - Ｂ．2(1)n + Ｃ．2n Ｄ．2(1)n -5．给定下列四个命题：①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行； ②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直； ③垂直于同一直线的两条直线相互平行； ④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．其中，为真命题的是Ａ．①和② Ｂ．②和③ Ｃ．.③和④ Ｄ．②和④ 6．一质点受到平面上的三个力123,,F F F （单位：牛顿）的作用而处于平衡状态．已知12,F F 成060角，且12,F F 的大小分别为２和４，则3F 的大小为Ａ．６Ｂ．２Ｃ．Ｄ．7．2010年广州亚运会组委会要从小张、小赵、小李、小罗、小王五名志愿者中选派四人分别从事翻译、导游、礼仪、司机四项不同工作，若其中小张和小赵只能从事前两项工作，其余三人均能从事这四项工作，则不同的选派方案共有Ａ．36种Ｂ．12种Ｃ．18种Ｄ．48种8．已知甲、乙两车由同一起点同时出发,并沿同一路线〈假定为直线）行驶．甲车、乙车的速度曲线分别为v v 乙甲和（如图2所示）．那么对于图中给定的01t t 和，下列判断中一定正确的是A ．在1t时刻，甲车在乙车前面 B ．1t时刻后，甲车在乙车后面 C ．在0t 时刻，两车的位置相同D ．0t 时刻后，乙车在甲车前面二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分．（一）必做题（９～１２题）９．随机抽取某产品n 件，测得其长度分别为12,,,n a a a ，则图3所示的程序框图输出的s = ，s 表示的样本的数字特征是．（注：框图中的赋值符号“=”也可以写成“←”“：=”）１０．若平面向量,a b 满足1a b +=，a b +平行于x 轴，(2,1)b =-，则a = ．11．巳知椭圆G 的中心在坐标原点，长轴在x 轴上，离心率为，且G 上一点到G 的两个焦点的距离之和为12，则椭圆G 的方程为．12．已知离散型随机变量X 的分布列如右表．若0EX =，1DX =，则a = ，b = ．（二）选做题（13 ~ 15题，考生只能从中选做两题）13．（坐标系与参数方程选做题）若直线112,:()2.x t l t y kt =-⎧⎨=+⎩为参数与直线2,:12.x s l y s =⎧⎨=-⎩（s 为参数）垂直，则k = ．14．（不等式选讲选做题）不等式112x x +≥+的实数解为．15．(几何证明选讲选做题）如图4，点,,A B C 是圆O 上的点，且04,45AB ACB =∠=，则圆O 的面积等于．三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤， 16．(本小题满分12分）已知向量(sin ,2)(1,cos )a b θθ=-=与互相垂直，其中(0,)2πθ∈．（1）求sin cos θθ和的值；（2）若sin()2πθϕϕ-=<<，求cos ϕ的值．17．（本小题满分12分）根据空气质量指数API （为整数）的不同，可将空气质量分级如下表:对某城市一年（365天）的空气质量进行监测，获得的API 数据按照区间[0,50],(50,100],(100,150],(150,200],(200,250],(250,300]进行分组，得到频率分布直方图如图5 （1）求直方图中x 的值；（2）计算一年屮空气质量分别为良和轻微污染的天数；（3）求该城市某一周至少有2天的空气质量为良或轻微污染的概率. (结果用分数表示．已知7732738123578125,2128,,36573518253651825182591259125==++++==⨯）18．（本小题满分１４分）如图６，已知正方体1111ABCD A B C D -的棱长为２，点Ｅ是正方形11BCC B 的中心，点Ｆ、Ｇ分别是棱111,C D AA 的中点．设点11,E G 分别是点Ｅ，Ｇ在平面11DCC D 内的正投影．（１）求以Ｅ为顶点，以四边形FGAE 在平面11DCC D 内的正投影为底面边界的棱锥的体积；（２）证明：直线11FG FEE ⊥平面；（３）求异面直线11E G EA 与所成角的正统值19．（本小题满分１４分）已知曲线2:C y x =与直线:20l x y -+=交于两点(,)A A A x y 和(,)B B B x y ，且A B x x <．记曲线C 在点A 和点B 之间那一段L 与线段AB 所围成的平面区域（含边界）为D ．设点(,)P s t 是L 上的任一点，且点P 与点A 和点B 均不重合．（１）若点Q 是线段AB 的中点，试求线段PQ 的中点M 的轨迹方程；（２）若曲线22251:24025G x ax y y a -+-++=与点D 有公共点，试求a 的最小值．20．（本小题满分１４分）已知二次函数()y g x =的导函数的图像与直线2y x =平行，且()y g x =在1x =-处取得极小值1(0)m m -≠．设()()g x f x x =．（１）若曲线()y f x =上的点P 到点(0,2)Qm 的值；（２）()k k R ∈如何取值时，函数()y f x kx =-存在零点，并求出零点． 21．（本小题满分１４分）已知曲线22:20(1,2,)n C x nx y n -+==．从点(1,0)P -向曲线n C 引斜率为(0)n n k k >的切线n l ，切点为(,)n n n P x y ．（１）求数列{}{}n n x y 与的通项公式；（２）证明：13521nn nxx x x x y -⋅⋅⋅⋅<<2009年普通高等学校招生全国统一考试（广东卷）数学（理科）参考答案选择题1-8 B .C. B. C D. D A A. 二。

江门09调研

江门市2009届普通高中高三调研测试化学本试卷分选择题和非选择题两部分，共10页，满分为150分，考试时间120分钟。

注意事项：1、答卷前，考生务必用黑色字迹钢笔或签字笔将自己的姓名和考生号填写在答题卡上，用2B铅笔将试卷类型填涂在答题卡上。

2、选择题每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号，不能答在试题卷上。

3、非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后写出新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4、考生必须保持答题卡的整洁，考试结束后，将答题卡交回。

可能用到的相对原子质量：H：1 C：12 N：14 O：16 S：32 Cl：35.5 I：127Na：23 Mg：24 Al：27 Fe：56 Cu：64 Ag：108一、选择题（本题包括9小题，每小题3分，共27分。

每小题只有一个选项．．．．．．符合题意）1．环境是人类生存和活动的场所。

下列有关人类满足生活和生产活动需求的做法的说法中，不正确的是：A．为举办“绿色奥运”，北京市将冬季燃煤取暖改用天然气做燃料，以改善空气质量B．研究人员用碳水化合物制造出了柴油燃料，属清洁的可再生资源C．光化学烟雾的产生与人为排放碳氢化合物、氮氧化物有关D．“长征”系列火箭为我国的航天事业立下了汗马功劳，其推进剂（偏二甲肼/四氧化二氮）属于环保燃料2．下列各组物质相互混合反应，既有气体生成，最终又有沉淀生成的是：①金属钠投入到FeCl3溶液②过量NaOH溶液和明矾溶液③少量电石投入过量NaHCO3溶液④Na2O2投入FeCl2溶液A．①B．③C．②③D．①③④3．近年来，我国储氢碳纳米管研究获重大进展，电弧法合成的碳纳米管，常伴有大量物质——碳纳米颗粒。

这种碳纳米颗粒可用氧化气化法提纯。

其反应的离子方程式为（其中a、b、c、d、e 、f为反应的系数）：aC + bCr2O72- + cH+ == dCO2↑ + eCr3+ + fH2O。

{高中试卷}广东省江门市高三调研测试数学(理)试题

20XX年高中测试高中试题试卷科目：年级：考点：监考老师：日期：江门市20XX年普通高中高三调研测试数学理科试题本试卷共4页，21题，满分150分，测试用时120分钟．参考公式：锥体的体积公式，其中是锥是锥体的底面积，体的高．如果事件、互斥，那么．一、选择题：本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的．⒈已知，，则A．B．C．D．⒉已知，，则A．B．C．D．⒊已知命题：；命题：复平面内表示复数（，是虚数单位）的点位于直线上。

则命题是命题的A．充分非必要条件 B．必要非充分条件C．非充分非必要条件 D．充要条件⒋函数在其定义域上是A．周期为的奇函数B．周期为的奇函数C．周期为的偶函数D．周期为的偶函数⒌某种饮料每箱装6听，如果其中有2听不合格。

质检人员从中随机抽出2听，检出不合格产品的概率A．B．C．D．⒍以抛物线的顶点为中心、焦点为一个顶点且离心率的双曲线的标准方程是A．B．C．D．⒎已知一个几何体的三视图及其大小如图1，这个几何体的体积A．B． C．D．⒏输入正整数（）和数据，，…，，如果执行如图2的程序框图，输出的是数据，，…，的平均数，则框图的处理框★中应填写的是A．B．C．D．二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分．(一)必做题（9～13题）⒐已知等差数列的首项，前三项之和，则的通项．图⒑已知、满足约束条件，则的最大值是．⒒已知是正整数，若，则的取值范围是． ⒓与圆：关于直线：对称的圆的方程是． ⒔曲线上任意一点到直线的距离的最小值是．(二)选做题（14、15题，考生只能从中选做一题）⒕（几何证明选讲选做题）如图3，圆的割线交圆于、两点，割线经过圆心。

已知，，。

则圆的半径．⒖（坐标系与参数方程选做题）在极坐标系（）中，直线被圆截得的弦的长是．三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤． ⒗（本小题满分12分）在中，角、、所对的边长分别为、、，已知．⑴求角的大小； ⑵若，，求的值．⒘（本小题满分12分）在平面直角坐标系中，，，是平面上一点，使三角形的周长为．⑴求点的轨迹方程；图4⑵在点的轨迹上是否存在点、，使得顺次连接点、、、所得到的四边形是矩形？若存在，请求出点、的坐标；若不存在，请简要说明理由．⒙（本小题满分14分）如图4，四棱锥中，底面，是直角梯形，为的中点，，，，．⑴求证：平面；⑵求与平面所成角的正弦值．⒚（本小题满分14分）如图5所示，有两个独立的转盘（A）、（B），其中三个扇形区域的圆心角分别为、、。

2009年广东高考(理科)数学试题及答案

绝密★启用前试卷类型：B2009年普通高等学校招生全国统一考试（广东卷）数学（理科）本试卷共4页，21小题，满分150分。

考试用时120分钟。

注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签宇笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。

用2B 铅笔将试卷类型（B ）填涂在答题卡相应位置上。

将条形码横贴在答题卡右上角“条形码粘贴处”。

2．选择题目每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。

答案不能答在试卷上。

3．非选择题目必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4．作答选做题时，请先用2B 铅笔填涂选做题的题组号对应的信息点，再作答。

漏涂、错涂、多涂的，答案无效。

5．考生必须保持答题卡的整洁。

考试结束后，将试卷和答题卡一并交回。

参考公式：锥体的体积公式13V sh ，其中S 是锥体的底面积，h 是锥体的高一、选择题目：本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的．１．巳知全集U R ，集合{212}M x x 和{21,1,2,}N x x k k 的关系的韦恩（Ｖenn ）图如图1所示，则阴影部分所示的集合的元素共有A ．３个Ｂ．２个Ｃ．１个Ｄ．无穷个２．设z 是复数，()a z 表示满足1n z 的最小正整数n ，则对虚数单位i ，()a iＡ．８Ｂ．６Ｃ．４Ｄ．２３．若函数()y f x 是函数(0,1)x y a a a 且的反函数，其图像经过点)a ，则()f xＡ．2log x Ｂ．12log x Ｃ．12x Ｄ．2x 3。

４．巳知等比数列{}n a 满足0,1,2,n a n ，且25252(3)n n a a n ，则当1n 时，2123221log log log n a a aＡ．(21)n n Ｂ．2(1)n Ｃ．2n Ｄ．2(1)n 45．给定下列四个命题：①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行；②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直；③垂直于同一直线的两条直线相互平行；④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．其中，为真命题的是Ａ．①和②Ｂ．②和③Ｃ．.③和④Ｄ．②和④6．一质点受到平面上的三个力123,,F F F （单位：牛顿）的作用而处于平衡状态．已知12,F F 成060角，且12,F F 的大小分别为２和４，则3FＡ．６Ｂ．２Ｃ．Ｄ．7．2010年广州亚运会组委会要从小张、小赵、小李、小罗、小王五名志愿者中选派四人分别从事翻译、导游、礼仪、司机四项不同工作，若其中小张和小赵只能从事前两项工作，其余三人均能从事这四项工作，则不同的选派方案共有Ａ．36种Ｂ．12种Ｃ．18种Ｄ．48种8．已知甲、乙两车由同一起点同时出发,并沿同一路线〈假定为直线）行驶．甲车、乙车的速度曲线分别为v v 乙甲和（如图2所示）．那么对于图中给定的01t t 和，下列判断中一定正确的是A ．在1t 时刻，甲车在乙车前面B ．1t 时刻后，甲车在乙车后面C ．在0t 时刻，两车的位置相同D ．0t 时刻后，乙车在甲车前面二、填空题目：本大题共7小题，考生作答6小题，每小题5分，满分30分．（一）必做题（９～１２题）９．随机抽取某产品n 件，测得其长度分别为12,,,n a a a ，则图3所示的程序框图输出的s ，表示的样本的数字特征是．（注：框图中的赋值符号“=”也可以写成“←”“：=”）１０．若平面向量,a b 满足1a b ，a b 平行于x 轴，(2,1)b ，则a ．11．巳知椭圆G 的中心在坐标原点，长轴在x 轴上，离心率为2，且G 上一点到G 的两个焦点的距离之和为12，则椭圆G 的方程为_________________．12．已知离散型随机变量X 的分布列如右表．若0EX ，1DX ，则a ，b ．（二）选做题（13~15题，考生只能从中选做两题）13．（坐标系与参数方程选做题）若直线112,:()2.x t l t y kt 为参数与直线2,:12.x s l y s （s 为参数）垂直，则k ．F 1F 2F 3O A B C D的实数解为．15．(几何证明选讲选做题）如图4，点,,A B C 是圆O 上的点，且04,45AB ACB ，则圆O 的面积等于．三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤，16．(本小题满分12分）已知向量(sin ,2)(1,cos )a b 与互相垂直，其中(0,)2．（1）求sin cos和的值；（2）若sin()102 ，求cos 的值．17．（本小题满分12分）根据空气质量指数API（为整数）的不同，可将空气质量分级如下表:对某城市一年（365天）的空气质量进行监测，获得API数据按照区间[0,50],(50,100],(100,150],(150,200],(200,250],(250,300]进行分组，得到频率分布直方图如图5（1）求直方图中x 的值；（2）计算一年中空气质量分别为良和轻微污染的天数；（3）求该城市某一周至少有2天的空气质量为良或轻微污染的概率.(结果用分数表示．已知57=78125,27=128,31825+2365+71825+31825+89125=1239125,365=73×5）18．（本小题满分１４分）如图６，已知正方体1111ABCD A B C D 的棱长为２，点Ｅ是正方形11BCC B 的中心，点Ｆ、Ｇ分别是棱111,C D AA 的中点．设点11,E G 分别是点Ｅ、Ｇ在平面11DCC D 内的正投影．（１）求以Ｅ为顶点，以四边形FGAE 在平面11DCC D 内的正投影为底面边界的棱锥的体积；（２）证明：直线11FG FEE 平面；19．（本小题满分１４分）已知曲线2:C y x 与直线:20l x y 交于两点(,)A A A x y 和(,)B B B x y ，且A B x x ．记曲线C 在点A 和点B 之间那一段L 与线段AB 所围成的平面区域（含边界）为D ．设点(,)P s t 是L 上的任一点，且点P 与点A 和点B 均不重合．（１）若点Q 是线段AB 的中点，试求线段PQ 的中点M 的轨迹方程；（２）若曲线22251:24025G x ax y y a 与D 有公共点，试求a 的最小值．20．（本小题满分１４分）已知二次函数()y g x 的导函数的图像与直线2y x 平行，且()y g x 在1x 处取得极小值1(0)m m ．设()()g x f x x ．（１）若曲线()y f x 上的点P 到点(0,2)Q ，求m 的值；（２）()k k R 如何取值时，函数()y f x kx 存在零点，并求出零点．21．（本小题满分１４分）已知曲线22:20(1,2,)n C x nx y n ．从点(1,0)P 向曲线n C 引斜率为(0)n n k k 的切线n l ，切点为(,)n n n P x y ．（１）求数列{}{}n n x y 与（２）证明：13521n n nx x x x x y答案1.解：�=�|−1≤�≤3，�=1,3,5,⋯，所以�∩�=1,3故，选B2.解：因为�2=−1，�3=−�，�4=1，所以满足��=1的最小正整数n 的值是4。

2009年广东高考数学理科卷带详解

2009年普通高等学校招生全国统一考试（广东卷）数学（理科）一、选择题：本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1.已知全集U R =，集合{}212M x x =--和{}21,1,2N x x k k ==-=的关系的韦恩（V enn ）图如图所示，则阴影部分所示的集合的元素共有 ( )第1题图A. 3个B. 2个C. 1个D. 无穷多个【测量目标】集合的表示方法（描述法），集合的并集.【考查方式】给出2个集合，通过并集运算求出集合的元素共有几个. 【难易程度】容易【参考答案】B【试题解析】由{}212M x x =--得{|13}M x x =-，{1,3,5,}N =则{1,3}M N =，有2个，选B.2.设z 是复数，()a z 表示满足1nz =的最小正整数n ，则对虚数单位i ，()i a = ( ) A. 8 B. 6 C. 4 D. 2 【测量目标】复数的基本概念.【考查方式】给出相关信息，求解出满足i 1n=最小正整数n 【难易程度】容易【参考答案】C【试题解析】()i i 1na ==，则最小正整数n 为4，选C.3.若函数()y f x =是函数(0,xy aa =>且)1a ≠的反函数，其图象经过点),,a a 则()f x = （）A.2log xB. 12log x C.12x D. 2x 【测量目标】反函数.【考查方式】给出反函数的原函数的方程和其图象经过点(),a a ，求解出反函数的方程.【难易程度】容易【参考答案】B【试题解析】()log ,a f x x =代入(),,a a 解得1,2a =所以()12log ,f x x =选B.4.已知等比数列{}n a 满足0,1,2,n a n >=且()252523,n n a a n -=则当1n 时，2123221log log log n a a a -+++= （）A.()21n n -B. ()21n + C. 2n D.()21n - 【测量目标】已知递推关系求通项.【考查方式】给出相关信息，先求出通项n a ，再利用对数函数化简，求解. 【难易程度】中等【参考答案】C【试题解析】由()252523nn a a n -=得222,0,n nn a a =>（步骤1）则2,nn a = ()22123221log log log 1321,n a a a n n -+++=+++-=选C.（步骤2）5.给定下列四个命题：①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行； ②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直； ③垂直于同一直线的两条直线相互平行；④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．其中，为真命题的是（）A. ①和②B. ②和③C. ③和④D. ②和④ 【测量目标】平行与垂直关系的综合问题.【考查方式】给出4个命题，通过直线与直线、面，面与面之间的位置关系判断其真假. 【难易程度】容易【参考答案】D【试题解析】显然 ①和③是假命题，故否定A,B,C,选D.6.一质点受到平面上的三个力123,,F F F （单位：牛顿）的作用而处于平衡状态．已知12,F F 成60角，且12,F F 的大小分别为2和4，则3F 的大小为（）A. 6B. 2C. 25D. 27【测量目标】余弦定理.【考查方式】给出物理学相关信息，通过余弦定理求解. 【难易程度】容易【参考答案】D【试题解析】()222312122cos 1806028,F F F F F =+--=所以327F =，选D.7.2010年广州亚运会组委会要从小张、小赵、小李、小罗、小王五名志愿者中选派四人分别从事翻译、导游、礼仪、司机四项不同工作，若其中小张和小赵只能从事前两项工作，其余三人均能从事这四项工作，则不同的选派方案共有 ( )A. 36种B. 12种C. 18种D. 48种【测量目标】排列组合及其应用..【考查方式】给出相关信息，考查了排列组合的公式. 【难易程度】中等【参考答案】A【试题解析】分两类：若小张或小赵入选，则有选法113223C C A 24,=若小张、小赵都入选，则有选法2223A A 12,=共有选法36种，选A.8.已知甲、乙两车由同一起点同时出发,并沿同一路线（假定为直线）行驶．甲车、乙车的速度曲线分别为v 甲和v 乙（如图所示）．那么对于图中给定的0t 和1t ，下列判断中一定正确的是（）第8题图A.在1t 时刻，甲车在乙车前面B.1t 时刻后，甲车在乙车后面C.在0t 时刻，两车的位置相同D.0t 时刻后，乙车在甲车前面【测量目标】函数图象的应用. 【考查方式】给出相关图象，再求解. 【难易程度】中等【参考答案】A【试题解析】由图象可知，曲线v 甲比v 乙在0100t t ～、～与x 轴所围成图形面积大，则在01t t 、时刻，甲车均在乙车前面，选A.二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分．（一）必做题（9 ~ 12题）9.随机抽取某产品n 件，测得其长度分别为12,,,,n a a a 则如图所示的程序框图输出的s = ，s 表示的样本的数字特征是．（注：框图中的赋值符号“=”也可以写成“←”“：=”）第9题图【测量目标】循环结构的程序框图.【考查方式】给出算法流程图，阅读框图，运行程序，得出结果. 【难易程度】容易【参考答案】12na a a n+++ 平均数【试题解析】第一次当i =1时,1;s a =第二次当i =2时,12;2a a s +=最后输出12+;na a a s n++=s =平均数.10.若平面向量,a b 满足1,+=+a b a b 平行于x 轴，()2,1,=-b 则=a .【测量目标】向量的坐标运算.【考查方式】考查向量的基本概念及向量的坐标运算. 【难易程度】中等【参考答案】()1,1-或()3,1-【试题解析】设(,)x y =a ，则(2,1)x y +=+-a b ，依题意，得⎪⎩⎪⎨⎧=-=-++011)1()2(22y y x ，（步骤1）解得⎩⎨⎧=-=11y x 或⎩⎨⎧=-=13y x ，所以(1,1)=-a 或(3,1)=-a .（步骤2） 11.已知椭圆G 的中心在坐标原点，长轴在x 轴上，离心率为32，且G 上一点到G 的两个焦点的距离之和为12，则椭圆G 的方程为．【测量目标】椭圆的标准方程.【考查方式】给出相关信息，通过离心率公式，长短轴间的关系，求解出标准方程. 【难易程度】中等【参考答案】221369x y += 【试题解析】3,212,6,3,2e a a b ====则所求椭圆方程为22 1.369x y += 12.已知离散型随机变量X 的分布列如右表．若0,1,EX DX ==则a = ，b = ．第12题图【测量目标】离散型随机变量的分布列.【考查方式】给出离散型随机变量的分布列，通过公式求解. 【难易程度】中等【参考答案】51,124【试题解析】由题知2221111,0,1121,12612a b c a c a c ++=-++=⨯+⨯+⨯= 解得51,124a b ==. （二）选做题（13 ~ 15题，考生只能从中选做两题） 13．（坐标系与参数方程选做题）若直线112,:2,x t l y kt =-⎧⎨=+⎩（t 为参数）与直线2,:12,x s l y s =⎧⎨=-⎩（s 为参数）垂直，则k = ．【测量目标】坐标系与参数方程.【考查方式】给出两条直线的参数方程，且两条直线垂直，求解. 【难易程度】较难【参考答案】1-【试题解析】直线112,:2,x t l y kt =-⎧⎨=+⎩（t 为参数）化为普通方程是)1(22--=-x ky ，该直线的斜率为2k-，（步骤1）直线2,:12,x s l y s =⎧⎨=-⎩（s 为参数）化为普通方程是12+-=x y ，该直线的斜率为2-，（步骤2）则由两直线垂直的充要条件，得()212k ⎛⎫--=- ⎪⎝⎭， 1.k =-（步骤3） 14．（不等式选讲选做题）不等式112x x ++的实数解为．【测量目标】解一元二次不等式【考查方式】给出不等式方程，先求定义域，再把它换成整数不等式求解. 【难易程度】中等【参考答案】{x |32x-且2-≠x }【试题解析】112xx++1220x xx⎧++⎪⇔⎨+≠⎪⎩22(1)(2)2x xx⎧++⇔⎨≠-⎩2302xx+⎧⇔⎨≠-⎩解得32x-且2-≠x.所以原不等式的解集为{x|32x-且2-≠x}. 15．（几何证明选讲选做题）如图，点,,A B C是圆O上的点，且4,45AB ACB=∠=，则圆O的面积等于．第15题图【测量目标】几何证明选讲.【考查方式】给出圆上线段长，角度大小，求解圆的面积.【难易程度】容易【参考答案】8π【试题解析】解法一：连结,,OA OB则902,AOB ACB∠==∠（步骤1）所以AOB△为等腰直角三角形，又4AB=，（步骤2）所以，圆O的半径22R=O的面积等于22ππ(22)8πR=⨯=（步骤3）解法二：设圆O的半径为R，在ABC△中，由正弦定理，得42sin45R=，解得22R=（步骤1）所以，圆O的面积等于22ππ(22)8πR=⨯=.（步骤2）三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤.16.(本小题满分12分）已知向量(sin,2)θ=-a与(1,cos)θ=b互相垂直，其中π(0,)2θ∈．（1）求sinθ和cosθ的值；（2）若10πsin()102θϕϕ-=<<，求cosϕ的值．【测量目标】余弦定理.【考查方式】利用两向量垂直公式、诱导公式、余弦定理求解.【难易程度】中等【试题解析】（1）∵向量()sin,2θ=-a与()1cosθ，b=互相垂直，∴ sin 2cos 0θθ=-=a b ，即θθcos 2sin =①，（步骤1）又 1cos sin 22=+θθ ② ① 代入②，整理，得51cos 2=θ，（步骤2）由π0,2θ⎛⎫∈ ⎪⎝⎭，可知0cos >θ， ∴55cos =θ，（步骤3）代入①得552sin =θ. 故55cos =θ， 552sin =θ.（步骤4）（2）ππππ0,0,,2222ϕθθϕ<<<<∴-<-<（步骤5）则()()2310cos 1sin ,10θϕθϕ-=--=（步骤6）()()()2cos cos cos cos sin sin .2ϕθθϕθθϕθθϕ∴=--=-+-=⎡⎤⎣⎦（步骤7） 17．（本小题满分12分）根据空气质量指数API （为整数）的不同，可将空气质量分级如下表：API0~50 51~100 101~150 151~200 201~250 251~300 >300 级别 I II 1III2III1IV2IVV状况优良轻微污染轻度污染中度污染中度重污染重度污染xy67 xy68xy69xy70xy71对某城市一年（365天）的空气质量进行监测，获得的API 数据按照区间[0,50],(50,100],(100,150],(150,200],(200,250],(250,300]进行分组，得到频率分布直方图如图所示. （1）求直方图中x 的值；（2）计算一年中空气质量分别为良和轻微污染的天数；（3）求该城市某一周至少有2天的空气质量为良或轻微污染的概率. （结果用分数表示．已知77578125,2128,==32738123,18253651825182591259125++++=365735=⨯)第17题图【测量目标】频率分布直方图.【考查方式】给出直方图，阅读，从图中找到相关信息，利用公式定理求解. 【难易程度】中等【试题解析】（1）因为，在频率分布直方图中，各个小矩形的面积之和等于1，依题意，得327385011825365182518259125x ⎛⎫+++++=⎪⎝⎭（步骤1）又 9125123912581825318257365218253=++++ 所以 182501199125123501=-=x .（步骤2）（2）一年中空气质量为良的天数为 1195018250119365=⨯⨯（天）；（步骤3）一年中空气质量为轻微污染的天数为 100503652365=⨯⨯（天）；（步骤4）（3）由（2）可知，在一年之中空气质量为良或轻微污染的天数共有119+100=219（天）所以，在一年之中的任何一天空气质量为良或轻微污染的概率是21933655P ==，（步骤5）设一周中的空气质量为良或轻微污染的天数为ξ，则ξ~B （7，53） 7733()C 155kkk P k ξ-⎛⎫⎛⎫==- ⎪⎪⎝⎭⎝⎭，（k =0,1,2,…,7）（步骤6）设“该城市某一周至少有2天的空气质量为良或轻微污染”为事件A ，则)1()0(1)(=-=-=ξξP P A P =-1070733C 155⎛⎫⎛⎫- ⎪⎪⎝⎭⎝⎭161733C 155⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭=6752537521⎪⎭⎫ ⎝⎛⨯⨯-⎪⎭⎫⎝⎛-=78125766537812513441281522121767=+-=⨯+-.（步骤7） 18．（本小题满分14分）如图，已知正方体1111ABCD A B C D -的棱长为2，点E 是正方形11BCC B 的中心，点F G 、分别是棱111,C D AA 的中点．设点1,1E G 分别是点,E G 在平面11DCC D 内的正投影．（1）求以E 为顶点，以四边形FGAE 在平面11DCC D 内的正投影为底面边界的棱锥的体积；（2）证明：直线1FG ⊥平面1FEE ；（3）求异面直线11E G EA 与所成角的正弦值.第18题图【测量目标】锥的体积、空间直角坐标系.【考查方式】考查了锥的体积、线面垂直的判定、异面直线所成的角，建立空间直角坐标系求解【难易程度】较难【试题解析】（1）依题得所求为四棱锥11FG DE E -的体积，其底面11FG DE 面积为111111Rt Rt E FG DG E DE FG S S S =+△△四边形221212221=⨯⨯+⨯⨯=，（步骤1）又⊥1EE 面11FG DE ，11=EE ，∴111111233E DE FG DE FG V S EE -==四边形.（步骤2）（2）以D 为坐标原点，DA 、DC 、1DD 所在直线分别作x 轴，y 轴，z 轴，得)1,2,0(1E ,)1,0,0(1G ，又因为)1,0,2(G ，)2,1,0(F ，)1,2,1(E ，则)1,1,0(1--=FG ，)1,1,1(-=FE ，)1,1,0(1-=FE ，（步骤3） ∴10(1)10FG FE =+-+=，110(1)10FG FE =+-+=，即FE FG ⊥1，11FE FG ⊥，（步骤4）又1FE FE F =，∴⊥1FG 平面1FEE .（步骤5）第18(2)题图（3）)0,2,0(11-=G E ，)1,2,1(--=EA ，则111111cos ,6E G EA E G EA E G EA<>==（步骤6）设异面直线11E G EA 与所成角为θ，则33321sin =-=θ.（步骤7）19.（本小题满分14分）已知曲线2:C y x =与直线:20l x y -+=交于两点(,)A A A x y 和(,)B B B x y ，且A B x x <．记曲线C 在点A 和点B 之间那一段L 与线段AB 所围成的平面区域（含边界）为D ．设点(,)P s t 是L 上的任一点，且点P 与点A 和点B 均不重合．（1）若点Q 是线段AB 的中点，试求线段PQ 的中点M 的轨迹方程；（2）若曲线22251:24025G x ax y y a -+-++=与D 有公共点，试求a 的最小值．【测量目标】直线与抛物线的位置关系，圆锥曲线中的探索性问题. 【考查方式】给出了抛物线方程与直线方程，利用公式、定理求解. 【难易程度】较难【试题解析】曲线C 与直线l 的联立方程组⎩⎨⎧=+-=022y x x y ,得⎩⎨⎧=-=1111y x ,⎩⎨⎧==4222y x ,（步骤1）又A B x x <，所以点,A B 的坐标分别为)4,2(),1,1(B A -（步骤2） ∵点Q 是线段AB 的中点∴点Q 的坐标为⎪⎭⎫⎝⎛25,21Q （步骤3）∵点(,)P s t 是L 上的任一点，且点P 与点A 和点B 均不重合．∴2s t = ，即),(2s s P ，且21<<-s （步骤4）设线段PQ 的中点为(),M x y ,则点M 的轨迹的参数方程为⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=2252212s y s x （s 为参数，且21<<-s ）；消去s 整理，得454122+⎪⎭⎫ ⎝⎛-=x y ，且⎪⎭⎫ ⎝⎛<<-4541x所以，线段PQ 的中点M 的轨迹方程是454122+⎪⎭⎫ ⎝⎛-=x y ，⎪⎭⎫ ⎝⎛<<-4541x ；（步骤5）（２)曲线22251:24025G x ax y y a -+-++=可化为()()222572⎪⎭⎫ ⎝⎛=-+-y a x ，它是以(),2G a 为圆心，以57为半径的圆，（步骤6）设直线:20l x y -+=与y 轴相交于点E ，则E 点的坐标为()0,2E ；自点A 做直线:20l x y -+=的垂线，交直线2y =于点F ，在Rt △EAF 中，45,AEF ∠=2=AE ，所以2=AF ，∵257<， ∴当0<a 且圆G 与直线l 相切时，圆心G 必定在线段FE 上，且切点必定在线段AE 上，（步骤7）于是，此时的a 的值就是所求的最小值. 当圆G 与直线:20l x y -+=相切时 571122=++-a ，解得527-=a ，或者527=a （舍去）所以，使曲线G 与平面区域D 有公共点的a 的最小值是527-．（步骤8）第19(2)题图20．（本小题满分14分）已知二次函数()y g x =的导函数的图象与直线2y x =平行，且()y g x =在1x =-处取得极小值1(0)m m -≠．设()()g x f x x=．（1）若曲线()y f x =上的点P 到点()0,2Q 2，求m 的值；（2）()k k ∈R 如何取值时，函数()y f x kx =-存在零点，并求出零点．【测量目标】函数零点的应用.【考查方式】利用导数求函数的极值、两点间距离公式、函数零点的判断等求解. 【难易程度】较难【试题解析】设二次函数()y g x =的解析式为)0()(2≠++=a c bx ax x g则它的导函数为)0(2)(≠+='a b ax x g ，（步骤1）∵函数)0(2)(≠+='a b ax x g 的图象与直线x y 2=平行， ∴22a = ，解得1a =,所以c bx x x g ++=2)(，b x x g +='2)(（步骤2）∵()y g x =在1x =-处取得极小值1(0)m m -≠∴⎩⎨⎧-=-=-'1)1(0)1(m g g ，即⎩⎨⎧-=+-=+-1102m c b b ，解得⎩⎨⎧==mc b 2.所以m x x x g ++=2)(2，()()g x f x x ==2++xm x （0≠x ）（步骤3）（1）设点P ⎪⎭⎫⎝⎛++2,x m x x （0≠x ，0≠m ）为曲线()y f x =上的任意一点则点P 到点(0,2)Q 的距离为m x m x x m x x PQ 2222222++=⎪⎭⎫ ⎝⎛++=（步骤4）22m当且仅当222m x =时，等号成立，此时min PQ =m m 222+（步骤5）又已知点P 到点(0,2)Q 2222=+m m两边平方整理，得12=+m m当0>m 时，12=+m m ，解得12-=m当0<m 时，12=+-m m ，解得12--=m 所以m 的值为12-或者12--；（步骤6）（2）函数令kx x f x h -=)()(=2)1(2++-=-++xmx k kx x m x （0≠x ）令0)(=x h ，即02)1(=++-xmx k （0≠x ），整理，得02)1(2=++-m x x k （0≠x ），①（步骤7）函数kx x f x h -=)()(存在零点，等价于方程①有非零实数根，由0≠m 可知，方程①不可能有零根，当1k =时，方程①变为02=+m x ，解得02≠=mx ，方程①有唯一实数根，此时，函数kx x f x h -=)()(存在唯一的零点2mx =；（步骤8）当1k ≠时，方程①根的判别式为)1(44k m --=∆，0≠m令)1(44k m --=∆=0，解得mk 11-=，方程①有两个相等的实数根m x x -==21，（步骤9）此时，函数kx x f x h -=)()(存在唯一的零点m x -=；令44(1)0m k ∆=-->，得()11m k -<,当0m >时，解得mk 11->，当0m <时，解得mk 11-<，以上两种情况下，方程①都有两个不相等的实数根kk m x ---+-=1)1(111，k k m x -----=1)1(112此时，函数kx x f x h -=)()(存在两个零点k k m x ---+-=1)1(111，kk m x -----=1)1(112（步骤10）综上所述，函数()y f x kx =-存在零点的情况可概括为当1k =时，函数kx x f x h -=)()(存在唯一的零点2mx =；当mk 11-=时，函数kx x f x h -=)()(存在唯一的零点m x -=；当0m >且m k 11->，或者0m <且mk 11-<时，函数kx x f x h -=)()(存在两个零点 k k m x ---+-=1)1(111，kk m x -----=1)1(112.（步骤11）21．（本小题满分14分）已知曲线22:20(1,2,)n C x nx y n -+==,从点(1,0)P -向曲线n C 引斜率为(0)n n k k >的切线n l ，切点为(,)n n n P x y ．（１）求数列{}{}n n x y 与的通项公式；（２）证明：13521n n nxx x x x y -<< 【测量目标】数列的实际应用，间接证明.【考查方式】利用圆锥曲线性质求通项公式，放缩法等求解. 【难易程度】较难【试题解析】曲线22:20(1,2,)n C x nx y n -+==可化为222)(n y n x =+-，所以，它表示以)0,(n C n 为圆心，以n 为半径的圆，切线n l 的方程为)1(+=x k y n ，联立⎩⎨⎧=+-+=02)1(22y nx x x k y n ，消去y 整理，得 0)22()1(2222=+-++n n n k x n k x k ，①（步骤1）222222)12(44)1(4)22(n n n n k n n k k n k +-=+--=∆，0>n k 令0=∆，解得1222+=n n k n， 12+=n n k n （步骤2）此时，方程①化为012)2122()121(2222=++-++++n n x n n n x n n整理，得[]0)1(2=-+n x n ，解得1+=n n x x ，（步骤3）所以121)11(12++=+++=n n n n n n ny n∴数列}{n x 的通项公式为1+=n nx x数列}{n y 的通项公式为121++=n n ny n .（步骤4）（２）证明：∵121111111+=+++-=+-n n n n n x x n n ，212n n -=<=135211352113521246235721n n n x x x x n n ---∴=⨯⨯⨯⨯<⨯⨯⨯⨯+ =121+n =nn x x +-11（步骤5）∵121+=n y x nn=n n x x +-11，又因为π043<< 令x y x n n =，则π04x <<，要证明n n n n y x y x sin 2<，只需证明当π04x <<时，x x sin 2<恒成立即可. （步骤6）设函数x x x f sin 2)(-=，π04x <<则x x f cos 21)(-='，π04x <<（步骤7）∵在区间π0,4⎛⎫⎪⎝⎭上x x f cos 21)(-='为增函数，∴当π04x <<时，π()1104f x x '=<=，（步骤8）∴x x x f sin 2)(-=在区间π0,4⎛⎫⎪⎝⎭上为单调递减函数，∴ x x x f sin 2)(-=0)0(=<f 对于一切π04x <<恒成立，（步骤9）∴x x sin 2<，即n n x x +-11=n n nny x y x sin 2< 综上，得13521n n nxx x x x y -<<（步骤10）。

2009年高考试题——数学理(广东卷)解析版

2009年普通高等学校招生全国统一考试（广东卷）数学（理科）参考答案一、选择题：本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 已知全集U R =，集合{212}M x x =-≤-≤和{21,1,2,}N x x k k ==-=的关系的韦恩（Venn ）图如图1所示，则阴影部分所示的集合的元素共有 A. 3个 B. 2个 C. 1个 D. 无穷多个【解析】由{212}M x x =-≤-≤得31≤≤-x ，则{}3,1=⋂N M ，有2个，选B. 2. 设z 是复数，()a z 表示满足1nz =的最小正整数n ，则对虚数单位i ，()a i = A. 8 B. 6 C. 4 D. 2 【解析】()a i =1=ni ，则最小正整数n 为4，选C.3. 若函数()y f x =是函数(0,1)xy a a a =>≠且的反函数，其图像经过点(,)a a ，则()f x =A. 2log xB. 12log x C.12xD. 2x 【解析】x x f a log )(=，代入(,)a a ，解得21=a ，所以()f x =12log x ，选B. 4.已知等比数列{}n a 满足0,1,2,n a n >=，且25252(3)nn a a n -⋅=≥，则当1n ≥时，2123221log log log n a a a -+++=A. (21)n n -B. 2(1)n + C. 2n D. 2(1)n - 【解析】由25252(3)nn a a n -⋅=≥得n n a 222=，0>n a ，则n n a 2=， +⋅⋅⋅++3212log log a a2122)12(31log n n a n =-+⋅⋅⋅++=-，选C.5. 给定下列四个命题：①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行；②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直； ③垂直于同一直线的两条直线相互平行；④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．其中，为真命题的是A. ①和②B. ②和③C. ③和④D. ②和④ 【解析】选D.6. 一质点受到平面上的三个力123,,F F F （单位：牛顿）的作用而处于平衡状态．已知1F ，2F 成060角，且1F ，2F 的大小分别为2和4，则3F 的大小为A. 6B. 2C. 25D. 27【解析】28)60180cos(20021222123=--+=F F F F F ，所以723=F ，选D.7．2010年广州亚运会组委会要从小张、小赵、小李、小罗、小王五名志愿者中选派四人分别从事翻译、导游、礼仪、司机四项不同工作，若其中小张和小赵只能从事前两项工作，其余三人均能从事这四项工作，则不同的选派方案共有A. 36种B. 12种C. 18种D. 48种【解析】分两类：若小张或小赵入选，则有选法24331212=A C C ；若小张、小赵都入选，则有选法122322=A A ，共有选法36种，选A.8．已知甲、乙两车由同一起点同时出发,并沿同一路线（假定为直线）行驶．甲车、乙车的速度曲线分别为v v 乙甲和（如图2所示）．那么对于图中给定的01t t 和，下列判断中一定正确的是 A. 在1t 时刻，甲车在乙车前面 B. 1t 时刻后，甲车在乙车后面 C. 在0t 时刻，两车的位置相同 D. 0t 时刻后，乙车在甲车前面【解析】由图像可知，曲线甲v 比乙v 在0～0t 、0～1t 与x 轴所围成图形面积大，则在0t 、1t 时刻，甲车均在乙车前面，选A.二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分．（一）必做题（9 ~ 12题）9. 随机抽取某产品n 件，测得其长度分别为12,,,n a a a ，则图3所示的程序框图输出的s = ，s 表示的样本的数字特征是．（注：框图中的赋值符号“=”也可以写成“←”“：=”）【解析】s =na a a n+⋅⋅⋅++21；平均数10. 若平面向量a ，b 满足1=+b a ，b a +平行于x 轴，)1,2(-=b ，则=a .【解析】)0,1(=+b a 或)0,1(-，则)1,1()1,2()0,1(-=--=a 或)1,3()1,2()0,1(-=---=a . 11．巳知椭圆G 的中心在坐标原点，长轴在x 3，且G 上一点到G 的两个焦点的距离之和为12，则椭圆G 的方程为．【解析】23=e ，122=a ，6=a ，3=b ，则所求椭圆方程为193622=+y x . 12．已知离散型随机变量X 的分布列如右表．若0EX =，1DX =，则a = ，b = ．【解析】由题知1211=++c b a ，061=++-c a ，1121211222=⨯+⨯+⨯c a ，解得125=a ，41=b . （二）选做题（13 ~ 15题，考生只能从中选做两题） 13．（坐标系与参数方程选做题）若直线⎩⎨⎧+=-=.2,21:1kt y t x l （t 为参数）与直线2,:12.x s l y s =⎧⎨=-⎩（s为参数）垂直，则k = ．【解析】1)2(2-=-⨯-k，得1-=k . 14．（不等式选讲选做题）不等式112x x +≥+的实数解为．【解析】112x x +≥+2302)2()1(022122-≤⇔⎩⎨⎧≠++≥+⇔⎩⎨⎧≠++≥+⇔x x x x x x x 且2-≠x . 15．（几何证明选讲选做题）如图4，点,,A B C 是圆O 上的点，且04,45AB ACB =∠=，则圆O 的面积等于．【解析】解法一：连结OA 、OB ，则090=∠AOB ，∵4=AB ，OB OA =，∴22=OA ，则ππ8)22(2=⨯=圆S ；解法二：222445sin 420=⇒==R R ，则ππ8)22(2=⨯=圆S .三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤. 16．(本小题满分12分）已知向量)2,(sin -=θa 与)cos ,1(θ=b 互相垂直，其中(0,)2πθ∈．（1）求θsin 和θcos 的值；（2）若10sin(),0102πθϕϕ-=<<，求cos ϕ的值．解：（1）∵a 与b 互相垂直，则0cos 2sin =-=⋅θθb a ，即θθcos 2sin =，代入1cos sin 22=+θθ得55cos ,552sin ±=±=θθ，又(0,)2πθ∈，∴55cos ,552sin ==θθ. （2）∵20πϕ<<，20πθ<<，∴22πϕθπ<-<-，则10103)(sin 1)cos(2=--=-ϕθϕθ，∴cos ϕ22)sin(sin )cos(cos )](cos[=-+-=--=ϕθθϕθθϕθθ. 17．（本小题满分12分）根据空气质量指数API （为整数）的不同，可将空气质量分级如下表：对某城市一年（365天）的空气质量进行监测，获得的API 数据按照区间]50,0[，]100,50(，]150,100(，]200,150(，]250,200(，]300,250(进行分组，得到频率分布直方图如图5.（1）求直方图中x 的值；（2）计算一年中空气质量分别为良和轻微污染的天数；（3）求该城市某一周至少有2天的空气质量为良或轻微污染的概率. （结果用分数表示．已知7812557=，12827=，++3652182531825791251239125818253=++，573365⨯=）解：（1）由图可知-=150x ++365218253(182********123150)9125818253⨯-=⨯++，解得18250119=x ；（2）219)5036525018250119(365=⨯+⨯⨯；（3）该城市一年中每天空气质量为良或轻微污染的概率为533652195036525018250119==⨯+⨯，则空气质量不为良且不为轻微污染的概率为52531=-，一周至少有两天空气质量为良或轻微污染的概率为7812576653)53()52()53()52(116670777=--C C .18．（本小题满分14分）如图6，已知正方体1111ABCD A B C D -的棱长为2，点E 是正方形11BCC B 的中心，点F 、G 分别是棱111,C D AA 的中点．设点11,E G 分别是点E ，G 在平面11DCC D 内的正投影．（1）求以E 为顶点，以四边形FGAE 在平面11DCC D 内的正投zy xE 1G 1影为底面边界的棱锥的体积；（2）证明：直线⊥1FG 平面1FEE ；（3）求异面直线11E G EA 与所成角的正弦值.解：（1）依题作点E 、G 在平面11DCC D 内的正投影1E 、1G ，则1E 、1G 分别为1CC 、1DD 的中点，连结1EE 、1EG 、ED 、1DE ，则所求为四棱锥11FG DE E -的体积，其底面11FG DE 面积为111111E DG Rt FG E Rt FG DE S S S ∆∆+= 221212221=⨯⨯+⨯⨯=，又⊥1EE 面11FG DE ，11=EE ，∴323111111=⋅=-EE S V FG DE FG DE E .（2）以D 为坐标原点，DA 、DC 、1DD 所在直线分别作x 轴，y 轴，z 轴，得)1,2,0(1E 、)1,0,0(1G ，又)1,0,2(G ，)2,1,0(F ，)1,2,1(E ，则)1,1,0(1--=FG ，)1,1,1(-=FE ，)1,1,0(1-=FE ，∴01)1(01=+-+=⋅FE FG ，01)1(011=+-+=⋅FE FG ，即FE FG ⊥1，11FE FG ⊥，又F FE FE =⋂1，∴⊥1FG 平面1FEE .（3）)0,2,0(11-=G E ，)1,2,1(--=EA，则62,cos 11=>=<EA G E EA G E ，设异面直线11E G EA 与所成角为θ，则33321sin =-=θ. 19．（本小题满分14分）已知曲线2:C y x =与直线:20l x y -+=交于两点(,)A A A x y 和(,)B B B x y ，且A B x x <．记曲线C 在点A 和点B 之间那一段L 与线段AB 所围成的平面区域（含边界）为D ．设点(,)P s t 是L 上的任一点，且点P 与点A 和点B 均不重合．（1）若点Q 是线段AB 的中点，试求线段PQ 的中点M 的轨迹方程；（2）若曲线22251:24025G x ax y y a -+-++=与D 有公共点，试求a 的最小值．解：（1）联立2x y =与2+=x y 得2,1=-=B A x x ，则AB 中点)25,21(Q ，设线段PQ 的中点M 坐标为),(y x ，则225,221ty s x +=+=，即252,212-=-=y t x s ，又点P 在曲线C 上， ∴2)212(252-=-x y 化简可得8112+-=x x y ，又点P 是L 上的任一点，且不与点A 和点B 重合，则22121<-<-x ，即4541<<-x ，∴中点M 的轨迹方程为8112+-=x x y （4541<<-x ）.（2）曲线22251:24025G x ax y y a -+-++=，即圆E ：2549)2()(22=-+-y a x ，其圆心坐标为)2,(a E ，半径57=r由图可知，当20≤≤a 时，曲线22251:24025G x ax y y a -+-++=与点D 有公共点；当0<a 时，要使曲线22251:24025G x ax y y a -+-++=与点D 有公共点，只需圆心E 到直线:20l x y -+=的距离572||2|22|≤=+-=a a d ，得0527<≤-a ，则a 的最小值为527-. 20．（本小题满分14分）已知二次函数()y g x =的导函数的图像与直线2y x =平行，且()y g x =在1x =-处取得极小值1(0)m m -≠．设()()g x f x x=．（1）若曲线()y f x =上的点P 到点(0,2)Qm 的值；（2）()k k R ∈如何取值时，函数()y f x kx =-存在零点，并求出零点．解：（1）依题可设1)1()(2-++=m x a x g (0≠a )，则a ax x a x g 22)1(2)('+=+=；又()g x '的图像与直线2y x =平行 22a ∴= 1a = m x x m x x g ++=-++=∴21)1()(22， ()()2g x mf x x x x ==++，设(),o o P x y ，则202020202)()2(||x m x x y x PQ ++=-+=当且仅当202202x m x =时，2||PQ 取得最小值，即||PQ 取得最小值2当0>m 时，2)222(=+m 解得12-=m 当0<m 时，2)222(=+-m 解得12--=m（2）由()()120my f x kx k x x =-=-++=(0≠x )，得()2120k x x m -++= ()* 当1k =时，方程()*有一解2m x =-，函数()y f x kx =-有一零点2mx =-；当1k ≠时，方程()*有二解()4410m k ⇔∆=-->，若0m >，11k m>-，函数()y f x kx =-有两个零点)1(2)1(442k k m x ---±-=，即1)1(11---±=k k m x ；若0m <，11k m<-，函数()y f x kx =-有两个零点)1(2)1(442k k m x ---±-=，即1)1(11---±=k k m x ；当1k ≠时，方程()*有一解()4410m k ⇔∆=--=, 11k m=-, 函数()y f x kx =-有一零点m k x -=-=11综上，当1k =时, 函数()y f x kx =-有一零点2m x =-；当11k m >-(0m >)，或11k m<-（0m <）时，函数()y f x kx =-有两个零点1)1(11---±=k k m x ；当11k m =-时，函数()y f x kx =-有一零点m k x -=-=11. 21．（本小题满分14分）已知曲线22:20(1,2,)n C x nx y n -+==．从点(1,0)P -向曲线n C 引斜率为(0)n n k k >的切线n l ，切点为(,)n n n P x y ．（1）求数列{}{}n n x y 与的通项公式；（2）证明：1352112sin 1n n n n nx xx x x x x y --⋅⋅⋅⋅<<+. 解：（1）设直线n l ：)1(+=x k y n ，联立0222=+-y nx x 得)22()1(2222=+-++n n n k x n k x k ，则)1(4)22(2222=+--=∆n n n k k n k ，∴12+=n n k n （12+-n n 舍去）22222)1(1+=+=n n k k x n n n，即1+=n n x n ，∴112)1(++=+=n n n x k y n n n （2）证明：∵121111111+=+++-=+-n n n n nx x nn∴nnn x x x x x x +-<⋅⋅⋅⋅⋅⋅⋅-1112531 由于nn n n x x n y x +-=+=11121，可令函数x x x f sin 2)(-=，则x x f cos 21)('-=，令0)('=x f ，得22cos =x ，给定区间)4,0(π，则有0)('<x f ，则函数)(x f 在)4,0(π上单调递减，∴0)0()(=<f x f ，即x x sin 2<在)4,0(π恒成立，又4311210π<≤+<n ，则有121sin 2121+<+n n ，即nn n n y x x x sin 211<+-.。

广东省江门市普通高中高三数学调研测试试题理(含解析)(最新整理)

江门市2018年普通高中高三调研测试数学(理科）第Ⅰ卷一、选择题:本大题共12个小题,每小题5分,共60分。

在每小题给出的四个选项中,只有一项是符合题目要求的。

1。

已知集合，，则( ）A。

B。

C。

D.【答案】D【解析】【分析】分别求得集合A和B，取交集即可得到答案．【详解】依题意，A={x|-3＜x＜1｝, B=｛x|x0｝，所以A∩B=,故选:D．【点睛】本题考查集合的交集运算.2。

是虚数单位，是实数集,，若，则（ )A。

B。

C. 2 D。

-2【答案】B【解析】【分析】直接由复数代数形式的乘除运算化简，结合已知条件列出方程，求解即可得答案．【详解】∵=∴,即a=−,故选:B．【点睛】本题考查了复数代数形式的乘除运算，考查了复数的基本概念.3.已知；，则是的( )A. 必要不充分条件B. 充分不必要条件 C。

充要条件 D。

既不充分也不必要【答案】B【解析】试题分析：由已知得条件，条件，显然充分性不成立，如当,不成立;又由，所以必要性成立.故选B。

考点:1.命题的充分条件、必要条件；2.二次不等式。

4.是自然对数的底数，若,，，，则（）A. B. C。

D.【答案】C【解析】【分析】利用指数和对数函数的单调性即可得到a，b,c的大小关系。

【详解】∵对数函数y=lnx在上单调递增，∴a=lnx〈ln1=0，∵指数函数在上单调递减,∴∵指数函数在上单调递增，∴由幂函数的性质可知即a<b<c,故选：C.【点睛】本题考查指数函数和对数函数性质的应用.5.若，,，则向量与的夹角为（ )A。

B. C。

D。

【答案】C【解析】【分析】由已知条件可得，再由两个向量夹角的余弦公式，即可求出夹角的余弦，进而得解．【详解】由已知，解得，则两个向量夹角的余弦值,所以两向量夹角为。

故选：C.【点睛】本题考查了平面向量的运算和利用平面向量的数量积求向量的夹角.6.若抛物线的焦点是双曲线的右焦点,则此双曲线的离心率为( )A. B. C。

(英语)09届江门市普通高中高三调研测试

江门市2009届普通高中高三调研测试英语本试卷共12页，四大题，满分为150分。

考试用时120分钟。

注意事项:1．答卷前考生务必用黑色字迹的墨水笔将自己的姓名和考生号填写在答题卷上。

2．选择题每小题选出答案后，用2B铅笔把答题卷上对应题目的答案标号涂黑。

3．非选择题必须用黑色字迹的墨水笔作答，答案必须写在答题卷各题目指定区域内相应位置上。

I 听力（共两节，满分35分）第一节听力理解（5段，共15小题；每小题2分，满分30分）听下面5段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C项中，选出最佳选项，并在答题卷上将该项涂黑。

听每段对话或独白前，你将有时间阅读各个小题，每小题5秒钟；听完后，各小题将给出5秒钟的作答时间。

每段对话或独白读两遍。

听第一段对话，回答第1—3题。

1. How does the woman know that all Americans have air conditioners?A. One of her Chinese friends told her.B. One of her American friends told her.C. She learned about it in the newspaper.2. What is the good news?A. They have many air conditioners in the apartment.B. They can get on an air conditioned bus.C. Many places are air conditioned.3. What do they decide to do at last?A. They will stay at home.B. They will go out into the city.C. They will stay on an air conditioned bus.听第二段对话，回答第4--6题。

江门市2009-2010学年度第二学期教学调研考试

7 89 94 4 6 4 7 3江门市2010-2011学年度第二学期教学调研考试高一数学模拟试题(2010.6.17)一、选择题（10小题，每小题5分，共50分。

1、设全集{}N x x x U ∈<≤=,61|，集合M=}4,2,1{，N={3，4，5}，则(C U A ．φ B ． U C ．{4} D ． {1，2，3，5}2、下列三个数：3.0log ,3,3.033.03===c b a 的大小顺序是（）A.c b a << B.b c a << C.b a c << D.c a b <<3、如图2，一个空间几何体的主视图和左视图都是边长为1的正三角形，俯视图是一个圆，那么这个几何体的侧面积．．．为（）D A .4π B . 4 C . 2 D . 12π 4. 01)1(=+++y x a 与圆0222=-+x y x 相切，则=a （）BA ．1B ．-1C ．2D ．-25、右图所示是一个算法流程图，则与输出的值相等的式子为（）A ．100321++++B ．99321++++C ．100D ．99 6、如图3是某一年中央电视台举办的挑战主持人大赛上，七位评委为某选手打出的分数的茎叶统计图，去掉一个最高分和一个最低分后，所剩数据的平均数和方差分别为（）A ．84，84.4B ．84，6.1C ．85，6.1D ．85，47、同时转动如图1所示的两个转盘，记转盘（甲）得到的数为x ，转盘（乙）得到的数为y ，则事件x+y=6的概率为（）C A.43 B.165 C.83 D.163 8． sin(-196π)的值等于（）B A. 21- B.12 C.23- D. 239102,a b ==2b A .二、填空题：本题共4小题，每题5分，满分20分。

1111213（14、在空间直角坐标系中,给定点P(2,-1,3)，若点Q 与P 关于坐标平面xoy 对称，则|PQ|=______.图2 图415、观察以下等式：,4360cos 30sin 60cos 30sin 22=︒︒+︒+︒ ,4350cos 20sin 50cos 20sin 22=︒︒+︒+︒,4340cos 10sin 40cos 10sin 22=︒︒+︒+︒ 猜想一般结论：____________________________________________.三、解答题（6道题，共80分, 要求写出完整的解题过程） 15、（本题满分12分）已知函数()2sin()2cos 6f x x x π=+-.(Ⅰ)求函数 ()f x 的最小正周期和单调递增区间；(Ⅱ)指出函数f(x)的图像是由y=sinx 的图像经过怎样的变换得到？16、（本题满分12分）某单位要在甲、乙、丙、丁4人中安排2人分别担任周六、周日的值班任务（每人被安排是等可能的，每天只安排一人）．（Ⅰ）其中甲、乙两人都被安排的概率是多少？（Ⅱ）甲、乙两人中至少有一人被安排的概率是多少？17、（本题满分14分）如图，四棱锥P —ABCD 中， PA ⊥平面ABCD ，底面ABCD 是直角梯形，AB ⊥AD ，CD ⊥AD ，CD=2AB ，E 为PC 中点． (I) 求证：平面PDC ⊥平面PAD ； (II) 求证：BE//平面PAD ．A B CD EP18、（本题满分14分）已知圆C 的方程为：2222440,()x y mx y m m R +--+-=∈．（1）试求m 的值，使圆C 的面积最小；（2）求与满足（1）中条件的圆C 相切，且过点(1,2)-的直线方程． 19、（本题满分14分）已知A 、B 、C 三点的坐标分别是A （3，0），B （0，3），C (sin ,cos )αα，（1）若1-=⋅，求α2sin 的值；（2）若13||=+，),0(πα∈求与的夹角。

(历史)09届江门市普通高中高三调研测试

江门市2009届普通高中毕业班调研测试历史本试卷分两部分。

满分为150分，考试用时120分钟。

注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的班别、考生号、姓名分别填写在答题卡和答题卷上。

2．选择题每小题选出答案后，请用2B铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡上各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4．考生必须保持答题卷的整洁，考试结束后。

只需交回答题卡和答题卷。

第I卷(选择题共75分)一、选择题：(本大题共25小题，每小题3分，共计75分。

在每小题列出的四个选项中，只有一项是符合题目要求的。

)1．生活在唐代长安的人，能见到的政治现象是A．宰相们到政事堂参加会议 B．长安城里禁军越来越多C．各行省的长官进城来述职 D．朱雀大街出现内阁衙门2．“介石先生慧鉴：恩来诸同志回延安称述先生盛德，钦佩无余。

先生领导全国民族进行空前伟大的民族革命战争，凡我国人无不崇仰。

……此物此志，知先生必有同心也。

敬祝健康!并致民族革命之礼!毛泽东谨启。

民国二十七年九月二十九日。

”根据材料判断，这封信写于A．北伐战争时期 B．国共十年对峙时期 C．抗日战争时期 D．重庆谈判后3．中国共产党人为了改变中国半殖民地半封建社会状况，在领导新民主主义革命的过程中，曾召开许多重要的会议，下列表述完全正确的是①中共一大确定党的中心工作是领导工人运动②中共二大第一次在全国人民面前明确提出反帝反封建的民主革命纲领③遵义会议事实上确立了以毛泽东为核心的党中央的正确领导④中共七届二中全会决定党的工作重心由乡村转移到城市A．①②③④ B．②③④ C．①②③ D．①④4．1965年，中央人民政府正式设立西藏自治区。