2018年数学同步优化指导必修3练习:3-习题课 随机事件
2018年数学同步优化指导必修3练习:3-2-2 整数值随机

第三章 3.2 3.2.21.利用抛硬币产生随机数1和2,出现正面表示产生的随机数为1,出现反面表示产生的随机数为2,小王抛两次,则出现的随机数之和为3的概率为( )A .12B .13C .14D .15解析:抛掷硬币两次,产生的随机数的情况有:(1,1),(1,2),(2,1),(2,2),共四种,其中随机数之和为3的情况有(1,2),(2,1)两种,故所求概率为24=12. 答案:A2.用计算器或计算机随机模拟掷骰子的试验,估计出现2点的概率,下列步骤中不正确的是( )A .用计算器的随机函数RANDI(1,7)或计算机的随机函数RANDBETWEEN(1,7)产生6个不同的1到6之间的取整数值的随机数x ,如果x =2,我们认为出现2点B .我们通常用计数器n 记录做了多少次掷骰子试验,用计数器m 记录其中有多少次出现2点,置n =0,m =0C .出现2点,则m 的值加1,即m =m +1;否则m 的值保持不变D .程序结束,出现2点的频率m n作为概率的近似值 解析:计算器的随机函数RANDI(1,7)或计算机的随机函数RANDBETWEEN(1,7)产生的是1到7之间的整数,包括7,共7个整数.答案:A3.先后抛掷两枚均匀的正方体骰子(它们的六个面分别标有点数1,2,3,4,5,6),骰子朝上的面的点数分别为X ,Y ,则log 2X Y =1的概率为( )A .16B .536C .112D .12解析:由题设,骰子朝上的面的点数X ,Y 满足Y =2X ,就是说朝上的面的点数只能是1,2;2,4;3,6.故所求概率为336=112. 答案:C4.一个正方体,它的表面涂满了红色,在它的每个面上切两刀,可得27个小正方体,从中任取一个,它恰有一个面涂有红色的概率是________.解析:恰有一个面涂有红色的小正方体在原正方体的每一个侧面上只有一个,共有6个,故所求概率为29. 答案:295.小明与同学都想知道每6个人中有2个人生肖相同的概率,他们想设计一个模拟试验来估计6个人中恰有2个人生肖相同的概率,你能帮他们设计这个模拟方案吗?解:用12个完全相同的小球分别编上号码1~12,代表12个生肖,放入一个不透明的袋中摇匀后,从中随机抽取一球,记下号码后放回,再摇匀后取出一球记下号码……连续取出6个球为一次试验,重复上述试验过程多次,统计恰出现2个相同号码的试验次数,再除以总的试验次数,得到试验频率,可估计每6个人中有2个人生肖相同的概率等于该频率.。
2018年数学同步优化指导北师大版必修3练习:2-2-3 循
第二章§2 2.3
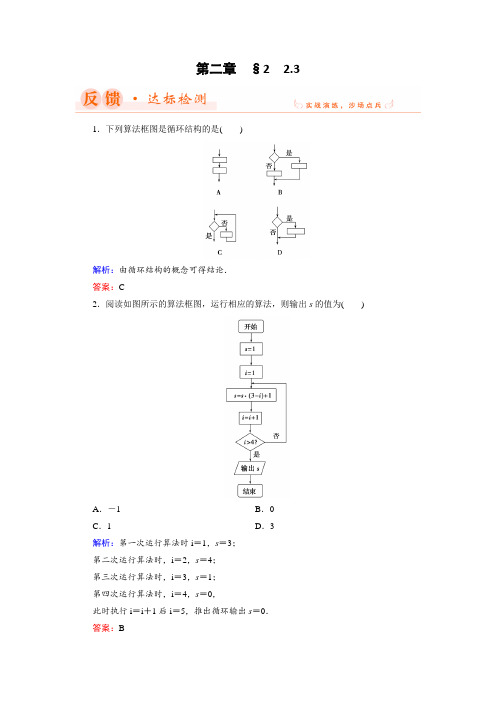
1.下列算法框图是循环结构的是()
解析:由循环结构的概念可得结论.
答案:C
2.阅读如图所示的算法框图,运行相应的算法,则输出s的值为()
A.-1B.0
C.1 D.3
解析:第一次运行算法时i=1,s=3;
第二次运行算法时,i=2,s=4;
第三次运行算法时,i=3,s=1;
第四次运行算法时,i=4,s=0,
此时执行i=i+1后i=5,推出循环输出s=0.
答案:B
3.如图所示的算法框图中,循环体是________.(只填序号)
解析:根据循环体的概念可知,循环体是反复执行的程序,故②正确.答案:②
4.如图是一个算法的程序框图,则输出的k的值是________.
解析:由条件为k>4,知k=5时满足条件,故输出5.
答案:5。
【教学参考】高一北师大版数学必修3同步作业:第3章 第1节 随机事件的概率 频率与概率 (1) Word版含答案[
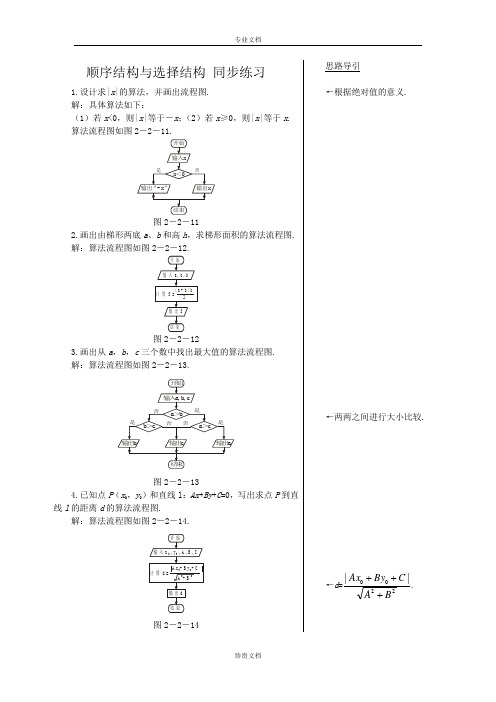
顺序结构与选择结构 同步练习
思路导引
1.设计求|x |的算法,并画出流程图. 解:具体算法如下:
(1)若x <0,则|x |等于-x ;(2)若x ≥0,则|x |等于x . 算法流程图如图2-2-11.
图2-2-11
2.画出由梯形两底a 、b 和高h ,求梯形面积的算法流程图. 解:算法流程图如图2-2-12.
图2-2-12
3.画出从a ,b ,c 三个数中找出最大值的算法流程图. 解:算法流程图如图2-2-13.
图2-2-13
4.已知点P (x 0,y 0)和直线l :Ax +By
+C =0,写出求点P 到直线l 的距离d 的算法流程图.
解:算法流程图如图2-2-14.
图2-2-14
←根据绝对值的意义.
←两两之间进行大小比较. ←d =
2
2
00|
|B
A C By Ax +++.
5.设汽车托运重量为P kg 的货物时,托运每千米的费用标准为
⎩⎨
⎧+⨯=时,当),-(
时,当,
kg 20201.1203.0kg 202.0P P P P y 画出行李托运费用的算法流程图.
5.解:算法流程图如图2-2-15.(x 为托运路程)
图2-2-15
←分段函数函数值的算法一般用选择结构.
≤ >。
2018年数学同步优化指导必修3练习:3-1-1 随机事件的

活页作业(十五)随机事件的概率(15分钟,30分)一、选择题(每小题4分,共12分)1.下列试验能够构成事件的是()A.掷一次硬币B.射击一次C.水烧至100 ℃D.摸彩票中头奖解析:作为一个事件,必须由条件和结果组成,故选D.答案:D2.将一根长为a的铁丝随意截成三段,构成一个三角形,此事件是()A.必然事件B.不可能事件C.随机事件D.不能判定解析:当截得的三段铁丝,任意两段长度之和大于第三段的长度时,构成一个三角形,否则不能构成三角形.答案:C3.袋内装有一个黑球与一个白球,从袋中取出一球,在100次摸球中,摸到黑球的频率为0.49,则摸到白球的次数为()A.49 B.51C.0.49 D.0.51解析:由于摸到黑球的频率为0.49,所以摸到白球的频率为0.51.从而摸到白球的次数为100×0.51=51.答案:B二、填空题(每小题4分,共8分)4.在200件产品中,有192件一级品,8件二级品,则下列事件:①在这200件产品中任意选出9件,全部是一级品;②在这200件产品中任意选出9件,全部是二级品;③在这200件产品中任意选出9件,不全是一级品;④在这200件产品中任意选出9件,其中不是一级品的件数小于9.其中,________是必然事件;________是不可能事件;________是随机事件.(只填事件的序号即可)解析:根据事件的有关概念可以判断④是必然事件,②是不可能事件;①③是随机事件.答案:④②①③5.某人捡到不规则形状的五面体石块,他在每个面上用数字1~5进行了标记,投掷100次,记录下落在桌面上的数字,得到如下频数表:解析:落在桌面的数字不小于4,即4,5的频数共13+22=35.所以频率为35100=0.35.答案:0.35 三、解答题6.(本小题满分10分)某个地区从某年起几年内的新生婴儿数及其中男婴数如表(结果精确到0.01):(1)(2)求这一地区男婴出生的概率.解:(1)利用公式,频率=n An ,可计算出1年内、2年内、3年内、4年内的男婴出生频率分别为0.49,0.54,0.50,0.50.(2)多次试验中,频率的近似稳定值就是该事件发生的概率,由(1)可知,这一地区男婴出生的概率为0.5.(15分钟,30分)一、选择题(每小题5分,共10分)1.从12个同类产品(其中10个是正品,2个是次品)中任意抽取3个的必然事件是( ) A .3个都是正品 B .至少有1个是次品 C .3个都是次品D .至少有1个是正品 解析:任意抽取3个的可能情况是3个正品;2个正品1个次品;1个正品2个次品.由于只有2个次品,不会有3个次品的情况.3种可能的结果中,都至少有1个正品,所以至少有1个是正品是必然发生的,必然事件应该是“至少有1个是正品”.答案:D2.随机事件A 的频率mn 满足( )A .mn=0B .m n=1C . mn >1D .0≤mn≤1解析:当n 次试验中,事件A 不发生时,频率为0,当事件A 发生n 次时,频率为1,当发生次数为m,0<m <n 时,频率m n 满足0<mn<1,故D 正确.答案:D二、填空题(每小题5分,共10分)3.一家保险公司想了解汽车的挡风玻璃在一年时间里破碎的概率,公司收集了20 000辆汽车,时间从某年的5月1日到下一年的5月1日,共发现有600辆汽车的挡风玻璃破碎,则一辆汽车在一年时间里挡风玻璃破碎的概率约为________.解析:p =60020 000=0.03.答案:0.034.对某厂生产的某种产品进行抽样检查,数据如下:大约需抽查________件产品.解析:抽查的产品总件数为1 150,合格品件数为1 094,故合格率为1 0941 150≈0.95.950÷0.95=1 000.答案:1 000 三、解答题5.(本小题满分10分)某水产试验厂实行某种鱼的人工孵化,10 000个鱼卵能孵出8 513条鱼苗,根据概率的统计定义解答下列问题:(1)这种鱼卵的孵化概率(孵化率)是多少? (2)30 000个鱼卵大约能孵化多少条鱼苗?(3)要孵化5 000条鱼苗,大约需准备多少个鱼卵(精确到百位)? 解:(1)由题意知,孵化率p =8 51310 000=0.851 3.(2)设30 000个鱼卵大约能孵化x 条鱼苗,则有 x30 000=0.851 3. 所以x =25 539,即30 000个鱼卵大约能孵化25 539条鱼苗.(3)设大约需准备y 个鱼卵,则5 000y=0.851 3,所以y ≈5 900,即大约需准备5 900个鱼卵.。
人教A版高中数学必修3课后习题 3.1.1 随机事件的概率

第三章概率3.1 随机事件的概率3.1.1 随机事件的概率课后篇巩固提升基础巩固①若任取x∈A,则x∈B是必然事件;②若任取x∉A,则x∈B是不可能事件;③若任取x∈B,则x∈A是随机事件;④若任取x∉B,则x∉A是必然事件.A.1个B.2个C.3个D.4个A是集合B的真子集,∴A中的任意一个元素都是B中的元素,而B中至少有一个元素不在A中,因此①正确,②错误,③正确,④正确.2.从含有8件正品、2件次品的10件产品中,任意抽取3件,则必然事件是( )A.3件都是正品B.至少有1件次品C.3件都是次品D.至少有1件正品8件正品2件次品的10件产品中,任意抽取3件, 在A中,3件都是正品是随机事件,故A错误;在B中,至少有1件次品是随机事件,故B错误;在C中,3件都是次品是不可能事件,故C错误;在D中,至少有1件正品是必然事件,故D正确.3.某人将一枚硬币连续抛掷了10次,正面朝上的情形出现了6次,则( )A.正面朝上的概率为0.6B.正面朝上的频率为0.6C.正面朝上的频率为6D.正面朝上的概率接近于0.6是正面朝上的频率不是概率.4.一个家庭前后育有两个小孩儿,则可能的结果为( )A.{(男,女),(男,男),(女,女)}B.{(男,女),(女,男)}C.{(男,男),(男,女),(女,男),(女,女)}D.{(男,男),(女,女)}.两小孩儿有大小之分,所以(男,女)与(女,男)是不同的结果,故选C.5.袋内装有一个黑球与一个白球,从袋中取出一球,在100次摸球中,摸到黑球的频率为0.49,则摸到白球的次数为( )A.49B.51C.0.49D.0.510.49,所以摸到白球的频率为0.51,从而摸到白球的次数为100×0.51=51.6.我国古代数学有“米谷粒分”题:发仓募粮,所募粒中秕不百三则收之(不超过3%).现抽样取米一把,取得235粒米中夹秕n粒,若这批米合格,则n不超过( )A.6B.7C.8D.9,n≤3%,解得n≤7.05,所以若这批米合格,则n不超过7.2357.一家保险公司想了解汽车的挡风玻璃破碎的概率,公司收集了20 000部汽车的相关信息,时间是从某年的5月1日到下一年的5月1日,共发现有600部汽车的挡风玻璃破碎,则一部汽车在一年内挡风玻璃破碎的概率近似是.=0.03.P=6008.某人捡到不规则形状的五面体石块,他在每个面上用数字1~5进行了标记,投掷100次,记录下落在桌面上的数字,得到如下频数表:则落在桌面的数字不小于4的频率为.4,即4,5的频数为13+22=35.所以频率为35=0.35.100①集合{x||x|<0}为空集是必然事件;②y=f(x)是奇函数,则f(0)=0是随机事件;③若log a(x-1)>0,则x>1是必然事件;④对顶角不相等是不可能事件.恒成立,∴①正确;奇函数y=f(x)只有当x=0有意义时才有f(0)=0,∴②正确;由log a(x-1)>0知,当a>1时,,(a,b)是一个基本事件.(1)“a+b=5”这一事件包含哪几个基本事件?“a<3且b>1”呢?(2)“ab=4”这一事件包含哪几个基本事件?“a=b”呢?(3)“直线ax+by=0的斜率k>-1”这一事件包含哪几个基本事件?Ω={(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2) ,(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)}.(1)“a+b=5”这一事件包含以下4个基本事件:(1,4),(2,3),(3,2),(4,1).“a<3且b>1”这一事件包含以下6个基本事件:(1,2),(1,3),(1,4),(2,2),(2,3),(2,4).(2)“ab=4”这一事件包含以下3个基本事件:(1,4),(2,2),(4,1);“a=b”这一事件包含以下4个基本事件:(1,1),(2,2),(3,3),(4,4).(3)直线ax+by=0的斜率k=-ab>-1,即a<b,所以包含以下6个基本事件:(1,2),(1,3),(1,4),(2,3),(2,4),(3,4).能力提升1.随机事件A的频率mn满足( )A.mn =0 B.mn=1 C.mn>1 D.0≤mn≤1n次试验中,事件A不发生时,频率mn=0;当事件A发生n次时,频率m n =1;当发生次数为m,0<m<n时,频率mn满足0<mn<1,故D正确.2.从存放号码分别为1,2,…,10的卡片的盒子里,有放回地取100次,每次取一张卡片,并记下号码,统计结果如下:卡1 2 3456 7 8 9 10则取到号码为奇数的频率是( ) A.0.53 B.0.5 C.0.47 D.0.37=53100=0.53.3.某个地区从某年起n 年内的新生婴儿数及其中男婴数如表所示(单位:个):时间范围 1年内 2年内 3年内 4年内(1)填写表中的男婴出生频率(结果精确到0.01); (2)这一地区男婴出生的概率约是 . 频率f(A)=nA n ,各频率为0.49,0.54,0.50,0.50.(2)可以利用频率来求近似概率.由(1)得概率约为0.50. 0.54 0.50 0.50 (2)0.504.某公司有5万元资金用于投资开发项目,如果成功,一年后可获收益12%,一旦失败,一年后将丧失全部资金的50%,下表是去年200例类似项目开发的实施结果:投资成功 投资失败 192次8次则该公司一年后估计可获收益的平均数是 元.x,如果成功,x 的取值为5×12%,如果失败,x 的取值为-5×50%,一年后公司成功的概率为192200=2425,失败的概率为8200=125,所以一年后公司收益的平均数是(5×12%×2425-5×50%×125)×10000=4760(元).5.为了估计某自然保护区中天鹅的数量,可以使用以下方法:先从该保护区中捕出一定数量的天鹅,例如200只,给每只天鹅做上不影响其存活的记号,然后放回保护区,经过适当的时间,让其和保护区中其余的天鹅充分混合,再从保护区中捕出一定数量的天鹅,例如150只,查看其中有记号的天鹅,设有20只,试根据上述数据,估计该自然保护区中天鹅的数量.n,假定每只天鹅被捕到的可能性是相等的,从保护区中任捕一只,设事件A={带有记号的天鹅},则P(A)=200n, ①第二次从保护区中捕出150只天鹅,其中有20只带有记号,由概率的统计定义可知P(A)=20150, ②由①②两式,得200n =20150,解得n=1500,所以该自然保护区中天鹅的数量约为1500只.6.李老师在某大学连续3年主讲经济学院的《高等数学》,下表是李老师统计的这门课3年来的学生考试成绩分布:经济学院一年级的学生王小慧下学期将选修李老师的《高等数学》,用已有的信息估计她得以下分数的概率(结果保留到小数点后三位).(1)90分以上;(2)60分~69分;(3)60分以上.43+182+260+90+62+8=645,根据公式可计算出选修李老师的《高等数学》的人的考试成绩在各个段上的频率依次为:43645≈0.067,182645≈0.282,260645≈0.403,90645≈0.140,62645≈0.096,8645≈0.012.用已有的信息,可以估计出王小慧下学期选修李老师的《高等数学》得分的概率如下:(1)将“90分以上”记为事件A,则P(A)≈0.067.(2)将“60分~69分”记为事件B,则P(B)≈0.140.(3)将“60分以上”记为事件C,则P(C)≈0.067+0.282+0.403+0.140=0.892.。
2018年数学同步优化指导必修3练习:3-1-2 概率的意义

活页作业(十六)概率的意义(15分钟,30分)一、选择题(每小题4分,共12分)1.事件A发生的概率接近于0,则()A.事件A不可能发生B.事件A也可能发生C.事件A一定发生D.事件A发生的可能性很大解析:不可能事件的概率为0,但概率接近于0的事件不一定是不可能事件.答案:B2.从一批准备出厂的电视机中随机抽取10台进行质量检查,其中有1台是次品,若用C表示抽到次品这一事件,则对C的说法正确的是()A.概率为110B.频率为110C.概率接近110D.每抽10台电视机,必有1台次品解析:事件C发生的频率为110,由于只做了一次试验,故不能得出概率接近110的结论.答案:B3.投掷一枚普通的正方体骰子,四名同学各自发表了以下见解:①出现“点数为奇数”的概率等于出现“点数为偶数”的概率;②只要连掷6次,一定会“出现1点”;③投掷前默念几次“出现6点”,投掷结果“出现6点”的可能性就会加大;④连续投掷3次,出现的点数之和不可能等于19.其中正确的见解有()A.1个B.2个C.3个D.4个解析:①因为奇数点与偶数点的数量相同,所以概率相等,正确;②每个点每次投掷出现的概率相等,连掷6次,不一定出现1点,错误;③出现6点的可能性大小只与概率有关,默念几次不能增大其概率,错误;④连掷3次,点数之和最多为18,正确.正确的有2个,故选B.答案:B二、填空题(每小题4分,共8分)4.如果袋中装有数量差别很大而大小相同的白球和黑球(只是颜色不同),从中任取一球,取了10次有9个白球,估计袋中数量最多的是________.解析:根据极大似然法,可以估计袋中数量最多的是白球.答案:白球5.某单位上级分给该单位职工一套房,而该单位符合分房条件的有8名职工.现抽签决定房主人选,则甲同志入选的可能性为__________.解析:8名职工抽出一人住房,故可能性为18.答案:18三、解答题6.(本小题满分10分)某高中学校共有学生2 000名,各年级男、女生人数如下表:(1)求x 的值.(2)已知y ≥245,z ≥245,且在高三年级任意抽取一人,抽到男生的概率大于抽到女生的概率,试写出y ,z 的所有取值.解:(1)由x2 000=0.19,得x =380.(2)高三年级人数为y +z =2 000-(373+377+380+370)=500.设高三年级女生、男生数记为(y ,z ),因为在高三年级任意抽取一人,抽到男生的概率大于抽到女生的概率,所以z >y .又因为y +z =500,y ≥245,z ≥245且y ,z ∈N ,所以(y ,z )所有的取值情况为(249,251),(248,252),(247,253),(246,254),(245,255).(15分钟,30分)一、选择题(每小题5分,共10分)1.某市交警部门在调查一起车祸过程中,所有的目击证人都指证肇事车是一辆普通桑塔纳出租车,但由于天黑,均未看清该车的车牌号码及颜色,而该市有两家出租车公司,其中甲公司有100辆桑塔纳出租车,3 000辆帕萨特出租车,乙公司有3 000辆桑塔纳出租车,100辆帕萨特出租车.交警部门应先调查哪家公司的车辆较合理?( )A .甲公司B .乙公司C .甲与乙公司D .以上都对解析:由于甲公司桑塔纳的比例为100100+3 000=131,乙公司桑塔纳的比例为 3 0003 000+100=3031,根据极大似然法可知应选B . 答案:B2.高考数学试题中,有12道选择题,每道选择题有4个选项,其中只有1个选项是正确的,则随机选择其中一个选项正确的概率是14,某家长说:“要是都不会做,每题都随机选择其中一个选项,则一定有3道题答对.”这句话( )A .正确B .错误C .不一定正确D .无法解释解析:把解答一个选择题作为一次试验,答对的概率是14说明了对的可能性大小是14.做12道选择题,即进行了12次试验,每个结果都是随机的,那么答对3道题的可能性较大,但是并不一定答对3道题,也可能都选错,或答对1,2,4,…道题,甚至12道题都答对.答案:B二、填空题(每小题5分,共10分)3.某地区牛患某种病的概率为0.25,且每头牛患病与否是互不影响的,今研制一种新的预防药,任选12头牛做试验,结果12头服用这种药后均未患病,则此药________.(填“有效”或“无效”)解析:若此药无效,则12头牛都不患病的概率为(1-0.25)12≈0.032,这个概率很小,故该事件基本上不发生,所以此药有效.答案:有效4.将一枚质地均匀的硬币连掷两次,则“至少出现一次正面”与“两次均出现反面”的概率比为________________.解析:将一枚质地均匀的硬币连掷两次有以下情形,(正,正),(正,反),(反,正),(反,反).“至少出现一次正面”有3种情形,“两次均出现反面”有1种情形,故答案为3∶1.答案:3∶1 三、解答题5.(本小题满分10分)在“六一”儿童节来临之际,某妇女儿童用品商场为吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成20份),并规定:顾客每购物满100元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得80元、50元、20元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可直接获得15元的购物券.转转盘和直接获得购物券,你认为哪种方式对顾客更划算?请说明理由.解:由题意可得转转盘所获得的购物券为80×120+50×320+20×520=16.5(元).因为16.5元>15元,所以选择转转盘对顾客更划算.。
2018年数学同步优化指导必修3练习:3-3-1 几何概型活

活页作业(二十) 几何概型(25分钟,60分)一、选择题(每小题5分,共25分)1.(2016·高考全国卷Ⅰ)某公司的班车在7:30,8:00,8:30发车,小明在7:50至8:30之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过10 min 的概率是( )A .13B .12C .23D .34解析:设小明到达时间为y ,当y 在7:50至8:00,或8:20至8:30时,小明等车时间不超过10 min ,因此所求概率P =2040=12.故选B .答案:B2.如图,矩形ABCD 中,点E 为边CD 的中点,若在矩形ABCD 内部随机取一个点Q ,则点Q 取自△ABE 内部的概率等于( )A .14B .13C .12D .23解析:△ABE 的面积是矩形ABCD 面积的一半,由几何概型,点Q 取自△ABE 内部的概率为12.答案:C3.(2015·高考山东卷)在区间[0,2]上随机地取一个数x ,则事件“-1≤log 12⎝⎛⎭⎫x +12≤1”发生的概率为 ( )A .34B .23C .13D .1解析:先利用对数函数的单调性解出不等式,再根据几何概型的概率公式求出概率.不等式-1≤log 12⎝⎛⎭⎫x +12≤1可化为log 122≤log 12⎝⎛⎭⎫x +12≤log 1212,即12≤x +12≤2,解得0≤x ≤32.故由几何概型的概率公式得P =32-02-0=34.答案:A4.如图,在正方形围栏内均匀撒米粒,一只小鸡在其中随意啄食,此刻小鸡正在正方形的内切圆中的概率是( )A .14B .π4C .13D .π3解析:设事件A ={小鸡正在正方形的内切圆中},则事件A 的几何区域为内切圆的面积S =πR 2(2R 为正方形的边长),全体基本事件的几何区域为正方形的面积,由几何概型的概率公式可得P (A )=πR 2(2R )2=π4,即小鸡正在正方形的内切圆中的概率为π4. 答案:B5.在区间[0,1]内任取两个数,则这两个数的平方和也在[0,1]内的概率是( ) A .π4B .π10C .π20D .π40解析:设在[0,1]内取出的数为a ,b ,若a 2+b 2也在[0,1]内,则有0≤a 2+b 2≤1.如右图,试验的全部结果所构成的区域为边长为1的正方形,满足a 2+b 2在[0,1]内的点在14的单位圆内(如阴影部分所示),故所求概率为14π1=π4.答案:A二、填空题(每小题5分,共15分)6.如图,甲、乙两人玩转盘游戏,规定当指针指向阴影所示区域时甲胜,否则乙胜,则甲获胜的概率是________________.解析:转盘共分为8部分,阴影占5部分,故甲获胜概率为58.答案:587.正方体ABCD -A 1B 1C 1D 1的棱长为a ,在正方体内随机取点M ,点M 落在三棱柱ABC -A 1B 1C 1内的概率为__________.解析:∵V 正方体=a 3,V 三棱柱=12a 3,∴所求概率P =12.答案:128.已知正方体ABCD -A 1B 1C 1D 1内有一个内切球O ,则在正方体ABCD -A 1B 1C 1D 1内任取点M ,点M 在球O 内的概率是________.解析:设正方体边长为1,则V 正方体=1,其内切球半径为12,故V 球=43πR 3=π6.故所求概率P =V 球V 正方体=π6.答案:π6三、解答题(每小题10分,共20分)9.设A 为圆周上一定点,在圆周上等可能地任取一点与A 连接,求弦长超过半径的2倍的概率.解:如图所示,在⊙O 上有一定点A ,任取一点B 与A 连接,则弦长超过半径的2倍,即为∠AOB 的度数大于90°,而小于270°.记“弦长超过半径的2倍”为事件C ,则C 表示的范围是∠AOB ∈(90°,270°). ∵270°-90°=180°.∴试验的的全部结果是圆周长,满足要求的结果是半圆周长,则由几何概型的概率公式,得P (C )=12.10.平面上画了一些彼此相距2a 的平行线,把一枚半径r <a 的硬币任意掷在这个平面上,求硬币不与任一条平行线相碰的概率.解:设事件A 为“硬币不与任一条平行线相碰”.为了确定硬币的位置,由硬币中心O 向靠得最近的平行线引垂线OM ,垂足为M ,参看图,这样线段OM 长度(记作|OM |)的取值范围是[0,a ],只有当r <|OM |≤a 时,硬币不与平行线相碰,其长度范围是(r ,a ].所以P (A )= r ,a ]的长度[0,a ]的长度=a -ra .(20分钟,40分)一、选择题(每小题5分,共10分)1.如下四个游戏盘(各正方形边长和圆的直径都是单位1),如果撒一粒黄豆落在阴影部分,那么可中奖.小明希望中奖,则应选择的游戏盘是( )解析:P (A )=38,P (B )=26=13,P (C )=1-π41=1-π4,P (D )=1π,则P (A )最大,故选A .答案:A2.(2013·高考湖南卷)已知事件“在矩形ABCD 的边CD 上随机取一点P ,使△APB 的最大边是AB ”发生的概率为12,则ADAB=( )A .12B .14C .32D .74解析:如图,不妨设AB =1,AD =x ,则ADAB =x .由图形的对称性和题意知,点P 应在EF 之间(BE =AB ,AF =AB ),EF =12,DE =CF =14.当点P 在点E 时,BP 最大为x 2+916,∴x 2+916=1.∴x =74.答案:D二、填空题(每小题5分,共10分)3.《广告法》对插播广告的时间有一定的规定,某人对某台的电视节目做了长期的统计后得出结论,他任意时间打开电视机看该台节目,看不到广告的概率为910,那么该台每小时约有________________ min 的广告.解析:60×⎝⎛⎭⎫1-910=6(min). 答案:64.设不等式组⎩⎪⎨⎪⎧0≤x ≤2,0≤y ≤2表示的平面区域为D ,在区域D 内随机取一个点,则此点到坐标原点的距离大于2的概率是________.解析:平面区域D 的面积为4,到原点距离大于2的点位于图中阴影部分,其面积为4-π,所以所求概率为4-π4.答案:4-π4三、解答题(每小题10分,共20分)5.如图,∠AOB =60°,OA =2,OB =5,在线段OB 上任取一点C ,试求:(1)△AOC 为钝角三角形的概率; (2)△AOC 为锐角三角形的概率. 解:如题图,由平面几何知识可知,当AD ⊥OB 时,OD =1;当OA ⊥AE 时,OE =4,BE =1.(1)当且仅当点C 在线段OD 或BE 上时,△AOC 为钝角三角形,记“△AOC 为钝角三角形”为事件M ,则P (M )=OD +BE OB =1+15=0.4,即△AOC 为钝角三角形的概率为0.4.(2)当且仅当点C 在线段DE 上时,△AOC 为锐角三角形,记“△AOC 为锐角三角形”为事件N ,则P (N )=DE OB =35=0.6.6.设关于x 的一元二次方程x 2+2ax +b 2=0.(1)若a 是从0,1,2,3四个数中任取的一个数,b 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率.(2)若a 是从区间[0,3]上任取的一个数,b 是从区间[0,2]上任取的一个数,求上述方程有实根的概率.解:设事件A 为“方程x 2+2ax +b 2=0有实根”.当a ≥0,b ≥0时,方程x 2+2ax +b 2=0有实根的充要条件是a ≥b .(1)基本事件共有12个:(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2).其中第一个数表示a 的取值,第二个数表示b 的取值.事件A 包含9个基本事件:(0,0),(1,0),(1,1),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2),故事件A 发生的概率为P (A )=912=34.(2)试验的全部结果所构成的区域为 {(a ,b )|0≤a ≤3,0≤b ≤2}.构成事件A 的区域为{(a ,b )|0≤a ≤3,0≤b ≤2,a ≥b }. 所以所求的概率为 P (A )=3×2-12×223×2=23.。
2018年数学同步优化指导必修3练习:3-3-2 均匀随机数

活页作业(二十一)均匀随机数的产生(25分钟,60分)一、选择题(每小题5分,共25分)1.X服从[3,40]上的均匀分布,则X的值不能等于()A.15B.25C.35D.45解析:由于X∈[3,40],因此3≤X≤40.故X≠45.答案:D2.将[0,1]内的均匀随机数转化为[-3,4]内的均匀随机数,需要实施的变换为() A.a=a1*7 B.a=a1*7+3C.a=a1*7-3 D.a=a1*4解析:根据伸缩平移变换,a=a1*[4-(-3)]+(-3)=a1*7-3.故选C.答案:C3.设x1是[0,1]内的均匀随机数,x2是[-2,1]内的均匀随机数,则x1与x2的关系是() A.x2=2x1-2B.x2=3x1-2C.x2=3x1+2 D.x2=x1-2解析:∵0≤x1≤1,∴0≤3x1≤3.∴-2≤3x1-2≤1.而-2≤x2≤1,∴x2=3x1-2.答案:B4.要产生[-3,3]上的均匀随机数y,现有[0,1]上的均匀随机数x,则y不可取为() A.-3x B.3xC.6x-3 D.-6x-3解析:方法一利用伸缩和平移变换进行判断.方法二由0≤x≤1,得-9≤-6x-3≤-3,故y不能取-6x-3.答案:D5.欧阳修《卖油翁》中写道:“(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿.”可见“行行出状元”,卖油翁的技艺让人叹为观止.若铜钱是直径为2.5 cm的圆,中间有边长为0.8 cm的正方形孔,若你随机向铜钱上滴一滴油,则油(油滴的大小忽略不计)正好落入孔中的概率为()A.89πB.1625πC.256625πD.6425π解析:由题意所求得概率为P =0.8×0.8π×⎝⎛⎭⎫2.522=256625π.答案:C二、填空题(每小题5分,共15分)6.b 1是[0,1]上的均匀随机数,b =6(b 1-0.5),则b 是__________上的均匀随机数. 解析:∵b 1∈[0,1], ∴b 1-0.5∈[-0.5,0.5]. ∴6(b 1-0.5)∈[-3,3]. 答案:[-3,3]7.如图,四边形ABCD 为矩形,AB =3,BC =1,以A 为圆心,1为半径作四分之一圆弧DE ,在∠DAB 内任作射线AP ,则射线AP 与线段BC 有公共点的概率为________.解析:因为在∠DAB 内任作射线AP ,则等可能基本事件为“∠DAB 内作射线AP ”,所以它的所有等可能事件所在的区域H 是∠DAB .当射线AP 与线段BC 有公共点时,射线AP 落在∠CAB 内,区域h 为∠CAB ,所以射线AP 与线段BC 有公共点的概率为∠CAB ∠DAB =30°90°=13. 答案:138.封闭图形ABC 如图所示,为了求其面积,小明在封闭的图中找出了一个半径为1 m 的圆,在不远处向圈内掷石子,且记录如下:解析:由记录mn≈1∶2,可得P (落在⊙O 内)=m n +m ≈13.又P (落在⊙O 内)=⊙O 的面积阴影面积+⊙O 的面积,所以S ⊙O S ABC ≈13.又S ⊙O =π(m 2),故S ABC ≈3π(m 2).答案:3π三、解答题(每小题10分,共20分)9.在长为12 cm 的线段AB 上任取一点M ,并以线段AM 为边作正方形,用随机模拟法估算该正方形的面积介于36 cm 2与81 cm 2之间的概率.解:因为正方形的面积只与边长有关,所以本题可转化为在线段AB 上任取一点M ,使线段AM 的长度介于6到9之间.设事件A ={正方形的面积介于36 cm 2与81 cm 2之间},则:(1)利用计算器或计算机产生一组0到1区间的均匀随机数,a 1=RAND ; (2)经过伸缩变换,a =a 1*12;(3)统计出试验总次数N 和[6,9]内的随机数个数N 1(即满足6≤a ≤9的个数); (4)计算频率f n (A )=N 1N,即为概率P (A )的近似值.10.利用随机模拟方法计算如图中阴影部分(曲线y =2x 与x 轴、x =±1围成的部分)的面积.解:(1)利用计算机产生两组[0,1]上的均匀随机数,a 1=RAND ,b 1=RAND.(2)经过平移和伸缩变换,a =(a 1-0.5)*2,b =b 1*2,得到一组[-1,1]上的均匀随机数和一组[0,2]上的均匀随机数.(3)统计试验总次数N 和落在阴影内的点数N 1.(4)计算频率N 1N,即为点落在阴影部分的概率的近似值.(5)用几何概型的概率公式求得点落在阴影部分的概率为P =S 4,又N 1N ≈S 4,所以S ≈4N 1N ,即为阴影部分的面积值.(20分钟,40分)一、选择题(每小题5分,共10分)1.已知函数RAND 可以产生[0,1]区间上的均匀随机数,现在利用均匀随机数产生坐标为(x ,y )的点M ,已知x =10]( )A .12B .34C .18D .38解析:(1)若x ∈[-5,0]⎝⎛⎭⎫概率是12,则y >x 的概率为1,y <x +5的概率是12. 故满足x <y <x +5的概率是12×1×12=14.(2)若x ∈[0,5]⎝⎛⎭⎫概率是12, 则y >x 概率为12,y <x +5的概率是12.故满足x <y <x +5的概率是12×12×12=18.综合(1)(2)知,满足x <y <x +5的概率是14+18=38.答案:D2.若a ,b 均为实数,且方程x 2-2(a +1)x -b 2+2b =0无实根,则函数y =log (a +b )x 是增函数的概率是( )A .14-12πB .π4-12C .12πD .12-14π解析:方程无实根,则4(a +1)2-4(-b 2+2b )<0,即(a +1)2+(b -1)2<1.函数y =log (a +b )x 为增函数,∴a +b >1.如图,由几何概型知图中阴影部分即为所求概率,故P =π4-12π=14-12π.答案:A二、填空题(每小题5分,共10分)3.利用计算机随机模拟方法计算图中阴影面积(如图所示).第一步:利用计算机产生两个均匀随机数x ,y ,其中-1<x <1,0<y <1;第二步:拟(x ,y )为点的坐标.共做此试验N 次.若落在阴影部分的点的个数为N 1,则可以计算阴影部分的面积S . 例如,做了2 000次试验,即N =2 000,模拟得到N 1=1 396, 所以S ≈__________.解析:根据题意,点落在阴影部分的概率可估计为1 3962 000,矩形的面积为2,故S 2≈1 3962 000.所以S ≈1.396.答案:1.3964.利用随机模拟方法计算如图所示的阴影部分(y =x 3和x =2以及x 轴所围成的部分)的面积.步骤:(1)利用计算器或计算机产生两组0~1之间的均匀随机数,a 1=RAND ,b 1=RAND .(2)进行伸缩变换a =2a 1, b =8b 1.(3)数出试验总次数N 和落在阴影内的样本点数N 1(满足b <a 3的点(a ,b )的个数),用几何概型的求概率公式计算阴影部分的面积.例如,做1 000次试验,即N =1 000,模拟得到N 1=250. 由S 阴影S 矩≈N 1N,得S 阴影≈________. 解析:由条件知,a ∈[0,2],b ∈[0,8],所以S 矩=2×8=16.又由N =1 000时模拟得到N 1=250,所以S 阴影≈N 1N ·S 矩=2501 000×16=4.答案:4三、解答题(每小题10分,共20分)5.从甲地到乙地有一班车在9:30到10:00到达,若某人从甲地坐该班车到乙地转乘9:45到10:15出发的汽车到丙地去,问他能赶上车的概率是多少?解:能赶上车的条件是到达乙地时汽车没有出发,我们可以用两组均匀随机数x 和y 来表示到达乙地的时间和汽车从乙地出发的时间,当x ≤y 时能赶上车.设事件A :“他能赶上车”.①利用计算器或计算机产生两组[0,1]上的均匀随机数,x 1=RNAD ,y 1=RAND . ②经过变换x =0.5x 1+9.5,y =0.5y 1+9.75.③统计出试验总次数N 和满足条件x ≤y 的点(x ,y )的个数N 1. ④计算频率f n (A )=N 1N ,则N 1N即为概率P (A )的近似值.6.小明家订了一份报纸,送报人可能在早上6:30到7:30之间把报纸送到小明家,小明妈妈离开家去工作的时间在早上7:00到8:00之间,若“小明妈妈在离开家前能得到报纸”记为事件A ,试用随机模拟方法估计事件A 发生的概率.写出操作过程.解:以Excel 软件为例.(1)选定A1格,键入“=RANDBETWEEN (0,1)”,按Enter 键,则在此格中的数是随机产生的[0,1]之间的均匀随机数.(2)选定A1格,按Ctrl +C 快捷键.选定A2至A50,B1至B50,按Ctrl +V 快捷键,则在A2至A50,B1至B50的数均为[0,1]之间的均匀随机数.用A 列的数加7表示小明妈妈离开家的时间,B 列的数加6.5表示报纸到达的时间.这样我们相当于做了50次随机试验.(3)如果A +7>B +6.5,即A -B >-0.5,则表示小明妈妈在离开家前能得到报纸. (4)选定D1格,键入“=A1-B1”;再选定D1,按Ctrl +C ,选定D2至D50,按Ctrl +V .(5)选定E1格,键入频数函数“=FREQUENCY(D1∶D50,-0.5)”,按Enter 键,此数是统计D 列中,比-0.5小的数的个数,即小明妈妈在离开家前不能得到报纸的频数.(6)选定F1格,键入“=1-E1/50”,按Enter 键,此数是表示统计50次试验中,小明妈妈在离开家前能得到报纸的频率,也就是所求事件A 的概率的近似值.。
2018年数学同步优化指导北师大版必修3练习:3-3 模拟

第三章 §3
1.若向面积为2的△ABC 内任取一点P ,并连接PB ,PC ,则△PBC 的面积小于1的概率为( )
A .14
B .12
C .23
D .34
解析:设△ABC ,△PBC 在BC 边上的高分别为h ,h ′,则h ′h =S △PBC S △ABC =12
∴P =1-⎝⎛⎭⎫122=34.
答案:D
2.在区间[0,1]任取两个数x 、y ,则满足x +2y ≤1的概率P =( )
A .12
B .13
C .14
D .15
解析:在区间[0,1]任取两个数x 、y ,对应的区域为边长是1的正方形,面积为1,则满
足x +2y ≤1的区域为三角形,如图,由几何概型的个数得到概率P =12×1×121=14
.
答案:C
3.利用计算机产生0~2之间的均匀随机数a ,则事件“3a -2<0”发生的概率为________.
解析:由3a -2<0得:a <23
, 数集⎝⎛⎭⎫0,23的长度为23
,数集(0,2)的长度为2, ∴事件“3a -2<0”发生的概率为232=13
.
答案:13
4.如图所示,四个相同的直角三角形与中间的小正方形拼成的一个边长为2的大正方
形,若直角三角形中较小的锐角θ=π6
,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内概率是____________.
解析:观察这个图可知:大正方形的边长为2,总面积为4,而阴影区域的边长为3-1,面积为4-23; 故飞镖落在阴影区域的概率
4-234=1-32
. 答案:1-32.。
2018年数学同步优化指导北师大版必修3课件:3-2-3 互

率
§2 2.3
古典概型 互斥事件
1 .理解互斥事件、对立事件的概念,明确互斥事件与对 立事件的联系,并能正确判断. 2.理解互斥事件、对立事件的概率加法公式.(重点)
3 .能利用互斥事件、对立事件的概率加法公式解决较复
杂的古典概型的概率计算问题.(难点)
一、阅读教材:提出问题~例5,完成下列问题. 1.互斥事件 不能同时发生 的 在一个随机试验中,我们把一次试验下______________ 两个事件A与B称作互斥事件. 2.互斥事件的概率加法公式 (1) 事件 A + B :给定事件 A , B ,我们规定 A + B 为一个事 事件A和B至少有一个发生 对于三个 件,事件 A + B 发生是指 ________________________.
解析: 由题意,该十字路口红灯亮起时至多有 2 辆车排队
等候即排队等候的车辆数为 0,1,2 ,所以 P = 1 - (0.2 + 0.1) =
0.7. 答案:0.7
事件关系的判断
某小组有3名男生和2名女生,从中任选2名同学参 加演讲比赛.判断下列每对事件是不是互斥事件,如果是,再 判别它们是不是对立事件. (1)恰有1名男生与恰有2名男生;
利用互斥事件概率加法公式求概率的基本步骤如下: (1) 将欲求事件 A 分为两个或几个互斥事件的和,即 A = A1 +A2+„+An,其中A1,A2,„,An彼此互斥; (2)分别求出事件A1,A2,„,An的概率; (3) 利用概率加法公式 P(A) = P(A1) + P(A2)+„ + P(An) ,进 而求出P(A).
是对立事件的是________.
解析:(1)共有三个基本事件:“两次都击中敌机”“两次 都没击中敌机”“恰有一次击中敌机”.显然A与B,B与C,A 与C,B与D为彼此互斥的事件. (2)①②④不互斥,③是对立事件. 答案:(1)A与B,B与C,A与C,B与D (2)③
2018年数学同步优化指导北师大版必修3练习:3-3 课时

课时作业(二十) 模拟方法——概率的应用基础达标一、选择题1.下列概率模型中,是几何概型的有( )①从区间[-10,10]内任取出一个数,求取到1的概率;②从区间[-10,10]内任取出一个数,求取到绝对值不大于1的数的概率;③从区间[-10,10]内任取出一个整数,求取到大于1而小于2的数的概率;④向一个边长为4 cm 的正方形内投一点P ,求点P 离正方形中心不超过1 cm 的概率.A .1个B .2个C .3个D .4个解析:只有②和④符合几何概型特征,是几何概型. 答案:B2.在区间[0,10]中任意取一个数,则它与4之和大于10的概率为( ) A .15B .25C .35D .27解析:在区间[0,10]中任意取一个数x ,则它与4之和大于10的x 满足x +4>10, 解得6<x ≤10,∴所求概率为10-610=25.答案:B3.用随机模拟方法估计概率时,其精确程度决定于( ) A .产生的随机数的大小 B .产生的随机数的个数 C .随机数对应的结果D .产生随机数的方法解析:用模拟法估计概率时,关键是统计产生的随机数的个数,利用产生的随机数的频率来估计概率.答案:B4.在区间[0,1]内任取两个数,则这两个数的平方和在区间[0,1]内的概率是( ) A .π4B .π10C .π20D .π40解析:设任在[0,1]中取出的数为a ,b ,若a 2+b 2也在[0,1]中,则有0≤a 2+b 2≤1(如图),试验的全部结果所构成的区域为边长为1的正方形,满足a 2+b 2在[0,1]内的点在14单位圆内(如图阴影部分),故所求概率P =14π1=π4.答案:A 二、填空题5.如图所示,在直角坐标系内,射线OT 落在60°角的终边上,任作一条射线OA ,则射线OA 落在∠xOT 内的概率为________.解析:以O 为起点作射线OA 是随机的,因而射线OA 落在任何位置都是等可能的.落在∠xOT 内的概率只与∠xOT 的大小有关,符合几何概型的条件.记事件B ={射线OA 落在∠xOT 内},因为∠xOT =60°,所以P (B )=60°360°=16.答案:166.欧阳修《卖油翁》中写到:(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔人,而钱不湿.可见“行行出状元”,卖油翁的技艺让人叹为观止.若铜钱是直径为3 cm 的圆,中间有边长为1 cm 的正方形孔,若随机向铜钱上滴一滴油,则油(油滴的大小忽略不计)正好落入孔中的概率是____________.解析:如图所示:∵S 正=1,S 圆=π⎝⎛⎭⎫322=9π4, ∴P =S 正S 圆=49π.则油(油滴的大小忽略不计)正好落入孔中的概率是49π.答案:49π三、解答题7.一个路口的红绿灯,红灯亮的时间为30秒,黄灯亮的时间为5秒,绿灯亮的时间为40秒(没有两灯同时亮),当你到达路口时,看见下列三种情况的概率各是多少?(1)红灯 (2)黄灯 (3)不是红灯解:在75秒内,每一时刻到达路口是等可能的,属于几何概型. (1)P =亮红灯的时间全部时间=3030+40+5=25;(2)P =亮黄灯的时间全部时间=575=115;(3)P =不是红灯亮的时间全部时间=黄灯或绿灯亮的时间全部时间=4575=35. 8.在一个大型商场的门口,有一种游戏是向一个画满边长为5 cm 的均匀方格的大桌子上掷直径为2 cm 的硬币,如果硬币完全落入某个方格中,则掷硬币者赢得一瓶洗发水,请问随机掷一个硬币正好完全落入方格的概率有多大?解:如图,边长为5 cm 的正方形形成的区域表示试验的所有基本事件构成的区域,当硬币的中心落入图中以3 cm 为边长的正方形区域时,则试验成功,所以,随机地投一个硬币正好完全落入方格的概率为P =3252=925.能力提升一、选择题1.长郡中学早上8点开始上课,若学生小张与小王均在早上7:40至8:00之间到校,且两人在该时间段的任何时刻到校都是等可能的,则小张比小王至少早5分钟到校的概率为( )A .932B .12C .364D .564解析:设小张到校的时间为x ,小王到校的时间为y .(x ,y )可以看成平面中的点试验的全部结果所构成的区域为Ω={(x ,y |40≤x ≤60,40≤y ≤60}是一个矩形区域,对应的面积S =20×20=400,则小张比小王至少早5分钟到校事件A ={x |y -x ≥5}作出符合题意的图象,则符合题意的区域为△ABC ,联立⎩⎪⎨⎪⎧ y -x =5y =60得C (55,60),由⎩⎪⎨⎪⎧y -x =5x =40得B (40,45),则S △ABC =12×15×15,由几何概率模型可知小张比小王至少早5分钟到校的概率为12×15×1520×20=932. 答案:A2.已知△ABC 内一点O 满足OA →+2OB →+3OC →=0,若△ABC 内任意投一个点,则该点落在△OAC 内的概率为( )A .16B .14C .13D .12解析:以OB →,OC →为邻边作平行四边形OBDC ,则OB →+OC →=OD →∵OA →+2OB →+3OC →=0, ∴3OD →=AB →,作AB 的两个三等分点E ,F ,则OC →=BD →=EO →,∴O 到AC 的距离是E 到AC 距离的一半,B 到AC 的距离是O 到AC 距离的3倍,如图所示.∴S △AOC =13S △ABC .故△ABC 内任意投一个点,则该点落在△OAC 内的概率为13.答案:C二、填空题3.广告法对插播广告时间有规定,某人对某台的电视节目作了长期的统计后得出结论,他任意时间打开电视机看该台节目,看不到广告的概率约为910,那么该台每小时约有________分钟广告.解析:这是一个与时间有关的几何概型,这人看不到广告的概率约为910,则看到广告的概率约为110,故60×110=6(分钟).答案:64.已知事件“在矩形ABCD 的边CD 上随机取一点P ,使△APB 的最大边是AB ”发生的概率为12,则ADAB=________.解析:矩形ABCD 如图所示,在点P 从D 点向C 点运动的过程中,DP 在增大,AP 也在增大,而BP 在逐渐减小,当P 点到P 1位置时,BA =BP 1,当P 点到P 2位置时,AB =AP 2,故点P 在线段P 1P 2上时,△ABP 中边AB 最大,由题意可得P 1P 2=12CD .在Rt △BCP 1中,BP 21=916CD 2+BC 2=916AB 2+AD 2=AB 2.即AD 2=716AB 2,所以AD AB =74. 答案:74三、解答题5.某同学到公共汽车站等车上学,可乘坐8路、23路,8路车10分钟一班,23路车15分钟一班.求这位同学等车不超过8分钟的概率.解:设x 轴表示23路车的到站时间,y 轴表示8路车的到站时间,记“8分钟内乘坐8路车或23路车”为事件A .如图所示,则A 所占区域面积为8×10+7×8=136,整个区域的面积为10×15=150,那么,等车不超过8分钟的概率P (A )=136150≈0.91.即这位同学等车不超过8分钟的概率约为0.91.6.已知关于x 的一元二次方程x 2+2ax +b 2=0.(1)若a 是从0,1,2,3四个数中任取的一个数,b 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;(2)若a 是从区间[0,3]内任取的一个数,b 是从区间[0,2]内任取的一个数,求上述方程有实根的概率.解:设事件A 为“方程x 2+2ax +b 2=0有实根”,此方程有实根的条件是(2a )2-4b 2≥0,即a ≥b .(1)基本事件共有12个,分别是(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2),其中括号内第一个数表示a 的取值,第二个数表示b 的取值.事件A 中包含9个基本事件,故事件A 发生的概率为P (A )=912=34.(2)试验的全部结果所构成的区域为{(a ,b )|0≤a ≤3,0≤b ≤2,a ≥b },如图所示的阴影部分,所以P (A )=3×2-12×223×2=23.。
2018年数学同步优化指导必修3练习:3-2-2 整数值随机

活页作业(十九) (整数值)随机数(random numbers)的产生(25分钟,60分)一、选择题(每小题5分,共25分)1.关于随机数的说法正确的是( )A .随机数就是随便取的一些数字B .随机数是用计算机或计算器随便按键产生的数C .用计算器或计算机产生的随机数为伪随机数D .不能用伪随机数估计概率答案:C2.袋中有2个黑球,3个白球,除颜色外小球完全相同,从中有放回地取出一球,连取三次,观察球的颜色.用计算机产生0到9的数字进行模拟试验,用0,1,2,3代表黑球,4,5,6,7,8,9代表白球,在下列随机数中表示结果为二白一黑的组数为( )160 288 905 467 589 239 079 146 351A .3B .4C .5D .6解析:二白一黑的组为288,905,079,146,共四组.答案:B3.池州九华山是著名的旅游胜地.天气预报8月1日后连续四天,每天下雨的概率为0.6.现用随机模拟的方法估计四天中恰有三天下雨的概率:在0~9十个整数值中,假定0,1,2,3,4,5表示当天下雨,6,7,8,9表示当天不下雨.在随机数表中从某位置按从左到右的顺序读取如下40组四位随机数:9533 9522 0018 7472 0018 3879 5869 3281 7890 26928280 8425 3990 8460 7980 2436 5987 3882 0753 89359635 2379 1805 9890 0735 4640 6298 8054 9720 56951574 8008 3216 6470 5080 6772 1642 7920 3189 0343据此估计四天中恰有三天下雨的概率为( )A .34B .25C .2140D .1740解析:在40组四位随机数中,0~5的整数恰出现3次的四位数有16组,故四天中恰有三天下雨的概率的估计值为1640=25. 答案:B4.袋子中有四个小球,分别写有“金、榜、书、业”四个字,从中任取一个小球,取到“书”就停止,用随机模拟的方法估计直到第二次停止的概率:先由计算器产生1到4之间取整数值的随机数,且用1,2,3,4表示取出小球上分别写有“金、榜、书、业”四个字,以每两个随机数为一组,代表两次的结果,经随机模拟产生了20组随机数:13 24 12 32 43 14 24 32 31 2123 13 32 21 24 42 13 32 21 34据此估计,直到第二次就停止的概率为( )A .15B .14C .13D .12解析:在20组随机模拟数中,表示第二次就停止的有13,43,23, 13,13,共5组.故模拟概率为520=14. 答案:B5.从自然数1,2,3,4,5中任意取出两个数组成两位的自然数,则在两位自然数中个位数字与十位数字恰好是相邻数字的概率为( )A .25B .15C .310D .12解析:从自然数1,2,3,4,5中任意取出两个数组成两位的自然数,有12,21,13,31,14,41,15,51,23,32,24,42,25,52,34,43,35,53,45,54,共20种情况,记“在两位自然数中个位数字与十位数字恰好是相邻数字”为事件A ,则事件A 所包含的情况有12,21,23,32,34,43,45,54,共8种情况,所以所求概率为P (A )=820=25.故选A . 答案:A二、填空题(每小题5分,共15分)6.已知某运动员每次投篮命中的概率低于40%.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中,再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了20组随机数:907 966 191 925 271 932 812 458569 683 431 257 393 027 556 488730 113 537 989其中,表示三次投篮恰好中两次的有________________组.解析:有191,271,932,812,393,共5组.答案:57.通过模拟试验,产生了20组随机数:6 830,3 013,7 055,7 430,7 740,4 422,7 884,2 604,3 346,0 952,6 807,9 706,5 774,5 725,6 576,5 929,9 768,6 071,9 138,6 754.如果恰有三个数在1,2,3,4,5,6中,表示恰有三次击中目标,那么四次射击中恰有三次击中目标的概率约为__________.解析:表示恰有三次击中目标的情况有3 013,2 604,5 725,6 576,6 754,共5组数,而随机数总共20组,所以所求的概率近似为520=14. 答案:148.甲、乙两人随意入住三间空房,则甲、乙两人各住一间房的概率是__________. 解析:设房间的编号分别为A ,B ,C ,甲、乙两人各住一间房包含的基本事件为:甲A 乙B ,甲B 乙A ,甲B 乙C ,甲C 乙B ,甲A 乙C ,甲C 乙A ,共6个,基本事件总数为3×3=9,所以所求的概率为69=23. 答案:23三、解答题(每小题10分,共20分)9.某种心脏手术,成功率为0.6,现准备进行3例此种手术,试估计;(1)恰好成功1例的概率.(2)恰好成功2例的概率.解:利用计算器或计算机产生0到9之间取整数值的随机数,我们用0,1,2,3代表手术不成功,用4,5,6,7,8,9代表手术成功,这样可以体现成功的概率为0.6.因为做3例手术,所以每3个随机数作为一组.例如产生907,966,191,925,…,730,113,537,989共100组随机数.(1)若出现4,5,6,7,8,9中1个数的数组个数为N 1,则恰好成功1例的概率近似为N 1100. (2)若出现4,5,6,7,8,9中2个数的数组个数为N 2,则恰好成功2例的概率近似为N 2100. 10.盒中有大小形状相同的5个白球、2个黑球,用随机模拟法求下列事件的概率:(1)任取一球,得到白球;(2)任取三球,恰有2个白球;(3)任取三球(分三次,每次放回再取),恰有3个白球.解:用计算器或计算机产生1到7之间的取整数值的随机数.用1,2,3,4,5表示白球,6,7表示黑球.(1)统计随机数个数N 及小于6的个数N 1,则N 1N即为任取一球,得到白球的概率的近似值.(2)3个数为一组(每组内数字不重复),统计总组数M 及恰有2个小于6的组数M 1,则M 1M即为任取三个,恰有2个白球的概率的近似值.(3)3个数为一组(每组内数字可重复),统计总组数K 及3个数都小于6的组数K 1,则K 1K即为恰有3个白球的概率的近似值.(20分钟,40分)一、选择题(每小题5分,共10分)1.将一枚骰子投掷两次,第一次出现的点数记为a ,第二次出现的点数记为b ,设两条直线l 1:ax +by =2与l 2:x +2y =2平行的概率为P 1,相交的概率为P 2,则点P (36P 1,36P 2)与圆C :x 2+y 2=1 098的位置关系是( )A .点P 在圆C 上B .点P 在圆C 外 C .点P 在圆C 内D .不能确定 解析:易知当且仅当a b ≠12时两条直线相交,而a b =12的情况有三种,a =1,b =2,此时两直线重合;a =2,b =4,此时两直线平行.a =3,b =6,此时两直线平行.而投掷两次的所有情况有36种,所以两条直线平行的概率P 1=236=118,两条直线相交的概率P 2=1-336=1112.所以点P 为(2,33),点P 与圆心(0,0)的距离为22+332= 1 093< 1 098,故点P 在圆C 内.答案:C2.天气预报说,在今后的三天中每一天下雨的概率均为30%,用随机模拟的方法进行试验,由1,2,3表示下雨,由4,5,6,7,8,9,0表示不下雨,利用计算器中的随机函数产生0~9之间随机整数的20组数据如下:907 966 191 925 271 932 812 458 569 683431 257 393 027 556 488 730 113 537 989通过以上数据可知三天都不下雨的概率近似为( )A .0.05B .0.35C .0.4D .0.7解析:由题意知利用计算器模拟求三天都不下雨的概率,产生的20组随机模拟数据中代表三天都不下雨的随机数,应该由4,5,6,7,8,9,0中的三个组成,这样的随机数有907,966,458,569,556,488,989,共7组随机数,所以所求概率为720=0.35.故选B .答案:B二、填空题(每小题5分,共10分)3.在利用整数随机数进行随机模拟试验中,整数a 到整数b 之间的每个整数出现的可能性是________________.解析:[a ,b ]中共有b -a +1个整数,每个整数出现的可能性相等,所以每个整数出现的可能性是1b -a +1. 答案:1b -a +14.有五名同学分别来自高一年级(1)至(5)班,现从中任选两人担任学生会干部,则选出的两人所在班级编号之差恰好为1的概率是________.解析:用带有编号1,2,3,4,5的5个小球分别代表1,2,3,4,5班的五名同学,放入箱子内搅拌均匀后取出两球观察结果,共有10种不同的结果,(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5),其中班级编号之差为1的有(1,2),(2,3),(3,4),(4,5),共4种,所以所求概率为410=0.4. 答案:0.4三、解答题(每小题10分,共20分)5.在10件产品中有7件正品,3件次品,从中任取一件,试用计算机或计算器进行随机模拟试验,写出试验过程,并求取出的一件产品恰为次品的概率.解:(1)用计算机的随机函数RANDBETWEEN(1,10)或计算器的随机函数RANDI(1,10)产生1到10之间的10个整数值随机数,分别用1,2,3表示次品,4,5,6,7,8,9,10表示正品.(2)统计试验总次数N ,统计其中出现1到3之间数的次数N 1.(3)计算频率N 1N,即为“取出一件产品恰为次品”的概率的近似值. 6.某人有5把钥匙,其中2把能打开门.现随机地抽1把钥匙试着开门,不能开门就扔掉,问“第三次才打开门”的概率是多少?如果试过的钥匙不扔掉,这个概率又是多少?设计一个试验,随机模拟估计上述概率.解:由题意,得随机地抽1把钥匙试着开门,不能开门就扔掉,第三次才打开门的概率为P =35×24×23=15.如果试过的钥匙不扔掉,这个概率为P =35×35×25=18125.随机模拟试验的步骤如下.用计算器或计算机产生1到5之间的整数随机数,1,2表示能打开门,3,4,5表示不能打开门.(1)三个数一组(每组数字不重复),统计总组数N 及前两个大于2,第三个是1或2的组数N 1,则N 1N即为“不能打开门即扔掉,第三次才打开门”的概率的近似值. (2)三个数一组(每组数字可重复),统计总组数M 及前两个大于2,第三个为1或2的组数M 1,则M 1M即为“试过的钥匙不扔掉,第三次才打开门”的概率的近似值.。
2018年数学同步优化指导必修3练习:3-1-3 概率的基本

活页作业(十七) 概率的基本性质(25分钟,60分)一、选择题(每小题5分,共25分)1.如果事件A ,B 互斥,且事件C ,D 分别是A ,B 的对立事件,那么( ) A .A ∪B 是必然事件 B .C ∪D 是必然事件 C .C 与D 一定互斥D .C 与D 一定不互斥解析:由于事件A 与B 互斥,即A ∩B =∅,则C ∪D =U (U 为全集)是必然事件. 答案:B2.设A ,B 为两个事件,且P (A )=0.3,则当________________时一定有P (B )=0.7.( ) A .A 与B 互斥 B .A 与B 对立 C .A ⊆BD .A 不包含B解析:∵A ,B 对立时P (A )+P (B )=1,∴此时,P (B )=1-P (A )=0.7. 答案:B3.从一批产品中取出三件产品,设A =“三件产品全不是次品”,B =“三件产品全是次品”,C =“三件产品有次品,但不全是次品”,则下列结论中错误的是( )A .A 与C 互斥B .B 与C 互斥 C .任何两个都互斥D .任何两个都不互斥解析:由题意知事件A ,B ,C 两两不可能同时发生,因此两两互斥. 答案:D4.围棋盒子中有多粒黑子和白子,已知从中取出2粒都是黑子的概率为17,从中取出2粒都是白子的概率是1235.则从中任意取出2粒恰好是同一色的概率是( )A .17B .1235C .1735D .1解析:设“从中取出2粒都是黑子”为事件A ,“从中取出2粒都是白子”为事件B ,“任意取出2粒恰好是同一色”为事件C ,则C =A ∪B ,且事件A 与B 互斥.所以P (C )=P (A )+P (B )=17+1235=1735,即任意取出2粒恰好是同一色的概率为1735.答案:C5.某产品分甲、乙、丙三级,其中乙、丙两级均属次品,若生产中出现乙级品的概率为0.03,丙级品的概率为0.01,则对成品抽查一件抽得正品的概率为( )A .0.09B .0.98C .0.97D .0.96解析:设“抽得正品”为事件A ,“抽得乙级品”为事件B ,“抽得丙级品”为事件C .由题意,P (A )=1-P (B ∪C )=1-P (B )-P (C )=1-0.03-0.01=0.96.答案:D二、填空题(每小题5分,共15分)6.某人在打靶中连续射击2次,事件“至少有一次中靶”的互斥事件是________________________________.解析:连续射击2次,共有以下情形,第一次中第二次中,第一次中第二次不中,第一次不中第二次中,第一次不中第二次不中.因此“至少有一次中靶”的互斥事件是“两次都不中靶”.答案:两次都不中靶7.若随机事件A ,B 互斥,A ,B 发生的概率均不等于0,且分别为P (A )=2-a ,P (B )=3a -4,则实数a 的取值范围为____________________.解析:∵由题意可得⎩⎪⎨⎪⎧0<P (A )<1,0<P (B )<1,P (A )+P (B )≤1,∴⎩⎪⎨⎪⎧0<2-a <1,0<3a -4<1,2a -2≤1.解得43<a ≤32.答案:⎝⎛⎦⎤43,328.掷一枚均匀的正六面体骰子,设A 表示事件“出现3点”,B 表示事件“出现偶数点”,则P (A ∪B )等于________.解析:P (A ∪B )=P (A )+P (B )=16+36=23.答案:23三、解答题(每小题10分,共20分)9.某县城有甲、乙两种报纸供居民订阅,记事件A 为“只订甲报”,事件B 为“至少订一种报”,事件C 为“至多订一种报”,事件D 为“不订甲报”,事件E 为“一种报纸也不订”.判断下列每对事件是不是互斥事件.如果是,再判断它们是不是对立事件.(1)A 与C . (2)B 与E . (3)B 与D . (4)B 与C . (5)C 与E .解:(1)由于事件C “至多订一种报”中有可能只订甲报,即事件A 与事件C 有可能同时发生,故A与C不是互斥事件.(2)事件B“至少订一种报”与事件E“一种报也不订”是不可能同时发生的,故B与E 是互斥事件.由于事件B不发生可导致事件E一定发生,且事件E不发生会导致事件B一定发生,故B与E还是对立事件.(3)事件B“至少订一种报”中有可能只订乙报,即有可能不订甲报,也就是说事件B 发生,事件D也可能发生,故B与D不互斥.(4)事件B“至少订一种报”中有这些可能:“只订甲报”“只订乙报”“订甲、乙两种报”.事件C“至多订一种报”中有这些可能:“什么也不订”“只订甲报”“只订乙报”.由于这两个事件可能同时发生,故B与C不是互斥事件.(5)由(4)的分析,事件E“一种报纸也不订”只是事件C的一种可能,即事件C与事件E有可能同时发生,故C与E不互斥.10.某商场有奖销售中,购满100元商品得一张奖券,多购多得,每1 000张奖券为一个开奖单位.设特等奖1个,一等奖10个,二等奖50个.设1张奖券中特等奖、一等奖、二等奖的事件分别为A,B,C,求:(1)P(A),P(B),P(C);(2)抽取1张奖券中奖概率;(3)抽取1张奖券不中特等奖或一等奖的概率.解:(1)∵每1 000张奖券中设特等奖1个,一等奖10个,二等奖50个,∴P(A)=11 000,P(B)=101 000=1 100,P(C)=501 000=120.(2)设“抽取1张奖券中奖”为事件D,则P(D)=P(A)+P(B)+P(C)=11 000+1100+120=611 000.(3)设“抽取1张奖券不中特等奖或一等奖”为事件E,则P(E)=1-P(A)-P(B)=1-11 000-1100=9891 000.(20分钟,40分)一、选择题(每小题5分,共10分)1.已知100件产品中有5件次品,从这100件产品中任意取出3件,设E表示事件“3件产品全不是次品”,F表示事件“3件产品全是次品”,G表示事件“3件产品中至少有1件次品”,则下列结论正确的是()A.F与G互斥B .E 与G 互斥但不对立C .E ,F ,G 任意两个事件均互斥D .E 与G 对立解析:本题主要考查互斥事件、对立事件的概念.由题意得事件E 与事件F 不可能同时发生,是互斥事件;事件E 与事件G 不可能同时发生,是互斥事件;当事件F 发生时,事件G 一定发生,所以事件F 与事件G 不是互斥事件,故A 、C 错.事件E 与事件G 中必有一个发生,所以事件E 与事件G 对立,所以B 错误,D 正确.答案:D2.某城市2016的空气质量状况如下表所示:T ≤150时,空气质量为轻微污染.则该城市2016年空气质量达到良或优的概率为( )A .15B .25C .35D .45解析:由题意可知2016年空气质量达到良或优的概率为P =110+16+13=35.答案:C二、填空题(每小题5分,共10分)3.袋中有12个小球,分别是红球、黑球、黄球(这些小球除颜色外其他都相同),从中任取一球,得到红球的概率为13,得到黑球的概率比得到黄球的概率多16,则得到黑球、黄球的概率分别是________.解析:∵得红球的概率为13,∴得黑球或黄球的概率为23.记“得到黄球”为事件A ,“得到黑球”为事件B ,则⎩⎨⎧P (A )+P (B )=23,P (B )-P (A )=16,∴P (A )=14,P (B )=512.答案:512,144.如图所示,靶子由一个中心圆面Ⅰ和两个同心圆环Ⅱ、Ⅲ构成,射手命中Ⅰ、Ⅱ、Ⅲ的概率分别为0.15,0.20,0.45,则不中靶的概率是________.解析:设射手“命中圆面Ⅰ”为事件A ,“命中圆环Ⅱ”为事件B ,“命中圆环Ⅲ”为事件C ,“不中靶”为事件D ,则A ,B ,C 互斥,故射手中靶的概率为P (A ∪B ∪C )=P (A )+P (B )+P (C )=0.15+0.20+0.45=0.80.因为中靶和不中靶是对立事件,所以不中靶的概率为P (D )=1-P (A ∪B ∪C )=1-0.80=0.20.答案:0.20三、解答题(每小题10分,共20分)5.三个臭皮匠顶上一个诸葛亮,能顶得上吗?在一次有关“三国演义”的知识竞赛中,三个臭皮匠A ,B ,C 能答对题目的概率P (A )=13,P (B )=14,P (C )=15,诸葛亮D 能答对题目的概率P (D )=23.如果将三个臭皮匠A ,B ,C 组成一组与诸葛亮D 比赛,答对题目多者为胜方,问哪方胜?解:若三个臭皮匠A ,B ,C 能答对的题目彼此互斥(他们能答对的题目不重复), 则P (A ∪B ∪C )=P (A )+P (B )+P (C ) =4760>P (D )=23, 故三个臭皮匠方为胜方,那么三个臭皮匠顶上一个诸葛亮;如果三个臭皮匠A ,B ,C 能答对的题目不互斥,那么三个臭皮匠未必能顶上一个诸葛亮.6.某医院一天派出医生下乡医疗,派出医生人数及其概率如下:(1)(2)若派出医生最多4人的概率为0.96,最少3人的概率为0.44,求y ,z 的值. 解:(1)由派出医生不超过2人的概率为0.56,得0.1+0.16+x =0.56.∴x =0.3. (2)由派出医生最多4人的概率为0.96,得0.96+z =1.∴z =0.04.由派出医生最少3人的概率为0.44.得y +0.2+0.04=0.44.∴y =0.44-0.2-0.04=0.2.。
2018年数学同步优化指导必修3练习:章末质量评估三 概

章末质量评估(三) 概 率A 基础达标卷(时间:45分钟 满分:75分)一、选择题(本大题共6小题,每小题5分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.把黑、红、白3张纸牌分给甲、乙、丙三人,则事件“甲分得红牌”与“乙分得红牌”是( )A .对立事件B .互斥但不对立事件C .不可能事件D .必然事件解析:根据题意,把黑、红、白3张纸牌分给甲、乙、丙三人,事件“甲分得红牌”与“乙分得红牌”不会同时发生,故两者是互斥事件,但除了“甲分得红牌”与“乙分得红牌”之外,还有“丙分得红牌”,故两者不是对立事件,所以事件“甲分得红牌”与“乙分得红牌”是互斥但不对立事件.答案:B2.根据多年气象统计资料,某地6月1日下雨的概率为0.45,阴天的概率为0.2,则该日晴天的概率为( )A .0.65B .0.55C .0.35D .0.75解析:P =1-0.45-0.2=0.35.故选C . 答案:C3.(2015·高考江苏卷)袋中有形状、大小都相同的4个球,其中1个白球,1个红球,2个黄球,从中一次随机摸出2个球,则这2个球颜色不同的概率为( )A .56B .23C .45D .12解析:从4个球中一次随机摸出2个,共有6种摸法,其中2个球颜色不同的共有5种,所以其概率为56.答案:A4.已知集合A ={-1,0,1},点P 的坐标为(x ,y ),其中x ∈A ,y ∈A .记点P 落在第一象限为事件M ,则P (M )等于( )A .13B .16C .19D .29解析:点P 的坐标可能为(-1,-1),(-1,0),(-1,1),(0,0),(0,1),(1,0),(1,-1),(0,-1),(1,1),共9种,其中落在第一象限的点的坐标为(1,1),故选C .答案:C5.如图,两个正方形的边长均为2a ,左边正方形内四个半径为a2的圆依次相切,右边正方形内有一个半径为a 的内切圆,在这两个圆形上各随机撒一粒黄豆,落在阴影内的概率分别为P 1,P 2,则P 1,P 2的大小关系是( )A .P 1=P 2B .P 1>P 2C .P 1<P 2D .无法比较解析:由题意知正方形的边长为2a .左图中圆的半径为正方形边长的14,故四个圆的面积和为πa 2.右图中圆的半径为正方形边长的一半,圆的面积也为πa 2.故P 1=P 2.答案:A6.(2014·高考湖北卷)随机掷两枚质地均匀的骰子,它们向上的点数之和不超过5的概率记为p 1,点数之和大于5的概率记为p 2,点数之和为偶数的概率记为p 3,则( )A .p 1<p 2<p 3B .p 2<p 1<p 3C .p 1<p 3<p 2D .p 3<p 1<p 2解析:总的基本事件个数为36,向上的点数之和不超过5的有(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(3,1),(3,2),(4,1),共10个,则向上的点数之和不超过5的概率p 1=1036=518;向上的点数之和大于5的概率p 2=1-518=1318;向上的点数之和为偶数与向上的点数之和为奇数的个数相等,故向上的点数之和为偶数的概率p 3=12.故p 1<p 3<p 2,选C .答案:C二、填空题(本大题共4小题,每小题5分,共20分,请把正确答案填在题中的横线上) 7.若A , B 为互斥事件,P (A )=0.4,P (A ∪B )=0.7,则P (B )=________. 解析:∵A ,B 为互斥事件, ∴P (A ∪B )=P (A )+P (B ).∴P (B )=P (A ∪B )-P (A )=0.7-0.4=0.3. 答案:0.38.(2013·高考福建卷)利用计算机产生0~1之间的均匀随机数a ,则事件“3a -1<0”发生的概率为________________.解析:设事件A 为“3a -1<0”,则a ∈⎣⎡⎭⎫0,13,所以P (A )=13-01=13. 答案:139.如图是某市3月1日至14日的空气质量指数趋势图.空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.此人到达当日空气质量优良的概率是________.解析:由图知,3月1日至3月13日这13天中,1日、2日、3日、7日、12日、13日共6天的空气质量优良,所以此人到达当日空气质量优良的概率为613.答案:61310.任意一个△ABC 的面积为S ,D 为△ABC 内任取的一个点,则△DBC 的面积和△ADC 的面积都大于S3的概率为________.解析:如图,在AB 上取三等分点E ,F ,过点E 作EM ∥BC 交AC 于M ,过点F 作FN ∥AC 交BC 于N ,则当点D 在△AEM 内时,满足S △DBC >S3.当点D 在△BFN 内时,满足S △ADC >S3.设EM 与FN 的交点为G ,则当点D 在△EFG 内时,同时满足S △DBC >S 3,S △ADC >S3,∴所求概率P =S △EFG S △ABC =19.答案:19三、解答题(本大题共2小题,共25分,解答应写出文字说明、证明过程或演算步骤) 11.(本小题满分12分) (2015·高考四川卷)一辆小客车上有5个座位,其座位号为1,2,3,4,5,乘客P 1,P 2,P 3,P 4,P 5的座位号分别为1,2,3,4,5,他们按照座位号从小到大的顺序先后上车,乘客P 1因身体原因没有坐自己的1号座位,这时司机要求余下的乘客按以下规则就座,如果自己的座位空着,就只能坐自己的座位,如果自己的座位已有乘客就座,就在这5个座位的剩余空位中任意选择座位.(1)若乘客P 1坐到了3号座位,其他乘客按规则就座,此时共有4种坐法,下表给出了其中两种坐法,请填入余下两种坐法(将乘客就座的座位号填入表格空格处);15 解:(1)余下两种坐法如下表所示. 1则所有可能的坐法可用下表表示.设“乘客P 5坐到5号座位”为事件A ,则事件A 中的基本事件的个数为4. 所以P (A )=48=12.12.(本小题满分13分) (2015·高考全国卷Ⅱ)某公司为了解用户对其产品的满意度,从A ,B 两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A 地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表.B地区用户满意度评分的频数分布表区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可).(2)根据用户满意度评分,将用户的满意度分为三个等级:解:(1)B地区用户满意度评分的频率分布直方图如图所示.通过两地区用户满意度评分的频率分布直方图可以看出,B地区用户满意度评分的平均值高于A地区用户区满意度评分的平均值;B地区用户满意度评分比较集中,而A地区用户满意度评分比较分散.(2)A地区用户的满意度等级为不满意的概率大.记C A表示事件:“A地区用户的满意度等级为不满意”;C B表示事件:“B地区用户的满意度等级为不满意”.由直方图得P (C A )的估计值为(0.01+0.02+0.03)×10=0.6, P (C B )的估计值为(0.005+0.02)×10=0.25. 所以A 地区用户的满意度等级为不满意的概率大.B 能力提升卷(时间:45分钟 满分:75分)一、选择题(本大题共6小题,每小题5分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.从一箱产品中随机地抽取一件,设事件A ={抽到一等品},事件B ={抽到二等品},事件C ={抽到三等品},且已知P (A )=0.65,P (B )=0.2,P (C )=0.1.则事件“抽到的是二等品或三等品”的概率为( )A .0.7B .0.65C .0.35D .0.3解析:由题意知,事件A ,B ,C 互为互斥事件,记事件D =“抽到的是二等品或三等品”,则P (D )=P (B ∪C )=P (B )+P (C )=0.2+0.1=0.3,故选D .答案:D2.(2016·高考全国卷Ⅰ)某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40 s .若一名行人来到该路口遇到红灯,则至少需要等待15 s 才出现绿灯的概率为( )A .710B .58C .38D .310解析:利用几何概型的概率公式求解.如图,若该行人在时间段AB 的某一时刻来到该路口,则该行人至少等待15 s 才出现绿灯.AB 长度为40-15=25.由几何概型的概率公式知,至少需要等待15 s 才出现绿灯的概率为40-1540=58,故选B .答案:B3.掷一枚质地均匀的硬币两次,设事件M =“一次正面向上,一次反面向上”,事件N =“至少一次正面向上”.则下列结果正确的是( )A .P (M )=13,P (N )=12B .P (M )=12,P (N )=34C .P (M )=13,P (N )=34D .P (M )=12,P (N )=12解析:所有等可能的结果有(正,正),(正,反),(反,正),(反,反),所以P (M )=12,P (N )=34.答案:B4.(2015·高考福建卷)如图,矩形ABCD 中,点A 在x 轴上,点B 的坐标为(1,0),且点C 与点D 在函数f (x )=⎩⎪⎨⎪⎧x +1,x ≥0,-12x +1,x <0的图象上.若在矩形ABCD 内随机取一点,则此点取自阴影部分的概率等于()A .16B .14C .38D .12解析:由图形知C (1,2),D (-2,2), ∴S 四边形ABCD =6,S 阴=12×3×1=32.∴P =326=14.答案:B5.有3个兴趣小组,甲、乙两名同学各自参加其中一个小组,每名同学参加各个小组的可能性相同,则这两名同学参加同一个兴趣小组的概率为( )A .13B .12C .23D .34解析:记3个兴趣小组分别为1,2,3,甲参加1组记为“甲1”,则基本事件为“甲1,乙1;甲1,乙2;甲1,乙3;甲2,乙1;甲2,乙2;甲2,乙3;甲3,乙1;甲3,乙2;甲3,乙3”,共9个.记事件A 为“甲、乙两名同学参加同一个兴趣小组”,则包含的基本事件有“甲1,乙1;甲2,乙2;甲3,乙3”,共3个.因此P (A )=39=13.答案:A6.为了调查某厂2 000名工人生产某种产品的能力,随机抽查了20名工人某天生产该产品的数量,产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35],频率分布直方图如图所示.工厂规定从生产低于20件产品的工人中随机地选取2名工人进行培训,则这2名工人不在同一组的概率是( )A .110B .715C .815D .1315解析:根据题中频率分布直方图可知产品件数在[10,15),[15,20)内的人数分别为5×0.02×20=2,5×0.04×20=4.设生产产品件数在[10,15)内的2人分别是A ,B ,设生产产品件数在[15,20)内的4人分别是C ,D ,E ,F ,则从生产低于20件产品的工人中随机地选取2名工人的结果有(A ,B ),(A ,C ),(A ,D ),(A ,E ),(A ,F ),(B ,C ),(B ,D ),(B ,E ),(B ,F ),(C ,D ),(C ,E ),(C ,F ),(D ,E ),(D ,F ),(E ,F ),共15种.2名工人不在同一组的结果有(A ,C ),(A ,D ),(A ,E ),(A ,F ),(B ,C ),(B ,D ),(B ,E ),(B ,F ),共8种.则选取这2人不在同一组的概率为815.答案:C二、填空题(本大题共4小题,每小题5分,共20分,请把正确答案填在题中的横线上) 7.已知某台纺纱机在1 h 内发生0次、1次、2次断头的概率分别是0.8,0.12,0.05,则这台纺纱机在1 h 内断头不超过两次的概率和断头超过两次的概率分别为____________,________.解析:断头不超过两次的概率P 1=0.8+0.12+0.05=0.97.于是,断头超过两次的概率P 2=1-P 1=1-0.97=0.03.答案:0.97 0.038.用两种不同的颜色给图中三个矩形随机涂色,每个矩形只涂一种颜色,则相邻两个矩形涂不同颜色的概率是________.解析:由于只有两种颜色,不妨将其设为1和2,若只用一种颜色,有111;222. 若用两种颜色,有122;212;221;211;121;112.所以基本事件共有8种.又相邻颜色各不相同的有2种,故所求概率为14.答案:149.已知平面区域A ={(x ,y )|x 2+y 2≤9,x ,y ∈R },B ={(x ,y )||x |+|y |≤3,x ,y ∈R }.在A 内随机取一点,此点取自B 的概率为________.解析:如图所示,分别画出A ,B 表示的区域,A 表示的区域为圆及其内部,B 表示的区域为正方形及其内部,根据几何概型可知,所求概率为18π·32=2π.答案:2π10.在箱子中装有十张卡片,分别写有1到10的十个整数;从箱子中任取一张卡片,记下它的读数x ,然后放回箱子中;第二次再从箱子中任取一张卡片,记下它的读数y ,则x +y 是10的倍数的概率为________.解析:先后两次取卡片,形成的有序数对有(1,1),(1,2),(1,3),…,(1,10),…,(10,10).共计100个.因为x +y 是10的倍数,这些数对应该是(1,9),(2,8),(3,7),(4,6),(5,5),(6,4),(7,3),(8,2),(9,1),(10,10),共10个,故x +y 是10的倍数的概率为P =10100=110.答案:110三、解答题(本大题共2小题,共25分,解答应写出文字说明、证明过程及演算步骤) 11.(本小题满分12分)PM2.5是指大气中直径小于或等于2.5 μm 的颗粒物,也称为可入肺颗粒物,我国PM2.5标准采用世卫组织设定的最宽限值,PM2.5日均值在35 μg /m 3以下空气质量为一级;在35 μg/m 3~75 μg /m 3之间空气质量为二级;在75 μg/m 3及其以上空气质量为超标.某试点城市环保局从该市市区2016年全年每天的PM2.5监测数据中随机抽取6天的数据作为样本,监测值茎叶图如图(十位为茎,个位为叶),若从这6天的数据中随机抽出2天,(1)求恰有一天空气质量超标的概率;(2)求至多有一天空气质量超标的概率.解:由茎叶图知,6天中有4天空气质量未超标,有2天空气质量超标.记未超标的4天为a,b,c,d,超标的两天为e,f,则从6天中抽取2天的所有情况为ab,ac,ad,ae,af,bc,bd,be,bf,cd,ce,cf,de,df,ef,基本事件数为15.(1)记“6天中抽取2天,恰有一天空气质量超标”为事件A,可能结果为ae,af,be,bf,ce,cf,de,df,基本事件数为8,∴P(A)=815.(2)记“至多有一天空气质量超标”为事件B,“2天都超标”为事件C,其可能结果为ef,故P(C)=1 15.∴P(B)=1-P(C)=1-115=1415.12.(本小题满分13分)(2015·高考湖南卷)某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖.抽奖方法是从装有2个红球A1,A2和1个白球B的甲箱与装有2个红球a1,a2和2个白球b1,b2的乙箱中,各随机摸出1个球,若摸出的2个球都是红球则中奖,否则不中奖.(1)用球的标号列出所有可能的摸出结果;(2)有人认为:两个箱子中的红球比白球多,所以中奖的概率大于不中奖的概率,你认为正确吗?请说明理由.解:(1)所有可能的摸出结果是{A1,a1},{A1,a2},{A1,b1},{A1,b2},{A2,a1},{A2,a2},{A2,b1},{A2,b2},{B,a1},{B,a2},{B,b1},{B,b2}.(2)不正确.理由如下:由(1)知,所有可能的摸出结果共12种,其中摸出的2个球都是红球的结果为{A1,a1},{A1,a2},{A2,a1},{A2,a2},共4种,所以中奖的概率为412=13,不中奖的概率为1-13=23.因为23>13,所以这种说法不正确.。
【高中数学】2018-2019学年度最新北师大版必修三教学案:第三章§1 随机事件的概率 Word版含答案

[核心必知]1.概率在相同的条件下,大量重复进行同一试验时,随机事件A发生的频率会在某个常数附近摆动,即随机事件A发生的频率具有稳定性.这时,我们把这个常数叫作随机事件A的概率,记为P(A).2.频率与概率的关系频率反映了一个随机事件出现的频繁程度,但频率是随机的,而概率是一个确定的值,因此,人们用概率来反映随机事件发生的可能性的大小.在实际问题中,某些随机事件的概率往往难以确切得到,常常通过做大量的重复试验,用随机事件发生的频率作为它的概率的估计值.3.随机事件在一次试验中发生与否是随机的,但是随机性中含有规律性.认识了这种随机性中的规律性,就能使我们比较准确地预测随机事件发生的可能性.概率只是度量事件发生的可能性的大小,不能确定是否发生.4.任何事件的概率是区间[0,1]上的一个确定数,它度量该事件发生的可能性大小.小概率(接近于0)事件不是不发生,而是很少发生,大概率(接近于1)事件不是一定发生,而是经常发生.[问题思考]1.把一枚质地均匀的硬币连续掷1 000次,其中有498次正面朝上,502次反面朝上,那么说此次试验正面朝上的频率为0.498,掷一次硬币正面朝上的概率为0.5,这样理解正确吗?提示:正确.由题意,正面朝上的频率为4981 000=0.498,通过做大量的试验可以发现,正面朝上的频率都在0.5附近摆动,故掷一次硬币,正面朝上的概率是0.5.即0.498是1 000次试验中正面朝上的频率;而概率是一个确定的常数,是客观存在的,与每次试验无关.2.如果某种病治愈的概率是0.3,那么10个人中,前7个人没有治愈,后3个人一定能够治愈吗?如何理解治愈的概率是0.3?提示:如果把治疗一个病人作为一次试验,对于一次试验来说,其结果是随机的,因此前7个人没有治愈是可能的,对后3个人来说,其结果仍然是随机的,有可能治愈,也可能没有治愈.“治愈的概率是0.3”指随着试验次数的增加,即治疗人数的增加,大约有30%的人能够治愈,如果患病的有1 000人,那么我们根据治愈的频率应在治愈的概率附近摆动这一前提,就可。
2018年数学同步优化指导必修3练习:3-1-1 随机事件的概率 含解析 精品

第三章 3.1 3.1.1
1.下面的事件是必然事件的是( )
①掷一枚硬币,出现反面;②异性电荷相互吸引;③3+5>10. A .② B .③ C .① D .②③
答案:A
2.下列事件不是随机事件的是( ) A .东方日出西边雨 B .下雪不冷化雪冷 C .清明时节雨纷纷
D .梅子黄时日日晴 解析:结合三种事件的概念可知B 是必然事件,其余均为随机事件. 答案:B
3.已知随机事件A 发生的频率是0.02,事件A 出现了10次,那么共进行了________________次试验.
解析:设进行了n 次试验,则有10
n =0.02,解得n =500.故进行了500次试验.
答案:500
4.下列随机事件中,一次试验各指什么?它们各有几次试验? (1)一天中,从北京开往沈阳的7列列车,全部正点到达. (2)抛10次质地均匀的硬币,硬币落地时有5次正面向上. 解:(1)一次列车开出,就是一次试验,共有7次试验. (2)抛一次硬币,就是一次试验,共有10次试验. 5.某篮球运动员在最近几场大赛中罚球投篮的结果如下:
(1)(2)该运动员投篮的命中率约为多少?
解:(1)该运动员投篮的频率值依次为34,45,34,79,710,3
4
.
(2)由(1)可知频率总在34的附近摆动,可知运动员的进球概率约为3
4,也就是其投篮的命
中率约为3
4
.。
2018年数学同步优化指导必修3练习:3-3-2 均匀随机数

第三章 3.3 3.3.21.与均匀随机数特点不符的是( )A .它是[0,1]内的任何一个实数B .它是一个随机数C .出现的每一个实数都是等可能的D .是随机数的平均数解析:A 、B 、C 是均匀随机数的定义,均匀随机数的“均匀”是“等可能”的意思,并不是“随机数的平均数”.答案:D2.若-4≤x ≤2,则x 是负数的概率是( )A .14B .34C .13D .23解析:P =0-(-4)2-(-4)=46=23. 答案:D3.两根电线杆相距100 m ,若遭遇雷击,且雷击点距离电线杆10 m 之内时,电线杆上的输电设备将受损,则遭受雷击时设备受损的概率为 ( )A .0.1B .0.2C .0.05D .0.5 解析:如图所示,AB =100 m ,AC =DB =10 m ,则当雷击点位于AC 或BD 上时,设备受损.记“遭受雷击时设备受损”为事件A ,故所求的概率为P (A )=AC +DB AB=0.2.答案:B4.在半径为1的圆内一条直径上任取一点,过这个点作垂直于直径的弦,则弦长超过圆内接等边三角形边长的概率是________.解析:记事件A 为“弦长超过圆内接等边三角形的边长”,如图,不妨在过等边三角形BCD 的顶点B 的直径BE 上任取一点F 作垂直于直径的弦,当弦为CD 时,就是等边三角形的边长(此时F 为OE 中点),弦长大于CD 的充要条件是圆心O 到弦的距离小于OF ,由几何概型公式得,P (A )=12×22=12.答案:125.利用计算机产生100个[2,6]上的均匀随机数,具体如何操作?解:(1)在A1~A100产生100个0~1之间的均匀随机数.(2)选定B1格,键入“=A1*4+2”,按Enter 键,则在此格中的数是随机产生的[2,6]上的均匀随机数.(3)选定B1格,拖动至B100,则在B1~B100的数都是[2,6]上的均匀随机数.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 习题课
(时间:45分钟 满分:75分)
一、选择题(每小题5分,共30分)
1.把一枚骰子投掷两次,观察出现的点数,并记第一次出现的点数为a ,第二次出现的点数为b ,向量m =(a ,b ),n =(1,-2),则向量m 与向量n 垂直的概率是( )
A .1
6
B .1
12
C .1
9
D .118
解析:∵m ⊥n ,∴m ·n =0,即a -2b =0.∴a =2b .掷骰子两次,共有36个基本事件,其中第一次点数是第二次点数2倍的情况有(2,1),(4,2),(6,3),
∴概率P =336=112.
答案:B
2.已知集合A ={-9,-7,-5,-3,-1,0,2,4,6,8},从集合A 中选取两个不相同的数,构成平面直角坐标系上的点,观察点的位置,则事件A ={点落在x 轴上}与事件B ={点落在y 轴上}的概率关系为( )
A .P (A )>P (
B ) B .P (A )<P (B )
C .P (A )=P (B )
D .不确定
解析:横坐标为0与纵坐标为0的可能性是一样的. 答案:C
3.袋中有大小相同的黄、红、白球各一个,每次任取一个,有放回地取3次,则概率为8
9
的事件是( ) A .颜色全同 B .颜色不全同 C .颜色全不同
D .无红球
解析:有放回地取球3次,共27种可能结果,其中颜色全相同的结果有3种,其概率为327=19;颜色不全相同的结果有24种,其概率为2427=8
9;颜色全不同的结果有6种,其概率为627=29;无红球的情况有8种,其概率为8
27
,故选B .
答案:B
4.(2015·高考全国卷Ⅰ)如果3个正整数可作为一个直角三角形三条边的边长,那么称这3个数为一组勾股数.从1,2,3,4,5中任取3个不同的数,则这3个数构成一组勾股数的概
率为( )
A .310
B .15
C .110
D .120
解析:列举出所有结果,并分析其中的勾股数,根据古典概型求解.
从1,2,3,4,5中任取3个不同的数共有如下10个不同的结果:(1,2,3),(1,2,4),(1,2,5),(1,3,4),(1,3,5),(1,4,5),(2,3,4),(2,3,5),(2,4,5),(3,4,5),其中勾股数只有(3,4,5),所以概率为1
10
.故选C .
答案:C
5.现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率:先由计算器给出0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7,8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数:
7527 0293 7140 9857 0347 4373 8636 6947 1417 4698 0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
根据以上数据估计该运动员射击4次至少击中3次的概率为( ) A .0.852 B .0.819 2 C .0.8
D .0.75
解析:本题主要考查随机模拟法,考查学生的逻辑思维能力.因为射击4次至多击中2次对应的随机数组为7140,1417,0371,6011,7610,共5组,所以射击4次至少击中3次的概率为1-520=3
4
.
答案:D
6.甲、乙两人有三个不同的学习小组A ,B ,C 可以参加,若每人必须参加且仅能参加一个学习小组,则两人参加同一个小组的概率为( )
A .13
B .14
C .15
D .16
解析:∵甲、乙两人参加学习小组的所有事件有(A ,A),(A ,B),(A ,C),(B ,A),(B ,B),(B ,C),(C ,A),(C ,B),(C ,C),共9个,其中两人参加同一个小组的事件有(A ,A),(B ,B),(C ,C),共3个,∴两人参加同一个小组的概率为39=1
3
.
答案:A
二、填空题(每小题5分,共20分)
7.在1,3,5,8路公共汽车都要停靠的一个站(假定这个站只能停靠一辆公共汽车),有一位乘客等候1路或3路公共汽车,假定当时各路公共汽车首先到站的可能性相等,则首先到站的正好是这位乘客所要乘的公共汽车的概率是________.
解析:∵4种公共汽车先到站有4个结果,且每种结果出现的可能性相等,“首先到站的车正好是所乘车”的结果有2个,∴P =24=12
.
答案:12
8.从含有3件正品、1件次品的4件产品中不放回地任取两件,则取出的两件中恰有一件次品的概率是________________.
解析:从4件产品中不放回地任取两件,共有6个基本事件,事件“取出的两件中恰有一件次品”的基本事件有3个,故概率为1
2
.
答案:12
9.(2014·高考广东卷)从字母a ,b ,c ,d ,e 中任取两个不同字母,则取到字母a 的概率为________.
解析:从a ,b ,c ,d ,e 中任取两个不同字母的所有基本事件为ab ,ac ,ad ,ae ,bc ,bd ,be ,cd ,ce ,de ,共10个,其中取到字母a 的有4个,故所求概率为4
10
=0.4.
答案:0.4
10.在集合{1,2,3}中有放回地先后随机取两个数,若把这两个数按照取的先后顺序组成一个两位数,则“个位数与十位数不相同”的概率是________.
解析:根据题意,在集合{1,2,3}中有放回地先后随机取两个数,基本事件有(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),共9种情况;按照取的先后顺序组成一个两位数后,其中个位数与十位数相同的有3种,即(1,1),(2,2),(3,3),则“个位数与十位数不相同”的有9-3=6种,则其概率为69=23
.
答案:23
三、解答题
11.(本小题满分12分)(2014·高考天津卷)某校夏令营有3名男同学A ,B ,C 和3名女同学X ,Y ,Z ,其年级情况如下表:
(1)用表中字母列举出所有可能的结果.
(2)设M 为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件M 发生的概率.
解:(1)从6名同学中随机选出2人参加知识竞赛的所有可能结果为{A ,B},{A ,C},{A ,X},{A ,Y},{A ,Z},{B ,C},{B ,X},{B ,Y},{B ,Z},{C ,X},{C ,Y},{C ,Z},{X ,Y},{X ,Z},{Y ,Z},共15种.
(2)选出的2人来自不同年级且恰有1名男同学和1名女同学的所有可能结果为{A ,Y},{A ,Z},{B ,X},{B ,Z},{C ,X},{C ,Y},共6种.
因此,事件M 发生的概率P (M )=615=25
.
12.(本小题满分13分)班级联欢时,主持人拟出了如下一些节目:跳双人舞、独唱、朗诵等,指定3个男生和2个女生来参与,把5个人分别编号为1,2,3,4,5,其中1,2,3号是男生,4,5号是女生,将每个人的号分别写在5张相同的卡片上,并放入一个箱子中充分混合,每次从中随机地取出一张卡片,取出谁的编号谁就参与表演节目.
(1)为了选出2人来表演双人舞,连续抽取2张卡片,求取出的2人不全是男生的概率. (2)为了选出2人分别表演独唱和朗诵,抽取并观察第一张卡片后,又放回箱子中,充分混合后再从中抽取第二张卡片,求独唱和朗诵由同一个人表演的概率.
解: (1)利用树形图我们可以列出连续抽取2张卡片的所有可能结果(如图所示).
由上图可以看出,试验的所有可能结果数为20,因为每次都随机抽取,所以这20种结果出现的可能性是相同的,试验属于古典概型.
用A 1表示事件“连续抽取2人是一男一女”,A 2表示事件“连续抽取2人都是女生”,则A 1与A 2互斥,并且A 1∪A 2表示事件“连续抽取2张卡片,取出的2人不全是男生”,由列出的所有可能结果可以看出,A 1的结果有12种,A 2的结果有2种,故由互斥事件的概率加法公式,可得P (A 1∪A 2)=P (A 1)+P (A 2)=1220+220=7
10=0.7,即连续抽取2张卡片,取出
的2人不全是男生的概率为0.7.
(2)有放回地连续抽取2张卡片,需注意同一张卡片可再次被取出,并且它被取出的可能性和其他卡片相等,我们用一个有序实数对表示抽取的结果,例如“第一次取出2号,第二次取出4号”就用(2,4)来表示,所有的可能结果可以用下表列出.
概型.
用A 表示事件“独唱和朗诵由同一个人表演”,由上表可以看出,A 的结果共有5种,因此独唱和朗诵由同一个人表演的概率P (A )=525=1
5
=0.2.。
