压轴2014天津

合集下载

天津市中考20年物理试题汇编综合训练压轴题

天津市2020年中考物理百分训练最后一道综合题1.（2000天津）（6分）质量和初温都相同的甲、乙两个物体，先把甲放在一杯冷水中，热平衡后水的温度升高了△t℃，把甲取出后再立即把乙放入此杯水中，热平衡后水温又升高了△t℃，若忽略热损失，问甲、乙两种物质的比热哪个大？请加以论证说明.2. (2001年天津) (7分)一个内部含有石块的冰块放在密度为ρ0＝0.95×103ks／m3的液体中恰好能悬浮。

一个底面积为S ＝100cm2的圆柱形容器中装有水，将这个含有石块的冰块放入水中后，容器中的水面较原来升高了h1＝2.09cm。

待冰熔化后，水面又下降了h2＝0.1cm。

求冰块内石块的密度为多少(冰的密度为0.9×103kg／m3)?S b3.(2002年天津)（7分）如图13所示，底面积为的圆柱形容S a器内盛有适量的水，另一底面积为S b自圆柱体A有部分体积浸在水中，当圆柱体A相对于容器下降高度为h时（水没有溢出，圆柱体A也未全部没入水中），求物体A所受水的浮力的增加量为多少?S a4.(2003年天津)（6分）某校科技小组自制一台可以测量电阻阻值的欧姆表，如图13所示，欧姆表电路由一只灵敏电流表G，定值电阻，滑动变阻器和干电池（设电压不变）组成。

使用时可把待测电阻接在A、B两端。

为了能直接从灵敏电流表盘上读出A、B端接入的电阻的阻值，需在表盘上重新标注A、B间所测得电阻的阻值数。

当将A、B两端直接连接在一起时，调节滑动变阻器使灵敏电流表指针偏转到最大位置处（满偏），已知此时灵敏电流表内阻、滑动变阻器的有效值和定值电阻的总阻值为15Ω。

问：（1）在该欧姆表指针满偏的位置处，盘面应标注的示数是多少？（2）当A、B间断开时，该欧姆表指针所指的位置处，盘面应标注的示数是多少？（3）该欧姆表表盘正中间位置处应标注的示数是多少？简要说明为什么。

（4）该欧姆表盘上的刻度值是否均匀？请从电路原理上说明理由。

2014年天津市高考化学压轴卷含解析

2014年天津市高考化学压轴卷含解析以下数据可供解题时参考：相对原子质量（原子量）：Al 27 Fe 56 Ba 137 S 32 O 16 Cl 35.5第Ⅰ卷本卷共6题，每题6分，共36分。

在每题给出的四个选项中，只有一项是最符合题目要求的。

1. 化学无处不在，运用化学知识判断下列与化学有关的说法正确的是（）A．地沟油的主要成分是高级脂肪酸甘油酯，可用于制肥皂和加工食用油B. SO2能漂白纸浆等，故可广泛用于食品的漂白C. 高空臭氧层吸收太阳紫外线，保护地球生物；低空过量臭氧是污染气体，对人体有害D.为防止富脂食品氧化变质，常在包装袋中放入生石灰2. 下列与有机物结构、性质相关的叙述中，正确的是（）A.淀粉、纤维素都属于天然高分子化合物，二者分子式相同，互为同分异构体B.粮食酿造的酒一定温度下密封存放时间越长香味越浓，是因为有酯生成C.鸡蛋清中加入CuSO4溶液会产生盐析现象，析出的蛋白质可再溶于水D.石油化工中的分馏、裂化、裂解都是通过化学反应来获得轻质油、气体烯烃3. 下列有关元素的性质及其递变规律，说法正确的是（）A．短周期元素都是主族元素B．第ⅦA族元素从上到下，其氢化物的稳定性逐渐增强C．构成单质的分子中一定含有共价键D．硅、锗都位于金属与非金属的交界处，都可以做半导体材料4. 下列根据实验操作和现象所得出的结论正确的是（）A. 将等物质的量浓度的NaHCO3与Na2CO3溶液等体积混合，所得混合液中有：c(CO32-)+2c(OH-)＝2c(H+)+c(HCO3-)+3c(H2CO3)B. 1L pH=3的H2SO4溶液与10L Ba(OH)2溶液恰好完全反应，则Ba(OH)2溶液的pH一定等于10C. NaHS溶液呈碱性，是因HS-发生水解，其水解离子方程式为：HS-+H2O S2-+H3O+D. pH＝9的CH3COONa溶液和pH＝9的NH3·H2O溶液，两溶液中水的电离程度相同6.将图1所示装置中的盐桥（琼脂-饱和KCl溶液）换成铜导线与石墨棒连接得到图2所示装置，发现电流表指针仍然有偏转，下列说法正确的是（）A.图1中，铁棒质量减少5.6g，则甲池NaCl溶液的质量增加5.6gB.图1中的石墨电极与图2中乙池石墨a电极的电极反应式相同C.两图所示装置的能量变化均是将化学能转化为电能D.图2中电子流向为：Fe→电流计→石墨a→石墨b→铜丝→石墨c→Fe第Ⅱ卷本卷共4题，共64分。

中考物理真题分类汇编专题23力学压轴题含解析

专题23力学压轴题1.（2006天津，34）在日常生活中，为了提高烹煮食物的温度，缩短烹煮的时间，人们利用水的沸点随气压的升高而升高的性质制造出了高压锅.某种规格的高压锅出气口的直径为3.2 mm ，计算出它的面积约为8 mm 2.要使锅内的气压达到2个标准大气压，请你帮助计算该高压锅应配的限压阀的质量为多少克?(设外界气压为1个标准大气压，1个标准大气压取105Pa ，g 取10 N ／kg)【答案】80g【解析】p 阀=p 内-p 外=2p 0-p 0=p 0=105Pa 因为SmgS G S F p ===阀所以g g S p m 80kg 108N/kg10m 108Pa 102265=⨯=⨯⨯==--阀所以限压阀的质量为80g 。

2.（2009天津，28）天津在支援四川德阳地区抗震救灾活动中，一辆满载物资的总重为G 牛顿的运输车，将物资沿ABCD 路线运至D 处，AB 段海拔高度为h 1米，CD 段海拔高度为h 2米，如图甲所示。

在整个运输过程中，汽车以恒定速度v 米／秒运动，汽车t =0时经过A 处，t l 时经过B 处，t 2时经过C 处，在此过程中汽车牵引力功率P 随时间，变化的图象可简化为图乙所示(P 1、P 2、t l 和t 2也为已知量)。

（1）请分析说明汽车在AB 段和BC 段运动时牵引力的大小关系。

（2）请用已知量求汽车沿斜坡BC 段运动时所受总阻力的表达式(总阻力包括摩擦力和空气阻力)。

【答案】（1）BC 段运动时牵引力较大；（2）)()()()(1212122牛t t v h h G t t P f ----=【解析】（1）设汽车的牵引力为F ，根据Fv t Fs t W P ===，得vPF =，又因为P 2大于P l 且速度一定，所以汽车在BC 段运动时牵引力较大。

（2）汽车沿斜坡BC 段运动时所受总阻力为f ，BC 段长为L 、高为h ，由功的关系可得：)()()()()()()()()(1212122121212212122牛t t v h h G t t P f t t fv h h G t t P fL h h G t t P fLGh W F ----=-+-=-+-=-+= 即汽车沿斜坡BC 段运动时所受总阻力)()()()(1212122牛t t v h h G t t P f ----=3.（2011天津，28）如图1所示，某桥梁工程部门在一次工程作业中，利用汽车将重为G ，高为h 0的柱形实心铁块，从水深为h 1的河底竖直打捞上来。

天津市2014高考数学压轴卷文(含解析)

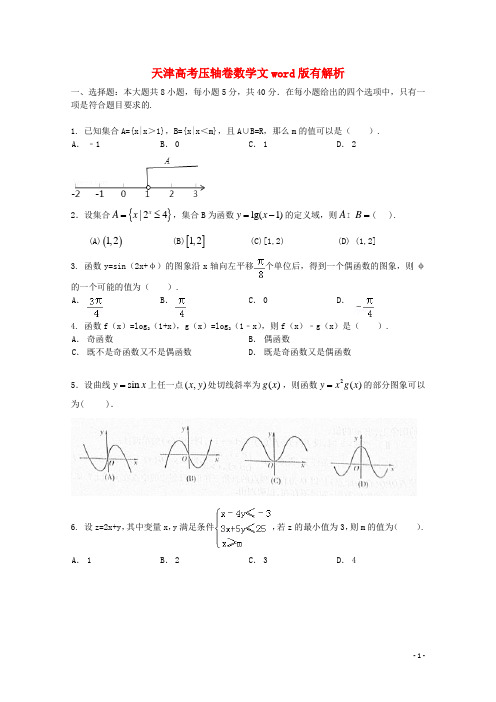
天津高考压轴卷数学文word 版有解析一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的.2．设集合{}|24xA x =≤，集合B 为函数lg(1)y x =-的定义域，则AB =( ).(A)()1,2 (B)[]1,2 (C)[1,2) (D) (1,2] 3. 函数y=sin （2x+φ）的图象沿x 轴向左平移个单位后，得到一个偶函数的图象，则φBC5．设曲线sin y x =上任一点(,)x y 处切线斜率为()g x ，则函数2()y x g x =的部分图象可以为( )．6. 设z=2x+y ，其中变量x ，y 满足条件，若z 的最小值为3，则m 的值为（）.7. 已知点P（x，y）在直线x+2y=3上移动，当2x+4y取最小值时，过P点（x，y）引圆C：=1的切线，则此切线长等于（）.C D①f（0）f（1）＞0；②f（0）f（1）＜0；③f（0）f（3）＞0；④f（0）f（3）＜0．9. 已知平面向量=（2，4），=（1，﹣2），若=﹣（•），则||=_____________．10. 已知tanα=，tanβ=﹣，且0＜α＜，＜β＜π，则2α﹣β的值________________．11. 记等差数列{a n}的前n项和为S n，已知a2+a4=6，S4=10．则a10=___________ ．12. 棱长为2的正方体被一平面截成两个几何体，其中一个几何体的三视图如图所示，那么该几何体的体积是___________.13.已知圆的方程为x2+y2﹣6x﹣8y=0，设该圆过点（3，5）的最长弦和最短弦分别为AC和BD，则四边形ABCD的面积为________________.14. 球面上有四个点P、A、B、C，若PA，PB，PC两两互相垂直，且PA=PB=PC=1，则该球的表面积是_______________．15. △ABC中，AB=3，∠A=60°，∠A的平分线AD交边BC于点D，且，则AD 的长为____________．16. 在△ABC中，BC=a，AC=b，a、b是方程的两个根，且A+B=120°，求△ABC 的面积及AB的长．三、解答题：本大题共6小题，共80分．解答应写出文字说明、证明过程或演算步骤．解答写在答题卡上的指定区域内．17. 如图，在四棱台ABCD﹣A1B1C1D1中，下底ABCD是边长为2的正方形，上底A1B1C1D1是边长为1的正方形，侧棱DD1⊥平面ABCD，DD1=2．（1）求证：B1B∥平面D1AC；（2）求证：平面D1AC⊥平面B1BDD1．18. 数列{a n}是递增的等差数列，且a1+a6=﹣6，a3•a4=8．（1）求数列{a n}的通项公式；（2）求数列{a n}的前n项和S n的最小值；（3）求数列{|a n|}的前n项和T n．19. 已知椭圆C：的右焦点为F（1，0），且点（﹣1，）在椭圆C上．（1）求椭圆C的标准方程；（2）已知动直线l过点F，且与椭圆C交于A，B两点，试问x轴上是否存在定点Q，使得恒成立？若存在，求出点Q的坐标，若不存在，请说明理由．20. 已知函数已知函数f（x）=e x+ln（x+1）（Ⅰ）求函数y=f（x）图象在点（0，f（0））处的切线方程；（Ⅱ）若a≤2，证明：当x≥0时，有f（x）≥ax+1．天津高考压轴卷数学文word 版参考答案 1.【答案】D.【解析】解：根据题意，若集合A={x|x ＞1}，B={x|x ＜m}，且A∪B=R，必有m ＞1，分析选项可得，D 符合；故选D ． 2. 【答案】D.【解析】解：{}|24{2}xA x x x =≤=≤，由10x ->得1x >，即{1}B x x =>,所以{12}A B x x =<≤，所以选D. 3. 【答案】B.【解析】解：令y=f （x ）=sin （2x+φ），则f （x+）=sin[2（x+）+φ]=sin （2x++φ），∵f （x+）为偶函数，∴+φ=k π+，∴φ=k π+，k ∈Z ，∴当k=0时，φ=．故φ的一个可能的值为．故选B ．4. 【答案】A.【解析】解：∵f（x ）=log 2（1+x ），g （x ）=log 2（1﹣x ）， ∴f（x ）﹣g （x ）的定义域为（﹣1，1）记F （x ）=f （x ）﹣g （x ）=log 2，则F （﹣x ）=log 2=log 2（）﹣1=﹣log 2=﹣F （x ）故f （x ）﹣g （x ）是奇函数．故选A.5. 【答案】C.【解析】解：'cos y x =,即()cos g x x =，所以22()cos y x g x x x ==，为偶函数，图象关于y 轴对称，所以排除A,B.当2cos 0y x x ==，得0x =或,2x k k Z ππ=+∈，即函数过原点，所以选C.6. 【答案】A.【解析】解：作出不等式组对应的平面区域， ∵若z 的最小值为3， ∴2x+y=3，由，解得，同时（1，1）都在直线x=m 上， ∴m=1．故选A ．7. 【答案】D.【解析】解：∵x+2y=3，2x+4y=2x+22y≥2x+2y=23=8，当且仅当 x=2y=时，等号成立，∴当2x+4y取最小值8时，P 点的坐标为（，），点P 到圆心C 的距离为CP==，大于圆的半径1，故切线长为==2，故选D ．8. 【答案】C.【解析】解：求导函数可得f′（x ）=3x 2﹣12x+9=3（x ﹣1）（x ﹣3） ∵a ＜b ＜c ，且f （a ）=f （b ）=f （c ）=0． ∴a ＜1＜b ＜3＜c设f （x ）=（x ﹣a ）（x ﹣b ）（x ﹣c ）=x 3﹣（a+b+c ）x 2+（ab+ac+bc ）x ﹣abc∵f （x ）=x 3﹣6x 2+9x ﹣abc ∴a+b+c=6，ab+ac+bc=9 ∴b+c=6﹣a ∴bc=9﹣a （6﹣a ）＜∴a 2﹣4a ＜0 ∴0＜a ＜4∴0＜a ＜1＜b ＜3＜c∴f （0）＜0，f （1）＞0，f （3）＜0∴f（0）f（1）＜0，f（0）f（3）＞0故选C．9. 【答案】.【解析】解：∵向量=（2，4），=（1，﹣2），∴=2×1+4×（﹣2）=﹣6．∴=（2，4）﹣（﹣6）（1，﹣2）=（8，﹣8），∴=．故答案为．10. 【答案】﹣．【解析】解：∵0＜α＜，tanα=＜1=tan，y=tanx在（0，）上单调递增，∴0＜α＜，又＜β＜π，∴﹣π＜2α﹣β＜﹣，∵tan2α===，tanβ=﹣，∴ta n（2α﹣β）===1，∴2α﹣β=﹣．11. 【答案】10．【解析】解：等差数列{a n}的前n项和为S n，∵a2+a4=6，S4=10，设公差为d，∴，解得a1=1，d=1，∴a10=1+9=10．故答案为10．12. 【答案】4．【解析】解：由三视图知余下的几何体如图示：∵E、F都是侧棱的中点，∴上、下两部分的体积相等，∴几何体的体积V=×23=4．13. 【答案】．【解析】解：圆的方程为x2+y2﹣6x﹣8y=0化为（x﹣3）2+（y﹣4）2=25．圆心坐标（3，4），半径是5．最长弦AC是直径，最短弦BD的中点是E．S ABCD=故答案为.14.【答案】3π．【解析】解：∵PA、PB、PC两两互相垂直，且PA=PB=PC=1，∴分别以PA、PB、PC为长、宽、高，作出正方体设所得正方体的外接球为球O，则P、A、B、C四点所在的球面就是球O表面就是正方体的对角线长等于球O的直径即2R==，得R=∴球O的表面积为S=4πR2=4π（）2=3π故答案为3π.15. 【答案】2．【解析】解：△ABC中，∵AB=3，∠A=60°，∠A的平分线AD交边BC于点D，且，取AC的一个三等分点E，满足AE=AC，作DF平行于AE，则由条件可得四边形AEDF为平行四边形，∴∠AFD=120°，∠FAD=30°，∠FDA=30°，故△AFD为等腰三角形，∴AF=DF=AC，故四边形AEDF为菱形．再由AF=λAB=3λ=DF=AC，可得 AC=9λ，菱形AEDF的边长为3λ．△AFD中，由余弦定理可得AD2=（3λ）2+（3λ）2﹣2•3λ•3λ•cos120°=27λ2，∴AD=3λ．△ABD中，由余弦定理可得BD2=32+27λ2﹣2×3×3λ×cos30°=27λ2﹣27λ+9，∴BD=3．△ACD中，由余弦定理可得 CD2=81λ2+27λ2﹣2×9λ×3λ×cos30°=27λ2=3λ．再由三角形的内角平分线性质可得，即=，解得λ=，或λ=（舍去）．故AD=3λ=3×=2，故答案为 2．16. 【解析】∵A+B=120°，∴C=60°．∵a、b是方程的两个根，∴a+b=，ab=2，∴S△ABC==，AB=c====．17. 【解析】证明：（1）设AC∩BD=E，连接D1E，∵平面ABCD∥平面A1B1C1D1．∴B1D1∥BE，∵B1D1=BE=，∴四边形B1D1EB是平行四边形，所以B1B∥D1E．又因为B1B⊄平面D1AC，D1E⊂平面D1AC，所以B1B∥平面D1AC（2）证明：侧棱DD1⊥平面ABCD，AC⊂平面ABCD，∴AC⊥DD1．∵下底ABCD是正方形，AC⊥BD．∵DD1与DB是平面B1BDD1内的两条相交直线，∴AC⊥平面B1BDD1∵AC⊂平面D1AC，∴平面D1AC⊥平面B1BDD1．18. 【解析】（1）由得：，∴a3、a4是方程x2+6x+8=0的二个根，∴x1=﹣2，x2=﹣4；∵等差数列{a n}是递增数列，∴a3=﹣4，a4=﹣2，∴公差d=2，a1=﹣8．∴a n=2n﹣10；（2）∵S n==n2﹣9n=﹣，∴（S n）min=S4=S5=﹣20；（3）由a n≥0得2n﹣10≥0，解得n≥5，此数列前四项为负的，第五项为0，从第六项开始为正的．当1≤n≤5且n∈N*时，T n=|a1|+|a2|+…+|a n|=﹣（a1+a2+…+a n）=﹣S n=﹣n2+9n；当n≥6且n∈N*时，T n=|a1|+|a2|+…+|a5|+|a6|+…+|a n|=﹣（a1+a2+…+a5）+（a6+…+a n）=S n﹣2S5=n2﹣9n﹣2（25﹣45）=n2﹣9n+40．∴T n=．19. 【解析】（1）由题意，c=1∵点（﹣1，）在椭圆C上，∴根据椭圆的定义可得：2a=，∴a=∴b2=a2﹣c2=1，∴椭圆C的标准方程为；（2）假设x轴上存在点Q（m，0），使得恒成立当直线l的斜率为0时，A（，0），B（﹣，0），则=﹣，∴，∴m=①当直线l的斜率不存在时，，，则•=﹣，∴∴m=或m=②由①②可得m=．下面证明m=时，恒成立当直线l的斜率为0时，结论成立；当直线l的斜率不为0时，设直线l的方程为x=ty+1，A（x1，y1），B（x2，y2）直线方程代入椭圆方程，整理可得（t2+2）y2+2ty﹣1=0，∴y1+y2=﹣，y1y2=﹣∴=（x1﹣，y1）•（x2﹣，y2）=（ty1﹣）（ty2﹣）+y1y2=（t2+1）y1y2﹣t（y1+y2）+=+=﹣综上，x轴上存在点Q（，0），使得恒成立．20. 【解析】（Ⅰ）解：∵f（x）=e x+ln（x+1），∴，则f'（0）=2又f（0）=e0+ln1=1∴函数y=f（x）图象在点（0，f（0））处的切线方程为：y﹣f（0）=f'（0）x，即函数y=f（x）图象在点（0，f（0））处的切线方程为y=2x+1；（Ⅱ）证明：当a≤2时，则2﹣a≥0…①令g（x）=f（x）﹣ax﹣1，则令φ（x）=e x﹣x﹣1（x∈R），则φ'（x）=e x﹣1（x∈R），由φ'（x）=0，得x=0当x≤0时，e x≤1，即e x﹣1≤0；当x＞0时，e x＞1，即e x﹣1＞0∴函数φ（x）=e x﹣x﹣1在（﹣∞，0]为减函数，在（0，+∞）为增函数∴φ（x）min=φ（0）=0，即φ（x）≥0∴对∀x∈R，都有e x≥x+1故当x≥0时，x+1＞0，∴，∴g'（x）≥0，∴若a≤2，函数y=g（x），在[0，+∞）为增函数，∴当x≥0时，g（x）≥g（0）=0∴当a≤2时，x≥0，有f（x）≥ax+1成立．。

2014年中考真题精品解析语文(天津卷)精编word版(原卷版)

第|一卷一、选择题(本大题共11小题,共30分.1～3小题,每题2分；4～11小题,每题3分)1．下面各组词语中加点字的注音,完全正确的一项为哪一项( )A．匀称．(chèn) 干涸．(gù) 吹毛求疵．(cī)B．归省．(shěng) 娴．熟(xián) 义愤填膺．(yīng)C．伫．立(zhù) 眷．念(juàn) 相得益彰．(zhāng)D．阴霾．(mái) 拮据．(jū) 忍俊不禁．(jìn)2．依次填入下面一段文字横线处的词语,最||恰当的一项为哪一项( )生命的历程中,人们往往丢掉当时觉得不重要的东西,抛掷时毫不；等到时光逐渐流去,失去的东西在流光中却不停地,在回忆里逐步被放大 .时光虽缓,渐渐也远逝了,等有一天终于,光阴却已永不回头 .A．惋惜闪烁醒悟B．怜惜闪耀醒悟C．怜惜闪烁悔恨D．惋惜闪耀悔恨5．下面情境中,小晨表达得体的一项为哪一项( )【情境】小晨和小鹏约好周末一同去科技馆参观.小晨去小鹏家找他,小鹏的奶奶开了门.A．我要找一下小鹏,我和他去科技馆参观.B．您是谁啊?小鹏在家吗?我和找他有事.C．您好!是奶奶吧?我是小晨,我和小鹏约好去科技馆,他在家吗? .D．您好!我想找小鹏去科技馆,你让他马上出来.6．下面对诗句的赏析,不恰当．．．的一项为哪一项( )A．日月之行,假设出其中；星汉灿烂,假设出其里. (曹操?观沧海? )B．落红不是无情物,化作春泥更护花. (龚自珍?己亥杂诗? )诗人从落花、春泥展开联想,表达了自己变革现实的理想无法实现的伤感与失望.C．江塞下秋来风景异,衡阳雁去无留意. (范仲淹?渔家傲·秋思? )这两句描写极其寒冷的边塞秋天,秋雁毫无逗留之意,如此景物与词人家乡大不相同.D．因为只有那里我们不像牲口一样活,蝼蚁一样死……那里,永恒的中国! (戴望舒?我用残损的手掌? )诗句中两个比喻用沦陷区反衬解放区,表达出诗人对解放区的深情向往和真挚情感.阅读?看云识天气?的节选文字,答复7～8题.我们还可以根据云上的荣耀现象,推测天气的情况 .在太阳和月亮的周围,有时会出现一种美丽的七彩光圈,里层是红色的,外层是紫色的 .这种光圈叫做晕 .日晕和月晕常常产生在卷层云上,卷层云后面的大片高层云和雨层云,是大风雨的征兆 .所以有"日晕三更雨,月晕午时风〞的说法 .说明出现卷层云,并且伴有晕,天气就会变坏 .另有一种比晕小的彩色光环,叫做"华〞 .颜色的排列是里紫外红,跟晕刚好相反 .日华和月华大多产生在高积云的边缘局部 .华环由小变大,天气趋向晴好 .华环由大变小,天气可能转为阴雨 .夏天,雨过天晴,太阳对面的云幕上,常会挂上一条彩色的圆弧,这就是虹 .人们常说："东虹轰隆西虹雨 .〞意思是说,虹在东方,就有雷无雨；虹在西方,将有大雨 .还有一种云彩常出现在清晨或黄昏 .太阳照到天空,使云层变成红色,这种云彩叫做霞 .朝霞在西,说明阴雨天气在向我们进袭；晚霞在东,表示最||近几天里天气晴朗 .所以有"朝霞不出门,晚霞行千里〞的谚语 .7．下面对选文说明的主要内容,概括正确的一项为哪一项( )A．云的荣耀与天气的关系. B．云的形态与天气的关系.C．晴天的云荣耀富于变化. D．雨雪天气的云出现的位置较高.A．日晕和月晕颜色非常美丽,如果出现在卷层云上,往往带来风雨天气.B．日华与月华大多产生在高积云边缘局部,颜色的排列是里红外紫.C．作者将晕、华、虹、霞进行了比较说明,突出了各自的特点.D．选文按照总分的逻辑顺序,分类依次介绍,层次清晰.阅读?生于忧患,死于安乐? ,答复9～11题.舜发于畎亩之中,傅说举．于版筑之间,胶鬲举于鱼盐之中,管夷吾举于士,孙叔敖举于海,百里奚举于市 .故天将降大任．于是人也,必先苦其心志,劳其筋骨,饿其体肤,空乏其身,行拂乱其所为,所以动心忍性,曾益其所不能 .人恒过．然后能改,困于心衡于虑而后作,征于色发于声而后喻 .入那么无法家拂士,出．那么无敌国外患者,国恒亡 .然后知生于忧患,而死于安乐也 .9．下面句子中加点词语的解释,不正确．．．的一项为哪一项( )B．故天将降大任．于是人也任：责任,使命C．人恒过．然后能改正：犯错误D．出．那么无敌国外患者出：指在国外10．下面句子中加点字的词语,不是．．通假字的一项为哪一项( )11．下面对选文的分析,不正确．．．的一项为哪一项( )A．选文第|一自然段列举古代贤士的事例,说明有成就的人必先经历苦难的磨炼.B．选文第二自然段先提出中|心论点,再论述一个国|家如果没有内忧外患将导致灭亡.C．从选文可以看出, "困于心衡于虑而后作〞是造就人才的主观因素.D．选文善用排比,而且句式灵活,既增添了气势,也给人以美感.第二卷二、(本大题共1小题,共8分)12．请将下面古诗文语句补充完整(8分)(1 )感时花溅泪 , . (杜甫?春望? )(2 )夕阳西下 , . (马致远?天净沙·秋思? )(3 )大漠孤烟直 , . (||王维?使至||塞上? )(4 )只恐双溪舴艋舟 , . (李清照?武陵春? )(5 ) ?留取丹心照汗青 . (文天祥?过零丁洋? )(6 )山随平野尽 , . (李白?渡荆门送别? )(8 )人有悲欢离合 , .此事古难全 . (苏轼?水调歌头·明月几时有? )三、 (本大题共3小题 ,共7分 )阅读下面文言文 ,答复13～15题 .楚庄||王问詹何①曰： " (治|国 )奈何 ?〞詹何对．曰： "臣明于治身而不明于 (治|国 )也 .〞楚庄||王曰： "寡人得奉宗庙社稷② ,愿学所以守之 .〞詹何对曰： "臣未尝闻身治③而国乱者也 ,又未尝闻身乱而国治者也 .故本．在身 ,不敢对以末④ .〞楚||王曰： "善 .〞 (选自?列子·说符篇? ) 【注释】①詹何：古代哲学家 .②社稷：指国|家 .③身治：自身修养好 .④末：末节 ,次要的事情 .13．解释文中加点词语的含义 . (2分 )(1 )詹何对．曰对： (2 )故本．在身本：臣明于治身而不明于 (治|国 )也 .15．楚庄||王在与詹何的对话中得到了怎样的启示 ?请用自己的话概括 . (3分 )四、 (本大题共4小题 ,共15分 )阅读?几生修得到梅花? ,答复16～19题 .李榕桦②江南的冬天还未过去 ,寒风肆虐 ,雪花纷飞 ,万木都在沉睡之中 ,而梅花却在这时 ,绽开一树树的花朵 ,向人们报告着春之将至||的讯息 .她不管桃儿、杏儿们嫉妒的流言 ,也不贪图蜂儿、蝶儿们嗡嗡的追捧 ,孤傲豪迈地开在漫天飞雪中 ,不畏严寒 ,独步早春 .③怒号的狂风不是不想．．．．吹灭她的火焰 ,漫天的大雪不是不想．．．．掩息她的娇媚 ,而她却在凌霜斗雪中更加灼灼有神 .那纷纷扬扬从天而降的雪花 ,似乎成了他玉洁冰清的知音 ,心魂相印的伴侣 .④在无锡梅园欣赏过梅花 ,走进梅花 ,你会感到诗意像湖水一样漫上心头 .润如凝脂的红梅 ,洁如瑞雪的白眉 ,碧光盈盈的绿梅 ,明艳灿灿的黄梅 ,构成了一个缤纷多彩的梅的世|界 .小小的花朵似乎不受半点尘埃的浸染 ,宛假设悄然飘落凡尘的仙子 ,真正是冰肌玉骨 .你假设拿俗常的桃花、杏花和她们对照 ,越发显得梅花的脱俗 .置身花下 ,你会被随之而来的清幽的芳馨环绕 ,使你立刻想到 "暗香浮动〞 .梅花的香气不像梨花、水仙花那样肥硕袭人 ,她假设有假设无 ,清逸幽雅 ,它是那么婉约和内敛 .欣赏梅的枝干 ,姿态极美 ,有的疏影横斜 ,有的奇崛突兀 ,有的苍劲朴拙 ,有的狂放洒脱 .怪不得古人说 "梅以形势为第|一〞 .⑤最||喜欢看那棵古梅,虬曲盘错,势如游龙 .铁骨嶙峋、古朴苍劲的枝头,绽放着朵朵温润率真的红梅,那种强烈的比照给你以心灵的撞击,无法用语言描述 .仿佛眼前的梅花是从悠远的历史深处走来,她曾与宋代林和靖①相伴相守,在西湖孤山朦胧的月色下, "疏影横斜水清浅,暗香浮动月黄昏〞；她曾和画家||王冕相交,是||王冕笔下"不要人夸颜色好,只留清气满乾坤〞的那幅墨梅的范本,在||王冕精心经营的梅园里度过许多春夏秋冬 .她是陆游一生痴迷的梅花,她是||王维、苏轼、杨万里、范大成他们曾经反复歌咏的梅花,她是被鲁迅识为"只有梅花是知己〞的那一树,她是历代有道的君子仰慕钦敬,视为修养的典范,感慨"几生修得到梅花〞那一树 .⑥特立独行的梅花从历史深处走来,那冰肌玉骨的韵致,高标清雅的圣洁,横斜疏美的仙姿,傲岸坚贞的风骨,凌霜斗雪的意志,独步早春的气魄,铸成了华夏民族的心魂,成为了中华民族代代相袭的品格和精神 .站在梅花前,无法用语言表达自己的心境,还是陆游说的好啊, "何方化身千亿?一树梅花一放翁〞 .(选自?青海湖?2021年第2期,原文有删改) 【注释】①林和靖：林逋(968 -1028 ) .字君复,谥号和靖先生.E．文章引用大量诗句,既表达了作者的心境,又丰富了文章的意蕴,语言典雅,令人回味.19．文章第⑥段在全文有怎样的作用?请分别从结构和内容角度具体分析. (4分)五、(本大题共4小题,共10分)(一)综合性学习(4分)某班开展了"美丽天津〞综合性学习活动,请你按照要求,答复20～21题.【材料一】蓟北雄关- -黄崖关长城,自古为兵家必争之地,城墙石垒砖包,坚如铜墙铁壁 .层峦叠嶂之中,战台林立,高地相连,前后照应,置身其间,仿佛又回到了那战火纷飞的年代 .【材料二】将在我市举行的第三届绿博会,日前已经完成基建工程,48家参展单位被分别划分到六大主题区域,各参展单位已于6月陆续进场施工 .【材料三】还和风景线宛如一幅长长的风景画卷,装扮着美丽的天津,夜幕降临,两岸假设明假设暗的各色灯光,倒映在河水中,似绚丽的彩霞,使人们产生无限的遐思 .【材料四】高度位列世|界第四,亚洲第二的天塔,坐落在波光粼粼的天塔胡(中|央) ,犹如一剑穿天,直插云霄 .这里地势开阔,花草繁茂,湖光塔影,相映生辉 .【材料五】"美丽天津一号工程〞,内容包括清新大气、清水河道、清洁村庄、清洁社区和绿化美化 .通过"四清一化〞行动,市民将享受到更多的碧水蓝天 .【材料五】"美丽天津一号工程〞,内容包括清新大气、清水河道、清洁村庄、清洁社区和绿化美化 .通过"四清一化〞行动,市民将享受到更多的碧水蓝天 .20．上面是某同学以"寻找津城最||美风景〞为主题搜集的一组材料,不符合．．．这一主题的两那么材料是、. (2分)21．请你仿照加点局部的句式,将后面的句子补充完整. (2分),；, .(二)名著阅读(6分) .请根据你的阅读积累,答复22～23题.22．请在横线处填写对应的人物. (3分)阅读名著能启迪思想,引领人生 .读施耐庵的?水浒传? ,能让我们深切地感受到"景阳冈打虎〞的①等梁山好汉的英雄气概；读鲁迅的?朝花夕拾? ,能让我们从②身上,学到严谨、正直、热诚、没有民族偏见的高尚品质；读罗曼·罗兰的?名人传? ,能让我们在贝多芬、米开朗琪罗、③三位伟人身上,体会到与命运抗争的崇高勇气和勇于担当的伟大情怀；读?傅雷家书? ,能让我们领悟到遇困难不气馁,要有国|家民族荣誉感的人生道理 .①②③23．?钢铁是怎样炼成的?是一部影响了几代人的史诗性长篇小说,主人公保尔被视为精神楷模.请结合保尔的经历,举一例谈谈保尔身上据有怎样的精神品质 . (3分)[来源:Z,xx,k．Com]六、(本大题共1小题,共50分)24．作文. (50分)什么是滋养你心灵的甘露呢?请以"我心灵的甘露〞为题目,写一篇文章.。

2014年高考数学压轴卷及答案

绝密★启用前试卷类型：A2014年高考数学压轴卷22()x x -++第Ⅰ卷（选择题共50分）一、选择题（本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的）1、定义集合运算：A ⊙B ={z ︳z =xy ,x ∈A ,y ∈B },设集合A ={—2013,0,2013},B ={ln a ,e a },则集合A ⊙B 的所有元素之和为【】 A. 2013 B. 0 C. —2013 D. ln2013+e 20132、奇函数f (x )在（0，+∞）上的解析式是f (x )= x (1—x )，则在（-∞，0）上，f (x )的函数解析式是【】A. f (x )= —x (1—x )B. f (x )= x(1+x ) C. f (x )= —x (1+x ) D. f (x )= x (x —1) 3、若复数221z i i=++，其中i 是虚数单位，则复数z 的模为【】 A.2B.C. D. 24、设a ∈R ，则“a =1”是“直线l 1：ax +2y —1=0与直线l 2：x +（a +1）y +4=0平行的【】A.充分不必要条件B.必要不充分条件 C. 充分必要条件 D. 既不充分不必要条件 5、若一个螺栓的底面是正六边形，它的主视图和俯视图如图所示，则它的体积是【】 A ． B ． π C ．D ．6、为得到函数πcos 23y x ⎛⎫=+ ⎪⎝⎭的图像，只需将函数sin 2y x =的图像【】 A ．向左平移5π12个长度单位B ．向右平移5π12个长度单位C ．向左平移5π6个长度单位 D ．向右平移5π6个长度单位7、若程序框图如图所示,则该程序运行后输出k 的值是( ) A. 4 B. 5C. 6D. 7容器8、从某高中随机选取5名高三男生，其身高和体重的数据如下表所示：根据上表可得回归直线方程0.56y x a =+，据此模型预报身高为172 cm 的高三男生的体重为【】A ． 70.09B ． 70.12C ． 70.55D ． 71.059、在棱长分别为1，2，3的长方体上随机选取两个相异顶点，若每个顶点被选的概率相同，则选到两个顶点的距离大于3的概率为【】A.47 B.37 C.27 D.31410、设等差数列{}n a 满足：22222233363645sin cos cos cos sin sin 1sin()a a a a a a a a -+-=+，公差(1,0)d ∈-. 若当且仅当9n =时，数列{}n a 的前n 项和n S 取得最大值，则首项1a 的取值范围是【】 A. 74,63ππ⎛⎫ ⎪⎝⎭B. 43,32ππ⎛⎫⎪⎝⎭ C. 74,63ππ⎡⎤⎢⎥⎣⎦D.43,32ππ⎡⎤⎢⎥⎣⎦第Ⅱ卷（非选择题共100分）二、填空题：（本大题共5小题，每小题5分，共25分．把答案值填在答题卡的相应位置） 11、给n 个自上而下相连的正方形着黑色或白色，当n≤4时，在所有不同的着色方案中，黑色正方形互不相邻的着色方案如图1所示，由此推断，当n=6时，黑色正方形互不相邻的着色方案共有____________种，至少有两个黑色正方形相邻的着色方案共有____________.(结果用数值表示) 12、设(5nx 的展开式的各项系数之和为M ，二项式系数之和为N ，若M —N=240，则展开式中3x 的系数为13、如图是一种加热水和食物的太阳灶，上面装有可旋转的抛物面形的反光镜，镜的轴截面是抛物线的一部分，盛水和食物的容器放在抛物线的焦点处，容器由若干根等长的铁筋焊接在一起的架子支撑。

2014年天津市高考历史压轴卷(含解析)

绝密★启用前2014天津市高考压轴卷文综历史1．《孟子·尽心》载：“善政不如善教之得民也。

善政，民畏之；善教，民爱之。

善政得民财，善教得民心。

”据此可知，孟子强调A．道德教化 B．兴办教育 C．克已复礼 D．礼法并用2．“元代行省长官在忽必烈时期主要职掌钱粮、户口、屯种、漕运等事务，成宗时，可就领本省军队。

同时，没有中书省、枢密院转发的诏旨，行省官员既不能更改赋税，也不能调动军队。

”据此可知元代A．地方长官有较大独立性 B．重视对地方官员的监察C．行省权力受到中央节制 D．专制主义皇权达到顶峰3．近代有学者说，“文人画不仅形于山水，无物不可寓文人之兴味也明矣”、“西洋画可谓形似极矣！而立体派之思想转变，亦足见形似之不足尽艺术之长”。

该学者这一认识的主旨是A．西方画作都以形似为重 B．文人画和西洋画可以取长补短C．文人画有形似的不足 D．文人画与立体派都重精神表达4．标语具有战斗力，在战争年代尤为如此。

下列标语与其它三个不属于同一时期的是A B C D5．1904年，商部头等顾问张謇上书皇帝，提出划定捕鱼区建议，并区别近海和远洋，主张“以内外渔界，定新旧渔业行渔范围”，保护中国近海“本国自主之权”。

后清政府绘制了《江海渔界全图》。

这一史实A．推动了中国近代海军的发展 B．遏制了列强对渔业资源的掠夺C．有利于发展实业与维护海权 D．收回了帝国主义在华侵略权益6．1694年，英国议会通过了《三年法案》，规定每三年必须召开一届议会，每届议员的最长任期不超过三年。

该规定A．标志英国君主立宪制的确立 B．保障了内阁在政治生活中的地位C．使工业资产阶级获得更多席位 D．使议会成为限制王权的常设机构7.马丁·路德提出“每个人都是自己的牧师”的观点。

对这一观点理解正确的是A.人们应严格遵守基督教的仪式B.在宗教信仰上应遵循牧师指导C.每个人都可以和上帝直接沟通D.人们应自觉传播基督教的教义8．英国史学家彼得·伯克强调写作《图像证史》一书的目的：一是鼓励图像证据的使用；二是告知使用者某些存在的陷阱。

天津市七年级数学压轴题专题

天津市七年级数学压轴题专题一、七年级上册数学压轴题1．（概念提出）数轴上不重合的三个点，若其中一点到另外两点的距离的比值为n（n≥1），则称这个点是另外两点的n阶伴侣点．如图，O是点A、B的1阶伴侣点；O是点A、C的2阶伴侣点；O也是点B、C的2阶伴侣点．（初步思考）（1）如图，C是点A、B的阶伴侣点；（2）若数轴上两点M、N分别表示－1和4，则M、N的32阶伴侣点所表示的数为；（深入探索）（3）若数轴上A、B、C三点表示的数分别为a、b、c，且点C是点A、B的n阶伴侣点，请直接用含a、b、n的代数式表示c．2．如图一，点C在线段AB上，图中有三条线段AB、AC和BC，若其中一条线段的长度是另外一条线段长度的2倍，则称点C是线段AB的“巧点”．（1）填空：线段的中点这条线段的巧点（填“是”或“不是”或“不确定是”）（问题解决）（2）如图二，点A和B在数轴上表示的数分别是20和40，点C是线段AB的巧点，求点C在数轴上表示的数。

（应用拓展）（3）在（2）的条件下，动点P从点A处，以每秒2个单位的速度沿AB向点B匀速运动，同时动点Q从点B出发，以每秒4个单位的速度沿BA向点A匀速运动，当其中一点到达中点时，两个点运动同时停止，当A、P、Q三点中，其中一点恰好是另外两点为端点的线段的巧点时，直接写出运动时间()t s的所有可能值．3．已知数轴上，M表示－10，点N在点M的右边，且距M点40个单位长度，点P，点Q是数轴上的动点．（1）直接写出点N所对应的数；（2）若点P从点M出发，以5个单位长度/秒的速度向右运动，同时点Q从点N出发，以3个单位长度/秒向左运动，设点P、Q在数轴上的D点相遇，求点D的表示的数；（3）若点P从点M出发，以5个单位长度/秒的速度向右运动，同时点Q从点N出发，以3个单位长度/秒向右运动，问经过多少秒时，P，Q两点重合？4．如图，在数轴上A 点表示数a ，B 点表示数b ，C 点表示数c ，其中39a c ==、．若点A 与点B 之间的距离表示为AB a b ，点B 与点C 之间的距离表示为BC b c =-，点B 在点A C 、之间，且满足2BC AB = ．（1）b = ；（2）若点M N 、分别从A 、C 同时出发，相向而行，点M 的速度是1个单位/秒，点N 的速度是2个单位秒，经过多久后M N 、相遇．（3）动点M 从A 点位置出发，沿数轴以每秒1个单位的速度向终点C 运动，设运动时间为t 秒，当点M 运动到B 点时，点N 从A 点出发，以每秒2个单位的速度沿数轴向C 点运动，N 点到达C 点后，再立即以同样的速度返回，运动到终点A ，问：在点N 开始运动后，M N 、两点之间的距离能否为2个单位？如果能，请求出运动的时间t 的值以及此时对应的M 点所表示的数；如果不能，请说明理由．5．已知实数a ，b ，c 在数轴上所对应的点分别为A ，B ，C ，其中b 是最小的正整数，且a ，b ，c 满足()2520c a b -++=．两点之间的距离可用这两点对应的字母表示，如：点A 与点B 之间的距离可表示为AB ．（1）a = ，b = ，c = ；（2）点A ，B ，C 开始在数轴上运动，若点A 以每秒1个单位长度的速度向左运动，同时，点B 以每秒2个单位长度的速度向右运动，点C 以每秒5个单位长度的速度向右运动，假设运动时间为t 秒，则AB = ，BC = ；（结果用含t 的代数式表示）这种情况下，BC AB -的值是否随着时间t 的变化而改变？若变化，请说明理由；若不变，请求其值；（3）若A ，C 两点的运动和（2）中保持不变，点B 变为以每秒n （0n >）个单位长度的速度向右运动，当3t =时，2AC BC =，求n 的值．6．在数轴上，点A 代表的数是-12，点B 代表的数是2，AB 表示点A 与点B 之间的距离．（1）①若点P 为数轴上点A 与点B 之间的一个点，且AP=6，则BP=_____； ②若点P 为数轴上一点，且BP=2，则AP=_____；（2）若C 点为数轴上一点，且点C 到点A 点的距离与点C 到点B 的距离的和是20，求C 点表示的数；（3）若点M 从点A 出发，点N 从点B 出发，且M 、N 同时向数轴负方向运动，M 点的运动速度是每秒6个单位长度，N 点的运动速度是每秒8个单位长度，当MN=2时求运动时间t 的值．7．如图，在数轴上，点O 是原点，点A ，B 是数轴上的点，已知点A 对应的数是a ，点B对应的数是b ，且a ，b 满足25(6)03a b b ++-=．（1）在数轴上标出点A ，B 的位置．（2）在数轴上有一个点C ，满足92CA CB -=，则点C 对应的数为________．（3）动点P ，Q 分别从A ，B 同时出发，点P 以每秒6个单位长度的速度沿数轴向右匀速运动，点Q 以每秒3个单位长度的速度沿数轴向左匀速运动设运动时间为t 秒（0t >）． ①当t 为何值时，原点O 恰好为线段PQ 的中点．②若M 为AP 的中点，点N 在线段BQ 上，且13BN BQ =，若3MN =时，请直接写出t 的值．8．如图，数轴上有三个点A 、B 、C ，表示的数分别是4-、2-、3，请回答：（1）若使C 、B 两点的距离与A 、B 两点的距离相等，则需将点C 向左移动______个单位．（2）若移动A 、B 、C 三点中的两个点，使三个点表示的数相同，移动方法有种，其中移动所走的距离和最小的是_______个单位；（3）若在表示1-的点处有一只小青蛙，一步跳1个单位长．小青蛙第1次先向左跳1步，第2次再向右跳3步，然后第3次再向左跳5步，第4次再向右跳7步按此规律继续跳下去，那么跳第99次时，应跳_______步，落脚点表示的数是_______．（4）数轴上有个动点表示的数是x ，则|1||4||5|x x x ++-++的最小值是_______． 9．如图，在数轴上A 点表示数a ，B 点示数b ，C 点表示数c ，b 是最小的正整数，且a 、c 满足|a+2|+（c ﹣7）2=0．（1）a= ，b= ，c= ；（2）若将数轴折叠，使得A 点与C 点重合，则点B 与数表示的点重合；（3）点A 、B 、C 开始在数轴上运动，若点A 以每秒1个单位长度的速度向左运动，同时，点B 和点C 分别以每秒2个单位长度和4个单位长度的速度向右运动，假设t 秒钟过后，若点A 与点B 之间的距离表示为AB ，点A 与点C 之间的距离表示为AC ，点B 与点C 之间的距离表示为BC ．则AB= ，AC= ，BC= ．（用含t 的代数式表示）（4）请问：3BC ﹣2AB 的值是否随着时间t 的变化而改变？若变化，请说明理由；若不变，请求其值．10．定义：若A ，B ，C 为数轴上三点，若点C 到点A 的距离是点C 到点B 的距离2倍，我们就称点C 是[],A B 的美好点．例如；如图1，点A 表示的数为1-，点B 表示的数为2．表示1的点C 到点A 的距离是2，到点B 的距离是1，那么点C 是[,]A B 的美好点；又如，表示0的点D 到点A 的距离是1，到点B 的距高是2，那么点D 就不是[,]A B 的美好点，但点D 是[,]B A 的美好点．如图2，M ，N 为数轴上两点，点M 所表示的数为7-，点N 所表示的数为2．（1）点E ，F ，G 表示的数分别是3-，6.5，11，其中是[,]M N 美好点的是________；写出[,]N M 美好点H 所表示的数是___________．（2）现有一只电子蚂蚁P 从点N 开始出发，以2个单位每秒的速度向左运动．当t 为何值时，点P 恰好为M 和N 的美好点？11．综合与探究：射线OC 是AOB ∠内部的一条射线，若12C A BO O C ∠=∠，则我们称射线OC 是射线OA 的伴随线．例如，如图1，60AOB ∠=︒，20AOC COD BOD ∠=∠=∠=︒，则12AOC BOC ∠=∠，称射线OC 是射线OA 的伴随线；同时，由于12BOD AOD ∠=∠，称射线OD 是射线OB 的伴随线．完成下列任务：（1）如图2，150AOB ∠=︒，射线OM 是射线OA 的伴随线，则AOM ∠= ︒，若AOB ∠的度数是x ，射线ON 是射线OB 的伴随线，射线OC 是AOB ∠的平分线，则NOC ∠的度数是．（用含x 的代数式表示）（2）如图3，如180AOB ∠=︒，射线OC 与射线OA 重合，并绕点O 以每秒6︒的速度逆时针旋转，射线OD 与射线OB 重合，并绕点O 以每秒10︒的速度顺时针旋转，当射线OD 与射线OA 重合时，运动停止．①是否存在某个时刻t （秒），使得COD ∠的度数是20︒，若存在，求出t 的值，若不存在，请说明理由；②当t 为多少秒时，射线OC ，OD ，OA 中恰好有一条射线是其余两条射线的伴随线．请直接写出结果．12．如图，O 为直线AB 上的一点，过点O 作射线OC ，∠AOC=30°，将一直角三角板（∠M=30°），的直角顶点放在O 处，一边ON 在射线OA 上，另一边OM 与OC 都在直线AB 的上方，将图1中的三角板绕点O 以每秒3°的速度沿顺时针方向旋转一周．（1）几秒后ON 与OC 重合？（2）如图2，经过t 秒后，OM 恰好平分∠BOC ，求此时t 的值．（3）若三角板在转动的同时，射线OC 也绕O 点以每秒6°的速度沿顺时针方向旋转一周，那么经过多长时间OC 平分∠MOB ？请画出图并说明理由．13．如图①，直线AB ､CD 相交于点O ，射线OE CD ⊥，垂足为点O ，过点O 作射线OF 使130BOF ∠=︒．（1）将图①中的直线CD 绕点O 逆时针旋转至图②，OE 在BOF ∠的内部，当OE 平分BOF ∠时，OC 是否平分AOF ∠，请说明理由；（2）将图①中的直线CD 绕点O 逆时针旋转至图③，OD 在AOF ∠的内部，探究AOE ∠与DOF ∠之间的数量关系，并说明理由；（3）若20BOE ∠=︒，将图①中的直线CD 绕点O 按每秒5°的速度逆时针旋转α度()0180a ︒<<︒设旋转的时间为t 秒，当AOC ∠与EOF ∠互余时，求t 的值．14．已知()()32162025a x x b x -++++是关于x 的二次二项式，A ，B 是数轴上两点，且A ，B 对应的数分别为a ，b ．（1）求线段AB 的中点C 所对应的数；（2）如图，在数轴上方从点C 出发引出射线CD ，CE ，CF ，CG ，且CF 平分∠ACD ，CG 平分∠BCE ，试猜想∠DCE 与∠FCG 之间是否存在确定的数量关系，并说明理由；（3）在（2）的条件下，已知∠DCE =20°，∠ACE =30°，当∠DCE 绕着点C 以2°/秒的速度逆时针旋转t 秒(065t <<)时，∠ACF 和∠BCG 中的一个角的度数恰好是另一个角度数的两倍，求t 的值15．如图1，在平面内，已知点O 在直线AB 上，射线OC 、OE 均在直线AB 的上方，AOC α∠=（030α︒<<︒），2COE α∠=，OD 平分COE ∠，DOF ∠与AOC ∠互余．（1）若:1:5AOE BOE ∠∠=，则α=________°；（2）当OF 在BOC ∠内部时①若20α=︒，请在图2中补全图形，求EOF ∠的度数；②判断射线OF 是否平分BOD ∠，并说明理由；（3）若4EOF AOC ∠=∠，请直接写出α的值． 16．如图，点O 在直线AB 上，90COD ∠=︒．（1）如图①，当COD ∠的一边射线OC 在直线AB 上（即OC 与OA 重合），另一边射线OD 在直线AB 上方时，OF 是BOD ∠的平分线，则COF ∠的度数为_______．（2）在图①的基础上，将COD ∠绕着点O 顺时针方向旋转（旋转角度小于360︒），OE 是AOC ∠的平分线，OF 是BOD ∠的平分线，试探究EOF ∠的大小．①如图②，当COD ∠的两边射线OC 、OD 都在直线AB 的上方时，求EOF ∠的度数．小红、小英对该问题进行了讨论：小红：先求出AOC ∠与BOD ∠的和，从而求出EOC ∠与FOD ∠的和，就能求出EOF ∠的度数．小英：可设AOC ∠为x 度，用含x 的代数式表示EOC ∠、FOD ∠的度数，也能求出EOF ∠的度数．请你根据她们的讨论内容，求出EOF ∠的度数．②如图③，当COD ∠的一边射线OC 在直线AB 的上方，另一边射线OD 在直线AB 的下方时，小红和小英认为也能求出EOF ∠的度数．你同意她们的看法吗?若同意，请求出EOF ∠的度数；若不同意，请说明理由．③如图④，当COD ∠的两边射线OC 、OD 都在直线AB 的下方时，能否求出EOF ∠的度数?若不能求出，请说明理由；若能求出，请直接写出EOF ∠的度数．17．如图，点A ，B 在数轴上所对应的数分别为－5，7（单位长度为1cm ），P 是A ，B 间一点，C ，D 两点分别从点P ，B 出发，以1cm/s ，2cm /s 的速度沿直线AB 向左运动（点C 在线段AP 上，点D 在线段BP 上），运动的时间为s t ．（1）AB =______cm ．（2）若点C ，D 运动到任一时刻时，总有2PD AC =，请求出AP 的长．（3）在（2）的条件下，Q 是数轴上一点，且AQ BQ PQ -=，求PQ 的长．18．已知150AOB ∠=︒，OD 为∠AOB 内部的一条射线．（1）如图（1），若60BOC ∠=︒，OD 为∠AOB 内部的一条射线，13COD BOC ∠=∠，OE 平分∠AOB ，求∠DOE 的度数；（2）如图（2），若OC 、OD 是∠AOB 内部的两条射线，OM 、ON 分别平分∠AOD ，∠BOC ，且MOC NOD ∠≠∠，求AOC BOD MOC NOD∠-∠∠-∠的值；（3）如图（3），C 1为射线OB 的反向延长线上一点，将射线OB 绕点O 顺时针以6°/s 的速度旋转，旋转后OB 对应射线为OB 1，旋转时间为t 秒（0＜t 35），OE 平分∠AOB 1，OF 为∠C 1OB 1的三等分线，11113C OF C OB ∠=∠，若130∠-∠=︒C OF AOE ，直接写出t 的值为_________．19．如图1，P 点从点A 开始以2cm /s 的速度沿A B C →→的方向移动，Q 点从点C 开始以1cm/s 的速度沿C A B →→的方向移动，在直角三角形ABC 中，90A ∠=︒，若16cm AB =，12cm AC =，20cm BC =，如果P ，Q 同时出发，用t （秒）表示移动时间．（1）如图1，若点P 在线段AB 上运动，点Q 在线段CA 上运动，当t 为何值时，QA AP =；（2）如图2，点Q 在CA 上运动，当t 为何值时，三角形QAB 的面积等于三角形ABC 面积的14；（3）如图3，当P 点到达C 点时，P ，Q 两点都停止运动，当t 为何值时，线段AQ 的长度等于线段BP 的长．20．点A ，B 为数轴上的两点，点A 对应的数为a ，点B 对应的数为3，a 3＝﹣8．（1）求A ，B 两点之间的距离；（2）若点C 为数轴上的一个动点，其对应的数记为x ，试猜想当x 满足什么条件时，点C 到A 点的距离与点C 到B 点的距离之和最小．请写出你的猜想，并说明理由；（3）若P ，Q 为数轴上的两个动点（Q 点在P 点右侧），P ，Q 两点之间的距离为m ，当点P 到A 点的距离与点Q 到B 点的距离之和有最小值4时，m 的值为．【参考答案】***试卷处理标记，请不要删除一、七年级上册数学压轴题1．（1）3；（2）－11，1，2，14；（3）当n ＝1时，c ＝，当n ＞1时，点C 在点A 、B 之间且靠近点B 时，c ＝a ＋ (b －a)；点C 在点A 、B 之间且靠近点A 时，c ＝a ＋ (b －a)；点C 在点A 、B 之解析：（1）3；（2）－11，1，2，14；（3）当n ＝1时，c ＝2a b +，当n ＞1时，点C 在点A 、B 之间且靠近点B 时，c ＝a ＋1n n + (b －a )；点C 在点A 、B 之间且靠近点A 时，c ＝a ＋11n + (b －a )；点C 在点A 、B 之外且靠近点B 时，c ＝a ＋1n n - (b －a )；点C 在点A 、B 之外且靠近点A 时，c ＝a －11n - (b －a )．【分析】初步思考：（1）可根据n 阶伴侣点的概念判断即可；（2）根据n 阶伴侣点的概念分类讨论即可；深入探究：（3）根据n 阶伴侣点的概念分类讨论即可．【详解】解：（1）∵O 是点A 、B 的1阶伴侣点；O 是点A 、C 的2阶伴侣点；O 也是点B 、C 的2阶伴侣点，∴OA =OB ,OC =2OA ,OC =2OB ，∴AC =3BC ，∴C 是点A 、B 的3阶伴侣点；故答案是：3（2）设表示的数为x ,由题意有： ①|x+1|=23|x-4|，解得，x=1或x=-11，②|x -4|=23|x +1|，解得，x=2或x=14，综上所述，M 、N 的32阶伴侣点所表示的数为－11，1，2，14；（3）①当n ＝1时，c ＝2a b +． ②当n ＞1时，无论a ＞b 或a ＜b ，均有下列四种情况：点C 在点A 、B 之间且靠近点B 时，c ＝a ＋1n n + (b －a )；点C 在点A 、B 之间且靠近点A 时，c ＝a ＋11n + (b －a )；点C 在点A 、B 之外且靠近点B 时，c ＝a ＋1n n - (b －a )；点C 在点A 、B 之外且靠近点A 时，c ＝a －11n - (b －a )．【点睛】本题主要考查新定义“n 阶伴侣点”，解题的关键是灵活运用所学知识，结合分类讨论思想解决问题． 2．（1）是；（2）10或0或20；(3) ；t=6；；t=12；；．【分析】（1）根据新定义，结合中点把原线段分成两短段，满足原线段是短线段的2倍关系，进行判断即可；（2）由题意设C 点表示的数为解析：（1）是；（2）10或0或20；(3) 152t =；t=6；607t =；t=12；907t =；454t =．【分析】（1）根据新定义，结合中点把原线段分成两短段，满足原线段是短线段的2倍关系，进行判断即可；（2）由题意设C 点表示的数为x ，再根据新定义列出合适的方程即可；（3）根据题意先用t 的代数式表示出线段AP ，AQ ，PQ ，再根据新定义列出方程，得出合适的解即可求出t 的值．【详解】解：（1）因原线段是中点分成的短线段的2倍，所以线段的中点是这条线段的巧点，故答案为：是；（2）设C 点表示的数为x ，则AC=x+20，BC=40-x ，AB=40+20=60，根据“巧点”的定义可知：①当AB=2AC 时，有60=2（x+20），解得，x=10；②当BC=2AC 时，有40-x=2（x+20），解得，x=0；③当AC=2BC 时，有x+20=2（40-x ），解得，x=20．综上，C 点表示的数为10或0或20；（3）由题意得()()60601026046601015t t AP t AQ t PQ t t -≤≤⎧⎪==-=⎨-≤⎪⎩，，＜，（i ）、若0≤t≤10时，点P 为AQ 的“巧点”，有①当AQ=2AP 时，60-4t=2×2t ，解得，152t =， ②当PQ=2AP 时，60-6t=2×2t ，解得，t=6；③当AP=2PQ 时，2t=2（60-6t ），解得，607t =；综上，运动时间()t s 的所有可能值有152t =；t=6；607t =；（ii ）、若10＜t≤15时，点Q 为AP 的“巧点”，有①当AP=2AQ 时，2t=2×（60-4t ），解得，t=12；②当PQ=2AQ 时，6t-60=2×（60-4t ），解得，907t =； ③当AQ=2PQ 时，60-4t=2（6t-60），解得，454t =．综上，运动时间()t s 的所有可能值有：t=12；907t =；454t =．故，运动时间()t s 的所有可能值有：152t =；t=6；607t =；t=12；907t =；454t =．【点睛】本题是新定义题，是数轴的综合题，主要考查数轴上的点与数的关系，数轴上两点间的距离，一元一次方程的应用，解题的关键是根据新定义列出方程并进行求解．3．（1）30；（2）15；（3）20秒【分析】（1）根据数轴上两点之间的距离得出结果；（2）利用时间=路程÷速度和算出相遇时间，再计算出点D 表示的数；（3）利用时间=路程÷速度差算出相遇时间即解析：（1）30；（2）15；（3）20秒【分析】（1）根据数轴上两点之间的距离得出结果；（2）利用时间=路程÷速度和算出相遇时间，再计算出点D 表示的数；（3）利用时间=路程÷速度差算出相遇时间即可．【详解】解：（1）-10+40=30，∴点N 表示的数为30；（2）40÷（3+5）=5秒，-10+5×5=15，∴点D 表示的数为15；（3）40÷（5-3）=20，∴经过20秒后，P ，Q 两点重合．【点睛】本题考查了数轴上两点之间的距离，解题的关键是掌握相遇问题和追击问题之间的数量关系．4．（1）5；（2）2秒；（3）当t 的值为6或2时，M 、N 两点之间的距离为2个单位，此时点M 表示的数为5或9．【分析】（1）用b 表示BC 、AB 的长度，结合BC=2AB 可求出b 值；（2）根据相遇时间解析：（1）5；（2）2秒；（3）当t 的值为6或2时，M 、N 两点之间的距离为2个单位，此时点M 表示的数为5或9．【分析】（1）用b 表示BC 、AB 的长度，结合BC=2AB 可求出b 值；（2）根据相遇时间=相遇路程÷速度和，即可得出结论；（3）用含t 的代数式表示出点M ，N 表示的数，结合MN=2，即可得出关于t 的含绝对值符号的一元一次方程，解之即可得出结论．【详解】（1）∵39a c ==、．又∵点B 在点A 、C 之间，且满足BC=2AB ，∴9-b=2（b-3），∴b=5．（2）AC=9-3=66÷（2+1）=2，即两秒后相遇．（3）M 到达B 点时t=（5-3）÷1=2（秒）；M 到达C 点时t=（9-3）÷1=6（秒）；N 到达C 时t=（9-3）÷2+2=5（秒）N 回到A 点用时t=（9-3）÷2×2+2=8（秒）当0≤t≤5时，N 没有到达C 点之前，此时点N 表示的数为3+2（t-2）=2t-1；M 表示的数为3+t MN=21(3)4t t t --+=-=2解得6t = （舍去）或2t =此时M 表示的数为5当5≤t≤6时，N 从C 点返回，M 还没有到达终点C点N 表示的数为9-2（t-5）=-2t+19；M 表示的数为3+t MN=219(3)316t t t -+-+=-=2解得6t =或143t =（舍去）此时M 表示的数为9当6≤t≤8时，N 从C 点返回，M 到达终点C此时M 表示的数是9点N 表示的数为9-2（t-5）=-2t+19；MN=9(219)210t t --+=-=2解得6t =此时M 表示的数是9综上所述：当t 的值为6或2时，M 、N 两点之间的距离为2个单位，此时点M 表示的数为5或9．【点睛】本题考查了数轴上两点间的距离以及一元一次方程的应用，解题的关键是找准等量关系，正确列出一元一次方程．5．（1）-2，1，5；（2）不变，值为1；（3）或【分析】（1）根据b 是最小的正整数，即可确定b 的值，然后根据非负数的性质，几个非负数的和是0，则每个数是0，即可求得a ，b ，c 的值；（2）用关于解析：（1）-2，1，5；（2）不变，值为1；（3）136或212 【分析】（1）根据b 是最小的正整数，即可确定b 的值，然后根据非负数的性质，几个非负数的和是0，则每个数是0，即可求得a ，b ，c 的值；（2）用关于t 的式子表示BC 和AB 即可求解；（3）分别求出当t=3时，A 、B 、C 表示的数，得到AC 和BC ，根据AC=2BC 列出方长，解之即可．【详解】解：（1）∵()2520c a b -++=，b 是最小的正整数，∴c-5=0，a+2b=0，b=1，∴a=-2，b=1，c=5，故答案为：-2，1，5；（2）∵点A 以每秒1个单位长度的速度向左运动，同时，点B 和点C 分别以每秒2个单位长度和5个单位长度的速度向右运动，∴t 秒后，A 表示的数为-t-2，B 表示的数为2t+1，C 表示的数为5t+5，∴BC=5t+5-（2t+1）=3t+4，AB=2t+1-（-t-2）=3t+3，∴BC-AB=3t+4-（3t+3）=1，∴BC-AB 的值不会随着时间t 的变化而改变，BC-AB=1；（3）当t=3时，点A 表示-2-3=-5，点B 表示1+3n ，点C 表示5+5×3=20，∴AC=20-（-5）=25，BC=2013n --=193n -，∵AC=2BC ，则25=2193n -，则25=2（19-3n ），或25=2（3n-19），解得：n=136或212．【点睛】此题考查一元一次方程的实际运用，以及数轴与绝对值，正确理解AB ，BC 的变化情况是关键．6．（1）①8；②16；（2）-15或5；（3）6或8【分析】（1）①根据题目要求，P 在数轴上点A 与B 之间，所以根据BP=AB-AP 进行求解②需要考虑两种情况，即P在数轴上点A与B之间时和当P不在解析：（1）①8；②16；（2）-15或5；（3）6或8【分析】（1）①根据题目要求，P在数轴上点A与B之间，所以根据BP=AB-AP进行求解②需要考虑两种情况，即P在数轴上点A与B之间时和当P不在数轴上点A与B之间时．当P在数轴上点A与B之间时，AP=AB-BP．当P不在数轴上点A与B之间时，此时有两种情况，一种是超越A点，在A点左侧，此时BP＞14，不符合题目要求．另一种情况是P在B点右侧，此时根据AP=AB+BP作答．（2）根据前面分析，C不可能在AB之间，所以，C要么在A左侧，要么在B右侧．根据这两种情况分别进行讨论计算．（3）分点M在点N的左侧和点M在点N的右侧，两种情况分别列出方程求解．【详解】解：（1）①∵AB总距离是2-（-12）=14，P在数轴上点A与B之间，∴BP=AB-AP=14-6=8，故答案为：8．②P在数轴上点A与B之间时，AP=AB-BP=14-2=12；当P不在数轴上点A与B之间时，因为AB=14，所以P只能在B右侧，此时BP=2，AP=AB+BP=14+2=16，故答案为：16．（2）假设C为x，当C在A左侧时，AC=-12-x，BC=2-x，AC+BC=20，则-12-x+2-x=20，解得x=-15，当C在B右侧时，AC=x-（-12），BC=x-2，AC+BC=20，则x-（-12）+x-2=20，解得x=5，∴点C表示的数为-15或5；（3）当M在点N左侧时，2-8t-（-12-6t）=2，解得：t=6；当M在点N右侧时，-12-6t-（2-8t）=2，解得：t=8，∴MN=2时，t的值为6或8．【点睛】本题考查了动点问题，一元一次方程的应用．在充分理解题目要求的基础上，可借助数轴用数形结合的方法求解．在解答过程中，注意动点问题的多解可能，并针对每一种可能进行讨论分析．7．（1）见解析；（2）；（3）①时，点O恰好为线段PQ的中点；②当MN=3时 ,的值为或秒．【分析】（1）由绝对值和偶次方的非负性质得出，，得出，，画出图形即可；（2）设点C 对应的数为x ，分两解析：（1）见解析；（2）14；（3）①43t =时，点O 恰好为线段PQ 的中点；②当MN=3时 ,t 的值为194或134秒．【分析】（1）由绝对值和偶次方的非负性质得出503a b +=，60b -=，得出10a =-，6b =，画出图形即可；（2）设点C 对应的数为x ，分两种情况，画出示意图，由题意列出方程，解方程即可；（3）①分相遇前和相遇后两种情况，画出示意图，由题意列出方程，解方程即可； ②根据题意得到点Q 、点N 对应的数，列出绝对值方程即可求解．【详解】（1）∵25(6)03a b b ++-=， ∴503a b +=，60b -=， ∴10a =-，6b =，点A ，B 的位置如图所示：（2）设点C 对应的数为x ，由题意得：C 应在A 点的右侧，∴CA=()10x --=10x +，①当点C 在线段AB 上时，如图所示：则CB=6x -，∵CA-CB=92， ∴()91062x x +--=，解得：14x =； ②当点C 在线段AB 延长线上时，如图所示：则CB=6x -，∵CA-CB=92， ∴()91062x x +--=，方程无解；综上，点C 对应的数为14；故答案为：14；（3）①由题意得：6AP t =，3BQ t =，分两种情况讨论：相遇前，如图：106OP t =-，63OQ t =-，∵点O 恰好为线段PQ 的中点，∴10663t t -=-，解得：43t =；相遇后，如图：610OP t =-，36OQ t =-，∵点O 恰好为线段PQ 的中点，∴61036t t -=-，解得：43t =，此时，468103AP =⨯=<，不合题意；故43t =时，点O 恰好为线段PQ 的中点； ②当运动时间为t 秒时，点P 对应的数为(610t -)，点Q 对应的数为(63t -)，∵M 为AP 的中点，点N 在线段BQ 上，且13BN BQ =， ∴点M 对应的数为6t 10103t 102--=-，点N 对应的数为()663t 66t 3---=-，∵3MN =， ∴()3t 106t 3---=，∴4316t =±+，∴194t =或134，答：当t 的值为194或134秒时，3MN =．【点睛】本题考查了一元一次方程的应用、绝对值和偶次方的非负性以及数轴，解题的关键是根据题意正确画出图形，要考虑全面，分类讨论，不要遗漏．8．（1）3；（2）3，7；（3）197，；（4）9．【分析】（1）设需将点C 向左移动x 个单位，再根据数轴的定义建立方程，解方程即可得；（2）分为三种：移动点B 、C ；移动点A 、C ；移动点A 、B ，再解析：（1）3；（2）3，7；（3）197，100-；（4）9．【分析】（1）设需将点C 向左移动x 个单位，再根据数轴的定义建立方程，解方程即可得；（2）分为三种：移动点B 、C ；移动点A 、C ；移动点A 、B ，再利用数轴的定义分别求出移动所走的距离和即可得；（3）先根据前4次归纳类推出一般规律，再列出运算式子，计算有理数的加减法即可得；（4）分5x ≤-，51x -<≤-，14x -<≤和4x >数四种情况，再分别结合数轴的定义、化简绝对值即可得．【详解】（1）设需将点C 向左移动x 个单位，由题意得：()()3224x ---=---，解得3x =，即需将点C 向左移动3个单位，故答案为：3；（2）()242AB =---=，()347AC =--=，()325BC =--=，由题意，分以下三种情况：①移动点B 、C ，把点B 向左移动2个单位，点C 向左移动7个单位，此时移动所走的距离和为279+=；②移动点A 、C ，把点A 向右移动2个单位，点C 向左移动5个单位，此时移动所走的距离和为257+=；③移动点A 、B ，把点A 向右移动7个单位，点B 向右移动5个单位，此时移动所走的距离和为7512+=；综上，移动方法有3种，其中移动所走的距离和最小的是7个单位，故答案为：3，7；（3）第1次跳的步数为1211=⨯-，第2次跳的步数为3221=⨯-，第3次跳的步数为5231=⨯-，第4次跳的步数为7241=⨯-，归纳类推得：第n 次跳的步数为(21)n -，其中n 为正整数，则第99次跳的步数为2991197⨯-=，落脚点表示的数为11357195197--+-+-+-，()()()()113579195197=--+-+-++-，10022=-⨯， 100=-，故答案为：197，100-；（4）由题意，分以下四种情况：①当5x ≤-时，则1451453213x x x x x x x ++-++=--+---=--≥；②当51x -<≤-时，则1451458x x x x x x x ++-++=--+-++=-+，51x -<≤-，9813x ∴≤-+<；③当14x -<≤时，则14514510x x x x x x x ++-++=++-++=+，14x -<≤，91014x ∴<+≤；④当4x >时，则1451453214x x x x x x x ++-++=++-++=+>；综上，1459x x x ++-++≥，则145x x x ++-++的最小值是9，故答案为：9．【点睛】本题考查了数轴、化简绝对值、一元一次方程的应用等知识点，熟练掌握数轴的定义是解题关键．9．（1）-2， 1，c=7；（2）4；（3）3t+3， 5t+9， 2t+6；（4）不变，3BC ﹣2AB=12．【分析】（1）利用|a＋2|＋（c−7）2＝0，得a＋2＝0，c−7＝0，解得a，c解析：（1）-2， 1，c=7；（2）4；（3）3t+3， 5t+9， 2t+6；（4）不变，3BC﹣2AB=12．【分析】（1）利用|a＋2|＋（c−7）2＝0，得a＋2＝0，c−7＝0，解得a，c的值，由b是最小的正整数，可得b＝1；（2）先求出对称点，即可得出结果；（3）AB原来的长为3，所以AB＝t＋2t＋3＝3t＋3，再由AC＝9，得AC＝t＋4t＋9＝5t＋9，由原来BC＝6，可知BC＝4t−2t＋6＝2t＋6；（4）由3BC−2AB＝3（2t＋6）−2（3t＋3）求解即可．【详解】（1）∵|a＋2|＋（c−7）2＝0，∴a＋2＝0，c−7＝0，解得a＝−2，c＝7，∵b是最小的正整数，∴b＝1；故答案为：−2；1；7．（2）（7＋2）÷2＝4.5，对称点为7−4.5＝2.5，2.5＋（2.5−1）＝4；故答案为：4．（3）依题意可得AB＝t＋2t＋3＝3t＋3，AC＝t＋4t＋9＝5t＋9，BC＝2t＋6；故答案为：3t＋3；5t＋9；2t＋6．（4）不变．3BC−2AB＝3（2t＋6）−2（3t＋3）＝12．【点睛】本题主要考查了一元一次方程的应用、数轴及两点间的距离，解题的关键是利用数轴的特点能求出两点间的距离．10．（1）G，-4或-16；（2）1.5或3或9【分析】（1）根据美好点的定义，结合图2，直观考察点E，F，G到点M，N的距离，只有点G符合条件．结合图2，根据美好点的定义，在数轴上寻找到点N的距离解析：（1）G，-4或-16；（2）1.5或3或9【分析】（1）根据美好点的定义，结合图2，直观考察点E，F，G到点M，N的距离，只有点G符合条件．结合图2，根据美好点的定义，在数轴上寻找到点N的距离是到点M的距离2倍的点，在点的移动过程中注意到两个点的距离的变化．（2）根据美好点的定义，分情况分别确定P点的位置，进而可确定t的值．【详解】解：（1）根据美好点的定义，结合图2，直观考察点E ，F ，G 到点M ，N 的距离，只有点G 符合条件，故答案是：G ．结合图2，根据美好点的定义，在数轴上寻找到点N 的距离是到点M 的距离2倍的点，点N 的右侧不存在满足条件的点，点M 和N 之间靠近点M 一侧应该有满足条件的点，进而可以确定-4符合条件．点M 的左侧距离点M 的距离等于点M 和点N 的距离的点符合条件，进而可得符合条件的点是-16．故答案是：-4或-16．（2）根据美好点的定义，P ，M 和N 中恰有一个点为其余两点的美好点分6种情况，第一情况：当P 为【M ，N 】的美好点，点P 在M ，N 之间，如图1，当MP =2PN 时，PN =3，点P 对应的数为2-3=-1，因此t =1.5秒；第二种情况，当P 为【N ，M 】的美好点，点P 在M ，N 之间，如图2，当2PM =PN 时，NP =6，点P 对应的数为2-6=-4，因此t =3秒；第三种情况，P 为【N ，M 】的美好点，点P 在M 左侧，如图3，当PN =2MN 时，NP =18，点P 对应的数为2-18=-16，因此t =9秒；综上所述，t 的值为：1.5或3或9．【点睛】本题考查实数与数轴、美好点的定义等知识，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考创新题目．11．（1），；（2）①存在，当秒或12.5秒时，的度数是；②秒或秒或秒或15秒【分析】（1）根据伴随线和角平分线的性质求解即可；（2）分为若OC 与OD 在相遇之前、OC 与OD 在相遇之后两种情况求解解析：（1）50，6x ；（2）①存在，当10t =秒或12.5秒时，COD ∠的度数是20︒；②457t =秒或18019秒或907秒或15秒【分析】（1）根据伴随线和角平分线的性质求解即可；（2）分为若OC 与OD 在相遇之前、OC 与OD 在相遇之后两种情况求解即可；（3）分为（Ⅰ）OC 、OD 未相遇之前：当OC 是OA 的伴随线时，当OC 是OD 的伴随线。

近10年2005-2014天津中考数学卷压轴题详解

（25）（本小题10分）在△ABC 中，∠A 、∠B 、∠C 所对的边分别用a 、b 、c 表示。

（Ⅰ）如图，在△ABC 中，∠A＝2∠B ，且∠A ＝60°。

求证：a 2＝b （b ＋c ）（Ⅱ）如果一个三角形的一个内角等于另一个内角的2 倍，我们称这样的三角形为“倍角三角形”。

本题第一问中的三角形是一个特殊的倍角三角形，那么对于任意的倍角三角形ABC ，其中∠A ＝2∠B ，关系式 a 2＝b （b ＋c ）是否仍然成了？并证明你的结论；（Ⅲ）试求出一个倍角三角形的三条边的长，使这三条边长恰为三个连续的正整数。

(26) (本小题10分)已知二次函数y ＝ax 2＋bx ＋c .（Ⅰ）若a ＝2，c ＝－3，且二次函数的图象经过点（－1，－2），求b 的值（Ⅱ）若a ＝2，b ＋c ＝－2，b ＞c ，且二次函数的图象经过点（p ，－2），求证：b ≥0；（Ⅲ）若a ＋b ＋c ＝0，a ＞b ＞c ，且二次函数的图象经过点（q ，－a ），试问自变量x ＝q ＋4时，二次函数y ＝ax 2＋bx ＋c 所对应的函数值y 是否大于0？并证明你的结论。

（25）（本小题10分）已知Rt △ABC 中，∠ACB ＝90°，AC ＝6，BC ＝8。

（Ⅰ）如图①，若半径为r 1的⊙O 1是Rt △ABC 的内切圆，求r 1；（Ⅱ）如图②，若半径为r 2的两个等圆⊙O 1、⊙O 2外切，且⊙O 1与AC 、AB 相切，⊙O 2与BC 、AB 相切，求r 2；（Ⅲ）如图③，当n 大于2的正整数时，若半径r n 的n 个等圆⊙O 1、⊙O 2、…、⊙O n依次外切，且⊙O 1与AC 、BC 相切，⊙O n 与BC 、AB 相切，⊙O 1、⊙O 2、⊙O 3、…、⊙O n －1均与AB 边相切，求r n . (26) (本小题10分)已知抛物线y ＝ax 2＋bx ＋c 的定点坐标为(2,4). （Ⅰ）试用含a 的代数式分别表示b ，c ；（Ⅱ）若直线y ＝kx ＋4（k ≠0）与y 轴及该抛物线的交点依次为D 、E 、F ，且13ODEOEFS S＝，其中O 为坐标原点，试用含a 的代数式表示k ；（Ⅲ）在（Ⅱ）的条件下，若线段EF 的长m 满足m ≤≤a 的取值范围。

数学_2014年天津市高考数学压轴试卷(理科)(含答案)

2014年天津市高考数学压轴试卷（理科）一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的1. 已知集合A ＝{x|x >1}，B ＝{x|x <m}，且A ∪B ＝R ，那么m 的值可以是（）A −1B 0C 1D 22. 设集合A ={x|2x ≤4}，集合B 为函数y =lg(x −1)的定义域，则A ∩B =( )A (1, 2)B [1, 2]C [1, 2)D (1, 2]3. 函数y =sin(2x +φ)的图象沿x 轴向左平移π8个单位后，得到一个偶函数的图象，则φ的一个可能的值为( )A 3π4B π4C 0D −π4 4. 函数f(x)=log 2(1+x)，g(x)=log 2(1−x)，则f(x)−g(x)是（）A 奇函数B 偶函数C 既不是奇函数又不是偶函数D 既是奇函数又是偶函数5. （江西师大附中期末考试）设曲线y =sinx 上任一点(x, y)处切线斜率为g(x)，则函数y =x 2g(x)的部分图象可以为（）A B C D6. 设z =2x +y ，其中变量x ，y 满足条件{x −4y ≤−33x +5y ≤25x ≥m，若z 的最小值为3，则m 的值为（）A 1B 2C 3D 47. 已知点P(x, y)在直线x +2y =3上移动，当2x +4y 取最小值时，过P 点(x, y)引圆C ：(x −12)2+(y +54)2=1的切线，则此切线长等于（） A 1 B √2 C √3 D 28. 已知函数f(x)=ln(e x −1)(x >0)( )A 若f(a)+2a =f(b)+3b ，则a >bB 若f(a)+2a =f(b)+3b ，则a <bC 若f(a)−2a =f(b)−3b ，则a >bD 若f(a)−2a =f(b)−3b ，则a <b二、填空题：本大题共6小题，每小题5分，共30分．把答案填在答题卡的相应位置．9. 设常数a ∈R ，若(x 2+a x )5的二项展开式中x 4项的系数为20，则a =________．10. 已知tanα=13，tanβ=−17，且0<α<π2，π2<β<π，则2α−β的值________． 11. 记等差数列{a n }的前n 项和为S n ，已知a 2+a 4=6，S 4=10．则a 10=________．12. 棱长为2的正方体被一平面截成两个几何体，其中一个几何体的三视图如图所示，那么该几何体的体积是________．13. 已知圆的方程为x 2+y 2−6x −8y =0，设该圆过点(3, 5)的最长弦和最短弦分别为AC 和BD ，则四边形ABCD 的面积为________．14. 等腰Rt △ACB ，AB =2，∠ACB =π2．以直线AC 为轴旋转一周得到一个圆锥，D 为圆锥底面一点，BD ⊥CD ，CH ⊥AD 于点H ，M 为AB 中点，则当三棱锥C −HAM 的体积最大时，CD 的长为________．三、解答题：本大题共6小题，共80分．解答应写出文字说明、证明过程或演算步骤．解答写在答题卡上的指定区域内．15. 袋中装有黑球和白球共7个，从中任取2个球都是黑球的概率为27，现有甲、乙两人从袋中轮流摸取1球，甲先取，乙后取，然后甲再取…，取球后不放回，直到两人中有一人取到白球时终止，每个球在每一次被取出的机会是等可能的，用ξ表示取球终止所需要的取球次数．（1）求随机变量ξ的分布列及数学期望；（2）求乙取到白球的概率．16. 在△ABC 中，BC =a ，AC =b ，a 、b 是方程x 2−2√3x +2=0的两个根，且A +B =120∘，求△ABC 的面积及AB 的长．17. 如图，在棱长为1的正方体ABCD −A 1B 1C 1D 1中，点E 是棱AB 上的动点．（1）求证：DA 1⊥ED 1；（2）若直线DA 1与平面CED 1成角为45∘，求AEAB 的值；（3）写出点E 到直线D 1C 距离的最大值及此时点E 的位置（结论不要求证明）．18. 数列{a n }是递增的等差数列，且a 1+a 6=−6，a 3⋅a 4=8．（1）求数列{a n }的通项公式；（2）求数列{a n }的前n 项和S n 的最小值；（3）求数列{|a n |}的前n 项和T n ．19. 已知椭圆C:x 2a 2+y 2b 2=1(a >b >0)的右焦点为F(1, 0)，且点(−1, √22)在椭圆C 上．（1）求椭圆C 的标准方程；（2）已知动直线l 过点F ，且与椭圆C 交于A ，B 两点，试问x 轴上是否存在定点Q ，使得QA →⋅QB →=−716恒成立？若存在，求出点Q 的坐标，若不存在，请说明理由．20. 已知f(x)=lnx ，g(x)=af(x)+f′(x)，（1）求g(x)的单调区间；（2）当a =1时，①比较g(x)与g(1x )的大小； ②是否存在x 0>0，使得|g(x)−g(x 0)|<1x 对任意x >0成立？若存在，求出x 0的取值范围；若不存在，请说明理由．2014年天津市高考数学压轴试卷（理科）答案1. D2. D3. B4. A5. C6. A7. D8. A9. ±√210. −3π411. 1012. 413. 20√614. √6315. 乙取到白球的概率为1335．…16. 解：∵ A +B =120∘，∴ C =60∘．∵ a 、b 是方程x 2−2√3x +2=0的两个根，∴ a +b =2√3，ab =2，∴ S △ABC =12absinC =12×2×sin60∘=√32，AB =c =√a 2+b 2−2abcosC =√(a +b)2−3ab =√(2√3)2−6=√6． 17.解：以D 为坐标原点，建立如图所示的坐标系，则D(0, 0, 0)，A(1, 0, 0)，B(1, 1, 0)，C(0, 1, 0)，D 1(0, 0, 1)，A 1(1, 0, 1)，设E(1, m, 0)(0≤m ≤1)(I)证明：DA 1→=(1, 0, 1)，ED 1→=(−1, −m, 1)∴ DA 1→⋅ED 1→=0∴ DA 1⊥ED 1；（2）解：设平面CED 1的一个法向量为v →=(x, y, z)，则∵ CD 1→=(0, −1, 1)，CE →=(1, m −1, 0)∴ {−y +z =0x +(m −1)y =0．取z =1，得y =1，x =1−m ，得v →=(1−m, 1, 1)．∵ 直线DA 1与平面CED 1成角为45∘，∴ sin45∘=|cos <DA 1→，v →>|=√22， ∴ |2−m|⋅=√22，解得m =12．-----（3）解：点E 到直线D 1C 距离的最大值为√62，此时点E 在A 点处．------18. 解：（1）由{a 1+a 6=−6⋅得：{a 3+a 4=−6⋅， ∴ a 3、a 4是方程x 2+6x +8=0的二个根，∴ x 1=−2，x 2=−4；∵ 等差数列{a n }是递增数列，∴ a 3=−4，a 4=−2，∴ 公差d =2，a 1=−8．∴ a n =2n −10；（2）∵ S n =n(a 1+a n )2=n 2−9n =(n −92)2−814，∴ (S n )min =S 4=S 5=−20；（3）由a n ≥0得2n −10≥0，解得n ≥5，此数列前四项为负的，第五项为0，从第六项开始为正的．当1≤n ≤5且n ∈N ∗时，T n =|a 1|+|a 2|+...+|a n |=−(a 1+a 2+...+a n )=−S n=−n 2+9n ；当n ≥6且n ∈N ∗时，T n =|a 1|+|a 2|+...+|a 5|+|a 6|+...+|a n |=−(a 1+a 2+...+a 5)+(a 6+...+a n )=S n −2S 5=n 2−9n −2(25−45)=n 2−9n +40．∴ T n ={9n −n 2，1≤n ≤5，n ∈N ∗n 2−9n +40，n ≥6，n ∈N ∗．19. 由题意，c ＝1∵ 点(−1, √22)在椭圆C 上，∴ 根据椭圆的定义可得：2a =(√22)+√22，∴ a =√2∴ b 2＝a 2−c 2＝1，∴ 椭圆C 的标准方程为x 22+y 2=1；假设x 轴上存在点Q(m, 0)，使得QA →⋅QB →=−716恒成立当直线l 的斜率为0时，A(√2, 0)，B(−√2, 0)，则(√2−m,0)⋅(−√2−m,0)=−716，∴ m 2=2516，∴ m =±54① 当直线l 的斜率不存在时，A(1,√22)，B(1,−√22)，则(1−m,√22)⋅(1−m,−√22)=−716， ∴ (1−m)2=116∴ m =54或m =34②由①②可得m =54．下面证明m =54时，QA →⋅QB →=−716恒成立当直线l 的斜率为0时，结论成立；当直线l 的斜率不为0时，设直线l 的方程为x ＝ty +1，A(x 1, y 1)，B(x 2, y 2) 直线方程代入椭圆方程，整理可得(t 2+2)y 2+2ty −1＝0，∴ y 1+y 2=−2tt 2+2，y 1y 2=−1t 2+2∴ QA →⋅QB →=(x 1−54, y 1)⋅(x 2−54, y 2)＝(ty 1−14)(ty 2−14)+y 1y 2＝(t 2+1)y 1y 2−1 4t(y1+y2)+116=−2t2−2+t22(t2+2)+116=−716综上，x轴上存在点Q(54, 0)，使得QA→⋅QB→=−716恒成立．20. 解：（1）∵ f′(x)=1x ，g(x)=alnx+1x，g(x)的定义域为(0, +∞)．g′(x)=ax−1x2=ax−1x2①当a≤0时，g′(x)<0，(0, +∞)是g(x)的单调区间；②当a>0时，由g′(x)>0，得x>1a ；由g′(x)<0，得0<x<1a，即增区间是(1a ，+∞)，减区间是(0,1a)．（2）g(x)=lnx+1x ，g(1x)=ln1x+x=−lnx+x∴ g(x)−g(1x )=2lnx+1x−x=μ(x)μ′(x)=2x−1x2−1=−x2+2x−1x2=−(x−1)2x2①当x=1时，μ(x)=0，此时g(x)=g(1x)②当0<x<1时，μ′(x)<0，∴ μ(x)>μ(1)=0．∴ g(x)>g(1x)③当x>1时，μ′(x)<0，∴ μ(x)<μ(1)=0．∴ g(x)<g(1x)．(3)|g(x)−g(x0)|<1x⇔−1x<g(x0)−g(x)<1x⇔lnx<g(x0)<lnx+2 x∵ lnx∈(−∞, +∞)，∴ g(x0)>lnx不能恒成立．故x0不存在．。

天津中考数学压轴题全搞定.doc

九年级数学冲刺讲义二次函数12题1. 已知关于x的函数同时满足下列三个条件：①函数的图象不经过第二象限；②当x＜2时，对应的函数值y＜0；③当x＜2时，函数值y随x的增大而增大．你认为符合要求的函数的解析式可以是：（写出一个即可，答案不唯一）．2．已知抛物线y=ax2+bx+c（b＞a＞0）与x轴最多有一个交点，现有以下四个结论：①该抛物线的对称轴在y轴左侧；②关于x的方程ax2+bx+c+2=0无实数根；③a﹣b+c≥0；④的最小值为3．其中，正确结论的个数为（）A．1个B．2个C．3个D．4个3．已知抛物线y=﹣x2+x+6与x轴交于点A，点B，与y轴交于点C．若D为AB的中点，则CD的长为（）A．B．C．D．4．已知二次函数y=（x﹣h）2+1（h为常数），在自变量x的值满足1≤x≤3的情况下，与其对应的函数值y的最小值为5，则h的值为（）A．1或﹣5 B．﹣1或5 C．1或﹣3 D．1或35．已知二次函数y=ax2+bx+c（a≠0）的图象如图，且关于x的一元二次方程ax2+bx+c﹣m=0没有实数根，有下列结论：①b2﹣4ac＞0；②abc＜0；③m＞2．其中，正确结论的个数是（）A．0 B．1 C．2 D．36．若关于x的一元二次方程（x﹣2）（x﹣3）=m有实数根x1、x2，且x1≠x2，有下列结论：①x1=2，x2=3；②m＞﹣；③二次函数y=（x﹣x1）（x﹣x2）+m的图象与x轴交点的坐标为（2，0）和（3，0）．其中，正确结论的个数是（）A．0 B．1 C．2 D．37．已知二次函数y=ax 2+bx+c （a≠0）的图象如图所示，有下列结论：①b 2﹣4ac ＞0；②abc ＞0；③8a+c ＞0；④9a+3b+c ＜0其中，正确结论的个数是（）A ．1B ．2C ．3D ．48．已知二次函数y=ax 2+bx+c （a≠0）的图象如图所示，有下列5个结论：①abc ＞0；②b ＜a+c ；③4a+2b+c ＞0；④2c ＜3b ；⑤a+b ＞m （am+b ）（m≠1的实数）．其中正确的结论有（）A ．2个B ．3个C ．4个D ．5个9. 已知抛物线y=x 2-(2m-1)x+2m 不经过第三象限，且当x>2时，函数值y 随x 的增大而增大，则实数m 的取值范围是（）A.0≤m≤1.5B.m≥1.5C.0≤m≤1D.0<m≤1.5网格题18题1. 如图，在下列网格中，每个小正方形的边长都是1，点A 、B 、Q 、P 均为格点。

2014年天津市高考压轴卷英语带解析

2014年天津市高考压轴卷含解析英语第I卷第一部分：英语知识运用(共两节，满分45分)第一节：单项填空(共15小题；每小题l分，满分l5分)从A、B、C、D四个选项中，选出可以填入空白处的最佳选项。

例：Stand over there you’ll be able to see it better．A．or B．and C．but D．while答案是B。

1.Cheer up! It won’t be ______ we can meet again.A. before longB. long beforeC. after longD. long since2.----Peter works hard and is considered to be the presidential candidate(候选人) of the class.------________________________ Tom.A. So doesB. So asC. It’s the same withD. So it was with3.They suspected that the secret had been _____ by one of their friends.A. given offB. given inC. given outD. given away4.He suggested the problem worth paying attention _______ at the meeting.A. to be discussedB. to being discussedC. to discussD. to discussing5.During the winter vacation we will go back to the school especially to pay _____visit to our teachers though it is such _____cold weather.A. a; aB. the; theC. a; 不填D. 不填；不填6.— Mary's been offered a job in a university, but she doesn't want to take it.— ________? It's a very good chance.A. Guess whatB. So whatC. Who caresD. But why7.The story is about an old Indian village r and an American tourist in India, ________ understanding the other’s language.A. none of whomB. both of themC. none of themD. neither of whom8.The weather turned out to be fine yesterday. I __________ the trouble to take my umbrella with me.A. should have takenB. could have takenC. couldn’t have takenD. needn’t have taken9.Chinese scientists have produced an embryo of a giant panda through cloning technology,_____ is a breakthrough ______ could save the endangered animals.A. that; whichB. which; thatC. which; whatD. that; what10.The new stadium being built for the Asian Games will be_____the present one.A.as three times big asB.three times as big asC.as big three timesD.as big three times as11. for several weeks, the city needed food.A. As having floodedB. Being floodedC. Having been floodedD. To flood12.The rescue team __________ 15 countries has come to aid..A. consists ofB. is made up ofC. consisting ofD. make up13.________you were coming，I would have stayed at home.A．If I know B．Should I knowC．Had I known D. If I should have known14.I know he failed his last test, but really he’s ________ stupid.A. something butB. anything butC. nothing butD. not but15.________ of the land in that area ________ covered with trees and grass.A. Two fifth; isB. Two fifth; areC. Two fifths; isD. Two fifths; are第二节：完形填空(共20小题；每小题l．5分，满分30分)阅读下面短文，掌握其大意，然后从16～35各题所给的A、B、C、D四个选项中，选出最佳选项。

天津市高考压轴卷语文 Word版含解析

GKXX2014年天津市高考压轴卷语文学科Word版含解析第Ⅰ卷（选择题，共36分）一、（15分） 1．下列词语中加点字的读音，全都正确的—组是（） A．骁勇（xiāo）氛（fèn）围自给（jǐ）自足悄无声息（qiǎo） B．挫折（cuò）皈依（guī）妄自菲（fēi）薄高屋建瓴（lǐng） C．咋舌（zé）强劲（jìng）揠（yà）苗助长济济一堂（jǐ） D．质量（zhǐ）刹那（shà）自怨自艾（yì）鞭辟入里（pì） 2．下列词语中，没有错别字的一组是（） A．笔画不粘锅轻车简从一年之季在于春 B．渔具功夫茶以德抱怨是可忍孰不可忍 C．泄秘一番话惹是生非制之死地而后生 D．蛰伏爆发力牟取暴利多行不义必自毙 3．依次填入下列横线处的词语，最恰当的一组是（） ①奥巴马即将展开的亚洲之行绕过中国，在很大程度上也是要突出美国对盟友的重视，强调盟友关系仍是美“亚太再平衡”的重要支柱。

②为应对区域范围内的重污染天气，今年将搭建起京津冀及周边地区空气质量预报预警平台，建立区域空气重污染预警会商机制，共同应对区域大范围空气重污染。

③专案组成员经过仔细观察发现，一名可疑的男子拎着不明物品，在街边蹲着休息，行为相当鬼祟。

A．刻意逐步行迹 B．蓄意逐渐形迹 C．蓄意逐渐行迹 D．刻意逐步形迹 4.下列各句中，加点的词语使用恰当的一项是（） A.“土豪”炫富虽属个人举动，但给社会带来的负能量却不可忽略一一极容易加剧人们的仇富心理，也助推了“拜金丰义”的蔓延。

B.4月15日上午，“国际奥比斯飞机眼科医院中国济南项目”学术交流活劫起动仪式在济南国际机场举行。

C.《百年孤独》堪称世上奇书，艰涩婉转，高深莫测，初读感觉或许不知所云，深读才知寓意深遂，曲径通幽。

2014天津高考压轴卷文科综合

绝密★启用前2014天津高考压轴卷文科综合注意事项：注意事项：1．答卷前，考生务必用黑色字迹钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上．用2B 铅笔将试卷类型（A ）填涂在答题卡相应位置上． 2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上．3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．4．作答选做题时，请先用2B 铅笔填涂选做题的题号对应的信息点，再作答．漏涂、错涂、多涂的，答案无效．5．考生必须保持答题卡的整洁．考试结束后，将试卷和答题卡一并交回．一、选择题：本题共35小题，每小题4分，共140分。

每小题给出的四个选项中，只有一个选项符合题目要求。

我国某校地理兴趣小组对教大楼四周日照情况进行观测。

下图示意某日教大楼日出、日落楼影分布，读图回答1、2题。

1．该日接受日照时间最长的地点是（） A ．甲 B ．乙 C ．丙 D ．丁 2．该日当地的昼长约为（）A ．3／小时 8．15／小时 C ．9／小时 D ．18／小时下图为我国部分地区7月气温及年均降水量分布图。

读图，回答3、4题。

试卷第2页，总6页3．该地区7月气温分布状况是（）A．各城市均高于24℃B．①处气温低于24℃C．太原与石家庄最大温差小于4℃D．①与②处气温相同4．关于该地区年均降水量的叙述，正确的是（）A．北京的年均降水量小于郑州B．④处的年均降水量大于③处C．山区、高原年均降水量大于平原D．太原、石家庄年均降水量均小于600 mm读图，回答小题。

5下列因素中对A区域工业布局发挥重要作用的有()。

①原料②技术③交通运输④环境因素⑤劳动力数量⑥劳动力素质A．①②③④B．③④⑤⑥C．①③⑤⑥D．②③④⑥6.B区域以完善的服务体系打造成了世界著名的新工业区代表，下列因素中对该工业区的形成影响较小的是()。

天津高考物理压轴大题

天津近5年高考物理压轴大题汇编1.(天津2013）超导现象是20世纪人类重大发现之一，日前我国己研制出世界传输电流最大的高温超导电缆并成功示范运行。

(l ）超导体在温度特别低时电阻可以降到几乎为零，这种性质可以通过实验研究．将一个闭合超导金属圈环水平放置在匀强磁场中，磁感线垂直于圈环平面向上，逐渐降低温度使环发生由正常态到超导态的转变后突然撤去磁场，若此后环中的电流不随时间变化．则表明其电阻为零。

请指出自上往下看环中电流方向，并说明理由。

（2）为探究该圆环在超导状态的电阻率上限ρ，研究人员测得撤去磁场后环中电流为I,并经一年以上的时间t 未检测出电流变化。

实际上仪器只能检测出大于ΔI 的电流变化，其中△I<<I ，当电流的变化小于△I 时，仪器检测不出电流的变化，研究人员便认为电流没有变化。

设环的横截面积为S ，环中定向移动电子的平均速率为v ，电子质量为m 、电荷量为e ．试用上述给出的各物理量，推导出ρ的表达式。

(3）若仍使用上述测量仪器，实验持续时间依旧为t ．为使实验获得的该圆环在超导状态的电阻率上限ρ的准确程度更高，请提出你的建议，并简要说明实现方法．2.（天津2012）对铀235的进一步研究在核能的开发和利用中具有重要的意义。

如图所示，质量为m 、电荷量为q 的铀235离子，从容器A 下方的小孔S 1不断飘入加速电场，其初速度可视为零，然后经过小孔S 2垂直与磁场方向进入磁感应强度为B 的均强磁场中，做半径为R 的均速圆周运动，离子行进半个圆周后离开磁场并被收集，离开磁场时离子束的等效电流I 。

不考虑离子重力及离子间的相互作用。

（1）求加速电场的电压U ；（2）求出在离子被收集的过程中任意间t 内收集到离子的质量M ；（3）实际上加速电压的大小在U ±ΔU 范围内微小变化。

若容器A 中有电荷量相同的铀235和铀238两种离子，如前述情况它们经电场加速后进入磁场中发生分离，为使这两种离子在磁场中运动的轨迹不发生交叠，UU 应小于多少？（结果用百分数表示，保留两位有效数字）3.（天津2011）回旋加速器在核科学、核技术、核医学等高新技术领域得到了广泛应用，有力地推动了现代科学技术的发展。

天津市人教版七年级上册数学压轴题期末复习试卷及答案-百度文库

天津市人教版七年级上册数学压轴题期末复习试卷及答案-百度文库一、压轴题1．如图1，O 为直线AB 上一点，过点O 作射线OC ，∠AOC ＝30°，将一直角三角板（其中∠P ＝30°）的直角顶点放在点O 处，一边OQ 在射线OA 上，另一边OP 与OC 都在直线AB 的上方．将图1中的三角板绕点O 以每秒3°的速度沿顺时针方向旋转一周．（1）如图2，经过t 秒后，OP 恰好平分∠BOC ． ①求t 的值；②此时OQ 是否平分∠AOC ？请说明理由；（2）若在三角板转动的同时，射线OC 也绕O 点以每秒6°的速度沿顺时针方向旋转一周，如图3，那么经过多长时间OC 平分∠POQ ？请说明理由；（3）在（2）问的基础上，经过多少秒OC 平分∠POB ？（直接写出结果）．2．小刚运用本学期的知识，设计了一个数学探究活动.如图1，数轴上的点M ，N 所表示的数分别为0，12.将一枚棋子放置在点M 处，让这枚棋子沿数轴在线段MN 上往复运动（即棋子从点M 出发沿数轴向右运动，当运动到点N 处，随即沿数轴向左运动，当运动到点M 处，随即沿数轴向右运动，如此反复⋯）.并且规定棋子按照如下的步骤运动：第1步，从点M 开始运动t 个单位长度至点1Q 处；第2步，从点1Q 继续运动2t 单位长度至点2Q 处；第3步，从点2Q 继续运动3t 个单位长度至点3Q 处…例如：当3t =时，点1Q 、2Q 、3Q 的位置如图2所示.解决如下问题：（1）如果4t =，那么线段13Q Q =______；（2）如果4t <，且点3Q 表示的数为3，那么t =______；（3）如果2t ≤，且线段242Q Q =，那么请你求出t 的值.3．已知数轴上，点A 和点B 分别位于原点O 两侧，AB=14，点A 对应的数为a ，点B 对应的数为b.(1) 若b ＝－4，则a 的值为__________. (2) 若OA ＝3OB ，求a 的值.(3) 点C 为数轴上一点，对应的数为c ．若O 为AC 的中点，OB ＝3BC ，直接写出所有满足条件的c 的值.4．已知∠AOB ＝110°，∠COD ＝40°，OE 平分∠AOC ，OF 平分∠BOD ．（1）如图1，当OB 、OC 重合时，求∠AOE ﹣∠BOF 的值；（2）如图2，当∠COD 从图1所示位置绕点O 以每秒3°的速度顺时针旋转t 秒（0＜t ＜10），在旋转过程中∠AOE ﹣∠BOF 的值是否会因t 的变化而变化？若不发生变化，请求出该定值；若发生变化，请说明理由．（3）在（2）的条件下，当∠COF ＝14°时，t ＝秒．5．综合试一试（1）下列整数可写成三个非0整数的立方和：45=_____；2=______．（2）对于有理数a ，b ，规定一种运算：2a b a ab ⊗=-．如2121121⊗=-⨯=-，则计算()()532-⊗⊗-=⎡⎤⎣⎦______．（3）a 是不为1的有理数，我们把11a-称为a 的差倒数．如：2的差倒数是1112=--，1-的差倒数是()11112=--．已知12a =，2a 是1a 的差倒数，3a 是2a 的差倒数，4a 是3a 的差倒数，……，以此类推，122500a a a ++⋅⋅⋅+=______．（4）10位裁判给一位运动员打分，每个人给的分数都是整数，去掉一个最高分，再去掉一个最低分，其余得分的平均数为该运动员的得分．若用四舍五入取近似值的方法精确到十分位，该运动员得9.4分，如果精确到百分位，该运动员得分应当是_____分．（5）在数1.2.3...2019前添加“+”，“-”并依次计算，所得结果可能的最小非负数是______（6）早上8点钟，甲、乙、丙三人从东往西直行，乙在甲前400米，丙在乙前400米，甲、乙、丙三人速度分别为120米/分钟、100米/分钟、90米/分钟，问：______分钟后甲和乙、丙的距离相等.6．如图，已知数轴上点A 表示的数为8，B 是数轴上位于点A 左侧一点，且AB =22，动点P从A点出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．（1）出数轴上点B表示的数；点P表示的数（用含t的代数式表示）（2）动点Q从点B出发，以每秒3个单位长度的速度沿数轴向右匀速运动，若点P、Q同时出发，问多少秒时P、Q之间的距离恰好等于2？（3）动点Q从点B出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，问点P运动多少秒时追上点Q？（4）若M为AP的中点，N为BP的中点，在点P运动的过程中，线段MN的长度是否发生变化？若变化，请说明理由，若不变，请你画出图形，并求出线段MN的长．7．已知多项式3x6﹣2x2﹣4的常数项为a，次数为b．（1）设a与b分别对应数轴上的点A、点B，请直接写出a＝，b＝，并在数轴上确定点A、点B的位置；（2）在（1）的条件下，点P以每秒2个单位长度的速度从点A向B运动，运动时间为t 秒：①若PA﹣PB＝6，求t的值，并写出此时点P所表示的数；②若点P从点A出发，到达点B后再以相同的速度返回点A，在返回过程中，求当OP＝3时，t为何值？8．已知数轴上有A、B、C三个点对应的数分别是a、b、c，且满足|a+24|+|b+10|+（c-10）2=0；动点P从A出发，以每秒1个单位的速度向终点C移动，设移动时间为t秒．（1）求a、b、c的值；（2）若点P到A点距离是到B点距离的2倍，求点P的对应的数；（3）当点P运动到B点时，点Q从A点出发，以每秒2个单位的速度向C点运动，Q点到达C点后．再立即以同样的速度返回，运动到终点A，在点Q开始运动后第几秒时，P、Q两点之间的距离为8？请说明理由．9．（1）探究：哪些特殊的角可以用一副三角板画出？在①135︒，②120︒，③75︒，④25︒中，小明同学利用一副三角板画不出来的特殊角是_________；（填序号）（2）在探究过程中，爱动脑筋的小明想起了图形的运动方式有多种.如图，他先用三角板∠）的顶点与60角画出了直线EF，然后将一副三角板拼接在一起，其中45角（AOB∠）的顶点互相重合，且边OA、OC都在直线EF上.固定三角板COD不动，将（COD三角板AOB绕点O按顺时针方向旋转一个角度α，当边OB与射线OF第一次重合时停止.①当OB 平分EOD ∠时，求旋转角度α；②是否存在2BOC AOD ∠=∠？若存在，求旋转角度α；若不存在，请说明理由. 10．如图，已知数轴上点A 表示的数为6，B 是数轴上在A 左侧的一点，且A ，B 两点间的距离为10．动点P 从点A 出发，以每秒5个单位长度的速度沿数轴向左匀速运动，动点Q 从点B 出发，以每秒3个单位长度的速度沿数轴向左匀速运动．（1）设运动时间为t （t ＞0）秒，数轴上点B 表示的数是，点P 表示的数是（用含t 的代数式表示）；（2）若点P 、Q 同时出发，求：①当点P 运动多少秒时，点P 与点Q 相遇？②当点P 运动多少秒时，点P 与点Q 间的距离为8个单位长度？11．已知，如图，A 、B 、C 分别为数轴上的三点，A 点对应的数为60，B 点在A 点的左侧，并且与A 点的距离为30，C 点在B 点左侧，C 点到A 点距离是B 点到A 点距离的4倍．（1）求出数轴上B 点对应的数及AC 的距离．（2）点P 从A 点出发，以3单位/秒的速度向终点C 运动，运动时间为t 秒． ①当P 点在AB 之间运动时，则BP ＝．（用含t 的代数式表示）②P 点自A 点向C 点运动过程中，何时P ，A ，B 三点中其中一个点是另外两个点的中点？求出相应的时间t ．③当P 点运动到B 点时，另一点Q 以5单位/秒的速度从A 点出发，也向C 点运动，点Q 到达C 点后立即原速返回到A 点，那么Q 点在往返过程中与P 点相遇几次？直．接．写．出．相遇时P 点在数轴上对应的数12．在数轴上，图中点A 表示－36，点B 表示44，动点P 、Q 分别从A 、B 两点同时出发，相向而行，动点P 、Q 的运动速度比之是3∶2（速度单位：1个单位长度/秒）．12秒后，动点P 到达原点O ，动点Q 到达点C ，设运动的时间为t （t ＞0）秒．（1）求OC 的长；（2）经过t 秒钟，P 、Q 两点之间相距5个单位长度，求t 的值；（3）若动点P 到达B 点后，以原速度立即返回，当P 点运动至原点时，动点Q 是否到达A 点，若到达，求提前到达了多少时间，若未能到达，说明理由．13．数轴上线段的长度可以用线段端点表示的数进行减法运算得到，例如：如图①，若点A ，B 在数轴上分别对应的数为a ，b (a <b )，则AB 的长度可以表示为AB =b －a ．请你用以上知识解决问题：如图②，一个点从数轴上的原点开始，先向左移动2个单位长度到达A点，再向右移动3个单位长度到达B点，然后向右移动5个单位长度到达C点．（1）请你在图②的数轴上表示出A，B，C三点的位置．（2）若点A以每秒1个单位长度的速度向左移动，同时，点B和点C分别以每秒2个单位长度和3个单位长度的速度向右移动，设移动时间为t秒．①当t=2时，求AB和AC的长度；②试探究：在移动过程中，3AC－4AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值．14．如图，数轴上有A、B两点，且AB=12，点P从B点出发沿数轴以3个单位长度/s的速度向左运动，到达A点后立即按原速折返，回到B点后点P停止运动，点M始终为线段BP的中点(1)若AP=2时，PM=____；(2)若点A表示的数是-5，点P运动3秒时，在数轴上有一点F满足FM=2PM，请求出点F 表示的数；(3)若点P从B点出发时，点Q同时从A点出发沿数轴以2.5个单位长度/s的速度一直．．向右运动，当点Q的运动时间为多少时，满足QM=2PM.15．如图所示，已知数轴上A，B两点对应的数分别为－2，4，点P为数轴上一动点，其对应的数为x.(1)若点P到点A，B的距离相等，求点P对应的数x的值．(2)数轴上是否存在点P，使点P到点A，B的距离之和为8？若存在，请求出x的值；若不存在，说明理由．(3)点A，B分别以2个单位长度/分、1个单位长度/分的速度向右运动，同时点P以5个单位长度/分的速度从O点向左运动．当遇到A时，点P立即以同样的速度向右运动，并不停地往返于点A与点B之间．当点A与点B重合时，点P经过的总路程是多少？【参考答案】***试卷处理标记，请不要删除一、压轴题1．（1）①5；②OQ平分∠AOC，理由详见解析；（2）5秒或65秒时OC平分∠POQ；（3）t＝703秒．【解析】【分析】（1）①由∠AOC＝30°得到∠BOC＝150°，借助角平分线定义求出∠POC度数，根据角的和差关系求出∠COQ度数，再算出旋转角∠AOQ度数，最后除以旋转速度3即可求出t 值；②根据∠AOQ和∠COQ度数比较判断即可；（2）根据旋转的速度和起始位置，可知∠AOQ＝3t，∠AOC＝30°+6t，根据角平分线定义可知∠COQ＝45°，利用∠AOQ、∠AOC、∠COQ角之间的关系构造方程求出时间t；（3）先证明∠AOQ与∠POB互余，从而用t表示出∠POB＝90°﹣3t，根据角平分线定义再用t表示∠BOC度数；同时旋转后∠AOC＝30°+6t，则根据互补关系表示出∠BOC度数，同理再把∠BOC度数用新的式子表达出来．先后两个关于∠BOC的式子相等，构造方程求解．【详解】（1）①∵∠AOC＝30°，∴∠BOC＝180°﹣30°＝150°,∵OP平分∠BOC，∴∠COP＝12∠BOC＝75°,∴∠COQ＝90°﹣75°＝15°,∴∠AOQ＝∠AOC﹣∠COQ＝30°﹣15°＝15°, t＝15÷3＝5；②是，理由如下：∵∠COQ＝15°，∠AOQ＝15°，∴OQ平分∠AOC；（2）∵OC平分∠POQ，∴∠COQ＝12∠POQ＝45°．设∠AOQ＝3t，∠AOC＝30°+6t，由∠AOC﹣∠AOQ＝45°，可得30+6t﹣3t＝45，解得：t＝5，当30+6t﹣3t＝225，也符合条件，解得：t＝65，∴5秒或65秒时，OC平分∠POQ；（3）设经过t秒后OC平分∠POB，∵OC平分∠POB，∴∠BOC＝12∠BOP，∵∠AOQ+∠BOP＝90°，∴∠BOP ＝90°﹣3t ，又∠BOC ＝180°﹣∠AOC ＝180°﹣30°﹣6t ， ∴180﹣30﹣6t ＝12（90﹣3t ），解得t ＝703．【点睛】本题主要考查一元一次方程的应用，根据角度的和差倍分关系，列出方程，是解题的关键. 2．(1)4；(2)12或72；(3)27或2213或2 【解析】【分析】(1)根据题目得出棋子一共运动了t+2t+3t=6t 个单位长度，当t=4时，6t=24,为MN 长度的整的偶数倍，即棋子回到起点M 处，点3Q 与M 点重合，从而得出13Q Q 的长度.(2)根据棋子的运动规律可得，到3Q 点时，棋子运动运动的总的单位长度为6t,,因为t<4,由(1)知道，棋子运动的总长度为3或12+9=21，从而得出t 的值.(3)若t 2,≤则棋子运动的总长度10t 20≤,可知棋子或从M 点未运动到N 点或从N 点返回运动到2Q 的左边或从N 点返回运动到2Q 的右边三种情况可使242Q Q = 【详解】解：(1)∵t+2t+3t=6t, ∴当t=4时，6t=24, ∵24122=⨯, ∴点3Q 与M 点重合， ∴134Q Q =(2)由已知条件得出：6t=3或6t=21,解得：1t 2=或7t 2= (3)情况一：3t+4t=2,解得：2t 7=情况二：点4Q 在点2Q 右边时：3t+4t+2=2(12-3t) 解得：22t 13=情况三：点4Q 在点2Q 左边时：3t+4t-2=2(12-3t) 解得：t=2.综上所述：t 的值为，2或27或2213.【点睛】本题是一道探索动点的运动规律的题目，考查了学生数形结合的能力，探索规律的能力，用一元一次方程解决问题的能力.最后要注意分多种情况讨论.3．(1)10；(2)212±；(3)288.5±±，【解析】【分析】(1)根据题意画出数轴，由已知条件得出AB=14,OB=4,则OA=10,得出a的值为10.(2)分两种情况,点A在原点的右侧时,设OB=m,列一元一次方程求解,进一步得出OA的长度,从而得出a的值.同理可求出当点A在原点的左侧时,a的值.(3)画数轴,结合数轴分四种情况讨论计算即可.【详解】(1)解：若b＝－4，则a的值为 10(2)解：当A在原点O的右侧时（如图）：设OB=m,列方程得：m+3m=14，解这个方程得，7m2 =，所以，OA=212，点A在原点O的右侧，a的值为212.当A在原点的左侧时（如图)，a=－21 2综上，a的值为±212.(3)解：当点A在原点的右侧，点B在点C的左侧时（如图), c=－28 5.当点A在原点的右侧，点B在点C的右侧时（如图), c=－8.当点A在原点的左侧，点B在点C的右侧时，图略，c=28 5.当点A在原点的左侧，点B在点C的左侧时,图略，c=8.综上，点c 的值为：±8，±285. 【点睛】本题考查的知识点是通过画数轴,找出数轴上各线段间的数量关系并用一元一次方程来求解,需要注意的是分情况讨论时要考虑全面,此题充分锻炼了学生动手操作能力以及利用数行结合解决问题的能力.4．（1）35°；（2）∠AOE ﹣∠BOF 的值是定值，理由详见解析；（3）4．【解析】【分析】（1）首先根据角平分线的定义求得∠AOE 和∠BOF 的度数，然后根据∠AOE ﹣∠BOF 求解；（2）首先由题意得∠BOC ＝3t°，再根据角平分线的定义得∠AOC ＝∠AOB+3t°，∠BOD ＝∠COD+3t°，然后由角平分线的定义解答即可；（3）根据题意得∠BOF ＝（3t+14）°，故3314202t t +=+，解方程即可求出t 的值．【详解】解：（1）∵OE 平分∠AOC ，OF 平分∠BOD ， ∴11AOE AOC 11022︒∠=∠=⨯＝55°，11AOF BOD 402022︒︒∠=∠=⨯=， ∴∠AOE ﹣∠BOF ＝55°﹣20°＝35°；（2）∠AOE ﹣∠BOF 的值是定值由题意∠BOC ＝3t°，则∠AOC ＝∠AOB+3t°＝110°+3t°，∠BOD ＝∠COD+3t°＝40°+3t°， ∵OE 平分∠AOC ，OF 平分∠BOD ，()11AOE AOC 1103t =22︒︒∴∠=∠=⨯+3552t ︒︒+ ∴()113BOF BOD 403t 20t 222︒︒︒︒∠=∠=+=+， ∴33AOE BOF 55t 20t 3522︒︒︒︒︒⎛⎫⎛⎫∠-∠=+-+= ⎪ ⎪⎝⎭⎝⎭， ∴∠AOE ﹣∠BOF 的值是定值，定值为35°；（3）根据题意得∠BOF ＝（3t+14）°， ∴3314202t t +=+，解得4t =．故答案为4．【点睛】本题考查了角度的计算以及角的平分线的性质，理解角度之间的和差关系是关键．5．（1）23+(-3)3+43，73+(-5)3+(-6)3；（2）100；（3）25032；（4）9.38；（5）0；（6）24或40 【解析】【分析】（1）把45分解为2、-3、4三个整数的立方和，2分解为7、-5、-6三个整数的立方和即可的答案；（2）按照新运算法则，根据有理数混合运算法则计算即可得答案；（3）根据差倒数的定义计算出前几项的值，得出规律，计算即可得答案；（4）根据精确到十分位得9.4分可知平均分在9.35到9.44之间，可求出总分的取值范围，根据裁判打分是整数即可求出8个裁判给出的总分，再计算出平均分，精确到百分位即可；（5）由1+2-3=0，连续4个自然数通过加减运算可得0，列式计算即可得答案；（6）根据题意得要使甲和乙、甲和丙的距离相等就可以得出甲在乙、丙之间，设x 分钟后甲和乙、甲和丙的距离相等，就有甲走的路程-乙走的路程-400=丙走的路程+800-甲走的路程建立方程求出其解，就可以得出结论．当乙追上丙时，甲和乙、丙的距离相等，求出乙追上丙的时间即可.综上即可的答案. 【详解】（1）45=23+(-3)3+43，2=73+(-5)3+(-6)3，故答案为23+(-3)3+43，73+(-5)3+(-6)3 （2）∵2a b a ab ⊗=-，∴()()532-⊗⊗-=⎡⎤⎣⎦(-5)⊗[32-3×(-2)]=(-5)⊗15 =(-5)2-(-5)×15 =100. （3）∵a 1=2， ∴a 2=1112=--， a 3=11(1)--=12， 412112a ==-a 5=-1 ……∴从a 1开始，每3个数一循环， ∵2500÷3=833……1， ∴a 2500=a 1=2，∴122500a a a ++⋅⋅⋅+=833×(2-1+12)+2=25032. （4）∵10个裁判打分，去掉一个最高分，再去掉一个最低分，∴平均分为中间8个分数的平均分，∵平均分精确到十分位的为9.4，∴平均分在9.35至9.44之间，9.35×8=74.8，9.44×8=75.52，∴8个裁判所给的总分在74.8至75.52之间，∵打分都是整数，∴总分也是整数，∴总分为75，∴平均分为75÷8=9.375，∴精确到百分位是9.38.故答案为9.38（5）2019÷4=504……3，∵1+2-3=0，4-5-6+7=0，8-9-10+11=0，……∴(1+2-3)+(4-5-6+7)+……+(2016-2017-2018+2019)=0∴所得结果可能的最小非负数是0，故答案为0（6）设x分钟后甲和乙、丙的距离相等，∵乙在甲前400米，丙在乙前400米，速度分别为120米/分钟、100米/分钟、90米/分钟，∴120x-400-100x=90x+800-120x解得：x=24.∵当乙追上丙时，甲和乙、丙的距离相等，∴400÷(100-90)=40(分钟)∴24分钟或40分钟时甲和乙、丙的距离相等.故答案为24或40.【点睛】本题考查数字类的变化规律、有理数的混合运算、近似数及一元一次方程的应用，熟练掌握相关知识是解题关键.6．（1）﹣14，8﹣5t；（2）2.5或3秒时P、Q之间的距离恰好等于2；（3）点P运动11秒时追上点Q；（4）线段MN的长度不发生变化，其值为11，见解析.【解析】【分析】（1）根据已知可得B点表示的数为8﹣22；点P表示的数为8﹣5t；（2）设t秒时P、Q 之间的距离恰好等于2．分①点P、Q相遇之前和②点P、Q相遇之后两种情况求t值即可；（3）设点P运动x秒时，在点C处追上点Q，则AC=5x，BC=3x，根据AC﹣BC=AB，列出方程求解即可；（3）分①当点P在点A、B两点之间运动时，②当点P运动到点B的左侧时，利用中点的定义和线段的和差求出MN的长即可．【详解】（1）∵点A表示的数为8，B在A点左边，AB=22，∴点B表示的数是8﹣22=﹣14，∵动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t （t＞0）秒，∴点P表示的数是8﹣5t．故答案为：﹣14，8﹣5t；（2）若点P、Q同时出发，设t秒时P、Q之间的距离恰好等于2．分两种情况：①点P、Q相遇之前，由题意得3t+2+5t=22，解得t=2.5；②点P、Q相遇之后，由题意得3t﹣2+5t=22，解得t=3．答：若点P、Q同时出发，2.5或3秒时P、Q之间的距离恰好等于2；（3）设点P运动x秒时，在点C处追上点Q，则AC=5x，BC=3x，∵AC﹣BC=AB，∴5x﹣3x=22，解得：x=11，∴点P运动11秒时追上点Q；（4）线段MN的长度不发生变化，都等于11；理由如下：①当点P在点A、B两点之间运动时：MN=MP+NP=12AP+12BP=12（AP+BP）=12AB=12×22=11；②当点P运动到点B的左侧时：MN=MP﹣NP=12AP﹣12BP=12（AP﹣BP）=12AB=11，∴线段MN的长度不发生变化，其值为11．【点睛】本题考查了数轴一元一次方程的应用，用到的知识点是数轴上两点之间的距离，关键是根据题意画出图形，注意分两种情况进行讨论．7．（1）﹣4，6；（2）①4；②1319,22或【解析】【分析】（1）根据多项式的常数项与次数的定义分别求出a，b的值，然后在数轴上表示即可；（2）①根据PA﹣PB＝6列出关于t的方程，解方程求出t的值，进而得到点P所表示的数；②在返回过程中，当OP＝3时，分两种情况：（Ⅰ）P在原点右边；（Ⅱ）P在原点左边．分别求出点P运动的路程，再除以速度即可．【详解】（1）∵多项式3x6﹣2x2﹣4的常数项为a，次数为b，∴a＝﹣4，b＝6．如图所示：故答案为﹣4，6；（2）①∵PA＝2t，AB＝6﹣（﹣4）＝10，∴PB＝AB﹣PA＝10﹣2t．∵PA﹣PB＝6，∴2t﹣（10﹣2t）＝6，解得t＝4，此时点P所表示的数为﹣4+2t＝﹣4+2×4＝4；②在返回过程中，当OP＝3时，分两种情况：（Ⅰ）如果P在原点右边，那么AB+BP＝10+（6﹣3）＝13，t＝132；（Ⅱ）如果P在原点左边，那么AB+BP＝10+（6+3）＝19，t＝192．【点睛】本题考查了一元一次方程的应用，路程、速度与时间关系的应用，数轴以及多项式的有关定义，理解题意利用数形结合是解题的关键．8．(1) a=-24，b=-10，c=10；(2) 点P的对应的数是-443或4；(3) 当Q点开始运动后第6、21秒时，P、Q两点之间的距离为8，理由见解析【解析】【分析】（1）根据绝对值和偶次幂具有非负性可得a+24=0，b+10=0，c-10=0，解可得a、b、c的值；（2）分两种情况讨论可求点P的对应的数；（3）分类讨论：当P点在Q点的右侧，且Q点还没追上P点时；当P在Q点左侧时，且Q点追上P点后；当Q点到达C点后，当P点在Q点左侧时；当Q点到达C点后，当P 点在Q点右侧时，根据两点间的距离是8，可得方程，根据解方程，可得答案．【详解】（1）∵|a+24|+|b+10|+（c-10）2=0，∴a+24=0，b+10=0，c-10=0，解得：a=-24，b=-10，c=10；（2）-10-（-24）=14，①点P在AB之间，AP=14×221=283，-24+283=-443，点P 的对应的数是-443； ②点P 在AB 的延长线上，AP =14×2=28，-24+28=4，点P 的对应的数是4；（3）∵AB =14，BC =20，AC =34，∴t P =20÷1=20（s ），即点P 运动时间0≤t ≤20，点Q 到点C 的时间t 1=34÷2=17（s ），点C 回到终点A 时间t 2=68÷2=34（s ），当P 点在Q 点的右侧，且Q 点还没追上P 点时，2t +8=14+t ，解得t =6；当P 在Q 点左侧时，且Q 点追上P 点后，2t -8=14+t ，解得t =22＞17（舍去）；当Q 点到达C 点后，当P 点在Q 点左侧时，14+t +8+2t -34=34，t =463＜17（舍去）；当Q 点到达C 点后，当P 点在Q 点右侧时，14+t -8+2t -34=34，解得t =623＞20（舍去），当点P 到达终点C 时，点Q 到达点D ，点Q 继续行驶（t -20）s 后与点P 的距离为8，此时2（t -20）+（2×20-34）=8，解得t =21；综上所述：当Q 点开始运动后第6、21秒时，P 、Q 两点之间的距离为8．【点睛】此题主要考查了一元一次方程的应用，关键是正确理解题意，掌握非负数的性质，再结合数轴解决问题．9．（1）④；（2）①15α=︒；②当105α=，125α=时，存在2BOC AOD ∠=∠.【解析】【分析】（1）根据一副三角板中的特殊角，运用角的和与差的计算，只要是15°的倍数的角都可以画出来；（2）①根据已知条件得到∠EOD=180°-∠COD=180°-60°=120°，根据角平分线的定义得到∠EOB=12∠EOD=12×120°=60°，于是得到结论； ②当OA 在OD 的左侧时，当OA 在OD 的右侧时，根据角的和差列方程即可得到结论．【详解】解：（1）∵135°=90°+45°，120°=90°+30°，75°=30°+45°，∴只有25°不能写成90°、60°、45°、30°的和或差，故画不出；故选④；（2）①因为COD 60∠=，所以EOD 180COD 18060120∠∠=-=-=.因为OB 平分EOD ∠，所以11EOB EOD 1206022∠∠==⨯=. 因为AOB 45∠=，所以αEOB AOB 604515∠∠=-=-=.②当OA 在OD 左侧时，则AOD 120α∠=-，BOC 135α∠=-.因为BOC 2AOD ∠∠=，所以()135α2120α-=-.解得α105=.当OA 在OD 右侧时，则AOD α120∠=-，BOC 135α∠=-.因为BOC 2AOD ∠∠=，所以()135α2α120-=-.解得α125=.综合知，当α105=，α125=时，存在BOC 2AOD ∠∠=.【点睛】本题考查角的计算，角平分线的定义，正确的理解题意并分类讨论是解题关键．10．（1）﹣4，6﹣5t ；（2）①当点P 运动5秒时，点P 与点Q 相遇；②当点P 运动1或9秒时，点P 与点Q 间的距离为8个单位长度．【解析】【分析】（1）根据题意可先标出点A ，然后根据B 在A 的左侧和它们之间的距离确定点B ，由点P 从点A 出发向左以每秒5个单位长度匀速运动，表示出点P 即可；（2）①由于点P 和Q 都是向左运动，故当P 追上Q 时相遇，根据P 比Q 多走了10个单位长度列出等式，根据等式求出t 的值即可得出答案；②要分两种情况计算：第一种是点P 追上点Q 之前，第二种是点P 追上点Q 之后.【详解】解：（1）∵数轴上点A 表示的数为6，∴OA ＝6，则OB ＝AB ﹣OA ＝4，点B 在原点左边，∴数轴上点B 所表示的数为﹣4；点P 运动t 秒的长度为5t ，∵动点P 从点A 出发，以每秒5个单位长度的速度沿数轴向左匀速运动，∴P 所表示的数为：6﹣5t ，故答案为﹣4，6﹣5t ；（2）①点P 运动t 秒时追上点Q ，根据题意得5t ＝10+3t ，解得t ＝5，答：当点P运动5秒时，点P与点Q相遇；②设当点P运动a秒时，点P与点Q间的距离为8个单位长度，当P不超过Q，则10+3a﹣5a＝8，解得a＝1；当P超过Q，则10+3a+8＝5a，解得a＝9；答：当点P运动1或9秒时，点P与点Q间的距离为8个单位长度．【点睛】在数轴上找出点的位置并标出，结合数轴求追赶和相遇问题是本题的考点，正确运用数形结合解决问题是解题的关键，注意不要漏解.11．（1）30，120（2）①30﹣3t②5或20③﹣15或﹣483 4【解析】【分析】（1）根据A点对应的数为60，B点在A点的左侧，AB＝30求出B点对应的数；根据AC＝4AB求出AC的距离；（2）①当P点在AB之间运动时，根据路程＝速度×时间求出AP＝3t，根据BP＝AB﹣AP 求解；②分P点是A、B两个点的中点；B点是A、P两个点的中点两种情况讨论即可；③根据P、Q两点的运动速度与方向可知Q点在往返过程中与P点相遇2次．设Q点在往返过程中经过x秒与P点相遇．第一次相遇是点Q从A点出发，向C点运动的途中．根据AQ ﹣BP＝AB列出方程；第二次相遇是点Q到达C点后返回到A点的途中．根据CQ+BP＝BC列出方程，进而求出P点在数轴上对应的数．【详解】（1）∵A点对应的数为60，B点在A点的左侧，并且与A点的距离为30，∴B点对应的数为60﹣30＝30；∵C点到A点距离是B点到A点距离的4倍，∴AC＝4AB＝4×30＝120；（2）①当P点在AB之间运动时，∵AP＝3t，∴BP＝AB﹣AP＝30﹣3t．故答案为30﹣3t；②当P点是A、B两个点的中点时，AP＝12AB＝15，∴3t＝15，解得t＝5；当B点是A、P两个点的中点时，AP＝2AB＝60，∴3t＝60，解得t＝20．故所求时间t的值为5或20；③相遇2次．设Q点在往返过程中经过x秒与P点相遇．第一次相遇是点Q从A点出发，向C点运动的途中．∵AQ﹣BP＝AB，∴5x﹣3x＝30，解得x＝15，此时P点在数轴上对应的数是：60﹣5×15＝﹣15；第二次相遇是点Q到达C点后返回到A点的途中．∵CQ+BP＝BC，∴5（x﹣24）+3x＝90，解得x＝1054，此时P点在数轴上对应的数是：30﹣3×1054＝﹣4834．综上，相遇时P点在数轴上对应的数为﹣15或﹣4834．【点睛】本题考查了一元一次方程的应用，行程问题相等关系的应用，线段中点的定义，进行分类讨论是解题的关键．12．（1）20；（2）t=15s或17s （3）4 3 s.【解析】【分析】（1）设P、Q速度分别为3m、2m，根据12秒后，动点P到达原点O列方程，求出P、Q 的速度，由此即可得到结论．（2）分两种情况讨论：①当A、B在相遇前且相距5个单位长度时；②当A、B在相遇后且相距5个单位长度时；列方程，求解即可．（3）算出P运动到B再到原点时，所用的时间，再算出Q从B到A所需的时间，比较即可得出结论．【详解】（1）设P、Q速度分别为3m、2m，根据题意得：12×3m=36，解得：m=1，∴P、Q速度分别为3、2，∴BC=12×2=24，∴OC=OB－BC=44－24=20．（2）当A、B在相遇前且相距5个单位长度时：3t＋2t＋5=44＋36，5t=75，∴t=15（s）；当A、B在相遇后且相距5个单位长度时：3t＋2t－5=44＋36，5t=85，∴t=17（s）．综上所述：t=15s或17s．（3）P运动到原点时，t=3644443++=1243s，此时QB=2×1243=2483＞44+38=80，∴Q点已到达A点，∴Q点已到达A点的时间为：3644804022+==（s），故提前的时间为：1243－40=43（s）．【点睛】本题考查了一元一次方程的应用-行程问题以及数轴上的动点问题．解题的关键是找出等量关系，列出方程求解．13．（1）详见解析；（2）①16；②在移动过程中，3AC ﹣4AB 的值不变【解析】【分析】（1）根据点的移动规律在数轴上作出对应的点即可；（2）①当t =2时，先求出A 、B 、C 点表示的数，然后利用定义求出AB 、AC 的长即可； ②先求出A 、B 、C 点表示的数，然后利用定义求出AB 、AC 的长，代入3AC －4AB 即可得到结论．【详解】（1）A ，B ，C 三点的位置如图所示：．（2）①当t =2时，A 点表示的数为－4，B 点表示的数为5，C 点表示的数为12，∴AB =5－(－4)=9，AC =12－(－4)=16．②3AC －4AB 的值不变．当移动时间为t 秒时，A 点表示的数为－t －2，B 点表示的数为2t ＋1，C 点表示的数为3t ＋6，则：AC =(3t ＋6)－(－t －2)=4t ＋8，AB =(2t ＋1)－(－t －2)=3t ＋3，∴3AC －4AB =3(4t ＋8)－4(3t ＋3)=12t ＋24－12t －12=12．即3AC ﹣4AB 的值为定值12，∴在移动过程中，3AC ﹣4AB 的值不变．【点睛】本题考查了数轴上的动点问题．表示出对应点所表示的数是解答本题的关键．14．(1)5 ；(2)点F 表示的数是11.5或者-6.5；(3)127t =或6t =. 【解析】【分析】（1）由AP=2可知PB=12-2=10，再由点M 是PB 中点可知PM 长度；（2）点P 运动3秒是9个单位长度，M 为PB 的中点，则可求解出点M 表示的数是2.5，再由FM=2PM 可求解出FM=9，此时点F 可能在M 点左侧，也可能在其右侧；（3）设Q 运动的时间为t 秒，由题可知t=4秒时，点P 到达点A ，再经过4秒点P 停止运动；则分04t ≤≤和48t <≤两种情况分别计算，由题可知即可QM=2PM=BP ，据此进行解答即可.【详解】(1)5 ；(2)∵点A 表示的数是5-∴点B 表示的数是7∵点P 运动3秒是9个单位长度，M 为PB 的中点∴PM=12PB=4.5，即点M 表示的数是2.5∵FM=2PM∴FM=9∴点F 表示的数是11.5或者-6.5(3)设Q 运动的时间为t 秒，当04t ≤≤时，由题可知QM=2PM=BP ，故点Q 位于点P 左侧，则AB=AQ+QP+PB ，而QP=QM-PM=2PM-PM=12BP ，则可得12=2.5t+12⨯3t+3t=7t ，解得t=127；当48t <≤时，由题可知QM=2PM=BP ，故点Q 位于点B 右侧，则PB=2QB ，则可得，()()123422.512t t --=-，整理得8t=48，解得6t =.【点睛】本题结合数轴上的动点问题考查了一元一次方程的应用，第3问要根据题干条件分情况进行讨论，作出图形更易理解.15．(1)x=1;(2) x ＝－3或x ＝5;(3) 30.【解析】【分析】（1）根据题意可得4－x ＝x －（－2），解出x 的值；（2）此题分为两种情况，当点P 在B 的右边时，当点P 在B 的左边时，分别列出方程求解即可；（3）设经过x 分钟点A 与点B 重合，根据题意得：2x ＝6＋x 进而求出即可.【详解】（1）4－x ＝x －（－2），解得：x ＝1，（2）①当点P 在B 的右边时得：x －（－2）＋x －4＝8，解得：x ＝5，②当点P 在B 的左边时得：－2－x ＋4－x ＝8，解得：x ＝－3，则x ＝－3或x ＝5.（3）设经过x 分钟点A 与点B 重合，根据题意得：2x ＝6＋x ，解得：x ＝6，则5x ＝30，故答案为30个单位长度.【点睛】本题主要考查了一元二次方程的应用，解此题的要点在于根据数轴得出点的位置.。

2014年新课标II高考压轴卷语

2014年新课标II高考压轴卷语文第I卷阅读题甲必考题一、现代文阅读（9分，每小题3分）阅读下面的文字，完成1～3题庸片高票房折射发行环节的膨胀葛颖自中国电影产业化以来，对发行环节的研究与探索成了我们向先进国家学习产业经验的主要方向。

如何包装产品、如何投放产品、如何掌握吆喝的分寸和时机，都在很大程度上决定了产品流通的范围和速度。

在美国，六大电影公司之所以举足轻重，是因为它们拥有庞大的影片分销渠道，它们能够基本保证影片抵达目标市场，与目标受众见面。

它们其实都是发行公司。

这在一个高度商业化的时代是再自然不过的事情，谁拥有销售渠道，谁就有可能把任何产品卖出去。

由之，发行在产业链中就握有了绝对的话语权。

凸显发行的主导性，在影片的策划阶段就导入市场概念，就能将传统制片环节的相对盲目性改变成为特定市场、特定人群的订制服务；同样，发行渗透放映环节，也会使放映服务更具针对性和特色。

但在一个尚不成熟的电影市场环境中，急速膨胀的发行端，由于没有相应的制衡机制，就容易出现独大独霸的卖方市场格局。

成熟市场中的电影产品，其质量评价体系有一个相对长期的验收过程，首轮票房只是对影片评价的第一个参数，更重要的还有口碑的检验（其海外放映、DVD发行、数字点播、衍生品售卖等，通常均在本土首轮放映之后）。

即使出现好片低票房、烂片高票房的情况，成熟的电影市场也能做一些补偿，比如每年年初的金球奖和奥斯卡奖就是对上一年度在北美公映的影片的内容检验。

通过奖项的肯定，许多被湮没的影片进入了公众的视野，或得以二次发行，或在音像等版权衍生市场上一炮打响。

而在目下的中国电影市场，本土票房基本是一部电影的全部收入。

尤其只要在前三天确保放映场次足够多，平均一周时间即可回本且赢利的市场条件下，如何开动发行机器就成了大多数电影决胜的要义。

一些内容质量不佳的影片便可能经过一番改头换面的包装，在口碑尚未构成对市场的决定性影响之前，攫取到第一桶金。

此外，影评缺失权威性，奖项对市场基本不具指导意义，全国影院的采片趣味趋同，都是酿成当前内地市场无法制衡强势的发行端的症结。