初三年级第一学期期中测试题十一

合集下载

广东省深圳市深圳高级中学(集团)2024--2025学年九年级上学期期中测试化学试题(含答案)

深圳高级中学（集团）2024-2025学年第一学期期中测试初三年级化学（学科）本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷为1-12题，共20分，第Ⅱ卷为13-16题，共30分。

全卷共计50分。

考试时间为40分钟。

注意事项：1、答题前，请将学校、姓名、班级、考场和座位号写在答题卡指定位置。

2、选择题答案，用2B铅笔把答题卡上对应题目的答案标号涂黑。

如需改动请用2B橡皮擦干净后，再涂其它答案，不能答在试题卷上。

非选择题，答题不能超出题目指定区域。

3、考试结束，监考人员将答题卡收回。

第Ⅰ卷（本卷共计20 分）一、选择题I（每小题只有一个选项符合题意，每小题1.5分，共计12分）1．2024年5月3日，嫦娥六号探测器由长征五号运载火箭在中国文昌航天发射场成功发射，开启世界首次月球背面采集月壤样品之旅。

下列探月过程属于化学变化的是（）A．点火起航B．箭器分离C．月背着陆D．采集月壤2．以下是常用的危险品标志，装运酒精的包装箱应贴的标志是（）A．B．C．D．3．正确操作是化学实验成功的基础，下列操作正确的是（）A．用滴管取液体B．氧气的验满C ．过滤泥水D．取用固体粉末4.“证据推理与模型认知”是科学思维的重要组成部分。

下列推理正确的是（ )A．物体受热时膨胀，所以分子的体积变大B．分子能保持物质的化学性质，所以保持物质化学性质的一定是分子C．化合物由不同种元素组成，所以由同种元素组成的物质一定不是化合物D．有氧气参与的化合反应一定是氧化反应，所以氧化反应一定是化合反应5．下列化学用语表达不正确的是（）A ．Al 3+的结构示意图：B. 2O ：表示两个氧原子C ．一个硫离子：S +2D.构成氯化钠的微粒：Na +和Cl ﹣6．科学家采用“组合转化”技术，可将CO 2在一定条件下转化为重要的化工原料乙烯，其反应的微观过程如图所示。

下列说法正确的是（）A.一个二氧化碳分子由一个碳原子和两个氧原子构成B ．“ ”是由原子构成的物质C ．参加反应的H 2和CO 2的分子个数比为4：1D ．反应前后原子和分子的种类、数目改变7．5G 通信技术是近期社会发展的一大科技亮点，其芯片是由氮化镓（GaN ）等材料制成。

人教版2022--2023学年度第一学期九年级数学上册期中测试卷及答案

（2）若点P为⊙O的"等直顶点"，且点P在直线yx上，求点P的横坐标的取值范围；
（3）设⊙C的圆心C在x轴上，半径为2，若直线yx上存在点D，使得半径为1的⊙D上存在点P是⊙C的等直顶点，求圆心C的横坐标的取值范围；
（4）直线y4x4分别和两坐标轴交于E，F两点，若线段EF上的所有点均为⊙O的等直顶点，求⊙O的半径的最大值与最小值．
(1)在如图所示的坐标系中求抛物线的解析式；
(2)若洪水到来时，水位以每小时0.3 m的速度上升，从正常水位开始，持续多少小时到达警戒线？
23.（5分）第二十四届冬季奥林匹克运动会于2022年2月4日至2月20日在北京举行，赛后，越来越多的青少年走向冰场、走进雪场、了解冰雪运动知识．某校开展了一次冬奥知识答题竞赛，七、八年级各有200名学生参加了本次活动，为了解两个年级的答题情况，从两个年级各随机抽取了20名学生的成绩进行调查分析，过程如下（数据不完整）．
【解析】
【分析】圆周角定理：在同圆或等圆中，一条弧所对的圆周角是它所对的圆心角的一半，根据圆周角定理即可得出答案．
【详解】解：∵∠ACB＝43°，
∴∠AOB＝2∠ACB＝86°，
故选：C．
【点睛】本题考查的是圆周角定理，掌握圆周角定理求解圆心角或圆周角是解题的关键.
3. C
【解析】
【详解】已知⊙O的半径为5，圆心O到直线l的距离为6，因6＞5，即d＜r，所以直线l与⊙O的位置关系是相离.
【详解】解：A. 化为一般形式为，，该方程有两个不相等的实数根，不符合题意；
B. 化为一般形式为，，该方程没有实数根，符合题意；
C. ，，该方程有两个不相等的实数根，不符合题意；
D. ，化为一般形式为，，该方程有两个不相等的实数根，不符合题意．

人教版2022--2023学年度第一学期九年级数学上册期中测试卷及答案(含两套题)

25.（12分）在正方形ABCD中，点E在射线BC上（不与点B、C重合），连接DB，DE，将DE绕点E逆时针旋转90°得到EF，连接BF．
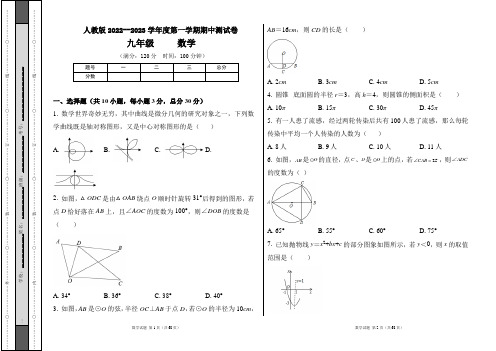
（1）如图1，点E在BC边上．
①依题意补全图1；
②若AB＝6，EC＝2，求BF的长；
（2）如图2，点E在BC边的延长线上，用等式表示线段BD，BE，BF之间的数量关系．
∴∠ODA=90°，AD=BD=8cm，
在Rt△ODA中，由勾股定理得
OD= cm，
∵OC=10cm，
∴CD=OC-OD=4cm，故选C．
【点睛】本题考查了垂径定理，勾股定理．能根据垂径定理求出AD的长是解题的关键．
4. B
【解析】
【分析】先求圆锥的母线，再根据公式求侧面积．
【详解】由勾股定理得：母线，
（1）如图1，MA＝6，MB＝8，∠NOB＝60°，求NB的长；
（2）如图2，过点M作MC⊥AB于点C，P是MN的中点，连接MB，NA，PC，试探究∠MCP，∠NAB，∠MBA之间的数量关系，并证明.
24.（12分）已知：如图1，在平面直角坐标系中，⊙P的圆心，半径为5，⊙P与抛物线的交点A、B、C刚好落在坐标轴上．
三、解答题（共9小题，总分72分）
17.（6分）已知△ABC的顶点A、B、C在格点上，按下列要求在网格中画图．
（1）△ABC绕点C顺时针旋转90°得到△A1B1C；
（2）画△A1B1C关于点O的中心对称图形△A2B2C2．
18.（6分）如图，A，P，B，C是⊙O上的四个点，∠APC＝∠CPB＝60°．
人教版2022--2023学年度第一学期期中测试卷
九年级数学
（满分：120分时间：100分钟）
题号
一
二

人教版2022--2023学年度第一学期九年级数学上册期中测试卷及答案

【详解】解：A、是轴对称图形，不是中心对称图形，故A选项错误；
B、既是轴对称图形，又是中心对称图形，故B选项错误；
C、是中心对称图形，不是轴对称图形，故C选项正确；
D、是轴对称图形，不是中心对称图形，故D选项错误；故选C.
【点睛】本题主要考查了中心对称与轴对称图形的概念，解题的关键在于能够熟练掌握中心对称图形与轴对称图形的相关知识.
14.从一块直径是的圆中剪出一个圆心角为90°的扇形，将减下来的扇形围成一个圆锥，圆锥底面圆的半径是___________．
15.如图，AB是⊙O的一条弦，点C是⊙O上一动点，且∠ACB=30°，点E、F分别是AC、BC的中点，直线EF与⊙O交于G、H两点，若⊙O的半径为7，则GE+FH的最大值为_______．
A. B.
C. D.
8.如图，是的内接三角形，，是直径，，则的长为（）
A.4B. C. D.
9.二次函数y＝ax2+bx+c（a≠0）的大致图象如图所示，顶点坐标为(1，﹣4a)，点A(4，y1)是该抛物线上一点，若点D(x2，y2)是抛物线上任意一点，有下列结论：①4a﹣2b+c＞0；②若y2＞y1，则x2＞4；③若0≤x2≤4，则0≤y2≤5a；④若方程a(x+1)(x﹣3)＝﹣1有两个实数根x1和x2，且x1＜x2，则﹣1＜x1＜x2＜3．其中正确结论的个数是（）
【详解】如图，连接，
分别与相切于两点,
,
，
，
，
．故选B．
【点睛】本题考查了圆的切线的性质，圆周角定理，求得是解题的关键．
7. B
【解析】
【分析】逐一分析四个选项，根据二次函数图象的开口以及对称轴与y轴的关系即可得出a、b的正负，由此即可得出一次函数图象经过的象限，再与函数图象进行对比即可得出结论．

福建省泉州市成功中学2025届九年级物理第一学期期中监测试题含解析

福建省泉州市成功中学2025届九年级物理第一学期期中监测试题题注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、单选题1．如图所示的电路中，电源电压不变，当电键S由闭合到断开时，下列判断正确的是A．V1变大，A变小B．V1不变，A变大C．V1变大，A变大D．V2变小，A变小2．在综合实践活动中，小明做了一个能自动回转的“魔罐”，如图甲所示．他将小铁块绑在橡皮筋中部，让橡皮筋穿入铁罐，两端分别固定在罐盖和罐底上，如图乙所示．实验装置做好后让它从不太陡的斜面上滚下，发现橡皮筋被铁块卷紧了，接着铁罐居然能从斜面底部自动滚上去．以下有关能量转化的判断，正确的是A．铁罐在斜面上从最高处滚到最低处，主要是重力势能转化为动能B．铁罐在斜面上从最高处滚到最低处，主要是弹性势能转化为动能C．铁罐在斜面上从最低处滚到最高处，主要是动能转化为重力势能D．铁罐在斜面上从最低处滚到最高处，主要是弹性势能转化为重力势能3．下列有关热的说法正确的是A．晶体在熔化过程中温度不变，内能也不变B．内燃机的压缩冲程，主要是用热传递的方法增加了气缸内的物质的内能C．用水作汽车冷却液，是因为水的比热容大D．物体吸收热量，温度一定升高4．已知有三个小球，A与毛皮摩擦过的橡胶棒相吸引，A和B相排斥，B和C相吸引，则C的带电情况是A．带正电B．带负电C．带正电或不带电D．带负电或不带电5．“海斗号”潜水器的最大潜深达10767米，使我国成为世界第三个拥有万米级深潜器的国家。

当“海斗号”在万米深处继续下潜时，受到海水的A．压强和浮力都增大B．压强和浮力都不变C．压强增大，浮力不变D．压强不变，浮力增大6．在如图所示的各电路中，开关S闭合后，小灯泡L1、L2都能发光的是（）A．B．C．D．7．李海同学骑车上学，因为赶时间经常忘记收起自行车支架便骑车或没有锁车就离开，因此他想设计提醒收支架和锁车的电路．在兴趣小组活动中，他请同学们一道设计提醒锁车的电路，要求：当车的支架支起（开关S1闭合）时，蜂鸣器响起，提醒锁车；当车上锁（开关S2断开）后，蜂鸣器停止发声．他们设计了如图所示的四个电路，其中符合要求的是A．B．C．D．8．如图所示工具，在使用时费力的是A．B．C．D．二、多选题9．如图所示，当开关S闭合后，下列说法正确的是（）A．灯L1与灯L2是串联，且灯L1被短路B．电压表可测出灯L1两端的电压C．电流表A1测的是灯L1的电流D．电流表A2测的是灯L2的电流10．下列几组现象及其中所蕴含的物理知识，对应正确的是（）A．扫地时尘土飞扬--分子是运动的B．搓手取暖--做功可以改变物体内能C．化纤衣服表面容易吸附灰尘--分子间存在引力D．验电器带电时两片金属箔会张开--同种电荷相互排斥三、填空题11．如图所示，当滑片向右移动时，接入电路的电阻减小，则应该选用的接线柱是___________．12．家用轿车日渐普及，到加油站给车加油时，能闻到汽油味，说明分子在_____；在烈日下，车体温度升高，这是通过_____的方式来改变物体内能的.13．如图所示电源两极间的电压不变.R1=4Ω，R2= 8Ω.当S1闭合时、S2断开①②都是电流表时两表的示数之比为____________；当S1、S2都闭合①②都是电压表时两表示数之比为____________.14．如图所示，赛艇的船桨是一种杠杆，划船时它是一支_____力杠杆，手移动的距离_____（选填：大于、小于）桨在水中移动的距离．15．如图所示的电路中，R1、R2均为定值电阻，电源电压不变，闭合开关S1、S2，两电表均有示数；再断开开关S2，则电流表示数_____，电压表与电流表示数之比_____（选填“变大”“变小”或“不变”）。

人教版2022--2023学年度第一学期九年级数学上册期中测试卷及答案

（1）若要建的矩形养鸡场面积为90m2，求鸡场的长(AB)和宽(BC)；
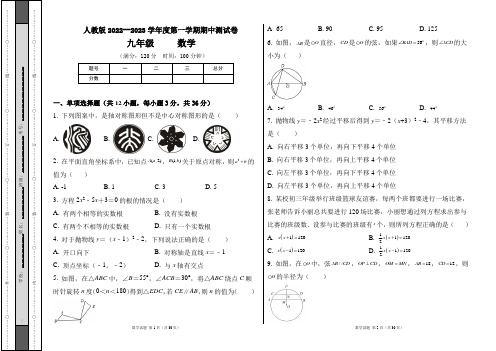
（2）该扶贫单位想要建一个100m2的矩形养鸡场，这一想法能实现吗？请说明理由．
23.（10分）某电商销售某种商品一段时间后，发现该商品每天的销售量y（单位：千克）和每千克的售价x（单位：元）满足一次函数关系（如图所示），其中，
【详解】由y＝（x﹣1）2﹣2，可知，，则抛物线的开口向上，
A选项不正确，
对称轴为，
B选项不正确，
顶点坐标为，
C选项不正确，
令，则
与轴的交点为：
D选项正确，符合题意；
故选D．
【点睛】本题考查了二次函数顶点式的性质，掌握的图象与性质是解题的关键．
5. C
【解析】
【分析】先根据三角形内角和求出∠A，根据平行线性质与旋转的性质及题意易得∠ACE的度数即可．
（1）求∠AOB的度数；
（2）求弦BC的长．
21.（8分）如图1，在圆O中，AB＝AC，∠ACB＝75°，点E在劣弧AC上运动，连接EC、BE，交AC于点F．
（1）求∠E的度数；
（2）当点E运动到使BE⊥AC时，如图2，连接AO并延长，交BE于点G，交BC于点D，交圆O于点M，求证：D为GM中点．
22.（8分）某扶贫单位为了提高贫困户经济收入，购买了33m的铁栅栏，准备用这些铁栅栏为贫困户靠墙(墙长15m)围建一个中间带有铁栅栏的矩形养鸡场(如图所示)，
【详解】解：过点作 C⊥x轴于C，
∵点A 坐标为，∠ABO＝90°，
∴ ，
∴
∴
∴ ，
由旋转的性质可得，
∴∠ OC=60°，
∴OC= Ocos60°=1， C= Osin60°= ，

人教版2022--2023学年度第一学期九年级物理上册期中测试卷及答案

物理试题第1页（共26页）物理试题第2页（共26页）………………○………………内………………○………………装………………○………………订………………○………………线………………○………………………………○………………外………………○………………装………………○………………订………………○………………线………………○………………… 学校：______________姓名：_____________班级：_______________考号：______________________人教版2022--2023学年度第一学期期中测试卷九年级物理（满分：70分时间：60分钟）题号一二总分分数第Ⅰ卷一、选择题（本题包括12小题，每小题3分，共30分。

每小题只有一个选项符合题意。

）1．对下列图片中的现象分析不正确的是（）A ．图中迅速向左推动活塞时，针筒内气体温度升高，表明压缩气体做功，气体内能增加B ．图中两个铅柱经压后就会结合在一起，说明分子间存在相互作用的引力C ．图中弹簧测力计的示数大于玻璃板的重力，是因为大气压的作用D ．图中向烧瓶中打气，当瓶塞被冲开时，瓶内出现白雾是瓶内水蒸气液化产生的2．依据表格中的数据，下列说法正确的是（）物质比热容c/J/（kg •℃）水 4.2×103 煤油 2.1×103 砂石约0.92×103A ．一杯水倒出一半，杯内剩余水的比热容变小B ．质量相等的水和砂石放出相等热量，水的温度降低得较少C ．水的比热容表示水的温度升高1℃吸收的热量是4.2×103JD ．水和煤油，吸收相等热量，煤油温度升高得较多3．如图是汽油机工作过程中的四个冲程，下列说法中错误的是（）A ．甲图是做功冲程，工作过程中主要是内能转化为机械能B ．这四个冲程的顺序是丁、丙、甲、乙C ．丙图是压缩冲程，工作过程中气缸内气体内能增加D ．丁图是吸气冲程，此冲程只将空气吸进汽缸4．如图是某地区使用的“风光互补”景观照明灯，它“头顶”小风扇，“肩扛”光电池板，“腰挎”照明灯，“脚踏”蓄电池。

人教版九年级数学(上册)期中测试卷(附参考答案)

九年级数学（上册）期中测试卷（测试时间：120分钟满分12分）一、选择题（本题共7个小题，每个小题只有一个正确选项，每小题3分，满分21分）1.a 的取值范围是（）A.0a ≥B.0a ≤C.3a ≥D. 3a ≤2.如图1所示,将正方形图案绕中心O 旋转180°后,得到的图案是 ( )图13.下列计算正确的是（）A ．224=-B =3=- 4.一元二次方程0452=-+x x 根的情况是（） A. 两个不相等的实数根 B. 两个相等的实数根C. 没有实数根D. 不能确定5.方程0562=-+x x 的左边配成完全平方后所得方程为（）A.14)3(2=+xB.14)3(2=-xC.4)3(2=+xD.4)3(2=-x 6.如图2所示，平面直角坐标系内Rt △AB O 的顶点A 坐标为（3，1），将△AB O 绕O 点逆时针旋转90°后，顶点A 的坐标为（） A. （-1，3） B. （1，-3）C. （3,1）D. (-3, 1)ODCBA图27.三角形两边长分别是8和6，第三边长是一元二次方程x 2-16x+60=0一个实数根，则该三角形的面积是（） A ．24 B ．48 C ．24或．二、填空题（本大题共8小题，每小题3分，满分24分）8.最简二次根式12+b 与17--a b 是同类二次根式，则a= b= .9.=2，且ab<0，则a-b= ．10.关于x 的方程032=--a ax x 的一个根是2-，则a 的值为_______.11.已知a 、b 是方程的两个实数根，则的值为_____. 12.已知a ，b ，则ab=_______．13.已知关于x 的一元二次方程22)210m x x -++=（有实数根，则m 的取值范围是．14.点P （—1，3）关于原点对称的点的坐标是。

15.将两块直角三角尺的直角顶点重合为如图3所示的位置, 若∠AOD=110°，则∠BOC= .图32250x x +-=22a ab a ++2690b b -+=三、解答题：（本大题共8个小题，满分75分）16、（本小题8分）化简。

人教版2022--2023学年度第一学期九年级数学上册期中测试卷及答案

A. B. C. D.
2.如图所示的正三棱柱的主视图是（）
A. B. C. D.
3.疫情期间进入学校都要进入测温通道，体温正常才可进入学校，昌平某校有2个测温通道，分别记为A、B通道，学生可随机选取其中一个通道测温进校园．某日早晨该校所有学生体温正常．小王和小李两同学该日早晨进校园时，选择同一通道测温进校园的概率是（）
A.11.5米B.11.75米C.11.8米D.12.25米
13.已知（x2+y2）2﹣y2＝x2+6，则x2+y2的值是（）
A.﹣2B.3C.﹣2或3D.﹣3或2
14.如图，AD//BC，∠D=90°，AD=3，BC=4，DC=6，若在边DC上有点P，使△PAD与△PBC相似，则这样的点P有（）
【详解】解：列表格如下：
A
B
A
A，A
B，A
B
A，B
B，B
由表可知，共有4种等可能的结果，其中小王和小李从同一个测温通道通过的有2种可能，
所以小王和小李从同一个测温通道通过的概率为．故选：C
【点睛】本题考查的是用列表法或画树状图法求概率．注意列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，用到的知识点为：概率=所求情况数与总情况数之比．
22.（8分）解方程：
（1）（2x﹣5）2﹣9＝0；
（2）4x2+2x﹣1＝0；
（3）（x+3）（x﹣1）＝5；
（4）2（x﹣3）2＝x2﹣9．
23.（4分）如图，△ABC三个顶点的坐标分别为A（0，﹣3）、B（3，﹣2）、C（2，﹣4），正方形网格中，每个小正方形的边长是1个单位长度．以点C为位似中心，在网格中画出△A2B2C，使△A2B2C与△ABC位似，且位似比为2：1，并直接写出△A2B2C的面积．

部编人教版2024--2025学年度第一学期九年级语文期中测试卷及答案

部编人教版2024--2025学年度第一学期期中测试卷九年级语文（满分：150分时间：120分钟）第一部分（30分）1.（12分）为了对“自强不息”精神有更多的了解，小苏制作了一张阅读积累卡，请帮他完善卡片内容。

○………………内………………○………………装………………○………………订………………○………………线………………○题不太契合主题需要删掉？（）A ．工厂里现在有二十多位残疾员工了，招收第一位残疾员工时您是怎么想的?B ．身体残疾对工作肯定会有一定影响的，您为什么坚持要招残疾员工，还招这么多?C ．您获评《感动中国》年度人物之后，家里人是什么反应? 6．（2分）小苏和陆鸿约定在1月23日上午10点进行采访。

22日小苏给他发短信，再次确定采访事宜。

短信中有两处内容需要修改，请你提出修改意见。

陆鸿，您好。

我是小苏。

之前跟您联系过，1月23日上午10点，我将莅临您的工厂对您进行“社会责任”主题采访。

请问见面的时间是否有变化？（1）改为（2）改为2.（9分）我校初三学生开展“春节习俗知多少”的活动，请你参与其中。

(1)（2分）请列举两种有关春节的民俗活动。

民俗活动：① ②(2)（4分）12月21日，宿迁市发布《关于调整燃放烟花爆竹范围的通告》，扩大主城区禁放区域范围。

“任何单位和个人不得以任何理由在禁放区域和场所燃放烟花爆竹”，“禁放令”颁布以后，城市中少见烟花爆竹的影子。

针对“禁放令”，请你列举两点支持的理由。

(3)（3分）校团委拟邀请民俗研究专家李教授1月5日来学校报告厅不当，请你帮忙修改。

邀请函尊敬的李教授：您好！为了让同学们领略春节文化习俗的魅力，我校邀请您于1月5日到我校作传统文化讲座。

希望你按时参加。

此致敬礼希望中学校团委 2024年1月3日①格式方面 ②内容方面 ③语言方面3.（9分）迁客骚人，情蕴诗中。

请用课文原句填空。

这里有陆游《十一月四日风雨大作（其二）》“僵卧孤村不自哀，① ”的坚定信念；有李白《行路难（其一）》“② ，直挂云帆济沧海”的奔放意志：有苏轼《江城子•密州出猎》“③ ，西北望，射天狼”的宏伟抱负；有辛弃疾《破阵子•为陈同甫赋壮词以寄之》“了却君王天下事，④ ”的雄心壮志；有王安石《登飞来峰》“不畏浮云遮望眼，⑤ ”的进取精神；有刘禹锡《酬乐天扬州初逢席上见赠》中“⑥ ， ”的昂扬之气；有范仲淹《岳阳楼记》中古仁人“⑦ ， ”的人生态度。

人教版2022--2023学年度第一学期九年级物理上册期中测试卷及答案

物理试题第1页（共24页）物理试题第2页（共24页）………………○………………内………………○………………装………………○………………订………………○………………线………………○………………………………○………………外………………○………………装………………○………………订………………○………………线………………○………………… 学校：______________姓名：_____________班级：_______________考号：______________________人教版2022--2023学年度第一学期期中测试卷九年级物理（满分：100分时间：60分钟）题号一二三四五六总分分数第Ⅰ卷一、选择题：（本题共8小题，每小题3分，共24分。

给出的四个选项中，只有一项符合题目要求，选对的得3分，有选错或不答的得0分。

）1．毛皮摩擦过的橡胶棒带负电，说明摩擦过程中橡胶棒（） A ．得到负电荷 B ．失去负电荷 C ．得到正电荷 D ．失去正电荷 2．下列选项可能符合汽车等热机能量流向的是（）A ．B ．C ．D ．3．下列说法中正确的是（） A ．摩擦起电的实质是产生电子B ．电压表不能直接测量电源两端的电压C ．通常情况下，即使通过导体的电流为零，导体的电阻一般也不为零D ．导线越长，其电阻一定也越大4．在如图所示的物理学家中，以其名字命名为电流单位的是( )A ．B ．C ．D ．5．下列关于四冲程内燃机的说法中正确的是（） A ．一个工作循环对外做功一次B ．汽油机在吸气冲程中吸入气缸的是空气C ．压缩冲程中将内能转化为机械能D ．热机效率越高，所做的有用功就越多6．某同学探究不同物质的吸热能力，用相同的酒精灯给质量相同的甲、乙两种液体加热，获得如图所示的甲、乙升温与加热时间之间关系的图像，甲、乙两种液体中有一种是水，下列说法中正确的是（）A ．甲液体是水B ．甲液体的比热容是()31.410J/kg ⨯⋅℃C ．质量相同的甲、乙下降相同的温度，甲放出的热量多D ．质量相同的甲、乙吸收相同的热量，乙升高的温度多7．如图所示电路，闭合开关S 1、S 2，小灯泡L 1和L 2均正常发光，两电表都有示数，下列判断正确的是（）物理试题第3页（共24页）物理试题第4页（共24页）……○………………内………………○………………装………………○………………订………………○………………线………………○………………此卷只装订不密封……○………………外………………○………………装………………○………………订………………○………………线………………○………………A．电流表A1只测量灯L2的电流B．电流表A2的示数比A1的大C．灯L 1被短路时，L2正常发光D．仅断开S1只有一个表有示数8．分别将下列物体接在如图所示电路的A、B两点间，闭合开关，能使灯泡发光的是（）A．干木条B．铅笔芯C．塑料棒D．陶瓷棒第Ⅱ卷二、填空题（每空1分，共计23分）9．烈日炎炎的夏季，白天河岸上沙土热得烫脚，但河水却非常凉爽，是由于水的比热容较____（“大”或“小”）；清澈河水看起来比实际深度要____（选填“深”或“浅”），容易造成误判，因此不要贸然下水，以免发生溺水事故｡10．昆明的阳春三月，春光明媚，乐乐和同学去郊外烧烤，烤肉散发出香味，这是___________现象；使用筷子夹烤豆腐时，筷子实质上是一种___________杠杆．11．两个相同的容器中分别装入质量相同的甲、乙两种液体，使用相同的热源为其加热，液体温度与加热时间的关系如图所示，若甲、乙两液体吸收相同的热量，则__________液体升高的温度较多；两者比较，__________液体更适合作汽车的冷却剂。

【人教版】九年级上期中数学试卷11含答案

【人教版】九年级上期中数学试卷11含答案一、选择题：（在各小题给出的四个选项中，只有一项是符合题目要求的，请在答题卡上指定的位置填涂符合要求的选项前面的字母代号·本大题共15小题，每小题3分，计45分）1．通过平移，可将如图移动到下列（）A．B．C．D．2．点P（1，2）关于原点的对称点P′的坐标为（）A．（2，1） B．（﹣1，﹣2） C．（1，﹣2）D．（﹣2，﹣1）3．用配方法解方程x2﹣2x﹣1=0，经过配方，得到（）A．（x+1）2=3 B．（x﹣1）2=2 C．（x﹣1）2=3 D．（x﹣2）2=54．方程x2﹣9=0的解是（）A．x=3 B．x=9 C．x=±3 D．x=±95．对于二次函数y=（x﹣1）2+2的图象，下列说法正确的是（）A．开口向下 B．顶点坐标是（1，2）C．对称轴是x=﹣1 D．有最大值是26．如图，一块等腰直角的三角板ABC，在水平桌面上绕点C按顺时针方向旋转到A′B′C 的位置，使A、C、B′三点共线，那么旋转角度的大小为（）A．45° B．90° C．120°D．135°7．若二次函数y=ax2的图象经过点P（﹣3，2），则a的值为（）A．B．C．D．8．已知方程x2+x﹣6=0的两个根是a，b，则ab的值为（）A．1 B．﹣1 C．6 D．﹣69．如图，△ABC由△A′B′C′绕O点旋转180°而得到，则下列结论不成立的是（）A．点A与点A′是对应点B．BO=B′OC．∠ACB=∠C′A′B′D．AB∥A′B′10．下列方程中有实数根的是（）A．x2+x+2=0 B．x2﹣x+2=0 C．x2﹣x﹣1=0 D．x2﹣x+3=011．有一人患了流感，经过两轮传染后共有100人患了流感，每轮传染中平均一个人传染的人数x满足的方程为（）A．1+x+x（1+x）=100 B．x（1+x）=100 C．1+x+x2=100 D．x2=10012．如图，二次函数y=ax2+bx+c的图象与x轴相交于（﹣2，0）和（4，0）两点，当函数值y＞0时，自变量x的取值范围是（）A．x＜﹣2 B．﹣2＜x＜4 C．x＞0 D．x＞413．下面表格列出了函数y=ax2+bx+c（a，b、c是常数，且a≠0），部分x与y对应值，那么方程ax2+bx+c=0的一个根x的取值范围是（）x 6·17 6·18 6·19 6·20y ﹣0·03 ﹣0·01 0·02 0·04 A．6＜x＜6·7 B．6·7＜x＜6·18 C．6·18＜x＜6·19 D．6·9＜x＜9·20 14．如图是一张长8cm、宽5cm的矩形纸板，将纸板四个角各剪去一个同样的正方形，可制成底面积是18cm2的一个无盖长方体纸盒，设剪去的正方形边长为xcm，那么x满足的方程是（）A．40﹣4x2=18 B．（8﹣2x）（5﹣2x）=18 C．40﹣2（8x+5x）=18 D．（8﹣2x）（5﹣2x）=915．如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为直线x=﹣1，给出四个结论，其中正确结论是（）A．b2＜4acB．2a+b=0C．a+b+c＞0D．若点B（，y1）、C（，y2）为函数图象上的两点，则y1＜y2二、解答题：（请将解答结果书写在答题卡上指定的位置．本大题共9小题，16～17每小题6分，18～19每小题6分，20～21每小题6分，22题10分，23题11分，24题12分，合计75分）16．解方程：（1）2x2﹣7x+3=0（2）x（x﹣2）=x．17．关于x的一元二次方程x2+2x+k+1=0的实数解是x1和x2．（1）求k的取值范围；（2）如果x1+x2﹣x1x2＜﹣1且k为整数，求k的值．18．△ABC在平面直角坐标系中的位置如图所示，其中每个小正方形的边长为1个单位长度．按要求作图：①画出△ABC关于原点O的中心对称图形△A1B1C1；②画出将△ABC绕点A逆时针旋转90°得到△AB2C2，③△A1B1C1中顶点A1坐标为．19．如图，已知四边形ABCD是正方形，E、F分别是DC和CB的延长线上的点，且DE=BF，连接AE、AF、EF．（1）填空：△ABF可以由△ADE绕旋转中心点，按逆时针方向旋转度得到；（2）若BC=8，DE=6，求△AEF的面积．20．如图，在水平地面点A处有一网球发射器向空中发射网球，网球飞行路线是一条抛物线，在地面上落点为B．有人在直线AB上点C（靠点B一侧）竖直向上摆放无盖的圆柱形桶，试图让网球落入桶内．已知AB=4米，AC=3米，网球飞行最大高度OM=5米，圆柱形桶的直径CD为0·5米，高为0·3米（网球的体积和圆柱形桶的厚度忽略不计）．（1）如图，建立直角坐标系，求此抛物线的解析式；（2）如果竖直摆放7个圆柱形桶时，网球能不能落入桶内？（3）当竖直摆放圆柱形桶至多多少个时，网球可以落入桶内？21．已知，如图，直线l经过A（4，0）和B（0，4）两点，抛物线y=a（x﹣h）2的顶点为P（1，0），直线l与抛物线的交点为M．（1）求直线l的函数解析式；（2）若S=3，求抛物线的解析式．△AMP22．宜兴科技公司生产销售一种电子产品，该产品总成本包括技术成本、制造成本、销售成本三部分，经核算，2013年该产品各部分成本所占比例约为2：a：1．且2013年该产品的技术成本、制造成本分别为400万元、1400万元．（1）确定a的值，并求2013年产品总成本为多少万元；（2）为降低总成本，该公司2014年及2015年增加了技术成本投入，确保这两年技术成本都比前一年增加一个相同的百分数m（m＜50%），制造成本在这两年里都比前一年减少一个相同的百分数2m；同时为了扩大销售量，2015年的销售成本将在2013年的基础上提高10%，经过以上变革，预计2015年该产品总成本达到2013年该产品总成本的，求m的值．23．如图1，在△ABC中，点P为BC边中点，直线a绕顶点A旋转，若点B，P在直线a的异侧，BM⊥直线a于点M．CN⊥直线a于点N，连接PM，PN．（1）延长MP交CN于点E（如图2）．①求证：△BPM≌△CPE；②求证：PM=PN；（2）若直线a绕点A旋转到图3的位置时，点B，P在直线a的同侧，其它条件不变，此时PM=PN还成立吗？若成立，请给予证明；若不成立，请说明理由；（3）若直线a绕点A旋转到与BC边平行的位置时，其它条件不变，请直接判断四边形MBCN 的形状及此时PM=PN还成立吗？不必说明理由．24．在平面直角坐标系xOy中，已知抛物线y=x2﹣2mx+m2﹣9．（1）求证：无论m为何值，该抛物线与x轴总有两个交点；（2）该抛物线与x轴交于A，B两点，点A在点B的左侧，且OA＜OB，与y轴的交点坐标为（0，﹣5），求此抛物线的解析式；（3）在（2）的条件下，抛物线的对称轴与x轴的交点为N，若点M是线段AN上的任意一点，过点M作直线MC⊥x轴，交抛物线于点C，记点C关于抛物线对称轴的对称点为D，点P是线段MC上一点，且满足MP=MC，连结CD，PD，作PE⊥PD交x轴于点E，问是否存在这样的点E，使得PE=PD？若存在，求出点E的坐标；若不存在，请说明理由．九年级（上）期中数学试卷参考答案与试题解析一、选择题：（在各小题给出的四个选项中，只有一项是符合题目要求的，请在答题卡上指定的位置填涂符合要求的选项前面的字母代号·本大题共15小题，每小题3分，计45分）1．通过平移，可将如图移动到下列（）A．B．C．D．【考点】利用平移设计图案．【分析】根据平移的性质，不改变图形的形状和大小，经过平移，对应点所连的线段平行且相等，对应线段平行且相等．【解答】解：通过图案平移得到必须与题中已知图案完全相同，角度也必须相同，观察图形可知B可以通过题中已知图案平移得到．故选B．【点评】本题考查平移的基本性质是：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．2．点P（1，2）关于原点的对称点P′的坐标为（）A．（2，1） B．（﹣1，﹣2） C．（1，﹣2）D．（﹣2，﹣1）【考点】关于原点对称的点的坐标．【分析】根据两个点关于原点对称时，它们的坐标符号相反可得答案．【解答】解：点P（1，2）关于原点的对称点P′的坐标为（﹣1，﹣2），故选：B．【点评】此题主要考查了关于原点对称的点的坐标，关键是掌握点的坐标的变化规律．3．用配方法解方程x2﹣2x﹣1=0，经过配方，得到（）A．（x+1）2=3 B．（x﹣1）2=2 C．（x﹣1）2=3 D．（x﹣2）2=5【考点】解一元二次方程-配方法．【分析】先把常数项﹣1移项后，再在方程的左右两边同时加上一次项系数﹣2的一半的平方．【解答】解：把方程x2﹣2x﹣1=0的常数项移到等号的右边，得到x2﹣2x=1方程两边同时加上一次项系数一半的平方，得到x2﹣2x+1=1+1配方得（x﹣1）2=2．故选：B．【点评】本题考查了配方法解方程．用配方法解一元二次方程的步骤：（1）形如x2+px+q=0型：第一步移项，把常数项移到右边；第二步配方，左右两边加上一次项系数一半的平方；第三步左边写成完全平方式；第四步，直接开方即可．（2）形如ax2+bx+c=0型，方程两边同时除以二次项系数，即化成x2+px+q=0，然后配方．4．方程x2﹣9=0的解是（）A．x=3 B．x=9 C．x=±3 D．x=±9【考点】解一元二次方程-直接开平方法．【分析】首先把﹣9移到方程右边，再两边直接开平方即可．【解答】解：移项得；x2=9，两边直接开平方得：x=±3，故选：C．【点评】此题主要考查了直接开平方法解一元二次方程，解这类问题要移项，把所含未知数的项移到等号的左边，把常数项移项等号的右边，化成x2=a（a≥0）的形式，利用数的开方直接求解．5．对于二次函数y=（x﹣1）2+2的图象，下列说法正确的是（）A．开口向下 B．顶点坐标是（1，2）C．对称轴是x=﹣1 D．有最大值是2【考点】二次函数的性质．【分析】根据二次函数的性质对各开口方向、顶点坐标、对称轴与最值进行判断即可．【解答】解：二次函数y=（x﹣1）2+2的图象的开口向上，对称轴为直线x=1，顶点坐标为（1，2），函数有最小值2．故选：B．【点评】本题考查了二次函数的性质，掌握利用顶点式求抛物线的开口方向、顶点坐标、对称轴与最值是解决问题的关键．6．如图，一块等腰直角的三角板ABC，在水平桌面上绕点C按顺时针方向旋转到A′B′C 的位置，使A、C、B′三点共线，那么旋转角度的大小为（）A．45° B．90° C．120°D．135°【考点】旋转的性质．【专题】计算题．【分析】根据等腰直角三角形的性质得∠ACB=45°，再根据旋转的性质得∠A′CB′=∠ACB=45°，∠ACA′等于旋转角，由于点A、C、B′三点共线，则∠ACB′=180°，于是∠ACA′=180°﹣∠A′CB′=135°．【解答】解：∵三角板ABC为等腰三角形，∴∠ACB=45°，∵在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置，使A、C、B′三点共线，∴∠A′CB′=∠ACB=45°，∠ACA′等于旋转角，∵点A、C、B′三点共线，∴∠ACB′=180°，∴∠ACA′=180°﹣∠A′CB′=135°，即旋转角为135°．故选D．【点评】本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角．也考查了等腰直角三角形的性质．7．若二次函数y=ax2的图象经过点P（﹣3，2），则a的值为（）A．B．C．D．【考点】二次函数图象上点的坐标特征．【分析】将点P的坐标代入函数解析式，然后解方程即可．【解答】解：∵二次函数y=ax2的图象经过点P（﹣3，2），∴a（﹣3）2=2，即9a=2，所以，a=．故选A ．【点评】本题考查了二次函数图象上点的坐标特征，是基础题，准确计算是解题的关键．8．已知方程x 2+x ﹣6=0的两个根是a ，b ，则ab 的值为（）A ．1B ．﹣1C ．6D ．﹣6【考点】根与系数的关系．【分析】直接利用根与系数的关系得出x 1x 2=，进而求出答案．【解答】解：∵方程x 2+x ﹣6=0的两个根是a ，b ，∴ab=﹣6．故选：D ．【点评】此题主要考查了根与系数的关系，正确把握根与系数关系是解题关键．9．如图，△ABC 由△A′B′C′绕O 点旋转180°而得到，则下列结论不成立的是（）A ．点A 与点A′是对应点B ．BO=B′OC ．∠ACB=∠C′A′B′D ．AB ∥A′B′【考点】旋转的性质．【分析】根据旋转的性质，图形的旋转是图形上的每一点在平面上绕某个固定点旋转固定角度的位置移动，其中对应点到旋转中心的距离相等，旋转前后图形的大小和形状没有改变；依次分析可得答案．【解答】解：根据旋转的性质，△ABC 由△A′B′C′绕O 点旋转180°，∠ACB 的对应角是∠A′C′B′，因此C 不正确．故选C ．【点评】根据旋转的性质，图形的旋转是图形上的每一点在平面上绕某个固定点旋转固定角度的位置移动，其中对应点到旋转中心的距离相等，旋转前后图形的大小和形状没有改变．10．下列方程中有实数根的是（）A ．x 2+x+2=0B ．x 2﹣x+2=0C ．x 2﹣x ﹣1=0D ．x 2﹣x+3=0【考点】根的判别式．【分析】根据题意对各选项进行逐一分析即可．【解答】解：A、∵△=12﹣8=﹣7＜0，∴此方程无实数根，故本选项错误；B、∵△=（﹣1）2﹣8=﹣7＜0，∴此方程无实数根，故本选项错误；C、∵△=（﹣1）2+4=5＞0，∴此方程有实数根，故本选项正确；D、∵△=（﹣1）2﹣12=﹣11＜0，∴此方程无实数根，故本选项错误．故选C．【点评】本题考查的是根的判别式，熟知一元二次方程ax2+bx+c=0（a≠0）中的根与△的关系是解答此题的关键．11．有一人患了流感，经过两轮传染后共有100人患了流感，每轮传染中平均一个人传染的人数x满足的方程为（）A．1+x+x（1+x）=100 B．x（1+x）=100 C．1+x+x2=100 D．x2=100【考点】由实际问题抽象出一元二次方程．【分析】由于每轮传染中平均一个人传染的人数是x人，那么经过第一轮后有（1+x）人患了流感，经过第二轮后有[（1+x）+x（1+x）]人患了流感，再根据经过两轮传染后共有100人患了流感即可列出方程．【解答】解：依题意得（1+x）+x（1+x）=100．故选A．【点评】本题考查了一元二次方程的运用，解此类题关键是根据题意分别列出不同阶段患了流感的人数．12．如图，二次函数y=ax2+bx+c的图象与x轴相交于（﹣2，0）和（4，0）两点，当函数值y＞0时，自变量x的取值范围是（）A．x＜﹣2 B．﹣2＜x＜4 C．x＞0 D．x＞4【考点】抛物线与x轴的交点．【分析】利用当函数值y＞0时，即对应图象在x轴上方部分，得出x的取值范围即可．【解答】解：如图所示：当函数值y＞0时，自变量x的取值范围是：﹣2＜x＜4．故选：B．【点评】此题主要考查了抛物线与x轴的交点，利用数形结合得出是解题关键．13．下面表格列出了函数y=ax2+bx+c（a，b、c是常数，且a≠0），部分x与y对应值，那么方程ax2+bx+c=0的一个根x的取值范围是（）x 6·17 6·18 6·19 6·20y ﹣0·03 ﹣0·01 0·02 0·04 A．6＜x＜6·7 B．6·7＜x＜6·18 C．6·18＜x＜6·19 D．6·9＜x＜9·20【考点】图象法求一元二次方程的近似根．【分析】根据二次函数的增减性，可得答案．【解答】解：由表格中的数据，得在6·17＜x＜6·20范围内，y随x的增大而减小，当x=6·18时，y=﹣0·01，当x=6·19时，y=0·02，方程ax2+bx+c=0的一个根x的取值范围是6·18＜x＜6·19，故选：C．【点评】本题考查了图象法求一元二次方程的近似解，解答此题的关键是利用函数的增减性．14．如图是一张长8cm、宽5cm的矩形纸板，将纸板四个角各剪去一个同样的正方形，可制成底面积是18cm2的一个无盖长方体纸盒，设剪去的正方形边长为xcm，那么x满足的方程是（）A．40﹣4x2=18 B．（8﹣2x）（5﹣2x）=18 C．40﹣2（8x+5x）=18 D．（8﹣2x）（5﹣2x）=9【考点】一元二次方程的应用．【分析】由于剪去的正方形边长为xcm，那么长方体纸盒的底面的长为（8﹣2x），宽为（5﹣2x），然后根据底面积是18cm2即可列出方程．【解答】解：设剪去的正方形边长为xcm，依题意得（8﹣2x）•（5﹣2x）=18，故选：B．【点评】此题主要考查了一元二次方程的应用，首先要注意读懂题意，正确理解题意，然后才能利用题目的数量关系列出方程．15．如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为直线x=﹣1，给出四个结论，其中正确结论是（）A．b2＜4acB．2a+b=0C．a+b+c＞0D．若点B（，y1）、C（，y2）为函数图象上的两点，则y1＜y2【考点】二次函数图象与系数的关系．【分析】根据抛物线与x轴交点个数可判断选项A；根据抛物线对称轴可判断选项B；根据抛物线与x轴的另一个交点坐标可判断选项C；根据函数图象的性质可判断选项D．【解答】解：A、∵由函数图象可知抛物线与x轴有2个交点，∴b2﹣4ac＞0即b2＞4ac，故本题选项错误；B、∵对称轴为直线x=﹣1，∴﹣=﹣1，即2a﹣b=0，故本选项错误；C、∵抛物线与x轴的交点A坐标为（﹣3，0）且对称轴为x=﹣1，∴抛物线与x轴的另一交点为（1，0），∴将（1，0）代入解析式可得，a+b+c=0，故本选项错误；D、∵抛物线的对称轴是直线x=﹣1，抛物线的开口向下，∴当x＞﹣1时，y随x的增大而减小，∵﹣1＜＜，点B（，y1）、C（，y2）为函数图象上的两点，∴y1＜y2，故本选项正确；故选D．【点评】本题考查了二次函数图象与系数的关系，二次函数y=ax2+bx+c（a≠0），a的符号由抛物线开口方向决定；b的符号由对称轴的位置及a的符号决定；c的符号由抛物线与y轴交点的位置决定；抛物线与x 轴的交点个数，决定了b 2﹣4ac 的符号，此外还要注意x=1，﹣3对应函数值的正负来判断其式子的正确与否．二、解答题：（请将解答结果书写在答题卡上指定的位置．本大题共9小题，16～17每小题6分，18～19每小题6分，20～21每小题6分，22题10分，23题11分，24题12分，合计75分）16．解方程：（1）2x 2﹣7x+3=0（2）x （x ﹣2）=x ．【考点】解一元二次方程-因式分解法．【分析】（1）直接利用十字相乘法分解因式得出答案；（2）直接利用提取公因式法分解因式得出答案．【解答】解：（1）2x 2﹣7x+3=0（2x11）（x ﹣3）=0，解得：x 1=0，x 2=3；（2）x （x ﹣2）=xx （x ﹣3）=0，解得：x 1=0，x 2=3．【点评】此题主要考查了因式分解法解方程，正确分解因式是解题关键．17．关于x 的一元二次方程x 2+2x+k+1=0的实数解是x 1和x 2．（1）求k 的取值范围；（2）如果x 1+x 2﹣x 1x 2＜﹣1且k 为整数，求k 的值．【考点】根与系数的关系；根的判别式；解一元一次不等式组．【专题】代数综合题；压轴题．【分析】（1）方程有两个实数根，必须满足△=b 2﹣4ac ≥0，从而求出实数k 的取值范围；（2）先由一元二次方程根与系数的关系，得x 1+x 2=﹣2，x 1x 2=k+1．再代入不等式x 1+x 2﹣x 1x 2＜﹣1，即可求得k 的取值范围，然后根据k 为整数，求出k 的值．【解答】解：（1）∵方程有实数根，∴△=22﹣4（k+1）≥0，解得k ≤0．故K 的取值范围是k ≤0．（2）根据一元二次方程根与系数的关系，得x 1+x 2=﹣2，x 1x 2=k+1，x 1+x 2﹣x 1x 2=﹣2﹣（k+1）．由已知，得﹣2﹣（k+1）＜﹣1，解得k ＞﹣2．又由（1）k ≤0，∴﹣2＜k ≤0．∵k 为整数，∴k 的值为﹣1或0．【点评】本题综合考查了根的判别式和根与系数的关系．在运用一元二次方程根与系数的关系解题时，一定要注意其前提是此方程的判别式△≥0．18．△ABC 在平面直角坐标系中的位置如图所示，其中每个小正方形的边长为1个单位长度．按要求作图：①画出△ABC 关于原点O 的中心对称图形△A 1B 1C 1；②画出将△ABC 绕点A 逆时针旋转90°得到△AB 2C 2，③△A 1B 1C 1中顶点A 1坐标为（1，﹣2）．【考点】作图-旋转变换；中心对称．【分析】①把△ABC 绕着点O 旋转180°，得到△A 1B 1C 1，那么这两个三角形关于这个点成中心对称；②按照旋转角度、旋转方向、旋转中心进行作图即可；③在直角坐标系中，点A 1在第四象限，距离x 轴2个单位，距离y 轴1个单位，据此求得其坐标．【解答】解：①如图，△ABC 与△A 1B 1C 1关于原点O 的中心对称；②如图，△AB2C2是由△ABC绕点A逆时针旋转90°得到的三角形；③由图可得，△A1B1C1中顶点A1坐标为（1，﹣2）．【点评】本题主要考查了利用旋转变换进行作图，旋转作图有自己独特的特点，决定图形位置的因素有旋转角度、旋转方向、旋转中心，得到的图形与原图形全等．19．如图，已知四边形ABCD是正方形，E、F分别是DC和CB的延长线上的点，且DE=BF，连接AE、AF、EF．（1）填空：△ABF可以由△ADE绕旋转中心点 A ，按逆时针方向旋转270 度得到；（2）若BC=8，DE=6，求△AEF的面积．【考点】旋转的性质；正方形的性质．【分析】（1）根据旋转的定义可得到△ABF可以由△ADE绕旋转中心 A点，按逆时针方向旋转270度得到；（2）先利用勾股定理可计算出AE=10，再根据△ABF可以由△ADE绕旋转中心A点，按逆时针方向旋转270度得到AE=AF，∠EAF=90°，然后根据直角三角形的面积公式计算即可．【解答】解：（1）△ABF可以由△ADE绕旋转中心点A，按逆时针方向旋转 270度得到．故答案为：A，270；（2）∵四边形ABCD是正方形，BC=8，∴AD=8，在Rt△ADE中，DE=6，AD=8，∴AE==10，∵△ABF可以由△ADE绕旋转中心 A点，按顺时针方向旋转90 度得到，∴AE=AF，∠EAF=90°，∴△AEF的面积=AE2=×100=50（平方单位）．【点评】本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角．也考查了勾股定理．20．如图，在水平地面点A处有一网球发射器向空中发射网球，网球飞行路线是一条抛物线，在地面上落点为B．有人在直线AB上点C（靠点B一侧）竖直向上摆放无盖的圆柱形桶，试图让网球落入桶内．已知AB=4米，AC=3米，网球飞行最大高度OM=5米，圆柱形桶的直径CD为0·5米，高为0·3米（网球的体积和圆柱形桶的厚度忽略不计）．（1）如图，建立直角坐标系，求此抛物线的解析式；（2）如果竖直摆放7个圆柱形桶时，网球能不能落入桶内？（3）当竖直摆放圆柱形桶至多多少个时，网球可以落入桶内？【考点】二次函数的应用．【分析】（1）以抛物线的对称轴为y轴，水平地面为x轴，建立平面直角坐标系，设解析式，结合已知确定抛物线上点的坐标，代入解析式确定抛物线的解析式；（2）利用当x=1时，y=；当x=1·5 时，y=．得出当竖直摆放5个圆柱形桶时，得出桶高进而比较；即可得出答案；（3）由圆桶的直径，求出圆桶两边缘纵坐标的值，确定m的范围，根据m为正整数，得出m的值，即可得到当网球可以落入桶内时，竖直摆放圆柱形桶个数．【解答】解：（1）M（0，5），B（2，0），C（1，0），D（，0），设抛物线的解析式为y=ax2+k，∵抛物线过点M和点B，则k=5，．即抛物线解析式为；（2）当x=1时，y=；当x=时，y=．即P（1，），Q（，）当竖直摆放7个圆柱形桶时，桶高=×7=2·1．∵2·1＜且2·1＜，∴网球不能落入桶内；（3）设竖直摆放圆柱形桶m个时网球可以落入桶内，由题意，得，≤0·3m≤，解得：≤m≤；∵m为整数，∴m的值为8，9，10，11，12．∴当竖直摆放圆柱形桶至多12个时，网球可以落入桶内．【点评】此题考查了抛物线的问题，需要建立适当的平面直角坐标系，根据已知条件，求出相关点的坐标，确定解析式，这是解答其它问题的基础．21．已知，如图，直线l经过A（4，0）和B（0，4）两点，抛物线y=a（x﹣h）2的顶点为P（1，0），直线l与抛物线的交点为M．（1）求直线l的函数解析式；=3，求抛物线的解析式．（2）若S△AMP【考点】二次函数的性质；待定系数法求一次函数解析式；待定系数法求二次函数解析式．【分析】（1）设出函数解析式为y=kx+b，利用待定系数法解答即可；（2）根据三角形的面积求出M点的纵坐标，代入直线解析式求出M的横坐标，再利用P、M 的值求出函数解析式．【解答】解：（1）设一次函数解析式为y=kx+b，把A（4，0），B（0，4）分别代入解析式得，解得，解析式为y=﹣x+4．（2）设M点的坐标为（m，n），∵S=3，△AMP∴（4﹣1）n=3，解得，n=2，把M（m，2）代入为2=﹣m+4得，m=2，M（2，2），∵抛物线y=a（x﹣h）2的顶点为P（1，0），可得y=a（x﹣1）2，把M（2，2）代入y=a（x﹣1）2得，2=a（2﹣1）2，解得a=2，函数解析式为y=2（x﹣1）2．【点评】本题考查了二次函数的性质和待定系数法求二次函数解析式、求一次函数解析式，要熟练运用二次函数与一次函数与坐标的特点．22．宜兴科技公司生产销售一种电子产品，该产品总成本包括技术成本、制造成本、销售成本三部分，经核算，2013年该产品各部分成本所占比例约为2：a：1．且2013年该产品的技术成本、制造成本分别为400万元、1400万元．（1）确定a的值，并求2013年产品总成本为多少万元；（2）为降低总成本，该公司2014年及2015年增加了技术成本投入，确保这两年技术成本都比前一年增加一个相同的百分数m（m＜50%），制造成本在这两年里都比前一年减少一个相同的百分数2m ；同时为了扩大销售量，2015年的销售成本将在2013年的基础上提高10%，经过以上变革，预计2015年该产品总成本达到2013年该产品总成本的，求m 的值．【考点】一元二次方程的应用．【分析】（1）由2：a=400：1400得出方程求得a 的数值，进一步求得总成本即可；（2）分别求得2015年的技术成本、制造成本、销售成本，进一步利用预计2015年该产品总成本达到2013年该产品总成本的，建立方程解决问题．【解答】解：（1）由题意得2：a=400：1400，解得a=7．则销售成本为400÷2=200万元，2013年产品总成本为400+1400+200=2000万元．（2）由题意可得400（1+m ）2+1400（1﹣2m ）2+200（1+10%）=2000×，整理得300m 2﹣240m+21=0，解得m 1=0·1，m 2=0·7（m ＜50%，不合题意舍去）．答：m 的值是10%．【点评】本题考查了列一元一次方程解实际问题的运用，一元二次方程的实际运用，增长率问题的数量关系的运用，解答时根据预计2015年该产品总成本达到2013年该产品总成本的建立方程是关键．23．（2010•沈阳）如图1，在△ABC 中，点P 为BC 边中点，直线a 绕顶点A 旋转，若点B ，P 在直线a 的异侧，BM ⊥直线a 于点M ．CN ⊥直线a 于点N ，连接PM ，PN ．（1）延长MP 交CN 于点E （如图2）．①求证：△BPM ≌△CPE ；②求证：PM=PN ；（2）若直线a 绕点A 旋转到图3的位置时，点B ，P 在直线a 的同侧，其它条件不变，此时PM=PN 还成立吗？若成立，请给予证明；若不成立，请说明理由；（3）若直线a 绕点A 旋转到与BC 边平行的位置时，其它条件不变，请直接判断四边形MBCN 的形状及此时PM=PN 还成立吗？不必说明理由．【考点】旋转的性质；全等三角形的判定；矩形的判定．【专题】几何综合题；压轴题．【分析】（1）①根据平行线的性质证得∠MBP=∠ECP再根据BP=CP，∠BPM=∠CPE即可得到；②由△BPM≌△CPE，得到PM=PE则PM=ME，而在Rt△MNE中，PN=ME，即可得到PM=PN．（2）证明方法与②相同．（3）四边形MBCN是矩形，则PM=PN成立．【解答】（1）证明：①如图2：∵BM⊥直线a于点M，CN⊥直线a于点N，∴∠BMA=∠CNM=90°，∴BM∥CN，∴∠MBP=∠ECP，又∵P为BC边中点，∴BP=CP，又∵∠BPM=∠CPE，∴△BPM≌△CPE，②∵△BPM≌△CPE，∴PM=PE∴PM=ME，∴在Rt△MNE中，PN=ME，∴PM=PN．（2）解：成立，如图3．证明：延长MP与NC的延长线相交于点E，∵BM⊥直线a于点M，CN⊥直线a于点N，∴∠BMN=∠CNM=90°∴∠BMN+∠CNM=180°，∴BM∥CN∴∠MBP=∠ECP，又∵P为BC中点，∴BP=CP，又∵∠BPM=∠CPE，在△BPM和△CPE中，，∴△BPM≌△CPE，∴PM=PE，∴PM=ME，则Rt△MNE中，PN=ME，∴PM=PN．（3）解：如图4，四边形M′BCN′是矩形，根据矩形的性质和P为BC边中点，得到△M′B P≌△N′CP，得PM′=PN′成立．即“四边形MBCN是矩形，则PM=PN成立”．【点评】本题考查旋转的性质．旋转变化前后，对应线段、对应角分别相等，图形的大小、形状都不改变．24．在平面直角坐标系xOy 中，已知抛物线y=x 2﹣2mx+m 2﹣9．（1）求证：无论m 为何值，该抛物线与x 轴总有两个交点；（2）该抛物线与x 轴交于A ，B 两点，点A 在点B 的左侧，且OA ＜OB ，与y 轴的交点坐标为（0，﹣5），求此抛物线的解析式；（3）在（2）的条件下，抛物线的对称轴与x 轴的交点为N ，若点M 是线段AN 上的任意一点，过点M 作直线MC ⊥x 轴，交抛物线于点C ，记点C 关于抛物线对称轴的对称点为D ，点P 是线段MC 上一点，且满足MP=MC ，连结CD ，PD ，作PE ⊥PD 交x 轴于点E ，问是否存在这样的点E ，使得PE=PD ？若存在，求出点E 的坐标；若不存在，请说明理由．【考点】二次函数综合题；全等三角形的判定与性质；直角三角形的性质．【专题】代数几何综合题．【分析】（1）令y=0，则x 2﹣2mx+m 2﹣9=0，根据根的判别式b 2﹣4ac=（﹣2m ）2﹣4（m 2﹣9）=36＞0，所以无论m 为何值，该抛物线与x 轴总有两个交点．（2）直接将C 点（0，﹣5）代入y=x 2﹣2mx+m 2﹣9根据抛物线与x 轴交于A ，B 两点（点A 在点B 的左侧，且OA ＜OB ），求出m 的值即可；（3）假设E 点存在由直角三角形的性质可以得出∠MEP=∠CPD ．再根据条件可以得出△EPM ≌△PDC 就有PM=DC ，EM=PC ，设C （x 0，y 0），则D （4﹣x 0，y 0），P （x 0， y 0）．根据PM=DC 就有2x 0﹣4=﹣y 0，由C 点在抛物线上有2x 0﹣4=﹣（ x 02﹣4x 0﹣5），求出x 0的值就可以得出结论．【解答】解：（1）令y=0，则x 2﹣2mx+m 2﹣9=0，∵△=（﹣2m ）2﹣4m 2+36＞0，∴无论m 为何值时方程x 2﹣2mx+m 2﹣9=0总有两个不相等的实数根，。

山东省潍坊市2023年九年级化学第一学期期中学业水平测试试题含解析

山东省潍坊市2023年九年级化学第一学期期中学业水平测试试题注意事项：1．答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。

2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。

3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、单选题（本大题共10小题，共20分）1．属于化学性质的是A．溶解性B．挥发性C．助燃性D．吸附性2．物质的性质决定了物质的用途．下列物质的用途，既利用了物质的物理性质又利用了物质的化学性质的是（）A．用氮气填充灯泡B．用氢气制造燃料电池C．用铜丝制作导线D．用干冰灭火3．下列有关化学实验的做法，错误的是A．给试管里的液体加热时，试管里的液体体积不应超过试管容积的1 3B．滴瓶上的滴管使用后不必清洗，不会污染整瓶试剂C．除易潮解、有腐蚀性的药品外，可将药品直接放在托盘上称量D．量筒读数时，量筒放平稳，视线应与凹液面的最低处保持水平4．如图所示装置可用于测定空气中氧气的含量，实验前在集气瓶内加入少量水，并做上记号．下列说法中不正确的是A．该实验证明空气中氧气的含量约占其体积的1 5B．该实验操作时红磷一定要足量，目的是把装置内的氧气消耗完C．实验开始前一定要检验装置的气密性D．红磷燃烧产生大量的白雾，火焰熄灭后立刻打开弹簧夹，让烧杯中的水沿导管进入集气瓶5．对MnO2、SO2、O2三种物质的宏观组成叙述中正确的是（）A．都含有氧气B．都含有氧元素C．都含有氧分子D．都含有2个氧原子6．下列物质中，由原子直接构成的是（）A．二氧化碳B．汞C．氮气D．氯化钠7．物质的性质决定其用途，下列物质的用途与其依据的性质不相符合的是（）A．焊接金属时用氮气做保护气﹣氮气的化学性质不活泼B．制糖工业中用活性炭脱色制白糖﹣活性炭具有可燃性C．铜丝作导线﹣铜有良好的导电性D．干冰作制冷剂一干冰升华时吸收大量的热量8．下列关于水的说法中正确的是A．经过沉淀、过滤后得到的矿泉水是纯净物B．常温下，1L水与1L酒精混合后的体积等于2LC．如果将水样蒸干后有固体析出，这种水样中一定含有杂质D．电解水的实验证明水是由氢气和氧气组成的9．某同学在一段时间化学学习后梳理了以下知识：①同种元素组成的物质一定不是化合物；②某物质在空气中燃烧生成二氧化碳和水，说明该物质中一定含有碳元素、氢元素和氧元素；③在同一化合物中，若金属元素显正价，则非金属元素一定显负价；④最外层电子数为8 的粒子一定是稀有气体的原子；⑤质子数相同的微粒一定属于同种元素；⑥物质与氧气的反应一定是氧化反应。

初三年级第一学期语文期中考试题十一

初三年级第一学期语文期中考试题十一第一部分（25分）1．根据汉语拼音写出汉字。

（4分）①(j ǜn) 工 ②(w ǎng) 然 ③滑（j ī） ④繁（y ǎn ）2．下面的句子中每句都有两个错别字，把它们找出来填入表中，然后改正。

（4分）①这水湾周围的小水蛙里长满了花草，早春柳树的枝条也已开花，茸茸的向小黄毛小鸡。

②刚才出力摇船尤如赛龙船似的一股劲儿，现在在每个人的身体里松泄下来了。

3．默写古诗文名句，并在括号内的横线上填写相应的作家、篇名。

（10分）① ，春风不度玉门关（王之涣《》） ②晓战随金鼓，。

（李白《塞下曲》）③ ，大雪满弓刀。

（《塞下曲》）④ 蒌蒿满地芦芽短，。

（苏轼《惠崇〈春江晚景〉二首》）⑤死即举大名耳，（司马迁《陈涉世家》） ⑥阡陌交通，鸡犬相闻，。

（陶渊明《桃花源记》）⑦ ，。

所谓伊人，在水之湄。

《诗经·蒹葭》4．社会经济的发展促进了词语内涵的日益丰富，请根据下列一段话，给“火星文”下个定义。

（4分)曾几何时，在网游中渐渐出现了一些诡异的符号和字体，据说最开始是为了用外挂不被封，后来却渐渐成了流行，以至于现在游戏中的怪异名字比比皆是。

比如：“宥时候卜知道脑子哩菑想什麽……”“狠嫘。

狠想停下麳歇歇。

狠想长眠卜起。

”这类文字大多由汉字中的生僻字，异体字、繁体字以及符号组成，由于大多数字体不常见，网友只能通过文字的偏旁或字型猜测其对照读音，因此被很多网友痛斥为“看不懂，没文化，糟蹋传统汉字”，并将此类字体贬为“脑残体”、“火星文字”。

而“火星文字”在年轻一代中会流行，自然有他的理由，比如说觉得“有个性”，我会打你不会打，就能更显示我的独特，此外还出现了“火星文字输入攻略”等秘籍，专门收集此类文字的话语。

________________________________ ____________________5．请阅读（填作者名）在《格列佛游记》中的一段文字，思考文中两类人物的观点各是什么？（3分）我们到了语言学校。

安徽阜阳十一中九年级上期中数学卷(解析版)(初三)期中考试.doc

安徽阜阳十一中九年级上期中数学卷（解析版）（初三）期中考试姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题（每空xx 分，共xx分）【题文】下列生态环保标志中，是中心对称图形的是（）A. B. C. D.【答案】B【解析】试题分析：A、不是中心对称图形，故本选项错误；B、是中心对称图形，故本选项正确；C、不是中心对称图形，故本选项错误；D、不是中心对称图形，故本选项错误．故选B．【考点】中心对称图形．【题文】如图，A、B、C是⊙O上的三点，∠B=75°，则∠AOC的度数是（）A．150° B．140° C．130° D．120°【答案】A．【解析】试题分析：∵A、B、C是⊙O上的三点，∠B=75°，∴∠AOC=2∠B=150°．故选A．【考点】圆周角定理．【题文】已知1是关于x的一元二次方程（m﹣1）x2+x+1=0的一个根，则m的值是（）A．1 B．﹣1 C．0 D．无法确定【答案】B．【解析】试题分析：把x=1代入方程，即可得到一个关于m的方程，（m﹣1）+1+1=0，解得：m=﹣1．故选B．【考点】一元二次方程的解；一元二次方程的定义．评卷人得分【题文】已知半径为5的圆，其圆心到直线的距离是3，此时直线和圆的位置关系为（）A．相离 B．相切 C．相交 D．无法确定【答案】C．【解析】试题分析：半径r=5，圆心到直线的距离d=3，∵5＞3，即r＞d，∴直线和圆相交，故选C．【考点】直线与圆的位置关系．【题文】下列四个圆形图案中，分别以它们所在圆的圆心为旋转中心，顺时针旋转120°后，能与原图形完全重合的是（）A． B． C． D．【答案】A．【解析】试题分析：A、最小旋转角度==120°；B、最小旋转角度==90°；C、最小旋转角度==180°；D、最小旋转角度==72°；综上可得：顺时针旋转120°后，能与原图形完全重合的是A．故选：A．【考点】旋转对称图形．【题文】抛物线y=﹣3x2﹣x+4与坐标轴的交点个数是（）A．3 B．2 C．1 D．0【答案】A．【解析】试题分析：抛物线解析式y=﹣3x2﹣x+4，令x=0，解得：y=4，∴抛物线与y轴的交点为（0，4），令y=0，得到﹣3x2﹣x+4=0，即3x2+x﹣4=0，分解因式得：（3x+4）（x﹣1）=0，解得：x1=﹣，x2=1，∴抛物线与x轴的交点分别为（﹣，0），（1，0），综上，抛物线与坐标轴的交点个数为3．故选：A．【考点】抛物线与x轴的交点．【题文】如图为二次函数y=ax2+bx+c（a≠0）的图象，则下列说法：①a＞0②2a+b=0③a+b+c＞0④当﹣1＜x＜3时，y＞0其中正确的个数为（）A．1 B．2 C．3 D．4【答案】C．【解析】试题分析：①图象开口向下，能得到a＜0；②对称轴在y轴右侧，x==1，则有﹣=1，即2a+b=0；③当x=1时，y＞0，则a+b+c＞0；④由图可知，当﹣1＜x＜3时，y＞0．故选C．【考点】二次函数图象与系数的关系．【题文】某单位要组织一次篮球联赛，赛制为单循环形式（2016•海南）如图，AB是⊙O的直径，直线PA 与⊙O相切于点A，PO交⊙O于点C，连接BC．若∠P=40°，则∠ABC的度数为（）A．20° B．25° C．40° D．50°【答案】B．【解析】试题分析：如图，∵AB是⊙O的直径，直线PA与⊙O相切于点A，∴∠PAO=90°．又∵∠P=40°，∴∠POA=50°，∴∠ABC=∠POA=25°．故选：B．【考点】切线的性质．【题文】如图，过⊙O外一点P引⊙O的两条切线PA、PB，切点分别是A、B，OP交⊙O于点C，点D是优弧上不与点A、点C重合的一个动点，连接AD、CD，若∠APB=80°，则∠ADC的度数是（）A．15° B．20° C．25° D．30°【答案】C．【解析】试题分析：如图，由四边形的内角和定理，得∠BOA=360°﹣90°﹣90°﹣80°=100°，由=，得∠AOC=∠BOC=50°．由圆周角定理，得∠ADC=∠AOC=25°，故选：C．【考点】切线的性质．【题文】如图，在Rt△ABC中，∠BAC=90°．将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C ，点A在边B′C上，则∠B′的大小为．【答案】42°．【解析】试题分析：根据题意：Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C，即旋转角为48°，则：∠ACA′=48°，根据直角三角形的两锐角互余求出∠B′=90°﹣48°=42°，故答案为：42°．【考点】旋转的性质；直角三角形的性质；两直角三角形的两锐角互余．【题文】把抛物线y=x2+bx+4的图象向右平移3个单位，再向上平移2个单位，所得到的图象的解析式为y=x2﹣2x+3，则b的值为．【答案】4．【解析】试题分析：∵y=x2﹣2x+3=（x﹣1）2+2，∴新抛物线的顶点为（1，2），∵向右平移3个单位，再向上平移2个单位，∴原抛物线的顶点坐标为（﹣2，0），∴原抛物线解析式为y=（x+2）2=x2+4x+4，∴b=4．故答案为：4．【考点】二次函数图象与几何变换．【题文】如图，AB是⊙O的直径，AC切⊙O于点A，BC交着⊙O于点D，连接OD，∠C=70°，则∠AOD的度数为．【答案】40°．【解析】试题分析：由AB是⊙O的直径，AC切⊙O于点A，可得AB⊥AC，又由∠C=70°，可求得∠B=90°﹣∠C=20°，∴∠AOD=2∠B=40°．故答案为：40°．【考点】切线的性质；圆心角、弧、弦的关系．【题文】解方程（x﹣1）2﹣5（x﹣1）+4=0时，我们可以将x﹣1看成一个整体，设x﹣1=y，则原方程可化为y2﹣5y+l所以原方程的解为：x1=﹣2，x2=﹣1．故答案为：x1=﹣2，x2=﹣1．【考点】换元法解一元二次方程．【题文】解方程：x2﹣4x+1=0．【答案】原方程的解是：x1=2+，x2=2﹣．【解析】试题分析：移项后配方得到x2﹣4x+4=﹣1+4，推出（x﹣2）2=3，开方得出方程x﹣2=±，求出方程的解即可．试题解析：移项得：x2﹣4x=﹣1，配方得：x2﹣4x+4=﹣1+4，即（x﹣2）2=3，开方得：x﹣2=±，∴原方程的解是：x1=2+，x2=2﹣．【考点】解一元二次方程-配方法．【题文】已知：抛物线．（1）写出抛物线的对称轴；（2）完成下表；x…﹣713…y…﹣9﹣1…（3）在下面的坐标系中描点画出抛物线的图象．【答案】（1）抛物线的对称轴为直线x=﹣1．（2）见试题解析；（3）见试题解析【解析】试题分析：（1）根据抛物线，直接得出对称轴即可；（2）根据直线解析式分别得出对应函数的值即可；（3）利用（2）中所求的点，画出图象即可．试题解析：（1）抛物线的对称轴为直线x=﹣1．（2）填表如下：x…﹣7﹣5﹣3﹣1135y…﹣9﹣4﹣1﹣1﹣4﹣9…（3）描点作图如下：【考点】二次函数的性质；二次函数的图象．【题文】如图，点E是△ABC的内心，AE的延长线与BC相交于点F，与△ABC的外接圆相交于点D．（1）求证：∠BAD=∠CBD；（2）求证：DE=DB．【答案】（1）∠BAD=∠CBD；（2）DE=DB．【解析】试题分析：（1）由内心的性质和圆周角定理可证得结论；（2）连接BE，由内心的性质及三角形外角的性质可证得∠DBE=∠DEB，可证得DE=DB．试题解析：（1）∵E是△ABC的内心，∴∠BAD=∠CAD，∵∠CAD=∠CBD，∴∠BAD=∠CBD；（2）连接BF，如图，{{38}l【解析】试题分析：先根据已知条件得：△D1CE1各角的度数，由旋转得：∠BCE1=15°，证明△ABC≌△CBD1，可以得出结论．试题解析：由题意得：∠CD1E1=∠D=30°，∠D1CE1=∠DCE=90°﹣30°=60°，∵把△DCE绕点C顺时针旋转15°得到△D1CE1，∴∠BCE1=15°，∴∠D1CB=60°﹣15°=45°，在△ACB和△CBD1中，∵，∴△ABC≌△CBD1，∴∠CD1B=∠A=45°，∴∠E1D1B=∠CD1B﹣∠CD1E1=45°﹣30°=15°．【考点】旋转的性质；全等三角形的判定与性质．【题文】（2012•乐山）菜农李伟种植的某蔬菜计划以每千克5元的单价对外批发销售，由于部分菜农盲目扩大种植，造成该蔬菜滞销．李伟为了加快销售，减少损失，对价格经过两次下调后，以每千克3.2元的单价对外批发销售．（1）求平均每次下调的百分率；（2）小华准备到李伟处购买5吨该蔬菜，因数量多，李伟决定再给予两种优惠方案以供选择：方案一：打九折销售；方案二：不打折，每吨优惠现金200元l答：平均每次下调的百分率是20%．（2）小华选择方案一购买更优惠．理由：方案一所需费用为：3.2×0.9×5000=14400（元），方案二所需费用为：3.2×5000﹣200×5=15000（元）．∵14400＜15000，∴小华选择方案一购买更优惠．【考点】一元二次方程的应用．【题文】如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣3，5），B（﹣2，1），C （﹣1，3）．（1）若△ABC经过平移后得到△A1B1C1，已知点C1的坐标为（4，0），写出顶点A1，B1的坐标；（2）若△ABC和△A2B2C2关于原点O成中心对称图形，写出△A2B2C2的各顶点的坐标；（3）将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3，写出△A3B3C3的各顶点的坐标．【答案】（1）点A1的坐标为（2，2），B1点的坐标为（3，﹣2）；（2）A2（3，﹣5），B2（2，﹣1），C2（1，﹣3）；（3）△A2B3C3为所作，A3（5，3），B3（1，2），C3（3，1）；【解析】试题分析：（1）利用点C和点C1的坐标变化得到平移的方向与距离，然后利用此平移规律写出顶点A1，B1的坐标；（2）根据关于原点对称的点的坐标特征求解；（3）利用网格和旋转的性质画出△A2B3C3，然后写出△A2B3C3的各顶点的坐标．试题解析：（1）如图，△A1B1C1为所作，因为点C（﹣1，3）平移后的对应点C1的坐标为（4，0），所以△ABC先向右平移5个单位，再向下平移3个单位得到△A1B1C1，所以点A1的坐标为（2，2），B1点的坐标为（3，﹣2）；（2）因为△ABC和△A1B2C2关于原点O成中心对称图形，所以A2（3，﹣5），B2（2，﹣1），C2（1，﹣3）；（3）如图，△A2B3C3为所作，A3（5，3），B3（1，2），C3（3，1）；【考点】坐标与图形变化-旋转；坐标与图形变化-平移．【题文】某网店销售某款童装，每件售价60元，每星期可卖300件，为了促销，该网店决定降价销售．市场调查反映：每降价1元，每星期可多卖30件．已知该款童装每件成本价40元，设该款童装每件售价x 元，每星期的销售量为y件．（1）求y与x之间的函数关系式；（2）当每件售价定为多少元时，每星期的销售利润最大，最大利润多少元？（3）若该网店每星期想要获得不低于6480元的利润，每星期至少要销售该款童装多少件？【答案】（1）y=﹣30x+2100．（2）每件售价定为55元时，每星期的销售利润最大，最大利润6750元．（3）每星期至少要销售该款童装360件．【解析】试题分析：（1）根据售量y（件）与售价x（元/件）之间的函数关系即可得到结论．（2））设每星期利润为W元，构建二次函数利用二次函数性质解决问题．（3）列出不等式先求出售价的范围，再确定销售数量即可解决问题．试题解析：（1）y=300+30（60﹣x）=﹣30x+2100．（2）设每星期利润为W元，W=（x﹣40）（﹣30x+2100）=﹣30（x﹣55）2+6750．∴x=55时，W最大值=6750．∴每件售价定为55元时，每星期的销售利润最大，最大利润6750元．（3）由题意（x﹣40）（﹣30x+2100）≥6480，解得52≤x≤58，当l【解析】试题分析：（1）直接利用角平分线的性质结合等腰三角形的性质得出OC⊥MN，进而得出答案；（2）利用相似三角形的判定与性质得出AB的长．试题解析：（1）连接OC，∵OA=OC，∴∠OAC=∠OCA，∵AC平分∠BAD，∴∠CAB=∠DAC，∴∠OCA=∠DAC，∴OC∥AD．∵AD⊥MN，∴OC⊥MN．∵OC为半径，∴MN是⊙O切线．（2）∵∠ADC=90°，AC=5，DC=4，∴AD=3，∵AB是⊙O的直径，∴∠ACB=90°，∴∠ADC=∠ACB，又∵∠CAB=∠DAC，∴△ADC∽△ACB，∴=，∴=，解得：AB=，即⊙O的直径长为．【考点】切线的判定；圆周角定理；相似三角形的性质和判定；勾股定理；平行线性质和判定；等腰三角形性质．【题文】已知，AB是⊙O的直径，点P在弧AB上（不含点A、B），把△AOP沿OP对折，点A的对应点C 恰好落在⊙O上．（1）当P、C都在AB上方时（如图1），判断PO与BC的位置关系（只回答结果）；（2）当P在AB上方而C在AB下方时（如图2），（1）中结论还成立吗？证明你的结论；（3）当P、C都在AB上方时（如图3），过C点作CD⊥直线AP于D，且CD是⊙O的切线，证明：AB=4PD ．【答案】（1）PO与BC的位置关系是PO∥BC；（2）中的结论成立，理由见试题解析；（3）证明见试题解析．【解析】试题分析：（1）PO与BC的位置关系是平行；（2）中的结论成立，理由为：由折叠可知三角形APO与三角形CPO全等，根据全等三角形的对应角相等可得出∠APO=∠CP O，再由OA=OP，利用等边对等角得到∠A=∠APO，等量代换可得出∠A=∠CPO，又根据同弧所对的圆周角相等得到∠A=∠PCB，再等量代换可得出∠CPO=∠PCB，利用内错角相等两直线平行，可得出PO与BC平行；（3）由CD 为圆O的切线，利用切线的性质得到OC垂直于CD，又AD垂直于CD，利用平面内垂直于同一条直线的两直线平行得到OC与AD平行，根据两直线平行内错角相等得到∠APO=∠COP，再利用折叠的性质得到∠AOP=∠COP，等量代换可得出∠APO=∠AOP，再由OA=OP，利用等边对等角可得出一对角相等，等量代换可得出三角形AOP三内角相等，确定出三角形AOP为等边三角形，根据等边三角形的内角为60°得到∠AOP 为60°，由OP平行于BC，利用两直线平行同位角相等可得出∠OBC=∠AOP=60°，再由OB=OC，得到三角形OBC为等边三角形，可得出∠COB为60°，利用平角的定义得到∠POC也为60°，再加上OP=OC，可得出三角形POC为等边三角形，得到内角∠OCP为60°，可求出∠PCD为30°，在直角三角形l（3）∵CD为圆O 的切线，∴OC⊥CD，又AD⊥CD，∴OC∥AD，∴∠APO=∠C OP，由折叠可得：∠AOP=∠COP，∴∠APO=∠AOP，又OA=OP，∴∠A=∠APO，∴∠A=∠APO=∠AOP，∴△APO为等边三角形，∴∠AOP=60°，又∵OP∥BC，∴∠OBC=∠AOP=60°，又OC=OB，∴△BCO为等边三角形，∴∠COB=60°，∴∠POC=180°﹣（∠AOP+∠COB）=60°，又OP=OC，∴△POC也为等边三角形，∴∠PCO=60°，PC=OP=OC，又∵∠OCD=90°，∴∠PCD=30°，在Rt△PCD中，PD=PC，又∵PC=OP=AB，∴PD=AB，即AB=4PD．【考点】切线的性质；等边三角形的判定与性质；含30度角的直角三角形；圆心角、弧、弦的关系；圆周角定理．。

通辽十一中初三数学上册期中测试卷(含答案解析)

通辽十一中2021初三数学上册期中测试卷(含答案解析)通辽十一中2021初三数学上册期中测试卷(含答案解析)一、选择题〔本大题共10个小题，每题3分，共30分．在每题给出的四个选项中，只有一项为哪一项符合题目要求的〕1．4的算术平方根是〔〕A．﹣4 B． 4 C．﹣2 D． 22．我国经济飞速开展，2021年的GDP为63.6万亿元，用科学记数法表示63.6万亿元为〔〕A．0.636×106亿元 B． 6.36×105亿元C． 6.36×104亿元 D．63.6×105亿元3．以下计算结果正确的选项是〔〕A．﹣3x2y?5x2y=2x2y B．﹣2x2y3?2x3y=﹣2x5y4 C．35x3y2÷5x2y=7xy D．〔﹣2x﹣y〕〔2x+y〕=4x2﹣y2 4．为理解某社区居民的用电情况，随机对该社区10户居民进展了调查，下表是这10户居民2021年4月份用电量的调查结果：那么关于这10户居民用电量〔单位：度〕，以下说法错误的选项是〔〕居民 1 3 2 4月用电量〔度/户〕 40 50 55 60A．中位数是55 B．众数是60 C．平均数是54 D．方差是295．用一个圆心角为120°，半径为3的扇形作一个圆锥的侧面，那么这个圆锥的底面半径为〔〕A． 1 B． 26．以下一元二次方程没有实数根的是〔〕A． x2﹣9=0 B． x2﹣x﹣1=0 C．﹣x2+3x﹣ =0 D． x2+x+1=0 7．?ABCD的周长为40，AB=BC﹣2，那么对角线AC的取值范围为〔〕A． 2＜AC＜20 B． 2＜AC＜40 C． 10＜AC＜20 D． 5＜AC ＜218．M、N两点关于y轴对称，且点M在双曲线y= 上，点N在直线y=x+3上，设点M的坐标为〔a，b〕，那么二次函数y=﹣abx2+〔a+b〕x〔〕A．有最大值﹣4.5 B．有最大值4.5 C．有最小值4.5 D．有最小值﹣4.59．如图，在矩形ABCD中，AB=6，BC=8，点E是BC中点，点F是边CD上的任意一点，当△AEF的周长最小时，那么DF的长为〔〕A． 1 B． 2 C． 3 D． 410．如图，在△ABC中，AB=AC=10，点D是边BC上一动点〔不与B，C重合〕，∠ADE=∠B=α，DE交AC于点E，且cosα= ．以下给出的结论中，正确的有〔〕①△ADE∽△AC D；②当BD=6时，△ABC与△DCE全等；③△DCE为直角三角形时，BD为8或12.5；④0＜CE≤6.4．A． 1个 B． 2个 C． 3个 D． 4个二、填空题〔每题3分，共21分〕11．分解因式：ax2﹣4a=．12．函数y= 的自变量x的取值范围．13．关于x的一元二次方程x2+〔3﹣k〕x﹣3k=0有一个实数根是1，那么这个方程的另一个实数根是．14．点A〔x1，y1〕、B〔x2，y2〕在二次函数y=〔x﹣1〕2+1的图象上，假设x1＞x2＞1，那么y1y2〔填“＞〞、“＜〞或“=〞〕．15．不等式组的解集是．16．在Rt△ABC中，∠C=90°，AD平分∠CAB，AC=6，BC=8，CD=．17．如图，四个边长为1的小正方形拼成一个大正方形，A、B、O是小正方形顶点，A、B、P是⊙O上的点，那么tan∠APB=．三、解答题〔共9小题，69分〕18．计算：|1﹣2sin60°|+ +〔﹣tan30°〕﹣1．19．先化简，再求值：，其中x=3．20．甲、乙两人玩猜数字游戏，游戏规那么如下：有四个数字0、1、2、3，先由甲心中任选一个数字，记为m，再由乙猜甲刚刚所选的数字，记为n．假设m、n满足|m﹣n|≤1，那么称甲、乙两人“心有灵犀〞．画树状图〔或列表〕求甲、乙两人“心有灵犀〞的概率．21．：平行四边形ABCD中，E、F是BC、AB的中点，DE、DF 分别交AB、CB的延长线于H、G；〔1〕求证：BH=AB；〔2〕假设四边形ABCD为菱形，试判断∠G与∠H的大小，并证明你的结论．22．如图，某校综合理论活动小组的同学欲测量公园内一棵树DE的高度．他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°，朝着这棵树的方向走到台阶下的点C处，测得树顶端D的仰角为60°．A点的高度AB 为2米，台阶AC的坡度为〔即AB：BC= 〕，且B、C、E三点在同一条直线上．请根据以上条件求出树DE的高度〔测倾器的高度忽略不计〕．23．2021年10月，雾霾天气覆盖中国中东部大局部地区，北京及全国多个城市PM2.5严重超标，多地空气质量达严重污染，环境治理已成为民生中的热点问题，小强为了理解本市空气质量情况，从“中国环境保护网〞数据中心查询到本市2021年全年的空气质量级别资料，用简单随机抽样的方法选取60天，并得出如下所示的统计表和扇形统计图：空气质量级别优良细微污染轻度污染中度污染重度污染天数 10 a 4 b 3 2请你根据所给信息解答以下问题：〔1〕求a，b的值；〔2〕这次抽样中，“空气质量不低于良〞的频率为；〔3〕画出本市60天空气质量情况条形统计图；〔4〕根据这次抽样结果，请你估计2021年全年〔共365天〕空气质量为优良的天数是多少？24．某商品每件的本钱为20元，第x天〔x≤90〕的售价和销量分别为y元/件和〔180﹣2x〕件，设第x天该商品的销售利润为w元，请根据所给图象解决以下问题：〔1〕求出w与x的函数关系式；〔2〕问销售该商品第几天时，当天销售利润最大？最大利润是多少？〔3〕该商品在销售过程中，共有多少天当天的销售利润不低于4200元？25．如图，AB是⊙O的直径，BC切⊙O于点B，连接CO并延长交⊙O于点D、E，连接AD并延长交BC于点F．〔1〕试判断∠CBD与∠CEB是否相等，并证明你的结论；〔2〕求证： = ；〔3〕假设BC= AB，求tan∠CDF的值．26．〔12分〕△ABC的三个顶点坐标分别为A〔﹣4，0〕、B 〔1，0〕、C〔﹣2，6〕．〔1〕求经过A、B、C三点的抛物线解析式；〔2〕设直线BC交y轴于点E，连接AE，求证：AE=CE；〔3〕设抛物线与y轴交于点D，连接AD交BC于点F，试问以A、B、F为顶点的三角形与△ABC相似吗？通辽十一中2021初三数学上册期中测试卷(含答案解析)参考答案与试题解析一、选择题〔本大题共10个小题，每题3分，共30分．在每题给出的四个选项中，只有一项为哪一项符合题目要求的〕1．4的算术平方根是〔〕A．﹣4 B． 4 C．﹣2 D． 2考点：算术平方根．分析：根据算术平方根的定义解答即可．解答：解：∵22=4，∴4的算术平方根是2，即 =2．应选D．点评：此题考察了算术平方根的定义，是根底题，熟记概念是解题的关键．2．我国经济飞速开展，2021年的GDP为63.6万亿元，用科学记数法表示63.6万亿元为〔〕A．0.636×106亿元 B． 6.36×105亿元C． 6.36×104亿元 D．63.6×105亿元考点：科学记数法—表示较大的数．分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点挪动了多少位，n的绝对值与小数点挪动的位数一样．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．解答：解：63.6万=63 6000=6.36×105，应选：B．点评：此题考察科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值3．以下计算结果正确的选项是〔〕A．﹣3x2y?5x2y=2x2y B．﹣2x2y3?2x3y=﹣2x5y4C．35x3y2÷5x2y=7xy D．〔﹣2x﹣y〕〔2x+y〕=4x2﹣y2 考点：整式的除法；单项式乘单项式；平方差公式．专题：计算题．分析： A、原式利用单项式乘以单项式法那么计算得到结果，即可做出判断；B、原式利用单项式乘以单项式法那么计算得到结果，即可做出判断；C、原式利用单项式除以单项式法那么计算得到结果，即可做出判断；D、原式利用完全平方公式展开得到结果，即可做出判断．解答：解：A、﹣3x2y?5x2y=﹣15x4y2，故A选项错误；B、﹣2x2y3?2x3y=﹣4x5y4，故B选项错误；C、35x3y2÷5x2y=7xy，故C选项正确；D、〔﹣2x﹣y〕〔2x+y〕=﹣〔2x+y〕2=﹣4x2﹣4xy﹣y2，故D 选项错误．应选：C．点评：此题考察了整式的除法，单项式乘除单项式，以及平方差公式，纯熟掌握运算法那么是解此题的关键．4．为理解某社区居民的用电情况，随机对该社区10户居民进展了调查，下表是这10户居民2021年4月份用电量的调查结果：那么关于这10户居民用电量〔单位：度〕，以下说法错误的选项是〔〕居民 1 3 2 4月用电量〔度/户〕 40 50 55 60A．中位数是55 B．众数是60 C．平均数是54 D．方差是29考点：众数；加权平均数；中位数；方差．分析：根据众数、平均数、众数和方差的概念，求出该组数据的众数、平均数、众数和方差，然后选择错误选项．解答：解：这组数据按照从小到大的顺序排列为：40，50，50，50，55，55，60，60，60，60，那么众数为：60，中位数为：55，平均数为： =54，方差为： =39．应选D．点评：此题考察了众数、中位数、平均数和方差的知识，解答此题的关键是掌握各知识点的概念．5．用一个圆心角为120°，半径为3的扇形作一个圆锥的侧面，那么这个圆锥的底面半径为〔〕A． 1 B． 2考点：圆锥的计算．分析：根据扇形的弧长公式求出弧长，根据圆锥的底面周长等于展开后扇形的弧长，根据周长公式求出半径即可．解答：解：扇形的弧长==2π，圆锥的底面半径为：2π÷2π=1．应选：B．点评：考察了扇形的弧长公式、圆的周长公式，理解圆锥的底面周长等于展开后扇形的弧长是解题的关键．6．以下一元二次方程没有实数根的是〔〕A． x2﹣9=0 B． x2﹣x﹣1=0 C．﹣x2+3x﹣ =0 D． x2+x+1=0 考点：根的判别式．分析：分别求出各个一元二次方程的根的判别式，再作出判断即可．解答：解：A、x2﹣9=0有两个相等的根，此选项错误；B、x2﹣x﹣1=0，△=5，方程有两个不相等的实数根，此选项错误；C、﹣x2+3x﹣ =0，△=9﹣4×〔﹣1〕×〔﹣〕=0，方程有两个相等的实数根，此选项错误；D、x2+x+1=0，△=1﹣4=﹣3＜0，方程没有实数根，此选项正确；应选D．点评：此题考察了一元二次方程ax2+bx+c=0〔a≠0〕的根的判别式△=b2﹣4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．7．?ABCD的周长为40，AB=BC﹣2，那么对角线AC的取值范围为〔〕A． 2＜AC＜20 B． 2＜AC＜40 C． 10＜AC＜20 D． 5＜AC ＜21考点：平行四边形的性质；三角形三边关系．分析：由平行四边形的性质和条件得出AB+BC=20，再由BC ﹣AB=2，由三角形的三边关系定理，即可得出结果．解答：解：如下图：∵四边形ABCD是平行四边形，∴AB=CD，AD=BC，∵?ABCD的周长为40，∴AB+BC=20，∵AB=BC﹣2，∴BC﹣AB=2，在△ABC中，由三角形的三边关系定理得：BC﹣AB＜AC＜BC+AB，∴对角线AC的取值范围为2＜AC＜20；应选：A．点评：此题考察了平行四边形的性质、三角形的三边关系定理；纯熟掌握平行四边形的性质，并能进展推理计算是解决问题的关键．8．M、N两点关于y轴对称，且点M在双曲线y= 上，点N 在直线y=x+3上，设点M的坐标为〔a，b〕，那么二次函数y=﹣abx2+〔a+b〕x〔〕A．有最大值﹣4.5 B．有最大值4.5 C．有最小值4.5 D．有最小值﹣4.5考点：二次函数的最值；一次函数图象上点的坐标特征；反比例函数图象上点的坐标特征；关于x轴、y轴对称的点的坐标．分析：可先求得N点坐标，再把M和N的坐标分别代入所满足的函数解析式，整理可求得ab和a+b的值，代入可求得二次函数解析式，可求得其最值．解答：解：∵M、N两点关于y轴对称，点M的坐标为〔a，b〕，∴N点坐标为〔﹣a，b〕，∵点M在双曲线y= 上，∴2ab=1，解得ab= ，∵点N在直线y=x+3上，∴b=﹣a+3，解得a+b=3，∴二次函数解析式为y=﹣ x2+3x，∴当x=﹣ =3时，函数有最大值，ymax=﹣×9+9=4.5．应选B．点评：此题主要考察二次函数的最值，根据点的对称及点的坐标与函数解析式的关系求得ab和a+b的值是解题的关键．9．如图，在矩形ABCD中，AB=6，BC=8，点E是BC中点，点F是边CD上的任意一点，当△AEF的周长最小时，那么DF的长为〔〕A． 1 B． 2 C． 3 D． 4考点：轴对称-最短道路问题；矩形的性质．专题：压轴题；探究型．分析：作点E关于直线CD的对称点E′，连接AE′交CD 于点F，再根据△CEF∽△BEA即可求出CF的长，进而得出DF的长．解答：解：作点E关于直线CD的对称点E′，连接AE′交CD于点F，∵在矩形ABCD中，AB=6，BC=8，点E是BC中点，∴BE=CE=CE′=4，∵AB⊥BC，CD⊥BC，∴ = ，即 = ，解得CF=2，∴DF=CD﹣CF=6﹣2=4．应选D．点评：此题考察的是轴对称﹣最短道路问题及相似三角形的断定与性质，根据题意作出E点关于直线CD的对称点，再根据轴对称的性质求出CE′的长，利用相似三角形的对应边成比例即可得出结论．10．如图，在△ABC中，AB=AC=10，点D是边BC上一动点〔不与B，C重合〕，∠ADE=∠B=α，DE交AC于点E，且cosα= ．以下给出的结论中，正确的有〔〕①△ADE∽△ACD；②当BD=6时，△ABC与△DCE全等；③△DCE为直角三角形时，BD为8或12.5；④0＜CE≤6.4．A． 1个 B． 2个 C． 3个 D． 4个考点：相似三角形的断定与性质；全等三角形的断定与性质．分析：①根据有两组对应角相等的三角形相似即可证明．②由BD=6，那么DC=10，然后根据有两组对应角相等且夹边也相等的三角形全等，即可证得．③分两种情况讨论，通过三角形相似即可求得．④根据相似三角形对应边成比例即可求得．解答：解：①∵AB=AC，∴∠B=∠C，又∵∠ADE=∠B∴∠ADE=∠C，∴△ADE∽△ACD；故①正确，②作AG⊥BC于G，∵AB=AC=10，∠ADE=∠B=α，cosα= ，∴BG=ABcosB，∴BC=2BG=2ABcosB=2×10× =16，∵BD=6，∴DC=10，∴AB=DC，在△ABD与△DCE中，∴△ABD≌△DCE〔ASA〕．故②正确，③当∠AED=90°时，由①可知：△ADE∽△ACD，∴∠ADC=∠AED，∵∠AED=90°，∴∠ADC=90°，即AD⊥BC，∵AB=AC，∴BD=CD，∴∠ADE=∠B=α且cosα= ，AB=10，BD=8．当∠CDE=90°时，易△CDE∽△BAD，∵∠CDE=90°，∴∠BAD=90°，∵∠B=α且cosα= ．AB=10，∴cosB= = ，∴BD=12.5．故③正确．④易证得△CDE∽△BAD，由②可知BC=16，设BD=y，CE=x，整理得：y2﹣16y+64=64﹣10x，即〔y﹣8〕2=64﹣10x，∴0＜x≤6.4．故④正确．正确的有①②③④．应选：D．点评：此题考察了相似三角形的断定和性质，全等三角形的断定和性质以及利用三角函数求边长等．二、填空题〔每题3分，共21分〕11．分解因式：ax2﹣4a= a〔x+2〕〔x﹣2〕．考点：提公因式法与公式法的综合运用．分析：先提取公因式a，再对余下的多项式利用平方差公式继续分解．解答：解：ax2﹣4a，=a〔x2﹣4〕，=a〔x+2〕〔x﹣2〕．点评：此题考察用提公因式法和公式法进展因式分解的才能，一个多项式有公因式首先提取公因式，然后再用其他方法进展因式分解，同时因式分解要彻底，直到不能分解为止．12．函数y= 的自变量x的取值范围x＞1 ．考点：函数自变量的取值范围．分析：根据二次根式被开放数大于等于0和分式的分母不为0答复即可．解答：解：由题意得：x﹣1≥0，且x﹣1≠0．解得：x＞1．故答案为：x＞1．点评：此题主要考察的函数自变量的取值范围问题，明确二次根式被开放数大于等于0和分式的分母不为0是解题的关键．13．关于x的一元二次方程x2+〔3﹣k〕x﹣3k=0有一个实数根是1，那么这个方程的另一个实数根是﹣3 ．考点：根与系数的关系；根的判别式．专题：计算题．分析：先根据一元二次方程的解的定义，把x=1代入方程1+3﹣k﹣3k=0求出k的值，那么原方程化为x2+2x﹣3=0，设另一个根为t，根据根与系数的关系得到那么1?t=﹣3，然后解此方程即可．解答：解：把x=1代入方程得1+3﹣k﹣3k=0，解得k=1，那么原方程化为x2+2x﹣3=0，设另一个根为t，那么1?t=﹣3，解得t=﹣3，所以这个方程的另一个实数根为﹣3．故答案为﹣3．点评：此题考察了根与系数的关系：假设x1，x2是一元二次方程ax2+bx+c=0〔a≠0〕的两根时，x1+x2=﹣，x1x2= ．也考察了一元二次方程的解．14．点A〔x1，y1〕、B〔x2，y2〕在二次函数y=〔x﹣1〕2+1的图象上，假设x1＞x2＞1，那么y1 ＞y2〔填“＞〞、“＜〞或“=〞〕．考点：二次函数图象上点的坐标特征．分析：先根据二次函数的解析式得出函数图象的对称轴，再判断出两点的位置及函数的增减性，进而可得出结论．解答：解：∵a=1＞0，∴二次函数的图象开口向上，由二次函数y=〔x﹣1〕2+1可知，其对称轴为x=1，∵x1＞x2＞1，∴两点均在对称轴的右侧，∵此函数图象开口向上，∴在对称轴的右侧y随x的增大而增大，∵x1＞x2＞1，∴y1＞y2．故答案为：＞．点评：此题考察的是二次函数图象上点的坐标特点，根据题意判断出A、B两点的位置是解答此题的关键．15．不等式组的解集是﹣≤x＜4 ．考点：解一元一次不等式组．分析：分别求出各不等式的解集，再求出其公共解集即可．解答：解：，由①得，x≥﹣，由②得，x＜4，故不等式组的解集为：﹣≤x＜4．故答案为：﹣≤x＜4．点评：此题考察的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到〞的原那么是解答此题的关键．16．在Rt△ABC中，∠C=90°，AD平分∠CAB，AC=6，BC=8，CD= 3 ．考点：角平分线的性质；勾股定理．分析：过点D作DE⊥AB于E，利用勾股定理列式求出AB，再根据角平分线上的点到角的两边间隔相等可得CD=DE，然后根据△ABC的面积列式计算即可得解．解答：解：如图，过点D作DE⊥AB于E，∵∠C=90°，AC=6，BC=8，∴AB= = =10，∵AD平分∠CAB，∴CD=DE，∴S△ABC= AC?CD+ AB?DE= AC?BC，即×6?CD+ ×10?CD= ×6×8，解得CD=3．故答案为：3．点评：此题考察了角平分线上的点到角的两边间隔相等的性质，熟记性质并利用三角形的面积列出方程是解题的关键．17．如图，四个边长为1的小正方形拼成一个大正方形，A、B、O是小正方形顶点，A、B、P是⊙O上的点，那么tan∠APB=1 ．考点：圆周角定理；锐角三角函数的定义．专题：网格型．分析：先根据圆周角定理得到∠APB= ∠AOB=45°，然后根据特殊角的三角函数值求解．解答：解：∵∠AOB=90°，∴∠APB= ∠AOB=45°，∴tan∠APB=tan45°=1．故答案为1．点评：此题考察了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆〔或直径〕所对的圆周角是直角，90°的圆周角所对的弦是直径．也考察了锐角三角函数的定义．三、解答题〔共9小题，69分〕18．计算：|1﹣2sin60°|+ +〔﹣ta n30°〕﹣1．考点：特殊角的三角函数值；负整数指数幂．分析：将特殊角的三角函数值代入求解即可．解答：解：原式= ﹣1+1﹣=0．点评：此题考察了特殊角的三角函数值，解答此题的关键是掌握几个特殊角的三角函数值．19．先化简，再求值：，其中x=3．考点：分式的化简求值．分析：先根据分式混合运算的法那么把原式进展化简，再把x的值代入进展计算即可．解答：解：将x=3代入原式得：原式= =1．点评：此题考察的是分式的化简求值，在解答此类题目时要注意通分及约分的灵敏应用．20．甲、乙两人玩猜数字游戏，游戏规那么如下：有四个数字0、1、2、3，先由甲心中任选一个数字，记为m，再由乙猜甲刚刚所选的数字，记为n．假设m、n满足|m﹣n|≤1，那么称甲、乙两人“心有灵犀〞．画树状图〔或列表〕求甲、乙两人“心有灵犀〞的概率．考点：列表法与树状图法．分析：首先根据题意画出树状图，然后由树状图求得所有等可能的结果与m、n满足|m﹣n|≤1情况，再利用概率公式即可求得答案．解答：解：画树状图得：∵共有16种等可能的结果，m、n满足|m﹣n|≤1的有10种情况，∴甲、乙两人“心有灵犀〞的概率为： = ．点评：此题考察的是用列表法或画树状图法求概率．注意列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法合适于两步完成的事件，树状图法合适两步或两步以上完成的事件．注意概率=所求情况数与总情况数之比．21．：平行四边形ABCD中，E、F是BC、AB的中点，DE、DF 分别交AB、CB的延长线于H、G；〔1〕求证：BH=AB；〔2〕假设四边形ABCD为菱形，试判断∠G与∠H的大小，并证明你的结论．考点：平行四边形的性质；平行线的性质；全等三角形的断定与性质；菱形的性质．专题：证明题；几何综合题．分析：〔1〕根据平行四边形性质推出DC=AB，DC∥AB，得出∠C=∠EBH，∠CDE=∠H，根据AAS证△CDE≌△BHE即可；〔2〕根据菱形的性质推出AD=CD，AF=CE，∠A=∠C，推出△ADF≌△CDE，得出∠CDE=∠ADF，根据平行线性质推出∠CDE=∠H，∠ADF=∠G，即可得到答案．解答：解：〔1〕证明：∵四边形ABCD是平行四边形，∴DC=AB，DC∥AB，∴∠C=∠EBH，∠CDE=∠H，又∵E是CB的中点，∴CE=BE，在△CDE和△BHE中∴△CDE≌△BHE，∴BH=DC，∴BH=AB．〔2〕∠G=∠H，证明：∵四边形ABCD是平行四边形，∴AD∥CB，∴∠ADF=∠G，∵四边形ABCD是菱形，∴AD=DC=CB=AB，∠A=∠C，∵E、F分别是CB、AB的中点，∴AF=CE，在△ADF和△CDE中∴△ADF≌△CDE，∴∠CDE=∠ADF，∴∠H=∠G．点评：此题考察了平行线的性质，平行四边形性质，菱形性质，全等三角形的性质和断定等知识点的应用，主要培养了学生运用定理进展推理的才能，题目比拟典型，难度也适中．22．如图，某校综合理论活动小组的同学欲测量公园内一棵树DE的高度．他们在这棵树正前方一座楼亭前的台阶上A 点处测得树顶端D的仰角为30°，朝着这棵树的方向走到台阶下的点C处，测得树顶端D的仰角为60°．A点的高度AB 为2米，台阶AC的坡度为〔即AB：BC= 〕，且B、C、E三点在同一条直线上．请根据以上条件求出树DE的高度〔测倾器的高度忽略不计〕．考点：解直角三角形的应用-仰角俯角问题；解直角三角形的应用-坡度坡角问题．专题：应用题．分析：通过构造直角三角形分别表示出BC和AM，得到有关的方程求解即可．解答：解：如图，过点A作AM⊥DE于点M，交CD于点F，那么四边形ABEM为矩形，∴AM=BE，EM=AB=2，设DE=x，在Rt△CDE中，CE= = ，在Rt△ABC中，∵ ，AB=2，∴BC=2 ，在Rt△AMD中，DM=DE﹣EM=x﹣2，∴AM= = 〔x﹣2〕，∵AM=BE=BC+CE，∴ 〔x﹣2〕=2 + ，解得x=6．答：树高为6米．点评：此题考察理解直角三角形的知识，解题的关键是正确的构造直角三角形并选择正确的边角关系求解．23．2021年10月，雾霾天气覆盖中国中东部大局部地区，北京及全国多个城市PM2.5严重超标，多地空气质量达严重污染，环境治理已成为民生中的热点问题，小强为了理解本市空气质量情况，从“中国环境保护网〞数据中心查询到本市2021年全年的空气质量级别资料，用简单随机抽样的方法选取60天，并得出如下所示的统计表和扇形统计图：空气质量级别优良细微污染轻度污染中度污染重度污染天数 10 a 4 b 3 2请你根据所给信息解答以下问题：〔1〕求a，b的值；〔2〕这次抽样中，“空气质量不低于良〞的频率为；〔3〕画出本市60天空气质量情况条形统计图；〔4〕根据这次抽样结果，请你估计2021年全年〔共365天〕空气质量为优良的天数是多少？考点：条形统计图；用样本估计总体；扇形统计图．分析：〔1〕根据轻度污染所占的百分比，即可求出b的值，a═60﹣10﹣4﹣3﹣2﹣3=38〔天〕；〔2〕用优、良的天数除以总天数，即可解答；〔3〕根据表格，即可补全统计图；〔4〕用365乘以，即可解答．解答：解：〔1〕b=60×5%=3〔天〕，a=60﹣10﹣4﹣3﹣2﹣3=38〔天〕；〔2〕这次抽样中，“空气质量不低于良〞的频率为：，故答案为：；〔3〕如下图：〔4〕365× =372，答：估计2021年全年〔共365天〕空气质量为优良的天数是372天．点评：此题考察统计知识的应用，试题以图表为载体，要求学生能从中提取信息来解题，与实际生活息息相关，符合新课标的理念．24．某商品每件的本钱为20元，第x天〔x≤90〕的售价和销量分别为y元/件和〔180﹣2x〕件，设第x天该商品的销售利润为w元，请根据所给图象解决以下问题：〔1〕求出w与x的函数关系式；〔2〕问销售该商品第几天时，当天销售利润最大？最大利润是多少？〔3〕该商品在销售过程中，共有多少天当天的销售利润不低于4200元？考点：二次函数的应用．分析：〔1〕根据单价乘以数量，可得利润，可得答案；〔2〕根据分段函数的性质，可分别得出最大值，根据有理数的比拟，可得答案；〔3〕根据二次函数值大于或等于4200，一次函数值大于或等于4200，可得不等式，根据解不等式组，可得答案．解答：解：〔1〕当1≤x≤50时，设y与x的函数关系式为y=kx+b，∵当x=1时，y=31，当x=50，y=80，解得：∴y=x+30，∴当1≤x≤50时，w=〔x+30﹣20〕〔180﹣2x〕=﹣2x2+160x+1800；当50＜x≤90时，w=〔80﹣20〕〔180﹣2x〕=﹣120x+10800；〔2〕w=﹣2x2+180x+1800=﹣2〔x﹣40〕2+5000，∴当x=40时获得最大值5000元；∵w=﹣120x+10800；∴当50≤x≤90时，y随x的增大而减小，当x=50时，y最大=4800，综上所述，该商品第45天时，当天销售利润最大，最大利润是5000元；〔3〕当1≤x＜50时，y=﹣2x2+160x+1800≥4200，解得20≤x≤60，因此利润不低于4800元的天数是20≤x＜50，共30天；当50≤x≤90时，y=﹣120x+10800≥4200，解得x≤55，因此利润不低于4800元的天数是50≤x≤55，共6天，所以该商品在销售过程中，共36天每天销售利润不低于4200元．点评：此题考察了二次函数的应用，利用单价乘以数量求函数解析式，利用了函数的性质求最值．25．如图，AB是⊙O的直径，BC切⊙O于点B，连接CO并延长交⊙O于点D、E，连接AD并延长交BC于点F．〔1〕试判断∠CBD与∠CEB是否相等，并证明你的结论；〔2〕求证： = ；〔3〕假设BC= AB，求tan∠CDF的值．考点：切线的性质；圆周角定理；相似三角形的断定与性质；锐角三角函数的定义．专题：几何综合题；压轴题．分析：〔1〕根据题意即可推出∠CBD=∠BAD，由∠BAD=∠CEB，即可推出∠CBD与∠CEB相等；〔2〕根据〔1〕所推出的结论，通过求证△EBC∽△BDC，即可推出结论；〔3〕通过设BC=3x，AB=2x，根据题意，推出OC和CD的长度，然后通过求证△DCF∽△BCD，即可推出DF：BD的值，即∠DBF的正切值，由∠DBF=∠CDF，即可推出∠CDF的正切值．解答：〔1〕解：∠CBD与∠CEB相等，证明：∵BC切⊙O于点B，∴∠CBD=∠BAD，∵∠BAD=∠CEB，∴∠CEB=∠CBD，〔2〕证明：∵∠C=∠C，∠CEB=∠CBD，∴∠EBC=∠BDC，∴△EBC∽△BDC，〔3〕解：∵AB、ED分别是⊙O的直径，∴AD⊥BD，即∠ADB=90°，∵BC切⊙O于点B，∴AB⊥BC，∵BC= ，设BC=3x，AB=2x，∴OB=OD=x，∴OC= ，∴CD=〔﹣1〕x，∵AO=DO，∴∠CDF=∠A=∠DBF，∴△DCF∽△BCD，∵tan∠DBF= = ，∴tan∠CDF= ．点评：此题主要考察切线的性质、相似三角形的断定与性质、圆周角定理、锐角三角函数定义等知识点，关键在于：〔1〕纯熟运用圆周角定理，切线的性质；〔2〕根据〔1〕的结论和条件推出△EBC∽△BDC；〔3〕关键在于通过求证△DCF∽△BCD，根据对应边成比例的性质求出tan∠DBF的值．26．〔12分〕△ABC的三个顶点坐标分别为A〔﹣4，0〕、B 〔1，0〕、C〔﹣2，6〕．〔1〕求经过A、B、C三点的抛物线解析式；〔2〕设直线BC交y轴于点E，连接AE，求证：AE=CE；〔3〕设抛物线与y轴交于点D，连接AD交BC于点F，试问以A、B、F为顶点的三角形与△ABC相似吗？考点：二次函数综合题．专题：综合题；压轴题．分析：〔1〕利用待定系数发求解即可得出抛物线的解析式；〔2〕求出直线BC的函数解析式，从而得出点E的坐标，然后分别求出AE及CE的长度即可证明出结论；〔3〕求出AD的函数解析式，然后结合直线BC的解析式可得出点F的坐标，由题意得∠ABF=∠CBA，然后判断出是否等于即可作出判断．解答：解：〔1〕设函数解析式为：y=ax2+bx+c，由函数经过点A〔﹣4，0〕、B〔1，0〕、C〔﹣2，6〕，可得，解得：，故经过A、B、C三点的抛物线解析式为：y=﹣x2﹣3x+4；〔2〕设直线BC的函数解析式为y=kx+b，由题意得：，解得：，即直线BC的解析式为y=﹣2x+2．故可得点E的坐标为〔0，2〕，从而可得：AE= =2 ，CE= =2 ，故可得出AE=CE；〔3〕相似．理由如下：设直线AD的解析式为y=kx+b，那么，解得：，即直线AD的解析式为y=x+4．联立直线AD与直线BC的函数解析式可得：，解得：，即点F的坐标为〔﹣，〕，那么BF= = ，又∵AB=5，BC= =3 ，又∵∠ABF=∠CBA，∴△ABF∽△CBA．故以A、B、F为顶点的三角形与△ABC相似．点评：此题属于二次函数的综合题目，涉及了相似三角形的断定与性质、待定系数法求二次函数解析式，两点间的间隔公式，解答此题要求我们仔细审题，将所学知识联络起来，综合解答．。

稠江中学11月九年级语文上册期中试题及答案

稠江中学2021年11月九年级语文上册期中试题及答案内容预览：九年级期中考试语文检测卷2021.11卷首寄语：亲爱的同学们，当你走进考场，你就是这里的主人。

只要心境平静，只要细心、认真地阅读、考虑，你就会感到试题并不难，一切都在你的掌握之中。

别忘了，对自己说一声：我能行！祝大家考出好成绩！一、语文知识积累与运用〔22分〕1、阅读下面文字，根据拼音写出汉字。

〔3分〕假如说奥斯卡是jiǎn〔1〕验好莱坞商业电影的标尺，那么“义博会〞就无可争议的成为全球小商品的一次行业盛典。

没有娱乐产业的喧xiāo〔2〕与急躁，这里尽是商业智huì〔3〕的博弈，机遇与财富编织的梦想让来自国内超过10万、境外1.8万人聚集义乌国际博览中心 (2021)年组委会给出了的数据显示首日成交额50.38亿元，同比增长11.7%，125个国家和地区的采购商到场采购。

2、以下各句中，加点的成语使用恰当的一项为哪一项〔▲〕〔2分〕A、电视剧?蜗居?播出时，几乎万人空巷，人们在家守着荧屏，街市冷清。

B、眼前这位老太太，脸上虽有不少皱纹，一身名牌装束却装戴得一尘不染。

C、房屋倒塌，道路扭曲，电力和通讯中断，触目惊心的震后景象凸现了地震的威力。

D、中国女子短道速滑队赢大满贯！当普天弹冠相庆时，人们不得不佩服教练李琰了。

3、古诗词填空。

〔6分〕(1)足蒸暑土气，。

〔白居易?观刈麦?〕(2)零落成泥碾作尘，。

(陆游?卜算子?)(3)梦是一种愿望达成，是清醒状态精神活动的延续。

苏轼把对亡妻的思念诉诸于梦：“夜来幽梦忽还乡，小轩窗，正梳妆〞；辛弃疾将渴望建功立业的雄心壮志尽显于梦：“▲，▲〞。

(?破阵子?)(4)文学史上“酒〞与“诗〞一路同行，请默写一联含有“酒〞字的古诗词名句：“▲，▲。

〞4、依次填入下面横线上的句子，排列恰当的一项为哪一项〔▲〕〔2分〕最动人的是秋林映着落日。

，而情愿把奔放的情感凝结。

①让你想流几行感怀身世之泪②却又被那逐渐淡去的酡红所慑住③晚风带着清澈的凉意，随着暮色浸染，那是一种非常艳丽的凄楚之美④那酡红如醉，衬托着天边加深的暮色A 、③④①② B、④③①② C 、④①③② D、③①②④5、名著阅读。

湖北省武汉市十一初级中学2021-2022学年九年级上学期期中英语试卷

2021---2022 学年度第一学期期中质量检测九年级英语试卷区教研室命制2021. 11. 12第I 部分选择题（85 分）一. 听力测试(本题共25 分，每小题1 分)第一节(共5 小题, 每小题1 分，满分5 分)听下面5 个问题，每个问题后有三个答语，从题中所给的A、B、C 三个选项中选出最佳选项。

听完每个问题后，你都有5 秒钟的时间来作答和阅读下一小题。

每个问题仅读一遍。

1.A. Farmers. B. Wuhan city. C. Glass.2.A. Three. B. Once a week. C. Mr. Dean.3.A. Last Sunday. B. Turn left. C. Kunming.4.A. 6:30 pm. B. Black. C. On foot.5.A. By reading. B. Sky lanterns. C. The big one.第二节(共7 题, 每小题1 分，满分7 分)听下面7 段对话，每段对话后有一个小题，从题中所给的A、B、C 三个选项中选出最佳选项。

听完每段对话后，你都有10 秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

6.What are the speakers doing?A. Drawing a picture.B. Taking a photo.C. Playing a joke.7. Where are the speakers?B. In a shop.C. In the street.A. At home.8. Who is the girl?A. A waitress.B. A doctor.C. A teacher.9.What did the man use to play?A. Tennis.B. Soccer.C. Golf.10.How much did the girl spend on her trousers?A. $46.B. $33.C. $13.11.What does the man want to do?A. To see the doctor.B. To buy a book.C. To get some medicine.12.What time can the man meet the girl?A. 5:20.B. 5:30.C. 5:40.第三节(共13 小题，每小题 1 分，满分13 分)听下面4 段对话或独白，每段对话或独白后有几个小题，根据所听材料内容，从题中所给的A、B、C 三个选项中选出最佳选项。