兰生复旦初三练习卷
上海民办兰生复旦中学初三化学上册期中初三化学试卷
上海民办兰生复旦中学化学上册期中化学试卷一、选择题(培优题较难)1.下列微观模拟图中●和○分别表示不同元素的原子,其中表示单质的是A.B.C.D.2.某反应的微观示意图如下,其中“”和“”表示不同元素的原子,下列说法不正确的是( )A.反应物有4种分子B.反应前后原子个数不变C.反应前后元素种类不变D.化学变化中的最小粒子是原子3.2017年10月27日央视财经报道:王者归“铼”,中国发现超级金属铼,制造出航空发动机核心部件。
如图是铼在元素周期表中的相关信息,下列有关说法不正确的是()A.铼原子的核内质子数为75 B.铼的相对原子质量为186.2gC.铼的元素符号是Re D.铼原子的核外电子数为754.实验室常用加热高锰酸钾固体制取氧气,化学方程式为2KMnO4K2MnO4+MnO2+O2↑,现对一定量的高锰酸钾固体进行加热,加热过程中涉及的相关量随时间变化的图象正确的是A.B.C.D.5.碳酸乙烯酯(C3H4O3)可用作锂电池电解液,下列有关碳酸乙烯酯的说法正确的是A.碳酸乙烯酯的相对分子质量为(12×3+1×4+16×3)gB.碳酸乙烯酯中C、H、O三种元素的质量比为12:1:16C.碳酸乙烯酯中C、H、O三种原子的个数比为3:4:3D.碳酸乙烯酯中碳元素的质量分数= ×100%6.以下是四种微粒的结构示意图,下列有关各微粒的说法中,错误的是A.①的化学性质比较稳定B.③④属于同种元素C.④是一种阴离子D.②容易得到电子7.实验室里制取氧气大致可分为下列步骤:①点燃酒灯,加热试管;②检查装置的气密性;③将药品装入试管,用带导管的塞子塞紧试管并固定在铁架台上;④用排水法收集氧气;⑤连接好装置;⑥熄灭酒精灯;⑦将导管从水槽中取出。
正确的操作顺序是()A.⑤②③①④⑦⑥B.③④⑤⑥⑦①②C.②③⑤①④⑦⑥D.②④③⑤①⑥⑦8.下图表示某化学反应的微观示意图,依据图分析判断,下列说法正确的是A.甲物质由5个原子构成B.化学变化的后硅元素的化合价不变C.参加反应的乙的质量和生成的丁中氢元素的质量相等D.参加反应的甲、乙两种物质的分子个数比为l:19.中华传统文化博大精深。
上海兰生复旦化学初三化学上册期末试卷(带解析)

上海兰生复旦化学上册期末试卷(带解析)一、九年级化学上册选择题1.下列图象能正确反映其对应关系的是()A.电解水B.加热一定质量的KClO3C.两份完全相同的双氧水在有无MnO2的情况下产生O2D.红磷在密闭容器中燃烧2.一定条件下,能与二氧化碳反应的是A.木炭B.一氧化碳C.氧化铜D.氧气3.在一定条件下,在一个密闭容器内发生某反应,测得反应过程中各物质的质量如下表所示,下列说法错误的是物质a b c d反应前质量1010102(g)反应后质量待测2212(g)A.该反应是化合反应,d可能是催化剂B.a、b两种物质中元素种类一定与c物质中元素种类相同C.b物质可能是单质D.反应后a物质的质量为3g4.推理是学习化学的一种重要方法,以下推理合理的是()A.组成CO和CO2的元素相同,它们的分子构成不同,所以它们的化学性质不同B.煤既是燃料,也是重要的化工原料,所以煤对人类有利而无害C.同种化合物中,金属元素显正价,非金属元素一定显负价D.一定条件下,碳和一氧化碳都能夺取氧化铜中的氧,都具有氧化性5.下列四个图像分别表示四个化学兴趣小组活动中的数据及处理情况,其中正确的是A.高温煅烧一定质量的石灰石B.加热一定质量的高锰酸钾固体C.相同质量的铁粉和锌粉分别加入到足量的稀硫酸中D.向一定质量的过氧化氢溶液加入二氧化锰固体6.除去下列物质中的少量杂质,实验方案不能达到除杂目的的是物质(括号内为杂质)实验方案A氮气(氧气)通过足量灼热铜网B氧化铜(木炭粉)在空气中充分灼烧C碳酸钙粉末(氯化钙)加入足量的水,过滤,洗涤,干燥D硫酸铁溶液(硫酸)加入足量铁粉,过滤A.A B.B C.C D.D7.将2.8 g铁粉放入一定量的硫酸与硫酸铜的混合溶液中,三者恰好完全反应,除去其中的不溶物,再将所得的溶液蒸干,最后可得固体( )A.3.2 g B.7.6 g C.8.0 g D.15.2 g8.完全燃烧2. 8g某有机物,生成8. 8gCO2和3. 6gH2O。
【物理】上海兰生复旦九年级上册期末精选试卷检测题

【物理】上海兰生复旦九年级上册期末精选试卷检测题一、初三物理电流和电路易错压轴题(难)1.小敏和小英通过实验探究“并联电路中干路电流与各支路电流的关系”.她们连接的电路如图所示.(1)当小敏用开关“试触”时,发现电流表A1无示数、电流表A2的指针快速右偏,两灯均不发光.由此可知,她们连接的电路发生了________故障;若闭合开关S,可能造成的后果是________.(2)小英只改接了电路中的一根导线,电路便连接正确了,请你在图中画出她的改法.(在错接的导线上画×,然后画出正确的接线)(___________)(3)她们利用改正后的电路进行实验:闭合开关S后,读出两块电流表的示数,得出的初步结论是:________.【答案】短路电流表A2被烧坏在并联电路中,干路电流大于支路电流【解析】【分析】【详解】(1)电流表A1无示数、电流表A2的指针快速右偏,两灯均不发光,由此可知电路发生了短路故障,若闭合开关S,由于电路发生短路,电路中电流过大,可能造成的后果是电流表A2被烧坏.(2)改正电路如图:(3)利用改正后的电路进行实验,闭合开关S后,读出两块电流表的示数,得出的初步结论是:在并联电路中,干路电流大于支路电流.【点睛】电路中发生短路的危害,可能烧毁电流表或电源,为避免短路发生,可采用试触法.2.小明利用如图所示的电路“探究串、并联电路中电流的关系“.(1)探究串联电路中电流的关系.①用笔画线代替导线将开关S3连入电路中________.(要求:只闭合开关S3后,R1、R2以及电流表串联;导线不许交叉)②小明将S3闭合后,发现电流表均无示数.于是他用一只电压表对电路故障(电路中只有一处故障)进行了检测,将电压表接在R1两端时,电压表与电流表均无示数;接在R2两端时,电压表有示数,电流表无示数.电路中的故障是________.小明排除故障后继续实验,读出了电路中各电流表的示数,得到了串联电路中电流的关系是:串联电路中各处电流相等.(2)完成上述实验后,小明继续探究并联电路中电流的关系.①各开关的连接情况是________(填写各开关断开或闭合).②分析实验中各电流表的读数(如图所示),可知并联电路中电流的关系是________:.③电阻R1:R2=________.(3)为了验证结论的普遍性,你可以采用的方法是:________.(拓展)在电源电压不变的情况下,小明两次实验中电路消耗的最大功率与最小功率之比P最大:P最小=________.【答案】R2断路闭合S1、S2断开S3并联电路干路电流等于各支路电流的和1:2改变电源电压9:2【解析】【分析】(1)按从电源正极依次连接,一条路径将所有用电器连接起来;(2)闭合开关后,电流表无示数,说明电路故障为断路;电压表的示数接近电源电压,说明电压表的正负接线柱与电源两极相连;(3)通过开关的断开与闭合判断出并联电路;(4)根据实验数据得到并联电路电流的规律;(5)多次测量找普遍规律,可以改变电源电压;(6)根据电功率的公式算出两次电功率的比值。
上海市民办兰生复旦中学初三物理电学练习题8.1电功率(2)电功率(1)

8.1电功率(2)电功率一、选择题1.下列说法中不正确的是()A.电流做功的过程是电能转化为其他形式能的过程B.做功多的用电器消耗的电能多C.电功率大的用电器消耗的电能多D.电功率表示电流做功的快慢2、下列判断中正确的是()A.根据P=I2R可知,电阻越大,电功率也越大B.根据P=U2/R可知,电阻越大,电功率反而越小C.根据P=UI可知,同一导体两端的电压越小,电功率也越小D.根据P=W/t可知,电流做的功越多,电功率也越大3、一只普通的家用白炽灯正常发光时,电流每秒做功为()A.400焦B.40焦C.4焦D.0.6焦4、亮度与60瓦的白炽灯相当的节能灯,它的额定功率约为()A.0.11瓦B.1.1瓦C.11瓦D.110瓦5、标有“100瓦“字样的家用电电器可能是()A.白炽灯B.电视机C.洗衣机D.空调6、标有“220伏25瓦”、“110伏25瓦”、“36伏25瓦”字样的三盏灯,各自在额定电压下工作,则()A.“220伏25瓦”的灯最亮B.“110伏25瓦”的灯最亮C.“36伏25瓦“的灯最亮D.一样亮7、甲、乙两用电器上分别标有“220V25W”、“110V40W”则下列判断中不正确的是()A.乙用电器做功一定多B.乙用电器做功一定快C.完成相同的功,中用电器所用的时间一定多D.相同时间内,甲用电器完成的功一定少8、为使某用电器的功率变为原来的一半,下列方法中正确的是()A.保持电压不变,电阻变为原来的1/2B.保持电阻不变,电压变为原来的1/2C.使电压为原来的1/4,电阻变为原来的1/2D.电压和电阻都变为原来的1/29、两只灯泡串联在电路中,其中一只灯亮,另一只不亮,原因可能是()A.两只灯泡相比较,流过不亮的灯泡的电流较小B.不亮的灯泡的灯丝断了C.两只灯泡相比较,亮的灯泡电阻太小D.两只灯泡相比较,不亮的灯泡电阻太小10、额定电压相同的甲、乙两盏电灯,其额定功率之比为5:3,如果将它们串联接入电压与额定电压相同的电路中,下列叙述正确的是()A.两灯实际消耗功率之比为5:3B.两灯都能正常发光C.两灯实际通过电流之比为3:5D.两灯实际电压之比为3:511、如图所示电路,阻值为6Ω的电阻与一个“6V3W”的小灯泡串联后接到9V的电路中,小灯泡恰能正常发光如果在此电路中将“6V3W”的小灯泡换成“6V4.5W”的小灯泡,那么该小灯泡的实际功率(设电源电压不变)()A.等于4.5W B.小于4.5W C.大于4.5W D.等于3W12、两个定值电阻R1和R2,,阻值分别为10Ω和20Ω允许通过的电流分别为1A租0.5A,将它们事联在电路中,下列说法中正确的是()A.加在它们两端的电压最大值为20VB.通过电路的电流最大值为1AC.通过电路的电流最大值为0.5AD.他们的总功货功率最大值是15W二、填空题13、____________________________叫做电功率,是表示____________________________的物理量,它的定义式是____________,某电动机的电功率为250瓦,它表示____________________________14、电功率等于用电器两端的____________和通过它的____________的乘积。
上海民办兰生复旦中学语文中考九年级文言文试卷

上海民办兰生复旦中学语文中考九年级文言文试卷一、文言文1.阅读下面的文字,回答问题。
【甲】侍中、侍郎郭攸之、费祎、董允等,此皆良实,志虑忠纯,是以先帝简拔以遗陛下。
愚以为宫中之事,事无大小,悉以咨之,然后施行,必能裨补阙漏,有所广益。
将军向宠,性行淑均,晓畅军事,试用于昔日,先帝称之曰能,是以众议举宠为督。
愚以为营中之事,悉以咨之,必能使行阵和睦,优劣得所。
(节选自诸葛亮《出师表》)【乙】高祖①曰:“吾所以有天下者何?项氏所以失天下者何?”高起②等对曰:“陛下使人攻城略③地,所降下者因以予之,与天下④同利也。
项羽妒贤嫉能,战胜而不予人功,得地而不予人利,此所以失天下也。
”高祖曰:“运筹帷幄之中,决胜千里之外,吾不如子房⑤;镇国家,抚百姓,吾不如萧何;连⑥百万之军,战必胜,吾不如韩信。
此三杰,吾能用之。
项羽有一范增而不能用,此其所以为我擒也。
”(节选自《史记·高祖本纪》,有删改)【注】①高祖:指汉高祖刘邦。
②高起:高祖臣子。
③略:攻占。
④天下:这里指刘邦的部属。
⑤子房:西汉谋士张良。
⑥连:率领。
(1)解释下列划线词在文中的意思。
①事无大小,悉以咨之悉:________②性行淑均,晓畅军事晓:________③战胜而不予人功予:________(2)把下面的句子翻译成现代汉语。
①先帝称之曰能,是以众议举宠为督。
①项羽有一范增而不能用,此其所以为我擒也。
(3)下面对【甲】【乙】两个文段理解不正确的一项是( )A.【甲】文中诸葛亮两次提到“先帝”是希望刘禅谨记先帝遗志,谨遵先帝安排,言辞恳切,拳拳之心,溢于言表。
B.【乙】文中,司马迁通过对话描写,将高祖取胜与项羽失败进行对比,刻画了高祖睿智英明的形象。
C.【甲】文中诸葛亮向刘禅举荐郭攸之、费祎、董允等管理“营中”之事,向宠管理“宫中”之事,安排得十分细致周到。
D.【乙】文中高祖非常有自知之明,他能够很清晰地认识到张良、萧何、韩信各自的长处,并让他们各得其所。
上海民办兰生复旦中学九年级上册期末数学试题(word版,含解析)

上海民办兰生复旦中学九年级上册期末数学试题(word 版,含解析)一、选择题1.关于x 的一元一次方程122a x m -+=的解为1x =,则a m -的值为( )A .5B .4C .3D .22.某大学生创业团队有研发、管理和操作三个小组,各组的日工资和人数如下表所示.现从管理组分别抽调1人到研发组和操作组,调整后与调整前相比,下列说法中不正确的是( )A .团队平均日工资不变B .团队日工资的方差不变C .团队日工资的中位数不变D .团队日工资的极差不变3.要得到函数y =2(x -1)2+3的图像,可以将函数y =2x 2的图像( ) A .向左平移1个单位长度,再向上平移3个单位长度 B .向左平移1个单位长度,再向下平移3个单位长度 C .向右平移1个单位长度,再向上平移3个单位长度 D .向右平移1个单位长度,再向下平移3个单位长度4.在平面直角坐标系中,点A(0,2)、B(a ,a +2)、C(b ,0)(a >0,b >0),若AB=42且∠ACB 最大时,b 的值为( ) A .226+B .226-+C .242+D .2425.一枚质地匀均的骰子,其六个面上分别标有数字:1,2,3,4,5,6,投掷一次,朝上面的数字大于4的概率是( ) A .12B .13C .23D .166.已知a 是方程x 2+3x ﹣1=0的根,则代数式a 2+3a+2019的值是( ) A .2020 B .﹣2020 C .2021 D .﹣2021 7.下列方程是一元二次方程的是( )A .2321x x =+B .3230x x --C .221x y -=D .20x y +=8.用配方法解方程2890x x ++=,变形后的结果正确的是( ) A .()249x +=-B .()247x +=-C .()2425x +=D .()247x +=9.如图,在□ABCD 中,E 、F 分别是边BC 、CD 的中点,AE 、AF 分别交BD 于点G 、H ,则图中阴影部分图形的面积与□ABCD 的面积之比为( )A .7 : 12B .7 : 24C .13 : 36D .13 : 7210.某同学在解关于x 的方程ax 2+bx +c =0时,只抄对了a =1,b =﹣8,解出其中一个根是x =﹣1.他核对时发现所抄的c 是原方程的c 的相反数,则原方程的根的情况是( )A .有两个不相等的实数根B .有两个相等的实数根C .有一个根是x =1D .不存在实数根11.下列方程中,关于x 的一元二次方程是( ) A .2x ﹣3=xB .2x +3y =5C .2x ﹣x 2=1D .17x x+= 12.已知在△ABC 中,∠ACB =90°,AC =6cm ,BC =8cm ,CM 是它的中线,以C 为圆心,5cm 为半径作⊙C ,则点M 与⊙C 的位置关系为( ) A .点M 在⊙C 上B .点M 在⊙C 内 C .点M 在⊙C 外D .点M 不在⊙C 内13.已知函数2y x bx c =-++的部分图像如图所示,若0y >,则的取值范围是( )A .41x -<<B .21x -<<C .31x -<<D .31x x <->或14.如图,△ABC 中AB 两个顶点在x 轴的上方,点C 的坐标是(﹣1,0),以点C 为位似中心,在x 轴的下方作△ABC 的位似图形△A′B′C′,且△A′B′C′与△ABC 的位似比为2:1.设点B 的对应点B′的横坐标是a ,则点B 的横坐标是( )A .12a -B .1(1)2a -+ C .1(1)2a -- D .1(3)2a -+ 15.二次函数y=ax 2+bx+c (a≠0)的图象如图,给出下列四个结论:①4ac ﹣b 2<0;②4a+c <2b ;③3b+2c <0;④m (am+b )+b <a (m≠﹣1),其中正确结论的个数是( )A .4个B .3个C .2个D .1个二、填空题16.如图,将△ABC 绕点C 顺时针旋转90°得到△EDC ,若点A 、D 、E 在同一条直线上,∠ACD =70°,则∠EDC 的度数是_____.17.如图,△ABC 周长为20cm ,BC=6cm,圆O 是△ABC 的内切圆,圆O 的切线MN 与AB 、CA 相交于点M 、N ,则△AMN 的周长为________cm.18.若记[]x 表示任意实数的整数部分,例如:[]4.24=,21⎡⎤=⎣⎦,…,则123420192020⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤-+-+⋅⋅⋅⋅⋅⋅+-⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦(其中“+”“-”依次相间)的值为______.19.已知点P 是线段AB 的黄金分割点,PA >PB ,AB =4 cm ,则PA =____cm . 20.某企业2017年全年收入720万元,2019年全年收入845万元,若设该企业全年收入的年平均增长率为x ,则可列方程____. 21.抛物线y =3(x+2)2+5的顶点坐标是_____.22.如图,在平面直角坐标系中,直线l :28y x =+与坐标轴分别交于A ,B 两点,点C 在x 正半轴上,且OC =O B .点P 为线段AB (不含端点)上一动点,将线段OP 绕点O 顺时针旋转90°得线段OQ ,连接CQ ,则线段CQ 的最小值为___________.23.抛物线21(5)33y x =--+的顶点坐标是_______. 24.如图,D 、E 分别是△ABC 的边AB ,AC 上的点,AD AB =AEAC,AE =2,EC =6,AB =12,则AD 的长为_____.25.如图(1),在矩形ABCD 中,将矩形折叠,使点B 落在边AD 上,这时折痕与边AD 和BC 分别交于点E 、点F .然后再展开铺平,以B 、E 、F 为顶点的△BEF 称为矩形ABCD 的“折痕三角形”.如图(2),在矩形ABCD 中,AB=2,BC=4,当“折痕△BEF”面积最大时,点E 的坐标为_________________________.26.已知关于x 的一元二次方程2230x x k -+=有两个不相等的实数根,则k 的取值范围是________.27.在Rt △ABC 中,两直角边的长分别为6和8,则这个三角形的外接圆半径长为_____. 28.如图,在△ABC 中,AC :BC :AB =3:4:5,⊙O 沿着△ABC 的内部边缘滚动一圈,若⊙O 的半径为1,且圆心O 运动的路径长为18,则△ABC 的周长为_____.29.若关于x 的一元二次方程22(1)0k x x k -+-=的一个根为1,则k 的值为__________. 30.如图,四边形ABCD 中,∠A =∠B =90°,AB =5cm ,AD =3cm ,BC =2cm ,P 是AB 上一点,若以P 、A 、D 为顶点的三角形与△PBC 相似,则PA =_____cm .三、解答题31.某商店专门销售某种品牌的玩具,成本为30元/件,每天的销售量y (件)与销售单价x (元)之间存在着如图所示的一次函数关系.(1)求y与x之间的函数关系式;(2)当销售单价为多少元时,每天获取的利润最大,最大利润是多少?(3)为了保证每天的利润不低于3640元,试确定该玩具销售单价的范围.32.如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.(1)求证:DP是⊙O的切线;(2)若⊙O的半径为3cm,求图中阴影部分的面积.33.如图,AB为O的直径,PD切O于点C,交AB的延长线于点D,且D A∠=∠.2∠的度数.(1)求D(2)若O的半径为2,求BD的长.34.超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加x元,每天售出y件.(1)请写出y与x之间的函数表达式;(2)当x为多少时,超市每天销售这种玩具可获利润2250元?(3)设超市每天销售这种玩具可获利w元,当x为多少时w最大,最大值是多少?⊥交AB于点P,过点B的直线交OP的延长线于35.如图,AB是⊙O的弦,OP OA点C,且BC是⊙O的切线.(1)判断CBP ∆的形状,并说明理由; (2)若6,2OA OP ==,求CB 的长;(3)设AOP ∆的面积是1,S BCP ∆的面积是2S ,且1225S S =.若⊙O 的半径为6,45BP =,求tan APO ∠.四、压轴题36.如图,在Rt △ABC 中,∠A=90°,0是BC 边上一点,以O 为圆心的半圆与AB 边相切于点D ,与BC 边交于点E 、F ,连接OD ,已知BD=3,tan ∠BOD=34,CF=83.(1)求⊙O 的半径OD ; (2)求证:AC 是⊙O 的切线; (3)求图中两阴影部分面积的和.37.如图1,ABC ∆是⊙O 的内接等腰三角形,点D 是弧AC 上异于,A C 的一个动点,射线AD 交底边BC 所在的直线于点E ,连结BD 交AC 于点F . (1)求证:ADB CDE ∠=∠;(2)若7BD =,3CD =,①求AD DE •的值;②如图2,若AC BD ⊥,求tan ACB ∠;(3)若5tan 2CDE ∠=,记AD x =,ABC ∆面积和DBC ∆面积的差为y ,直接写出y 关于x 的函数关系式.38.在平面直角坐标系xOy 中,对于任意三点A ,B ,C ,给出如下定义:如果矩形的任何一条边均与某条坐标轴平行,且A ,B ,C 三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形.例如,下图中的矩形A1B1C1D1,A2B2C2D2,AB3C3D3都是点A,B,C的覆盖矩形,其中矩形AB3C3D3是点A,B,C的最优覆盖矩形.(1)已知A(﹣2,3),B(5,0),C(t,﹣2).①当t=2时,点A,B,C的最优覆盖矩形的面积为;②若点A,B,C的最优覆盖矩形的面积为40,求直线AC的表达式;(2)已知点D(1,1).E(m,n)是函数y=4x(x>0)的图象上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.39.如图,在⊙O中,弦AB、CD相交于点E,AC=BD,点D在AB上,连接CO,并延长CO交线段AB于点F,连接OA、OB,且OA=5,tan∠OBA=12.(1)求证:∠OBA=∠OCD;(2)当△AOF是直角三角形时,求EF的长;(3)是否存在点F,使得S△CEF=4S△BOF,若存在,请求EF的长,若不存在,请说明理由.40.如图,PA切⊙O于点A,射线PC交⊙O于C、B两点,半径OD⊥BC于E,连接BD、DC和OA,DA交BP于点F;(1)求证:∠ADC+∠CBD=12∠AOD;(2)在不添加任何辅助线的情况下,请直接写出图中相等的线段.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【解析】 【分析】满足题意的有两点,一是此方程为一元一次方程,即未知数x 的次数为1;二是方程的解为x=1,即1使等式成立,根据两点列式求解. 【详解】 解:根据题意得, a-1=1,2+m=2, 解得,a=2,m=0, ∴a-m=2. 故选:D. 【点睛】本题考查一元一次方程的定义及方程解的定义,对定义的理解是解答此题的关键.2.B解析:B 【解析】 【分析】根据平均数、方差、中位数和众数的定义分别对每一项进行分析,即可得出答案. 【详解】解:调整前的平均数是:26042804300443⨯+⨯+⨯⨯=280;调整后的平均数是:260528023005525⨯+⨯+⨯++=280; 故A 正确;调整前的方差是:()()()222142602804280280430028012⎡⎤-+-+-⎣⎦=8003; 调整后的方差是:()()()222152602802280280530028012⎡⎤-+-+-⎣⎦=10003; 故B 错误;调整前:把这些数从小到大排列为:260,260,260,260,280,280,280,280,300,300,300,300;最中间两个数的平均数是:280,则中位数是280,调整后:把这些数从小到大排列为:260,260,260,260,260,280,280,300,300,300,300,300;最中间两个数的平均数是:280,则中位数是280, 故C 正确;调整前的极差是40,调整后的极差也是40,则极差不变, 故D 正确. 故选B. 【点睛】此题考查了平均数、方差、中位数和极差的概念,掌握各个数据的计算方法是关键.3.C解析:C 【解析】 【分析】找到两个抛物线的顶点,根据抛物线的顶点即可判断是如何平移得到. 【详解】解:∵y =2(x -1)2+3的顶点坐标为(1,3),y=2x 2的顶点坐标为(0,0),∴将抛物线y=2x 2向右平移1个单位,再向上平移3个单位,可得到抛物线y =2(x -1)2+3 故选:C . 【点睛】本题考查了二次函数图象与几何变换,解答时注意抓住点的平移规律和求出关键点顶点坐标.4.B解析:B 【解析】 【分析】根据圆周角大于对应的圆外角可得当ABC ∆的外接圆与x 轴相切时,ACB ∠有最大值,此时圆心F 的横坐标与C 点的横坐标相同,并且在经过AB 中点且与直线AB 垂直的直线上,根据FB=FC 列出关于b 的方程求解即可. 【详解】解:∵AB=A(0,2)、B(a ,a +2)= 解得a =4或a =-4(因为a >0,舍去) ∴B(4,6),设直线AB 的解析式为y=kx+2, 将B(4,6)代入可得k =1,所以y=x+2,利用圆周角大于对应的圆外角得当ABC ∆的外接圆与x 轴相切时,ACB ∠有最大值. 如下图,G 为AB 中点,()2,4G ,设过点G 且垂直于AB 的直线:l y x m =-+, 将()2,4G 代入可得6m =,所以6y x =-+.设圆心(),6F b b -+,由FC FB =,可知()()()2226466b b b -+=-+-+-,解得262b =(已舍去负值).故选:B. 【点睛】本题考查圆的综合题,一次函数的应用和已知两点坐标,用勾股定理求两点距离.能结合圆的切线和圆周角定理构建图形找到C 点的位置是解决此题的关键.5.B解析:B 【解析】 【分析】直接得出朝上面的数字大于4的个数,再利用概率公式求出答案. 【详解】∵一枚质地均匀的骰子,其六个面上分别标有数字1,2,3,4,5,6,投掷一次, ∴共有6种情况,其中朝上面的数字大于4的情况有2种, ∴朝上一面的数字是朝上面的数字大于4的概率为:2163=, 故选:B . 【点睛】本题考查简单的概率求法,概率=所求情况数与总情况数的比;熟练掌握概率公式是解题关键.解析:A【解析】【分析】根据一元二次方程的解的定义,将a 代入已知方程,即可求得a 2+3a 的值,然后再代入求值即可.【详解】解:根据题意,得a 2+3a ﹣1=0,解得:a 2+3a =1,所以a 2+3a+2019=1+2019=2020.故选:A.【点睛】此题考查的是一元二次方程的解,掌握一元二次方程解的定义是解决此题的关键7.A解析:A【解析】【分析】根据一元二次方程的定义逐一判断即可.【详解】解:A . 2321x x =+是一元二次方程,故本选项符合题意;B . 3230x x --是一元三次方程,故本选项不符合题意;C . 221x y -=是二元二次方程,故本选项不符合题意;D . 20x y +=是二元一次方程,故本选项不符合题意;故选A .【点睛】此题考查的是一元二次方程的判断,掌握一元二次方程的定义是解决此题的关键.8.D解析:D【解析】【分析】先将常数项移到右侧,然后两边同时加上一次项系数一半的平方,配方后进行判断即可.【详解】2890x x ++=,289x x +=-,2228494x x ++=-+,所以()247x +=,【点睛】本题考查了配方法解一元二次方程,熟练掌握配方法的一般步骤以及注意事项是解题的关键.9.B解析:B【解析】【分析】根据已知条件想办法证明BG=GH=DH ,即可解决问题;【详解】解:∵四边形ABCD 是平行四边形,∴AB ∥CD ,AD ∥BC ,AB=CD ,AD=BC ,∵DF=CF ,BE=CE , ∴12DH DF HB AB ==,12BG BE DG AD ==, ∴13DH BG BD BD ==, ∴BG=GH=DH ,∴S △ABG =S △AGH =S △ADH ,∴S 平行四边形ABCD =6 S △AGH ,∴S △AGH :ABCD S 平行四边形=1:6,∵E 、F 分别是边BC 、CD 的中点, ∴12EF BD =, ∴14EFC BCDD S S =, ∴18EFC ABCD SS =四边形, ∴1176824AGH EFC ABCD S S S +=+=四边形=7∶24, 故选B.【点睛】本题考查了平行四边形的性质、平行线分线段成比例定理、等底同高的三角形面积性质,题目的综合性很强,难度中等.10.A解析:A【解析】【分析】直接把已知数据代入进而得出c 的值,再解方程根据根的判别式分析即可.【详解】∵x =﹣1为方程x 2﹣8x ﹣c =0的根,1+8﹣c =0,解得c =9,∴原方程为x 2-8x +9=0,∵24b ac ∆=-=(﹣8)2-4×9>0,∴方程有两个不相等的实数根.故选:A .【点睛】本题考查一元二次方程的解、一元二次方程根的判别式,解题的关键是掌握一元二次方程根的判别式,对于一元二次方程()200++=≠ax bx c a ,根的情况由24b ac ∆=-来判别,当24b ac ->0时,方程有两个不相等的实数根,当24b ac -=0时,方程有两个相等的实数根,当24b ac -<0时,方程没有实数根.11.C解析:C【解析】【分析】利用一元二次方程的定义判断即可.【详解】A 、方程2x ﹣3=x 为一元一次方程,不符合题意;B 、方程2x +3y =5是二元一次方程,不符合题意;C 、方程2x ﹣x 2=1是一元二次方程,符合题意;D 、方程x +1x=7是分式方程,不符合题意, 故选:C .【点睛】本题考查了一元一次方程的问题,掌握一元一次方程的定义是解题的关键.12.A解析:A【解析】【分析】根据题意可求得CM 的长,再根据点和圆的位置关系判断即可.【详解】如图,∵由勾股定理得2268 ,∵CM 是AB 的中线,∴CM=5cm ,∴d=r ,所以点M 在⊙C 上,故选A .【点睛】本题考查了点和圆的位置关系,解决的根据是点在圆上⇔圆心到点的距离=圆的半径.13.C解析:C【解析】【分析】根据抛物线的对称性确定抛物线与x 轴的另一个交点为(−3,0),然后观察函数图象,找出抛物线在x 轴上方的部分所对应的自变量的范围即可.【详解】∵y =ax 2+bx +c 的对称轴为直线x =−1,与x 轴的一个交点为(1,0),∴抛物线与x 轴的另一个交点为(−3,0),∴当−3<x <1时,y >0.故选:C .【点睛】此题主要考查二次函数的图像与性质,解题的关键是根据函数对称轴找到抛物线与x 轴的交点.14.D解析:D【解析】【分析】设点B 的横坐标为x ,然后表示出BC 、B′C 的横坐标的距离,再根据位似变换的概念列式计算.【详解】设点B 的横坐标为x ,则B 、C 间的横坐标的长度为﹣1﹣x ,B′、C 间的横坐标的长度为a+1,∵△ABC 放大到原来的2倍得到△A′B′C ,∴2(﹣1﹣x )=a+1,解得x=﹣12(a+3),故选:D.【点睛】本题考查了位似变换,坐标与图形的性质,根据位似变换的定义,利用两点间的横坐标的距离等于对应边的比列出方程是解题的关键.15.B解析:B【解析】【分析】【详解】解:∵抛物线和x轴有两个交点,∴b2﹣4ac>0,∴4ac﹣b2<0,∴①正确;∵对称轴是直线x﹣1,和x轴的一个交点在点(0,0)和点(1,0)之间,∴抛物线和x轴的另一个交点在(﹣3,0)和(﹣2,0)之间,∴把(﹣2,0)代入抛物线得:y=4a﹣2b+c>0,∴4a+c>2b,∴②错误;∵把(1,0)代入抛物线得:y=a+b+c<0,∴2a+2b+2c<0,∵b=2a,∴3b,2c<0,∴③正确;∵抛物线的对称轴是直线x=﹣1,∴y=a﹣b+c的值最大,即把(m,0)(m≠0)代入得:y=am2+bm+c<a﹣b+c,∴am2+bm+b<a,即m(am+b)+b<a,∴④正确;即正确的有3个,故选B.考点:二次函数图象与系数的关系二、填空题16.115°【解析】【分析】根据∠EDC=180°﹣∠E﹣∠DCE,想办法求出∠E,∠DCE即可.【详解】由题意可知:CA=CE,∠ACE=90°,∴∠E=∠CAE=45°,∵∠ACD=7解析:115°【解析】【分析】根据∠EDC=180°﹣∠E﹣∠DCE,想办法求出∠E,∠DCE即可.【详解】由题意可知:CA=CE,∠ACE=90°,∴∠E=∠CAE=45°,∵∠ACD=70°,∴∠DCE=20°,∴∠EDC=180°﹣∠E﹣∠DCE=180°﹣45°﹣20°=115°,故答案为115°.【点睛】本题考查了旋转的性质,等腰直角三角形的性质,三角形的内角和定理等知识,解题的关键是灵活运用所学知识,问题,属于中考常考题型.17.8【解析】【分析】先作出辅助线,连接切点,利用内切圆的性质得到BE=BF,CE=CG,ME=MH,NG=NH,再利用等量代换即可解题.【详解】解:∵圆O是△ABC的内切圆,MN是圆O的切线解析:8【解析】【分析】先作出辅助线,连接切点,利用内切圆的性质得到BE=BF,CE=CG,ME=MH,NG=NH,再利用等量代换即可解题.【详解】解:∵圆O是△ABC的内切圆,MN是圆O的切线,如下图,连接各切点,有切线长定理易得,BE=BF,CE=CG,ME=MH,NG=NH,∵△ABC周长为20cm, BC=6cm,∴BC=CE+BE=CG+BF=6cm,∴△AMN 的周长=AM+AN+MN=AM+AN+FM+GN=AF+AG,又∵AF+AG=AB+AC-(BF+CG)=20-6-6=8cm故答案是8【点睛】本题考查了三角形内接圆的性质,切线长定理的应用,中等难度,熟练掌握等量代换的方法是解题关键.18.-22【解析】【分析】先确定的整数部分的规律,根据题意确定算式的运算规律,再进行实数运算.【详解】解:观察数据12=1,22=4,32=9,42=16,52=25,62=36的特征,得出数 解析:-22【解析】【分析】 1,2,32020的整数部分的规律,根据题意确定算式123420192020⎡⎡⎡⎤⎡-+-+⋅⋅⋅⋅⋅⋅+-⎣⎣⎣⎦⎣的运算规律,再进行实数运算. 【详解】解:观察数据12=1,22=4,32=9,42=16,52=25,62=36的特征,得出数据1,2,3,4……2020中,算术平方根是1的有3个,算术平方根是2的有5个,算数平方根是3的有7个,算数平方根是4的有9个,…其中432=1849,442=1936,452=2025,所以在1⎡⎤⎣⎦、22020⎡⋅⋅⋅⋅⋅⋅⎣中,算术平方根依次为1,2,3……43的个数分别为3,5,7,9……个,均为奇数个,最大算数平方根为44的有85个,所以123420192020⎡⎡⎡⎤⎡-+-+⋅⋅⋅⋅⋅⋅+-⎣⎣⎣⎦⎣=1-2+3-4+…+43-44= -22 【点睛】本题考查自定义运算,通过正整数的算术平方根的整数部分出现的规律,找到算式中相同加数的个数及符号的规律,方能进行运算.19.2-2【解析】【分析】根据黄金分割点的定义,知AP 是较长线段;则AP=AB ,代入运算即可.【详解】解:由于P 为线段AB=4的黄金分割点,且AP 是较长线段;则AP=4×=cm ,故答案为解析:2【解析】【分析】根据黄金分割点的定义,知AP 是较长线段;则AB ,代入运算即可. 【详解】解:由于P 为线段AB=4的黄金分割点,且AP 是较长线段;则AP=4×12=)21cm ,故答案为:(2)cm.【点睛】此题考查了黄金分割的定义,应该识记黄金分割的公式:较短的线段=,难度一般. 20.720(1+x )2=845.【解析】【分析】增长率问题,一般用增长后的量=增长前的量×(1+增长率),参照本题,如果该企业全年收入的年平均增长率为x ,根据2017年全年收入720万元,2019 解析:720(1+x )2=845.【解析】【分析】增长率问题,一般用增长后的量=增长前的量×(1+增长率),参照本题,如果该企业全年收入的年平均增长率为x ,根据2017年全年收入720万元,2019年全年收入845万元,即可得出方程.【详解】解:设该企业全年收入的年平均增长率为x ,则2018的全年收入为:720×(1+x )2019的全年收入为:720×(1+x)2.那么可得方程:720(1+x)2=845.故答案为:720(1+x)2=845.【点睛】本题考查了一元二次方程的运用,解此类题的关键是掌握等量关系式:增长后的量=增长前的量×(1+增长率).21.(﹣2,5)【解析】【分析】已知抛物线的顶点式,可直接写出顶点坐标.【详解】解:由y=3(x+2)2+5,根据顶点式的坐标特点可知,顶点坐标为(﹣2,5).故答案为:(﹣2,5).【点解析:(﹣2,5)【解析】【分析】已知抛物线的顶点式,可直接写出顶点坐标.【详解】解:由y=3(x+2)2+5,根据顶点式的坐标特点可知,顶点坐标为(﹣2,5).故答案为:(﹣2,5).【点睛】本题考查二次函数的性质,熟知二次函数的顶点式是解题的关键,即在y=a(x-h)2+k中,顶点坐标为(h,k),对称轴为x=h.22.【解析】【分析】在OA上取使,得,则,根据点到直线的距离垂线段最短可知当⊥AB时,CP最小,由相似求出的最小值即可.【详解】解:如图,在OA上取使,∵,∴,在△和△QOC中,,解析:455【解析】【分析】在OA上取'C使'OC OC=,得'OPC OQC≅,则CQ=C'P,根据点到直线的距离垂线段最短可知当'PC⊥AB时,CP最小,由相似求出C'P的最小值即可.【详解】解:如图,在OA上取'C使'OC OC=,∵90AOC POQ∠=∠=︒,∴'POC QOC∠=∠,在△'POC和△QOC中,''OP OQPOC QOCOC OC=⎧⎪∠=∠⎨⎪=⎩,∴△'POC≌△QOC(SAS),∴'PC QC=∴当'PC最小时,QC最小,过'C点作''C P⊥AB,∵直线l:28y x=+与坐标轴分别交于A,B两点,∴A坐标为:(0,8);B点(-4,0),∵'4OC OC OB===,∴22228445AB OA OB++=''4AC OA OC=-=.∵'''OB C Psin BAOAB AC∠==,''445C P=,∴4''55C P=∴线段CQ455【点睛】 本题主要考查了一次函数图像与坐标轴的交点及三角形全等的判定和性质、垂线段最短等知识,解题的关键是正确寻找全等三角形解决问题,学会利用垂线段最短解决最值问题,属于中考压轴题.23.(5,3)【解析】【分析】根据二次函数顶点式的性质直接求解.【详解】解:抛物线的顶点坐标是(5,3)故答案为:(5,3).【点睛】本题考查二次函数性质其顶点坐标为(h ,k ),题目比较解析:(5,3)【解析】【分析】根据二次函数顶点式2()y a x h k =-+的性质直接求解.【详解】 解:抛物线21(5)33y x =--+的顶点坐标是(5,3)故答案为:(5,3).【点睛】本题考查二次函数性质2()y a x h k =-+其顶点坐标为(h ,k ),题目比较简单. 24.3【解析】【分析】把AE =2,EC =6,AB =12代入已知比例式,即可求出答案.【详解】解:∵=,AE =2,EC =6,AB =12,∴=,解得:AD =3,故答案为:3.【点睛】本题解析:3 【解析】【分析】把AE =2,EC =6,AB =12代入已知比例式,即可求出答案.【详解】解:∵AD AB =AE AC,AE =2,EC =6,AB =12, ∴12AD =226, 解得:AD =3,故答案为:3.【点睛】 本题考查了成比例线段,灵活的将已知线段的长度代入比例式是解题的关键.25.(,2).【解析】【分析】【详解】解:如图,当点B 与点D 重合时,△BEF 面积最大,设BE=DE=x ,则AE=4-x ,在RT △ABE 中,∵EA2+AB2=BE2,∴(4-x )2+22=解析:(32,2). 【解析】【分析】【详解】解:如图,当点B 与点D 重合时,△BEF 面积最大,设BE=DE=x ,则AE=4-x ,在RT △ABE 中,∵EA 2+AB 2=BE 2,∴(4-x )2+22=x 2,∴x=52,∴BE=ED=52,AE=AD-ED=32,∴点E坐标(32,2).故答案为:(32,2).【点睛】本题考查翻折变换(折叠问题),利用数形结合思想解题是关键.26.【解析】【分析】根据一元二次方程的根的判别式,建立关于k的不等式,求出k的取值范围.【详解】根据一元二次方程的根的判别式,建立关于k的不等式,求出k的取值范围. ,,方程有两个不相等的实数解析:3k<【解析】【分析】根据一元二次方程的根的判别式,建立关于k的不等式,求出k的取值范围.【详解】根据一元二次方程的根的判别式,建立关于k的不等式,求出k的取值范围.1a,b=-,c k=方程有两个不相等的实数根,241240b ac k∴∆=-=->,3k∴<.故答案为:3k<.【点睛】本题考查了根的判别式.总结:一元二次方程根的情况与判别式△的关系:(1)△>0⇔方程有两个不相等的实数根;(2)△=0⇔方程有两个相等的实数根;(3)△<0⇔方程没有实数根.27.5【解析】【分析】根据直角三角形外接圆的直径是斜边的长进行求解即可.【详解】由勾股定理得:AB==10,∵∠ACB=90°,∴AB是⊙O的直径,∴这个三角形的外接圆直径是10;∴这解析:5【解析】【分析】根据直角三角形外接圆的直径是斜边的长进行求解即可.【详解】由勾股定理得:AB=22=10,68∵∠ACB=90°,∴AB是⊙O的直径,∴这个三角形的外接圆直径是10;∴这个三角形的外接圆半径长为5,故答案为5.【点睛】本题考查了90度的圆周角所对的弦是直径,熟练掌握是解题的关键.28.30【解析】【分析】如图,首先利用勾股定理判定△ABC是直角三角形,由题意得圆心O所能达到的区域是△DEG,且与△ABC三边相切,设切点分别为G、H、P、Q、M、N,连接DH、DG、EP、EQ解析:30【解析】【分析】如图,首先利用勾股定理判定△ABC是直角三角形,由题意得圆心O所能达到的区域是△DEG,且与△ABC三边相切,设切点分别为G、H、P、Q、M、N,连接DH、DG、EP、EQ、FM、FN,根据切线性质可得:AG=AH,PC=CQ,BN=BM,DG、EP分别垂直于AC,EQ、FN分别垂直于BC,FM、DH分别垂直于AB,继而则有矩形DEPG、矩形EQNF、矩形DFMH,从而可知DE=GP,EF=QN,DF=HM,DE∥GP,DF∥HM,EF∥QN,∠PEF =90°,根据题意可知四边形CPEQ是边长为1的正方形,根据相似三角形的判定可得△DEF ∽△ACB ,根据相似三角形的性质可知:DE ∶EF ∶FD =AC ∶CB ∶BA =3∶4∶5,进而根据圆心O 运动的路径长列出方程,求解算出DE 、EF 、FD 的长,根据矩形的性质可得:GP 、QN 、MH 的长,根据切线长定理可设:AG =AH =x ,BN =BM =y ,根据线段的和差表示出AC 、BC 、AB 的长,进而根据AC ∶CB ∶BA =3∶4∶5列出比例式,继而求出x 、y 的值,进而即可求解△ABC 的周长.【详解】∵AC ∶CB ∶BA =3∶4∶5,设AC =3a ,CB =4a ,BA =5a (a >0)∴()()()222222=345AC CB a a a BA ++==∴△ABC 是直角三角形,设⊙O 沿着△ABC 的内部边缘滚动一圈,如图所示,连接DE 、EF 、DF ,设切点分别为G 、H 、P 、Q 、M 、N ,连接DH 、DG 、EP 、EQ 、FM 、FN ,根据切线性质可得:AG =AH ,PC =CQ ,BN =BMDG 、EP 分别垂直于AC ,EQ 、FN 分别垂直于BC ,FM 、DH 分别垂直于AB ,∴DG ∥EP ,EQ ∥FN ,FM ∥DH ,∵⊙O 的半径为1∴DG =DH =PE =QE =FN =FM =1,则有矩形DEPG 、矩形EQNF 、矩形DFMH ,∴DE =GP ,EF =QN ,DF =HM ,DE ∥GP ,DF ∥HM ,EF ∥QN,∠PEF =90°又∵∠CPE =∠CQE =90°, PE =QE =1∴四边形CPEQ 是正方形,∴PC =PE =EQ =CQ =1,∵⊙O 的半径为1,且圆心O 运动的路径长为18,∴DE +EF +DF =18,∵DE ∥AC ,DF ∥AB ,EF ∥BC ,∴∠DEF =∠ACB ,∠DFE =∠ABC ,∴△DEF ∽△ABC ,∴DE :EF :DF =AC :BC :AB =3:4:5,设DE =3k (k >0),则EF =4k ,DF =5k ,∵DE +EF +DF =18,∴3k +4k +5k =18,解得k =32, ∴DE =3k =92,EF =4k =6,DF =5k =152, 根据切线长定理,设AG =AH =x ,BN =BM =y ,则AC =AG +GP +CP =x +92+1=x +5.5, BC =CQ +QN +BN =1+6+y =y +7,AB =AH +HM +BM =x +152+y =x +y +7.5, ∵AC :BC :AB =3:4:5, ∴(x +5.5):(y +7):(x +y +7.5)=3:4:5,解得x =2,y =3,∴AC =7.5,BC =10,AB =12.5,∴AC +BC +AB =30.所以△ABC 的周长为30.故答案为30.【点睛】本题是一道动图形问题,考查切线的性质定理、相似三角形的判定与性质、矩形的判定与性质、解直角三角形等知识点,解题的关键是确定圆心O 的轨迹,学会作辅助线构造相似三角形,综合运用上述知识点.29.0【解析】把x =1代入方程得,,即,解得.此方程为一元二次方程,,即,故答案为0.解析:0【解析】把x =1代入方程得,2110k k -+-=,即20k k -=,解得120,1k k ==.此方程为一元二次方程,10k ∴-≠,即1k ≠,0.k ∴=故答案为0.30.2或3【解析】【分析】根据相似三角形的判定与性质,当若点A ,P ,D 分别与点B ,C ,P 对应,与若点A ,P ,D 分别与点B ,P ,C 对应,分别分析得出AP 的长度即可.【详解】解:设AP =xcm .则解析:2或3【解析】【分析】根据相似三角形的判定与性质,当若点A ,P ,D 分别与点B ,C ,P 对应,与若点A ,P ,D 分别与点B ,P ,C 对应,分别分析得出AP 的长度即可.【详解】解:设AP =xcm .则BP =AB ﹣AP =(5﹣x )cm以A ,D ,P 为顶点的三角形与以B ,C ,P 为顶点的三角形相似,①当AD :PB =PA :BC 时,352x x =-, 解得x =2或3.②当AD :BC =PA +PB 时,3=25x x-,解得x =3, ∴当A ,D ,P 为顶点的三角形与以B ,C ,P 为顶点的三角形相似,AP 的值为2或3. 故答案为2或3.【点睛】本题考查了相似三角形的问题,掌握相似三角形的性质以及判定定理是解题的关键.三、解答题31.(1)10700y x =-+;(2)销售单价为50元时,每天获取的利润最大,最大利润是4000元;(3)44≤x ≤56【解析】【分析】(1)直接利用待定系数法求出一次函数解析式即可;(2)利用w=销量乘以每件利润进而得出关系式求出答案;(3)利用w=3640,进而解方程,再利用二次函数增减性得出答案.【详解】解:(1)y 与x 之间的函数关系式为:y kx b =+把(35,350),(55,150)代入得:由题意得:3503515055k b k b =+⎧⎨=+⎩解得:10700k b =-⎧⎨=⎩∴y 与x 之间的函数关系式为:10700y x =-+.(2)设销售利润为W 元则W=(x ﹣30)•y =(x ﹣30)(﹣10x +700),W =﹣10x 2+1000x ﹣21000W =﹣10(x ﹣50)2+4000∴当销售单价为50元时,每天获取的利润最大,最大利润是4000元.(3)令W =3640∴﹣10(x ﹣50)2+4000=3640∴x 1=44,x 2=56如图所示,由图象得:当44≤x ≤56时,每天利润不低于3640元.【点睛】此题主要考查了二次函数的应用以及待定系数法求一次函数解析式,正确掌握二次函数的性质是解题关键.32.(1)证明见解析;(22933()22cm . 【解析】【分析】(1)连接OD ,求出∠AOD ,求出∠DOB ,求出∠ODP ,根据切线判定推出即可. (2)求出OP 、DP 长,分别求出扇形DOB 和△ODP 面积,即可求出答案.【详解】解:(1)证明:连接OD ,。
上海民办兰生复旦中学初三化学上册期中化学试题(word版,含解析)

上海民办兰生复旦中学上册期中化学试题(word版,含解析)一、选择题(培优题较难)1.运用推理、归纳、类比、对比的方法得出下列结论,其中合理的是()A.因为化学变化都遵循质量守恒定律,所以质量不发生改变的变化一定是化学变化B.水和过氧化氢的组成元素相同,则两者的化学性质相同C.Na+、Mg2+、Cl-的最外层电子数均为8,由此得出离子的最外层电子数均为8D.过氧化氢溶液加催化剂的反应速率快,说明催化剂可以改变反应速率2.四种物质在一定的条件下充分混合反应,测得反应前后各物质的质量分数如图所示.则有关说法中不正确的()A.丁一定是化合物B.乙可能是这个反应的催化剂C.生成的甲、丙两物质的质量比为8: 1D.参加反应的丁的质量一定等于生成甲和丙的质量之和3.锌是促进人体生长发育的必须微量元素。
下图为锌元素在元素周期表中的相关信息及原子结构示意图。
下列说法正确的是()A.锌属于非金属元素B.锌原子的中子数为30C.锌的相对原子质量为65.38g D.锌原子在化学反应中易失去电子形成Zn2+ 4.如图所示有关二氧化碳的实验中,只与二氧化碳物理性质有关的实验是()A. B. C. D.5.下列实验操作正确的是A.塞紧橡皮塞B.加热液体C.取用液体D.读出液体的体积6.下列各图中和分别表示不同元素的原子,则其中表示化合物的是( ) A.B.C.D.7.碳12是指含6个中子的碳原子。
下列对氧16和氧18两种氧原子的说法正确的是A.质子数相同B.质量相同C.电子数不相同D.16和18表示原子个数8.以下是四种微粒的结构示意图,下列有关各微粒的说法中,错误的是A.①的化学性质比较稳定B.③④属于同种元素C.④是一种阴离子D.②容易得到电子9.下列古代文明或工艺一定包含化学变化的是A.在甲骨上刻文字B.指南针指引航海C.用泥土烧制陶瓷D.用石块修筑长城10.实验小组用如图装置测定空气中的氧气含量,锥形瓶中空气的体积为100mL,注射器中水的体积为25 mL,装置气密性良好。
上海兰生复旦数学九年级上册期末试卷(带解析)

27.抛物线 与x轴只有一个公共点,则m的值为________.
28.如图,⊙O是正五边形ABCDE的外接圆,则∠CAD=_____.
A.70°B.72°C.74°D.76°
3.在平面直角坐标系中,如图是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③方程ax2+bx+c=0的两根分别为﹣3和1;④b2﹣4ac>0,其中正确的命题有( )
A.1个B.2个C.3个D.4个
4.分别写有数字0,﹣1,﹣2,1,3的五张卡片,除数字不同外其他均相同,从中任抽一张,那么抽到负数的概率是()
17.如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD.若AC=2,则cosD=________.
18.如图,Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AB边上一点(不与A、B重合),若过点D的直线截得的三角形与△ABC相似,并且平分△ABC的周长,则AD的长为____.
上海兰生复旦数学九年级上册期末试卷(带解析)
一、选择题
1.在半径为3cm的⊙O中,若弦AB=3 ,则弦AB所对的圆周角的度数为( )
A.30°B.45°C.30°或150°D.45°或135°
2.如图,OA、OB是⊙O的半径,C是⊙O上一点.若∠OAC=16°,∠OBC=54°,则∠AOB的大小是()
25.如图(1),在矩形ABCD中,将矩形折叠,使点B落在边AD上,这时折痕与边AD和BC分别交于点E、点F.然后再展开铺平,以B、E、F为顶点的△BEF称为矩形ABCD的“折痕三角形”.如图(2),在矩形ABCD中,AB=2,BC=4,当“折痕△BEF”面积最大时,点E的坐标为_________________________.
兰生复旦九年级月考卷真题

兰复 学
学
学
阶试
ė ń
ö
ş è
ș
ė
ū İ
ū ńĄ ť
由 扫描全能王 扫描创建
兰窆复 学
学
ą
ņ ï
学
阶试
ì
Ī
ä
Ř
ş
厂
ċ İ ť ū
题卡
Į
由 扫描全能王 扫描创建
兰复 学
学
学
阶试
į ţ
ď
ī ś
ę Ë
ä
ľ ń
ď ķ
由 扫描全能王 扫描创建
学
学
兰
学
阶试
ė
ė
ū
ń
ö
ť
ń
ť
à
ė
ť
ń
Ċ ĺ
题纸
由 扫描全能王 扫描创建
兰复 学
学
学
阶试
兰复 学
学
学
阶
级 语测试 试
总
时间
钟
听
国
Ţ
国
对
删
国
ĺ
话 题选
当
»
你听
ý ù
由 扫描全能王 扫描创建
由 扫描全能王 扫描创建
兰复 学
学
学
阶试
é Ĥ
ï
题纸
ī
ų ę
ę
由 扫描全能王 扫描创建
由 扫描全能王扫描创建
兰复
学
学
学
阶
题卡
ş
几 严
ńĄ
炉
Ė ș
由 扫描全能王 扫描创建
由 扫描全能王 扫描创建
复学
学
学
阶试
ĵ
ė
上海市兰生复旦中学2021学年英语九年级阶段练习卷

上海市兰生复旦中学2021学年英语九年级阶段练习卷一、听力(一). 听句子在每小题内,你将听到一个句子,并看到供你选择的3个单词或短语。
每个句子读一遍。
请在每小题A、B、C三个选项中选出你所听到的单词或短语。
( )1. A. lamb B. name C. time( )2. A. luck B. leg C. neck( )3. A. sounds B. sons C. salad( )4. A. word B. walk C. work( )5. A. how about B. think about C. ask about(二)情景反应:根据你听到的句子选择适当答语。
( )6. A. I’m glad. B. I have a stomachache. C. I don’t know.( )7. A. Once. B. Once a week. C. A week.( )8. A. Yes, I do. B. Yes, I can. C. Yes, I have.( )9. A. I’m tired. B. No, you are tired. C. Yes, very much.( )10. She can’t sleep. B. He can’t sleep. C. I can’t sleep.(三)听句子。
在每小题内,你将听到一个句子,请在每小题A、B、C三个选项中选出1个与你所听到的句子意义最接近的句子。
( )11. A. They often go to the movies every day. B. they often go to the movies once a week.C. They often go to the movies on Saturdays.( )12. A. What’s wrong with you ? B. What’s your name ?C. What meat is in your Pizza ?( )13. A. Mary and Jim are in the same class. B. Mary and Jim are not in different grades.C. Mary and Jim are not in the same grade.( )14. A. I am going to Paris. B. Tom and I are going to Paris. C. Tom is going to Paris.( )15. A. We had a good time in the park last Sunday. B. We loved the park very much.C. Last Sunday we were in the park.(四)对话理解。
【物理】上海民办兰生复旦中学九年级上册期中精选试卷检测题
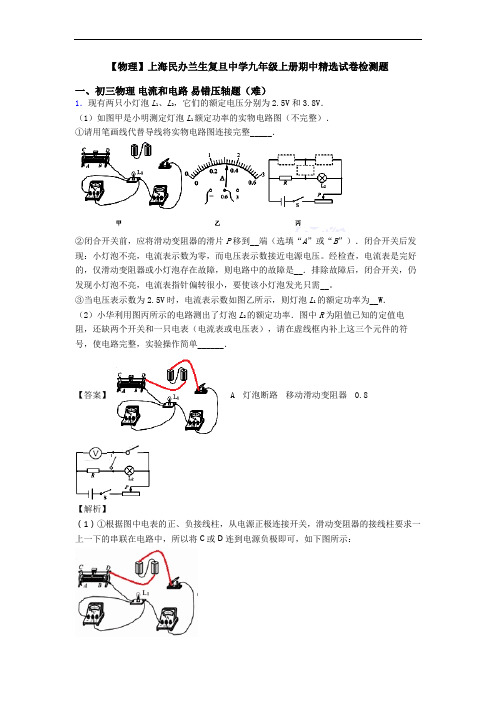
【物理】上海民办兰生复旦中学九年级上册期中精选试卷检测题一、初三物理电流和电路易错压轴题(难)1.现有两只小灯泡L1、L2,它们的额定电压分别为2.5V和3.8V.(1)如图甲是小明测定灯泡L1额定功率的实物电路图(不完整).①请用笔画线代替导线将实物电路图连接完整_____.②闭合开关前,应将滑动变阻器的滑片P移到__端(选填“A”或“B”).闭合开关后发现:小灯泡不亮,电流表示数为零,而电压表示数接近电源电压。
经检查,电流表是完好的,仅滑动变阻器或小灯泡存在故障,则电路中的故障是__.排除故障后,闭合开关,仍发现小灯泡不亮,电流表指针偏转很小,要使该小灯泡发光只需__。
③当电压表示数为2.5V时,电流表示数如图乙所示,则灯泡L1的额定功率为__W.(2)小华利用图丙所示的电路测出了灯泡L2的额定功率.图中R为阻值已知的定值电阻,还缺两个开关和一只电表(电流表或电压表),请在虚线框内补上这三个元件的符号,使电路完整,实验操作简单______.【答案】A灯泡断路移动滑动变阻器0.8【解析】(1)①根据图中电表的正、负接线柱,从电源正极连接开关,滑动变阻器的接线柱要求一上一下的串联在电路中,所以将C或D连到电源负极即可,如下图所示:②电压表有示数,说明电压表与电源连通;电流表示数几乎为零,灯泡不发光,说明电路断路或电路的总电阻很大,导致这一现象的原因可能是小灯泡断路而导致电压表串联在电路中;③为了保护电路,闭合开关前,滑片P应处在使电路中电阻最大位置A端;由乙图,电流表使用0-0.6A量程,分度值为0.02A,示数为0.32A,所以灯泡L1的额定功率:;(2)由上面的分析知,右上边的是电压表;左边两虚线框内是开关,如图所示:①只闭合S和中间的开关,移动滑片使电压表示数为3.8V;②保持滑片位置不动,断开中间开关,闭合左上边开关,测出灯与R的总电压,根据串联电路的电压特点计算出R两端电压U R;③由计算出R的电流,即灯泡此时的电流,由P=U额I额计算灯泡L2电功率即可.故答案为:(1). (2). A (3). 灯泡断路 (4). 移动滑动变阻器(5). 0.8 (6).【点睛】本题是测灯泡额定功率的实验,考查了电路连接、变阻器的使用、电表读数和功率计算以及特殊方法测功率的电路设计.特殊方法测功率时,只给电流表通常会使用并联电路,只给电压表时通常使用并联电路,利用已知阻值的电阻与电表的组合间接测电压或电流达到实验目的。
上海兰生复旦九年级上册期末精选试卷检测题

上海兰生复旦九年级上册期末精选试卷检测题一、初三数学 一元二次方程易错题压轴题(难)1.元旦期间,某超市销售两种不同品牌的苹果,已知1千克甲种苹果和1千克乙种苹果的进价之和为18元.当销售1千克甲种苹果和1千克乙种苹果利润分别为4元和2元时,陈老师购买3千克甲种苹果和4千克乙种苹果共用82元.(1)求甲、乙两种苹果的进价分别是每千克多少元?(2)在(1)的情况下,超市平均每天可售出甲种苹果100千克和乙种苹果140千克,若将这两种苹果的售价各提高1元,则超市每天这两种苹果均少售出10千克,超市决定把这两种苹果的售价提高x 元,在不考虑其他因素的条件下,使超市销售这两种苹果共获利960元,求x 的值.【答案】(1)甲、乙两种苹果的进价分别为10元/千克,8元/千克;(2)x 的值为2或7.【解析】【分析】(1)根据题意列二元一次方程组即可求解,(2)根据题意列一元二次方程即可求解.【详解】(1)解:设甲、乙两种苹果的进价分别为a 元/千克, b 元/千克.由题得:()()18344282a b a b +=⎧⎨+++=⎩解之得:108a b =⎧⎨=⎩ 答:甲、乙两种苹果的进价分别为10元/千克,8元/千克(2)由题意得:()()()()410010214010960x x x x +-++-=解之得:12x =,27x =经检验,12x =,27x =均符合题意答:x 的值为2或7.【点睛】本题考查了二元一次方程组和一元二次方程的实际应用,中等难度,列方程是解题关键.2.阅读以下材料,并解决相应问题:材料一:换元法是数学中的重要方法,利用换元法可以从形式上简化式子,在求解某些特殊方程时,利用换元法常常可以达到转化的目的,例如在求解一元四次方程42210x x -+=,就可以令21x =,则原方程就被换元成2210t t -+=,解得 t = 1,即21x =,从而得到原方程的解是 x = ±1材料二:杨辉三角形是中国数学上一个伟大成就,在中国南宋数学家杨辉 1261 年所著的《详解九章算法》一书中出现,它呈现了某些特定系数在三角形中的一种有规律的几何排列,下图为杨辉三角形:……………………………………(1)利用换元法解方程:()()222312313+-++-=x x x x(2)在杨辉三角形中,按照自上而下、从左往右的顺序观察, an 表示第 n 行第 2 个数(其中 n≥4),bn 表示第 n 行第 3 个数,n c 表示第(n )1-行第 3 个数,请用换元法因式分解:()41-⋅+n n n b a c【答案】(1)317x -+=或317x --= 或x=-1或x=-2;(2)()41-⋅+n n n b a c =(n 2-5n+5)2【解析】【分析】(1)设t=x 2+3x-1,则原方程可化为:t 2+2t=3,求得t 的值再代回可求得方程的解; (2)根据杨辉三角形的特点得出a n ,b n ,c n ,然后代入4(b n -a n )•c n +1再因式分解即可.【详解】(1)解:令t=x 2+3x-1则原方程为:t 2+2t=3解得:t=1 或者 t=-3当t=1时,x 2+3x-1=1 解得:3172x -+= 或3172x -= 当t=-3时,x 2+3x-1=-3解得:x=-1或x=-2 ∴方程的解为:317x -+=或317x --=或x=-1或x=-2 (2)解:根据杨辉三角形的特点得出:a n =n-1(1)(2)2n n n b --= (2)(3)2n n n c --= ∴4(b n -a n )•c n +1=(n-1)(n-4)(n-2)(n-3)+1=(n 2-5n+4)(n 2-5n+6)+1=(n 2-5n+4)2+2(n 2-5n+4)+1=(n 2-5n+5)2【点睛】本题主要考查因式分解的应用.解一些复杂的因式分解问题,常用到换元法,即对结构比较复杂的多项式,若把其中某些部分看成一个整体,用新字母代替(即换元),则能使复杂的问题简单化,明朗化,在减少多项式项数,降低多项式结构复杂程度等方面有独到作用.3.有n 个方程:x 2+2x ﹣8=0;x 2+2×2x ﹣8×22=0;…x 2+2nx ﹣8n 2=0.小静同学解第一个方程x 2+2x ﹣8=0的步骤为:“①x 2+2x=8;②x 2+2x+1=8+1;③(x+1)2=9;④x+1=±3;⑤x=1±3;⑥x 1=4,x 2=﹣2.” (1)小静的解法是从步骤 开始出现错误的.(2)用配方法解第n 个方程x 2+2nx ﹣8n 2=0.(用含有n 的式子表示方程的根)【答案】(1)⑤;(2)x 1=2n ,x 2=﹣4n .【解析】【分析】(1)根据移项要变号,可判断;(2)先把常数项移到方程的右边,再把方程两边都加上一次项系数的一半,使左边是一个完全平方式,然后用直接开平方法求解.【详解】解:(1)小静的解法是从步骤⑤开始出现错误的,故答案为⑤;(2)x 2+2nx ﹣8n 2=0,x 2+2nx=8n 2,x 2+2nx+n 2=8n 2+n 2,(x+n )2=9n 2,x+n=±3n ,x 1=2n ,x 2=﹣4n .4.使得函数值为零的自变量的值称为函数的零点.例如,对于函数1y x =-,令y=0,可得x=1,我们就说1是函数1y x =-的零点. 己知函数222(3)y x mx m =--+(m m 为常数). (1)当m =0时,求该函数的零点;(2)证明:无论m 取何值,该函数总有两个零点;(3)设函数的两个零点分别为1x 和2x ,且121114x x +=-,此时函数图象与x 轴的交点分 别为A 、B(点A 在点B 左侧),点M 在直线10y x =-上,当MA+MB 最小时,求直线AM 的函数解析式.【答案】(1)当m =06和6-(2)见解析,2【解析】【分析】 (1)根据题中给出的函数的零点的定义,将m=0代入y=x 2-2mx-2(m+3),然后令y=0即可解得函数的零点;(2)令y=0,函数变为一元二次方程,要想证明方程有两个解,只需证明△>0即可; (3)根据题中条件求出函数解析式进而求得A 、B 两点坐标,个、作点B 关于直线y=x-10的对称点B′,连接AB′,求出点B′的坐标即可求得当MA+MB 最小时,直线AM 的函数解析式【详解】(1)当m =0时,该函数的零点为6和6-.(2)令y=0,得△=∴无论m 取何值,方程总有两个不相等的实数根. 即无论m 取何值,该函数总有两个零点.(3)依题意有, 由解得.∴函数的解析式为. 令y=0,解得∴A(),B(4,0) 作点B 关于直线10y x =-的对称点B’,连结AB’,则AB’与直线10y x =-的交点就是满足条件的M 点.易求得直线10y x =-与x 轴、y 轴的交点分别为C (10,0),D (0,10).连结CB’,则∠BCD=45°∴BC=CB’=6,∠B’CD=∠BCD=45°∴∠BCB’=90°即B’(106-,)设直线AB’的解析式为y kx b =+,则20{106k b k b -+=+=-,解得112k b =-=-,2即AM的解析式为112y x=--.5.如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA、OB的长分别是一元二次方程x2﹣7x+12=0的两个根(OA>OB).(1)求点D的坐标.(2)求直线BC的解析式.(3)在直线BC上是否存在点P,使△PCD为等腰三角形?若存在,请直接写出点P的坐标;若不存在,说明理由.【答案】(1)D(4,7)(2)y=3944x-(3)详见解析【解析】试题分析:(1)解一元二次方程求出OA、OB的长度,过点D作DE⊥y于点E,根据正方形的性质可得AD=AB,∠DAB=90°,然后求出∠ABO=∠DAE,然后利用“角角边”证明△DAE 和△ABO全等,根据全等三角形对应边相等可得DE=OA,AE=OB,再求出OE,然后写出点D的坐标即可;(2)过点C作CM⊥x轴于点M,同理求出点C的坐标,设直线BC的解析式为y=kx+b (k≠0,k、b为常数),然后利用待定系数法求一次函数解析式解答;(3)根据正方形的性质,点P与点B重合时,△PCD为等腰三角形;点P为点B关于点C 的对称点时,△PCD为等腰三角形,然后求解即可.试题解析:(1)x2﹣7x+12=0,解得x1=3,x2=4,∵OA>OB,∴OA=4,OB=3,过D作DE⊥y于点E,∵正方形ABCD,∴AD=AB,∠DAB=90°,∠DAE+∠OAB=90°,∠ABO+∠OAB=90°,∴∠ABO=∠DAE,∵DE⊥AE,∴∠AED=90°=∠AOB,∵DE⊥AE∴∠AED=90°=∠AOB,∴△DAE≌△ABO(AAS),∴DE=OA=4,AE=OB=3,∴OE=7,∴D(4,7);(2)过点C作CM⊥x轴于点M,同上可证得△BCM≌△ABO,∴CM=OB=3,BM=OA=4,∴OM=7,∴C(7,3),设直线BC的解析式为y=kx+b(k≠0,k、b为常数),代入B(3,0),C(7,3)得,,解得,∴y=x﹣;(3)存在.点P与点B重合时,P1(3,0),点P与点B关于点C对称时,P2(11,6).考点:1、解一元二次方程;2、正方形的性质;3、全等三角形的判定与性质;4、一次函数二、初三数学二次函数易错题压轴题(难)6.如图1,抛物线y=mx2﹣3mx+n(m≠0)与x轴交于点C(﹣1,0)与y轴交于点B (0,3),在线段OA上有一动点E(不与O、A重合),过点E作x轴的垂线交直线AB 于点N,交抛物线于点P,过点P作PM⊥AB于点M.(1)分别求出抛物线和直线AB的函数表达式;(2)设△PMN的面积为S1,△AEN的面积为S2,当1236 25SS=时,求点P的坐标;(3)如图2,在(2)的条件下,将线段OE绕点O逆时针旋转的到OE′,旋转角为α(0°<α<90°),连接E′A、E′B,求E'A+23E'B的最小值.【答案】(1)抛物线y=﹣34x2+94x+3,直线AB解析式为y=﹣34x+3;(2)P(2,3 2);(3410【解析】【分析】(1)由题意令y=0,求出抛物线与x轴交点,列出方程即可求出a,根据待定系数法可以确定直线AB解析式;(2)根据题意由△PNM∽△ANE,推出65PNAN=,以此列出方程求解即可解决问题;(3)根据题意在y轴上取一点M使得OM′=43,构造相似三角形,可以证明AM′就是E′A+23E′B的最小值.【详解】解:(1)∵抛物线y=mx2﹣3mx+n(m≠0)与x轴交于点C(﹣1,0)与y轴交于点B (0,3),则有330nm m n⎧⎨⎩++==,解得433mn⎧⎪⎨⎪-⎩==,∴抛物线239344y x x =-++, 令y =0,得到239344x x -++=0, 解得:x =4或﹣1,∴A (4,0),B (0,3),设直线AB 解析式为y =kx+b ,则340b k b +⎧⎨⎩==, 解得334k b ⎧-⎪⎨⎪⎩==,∴直线AB 解析式为y =34-x+3. (2)如图1中,设P (m ,239344m m -++),则E (m ,0),∵PM ⊥AB ,PE ⊥OA ,∴∠PMN =∠AEN ,∵∠PNM =∠ANE ,∴△PNM ∽△ANE ,∵△PMN 的面积为S 1,△AEN 的面积为S 2,123625S S =, ∴65PN AN =, ∵NE ∥OB , ∴AN AE AB OA =, ∴AN =54545454(4﹣m ), ∵抛物线解析式为y =239344x x -++,∴PN =239344m m -++﹣(34-m+3)=34-m 2+3m , ∴2336455(4)4m m m -+=-, 解得m =2或4(舍弃), ∴m =2,∴P (2,32). (3)如图2中,在y 轴上 取一点M′使得OM′=43,连接AM′,在AM′上取一点E′使得OE′=OE .∵OE′=2,OM′•OB =43×3=4, ∴OE′2=OM′•OB ,∴OE OB OM OE '='', ∵∠BOE′=∠M′OE′,∴△M′OE′∽△E′OB ,∴M E OE BE OB '''='=23, ∴M′E′=23BE′, ∴AE′+23BE′=AE′+E′M′=AM′,此时AE′+23BE′最小(两点间线段最短,A 、M′、E′共线时), 最小值=AM′2244()3+=4103. 【点睛】本题属于二次函数综合题,考查相似三角形的判定和性质、待定系数法、最小值问题等知识,解题的关键是构造相似三角形,找到线段AM′就是AE′+23BE′的最小值,属于中考压轴题.7.在平面直角坐标系中,将函数y=x2﹣2mx+m(x≤2m,m为常数)的图象记为G,图象G的最低点为P(x0,y0).(1)当y0=﹣1时,求m的值.(2)求y0的最大值.(3)当图象G与x轴有两个交点时,设左边交点的横坐标为x1,则x1的取值范围是.(4)点A在图象G上,且点A的横坐标为2m﹣2,点A关于y轴的对称点为点B,当点A不在坐标轴上时,以点A、B为顶点构造矩形ABCD,使点C、D落在x轴上,当图象G 在矩形ABCD内的部分所对应的函数值y随x的增大而减小时,直接写出m的取值范围.【答案】(1)51+或﹣1;(2)14;(3)0<x1<1;(4)m=0或m>43或23≤m<1【解析】【分析】(1)分m>0,m=0,m<0三种情形分别求解即可解决问题;(2)分三种情形,利用二次函数的性质分别求解即可;(3)由(1)可知,当图象G与x轴有两个交点时,m>0,求出当抛物线顶点在x轴上时m的值,利用图象法判断即可;(4)分四种情形:①m<0,②m=0,③m>1,④0<m≤1,分别求解即可解决问题.【详解】解:(1)如图1中,当m>0时,∵y=x2﹣2mx+m=(x﹣m)2﹣m2+m,图象G是抛物线在直线y=2m的左侧部分(包括点D),此时最底点P(m,﹣m2+m),由题意﹣m2+m=﹣1,解得m=512或512(舍弃),当m=0时,显然不符合题意,当m<0时,如图2中,图象G是抛物线在直线y=2m的左侧部分(包括点D),此时最底点P是纵坐标为m,∴m=﹣1,综上所述,满足条件的m 51或﹣1;(2)由(1)可知,当m>0时,y0=﹣m2+m=﹣(m﹣12)2+14,∵﹣1<0,∴m=12时,y0的最大值为14,当m=0时,y0=0,当m<0时,y0<0,综上所述,y0的最大值为14;(3)由(1)可知,当图象G与x轴有两个交点时,m>0,当抛物线顶点在x轴上时,4m2﹣4m=0,∴m=1或0(舍弃),∴观察观察图象可知,当图象G与x轴有两个交点时,设左边交点的横坐标为x1,则x1的取值范围是0<x1<1,故答案为0<x1<1;(4)当m<0时,观察图象可知,不存在点A满足条件,当m=0时,图象G在矩形ABCD内的部分所对应的函数值y随x的增大而减小,满足条件,如图3中,当m>1时,如图4中,设抛物线与x轴交于E,F,交y轴于N,观察图象可知当点A在x轴下方或直线x=﹣m和y轴之间时(可以在直线x=﹣m上)时,满足条件.则有(2m﹣2)2﹣2m(2m﹣2)+m<0,解得m>43,或﹣m≤2m﹣2<0,解得23≤m<1(不合题意舍弃),当0<m≤1时,如图5中,当点A在直线x=﹣m和y轴之间时(可以在直线x=﹣m上)时,满足条件.即或﹣m≤2m﹣2<0,解得23≤m<1,综上所述,满足条件m的值为m=0或m>43或23≤m<1.【点睛】本题属于二次函数综合题,考查了二次函数的性质,矩形的性质,最值问题,不等式等知识,解题的关键是理解题意,学会用分类讨论的思想思考问题,学会用转化的思想思考问题,属于中考压轴题.8.如图,在平面直角坐标系x O y中,抛物线y = ax2+ bx + c经过A、B、C三点,已知点A (-3,0),B(0,3),C(1,0).(1)求此抛物线的解析式;(2)点P是直线AB上方的抛物线上一动点,(不与点A、B重合),过点P作x轴的垂线,垂足为F,交直线AB于点E,作PD⊥AB于点D.动点P在什么位置时,△PDE的周长最大,求出此时P点的坐标;(3)在直线x = -2上是否存在点M,使得∠MAC = 2∠MCA,若存在,求出M点坐标.若不存在,说明理由.【答案】(1)y=-x2-2x+3;(2)点(-32,154),△PDE的周长最大;(3)点M(-2,3)或(-2,3【解析】【分析】(1)将A、B、C三点代入,利用待定系数法求解析式;(2)根据坐标发现,△AOB是等腰直角三角形,故只需使得PD越大,则△PDE的周长越大.联立直线AB与抛物线的解析式可得交点P坐标;(3)作点A关于直线x=-2的对称点D,利用∠MAC = 2∠MCA可推导得MD=CD,进而求得ME的长度,从而得出M坐标【详解】解:(1)∵抛物线y=ax2+bx+c经过点A(-3,0),B(0,3),C(1,0),∴9303a b cca b c-+=⎧⎪=⎨⎪++=⎩,解得:123abc=-⎧⎪=-⎨⎪=⎩,所以,抛物线的解析式为y=-x2-2x+3;(2)∵A(-3,0),B(0,3),∴OA=OB=3,∴△AOB 是等腰直角三角形,∴∠BAO=45°, ∵PF ⊥x 轴,∴∠AEF=90°-45°=45°, 又∵PD ⊥AB ,∴△PDE 是等腰直角三角形,∴PD 越大,△PDE 的周长越大,易得直线AB 的解析式为y=x+3, 设与AB 平行的直线解析式为y=x+m ,联立223y x m y x x =+⎧⎨=--+⎩,消掉y 得,x 2+3x+m-3=0, 当△=9-4(m-3)=0,即m=214时,直线与抛物线只有一个交点,PD 最长, 此时x=-32,y=154,∴点(-32,154),△PDE 的周长最大;(3)设直线x=-2与x 轴交于点E ,作点A 关于直线x=-2的对称点D ,则D (-1,0),连接MA ,MD ,MC .∴MA=MD ,∠MAC=∠MDA=2∠MCA , ∴∠CMD=∠DCM∴MD=CD=2 , ∴3∴点M (-23)或(-2,3 【点睛】本题是动点和最值的考查,在解决动点问题时,寻找出不变量来分析是解题关键,最值问题,通常利用对称来简化分析9.如图,若抛物线y =x 2+bx+c 与x 轴相交于A ,B 两点,与y 轴相交于点C ,直线y =x ﹣3经过点B ,C . (1)求抛物线的解析式;(2)点P 是直线BC 下方抛物线上一动点,过点P 作PH ⊥x 轴于点H ,交BC 于点M ,连接PC .①线段PM 是否有最大值?如果有,求出最大值;如果没有,请说明理由;②在点P 运动的过程中,是否存在点M ,恰好使△PCM 是以PM 为腰的等腰三角形?如果存在,请直接写出点P 的坐标;如果不存在,请说明理由.【答案】(1)y=x2﹣2x﹣3;(2)①有,94;②存在,(2,﹣3)或(32,2﹣2)【解析】【分析】(1)由直线表达式求出点B、C的坐标,将点B、C的坐标代入抛物线表达式,即可求解;(2)①根据PM=(x﹣3)﹣(x2﹣2x﹣3)=﹣(x﹣32)2+94即可求解;②分PM=PC、PM=MC两种情况,分别求解即可.【详解】解:(1)对于y=x﹣3,令x=0,y=﹣3,y=0,x=3,故点B、C的坐标分别为(3,0)、(0,﹣3),将点B、C的坐标代入抛物线表达式得:9303b cc++=⎧⎨=-⎩,解得:32 cb=-⎧⎨=-⎩,故抛物线的表达式为:y=x2﹣2x﹣3;(2)设:点M(x,x﹣3),则点P(x,x2﹣2x﹣3),①有,理由:PM=(x﹣3)﹣(x2﹣2x﹣3)=﹣(x﹣32)2+94,∵﹣1<0,故PM有最大值,当x=32时,PM最大值为:94;②存在,理由:PM2=(x﹣3﹣x2+2x+3)2=(﹣x2+3x)2;PC2=x2+(x2﹣2x﹣3+3)2;MC2=(x﹣3+3)2+x2;(Ⅰ)当PM=PC时,则(﹣x2+3x)2=x2+(x2﹣2x﹣3+3)2,解得:x=0或2(舍去0),故x=2,故点P(2,﹣3);(Ⅱ)当PM=MC时,则(﹣x2+3x)2=(x﹣3+3)2+x2,解得:x=0或2(舍去0和2),故x =3﹣2,则x 2﹣2x ﹣3=2﹣42, 故点P (3﹣2,2﹣42).综上,点P 的坐标为:(2,﹣3)或(3﹣2,2﹣42). 【点睛】本题考查的是二次函数综合运用,涉及到一次函数的性质、等腰三角形的性质等,其中(2)②,要注意分类求解,避免遗漏.10.如图1所示,抛物线223y x bx c =++与x 轴交于A 、B 两点,与y 轴交于点C ,已知C 点坐标为(0,4),抛物线的顶点的横坐标为72,点P 是第四象限内抛物线上的动点,四边形OPAQ 是平行四边形,设点P 的横坐标为m . (1)求抛物线的解析式;(2)求使△APC 的面积为整数的P 点的个数;(3)当点P 在抛物线上运动时,四边形OPAQ 可能是正方形吗?若可能,请求出点P 的坐标,若不可能,请说明理由;(4)在点Q 随点P 运动的过程中,当点Q 恰好落在直线AC 上时,则称点Q 为“和谐点”,如图(2)所示,请直接写出当Q 为“和谐点”的横坐标的值.【答案】(1)2214433y x x =-+;(2)9个 ;(3)33,22或44,;(4)33【解析】 【分析】(1)抛物线与y 轴交于点C ,顶点的横坐标为72,则472223cb ,即可求解; (2)APC ∆的面积PHAPHCSSS,即可求解;(3)当四边形OPAQ 是正方形时,点P 只能在x 轴的下方,此时OAP 为等腰直角三角形,设点(,)P x y ,则0x y +=,即可求解; (4)求出直线AP 的表达式为:2(1)(6)3ym x ,则直线OQ 的表达式为:2(1)3ymx ②,联立①②求出Q 的坐标,又四边形OPAQ 是平行四边形,则AO 的中点即为PQ 的中点,即可求解. 【详解】解:(1)抛物线与y 轴交于点C ,顶点的横坐标为72,则472223cb ,解得1434bc,故抛物线的抛物线为:2214433y x x =-+; (2)对于2214433y x x =-+,令0y =,则1x =或6,故点B 、A 的坐标分别为(1,0)、(6,0);如图,过点P 作//PH y 轴交AC 于点H ,设直线AC 的表达式为:y kx b =+ 由点A (6,0)、C (0,4)的坐标得460b kb,解得423b k, ∴直线AC 的表达式为:243y x =-+①, 设点2214(,4)33P x x x ,则点2(,4)3H x x ,APC ∆的面积221122146(44)212(16)22333PHAPHCSSSPH OA x x x x x,当1x =时,10S =,当6x =时,0S =, 故使APC ∆的面积为整数的P 点的个数为9个;(3)当四边形OPAQ 是正方形时,点P 只能在x 轴的下方, 此时OAP 为等腰直角三角形,设点(,)P x y ,则0x y +=, 即2214433yx x x ,解得:32x =或4, 故点P 的坐标为3(2,3)2或(4,4)-;(4)设点2214(,4)33P m m m ,为点(6,0)A ,设直线AP 的表达式为:y kx t =+,由点A ,P 的坐标可得260214433kt kmt m m ,解之得:2(1)326(1)3km tm∴直线AP 的表达式为:2(1)(6)3ym x , //AP OQ ,则AP 和OQ 表达式中的k 值相同,故直线OQ 的表达式为:2(1)3ym x ②, 联立①②得:2(1)3243ym x yx ,解得:446mm y x ,则点6(Q m ,44)m, 四边形OPAQ 是平行四边形,则AO 的中点即为PQ 的中点, 如图2,作QC x ⊥轴于点C ,PD x ⊥轴于点D ,∴OC AD =, 则有,66m m ,解得:33m,经检验,33m 是原分式方程得跟,则633m,故Q 的横坐标的值为33 【点睛】本题考查的是二次函数综合运用,涉及到一次函数的性质、平行四边形正方形的性质、面积的计算等,能熟练应用相关性质是解题的关键.三、初三数学 旋转易错题压轴题(难)11.阅读材料并解答下列问题:如图1,把平面内一条数轴x 绕原点O 逆时针旋转角00)90(θ︒︒<<得到另一条数轴,y x 轴和y 轴构成一个平面斜坐标系.xOy规定:过点P 作y 轴的平行线,交x 轴于点A ,过点P 作x 轴的平行线,交y 轴于点B ,若点A 在x 轴对应的实数为a ,点B 在y 轴对应的实数为b ,则称有序实数对(),a b 为点P 在平面斜坐标系xOy 中的斜坐标.如图2,在平面斜坐标系xOy 中,已知60θ︒=,点P 的斜坐标是()3,6,点C 的斜坐标是()0,6.(1)连接OP ,求线段OP 的长;(2)将线段OP 绕点O 顺时针旋转60︒到OQ (点Q 与点P 对应),求点Q 的斜坐标; (3)若点D 是直线OP 上一动点,在斜坐标系xOy 确定的平面内以点D 为圆心,DC 长为半径作D ,当⊙D 与x 轴相切时,求点D 的斜坐标,【答案】(1)37OP =2)点Q 的斜坐标为(9,3-);(3)点D 的斜坐标为:(32,3)或(6,12). 【解析】 【分析】(1)过点P 作PC ⊥OA ,垂足为C ,由平行线的性质,得∠PAC=60θ=︒,由AP=6,则AC=3,33PC =OP 的长度;(2)根据题意,过点Q 作QE ∥OC ,QF ∥OB ,连接BQ ,由旋转的性质,得到OP=OQ ,∠COP=∠BOQ ,则△COP ≌△BOQ ,则BQ=CP=3,∠OCP=∠OBQ=120°,然后得到△BEQ 是等边三角形,则BE=EQ=BQ=3,则OE=9,OF=3,即可得到点Q 的斜坐标;(3)根据题意,可分为两种情况进行分析:①当OP 和CM 恰好是平行四边形OMPC 的对角线时,此时点D 是对角线的交点,求出点D 的坐标即可;②取OJ=JN=CJ ,构造直角三角形OCN ,作∠CJN 的角平分线,与直线OP 相交与点D ,然后由所学的性质,求出点D 的坐标即可.【详解】解:(1)如图,过点P作PC⊥OA,垂足为C,连接OP,∵AP∥OB,∴∠PAC=60θ=︒,∵PC⊥OA,∴∠PCA=90°,∵点P的斜坐标是()3,6,∴OA=3,AP=6,∴1 cos602ACAP︒==,∴3AC=,∴226333PC=-=,336OC=+=,在Rt△OCP中,由勾股定理,得226(33)37OP=+=;(2)根据题意,过点Q作QE∥OC,QF∥OB,连接BQ,如图:由旋转的性质,得OP=OQ,∠POQ=60°,∵∠COP+∠POA=∠POA+∠BOQ=60°,∴∠COP=∠BOQ,∵OB=OC=6,∴△COP≌△BOQ(SAS);∴CP=BQ=3,∠OCP=∠OBQ=120°,∴∠EBQ=60°,∵EQ∥OC,∴∠BEQ=60°,∴△BEQ是等边三角形,∴BE=EQ=BQ=3,∴OE=6+3=9,OF=EQ=3,∵点Q在第四象限,∴点Q的斜坐标为(9,3 );(3)①取OM=PC=3,则四边形OMPC是平行四边形,连接OP、CM,交点为D,如图:由平行四边形的性质,得CD=DM,OD=PD,∴点D为OP的中点,∵点P的坐标为(3,6),∴点D的坐标为(32,3);②取OJ=JN=CJ,则△OCN是直角三角形,∵∠COJ=60°,∴△OCJ是等边三角形,∴∠CJN=120°,作∠CJN的角平分线,与直线OP相交于点D,作DN⊥x轴,连接CD,如图:∵CJ=JN ,∠CJD=∠NJD ,JP=JP ,∴△CJD ≌△NJD (SAS ),∴∠JCD=∠JND=90°,则由角平分线的性质定理,得CD=ND ;过点D 作DI ∥x 轴,连接DJ ,∵∠DJN=∠COJ=60°,∴OI ∥JD ,∴四边形OJDI 是平行四边形,∴ID=OJ=JN=OC=6,在Rt △JDN 中,∠JDN=30°,∴JD=2JN=12;∴点D 的斜坐标为(6,12);综合上述,点D 的斜坐标为:(32,3)或(6,12). 【点睛】本题考查了坐标与图形的性质,解直角三角形,旋转的性质,全等三角形的判定和性质,角平分线的性质等知识,解题的关键是理解题意,正确寻找圆心D 的位置来解决问题,属于中考创新题型.注意运用分类讨论的思想进行解题.12.已知如图1,在ABC 中,90ABC ∠=︒,BC AB =,点D 在AC 上,DF AC ⊥交BC 于F ,点E 是AF 的中点.(1)写出线段ED 与线段EB 的关系并证明;(2)如图2,将CDF 绕点C 逆时针旋转()090a α︒<<︒,其它条件不变,线段ED 与线段EB 的关系是否变化,写出你的结论并证明;(3)将CDF 绕点C 逆时针旋转一周,如果6BC =,32CF =,直接写出线段CE 的范围.【答案】(1)ED EB =,DE BE ⊥,证明见解析;(2)结论不变,理由见解析;(3)最大值922=最小值322=.【解析】【分析】(1)在Rt△ADF中,可得DE=AE=EF,在Rt△ABF中,可得BE=EF=EA,得证ED=EB;然后利用等腰三角形的性质以及四边形ADFB的内角和为180°,可推导得出∠DEB=90°;(2)如下图,先证四边形MFBA是平行四边形,再证△DCB≌△DFM,从而推导出△DMB 是等腰直角三角形,最后得出结论;(3)如下图,当点F在AC上时,CE有最大值;当点F在AC延长线上时,CE有最小值.【详解】(1)∵DF⊥AC,点E是AF的中点∴DE=AE=EF,∠EDF=∠DFE∵∠ABC=90°,点E是AF的中点∴BE=AE=EF,∠EFB=∠EBF∴DE=EB∵AB=BC,∴∠DAB=45°∴在四边形ABFD中,∠DFB=360°-90°-45°-90°=135°∠DEB=∠DEF+∠FEB=180°-2∠EFD+180°-2∠EFB=360°-2(∠EFD+∠EFB)=360°-2×135°=90°∴DE⊥EB(2)如下图,延长BE至点M处,使得ME=EB,连接MA、ME、MF、MD、FB、DB,延长MF交CB于点H∵ME=EB,点E是AF的中点∴四边形MFBA是平行四边形∴MF∥AB,MF=AB∴∠MHB=180°-∠ABC=90°∵∠DCA=∠FCB=a∴∠DCB=45°+a,∠CFH=90°-a∵∠DCF=45°,∠CDF=90°∴∠DFC=45°,△DCF是等腰直角三角形∴∠DFM=180°-∠DFC-∠CFH=45°+a∴∠DCB=∠DFM∵△ABC和△CDF都是等腰直角三角形∴DC=DF,BC=AB=MF∴△DCB≌△DFM(SAS)∴∠MDF=∠BDC,DB=DM∴∠MDF+∠FDB=∠BDC+∠FDB=90°∴△DMB是等腰直角三角形∵点E是MB的中点∴DE=EB,DE⊥EB(3)当点F在AC上时,CF有最大值,图形如下:∵BC=6,∴在等腰直角△ABC中,2∵2,∴2∴CE=CF+FE=CF+12AF922当点F在AC延长线上时,CE有最小值,图形如下:同理,CE=EF-CF32【点睛】本题考查三角形的旋转变换,用到了等腰直角三角形的性质和平行四边形的性质,解题关键是构造并证明△BDM是等腰直角三角形.13.综合与实践问题情境在一节数学活动课上,老师带领同学们借助几何画板对以下题目进行了研究.如图1,MN是过点A的直线,点C为直线MN外一点,连接AC,作∠ACD=60°,使AC=DC,在MN上取一点B,使∠DBN=60°.观察发现(1)根据图1中的数据,猜想线段AB、DB、CB之间满足的数量关系是;(2)希望小组认真思考后提出一种证明方法:将CB所在的直线以点C为旋转中心,逆时针旋转60°,与直线MN交于点E,即可证明(1)中的结论. 请你在图1中作出线段CE,并根据此方法写出证明过程;实践探究(3)奋进小组在继续探究的过程中,将点C绕点A逆时针旋转,他们发现当旋转到图2和图3的位置时,∠DBN=120°,线段AB、BD、CB的大小发生了变化,但是仍然满足一定的数量关系,请你直接写出这两种关系:在图2中,线段AB、DB、CB之间满足的数量关系是;在图3中,线段AB、DB、CB之间满足的数量关系是;提出问题(4)智慧小组提出一个问题:若图3中BC⊥CD于点C时,BC=2,则AC为多长?请你解答此问题.【答案】(1)AB+DB=CB;(2)见解析;(3)AB-DB=CB;DB-AB=CB;(4)23【解析】【分析】(1)根据图中数据直接猜想AB+DB=CB(2)在射线AM上一点E,使得∠ECB=60°,证明△ACE≌△DCB,推出EB=CB从而得出(1)中的结论;(3)利用旋转的性质和线段的和差关系以及全等三角形的性质得出线段关系;(4)过点C作∠BCE=60º,边CE与直线MN交于点E,设AC与BD交于点F.证明△ACE≌△DCB,得出BC=EC,结合△ECB为等边三角形,得出∠ECA=90°,在Rt△AEC中根据边长计算出AC的长度.【详解】综合与实践(1)AB+DB=CB(2)线段CE如图所示.证明:∵∠ECB=∠ACD=60º,∴∠2+∠ACB=∠1+∠ACB,∴∠2=∠1.∵∠ACD=∠DBN=60º, ∠ABD+∠DBN=180º,∴∠ABD+∠ACD=180º,∴在四边形ACDB中,∠CAB+∠3=180º.∵∠CAB+∠4=180º,∴∠4=∠3.又∵AC=DC,∴△ACE≌△DCB(ASA)∴EA=BD,EC=BC.又∵∠ECB=60°,∴△ECB为等边三角形,∴EB=CB.而EB=EA+AB=DB+AB,∴CB=DB+AB.(3) AB-DB=CB;DB-AB=CB;(4)证明:如图,过点C作∠BCE=60º,边CE与直线MN交于点E,设AC与BD交于点F.∵∠DCA=60º∴∠ECB+∠BCA=∠DCA+∠BCA即∠ECA=∠BCD∵∠DBN=120º∴∠DBA=60º又∵∠AFB=∠DFC∴∠EAF=∠BDC又∵AC=DC∴△ACE ≌△DCB (ASA )∴BC=EC∴△ECB 为等边三角形∴∠CEB=60º∵BC ⊥CD∴∠ECA=∠BCD=90º∴在Rt △AEC 中,∠CAE=30º∵BC=2,EC=BC∴AC=EC·tan60º= 23 【点睛】本题考查了全等三角形的判定和性质,旋转的性质,根据题中条件适当添加辅助线构造全等三角形,利用全等的性质得出线段关系是本题的关键.14.两块等腰直角三角形纸片AOB 和COD 按图1所示放置,直角顶点重合在点O 处,25AB =,17CD =.保持纸片AOB 不动,将纸片COD 绕点O 逆时针旋转(090)αα<<角度,如图2所示.()1利用图2证明AC BD =且AC BD ⊥;()2当BD 与CD 在同一直线上(如图3)时,求AC 的长和α的正弦值.【答案】(1)详见解析;(2)7,725. 【解析】【分析】 (1)图形经过旋转以后明确没有变化的边长,证明AOC BOD ≅,得出AC=BD , 延长BD 交AC 于E ,证明∠AEB=90︒,从而得到BD AC ⊥.(2) 如图3中,设AC=x ,在Rt △ABC 中,利用勾股定理求出x ,再根据sinα=sin ∠ABC=AC AB即可解决问题【详解】 ()1证明:如图2中,延长BD 交OA 于G ,交AC 于E .∵90AOB COD ∠=∠=,∴AOC DOB ∠=∠, 在AOC 和BOD 中,OA OB AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩,∴AOC BOD ≅,∴AC BD =,CAO DBO ∠=∠,∵90DBO GOB ∠+∠=,∵OGB AGE ∠=∠,∴90CAO AGE ∠+∠=,∴90AEG ∠=,∴BD AC ⊥.()2解:如图3中,设AC x =,∵BD 、CD 在同一直线上,BD AC ⊥, ∴ABC 是直角三角形,∴222AC BC AB +=,∴222(17)25x x ++=,解得7x =,∵45ODC DBO α∠=∠+∠=,45ABC DBO ∠+∠=,∴ABC α∠=∠, ∴7sin sin 25AC ABC AB α=∠==. 【点睛】本题考查旋转的性质、全等三角形的判定和性质、勾股定理、等腰直角三角形的性质等知识,解题的关键是正确寻找全等三角形,利用全等三角形的性质解决问题,第二个问题的关键是利用(1)的结论解决问题,属于中考常考题型.15.如图,△ABC 和△DEC 都是等腰三角形,点C 为它们的公共直角顶点,连接AD 、BE ,F为线段AD的中点,连接CF.(1)如图1,当D点在BC上时,BE与CF的数量关系是__________;(2)如图2,把△DEC绕C点顺时针旋转90°,其他条件不变,问(1)中的关系是否仍然成立?请说明理由;(3)如图3,把△DEC绕C点顺时针旋转一个钝角,其他条件不变,问(1)中的关系是否仍然成立?如成立,请证明;如果不成立,请写出相应的正确的结论并加以证明.【答案】(1)BE=2CF;(2)(1)中的关系是仍然成立,理由见解析;(3)(1)中的关系是仍然成立,理由见解析.【解析】试题分析:(1)根据“SAS”证明△ACD≌△BCE,可得AD=BE,又因为AD=2CF,从而BE=2CF;(2)由点F是AD中点,可得AD=2DF,从而AC= 2DF+CD,又由△ABC和△CDE是等腰直角三角形,可知BC=2DF+CE,所以BE= 2(DF+CE),CF= DF+CD,从而BE=2CF;(3)延长CF至G使FG=CF,即:CG=2CF,可证△CDF≌△GAF,再证明△BCE≌△ACG,从而BE=CG=2CF成立.解:(1)∵△ABC是等腰直角三角形,∴AC=BC,∵△CDE是等腰直角三角形,∴CD=CE,在△ACD和△BCE中,,∴△ACD≌△BCE,∴AD=BE,在Rt△ACD中,点F是AD中点,∴AD=2CF,∴BE=2CF,故答案为BE=2CF;(2)(1)中的关系是仍然成立,理由:∵点F是AD中点,∴AD=2DF,∴AC=AD+CD=2DF+CD,∵△ABC和△CDE是等腰直角三角形,∴AC=BC,CD=CE,∴BC=2DF+CE,∴BE=BC+CE=2DF+CE+CE=2(DF+CE),∵CF=DF+CD=DF+CD,∴BE=2CF;(3)(1)中的关系是仍然成立,理由:如图3,延长CF至G使FG=CF,即:CG=2CF,∵点F是AD中点,∴AF=DF,在△CDF和△GAF中,,∴△CDF≌△GAF,∴AG=CD=CE,∠CDF=∠GAF,∴∠CAG=∠CAD+∠GAF=∠CAD+∠ADC=180°﹣∠ACD,∵∠ACB=∠DCE=90°,∴∠BCE=360°﹣∠ACB﹣∠DCE﹣∠ACD=180°﹣∠ACD,∴∠CAG=∠BCE,连接BE,在△BCE和△ACG中,,∴△BCE≌△ACG,∴BE=CG=2CF,即:BE=2CF.点睛:本题主要考查了等腰直角三角形的性质、全等三角形的判定与性质和旋转的性质,考查了学生综合运用知识的能力,熟练掌握旋转的性质、全等三角形的判定与性质是解答本题的关键.四、初三数学圆易错题压轴题(难)16.在直角坐标系中,A(0,4),B(4,0).点C从点B出发沿BA方向以每秒2个单位的速度向点A匀速运动,同时点D从点A出发沿AO方向以每秒1个单位的速度向点O匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点C、D运动的时间是t秒(t>0).过点C作CE⊥BO于点E,连结CD、DE.⑴当t为何值时,线段CD的长为4;⑵当线段DE与以点O为圆心,半径为的⊙O有两个公共交点时,求t的取值范围;⑶当t为何值时,以C为圆心、CB为半径的⊙C与⑵中的⊙O相切?【答案】(1); (2) 4-<t≤; (3)或.【解析】试题分析:(1)过点C作CF⊥AD于点F,则CF,DF即可利用t表示出来,在Rt△CFD中利用勾股定理即可得到一个关于t的方程,从而求得t的值;(2)易证四边形ADEC是平行四边形,过点O作OG⊥DE于点G,当线段DE与⊙O相切时,则OG=,在直角△OEG中,OE可以利用t表示,则OG也可以利用t表示出来,当OG<时,直线与圆相交,据此即可求得t的范围;(3)分两圆外切与内切两种情况进行讨论,当外切时,圆心距等于两半径的和,当内切时,圆心距等于圆C的半径减去圆O的半径,列出方程即可求得t的值.(1)过点C作CF⊥AD于点F,在Rt△AOB中,OA=4,OB=4,∴∠ABO=30°,由题意得:BC=2t,AD=t,∵CE⊥BO,。
上海民办兰生复旦中学化学初三化学上册期末化学试卷

上海民办兰生复旦中学化学上册期末化学试卷一、九年级化学上册选择题1.相同质量的H2、CH4和CO完全燃烧需要氧气的质量()A.CO最多,H2最少B.H2最多,CH4最少C.H2最多,CO最少D.CH4最多,CO最少2.下列实验操作中,能达到实验目的的是选项实验目的实验操作A鉴别二氧化碳和氮气将燃着的木条伸入集气瓶中B除去CO2中的少量CO点燃C检验H2中混有的CH4点燃,在火焰上方罩一个干冷烧杯D鉴别H2O2溶液和H2O分别加入二氧化锰A.A B.B C.C D.D3.取2%的NaOH溶液20g和2%的HCl溶液20g,使其充分反应,所得到的溶液能使紫色石蕊试液显A.红色B.蓝色C.无色D.紫色4.已知:2KClO3=2KCl + 3O2↑,下列图像表示一定质量的KClO3和MnO2固体混合物受热过程中某些量随加热时间的变化趋势,其中不正确...的是A.A B.B C.C D.D5.下列除去少量杂质的方法正确的是()A.CO2气体(CO):点燃 B.MnO2固体(KCl):加水过滤C.Fe粉中含少量铜:加盐酸 D.CO气体(CO2):通入水6.能正确反映相关实验过程中量的变化的图像是A.A B.B C.C D.D7.下列图像对应的关系正确的是A.表示水通电分解产生的气体质量m与反应时间t的关系B.表示两份完全相同的双氧水在有无MnO2的情况下,产生O2的质量m与反应时间t的关系C.表示硫在密闭容器内燃烧,容器内物质的总质量m与反应时间t的关系D.表示加热一定质量的氯酸钾和二氧化锰混合物,产生氧气的质量m与时间t的关系8.在由CO2和O2组成的混合气体中,测得碳元素的质量分数为24%,则混合气体中CO2和O2的质量比为A.2∶1 B.1∶2 C.22∶3 D.22∶79.在一定的条件下,向一密闭的容器内加入A、B、C、D四种物质各20g,充分反应后,测定其质量,得到数据如下:物 质 A BC D 反应前质量(g ) 20 2020 20 反应后质量(g ) 2030 未知 14下列说法不正确的是A .物质A 可能是该反应的催化剂B .容器内发生了化合反应C .其化学方程式为:2C+3D=5BD .反应后容器内C 的质量为16g 10.美国普度大学研发出一种制备氢气的新工艺,流程如图所示。
上海民办兰生复旦中学初三化学上册期中初三化学试卷

上海民办兰生复旦中学化学上册期中化学试卷一、选择题(培优题较难)1.下列图示中的“错误实验操作”与图下面对应的“可能产生的后果”不一致的是()A.液体喷出B.污染试剂C.酒精溅出D.读数偏大2.下列说法正确的是()A.原子的质量主要集中在原子核上B.相同的原子无法构成不同的分子C.温度计内汞柱液面上升说明汞原子体积变大D.原子呈电中性是因为原子中质子数与中子数相等3.下列古代文明或工艺一定包含化学变化的是A.在甲骨上刻文字B.指南针指引航海C.用泥土烧制陶瓷D.用石块修筑长城4.在一密闭的容器中,一定质量的碳粉与过量的氧气在点燃的条件下充分反应,容器内各相关量与时间(从反应开始计时)的对应关系正确的是( )A.B.C.D.5.科学家用单个分子制戚的“纳米车”能在人工操纵下运输药物分子到病源处释放,杀死癌细胞。
下列叙述错误的是()A.分子是由原子构成的B.分子之间有间隙C.分子是肉眼不能够直接看见的D.分子在人为外力作用下才能运动6.锌是促进人体生长发育的必须微量元素。
下图为锌元素在元素周期表中的相关信息及原子结构示意图。
下列说法正确的是()A.锌属于非金属元素B.锌原子的中子数为30C.锌的相对原子质量为65.38g D.锌原子在化学反应中易失去电子形成Zn2+ 7.下列实验操作正确的是A.塞紧橡皮塞B.加热液体C.取用液体D.读出液体的体积8.2017年10月27日央视财经报道:王者归“铼”,中国发现超级金属铼,制造出航空发动机核心部件。
如图是铼在元素周期表中的相关信息,下列有关说法不正确的是()A.铼原子的核内质子数为75 B.铼的相对原子质量为186.2gC.铼的元素符号是Re D.铼原子的核外电子数为759.硼是作物生长必需的微量营养元素,硼元素的相关信息如图所示。
下列有关硼的说法正确的是A.相对原子质量为10.81g B.属于金属元素C.原子的核电荷数为5D.原子核外有6个电子10.丙烷(C3H8)是液化石油气的主要成分之一,燃烧前后分子种类变化的微观示意图如下。
上海民办兰生复旦中学初三化学上册期末化学试题(word版,含解析)

上海民办兰生复旦中学上册期末化学试题(word版,含解析)一、九年级化学上册选择题1.某露置于空气中的CaO固体,测得其中Ca元素质量分数为50%,取10g该CaO固体样品,向其中加入足量稀盐酸使其完全溶解。
正确的说法是( )A.加入稀盐酸后一定没有气泡产生B.该CaO样品的成分可能是CaO和Ca(OH)2C.生成CaCl2的质量为11.1gD.该CaO样品的成分可能是Ca(OH)2和CaCO32.有一氧化碳和二氧化碳的混合气体40g,其中碳元素的质量分数为30%。
使该混合气体通过足量的灼热氧化铜充分反应后。
再将气体通入过量的石灰水中,能得到白色沉淀的质量为()A.30g B.50g C.100g D.150g3.法拉第曾以《蜡烛的故事》为题为青少年连续开展了多次报告。
下表列举了报告中涉及的问题及对问题的回答,其中“对问题的回答”属于“设计实验方案”的是A.A B.B C.C D.D4.下列实验操作中,能达到实验目的的是A.A B.B C.C D.D5.某有机物6.2g在空气中完全燃烧,共得到17.6g二氧化碳和10.8g水,则该化合物的组成元素是()A.一定只含有碳元素B.一定只含有碳、氢两种元素C.一定含有碳、氢、氧三种元素D.一定含有碳、氢元素,可能含有氧元素6.推理是研究和学习化学的一种重要方法。
正电子、负质子都是反粒子,它们跟通常所说的电子、质子相比较,质量相等,但电性相反。
科学家已发现反氢原子。
推测出反氢原子的结构可能是()A.由一个带负电的质子和一个电子构成B.由一个质子和一个电子构成C.由一个带负电的质子和一个带正电的电子构成D.由一个质子和一个带正电的电子构成7.电解水时为了增强水的导电性可加入少量氢氧化钠溶液(氢氧化钠栄参与反应),电解一定质量氢氧化钠稀溶液的过程中,下列说法正确的是A.生成氢气和氧气的质量比为2:1 B.溶液中钠元素质量变大C.溶液中氢、氧元素质量比不变 D.溶液中氢元素质量分数减小8.除去下列物质中的少量杂质,实验方案不能达到除杂目的的是物质(括号内为杂质)实验方案A氮气(氧气)通过足量灼热铜网B氧化铜(木炭粉)在空气中充分灼烧C碳酸钙粉末(氯化钙)加入足量的水,过滤,洗涤,干燥D硫酸铁溶液(硫酸)加入足量铁粉,过滤A.A B.B C.C D.D9.某化学反应的微观示意图如下(反应条件已省略),根据该图得出的结论正确的是A.化学反应前后分子种类没有发生变化B.乙、丙、丁三种物质都属于氧化物C.甲物质中氮、氢元素的质量比为1:3D.生成物中丙、丁分子个数比为2:310.实验室中有一瓶气体,它由氢气、一氧化碳、二氧化碳、甲烷中的一种或几种组成(甲烷燃烧生成水和二氧化碳),用它进行如图所示实验,对该瓶气体中可能有哪些气体,某同学做了如下判断:a.可能是甲烷b.可能是甲烷和氢气c.可能是甲烷和一氧化碳d.可能是氢气和一氧化碳e.可能是甲烷、氢气和一氧化碳,其中判断正确的个数为()A.1个B.3个C.4个D.5个11.A、B、C三种物质各15 g,它们化合时只能生成30 g新物质D;若增加10 gA,则反应停止后,原反应物中只剩余C。
上海市民办兰生复旦中学沪教版初三物理电学练习题 7.2欧姆定律(2)

7.2欧姆定律 电阻(2)——电阻一、选择题:1、在下列科学家中,为了纪念他的贡献,将其名字作为物理量单位的是( )A 、阿基米德B 、爱因斯坦C 、欧姆D 、托里拆利2、根据欧姆定律,下列说法中正确的是( )A 、通过导体的电流越大,这段导体的电阻就越小B 、导体两端的电压越大,这段导体的电阻就越大C 、导体两端的电压越大,这段导体中的电流就越大D 、导体的电阻与电压成正比,与电流成反比3、如图所示为导体甲、乙的电流与电压的关系图象,下列根据图像的分析中,正确的是( )A 、甲的电阻大于乙的电阻B 、当通过甲、乙的电流相同时,甲两端的电压大C 、当甲、乙两端的电压相同时,通过甲的电流大D 、通过甲的电流与它两端的电压成反比4、如图所示是探究“通过同一导体中的电流与导体两端电压之间的关系”的实验电路。
为了得出普遍的物理规律,需要多次实验,下列方法可行的是( )A 、改变导体B 、改变电源电压C 、改变电流表量程D 、改变电压表量程5、对于欧姆定律的理解,下列说法中错误的是( )A 、对同一导体,导体中的电流与这段导体两端的电压成正比B 、在电压相同时,导体的电阻越大,通过导体的电流越小C 、对同一导体,导体两端的电压与通过电流的比值不变D 、在电压相同时,导体的电阻与电流成反比6、关于公式R=I U ,以下说法中正确的是( ) A 、加在导体两端的电压越大,导体的电阻就越大B 、通过导体的电流越大,导体的电阻就越小C 、导体的电阻在数值上等于导体两端的电压与通过该导体的电流之比D 、导体的电阻与导体两端的电压成正比,与通过导体的电流成反比7、下列说法正确的是( )A、导体中的电荷量越大,电阻一定越大B、导体中电流越小,电阻越大C、导体两端电压为零时,导体的电阻为零D、导体对电流的阻碍作用越大,电阻也越大8、下列物理量中属于导体本身的性质的是()A、电流B、电荷量C、电压D、电阻9、对于某个导体电阻的大小,以下说法正确的是( )A、加在导体两端的电压增大两倍,导体的电阻也增大两倍B、通过导体的电流减小一半,则导体的电阻增大两倍C、当导体的电压和通过导体的电流为零时,导体的电阻为零D、导体的电阻等于导体两端电压与通过它的电流之比10、甲、乙两导体的阻值之比为3:2,将它们先后接在同一电源上,则通过甲、乙两导体的电流之比是()A、3:2B、2:3C、1:1D、4:9二、填空题:1、在温度不变时,通过实验探究发现:通过导体的电流跟这段导体两端的电压成比;通过导体的电流与这段导体两端的电压之间的关系可用如图所示的U-I图象来表示:它是一条通过坐标原点的,电压跟电流的比值是一个,它与导体两端的电压和通过的电流大小,反映了导体对电流的,在物理学中用和的比值来表示导体的电阻,导体的电阻是导体本身的。
上海民办兰生复旦中学初三化学上册期中化学试题(word版,含解析)
上海民办兰生复旦中学上册期中化学试题(word版,含解析)一、选择题(培优题较难)1.在密闭容器内,有甲、乙、丙、丁四种物质,在一定条件下充分反应,测得反应前后各物质的质量分数如图所示,下列说法错误的是()A.该反应符合质量守恒定律B.生成的甲,丙两物质的质量比为8:1C.乙可能是该反应的催化剂D.参加反应的丁的质量等于生成的甲和丙的质量之和2.四种物质在一定的条件下充分混合反应,测得反应前后各物质的质量分数如图所示.则有关说法中不正确的()A.丁一定是化合物B.乙可能是这个反应的催化剂C.生成的甲、丙两物质的质量比为8: 1D.参加反应的丁的质量一定等于生成甲和丙的质量之和3.如图所示有关二氧化碳的实验中,只与二氧化碳物理性质有关的实验是()A. B. C. D.4.下列实验操作正确的是A.塞紧橡皮塞B.加热液体C.取用液体D.读出液体的体积5.最近,我国科学家成功合成新型催化剂,将CO2高效转化为甲醇(CH3OH)。
这不仅可以缓解碳排放引起的温室效应,还将成为理想的能源补充形式。
该化学反应的微观过程如下图所示。
下列说法正确的是A.该反应中四种物质均为化合物B.反应前后H元素的化合价不变C.参加反应的甲、乙分子个数比为1:3D.反应前后原子数目发生改变6.某工地发生多人食物中毒,经化验为误食工业用盐亚硝酸钠(NaNO2)所致。
NaNO2中氮元素的化合价是()A.+4B.+3C.+2D.+57.下列有关氧气的说法,错误的是()A.氧气能支持燃烧B.细铁丝在氧气中燃烧,生成氧化铁C.在通常状况下,氧气的密度比空气大D.氧气的化学性质比较活泼,能跟许多物质发生反应8.下列物质含有氢分子的是()A.H2B.H2O2C.H2CO3D.H2O9.下列说法正确的是()A.原子的质量主要集中在原子核上B.相同的原子无法构成不同的分子C.温度计内汞柱液面上升说明汞原子体积变大D.原子呈电中性是因为原子中质子数与中子数相等10.在一个密闭容器中放入甲、乙、丙、丁四种物质,在一定条件下充分反应,测得反应前后各物质的质量如下表所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
I. Choose the word or expression in the box which is closest in meaning to the underlinedpart in each sentence(选择方框中与划线部分意思相近的词)A)tell other people that something is good B).the place where she was bornC)a machine that drives a car D)below the surface of water E)in front ofF)connected G) the glass at the front of usl.I had to wait half an hour because there were so many people ahead of me.2. It is clear that my computer is linked to the Internet.3. After a few years, she was sent back to her native country.4. Cars in the future will have a clean engine that will not pollute the air.5. Can you recommend a good restaurant for Sichuan food?6. Do you think there are any underwater palaces in the world?7.It is important that you keep the windscreen of your car clean so that you can see the traffic clearly.plete the sentences with the given words in their proper forms(用括号中所给单词的适当形式完成下列句)1.They will enjoy _____ when they drive new car. (they)2. It seems that those foreigners have _______understood the introduction of tourist guide.(complete)3. It is easier for new drivers to find their ways with the help of______maps on their cars.(electricity)4.The____ clothes attracted the lady so much that she spent almost all her salary.(design)5.He always feel_____ when he sees the sick brother.(guilt)6.We should buy hydrogen cars which cause _____ air pollution. (little)7.Look!Some chemicals are ____ into the water. What may happen?(mixture)8.____is one of the most serious problems nowadays. (pollute)III Complete the sentences(首字母已给,填单词完成句子)1. I would like to r____ this article to all my students because it is worth reading.2.I really want to share these t____ on study with you, my English has improved a lot.3. The houses were situated in an a_____ spot, which attracted thousands of tourists.4. My cousin got an A for the final exam and his parents were s_____ with it.5.The road a_____ was blocked and hundreds of cars had to wait impatiently.6. The record sounds so h_____ that the room is full of noise.7. The boy was so clever, and he could use several m____to solve the problem.8.The scientist should improve the machines’ f____ but not their appearance.I Complete the following sentences as required(根据所给要求,完成下列句子)1.We were asking him for some advice this time yesterday(改为否定句)We ________ him some advice this time yesterday.2.Mr Green never went to see a doctor.(改为反意疑问句)Mr green never went to see a doctor,_____he?3.The windscreen is made of glass(对划线部分提问)_____ ______ the windscreen made of?4.The weather was horrible when we were at the beach.(改为感叹句)_____ ______ weather was when we were at the beach!5.You can watch the fish closely in an underwater hotel.(保持句意基本不变)You can get a ____ _____ at the fish in an the underwater hotel.6.We will have no water to drink unless we learn to save water.(保持句意基本不变) We will have no water to drink ___ we ____ learn to save water.7. We know the Oriental Pearl TV Tower well。
(保持句意基本不秒)We are _____ _____ the Oriental Pearl TV Tower.II Choose the best answer(选择最恰当的答案)1.The number of the trees in our neighbourhood is getting ____.A)more and more B)less and lessC)more and less D)larger and larger2. The plan for the summer holidays soundsA)like fun B)like funnyC)a lot of fun D)interested3.Tom______ from his chair to answer the question that was_____.A)rose. risen B) raised..raisedC)rose.. raised D)raised.risen4. It's time for Tim and _____to the Palace MuseumA) I to go B)I goingC)me to go D)me going5. Look at this apple, three quarters of it is red, the rest _____ green.A)is B)hasC)are D)has been6. Half of the students on the playground are playing basketball, the rest____ running.A)is B)hasC)are D ) has been7. Jane can speak French___. Mike can also speak_____A)good good B)well.well.C)good.well D)well.good8.He_____ down on his bed and soon____ asleep.A)lied.. fall B)lied.fellC)lay...fell D).lay..felt9.I bought ____of these books because I didn’t know which one was the best.A)none B)noC)neither D)bothI.Choose the best answer(选择最恰当的答案)1.I ______a lot from the farmers. I still remember the days when I was with them.A)learn B)was learning C)have learned D) had learned2. I met my English teacher yesterday afternoon while I______A)walk B)am walking C)to walk D) was walking3.I went to see Alice this morning, she ______the piano.A)play B)is playingC)has played D)was playing4. When I got home, my parents ______videos in the living room.A) are watching B)were watching C)watched D)watch5.-Did you hear someone shouting?-No, I didn' t because I_____to the music with earphone(耳机)A).listened B)have listenedC)was listening D)was listened6.Shirley ______a book about China last year, but I don’t know whether she has finished itA)has written B )was writingC)wrote D)had written7. While I was writing a letter,my parents _____about the holiday plan.A)talk B)is takingC)takes D)were talking8.Henry _____a nap when I met him for the first time.A)took B)is takingC)takes D)was taking9. As soon as they sat down, they______with steaming bowls of soup.A)are served B )have servedC)served D)were served10.Stop making any noise.Tommy _____ in the next room.A)is sleeping B)has sleptC)slept D)was sleeping11. By the age of sixteen, Jack ______his first science fiction. He is now very famous.A)has published B)publishedC)was publishing D)had published12. Professor Li _____to us before his speech at the meeting last Sunday.A)introduced B)was introducingC)was introduced D)had introduced13. Mr Ma__many school rules since he became our headmaster last SeptemberA)changed B)would changeC)was changing D)has changedII. Complete the sentences with suitable verbs(用恰当的动词形式填空)1. When Mary ______(help) her mother do the washing up, she _____(break)a dish2 We ______(sleep) when a fire ____ (break) out in our building.3. A the picnic,some of the students______(fish) while others ______(play) badminton4. When the robber ______(see)the policemen, he______ (run) away5. While I_____ (lie) on the beach, somebody _____( shout).’ Shark!’6.A bird ____(fly) into the room when I ____(open) the window.7.My brother _____( help) me at all while I _____(tidy)up our flat yesterday8.The telephone ___ (ring) while I ____(do) some English grammar exercisesI. Read the passage and fill in the blanks with proper words(在短文的空格内填入适当的词,使其内容通顺,每空格限填一词)What will man be like in the future? In 5, 000 or even 50 000 years from now? We can only make a guess, of course, but we can be sure that he will be different from what he is today.Let us make an example. Man, even five hundred years ago, was shorter than he ison the average, men are about three inches taller. Five hundred years is' a relatively(相对地)short period of time, so we may suppose that man will continue to grow t___1__.Again, in the modern world we use our brains a great deal. Even so, we still make use of o_2__about 20% of the brain’s capacity(容量). As time goes on, however, we will use our brains more and more and f ___3_ we shall need a larger one! This is likely to bring a physical change, too. The head, especially the forehead, will grow larger.Nowadays our eyes are being used too much. In fact, we use them so much that very often they become weaker and we have to wear g__4__. But over a very long period of time it is likely that man’s eyes will grow stronger.On the other band, we tend to make less use of our arms and legs. These as a result, are likely to grow weaker. At the same time. however, our fingers will grow more sensitive b __5___ they are used a great deal in modern life.Another change maybe surprises you. Hair will not be useful any longer and this will make it d __6___from the body. Both future man and woman will probably be hairless!Besides these changes, future man will still have a lot in c__7__ with us. He will still be a human being, with thoughts and feelings similar to our own.II.write a passage on the topic“ Life in the future” according to the situation given。
