精选最新版2019年高中一年级数学单元测试卷《函数的概念和基本初等函数》完整考试题(含标准答案)
最新版精选2019年高中一年级数学单元测试卷《函数的概念和基本初等函数》完整考题(含答案)

2019年高中数学单元测试试题 函数的概念和基本初等函数(含答案)学校:__________第I 卷(选择题)请点击修改第I 卷的文字说明一、选择题1.已知函数M ,最小值为m ,则mM 的值为__2_____2.若函数f(x)=x 2+b x +c 的图象的顶点在第四象限,则函数f /(x)的图象是()(2004湖南文).3.函数y =log 2x 的图象大致是( )(2010四川文2)(A ) (B ) (C ) (D )4.设函数()f x 和)(x g 分别是R 上的偶函数和奇函数,则下列结论恒成立的是( )A .()f x +|)(x g |是偶函数B .()f x -|)(x g |是奇函数C .|()f x | +)(x g 是偶函数D .|()f x |- )(x g 是奇函数(2011广东理4)5.定义在R 上的偶函数()f x 的部分图像如右图所示,则在()2,0-上,下列函数中与()f x 的单调性不同的是A .21y x =+B. ||1y x =+C. 321,01,0x x y x x +≥⎧=⎨+<⎩D .,,0x x e x o y e x -⎧≥⎪=⎨<⎪⎩ 解析 解析 根据偶函数在关于原点对称的区间上单调性相反,故可知求在()2,0-上单调递减,注意到要与()f x 的单调性不同,故所求的函数在()2,0-上应单调递增。
而函数21y x =+在(],1-∞上递减;函数1y x =+在(],0-∞时单调递减;函数⎩⎨⎧++=0,10,123 x x x x y 在(]0,∞-上单调递减,理由如下y ’=3x 2>0(x<0),故函数单调递增,显然符合题意;而函数⎪⎩⎪⎨⎧≥=-0,0, x e x e y x x ,有y ’=-x e -<0(x<0),故其在(]0,∞-上单调递减,不符合题意,综上选C 。
6.已知2()82f x x x =+-,如果2()(2)g x f x =-,那么()g x ------------------------------( )A.在区间(-1,0)上是减函数B.在区间(0,1)上是减函数C.在区间(-2,0)上是增函数D.在区间(0,2)上是增函数7.若)(x f 在[-5,5]上是奇函数,且)()(13f f <,则--------------------------------------------------------( )(A))()(31-<-f f (B))()(10f f > (C))()(11f f <- (D))()(53->-f f1 第II 卷(非选择题)请点击修改第II 卷的文字说明二、填空题8.函数xx y --=112的单调区间为____________________ 9.已知奇函数()f x 是定义在R 上的减函数,其图像经过A (3,-2),则不等式︱f(2x+1)︱<2的解集10.若函数()x f 是定义在R 上的奇函数,且在),0(+∞上是单调减函数,若()02=f ,则不等式()0≤⋅x f x 的解集是________________。
新版精选2019年高中一年级数学单元测试卷《函数的概念和基本初等函数》测试题(含标准答案)

2019年高中数学单元测试试题 函数的概念和基本初等函数(含答案)学校:__________第I 卷(选择题)请点击修改第I 卷的文字说明 一、选择题1.下列函数中,在其定义域内既是奇函数又是减函数的是( )A. R x x y ∈-=,3B. R x x y ∈=,sinC. R x x y ∈=,D. R x x y ∈=,)21((2006广东)2.设f (x )是定义在R 上以6为周期的函数,f (x )在(0,3)内单调递增,且y f (x )的图象关于直线x 3对称,则下面正确的结论是( ) (A) f (1.5)<f (3.5)<f (6.5) (B) f (3.5)<f (1.5)<f (6.5) (C) f (6.5)<f (3.5)<f (1.5)(D) f (3.5)<f (6.5)<f (1.5)(2005天津文)3.若对任意∈x R,不等式x ≥ax 恒成立,则实数a 的取值范围是( ) A . a <-1B . a ≤1C .a <1D .a ≥1(2007安徽)4.函数f(x)=|x-1|的图象是( )(2005北京春季文)5.下列函数()f x 中,满足“对任意1x ,2x ∈(0,+∞),当1x <2x 时,都有1()f x >2()f x的是 A .()f x =1xB. ()f x =2(1)x - C .()f x =xe D ()ln(1)f x x =+(2009福建卷理)6.已知3123(),,,,f x x x x x x R =--∈且1223310,0,0x x x x x x +>+>+>,则123()()()f x f x f x ++的值为 ( )A 一定大于0B 一定小于0C 等于0D 正负都有可能第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题7.若函数f(x)值域为 [-2,2],则函数f (x+1)的值域是____________ 8.已知函数2(),([2,2])f x x x ∈-=,2()sin(2)3,[0,]62g x a x a x ππ=++∈, 1[2,2]x ∀∈-,001[0,],()()2x g x f x π∃∈=总使得成立,则实数a 的取值范围是 .9.设()f x 是定义在R 上的奇函数,当x ≤0时,()f x x x 2=2-,则()f 1= ▲ ;10. 函数()f x ==)2(f ____▲______11.解析式为2()f x x =且值域为{4,9}的函数的个数是 . 12.已知()f x 是定义在(3,3)-上的偶函数, 当03x ≤<时, ()f x 的图像如右图,则不等式(1)()0x f x -⋅≤的解集是13.若(1)f x +为奇函数,当1x <时,2()21f x x x =-+,那么1x >时,()f x 的单调递减区间为______________________ 14.设函数()()()1x x a f x x++=为奇函数,则实数=a 。
精选新版2019年高中一年级数学单元测试卷《函数的概念和基本初等函数》考核题完整版(含答案)

2019年高中数学单元测试试题 函数的概念和基本初等函数(含答案)学校:__________第I 卷(选择题)请点击修改第I 卷的文字说明 一、选择题1.已知)(x f y =是定义在R 上的单调函数,实数21x x ≠,,1,121λλλ++=-≠x x aλλβ++=112x x ,若|)()(||)()(|21βαf f x f x f -<-,则( )A .0<λB .0=λC .10<<λD .1≥λ(2005辽宁) 2.用表示a ,b 两数中的最小值。
若函数的图像关于直线x=12-对称,则t 的值为( ) A .-2 B .2 C .-1 D .1(2010湖南理8)3.若函数f (x )=3x +3-x 与g (x )=3x -3-x 的定义域均为R ,则( ) A .f (x )与g (x )均为偶函数 B . f (x )为偶函数,g (x )为奇函数 C .f (x )与g (x )均为奇函数 D . f (x )为奇函数,g (x )为偶函数(2010广东理3)()33(),()33()x x x x f x f x g x g x ---=+=-=-=-.4.下列函数中,既是偶函数又在()0,+∞单调递增的函数是( )A. 3y x = B. 1y x =+ C. 21y x =-+ D. 2xy -=(2011全国文3)5.定义在(-∞,+∞)上的任意函数f (x )都可以表示成一个奇函数g (x )和一个偶函数h (x )之和,如果f (x )=lg (10x+1),x ∈(-∞,+∞),那么( ) A .g (x )=x ,h (x )=lg (10x+10-x+2) B .g (x )=21lg [(10x +1)+x ],h (x )=21lg [(10x+1)-x ] C .g (x )=2x ,h (x )=lg (10x+1)-2x D .g (x )=-2x ,h (x )=lg (10x+1)+2x (1994全国15) 6.已知2()82f x x x =+-,如果2()(2)g x f x =-,那么()g x ------------------------------( )A.在区间(-1,0)上是减函数B.在区间(0,1)上是减函数C.在区间(-2,0)上是增函数D.在区间(0,2)上是增函数第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题7.函数y=x 2—2x (x ∈[0,3]的值域是8.已知函数f (x )=x 2+2(a -1)x +2在区间(-∞,4)上是减函数,则a 的取值范围是9.函数()f x 在[0,)+∞上单调递减,则f 的单调递减区间为 . 10.若函数2()1f x x mx =++在区间[1,2]上单调,则实数m 的取值范围是 .11.定义在R 上的偶函数()f x 在[0,)+∞上单调递增,且(2)0f -=,则不等式()0xf x >的解集为 .12.若函数f(x)值域为 [-2,2],则函数f (x+1)的值域是____________13.若3)1(4)54()(22+---+=x a x a a x f 的图象都在x 轴的上方,则实数a 的取值范围是 . 114.函数f (x )=4x 2-mx +5在区间[-2,+∞]上是增函数,在区间(-∞,-2)上是减函数,则f (1)等于__________15.函数()()()01log 09c ax b x f x x x +≤⎧⎪=⎨⎛⎫+> ⎪⎪⎝⎭⎩的图象如图所示,则 a b c ++= 。
精选2019年高中一年级数学单元测试卷《函数的概念和基本初等函数》完整考试题(含答案)

2019年高中数学单元测试试题 函数的概念和基本初等函数(含答案)学校:__________第I 卷(选择题)请点击修改第I 卷的文字说明 一、选择题1.已知函数()f x 是定义在R 上的偶函数,且在区间[)0+,∞上是增函数.令2sin 7a f π⎛⎫= ⎪⎝⎭,5cos 7b f π⎛⎫= ⎪⎝⎭,5tan 7c f π⎛⎫= ⎪⎝⎭,则( )A .b a c <<B .c b a <<C .b c a <<D .a b c <<(2008天津理)2.若函数f(x)=x 2+b x +c 的图象的顶点在第四象限,则函数f /(x)的图象是( )(2004湖南文).3.函数()y f x =的图像与函数2()log (0)g x x x =>的图像关于原点对称,则()f x 的表达式为( ) A .21()(0)log f x x x=> B .21()(0)log ()f x x x =<-C .2()log (0)f x x x =->D .2()log ()(0)f x x x =--<(2006)4.若对任意∈x R,不等式x ≥ax 恒成立,则实数a 的取值范围是( ) A . a <-1B . a ≤1C .a <1D .a ≥1(2007安徽)5.设0abc >,二次函数()2f x ax bx c =++的图象可能是6.下列函数中,与函数y=有相同定义域的是 A .()ln f x x = B.1()f x x= C. ()||f x x = D.()xf x e = (2009福建卷文) 解析 解析 由y=可得定义域是0.()ln x f x x >=的定义域0x >;1()f x x =的定义域是x ≠0;()||f x x =的定义域是;()xx R f x e ∈=定义域是x R ∈。
精选最新2019年高中一年级数学单元测试卷《函数的概念和基本初等函数》完整考题(含标准答案)

2019年高中数学单元测试试题 函数的概念和基本初等函数(含答案)学校:__________第I 卷(选择题)请点击修改第I 卷的文字说明一、选择题1.若()f x 是R 上周期为5的奇函数,且满足()()11,22f f ==,则()()34f f -=( )A 、-1B 、1C 、-2D 、2(2010安徽理)2.若对任意∈x R,不等式x ≥ax 恒成立,则实数a 的取值范围是( )A . a <-1B . a ≤1C .a <1D .a ≥1(2007安徽)3.下列函数中,不是偶函数的是------------------------------------------------------------------------------------( )(A) 23x y -= (B) 23x y = (C) 2)()(x f x f y +-= (D) 12-+=x x y 4.已知奇函数)(x f y =在其定义域上是增函数,那么)(x f y -=在它的定义域上--------------------( )(A) 既是奇函数,又是增函数 (B) 既是奇函数,又是减函数(C) 既是偶函数,又是先减后增的函数 (D) 既是偶函数,又事先增后减的函第II 卷(非选择题)请点击修改第II 卷的文字说明二、填空题5.若(1)f x +为奇函数,当1x <时,2()21f x x x =-+,那么1x >时,()f x 的单调递减区间为______________________6.函数y =lncos x (-2π<x <)2π的图象是A7.函数f (x )=x (2-x )的单调递减区间是___ ___.8.设2()lg()1f x a x=+-是奇函数,则使()0f x <的x 的取值范围是 . 9.当228x x -<时,函数252x x y x --=+的最小值是 . 10.已知函数()c f x x x=+的定义域为(0,)+∞,若对任意*x N ∈,都有()(3)f x f ≥,则实数c 的取值范围是11.下列各组函数中,表示同一函数的序号是 ▲ .①1y x =+ 和 211x y x -=+ ②0y x = 和 1y =③2()f x x = 和()2()1g x x =+ ④2()f xx = 和 ()g x =12.已知偶函数f :→Z Z 满足(1)1f =,(2011)1f ≠,对任意的a b ∈Z 、,都有()f a b +≤ {}max ()()f a f b , ,(注:{}max x y , 表示x y , 中较大的数),则(2012)f 的可能值是 ▲ .13.“龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点,用12,S S 分别表示乌龟和兔子所行的路程,t 为时间,则下图与故事情节相吻合的是___ ▲ .14.奇函数()()f x x R ∈满足:()30f -=,且在区间[]0,2与[)2,+∞上分别递减和递增,则不等式()0xf x <的解集为______________.15.已知x x x f 2122-=+)(,则)(2f =_______________16.已知函数2()2(1)2f x x a x =+-+在区间(,4]-∞上是减函数,则实数k 的取值范围是______17.已知753()5f x ax bx cx dx =++++(,,,a b c d 为常数),若(7)7f -=-,则(7)f = .18.如果函数12-+=ax x y 在闭区间[]3,0上有最小值2-,那么a 的值是 。
精选新版2019年高中一年级数学单元测试卷《函数的概念和基本初等函数》完整题(含标准答案)

2019年高中数学单元测试试题 函数的概念和基本初等函数(含答案)学校:__________第I 卷(选择题)请点击修改第I 卷的文字说明 一、选择题1.某地一年的气温Q (t )(单位:ºc )与时间t (月份)之间的关系如图(1)所示,已知该年的平均气温为10ºc ,令G (t )表示时间段〔0,t 〕的平均气温,G (t )与t 之间的函数关系用下列图象表示,则正确的应该是( )(2006江西理)2.函数)34(log 1)(22-+-=x x x f 的定义域为( )A .(1,2)∪(2,3)B .),3()1,(+∞⋃-∞C .(1,3)D .[1,3] (2005江西)3.函数()f x 的定义域为R ,若(1)f x +与(1)f x -都是奇函数,则( D ) (A) ()f x 是偶函数 (B) ()f x 是奇函数 (C) ()(2)f x f x =+ (D) (3)f x +是奇函数4.已知ω是正实数,函数()2sin f x x ω=在[,]34ππ-上递增,那么----------------------------------------( ) A .302ω<≤B .02ω<≤C .2407ω<≤ D .2ω≥ 5.已知二次函数2()(0)f x x x a a =++>,若()0f m <,则(1)f m +的值( ) (A )正数 (B )负数 (C )零 (D )符号与a 有关第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题6.定义在R 上的偶函数()f x 在[0,)+∞上单调递增,且(2)0f -=,则不等式()0xf x >的解集为 .7.已知函数y =tan x ω在(-π2,π2)内是减函数,则ω范围 .8.“龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点,用12,S S 分别表示乌龟和兔子所行的路程,t 为时间,则下图与故事情节相吻合的是___ ▲ .9.已知函数22()1x f x x =+,则①② ③ ④111(1)(2)()(3)()(4)()234f f f f f f f ++++++=_____________;10.下列几个命题:①方程x 2+(a-3)x+a=0的有一个正解,一个负实根,则a<0;②若f(x)的定义域为[0,1],则f(x+2)的定义域为[-2,1]③函数y=log 2(x+1)+2的图像可由y=log 2(x-1)-2的图像向上平移4个单位,向右平移2个单位得到④若关于x 的方程式∣x 2-2x-3∣=m 有两解,则m=0或m>4;其中正确的有。
精选最新版2019年高中一年级数学单元测试卷《函数的概念和基本初等函数》完整题(含标准答案)

2019年高中数学单元测试试题 函数的概念和基本初等函数(含答案)学校:__________第I 卷(选择题)请点击修改第I 卷的文字说明 一、选择题1.已知函数()f x 是定义在R 上的偶函数, 且在区间[0,)+∞单调递增. 若实数a 满足212(log )(log )2(1)f a f f a ≤+, 则a 的取值范围是( )A .[1,2]B .10,2⎛⎤ ⎥⎝⎦C .1,22⎡⎤⎢⎥⎣⎦D .(0,2] (2013年高考天津卷(文))2.已知函数M ,最小值为m ,则mM的值为__2_____3.函数ln cos ()22y x x ππ=-<<的图象是 ( )(2008山东)4.函数1()lg(1)1f x x x=++-的定义域是( )A .(-∞,1)B .(1,+∞)C .(-1,1)∪(1,+∞)D .(-∞,+∞)(2011广东文4)要使函数有意义当且仅当⎩⎨⎧>+≠-0101x x 解得1->x 且1≠x ,从而定义域为),(),(∞+-111 ,故选C. 5.函数y =11+x 的图象是( )(1995全国文2)6.当a >1时,在同一坐标系中,函数y=a -x与y =log a x 的图象是( )(1996全国2)7.函数()sin f x x x m n =++为奇函数的充要条件是………………………………………( ) A 、220m n += B 、0mn = C 、0m n +=D 、0m n -=8.在(,0)-∞上是增函数的是---------------------------------------------------------------------( )A.2(1)y x =-- B.23y x = C .12y x =- D.1y x=第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题9.反比例函数:函数f (x )=1x,当x ∈[-2,-1]∪(3,4]时,则f (x )的值域 10.函数)53(log )(21-=x x f 的定义域为 .11.函数322+-=mx x x f )(,当),[+∞-∈2x 时是增函数,当],(2--∞∈x 时是减函数,则)(1f =__________________12.已知(21)f x +是偶函数,则函数(2)f x 图像的对称轴为____________13.函数||||x x y -++=21的递增区间是_______________,递减区间是_______________14.已知)(12-x f 的定义域为),[10,求)(x f 31-的定义域15.已知1271515n n C C +-=(N n ∈),则n = .78n =或16.“龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点,用12,S S 分别表示乌龟和兔子所行的路程,t 为时间,则下图与故事情节相吻合的是___ ▲ .17. 函数)3(log 22x x y -=的定义域是___________.①② ③ ④18.给定映射),2(),(:xy y x y x f +→,点(61,61-)的原象是 。
新版精选2019年高中一年级数学单元测试卷《函数的概念和基本初等函数》完整考题(含标准答案)

2019年高中数学单元测试试题 函数的概念和基本初等函数(含答案)学校:__________第I 卷(选择题)请点击修改第I 卷的文字说明 一、选择题1.设()f x 是R 上的任意函数,则下列叙述正确的是( ) (A)()()f x f x -是奇函数 (B)()()f x f x -是奇函数(C) ()()f x f x --是偶函数 (D) ()()f x f x +-是偶函数(2006辽宁理)2.若关于x 的不等式x k )1(2+≤4k +4的解集是M ,则对任意实常数k ,总有( )A .2∈M ,0∈M ;B .2∉M ,0∉M ;C .2∈M ,0∉M ;D .2∉M ,0∈M .第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题3.函数2x y =在(0,+∞)上为单调 函数,函数x y =在(0,+∞)上为单调函数,函数x y -=在(0,+∞)上为单调 函数;4.已知])9,1[(2log )(3∈+=x x x f ,则函数)()]([22x f x f y +=的最大值是 .5.函数()y f x =的定义域为[]0,5,则函数()y f x m =+的定义域为______________.6.给定集合{1,2,3,...,}n A n =,映射:n n f A A →满足: ①当,,n i j A i j ∈≠时,()()f i f j ≠;②任取,n m A ∈若2m ≥,则有m {(1),(2),..,()}f f f m ∈..则称映射f :n n A A →是一个“优映射”.例如:用表1表示的映射f :33A A →是一个“优映射”.表1 表2(1)已知表2表示的映射f : 44A A →是一个优映射,请把表2补充完整(只需填出一个满足条件的映射);(2)若映射f :1010A A →是“优映射”,且方程()f i i =的解恰有6个,则这样的“优映射”的个数是_____.84.7.定义在R 上的奇函数)(x f ,当0<x 时,11)(+=x x f ,则)21(f = ▲ .8.若函数2(21)1y x a x =+++在区间]2,(-∞上是减函数,则实数a 的取值范围是___ ▲ .9.“龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点,用12,S S 分别表示乌龟和兔子所行的路程,t 为时间,则下图与故事情节相吻合的是___ ▲ .10.已知()f x 为R 上的奇函数,且(2)()f x f x +=,若(1)1f a +=,则(1)f a -=11.若函数)2(xf 的定义域是)1,21(,则函数)(x f 的定义域是______________. 12.设集合M={x|0≤x -≤1},函数()f x =的定义域为N ,则M∩N= 。
最新精选2019年高中一年级数学单元测试卷《函数的概念和基本初等函数》完整题(含标准答案)

2019年高中数学单元测试试题 函数的概念和基本初等函数(含答案)学校:__________第I 卷(选择题)请点击修改第I 卷的文字说明 一、选择题1.若不等式x 2+ax +1≥0对于一切x ∈(0,12)成立,则a 的取值范围是( ) A .0 B. –2 C.-52D.-3(2006江西理)2.设f(x)为定义在R 上的奇函数,当x ≥0时,f(x)=2x+2x+b(b 为常数),则f(-1)= ( )(A) 3 (B) 1 (C)-1 (D)-3(2010山东理4)3.已知函数f (x)=1-xe ,g(x)=.342-+-x x 若有f(a)=g(b),则b 的取值范围为( ) (A ).]22,22[+- (B ).)22,22(+- (C ).[1,3](D ).(1,3) (2011湖南文8) 4.函数2log 2-=x y 的定义域是( )A .),3(+∞B .),3[+∞C .),4(+∞D .),4[+∞ (2006湖南理)5.若对任意∈x R,不等式x ≥ax 恒成立,则实数a 的取值范围是( ) A . a <-1B . a ≤1C .a <1D .a ≥1(2007安徽)6.已知二次函数2()(0)f x x x a a =++>,若()0f m <,则(1)f m +的值( ) (A )正数 (B )负数 (C )零 (D )符号与a 有关第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题7.对于任意实数x ,符号[x ]表示x 的整数部分,即[x ]是不超过x 的最大整数”.在实数轴R (箭头向右)上[x ]是在点x 左侧的第一个整数点,当x 是整数时[x ]就是x .这个函数[x ]叫做“取整函数”,它在数学本身和生产实践中有广泛的应用.那么不等式[][]03log 2log 323≤--xx 的解集为 _________ .8.定义在R 上的函数()f x 满足()()f x f x -=-,且(1)(1)f x f x -=+,当[]1,1x ∈-时,3()f x x =,则(2008)f = .9.已知定义域为D 的函数()f x ,对任意x D ∈,存在正数K ,都有()f x K ≤成立,则称函数()f x 是D 上的“有界函数”。
新版精选2019年高中一年级数学单元测试卷《函数的概念和基本初等函数》完整题(含标准答案)

2019年高中数学单元测试试题 函数的概念和基本初等函数(含答案)学校:__________第I 卷(选择题)请点击修改第I 卷的文字说明 一、选择题1.若函数)1,0)((log ≠>+=a a b x y a 的图象过两点(-1,0)和(0,1),则 ( ) (A)a=2,b=2 (B)a= 2 ,b=2 (C)a=2,b=1 (D)a= 2 ,b= 2 (2004江苏)2.已知函数y= f (x) 的周期为2,当x ∈[]11,-时 f (x) =x 2,那么函数y = f (x) 的图象与函数y =x lg 的图象的交点共有( )A .10个 B.9个 C.8个 D.1个(2011全国文12)3.在区间上),(+∞0不是增函数的是------------------------------------------------------------------------------------( )(A) 12+=x y (B) 132+=x y (C) xy 2=(D) 122++=x x y 4.已知ω是正实数,函数()2sin f x x ω=在[,]34ππ-上递增,那么----------------------------------------( ) A .302ω<≤B .02ω<≤C .2407ω<≤ D .2ω≥ 5.已知函数()f x 在[,]a b 上单调,且()()0f a f b ⋅<,则方程()0f x =在[,]a b 上( ) A.至少有一实根 B.至多有一实根 C.无实根 D.必有唯一实根第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题6.若函数2()1f x x mx =++在区间[1,2]上单调,则实数m 的取值范围是 . 7.函数xx y -=2)31(的单调递减区间是__________;函数y=|lg(x-1)|的增区间是____8.若函数()[]2log (3)24a f x ax x =-+在,上是增函数,则实数a 的取值范围是 ;9.若二次函数2()4f x x ax =--+在区间[)1+∞,上单调递减,则a 的取值范围为▲ ;10.定义域为R 的函数()y f x =的值域为[,]a b ,则函数()y f x a =+的值域为_______________ 11.求函数的定义域 (1)xx x y -+=||)(01; (2)6542-+--=x x x y ;(3)xy 111+=; (4)12||y x =+-(5)20(54)lg(43)x y x x =+-+; (6)lg(cos )y x =12.已知函数()y f x =的图像关于直线1x =-对称,且(0,)x ∈+∞时,1()f x x=,则当(,2)x ∈-∞-时,()f x 的解析式为_________________13.若函数m x x x g -+=2)(为偶函数,则实数=m _____________________. 14.一次函数:函数f (x )=-2x +1,当x ∈[-2,3]时, 则f (x )的值域 。
新版精选2019年高中一年级数学单元测试卷《函数的概念和基本初等函数》完整题(含答案)
2019年高中数学单元测试试题 函数的概念和基本初等函数(含答案)学校:__________第I 卷(选择题)请点击修改第I 卷的文字说明 一、选择题1.函数()y f x =的图像与函数2()log (0)g x x x =>的图像关于原点对称,则()f x 的表达式为( ) A .21()(0)log f x x x=> B .21()(0)log ()f x x x =<-C .2()log (0)f x x x =->D .2()log ()(0)f x x x =--<(2006)2.已知函数y= f (x) 的周期为2,当x ∈[]11,-时 f (x) =x 2,那么函数y = f (x) 的图象与函数y =x lg 的图象的交点共有( )A .10个 B.9个 C.8个 D.1个(2011全国文12)3.定义在R 上的偶函数()f x 满足:对任意的1212,(,0]()x x x x ∈-∞≠,有2121()(()())0x x f x f x -->.则当*n N ∈时,有(A)()(1)(1)f n f n f n -<-<+ (B) (1)()(1)f n f n f n -<-<+ (C) (C)(1)()(1)f n f n f n +<-<- (D) (1)(1)()f n f n f n +<-<-4.已知二次函数2()(0)f x x x a a =++>,若()0f m <,则(1)f m +的值( ) (A )正数 (B )负数 (C )零 (D )符号与a 有关5.下列函数中是偶函数,且又在区间(,0)-∞上是增函数的是( )(A) 2y x x =- (B) 65y x -= (C) 1()4xy -= (D)653log y x =第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题6.若函数∈+++=x x a x y ,3)2(2[a ,b]的图象关于直线1=x 对称,则_________=b . 7.将函数23x y =的图像向上平移1个单位,得函数_______________的图像,再将所得图像向左平移2个单位,得函数_____________________的图像8.设函数2()([1,1])f x ax x a x =+-∈-的最大值为()M a ,则对于一切[1,1]a ∈-,()M a 的最大值为 .9. 已知函数2()(2f x x b x a b =++-是偶函数,则函数图像与y 轴交点的纵坐标的最大值是 .10.已知函数()log (21)(01)xa f xb a a =+->≠,的图象如右图所示,则a b ,,1a -,1b -的从小到大的 顺序是11.若1()21xf x a =+-是奇函数,则a = .12.函数322+-=mx x x f )(,当),[+∞-∈2x 时是增函数,当],(2--∞∈x 时是减函数,则)(1f =__________________13.关于函数),0(||1lg)(2R x x x x x f ∈≠+=有下列命题: ①函数)(x f y =的图象关于y 轴对称;②在区间)0,(-∞上,函数)(x f y =是减函数; ③函数)(x f 的最小值为2lg ;④在区间),1(∞上,函数)(x f 是增函数. 其中正确命题序号为_______________14.函数)()(11>+=x xxx f 的值域____________ 15.已知定义域为D 的函数()f x ,对任意x D ∈,存在正数K ,都有()f x K ≤成立,则称函数()f x 是D 上的“有界函数”。
精选最新2019年高中一年级数学单元测试卷《函数的概念和基本初等函数》完整版考核题(含答案)

2019年高中数学单元测试试题 函数的概念和基本初等函数(含答案)学校:__________第I 卷(选择题)请点击修改第I 卷的文字说明 一、选择题1.函数ln cos ()22y x x ππ=-<<的图象是 ( )(2008山东)2.已知函数()|lg |f x x =.若a b ≠且,()()f a f b =,则a b +的取值范围是( ) (A)(1,)+∞ (B)[1,)+∞(C) (2,)+∞ (D) [2,)+∞(2010全国1文7) 【解析1】因为 f(a)=f(b),所以|lga|=|lgb|,所以a=b(舍去),或1b a =,所以a+b=1a a+ 又0<a<b,所以0<a<1<b ,令()f a a=1a +由“对勾”函数的性质知函数()f a 在a ∈(0,1)上为减函数,所以f(a)>f(1)=1+1=2,即a+b 的取值范围是(2,+∞).【解析2】由0<a<b,且f (a )=f (b )得:0111a b ab <<⎧⎪<⎨⎪=⎩,利用线性规划得:0111x y xy <<⎧⎪<⎨⎪=⎩,化为求z x y =+的取值范围问题,z x y y x z =+⇒=-+,2111y y x x'=⇒=-<-⇒过点()1,1时z 最小为2,∴(C) (2,)+∞3.下列函数中,既是偶函数又在()0,+∞单调递增的函数是( )A. 3y x = B. 1y x =+ C. 21y x =-+ D. 2xy -=(2011全国文3)4.设函数()y f x =()x R ∈的图象关于直线0x =及直线1x =对称,且[0,1]x ∈时,2()f x x =,则3()2f -=( )A .12B .14C .34D .94(2008四川理11文11)5.函数x x y 22-=在区间],[b a 上的值域是]3,1[-,则点),(b a 的 轨迹是图中的线段( )(A )AB 和AD (B )AB 和CD (C )AD 和BC (D )AC 和BD6.函数)(x f 在定义域R 内可导,若)2()(x f x f -=,且当)1,(-∞∈x 时,0)()1(<'-x f x ,设).3(),21(),0(f c f b f a ===则BA .c b a <<B .b a c <<C .a b c <<D .a c b <<第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题7.已知函数2(),([2,2])f x x x ∈-=,2()sin(2)3,[0,]62g x a x a x ππ=++∈, 1[2,2]x ∀∈-,001[0,],()()2x g x f x π∃∈=总使得成立,则实数a 的取值范围是 .8.已知函数M,最小值为m,则mM的值为( ) A .14B .12C.2 D2008重庆理4)9.将函数222y x x =++的图象沿直线0x y +=()y f x = 的图象,则()y f x =的表达式为10.在股票买卖过程中,经常用两种曲线来描述价格变化情况:一种是即时价格曲线y=f (x ),另一种平均价格曲线y=g(x ),如f (2)=3表示股票开始卖卖后2小时的即时价格为3元;g(2)=3表示2小时内的平均价格为3元。
最新版精选2019年高中一年级数学单元测试卷《函数的概念和基本初等函数》考核题完整版(含答案)

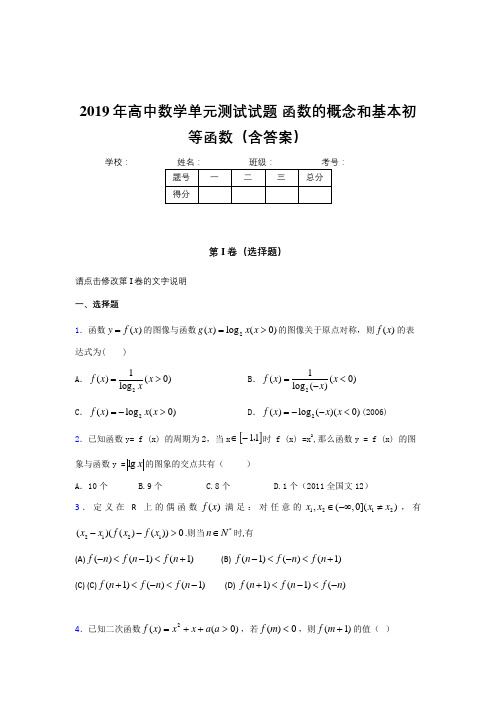
2019年高中数学单元测试试题 函数的概念和基本初等函数(含答案)学校:__________第I 卷(选择题)请点击修改第I 卷的文字说明 一、选择题1.如图所示,单位圆中AB 的长为x ,()f x 表示弧AB 与弦AB 所围成的弓形面积的2倍,则函数()y f x =的图像是( )(2003)2.已知奇函数)(x f 在区间],[a b --上为减函数,且在此区间上)(x f 的最小值为2,则)()(x f x g -=在区间],[b a 上是-------------------------------------------------------------------------------------------------------------( )A .增函数且最大值为2-B . 增函数且最小值为2-C .减函数且最大值为2-D . 减函数且最小值为2-3.若函数()f x 是R上的增函数,对实数a ,b ,若a +b >0,则有------------ ----------( )A.()()()()f a f b f a f b +>-+- B.()()()()f a f b f a f b +<-+- C.()()()()f a f b f a f b ->--- D.()()()()f a f b f a f b -<---第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题4.若13x ≤≤,则(1)函数232y x x =++的值域为 ;(2)函数232y x x =-+的值域为 ;(3)函数282y x x =-+的值域为 ;(4)函数4y x x =+的值域为 ;(5)函数16y x x =+的值域为 ; (6)函数14y x x=+的值域为 .5.设ax x f x21)13(log )(3++=是偶函数,则a 的值为 1-6.函数x x f 3log 1)(-=的定义域是 。
精选新版2019年高中一年级数学单元测试卷《函数的概念和基本初等函数》测试题(含答案)

2019年高中数学单元测试试题 函数的概念和基本初等函数(含答案)学校:__________第I 卷(选择题)请点击修改第I 卷的文字说明 一、选择题1.已知()f x 是周期为2的奇函数,当01x <<时,()lg .f x x =设63(),(),52a f b f ==5(),2c f =则( )A .a b c <<B .b a c <<C .c b a <<D .c a b <<(2006)2.设0>b ,二次函数122-++=a bx ax y 的图像为下列之一则a 的值为( ) (A )1(B )1-(C )251-- (D )251+-(2005全国1理) 3.函数)13lg(13)(2++-=x xx x f 的定义域是( )A.),31(+∞- B. )1,31(- C. )31,31(- D. )31,(--∞(2006广东)4.函数y =11+x 的图象是( )(1995全国文2)5.函数()sin f x x x m n =++为奇函数的充要条件是………………………………………( ) A 、220m n += B 、0mn =C 、0m n +=D 、0m n -=6.已知函数()f x 满足:x ≥4,则()f x =1()2x;当x <4时()f x =(1)f x +,则2(2lo g 3)f += (A )124 (B )112 (C )18 (D )38(2009辽宁卷文)7.函数22)24()2cos x x xf x x xπ+++=+的最大值为M ,最小值为m ,则--------------------------------( )A .4M m -=B .4M m +=C .2M m -=D .2M m +=第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题8.定义在R 上的奇函数()f x 在[0,)+∞上单调递增,且(2)0f -=,则不等式()0xf x >的解集为 .9.已知:753()5f x ax bx cx dx =++++,其中,,,a b c d 为常数,若(7)7f -=-,则(7)f =________10.已知函数f(n)=,则f(3)的值是 。
新版精选2019年高中一年级数学单元测试卷《函数的概念和基本初等函数》考核题完整版(含标准答案)

2019年高中数学单元测试试题 函数的概念和基本初等函数(含答案)学校:__________第I 卷(选择题)请点击修改第I 卷的文字说明一、选择题1.下列函数中,既是偶函数,又在区间(1,2)内是增函数的为( )A .cos 2y x =B .2log ||y x =C .2x x e e y --= D .31y x =+(2012天津文)2.对于任意的两个实数对(a ,b )和(c,d),规定(a ,b )=(c,d)当且仅当a =c,b =d;运算“⊗”为:),(),(),(ad bc bd ac d c b a +-=⊗,运算“⊕”为:),(),(),(d b c a d c b a ++=⊕,设R q p ∈,,若)0,5(),()2,1(=⊗q p 则=⊕),()2,1(q pA. )0,4(B. )0,2(C.)2,0(D.)4,0(- (2006广东)由)0,5(),()2,1(=⊗q p 得⎩⎨⎧-==⇒⎩⎨⎧=+=-210252q p q p q p , 所以)0,2()2,1()2,1(),()2,1(=-⊕=⊕q p ,故选B.3.下列函数中,在其定义域内既是奇函数又是减函数的是( )A. R x x y ∈-=,3B. R x x y ∈=,sinC. R x x y ∈=,D. R x xy ∈=,)21((2006广东)4.若函数)(x f =))(12(a x x x -+为奇函数,则a =( ) (A )21 (B )32 (C )43 (D )1(2011辽宁文6) 5.已知函数⎩⎨⎧<-≥+=0,40,4)(22x x x x x x x f 若2(2)(),f a f a ->则实数a 的取值范围是 A (,1)(2,)-∞-⋃+∞ B (1,2)- C (2,1)- D (,2)(1,)-∞-⋃+∞【考点定位】本小题考查分段函数的单调性问题的运用。
精选最新版2019年高中一年级数学单元测试卷《函数的概念和基本初等函数》考核题完整版(含标准答案)

2019年高中数学单元测试试题 函数的概念和基本初等函数(含答案)学校:__________第I 卷(选择题)请点击修改第I 卷的文字说明 一、选择题1.下列函数中,既是偶函数,又在区间(1,2)内是增函数的为( )A .cos 2y x =B .2log ||y x =C .2x x e e y --= D .31y x =+(2012天津文)2.对于任意的两个实数对(a ,b )和(c,d),规定(a ,b )=(c,d)当且仅当a =c,b =d;运算“⊗”为:),(),(),(ad bc bd ac d c b a +-=⊗,运算“⊕”为:),(),(),(d b c a d c b a ++=⊕,设R q p ∈,,若)0,5(),()2,1(=⊗q p 则=⊕),()2,1(q pA. )0,4(B. )0,2(C.)2,0(D.)4,0(- (2006广东) 由)0,5(),()2,1(=⊗q p 得⎩⎨⎧-==⇒⎩⎨⎧=+=-210252q p q p q p , 所以)0,2()2,1()2,1(),()2,1(=-⊕=⊕q p ,故选B.3.一给定函数)(x f y =的图象在下列图中,并且对任意)1,0(1∈a ,由关系式)(1n n a f a =+得到的数列}{n a 满足)(*1N n a a n n ∈>+,则该函数的图象是( )( 2005辽宁)A B C D4.若对任意∈x R,不等式x≥ax恒成立,则实数a的取值范围是()A. a<-1 B.a≤1 C.a<1 D.a≥1(2007安徽)5.设函数()y f x=()x R∈的图象关于直线0x=及直线1x=对称,且[0,1]x∈时,2()f x x=,则3()2f-=()A.12B.14C.34D.94(2008四川理11文11)6.如图所示,单位圆中AB的长为x,()f x表示弧AB与弦AB所围成的弓形面积的2倍,则函数()y f x=的图像是()(2006重庆理)7.若)(xf在[-5,5]上是奇函数,且)()(13ff<,则--------------------------------------------------------( )(A))()(31-<-f f (B))()(10f f > (C))()(11f f <- (D))()(53->-f f 18.若二次函数f(x)=ax 2+bx+c 的最大值等于(1)f ,设q f p f xx ==)2(,)3(,则 ( ) A .当x<0时p>q ;当x>0时p<q B .当x<0时p<q ;当x>0时p>q C .当x ≠0时,总有p<q D .当x ≠0时,总有p>q9.已知3123(),,,,f x x x x x x R =--∈且1223310,0,0x x x x x x +>+>+>,则123()()()f x f x f x ++的值为 ( )A 一定大于0B 一定小于0C 等于0D 正负都有可能10.设f (x )=(x +2)3,则函数y =f (x -2) ()A 、是偶函数(B )是减函数(C )是奇函数(D )图象关于(1,0)对称11.已知函数2()22(4)1f x mx m x =--+,()g x mx =,若对于任一实数x ,()f x 与()g x 至少有一个为正数,则实数m 的取值范围是( )A . (0,2)B .(0,8)C .(2,8)D . (,0)-∞(2008江西理12文12)第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题12.已知函数y=f(2x-1)的定义域为[-1,2],则f(x) 的定义域为13.已知奇函数()f x 是定义在R 上的减函数,其图像经过A (3,-2),则不等式 ︱f(2x+1)︱<2的解集14.已知定义在R 上的函数()f x 的图象关于点3(,0)4-对称,且满足3()()2f x f x =-+,又(1)1f -=,(0)2f =-,则(1)(2)(3)(2008)f f f f ++++= .115.已知奇函数()x f 在()0,∞-上单调递减,且()02=f ,则不等式()()11--x f x >0的解集是16.已知函数()f x 是偶函数,并且对于定义域内任意的x ,满足()()12f x f x +=-, 若当23x <<时,()f x x =,则)5.2007(f =__________ _17.已知函数(1)f x +为奇函数,函数(1)f x -为偶函数,且(0)2f =,则(4)f =______ 18.定义在[-a ,2]奇函数()f x 在[0,2]x ∈上递增,则(0)f = ,a = ;在[,0]x a ∈- 上增减性为 。
新版精选2019年高中一年级数学单元测试卷《函数的概念和基本初等函数》考核题完整版(含标准答案)
2019年高中数学单元测试试题 函数的概念和基本初等函数(含答案)学校:__________第I 卷(选择题)请点击修改第I 卷的文字说明 一、选择题1.已知函数()f x 是定义在R 上的偶函数, 且在区间[0,)+∞单调递增. 若实数a 满足212(log )(log )2(1)f a f f a ≤+, 则a 的取值范围是( )A .[1,2]B .10,2⎛⎤ ⎥⎝⎦C .1,22⎡⎤⎢⎥⎣⎦D .(0,2] (2013年高考天津卷(文))2.下列函数中,既是奇函数又是增函数的为 ( )A .1y x =+B .2y x =-C .1y x=D .||y x x =(2012陕西文) 3.用表示a ,b 两数中的最小值。
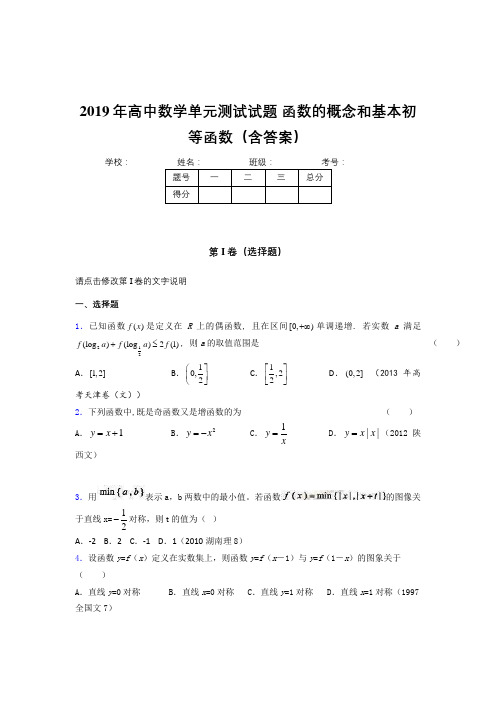
若函数的图像关于直线x=12-对称,则t 的值为( ) A .-2 B .2 C .-1 D .1(2010湖南理8)4.设函数y =f (x )定义在实数集上,则函数y =f (x -1)与y =f (1-x )的图象关于( ) A .直线y =0对称 B .直线x =0对称 C .直线y =1对称D .直线x =1对称(1997全国文7)5.设()f x 是定义在R 上的奇函数,当x ≤0时,()f x x x 2=2-,则()f 1=( ) (A )-3 (B) -1 (C)1 (D)3(2011安徽理3)6.如图所示,一质点(,)P x y 在xOy 平面上沿曲线运动,速度大小不 变,其在x 轴上的投影点(,0)Q x 的运动速度()V V t =的图象大致为A B C D (2009江西卷文)7.如图,函数cos y x x =-的部分图象是-------------------------------------------------( )第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题8.设函数)(x f 定义在R 上,且)1(+x f 是偶函数,)1(-x f 是奇函数,则)2003(f =____(V((V (9.若二次函数3222+-+-=m mx x x f )(的图像的对称轴为02=+x ,则m =________________顶点坐标为____________10.函数y =的定义域是11.函数)86(log 221+-=x x y 的定义域是12.已知)(x f y =是定义在实数集R 上的偶函数,且在[)+∞,0上单调递增。
最新2019年高中一年级数学单元测试卷《函数的概念和基本初等函数》完整题(含答案)

2019年高中数学单元测试试题 函数的概念和基本初等函数(含答案)学校:__________第I 卷(选择题)请点击修改第I 卷的文字说明 一、选择题1.下列函数中,与函数( )A .y=1sin xB .y=1nxxC .y=xe xD .sin xx(2012江西理)D2.若()f x 是R 上周期为5的奇函数,且满足()()11,22f f ==,则()()34f f -=( ) A 、-1B 、1C 、-2D 、2(2010安徽理)3.函数f (x )=x 2+mx +1的图像关于直线x =1对称的充要条件是( )(A )2m =- (B )2m = (C )1m =- (D )1m =(2010四川理4)解析:函数f (x )=x 2+mx +1的对称轴为x =-2m 于是-2m=1 ⇒ m =-24.函数22xy x =-的图像大致是( )(2010山东文11)5.下列函数()f x 中,满足“对任意1x ,2(0,)x ∈+∞,当12x x <时,都有12()()f x f x >的是( )A .1()f x x =B . 2()(1)f x x =-C .()x f x e =D ()ln(1)f x x =+(2009福建理)[解析]依题意可得函数应在(0,)x ∈+∞上单调递减,故由选项可得A 正确 6.若()f x =,则()f x 的定义域为( )A . 1,02⎛⎫-⎪⎝⎭ B . 1,02⎛⎤- ⎥⎝⎦C . 1,2⎛⎫-+∞ ⎪⎝⎭ D . ()0,+∞(2011江西理3)【精讲精析】选A.2x 1)2x 1)11221log 0x 0.log 02++⎧⎪≠<⎨>⎪⎩((2x+1>0由题意得:且,得-< 7.若0<a<1,则函数y=log a (x+5)的图象不经过( ) A .第一象限 B .第二象限C .第三象限D .第四象限(1998上海理13)8.设函数y =f (x )定义在实数集上,则函数y =f (x -1)与y =f (1-x )的图象关于( ) A .直线y =0对称 B .直线x =0对称 C .直线y =1对称D .直线x =1对称(1997全国文7)9.已知定义在R 上的奇函数f (x )满足f (x+2)=-f (x ),则,f (6)的值为( ) (A)-1 (B) 0 (C) 1 (D)2(2006山东理)10.函数()sin f x x x m n =++为奇函数的充要条件是………………………………………( )A 、220m n +=B 、0mn =C 、0m n +=D 、0m n -=11.下列函数()f x 中,满足“对任意1x ,2x ∈(0,+∞),当1x <2x 时,都有1()f x >2()f x的是 A .()f x =1xB. ()f x =2(1)x - C .()f x =xe D ()ln(1)f x x =+(2009福建卷理)12.函数2()||(0)f x ax bx c a =++≠的定义域分成四个单调区间的充要条件是--------------------------( )A .0a >且240b ac -> B .02b a -> C .240b ac -> D .02b a-< 13.已知奇函数)(x f y =在其定义域上是增函数,那么)(x f y -=在它的定义域上--------------------( )(A) 既是奇函数,又是增函数 (B) 既是奇函数,又是减函数(C) 既是偶函数,又是先减后增的函数 (D) 既是偶函数,又事先增后减的函14.已知f (x )是奇函数,且当x ∈(0,+∞)时,f (x )=x 2-2,那么当x ∈(-∞,0)时,f (x )等于x 2-2(B )-x 2-2(C )2-x 2(D )x 2+2第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题15.设()y f x =定义域R ,对于给的正数k ,定义函数()()()()k f x f x k f x kf x k≤⎧=⎨>⎩ 取函数x x f 2log )(=,当21=k 时,函数()k f x 的单调递增区间为 ▲ 。
最新2019年高中一年级数学单元测试卷《函数的概念和基本初等函数》考核题完整版(含答案)
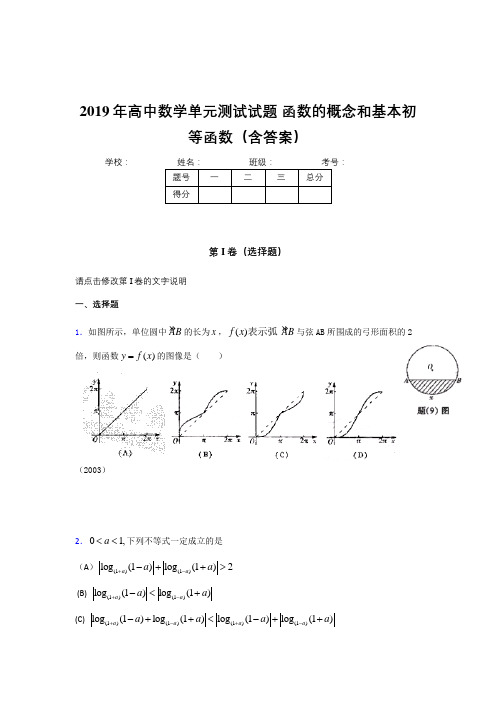
2019年高中数学单元测试试题 函数的概念和基本初等函数(含答案)学校:__________第I 卷(选择题)请点击修改第I 卷的文字说明 一、选择题1.如图所示,单位圆中AB 的长为x ,()f x 表示弧AB 与弦AB 所围成的弓形面积的2倍,则函数()y f x =的图像是( )(2003)2.01,a <<下列不等式一定成立的是 (A )(1)(1)log (1)log (1)2a a a a +--++> (B) (1)(1)log (1)log (1)a a a a +--<+(C) (1)(1)(1)(1)log (1)log (1)log (1)log (1)a a a a a a a a +-+--++<-++(D) (1)(1)(1)(1)log (1)log (1)log (1)log (1)a a a a a a a a +-+---+>--+(2005山东理) 3.设集合044|{},01|{2<-+∈=<<-=mx mx R m Q m m P 对任意实数x 恒成立},则下列关系中成立的是( )(A .P QB .Q PC .P=QD .P Q=(2004湖北理)4.函数y =log 2x 的图象大致是( )(2010四川文2)(A ) (B ) (C ) (D )5.若定义在区间(-1,0)内的函数f (x )=log 2a (x +1)满足f (x )>0,则a 的取值范围是 ( ) A.⎝⎛⎭⎫0,12 B.⎝⎛⎦⎤0,12 C.⎝⎛⎭⎫12,+∞ D .(0,+∞) 解析:∵-1<x <0, ∴0<x +1<1.又f (x )=log 2a (x +1)>0, ∴0<2a <1,即0<a <12.6.已知函数y= f (x) 的周期为2,当x ∈[]11,-时 f (x) =x 2,那么函数y = f (x) 的图象与函数y =x lg 的图象的交点共有( )A .10个 B.9个 C.8个 D.1个(2011全国文12) 7.函数()sin f x x x m n =++为奇函数的充要条件是………………………………………( ) A 、220m n +=B 、0mn =C 、0m n +=D 、0m n -=8.若)(x f 在[-5,5]上是奇函数,且)()(13f f <,则--------------------------------------------------------( )(A))()(31-<-f f (B))()(10f f > (C))()(11f f <- (D))()(53->-f f 19.已知函数()sin(2)f x x ϕ=+,满足()()f x f a ≤对x R ∈恒成立,则----------------------------------( )(A)函数()f x a -一定为奇函数 (B) 函数()f x a -一定为偶函数 (C)函数()f x a +一定为奇函数 (D)函数()f x a +为偶函数第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题10.已知函数3()(,,)1bx c f x a b c a >0ax +=∈+R,是奇函数,若()f x 的最小值为12-,且2(1)5f >,则b 的取值范围是__________. 11.老师给出一个函数y=f (x ).四个学生甲、乙、丙、丁各指出这个函数的一个性质: 甲:对于x ∈R,都有f (1+x )=f (1-x ); 乙:在(-∞, 0)上函数递减; 丙:在(0,+∞)上函数递增; 丁:f (0)不是函数的最小值. 如果其中恰有三个学生说得正确,请写出一个这样的函数: . 12.奇函数()f x 在[3,6]上单调递增,且在[3,6]上的最大值为8,最小值为1-,则2(6)(3)f f -+-= .13.已知函数||y x a =-在区间[)+∞,2上是增函数,那么a 的取值范围是__________. 14.函数y=322--x x 的递增区间为__________.15.一次函数:函数f (x )=-2x +1,当x ∈[-2,3]时, 则f (x )的值域 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019年高中数学单元测试试题 函数的概念和基本初等函数(含答案)学校:__________第I 卷(选择题)请点击修改第I 卷的文字说明 一、选择题1.函数y=x 2+bx+c (x ∈[0,+∞))是单调函数的充要条件是( ) A .b ≥0 B .b ≤0C .b >0D .b <0(2002全国文10,理9)2.设函数()f x 定义在实数集上,它的图像关于直线1x =对称,且当1x ≥时,()31x f x =-,则有( )A .132()()()323f f f <<B .231()()()323f f f <<C .213()()()332f f f <<D .321()()()233f f f <<(2006江苏6)3.二次函数c bx ax y ++=2)0(<ac 的值域为M ,a bx cx y ++=2的值域为N ,则NM ,的关系为( )(A)M N M = B .N N M = C .φ=N M D .φ≠N M 4.函数()||f x x =和()(2)g x x x =-的递增区间分别是_________________ 5.函数)(x f 在定义域R 内可导,若)2()(x f x f -=,且当)1,(-∞∈x 时,0)()1(<'-x f x ,设).3(),21(),0(f c f b f a ===则BA .c b a <<B .b a c <<C .a b c <<D .a c b <<第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题6.二次函数)(x f 满足,1)1()2(-=-=f f 且)(x f 的最大值是8,求此二次函数.7.已知函数⎩⎨⎧≥-+--<+=0x ,a 32x )1a 2(x 0x ,1ax )x (f 2在),(+∞-∞上是增函数,则实数a 的取值范围是 ▲8.函数)13lg(1132++-+=x xx y 的定义域为 ▲ .9.函数)(x f 在),(+∞-∞上为奇函数,且当],(0-∞∈x 时,)()(1-=x x x f ,则当),(+∞∈0x 时,)(x f =___________________________10.函数xx y --=112的单调区间为____________________ 11.设函数)(x f 定义在R 上,且)1(+x f 是偶函数,)1(-x f 是奇函数,则)2003(f =____12.函数1)2(log )(2-+-=x x x f 的定义域是 。
13.函数()1f x ax a =+-在[]1,2上有最大值5,则实数a =14.若奇函数)(x f y =的图象上有一点(3,—2),则另一点 必在)(x f y =的图象上;若偶函数)(x f y =的图象上有一点(3,—2),则另一点 必在)(x f y =的图象上;15.已知:函数()()2411f x x a x =+-+在[)1,+∞上是增函数,则a 的取值范围是16.已知22()(1)(1)2f x m x m x n =-+-++,当,m n 为 时为奇函数。
17.已知函数||y x a =-在区间[)+∞,2上是增函数,那么a 的取值范围是__________. 18.已知函数(1)f x +为奇函数,函数(1)f x -为偶函数,且(0)2f =,则(4)f =______ 19.老师给出一个函数y=f (x ).四个学生甲、乙、丙、丁各指出这个函数的一个性质: 甲:对于x ∈R,都有f (1+x )=f (1-x ); 乙:在(-∞, 0)上函数递减; 丙:在(0,+∞)上函数递增; 丁:f (0)不是函数的最小值. 如果其中恰有三个学生说得正确,请写出一个这样的函数: .20.函数32)(2--=ax x x f 在区间(–∞,2)上为减函数,则a 的范围是21.已知函数y =x +xa有如下性质:若常数0a >,则该函数在区间上是减函数,在区间)+∞上是增函数;函数y =2x +2b x有如下性质:若常数c >0,则该函数在区间上是减函数,在区间[)+∞上是增函数;则函数y =nn c x x+(常数0c >, n 是正奇数)的单调增区间为 ▲ .22.函数()2px p x x f +-=在(1,+∞)上是增函数,则实数p 的取值范围是__________23.函数2()lg(1)f x mx mx =++的定义域为R ,则m 的取值范围是 . 24.若12sin a x x a x ≤≤对任意的π02x ⎡⎤∈⎢⎥⎣⎦,都成立,则21a a -的最小值为 ▲ . 关键字:恒成立问题;不能参变分离;数形结合;最值25.若函数xxk k x f 212)(⋅+-=在其定义域上为奇函数,则实数=k ▲ .26.设a 为实常数,()y f x =是定义在R 上的奇函数,当0x <时,2()97a f x x x=++,若()1f x a ≥+对一切0x ≥成立,则a 的取值范围为________(2013年高考上海卷(理))27.设函数()ln f x x =的定义域为(),M +∞,且0M >,对于任意a ,b ,(,)c M ∈+∞,若a ,b ,c 是直角三角形的三条边长,且()f a ,()f b ,()f c 也能成为三角形的三条边长,那么M 的最小值为 ▲ .28.设函数e ()1exx a f x a -=+(a 为常数)在定义域上是奇函数,则a = ▲ .29.已知函数],1,1[,12)(2-∈--=x x x x f 则函数)(x f 的值域是 .30.函数221)(x xx f +=的最小值是 ▲ .31.已知偶函数()()()2f x x a bx a =++(,a b R ∈)的值域为(]4-∞,,则该函数的解析式为 .32.设()f x 是定义在R 上的奇函数,当x ≤0时,()f x x x 2=2-,则()f 1= ▲ ;33.将函数y =sin (2x +56π)的图象向左平移至少 ▲ 个单位,可得一个偶函数的图象.34.已知函数23()f x x =,[]1,8x ∈-,函数()2g x ax =+,[]1,8x ∈-.若对任意[]11,8x ∈-,总存在[]21,8x ∈-,使12()()f x g x =成立.则实数a 的取值范围是 .35.若a 为正整数,2()(2)1f x ax a x =-++在[0,1]上的最小值为1-,则a = .36.设二次函数2()4(0)f x ax x c a =-+≠的值域为[)0,+∞,且(1)4f ≤,则2244a cu c a =+++的最大值是 。
37.若函数2()f x x x a =-+为偶函数,则实数a = 。
38.定义:区间)](,[2121x x x x <的长度为12x x -.已知函数2|28|y x x =+-定义域为],[b a ,值域为[0,5],则区间],[b a 的长度的最大值为 ▲ . 学科39.已知)(x f 为偶函数,当[)+∞∈,0x 时,1)(-=x x f ,则()0f x <的解集是 40.设函数2()([1,1])f x ax x a x =+-∈-的最大值为()M a ,则对于一切[1,1]a ∈-,()M a 的最大值为 .41.若()22f x x ax =-+与()1ag x x =+在区间[1,2]上都是减函数,则a 的取值范围是 ▲ .42.设()f x 为定义在R 上的奇函数,当0x ≥时,()2x f x x a =++,则(1)f -= ▲ .三、解答题43.设函数2()45f x x x =--. (Ⅰ)画出)(x f y =的图象; (Ⅱ)设A ={}|()7,x f x ≥求集合 A ;(Ⅲ)方程()1f x k =+有两解,求实数k 的取值范围.44.已知R a ∈,函数a x x x f -=)(,(Ⅰ)当a =2时,写出函数)(x f y =的单调递增区间; (Ⅱ)求函数)(x f y =在区间[]2,1上的最小值;(Ⅲ)设0≠a ,函数)(x f 在),(n m 上既有最大值又有最小值,请分别求出n m 、的取值范围(用a 表示).(本题满分18分)45.判断下列函数的奇偶性(1)|1||1|)(-++=x x x f (2)⎪⎩⎪⎨⎧<->--=0,10,1)(33x x x x x f46.已知2()3f x x ax =++(1)当x R ∈时,()f x a ≥恒成立,求实数a 的取值范围; (2)当[2,2]x ∈-时,()f x a ≥恒成立,求实数a 的取值范围; (3)当[2,2]x ∈-时,()3f x a ≤恒成立,求实数a 的取值范围.47.设βα、是关于x 的方程012=+-ax x 的两根,且21,10<<<<βα,求实数a 的取值范围. 5(2,)248.设,x y 是关于m 的方程2260m am a -++=的两个实根,求()()2211x y -+-的最小值。
49.已知()f x 为定义在R 上的奇函数,当0x >时,2()231f x x x =+-,求()f x . 50.二次函数()f x 满足(1)()2,f x f x x +-=且(0)1f =. (1)求()f x 的解析式;(2)在区间[]1,1-上,()y f x =的图象恒在2y x m =+的图象上方,试确定实数m 的范围.。
