05级EDA_B卷+
EDA技术精品课件

高级综合工具是EDA技术中最核心的工具之一,它可以将高层次设计转换成硬件描述语言,如Verilog和VHDL。
1
布局布线工具
2
3
布局布线工具是EDA技术中用于芯片物理设计的工具。
布局布线工具可以将高层次的设计转换成实际的芯片物理设计,包括芯片的布局、布线和验证等。
eda技术精品课件
2023-10-28
目录
contents
EDA技术概述EDA技术的基本原理EDA技术的关键技术EDA技术的设计案例EDA技术的未来趋势
01
EDA技术概述
定义
EDA技术是指电子设计自动化技术,它利用计算机辅助设计软件来完成集成电路的设计、验证和模拟。
特点
自动化程度高,可以大大缩短设计周期;设计灵活,可以适应不同的设计需求;设计成本低,可以提高芯片的竞争力。
布局布线工具能够优化芯片的性能和功耗,并且可以检查芯片设计的可制造性和可靠性。
03
IP核复用技术可以提高设计的可靠性和性能,并且可以缩短设计周期和降低成本。
IP核复用技术
01
IP核复用技术是EDA技术中用于提高设计效率和可靠性的重要技术之一。
02
IP核复用技术可以将已经经过验证的硬件设计模块化,从而避免重复设计和错误。
VS
随着集成电路和半导体技术的不断发展,EDA技术将覆盖更多的应用领域。例如,在物联网、人工智能、5G通信等领域,EDA技术将被广泛应用于各种芯片设计,包括处理器、存储器、传感器等。
扩大EDA技术的应用领域需要不断加强技术研发和市场开拓,以实现技术的广泛应用和商业化落地。
集成电路设计的EDA系统概述

集成电路设计实例
要点一
总结词
集成电路设计是EDA系统的核心应用之一,通过使用EDA 系统,设计师可以完成集成电路的物理设计、验证和优化 。
要点二
详细描述
集成电路设计实例包括微处理器芯片、数字信号处理芯片 等复杂集成电路。EDA系统提供了集成电路物理设计、布 局布线、DRC/LVS检查等功能,确保了集成电路设计的正 确性和可靠性,缩短了产品上市时间。
随着云计算技术的发展,EDA系统将更加 云化,能够提供更加灵活和高效的设计服 务。
协同设计
可定制化设计
随着多项目和跨领域协同设计的需求增加 ,EDA系统将更加注重协同设计功能的建 设和完善。
随着集成电路设计的多样化和个性化需求 增加,EDA系统将更加注重可定制化设计 功能的建设和完善。
05
EDA系统的应用实例
THANKS ห้องสมุดไป่ตู้OR WATCHING
感谢您的观看
物理设计
布图规划
根据电路设计和仿真结果,进行版图规划,确定元件布局和布线策略。
布线设计
根据布图规划结果,进行实际的布线设计,生成物理版图。
布图规划
自动布线
布线优化
支持自动布线功能,提高布线效率和准确性。
对布线结果进行优化,降低信号延迟和功耗。
验证和测试
形式验证
通过数学方法验证电路设计的正确性。
系统复杂性高
EDA系统的功能和模块越来越多,系 统复杂性也越来越高,使用和维护的 难度也随之增加。
数据安全风险
EDA系统涉及大量的设计数据和知识 产权,需要采取有效的安全措施以保 障数据安全。
未来的发展趋势
智能化设计
云化服务
随着人工智能和机器学习技术的发展, EDA系统将更加智能化,能够自动学习和 优化设计过程。
EDA技术实验报告完整版

福建农林大学金山学院信息工程类实验报告课程名称:EDA技术姓名:邱彬彬系:信息与机电工程系专业:电子信息工程专业年级:2010级学号:100201079指导教师:蔡剑卿职称:讲师2013年05月03日实验项目列表福建农林大学金山学院信息工程类实验报告系:信息与机电工程系专业:电子信息工程年级: 2010级姓名:邱彬彬学号: 100201079 实验课程: EDA技术实验室号:__田实405 实验设备号: 2B 实验时间: 2013年4月13日指导教师签字:成绩:实验一Quartus II 9.0软件的使用1.实验目的和要求本实验为验证性实验,其目的是熟悉Quartus II 9.0软件的使用,学会利用Quartus II 9.0软件来完成整个EDA开发的流程。
2.实验原理利用VHDL完成电路设计后,必须借助EDA工具中的综合器、适配器、时序仿真器和编程器等工具进行相应的处理后,才能使此项设计在FPGA上完成硬件实现,并得到硬件测试,从而使VHDL设计得到最终的验证。
Quartus II是Altera提供的FPGA/CPLD开发集成环境,包括模块化的编译器,能满足各种特定设计的需要,同时也支持第三方的仿真工具。
3.主要仪器设备(实验用的软硬件环境)实验的硬件环境是:微机一台GW48 EDA实验开发系统一套电源线一根十芯JTAG口线一根USB下载线一根USB下载器一个实验的软件环境是:Quartus II 9.0软件4.操作方法与实验步骤利用Quartus II 9.0软件实现EDA的基本设计流程:创建工程、编辑文本输入设计文件、编译前设置、全程编译、功能仿真。
利用Quartus II 9.0软件实现引脚锁定和编译文件下载。
利用Quartus II 9.0软件实现原理图输入设计文件的编辑和产生相应的原理图符号元件。
5.实验内容及实验数据记录安装QUARTUSII软件;因为实验时我的机器了已经有QUARTUSII软件,所以我并没有进行安装软件的操作。
冀教版五年级上册期末模拟测试数学试卷(B卷)(含解析)

冀教版五年级上册期末模拟测试数学试卷(B卷)一、认真填空。
(每空1分,共16分)1.在括号里填上合适的面积单位。
我们教室的面积约是48( )。
我们伟大祖国的陆地面积约是960万( )。
北京故宫是世界上最大的宫殿建筑群,占地面积约是72( )。
2.8.495495…是( )小数,保留两位小数后的近似值是( )。
3.36000平方米=( )公顷9.05吨=( )吨( )千克4.25时=( )分1平方千米40公顷=( )公顷4.小明今年a岁,爸爸的年龄比他的3倍大b岁,爸爸今年_____岁。
5.一个平行四边形的底是10厘米,高是6.4厘米,这个平行四边形的面积是( )平方厘米,与这个平行四边形等底等高的三角形的面积是( )平方厘米。
6.王鹏8分钟跑完1.5千米,他平均每分钟跑( )千米。
7.下图是一个直角三角形,已知两条直角边分别是6厘米和8厘米,这个三角形斜边上对应的高是4.8厘米,它的斜边长是( )厘米。
8.财务室会计结账时,发现账面上少了890.1元钱,经核对发现把一笔钱的小数点点错了一位,原来这笔钱是( )元。
二、仔细判断,正确的在括号里画“√”,错误的画“×”。
(10分)9.0.05乘一个小数,所得的积一定比0.05小。
( )10.甲地在乙地北偏东40°方向,则乙地在甲地南偏西40°方向。
( )11.一个盒子里放有4个红球和4个白球,任意摸出1个球,摸到红球和白球的可能性相等。
( )12.小明今年a岁,小华今年(a-b)岁,再过x年后,他们相差x岁。
( ) 13.两个三角形的面积相等,则这两个三角形一定等底等高。
( )三、慎重选择,把正确答案的序号填在括号里。
(12分)14.下列图形中,不能密铺的是()。
15.一个三位小数四舍五入后是3.50,这个三位小数最大和最小相差()。
A.0.007B.0.008C.0.00916.如图,边长相等的两个正方形中,画了甲、乙两个三角形(用阴影表示),它们的面积相比()A.甲的面积大B.乙的面积大C.相等17.王老师带着90元钱去书店买《新华字典》,该书的单价是6.5元。
电路与电子技术-电子设计自动化(eda)简介

HDL描述可以被EDA工具转换成可执行的硬件配置,从而在FPGA或ASIC上实现。
逻辑合成
01
逻辑合成是将HDL描述转换为门级网表的自动化过程
。
02
逻辑合成工具使用优化算法和库技术,将HDL代码转
换为低层次的逻辑门级描述,以便于物理实现。
成熟阶段
20世纪80年代以后,随着计算机技 术的飞速发展,EDA技术逐渐成熟, 出现了许多功能强大的EDA软件, 广泛应用于电子设计领域。
EDA技术的应用领域
集成电路设计
EDA技术广泛应用于集成电路 设计领域,包括逻辑设计、物 理设计、布线设计和可靠性分
析等环节。
电路板设计
EDA技术可以帮助设计师完成 电路板的设计、布局、布线和 仿真等任务,提高设计效率和 产品质量。
大数据分析
通过大数据技术,对电路设计过 程中的数据进行分析,挖掘设计 规律和优化方向,提高设计效率 和质量。
实时计算与仿真
利用云计算的强大计算能力,实 现电路设计的实时仿真和计算, 提高设计的实时性和准确性。
5G通信技术在EDA中的应用
远程协同设计
利用5G高速网络,实现 远程协同设计,让团队 成员在全球范围内进行 实时沟通和协作。
特点
EDA技术具有自动化、智能化、高精度和高效率等特点,能够大大提高电路和 电子系统的设计和生产效率,降低成本,缩短研发周期。
EDA技术的发展历程
初级阶段
20世纪60年代,人们开始使用计 算机辅助设计(CAD)软件进行 简单的电路原理图绘制和布局。
发展阶段
20世纪70年代,随着集成电路的 出现,EDA技术逐渐发展,出现了 电路仿真和版图自动布局布线等工 具。
EDA技术及应用-VHDL版(第三版)(潭会生)第7章详解

第7章 EDA技术实验
CLK CLR ENA
CNT10
CLK
U0
CLR
ENA
CQ[3..0] CO
DOUT[3..0] S0
CNT10
CLK
U1
CLR
ENA
CQ[3..0] CO
DOUT[7..4] S1
CNT10
CLK CLR ENA
U2 CQ[3..0] CO
DOUT[11..8] S2
CNT10 U3
第7章 EDA技术实验
ห้องสมุดไป่ตู้验证清零功能
验证使能有效
验证计数功能
预计可能结果
图7.2 CNT10仿真输入设置及可能结果估计图
第7章 EDA技术实验
4) 管脚锁定文件 根据图7.1所示的CNT9999电路原理图,本设计实体的 输入有时钟信号CLK、清零信号CLR和计数使能信号ENA, 输出为DOUT[15..0],据此可选择实验电路结构图NO.0,对 应实验模式0。 根据图7.5所示的实验电路结构图NO.0和图7.1确定引脚 的锁定。选用EPM7128S-PL84芯片,其引脚锁定过程如表 7.1所示,其中CLK接CLOCK2,CLR接键3,ENA接键4, 计数结果DOUT[3..0]、DOUT[7..4]、DOUT[11..8]、 DOUT[15..12]经外部译码器译码后,分别在数码管1、数码 管2、数码管3、数码管4上显示。
第7章 EDA技术实验
3.实验要求 (1) 画出系统的原理框图,说明系统中各主要组成部分 的功能。 (2) 编写各个VHDL源程序。 (3) 根据系统的功能,选好测试用例,画出测试输入信 号波形或编好测试程序。 (4) 根据选用的EDA实验开发装置编好用于硬件验证的 管脚锁定表格或文件。 (5) 记录系统仿真、逻辑综合及硬件验证结果。 (6) 记录实验过程中出现的问题及解决办法。
数字电子技术三个教学环节教改创新情况.doc
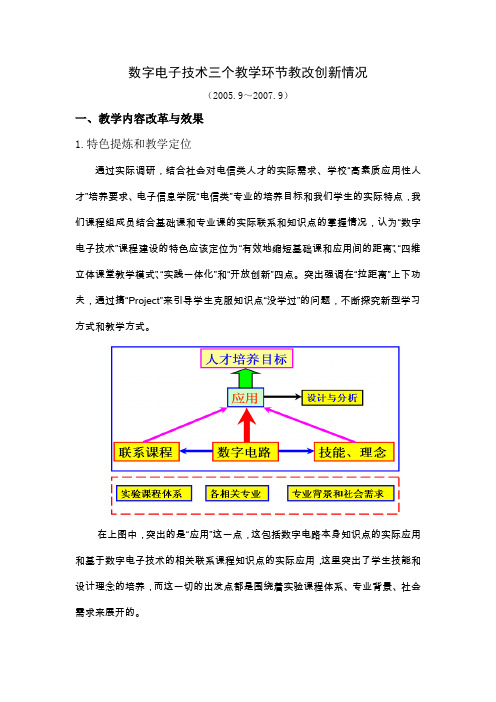
数字电子技术三个教学环节教改创新情况(2005.9~2007.9)一、教学内容改革与效果1.特色提炼和教学定位通过实际调研,结合社会对电信类人才的实际需求、学校“高素质应用性人才”培养要求、电子信息学院“电信类”专业的培养目标和我们学生的实际特点,我们课程组成员结合基础课和专业课的实际联系和知识点的掌握情况,认为“数字电子技术”课程建设的特色应该定位为“有效地缩短基础课和应用间的距离”、“四维立体课堂教学模式”、“实践一体化”和“开放创新”四点。
突出强调在“拉距离”上下功夫,通过搞“Project”来引导学生克服知识点“没学过”的问题,不断探究新型学习方式和教学方式。
在上图中,突出的是“应用”这一点,这包括数字电路本身知识点的实际应用和基于数字电子技术的相关联系课程知识点的实际应用,这里突出了学生技能和设计理念的培养,而这一切的出发点都是围绕着实验课程体系、专业背景、社会需求来展开的。
与此同时,从数字电路的角度,理顺了教学内容、知识点的落实和后续应用的关系,构建了一下的模式,并确定了相互间的联系。
另外结合相关课程的任课教师情况,确立了前后内容的责任教师。
另外其他相关教师在实践教学中发挥一定的作用,并有所侧重。
2.教学内容组织方式具体实施中,体现“大班教学,小班讨论”的教学思想,以分组讨论,提问式、小组协作式等方式展开学习交流和讨论,同时通过网上教学BBS载体展开教学活动。
课堂教学中,贯彻探究型课堂教学模式的应用,主要从四个方面入手,突出学生的主体地位,教师就是服务和引导。
改变中最突出的一点就是,让学生学会学习,同时通过实验实践教学活动的一系列教学规范措施,让学生学会“如何做人”、“如何养成良好的工程习惯”和“如何展示自我”。
具体确立的总体方案如下图所示,突出的是“有机结合”和“精品课件”。
1)理论教学理论教学具体实施模式如下图所示,突出“黑板+PPT+EDA仿真+网络课程”的四维模式,同时结合“提问式”、“分组式”、“问题探究式”等过程实施。
《eda技术》课程教学

VHDL编程实例分析
1 2
组合逻辑电路设计
通过实例分析,讲解如何使用VHDL语言设计组 合逻辑电路,如编码器、译码器、数据选择器等。
时序逻辑电路设计
通过实例分析,讲解如何使用VHDL语言设计时 序逻辑电路,如触发器、计数器、寄存器等。
3
状态机设计
通过实例分析,讲解如何使用VHDL语言设计状 态机,包括Moore型状态机和Mealy型状态机。
05
CPLD/FPGA应用与开发
CPLD/FPGA器件概述
CPLD(Complex Programmable Logic Device)和FPGA(Field Programmable Gate Array)的基本概念和原理
CPLD和FPGA的结构和特点
CPLD和FPGA的编程方式和编程语言
CPLD/FPGA开发流程
综合与优化
将设计转换为门级网表,并进 行优化
仿真与验证
对设计进行功能仿真和时序仿 真,确保设计的正确性
设计输入
使用硬件描述语言(HDL)或 原理图输入设计
布局与布线
将门级网表映射到 CPLD/FPGA器件上,并进行 布局和布线
下载与调试
将设计下载到CPLD/FPGA器 件中,并进行调试和测试
典型应用案例分析
用操作。
合理利用图层
02
通过图层管理可以方便地组织和编辑复杂的原理图,提高可读
性。
灵活运用编辑工具
03
掌握各种编辑工具的使用技巧,如选择、移动、旋转、镜像等。
层次化设计思想
自顶向下设计
从系统最高层次开始,逐 步细化到低层次的设计方 法。
模块化设计
将复杂的系统划分为若干 个相对独立的模块,分别 进行设计。
五年级英语补充答案下册05网

五年级英语补充答案下册05网第一部分听力技能(共两节,满分20分)做题时,先在试题卷上作答。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节 (共5小题;每小题1分,满分5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、c三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话读两遍。
1. Where is the woman going?A. To the factory.B. To the store.C. To the hospital.2. How often does the subway run?A. Every 10 minutes.B. Every 20 minutes.C. Every 30 minutes.3. What was the weather like in Shanghai?A. Sunny.B. Rainy.C. Cloudy.4. Who made a call half an hour ago?A. Jim's friend.B. Jim's aunt.C. Jim's uncle.5. What does the man think of the CD?A. It's very good.B. It's too expensive.C. It deserves the price.第二节 (共15小题;每小题1分,满分15分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、c三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
听下面一段对话,回答第6和第7两个小题。
6. How many people will go hiking tomorrow?A. Two.B. Three.C. Four.7. Why will they start early?A. Because it is far.B. Because it is hot.C. Because it will rain.听下面一段对话,回答第8和第10两个小题。
电子设计自动化EDA

可测试性设计
EDA技术可以帮助设计师进行 可测试性设计,提高产品的可
测试性和可靠性。
02
EDA工具分类与功能
硬件描述语言(HDL)工具
总结词
用于描述数字电路和系统的行为和结构。
详细描述
HDL工具包括Verilog和VHDL等,用于描述数字电路和系统的行为和结构。这 些工具支持逻辑设计、模拟、验证等功能,是电子设计过程中不可或缺的一部 分。
05
EDA发展趋势与未来展望
AI与机器学习在EDA中的应用
自动化设计优化
利用机器学习算法对电路设计进行自动优化, 提高设计的性能和可靠性。
智能物理设计
通过机器学习技术实现物理设计的自动化, 提高设计的效率和质量。
自动化布线
利用机器学习技术实现布线的自动化,提高 布线的准确性和效率。
自动化测试
通过机器学习技术实现测试的自动化,提高 测试的准确性和效率。
特点
EDA技术具有自动化程度高、设计灵 活、精度高、可重复性好等优点,能 够大大提高设计效率,缩短产品上市 时间。
EDA技术的发展历程
起源
20世纪60年代,随着集成电路的出现, 人们开始使用计算机辅助设计工具进 行电子系统设计。
发展
现状
目前,EDA技术已经成为电子系统设 计不可或缺的重要工具,广泛应用于 集成电路、印刷电路板、系统级等多 个领域。
云计算与高性能计算在EDA中的应用
01
云计算资源共享
02
高性能计算加速
03
云端协同设计
通过云计算技术实现EDA资源的 共享,提高资源的利用率和效率。
利用高性能计算技术加速EDA的 计算过程,提高设计的速度和效 率。
人教版2022--2023学年度第一学期五年级英语期中测试卷及答案(含三套题)

…○………………内………………○………………装………………○………………订………………○………………线………………○…………………○………………外………………○………………装………………○………………订………………○………………线………………○………………… 学校:______________姓名:_____________班级:_______________考号:______________________人教版2022--2023学年度第一学期期中测试卷五年级 英语本试卷总分100分,考试时间60分钟。
题号 一二 三 四 五 六 七 八 九 十 十一 十二 总分 得分听力部分(30分)一、听录音,选出你所听到的单词。
(每小题1分,共5分) ( )1. A. Friday B. funny C. sunny ( )2. A. fish B. shyC. fresh( )3. A. thirstyB. ThursdayC. thirty( )4. A. sweetB. windyC. weekend ( )5. A. healthyB. happyC. Saturday二、听录音,判断下列图片与所听内容是否相符。
相符的打(√),不相符的打(×)。
(每小题1分,共5分)1. ( )2.( )3.( )4. ( )5.( ) 三、听问句,选答语。
(每小题2分,共10分) ( )1. A. Yes. I am. B. No. he isn’t.C. Yes, she is.( )2. A. Yes. I do.B. I have English and PE.C. I watch TV.( )3. A. I like some beef. B. Noodles, please. C. I’d like some milk. ( )4. A. Yes, I do. B. No, I am not.C. No, I can’t.( )5. A. He likes art. B. He can swim. C. He is hard-working. 四、听对话,根据对话内容选择正确答案。
05_EDA工具课程之PrimeTime

Company Logo
三、PrimeTime进行时序分析的流程
4、 进行分析和生成报告
-时序约束检查 -生成约束报告( constraint reports ) -生成瓶颈分析报告( bottleneck reports ) -生成路径时序报告( path timing reports )。
Company Logo
五、PrimeTime命令简介
创建时钟
create_clock -period period_value [-waveform edge_list] [-name clock_name] [source_objects]
pt_shell>create_clock -period 4 -waveform [list 0 2] – name\ clk [get_ports clk]
rimeTime的用户界面
PrimeTime 提供两种用户界面,图形用户界面GUI(Graphical User Interface)和基于Tcl 的命令行界面pt_shell,其运行方式分别是:
% PrimeTime
% pt_shell
Company Logo
三、PrimeTime进行时序分析的流程
1、 建立设计环境 - 建立搜索路径(search path)和链接路径(link path) - 读入设计和库 (read_verilog和read_db) - 链接顶层设计 -建立运作条件、连线负载模型、端口负载、驱动和传输时间
Company Logo
五、PrimeTime命令简介
设计输入 PT不能读取RTL源文件,它是静态分析引擎,只能读取映射后的 设计,包括db、verilog、vhdl和edif等格式的文件。
eda论文【范本模板】

摘要:随着基于PLD的EDA技术的发展和应用领域的扩大与深入,EDA技术在电子信息、通信、自动控制及计算机应用等领域的重要性日益突出。
从而使它成为当今电子技术发展的前沿之一;本文详细介绍EDA课程设计及相关内容,阐述了EDA的基本概念及发展过程。
关键词: EDA 发展与应用自动售货机1。
EDA概况及特点EDA是电子设计自动化(Electronic Design Automation)缩写,是90年代初从CAD(计算机辅助设计)、CAM(计算机辅助制造)、CAT(计算机辅助测试)和CAE(计算机辅助工程)的概念发展而来的。
EDA技术是以计算机为工具,根据硬件描述语言HDL( Hardware Description language)完成的设计文件,自动地完成逻辑编译、化简、分割、综合及优化、布局布线、仿真以及对于特定目标芯片的适配编译和编程下载等工作。
EDA技术作为现代电子设计技术的核心,它依赖强大的计算机,在EDA工具软件平台上,对以硬件描述语言HDL 为系统逻辑描述手段完成的设计文件,自动地完成逻辑编译、逻辑简化、逻辑分割、逻辑综合,以及逻辑优化和仿真测试,直至实现既定的电子线路系统功能。
它的基本特征是:设计人员按照“自顶向下”的设计方法,对整个系统进行方案设计和功能划分,系统的关键电路用一片或几片专用集成电路(ASIC)实现,然后采用硬件描述语言(HDL)完成系统行为级设计,最后通过综合器和适配器生成最终的目标器件,这样的设计方法被称为高层次的电子设计方法。
下面介绍与EDA基本特征有关的几个概念。
1.“自顶向下"的设计方法10年前,电子设计的基本思路还是选用标准集成电路“自底向上”地构造出一个新的系统,这样的设计方法就如同一砖一瓦建造金字塔,不仅效率低、成本高而且容易出错。
高层次设计是一种“自顶向下"的全新设计方法,这种设计方法首先从系统设计入手,在顶层进行功能方框图的划分和结构设计。
部编数学八年级上册专题05模型方法课之三垂直模型压轴题专练(解析版)(人教版)含答案

答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的小朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!专题05模型方法课之三垂直模型压轴题专练(解析版)学校:___________姓名:___________班级:___________考号:___________一、单选题1.如图,在等腰直角ABC V 中,4AC BC ==,EDF Ð的直角顶点D 与AB 的中点重合,两边分别交AC ,BC 于点E ,F ,有以下结论:①CE BF =;②12ABC CFDE S S =V 四边形;③14DEF S ££V ;④2222BF CF DF +=.上述结论错误的是( )A .①B .②C .③D .④【答案】C【分析】①证明△CDE ≌△BDF ,即可得出CE= BF ,故①正确;②根据△CDE ≌△BDF ,得出S △DCE =S △BDF ,即可得出答案,故②正确;③由①可知DE=DF ,推出△DEF 是等腰直角三角形,得出S △DEF =12·DE·DF ,根据当DE 最短时,S △DEF 最小,当DE 最长时,S △DEF 最大,然后分类讨论即可2≤S △DEF ≤4,故③错误;④由①得BF=CE ,根据在Rt △ECF 中,EC 2+CF 2=EF 2和在Rt △DEF 中,DE 2+DF 2=EF 2,根据DE=DF ,即可得出BF 2+CF 2=2DF 2,故④正确,即可得出答案.【详解】①∵ AC= BC ,D 是AB 的中点,∴CD ⊥AB ,∴∠CDB = 90°,∵∠EDF=90°,∴∠CDE+∠CDF=∠BDF+∠CDF ,∴∠CDE=∠BDF ,∵D 是Rt △ABC 斜边AB 上的中点,AC= BC ,∴CD=BD=AD=12АВ,∠ACD=∠B=45°,在△CDE 和△BDF 中=CDE BDF CD BDDCE B =ìî=ïíï∠∠∠∠∴△CDE ≌△BDF (AAS ),∴DE= DF ,CE= BF ,故①正确;②∵△CDE ≌△BCF ,∴S △DCE =S △BDF ,S 四边形CDFE = S △CDF +S △BDF =S △BDC =12S △ABC ,故②正确;③由①可知DE=DF ,∵∠EDF=90°,∴△DEF 是等腰直角三角形,∴S △DEF =12·DE·DF ,则当DE 最短时,S △DEF 最小,当DE 最长时,S △DEF 最大,当DE ⊥AC 时,DE 最小,此时DE ∥BC ,∵DE 是AB 中点,∴DE 是△ABC 的中位线,∴DE=12BC=2,∴S △DEF 的最小值为12×2×2=2,当E 与A 重合,F 与C 重合时,DE 最大,此时DE=AD=12AB ,=2则DE=∴S △DEF 的最小值为12××,∴2≤S △DEF ≤4,故③错误;④由①得BF=CE ,∴在Rt △ECF 中,EC 2+CF 2=EF 2,又∵在Rt △DEF 中,DE 2+DF 2=EF 2,∵DE=DF ,∴EC 2+CF 2=2DF 2,∴BF 2+CF 2=2DF 2,故④正确;故选:C .【点睛】本题考查了全等三角形的判定和性质,等腰三角形的判定和性质,勾股定理,三角形的中位线的性质,题目综合性很强,掌握这些知识点是解题关键.2.在正方形ABCD 中,直线m 经过对角线AC ,BD 的交点O ,过A ,B 两点分别作直线m 的垂线,交直线m 于点E ,F .若2AE =,5BF =,则EF 长为()A .2B .3C .2或6D .3或7【答案】D【分析】依据已知条件求出90AEO BFO Ð=Ð=°,EAO FOB Ð=Ð,根据AAS 证EAO FOB @V V ,推出2AE OF ==,5OE BF ==,即可得到EF 的长.【详解】解:如图,当直线m 与线段AB 不相交时,AE m ^Q ,BF m ^,90AOB Ð=°,90AOE EAO AOE BOF \Ð+Ð=°=Ð+Ð,AEO OFB Ð=Ð,EAO FOB \Ð=Ð,又Q 正方形ABCD 中,AO OB =,()EAO FOB AAS \@V V ,2AE OF \==,5BF EO ==,527EF EO FO \=+=+=;如图,当直线m 与线段AB 相交时,AE m ^Q ,BF m ^,90AOB Ð=°,90AOE EAO AOE BOF \Ð+Ð=°=Ð+Ð,AEO OFB Ð=Ð,EAO FOB \Ð=Ð,又Q 正方形ABCD 中,AO OB =,()EAO FOB AAS \@V V ,2AE OF \==,5BF EO ==,523EF EO FO \=-=-=;故选D .【点睛】本题考查三角形全等的判定方法和全等三角形的性质的运用,判定两个三角形全等的一般方法有:SSS 、SAS 、SSA 、HL .本题要注意思考全面,直线m 与线段AB 有两种情况(相交、不相交),不能遗漏.3.如图,正方形ABCD 中,E ,F 分别为AB ,AD 上的点,AF BE =,CE ,BF 交于点H ,BF 交AC 于点M ,O 为AC 的中点,OB 交CE 于点N ,连接OH .下列结论:①BF CE ^;②BM CN =;③45FHO Ð=°;④CH BH -,正确的个数是( )A .1B .2C .3D .4【答案】D【分析】①可证ABF BEC @V V 得BCE ABF Ð=Ð,所以90HBC HCB Ð+Ð=°,由此得证.②由题意正方形中ABO BCO Ð=Ð,在上面所证BCE ABF Ð=Ð,得ECO FBO Ð=Ð,结合正方形性质易证OBM ONC @V V (AAS )得到BM CN =即得证.③过O 点作OG 垂直于OH ,OG 交CH 于G 点,可证得OGC OHB @V V . 得OHG V 是等腰直角三角形,由45FHO FHC OHC Ð=Ð-Ð=°,④由OGC OHB @V V 得CG BH =,所以=CH BH HG -=.【详解】解:AF BE =Q ,AB BC =,90ABC BAD Ð=Ð=°,()ABF BEC SAS \@V V ,BCE ABF \Ð=Ð,又∵90ABC ABH HBC Ð=Ð+Ð=°,∴90HBC HCB Ð+Ð=°,即BF EC ^,故结论①正确;Q 四边形是正方形,BO AC \^,BO OC =,由题意正方形中ABO BCO Ð=Ð,在上面所证BCE ABF Ð=Ð,ECO FBO \Ð=Ð,OBM ONC \@V V (AAS ),BM CN \=,即结论②正确;过O 点作OG 垂直于OH ,OG 交CH 与G 点,∵HON NOG NOG GOC Ð+Ð=Ð+Ð,∴HON GOC Ð=Ð,在OGC V 与OHB V 中,OCN OBH OC OBHON GOC Ð=Ðìï=íïÐ=Ðî,故OGC OHB @V V (ASA ),∴=OH OG ,OH OG ^Q ,=45OHG \а,∴904545FHO FHC OHC Ð=Ð-Ð=°-°=°,故结论③正确;∵OGC OHB @V V ,BH CG \=,∴CH BH CH CG HG -=-=,90HOG Ð=°Q ,=OH OG ,∴=CH BH HG -=,故结论④正确;综上所述,①②③④正确.【点睛】本题考查了正方形的性质,全等三角形的证明以及等腰直角三角形性质,充分利用线段和角证明三角形全等,转化线段和角的关系是解题关键,比较综合,有一定难度.二、填空题4.如图,已知△ABC 中,∠ABC=45°,AD 与BE 为△ABC 的高,交点为F ,CD=4,则线DF=___________.【答案】4【分析】求出AD=BD ,求出∠ADC=∠ADB=90°,∠CAD=∠FBD ,根据ASA 证△BDF ≌△ADC ,根据全等三角形的性质推出DF=DC 即可.【详解】解:∵AD ⊥BC ,BE ⊥AC ,∴∠ADC=∠ADB=∠BEA=90°,∴∠CAD+∠AFE=90°,∠BFD+∠DBF=90°,∵∠AFE=∠DFB ,∴∠CAD=∠FBD ,∵∠ADB=90°,∠ABC=45°,∴∠BAD=∠ABD=45°,∴AD=BD ,在△BDF 和△ADC 中FBD DAC BD ADBDF ADC Ð=Ðìï=íïÐ=Ðî, ∴△BDF ≌△ADC (ASA ),∴DF=DC=4,故答案为:4.本题考查了垂直定义,余角的性质,等腰直角三角形的判定与性质,全等三角形的性质和判定,掌握全等三角形的判定方法(即SSS 、SAS 、ASA 、AAS 和HL )是解题的关键.5.如图,已知正方形ABCD 的边长为4,点E 是AB 边上一动点,连接ED ,将ED 绕点E 顺时针旋转90°到EF ,连接,DF CF ,则DF CF +的最小值是_____.【答案】【分析】如图所示,根据题意构造出△AED 和△GFE 全等,分析出点F 的轨迹,然后根据D 、F 、C 三点共线时求出最小值即可.【详解】解:连接BF ,过点F 作FG ⊥AB 交AB 延长线于点G ,∵将ED 绕点E 顺时针旋转90°到EF ,∴EF ⊥DE ,且EF =DE ,∵90ADE AED Ð+Ð=°,90GEF AED +=°∠∠,∴∠EDA =∠FEG ,∴在△AED 和△GFE 中,A EGF ADE FEGDE EF Ð=ÐìïÐ=Ðíï=î∴△AED ≌△GFE (AAS ),∴FG =AE ,AD GE =,又∵AD AB =,∴GE AB =,∴AE BG =,∴FG BG =,又∵FG BG ^,∴BGF V 是等腰直角三角形,∴45GBF Ð=°,∴BF 是∠CBC ′的角平分线,即F 点在∠CBC ′的角平分线上运动,过点C 作BF 的对称点C ¢,则4,BC BC ¢==∴C 点在AB 的延长线上,CBC ¢△是等腰直角三角形,∴当D 、F 、C 三点共线时,DF +CF =DC ¢最小,∴在DAC ¢△中,AD =4,8AC AB BC AB BC ¢¢=+=+=,∴DC AD ¢===,∴DF +CF 的最小值为,故答案为:【点睛】本题考查了旋转的性质,正方形的性质,轴对称求最短路径,能够将线段的和通过轴对称转化为共线线段是解题的关键.6.如图,正方形ABCD 中,E 为DC 边上一点,且2DE =,将AE 绕点E 逆时针旋转90°得到EF ,连接AF 、FC ,则线段FC 的长度是_________.【答案】.【分析】作FH CD ^于点H ,如图,利用正方形的性质得DA CD =, 90D Ð=°,再根据旋转的性质得EA EF =, 90AEF Ð=°,接着证明 ADE EHF @V V ,得到 2DE FH ==,AD EH =,所以 EH DC =,则 2DE CH ==,然后利用勾股定理计算FC 的长.【详解】如图,作FH CD ^于点H ,∵四边形ABCD 为正方形,∴DA CD =,90D Ð=°,∵AE 绕点E 顺时针旋转90°得到EF ,∴EA EF =, 90AEF Ð=°,∵90DAE AED Ð+=°,90FEH AED Ð+Ð=°,∴EAD FEH Ð=Ð,在ADE V 和EHF V 中,D FHE EAD FEH AE EF Ð=ÐìïÐ=Ðíï=î,∴()ADE EHF AAS @V V ,∴2DE FH ==,AD EH =,∴EH DC =,即DE CE CH EC +=+,∴2DE CH ==,在Rt CFH V中,FC ===故答案为:【点睛】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等,也考查了正方形的性质.7.如图,在四边形ABCD 中,45B C Ð=Ð=°,P 是BC 上一点,PA PD =,90APD Ð=°,AB CD BC +=______.【分析】通过等腰直角三角形构建一线三等角模型求解即可.【详解】解:如图所示,分别过A 、D 作AE BC ^于E ,DF BC ^于F∴90AEP DFP Ð=Ð=°∴90APE PAE Ð+Ð=°,90DPF PDF Ð+Ð=°∵90APD Ð=°∴90APE DPF +=°∠∠∴APE DPF Ð=Ð ,PAE DPF Ð=Ð在AEP △与DFP △中APE DPFPA PDPAE DPFÐ=Ðìï=íïÐ=Ðî∴()AEP DPF ASA @△△∴AE PF = ,PE DF =45,C Ð=°Q45,FDC C \Ð=Ð=°,DF FC PE \==在Rt ABE △中,45B Ð=°∴AB===同理可得:CD==∴AB CDBC+===.【点睛】本题考察特殊的直角三角形,灵活运用一线三等角模型及特殊直角三角形三边关系是解题的关键.三、解答题8.如图1,在△ABC中,∠ACB=90°,AC=BC,过C在△ABC外作直线MN,AM⊥MN于点M,BN⊥MN于点N.(1)求证:MN=AM+BN;(2)如图2,若过点C作直线MN与线段AB相交,AM⊥MN于点M,BN⊥MN于点N(AM>BN),(1)中的结论是否仍然成立?说明理由.【答案】(1)见解析;(2)不成立,理由见解析【分析】(1)根据垂直的定义得到∠AMC=∠CNB=90°,则∠MAC+∠ACM=90°,又∠ACB=90°,则∠ACM+∠NCB=90°,于是根据等量代换得到∠MAC=∠NCB,根据“AAS”可证明△ACM≌△CBN,根据全等的性质得到AM=CN,CM=BN,则MN=MC+CN=AM+BN.(2)根据已知条件能证得△ACM≌△CBN,利用全等的性质得到AM=CN,CM=BN,而MN=CN-CM=AM-BN.【详解】解:(1)∵AM⊥MN于点M,BN⊥MN于点N,∴∠AMC=∠CNB=90°,∴∠MAC+∠ACM=90°,∵∠ACB=90°,∴∠ACM+∠NCB=90°,∴∠MAC=∠NCB ,在△ACM 和△CBN 中,AMC CNB MAC NCB AC BC Ð=ÐìïÐ=Ðíï=î\∴ACM ≌△CBN ,∴AM=CN ,CM=BN ,∴MN=MC+CN=AM+BN .(2)题(1)中的结论不成立,同题(1)证明可知:ACM ≌△CBN ,∴AM=CN ,CM=BN ,∴MN=CN-CM=AM-BN ,【点睛】本题主要考查的是全等三角形的性质与判断,正确的掌握全等三角形的性质与判断是解题的关键.9.如图,90BCA Ð=°,AC BC =,BE CF ^于点E ,AF CF ^于点F ,其中045ACF °<Ð<°.(1)求证:BEC CFA @V V ;(2)若5AF =,8EF =,求BE 的长;(3)连接AB ,取AB 的中点为Q ,连接QE ,QF ,判断QEF △的形状,并说明理由.【答案】(1)证明见解析;(2)13;(3)QEF △是等腰直角三角形,理由见解析.【分析】(1)先根据垂直的定义可得90BEC CFA Ð=Ð=°,再根据直角三角形的两锐角互余、角的和差可得CBE ACF Ð=Ð,然后根据三角形全等的判定定理即可得证;(2)先根据三角形全等的性质可得,5BE CF CE AF ===,再根据线段的和差可得13CF =,由此即可得;(3)如图(见解析),先根据等腰直角三角形的判定与性质可得45,,BAC BCQ CQ AQ CQ AB Ð=Ð=°=^,再根据三角形全等的性质可得,CE AF BCE CAF =Ð=Ð,从而可得ECQ FAQ Ð=Ð,然后根据三角形全等的判定定理与性质可得,CQE QE Q A F F Q =Ð=Ð,最后根据等腰直角三角形的判定即可得.【详解】(1),B AF CF E CF ^^Q ,90BEC CFA \Ð=Ð=°,90CBE BCE \Ð+Ð=°,90BCA Ð=°Q ,90ACF BCE \Ð+Ð=°,CBE ACF \Ð=Ð,在BEC △和CFA △中,BEC CFA CBE ACF BC CA Ð=ÐìïÐ=Ðíï=î,()BEC CFA AAS \@V V ;(2)由(1)已证:BEC CFA @V V ,,BE CF CE AF \==,5AF =Q ,5CE \=,8EF =Q ,5813CF CE EF \=+=+=,13BE \=;(3)QEF △是等腰直角三角形,理由如下:如图,连接CQ ,90,A CA C BC B °==ÐQ ,ABC \V 是等腰直角三角形,45BAC Ð=°,Q 点Q 是斜边AB 的中点,1,,452CQ AQ CQ AB BCQ B A AC BC \=^==°=ÐÐÐ,90CQE AQE AQC \Ð+Ð=Ð=°,由(1)已证:BEC CFA @V V ,,CE AF BCE CAF \=Ð=Ð,BCQ B B F C CE CA A \Ð-=ÐÐ-Ð,即ECQ FAQ Ð=Ð,在CEQ V 和AFQ △中,CQ AQ ECQ FAQ CE AF =ìïÐ=Ðíï=î,()CEQ AFQ SAS \@V V ,,CQ QE E Q AQF F =Ð\=Ð,QEF \V 是等腰三角形,又90CQE AQE Ð+Ð=°Q ,90AQF AQE \Ð+Ð=°,即90EQF Ð=°,QEF \V 是等腰直角三角形..【点睛】本题考查了三角形全等的判定定理与性质、等腰直角三角形的判定与性质、直角三角形斜边上的中线等知识点,较难的是题(3),通过作辅助线,构造全等三角形是解题关键.10.如图,三角形ABC 中,AD BC ^于D ,若BD AD =,FD CD =.(1)求证:FBD CAD Ð=Ð;(2)延长BF 交AC 于点E ,求证:BE AC ^.【答案】(1)见解析;(2)见解析.【分析】(1)求出∠ADC=∠BDF=90°,根据SAS 证△ADC ≌△BDF ,根据全等三角形的性质推出∠FBD=∠CAD 即可;(2)根据三角形的内角和定理求出∠FBD+∠BFD=90°,推出∠AFE+∠EAF=90°,在△AFE 中,根据三角形的内角和定理求出∠AEF 即可.【详解】证明:(1)∵AD ⊥BC ,∴∠ADC=∠BDF=90°,∵在△ADC 和△BDF 中BD AD ADC BDF DF CD =ìïÐ=Ðíï=î,∴△ADC ≌△BDF (SAS ),∴∠FBD=∠CAD ;(2)∵∠BDF=90°,∴∠FBD+∠BFD=90°,∵∠AFE=∠BFD ,由(1)知:∠FBD=∠CAD ,∴∠CAD+∠AFE=90°,∴∠AEF=180°-(∠CAD+∠AFE )=90°,∴BE ⊥AC .【点睛】本题考查了全等三角形的性质和判定,垂直定义,三角形的内角和定理等知识点的应用,关键是推出△ADC ≌△BDF .11.问题1:在数学课本中我们研究过这样一道题目:如图1,∠ACB =90°,AC =BC ,BE ⊥MN ,AD ⊥MN ,垂足分别为E 、D .图中哪条线段与AD 相等?并说明理由.问题2:试问在这种情况下线段DE 、AD 、BE 具有怎样的等量关系?请写出来,不需要说明理由.问题3:当直线CE 绕点C 旋转到图2中直线MN 的位置时,试问DE 、AD 、BE 具有怎样的等量关系?请写出这个等量关系,并说明理由.【答案】问题1,AD=EC,证明见解析;问题2:DE+BE=AD;问题3:DE=AD+BE,证明见解析.【分析】(1)由已知推出∠ADC=∠BEC=90°,因为∠ACD+∠BCE=90°,∠DAC+ACD=90°,推出∠DAC=∠BCE,根据AAS即可得到△ADC≌△CEB,即可得出AD=EC;(2)由(1)得到AD=CE,CD=BE,即可求出答案;(3)与(1)证法类似可证出∠ACD=∠EBC,能推出△ADC≌△CEB,得到AD=CE,CD=BE,即可得到DE、AD、BE之间的等量关系.【详解】解:(1)AD=EC;证明:∵AD⊥MN,BE⊥MN,∴∠ADC=∠BEC=90°,∵∠ACB=90°,∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,∴∠DAC=∠BCE,∵∠ADC=∠BEC,AC=BC,∴△ADC≌△CEB,∴AD=EC;(2)DE+BE=AD;由(1)已证△ADC≌△CEB,∴AD=EC,CD=EB,CE=AD∴CE=CD+DE=BE+DE=AD即DE+BE=AD;(3)DE=AD+BE.证明:∵BE⊥BC,AD⊥CE,∴∠ADC=90°,∠BEC=90°,∴∠EBC+∠ECB=90°,∵∠ACB =90°,∴∠ECB +∠ACD =90°,∴∠ACD =∠CBE ,∵∠ADC =∠BEC ,AC =BC ,∴△ADC ≌△CEB ,∴AD =CE ,CD =BE ,∵CD +CE =DC ,∴DE =AD +BE .【点睛】此题主要考查了邻补角的意义,全等三角形的性质和判定等知识点,能根据已知证出符合全等的条件是解此题的关键,题型较好,综合性比较强.12.如图,已知:ABC V 中,AB AC =,BAC 90Ð=°,分别过B ,C 向经过点A 的直线EF 作垂线,垂足为E ,F .(1)当EF 与斜边BC 不相交时,请证明EF BE CF(=+如图1);(2)如图2,当EF 与斜边BC 这样相交时,其他条件不变,证明:EF BE CF =-;【答案】(1)见解析;(2)见解析.【分析】(1)根据已知条件容易证明△BEA ≌△AFC ,然后利用对应边相等就可以证明题目的结论;(2)根据(1)知道△BEA ≌△AFC 仍然成立,则BE=AF ,AE=CF ,就可以求出EF=BE-CF .【详解】解:(1)BE EA ^Q ,CF AF ^,BAC BEA CFE 90ÐÐÐ\===°,EAB CAF 90ÐÐ\+=°,EBA EAB 90ÐÐ+=°,CAF EBA ÐÐ\=,在ABE V 和CAF V 中,BEA AFC EBA FACAB AC Ð=ÐìïÐ=Ðíï=îBEA \V ≌()AFC AAS V ,EA FC \=,BE AF =,EF EA AF BE CF \=+=+.(2)BE EA ^Q ,CF AF ^,BAC BEA CFE 90ÐÐÐ\===°,EAB CAF 90ÐÐ\+=°,ABE EAB 90ÐÐ+=°,CAF ABE ÐÐ\=,在ABE V 和ACF V 中,EBA FAC BEA CFAAB AC Ð=ÐìïÐ=Ðíï=îBEA \V ≌()AFC AAS V ,EA FC \=,BE AF =,∵EF AF AE =-,∴EF BE CF=-【点睛】本题主要考查了全等三角形的性质与判定,利用它们解决问题,经常用全等来证线段和的问题.13.(1)问题:如图①,在四边形ABCD 中,90B C Ð=Ð=°,P 是BC 上一点,PA PD =,AB BP BC +=.求证:90APD Ð=°;(2)问题:如图②,在三角形ABC 中,45B C Ð=Ð=°,P 是AC 上一点,PE PD =,且90EPD Ð=°.求AE AP PC+的值.【答案】(1)见解析;(2)1【分析】(1)先证明()ABP PCD HL @△△,从而得APB PDC ÐÐ=,进而即可得到结论;(2)过D 点做DF AC ^于点F ,易证()APE FDP AAS @△△,DPC △是等腰直角三角形,进而即可求解.【详解】(1)∵BP PC BC +=,BP AB BC +=,∴PC AB =,在t R ABP △与t R PCD V 中∵AP PD AB PC =ìí=î,∴()ABP PCD HL @△△,∴APB PDC ÐÐ=,∴180APD APB DPC Ð=°-Ð-Ð180()PDC DPC =°-Ð+Ð18090=°-°90=°;(2)过D 点做DF AC ^于点F ,在ABC 中,18090A B C Ð=°-Ð-Ð=°,∴A PFD ÐÐ=,∵90APE DPF +=°∠∠ ,90AEP APE Ð+Ð=°,∴DPF AEP ÐÐ=,在APE V 与FDP V 中A DFP DPE AEP PE PD Ð=ÐìïÐ=Ðíï=î,∴()APE FDP AAS @△△,∴AE PF =,AP DF =,∵在DPC △中,90904545FDC C Ðа°°°=-=-=,∴DF FC =,∴AP FC =,∴PC PF FC AE AP =+=+,∴1AE AP PC+=.【点睛】本题主要考查全等三角形的判定和性质,等腰直角三角形的判定和性质,熟练掌握“一线三等角”模型,添加合适的辅助线,构造全等三角形,是解题的关键.14.在△ABC 中,AC=BC ,直线MN 经过点C ,AD ⊥MN 于点D ,BE ⊥MN 于点E ,且AD=CE ;(1)当直线MN 绕点C 旋转到如图1的位置时,求证:AC ⊥BC .(2)判断AD 、BE 、DE 这三条线段之间的数量关系,并说明理由.(3)当直线MN 绕点C 旋转到如图2的位置时,线段DE 、AD 、BE 之间又有什么样的数量关系?请你直接写出这个数量关系,不必证明.【答案】(1)见解析;(2)DE =AD +BE ;见解析;(3)AD =DE +BE【分析】(1)利用垂直的定义得∠ADC =∠CEB =90°,再利用HL 证明Rt △ADC ≌Rt △CEB ,得到∠DAC =∠BCE ,再根据余角的定义得到∠ACD +∠BCE =∠ACB =90°,可得结论;(2)根据Rt △ADC ≌Rt △CEB 得到DC =BE ,从而利用等量代换得到DE =AD +BE ;(3)同理可证:Rt △ADC ≌Rt △CEB ,利用等量代换可得AD =DE +BE .【详解】解:(1)证明:∵AD ⊥MN ,BE ⊥MN ,∴∠ADC =∠CEB =90°,在Rt △ADC 和Rt △CEB 中,AC BC AD CE =ìí=î,∴Rt △ADC ≌Rt △CEB (HL ),∴∠DAC =∠BCE ,∵∠ADC =90°,即∠DAC +∠ACD =90°,∴∠ACD +∠BCE =90°,即∠ACB =90°,∴AC ⊥BC ;(2)DE =AD +BE ,理由如下:∵Rt △ADC ≌Rt △CEB ,∴DC =BE ,∵AD =CE ,∴DE =DC +CE =AD +BE ;(3)AD =DE +BE ,同理可证:Rt △ADC ≌Rt △CEB (HL ),∴CD =BE ,∴AD =CE =DE +CD =DE +BE ,∴即AD =DE +BE .【点睛】本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS ”、“SAS ”、“ASA ”、“AAS ”、“HL ”;全等三角形的对应边、对应角相等.15.(1)(问题原型)如图,在等腰直角三角形ABC 中,90ACB Ð=°,8BC =.过B 作BD AB ^,且BD AB =,连结CD ,过点D 作BCD D 的BC 边上的高DE ,易证ABC BDE D D ≌,从而得到BCD D 的面积为_________.(2)(初步探究)如图,在Rt ABC D 中,90ACB Ð=°,BC a =,过B 作BD AB ^,且BD AB =,连结CD .用含a 的代数式表示BCD D 的面积并说明理由.(3)(简单应用)如图,在等腰ABC D 中,AB AC =,BC m =,过B 作BD AB ^,且BD AB =,连结CD ,求BCD D 的面积(用含m 的代数式表示).【答案】(1)32;(2)212BCD S a D =;答案见解析;(3)214m .【分析】(1)【问题原型】根据AAS 证明出△ABC ≌△BDE ,就有DE =BC =8.进而由三角形的面积公式得出结论(2)【初步探究】过点D 作BC 的垂线,与BC 的延长线交于点E ,由垂直的性质就可以得出△ABC ≌△BDE ,就有DE =BC =a .进而由三角形的面积公式得出结论.(3)【简单应用】过点A 作AF ⊥BC 与F ,过点D 作DE ⊥BC 的延长线于点E ,由等腰三角形的性质可以得出12BF BC =,由条件可以得出△AFB ≌△BED 就可以得出BF =DE ,由三角形的面积公式就可以得出结论.【详解】解:(1)【问题原型】如图,∵过点D 作BC 的垂线,与BC 的延长线交于点E .∴∠BED =∠ACB =90°,∵线段AB 绕点B 顺时针旋转90°得到线段BD ,∴AB =BD ,∠ABD =90°.∴∠ABC +∠DBE =90°.∵∠A +∠ABC =90°.∴∠A =∠DBE .在△ABC 和△BDE 中,ACB BED A DBEAB BD Ð=ÐìïÐ=Ðíï=î∴△ABC ≌△BDE (AAS )∴BC =DE =8.12D =×BCD S BC DE ∴S △BCD =32,(2)【初步探究】212S a =.理由:过D 做DE 上以C 垂足为E ,∵90ACB Ð=°,∴90A ABC Ð+Ð=°.∵AB BD ^,∴90ABC DBE Ð+Ð=°.∴A BDE Ð=Ð.在△ABC 和△BDE 中,,ACB BED A DBE AB BD Ð=ÐìïÐ=Ðíï=î∵ABC BDE D D ≌.∴DE BC ==a .∴22111222D ×===BCD S BC DE BC a (3)【简单应用】过A 做AF BC ^于F ,过D 做DE BC ^于E.∴∠AFB =∠E =90°,∴∠FAB +∠ABF =90°.∵∠ABD =90°,∴∠ABF +∠DBE =90°,∴∠FAB =∠EBD .∵线段BD 是由线段AB 旋转得到的,∴AB =BD .在△AFB 和△BED 中,AFB E FAB EBDAB BD Ð=ÐìïÐ=Ðíï=î∴△AFB ≌△BED (AAS ),∴FB DE =.∵AB AC =,BC m =,AF BC ^,∴11m 22==BF BC ∴12DE BC =.∴12D =×BCD S BC DE 1122BC BC =×221144BC m ==.【点睛】本题考查了直角三角形的性质的运用,等腰三角形的性质的运用,全等三角形的判定及性质的运用,三角形的面积公式的运用,解答时证明三角形全等是关键.16.如图,已知ABC V 和CDE △均是直角三角形,Rt ACB CED Ð=Ð=Ð,AC CE =,AB CD ^于点F.(1)求证:ABC V ≌CDE △;(2)若点B 是EC 的中点,10cm DE =,求AE 的长.【答案】(1)见解析;(2)cm【分析】(1)根据ASA 即可证明结论;(2)结合(1)可得10DE BC ==cm ,根据点B 是EC 的中点,可得220EC BC ==cm ,根据勾股定理即可求出AE 的长.【详解】解:(1)证明:AB CD ^Q ,90FAC ACF \Ð+Ð=°,90ACE Ð=°Q ,90DCB ACF \Ð+Ð=°,FAC DCB \Ð=Ð,AC EC \=,在ABC D 和CDE D 中,90FAC DCB AC ECACB CED Ð=Ðìï=íïÐ=Ð=°î,()ABC CDE ASA \D @D ;(2)ABC CDE D @D Q ,10DE BC \==cm ,Q 点B 是EC 的中点,220EC BC \==cm ,20AC EC \==cm ,在Rt AEC △中,根据勾股定理,得AE ==.【点睛】本题考查了全等三角形的判定与性质,勾股定理,解决本题的关键是掌握全等三角形的判定与性质.17.(提出问题)如图1,在直角ABC V 中,∠BAC =90°,点A 正好落在直线l 上,则∠1、∠2的关系为(探究问题)如图2,在直角ABC V 中,∠BAC =90°,AB =AC ,点A 正好落在直线l 上,分别作BD ⊥l 于点D ,CE ⊥l 于点E ,试探究线段BD 、CE 、DE 之间的数量关系,并说明理由.(解决问题)如图3,在ABC V 中,∠CAB 、∠CBA 均为锐角,点A 、B 正好落在直线l 上,分别以A 、B 为直角顶点,向ABC V 外作等腰直角三角形ACE 和等腰直角三角形BCF ,分别过点E 、F 作直线l 的垂线,垂足为M 、N .①试探究线段EM 、AB 、FN 之间的数量关系,并说明理由;②若AC =3,BC =4,五边形EMNFC 面积的最大值为【答案】提出问题:1290Ð+Ð=°;探究问题:BD CE DE +=,理由见解析;解决问题:①EM FN AB +=,理由见解析;②492.【分析】提出问题:根据平角的定义、角的和差即可得;探究问题:先根据垂直的定义可得90ADB CEA Ð=Ð=°,再根据直角三角形的两锐角互余、角的和差可得2ABD Ð=Ð,然后根据三角形全等的判定定理与性质可得,BD AE AD CE ==,最后根据线段的和差即可得;解决问题:①如图(见解析),同探究问题的方法可得,EM AD FN BD ==,再根据线段的和差即可得;②如图(见解析),同探究问题的方法可得,ACD EAM BCD FBN @@V V V V ,再根据三角形全等的性质可得,ACD EAM BCD FBN S S S S ==V V V V ,然后利用三角形的面积公式将五边形EMNFC 面积表示出来,由此即可得出答案.【详解】提出问题:12180,90BAC BAC Ð+Ð+Ð=°Ð=°Q ,2190\Ð+Ð=°,故答案为:1290Ð+Ð=°;探究问题:BD CE DE +=,理由如下:,BD l CE l ^^Q ,90ADB CEA \Ð=Ð=°,190ABD \Ð+Ð=°,由提出问题可知,1290Ð+Ð=°,2ABD \Ð=Ð,在ABD △和CAE V 中,2ADB CEA ABD AB CA Ð=ÐìïÐ=Ðíï=î,()ABD CAE AAS \@V V ,,BD AE AD CE \==,DE AE AD BD CE \=+=+,即BD CE DE +=;解决问题:①EM FN AB +=,理由如下:同探究问题的方法可证:,EM AD FN BD ==,AB AD BD EM FN \=+=+,即EM FN AB +=;②如图,过点C 作CD l ^于点D ,同探究问题的方法可证:,ACD EAM BCD FBN @@V V V V ,,ACD EAM BCD FBN S S S S \==V V V V ,ACE QV 和BCF △都是等腰直角三角形,且3,4AC BC ==,3,4AE AC BF BC \====,191,8222ACE BCF S AC AE S BC BF \=×==×=V V ,\五边形EMNFC 面积为EAM ACE ACD BCD BCF FBN S S S S S S +++++V V V V V V ,982ACD ACD BCD BCD S S S S =+++++V V V V ,()2522ACD BCD S S =++V V ,2522ABC S =+V ,则当ABC V 面积取得最大值时,五边形EMNFC 面积最大,设ABC V 的BC 边上的高为h ,则122ABC S BC h h =×=V ,Q 在ABC V 中,CAB Ð、CBA Ð均为锐角,\当90ACB Ð=°时,h 取得最大值,最大值为3AC =,ABC \V 面积的最大值为236ABC S =´=V ,则五边形EMNFC 面积的最大值为25492622´+=,故答案为:492.【点睛】本题考查了垂直的定义、三角形全等的判定定理与性质、等腰直角三角形的定义等知识点,熟练掌握三角形全等的判定定理与性质是解题关键.18.综合与实践.积累经验我们在第十二章《全等三角形》中学习了全等三角形的性质和判定,在一些探究题中经常用以上知识转化角和边,进而解决问题.例如:我们在解决:“如图1,在ABC D 中,90ACB Ð=°,AC BC =,线段DE 经过点C ,且AD DE ^于点D ,BE DE ^于点E .求证:AD CE =,CD BE =”这个问题时,只要证明ADC CEB D D ≌,即可得到解决,(1)请写出证明过程;类比应用(2)如图2,在平面直角坐标系中,ABC D 中,90ACB Ð=°,AC BC =,点A 的坐标为()0,2,点C 的坐标为()1,0,求点B 的坐标.拓展提升(3)如图3,ABC D 在平面直角坐标系中,90ACB Ð=°,AC BC =,点A 的坐标为()2,1,点C 的坐标为()4,2,则点B 的坐标为____________.【答案】(1)见解析;(2)B 的坐标(3,1);(3)(3,4)【分析】(1)根据AD ⊥DE 、BE ⊥DE 得到∠D=∠E=90°再根据直角三角形的性质以及同角的余角相等,推出∠DAC=∠BCE ,进而证明ADC CEB @V V ,最后再根据全等三角形对应边相等得出AD=CE ,CD=BE ;(2)如图4,过点B 作BE ⊥x 轴于点E ,通过证明AOC CEB @V V ,进而得出AO=CE ,CO=BE ,再根据点A 的坐标为(0,2),点C 的坐标(1,0),求得OE=3,最后得出B 的坐标(3,1);(3)如图5,过点C 做CF ⊥x 轴与点F ,再过点A 、B 分别做AE ⊥CF ,BD ⊥CF ,通过证明CDB AEC @V V ,进而得出BD=CE=,AE=CD ,最后根据点A 的坐标为()2,1,点C 的坐标为()4,2,得出B 坐标(3,4).【详解】(1)证明:∵AD ⊥DE ,BE ⊥DE∴∠D=∠E=90°∴∠DAC+∠ACD=90°又∵∠ACB=90°∴∠ACD+∠BCE=90°∴∠DAC=∠BCE在△ADC 和△CEB 中D E DAC BCEAC BC Ð=ÐìïÐ=Ðíï=î∴△ADC ≌△CEB∴AD=CE ,CD=BE(2)解:如图,过点B 作BE ⊥x 轴于点E∵∠AOC=90°∴∠OAC+∠ACO=90°又∵∠ACB=90°∴∠ACO+∠BCE=90°∴∠OAC=∠BCE在△AOC 和△CEB 中90AOC CEB OAC ECBAC BC ìÐ=Ð=ïÐ=Ðíï=îo∴△AOC ≌△CEB∴AO=CE ,CO=BE又∵点A 的坐标为(0,2),点C 的坐标(1,0)∴AO=2,CO=1∴CE=2,BE=1∴OE=3∴B 的坐标(3,1)(3)(3,4)解:如图5,过点C 做CF ⊥x 轴与点F ,再过点A 、B 分别做AE ⊥CF ,BD ⊥CF ,∵AE ⊥CF ,BD ⊥CF∴90AEC CDB Ð=Ð=°,∴90ACE CAE Ð+Ð=°,又∵90ACB Ð=°,∴90ACE BCD Ð+Ð=°,∴CAE BCD Ð=Ð,∴在ACE △和BCD △中AEC CDB CAE BCD AC BC Ð=ÐìïÐ=Ðíï=î,∴ACE BCD @V V (AAS )∴BD=CE ,AE=CD ,又∵A 的坐标为()2,1,点C 的坐标为()4,2,∴CE=BD=2-1=1,CD=AE=4-2=2设B 点坐标为(a ,b ),则a =4-1=3,b =2+2=4,∴B 坐标(3,4).【点睛】本题综合考查了全等三角形的证明以及平面直角坐标系中求点坐标的综合应用问题;通过构建“一线三等角”模型,再利用直角三角形的性质以及同角的余角相等解决角关系是本题的关键.19.如图,等腰Rt ABC V 中,90ABC Ð=°,AB BC =,点A ,B 分别在坐标轴上.(1)如图1,若点C 的横坐标为5,直接写出点B 的坐标_______;图1(2)如图2,若点A 的坐标为()6,0-,点B 在y 轴的正半轴上运动时,分别以OB ,AB 为边在第一、第二象限作等腰Rt OBF V ,等腰Rt ABE △,连接EF 交y 轴于点P ,当点B 在y 轴的正半轴上移动时,PB 的长度是否发生改变?若不变,求出PB 的值;若变化,求PB 的取值范围.图2【答案】(1)()05,;(2)不变,PB 的值为3【分析】(1)作CD ⊥BO ,可证△ABO 全等于△BCD ,根据全等三角形对应边相等的性质即可解题;(2)作EG ⊥y 轴,可证△BAO 全等于△EBG 全等于△EGP 全等于△FBP ,可得BG=OA 和PB=PG,即可求得PB 是AO 的2倍,即可得到结论.【详解】(1)如图,作CD ⊥BO 于D ,∵∠CBD+∠ABO=90°,∠ABO+∠BAO=90°,∴∠CBD=∠BAO,在△ABO 和△BCD 中,90BOA BDC CBD BAOAB BC Ð=Ð=°ìïÐ=Ðíï=î∴△ABO ≌△BCD,∴CD=BO=5,∴B 点的坐标(0,5)故答案为:()05,.(2)不发生改变,理由如下:作EG y ^轴于G ,90BAO OBA Ð+Ð=°Q ,90OBA EBG Ð+Ð=°,BAO EBG \Ð=Ð.在BAO D 和EBG D 中,90AOB BGE BAO EBGAB BE Ð=Ð=°ìïÐ=Ðíï=î()BAO EBG AAS \D @D AO BG \=,OB EG=OB BF =Q ,BF EG\=在EGP D 和FBP D 中,90EPG FPB EGP FBP EG FB Ð=ÐìïÐ=Ð=°íï=î()EGP FBP AAS \D @D PG PB \=.11322PB BG AO \===.∴不变,PB 的值为3.【点睛】本题考查三角形全等、等腰直角三角形性质、勾股定理、角平分线性质,熟练掌握添加辅助线证明三角形全等是解题的关键.20.在直角坐标系中,A 为x 轴负半轴上的点,B 为y轴负半轴上的点.(1)如图①,以A 点为顶点,AB 为腰在第三象限作等腰Rt ABC V ,若已知()2,0A -,()0,4B -,试求C 点的坐标.(2)如图②,若点A的坐标为()-,点B 的坐标为()0,a ,点D 的纵坐标为b ,以B 为顶点,BA 为腰作等腰Rt ABD △,当B 点沿y 轴负半轴向下运动且其他条件都不变时,求式子22b a --(3)如图③,E 为x 轴负半轴上的一点,且OB OE =,OF EB ^于点F ,以OB 为边作等边OBM V ,连接EM 交OF 于点N ,求式子EM ON EN-的值.【答案】(1)(6,2)C --;(2)0;(3)2【分析】(1)作CQ ⊥OA 于点Q ,可以证明△AQC ≌△BOA ,由QC =AO ,AQ =BO ,再由条件就可以求出C 的坐标.(2)作DP ⊥OB 于点P ,可以证明△AOB ≌△BPD ,则有AO =BP =OB−PO =−a−(−b )=b−a 为定值.(3)作BH ⊥EB 于B ,由条件可以得出∠1=30°,∠2=∠3=∠EMO =15°,∠EOF =∠BMG =45°,EO =BM ,可以证明△ENO ≌△BGM ,则GM =ON ,就有EM−ON =EM−GM =EG ,最后由含30°的直角三角形的性质就可以得出EN =EM−ON 的一半即可得.【详解】(1)如图(1)作CQ OA ^于点Q ,∴90AQC Ð=°∵ABC V 是等腰直角三角形,∴AC AB =,90CAB Ð=°,∴ACQ BAO Ð=Ð,在AQC V 与BOA △中,AQC AOB QAC ABO AC AB Ð=ÐìïÐ=Ðíï=î,∴AQC BOA △≌△,∴CQ AO =,AQ BO =.∵(2,0)A -,(0,4)B -,∴2OA =,4OB =,∴2CQ =,4AQ =,∴6OQ =,∴(6,2)C --,故答案为:(6,2)C --.(2)如图(2)作DP OB ^于点P ,∴90BPD Ð=°,∵ABD △是等腰直角三角形,∴AB BD =,90ABD ABO OBD Ð=Ð+Ð=°,∵90OBD PDB Ð+Ð=°,∴ABO BDP Ð=Ð,在AOB V 与BPD △中,AOB DPB ABO PDB AB BD Ð=ÐìïÐ=Ðíï=î,∴AOB BPD △≌△,∴AO BP =,∵()BP OB PO a b b a =-=---=-,∵(A -,∴=OA∴b a -=,∴当B 点沿y轴负半轴向下运动时,AO BP b a ==-=,∴22b a --的值不变为0,故答案为:0.(3)解:如图(3)在ME 上截取MG ON =,连接BG ,∵OBM V 是等边三角形,OB OE =,∴BO BM MO ==,60OBM OMB BOM Ð=Ð=Ð=°,∴EO MO BM ==,105EBM Ð=°,130Ð=°,∴315EMO Ð=Ð=°,∴30BEM Ð=°,45BME Ð=°,∵OF EB ^,∴45EOF Ð=°,∴EOF BME Ð=Ð,在ENO △与BGM V 中,OE BM EON BMG ON MG =ìïÐ=Ðíï=î,∴()ENO BGM SAS △≌△,∴BG EN =,∵ON MG =,∴23ÐÐ=,∴215Ð=°,∴90EBG Ð=°,∴12BG EG =,∴12EN EG =,∵EG EM GM =-,∴1()2EN EM GM =-,∴1()2EN EM ON =-,∴2EM ON EN-=,故答案为:2.【点睛】本题考查了等腰直角三角形的性质,等边三角形的性质,等腰三角形的性质,三角形的外角与内角的关系,全等三角形的判定与性质的运用.21.在ABC V 中,90,ACB AC BC Ð=°=,直线MN 经过点C ,且AD MN ^于D ,BE MN ^于E ,(1)当直线MN 绕点C 旋转到图1的位置时,显然有:DE AD BE =+(不必证明);(2)当直线MN 绕点C 旋转到图2的位置时,求证:DE AD BE =-;(3)当直线MN MN 绕点C 旋转到图3的位置时,试问DE 、AD 、BE 具有怎样的等量关系?请直接写出这个等量关系.【答案】(1)见解析;(2)见解析;(3)DE =BE -AD【分析】(1)由于△ABC 中,∠ACB =90°,AC =BC ,直线MN 经过点C ,且AD ⊥MN 于D ,BE ⊥MN 于E ,由此即可证明△ADC ≌△CEB ,然后利用全等三角形的性质即可解决问题;(2)由于△ABC 中,∠ACB =90°,AC =BC ,直线MN 经过点C ,且AD ⊥MN 于D ,BE ⊥MN 于E ,由此仍然可以证明△ADC ≌△CEB ,然后利用全等三角形的性质也可以解决问题;(3)当直线MN 绕点C 旋转到图(3)的位置时,仍然△ADC ≌△CEB ,然后利用全等三角形的性质可以得到DE =BE -A D .【详解】。
EDA的概念

一、 EDA的概念1、定义:电子(系统)设计的自动化,或电子线路或系统的计算机辅助设计。
是基于计算机平台的一整套先进的设计电子系统的软件工具。
2、研究对象:电子电路与系统设计的全过程:低频、高频、微波电路、线性与非线性电路、模拟和数字电路、分离电路和集成电路。
3、三个层次:设计的层次系统级;电路级;物理实现级。
4、EDA技术发展的三个阶段CAD阶段(70s):EDA的初级阶段。
利用功能有限的计算机进行简单的电路性能分析和预测,PCB的计算机辅助布局布线,如smart work。
CAE阶段(80s):CAD工具逐步完善和发展,将许多单点工具集成在一起使用,大大提高了效率。
如ORCAD,PROTEL, PSPICE等;aEDA阶段(90s):超大规模集成电路时代,集成电路工艺水平达到深亚微米,一个芯片可集成上千万个晶体管,速度达giga bit/s,对电子设计的工具提出了更高的要求,同时也促进了设计工具的发展。
出现了众多的ICCAD工具,如CADENCE,MENTOR GRAPHICS,SYNOPSIS等著名公司的EDA软件;中国的熊猫系统等。
5、现代EDA 技术的特点1)采用硬件描述语言(HDL)。
具有如下突出优点:语言的公开性和可利用性、设计与工艺无关、宽范围的描述能力、便于大规模系统设计和设计的可复用、交流、保存、修改;2)高层综合和优化。
开发工具支持系统级的综合和仿真,可更好地支持自上而下的设计方法;3)并行工程。
系统化的、集成化的、并行的产品及相关过程的开发模式,支持多人同时并行进行设计工作。
4)开放性和标准化。
EDA工具的相互兼容,有利于资源共享。
6、设计方法自上而下的设计设计需要经过“设计-验证-修改-再验证”的过程。
优点:对复杂系统通盘考虑,合理划分和优化,是目前主流的设计方法。
✓正向设计:由概念到产品的设计过程,自上而下的芯片设计。
如右图所示。
✓反向设计:剖析别人已有设计,由版图得到原理图、功能和工作原理,再转入正向设计的方法。
EDA试卷及答案

EDA试卷及答案一、单项选择题:(20分)1.IP核在EDA技术和开发中具有十分重要的地位;提供用VHDL等硬件描述语言描述的功能块,但不涉及实现该功能块的具体电路的IP核为_____ D_____。
A .瘦IP B.固IP C.胖IP D.都不是2.综合是EDA设计流程的关键步骤,在下面对综合的描述中,____ D _____是错误的。
A.综合就是把抽象设计层次中的一种表示转化成另一种表示的过程;B.综合就是将电路的高级语言转化成低级的,可与FPGA / CPLD的基本结构相映射的网表文件;C.为实现系统的速度、面积、性能的要求,需要对综合加以约束,称为综合约束;D.综合可理解为一种映射过程,并且这种映射关系是唯一的,即综合结果是唯一的。
3.大规模可编程器件主要有FPGA、CPLD两类,下列对FPGA结构与工作原理的描述中,正确的是__C__。
A. FPGA全称为复杂可编程逻辑器件;B. FPGA是基于乘积项结构的可编程逻辑器件;C.基于SRAM的FPGA器件,在每次上电后必须进行一次配置;D.在Altera公司生产的器件中,MAX7000系列属FPGA结构。
4.进程中的信号赋值语句,其信号更新是___C____。
A.按顺序完成;B.比变量更快完成;C.在进程的最后完成;D.都不对。
5. VHDL语言是一种结构化设计语言;一个设计实体(电路模块)包括实体与结构体两部分,结构体描述_____B______。
A.器件外部特性;B.器件的内部功能;C.器件的综合约束;D.器件外部特性与内部功能。
6.不完整的IF语句,其综合结果可实现____ A ____。
A. 时序逻辑电路B. 组合逻辑电路C. 双向电路D. 三态控制电路7.子系统设计优化,主要考虑提高资源利用率减少功耗(即面积优化),以及提高运行速度(即速度优化);指出下列哪些方法是面积优化_____ B____。
①流水线设计②资源共享③逻辑优化④串行化⑤寄存器配平⑥关键路径法A. ①③⑤ B. ②③④C. ②⑤⑥ D. ①④⑥8.下列标识符中,_____B_____是不合法的标识符。
