热点专题突破8a

合集下载

英—8寒(新世纪版)—07—8A U7复习—8B U7单词预习—形容词副词—阅读综合类

八年级英语寒假班（新世纪版）教师日期学生课程编号07 课型复习/预习+专题课题8A U7复习+8B U7单词预习+形容词副词+阅读综合训练教学目标1．形容词和副词专题2．分类综合阅读（环境保护类）3. 复习8A U7&8B U7预习教学重点1．形容词和副词的考查重点和常考考点；2．关于环境保护主题的综合阅读，掌握文章的脉络以及文章中的高频词汇和句型。

教学安排版块时长1形容词和副词2师生总结3环境保护类综合阅读4复习8A U7&8B U7预习5作业布置61、8A U7复习I. Fill in the blanks with the proper words. （填入适当的单词，首字母已给）1.Our English teacher told us that the e____________ would be hold in five days.2.Friendship is p___________ in the world, so we should value our friends.3.The class teacher let us meet at the e_____________ of our school.4.We often e_____________ ideas with our parents.5.My friend showed us her new house with great p____________ last weekend.II.Fill in the blanks with the following words in their proper forms. （用所给单词的适当形式填空）1.Be careful. The picture from the Song Dynasty is _____________ (price).2.Could you tell me the _____________ to the exhibition hall? (enter)3.Peter is an ______________ student from Korean. (change)4.This is the first time a _____________ country will hold such a great event. (develop)5.____________ are busy doing research in the labs these days. (science)2、8B U7单词预习8B Unit 7 Vocabulary（新世纪）序号英文音标词性中文1 ['muːnlaɪt] n. 月光2 [sə'nɑːtə]n. 奏鸣曲3 ['ɪnstrʊm(ə)nt] n. 乐器4 [ə'kɔːdɪən] n. 手风琴5 [drʌm] n. 鼓6 [fluːt]n. 长笛7 [ˈsʌdnlɪ] ad. 突然8 [aʊt'saɪd] prep. 在外面9 [wɪʃ] v. 希望10 [ə'fɔːd]v. 买得起11 [fə'get] v. 忘记12 ['kænd(ə)l] n. 蜡烛13 [θruː]prep. 穿过14 ['kreɪzɪ] a. 疯狂的15 ['kɒpɪ] v. 复制16 ['ti:neidʒ] a. 十几岁的17 ['ɪnflʊəns] n. 影响18 [kəm'baɪn] v. 结合19 乐器20 令人惊讶的是21 仰视22 沉湎，沉浸PracticeComplete the sentences with the given words in their proper forms.(用所给单词的适当形式填空）1._____________, my daughter began to cry. (sudden)2.The boy was ____________ hurt. The doctor saved him. (serious)3.Beethoven was _____________ to see that the girl was blind. (surprise)4.My grandfather is so ______________ that he often leaves things behind. (forget)5.The firemen have saved the boy from the fire _____________.(success)6.The children went ______________ when they saw their favourite characters. (craze)7.With the ____________ of science and technology, life has become easier. (develop)8.Tom and Jerry lost _____________ in the funny game. (they)9.That young man looked at us in ____________ when we had an argument. (surprised)10.How many birthday ___________ do you need in all? (candle)3、形容词-副词形容词和副词专题Presentation-形容词和副词(一)形容词和副词的概述：形容词是指那些用来描述或修饰名词（或代词）的一类词。

电功率知识总结及复习1

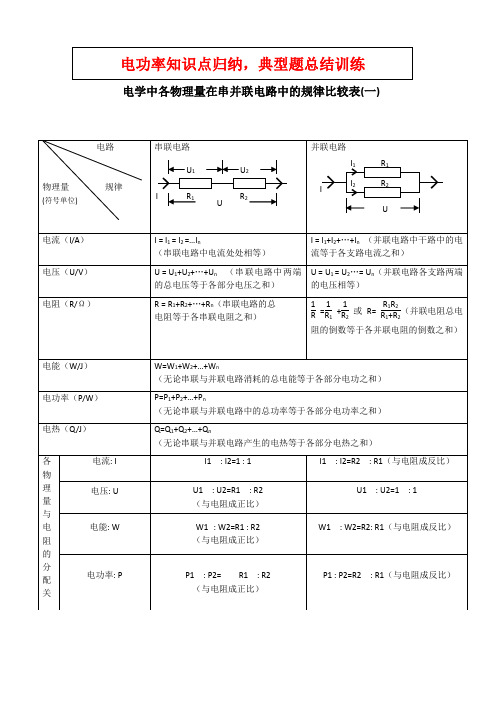
电学中各物理量在串并联电路中的规律比较表(一)二、电学中各物理量求解公式表（二）分析：1.对于电功、电功率、电热三个物理量, 它们无论是在串联电路还是并联电路中, 都是总量等于各部分之和。

同学们在解答这类题时应灵活选取公式进行计算。

如以计算电路中的总功率为例, 既可以根据P=P1+P2,也可以跟据P=UI进行计算, 其它几个物理量的求解也与之类似。

2.用欧姆定律Ｉ= 求电路中的电流, 让学生明白此公式是由实验得出, 是电学中最基本的公式, 但此公式只适合于纯电阻电路(所谓纯电阻电路即电路中电能全部转化为热能的电路)。

3.电功率求解公式P = 与P=UI这两个公式为电学中计算电功率时普遍适用最基本的两个公式, 第一个为电功率的定义式, 也常常作为用电能表和钟表测记家用电器电功率的公式。

第二个公式是实验室用伏安法小灯泡功率的原理, 也是计算用电器电功率的最基本公式。

4、虽然表中公式繁多, 但电学基本公式只有4个, 即：Ｉ= 、P = 、P = UI、Q = I2Rt 。

其他公式都是导出公式, 同学们可以在掌握这4个公式的基础上进行推导练习, 很快就会熟悉并掌握。

5、应熟练掌握的几个比较重要的导出公式。

具体公式：在表中分别是如下八个公式（2）I = （5）U = IR （6）R = （7）R = （12）P = (13) P = I2R (14) W = Pt (17) Q = I2Rt 这八个公式在电学解题中使用的频率也较高, 要求学生能熟练掌握。

专题一典题解析设疑: 电能表是电功、电功率知识点在生活实际中的一个最常规“落脚点”, 你了解电能表吗？1（11河源）小明同学在家中拍到一张电能表照片, 如图1所示, 他仔细观察照后, 得到下列四个结论, 你认为正确的是A. 电能表的额定功率为2500WB. 电能表的标定电流为5AC. 拍照片时, 小明家已消耗的电能为9316kW•hD．拍照片时, 小明家已消耗的电能为931.6J设计意图：本题考察学生对电能表各个参数的基本认知。

第7讲解题技巧专题：二次根式中的化简求值(6类热点题型讲练)(原卷版)--初中数学北师大版8年级上册

(1)
1 3
______ ； 2
(2)化简
1 2 1
1 3
2
1 4
3
1 10
； 9
(3)若 a
1 5
2
，求
a2
4a
3 的值．
4．（2023 春·河北邢台·八年级校考期中）【阅读材料】在二次根式中，如： 3 2 3 2 1， 3 3 3 3 6 ，它们的积不含根号，我们称这样的两个二次根式互为有理化因式．于是我们可以利用
m
*
n
m m
n m n n m n ，则计算 3*8 27 * 2 的结果为
．
【变式训练】
1．（2023 春·广西南宁·七年级校联考期中）对于两个不相等的实数 a、b，定义一种新的运算如下，
ab
ab ab
(
a
b
0)
，如：
3
*
2
32 32
5 ，那么 5 4
．
2．（2023 秋·河北保定·七年级统考期末）定义一种对正整数 n 的“F 运算”：①当 n 为奇数时，结果为 3n 5；
2．（2023 春·广东肇庆·七年级校考期中）已知 | a 1| 7 b 0，则 2a 2b 的算术平方根是
．
3．（2023·全国·八年级假期作业）如果实数 x 、 y 满足 y x 3 3 x 2 ，则 x 3y 的平方根为．
4．（2023 春·安徽池州·八年级统考期末）已知直角三角形两边 x、y 的长满足 x2 4 y2 5 y 6 0 ，则第
第 2 章第 07 讲解题技巧专题：二次根式中的化简求值(6 类热点题型讲练)
目录【类型一利用二次根式的非负性求值】 ..........................................................................................................1 【类型二利用乘法公式进行计算】 ..................................................................................................................2 【类型三整体代入求值】 .................................................................................................................................. 2 【类型四新定义型运算】 .................................................................................................................................. 3 【类型五二次根式的分母有理化】 ..................................................................................................................4 【类型六复合二次根式的化简】 ......................................................................................................................7

第02讲整式(单项式与多项式)(9类热点题型讲练)(原卷版)--初中数学北师大版7年级上册

第02讲整式(单项式与多项式)1.掌握单项式、多项式、整式的概念；2.掌握单项式的系数与次数和多项式的项数、系数与次数；3.掌握单项式的规律题的方法；4.掌握多项式的升幂、降幂排列方法.知识点01单项式的概念如mn 2-，23xy π，0，它们都是数与字母的积，像这样的式子叫单项式，单独的一个数或一个字母也是单项式．【注意】（1）单项式包括三种类型：①数字与字母相乘或字母与字母相乘组成的式子；②单独的一个数；③单独的一个字母．（2）单项式中不能含有加减运算，但可以含有除法运算．如：2mn 可以写成mn 21。

但若分母中含有字母，如x 1就不是单项式，因为它无法写成数字与字母的乘积．知识点02单项式的系数与次数1.单项式的系数：单项式中的数字因数叫做这个单项式的系数．（1）确定单项式的系数时，最好先将单项式写成数与字母的乘积的形式，再确定其系数；（2）圆周率π是常数．单项式中出现π时，应看作系数；（3）当一个单项式的系数是1或-1时，“1”通常省略不写；（4）单项式的系数是带分数时，通常写成假分数.2.单项式的次数：一个单项式中，所有字母的指数的和叫做这个单项式的次数．单项式的次数是计算单项式中所有字母的指数和得到的，计算时要注意以下两点：（1）没有写指数的字母，实际上其指数是1，计算时不能将其遗漏；（2）不能将数字的指数一同计算．知识点03多项式1.多项式的概念：几个单项式的和叫做多项式．2.多项式的项：每个单项式叫做多项式的项，不含字母的项叫做常数项．【注意】（1）多项式的每一项包括它前面的符号．（2）一个多项式含有几项，就叫几项式，如：1-xx是一个三项式．22+33.多项式的次数：多项式里次数最高项的次数，叫做这个多项式的次数．【注意】（1）多项式的次数不是所有项的次数之和，而是多项式中次数最高的单项式的次数．（2）一个多项式中的最高次项有时不止一个，在确定最高次项时，都应写出．知识点04整式单项式与多项式统称为整式．【注意】（1）单项式、多项式、整式这三者之间的关系如图所示．即单项式、多项式必是整式，但反过来就不一定成立．（2）分母中含有字母的式子一定不是整式．题型01单项式的判断题型02单项式的系数、次数题型03写出满足某些特征的单项式题型04单项式规律题题型05多项式的判断题型06多项式的项、项数或次数题型07多项式系数、指数中字母求值的值是题型08将多项式按某个字母升幂(降幂)排列题型09整式的判断一、单选题。

第04讲探索与表达规律(6类热点题型讲练)(原卷版)--初中数学北师大版7年级上册

第04讲探索与表达规律(6类热点题型讲练)1.探索运用符号表示数字规律和图形规律的方法.2.提高观察图形、探索规律的能力，培养创新意识.知识点01规律探究常见的数字规律知识点02规律探究方法总结1.规律探究的核心是找出每个数与对应的位次（即n ）之间的关系；2.若数列为分数数列，则分子分母分开找规律；3.若数列是正负交替排列，则在答案前加上n )1(-；若数列是负正交替排列，则在答案前加上1)1(+-n ；4.若是选择题，则可以用代值法，再利用排除法选出正确答案即可.知识点03高斯求和定理2)1(2)(14321nn n n ⋅+=⨯+=+-+⋅⋅⋅++++项数末项首项.题型01数字类规律探索之排列问题（1）第5行第10列的数字是．题型02数字类规律探索之末尾数字问题【典例2】（2022秋·江苏连云港·七年级校考阶段练习）观察下列算式：031=，133=，239=，3327=，4381=，53243=，63729=，732187=…归纳各计算结果中个位数字的规律，可得20033的个位数字是（）A ．1B ．3C ．9D ．7【变式1】（2023春·江苏南京·七年级校考阶段练习）观察下列算式：①2(1)(1)1x x x -+=-；②23(1)(1)1x x x x -++=-；③324(1)(1)1x x x x x -+++=-寻找规律，并判断(2011)(2017)222221++⋯+++的值的末位数字为（）A ．1B ．3C ．5D ．7【变式2】（2023春·江苏泰州·七年级统考期中）发现规律解决问题是常见解题策略之一．已知数5555551234529a =++++++ ，则这个数a 的个位数为（）A ．3B ．4C ．5D ．6【变式3】（2023春·江苏连云港·七年级统考期末）生物学中，描述、解释和预测种群数量的变化，常常需要建立数学模型．在营养和生存空间没有限制的情况下，某种细胞可通过分裂来繁殖后代，我们就用数学模型2n 来表示，即：122=，224=，328=，4216=，5232=，……，请你推算123452023222222+++++⋅⋅⋅⋅⋅⋅+的个位数字是（）A ．8B ．6C ．4D ．2题型03数字类规律探索之新运算问题题型04数字类规律探索之等式问题题型05图形类规律探索之数字问题【典例5】（2022秋·湖北黄冈·七年级校考阶段练习）如图，根据图形中数的规律，可推断出a 的值为（）A ．128B ．216C ．226D ．240【变式1】（2023春·贵州毕节·七年级统考期末）根据图中数字的规律，若第n 个图中A B C D ++-的值为196，则n =（）A ．12B ．13C ．14D ．15【变式2】（2022秋·河南周口·七年级校考期中）如图所示，下列各三角形中的三个数之间均具有相同的规律，根据此规律，则第n （n 为正整数）个三角形中，用n 表示y 的式子为（）A ．21n +B ．2n n +C ．12n n ++D ．21n n ++题型06图形类规律探索之数量问题【变式2】（2023·安徽淮北·淮北市第二中学校考二模）如图，利用黑白两种颜色的五边形组成的图案，根据图案组成的规律回答下列问题：(1)图案④中黑色五边形有______个，白色五边形有(2)图案n中黑色五边形有______个，白色五边形有(3)图案n中的白色五边形可能为2023个吗？若可能，请求出A．72B．66C．564．（2023春·云南临沧·七年级统考期末）如图，用字母有4个H，第2个图案中有6个H，第3个图案中有A．4044B．4046C．60695．（2023春·福建宁德·七年级校联考期中）我国宋代数学文杨辉所著《详解九章算法》中记载了用如图所示的一角形解释了二项和的乘方展开式中的系数规律，我们把这种数字三角形叫做【分析】根据图中规律，可得()2a b +的展开式中含3b 项的系数，再根据()6a b -的展开式中，系数的绝对值与()2a b +的展开式中的系数相同，符号从左往后为奇数项为正，偶数项为负．【详解】解：由题意可知，下排每个数等于上方两个数字的绝对值之和，∴5()a b +的展开式系数从左往右分别是1,5,10,10,5,1，6()a b ∴+的展开式系数从左往右分别是1,6,15,20,15,6,1，根据图中，可知()6a b -含有3b 项的项为从左往右第四项，且符号为负，故()6a b -的展开式中，含3b 项的系数是20-，故选：C ．【点睛】本题考查了数字变化规律，通过观察、分析、归纳发现其中规律，并应用发现的规律是解题的关键．7．（2023春·山东泰安·六年级校考期中）观察下列各式，探索规律：21321⨯=-；23541⨯=-；25761⨯=-；27981⨯=-；911⨯=用含正整数n 的等式表示你所发现的规律为8．（2023春·黑龙江绥化·七年级校考期末）观察下列算式：13=根据上述算式中的规律，你认为20233的末位数字是．9．（2023春·河北石家庄·七年级行唐一中校考开学考试）观察下列图形的构成规律，按此规律，第中棋子的个数为个，第n 个图形中棋子的个数为个．10．（2022秋·江苏宿迁·七年级校考阶段练习）已知整数(1)数一数，完成下列表格．直线的条数23452+==13422++== 135932 +++== 1357164 ++++== 13579255(1)填写下表：每条边上摆放的盆数（n）23456…。

2014高考数学理(真题讲练规律总结名师押题)热点专题突破：第五讲导数及其应用

第五讲导数及其应用变化率导数定义导函数定积分微积分基本定理定积分应用在几何中的应用在物理中的应用导数的计算基本初等函数的导数公式简单复合函数求导导数四则运算导数的应用函数单调性曲线的切线极值与最值优化问题几何意义曲边梯形面积变速运动行程1．(导数的几何意义)若函数f (x )＝2xx 2＋1在点(2，f (2))处的切线为l ，则直线l 与y 轴的交点坐标为________．【解析】 f ′(x )＝2(x 2＋1)－2x ·2x (x 2＋1)2＝－2x 2＋2(x 2＋1)2，则f ′(2)＝－625，又f (2)＝45，故直线l 的方程为y －45＝－625(x －2)，令x ＝0得y ＝3225，即直线l 与y 轴的交点坐标为⎝⎛⎭⎫0，3225. 【答案】 ⎝⎛⎭⎫0，3225 2．(导数与单调性的关系)函数y ＝12x 2－ln x 的单调递减区间为________．【解析】 y ′＝x －1x ，且x >0.令y ′＝x －1x ≤0，解之得0<x ≤1，∴函数的单调减区间为(0,1]．【答案】 (0,1]3．(定积分)定积分(x 2＋sin x )d x ＝________.【解析】(x 2＋sin x )d x ＝⎝⎛⎭⎫13x 3－cos x |1－1＝⎝⎛⎭⎫13－cos 1－⎣⎡⎦⎤－13－cos (－1)＝23. 【答案】 234．(函数的最值)已知f (x )＝2x 3－6x 2＋m (m 为常数)，在[－2,2]上有最大值3，那么此函数在[－2,2]上的最小值为__________．【解析】 ∵f ′(x )＝6x 2－12x ＝6x (x －2)，由f ′(x )＝0，得x ＝0或x ＝2.∵f (0)＝m ，f (2)＝－8＋m ，f (－2)＝－40＋m ，有f (0)>f (2)>f (－2)． ∴m ＝3，最小值为f (－2)＝－37. 【答案】－375．(导数的实际应用)放射性元素由于不断有原子放射出微粒子而变成其他元素，其含量不断减少，这种现象称为衰变．假设在放射性同位素铯137的衰变过程中，其含量M (单位：太贝克)与时间t (单位：年)满足函数关系．M (t )＝M 0·2－t30，其中M 0为t ＝0时铯137含量．已知t ＝30时，铯137含量的变化率是－10ln 2(太贝克/年)，则M (60)＝________太贝克．【解析】由题意，M ′(t )＝M 0·2－t 30(－130)ln 2.∴M ′(30)＝M 0·2－1(－130)ln 2＝－10ln 2，则M 0＝600，故M (60)＝600×2－2＝150.【答案】 150(2013·山东高考)已知函数f (x )＝ax 2＋bx －ln x (a ，b ∈R )．(1)设a ≥0，求f (x )的单调区间；(2)设a ＞0，且对任意x ＞0，f (x )≥f (1)，试比较ln a 与－2b 的大小．【思路点拨】 (1)求f ′(x )，分a ＝0与a ＞0两种情况求f ′(x )＞0与f ′(x )＜0的解集．同时注意b 对解集的影响；(2)由f (x )≥f (1)知，f (1)是函数f (x )的最小值，由此可建立等量关系寻找a 、b 的关系，进而构造函数比较大小．【自主解答】 (1)由f (x )＝ax 2＋bx －ln x ，x ∈(0，＋∞)，得 f ′(x )＝2ax 2＋bx －1x .①当a ＝0时，f ′(x )＝bx －1x.a ．若b ≤0，当x ＞0时，f ′(x )＜0恒成立，所以函数f (x )的单调递减区间是(0，＋∞)．b ．若b ＞0，当0＜x ＜1b 时，f ′(x )＜0，函数f (x )单调递减，当x ＞1b时，f ′(x )＞0，函数f (x )单调递增．所以函数f (x )的单调递减区间是⎝⎛⎭⎫0，1b ，单调递增区间是⎝⎛⎭⎫1b ，＋∞. ②当a ＞0时，令f ′(x )＝0，得2ax 2＋bx －1＝0. 由Δ＝b 2＋8a ＞0，得x 1＝－b －b 2＋8a 4a ，x 2＝－b ＋b 2＋8a4a .显然x 1＜0，x 2＞0.当0＜x ＜x 2时，f ′(x )＜0，函数f (x )单调递减；当x ＞x 2时，f ′(x )＞0，函数f (x )单调递增．所以函数f (x )的单调递减区间是⎝ ⎛⎭⎪⎫0，－b ＋b 2＋8a 4a ，单调递增区间是⎝ ⎛⎭⎪⎫－b ＋b 2＋8a 4a ，＋∞.综上所述，当a ＝0，b ≤0时，函数f (x )的单调递减区间是(0，＋∞)；当a ＝0，b ＞0时，函数f (x )的单调递减区间是⎝⎛⎭⎫0，1b ，单调递增区间是⎝⎛⎭⎫1b ，＋∞；当a ＞0时，函数f (x )的单调递减区间是⎝ ⎛⎭⎪⎫0，－b ＋b 2＋8a 4a ，单调递增区间是⎝ ⎛⎭⎪⎫－b ＋ b 2＋8a 4a ，＋∞.(2)由题意知函数f (x )在x ＝1处取得最小值．由(1)知－b ＋b 2＋8a4a 是f (x )的唯一极小值点，故－b ＋b 2＋8a 4a ＝1.整理，得2a ＋b ＝1，即b ＝1－2a .令g (x )＝2－4x ＋ln x ，则g ′(x )＝1－4xx .令g ′(x )＝0，得x ＝14.当0＜x ＜14时，g ′(x )＞0，g (x )单调递增；当x ＞14时，g ′(x )＜0，g (x )单调递减．因此g (x )≤g ⎝⎛⎭⎫14＝1＋ln 14＝1－ln 4＜0. 故g (a )＜0，即2－4a ＋ln a ＝2b ＋ln a ＜0，即ln a ＜－2b .1．解答第(2)题的关键是根据b ＝1－2a ，构造函数g (x )＝2－4x ＋ln x ，再求函数g (x )的最大值．2．根据函数的单调性求参数取值范围的思路． (1)求f ′(x )．(2)将单调性转化为f ′(x )≥0或f ′(x )≤0恒成立问题求解，要注意“＝”是否可以取到，应加以检验．变式训练1 (2013·宜昌模拟)已知函数f (x )＝a ln x －2ax ＋3(a ≠0)． (1)求函数f (x )的单调增区间；(2)函数y ＝f (x )的图象在x ＝2处的切线的斜率为32.若函数g (x )＝13x 3＋x 2[f ′(x )＋m ]在区间(1,3)上不是单调函数．求实数m 的取值范围．【解】 (1)f (x )的定义域为(0，＋∞)．又f ′(x )＝ax －2a ＝a (1－2x )x ，∴当a >0时，由f ′(x )>0，得0<x <12.当a <0时，由f ′(x )>0，得x >12，∴当a >0时，f (x )的增区间为(0，12)；当a <0时，f (x )的增区间为(12，＋∞)．(2)∵f (x )在x ＝2处的切线斜率为32，∴f ′(2)＝－32a ＝32，∴a ＝－1.此时f ′(x )＝2－1x ，因此g (x )＝13x 3＋x 2(2－1x ＋m )＝13x 3＋(2＋m )x 2－x . ∴g ′(x )＝x 2＋2(2＋m )x －1. ∵g (x )在区间(1,3)上不是单调函数，则g ′(x )在(1,3)内有零点．又g ′(0)＝－1，∴结合g ′(x )的图象知⎩⎪⎨⎪⎧g ′(1)<0，g ′(3)>0.即⎩⎪⎨⎪⎧1＋2(2＋m )－1<0，9＋6(2＋m )－1>0，解之得－103<m <－2.故实数m 的取值范围为(－103，－2).【命题要点】 ①已知函数，求极值或最值；②已知极值或最值，求参数的取值范围.(2013·广东高考)设函数f (x )＝(x －1)e x －kx 2(k ∈R )．(1)当k ＝1时，求函数f (x )的单调区间；(2)当k ∈⎝⎛⎦⎤12，1时，求函数f (x )在[0，k ]上的最大值M .【思路点拨】 (1)求函数的单调区间，就是求不等式f ′(x )>0和f ′(x )<0的解集．(2)求函数在给定区间上的最大值，要结合函数单调性求出极值，并和区间端点函数值进行比较，因含有参数，故需要分类讨论．【自主解答】 (1)当k ＝1时，f (x )＝(x －1)e x －x 2， f ′(x )＝e x ＋(x －1)e x －2x ＝x (e x －2)．由f ′(x )＝0，解得x 1＝0，x 2＝ln 2>0. 由f ′(x )>0，得x <0或x >ln 2. 由f ′(x )<0，得0<x <ln 2.所以函数f (x )的单调增区间为(－∞，0)和(ln 2，＋∞)，单调减区间为(0，ln 2)． (2)因为f (x )＝(x －1)e x －kx 2，所以f ′(x )＝x e x －2kx ＝x (e x －2k )．令f ′(x )＝0，解得x 1＝0，x 2＝ln(2k )，因为k ∈⎝⎛⎦⎤12，1，所以2k ∈(1,2]，所以0<ln(2k )≤ln 2. 设g (k )＝k －ln(2k )，k ∈⎝⎛⎦⎤12，1， g ′(k )＝1－1k ＝k －1k ≤0，所以g (k )在⎝⎛⎦⎤12，1上是减函数，所以g (k )≥g (1)＝1－ln 2>0，即0<ln(2k )<k . 所以f ′(x )，f (x )随x 的变化情况如下表：f (0)＝－1，f (k )＝(k －1)e k －k 3，f (k )－f (0)＝(k －1)e k －k 3＋1＝(k －1)e k －(k 3－1) ＝(k －1)e k －(k －1)(k 2＋k ＋1) ＝(k －1)[e k －(k 2＋k ＋1)]．因为k ∈⎝⎛⎦⎤12，1，所以k －1≤0.令h (k )＝e k －(k 2＋k ＋1)，则h ′(k )＝e k －(2k ＋1)．对任意的k ∈⎝⎛⎦⎤12，1，y ＝e k 的图象恒在y ＝2k ＋1的图象的下方，所以e k －(2k ＋1)<0，即h ′(k )<0，所以函数h (k )在⎝⎛⎦⎤12，1上为减函数，故h (1)≤h (k )<h (12)＝e 12－⎝⎛⎭⎫14＋12＋1＝e －74<0，所以f (k )－f (0)≥0，即f (k )≥f (0)．所以函数f (x )在[0，k ]上的最大值M ＝f (k )＝(k －1)e k －k 3.1．解答本题第(2)小题时，需要判断f (0)与f (k )的大小，采用作差比较法，对于不能判断正负的因式，构造函数利用导数求解．2．(1)求闭区间上可导函数的最值，对于极大值还是极小值，可不作判断，只需要将其与端点的函数值比较．(2)本题充分考查分类讨论的数学思想，分类标准要明确，讨论要彻底，这才能有效地避免错误．变式训练2 (2013·浙江高考)已知a ∈R ，函数f (x )＝2x 3－3(a ＋1)x 2＋6ax . (1)若a ＝1，求曲线y ＝f (x )在点(2，f (2))处的切线方程； (2)若|a |>1，求f (x )在闭区间[0,2|a |]上的最小值．【解】 (1)当a ＝1时，f ′(x )＝6x 2－12x ＋6，所以f ′(2)＝6. 又因为f (2)＝4，所以切线方程为y －4＝6(x －2)，即6x －y －8＝0.(2)记g (a )为f (x )在闭区间[0,2|a |]上的最小值． f ′(x )＝6x 2－6(a ＋1)x ＋6a ＝6(x －1)(x －a )．令f ′(x )＝0，得x 1＝1，x 2＝a . 当a >1时，g (a )＝⎩⎪⎨⎪⎧0，1<a ≤3，a 2(3－a )，a >3.当a <－1时，综上所述，f (x )在闭区间[0,2|a |]上的最小值为g (a )＝⎩⎪⎨⎪⎧3a －1，a <－1，0，1<a ≤3，a 2(3－a )，a >3.(2013·济南模拟)设f (x )＝(x ＋a )ln xx ＋1，曲线y ＝f (x )在点(1，f (1))处的切线与直线2x ＋y ＋1＝0垂直．(1)求a 的值；(2)若∀x ∈[1，＋∞)，f (x )≤m (x －1)恒成立，求m 的范围．(3)求证：ln 42n ＋1＜∑ni ＝1i4i 2－1.(n ∈N *)．【思路点拨】 (1)利用f ′(1)＝12求解．(2)把f (x )≤m (x －1)进行等价转化，构造函数，利用导数判断不等式是否恒成立． (3)根据第(2)题的结论可得ln x ＜12⎝⎛⎭⎫x －1x ，令x ＝2k ＋12k －1可得到ln 2k ＋12k －1＜4k 4k 2－1，即14[ln(2k ＋1)－ln(2k －1)]＜k4k 2－1，k ∈N *，累加求和，可证明结论．【自主解答】(1)f ′(x )＝⎝⎛⎭⎫x ＋a x ＋ln x (x ＋1)－(x ＋a )ln x (x ＋1)2，由题设f ′(1)＝12，∴2(1＋a )4＝12.∴1＋a ＝1，∴a ＝0.(2)f (x )＝x ln xx ＋1，∀x ∈[1，＋∞)，f (x )≤m (x －1)，即ln x ≤m ⎝⎛⎭⎫x －1x . 设g (x )＝ln x －m ⎝⎛⎭⎫x －1x ，即∀x ∈[1，＋∞)，g (x )≤0. g ′(x )＝1x －m ⎝⎛⎭⎫1＋1x 2＝－mx 2＋x －m x 2.①若m ≤0，g ′(x )＞0，g (x )≥g (1)＝0，这与题设g (x )≤0矛盾②若m ＞0，方程－mx 2＋x －m ＝0的判别式Δ＝1－4m 2.当Δ≤0，即m ≥12时，g ′(x )≤0，∴g (x )在(0，＋∞)上单调递减，∴g (x )≤g (1)＝0，即不等式成立．当0＜m ＜12时，方程－mx 2＋x －m ＝0，其根x 1＝1－1－4m 22m ＞0，x 2＝1＋1－4m 22m＞1，当x ∈(1，x 2)，g ′(x )＞0，g (x )单调递增，g (x )＞g (1)＝0，与题设矛盾．综上所述，m ≥12.(3)由(2)知，当x ＞1时，m ＝12时，ln x ＜12⎝⎛⎭⎫x －1x 成立．不妨令x ＝2k ＋12k －1，k ∈N *所以ln 2k ＋12k －1＜12⎝ ⎛⎭⎪⎫2k ＋12k －1－2k －12k ＋1＝4k4k 2－1， 14[ln(2k ＋1)－ln(2k －1)]＜k4k 2－1，k ∈N * ⎩⎪⎨⎪⎧14(ln 3－ln 1)＜14×12－1，14(ln 5－ln 3)＜24×22－1，…………14[(ln (2n ＋1)－ln (2n －1)]＜n 4×n 2－1，累加可得14ln(2n ＋1)＜∑ni ＝1 i 4i 2－1(n ∈N *)．即ln 42n ＋1＜∑ni ＝1i4i 2－1(n ∈N *)．1．本题失分原因主要有：(1)对不等式f (x )≤m (x －1)不能正确转化，或对m 不能进行分类讨论求解．(2)思维能力差，不能根据第(2)题的结论得到ln x ＜12⎝⎛⎭⎫x －1x ，或不能根据结论，令x ＝2k ＋12k －1，从而得不到14[ln(2k ＋1)－(2k －1)]＜k4k 2－1，k ∈N *.2．涉及不等式证明或不等式恒成立问题，常根据题目的特征，恰当构建函数，利用导数研究函数的单调性，转化为求函数的最值、极值问题，解题中要注意转化的等价性．对于含参数的不等式，注意分离参数与分类讨论；必要时，可作出函数图象草图，借助几何直观分析转化．变式训练3 (2013·黄冈模拟)已知函数f (x )＝－x 3＋x 2，g (x )＝a ln x (a ≠0，a ∈R )． (1)若对任意x ∈[1，＋∞)，使得f (x )＋g (x )≥－x 3＋(a ＋2)x 恒成立，求实数a 的取值范围；(2)证明：对n ∈N *，不等式1ln (n ＋1)＋1ln (n ＋2)＋…＋1ln (n ＋2 013)＞ 2 013n (n ＋2 013)成立．【解】 (1)f (x )＋g (x )≥－x 3＋(a ＋2)x 转化为a (ln x －x )≥2x －x 2，易知ln x ＜x ，∴a ≤x 2－2x x －ln x ，设φ(x )＝x 2－2xx －ln x，φ′(x )＝(x －1)(x ＋2－2ln x )(x －ln x )2，设h (x )＝x ＋2－2ln x ，h ′(x )＝1－2x.∵h (x )在(1,2)单调递减，(2，＋∞)单调递增， ∴h (x )min ＝h (2)＝4－2ln 2＞0.∴φ′(x )≥0，∴φ(x )在[1，＋∞)上是增函数， φ(x )min ＝φ(1)＝－1. ∴a ≤－1.(2)由(1)知：a ln x －(a ＋2)x ＋x 2≥0对x ≥1恒成立，令a ＝－1，则ln x ≤x 2－x ， ∴1ln x ＞1x (x －1)＝1x －1－1x. 取x ＝n ＋1，n ＋2，…，n ＋2 013得1ln (n ＋1)＞1n －1n ＋1，1ln (n ＋2)＞1n ＋1－1n ＋2，…，1ln (n ＋2 013)＞1n ＋2 012－1n ＋2 013.相加得：1ln (n ＋1)＋1ln (n ＋2)＋…＋1ln (n ＋2 013)＞⎝⎛⎭⎫1n －1n ＋1＋⎝⎛⎭⎫1n ＋1－1n ＋2＋…＋⎝⎛⎭⎫1n ＋2 012－1n ＋2 013＝1n －1n ＋2 013＝ 2 013n (n ＋2 013).从近两年高考题来看，导数的应用是高考考查的热点，重点考查利用导数判断函数的单调性，证明不等式．解决恒成立等问题，其中利用导数研究方程根的个数问题，2013年山东高考对此做了考查，在复习备考时应高度重视．导数在研究函数图象公共点中的应用(12分)已知f (x )＝x 2＋3x ＋1，g (x )＝a －1x －1＋x .(1)a ＝2时，求y ＝f (x )和y ＝g (x )图象的公共点个数； (2)a 为何值时，y ＝f (x )和y ＝g (x )的公共点个数恰为两个．【规范解答】 (1)当a ＝2时，联立⎩⎪⎨⎪⎧y ＝f (x )，y ＝g (x )，得x 2＋3x ＋1＝1x －1＋x ，2分整理得x 3＋x 2－x －2＝0(x ≠1)，即联立⎩⎪⎨⎪⎧y ＝0，y ＝x 3＋x 2－x －2(x ≠1)， 4分求导得y ′＝3x 2＋2x －1＝0得x 1＝－1，x 2＝13，得到极值点分别在－1和13处，且极大值、极小值都是负值，图象如图，故交点只有一个.6分(2)联立⎩⎪⎨⎪⎧y ＝f (x )，y ＝g (x )，得x 2＋3x ＋1＝a －1x －1＋x ，整理得a ＝x 3＋x 2－x (x ≠1)，8分即联立⎩⎪⎨⎪⎧y ＝a ，y ＝h (x )＝x 3＋x 2－x (x ≠1)，对h (x )求导可以得到极值点分别在－1和13处，画出草图如图．h (－1)＝1，h ⎝⎛⎭⎫13＝－527，10分当a ＝h (－1)＝1时，y ＝a 与y ＝h (x )仅有一个公共点(因为(1,1)点不在y ＝h (x )曲线上)，故a ＝－527时恰有两个公共点.12分【阅卷心语】易错提示 (1)第(1)小题中不能把两函数图象的交点个数问题转化为函数的零点个数问题求解或不能利用函数的极值及变化趋势画出函数的大致图象，从而无法求解．(2)第(2)小题中，未能分离参数a ，使问题进一步转化，从而无法求解．防范措施 (1)函数图象有公共点⇔方程有解⇔函数有零点，它们之间的相互转化是解决此类问题的关键．(2)分离参数是求参数的值或参数范围的常用方法，应切实掌握．1．若函数f (x )＝log a (x 3－ax )(a ＞0，a ≠1)在区间⎝⎛⎭⎫－12，0内单调递增，则a 的取值范围是( )A.⎣⎡⎭⎫14，1 B.⎣⎡⎭⎫34，1 C.⎝⎛⎭⎫94，＋∞D.⎝⎛⎭⎫1，94 【解析】由x 3－ax ＞0得x (x 2－a )＞0，则有⎩⎪⎨⎪⎧ x ＞0，x 2－a ＞0或⎩⎪⎨⎪⎧x ＜0，x 2－a ＜0，∴x ＞a 或－a ＜x ＜0，即函数f (x )的定义域为(a ，＋∞)∪(－a ，0)．令g (x )＝x 3－ax ，则g ′(x )＝3x 2－a .由g ′(x )＜0得－3a3＜x ＜0. 从而g (x )在x ∈⎝⎛⎭⎫－3a 3，0上是减函数，又函数f (x )在x ∈⎝⎛⎭⎫－12，0内单调递增，则有⎩⎨⎧0＜a ＜1，－a ≤－12，－3a 3≤－12，∴34≤a ＜1. 【答案】 B 2．已知函数f (x )＝x 3＋x ，对任意的m ∈[－2,2]，f (mx －2)＋f (x )＜0恒成立，则x 的取值范围是________．【解析】 ∵f ′(x )＝3x 2＋1＞0恒成立， ∴函数f (x )在R 上是增函数．又f (－x )＝(－x )3＋(－x )＝－(x 3＋x )＝－f (x )， ∴函数f (x )是奇函数．由f (mx －2)＋f (x )＜0得f (mx －2)＜－f (x )＝f (－x )， ∴mx －2＜－x ，即xm －2＋x ＜0在m ∈[－2,2]上恒成立．记g (m )＝xm －2＋x ，则⎩⎪⎨⎪⎧ g (－2)＜0，g (2)＜0，即⎩⎪⎨⎪⎧－2x －2＋x ＜0，2x －2＋x ＜0得－2＜x ＜23.【答案】 ⎝⎛⎭⎫－2，23。

2020中考数学复习测试：热点专题突破专题六%E3%80%80开放型

专题六开放型条件开放类[类型解读]条件开放类问题的三种类型(1)补充条件型:题目给出部分条件,然后再添加一个(或几个)条件,使结论成立.(2)探索条件型:题目只给出结论,通过分析给出的结论特征,发现使结论成立的条件.(3)条件变化型:在原有条件与结论的基础上,题目的结论发生变化,需要补充条件.[例1](2019绍兴)在屏幕上有如下内容:如图,△ABC内接于☉O,直径AB的长为2,过点C的切线交AB的延长线于点D.张老师要求添加条件后,编制一道题目,并解答.(1)在屏幕内容中添加条件∠D=30°,求AD的长.请你解答.(2)以下是小明、小聪的对话:小明:我加的条件是BD=1,就可以求出AD的长.小聪:你这样太简单了,我加的是∠A=30°,连接OC,就可以证明△ACB与△DCO全等.参考此对话,在屏幕内容中添加条件,编制一道题目(可以添线添字母),并解答.解决条件开放型问题的一般思路:从结论出发,执果索因,逆向思维,逐步探求结论成立的条件.强化运用1:(2019齐齐哈尔)如图,已知在△ABC和△DEF中,∠B=∠E,BF=CE,点B,F,C,E在同一条直线上,若使△ABC≌△DEF,则还需添加的一个条件是(只填一个即可).结论开放类[类型解读]结论开放型问题的两种类型(1)结论是否成立型:这类探索问题的设问,常以适合某种条件的结论“成立”“不成立”等语句加以表述.从给出的已知条件出发,经过推理证明能够推出结论是否成立.(2)判断猜想型:这类问题设问通常有两条线段有何关系(探索相等、平行或垂直),两个角是否相等,这个三角形是什么特殊的三角形,这个四边形是什么特殊的四边形等.它与传统题的区别在于:探索问题的结论过程往往也是解题过程.[例2]小敏思考解决如下问题:原题:如图1,点P,Q分别在菱形ABCD的边BC,CD上,∠PAQ=∠B,求证:AP=AQ.(1)小敏进行探索,若将点P,Q的位置特殊化:把∠PAQ绕点A旋转得到∠EAF,使AE⊥BC,点E,F分别在边BC,CD上,如图2.此时她证明了AE=AF,请你证明;(2)受以上(1)的启发,在原题中,添加辅助线:如图3,作AE⊥BC,AF⊥CD,垂足分别为E,F.请你继续完成原题的证明.解决结论开放型问题,要充分利用题目中给出的条件合理地猜想,正确地推理,就会获得所求的结论.强化运用2:(2019贵阳)(1)数学理解:如图①,△ABC是等腰直角三角形,过斜边AB的中点D 作正方形DECF,分别交BC,AC于点E,F,求AB,BE,AF之间的数量关系;(2)问题解决:如图②,在任意直角△ABC内,找一点D,过点D作正方形DECF,分别交BC,AC于点E,F,若AB=BE+AF,求∠ADB的度数;(3)联系拓广:如图③,在(2)的条件下,分别延长ED,FD,交AB于点M,N,求MN,AM,NB的数量关系.存在性开放类[类型解读]存在性开放问题常见的四种类型(1)特殊点存在性开放问题:图形中存在特殊的点,该点满足题目中的某些条件,通过探索,推理证明或运算说明该点存在.(2)特殊三角形存在性开放问题:图形中存在着特殊的三角形(等腰三角形或直角三角形),通过探索,推理证明或运算说明该特殊三角形存在.(3)相似三角形存在性开放问题:图形中存在着与原三角形相似的三角形,通过探索,推理证明说明该三角形存在.(4)特殊四边形存在性开放问题:图形中存在着特殊的四边形,通过探索,推理证明或运算说明该特殊四边形存在.[例3](2019辽阳)如图,在平面直角坐标系中,Rt△ABC 的边BC在x轴上,∠ABC=90°,以A 为顶点的抛物线y=-x2+bx+c经过点C(3,0),交y轴于点E(0,3),动点P在对称轴上.(1)求抛物线的解析式;(2)若点P从A点出发,沿A→B方向以1个单位/秒的速度匀速运动到点B停止,设运动时间为t秒,过点P作PD⊥AB交AC于点D,过点D作平行于y轴的直线l交抛物线于点Q,连接AQ,CQ,当t为何值时,△ACQ的面积最大?最大值是多少?(3)若点M是平面内的任意一点,在x轴上方是否存在点P,使得以点P,M,E,C为顶点的四边形是菱形,若存在,请求出符合条件的M点坐标;若不存在,请说明理由.解决存在性问题,需先假设存在,再进行推演,若得出推演结果,则说明结论存在;若推出矛盾,则推翻假设,说明结论不存在.2+bx+c(a≠0)经过点A(3,0),B(-1,0),C(0,-3).(1)求该抛物线的解析式;(2)若以点A为圆心的圆与直线BC相切于点M,求切点M的坐标;(3)若点Q在x轴上,点P在抛物线上,是否存在以点B,C,Q,P为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.1.(2019咸宁)若整式x2+my2(m为常数,且m≠0)能在有理数范围内分解因式,则m的值可以是(写一个即可).2.如图,在平面直角坐标系中,点A,B的坐标分别为(1,3),(n,3),若直线y=2x与线段AB有公共点,则n的值可以为.(写出一个即可)3.如图,在△ABC中,AB≠AC,D,E分别为边AB,AC上的点,AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件: ,可以使得△FDB与△ADE相似.(只需写出一个)第2题图第3题图4.(2019舟山)如图,在矩形ABCD中,点E,F在对角线BD上.请添加一个条件,使得结论“AE=CF”成立,并加以证明.5.(2019温州)如图,在7×5的方格纸ABCD中,请按要求画图,且所画格点三角形与格点四边形的顶点均不与点A,B,C,D重合.(1)在图1中画一个格点△EFG,使点E,F,G分别落在边AB,BC,CD上,且∠EFG=90°.(2)在图2中画一个格点四边形MNPQ,使点M,N,P,Q分别落在边AB,BC,CD,DA上,且MP=NQ.6.如图,已知二次函数的图象过点O(0,0),A(8,4),与x轴交于另一点B,且对称轴是直线x=3.(1)求该二次函数的解析式;(2)若M是OB上的一点,作MN∥AB交OA于点N,当△ANM面积最大时,求点M的坐标;(3)P是x轴上的点,过P作PQ⊥x轴,与抛物线交于点Q.过A作AC⊥x轴于点C,当以点O,P,Q 为顶点的三角形与以点O,A,C为顶点的三角形相似时,求P点的坐标.专题六开放型专题突破[例1]解:(1)如图,连接OC,∵CD为切线,∴OC⊥CD,∴∠OCD=90°,∵∠D=30°,∴OD=2OC=2,∴AD=AO+OD=1+2=3.(2)(答案不唯一)添加∠DCB=30°,求AC的长.解:∵AB为直径,∴∠ACB=90°,∵∠ACO+∠OCB=90°,∠OCB+∠DCB=90°,∴∠ACO=∠DCB,∵∠ACO=∠A,∴∠A=∠DCB=30°,在Rt△ACB中,BC=AB=1,∴AC=BC=.强化运用1:AB=DE(答案不唯一)[例2]证明:(1)∵四边形ABCD是菱形,∴∠B+∠C=180°,∠B=∠D,AB=AD,∵∠EAF=∠B,∴∠EAF+∠C=180°,∴∠AEC+∠AFC=180°,∵AE⊥BC,∴∠AEB=90°,∴∠AFC=∠AFD=90°,在△AEB和△AFD中,∴△AEB≌△AFD,∴AE=AF.(2)由(1)得∠PAQ=∠EAF=∠B,AE=AF,∴∠EAP=∠FAQ,在△AEP和△AFQ中,∴△AEP≌△AFQ(ASA),∴AP=AQ.强化运用2:解:(1)AB=(AF+BE).理由如下:∵△ABC是等腰直角三角形,∴AC=BC,∠A=∠B=45°,AB=AC,∵四边形DECF是正方形,∴DE=DF=CE=CF,∠DFC=∠DEC=90°,∴∠A=∠ADF=45°,∴AF=DF=CE,∴AF+BE=BC=AC,∴AB=(AF+BE).(2)如图,延长AC到点M,使FM=BE,连接DM,∵四边形DECF是正方形,∴DF=DE,∠DFC=∠DEC=90°,∵BE=FM,∠DFC=∠DEB=90°,DF=ED,∴△DFM≌△DEB(SAS),∴DM=DB,∵AB=AF+BE,AM=AF+FM,FM=BE,∴AM=AB,又DM=DB,AD=AD,∴△ADM≌△ADB(SSS).∴∠DAC=∠DAB=∠CAB,同理,得∠ABD=∠CBD=∠ABC,∵∠ACB=90°,∴∠CAB+∠CBA=90°,∴∠DAB+∠ABD=(∠CAB+∠CBA)=45°,∴∠ADB=180°-(∠DAB+∠ABD)=135°. (3)∵四边形DECF是正方形,∴DE∥AC,DF∥BC,∴∠CAD=∠ADM,∠CBD=∠NDB,∠MDN=∠AFD=90°,∵∠DAC=∠DAB,∠ABD=∠CBD,∴∠DAB=∠ADM,∠NDB=∠ABD,∴AM=MD,DN=NB,在Rt△DMN中,MN2=MD2+DN2,∴MN2=AM2+NB2.[例3]解:(1)将点C(3,0),E(0,3)的坐标分别代入二次函数解析式,得解得故抛物线的解析式为y=-x2+2x+3.(2)由(1)知y=-x2+2x+3=-(x-1)2+4,∴点A的坐标为(1,4),设直线AC的解析式为y=kx+b,把A(1,4),C(3,0)代入,得解得∴直线AC的解析式为y=-2x+6,由题意,知AP=t,∴BP=4-t(0≤t≤4).把y=4-t代入y=-2x+6得4-t=-2x+6,解得x=1+.∴点D的坐标为1+,4-t.把x=1+代入y=-x2+2x+3,得y=-1+2+2×1++3=-+4,∴点Q的坐标为1+,-+4.∴QD=y Q-y D=-+4-(4-t)=-+t,∴S△ACQ=S△ADQ+S△CDQ=QD·(x Q-x A)+QD·(x C-x Q)=QD·(x C-x A)=×-+t×(3-1)=-+t=-(t-2)2+1(0≤t≤4).∴当t=2时,△ACQ的面积最大,最大面积为1.(3)设点P的坐标为(1,m),点M的坐标为(x,y),①当EC是菱形一条边时,且点M在直线AB右侧时,点E向右平移3个单位、向下平移3个单位得到C,则点P向右平移3个单位、向下平移3个单位得到M,则1+3=x,m-3=y,而MP=EP,得1+(m-3)2=(x-1)2+(y-m)2,解得y=m-3=,故点M的坐标为(4,);当点M在直线AB左侧时,同理,得点M的坐标为(-2,3+);②当EC是菱形一对角线时,则EC的中点即为PM的中点,则x+1=3,y+m=3,而PE=PC,即1+(m-3)2=4+m2,解得m=1,故x=2,y=3-m=3-1=2,故点M的坐标为(2,2).综上,点M的坐标为(4,)或(-2,3+)或(2,2).强化运用3:解:(1)把A(3,0),B(-1,0),C(0,-3)代入抛物线解析式,得解得则该抛物线的解析式为y=x2-2x-3.(2)设直线BC的解析式为y=kx-3,把B(-1,0)代入得-k-3=0,即k=-3,∴直线BC的解析式为y=-3x-3,∵A(3,0),B(-1,0),C(0,-3),∴AB=4,BC=,BO=1,如图,∵以点A为圆心的圆与直线BC相切于点M,∴AM⊥BC,∴∠AMB=∠COB=90°.∵∠ABM=∠CBO,∴△ABM∽△CBO,∴=,∴=,∴BM=,设M点的坐标为(m,-3m-3).则BM2=(-1-m)2+(3m+3)2=,解得m1=-,m2=-(不合题意,舍去)∴M点的坐标为-,-.(3)存在以点B,C,Q,P为顶点的四边形是平行四边形.设Q(x,0),P(n,n2-2n-3),当四边形BCQP为平行四边形时,由B(-1,0),C(0,-3),则-1+x=0+n,0+0=-3+n2-2n-3,解得n1=1+,n2=1-,当n=1+时,n2-2n-3=3,即P1(1+,3);当n=1-时,n2-2n-3=3,即P2(1-,3).当四边形BCPQ为平行四边形时,则-1+n=0+x,0+n2-2n-3=-3+0,解得n3=0,n4=2,当n=0时,不合题意,舍去;当n=2时,n2-2n-3=-3,即P3(2,-3).当四边形BQCP为平行四边形时,x+n=-1+0,0+n2-2n-3=-3+0,解得n5=0,n6=2,则P4(2,-3).综上可得,存在以点B,C,Q,P为顶点的四边形是平行四边形,点P的坐标为(1+,3)或(1-,3)或(2,-3).专题精练1.-1(答案不唯一)2.2(答案不唯一)3.∠BDF=∠A(答案不唯一)4.解:(答案不唯一)添加的条件是BE=DF.证明:∵四边形ABCD是矩形,∴AB∥CD,AB=CD,∴∠ABD=∠BDC,又∵BE=DF,∴△ABE≌△CDF(SAS),∴AE=CF.5.解:(1)(答案不唯一)满足条件的△EFG,如图1,2所示.(2)(答案不唯一)满足条件的四边形MNPQ如图所示.6.解:(1)∵抛物线过原点,对称轴是直线x=3,∴点B的坐标为(6,0),设抛物线解析式为y=ax(x-6),把A(8,4)代入,得4=8a(8-6),解得a=,∴抛物线解析式为y=x(x-6)=x2-x.(2)设M(t,0),直线OA的解析式为y=x,设直线AB的解析式为y=kx+b,把B(6,0),A(8,4)代入得,解得∴直线AB的解析式为y=2x-12,∵MN∥AB,∴设直线MN的解析式为y=2x+n,把M(t,0)代入得2t+n=0,解得n=-2t,∴直线MN的解析式为y=2x-2t,解方程组得则N t,t,∴S△AMN=S△AOM-S△NOM=×4t-t×t=-t2+2t=-(t-3)2+3,当t=3时,S△AMN有最大值3,此时M点坐标为(3,0).(3)设点P(m,0),则点Q m,m2-m,当△PQO∽△COA时,=,即=,∴PQ=2PO,即m2-m=2|m|,解方程m2-m=2m,得m1=0(舍去),m2=14,此时P点坐标为(14,0);解方程m2-m=-2m,得m3=0(舍去),m4=-2,此时P点坐标为(-2,0).当△PQO∽△CAO时,=,即=,∴PQ=PO,即m2-m=|m|,解方程m2-m=m,得m5=0(舍去),m6=8(舍去),解方程m2-m=-m,得m7=0(舍去),m8=4,此时P点坐标为(4,0).综上所述,P点坐标为(14,0)或(-2,0)或(4,0).。

关于新形势下的电视专题片创作分析

关于新形势下的电视专题片创作分析1. 引言1.1 新形势下电视专题片创作的重要性新形势下的电视专题片创作可以帮助观众深刻了解当下社会、经济、文化等方面的实际情况。

通过专题片的形式，可以深入挖掘问题的根源，解析复杂的社会现象，为观众提供更为全面、深入的信息。

这不仅可以丰富观众的知识储备，还能够引导他们客观、理性地看待社会现实，提升社会文明程度。

新形势下的电视专题片创作具有重要的意义，它不仅是传递信息、展现事实的工具，更是引导社会关注、促进沟通交流的重要途径。

我们需要重视和支持电视专题片创作，在新形势下不断创新，为社会发展和进步贡献力量。

1.2 当前电视专题片创作面临的挑战当前电视专题片创作面临的挑战主要包括以下几个方面：随着互联网和新媒体的快速发展，传统电视专题片的传播渠道受到影响，观众的选择面更加广泛，如何吸引观众的注意成为创作者们面临的难题。

随着社会对品质内容的需求不断提升，电视专题片创作越来越需要深入挖掘独特的价值观念和创意元素，但受到制作周期长、制作成本高等因素的制约，如何在保证质量的同时有效控制成本成为制作团队的挑战。

信息传播日益快速，观众的关注点也在不断变化，如何及时把握时事热点，创作出具有时代性、前瞻性的电视专题片成为创作者们亟待解决的问题。

受政策法规和市场环境等因素的影响，电视专题片创作面临着政策导向性、市场竞争等方面的挑战。

面对这些挑战，创作者们需要不断提升自身素养，加强团队合作，积极拓展创作思路，才能在新形势下取得更好的发展。

2. 正文2.1 新形势下电视专题片创作的特点1. 多样化题材：新形势下，电视专题片创作呈现出题材多样化的特点，涵盖了政治、社会、文化、科技等各个领域，不再局限于传统的纪录片题材。

创作者通过多样化的题材创作出更具吸引力和观赏性的作品。

2. 多元化表现形式：随着时代的发展，电视专题片创作形式也在不断创新与变化。

除了传统的纪录片形式外，还出现了互动式、虚拟现实等多种表现形式，给观众带来更加丰富多彩的观影体验。

语文专题复习+九年级全册+专题1-7课件+新人教版_图

语文专题复习+九年级全册+专题 1-7课件+新人教版_图
专题复习一┃ 名句默写
┃备考方略┃
针对默写名篇名句的题型特点，结合中考的发展变化趋势，在复习这一考点时应注意： 1．辨明名句(篇)的特征，抓住复习重点。 2．重视平时积累与考前强化结合，文句记忆与字形辨析并重。平时积累，主要是：(1)要化整为零，减轻积累记忆的压力；(2)要寻找规律，提高识记的效率；(3)要口手并用，读抄结合，适应识记题的默写式考查方式。
专题复习三┃病句的辨析与修改
6.不合逻辑 (1)自相矛盾如：他是多少个死难者中幸免的一个。(既然“幸免”，自然是没有死，怎么能说是“死难者”中的一个呢？应改为：多少人死难了，他是幸免的一个) (2)范围不清如：从事业的发展上看，还缺乏各项科学专家与各项人才。(各项人才包括科学专家，不宜并列，应说“各学科的专家与其他人才”)
专题复习三病句的辨析与修改
专题复习三┃病句的辨析与修改
┃备考方略┃
病句主要包括6种类型：语序不当、搭配不当、成分残缺或赘余、结构混乱、表意不明、不合逻辑。其中前四类是语法结构方面的问题，后两类是句意方面的问题。
1．语序不当如：一位优秀的有20多年教学经验的佛山一中的语文教师。正确顺序：佛山一中的(领属性的)一位(数量)有20多年教学经验的(动词短语)优秀的(形容)语文(名词) 教师。 2．搭配不当 (1)主谓搭配不当如：我国棉花的生产，过去不能自给。(不能自给的是“棉花”而不是“生产”)
专题复习三┃病句的辨析与修改
(2)他的眼神即使到美国治好后也还是不大好，走起路来有点深一脚浅一脚。这个句子应该做点修改，表达的意思才能清楚。请写出你修改后的句子。 [答案] “即使”改为“虽然”，“治好后”改为“治疗过”，“也”改为“但”。

2022版高考数学二轮专题突破(浙江专用理科)文档：专题六自选模块第1讲 Word版含答案

第1讲导数及其应用1．(2021·浙江)已知函数y ＝f (x )的图象是下列四个图象之一，且其导函数y ＝f ′(x )的图象如图所示，则该函数的图象是( )2．(2022·陕西)如图，修建一条大路需要一段环湖弯曲路段与两条直道平滑连接(相切)．已知环湖弯曲路段为某三次函数图象的一部分，则该函数的解析式为( )A ．y＝12x 3－12x 2－xB ．y ＝12x 3＋12x 2－3xC ．y ＝14x 3－xD ．y ＝14x 3＋12x 2－2x3．(2022·辽宁)当x ∈[－2,1]时，不等式ax 3－x 2＋4x ＋3≥0恒成立，则实数a 的取值范围是( ) A ．[－5，－3] B ．[－6，－98]C ．[－6，－2]D ．[－4，－3]4．(2021·课标全国Ⅱ)已知曲线y ＝x ＋ln x 在点(1,1)处的切线与曲线y ＝ax 2＋(a ＋2)x ＋1相切，则a ＝______________.1.导数的意义和运算是导数应用的基础，是高考的一个热点.2.利用导数解决函数的单调性与极值(最值)是高考的常见题型.热点一导数的几何意义1．函数f (x )在x 0处的导数是曲线f (x )在点P (x 0，f (x 0))处的切线的斜率，曲线f (x )在点P 处的切线的斜率k ＝f ′(x 0)，相应的切线方程为y －f (x 0)＝f ′(x 0)(x －x 0)．2．求曲线的切线要留意“过点P 的切线”与“在点P 处的切线”的不同．例1 (1)(2021·课标全国Ⅰ)已知函数f (x )＝ax 3＋x ＋1的图象在点(1，f (1))处的切线过点(2,7)，则a ＝____________.(2)(2021·宁波模拟)设函数f (x )＝ax 3＋3x ，其图象在点(1，f (1))处的切线l 与直线x －6y －7＝0垂直，则直线l 与坐标轴围成的三角形的面积为( ) A ．1 B ．3 C ．9D ．12思维升华 (1)求曲线的切线要留意“过点P 的切线”与“在点P 处的切线”的差异，过点P 的切线中，点P 不愿定是切点，点P 也不愿定在已知曲线上，而在点P 处的切线，必以点P 为切点．(2)利用导数的几何意义解题，主要是利用导数、切点坐标、切线斜率之间的关系来进行转化．以平行、垂直直线斜率间的关系为载体求参数的值，则要求把握平行、垂直与斜率之间的关系，进而和导数联系起来求解．跟踪演练1 在平面直角坐标系xOy 中，设A 是曲线C 1：y ＝ax 3＋1(a >0)与曲线C 2：x 2＋y 2＝52的一个公共点，若C 1在A 处的切线与C 2在A 处的切线相互垂直，则实数a 的值是________．热点二利用导数争辩函数的单调性1．f ′(x )>0是f (x )为增函数的充分不必要条件，如函数f (x )＝x 3在(－∞，＋∞)上单调递增，但f ′(x )≥0. 2．f ′(x )≥0是f (x )为增函数的必要不充分条件，当函数在某个区间内恒有f ′(x )＝0时，则f (x )为常函数，函数不具有单调性．例2 (2021·重庆)设函数f (x )＝3x 2＋axe x(a ∈R )．(1)若f (x )在x ＝0处取得极值，确定a 的值，并求此时曲线y ＝f (x )在点(1，f (1))处的切线方程； (2)若f (x )在[3，＋∞)上为减函数，求a 的取值范围．思维升华利用导数争辩函数单调性的一般步骤： (1)确定函数的定义域； (2)求导函数f ′(x )；(3)①若求单调区间(或证明单调性)，只要在函数定义域内解(或证明)不等式f ′(x )>0或f ′(x )<0. ②若已知函数的单调性，则转化为不等式f ′(x )≥0或f ′(x )≤0在单调区间上恒成立问题来求解．跟踪演练2 (1)函数f (x )＝12x 2－ln x 的单调递减区间为( )A ．(－1,1]B ．(0,1]C ．[1，＋∞)D ．(0，＋∞)(2)若函数f (x )＝－13x 3＋12x 2＋2ax 在[23，＋∞)上存在单调递增区间，则a 的取值范围是________．热点三利用导数求函数的极值、最值1．若在x 0四周左侧f ′(x )>0，右侧f ′(x )<0，则f (x 0)为函数f (x )的极大值；若在x 0四周左侧f ′(x )<0，右侧f ′(x )>0，则f (x 0)为函数f (x )的微小值．2．设函数y ＝f (x )在[a ，b ]上连续，在(a ，b )内可导，则f (x )在[a ，b ]上必有最大值和最小值且在极值点或端点处取得．例3 (2021·北京改编)设函数f (x )＝x 22－k ln x ，k >0.(1)求f (x )的单调区间和极值；(2)当x ∈[1，e]时，求f (x )的最小值．思维升华 (1)求函数f (x )的极值，则先求方程f ′(x )＝0的根，再检查f ′(x )在方程根的左右函数值的符号．(2)若已知极值大小或存在状况，则转化为已知方程f ′(x )＝0根的大小或存在状况来求解．(3)求函数f (x )在闭区间[a ，b ]的最值时，在得到极值的基础上，结合区间端点的函数值f (a )，f (b )与f (x )的各极值进行比较得到函数的最值．跟踪演练3 已知函数f (x )＝ln x ＋ax －a 2x 2(a ≥0)． (1)若x ＝1是函数y ＝f (x )的极值点，求a 的值； (2)若f (x )<0在定义域内恒成立，求实数a 的取值范围．1．已知曲线y ＝ln x 的切线过原点，则此切线的斜率为( )A ．eB ．－e C.1eD ．－1e2．已知函数f (x )＝x 3＋ax 2＋bx －a 2－7a 在x ＝1处取得极大值10，则ab 的值为( )A ．－23B ．－2C ．－2或－23D ．2或－233．已知函数f (x )＝x 2－ax ＋3在(0,1)上为减函数，函数g (x )＝x 2－a ln x 在(1,2)上为增函数，则a 的值等于________． 4．已知函数f (x )＝x －1x ＋1，g (x )＝x 2－2ax ＋4，若任意x 1∈[0,1]，存在x 2∈[1,2]，使f (x 1)≥g (x 2)，则实数a的取值范围是__________．提示：完成作业专题六第1讲二轮专题强化练专题六第1讲导数及其应用A 组专题通关1.若函数y ＝f (x )的导函数y ＝f ′(x )的图象如图所示，则y ＝f (x )的图象可能为( )2．(2021·云南第一次检测)函数f (x )＝ln x －2xx 的图象在点(1，－2)处的切线方程为( )A ．2x －y －4＝0B ．2x ＋y ＝0C ．x －y －3＝0D ．x ＋y ＋1＝03．(2021·福建)若定义在R 上的函数f (x )满足f (0)＝－1，其导函数f ′(x )满足f ′(x )＞k ＞1，则下列结论中确定错误的是( ) A ．f ⎝⎛⎭⎫1k ＜1k B ．f ⎝⎛⎭⎫1k ＞1k －1 C ．f ⎝⎛⎭⎫1k －1＜1k －1D ．f ⎝⎛⎭⎫1k －1＞k k －14．设f (x )＝13x 3＋ax 2＋5x ＋6在区间[1,3]上为单调函数，则实数a 的取值范围为( )A ．[－5，＋∞)B ．(－∞，－3]C ．(－∞，－3]∪[－5，＋∞)D ．[－5，5]5．已知a ≤1－x x ＋ln x 对任意x ∈[12，2]恒成立，则a 的最大值为( )A ．0B ．1C ．2D ．36．(2021·陕西)函数y ＝x e x 在其极值点处的切线方程为________．7．若函数f (x )＝ax ＋1x ＋2在x ∈(2，＋∞)上单调递减，则实数a 的取值范围是________．8．已知函数f (x )＝4ln x ＋ax 2－6x ＋b (a ，b 为常数)，且x ＝2为f (x )的一个极值点，则a 的值为________． 9．(2021·重庆)已知函数f (x )＝ax 3＋x 2(a ∈R )在x ＝－43处取得极值．(1)确定a 的值；(2)若g (x )＝f (x )e x ，争辩g (x )的单调性．10．已知函数f (x )＝x 28－ln x ，x ∈[1,3]．(1)求f (x )的最大值与最小值；(2)若f (x )<4－at 对任意的x ∈[1,3]，t ∈[0,2]恒成立，求实数a 的取值范围．B组力气提高11．函数f(x)＝x3－3x－1，若对于区间[－3,2]上的任意x1，x2，都有|f(x1)－f(x2)|≤t，则实数t的最小值是() A．20 B．18 C．3 D．012．已知函数f(x)＝x(ln x－ax)有两个极值点，则实数a的取值范围为________．13．设函数f(x)＝a e x(x＋1)(其中，e＝2.718 28…)，g(x)＝x2＋bx＋2，已知它们在x＝0处有相同的切线．(1)求函数f(x)，g(x)的解析式；(2)求函数f(x)在[t，t＋1](t>－3)上的最小值；(3)若对∀x≥－2，kf(x)≥g(x)恒成立，求实数k的取值范围．同学用书答案精析专题六自选模块第1讲导数及其应用高考真题体验1．B [从导函数的图象可以看出，导函数值先增大后减小，x ＝0时最大，所以函数f (x )的图象的变化率也先增大后减小，在x ＝0时变化率最大．A 项，在x ＝0时变化率最小，故错误；C 项，变化率是越来越大的，故错误；D 项，变化率是越来越小的，故错误．B 项正确．]2．A [A 选项中，y ′＝f ′(x )＝32x 2－x －1，f ′(0)＝－1，f ′(2)＝3.曲线在(0,0)和(2,0)处分别与直线y ＝－x ，y ＝3x －6相切，且在(0，1＋73)上单调递减，在(1＋73，2)上单调递增，符合题意．对B 、C 、D 选项可验证曲线在(0,0)或(2,0)处不与直线y ＝－x ，y ＝3x －6相切．故选A.] 3．C [当x ＝0时，ax 3－x 2＋4x ＋3≥0变为3≥0恒成立，即a ∈R . 当x ∈(0,1]时，ax 3≥x 2－4x －3，a ≥x 2－4x －3x 3，∴a ≥⎣⎢⎡⎦⎥⎤x 2－4x －3x 3max . 设φ(x )＝x 2－4x －3x 3，φ′(x )＝(2x －4)x 3－(x 2－4x －3)3x 2x 6＝－x 2－8x －9x 4＝－(x －9)(x ＋1)x 4>0，∴φ(x )在(0,1]上递增，φ(x )max ＝φ(1) ＝－6，∴a ≥－6.当x ∈[－2,0)时，a ≤x 2－4x －3x 3，∴a ≤⎣⎢⎡⎦⎥⎤x 2－4x －3x 3min .仍设φ(x )＝x 2－4x －3x 3，φ′(x )＝－(x －9)(x ＋1)x 4.当x ∈[－2，－1)时，φ′(x )<0，当x ∈(－1,0)时，φ′(x )>0.∴当x ＝－1时，φ(x )有微小值，即为最小值．而φ(x )min ＝φ(－1)＝1＋4－3－1＝－2，∴a ≤－2.综上知－6≤a ≤－2.]4．8解析由y ＝x ＋ln x ，得y ′＝1＋1x ，得曲线在点(1,1)的切线的斜率为k ＝y ′|x ＝1＝2，所以切线方程为y －1＝2(x －1)，即y ＝2x －1，此切线与曲线y ＝ax 2＋(a ＋2)x ＋1相切，消去y 得ax 2＋ax ＋2＝0，得a ≠0且Δ＝a 2－8a ＝0，解得a ＝8. 热点分类突破例1 (1)1 (2)B解析 (1)f ′(x )＝3ax 2＋1，f ′(1)＝1＋3a ，f (1)＝a ＋2. (1，f (1))处的切线方程为y －(a ＋2)＝(1＋3a )(x －1)．将(2,7)代入切线方程，得7－(a ＋2)＝(1＋3a )，解得a ＝1.(2)f ′(x )＝3ax 2＋3，由题设得f ′(1)＝－6，所以3a ＋3＝－6，a ＝－3.所以f (x )＝－3x 3＋3x ，f (1)＝0，切线l 的方程为y －0＝－6(x －1)，即y ＝－6x ＋6.所以直线l 与坐标轴围成的三角形的面积为S ＝12×1×6＝3.选B.跟踪演练1 4解析设A (x 0，y 0)，则C 1在A 处的切线的斜率为f ′(x 0)＝3ax 20，C 2在A 处的切线的斜率为－1k OA ＝－x 0y 0，又C 1在A 处的切线与C 2在A 处的切线相互垂直，所以(－x 0y 0)·3ax 20＝－1，即y 0＝3ax 30，又ax 30＝y 0－1，所以y 0＝32，代入C 2：x 2＋y 2＝52，得x 0＝±12，将x 0＝±12，y 0＝32代入y ＝ax 3＋1(a >0)，得a ＝4.例2 解 (1)对f (x )求导得f ′(x )＝(6x ＋a )e x －(3x 2＋ax )e x(e x )2＝－3x 2＋(6－a )x ＋ae x，由于f (x )在x ＝0处取得极值，所以f ′(0)＝0，即a ＝0.当a ＝0时，f (x )＝3x 2e x ，f ′(x )＝－3x 2＋6x e x，故f (1)＝3e ，f ′(1)＝3e ，从而f (x )在点(1，f (1))处的切线方程为y －3e＝3e (x －1)，化简得3x －e y ＝0. (2)由(1)知f ′(x )＝－3x 2＋(6－a )x ＋ae x .令g (x )＝－3x 2＋(6－a )x ＋a ，由g (x )＝0，解得x 1＝6－a －a 2＋366，x 2＝6－a ＋a 2＋366.当x ＜x 1时，g (x )＜0，即f ′(x )＜0，故f (x )为减函数；当x 1＜x ＜x 2时，g (x )＞0，即f ′(x )＞0，故f (x )为增函数；当x ＞x 2时，g (x )＜0，即f ′(x )＜0，故f (x )为减函数．由f (x )在[3，＋∞)上为减函数，知x 2＝6－a ＋a 2＋366≤3，解得a ≥－92，故a 的取值范围为⎣⎡⎭⎫－92，＋∞. 跟踪演练2 (1)B (2)(－19，＋∞)解析 (1)由题意知，函数的定义域为 (0，＋∞)，又由f ′(x )＝x －1x ≤0，解得0<x ≤1，所以函数f (x )的单调递减区间为(0,1]．(2)对f (x )求导，得f ′(x )＝－x 2＋x ＋2a ＝－(x －12)2＋14＋2a .当x ∈[23，＋∞)时，f ′(x )的最大值为f ′(23)＝29＋2a .令29＋2a >0，解得a >－19. 所以a 的取值范围是(－19，＋∞)．例3 解 (1)函数的定义域为(0，＋∞)．由f (x )＝x 22－k ln x (k >0)得f ′(x )＝x －k x ＝x 2－kx.由f ′(x )＝0解得x ＝k (负值舍去)．f (x )与f ′(x )在区间(0，＋∞)上的变化状况如下表：↘↗所以，f (x )的单调递减区间是(0，k )，单调递增区间是(k ，＋∞)．f (x )在x ＝k 处取得微小值f (k )＝k (1－ln k )2.(2)由(1)知，当k >e 即k >e 时， f (x )min ＝f (e)＝e 2－k2.当1≤k ≤e 即1≤k ≤e 时， f (x )min ＝f (k )＝k (1－ln k )2.当k <1即0<k <1时， f (x )min ＝f (1)＝12.故函数f (x )在[1，e]上的最小值f (x )min＝⎩⎪⎨⎪⎧12， 0<k <1，k (1－ln k )2， 1≤k ≤e ，e 2－k 2， k >e.跟踪演练3 解 (1)函数的定义域为 (0，＋∞)，f ′(x )＝－2a 2x 2＋ax ＋1x.由于x ＝1是函数y ＝f (x )的极值点，所以f ′(1)＝1＋a －2a 2＝0，解得a ＝－12(舍去)或a ＝1.经检验，当a ＝1时，x ＝1是函数y ＝f (x )的极值点，所以a ＝1.(2)当a ＝0时，f (x )＝ln x ，明显在定义域内不满足f (x )<0；当a >0时，令f ′(x )＝(2ax ＋1)(－ax ＋1)x＝0，得x 1＝－12a (舍去)，x 2＝1a ，所以f ′(x )，f (x )的变化状况如下表：↗↘所以f (x )max ＝f (1a )＝ln 1a <0，所以a >1.综上可得a 的取值范围是(1，＋∞)．高考押题精练1．C [y ＝f (x )＝ln x 的定义域为(0，＋∞)，设切点为(x 0，y 0)，则切线斜率k ＝f ′(x 0)＝1x 0.∴切线方程为y －y 0＝1x 0(x －x 0)，又切线过点(0,0)，代入切线方程得y 0＝1，则x 0＝e ，∴k ＝1x 0＝1e .] 2．A [由题意知f ′(x )＝3x 2＋2ax ＋b ，f ′(1)＝0，f (1)＝10，即⎩⎪⎨⎪⎧3＋2a ＋b ＝0，1＋a ＋b －a 2－7a ＝10，解得⎩⎪⎨⎪⎧ a ＝－2，b ＝1或⎩⎪⎨⎪⎧a ＝－6，b ＝9，经检验⎩⎪⎨⎪⎧a ＝－6，b ＝9满足题意，故a b ＝－23.]3．2解析 ∵函数f (x )＝x 2－ax ＋3在(0,1)上为减函数， ∴a2≥1，得a ≥2. 又∵g ′(x )＝2x －ax ，依题意g ′(x )≥0在x ∈(1,2)上恒成立，得2x 2≥a 在x ∈(1,2)上恒成立，有a ≤2，∴a ＝2.4.⎣⎡⎭⎫94，＋∞解析由于f ′(x )＝1＋1(x ＋1)2>0，因此函数f (x )在[0,1]上单调递增，所以x ∈[0,1]时，f (x )min ＝f (0)＝－1. 依据题意可知存在x ∈[1,2]，使得g (x )＝x 2－2ax ＋4≤－1，即x 2－2ax ＋5≤0，即a ≥x 2＋52x 能成立，令h (x )＝x 2＋52x，则要使a ≥h (x )在x ∈[1,2]能成立，只需使a ≥h (x )min ，又函数h (x )＝x 2＋52x在x ∈[1,2]上单调递减，所以h (x )min ＝h (2)＝94，故只需a ≥94.二轮专题强化练答案精析专题六自选模块第1讲导数及其应用1．C [依据f ′(x )的符号，f (x )图象应当是先下降后上升，最终下降，排解A 、D ；从适合f ′(x )＝0的点可以排解B.]2．C [f ′(x )＝1－ln xx 2，则f ′(1)＝1，故该切线方程为y －(－2)＝x －1，即x －y －3＝0.]3．C [∵导函数f ′(x )满足f ′(x )＞k ＞1，∴f ′(x )－k ＞0，k －1＞0，1k －1＞0，可构造函数g (x )＝f (x )－kx ，可得g ′(x )＞0，故g (x )在R 上为增函数，∵f (0)＝－1，∴g (0)＝－1，∴g ⎝ ⎛⎭⎪⎫1k －1＞g (0)，∴f ⎝ ⎛⎭⎪⎫1k －1－k k －1＞－1，∴f ⎝ ⎛⎭⎪⎫1k －1＞1k －1，∴选项C 错误，故选C.] 4．C [f ′(x )＝x 2＋2ax ＋5，当f (x )在[1,3]上单调递减时，由⎩⎨⎧f ′1≤0，f ′3≤0得a ≤－3；当f (x )在[1,3]上单调递增时，f ′(x )≥0恒成立，则有Δ＝4a 2－4×5≤0或⎩⎨⎧Δ>0，－a <1f ′1≥0或⎩⎪⎨⎪⎧Δ>0，－a >3，f ′3≥0，得a ∈[－5，＋∞)．综上a 的取值范围为(－∞，－3]∪[－5，＋∞)，故选C.]5．A [令f (x )＝1－x x ＋ln x ，则f ′(x )＝x －1x 2，当x ∈[12，1)时，f ′(x )<0，当x ∈(1,2]时，f ′(x )>0，∴f (x )在[12，1]上单调递减，在[1,2]上单调递增，∴[f (x )]min ＝f (1)＝0，∴a ≤0.]6．y ＝－1e解析设y ＝f (x )＝x e x ，令y ′＝e x ＋x e x ＝e x (1＋x )＝0，得x ＝－1.当x ＜－1时，y ′＜0；当x ＞－1时，y ′＞0，故x ＝－1为函数f (x )的极值点，切线斜率为0，又f (－1)＝－e －1＝－1e ，故切点坐标为⎝⎛⎭⎫－1，－1e ，切线方程为y ＋1e ＝0(x ＋1)，即y ＝－1e . 7．a ≤12解析 f ′(x ) ＝ax ＋1′x ＋2－x ＋2′ax ＋1x ＋22＝ax ＋2－ax ＋1x ＋22＝2a －1x ＋22，令f ′(x )≤0，即2a －1≤0，解得a ≤12.8．1解析由题意知，函数f (x )的定义域为(0，＋∞)， ∵f ′(x )＝4x＋2ax －6，∴f ′(2)＝2＋4a －6＝0，即a ＝1.9．解 (1)对f (x )求导得f ′(x )＝3ax 2＋2x ，由于f (x )在x ＝－43处取得极值，所以f ′⎝⎛⎭⎫－43＝0，即3a ·169＋2·⎝⎛⎭⎫－43 ＝16a 3－83＝0，解得a ＝12. (2)由(1)得g (x )＝⎝⎛⎭⎫12x 3＋x 2e x，故g ′(x )＝⎝⎛⎭⎫32x 2＋2x e x ＋⎝⎛⎭⎫12x 3＋x 2e x＝⎝⎛⎭⎫12x 3＋52x 2＋2x e x＝12x (x ＋1)(x ＋4)e x . 令g ′(x )＝0，解得x ＝0，x ＝－1或x ＝－4. 当x ＜－4时，g ′(x )＜0，故g (x )为减函数；当－4＜x ＜－1时，g ′(x )＞0，故g (x )为增函数；当－1＜x ＜0时，g ′(x )＜0，故g (x )为减函数；当x ＞0时，g ′(x )＞0，故g (x )为增函数．综上知g (x )在(－∞，－4)和(－1,0)内为减函数，在(－4，－1)和(0，＋∞)内为增函数． 10．解 (1)∵函数f (x )＝x 28－ln x ，∴f ′(x )＝x 4－1x ，令f ′(x )＝0得x ＝±2， ∵x ∈[1,3]，当1<x <2时，f ′(x )<0；当2<x <3时，f ′(x )>0； ∴f (x )在(1,2)上是单调减函数，在(2,3)上是单调增函数， ∴f (x )在x ＝2处取得微小值 f (2)＝12－ln 2；又f (1)＝18，f (3)＝98－ln 3，∵ln 3>1，∴18－(98－ln 3)＝ln 3－1>0， ∴f (1)>f (3)，∴x ＝1时f (x )的最大值为18，x ＝2时函数取得最小值为12－ln 2.(2)由(1)知当x ∈[1,3]时，f (x )≤18，故对任意x ∈[1,3]，f (x )<4－at 恒成立，只要4－at >18对任意t ∈[0,2]恒成立，即at <318恒成立，记g (t )＝at ，t ∈[0,2]．∴⎩⎨⎧g0<318，g2<318，解得a <3116，∴实数a 的取值范围是(－∞，3116)．11．A [由于f ′(x )＝3x 2－3＝3(x －1)(x ＋1)，令f ′(x )＝0，得x ＝±1，可知－1,1为函数的极值点．又f (－3)＝－19，f (－1)＝1，f (1)＝－3，f (2)＝1，所以在区间[－3,2]上f (x )max ＝1，f (x )min ＝－19.由题设知在区间[－3,2]上f (x )max －f (x )min ≤t ，从而t ≥20，所以t 的最小值是20.] 12．(0，12)解析 f ′(x )＝ln x ＋1－2ax (a >0)，问题转化为a ＝ln x ＋12x 在(0，＋∞)上有两个实数解．设g (x )＝ln x ＋12x ，则g ′(x )＝－ln x2x2.所以g (x )在(0,1)上单调递增，在(1，＋∞)上单调递减，g (x )在x ＝1处取得极大值也是最大值，即g (x )max ＝ g (1)＝12.留意g (1e )＝0，当x >1时，g (x )>0，则g (x )的大致图象如图所示．由图象易知0<a <12时，a ＝ln x ＋12x 在(0，＋∞)上有两个实数解．13．解 (1)f ′(x )＝a e x (x ＋2)，g ′(x )＝2x ＋b . 由题意，得两函数在x ＝0处有相同的切线． ∴f ′(0)＝2a ，g ′(0)＝b ， ∴2a ＝b ，f (0)＝a ，g (0)＝2， ∴a ＝2，b ＝4，∴f (x )＝2e x (x ＋1)，g (x )＝x 2＋4x ＋2.(2)由(1)知f ′(x )＝2e x (x ＋2)，由f ′(x )>0得x >－2，由f ′(x )<0得x <－2，∴f (x )在(－2，＋∞)单调递增，在(－∞，－2)单调递减．∵t >－3， ∴t ＋1>－2.①当－3<t <－2时，f (x )在[t ，－2]单调递减，在[－2，t ＋1]单调递增， ∴f (x )min ＝f (－2)＝－2e －2.②当t ≥－2时，f (x )在[t ，t ＋1]单调递增， ∴f (x )min ＝f (t )＝2e t (t ＋1)；∴f (x )＝⎩⎪⎨⎪⎧－2e －2－3<t <－2，2e tt ＋1t ≥－2.(3)令F (x )＝kf (x )－g (x )＝2k e x (x ＋1)－x 2－4x －2，由题意当x ≥－2时，F (x )min ≥0. ∵∀x ≥－2，kf (x )≥g (x )恒成立， ∴F (0)＝2k －2≥0，∴k ≥1.F ′(x )＝2k e x (x ＋1)＋2k e x －2x －4 ＝2(x ＋2)(k e x －1)，∵x ≥－2，由F ′(x )>0得e x >1k ，∴x >ln 1k；由F ′(x )<0得x <ln 1k，∴F (x )在(－∞，ln 1k )单调递减，在[ln 1k ，＋∞)单调递增．①当ln 1k<－2，即k >e 2时，F (x )在[－2，＋∞)单调递增， F (x )min ＝F (－2)＝－2k e －2＋2＝2e 2(e 2－k )<0，不满足F (x )min ≥0.②当ln 1k ＝－2，即k ＝e 2时，由①知，F (x )min ＝F (－2)＝2e 2(e 2－k )＝0，满足F (x )min ≥0.③当ln 1k >－2，即1≤k <e 2时，F (x )在[－2，ln 1k )单调递减，在[ln 1k ，＋∞)单调递增．F (x )min ＝F (ln 1k )＝ln k (2－ln k )>0，满足F (x )min ≥0.综上所述，满足题意的k 的取值范围为[1，e 2]．。

【师说】2015-2016高中历史人教版必修1 第2单元专题二

2.内容 (1)经历了民主制度不断完善的过程：梭伦改革奠定基础、克利斯提尼改革正式确立、伯利克里改革达到顶峰。 (2)经历了民主范围不断扩大过程：由血缘世袭到财产、地域为主，由财产等级限制到逐步取消，由贵族共和到公民广泛参与、人民主权、轮番而治。 (3)民主制度不断创新：抽签选举、差额选举制，立法、行政、司法分权制的尝试(公民大会为最高权力机关、五百人议事会和十将军委员会为行政机构、陪审法庭为司法机构)。 (4)少数人的民主：以城邦制为基础，适合小国寡民，民主只属于雅典少数有一定经济能力的成年男性公民，妇女、外邦人则无法享有。
解析：梭伦实行财产等级制度，只有公民大会和陪审法庭这两个机构任何公民都可以参加，并参与国政。材料中肯定了这两种权利的重要性，说明平民在城邦事务中取得了一定的参与权，B 项正确。A、C、D 三项均与史实不符。答案：B
专题 2 全面认识罗马法 1．形成 (1)政治条件：罗马不断发展与对外扩张。(2)社会条件：平民的不断斗争，迫使统治者不断调整法律。(3)经济条件：罗马奴隶制经济的发展与繁荣。(4)思想条件：古罗马人“自然法则”思想的存在和发展。(5)主观条件：统治者的重视。 2．核心：承认私有财产神圣不可侵犯。其中最重要的是对债权的规定和解释，规定了解决各类债务适用的法律条款，特别清晰地规定了契约的各种形式，以及契约双方的权利和义务。 3.特点：罗马法中渗透着自然法思想，如理性、自由、平等、正义等。 4.实质：保障和维护罗马奴隶主的地位和统治。
解析：根据题干提供的信息和所学史实，罗马法包括起源、发展和形成三个阶段，这些属于归纳整理。故选 C 项。答案：C
解析：材料中雅典国家机构权限的相互交叉和公职人员权限的部分交叉，体现了权力的制约与平衡，C 项正确。雅典民主是奴隶主阶级的民主，公民大会是其最高权力机构，首席执政官是其最高行政首脑，故 A、B、D 三项均错误。答案：C

分式的乘除法(6类热点题型讲练)(原卷版) 八年级数学下册

第02讲分式的乘除法(6类热点题型讲练)
1.掌握分式的乘除运算法则；
2.能够进行分子、分母为多项式的分式乘除法运算.
知识点01分式的乘法
乘法法则：分式乘分式，用分子的积作为积的分子，分母的积作为积的分母．用式子表示为：a c a c
b d b d
⋅⋅
=⋅．知识点02分式的除法
除法法则：分式除以分式，把除式的分子、分母颠倒位置后与被除式相乘．用式子表示为：
a c a d a d
b d b
c b c
⋅÷=⋅=⋅．知识点03分式的乘方
乘方法则：分式的乘方，把分子、分母分别乘方．用式子表示为：((n
n n a a n b b
=为正整数，0)b ≠．
题型01分式的乘法运算
【变式训练】
题型02分式的除法运算
【变式训练】
题型03分式乘除混合运算
【变式训练】
题型04分式的乘方运算
【变式训练】
题型05含乘方的分式乘除混合运算
【变式训练】
题型06分式乘除混合运算中化简求值
【变式训练】
则第4次运算的结果4y=．三、解答题。

八年级英语寒假班(新世纪版)—07—8A U7复习—8B U7单词预习—形容词副词—阅读综合类

1、8A U7复习I. Fill in the blanks with the proper words. （填入适当的单词，首字母已给）1.Our English teacher told us that the e____________ would be hold in five days.2.Friendship is p___________ in the world, so we should value our friends.3.The class teacher let us meet at the e_____________ of our school.4.We often e_____________ ideas with our parents.5.My friend showed us her new house with great p____________ last weekend.II.Fill in the blanks with the following words in their proper forms. （用所给单词的适当形式填空）1.Be careful. The picture from the Song Dynasty is _____________ (price).2.Could you tell me the _____________ to the exhibition hall? (enter)3.Peter is an ______________ student from Korean. (change)4.This is the first time a _____________ country will hold such a great event. (develop)5.____________ are busy doing research in the labs these days. (science)2、8B U7单词预习8B Unit 7 Vocabulary（新世纪）序号英文音标词性中文1 ['muːnlaɪt] n. 月光2 [sə'nɑːtə]n. 奏鸣曲3 ['ɪnstrʊm(ə)nt] n. 乐器4 [ə'kɔːdɪən] n. 手风琴5 [drʌm] n. 鼓6 [fluːt]n. 长笛7 [ˈsʌdnlɪ] ad. 突然8 [aʊt'saɪd] prep. 在外面9 [wɪʃ] v. 希望10 [ə'fɔːd]v. 买得起11 [fə'get] v. 忘记12 ['kænd(ə)l] n. 蜡烛13 [θruː]prep. 穿过14 ['kreɪzɪ] a. 疯狂的15 ['kɒpɪ] v. 复制16 ['ti:neidʒ] a. 十几岁的17 ['ɪnflʊəns] n. 影响18 [kəm'baɪn] v. 结合19 乐器20 令人惊讶的是21 仰视22 沉湎，沉浸PracticeComplete the sentences with the given words in their proper forms.(用所给单词的适当形式填空）1._____________, my daughter began to cry. (sudden)2.The boy was ____________ hurt. The doctor saved him. (serious)3.Beethoven was _____________ to see that the girl was blind. (surprise)4.My grandfather is so ______________ that he often leaves things behind. (forget)5.The firemen have saved the boy from the fire _____________.(success)6.The children went ______________ when they saw their favourite characters. (craze)7.With the ____________ of science and technology, life has become easier. (develop)8.Tom and Jerry lost _____________ in the funny game. (they)9.That young man looked at us in ____________ when we had an argument. (surprised)10.How many birthday ___________ do you need in all? (candle)3、形容词-副词形容词和副词专题Presentation-形容词和副词(一)形容词和副词的概述：形容词是指那些用来描述或修饰名词（或代词）的一类词。

专题07 函数中的双变量问题(学生版) -2025年高考数学压轴大题必杀技系列导数

专题7 函数中的双变量问题函数与导数一直是高考中的热点与难点, 近几年高考试卷及各地模拟试卷中常出现在函数背景下借组导数处理含有两个变量的等式与不等式问题,这类问题由于变量多,不少同学不知如何下手,其实如能以函数思想为指导,把双变量问题转化为一个或两个一元函数问题,再利用导数就可有效地加以解决.(一) 与函数单调性有关的双变量问题此类问题一般是给出含有()()1212,,,x x f x f x 的不等式,若能通过变形,把不等式两边转化为同源函数,可利用函数单调性定义构造单调函数,再利用导数求解.常见结论：(1)若对任意12,x x D Î,当12x x ¹时恒有()()12120f x f x x x ->-,则()y f x =在D 上单调递增；(2)若对任意12,x x D Î,当12x x ¹时恒有()()1212f x f x k x x ->-,则()y f x kx =-在D 上单调递增；(3)若对任意12,x x D Î,当12x x ¹时恒有()()121212f x f x kx x x x ->-,则()k y f x x =+在D 上单调递增；(4)若对任意12,x x D Î,当12x x ¹时恒有()()121212f x f x x x x x ->+-,则()2y f x x =-在D 上单调递增.【例1】（2024届四川省仁寿第一中学校高三上学期调研）已知函数212ln ()xf x x +=．(1)求()f x 的单调区间；(2)存在12,(1,)x x Î+¥且12x x ¹，使()()1212ln ln f x f x k x x -³-成立，求k 的取值范围．【解析】（1）由题意得()34ln xf x x -¢=，令()0f x ¢=得1x =，(01),x Î时，()0f x ¢>，()f x 在(0,1)上单调递增；,(1)x Î+¥时，()0f x ¢<，()f x 在(1,)+¥上单调递减；综上，()f x 单调递增区间为(0,1)，单调递减区间为(1,)+¥．（2）由题意存在12,(1,)x x Î+¥且12x x ¹，不妨设121x x >>，由（1）知,(1)x Î+¥时，()f x 单调递减．()()1212ln ln f x f x k x x -³-等价于()()()2112ln ln f x f x k x x -³-，即()()2211ln ln f x k x f x k x +³+，即存在12,(1,)x x Î+¥且12x x >，使()()2211ln ln f x k x f x k x +³+成立．令()()ln h x f x k x =+，则()h x 在(1,)+¥上存在减区间．即234ln ()0kx x h x x-¢=<在(1,)+¥上有解集，即24ln x k x <在(1,)+¥上有解，即2max 4ln x k x æö<ç÷èø，(1,)x Î+¥；令()24ln x t x x =，(1,)x Î+¥，()()3412ln x t x x -¢=，(x Î时，()0t x ¢>，()t x在(上单调递增，)x ¥Î+时，()0t x ¢<，()t x在)+¥单调递减，∴max 2()e t x t ==，∴2ek <． (二) 与极值点有关的双变量问题与极值点12,x x 有关的双变量问题,一般是根据12,x x 是方程()0f x ¢=的两个根,确定12,x x 的关系,再通过消元转化为只含有1x 或2x 的关系式,再构造函数解题,有时也可以把所给条件转化为12,x x 的齐次式,然后转化为关于21x x 的函数，此外若题中含有参数也可考虑把所给式子转化为关于参数的表达式.【例2】（2024届黑龙江省双鸭山市高三下学期第五次模拟）已知函数2()ln (1)(R)f x x a x a x=+-+Î.(1)当1a =-时，讨论()f x 的单调性；(2)若()1212,x x x x <是()f x 的两个极值点，证明：()()21f x f x -<【解析】（1）当1a =-时，2()ln 1,()f x x x f x x=+++的定义域为(0,)+¥，所以2222122(2)(1)()1x x x x f x x x x x¢+-+-=-+==，令()0f x ¢=，解得1x =，当(0,1)x Î时，()0f x ¢<，当(1,)x Î+¥时，()0f x ¢>，故()f x 在(0,1)上单调递减，在(1,)+¥上单调递增．（2）222122()ax x f x a x x x ¢-+-=--=，由题意可知，()1212,x x x x <是方程220ax x -+-=的两根，则102180a a ì>ïíïD =->î，解得108a <<，所以121x x a +=，122x x a =，要证()()21f x f x -<====即证()()22112122ln 1ln 1x a x x a x x x éù+-+-+-+êúëû只需证()()122211122lnx x x a x x x x x -+--<需证()()212211122ln2x x x a x x x x x -<-=++令21(1)x t t x =>，则需证2(1)ln 1t t t -<++，设()ln 1)g t t t =>，则2111111442222111(1)11222()02t t t t t t t g t t t tt---¢æö-ç÷----+èø=-==-<，所以函数()g t 在(1,)+¥上单调递减，所以()(1)0g t g <=，因此ln t <由1t >得，2(1)01t t ->+，所以2(1)ln 1t t t -<+，故()()21f x f x -<,【例3】（2023届云南省曲靖市高三下学期第二次联考）已知函数()()21ln 402f x x a x x a =+->.(1)当3a =时，试讨论函数()f x 的单调性；(2)设函数()f x 有两个极值点()1212,x x x x <，证明：()()12ln 10f x f x a +>-.【解析】（1）当3a =时，()213ln 42f x x x x =+-定义域为()0,x Î+¥，()()()2133434x x x x f x x x x x---+=+-==¢，令()0f x ¢=解得1x =或3，且当01x <<或3x >时，()0f x ¢>，当13x <<时，()0f x ¢<，所以当01x <<或3x >时，()f x 单调递增，当13x <<时，()f x 单调递减，综上()f x 在区间()0,1，()3,+¥上单调递增，()f x 在区间()1,3单调递减.（2）由已知()21ln 42f x x a x x =+-，可得()244a x x af x x x x-+=+-=¢，函数()f x 有两个极值点()1212,x x x x <，即240x x a -+=在()0,¥+上有两个不等实根，令()24h x x x a =-+，只需()()00240h a h a ì=>ïí=-<ïî，故04a <<，又124x x +=，12x x a =，所以()()221211122211ln 4ln 422f x f x x a x x x a x x æöæö+=+-++-ç÷ç÷èøèø()()()2212121214ln ln ln 82x x a x x x x a a a =-+++++=--，要证()()12ln 10f x f x a +>-，即证ln 8ln 10a a a a -->-，只需证()1ln 20a a a -+-<，令()()1ln 2m a a a a =-+-，()0,4a Î，则()11ln 1ln a m a a a a a-=-++=-¢，令()()n a m a ¢=，则()2110n a a a¢=--<恒成立，所以()m a ¢在()0,4a Î上单调递减，又()110m ¢=>，()12ln202m =-<¢，由零点存在性定理得，()01,2a $Î使得()00m a ¢=，即001ln a a =，所以()00,a a Î时，()0m a ¢>，()m a 单调递增，()0,4a a Î时，()0m a ¢<，()m a 单调递减，则()()()()0000000max 00111ln 2123m a m a a a a a a a a a ==-+-=-+-=+-，又由对勾函数知0013y a a =+-在()01,2a Î上单调递增，所以00111323022a a +-<+-=-<，所以()0m a <，即()()12ln 10f x f x a +>-得证.(三) 与零点有关的双变量问题与函数零点12,x x 有关的双变量问题,一般是根据12,x x 是方程()0f x =的两个根,确定12,x x 的关系,再通过消元转化为只含有1x 或2x 的关系式,再构造函数解题,有时也可以把所给条件转化为12,x x 的齐次式,然后转化为关于21x x 的函数,有时也可转化为关于12x x -的函数,若函数中含有参数,可考虑把参数消去,或转化为以参数为自变量的函数.【例4】（2024届四川省南充高中高三下学期月考）已知函数())ln 2f x x a =-ÎR .(1)讨论函数()f x 的单调性，并求()f x 的极值；(2)若函数()f x 有两个不同的零点12,x x （12x x <），证明：1e a<<.【解析】（1）函数()f x 的定义域为(0,)+¥，由题意，()1f x x ==¢，当0a £时，()0f x ¢>，函数()f x 在(0,)+¥单调递增，无极值.当0a >时，令()0f x ¢=，得21x a =∴()f x 在210,a æöç÷èø单调递增，在21,a ¥æö+ç÷èø单调递减，所以函数()f x 在21x a =时取极大值，极大值为212ln 2f a a æö=--ç÷èø，无极小值.x210,a æöç÷èø21a 21,a ¥æö+ç÷èø()f x ¢+-()f x 递增极大值递减（212t t ==，且12x x <，则有1122ln ln t at t at =ìí=î，两式相减可得，1212ln ln t t a t t-=-1a <.12121ln ln t t a t t-<=-12ln 0t t Û>，令u =121ln02ln 0(01)t u u u t u >Û-+><<，设()12ln g u u u u =-+，则()222212110u u g u u u u -+-=--=<¢，所以()g u 在()0,1上单调递减，所以()()10g u g >=1a<.1122ln ln t at t at =ìí=î，两式子相加得，()1212ln t t a t t =+e >，即证212e t t >，由上式只需证()122a t t +>，即证()1121212112221ln ln 2ln 201t t t t t t t t t t t t --×+>Û-<-+，令12t v t =，11212211ln 20ln 20(01)11t t t v v v t t v t --æö-<Û-<<<ç÷+èø+，设()()1ln 2011v h v v v v -æö=-<<ç÷+èø，则()22(1)0(1)v h v v v +¢-=>，所以()h v 在()0,1上单调递增，所以()()10h v h <=e >.综上：1e a<<. (四) 独立双变量,各自构造一元函数此类问题一般是给出两个独立变量,通过变形,构造两个函数,再利用导数知识求解.【例5】（2024届陕西省宝鸡实验高中高三一模）已知函数2()ln (,,1)x f x a x x a b a b R a =+--Î>，e 是自然对数的底数.(1)当e,4a b ==时，求整数k 的值，使得函数()f x 在区间(,1)k k +上存在零点；(2)若存在12,[1,1],x x Î-使得12|()()|e 1f x f x -³-，试求a 的取值范围.【解析】（1）2()e 4x f x x x =+--，()e 21x f x x ¢\=+-，(0)0f ¢\=当0x >时，e 1x >，()0f x ¢\>，故()f x 是(0,)+¥上的增函数，同理()f x 是(,0)-¥上的减函数，2(0)30,(1)e 40,(2)e 20f f f =-<=-<=->，且2x >时，()0f x >，故当0x >时，函数()f x 的零点在()1,2内，1k \=满足条件．同理，当0x <时，函数()f x 的零点在()2,1--内，2k \=-满足条件，综上1,2k =-．（2）问题Û当[1,1]x Î-时，max min max min |()()|()()e 1f x f x f x f x -=-³-，()ln 2ln 2(1)ln x x f x a a x a x a a ¢=+-=+-，①当0x >时，由1a >，可知10,ln 0,()0x a a f x ¢->>\>；②当0x <时，由1a >，可知10,ln 0,()0x a a f x ¢-<>\<；③当0x =时，()0f x ¢=，()f x \在[1,0]-上递减，[0,1]上递增，\当[1,1]x Î-时，min max ()(0),()max{(1),(1)}f x f f x f f ==-，而1(1)(1)2ln f f a a a--=--，设1()2ln (0),g t t t t t =-->22121()1(1)0g t t t t¢=+-=-³Q （仅当1t =时取等号），()g t \在(0,)+¥上单调递增，而(1)0g =，\当1t >时，()0g t >即1a >时，12ln 0a a a-->，(1)(1),(1)(0)e 1f f f f \>-\-³-即ln e 1e ln e a a -³-=-，构造()ln (1)h a a a a =->，易知()0¢>h a ，()h a \在(1,)+¥递增，e a \³，即a 的取值范围是[e,)+¥．(五) 构造一元函数求解双变量问题当两个以上的变元或是两个量的确定关系在解题过程中反复出现.通过变量的四则运算后,把整体处理为一个变量,从而达到消元的目的.【例6】（2024届山东省菏泽市高考冲刺押题卷）已知函数2()ln 1(02)f x tx x x t =-+<£．(1)求函数()f x 的单调区间(2)若0a b >>，证明:2244a b a b <-．【解析】（1）()ln 2,0f x t x t x x ¢=+->，令()()ln 2g x f x t x t x ¢==+-，所以()2,0tg x x x¢=->，由()0g x ¢>可得02t x <<，由()0g x ¢<可得2t x >，所以()f x ¢在(0,)2t 上单调递增，在(,)2t+¥上单调递减，所以max ()(ln ln 222t t tf x f t t t t ¢¢==+-=.又因为02t <£，所以ln02t£，即()0f x ¢£，且()f x ¢至多在一个点处取到0.所以()f x 在(0,)+¥上单调递减，故()f x 的单调递减区间为()0,+¥，没有单调递增区间.（2）证明2244a b a b <-，只需证：22222222222222+)))()11((ln 24(a b a b a b a b a b a b --<-++-，即证：2222222222222ln a b a b a b a b a b a b ++-<---+，令2222,0a b x a b a b +=>>-，所以1x >，只需证：12ln x x x<-，即证：22ln 10x x x -+<，由（1）知，当2t =时，2()2ln 1f x x x x =-+在(0,)+¥上单调递减，1x >()(1)0f x f <=，即22ln 10x x x -+<，所以2244a b a b<-.(六) 独立双变量,把其中一个变量看作常数若问题中两个变量没有明确的数量等式关系,有时可以把其中一个当常数,另外一个当自变量【例7】已知函数，(1)若函数在处的切线也是函数图像的一条切线，求实数a 的值；(2)若函数的图像恒在直线的下方，求实数a 的取值范围；(3)若，且，证明：>【解析】 (1)，在处切线斜率，，所以切线，又，设与相切时的切点为，则斜率，则切线的方程又可表示为，由，解之得．(2)由题可得对于恒成立，即对于恒成立，令，则，由得，x20,e a æöç÷èø2e a2e a æö+¥ç÷èø，()h x ¢+0-()h x ↗极大值↘则当时，，由，得：，即实数的取值范围是．(3)由题知，由得，当时，，单调递减，因为，所以，即，所以，①同理，②①+②得，()ln (0)af x x a x=×>()e xg x =0x =()f x ()f x 10x y -+=12,(,)e 2a a x x Î12x x ¹412()x x +212a x x ()e xg x ¢=()g x 0x =()01k g ¢==()01g =:1l y x =+()ln1af x x =¢-l ()f x 000,ln a x x x æöç÷èø()00ln 1a k f x x ¢==-l ()000000ln 1ln ln 1a a ay x x x x x x x x æöæö=--+=-+ç÷ç÷èøèø00ln 111ax x ì-=ïíï=î2e a =()10f x x --<0x >ln 10ax x x--<0x >()ln 1a h x x x x =--()ln 2ah x x =¢-()0h x ¢=2ea x =0x >()22max 1e ea a h x h æö==-ç÷èø210e a -<20e a <<a ()20,e ()ln 1af x x=¢-()0f x ¢=e a x =e a x a <<()0f x ¢<()()ln 0af x x a x=>112x x x a +<<()()112f x f x x >+()112112ln ln a ax x x x x x >++121112lnln x x a a x x x x +>+122212ln ln x x a ax x x x +>+1212121212lnln ln x x x x a a ax x x x x x æöç÷èø>+++++因为，由得，即，所以，即，所以．(七) 双变量,通过放缩消元转化为单变量问题此类问题一般是把其中一个变量的式子放缩成常数,从而把双变量问题转化为单变量问题【例8】（2024届河北省衡水市高三下学期联合测评）过点(),P a b 可以作曲线e x y x =+的两条切线，切点为,A B .(1)证明：()1ea b a ->-；(2)设线段AB 中点坐标为()00,x y ，证明：00a y b x +>+.【解析】（1）证明：设切点(),e tA t t +，1e xy ¢=+，所以e 1e t tPAt bk t a+-=+=-，即关于t 的方程()1e 0tt a b a --+-=有两个不相等的实数根.设()()1e t f t t a b a =--+-，则()()e 0tf t t a =-=¢，t a =.当t a <时，()0f t ¢<，则()f t 在(),a ¥-上单调递减；当t a >时，()0f t ¢>，则()f t 在(),a ¥+上单调递增，所以()f t 在t a =处取值得最小值，即()e af a b a =--.当t ®+¥时，()f t ¥®+，当t ®-¥时，()f t b a ®-，若满足方程有两个不相等的实数根，则0e 0ab a b a ->ìí--<î，于是0e a b a <-<，即()ln b a a -<，得()()()ln b a b a b a a --<-,设()ln g x x x =，()ln 10g x x +¢==，得1ex =，在10,e æöç÷èø上，()0g x ¢<，则()g x 单调递减，在1,e ¥æö+ç÷èø上，()0g x ¢>，则()g x 单调递增，所以()ln g x x x =，在1e x =处取得最小值，即11e e g æö=-ç÷èø，所以()1e a b a ->-.（2）证明：设()()1122,,,A x y B x y ，则()()12012011e e 22x x y y y x =+=++，即()()12001211e e 22x x y x y y -=+=+，121221121224x x x x x x x x x x +++=++³12x x a +<121a x x +>12ln 0ax x >+1212ln ln 4ln a a a x x x x +>+421212a a x x x x æö>ç÷+èø()421212x x a x x +>在点()()1122,,,A x y B x y 处的切线方程都过(),P a b ，于是，由()()1111e 1e x xb x a x --=+-，得()1110e x b a x a --++=，由()()2222e 1e x xb x a x --=+-，得()2210e x b a x a --++=两式相减整理得：()121212e e e x x x x x x b a +--=-，()()()()1212121200e 1e ee e 2x x x x x x x x b a y x +----=-+-()()121212122212e e e 2e 2e e x x x x x x x x x x ++éù-=--êú-ëû()()1212121212e 12e e 2e e x x x x x x x x x x +--éù=--+êú-ëû，不妨设1212,0x x m x x >=->，所以()1212e 02e e x x x x +>-，则()12e e m mh m m =-+，()12e 220e m mh m ¢=--£-=，所以()h m 在()0,¥+上单调递减，于是()()00h m h <=，于是()()000b a y x ---<，即00a y b x +>+.【例1】（2024届陕西省西安市一中高三考前模拟）已知函数()2e 2xx f x a =++.(1)若4a =-，求()f x 的极值；(2)若0a >，不相等的实数,m n 满足()()228f m f n m n +=++，求证：0m n +<.【解析】（1）依题意，()2e 42x f x x =-+，则()2e 4xf x =¢-，令()0f x ¢=，解得ln 2x =，故当(),ln 2x ¥Î-时，()0f x ¢<，当()ln 2,x ¥Î+时，()0f x ¢>，故函数()f x 在(),ln 2¥-上单调递减，在()ln 2,¥+上单调递增，故函数()f x 的极小值为()ln 244ln 2264ln 2f =-+=-，无极大值；（2）令()()222e 2x g x f x x ax x =-=+-+，则()2e 2xg x x a =¢-+，令()e xt x x =-，则()e 1x t x ¢=-，当0x <时，()0t x ¢<，当0x >时，()0t x ¢>，所以函数()t x 在(),0¥-上单调递减，在()0,¥+上单调递增，所以()()e 010x t x x t =-³=>，又0a >，所以()()2e 0xg x x a =-+>¢，所以()g x 在R 上单调递增，()()228f m f n m n +=++，即()()8g m g n +=，因为()04g =，所以,0m n ¹，要证0m n +<，即证n m <-，只需证()()g n g m <-，即()()8g m g m -<-，即()()8g m g m +->，令函数()()()22e 2e 24x x h x g x g x x -=+-=+-+，则()2e 2e 4x x h x x -=--¢，令()()x h x j =¢，则()2e 2e 40xx x j -=-¢+³，所以()h x ¢为R 上的增函数，当0x <时，()()00h x h ¢¢<=，当0x >时，()()00h x h ¢¢>=，所以()h x 在(),0¥-上单调递减，在()0,¥+上单调递增，所以对任意0m ¹，都有()()()()08h m g m g m h =+->=，从而原命题得证.【例2】（2024届河北省衡水市部分示范性高中高三下学期三模）已知()e xf x x =-．(1)求()f x 的单调区间和最值；(2)定理：若函数()f x 在(,)a b 上可导，在[]a b ，上连续，则存在(,)a b x Î，使得()()()f b f a f ξb a-¢=-．该定理称为“拉格朗日中值定理”，请利用该定理解决下面问题：若0m n <<，求证：()2e e 111m n m n m n m æö-<+-ç÷èø．【解析】（1）()e 1x f x ¢=-，令()0f x ¢=，解得0x =，当(,0)x Î-¥时，()0,()¢<f x f x 单调递减；当,()0x Î+¥时，()0,()¢>f x f x 单调递增．当0x =时，()f x 取得最小值1，无最大值；（2）要证2e e 11(1)m n m n m n m æö-<+-ç÷èø，只需证2e e (1)()m n m n m m n -<+-，因为0m n <<，故只需证2e e (1)m nm n m m n->+-．令()e (0)x g x x x =>，显然()g x 在(,)m n 上可导，在[]m n ，上连续，故由拉格朗日中值定理知存在(,)m n x Î，使得e e()m nm n g m nx ¢-=-，而()(1)e 0,()x g x x g x ¢¢=+>在(0,)+¥上单调递增，因为m n x <<，故()()g g m x ¢¢>，即()(1)e m g m x ¢>+，故只需证2(1)e (1)m m m +³+即可，因为0m >，故只需证e 1m m ³+．由（1）知e 1x x ³+恒成立，因此原命题得证．【例3】（2024届天津市部分区高三二模）已知,R a b Î，函数()sin ln f x x a x b x =++．(1)当0,1a b ==-时，求()f x 的单调区间；(2)当1,02a b =-¹时，设()f x 的导函数为()f x ¢，若()0f x ¢>恒成立，求证：存在0x ，使得()01f x <-；(3)设01,0a b <<<，若存在()12,0,x x Î+¥，使得()()()1212f x f x x x =¹>．【解析】（1）由函数()sin ln f x x a x b x =++，可得其定义域为()0,¥+，当0,1a b ==-时，可得()ln f x x x =-，则()111x f x x x¢-=-=，当()0,1x Î时，可得()0f x ¢<，()f x 单调递减；当()1,x ¥Î+时，可得()0f x ¢>，()f x 单调递增，\函数()f x 的单调递增区间为()1,¥+，单调递减区间为()0,1．（2）当1,02a b =-¹时，可得()1sin ln 2f x x x b x =-+，则()11cos 2bf x x x =-+¢，Q ()0f x ¢>恒成立，即11cos 02b x x -+>恒成立，令()11cos ,02bh x x x x=-+>，若0b <，则0b x <，存在2b x =-，使得111cos 21cos 022222b b b h æöæöæö-=---=---<ç÷ç÷ç÷èøèøèø，即()0f x ¢<，不符合题意，>0b \，取30e bx -=，则001x <<，可得()3301esin e 312bb f x --=--<-，即存在0x ，使得()01f x <-．（3）由函数()sin ln f x x a x b x =++，可得()1cos bf x a x x ¢=++，设12x x <，由()()12f x f x =，可得111222sin ln sin ln x a x b x x a x b x ++=++，则()()()22121211sin sin ln ln lnx x x a x x b x x b x -+-=--=-，又由sin y x x =-，可得'1cos 0y x =-³，\函数sin y x x =-为单调递增函数，\2211sin sin x x x x ->-，即2121sin sin x x x x -<-，\()()2211ln1x b a x x x -<+-，设()1ln 21x h x x x -=-´+，可得()()()()222114011x h x x x x x -=-=+¢³+，\当1x >时，()()10h x h >=，即ln 2x >\2>即ln 4x =>\21ln 44x x >=代入可得：()()()()21411b a x x a ×-<+-=+，则()241b a -×<++，\>【例4】（2024届四川省百师联盟高三联考三）已知函数()214ln 2f x x x a x =-+.(1)当1a =时，求曲线()f x 在点()()1,1f 处的切线方程；(2)设函数()y f x =有两个不同的极值点1x ，2x .证明：()()2121135ln 244f x f x a a +--≥.【解析】（1）当1a =时()214ln 2x f x x x =-+，()14f x x x ¢=-+，()171422f =-=-，()14121f ¢=-+=-，则切线方程为()7212y x +=--，化简得4230x y ++=.（2）证明：由题()244a x x af x x x x=¢-+=-+，函数()f x 有两个极值点1x ，2x ，即240x x a -+=在()0,¥+上有两个不等实根，令()24h x x x a =-+，只需故()()00240h a h a ì=>ïí=-<ïî，故04a <<.又124x x +=，12x x a =，所以()()221211122211ln 4ln 422f x f x x a x x x a x x æöæö+=+-++-ç÷ç÷èøèø()()()2212121214ln ln ln 82x x a x x x x a a a =-+++++=--.若证()()2121135ln 244f x f x a a +--≥，即证21135ln 8ln 244a a a a a ----≥，即2113ln ln 0244a a a a a --++≥.令()2113ln ln 244x x x x x x j =--++，()0,4x Î，()11ln 2x x xx j æö¢=+-ç÷èø，则()x j ¢在()0,4上递增，且有()01j ¢=，当()0,1x Î时，()0x j ¢<，所以()x j 在()0,1上递减；当()1,4x Î时，()0x j ¢>，所以()x j 在()1,4上递增；所以()()113ln11ln101244x j j =--++=≥，()0,4x Î.即()()2121135ln 244f x f x a a +--≥得证.【例5】（2024陕西省西安八校高三下学期联考）已知函数的图象在处的切线过原点．(1)求的值；(2)设，若对总，使成立，求整数的最大值．【解析】（1）易知的定义域为，又，的图象在处的切线方程为，将代入，得；（2）．当时，取得最小值，．由（1）知，．，得的定义域为．则，易知单调递增，又．即在上有唯一解，故．()()()e ln 1R ,xf x m x x m f x =-+-Î()()1,1f m ()()()2,2g x f x x h x x x a =-=-+()10,x ¥"Î+2x $ÎR ()1g x >()2h x a ()f x ()()0,,1e f ¥+=()()e 1,1e 1x mf x f m x¢¢=-+=-+()f x \()()1,1f ()()e e 11y m x -=-+-0,0x y ==1m =()222(1)1h x x x a x a =-+=-+-\1x =()h x ()()min []11h x h a ==-1m =()e ln 1x f x x x \=-+-()()e ln 1,x g x x g x =--()0,¥+()1e xg x x =¢-()1e 0xy x x=->()120,1e 102g g æö¢¢=-ç÷èø()0g x ¢=1,12æöç÷èø0x 000011e ,e x x x x ==于是当时，在上单调递减；当时，在上单调递增．在处取得极小值也是最小值．则，对总，使成立，只需，得．故整数的最大值为．1．（2024届广东省汕头市第二次模拟）设M 是由满足下列条件的函数()f x 构成的集合：①方程()0fx x-=有实根；②()f x 在定义域区间D 上可导，且()f x ¢满足()01f x ¢<<.(1)判断()ln 322x xg x =-+，()1,x Î+¥是否是集合M 中的元素，并说明理由；(2)设函数()f x 为集合M 中的任意一个元素，证明：对其定义域区间D 中的任意a 、b ，都有()()a b a b -£-f f .2．（2024届山东省滨州市高三下学期二模）定义：函数()f x 满足对于任意不同的12,[,]x x a b Î，都有()()1212f x f x k x x -<-，则称()f x 为[],a b 上的“k 类函数”．(1)若2()13x f x =+，判断()f x 是否为[]1,3上的“2类函数”；(2)若2()(1)e ln 2xx f x a x x x =---为[1,e]上的“3类函数”，求实数a 的取值范围；(3)若()f x 为[1,2]上的“2类函数”，且(1)(2)f f =，证明：1x "，2[1,2]x Î，()()121f x f x -<．3．（2024届辽宁省沈阳市第一二〇中学高三最后一卷）设函数()21ln 2f x x x x ax =--的两个极值点分别为()1212,x x x x <．(1)求实数a 的取值范围；(2)若不等式()12a x x l <+恒成立，求正数l 的取值范围（其中e 271828=L ．为自然对数的底数）．00x x <<()()0,g x g x ¢<()00,x 0x x >()()0,g x g x ¢>()0,x ¥+()g x \0x x =()000min 015e ln 112,2xg x x x x æö=--=+-Îç÷èø\()10,x ¥"Î+2x $ÎR ()()12g x h x >11a ³-2a £a 24．（2024届湖南省高三“一起考”大联考下学期模拟）已知函数()2f x ax =，()lng x x =，函数()f x ，()g x 有两条不同的公切线（与()f x ，()g x 均相切的直线）1l ，2l .(1)求实数a 的取值范围；(2)记1l ，2l 在y 轴上的截距分别为1d ，2d ，证明：121d d +<-.5．（2024届天津市民族中学高三下学期4月模拟）已知函数()()22ln 0f x x x a x a =-+>．(1)当2a =时，试求函数图象在点()()1,1f 处的切线方程；(2)若函数()f x 有两个极值点1x 、()212x x x <；（ⅰ）求a 的取值范围；（ⅱ）不等式()12f x mx ³恒成立，试求实数m 的取值范围．6．（2024届陕西省部分学校（菁师联盟）高三下学期5月份高考适应性考试）已知函数()2ln f x x x x =-.(1)求曲线()y f x =在2e x =处的切线方程；(2)若()()12f x f x =，且12x x <.求证：212e x x +<.7．（2024届广东省广州市二模）已知函数()()21e x f x a x x -=++．(1)讨论()f x 的零点个数；(2)若()f x 存在两个极值点，记0x 为()f x 的极大值点，1x 为()f x 的零点，证明：0122x x ->．8．（2024届重庆市名校联盟高三下学期全真模拟）T 性质是一类重要的函数性质，具有T 性质的函数被称为T 函数，它可以从不同角度定义与研究.人们探究发现，当()y f x =的图像是一条连续不断的曲线时，下列两个关于T 函数的定义是等价关系．定义一：若()y f x =为区间(),a b 上的可导函数，且()y f x ¢=为区间(),a b 上的增函数，则称()y f x =为区间(),a b 上的T 函数．定义二：若对()12,,x x a b "Î，()0,1l "Î，都有()()()()121211f x x f x f x l l l l éù+-£+-ëû恒成立，则称()y f x =为区间(),a b 上的T 函数．请根据上述材料，解决下列问题：(1)已知函数()πtan 02f x x x æö=Îç÷èø，,．①判断()y f x =是否为π0,2x æöÎç÷èø上的T 函数，并说明理由；②若π0,2a b æöÎç÷èø，且π22a b +=，求()()2f f a b +的最小值(2)设11111m n m n >>+=，，，当00a b >>，时，证明：11m na b ab m n+³．9．（2024届河南省九师联盟高三下学期5月联考）已知函数1()ln (0)f x a x a x=+¹．(1)若()f x a >对,()0x Î+¥恒成立，求a 的取值范围；(2)当3a =时，若关于x 的方程211()42f x x x b x =-++有三个不相等的实数根1x ，2x ，3x ，且1x <23x x <，求b 的取值范围，并证明：314x x -<．10．（2024届湖北省宜荆荆随恩高三5月联考）设函数，(1)讨论的单调性．(2)若函数存在极值，对任意的，存在正实数，使得（ⅰ）证明不等式．（ⅱ）判断并证明与的大小．11．（2024届江西省上饶市六校高三5月第二次联合考试）已知函数．(1)若，求的极值；(2)若，求的最大值．12．（2024届山西省临汾市高三下学期考前适应性训练）已知函数．(1)求在处的切线方程；(2)若曲线与直线有且仅有一个交点，求的取值范围；(3)若曲线在处的切线与曲线交于另外一点，求证：．13．（2024届江苏省扬州市仪征市四校高三下学期4月联合学情检测）已知函数．()()24ln 42f x x ax a x =-+-a ÎR()f x ()f x 120x x <<0x ()()()()21021f x f x f x x x ¢-=-212121ln ln 2x x x x x x ->-+122x x +0x ()()ln ,,0f x x a x b a b a =--Î¹R 1a b ==()f x ()0f x ³ab ()()21ln 12=++f x x x ()f x 0x =()y f x =y ax =a ()y f x =()()(),0m f m m >()y f x =()(),n f n 21mm n m -<<-+()()()ln 0f x mx x m =->(1)若恒成立，求的取值范围；(2)若有两个不同的零点，证明．14．（2024届河北省保定市高三下学期第二次模拟）已知函数为其导函数．(1)若恒成立，求的取值范围；(2)若存在两个不同的正数，使得，证明：．15．（2024届云南省高中毕业生第二次复习统一检测）已知常数，函数.(1)若，求的取值范围;(2)若、是的零点，且，证明:.()0f x £m ()f x 12,x x 122x x +>()ln ,()f x ax x x f x ¢=-()1f x £a 12,x x ()()12f x f x=0f ¢>0a >221()2ln 2f x x ax a x =--20,()4x f x a ">>-a 1x 2x ()f x 12x x ¹124x x a +>。

专题八文化的传承与创新(初改)

从命题内容看，考查的重点有：文化多样性的表现、
本如何对待文化的多样性、如何对待传统文化与外来文化、
专题栏
如何进行文化创新。在复习备考中要注意： (1)保护文化遗产是命题的热点，
目开关
尤其注重保护非物质文化遗产。(2)以中外文化交流为背景材料考查文化的多样性、文化交流、文化创新等知识。
【网络构建】
的发展起积极作用
开
取其精华，去其糟粕，批
关
态度
推陈出新、革故鼎新
判继承，古为今用
对于符合社会发展要求的、积极在继承的基础上发展，
向上的内容，应该保持和发扬；在发展的过程中继承，
本做法对于不符合社会发展要求的、落不断革除陈旧的、过时
专
后的、腐朽的东西，必须加以改的旧文化，推出体现时
题
栏
造或剔除
题栏
B．对传统文化需要继承与发扬
目开
C．不同民族文化各具特色，又具有共通性
关
D．优秀文化能激励人们创造美好生活
(C)
解析文化是民族的，又是世界的，中国媳妇处理婆媳关系时的善
良和智慧体现了中华文化的民族特色，坦桑尼亚观众在感动中体会
中国“和”文化的美好，说明了世界各民族文化具有共性和普遍规
律，C 项正确。
设
创新、反对迷信和伪科学的良好氛围
1．必须尊重和认同传统文化。
()
(2013·安徽高考，8A)
提示 ×。传统文化中有糟粕，不能一味认同。
本专
2．繁荣我国文化的关键是继承我国的传统文化。
()
题栏目
(2012·浙江高考，31③) 提示 ×。文化发展的关键是立足于社会实践，发展中国特色

第一章第05讲整式的乘法(10类热点题型讲练)(解析版)--初中数学北师大版7年级下册

第05讲整式的乘法(10类热点题型讲练)1．复习幂的运算性质，探究并掌握单项式乘以单项式的运算法则；2．能够熟练运用单项式乘以单项式的运算法则进行计算并解决实际问题；3．能根据乘法分配律和单项式与单项式相乘的法则探究单项式与多项式相乘的法则；4．理解多项式乘以多项式的运算法则，能够按多项式乘法步骤进行简单的乘法运算；5．掌握单项式与多项式、多项式与多项式的乘法法则的应用．知识点01单项式与单项式相乘单项式乘法法则：单项式相乘，把它们的系数、相同字母分别相乘，对于只在一个单项式里含有的字母，连同它的指数作为积的一个因式.单项式乘法法则在运用时要注意以下几点：①积的系数等于各因式系数积，先确定符号，再计算绝对值.这时容易出现的错误的是，将系数相乘与指数相加混淆；②相同字母相乘，运用同底数的乘法法则；③只在一个单项式里含有的字母，要连同它的指数作为积的一个因式；④单项式乘法法则对于三个以上的单项式相乘同样适用；⑤单项式乘以单项式，结果仍是一个单项式.知识点02单项式与多项式相乘单项式乘以多项式，是通过乘法的分配律，把它转化为单项式乘以单项式，即单项式与多项式相乘，就是用单项式去乘多项式的每一项，再把所得的积相加.即（a+b+c)m=am+bm+cm单项式与多项式相乘时要注意以下几点：①单项式与多项式相乘，积是一个多项式，其项数与多项式的项数相同；②运算时要注意积的符号，多项式的每一项都包括它前面的符号；③在混合运算时，要注意运算顺序.知识点03多项式与多项式相乘多项式与多项式相乘，先用一个多项式中的每一项乘以另一个多项式的每一项，再把所得的积相加.即（a+b)(m+n)=am+an+bm+bn多项式与多项式相乘时要注意以下几点：①多项式与多项式相乘要防止漏项，检查的方法是：在没有合并同类项之前，积的项数应等于原两个多项式项数的积；②多项式相乘的结果应注意合并同类项；③对含有同一个字母的一次项系数是1的两个一次二项式相乘，其二次项系数为1，一次项系数等于两个因式中常数项的和，常数项是两个因式中常数项的积.即(x+a)(x+b)=x²+（a+b)x+ab对于一次项系数不为1的两个一次二项式(mx+a)和(nx+b)相乘可以得到.题型01计算单项式乘单项式题型02利用单项式乘法求字母或代数式的值题型03计算单项式乘多项式及求值【例题】（2023上·福建龙岩·八年级校考期中）（1）计算：()2232xy xy xy⋅－（2）先化简，再求值：(2)(22)(2)x x x x -+--，其中2x =-．【答案】（1）232246x y x y -；（2）24x -；0【分析】本题考查整式的乘法，化简求解．（1）根据单项式乘多项式的法则计算即可；（2）根据整式的乘法，合并同类项进行计算，再代入求值．【详解】（1）()2232223246xy xy xy x y x y =-⋅－；（2）(2)(22)(2)x x x x -+--()()222242x x x x =----222242x x x x =---+24x =-，当2x =-时，原式()224240x =-=--=．【变式训练】题型04计算多项式乘多项式【例题】（2023上·八年级课时练习）计算：(1)()()342x y x y -+；(2)()()211x x x -++．【答案】(1)22328x xy y +-(2)31x -【分析】（1）根据多项式与多项式的乘法法则计算；（2）根据多项式与多项式的乘法法则计算．【详解】（1）()()342x y x y -+223648x xy xy y =+--22328x xy y =+-（2）()()211x x x -++3221x x x x x =++---31x =-【点睛】本题考查了多项式与多项式的乘法运算，多项式与多项式相乘，先用一个多项式的每一项分别乘另一个多项式的每一项，再把所得的积相加．【变式训练】1．（2023上·八年级课时练习）计算：题型05(x+p)(x+q)型多项式乘法题型06已知多项式乘积不含某项求字母的值题型07多项式乘多项式——化简求值1．（2023上·黑龙江哈尔滨·八年级哈尔滨市第十七中学校校考期中）化简求值：题型08单项式乘多项式、多项式乘多项式与图形面积【例题】（2023上·重庆巴南·七年级校联考期中）三张大小不一的正方形纸片按如图1和图2方式分别置于相同的长方形中，它们既不重叠也无空隙．已知正方形A的边长为a，正方形B的边长为b，正方形C的边长为c．(1)用代数式表示图1中阴影部分的面积，并计算当5a =，3b =，1c =时阴影部分的面积．(2)记图1中阴影部分周长为m ，图2阴影部分周长之和为n ，判断m n -的值是否与正方形A 、B 、C 的边长有关，若有关请说明理由，若无关，求出m n -的值．【答案】(1)13(2)m n -的值与三个小正方形的边长无关，值为0【分析】本题考查了多项式乘以多项式，整式的加减，解题的关键是掌握运算法则．（1）用长方形的面积减去3个正方形的面积即可；（2）分别求出m ，n 的值相减即可．【详解】（1）由题意知：长方形的长为()a b +，宽为()a c +∴长方形的面积()()a b a c =++∴所以图1中阴影部分的面积222()()S a b a c a b c =++---当5a =，3b =，1c =时，阴影部分的面积222(53)(51)531S =+⨯+---13=（2）图1中阴影部分的周长2()2()242m a b a b c a c =++-+=+图2中阴影部分的周长2()22()42n a c b c a c b a c=-++++-=+0m n ∴-=即m n -的值与三个小正方形的边长无关，值为0．【变式训练】1．（2023上·吉林长春·八年级校考期末）如图，某社区有两块相连的长方形空地，一块长为()32m a b +，宽为()2m a b +；另一块长为()m a b +，宽为()m a b -．现将两块空地进行改造，计划在中间边长为()m a b -的正方形（阴影部分）中种花，其余部分种植草坪．(1)求计划种植草坪的面积；(2)已知30a =，10b =，若种植草坪的价格为30元/2m ，求种植草坪应投入的资金是多少元？【答案】(1)计划种植草坪的面积为()2269ma ab +(2)种植草坪应投入的资金是243000元【分析】本题考查了列代数式，多项式乘多项式，以及整式的混合运算-化简求值，弄清楚题意是解答本题的关键．（1）计划种植草坪的面积等于2个矩形的面积减去阴影部分的面积，利用多项式乘多项式法则，平方差公式和完全平方公式化简，去括号合并得到最简结果即可；（2）将a 与b 的值代入（1）中求得的栽花面积和草坪面积，再根据总价=单价×数量计算即可求解．【详解】（1）解：（1）两块空地总面积：()()()()322a b a b a b a b ⨯+++⨯-＋，2222672a ab b a b =-＋＋＋2277a ab b =＋＋，栽花面积：()2222a b a ab b --＝＋，草坪面积：()2222277269a ab b a ab b a ab ++--+=＋．（2）30a =，10b =，草坪价格为30元/2m ，应投入的资金()()2269306309301030243000a ab =+⨯=⨯+⨯⨯⨯=元．2．（2023上·江西上饶·七年级统考期中）如图，一个长方形运动场被分隔成A ，B ，A ，B ，C ，C 共6个区，A 区是边长为m a 的正方形，B 区是边长为m b 的正方形．(1)列式表示每个C 区长方形场地的周长，并将式子化简；（用含a 、b 的代数式表示）(2)列式表示整个长方形运动场的周长，并将式子化简；（用含a 、b 的代数式表示）(3)如果30a =，10b =，求整个长方形运动场的面积．【答案】(1)右上方C 区长方形场地的周长为：()42m a b +，左下角C 区长方形场地的周长为：()42m a b +(2)整个长方形运动场的周长为：()4m a b +(3)整个长方形运动场的面积为4000m【分析】本题主要考查整式的混合运算与图形周长、面积的计算，掌握整式的混合运算，代入求值是解题的关键．（1）A 区是边长为m a 的正方形，B 区是边长为m b 的正方形，图形结合即可求解；（2）根据长方形的周长的计算方法，整式的加减运算进行化简即可求解；（3）根据长方形的面积的计算方法列式，代入30a =，10b =计算即可．【详解】（1）解：A 区是边长为m a 的正方形，B 区是边长为m b 的正方形，∴C 区长方形场地的长为：()2m a b +，宽为：()m a b -，∴右上方C 区长方形场地的周长为：()()()2242m a b a b a b ++-⨯=+⎡⎤⎣⎦，左下角C 区长方形场地的周长为：()()()2242m a b a b a b ++-⨯=+⎡⎤⎣⎦．（2）解：由（1）可知，C 区长方形场地的长为：()2m a b +，宽为()m a b -，∴整个长方形运动场的长为：()()222m a b a a b ++=+，宽为：()()2m a b a a b -+=-，∴整个长方形运动场的周长为：()()222282m a b a b a b ++-⨯=+．（3）解：整个长方形运动场的长为：()22m a b +，宽为：()2m a b -，∴整个长方形运动场的面积为：()()22222422a b a b a ab b +⨯-=+-，当30a =，10b =时，原式()22430230102104000m =⨯+⨯⨯-⨯=，∴整个长方形运动场的面积为4000m ．题型09多项式乘法中的规律性问题1．我国宋朝数学家杨辉在其著作《详解九章算法》中提出“杨辉三角”（如图），下图揭示了()na b +（n 为非负整数）展开式的项数及各项系数的有关规律：杨辉三角两腰上的数都是1，其余每个数为它的上方（左右）两数之和，例如：()1a b +=，它只有一项，系数为1()1a b a b +=+，它有两项，系数分别为1，1，系数和为2；()2222a b a ab b +=++，它有三项，中间项系数2等于上方数字1加1，系数分别为1，2，1，系数和为4；()3322333a b a a b ab b +=+++，它有四项，中间项系数3等于上方数字1加2，系数分别为1，3，3，1，系数和为8；……(1)写出()4a b +的展开式______请利用整式的乘法验证你的结果．(2)()5a b +的展开式的系数分别为______，系数和为______．(3)()na b +展开式共有______项，系数和为______，请说明你是怎样得到这个结果的？【详解】（1）解：如图，根据杨辉三角可知，()4432234464a b a a b a b ab b +=++++；用整式乘法验证：()4a b +()22a b ⎡⎤=+⎣⎦()2222a ab b =++()()222222a ab b aab b =++++43223223223422422a a b a b a b a b ab a b ab b =++++++++432234464a a b a b ab b =++++；故答案为：++++432234a 4a b 6a b 4ab b ．（2）解：如图，根据杨辉三角可知，()543225345510105a a b a b a a a b b b b =++++++，∴()5a b +的展开式的系数分别为1，5，10，10，5，1，∴系数和为：515101051322+++++==；故答案为：1，5，10，10，5，1；52．（3）解：()1a b a b +=+，共有2项，系数分别为1，1，()2222a b a ab b +=++，共有3项，系数分别为1，2，1，()3322333a b a a b ab b +=+++，共有4项，系数分别为1，3，3，1，()4432234464a b a a b a b ab b +=++++，共有5项，系数分别为1，4，6，4，1，…∴()na b +展开式中共有1n +项，令()na b +中1a =，1b =，则()na b +的展开式中的每一项正好是每一项的系数，∴()na b +的展开式中各项的系数和为()112nn +=．故答案为：1n +；2n ．题型10整式乘法混合运算1．（2023下·湖南岳阳·七年级岳阳市弘毅新华中学校考阶段练习）计算：一、单选题1．（2023上·河北廊坊·八年级校考阶段练习）计算22()a a ⋅-的结果是（）A ．32aB ．32-aC ．22a -D ．22a 【答案】B【分析】本题主要考查了单项式乘以单项式，在解题时要注意单项式的乘法法则的灵活应用是本题的关键．【详解】解：232()2a a a ⋅-=-，故选B ．2．（2023上·四川宜宾·八年级统考期中）若()()2428x x x mx ++=++，则m 的值是（）A ．6B ．6-C ．8D ．8-【答案】A【分析】本题考查的是多项式乘以多项式，再比较各项的系数即可得到答案；熟记多项式乘以多项式的运算法则是解本题的关键．【详解】解：∵()()2242688x x x x x mx ++=++=++，则m 的值为6．故选：A ．3．（2023上·河北石家庄·八年级统考期末）下列正确的是（）A ．23263236a b a b a b ⋅=B ．40.000767.610=⨯C ．()2222a a b a ab-+=-+D ．()()2212232x x x x +-=--【答案】D【分析】根据单项式乘单项式，科学记数法，单项式乘以多项式，，多项式乘以多项式的计算法则计算即可．【详解】解：A 、53232236a b a b a b ⋅=，故选项A 错误，不符合题意；B 、40.000767.610-=⨯，故选项B 错误，不符合题意；C 、()2222a a b a ab -+=--，故选项C 错误，不符合题意；D 、()()2212232x x x x +-=--，故选项D 正确，符合题意．故选：D ．【点睛】本题主要考查单项式乘单项式，科学记数法，单项式乘以多项式，，多项式乘以多项式，熟练掌握运算法则计算即可．4．（2023上·河南洛阳·八年级校考期中）22(3)(3)x nx x x m ++-+的乘积中不含2x 和3x 项，则m n 、的值为（）A ． 3m = 6n =B ． 3m =5n =C ．6m =3n =D ．6m =4n =【答案】C【分析】本题考查了多项式乘多项式，根据多项式乘以多项式的法则先把要求的式子进行整理，再根据多项式展开后不含2x 和3x 的项，得出30,330n m n -=-+=，求出m n 、的值即可．【详解】解：22(3)(3)x nx x x m ++-+43232233393x x mx nx nx mnx x x m=-++-++-+()()()43233393x n x m n x mn x m=+-+-++-+∴30,330n m n -=-+=，解得：3,6n m ==故选：C ．5．（2023上·山东临沂·八年级校考阶段练习）通过计算比较图中图①，图②中阴影部分的面积，可以验证的计算式子是（）A ．()a b x ab a -=-B ．()b a x ab bx -=-C ．()()a x b x ab ax bx --=--D ．()()2a xb x ab ax bx x --=--+【答案】D【分析】本题主要考查了多项式乘多项式、单项式乘多项式、整式运算等知识点，先根据图1和图2，分别用两种方法表示出阴影部分面积，然后列出等式即可；掌握数形结合思想成为解题的关键．【详解】解：图1中的阴影部分的面积为()()a x b x --，图2中的阴影部分的面积为2ab ax bx x --+，∴()()2a xb x ab ax bx x --=--+．故选：D ．二、填空题∵2230m m --=，∴223m m =+，223m m -=，∴()()3227323732432232339m m m m m m m m m -+=+-+=-+=-+=⨯+=，故答案为：9．三、解答题11．（2023上·重庆渝北·八年级校联考期中）计算：(1)()223321a b ab ⋅-+；(2)()()22a b a ab b -++．【答案】(1)352263a b a b -+(2)33a b -【分析】本题主要考查了整式的有关运算，解题关键是熟练掌握单项式乘单项式法则和多项式乘多项式法则．（1）根据单项式乘单项式法则，让单项式乘多项式的每一项，再把所得的积相加即可；（2）根据多项式乘多项式法则进行计算即可；【详解】（1）解：原式()223223231a b ab a b =⋅-+⋅352263a b a b =-+；（2）原式()()()2222a a a ab a b b a b ab b b=⋅+⋅+⋅+-⋅+-⋅+-⋅32222333a a b ab a b ab b a b =++---=-．12．（2023下·陕西西安·七年级交大附中分校校考期末）计算：(1)()()3227x y xy ⋅-；(2)()()()()21233a a a a +--+-．【答案】(1)757x y -(2)237a a -+【分析】（1）先计算积的乘方，再计算单项式乘以单项式即可；（2）先计算多项式乘以多项式，再合并同类项即可．【详解】（1）原式()3267x y xy ⋅-=757x y =-；（2）原式222429a a a a =-+--+【分析】（1）先根据多项式乘多项式运算法则展开，再合并同类项，然后根据题意得出关于m n 、的方程，解之即可求解；（2）先根据多项式乘多项式运算法则展开，再合并同类项，再代入m n 、值计算即可；本题考查了多项式乘多项式不含某项问题、多项式乘多项式化简求值，掌握多项式乘多项式的运算法则是解题的关键．【详解】（1）解：原式32222x x mx mx nx n =-+--+，()()3222x m x m n x n =+--++，∵()22(1)x mx n x +--展开的结果中，不含2x 和x 项，∴20m -=，0m n +=，∴2m =，2n =-；（2）解：()()22m n m mn n -++322223m m n mn m n mn n =++---，33m n =-，把2m =，2n =-代入得，原式()3322=--，()88=--，16=．16．（2023上·陕西安康·八年级校联考阶段练习）如图，在一个长方形空地中，沿它的两个角用栅栏围成两个大小相同的正方形（有关线段的长如图所示），留下一个“T ”型的图形（阴影部分）．(1)用含x ，y 的式子表示“T ”型图形的面积并化简；(2)若30y =米，20x =米，计划在“T ”型区域铺上价格为每平方米25元的草坪，请计算草坪的造价．（不考虑其他费用）【答案】(1)225x xy+(2)95000元【分析】本题考查多项式乘多项式与几何图形的面积．(1)小李同学拼成一个宽为()a b +，长为(2)a b +的长方形（如图2），并用不同的方法计算面积，从而得出相应的等式：（答案直接填写到横线上）；(2)如果用这三种纸片拼出一个面积为(2)(3)a b a b ++的大长方形，求需要A ，(3)利用上述方法，画出面积为22252a ab b ++的长方形，并求出此长方形的周长【答案】(1)22()(2)32a b a b a ab b ++=++这个长方形的周长为：2[(2⨯答：此长方形的周长为6a 18．（2023上·福建龙岩·八年级校考阶段练习）做整式的乘法运算时利用几何直观的方法获取结论，在解决整式运算问题时经常运用．例1：如图1，可得等式：(1)如图3，将几个面积不等的小正方形与小长方形拼成一个边长为a b c ++的正方形，从中你发现的结论用等式表示为；(2)利用（1）中所得到的结论，解决下面的问题：已知75a x =-，42b x =-+，c =-ab bc ac ++的值；(3)如图4，拼成AMGN 为大长方形，记长方形ABCD 的面积与长方形EFGH 的面积差为（1）正方形的面积为()2a b c ++，各小块面积总和为：222222a b c ab bc ac +++++，再由面积相等，即可得出答案；（2）由题意可得1a b c ++=，由（1）可得：()2222222a b c a b c ab bc ac ++=+++++，结合22237a b c ++=可得2137222ab bc ac =+++，进行计算即可得出答案；（3）由图可得：2BC a =，3DE a =，EH CF b ==，从而得出3EF x b a =+-，根据ABCD EFGH S S S =-长方形长方形，表示出()223S a b x b ab =--+，最后由S 的值与CD 无关，可得20a b -=，即可得出答案．【详解】（1）解：由图可得：正方形的面积为()2a b c ++，各小块面积总和为：222222a b c ab bc ac +++++，面积相等，()2222222a b c a b c ab bc ac ∴++=+++++，故答案为：()2222222a b c a b c ab bc ac ++=+++++；（2）解： 75a x =-，42b x =-+，34c x =-+，()()7542347542341a b c x x x x x x ∴++=-+-++-+=--+-+=，由（1）可得：()2222222a b c a b c ab bc ac ++=+++++， 22237a b c ++=，2137222ab bc ac ∴=+++，()236ab bc ac ∴++=-，18ab bc ac ∴++=-；（3）解：由图可得：2BC a =，3DE a =，EH CF b ==，DC x = ，3EF CD CF DE x b a ∴=+-=+-，ABCD EFGH S S S =- 长方形长方形，S CD BC EF EH∴=⋅-⋅()23x a x b a b=⋅-+-⋅223ax bx b ab=--+()223a b x b ab =--+，S 的值与CD 无关，20a b ∴-=，2a b ∴=．。

第十四章考试热点突破(遵义题组)

遵义学练考数学 8上【R】
第十四章整式的乘法与因式分解
第十四章考试热点突破（遵义题组）
•
9、要学生做的事，教职员躬亲共做；要学生学的知识，教职员躬亲共学；要学生守的规则，教职员躬亲共守。21.8.3021.8.30Monday, August 30, 2021
•
10、阅读一切好书如同和过去最杰出的人谈话。02:51:4702:51:4702:518/30/2021 2:51:47 AM
•
17、儿童是中心，教育的措施便围绕他们而组织起来。上午2时51分47秒上午2时51分02:51:4721.8.30
•
You have to believe in yourself. That's the secret of success. 人必须相信自己，这是成功的秘诀。
•
13、He who seize the right moment, is the right man.谁把握机遇，谁就心想事成。21.8.3021.8.3002:51:4702:51:47August 30, 2021
•
14、谁要是自己还没有发展培养和教育好，他就不能发展培养和教育别人。2021年8月30日星期一上午2时51分47秒02:51:4721.8.30
•
15、一年之计，莫如树谷；十年之计，莫如树木；终身之计，莫如树人。2021年8月上午2时51分21.8.3002:51August 30, 2021
•
16、教学的目的是培养学生自己学习，自己研究，用自己的头脑来想，用自己的眼睛看，用自己的手来做这种精神。2021年8月30日星期一2时51分47秒02:51:4730 August 2021
Байду номын сангаас

热点强化突破(六)课件人教版课件

解析：设船移动距离为 x，则人移动距离为 l－x，以船行方向为正方向，船对地的平均速度为xt ，人对地的平均速度为－ l－x，由动量守恒定律有
t M·xt －ml－t x＝0 即 Mx－m(l－x)＝0 解得船移动的距离为 x＝Mm＋lm＝15500×＋450 m＝1 m.
答案：1 m
2．(2010·高考重庆卷)某兴趣小组用如图所示的装置进行实验研究．他们在水平桌面上固定一内径为 d 的圆柱形玻璃杯，杯口上放置一直径为32d、质量为 m 的匀质薄圆板，板上放一质量为 2m 的小物块．板中心、物块均在杯的轴线上．物块与板间动摩擦因数为 μ，不计板与杯口之间的摩擦力，重力加速度为 g，不考虑板翻转．
热点强化突破（六）
热点1 动量守恒定律应用中的常见模型人船模型：此类问题关键在于确定物体位移间的关系，并结合动量守恒求解． “滑块—木板”模型：“滑块”问题是动量和能量的综合应用之一，由于滑块与木板之间常存在一对相互作用的摩擦力，这对摩擦力使滑块、木板的动量发生变化，也使它们的动能发生改变，但若将两者视为系统，则这对摩擦力是系统的内力，它不影响系统的总动量，但克服它做功，使系统机械能损失，所以解决“滑块”问题常用到动量守恒定律．
木块的动能 Ek＝12mv2块＝2 J.
(3)木块往返过程中克服摩擦力做功，系统损失的机械能为 ΔE ＝12mv20－12(M＋m)v2＝4系统克服摩擦力做功损失的机械能为12ΔE＝20 J．对这个过程由能量转化与守恒定律有：12mv20＝12(M＋m)v2＋12ΔE＋Epm，解得弹簧压缩到最短时获得的最大弹性势能 Epm＝20 J. 答案：(1)2 m/s 方向向右 (2)2 J (3)20 J
因为 s 相＝0.75 m＜1.08 m，故假设成立，滑块 C 在平板车上滑行的距离为 0.75 m.