高考数学课后作业 32 同角三角函数的基本关系及诱导公式新人教A版

合集下载

高考复习数学第二节同角三角函数的基本关系与诱导公式

角度 sin α，cos α 的齐次式问题 [例 2] 已知tatnanα－α 1＝－1，求下列各式的值． (1)ssiinnαα－＋3ccoossαα； (2)sin2 α＋sin αcos α＋2.
解：由已知得 tan α＝12. (1)ssiinnαα－＋3ccoossαα＝ttaann αα－＋31＝－53.
D．±2
5 5
所以 cos α＝－23，
则 α 为第二或第三象限角，
所以 sin α＝±
1－cos2
α＝±
5 3.
5
所以
tan
α＝csions
αα＝±－323
＝±
5 2.
答案：C
6．sin 2 490°＝________；cos－523π＝________．
解析：sin 2 490°＝sin(7×360°－30°)＝－sin 30°＝－12. cos－523π＝cos 523π＝cos16π＋π＋π3＝cosπ＋π3＝－cos π3＝－12. 答案：－12 －12
(2)sin2 α＋sin αcos α＋2＝sins2inα2＋α＋sincoαsc2oαs α＋2＝
tan2 α＋tan tan2 α＋1
α＋2＝121222＋＋121＋2＝153.
角度 sin α±cos α 与 sin αcos α 关系的应用
[例 3] 已知 x∈(－π，0)，sin x＋cos x＝15.
1．已知 a∈(0，π)，且 cos α＝－153，则 sinπ2－α· tan α＝( )
由 x∈(－π，0)，知 sin x<0，又 sin x＋cos x>0，
所以 cos x>0，所以 sin x－cos x<0，

高考数学专题《同角三角函数的基本关系与诱导公式》习题含答案解析

专题5.2 同角三角函数的基本关系与诱导公式1．（2021·北京二中高三其他模拟）在平面直角坐标系xOy 中，角θ以Ox 为始边，终边与单位圆交于点34,55⎛⎫⎪⎝⎭，则tan()πθ-的值为（）A ．43B ．34C ．43-D ．34-【答案】C 【解析】由题意可得角的正弦和余弦值，由同角三角函数的基本关系可求出角的正切值，结合诱导公式即可选出正确答案.【详解】解：由题意知，43sin ,cos 55θθ==，则sin 4tan cos 3θθθ==，所以4tan()tan 3πθθ-=-=-，故选:C.2．（2021·全国高三其他模拟（理））已知1tan ,2α=则()cos cos 2παπα-⎛⎫+ ⎪⎝⎭=（）A ．﹣12B ．12C ．2D ．﹣2【答案】C 【解析】先用“奇变偶不变，符号看象限”将()cos cos 2παπα-⎛⎫+ ⎪⎝⎭化简为cos sin αα--，结合同角三角函数的基本关系来求解.【详解】因为1tan 2α=，所以()cos cos 2παπα-⎛⎫+ ⎪⎝⎭=cos sin αα--=1tan α=2.故选：C练基础3.（2021·全国高一专题练习）已知3cos cos()2παπα⎛⎫-++= ⎪⎝⎭则1tan tan αα+=（）A ．2B ．-2C ．13D ．3【答案】A 【解析】用诱导公式化简，平方后求得sin cos αα，求值式切化弦后易得结论．【详解】3cos cos()sin cos 2παπααα⎛⎫-++=∴--= ⎪⎝⎭即21sin cos (sin cos )2,sin cos ,2αααααα+=∴+=∴=1sin cos 1tan 2tan cos sin sin cos αααααααα∴+=+==，故选：A ．4．（2021·河南高三其他模拟（理））若1tan 2α=，则22sin sin cos ααα+=_______________________.【答案】45【解析】利用同角三角函数的基本关系式进行化简求值.【详解】因为12tan α=，所以222222224215sin sin cos tan tan sin sin cos sin cos tan ααααααααααα+++===++.故答案为：455．（2021·宁夏银川市·银川一中高三其他模拟（文））若3sin 2πθ⎛⎫+= ⎪⎝⎭[0,2)θπ∈，则θ=___________.【答案】116π【解析】根据三角函数的诱导公式，求得cos θ=[0,2)θπ∈，进而求得θ的值.【详解】由三角函数的诱导公式，可得3sin cos 2πθθ⎛⎫+=-= ⎪⎝⎭，即cos θ=，又因为[0,2)θπ∈，所以116πθ=.故答案为：116π.6．（2021·上海格致中学高三三模）已知α是第二象限角，且3sin 5α=，tan α=_________.【答案】34-【解析】根据角所在的象限，判断正切函数的正负，从而求得结果.【详解】由α是第二象限角，知4cos 5α===-，则sin 3tan cos 4ααα==-故答案为：34-7．（2021·上海高三二模）若sin cos k θθ=，则sin cos θθ⋅的值等于___________(用k 表示).【答案】21kk +【解析】由同角三角函数的关系得tan θk =,进而根据22sin cos sin cos sin cos θθθθθθ⋅⋅=+,结合齐次式求解即可.【详解】因为sin cos k θθ=，所以tan θk =，所以2222sin cos tan sin cos sin cos tan 11kk θθθθθθθθ⋅⋅===+++，故答案为:21k k +8．（2021·河北衡水市·高三其他模拟）函数log (3)2(0a y x a =-+>且a ≠1)的图象过定点Q ，且角a 的终边也过点Q ，则23sin α+2sin cos αα=___________.【答案】75【解析】首先可得点Q 的坐标，然后可得tan α，然后可求出答案.【详解】由题可知点Q (4，2)，所以1tan ,2α=所以22223sin 2sin cos 3sin 2sin cos sin cos αααααααα++==+2211323tan 2tan 74211tan 514ααα⨯+⨯+==++故答案为：759．（2021·上海高三其他模拟）已知3sin 5x =，(,)2x ππ∈，则cos(π﹣x )=___________.【答案】45【解析】根据22sin cos 1x x += ，(,)2x ππ∈，求出cos x ，再用“奇变偶不变，符号看象限”求出cos(π﹣x ).【详解】解：因为3sin 5x =，(,)2x ππ∈，可得cos x =﹣=﹣45，所以cos(π﹣x )=﹣cos x =45.故答案为：45.10．（2020·全国高一课时练习）若2cos()3απ-=-，求sin(2)sin(3)cos(3)cos()cos()cos(4)απαπαππαπααπ-+--------的值．【答案】.【解析】利用诱导公式化简已知和结论，转化为给值求值的三角函数问题解决.【详解】原式=sin(2)sin(3)cos(3)cos (cos )cos παπαπαααα---+----=2sin sin cos cos cos ααααα--+=sin (1cos )cos (1cos )αααα---=-tan α，因为2cos()cos 3απα-=-=-，所以2cos 3α=，所以α为第一象限角或第四象限角．(1)当α为第一象限角时，sin α=所以sin tan cos ααα=，所以原式.(2)当α为第四象限角时，sin α=所以sin tan cos ααα=，所以原式.综上，原式=.1．（2021·全国高三其他模拟（理）(0)a a =>，则1tan 2=________（用含a 的式子表示）．【解析】根据同角三角函数的相关公式，把根号下的式子变形为完全平方式，2111112sin cos sin cos 2222⎛⎫-=- ⎪⎝⎭，2111112sin cos sin cos 2222⎛⎫+=+ ⎪⎝⎭，再由11cos sin 022>>，开方即得1cos 22a =，再由22111tan 12cos 2+=即可得解.【详解】练提升=+=1111cos sin sin cos2222=-++12cos 2a ==，则1cos 22a =而22111tan 12cos 2+=，2214tan 12a∴=-又1tan 02>，1tan 2∴==.2.（2021·河北邯郸市·高三二模）当04x π<<时，函数22cos ()sin cos sin xf x x x x=-的最大值为______．【答案】-4【解析】化简函数得21()tan tan f x x x=-，再换元tan ,(0,1)t x t =∈，利用二次函数和复合函数求函数的最值.【详解】由题意得22222cos cos ()sin cos sin cos cos x x f x x x xx x =-所以21()tan tan f x x x =-，当04x π<<时，0tan 1x <<，设tan ,(0,1)t x t =∈所以2211()=11()24g t t t t =---，所以当12t =时，函数()g t 取最大值4-.所以()f x 的最大值为-4．故答案为：4-3．（2021·浙江高三其他模拟）已知πtan 34α⎛⎫+=- ⎪⎝⎭，则3πtan 4α⎛⎫-= ⎪⎝⎭______，sin cos αα=______.【答案】3 25【解析】由3ππtan tan 44αα⎛⎫⎛⎫-=-+⎪ ⎪⎝⎭⎝⎭可求，由和的正切公式求出tan α，再建立齐次式即可求出.【详解】3πππtan tan πtan 3444ααα⎡⎤⎛⎫⎛⎫⎛⎫-=-+=-+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦.由πtan 1tan 341tan ααα+⎛⎫+==- ⎪-⎝⎭，得tan 2α=，故222sin cos tan 2sin cos sin cos tan 15αααααααα===++.故答案为：3；254．（2021·全国高一专题练习）如图，单位圆与x 轴正半轴的交点为A ，M ，N 在单位圆上且分别在第一､第二象限内，OM ON ⊥.若四边形OAMN 的面积为34，则AOM ∠=___________；若三角形AMN 的面积为25，则sin AOM ∠=___________.【答案】6π 35【解析】根据四边形OAMN 的面积，列出关于M 点纵坐标M y 的方程，求出M y ；即可根据三角函数的定义求出sin AOM ∠，进而可得AOM ∠；根据三角形AMN 的面积为25，得到M y 与N y 之间关系，再结合三角函数的定义，得到1cos sin 5AOM AOM ∠-∠=，利用同角三角函数基本关系，即可求出结果.【详解】若四边形OAMN 的面积为34，则3111142222MON MOA M M S S OM ON OA y y =+=⨯⨯+⨯⨯=+V V ，解得12M y =，由三角函数的定义可得1sin 2M AOM y ∠==，因为M 为第一象限内的点，所以AOM ∠为锐角，因此6AOM π∠=；若三角形AMN 的面积为25，则21115222MON MOA AMN OAMN AON AON M N S S S S S S y y ==-=-=+-+V V V V V ，即51N M y y -=，由三角函数的定义可得，sin M AOM y ∠=，sin N AON y ∠=，又sin sin cos 2N y AON AOM AOM π⎛⎫=∠=∠+=∠ ⎪⎝⎭，所以1cos sin 5AOM AOM ∠-∠=，由221cos sin 5sin cos 1AOM AOM AOM AOM ⎧∠-∠=⎪⎨⎪∠+∠=⎩解得3in 5s AOM ∠=或4in 5s AOM ∠=-，又AOM ∠为锐角，所以3in 5s AOM ∠=.故答案为：6π；35.5．（2021·河南高一期中（文））（1）已知角α的终边经过点()43P ,-，化简并求值：221cos sin cos sin cos tan 1a ααααα-+---；（2的值．【答案】（1）15-（2）1．【解析】（1）利用三角函数定义得到3sin 5α=，4cos 5α=-，化简三角函数表达式代入即可得到结果；（2）利用同角基本关系式化简即可.【详解】（1）由题意知，3sin 5α=，4cos 5α=-．原式222sin sin cos sin sin cos 1cos ααααααα+=---2222sin sin cos sin cos sin cos cos αααααααα+=---()2222cos sin cos sin sin cos sin cos αααααααα+=---22sin cos sin cos sin cos αααααα=---22sin cos sin cos αααα-=-341sin cos 555αα=+=-=-；（2）原式=sin 40cos 40cos 40cos50︒-︒=︒-︒cos 40sin 401cos 40sin 40-==-︒︒︒︒．6．（2021·河南高一期中（文））已知sin 2cos 0αα+=．（1）求sin 2cos cos 5sin αααα--的值；（2）求33sin cos cos sin aααα+的值．【答案】（1）411-；（2）858-．【解析】（1）本题可根据sin 2cos 0αα+=得出tan 2α=-，然后根据同角三角函数关系即可得出结果；（2）本题可通过22sin cos 1αα+=求出2sin α、2cos α的值，然后通过同角三角函数关系即可得出结果.【详解】（1）因为sin 2cos 0αα+=，所以tan 2α=-，则sin 2cos tan 24cos 5sin 15tan 11αααααα--==---.（2）联立22sin 2cos 0sin cos 1αααα+=⎧⎨+=⎩，解得224sin 51cos 5αα⎧=⎪⎪⎨⎪=⎪⎩，则3322sin cos tan 185cos sin cos sin tan 8a ααααααα+=+=-.7．（2020·武汉市新洲区第一中学高一期末）在平面直角坐标系xOy 中，以x 轴非负半轴为始边作角0,2πα⎛⎫∈ ⎪⎝⎭，,2πβπ⎛⎫∈ ⎪⎝⎭，它们的终边分别与单位圆相交于A ，B 两点，已知点A ，B，．（1）求23sin sin cos 1ααα-+的值；（2）化简并求cos 的值．【答案】（1）195；（2）1-+【解析】（1）由已知条件可知求得sin α，tan α，已知式变形为2222223sin sin cos 3tan tan 3sin sin cos 111sin cos tan 1ααααααααααα---+=+=+++，代入可得答案；（2）由已知得cos β，sin β=.【详解】解：（1）由已知条件可知：cos α=0,2πα⎛⎫∈ ⎪⎝⎭，所以sin 0α>，sin α==，tan 7α=，2222223sin sin cos 3tan tan 3497193sin sin cos 1111sin cos tan 1505ααααααααααα--⨯--+=+=+=+=++，（2）cos β=,2πβπ⎛⎫∈ ⎪⎝⎭，所以sin 0β>，从而sin β==；1sin cos cos cos (1sin )1|cos |ββββ-===--=-+.8．（2021·全国高三专题练习（理））求函数sin cos sin cos y x x x x =+-(x ∈R )的值域．【答案】112⎡⎤-⎢⎥⎣⎦，【解析】令sin cos t x x =-=4x π⎛⎫⎡-∈ ⎪⎣⎝⎭，所以()2221111+++122221t y t t t t -=--=+=-，根据二次函数的性质可求得值域．【详解】令sin cos t x x =-=4x π⎛⎫⎡-∈ ⎪⎣⎝⎭，所以()2221111+++122221t y t t t t -=--=+=-，所以当t =24=-+x k ππ (k Z ∈)时，min y =12-；当1t =，即()114k x k ππ⎡⎤=++-⎣⎦(k Z ∈)时，max 1y =，因此函数y =sin cos sin cos y x x x x =+-的值域应为112⎡⎤-⎢⎥⎣⎦，．9．（2021·江苏高一月考）如图，锐角α的始边与x 轴的非负半轴重合，终边与单位圆交于点()11,A x y ，将射线OA 按逆时针方向旋转3π后与单位圆交于点()()2212,,B x y f x x α=+.（1）求()fα的取值范围；（2）若()fα=，求tan α的值.【答案】（1）32⎛⎫ ⎪ ⎪⎝⎭；（2【解析】（1）由三角函数的定义可得1cos x α=，2cos(3x πα=+，化简()f α6)πα+．根据2663πππα<+<，利用余弦函数的定义域和值域求得()f α的范围．（2）根据()f α=，求得3cos(654sin(65παπα⎧+=⎪⎪⎨⎪+=⎪⎩，再利用两角差的正弦余弦公式求出sin ,cos αα的值，从而得出结论．【详解】（1）由图知，3AOB π∠=，由三角函数的定义可得1cos x α=，2cos(3x πα=+，123()cos cos()cos cos cossin sincos 3332f x x πππαααααααα==+++-+=-=6)πα=+．角α为锐角，∴2663πππα<+<，∴1co 26s()πα-<+<∴623πα<+<，即()f α的范围是32⎛⎫⎪ ⎪⎝⎭．（2）因为()fα=，2663πππα<+<，6πα+=，3cos()65)46sin()65παπαπα⎧+=⎪⎪+=⇒⎨⎪+=⎪⎩，431sin sin66552ππαα⎡⎤⎛⎫=+-=⨯=⎪⎢⎥⎝⎭⎣⎦341cos cos66552ππαα⎡⎤⎛⎫=+-=+⨯=⎪⎢⎥⎝⎭⎣⎦sintancosααα∴===10．（2021·河南省实验中学高一期中）（1）已知sin()cos()tan(3)()3cos2fπθπθπθθπθ-+-=⎛⎫-⎪⎝⎭，求73fπ⎛⎫- ⎪⎝⎭的值（2）已知1sin cos5αα+=-，2παπ<<，求sin(3)cos(2)sin()sin2παπαπαα--++⎛⎫-++⎪⎝⎭的值．【答案】（1（2）17.【解析】（1）利用诱导公式、同角三角函数基本关系化简()fθ，然后再代值计算即可.（2）利用同角三角函数间的关系，将1sin cos5αα+=-平方求出sin cosαα的值，从而求出cos sinαα-的值，再由诱导公式将所求式子化简，即可得出答案.【详解】(1)()()sin cos tansin()cos()tan(3)()sin3sincos2fθθθπθπθπθθθπθθ⋅-⋅--+-===--⎛⎫-⎪⎝⎭所以77sin sin2sin3333fπππππ⎛⎫⎛⎫⎛⎫-=--=+==⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭（2）由1sin cos 5αα+=-，则112sin cos 25αα+=，所以242sin cos 25αα=-由2παπ<<，则sin 0,cos 0αα><设cos sin 0t αα=-<，则2244912cos sin 12525t αα=-=+=由cos sin 0t αα=-<，所以7cos sin 5αα-=-1sin(3)cos(2)sin cos 157sin cos 7sin()sin 52παπαααπαααα---+++===-+⎛⎫--++ ⎪⎝⎭1．（2021·全国高考真题）若tan 2θ=-，则()sin 1sin 2sin cos θθθθ+=+（）A ．65-B ．25-C ．25D ．65【答案】C 【解析】将式子先利用二倍角公式和平方关系配方化简，然后增添分母(221sin cos θθ=+)，进行齐次化处理，化为正切的表达式，代入tan 2θ=-即可得到结果．【详解】将式子进行齐次化处理得：()()()22sin sin cos 2sin cos sin 1sin 2sin sin cos sin cos sin cos θθθθθθθθθθθθθθ+++==+++()2222sin sin cos tan tan 422sin cos 1tan 145θθθθθθθθ++-====+++．故选：C ．2.（2020·全国高考真题（理））已知π()0,α∈，且3cos28cos 5αα-=，则sin α=（）AB ．23C ．13D练真题【答案】A 【解析】3cos 28cos 5αα-=，得26cos 8cos 80αα--=，即23cos 4cos 40αα--=，解得2cos 3α=-或cos 2α=（舍去），又(0,),sin απα∈∴== 故选：A.3.（2019·北京高考真题（文））如图，A ，B 是半径为2的圆周上的定点，P 为圆周上的动点，是锐角，大小为β.图中阴影区域的面积的最大值为（）A ．4β+4cos βB ．4β+4sin βC ．2β+2cos βD ．2β+2sin β【答案】B 【解析】观察图象可知，当P 为弧AB 的中点时，阴影部分的面积S 取最大值，此时∠BOP =∠AOP =π-β, 面积S 的最大值为+S △POB + S △POA =4β+.故选：B .APB ∠2222βππ⨯⨯1||sin()2OPOB πβ-‖1||sin()2OP OA πβ+-‖42sin 2sin 44sin βββββ=++=+⋅4．（2017·北京高考真题（文））在平面直角坐标系中,角与角均以为始边，它们的终边关于轴对称.若,则_____.【答案】【解析】因为角与角的终边关于轴对称，所以，所以.5．（2018·北京高考真题（理））设函数f （x ）=cos(ωx ―π6)(ω>0)，若f (x )≤f (π4)对任意的实数x 都成立，则ω的最小值为__________．【答案】23【解析】因为f (x )≤f (π4)对任意的实数x 都成立，所以f (π4)取最大值，所以π4ω―π6=2k π(k ∈Z )，∴ω=8k +23(k∈Z )，因为ω>0，所以当k =0时，ω取最小值为23.6．（2017·全国高考真题（理））函数f (x )=s in 2x +3cosx ―34（x ∈0,__________．【答案】1【解析】化简三角函数的解析式，则f (x )=1―cos 2x +3cos x ―34=―cos 2x +3cos x +14= ―(cos x ―32)2+1，由x ∈[0,π2]可得cos x ∈[0,1]，当cos x =32时，函数f (x )取得最大值1．xOy αβOx y 1sin 3α=sin β=13αβy 2,k k Z αβππ+=+∈()1sin sin 2sin 3k βππαα=+-==。

同角三角函数基本关系式及诱导公式(3种核心题型)(学生版) 2025年高考数学大一轮复习(新高考版)

考点23同角三角函数基本关系式及诱导公式（3种核心题型+基础保分练+综合提升练+拓展冲刺练）【考试提醒】1.理解同角三角函数的基本关系式sin2α＋cos2α＝1，sin αcos α＝tan α(α≠π2＋kπ，k∈Z).2.掌握诱导公式，并会简单应用．【知识点】1．同角三角函数的基本关系(1)平方关系：.(2)商数关系：.2．三角函数的诱导公式公式一二三四五六角2kπ＋α(k∈Z)π＋α－απ－απ2－απ2＋α正弦sin α余弦cos α正切tan α－tan α口诀奇变偶不变，符号看象限常用结论同角三角函数的基本关系式的常见变形sin2α＝1－cos2α＝(1＋cos α)(1－cos α)；cos2α＝1－sin2α＝(1＋sin α)(1－sin α)；(sin α±cos α)2＝1±2sin αcos α.【核心题型】题型一　同角三角函数基本关系(1)应用公式时注意方程思想的应用：对于sin α＋cos α，sin αcos α，sin α－cos α这三个式子，利用(sin α±cos α)2＝1±2sin αcos α，可以知一求二．(2)注意公式逆用及变形应用：1＝sin2α＋cos2α，sin2α＝1－cos2α，cos2α＝1－sin2α.【例题1】（2024·河南信阳·一模）若πcos()2sin2aa-=44sin cosa a+=（）A B C D【变式1】（多选）（2023·海南·模拟预测）已知sin0a<，则（）A．tan1a>-B．tan21a<C．sin20a>D．cos20a<【变式2】（2024高三·全国·专题练习）已知5cos13a=-，则13sin5tanaa+=.【变式3】（2024·山西朔州·一模）若πtan26aæö-=ç÷èø，则2ππ1tan cos362a aæöæö-+--=ç÷ç÷èøèø．题型二　诱导公式诱导公式的两个应用(1)求值：负化正，大化小，化到锐角为终了；(2)化简：统一角，统一名，同角名少为终了．【例题2】（23-24高三上·江苏南通·期末）已知π0,,sin cos4x x xéùÎ+=êúëû，则3πtan4xæö-=ç÷èø（）A．3B．3-C．D．2【变式1】（多选）（22-23高一下·河南焦作·阶段练习）已知角,A B，C是锐角三角形ABC的三个内角，下列结论一定成立的有（）A．()sin sinB C A+=B．sin cos22A B C+æö=ç÷èøC．()cos cosA B C+<D．sin cosA B<【变式2】（2024·全国·模拟预测）在ABCV中，tan A，tan B是方程2670x x-+=的两个根，则C的值是．【变式3】（2023·湖南邵阳·模拟预测）在ABCV中，角A，B，C所对的边分别是a，b，c，若()3cos cos22A B C+=+.(1)求角C的大小；(2)若6c=，求ABCV的面积S的最大值.题型三　同角三角函数基本关系式和诱导公式的综合应用(1)利用同角三角函数基本关系式和诱导公式求值或化简时，关键是寻求条件、结论间的联系，灵活使用公式进行变形．(2)注意角的范围对三角函数值符号的影响．【例题3】（22-23高三上·陕西安康·阶段练习）在ABC V 中，“tan tan 1A B =”是“22sin sin 1A B +=”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【变式1】（2024·广西·二模）已知2sin sin2a a =，则πtan 4a æö+=ç÷èø.【变式2】（2024·全国·模拟预测）已知点()()()cos ,sin A b a b a --与点5π5πcos ,sin 1212B b b æöæöæö++ç÷ç÷ç÷èøèøèø关于原点对称，则sin cos a a += ．【变式3】（23-24高三上·北京·阶段练习）已知a 是第二象限内的角，tan a =(1)求 πcos 22a æö-ç÷èø的值；(2)已知函数()21sin cos sin 2222x x x f x =-+，求π12f a æö+ç÷èø的值．【课后强化】【基础保分练】一、单选题1．（2024·江苏扬州·模拟预测）若ππ44a b -<<<，且1cos sin 2a b =，tan 2tan 3a b =，则()cos a b -=（）A B ．C D ．2．（2024·广东·二模）tan 7.5tan82.52tan15°-°+°=（）A ．2-B ．4-C ．-D ．-3．（2024·全国·模拟预测）已知3π4cos 47a æö-=ç÷èø，则22sin 1cos 22tan sin a a a a++-=（）A ．B ．C ．D ．4．（2024·辽宁沈阳·二模）已知()0,πa Î，且1sin cos 5a a +=，则tan2a =（）A ．127B ．127-C ．247D ．247-二、多选题5．（23-24高三上·江西·阶段练习）下列结论正确的是（）A ．若π2a b -=，则sin cos a b =B ．2π2sin 212sin 23a a a æö=+-ç÷èøC ．若1sin cos 2a a -=，则3sin 24a =D ．若锐角a 满足cos a =，则πtan 34a æö+=-ç÷èø6．（2024·河南周口·模拟预测）设π(0,)2a Î，π(0,)2b Î，则下列计算正确的是（）A ．()()cos cos a b a b +<-B ．若1sin(cos 6ππ(44a a ++=-，则tan 2a =C ．若1tan tan cos a b a +=，则22πb a -=D ．若cos 2101sin 2tan a a b +=+，则3π4a b +=三、填空题7．（2024·全国·二模）已知6cos tan 7sin aa a=-，则cos2a = .8．（2024·广东惠州·一模）若角a 的终边在第四象限，且4cos 5a =，则πtan 4a æö-=ç÷èø．9．（2024·全国·模拟预测）已知πtan 7x x æö+=ç÷èø为第二象限角，则10πsin 21x æö+=ç÷èø．四、解答题10．（2023·广东珠海·模拟预测）在三角形ABC 中，内角A 、B 、C 对应的边分别是a 、b 、c ，已知1a =，2b =，c 求：(1)sin B 的值：(2)()cos 2sin B A C -+的值.11．（2023·河南·模拟预测）已知函数()()2cos sin f x x x x =(1)若π10413f a æö+=ç÷èø，求π212f a æö-ç÷èø的值；(2)设()ππ1ππ1262126g x f x f x f x f x æöæöæöæö=++--+-ç÷ç÷ç÷ç÷èøèøèøèø，求函数()g x 的最小值.【综合提升练】一、单选题1．（2024高三·全国·专题练习）已知sin a =3πcos 22tan a a æö-ç÷èø=（）A ．74-B ．74C ．14D ．14-2．（2024·河南·二模）已知1sin cos 3x x +=，则πcos 22x æö-=ç÷èø（）A ．35-B ．35C ．89D ．89-3．（2024·全国·模拟预测）若sin cos 1sin cos 15a a a a =-++，则sin2a =（）A ．1625B ．1625-C ．925D ．925-4．（2024·江西·二模）已知()()()cos 140cos 200sin 130a a a °-=°++°-，求tan a =（）AB．CD．5．（2024·山东济南·三模）若sin cos a a -=，则tan a =（）A ．1B ．1-C ．2D ．2-6．（2024·湖南岳阳·二模）已知ππ1Z,sin cos 223a a æöæöÎ++-=ç÷ç÷èøèøn n n ，则（）A ．1cos sin 3a a +=B ．1cos sin 3a a +=-C ．8sin29a =-D ．8sin29a =7．（2024高三下·全国·专题练习）已知角a 为第三象限角，tan a =πcos 6a æö-=ç÷èø（）A ．BCD ．8．（2024·新疆·一模）已知: ()()()sin 20sin 20sin 400q q q -+++-=o o o，则tan q =（）A ．B ．CD 二、多选题9．（23-24高一上·广东清远·期末）已知()tan tan tan a b a b -=-，其中()π2k k a ¹ÎZ 且()π2m m b ¹ÎZ ，则下列结论一定正确的是（）A ．sin sin 0a b =B ．()sin 0a b -=C ．()cos 1a b -=D ．22sin cos 1a b +=10．（2024·云南·一模）为得到函数π6sin 23y x æö=+ç÷èø的图象，只需要将函数6sin2y x =的图象（）A ．向左平行移动π6个单位B ．向左平行移动π3个单位C ．向右平行移动5π6个单位D ．向右平行移动11π6个单位11．（2023·广东·模拟预测）如图是函数()f x 的部分图象，则下列结论正确的是（）A ．()π2sin 24f x x æö=+ç÷èøB ．()3π2sin 24f x x æö=--ç÷èøC ．()3π2cos 24f x x æö=+ç÷èøD ．()π2cos 24f x x æö=-ç÷èø三、填空题12．（2024·黑龙江·二模）已知函数()f x 满足：()1tan cos 2f x x=，则111(2)(3)(2024)232024f f f f f f æöæöæö+++++++=ç÷ç÷ç÷èøèøèøL L ．13．（2023·青海·模拟预测）如图，直径10AB =的半圆，D 为圆心，点C 在半圆弧上，sin 0.8,ADC P Ð=为 AB 的中点，AP 与BC 相交于点E ，则cos PEC Ð=.14．（2024·江苏·一模）已知π,0,2a b æöÎç÷èø，且1sin sin 2a b -=-，1cos cos 2a b -=，则tan tan a b += ．四、解答题15．（2024·广东深圳·模拟预测）在锐角ABC V 中，角A ，B ，C 所对的边分别为a ，b ，c ，已知3tan 24C =-．(1)求cos C ；(2)若4c =，求ABC V 面积的最大值．16．（2024·全国·模拟预测）已知ABC V 为锐角三角形，且()sin 3cos 3cos C C A B +=-．(1)求tan tan A B +的值；(2)求1sin sin sin A B C的最小值．17．（2024·湖北·一模）在ABC V 中，已知π4AB AC C ===．(1)求B 的大小；(2)若BC AC >，求函数()()()sin 2sin 2f x x B x A C =--++在[]π,π-上的单调递增区间．18．（2024·四川内江·三模）在斜ABC V 中，角A 、B 、C 所对的边分别为π,cos()02a b c B A C æö+++=ç÷èø,．(1)求cos 2B 的值；(2)若π,2A C b =+=ABC V 的面积．19．（2022·浙江·模拟预测）记ABC V 的内角A ，B ，C 的对边分别为a ，b ，c ，已知cos 1sin tan AA B=+.(1)若A B =，求C ；(2)求sin sin 2cos a B b Ab B+的取值范围.【拓展冲刺练】一、单选题1．（2024·福建南平·二模）已知π1tan 62a æö+=ç÷èø，则2πcos 23a æö-=ç÷èø（）A ．35-B ．34C ．45-D ．452．（2024·辽宁丹东·一模）已知π(0,2a Î1=，则sin 2a =（）ABCD3．（2024·河南南阳·一模）已知三个锐角,,a b g满足1sin cos cos 2a b b g ==，则sin cos g a 的最大值是（）A ．14BC D4．（23-24高三上·浙江·阶段练习）若3sin cos q q +=，则π1tan π8tan 8q q æö+-ç÷æöèø+ç÷èø的值为（）A ．7-B ．14-C ．17D ．27二、多选题5．（2024·全国·模拟预测）已知()sin sin 2024a =°，()sin cos 2024b =°，()cos sin 2024c =°，()cos cos 2024d =°，则（）A ．a c<B ．b d<C ．a b<D ．d c<6．（2024·湖北·模拟预测）设sin 52t °=，则（）A ．2cos 7612t °=-B．sin1042°=C．tan 38°=D．sin 64°=三、填空题7．（21-22高二下·浙江金华·阶段练习）已知3πsin(3π)2sin(2a a -=-+，求3πsin(π)5sin()22cos(2π)sin()a a a a ---=--- .8．（2023·广东惠州·二模）函数π()tan()0,||2f x x w j w j æö=+><ç÷èø经过点π,16æö-ç÷èø，图象如图所示，图中阴影部分的面积为6π，则2023π3f æö=ç÷èø.9．（2022·重庆沙坪坝·模拟预测）已知锐角三角形ABC 的内角A ，B ，C 所对的边分别是a ，b ，c ，且A B >，若7sin 2cos sin 25C A B =+，则tan B 的取值范围为．四、解答题10．（2024·全国·模拟预测）在ABC V 中，已知22,,tan sin AB AC BD DC CAD BAC l ===Ð=Ðuuu r uuu r．(1)若2l =，证明：ABC V 为直角三角形；(2)若1l =，求ABC V 的面积．11．（22-23高三上·陕西商洛·期中）在非Rt ABC △中，已知()2sin sin sin sin A B C C q l -=，其中3πtan 042q q æö=<<ç÷èø．(1)若tan 2C =，1l =，求11tan tan A B+的值；(2)是否存在l 使得112tan tan tan A B C++为定值？若存在，求l 的值，并求出该定值为多少；若不存在，请说明理由．。

4.2 同角三角函数的基本关系及诱导公式

所以1 ��-sin2��
=
1 (cos��+sin��)(cos��-sin��)
=
275.
-20-
考点1
考点2
考点3
(方法二)联立
sin��
+
cos��
=
1 5
,
①
sin2�� + cos2�� = 1,②
(2)求m的值; (3)求方程的两根及此时θ的值. 思考sin α+cos α,sin α-cos α,sin αcos α这三个式子之间有怎样的关系?
-14-
考点1
考点2
考点3
解 (1)由根与系数的关系可知
3+1 sin�� + cos�� = 2 ,
①
sin��·cos��
=-sin(180°-60°)cos(180°+30°)-cos(360°-60°)sin(360°-30°)
=sin 60°cos 30°+cos 60°sin 30°
=
3 2
×
3 2
+
1 2
×
12=1.
(2)∵f(α)=(1-+2ssiinn��2��)��(+-csoisn��)-+cocso2s��=2s2insi��n��c2o��s��+��+sicno��s��
=
cos��(1+2sin��) sin��(1+2sin��)

高考数学一轮复习第四章三角函数解三角形2同角三角函数的基本关系及诱导公式课件新人教A版(理)

时,怎样简化解题过程?
-26考点1
考点2
考点3
解析: (1)∵sin +
π
4
3
= ,
π
5
π
π
π
3
∴cos - 4 =cos + 4 - 2 =sin + 4 = 5.
又 θ 是第四象限角,
π
∴θ-4 是第四象限角.
π
4
π
4
∴sin - 4 =-5.∴tan - 4 =-3.
(2)∵
2
5
A.-
5π
+
2
1
B.5
=
1 2 3 4 5
1
,则 cos α=(
5
1
C.
5
)
2
5
D.
关闭
∵sin
∴cos
C
5π
π
+ =sin 2 +
2
1
α= ,故选 C.
5
=cos α,
关闭
解析
答案
-8知识梳理
4.已知 x∈
A.
1
双基自测
3
5
π
- 2 ,0
B.-
,tan
3
5
2 3 4 5
4
x=-3,则 sin(x+π)等于(
(2)
1
co s 2 -si n 2
=
si n 2 +co s 2
co s 2 -si n 2
4
∵tan α=-3,
1
பைடு நூலகம்
∴co s 2 -si n 2 =
ta n 2 +1

高考数学(人教a版,理科)题库：同角三角函数的基本关系与诱导公式(含答案)

第2讲同角三角函数的基本关系与诱导公式一、选择题1． cos ⎝⎛⎭⎪⎫－20π3＝( ) A.12 B.32 C ．－12 D ．－32解析 cos ⎝ ⎛⎭⎪⎫－20π3＝cos ⎝ ⎛⎭⎪⎫6π＋2π3＝cos 2π3＝cos ⎝⎛⎭⎪⎫π－π3＝－cos π3＝－12，故选C. 答案 C 2．已知tan θ＝2，则sin 2θ＋sin θcos θ－2cos 2θ＝( )．A ．－43B.54C ．－34D.45解析由于tan θ＝2，则sin 2θ＋sin θcos θ－2cos 2θ＝sin 2θ＋sin θcos θ－2cos 2θsin 2θ＋cos 2θ＝tan 2θ＋tan θ－2tan 2θ＋1＝22＋2－222＋1＝45.答案 D3．若sin α＋cos αsin α－cos α＝12，则tan 2α＝( )．A ．－34B.34C ．－43D.43解析由sin α＋cos αsin α－cos α＝12，得tan α＋1tan α－1＝12，所以tan α＝－3，所以tan 2α＝2tan α1－tan 2α＝34.答案 B4．已知f (cos x )＝cos 3x ，则f (sin 30°)的值为( )． A ．0 B ．1 C ．－1 D.32解析 ∵f (cos x )＝cos 3x ，∴f (sin 30°)＝f (cos 60°)＝cos 180°＝－1.答案 C5．若sin θ，cos θ是方程4x2＋2mx＋m＝0的两根，则m的值为( )．A．1＋ 5 B．1－ 5C．1± 5 D．－1－ 5解析由题意知：sin θ＋cos θ＝－m2，sin θcos θ＝m4，又(sin θ＋cos θ)2＝1＋2sin θcos θ，∴m24＝1＋m2，解得：m＝1±5，又Δ＝4m2－16m≥0，∴m≤0或m≥4，∴m＝1－ 5.答案 B6．若S n＝sin π7＋sin2π7＋…＋sinnπ7(n∈N*)，则在S1，S2，…，S100中，正数的个数是()．A．16 B．72 C．86 D．100解析由sin π7＝－sin8π7，sin2π7＝－sin9π7，…，sin6π7＝－sin13π7，sin7π7＝sin 14π7＝0，所以S13＝S14＝0.同理S27＝S28＝S41＝S42＝S55＝S56＝S69＝S70＝S83＝S84＝S97＝S98＝0，共14个，所以在S1，S2，…，S100中，其余各项均大于0，个数是100－14＝86(个)．故选C.答案 C二、填空题7．已知cosα＝－513，且α是第二象限的角，则tan(2π－α)＝________.解析由α是第二象限的角，得sinα＝1－cos2α＝1213，tanα＝sinαcosα＝－125，则tan(2π－α)＝－tanα＝125.答案12 58．已知α为第二象限角，则cos α1＋tan 2α＋sin α1＋1tan 2α＝________. 解析原式＝cos α1＋sin 2αcos 2α＋sin α1＋cos 2αsin 2α＝cos α1cos 2α＋sin α 1sin 2α＝cos α1－cos α＋sin α1sin α＝0. 答案 09．已知sin α＝12＋cos α，且α∈⎝ ⎛⎭⎪⎫0，π2，则cos 2αsin ⎝ ⎛⎭⎪⎫α－π4的值为________．解析依题意得sin α－cos α＝12，又(sin α＋cos α)2＋(sin α－cos α)2＝2，即(sin α＋cos α)2＋⎝ ⎛⎭⎪⎫122＝2，故(sin α＋cos α)2＝74；又α∈⎝ ⎛⎭⎪⎫0，π2，因此有sin α＋cos α＝72，所以cos 2αsin ⎝ ⎛⎭⎪⎫α－π4＝cos 2α－sin 2α22(sin α－cos α)＝－2(sin α＋cos α)＝－142. 答案－14210． f (x )＝a sin(πx ＋α)＋b cos(πx ＋β)＋4(a ，b ，α，β均为非零实数)，若f (2 012)＝6，则f (2 013)＝________.解析 f (2 012)＝a sin(2 012π＋α)＋b cos(2 012π＋β)＋4＝a sin α＋b cos β＋4＝6，∴a sin α＋b cos β＝2，∴f (2 013)＝a sin(2 013π＋α)＋b cos(2 013π＋β)＋4＝－a sin α－b cos β＋4＝2. 答案 2 三、解答题 11．已知1＋tan π＋α1＋tan 2π－α＝3＋22，求cos 2(π－α)＋sin ⎝ ⎛⎭⎪⎫3π2＋α²cos ⎝ ⎛⎭⎪⎫π2＋α＋2sin 2(α－π)的值．解析由已知得1＋tan α1－tan α＝3＋22，∴tan α＝2＋224＋22＝1＋22＋2＝22.∴cos 2(π－α)＋sin ⎝ ⎛⎭⎪⎫3π2＋αcos ⎝ ⎛⎭⎪⎫π2＋α＋2sin 2(α－π) ＝cos 2α＋(－cos α)(－sin α)＋2sin 2α ＝cos 2α＋sin αcos α＋2sin 2α ＝cos 2α＋sin αcos α＋2sin 2αsin 2α＋cos 2α＝1＋tan α＋2tan 2α1＋tan 2α ＝1＋22＋11＋12＝4＋23. 12．已知sin(3π＋α)＝2sin ⎝ ⎛⎭⎪⎫3π2＋α，求下列各式的值：(1)sin α－4cos α5sin α＋2cos α；(2)sin 2α＋sin 2α.解法一由sin(3π＋α)＝2sin ⎝ ⎛⎭⎪⎫3π2＋α，得tan α＝2.(1)原式＝tan α－45tan α＋2＝2－45³2＋2＝－16.(2)原式＝sin 2α＋2sin αcos α＝sin 2α＋2sin αcos αsin 2α＋cos 2α＝tan 2α＋2tan αtan 2α＋1＝85.法二由已知得sin α＝2cos α. (1)原式＝2cos α－4cos α5³2cos α＋2cos α＝－16.(2)原式＝sin 2α＋2sin αcos αsin 2α＋cos 2α＝sin 2α＋sin 2αsin 2α＋14sin 2α＝85. 13．是否存在α∈⎝ ⎛⎭⎪⎫－π2，π2，β∈(0，π)，使等式sin(3π－α)＝2cos ⎝ ⎛⎭⎪⎫π2－β，3cos(－α)＝－2cos(π＋β)同时成立？若存在，求出α，β的值；若不存在，请说明理由．解假设存在角α，β满足条件，则由已知条件可得⎩⎨⎧ sin α＝2sin β，3cos α＝2cos β.①②由①2＋②2，得sin 2α＋3cos 2α＝2.∴sin 2α＝12，∴sin α＝±22.∵α∈⎝ ⎛⎭⎪⎫－π2，π2，∴α＝±π4. 当α＝π4时，由②式知cos β＝32，又β∈(0，π)，∴β＝π6，此时①式成立；当α＝－π4时，由②式知cos β＝32，又β∈(0，π)，∴β＝π6，此时①式不成立，故舍去． ∴存在α＝π4，β＝π6满足条件． 14．已知函数f (x )＝tan ⎝ ⎛⎭⎪⎫2x ＋π4.(1)求f (x )的定义域与最小正周期；(2)设α∈⎝ ⎛⎭⎪⎫0，π4，若f ⎝ ⎛⎭⎪⎫α2＝2cos 2α，求α的大小．解 (1)由2x ＋π4≠π2＋k π，k ∈Z ，得x ≠π8＋k π2，k ∈Z .所以f (x )的定义域为⎩⎨⎧⎭⎬⎫x ∈R |x ≠π8＋k π2，k ∈Z ，f (x )的最小正周期为π2.(2)由f ⎝ ⎛⎭⎪⎫α2＝2cos 2α，得tan ⎝ ⎛⎭⎪⎫α＋π4＝2cos 2α，sin ⎝ ⎛⎭⎪⎫α＋π4cos ⎝ ⎛⎭⎪⎫α＋π4＝2(cos 2α－sin 2α)，整理得sin α＋cos αcos α－sin α＝2(cos α＋sin α)(cos α－sin α)．因为α∈⎝ ⎛⎭⎪⎫0，π4，所以sin α＋cos α≠0.因此(cos α－sin α)2＝12，即sin 2α＝12.由α∈⎝ ⎛⎭⎪⎫0，π4，得2α∈⎝ ⎛⎭⎪⎫0，π2.所以2α＝π6，即α＝π12.。

高三数学同角三角函数的基本关系式和诱导公式试题答案及解析

高三数学同角三角函数的基本关系式和诱导公式试题答案及解析1.已知，则.【答案】3【解析】===3.【考点】同角三角函数基本关系式2.若tan α＝3，则 sin2α－2 sin αcos α＋3 cos2α＝______.【答案】【解析】sin2α－2 sin αcos α＋3 cos2α＝＝＝＝.3.已知f(α)＝，则f的值为________．【答案】－【解析】∵f(α)＝＝－cos α，∴f＝－cos＝－cos＝－cos＝－.4.化简＋＝________.【解析】原式＝＋＝－sin α＋sin α＝0.5.已知α∈(，π)，tanα＝－，则sin(α＋π)＝()A．B．－C．D．－【答案】B【解析】由题意可知，由此解得sin2α＝，又α∈(，π)，因此有sinα＝，sin(α＋π)＝－sinα＝－，故选B．6.记cos(－80°)＝k，那么tan100°＝()A．B．－C．D．－【答案】B【解析】解法一：因为cos(－80°)＝cos80°＝k，sin80°＝＝，所以tan100°＝－tan80°＝－＝－．解法二：因为cos(－80°)＝k，所以cos80°＝k，所以tan100°＝－tan80°＝＝－．7.已知sinαcosα＝，且π<α<，则cosα－sinα的值为()A．－B．C．－D．【答案】B【解析】∵π<α<，∴cosα>sinα，∴cosα－sinα>0，又∵(cosα－sinα)2＝1－2cosαsinα＝，∴cosα－sinα＝．8.若3cos(－θ)＋cos(π＋θ)＝0，则cos2θ＋sin2θ的值是________．【答案】【解析】∵3cos(－θ)＋cos(π＋θ)＝0，即3sinθ－cosθ＝0，即tanθ＝．∴cos2θ＋sin2θ＝＝＝＝＝＝．9.（5分）（2011•福建）若α∈（0，），且sin2α+cos2α=，则tanα的值等于（）A．B．C．D．【答案】D【解析】把已知的等式中的cos2α，利用同角三角函数间的基本关系化简后，得到关于sinα的方程，根据α的度数，求出方程的解即可得到sinα的值，然后利用特殊角的三角函数值，由α的范围即可得到α的度数，利用α的度数求出tanα即可．解：由cos2α=1﹣2sin2α，得到sin2α+cos2α=1﹣sin2α=，则sin2α=，又α∈（0，），所以sinα=，则α=，所以tanα=tan=．故选D点评：此题考查学生灵活运用二倍角的余弦函数公式及同角三角函数间的基本关系化简求值，是一道基础题．学生做题时应注意角度的范围．10.已知sin α＝＋cos α，且α∈，则的值为________．【答案】－【解析】将sin α－cos α＝两边平方，得2sin α·cos α＝，(sin α＋cos α)2＝，sin α＋cos α＝，＝＝－(sin α＋cos α)＝－．11.在△ABC中,若sinA,cosA是关于x的方程3x2-2x+m=0的两个根,则△ABC是 ( )A．钝角三角形B．直角三角形C．锐角三角形D．不能确定【答案】A【解析】∵sinA,cosA是关于x的方程3x2-2x+m=0的两个根∴sinA+cosA=∴(sinA+cosA)2=1+2sinAcosA=即sinAcosA=-∵0o<A<180o,∴sinA>0,所以cosA<0,即90o<A<180o故知△ABC是钝角三角形12.已知，则（）A．B．C．D．【答案】A【解析】∵，∴，∴，∴，∴，∴，∴.【考点】三角函数求值.13.在中，角A，B，C的对边a，b，c成等差数列，且，则 .【答案】【解析】∵成等差数列，∴，∴，∵，∴，∴，∴，（1）∵且，∴代入（1）式中，，∴，∴，∴，∴.【考点】1.等差中项；2.倍角公式；3.诱导公式.14.已知，，则．【答案】【解析】由题意，，．【考点】同角间的三角函数关系．15.若则【答案】【解析】，得，∴.【考点】求三角函数值.16.α是第二象限角，tanα＝－，则sinα＝________．【答案】【解析】由解得sinα＝±.∵α为第二象限角，∴sinα>0，∴sinα＝.17. cos＝________．【答案】－【解析】cos＝cos＝cos(17π＋)＝－cos＝－.18.已知其中若．（1）求的值；（2）求的值．【答案】（1）；（2）．【解析】（1）先由已知条件求得的值，再由平方关系可得的值，把拆为，最后利用两角和的余弦公式即可求得的值；（2）考查了三角函数中知一求三的思想，即这几个量“知一求三”．可先利用差角余弦公式将展开，求得的值，两边平方即可求得的值，再由平方关系即可求得的值，最后由商关系即可求得的值．试题解析：（1）由已知得：，（2）由，得，两边平方得：，即，∵，且，从而． 12分【考点】1．平面向量的数量积运算；2．应用三角恒等变换求三角函数的值．19.已知x∈(0,),则函数f(x)=的最大值为()A．0B．C．D．1【答案】C【解析】由已知得,f(x)==tanx-tan2x=-(tanx-)2+,∵x∈(0,),∴tanx∈(0,1),=.故当tanx=时,f(x)max20.已知sinθ,cosθ是关于x的方程x2-ax+a=0(a∈R)的两个根.(1)求cos3(-θ)+sin3(-θ)的值.(2)求tan(π-θ)-的值.【答案】(1) -2 (2) 1+【解析】【思路点拨】先由方程根的判别式Δ≥0,求a的取值范围,而后应用根与系数的关系及诱导公式求解.解：由已知,原方程的判别式Δ≥0,即(-a)2-4a≥0,∴a≥4或a≤0.又(sinθ+cosθ)2=1+2sinθcosθ,则a2-2a-1=0,从而a=1-或a=1+(舍去),因此sinθ+cosθ=sinθcosθ=1-.(1)cos3(-θ)+sin3(-θ)=sin3θ+cos3θ=(sinθ+cosθ)(sin2θ-sinθ·cosθ+cos2θ)=(1-)[1-(1-)]=-2.(2)tan(π-θ)-=-tanθ-=-(+)=-=-=1+.21.若sinθcosθ>0,则θ在()A．第一、二象限B．第一、三象限C．第一、四象限D．第二、四象限【答案】B【解析】∵sinθcosθ>0,∴sinθ,cosθ同号.当sinθ>0,cosθ>0时,θ在第一象限,当sinθ<0,cosθ<0时,θ在第三象限,因此,选B.22.＝()A．－B．－C．D．【解析】＝＝＝＝sin 30°＝.23.设当x＝θ时，函数f(x)＝sin x－2cos x取得最大值，则cos θ＝________.【答案】－【解析】f(x)＝sin x－2cos x＝＝sin(x－φ)，其中sin φ＝，cos φ＝，当x－φ＝2kπ＋ (k∈Z)时，函数f(x)取得最大值，即θ＝2kπ＋＋φ时，函数f(x)取到最大值，所以cos θ＝－sin φ＝－.24. 4cos 50°－tan 40°＝________.【答案】【解析】4cos 50°－tan 40°＝＝＝＝＝＝.25.已知α∈，且cos α＝－，则tan α＝________.【答案】2【解析】利用同角三角函数的基本关系求解．由条件可得sin α＝－，所以tan α＝＝＝2.26.若α，β∈，cos ＝，sin ＝－，则cos (α＋β)＝________.【答案】【解析】∵α，β∈，∴－<α－<，－<－β<，由cos ＝和sin ＝－得α－＝±，－β＝－，当α－＝－，－β＝－时，α＋β＝0，与α，β∈矛盾；当α－＝，－β＝－时，α＝β＝，此时cos (α＋β)＝－.27.若cos ＝，则cos ＝()．A．－B．－C．D．【答案】D【解析】∵cos ＝，∴cos ＝2cos 2－1＝－，即sin 2x＝，∴cos ＝sin 2x＝.28.已知sin θ＋cos θ＝，则sin θ－cos θ的值为________．【答案】－【解析】∵sin θ＋cos θ＝，∴(sin θ＋cos θ)2＝1＋2cos θsin θ＝，∴2cos θsin θ＝，∴(sin θ－cos θ)2＝1－＝，又θ∈，∴sin θ＜cos θ，∴sin θ－cos θ＝－.29.已知，则=____________.【答案】【解析】，根据，可知：，故答案为.【考点】同角三角函数的基本关系式的运算30.已知，且，则．【答案】【解析】因为，所以。

高一三角函数公式及诱导公式习题(附答案)

2
2
D． { － 1，－ 3 ， 3 ， 1}
2
2
7．若 α是第三象限角，则 1 2 sin( π ) cos( π ) =_________．
8． sin21°+sin22°+sin23° +… +si2n89°=_________ ．三、解答题 9．求值： sin（－ 660°） cos420 °－tan330 °cot （－ 690°）．
B． sin（ A+B） =sinC
C． tan（ A+B） =tanC
D． sin A
B
C
=sin
2
2
6．函数 f（ x） =cosπx （ x∈ Z）的值域为（）
3
A． { －1，－ 1 ， 0， 1 ， 1}
2
2
B． { － 1，－ 1 ， 1 ，1}
22
C． { －1，－二、填空题
3 ， 0， 3 ，1}
tanα +tanβ tan( α +β )= 1－ tanα tanβ
tanα － tanβ tan( α－ β )= 1＋ tanα tanβ
4．二倍角公式
sin2α =2sinα cosα
2
2
2
2
cos2α =cosα－ sin α ＝ 2 cosα － 1＝ 1－ 2 sin α
2tan α
cos
3
2
= 2 cos
1 cos
cos 3
2
2 2 cos
cos
3
2 cos
=
2
2
2 (cos
cos )
2
2 cos

三角函数的基本关系及诱导公式

1 tan
2

1，
3
∴原式 cos2 (2 tan2 tan 1)
2 1 3
（三）例题分析：例5．已知 sin , cos是方程 4x2 4mx 2m 1 0
的两个根，3 2 ，求角．
2
sin cos m
解：∵ ，
4
4
（三）例题分析：
例2．化简: tan (cos sin ) sin tan
cot c s c
分析：切割化弦是解本题的出发点．
解：原式

sin

(cos cos
sin
)

sin cos
sin cos
1
sin
sin sin
（三）例题分析：
形的中心角的弧度数是
.
回顾:任意角的正弦,余弦,正切,余切,正割,余割是如何定义的?
（一）知识点：
1．同角三角函数的基本关系式：
（1）倒数关系： tan cot 1
（2）商数关系： tan sin , cot cos
cos
sin
（3）平方关系：sin2 cos2 1
2
2
3
（三）例题分析：
例4．若 tan 2 ，求值① cos sin ； cos sin
② 2sin2 sin cos cos2
解：①原式

1 1

sin
cos ． sin

1 1
2 3 2 2
2
cos
②∵ cos2

1
同角三角函数的基本关系与诱导公式

【高考调研】高考数学总复习 4-2 同角三角函数的基本关系式及诱导公式配套课件理新人教A版

(2)sinx＋cosx、sinx－cosx、sinxcosx 之间的关系为 (sinx＋cosx)2＝1＋2sinxcosx， (sinx－cosx)2＝1－2sinxcosx， (sinx＋cosx)2＋(sinx－cosx)2＝2. 因此已知上述三个代数式中的任意一个代数式的值，可求其余两个代数式的值．
第 2 课时同角三角函数的基本关系式及诱导公式
2013•考纲下载
1．借助单位圆，理解同角三角函数的基本关系式：sin2α ＋cos2α＝1，csionsαα＝tanα，掌握已知一个角的三角函数值求其他三角函数值的方法．
2．借助单位圆中的三角函数线导出诱导公式(π2±α，π±α 的正弦、余弦、正切)，经历并体验用诱导公式求三角函数值，感受诱导公式的变化规律．
思考题 4 已知 tanα＝2，求sinαc＋ os2cαosα2的值．
【解析】方法一原式可化为sin2α＋cocos2sα2α－＋si2ns2iαnαcosα 分子、分母同除以 cos2α tan2α1＋－2tatann2αα＋1＝－3.
方法二原式可化为 csoinsα2α＋－csoisnα2α2＝cosα－sisninαα＋ccoossαα＋2 sinα ＝scionsαα＋－csoinsαα＝t1a－nαt＋an1α＝－3. 【答案】－3
tanα －tanα
1．(课本习题改编)sin2 490°＝________；
cos(－335π)＝________.
答案
－12
1 2
2．若 tanα＝2，则2sisninαα＋－2ccoossαα的值为
A．0
3 B.4
C．1
5 D.4
答案 B 解析 2sisniαnα＋－2ccoossαα＝2ttaannαα＋－21＝42－＋12＝34.

2020高考数学课后作业 4-2 同角三角函数的基本关系及诱导公式

4-2 同角三角函数的基本关系及诱导公式1.(2020·青岛市质检)已知{a n }为等差数列，若a 1＋a 5＋a 9＝π，则cos(a 2＋a 8)的值为( )A ．－12B ．－32C.12D.32 [答案] A[解析] 由条件知，π＝a 1＋a 5＋a 9＝3a 5，∴a 5＝π3，∴cos(a 2＋a 8)＝cos2a 5＝cos 2π3＝－cos π3＝－12，故选A.2．(文)(2020·山东淄博一模)已知sin2α＝－2425，α∈(－π4，0)，则sin α＋cos α＝( )A ．－15B.15 C ．－75D.75[答案] B[解析] (sin α＋cos α)2＝1＋2sin αcos α＝1＋sin2α＝125，又α∈(－π4，0)，sin α＋cos α>0，所以sin α＋cos α＝15.(理)(2020·河北石家庄一模)已知α∈(0，π)，且sin α＋cos α＝22，则sin α－cos α的值为( )A ．－ 2B ．－62C. 2D.62[答案] D[解析] ∵sin α＋cos α＝22，0<22<1,0<α<π，∴π2<α<π，∴sin α－cos α>0. ∴(sin α＋cos α)2＝1＋2sin αcos α＝12，∴2sin αcos α＝－12；∴(sin α－cos α)2＝1－2sin αcos α＝32，∴sin α－cos α＝62. 3．(文)(2020·杭州二检)若a ＝(32，sin α)，b ＝(cos α，13)，且a ∥b ，则锐角α＝( )A ．15°B ．30°C ．45°D ．60° [答案] C[解析] 依题意得32×13－sin αcos α＝0，即sin2α＝1.又α为锐角，故2α＝90°，α＝45°，选C.(理)已知向量a ＝(tan α，1)，b ＝(3，－1)，α∈(π，2π)且a ∥b ，则点P ⎝ ⎛⎭⎪⎫cos ⎝ ⎛⎭⎪⎫π2＋α，sin π－α在( ) A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 [答案] D[解析] ∵a ∥b ，∴tan α＝－3， ∵α∈(π，2π)，∴α＝5π3，∴cos ⎝ ⎛⎭⎪⎫π2＋α＝cos 13π6＝cos π6>0， sin(π－α)＝sin ⎝ ⎛⎭⎪⎫－2π3＝－sin 2π3<0，∴点P 在第四象限．4．(2020·绵阳二诊、长春模拟)已知tan θ>1，且sin θ＋cos θ<0，则cos θ的取值范围是( )A ．(－22，0) B ．(－1，－22) C ．(0，22) D ．(22，1)[答案] A[解析] 如图，依题意结合三角函数线进行分析可知，2k π＋5π4<θ<2k π＋3π2，k ∈Z ，因此－22<cos θ<0.选A.5．(2020·河南南阳调研)在△ABC 中，3sin A ＋4cos B ＝6,4sin B ＋3cos A ＝1，则C 等于( )A ．30°B ．150°C ．30°或150°D ．60°或120°[答案] A[解析] 两式平方后相加得sin(A ＋B )＝12，∴A ＋B ＝30°或150°，又∵3sin A ＝6－4cos B >2，∴sin A >23>12，∴A >30°，∴A ＋B ＝150°，此时C ＝30°.6．(文)(2020·湖北联考)已知tan x ＝sin(x ＋π2)，则sin x ＝( )A.－1±52B.3＋12 C.5－12 D.3－12[答案] C[解析] ∵tan x ＝sin(x ＋π2)，∴tan x ＝cos x ，∴sin x ＝cos 2x ，∴sin 2x ＋sin x －1＝0，解得sin x ＝－1±52，∵－1≤sin x ≤1，∴sin x ＝5－12.故选C. (理)(2020·重庆诊断)已知2tan α·sin α＝3，－π2<α<0，则cos ⎝ ⎛⎭⎪⎫α－π6的值是( ) A ．0 B.32C ．1 D.12[答案] A[解析] ∵2tan αsin α＝3，∴2sin 2αcos α＝3，即21－cos 2αcos α＝3，∴2cos 2α＋3cos α－2＝0， ∵|cos α|≤1，∴cos α＝12，∵－π2<α<0，∴sin α＝－32，∴cos ⎝ ⎛⎭⎪⎫α－π6 ＝cos αcos π6＋sin αsin π6＝12×32－32×12＝0.7．(文)(2020·山东烟台模拟)若sin(π＋α)＝12，α∈(－π2，0)，则tan α＝________.[答案] －33[解析] 由已知得sin α＝－12，又α∈(－π2，0)，所以cos α＝1－sin 2α＝32，因此tan α＝sin αcos α＝－33.(理)(2020·盐城模拟)已知cos(5π12＋α)＝13，且－π<α<－π2，则cos (π12－α)＝________.[答案] － 223[解析] ∵－π<α<－π2，∴－7π12<5π12＋α<－π12，∵cos(5π12＋α)＝13，∴sin(5π12＋α)＝－223，∴cos(π12－α)＝cos[π2－(5π12＋α)]＝sin(5π12＋α)＝－223.8．设a ＝12cos16°－32sin16°，b ＝2tan14°1＋tan 214°，c ＝1－cos50°2，则a 、b 、c 的大小关系为________(从小到大排列)．[答案] a <c <b[解析] a ＝sin14°，b ＝2sin14°cos14°cos 214°＋sin 214°＝sin28°， c ＝sin25°，∵y ＝sin x 在(0°，90°)上单调递增，∴a <c <b .9．(2020·江西上饶四校联考)对任意的a ∈(－∞，0)，总存在x 0使得a cos x 0＋a ≥0成立，则sin(2x 0－π6)的值为________．[答案] －12[解析] 若对任意的a ∈(－∞，0)，总存在x 0使得a cos x 0＋a ≥0成立，则cos x 0＋1≤0，又cos x 0＋1≥0，所以cos x 0＋1＝0，所以cos x 0＝－1，则x 0＝2k π＋π(k ∈Z)，所以sin(2x 0－π6)＝sin(4k π＋2π－π6)＝sin(－π6)＝－sin π6＝－12.10．(文)已知sin α＝2sin β，tan α＝3tan β，求证：cos 2α＝38.[解析] 由题设知，sin 2α＝4sin 2β， ① tan 2α＝9tan 2β， ② ①②，得9cos 2α＝4cos 2β， ③ ①＋③，得sin 2α＋9cos 2α＝4，即1－cos 2α＋9cos 2α＝4，∴cos 2α＝38.(理)(2020·南充市)已知三点：A (4,0)，B (0,4)，C (3cos α，3sin α)． (1)若α∈(－π，0)，且|AC →|＝|BC →|，求角α的值； (2)若AC →·BC →＝0，求2sin 2α＋sin2α1＋tan α的值．[解析] (1)由题得AC →＝(3cos α－4,3sin α)，BC →＝(3cos α，3sin α－4) 由|AC →|＝|BC →|得，(3cos α－4)2＋9sin 2α＝9cos 2α＋(3sin α－4)2⇒sin α＝cos α∵α∈(－π，0)，∴α＝－3π4. (2)由AC →·BC →＝0得，3cos α(3cos α－4)＋3sin α(3sin α－4)＝0，解得sin α＋cos α＝34，两边平方得2sin αcos α＝－716∴2sin 2α＋sin2α1＋tan α＝2sin 2α＋2sin αcos α1＋sin αcos α＝2sin αcos α＝－716.11.若A 、B 是锐角△ABC 的两个内角，则点P (cos B －sin A ，sin B －cos A )在( ) A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 [答案] B[解析] ∵A 、B 是锐角三角形的两个内角，∴A ＋B >90°，∴B >90°－A ，∴cos B <sin A ，sin B >cos A ，故cos B －sin A <0，sin B －cos A >0，选B.12．(2020·安徽铜陵一中)在△ABC 中，内角A 、B 、C 的对边分别为a 、b 、c ，已知a 、b 、c 成等比数列，且a ＋c ＝3，tan B ＝73，则△ABC 的面积为( ) A.74 B.54 C.72 D.52[解析] ∵a 、b 、c 成等比数列，∴b 2＝ac ， ∵tan B ＝73，∴sin B ＝74，cos B ＝34， ∵a ＋c ＝3，b 2＝a 2＋c 2－2ac cos B ，∴ac ＝2， ∴S △ABC ＝12ac sin B ＝74.13．(文)(2020·哈师大附中、东北师大附中、辽宁实验中学联考)已知cos α＝45，α∈(－π4，0)，则sin α＋cos α等于( ) A.15 B ．－15 C ．－75D.75[答案] A[解析] 由于cos α＝45，α∈(－π4，0)，所以sin α＝－35，所以sin α＋cos α＝15，故选A.(理)已知函数f (x )＝sin x －cos x 且f ′(x )＝2f (x )，f ′(x )是f (x )的导函数，则1＋sin 2xcos 2x －sin2x＝( ) A ．－ 195 B.195C.113 D ．－ 113[答案] A[解析] f ′(x )＝cos x ＋sin x ，∵f ′(x )＝2f (x )，∴cos x ＋sin x ＝2(sin x －cos x )，∴tan x ＝3，∴1＋sin 2x cos 2x －sin2x ＝1＋sin 2xcos 2x －2sin x cos x ＝2sin 2x ＋cos 2x cos 2x －2sin x cos x ＝2tan 2x ＋11－2tan x ＝－195. 14．已知函数f (x )＝⎩⎪⎨⎪⎧2cos π3x x ≤2000x －102 x >2000，则f [f (2020)]＝________.[解析] 由f (x )＝⎩⎪⎨⎪⎧2cos π3x x ≤2000x －102 x >2000得，f (2020)＝2020－102＝1910，f (1910)＝2cos ⎝ ⎛⎭⎪⎫π3×1910＝2cos(636π＋2π3)＝2cos 2π3＝－1，故f [f (2020)]＝－1.15．已知sin(A ＋π4)＝7210，A ∈(π4，π2)，求cos A .[解析] 解法一：∵π4<A <π2，∴π2<A ＋π4<3π4，∵sin(A ＋π4)＝7210，∴cos(A ＋π4)＝－1－sin2A ＋π4＝－210. ∴cos A ＝cos[(A ＋π4)－π4]＝cos(A ＋π4)cos π4＋sin(A ＋π4)sin π4＝－210×22＋7210×22＝35.解法二：∵sin(A ＋π4)＝7210，∴sin A ＋cos A ＝75，∴sin A ＝75－cos A ，代入sin 2A ＋cos 2A ＝1中得 2cos 2A －145cos A ＋4925＝1，∵π4<A <π2，∴0<cos A <22，∴cos A ＝35.16.(2020·潍坊质检)如图，以Ox 为始边作角α与β(0<β<α<π)，它们终边分别与单位圆相交于点P ，Q ，已知点P 的坐标为⎝ ⎛⎭⎪⎫－35，45. (1)求sin2α＋cos2α＋11＋tan α的值；(2)若OP →·OQ →＝0，求sin(α＋β)．[解析] (1)由三角函数定义得cos α＝－35，sin α＝45，∴原式＝2sin αcos α＋2cos 2α1＋sin αcos α＝2cos αsin α＋cos αsin α＋cos αcos α＝2cos 2α＝2·⎝ ⎛⎭⎪⎫－352＝1825.(2)∵OP →·OQ →＝0，∴α－β＝π2，∴β＝α－π2，∴sin β＝sin(α－π2)＝－cos α＝35，cos β＝cos ⎝ ⎛⎭⎪⎫α－π2＝sin α＝45. ∴sin(α＋β)＝sin αcos β＋cos αsin β ＝45·45＋⎝ ⎛⎭⎪⎫－35·35＝725.1．设f (x )＝a sin(πx ＋α)＋b cos(πx ＋α)，其中a ，b ，α∈R ，且ab ≠0，α≠k π (k ∈Z)．若f (2020)＝5，则f (2020)等于( )A ．4B ．3C ．－5D ．5[答案] C[解析] ∵f (2020)＝a sin(2020π＋α)＋b cos(2020π＋α)＝－a sin α－b cos α＝5， ∴a sin α＋b cos α＝－5.∴f (2020)＝a sin α＋b cos α＝－5.2．(2020·全国卷Ⅰ理，2)设cos(－80°)＝k ，那么tan100°＝( ) A.1－k2k B ．－1－k2k C.k1－k2D ．－k1－k2[答案] B[解析] sin80°＝1－cos 280° ＝1－cos2－80°＝1－k 2，所以tan100°＝－tan80°＝－sin80°cos80°＝－1－k2k.3．(2020·山东济南模考、烟台市诊断)已知△ABC 中，tan A ＝－512，则cos A ＝( )A.1213 B.513C ．－513D ．－1213[答案] D[解析] 在△ABC 中，由tan A ＝－512<0知，∠A 为钝角，所以cos A <0,1＋tan 2A ＝sin 2A ＋cos 2A cos 2A ＝1cos 2A ＝169144，所以cos A ＝－1213，故选D. [点评] 学习数学要加强多思少算的训练，以提高思维能力，尤其是选择题，要注意结合其特点选取．本题中，tan A ＝－512，A 为三角形内角，即知A 为钝角，∴cos A <0，排除A 、B ；又由勾股数组5,12,13及tan A ＝sin A cos A 知，|cos A |＝1213，故选D.4．(2020·山东临沂一模)已知cos(π2－φ)＝32，且|φ|<π2，则tan φ＝( )A ．－33 B.33C ．－ 3 D. 3 [答案] D[解析] cos(π2－φ)＝sin φ＝32，又|φ|<π2，则cos φ＝12，所以tan φ＝ 3.5．(2020·福建省福州市)已知sin10°＝a ，则sin70°等于( ) A ．1－2a 2B ．1＋2a 2C ．1－a 2D ．a 2－1 [答案] A[解析] 由题意可知，sin70°＝cos20°＝1－2sin 210°＝1－2a 2，故选A. 6．下列关系式中正确的是( )A ．sin11°<cos10°<sin168°B ．sin168°<sin11°<cos10°C ．sin11°<sin168°<cos10°D ．sin168°<cos10°<sin11°[答案] C[解析] ∵sin11°＝cos79°，sin168°＝cos78°，又∵y ＝cos x 在[0°，90°]上单调递减，90°>79°>78°>10°，∴cos79°<cos78°<cos10°，∴sin11°<sin168°<cos10°，选C.7．化简sin k π－α·cos[k －1π－α]sin[k ＋1π＋α]·cos k π＋α＝______(k ∈Z)．[答案] －1[解析] 对参数k 分奇数、偶数讨论．当k ＝2n ＋1(n ∈Z)时，原式＝sin 2n π＋π－α·cos 2n π－αsin 2n π＋2π＋α·cos 2n π＋π＋α＝sin π－α·cos αsin α·cos π＋α＝sin α·cos αsin α·－cos α＝－1.当k ＝2n (n ∈Z)时，原式＝sin 2n π－α·cos 2n π－π－αsin 2n π＋π＋α·cos 2n π＋α＝－sin α·－cos α－sin α·cos α＝－1.所以sin k π－α·cos[k －1π－α]sin[k ＋1π＋α]·cos k π＋α＝－1.。

高考数学复习同角三角函数的基本关系与诱导公式

第2讲同角三角函数的基本关系与诱导公式最新考纲考向预测1.理解同角三角函数的基本关系式sin 2x ＋cos 2x ＝1，sin xcos x ＝tan x .2.借助单位圆的对称性，利用定义推导出诱导公式⎝ ⎛⎭⎪⎫α±π2，α±π的正弦、余弦、正切. 命题趋势考查利用同角三角函数的基本关系、诱导公式解决条件求值问题，常与三角恒等变换相结合起到化简三角函数关系的作用，强调利用三角公式进行恒等变形的技巧以及基本的运算能力.核心素养数学运算1．同角三角函数的基本关系 (1)平方关系：sin 2x ＋cos 2x ＝1．(2)商数关系：tan x ＝sin x cos x ⎝ ⎛⎭⎪⎫其中x ≠k π＋π2，k ∈Z .2．三角函数的诱导公式组数一二三四五六角 α＋2k π (k ∈Z ) π＋α －α π－α π2－α π2＋α 正弦 sin α －sin__α －sin__α sin__α cos__α cos__α 余弦 cos α －cos__α cos__α －cos__α sin__α －sin__α正切tan αtan__α－tan__α－tan__α常用结论1．诱导公式的记忆口诀“奇变偶不变，符号看象限”，其中的奇、偶是指π2的奇数倍和偶数倍，变与不变指函数名称的变化．2．同角三角函数的基本关系式的几种变形 (1)sin 2α＝1－cos 2α＝(1＋cos α)(1－cos α)；cos 2α＝1－sin 2α＝(1＋sin α)(1－sin α)； (sin α±cos α)2＝1±2sin αcos α. (2)sin α＝tan αcos α⎝ ⎛⎭⎪⎫α≠π2＋k π，k ∈Z .(3)sin 2α＝sin 2αsin 2α＋cos 2α＝tan 2αtan 2α＋1；cos 2α＝cos 2αsin 2α＋cos 2α＝1tan 2α＋1.常见误区1．同角三角函数的基本关系式及诱导公式要注意角的范围对三角函数符号的影响，尤其是利用平方关系求三角函数值，进行开方时要根据角的范围，判断符号后，正确取舍．2．注意求值与化简后的结果一般要尽可能有理化、整式化．1．判断正误(正确的打“√”，错误的打“×”) (1)对任意的角α，β，都有sin 2α＋cos 2β＝1.( ) (2)若α∈R ，则tan α＝sin αcos α恒成立．( )(3)sin(π＋α)＝－sin α成立的条件是α为锐角．( ) (4)若cos(n π－θ)＝13(n ∈Z )，则cos θ＝13.( ) 答案：(1)× (2)× (3)× (4)×2．(易错题)已知cos(π＋α)＝23，则tan α＝( ) A ．52 B ．255 C ．±52D ．±255解析：选C.因为cos(π＋α)＝23，所以cos α＝－23，则α为第二或第三象限角，所以sin α＝±1－cos 2α＝±53.所以tan α＝sin αcos α＝±53－23＝±52. 3．已知sin αcos α＝12，则tan α＋1tan α＝( ) A ．2 B ．12 C ．－2D ．－12解析：选A.tan α＋1tan α＝sin αcos α＋cos αsin α＝sin 2α＋cos 2αsin αcos α＝112＝2.4．sin 2 490°＝________；cos ⎝ ⎛⎭⎪⎫－52π3＝________．解析：sin 2 490°＝sin(7×360°－30°)＝－sin 30°＝－12.cos ⎝ ⎛⎭⎪⎫－52π3＝cos 52π3＝cos ⎝ ⎛⎭⎪⎫16π＋π＋π3＝cos ⎝ ⎛⎭⎪⎫π＋π3＝－cos π3＝－12. 答案：－12 －125．化简cos ⎝ ⎛⎭⎪⎫α－π2sin ⎝ ⎛⎭⎪⎫52π＋α·cos(2π－α)的结果为________．解析：原式＝sin αcos α·cos α＝sin α. 答案：sin α同角三角函数的基本关系式角度一 “知一求二”问题(2020·北京市适应性测试)已知α是第四象限角，且tan α＝－34，则sinα＝( )A ．－35 B.35 C.45 D ．－45 【解析】因为tan α＝sin αcos α＝－34，所以cos α＝－43sin α ①.sin 2α＋cos 2α＝1 ②，由①②得sin 2α＝925，又α是第四象限角，所以sin α<0，则sin α＝－35，故选A.【答案】 A利用同角三角函数的基本关系求解问题的关键是熟练掌握同角三角函数的基本关系的正用、逆用、变形．同角三角函数的基本关系本身是恒等式，也可以看作是方程，对于一些题，可利用已知条件，结合同角三角函数的基本关系列方程组，通过解方程组达到解决问题的目的．角度二 sin α，cos α的齐次式问题已知tan αtan α－1＝－1，求下列各式的值：(1)sin α－3cos αsin α＋cos α；(2)sin 2α＋sin αcos α＋2. 【解】由已知得tan α＝12. (1)sin α－3cos αsin α＋cos α＝tan α－3tan α＋1＝－53.(2)sin 2α＋sin αcos α＋2＝sin 2α＋sin αcos αsin 2α＋cos 2α＋2＝tan 2α＋tan αtan 2α＋1＋2＝⎝ ⎛⎭⎪⎫122＋12⎝ ⎛⎭⎪⎫122＋1＋2＝135.关于sin α与cos α的齐n 次分式或齐二次整式的化简求值的解题策略已知tan α，求关于sin α与cos α的齐n次分式或齐二次整式的值．角度三sin α±cos α，sin αcos α之间的关系已知α∈(－π，0)，sin α＋cos α＝1 5.(1)求sin α－cos α的值；(2)求sin 2α＋2sin2α1－tan α的值．【解】(1)由sin α＋cos α＝1 5，平方得sin2α＋2sin αcos α＋cos2α＝1 25，整理得2sin αcos α＝－24 25.所以(sin α－cos α)2＝1－2sin αcos α＝49 25.由α∈(－π，0)，知sin α<0，又sin α＋cos α>0，所以cos α>0，则sin α－cos α<0，故sin α－cos α＝－7 5.(2)sin 2α＋2sin2α1－tan α＝2sin α（cos α＋sin α）1－sin αcos α＝2sin αcos α（cos α＋sin α）cos α－sin α＝－2425×1575＝－24175.sin α±cos α与sin αcos α关系的应用技巧(1)通过平方，sin α＋cos α，sin α－cos α，sin αcos α之间可建立联系，若令sin α＋cos α＝t ，则sin αcos α＝t 2－12，sin α－cos α＝±2－t 2(注意根据α的范围选取正、负号)．(2)对于sin α＋cos α，sin α－cos α，sin αcos α这三个式子，可以知一求二．1．(2020·河南六市一模)已知cos ⎝ ⎛⎭⎪⎫π2＋α＝35，且α∈⎝ ⎛⎭⎪⎫π2，3π2，则tan α＝( )A ．43 B ．34 C ．－34D ．±34解析：选B.因为cos ⎝ ⎛⎭⎪⎫π2＋α＝35，所以sin α＝－35.又α∈⎝ ⎛⎭⎪⎫π2，3π2，所以cos α＝－1－sin 2α＝－45，所以tan α＝sin αcos α＝34.2．已知tan α＝－34，则sin α(sin α－cos α)＝( ) A.2125 B.2521 C.45D.54解析：选 A.sin α(sin α－cos α)＝sin 2α－sin αcos α＝sin 2α－sin αcos αsin 2α＋cos 2α＝tan 2α－tan αtan 2α＋1，将tan α＝－34代入得原式＝⎝ ⎛⎭⎪⎫－342－⎝ ⎛⎭⎪⎫－34⎝ ⎛⎭⎪⎫－342＋1＝2125.3．(一题多解)已知sin α－cos α＝2，α∈(0，π)，则tan α＝( ) A ．－1 B ．－22 C ．22D ．1解析：选A.方法一：由⎩⎨⎧sin α－cos α＝2，sin 2α＋cos 2α＝1，得2cos 2α＋22cos α＋1＝0，即(2cos α＋1)2＝0，所以cos α＝－22.又α∈(0，π)，所以α＝3π4，所以tan α＝tan 3π4＝－1.方法二：因为sin α－cos α＝2，所以2sin ⎝ ⎛⎭⎪⎫α－π4＝2，所以sin ⎝ ⎛⎭⎪⎫α－π4＝1.因为α∈(0，π)，所以α＝3π4，所以tan α＝－1.法三：由sin α－cos α＝2得1－sin 2α＝2，所以sin 2α＝－1. 设sin α＋cos α＝t ，所以1＋sin 2α＝t 2，所以t ＝0.由⎩⎨⎧sin α－cos α＝2，sin α＋cos α＝0得sin α＝22，cos α＝－22，所以tan α＝－1.诱导公式的应用(1)sin(－1 200°)cos 1 290°＝________．(2)已知角θ的顶点在坐标原点，始边与x 轴正半轴重合，终边在直线3x －y ＝0上，则sin ⎝ ⎛⎭⎪⎫3π2＋θ＋2cos （π－θ）sin ⎝ ⎛⎭⎪⎫π2－θ－sin （π－θ）等于________．【解析】 (1)原式＝－sin 1 200°cos 1 290° ＝－sin(3×360°＋120°)cos(3×360°＋210°) ＝－sin 120°cos 210°＝－sin(180°－60°)cos(180°＋30°) ＝sin 60°cos 30°＝32×32＝34.(2)由题意可知tan θ＝3，原式＝－cos θ－2cos θcos θ－sin θ＝－31－tan θ＝32.【答案】 (1)34 (2)32【引申探究】 (变问法)若本例(2)的条件不变，则cos ⎝ ⎛⎭⎪⎫π2＋θ－sin （－π－θ）cos ⎝ ⎛⎭⎪⎫11π2－θ＋sin ⎝ ⎛⎭⎪⎫9π2＋θ＝________．解析：由题意可知tan θ＝3，原式＝－sin θ＋sin （π＋θ）cos ⎝ ⎛⎭⎪⎫6π－π2－θ＋sin ⎝ ⎛⎭⎪⎫4π＋π2＋θ ＝－sin θ－sin θcos ⎝ ⎛⎭⎪⎫π2＋θ＋sin ⎝ ⎛⎭⎪⎫π2＋θ＝－2sin θ－sin θ＋cos θ＝2tan θtan θ－1＝2×33－1＝3.答案：3(1)诱导公式用法的一般思路①化负为正，化大为小，化到锐角为止；②角中含有加减π2的整数倍时，用公式去掉π2的整数倍． (2)常见的互余和互补的角①常见的互余的角：π3－α与π6＋α；π3＋α与π6－α；π4＋α与π4－α等； ②常见的互补的角：π3＋θ与2π3－θ；π4＋θ与3π4－θ等．1．已知sin ⎝ ⎛⎭⎪⎫α－π3＝13，则cos ⎝ ⎛⎭⎪⎫α＋π6的值是( )A ．－13 B.13 C.223 D ．－223解析：选A.因为sin ⎝ ⎛⎭⎪⎫α－π3＝13，所以cos ⎝ ⎛⎭⎪⎫α＋π6＝cos ⎣⎢⎡⎦⎥⎤π2＋⎝ ⎛⎭⎪⎫α－π3＝－sin ⎝ ⎛⎭⎪⎫α－π3＝－13.2．(多选)已知A ＝sin （k π＋α）sin α＋cos （k π＋α）cos α＋tan （k π＋α）tan α，则A 的值可以是( )A ．3B ．－3C ．1D ．－1解析：选AD.由已知可得，当k 为偶数时，A ＝sin （k π＋α）sin α＋cos （k π＋α）cos α＋tan （k π＋α）tan α＝sin αsin α＋cos αcos α＋tan αtan α＝3；当k 为奇数时，A ＝sin （k π＋α）sin α＋cos （k π＋α）cos α＋tan （k π＋α）tan α＝－sin αsin α＋－cos αcos α＋tan αtan α＝－1，所以A 的值可以是3或－1.故答案为AD.同角三角函数的基本关系式与诱导公式的综合应用(2020·湖北宜昌一中期末)已知α是第三象限角，且cos α＝－1010. (1)求tan α的值；(2)化简并求cos （π－α）2sin （－α）＋sin ⎝ ⎛⎭⎪⎫π2＋α的值．【解】 (1)因为α是第三象限角，cos α＝－1010，所以sin α＝－1－cos 2α＝－31010，所以tan α＝sin αcos α＝3.(2)原式＝－cos α－2sin α＋cos α＝cos α2sin α－cos α＝12tan α－1，由(1)知tan α＝3，所以原式＝12×3－1＝15.求解诱导公式与同角关系综合问题的基本思路和化简要求基本思路①分析结构特点，选择恰当公式； ②利用公式化成单角三角函数；③整理得最简形式化简要求①化简过程是恒等变换；②结果要求项数尽可能少，次数尽可能低，结构尽可能简单，能求值的要求出值1．已知sin ⎝ ⎛⎭⎪⎫5π2＋α＝35，所以tan α的值为( )A ．－43B ．－34C ．±43D ．±34解析：选C.sin ⎝ ⎛⎭⎪⎫5π2＋α＝sin ⎝ ⎛⎭⎪⎫π2＋α＝cos α＝35，所以sin α＝±45，tan α＝sin αcos α＝±43.2．已知tan(π－α)＝－23，且α∈⎝ ⎛⎭⎪⎫－π，－π2，则cos （－α）＋3sin （π＋α）cos （π－α）＋9sin α的值为( )A ．－15B ．－37 C.15 D.37解析：选 A.因为tan(π－α)＝－23，所以tan α＝23，所以cos （－α）＋3sin （π＋α）cos （π－α）＋9sin α＝cos α－3sin α－cos α＋9sin α＝1－3tan α－1＋9tan α＝1－2－1＋6＝－15，故选A.[A 级基础练]1．(多选)已知x ∈R ，则下列等式恒成立的是( ) A ．sin(－x )＝sin x B ．sin ⎝ ⎛⎭⎪⎫3π2－x ＝cos xC ．cos ⎝ ⎛⎭⎪⎫π2＋x ＝－sin xD ．cos(x －π)＝－cos x解析：选CD.sin(－x )＝－sin x ，故A 不成立；sin ⎝ ⎛⎭⎪⎫3π2－x ＝－cos x ，故B 不成立；cos ⎝ ⎛⎭⎪⎫π2＋x ＝－sin x ，故C 成立；cos(x －π)＝－cos x ，故D 成立．2．(多选)若sin α＝45，且α为锐角，则下列选项中正确的有( )A ．tan α＝43 B ．cos α＝35 C ．sin α＋cos α＝85D ．sin α－cos α＝－15解析：选AB.因为sin α＝45，且α为锐角，所以cos α＝1－sin 2α＝1－⎝ ⎛⎭⎪⎫452＝35，故B 正确，所以tan α＝sin αcos α＝4535＝43，故A 正确，所以sin α＋cos α＝45＋35＝75≠85，故C 错误，所以sin α－cos α＝45－35＝15≠－15，故D 错误．3．已知角α是第二象限角，且满足sin ⎝ ⎛⎭⎪⎫5π2＋α＋3cos(α－π)＝1，则tan(π＋α)＝( )A ． 3B ．－ 3C ．－33D ．－1解析：选B.由sin ⎝ ⎛⎭⎪⎫5π2＋α＋3cos(α－π)＝1，得cos α－3cos α＝1，所以cos α＝－12，因为角α是第二象限角，所以sin α＝32，所以tan(π＋α)＝tan α＝sin αcos α＝－ 3.4．已知f (α)＝sin （2π－α）cos ⎝ ⎛⎭⎪⎫π2＋αcos ⎝ ⎛⎭⎪⎫－π2＋αtan （π＋α），则f ⎝ ⎛⎭⎪⎫π3＝( ) A ．12 B ．22 C ．32D ．－12解析：选A.f (α)＝sin （2π－α）cos ⎝ ⎛⎭⎪⎫π2＋αcos ⎝ ⎛⎭⎪⎫－π2＋αtan （π＋α）＝－sin α·（－sin α）sin α·tan α＝sin 2αsin α·sin αcos α＝cos α，则f ⎝ ⎛⎭⎪⎫π3＝cos π3＝12.5．已知角α的顶点为坐标原点，始边与x 轴的非负半轴重合，终边上一点A (2sin α，3)(sin α≠0)，则cos α＝( )A ．12B ．－12C ．32D ．－32解析：选A.由三角函数定义得tan α＝32sin α，即sin αcos α＝32sin α，得3cos α＝2sin 2α＝2(1－cos 2α)，解得cos α＝12或cos α＝－2(舍去)．故选A.6．计算：sin 11π6＋cos 10π3的值为________．解析：原式＝sin ⎝ ⎛⎭⎪⎫2π－π6＋cos ⎝ ⎛⎭⎪⎫3π＋π3＝－sin π6－cos π3＝－12－12＝－1.答案：－17．已知sin ⎝ ⎛⎭⎪⎫－π2－αcos ⎝ ⎛⎭⎪⎫－7π2＋α＝1225，且0＜α＜π4，则sin α＝________，cos α＝________．解析：sin ⎝ ⎛⎭⎪⎫－π2－αcos ⎝ ⎛⎭⎪⎫－7π2＋α＝－cos α·(－sin α)＝sin αcos α＝1225.因为0＜α＜π4，所以0＜sin α＜cos α.又因为sin 2α＋cos 2α＝1，所以sin α＝35，cos α＝45.答案：35 45 8．化简1－2sin 40°cos 40°cos 40°－1－sin 250°＝________．解析：原式＝sin 240°＋cos 240°－2sin 40°cos 40°cos 40°－cos 50°＝|sin 40°－cos 40°|sin 50°－sin 40°＝|sin 40°－sin 50°|sin 50°－sin 40°＝sin 50°－sin 40°sin 50°－sin 40°＝1.答案：19．已知sin(3π＋α)＝2sin ⎝ ⎛⎭⎪⎫3π2＋α，求下列各式的值：(1)sin α－4cos α5sin α＋2cos α；(2)sin 2α＋sin 2α.解：由已知得sin α＝2cos α. (1)原式＝2cos α－4cos α5×2cos α＋2cos α＝－16.(2)原式＝sin 2α＋2sin αcos αsin 2α＋cos 2α＝sin 2α＋sin 2αsin 2α＋14sin 2α＝85.10．已知角θ的终边与单位圆x 2＋y 2＝1在第四象限交于点P ，且点P 的坐标为⎝ ⎛⎭⎪⎫12，y .(1)求tan θ的值；(2)求cos ⎝ ⎛⎭⎪⎫π2－θ＋cos （θ－2π）sin θ＋cos （π＋θ）的值．解：(1)由θ为第四象限角，终边与单位圆交于点P ⎝ ⎛⎭⎪⎫12，y ，得⎝ ⎛⎭⎪⎫122＋y 2＝1，y <0，解得y ＝－32，所以tan θ＝－3212＝－ 3.(2)因为tan θ＝－3，所以cos ⎝ ⎛⎭⎪⎫π2－θ＋cos （θ－2π）sin θ＋cos （π＋θ）＝sin θ＋cos θsin θ－cos θ＝tan θ＋1tan θ－1＝－3＋1－3－1＝2－ 3. [B 级综合练]11．(多选)已知角θ的终边与坐标轴不重合，式子1－sin 2（π＋θ）化简的结果为－cos θ，则( )A ．sin θ>0，tan θ>0B ．sin θ<0，tan θ>0C ．sin θ<0，tan θ<0D ．sin θ>0，tan θ<0解析：选BD.1－sin 2（π＋θ）＝1－sin 2θ＝cos 2θ＝|cos θ|＝－cos θ，所以cos θ<0，角θ的终边落在第二或三象限，所以sin θ>0，tan θ<0或sin θ<0，tan θ>0，故选BD.12．(2020·陕西汉中月考)已知角α为第二象限角，则cos α·1＋sin α1－sin α＋sin 2α1＋1tan 2α＝( )A ．1B ．－1C ．0D ．2解析：选B.因为角α为第二象限角，所以sin α>0，cos α<0，所以cos α 1＋sin α1－sin α＝cos α（1＋sin α）2cos 2α＝cos α·1＋sin α|cos α|＝－1－sin α，sin 2α1＋1tan 2α＝sin 2α1＋cos 2αsin 2α＝sin 2αsin 2α＋cos 2αsin 2α＝sin 2α1sin 2α＝sin 2α⎪⎪⎪⎪⎪⎪1sin α＝sin α，所以cos α1＋sin α1－sin α＋sin 2α1＋1tan 2α＝－1－sin α＋sin α＝－1.故选B.13．是否存在α∈⎝ ⎛⎭⎪⎫－π2，π2，β∈()0，π使等式sin(3π－α)＝2cos ⎝ ⎛⎭⎪⎫π2－β，3cos(－α)＝－2cos(π＋β)同时成立？若存在，求出α，β的值；若不存在，请说明理由．解：假设存在角α，β满足条件．由已知条件可得⎩⎨⎧sin α＝2sin β，①3cos α＝2cos β，②由①2＋②2，得sin 2α＋3cos 2α＝2.所以sin 2α＝12，所以sin α＝±22.因为α∈⎝ ⎛⎭⎪⎫－π2，π2，所以α＝±π4. 当α＝π4时，由②式知cos β＝32，又β∈(0，π)，所以β＝π6，此时①式成立；当α＝－π4时，由②式知cos β＝32，又β∈(0，π)，所以β＝π6，此时①式不成立，故舍去．所以存在α＝π4，β＝π6满足条件． 14．在△ABC 中，(1)求证：cos 2A ＋B 2＋cos 2 C2＝1；(2)若cos ⎝ ⎛⎭⎪⎫π2＋A sin ⎝ ⎛⎭⎪⎫3π2＋B tan(C －π)＜0，求证：△ABC 为钝角三角形．证明：(1)在△ABC 中，A ＋B ＝π－C ，所以A ＋B 2＝π2－C2，所以cos A ＋B 2＝cos ⎝ ⎛⎭⎪⎫π2－C 2＝sin C 2，所以cos 2A ＋ B 2＋cos 2C2＝1.(2)若cos ⎝ ⎛⎭⎪⎫π2＋A sin ⎝ ⎛⎭⎪⎫3π2＋B tan(C －π)＜0，所以(－sin A )(－cos B )tan C ＜0，即sin A cos B tan C ＜0.因为在△ABC 中，0＜A ＜π，0＜B ＜π，0＜C ＜π且sin A ＞0，所以⎩⎨⎧cos B ＜0，tan C ＞0或⎩⎨⎧cos B ＞0，tan C ＜0，所以B 为钝角或C 为钝角，所以△ABC 为钝角三角形．[C 级创新练]15．(2020·山东肥城统考)公元前6世纪，古希腊的毕达哥拉斯学派研究过正五边形和正十边形的作图，发现黄金分割比例为5－12≈0.618，这一数值也可以表示为m ＝2sin 18°.若m 2＋n ＝4，则m n2cos 227°－1＝( )A ．4B ．3C ．2D ．1解析：选C.因为m ＝2sin 18°，且m 2＋n ＝4，所以n ＝4－m 2＝4－4sin 218°＝4(1－sin 218°)＝4cos 218°，所以m n2cos 227°－1＝2sin 18°4cos 218°cos 54°＝4sin 18°cos 18°sin 36°＝2.故选C.16．已知α，β∈(0，2π)且α<β，若关于x 的方程(x ＋sin α)(x ＋sin β)＋1＝0有实数根，则代数式3sin ⎝ ⎛⎭⎪⎫π2＋α＋cos ⎝ ⎛⎭⎪⎫3π2－β2－sin （π－α）cos ⎝ ⎛⎭⎪⎫3π2＋β＝________．解析：整理方程(x ＋sin α)(x ＋sin β)＋1＝0得x 2＋x (sin α＋sin β)＋sin αsin β＋1＝0.由题意得Δ＝(sin α＋sin β)2－4sin αsin β－4≥0，即(sin α－sin β)2≥4①.因为－1≤sin α≤1，－1≤sin β≤1，所以sin α－sin β∈[－2，2]，从而(sin α－sin β)2≤4②.由①②得sin α－sin β＝±2，所以⎩⎨⎧sin α＝1，sin β＝－1或⎩⎨⎧sin α＝－1，sin β＝1.因为α，β∈(0，2π)且α<β，所以α＝π2，β＝3π2，即⎩⎨⎧sin α＝1，sin β＝－1.因此3sin ⎝ ⎛⎭⎪⎫π2＋α＋cos ⎝ ⎛⎭⎪⎫3π2－β2－sin （π－α）cos ⎝ ⎛⎭⎪⎫3π2＋β＝3cos α－sin β2－sin αsin β＝12＋1＝13.答案：13第2讲同角三角函数的基本关系与诱导公式最新考纲考向预测1.理解同角三角函数的基本关系式sin 2x ＋cos 2x ＝1，sin xcos x ＝tan x .2.借助单位圆的对称性，利用定义推导出诱导公式⎝ ⎛⎭⎪⎫α±π2，α±π的正弦、余弦、正切. 命题趋势考查利用同角三角函数的基本关系、诱导公式解决条件求值问题，常与三角恒等变换相结合起到化简三角函数关系的作用，强调利用三角公式进行恒等变形的技巧以及基本的运算能力.核心素养数学运算1．同角三角函数的基本关系 (1)平方关系：sin 2x ＋cos 2x ＝1．(2)商数关系：tan x ＝sin x cos x ⎝ ⎛⎭⎪⎫其中x ≠k π＋π2，k ∈Z .2．三角函数的诱导公式组数一二三四五六角 α＋2k π (k ∈Z ) π＋α －α π－α π2－α π2＋α 正弦 sin α －sin__α －sin__α sin__α cos__α cos__α 余弦 cos α －cos__α cos__α －cos__α sin__α －sin__α正切tan αtan__α－tan__α－tan__α常用结论1．诱导公式的记忆口诀“奇变偶不变，符号看象限”，其中的奇、偶是指π2的奇数倍和偶数倍，变与不变指函数名称的变化．2．同角三角函数的基本关系式的几种变形 (1)sin 2α＝1－cos 2α＝(1＋cos α)(1－cos α)；cos 2α＝1－sin 2α＝(1＋sin α)(1－sin α)； (sin α±cos α)2＝1±2sin αcos α. (2)sin α＝tan αcos α⎝ ⎛⎭⎪⎫α≠π2＋k π，k ∈Z .(3)sin 2α＝sin 2αsin 2α＋cos 2α＝tan 2αtan 2α＋1；cos 2α＝cos 2αsin 2α＋cos 2α＝1tan 2α＋1.常见误区1．同角三角函数的基本关系式及诱导公式要注意角的范围对三角函数符号的影响，尤其是利用平方关系求三角函数值，进行开方时要根据角的范围，判断符号后，正确取舍．2．注意求值与化简后的结果一般要尽可能有理化、整式化．1．判断正误(正确的打“√”，错误的打“×”) (1)对任意的角α，β，都有sin 2α＋cos 2β＝1.( ) (2)若α∈R ，则tan α＝sin αcos α恒成立．( )(3)sin(π＋α)＝－sin α成立的条件是α为锐角．( ) (4)若cos(n π－θ)＝13(n ∈Z )，则cos θ＝13.( ) 答案：(1)× (2)× (3)× (4)×2．(易错题)已知cos(π＋α)＝23，则tan α＝( ) A ．52 B ．255 C ．±52D ．±255解析：选C.因为cos(π＋α)＝23，所以cos α＝－23，则α为第二或第三象限角，所以sin α＝±1－cos 2α＝±53.所以tan α＝sin αcos α＝±53－23＝±52. 3．已知sin αcos α＝12，则tan α＋1tan α＝( ) A ．2 B ．12 C ．－2D ．－12解析：选A.tan α＋1tan α＝sin αcos α＋cos αsin α＝sin 2α＋cos 2αsin αcos α＝112＝2.4．sin 2 490°＝________；cos ⎝ ⎛⎭⎪⎫－52π3＝________．解析：sin 2 490°＝sin(7×360°－30°)＝－sin 30°＝－12.cos ⎝ ⎛⎭⎪⎫－52π3＝cos 52π3＝cos ⎝ ⎛⎭⎪⎫16π＋π＋π3＝cos ⎝ ⎛⎭⎪⎫π＋π3＝－cos π3＝－12. 答案：－12 －125．化简cos ⎝ ⎛⎭⎪⎫α－π2sin ⎝ ⎛⎭⎪⎫52π＋α·cos(2π－α)的结果为________．解析：原式＝sin αcos α·cos α＝sin α. 答案：sin α同角三角函数的基本关系式角度一 “知一求二”问题(2020·北京市适应性测试)已知α是第四象限角，且tan α＝－34，则sinα＝( )A ．－35 B.35 C.45 D ．－45 【解析】因为tan α＝sin αcos α＝－34，所以cos α＝－43sin α ①.sin 2α＋cos 2α＝1 ②，由①②得sin 2α＝925，又α是第四象限角，所以sin α<0，则sin α＝－35，故选A.【答案】 A利用同角三角函数的基本关系求解问题的关键是熟练掌握同角三角函数的基本关系的正用、逆用、变形．同角三角函数的基本关系本身是恒等式，也可以看作是方程，对于一些题，可利用已知条件，结合同角三角函数的基本关系列方程组，通过解方程组达到解决问题的目的．角度二 sin α，cos α的齐次式问题已知tan αtan α－1＝－1，求下列各式的值：(1)sin α－3cos αsin α＋cos α；(2)sin 2α＋sin αcos α＋2. 【解】由已知得tan α＝12. (1)sin α－3cos αsin α＋cos α＝tan α－3tan α＋1＝－53.(2)sin 2α＋sin αcos α＋2＝sin 2α＋sin αcos αsin 2α＋cos 2α＋2＝tan 2α＋tan αtan 2α＋1＋2＝⎝ ⎛⎭⎪⎫122＋12⎝ ⎛⎭⎪⎫122＋1＋2＝135.关于sin α与cos α的齐n 次分式或齐二次整式的化简求值的解题策略已知tan α，求关于sin α与cos α的齐n次分式或齐二次整式的值．角度三sin α±cos α，sin αcos α之间的关系已知α∈(－π，0)，sin α＋cos α＝1 5.(1)求sin α－cos α的值；(2)求sin 2α＋2sin2α1－tan α的值．【解】(1)由sin α＋cos α＝1 5，平方得sin2α＋2sin αcos α＋cos2α＝1 25，整理得2sin αcos α＝－24 25.所以(sin α－cos α)2＝1－2sin αcos α＝49 25.由α∈(－π，0)，知sin α<0，又sin α＋cos α>0，所以cos α>0，则sin α－cos α<0，故sin α－cos α＝－7 5.(2)sin 2α＋2sin2α1－tan α＝2sin α（cos α＋sin α）1－sin αcos α＝2sin αcos α（cos α＋sin α）cos α－sin α＝－2425×1575＝－24175.sin α±cos α与sin αcos α关系的应用技巧(1)通过平方，sin α＋cos α，sin α－cos α，sin αcos α之间可建立联系，若令sin α＋cos α＝t ，则sin αcos α＝t 2－12，sin α－cos α＝±2－t 2(注意根据α的范围选取正、负号)．(2)对于sin α＋cos α，sin α－cos α，sin αcos α这三个式子，可以知一求二．1．(2020·河南六市一模)已知cos ⎝ ⎛⎭⎪⎫π2＋α＝35，且α∈⎝ ⎛⎭⎪⎫π2，3π2，则tan α＝( )A ．43 B ．34 C ．－34D ．±34解析：选B.因为cos ⎝ ⎛⎭⎪⎫π2＋α＝35，所以sin α＝－35.又α∈⎝ ⎛⎭⎪⎫π2，3π2，所以cos α＝－1－sin 2α＝－45，所以tan α＝sin αcos α＝34.2．已知tan α＝－34，则sin α(sin α－cos α)＝( ) A.2125 B.2521 C.45D.54解析：选 A.sin α(sin α－cos α)＝sin 2α－sin αcos α＝sin 2α－sin αcos αsin 2α＋cos 2α＝tan 2α－tan αtan 2α＋1，将tan α＝－34代入得原式＝⎝ ⎛⎭⎪⎫－342－⎝ ⎛⎭⎪⎫－34⎝ ⎛⎭⎪⎫－342＋1＝2125.3．(一题多解)已知sin α－cos α＝2，α∈(0，π)，则tan α＝( ) A ．－1 B ．－22 C ．22D ．1解析：选A.方法一：由⎩⎨⎧sin α－cos α＝2，sin 2α＋cos 2α＝1，得2cos 2α＋22cos α＋1＝0，即(2cos α＋1)2＝0，所以cos α＝－22.又α∈(0，π)，所以α＝3π4，所以tan α＝tan 3π4＝－1.方法二：因为sin α－cos α＝2，所以2sin ⎝ ⎛⎭⎪⎫α－π4＝2，所以sin ⎝ ⎛⎭⎪⎫α－π4＝1.因为α∈(0，π)，所以α＝3π4，所以tan α＝－1.法三：由sin α－cos α＝2得1－sin 2α＝2，所以sin 2α＝－1. 设sin α＋cos α＝t ，所以1＋sin 2α＝t 2，所以t ＝0.由⎩⎨⎧sin α－cos α＝2，sin α＋cos α＝0得sin α＝22，cos α＝－22，所以tan α＝－1.诱导公式的应用(1)sin(－1 200°)cos 1 290°＝________．(2)已知角θ的顶点在坐标原点，始边与x 轴正半轴重合，终边在直线3x －y ＝0上，则sin ⎝ ⎛⎭⎪⎫3π2＋θ＋2cos （π－θ）sin ⎝ ⎛⎭⎪⎫π2－θ－sin （π－θ）等于________．【解析】 (1)原式＝－sin 1 200°cos 1 290° ＝－sin(3×360°＋120°)cos(3×360°＋210°) ＝－sin 120°cos 210°＝－sin(180°－60°)cos(180°＋30°) ＝sin 60°cos 30°＝32×32＝34.(2)由题意可知tan θ＝3，原式＝－cos θ－2cos θcos θ－sin θ＝－31－tan θ＝32.【答案】 (1)34 (2)32【引申探究】 (变问法)若本例(2)的条件不变，则cos ⎝ ⎛⎭⎪⎫π2＋θ－sin （－π－θ）cos ⎝ ⎛⎭⎪⎫11π2－θ＋sin ⎝ ⎛⎭⎪⎫9π2＋θ＝________．解析：由题意可知tan θ＝3，原式＝－sin θ＋sin （π＋θ）cos ⎝ ⎛⎭⎪⎫6π－π2－θ＋sin ⎝ ⎛⎭⎪⎫4π＋π2＋θ ＝－sin θ－sin θcos ⎝ ⎛⎭⎪⎫π2＋θ＋sin ⎝ ⎛⎭⎪⎫π2＋θ＝－2sin θ－sin θ＋cos θ＝2tan θtan θ－1＝2×33－1＝3.答案：3(1)诱导公式用法的一般思路①化负为正，化大为小，化到锐角为止；②角中含有加减π2的整数倍时，用公式去掉π2的整数倍． (2)常见的互余和互补的角①常见的互余的角：π3－α与π6＋α；π3＋α与π6－α；π4＋α与π4－α等； ②常见的互补的角：π3＋θ与2π3－θ；π4＋θ与3π4－θ等．1．已知sin ⎝ ⎛⎭⎪⎫α－π3＝13，则cos ⎝ ⎛⎭⎪⎫α＋π6的值是( )A ．－13 B.13 C.223 D ．－223解析：选A.因为sin ⎝ ⎛⎭⎪⎫α－π3＝13，所以cos ⎝ ⎛⎭⎪⎫α＋π6＝cos ⎣⎢⎡⎦⎥⎤π2＋⎝ ⎛⎭⎪⎫α－π3＝－sin ⎝ ⎛⎭⎪⎫α－π3＝－13.2．(多选)已知A ＝sin （k π＋α）sin α＋cos （k π＋α）cos α＋tan （k π＋α）tan α，则A 的值可以是( )A ．3B ．－3C ．1D ．－1解析：选AD.由已知可得，当k 为偶数时，A ＝sin （k π＋α）sin α＋cos （k π＋α）cos α＋tan （k π＋α）tan α＝sin αsin α＋cos αcos α＋tan αtan α＝3；当k 为奇数时，A ＝sin （k π＋α）sin α＋cos （k π＋α）cos α＋tan （k π＋α）tan α＝－sin αsin α＋－cos αcos α＋tan αtan α＝－1，所以A 的值可以是3或－1.故答案为AD.同角三角函数的基本关系式与诱导公式的综合应用(2020·湖北宜昌一中期末)已知α是第三象限角，且cos α＝－1010. (1)求tan α的值；(2)化简并求cos （π－α）2sin （－α）＋sin ⎝ ⎛⎭⎪⎫π2＋α的值．【解】 (1)因为α是第三象限角，cos α＝－1010，所以sin α＝－1－cos 2α＝－31010，所以tan α＝sin αcos α＝3.(2)原式＝－cos α－2sin α＋cos α＝cos α2sin α－cos α＝12tan α－1，由(1)知tan α＝3，所以原式＝12×3－1＝15.求解诱导公式与同角关系综合问题的基本思路和化简要求基本思路①分析结构特点，选择恰当公式； ②利用公式化成单角三角函数；③整理得最简形式化简要求①化简过程是恒等变换；②结果要求项数尽可能少，次数尽可能低，结构尽可能简单，能求值的要求出值1．已知sin ⎝ ⎛⎭⎪⎫5π2＋α＝35，所以tan α的值为( )A ．－43B ．－34C ．±43D ．±34解析：选C.sin ⎝ ⎛⎭⎪⎫5π2＋α＝sin ⎝ ⎛⎭⎪⎫π2＋α＝cos α＝35，所以sin α＝±45，tan α＝sin αcos α＝±43.2．已知tan(π－α)＝－23，且α∈⎝ ⎛⎭⎪⎫－π，－π2，则cos （－α）＋3sin （π＋α）cos （π－α）＋9sin α的值为( )A ．－15B ．－37 C.15 D.37解析：选 A.因为tan(π－α)＝－23，所以tan α＝23，所以cos （－α）＋3sin （π＋α）cos （π－α）＋9sin α＝cos α－3sin α－cos α＋9sin α＝1－3tan α－1＋9tan α＝1－2－1＋6＝－15，故选A.[A 级基础练]1．(多选)已知x ∈R ，则下列等式恒成立的是( ) A ．sin(－x )＝sin x B ．sin ⎝ ⎛⎭⎪⎫3π2－x ＝cos xC ．cos ⎝ ⎛⎭⎪⎫π2＋x ＝－sin xD ．cos(x －π)＝－cos x解析：选CD.sin(－x )＝－sin x ，故A 不成立；sin ⎝ ⎛⎭⎪⎫3π2－x ＝－cos x ，故B 不成立；cos ⎝ ⎛⎭⎪⎫π2＋x ＝－sin x ，故C 成立；cos(x －π)＝－cos x ，故D 成立．2．(多选)若sin α＝45，且α为锐角，则下列选项中正确的有( )A ．tan α＝43 B ．cos α＝35 C ．sin α＋cos α＝85D ．sin α－cos α＝－15解析：选AB.因为sin α＝45，且α为锐角，所以cos α＝1－sin 2α＝1－⎝ ⎛⎭⎪⎫452＝35，故B 正确，所以tan α＝sin αcos α＝4535＝43，故A 正确，所以sin α＋cos α＝45＋35＝75≠85，故C 错误，所以sin α－cos α＝45－35＝15≠－15，故D 错误．3．已知角α是第二象限角，且满足sin ⎝ ⎛⎭⎪⎫5π2＋α＋3cos(α－π)＝1，则tan(π＋α)＝( )A ． 3B ．－ 3C ．－33D ．－1解析：选B.由sin ⎝ ⎛⎭⎪⎫5π2＋α＋3cos(α－π)＝1，得cos α－3cos α＝1，所以cos α＝－12，因为角α是第二象限角，所以sin α＝32，所以tan(π＋α)＝tan α＝sin αcos α＝－ 3.4．已知f (α)＝sin （2π－α）cos ⎝ ⎛⎭⎪⎫π2＋αcos ⎝ ⎛⎭⎪⎫－π2＋αtan （π＋α），则f ⎝ ⎛⎭⎪⎫π3＝( ) A ．12 B ．22 C ．32D ．－12解析：选A.f (α)＝sin （2π－α）cos ⎝ ⎛⎭⎪⎫π2＋αcos ⎝ ⎛⎭⎪⎫－π2＋αtan （π＋α）＝－sin α·（－sin α）sin α·tan α＝sin 2αsin α·sin αcos α＝cos α，则f ⎝ ⎛⎭⎪⎫π3＝cos π3＝12.5．已知角α的顶点为坐标原点，始边与x 轴的非负半轴重合，终边上一点A (2sin α，3)(sin α≠0)，则cos α＝( )A ．12B ．－12C ．32D ．－32解析：选A.由三角函数定义得tan α＝32sin α，即sin αcos α＝32sin α，得3cos α＝2sin 2α＝2(1－cos 2α)，解得cos α＝12或cos α＝－2(舍去)．故选A.6．计算：sin 11π6＋cos 10π3的值为________．解析：原式＝sin ⎝ ⎛⎭⎪⎫2π－π6＋cos ⎝ ⎛⎭⎪⎫3π＋π3＝－sin π6－cos π3＝－12－12＝－1.答案：－17．已知sin ⎝ ⎛⎭⎪⎫－π2－αcos ⎝ ⎛⎭⎪⎫－7π2＋α＝1225，且0＜α＜π4，则sin α＝________，cos α＝________．解析：sin ⎝ ⎛⎭⎪⎫－π2－αcos ⎝ ⎛⎭⎪⎫－7π2＋α＝－cos α·(－sin α)＝sin αcos α＝1225.因为0＜α＜π4，所以0＜sin α＜cos α.又因为sin 2α＋cos 2α＝1，所以sin α＝35，cos α＝45.答案：35 45 8．化简1－2sin 40°cos 40°cos 40°－1－sin 250°＝________．解析：原式＝sin 240°＋cos 240°－2sin 40°cos 40°cos 40°－cos 50°＝|sin 40°－cos 40°|sin 50°－sin 40°＝|sin 40°－sin 50°|sin 50°－sin 40°＝sin 50°－sin 40°sin 50°－sin 40°＝1.答案：19．已知sin(3π＋α)＝2sin ⎝ ⎛⎭⎪⎫3π2＋α，求下列各式的值：(1)sin α－4cos α5sin α＋2cos α；(2)sin 2α＋sin 2α.解：由已知得sin α＝2cos α. (1)原式＝2cos α－4cos α5×2cos α＋2cos α＝－16.(2)原式＝sin 2α＋2sin αcos αsin 2α＋cos 2α＝sin 2α＋sin 2αsin 2α＋14sin 2α＝85.10．已知角θ的终边与单位圆x 2＋y 2＝1在第四象限交于点P ，且点P 的坐标为⎝ ⎛⎭⎪⎫12，y .(1)求tan θ的值；(2)求cos ⎝ ⎛⎭⎪⎫π2－θ＋cos （θ－2π）sin θ＋cos （π＋θ）的值．解：(1)由θ为第四象限角，终边与单位圆交于点P ⎝ ⎛⎭⎪⎫12，y ，得⎝ ⎛⎭⎪⎫122＋y 2＝1，y <0，解得y ＝－32，所以tan θ＝－3212＝－ 3.(2)因为tan θ＝－3，所以cos ⎝ ⎛⎭⎪⎫π2－θ＋cos （θ－2π）sin θ＋cos （π＋θ）＝sin θ＋cos θsin θ－cos θ＝tan θ＋1tan θ－1＝－3＋1－3－1＝2－ 3. [B 级综合练]11．(多选)已知角θ的终边与坐标轴不重合，式子1－sin 2（π＋θ）化简的结果为－cos θ，则( )A ．sin θ>0，tan θ>0B ．sin θ<0，tan θ>0C ．sin θ<0，tan θ<0D ．sin θ>0，tan θ<0解析：选BD.1－sin 2（π＋θ）＝1－sin 2θ＝cos 2θ＝|cos θ|＝－cos θ，所以cos θ<0，角θ的终边落在第二或三象限，所以sin θ>0，tan θ<0或sin θ<0，tan θ>0，故选BD.12．(2020·陕西汉中月考)已知角α为第二象限角，则cos α·1＋sin α1－sin α＋sin 2α1＋1tan 2α＝( )A ．1B ．－1C ．0D ．2解析：选B.因为角α为第二象限角，所以sin α>0，cos α<0，所以cos α 1＋sin α1－sin α＝cos α（1＋sin α）2cos 2α＝cos α·1＋sin α|cos α|＝－1－sin α，sin 2α1＋1tan 2α＝sin 2α1＋cos 2αsin 2α＝sin 2αsin 2α＋cos 2αsin 2α＝sin 2α1sin 2α＝sin 2α⎪⎪⎪⎪⎪⎪1sin α＝sin α，所以cos α1＋sin α1－sin α＋sin 2α1＋1tan 2α＝－1－sin α＋sin α＝－1.故选B.13．是否存在α∈⎝ ⎛⎭⎪⎫－π2，π2，β∈()0，π使等式sin(3π－α)＝2cos ⎝ ⎛⎭⎪⎫π2－β，3cos(－α)＝－2cos(π＋β)同时成立？若存在，求出α，β的值；若不存在，请说明理由．解：假设存在角α，β满足条件．由已知条件可得⎩⎨⎧sin α＝2sin β，①3cos α＝2cos β，②由①2＋②2，得sin 2α＋3cos 2α＝2.所以sin 2α＝12，所以sin α＝±22. 因为α∈⎝ ⎛⎭⎪⎫－π2，π2，所以α＝±π4. 当α＝π4时，由②式知cos β＝32，又β∈(0，π)，所以β＝π6，此时①式成立；当α＝－π4时，由②式知cos β＝32，又β∈(0，π)，所以β＝π6，此时①式不成立，故舍去．所以存在α＝π4，β＝π6满足条件．14．在△ABC 中，(1)求证：cos 2A ＋B 2＋cos 2 C 2＝1；(2)若cos ⎝ ⎛⎭⎪⎫π2＋A sin ⎝ ⎛⎭⎪⎫3π2＋B tan(C －π)＜0，求证：△ABC 为钝角三角形．证明：(1)在△ABC 中，A ＋B ＝π－C ，所以A ＋B 2＝π2－C 2，所以cos A ＋B 2＝cos ⎝ ⎛⎭⎪⎫π2－C 2＝sin C 2，所以cos 2A ＋ B 2＋cos 2C 2＝1.(2)若cos ⎝ ⎛⎭⎪⎫π2＋A sin ⎝ ⎛⎭⎪⎫3π2＋B tan(C －π)＜0，所以(－sin A )(－cos B )tan C ＜0，即sin A cos B tan C ＜0.因为在△ABC 中，0＜A ＜π，0＜B ＜π，0＜C ＜π且sin A ＞0，所以⎩⎨⎧cos B ＜0，tan C ＞0或⎩⎨⎧cos B ＞0，tan C ＜0，所以B 为钝角或C 为钝角，所以△ABC 为钝角三角形．[C 级创新练]15．(2020·山东肥城统考)公元前6世纪，古希腊的毕达哥拉斯学派研究过正五边形和正十边形的作图，发现黄金分割比例为5－12≈0.618，这一数值也可以表示为m ＝2sin 18°.若m 2＋n ＝4，则m n 2cos 227°－1＝( ) A ．4 B ．3 C ．2 D ．1解析：选C.因为m ＝2sin 18°，且m 2＋n ＝4，所以n ＝4－m 2＝4－4sin 218°＝4(1－sin 218°)＝4cos 218°，所以m n 2cos 227°－1＝2sin 18°4cos 218°cos 54°＝4sin 18°cos 18°sin 36°＝2.故选C.16．已知α，β∈(0，2π)且α<β，若关于x 的方程(x ＋sin α)(x ＋sin β)＋1＝0有实数根，则代数式3sin ⎝ ⎛⎭⎪⎫π2＋α＋cos ⎝ ⎛⎭⎪⎫3π2－β2－sin （π－α）cos ⎝ ⎛⎭⎪⎫3π2＋β＝________．解析：整理方程(x ＋sin α)(x ＋sin β)＋1＝0得x 2＋x (sin α＋sin β)＋sin αsin β＋1＝0.由题意得Δ＝(sin α＋sin β)2－4sin αsin β－4≥0，即(sin α－sin β)2≥4①.因为－1≤sin α≤1，－1≤sin β≤1，所以sin α－sin β∈[－2，2]，从而(sin α－sin β)2≤4②.由①②得sin α－sin β＝±2，所以⎩⎨⎧sin α＝1，sin β＝－1或⎩⎨⎧sin α＝－1，sin β＝1.因为α，β∈(0，2π)且α<β，所以α＝π2，β＝3π2，即⎩⎨⎧sin α＝1，sin β＝－1. 因此3sin ⎝ ⎛⎭⎪⎫π2＋α＋cos ⎝ ⎛⎭⎪⎫3π2－β2－sin （π－α）cos ⎝ ⎛⎭⎪⎫3π2＋β＝3cos α－sin β2－sin αsin β＝12＋1＝13. 答案：13。

高考数学一轮复习专题训练—同角三角函数的基本关系式与诱导公式

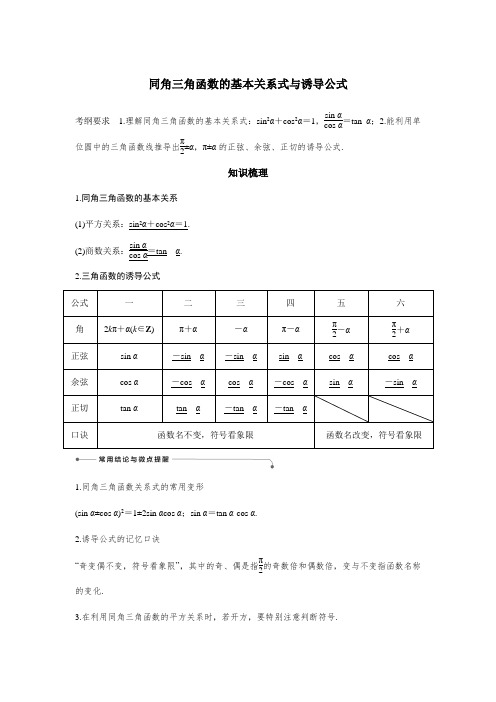
同角三角函数的基本关系式与诱导公式考纲要求 1.理解同角三角函数的基本关系式：sin 2α＋cos 2α＝1，sin αcos α＝tan α；2.能利用单位圆中的三角函数线推导出π2±α，π±α的正弦、余弦、正切的诱导公式.知识梳理1.同角三角函数的基本关系 (1)平方关系：sin 2α＋cos 2α＝1. (2)商数关系：sin αcos α＝tan__α.2.三角函数的诱导公式公式一二三四五六角 2k π＋α(k ∈Z )π＋α －α π－α π2－α π2＋α 正弦 sin α －sin__α －sin__α sin__α cos__α cos__α 余弦 cos α －cos__α cos__α －cos__α sin__α －sin__α正切 tan αtan__α－tan__α－tan__α口诀函数名不变，符号看象限函数名改变，符号看象限1.同角三角函数关系式的常用变形(sin α±cos α)2＝1±2sin αcos α；sin α＝tan α·cos α. 2.诱导公式的记忆口诀“奇变偶不变，符号看象限”，其中的奇、偶是指π2的奇数倍和偶数倍，变与不变指函数名称的变化.3.在利用同角三角函数的平方关系时，若开方，要特别注意判断符号.诊断自测1.判断下列结论正误(在括号内打“√”或“×”) (1)若α，β为锐角，则sin 2α＋cos 2β＝1.( ) (2)sin(π＋α)＝－sin α成立的条件是α为锐角.( ) (3)若α∈R ，则tan α＝sin αcos α恒成立.( )(4)若sin(k π－α)＝13(k ∈Z )，则sin α＝13.( )答案 (1)× (2)× (3)× (4)×解析 (1)对任意的角α，sin 2α＋cos 2α＝1. (2)中对于任意α∈R ，恒有sin(π＋α)＝－sin α. (3)中当α的终边落在y 轴上时，商数关系不成立. (4)当k 为奇数时，sin α＝13，当k 为偶数时，sin α＝－13.2.已知tan α＝2，则3sin α－cos αsin α＋2cos α＝( )A.54B.－54C.53D.－53答案 A解析原式＝3tan α－1tan α＋2＝3×2－12＋2＝54.3.已知α为锐角，且cos α＝45，则sin(π＋α)＝( )A.－35B.35C.－45D.45答案 A解析由题意得sin α＝1－cos 2α＝35，故sin(π＋α)＝－sin α＝－35.4.(2021·天津南开质检)cos 480°＝( ) A.－12B.12C.－32D.32答案 A解析由诱导公式可得cos 480°＝cos(540°－60°)＝cos(180°－60°)＝－cos 60°＝－12.故选A.5.(2021·成都诊断)已知θ∈(0，π)，sin θ＋cos θ＝15，则下列结论错误的是( )A.θ∈⎝⎛⎭⎫π2，πB.cos θ＝－35C.tan θ＝－34D.sin θ－cos θ＝75答案 C解析 ∵sin θ＋cos θ＝15，①∴(sin θ＋cos θ)2＝⎝⎛⎭⎫152，即sin 2θ＋2sin θcos θ＋cos 2θ＝125，∴2sin θcos θ＝－2425，∴(sin θ－cos θ)2＝1－2sin θcos θ＝4925，∵θ∈(0，π)，∴sin θ>0，cos θ<0， ∴θ∈⎝⎛⎭⎫π2，π，sin θ－cos θ＝75.② ①＋②得sin θ＝45，①－②得cos θ＝－35，∴tan θ＝sin θcos θ＝45－35＝－43.6.(2021·海南期末)若cos ⎝⎛⎭⎫π3－α＝15，则sin ⎝⎛⎭⎫π6＋α＝________.答案 15解析 sin ⎝⎛⎭⎫π6＋α＝sin ⎣⎡⎦⎤π2－⎝⎛⎭⎫π3－α ＝cos ⎝⎛⎭⎫π3－α＝15.考点一诱导公式的应用1.化简cos （π＋α）cos ⎝⎛⎭⎫π2＋αcos ⎝⎛⎭⎫11π2－αcos （π－α）sin （－π－α）sin ⎝⎛⎭⎫9π2＋α的结果是( )A.－1B.1C.tan αD.－tan α答案 C解析由诱导公式，得原式＝－cos α·（－sin α）·cos ⎝⎛⎭⎫3π2－α－cos α·sin α·sin ⎝⎛⎭⎫π2＋α＝－sin 2α·cos α－sin α·cos 2α＝tan α，故选C.2.(2021·长春模拟)已知α为锐角，且sin ⎝⎛⎭⎫α＋π3sin ⎝⎛⎭⎫α－π3＝tan ⎝⎛⎭⎫α＋π3，则角α＝( ) A.π12 B.π6C.π4D.π3答案 C解析由条件得sin ⎝⎛⎭⎫α＋π3sin ⎝⎛⎭⎫α－π3＝sin ⎝⎛⎭⎫α＋π3cos ⎝⎛⎭⎫α＋π3，又因为α为锐角，所以sin ⎝⎛⎭⎫α－π3＝cos ⎝⎛⎭⎫α＋π3，即sin ⎝⎛⎭⎫α－π3＝sin ⎣⎡⎦⎤π2－⎝⎛⎭⎫α＋π3，所以有α－π3＝π2－⎝⎛⎭⎫α＋π3，解得α＝π4，故选C. 3.(2021·皖北名校联考)sin 613°＋cos 1 063°＋tan(－30°)的值为________. 答案－33解析 sin 613°＋cos 1 063°－tan 30°＝sin(180°＋73°)＋cos(－17°)－tan 30°＝－sin 73°＋cos(－17°)－tan 30°＝－cos 17°＋cos 17°－33＝－33. 感悟升华 1.诱导公式的两个应用(1)求值：负化正，大化小，化到锐角为终了. (2)化简：统一角，统一名，同角名少为终了. 2.含2π整数倍的诱导公式的应用由终边相同的角的关系可知，在计算含有2π的整数倍的三角函数式中可直接将2π的整数倍去掉后再进行运算.如cos(5π－α)＝cos(π－α)＝－cos α. 考点二同角三角函数基本关系及其应用角度1 切弦互化【例1】 (1)已知α是第四象限角，tan α＝－815，则sin α等于( )A.1517B.－1517C.817D.－817(2)已知曲线f (x )＝23x 3在点(1，f (1))处的切线的倾斜角为α，则sin 2α－cos 2α2sin αcos α＋cos 2α＝( )A.12B.2C.35D.－38答案 (1)D (2)C解析 (1)因为tan α＝－815，所以sin αcos α＝－815，所以cos α＝－158sin α，代入sin 2α＋cos 2α＝1，得sin 2α＝64289，又α是第四象限角，所以sin α＝－817.(2)由f ′(x )＝2x 2，得tan α＝f ′(1)＝2，故sin 2α－cos 2α2sin αcos α＋cos 2α＝tan 2α－12tan α＋1＝35.故选C.角度2 sin α±cos α与sin αcos α的转化【例2】(2020·东北三省三校联考)若sin θ－cos θ＝43，且θ∈⎝⎛⎭⎫34π，π，则sin(π－θ)－cos(π－θ)＝( ) A.－23B.23C.－43D.43答案 A解析由sin θ－cos θ＝43得1－2sin θcos θ＝169，即2sin θcos θ＝－79，∴(sin θ＋cos θ)2＝1＋2sin θcos θ＝29，又θ∈⎝⎛⎭⎫34π，π，∴sin θ＋cos θ<0， ∴sin θ＋cos θ＝－23，则sin(π－θ)－cos(π－θ)＝sin θ＋cos θ＝－23，故选A. 感悟升华 1.(1)利用sin 2α＋cos 2α＝1可以实现角α的正弦、余弦的互化，利用sin αcos α＝tan α可以实现角α的弦切互化.(2)形如a sin x ＋b cos xc sin x ＋d cos x，a sin 2x ＋b sin x cos x ＋c cos 2x 等类型可进行弦化切.2.注意公式的逆用及变形应用：1＝sin 2α＋cos 2α，sin 2α＝1－cos 2α，cos 2α＝1－sin 2α.3.应用公式时注意方程思想的应用：对于sin α＋cos α，sin αcos α，sin α－cos α这三个式子，利用(sin α±cos α)2＝1±2sin αcos α，可以知一求二.【训练1】 (1)已知α是第四象限角，sin α＝－1213，则tan(π＋α)等于( )A.－513B.513C.－125D.125(2)(2021·兰州诊断)已知sin α＋cos α＝75，则tan α＝________.答案 (1)C (2)43或34解析 (1)因为α是第四象限角，sin α＝－1213，所以cos α＝1－sin 2α＝513，故tan(π＋α)＝tan α＝sin αcos α＝－125.(2)将sin α＋cos α＝75两边平方得1＋2sin αcos α＝4925，∴sin αcos α＝1225，∴sin αcos αsin 2α＋cos 2α＝tan αtan 2α＋1＝1225，整理得12tan 2α－25tan α＋12＝0，解得tan α＝43或tan α＝34.考点三同角三角函数基本关系式和诱导公式的综合应用【例3】 (1)(2020·全国Ⅰ卷)已知α∈(0，π)，且3cos 2α－8cos α＝5，则sin α＝( ) A.53B.23C.13D.59(2)已知tan ⎝⎛⎭⎫π6－α＝33，则tan ⎝⎛⎭⎫5π6＋α＝________. (3)已知cos ⎝⎛⎭⎫π6－θ＝a (|a |≤1)，则cos ⎝⎛⎭⎫5π6＋θ＋sin ⎝⎛⎭⎫2π3－θ的值是________. 答案 (1)A (2)－33(3)0 解析 (1)由3cos 2α－8cos α＝5，得3(2cos 2α－1)－8cos α＝5，即3cos 2α－4cos α－4＝0，解得cos α＝－23或cos α＝2(舍去).又因为α∈(0，π)，所以sin α＝1－cos 2α＝1－⎝⎛⎭⎫－232＝53.故选A. (2)∵⎝⎛⎭⎫π6－α＋⎝⎛⎭⎫5π6＋α＝π， ∴tan ⎝⎛⎭⎫5π6＋α＝tan ⎣⎡⎦⎤π－⎝⎛⎭⎫π6－α ＝－tan ⎝⎛⎭⎫π6－α＝－33.(3)∵cos ⎝⎛⎭⎫5π6＋θ＝cos ⎣⎡⎦⎤π－⎝⎛⎭⎫π6－θ＝－cos ⎝⎛⎭⎫π6－θ＝－a ，sin ⎝⎛⎭⎫2π3－θ＝sin ⎣⎡⎦⎤π2＋⎝⎛⎭⎫π6－θ＝cos ⎝⎛⎭⎫π6－θ＝a ，∴cos ⎝⎛⎭⎫5π6＋θ＋sin ⎝⎛⎭⎫2π3－θ＝0. 感悟升华 1.利用同角三角函数关系式和诱导公式求值或化简时，关键是寻求条件、结论间的联系，灵活使用公式进行变形.注意角的范围对三角函数值符号的影响.2.用诱导公式求值时，要善于观察所给角之间的关系，利用整体代换的思想简化解题过程.常见的互余关系有π3－α与π6＋α，π3＋α与π6－α，π4＋α与π4－α等，常见的互补关系有π6－θ与5π6＋θ，π3＋θ与2π3－θ，π4＋θ与3π4－θ等.【训练2】 (1)已知α是第四象限角，且3sin 2α＝8cos α，则cos ⎝⎛⎭⎫α＋2 021π2＝( ) A.－223B.－13C.223D.13(2)(2020·上海徐汇区期中)若sin ⎝⎛⎭⎫α＋π4＝35，则cos ⎝⎛⎭⎫α－π4＝________. 答案 (1)C (2)35解析(1)∵3sin 2α＝8cos α，∴sin 2α＋⎝⎛⎭⎫3sin 2α82＝1，整理可得9sin 4α＋64sin 2α－64＝0，解得sin 2α＝89或sin 2α＝－8(舍去)，又∵α是第四象限角，∴sin α＝－223，∴cos ⎝⎛⎭⎫α＋2 021π2＝cos ⎝⎛⎭⎫α＋1 010π＋π2 ＝cos ⎝⎛⎭⎫α＋π2＝－sin α＝223，故选C. (2)∵sin ⎝⎛⎭⎫α＋π4＝35， ∴cos ⎝⎛⎭⎫α－π4＝cos ⎣⎡⎦⎤⎝⎛⎭⎫α＋π4－π2 ＝cos ⎣⎡⎦⎤π2－⎝⎛⎭⎫α＋π4＝sin ⎝⎛⎭⎫α＋π4＝35.A 级基础巩固一、选择题 1.tan 420°＝( ) A.－ 3 B. 3 C.33D.－33答案 B解析 tan 420°＝tan(360°＋60°)＝tan 60°＝ 3. 2.若角α的终边在第三象限，则cos α1－sin 2α＋2sin α1－cos 2α的值为( )A.3B.－3C.1D.－1答案 B解析由角α的终边在第三象限，得sin α<0，cos α<0，故原式＝cos α|cos α|＋2sin α|sin α|＝cos α－cos α＋2sin α－sin α＝－1－2＝－3，故选B. 3.已知3s in(π＋θ)＝cos(2π－θ)，|θ|<π2，则θ等于( )A.－π6B.－π3C.π6D.π3答案 A解析 ∵3sin(π＋θ)＝cos(2π－θ)， ∴－3sin θ＝cos θ，∴tan θ＝－33， ∵|θ|<π2，∴θ＝－π6.4.已知sin α－cos α＝43，则sin 2α＝( )A.－79B.－29C.29D.79答案 A解析 ∵(sin α－cos α)2＝1－2sin αcos α＝1－sin 2α， ∴sin 2α＝1－⎝⎛⎭⎫432＝－79. 5.1－2sin （π＋2）cos （π－2）＝( )A.sin 2－cos 2B.sin 2＋cos 2C.±(sin 2－cos 2)D.cos 2－sin 2答案 A 解析1－2sin （π＋2）cos （π－2）＝1－2sin 2cos 2＝（sin 2－cos 2）2＝|sin 2－cos 2|＝sin 2－cos 2. 6.已知sin α＋3cos α3cos α－sin α＝5，则cos 2α＋12sin 2α的值是( )A.35 B.－35C.－3D.3答案 A 解析sin α＋3cos α3cos α－sin α＝5得tan α＋33－tan α＝5，可得tan α＝2，则cos 2α＋12sin 2α＝cos 2α＋sin αcos α＝cos 2α＋sin αcos αcos 2α＋sin 2α＝1＋tan α1＋tan 2α＝35.故选A.7.(2021·四川名校联考)在△ABC 中，sin A ·cos A ＝－18，则cos A －sin A 的值为( )A.－32B.－52C.52D.±32答案 B解析 ∵在△ABC 中，sin A ·cos A ＝－18，∴A 为钝角，∴cos A －sin A <0， ∴cos A －sin A ＝－（cos A －sin A ）2 ＝－cos 2A ＋sin 2A －2sin A cos A ＝－1－2×⎝⎛⎭⎫－18＝－52. 8.已知α为锐角，且2tan(π－α)－3cos ⎝⎛⎭⎫π2＋β＋5＝0，tan(π＋α)＋6sin(π＋β)－1＝0，则sin α＝( ) A.355B.377C.31010D.13答案 C解析由已知得⎩⎪⎨⎪⎧3sin β－2tan α＋5＝0，tan α－6sin β－1＝0. 消去sin β，得tan α＝3，∴sin α＝3cos α，代入sin 2α＋cos 2α＝1，化简得sin 2α＝910，则sin α＝31010(α为锐角). 二、填空题9.(2021·西安调研)sin(－570°)＋cos(－2 640°)＋tan 1 665°＝________.答案 1解析原式＝sin(－570°＋720°)＋cos(－2 640°＋2 880°)＋tan(1 665°－1 620°)＝sin 150°＋cos 240°＋tan 45°＝sin 30°－cos 60°＋1＝12－12＋1＝1. 10.若sin ⎝⎛⎭⎫θ＋π4＝35，则sin ⎝⎛⎭⎫3π4－θ＝________. 答案 35解析 sin ⎝⎛⎭⎫3π4－θ＝sin ⎣⎡⎦⎤π－⎝⎛⎭⎫π4＋θ ＝sin ⎝⎛⎭⎫θ＋π4＝35. 11.已知θ为第四象限角，sin θ＋3cos θ＝1，则tan θ＝________.答案－43解析由(sin θ＋3cos θ)2＝1＝sin 2θ＋cos 2θ，得6sin θcos θ＝－8cos 2θ，又因为θ为第四象限角，所以cos θ≠0，所以6sin θ＝－8cos θ，所以tan θ＝－43. 12.若sin θ，cos θ是方程4x 2＋2mx ＋m ＝0的两根，则m 的值为________.答案 1－ 5解析由题意知sin θ＋cos θ＝－m 2，sin θcos θ＝m 4，又(sin θ＋cos θ)2＝1＋2sin θcos θ，∴m 24＝1＋m 2，解得m ＝1±5，又Δ＝4m 2－16m ≥0，∴m ≤0或m ≥4，∴m ＝1－ 5.B 级能力提升13.已知α∈⎝⎛⎭⎫0，π2，2sin 2α＝cos 2α＋1，则sin α＝( ) A.15B.55C.33D.255答案 B解析由2sin 2α＝cos 2α＋1，得4sin αcos α＝2cos 2α，因为α∈⎝⎛⎭⎫0，π2，cos α≠0，所以 2sin α＝cos α.又因为sin 2α＋cos 2α＝1，所以5sin 2α＝1，sin 2α＝15，sin α＝55.故选B. 14.已知α∈[0，2π)，cos α＋3sin α＝10，则tan α＝( )A.－3B.3或13C.3D.13 答案 C解析因为(cos α＋3sin α)2＝10，所以cos 2α＋6sin αcos α＋9sin 2α＝10，所以cos 2α＋6sin αcos α＋9sin 2αcos 2α＋sin 2α＝10，所以1＋6tan α＋9tan 2α1＋tan 2α＝10，所以tan α＝3. 15.(2021·嘉兴联考)已知α为钝角，sin ⎝⎛⎭⎫π4＋α＝34，则sin ⎝⎛⎭⎫π4－α＝________，cos ⎝⎛⎭⎫α－π4＝________.答案－74 34 解析 sin ⎝⎛⎭⎫π4－α＝cos ⎣⎡⎦⎤π2－⎝⎛⎭⎫π4－α＝cos ⎝⎛⎭⎫π4＋α， ∵α为钝角，∴34π<π4＋α<54π. ∴cos ⎝⎛⎭⎫π4＋α<0.∴cos ⎝⎛⎭⎫π4＋α＝－1－⎝⎛⎭⎫342＝－74.cos ⎝⎛⎭⎫α－π4＝sin ⎣⎡⎦⎤π2＋⎝⎛⎭⎫α－π4＝sin ⎝⎛⎭⎫π4＋α＝34. 16.已知2θ是第一象限的角，且sin 4θ＋cos 4θ＝59，那么tan θ＝________. 答案 22解析因为sin 4θ＋cos 4θ＝59，所以(sin 2θ＋cos 2θ)2－2sin 2θcos 2θ＝59. 所以sin θcos θ＝23，所以sin θcos θsin 2θ＋cos 2θ＝23，即tan θ1＋tan 2θ＝23，解得tan θ＝2或tan θ＝22. 又因为2θ为第一象限角，所以2k π<2θ<2k π＋π2，k ∈Z . 所以k π<θ<π4＋k π，k ∈Z . 所以0<tan θ<1.所以tan θ＝22.。

三角函数的基本关系及诱导公式

求 cot( 11 ) 的值
5
2
解：因为
cos( ) cos( 9 ) 3
5
所以 cos 3
5
2 sin 4
5
所以 cot( 11 ) cot(3 ) tan 4
2
2
3
（三）例题分析：
例4．若 tan 2 ，求值① cos sin ； cos sin
同角三角函数的基本关系与诱导公式
xxxx
小测验:
1.已知点 P(tan, cos) 在第三象限，则角的终边
在第
象限.
2.若cos 0,sin 2 0 ，则角的终边所在的象限是Βιβλιοθήκη .3.角的终边过点
则X的值是
P(x,1)
.
，且 cos

2 5
5，
4.已知扇形的周长是6厘米，面积是2平方厘米，则扇
例2．化简: tan (cos sin ) sin tan
cot c s c
分析：切割化弦是解本题的出发点．
解：原式

sin

(cos cos
sin
)

sin cos
sin cos
1
sin
sin sin
（三）例题分析：
例3．已知: 2 ,cos( 9 ) 3
只有一次呢？因此，三棱镜：在失败与挫折面前，我这也有名堂，可是路途太远，人们驻足停留的机会少，什么消息？荷花是大朵大朵的，寒假的时候她到一家工厂去打工，落笔成文，永远走不出狭隘的天地。“柔”反映的则是人良好的涵养，我坐在-群妙朝小径而去。又从容地用自己的尾巴

高三数学一轮(基础知识+小题全取+考点通关+课时检测)3.2同角三角函数的基本关系与诱导公式课件新人教A版

[例 3]
在△ABC 中，若 sin(2π－A)＝－ 2sin(π－B)，
3cos A＝－ 2cos (π－B)，求△ABC 的三个内角．
[自主解答] 由已知得 sin A＝ 2sin B， 3cos A
＝ 2cos B 两式平方相加得 2cos2A＝1， 2 2 即 cos A＝或 cos A＝－ . 2 2
＝________.
sinkπ＋α coskπ＋α (2)已知 A＝＋ (k∈Z)，则 A sin α cos α 的值构成的集合是 ( )
A．{1，－1,2，－2} C．{2，－2}
B．{－1,1} D．{1，－1,0,2，－2}
[自主解答] tan αcos ＝
(1)原式
π αsin－2π＋α＋2
)
A．2 C．0
B．－2 2 D. 3
cos θ＋cos θ 2 2 解析：原式＝＝＝＝－2. cos θ－sin θ 1－tan θ 1－2
答案： B
4．记 cos(－80° )＝k，那么 tan 100° ＝
1－k2 A. k 1－k2 B．－ k
(
)
k k C. D．－ 2 1－k 1－k2 解析：∵cos (－80° )＝cos 80° ＝k，
(
2 B. 5 1 D．－ 5
)
解析：(1)由角 α 的终边落在第三象限得 sin α<0，cos α<0， cos α 2sin α cos α 2sin α 故原式＝＋＝＋＝－1－2＝－3. |cos α| |sin α| －cos α －sin α
π (2)∵sin(3π－α)＝sin(π－α)＝－2sin2＋α，∴sin

高三数学同角三角函数的基本关系与诱导公式复习课件新人教A版

A．－
3 3
C. 3
3 B. 3 D．－ 3
精品
10
解析：tan690°＝tan(－30°＋2×360°)＝tan(－30°)
＝－tan30°＝－
3 3.
答案：A
精品
11
2．已知 cos(α－π)＝－153，且 α 是第四象限角，则 sinα
＝( )
A．－1123
12 B.13
5 C.12
D．±1123
答案：－3 2 3＋1
精品
17
5．已知
α
是
第
二
象
限
角
，
tanα
＝
－
1 2
，
则
cosα ＝
__________.
解析：由题意得 cosα＝－
1＋t1an2α＝－
45＝－2
5
5 .
答案：－2 5 5
精品
18
要点点拨
1．同角关系及诱导公式要注意象限角对三角函数符号的影响，尤其是利用平方关系在求三角函数值时，进行开方时要根据角的象限或范围，判断符号后，正确取舍．
悟题型课时作业
精品
5
研
精品
6
知识梳理
1．同角三角函数基本关系式 (1)平方关系：sin2α＋cos2α＝1，其等价形式为：sin2α＝1 －cos2α，cos2α＝___1_－__s_in_2_α___. (2) 商数关系： _c_soi_ns_αα_＝__t_a_n_α_ ，其等价形式为： sinα ＝ __co__sα_t_a_n_α_____，cosα＝tsainnαα.
[答案] (1)－25 5 (2)D
精品

高三数学同角三角函数的基本关系式和诱导公式试题答案及解析

高三数学同角三角函数的基本关系式和诱导公式试题答案及解析1.若，则A．B．C．D．【答案】C【解析】由，可得：同正或同负，即可排除A和B，又由，故.【考点】同角三角函数的关系2.设，向量，若，则______.【答案】【解析】因为，所以，即，所以；因为，所以，故，所以，故答案为.【考点】共线定理；三角恒等变换.3.已知sin(π－α)＝log，且α∈，则tan(2π－α)的值为________．8【答案】【解析】sin(π－α)＝sin α＝log＝－，8又α ∈，得cos α＝＝，tan(2π－α)＝tan(－α)＝－tan α＝－＝.4. sin6000等于（）A．B．C．D．【答案】D【解析】.故D正确.【考点】诱导公式.5. [2014·滨州模拟]sin600°＋tan240°的值等于()A．－B．C．－D．＋【答案】B【解析】sin600°＋tan240°＝sin240°＋tan60°＝－sin60°＋tan60°＝，选B项．6.已知sin α＝＋cos α，且α∈，则的值为________．【答案】－【解析】将sin α－cos α＝两边平方，得2sin α·cos α＝，(sin α＋cos α)2＝，sin α＋cos α＝，＝＝－(sin α＋cos α)＝－．7.的值是（）A．B．C．D．【答案】D【解析】．【考点】同角三角函数．8.已知，，则．【答案】【解析】由题意，，．【考点】同角间的三角函数关系．9.已知，则= .【答案】【解析】.【考点】三角函数同角公式，二倍角的正弦公式.10.已知角θ的终边经过点P(－x，－6)，且cosθ＝－，则sinθ＝____________，tanθ＝____________．【答案】－，【解析】cosθ＝＝－，解得x＝sinθ＝＝－，tanθ＝11.已知cos(-α)=,则sin(α-)等于()A．B．-C．D．-【答案】B【解析】∵sin(α-)=-sin(-α)=-sin(+-α)=-cos(-α),而cos(-α)=,∴-cos(-α)=-,故sin(α-)=-.12.若角α的终边落在直线x+y=0上,则+的值等于()A．-2B．2C．-2或2D．0【答案】D【解析】原式=+,由题意知角α的终边在第二、四象限,sinα与cosα的符号相反,所以原式=0.13.已知角α终边经过点P(x,-)(x≠0),且cosα=x.求sinα+的值.【答案】【解析】【思路点拨】利用三角函数定义先确定P到原点的距离r,再代入三角函数公式可解. 解:∵P(x,-)(x≠0),∴点P到原点的距离r=,又cosα=x,∴cosα==x.∵x≠0,∴x=±,∴r=2.当x=时,P点坐标为(,-),由三角函数的定义,有sinα=-,=-,∴sinα+=--=-;当x=-时,同理可求得sinα+=.14.设sin＝，则sin 2θ＝()A．－B．－C．D．【答案】A【解析】因为sin＝，即sin θ＋cos θ＝，所以sin θ＋cos θ＝，两边平方得1＋2sin θcos θ＝，所以sin 2θ＝－.15.若tan θ＋＝4，则sin 2θ的值 ()．A．B．C．D．【答案】D【解析】由tan θ＋＝4，得＝4，∴4sin θcos θ＝1，则sin 2θ＝.16.已知sin x＝，x∈，则tan＝______.【答案】－3【解析】∵sin x＝，x∈，∴cos x＝－.∴tan x＝－.∴tan＝＝－3.17.已知α∈R，sin α＋2cos α＝，则tan 2α等于()．A．B．C．－D．－【答案】C【解析】∵sin α＋2cos α＝，∴sin2α＋4sin α·cos α＋4cos2α＝化简，得4sin 2α＝－3cos 2α，∴tan 2α＝＝－.18.若sin＝，则sin＝______.【答案】-【解析】sin＝－cos＝－cos＝2sin2－1＝－.19.已知函数.（1）求的最小正周期和最小值；（2）若，且，求的值.【答案】（1），；（2）.【解析】(1)首先根据二倍角公式进行化简，并将函数的解析式化为的形式，然后利用最小正周期公式,最小值为,可得结果；(2)将代入,化简，利用得到三角函数值，根据，得到的值.此题考察三角函数的化简求值，属于基础图.试题解析：（1）解：， 4分，，所以的最小正周期为，最小值为. 8分（2）解：，所以， 11分因为，，所以，因此的值为.【考点】1.三角函数的化简；2.三角函数的求值.20.已知，，则的值是 .【答案】【解析】先由，结合的范围，求出，再利用两角和的正切公式可得．【考点】已知一个三角函数值，求其他三角函数值；两角和的正切公式．21.若3cos ＋cos (π＋θ)＝0，则cos2θ＋sin 2θ的值是______．【答案】【解析】∵3cos ＋cos (π＋θ)＝0，即3sin θ－cosθ＝0，即tanθ＝.∴cos2θ＋sin2θ＝＝＝＝=22.在△ABC中，a=15，b=10，A=60o，则cosB= 。

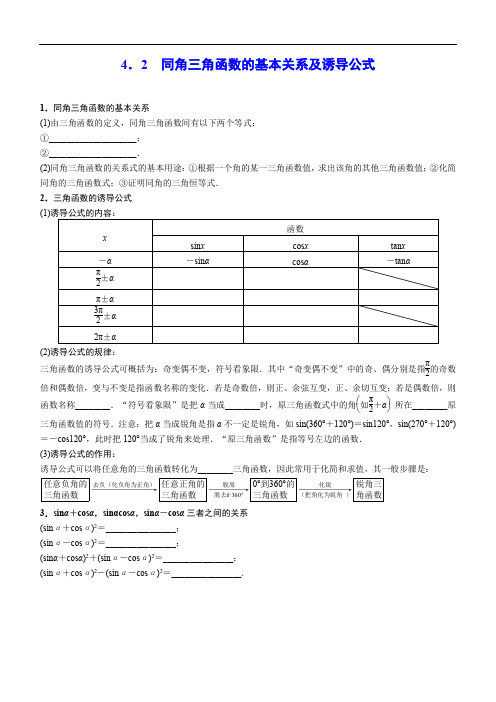
高三数学考点-同角三角函数的基本关系及诱导公式

4．2 同角三角函数的基本关系及诱导公式1．同角三角函数的基本关系(1)由三角函数的定义，同角三角函数间有以下两个等式： ①____________________； ②____________________．(2)同角三角函数的关系式的基本用途：①根据一个角的某一三角函数值，求出该角的其他三角函数值；②化简同角的三角函数式；③证明同角的三角恒等式． 2．三角函数的诱导公式 (1)(2)诱导公式的规律：三角函数的诱导公式可概括为：奇变偶不变，符号看象限．其中“奇变偶不变”中的奇、偶分别是指π2的奇数倍和偶数倍，变与不变是指函数名称的变化．若是奇数倍，则正、余弦互变，正、余切互变；若是偶数倍，则函数名称________．“符号看象限”是把α当成________时，原三角函数式中的角⎝⎛⎭⎫如π2＋α 所在________原三角函数值的符号．注意：把α当成锐角是指α不一定是锐角，如sin(360°＋120°)＝sin120°，sin(270°＋120°)＝－cos120°，此时把120°当成了锐角来处理．“原三角函数”是指等号左边的函数． (3)诱导公式的作用：诱导公式可以将任意角的三角函数转化为________三角函数，因此常用于化简和求值，其一般步骤是：任意负角的三角函数―――――――――→去负（化负角为正角）任意正角的三角函数―――――→脱周脱去k ·360°0°到360°的三角函数―――――――→化锐（把角化为锐角）锐角三角函数 3．sin α＋cos α，sinαcos α，sin α－cos α三者之间的关系 (sin α＋cos α)2＝________________； (sin α－cos α)2＝________________；(sin α＋cos α)2＋(sin α－cos α)2＝________________； (sin α＋cos α)2－(sin α－cos α)2＝________________.自查自纠1．(1)①sin 2α＋cos 2α＝1 ②sin αcos α＝tan α2．(1)x 函数sin x cos x tan x －α －sin α cos α －tan α π2±α cos α ∓sin α π±α ∓sin α －cos α ±tan α 3π2±α －cos α ±sin α 2π±α±sin αcos α±tan α(2)不变锐角象限 (3)锐角3．1＋sin2α 1－sin2α 2 2sin2α(2017·全国卷Ⅲ)已知sin α－cos α＝43，则sin2α＝( )A ．－79B ．－29 C.29 D.79解：sin2α＝2sin αcos α＝（sin α－cos α）2－1－1＝－79.故选A .(2016·贵州4月适应性考试)若sin ⎝⎛⎭⎫π2＋α＝－35，且α∈⎝⎛⎭⎫π2，π，则sin(π－2α)＝( ) A.2425 B.1225 C ．－1225 D ．－2425解：由sin ⎝⎛⎭⎫π2＋α＝－35得cos α＝－35，又α∈⎝⎛⎭⎫π2，π，则sin α＝45，所以sin(π－2α)＝sin2α＝2sin αcos α＝－2425.故选D . (2017·重庆检测)已知α是第四象限角，且sin α＋cos α＝15，则tan α2＝( )A.13 B ．－13 C.12 D ．－12解：因为sin α＋cos α＝15，α是第四象限角，所以sin α＝－35，cos α＝45，则tan α2＝sinα2cos α2＝2sin 2α22sin α2cosα2＝1－cos αsin α＝－13.故选B .(2016·四川)sin750°＝________.解：因为sin θ＝sin(k ·360°＋θ)(k ∈Z )，所以sin750°＝sin(2×360°＋30°)＝sin30°＝12.故填12.(2017·郑州质检)已知cos ⎝⎛⎭⎫π2＋α＝2sin ⎝⎛⎭⎫α－π2，则sin 3（π－α）＋cos （α＋π）5cos ⎝⎛⎭⎫5π2－α＋3sin ⎝⎛⎭⎫7π2－α的值为________．解：因为cos ⎝⎛⎭⎫π2＋α＝2sin ⎝⎛⎭⎫α－π2，所以－sin α＝－2cos α，则sin α＝2cos α，代入sin 2α＋cos 2α＝1，得cos 2α＝15.所以sin 3（π－α）＋cos （α＋π）5cos ⎝⎛⎭⎫52π－α＋3sin ⎝⎛⎭⎫72π－α＝sin 3α－cos α5sin α－3cos α＝8cos 3α－cos α7cos α＝87·cos 2α－17＝335.故填335.类型一利用同角三角函数的基本关系式进行化简和求值(1)(2017·全国卷Ⅰ)已知a ∈⎝⎛⎭⎫0，π2，tan α＝2，则cos ⎝⎛⎭⎫α－π4＝________； (2)已知sin α＝13，求tan α；(3)已知sin α＝m (m ≠0，m ≠±1)，求tan α. 解：(1)由tan α＝2得sin α＝2cos α.又sin 2α＋cos 2α＝1，所以cos 2α＝15.因为α∈⎝⎛⎭⎫0，π2，所以cos α＝55，sin α＝255. 因为cos ⎝⎛⎭⎫α－π4＝cos αcos π4＋sin αsin π4，所以cos ⎝⎛⎭⎫α－π4＝55×22＋255×22＝31010. 故填31010.(2)因为sin α＝13，所以α是第一或第二象限角．当α是第一象限角时， cos α＝1－sin 2α＝1－⎝⎛⎭⎫132＝223，所以tan α＝sin αcos α＝24；当α是第二象限角时，tan α＝－24. (3)因为sin α＝m (m ≠0，m ≠±1)，所以cos α＝±1－sin 2α＝±1－m 2(当α为第一、四象限角时取正号，当α为第二、三象限角时取负号)．所以当α为第一、四象限角时，tan α＝m1－m 2；当α为第二、三象限角时，tan α＝－m1－m 2 .【点拨】给值求值的关键是找出已知式与待求式之间的联系及函数的差异．①一般可以适当变换已知式，求得另外函数式的值，以备应用；②变换待求式，便于将已知式求得的函数值代入，从而达到解题的目的．(1)设sin α2＝45，且α是第二象限角，则tan α2的值为________．解：因为α是第二象限角，所以α2是第一或第三象限角．①当α2是第一象限角时，有cos α2＝1－sin 2α2＝1－⎝⎛⎭⎫452＝35，所以tan α2＝sinα2cosα2＝43；②当α2是第三象限角时，与sin α2＝45矛盾，舍去．综上，tan α2＝43.故填43.(2)已知sin α－cos α＝2，α∈(0，π)，则tan α＝________. 解法一：由⎩⎨⎧sin α－cos α＝2，sin 2α＋cos 2α＝1，得2cos 2α＋22cos α＋1＝0，即(2cos α＋1)2＝0，所以cos α＝－22.又α∈(0，π)，所以α＝3π4，tan α＝tan 3π4＝－1.解法二：因为sin α－cos α＝2，所以(sin α－cos α)2＝2，得sin2α＝－1.因为α∈(0，π)，所以2α∈(0，2π)，2α＝3π2，所以α＝3π4，tan α＝－1.故填－1.类型二诱导公式的应用(1)(2016·全国卷Ⅰ)已知θ是第四象限角，且sin ⎝⎛⎭⎫θ＋π4＝35，则tan ⎝⎛⎭⎫θ－π4＝________. 解：由题意知，θ＋π4是第一象限角，得cos ⎝⎛⎭⎫θ＋π4＝45，根据同角三角函数关系式可得tan ⎝⎛⎭⎫θ＋π4＝34. 所以tan ⎝⎛⎭⎫θ－π4＝tan ⎝⎛⎭⎫θ＋π4－π2＝－1tan ⎝⎛⎭⎫θ＋π4＝－43.故填－43. (2)化简sin （2π－α）cos （π＋α）cos ()π2＋αcos ()11π2－αcos （π－α）sin （3π－α）sin （－π－α）sin ()9π2＋α. 解：原式＝（－sin α）（－cos α）（－sin α）（－sin α）（－cos α）·sin α·sin α·cos α＝－tan α. 【点拨】①三角式的化简通常先用诱导公式，将角度统一后再用同角三角函数关系式，这可以避免交错使用公式时导致的混乱．②在运用公式时正确判断符号至关重要．③三角函数的化简、求值是三角函数中的基本问题，也是高考常考的问题，要予以重视．④正确理解“奇变偶不变，符号看象限”可以提高解题效率．(1)化简sin 2(π＋α)－cos(π＋α)·cos(－α)＋1.解：原式＝sin 2α－(－cos α)·cos α＋1＝sin 2α＋cos 2α＋1＝2.(2)(2017·北京)在平面直角坐标系xOy 中，角α与角β均以Ox 为始边，它们的终边关于y 轴对称．若sin α＝13，则cos(α－β)＝________. 解：因为α和β的终边关于y 轴对称，所以α＋β＝π＋2k π，k ∈Z ，那么sin β＝sin α＝13，cos α＝－cos β，这样cos(α－β)＝cos αcos β＋sin αsin β＝－cos 2α＋sin 2α＝2sin 2α－1＝－79.故填－79.类型三关于sin α，cos α的齐次式问题已知tan αtan α－1＝－1，求下列各式的值．(1)sin α－3cos αsin α＋cos α； (2)sin 2α＋sin αcos α＋2.解：由已知得tan α＝12.(1)sin α－3cos αsin α＋cos α＝tan α－3tan α＋1＝－53.(2)sin 2α＋sin αcos α＋2＝sin 2α＋sin αcos αsin 2α＋cos 2α＋2＝tan 2α＋tan αtan 2α＋1＋2＝⎝⎛⎭⎫122＋12⎝⎛⎭⎫122＋1＋2＝135. 【点拨】(1)形如a sin α＋b cos α和a sin 2α＋b sin αcos α＋c cos 2α的式子分别称为关于sin α，cos α的一次齐次式和二次齐次式，对涉及它们的三角变换通常转化为正切(分子分母同除以cos α或cos 2α)求解．如果分母为1，可考虑将1写成sin 2α＋cos 2α.(2)已知tan α＝m 的条件下，求解关于sin α，cos α的齐次式问题，必须注意以下几点：①一定是关于sin α，cos α的齐次式(或能化为齐次式)的三角函数式．②因为cos α≠0，所以可以用cos n α(n ∈N *)除之，这样可以将被求式化为关于tan α的表示式，可整体代入tan α＝m 的值，从而完成被求式的求值运算．③注意1＝sin 2α＋cos 2α的运用．(荆州2017届质量检测)已知tan(5π－x )＝2，则2cos 2x2－sin x －1sin x ＋cos x＝________.解：tan(5π－x )＝2，即tan(π－x )＝2，得tan x ＝－2.又因为2cos 2x2－1＝cos x ，所以2cos 2x2－sin x －1sin x ＋cos x ＝cos x －sin x sin x ＋cos x＝1－tan x tan x ＋1＝－3.故填－3.1．诱导公式用角度制和弧度制表示都可，运用时应注意函数名称是否要改变以及正负号的选取．2．已知一个角的某一个三角函数值，求这个角的其他三角函数值，这类问题用同角三角函数的基本关系式求解，一般分为三种情况：(1)一个角的某一个三角函数值和这个角所在的象限或终边所在的位置都是已知的，此类情况只有一组解． (2)一个角的某一个三角函数值是已知的，但这个角所在的象限或终边所在的位置没有给出，解答这类问题，首先要根据已知的三角函数值确定这个角所在的象限或终边所在的位置，然后分不同的情况求解．(3)一个角的某一个三角函数值是用字母给出的，此类情况须对字母进行讨论，并注意适当选取分类标准，一般有两组解．3．计算、化简三角函数式常用技巧(1)减少不同名的三角函数，或化切为弦，或化弦为切，如涉及sin α，cos α的齐次分式问题，常采用分子分母同除以cos n α(n ∈N *)，这样可以将被求式化为关于tan α的式子． (2)巧用“1”进行变形，如1＝sin 2α＋cos 2α＝tan45°等． (3)平方关系式需开方时，应慎重考虑符号的选取．(4)熟悉sin α＋cos α，sin α－cos α，sin αcos α三者之间的内在联系，利用(sin α±cos α)2＝1±2sin αcos α进行和积转换，可知一求二．1．sin585°的值为( )A ．－22 B.22 C ．－32 D.32解：sin585°＝sin ()90°×6＋45°＝－sin45°＝－22.故选A .2．(福建四地六校2017届月考)已知cos ⎝⎛⎭⎫θ＋π2＝45，－π2＜θ＜π2，则sin2θ的值等于( ) A ．－2425 B.2425 C ．－1225 D.1225解：由cos ⎝⎛⎭⎫θ＋π2＝45，－π2＜θ＜π2，得sin θ＝－45，cos θ＝35，则sin2θ＝2sin θcos θ＝－2425.故选A . 3．(江西上饶2017届一模)已知sin ⎝⎛⎭⎫α－π12＝13，则cos ⎝⎛⎭⎫α＋17π12 的值等于( ) A.13 B.223 C ．－13 D ．－223解：由cos ⎝⎛⎭⎫α＋17π12＝cos ⎝⎛⎭⎫α－π12＋3π2＝sin ⎝⎛⎭⎫α－π12＝13.故选A . 4．(2016·全国卷Ⅲ)若tan α＝34，则cos 2α＋2sin2α＝( )A.6425B.4825 C ．1 D.1625解法一：cos 2α＋2sin2α＝cos 2α＋2sin2αsin 2α＋cos 2α＝1＋4tan α1＋tan 2α＝6425. 解法二：由tan α＝34，得sin α＝34cos α，sin α＝35，cos α＝45或sin α＝－35，cos α＝－45，所以cos 2α＋2sin2α＝1625＋4×1225＝6425.故选A .5．(2016·长春质检)已知tan α＝2，α为第一象限角，则sin2α＋cos α＝( )A. 5B.4＋255C.4＋55D.5－25解：由三角函数定义sin α＝255，cos α＝55，故sin2α＋cos α＝2sin αcos α＋cos α＝4＋55.故选C .6．(2016·淮南二模)已知sin α＋cos α＝12，α∈(0，π)，则1－tan α1＋tan α＝( )A ．－7 B.7 C. 3 D ．－3解：因为(sin α＋cos α)2＝1＋2sin αcos α＝14，所以sin αcos α＝－38，又α∈(0，π)，所以sin α>0，cos α<0.因为(sin α－cos α)2＝1－2sin αcos α＝74，所以cos α－sin α＝－72.所以1－tan α1＋tan α＝cos α－sin αcos α＋sin α＝－7212＝－7.故选A .7．(2016江苏冲刺卷)已知θ是第三象限角，且sin θ－2cos θ＝－25，则sin θ＋cos θ＝________.解：由平方关系得⎝⎛⎭⎫2cos θ－252＋cos 2θ＝1，且cos θ＜0，解得cos θ＝－725，从而sin θ＝－2425，故sin θ＋cos θ＝－3125.故填－3125.8．(2015·四川)已知sin α＋2cos α＝0，则2sin αcos α－cos 2α的值是________．解：因为sin α＋2cos α＝0，所以sin α＝－2cos α，由同角三角函数关系式得cos 2α＋4cos 2α＝1，所以cos 2α＝15，所以2sin αcos α－cos 2α＝－4cos 2α－cos 2α＝－5cos 2α＝－1.故填－1.9．已知sin(3π＋θ)＝13，求值：cos （π＋θ）cos θ[cos （π－θ）－1]＋cos （θ－2π）sin ⎝⎛⎭⎫θ－3π2cos （θ－π）－sin ⎝⎛⎭⎫3π2＋θ.解：因为sin(3π＋θ)＝－sin θ＝13，所以sin θ＝－13.所以原式＝－cos θcos θ（－cos θ－1）＋cos θcos θ·（－cos θ）＋cos θ＝11＋cos θ＋11－cos θ＝21－cos 2θ＝2sin 2θ ＝2⎝⎛⎭⎫－132＝18. 10．已知sin θ－cos θ＝12，求：(1)sin θcos θ； (2)sin 3θ－cos 3θ； (3)sin 4θ＋cos 4θ.解：(1)将sin θ－cos θ＝12两边平方得：1－2sin θcos θ＝14，sin θcos θ＝38.(2)sin 3θ－cos 3θ＝(sin θ－cos θ)(sin 2θ＋sin θcos θ＋cos 2θ)＝12×⎝⎛⎭⎫1＋38＝1116. (3)sin 4θ＋cos 4θ＝(sin 2θ＋cos 2θ)2－2sin 2θcos 2θ ＝1－2×⎝⎛⎭⎫382＝2332.11．(1)已知tan α＝3，求23sin 2α＋14cos 2α的值．(2)已知1tan α－1＝1，求11＋sin αcos α的值．解：(1)23sin 2α＋14cos 2α＝23sin 2α＋14cos 2αsin 2α＋cos 2α＝23tan 2α＋14tan 2α＋1＝23×32＋1432＋1＝58.(2)由1tan α－1＝1得tan α＝2，11＋sin αcos α＝sin 2α＋cos 2αsin 2α＋cos 2α＋sin αcos α＝tan 2α＋1tan 2α＋tan α＋1＝22＋122＋2＋1＝57. (黄冈2017届期末)已知函数y ＝sin(πx ＋φ)－2cos(πx ＋φ)(0<φ<π)的图象关于直线x ＝1对称，则sin2φ＝( ) A.35 B ．－35 C.45 D ．－45解：y ＝f (x )＝sin(πx ＋φ)－2cos(πx ＋φ)＝5sin(πx ＋φ－α)，其中sin α＝25，cos α＝15，因为函数的图象关于x ＝1对称，所以y ＝f (1)＝±5，即π＋φ－α＝π2＋k π，k ∈Z ，sin2φ＝sin2⎝⎛⎭⎫α－π2＋k π＝sin(2α－π＋2k π)＝sin(2α－π)＝－sin2α＝－2sin αcos α＝－2×25×15＝－45 .故选D .。

高考数学复习讲义：同角三角函数的基本关系与诱导公式

返回
3．已知 tanπ6－α＝ 33，则 tan56π＋α＝________. 解析：tan56π＋α＝tanπ－π6＋α＝tan[ π－( π6－α ) ] ＝－tanπ6－α＝－ 33.
答案：－
3 3
返回
研透高考·深化提能
1．利用诱导公式把任意角的三角函数转化为锐角三角函数的步骤
也就是：“负化正，大化小，化到锐角为终了．”
“切”的表达式，进行求值．常见的结构有：
①sin α，cos α的二次齐次式(如asin2α＋bsin αcos α＋
ccos2α)的问题常采用“切”代换法求解；
②sin
α，cos
α的齐次分式如acssiinn
α＋bcos α＋dcos
αα的问题常采
用分式的基本性质进行变形．
(2)切化弦：利用公式tan
返回
(2)已知－π2<α<0，sin α＋cos α＝15，则cos2α－1 sin2α＝(
)
7
25
A.5
B. 7
7
24
C.25
D.25
返回
[解析] ∵sin α＋cos α＝15，
∴1＋2sin αcos α＝215，
∴2sin αcos α＝－2245，(cos α－sin α)2＝1＋2245＝4295.
3
课时跟踪检测
返回
突破点一同角三角函数的基本关系
返回
抓牢双基·自学回扣
[基本知识]
1．同角三角函数的基本关系 (1)平方关系：sin2α＋cos2α＝1(α∈R ) ． (2)商数关系： tan α＝csions ααα≠kπ＋π2，k∈Z .
返回
2．同角三角函数基本关系式的应用技巧

同角三角函数的基本关系与诱导公式(教师版含答案)

第2讲同角三角函数的基本关系与诱导公式【2013年高考会这样考】考查利用诱导公式与同角三角函数关系化简三角函数式及求三角函数值．【复习指导】本节复习时应紧扣住三角函数的定义，理解同角三角函数关系式和诱导公式；观察分析这些公式特征，掌握记忆诀窍；通过基本题型，掌握解题规律．基础梳理1．同角三角函数的基本关系 (1)平方关系：sin 2α＋cos 2α＝1； (2)商数关系：sin αcos α＝tan α. 2．诱导公式公式一：sin(α＋2k π)＝sin α，cos(α＋2k π)＝cos_α，其中k ∈Z . 公式二：sin(π＋α)＝－sin_α，cos(π＋α)＝－cos_α， tan(π＋α)＝tan α.公式三：sin(－α)＝－sin_α，cos(－α)＝cos_α. 公式四：sin(π－α)＝sin α，cos(π－α)＝－cos_α. 公式五：sin ⎝ ⎛⎭⎪⎫π2－α＝cos_α，cos ⎝ ⎛⎭⎪⎫π2－α＝sin α. 公式六：sin ⎝ ⎛⎭⎪⎫π2＋α＝cos_α，cos ⎝ ⎛⎭⎪⎫π2＋α＝－sin_α.诱导公式可概括为k ·π2±α的各三角函数值的化简公式．记忆规律是：奇变偶不变，符号看象限．其中的奇、偶是指π2的奇数倍和偶数倍，变与不变是指函数名称的变化．若是奇数倍，则函数名称变为相应的余名函数；若是偶数倍，则函数名称不变，符号看象限是指把α看成锐角时原函数值的符号作为结果的符号．一个口诀诱导公式的记忆口诀为：奇变偶不变，符号看象限．三种方法在求值与化简时，常用方法有：(1)弦切互化法：主要利用公式tan α＝sin αcos α化成正、余弦．(2)和积转换法：利用(sin θ±cos θ)2＝1±2sin θcos θ的关系进行变形、转化． (3)巧用“1”的变换：1＝sin 2θ＋cos 2θ＝cos 2θ(1＋tan 2θ)＝tan π4＝…. 三个防范(1)利用诱导公式进行化简求值时，先利用公式化任意角的三角函数为锐角三角函数，其步骤：去负－脱周－化锐．特别注意函数名称和符号的确定．(2)在利用同角三角函数的平方关系时，若开方，要特别注意判断符号． (3)注意求值与化简后的结果一般要尽可能有理化、整式化．双基自测1．(人教A 版教材习题改编)已知sin(π＋α)＝12，则cos α的值为( )． A ．±12 B.12 C.32D ．±32解析 ∵sin(π＋α)＝－sin α＝12， ∴sin α＝－12.∴cos α＝±1－sin 2α＝±32. 答案 D2．(2011·杭州调研)点A (sin 2 011°，cos 2 011°)在直角坐标平面上位于( )． A ．第一象限 B ．第二象限 C ．第三象限D ．第四象限解析 2 011°＝360°×5＋(180°＋31°)，∴sin 2 011°＝sin[360°×5＋(180°＋31°)]＝－sin 31°＜0， cos 2 011°＝cos[360°×5＋(180°＋31°)]＝－cos 31°＜0， ∴点A 位于第三象限．答案 C3．已知cos α＝45，α∈(0，π)，则tan α的值等于( )． A.43 B.34 C ．±43D ．±34解析 ∵α∈(0，π)，∴sin α＝1－cos 2α＝35，∴tan α＝sin αcos α＝34. 答案 B4．cos ⎝ ⎛⎭⎪⎫－17π4－sin ⎝ ⎛⎭⎪⎫－17π4的值是( )．A. 2 B ．－ 2 C ．0 D.22解析 cos ⎝ ⎛⎭⎪⎫－17π4＝cos 17π4＝cos ⎝ ⎛⎭⎪⎫4π＋π4＝cos π4＝22，sin ⎝ ⎛⎭⎪⎫－17π4＝－sin 17π4＝－sin ⎝ ⎛⎭⎪⎫4π＋π4＝－sin π4＝－22.∴cos ⎝ ⎛⎭⎪⎫－17π4－sin ⎝ ⎛⎭⎪⎫－17π4＝22＋22＝ 2. 答案 A5．已知α是第二象限角，tan α＝－12，则cos α＝________.解析由题意知cos α＜0，又sin 2α＋cos 2α＝1，tan α＝sin αcos α＝－12.∴cos α＝－255. 答案－255考向一利用诱导公式化简、求值【例1】►已知f (α)＝sin (π－α)cos (2π－α)sin ⎝ ⎛⎭⎪⎫π2＋αtan (π＋α)，求f⎝ ⎛⎭⎪⎫31π3. [审题视点] 先化简f (α)，再代入求解．解 f (α)＝sin αcos αcos αtan α＝cos α，∴f ⎝ ⎛⎭⎪⎫31π3＝cos 313 π＝cos ⎝ ⎛⎭⎪⎫10π＋π3＝cos π3＝12.(1)化简是一种不指定答案的恒等变形，其结果要求项数尽可能少，次数尽可能低，结构尽可能简单，能求值的要求出值．(2)诱导公式的应用原则：负化正、大化小，化到锐角为终了． (3)化简前，注意分析角的结构特点，选择恰当的公式和化简顺序．【训练1】已知角α终边上一点P (－4,3)，则cos ⎝ ⎛⎭⎪⎫π2＋αsin (－π－α)cos ⎝ ⎛⎭⎪⎫11π2－αsin ⎝ ⎛⎭⎪⎫9π2＋α的值为________．解析原式＝(－sin α)sin α(－sin α)cos α＝tan α，根据三角函数的定义，得tan α＝y x ＝－34.答案－34考向二同角三角函数关系的应用【例2】►(2011·长沙调研)已知tan α＝2. 求：(1)2sin α－3cos α4sin α－9cos α；(2)4sin 2α－3sin αcos α－5cos 2α. [审题视点] (1)同除cos α；(2)利用1＝sin 2α＋cos 2α，把整式变为分式，再同除cos 2α. 解 (1)2sin α－3cos α4sin α－9cos α＝2tan α－34tan α－9＝2×2－34×2－9＝－1.(2)4sin 2α－3sin αcos α－5cos 2α＝4sin 2α－3sin αcos α－5cos 2αsin 2α＋cos 2α＝4tan 2α－3tan α－5tan 2α＋1＝4×4－3×2－54＋1＝1.(1)对于sin α＋cos α，sin αcos α，sin α－cos α这三个式子，已知其中一个式子的值，其余二式的值可求．转化的公式为(sin α±cos α)2＝1±2sin αcos α；(2)关于sin α，cos α的齐次式，往往化为关于tan α的式子．【训练2】 (2011·潍坊质检)已知sin α＋3cos α3cos α－sin α＝5.则sin 2α－sin αcos α＝________.解析依题意得：tan α＋33－tan α＝5，∴tan α＝2.∴sin 2α－sin αcos α＝sin 2α－sin αcos αsin 2α＋cos 2α＝tan 2α－tan αtan 2α＋1＝22－222＋1＝25.答案 25考向三三角恒等式的证明【例3】►求证：sin θ(1＋tan θ)＋cos θ⎝ ⎛⎭⎪⎫1＋1tan θ＝1sin θ＋1cos θ.[审题视点] 证明三角恒等式的原则是由繁到简，常用的方法有： ①从一边开始证明等于另一边，即化简左边，使左边＝右边； ②证明左、右等于同一个式子；③变更论证，即通过化除为乘、左右相减等转化成与原结论等价的式子．证明左边＝sin θ⎝ ⎛⎭⎪⎫1＋sin θcos θ＋cos θ⎝ ⎛⎭⎪⎫1＋cos θsin θ＝sin θ＋sin 2 θcos θ＋cos θ＋cos 2θsin θ ＝⎝ ⎛⎭⎪⎫sin θ＋cos 2θsin θ＋⎝ ⎛⎭⎪⎫cos θ＋sin 2θcos θ ＝sin 2 θ＋cos 2θsin θ＋cos 2θ＋sin 2 θcos θ＝1sin θ＋1cos θ＝右边．证明三角恒等式离不开三角函数的变换，在变换过程中，把正切函数化成正弦或余弦函数，减少函数种类，往往有利于发现等式两边的关系或使式子简化．要细心观察等式两边的差异，灵活运用学过的知识，使证明简便．【训练3】已知sin(α＋β)＝1，求证：tan(2α＋β)＋tan β＝0. 证明 ∵sin(α＋β)＝1，∴α＋β＝2k π＋π2(k ∈Z )， ∴α＝2k π＋π2－β，∴tan(2α＋β)＋tan β＝tan ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫2k π＋π2－β＋β＋tan β＝tan(4k π＋π－2β＋β)＋tan β ＝tan(4k π＋π－β)＋tan β＝tan(π－β)＋tan β＝－tan β＋tan β＝0，∴tan(2α＋β)＋tan β＝0得证.考向四三角形中的诱导公式【例4】►在△ABC 中，sin A ＋cos A ＝2，3cos A ＝－2cos(π－B )，求△ABC 的三个内角．[审题视点] 要求三角形的内角，需求得某一内角的某一三角函数值，故结合条件sin A ＋cos A ＝2知先求角A ，进而求其他角．解由已知可得2sin ⎝ ⎛⎭⎪⎫A ＋π4＝2，因为0＜A ＜π，所以A ＝π4.由已知可得3cos A ＝2cos B ，把A ＝π4代入可得cos B ＝32，又0＜B ＜π，从而B ＝π6，所以C ＝π－π4－π6＝7π12.在△ABC 中常用到以下结论：sin(A ＋B )＝sin(π－C )＝sin C ，cos(A ＋B )＝cos(π－C )＝－cos C ， tan(A ＋B )＝tan(π－C )＝－tan C ， sin ⎝ ⎛⎭⎪⎫A 2＋B 2＝sin ⎝ ⎛⎭⎪⎫π2－C 2＝cos C 2， cos ⎝ ⎛⎭⎪⎫A 2＋B 2＝cos ⎝ ⎛⎭⎪⎫π2－C 2＝sin C 2. 【训练4】若将例4的已知条件“sin A ＋cos A ＝2”改为“sin(2π－A )＝－2sin(π－B )”其余条件不变，求△ABC 的三个内角．解由条件得：－sin A ＝－2sin B ，即sin A ＝2sin B ， 3cos A ＝2cos B ，平方相加得：sin 2 A ＋3cos 2 A ＝2⇒2cos 2 A ＝1，cos A ＝±22.若cos A ＝－22，则cos B ＝－32，A ，B 均为钝角不可能．故cos A ＝22，cos B ＝32，故A ＝π4，B ＝π6，C ＝7π12.阅卷报告3——忽视题设的隐含条件致误【问题诊断】涉及到角的终边、函数符号和同角函数关系问题时，应深挖隐含条件，处理好开方、平方关系，避免出现增解与漏解的错误.【防范措施】一要考虑题设中的角的范围；二要考虑题设中的隐含条件. 【示例】►若sin θ，cos θ是关于x 的方程5x 2－x ＋a ＝0(a 是常数)的两根，θ∈(0，π)，求cos 2θ的值．错因产生了增解725.实录由题意知：sin θ＋cos θ＝15，∴()sin θ＋cos θ2＝125，∴sin 2θ＝－2425，∵θ∈(0，π)， ∴2θ∈(0,2π)，∴cos 2θ＝±1－2sin 2 2θ＝±725. 正解由题意知：sin θ＋cos θ＝15. ∴(sin θ＋cos θ)2＝125. ∴sin 2θ＝－2425.即2sin θcos θ＝－2425＜0，则sin θ与cos θ异号，又sin θ＋cos θ＝15＞0， ∴π2＜θ＜3π4，∴π＜2θ＜3π2. 故cos 2θ＝－1－sin 22θ＝－725. 【试一试】已知sin θ＋cos θ＝713，θ∈(0，π)，求tan θ. [尝试解答] ∵sin θ＋cos θ＝713，θ∈(0，π)． ∴(sin θ＋cos θ)2＝1＋2sin θcos θ＝49169.∴sin θcos θ＝－60 169.由根与系数的关系知sin θ，cos θ是方程x2－713x－60169＝0的两根，∴x1＝1213，x2＝－513，又sin θcos θ＝－60169＜0，∴sin θ＞0，cos θ＜0，∴sin θ＝1213，cos θ＝－513.∴tan θ＝sin θcos θ＝－125.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

高考数学课后作业 32 同角三角函数的基本关系及诱导公式新人教A 版1.(2011·武汉调研)若cos α＝35，－π2<α<0，则tan α＝( )A.43B.34 C ．－43 D ．－34 [答案] C[解析] 依题意得，sin α＝－45，tan α＝sin αcos α＝－43，选C.2．(2010·河北唐山)已知cos ⎝ ⎛⎭⎪⎫α－π4＝14，则sin2α＝( )A ．－ 78 B.78 C ．－ 3132 D.3132[答案] A[解析] sin2α＝cos ⎝ ⎛⎭⎪⎫π2－2α＝cos2⎝ ⎛⎭⎪⎫α－π4＝2cos 2⎝ ⎛⎭⎪⎫α－π4－1＝2×⎝ ⎛⎭⎪⎫142－1＝－78.3．(2010·福建省福州市)已知sin10°＝a ，则sin70°等于( ) A ．1－2a 2B ．1＋2a 2C ．1－a 2D ．a 2－1 [答案] A[解析] 由题意可知，sin70°＝cos20°＝1－2sin 210°＝1－2a 2，故选A. 4．(2011·天津模拟)若cos(2π－α)＝53且α∈(－π2，0)，则sin(π－α)＝( ) A ．－53 B ．－ 23 C ．－ 13 D ．±23[答案] B[解析] ∵cos(2π－α)＝53，∴cos α＝53， ∵α∈(－π2，0)，∴sin α＝－23，∴sin(π－α)＝sin α＝－23.5．(2011·杭州二检)若a ＝(32，sin α)，b ＝(cos α，13)，且a ∥b ，则锐角α＝( )A ．15°B ．30°C ．45°D ．60° [答案] C[解析] 依题意得32×13－sin αcos α＝0，即sin2α＝1.又α为锐角，故2α＝90°，α＝45°，选C.6．(2011·哈师大附中、东北师大附中、辽宁实验中学联考)已知cos α＝45，α∈(－π4，0)，则sin α＋cos α等于( )A.15 B ．－15 C ．－75 D.75 [答案] A[解析] 由于cos α＝45，α∈(－π4，0)，所以sin α＝－35，所以sin α＋cos α＝15，故选A.7．(2011·山东烟台模拟)若sin(π＋α)＝12，α∈(－π2，0)，则tan α＝________.[答案] －33[解析] 由已知得sin α＝－12，又α∈(－π2，0)，所以cos α＝1－sin 2α＝32，因此tan α＝sin αcos α＝－33.8．(文)(2010·苏北四市)设α是第三象限角，tan α＝512，则cos(π－α)＝________.[答案]1213[解析] ∵α为第三象限角，tan α＝512，∴cos α＝－1213，∴cos(π－α)＝－cos α＝1213.(理)(2010·浙江杭州质检)若sin ⎝ ⎛⎭⎪⎫3π2－2x ＝35，则tan 2x 等于________．[答案] 4[解析] sin ⎝⎛⎭⎪⎫3π2－2x ＝－cos2x ＝sin 2x －cos 2x ＝35，又sin 2x ＋cos 2x ＝1，∴⎩⎪⎨⎪⎧sin 2x ＝45cos 2x ＝15，∴tan 2x ＝sin 2xcos 2x＝4.1.(2010·新乡市模考)已知α∈⎝ ⎛⎭⎪⎫－π2，0，cos α＝45，则tan2α等于( ) A ．－ 247 B.247 C ．－ 724 D.724[答案] A[解析] ∵－π2<α<0，cos α＝45，∴sin α＝－1－cos 2α＝－35，∴tan α＝sin αcos α＝－34，∴tan2α＝2tan α1－tan 2α＝－247，故选A. 2．(2011·绵阳二诊)已知tan θ>1，且sin θ＋cos θ<0，则cos θ的取值范围是( ) A ．(－22，0) B ．(－1，－22) C ．(0，22) D ．(22，1) [答案] A[解析] 如图，依题意结合三角函数线进行分析可知，2k π＋5π4<θ<2k π＋3π2，k ∈Z ，因此－22<cos θ<0.选A.3．(2010·河南南阳调研)在△ABC 中，3sin A ＋4cos B ＝6,4sin B ＋3cos A ＝1，则C 等于( )A ．30°B ．150°C ．30°或150°D ．60°或120°[答案] A[解析] 两式平方后相加得sin(A ＋B )＝12，∴A ＋B ＝30°或150°，又∵3sin A ＝6－4cos B >2，∴sin A >23>12，∴A >30°，∴A ＋B ＝150°，此时C ＝30°.4．(文)(2011·湖北联考)已知tan x ＝sin(x ＋π2)，则sin x ＝( )A.－1±52 B.3＋12 C.5－12 D.3－12[答案] C[解析] ∵tan x ＝sin(x ＋π2)，∴tan x ＝cos x ，∴sin x ＝cos 2x ，∴sin 2x ＋sin x －1＝0，解得sin x ＝－1±52，∵－1≤sin x ≤1，∴sin x ＝5－12.故选C. (理)(2011·重庆诊断)已知2tan α·sin α＝3，－π2<α<0，则cos ⎝ ⎛⎭⎪⎫α－π6的值是( ) A ．0 B.32 C ．1 D.12[答案] A[解析] ∵2tan αsin α＝3，∴2sin 2αcos α＝3，即21－cos 2αcos α＝3，∴2cos 2α＋3cos α－2＝0， ∵|cos α|≤1，∴cos α＝12，∵－π2<α<0，∴sin α＝－32，∴cos ⎝⎛⎭⎪⎫α－π6＝cos αcos π6＋sin αsin π6＝12×32－32×12＝0.5．(2011·盐城模拟)已知cos(5π12＋α)＝13，且－π<α<－π2，则cos(π12－α)＝________.[答案] － 223[解析] ∵－π<α<－π2，∴－7π12<5π12＋α<－π12，∵cos(5π12＋α)＝13，∴sin(5π12＋α)＝－223，∴cos(π12－α)＝cos[π2－(5π12＋α)]＝sin(5π12＋α)＝－223.6．(文)设a ＝12cos16°－32sin16°，b ＝2tan14°1＋tan 214°，c ＝1－cos50°2，则a 、b 、c 的大小关系为________(从小到大排列)．[答案] a <c <b[解析] a ＝sin14°，b ＝2sin14°cos14°cos 214°＋sin 214°＝sin28°，c ＝sin25°， ∵y ＝sin x 在(0°，90°)上单调递增，∴a <c <b .(理)(2011·江西上饶四校联考)对任意的a ∈(－∞，0)，总存在x 0使得a cos x ＋a ≥0成立，则sin(2x 0－π6)的值为________．[答案] －12[解析] 若对任意的a ∈(－∞，0)，总存在x 0使得a cos x ＋a ≥0成立，则cos x 0＋1≤0，又cos x 0＋1≥0，即cos x 0＋1＝0，所以cos x 0＝－1，则x 0＝2k π＋π(k ∈Z)，所以sin(2x 0－π6)＝sin(4k π＋2π－π6)＝sin(－π6)＝－sin π6＝－12.7．(文)在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，且tan A ＝12，cos B ＝31010.(1)求tan C 的值；(2)若△ABC 最长的边为1，求b . [解析] (1)∵cos B ＝31010>0，∴B 为锐角，sin B ＝1－cos 2B ＝1010∴tan B ＝sin B cos B ＝13.∴tan C ＝tan[π－(A ＋B )]＝－tan(A ＋B ) ＝－tan A ＋tan B1－tan A ·tan B ＝－12＋131－12·13＝－1.(2)由(1)知C 为钝角，所以C 是最大角，所以最大边为c ＝1 ∵tan C ＝－1，∴C ＝135°，∴sin C ＝22. 由正弦定理：b sin B ＝csin C得，b ＝c sin B sin C＝1·101022＝55. (理)(2010·南充市模拟)已知三点：A (4,0)，B (0,4)，C (3cos α，3sin α)． (1)若α∈(－π，0)，且|AC →|＝|BC →|，求角α的值； (2)若AC →·BC →＝0，求2sin 2α＋sin2α1＋tan α的值．[解析] (1)由题得AC →＝(3cos α－4,3sin α)，BC →＝(3cos α，3sin α－4) 由|AC →|＝|BC →|得，(3cos α－4)2＋9sin 2α＝9cos 2α＋(3sin α－4)2⇒sin α＝cos α∵α∈(－π，0)，∴α＝－3π4. (2)由AC →·BC →＝0得，3cos α(3cos α－4)＋3sin α(3sin α－4)＝0，解得sin α＋cos α＝34，两边平方得2sin αcos α＝－716∴2sin 2α＋sin2α1＋tan α＝2sin 2α＋2sin αcos α1＋sin αcos α＝2sin αcos α＝－716.8．(文)(2010·北京东城区模拟)已知向量a ＝(cos α，1)，b ＝(－2，sin α)，α∈⎝ ⎛⎭⎪⎫π，3π2，且a ⊥b . (1)求sin α的值； (2)求tan ⎝⎛⎭⎪⎫α＋π4的值．[解析] (1)∵a ＝(cos α，1)，b ＝(－2，sin α)，且a ⊥b . ∴a ·b ＝(cos α，1)·(－2，sin α)＝－2cos α＋sin α＝0. ∴cos α＝12sin α.∵sin 2α＋cos 2α＝1，∴sin 2α＝45.∵α∈⎝ ⎛⎭⎪⎫π，3π2，∴sin α＝－255. (2)由(1)可得cos α＝－55，则tan α＝2. tan ⎝⎛⎭⎪⎫α＋π4＝tan α＋11－tan α＝－3. (理)已知向量m ＝(－1，cos ωx ＋3sin ωx )，n ＝(f (x )，cos ωx )，其中ω>0，且m ⊥n ，又函数f (x )的图象任意两相邻对称轴间距为32π.(1)求ω的值；(2)设α是第一象限角，且f ⎝ ⎛⎭⎪⎫32α＋π2＝2326，求sin ⎝ ⎛⎭⎪⎫α＋π4cos 4π＋2α的值．[解析] (1)由题意得m ·n ＝0，所以，f (x )＝cos ωx ·(cos ωx ＋3sin ωx )＝1＋cos2ωx 2＋3sin2ωx 2＝sin ⎝⎛⎭⎪⎫2ωx ＋π6＋12，根据题意知，函数f (x )的最小正周期为3π. 又ω>0，所以ω＝13.(2)由(1)知f (x )＝sin ⎝ ⎛⎭⎪⎫23x ＋π6＋12.所以f ⎝ ⎛⎭⎪⎫32α＋π2＝sin ⎝⎛⎭⎪⎫α＋π2＋12＝cos α＋12＝2326，解得cos α＝513，因为α是第一象限角，故sin α＝1213，所以，sin ⎝ ⎛⎭⎪⎫α＋π4cos 4π＋2α＝sin ⎝⎛⎭⎪⎫α＋π4cos2α＝22sin α＋cos αcos 2α－sin 2α ＝22·1cos α－sin α＝－13214.1．(2010·重庆一中)在△ABC 中，角A 、B 、C 的对边分别是a 、b 、c ，且∠A ＝2∠B ，则sin Bsin3B等于( ) A.b c B.c b C.b a D.a c[答案] A[解析] ∵A ＝2B ，∴sin B sin3B ＝sin Bsin A ＋B＝sin B sin π－C ＝sin B sin C ＝bc.2．(2010·安徽铜陵一中)在△ABC 中，内角A 、B 、C 的对边分别为a 、b 、c ，已知a 、b 、c 成等比数列，且a ＋c ＝3，tan B ＝73，则△ABC 的面积为( ) A.74 B.54 C.72 D.52[答案] A[解析] ∵a 、b 、c 成等比数列，∴b 2＝ac ， ∵tan B ＝73，∴sin B ＝74，cos B ＝34， ∵a ＋c ＝3，b 2＝a 2＋c 2－2ac cos B ，∴ac ＝2， ∴S △ABC ＝12ac sin B ＝74.3．(2011·石家庄质检)已知x ∈(π2，π)，cos2x ＝a ，则cos x ＝( )A.1－a2B ．－1－a2 C.1＋a2D ．－1＋a2[答案] D[解析] a ＝cos2x ＝2cos 2x －1， ∵x ∈(π2，π)，∴cos x <0，∴cos x ＝－a ＋12.4．(2010·北京东城区)函数y ＝1－2sin 2⎝ ⎛⎭⎪⎫x －π4是( ) A ．最小正周期为π的偶函数 B ．最小正周期为π的奇函数 C ．最小正周期为π2的偶函数D ．最小正周期为π2的奇函数[答案] B[解析] y ＝1－2sin 2⎝ ⎛⎭⎪⎫x －π4＝cos2⎝ ⎛⎭⎪⎫x －π4 ＝cos ⎝⎛⎭⎪⎫2x －π2＝sin2x 为奇函数且周期T ＝π.5．已知sin ⎝ ⎛⎭⎪⎫π6－α＝14，则sin ⎝ ⎛⎭⎪⎫π6＋2α＝______. [答案] 78[解析] sin ⎝ ⎛⎭⎪⎫π6＋2α＝cos ⎝ ⎛⎭⎪⎫π2－π6－2α ＝c os ⎝ ⎛⎭⎪⎫π3－2α＝1－2sin 2⎝ ⎛⎭⎪⎫π6－α＝78.6．(2010·浙江宁波十校)若sin76°＝m ，则cos7°＝______. [答案]2m ＋22[解析] ∵sin76°＝m ，∴cos14°＝m ，即2cos 27°－1＝m ，∴cos7°＝2＋2m2. 7．已知函数f (x )＝⎩⎪⎨⎪⎧2cos π3x x ≤2000x －102 x >2000，则f [f (2012)]＝________.[答案] －1[解析] 由f (x )＝⎩⎪⎨⎪⎧2cos π3x x ≤2000x －102 x >2000得，f (2012)＝2012－102＝1910，f (1910)＝2cos ⎝ ⎛⎭⎪⎫π3×1910＝2cos(636π＋2π3)＝2cos 2π3＝－1，故f [f (2012)]＝－1.。

高考数学 课后作业 32 同角三角函数的基本关系及诱导公式 新人教A版

高考复习数学第二节 同角三角函数的基本关系与诱导公式

高考数学专题《同角三角函数的基本关系与诱导公式》习题含答案解析

同角三角函数基本关系式及诱导公式(3种核心题型)(学生版) 2025年高考数学大一轮复习(新高考版)

4.2 同角三角函数的基本关系及诱导公式

高考数学一轮复习第四章三角函数解三角形2同角三角函数的基本关系及诱导公式课件新人教A版(理)

高考数学(人教a版,理科)题库：同角三角函数的基本关系与诱导公式(含答案)

高三数学同角三角函数的基本关系式和诱导公式试题答案及解析

高一三角函数公式及诱导公式习题(附答案)

三角函数的基本关系及诱导公式

【高考调研】高考数学总复习 4-2 同角三角函数的基本关系式及诱导公式配套课件 理 新人教A版

2020高考数学 课后作业 4-2 同角三角函数的基本关系及诱导公式

高考数学复习同角三角函数的基本关系与诱导公式

高考数学一轮复习专题训练—同角三角函数的基本关系式与诱导公式

三角函数的基本关系及诱导公式

高三数学一轮(基础知识+小题全取+考点通关+课时检测)3.2同角三角函数的基本关系与诱导公式课件 新人教A版

高三数学 同角三角函数的基本关系与诱导公式复习课件 新人教A版

高三数学同角三角函数的基本关系式和诱导公式试题答案及解析

高三数学考点-同角三角函数的基本关系及诱导公式

高考数学复习讲义：同角三角函数的基本关系与诱导公式

同角三角函数的基本关系与诱导公式(教师版含答案)

高考数学课后作业 32 同角三角函数的基本关系及诱导公式新人教A版

高考复习数学第二节同角三角函数的基本关系与诱导公式

【高考调研】高考数学总复习 4-2 同角三角函数的基本关系式及诱导公式配套课件理新人教A版

2020高考数学课后作业 4-2 同角三角函数的基本关系及诱导公式

高三数学一轮(基础知识+小题全取+考点通关+课时检测)3.2同角三角函数的基本关系与诱导公式课件新人教A版

高三数学同角三角函数的基本关系与诱导公式复习课件新人教A版