大物答案8
大物课后习题 答案

1-3 一质点在xOy 平面上运动,运动方程为x =3t +5, y =21t 2+3t -4.式中t 以 s 计,x ,y 以m 计.(1)以时间t 为变量,写出质点位置矢量的表示式;(2)求出t =1 s 时刻和t =2s 时刻的位置矢量,计算这1秒内质点的位移;(3)计算t =0 s 时刻到t =4s 时刻内的平均速度;(4)求出质点速度矢量表示式,计算t =4 s 时质点的速度;(5)计算t =0s 到t =4s 内质点的平均加速度;(6)求出质点加速度矢量的表示式,计算t =4s 时质点的加速度(请把位置矢量、位移、平均速度、瞬时速度、平均加速度、瞬时加速度都表示成直角坐标系中的矢量式).解:(1) j t t i t r)4321()53(2-+++=m (4) 1s m )3(3d d -⋅++==j t i tr v则 j i v734+= 1s m -⋅(6) 2s m 1d d -⋅==j tv a这说明该点只有y 方向的加速度,且为恒量。
1-4 在离水面高h 米的岸上,有人用绳子拉船靠岸,船在离岸S 处,如题1-4图所示.当人以0v (m ·1-s)的速率收绳时,试求船运动的速度和加速度的大小.图1-4解: 设人到船之间绳的长度为l ,此时绳与水面成θ角,由图可知 222s h l +=将上式对时间t 求导,得ts stl ld d 2d d 2= 题1-4图根据速度的定义,并注意到l ,s 是随t 减少的, ∴ ts v v tl v d d ,d d 0-==-=船绳即 θcos d d d d 00v v sl tl s l ts v ==-=-=船或 sv s h slv v 02/1220)(+==船将船v 再对t 求导,即得船的加速度32022222002)(d d d d d d sv h sv sls v slv s v v st s l tl s tv a =+-=+-=-==船船1-6 已知一质点作直线运动,其加速度为 a =4+3t 2s m -⋅,开始运动时,x =5 m , v =0,求该质点在t =10s 时的速度和位置. 解:∵ t tv a 34d d +==分离变量,得 t t v d )34(d += 积分,得12234c t t v ++=由题知,0=t ,00=v ,∴01=c 故 2234t t v += 又因为 2234d d t t tx v +==分离变量, t t t x d )234(d 2+=积分得 232212c t t x ++=由题知 0=t ,50=x ,∴52=c 故 521232++=t t x所以s 10=t 时m70551021102sm 190102310432101210=+⨯+⨯=⋅=⨯+⨯=-x v1-8 质点沿半径为R 的圆周按s =2021bt t v -的规律运动,式中s 为质点离圆周上某点的弧长,0v ,b 都是常量,求:(1)t 时刻质点的加速度;(2) t 为何值时,加速度在数值上等于b . 解:(1) bt v ts v -==0d dRbt v Rva b t v a n 202)(d d -==-==τ则 240222)(Rbt v b aa a n-+=+=τ加速度与半径的夹角为20)(arctanbt v Rb a a n--==τϕ(2)由题意应有2402)(Rbt v b b a -+==即 0)(,)(4024022=-⇒-+=bt v Rbt v b b∴当bv t 0=时,b a =1-10 以初速度0v =201s m -⋅抛出一小球,抛出方向与水平面成幔 60°的夹角,求:(1)球轨道最高点的曲率半径1R ;(2)落地处的曲率半径2R . (提示:利用曲率半径与法向加速度之间的关系)解:设小球所作抛物线轨道如题1-10图所示.题1-10图(1)在最高点,o0160cos v v v x == 21sm 10-⋅==g a n又∵ 1211ρv a n =∴m1010)60cos 20(22111=︒⨯==n a v ρ(2)在落地点,2002==v v 1sm -⋅,而 o60cos 2⨯=g a n ∴ m 8060cos 10)20(22222=︒⨯==n a v ρ2-3 283166-⋅===sm m f a x x2167-⋅-==s m mf a y y(1)⎰⎰--⋅-=⨯-=+=⋅-=⨯+-=+=2101200872167452832sm dt a v v s m dt a v v y y y x x x于是质点在2s 时的速度18745-⋅--=sm ji v(2) mji j i jt a i t a t v r y x 874134)167(21)4832122(21)21(220--=⨯-+⨯⨯+⨯-=++= 2-4 (1)∵dtdv mkv a =-=分离变量,得m kdt v dv -=即⎰⎰-=vv tmkdt v dv 0mkt ev v -=ln ln∴ tmk e v v -=0(2)⎰⎰---===tttmk mk ekmv dt ev vdtx 000)1((3)质点停止运动时速度为零,即t →∞, 故有⎰∞-=='000kmv dt ev x tmk(4)当t=km 时,其速度为ev ev ev v km m k 0100===-⋅-即速度减至v 0的e1.2-7由题知,小球落地时间为0.5s .因小球为平抛运动,故小球落地的瞬时向下的速度大小为v 1=gt=0.5g ,小球上跳速度的大小亦为v 2=0.5g .设向上为y 轴正向,则动量的增量 Δp=mv 2-mv 1 方向竖直向上,大小 |Δp |=mv 2-(-mv 1)=mg碰撞过程中动量不守恒.这是因为在碰撞过程中,小球受到地面给予的冲力作用.另外,碰撞前初动量方向斜向下,碰后末动量方向斜向上,这也说明动量不守恒. 2-12 (1)由题知,F 合为恒力,∴ A 合=F ·r=(7i-6j)·(-3i+4j+16k)=-21-24=-45 J (2)w tA N 756.045==∆=(3)由动能定理,ΔE k =A=-45 J2-15 弹簧A 、B 及重物C 受力如题2-15图所示平衡时,有题2-15图 F A =F B =Mg 又 F A =k 1Δx 1 F B =k 2Δx 2所以静止时两弹簧伸长量之比为 1221k k x x =∆∆弹性势能之比为12222211121212k k x k x k E E p p=∆∆=2-20 两小球碰撞过程中,机械能守恒,有222120212121mv mv mv +=即 222120v v v += ①3-7 观测者甲乙分别静止于两个惯性参考系S 和S '中,甲测得在同一地点发生的两事件的时间间隔为 4s ,而乙测得这两个事件的时间间隔为 5s .求: (1) S '相对于S 的运动速度.(2)乙测得这两个事件发生的地点间的距离.解: 甲测得0,s 4==x t ∆∆,乙测得s 5=t ∆,坐标差为12x x x '-'='∆′ (1)∴ t cv tx cv t t ∆-∆=∆+∆='∆22)(11)(λγ54122='∆∆=-t t cv解出 c c t t c v 53)54(1)(122=-='∆∆-=8108.1⨯= 1s m -⋅(2) ()0,45,=∆=∆'∆=∆-∆='∆x tt t v x x γγ∴ m 1093453458⨯-=-=⨯⨯-=-='c c t v x ∆γ∆负号表示012<'-'x x . 3-8 一宇航员要到离地球为5光年的星球去旅行.如果宇航员希望把这路程缩短为3光年,则他所乘的火箭相对于地球的速度是多少? 解: 2220153,1513βββ-=-=-=='则l l∴ c c v 542591=-=3-11 根据天文观测和推算,宇宙正在膨胀,太空中的天体都远离我们而去.假定地球上观察到一颗脉冲星(发出周期无线电波的星)的脉冲周期为 0.50s ,且这颗星正沿观察方向以速度0.8c 离我们而去.问这颗星的固有周期为多少?解: 以脉冲星为S '系,0='∆x ,固有周期0τ='∆t .地球为S 系,则有运动时t t '∆=∆γ1,这里1t ∆不是地球上某点观测到的周期,而是以地球为参考系的两异地钟读数之差.还要考虑因飞行远离信号的传递时间,ct v 1∆∴ t cv t c t v t t ∆+'∆=∆+∆=∆γγ11′)1(cv t +'=∆γ6.01)8.0(112=-=c c γ则 γλτ)8.01(5.0)1(0c c cv t t +++∆='∆=s 1666.08.13.06.01)8.01(5.0==+=3-16 静止在S 系中的观测者测得一光子沿与x 轴成︒60角的方向飞行.另一观测者静止于S ′系,S ′系的x '轴与x 轴一致,并以0.6c 的速度沿x 方向运动.试问S ′系中的观测者观测到的光子运动方向如何? 解: S 系中光子运动速度的分量为c c v x 500.060cos ο==c c v y 866.060sin ο==由速度变换公式,光子在S '系中的速度分量为c ccc c c v cu u v v xx x143.05.06.016.05.0122-=⨯--=--='c ccc c v cu v cu v xyy 990.05.06.01866.06.011122222=⨯-⨯-=--='光子运动方向与x '轴的夹角θ'满足692.0tan -=''='xy v v θθ'在第二象限为ο2.98='θ在S '系中,光子的运动速度为c v v v y x='+'='22 正是光速不变. 3-17 (1)如果将电子由静止加速到速率为0.1c ,须对它作多少功?(2)如果将电子由速率为0.8c 加速到0.9c ,又须对它作多少功?解: (1)对电子作的功,等于电子动能的增量,得)111()1(222020202--=-=-==cv c m c m cm mcE E k k γ∆)11.011()103(101.922831--⨯⨯⨯=-161012.4-⨯=J=eV 1057.23⨯(2) )()(2021202212c m c m c m c m E E E k k k---=-='∆)1111(221222202122cv cv c m cm c m ---=-=))8.0119.011(103101.92216231---⨯⨯⨯=-J 1014.514-⨯=eV 1021.35⨯=4-2 劲度系数为1k 和2k 的两根弹簧,与质量为m 的小球按题4-2图所示的两种方式连 接,试证明它们的振动均为谐振动,并分别求出它们的振动周期.题4-2图解:(1)图(a)中为串联弹簧,对于轻弹簧在任一时刻应有21F F F ==,设串联弹簧的等效倔强系数为串K 等效位移为x ,则有111x k F x k F -=-=串222x k F -=又有 21x x x +=2211k F k F k F x +==串所以串联弹簧的等效倔强系数为2121k k k k k +=串即小球与串联弹簧构成了一个等效倔强系数为)/(2121k k k k k +=的弹簧振子系统,故小球作谐振动.其振动周期为2121)(222k k k k m k m T +===ππωπ串(2)图(b)中可等效为并联弹簧,同上理,应有21F F F ==,即21x x x ==,设并联弹簧的倔强系数为并k ,则有2211x k x k x k +=并故 21k k k +=并 同上理,其振动周期为212k k m T +='π4-5 一个沿x 轴作简谐振动的弹簧振子,振幅为A ,周期为T ,其振动方程用余弦函数表示.如果0=t 时质点的状态分别是:(1)A x -=0;(2)过平衡位置向正向运动; (3)过2A x =处向负向运动; (4)过2A x -=处向正向运动.试求出相应的初位相,并写出振动方程. 解:因为 ⎩⎨⎧-==000sin cos φωφA v A x将以上初值条件代入上式,使两式同时成立之值即为该条件下的初位相.故有)2cos(1πππφ+==t TA x)232cos(232πππφ+==t T A x)32cos(33πππφ+==t TA x)452cos(454πππφ+==t TA x4-7 有一轻弹簧,下面悬挂质量为g 0.1的物体时,伸长为cm 9.4.用这个弹簧和一个质量为g 0.8的小球构成弹簧振子,将小球由平衡位置向下拉开cm 0.1后 ,给予向上的初速度10scm 0.5-⋅=v ,求振动周期和振动表达式.解:由题知 12311mN 2.0109.48.9100.1---⋅=⨯⨯⨯==x g m k而0=t 时,-12020s m 100.5m,100.1⋅⨯=⨯-=--v x ( 设向上为正)又 s 26.12,51082.03===⨯==-ωπωT mk 即m102)5100.5()100.1()(22222220---⨯=⨯+⨯=+=∴ωv x A45,15100.1100.5tan 022000πφωφ==⨯⨯⨯=-=--即x v∴ m )455cos(1022π+⨯=-t x4-8 图为两个谐振动的t x -曲线,试分别写出其谐振动方程.题4-8图解:由题4-8图(a),∵0=t 时,s 2,cm 10,,23,0,0000===∴>=T A v x 又πφ即 1s rad 2-⋅==ππωT故 m )23cos(1.0ππ+=t x a由题4-8图(b)∵0=t 时,35,0,2000πφ=∴>=v A x01=t 时,22,0,0111ππφ+=∴<=v x又 ππωφ253511=+⨯=∴ πω65=故 m t x b )3565cos(1.0ππ+=4-12 试用最简单的方法求出下列两组谐振动合成后所得合振动的振幅:(1) ⎪⎩⎪⎨⎧+=+=cm )373cos(5cm )33cos(521ππt x t x (2)⎪⎩⎪⎨⎧+=+=cm)343cos(5cm )33cos(521ππt x t x 解: (1)∵ ,233712πππφφφ=-=-=∆∴合振幅 cm 1021=+=A A A (2)∵ ,334πππφ=-=∆∴合振幅 0=A4-13 一质点同时参与两个在同一直线上的简谐振动,振动方程为⎪⎩⎪⎨⎧-=+=m)652cos(3.0m )62cos(4.021ππt x t x 试分别用旋转矢量法和振动合成法求合振动的振动幅和初相,并写出谐振方程。
华理大物实验标准答案(误差与有效数字,基本测量)

1 / 6误差与有效数字练习题答案1.1.有甲、有甲、乙、丙、丁四人,用螺旋测微计测量一个铜球的直径,各人所得的结果表达如下:d 甲 =(1.2832±0.00030.0003))cm ,d 乙 =(1.2831.283±±0.00030.0003))cm ,d 丙 =(1.281.28±±0.00030.0003))cm ,d 丁 =(1.31.3±±0.00030.0003))cm ,问哪个人表达得正确?其他人错在哪里?问哪个人表达得正确?其他人错在哪里?答:甲对。
其他人测量结果的最后位未与不确定度所在位对齐。
2.一学生用精密天平称一物体的质量m ,数据如下表所示,数据如下表所示 : Δ仪 =0.0002g 次数次数次数 1 2 3 4 5 6m /g 3.61243.61273.61223.61213.61203.6125请计算这一测量的算术平均值,测量标准误差及相对误差,写出结果表达式。
3.61232im m g nS ==A 类分量: ()()()20.683-1 1.110.0001080.000120-1i m mS t n g n n S =-=´=B 类分量:0.6830.6830.00020.00u g =D =´=仪合成不确定度:22220.001200.0001370.000182U S u g =+=+==0.00018g取0.00018g ,测量结果为:,测量结果为:(3.612320.00018)m U g ±=±( P=0.683 ) 相对误差相对误差:: 0.000180.005%3.61232U E m === 3.3.用米尺测量一物体的长度,测得的数值为用米尺测量一物体的长度,测得的数值为 次数次数次数 1 2 3 4 5 678 9 10 L /cm 98.98 98.94 98.96 98.97 99.00 98.95 98.9798.9698.9898.94试求其算术平均值,试求其算术平均值,A A 类不确定度、类不确定度、B B 类不确定度、合成不确定度及相对误差,写出结果表达式。
大物习题册答案及详解(山东理工大学大二上学期2020版)

4.如图所示,一点电荷q位于正立方体的A角上,则通过侧面abcd的电通量Φe=q/24ε0
考点: 高斯定理公式 (课本118页 6-18) 解法:1.建立一正方体高斯面(补7个如图正方体),使A点位于正中心
考点:电势是一个与引进电荷无关,完全由电场自身的性质和相对位置决定的物理量。电场中某点电势的大小与零 电势点的选取有关。
2.在边长为a的正方体中心处放置一电量为Q的点电荷,设无穷远处为电势零点,则在一个侧面的中心处的电势为
(B)
(A)Q/4πε0a
(B)Q/2πε0a
(C)Q/πε0a
(D)Q/2√2πε0a
q/(1/r-1/r0)/4πε0
考点:电势的计算
解法:U=∫
r0 r
E·dr
=∫
r0 qdr r 4πε0r
2
=q/(1/r-1/r0)/4πε0
(课本122页
6-29b)
பைடு நூலகம்
3.一质量为m、电量为q的小球,在电_场__力__作__用下,从电势为U的a点移动到电势为零的b点,若已知小球在b点的 速率为Vb,则小球在a点的速率Va=√Vb2-2qU/m
②均匀带电球面内的电势UP2=Q/4πε0R(课本123页例6-8结论得), ③UP=UP1+UP2.
6.在带电量为-Q的点电荷A的静电场中,将另一带电量为q的点电荷B从a点移到b点,a、b两点距离点电荷A的距 离分别为r1和r2,如图所示,则移动过程中电场力做的功为(C) (A)-Q(1/r1-1/r2)/4πε0 (B)qQ(1/r1-1/r2)/4πε0 (C)-qQ(1/r1-1/r2)/4πε0 (D)-qQ/4πε0(r2-r1) 考点:电场力的功 解法:Aeab=q(UA-UB)=q(-Q/4πε0r1— -Q/4πε0r2)=-qQ(1/r1-1/r2)/4πε0 (课本123页 6-31)
大物b课后题08-第八章电磁感应电磁场

习题8-6 一根无限长直导线有交变电流0sin i I t ω=,它旁边有一与它共面的矩形线圈ABCD ,如图所示,长为l 的AB 和CD 两边与直导向平行,它们到直导线的距离分别为a 和b ,试求矩形线圈所围面积的磁通量,以及线圈中的感应电动势。
解 建立如图所示的坐标系,在矩形平面上取一矩形面元dS ldx =,载流长直导线的磁场穿过该面元的磁通量为02m id B dS ldx xμφπ=⋅=通过矩形面积CDEF 的总磁通量为0000ln ln sin 222bm ai il I l b bldx t x a aμμμφωπππ===⎰由法拉第电磁感应定律有00ln cos 2m d I l bt dt aφμωεωπ=-=- 8-7 有一无限长直螺线管,单位长度上线圈的匝数为n ,在管的中心放置一绕了N 圈,半径为r 的圆形小线圈,其轴线与螺线管的轴线平行,设螺线管内电流变化率为dI dt,球小线圈中感应的电动势。
解 无限长直螺线管内部的磁场为0B nI μ=通过N 匝圆形小线圈的磁通量为20m NBS N nI r φμπ==由法拉第电磁感应定律有20m d dIN n r dt dtφεμπ=-=- 8-8 一面积为S 的小线圈在一单位长度线圈匝数为n ,通过电流为i 的长螺线管内,并与螺线管共轴,若0sin i i t ω=,求小线圈中感生电动势的表达式。
解 通过小线圈的磁通量为0m BS niS φμ==由法拉第电磁感应定律有000cos m d dinS nSi t dt dtφεμμωω=-=-=- 8-9 如图所示,矩形线圈ABCD 放在16.010B T -=⨯的均匀磁场中,磁场方向与线圈平面的法线方向之间的夹角为60α=︒,长为0.20m 的AB 边可左右滑动。
若令AB 边以速率15.0v m s -=•向右运动,试求线圈中感应电动势的大小及感应电流的方向。
解 利用动生电动势公式0.20()50.6sin(60)0.30()2B Av B dl dl V πε=⨯•=⨯⨯-︒=⎰⎰感应电流的方向从A B →.8-10 如图所示,两段导体AB 和BC 的长度均为10cm ,它们在B 处相接成角30︒;磁场方向垂直于纸面向里,其大小为22.510B T -=⨯。
大物解答题及其答案

热学部分:1.等(定)压摩尔热容和等(定)容摩尔热容的物理含义是什么?它们分别取决于哪些因素?答:1mol物质在等压过程中温度升高1K时所吸收的热量称为等压摩尔热容,同理,1mol物质在等容过程中温度升高1K时所吸收的热量称为等容摩尔热容。
理想气体的等压摩尔热容和等容摩尔热容只与气体分子的自由度有关。
2.理想气体等压过程的特征是什么?在此过程中热量、作功和内能如何表示?答:理想气体的等压过程的特征是压强为恒量,改变温度;热量、内能和功都在变化。
且热量:内能增量:气体对外作的功:3.理想气体等容过程的特征是什么?在此过程中热量、作功和内能如何表示?答:理想气体等容过程的特征是,体积为恒量,改变温度;对外作功为零,热量等于内能的增量。
热量和内能增量:气体对外作的功:4.理想气体等温过程的特征是什么?在此过程中热量、作功和内能如何表示?答:理想气体等温过程的特征是温度是恒量,改变压强;内能变化为0.系统吸收的热量等于对外做的功。
吸收热量和对外作功:内能增量:5.简述卡诺循环过程;提高热机效率的途径有哪些?答:卡诺循环是在两个温度恒定的热源(一个高温热源,一个低温热源)之间工作的循环过程,它是由两个等温和两个绝热的平衡过程组成。
按照循环方向的不同,分为卡诺正循环和卡诺负循环,分别对应热机和制冷机。
以卡诺正循环为例,第一过程是等温膨胀,从高温热库吸入热量,第二过程是绝热膨胀,第三过程是等温压缩过程,系统向低温热库放出热量,第四过程是绝热压缩过程。
提高热机效率的方式主要有两种,提高高温热库温度,降低低温热库温度。
6.给出热力学第二定律的两种以上叙述方式。
证明能否用一个等温过程和一个绝热过程构成一个循环过程。
答:开尔文表述:不可能制成一种循环动作的热机,只从单一热源吸收热量,使之完全变为有用的功,而不引起其他变化。
(或者,第二类永动机是不可能实现的。
)克劳修斯描述:热量不能自动的从低温物体传到高温物体。
由一个等温过程和绝热过程不能构成一个循环过程,理由如下:假设有一热机等温过程中吸收热量并在绝热膨胀过程中将吸收的热量完全转化为功,这显然与热力学第二定律的开氏表述矛盾,同理,再假设有一制冷机,经历一次绝热压缩后向低温热库吸热并在等温过程完全用于制冷,将这两个过程做成一个复合热机,一次循环后,外界没有作功,二热量却自动的从低温热源传到高温热源,与热力学第二定律的克氏表述矛盾。
大物下习题答案

习题1111-3.将一“无限长”带电细线弯成图示形状,设电荷均匀分布,电荷线密度为λ,四分之一圆弧AB的半径为R,试求圆心O点的场强。
解:以O为坐标原点建立xOy坐标,如图所示。
①对于半无限长导线A∞在O点的场强:有:(cos cos)42(sin sin)42AxA yERERλπππελπππε=-=-⎧⎪⎪⎨⎪⎪⎩②对于半无限长导线B∞在O点的场强:有:(sin sin)42(cos cos)42B xB yERERλπππελπππε=-=-⎧⎪⎪⎨⎪⎪⎩③对于AB圆弧在O点的场强:有:200200cos(sin sin)442sin(cos cos)442AB xAB yE dR RE dR Rππλλπθθππεπελλπθθππεπε==-=⎧⎪⎪⎨⎪⎪=--⎩⎰⎰∴总场强:04O xERλπε=,04O yERλπε=,得:0()4OE i jRλπε=+。
或写成场强:0E==,方向45。
11-5.带电细线弯成半径为R的半圆形,电荷线密度为0sinλλϕ=,式中λ为一常数,ϕ为半径R与x轴所成的夹角,如图所示.试求环心O处的电场强度。
解:如图,200sin44ddldER Rλϕϕλπεπε==,cossinxydE dEdE dEϕϕ==⎧⎪⎨⎪⎩考虑到对称性,有:0=xE;∴200000000sin(1cos2)sin4428yd dE dE dER R Rππλϕϕλλϕϕϕπεπεε-=====⎰⎰⎰⎰,方向沿y轴负向。
11-15.图示为一个均匀带电的球壳,其电荷体密度为ρ,球壳内表面半径为1R,外表面半径为2R .设无穷远处为电势零点,xyE求空腔内任一点的电势。
解:当1r R <时,因高斯面内不包围电荷,有:10E =,当12R r R <<时,有:203132031323)(4)(34r R r r R r E ερπεπρ-=-=,当2r R >时,有:20313220313233)(4)(34r R R r R R E ερπεπρ-=-=,以无穷远处为电势零点,有:21223R R R U E d r E d r ∞=⋅+⋅⎰⎰⎰⎰∞-+-=2R dr r R R dr r R r R R203132203133)(3)(21ερερ)(221220R R -=ερ。
大物习题答案第3章连续物体的运动

第3章 连续物体的运动一 基本要求1 理解描写刚体定轴转动的物理量,并掌握角量与线量的关系。
2 理解力矩和转动惯量概念,掌握刚体绕定轴转动的转动定律。
3理解角动量概念,掌握质点在平面内运动以及刚体绕定轴转动情况下的角动量守恒定律。
4理解刚体定轴转动的转动动能概念,能载有刚体绕定轴转动的问题中正确的应用机械能守恒定律。
5了解流体的特点,掌握理想流体的概念。
6掌握理想流体的连续性方程和伯努利方程。
7了解伯努利方程的应用。
二 基本概念1连续介质 在宏观力学的范围内如果能忽视物体内部的不连续性,把物体看作质量连续分布的质点系。
2刚体 大小和形状的变化可以忽略的连续介质。
3F 对定轴Z 的力矩:力F 的大小与O 点到力F 的作用线的垂直距离的d (力臂)乘积。
sin M Fd Fr θ== 或 M =r ×F4转动惯量 转动惯量是描述刚体在转动中惯性大小的物理量。
对于质点系的转动惯量1ni i i J m r ==∆∑ 。
如果物体的质量是连续分布的,上式可写为 2J r dm =⎰ 。
5 质点的角动量 质点m 对固定点O 的位矢为r ,质点m 对原点O 的角动量为 m =⨯=⨯L r p r υ6 冲量矩 力矩和作用时间的乘积,记作21t t t ⎰Md 。
7刚体定轴转动的角动量 21ni i i m r ==∑L ωJ =ω8力矩的功 W Md θ=⎰ 9力矩的功率 dW Md P M dt dtθω===10刚体的转动动能 221ωJ E k =11流体 处于液态和气态的物体的统称。
特点是物体各部分之间很容易发生相对运动,即流动性。
12理想流体 绝对不可压缩和完全没有黏性的流体。
13定常流动 流体流经空间任一给定点的速度是确定的,并且不随时间变化。
在流速较低时定常流动的条件是能够得到满足的。
14流线 为了形象地描述流体的运动, 在流体中画出一系列曲线,使曲线上每一点的切线方向与流经该点流体质点的速度方向相同, 这种曲线称为流线。
大物实验理论题库及答案—精选的八套题

大物实验理论题库及答案Metaphorl一、填空题(20分,每题2分)1 •依照测量方法的不同,可将测量分为_________________ 和_______________ 两大类。
2•误差产生的原因很多,按照误差产生的原因和不同性质,可将误差分为疏失误差、和随机误差系统误差。
3. _________________________测量中的视差多属__ 随机_____________________________________ 误差;天平不等臂产生的误差属于____________ 系统误差。
4. 已知某地重力加速度值为9.794 m/s2,甲、乙、丙三人测量的结果依次分别为:9.790 ± 0.024m/s 2、9.811 ± 0.004m/s2、9.795 ±0.006m/s 2,其中精密度最高的是 _乙 _____ ,准确度最高的是丙。
5 •累加放大测量方法用来测量微小等量物理量,使用该方法的目的是减小仪器造成的误差从而减小不确定度。
若仪器的极限误差为0.4,要求测量的不确定度小于0.04,则累加倍数N>6 。
6. 示波器的示波管主要由电子枪、偏转板和荧光屏组成。
7. 已知y=2X1-3X2+5%,直接测量量X,%,X3的不确定度分别为△ X、△X3,则间接测量量的不I 2 2 2确定度△ y= 4X1 9X2 25X3。
&用光杠杆测定钢材杨氏弹性模量,若光杠杆常数(反射镜两足尖垂直距离) d=7.00cm,标尺至平面镜面水平距离D=105.0 cm,求此时光杠杆的放大倍数 K=30o9、对于0.5级的电压表,使用量程为3V,若用它单次测量某一电压U,测量值为2.763V,则测量结果应表示为 U= 2.763 ± 0.009V,相对不确定度为 B= 0.3 %。
10、滑线变阻器的两种用法是接成分压线路或限流线路。
二、判断题(“对”在题号前( )中打V, “错”打X) (10分)(t ) 1、误差是指测量值与真值之差,即误差 =测量值-真值,如此定义的误差反映的是测量值偏离真值的大小和方向,既有大小又有正负符号。
重庆大学大物实验答案网上-分光计Word版

《分光计的调整和玻璃折射率的测定》实验预习自测随机试卷离考试结束还有:一、选择题(共11题)1. 选出下列说法正确的是A:光线入射三棱镜的入射角愈小,其偏向角愈小B:日光灯经过三棱镜二次折射后,各单色光偏离入射光方向的顺序是从黄到紫 C:一束复色光经过三棱镜折射成为有序排列的单色光,当改变入射角时,都可使各色单色光同时出现最小偏向角 D:日光灯经过三棱镜二次折射后,各单色光偏离入射光方向的顺序是从紫到黄请选择:2. 下列说法正确的是A:分光计调节中,只要从望远镜中看到清晰的狭缝像,就证明平行光管已产生了平行光束。
B:分光计调节中,如果由载物台上面的的双面反射镜反射回来的亮十字象能与实物亮十字重合,就表明望远镜轴已与仪器主轴垂直。
C:分光计载物台已垂直于分光计主轴的严格说法是,双面反射镜在载物台上任一位置都能使其两面反射回来的亮十字象与上放十字叉丝重合。
D:如果看到的望远镜的叉丝清晰,并且看到经平面反射镜反射回来的亮十字象清晰,此时望远镜即没有聚集无穷远了。
请选择:3. 在测量三棱镜折射率的实验中,可以看清日光灯的主要谱线有A:紫、绿、黄 B:紫、蓝、青 C:黄、红、蓝 D:蓝、青、红请选择:1112224. 分光计是一种能够精确测量角度的光学仪器,以下不是它的组成部分的是A:望远镜 B:平行光管 C:载物台D:三棱镜请选择:1112225. 光栅是一种分光元件,光栅衍射时,绿光的衍射角____黄光的衍射角;棱镜折射时,绿光的折射角____紫光的折射角。
A:大于、小于 B:小于、大于 C:大于、大于D:小于、小于请选择:6. 在分光计实验中,仪器调节的步骤顺序是: a、粗调 b、调节平行光管,使其发出平行光 c、用自准直法对望远镜调焦 d、调处两侧面反射回来的亮十字象e、用逐渐逼近方法将亮十字象都调至与上方十字横叉丝重合A:a b c d e B:b c d a e C:c b a d e D:e d b c a请选择:7. 用自准直法测三棱镜顶角A,是在望远镜调节达到要求后,固定刻度盘转动游标盘,分别读出三棱镜两个光学面与望远镜光轴垂直是的角位置则可以求的A 了,转动游标盘时要放松制动螺钉。
大物磁场答案
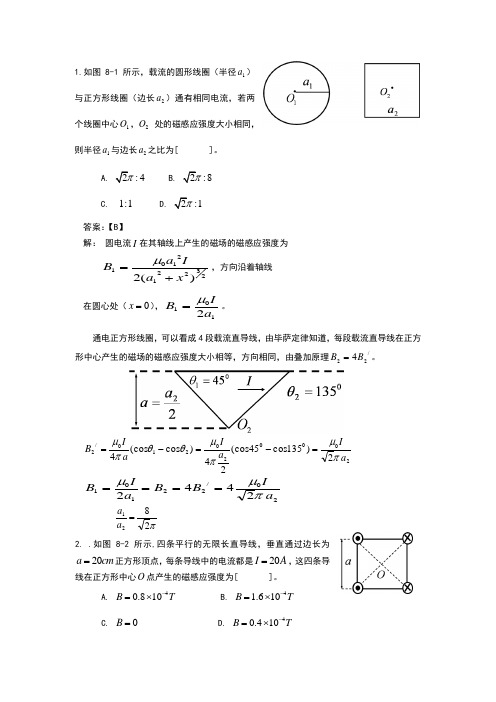
1.如图8-1所示,载流的圆形线圈(半径1a )与正方形线圈(边长2a )通有相同电流,若两个线圈中心1O ,2O 处的磁感应强度大小相同,则半径1a 与边长2a 之比为[ ]。
A. 2:4πB. 2:8πC. 1:1D. 2:1π答案:【B 】解: 圆电流I 在其轴线上产生的磁场的磁感应强度为232212101)(2x a Ia B +=μ,方向沿着轴线 在圆心处(0=x ),1012a IB μ=。
通电正方形线圈,可以看成4段载流直导线,由毕萨定律知道,每段载流直导线在正方形中心产生的磁场的磁感应强度大小相等,方向相同,由叠加原理/224B B =。
200020210/22)135cos 45(cos 24)cos (cos 4a I a I a I B πμπμθθπμ=-=-= 20/221012442a I B B a IB πμμ====π2821=a a 2. .如图8-2所示,四条平行的无限长直导线,垂直通过边长为20a cm =正方形顶点,每条导线中的电流都是20I A =,这四条导线在正方形中心O 点产生的磁感应强度为[ ]。
A. 40.810B T -=⨯B. 41.610B T -=⨯C. 0B =D. 40.410B T -=⨯答案:【A 】解:建立直角坐标系,则4根无限长载流直导线在正方形中心产生的磁感应强度为i a I B 45cos 201πμ=,j a I B 45cos 202πμ= i a IB 45cos 203πμ=,j a I B45cos 204πμ= )(45cos 2204321j i a I B B B B B+=+++=πμ T B 5108-⨯= 3.一根无限长直导线abcde 弯成图8-3所示的形状,中部bcd 是半径为R 、对圆心O 张角为0120的圆弧,当通以电流I 时,O 处磁感应强度的大小B = ,方向为 。
a 答案:)32(2600-=RI R IB πμμ+, 方向垂直纸面向里解:将整个载流导线分为三段:直线ab 、圆弧bcd 、直线de 。
大物课后答案

0-1已知m 412j i a+=,m 10i b -=,试分别用作图法和解析法求解:(1)b a +;(2)b a -。
解:(1) m )42(m )10412(j i i j i b a+=-+=+204222=+=+b a︒==4.6324arctan θ(2) m )422(m )10412(j i i j i b a+=++=-51042222=+=-b a︒==3.10224arctan θ (图略)0-2两矢量j i a126+=,m 68j i b --=,试求:(1)b a ⋅;(2)b a ⨯。
解:(1) 1207248)68()126(-=--=--⋅+=⋅j i j i b a(2) k k k j i j i b a609636)68()126(=+-=--⨯+=⨯0-3三矢量构成一个三角形,如图0-3所示。
已知m 3||=a ,m 4||=b ,m 5||=c ,求:(1)||b a+; (2)b a ⋅;(3)b a⨯。
解:(1) m 5==-=+c c b a(2) b a ⊥,0=⋅∴b a(3) k i j b a1243-=⨯=⨯0-4已知k t j e i t t r t5sin 23)2(23+-+=-,求下列各式在0=t 时的值:(1)t r d d ;(2)t r d d ;(3)tr r d d ⋅;(4)t r r d d⨯。
解:(1) k t j e i t t r t5cos 106)23(d d 22+++=-,0=t 时,j r 3-=,k j i t r 1062d d ++=(2) 1401062d d 222=++=tr(3) 18)1062()3(d d -=++⋅-=⋅k j i j t rr(4) i k k j i j trr 306)1062()3(d d -=++⨯-=⨯运动量1-1质点在xOy 平面内的运动方程为 x =3t ,y =2t 2+3。
大物实验预习题与思考题答案周岚版

实验七 单摆设计【思考题】1.用秒表手动测量单摆周期时,从测量技巧上来考虑,应注意哪些方面才能使周期测得更准确些?答:(1)注意定点观察,在摆线通过平衡位置时开、停秒表。
(2)适当增加单摆振动次数,及重复测量。
2.在室天棚上挂一单摆,摆长很长无法用尺直接测出来,请设计用简单的工具和方法测量其摆长。
答:测出单摆振动的周期T ,查出本地重力加速度g ,即可通过gl T π2=计算出摆长l 。
实验八 用直流电桥测量电阻【预习题】1.怎样消除比例臂两只电阻不准确相等所造成的系统误差?答:可以交换0R 和x R ,进行换臂测量,这样最终'00R R R x ⋅=,就与比例臂没有关系了。
【思考题】1.改变电源极性对测量结果有什么影响?答:在调节检流计平衡时,改变极性对未知电阻的测量没有影响。
测量电桥灵敏度时,改变电源极性会改变指针偏转方向,但对偏转格数没有影响。
总之,改变电源极性对测量结果没有影响。
2.影响单臂电桥测量误差的因素有哪些?答: (1)电桥灵敏度的限制,(2)电阻箱各旋钮读数的准确度等级(3)电阻箱各旋钮的残余电阻(接触电阻)实验九 液体粘滞系数的测定【预习题】1.在一定的液体中,若减小小球直径,它下落的收尾速度怎样变化?减小小球密度呢?答:在一定的液体中,小球下落的收尾速度与小球的质量和小球最大截面积有关。
即 23234r r K r V K s m Kv ππρπρ⋅===收尾 化简后得: ρr K v 32=收尾从上式可见,小球的收尾速度与小球半径和密度的平方根成正比,其中K 为比例系数。
2.试分析实验中造成误差的主要原因是什么?若要减小实验误差,应对实验中哪些量的测量方法进行改进?答:在实验中,小球的半径r 和下落速度收尾v 是对粘滞系数η测量误差影响最大的两个因素。
(1)小球直径的测量:因为该量的绝对量值较小,如测量仪器选用不当或测量方法不当都会造成测量的相对误差较大。
应选用规则的小球,小球直径尽量小些。
西南交通大学大物参考答案NO导体介质中的静电场

A 球电势 U A
= q1 4πε 0r1
+
q内 4πε 0r2
+
q外 4πε 0 r3
= 5400 V
B 球电势 U B
= q1 4πε 0r3
+
q内 4πε 0r3
+
q外 4πε 0 r3
=
q外 4πε 0r3
= 3600 V
4.一平行板电容器,充电后与电源保持联接,然后使两极板间充满相对介电常量为εr 的
电场强度 E′ = σ ′ / ε 0ε r = Q′ / S / ε 0ε r = ε rQ / S / ε 0ε r = E
电场能量W ′
=
1 C′V 2 2
=
1 2 ε rCV
2
= ε rW
即分别为 ε r ,1, ε r 倍
5.一空气平行板电容器,电容为 C,两极板间距离为 d。充电后,两极板间相互作用力
分布为
E = λ /(2πε r)
设电容器内外两极板半径分别为 r0,R,则极板间电压为
∫ ⋅ ∫ R � � R
U = E dr =
λ
λR d r = ln
r
r 2πε r
2πε r0
电介质中场强最大处在内柱面上,当这里场强达到 E0 时电容器击穿,这时应有
λ = 2πε r0 E0
R U = r0 E0 ln r0
适当选择 r0 的值,可使 U 有极大值,即令
dU /d r0 = E0 ln(R / r0 ) − E0 = 0
得 显然有
r0 = R / e
d2 U
< 0, 故当
d r0 2
r0 = R / e
大物试题答案

大物试题答案一、选择题1. 根据牛顿第二定律,一个质量为2kg的物体,受到10N的力作用,加速度大小为:A. 2 m/s²B. 5 m/s²C. 10 m/s²D. 20 m/s²答案:B解析:根据牛顿第二定律 \( F = ma \),其中 \( F \) 为作用力,\( m \) 为物体质量,\( a \) 为加速度。
代入已知数值,\( a =\frac{F}{m} = \frac{10N}{2kg} = 5 m/s² \)。
2. 一个物体从静止开始做匀加速直线运动,经过10秒后速度达到20 m/s,求物体的加速度:A. 1 m/s²B. 2 m/s²C. 5 m/s²D. 20 m/s²答案:B解析:根据速度与加速度的关系 \( v = at \),其中 \( v \) 为速度,\( a \) 为加速度,\( t \) 为时间。
代入已知数值,\( a =\frac{v}{t} = \frac{20 m/s}{10 s} = 2 m/s² \)。
3. 一个质量为0.5kg的物体,受到的重力为多少?A. 1 NB. 2.5 NC. 4.5 ND. 9.8 N答案:C解析:重力 \( G = mg \),其中 \( m \) 为物体质量,\( g \) 为重力加速度,一般取9.8 m/s²。
代入数值,\( G = 0.5kg \times9.8 m/s² = 4.9 N \),约等于4.5 N。
4. 一个弹簧秤挂在天花板上,下面挂一个10N的重物,如果将重物向下拉,使弹簧秤的读数增加到15N,求拉力的大小:A. 5 NB. 10 NC. 15 ND. 20 N答案:A解析:弹簧秤的读数等于作用在其上的力。
初始时,弹簧秤读数为10N,表示重物的重力。
当读数增加到15N时,额外的5N即为施加的拉力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
©物理系_2014_09《大学物理AII 》作业 No.8 量子力学基础班级 ________ 学号 ________ 姓名 _________ 成绩 _______一、判断题:(用“T ”和“F ”表示)[ F ] 1.根据德存布罗意假设,只有微观粒子才有波动性。
解:教材188页表16.1.1,宏观物体也有波动性,不过是其物质波波长太小了,所以其波动性就难以显示出来,而微观粒子的物质波波长可以与这些例子本身的大小相比拟,因此在原子大小的范围内将突出表现其波动性。
[ F ] 2.关于粒子的波动性,有人认为:粒子运行轨迹是波动曲线,或其速度呈波动式变化。
解:例如电子也有衍射现象,这是微观粒子波动性的体现。
与其轨迹、速度无关。
[ T ] 3.不确定关系表明微观粒子不能静止,必须有零点能存在。
解:教材202页。
因为如果微观粒子静止了,它的动量和位置就同时确定了,这违反了不确定关系。
[ F ] 4.描述微观粒子运动状态的波函数不满足叠加原理。
解:教材207页。
[ F ] 5.描述微观粒子运动状态的波函数在空间中可以不满足波函数的标准条件。
解:教材208页,波函数必须是单值、有限、连续的函数,只有满足这些标准条件的波函数才有物理意义。
二、选择题:1.静止质量不为零的微观粒子作高速运动,这时粒子物质波的波长λ与速度v 有如下关系:[ C ] (A) v ∝λ(B) v1∝λ(C)2211cv -∝λ (D) 22v c -∝λ 解:由德布罗意公式和相对论质 — 速公式有 2201cv v m m v h p -===λ得粒子物质波的波长22011c v m h -=λ,即2211cv -∝λ 故选C2.不确定关系式 ≥∆⋅∆x p x 表示在x 方向上[ D ] (A) 粒子位置不能确定 (B) 粒子动量不能确定(C) 粒子位置和动量都不能确定 (D) 粒子位置和动量不能同时确定解:不确定关系式 ≥∆⋅∆x p x 微观粒子的位置和动量不能同时准确确定。
3. 将波函数在空间各点的振幅同时增大D 倍,则粒子在空间的分布概率将 [ D ] (A) 增大2D 倍。
(B) 增大2D 倍。
(C) 增大D 倍。
(D) 不变。
4. 已知粒子在一维矩形无限深势阱中运动,其波函数为:)(23cos 1)(a x a a x a x ≤≤-=πψ那么粒子在65ax =处出现的概率密度为[ A ] a 21(A) a 1(B) a21(C) a 1(D)解:概率密度 )23(cos 1)(22ax a x πψ= 将65a x =代入上式,得 aa a a x 21)6523(cos 1)(22=⋅=πψ5. 波长 λ = 5000 Å的光沿x 轴正方向传播,若光的波长的不确定量∆λ=103-Å,则利用不确定关系h p x x ≥∆⋅∆可得光子的x 坐标的不确定量至少为:[ C ] (A) 25cm (B )50cm (C) 250cm (D) 500cm 解:由公式p =λh知, △322105000-⨯-=∆-=h hp λλ 利用不确定关系h p x x ≥∆⋅∆,可得光子的x 坐标满足91025⨯=∆≥∆xp h x Å=250cm三、填空题:1. 低速运动的质子P 和α粒子,若它们的德布罗意波长相同,则它们的 动量之比αp p :p = 1:1 ;动能之比αE E :p = 4:1 。
解:由λhp =,二者λ相同,所以1:1:p =αp p 。
由经典关系,动能mp E 22=,所以1:4::p p ==m m E E αα2.热中子平均动能为kT 23。
则当温度为K 003时,一个热中子的动能为 J ,相应的德布罗意波长为 。
(波尔兹曼常数123K J 10381--⋅⨯=.k ,普朗克常量s J 1063.634⋅⨯=-h ,中子质量kg 1067.127-⨯=m )解:一个热中子的动能为(J)1021.63001038.123kT 232123--⨯=⨯⨯⨯==k E 相应的德布罗意波长kmE hp h 2==λnm 6.14)m (1046.11021.61067.121063.610212734=⨯=⨯⨯⨯⨯⨯=----3.在如果电子被限制在边界x 与x x ∆+之间,5.0=∆x Å则电子动量的x 分量的不确定量近似地为 -1s m kg ⋅⋅。
(不确定关系式h p x x ≥∆⋅∆,普朗克常量s J 1063.634⋅⨯=-h )解:由不确定关系式h p x x ≥∆⋅∆得电子动量的x 分量的不确定量近似地为()1231034s m kg 1033.1105.01063.6----⋅⋅⨯=⨯⨯=∆≥∆x h p x4.若一个电子处于原子某能态的时间s t 810-=∆ ,这个原子能态的能量的最小不确定值=∆E 。
解:根据不确定关系ht E ≥∆⋅∆得到: J t h E 26341063.6101063.6--⨯=⨯=∆≥∆ 如果用不确定关系≥∆⋅∆tE ,那么J t E 263410055.11021063.6--⨯=⨯⨯=∆≥∆π5.微观粒子的下述性质分别由哪个式子给出?1) 微观粒子永远不可能静止h p x x ≥∆⋅∆或者 ≥∆⋅∆x p x 。
2) 原子光谱存在自然宽度h tE ≥∆⋅∆或者 ≥∆⋅∆t E 。
四、计算题:1、在宽为a 的一维无限深势阱中运动的粒子,它的一个定态波函数如图(a)所示,对应的总能量为4eV ,若它处于另一个波函数如图(b)的态上,它的总能量是多少?粒子的零点能又是多少? 解:一维无限深势阱的能级表达式为:12E n E n=由(a )图知:n =2,即 eV 1eV 44211122=⇒===E E E E由(b )图知:n =3,即eV 9931123===E E E2.同时测量动能为1keV 的作一维运动的电子的位置与动量时,若位置的不确定值在0.1nm ()m 10nm 19-=内,则动量的不确定值的百分比p p /∆至少为何值 ?(电子质量kg 1011.931-⨯=e m ,J 1060.1eV 119-⨯=,普朗克常量s J 1063.634⋅⨯=-h )解:电子的动能()J 106.1keV 116-⨯==k E ,又ek m P E 22=,得电子的动量大小()1231631s m kg 1071.1106.11011.922----⋅⋅⨯=⨯⨯⨯⨯==k e E m p根据不确定关系 ≥∆⋅∆x p x ,得动量不确定量()124934s m kg 1006.1101.014.321063.6----⋅⋅⨯=⨯⨯⨯=∆≥∆x p 所以有 %2.6062.01071.11006.12324==⨯⨯=∆--p p 如果用h p x x ≥∆⋅∆,得到动量不确定量为:()124934sm kg 1063.6101.01063.6----⋅⋅⨯=⨯⨯=∆≥∆x h p%3939.01071.11063.62324==⨯⨯=∆--p p3.粒子在宽度为 a 的一维无限深势阱中运动,其波函数为:)0(3sin 2)(a x ax a x <<=πψ试求粒子出现概率最大的各个位置及在区间)26(ax a <<的概率。
解:第一个问:a)较复杂的方法()ax a x πψ3sin 2223=, 要求求粒子出现概率最大的各个位置,就有:0d d ,0d d 22<=x P x P ,根据()0d d d d ,0d d 23==⇒=xx x P x P ψ,得到()取整数。
n n ax a x a xa a x a a x a x x ,606sin 06sin 63cos 3.3sin .2.2d d 223ππππππππψ=⇒=⇒=== (1)a aa a a a x ,65,32,2,3,6,0=处,概率密度有极值。
要取极大值,得有23262206cos 06cos 6.60d d 222πππππππππ+<<+⇒<⇒<⇒<n a x n axa x a a x P (2)当0=n 时,有a x a 123121<<当1=n 时,有a x a 127125<< 当2=n时,有a x a 121143<<由上面的分析,得出,在65,2,6aa a x =处,粒子出现的概率最大。
b)简单方法:()a a x a x a a x a x πππψ6c o s126c o s 123s in 2223-=⎪⎪⎪⎪⎭⎫⎝⎛-==,上式要取极大值,只有()65,2,661212616cos a a a x an x n a x a x =⇒+=⇒+=⇒-=πππ第二个问题:()x xax a xa x x P a a a a a a ⎰⎰⎰===262622623d 2a 6cos-12d 3sin 2d ππψ%33.330316sin 6126=-=⎥⎦⎤⎢⎣⎡-=aa a x a x a ππ。
