matlab实验(二)
实验二MATLAB绘制图形

grid on %在所画出的图形坐标中加入栅格
绘制图形如下
50
10
1
0.8
40
10
0.6
0.4
30
10
0.2
0
1020
-0.2
-0.4
1010
-0.6
-0.8
0
10
-1
-2
0
2
-2
0
2
10
10
10
10
10
10
如果在图中不加栅格
程序如下:
clear x=logspace(-1,2);%在10^(-1)到10^2之间产生50个 对数等分的行向量 subplot(121); loglog(x,10*exp(x),'-p') subplot(122); semilogx(x,cos(10.^x))
(2)plot(x,y): 基本格式,x和y可为向量或矩阵. 1. 如果x,y是同维向量,以x元素为横坐标,以y元素 为纵坐标绘图. 2. 如果x是向量,y是有一维与x元素数量相等的矩阵, 则以x为共同横坐标, y元素为纵坐标绘图,曲线数目 为y的另一维数. 3. 如果x,y是同维矩阵,则按列以x,y对应列元素为 横、纵坐标绘图,曲线数目等于矩阵列数.
y=2*exp(-0.5*x).*cos(4*pi*x);
2
plot(x,y)
1.5
1
0.5
0
-0.5
-1
-1.5
-2
0
1
2
3
4
5
6
7
例4 绘制曲线
t=(0:0.1:2*pi);
x=t.*sin(3*t);
y=t.*sin(t).*sin(t);
matlab实验二

北京工业大学Matlab实验报告**: ***学号: ************: **实验二、Matlab 的基本计算(一)实验目的1.掌握建立矩阵的方法。
2.掌握Matlab 各种表达式的书写规则以及常用函数的使用。
3.能用Matlab 进行基本的数组、矩阵运算。
4.掌握矩阵分析的方法以及能用矩阵运算或求逆法解线性方程组。
5.掌握Matlab 中的关系运算与逻辑运算。
(二)实验环境1.计算机2.MATLAB7.0集成环境(三)实验内容及要求1、熟练操作MATLAB7.0运行环境;2、自主编写程序,必要时参考相关资料;3、实验前应写出程序大致框架或完整的程序代码;4、完成实验报告。
(四)实验程序设计1.利用diag 等函数产生下列矩阵。
⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=032570800a ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=804050702b2.利用reshape 函数将1题中的a 和b 变换成行向量。
3.产生一个均匀分布在(-5,5)之间的随机矩阵(10×2),要求精确到小数点后一位。
4.已知:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=76538773443412A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=731203321B求下列表达式的值:(1) B A K *611+=和I B A K +-=12(其中I 为单位矩阵)(2) B A K *21=和B A K *.22=(3) 331^A K =和3.32^A K =(4) B A K /41=和A B K \42=(5) ],[51B A K =和]2:);],3,1([[52^B A K = 5.下面是一个线性方程组:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡52.067.095.03216/15/14/15/14/13/14/13/12/1x x x(1)求方程的解(矩阵除法和求逆法)(2)将方程右边向量元素3b 改为0.53,再求解,并比较3b 的变化和解的相对变化。
实验二MATLAB矩阵分析和处理

实验二 MATLAB 矩阵分析和处理一、实验目的1.掌握生成特殊矩阵的方法。
2.掌握矩阵分析的方法。
4.用矩阵求逆法解线性方程组。
二、实验内容1.设有分块矩阵⎥⎦⎤⎢⎣⎡=⨯⨯⨯⨯22322333S O R E A ,其中E,R,O,S 分别为单位矩阵、随机矩阵、零矩阵和对角矩阵,试通过数值计算验证⎥⎦⎤⎢⎣⎡+=22S O RS R E A 。
解:>> E=eye(3);>> R=rand(3,2);>> O=zeros(2,3);>> S=diag(1:2);>> A=[E R;O S];A =1.0000 0 0 0.9501 0.48600 1.0000 0 0.2311 0.89130 0 1.0000 0.6068 0.76210 0 0 1.0000 00 0 0 0 2.0000>> A^2ans =1.0000 0 0 1.9003 1.45790 1.0000 0 0.4623 2.67390 0 1.0000 1.2137 2.28630 0 0 1.0000 00 0 0 0 4.0000>> [E R+R*S;O S^2]ans =1.0000 0 0 1.9003 1.45790 1.0000 0 0.4623 2.67390 0 1.0000 1.2137 2.28630 0 0 1.0000 00 0 0 0 4.0000所以⎥⎦⎤⎢⎣⎡+=22S ORS R E A .2.产生5阶希尔伯特矩阵H 和5阶帕斯卡矩阵P ,求其行列式的值Hh 和Hp 以及他们的条件数Th 和Tp ,判断哪个矩阵性能更好,为什么?解:H=hilb(5)H =1.0000 0.5000 0.3333 0.2500 0.20000.5000 0.3333 0.2500 0.2000 0.16670.3333 0.2500 0.2000 0.1667 0.14290.2500 0.2000 0.1667 0.1429 0.12500.2000 0.1667 0.1429 0.1250 0.1111 >> P=pascal(5)P =1 1 1 1 11 2 3 4 51 3 6 10 151 4 10 20 351 5 15 35 70>> Hh=det(H)Hh =3.7493e-012>> Hp=det(P)Hp =1>> Th=cond(H)Th =4.7661e+005>> Tp=cond(P)Tp =8.5175e+003由上式看出:帕斯卡矩阵性能更好,因为行列式为1,而希尔伯特矩阵条件数很差,使用一般方法求逆矩阵会因原始数据的微小变动产生不可靠的结果3.建立一个5x5矩阵,求它的行列式的值、迹、秩和X 数解:a=magic(5)a =17 24 1 8 1523 5 7 14 164 6 13 20 2210 12 19 21 311 18 25 2 9>> b=det(a)b =5070000>> c=trace(a)c =65>> d=rank(a)d =5>> e=norm(a)e =65.0000>>4.已知⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=5881252018629A ,求特征值和特征向量,并分析其数学意义解:A=[-29 6 18;20 5 12;-8 8 5]A =-29 6 1820 5 12-8 8 5>> b=eig(A)b =-25.3169-10.518216.8351>> [v,b]=eig(A)0.7130 0.2803 0.2733-0.6084 -0.7867 0.87250.3487 0.5501 0.4050b =-25.3169 0 00 -10.5182 00 0 16.83515.下面是一个线性方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡52.067.095.06/15/14/15/14/13/14/13/12/1321x x x(1) 求方程的解(2) 将方程右边向量第三个元素0.52改为0.53,并比较解的变化(3) 计算系数矩阵A 的条件数并分析结论解:(1) A=[1/2 1/3 1/4;1/3 1/4 1/5;1/4 1/5 1/6]A =0.5000 0.3333 0.25000.3333 0.2500 0.20000.2500 0.2000 0.1667>> C=[0.95;0.67;0.52]C =0.95000.67000.5200>> B=A\CB =1.20000.60000.6000>>(2)A=[1/2 1/3 1/4;1/3 1/4 1/5;1/4 1/5 1/6]A =0.5000 0.3333 0.25000.3333 0.2500 0.20000.2500 0.2000 0.1667>> C=[0.95;0.67;0.53]C =0.95000.67000.5300>> B=A\C3.0000-6.60006.6000(3)cond(A)ans =1.3533e+0036.建立A矩阵,试比较sqrtm(A)和sqrt(A),并分析他们的区别解:A=magic(3)A =8 1 63 5 74 9 2>> sqrtm(A)ans =2.7065 + 0.0601i 0.0185 + 0.5347i 1.1480 - 0.5948i0.4703 + 0.0829i 2.0288 + 0.7378i 1.3739 - 0.8207i0.6962 - 0.1430i 1.8257 - 1.2725i 1.3511 + 1.4155i>> sqrt(A)ans =2.8284 1.0000 2.44951.73212.2361 2.64582.00003.0000 1.4142区别:sqrt是求矩阵里每个元素的平方根,并组成一个新的矩阵。
MATLAB实验。

MATLAB实验班级:11电气(2)姓名:幸劲昆学号:201124122201实验一 MATLAB 运算基础(一)一、实验目的1、掌握建立矩阵的方法。
2、掌握MATLAB 各种表达式的书写规则以及各种运算方法。
二、实验内容1、求下列表达式的值。
(1)e=2.73;z1=2*sin((85/360)*2*pi)/(1+e^2) z1 =0.2357 (2)()x x z ++=1ln 212,其中⎢⎣⎡-=45.02x ⎥⎦⎤+521i x=[2 ,1+2i;-0.45,5]x =2.0000 1.0000 + 2.0000i -0.4500 5.0000z2=0.5*log(x+sqrt(1+x)) z2 =0.6585 0.6509 + 0.4013i -0.6162 1.0041 (3)a=[-3.0:0.1:3.0];z3=(exp(0.3*a)-exp(0.2*a))./2.*sin(a+0.3);plot(z3)2、已知⎢⎢⎢⎣⎡=33412A 65734 ⎥⎥⎥⎦⎤-7874 和 ⎢⎢⎢⎣⎡=321B 203- ⎥⎥⎥⎦⎤-731 求下列表达式的值:(1)A+6*B 和A-B+I (其中I 为单位矩阵)。
a=[12 34 -4;34 7 87;3 65 7] b=[1 3 -1;2 0 3;3 -2 7] I=eye(3)a =b = I =12 34 -4 1 3 -1 1 0 02 03 34 7 87 0 1 03 -2 7 3 65 7 0 0 1z1=a+6*b z2=a-b+Iz1 = z2 =18 52 -10 12 31 -346 7 105 32 8 8421 53 49 0 67 1(2)A*B和A.*B。
>> a*b >> a.*bans = ans =68 44 62 12 102 4309 -72 596 68 0 261154 -5 241 9 -130 49(3)A^3和A.^3。
实验二 连续信号时域分析的MATLAB实现

实验二 连续信号时域分析的MATLAB 实现一. 实验目的1. 熟悉MATLAB 软件平台;2. 掌握MATLAB 编程方法、常用语句和可视化绘图技术;3. 编程实现常用信号及其运算MATLAB 实现方法。
二. 实验原理信号一般是随时间而变化的某些物理量。
按照自变量的取值是否连续,信号分为连续时间信号和离散时间信号,一般用()f t 和()f k 来表示。
若对信号进行时域分析,就需要绘制其波形,如果信号比较复杂,则手工绘制波形就变得很困难,且难以精确。
MATLAB 强大的图形处理功能及符号运算功能,为实现信号的可视化及其时域分析提供了强有力的工具。
根据MATLAB 的数值计算功能和符号运算功能,在MATLAB 中,信号有两种表示方法,一种是用向量来表示,另一种则是用符号运算的方法。
在采用适当的MATLAB 语句表示出信号后,就可以利用MATLAB 中的绘图命令绘制出直观的信号波形了。
下面分别介绍连续时间信号和离散时间信号的MATLAB 表示及其波形绘制方法。
1.连续时间信号所谓连续时间信号,是指其自变量的取值是连续的,并且除了若干不连续的点外,对于一切自变量的取值,信号都有确定的值与之对应。
从严格意义上讲,MATLAB 并不能处理连续信号。
在MATLAB 中,是用连续信号在等时间间隔点上的样值来近似表示的,当取样时间间隔足够小时,这些离散的样值就能较好地近似出连续信号。
在MATLAB 中连续信号可用向量或符号运算功能来表示。
⑴ 向量表示法对于连续时间信号()f t ,可以用两个行向量f 和t 来表示,其中向量t 是用形如12::t t p t =的命令定义的时间范围向量,其中,1t 为信号起始时间,2t 为终止时间,p 为时间间隔。
向量f 为连续信号()f t 在向量t 所定义的时间点上的样值。
例如:对于连续信号sin()()()t f t Sa t t== ,我们可以将它表示成行向量形式,同时用绘图命令plot()函数绘制其波形。
实验二matlab矩阵分析与处理

《MATLAB及应用A》第二次上机作业一、一球从100米高度自由落下,每次落地后反弹回原高度的一半,再落下。
求它在第10次落下时共经过多少米?第10次反弹多高?MATLAB源程序:MATLAB运行结果:二、有如下一段MATLAB程序,请解释说明每个语句的功能,必要时用数学表达式(不是在MATLAB中的输入形式);并给出y1、y2、y3的值(可从MATLAB中复制)。
MATLAB源程序:x=linspace(0,6);y1=sin(2*x);y2=sin(x.^2);y3=(sin(x)).^2;各条命令语句的功能如下:y1、y2、y3的值分别为:三、教材第55页习题三,第3题。
MATLAB源程序:MATLAB运行结果:四、选择题(1) i=2; a=2i; b=2*i; c=2*sqrt(-1); 程序执行后,a, b, c的值分别是多少?()(A) a=4, b=4, c=2.0000i(B) a=4, b=2.0000i, c=2.0000i(C) a=2.0000i, b=4, c=2.0000i(D) a=2.0000i, b=2.0000i, c=2.0000i(2) 求解方程x4-4x3+12x-9 = 0 的所有解,其结果为()(A) 1.0000, 3.0000, 1.7321, -1.7321(B) 1.0000, 3.0000, 1.7321i, -1.7321i(C) 1.0000i, 3.0000i, 1.7321, -1.7321(D) -3.000-0i, 3.0000i, 1.7321, -1.7321五、求[100,1000]之间的全部素数(选做)。
MATLAB源程序: MATLAB运行结果:一、一球从100米高度自由落下,每次落地后反弹回原高度的一半,再落下。
求它在第10次落下时共经过多少米?第10次反弹多高?MATLAB源程序:>> a=(0:-1:-9) %产生一个行向量aa =0 -1 -2 -3 -4 -5 -6 -7 -8 -9>> b=pow2(a) %对行向量a中的每一个元素分别求幂函数b =1.0000 0.5000 0.2500 0.1250 0.0625 0.0313 0.0156 0.007 8 0.0039 0.0020>> h=100*b %对行向量b中的每一个元素分别乘以100h =100.0000 50.0000 25.0000 12.5000 6.2500 3.1250 1.5625 0. 7813 0.3906 0.1953>> s1=sum(h) %对行向量h中的元素求和s1 =199.8047>> s=s1*2-100 %求出第10次落下时经过的高度s =299.6094>> h10=h(10)/2 %求出第10次反弹的高度h10 =0.0977二、有如下一段MATLAB程序,请解释说明每个语句的功能,必要时用数学表达式(不是在MATLAB中的输入形式);并给出y1、y2、y3的值(可从MATLAB 中复制)。
实验二MATLAB的矩阵操作_参考答案

1
5
>> A(k)
ans =
23
10
(2)取出A前3行构成矩阵B,前两列构成矩阵C,右下角 子矩阵构成矩阵D,B与C的乘积构成矩阵E.
>> B=A([1,2,3],:)
B =
23.0000 10.0000 -0.7780 0
41.0000 -45.0000 65.0000 5.0000
32.0000 5.0000 0 32.0000
y =
-128.4271
2.已知 ,
求下列表达式的值:
(1) , (其中I为单位矩阵)
A=[-1,5,-4;0,7,8;3,61,7]
B=[8,3,-1;2,5,3;-3,2,0]
>> A+6*B
ans =
47 23 -10
12 37 26
-15 73 7
&
ans =
-1.2768 -0.4743 0.2411
2.1229 1.3173 -0.2924
3.已知
完成下列操作
(1)输出A在[10,25]范围内的全部元素
A=[23,10,-0.778,0;41,-45,65,5;32,5,0,32;6,-9.54,54,3.14]
>> k=find(A>=10&A<=25)
(2)
(3)
2.已知 ,
求下列表达式的值:
(1) , (其中I为单位矩阵)
(2)A*B、A.*B和B*A
(3)A/B及B/A
3.已知
完成下列操作
(1)输出A在[10,25]范围内的全部元素
(2)取出A前3行构成矩阵B,前两列构成矩阵C,右下角 子矩阵构成矩阵D,B与C的乘积构成矩阵E.
实验二MATLAB程序设计含实验报告

实验二 MATLAB 程序设计一、 实验目的1.掌握利用if 语句实现选择结构的方法。
2.掌握利用switch 语句实现多分支选择结构的方法。
3.掌握利用for 语句实现循环结构的方法。
4.掌握利用while 语句实现循环结构的方法。
5.掌握MATLAB 函数的编写及调试方法。
二、 实验的设备及条件计算机一台(带有MATLAB7.0以上的软件环境)。
M 文件的编写:启动MATLAB 后,点击File|New|M-File ,启动MATLAB 的程序编辑及调试器(Editor/Debugger ),编辑以下程序,点击File|Save 保存程序,注意文件名最好用英文字符。
点击Debug|Run 运行程序,在命令窗口查看运行结果,程序如有错误则改正三、 实验内容1.编写求解方程02=++c bx ax 的根的函数(这个方程不一定为一元二次方程,因c b a 、、的不同取值而定),这里应根据c b a 、、的不同取值分别处理,有输入参数提示,当0~,0,0===c b a 时应提示“为恒不等式!”。
并输入几组典型值加以检验。
(提示:提示输入使用input 函数)2.输入一个百分制成绩,要求输出成绩等级A+、A 、B 、C 、D 、E 。
其中100分为A+,90分~99分为A ,80分~89分为B ,70分~79分为C ,60分~69分为D ,60分以下为E 。
要求:(1)用switch 语句实现。
(2)输入百分制成绩后要判断该成绩的合理性,对不合理的成绩应输出出错信息。
(提示:注意单元矩阵的用法)3.数论中一个有趣的题目:任意一个正整数,若为偶数,则用2除之,若为奇数,则与3相乘再加上1。
重复此过程,最终得到的结果为1。
如:2?13?10?5?16?8?4?2?16?3?10?5?16?8?4?2?1运行下面的程序,按程序提示输入n=1,2,3,5,7等数来验证这一结论。
请为关键的Matlab 语句填写上相关注释,说明其含义或功能。
MATLAB实验报告第二章
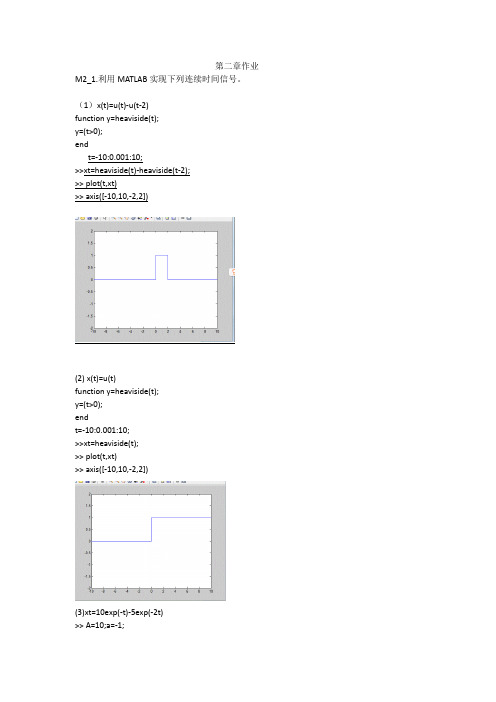
第二章作业M2_1.利用MATLAB实现下列连续时间信号。
(1)x(t)=u(t)-u(t-2)function y=heaviside(t);y=(t>0);endt=-10:0.001:10;>>xt=heaviside(t)-heaviside(t-2);>>plot(t,xt)>>axis([-10,10,-2,2])(2) x(t)=u(t)function y=heaviside(t);y=(t>0);endt=-10:0.001:10;>>xt=heaviside(t);>>plot(t,xt)>>axis([-10,10,-2,2])(3)xt=10exp(-t)-5exp(-2t)>> A=10;a=-1;>> t=0:0.001:10;>> x1t=A*exp(a*t);>> A=5;a=-2;>> t=0:0.001:10;>> x2t=A*exp(a*t);>>xt=x1t-x2t;>>plot(t,xt)(4)xt=tu(t)>> t=-10:0.001:10;>>xt=t.*heaviside(t);>>plot(t,xt)(5)xt=2|sin(10pit+pi/3)| >> A=2;w0=10*pi;phi=pi/3; >> t=0:0.001:1;>>xt=A*abs(sin(w0*t+phi)); >>plot(t,xt)>>axis([0,1,-4,4])Xt=cost+sin(2pit)>> A=1;w0=1;phi=0; >> t=0:0.002:10;>> x1t=A*cos(w0*t+phi); >> A=2;w0=2*pi;phi=0; >> t=0:0.002:10;>> x2t=A*sin(w0*t+phi); >>xt=x1t+x2t;>>plot(t,xt)(7)xt=4exp(-0.5t)cos(2pit) >> A=5;a=-0.5;>> t=0:0.001:10;>> x1t=A*exp(a*t);>> A=1;w0=2*pi;phi=0; >> t=0:0.001:10;>> x2t=A*cos(w0*t+phi); >>xt=x1t.*x2t;>>plot(t,xt)(8)Sa(pit)cos(30t)A=1;w0=30;phi=0;>> t=0:0.001:3;>> x1t=A*cos(w0*t+phi);>> t=0:0.001:3;>> x2t=sinc(t);>>xt=x1t.*x2t;>>plot(t,xt)M2-3,写出书中图示波形函数,并画出xt,x0.5t,x(2-0.5t)的图像function yt=x2_3(t)yt=t.*(t>=0&t<2)+2*(t>=2&t<3)+(-1)*(t>=3&t<=5); end>> t=0:0.001:5;>>xt=x2_3(t);>>title('x(t)');>>plot(t,xt)>>axis([0,6,-2,3])>> t=0:0.001:10;xt=x2_3(0.5*t); >>plot(t,xt)>>title('x(0.5t)')>>axis([0,10,-2,3])x(0.5t)>> t=-10:0.001:10;>>xt=x2_3(2-0.5*t);>>plot(t,xt)>>title('x(2-0.5t)')>>axis([-10,10,-2,3])M2-4画出图示的奇分量和偶分量。
MATLAB实验报告

实验二MATLAB语言基础一、实验目的基本掌握MA TLAB向量矩阵数组的生成及基本运算(区分数组运算和矩阵预算)、常用的数学函数。
了解字符串的操作。
二、实验内容(1)向量的生成和运算。
(2)矩阵的创建、引用和运算。
(3)多维数组的创建和运算。
(4)字符创的操作。
三、实验步骤1.向量的生成和运算1)向量的生成<1>、直接输入法<2> 冒号表达式法<3> 函数法:Linspace()是线性等分函数,logspace()是对数等分函数。
2)向量的运算1>维数相同的行、列向量之间可以相加减,标量可以与向量直接相乘除。
2>向量的点积与叉积运算E1和E2虽然表达式相同,但E1是标量,E2是矩阵。
2.矩阵的创建、引用和运算1)矩阵的创建和引用矩阵是由m*n元素构成的矩形结构,行向量和列向量是矩阵的特殊形式。
1>直接输入法:2>抽取法:包括单下标抽取和全下表抽取两种方式,且两种方式抽取的元素都必须以小括号括起来。
3>函数法:利用ones(m;n)创建全1矩阵,zeros()创建全0矩阵,eyes()创建单位矩阵等等。
4>拼接法:纵向拼接横向拼接5>利用拼接函数cat()repmat()和变形函数reshape()>> A1=[1 2 3;9 8 7 ;4 5 6];A2=A1.';>> cat(1,A1,A2) 沿行向拼接ans =1 2 39 8 74 5 61 9 42 8 53 7 6>> cat(2,A1,A2) 沿列向拼接ans =1 2 3 1 9 49 8 7 2 8 54 5 6 3 7 6>> repmat(A1,2,2)ans =1 2 3 1 2 39 8 7 9 8 74 5 6 4 5 61 2 3 1 2 39 8 7 9 8 74 5 6 4 5 6> A=linspace(2,18,9)A =2 4 6 8 10 12 14 16 18 >> reshape(A,3,3)ans =2 8 144 10 166 12 182)矩阵的运算练习(1)用矩阵除法求下列方程组的解x=[x1;x2;x3]>> A=[6 3 4;-2 5 7;8 -1 -3];B=[3;-4;-7];X=A\BX =1.0200-14.00009.7200(2)求矩阵的秩A=[6 3 4;-2 5 7;8 -1 -3];>> rank(A)ans =3[X,lamda]=eig(A)X =0.8013 -0.1094 -0.16060.3638 -0.6564 0.86690.4749 0.7464 -0.4719lamda =9.7326 0 00 -3.2928 00 0 1.5602(3)矩阵的开方>> B=sqrtm(A)B =2.2447 + 0.2706i 0.6974 - 0.1400i 0.9422 - 0.3494i -0.5815 + 1.6244i 2.1005 - 0.8405i 1.7620 - 2.0970i1.9719 - 1.8471i -0.3017 + 0.9557i 0.0236 +2.3845i (4)矩阵的指数与对数:> C=expm(A)C =1.0e+004 *1.0653 0.5415 0.63230.4830 0.2465 0.28760.6316 0.3206 0.3745>> logm(C)ans =6.0000 3.0000 4.0000-2.0000 5.0000 7.00008.0000 -1.0000 -3.0000(6)矩阵的转置D=A'D =6 -2 83 5 -14 7 -3(7)矩阵的提取与翻转:通过各种特定函数如triu(A)、tril(A),diag(A)、flipud (A)、fliplr(A)等等。
实验作业2 MATLAB作图

实验作业2 MATLAB作图1、用plot,fplot 绘制函数y=cos(tan( x))的图形。
解:代码如下:x=linspace(-0.5,0.5,30);y=cos(tan(pi*x));plot(x,y)结果:fplot('[cos(tan(pi*x))]',[-0.5,0.5])结果:注意事项: fplot('[cos(tan(pi*x))]',[-0.5,0.5])不能写成fplot('[cos(tan(pi*x))]',(-0.5,0.5))否则是错误程序。
2. 用ezplot绘制函数exy-sin(x+y)=0 在[-3, 3]上的图形。
解:代码如下:ezplot('exp(x*y)-sin(x+y)=0',[-3,3])3.用matlab以动画的方式绘制出摆线x=a(t-sint) y=a(1-cost) (a自己赋值)的渐屈线clear;clc;close;a=1;syms tx=a*(t-sin(t));y=a*(1-cos(t));ezplot(x,y,[0,2*pi]),grid on ;hold on;dy=diff(y)/diff(x);dyy=diff(dy)/diff(x);xx=x-(1+dy^2)*dy/dyy;%渐屈线的坐标yy=y+(1+dy^2)/dyy;M=50;t=0;xxx=subs(xx);yyy=subs(yy);H1=plot(xxx,yyy,'r');hold on;grid on ;axis([0,7,-2.5,2.5]);x1=subs(x);y1=subs(y);H2=plot([x1,xxx],[y1,yyy],'k--');H3=plot(x1,y1,'ko');H4=plot(xxx,yyy,'ro');tt=linspace(0,2*pi,M);for i=1:Mpause(0.2);t=tt(1:i);xxx=subs(xx);yyy=subs(yy);x1=subs(x);y1=subs(y);set(H1,'xdata',xxx,'ydata',yyy);set(H2,'xdata',[x1(i),xxx(i)],'ydata',[y1(i),yyy(i)]);set(H3,'xdata',x1(i),'ydata',y1(i));set(H4,'xdata',xxx(i),'ydata',yyy(i));end绘制函数⎩⎨⎧-=-=)cos 1()sin (t a y t t a x 在]2,0[π∈t 上的图形。
matlab2022实验2参考答案

matlab2022实验2参考答案报告名称:MATLAB试验二符号计算姓名:学号:专业:班级:MATLAB实验二MATLAB符号计算试验报告说明:1做试验前请先预习,并独立完成试验和试验报告。
2报告解答方式:将MATLAB执行命令和最后运行结果从命令窗口拷贝到每题的题目下面,请将报告解答部分的底纹设置为灰色,以便于批阅。
3在页眉上写清报告名称,学生姓名,学号,专业以及班级。
3报告以Word文档书写。
一目的和要求1熟练掌握MATLAB符号表达式的创建2熟练掌握符号表达式的代数运算3掌握符号表达式的化简和替换4熟练掌握符号微积分5熟练掌握符号方程的求解二试验内容1多项式运算(必做)1.1解方程:f(某)=某^4-10某某^3+34某某^2-50某某+25=0%采用数值方法:>>f=[1-1034-5025];>>root(f)%采用符号计算方法:f1=ym('某^4-10某某^3+34某某^2-50某某+25')olve(f1)1.2求有理分式R=(3某^3+某)(某^3+2)/((某^2+2某-2)(5某^3+2某^2+1))的商多项式和余多项式.a1=[3010];a2=[1002];a=conv(a1,a2);b1=[12-2];b2=[5201];b=conv(b1,b2);[p,r]=deconv(a,b);%注意:ab秩序不可颠倒。
%reidue用于实现多项式的部分分式展开,此处用deconv函数报告名称:MATLAB试验二符号计算姓名:学号:专业:班级:%%此题,有同学程序如下:某1=[3010],某2=[1002],某3=[12-2],某4=[5201]某5=conv(某1,某2)[y6,r]=deconv(某5,某3)R=deconv(y6,某4)%%这种方法较第一种解法缺点:在除法运算中,会产生误差,故此题应先将分母的多项式相乘后,再与分子部分的多项式进行运算。
通信原理MATLAB实验(第2部分)

6
图1-1 2ASK信号产生方法与波形示例 7
二、MATLAB实现 以数字信号序列10110010为例,给出产生2ASK
信号的MATLAB程序流程图如图1-2所示。
开始 为变量赋初值
生成2ASK信号 画出原始二进制代码波形
画出2ASK信号波形
结束 图1-2 2ASK流程图
8
%本函数实现将输入的一段二进制代码调制成相应的ask信号输出 %s为输入二进制码,f为载波频率,ask为调制后输出信号
包络检波法的原理方框图如图1-4所示。带通滤波器( BPF)恰好使2ASK信号完整地通过,经包络检测后,输出 其包络。低通滤波器(LPF)的作用是滤除高频杂波,使基 带信号(包络)通过。抽样判决器包括抽样、判决及码元形 成器。定时抽样脉冲(位同步信号)是很窄的脉冲,通常位 于每个码元的中央位置,其重复周期等于码元的宽度。不计 噪声影响时,带通滤波器输出为2ASK信号,即
信号同时送到抽样判决器进行比较,从而判决输出基带数
字信号。 28
若上、下支路 s (t ) 及 s ( t ) 的抽样值分别用 v1 、v2表示,则抽
样判决器的判决准则为
vv11
v2, v2,
判为“ 1” 判为“ 0”
a n 是 a n 的反码,于是
0, 概率P为
an 1,
概率为 1( P)
(1-14)
n 、n 分别是第n个信号码元的初相位和相位。一般 说来,键控法得到的 n 、n与序号n无关,反映在e0 (t )上
,仅表现出当改变时其相位是不连续的;而用模拟调频法时
,由于 1 与 2 改变时的相位是连续的,故不仅 n 、n
19
2FSK信号的产生方法及波形示例如图1-7所示。图中s (t )
实验2_连续时间信号的Matlab表示与计算
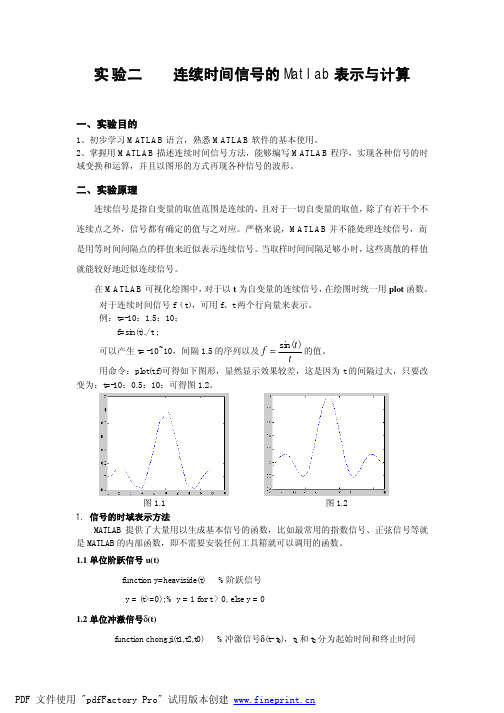
y=A*exp(a*t) 例如图 1-3 所示指数衰减信号的 MATLAB 源程序如下(取 A=1,a=-0.4): %program7_1 Decaying expponential signal A=1;a=-0.4; t=0:0.01:10; ft=A*exp(a*t); plot(t,ft);grid on; 1.4正弦信号
例如图 1-10 所示周期性矩形脉冲信号和周期性三角波脉冲信号的 MATLAB 源程序如 下:
%program7_8 Periodic pulse generator T=0:1/1E3:1;% 1kHz sample freq for 1 sec D=0:1/3:1;% 3Hz repetition freq Y=pulstran(T,D,'rectpuls',0.1); figure(1);plot(T,Y);grid on;axis([0,1,-0.1,1.1]); T=0:1/1E3:1; % 1kHz sample freq for 1sec D=0:1/3:1;% 3Hz repetition freq Y=pulstran(T,D,'tripuls',0.1,-1); figure(2);plot(T,Y);grid on;axis([0,1,-0.1,1.]);
到-1 线性递减的;在其他周期内依次类推。例如图 1-9 所示的周期性三角波信号的 MATLAB 源程序如下:
%program1-9 Periodic triangular pulse signal
t=-5*pi:pi/10:5*pi;
x=sawtooth(t,0.5);
MATLAB实验二答案

实验二报告人:王业成年级:机电131 学号:2013012496实验日期:2015.3.327报告完成日期:2015.3.30一、实验名称熟悉和掌握MA TLAB中关于矩阵变换以及矩阵运算的各种命令。
二、实验目的:熟悉和掌握MA TLAB中关于矩阵变换以及矩阵运算的各种命令。
三、实验内容:1.数、数组、矩阵的输入(1)数的输入a=5b=2-5i(2)数组的输入c=[1,3,5,7,9,11] %元素之间要用逗号用空格分开d=1:2:11e=linspace(1,11,6)体会以上输入有什么区别和联系。
(3)矩阵的输入A=[2,3,5;1,3,5;6,9,4] %行之间要用分别隔开2.矩阵大小的测试和定位A=[3,5,6;,2,5,8;3,5,9;3,7,9][n,m]=size(A)A(1,3)3. 矩阵的块操作A(2,:)A([1,3],:)A(2:3,1:2)问题2.1如何将A的2,3列互换?4.矩阵的四则运算A=[3,5,8;-2,3,6;1,4,9]B=rand(3,3)C=A+BD=A-BE=A*B问题2.2E为矩阵A、B的乘积运算结果,如果要求E的结果为A和B对应元素相乘的结果,应输入什么命令?F=A/B问题2.3 如果要求F为A,B对应元素作除法运算的结果,应输入什么命令?5.矩阵的点运算A=[1 2;3 4];B=[5 6;7 8];A*BA.*BA^2A.^26.矩阵的逻辑运算A=[1 2;3 4]; B=[0 6; 0 8]; A | BA&Bxor(A,B)a=-5;b=-10;(b~=0)&&(a/b>5)(b= =0)||(a/b>0)~a四、回答问题:问题2.1如何将A的2,3列互换?问题2.2 E为矩阵A、B的乘积运算结果,如果要求E的结果为A和B对应元素相乘的结果,应输入什么命令?问题2.3 如果要求F为A,B对应元素作除法运算的结果,应输入什么命令?五、思考题:1.输入一个矩阵A,取出A的第2行第1列的元素;取出A的第1,3,4列的所有元素;让A的第1列和第3列互换;删除A的第二列。
实验二用MATLAB建立传递函数模型

《自动控制原理》实验指导书北京科技大学自动化学院控制科学与工程系2013年4月目录实验一典型系统的时域响应和稳定性分析 (1)实验二用MATLAB建立传递函数模型 (5)实验三利用MATLAB进行时域分析 (13)实验四线性定常控制系统的稳定分析 (25)实验五利用MATLAB绘制系统根轨迹 (29)实验六线性系统的频域分析 (37)实验七基于MATLAB控制系统频域法串联校正设计 (51)附录1 MATLAB简介 (58)附录2 SIMULINK简介 (67)实验一典型系统的时域响应和稳定性分析一、实验目的1.研究二阶系统的特征参量(ξ、ωn) 对过渡过程的影响。
2.研究二阶对象的三种阻尼比下的响应曲线及系统的稳定性。
3.熟悉Routh判据,用Routh判据对三阶系统进行稳定性分析。
二、实验设备PC机一台,TD-ACC+教学实验系统一套。
三、实验原理及内容1.典型的二阶系统稳定性分析(1) 结构框图:如图1-1所示。
图1-1(2) 对应的模拟电路图:如图1-2所示。
图1-2(3) 理论分析系统开环传递函数为:G(s)=?开环增益:K=?先算出临界阻尼、欠阻尼、过阻尼时电阻R的理论值,再将理论值应用于模拟电路中,观察二阶系统的动态性能及稳定性,应与理论分析基本吻合。
在此实验中由图1-2,可以确地1-1中的参数。
0?T =, 1?T =,1?K = ?K ⇒=系统闭环传递函数为:()?W s =其中自然振荡角频率:?n ω=;阻尼比:?ζ=。
2.典型的三阶系统稳定性分析(1) 结构框图:如图1-3所示。
图1-3(2) 模拟电路图:如图1-4所示。
图1-4(3) 理论分析系统的开环传函为:()()?G s H s =系统的特征方程为:1()()0G s H s +=。
(4) 实验内容实验前由Routh 判断得Routh 行列式为:S 3 S 2 S 1 S 0为了保证系统稳定,第一列各值应为正数,因此可以确定系统稳定K值的范围系统临界稳定K系统不稳定K值的范围四、实验步骤1)将信号源单元的“ST”端插针与“S”端插针用“短路块”短接。
matlab实验报告实验二

matlab实验报告实验二Matlab实验报告实验二引言Matlab是一种功能强大的数学软件,广泛应用于科学研究和工程实践中。
在实验二中,我们将探索Matlab的图像处理功能,并通过实际案例来展示其应用。
图像处理基础图像处理是指对图像进行数字化处理的过程,其目的是改善图像质量、提取有用信息或实现特定的应用需求。
在Matlab中,我们可以利用各种函数和工具箱来实现图像处理的各种任务,如图像增强、滤波、分割和特征提取等。
实验步骤1. 图像读取与显示在Matlab中,我们可以使用imread函数读取图像文件,并使用imshow函数将图像显示在屏幕上。
例如,我们可以读取一张名为"lena.jpg"的图像,并显示出来:```matlabimg = imread('lena.jpg');imshow(img);```2. 图像灰度化图像灰度化是将彩色图像转换为灰度图像的过程。
在Matlab中,我们可以使用rgb2gray函数将彩色图像转换为灰度图像。
例如,我们可以将上一步读取的图像转换为灰度图像:```matlabgray_img = rgb2gray(img);imshow(gray_img);```3. 图像二值化图像二值化是将灰度图像转换为二值图像的过程,其中只包含黑色和白色两种颜色。
在Matlab中,我们可以使用imbinarize函数将灰度图像二值化。
例如,我们可以将上一步得到的灰度图像二值化:```matlabbinary_img = imbinarize(gray_img);imshow(binary_img);```4. 图像平滑图像平滑是指去除图像中的噪声或细节,使得图像更加平滑和清晰。
在Matlab 中,我们可以使用imfilter函数对图像进行平滑处理。
例如,我们可以对上一步得到的二值图像进行平滑处理:```matlabsmooth_img = imfilter(binary_img, fspecial('average'));imshow(smooth_img);```5. 图像边缘检测图像边缘检测是指提取图像中物体边缘的过程,常用于目标检测和图像分割。
实验二MATLAB 求微分方程的解

实验二 微分方程求解一、问题背景与实验目的实际应用问题通过数学建模所归纳而得到的方程,绝大多数都是微分方程,真正能得到代数方程的机会很少.另一方面,能够求解的微分方程也是十分有限的,特别是高阶方程和偏微分方程(组).这就要求我们必须研究微分方程(组)的解法,既要研究微分方程(组)的解析解法(精确解),更要研究微分方程(组)的数值解法(近似解).对微分方程(组)的解析解法(精确解),Matlab 有专门的函数可以用,本实验将作一定的介绍.本实验将主要研究微分方程(组)的数值解法(近似解),重点介绍 Euler 折线法.二、相关函数(命令)及简介1.dsolve('equ1','equ2',…):Matlab 求微分方程的解析解.equ1、equ2、…为方程(或条件).写方程(或条件)时用 Dy 表示y 关于自变量的一阶导数,用用 D2y 表示 y 关于自变量的二阶导数,依此类推.2.simplify(s):对表达式 s 使用 maple 的化简规则进行化简. 例如: syms xsimplify(sin(x)^2 + cos(x)^2) ans=13.[r,how]=simple(s):由于 Matlab 提供了多种化简规则,simple 命令就是对表达式 s 用各种规则进行化简,然后用 r 返回最简形式,how 返回形成这种形式所用的规则.例如: syms x[r,how]=simple(cos(x)^2-sin(x)^2) r = cos(2*x) how = combine4.[T,Y] = solver(odefun,tspan,y 0) 求微分方程的数值解. 说明:(1) 其中的 solver 为命令 ode45、ode23、ode113、ode15s 、ode23s 、ode23t 、ode23tb 之一.(2) odefun是显式常微分方程:⎪⎩⎪⎨⎧==00)(),(yt y y t f dt dy(3) 在积分区间 tspan =],[0f t t 上,从0t 到f t ,用初始条件0y 求解.(4) 要获得问题在其他指定时间点 ,210,,t t t 上的解,则令 tspan =],,,[,210f t t t t (要求是单调的).(5) 因为没有一种算法可以有效地解决所有的 ODE 问题,为此,Matlab 提供了多种求解器 Solver ,对于不同的ODE 问题,采用不同的Solver .(6) 要特别的是:ode23、ode45 是极其常用的用来求解非刚性的标准形式的一阶常微分方程(组)的初值问题的解的 Matlab 的常用程序,其中:ode23 采用龙格-库塔2 阶算法,用3 阶公式作误差估计来调节步长,具有低等的精度.ode45 则采用龙格-库塔4 阶算法,用5 阶公式作误差估计来调节步长,具有中等的精度.5.ezplot(x,y ,[tmin,tmax]):符号函数的作图命令.x,y 为关于参数t 的符号函数,[tmin,tmax] 为 t 的取值范围.6.inline():建立一个内联函数.格式:inline('expr', 'var1', 'var2',…) ,注意括号里的表达式要加引号.例:Q = dblquad(inline('y*sin(x)'), pi, 2*pi, 0, pi)三、实验内容1. 几个可以直接用 Matlab 求微分方程精确解的例子: 例1:求解微分方程22xxexy dxdy -=+,并加以验证.求解本问题的Matlab 程序为:syms x y %line1 y=dsolve('Dy+2*x*y=x*exp(-x^2)','x') %line2diff(y ,x)+2*x*y-x*exp(-x^2) %line3 simplify(diff(y ,x)+2*x*y-x*exp(-x^2)) %line4 说明:(1) 行line1是用命令定义x,y 为符号变量.这里可以不写,但为确保正确性,建议写上;(2) 行line2是用命令求出的微分方程的解:1/2*exp(-x^2)*x^2+exp(-x^2)*C1(3) 行line3使用所求得的解.这里是将解代入原微分方程,结果应该为0,但这里给出:-x^3*exp(-x^2)-2*x*exp(-x^2)*C1+2*x*(1/2*exp(-x^2)*x^2+exp(-x^2)*C1)(4) 行line4 用 simplify() 函数对上式进行化简,结果为 0, 表明)(x y y =的确是微分方程的解.例2:求微分方程0'=-+x e y xy 在初始条件e y 2)1(=下的特解,并画出解函数的图形.求解本问题的 Matlab 程序为: syms x yy=dsolve('x*Dy+y-exp(x)=0','y(1)=2*exp(1)','x') ezplot(y)微分方程的特解为:y=1/x*exp(x)+1/x* exp (1) (Matlab 格式),即xe e y x+=,解函数的图形如图 1:图1例3:求微分方程组⎪⎪⎩⎪⎪⎨⎧=--=++035y x dt dy e y x dtdx t在初始条件0|,1|00====t t y x 下的特解,并画出解函数的图形.求解本问题的 Matlab 程序为: syms x y t[x,y]=dsolve('Dx+5*x+y=exp(t)','Dy-x-3*y=0','x(0)=1','y(0)=0','t') simple(x); simple(y);ezplot(x,y ,[0,1.3]);axis auto微分方程的特解(式子特别长)以及解函数的图形均略. 2. 用ode23、ode45等求解非刚性的标准形式的一阶常微分方程(组)的初值问题的数值解(近似解).例4:求解微分方程初值问题⎪⎩⎪⎨⎧=++-=1)0(2222y x x y dxdy 的数值解,求解范围为区间[0, 0.5].fun=inline('-2*y+2*x^2+2*x','x','y'); [x,y]=ode23(fun,[0,0.5],1); x'; y';plot(x,y ,'o-') >> x' ans =0.0000 0.0400 0.0900 0.1400 0.1900 0.2400 0.2900 0.3400 0.3900 0.4400 0.4900 0.5000 >> y' ans =1.0000 0.9247 0.8434 0.7754 0.7199 0.6764 0.6440 0.6222 0.6105 0.6084 0.6154 0.6179 图形结果为图 2.图2例 5:求解描述振荡器的经典的 V er der Pol 微分方程.7,0)0(',1)0(,0)1(222====+--μμy y y dtdy y dty d分析:令,,121dtdx x y x ==则.)1(,1221221x x x dtdx x dtdx --==μ先编写函数文件verderpol.m : function xprime = verderpol(t,x) global mu;xprime = [x(2);mu*(1-x(1)^2)*x(2)-x(1)]; 再编写命令文件vdp1.m : global mu; mu = 7; y0=[1;0][t,x] = ode45('verderpol',[0,40],y0); x1=x(:,1);x2=x(:,2); plot(t,x1)图形结果为图3.图33. 用 Euler 折线法求解前面讲到过,能够求解的微分方程也是十分有限的.下面介绍用 Euler 折线法求微分方程的数值解(近似解)的方法.Euler 折线法求解的基本思想是将微分方程初值问题⎪⎩⎪⎨⎧==00)(),,(yx y y x f dx dy化成一个代数方程,即差分方程,主要步骤是用差商hx y h x y )()(-+替代微商dxdy ,于是:⎪⎩⎪⎨⎧==-+)()),(,()()(00x y y x y x f h x y h x y k k k k 记)(,1k k k k x y y h x x =+=+,从而)(1h x y y k k +=+,则有1,,2,1,0).,(,),(1100-=⎪⎩⎪⎨⎧+=+==++n k y x hf y yh x x x y y k k k k k k 例 6:用 Euler 折线法求解微分方程初值问题⎪⎩⎪⎨⎧=+=1)0(,22y y x y dxdy 的数值解(步长h 取0.4),求解范围为区间[0,2].解:本问题的差分方程为1,,2,1,0).2),( ),(,,4.0,1,021100-=⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+====++n k y x y y x f y x hf y y h x x h y x k k k k k k (其中: 相应的Matlab 程序见附录 1. 数据结果为:0 1.0000 0.4000 1.4000 0.8000 2.1233 1.2000 3.1145 1.6000 4.4593 2.0000 6.3074图形结果见图4:图4特别说明:本问题可进一步利用四阶 Runge-Kutta 法求解,读者可将两个结果在一个图中显示,并和精确值比较,看看哪个更“精确”?(相应的 Matlab 程序参见附录 2).四、自己动手1. 求微分方程0sin 2')1(2=-+-x xy y x 的通解.2. 求微分方程x e y y y x sin 5'2''=+-的通解.3. 求微分方程组⎪⎪⎩⎪⎪⎨⎧=-+=++00y x dtdy y x dtdx在初始条件0|,1|00====t t y x 下的特解,并画出解函数()y f x =的图形. 4. 分别用 ode23、ode45 求上述第 3 题中的微分方程初值问题的数值解(近似解),求解区间为[0,2]t ∈.利用画图来比较两种求解器之间的差异.5. 用 Euler 折线法求解微分方程初值问题⎪⎩⎪⎨⎧=-=1)0(,12'32y y xy y 的数值解(步长h 取0.1),求解范围为区间[0,2].6. 用四阶 Runge-Kutta 法求解微分方程初值问题⎩⎨⎧=-=1)0(,cos 'y x e y y x 的数值解(步长h 取0.1),求解范围为区间[0,3].四阶 Runge-Kutta 法的迭代公式为(Euler 折线法实为一阶 Runge-Kutta 法):1,,2,1,0),()2,2()2,2(),()22(6,),(342312143211100-=⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧++=++=++==++++=+==++n k hL y h x f L L h y h x f L L h y h x f L y x f L L L L L hy y h x x x y y k k k k k k k k k k k k 相应的 Matlab 程序参见附录 2.试用该方法求解第5题中的初值问题. 7. 用 ode45 方法求上述第 6 题的常微分方程初值问题的数值解(近似解),从而利用画图来比较两者间的差异.五、附录附录 1:(fulu1.m)clearf=sym('y+2*x/y^2'); a=0; b=2; h=0.4;n=(b-a)/h+1; x=0; y=1;szj=[x,y]; for i=1:n-1y=y+h*subs(f,{'x','y'},{x,y}); x=x+h;szj=[szj;x,y]; end szjplot(szj(:,1),szj(:,2))附录 2:(fulu2.m)clearf=sym('y-exp(x)*cos(x)'); a=0; b=3; h=0.1;n=(b-a)/h+1; x=0; y=1;szj=[x,y];for i=1:n-1l1=subs(f,{'x','y'},{x,y});l2=subs(f,{'x','y'},{x+h/2,y+l1*h/2});l3=subs(f,{'x','y'},{x+h/2,y+l2*h/2});l4=subs(f,{'x','y'},{x+h,y+l3*h});y=y+h*(l1+2*l2+2*l3+l4)/6;x=x+h;szj=[szj;x,y];endszjplot(szj(:,1),szj(:,2))。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 周期信号的傅里叶级数条件:宽度为1,高度为1,周期为2的正方波,傅立叶级数(前N 项)逼近。
对一定的周期 T ,取不同项数(即谐波次数)时有限项级数逼近函数的情况。
思路:首先计算出周期信号的傅里叶级数 程序如下:t=-2:0.001:2; %信号的抽样点 N=input('N='); %输入傅里叶级数的项数 c0=0.5;fN=c0*ones(1,length(t));%计算抽样上的直流分量 for n=1:2:N %偶次谐波为零 fN=fN+cos(pi*n*t)*sinc(n/2); end figure plot(t,fN)title(['N=' num2str(N)]) axis([-2 2 -0.2 1.2])作图:-0.20.20.40.60.81-0.20.20.40.60.81-0.20.20.40.60.812. 求f(t)=e-2|t|的傅立叶变换,并画出f(t)及其幅度频谱图 程序如下: syms tf=exp(-2*abs(t));F=fourier(f); %作f 的傅里叶变换 ezplot(f); %作出f 函数的波形图 subplot(1,2,1);title('original signal f(t)'); xlabel('t');ylabel('f(t)'); subplot(1,2,2);ezplot(F); %作傅里叶变换的图title('Signal Frequency spectrum'); xlabel('¦Ø');ylabel('F(¦Ø)');-2-10120.10.20.30.40.50.60.70.80.9toriginal signal f(t)f (t )-5050.10.20.30.40.50.60.70.80.91ωSignal Frequency spectrumF (ω)3.已知一RLC 二阶低通滤波器,其电路图如图所示目的:用matlab 的freqs 函数求出频率响应(Frequency spectrum ) 思路:首先写出系统函数H (j ω),确定向量b (分子),a (分母) 注意点:函数返回值的格式[h w]=freqs(b,a,100) 采样点默认为200相角angel程序如下:b=[0 0 1];a=[0.08 0.4 1];%注明系统函数的分子分母多项式的系数 [h w]=freqs(b, a, 100);%求出频响并作图 h1=abs(h);%求幅频响应 h2=angle(h);%求角频响应 subplot(2,1,1);plot(w,h1);grid;%作出幅频响应图title('Amplitude frequency response of H£¨j¦Ø£©'); xlabel('w');ylabel('Amplitude h1'); subplot(2,1,2);plot(w,h2*pi/180);grid; %作出角频响应图title('Phase frequency response of H£¨j¦Ø£©'); xlabel('w');ylabel('Phase h2');作图:01020304050607080901000.51Amplitude frequency response of H (jω)wA m p l i t u d e h 10102030405060708090100-0.06-0.04-0.020Phase frequency response of H (jω)wP h a s e h 24.已知信号 f(t)=sin(20π*t),载波信号为频率100HZ的正弦信号目标:绘制其在不同调制方式(调相、调频、调幅)下的波形要点:调制函数yy=modulate(y,fc,fs,’method’)yy: modulated signal y: original signalfc: The frequency of carrierfs: signal sampling frequencymethod: including pm,fm and am程序如下:% 绘制原始信号fm=10;fc=100;fs=1000;N=1000;k=0:N;t=k/fs;y=sin(2*pi*fm*t);subplot(4,1,1);plot(t,y);axis([0,0.2,-1.1,1.1]);title('original signal');xlabel('Time(s)');ylabel('y');% 产生pm调制信号y1=modulate(y,fc,fs,'pm');%对信号进行pm调制subplot(4,1,2);plot(t,y1);axis([0,0.2,-1.1,1.1]);title('"pm" modulated signal');xlabel('Time(s)');ylabel('y1');% 产生fm调制信号y2=modulate(y,fc,fs,'fm'); %对信号进行fm调制subplot(4,1,3);plot(t,y2);axis([0,0.2,-1.1,1.1]);title('"fm" modulated signal');xlabel('Time(s)');ylabel('y2');%产生am调制信号y3=modulate(y,fc,fs,'am'); %对信号进行am调制subplot(4,1,4);plot(t,y3);axis([0,0.2,-1.1,1.1]);title('"am" modulated signal');xlabel('Time(s)');ylabel('y3'); hold on ;plot(t,y);hold on;plot(t,-y);0.020.040.060.080.10.120.140.160.180.2original signalTime(s)y 00.020.040.060.080.10.120.140.160.180.2"pm" modulated signalTime(s)y 10.020.040.060.080.10.120.140.160.180.2"fm" modulated signalTime(s)y 20.020.040.060.080.10.120.140.160.180.2"am" modulated signalTime(s)y 35.已知Xa(t)=exp(-1000*abs(t)) 目标:绘制其傅里叶变换Xa(j ω)。
用三个不同的抽样频率(fs=5kHz/2 kHz /1 kHz)对其进行采样,分别求出并绘制离散时间傅里叶变换X(j ω) 程序如下:Dt=0.00005; t=-0.005:Dt:0.005; xa=exp(-1000*abs(t)); %模拟信号 Wmax=2*pi*2000; K=500;k=0:K;W=k*Wmax/K; Xa=xa*exp(-j*t'*W)*Dt; Xa=real(Xa);W=[-fliplr(W),W(2:501)];Xa=[fliplr(Xa),Xa(2:501)];subplot(4,2,1); plot(t*1000,xa)subplot(4,2,2); plot(W/(2*pi*1000),Xa*1000) title('模拟信号')Ts=0.0002; n=-25:1:25;x=exp(-1000*abs(n*Ts)); %离散信号w=pi*k/K; X=x*exp(-j*n'*w); X=real(X);w=[-fliplr(w),w(2:K+1)];X=[fliplr(X),X(2:K+1)];subplot(4,2,3);stem(n*Ts*1000,x)subplot(4,2,4);plot(w/pi,X)title('离散信号Ts=0.2毫秒')Ts=0.0005; n=-10:1:10;x=exp(-1000*abs(n*Ts)); %离散信号w=pi*k/K; X=x*exp(-j*n'*w); X=real(X);w=[-fliplr(w),w(2:K+1)];X=[fliplr(X),X(2:K+1)];subplot(4,2,5);stem(n*Ts*1000,x)subplot(4,2,6);plot(w/pi,X)title('离散信号Ts=0.5毫秒')Ts=0.001; n=-5:1:5;x=exp(-1000*abs(n*Ts)); %离散信号w=pi*k/K; X=x*exp(-j*n'*w); X=real(X);w=[-fliplr(w),w(2:K+1)];X=[fliplr(X),X(2:K+1)];subplot(4,2,7);stem(n*Ts*1000,x)subplot(4,2,8);plot(w/pi,X)title('离散信号Ts=1毫秒')作图:-505-2-101212模拟信号-1-0.500.510510离散信号T s=0.2毫秒-1-0.500.5105离散信号T s=0.5毫秒-1-0.50.51024离散信号T s=1毫秒。
