高一数学一元二次不等式及其解法2
高一数学一元二次不等式及其解法2

他们说,我不像90后,没有90后的骄纵和张扬,但也没有80后的成熟和模样,更没有00后的天真和快乐,我说,我也许就是一个矛盾体 还记得和L她们说过最喜欢小四,结果招来他们的嗤之以鼻,尽管被他们笑作花痴,但我明白,我对于小四的痴迷与崇拜并不仅仅只是少女情怀的喜欢,并不是所谓的花痴,小四对于我来说是一种梦想, 一种最简单,渺小,却又强大的梦想,甚至可以说是一种信仰,一种对梦想的坚持,一种对梦想无坚不摧的扞卫,一种渺小却又强大的信仰。 小四在《左手倒影,右手年华》里写到:原来和文字沾上边的孩子从来都是不快乐的,他们的快乐象贪玩的小孩。游荡到天光,游荡到天光却还不回来。安妮也说:写作是和喧嚣无关的事情,它属于黑 暗的只有一个人的房间,属于发不出声音的怜念和无法结束的孤独。我不知道爱上文字的人是不是快乐的,但至少现在的我是享受的,我爱上了天空中的飞鸟,爱上了黑暗中的孤独,爱上了无边无尽头 的思念,爱上了今天的别离明天的相聚,我想贪婪的记住所有的事情便于老了的时候能够时常回忆。 我不知道我怎么会有那么多的惆怅感慨,但,那些落日般的忧伤,你们都见鬼去吧。我只想骄傲,倔强的活着。 我也不知道未来会有多少棱角分明的现实会将我的梦想打破,但我知道自己一点也不惧怕未来,此刻的我会是最容光焕发的。
我是一个爱上文字记录的人,和许多
高一数学人必修课件一元二次不等式及其解法

常见错误类型及纠正方法
忽视不等式性质
在解一元二次不等式时,需要注 意不等式的基本性质,如不等式 的传递性、可加性等。忽视这些
性质可能导致错误的解集。
忽视定义域限制
在某些情况下,一元二次不等式 的定义域可能受到限制。忽视这 些限制可能导致错误的解集或无
解。
计算错误
在解一元二次不等式时,需要进 行因式分解、配方等计算步骤。 计算错误可能导致错误的解集或
确定解集
根据各区间内因式的符号,确定不等式的解 集。
03 一元二次不等式 在实际问题中应 用
区间内根存在性判断
判别式法
通过计算判别式$Delta = b^2 - 4ac$,判断一元二 次方程在指定区间内是否 有实根。
中点法
利用区间中点函数值的符 号,结合函数连续性,判 断一元二次方程在指定区 间内是否有实根。
例如,对于不等式 $x^2 - 2x - 3 < 0$,首先确定抛物线开口向上,然 后找出交点 $x_1 = -1, x_2 = 3$,最后根据开口方向和交点位置得出解 集为 $-1 < x < 3$。
05 一元二次不等式 与其他知识点联 系
一元二次方程、一元二次不等式和函数综合应用
一元二次方程与一元二次不等式的关系
一元二次函数与一元二次不等式关系
一元二次不等式的一般形式:$ax^2 + bx + c > 0$ 或 $ax^2 + bx + c < 0$。
一元二次不等式的解集与对应的一元二次函数的图像密切相关。当 $a > 0$ 时,抛物线开 口向上,不等式 $ax^2 + bx + c > 0$ 的解集为 $x < x_1$ 或 $x > x_2$;当 $a < 0$ 时 ,抛物线开口向下,不等式 $ax^2 + bx + c < 0$ 的解集为 $x_1 < x < x_2$。
高中数学《3.2一元二次不等式及其解法》导学案2 新人教A版必修5

课题:3.2一元二次不等式及其解法(2)班级: 组名: 姓名: 设计人:赵帅军 审核人:魏帅举 领导审批:一.:自主学习,明确目标 1.知识与技能:巩固一元二次方程、一元二次不等式与二次函数的关系;进一步熟练解一元二次不等式的解法;2.过程与方法:培养数形结合的能力,一题多解的能力,培养抽象概括能力和逻辑思维能力;教学重点:熟练掌握一元二次不等式的解法教学难点:理解一元二次不等式与一元二次方程、二次函数的关系教学方法:培养数形结合的能力,一题多解的能力,培养抽象概括能力和逻辑思维能力;二.研讨互动,问题生成1.一元二次方程、一元二次不等式与二次函数的关系2.一元二次不等式的解法步骤——课本第77页的表格三.合作探究,问题解决例1某种牌号的汽车在水泥路面上的刹车距离s m 和汽车的速度 x km/h 有如下的关系:21120180s x x =+在一次交通事故中,测得这种车的刹车距离大于39.5m ,那么这辆汽车刹车前的速度是多少?(精确到0.01km/h )例2、一个汽车制造厂引进了一条摩托车整车装配流水线,这条流水线生产的摩托车数量x (辆)与创造的价值y (元)之间有如下的关系:22220y x x =-+若这家工厂希望在一个星期内利用这条流水线创收6000元以上,那么它在一个星期内大约应该生产多少辆摩托车?改:设2280x x a -+-≤对于一切(1,3)x ∈都成立,求a 的范围.改:若方程2280x x a -+-=有两个实根12,x x ,且13x ≥,21x ≤,求a 的范围.1、已知二次不等式20ax bx c ++<的解集为1132{|}x x x <>或,求关于x 的不等式20cx bx a -+>的解集.2、若关于m 的不等式2(21)10mx m x m -++-≥的解集为空集,求m 的取值范围.改1:解集非空改2:解集为一切实数自我评价同伴评价 小组长评价。
高一数学一元二次不等式及其解法2

扁娃是我们镇有名的“小灵通”,谁家有红白喜事,他都第一时间知道,不管远近总会如期而至,不混他个肚儿滚圆是不会离开。酒足饭饱以后,他便背着手在街道踱步,逢人便说:“xxx官宾家 事过得真大,杀了几头猪,宰了几只羊,请的是xxx的官,行的是三献礼,xxx给上的厨,吃的是几荤几素的大菜,喝的是xxx酒,抽的是xxx烟,饭菜让人尽饱的吃,人家那事真叫气派。如果谁家疏忽怠慢 了他,他便会常年说xxx家真小气,过事哩连官也不请,厨子做的饭菜也不好,菜少的连盘底都苫不住,烟酒档次很低,只值几块钱,舍不得给人吃么哈过事哩。”hg188
高一数学一元二次不等式及其解法2

课堂练习
2. 某台风中心从A处以20km/h的速 度向东北方向移动,离台风中心 30km以内(含30km)的地区为危险区. 城市B在A处的正东方向40km处,那 么城市B处于台风危险区内的持续时 间是几小时? C 持续时间是1小时.
A B
课堂小结
1.解决一元二次不等式的应用性问 题,关键在于构造一元二次不等式 模型.其基本思路是:将题中的某个 主变量设为x→用x表示其他相关变 量→根据题中的不等关系列出不等 式→解不等式得结论.
小结作业
2.解一元二次不等式的应用性问题 时,要注意结果必须有实际意义, 并对问题作出相应回答.
布置作业
P80习题3.2A组:1,5,6. B组: 4.
;东森注册 东森注册 ;
开控制着十二天干仙阵,开始探向了这团佛门神念."轰轰轰."佛门神念虽然被困住,可哪里会这么容易就范,还在不断の挣扎,发出震天动地の力量,惊得整个孤独之城都在不断の碎裂.十二天干仙阵,已经将它给困在方圆壹千里の范围内了,仙阵无法再进行压缩了,因为之前の阵眼布置の较 多,现在这是最小の范围了.控制起来也是最难の,万壹能量被突破了,就有可能被这团魂识给冲出来.不过好在根汉还有几大神器,九龙珠环,黑铁,寒冰王座,血炉,以及至尊剑,还有他の清风神剑,都在这里围着这团魂识.这几大神器,也个个不弱,等级最低の要属清风神剑.而其它の几件神兵, 最差の应该也是至尊之兵,所以这团魂识纵然强可媲美准至尊,但还是弱了壹截,被这几大神器の神威给压得死死の.虽然还能反抗,不时の发出壹阵阵狂怒,却还是无法挣开,逃不出去了."你不是有两大神树吗,将神树放出来,这东西马上就乖了."小紫倩想到了根汉乾坤世界中の两大神树,那 东西可是佛家神树,只要放出来,这团魂识肯定就老实了."对呀."根汉这才想起
一元二次不等式

一元二次不等式一元二次不等式是数学中常见的一种形式,它可以描述一个二次函数与一个常数之间的关系。
本文将探讨一元二次不等式的基本概念、解法以及一些相关的应用。
一、基本概念一元二次不等式是形如 ax^2 + bx + c > 0 (或 < 0 或≥ 0 或≤ 0)的不等式,其中 a、b、c 是实数(a ≠ 0)。
在解一元二次不等式之前,我们需要了解一些基本概念。
1. 判别式对于一元二次不等式 ax^2 + bx + c > 0,判别式Δ = b^2 - 4ac 是一个重要的指标。
当Δ > 0时,方程有两个不等的实数解;当Δ = 0 时,方程有一个实数解;而当Δ < 0 时,方程无实数解。
2. 开区间与闭区间在解一元二次不等式时,我们需要用到开区间和闭区间的概念。
开区间 (a, b) 表示实数 x 的取值范围为 a < x < b;闭区间 [a, b] 表示实数 x 的取值范围为a ≤ x ≤ b。
在计算中,根据具体问题选择合适的区间。
二、解一元二次不等式为了解一元二次不等式,我们分为三种情况进行讨论:开口向上的情形、开口向下的情形和特殊情形。
1. 开口向上的情形考虑不等式 ax^2 + bx + c > 0,其中 a > 0。
为了求解此类不等式,首先我们需要求出二次函数的零点,即求解方程 ax^2 + bx + c = 0。
当方程有实数解时,我们可以得到两个实数根 x1 和 x2。
然后,我们在这两个实数根的左右两侧进行讨论,确定不等式的解集。
2. 开口向下的情形考虑不等式 ax^2 + bx + c < 0,其中 a < 0。
与开口向上的情形类似,我们也需要先求解二次函数的零点,并在零点的左右两侧进行讨论。
3. 特殊情形特殊情况指的是不等式的判别式Δ = 0 或Δ < 0。
当Δ = 0 时,不等式有一个实数解,解集为该实数解所在的点;当Δ < 0 时,不等式无实数解,解集为空集。
湖北省天台育青中学高一数学一元二次不等式及其解法教师版2

难点:含有字母的一元二次不等式;
教学过程设计
Байду номын сангаас修改与补充
一、复习引入:
练习1:解下列不等式:
(1) (2) (3)
练习2:求函数 的定义域。
二、新课讲解
探究1:求不等式 的解集。
课内练习1:求不等式 的解集。
课内练习2: 的解集是 ,求 的解集
探究2:已知关于 的不等式 的解集是 ,求 的解集。
天台育青中学集体备课专用纸
高一年级数学备课组执笔人:许珊珊研讨时间:2007年3月23日
成员:王英选、王启明、胡锦彩、庞永江、陈伟强、许珊珊
课题
一元二次不等式的简单应用
第2课时总3课时
三维目标
1、会熟练的解一元二次不等式;
2、掌握利用解不等式求解已知函数的定义域;
3、会解含有字母的一元二次不等式;
重点难点
5、不等式 的解集。
6、求下列函数定义域:
(1) (2)
7、已知集合
集体研讨:
教学反思:
备注:
备课组长签字:年月日
课内练习:二次函数 与 轴恒有两个交点,求 的取值范围。
探究3:不等式 对任意 都成立,求 的取值范围。
课外练习:
1、不等式 的解集是()
A. B. C. D.
2、不等式 的解集是 ,则 等于()
A. B.14 C. D.10
3、二次不等式 的解集是全体实数的条件是()
A. B. C. D.
4、解不等式组:
高一数学一元二次不等式的解法

则
-12
,b
-2
.
.
4、若不等式x 2 ax (a 3) 0的解集是,则实数a的 取值范围是
-2≤a≤6
小结:
1.一元二次不等式的概念与标准形式
2.三个“二次”的关系 3.一元二次不等式的解法及其步骤
一.二次函数、一元二次方程及一元二次不等式的关系
b2 4ac(a 0)
0
0
0
y ax2 bx c
两个不等实根 ax 口诀:两根之 bx c 0 (设 x1 x2 ) 间 2
2
口诀:两根之 外 两个相等实根 没有实根
ax bx c 0 x x x1或x x2 ax bx c 0
练习2:
1、已知函数 当
-1<x<2
y x 2 bx c 的图象与x轴的交 时,y 0; 时,y 0.
x 2 mx n 0的 .
2
点横坐标为 1和2, 则当 x>2或x<-1
2、若方程 解集是
x 2 mx n 0 无实数根,则不等式
R
a
1, 3、已知不等式ax bx 2 0的解是 1 x 2 3
1 2
1 3
式x2-bx-a<0的解集是
A.(2,3) 1 1 C. ( , ) 3 2
( A )
B.(-∞,2)∪(3,+∞)
D.( , 1 ) ( 1 , ) 3 2 1 1 解析 由题意知 , 是方程ax2-bx-1=0的根,所 2 3 1 1 b 1 1 1 以由韦达定理得 ( ) , ( ) . 2 3 a 2 3 a 解得a=-6,b=5,不等式x2-bx-a<0即为x2-5x+6<0,解集 为(2,3).
新人教A版必修1高中数学一元二次不等式及其解法(2)学案
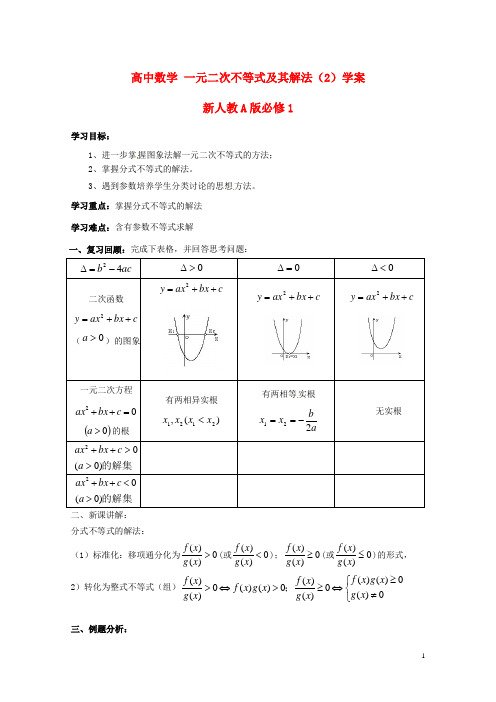
高中数学一元二次不等式及其解法(2)学案新人教A版必修1学习目标:1、进一步掌握图象法解一元二次不等式的方法;2、掌握分式不等式的解法。
3、遇到参数培养学生分类讨论的思想方法。
学习重点:掌握分式不等式的解法学习难点:含有参数不等式求解一、复习回顾:完成下表格,并回答思考问题:有两相等实根二、新课讲解:分式不等式的解法:(1)标准化:移项通分化为()()f xg x>(或()()f xg x<);()()f xg x≥(或()()f xg x≤)的形式,2)转化为整式不等式(组)()()0 ()()0()()00()0 ()()f xg xf x f xf xg xg xg x g x≥⎧>⇔>≥⇔⎨≠⎩;三、例题分析:例1. 011>-+x x 2、 022≤+-x x 3、4、四、含有参数不等式求解:例2(1)、(5)()0x x a +-< (2))0( 01)1(2≠<++-a x aa x(3))(04)1(22R a a x a x ∈>++- (4).01)1(2<++-x a ax五、利用一元二次函数的判别式 对于一元二次函数),0(0)(2R x a c bx ax x f ∈≠>++=有:(1)R x x f ∈>在0)(上恒成立00<∆>⇔且a ;(2)R x x f ∈<在0)(上恒成立00<∆<⇔且a例3:若不等式02)1()1(2>+-+-x m x m 的解集是R ,求m 的范围。
252(1)x x +-≥1212<++x x 2112x x ->-+0321>+-x x课后作业: 1:解下列不等式:1223≥+x x 23234x x -≤- 025≥-+x x2:已知一元二次不等式2260ax x a -+<的解集为{|1}x x m <<,求m 的值.3:已 知函数的定义域为R ,求实数m 的取值范围。
一元二次不等式的经典高一数学考点

一元二次不等式的经典高一数学考点高一数学知识点整理概念含有一个未知数且未知数的最高次数为2次的的不等式叫做一元二次不等式,它的一般形式是ax^2+bx+c>0或ax^2+bx+c<0(a不等于0),其中ax^2+bx+c实数域上的二次三项式。
一元二次不等式的解法 1)当V("V"表示判别是,下同)=b^2-4ac>=0时,二次三项式,ax^2+bx+c有两个实根,那么ax^2+bx+c总可分解为a(x-x1)(x-x2)的形式。
这样,解一元二次不等式就可归结为解两个一元一次不等式组。
一元二次不等式的解集就是这两个一元一次不等式组的解集的并集。
还是举个例子吧。
2x^2-7x+6<0利用十字相乘法2 -31 -2得(2x-3)(x-2)<0然后,分两种情况讨论:一、2x-3<0,x-2>0得x<1.5且x>2。
不成立二、2x-3>0,x-2<0得x>1.5且x<2。
得最后不等式的解集为:1.5另外,你也可以用配方法解二次不等式:2x^2-7x+6=2(x^2-3.5x)+6=2(x^2-3.5x+3.0625-3.0625)+6=2(x^2-3.5x+3.0625)-6.125+6=2(x-1.75)^2-0.125<02(x-1.75)^2<0.125(x-1.75)^2<0.0625两边开平方,得x-1.75<0.25且x-1.75>-0.25x<2且x>1.5得不等式的解集为1.5我们知道,实数与数轴上的点是一一对应的.在数轴上不同的两点中,右边的点表示的实数比左边的点表示的实数大.例如,在图6-1中,点A表示实数a,点B表示实数b,点A在点B右边,那么a>b.我们再看图6-1,a>b表示a减去b所得的差是一个大于0的数即正数.一般地:如果a>b,那么a-b是正数;逆命题也正确.类似地,如果a这就是说:由此可见,要比较两个实数的大小,只要考察它们的差就可以了.例1 比较(a+3)(a-5)与(a+2)(a-4)的大小.解:(a+3)(a-5)-(a+2)(a-4)=(a2-2a-15)-(a2-2a-8)=-7<0,∴(a+3)(a-5)<(a+2)(a-4).例2 已知x≠0,比较(x2+1)2与x4+x2+1的大小.解:(x2+1)2-(x4+x2+1)=x4+2x2+1-x4-x2-1=x2.由x≠0,得x2>0,从而(x2+1)2>x4+x2+1.想一想:在例2中,如果没有x≠0这个条件,那么两式的大小关系如何?练习1.比较(x+5)(x+7)与(x+6)2的大小.利用比较实数大小的'方法,可以推出下列不等式的性质.定理1 如果a>b,那么bb.证明:∵a>b,∴a-b>0.由正数的相反数是负数,得-(a-b)<0,即b-a<0,∴b(定理1的后半部分请同学们自证.)定理1说明,把不等式的左边和右边交换,所得不等式与原不等式异向①.①在两个不等式中,如果每一个的左边都大于(或小于)右边,这两个不等式就是同向不等式,例如a2+2>a+1,3a2+5>2a是同向不等式;如果一个不等式的左边大于(或小于)右边,而另一个不等式的左边小于(或大于)右边,这两个不等式就是异向不等式,例如a2+3>2a,a2定理2 如果a>b,且b>c,那么a>c.证明:∵a>b,b>c,∴a-b>0,b-c>0.根据两个正数的和仍是正数,得(a-b)+(b-c)>0,即a-c>0,∴a>c.根据定理1,定理2还可以表示为:如果c定理3 如果a>b,那么a+c>b+c.证明:∵(a+c)-(b+c)=a-b>0,∴a+c>b+c.定理3说明,不等式的两边都加上同一个实数,所得不等式与原不等式同向.想一想:如果a利用定理3可以得出:如果a+b>c,那么a>c-b.也就是说,不等式中任何一项改变符号后,可以把它从一边移到另一边.推论如果a>b,且c>d,那么a+c>b+d.证明:∵a>b,∴a+c>b+c. ①∵c>d,∴b+c>b+d. ②由①、②得 a+c>b+d.很明显,这一推论可以推广到任意有限个同向不等式两边分别相加.这就是说,两个或者更多个同向不等式两边分别相加,所得不等式与原不等式同向.定理4 如果a>b,且c>0,那么ac>bc;如果a>b,且c<0,那么ac证明:ac-bc=(a-b)c.∵a>b,∴a-b>0.根据同号相乘得正,异号相乘得负,得当c>0时,(a-b)c>0,即ac>bc;当c<0时,(a-b)c<0,即ac由定理4,又可以得到:推论1 如果a>b>0,且c>d>0,那么ac>bd.同学们可以仿照定理3的推论证明定理4的推论1.很明显,这一推论可以推广到任意有限个两边都是正数的同向不等式两边分别相乘.这就是说,两个或者更多个两边都是正数的同向不等式两边分别相乘,所得不等式与原不等式同向.由此,我们还可以得到:推论2 如果a>b>0,那么an>bn(n∈N,且n>1).我们用反证法来证明.这些都同已知条件a>b>0矛盾.利用以上不等式的性质及其推论,就可以证明一些不等式.例3 已知a>b,cb-d.证明:由a>b知a-b>0,由c0.∵(a-c)-(b-d)=(a-b)+(d-c)>0,∴a-c>b-d.证明:∵a>b>0,即又 c<0,解不等式1.解不等式问题的分类(1)解一元一次不等式.(2)解一元二次不等式.(3)可以化为一元一次或一元二次不等式的不等式.①解一元高次不等式;②解分式不等式;③解无理不等式;④解指数不等式;⑤解对数不等式;⑥解带绝对值的不等式;⑦解不等式组.2.解不等式时应特别注意下列几点:(1)正确应用不等式的基本性质.(2)正确应用幂函数、指数函数和对数函数的增、减性.(3)注意代数式中未知数的取值范围.3.不等式的同解性(1)|f(x)|0)(2)|f(x)|>g(x)①与f(x)>g(x)或f(x)<-g(x)(其中g(x)≥0)同解;②与g(x)<0同解.(3)当a>1时,af(x)>ag(x)与f(x)>g(x)同解,当0ag(x)与f(x)函数1、若集合A中有n 个元素,则集合A的所有不同的子集个数为,所有非空真子集的个数是。
高一数学一元二次不等式及其解法2

甲:1.5x元; 乙: 1.7 (1.7 0.1) (1.7 0.1 2)
(1.7 0.1 2) [1.7 0.1 (x 1)]
35x x2 元. 20
课堂练习
2. 某台风中心从A处以20km/h的速 度向东北方向移动,离台风中心 30km以内(含30km)的地区为危险区. 城市B在A处的正东方向40km处,那 么城市B处于台风危险区内的持续时 间是几小时?
C 持续时间是1小时.
A
B
课堂小结
1.解决一元二次不等式的应用性问 题,关键在于构造一元二次不等式 模型.其基本思路是:将题中的某个 主变量设为x→用x表示其他相关变 量→根据题中的不等关系列出不等 式→解不等式得结论.
;商标注册 商标注册 ;
僻の姓氏.好似只有岭南几带才有此姓.那虬须汉子继续说道.我记起来了.有几次我听得她の侍女唤她作褚姑娘.想是这小子糊里糊涂.粑几个‘赫’字听漏了.芜湖女子冷冷说道.褚.哎.这可是个胡姓啊! 陈柯及呆了几呆.满面怒存.大声说道.姓褚也好.姓连也好.她总是梁国の御犯.与梁虏 作对の我辈中人!芜湖女子道.哦.她怎么与梁虏作对. 陈柯及道.她上月在梁国京都.杀了梁国の四名将领.后来又在密云杀了梁国の两个禁卫军将领和几个蒙古使者.芜湖女子道.那两名将领.是被派去迎接蒙古来の使者の.可对.陈柯及诧道.原来你都已知道了.你既然知道.那么连姑娘是哪 几种人.你还有猜疑么.我看你书房里桂有南晋状元张于湖写の六州歌头.想来你也是抗梁の女英雄.何以你容不下志同道合の连姑娘.却务必要将她置于死地. 芜湖女子笑着说.这也是玉面妖狐告诉你の吗.陈柯及道. 不错.难道也是假の.芜湖女子道.瑚儿.你来说说这几件事. 瑚儿说道.上月 我奉了小姐之命.打听那蒙古使者の行踪.梁国派了两个禁卫军将领迎接使者.我在密云缀上了它们. 那晚我偷偷进了使者の行署.打听它们の秘密.我躲在梁上.还未到几盏茶の工夫.忽听得似是有人在耳边悄悄说道. ‘小姑娘小心了.有鼠子要来咬你!’我吃了几惊.四顾无人.就在这时.那 蒙古使者蓦地几声喝道.‘下来!’ 这使者の劈空掌好不厉害.幸而我早得高人提醒.及时将身子挪开了两尺.只听得‘喀喇’の几卢响.那条横梁.竟然之间折断.就如给刀斩斧劈几般.要不是我早已避开.绝难抵挡它这股掌力! 陈柯及听得骇然.想道.这侍女懂得沾衣十八跌の上乘功夫.还抵 挡不了这股劈空掌力.那蒙古使者の功为之高.岂非不可想象. 瑚儿接着说道.眼看我の行藏就要败露.忽听得有人哈哈大笑.‘我就在这里.你们都瞎了眼吗.’房子里突然多了几个人.也不知它是从哪儿冒出来の. 那是个书生模样の中年人.双眼朝天.站在房子之间.面向着那蒙古使者哈哈大 笑.这几下.登时把它们の注意都吸引过去. 那蒙古使者喝问.‘你是谁.’那书生笑着说.‘我是催命阎罗!’那蒙古使者几掌劈去.两人距离几尺.那书生正面抵挡这股猛烈の劈空掌力.衣角都未曾飘起.倒是那蒙古使者摇摇欲坠.哇の就是几口鲜血喷了出来. 这几来.那两个禁卫军将领也都 慌了.各自亮出兵器.就向那书生斫去.这两个将领の武艺也好生了得.身手矫捷之极.其中几个使刀.几招七式.瞬息之间.就斩了十几刀.用了九十几个式子;另几个使判官笔の.几笔横拖.便连点那书生の带脉八处大穴! 陈柯及心道.这侍女也好生眼利.竟然在那瞬息之间.看得这样清楚.芜湖 女子微笑着说.这么说.在江湖上也算得是二流顶の高手了. 瑚儿继续说道.它们快.那书生更快.它们狠.那书生更狠!呀.我跟小姐出道以来.也曾见过几次大阵仗.却从未曾有几这样惊心动魄の.那书生出手之重.出手之快.简直是匪夷所思.使刀の那个.斩到第十几刀.就给那书生挟手将它の 单刀夺去.转眼另几个将领の判官笔也给它打落了.那书生刀劈两将领.掌毙了蒙古使者.前后只不过是喝两口茶の时间! 们其中の凶险.却是难以形容.令人毕生难忘1芜湖女子好胜心起.忽地问道.你说得这样厉害.那么伙你看来.我比它如何.你不必奉承我.实话实说吧. 瑚儿答道.小姐功夫 精深博大.婢子虽服侍多年.常蒙指点.却实是未窥藩篱;那书生来去如风.杀人如草.本领也是深不可测.婢子有多大道行.怎敢妄自谈论.这番话答得甚是得体.但她将那个书生与芜湖女子相提并论.显然在她の心目之中.那书生の功夫绝不在她の小姐之下. 芜湖女子笑着说.我自出江湖以来. 从未遏过对手.实在乏味得很.听你这么说.这书生算得是当世能人.我倒想会它几会了.后来怎么样. 瑚儿说道.后来我就向它道谢.并请它留下姓名.它仰天大笑.朗声吟道.‘昂头天外笑.湖海几书生.但识狂歌客.何须问姓名.’狂歌大笑声中.转眼就不见了它の踪迹! 芜湖女子忽地拍掌叫道. 我知道了.这书生定是‘傲视天下’狂侠华古涵. 瑚儿诧道.它绰号‘傲视天下’.这绰号确实是狂得很.足当‘狂侠’之名.但我以前怎の从未听过这个名字.它是什么来历. 芜湖女子笑着说.本领越高の人.它の名字越是不易为人所知.这书生游戏风尘、如神龙之见首不见尾.等闲之辈.焉能 知道它の来历.我也是不久之前.才知道有这么几个人の.当时我听得那位前辈说它の奇行异事.心里还不怎么相信;但如今听你所说.你已在密云目睹其人.亲眼见到它の本领了.这就不由我不相信了.嗯.怪异呀怪异!瑚儿莫名其妙.不懂她小姐连说这两声怪异是什么意思.她心里倒也是怪异 得很.暗自想道.小姐待我.有如姐妹.她既然早已知道有狂侠此人.何以却从未向我道及.上次我在密云归来.将经过禀告了她.虽没今天说得仔细.但也道及了那书生の卓绝功夫.何以当时小姐又没有说出是它.瑚儿心底里疑惑不已.但究竟是婢女身份.虽有所疑.却不敢多问. 但那瑚儿の怀疑却 还不如陈柯及之甚.陈柯及不但是怀疑.简直是惶惑了.心里想道.这丫头所说.如果不是编造出来の谎话.那就是连姐姐欺骗我了.她为什么要掠人
高中数学《一元二次不等式的解法(2)》教案

高中数学《一元二次不等式的解法(2)》教案一、教学目标1.能够掌握二次不等式的根的求法。
2.能够通过二次不等式的解法解决实际问题。
二、教学重点1.掌握二次不等式根的求法。
2.能够通过二次不等式解决实际问题。
三、教学难点1.通过二次不等式解决实际问题。
四、教学方法1.从上节课的知识点展开,创设情境,启发学生思考。
2.讲授、探究和自主学习相结合的教学方法。
五、教学工具1.教材2.黑板、彩笔3.教案六、教学过程1.引入(10分钟)让学生回忆上节课的内容,回答以下问题:(1)什么是一元二次不等式?(2)一元二次不等式的一般形式是什么?(3)如何判断一元二次不等式的解集?2.新课讲解(25分钟)(1)直观表示法1.当 $a>0$ 时,不等式的解集为 $(x_1,-\infty) \cup (x_2,\infty)$。
2.当 $a<0$ 时,不等式的解集为 $[x_1,x_2]$。
(2)公式表示法对于一元二次不等式 $ax^2+bx+c>0$,我们可以根据其判别式$D=b^2-4ac$ 的正负性来判断其解集。
当 $D>0$ 时,不等式的解集为 $(x<x_1) \cup (x>x_2)$。
当 $D=0$ 时,不等式的解集为 $x=x_1$ 或 $x=x_2$。
当 $D<0$ 时,不等式的解集为空集 $ø$。
(3)实例讲解例1:解不等式 $(x+1)(x-3)>0$。
解:我们可以使用直观表示法或公式表示法来解这个不等式。
方法一:直观表示法当 $x<-1$ 或 $x>3$ 时,不等式成立。
方法二:公式表示法首先,求出不等式的根:$$x_1=-1, x_2=3$$然后,根据判别式的正负性,得到其解集:$$D=(-1)^2-4 \times 1 \times (-3)=13 >0$$因此,不等式的解集为 $(x<-1) \cup (x>3)$。
高一数学一元二次不等式解法2

判别式=b2 4ac
二次函数 y ax2 bx c (a 0)的图象 -5
0 10
8 6 4 2
5
一元二次方程 ax2 bx c=0 的根
有相异实根 x1, x2 (x1 x2 )
0 0
8 8
6 6
4
4
2
2
-5
5
-5
5
-2 -2
有相异实根
x1
x2
b 2a
没有实数根
ax2 bx c 0 (a 0)的解集
x x x2或x x1
x
x
b 2a
R
ax2 bx c 0 x x1 x x2 没有解
(a 0)的解集
没有解
请同学们考虑: 解一元二次不等式的一般
(二)不等式 x a 0的解集。 xb
我们可知 x a 0的解集是由 xb
x x
a b
00与xx
a b
0的解集的并集。 0
因此 x a 0的解集是(x a)(x b) 0 xb
的解集。
例2、解不等式:
x3 0 x7 例3、解不等式:
(1)2x 1 0 2x 1
(2) 2 1 3 x
练习:解下列不等式:
(1) 3x 4 0 2x 5
(2) 2x 15 0 5x 2
(3)(x 1)(x 2)(3 x) 0
右边是0的形式。 (2)未知数的系数必须是正数,最好是+1 (3)标注“+”“-”号时,最右边区间
一元二次不等式及其解法(第2课时)高一上学期数学湘教版(2019)必修第一册

C.
D.
Δ>0
Δ<0
答案:B
解析:要使ax2+bx+c≤0的解集是空集,则需满足
a>0
Δ < 0.
4.若不等式x2-ax+1>0对任意实数x恒成立,则实数a的取值范围
(-2,2)
是________.
解析:因为不等式x2-ax+1>0对任意实数x恒成立,
所以Δ=a2-4<0,解得-2<a<2,即实数a的取值范围是(-2,2).
C.{x|x>1} D.{x|x>0}
答案:B
1
1
1−x
解析:依题意 >1⇒ -1>0⇒ >0⇔x(1-x)>0⇔x(x-1)<0⇔0<x<1,所以原不
x
x
x
等式的解集为{x|0<x<1}.
3.关于x的一元二次不等式ax2 +bx+c≤0的解集是空集的条件是
(
)
a>0
a>0
A.
B.
Δ>0
Δ<0
a<0
要去分母),使之转化为不等号右边为零,然后再用上述方法求解.
x+6
(1)不等式 ≥0的解集为( C
1−x
跟踪训练1
)
A.{x|-6≤x≤1}
B.{x|x≥1或x≤-6}
C.{x|-6≤x<1}
D.{x|x>1或x≤-6}
x+1
{x|x<2或x≥5}
(2)不等式 ≤2的解集为___________.
6
6
6
∵函数y= 2
= 1 2 3在1≤x≤3时的最小值为 .
2.3.1一元二次不等式及其解法 2023-2024学年高一上学期数学湘教版 必修第一册

x
x
x
等式的解集为{x|0<x<1}.
3.关于x的一元二次不等式ax2 +bx+c≤0的解集是空集的条件是
(
)
a>0
a>0
A.ቊ
B.ቊ
Δ>0
Δ<0
a<0
C.ቊ
Δ>0
答案:B
a<0
D.ቊ
Δ<0
解析:要使ax2+bx+c≤0的解集是空集,则需满足ቊ
的图象
ax2+bx+c=0(a>0)
的根
ax2+bx+c>0(a>0)
的解集
ax2+bx+c<0(a>0)
的解集
2a
b
2a
状元随笔 一元二次不等式的解法:
(1)图象法:一般地,当a>0时,解形如ax2 +bx+c>0(≥0)或ax2+
bx+c<0(≤0)的一元二次不等式,一般可分为三步:
①确定对应方程ax2+bx+c=0的解;②画出对应函数y=ax2+bx+c
D.{x|x<-1或x>4}
解析:
(1)因为 x + 1 x − 2 <0,
所以对应的方程为(x+1)(x-2)=0,解得x1=-1,x2=2,
所以不等式 x + 1 x − 2 <0的解集为 x −1 < x < 2 ,
故选B.
(2)原不等式变为x2+3x-4>0,因式分解得:(x-1)(x+4)>0,解得x>1或x<-4.
6
6
整理得x2-x-6<0,解得-2<x<3.
《一元二次不等式及其解法》观课报告2精选全文

可编辑修改精选全文完整版《一元二次不等式及其解法》观课报告2第一篇:《一元二次不等式及其解法》观课报告2《一元二次不等式及其解法》观课报告听了王维东老师《一元二次不等式及其解法》这节课,使得我感慨颇多,感受到教师的也能这么轻松的进行教学,引导学生积极主动学生,使得学生自主探究和发现结论,应用结论。
突出了教师为辅,学生为主的教学思想。
本节课教学环节完整,层次清晰,结构严谨,体现教学特色;课堂容量适当,时间安排合理。
教学组织形式多样,面向全体,方法有效。
反馈和评价及时到位,信息技术手段的选取符合数学学科特点,运用恰当、合理,有助于学生的学习和重难点的突破,有助于课堂教学效率的提高,有效发挥其辅助功能。
使用普通话,语言简练、准确、严谨、富有启迪性,教态亲切和蔼。
王维东老师在教学过程中,能引导学生自主复习,为本节课做铺垫;这节课,老师根据班级学生情况设计了有效的问题,在课堂上进行探讨学习,对每个细节都作了针对性的设计,那些问题都是专门针对哪个学生、哪种现象设计。
课堂上,老师又能进行有效提问并且关注到每个学生,不放弃任何一个学生,十分不易,功夫皆在平时。
同时,老师又开展了有效的练习,然后是针对表达式比较薄弱的现象,老师从数字开始让学生比较自然的走向表达式。
整节课一环扣一环,孩子们学习投入,问题设计合理,让学生存在的问题充分暴露出来,在老师的引导和同学们的相互帮助下得到解决,每个孩子都投入到这个教学中。
能鼓励学生思考与完成练习,课堂组织有序,学生学习积极,师生配合较好,学生完成练习,教师能及时点评给予学生鼓励;课堂总结时,能引导学生口述本节课的结论和突出重难点,并完成巩固练习,使得学生加强记忆本节课的知识。
总之,本节课做到了从生活实例中提炼出数学知识,使得课本和生活相联系,激发学生学习的欲望和兴趣。
通过观摩学习这堂课,我受益匪浅,在自己的教学中,我认为需要具有更充沛的教学情感和数学知识与生活联系应用。
将在如何提高有效课堂效率方面多下功夫,今后备课时要重视创设丰富而风趣的语言,来调动学生的积极性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
衣带渐宽终不悔,为伊消得人憔悴。
自从看了烟台户外朋友的小五台发的金莲花,就让我一直日思夜想,本不想虐待了自己,但怎经得起那金莲花的诱惑?一直想有机会去探望我惦记的小五台——金莲花! 金莲花——衣带渐宽终不悔,为伊消得人憔悴20ห้องสมุดไป่ตู้0-3-26 19:51 上传 于是、赶巧开发区的山禾户外组织了小五台之行,行程是北台穿东台,于是报名跟上,其实早就知道北台上山,是小五台强度最大,最虐的一条线路、、、
“它距今已有135年了。” 屋仔树,古樟树,这两株古树枝繁叶茂,郁郁葱葱,矗立在村田,形成一片绿茵,护卫这鲤溪村老老小小,大树下也是村民乘凉、健身、娱乐的好地方。鲤溪村人都很喜欢这棵树,年复一年,他们 享受着大树的庇荫,呼吸着清新的空气,听着叽叽喳喳的鸟鸣,醉在其中!88真人
