平行四边形上的几何概率研究
初中数学知识点思维导图

第八章
反比例函数
反比例函数图像与性质
1、反比例函数的定义
2、反比例函数的图像与对称性
3、反比例函数的性质
4、系数k的几何意义
5、反比例函数图像上点的坐标特征
6、待定系数法求反比例函数解析式
7、反比例函数与一次函数父点问题
反比例函数的应用
反比例函数的应用
从统计图分析数据的几种
趋势
3、扇形、条形、折线统计图及其选择
3、一次函数与一元一次方程
4、依据实际问题列一次函数关系式
一次函数的图像
1、一次函数、正比例函数的图像与性质
2、一次函数图像与系数的关系
3、一次函数图像上点的坐标特点
4、一次函数图像与几何变换
一次函数的应用
一次函数的应用与综合题
多边形与圆的初步认识
4、多边形与多边形的对角线
5、圆的认识〔圆心角、弧、弦的关系〕
1、轴对称的性质
2、轴对称--最短路径问题
3、翻折变换〔折叠问题〕
简单的轴对称图形
1、角平分线性质
2、线段垂直平分线的性质
3、等腰三角形的性质与判定
4、等边三角形的性质与判定
第八章概率初步
感受可能性
1、随机事件
2、可能性的大小
频率的稳定性
利用频率估量概率
等可能事件的概率
1、概率的意义、公式
2、几何概率
6、扇形面积的计算
第五章二元次方程组
认识二元次方程组
1、二兀一次防尘的定义、解
2、解二兀次方程
3、二元一次方程组的定义、解
求解二元次方程
1、解二兀一次方程组
2、同解方程组
二兀次方程的应用
1、鸡兔同笼
浙教版初中八年级数学上册全套教案

(3)板书布局合理,避免信息过载。
五、作业设计的针对性与答案的准确性
(1)作业题目要针对教学难点和重点,有助于巩固课堂所学;
(2)作业答案要准确无误,避免误导学生;
(3)作业量适中,既能巩固知识,又不增加学生负担。
六、课后反思与拓展延伸的深度
(1)教师要在课后反思本次课程的教学效果,分析学生的掌握情况,找出不足之处,为下一次教学做好准备;
2.几何图形:
(1)平行四边形;
(2)矩形、菱形、正方形;
(3)梯形。
3.概率初步:
(1)随机事件与概率;
(2)组合与概率的加法法则;
(3)条件概率与独立事件。
七、作业设计
1.作业题目:
(1)解一元二次方程:x^2 - 5x + 6 = 0;
(2)判断以下图形是否为平行四边形,若是,判断其是否为矩形、菱形、正方形或梯形;
浙教版初中八年级数学上册全套教案
一、教学内容
本教案依据浙教版初中八年级数学上册教材,主要涵盖以下章节内容:
1.第十一章:一元二次方程
1.1一元二次方程的定义与一般形式
1.2解一元二次方程的几种方法
1.3一元二次方程的根与系数的关系
2.第十二章:几何图形
2.1平行四边形
2.2矩形、菱形、正方形
2.3梯形
(1)让学生独立完成一元二次方程的求解;
(2)让学生绘制几何图形,并判断其性质;
(3)让学生计算给定概率问题。
4.小组讨论与合作:
(1)讨论一元二次方程的求解方法;
(2)探讨几何图形的性质与判定;
(3)研究概率的计算方法。
六、板书设计
1.一元二次方程:
初中数学几何概率试讲教案

教案:初中数学几何概率试讲教学目标:1. 知识与技能目标:学生能够理解几何概率的基本概念,学会使用几何概率的方法解决实际问题。
2. 过程与方法目标:通过实例分析,培养学生运用几何概率解决问题的能力,发展学生的逻辑思维和推理能力。
3. 情感态度与价值观目标:激发学生对几何概率的兴趣,体会数学在生活中的应用。
教学重难点:1. 重点:理解几何概率的基本概念,掌握几何概率的计算方法。
2. 难点:灵活运用几何概率解决实际问题。
教学准备:1. 教学工具:黑板、粉笔、多媒体设备。
2. 教学材料:几何概率相关案例、练习题。
教学过程:一、导入新课1. 利用多媒体展示几何概率的实例,引导学生思考:为什么在相同的条件下,某些事件发生的可能性会不同?2. 学生讨论,教师总结:在相同的条件下,某些事件发生的可能性会受到事件本身特征的影响。
二、新课讲解1. 教师引导学生回顾概率的基本概念,引出几何概率的定义。
2. 讲解几何概率的基本原理,引导学生理解几何概率的计算方法。
3. 通过实例分析,让学生掌握如何运用几何概率解决问题。
三、课堂练习1. 学生独立完成练习题,巩固所学知识。
2. 教师选取部分学生的练习题进行讲解,解答学生的疑问。
四、拓展与应用1. 学生分组讨论,尝试运用几何概率解决实际问题。
2. 各小组汇报讨论成果,教师点评并指导。
五、课堂小结1. 学生自主总结本节课所学内容,分享自己的学习收获。
2. 教师点评学生的总结,强调几何概率在生活中的应用。
六、布置作业1. 学生完成课后练习题,巩固所学知识。
2. 选择一个实际问题,运用几何概率的方法解决,并将解题过程写成报告。
教学反思:本节课通过实例引入几何概率的概念,让学生在实际问题中体会几何概率的应用。
通过课堂练习和拓展应用环节,培养学生运用几何概率解决问题的能力。
在教学过程中,要注意关注学生的学习情况,及时解答学生的疑问,提高学生的学习效果。
九年级数学上册第二十五章概率初步必考知识点归纳(带答案)

九年级数学上册第二十五章概率初步必考知识点归纳单选题1、在一个不透明的口袋中装有5个红球和若干个白球,它们除颜色外其他完全相同,通过多次摸球实验后发现,摸到红球的频率稳定在0.25附近,则估计口袋中大约共有白球()A.10B.15C.20D.都不对答案:B分析:由摸到红球的频率稳定在0.25附近,可以得出摸到红球的概率,即可求出白球个数.∵摸到红球的频率稳定在0.25附近,∴摸到红球的概率为0.25,∴总球数:5÷0.25=20(个)∴白球个数:20-5=15(个)所以答案是:B.小提示:本题考查了用频率估计概率、已知概率求数量,得出摸到红球的概率是本题的关键.2、在有25名男生和24名女生的班级中,随机抽签确定一名学生代表,则下列说法正确的是(). A.男、女生做代表的可能性一样大B.男生做代表的可能性较大C.女生做代表的可能性较大D.男、女生做代表的可能性的大小不能确定答案:B分析:根据题意,只要求出男生和女生当选的可能性,再进行比较即可解答.∵某班有25名男生和24名女生,∴用抽签方式确定一名学生代表,男生当选的可能性为2525+24=25 49,女生当选的可能性为2425+24=24 49,∴男生当选的可能性大于女生当选的可能性.故选B.小提示:此题考查可能性大小的比较:只要总情况数目相同,谁包含的情况数目多,谁的可能性就大;反之也成立;若包含的情况相当,那么它们的可能性就相等.3、某居委会组织两个检查组,分别对“垃圾分类”和“违规停车”的情况进行抽查.各组随机抽取辖区内某三个小区中的一个进行检查,则两个组恰好抽到同一个小区的概率是( ) A .19B .16C .13D .23答案:C分析:将三个小区分别记为A 、B 、C ,列举出所有情况即可,看所求的情况占总情况的多少即可. 详解:将三个小区分别记为A 、B 、C , 列表如下:3种, 所以两个组恰好抽到同一个小区的概率为39=13. 故选C .点睛:此题主要考查了列表法求概率,列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适用于两步或两步以上完成的事件;解题时还要注意是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.4、某市有6名教师志愿到四川地震灾区的甲、乙、丙三个镇去支教,每人只能去一个镇,则恰好其中一镇去4名,另两镇各去1名的概率为( ) A .2081B .1081C .5243D .10243答案:B分析:因为对于这六个人来说,会被随机分派到3个镇中的任何一个,所以一共有36种情况,而有4个人的镇可能是3个镇中的任何一个,剩下两个镇各派一个人的派法是3×C 64,根据概率公式求解.解:6名教师志愿随机派到3个镇中的任何一个共有36种情况,有4个人的镇可能是3个镇中的任何一个,另两镇各去1名的结果数为3×6×5,所以恰好其中一镇去4名,另两镇各去1名的概率=3×6×536=1081,故选:B .【小提示】选出符合事件A 或B 的结果数目m ,然后根据概率公式求出事件A 或B 的概率. 5、同时抛掷两枚质地均匀的硬币,则一枚硬币正面向上、一枚硬币反面向上的概率是( ) A .14B .13C .12D .23答案:C分析:根据题意可画出树状图,然后进行求解概率即可排除选项. 解:由题意得:∴一枚硬币正面向上、一枚硬币反面向上的概率是P =24=12; 故选C .小提示:本题主要考查概率,熟练掌握利用树状图求解概率是解题的关键.6、①三点确定一个圆; ②平分弦的直径平分弦所对的弧;③同圆或等圆中,相等的弦所对的圆心角相等;④在半径为4的圆中,30°的圆心角所对的弧长为π3;⑤方程x 2-x +3=0的两根之积是3,从上述5个命题中任取一个,是真命题的概率是( ) A .1B .35C .25D .15 答案:C分析:先根据确定圆的条件对①进行判断;根据垂径定理的推论对②进行判断;根据圆心角、弧、弦的关系对③进行判断;根据弧长公式对④进行判断;利用根与系数关系对⑤进行判断.然后利用概率公式进行计算即可.解:①不在同一直线上的三点可以确定一个圆,故①说法错误,是假命题; ②平分弦(非直径)的直径平分弦所对的弧,所以②错误,是假命题; ③在同圆或等圆中,弦相等,所对的圆心角相等,所以③正确,是真命题; ④在半径为4的圆中,30°的圆心角所对的弧长为2π3,所以④错误,是假命题;⑤方程x 2-x+3=0的两根之积是3,正确,是真命题, 其中真命题有2个,所以是真命题的概率是:25, 故选:C .小提示:本题考查了真假命题的判断及概率公式,解题的关键是:先判断命题的真假.7、不透明的袋子中装有红、绿小球各一个,除颜色外两个小球无其他差别,从中随机摸出一个小球,放回并摇匀,再从中随机摸出一个小球,那么第一次摸到红球、第二次摸到绿球的概率是( ) A .14B .13C .12D .34答案:A分析:首先根据题意画出树状图,由树状图求得所有等可能的结果与第一次摸到红球,第二次摸到绿球的情况,然后利用概率公式求解即可求得答案. 解:画树状图得:∵共有4种等可能的结果,第一次摸到红球,第二次摸到绿球有1种情况, ∴第一次摸到红球,第二次摸到绿球的概率为14,故选:A .小提示:本题考查了画树状法或列表法求概率,列出所有等可能的结果是解决本题的关键.8、如图是用七巧板拼成的正方形桌面,一个小球在桌面上自由地滚动,它最终停在黑色区域的概率是( )A .14B .18C .316D .23答案:C分析:先求出黑色区域的面积是正方形桌面的分率,再根据概率公式即可得出答案. 解:观察图形可知,黑色区域的面积是正方形桌面的316,∴最终停在黑色区域的概率是316,故选:C .小提示:本题考查几何概率,熟练掌握几何概率的计算方法是解题的关键.9、将一枚飞镖任意投掷到如图所示的正六边形镖盘上,飞镖落在白色区域的概率为( )A .12B .13C .25D .35答案:A分析:随机事件A 的概率P (A )=事件A 发生时涉及的图形面积÷一次试验涉及的图形面积,因为这是几何概率.解:设正六边形边长为a ,过A 作AD ⊥BC 于D ,过B 作BE ⊥CE 于E ,如图所示:∵正六边形的内角为180°−360°6=120°,∴在RtΔACD 中,∠ADC =90°,∠CAD =60°,AC =a ,则AD =12a,CD =√32a , ∴BC =2CD =√3a ,∴在RtΔBCE 中,∠BEC =90°,∠BCE =60°,BC =√3a ,则CE =√32a,BE =32a ,则灰色部分面积为3S ΔABC =3×12BC ⋅AD =3×12×√3a ×12a =34√3a 2,白色区域面积为2S ΔBCE =2×12CE ⋅BE =√32a ×32a =3√34a 2, 所以正六边形面积为两部分面积之和为32√3a 2,飞镖落在白色区域的概率P =34√3a 232√3a 2=12,故选:A .小提示:本题考查了几何概率,熟练掌握几何概率模型及简单概率公式是解决问题的关键.10、如图是一张矩形纸板,顺次连接各边中点得到菱形,再顺次连接菱形各边中点得到一个小矩形.将一个飞镖随机投掷到大矩形纸板上,则飞镖落在阴影区域的概率是( )A .13B .14C .16D .18答案:B分析:连接菱形对角线,设大矩形的长=2a ,大矩形的宽=2b ,可得大矩形的面积,根据题意可得菱形的对角线长,从而求出菱形的面积,根据“顺次连接菱形各边中点得到一个小矩形”,可得小矩形的长,宽分别是菱形对角线的一半,可求出小矩形的面积,根据阴影部分的面积=菱形的面积-小矩形的面积可求出阴影部分的面积,再求出阴影部分与大矩形面积之比即可得到飞镖落在阴影区域的概率. 解:如图,连接EG ,FH ,设AD=BC=2a ,AB=DC=2b , 则FH=AD=2a ,EG=AB=2b , ∵四边形EFGH 是菱形,∴S 菱形EFGH =12FH ⋅EG =12⋅2a ⋅2b =2ab , ∵M ,O ,P ,N 点分别是各边的中点,∴OP=MN=12FH=a ,MO=NP=12EG=b ,∵四边形MOPN 是矩形, ∴S 矩形MOPN =OP ⋅MO=ab ,∴S 阴影= S 菱形EFGH -S 矩形MOPN =2ab-ab=ab , ∵S 矩形ABCD =AB ⋅BC=2a ⋅2b=4ab , ∴飞镖落在阴影区域的概率是ab 4ab=14,故选B .小提示:本题考查了几何概率问题.用到的知识点是概率=相应的面积与总面积之比. 填空题11、小兰和小华两人做游戏,她们准备了一个质地均匀的正六面体骰子,骰子的六个面分别标有1,2,3,4,5,6,若掷出的骰子的点数为偶数,则小兰赢;若掷出的骰子的点数是3的倍数,则小华赢,游戏规则对______(填“小兰”或“小华”)有利. 答案:小兰分析:根据所出现的情况,分别计算两人能赢的概率,即可解答. 解:骰子的点数是偶数的有2,4,6,其概率为36=12,骰子的点数是3的倍数的有3,6,其概率为26=13,而12>13,∴游戏规则对小兰有利, 所以答案是:小兰.小提示:本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.12、甲、乙两人做游戏,他们准备了一个质量分布均匀的正六面体骰子,骰子的正六面分别标有1,2,3,4,5,6.若掷出的骰子的点数是偶数,则甲赢;若掷出的骰子的点数是3的倍数,则乙赢,这个游戏对甲、乙来说是_________的.(填“公平”或“不公平”) 答案:不公平分析:根据所出现的情况,分别计算两人能赢的概率,即可解答.解:∵骰子的点数是偶数的有2,4,6,其概率为36=12,骰子的点数是3的倍数的有3,6,其概率为26=13,故游戏规则对甲有利.所以答案是:不公平.小提示:本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.13、巧板是我国古代劳动人民的一项发明,被誉为“东方魔板”,它由五块等腰直角三角形、一块正方形和一块平行四边形组成.如图是利用七巧板拼成的正方形,随机向该图形内抛一枚小针,则针尖落在阴影部分的概率为 _____.答案:38分析:设大正方形的边长为2,先求出阴影区域的面积,然后根据概率公式即可得出答案.图,设小正方形的边长为1,根据等腰三角形和正方形的性质可求得AB=BE=2√2,FG=DC=√2,则空白的面积为:12×√2×√2+1×1+12×1×1×2+12×2×2=5;大正方形的面积是:2√2×2√2=8,阴影区域的面积为:8-5=3,所以针尖落在在阴影区域上的概率是:38.所以答案是:3.8小提示:本题考查几何概率,熟练掌握几何概率的计算方法是解题的关键.14、如图,在边长为1的小正方形组成的3×3网格中,A,B两点均在格点上,若在格点上任意放置点C,恰的概率为_________.好使得△ABC的面积为12##0.375答案:38分析:按照题意分别找出点C所在的位置,根据概率公式求出概率即可.的三角形,解:可以找到6个恰好能使△ABC的面积为12,则概率为:6÷16=38所以答案是:3.8小提示:此题主要考查了概率公式,解决此题的关键是正确找出恰好能使△ABC的面积为1的点.15、口袋内装有编号分别为1,2,3,4,5,6,7的七个球(除编号外都相同),从中随机摸出一个球,则摸出编号为偶数的球的概率是___.答案:37分析:用袋子中编号为偶数的小球的数量除以球的总个数即可得.解:∵从袋子中随机摸出一个球共有7种等可能结果,其中摸出编号为偶数的球的结果数为3,∴摸出编号为偶数的球的概率为3,7所以答案是:37.小提示:本题主要考查概率公式,解题的关键是掌握随机事件A 的概率P (A )=事件A 可能出现的结果数÷所有可能出现的结果数. 解答题16、在同升湖实验学校九年级的班级三人制篮球赛过程中,经过几轮激烈的角逐,最后由2班、5班、6班、9班进入了年级四强进行最后的名次争夺赛.现在葛老师规定先用抽签的方式决定将这4个班级分成2个小组,再由两个小组的胜出者争夺一二名,小组落败者争夺三四名. (1)直接写出9班和5班抽签到一个小组的概率;(2)若4个班级的实力完全相当,任何两个班级对决的胜率都是50%,求在年级四强的名次争夺赛中9班不与5班对决的概率. 答案:(1)13;(2)13分析:(1)利用列举法求解即可; (2)分类讨论,利用列举法即可求解.(1)分组:(2,5)和(6,9);(2,6)和(5,9);(2,9)和(5,6)共3种, 9班和5班抽签到一个小组只有一种情况, 故概率为:13;(2)①分组为(2,5)和(6,9),故概率为:3×4=6; ②分组为(2,9)和(5,6),故概率为:3×4=6;综上,在年级四强的名次争夺赛中9班不与5班对决的概率为16+16=13.小提示:本题考查了利用列举法求概率,通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.17、为落实“垃圾分类”,环保部门要求垃圾要按A,B,C,D四类分别装袋、投放,其中A类指废电池、过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料、废纸等可回收物,D类指其他垃圾.小明、小亮各投放了一袋垃圾.(1)小明投放的垃圾恰好是A类的概率为;(2)求小亮投放的垃圾与小明投放的垃圾是同一类的概率.答案:(1)14(2)14分析:(1)直接利用概率公式求出小明投放的垃圾恰好是A类的概率;(2)首先利用树状图法列举出所有可能,进而利用概率公式求出答案.(1)解:∵垃圾要按A,B,C,D四类分别装袋,小明投放了一袋垃圾,∴小明投放的垃圾恰好是A类的概率为:14;所以答案是:14;(2)解:如图所示:由图可知,共有16种可能结果,其中小亮投放的垃圾与小明投放的垃圾是同一类的结果有4种,所以小亮投放的垃圾与小明投放的垃圾是同一类的概率为416=14.小提示:此题主要考查了树状图法求概率,正确利用列举出所有可能并熟练掌握概率公式是解题关键.18、一个不透明的口袋中装有6个红球,9个黄球,3个白球,这些球除颜色外其他均相同.从中任意摸出一个球,(1)求摸到的球是白球的概率,(2)如果要使摸到白球的概率为14,需要在这个口袋中再放入多少个白球?答案:(1)16(2)2分析:(1)直接利用概率公式求解即可;(2)根据绿球的概率公式得到相应的方程,求解即可.(1)解:根据题意分析可得:口袋中装有红球6个,黄球9个,白球3个,共18个球,故P(摸到白球)=318=16(2)设需要在这个口袋中再放入x个白球,得:3+x18+x =14,解得:x=2.经检验x=2符合题意,所以需要在这个口袋中再放入2个白球.小提示:本题考查概率的求法与运用,一般方法为:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=mn.。
初中数学《用列举法求概率》教案
课时教学设计个因素(例如抛掷两枚骰子)改为“把一枚骰子掷两次”,(1)满足两枚骰子点数相同(记为事件A)的结果有6个(表中斜体加粗部分),所以P(A)=636=16;(2)满足两枚骰子的和是9(记为事件B)的结果有4个(表中的阴影部分),所以P(B)=436=19;(3)满足至少有一枚骰子的点数为2(记为事件C)的结果有11个(表中方框部分),所以P(C)=1136步骤列表;求出表中可能出现的结果的总数n;统计某种随机事件可能发生的结果的数目m;用公式P(A)=mn计算概率.个分支,在分支下的第三行分别写上H和I;④按竖向把各种可能的结果竖着写在下面,就可得出所有可能的结果的总数(即机会均等的结果的总数m),再找出符合要求的种数,就可以利用概率的意义计算概率了.依据题意,我们可以画出如下的树状图:从树状图中可以看出,所有可能出现的结果共有12个,且这些结果出现的可能性相等,只有一个元音字母的结果有5个,即ACI,ADH,BCI,BDI,BEH,所以P(一个元音)=5 12;全是辅音字母的结果有两个,即BCH,BDH,所以P(三个辅音)=21= 126.的值,,∵共有6种等可能的结果,抽取2名,恰好是1名女生和1名男生有4种情况,∴抽取2名,恰好是1名女生和1名男生概率为23.称为几何概型).小猫在如图所示的地板上自由地走来走去,并随意停留在某块方砖上(图中每一块方砖除颜色外完全相同),求它最终停留在黑色方砖上的概率.由于试验中等可能发生的结果无法计数,所以此时的概率可以用所关注区域(即所有黑色方砖)的面积除以可能发生的区域(即所有方砖)的面积.不妨设小方砖的面积为1,由几何概型的概率公式知,P(停留在黑砖上)=41=164.2.如图所示的扇形图给出的是地球上海洋、陆地的表面积约占地球表面积的百分比.若宇宙中有一块陨石落在地球上,则它落在海洋中的概率是 %.板书设计。
浅析分类讨论思想在高中数学解题中的应用

浅析分类讨论思想在高中数学解题中的应用在高中数学中,分类讨论思想是一个非常重要的解题方法。
通过将问题进行分类讨论,可以帮助我们更好地理解问题的本质,找到解题的方法,提高解题的效率。
本文将从基本概念、思维方法和实际应用三个方面来浅析分类讨论思想在高中数学解题中的应用。
一、基本概念分类讨论思想是指将问题按照某种特定的特征或性质进行分类,然后分别讨论各个类别的情况,最后将不同情况的结果进行综合。
这种思维方法在高中数学中尤为常见,可以应用于代数、几何、概率等各个领域的解题中。
分类讨论思想的关键在于合理地划分类别,确保每个类别都是互不重叠且全面覆盖的。
只有这样才能保证我们对问题的分析不会遗漏任何一种情况。
分类讨论也要求我们具备较强的逻辑推理能力,能够将不同类别的情况进行合理的比较和综合。
二、思维方法在实际解题过程中,如何正确运用分类讨论思想是非常重要的。
以下是几种常见的思维方法:1. 同时考虑全部情况:在某些问题中,我们可以将问题的所有情况列举出来,然后进行分类讨论。
在排列组合中,我们可以将排列或组合的条件进行分类讨论,然后分别计算不同类别的情况。
2. 构造特殊情况:有时候,我们可以通过构造特殊的情况来帮助我们理解问题。
在几何证明中,我们可以通过构造特殊的图形或角度来帮助我们理解问题的本质,然后再进行一般性的证明。
3. 排除法:有些问题可以通过排除法来简化解题过程。
在概率问题中,我们可以通过排除不可能发生的情况来简化计算过程,从而得出最终结果。
以上思维方法并不是孤立的,有时候我们需要结合使用,根据具体问题的情况来进行思考和运用。
三、实际应用现在我们以代数、几何和概率三个方面来举例说明分类讨论思想在高中数学解题中的应用。
1. 代数问题如何将一个三位数分解成其各位数字之和的问题。
我们可以将三位数的情况分为百位数、十位数和个位数三种情况,然后分别讨论。
通过这样的分类讨论,我们可以找到所有满足条件的三位数。
2. 几何问题如何证明一个四边形是平行四边形的问题。
人教版八年级数学下册-平行四边形-数学活动

F
B
C
∠ABN=60° ∠ABM=∠MBN=∠NBC=30°
那么,怎样得到15°,120°角?说说你的方法.
练习
1.如图,在直角三角形ABC中,若∠A=
30°,BC=1,则AB=( B )
A. 3
D.
B.2
3 C.
5
2
活动 2 黄金矩形
黄金矩形给我们以协调、匀称的美感.世界 各国许多著名的建筑,为取得最佳的视觉效果, 都采用了黄金矩形的设计.
---------八年级数学下册教材分析
一、人教版八年级数学下册内容的安排
四边形
勾股定理
反比例函 数
分式
数与代 数
统计与概率
实践活动
八 年
实践与运用
综合应用
级
课题学习
数
学
二、教材内容分析
性质 通分
约分
乘除 乘方 加减
整数指数幂
定义
解方程 方程的解 应用
第 分十 式六
意义 应用
定义
二、教材内容分析
数学活动
新课导入
同学们,如果我们身旁没有量角器,你能 用矩形纸片折出60°,30°,15°的角吗?同 时,你知道黄金矩形的概念吗?你能仅用矩形 的纸片,折叠出一个黄金矩形吗?
学习目标
1.能用矩形纸片折出60°,30°,15°角,折出 黄金矩形.
2.通过动手操作、搜索证明、总结归纳及交流反 思,逐步培养学生动手能力.
已知直角三角形的两边求第三 边在数轴上表示无理数 实际问 题
构造全等的直角三角 已形知三边判断形 状 实际问题
二、教材内容分析
一般 在平面内,四条线段 四边形 首
尾顺次相接组成的图
北师大版五年数学上册总复习图形与几何、统计与概率教案

图形与几何、统计与概率
轴对称和平移:
图形与几何、多边形的面积、组合图形的面积
统计与概率:可能性
【设计意图】回顾本节课的学习内容,让学生在归纳总结中进一步加深对所学知识系统的理解,获得学习数学的成功体验。
小结
通过这节课的学习,你有哪些收获?
(1):
(2):
(3):
反思
本节课复习了“图形与几何”“统计与概率”的相关知识。通过复习,让学生经历回顾、梳理、应用知识的过程,在整理知识的过程中,学生还能整合知识,总结学习方法,同时在由易到难的练习中进一步巩固和加深对知识的理解和应用。本节课的突出之处在于:(1)通过复习,将凌乱的知识梳理清楚,“图形与几何”“统计与概率”知识基本连成了线,经过应用与拓展,这些连成线的“知识珍珠”被穿了起来,使学生更易于理解。(2)注重知识网络的构建。通过师生的共同整理,学生对本册教材中所学的“图形与几何”“统计与概率”的知识融会贯通,找出了各知识点之间的联系,使所学知识系统化。(3)学生解决问题的能力得到提高。学生在练习中形成知识网络,在综合运用中体会到数学知识之间的联系,这样,学生综合解决问题的能力得到提升,解决问题的灵活性得到加强。
(二)复习“摸球游戏”
1.课件出示教材第107页“统计与概率”第2题。
(1)先想一想,再在小组里说一说你的想法。
(2)小组选派代表在全班汇报。
小结:摸出白球的总次数比摸出黄球的总次数多得多,所以盒子里白球多。
2.课件出示教材第112页“统计与概率”第2题。
(1)学生先独立思考,再小组交流,说说自己的想法。
(2)独立完成练习。
(3)听取汇报,集体订正。
【设计意图】通过复习,进一步了解计算组合图形面积的方法,理解“分割法”和“添补法”在计算组合图形面积中的重要作用,培养学生的发散性思维能力。
平行四边形的证明条件

平行四边形的证明条件
平行四边形是平面几何学中最基本的形状之一,它由四条平行边组成,每条边
成等腰形状及全等长,但是要证明一个四边形是一个平行四边形,需要使用不同的定义,如果不遵守定义,那么就无法确定是否为平行四边形。
一个多边形是平行四边形的证明条件,包括:
1. 四个顶点:平行四边形的一个重要的条件是,它有四个离散的顶点,不能
有其他顶点。
2. 平行直线:多边形中四条边都是平行的,平行的线段间没有其他直线存在,这是一个平行四边形的基本条件。
3. 等边长度:多边形中四条边的长度是一样的,四个顶点之间的距离是相同的,两个对角线的长度也相同,这是证明此四边形是平行四边形的必要条件。
4. 相同的内角:平行四边形的内角全部相等,有两种角,90°和180°,这
是证明四边形是平行四边形的另一个重要条件。
综上所述,证明一个多边形是平行四边形需要以上这四个条件,只有当多边形
满足这四个条件时,才可以确定这个多边形是平行四边形。
否则,出于纯概率的考虑,要么不能证明它是平行四边形,要么规范及上诉提到的一些条件无法满足。
九年级数学上册知识点归纳北师大版

九年级数学上册知识点归纳北师大版第一章特殊平行四边形第二章一元二次方程第三章概率的进一步认识第四章图形的相似第五章投影与视图第六章反比例函数八下前情回顾※平行四边的定义:两线对边分别平行的四边形叫做平行四边形.....,平行四边形不相邻的两顶点连成的线段叫做它的对角线...;※平行四边形的性质:平行四边形的对边相等,对角相等,对角线互相平分;※平行四边形的判别方法:两组对边分别平行的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两条对角线互相平分的四边形是平行四边形;※平行线之间的距离:若两条直线互相平行,则其中一条直线上任意两点到另一条直线的距离相等;这个距离称为平行线之间的距离;第一章特殊平行四边形1菱形的性质与判定菱形的定义:一组邻边相等的平行四边形叫做菱形;※菱形的性质:具有平行四边形的性质,且四条边都相等,两条对角线互相垂直平分,每一条对角线平分一组对角;菱形是轴对称图形,每条对角线所在的直线都是对称轴;※菱形的判别方法:一组邻边相等的平行四边形是菱形;对角线互相垂直的平行四边形是菱形;四条边都相等的四边形是菱形;2矩形的性质与判定※矩形的定义:有一个角是直角的平行四边形叫矩形..;矩形是特殊的平行四边形; ※矩形的性质:具有平行四边形的性质,且对角线相等,四个角都是直角;矩形是轴对称图形,有两条对称轴※矩形的判定:有一个内角是直角的平行四边形叫矩形根据定义;对角线相等的平行四边形是矩形;四个角都相等的四边形是矩形;※推论:直角三角形斜边上的中线等于斜边的一半;3正方形的性质与判定正方形的定义:一组邻边相等的矩形叫做正方形;※正方形的性质:正方形具有平行四边形、矩形、菱形的一切性质;正方形是轴对称图形,有两条对称轴※正方形常用的判定:有一个内角是直角的菱形是正方形;邻边相等的矩形是正方形;对角线相等的菱形是正方形;对角线互相垂直的矩形是正方形;正方形、矩形、菱形和平行边形四者之间的关系如图3所示:※梯形定义:一组对边平行且另一组对边不平行的四边形叫做梯形;※两条腰相等的梯形叫做等腰梯形;※一条腰和底垂直的梯形叫做直角梯形;※夹在两条平行线间的平行线段相等; ※在直角三角形中,斜边上的中线等于斜边的一半第二章 一元二次方程1认识一元二次方程※只含有一个未知数的整式方程,且都可以化为02=++c bx ax a 、b 、c 为 常数,a ≠0的形式,这样的方程叫一元二次方程......; ※把02=++c bx ax a 、b 、c 为常数,a ≠0称为一元二次方程的一般形式,a 为二次项系数;b 为一次项系数;c 为常数项;2用配方法求解一元二次方程①配方法 <即将其变为0)(2=+m x 的形式>※配方法解一元二次方程的基本步骤:①把方程化成一元二次方程的一般形式;②将二次项系数化成1;③把常数项移到方程的右边;④两边加上一次项系数的一半的平方;⑤把方程转化成0)(2=+m x 的形式;⑥两边开方求其根;3用公式法求解一元二次方程图3②公式法 aac b b x 242-±-= 注意在找abc 时须先把方程化为一般形式 4用因式分解法求解一元二次方程③分解因式法 把方程的一边变成0,另一边变成两个一次因式的乘积来求解;主要包括“提公因式”和“十字相乘”5一元二次方程的根与系数的关系※根与系数的关系:当b 2-4ac>0时,方程有两个不等的实数根;当b 2-4ac=0时,方程有两个相等的实数根;当b 2-4ac<0时,方程无实数根;※如果一元二次方程02=++c bx ax 的两根分别为x 1、x 2,则有:ac x x a bx x =⋅-=+2121; ※一元二次方程的根与系数的关系的作用:1已知方程的一根,求另一根;2不解方程,求二次方程的根x 1、x 2的对称式的值,特别注意以下公式:①2122122212)(x x x x x x -+=+ ②21212111x x x x x x +=+ ③212212214)()(x x x x x x -+=- ④21221214)(||x x x x x x -+=- ⑤||22)(|)||(|2121221221x x x x x x x x +-+=+⑥)(3)(21213213231x x x x x x x x +-+=+ ⑦其他能用21x x +或21x x 表达的代数式;3已知方程的两根x 1、x 2,可以构造一元二次方程:0)(21221=++-x x x x x x 4已知两数x 1、x 2的和与积,求此两数的问题,可以转化为求一元二次方程0)(21221=++-x x x x x x 的根6应用一元二次方程※在利用方程来解应用题时,主要分为两个步骤:①设未知数在设未知数时,大多数情况只要设问题为x ;但也有时也须根据已知条件及等量关系等诸多方面考虑;②寻找等量关系一般地,题目中会含有一表述等量关系的句子,只须找到此句话即可根据其列出方程;※处理问题的过程可以进一步概括为: 解答检验求解方程抽象分析问题→→第三章 概率的进一步认识用树状图或表格求概率相关知识点链接:频数与频率频数:在数据统计中,每个对象出现的次数叫做频数,频率:每个对象出现的次数与总次数的比值为频率;概率的意义和大小:概率就是表示每件事情发生的可能性大小,即一个时间发生的可能性大小的数值;必然事件发生的概率为1;不可能事件发生的概率为0;不确定事件发生的概率在0与1之间;知识点1频率与概率的含义在试验中,每个对象出现的频繁程度不同,我们称每个对象出现的次数为频数,而每个对象出现的次数与总次数的比值为频率,即=频数频率总次数把刻画事件A 发生的可能性大小的数值,称为事件A 发生的概率;知识点2通过实验运用稳定的频率来估计某一时间的概率在进行试验的时候,当试验的次数很大时,某个事件发生的频率稳定在相应的概率附近;我们可以通过多次试验,用一个事件发生的频率来估计这一事件发生的频率; 知识点3利用画树状图或列表法求概率重难点第四章 图形的相似1成比例线段一. 线段的比※1. 如果选用同一个长度单位量得两条线段AB, CD 的长度分别是m 、n,那么就说这两条线段的比AB:CD=m:n ,或写成nm B A =. ※2. 四条线段a 、b 、c 、d 中,如果a 与b 的比等于c 与d 的比,即d c b a=,那么这四条线段a 、b 、c 、d 叫做成比例线段,简称比例线段.※3. 注意点:①a:b=k,说明a 是b 的k 倍;②由于线段 a 、b 的长度都是正数,所以k 是正数;③比与所选线段的长度单位无关,求出时两条线段的长度单位要一致;④除了a=b 之外,a:b ≠b:a, b a 与a b 互为倒数; ⑤比例的基本性质:若d c b a =, 则ad=bc; 若ad=bc, 则dc b a = 2平行线分线段成比例 ※1. 平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.如图2, l 1 EF BC DE AB =二. 黄金分割 ※1. 如图1,点C 把线段AB 分成两条线段AC 和BC,如果AC BC AB AC =,那么称线段AB 被点C 黄金分割,点C 叫做线段AB 的黄金分割点,AC 与AB 的比叫做黄金比._ 图1 _B_C _A _ 图2 _ F _ E _ D _ C_ B _ A _l_3 _l _2 _l _11:618.0215:≈-=AB AC ※2.黄金分割点是最优美、最令人赏心悦目的点.3相似多边形1. 一般地,形状相同的图形称为相似图形.※2. 对应角相等、对应边成比例的两个多边形叫做相似多边形.相似多边形对应边的比叫做相似比.※1. 在相似多边形中,最为简单的就是相似三角形.※2. 对应角相等、对应边成比例的三角形叫做相似三角形.相似三角形对应边的比叫做相似比.※3. 全等三角形是相似三角的特例,这时相似比等于1. 注意:证两个相似三角形,与证两个全等三角形一样,应把表示对应顶点的字母写在对应的位置上. ※4. 相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比. ※5. 相似三角形周长的比等于相似比.※6. 相似三角形面积的比等于相似比的平方.※相似多边形的周长等于相似比;面积比等于相似比的平方.4探索三角形相似的条件※1. 相似三角形的判定方法:基本定理:平行于三角形的一边且和其他两边或两边的延长线相交的直线,所截得的三角形与原三角形相似.※2. 平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例. 如图2, l 1 EFBC DE AB ※3. 平行于三角形一边的直线与其他两边或两边的延长线相交,所构成的三角形与原三角形相似.5相似三角形的判定定理的证明6利用相似三角形测高7相似三角形的性质8图形的位似 第五章 投影与视图A 三视图主视图——从正面看到的图左视图——从左面看到的图俯视图——从上面看到的图画物体的三视图时,要符合如下原则:大小:长对正,高平齐,宽相等.虚实:在画图时,看的见部分的轮廓通常画成实线,看不见部分的轮廓线通常画成虚线.B 投影物体在光线的照射下,会在地面或墙壁上留下它的影子,这就是投影现象. 太阳光线可以看成平行光线,像这样的光线所形成的投影称为平行投影; 在同一时刻,物体高度与影子长度成比例.物体的三视图实际上就是该物体在某一平行光线垂直于投影面的平行光线下的平行投影.探照灯,手电筒,路灯,和台灯的光线可以看成是从一点出发的光线,像这样的光线所形成的投影称为中心投影皮影和手影都是在灯光照射下形成的影子.它们是中心投影;C 视点、视线、盲区的定义以及在生活中的应用;.眼睛所在的位置称为视点,.由视点发出的光线称为视线,.眼睛看不到的地方称为盲区第六章 反比例函数知识点1 反比例函数的定义一般地,形如xk y =k 为常数,0k ≠的函数称为反比例函数,它可以从以下几个方面来理解:⑴x 是自变量,y 是x 的反比例函数;⑵自变量x 的取值范围是0x ≠的一切实数,函数值的取值范围是0y ≠; ⑶比例系数0k ≠是反比例函数定义的一个重要组成部分;⑷反比例函数有三种表达式: ①x k y =0k ≠, ②1kx y -=0k ≠,③k y x =⋅定值0k ≠; ⑸函数xk y =0k ≠与y k x =0k ≠是等价的,所以当y 是x 的反比例函数时,x 也是y 的反比例函数;k 为常数,0k ≠是反比例函数的一部分,当k=0时,x k y =,就不是反比例函数了,由于反比例函数xk y =0k ≠中,只有一个待定系数,因此,只要一组对应值,就可以求出k 的值,从而确定反比例函数的表达式;知识点2用待定系数法求反比例函数的解析式 由于反比例函数xk y =0k ≠中,只有一个待定系数,因此,只要一组对应值,就可以求出k 的值,从而确定反比例函数的表达式;知识点3反比例函数的图像及画法反比例函数的图像是双曲线,它有两个分支,这两个分支分别位于第一、第三象限或第二、第四象限,它们与原点对称,由于反比例函数中自变量函数中自变量0x ≠,函数值0y ≠,所以它的图像与x 轴、y 轴都没有交点,即双曲线的两个分支无限接近坐标轴,但永远达不到坐标轴;反比例的画法分三个步骤:⑴列表;⑵描点;⑶连线;再作反比例函数的图像时应注意以下几点:①列表时选取的数值宜对称选取;②列表时选取的数值越多,画的图像越精确;③连线时,必须根据自变量大小从左至右或从右至左用光滑的曲线连接,切忌画成折线;④画图像时,它的两个分支应全部画出,但切忌将图像与坐标轴相交;知识点4反比例函数的性质☆关于反比例函数的性质,主要研究它的图像的位置及函数值的增减情况,如下表:k 的 符号 图像性质①x 的取值范围是0x ≠,y 的取值范围是0y ≠ ②当0k >时,函数图像的两个分支分别在第一、第三象限,在每个象限内,y 随x 的增大而减小; ①x 的取值范围是0x ≠,y的取值范围是0y ≠②当0k <时,函数图像的两个分支分别在第二、第四象限,在每个象限内,y 随x的增大而增大;注意:描述函数值的增减情况时,必须指出“在每个象限内……”否则,笼统地说,当0k >时,y 随x 的增大而减小“,就会与事实不符的矛盾;反比例函数图像的位置和函数的增减性,是有反比例函数系数k 的符号决定的,反过来,由反比例函数图像双曲线的位置和函数的增减性,也可以推断出k 的符号;如xk y =在第一、第三象限,则可知0k >; ☆反比例函数x k y =0k ≠中比例系数k 的绝对值k 的几何意义; 如图所示,过双曲线上任一点Px,y 分别作x 轴、y 轴的垂线,E 、F 分别为垂足, 则OEPF S PE PF y x xy 矩形=⋅=⋅==k☆ 反比例函数x k y =0k ≠中,k 越大,双曲线x k y =越远离坐标原点;k 越小,双曲线xk y =越靠近坐标原点; ☆ 双曲线是中心对称图形,对称中心是坐标原点;双曲线又是轴对称图形,对称轴是直线y=x 和直线y=-x;。
九年级数学上册第二十五章概率初步知识点归纳总结(精华版)(带答案)

九年级数学上册第二十五章概率初步知识点归纳总结(精华版)单选题1、七巧板是我国古代劳动人民的发明之一,被誉为“东方模板”,它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的.如图是一个用七巧板拼成的正方形,如果在此正方形中随机取一点,那么此点取自黑色部分的概率为( )A .932B .516C .38D .716答案:C分析:首先设正方形的面积,再表示出阴影部分面积,然后可得概率.解:设“东方模板”的面积为4,则阴影部分三角形面积为1,平行四边形面积为12,则点取自黑色部分的概率为:1+124=38,故选C .小提示:此题主要考查了概率,关键是表示图形的面积和阴影部分面积.2、在一个不透明的口袋中,放置3个黄球,1个红球和n 个蓝球,这些小球除颜色外其余均相同,课外兴趣小组每次摸出一个球记录下颜色后再放回,并且统计了蓝球出现的频率(如图所示),则n 的值最可能是( )A .4B .5C .6D .7 答案:C分析:根据图知,经过大量实验,蓝球出现的频率稳定在0.6附近,再根据频率公式逐项判断即可.解:根据图知,经过大量实验,蓝球出现的频率稳定在0.6附近, 则n1+3+n =0.6,当n =4时,41+3+4=0.5≠0.6,故A 不符合题意; 当n =5时,51+3+5=59≠0.6,故B 不符合题意; 当n =6时,61+3+6=0.6,故C 符合题意; 当n =7时,71+3+7=711≠0.6,故D 不符合题意;∴n 的值最可能是6, 故选:C .小提示:本题考查频数与频率,能从图中获取到蓝球出现的频率稳定在0.6附近是解答的关键.3、如图,电路连接完好,且各元件工作正常.随机闭合开关S 1,S 2,S 3中的两个,能让两个小灯泡同时发光的概率为( )A .16B .12C .23D .13答案:D分析:首先根据题意画出树状图,然后由树状图求得所有等可能的结果与能让两个小灯泡同时发光的情况,再利用概率公式求解即可求得答案. 解:画树状图得:∵共有6种等可能的结果,能让两个小灯泡同时发光的有2种情况,∴能让两个小灯泡同时发光的概率为26=13;故选:D.小提示:本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比.4、一只不透明的袋子中装有若干个白球和红球,共计20个,这些球除颜色外都相同.将球搅匀,每次从中随机摸出一个球,记下颜色后放回、再搅匀、再摸球,通过大量重复摸球试验后,发现摸到白球的频率稳定于0.3,由此可估计袋子中红球的个数约为()A.6B.14C.5D.20答案:B分析:根据白球的概率可估计红球的概率,即可求解.解:红球的个数为:20×(1−0.3)=14(个),故选:B.小提示:本题考查用频率估计概率,当进行大量重复试验时,频率稳定在概率附近.5、一个口袋中有3个黑球和若干个白球,在不允许将球倒出来数的前提下,小明为估计其中的白球数,采用了如下的方法:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色,再放回,不断重复上述过程.小明共摸了100次,其中80次摸到白球.根据上述数据,小明可估计口袋中的白球大约有()A.18个B.15个C.12个D.10个答案:C分析:小明共摸了100次,其中80次摸到白球,20次摸到黑球,摸到黑球与摸到白球的次数之比为1:4,由此可估计口袋中黑球和白球个数之比为1:4;即可计算出白球数.解:由题可得:3÷100−8080=12(个).所以答案是:12.小提示:本题考查的是通过样本去估计总体,只需将样本“成比例地放大”为总体即可.一般来说,用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确.6、小颖有两顶帽子,分别为红色和黑色,有三条围巾,分别为红色、黑色和白色,她随机拿出一顶帽子和一条围巾戴上,恰好为红色帽子和红色围巾的概率是( ) A .12B .23C .16D .56答案:C分析:利用列表法或树状图即可解决.分别用r 、b 代表红色帽子、黑色帽子,用R 、B 、W 分别代表红色围巾、黑色围巾、白色围巾,列表如下:1种,根据概率公式,恰好为红色帽子和红色围巾的概率是16. 故选:C .小提示:本题考查了简单事件的概率,常用列表法或画树状图来求解.7、不透明袋中装有除颜色外完全相同的a 个白球、b 个红球,则任意摸出一个球是红球的概率是( ) A .ba+b B .ba C .aa+b D .ab 答案:A分析:根据概率公式直接求解即可. ∵共有(a +b)个球,其中红球b 个∴从中任意摸出一球,摸出红球的概率是ba+b . 故选A .小提示:本题考查了简单概率公式的计算,熟悉概率公式是解题的关键.8、如图所示的是由8个全等的小正方形组成的图案,假设可以随意在图中取一点,那么这个点取在阴影部分的概率是( )A .38B .12C .58D .1 答案:A分析:根据阴影部分的面积所占比例得出概率即可. 解:由图知,阴影部分的面积占图案面积的38,即这个点取在阴影部分的概率是38,故选:A .小提示:本题主要考查几何概率的知识,熟练根据几何图形的面积得出概率是解题的关键. 9、如图,若随机向8×8正方形网格内投针,则针尖落在阴影部分的概率为( )A .12B .58C .9π64D .2564 答案:D分析:利用割补法求得阴影面积,再根据几何概率计算求值即可; 解:将上边和左边的弓形面积补到下边和右边可得阴影面积为5×5=25, 该图形总面积为8×8=64, ∴针尖落在阴影部分的概率=2564, 故选: D .小提示:本题考查了几何概率:事件的概率可以用部分线段的长度(部分区域的面积)和整条线段的长度(整个区域的面积)的比来表示.10、如图是一个游戏转盘.自由转动转盘,当转盘停止转动后,指针落在数字1,2,3,4所示区域内可能性最大的是( )A.1号B.2号C.3号D.4号答案:C分析:根据圆周角可得1区域的圆心角度数,然后计算各个区域的可能性,比较大小即可得.解:1区域的圆心角为:360°−50°−125°−65°=120°,∴落在1区域的可能性为:120°360°=13,落在2区域的可能性为:50°360°=536,落在3区域的可能性为:125°360°=2572,落在4区域的可能性为:65°360°=1372,∵536<1372<13<2572,∴落在3区域的可能性最大,故选:C.小提示:题目主要考查可能性的计算及大小比较,理解题意,掌握可能性的计算方法是解题关键.填空题11、一个事件经过500次的试验,某种结果发生的频率为0.32,那么在这一次试验中,该种结果发生的概率估计值是___________.答案:0.32分析:由题意依据大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率进行分析即可.解:一个事件经过500次的试验,某种结果发生的频率为0.32,那么在这一次试验中,该种结果发生的概率估计值是0.32.所以答案是:0.32.小提示:本题考查利用频率估计概率,解答本题的关键是掌握频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.12、如图,数学活动小组自制了一个飞镖盘.若向飞镖盘内投掷飞镖(落在边界线重新投掷),则飞镖落在阴影区域的概率是_____.答案:13分析:利用阴影部分面积除以总面积=投掷在阴影区域的概率,进而得出答案.解:由题意可得,投掷在阴影区域的概率是:39=13.所以答案是:13.小提示:此题主要考查了几何概率,求出阴影部分面积与总面积的比值是解题关键.13、疫情期间,进入学校都要进入测温通道,体温正常才可进入学校.某校有3个测温通道,分别记为A,B,C通道.学生可随机选取其中的一个通道测温进校园,某日早晨,小王和小李两位同学在进入校园时,恰好选择不同通道测温进校园的概率是_____________.答案:23分析:画树状图展示所有9种等可能的情况数,找出符合条件的情况数,然后根据概率公式求解即可.画树状图为:共有9种等可能的情况,其中小王和小李从不同通道测温进校园的有6种情况,侧小王和小李两位同学在进入校园时,恰好选择不同通道测温进校园的概率是69=23,所以答案是:23.小提示:本题考查了列表法与树状图法:利用列表法或树状图法展示所有可能的结果求出,再从中选出符合事件A 或B 的结果数目m ,然后根据概率公式计算事件A 或事件B 的概率.14、小强、小亮、小文三位同学玩投硬币游戏.三人同时各投出一枚均匀硬币,若出现三个正面向上或三个反面向上,则小强赢;若出现两个正面向上和一个反面向上,则小亮赢;若出现一个正面向上和两个反面向上,则小文赢.有下列说法:①小强赢的概率最小;②小文和小亮赢的概率相等;③小文赢的概率是38;④这是一个公平的游戏.其中,正确的是__________(填序号). 答案:①②③分析:利用树状图得出三人分别赢得概率,然后依次判断即可. 解:画树状图得:所以共有8种可能的情况.三个正面向上或三个反面向上的情况有2种,所以P (小强赢)=28=14;出现2个正面向上一个反面向上的情况有3种,所以P (小亮赢)=38;出现一个正面向上2个反面向上的情况有3种,,所以P (小文赢)=38, ∵14<38,∴小强赢的概率最小,①正确; 小亮和小文赢的概率均为38,②正确; 小文赢的概率为38,③正确;三个人赢的概率不一样,这个游戏不公平,④错误; 所以答案是:①②③.小提示:题目主要考查利用树状图求概率,熟练掌握运用树状图求概率的方法是解题关键.15、有三张完全一样正面分别写有字母A ,B ,C 的卡片.将其背面朝上并洗匀,从中随机抽取一张,记下卡片上的字母后放回洗匀,再从中随机抽取一张,则抽取的两张卡片上的字母相同的概率是_________. 答案:13分析:根据题意列出图表得出所有等情况数和抽取的两张卡片上的字母相同的情况数,然后根据概率公式即可得出答案.解:根据题意列表如下:3种情况, 所以P (抽取的两张卡片上的字母相同)=39=13.小提示:此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验. 解答题16、寒冬战疫,西安常安,感谢每一位为这座城拼命的人!一个不透明的口袋里装有分别标有汉字“西”、“安”、“常”、“安”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球. (1)若从中任取一球,球上的汉字刚好是“安”的概率为多少?(2)甲从中任取一球,不放回,再从中任取一球,请用画树状图或列表法,求出甲取出的两个球上的汉字恰能组成“西安”的概率。
(上)微专题十一概率与代数几何知识的综合(最新)人教版九年级数学全一册课件(28张)-公开课

解:(1)列表:
第一次 A B 第二次
x2+1
x2+1 -x2-2
3
x2+1 -x2-2 x2+1
3
-x2-2
-x2-2 x2+1
-x2-2 3
3
3 x2+1
3 -x2-2
(2)代数式BA所有可能的结果共有 6 种,每种结果出现的可能性相等,其中代数式 AB是分式的结果有 4 种,
[2018·呼和浩特]已知函数 y=(2k-1)x+4(k 为常数),若从-3≤k≤3 中任取 k 值,则得到的函数是具有性质“y 随 x 增加而增加”的一次函数的概率为
5 ___1_2___.
【解析】 当 2k-1>0 时,y 随 x 的增加而增加,∴k>12,从-3≤k≤3 中任取 k 的值,能满足“y 随 x 的增加而增加”的是12<k≤3,因此从-3≤k≤3 中任取 k 的 值,满足一次函数具有性质 y 随 x 的增加而增加的概率是3-3(--123)=152.
[2019·常州]将图 1 中的 A 型(正方形)、B 型(菱形)、C 型(等腰直角三角 形)纸片分别放在 3 个盒子中,盒子的形状、大小、质地都相同,再将这 3 个盒子装 入一只不透明的袋子中.根据以上信息,解决下列问题:
图1 (1)搅匀后从中摸出 1 个盒子,盒中的纸片既是轴对称图形又是中心对称图形的
[2018·株洲]从-5,-130,- 6,-1,0,2,π 这七个数中随机抽取一
个数,恰好为负整数的概率为( A )
A.27
B.37
C.47
D.57
【解析】 ∵负整数有-5 和-1,∴恰好为负整数的概率为27.故选 A.
2024年小学毕业质量监测数学试题分析报告

2024年小学毕业质量监测数学试题分析报告随着《义务教育课程标准(2022年版)》的推出,培养学生的综合素质成为教师的迫切任务,核心素养评价和学业质量检测也进一步成为教学研究和关注的重点。
在小学阶段,数学的学习不仅仅是理解概念,记忆公式,明确算理,掌握算法,学习解题技巧,更重要的是培养学生的数学思维和解决问题的能力,全面提升学生的数学素养。
xx县2024年小学毕业质量监测数学试题,基本覆盖了六年级上下册教材内容,题型灵活多样,内容紧密联系生活实际,注重实践性和创新性,难易适度,符合学生的认知水平。
试题重视基础知识、基本技能、解决问题以及数据分析能力的考查,具备一定的综合性和灵活性,试题指向学生对知识的本质理解,考查数学素养的落实情况,充分体现数学来源于生活,用于生活的价值观。
一、试题概述本次小学毕业质量监测数学试题全面评估了学生六年来的数学学习成果。
试题内容覆盖了数与代数、图形与几何、统计与概率、综合与实践四大领域,旨在通过多样化的题型和难易程度,考查学生对数学基础知识的掌握、应用能力和数学思维的发展。
本测试卷卷面总分120分,分为四个板块——“我会数学思考”(选择题10道题共10分,填空题10道题共20分)、“我能熟练运算”(7道题共40分)、“我会动手操作”(4道题共15分)和“我能综合应用”(6道题共35分),旨在检测学生的数学基础知识、基本技能和核心素养。
(一)基础概念理解试题中对单位换算、速度比、最大公因数和最小公倍数等基础概念的考查,反映了对学生基础数学知识掌握的重视。
通过这些题目,能够清晰了解学生对基本数学概念和定义的理解程度。
对于数轴上的点表示数、位置与方向等题目,考查了学生对空间位置关系的理解,体现了对学生空间思维能力的关注。
(二)计算能力考查试题中的直接写出得数、化简比、简算等题目,要求学生熟练掌握加减乘除等基本运算规则,并能快速准确地计算出结果。
这些题目不仅考查了学生的计算能力,还考查了学生的运算速度和准确性。
难点解析北师大版八年级数学下册第六章平行四边形重点解析试题(含解析)

北师大版八年级数学下册第六章平行四边形重点解析考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、在△ABC中,AD是角平分线,点E、F分别是线段AC、CD的中点,若△ABD、△EFC的面积分别为21、7,则ABAC的值为()A.14B.34C.23D.132、如图,点O是▱ABCD的对称中心,l是过点O的任意一条直线,它将平行四边形分成甲、乙两部分,在这个图形上做扎针试验,则针头扎在甲、乙两个区域的可能性的大小是()A.甲大B.乙大C.一样大D.无法确定3、如图,在平行四边形ABCD中,AE BC于点E,把BAE以点B为中心顺时针旋转一定角度后,得到BFG ,已知点F 在BC 上,连接DF .若70ADC ∠=︒,15CDF ∠=︒,则DFG ∠的大小为( )A .140°B .155°C .145°D .135°4、已知正多边形的一个外角等于45°,则该正多边形的内角和为( ) A .135°B .360°C .1080°D .1440°5、如图,正五边形ABCDE 点D 、E 分别在直线m 、n 上.若m ∥n ,∠1=20°,则∠2为( )A .52°B .60°C .58°D .56°6、四边形ABCD 中,如果270A C D ∠+∠+∠=︒,则B 的度数是( ) A .110°B .100°C .90°D .30°7、多边形每一个内角都等于150°,则从该多边形一个顶点出发,可引出对角线的条数为( ) A .9条B .8条C .7条D .6条8、如图,将三角形纸片ABC 沿DE 折叠,当点A 落在四边形BCED 的外部时,测量得∠1=70°,∠2=132°,则∠A为()A.40°B.22°C.30°D.52°9、正五边形的外角和是()A.180︒B.360︒C.540︒D.720︒10、在平面直角坐标系中,平行四边形ABCD的顶点A、B、D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是()A.(7,3)B.(8,2)C.(3,7)D.(5,3)第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、如图,在平行四边形ABCD中,AB=4,BC=5,以点C为圆心,适当长为半径画弧,交BC于点P,交CD于点Q,再分别以点P,Q为圆心,大于12PQ的长为半径画弧,两弧相交于点N,射线CN交BA的延长线于点E,则AE的长是 _____.2、如图,已知AB ∥CD ,ABE ∠和CDE ∠的平分线相交于F ,140E ∠=︒,求BFD ∠的度数_____.3、如图,在四边形ABCD 中,90A C ∠=∠=︒,34B ∠=︒,在边AB ,BC 上分别找一点E ,F 使DEF 周长最小,此时EDF ∠=______.4、如图,在Rt△ABC 中,∠ACB =90°,AB =5,BC =3,将△ABC 绕点B 顺时针旋转得到△A′B C′,其中点A ,C 的对应点分别为点,A C ''连接,AA CC '',直线CC '交AA '于点D ,点E 为AC 的中点,连接DE .则DE 的最小值为_________5、如图,在平行四边形ABCD 中,45ABC ∠=︒,E 、F 分别在CD 和BC 的延长线上,AE BD ∥,30EFC ∠=︒,AB =EF =______.三、解答题(5小题,每小题10分,共计50分)1、已知:如图,在ABC 中,AD DB =,BE EC =,AF FC =.求证:AE DF 、互相平分.2、△ABC 和△GEF 都是等边三角形.问题背景:如图1,点E 与点C 重合且B 、C 、G 三点共线.此时△BFC 可以看作是△AGC 经过平移、轴对称或旋转得到.请直接写出得到△BFC 的过程.迁移应用:如图2,点E 为AC 边上一点(不与点A ,C 重合),点F 为△ABC 中线CD 上一点,延长GF交BC 于点H ,求证:CE CH +=.联系拓展:如图3,AB =12,点D ,E 分别为AB 、AC 的中点,M 为线段BD 上靠近点B 的三等分点,点F 在射线DC 上运动(E 、F 、G 三点按顺时针排列).当12MG AG +最小时,则△MDG 的面积为_______.3、在等腰直角三角形ABC 中,90BAC ∠=︒,点E 、F 分别为AB ,AC 的中点,H 为线段EF 上一动点(不与点E ,F 重合),将线段AH 绕点A 逆时针方向旋转90°得到AG ,连接GC ,HB .(1)如图1,求证:AHB AGC ≌; (2)如图2,连接GF ,HG ,HG 交AF 于点Q . ①点H 在运动的过程中,求证:90HFG ∠=︒;②若44AB C ==,当AQG 为等腰三角形时,EH 的长为______. 4、已知:如图:五边形ABCDE 的内角都相等,DF ⊥AB . (1)则∠CDF =(2)若ED =CD ,AE =BC ,求证:AF =BF .5、如图,在Rt△OAB 中,∠OAB =90°,OA =AB =6,将△OAB 绕点O 沿逆时针方向旋转90°得到△OA 1B 1.(1)线段OA 1的长是 ,∠AOB 1的度数是 ; (2)连接AA 1,求证:四边形OAA 1B 1是平行四边形.-参考答案-一、单选题 1、B 【分析】过点A 作△ABC 的高,设为x ,过点E 作△EFC 的高为12x ,可求出42BD x =,28CF x=,再由点E 、F 分别是线段AC 、CD 的中点,可得出2CE CD CE CF =,进而求出56CD x=,再利用角平分线的性质可得出AB AC 的值为BDCD即可求解. 【详解】解:过点A 作△ABC 的高,设为x ,过点E 作△EFC 的高为12x ,∴1212ABDSx BD == ,11722EFCS x CF == ∴42BD x =,28CF x= ,∵点E 、F 分别是线段AC 、CD 的中点, ∴12CE EF CF CA AD CD === , ∴2CA CE = , ∵CE CD CA CF = , ∴2CE CD CE CF =, ∴56CD x=, 过点D 作DM ⊥AB ,DN ⊥AC , ∵AD 为BAC ∠平分线, ∴DM =DN , ∵1122ABD ACDSAB DM S AC DN =⋅=⋅,, ∴S ABD AB DM DB S ACD AC DN CD ⋅==⋅,即:AB DBAC CD=∴4242356564AB BD x AC CD x==== , 故选:B . 【点睛】本题考查角平分线性质定理及三角形中位线的性质,解题关键是求出AB BDAC CD=. 2、C 【分析】如图,连接,,AC BD 记过O 的直线交,AD BC 于,,N H 则O 为,AC BD 的中点,,,,OA OC OB OD AD BC ∥再证明,ANO CHO ≌ ,,DNO BHO AOB COD ≌≌ 可得,ANHB CHND S S 四边形四边形 从而可得答案.【详解】解:如图,连接,,AC BD 记过O 的直线交,AD BC 于,,N HO 为▱ABCD 的对称中心,O 为,AC BD 的中点,,,,OA OC OB OD AD BC ∥,,NAO HCO ANO CHO,ANO CHO ≌同理:,,DNO BHO AOB COD ≌≌,ANHBCHND S S 四边形四边形所以针头扎在甲、乙两个区域的可能性的大小是一样的, 故选C 【点睛】本题考查的是全等三角形的判定与性质,平行四边形的性质,随机事件发生的可能性的大小,几何概率的意义,理解几何概率的意义是解本题的关键. 3、C 【分析】根据题意求出∠ADF ,根据平行四边形的性质求出∠ABC 、∠BAE ,根据旋转变换的性质、结合图形计算即可.【详解】解:∵∠ADC=70°,∠CDF=15°,∴∠ADF=55°,∵四边形ABCD是平行四边形,∴∠ABC=∠ADC=70°,AD∥BC,∴∠BFD=125°,∵AE⊥BC,∴∠BAE=20°,由旋转变换的性质可知,∠BFG=∠BAE=20°,∴∠DFG=∠DFB+∠BFG=145°,故选:C.【点睛】本题考查的是平行四边形的性质、旋转变换的性质,掌握旋转前、后的图形全等是解题的关键.4、C【分析】先利用正多边形的每一个外角为45︒,求解正多边形的边数,再利用正多边形的内角和公式可得答案. 【详解】解:正多边形的一个外角等于45°,∴这个正多边形的边数为:3608, 45∴这个多边形的内角和为:821801080,故选C本题考查的是正多边形内角和与外角和的综合,熟练的利用正多边形的外角的度数求解正多边形的边数是解本题的关键.5、D【分析】延长AB 交直线n 于点F ,由正五边形ABCDE ,可得出五边形每个内角的度数,再由三角形外角的性质可得128EGB ∠=︒,根据平行线的性质可得52GFH ∠=︒,最后再利用一次三角形外角的性质即可得.【详解】解:如图所示,延长AB 交直线n 于点F ,∵正五边形ABCDE ,∴108A ABC C D AED ∠=∠=∠=∠=∠=︒,∵120∠=︒,∴1128EGB A ∠=∠+∠=︒,∵m n ∥,∴18052GFH EGB ∠=︒-∠=︒,∴256GBH GFH ∠=∠-∠=︒,故选:D .题目主要考查正多边形的内角,平行线的性质,三角形外角的性质等,理解题意,作出辅助线,综合运用这几个性质是解题关键.6、C【分析】根据四边形内角和是360°进行求解即可.【详解】 解:四边形的内角和是360°,+++=360A B C D ∴∠∠∠∠︒∵270A C D ∠+∠+∠=︒=360-270=90B ∴∠︒︒︒.故选:C .【点睛】本题考查四边形的内角和,是基础考点,难度较易,掌握相关知识是解题关键.7、A【分析】多边形从一个顶点出发的对角线共有(n-3)条.多边形的每一个内角都等于150°,多边形的内角与外角互为邻补角,则每个外角是30度,而任何多边形的外角是360°,则求得多边形的边数;再根据不相邻的两个顶点之间的连线就是对角线,则此多边形从一个顶点出发的对角线共有(n-3)条,即可求得对角线的条数.【详解】解:∵多边形的每一个内角都等于150°,∴每个外角是30°,∴多边形边数是360°÷30°=12,则此多边形从一个顶点出发的对角线共有12-3=9条.故选A .本题主要考查了多边形的外角和定理,已知外角求边数的这种方法是需要熟记的内容.8、B【分析】利用四边形的内角和定理求出B C ∠+∠,再利用三角形的内角和定理可得结果.【详解】∵1=70∠︒,2=132∠︒,∴3601236070132158B C ∠+∠=︒-∠-∠=︒-︒-︒=︒,∴180()18015822A B C ∠=︒-∠+∠=︒-︒=︒,故选:B .【点睛】本题主要考查了多边形的内角和定理及三角形的内角和定理,关键是运用多边形的内角和定理求出B C ∠+∠的度数.9、B【分析】根据多边形的外角和等于360°,即可求解.【详解】解:任意多边形的外角和都是360°,故正五边形的外角和的度数为360°.故选:B .【点睛】本题主要考查多边形的外角和定理,解答本题的关键是掌握任意多边形的外角和都是360°.10、A利用平行四边形的对边平行且相等的性质,先利用对边平行,得到D点和C点的纵坐标相等,再求出CD=AB=5,得到C点横坐标,最后得到C点的坐标.【详解】解:四边形ABCD为平行四边形。
判断平行四边形的五种方法

判断平行四边形的五种方法平行四边形,是几何中的常客。
它那对边平行、对角相等的特性让人一眼就能认出来。
不过,有时候我们需要从不同的角度来验证一个四边形是否真的符合平行四边形的定义。
今天,我们就来聊聊五种实用的方法,帮你把这些“疑点”搞个清楚。
1. 利用对边平行1.1 基本概念最直观的方法就是看看四边形的对边是否平行。
平行四边形的基本定义就是对边平行。
所以,你可以拿出直尺、量角器,甚至用眼睛观察一下。
如果两对对边分别平行,那它基本上就是平行四边形了。
1.2 小技巧有时候我们用眼睛观察不够准确,可以用一把直尺或量角器来帮助验证。
如果对边的测量结果显示它们平行,那基本上没错了。
特别是在实际操作中,这个方法简单直接,特别适合手头上没有复杂工具的时候。
2. 验证对边相等2.1 对边长度相等另一个很有用的方法是检查对边的长度是否相等。
平行四边形的一个重要特性是对边长度相等。
如果你测量出对边长度完全一样,那么这个四边形很可能就是平行四边形。
2.2 怎么测量用尺子量取对边的长度,记录下来。
然后比对这些长度,如果对边的长度一一对应,那么你的四边形就大概率是平行四边形。
这种方法适用于直观测量,也能在没有高科技工具的情况下进行验证。
3. 检查对角线的交点性质3.1 对角线的交点平行四边形的对角线在交点处互相平分。
这就像是在一个平行四边形中,两个对角线交叉成了四个角度一样的地方。
这是一个很特别的属性,用来判断一个四边形是否是平行四边形非常有效。
3.2 操作步骤用直尺或者量角器量取对角线的长度,然后检查它们的交点。
把交点分成两对等长的部分,这样你就能验证它们是否真的相互平分。
这个方法可以帮助你更准确地确认四边形的性质,特别是在绘图和实际操作中。
4. 检查内角和4.1 内角和平行四边形的内角和是360度。
这是因为平行四边形的每两个内角加起来都等于180度,所以四个内角加起来就是360度。
如果你的四边形内角和符合这个条件,那么它很可能是平行四边形。
河北省阜平一中2025届高三适应性调研考试数学试题含解析

河北省阜平一中2025届高三适应性调研考试数学试题考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。
选择题必须用2B 铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知六棱锥P ABCDEF -各顶点都在同一个球(记为球O )的球面上,且底面ABCDEF 为正六边形,顶点P 在底面上的射影是正六边形ABCDEF 的中心G ,若6PA =,2AB =,则球O 的表面积为( )A .163πB .94π C .6πD .9π2.若复数z 满足(1)12i z i +=+,则||z =( )A .22B .32C .102D .123.已知定义在R 上的可导函数()f x 满足()()()'10x f x x f x -⋅+⋅>,若3(2)y f x e=+-是奇函数,则不等式1()20x x f x e +⋅-<的解集是( ) A .(),2-∞B .(),1-∞C .()2,+∞D .()1,+∞4.如图,在平行四边形ABCD 中,O 为对角线的交点,点P 为平行四边形外一点,且AP OB ,BP OA ,则DP =( )A .2DA DC +B .32DA DC + C .2DA DC +D .3122DA DC +5.已知1F 、2F 分别是双曲线()2222:10,0x yC a b a b-=>>的左、右焦点,过2F 作双曲线C 的一条渐近线的垂线,分别交两条渐近线于点A 、B ,过点B 作x 轴的垂线,垂足恰为1F ,则双曲线C 的离心率为( ) A .2B 3C .3D 56.关于圆周率π,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯实验.受其启发,某同学通过下面的随机模拟方法来估计π的值:先用计算机产生2000个数对(),x y ,其中x ,y 都是区间()0,1上的均匀随机数,再统计x ,y 能与1构成锐角三角形三边长的数对(),x y 的个数m ﹔最后根据统计数m 来估计π的值.若435m =,则π的估计值为( ) A .3.12B .3.13C .3.14D .3.157.函数()5sin 20312f x x x ππ⎛⎫⎛⎫=+≤≤ ⎪⎪⎝⎭⎝⎭的值域为( )A .1,12⎡⎤-⎢⎥⎣⎦B .10,2⎡⎤⎢⎥⎣⎦C .[]0,1D .1,02⎡⎤-⎢⎥⎣⎦8.设全集U =R ,集合{|(1)(3)0}A x x x =--≥,11|24xB x ⎧⎫⎪⎪⎛⎫=>⎨⎬ ⎪⎝⎭⎪⎪⎩⎭.则集合()U A B 等于( )A .(1,2)B .(2,3]C .(1,3)D .(2,3)9.已知向量(22cos m x =,()1,sin2n x =,设函数()f x m n =⋅,则下列关于函数()y f x =的性质的描述正确的是( )A .关于直线12x π=对称B .关于点5,012π⎛⎫⎪⎝⎭对称 C .周期为2πD .()y f x =在,03π⎛⎫-⎪⎝⎭上是增函数 10.已知集合A {x x 0}︱=>,2B {x x x b 0}=-+=︱,若{3}A B ⋂=,则b =( ) A .6-B .6C .5D .5-11.已知等比数列{}n a 的前n 项和为n S ,且满足122n n S λ+=+,则λ的值是( )A .4B .2C .2-D .4-12.已知双曲线C :22221x y a b-=(0a >,0b >)的焦距为2c .点A 为双曲线C 的右顶点,若点A 到双曲线C 的渐近线的距离为12c ,则双曲线C 的离心率是( )AB C .2D .3二、填空题:本题共4小题,每小题5分,共20分。
数学趣味大挑战八年级上册数学趣味题解析

数学趣味大挑战八年级上册数学趣味题解析数学作为一门抽象的学科,在许多学生眼中常常给人一种难以驾驭的感觉。
然而,数学也可以充满趣味和挑战性。
下面,我们将为大家解析八年级上册一些有趣的数学题目,希望能够帮助大家更好地理解和掌握数学知识。
1. 扑克游戏中的数学扑克牌游戏是一种常见的娱乐方式,很多人喜欢通过扑克牌来挑战自己的运气和智慧。
在扑克游戏中,一副牌有52张牌,其中有4种花色(红心、方块、梅花、黑桃),每种花色有13张牌(A、2、3、4、5、6、7、8、9、10、J、Q、K)。
现在我们来解答以下两个问题:问题一:从一副扑克牌中随机抽取5张牌,问这5张牌全为黑桃的概率是多少?解析:一副牌中有52张牌,其中有13张黑桃牌。
因此,第一张牌抽到黑桃的概率为13/52,第二张牌(已经抽出一张黑桃牌)抽到黑桃的概率为12/51,以此类推,最后一张牌抽到黑桃的概率为9/48。
根据乘法原理,这5张牌全为黑桃的概率为(13/52)*(12/51)*(11/50)*(10/49)*(9/48)≈0.00018。
问题二:从一副扑克牌中随机抽取5张牌,问这5张牌中至少有两张黑桃牌的概率是多少?解析:利用补集原理,我们可以计算至少有两张黑桃牌的概率为1减去没有黑桃牌和只有一张黑桃牌的概率。
没有黑桃牌的概率可以用C(39, 5)/C(52, 5)来表示,其中C(n, m)表示从n个数中选择m个数的组合数。
只有一张黑桃牌的概率可以用C(13, 1)*C(39, 4)/C(52, 5)来表示。
因此,至少有两张黑桃牌的概率为1 - C(39, 5)/C(52, 5) - C(13, 1)*C(39, 4)/C(52, 5)≈0.3794。
2. 几何问题的解析几何问题是数学中的重要组成部分,通过解析几何问题可以帮助我们理解和掌握几何概念和定理。
下面我们来解析一个有关平行四边形的问题:问题:已知ABCD是一个平行四边形,P为边BC上的一点,连接AP并延长交边CD于点O,若AP=2BP,求证AO=2OC。
不同版本教材知识点设置的比较研究—以初中数学平行四边形为例

摘要随着课程改革不断推进,各地出现了各有特点的数学教材,教材的编写者有不同的思路,因此教材在各个方面也会存在一定的差异,同时不同版本的教材对比也有助于教师更好地教学与进行教学研究.通过对人教版、北师大版、苏科版中的“平行四边形”部分进行比较研究,从而帮助对该部分知识点的全面把握,以便更好地把握数学教材内容,优化教学设计.通过文献分析法、对比分析法、统计法、问卷调查法对不同版本初中数学教材从结构、引入、探究及习题设置进行了比较,从而发现三个版本教材的特色以及各自的异同点.通过对此课题的研究,提供一些有益的数学教学建议.关键词平行四边形教材对比人教版北师大版苏科版A comparative study on the set of knowledge points in different editionsof textbooks—— A case study of Parallelogram in junior middle schoolAbstract With the continuous advancement of the curriculum reform, mathematics textbooks with their own characteristics have appeared in various places. The compilers of the textbooks have different ideas, so there are certain differences in various aspects of the textbooks, at the same time, the comparison of different versions of teaching materials is helpful to teachers. This paper makes a comparative study of the "Parallelogram" section in the people s education press, the Beijing Normal University press and the Soviet section press, so as to help us grasp the knowledge points of this section in anall-round way, so as to better grasp the contents of the mathematics teaching materials and optimize the teaching design. Through literature analysis, Comparative Analysis, Statistics and Questionnaire survey, this paper compares the structure, Introduction, exploration and problem setting of different editions of junior middle school mathematics textbooks, thus discovered three edition teaching material's characteristic as well as respective similarities and differences. Through the research on this subject, some useful suggestions on mathematics teaching are provided.Key words Parallelogram textbook comparison People's Education Edition Beijing Normal University Edition Suke edition目录摘要 (II)Abstract (III)引言 (1)1绪论 (1)1.1问题的提出 (1)1.2国内外研究现状 (1)1.2.1国外研究概况 (1)1.2.2国内研究概况 (2)2研究对象、研究维度、研究思路与研究方法 (2)2.1研究对象 (2)2.2研究维度 (2)2.3研究思路 (2)2.4研究方法 (3)3平行四边形内容设置的比较研究 (3)3.1教材内容结构比较 (3)3.2引入的比较 (5)3.3探究活动的比较 (12)3.4习题的比较 (14)4初中不同版本数学教材比较的实证研究 (16)4.1问卷调查对象 (16)4.2问卷调查数据整理 (16)4.3问卷调查数据分析 (17)5结论 (17)5.1三个版本教材的横向比较 (17)5.2三个版本教材的纵向比较 (18)6建议 (18)6.1内容结构方面 (18)6.2引入方式方面 (18)6.3习题设置方面 (19)6.4探究活动方面 (19)结语 (20)参考文献 (21)致谢 (22)附录 (23)引言教育改革的核心是课程改革,课程改革促进了教材的优化 [1]P10.结合不同的地域特点和教育现状,国家支持相关部门编写不同特征的教材,不同教材的编写思路决定了教材在各个方面也会存在一定差异[2]P59-66.目前有很多专家学者对不同版本的初中数学教材进行了对比研究,很多一线教师也在关注不同教材下同一知识点的异同点.目前各种教材是怎样设计的,有什么样的优缺点、异同点,编写意图是什么?这些有待作进一步研究.在实际教学过程中应如何选用和使用教材是值得每一个基础教育工作者思考的问题.作为一名未来从事教育事业的毕业生,我结合自身学习的理论经验和实习期间的实践教学经验,对人民教育出版社[3]P41-67(以下简称人教版)、北京师范大学出版社[4]P135-140(以下简称北师版)、江苏风凰科学技术出版社[5]P56-90(以下简称苏科版)三个版本教材中“平行四边形”的内容进行比较研究,在研究过程中主要运用内容分析和统计分析法,并且结合一定的实践经验,通过对不同教材进行比较,希望可以深入的理解教材,找到不同之处,取长补短,对初中数学教材进行优化与反思.1绪论1.1问题的提出教科书是教师教和学生学的主要载体[6].现如今,越来越多的人去研究教材,新版本的初中数学教材有哪些特点,现在各种教材是怎样设计的,有什么样的优缺点、异同点?这些有待作进一步研究.平行四边形是四边形内容中的重要部分.它在教材中有着呈上启下的作用.研究发现,这部分研究较缺乏,因此,本文通过对三个版本初中数学教材中“平行四边形”部分进行对比研究,分析不同版本教材的特点.1.2 国内外研究现状现在对教材的研究较多,研究的方面也很多,作者搜集了大量的资料,通过分析整理,对国内外已有的教材对比研究现状进行了分析概括.1.2.1国外研究概况近年来,我国教育事业有了很大的发展,因为我们不断与国外教材进行比较研究,比较研究大多是对某一个具体的模块进行具体的分析比较,从而找出国内外教材之间的差异.2002年, Hoyles等学者,借助TIMSS这种手段对多国教材进行有针对性的比较,分析了这些国家的数学教科书与学生的成绩测试以及评价结果,对异同点进行了详细的比较[7]P61-P65;2006年,梁贯成等学者对日本、韩国等国家的教材进行了多方面比较,同时也对比了中澳数学教材中的价值观和中新数学教材的知识架构等等[8]P32-34;2007年,范良火等学者通过对三个国家的初中数学教材内容中的“问题解决步骤的呈现方式”进行比较,发现这三个国家在这方面的异同点,同时也提供了建议[9]P61-75;2013年,曹一鸣等人对不同国家初中数学的数与代数、统计与概率和图形与几何的整体布局进行了比较[10]P29-36。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.
P( 2 z 一
<
引 言
本 问题 源 于 一道 中学 数 学题 , 问题 为求 在 原 单 位面 积长 方形 四边 上任 意取 一点 , 连接 这 四点 ,
所 构 成 的 四 边 形 的 面 积 小 于 0 5的 概 率 是 多 少 。 .
0 + P( 。 z 一 一 < O ) z + 1 1 )
f
一
, < 0 <z 以
0其 他 ,
Tn0 m s + i
{ , <≤ 字 ~ zo a
l
故 F()一 P{ £G £ S FH< £ = P( )
小于其 原 面积妻 的概率为 0 5 且 四边 形面 积 .,
sF E H的概 率分 布 , F()一 P{ H< t 的结 G 即 SF G ) 果 ( 定理 证 明 中的 F()表达 式)如下 : 见 £
,
一
a ≥ b
。 < £< 曲
j c-( 卜 c 鲁 +c a+ 譬 + ~ 譬 2 t÷ 手 ) b
J 0 ,
一 曲 <
t 一 a ≤ b
80
第 2 第 1期 4卷
21 0 1年 2月
高等 函授 学报 ( 自然 科学 版)
J u n l fHi h rCo r s 0 d n e Ed c t n( t rlS in e ) o r a g e re p n e c u ai Na u a ce c s o o
叩 , 密度 函数 如下 : 叩 的
r ,
) b + t )- b 2 a + 1 )@ (- - - t( -
-
2 t
(一 1 + (_ ) n 譬 6 2 )
t
} (- +b (t 一 (一 )(+t了 a T) -(1 警_ ÷+ aI ) 1b t a + a- ) a t8 2 2 b t bn )h o
关 键 词 : 何 概 率 ;概 率 分 布 ;仿 真 几
中 图分 类 号 : 3 G6 3
文 献标 识 码 : A
文 章 编 号 : 0 6 7 5 ( 0 1 0 —0 7 —0 lO — 3 3 2 1 ) 1 0 9 3
)< 0 一 P( 。 z1 一 > 0 ) z + 一 1 )
.
P( 2 X4 0 , 于 z m > )由
,
。
~
均匀 分布 uE , ] z , ~ uE ,- o , z o 。 1
该 问题本 文 给予 了解 答 , 将 结 论 推 广 至平 行 四 并
边 形 , 出了其 面积 的概率 分布 , 求 主要用 到 了随机
变 量 的概 率 分布 进行 求 解 , 运 用 了 几何 概 率 的 并
Vo . 4 No 1 12 .
201 1
于 ( 一 {阳 < ) P叩 是F) PS 一 {
+ 罟<£一 {】 2 m/n) ) P 7 t )i , 2 - s 故 <(
m
知 L
一 I ^
一
/ 2
其中 一 (t—蚪 /i 0 lCI n 2 m)s , — , B n + 口 l B l= =b A :
m
一
一
dx  ̄
肛
f  ̄
川
型 如z+
4 - ( 一 已 ) a + 一 b sn 0 & ( ) i
厶
厶
专 型如 :
( (
一
由于 , 服从 均匀分 布 uE ,] , 服从 o6, & 均匀分 布 uE ,] on , 记叩 一 e + 一b 一 一 已, 。 。 , 由引理 2知
7 9
第 2 4卷第 1期
21 0 1年 2月
高 等 函授 学 报 ( 自然 科 学 版 )
J u n lo g rCo r s o d n eEd c t n Na u a ce e ) o r a fHihe r ep n e c u a i ( t r lS inc s o
Vo . 4 NO 1 12 .
2 1 01
・
大 学 生 园地 ・
平 行 四边形 上 的几 何 概 率 研 究
吴 贤 盛 乔 琦 花 张 聪
( 中师 范大 学 数 学 与 统 计 学 学 院 , 汉 4 0 7) 华 武 3 0 9
摘
要 : 文 主要 探 究 平 行 四 边 形 上 面 积 的概 率 分 布 , 验 证 了单 位 面积 长 方 形 四 边 上 任 意 本 先
Z
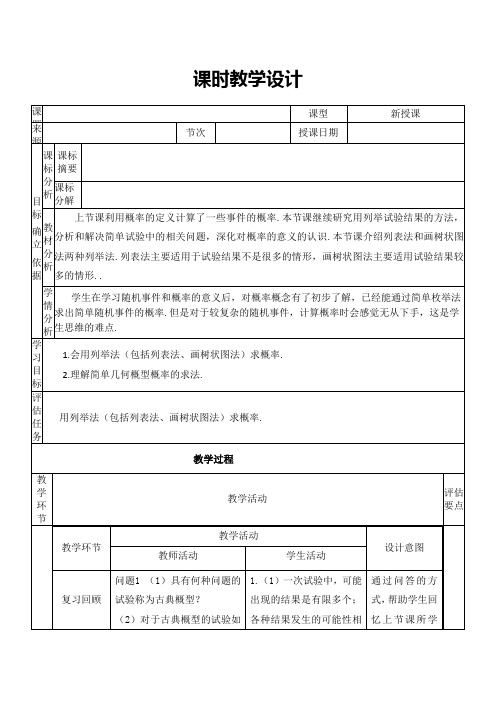
图 1
证明 设 lEl , F 一 邑, D l B — l CI I 一 G 已, D f a,B Ⅱ f B f 6ZA C 一 f H : 一 fCf ,A 一 , B
,
( 6 ) 2a ) ( 一 一詈 一/ 了一 + 十 ( 1 :  ̄
1_ 一
一
( 一: f 表 F( )的 仿 真 值 与 理论 值 )
生
”
由表 一可 知 , 论值 与仿 真值 很 接近 , 理 从侧 面验证 了分 布 函数 F £ ()的正确 性 , 至此 已求 出了任意平
行 四边形 四边 上任 意取 点所 构成 四边 形 面积 的概 率分 布分 布 。
s H: 唧 : =l一 ( .( 一 。 z )+ ( 一 。 . )
且 , 相互 独立 , 则 的密 度 函数 。
户 ) l P () —u d , 中P ( , ( 一 p ( )u 其 l )
P ( ) 别 为 。已 的 密 度 函 数 Ⅲ 。 :z 分 ,
第 2 4卷 第 1 期 21 0 1年 2月
高 等 函授 学 报 ( 自然 科 学 版 )
J u n lo ih rCo r s o d n eEd c t n Na u a ce c s o r a fH g e r e p n e c u a i ( t r l in e ) o S
分 布
乩一
一
(
一
一
正 方形 的仿 真验 算 。
M 曲
次, 最终 的 sn即为 P{ E H< t i SF G )的理 论 估计 值
( 真值 ) 仿 。
一 6 -方形 为例 , 出 F()的 璺 下 面 以单位 面 积的正 画 £
概 率分 布 曲线如 图 + t兰 范 围[ ,] 2 二6 , 曲 01。 H 的取值 ]
一
P{ £ < m/ ) sF G 2 一 , 即对任 意平行 四边 形在
。 ( _ . + : ~ . o 一 一 6 。
厶
条 边上 产生 4 服从 [ ,] 均匀 分布 的 随机数 , 个 O1 的
这 样点 E、 G、 的 位置 就 被 确 定 了 , 设 置 计 F、 H 并
其 边上 任 意取点 构 成 的四边形 的面积小 于其 原 面
1
积 的 概率 为 0 5 同 时还 算 出了其 面 积 的概 率 .,
厶
数 变 量 s初 值赋 为 0 若 某 次试 验 中 s H< t则 , , 聊 ,
将 s 1否 则 s 加 , 的值保 持 不 变 , 拟 一 1 0 0 模 0 00
的率 ÷ 概 为
证 明 设 长 方 形 A D 的 AB 边 为 ,则 BC
综 得 ( 丢一 , 面 为 的 上 P 肿 < ) 即 积 1 s 1在
长 方 形 的各 边 上任 取 一 点 , 次 将 各 点 连 接 所得 依
B C边 为 n, A B C D 上依 次取 点 E、 在 B、 C、 D、 A F、
取 所 四 形 面 小 原 积 的 率 0,推 至 意 行 边 的 形并 出 点 成 边 的 积 于 面 ÷ 概 为.再 广 任 平 四 形 情 ,求 了 5
其 面积 的概 率 分 布 , 针 对 单位 面 积 正 方 形利 用 计 算机 仿 真 进 行 验 证 , 论 值 与 仿 真 值 很 接 近 并 理
四边 形 的面积 小于 的概率 为 0 5 立 。 .成
1理 2 ( 1 随机变 量 的和差运 算 ) 叩一 + 若
,
G H, IE I z ,I Cl 。 lD l 。 、 设 — 。 — , — , B F G — IH I z D
则 记 四 边 形 E GH 的 面 积 F
z +zz + ( 2 3 4 n— z ) 一 z ) , 4( 1 ) 则
P(  ̄c < 1) S
一
证 明 设 (- )的 联合 密 度 函数 为 p( , x, z ) 由 于 , 相 互 独 立 ,故 p x , ) 一 z, (
P( z + z 一 ).( 一 (。
参 考 文 献
m <。 一 K /
其 中 “ 一 (t— m /i 0 lCf a 2 )s , — , n B
— lB I b A
一
2 c 如
a D
_ + ( 如 如 +肛 L
口。 D。
z
B
F
C
如。 )一 丽 ( 一 + Tb )+ 1 t a z 2 z
Vo . 4 N o 1 12 .
2 1 01
1 2 + <
J ] I
) d 一 仁 。 dx x z ,
一
f
, <6 0 <z
z d d。 d。 “ 1。 2x 。x x 一f xf px px) 一 ) () ( d
{ ,6z 一< ≤
知识。 引 理 1 面 积 为 1 长 方 形 A D 的 各 边 上 的 BC 任 取 一 点 ,依 次 连 接 各 点 所 得 四 边 形 的 面 积 小 于
1 2
结合 几 何 概 率 可 知 , z + z 一 < 0 , P( 。 。 )
