完整word版北师大版七年级数学下册第二章单元测试题及答案全套,文档.docx
北师大版七年级数学下册第二章检测卷及答案.docx

【本文档由书林工作坊整理发布,谢谢你的下载和关注!】第二章检测卷时间:120分钟满分:120分一、选择题(本大题共6小题,每小题3分,满分18分,每小题只有一个正确选项)1.如图,直线AB与直线CD相交于点O.若∠AOD=50°,则∠BOC的度数是()A.40°B.50°C.90°D.130°2.在我们常见的英文字母中,存在着同位角、内错角、同旁内角的现象.在下列几个字母中,不含同旁内角现象的字母是()A.E B.F C.N D.H3.如图,在三角形ABC中,D,E,F分别在AB,BC,AC上,且EF∥AB,要使DF∥BC,只需满足下列条件中的()A.∠1=∠2 B.∠2=∠AFDC.∠1=∠AFD D.∠1=∠DFE第3题图第4题图4.如图,已知OA⊥OB,OC⊥OD,∠BOA∶∠AOD=3∶4,则∠BOD的度数为() A.120°B.125°C.150°D.157.5°5.如图,将一副三角板叠放在一起,使直角的顶点重合于点O.若AB∥OC,DC与OB 交于点E,则∠DEO的度数为()A.85°B.70°C.75°D.60°第5题图第6题图6.一次数学活动中,检验两条完全相同的纸带①、②的边线是否平行,小明和小丽采用两种不同的方法:小明把纸带①沿AB折叠,量得∠1=∠2=50°;小丽把纸带②沿GH 折叠,发现GD与GC重合,HF与HE重合.则下列判断正确的是()A.纸带①的边线平行,纸带②的边线不平行B.纸带①的边线不平行,纸带②的边线平行C.纸带①、②的边线都平行D.纸带①、②的边线都不平行二、填空题(本大题共6小题,每小题3分,满分18分)7.一个角的度数为20°,则它的补角的度数为________.8.如图是李晓松同学在运动会跳远比赛中最好的一跳,甲、乙、丙三名同学分别测得P A=5.52米,PB=5.37米,MA=5.60米,那么他的跳远成绩应该为________米.第8题图第9题图9.如图,直线a,b与直线c,d相交,已知∠1=∠2,∠3=110°,则∠4的度数为________.10.一个安全用电标识如图①所示,此标识可以抽象为图②中的几何图形,其中AB∥CD,ED∥BF,点E,F在线段AC上.若∠A=∠C=17°,∠B=∠D=50°,则∠AED的度数为________.第10题图 第11题图11.如图,AB ∥CD ,OE 平分∠BOC ,OF ⊥OE ,OP ⊥CD ,∠ABO =a °.有下列结论:①∠BOE =12(180-a )°;②OF 平分∠BOD ;③∠POE =∠BOF ;④∠POB =2∠DOF .其中正确的是__________(填序号).12.已知OA ⊥OC ,∠AOB ∶∠AOC =2∶3,则∠BOC 的度数为__________. 三、解答题(本大题共5小题,每小题6分,满分30分)13.已知一个角的余角比它的补角的23还小55°,求这个角的度数.14.如图,点D 在射线AE 上,AB ∥CD ,∠CDE =140°,求∠A 的度数.15.如图,直线AB 与直线CD 相交于点O ,EO ⊥AB ,垂足为O ,∠EOC =35°,求∠AOD 的度数.16.如图,利用无刻度的直尺和圆规在三角形ABC的边AC上方作∠CAD=∠ACB,并说明AD与BC的位置关系(保留作图痕迹,不写作法).17.如图,在三角形ABC中,∠ACB=90°,将三角形ABC向下翻折,使点A与点C 重合,折痕为DE.试说明:DE∥BC.四、(本大题共3小题,每小题8分,共24分)18.如图,已知DE∥BC,BE平分∠ABC,∠C=65°,∠ABC=50°.(1)求∠BED的度数;(2)判断BE与AC的位置关系,并说明理由.19.如图,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COB,∠AOD∶∠DOE =4∶1.求∠AOF的度数.20.如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,试说明:CD⊥AB.解:∵DG⊥BC,AC⊥BC(已知),∴∠DGB=∠ACB=90°(垂直定义),∴DG∥AC(__________________________),∴∠2=∠________().∵∠1=∠2(已知),∴∠1=∠________(等量代换),∴EF∥CD(________________________),∴∠AEF=∠________(__________________________).∵EF⊥AB(已知),∴∠AEF=90°(________________),∴∠ADC=90°(________________),∴CD⊥AB(________________).五、(本大题共2小题,每小题9分,共18分)21.由于被墨水污染,一道几何题仅能见到如图所示的图形和文字:“如图,已知四边形ABCD中,AD∥BC,∠D=67°,…”(1)根据以上信息,你可以求出∠A,∠B,∠C中的哪个角?写出求解的过程;(2)若要求出其他的角,请你添上一个适当的条件:____________________________,并写出解题过程.22.如图,已知直线l1∥l2,A,B分别是l1,l2上的点,l3和l1,l2分别交于点C,D,P是线段CD上的动点(点P不与C,D重合).(1)若∠1=150°,∠2=45°,则∠3的度数是多少?(2)若∠1=α,∠2=β,用α,β表示∠APC+∠BPD.六、(本大题共12分)23.如图,已知BE平分∠ABD,DE平分∠BDC,且∠EBD+∠EDB=90°.(1)试说明:AB∥CD;(2)H是BE的延长线与直线CD的交点,BI平分∠HBD,写出∠EBI与∠BHD的数量关系,并说明理由.参考答案与解析1.B 2.C 3.D 4.C 5.C6.B解析:如图①,∵∠1=∠2=50°,∴∠3=∠1=50°,∠4=180°-∠2=130°.由折叠可知∠4=∠2+∠5,∴∠5=∠4-∠2=80°.∵∠3≠∠5,∴纸带①的边线不平行.如图②,∵GD与GC重合,HF与HE重合,∴∠CGH=∠DGH=90°,∠EHG=∠FHG=90°,∴∠CGH+∠EHG=180°,∴纸带②的边线平行.故选B.7.160°8.5.379.70°10.67°11.①②③12.30°或150°.解析:∵OA⊥OC,∴∠AOC=90°.∵∠AOB∶∠AOC=2∶3,∴∠AOB=60°.∵OB 的位置有两种,一种是在∠AOC 内,一种是在∠AOC 外,∴∠BOC 的度数应分两种情况讨论,如图.(1)当OB 在∠AOC 内时,∠BOC =90°-60°=30°;(2)当OB 在∠AOC 外时,∠BOC =90°+60°=150°.故∠BOC 的度数为30°或150°.13.解:设这个角的度数为x ,依题意有23(180°-x )-55°=90°-x ,(3分)解得x =75°.故这个角的度数为75°.(6分)14.解:∵∠CDE =140°,∴∠CDA =180°-∠CDE =40°.(3分)∵AB ∥CD ,∴∠A =∠CDA =40°.(6分)15.解:∵EO ⊥AB ,∴∠EOB =90°.(2分)又∵∠COE =35°,∴∠COB =∠COE +∠BOE =125°.(4分)∵∠AOD =∠COB ,∴∠AOD =125°.(6分)16.解:如图所示.(4分)∵∠CAD =∠ACB ,∴AD ∥BC .(6分) 17.解:∵将三角形ABC 向下翻折,使点A 与点C 重合,折痕为DE ,∴∠AED =∠CED ,∠AED +∠CED =180°,∴∠AED =∠CED =90°,(3分)∴∠AED =∠ACB =90°,∴DE ∥BC .(6分)18.解:(1)∵BE 平分∠ABC ,∠ABC =50°,∴∠EBC = 12∠ABC =25°.∵DE ∥BC ,∴∠BED =∠EBC =25°.(3分)(2)BE ⊥AC .(4分)理由如下:∵DE ∥BC ,∠C =65°,∴∠AED =∠C =65°.(6分)由(1)知∠BED =25°,∴∠AEB =∠AED +∠BED =65°+25°=90°,∴BE ⊥AC .(8分)19.解:∵OE 平分∠BOD ,∴∠DOE =∠EOB .(2分)又∵∠AOD ∶∠DOE =4∶1,∴∠AOD =4∠DOE .∵∠AOD +∠DOE +∠EOB =180°,∴∠DOE =∠EOB =30°,∠AOD =120°,∴∠COB =∠AOD =120°.(5分)∵OF 平分∠COB ,∴∠COF =60°.又∵∠AOC =∠BOD =∠DOE +∠EOB =60°,∴∠AOF =∠COF +∠AOC =60°+60°=120°.(8分)20.解:同位角相等,两直线平行 ACD 两直线平行,内错角相等 ACD 同位角相等,两直线平行(4分)ADC 两直线平行,同位角相等 垂直定义 等量代换 垂直定义(8分)21.解:(1)可以求出∠C .(1分)解法如下:∵AD ∥BC ,∠D =67°,∴∠C =180°-∠D =180°-67°=113°.(4分)(2)添加的条件是AB ∥CD .(5分)∵AB ∥CD ,∴∠B =180°-∠C =180°-113°=67°,∴∠A =180°-∠D =180°-67°=113°.(9分) 22.解:(1)过点P 向右作PE ∥l 1.∵l 1∥l 2,∴l 1∥PE ∥l 2,∴∠1+∠APE =180°,∠2=∠BPE .(2分)∵∠1=150°,∠2=45°,∴∠APE=180°-∠1=180°-150°=30°,∠BPE=∠2=45°,(4分)∴∠3=∠APE+∠BPE=30°+45°=75°.(5分)(2)若∠1=α,∠2=β,则∠APB=180°-∠1+∠2=180°-α+β,(7分)∴∠APC+∠BPD =180°-∠APB=180°-(180°-α+β)=α-β.(9分)23.解:(1)∵BE平分∠ABD,DE平分∠BDC,∴∠ABD=2∠EBD,∠BDC=2∠EDB.(3分)∵∠EBD+∠EDB=90°,∴∠ABD+∠BDC=2(∠EBD+∠EDB)=180°,∴AB∥CD.(6分)(2)∠EBI=12∠BHD.(8分)理由如下:∵BH平分∠ABD,∴∠ABH=∠EBD.∵AB∥CD,∴∠ABH=∠BHD.(10分)∵BI平分∠EBD,∴∠EBI=12∠EBD=12∠ABH=12∠BHD.(12分)中考数学知识点代数式一、重要概念分类:1.代数式与有理式用运算符号把数或表示数的字母连结而成的式子,叫做代数式。
北师大版数学七年级下册第二章单元测试卷(含答案)

北师大版数学七年级下册第二章单元测试卷一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个是符合要求的)1.下图中,∠1和∠2是对顶角的是()2.已知∠1=40°,则∠1的补角的度数是()A.100°B.140°C.50°D.60°3.下列选项中,不是运用“垂线段最短”这一性质的是()A.立定跳远时测量落点后端到起跳线的距离B.从一条河向一个村庄引一条最短的水渠C.把弯曲的公路改成直道可以缩短路程D.直角三角形中任意一条直角边的长度都比斜边短4.如图,∠1=20°,∠AOC=90°,点B,O,D在同一条直线上,则∠2的度数为()A.95°B.100°C.110°D.120°(第4题) (第5题)5.如图,∠B的同旁内角有()A.1个B.2个C.3个D.4个6.如图,一个合格的弯形管道ABCD要求AB∥CD.现测得∠ABC=135°,若这个弯形管道符合要求,则∠BCD的度数为()A.25°B.45°C.55°D.65°7.如图,直线a,b被直线c所截,下列条件中,不能判定a∥b的是()A.∠2=∠4 B.∠1+∠4=180°C.∠5=∠4 D.∠1=∠38.如图所示,若AB∥CD,则∠A,∠D,∠E之间的关系是()A.∠A+∠E+∠D=180°B.∠A-∠E+∠D=180°C.∠A+∠E-∠D=180°D.∠A+∠E+∠D=270°9.如图所示,∠BAC=90°,AD⊥BC,则下列结论中,正确的有()①AB⊥AC;②AD与AC互相垂直;③点C到AB的垂线段是线段AB;④点A到BC的距离是线段AD;⑤线段AB的长度是点B到AC的距离;⑥∠BAD =∠C.A.2个B.3个C.4个D.5个10.(1)如图①,AB∥CD,则∠A+∠E+∠C=180°;(2)如图②,AB∥CD,则∠E=∠A+∠C;(3)如图③,AB∥CD,则∠A+∠E-∠1=180°;(4)如图④,AB∥CD,则∠A=∠C+∠P.以上结论正确的是()A.(1)(2)(3)(4)B.(1)(2)(3)C.(2)(3)(4)D.(1)(2)(4)二、填空题(本题共6小题,每小题3分,共18分)11.若直线a∥b,a∥c,则____________,理由是_____________________.12.如图,ED∥AB,ED交AF于点C,若∠ECF=138°,则∠A=________.13.若∠A=45°,则∠A的余角等于________°.14.如图,请填写一个条件:______________,使得DE∥AB .15.如图,A,B之间是一座山,一条铁路要通过A,B两地,为此需要在A,B 之间修一条笔直的隧道,在A地测得铁路走向是北偏东63°,那么在B地按南偏西________的方向施工,才能保证铁路准确接通.16.如图,在△ABC中,∠ACB=90°,AC=5 ,BC=12 ,AB=13 .点P是线段AB上的一个动点,则CP的最小值为__________.3三、解答题(本题共6小题,共52分.解答应写出文字说明、证明过程或演算步骤)17.(8分)如图,已知∠B+∠BCD=180°,∠B=∠D,那么∠E=∠DFE成立吗?为什么?下面是彬彬同学进行的推理,请你将彬彬同学的推理过程补充完整.解:成立.因为∠B+∠BCD=180°(已知),所以__________(同旁内角互补,两直线平行).所以∠B=∠DCE(____________________________).又因为∠B=∠D(已知),所以∠DCE=∠D(等量代换).所以AD∥BE(____________________________).所以∠E=∠DFE(____________________________).18.(8分)一个角的余角比它的补角的23还小55°,求这个角的度数.19.(8分)如图,已知AB∥CD,∠B=100°,EF平分∠BEC,EG⊥EF,求∠BEG 和∠DEG的度数.20.(8分)如图,以点B为顶点,射线BC为一边,利用尺规作图法作∠EBC,使∠EBC=∠A,BE与AD平行吗?21.(10分)学习完平行线的性质与判定之后,我们发现借助构造平行线的方法可以帮我们解决许多问题.(1)小明遇到了下面的问题:如图①,l1∥l2,点P在l1,l2之间,探究∠A,∠APB,∠B之间的数量关系.小明过点P作l1的平行线,可得到∠APB,∠A,∠B之间的数量关系是__________________.(2)如图②,若AC∥BD,点P在AC,BD同侧,∠A,∠B,∠APB的数量关系如何?为此,小明进行了下面的推理.请将这个推理过程补充完整,并在括号内填上依据.解:过点P作PE∥AC,如图②,所以∠A=∠APE (______________________).因为AC∥BD,5所以BD∥PE(__________________________),所以∠B=∠BPE.因为∠APB=∠BPE-∠APE,所以∠APB=____________(____________).(3)随着以后的学习我们还会发现平行线的许多用途.如图③,在小学我们已知道,三角形ABC中,∠A+∠B+∠C=180°,试构造平行线说明理由.22.(10分)已知AB∥CD.(1)如图①,若∠B=30°,∠BEC=148°,求∠C的度数;(2)如图②,若CF∥EB,CF平分∠ECD,试判断∠ECD与∠B之间的数量关系,并说明理由.答案一、1.C 2.B 3.C 4.C 5.C 6.B7.D8.C 9.B10.C二、11.b∥c;平行于同一条直线的两条直线平行12.42°13.4514.∠ABD=∠D(答案不唯一)15.63°16.60 13三、17.AB∥CD;两直线平行,同位角相等;内错角相等,两直线平行;两直线平行,内错角相等18.解:设这个角的度数为x°.由题意得90-x=23(180-x)-55,解得x=75.答:这个角的度数为75°.19.解:因为AB∥CD,∠B=100°,所以∠BEC=80°.因为EF平分∠BEC,所以∠BEF=∠CEF=40°.因为EG⊥EF,所以∠GEF=90°.所以∠BEG=90°-∠BEF=90°-40°=50°,∠DEG=180°-∠GEF-∠CEF =180°-90°-40°=50°.20.解:如图,BE与AD不一定平行.21.解:(1) ∠APB=∠A+∠B(2)两直线平行,内错角相等;平行于同一条直线的两条直线平行;∠B-∠A;等量代换(3)过点A作直线DE∥BC,如图.因为DE∥BC,所以∠DAB=∠B,∠EAC=∠C (两直线平行,内错角相等).7因为∠DAB+∠BAC+∠EAC=180°,所以∠BAC+∠B+∠C=180°(等量代换).22.解:(1)如图①,过点E作EG∥AB,所以∠B=∠BEG.因为∠BEC=∠BEG +∠GEC=148°.所以∠B+∠GEC=148°.因为∠B=30°,所以∠GEC=148°-∠B=118°.因为AB∥CD,所以EG∥CD.所以∠GEC+∠C=180°.所以∠C =180°-∠GEC=62°.(2)∠B=12∠ECD.理由如下:如图②,过点E作EG∥AB,所以∠B=∠BEG.因为AB∥CD,所以EG∥CD.所以∠GEC+∠ECD=180°. 因为CF平分∠ECD,所以∠ECD=2∠ECF. 所以∠GEC+2∠ECF=180°.因为CF∥EB,所以∠BEC+∠ECF=180°.所以∠GEC+∠BEG+∠ECF=180°.所以∠BEG+∠ECF=2∠ECF.所以∠BEG=∠ECF.因为∠B=∠BEG,∠ECF=12∠ECD.所以∠B=12∠ECD.。
北师大版七年级数学下册第二章单元测试题及答案全套共20页word资料
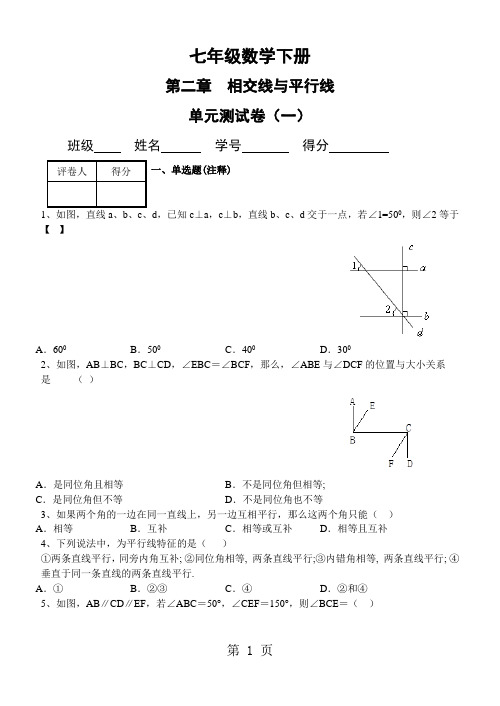
七年级数学下册第二章相交线与平行线单元测试卷(一)班级姓名学号得分评卷人得分一、单选题(注释)1、如图,直线a、b、c、d,已知c⊥a,c⊥b,直线b、c、d交于一点,若∠1=500,则∠2等于【】A.600B.500C.400D.3002、如图,AB⊥BC,BC⊥CD,∠EBC=∠BCF,那么,∠ABE与∠DCF的位置与大小关系是()A.是同位角且相等B.不是同位角但相等;C.是同位角但不等D.不是同位角也不等3、如果两个角的一边在同一直线上,另一边互相平行,那么这两个角只能()A.相等B.互补C.相等或互补D.相等且互补4、下列说法中,为平行线特征的是()①两条直线平行,同旁内角互补; ②同位角相等, 两条直线平行;③内错角相等, 两条直线平行; ④垂直于同一条直线的两条直线平行.A.①B.②③C.④D.②和④5、如图,AB∥CD∥EF,若∠ABC=50°,∠CEF=150°,则∠BCE=()A.60°B.50°C.30°D.20°6、如图,如果AB∥CD,则角α、β、γ之间的关系为()A.α+β+γ=360°B.α-β+γ=180°C.α+β-γ=180°D.α+β+γ=180°7、如图,由A到B 的方向是()A.南偏东30°B.南偏东60°C.北偏西30°D.北偏西60°8、如图,由AC∥ED,可知相等的角有()A.6对B.5对C.4对D.3对9、如图,直线AB、CD交于O,EO⊥AB于O,∠1与∠2的关系是( )更多功能介绍ykw18/zt/A.互余B.对顶角C.互补D.相等10、若∠1和∠2互余,∠1与∠3互补,∠3=120°,则∠1与∠2的度数分别为( ) A.50°、40°B.60°、30°C.50°、130°D.60°、120°11、下列语句正确的是( )A.一个角小于它的补角B.相等的角是对顶角C.同位角互补,两直线平行D.同旁内角互补,两直线平行12、图中与∠1是内错角的角的个数是( )A.2个B.3个C.4个D.5个13、如图,直线AB和CD相交于点O,∠AOD和∠BOC的和为202°,那么∠AOC的度数为( )A.89°B.101°C.79°D.110°14、如图,∠1和∠2是对顶角的图形的个数有( )A.1个B.2个C.3个D.0个15、如图,直线a、b被直线c所截,现给出下列四个条件:①∠1=∠5,②∠1=∠7,③∠2+∠3=180°,④∠4=∠7,其中能判定a∥b的条件的序号是( )A.①②B.①③C.①④D.③④评卷人得分二、填空题(注释)16、如图,∠ACD=∠BCD,DE∥BC交AC于E,若∠ACB=60°,∠B=74°,则∠EDC=___°,∠CDB=____°。
北师大版七年级数学下册第二章达标测试卷-带参考答案

北师大版七年级数学下册第二章达标测试卷-带参考答案一、选择题(本大题共10个小题,每小题3 分,共30 分,在每个小题给出的四个选项中,只有一项符合题目要求)1.在同一平面内两条直线的位置关系是()A.相交B.平行C.平行或相交D.以上答案都不对2.下列各图中,∠1与∠2是对顶角的是()3.如图,下列各组角中,互为同位角的是()A.∠2和∠3 B.∠1和∠3C.∠3和∠4 D.∠2和∠5(第3题)(第4题)4.如图,某污水处理厂要从A处把处理过的水引入排水渠PQ,为了节约用料,铺设垂直于排水渠PQ的管道AB.这种铺设方法蕴含的数学原理是()A.两点确定一条直线B.两点之间,线段最短C.过一点可以作无数条直线D.垂线段最短5.下列各图能表示点A到BC的距离的是()6.如图,DE∥BC,DF∥AC,∠C=72°,则∠EDF的度数是() A.70°B.72°C.80°D.82°(第6题)(第7题)7.如图,下列条件能判定直线l1∥l2的是()A.∠1=∠2 B.∠1+∠3=180°C.∠4=∠5 D.∠1+∠2=180°8.如图,将一副三角尺叠放在一起,使直角的顶点重合于点O,AB∥OC,DC 与OB交于点E,则∠DEO的度数为()A.85°B.70°C.75°D.60°(第8题)(第9题)9.如图,用尺规作出∠OBF=∠AOB,所画痕迹弧MN是()A.以点B为圆心,OD长为半径的弧B.以点C为圆心,DC长为半径的弧C.以点E为圆心,OD长为半径的弧D.以点E为圆心,DC长为半径的弧10.如图,若∠1=∠2,DE∥BC,则下列结论中:①FG∥DC;②∠AED=∠ACB;③CD平分∠ACB;④∠1+∠B=90°;⑤∠BFG=∠BDC;⑥∠FGC=∠DEC+∠DCE,正确的结论是()A.①②③B.①②⑤⑥C.①③④⑥ D.③④⑥(第10题)(第11题)二、填空题(本大题共5个小题,每小题3 分,共15 分)11.如图是一把剪刀,若∠AOB=41°,则∠COD=________.12.如图,直线AB,CD相交于点O,OE⊥AB,∠COB=145°,则∠DOE=________.(第12题)(第13题)13.如图,直线a与直线b交于点A,∠1=120°,∠2=40°.若要使直线b与直线c平行,则至少应将直线b绕点A逆时针旋转________°.14.如图,把一张长方形纸片沿AB折叠,若∠1=75°,则∠2的度数为________.(第14题)(第15题)15.如图,已知AB∥DE,∠B=135°,∠C=60°,则∠D的度数为________.三、解答题(本大题共8个小题,共75分.解答应写出文字说明或演算步骤) 16.(9分)如图,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河岸.(1)从火车站到码头怎样走最近?画图并说明理由;(第16题)(2)从码头到铁路怎样走最近?画图并说明理由;(3)从火车站到河岸怎样走最近?画图并说明理由.17.(6分)已知一个角的余角是这个角的补角的13,求这个角的度数.第3 页共10 页18.(8分)如图,已知三角形ABC,D为AB的中点,请你解决下列问题:(1)过点D作DE∥BC,交AC于点E,并说明作图的依据(尺规作图);(2)度量DE,BC的长度,直接写出DE,BC之间有何数量关系.(第18题)19.(8分)如图,已知∠1+∠2=180°,∠3=∠B.试说明:∠EDG+∠DGC=180°.(第19题)20.(9分)如图,已知∠1=∠BDC,∠2+∠3=180°.(1)请判断AD与EC的位置关系,并说明理由;(2)若DA平分∠BDC,CE⊥AE,∠1=70°,求∠F AB的度数.(第20题)21.(10分)如图,直线AB,CD相交于点O,∠COE=90°.(1)若∠AOC=36°,求∠BOE的度数;(2)若∠BOD∶∠BOC=1 ∶5,求∠AOE的度数;(3)在(2)的条件下,过点O作OF⊥AB,请直接写出∠EOF的度数.(第21题)第5 页共10 页22.(12分)综合与探究:如图,已知∠BAD+∠ADC=180°,AE平分∠BAD,CD与AE相交于点F,DG交BC的延长线于点G,∠CFE=∠AEB.(1)若∠B=87°,求∠DCG的度数;(2)AD与BC是什么位置关系?请说明理由;(3)若∠DAB=α,∠DGC=β,直接写出当α,β满足什么数量关系时,AE∥DG.(第22题)23.(13分)综合与实践:【问题情境】如图①,AB∥CD,∠P AB=130°,∠PCD=120°,求∠APC的度数.小明的思路是过点P向右作射线PE∥AB,利用平行线的性质求∠APC的度数.【初步探究】(1)按小明的思路,求∠APC的度数;【问题迁移】(2)如图②,AB∥CD,点P在B,D两点之间运动(不与点B,D重合),记∠P AB=α,∠PCD=β,则∠APC与α,β之间有何数量关系?请说明理由;【联想拓展】(3)在(2)的条件下,如果点P在线段OB,射线DM上运动(点P与点O不重合),其余条件不变,请你直接写出∠APC与α,β之间的数量关系;【解决问题】(4)我们发现借助构造平行线的方法可以解决许多问题,随着以后的学习你还会发现平行线的更多用途.试构造平行线解决以下问题:如图③,已知三角形ABC,试说明:∠A+∠B+∠C=180°.(第23题)第7 页共10 页答案一、1.C 2.A 3.B 4.D 5.B 6.B7.B8.C9.D10.B二、11.41°12.55°思路点拨:根据对顶角相等可得∠AOD=145°,再根据垂直的定义可得∠AOE=90°,最后根据角的和差关系即可得到答案.13.2014.30°15.105°三、16.解:(1)如图,沿BA走.理由:两点之间线段最短.(2)如图,沿AC走.理由:垂线段最短.(3)如图,沿BD走.理由:垂线段最短.(第16题)17.解:设这个角的度数为x°,则它的余角为(90-x)°,补角为(180-x)°,由题意得90-x=13(180-x)解得x=45.所以这个角的度数是45°.18.解:(1)如图.依据:同位角相等,两直线平行.(第18题)(2)DE=12BC.19.解:因为∠1+∠2=180°,∠1+∠DFE=180°所以∠2=∠DFE,所以EF∥AB,所以∠3=∠ADE.又因为∠3=∠B,所以∠B=∠ADE所以DE∥BC,所以∠EDG+∠DGC=180°. 20.解:(1)AD∥EC.理由:因为∠1=∠BDC,所以AB∥CD,所以∠2=∠ADC.又因为∠2+∠3=180°,所以∠ADC+∠3=180°所以AD∥EC.(2)因为DA平分∠BDC所以∠ADC=12∠BDC=12∠1=12×70°=35°.所以∠2=∠ADC=35°,因为AD∥EC所以∠F AD=∠AEC.又因为CE⊥AE,所以∠F AD=∠AEC=90°. 所以∠F AB=∠F AD-∠2=90°-35°=55°. 21.解:(1)因为∠AOC=36°,∠COE=90°所以∠BOE=180°-∠AOC-∠COE=54°.(2)因为∠BOD∶∠BOC=1∶5所以∠BOD=180°×11+5=30°,所以∠AOC=30°所以∠AOE=∠AOC+∠COE=30°+90°=120°.(3)∠EOF的度数是30°或150°.22.解:(1)因为∠BAD+∠ADC=180°所以AB∥CD,所以∠DCG=∠B=87°.(2)AD∥BC.理由如下:因为AB∥CD所以∠BAF=∠CFE.因为AE平分∠BAD,所以∠BAF=∠DAF所以∠DAF=∠CFE.因为∠CFE=∠AEB所以∠DAF=∠AEB,所以AD∥BC.(3)当α=2β时,AE∥DG.23.解:(1)因为AB∥CD,PE∥AB,所以PE∥CD,∠P AB+∠APE=180°所以∠PCD+∠CPE=180°.因为∠P AB=130°,∠PCD=120°所以∠APE=50°,∠CPE=60°所以∠APC=∠APE+∠CPE=50°+60°=110°.(2)∠APC=α+β.理由:如图①,过点P作PG∥AB交AC于点G则∠APG=∠P AB=α.因为AB∥CD,所以PG∥CD,所以∠CPG=∠PCD=β所以∠APC=∠APG+∠CPG=α+β.第9 页共10 页(第23题)(3)∠APC=|α-β|.(4)如图②,在BC边(端点除外)上任取一点D,过点D作DN∥AC交AB于点N,作DF∥AB交AC于点F.因为DN∥AC,所以∠C=∠BDN,∠CFD=∠NDF.因为DF∥AB,所以∠B=∠CDF,∠A=∠CFD所以∠A=∠NDF.因为∠BDN+∠NDF+∠CDF=180°所以∠A+∠B+∠C=180°.。
(完整版)北师大版七年级数学下册第二章测试题及答案,推荐文档

9.(1)∠NOD=90° (2)∠AOC=60°
∠MOD=15°10.∠AEC=90°
出题意图 本着对第二章内容全方位的考察为目的,特为学生设计此套测试 题,考察内容广泛,技巧灵活多样,让学生充分利用所学知识来解 决问题,有助于知识的升华。建议考试时间 100—120 分钟。
“
”
“
”
At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!
北师大版七年级下册数学第二章测试卷及答案共3套

第二章 相交线与平行线单元测试一、选择题l 、如果一个角的补角是 150,那么这个角的余角的度数是( )A.30B.60C.90D.1202、如图,下列条件中,能判定DE//AC 的是( )A.EDC=EFC ∠∠B.AFE ACD ∠=∠C.34∠=∠D.12∠=∠3、如图,//,AB CD 下列结论中错误的是( )A.12∠=∠B.25180∠+∠=C.23180∠+∠=D.34180∠+∠=4、如图,//D,1128,AB C ∠=FG 平分,EFD ∠则2∠的度数是( )A.46B.23C.26D.24 5、如图,,//,AD BC DE AB ⊥则B ∠和1∠的关系是( )A.相等B.互补C.互余D.不能确定6、将直尺与三角尺按如图所示的方式叠放在一起,在图中标记的角中,与∠1互余的角有( )个.A.2B.3C. 4D.57、如图,把矩形ABCD 沿EF 对折,若150,∠=则FED ∠等于( )A.50B.80C.65D.1158、已知两个角的两边互相平行,这两个角的差是o 40,则这两个角分别是( )A.140100和B.11070和C.7030和D.150110和9、一辆汽午在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是( )A.第一次右拐60,第二次左拐120 B.第一次左拐60,第二次右拐60 C.第一次左拐60,第二次左拐120 D.第一次右拐60,第二次右拐6010、把一张对面互相平行的纸条折成如图那样,EF 是折痕,若32EFB ∠=则下列结论正确有( )(1)32 (2)116'C EF AEC ∠=∠=(3)D 116 (4)=64BF BGE ∠=∠A 、1个B 、2个C 、3个D 、4个 二、填空题11、如图,已知直线a b 、被直线c 所截,//,1130,a b ∠=则2∠= .12、如图,//,AB CD 如果2,DHG AGE ∠=∠则DHG ∠= .13、一个角的余角是这个角的补角的1,3则这个角是 度.14、如图,40,60,ABC ACB ∠=∠=BO CO 、平分ABC ∠和ACB ∠,DE 过O 点,且//DE BC ,则BOC ∠= .15、如图,已知//,70AB DE B ∠=,CM 平分,BCE CN CM ∠⊥,那么DCN ∠= .16、如图,//,120,30AB CD BAE DCE ∠=∠=,则AEC ∠= .17、如图,直线AB 、CD 、EF 相交于点O ,140,70,AOD DOE ∠=∠=则AOF ∠= . 18、如图,DB 平分,//,80,ADE DE AB CDE ∠∠=则ABD ∠= ,A ∠= . 19、如图, 已知////,60,10,AB CD EF B D ∠=∠=EG 平分BED ∠,则GEF ∠= .20、如图,已知//,AB CD ABE ∠和CDE ∠的平分线相交于F ,140,E ∠=则BFD ∠的度数为 . 三、作图题(要求必须用尺规作图,不写作法,留下作图痕迹,要有结论)21、如图,一块大的三角板ABC ,D 是AB 上一点,现要求过点D 割出一块小的三角板ADE ,使//,DE BC 请作出DE.四、证明题22、已知,如图,//,,701150,EF BC A D AOB C ∠=∠∠=∠+∠=,求B ∠的度数.23、已知:如图,//D,D AC B A ∠=∠,求证:.E F ∠=∠24、如图,已知//,AB CD 猜想图1、图2、图3中,,B BED D ∠∠∠之间有什么关系?请用等式表示出它们的关系。
北师大七年级下数学第二章相交线与平行线单元测试(含答案)

第二章订交线与平行线一、选择题1.以下作图语句正确的选项是()A. 延伸线段AB 到 C,使 AB=BCB. 延伸射线ABC. 过点 A 作 AB∥ CD∥EF D作.∠ AOB 的均分线 OC2.以下四幅图中,∠ 1 和∠ 2 是同位角的是()A. ⑴⑵B. ⑶⑷C. ⑴⑵⑶D. ⑵、⑶⑷3.假如一个角的补角是150 °,那么这个角的余角的度数是()A.30 °B.60 °C.90 °D.120 °4.如图,以下说法错误的选项是()A. ∠A 与∠ EDC是同位角B∠. A 与∠ ABF 是内错角C. ∠ A 与∠ ADC是同旁内角D∠. A 与∠ C 是同旁内角5. 两条平行线被第三条直线所截,一对同旁内角的比为2: 7,则这两个角中较大的角的度数为()A.40 °B.70 °C. 100 °D. 140 °6. 以下说法正确的有 ( ) ① 对顶角相等;② 相等的角是对顶角;③ 若两个角不相等,则这两个角必定不是对顶角;④若两个角不是对顶角,则这两个角不相等.A. 1 个B. 个2C.个3D. 个47.如图, AB∥CD,则图中∠ 1、∠ 2、∠ 3关系必定建立的是()A. ∠1+∠ 2+∠ 3= 180 °B. ∠1+∠ 2+∠ 3= 360 °8.以下说法:①在同一平面内,不订交的两条线段叫做平行线;知直线;③ 两条平行直线被第三条直线所截,同位角相等;有()个.C.∠ 1+∠ 3=2∠ 2D.∠ 1+∠ 3=∠ 2② 过一点,有且只有一条直线平行于已④ 同旁内角相等,两直线平行.正确的个数9.如图,直线a, b 订交于点O, OE⊥ a 于点 O, OF⊥ b 于点 O,若∠ 1=40 °,则以下结论正确的选项是()A. ∠2=∠ 3=50 °B.∠ 2=∠ 3=40 °C.∠ 2=40 °,∠ 3=50 °D.∠2=50 °, 3=40 °10.如图,给出了过直线外一点作已知直线的平行线的方法,其依照是()A. 同位角相等,两直线平行B内.错角相等,两直线平行C. 同旁内角互补,两直线平行D. 两直线平行,同位角相等11.如图,已知∠1=∠ 2=∠ 3=∠ 4,则图形中全部平行的是()A. AB∥ CD∥ EFB. CD∥ EFC. AB∥EFD. AB∥ CD∥ EF, BC∥DE12.如图, AB∥ CD,∠ 1=58 °, FG 均分∠ EFD,则∠ FGB的度数等于()A. 122 °B. 151C. 116 °D. 97 °°二、填空题, b, c 是直线,且 a∥b ,b∥ c,则 ________ .14. 两个角的两边分别平行,此中一个角比另一个角的 4 倍少 30°,这两个角是 ________.15. 一个正方体中有一条棱是a,与 a 平行棱长有 ________ 条,与 a 垂直并订交的棱长有________ 条.16. 如图,∠ 1=75 °,∠ 2=120 °,∠ 3=75 °,则∠ 4=________17.如图,直线l1∥ l2,而且被直线l 3,l4所截,则∠ α=________18.图中的内错角是________ .19.假如一个角的余角是30°,那么这个角是________ .20.已知∠α的补角是它的 3 倍,则∠α=________.21.已知∠ A 与∠ B 互余,若∠ A=20° 15,′则∠ B 的度数为 ________ .22.如下图,已知AB∥ DC, AE 均分∠ BAD, CD 与 AE 订交于点F,∠ CFE=∠ E.试说明AD∥BC.达成推理过程:∵ AB∥ DC(已知)∴∠ 1=∠ CFE( ________)∵AE 均分∠ BAD(已知)∴∠ 1=∠ 2 (角均分线的定义)∵∠ CFE=∠ E(已知)∴∠ 2=________(等量代换)∴ AD∥ BC ( ________)三、解答题23.如下图, L1,L2,L3交于点O,∠ 1=∠ 2,∠ 3:∠ 1=8:1,求∠ 4的度数.24.一个角的补角加上24°,恰巧等于这个角的 5 倍,求这个角的度数.25.如图,已知射线AB 与直线 CD交于点 O, OF 均分∠ BOC, OG⊥ OF 于 O, AE∥ OF,且∠ A=30°.(1)求∠ DOF的度数;(2)试说明 OD 均分∠ AOG.26.如图 1, CE均分∠ ACD, AE 均分∠ BAC,∠ EAC+∠ ACE=90°( 1)请判断AB 与 CD 的地点关系并说明原因;( 2)如图 2,在( 1)的结论下,当∠E=90°保持不变,挪动直角极点点挪动时,问∠BAE与∠ MCD 能否存在确立的数目关系?E,使∠MCE=∠ ECD,当直角极点 E( 3)如图运动时(点3,在( 1)的结论下, P 为线段 AC 上必定点,点C 除外)∠ CPQ+∠CQP与∠ BAC 有何数目关系?Q 为直线( 2、3CD上一动点,当点 Q 在射线小题只要选一题说明原因)CD 上参照答案一、选择题D A B D D B D A C A D B二、填空题13.a ∥ c14.42°, 138 °或 10°, 10°15.3; 416.60°17.64°18.∠ A 与∠ AEC;∠ B 与∠ BED19.60°20.45°21.69.75 °22.两直线平行,同位角相等;∠ E;内错角相等,两直线平行三、解答题23.解:设∠ 1=x,则∠ 2=x,∠ 3=8x,依题意有x+x+8x=180 ,°解得 x=18°,则∠ 4=18°+18°=36°.故∠ 4 的度数是36°.24.解:设这个角的度数为 x°,180﹣ x+24=5x,解得, x=34.∴这个角的度数是34°.25.解:( 1)∵ AE∥ OF,∴∠ FOB=∠ A=30°,∵ OF 均分∠ BOC,∴∠ COF=∠ FOB=30°,∴∠ DOF=180°﹣∠ COF=150°;(2)∵ OF⊥OG,∴∠ FOG=90°,∴∠ DOG=∠ DOF﹣∠ FOG=150°﹣90°=60°,∵∠ AOD=∠ COB=∠ COF+∠FOB=60°,∴∠ AOD=∠ DOG,∴ OD 均分∠ AOG.26. ( 1)解:∵ CE均分∠ ACD,AE 均分∠ BAC,∴∠ BAC=2∠ EAC,∠ ACD=2∠ ACE,∵∠ EAC+∠ ACE=90°,∴∠ BAC+∠ ACD=180°,∴AB∥ CD;( 2)∠ BAE+∠ MCD=90° ;过E作EF∥ AB,∵AB∥ CD,∴EF∥ AB∥CD,∴∠ BAE=∠ AEF,∠ FEC=∠DCE,∵∠ E=90°,∴∠ BAE+∠ ECD=90°,∵∠ MCE=∠ ECD,∴∠ BAE+∠ MCD=90° ;( 3)∵ AB∥CD,∴∠ BAC+∠ ACD=180°,∵∠ QPC+∠ PQC+∠ PCQ=180°,∴∠ BAC=∠ PQC+∠ QPC.。
北师大版七年级数学下册第二章达标测试卷附答案

北师大版七年级数学下册第二章达标测试卷一、选择题(每题3分,共30分)1.下图中,∠1和∠2是对顶角的是()2.已知∠1=40°,则∠1的补角的度数是()A.100°B.140°C.50°D.60°3.如图,这是一条公路上人行横道线的示意图,小丽站在A点想穿过公路,如果小丽想尽快穿过,那么小丽前进的方向应该是()A.线段AB的方向B.线段AC的方向C.线段AD的方向D.线段AE的方向4.如图,已知OA⊥OB,OC⊥OD,则图中∠1和∠2的关系是()A.互余B.互补C.相等D.以上都不对5.如图,∠B的同旁内角有()A.1个B.2个C.3个D.4个6.如图,直线AB,CD相交于点O,OE⊥AB于O,若∠BOD=40°,则不正确...的结论是()A.∠AOC=40°B.∠COE=130°C.∠EOD=40°D.∠BOE=90°7.下图中由∠1=∠2能得到AB∥CD的是()8.在同一平面内有三条不同的直线a,b,c,如果a∥b,a与b的距离是2 cm,并且b上的点P到直线c的距离也是2 cm,那么a与c的位置关系是() A.平行B.相交C.垂直D.不能确定9.如图,将四边形纸片ABCD沿PR翻折得到三角形PC′R,恰好C′P∥AB,C′R ∥AD.若∠B=120°,∠D=50°,则∠C=()A.85°B.95°C.90°D.80°10.如图,若∠1=∠2,DE∥BC,则下列结论中正确的有()①FG∥DC;②∠AED=∠ACB;③CD平分∠ACB;④∠1+∠B=90°;⑤∠BFG=∠BDC.A.1个B.2个C.3个D.4个二、填空题(每题3分,共30分)11.三条直线a∥b,a∥c,则__________,理由是___________________________.12.一个角与它的余角的比是1∶2,则这个角的度数是________.13.如图,ED∥AB,ED交AF于点C,∠ECF=138°,则∠A=________.14.如图,已知直线AB和CD相交于点O,OE⊥AB,∠AOD=128°,则∠COE 的度数是________.15.已知∠AOB=60°,OC为∠AOB的平分线,以OB为始边,在∠AOB的外部作∠BOD=∠AOC,则∠COD的度数是________.16.如图,请填写一个条件:________________,使得DE∥AB.17.如图,已知AC⊥BC,CD⊥AB,AC=3,BC=4,则点B到直线AC的距离等于________,点C到直线AB的垂线段是线段________.18.如图,A,B之间是一座山,一条铁路要通过A,B两点,为此需要在A,B 之间修一条笔直的隧道,在A地测得铁路走向是北偏东63°,那么在B地按南偏西________的方向施工,才能保证铁路准确接通.19.如图,直线l∥m,将含有45°角的三角尺ABC的直角顶点C放在直线m上,若∠1=25°,则∠2的度数是________.20.如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=________.三、解答题(21,22题每题8分,26题14分,其余每题10分,共60分) 21.如图,已知∠B+∠BCD=180°,∠B=∠D,那么∠E=∠DFE成立吗?为什么?下面是彬彬同学进行的推理,请你将彬彬同学的推理过程补充完整.解:成立.因为∠B+∠BCD=180°(已知),所以__________(同旁内角互补,两直线平行).所以∠B=∠DCE(____________________________).又因为∠B=∠D(已知),所以∠DCE=∠D(等量代换).所以AD∥BE(____________________________).所以∠E=∠DFE(____________________________).22.一个角的余角比它的补角的23还小55°,求这个角的度数.23.如图,已知AB∥CD,∠B=100°,EF平分∠BEC,EG⊥EF,求∠BEG和∠DEG的度数.24.如图,以点B为顶点,射线BC为一边,利用尺规作图法作∠EBC,使∠EBC =∠A,BE与AD平行吗?请说明理由.25.如图,将一副三角尺的直角顶点重合在一起.(1)若∠DOB与∠DOA的度数比是2∶11,求∠BOC的度数;(2)若叠合所成的∠BOC=n°(0<n<90),则∠AOD的补角的度数与∠BOC的度数之比是多少?26.如图,∠B,∠D的两边分别平行.(1)在图①中,∠B与∠D的数量关系是什么?为什么?(2)在图②中,∠B与∠D的数量关系是什么?为什么?(3)由(1)(2)可得结论:_________________________________________.(4)应用:若两个角的两边分别平行,其中一个角比另一个角的2倍少30°,求这两个角的度数.答案一、1.C 2.B 3.B 4.C 5.C 6.C 7.D8.D点拨:分为两种情况:(1)如图①,直线a和直线c相交(此时直线a和直线c也可能垂直);(2)如图②,直线c和直线a平行.故不能确定a与c的位置关系.9.B点拨:因为C′P∥AB,所以∠C′PC=∠B=120°.因为C′R∥AD,所以∠C′RC=∠D=50°.由折叠的性质可知∠CPR=12∠C′PC=60°,∠CRP=12∠C′RC=25°.所以∠C=180°-60°-25°=95°.10.C二、11.b∥c;平行于同一条直线的两条直线平行12.30°13.42°14.38°15.60°16.∠ABD=∠D(答案不唯一)17.4;CD18.63°19.20°20.140°三、21.AB∥CD;两直线平行,同位角相等;内错角相等,两直线平行;两直线平行,内错角相等22.解:设这个角的度数为x°.由题意得90-x=23(180-x)-55,解得x=75.所以这个角的度数为75°.23.解:因为AB∥CD,∠B=100°,所以∠BEC=80°.因为EF平分∠BEC,所以∠BEF=∠CEF=40°.因为EG⊥EF,所以∠GEF=90°.所以∠BEG=90°-∠BEF=90°-40°=50°,∠DEG=180°-∠GEF-∠CEF =180°-90°-40°=50°.24.解:BE与AD不一定平行.理由如下:如图,可以作出两个符合要求的角.故BE与AD不一定平行.25.解:(1)设∠DOB=2x°,则∠DOA=11x°.因为∠AOB=∠COD=90°,所以∠AOC=∠DOB=2x°,∠BOC=7x°.又因为∠DOA=∠AOB+∠COD-∠BOC=180°-∠BOC,所以11x=180-7x,解得x=10.所以∠BOC=70°.(2)因为∠AOD=∠AOB+∠COD-∠BOC=180°-∠BOC,所以∠AOD与∠BOC互补,则∠AOD的补角等于∠BOC.故∠AOD的补角的度数与∠BOC的度数之比是1∶1. 26.解:(1)∠B=∠D.理由如下:如图①,因为AB∥CD,所以∠B=∠1.因为BE∥DF,所以∠1=∠D.所以∠B=∠D.(2)∠B+∠D=180°.理由如下:如图②,因为AB∥CD,所以∠B=∠2.因为BE∥DF,所以∠2+∠D=180°.所以∠B+∠D=180°.(3)如果两个角的两边分别平行,那么这两个角相等或互补(4)情况①:设一个角是x°,则另一个角也是x°.所以x=2x-30,解得x=30.情况②:设一个角是x°,则另一个角是(180-x)°. 所以x=2(180-x)-30,解得x=110.180-x=70.所以这两个角的度数是30°,30°或70°,110°.。
【北师大版】初一七年级数学下册《第二章检测卷》(附详细答案)

第二章检测卷分一、选择题(每小题3分,共30分) 1.下列图形中,∠1与∠2互为对顶角的是( )2.如图,O 是直线AB 上一点,若∠1=26°,则∠AOC 的度数为( ) A .154° B .144° C .116° D .26°或154°第2题图 第3题图3.如图,已知直线a ,b 被直线c 所截,那么∠1的同旁内角是( ) A .∠3 B .∠4 C .∠5 D .∠64.下列作图能表示点A 到BC 的距离的是( )5.如图,下列条件:①∠1=∠3;②∠2=∠3;③∠4=∠5;④∠2+∠4=180°中,能判断直线l 1∥l 2的有( )A .1个B .2个C .3个D .4个第5题图6.如图,直线a ,b 与直线c ,d 相交,已知∠1=∠2,∠3=110°,则∠4的度数为( ) A .70° B .80°C.110°D.100°第6题图第7题图7.如图,AB∥CD,CD∥EF,则∠BCE等于()A.∠2-∠1 B.∠1+∠2C.180°+∠1-∠2 D.180°-∠1+∠28.如图,将一副三角板叠放在一起,使直角的顶点重合于点O,AB∥OC,DC与OB 交于点E,则∠DEO的度数为()A.85°B.70°C.75°D.60°第8题图第9题图9.如图,E,F分别是AB,CD上的点,G是BC的延长线上一点,且∠B=∠DCG=∠D,则下列结论不一定成立的是()A.∠AEF=∠EFC B.∠A=∠BCFC.∠AEF=∠EBC D.∠BEF+∠EFC=180°10.一次数学活动中,检验两条完全相同的纸带①、②的边线是否平行,小明和小丽采用两种不同的方法:小明把纸带①沿AB折叠,量得∠1=∠2=50°;小丽把纸带②沿GH折叠,发现GD与GC重合,HF与HE重合.则下列判断正确的是()A.纸带①的边线平行,纸带②的边线不平行B.纸带①的边线不平行,纸带②的边线平行C.纸带①、②的边线都平行D.纸带①、②的边线都不平行第10题图二、填空题(每小题3分,共24分)11.如图,∠1和∠2是________角,∠2和∠3是________角.第11题图12.如图是李晓松同学在运动会跳远比赛中最好的一跳,甲、乙、丙三名同学分别测得P A =5.52米,PB =5.37米,MA =5.60米,那么他的跳远成绩应该为________米.第12题图第13题图13.如图,直线AB ,CD 交于点O ,OE ⊥AB ,OD 平分∠BOE ,则∠AOC =________°. 14.如图,条件:____________可使AC ∥DF ;条件:____________可使AB ∥DE (每空只填一个条件).第14题图第15题图15.如图是超市里的购物车,扶手AB 与车底CD 平行,∠2比∠3大10°,∠1是∠2的2011倍,则∠2的度数是________. 16.一个安全用电标识如图①所示,此标识可以抽象为图②中的几何图形,其中AB ∥CD ,ED ∥BF ,点E 、F 在线段AC 上.若∠A =∠C =17°,∠B =∠D =50°,则∠AED 的度数为________.第16题图第17题图17.如图,AB ∥CD ,OE 平分∠BOC ,OF ⊥OE ,OP ⊥CD ,∠ABO =a °.有下列结论:①∠BOE =12(180-a )°;②OF 平分∠BOD ;③∠POE =∠BOF ;④∠POB =2∠DOF .其中正确的结论是________(填序号).18.已知OA ⊥OC ,∠AOB ∶∠AOC =2∶3,则∠BOC 的度数为________. 三、解答题(共66分)19.(7分)已知一个角的余角比它的补角的23还小55°,求这个角的度数.20.(7分)用直尺和圆规作图:已知∠1,∠2,求作一个角,使它等于∠1+2∠2..21.(8分)如图,DG⊥BC,AC⊥BC,FE⊥AB,∠1=∠2,试说明:CD⊥AB解:∵DG⊥BC,AC⊥BC(已知),∴∠DGB=∠ACB=90°(垂直定义),∴DG∥AC(__________________________),∴∠2=∠________(____________________).∵∠1=∠2(已知),∴∠1=∠________(等量代换),∴EF∥CD(________________________),∴∠AEF=∠________(__________________________).∵EF⊥AB(已知),∴∠AEF=90°(________________),∴∠ADC=90°(________________),∴CD⊥AB(________________).22.(8分)如图,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COB,∠AOD∶∠DOE=4∶1,求∠AOF的度数.23.(10分)如图,已知直线l1∥l2,A,B分别是l1,l2上的点,l3和l1,l2分别交于点C,D,P是线段CD上的动点(点P不与C,D重合).(1)若∠1=150°,∠2=45°,求∠3的度数;.(2)若∠1=α,∠2=β,用α,β表示∠APC+∠BPD24.(12分)如图,已知BE平分∠ABD,DE平分∠BDC,且∠EBD+∠EDB=90°.(1)试说明:AB∥CD;(2)H是BE延长线与直线CD的交点,BI平分∠HBD,写出∠EBI与∠BHD的数量关系,并说明理由.25.(14分)如图,已知AB∥CD,AD∥BC,∠DCE=90°,点E在线段AB上,∠FCG =90°,点F在直线AD上,∠AHG=90°.(1)找出图中与∠D相等的角,并说明理由;(2)若∠ECF=25°,求∠BCD的度数;(3)在(2)的条件下,点C(点C不与B,H两点重合)从点B出发,沿射线BG的方向运动,其他条件不变,求∠BAF的度数.参考答案与解析1.C 2.A 3.B 4.B 5.C 6.A 7.C 8.C 9.C 10.B 解析:如图①,∵∠1=∠2=50°,∴∠3=∠1=50°,∠4=180°-∠2=130°.由折叠可知∠4=∠2+∠5,∴∠5=∠4-∠2=80°.∵∠3≠∠5,∴纸带①的边线不平行.如图②,∵GD 与GC 重合,HF 与HE 重合,∴∠CGH =∠DGH =90°,∠EHG =∠FHG =90°,∴∠CGH +∠EHG =180°,∴纸带②的边线平行.故选B.11.同位 同旁内 12.5.37 13.4514.∠ACB =∠EFD ∠B =∠E 15.55° 16.67° 17.①②③ 18.30°或150° 解析:∵OA ⊥OC ,∴∠AOC =90°.∵∠AOB ∶∠AOC =2∶3,∴∠AOB =60°.如图,∠AOB 的位置有两种情况:一种是在∠AOC 内,一种是在∠AOC 外.(1)当在∠AOC 内时,∠BOC =90°-60°=30°;(2)当在∠AOC 外时,∠BOC =90°+60°=150°.综上可知,∠BOC 的度数为30°或150°.19.解:设这个角的度数为x ,依题意有23(180°-x )-55°=90°-x ,(4分)解得x =75°.故这个角的度数为75°.(7分)20.解:略.(7分)21.解:同位角相等,两直线平行 ACD 两直线平行,内错角相等 ACD 同位角相等,两直线平行(4分) ADC 两直线平行,同位角相等 垂直的定义 等量代换 垂直的定义(8分)22.解:∵OE 平分∠BOD ,∴∠DOE =∠EOB .(2分)又∵∠AOD ∶∠DOE =4∶1,∠AOD +∠DOE +∠EOB =180°,∴∠DOE =∠EOB =30°,∠AOD =120°,∴∠COB =∠AOD =120°.(5分)∵OF 平分∠COB ,∴∠BOF =12∠COB =60°,∴∠AOF =180°-∠BOF =180°-60°=120°.(8分)23.解:(1)过点P 向右作PE ∥l 1.∵l 1∥l 2,∴l 1∥PE ∥l 2,∴∠1+∠APE =180°,∠2=∠BPE .(2分)∵∠1=150°,∠2=45°,∴∠APE =180°-∠1=180°-150°=30°,∠BPE =∠2=45°,∴∠3=∠APE +∠BPE =30°+45°=75°.(6分)(2)由(1)知∠1+∠APE =180°,∠2=∠BPE .∵∠1=α,∠2=β,∴∠APB =∠APE +∠BPE =180°-∠1+∠2=180°-α+β,(8分)∴∠APC +∠BPD =180°-∠APB =180°-(180°-α+β)=α-β.(10分)24.解:(1)∵BE 平分∠ABD ,DE 平分∠BDC ,∴∠ABD =2∠EBD ,∠BDC =2∠EDB .(3分)∵∠EBD +∠EDB =90°,∴∠ABD +∠BDC =2(∠EBD +∠EDB )=180°,∴AB ∥CD .(6分)(2)∠EBI =12∠BHD .(8分)理由如下:∵AB ∥CD ,∴∠ABH =∠EHD .(10分)∵BI 平分∠EBD ,∴∠EBI =12∠EBD =12∠ABH =12∠BHD .(12分)25.解:(1)与∠D 相等的角为∠DCG ,∠ECF ,∠B .(1分)理由如下:∵AD ∥BC ,∴∠D=∠DCG .∵∠FCG =90°,∠DCE =90°,∴∠ECF =∠DCG =∠D .∵AB ∥DC ,∴∠B =∠DCG =∠D ,∴与∠D 相等的角为∠DCG ,∠ECF ,∠B .(4分)(2)∵∠ECF =25°,∠DCE =90°,∴∠FCD =65°.又∵∠BCF =90°,∴∠BCD =65°+90°=155°.(7分)(3)分两种情况进行讨论:①如图a ,当点C 在线段BH 上时,点F 在DA 的延长线上,此时∠ECF =∠DCG =∠B =25°.∵AD ∥BC ,∴∠BAF =∠B =25°;(10分)②如图b ,当点C 在BH 的延长线上时,点F 在线段AD 上.∵∠B =25°,AD ∥BC ,∴∠BAF =180°-25°=155°.综上所述,∠BAF 的度数为25°或155°.(14分)。
七年级数学北师大版下册第2章《单元测试》01(含答案解析)

答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的小朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!北师大版七年级下单元测试第2单元班级________姓名________一、选择题(共10小题,每小题4分,共40分)1.如图,直线a,b被直线c所截,则∠1与∠2是()A.同位角B.内错角C.同旁内角D.邻补角2.已知∠A=25°,则∠A的余角、补角分别是()A.65°B.75°C.155°D.165°3.如图,某同学的家在P处,他想尽快赶到附近公路边搭公交车,他选择P→C 路线,用几何知识解释其道理正确的是()A.两点确定一条直线B.垂直线段最短C.两点之间线段最短D.过一点有且只有一条直线与已知直线垂直4.如图,已知OA⊥OB,OC⊥OD,则图中∠1和∠2的关系是()A.互余B.互补C.相等D.以上都不对5.如图,下列推理正确的是()A.因为∠1=∠2,所以DE∥BFB.因为∠1=∠2,所以CE∥AFC.因为∠CEF+∠AFE=180°,所以DE∥BFD.因为∠CEF+∠AFE=180°,所以CE∥AF6.如图,直线a,b被直线c所截,若a∥b,∠1=40°,∠2=70°,则∠3=()A.70°B.100°C.110°D.120°7.如图,下列判断错误的是()A.∵∠1=∠2,∴AE∥BDB.∵∠3=∠4,∴AB∥CDC.∵∠1=∠2,∴AB∥DED.∵∠5=∠BDC,∴AE∥BD8.如图,AB∥CD,DE⊥CE,∠1=34°,则∠DCE的度数为()A.34°B.56°C.66°D.54°9.如图,AB∥CD,则α,β,γ三个角之间的数量关系为()A.α-β+γ=180°B.α+β-γ=180°C.α+β+γ=360°D.α-β-γ=180°10.如图,一束光线与水平面成60°角照射到地面,现在地面AB上支放着一块平面镜CD,使这束光线经过平面镜反射后成水平光线射出(∠1=∠2),那么平面镜CD与地面AB所成∠DCA度数为()A.30°B.45°C.50°D.60°二.填空题(共6小题,每小题4分,共24分)11.已知在同一个平面内的三条直线l1,l2,l3,如果l1⊥l2,l2⊥l3,那么l1与l3的位置关系是________12.如图,已知∠1=∠2,则图中互相平行的线段是;理由是:__________________________________________;13.如图,B,A,E三点在同一直线上,请你添加一个条件,使AD∥BC,你所添加的条件是________________.(不允许添加任何辅助线)14.已知∠AOB=60°,OC为∠AOB的平分线,以OB为始边,在∠AOB的外部作∠BOD=∠AOC,则∠COD的度数是________.15.如图,m∥n,∠1=110°,∠2=100°,则∠3=________.16.如图,AD平分∠CAE,CF∥AD,∠1=80°,∠2=________.三.解答题(共6小题,56分)17.(6分)若一个角的余角是这个角的15,求这个角的补角的度数.18.(8分)如图,直线AB,CD相交于点O,OD平分∠AOF,OE⊥CD于点O,∠1=50°,求∠COB,∠BOF的度数.19.(8分)如图,在△ABC中,CD⊥AB,垂足为点D,点E在BC上,EF⊥AB,垂足为F;(1)CD与EF平行吗?为什么?(2)如果∠1=∠2,且∠3=105°,求∠ACB的度数;20.(10分)如图,直线AB和CD交于点O,OE⊥OD,OD平分∠BOF,∠BOE =50°.(1)求∠AOC的度数;(2)求∠EOF的度数.21.(12分)如图,将一副三角尺的直角顶点重合在一起.(1)若∠DOB与∠DOA的度数比是2∶11,求∠BOC的度数;(2)若叠合所成的∠BOC=n°(0<n<90),则∠AOD的补角的度数与∠BOC的度数之比是多少?22.(12分)观察发现:已知AB∥CD,点P是平面上一个动点.当点P在直线AB,CD的异侧,且在BC(不与点B,C重合)上时,如图①,容易发现:∠ABP +∠DCP=∠BPC.拓展探究:(1)当点P位于直线AB,CD的异侧,且在BC左侧时,如图②,∠ABP,∠DCP,∠BPC之间有何关系?并说明理由;(2)当点P位于直线AB,CD的异侧,且在BC右侧时,如图③,∠ABP,∠DCP,∠BPC之间有何关系?并说明理由;(3)当点P位于直线AB,CD的同侧,如图④,∠ABP,∠DCP,∠BPC之间有何关系?并说明理由.参考答案1-5BCBCD6-10CCBBA11.平行12.AD//BC,内错角相等,两直线平行13.∠EAD=∠B或∠DAC=∠C或∠DAB+∠B=180°14.60°15.150°16.100°17.解:设这个角的度数为x,则它的余角的度数为(90°-x).由题意得90°-x=15x,解得x=75°.所以这个角的补角为180°-x=180°-75°=105°. 18.解:因为OE⊥CD,所以∠DOE=90°,因为∠1=50°,所以∠DOA=40°,即∠BOC=∠DOA=40°,因为OD平分∠AOF,所以∠AOF=2∠DOA=80°,所以∠BOF=180°-∠AOF=100°19.解:(1)∵CD⊥AB,EF⊥AB,∴∠CDB=∠EFB=90°∴CD∥EF(2)∵EF∥DC∴∠2=∠BCD∵∠1=∠2,∴∠1=∠BCD xx+]∴DG∥BC∴∠ACB=∠3=105°20.解:(1)因为∠BOE=50°,∠COE=90°,∠AOC+∠COE+∠BOE=180°,所以∠AOC=180°-50°-90°=40°.(2)因为∠AOC=40°,所以∠BOD=∠AOC=40°,因为OD平分∠BOF,所以∠BOD=∠DOF=40°,所以∠EOF=50°+40°+40°=130°.21.解:(1)设∠DOB=2x°,则∠DOA=11x°.因为∠AOB=∠COD=90°,所以∠AOC=∠DOB=2x°,∠BOC=7x°.又因为∠DOA=∠AOB+∠COD-∠BOC=180°-∠BOC,所以11x=180-7x,解得x=10.所以∠BOC=70°.(2)因为∠AOD=∠AOB+∠COD-∠BOC=180°-∠BOC,所以∠AOD与∠BOC互补,则∠AOD的补角等于∠BOC.故∠AOD的补角的度数与∠BOC的度数之比是1∶1.22.解:(1)∠ABP+∠DCP=∠BPC.理由:如图,过点P作直线PQ∥AB,∴∠ABP=∠BPQ(两直线平行,内错角相等),∵AB∥CD(已知),∴DC∥PQ(如果两条直线和第三条直线平行,那么这两条直线平行),∴∠DCP=∠CPQ(两直线平行,内错角相等),∴∠ABP+∠DCP=∠BPQ+∠CPQ=∠BPC(等量代换)(2)∠ABP+∠BPC+∠DCP=360°,理由:如图③,过P作PQ∥AB,则DC∥PQ,∴∠ABP+∠BPQ=180°,∠DCP+∠CPQ=180°,∴∠ABP+∠BPC+∠DCP=360°(3)∠BPC=∠DCP-∠ABP,理由:如图④,过P作PQ∥AB,则PQ∥DC,∴∠DCP=∠CPQ,∠ABP=∠BPQ,∴∠BPC=∠CPQ-∠BPQ=∠DCP-∠ABP。
北师大版七年级数学下册第二章测试题

北师大版七年级数学下册第二章测试题(共6页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--七年级(下)第二章《平行线与相交线》单元测试题(满分:100分 时间:100分钟) 望远中学 命题人: 汤艳华姓 名 班 级 得分一、填空题(每题3分,共24分)1、若,则它的余角是_________,它的补角是________.2、若∠α与∠β是对顶角,且∠α+∠β=1200 ,则∠α= ,∠β=3、如图, 和 相交, 和 是______角, 和 是______角, 和 是______角, 和 是______角.(第3题) (第4题) (第5题) 4、如图:已知: ,则5、如图:已知: ,则6、如图,,则 .(第6题) (第7题)7、如图,已知∠AOB 、∠BOC 、∠COD 的顶点是一条直线上同一点,且∠AOB=65015’, ∠BOC=78030’,则∠COD=CBADO8、一个角的补角等于这个角的余角的4倍,这个角是________.二、选择题(每题3分,共24分)9、两条直线被第三条直线所截,则().A.同位角必相等 B.内错角必相等C.同旁内角必互补 D.同位角不一定相等10、如图,与是对顶角的为()11、如图,直线a,b都与c相交,由下列条件能推出的是()①②③④A.① B.①② C.①②③ D.①②③④(第11题)(第12题)12、如图,下列条件中能判定的是()A. B.C. D.13、如图,,则下列结论中,错误的是()(第13题)(第14题)A. B.C. D.14、如图,下列推理中正确的是()A.∴ B.∴C.∴D.∴15、如图,由已知条件推出的结论,正确的是().A.由,可推出 B.由,可推出C.由,可推出D.由,可推出16、下列角的平分线中,互相垂直的是()A.平行线的同旁内角的平分线 B.平行线的同位角的平分线C.平行线的内错角的平分线 D.对顶角的平分线三、解答题(每题4分,共16分)1、如图,,求的度数.2、作图题:如图,已知∠α,∠β,求作一个角使它等于∠α+∠β3、如图,已知DE∥AB,∠EAD =∠ADE,试问AD是∠BAC的平分线吗为什么4、如图:已知:,求∠4的度数四、解答题(每题5分,共20分)1、如图:找出互相平行的直线,并说明理由.2、如图,已知AB∥CD,∠A =1000,CB平分∠ACD.回答下列问题:(1)∠ACD等于多少度为什么(2)∠ACB、∠BCD 各等于多少度为什么(3)∠ABC等于多少度为什么3、如图:已知AB∥CD,∠α =450,∠D=∠C.你能求出∠D、∠C和∠B的度数吗4、如图,完成下列推理过程已知:DE⊥AO于E, BO⊥AO,∠CFB=∠EDO证明:CF∥DO证明:∵DE⊥AO, BO⊥AO(已知)∴∠DEA=∠BOA=900()∵DE∥BO ()∴∠EDO=∠DOF ()又∵∠CFB=∠EDO()五、解答题(每题8分,共16分)1、 DE ∥BC ,CD 是∠ACB 的平分线,∠B =80,∠ACB=500 ,求∠EDC ,∠CDB新 课 标 第一网2、如图,AB ∥EF ,∠B =1350,∠C=670,则求∠1的度数.EB ADC新课标第一网。
北师大版七年级数学(下)第二章测试卷

七年级数学(下)第二章测试卷学校 班别 姓名 学号 总分一、填空题。
(每空2分,共36分)1、判断两直线平行的三个条件是:① ② ③ 2、两直线平行的三个特征是:① ② ③3、一个角是52度,那么这个角的补角是 度,余角是 度。
4、如图1所示,直线a 、b 、c 两两相交,共构成 对对顶角。
5、如图2所示,已知CD AB //,AD 与BC 相交于点O ,∠A=∠AOB , ∠COD=66°,则∠A= ,∠C= 。
1= 时,AD//BC ;当∠1= 时,DC//AB 。
则∠B= 度,∠C= 度。
二、选择题。
(每题3分,共15分)1、如图6所示,∠1与∠2是一对( ) A 、同位角 B 、对顶角 C 、内错角 D 、同旁内角2、下列语句中正确的是( ) A 、 相等的角是对顶角B 、 有公共顶点且相等的角是对顶角C 、 有公共顶点的两个角是对顶角D 、 角的两边互为反向延长线的两个角是对顶角 3、下列说法正确的是( ) A 、 两直线平行,同旁内角相等 B 、 两直线平行,同位角相等C 、 两直线被第三条直线所截,内错角相等D 、 若一个角的两边分别与另一个角的两边平行,则这两个角相等 4、如图7,能与∠1构成同位角的角有( ) A 、2个 B 、3个 C 、4个 D 、5个 5、如图7,能与∠1构成同旁内角的角有( ) A 、2个 B 、3个 C 、4个 D 、5个三、利用尺规作图(共6分)①、b AB 、CD 使AB=a+b ;CD=2a-b②(在原图作图)以点B 为顶点,射线BC 为一边,作一角∠EBC ,使得∠EBC=∠A四、求值题。
(共13分)1、如图,AB//CD ,∠1=50°,∠D=∠C ,依次求出∠D 、∠C 、∠B 的度数(7分)2、 如图,已知AB//CD ,∠1=120°,∠3=50°,求∠2和∠4的度数。
(6分)五、在空格内填上推理的理由(每个空格1分,共261、如图,已知AB//DE ,∠B=∠E ,求证:BC//EF证明: AB//DE ( )∴ ∠B= ( )又 ∠B=∠E ( )∴ = (等量代换)∴ // ( )2、已知,如图,∠1=120°,∠2=120°,求证:AB//CD 。
七级数学下册第二章单元测试题及答案

北师大版七年级数学下册第二章 相交线与平行线单元测试卷(一)班级 姓名 学号 得分一、单选题(注释)1、如图,直线a 、b 、c 、d ,已知c ⊥a ,c ⊥b ,直线b 、c 、d 交于一点,若∠1=500,则∠2等于【 】A .600B .500C .400 D .3002、如图,AB ⊥BC ,BC ⊥CD ,∠EBC =∠BCF ,那么,∠ABE 与∠DCF 的位置与大小关系是 ( )A .是同位角且相等B .不是同位角但相等。
C .是同位角但不等D .不是同位角也不等3、如果两个角的一边在同一直线上,另一边互相平行,那么这两个角只能( ) A .相等 B .互补 C .相等或互补 D .相等且互补4、下列说法中,为平行线特征的是( )①两条直线平行,同旁内角互补。
②同位角相等, 两条直线平行。
③内错角相等, 两条直线平行。
④垂直于同一条直线的两条直线平行. A .① B .②③ C .④ D .②和④5、如图,AB∥CD∥EF,若∠ABC=50°,∠CEF=150°,则∠BCE=()A.60°B.50°C.30°D.20°6、如图,如果AB∥CD,则角α、β、γ之间的关系为()A.α+β+γ=360°B.α-β+γ=180°C.α+β-γ=180°D.α+β+γ=180°7、如图,由A到B 的方向是()A.南偏东30°B.南偏东60°C.北偏西30°D.北偏西60°8、如图,由AC∥ED,可知相等的角有()A.6对B.5对C.4对D.3对9、如图,直线AB、CD交于O,EO⊥AB于O,∠1与∠2的关系是( )更多功能介绍/zt/A.互余B.对顶角C.互补D.相等10、若∠1和∠2互余,∠1与∠3互补,∠3=120°,则∠1与∠2的度数分别为( ) A.50°、40°B.60°、30°C.50°、130°D.60°、120°11、下列语句正确的是( )A.一个角小于它的补角B.相等的角是对顶角C.同位角互补,两直线平行D.同旁内角互补,两直线平行12、图中与∠1是内错角的角的个数是( )A.2个B.3个C.4个D.5个13、如图,直线AB和CD相交于点O,∠AOD和∠BOC的和为202°,那么∠AOC的度数为( )A.89°B.101°C.79°D.110°14、如图,∠1和∠2是对顶角的图形的个数有( )A.1个B.2个C.3个D.0个15、如图,直线a、b被直线c所截,现给出下列四个条件:①∠1=∠5,②∠1=∠7,③∠2+∠3=180°,④∠4=∠7,其中能判定a∥b的条件的序号是( )A.①②B.①③C.①④D.③④二、填空题(注释)16、如图,∠ACD=∠BCD,DE∥BC交AC于E,若∠ACB=60°,∠B=74°,则∠EDC=___°,∠CDB=____°。
北师大七年级数学下册 第二章达标检测卷(含答案)
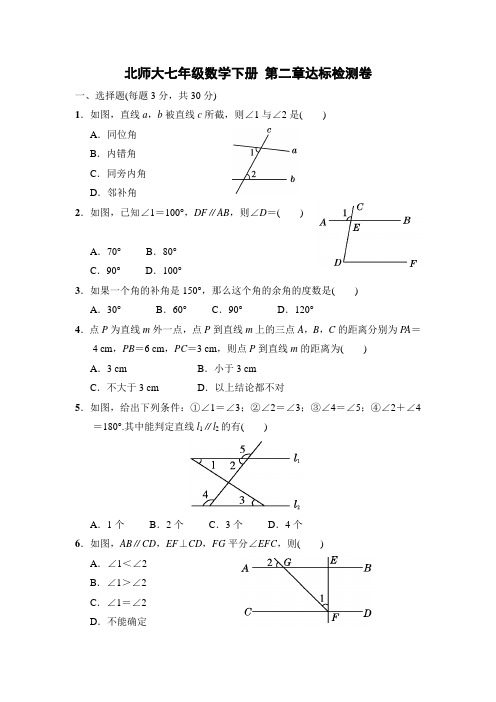
北师大七年级数学下册第二章达标检测卷一、选择题(每题3分,共30分)1.如图,直线a,b被直线c所截,则∠1与∠2是()A.同位角B.内错角C.同旁内角D.邻补角2.如图,已知∠1=100°,DF∥AB,则∠D=()A.70°B.80°C.90°D.100°3.如果一个角的补角是150°,那么这个角的余角的度数是() A.30°B.60°C.90°D.120°4.点P为直线m外一点,点P到直线m上的三点A,B,C的距离分别为P A=4 cm,PB=6 cm,PC=3 cm,则点P到直线m的距离为()A.3 cm B.小于3 cmC.不大于3 cm D.以上结论都不对5.如图,给出下列条件:①∠1=∠3;②∠2=∠3;③∠4=∠5;④∠2+∠4=180°.其中能判定直线l1∥l2的有()A.1个B.2个C.3个D.4个6.如图,AB∥CD,EF⊥CD,FG平分∠EFC,则()A.∠1<∠2B.∠1>∠2C.∠1=∠2D.不能确定7.如图,将长方形ABCD沿线段OG折叠,点B,C的对应点分别为B′,C′,若∠OGC′=100°,则∠AOB′的度数为()A.20°B.30°C.40°D.50°8.如图,将一副三角尺叠放在一起,使直角的顶点重合于点O,AB∥OC,DC与OB交于点E,则∠DEO的度数为()A.85°B.70°C.75°D.60°9.如图,AB∥CD,CD∥EF,则∠BCE等于()A. ∠2-∠1B. ∠1+∠2C.180°+∠1-∠2 D.180°-∠1+∠210.如图,已知A1B∥A n C,则∠A1+∠A2+…+∠A n等于() A.180°nB.(n+1)·180°C.(n-1)·180°D.(n-2)·180°二、填空题(每题3分,共24分)11.尺规作图是指用____________________________画图.12.如图,∠1=15°,∠AOC=90°.若点B,O,D在同一条直线上,则∠2=________.13.如图,某工程队计划把河水引到水池A中,他们先过点A作AB⊥CD,垂足为点B,然后沿AB开渠,可以节约人力、物力和财力,这样设计的数学依据是______________________________.14.用吸管吸易拉罐内的饮料时,示意图如图,AD∥BC,若∠1=110°,则∠2=________.15.同一平面内的三条直线a,b,c,若a⊥b,b⊥c,则a________c.若a∥b,b∥c,则a________c.若a∥b,b⊥c,则a________c.16.如图,把一块含有45°角的直角三角尺的两个顶点放在直尺的对边上,如果∠1=20°,那么∠2的度数是________.17.如图,某煤气公司安装煤气管道,他们从点A处铺设到点B处时,由于有一个人工湖挡住了去路,需要改变方向经过点C,再拐到点D,然后沿与AB 平行的DE方向继续铺设.已知∠ABC=135°,∠BCD=65°,则∠CDE=________.18.如图,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF =130°,则∠F=________.三、解答题(19~21题每题8分,25题12分,其余每题10分,共66分)19.若一个角的余角是这个角的15,求这个角的补角的度数.20.完成下列推理过程:如图,如果∠A=∠F,∠C=∠D,那么∠BMN与∠CNM互补.解:因为∠A=∠F(已知),所以________∥________(),所以∠D=∠________().又因为∠C=∠D(已知),所以∠C=∠________(),所以________∥________(),所以∠BMN与∠CNM互补().21.如图,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COB,∠AOD ∠DOE=4 1.求∠AOF的度数.22.将一副三角尺拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.(1)试说明:CF∥AB;(2)求∠DFC的度数.23.如图,在四边形ABCD中,AB∥CD,点P为BC上一点(点P与B,C不重合),设∠CDP=∠α,∠CPD=∠β,你能不能说明,不论点P在BC上怎样运动,总有∠α+∠β=∠B?24.如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.试说明:AD∥BC.25.如图①、图②,已知∠1+∠2=180°.(1)若图①中∠AEF=∠H L N,判断图中平行的直线,并说明理由;(2)如图②,∠PMB=3∠3,∠PND=3∠4,判断∠P与∠Q的数量关系,并说明理由.答案一、1.B 2.B 3.B 4.C 5.C 6.C7.A 8.C9.C10.C点拨:如图,过点A2作A2D∥A1B,过点A3作A3E∥A1B,……因为A 1B∥A n C,所以A3E∥A2D∥…∥A1B∥A n C.所以∠A1+∠A1A2D=180°,∠DA2A3+∠A2A3E=180°……所以∠A1+∠A1A2A3+…+∠A n-1A n C=(n-1)·180°.二、11.圆规和没有刻度的直尺12. 105°13.垂线段最短14.70°15.∥;∥;⊥16.25°17.110°点拨:如图,过点C作CF∥AB,因为AB∥DE,所以DE∥CF.所以∠CDE=∠FCD.因为AB∥CF,∠ABC=135°,所以∠BCF=180°-∠ABC =45°.又因为∠FCD=∠BCD+∠BCF,∠BCD=65°,所以∠FCD=110°.所以∠CDE=110°.18.9.5°点拨:过点F向左作FH∥BA,则AB∥CD∥HF,所以∠BED=∠CDE,∠AGF+∠GFH=180°,∠BEF=∠EFH,所以∠GFH=180°-∠AGF=50°.因为EF平分∠BED,所以∠BEF=12∠BED=12∠CDE=59.5°,所以∠EFH=59.5°,所以∠EFG=∠EFH-∠GFH=9.5°.三、19.解:设这个角的度数为x,则它的余角的度数为(90°-x).由题意,得90°-x=15x,解得x=75°,所以这个角的补角为180°-x =180°-75°=105°.20.DF ;AC ;内错角相等,两直线平行;DBA ;两直线平行,内错角相等;DBA ;等量代换;BD ;CE ;同位角相等,两直线平行;两直线平行,同旁内角互补21.解:因为OE 平分∠BOD ,所以∠DOE =∠EOB . 又因为∠AOD∠DOE =41,∠AOD +∠DOE +∠EOB =180°,所以∠DOE =∠EOB =180°×16=30°,∠AOD =120°.所以∠COB =∠AOD =120°. 因为OF 平分∠COB , 所以∠BOF =60°.所以∠AOF =180°-60°=120°. 22.解:(1)因为CF 平分∠DCE ,所以∠1=∠2=12∠DCE . 因为∠DCE =90°, 所以∠1=45°. 因为∠3=45°, 所以∠1=∠3.所以CF ∥AB (内错角相等,两直线平行). (2)因为∠D =30°,∠1=45°,所以∠DFC =180°-30°-45°=105°.23.解:能.过点P 作PE ∥CD 交AD 于E ,则∠DPE =∠α.因为AB ∥CD ,所以PE ∥AB .所以∠CPE =∠B ,即∠DPE +∠β=∠α+∠β=∠B .故不论点P 在BC 上怎样运动,总有∠α+∠β=∠B . 24.解:因为AE 平分∠BAD ,所以∠1=∠2.因为AB ∥CD ,∠CFE =∠E , 所以∠1=∠CFE =∠E .所以∠2=∠E.所以AD∥BC.25.解:(1)AB∥CD,EF∥H L.理由如下:因为∠2+∠MND=180°,∠1+∠2=180°,所以∠1=∠MND.所以AB∥CD.延长EF交CD于点G.因为AB∥CD,所以∠AEF=∠EGD.又因为∠AEF=∠HLN,所以∠EGD=∠HLN.所以EF∥HL.(2)∠P=3∠Q.理由如下:如图,过点P作PE∥AB.由(1)中可得AB∥CD,所以PE∥CD.过点Q作QF∥AB,则FQ∥CD.因为AB∥EP,所以∠7=∠BMP=3∠3.同理可得∠8=3∠4,所以∠MPN=∠7+∠8=3(∠3+∠4).因为AB∥FQ,所以∠3=∠5.因为FQ∥CD,所以∠6=∠4.所以∠MQN=∠5+∠6=∠3+∠4.所以∠MPN=3∠MQN.。
七年级数学北师大版下册第2章《单元测试》04(含答案解析)

2
证明:如图 ② 延长 线㤰 和 ‹ 的延长线交于点 ,
因为 线∥ ‹,
所以 ∠ 线㤰 = ∠ ,
因为 线㤰∥ ‹,
所以 ∠ = ∠‹ ‹,
因为 ‹ 平分 ∠㤰 ‹,
所以 ∠㤰 ‹ = ∠‹ ‹,
所以 1 ∠㤰 ‹ = ∠ = ∠ 线㤰,
2
所以
∠
线㤰
=
1 2
∠㤰
二、填空题(共 7 小题)
10. 如图,直线 , 相交,∠2 = 3∠1,则 ∠3 =
.
11. 如果 ∠ = 35∘,那么 ∠ 的余角等于
为
.
,∠ 的补角
12. 如 图 , 直 线 ∠线 ‹ =
线与
‹ 相交于点 .
, 㤰 ⊥ 线 , ∠ 㤰 = 60∘ , 则
13. 如图,如果 ∠ 据
=∠
,那么根
(1) ‹ 与 㤰‹ 平行吗?为什么? (2)如果 ∠1 = ∠2,且 ∠3 = 105∘,求 ∠ 线 的度数. 20. 已知 线∥ ‹. (1)如图 ①,若 ∠ 线㤰 = 30∘,∠线㤰 = 148∘,求 ∠㤰 ‹ 的度数;
(2)如图 ②,若 ‹∥㤰线, ‹ 平分 ∠㤰 ‹,试探究 ∠㤰 ‹ 与 ∠ 线㤰 之 间的数量关系,并证明.
(2) 因为 㤰‹∥‹ , 所以 ∠2 = ∠线 ‹. 因为 ∠1 = ∠2, 所以 ∠1 = ∠线 ‹. 所以 ‹ ∥线 . 所以 ∠ 线 = ∠3 = 105∘. 20. (1) 如图 ①,过点 㤰 作 㤰‹∥ 线,
因为 线∥ ‹, 所以 线∥㤰‹∥ ‹, 所以 ∠ 线㤰 = ∠线㤰‹,∠‹㤰 + ∠㤰 ‹ = 180∘, 因为 ∠ 线㤰 = 30∘,∠线㤰 = 148∘, 所以 ∠‹㤰 = 118∘, 所以 ∠㤰 ‹ = 180∘ − 118∘ = 62∘;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级数学下册第二章相交线与平行线单元测试卷(一)班级姓名学号得分评卷人得分一、单选题(注释)1、如图,直线 a、 b、c、 d,已知 c⊥ a, c⊥ b,直线 b、c、 d 交于一点,若∠ 1=50 0,则∠ 2 等于【】A. 600B. 500C.400D. 3002、如图, AB ⊥ BC , BC⊥CD ,∠ EBC =∠ BCF ,那么,∠ABE与∠ DCF的位置与大小关系是()A .是同位角且相等C.是同位角但不等B .不是同位角但相等D .不是同位角也不等;3、如果两个角的一边在同一直线上,另一边互相平行,那么这两个角只能(A .相等B.互补C.相等或互补D.相等且互补)4、下列说法中,为平行线特征的是()①两条直线平行,同旁内角互补 ; ②同位角相等 , 两条直线平行 ;③内错角相等 , 两条直线平行 ; ④垂直于同一条直线的两条直线平行 .A .①B.②③C.④D.②和④5、如图, AB ∥ CD ∥ EF,若∠ ABC = 50°,∠ CEF= 150 °,则∠ BCE =()A . 60°B. 50°C.30°D. 20°6、如图,如果AB ∥ CD,则角α、β、γ之间的关系为()A .α +β=+γ360 °C.α +β-γ= 180 °B .α-β +=γ180 °D .α +β=+γ180 °7、如图,由 A 到B的方向是()A .南偏东30°B.南偏东60°C.北偏西30°D.北偏西60°8、如图,由AC ∥ ED ,可知相等的角有()A.6对B.5 对C.4 对D.3 对9、如图,直线AB 、CD交于O, EO⊥ AB于 O,∠ 1 与∠ 2 的关系是()更多功能介绍/zt/A. 互余B. 对顶角C.互补D. 相等10、若∠ 1和∠ 2 互余,∠ 1 与∠ 3 互补,∠ 3=120 °,则∠ 1 与∠ 2 的度数分别为 ( )A . 50°、 40°B. 60°、 30°C.50°、 130 °D. 60°、 120 °11、下列语句正确的是( )A.一个角小于它的补角B.相等的角是对顶角D.同旁内角互补,两直线平行12、图中与∠ 1 是内错角的角的个数是( )A.2个B.3 个C.4 个D.5 个13、如图,直线AB和CD相交于点O,∠AOD和∠ BOC的和为202 °,那么∠ AOC的度数为()A. 89°B. 101 °C.79°D. 110 °14、如图,∠ 1 和∠ 2 是对顶角的图形的个数有()A.1个B.2 个C.3 个D.0 个15、如图,直线 a、b 被直线 c 所截,现给出下列四个条件:①∠ 1=∠ 5,②∠ 1=∠ 7,③∠ 2+∠3=180 °,④∠ 4= ∠7,其中能判定 a∥ b 的条件的序号是 ( )A .①②B.①③C.①④D.③④评卷人得分二、填空题 ( 注释 )16、如图,∠ ACD =∠ BCD ,DE∥BC 交 AC 于 E,若∠ ACB =60°,∠ B =74°,则∠ EDC = ___ °,∠CDB = ____°。
17、如图, BA ∥ DE,∠ B = 150 °,∠ D= 130 °,则∠ C 的度数是 __________ 。
18、如图,AD ∥ BC ,∠ A 是∠ ABC 的 2 倍,( 1)∠A = ____度;( 2)若 BD 平分∠ ABC ,则∠ ADB =____ 。
19、如图, DH ∥ EG∥ BC, DC ∥ EF,图中与∠ 1 相等的角有 ________________________ 。
20、如图, AB ∥ CD,直线 EF 分别交 AB 、 CD 于 E、 F, EG 平分∠ BEF ,若∠ 1= 72°,则∠ 2=_________。
21、如图, AB ⊥ EF, CD ⊥ EF,∠ 1=∠ F= 45°,那么与∠ FCD 相等的角有 ___个,它们分别是____。
22、如图, AB ∥ CD ,AF 分别交 AB 、CD 于 A 、C,CE 平分∠ DCF ,∠ 1=100 °,则∠ 2=_____.23、如图,∠ 1 与∠ 4 是 _____角,∠ 1 与∠ 3 是 _____角,∠3 与∠ 5 是 _____角,∠ 3 与∠ 4 是 _____角 .24、如图,∠ 1 的同旁内角是_____,∠ 2 的内错角是 _____.25、如图,已知∠ 2=∠ 3,那么 _____∥ _____,若∠ 1=∠ 4,则 _____∥ _____.26、如图,若∠ 1=∠2,则 _____∥ _____.若∠ 3+∠ 4=180 °,则 _____∥ _____.27、如图,已知直线AB 、CD 交于点 O,OE 为射线,若∠ 1+ ∠ 2=90 °,∠ 1=65 °,则∠ 3=_____.28、看图填空:∵直线AB 、 CD 相交于点O,∴∠ 1 与 _____是对顶角,∠2 与 _____是对顶角,∴∠ 1=_____,∠ 2=_____.理由是:29、如图,直线a,b 相交,∠ 1=55 °,则∠ 2=_____,∠ 3=_____,∠ 4=_____.30、若∠ A 与∠ B 互余,则∠ A+ ∠ B=_____ ;若∠ A 与∠ B 互补,则∠ A+ ∠ B=_____.31、如图,三条直线交于同一点,则∠1+∠ 2+∠3=_____.32、如果∠α与∠ β是对顶角,∠ α =30,°则∠β =_____.评卷人得分三、解答题 ( 注释 )33、如图,已知∠ 1+∠ 2= 180 °,∠ 3=∠ B ,试判断∠ AED 与∠ C 的关系。
34、如图, AB ∥ CD,∠ 1=∠ 2,∠ BDF 与∠ EFC 相等吗?为什么?35、如图,∠ 1=∠ 2,∠ C=∠ D,那么∠ A =∠ F,为什么?36、如图, DE∥ CB,试证明∠ AED =∠ A +∠ B。
37、如图,∠ CAB = 100 °,∠ ABF = 130 °, AC ∥MD ,BF ∥ME ,求∠ DME的度数.38、已知,如图,MN ⊥ AB ,垂足为 G, MN ⊥ CD,垂足为H,直线 EF 分别交 AB 、 CD 于 G、Q,∠ GQC= 120 °,求∠ EGB 和∠ HGQ 的度数。
39、如图,∠ ABD= 90 °,∠ BDC=90°,∠ 1+∠ 2=180 °, CD 与 EF 平行吗?为什么?40、如图, EF 交 AD 于 O, AB 交 AD 于 A , CD 交 AD 于 D,∠ 1=∠ 2,∠ 3=∠ 4,试判 AB 和CD 的位置关系,并说明为什么.41、已知直线a、 b、c 两两相交,∠1=2 ∠3,∠ 2=40 °,求∠ 4.单元测试卷(一)参考答案1.【解析】∵ c⊥ a, c⊥b,∴ a∥ b。
∵∠ 1=50 0,∴∠ 2=∠ 1=500。
故选 B。
2.【解析】试题分析:由 AB ⊥BC, BC⊥ CD ,∠ EBC=∠ BCF ,即可判断∠ ABE 据同位角的特征即可判断∠ ABE 与∠ DCF 的位置关系,从而得到结论与∠DCF .的大小关系,根∵AB ⊥ BC , BC ⊥CD ,∠ EBC=∠ BCF,∴∠ ABE= ∠ DCF ,∴∠ ABE 与∠ DCF 的位置与大小关系是不是同位角但相等,故选 B.考点:本题考查的是同位角点评:准确识别同位角、内错角、同旁内角的关键,是弄清哪两条直线被哪一条线所截.也就是说,在辨别这些角之前,要弄清哪一条直线是截线,哪两条直线是被截线.3.【解析】试题分析:根据平行线的性质即可得到结果.如果两个角的一边在同一直线上,另一边互相平行,那么这两个角相等或互补,故选 C.考点:本题考查的是平行线的性质点评:解答本题的关键是熟记如果两个角的一边在同一直线上,另一边互相平行,那么这两个角相等或互补 .4.【解析】试题分析:根据平行线的性质依次分析各小题即可.为平行线特征的是①两条直线平行,同旁内角互补,②同位角相等,两条直线平行;③内错角相等,两条直线平行;④垂直于同一条直线的两条直线平行,均为平行线的判定,故选 A.考点:本题考查的是平行线的性质点评:解答本题的关键是熟练掌握平行线的性质:两直线平行,同位角相等;两直线平行,内错角相等;两条直线平行,同旁内角互补.5.【解析】试题分析:根据两直线平行,内错角相等求出∠BCD等于55°;两直线平行,同旁内角互补求出∠ ECD 等于 30°,∠ BCE 的度数即可求出.∵ AB ∥ CD ,∠ ABC=50°,BCD= ABC=50∵ EF∥ CD,∴∠ ECD+ ∠ CEF=180°,∵∠ CEF=150°,∴∠ ECD=180° -∠ CEF=180° -150 °=30°,∴∠ BCE= ∠BCD- ∠ ECD=50° -30 °=20°.考点:此题考查了平行线的性质点评:解题的关键是注意掌握两直线平行,同旁内角互补,两直线平行,内错角相等.6.【解析】试题分析:首先过点 E 作 EF ∥AB ,由 AB ∥ CD,即可得EF∥AB ∥CD ,根据两直线平行,同旁内角互补与两直线平行,内错角相等,即可求得∠α+∠1=180°,∠2=∠ γ,继而求得α+β-γ=180°.过点 E 作 EF∥AB,∵AB ∥CD,∴EF∥AB ∥CD,∴∠ α+∠ 1=180°,∠ 2= ∠ γ,∵∠ β=∠ 1+∠ 2=180°-∠ α+∠ γ,∴ α+β-γ=180°.故选 C.考点:此题考查了平行线的性质点评:解题的关键是注意掌握两直线平行,同旁内角互补与两直线平行,内错角相等定理的应用,注意辅助线的作法.7.【解析】试题分析:根据方位角的概念和三角形的内角和即可得到结果.根据方位角的概念,由 A 测 B 的方向是南偏东90°-30 °=60°,故选 B.考点:本题考查的是方位角,三角形的内角和点评:解答本题的关键是要求同学们熟练掌握方位角的概念,再结合三角形的角的关系求解.8.【解析】试题分析:根据平行线的性质,对顶角相等即可判断.根据平行线的性质,对顶角相等可知相等的角有 5 对,故选 B.考点:本题考查的是平行线的性质,对顶角相等点评:解答本题的关键是熟练掌握两直线平行,同位角相等;两直线平行,内错角相等9.【解析】.试题分析:根据EO⊥AB 结合平角的定义即可得到结果.∵EO⊥ AB ,∴∠ 1+ ∠2=90°,故选 A.考点:本题考查的是平角的定义,互余的定义点评:解答本题的关键是熟记和为90°的两个角互余,平角等于180°.10.【解析】试题分析:先根据互补的定义求得∠1,再根据互余的定义求得∠ 2.∵∠ 1 与∠ 3 互补,∠ 3=120°,∴∠ 1=180°-∠ 3=60°,∵∠1和∠2互余,∴∠ 2=90°-∠ 1=30°,故选 B.若∠ A 与∠ B 互余,则∠ A+ ∠ B=90°;若∠ A 与∠ B 互补,则∠ A+ ∠ B=180°.考点:本题考查的是互余,互补点评:解答本题的关键是熟记和为90°的两个角互余,和为180°的两个角互补.11.【解析】试题分析:根据补角的性质,对顶角的性质,平行线的判定定理依次分析各项即可.A、直角的补角是直角,故本选项错误;B、直角都相等,但不一定是对顶角,故本选项错误;D、同旁内角互补,两直线平行,本选项正确;故选 D.考点:本题考查的是补角,对顶角,平行线的判定点评:解答本题的关键是熟记同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行 .12.【解析】试题分析:根据同内错角的概念即可判断.与∠ 1 是内错角的角的个数是 3 个,故选 B.考点:本题考查的是内错角的概念点评:准确识别同位角、内错角、同旁内角的关键,是弄清哪两条直线被哪一条线所截.也就是说,在辨别这些角之前,要弄清哪一条直线是截线,哪两条直线是被截线.13.【解析】.试题分析:根据对顶角相等及∠AOD 和∠ BOC 的和为 202°,即可求得结果由图可知∠ AOD= ∠ BOC,而∠ AOD+ ∠ BOC=202°,∴∠ AOD=101°,∴∠ AOC=180° -∠ AOD=79°,故选 C.考点:本题考查的是对顶角,邻补角点评:解答本题的关键是熟练掌握对顶角相等,邻补角之和等于180°.14.【解析】试题分析:根据对顶角的定义依次分析各个图形即可求得结果.是对顶角的图形只有③,故选 A.点评:解答本题的关键是熟练掌握对顶角的定义:两条直线相交形成的没有公共边的一对角叫对顶角 .15.【解析】试题分析:根据平行线的判定定理即可得到结果.能判定 a∥b 的条件是①∠1= ∠5,②∠ 1=∠ 7,故选 A.考点:本题考查的是平行线的判定点评:解答本题的关键是熟记同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行 .16.【解析】试题分析:由∠ ACD =∠ BCD ,∠ ACB=60°,根据 DE∥ BC,即可求得∠ EDC 的度数,再根据三角形的内角和定理即可求得∠ BDC 的度数.∵∠ ACD =∠ BCD ,∠ ACB=60°,∴∠ ACD =∠ BCD=30°,∵DE ∥ BC,∴∠ EDC =∠ BCD=30°,∴∠ CDB = 180°-∠ BCD- ∠B = 76°.考点:此题考查了平行线的性质点评:解答本题的关键是熟练掌握两直线平行,内错角相等,三角形的内角和为180°.17.【解析】试题分析:过 C 作 CF∥ AB ,把∠ C 分成两个角,根据平行线的性质即可求出两个角,相加就可以得到所求值.如图:过 C 作 CF∥ AB ,则 AB ∥ DE ∥CF,∠1=180°-∠ B=180°-150 °=30°,∠2=180°-∠ D=180°-130 °=50°∴∠ BCD= ∠ 1+∠ 2=30°+50°=80°.考点:本题考查的是平行线的性质点评:通过作辅助线,找出∠ B 、∠ D 与∠ C 的关系是解答本题的关键.18.【解析】试题分析:根据平行线的性质,角平分线的性质即可得到结果.∵AD ∥BC,∴∠ A+ ∠ ABC=180°;∵∠ A :∠ ABC=2 : 1,∴∠ A = 120°,∠ ABC=60°;∵BD 平分∠ ABC ,∴∠ DBC=30°,∵AD ∥BC,∴∠ADB=30° .考点:本题考查的是平行线的性质,角平分线的性质点评:解答本题的关键是熟练掌握两直线平行,内错角相等;两直线平行,同旁内角互补.19.【解析】试题分析:根据两直线平行,同位角相等,内错角相等,找出∠ 1 的同位角与内错角以及与∠1相等的角的同位角与内错角,从而得解.根据平行线的性质,与∠ 1 相等的角有∠ FEK ,∠ DCF ,∠ CKG ,∠ EKD ,∠ KDH.考点:本题考查的是平行线的性质点评:解答本题的关键是熟练掌握两直线平行,同位角相等;两直线平行,内错角相等;在图中标注上角更形象直观.20.【解析】试题分析:两直线平行,同旁内角互补,可求出∠ FEB ,再根据角平分线的性质,可得到∠ BEG,然后用两直线平行,内错角相等求出∠2.∵AB ∥CD,∴∠ BEF=180° -∠1=180°-72 °=108°,∠ 2=∠BEG ,又∵ EG 平分∠ BEF ,∴∠ BEG=∠ BEF=54°,∴∠ 2= ∠BEG=54° .考点:本题考查的是平行线的性质,角平分线的性质点评:解答本题的关键是熟练掌握两直线平行,内错角相等;两直线平行,同旁内角互补.21.【解析】试题分析:由AB ⊥EF,CD ⊥ EF,∠ 1=∠ F=45°,根据三角形的内角和为180°,平角的定义即可得到结果 .∵AB ⊥ EF, CD ⊥ EF,∠ 1=∠ F= 45°,∴∠ A= ∠ ABG= ∠ FCD= 45°,∴与∠ FCD 相等的角有 4 个,它们分别是∠F,∠ 1,∠ FAB ,∠ ABG.考点:本题考查的是三角形的内角和点评:解答本题的关键是熟练掌握三角形的内角和为180°,平角等于180°.22.【解析】.试题分析:先根据平行线的性质求得∠DCF 的度数,再根据角平分线的性质即可求得结果∵AB ∥CD,∴∠ DCF= ∠1= 100 °,∵ CE 平分∠ DCF ,∴∠ 2= 50°.考点:本题考查的是平行线的性质,角平分线的性质点评:解答本题的关键是熟练掌握两直线平行,同位角相等.23.【解析】试题分析:根据同位角、内错角、同旁内角的概念即可判断.∠ 1 与∠ 4 是同位角,∠ 1 与∠ 3 是对顶角,∠ 3 与∠ 5 是同旁内角,∠ 3 与∠ 4 是内错角 . 考点:本题考查的是同位角、内错角、同旁内角的概念点评:准确识别同位角、内错角、同旁内角的关键,是弄清哪两条直线被哪一条线所截.也就是说,在辨别这些角之前,要弄清哪一条直线是截线,哪两条直线是被截线.24.【解析】试题分析:根据同旁内角、内错角的特征即可判断 . ∠ 1的同旁内角是∠ B 、∠ C,∠ 2 的内错角是∠ C. 考点:本题考查的是同位角、内错角、同旁内角的概念点评:准确识别同位角、内错角、同旁内角的关键,是弄清哪两条直线被哪一条线所截.也就是说,在辨别这些角之前,要弄清哪一条直线是截线,哪两条直线是被截线.25.【解析】试题分析:根据平行线的判定定理即可得到结果.若∠ 2= ∠ 3,则 AB ∥ CD;若∠ 1=∠ 4,则 AD ∥ BC.考点:本题考查的是平行线的判定点评:解答本题的关键是熟记内错角相等,两直线平行.26.【解析】试题分析:根据平行线的判定定理即可得到结果.若∠ 1= ∠ 2,则 DE∥ BC;若∠ 3+∠4=180°,则 DE∥ BC.考点:本题考查的是平行线的判定点评:解答本题的关键是熟记同位角相等,两直线平行;同旁内角互补,两直线平行. 27.【解析】试题分析:先求出∠ 2 的度数,再根据对顶角相等即可得到结果.∵∠ 1+ ∠2=90°,∠ 1=65°,∴∠ 2=25°,∴∠ 3= ∠2=25°.考点:本题考查的是对顶角点评:解答本题的关键是熟练掌握对顶角相等.28.【解析】试题分析:根据对顶角的定义及对顶角相等即可求得结果.∵直线 AB 、 CD 相交于点 O,∴∠ 1 与∠ BOD 是对顶角,∠ 2 与∠ AOD 是对顶角,∴∠ 1= ∠BOD ,∠ 2= ∠ AOD ,理由是:对顶角相等 .考点:本题考查的是对顶角点评:解答本题的关键是熟练掌握对顶角的定义:两条直线相交形成的没有公共边的一对角叫对顶角,同时熟记对顶角相等 .29.【解析】试题分析:根据对顶角相等及平角的定义即可得到结果.∵∠ 1=55°,∴∠ 2=125°,∠ 3=55°,∠ 4=125°.考点:本题考查的是对顶角,平角的定义点评:解答本题的关键是熟练掌握对顶角相等,平角等于180°.30.【解析】试题分析:根据互余,互补的定义即可得到结果.若∠ A 与∠ B 互余,则∠ A+ ∠ B=90°;若∠ A 与∠ B 互补,则∠ A+ ∠ B=180°.考点:本题考查的是互余,互补点评:解答本题的关键是熟记和为90°的两个角互余,和为 180°的两个角互补 .31.【解析】试题分析:根据对顶角相等及平角的定义即可得到结果.由图可知∠ 1+∠ 2+∠ 3=180°.考点:本题考查的是对顶角,平角的定义点评:解答本题的关键是熟练掌握对顶角相等,平角等于180°.32.【解析】试题分析:根据对顶角相等即可得到结果。
