移动对象的连续k最优有序路径查询

合集下载

基于路网的移动对象k近邻查询方法

ｏｔｉａｉｎｏｓａｄＳｒｄｕ，ｗｈｃｓｅｉｉｎｏａｓｌｋｐｉｚｔｆＩｌｎ ’ ａｉｓｍｏｉｈｉｆｃｅｔｔｎｗｅＮＮｅｒｈｉｏｓｒｉｅｏｄｎｔｒＢｙｕｉｇｔａｓｔｏｔｉｅｅｅｔｔｎａｄｓａｃｎｃｎｔａｎｄｒａｅｗｏｋｓｎｒｎｉｉｎｍａｒｘｒｐｒｓｎａｉｏｎｒｄｕｓｏｔｍｉａｉｎｍｅｈｄｔｅｓａｃｆｉｉｎｙｉｂｔｅａｈｌｔｏｉｃｕｎｇｓａｃｉｎ／ｐｇｓａｃｓ．ａｉｐｉｚｔｏｔｏ，ｈｅｒｈｅｃｅｃｓｅｔｒｔｎｔｅｏｄｍｅｈｄ．ｎｌｄｉｅｒｈｔｈｍｅａｄＩ出了改进方法Ｉｌｎｓｄ，采用过度矩阵表示转向以及区域半径优化方法，结果证明提高了查询效率，查询时间和Ｉａ／Ｏ对磁盘页访
问次数明显少于原方法。
关健词：路网；Ｉｌｄ算法；交通堵塞探测；ｋ近邻ｓｎａ
ｋＮｅｒｓＮｉｈｏｅｉｓｆｖｎｊｃｓａｅｎＮｅｗｒｓａｅｔｅｇｂｒＱｕｒｅｉｇ０ＭｏｏｂｅｔＢｓｄ０ｔｏｋ
维普资讯
第３４卷第３期
、＿．４，ｔ３０
・
计
算
机
工
程
２００８年２月
Ｆｂｕｒ０８ｅｒａｙ２０
Ｎｏ３．
ＣｏｐｕｔｒＥｎｇｎｅｒｎｇｍｅｉｅｉ

地理信息科学B考试题库以及答案

1.什么是空间插值？空间插值就是利用离散点构建一个连续的曲面。

它的目的是使用有限的观测值，通过估计值对无数据的点进行填补。

（推论1）当只有内蕴量信息时，可通过地统计分析，弥补外蕴量信息缺口，运用HASM 构建高精度曲面。

空间插值常用于将离散点的测量数据转换为连续的数据曲面，以便与其它空间现象的分布模式进行比较，它包括了空间内插和外推两种算法。

（百科）尺度转换是指利用某一尺度上所获得的信息和知识来推测其它尺度的现象，包括升尺度和降尺度。

2.什么是空间降尺度？降尺度转换是指将粗分辨率数据向细分辨率转换。

（推论2）当粗分辨率宏观数据可用时，应补充地面观测信息，并运用HASM对此粗粉辨率数据进行降尺度处理，可获取更高精度的高分辨率曲面。

许多模型和数据由于空间分辨率太粗而无法用于分析区域尺度和局地尺度问题。

为了解决这个问题，需要研发降尺度方法，将粗分辨模型输出结果和粗分辨率数据降尺度为高空间分辨率数据。

3.什么是空间升尺度？升尺度是指将细分辨率数据向粗分辨率转换。

在许多情况下，为了节约计算成本，需要将细分辨率数据转换为粗分辨率数据，此过程称之为升尺度。

推论3（升尺度）：当运用HASM将细分变率曲面转化为较粗分辨率曲面时，引入地面细节数据可提高升尺度结果的精度。

4.什么是数据融合？数据融合是将表达同一现实对象的多源、多尺度数据和知识集成成为一个一致的有用形式，其主要目的是提高信息的质量，使融合结果比单独使用任何一个数据源都有更高精度。

推论4（数据融合）：卫星遥感信息可用时，必须补充来自地面观测信息，尚可运用HASM构建地球表层及其环境要素高精度曲面，得到较遥感信息更高精度的结果。

推论5（数据融合）：卫星遥感信息和地面观测信息可用时，可运用HASM构建地球表层及其环境要素高精度曲面，获得较卫星遥感信息和地面观测信息精度都高的结果。

5.什么是数据同化？数据同化就是将地面观测数据并入系统模型的过程，其目的是提高系统模型的精度。

【计算机应用】_距离函数_期刊发文热词逐年推荐_20140726

科研热词聚类无线传感器网络高维数据高斯变异算子频繁结构向量模型频繁子树隶属函数重新初始化配准遗传算法遗传模拟退火算法连续性边缘梯度距离阈值距离反比加权蚁群算法节点定位脉冲噪声聚类分析结构挖掘线性鉴别粒子群优化类约束算法性能离散度函数碱基对相似性度量相似性目标匹配熵潜在支持向量混合优化策略水平集模糊支持向量机模糊c均值模拟退火算法核函数权值无监督聚类支持度扩散张量张量重定向嵌入子树实验变差函数定位算法完全信息集多议题多属性效用理论多代理复相关系数图像分割噪声检测
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68
加权欧式距离八分域搜索保持邻域嵌入位置校正矢量人脸识别二次规划主动轮廓中值滤波两阶段协商丛聚效应三维栅格一类分类方法 powell算法 java3d hausdorff距离 dv-hop
推荐指数 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
推荐指数 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

位置不确定移动对象的连续概率反Skyline查询

ａｐｐｌｉｃａｔｉｏｎｓ．ＥｘｉｓｉｔｎｇｒｅｓｅａｒｃｈｅｓｆｏｃｕｓＯｎｓｔａｔｉｃｒｅｖｅｒｓｅｓｋｙｌｉｎｅｏＴｈｉｓｐａｐｅｒｃｏｎｓｉｄｅｒｅｄｒｅｖｅｒｓｅｓｋｙｌｉｎｅｑｕｅｒｉｅｓｐｒｏｃｅｓｓｉｎｇ
ＡｂｓｔｒａｃｔＲｅｖｅｒｓｅＳｋｙｌｉｎｅＱｕｅｒｉｅｓｈａｖｅｂｅｅｎｐｒｏｖｅｄｕｓｅｆｕｌｌｙｉｎｂｕｓｉｎｅｓｓｐｌａｎｎｉｎｇ，ｅｎｖｉｒｏｎｍｅｎｔａｌｍｏｎｉｔｏｍｎｇａｎｄｏｔｈｅｒ
ｏｎｍｏｖｉｎｇｔａｒｇｅｔｏｂｊｅｃｔｓｗｉｔｈｕｎｃｅｒｔａｉｎｔｙ．Ｏｎｔｈｅｂａｓｉｓｏｆａｄｅｔａｉｌｅｄａｎａｌｙｓｉｓｏｆｔｈｅｒｅｖｅｒｓｅｄｏｍｉｎａｎｔｒｅｌａｔｉｏｎｓｈｉｐｂｅ－
摘要反Ｓｋｙｌｉｎｅ查询现在已经被广泛用于商业规划、环境监测及其它领域。当前的研究多集中在目标对象静止条
件下的反Ｓｋｙｌｉｎｅ计算。对移动环境下的目标对象不断运动变化并且位置不确定情况下的连续概率反Ｓｋｙｌｉｎｅ计算进

移动对象在空间网络数据库上的kNN查询

Moving o b 改t Query k Near est Neighbor s in SPatiaI Network Databases j
Yin x iaolan， Ding zhimin扩， LI Jing，， 3， and
l ( 了减h n 0 ‘ ， n e o s 叮咖 r E” e r n ， s t t o S ) w r ， i e A‘ 1 )〕 t r f g o 飞 e glne i g I t u e f f a e C n s ni t h 口 dem少反i nc ， i ng lo 0 0 f o e e Bj s e o 8 ) 2( 7 飞ch n 01 9，Q nte o 压5￡S7 w r ， O r f c f a e Inst艺 e o 和户 r ， in， Academ，反￡ e ，延 100080) t tut f a w e C h f o enc 及红ng s
计算机研究与发展 Jour al o C冶 n f n1Pute Re r s a e
c r h and L艳 l o ment ve P
IS N 1000一 S 1239l CN l l 一 1777l TP 44( S ppl. ) : 55 一60 ， u 2007

移动对象在空间网络数据库上的 kNN 查询
3( Gr doat。 i馏￡ o C ine Ac 山my o 反i nc ， i ing l00049) a n U r t f h s a s y e f e e Bj s e
Abstract One o the most important kinds of queries in spatial network databas s ( SNDB) to support f e location一 based ser ices (LBS) is the k一 v nearest neighbor ( k一 s NN) query。 Given a ob ect in a netw rk ， .9. j o e a location of a car on a r ad network ， a set of ob ects of interests ， . hotels ， stat ion ，， o and j e.9 gas car etc. the k一 query returns the k ob ects of interest closest to the query ob ect . The network distance， a d NN j j inste of the Euclidean distance ， used in such a query. Pr 卯sed in this paper is a k一 algorithm with a set of is o NN index structures to support the sit uation of moving ob ects . Experimental evaluat ion with generated data j e s ts sh ws tha this Pr posal is m r efficient than the t raditional s lution t this pr blem . O t o o e o o o

移动对象的K个连续最近邻查询算法

维普资讯
第ｌ２卷
第６期
哈尔滨理工大学学报
ＪＯＵＲＮＡＬＨＡＲＢＮＵＮＩＩＶ．Ｓ．＆ＴＣＨ．ＣＩＥ
Ｖｏ２Ｎｏ６Ｌ１．
Ｄｅ．０７ｃ，２０
２００７年ｌ２月
移动对象的个连续最近邻查询算法
ｏｓａｆｃｅｔａｇｒｈｍａａｅｏｈｎｅｆｒＲｔｅａｄｕｅｏｐｕｉｅｈｉｅｔｅｏｖｅｐｏｌｍ．ｎｐｅｉｉｎｌｏｔｅｔｔｓｎｔｅｉｄｘｏＰ — ｅｎｓ【ｒｎｇｔｃｎｑｒｓｌｅｔｒｂｅＡｎｉｈｂｒｕｏｈ
黄敬良，郝忠孝
（哈尔滨理工大学计算机科学与技术学院，黑龙江哈尔滨１０８）５００
摘
要：给定一个移动查询点和一个移动对象集合，由于查询和数据对象的位置都是连续变
化的。因此不能依赖于给出的固定参考位置来解决查询问题．为了解决移动对象的个连续最近邻查询。ＴＲ树的基础上，出了分界时间的概念，剪枝技术给出了查询算法．在Ｐ提利用利用模拟
点只被访问一次．
树索引．４局限于回答一个最近邻查询．［］文［］文５提出一种基于ＴＲ树索引的查询算法，Ｐ］这种方法要多次对ＴＲ树进行搜索，Ｐ因此时间复杂度高．文
２基础知识
２１ＴＲ树．Ｐ
［］１虽对文［］５进行了改进，但是这种技术只适应于静态数据集合．［］文６等人提出的算法不能查询多

一种改进的连续k近邻查询处理方法

问整个ＴＲ树，响了查询的效率。本文基于动态增大的搜Ｐ影
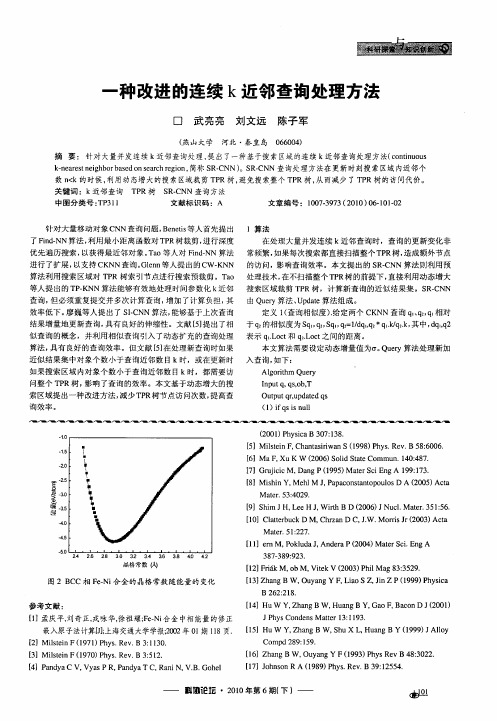
本文算法需要设定动态增量值为ａ。ｕｒＱｅｙ算法处理新加
ＡｌｏｔＱｅｙｇｒｈｉｍｕｒ
Ｉｐｔ，ｓｏ，ｎｕｑ，ｂＴｑＯｕｐｔｒｐａｅｓｔｕ，ｄｔｄｑｑｕ
Ｍａｅ．：２７ｔｒ５１２．
【１ｒ．ｏｌｄ。ｄｒ２０）ｔｒＳｉＥｇＡｌ】ｅＲＭＰｋｕａＪＡｎｅａＰ（０４Ｍａｅｃ．ｎ
３８３９：２３７— ８９．
【】ｒｔＭ，ｂＭ，ｉｋＶ（０３ＰｉＭａ３３２．１ＦｉｋｏＶｔ２０）ｈｌｇ８：５９２ｆｅ
数ｎｋ的时候，＜利用动态增大的搜索区域裁剪ＴＲ树，免搜索整个ＴＲ树，而减少了ＴＲ树的访问代价。Ｐ避ＰＴ３ｌ
ＴＲ树Ｐ
Ｓ．ＮＮ查询方法ＲＣ
文献标识码：Ａ文章编号：１０．９３２１０ —０ —２０７３７（００）６１１０
针对大量移动对象ＣＮＮ查询问题，ｅｅｓＢｎｔ等人首先提出ｉ了Ｆｎ — Ｎ算法，ｉｄＮ利用最小距离函数对ＴＲ树裁剪，Ｐ进行深度
１算法
在处理大量并发连续ｋ近邻查询时，查询的更新变化非
优先遍历搜索，以获得最近邻对象。ａＴｏ等人对Ｆｎ — Ｎ算法常频繁，ｉｄＮ如果每次搜索都直接扫描整个ＴＲ树，Ｐ造成额外节点

公路网上移动对象连续k近邻查询的一种方法

欧氏空间的近邻查询方法（Ｅ）（Ｉ），ＩＲ和１ＥＪ由于ｌＥＶＩＶ比ＩＲ的算法效率高，我们就只介绍一下ＩＥ方法．Ｅ这里Ｎ该
方法的主要思想是以发出查询的点为中心逐步进行扩张搜索，在扩张过程中比较所有遇到的移动对象到查询中心的距离，这种方法是对Ｄｉｔ￣ｓａ算法的一种多次使用，ｋｒ当扩张半径超过到第个对象的距离时，查询就结束了．ＮＩＥ算法
（（ｎ）、ｅｎ，）对象离它所在边的起点距离（ｉＤｓｔ
３９
）、）平均
Ｋｌｈｏｚｎ等人提出了Ｖ３方法Ｊ它是基于ｏｄｕａａＮ，
值之和）针对路网下的近邻查询，．一些学者首先提出了对
网络上的静态对象查询处理的算法－２
，而后又针对移动
的效率取决于要查询对象的密度，整个路网范围比较如果大，而要查询的对象又比较少且很分散，么该方法的效率那
就很低，因为要搜索大部分的路网．
然而在大多数现实场景中，查询者和移动对象被限制在一
个传输网络中．型的，典道路网络就是这样一类的传输网
络，由各路段组成，它们路段的权值对应于它们的长度或移动对象穿越它们所需要的行驶时间．在这种环境中，两个对
象之间的距离被定义为连接它们的最短路径的长度（即权
对象的ＣＮＫＮ查询给出了再计算的快照方法，以解决移
动对象的位置随时间变化而进行更新处理，而这种处理然

【计算机应用与软件】_静态_期刊发文热词逐年推荐_20140725

科研热词面向对象道路网软件路段连接算法路径规划视频检索蚁群算法自动配置脱机中文签名鉴定统一建模语言电站炉水生物测定特征提取模糊控制柔性化机器人服务流程挑战-应答机制拉普拉斯算子报表模板复用方法卓越绩效动态报表生成器动态口令加药处理功能构件关键帧不变矩三层架构 smith-pid自适应控制 rr-tree owc meanshift lsvm lscasc elgamal公钥密码体制 bp神经网络
2012年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
科研热词推荐指数面向对象 1 静态职责分离 1 静态生成 1 静态安全配置模型 1 阈值分割 1 道路识别 1 边缘检测 1 警务绩效 1 虚拟执行 1 蒙特卡洛算法 1 航迹规划 1 缓冲区溢出攻击 1 统一建模语言 1 累积帧差技术 1 目标检测混合高斯模型 1 特征线段 1 灰度不一致 1 模糊综合评价 1 模板匹配 1 模板 1 模型转换 1 模型 1 整合 1 数据网格 1 数据复制 1 数学形态学 1 报表 1 带宽 1 大地方位角 1 基于角色的访问控制 1 图像拼接 1 图像平滑 1 图像分割 1 可扩展访问控制标记语言 1 反汇编 1 动态职责分离 1 动态安全配置模型 1 动态下载 1 动作语言 1 切割 1 分级安全模型 1 入侵检测 1 交换系统 1 主动轮廓模型 1 一致性检测 1 yaffs文件系统 1 xml 1 uml 1 ssi 1 shellcode 1 nand flash 1 mumford-shah模型 1

一种道路网络中移动对象的k近邻多查询处理算法

algorithm .
Key wor s K nearest neighbor query ; multi queries pr cessing ; r ad network ; cluster d o o
摘要在实际应用中，服务器时常会收到许多查询请求，因此知何高效地进行多查询处理，并且获得良好的吞吐量具有重要的意义. 研究了道路网络中连续的 K 近部多查询处理技术. 在已知查询点位置和运动速度的情况下，将道路网络上的查询点进行聚类，出了基于聚类的 K 近邻多查询处理算法，提使同一聚类中的查询共享执行，从而大大提高多查询处理的效率. 算法还进一步利用扩展树存储查询结果，提高连续的 K 近邻多查询处理性能. 理论分析和实验结果表明提出的算法是可行的、高效的.
( &为 o l Z rmat勿， l o f sf o n Renm￡饰 1 it o C ina ， j i叹 100872) n 二 y f h 价i
Abstract
ln the 代 w rld applicat ions， al o severs often receive a lot of query reque ts ，s how to Pr ces s o o s
thes queries efficient1 and achieve better l/O efficiency is a challenging goal. Studied in this paper is the e y
multiPle KNN queries Processing f r moving ob ects in r ad netw rks . Assume that the location and o j o o velocity of the query 卯ints in the r ad network are given ， query points are clustered and a Clu一 o the MQN (clustering based multiple querie in r ad netw rk) algorithm is proposed which pr cesses the queries in the s o o o sa e cluster synchro ously ， the efficiency o query processing is greatly impro ed . Als the expansion m n o s f v o tree is us d to stor the query results in order to impr ve the efficiency of pr cessing multiple cont inuous K e e o o nearest neighb r queries. Theor tical and experimental analysis pr ves the feasibility and efficiency of the o e o

道路网络中的连续最近邻查询

ｑｅｙａｍｅｈｆｃｍｐｕｉｇＣＮＮｕｅｎｒａｅｗｏｋｉｏｏｅ．ｔｒｓｎｓｔｅｍｅｏｆｃｍｐｔｎｐｉｐｎｓａｄｔｅａｇｒｔｍｆＣＮＮ，ｕｒ，ｔｏｄｏｏｔｎｑｒｉｏｄｎｔｒｓｐｒｐｓｄＩｅｅｔｈｔｄｏｏｕｇｓｌｔｏｉｔｎｌｏｈｏｙｐｈｉｈｉａｄｐｏｉｅｈｒｏｆｔｅｃｒｅｔｎａｄｔｒｎｔｏｎｏｌｘｔｆｔｅＣＮＮｕｒｌｏｔｍ．ｏａｉｇｗｉｅａｅｌｏｉｍｓｔｎｒｖｄｓｔｅｐｏｆｏｈｏｒｃｉｎｅｍｉａｉｎａｄｃｍｐｅｉｏｈｏｙｑｅｙａｇｒｈｉＢｙｃｍｐｒｎｔｒｌｔｄａｇｒｔｈｈ，ｉ
［ｙｗｒｓｏｄｎｔｏｋＣｎｉｕｕｗｅｔｉｈｏ（ＮＮ）ｓｌｏｎｓｑｅｙａｇｒｈＫｅｏｄ］ｒａｅｗｒ；ｏｔｏｓｎＮｅｓＮｅｇｂｒｃ；ｐｉｐｉｔｕｒｌｏｔｍ中移动对象的连续最近邻查询和基于位置服
ｃｎｌｄｓａｉｉｍｏｅｓｉｂｅｆｒｒｃｉａｎｔｏｋｔｅｒｑｅｔｈｎｅｏｂｅｔｉｅｗｒｓｏｃｕｅｔｔｓｒｔｌｏａｔｌｅｗｒｓｈｔｅｕｎａｇｆｊｓｎｔｏｋ．ｈｔｕａｐｃｗｉｈｆｃｏｃｎ
第３卷第８期６
１１６１．ｏ３
・
计
算
机
工
程

移动点对象轨迹上k-最近邻查询

ｌｓｆｍｅｒｒｔｙｉｔｏｍｏｆｓｌ．Ｈｏｖｒｙｉｗｅｅ，ｗｈｅｈｐａｅｌｔｒａｈｓｔｘｍｕｖｌｅ，ｔｔｅｌｂｐｔｄ．ＩｎｔｅｕｄｔｉｅｃｅｈｅｍａｉｍａｕｓｈｅＲ・ｒｅｗｉｌｅｕｄａｅｎａｗｏｄ，ｔｅｐｐｒｅｅｔｅｙｒｄｃｓｔｅｄｓｃｅｓｓ，ａｓｍｐｏｅｈｆｃｅｃｆｑｅｅｈｉｋａｃｓｅｖｎｄａｏｉｒｖｓｔｅｅｉｎｙｏｕｒｓｌｉｉＫｅｗｏｄｓ：－ｅｒｓｅｇｂｒｔｏｙｒｋｎａｅｔｎｉｈｏｍｅｄ；ｐｅｉｔｄ・ｐｅｏｉｙ；ｕｄｔｒｔｙｓｏｅｎｍｅｒ；ｂｔｏｕｓｈｒｄｃｅｓｅｄｐｌｃｐａｅｆｓｌｔｒｄｉｍｏｉｙｏｔｍ－ｐ
ｔｅＴａｅｔｒｏｏｉｏｔｊｃｈｒｊｃｙｆｖｎＰｉｅｔｏＭｇＯｂｓｎ
ＦＡＮｏ・ｅ，ＨＡＯｏｇ・ｉｏＳｈｕｄＺｈｎｘａ
（ｃｏｌｆｏｕｅｃｅｃＳｈｏｍｐｔＳｉｅ＆Ｔｃｎｌｇ，ｒｉＵｉｒｔｏｉｎｅａｄＴｃｎｌｇ，Ｈｒｉ５００，ｈｎ）ｏＣｒｎｅｈｏｏｙＨａｂｎｎｖｓｙｆｅｃｎｅｈｏｏｙａｂｎ１０８ＣｉａｅｉＳｃ
ｓａｉ — ｍｐｒｌｑｅｅ．Ｔｉｐｐｒｐｏｏｅｅｍｅｈｄｏｎｔｒｎｅｋｎａｅｔｅｇｂｒ，ｗｉｈａｏｔｒ－ｐｔｔｏｅｏａｕｒｓｈｓａｅｒｐｓｓｔｔｏｆｉｈｍｏｉｉｇｔ－ｅｒｓｉｈｏｓｈｃｄｐｓａｐｅｏｈｎｄｃｅ —ｐｅｏｉｙａｄａｂｔｍ・ｐｕｄｔｔｅｎｅｉｎｕｄｔｒｔｔｒｄｉｍｏｙｉｔｄｓｅｄｐｌｎｏｔｕｐａｅＲ・ｅｉｄｘｗｔａｐａｅｆｓｌｓｏｅｎｍｅｒ．Ｗｈｎｔｅｓｅｄｃｏｒｈｉｙｅｈｐｅｓ

【计算机应用与软件】_最优搜索_期刊发文热词逐年推荐_20140723

2008年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14ห้องสมุดไป่ตู้15 16 17 18 19 20 21 22
科研热词遗传算法高斯分布遗传操作运动检测边缘检测视频监控系统自适应模式匹配最大方差法最优搜索改进遗传算法探测函数局部收敛多目标基因交叉概率块匹配图像分割双粒子群优化算法双混沌优化机制入侵检测人工免疫算法 pid整定
2012年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
科研热词人工鱼群算法预测模型蟑螂算法蜂群算法网络流量网格神经网络集成热带气旋强度混沌映射混沌变异泛化能力最优回路最优化时空折中支持向量机彩虹表并行图像插值方法差分进化局部最优密钥搜索图像插值剖分凹多面体任务调度三角网生长法 pdf文档 delaunay三角剖分
推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
科研热词马尔可夫模型量子粒子群算法蚁群算法自适应调整纹理特征粒子群算法粒子群优化环形邻域混合算法模拟退火最近节点选择智能蚁群算法旅行商问题序列生境奖罚策略多峰函数优化图像分类图像分割和声搜索分组信息素优化二维ostu方法中值迭代函数 mmas
推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

时空数据库中的轨迹数据挖掘与查询优化

时空数据库中的轨迹数据挖掘与查询优化随着移动设备和GPS技术的普及，轨迹数据的获取变得越来越容易。

这些轨迹数据包含了移动对象在时空中的移动轨迹信息，它们的应用广泛，如交通管理、城市规划、人群流动分析等。

然而，大规模的轨迹数据产生了数据量的爆炸性增长，如何高效地存储、管理和查询轨迹数据成为一个重要的问题。

本文将介绍时空数据库中的轨迹数据挖掘与查询优化的相关技术和方法。

在时空数据库中，轨迹数据通常以点、线、面等几何对象的形式存储。

为了更好地提取轨迹数据的空间和时间信息，需要进行轨迹数据的挖掘。

轨迹数据挖掘是指从轨迹数据中发现有价值的信息，如轨迹模式、聚类分析、异常检测等。

其中，轨迹模式是轨迹数据挖掘中的一个重要任务，它可以用来描述移动对象的典型移动行为。

常见的轨迹模式包括直线行进、环形行进、往返行进等。

轨迹聚类分析是将轨迹数据划分为若干个相似的聚类，可以用于群体行为分析和异常检测。

轨迹数据中的异常点可能是移动对象的异常行为，如交通事故、犯罪活动等。

因此，异常检测可以帮助我们识别和预测潜在的风险。

为了实现高效的轨迹数据挖掘，需要对时空数据库进行查询优化。

查询优化是指通过选择合适的查询计划和参数来提高查询性能。

在时空数据库中，轨迹数据的查询通常涉及到时空范围查询、k近邻查询和轨迹相似性查询等。

时空范围查询是指根据时间和空间的限制条件，查询在指定范围内的轨迹数据。

k近邻查询是指查询与指定轨迹数据最相似的k条轨迹数据。

轨迹相似性查询是指查询与指定轨迹数据相似度最高的轨迹数据。

这些查询通常需要计算轨迹数据的时空相似性，如欧氏距离、动态时间规整等。

对于轨迹数据的查询优化，可以采用索引结构的方法。

索引结构是一种数据结构，用于加速数据的检索和查询。

在时空数据库中，常用的索引结构包括R树、k-d树和四叉树等。

R树是一种多维索引结构，可以用于存储和查询空间对象。

k-d树是一种二叉树，可以用于存储和查询多维数据。

四叉树是一种四叉分割树，可以用于存储和查询二维数据。

道路网中的移动对象连续K近邻查询

（防科学技术大学电子科学与工程学院国（军工程大学电子工程学院武汉海长沙４０７）１０３４０３）３０３
摘要已有道路网中的连续ｋ近邻查询处理算法采用增量式的查询处理机制，数据频繁更新时性能急剧下当降．结合多核多线程技术，出了一种基于多线程的连续查询处理框架．框架周期性重计算所有查询结果，查提该将询处理分为顺序执行的数据更新阶段和查询执行阶段，别使用任务并行和数据并行了数据更新阶段使用的数据结构，出了查询处理阶段的ｋ近邻查询处理策略，含离线预计算和在线ｋ近提包邻查询处理算法两个部分．ｋ近邻算法复杂性及多线程处理框架的加速比进行了理论分析．验结果表明，出对实提的算法在数据频繁更新下，串行执行时性能优于已有算法，基于多线程处理框架的并行执行在任何参数配置下而性能均优于已有算法；基于多线程处理框架的并行执行具有较好的性能扩展性，速比可以达到１５～１７且加．１．．关键词移动对象；路网；续ｋ近邻查询；线程；繁更新道连多频
ｍｕｔｔｒａｉｇｂｓｄｆａｗｏｋｆｒｃｎｉｕｕＮＮｕｒｅｆｍｏｉｇｏｊｃｓｉｐｏｏｅ．Ｉｌ —ｈｅｄｎａｅｒｍｅｒｏｏｔｎｏｓｋｉｑｅｉｓｏｖｎｂｔｓｒｐｓｄｎｅ

路径搜寻算法

路径搜寻算法是计算机科学中的一种重要算法，用于在图或网络中寻找从一个节点到另一个节点的最短路径或最优路径。

常见的路径搜寻算法有深度优先搜索（DFS）、广度优先搜索（BFS）、Dijkstra 算法、A*算法等。

1. 深度优先搜索（DFS）：这是一种递归算法，沿着图的深度遍历路径，直到找到目标或到达无法进一步前进的位置。

2. 广度优先搜索（BFS）：这种算法会扩展所有的节点，即按宽度优先的顺序，因此它通常用于搜索无权重图。

3. Dijkstra算法：这是一种适用于带权重的图的寻路算法，它会找到从起点到所有其他点的最短路径。

4. A*算法：这是一种启发式搜索算法，结合了深度优先搜索和Dijkstra算法的优点。

它通过估计从当前节点到目标节点的距离，选择最有希望的节点进行搜索，以减少搜索范围。

A*算法的优点是能够找到最优路径，并且在搜索过程中能够动态调整搜索方向，提高搜索效率。

在实际应用中，路径搜寻算法有着广泛的应用，如地图导航、物流规划、网络路由等。

AE运动路径教程设置运动路径来控制对象移动

AE运动路径教程：设置运动路径来控制对象移动Adobe After Effects（简称AE）是一款专业的视频特效制作软件，被广泛应用于电影、电视、动画等领域。

在AE中，我们可以利用运动路径来控制对象的移动，实现各种炫酷的效果。

本文将介绍AE中如何设置运动路径来控制对象移动的方法。

1. 创建一个新项目并导入素材首先，打开AE软件并创建一个新项目。

然后，将需要操作的素材导入到项目中，可以使用“文件”菜单中的“导入”选项完成。

2. 创建一个图层并应用动画效果选中导入的素材，在菜单栏中选择“图层”->“新建”->“空白图层”，创建一个新的图层。

接下来，在“效果与预设”面板中找到你想要应用的动画效果，并将其拖拽到图层上。

3. 打开关键帧面板在AE中，关键帧用于控制对象的属性或动画效果随时间的变化。

我们需要打开关键帧面板来设置运动路径。

4. 添加第一个关键帧选中图层，在关键帧面板中找到你想要控制的属性（如位置或旋转），在该属性上点击右键，并选择“添加关键帧”或者直接按下快捷键“Ctrl+Shift+K”。

这将在当前时间点添加第一个关键帧。

5. 设置第二个关键帧在时间轴上移动播放头到你想要对象开始运动的时间点。

然后，调整图层在画布中的位置或其他属性，如旋转角度。

这将自动在该时间点上添加第二个关键帧。

6. 创建运动路径选择图层，在菜单栏中选择“图层”->“运动路径”->“添加飞行相机”或“添加路径”，这将在导航面板中创建一个新的飞行路径。

7. 编辑运动路径选中运动路径，在画布上会显示出一个编辑点和一条曲线。

你可以通过拖动编辑点来调整路径的形状。

此外，你还可以在导航面板的“路径”选项中调整路径的属性，如速度和方向。

8. 预览与调整在编辑完运动路径后，点击“空格”键预览动画效果。

如果需要调整路径或关键帧的位置，可以通过拖动编辑点或在关键帧面板中调整关键帧的数值来完成。

9. 添加其他效果通过在图层上添加其他AE效果，如调整颜色、应用滤镜等，可以进一步增强你的动画效果。

《2024年外包空间数据库中范围和移动k近邻skyline的查询验证》范文

《外包空间数据库中范围和移动k近邻skyline的查询验证》篇一一、引言随着空间数据库的广泛应用，查询验证技术显得尤为重要。

外包空间数据库的查询验证在确保数据的准确性和安全性方面具有不可替代的作用。

其中，范围和移动K近邻Skyline查询验证在许多场景中都有着广泛的应用。

本文旨在深入探讨这一领域的理论与实践，并为其在现实中的应用提供一定的指导。

二、背景及意义外包空间数据库的查询验证主要包括对查询结果准确性的验证以及对数据安全性的保障。

在空间数据库中，范围和移动K近邻Skyline查询是一种常见的查询方式，它可以用于寻找给定范围内的K个最近邻或最远邻对象，并在此基础上进行进一步的分析和操作。

因此，对于这种查询的验证不仅有助于提高查询结果的准确性，也有助于保障数据的安全性。

三、方法与步骤1. 定义问题：首先，我们需要明确范围和移动K近邻Skyline 查询的具体定义和要求。

这包括对空间范围、K值、近邻或远邻的定义等。

2. 数据准备：准备相应的空间数据集，包括点、线、面等空间对象以及其属性信息。

3. 算法设计：设计有效的算法来执行范围和移动K近邻Skyline查询。

这需要考虑到查询的效率、准确性以及数据的安全性。

4. 查询验证：通过对比算法执行结果与实际结果，验证查询的准确性。

同时，还需要对数据进行安全性的验证，确保数据在传输和存储过程中不会被篡改或泄露。

5. 结果分析：对验证结果进行分析，总结算法的优缺点，提出改进措施。

四、实践应用范围和移动K近邻Skyline查询验证在许多领域都有广泛的应用。

例如，在智能交通系统中，可以通过该查询验证来查找附近的最优路径；在地理信息系统中，可以用于查找特定范围内的地理对象；在移动计算和网络应用中，可以用于寻找移动对象的K近邻等。

这些应用都需要对查询结果进行准确的验证，以确保数据的准确性和安全性。

五、实验与结果为了验证范围和移动K近邻Skyline查询的准确性，我们进行了实验。

基于道路网的连续k近邻查询算法

其中的有效部分，从而避免了对道路网的盲目扩展；且在节点的网络扩展中，通过应用具有相同扩展方向的其他查询
的扩展结果，不仅减少了对道路网的重复扩展，还节省了计算代价。实验结果表明，所提算法同传统算法相比较，缩短了查询响应时间，提高了运行效率，并且适用于不同类型的ｋ近邻查询。关键词：增量式监测算法；移动对象；连续ｋ近邻查询；网络扩展；扩展树；道路网
刘德高 ’ ，李晓宇
（郑州大学信息工程学院，郑州４５０００１）（通信作者电子邮箱ｌｄｇ＿８０＠１６３．ｃｏｎｒ）
摘
要：针对增量式监测算法（ＩＭＡ）的冗余搜索问题，提出一种基于ＩＭＡ改进的移动对象连续ｋ近邻（Ｃｏｎｉｔｎｕｏｕｓ
Ａｂｓｔｒａｃｔ：ＣｏｎｃｅｍｉｎｇｔｈｅｐｒｏｂｌｅｍｏｆｒｅｄｕｎｄａｎｔｓｅｒｃａｈｏｆＩｎｃｒｅｍｅｎｔｌａＭｏｎｉｔｏｉｒｎｇＡｌｇｏｉｒｈｍ（ｔＩＭＡ），ｔｈｉｓｐａｐｅｒｐｒｏｐｏｓｅｄ
ａｎｅｗｌａｇｏｒｉｔｈｍｏｆｉｍｐｒｏｖｉｎｇＣｏｎｔｉｎｕｏｕｓｋＮｅａｒｅｓｔＮｅｉｇｈｂｏｒ（ＣｋＮＮ）ｑｕｅｉｒｅｓｆｏｒｍｏｖｉｎｇｏｂｊｅｃｔｓｂａｓｅｄｏｎＩＭＡ．Ｔｈｅ

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

度。称为基于序列的ｑ的最优有序路径，记作Ｑｑｇ）＝Ｒ（，
＝
随着查询对象ｑ的移动，它在序列Ｍ下的最优有序路径也在不断地发生变化，因此要求解ｑ在其运动期［ｔ］内的连续ｔ，ｋ优有序路径必须找到它的时间分界点。最由于ｑ在起始数据集中的最近邻不一定是ｇ的最优有序路径的起点，因此移动对象的单数据集连续最近邻查询方法无法适用于移动对象的连续ｋ最优有序路径查询。文在文献［］的基础上引入加权相对距本７离函数的概念，在此基础上给出移动对象的连续ｋ最优有序并路径查询算法。定义１给定二维空间中的移动对象ｑｘ，ｏ，１（。Ｙ）速度为ｖｖ，）ｎ个数据集为Ｕ，，… ，［，（，，序列Ｍ＝（，，ｇＭ２
第２８卷第７期
２１０１年７月
计算机应用与软件
ＣｏｐｔｒＡｐｐｉａｉｎｎｏｔｒｍｕｅｌｃｔｓａｄＳｆｗａｅｏ
Ｖ０．８Ｎｏ７１２．
Ｊ１０１ｕ．２１
移动对象的连续ｋ最优有序路径查询
ｄｔｎｅｆｎｔｎａｉｔｓｃａｅｓｗｔｏｉｇｑｅｙｏｊｃａｄａｓｔａｂｃ．Ｔｅａｄｔｅｙｗｉｔｅｔｅｄｓｎｅｉａｃｃｏｉｎａｕｈｃｓｓａｉａｍｖｕｒｂｔｎｔｉｄｔｏｊｔｈｄｉｖｌｅｈｅｒｌｉｉａｃｓｕｉｍｇｈｎｅａｃａｅｉｇｄａｖｔ
第７期
孙冬璞等：动对象的连续ｋ最优有序路径查询移
ｌ３３
则ｑ的最优有序路径查询Ｑ（，）义为：基于序列ｇ的所ｑＭ定在
［，，ｔｔ起始位置坐标为（Ｙ）速度为（，）个数据］ ‰，ｏ，，
ｆｎｔｎｅｗｅａａｐｉｔｎｖｎ —ｕｒｒａｃｌｔｄｂＣ０ＳｌｏｔｍｏｄｔｒｎｈｉｒｌｔｅｄｓａｃｓｅｔｃｉｇｓａｃｕｃｉｓｂｔｅｎｄｔｏｎｓａｄｍｏｉｇｑｅａｅｃｌｕａｅｙＳｋＲａｇｒｈｔｅｅｍｉｅｔｅｒｅａｉｉｎｅ．ＲｓｒｔｅｒｈｏｙｉｖｔｉｎａｅｓｕｅｎＤＣＯＳｇｒｈｅｕｅｔｅｑａｔｙｏｏｎｓｉｃｕｅｎｔｅｃｍｐｔｔｎｏｄｉｖｌｉｈｅｅａｉｅｄｓａｃｎｔｎ．ｒａｓｄｉｋＲａｏｔｍｒｄｃｈｕｎｉｆｉｔｎｌｄｄｉｈｏｕａｉｆａｄｔｅｙｗｅｇｔｄｒｌｔｉｔｎｅｆｃｉｓｌｉｔｐｏｉｖｕｏＥｐｒｍｅｔｌｅｕｔｓｏｂｔｒｐｒｏｍａｃｆｔｅＤＣ０ＲａｇｒｈｘｅｉｎａｓｌｈｗｅｔｅｒｎｅｏｋＳｌｏｔｍ．ｒｓｅｆｈｉ
顺序下的最优路径的求解。对该类查询及其同类查询问题的研
∑ｄｍ，，ｐＰ表示之的小（，）ｐＰ其中ｄ）点Ｐ和Ｐ间最距（，
离。ｒ＝１时，）＝０。当（定义４给定路径Ｒ＝（Ｐ，，，，Ｐ为路径Ｒ的起Ｐ， … Ｐ）称。点，记作ＳＲ＝Ｐ。（）．
若已知Ｒ＝（１Ｐ，，，，Ｐ① Ｒ＝（，１Ｐ，，，为Ｐ，２ … Ｐ）则ＰＰ，２… Ｐ）
一
究目前已经取得了一定的成果，但都是针对静态查询对象和静态数据对象的情况提出的方法，且只能求得一个结果。并
，）称Ｒ＝（Ｐ，，，ｒ，Ｐ， … Ｐ）为一条路径，其长度为ＬＲ＝（）
最近邻查询就是其中的一种，是对跨越多个数据集的最优路径
的求解。最优有序路径ＯＲ（ｐｉａＳｑｅｃｄＲｕ）询是ＳＯｔｌｅｕｎｅｏｔ查ｍｅ多类型最近邻查询的特例，是对在多个数据集的某种固定排列
２，… ，）若１≤ Ｍｎ（Ｍ， ≤ ｉ＝１２ ‘ ，，Ｍ＝（，，，。ｍ）称。Ｍ１
０引言
最近邻查询是时空数据库研究的重点之一，它在许多领域
占据着重要的位置，如地理信息系统、多媒体应用以及数据挖掘等。随着研究的深入，最近邻查询出现了许多变体形式，多类型
２ … ，，称Ｒ为基于序列的有序路径。基于序列的所，ｍ）则将
ＳｋＳＣ０Ｒ算法和ＤｋＳＣＯＲ算法，最后通过实验对算法进行了性
能验证。
有有序路径的集合记作Ｃ。
定义６给定对象ｇ以及序列Ｍ＝（，，，）ＭＭ２ … Ｍ，
ｏｔｌｓｑｅｃｄｒｕｅｑｅｙｈＣ０ＲｎｋＲａｇｒｈｒｒｐｓｄｂｎｒｄｃｎｈｏｃｐｆｄｉｖｌｉｈｅｅａｉｅｐｉｅｕｎｅｏｔｕｒ．ＴｅＳｋＳａｄＤＣ０Ｓｏｉｍｓａｅｐｏｏｅｙｉｔｏｕｉｇｔｅｃｎｅｔｏｄｔｅｙｗｅｇｔｄｒｌｔｍａｌｔａｉｖ
Ｋｅｗｒｓｙｏｄ
ＣｎｉｕｕｐｉｌｅｕｎｅｕｅｕｒＡｄｔｅｅｈｄｒｌｉｉａｃｎｔｎＭｏｉｇｂｅｔＱｅｙｌｒｈｏｔｏｓｋｏｔｑｅｃｄｒｔｑｅｙｄｉｖｌｗｉｔａｖｄｓｎｅｆｃｏｖｊｃｎｍａｓｏｉｙｇｅｅｔｅｔｕｉｎｏｕｒａｏｉｍｇｔ
ＴＥＣＨＯＮＴＮＩＵＯＵＳＫＴＭＡＥＥＣＤＲＴＥＹＦＯＮＧＯＢＥＣＳＯＰＩＬＳＱＵＮＥＯＵＥＱＵＲＯＲＭＶＩＪＴ
ＳｎＤｏｇｕｎｐｕＨａｏｇａｏＺｈｎｘｉｏ ’
鉴于此，文提出了移动对象的连续ｋ最优有序路径Ｃ０Ｒ本ｋＳ（ｏｔｕｕＯｔｌＳｑｅｃｄＲｕｅ查询的概念，提出加Ｃｎｉｏｓｐｉｅｕｎｅｏｔ）ｎｍａ并
权相对距离ＡＤ（ｄｉｖｌＷｅｈｅｅｔｅＤｓｎｅ函数ＷＲＡｄｔｅｙｉｔＲｌｉｉａｃ）ｉｇｄａｖｔ
（ｏｅｅＣｍｕｒｃｅｃｎｅｈｏｏ）Ｈａｂｎｖｓｙ０ＳｉｃｎｅｈｏｏｙＨｒｉ１０８Ｈｅｏ￣ｉｎＣｉａＣｌｇｏｐｔｉｅａｄＴｃｎｌｇ，ｒｉＵｉｒｔｃｎｅａｄＴｃｎｌ，ａｂ５００，ｉｎａｇ，ｈｎ）ｌｅＳｎｎｅｉ厂ｅｇｎｌ。Ｃｌｇ厂ＣｍｕｒｃｎｅａｄＴｃｎｌｇ，ａｂｎＩｓｔｔｏＴｃｎｌｙＨａｂ５０１Ｈｉｎｆｎ，ｈｎ）（ｏｌｅＤｏｐｔｉｃｎｅｈｏｙＨｒｉｎｔｕｅ厂ｅｈｏｏ，ｒｉ１００，ｅｏｇａｇＣｉｅｅＳｅｏｉｇｎｌｉａ
孙冬璞郝忠孝
（哈尔滨理工大学计算机科学与技术学院（哈尔滨工业大学计算机科学与技术学院黑龙江哈尔滨１０８）５００黑龙江哈尔滨Ｉ００）５０１
摘
要
针对最优有序路径查询问题，出了移动对象的连续最优有序路径查询问题，针对移动查询对象和静态数据对象的提并
Ａｓａｔｂｔｃｒ
Ｔｅｃｎｅｔｆｏｔｕｕｐｉａｓｑｅｃｄｒｕｅｕｒｆｒｏｉｂｅｔｉｐｔｏｗｒｏｓｅｔｎｏｅｐｏｌｆｈｏｃｐｎｉｏｓｏｔｌｅｕｎｅｔｑｅｖｇｏｊｓｓｕｆａｄｉｃｎｉｒｉｆｈｒｂｅｏｏｃｎｋｍｏｙｏｍｎｃｒｎｄａｏｔｍ
条以Ｐ为起点的新的路径，路径是在Ｊ加入新的起点形该Ｒ上
成的。
定义５给定序列Ｍ＝（，，， ” Ｍ …
）若路径Ｒ：，
的概念，对移动查询对象和静态数据对象的情况给出针
（Ｐ，…，）Ｐ，２Ｐ满足序列肘，Ｒ中的每个点Ｐ ∈ ．ｉ，即，（＝１
集分别为Ｕ，，… ，，数据集包含ｍ（＝１２ … ，）且ｉ，，ｎ个点。了讨论方便，妨求ｑ于序列Ｍ：（。为不基，，… ，）（，，：１２ … ，）的连续ｋ优有序路径。：，，ｎ最
有有序路径中，找到这样一条有序路径Ｒ＝（Ｐ，… ，，Ｐ，Ｐ）使等式ＬｑＲ）＝ｄｑＰ）＋（取得最小值，中，（，（，（，ＬＲ）其ＬｑＲ）
表示有序路径Ｒ＝ｑ① Ｒ的长度，（ＬＲ）表示有序路径Ｒ的长
情况，通过引入加权相对距离函数的概念提出了ＳｋＳＣ０Ｒ算法和ＤｋＳＣＯＲ算法。ＳｋＳＣ０Ｒ算法利用加权相对距离函数确定数据点与