2018年普通高等学校招生全国统一考试最后一卷 文科数学含精品解析
2018年普通高等学校招生全国统一考试文科数学试题(内含详细答案)

绝密★启用前2018年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.作答时,将答案写在答题卡上。
写在本试卷及草稿纸上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
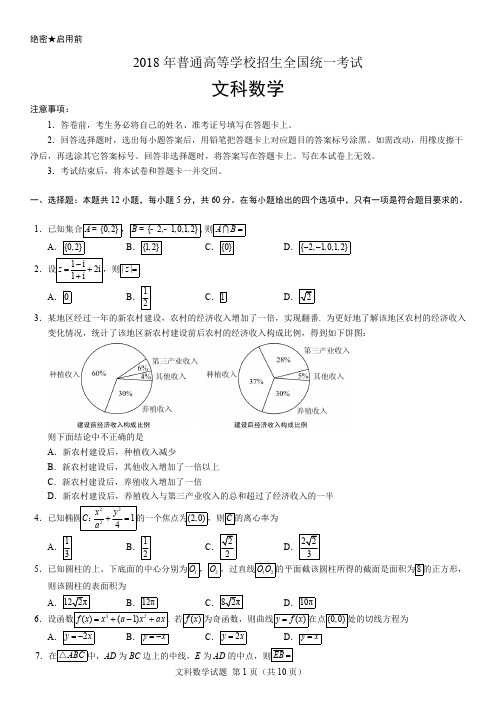
1.()i 23i += A .32i -B .32i +C .32i --D .32i -+2.已知集合{}1,3,5,7A =,{}2,3,4,5B =,则AB =A .{}3B .{}5C .{}3,5D .{}1,2,3,4,5,73.函数()2e e x xf x x --=的图像大致为4.已知向量a ,b 满足||1=a ,1⋅=-a b ,则(2)⋅-=a a b A .4B .3C .2D .05.从2名男同学和3名女同学中任选2人参加社区服务,则选中的2人都是女同学的概率为 A .0.6B .0.5C .0.4D .0.36.双曲线22221(0,0)x y a b a b-=>>A .y =B .y =C .y =D .y x =7.在ABC △中,cos 2C 1BC =,5AC =,则AB =A .BCD .8.为计算11111123499100S =-+-++-,设计了如图的程序框图,则在空白框中应填入A .1i i =+B .2i i =+C .3i i =+D .4i i =+9.在正方体1111ABCD A B C D -中,E 为棱1CC 的中点,则异面直线AE 与CD 所成角的正切值为 A .2B C D 10.若()cos sin f x x x =-在[0,]a 是减函数,则a 的最大值是A .π4B .π2C .3π4D .π11.已知1F ,2F是椭圆C 的两个焦点,P 是C 上的一点,若12PF PF ⊥,且2160PF F ∠=︒,则C 的离心率为 A .1B .2C D 112.已知()f x 是定义域为(,)-∞+∞的奇函数,满足(1)(1)f x f x -=+.若(1)2f =,则(1)(2)(3f f f++(50)f ++=A .50-B .0C .2D .50二、填空题:本题共4小题,每小题5分,共20分。
(完整版)2018年高考文科数学(全国I卷)试题及答案,推荐文档
2an n
,即 bn1
2bn
,又 b1
1 ,所以 {bn} 是首项为 1 ,公比为
2
的等比数列.
(3)由(2)可得
an n
2n1 ,所以 an
n 2n1 .
18.解:
(1)由已知可得, BAC 90 , BA AC .
又 BA AD ,所以 AB 平面 ACD .
又 AB 平面 ABC ,
文科数学试题 第 3 页(共 10 页)
19.(12 分)
某家庭记录了未使用节水龙头 50 天的日用水量数据(单位: m3 )和使用了节水龙头 50 天的日用水量数据, 得到频数分布表如下:
未使用节水龙头 50 天的日用水量频数分布表
日用水量 [0,0.1) [0.1,0.2 [0.2,0.3 [0.3,0.4 [0.4,0.5 [0.5,0.6 [0.6,0.7
2
2
(2)当 l 与 x 轴垂直时,AB 为 MN 的垂直平分线,所以 ABM ABN .
当 l 与 x 轴不垂直时,设 l 的方程为 y k(x 2) (k 0) , M (x1, y1) , N (x2 , y2 ) ,则 x1 0, x2 0 .
由
y k(x
y
2
2x
2),
得
ky 2
则 | a b |
1 A.
5
5 B.
5
25 C.
5
D. 1
12.设函数
f
(x)
2x ,
1,
x ≤ 0, 则满足 f (x 1) f (2x) 的 x 的取值范围是 x 0,
A. (, 1]
B. (0,)
C. (1, 0)
2018年高考真题文数全国卷Ⅲ 含解析 精品

绝密★启用前2018年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分.在每小题给的四个选项中,只有一项是符合题目要求的.1. 已知集合,,则A. B. C. D.【答案】C【解析】分析:由题意先解出集合A,进而得到结果。
详解:由集合A得,所以故答案选C.点睛:本题主要考查交集的运算,属于基础题。
2.A. B. C. D.【答案】D【解析】分析:由复数的乘法运算展开即可。
........................故选D.点睛:本题主要考查复数的四则运算,属于基础题。
3. 中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是A. AB. BC. CD. D【答案】A【解析】分析:观察图形可得。
详解:观擦图形图可知,俯视图为故答案为A.点睛:本题主要考擦空间几何体的三视图,考查学生的空间想象能力,属于基础题。
4. 若,则A. B. C. D.【答案】B【解析】分析:由公式可得。
详解:故答案为B.点睛:本题主要考查二倍角公式,属于基础题。
5. 若某群体中的成员只用现金支付的概率为0.45,既用现金支付也用非现金支付的概率为0.15,则不用现金支付的概率为A. 0.3B. 0.4C. 0.6D. 0.7【答案】B【解析】分析:由公式计算可得详解:设设事件A为只用现金支付,事件B为只用非现金支付,则因为所以故选B.点睛:本题主要考查事件的基本关系和概率的计算,属于基础题。
2018年数学真题及解析_2018年全国统一高考数学试卷(文科)(全国新课标ⅲ)

2018年云南省高考数学试卷(文科)(全国新课标Ⅲ)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5.00分)已知集合A={x|x﹣1≥0},B={0,1,2},则A∩B=()A.{0}B.{1}C.{1,2}D.{0,1,2}2.(5.00分)(1+i)(2﹣i)=()A.﹣3﹣i B.﹣3+i C.3﹣i D.3+i3.(5.00分)中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是()A. B. C. D.4.(5.00分)若sinα=,则cos2α=()A.B.C.﹣ D.﹣5.(5.00分)若某群体中的成员只用现金支付的概率为0.45,既用现金支付也用非现金支付的概率为0.15,则不用现金支付的概率为()A.0.3 B.0.4 C.0.6 D.0.76.(5.00分)函数f(x)=的最小正周期为()A.B.C.πD.2π7.(5.00分)下列函数中,其图象与函数y=lnx的图象关于直线x=1对称的是()A.y=ln(1﹣x)B.y=ln(2﹣x)C.y=ln(1+x) D.y=ln(2+x)8.(5.00分)直线x+y+2=0分别与x轴,y轴交于A,B两点,点P在圆(x﹣2)2+y2=2上,则△ABP面积的取值范围是()A.[2,6]B.[4,8]C.[,3]D.[2,3]9.(5.00分)函数y=﹣x4+x2+2的图象大致为()A.B.C.D.10.(5.00分)已知双曲线C:﹣=1(a>0,b>0)的离心率为,则点(4,0)到C的渐近线的距离为()A.B.2 C.D.211.(5.00分)△ABC的内角A,B,C的对边分别为a,b,c.若△ABC的面积为,则C=()A.B.C.D.12.(5.00分)设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且面积为9,则三棱锥D﹣ABC体积的最大值为()A.12B.18C.24D.54二、填空题:本题共4小题,每小题5分,共20分。
全国联考2018届高三最后一模数学(文科)卷

全国联考2018届高三最后一模数学(文科)本试题卷共6页,23题(含选考题)。
全卷满分150分。
考试用时120分钟。
★祝考试顺利★注意事项:1、答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。
2、选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3、填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4、选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑。
答案写在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
5、考试结束后,请将本试题卷和答题卡一并上交。
第I 卷 选择题(每题5分,共60分)本卷共12题,每题5分,共60分,在每题后面所给的四个选项中,只有一个是正确的。
1.已知集合{}{}212,0M x x N x x x =-<<=-4<,则M N ⋂= ( ) A .()0,4 B .()1,4- C .()1,2- D .()0,22.若复数z 满足iz=1+2i ,其中i 为虚数单位,则在复平面上复数z 对应的点的坐标为( ) A .(﹣2,﹣1) B .(﹣2,1) C .(2,1) D .(2,﹣1)3.设,则a ,b ,c 的大小关系为( )A .a >b >cB .a >c >bC .b >a >cD .c >b >a4.已知公差不为0的等差数列{a n }满足a 1,a 3,a 4成等比数列,S n 为数列{a n }的前n 项和,则的值为( )A .2B .3C .﹣2D .﹣35.将函数f (x )=sin2x+3cos2x 图象上所有点向右平移6π个单位长度,得到函数g (x )的图象,则g (x )图象的一个对称中心是( ) A .(3π,0) B .(4π,0) C .(12π-,0) D .(2π,0)6.设实数,x y满足301210x yy xx+-≤⎧⎪⎪-≥⎨⎪-≥⎪⎩,则y xux y=-的取值范围为()A.1,22⎡⎤⎢⎥⎣⎦B.2,23⎡⎤-⎢⎥⎣⎦C.23,32⎡⎤-⎢⎥⎣⎦D.33,22⎡⎤-⎢⎥⎣⎦7.程大位是明代著名数学家,他的《新编直指算法统宗》是中国历史上一部影响巨大的著作.它问世后不久便风行宇内,成为明清之际研习数学者必读的教材,而且传到朝鲜、日本及东南亚地区,对推动汉字文化圈的数学发展起了重要的作用.卷八中第33问是:“今有三角果一垛,底阔每面七个.问该若干?”如图是解决该问题的程序框图.执行该程序框图,求得该垛果子的总数S为()A.120 B.84 C.56 D.288.记集合A={(x,y)|x2+y2≤16},集合B={(x,y)|x+y﹣4≤0,(x,y)∈A}表示的平面区域分别为Ω1,Ω2.若在区域Ω1内任取一点P(x,y),则点P落在区域Ω2中的概率为()A.B.C.D.9.某几何体的三视图如图所示,其中俯视图中六边形ABCDEF是边长为1的正六边形,点G为AF的中点,则该几何体的外接球的表面积是()A. 316πB. 318πC. 48164π10.函数f (x )=x|x |ln 的图象大致形状是( )A .B .C .D .11.已知双曲线﹣=1(a >0,b >0)的左、右焦点分别为F 1、F 2,点P 在双曲线的右支上,且|PF 1|=4|PF 2|,则此双曲线的离心率e 的最大值为( )A .B .C .D .12.已知f (x )是定义在(0,+∞)上的非负可导函数,且满足xf'(x )+f (x )≤0,对任意的0<a <b ,则必有( )A.af(b)≤bf(a) B.bf(a)≤af(b) C.af(a)≤f(b)D.bf(b)≤f(a)第II卷非选择题(共90分)二.填空题(每题5分,共20分)13.已知向量45(2sin,cos)36aππ=,(),1b k=.若//a b,则k=.14.已知椭圆+=1(a>b>0)的左、右焦点分别为F1,F2,过F1且与x轴垂直的直线交椭圆于A、B两点,直线AF2与椭圆的另一个交点为C,若S△ABC=3S,则椭圆的离心率为.15.已知A,B是求O的球面上两点,且∠AOB=120°,C为球面上的动点,若三棱锥O﹣ABC体积的最大值为,则求O的表面积为.16.若函数f(x),g(x)满足:∀x∈(0,+∞),均有f(x)>x,g(x)<x成立,则称“f(x)与g(x)关于y=x分离”.已知函数f(x)=a x与g(x)=log a x(a>0,且a≠1)关于y=x分离,则a的取值范围是.三.解答题(共8题,共70分)17.(本题满分12分)在锐角△ABC中,角A,B,C的对边分别为a,b,c,向量,向量,且.(Ⅰ)求角B的大小;(Ⅱ)若sinAsinC=sin2B,求a﹣c的值.18.(本题满分12分)如图,三棱柱ABC﹣A1B1C1的所有棱长均相等,AA1⊥平面ABC,E为AA1的中点.(1)求证:平面BC1E⊥平面BCC1B1;(2)求直线BC1与平面BB1A1A所成角的正弦值.19.(本题满分12分)交强险是车主必须为机动车购买的险种.若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为a元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如表:某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:(Ⅰ)求一辆普通6座以下私家车在第四年续保时保费高于基本保费的频率;(Ⅱ)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元,且各种投保类型车的频率与上述机构调查的频率一致,完成下列问题:①若该销售商店内有六辆(车龄已满三年)该品牌二手车,某顾客欲在店内随机挑选两辆车,求这两辆车中恰好有一辆为事故车的概率;②若该销售商一次购进120辆(车龄已满三年)该品牌二手车,求一辆车盈利的平均值.20.(本题满分12分)如图,在平面直角坐标系xOy 中,已知椭圆C :22a x +22by =1(a >b >0)的离心率e= 23,在顶点为A (﹣2,0),过点A 作斜率为k (k≠0)的直线l 交椭圆C 于点D ,交y 轴于点E . (1)求椭圆C 的方程;(2)已知点P为AD的中点,是否存在定点Q,对于任意的k(k≠0)都有OP⊥EQ?若存在,求出点Q的坐标,若不存在,说明理由;(3)若过点O作直线l的平行线交椭圆C于点M,求|OM||AE||AD|的最小值.21.(本题满分12分)已知函数.(1)当a=﹣1时,求函数f(x)的单调增区间;(2)若函数f(x)在(0,+∞)上是增函数,求实数a的取值范围;(3)若a>0,且对任意x1,x2∈(0,+∞),x1≠x2,都有|f(x1)﹣f(x2)|>2|x1﹣x2|,求实数a的最小值.选做题请考生从22、23题中任选一题作答,共10分。
2018年全国统一高考数学试卷(文科)(新课标ⅰ)(含解析版)

2018年全国统一高考数学试卷(文科)(全国新课标Ⅰ)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)已知集合A={0,2},B={﹣2,﹣1,0,1,2},则A∩B=()A.{0,2}B.{1,2}C.{0}D.{﹣2,﹣1,0,1,2}2.(5分)设z=+2i,则|z|=()A.0B.C.1D.3.(5分)某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:则下面结论中不正确的是()A.新农村建设后,种植收入减少B.新农村建设后,其他收入增加了一倍以上C.新农村建设后,养殖收入增加了一倍D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半4.(5分)已知椭圆C:+=1的一个焦点为(2,0),则C的离心率为()A.B.C.D.5.(5分)已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为()A.12πB.12πC.8πD.10π6.(5分)设函数f(x)=x3+(a﹣1)x2+ax.若f(x)为奇函数,则曲线y=f(x)在点(0,0)处的切线方程为()A.y=﹣2x B.y=﹣x C.y=2x D.y=x7.(5分)在△ABC中,AD为BC边上的中线,E为AD的中点,则=()A.﹣B.﹣C.+D.+8.(5分)已知函数f(x)=2cos2x﹣sin2x+2,则()A.f(x)的最小正周期为π,最大值为3B.f(x)的最小正周期为π,最大值为4C.f(x)的最小正周期为2π,最大值为3D.f(x)的最小正周期为2π,最大值为49.(5分)某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M 在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为()A.2B.2C.3D.210.(5分)在长方体ABCD﹣A1B1C1D1中,AB=BC=2,AC1与平面BB1C1C所成的角为30°,则该长方体的体积为()A.8B.6C.8D.811.(5分)已知角α的顶点为坐标原点,始边与x轴的非负半轴重合,终边上有两点A(1,a),B(2,b),且cos2α=,则|a﹣b|=()A.B.C.D.112.(5分)设函数f(x)=,则满足f(x+1)<f(2x)的x的取值范围是()A.(﹣∞,﹣1]B.(0,+∞)C.(﹣1,0)D.(﹣∞,0)二、填空题:本题共4小题,每小题5分,共20分。
2018年全国普通高等学校招生统一考试文科数学(新课标III卷)(解析版)详细答案

绝密★启用前2018年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
学@科网一、选择题:本题共12小题,每小题5分,共60分.在每小题给的四个选项中,只有一项是符合题目要求的.1.A. B. C. D.【答案】C【解析】分析:由题意先解出集合A,进而得到结果。
详解:由集合A故答案选C.点睛:本题主要考查交集的运算,属于基础题。
2.C.【答案】D【解析】分析:由复数的乘法运算展开即可。
详解:故选D.点睛:本题主要考查复数的四则运算,属于基础题。
3. 中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是A. AB. BC. CD. D【答案】A【解析】分析:观察图形可得。
详解:观擦图形图可知,俯视图为故答案为A.点睛:本题主要考擦空间几何体的三视图,考查学生的空间想象能力,属于基础题。
4.B. D.【答案】B故答案为B.点睛:本题主要考查二倍角公式,属于基础题。
5. 若某群体中的成员只用现金支付的概率为0.45,既用现金支付也用非现金支付的概率为0.15,则不用现金支付的概率为A. 0.3B. 0.4C. 0.6D. 0.7【答案】B详解:设设事件A为只用现金支付,事件B为只用非现金支付,故选B.点睛:本题主要考查事件的基本关系和概率的计算,属于基础题。
6.B. C.【答案】C【解析】分析:的最小正周期故选C.点睛:本题主要考查三角函数的化简和最小正周期公式,属于中档题7.【答案】B1,0)关于x=1对称点,代入选项验证即可。
2018年全国高中高考文科数学试卷试题及答案解析全国卷

文科数学注意事项:1.答题前,考生务势必自己的姓名、准考据号填写在答题卡上。
2.回答选择题时,选出每题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需变动,用橡皮擦洁净后,再选涂其余答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每题5分,共60分。
在每题给出的四个选项中,只有一项为哪一项切合题目要求的。
1.已知会合A={1,2,3,4},B={2,4,6,8},则AIB中元素的个数为A.1B.2C.3D.42.复平面内表示复数z i(2 i)的点位于A.第一象限B.第二象限C.第三象限D.第四象限3.某城市为认识旅客人数的变化规律,提升旅行服务质量,采集并整理了2014年1月至2016年12月时期月招待旅客量(单位:万人)的数据,绘制了下边的折线图.依据该折线图,以下结论错误的选项是A.月招待旅客逐月增添B.年招待旅客量逐年增添C.各年的月招待旅客量顶峰期大概在7,8月D.各年1月至6月的月招待旅客量相关于7月至12月,颠簸性更小,变化比较安稳4.已知sincos 4=,则sin23A.7B.2C.2D.7 99993x 2y6 05.设x,y 知足拘束条件x 0 ,则zxy 的取值范围是yA .[-3,0]B .[-3,2]C .[0,2]D .[0,3]6.函数f(x)1sin(x) cos(x)的最大值为A .6536C .3D .1B .17.函数A . C .5 55sinx y1xx 2的部分图像大概为B . D .8.履行右边的程序框图,为使输出 S 的值小于 91,则输入的正 整数N 的最小值为A .5B .4C .3D .29.已知圆柱的高为 1,它的两个底面的圆周在直径为 2的同一个球的球面上,则该圆柱的体积为A .B .C .D .3 42410.在正方体 ABCD A 1B 1C 1D 1中,E 为棱CD 的中点,则A.A1E⊥DC1B.A1E⊥BD C.A1E⊥BC1D.A1E⊥AC x2y21(a b0)的左、右极点分别为A1,A2,且以线段A1A2为直径11.已知椭圆C:2b2a的圆与直线bx ay2ab0相切,则C的离心率为A.6B.3C.2D.1 3333 12.已知函数f(x)x22x a(e x1e x1)有独一零点,则a= 11C.A.B.23二、填空题:此题共4小题,每题5分,共20分。
2018年高考文科数学试卷及详解答案

如图,P是⊙O外一点,PA是切线,A为切点,割线PBC与⊙O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交⊙O于点E,证明:Zzz6ZB2Ltk
<I)BE=EC;
<II)AD·DE=2PB2。
【解读】
<1)
<2)
(23)<本小题满分10分)选修4-4:坐标系与参数方程
【答案】 3
【解读】
<16)数列 满足 = , =2,则 =_________.
【答案】
【解读】
(7)解答题:解答应写出文字说明过程或演算步骤。
(15)<本小题满分12分)
四边形ABCD的内角A与C互补,AB=1,BC=3, CD=DA=2.
(I>求C和BD;
(II>求四边形ABCD的面积。
【答案】 (1> (2>
3.回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
<1)已知集合A=﹛-2,0,2﹜,B=﹛ | - - ﹜,则A B=
(A> <B) <C) (D>
【答案】B
所以,市民对甲、乙部门的评分大于90的概率分别为0.1,0.16
(20)<本小题满分12分)
设F1 ,F2分别是椭圆C: <a>b>0)的左,右焦点,M是C上一点且MF2与x轴垂直,直线MF1与C的另一个交点为N。LDAYtRyKfE
<I)若直线MN的斜率为 ,求C的离心率;
2018年高考真题——文科数学(全国卷Ⅰ)+Word版含解析

绝密★启用前2018年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知集合,,则A. B. C. D.【答案】A【解析】分析:利用集合的交集中元素的特征,结合题中所给的集合中的元素,求得集合中的元素,最后求得结果.详解:根据集合交集中元素的特征,可以求得,故选A.点睛:该题考查的是有关集合的运算的问题,在解题的过程中,需要明确交集中元素的特征,从而求得结果.2. 设,则A. 0B.C.D.【答案】C【解析】分析:首先根据复数的运算法则,将其化简得到,根据复数模的公式,得到,从而选出正确结果.详解:因为,所以,故选C.点睛:该题考查的是有关复数的运算以及复数模的概念及求解公式,利用复数的除法及加法运算法则求得结果,属于简单题目.3. 某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:则下面结论中不正确的是A. 新农村建设后,种植收入减少B. 新农村建设后,其他收入增加了一倍以上C. 新农村建设后,养殖收入增加了一倍D. 新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半【答案】A【解析】分析:首先设出新农村建设前的经济收入为M,根据题意,得到新农村建设后的经济收入为2M,之后从图中各项收入所占的比例,得到其对应的收入是多少,从而可以比较其大小,并且得到其相应的关系,从而得出正确的选项.详解:设新农村建设前的收入为M,而新农村建设后的收入为2M,则新农村建设前种植收入为0.6M,而新农村建设后的种植收入为0.74M,所以种植收入增加了,所以A项不正确;新农村建设前其他收入我0.04M,新农村建设后其他收入为0.1M,故增加了一倍以上,所以B项正确;新农村建设前,养殖收入为0.3M,新农村建设后为0.6M,所以增加了一倍,所以C项正确;新农村建设后,养殖收入与第三产业收入的综合占经济收入的,所以超过了经济收入的一半,所以D正确;故选A.点睛:该题考查的是有关新农村建设前后的经济收入的构成比例的饼形图,要会从图中读出相应的信息即可得结果.4. 已知椭圆:的一个焦点为,则的离心率为A. B. C. D.【答案】C【解析】分析:首先根据题中所给的条件椭圆的一个焦点为,从而求得,再根据题中所给的方程中系数,可以得到,利用椭圆中对应的关系,求得,最后利用椭圆离心率的公式求得结果.详解:根据题意,可知,因为,所以,即,所以椭圆的离心率为,故选C.点睛:该题考查的是有关椭圆的离心率的问题,在求解的过程中,一定要注意离心率的公式,再者就是要学会从题的条件中判断与之相关的量,结合椭圆中的关系求得结果.5. 已知圆柱的上、下底面的中心分别为,,过直线的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为A.B.C.D.【答案】B【解析】分析:首先根据正方形的面积求得正方形的边长,从而进一步确定圆柱的底面圆半径与圆柱的高,从而利用相关公式求得圆柱的表面积. 详解:根据题意,可得截面是边长为的正方形,结合圆柱的特征,可知该圆柱的底面为半径是的圆,且高为,所以其表面积为,故选B.点睛:该题考查的是有关圆柱的表面积的求解问题,在解题的过程中,需要利用题的条件确定圆柱的相关量,即圆柱的底面圆的半径以及圆柱的高,在求圆柱的表面积的时候,一定要注意是两个底面圆与侧面积的和. 6. 设函数.若为奇函数,则曲线在点处的切线方程为A.B.C.D.【答案】D【解析】分析:利用奇函数偶此项系数为零求得,进而得到的解析式,再对求导得出切线的斜率,进而求得切线方程.详解:因为函数是奇函数,所以,解得,所以,,所以,所以曲线在点处的切线方程为,化简可得,故选D.点睛:该题考查的是有关曲线在某个点处的切线方程的问题,在求解的过程中,首先需要确定函数解析式,此时利用到结论多项式函数中,奇函数不存在偶次项,偶函数不存在奇次项,从而求得相应的参数值,之后利用求导公式求得,借助于导数的几何意义,结合直线方程的点斜式求得结果.7. 在△中,为边上的中线,为的中点,则A. B.C. D.【答案】A【解析】分析:首先将图画出来,接着应用三角形中线向量的特征,求得,之后应用向量的加法运算法则-------三角形法则,得到,之后将其合并,得到,下一步应用相反向量,求得,从而求得结果.详解:根据向量的运算法则,可得,所以,故选A.点睛:该题考查的是有关平面向量基本定理的有关问题,涉及到的知识点有三角形的中线向量、向量加法的三角形法则、共线向量的表示以及相反向量的问题,在解题的过程中,需要认真对待每一步运算.8. 已知函数,则A. 的最小正周期为π,最大值为3B. 的最小正周期为π,最大值为4C. 的最小正周期为,最大值为3D. 的最小正周期为,最大值为4【答案】B【解析】分析:首先利用余弦的倍角公式,对函数解析式进行化简,将解析式化简为,之后应用余弦型函数的性质得到相关的量,从而得到正确选项.详解:根据题意有,所以函数的最小正周期为,且最大值为,故选B.点睛:该题考查的是有关化简三角函数解析式,并且通过余弦型函数的相关性质得到函数的性质,在解题的过程中,要注意应用余弦倍角公式将式子降次升角,得到最简结果.9. 某圆柱的高为2,底面周长为16,其三视图如右图.圆柱表面上的点在正视图上的对应点为,圆柱表面上的点在左视图上的对应点为,则在此圆柱侧面上,从到的路径中,最短路径的长度为A. B.C. D. 2【答案】B【解析】分析:首先根据题中所给的三视图,得到点M和点N在圆柱上所处的位置,点M在上底面上,点N在下底面上,并且将圆柱的侧面展开图平铺,点M、N在其四分之一的矩形的对角线的端点处,根据平面上两点间直线段最短,利用勾股定理,求得结果.详解:根据圆柱的三视图以及其本身的特征,可以确定点M和点N分别在以圆柱的高为长方形的宽,圆柱底面圆周长的四分之一为长的长方形的对角线的端点处,所以所求的最短路径的长度为,故选B.点睛:该题考查的是有关几何体的表面上两点之间的最短距离的求解问题,在解题的过程中,需要明确两个点在几何体上所处的位置,再利用平面上两点间直线段最短,所以处理方法就是将面切开平铺,利用平面图形的相关特征求得结果.10. 在长方体中,,与平面所成的角为,则该长方体的体积为A. B. C. D.【答案】C【解析】分析:首先画出长方体,利用题中条件,得到,根据,求得,可以确定,之后利用长方体的体积公式详解:在长方体中,连接,根据线面角的定义可知,因为,所以,从而求得,所以该长方体的体积为,故选C.点睛:该题考查的是长方体的体积的求解问题,在解题的过程中,需要明确长方体的体积公式为长宽高的乘积,而题中的条件只有两个值,所以利用题中的条件求解另一条边的长久显得尤为重要,此时就需要明确线面角的定义,从而得到量之间的关系,从而求得结果.11. 已知角的顶点为坐标原点,始边与轴的非负半轴重合,终边上有两点,,且,则A. B. C. D.【答案】B【解析】分析:首先根据两点都在角的终边上,得到,利用,利用倍角公式以及余弦函数的定义式,求得,从而得到,再结合,从而得到,从而确定选项.详解:根据题的条件,可知三点共线,从而得到,因为,解得,即,所以,故选B.点睛:该题考查的是有关角的终边上点的纵坐标的差值的问题,涉及到的知识点有共线的点的坐标的关系,余弦的倍角公式,余弦函数的定义式,根据题中的条件,得到相应的等量关系式,从而求得结果.12. 设函数,则满足的x的取值范围是A. B. C. D.【答案】D【解析】分析:首先根据题中所给的函数解析式,将函数图像画出来,从图中可以发现若有成立,一定会有,从而求得结果.详解:将函数的图像画出来,观察图像可知会有,解得,所以满足的x的取值范围是,故选D.点睛:该题考查的是有关通过函数值的大小来推断自变量的大小关系,从而求得相关的参数的值的问题,在求解的过程中,需要利用函数解析式画出函数图像,从而得到要出现函数值的大小,绝对不是常函数,从而确定出自变量的所处的位置,结合函数值的大小,确定出自变量的大小,从而得到其等价的不等式组,从而求得结果.二、填空题(本题共4小题,每小题5分,共20分)13. 已知函数,若,则________.【答案】-7【解析】分析:首先利用题的条件,将其代入解析式,得到,从而得到,从而求得,得到答案.详解:根据题意有,可得,所以,故答案是.点睛:该题考查的是有关已知某个自变量对应函数值的大小,来确定有关参数值的问题,在求解的过程中,需要将自变量代入函数解析式,求解即可得结果,属于基础题目.14. 若满足约束条件,则的最大值为________.【答案】6【解析】分析:首先根据题中所给的约束条件,画出相应的可行域,再将目标函数化成斜截式,之后在图中画出直线,在上下移动的过程中,结合的几何意义,可以发现直线过B点时取得最大值,联立方程组,求得点B的坐标代入目标函数解析式,求得最大值.详解:根据题中所给的约束条件,画出其对应的可行域,如图所示:由可得,画出直线,将其上下移动,结合的几何意义,可知当直线过点B时,z取得最大值,由,解得,此时,故答案为6.点睛:该题考查的是有关线性规划的问题,在求解的过程中,首先需要正确画出约束条件对应的可行域,之后根据目标函数的形式,判断z的几何意义,之后画出一条直线,上下平移,判断哪个点是最优解,从而联立方程组,求得最优解的坐标,代入求值,要明确目标函数的形式大体上有三种:斜率型、截距型、距离型;根据不同的形式,应用相应的方法求解.15. 直线与圆交于两点,则________.【答案】【解析】分析:首先将圆的一般方程转化为标准方程,得到圆心坐标和圆的半径的大小,之后应用点到直线的距离求得弦心距,借助于圆中特殊三角形半弦长、弦心距和圆的半径构成直角三角形,利用勾股定理求得弦长.详解:根据题意,圆的方程可化为,所以圆的圆心为,且半径是2,根据点到直线的距离公式可以求得,结合圆中的特殊三角形,可知,故答案为.点睛:该题考查的是有关直线被圆截得的弦长问题,在解题的过程中,熟练应用圆中的特殊三角形半弦长、弦心距和圆的半径构成的直角三角形,借助于勾股定理求得结果.16. △的内角的对边分别为,已知,,则△的面积为________.【答案】【解析】分析:首先利用正弦定理将题中的式子化为,化简求得,利用余弦定理,结合题中的条件,可以得到,可以断定A为锐角,从而求得,进一步求得,利用三角形面积公式求得结果.详解:根据题意,结合正弦定理可得,即,结合余弦定理可得,所以A为锐角,且,从而求得,所以△的面积为,故答案是.点睛:该题考查的是三角形面积的求解问题,在解题的过程中,注意对正余弦定理的熟练应用,以及通过隐含条件确定角为锐角,借助于余弦定理求得,利用面积公式求得结果.三、解答题:共70分。
2018年高考真题——文科数学(全国卷Ⅰ)+Word版含解析

绝密★启用前2018年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知集合,,则A. B. C. D.【答案】A【解析】分析:利用集合的交集中元素的特征,结合题中所给的集合中的元素,求得集合中的元素,最后求得结果.详解:根据集合交集中元素的特征,可以求得,故选A.点睛:该题考查的是有关集合的运算的问题,在解题的过程中,需要明确交集中元素的特征,从而求得结果.2. 设,则A. 0B.C.D.【答案】C【解析】分析:首先根据复数的运算法则,将其化简得到,根据复数模的公式,得到,从而选出正确结果.详解:因为,所以,故选C.点睛:该题考查的是有关复数的运算以及复数模的概念及求解公式,利用复数的除法及加法运算法则求得结果,属于简单题目.3. 某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:则下面结论中不正确的是A. 新农村建设后,种植收入减少B. 新农村建设后,其他收入增加了一倍以上C. 新农村建设后,养殖收入增加了一倍D. 新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半【答案】A【解析】分析:首先设出新农村建设前的经济收入为M,根据题意,得到新农村建设后的经济收入为2M,之后从图中各项收入所占的比例,得到其对应的收入是多少,从而可以比较其大小,并且得到其相应的关系,从而得出正确的选项.详解:设新农村建设前的收入为M,而新农村建设后的收入为2M,则新农村建设前种植收入为0.6M,而新农村建设后的种植收入为0.74M,所以种植收入增加了,所以A项不正确;新农村建设前其他收入我0.04M,新农村建设后其他收入为0.1M,故增加了一倍以上,所以B项正确;新农村建设前,养殖收入为0.3M,新农村建设后为0.6M,所以增加了一倍,所以C项正确;新农村建设后,养殖收入与第三产业收入的综合占经济收入的,所以超过了经济收入的一半,所以D正确;故选A.点睛:该题考查的是有关新农村建设前后的经济收入的构成比例的饼形图,要会从图中读出相应的信息即可得结果.4. 已知椭圆:的一个焦点为,则的离心率为A. B. C. D.【答案】C【解析】分析:首先根据题中所给的条件椭圆的一个焦点为,从而求得,再根据题中所给的方程中系数,可以得到,利用椭圆中对应的关系,求得,最后利用椭圆离心率的公式求得结果.详解:根据题意,可知,因为,所以,即,所以椭圆的离心率为,故选C.点睛:该题考查的是有关椭圆的离心率的问题,在求解的过程中,一定要注意离心率的公式,再者就是要学会从题的条件中判断与之相关的量,结合椭圆中的关系求得结果.5. 已知圆柱的上、下底面的中心分别为,,过直线的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为A.B.C.D.【答案】B【解析】分析:首先根据正方形的面积求得正方形的边长,从而进一步确定圆柱的底面圆半径与圆柱的高,从而利用相关公式求得圆柱的表面积. 详解:根据题意,可得截面是边长为的正方形,结合圆柱的特征,可知该圆柱的底面为半径是的圆,且高为,所以其表面积为,故选B.点睛:该题考查的是有关圆柱的表面积的求解问题,在解题的过程中,需要利用题的条件确定圆柱的相关量,即圆柱的底面圆的半径以及圆柱的高,在求圆柱的表面积的时候,一定要注意是两个底面圆与侧面积的和. 6. 设函数.若为奇函数,则曲线在点处的切线方程为A.B.C.D.【答案】D【解析】分析:利用奇函数偶此项系数为零求得,进而得到的解析式,再对求导得出切线的斜率,进而求得切线方程.详解:因为函数是奇函数,所以,解得,所以,,所以,所以曲线在点处的切线方程为,化简可得,故选D.点睛:该题考查的是有关曲线在某个点处的切线方程的问题,在求解的过程中,首先需要确定函数解析式,此时利用到结论多项式函数中,奇函数不存在偶次项,偶函数不存在奇次项,从而求得相应的参数值,之后利用求导公式求得,借助于导数的几何意义,结合直线方程的点斜式求得结果.7. 在△中,为边上的中线,为的中点,则A. B.C. D.【答案】A【解析】分析:首先将图画出来,接着应用三角形中线向量的特征,求得,之后应用向量的加法运算法则-------三角形法则,得到,之后将其合并,得到,下一步应用相反向量,求得,从而求得结果.详解:根据向量的运算法则,可得,所以,故选A.点睛:该题考查的是有关平面向量基本定理的有关问题,涉及到的知识点有三角形的中线向量、向量加法的三角形法则、共线向量的表示以及相反向量的问题,在解题的过程中,需要认真对待每一步运算.8. 已知函数,则A. 的最小正周期为π,最大值为3B. 的最小正周期为π,最大值为4C. 的最小正周期为,最大值为3D. 的最小正周期为,最大值为4【答案】B【解析】分析:首先利用余弦的倍角公式,对函数解析式进行化简,将解析式化简为,之后应用余弦型函数的性质得到相关的量,从而得到正确选项.详解:根据题意有,所以函数的最小正周期为,且最大值为,故选B.点睛:该题考查的是有关化简三角函数解析式,并且通过余弦型函数的相关性质得到函数的性质,在解题的过程中,要注意应用余弦倍角公式将式子降次升角,得到最简结果.9. 某圆柱的高为2,底面周长为16,其三视图如右图.圆柱表面上的点在正视图上的对应点为,圆柱表面上的点在左视图上的对应点为,则在此圆柱侧面上,从到的路径中,最短路径的长度为A. B.C. D. 2【答案】B【解析】分析:首先根据题中所给的三视图,得到点M和点N在圆柱上所处的位置,点M在上底面上,点N在下底面上,并且将圆柱的侧面展开图平铺,点M、N在其四分之一的矩形的对角线的端点处,根据平面上两点间直线段最短,利用勾股定理,求得结果.详解:根据圆柱的三视图以及其本身的特征,可以确定点M和点N分别在以圆柱的高为长方形的宽,圆柱底面圆周长的四分之一为长的长方形的对角线的端点处,所以所求的最短路径的长度为,故选B.点睛:该题考查的是有关几何体的表面上两点之间的最短距离的求解问题,在解题的过程中,需要明确两个点在几何体上所处的位置,再利用平面上两点间直线段最短,所以处理方法就是将面切开平铺,利用平面图形的相关特征求得结果.10. 在长方体中,,与平面所成的角为,则该长方体的体积为A. B. C. D.【答案】C【解析】分析:首先画出长方体,利用题中条件,得到,根据,求得,可以确定,之后利用长方体的体积公式详解:在长方体中,连接,根据线面角的定义可知,因为,所以,从而求得,所以该长方体的体积为,故选C.点睛:该题考查的是长方体的体积的求解问题,在解题的过程中,需要明确长方体的体积公式为长宽高的乘积,而题中的条件只有两个值,所以利用题中的条件求解另一条边的长久显得尤为重要,此时就需要明确线面角的定义,从而得到量之间的关系,从而求得结果.11. 已知角的顶点为坐标原点,始边与轴的非负半轴重合,终边上有两点,,且,则A. B. C. D.【答案】B【解析】分析:首先根据两点都在角的终边上,得到,利用,利用倍角公式以及余弦函数的定义式,求得,从而得到,再结合,从而得到,从而确定选项.详解:根据题的条件,可知三点共线,从而得到,因为,解得,即,所以,故选B.点睛:该题考查的是有关角的终边上点的纵坐标的差值的问题,涉及到的知识点有共线的点的坐标的关系,余弦的倍角公式,余弦函数的定义式,根据题中的条件,得到相应的等量关系式,从而求得结果.12. 设函数,则满足的x的取值范围是A. B. C. D.【答案】D【解析】分析:首先根据题中所给的函数解析式,将函数图像画出来,从图中可以发现若有成立,一定会有,从而求得结果.详解:将函数的图像画出来,观察图像可知会有,解得,所以满足的x的取值范围是,故选D.点睛:该题考查的是有关通过函数值的大小来推断自变量的大小关系,从而求得相关的参数的值的问题,在求解的过程中,需要利用函数解析式画出函数图像,从而得到要出现函数值的大小,绝对不是常函数,从而确定出自变量的所处的位置,结合函数值的大小,确定出自变量的大小,从而得到其等价的不等式组,从而求得结果.二、填空题(本题共4小题,每小题5分,共20分)13. 已知函数,若,则________.【答案】-7【解析】分析:首先利用题的条件,将其代入解析式,得到,从而得到,从而求得,得到答案.详解:根据题意有,可得,所以,故答案是.点睛:该题考查的是有关已知某个自变量对应函数值的大小,来确定有关参数值的问题,在求解的过程中,需要将自变量代入函数解析式,求解即可得结果,属于基础题目.14. 若满足约束条件,则的最大值为________.【答案】6【解析】分析:首先根据题中所给的约束条件,画出相应的可行域,再将目标函数化成斜截式,之后在图中画出直线,在上下移动的过程中,结合的几何意义,可以发现直线过B点时取得最大值,联立方程组,求得点B的坐标代入目标函数解析式,求得最大值.详解:根据题中所给的约束条件,画出其对应的可行域,如图所示:由可得,画出直线,将其上下移动,结合的几何意义,可知当直线过点B时,z取得最大值,由,解得,此时,故答案为6.点睛:该题考查的是有关线性规划的问题,在求解的过程中,首先需要正确画出约束条件对应的可行域,之后根据目标函数的形式,判断z的几何意义,之后画出一条直线,上下平移,判断哪个点是最优解,从而联立方程组,求得最优解的坐标,代入求值,要明确目标函数的形式大体上有三种:斜率型、截距型、距离型;根据不同的形式,应用相应的方法求解.15. 直线与圆交于两点,则________.【答案】【解析】分析:首先将圆的一般方程转化为标准方程,得到圆心坐标和圆的半径的大小,之后应用点到直线的距离求得弦心距,借助于圆中特殊三角形半弦长、弦心距和圆的半径构成直角三角形,利用勾股定理求得弦长.详解:根据题意,圆的方程可化为,所以圆的圆心为,且半径是2,根据点到直线的距离公式可以求得,结合圆中的特殊三角形,可知,故答案为.点睛:该题考查的是有关直线被圆截得的弦长问题,在解题的过程中,熟练应用圆中的特殊三角形半弦长、弦心距和圆的半径构成的直角三角形,借助于勾股定理求得结果.16. △的内角的对边分别为,已知,,则△的面积为________.【答案】【解析】分析:首先利用正弦定理将题中的式子化为,化简求得,利用余弦定理,结合题中的条件,可以得到,可以断定A为锐角,从而求得,进一步求得,利用三角形面积公式求得结果.详解:根据题意,结合正弦定理可得,即,结合余弦定理可得,所以A为锐角,且,从而求得,所以△的面积为,故答案是.点睛:该题考查的是三角形面积的求解问题,在解题的过程中,注意对正余弦定理的熟练应用,以及通过隐含条件确定角为锐角,借助于余弦定理求得,利用面积公式求得结果.三、解答题:共70分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绝密 ★ 启用前2018年普通高等学校招生全国统一考试最后一卷文 科 数 学注意事项:1、本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答题前,考生务必将自己的姓名、考生号填写在答题卡上。
2、回答第Ⅰ卷时,选出每小题的答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在试卷上无效。
3、回答第Ⅱ卷时,将答案填写在答题卡上,写在试卷上无效。
4、考试结束,将本试卷和答题卡一并交回。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知a ∈R ,ia 的值为( ) A .1- B .0C .1D .2【答案】C【解析】则10a -=,即1a =,故选C . 2,则sin 2a 的值为()ABC.9D.9【答案】A【解析】 又因为sin 0α<,所以A . 3.某高校调查了320名学生每周的自习时间(单位:小时),制成了下图所示的频率分布直方图,其中自习时间的范围是[]17530.,,样本数据分组为[]17520.,,(]20225,.,(]22525.,,(]25275,.,(]27530.,.根据直方图,这320名学生中每周的自习时间不足225.小时的人数是( ) A .68 B .72C .76D .80【答案】B【解析】由频率分布直方图可得,320名学生中每周的自习时间不足225.小时的人数是()3200020072572⨯+⨯=...人.选B .4.正方形ABCD 中,点E ,F 分别是DC ,BC 的中点,那么EF =( )A .11+22AB ADB .1122AB AD --C .1122AB AD -+D .1122AB AD - 【答案】 D【解析】因为点E 是CD 的中点,所以12EC AB =,点F 是BC 的中点,所以1122CF CB AD ==-, 所以1122EF EC CF AB AD =+=-,故选D . 5.已知双曲线()222210,0x ya b a b-=>>F ,过点F 与x 轴垂直的直线与双曲线的两条渐近线分别交于点M ,N ,若O M N △的面积为20,其中O 是坐标原点,则该双曲线的标准方程为( )A .22128x y -=B .22148x y -=C .22182x y -=D .22184x y -=此卷只装订不密封班级 姓名 准考证号 考场号 座位号【答案】A 【解析】由c a=225c a =,∴2225a b a +=,故224ba =.∴双曲线的渐近线方程为2y x =±,由题意得(),2M c c -,(),2N c c --, ∴14202OMN S c c =⋅⋅=△,解得210c =,∴22a =,28b =, ∴双曲线的方程为22128x y -=.选A . 6.某空间几何体的三视图如图所示,则该几何体的体积为( )A .42π+B .26π+C .4π+D .24π+【答案】D【解析】由三视图可得,该几何体是一个三棱柱与一个圆柱的组合体(如图所示), 其体积2π21224πV =⨯+⨯=+.7.执行如下图的程序框图,若输入a 的值为2,则输出S 的值为( )A .3.2B .3.6C .3.9D .4.9【答案】C【解析】运行框图中的程序可得 ①1k =,2122S =+=,不满足条件,继续运行; ②2k =,282=33S =+,不满足条件,继续运行; ③3k =,8219+=346S =,不满足条件,继续运行; ④4k =,1921076530S =+=,不满足条件,继续运行; ⑤=5k ,1072117=+==3930630S .,满足条件,停止运行,输出=39S ..选C . 8.函数3y =)A .B .C .D .【答案】A【解析】由题意,函数满足()()33x f x f x --===-,所以函数()f x 为奇函数,图象关于原点对称,排除C ,又由102f ⎛⎫<⎪⎝⎭且()20f >,排除B 、D ,故选A . 9.已知函数()()πcos 20,2f x x ωϕωϕ⎛⎫=+><⎪⎝⎭的最小正周期为π,将其图象向右平移π6个单位后得函数()cos2g x x =的图象,则函数()f x 的图象( )A .关于直线2π3x =对称 B .关于直线π6x =对称 C .关于点2π03⎛⎫- ⎪⎝⎭,对称 D .关于点5π012⎛⎫-⎪⎝⎭,对称 【答案】D【解析】由题意得2ππ2ω=,故1ω=,∴()()cos 2f x x ϕ=+, ∴()ππcos 2cos 2cos 263g x x x x ϕϕ⎡⎤⎛⎫⎛⎫=-+=-+= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,∴π3ϕ=,∴()πcos 23f x x ⎛⎫=+ ⎪⎝⎭.∵2π2ππ5π1cos 2cos 133332f ⎛⎫⎛⎫=⨯+==≠±⎪ ⎪⎝⎭⎝⎭,πππ2π1cos 2cos 166332f ⎛⎫⎛⎫=⨯+==-≠± ⎪ ⎪⎝⎭⎝⎭,∴选项A ,B 不正确. 又()2π2ππcos 2cos π10333f ⎛⎫⎛⎫-=-⨯+=-=-≠ ⎪⎪⎝⎭⎝⎭, 5π5πππcos 2cos 0121232f ⎛⎫⎛⎫⎛⎫-=-⨯+=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,∴选项C 不正确,选项D 正确.选D .10.若m ,n 是两条不同的直线,α,β,γ是三个不同的平面,①m n ∥,m α⊥n α⇒⊥;②αβ∥,m α⊂,n β⊂//m n ⇒; ③αβ∥,m n ∥,m α⊥n β⇒⊥;④若m αγ=,n βγ=,m n ∥,则αβ∥;则以上说法中正确的有( )个. A .1 B .2C .3D .4【答案】B【解析】由m ,n 是两条不同的直线,α,β,γ是三个不同的平面,知:对于①,m n ∥,m α⊥,由线面垂直的判定定理得n α⊥,故①正确;对于②,αβ∥,m α⊂,n β⊂,则m 与n 平行或异面,故②错误;对于③,αβ∥,m n ∥,m α⊥,由线面垂直的判定定理得n β⊥,故③正确;对于④,若m αγ=,n βγ=,m n ∥,则α与β相交或平行,故④错误.故选B .11.已知椭圆()222210x y a b a b+=>>的短轴长为2,上顶点为A ,左顶点为B ,1F ,2F 分别是椭圆的左、右焦点,且1F AB △的面积为22-,点P 为椭圆上的任意一点,则1211PF PF +的取值范围为( ) A .[]12,B.C .⎤⎦D .[]14,【答案】D【解析】由已知得22b =,故1b =;∵1F AB △的面积为22-∴()12ac b -=,∴2a c -=-()()2221a c a c a c b -=-+==,∴2a =,c =()12212121111112444PF PF a PF PF PF PF PF PF PF PF ++===--+,又122PF ≤≤,∴211144PFPF ≤-+≤,∴121114PF PF ≤+≤.即1211PF PF +的取值范围为[]14,.选D . 12.已知函数()()()211e 2x f x ax x a =--∈R 若对区间[]01,内的任意实数1x、2x 、3x ,都有()()()123f x f x f x +≥,则实数a 的取值范围是( )A .[]1,2B .[]e,4C .[]1,4D .[)[]1,2e,4【答案】C【解析】由题得()()()e 1e e e x x x xf x ax x ax x x a '⎡⎤=-+-=-=-⎣⎦, 当1a <时,()0f x '<,所以函数()f x 在[]0,1单调递减,因为对区间[]0,1内的任意实数1x 、2x 、3x ,都有()()()123f x f x f x +≥,所以()()()110f f f +≥,所以11122a a +≥,故1a ≥,与1a <矛盾,故1a <不成立. 当1e a ≤<时,函数()f x 在[]0,ln a 单调递增,在(]ln ,1a 单调递减.所以()()2max 1ln ln ln 2f x f a a a a a a ==-+, 因为对区间[]0,1内的任意实数1x 、2x 、3x ,都有()()()123f x f x f x +≥,所以()()()01ln f f f a +≥,所以2111ln ln 22a a a a a a +≥-+,即211ln ln 1022a a a a a -+-≤, 令()211ln ln 122g a a a a a a =-+-,()1e a ≤<,所以()()21ln 102g a a '=-<,所以函数()g a 在()1,e 上单调递减,所以()()max 10ga g ==,所以当1e a ≤<时,满足题意.当e a ≥时,函数()f x 在()0,1单调递增,因为对区间[]0,1内的任意实数1x 、2x 、3x ,都有()()()123f x f x f x +≥,所以()()()001f f f+≥,故1112a +≥,所以4a ≤,故e 4a ≤≤;综上所述,[]1,4a ∈;故选C .第Ⅱ卷本卷包括必考题和选考题两部分。
第(13)~(21)题为必考题,每个试题考生都必须作答。
第(22)~(23)题为选考题,考生根据要求作答。
二、填空题:本大题共4小题,每小题5分。
13.设变量x ,y 满足约束条件00 34x y x y x y +⎧≥-≥+≤⎪⎨⎪⎩,则32x y +的最大值为__________.【答案】5【解析】画出不等式组所表示的平面区域,如图所示, 设目标函数32z x y =+,化简得322z y x =-+, 由图象可知,当直线322zy x =-+过点A 点时,直线在纵轴的截距最大, 此时目标函数取得最大值,由034x y x y -=+=⎧⎨⎩,解得11x y ==⎧⎨⎩,即()1,1A ,所以目标函数的最大值为31215⨯+⨯=.14.若函数()f x 是偶函数0x ≥时,()()lg 1f x x =+,则满足()211f x +<的实数x 取值范围是________.【答案】()54-,【解析】∵函数()f x 是偶函数,且0x ≥时,()()lg 1f x x =+, ∴0x ≥时,()f x 单调递增,∴0x <时,()f x 单调递减.又()()9lg 911f =+=,∴不等式()211f x +<可化为()()219f x f +<, ∴219x +<,∴9219x -<+<,解得54x -<<,∴实数x 取值范围是()54-,. 15.在锐角ABC △中,内角A ,B ,C 所对的边分别是a ,b ,c ,若2C B =,则cb的取值范围是________.【答案】【解析】由正弦定理得sin sin 22cos sin sin c C B B b B B ===,由于三角形为锐角三角形,所以π02C <<,所以π022B <<,π04B <<,而π32B C B +=>,π6B >2cos B < 16.数列{}n a 的前n 项和()212n n n S +⎡⎤=⎢⎥⎣⎦,数列{}nb 满足2n n a b n =,则对于任意的正整数n ,下列结论正确的是__________. ①112231n n n nb b b b b b b b ++++⋅⋅⋅+=; ②12112n b b bn++⋅⋅⋅+<; ③122225124n b b b n ++⋅⋅⋅+<; ④12111112n n n b b b b b +++⋅⋅⋅+=.【答案】①③④.【解析】由题可知,11b =,()2222121122n n n n b b b +⎡⎤++⋯+=⎢⎥⎣⎦,当2n ≥时,()()22221211112 +2n n n n b b b ---⎡⎤++⋯=⎢⎥⎣⎦,两式相减得1nb n =, 112231 +1n n n nb nb b b b b b n b ++++⋯==+成立,①正确;当1n =时,②不正确; ()()122223333111111+1212112311n b b b n n n n n ++⋯=++⋯<++⋯+⋅⋅-+ ()5154214n n =-<+,③正确; ()12111111+22n n n n n b b b b b ++++⋯==成立,④正确. 就答案为①③④.三、解答题:解答应写出文字说明、证明过程或演算步骤。
