基础知识的试题人教版高一数学必修1测试题(含答案)(可编辑修改word版)
人教版高一数学必修1测试题(含答案)(2)(K12教育文档)

人教版高一数学必修1测试题(含答案)(2)(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(人教版高一数学必修1测试题(含答案)(2)(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为人教版高一数学必修1测试题(含答案)(2)(word版可编辑修改)的全部内容。
一、选择题1、设集合{}{}{}1,2,3,4,5,1,2,3,2,5U A B ===,则()UA CB =( ) A 、{}2 B 、{}2,3C 、{}3D 、{}1,32、已知集合{}{}0,1,2,2,M N x x a a M ===∈,则集合 M N ( ) A 、{}0 B 、{}0,1 C 、{}1,2 D 、{}0,23、函数()21log ,4y x x =+≥的值域是 ( ) A 、[)2,+∞ B 、()3,+∞ C 、[)3,+∞ D 、(),-∞+∞4、关于A 到B 的一一映射,下列叙述正确的是 ( ) ① 一一映射又叫一一对应② A 中不同元素的像不同③ B 中每个元素都有原像④ 像的集合就是集合BA 、①②B 、①②③C 、②③④D 、①②③④5、在221,2,,y y x y x x y x ===+=,幂函数有 ( ) A 、1个 B 、2个 C 、3个 D 、4个6、已知函数()213f x xx +=-+,那么()1f x -的表达式是 ( ) A 、259x x -+ B 、23x x -- C 、259x x +- D 、21x x -+ 7、若方程0x ax a --=有两个解,则a 的取值范围是 ( ) A 、()0,+∞ B 、()1,+∞ C 、()0,1 D 、∅ 8、若21025x =,则10x -等于 ( ) A 、15-B 、15C 、150D 、1625 9、若()2log 1log 20a a a a +<<,则a 的取值范围是 ( )A 、01a <<B 、112a <<C 、102a << D 、1a > 10、设 1.50.90.4814,8,2abc -⎛⎫=== ⎪⎝⎭,则,,a b c 的大小顺序为 ( )A 、a b c >> B 、a c b >> C 、b a c >> D 、c a b >> 11、已知()()2212f x xa x =+-+在(],4-∞上单调递减,则a 的取值范围是( ) A 、3a ≤- B 、3a ≥- C 、3a =- D 、以上答案都不对12、若()lg f x x =,则()3f = ( )A 、lg 3B 、3C 、310D 、103 二、填空题13。
人教版高中一年级数学必修1测试题(含答案)

人教版数学必修I 测试题(含答案)一、选择题1、设集合{}{}{}1,2,3,4,5,1,2,3,2,5U A B ===,则()U AC B =( )A 、{}2B 、{}2,3C 、{}3D 、{}1,32、已知集合{}{}0,1,2,2,M N x x a a M ===∈,则集合 MN ( )A 、{}0B 、{}0,1C 、{}1,2D 、{}0,23、函数()21log ,4y x x =+≥的值域是 ( )A 、[)2,+∞B 、()3,+∞C 、[)3,+∞D 、(),-∞+∞4、关于A 到B 的一一映射,下列叙述正确的是 ( ) ① 一一映射又叫一一对应 ② A 中不同元素的像不同③ B 中每个元素都有原像 ④ 像的集合就是集合BA 、①②B 、①②③C 、②③④D 、①②③④5、在221,2,,y y x y x x y x===+=,幂函数有 ( ) A 、1个 B 、2个 C 、3个 D 、4个6、已知函数()213f x x x +=-+,那么()1f x -的表达式是 ( )A 、259x x -+B 、23x x --C 、259x x +-D 、21x x -+7、若方程0x a x a --=有两个解,则a 的取值范围是 ( )A 、()0,+∞B 、()1,+∞C 、()0,1D 、∅ 8、若21025x =,则10x -等于 ( )A 、15-B 、15C 、150D 、1625 9、若()2log 1log 20a a a a +<<,则a 的取值范围是 ( )A 、01a <<B 、112a <<C 、102a << D 、1a >10、设 1.50.90.4814,8,2a b c -⎛⎫=== ⎪⎝⎭,则,,a b c 的大小顺序为 ( )A 、a b c >>B 、a c b >>C 、b a c >>D 、c a b >> 11、已知()()2212f x x a x =+-+在(],4-∞上单调递减,则a 的取值范围是 ( )A 、3a ≤-B 、3a ≥-C 、3a =-D 、以上答案都不对 12、若()lg f x x =,则()3f = ( )A 、lg 3B 、3C 、310D 、103 二、填空题13、设{}{}12,0A x x B x x a =<<=-<,若A B Ø,则a 的取值范围是 ;14、函数y =的定义域为 ;15、若2x <,3x -的值是 ; 16、100lg 20log 25+= 。
人教版高一数学(必修1)基础知识试题选及答案

必修1高一数学基础知识试题选说明:本试卷分第Ⅰ卷和第Ⅱ卷两部分.第Ⅰ卷60分,第Ⅱ卷60分,共120分,答题时间90分钟.第Ⅰ卷(选择题,共60分)一、选择题:(每小题5分,共60分,请将所选答案填在括号内)1.已知集合M ⊂≠{4,7,8},且M 中至多有一个偶数,则这样的集合共有()(A)3个(B)4个(C)5个(D)6个2.已知S={x|x=2n,n ∈Z},T={x|x=4k ±1,k ∈Z},则()(A)S ⊂≠3P Q 等()}2y ≤4(A)16-5.已知(f 6.函数y 7.函数8.若函数(A)a 9(A)(B)(C)12(D)12 10.已知函数f(x)14x a -=+的图象恒过定点p ,则点p 的坐标是()(A )(1,5)(B )(1,4)(C )(0,4)(D )(4,0)11.函数y =的定义域是 ( ) (A )[1,+∞](B)(23,)+∞(C)[23,1](D)(23,1]12.设a,b,c 都是正数,且346a b c ==,则下列正确的是 ()(A)111c a b =+(B)221C a b =+(C)122C a b =+(D)212c a b =+第Ⅱ卷(非选择题,共60分)二、填空题:(每小题4分,共16分,答案填在横线上)13.已知(x,y )在映射f 下的象是(x-y,x+y),则(3,5)在f 下的象是,原象是。
14.已知函数f(x)的定义域为[0,1],则f(2x )的定义域为。
15.若log a 23<1,则a 的取值范围是161221718.19.20.(1(213.(17.略19.解:()f x 在R 2(4f x x --223x ++=由2(2x x ++∴解集为{|1}x x <-.20.(1)1a =-或3a =-(2)当A B A = 时,B A ⊆,从而B 可能是:{}{}{},1,2,1,2∅.分别求解,得3a ≤-;。
基础知识的试题人教版高一数学必修1测试题(含答案)

精品文档
人教版数学必修 I 测试题 高一数学 ( 答案卷 )
一、选择题(本大题共 12 道小题,每小题 5 分,共 60 分。在每小 题给出的四个选项中,只有一项是符合题目要求的) 题 1 2 3 4 5 6 7 8 9 10 11 12 号 答 DDCDB A A B CB A C 案
二、填空题(本大题共 4 道小题,每小题 5 分,共 20 分。把答案
ab
ab 。
b
.
证
明
:
由
----------------------------------------4
ab b a
则
左
边
-----------------------------------------6
a
ab
a bb
aa
知
:
分
=
分
精品文档
b
b aa
a
a
a b ab
b
a
bb
---------------------------------------- 10
填在题中横线上)
13、 2, ; 14 、 1,0 ; 15 、 1 ;
16
、
2。
三、解答题(本大题共 6 道小题,共 70 分。解答应写出文字说明、
证明过程或演算步骤) 17 、(本小题满分 10 分)设 A
4,2 a 1,a2 , B a 5,1 a,9 ,已知
AI B 9 ,求 a 的值。
解
:
a1
ab
ab
ab
分
右
边
-------------------------------------12
基础知识的试题人教版高一数学必修1测试题(含答案)

根底知识测试人教版数学必修I 测试题〔含答案〕一、选择题1、设集合{}{}{}1,2,3,4,5,1,2,3,2,5U A B ===,那么()U A C B =〔 〕A 、{}2B 、{}2,3C 、{}3D 、{}1,32、集合{}{}0,1,2,2,M N x x a a M ===∈,那么集合 MN 〔 〕A 、{}0B 、{}0,1C 、{}1,2D 、{}0,23、函数()21log ,4y x x =+≥的值域是 〔 〕A 、[)2,+∞B 、()3,+∞C 、[)3,+∞D 、(),-∞+∞4、关于A 到B 的一一映射,以下表达正确的选项是 〔 〕 ① 一一映射又叫一一对应 ② A 中不同元素的像不同③ B 中每个元素都有原像 ④ 像的集合就是集合BA 、①②B 、①②③C 、②③④D 、①②③④ 5、在221,2,,y y x y x x y x===+= 〔 〕A 、1个 B 、2个 C 、3个 D 、4个6、函数()213f x x x +=-+,那么()1f x -的表达式是 〔 〕A 、259x x -+B 、23x x --C 、259x x +-D 、21x x -+7、假设方程0x a x a --=有两个解,那么a 的取值范围是 〔 〕A 、()0,+∞B 、()1,+∞C 、()0,1D 、∅8、假设21025x =,那么10x -等于 〔 〕A 、15-B 、15C 、150D 、16259、假设()2log 1log 20a a a a +<<,那么a 的取值范围是 〔 〕A 、01a <<B 、112a <<C 、102a << D 、1a > 10、设 1.50.90.4814,8,2a b c -⎛⎫=== ⎪⎝⎭,那么,,a b c 的大小顺序为 〔 〕A 、a b c >>B 、a c b >>C 、b a c >>D 、c a b >>11、()()2212f x x a x =+-+在(],4-∞上单调递减,那么a 的取值范围是 〔 〕A 、3a ≤-B 、3a ≥-C 、3a =-D 、以上答案都不对12、假设()lg f x x =,那么()3f = 〔 〕 A 、lg 3B、3C、310D 、103二、填空题13、设{}{}12,0A x x B x x a =<<=-<,假设AB ,那么a 的取值范围是 ; 14、函数y =的定义域为 ; 15、假设2x <,那么3x-的值是 ; 16、100lg 20log 25+=。
(完整word版)高一数学必修1试题附答案详解

高一数学必修1试题1。
已知全集I ={0,1,2},且满足C I (A ∪B )={2}的A 、B 共有组数2。
如果集合A ={x |x =2k π+π,k ∈Z},B ={x |x =4k π+π,k ∈Z },则集合A,B 的关系3.设A ={x ∈Z ||x |≤2},B ={y |y =x 2+1,x ∈A },则B 的元素个数是4.若集合P ={x |3〈x ≤22},非空集合Q ={x |2a +1≤x 〈3a -5},则能使Q ⊆ (P ∩Q )成立的所 有实数a 的取值范围为5。
已知集合A =B =R ,x ∈A ,y ∈B ,f :x →y =ax +b ,若4和10的原象分别对应是6和9, 则19在f 作用下的象为6。
函数f (x )=错误! (x ∈R 且x ≠2)的值域为集合N ,则集合{2,-2,-1,-3}中不属于N 的元 素是7.已知f (x )是一次函数,且2f (2)-3f (1)=5,2f (0)-f (-1)=1,则f (x )的解析式为8。
下列各组函数中,表示同一函数的是 A.f (x )=1,g (x )=x 0B.f (x )=x +2,g (x )=错误!C.f (x )=|x |,g (x )=错误! D 。
f (x )=x ,g (x )=(错误!)29。
f (x )=⎩⎪⎨⎪⎧x 2 x >0π x =00 x <0,则f {f [f (-3)]}等于10。
已知2lg (x -2y )=lg x +lg y ,则错误!的11。
设x ∈R ,若a 〈lg (|x -3|+|x +7|)恒成立,则a 取值范围是12.若定义在区间(-1,0)内的函数f(x)=log2a(x+1)满足f(x)>0,则a的取值范围是高一数学必修1试题一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知全集I={0,1,2},且满足C I (A∪B)={2}的A、B共有组数A。
高一数学必修1基础试题附标准答案

高一数学必修1基础试题一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知全集I ={0,1,2},且满足C I (A ∪B )={2}的A 、B 共有组数 A.5 B.7 C.9 D.112.如果集合A ={x |x =2k π+π,k ∈Z},B ={x |x =4k π+π,k ∈Z},则A.A BB.B AC.A =BD.A ∩B =∅3.设A ={x ∈Z||x |≤2},B ={y |y =x 2+1,x ∈A },则B 的元素个数是 A.5 B.4 C.3 D.2 4.若集合P ={x |3<x ≤22},非空集合Q ={x |2a +1≤x <3a -5},则能使Q ⊆ (P ∩Q )成立的所有实数a 的取值范围为 A.(1,9) B.[1,9] C.[6,9)D.(6,9]5.已知集合A =B =R ,x ∈A ,y ∈B ,f :x →y =a x +b ,若4和10的原象分别对应是6和9,则19在f 作用下的象为 A.18B.30C. 272D.286.函数f (x )=3x -12-x (x ∈R 且x ≠2)的值域为集合N ,则集合{2,-2,-1,-3}中不属于N 的元素是 A.2 B.-2 C.-1 D.-3 7.已知f (x )是一次函数,且2f (2)-3f (1)=5,2f (0)-f (-1)=1,则f (x )的解析式为 A.3x -2 B.3x +2 C.2x +3 D.2x -3 8.下列各组函数中,表示同一函数的是 A.f (x )=1,g (x )=x 0B.f (x )=x +2,g (x )=x 2-4x -2C.f (x )=|x |,g (x )=⎩⎨⎧x x ≥0-x x <0D.f (x )=x ,g (x )=(x )29. f (x )=⎩⎪⎨⎪⎧x 2 x >0π x =00 x <0,则f {f [f (-3)]}等于A.0B.πC.π2D.910.已知2lg(x -2y )=lg x +lg y ,则xy 的值为A.1B.4C.1或4D. 14或4 11.设x ∈R ,若a <lg(|x -3|+|x +7|)恒成立,则 A.a ≥1 B.a >1 C.0<a ≤1 D.a <112.若定义在区间(-1,0)内的函数f (x )=log 2a (x +1)满足f (x )>0,则a 的取值范围是A.(0,12)B.(0,⎥⎦⎤21C.( 12,+∞)D.(0,+∞)二、填空题(本大题共6小题,每小题4分,共24分.把答案填在题中横线上) 13.若不等式x 2+ax +a -2>0的解集为R ,则a 可取值的集合为__________.14.函数y =x 2+x +1 的定义域是______,值域为__ ____.15.若不等式3ax x 22->(13)x +1对一切实数x 恒成立,则实数a 的取值范围为___ ___.16. f (x )=]()⎪⎩⎪⎨⎧+∞∈--∞∈---,1 231,( 2311x x x x ,则f (x )值域为_____ _. 17.函数y =12x +1的值域是__________.18.方程log 2(2-2x )+x +99=0的两个解的和是______.第Ⅱ卷一、选择题二、填空题13 14 15 16 17 18 三、解答题(本大题共5小题,共66分. 解答应写出文字说明、证明过程或演算步骤) 19.全集U =R ,A ={x ||x |≥1},B ={x |x 2-2x -3>0},求(C U A )∩(C U B ).20.已知f (x )是定义在(0,+∞)上的增函数,且满足f (xy )=f (x )+f (y ),f (2)=1. (1)求证:f (8)=3 (2)求不等式f (x )-f (x -2)>3的解集.21.某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出,当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需维护费150元,未租出的车每辆每月需要维护费50元.(1)当每辆车的月租金定为3600元时,能租出多少辆车?(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?22.已知函数f (x )=log 412x -log 41x +5,x ∈[2,4],求f (x )的最大值及最小值.23.已知函数f (x )=a a 2-2 (a x -a -x )(a >0且a ≠1)是R 上的增函数,求a 的取值范围.高一数学综合训练(一)答案二、填空题13. ∅ 14. R [32,+∞) 15. -12 < a < 3216. (-2,-1] 17. (0,1) 18. -99三、解答题(本大题共5小题,共66分. 解答应写出文字说明、证明过程或演算步骤) 19.全集U =R ,A ={x ||x |≥1},B ={x |x 2-2x -3>0},求(C U A )∩(C U B ).(C U A )∩(C U B )={x |-1<x <1}20.已知f (x )是定义在(0,+∞)上的增函数,且满足f (xy )=f (x )+f (y ),f (2)=1. (1)求证:f (8)=3 (2)求不等式f (x )-f (x -2)>3的解集. 考查函数对应法则及单调性的应用. (1)【证明】 由题意得f (8)=f (4×2)=f (4)+f (2)=f (2×2)+f (2)=f (2)+f (2)+f (2)=3f (2) 又∵f (2)=1 ∴f (8)=3(2)【解】 不等式化为f (x )>f (x -2)+3∵f (8)=3 ∴f (x )>f (x -2)+f (8)=f (8x -16) ∵f (x )是(0,+∞)上的增函数∴⎩⎨⎧->>-)2(80)2(8x x x 解得2<x <16721.某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出,当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需维护费150元,未租出的车每辆每月需要维护费50元.(1)当每辆车的月租金定为3600元时,能租出多少辆车?(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少? 考查函数的应用及分析解决实际问题能力.【解】 (1)当每辆车月租金为3600元时,未租出的车辆数为 3600-300050=12,所以这时租出了88辆.(2)设每辆车的月租金定为x 元,则公司月收益为 f (x )=(100-x -300050 )(x -150)-x -300050×50整理得:f (x )=-x 250 +162x -2100=-150 (x -4050)2+307050∴当x =4050时,f (x )最大,最大值为f (4050)=307050 元22.已知函数f (x )=log 412x -log 41x +5,x ∈[2,4],求f (x )的最大值及最小值.考查函数最值及对数函数性质.【解】 令t =log 41x ∵x ∈[2,4],t =log 41x 在定义域递减有log 414<log 41x <log 412, ∴t ∈[-1,-12]∴f (t )=t 2-t +5=(t -12 )2+194 ,t ∈[-1,-12 ]∴当t =-12 时,f (x )取最小值 234当t =-1时,f (x )取最大值7.23.已知函数f (x )=a a 2-2(a x -a -x )(a >0且a ≠1)是R 上的增函数,求a 的取值范围.考查指数函数性质.【解】 f (x )的定义域为R ,设x 1、x 2∈R ,且x 1<x 2 则f (x 2)-f (x 1)= aa 2-2(a 2x -a 2x --a 1x +a 1x -) =aa 2-2 (a 2x -a 1x )(1+211x x aa ⋅) 由于a >0,且a ≠1,∴1+211x x a a >0∵f (x )为增函数,则(a 2-2)( a 2x -a 1x )>0于是有⎪⎩⎪⎨⎧<-<-⎪⎩⎪⎨⎧>->-002002121222x x x x a a a a a a 或, 解得a > 2 或0<a <1. . .。
人教版高一数学必修一-第一章练习题与答案

集合与函数基础测试一、选择题(共12小题,每题5分,四个选项中只有一个符合要求)1.函数y ==x 2-6x +10在区间(2,4)上是( )A .递减函数B .递增函数C .先递减再递增D .选递增再递减.2.方程组20{=+=-y x y x 的解构成的集合是 ( )A .)}1,1{(B .}1,1{C .(1,1)D .}1{3.已知集合A ={a ,b ,c },下列可以作为集合A 的子集的是 ( )A 。
aB 。
{a ,c }C 。
{a ,e } D.{a ,b ,c ,d }4.下列图形中,表示N M ⊆的是 ( )5.下列表述正确的是 ( )A 。
}0{=∅B 。
}0{⊆∅ C. }0{⊇∅ D. }0{∈∅6、设集合A ={x |x 参加自由泳的运动员},B ={x|x 参加蛙泳的运动员},对于“既参加自由泳又参加蛙泳的运动员”用集合运算表示为 ( ) A 。
A∩B B.A ⊇B C 。
A ∪B D 。
A ⊆B7.集合A={x Z k k x ∈=,2} ,B={Z k k x x ∈+=,12} ,C={Z k k x x ∈+=,14}又,,B b A a ∈∈则有( )A.(a+b )∈ AB. (a+b) ∈B C 。
(a+b) ∈ C D 。
(a+b ) ∈ A 、B 、C 任一个8.函数f (x )=-x 2+2(a -1)x +2在(-∞,4)上是增函数,则a 的范围是( )A .a ≥5B .a ≥3C .a ≤3D .a ≤-59。
满足条件{1,2,3}⊂≠M ⊂≠{1,2,3,4,5,6}的集合M 的个数是( ) A 。
8 B 。
7 C. 6 D 。
510。
全集U = {1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 }, A= {3 ,4 ,5 }, B= {1 ,3 ,6 },那么集合 { 2 ,7 ,8}是 ( )A. A B B 。
B A C 。
人教版高一数学必修1测试题(含答案)

人教版高一数学必修1测试题(含答案)人教版数学必修I测试题(含答案)一、选择题1、设集合U 1,2,3,4,5 ,A 1,2,3 ,B 2,5 ,则A CUB ()A、2B、2,3C、3D、1,32、已知集合M 0,1,2 ,N xx 2a,a M ,则集合M N (A、0 B、0,1C、1,23、函数y 1 log2x, x 4 的值域是()A、2,B、3,C、3, ,4、关于A到B的一一映射,下列叙述正确的是()① 一一映射又叫一一对应② A中不同元素的像不同③ B中每个元素都有原像④ 像的集合就是集合BA、①②B、①②③C、②③④ ①②③④ 5、在y1x2,y 2x,y x2x,y (A、1个B、2个C、3个4个)D、0,2D、D、)D、6、已知函数f x 1 x2 x 3,那么f x 1 的表达式是()A、x2 5x 9B、x2 x 3C、x2 5x 9D、x2 x 17、若方程ax x a 0有两个解,则a的取值范围是()A、0,B、1,C、0,1D、8、若102x 25,则10 x等于()A、1B1 C1 D、55501 6259、若loga a2 1 loga2a 0,则a的取值范围是()11A、0 a 1 B a 1 C、a 1 0 a D、2210、设a 40.9,b 80.481,c21.5,则a,b,c的大小顺序为()A、a b cB、a c bC、b a cD、c a b11、已知f x x2 2 a 1 x 2在,4 上单调递减,则a的取值范围是()A、a 3B、a 3C、a 3D、以上答案都不对12、若f lgx x,则f 3 ()A、lg3B、3 C、103D、310二、填空题13、设A x x 2 ,B xx a 0 ,若AB,则a的取值范围是;14、函数y 的定义域为;15、若x2,则x4的3x 值是;16lg20 log*****、。
三、解答题17、(本小题满分10分)设A 4,2a 1,a2 ,B a 5,1 a,9 ,已知A B 9 ,求a的值。
人教版最新高一数学必修一复习测试题及参考答案

——教学资料参考参考范本——人教版最新高一数学必修一复习测试题及参考答案______年______月______日____________________部门人教版最新高一数学必修一复习测试题及参考答案(附参考答案)班级 姓名一、选择题。
(共10小题,每题5分) 1、设集合A={xQ|x>-1},则( )∈A 、B 、C 、D 、 A ∅∉2A ∉2A∈{}2⊆A2、设A={a ,b},集合B={a+1,5},若A∩B={2},则A∪B=( ) A 、{1,2} B 、{1,5} C 、{2,5} D 、{1,2,5}3、函数的定义域为( )21)(--=x x x fA 、[1,2)∪(2,+∞)B 、(1,+∞)C 、[1,2)D 、[1,+∞)4、设集合M={x|-2≤x ≤2},N={y|0≤y ≤2},给出下列四个图形,其中能表示以集合M 为定义域,N 为值域的函数关系的是( )5、三个数70。
3,0.37,,㏑0.3,的大小顺序是( )A 、 70。
3,0.37,,㏑0.3,B 、70。
3,,㏑0.3, 0.37C 、 0.37, , 70。
3,,㏑0.3,D 、㏑0.3, 70。
3,0.37,6、若函数f(x)=x3+x2-2x-2的一个正数零点附近的函数值用二分法逐次计算,参考数据如下表:f(1)=-2 f(1.5)=0.625 f(1.25)=-0.984 f(1.375)=-0.260 f(1.438)=0.165f(1.4065)=-0.052那么方程x3+x2-2x-2=0的一个近似根(精确到0.1)为( ) A 、1.2 B 、1.3 C 、1.4 D 、1.57、函数 的图像为( )2,02,0x x x y x -⎧⎪⎨⎪⎩≥=< 8、设(a>0,a ≠1),对于任意的正实数x ,y ,都有( )()log a f x x =A 、f(xy)=f(x)f(y)B 、f(xy)=f(x)+f(y)C 、f(x+y)=f(x)f(y)D 、f(x+y)=f(x)+f(y)9、函数y=ax2+bx+3在(-∞,-1]上是增函数,在[-1,+∞)上是减函数,则( )A 、b>0且a<0B 、b=2a<0C 、b=2a>0D 、a ,b 的符号不定10、某企业近几年的年产值如图,则年增长率最高的是( )(年增长率=年增长值/年产值)A 、97年B 、98年0099989796(年)2004006008001000(万元)C 、99年D 、00年二、填空题(共4题,每题5分) 11、f(x)的图像如下图,则f(x)的值域为 ; 12、计算机成本不断降低,若每隔3年计算机价格降低1/3,现在价格为8100元的计算机,则9年后价格可降为 ;13、若f(x)为偶函数,当x>0时,f(x)=x,则当x<0时,f(x)= ;14、计算:+= ;2391- ⎪⎭⎫ ⎝⎛326415、函数的递减区间为212log (45)y x x =--三、解答题(本大题共6小题,满分75分,解答题写出必要的文字说明、推演步骤。
人教版高一数学必修1测试题(含答案)

人教版数学必修I 测试题(含答案)一、选择题1、设集合{}{}{}1,2,3,4,5,1,2,3,2,5U A B ===,则()U AC B =( )A 、{}2B 、{}2,3C 、{}3D 、{}1,32、已知集合{}{}0,1,2,2,M N x x a a M ===∈,则集合 MN ( )A 、{}0B 、{}0,1C 、{}1,2D 、{}0,23、函数()21log ,4y x x =+≥的值域是 ( )A 、[)2,+∞B 、()3,+∞C 、[)3,+∞D 、(),-∞+∞4、关于A 到B 的一一映射,下列叙述正确的是 ( ) ① 一一映射又叫一一对应 ② A 中不同元素的像不同③ B 中每个元素都有原像 ④ 像的集合就是集合BA 、①②B 、①②③C 、②③④D 、①②③④5、在221,2,,y y x y x x y x===+= ( )A 、1个B 、2个C 、3个D 、4个 6、已知函数()213f x x x +=-+,那么()1f x -的表达式是 ( )A 、259x x -+B 、23x x --C 、259x x +-D 、21x x -+7、若方程0x a x a --=有两个解,则a 的取值范围是 ( )A 、()0,+∞B 、()1,+∞C 、()0,1D 、∅8、若21025x =,则10x -等于 ( )A 、15-B 、15C 、150D 、16259、若()2log 1log 20a a a a +<<,则a 的取值范围是 ( )A 、01a <<B 、112a << C 、102a << D 、1a > 10、设 1.50.90.4814,8,2a b c -⎛⎫=== ⎪⎝⎭,则,,a b c 的大小顺序为 ( )A 、a b c >>B 、a c b >>C 、b a c >>D 、c a b >>11、已知()()2212f x x a x =+-+在(],4-∞上单调递减,则a 的取值范围是 ( )A 、3a ≤-B 、3a ≥-C 、3a =-D 、以上答案都不对12、若()lg f x x =,则()3f = ( )A 、lg 3B 、3C 、310D 、103 二、填空题13、设{}{}12,0A x x B x x a =<<=-<,若A B Ø,则a 的取值范围是 ; 14、函数y =的定义域为 ; 15、若2x <,则3x -的值是 ; 16、100lg 20log 25+= 。
人教版高中数学必修一综合测试题(很基础,很全面)
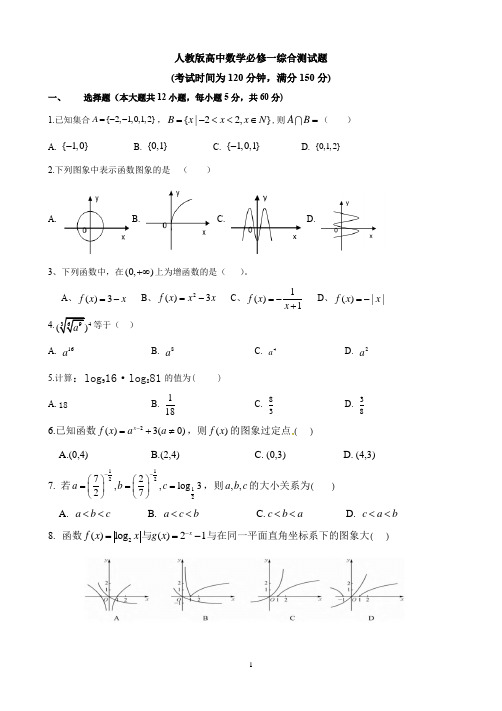
人教版高中数学必修一综合测试题(考试时间为120分钟,满分150分)一、 选择题(本大题共12小题,每小题5分,共60分)1.已知集合{2,1,0,1,2}A =--,{|22,}B x x x N =-<<∈,则AB =( ) A. {1,0}- B. {0,1} C. {1,0,1}- D. {0,1,2}2.下列图象中表示函数图象的是 ( )A. B. C. D.3、下列函数中,在(0,)+∞上为增函数的是( )。
A 、()3f x x =-B 、2()3f x x x =-C 、1()1f x x =-+ D 、()||f x x =-4.4等于( )A. 16aB. 8aC. 4aD. 2a 5.计算:log 916·log 881的值为( )A. 18B. 118C. 83D. 386.已知函数2()3(0)x f x a a -=+≠,则()f x 的图象过定点( )A.(0,4)B.(2,4)C. (0,3)D. (4,3) 7. 若11221272,,log 327a b c --⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭,则,,a b c 的大小关系为( ) A. a b c << B. a c b << C.c b a << D. c a b << 8. 函数2()log ()21x f x x g x -==-与与在同一平面直角坐标系下的图象大( )9.函数()f x = ) A. {}0x x > B. {}1x x > C. {}1x x ≥ D. {}01x x <≤ 10.如果函数2()2(1)2f x x a x =+-+在区间(],4-∞上是减函数,那么实数a 的取值范围是( )A. 3a ≤-B. 3a ≥-C. 5a ≤D. 5a ≥11、已知函数f(x)是R 上的减函数,A (0,1),B (2,-1)是其图象上的两点,那么∣f(x)∣<1的解集的补集是 ( )A.(-1,2)B.(1,4)C.(-∞,-1)∪[4,+∞)D.(∞,0]∪[2,+∞) 12.12R (),f x x ∈定义在上的偶函数满足:对任意的x (]12,0(),x x -∞≠有12)x x -•([]21()()0.)f x f x n N *->∈则当时,有( A.()(1)(1)f n f n f n -<-<+ B. (1)()(1)f n f n f n -<-<+C. (1)()(1)f n f n f n +<-<-D. (1)(1)()f n f n f n +<-<-二、填空题(本大题共4小题,每小题5分,共20分)13、210()20x x f x x x ⎧+≤=⎨->⎩ , , , ,若()10f x = ,则_______x =.14.使不等式31220x -->成立的x 的取值范围是 .15、已知函数3()8f x ax bx =+- ,且f(-2) =10,则f (2 ) =_______. 16.下列命题:①若函数()f x 是一个定义在R 上的函数,则函数h x f x f x 是奇函数; ②函数211x x y x 是偶函数; ②函数12x y -=的图象可由12x y的图象向右平移2个单位得到; ②函数1y x=在区间12,上既有最大值,又有最小值; 则上述正确命题的序号是________②.三、解答题(本大题共6小题,共70分)17.(本题满分10分)已知全集为U=R ,A={22|<<-x x } ,B={1,0|≥<x x x 或} 求:(1)A ⋂B ,(2)A ⋃B 。
高一数学必修1基础试题附答案

高一数学必修1基础试题附答案高一数学必修1基础试题一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知全集I={0,1,2},且满足C I (A∪B)={2}的A、B共有组数A.5B.7C.9D.112.如果集合A={x|x=2kπ+π,k∈Z},B={x|x =4kπ+π,k∈Z},则A.A BB.B AC.A=BD.A∩B=∅3.设A={x∈Z||x|≤2},B={y|y=x2+1,x∈A},则B的元素个数是A.5B.4C.3D.24.若集合P={x|3<x≤22},非空集合Q={x|2a+1≤x<3a-5},则能使Q ⊆(P∩Q)成立的所有实数a的取值范围为A.(1,9)B.[1,9]C.[6,9)D.(6,9]5.已知集合A=B=R,x∈A,y∈B,f:x→y=a x+b ,若4和10的原象分别对应是6和9,则19在f 作用下的象为A.18B.30C. 272D.286.函数f (x )=3x -12-x(x ∈R 且x ≠2)的值域为集合N ,则集合{2,-2,-1,-3}中不属于N 的元素是A.2B.-2C.-1D.-37.已知f (x )是一次函数,且2f (2)-3f (1)=5,2f (0)-f (-1)=1,则f (x )的解析式为A.3x -2B.3x +2C.2x +3D.2x -38.下列各组函数中,表示同一函数的是A.f (x )=1,g (x )=x 0B.f (x )=x+2,g (x )=x 2-4x -2C.f (x )=|x |,g (x )=⎩⎪⎨⎪⎧x x ≥0-x x <0D.f (x )=x ,g (x )=(x )29. f (x )=⎩⎪⎨⎪⎧x 2 x >0π x =00 x <0,则f {f [f (-3)]}等于 A.0 B.π C.π2D.9 10.已知2lg(x -2y )=lg x +lg y ,则x y 的值为A.1B.4C.1或4D. 14或4 11.设x ∈R ,若a <lg(|x -3|+|x +7|)恒成立,则A.a ≥1B.a >1C.0<a ≤1D.a <112.若定义在区间(-1,0)内的函数f (x )=log 2a (x+1)满足f (x )>0,则a 的取值范围是A.(0,12 )B.(0,⎥⎦⎤21C.( 12,+∞) D.(0,+∞)二、填空题(本大题共6小题,每小题4分,共24分.把答案填在题中横线上)13.若不等式x 2+ax +a -2>0的解集为R ,则a可取值的集合为__________.14.函数y =x 2+x +1 的定义域是______,值域为__ ____.15.若不等式3ax x 22->(13)x +1对一切实数x 恒成立,则实数a 的取值范围为___ ___. 16. f (x )=]()⎪⎩⎪⎨⎧+∞∈--∞∈---,1 231,( 2311x x x x ,则f (x )值域为_____ _. 17.函数y =12x +1的值域是__________. 18.方程log 2(2-2x )+x +99=0的两个解的和是______.第Ⅱ卷一、选择题二、填空题13 14 1516 1718三、解答题(本大题共5小题,共66分. 解答应写出文字说明、证明过程或演算步骤)19.全集U=R,A={x||x|≥1},B={x|x2-2x-3>0},求(C U A)∩(C U B).20.已知f(x)是定义在(0,+∞)上的增函数,且满足f(xy)=f(x)+f(y),f(2)=1.(1)求证:f(8)=3 (2)求不等式f(x)-f(x-2)>3的解集.21.某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出,当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需维护费150元,未租出的车每辆每月需要维护费50元.(1)当每辆车的月租金定为3600元时,能租出多少辆车?(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?22.已知函数f (x )=log 412x -log 41x +5,x ∈[2,4],求f (x )的最大值及最小值.23.已知函数f(x)=aa2-2(a x-a-x)(a>0且a≠1)是R上的增函数,求a的取值范围.高一数学综合训练(一)答案一、选择题二、填空题13. 14. R [32,+∞) 15. -12 < a < 3216. (-2,-1] 17. (0,1)18. -99三、解答题(本大题共5小题,共66分. 解答应写出文字说明、证明过程或演算步骤)19.全集U =R ,A ={x ||x |≥1},B ={x |x 2-2x -3>0},求(C U A )∩(C U B ).(C U A )∩(C U B )={x |-1<x <1}20.已知f (x )是定义在(0,+∞)上的增函数,且满足f (xy )=f (x )+f (y ),f (2)=1.(1)求证:f (8)=3 (2)求不等式f (x )-f (x -2)>3的解集.考查函数对应法则及单调性的应用.(1)【证明】 由题意得f (8)=f (4×2)=f (4)+f (2)=f (2×2)+f (2)=f (2)+f (2)+f (2)=3f (2)又∵f (2)=1 ∴f (8)=3(2)【解】 不等式化为f (x )>f (x -2)+3∵f (8)=3 ∴f (x )>f (x -2)+f (8)=f (8x -16)∵f (x )是(0,+∞)上的增函数 ∴⎩⎨⎧->>-)2(80)2(8x x x 解得2<x <16721.某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出,当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需维护费150元,未租出的车每辆每月需要维护费50元. (1)当每辆车的月租金定为3600元时,能租出多少辆车?(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?考查函数的应用及分析解决实际问题能力. 【解】 (1)当每辆车月租金为3600元时,未租出的车辆数为 3600-300050 =12,所以这时租出了88辆.(2)设每辆车的月租金定为x 元,则公司月收益为f (x )=(100-x -300050 )(x -150)-x -300050×50整理得:f (x )=-x 250 +162x -2100=-150 (x-4050)2+307050∴当x =4050时,f (x )最大,最大值为f (4050)=307050 元22.已知函数f (x )=log 412x -log 41x +5,x ∈[2,4],求f (x )的最大值及最小值.考查函数最值及对数函数性质.【解】 令t =log 41x ∵x ∈[2,4],t =log 41x 在定义域递减有log 414<log 41x <log 412, ∴t ∈[-1,-12]∴f (t )=t 2-t +5=(t -12 )2+194,t ∈[-1,-12] ∴当t =-12 时,f (x )取最小值 234当t =-1时,f (x )取最大值7.23.已知函数f (x )=a a 2-2(a x-a -x )(a >0且a ≠1)是R 上的增函数,求a 的取值范围.考查指数函数性质.【解】 f (x )的定义域为R ,设x 1、x 2∈R ,且x 1<x 2则f (x 2)-f (x 1)= aa 2-2(a 2x -a 2x --a 1x +a 1x -)=aa 2-2(a 2x -a 1x )(1+211x x a a⋅)由于a >0,且a ≠1,∴1+211x x a a >0 ∵f (x )为增函数,则(a 2-2)( a 2x -a 1x )>0于是有⎪⎩⎪⎨⎧<-<-⎪⎩⎪⎨⎧>->-02002121222x x x x a a a a a a 或,解得a > 2 或0<a <1 . . .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基础知识测试人教版数学必修I 测试题(含答案)一、选择题1、设集合U ={1, 2, 3, 4, 5}, A ={1, 2, 3}, B ={2, 5},则A (C U B)=()A 、{2}{1, 3}B 、{2, 3}C 、{3}D 、2、已知集合M ={0,1, 2}, N ={x x = 2a, a ∈M },则集合M N ()A 、{0}{0, 2}B 、{0,1}C 、{1, 2}D 、3、函数y =1+ log2x, (x≥ 4)的值域是()A 、[2, +∞)(-∞, +∞)B 、(3, +∞)C 、[3, +∞)D 、4、关于A 到B 的一一映射,下列叙述正确的是()① 一一映射又叫一一对应② A中不同元素的像不同③ B中每个元素都有原像④ 像的集合就是集合 BA 、①②D 、①②③④B 、①②③C 、②③④5、在y = 1 , y = 2x, y =x2+x, y =x2四个函数中,幂函数有()3 x5a a2 A 、 1 个 个B 、 2 个C 、 3 个D 、 46、已知函数 f ( x +1) = x 2 - x + 3 ,那么 f ( x -1) 的表达式是 ()A 、 x 2 - 5x + 9B 、 x 2 - x - 3C 、 x 2 + 5x - 9D 、x 2 - x +17、若方程a x - x - a = 0 有两个解,则a 的取值范围是 ()A 、(0, +∞)B 、(1, +∞)C 、(0,1)D 、∅8、若102x = 25 ,则10-x 等于 ()A 、 - 15 D 、 1625B 、 15C 、 1509、若log (a 2 +1) < log 2a < 0 ,则a 的取值范围是 ( )A 、0 < a < 1a > 110、设0.90.48B 、1 < a < 12⎛ 1 ⎫-1.5C 、0 < a <1 D 、2a = 4 ,b = 8 ,c = ⎪⎝ ⎭,则a , b , c 的大小顺序为 ()A 、a > b > cB 、a > c > bC 、b > a > cD 、c > a > b11、已知 f ( x ) = x 2 + 2 (a -1) x + 2 在(-∞, 4] 上单调递减,则a 的取值范围是 ()A 、a ≤ -3答案都不对B 、a ≥ -3C 、a = -3D 、以上b ⎪⎨ 12、若 f (lg x ) = x ,则 f (3) = ()A 、 lg 3B 、 3C 、 103D 、310二、填空题13、 设 A = {x 1 < x < 2}, B = {x x - a < 0}, 若 A Ø B , 则 a 的 取 值 范 围是 ;14、函数y的定 义 域为;15、若 x < 2 , 则 - 3 - x 的 值是 ;16、lg 20 + log 100 25 =。
三、解答题17、(本小题满分 10 分)设 A = {-4, 2a -1, a 2}, B = {a - 5,1- a , 9} ,已知 A B = {9} ,求a 的值。
18、(本小题满分 10 分)判断并证明 f ( x ) = xx 2+1 在(0, +∞) 的单调性。
19、(本小题满分 12 分)研究函数 y = lg1- x的定义域和奇偶性。
1+ x20、(本小题满分 12 分)已知: a> 0, b > 0 ,且a b= b a a ,求证: ⎛ a ⎫b= ⎝ ⎭a -ba b 。
21、(本小题满分 12 分)某商品最近 30 天的价格 f (t ) (元)与时间t 满足关系式⎧ f (t ) = ⎪⎪- ⎩ 1 t + 8,3 1t +18, 3(0 ≤ t < 15, t ∈ N + ),(15 ≤ t < 30, t ∈ N + )a a a a 且知销售量g (t ) 与时间t 满足关系式该商品的日销售额的最大值。
22、(本小题满分 14 分)已知g (t ) = -t + 30,(0 ≤ t ≤ 30, t ∈ N + ),求 log (x 2 + 4) + log ( y 2 +1) = log 5+ log (2xy -1), (a > 0,且a ≠ 1) , 求log y 的值。
8 x人教版数学必修 I 测试题高一数学(答案卷)一、选择题(本大题共 12 道小题,每小题 5 分,共 60 分。
在每小题给出的四个选项中,只有一项是符合题目要求的)二、填空题(本大题共 4 道小题,每小题 5 分,共 20 分。
把答案填在题中横线上) 13、 [2, +∞)16、 2 。
;14、 (-1, 0]; 15、 -1 ;三、解答题(本大题共 6 道小题,共 70 分。
解答应写出文字说明、 证明过程或演算步骤)17、(本小题满分 10 分)设 A = {-4, 2a -1, a 2}, B = {a - 5,1- a , 9} ,已知 A B = {9},求a 的值。
解: A B = {9},∴9 ∈ A 且9 ∈ B----1 分有2a -1 = 9 或a 2 = 9 ,解得: a = 5,或a = ±3----4 分当a = 5 时, A = {-4, 9, 25}, B = {0, -4, 9} ,-----------------则有 A B = {-4, 9} ,与题意不相符,∴ a = 5 舍去。
-----------6 分当a = 3 时, A = {-4, 9, 5}, a - 5 = 1- a = -2 ,则与B 中有 3 个元素不相符,∴ a = 3 舍去。
------------------8 分-10 分当a = -3 时, A = {-4, -7, 9}, B = {-8, 4, 9} , A B = {9}∴ a = 3-----18、(本小题满分 10 分)判断并证明 f ( x ) = x 2x 2 +1在(0, +∞) 的单调性。
解:判断: f ( x ) = ----2 分x 2x 2 +1在(0, +∞) 的单调递增。
----------------------证明:设>> ,则有 ( ) = x ( ) =x --------------x 1x 2 0f x 11, f x 2x 2 +1 2 x 2+1--3 分x 2 x 212x 2 •(x 2 +1) - x 2 •(x 2 +1) f ( x ) - f ( x ) = 1 - 2 = 1 2 2 1--------5 1 2x 2 +1 x 2 +1 (x 2 +1)•(x 2 +1)1212分2 21 212x⎝ ⎭ x 2 - x 2 =(x 2 +1)•(x2+1) = ( x 1 + x 2 ) •( x 1 - x 2 ) ---------- (x 2 +1)•(x 2 +1)---7 分1212x > x > 0 ,∴ x + x > 0, x - x > 0 ,又 x 2 +1 > 0, x 2 +1 > 0 ------------ 1012121212分∴( x 1 + x 2 ) •( x 1 - x 2 ) > 0 ,即 f( x ) - f ( x ) > 0(x 2 +1)•(x 2 +1)122故 f ( x ) =x 2+1在(0, +∞) 的单调递增。
19、(本小题满分 12 分)研究函数 y = lg 1- x 的定义域和奇偶性。
1+ x解:(1)依题意有: 1- x> 0 ,1+ x----------2 分解得: -1 < x < 1----------4 分所以,函数 y = lg 1- x 的定义域为(-1,1)1+ x(2) 设x ∈(-1,1) ,则-x ∈(-1,1)有: f (-x ) = lg1+ x1- x--------6 分⎛ 1- x ⎫-1= lg 1+ x ⎪= -lg 1- x1+ x----------10 分= - f ( x )所以函数 y = lg 1- x为奇函数-----------------------1+ x---------12 分b ⎪b ⎨ 20、(本小题满分 12 分)已知: a> 0, b >0 ,且a b= b aa,求证: ⎛ a ⎫b= ⎝ ⎭a -ba b 。
b证明:由a b = b a 知: b = a a--------4 分a a 则左边=⎛ a ⎫b= a b--------6 分⎪ a⎝ ⎭ b baaba⎛ b ⎫ba a ⎪ ⎝ ⎭10 分a -1a -b= ab-------12 分= ab= 右边21、(本小题满分 12 分)某商品最近 30 天的价格 f (t ) (元)与时 间t 满足关系式⎧ f (t ) = ⎪⎪- ⎩ 1 t + 8,3 1t +18, 3(0 ≤ t < 15, t ∈ N + ),(15 ≤ t < 30, t ∈ N + )且知销售量g (t ) 与时间t 满足关系式该商品的日销售额的最大值。
g (t ) = -t + 30, (0 ≤ t ≤ 30, t ∈ N + ),求解:设W (t ) 表示商品甲的日销售额(单位:元)与时间t 的函数关系。
--------1 分则有:W (t ) = ---------2 分f (t ) •g (t )=⎪ ⎨1 ⎨ 1max max a a a a ⎧ ⎛ 1 t + 8⎫•(-t + 30),(0 ≤ t < 15, t ∈ N + ) ⎪ 3⎪ = ⎪ ⎝ ⎭ ⎨⎪⎛ - ⎪ 1 t + 8⎫ •(-t + 30), 3 (15 ≤ t ≤ 30, t ∈ N + )⎩⎝⎭ ⎧ - 1 t 2+ 2t + 240,(0 ≤ t < 15, t ∈ N + ) = ⎪ ⎪ ⎪⎩33 t 2 - 28t + 540, (15 ≤ t ≤ 30, t ∈ N + )---------------------5 分⎧- 1(t - 3)2 + 243,(0 ≤ t < 15, t ∈ N + )-----7 分= ⎪ ⎪ ⎪⎩ 33 (t - 42)2- 48, (15 ≤ t ≤ 30, t ∈ N + )-------------------9 分--11 分当0 ≤ t < 15, t ∈ N + 时,易知t = 3 时,W (t ) = W (3) = 243当15 ≤ t ≤ 30, t ∈ N + 时,易知t = 15 时,W (t ) = W (15) = 195 ------所以,当t = 3 时,该商品的日销售额为最大值 243 元。
