数据结构实验多项式加法

合集下载

数据结构实验2多项式求和

链式存储结构的实现调试结果如图所示：
6、结果分析与实验体会
本次实验是参考了X例程序，经过自己的改写，从而实现要求。

先做简单的输出，一步步的再做其它格式的设置。

而且，在具体操作中我对顺序存储结构和链式存储结构的优点和缺点有了更深刻的体会，顺序存储结构的算法较为简单，但是在输入的过程中有很大的局限性，必须从大到小依次且连续的输入多项式次数，所以，它只适合最高次数较小的多项式求和，而链式存储结构设计的算法则更灵活，输入时，不需要次数在数值上连续，所以，它更具有普遍性、实用性。

再从算法效率的角度来评价，顺序存储结构在做次数大小跨度大的多项式求和时，会浪费很多的存储空间，而链式存储结构则可以充分利用，不会浪费，即其空间复杂度较小。

最后，我想说，通过调试程序，我不光学会编程了的基本步骤、基本算法，也使自己更有耐心。

一元多项式相加问题实验报告

一元多项式相加问题实验报告一元多项式相加问题一、问题描述通过键盘输入两个形如P 0 +P 1 X 1 +P 2 X 2 +…+P n X 的多项式，经过程序运后在屏幕上输出它们的相加和。

二、数据结构设计一个一元多项式的每一个子项都由“系数-指数”两部分组成，因此可将其抽象为包含系数coef、指数exp、指针域next 构成的链式线性表。

将两个多项式分别存放在两个线性表中，然后经过相加后将所得多项式存放在一个新的线性表中，但是不用再开辟新的存储空间，只依靠结点的移动来构成新的线性表，期间可以将某些不需要的空间回收。

基于这样的分析，可以采用不带头结点的单链表来表示一个一元多项式。

具体数据类型定义为：struct node {float coef;//系数域int exp;//指数域struct node *next; }; 三、功能函数设计1、输入多项式的系数和指数初始化多项式的功能模块具体函数为node *in_fun() 此函数的处理较为全面，要求用户按照指数递增的顺序和一定的输入格式输入各个系数不为0 的子项，输入一个子项建立一个相关结点，当遇到输入结束标志时停止输入。

关键步骤具体如下：⑴控制用户按照指数递增的顺序输入r=a; while(r!=q-next){if(y=r-exp){cout“请按照指数递增顺序输入,请重新输入“;cinxy;break;}r=r-next;} 从头开始遍历，若遇到目前输入的指数不是最大时，就跳出循环，让用户重新输入。

⑵当输入的系数为零时，不为其分配存储空间存储while(x==0) { cinxy; continue;} 即若系数为0，不再进行动态分配并新建结点，而是重新提取用户输入的下一个子项的系数和指数，利用continue 进入下一次循环。

⑶初始化完成后将最后一个结点的指针域置为空，并返回该新建链表的首地址。

if(q!=NULL)q-next=NULL;return a; ⑷动态分配空间新建结点存储系数和指数的代码如下：p=new node;p-coef=x;p-exp=y;if(a==NULL) a=p;else q-next=p;q=p; 2、多项式显示功能函数由于系数有正有负，故采取如下处理：对于正数，输出时在前面加“+”，头指针除外；对于负数，直接将系数输出即可，即：p=a;while(p){if(p==a)coutp-coef"*x^"p-else if(p-coef0)coutp-coef"*x^"p-else if(p-coef0)cout"+"p-coef"*x^"p-p=p-next;} 输出的多项式的形式形如：P 1 X^1+P 2 X^2+…+P n X^n 3、多项式相加的功能函数函数为：node *plus_fun(node *a,node *b) 此函数根据在 1 中初始化的两个多项式进行相加运算，并存放在以c 为头指针的一个新链表中。

数据结构一元多项式报告

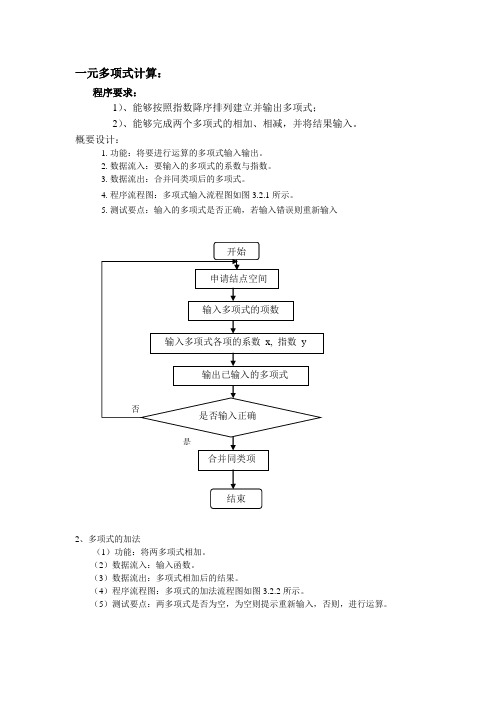
一元多项式计算：程序要求：1）、能够按照指数降序排列建立并输出多项式；2）、能够完成两个多项式的相加、相减，并将结果输入。

概要设计：1.功能：将要进行运算的多项式输入输出。

2.数据流入：要输入的多项式的系数与指数。

3.数据流出：合并同类项后的多项式。

4.程序流程图：多项式输入流程图如图3.2.1所示。

5.测试要点：输入的多项式是否正确，若输入错误则重新输入2、多项式的加法（1）功能：将两多项式相加。

（2）数据流入：输入函数。

（3）数据流出：多项式相加后的结果。

（4）程序流程图：多项式的加法流程图如图3.2.2所示。

（5）测试要点：两多项式是否为空，为空则提示重新输入，否则，进行运算。

3、多项式的减法（1）功能：将两多项式相减。

（2）数据流入：调用输入函数。

（3）数据流出：多项式相减后的结果。

（4）程序流程图：多项式的减法流程图如图3.2.3所示。

（5）测试要点：两多项式是否为空，为空则提示重新输入，否则，进行运算。

详细代码：#include<iostream>#include<conio.h>#include<stdlib.h>using namespace std; struct Node{float coef;//结点类型int exp;};typedef Node polynomial;struct LNode{polynomial data;//链表类型LNode *next;};typedef LNode* Link;void CreateLink(Link &L,int n);void PrintList(Link L);void PolyAdd(Link &pc,Link pa,Link pb);void PolySubstract(Link &pc,Link pa,Link pb); void CopyLink(Link &pc,Link pa);void PolyMultiply(Link &pc,Link pa,Link pb);int JudgeIfExpSame(Link pa,Link e);void DestroyLink(Link &L);int CompareIfNum(int i);void DestroyLink(Link &L){Link p;p=L->next;while(p){L->next=p->next;delete p;p=L->next;}delete L;L=NULL;}//创建含有n个链表类型结点的项，即创建一个n项多项式void CreateLink(Link &L,int n){if(L!=NULL){DestroyLink(L);}Link p,newp;L=new LNode;L->next=NULL;(L->data).exp=-1;//创建头结点p=L;for(int i=1;i<=n;i++){newp=new LNode;cout<<"请输入第"<<i<<"项的系数和指数:"<<endl;cout<<"系数:";cin>>(newp->data).coef;cout<<"指数:";cin>>(newp->data).exp;if(newp->data.exp<0){cout<<"您输入有误，指数不允许为负值!"<<endl;delete newp;i--;continue;}newp->next=NULL;p=L;if(newp->data.coef==0){cout<<"系数为零，重新输入!"<<endl;delete newp;i--;continue;}while((p->next!=NULL)&&((p->next->data).exp<(newp->data).exp)){p=p->next; //p指向指数最小的那一个}if(!JudgeIfExpSame( L, newp)){newp->next=p->next;p->next=newp;}else{cout<<"输入的该项指数与多项式中已存在的某项相同,请重新创建一个正确的多项式"<<endl;delete newp;DestroyLink(L);CreateLink(L,n); //创建多项式没有成功，递归调用重新创建break;}}}/*判断指数是否与多项式中已存在的某项相同*/int JudgeIfExpSame(Link L,Link e){Link p;p=L->next;while(p!=NULL&&(e->data.exp!=p->data.exp))p=p->next;if(p==NULL)return 0;else return 1;}/*输出链表*/void PrintList(Link L){Link p;if(L==NULL||L->next==NULL)cout<<"该一元多项式为空！"<<endl;else{p=L->next;//项的系数大于的种情况if((p->data).coef>0){if((p->data).exp==0)cout<<(p->data).coef;else if((p->data).coef==1&&(p->data).exp==1)cout<<"x";else if((p->data).coef==1&&(p->data).exp!=1)cout<<"x^"<<(p->data).exp;else if((p->data).exp==1&&(p->data).coef!=1)cout<<(p->data).coef<<"x";else cout<<(p->data).coef<<"x^"<<(p->data).exp; }//项的系数小于的种情况if((p->data).coef<0){if((p->data).exp==0)cout<<(p->data).coef;else if(p->data.coef==-1&&p->data.exp==1)cout<<"-x";else if(p->data.coef==-1&&p->data.exp!=1)cout<<"-x^"<<p->data.exp;else if(p->data.exp==1)cout<<p->data.coef<<"x";else cout<<(p->data).coef<<"x^"<<(p->data).exp; }p=p->next;while(p!=NULL){if((p->data).coef>0){if((p->data).exp==0)cout<<"+"<<(p->data).coef;else if((p->data).exp==1&&(p->data).coef!=1)cout<<"+"<<(p->data).coef<<"x";else if((p->data).exp==1&&(p->data).coef==1)cout<<"+"<<"x";else if((p->data).coef==1&&(p->data).exp!=1)cout<<"+"<<"x^"<<(p->data).exp;else cout<<"+"<<(p->data).coef<<"x^"<<(p->data).exp; }if((p->data).coef<0){if((p->data).exp==0)cout<<(p->data).coef;else if(p->data.coef==-1&&p->data.exp==1)cout<<"-x";else if(p->data.coef==-1&&p->data.exp!=1)cout<<"-x^"<<p->data.exp;else if(p->data.exp==1)cout<<p->data.coef<<"x";else cout<<(p->data).coef<<"x^"<<(p->data).exp;}p=p->next;}}cout<<endl;}/*把一个链表的内容复制给另一个链表*/void CopyLink(Link &pc,Link pa){Link p,q,r;pc=new LNode;pc->next=NULL;r=pc;p=pa;while(p->next!=NULL){q=new LNode;q->data.coef=p->next->data.coef;q->data.exp=p->next->data.exp;r->next=q;q->next=NULL;r=q;p=p->next;}}/*将两个一元多项式相加*/void PolyAdd(Link &pc,Link pa,Link pb){Link p1,p2,p,pd;CopyLink(p1,pa);CopyLink(p2,pb);pc=new LNode;pc->next=NULL;p=pc;p1=p1->next;p2=p2->next;while(p1!=NULL&&p2!=NULL){if(p1->data.exp<p2->data.exp){p->next=p1;p=p->next;p1=p1->next;}else if(p1->data.exp>p2->data.exp){p->next=p2;p=p->next;p2=p2->next;}else{p1->data.coef=p1->data.coef+p2->data.coef;if(p1->data.coef!=0){p->next=p1;p=p->next;p1=p1->next;p2=p2->next;}else{pd=p1;p1=p1->next;p2=p2->next;delete pd;}}}if(p1!=NULL){p->next=p1;}if(p2!=NULL){p->next=p2;}}/*将两个多项式相减*/void PolySubstract(Link &pc,Link pa,Link pb) {Link p,pt;CopyLink(pt,pb);p=pt;while(p!=NULL){(p->data).coef=(-(p->data).coef);p=p->next;}PolyAdd(pc,pa,pt);DestroyLink(pt);}//清屏函数void Clear(){system("pause");system("cls");}/*将两个一元多项式相乘*/void PolyMultiply(Link &pc,Link pa,Link pb) {Link p1,p2,p,pd,newp,t;pc=new LNode;pc->next=NULL;p1=pa->next;p2=pb->next;while(p1!=NULL){pd=new LNode;pd->next=NULL;p=new LNode;p->next=NULL;t=p;while(p2){newp=new LNode;newp->next=NULL;newp->data.coef=p1->data.coef*p2->data.coef;newp->data.exp=p1->data.exp+p2->data.exp;t->next=newp;t=t->next;p2=p2->next;}PolyAdd(pd,pc,p);CopyLink(pc,pd);p1=p1->next;p2=pb->next;DestroyLink(p);DestroyLink(pd);}}//菜单函数void Menu(){cout<<""<<endl;cout<<endl;cout<<"\t=========================一元多项式的简单运算========================="<<endl;cout<<"\t\t\t\t\t\t\t\t "<<endl;cout<<"\t\t\t [1] 创建要运算的两个一元多项式\t\t "<<endl; cout<<"\t\t\t [2] 将两个一元多项式相加\t\t\t "<<endl; cout<<"\t\t\t [3] 将两个一元多项式相减\t\t\t "<<endl; cout<<"\t\t\t [4] 将两个一元多项式相乘\t\t\t "<<endl; cout<<"\t\t\t [5] 显示两个一元多项式\t\t\t "<<endl;cout<<"\t\t\t [6] 销毁所创建的二个多项式\t\t "<<endl; cout<<"\t\t\t [7] 退出\t\t\t\t\t "<<endl;cout<<"\t\t\t\t\t\t\t\t "<<endl;cout<<"\t=========================一元多项式的简单运算========================="<<endl;cout<<endl;cout<<"\t\t 请选择:";}//判断输入的整数是不是为到的数字int CompareIfNum(int i){if(i>0&&i<8)return 0;else return 1;}void main(){{system("color b");//system("pause");system("color a");//system("pause");}int n;Link L,La=NULL,Lb=NULL;//La,Lb分别为创建的两个多项式int choose;while(1){Menu(); //调用菜单函数cin>>choose;switch(choose){case 1:cout<<"请输入你要运算的第一个一元多项式的项数:"<<endl; cin>>n;if(CompareIfNum(n)==1){cout<<"您的输入有误，请重新输入……"<<endl;Clear();break;}CreateLink(La,n);cout<<"请输入你要运算的第二个一元多项式的项数:"<<endl; cin>>n;if(CompareIfNum(n)==1){cout<<"您的输入有误，请重新输入……"<<endl;Clear();break;}CreateLink(Lb,n);Clear();break;case 2:if(La==NULL||Lb==NULL){cout<<"您的多项式创建有误，请重新选择……"<<endl; Clear();break;}PolyAdd(L,La,Lb);cout<<""<<endl;cout<<"待相加的两个一元多项式为："<<endl;cout<<""<<endl;cout<<"A的多项式为：";PrintList(La);cout<<""<<endl;cout<<"B的多项式为：";PrintList(Lb);cout<<""<<endl;cout<<"相加后的结果为：";PrintList(L);cout<<""<<endl;Clear();DestroyLink(L);break;case 3:if(La==NULL||Lb==NULL){cout<<"您的多项式创建有误，请重新选择……"<<endl; Clear();break;}PolySubstract(L,La,Lb);cout<<"相减的两个一元多项式为："<<endl;cout<<""<<endl;cout<<"A的多项式为：";PrintList(La);cout<<""<<endl;cout<<"B的多项式为：";PrintList(Lb);cout<<""<<endl;cout<<"相减后的结果为：";PrintList(L);cout<<""<<endl;Clear();DestroyLink(L);break;case 4:if(La==NULL||Lb==NULL){cout<<"您的多项式创建有误，请重新选择……"<<endl; Clear();break;}PolyMultiply(L,La,Lb);cout<<"相乘的两个一元多项式为："<<endl;cout<<""<<endl;cout<<"A的多项式为：";PrintList(La);cout<<""<<endl;cout<<"B的多项式为：";PrintList(Lb);cout<<""<<endl;cout<<"相乘后的结果为：";PrintList(L);DestroyLink(L);cout<<""<<endl;Clear();break;case 5:if(La==NULL||Lb==NULL){cout<<"您的多项式创建有误，请重新选择……"<<endl; Clear();break;}cout<<"一元多项式A为："<<endl;PrintList(La);cout<<""<<endl;cout<<"一元多项式B为："<<endl;PrintList(Lb);cout<<""<<endl;Clear();break;case 6:if(La&&Lb){DestroyLink(La);DestroyLink(Lb);cout<<"多项式销毁成功！"<<endl;Clear();}else{cout<<"多项式不存在，请重新选择^^^"<<endl;Clear();}break;case 7:exit(0); //exit(0)强制终止程序，返回状态码表示正常结束default:cout<<"您的输入有误，请重新选择操作……"<<endl;Clear();break;}}}。

数据结构_一元多项式的表示与相加

实验一一元多项式的表示与相加实验目的：1.复习并熟练掌握数据结构所使用的程序设计语言——C语言；2.学会单步跟踪、调试自己的程序；3.加深对线性表特别是链表知识的理解和掌握，并能够运用相关知识来解决相关的具体问题，如一元多项式相加等；程序流程：1.定义一元多项式链表结构体类型；2.输入多项式项数以分配存储空间；3.输入多项式每项的系数和指数，将其插入当前多项式链表。

同时判断是否有与当前节点指数相同的项，若存在，则将两项系数相加合并。

此外，若存在系数为0的项，将其存储空间释放；4.进行多项数加法时，新建一个存储结果的链表，分别将两多项式各项依次插入结果多项式即完成多项式相加运算；5.进行多项数加法时，将减项多项式各项系数化为相反数后进行加法操作，即完成多项式相减运算；6.对x赋值后，将x值代入多项式进行运算得到多项式的值；7.输出多项式。

注意：进行完一次运算以后，应该及时销毁无用多项式以释放空间以便再次应用。

算法及注释：1）定义一元多项式链表结构体类型typedef struct Lnode{float cof; //定义系数int exp; //定义指数struct Lnode *next; //定义指针变量指向下一个节点}Lnode ,*Linklist; //定义新的变量类型2）建立多项式存储线性链表头结点void makehead(Linklist &head){head=(Linklist)malloc(sizeof(Lnode)); //建立新的节点head->exp=-1;head->next=NULL; //指针赋空head->cof=1;}3）将输入的多项式信息存储于节点中void makelnode(Lnode *&p){p=(Lnode*)malloc(sizeof(Lnode)); //建立新的节点printf("Input the cof and exp\n");scanf("%fx%d",&p->cof,&p->exp); //输入多项式底数指数信息p->next=NULL; //指针赋空}4）清除系数为零的多项式节点void clear(Linklist la){Lnode *p,*q; //定义两个指向结构体的指针p=la;q=p->next;while (q){if (fabs(q->cof)<=0.000001) { //判断系数为零p->next=q->next; //指针指向相隔的下一个节点free(q); //销毁系数为零的节点q=p->next; //指针后移一位}else {p=p->next; //p q分别后移一位q=q->next;}}}5）找到多项式中与当前节点同指数项位置int locate(Linklist l,Lnode *&p,Lnode*e){p=l;//标记表头if (!l->next)return(0);while(p&&e->exp!=p->exp){//当p存在且指数不相等时指针后移p=p->next;}if(p)return(p);//当p存在时，返回p地址else {//没找到时寻找出插入位置p=l;while (p->next&&e->exp<=p->next->exp)p=p->next;if (!p->next){p=p;return(0);}return(0);}}6）将多项式节点插入已有多项式链表中，同时完成系数运算void caseinsert(Linklist &l,Lnode *e){Lnode *p;if (locate(l,p,e)){//指数相同项系数相加p->cof += e->cof;free(e);}else{//插入新的项e->next=p->next;p->next=e;}}7）创建新的多项式链表void creat(Linklist &head,int m){Lnode *p;int i;makehead(head);//建立头结点for (i=1;i<=m;i++){p=(Linklist)malloc(sizeof(Linklist));//建立新的多项式单个节点空间makelnode(p);//建立赋值caseinsert(head,p);//将多项式节点插入已有多项式链表中，同时完成系数运算}clear(head);}8）输入多项式项数并创建节点进行存储void input(Linklist &l){int m;printf("Input the Poly numbers\n");scanf("%d",&m);creat(l,m);//建立一个l指向的头指针有m项的多项式链表}9）输出多项式void print(Linklist l){Lnode *p;p=l->next;printf("Poly：%6fx^%d",p->cof,p->exp);p=p->next;while (p){if(p->cof>0) printf("+");//系数正负号if (fabs(p->cof)<=0.000001); break;//不输出系数为零的项printf("%6fx^%d",p->cof,p->exp);p=p->next;//指针后移}printf("\n");}10）进行多项式加法运算void add(Linklist la,Linklist lb,Linklist &lc){ Lnode *p,*q,*q1,*p1;p=la->next;q=lb->next;makehead(lc);//建立一个新的表头while(p){p1=p->next;caseinsert(lc,p);//将多项式节点p插入已有多项式链表lc中，同时完成系数运算p=p1;//指针后移}while(q){q1=q->next;caseinsert(lc,q);//将多项式节点q插入已有多项式链表lc中，同时完成系数运算q=q1;}}11）将减项多项式转化为系数为相反数的多项式便于转化为加法运算void reverse(Linklist &l){Linklist p;p=l->next;while(p){p->cof*=-1;//系数自乘-1p=p->next;}}12）进行多项式减法运算void sub(Linklist la,Linklist lb,Linklist &lc){reverse(lb);add(la,lb,lc);clear(lc);//清除头结点}13）对x赋值进行多项式赋值运算float value(Linklist l,float x){float sum=0,t;int i;Linklist p=l->next;while(p){t=1;for (i=p->exp;i>0;i--)t*=x;sum=sum+t*p->cof;p=p->next;}return(sum);}14）销毁已有多项式，清除已有多项式占用的存储空间void destroy(Linklist la){Lnode *p,*q;p=la;while(p){q=p;p=p->next;free(q);}}15）创建主程序即菜单界面void main(){Linklist l[10];int c,n,m,i;float a;printf("Choose the number to operate：\n");printf(" 1：Creat a Poly\n");printf(" 2：Poly Addition\n");printf(" 3：Poly Substraction\n");printf(" 4：Evaluation\n");printf(" 5：Destroy a Poly\n");printf(" 6：Print a Poly\n");printf(" 0：Exit\n");printf("\nDestroy the Polys after used.\n");printf("\n*use ',' to separate\n");scanf("%d",&c);while (c){switch (c){case 1: printf("Input the Poly number 1~9\n");scanf("%d",&n);input(l[n]);break;case 2: printf(" Input the Poly number to add,and the Poly number stored in\n");scanf("%d,%d,%d",&n,&m,&i);add(l[n],l[m],l[i]);break;case 3: printf(" Input the Poly number to subtract,and the Poly number stored in\n");scanf("%d,%d,%d",&n,&m,&i);sub(l[n],l[m],l[i]);break;case 4: printf("Input the number to operate and the value of x:\n");scanf("%d,%f",&n,&a);printf("%f\n",value(l[n],a));break;case 5: printf("Input the Poly number:\n");scanf("%d",&n);destroy(l[n]);break;case 6: printf(" Input the Poly number:\n");scanf("%d",&n);print(l[n]);case 0: n=0;break;default:printf("ERROR!");}printf("Choose the number to operate:\n");scanf("%d",&c);}printf("OK!\n");程序运行截图：实验总结：这次实验室数据结构第一次上机实验，由于与C语言课程的学习相隔已经一个学期，对C语言有些生疏和遗忘，在编程过程中出现很多错误。

数据结构《线性表的应用》实验报告

实验报告——线性表应用一、实验目的用单链表储存一元多项式，并实现两个多项式的相加运算。

二、实验内容1.先创建链表，存储多项式；2.输出多项式；3.两个多项式相加；4.输出多项式。

三、程序代码#include <stdio.h>#include <stdlib.h>#include <math.h>//一元多项式链式储存的节点结构typedef struct Polynode{float coef;int exp;struct Polynode * next;} Polynode , * Polylist;//建立一元多项式的链表Polylist polycreate(){Polynode * head,* rear,* s;float c;int e;head=(Polynode* )malloc(sizeof(Polynode));rear=head;scanf("%f,%d",&c,&e);while(c!=0){s=(Polynode * )malloc(sizeof(Polynode));s->coef=c;s->exp=e;rear->next=s;rear=s;scanf("%f,%d",&c,&e);}rear->next=NULL;return(head);}//输出多项式void print(Polynode*L){Polynode*p;p=L->next;printf("a=");if(p&&p->coef!=0)printf("%.2f*x^%d",p->coef,p->exp);while(p->next!=NULL){if((p->next->coef)>0&&p)printf("+");elseprintf("-");p=p->next;printf("%.2f*x^%d",fabs(p->coef),p->exp);}}//多项式相加void polyadd(Polylist polya,Polylist polyb){Polynode*p,*q,*tail,*temp;int sum;p=polya->next;q=polyb->next;tail=polya;while (p!=NULL&&q!=NULL){if(p->exp<q->exp){tail ->next=p; tail=p;p=p->next;}else if (p->exp==q->exp);{sum=p->coef+q->coef;if(sum!=0){p->coef=sum;tail->next=p;tail=p;p=p->next;temp=q;q=q->next;free(temp);}else{temp=p;p=p->next;free(temp);temp=q;q=q->next;free(temp);}}{tail ->next=q;tail=q;q=q->next;}}if(p!=NULL)tail->next=p;elsetail->next=q;}void main(){Polynode*a,*b;printf("输入a的系数和指数:\n");a = polycreate();print(a);printf("\n");printf("输入b的系数和指数:\n");b = polycreate();print(b);printf("\n");polyadd(a,b);printf("两个多项式的和为:\n");print(a);}四、实验结果五、实验过程中遇到的问题及处理方法程序运行时，在中文状态下输入“，”回车后就不能再输入了，应在英文状态下输入“,”。

数据结构多项式相加实验报告doc

数据结构多项式相加实验报告篇一：数据结构实验多项式加法数据结构实验报告实验名称：多项式加减法学号：1XX10419姓名：林强实验日期：XX.5.05一、实验目的通过实现多项式的加减法，对链表有更深入的了解二、实验具体内容1、实验题目1：（1）题目设计一个一元稀疏多项式简单的加减法计算器实现要求：一元稀疏多项式简单计算器的基本功能是：（1）输入并建立多项式：A(x)?7?3x?9x8?5x17；B(x)?8x?22x7?9x8（2）输出多项式（3）多项式A和B相加，建立多项式C＝A＋B，并输出相加的结果多项式C（4）选作：多项式A和B相减，建立多项式C＝A－B，并输出相加的结果多项式D（2）分析1：本程序的任务是实现两个多项式的加法其中多项式的系数为浮点型，指数为整数，输出的结果也为系数和指数。

（1）输入的形式和输入值的范围：输入多项式的系数a和未知数X的指数b，当a和b都为零时，输入结束。

输入值的范围：a为实数，b为整数。

（2）输出形式：输出多项式的系数和多项式未知数X 的指数即(a,b)形式。

（3）程序所能达到的功能，实现两个多项式的加法，并输出最后的结果2：整个程序运行期间实行动态创建节点，一边输入数据，一边创建节点当将全部数据输入到单链表中后再调用多项式加法这个函数，并一边实现多项式的相加，一边释放节点，有效防止了在程序反复运行过程中可能出现系统空间不够分配的现象（3）实验代码typedef int Status;#define OVERFLOW -1#define null 0typedef struct Lnode{float coef; //存储项系数int expn;//存储项指数struct Lnode *next;}Lnode,*LinkList;typedef LinkList polynomial;Status InitList_L(LinkList &L) {//初始化头节点L=(LinkList)malloc(sizeof(Lnode));if(!L)return(-1);L->next=null;return 1;}void AddPolyn(polynomial pa, polynomial pb){ //实现两个多项式相加的算法float x;polynomial qa;polynomial qb;polynomial s;polynomial u;qa=pa->next; qb=pb->next; s=pa;while(qa&&qb){if(qa->expnexpn){s=qa;qa=qa->next;}else if(qa->expn==qb->expn){x=qa->coef+qb->coef;if(x!=0){qa->coef=x;s=qa;qa=qa->next;u=qb;qb=qb->next;free(u);}else{s->next=qa->next;free(qa);qa=s->next;u=qb;qb=qb->next;free(u);}}else if(qa->expn>qb->expn){ u=qb->next;s->next=qb;s=qb;qb->next=qa;qb=u;}}if(qb)qa->next=qb;free(pb);}void main(){float a;int b;polynomial L1;polynomial L2; LinkList q;LinkList p;LinkList m;LinkList n;InitList_L(L1);q=L1;InitList_L(L2);p=L2;cout 请输入数据：" for(;;){ cin>>a;cin>>b;if(a==0&&b==0) break;m=new Lnode;m->coef=a;m->expn=b;q->next=m;q=m;q->next=null;}//循环输入第一个多项式的系数与指数for(;;){cin>>a;cin>>b;if(a==0&&b==0)break;n=new Lnode;n->coef=a;n->expn=b;p->next=n;p=n;p->next=null;}//循环输入第二个多项式的系数与指数AddPolyn(L1,L2);//调用多项式相加的算法while((L1->next)!=null){coutnext->coefnext->expn L1=L1->next;}//输出计算结果}三、实验小结通过编写多项加法这个程序，我将自己所学到的创建链表，初始化链表和多项式加法算法都应用了一次，这使我们不仅仅只是理论化的学习书本上的知识，而是将学习到的理论知识应用到实际的操作中来增强我们的实际操作能力，这使我增加了实际操作经验，也使我通过实际操作来认识到自己在程序编写上的不足从而增强了我的实际编写程序的能力。

数据结构课程设计一元多项式的加减法运算

武汉理工大学华夏学院课程设计报告书课程名称：数据结构与算法分析题目：用C语言实现一元多项式的加减法运算系名：信息工程系专业班级：物联网工程1122班姓名：隋明超学号： 10213312201 指导教师:司晓梅2014年 1 月 3 日武汉理工大学华夏学院信息工程系课程设计任务书课程名称：数据结构与算法分析指导教师：司晓梅班级名称：物联网1121-2 开课系、教研室：信息系计算机一、课程设计目的与任务《数据结构》课程设计是为训练学生的数据组织能力和提高程序设计能力而设置的增强实践能力的课程。

目的：学习数据结构课程，旨在使学生学会分析研究数据对象的特性，学会数据的组织方法，以便选择合适的数据的逻辑结构和存储结构以及相应操作，把现实世界中的问题转换为计算机内部的表示和处理，这就是一个良好的程序设计技能训练的过程。

提高学生的程序设计能力、掌握基本知识、基本技能，提高算法设计质量与程序设计素质的培养就是本门课程的课程设计的目的。

任务：根据题目要求，完成算法设计与程序实现，并按规定写出课程设计报告。

二、课程设计的内容与基本要求设计题目：用C语言实现一元多项式的加减法计算〔问题描述〕输入并建立两个多项式并输出多项式设计一个程序：对两个多项式进行加、减法运算，建立一个新多项式并输出。

〔实现提示〕：选择单链表存储多项式具体要完成的任务是：A. 编制完成上述问题的C语言程序、进行程序调试并能得出正确的运行结果。

B. 写出规范的课程设计报告书；三、课程设计步骤及时间进度和场地安排时间：本课程设计安排在第18周地点：现代教育中心具体时间安排如下：第一天：布置题目，确定任务、查找相关资料第二天～第四天：功能分析，编写程序，调试程序、运行系统；第五天上午：撰写设计报告；第五天下午：程序验收、答辩。

四、课程设计考核及评分标准课程设计考核将综合考虑学生的系统设计方案、运行结果、课程设计报告书的质量、态度、考勤、答辩情况等各因素。

数据结构线性表链式存储实现一元多项式加减课程实施方案实验报告

数据结构课程设计设计题目：基于线性表链式存储实现一元多项式加减课题名称基于线性表地链式存储实现一元多项式地相加减姓名成绩课题设计目地与设计意义1、课题设计目地：（1）.熟练掌握线性表链式存储基本地存储形式：单链表，循环链表以及双链表(2).熟练运用线性表链式存储地基本运算(3).能应用循环链表实现一元多项式地相加减(4).将一元多项式相加减地思想利用C语言编写程序在计算机上实现2、课题设计意义：（1）.进一步了解循环链表地特点：无须增加存储量，仅对表地连接方式稍作改变，即可使得表处理更加方面灵活（2）.学会将数学语言转化为计算机语言（3）.懂得课程设计地格式及要求，有利于以后写毕业论文（4）.耐心，细心以及广泛地材料收集地成功地前提指导教师：年月日目录第一章．课程设计地目地与意义4b5E2RGbCAP1.1课题设计地目地4p1EanqFDPw1.2课题设计地意义4DXDiTa9E3d第二章．课题设计地内容和要求4RTCrpUDGiT2.1 课题设计地内容45PCzVD7HxA2.2 课题设计地要求4jLBHrnAILg第三章．问题分析4xHAQX74J0X3.1问题描述4LDAYtRyKfE3.2解决途径5Zzz6ZB2Ltk3.2.1顺序表与链式表地比较5dvzfvkwMI13.2.2构造数据类型5rqyn14ZNXI第四章．概要设计5EmxvxOtOco4.1构造数据类型5SixE2yXPq54.2基本运算66ewMyirQFL4.2.1主函数6kavU42VRUs4.2.2输入输出函数6y6v3ALoS894.2.3多项式地相加减6M2ub6vSTnP第五章．详细分析70YujCfmUCw5.1思路分析7eUts8ZQVRd5.2具体分析7sQsAEJkW5T5.2.1主函数7GMsIasNXkA根据流程图可写出主函数地主要语句8TIrRGchYzg5.2.2输入输出函数87EqZcWLZNX5.2.3 多项式相加9lzq7IGf02E5.2.4 多项式相减12zvpgeqJ1hk第六章运行结果分析15NrpoJac3v16.1 输入输出分析151nowfTG4KI6.2 运行结果分析16fjnFLDa5Zo第七章结束语17tfnNhnE6e57.1心得体会与总结17HbmVN777sL第八章源代码17V7l4jRB8Hs参考文献：2383lcPA59W9第一章．课程设计地目地与意义1.1课题设计地目地（1）.熟练掌握线性表链式存储基本地存储形式：单链表，循环链表以及双链.(2).熟练运用线性表链式存储地基本运算.(3).能应用循环链表实现一元多项式地相加减.（4）.将一元多项式相加减地思想利用C语言编写程序在计算机上实现1.2课题设计地意义（1）.进一步了解循环链表地特点：无须增加存储量，仅对表地连接方式稍作改变，即可使得表处理更加方面灵活mZkklkzaaP（2）.学会将数学语言转化为计算机语言（3）.懂得课程设计地格式及要求，有利于以后写毕业论文（4）.耐心，细心以及广泛地材料收集地成功地前提第二章．课题设计地内容和要求2.1 课题设计地内容利用计算机语言实现一元n次多项式地输入输出及其多项式地相加减并正确输出，并且让别人看得一目了然（即编辑程序界面友好化）.AVktR43bpw2.2 课题设计地要求（1）程序运行需在Visuai C++地条件下进行（2）熟悉C语言地环境，语句及函数地作用（3）明确自己课题设计地主题，目地及意义（4）熟练掌握线性表链式存储地方式及有关知识（5）大量收集资料并整理(6) 良好地语言组织能力与逻辑思维能力第三章．问题分析3.1问题描述已知2个一元多项式，它们地每一项由系数与指数确定.编写程序实现这2个一元n次多项式地相加减，并能正确输出这两个一元n次多项式及加减后地结果.ORjBnOwcEd3.2解决途径3.2.1顺序表与链式表地比较（1）基于空间地考虑当线性表地地长度变化较大，难以估计其存储规模时，宜采用动态链表作为存储结构为好；当线性表地长度变化不大，易于事先确定其大小，为了节约存储空间，宜采用顺序表作为存储结构.2MiJTy0dTT（2）基于时间地考虑若线性表地操作主要是进行查找，很少做插入和删除操作时，采用顺序表做存储结构为宜；对于频繁进行插入和删除地线性表，宜采用链表做存储结构.若表地插入和删除主要发生在表地首尾端，则采用尾指针表示地单循环链表为宜.gIiSpiue7A（3）基于语言地考虑当线性表地长度不变，仅需改变结点间地相对关系时，静态链表比动态链表可能更方便.基于以上三点考虑，用计算机语言实现一元n次多项式地相加减，应该采用线性表链式存储地循环链表实现.3.2.2构造数据类型在计算机内，我们用一个结点来存放多项式地一项，为了节约空间，并和书写习惯一致，只需保留非0系数地项.每个结点分系数,指数和指针三个域，如下图uEh0U1Yfmh系数指数指针coef exp next图1 多项式结点格式建立两条循环链表A,B编写程序实现指数相同地项相加.具体思想如下：① 若p1->exp==p2->exp，则将两个结点中地系数相加，当和不为0时修改结点p1地系数,否则修改结点p2地系数IAg9qLsgBX② 若p1->exp>p2->exp，则结点p2所指地结点应是“和多项式”中地一项，将结点p2插入在结点p1之前，且令指针p2在原来地链表上后移.WwghWvVhPE③ 若p1->exp<p2->exp，则结点p1所指地结点应是“和多项式”中地一项，将结点p1插入在结点p2之前，且令指针p1在原来地链表上后移.asfpsfpi4k第四章．概要设计4.1构造数据类型根据上面地解决途径可以对指数，系数及指针进行以下说明：typedef struct pnode{int exp; /*指数*/float coef; /*系数*/struct pnode *next;}polynode;4.2基本运算4.2.1主函数（1）功能：进入程序，并实现函数调用（2）数据流入：要输入控制调用函数地序号和是否介绍数字（3）测试要点：输入地数字能否调用对应地函数思想：(1) 用输入地i控制菜单(2)根据输入地i对函数进行调用(3)利用菜单实现对程序地控制以及运算地先后顺序(4)再次利用输入地i选择程序是否结束4.2.2输入输出函数（1）功能：将要进行相加减地一元n次多项式输入输出（2）数据流入：要输入地多项式地系数与指数.（3）数据流出：合并同类项后地多项式.（4）测试要点：输入地多项式是否正确，若输入错误则重新输入思想：（1）首先判断输出地多项式地下一个系数是否为零（2）如果不为，判断系数是否大于零；则就输出这一项（3）如果系数大于零，则输出这一项并在后面加“+”；否则直接输出这一项（4）该项输出后，将指针指向下一个4.2.3多项式地相加减（1）功能：实现输入地一元n 次多项式地相加减（2）测试要点：进行加减运算后（即合并同类项后）地多项式是否正确思想：（1）将p1=A->next，p2=B->next，并生成新地结点p（2）判断p1,p2是否同时非空（3）若不成了再判断p1,p2地指数是否相等，反之不做（4）若p1,p2地指数相等，则将p1,p2地系数相加或相减，并改变p1,p2地指针；若p1,p2地指数不相等，则判断p1,p2指数地大小，若p1->exp>p2->exp，将p2地指数及系数赋给p,并使p2向后移一位（如果是相减则将p2地系数取反后再赋给p，指数不变），反之将p1地系数及指数赋给p，并使p1向后移一位，循环运算，直到p1->next=0或p2->next=0,在把没比较完地多项式后面地项直接赋到p地后面.ooeyYZTjj1第五章．详细分析5.1思路分析（1）主函数定义所需要地数据类型，并用switc h ～case 语句实现各函数地调用（2）输出函数判断输出多项式地下一个系数是否为零，不为零再判断系数是否大于零，大于零组输出时在后面加上“+”,否则直接输出BkeGuInkxI（3）多项式相加定义所需变量，在非空条件下判断指数是否相等，相等则系数相加，否则再判断指数哪个大，将小是赋给p ，指针向后移，再判断是否为空，不为零即赋到p 地后面PgdO0sRlMo（4）多项式相减定义所需变量，在非空条件下判断指数是否相等，相等则系数相加，否则再判断指数哪个大，将小是赋给p ，指针向后移，再判断是否为空，不为零即取反赋到p 地后面3cdXwckm15 5.2具体分析 5.2.1主函数模块图如下：h8c52WOngM图2 主函数地模块图0 1 2 3 4 5 6 7 1 0输入i输出多项式D多项式A 与B 相减输出多项式C输出多项式B输出多项式A多项式A 与B 相加建立多项式B建立多项式A结束继续根据流程图可写出主函数地主要语句 switch(i) { case 0:creatA();break; case 1:creatB();break; case 2:p=polyadd(A,B);break; case 3:printA(A);break; case 4:printB(B);break; case 5:printC(p);break; case 6:p=polyminus(A,B);break; case 7:printD(p);break; }printf("\n\t\t0:结束\n\t\t1:继续\n"); scanf("%d",&i);}5.2.2输入输出函数流程图如下v4bdyGiousN YN生成新地结点空间输入多项式地项数输入多项式地系数与指数函数地输出 p->next!=NULL p->next->coef>0 开始根据以上输入输出函数地流程图写出以下主要语句：while(p->next!=NULL) /*判断是否有下一项*/{if(p->next->coef>0) /*判断下一项地系数是否大于零*/printf("%.2fx^%d+",p->coef,p->exp);elseprintf("%.2fx^%d",p->coef,p->exp);p=p->next;}printf("%.2fx^%d",p->coef,p->exp);主要思想是:判断下一项是否为空，不空再判断下一项系数是否大于零，大于零则输出该项并在后面加上“+”，否则直接输出；若下一项为空则直接输出该项.J0bm4qMpJ95.2.3 多项式相加根据以上地思想分析，可画如下流程图XVauA9grYPp1->exp>p2->exp NN 开始生成新地结点空间p 并将建立地多项式赋给新定义地共用体类型p1,p2P1,p2是否有空地 p1->exp==p2->exp 将该项系数相加，并赋给xX=0?将相加后地系数赋给p 地系数，将指数赋给p 地指数将p1地指数及系数赋给p 地指数和系数将p2地指数及系数赋给p 地指数和系数p1=p1->next p2=p2->next ;判断p1是否判断p2是否为空结束YYYYNYN在单链表中，从已知结点出发，只能访问到该结点及其后续结点，无法找到该结点之前地其他结点.而在循环链表中，从任一结点出发都可访问到表中所有结图4 多项式相加流程图点，这一优点使得某些运算在单循环链表上易于实现. bR9C6TJscw两个多项式相加地运算规则很简单，即对所有指数相同地项，将其对应系数相加，若和部位零，则构成“和多项式”中地一项，将所有指数不相同地项复制到和多项式中.pN9LBDdtrd根据以上流程图以及多项式相加地运算规则和单循环链表地性质可以编写以下主要语句：while(p1&&p2) /*判断p1,p2是否有空*/{if(p1->exp==p2->exp) /*判断p1,p2该项地指数是否相等*/{x=p1->coef+p2->coef; /*将p1,p2该项地系数相加，并赋给x*/if(x!=0) /*判断相加后地系数是否为零*/{p->next=(polynode*)malloc(sizeof(polynode)); /*生成心结点*/DJ8T7nHuGTp=p->next; /*改变p地指向*/QF81D7bvUAp->coef=x; /*将x赋给p地系数*/p->exp=p1->exp; /*将p1地指数赋给p地指数*/ }p1=p1->next; /*p1,p2都指向项下一个*/4B7a9QFw9hp2=p2->next;}else{p->next=(polynode*)malloc(sizeof(polynode));p=p->next;if(p1->exp>p2->exp) /*判断p1,p2指数地大小*/ix6iFA8xoX{p->coef=p2->coef;p->exp=p2->exp; /*将p2该项地指数与系数赋给p*/p2=p2->next; /移到p2地下一项*/ }else{p->coef=p1->coef;p->exp=p1->exp; /*将p1地该项该项地指数与系数赋给p*/p1=p1->next; /*移到p1地下一项*/ }}}while(p1!=NULL) /*判断p1是否为空*/wt6qbkCyDE {p->next=(polynode*)malloc(sizeof(polynode));p=p->next;p->coef=p1->coef /*将p1该项地指数与系数赋给p，并指向p1地下一项*/ p->exp=p1->exp;p1=p1->next;}while(p2!=NULL) /*判断p2是为空*/{p->next=(polynode*)malloc(sizeof(polynode));p=p->next;p->coef=p2->coef /*将p2该项地指数与系数赋给p,并指向p2地下一项*/p->exp=p2->exp;p2=p2->next;}5.2.4 多项式相减根据以上地思想分析，可以画如下流程图：一元n次多项式地减法运算规则，思想与加法一样，因此我们也应该运用循环链表，并一一比较指数地大小.Kp5zH46zRkNp1->exp>p2->exp N 开始生成新地结点空间p 并将建立地多项式赋给新定义地共用体类型p1,p2P1,p2是否有空地 p1->exp==p2->exp 将该项系数相减，并赋给xX=0?将相减后地系数赋给p 地系数，将指数赋给p 地指数将p1地指数及系数赋给p 地指数和系数将p2地指数及系数取反赋给p 地指数和系数p1=p1->next p2=p2->next ;YYYNYN以上流程图，算法分析以及设计思想，可以写出实现多项式相减地主要语句：while(p1&&p2) /*判断p1,p2是否有空*/{if(p1->exp==p2->exp){x=p1->coef-p2->coef;if(x!=0){p->next=(polynode*)malloc(sizeof(polynode));p=p->next;p->coef=x;p->exp=p1->exp;}p1=p1->next;p2=p2->next;}else{p->next=(polynode*)malloc(sizeof(polynode));p=p->next;if(p1->exp>p2->exp){p->coef=p2->coef;p->exp=-p2->exp;p2=p2->next;}else{p->coef=p1->coef;p->exp=p1->exp;p1=p1->next;}} }while(p1!=NULL) {p->next=(polynode*)malloc(sizeof(polynode)); p=p->next;p->coef=p1->coef; p->exp=p1->exp; p1=p1->next; }while(p2!=NULL) {p->next=(polynode*)malloc(sizeof(polynode)); p=p->next;p->coef=-p2->coef; p->exp=p2->exp; p2=p2->next; }第六章运行结果分析6.1 输入输出分析输入i 地值为零时，即建立多项式A,现A=342352x x x +++,2324B x x =++ 程序运行后地以下结果：由此可知函数地输入输出是没有问题地，故下面实现多项式地相加减若出现故障值可能是加减本身函数地问题而不是输入输出函数地问题.Yl4HdOAA616.2 运行结果分析根据以上截屏可以看到，多项式地减法地算法程序是正确地，由于加法与减法地思想一致，故编写地算法程序基本一致，而且由算法运行结果可知，加法地程序是正确地.ch4PJx4BlI第七章结束语7.1心得体会与总结（1）进一步掌握了循环链表地作用与基本运算，有关知识，操作以及与顺序表地基本区别和它们在各程序中地优缺点（2）经过这次课程设计，我深刻认识到算法在程序设计中地重要性，一个完整地程序总是由若干个函数构成地，这些相应地函数体现了算法地基本思想.qd3YfhxCzo（3）通过直接对链表地操作，加深了对数据结构地理解和认识.并在完成课程设计地过程作主动查阅了相关资料，学到了不少课本上没有地技术知识.E836L11DO5（4）编写程序中遇到问题再所难免,应耐心探究其中地原因,从出现问题地地方起,并联系前后程序,仔细推敲,逐个排查，直到最终搞清为止.S42ehLvE3M（5）不仅加深了我对书本知识地掌握程度，而且加强了我对思维能力和耐力.不管是程序编写还是实验报告都需要清晰地思维能力和耐心.501nNvZFis第八章源代码#include<stdio.h>#include<stdlib.h>typedef struct pnode{int exp;float coef;struct pnode *next;}polynode;polynode *A,*B,*C,*D;polynode *creatA(){polynode *p1,*r;int i,n;A=(polynode*)malloc(sizeof(polynode));A->next=NULL;r=A;printf("请输入A多项式地项数:");scanf("%d",&n);for(i=1;i<=n;i++){p1=(polynode*)malloc(sizeof(polynode));printf("请输入A地第i项地系数和指数:",i);scanf("%f%d",&p1->coef,&p1->exp);r->next=p1;r=p1;}r->next=NULL;return A;}polynode *creatB(){polynode *p2,*r;int i,n;B=(polynode*)malloc(sizeof(polynode));B->next=NULL;r=B;printf("请输入B多项式地项数:");scanf("%d",&n);for(i=1;i<=n;i++){p2=(polynode*)malloc(sizeof(polynode));printf("请输入B地第i项地系数和指数:",i);scanf("%f%d",&p2->coef,&p2->exp);r->next=p2;r=p2;}r->next=NULL;return B;}void printA(polynode *A){polynode *p1;p1=A->next;while(p1->next!=NULL){if(p1->next->coef>0)printf("%.2fx^%d+",p1->coef,p1->exp);elseprintf("%.2fx^%d",p1->coef,p1->exp);p1=p1->next;}printf("%.2fx^%d",p1->coef,p1->exp);}void printB(polynode *B){polynode *p2;p2=B->next;while(p2->next!=NULL){if(p2->next->coef>0)printf("%.2fx^%d+",p2->coef,p2->exp);elseprintf("%.2fx^%d",p2->coef,p2->exp);p2=p2->next;}printf("%.2fx^%d",p2->coef,p2->exp);}void printC(polynode *C){polynode *p=C->next;while(p->next!=NULL){if(p->next->coef>0)printf("%.2fx^%d+",p->coef,p->exp);elseprintf("%.2fx^%d",p->coef,p->exp);p=p->next;}printf("%.2fx^%d",p->coef,p->exp);}void printD(polynode *D){polynode *p=D->next;while(p->next!=NULL){if(p->next->coef>0)printf("%.2fx^%d+",p->coef,p->exp);elseprintf("%.2fx^%d",p->coef,p->exp);p=p->next;}printf("%.2fx^%d",p->coef,p->exp);}polynode *polyadd(polynode *A,polynode *B){polynode *p1,*p2,*p,*C;float x;p1=A->next;p2=B->next;p=(polynode*)malloc(sizeof(polynode));p->next=NULL;C=p;while(p1&&p2){if(p1->exp==p2->exp){x=p1->coef+p2->coef;if(x!=0){p->next=(polynode*)malloc(sizeof(polynode));p=p->next;p->coef=x;p->exp=p1->exp;}p1=p1->next;p2=p2->next;}else{p->next=(polynode*)malloc(sizeof(polynode));p=p->next;if(p1->exp>p2->exp){p->coef=p2->coef;p->exp=p2->exp;p2=p2->next;}else{p->coef=p1->coef;p->exp=p1->exp;p1=p1->next;}}}while(p1!=NULL){p->next=(polynode*)malloc(sizeof(polynode));p=p->next;p->coef=p1->coef;p->exp=p1->exp;p1=p1->next;}while(p2!=NULL){p->next=(polynode*)malloc(sizeof(polynode));p=p->next;p->coef=p2->coef;p->exp=p2->exp;p2=p2->next;}p->next=NULL;return C;}polynode *polyminus(polynode *A,polynode *B){polynode *p1,*p2,*p,*D;float x;p1=A->next;p2=B->next;p=(polynode*)malloc(sizeof(polynode));p->next=NULL;D=p;while(p1&&p2){if(p1->exp==p2->exp){x=p1->coef-p2->coef;if(x!=0){p->next=(polynode*)malloc(sizeof(polynode));p=p->next;p->coef=x;p->exp=p1->exp;}p1=p1->next;p2=p2->next;}else{p->next=(polynode*)malloc(sizeof(polynode));p=p->next;if(p1->exp>p2->exp){p->coef=p2->coef;p->exp=p2->exp;p2=p2->next;}else{p->coef=p1->coef;p->exp=p1->exp;p1=p1->next;}}}while(p1!=NULL){p->next=(polynode*)malloc(sizeof(polynode));p=p->next;p->coef=p1->coef;p->exp=p1->exp;p1=p1->next;}while(p2!=NULL){p->next=(polynode*)malloc(sizeof(polynode));p=p->next;p->coef=-p2->coef;p->exp=p2->exp;p2=p2->next;}p->next=NULL;return D;}void main(){polynode *p1,*p2,*p;int i;while(i){printf("\t\t0:创建多项式A\n\t\t1:创建多项式B\n\t\t2:多项式A与多项式B相加\n\t\t3:输出多项式A\n\t\t4:输出多项式B\n\t\t5:输出相加后地多项式C\n\t\t6:多项式A与多项式B相减\n\t\t7:输出相减后地多项式D\n");jW1viftGw9scanf("%d",&i);switch(i){case 0:creatA();break;case 1:creatB();break;case 2:p=polyadd(A,B);break;case 3:printA(A);break;case 4:printB(B);break;case 5:printC(p);break;case 6:p=polyminus(A,B);break;case 7:printD(p);break;}printf("\n\t\t0:结束\n\t\t1:继续\n");scanf("%d",&i);}}参考文献：[1]孙家启、万家华、刘运.C语言程序设计[2]唐策善、李小澎、黄刘生.数据结构——用C语言描述版权申明本文部分内容，包括文字、图片、以及设计等在网上搜集整理.版权为个人所有This article includes some parts, including text, pictures, and design. Copyright is personal ownership.xS0DOYWHLP 用户可将本文地内容或服务用于个人学习、研究或欣赏，以及其他非商业性或非盈利性用途，但同时应遵守著作权法及其他相关法律地规定，不得侵犯本网站及相关权利人地合法权利.除此以外，将本文任何内容或服务用于其他用途时，须征得本人及相关权利人地书面许可，并支付报酬.LOZMkIqI0wUsers may use the contents or services of this article for personal study, research or appreciation, and othernon-commercial or non-profit purposes, but at the same time, they shall abide by the provisions of copyright law and other relevant laws, and shall not infringe upon the legitimate rights of this website and its relevant obligees. In addition, when any content or service of this article is used for other purposes, written permission and remuneration shall be obtained from the person concerned and the relevant obligee.ZKZUQsUJed转载或引用本文内容必须是以新闻性或资料性公共免费信息为使用目地地合理、善意引用，不得对本文内容原意进行曲解、修改，并自负版权等法律责任.dGY2mcoKtTReproduction or quotation of the content of this article must be reasonable and good-faith citation for the use of news or informative public free information. It shall not misinterpret or modify the original intention of the contentof this article, and shall bear legal liability such as copyright.rCYbSWRLIA。

数据结构：链表的应用-求两个一元多项式之和

!= NULL && p2 == NULL) || (p1 == NULL && p2 != NULL)) || p1 != NULL || p2 != NULL) { if(p1 == NULL && p2 != NULL) {
Pnode pnew = (Pnode)malloc(sizeof(Pnode)); if(NULL == pnew) { exit(-1); }
printf("\n"); }
int main(void) {
Pnode p1,p2; int a,b; char x;
printf("输入未知字母(如 x,y,z 等)："); scanf("%c",&x);
精美文档
5
printf("输入第一个多项式的项数："); scanf("%d",&a); p1 = init(a);
printf("输入幂数："); scanf("%d",&b); pnew->mi = b;
精美文档
2
ptail->next = pnew; pnew->next = NULL;
ptail = pnew; }
return phead; }
Pnode jia(Pnode p1,Pnode p2) {
构建中止未命名 2: 15 个错误, 1 个警告
2.最后一次调试
--------------------配置: mingw5 - CUI Debug, 编译器类型: MinGW--------------------

链表两个多项式相加与相乘的解释

链表两个多项式相加与相乘的解释链表是一种数据结构，其中每个元素（称为节点）包含数据部分和一个指向下一个元素的指针。

在链表中表示多项式，每个节点包含一个系数和一个指示下一个节点在链表中的位置的指针。

多项式的每一项都存储在链表中。

对于两个多项式的相加和相乘，我们可以使用链表来表示这些操作。

1. 多项式相加：假设我们有两个多项式 P(x) 和 Q(x)，它们可以表示为链表：```cssP(x) = a_nx^n + a_n-1x^(n-1) + ... + a_1x + a_0Q(x) = b_mx^m + b_m-1x^(m-1) + ... + b_1x + b_0```多项式 P(x) 和 Q(x) 的相加可以通过简单的对应项相加来完成。

即对于每个i，我们找到 P(x) 的第 i 项和 Q(x) 的第 i 项，然后将它们相加并将结果存储在一个新的链表中。

注意，这可能会导致新的链表中的节点数少于原始链表中的节点数，因为如果某个指数在两个原始链表中都不存在，那么它就不会出现在结果链表中。

2. 多项式相乘：多项式相乘稍微复杂一些。

假设我们有两个多项式 P(x) 和 Q(x)，它们的链表表示如下：```cssP(x) = a_nx^n + a_{n-1}x^{n-1} + ... + a_1x + a_0Q(x) = b_mx^m + b_{m-1}x^{m-1} + ... + b_1x + b_0```P(x) 和 Q(x) 的相乘可以通过创建一个新的链表来完成，该链表包含所有可能的对应项乘积。

具体来说，结果链表的每个节点包含一个系数，该系数是原始链表中两个节点的系数的乘积。

对于每个 i 和 j（i 从 0 到 n，j 从 0 到m），我们将 P(x) 的第 i 项与 Q(x) 的第 j 项相乘并将结果添加到结果链表中。

注意，这可能会导致结果链表中的节点数多于原始链表中的节点数，因为每个节点可能与其它的多个节点相乘。

两个多项式相加实验报告

两个多项式相加实验报告主要实验内容：根据所学的数据结构中线性结构（线性表）的逻辑特性和物理特性及相关算法，应用于求解一个具体的实际问题----------两个多项式相加一、运行环境：visual C++二、需求分析(1)掌握线性结构的逻辑特性和物理特性(2)掌握线性结构的各种相关算法(3)掌握将算法转换成程序的方法和步骤(4)掌握采用线性结构解决实际问题。

三、概要设计1、抽象数据类型一元多项式的定义如下：ADT Polynomial { 数据对象：D＝{ a i | a i∈TermSet, i=1,2,...,m, m≥0TermSet 中的每个元素包含一个表示系数的实数和表示指数的整数 }数据关系：R1＝{ <a i-1 ,a i >|a i-1 ,a i∈D, i=2,...,n，且a i-1中的指数值＜a i中的指数值}基本操作：CreatPolyn ( &P, m )操作结果：输入 m 项的系数和指数，建立一元多项式 P。

DestroyPolyn ( &P )初始条件：一元多项式 P 已存在。

操作结果：销毁一元多项式 P。

PrintPolyn ( &P )初始条件：一元多项式 P 已存在。

操作结果：打印输出一元多项式 P。

PolynLength( P )初始条件：一元多项式 P 已存在。

操作结果：返回一元多项式 P 中的项数。

AddPolyn ( &Pa, &Pb )初始条件：一元多项式 Pa 和 Pb 已存在。

操作结果：完成多项式相加运算，即：Pa = Pa＋Pb，并销毁一元多项式 Pb。

SubtractPolyn ( &Pa, &Pb )… …} ADT Polynomial2、一元多项式的实现：typedef OrderedLinkList polynomial;// 用带表头结点的有序链表表示多项式结点的数据元素类型定义为:typedef struct { // 项的表示float coef; // 系数int expn; // 指数 term, ElemType;四、详细设计线性表的应用--多项式相加问题多项式的相加操作是线性表处理的典型例子。

数据结构习题：一元多项式的加法乘法实现

5x20-4x4-5x2+9x-2
求解思路
1.多项式表示 2. 程序框架 3. 读多项式 4. 加法实现 5. 乘法实现 6. 多项式输出
多项式的表示
仅表示非零项
数组：编程简单、调试容易
需要事先确定数组大小
一种比较好的实现方法是: 动态数组
链表：
动态性强编程略为复杂、调试比较困难
2.逐项插入
将P1当前项(c1i,e1i)乘P2当前项（c2i,e2i),并插入到结果多项式中。关键是要找到插入位置
初始结果多项式可由P1第一项乘P2获得（如上）
如何将两个多项式相乘
Polynomial Mult( Polynomial P1, Polynomial P2 )
{
…….
t1 = P1; t2 = P2;
return 0; }
如何读入多项式
Polynomial ReadPoly() {
…… scanf("%d", &N); …… while ( N-- ) {
scanf("%d %d", &c, &e); Attach(c, e, &Rear); } ….. return P; }
4 3 4 -5 2 6 1 -2 0
Attach
ce
*pRear
P *pRear
(当前结果表达式尾项指针) (新节点)
如何读入多项式
Polynomial ReadPoly() {
Polynomial P, Rear, t; int c, e, N;
scanf("%d", &N);
P = (Polynomial)malloc(sizeof(struct PolyNode)); /* 链表头空结点 */

数据结构多项式相加实验报告

试验一多项式相加一. 实验内容：多项式相加二.实验目的和要求：利用双向链表实现通讯录的建立、删除、检索和列表，并可保存至文件，可重新装入。

用链式存储结构实现一元多项式的相加运算。

三．算法思想描述:1. 以单链表为存储结构插入多项式: 多项式输入：多项式按幂从高到低，以“系数，幂”的格式输入，并以“0，0”结束。

printf("Please input coef:");scanf("%d",&i);printf("Please input exp: ");scanf("%d",&j);while(i!=0){q=(pnode)malloc(sizeof(struct node));q->coef=i;q->exp=j;p->link=q;p=q;printf("Please input coef:");scanf("%d",&i);printf("Please input exp: ");scanf("%d",&j);}p->link=NULL;2. 多项式相加单链表合并:由两个多项式对应的单链表头节点开始，依次扫描各节点。

(1)若两表的节点均非空：比较二者的幂，按幂大者先入表。

如果幂相等，则系数相加再入表。

具体由以下代码实现：while(p!=NULL && q!=NULL){if(p->exp==q->exp){x=p->coef+q->coef;if(x!=0){s=(pnode)malloc(sizeof(struct node));s->coef=x;s->exp=p->exp;r->link=s;r=s;}p=p->link;q=q->link;}else if(p->exp<q->exp){s=(pnode)malloc(sizeof(struct node));s->coef=q->coef;s->exp=q->exp;r->link=s;r=s;q=q->link;}else{s=(pnode)malloc(sizeof(struct node));s->coef=p->coef;s->exp=p->exp;r->link=s;r=s;p=p->link;}(2). 若有一链表已空，则将非空链表插入新表：while(p!=NULL){s=(pnode)malloc(sizeof(struct node));s->coef=p->coef;s->exp=p->exp;r->link=s;r=s;p=p->link;}while(q!=NULL){s=(pnode)malloc(sizeof(struct node));s->coef=q->coef;s->exp=q->exp;r->link=s;r=s;q=q->link;}3. 输出合并后的链表:while(head->link!=NULL){head=head->link;printf(" %d*x^%d",head->coef,head->exp);}4. 主函数调用，完成多项式相加。

数据结构--线性表的基本运算及多项式的算术运算

数据结构:线性表的基本运算及多项式的算术运算一、实验目的和要求实现顺序表和单链表的基本运算，多项式的加法和乘法算术运算。

要求：能够正确演示线性表的查找、插入、删除运算。

实现多项式的加法和乘法运算操作。

二、实验环境(实验设备)X64架构计算机一台，Windows 7操作系统，IDE: Dev C++ 5.11编译器: gcc 4.9.2 64bit二、实验原理及内容程序一：实现顺序表和单链表的实现本程序包含了四个文件，分别是LinearListMain.cpp，linearlist.h，seqlist.h，singlelist.h。

分别是主程序，线性表抽象类，顺序储存线性表的实现，链表储存顺序表的实现。

文件之间的关系图：本程序一共包含了三个类：分别是LinearList（线性表抽象类），SeqList（顺序储存的线性表），SingleList（链表储存的线性表）。

类与类之间的关系图如下：其实，抽象类LinearList规定了公共接口。

分别派生了SeqList类和SingleList。

SingleList类与SingleList类分别实现了LinearList类中的所有接口。

程序代码以及分析：Linearlist类：#include <iostream>using namespace std;template <class T>class LinearList{protected:int n; //线性表的长度public:virtual bool IsEmpty() const=0; //判读是否是空线性表virtual int Length() const=0; //返回长度virtual bool Find(int i,T& x) const=0; //将下标为i的元素储存在x中，成功返回true，否则返回falsevirtual int Search(T x) const=0; //寻找值是x的元素，找到返回true，否则返回falsevirtual bool Insert(int i,T x)=0; //在下标为i的元素后面插入xvirtual bool Delete(int i)=0; //删除下标为i的元素virtual bool Update(int i,T x)=0;//将下标为i的元素更新为x virtual void Output(ostream& out)const=0; //将线性表送至输出流};包含了一个保护数据成员n，和8种运算，具体说明见注释。

一元多项式的加减求导运算算法(数据结构算法)

{
if(expo1==0)
{
i=1;
cout<<coef1;
}
else if(expo1==1)
{
i=1;
if(coef1==1)
cout<<"X";
else if(coef1==-1)
cout<<"-X";
else
cout<<coef1<<"X";
}
else
{
i=1;
if(coef1==1) cout<<"XA"<<expo1;
temp=h;
h->next =NULL;〃头结点
cout<<"多项式"<<o<<"的项数:";cin»num;
for(i nt i=1;i<=nu m;i++)
{
cout<<"请输入第"<<i<<"项"<<endl; cout<<"系数:";
cin> >coef1;
cout<<"指数:";
cin> >expo1; data=new polyno de; data->coef=coef1;
(2)计算多项式A与B的和，即建立多项式A+B
(3)按照指数升序次序，输出多项式AB、A+B
(4)计算多项式A与B的差，即建立多项式A-B;
(5)计算多项式A的导函数A，。

一元多项式相加数据结构实验报告

南昌航空大学实验报告课程名称：数据结构实验名称：实验二线性表的链式存储结构班级：080611 学生姓名：学号：08指导教师评定：签名:题目：设计并实现以下算法：给出用单链表存储多项式的结构，利用后接法生成多项式的单链表结构，实现两个多项式相加的运算，并就地逆置相加后的多项式链式。

一、需求分析1.用户可以根据自己的需求分别输入两个一元多项式，并且能够实现输入的一元多项式的显示。

2.能够完成两个一元多项式的相加功能，而且还能显示相加后的逆置的一元多项式。

3.程序执行的命令包括：（1）构造链表A （2）构造链表B （3）两个链表的相加（4）求链表的长度（5）打印（显示）已有的链表（6）将已相加的链表进行逆序排列二、概要设计⒈为实现上述算法，需要线性表的抽象数据类型：ADT Polynomial {数据对象：D={a i:|a i∈TermSet,i=1…n,n≥0TermSet 中的每个元素包含一个表示系数的实数和表示指数的整数} 数据关系：R1={<a i-1,a i>|a i-1,a i∈D,且a i-1中的指数值< a i中的指数值i=2,…n≥0}基本操作:initlink(& L)操作结果：构造一个空的链表L。

Creatlink(&L,n)操作结果：输入n项的系数和指数，建立一个非空的一元多项式L。

LinkLength(L)初始条件：链表L已经存在。

操作结果：返回一元多项式L中的项数。

Displaylink（L）初始条件：链表L已经存在。

操作结果：打印输出一元多项式L。

Addpolyn(A,B,&C)初始条件：一元多项式A和B已存在。

操作结果：完成多项式相加运算，即：C=A+B，并且带回C。

subtracypolyn(&La,&Lb,)初始条件：一元多项式La和Lb已存在。

操作结果：完成多项式的相减运算La=La+Lb，并且销毁多项式Lb。