2004全国初中数学联赛深圳赛区第一试
0Fhcso2004年深圳市中考数学试卷

生活需要游戏,但不能游戏人生;生活需要歌舞,但不需醉生梦死;生活需要艺术,但不能投机取巧;生活需要勇气,但不能鲁莽蛮干;生活需要重复,但不能重蹈覆辙。
-----无名深圳市2004年数学中考试题(说明:本试卷考试时间为90分钟,满分为100分)一、选择题:(本题共10小题,每题3分,共30分)每题给出4个答案,其中只有一个是正确的,请把选出的答案编号填在上面的答题表中,否则不给分.1、16的平方根是()A、4B、-4C、±4D、±22、下列等式正确的是()A、(-x2)3= -x5B、x8÷x4=x2C、x3+x3=2x3D、(xy)3=xy33、不等式组⎩⎨⎧≤-≥+12x 01x 的解集在数轴上的表示正确的是( )A BC D4、已知⊙O 1的半径是3,⊙O 2的半径是4,O 1O 2=8,则这两圆的位置关系是( ) A 、相交 B 、相切 C 、内含 D 、外离5、学校开展为贫困地区捐书活动,以下是八名学生捐书的册数:2,2,2,3,6,5,6,7,则这组数据的中位数为( )A 、2B 、3C 、4D 、4.56、下列图中:①线段;②正方形;③圆;④等腰梯形;⑤平行四边形是轴对称图形,但不是中心对称图形有( )A 、1个B 、2个C 、3个D 、4个 7、函数y=x 2-2x+3的图象顶点坐标是( )A 、(1,-4)B 、(-1,2)C 、(1,2)D 、(0,3)8、如图,⊙O 的两弦AB 、CD 相交于点M ,AB=8cm ,M 是AB 的中点,CM :MD=1:4,则CD=( )A 、12cmB 、10cmC 、8cmD 、5cm9、圆内接四边形ABCD 中,AC 平分∠BAD ,EF 切圆于C ,若∠BCD=120º,则∠BCE=( ) A 、30º B、40º C、45º D、60º-1-1-1-1(8) (9) (10) 10、抛物线过点A (2,0)、B (6,0)、C (1,3),平行于x 轴的直线CD 交抛物线于点C 、D ,以AB 为直径的圆交直线CD 于点E 、F ,则CE+FD 的值是( ) A 、2 B 、4 C 、5 D 、6二、填空题:(共5小题,每题3分,共15分) 11、分解因式:x 2-9y 2+2x-6y=______. 12、在函数式y=1x 1x -+中,自变量x 的取值范围是_______.13、计算:3tan30º+cot45º-2tan45º+2cos60º=_______.14、等腰三角形的两边长分别为2cm 和5cm ,则它的周长为________.15、在矩形ABCD 中,对角线AC 、BD 相交于点O ,过点O 作OE ⊥BC ,垂足为E ,连结DE 交AC 于点P ,过P 作PF ⊥BC ,垂足为F ,则CBCF 的值是_____.三、解答题:(本部分共6题,其中第16题7分,第17-18题各8分,第19-20题各10分,第21题12分,共55分)ABFCDOP16、计算:|1-2|+231++(π-2)0(7分)17、解方程组:⎩⎨⎧=+-=+05x 3y 5y x 2 (8分)18、在深圳“净畅宁”行动中,有一块面积为150亩的绿化工程面向全社会公开招标。
2004年深圳市数学中考试题

最大最全最精的教育资源网2007年湘潭市初中毕业学业考试数 学 试 卷亲爱的同学,你好!今天是展示你的才能的时候了,请你仔细审题,认真答题,发挥自己的正常水平,轻松一点,相信自己的实力!注意:本试卷共八个版面,考试时间:120分钟;满分100分. 一、填空题(本题共10个小题,每小题2分,共20分) 1.15-的相反数是 . 2.因式分解:23x x -= .3.温家宝总理有句名言:多么小的问题乘以13亿,都会变得很大;多么大的经济总量,除以13亿都会变得很小.将1 300 000 000用科学记数法表示为 .4.足球比赛前,裁判用抛一枚硬币猜正反面的方式让甲、乙两个队长选进攻方向,猜对正面的队长先选,则队长甲先选的概率是 .5.若反比例函数ky x=的图象过点(12)A -,,则k = . 6.如图,一轮船由南向北航行到O 处时,发现与轮船相距40海里的A 岛在北偏东33方向.已知A 岛周围20海里水域有暗礁, 如果不改变航向,轮船 (填“有”或“没有”)触暗礁的危险.(可使用科学计算器)7.有三个数59x ,,,它们的平均数为6,则x 为 .8.将一副三角板摆放成如图所示,图中1∠= 度.9.某市在端年节准备举行划龙舟大赛,预计15个队共330人参加.已知每个队一条船,每条船上人数相等,且每条船上有1人击鼓,1人掌舵,其余的人同时划桨.设每条船上划桨的有x 人,那么可列出一元一次方程为 . 10.如图,已知O 半径为5,弦AB 长为8,点P 为弦AB 上一 动点,连结OP ,则线段OP 的最小长度是 .OAB33北 (第6题图)1(第8题图) O BPA(第10题图)最大最全最精的教育资源网二、选择题(本题共10个小题,每小题2分,共20分)下列每小题都给出了标号为A ,B ,C ,D 四个结论,其中只有一个是正确的.每小题选对得分;不选、选错或多选的不得分,请将所选答案的标号填写在下面的表格内. 题号 11121314 15 16 17 18 19 20 答案11.下列计算正确的是( ) A .236x x x =B .22(1)1x x -=-C .2(3)3-=-D .22232x y x y x y -=12.从左面观察下图所示机器零件,看到的是( )13.2007年5月下旬,湘潭市的天气特点是潮湿、闷热.张小敏同学对这11天的最高气温进行统计,得到的数据如下表:日 期2122232425262728293031最高气温(单位:℃) 31 2831 32 34 29 32 33 313134 则五月下旬最高气温的众数和极差分别是( ) A .31,5 B .31,6 C .31,7 D .32,614.为庆祝“六一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示:按照上面的规律,摆n 个“金鱼”需用火柴棒的根数为( ) A .26n + B .86n + C .44n + D .8n15.不等式组10235x x +⎧⎨+<⎩≤,的解集在数轴上表示为( )16.小明和小亮做游戏,先是各自背着对方在纸上写一个正整数,然后都拿给对方看.他们约定:若两人所写的数都是奇数或都是偶数,则小明获胜;若两个人所写的数一个是奇数,另一个是偶数,则小亮获胜.这个游戏( )A .对小明有利B .对小亮有利C .游戏公平D .无法左面 A . B . C . D .…… ① ② ③ 1- 1 x 1- 1 x 1- 1 x 1- 1 x A . B . C . D .最大最全最精的教育资源网确定对谁有利17.如图,在Rt ABC △中,90ACB D E ∠=,,分别 为AC AB ,的中点,连DE CE ,.则下列结论中不一定... 正确的是( ) A .ED BC ∥ B .ED AC ⊥C .ACE BCE ∠=∠D .AE CE =18.一元二次方程240x x c ++=中,0c <,该方程的解的情况是( ) A .没有实数根 B .有两个不相等的实数根 C .有两个相等的实数根 D .不能确定 19.下列说法或计算正确的是( ) A .在将分式方程251x x=-化为整式方程时,可将方程两边同时乘以(1)x x - B .函数20075y x -=-中,自变量x 的取值范围是5x ≥ C .8与2不是同类二次根式 D .0(3sin30)0-=20.如图,用两根等长的钢条AC 和BD 交叉构成一个卡钳, 可以用来测量工作内槽的宽度.设OA OBm OC OD==,且量得 CD b =,则内槽的宽AB 等于( )A .mbB .mbC .b mD .1b m +`三、解答题(本题共8个小题,其中21~24题每小题6分,25、26题每小题8分,27、28题每小题10分,共60分)21.(本题满分6分)先化简,再求值:4()(2)(2)x y x x y x y -++-,其中122x y ==-,. 22.(本题满分6分)如图,在正五边形ABCDE 中, 连结对角线AC AD ,和CE AD ,交CE 于F .(1)请列出图中两对全等三角形 (不另外添加辅助线)(2)请选择所列举的一对全等三角形加以证明.AEBCD(第17题图)DCbA B(第20题图)ABEF最大最全最精的教育资源网23.(本题满分6分)如图,在ABC △中,AB AC E F =,,分别为AB AC ,上的点(E F ,不与A 重合),且EF BC ∥.将AEF △沿着直线EF 向下翻折,得到A EF '△,再展开. (1)请证明四边形AEA F '为菱形; (2)当等腰ABC △满足什么条件时,按上述方法操作,四边形AEA F '将变成正方形?(只写结果,不作证明)24.(本题满分6分)2008年,举世瞩目的第29届奥运盛会将在北京举行.奥运五环,环环相扣,象征着全世界人民的大团结.五环图中五个圆环均相等,其中上排三个、下排两个,且上排的三个圆心在同一直线上;五环图是一个轴对称图形.(1)请用尺规作图,在图24—1中补全奥运五环图,心怀奥运.(不写作法,保留作图痕迹) (2)五环图中五个圆心围一个等腰梯形.如图24—2,在等腰梯形ABCD 中,AD BC ∥.假设4845BC AD A ==∠=,,,求梯形的面积.25.(本题满分8分)星期天,七年级1、2两班部分同学相约去某公园玩碰碰车或划船.已知玩碰碰车的同学每人租用一辆车,划船的同学每4人合租一条船,两班各花了115元.活动人数如下表:A E F CB A ' A BC D 45 图24—2 图24—1最大最全最精的教育资源网班级 玩碰碰车的同学划船的同学 111人16人28人 20人 试求碰碰车每辆车租金多少元;游船每条船租金多少元.26.(本题满分8分)某中学为促进课堂教学,提高教学质量,对七年级学生进行了一次“你最喜欢的课堂教学方式”的问卷调查.根据收回的问卷,学校绘制了“频率分布表”和“频数分布条形图”.请你根据图表中提供的信息,解答下列问题.频率分布表 代号 教学方式 最喜欢的频数频率 1 老师讲,学生听 20 0.10 2 老师提出问题,学生探索思考 100 3 学生自行阅读教材,独立思考30 0.15 4分组讨论,解决问题0.25(1)补全“频率分布表”;(2)在“频数分布条形图”中,将代号为“4”的部分补充完整;(3)你最喜欢以上哪一种教学方式或另外的教学方式,请提出你的建议,并简要说明理由.(字数在20字以内)27.(本题满分10分)初三体能素质测试中的一项是考查同学们的握力.2007年3月初,小杨和小李在摸底检测时,握力分别为30千克和34千克,他们不太满意,决定加强训练,争取在5月中旬测试时有较好成绩.小杨计划每周提高握力1.5千克,小李计划每周提高握力1千克.(1)分别写出两同学的握力y (千克)与时间x (周)之间的函数关系式; (2)请在下面的平面直角坐标系中,分别 作出(1)中两个函数所在点的直线,并根 据图象回答:第几周时,两人计划达到的握 力一样?如果握力达到或超过45千克获得满 分,那么按计划,谁先达到满分水平?25 50 75100 最喜欢的人数(个) 教学方式代号1 2 3 4 频数分布条形图36 37 38 39 40 41 42 43 45 46 44 y (千克)最大最全最精的教育资源网28.(本题满分10分) 如图28—1,设抛物线2113424y x x =--交x 轴于A B ,两点,顶点为D .以BA 为直径作半圆,圆心为M ,半圆交y 轴负半轴于C . (1)求抛物线的对称轴;(2)将ACB △绕圆心M 顺时针旋转180,得到三角形APB ,如图28—2.求点P 的坐标;(3)有一动点Q 在线段AB 上运动,QCD △的周长在不断变化时是否存在最小值?若存在,求点Q 的坐标;若不存在,说明理由.ABMO CxyMOxyPC()B A()A B图28—1图28—2D。
2004年深圳中考数学试卷及答案解析

2004年深圳市初中毕业生学业考试数学试卷一、选择题:(本题共10小题,每题3分,共30分) 1、16的平方根是A 、4B 、-4C 、±4D 、±2 2、下列等式正确的是A 、(-x 2)3= -x 5B 、x 8÷x 4=x 2C 、x 3+x 3=2x 3D 、(xy)3=xy 33、不等式组⎩⎨⎧≤-≥+12x 01x 的解集在数轴上的表示正确的是C D4、已知⊙O 1的半径是3,⊙O 2的半径是4,O 1O 2=8,则这两圆的位置关系是 A 、相交B 、相切C 、内含 D、外离5、学校开展为贫困地区捐书活动,以下是八名学生捐书的册数:2,2,2,3,6,5,6,7,则这组数据的中位数为A 、2B 、3C 、4D 、4.56、下列图中:①线段;②正方形;③圆;④等腰梯形;⑤平行四边形是轴对称图形,但不是中心对称图形有A 、1个B 、2个C 、3个D 、4个7、函数y=x 2-2x+3的图象顶点坐标是 A 、(1,-4) B 、(-1,2) C 、(1,2) D 、(0,3)8、如图,⊙O 的两弦AB 、CD 相交于点M ,AB=8cm ,M 是AB 的中点,CM :MD=1:4,则CD= A 、12cm B 、10cm C 、8cm D 、5cm9、圆内接四边形ABCD 中,AC 平分∠BAD ,EF 切圆于C ,若∠BCD=120º,则∠BCE= A 、30º B、40º C、45º D、60º(8) (9) (10)-1 -1-1 -110、抛物线过点A (2,0)、B (6,0)、C (1,3),平行于x 轴的直线CD 交抛物线于点C 、D ,以AB 为直径的圆交直线CD 于点E 、F ,则CE+FD 的值是A 、2B 、4C 、5D 、6二、填空题:(共5小题,每题3分,共15分)11、分解因式:x 2-9y 2+2x-6y=______.12、在函数式y=1x 1x -+中,自变量x 的取值范围是_______. 13、计算:3tan30º+cot45º-2tan45º+2cos60º=_______.14、等腰三角形的两边长分别为2cm 和5cm ,则它的周长为________.15、在矩形ABCD 中,对角线AC 、BD 相交于点O ,过点O 作OE ⊥BC ,垂足为E ,连结DE 交AC 于点P ,过P作PF ⊥BC ,垂足为F ,则CBCF的值是_____.三、解答题:(本部分共6题,其中第16题7分,第17-18题各8分,第19-20题各10分,第21题12分,共55分)16、计算:|1-2|+231++(π-2)0(7分)17、解方程组:⎩⎨⎧=+-=+05x 3y 5y x 2 (8分)18、在深圳“净畅宁”行动中,有一块面积为150亩的绿化工程面向全社会公开招标。
深圳实验学校2004届初中毕业、选拔考试数学毕业卷

深圳实验学校2004届初中毕业、选拔考试数学试卷说明:1、试卷分为毕业卷和选拔卷两部分,每部分100分。
2、毕业卷与选拔卷应在150分钟内完成,考生应根据情况分配好答题时间。
注意事项:1、答毕业卷前,考生务必将自己的姓名、准考证号、考试科目、试卷类型A 用铅笔涂写在答题卡上;2、毕业卷由30道选择题构成,每小题给出A 、B 、C 、D 的结论中有且只有一个是正确的,选出答案后,用2B 铅笔把答题卡上对应题目的答案标题号涂黑,如需改动用橡皮擦干净后,再选涂其他答案,不能答在试题卷上;3、考试结束,将本试卷和答题卡一并交回。
(毕业卷)选择题(1-25题每小题3分,26-30每小题5分)1.下列运算正确的是A .6332x x x =+B .326x x x =÷C .6233)3(x x =-D .132--=x x x ⋅2.在下列二次根式中与2是同类二次根式的是A .8B . 10C .12D .273.下面有四种说法,其中正确的是A .—64的立方根是4B .49的算术平方根是±7C .271的立方根是31 D .9的平方根是±3 4.不等式组⎩⎨⎧01042<->+x x 的解为 A .x >1或x <-2 B .x >1 C .-2<x <1 D .x <-25.近似数0.03020的有效数字的个数和精确度分别是A .四个,精确到万分位B .三个,精确到十万分位C .四个,精确到十万分位D .三个,精确到万分位6.下列一元二次方程中,两根分别为51+-、51--的是A .0422=++x xB .0422=-+x xC .0422=+-x xD .0422=--x x7.已知⎩⎨⎧1,2==y x 是方程kx -y =3的解,那么k 的值是A .2B .-2C .1D .-18.如果2)2(2-=-x x ,那么x 的取值范围是A .x ≤2B .x <2C .x ≥2D .x >29.将抛物线y=2x 2如何平移可得到抛物线y = 2(x —4)2—1A .向左平移4个单位,再向上平移1个单位B .向左平移4个单位,再向下平移1个单位C .向右平移4个单位,再向上平移1个单位D .向右平移4个单位,再向下平移1个单位10.化简mm -+-21442的结果是 A .21+-m B .21+m C .462-+m m D .21+-m 11.如果圆柱的母线长为5cm ,底面半径为2cm ,那么这个圆柱的侧面积是 A. 102cm B. 102πcm C. 202cm D. 202πcm 12.下列说法中,正确的是A .到圆心的距离大于半径的点在圆内B .圆的半径垂直于圆的切线C .圆周角等于圆心角的一半D .等弧所对的圆心角相等13.如果一个角的余角和补角互补,那么这个角的度数是A .30°B .45°C .90°D .135°14.我国主要银行的商标设计基本上都融入了中国古代钱币的图案.下列我国四大银行的商标图案中是轴对称图形而不是中心对称图形的是15.已知△ABC 中,∠C=90°,∠A 、∠B 、∠C 所对的边分别是a 、b 、c 且c=3b ,则cosA=A .32B .322C .31D .310 16.已知一组数据—1,x ,0,1,—1的平均数是0,那么这组数据的方差是A .2B .0.8C .4D .217.下图中,分别给出了变量x 与y 之间的对应关系,y 不是x 的函数的是A B C D18.下列四个命题中错误的是A .两条对角线互相垂直且相等的四边形是正方形B .菱形的一条对角线平分一组对角C .顺次连结四边形的各边中点所得的四边形是平行四边形D .等腰梯形的两条对角线相等19.如图,在△ABC 中,若∠AED =∠B ,DE =6,AB =10,AE =8,则BC 的长为A .415B .7C .215D .524 20.如图,⊙O 中弦AB 、CD 相交于点F ,AB =10,AF =2.若CF ∶DF =1∶4,则CF 的长等于A .2B .2C .3D .22 21.已知一次函数y=kx —2,y 随x 的增大而减小,那么反比例函数xk y = A .当x>0时,y>0 B .在第二个象限内,y 随x 增大而减小C .图象在第一、三象限D .图象在第二、四象限22.关于x 的方程021)3(22=m m x m x -+-+的根的情况是A .有两个相等的实数根B .有两个不相等的实数根C .没有实数根D .有两个实数根23.将一张平行四边形的纸片折一次,使得折痕平分这个平行四边形的面积,则这样的折纸方法共有A .1种B .2种C .3种D .无数种24.如图,⊙O 的弦AB 垂直于直径MN ,C 为垂足.若OA =5 cm ,下面四个结论中可能成立的是第(24)题图第(20)题图第(19)题图A .AB =12 cm B .OC =6 cm C .MN =8 cmD .AC =2.5 cm25.计算()1999199902425.0513*******⨯-+⎪⎭⎫ ⎝⎛-+-÷⎪⎭⎫ ⎝⎛⨯⎪⎭⎫ ⎝⎛--的结果是 A .9 B .10 C .11 D .1226.如果两个等腰直角三角斜边的比是1︰2,那么它们面积的比是 A .1︰1 B .1︰2C .1︰2D .1︰4 27.星期六晚饭后,小红从家里出去散步,如图描述了她散步过程中离家的距离s (米)与散步所用时间t (分)之间的函数关系.依据图象,下面描述符合小红散步情景的是A .从家出发,到了一个公共阅报栏,看了一会儿报,就回家了B .从家出发,到了一个公共阅报栏,看了一会儿报后,继续向前走了一段,然后回家了C .从家出发,一直散步(没有停留),然后回家了D .从家出发,散了一会儿步,就找同学去了,18分钟后才开始返回.28.赵强同学借了一本书,共280页,要在两周借期内读完.当他读了一半时,发现平均每天要多读21页才能在借期内读完.他读前一半时,平均每天读多少页?如果设读前一半时,平均每天读x 页,则下面所列方程中,正确的是A .1421140140=-+x x B .1421280280=++x x C .1421140140=++x x D .1211010=++x x 29.将一张矩形纸对折再对折(如图),然后沿着图中的虚线剪下,得到①、②两部分,将①展开后得到的平面图形是A .矩形B .三角形C .梯形D .菱形30、如图,直角梯形ABCD 中,AD ∥BC ,∠B=900,AD +BC >DC ,若腰DC 上有点P ,使AP ⊥BP ,则这样的点A .不存在B .只有一个C .只有两个D .有无数个第(30)题图第(27)题图 第(29)题图。
2004年全国初中数学联赛试题及答案(修正版)

NABCDP2004年全国初中数学联合数学竞赛试题第一试一.选择题1.已知abc ≠0,且a +b +c =0, 则代数式 a 2bc +b 2ca +c 2ab的值是( )(A) 3 (B) 2 (C) 1 (D) 02.已知p ,q 均为质数,且满足5p 2+3q =59,则以p +3,1-p +q ,2p +q -4为边长的三角形是( )(A) 锐角三角形 (B) 直角三角形 (C) 钝角三角形 (D) 等腰三角形3. 一个三角形的边长分别为a ,a ,b ,另一个三角形的边长分别为b ,b ,a ,其中a >b ,若两个三角形的最小内角相等,则 a b的值等于( )(A)3+1 2 (B) 5+1 2 (C) 3+2 2 (D) 5+224.过点P (-1,3)作直线,使它与两坐标轴围成的三角形面积为5,这样的直线可以作( ) (A) 4条 (B) 3条 (C) 2条 (D) 1条5.已知b 2-4ac 是一元二次方程ax 2+bx +c =0(a ≠0)的一个实数根,则ab 的取值范围为( ) (A) ab ≥1 8(B) ab ≤1 8(C) ab ≥1 4(D) ab ≤1 46.如图,在2×3矩形方格纸上,各个小正方形的顶点称为格点,则以格点为顶点的等腰直角三角形的个数为( )(A) 24 (B) 38 (C) 46 (D) 50二.填空题1.计算1 1+2+1 2+3+1 3+4+……+12003+2004= .2.如图ABCD 是边长为a 的正方形,以D 为圆心,DA 为半径的圆弧与以BC 为直径的半圆交于另一点P ,延长AP 交BC 于点N ,则BNNC = .3.实数a ,b 满足a 3+b 3+3ab =1,则a +b = .4.设m 是不能表示为三个合数之和的最大整数,则m = .l G B C H F A E P QMD 第二试一、 已知方程x 2-6x -4n 2-32n =0的根都是整数,求整数n 的值。
全国初中数学联赛试题(含参考答案)

全国初中数学联合竞赛试题参考答案第一试一、选择题(本题满分42分,每小题7分) 1、设17-=a ,则=--+12612323a a a ( A )A 、24B 、 25C 、1074+D 、1274+ 2、在ABC ∆中,最大角A ∠是最小角C ∠的两倍,且7=AB ,8=AC ,则=BC ( C ) A 、27 B 、10 C 、105 D 、37 3、用[]x 表示不大于x 的最大整数,则方程[]0322=--x x 的解的个数为( C ) A 、1 B 、2 C 、3 D 、 44、设正方形ABCD 的中心为点O ,在以五个点A 、B 、C 、D 、O 为顶点所构成的所有三角形中任意取出两个,它们的面积相等的概率为 ( B )A 、143 B 、73 C 、21 D 、74 5、如图,在矩形ABCD 中,3=AB ,2=BC ,以BC 为直径在矩形内作半圆,自点A 作半圆的切线AE ,则=∠CBE sin ( D )A 、36 B 、32C 、31D 、10106、设n 是大于1909的正整数,使得nn --20091909为完全平方数的n 的个数是 ( B )A 、3B 、 4C 、 5D 、6 二、填空题(本题满分28分,每小题7分)1、已知t 是实数,若a ,b 是关于x 的一元二次方程0122=-+-t x x 的两个非负实根,则()()1122--b a的最小值是____________.答案:3-2、设D 是ABC ∆的边AB 上的一点,作BC DE //交AC 于点E ,作AC DF //交BC 于点F ,已知ADE ∆、DBF ∆的面积分别为m 和n ,则四边形DECF 的面积为______.答案:mn 23、如果实数a ,b 满足条件122=+b a ,2212|21|a b a b a -=+++-,则____=+b a . 答案:1-4、已知a ,b 是正整数,且满足⎪⎪⎭⎫ ⎝⎛+b a 15152是整数,则这样的有序数对(a ,b )共有_对。
2004年全国初中数学联赛答案

2004年全国初中数学联赛答案一、1、A 原式=()()()b c a a c b a b c bc ac ab -+-+-+++=a a b b c c b c a c a b ⎛⎫⎛⎫⎛⎫-+-+-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=3a b ca b c++= 2、B因为253p q +为奇数,故,p q 必为一奇一偶。
而,p q 均为质数,故,p q 中有一个为2。
若2q =,则2535p =,不合题意,舍去; 若2p =,则13q =。
此时,35,112,2413p p q p q +=-+=+-=。
因为22251213+=,所以,以5、12、13为边长的三角形为直角三角形。
3、B如图,设△ABC 中,AB =AC =a ,BC =b 。
D 是AB 上的一点,有AD =b 。
因为a b >,故∠A 是△ABC 的最小角,记∠A =θ。
则以,,b b a 为三边的三角形的最小角亦为θ。
从而,此三角形与△ADC 全等。
所以,DC =b ,∠ACD =θ。
又△ABC ∽△CBD ,于是,BC BD AB BC =,即b a b a b -=。
令ax b=,即得方程210x x --=解得a x b ==4、C设满足条件的直线l :k kx b =+。
因为P(-1,3)在直线l 上,所以,3k b =-+,故3b k =+ 因此,l 为3y kx k =++l 与两坐标轴的交点分别为3,0k A k +⎛⎫- ⎪⎝⎭,(0,3)B k +故l 与两坐标轴围成的三角形的面积1133522AOB k S OA OB k k∆+=⋅=-⋅+=,即2(3)10k k += ① 当0k >时,方程①即2490k k -+=,此时方程无实数解;当0k <时,方程①即21690k k ++=,此时方程有两个实数解1,28k =-因此,过点P(-1,3)且与坐标轴围成的三角形面积为5的直线有两条。
2004年全国初中数学竞赛

100
陈志敏
新塍镇中学
李科梅
101
朱立成
秀洲现代实验学校
袁天红
102
马瑶
嘉善四中
吴泉林
103
邱涛
嘉善四中
吴泉林
104
张严平
嘉善五中
陈华
105
孙晨良
嘉善杨庙中学
樊根平
106
王金花
嘉善姚庄中学
唐建红
107
成盖天
城关中学
蒋根荣
108
钱琰君
东湖中学
山引珠
109
俞山杰
林埭中学
孙跃平
110
沈燕
新仓中学
李洪根/朱川丽
秀洲现代实验学校
陆长林
270
葛佳伟
秀洲现代实验学校
高爱民
271
曹贇轩
秀洲现代实验学校
高爱民
272
郑晓辰
秀洲现代实验学校
高爱民
273
程丽斌
黄姑中学
陶国梁
274
董玉凤
羔羊中学
徐月江
275
庄煜顺
高桥初中
276
徐倩莲
南日初中
冯荣方
277
陈怡
邵逸夫中学
李伟昌
278
曹丽娟
桐乡十中
朱林祥
279
章瑰玮
桐乡四中
高月良
东湖中学
顾菊根
77
金必卿
东湖中学
蒋建强
78
施布恩
东湖中学
沈兴旺
79
缪芸
东湖中学
郭照明
80
顾立佳
海盐县沈荡中学
苏娟芳
81
2004年全国初中数学联合竞赛试题及解答

3 ,则 a
1 1 3 3 1 3 3 a 1 1 3= (a ) 3 2 3 6 2 2 a 2 a 2
S△ AOB S△ APC S△PDB S矩形PCOD
因此,二象限中不存在这样的三角形.故选 C. 5.已知 b2 4ac 是一元二次方程 ax2 bx c 0 (a 0) 的一个实数根,则 ab 的取值范围为 ( ) A. ab ≥ 【答】B.
a . 2
D C
因为 BC 为直径,所以∠BPC=90° . 易证△MBC≌△FAB≌△MAF, 所以 AF= MA=MB= 由 DE∥BC 可得: ∴BN= ∴
a ,AE=BC=a. 2
A F N P M B
BN BP BC 2 AF PF EF 3
a 2a ,NC= 3 3
BN 1 NC 2
第一试
一、选择题(本题满分 42 分,每小题 7 分) 1. 已知 abc 0 ,且 a b c 0 ,则代数式 A.3 【答】A. 原代数式
a 2 b 2 c 2 a 3 b3 c 3 . bc ca ab abc
a 2 b2 c 2 的值是( bc ca ab
l E P M Q K H A O D N R H B C F
G
6
三. (本题满分 25 分)已知点 A(0 , 3) , B(2 , 1) ,C (2 , 1) , P(t , t 2 ) 为抛物线 y x 2 上 位于三角形 ABC 内(包括边界)的一动点,BP 所在的直线交 AC 于 E,CP 所在的直线交 AB 于 F.将
a 2 b 2 c 2 a 3 b3 c 3 3 bc ca ab abc
2000年全国初中数学联赛第一试和第二试试题及答案

2000年全国初中数学联合竞赛试卷第一试(4月2日上午8:30----9:30)一、选择题(本题满分42分,每小题7分)1、计算的值是()。
(A)1;(B);(C);(D)5。
2、若,则的值是()。
(A);(B);(C)5;(D)6。
3、设是不相等的任意正数,又,则这两个数一定()。
(A)都不大于2;(B)都不小于2;(C)至少有1个大于2;(D)至少有1个小于2。
4、正整数小于100,并满足等式,其中表示不超过的最大整数,这样的正整数有()。
(A)2个;(B)3个;(C)12个;(D)16个。
5、已知一个梯形的四条边的长分别为1、2、3、4,则此梯形的面积等于()。
(A)4;(B)6;(C);(D)。
6、已知ABCD是一个半径为R的圆的内接四边形,AB=12,CD=6,分别延长AB 和DC,它们相交于P且BP=8,∠APD=60°,则R等于()。
(A)10;(B);(C);(D)14。
二、填空题(本题满分28分,每小题7分)1、是正数,并且抛物线和都与轴有公共点,则的最小值是________。
2、某果品店组合销售水果,甲种搭配:2千克A水果,4千克B水果;乙种搭配:3千克A水果,8千克B水果,1千克C水果;丙种搭配:2千克A水果,6千克B水果,l千克C水果。
A水果价格每千克2元,B水果价格每千克1.2元,C水果价格每千克10元。
某天该店销售三种搭配共得441.2元,其中A水果的销售额为116元,则C水果的销售额为________元。
3、实数满足和,则________。
4、设正三角形ABC的边长为2,M是AB边上的中点,P是边BC上的任意一点,PA+PM的最大值和最小值分别记为和,则________。
=============== =============== ===============第二试(4月2日上午10:30----11:30)一、(本题满分20分)设是实数,二次函数的图象与轴有两个不同的交点。
2004年全国初中数学联赛

23
解得 x = 4. C.
C卷
一、 ( 20 分 ) 同 A 卷第一题 . 二、 ( 25 分 ) 如图 6, 梯 形 ABCD 中 , AD ∃ BC , 分 别以 两 腰 AB 、CD 为边 向两 边作 正方 形 ABGE 和 正 方 形 DCHF , 连 结 EF , 设 线段 EF 的 中点 为 M . 求证 : MA = MD. 三、 ( 25 分 ) 同 A 卷第三题 .
22
中 等 数 学
竞赛之窗
2004 年全国初中数学联赛
第一试
一、 选择题 ( 每小题 7 分 , 共 42 分 ) 1. 已 知 abc 0, 且 a + b + c = 0. 则 代 数 式 a + b + c 的值为 ( bc ca ab ( A) 3 ( B) 2
2 2 2
4. 如 图 2, ABCD 是 边长 为 a 的 正 方 形, 以 D 为 圆 心、 DA 为 半 径 的 圆 弧 与 以 BC 为直 径 的半 圆交 于 另一 点 P . 延长 AP 交 BC 于点 N . BN = 则 NC .
24
中 等 数 学
2004 年第 4 期
25
2004 年四川省初中数学联赛
一、 选择题 ( 每小题 7 分 , 共 42 分 ) 1. 若 x < - 2, 则 y = | 1- | 1+ x | | 等于 ( (A) 2+ x * ∗ ( B) - 2- x * ∗ ( C) x 2. 如 图 1, M 是 & ABC 的边 BC 的 中 点 , AN 平分 + BAC , BN % AN 于 点 N , 且 AB = 10, BC = 15, MN = 3. 则 & ABC 的 周 长 等 于 ( ). ( A) 38 ( B) 39 ( C) 40
2004年广东省深圳市中考数学试卷

2004年广东省深圳市中考数学试卷一、选择题(共10小题,每小题3分,满分30分)1.(3分)16的平方根是()A.4 B.±4 C.﹣4 D.±82.(3分)下列等式正确的是()A.(﹣x2)3=﹣x5B.x8÷x4=x2C.x3+x3=2x3D.(xy)3=xy33.(3分)不等式组的解集在数轴上的表示正确的是()A. B.C.D.4.(3分)已知⊙O1的半径是3,⊙O2的半径是4,O1O2=8,则这两圆的位置关系是()A.相交 B.相切 C.内含 D.外离5.(3分)学校开展为贫困地区捐书活动,以下是八名学生捐书的册数:2,2,2,3,6,5,6,7,则这组数据的中位数为()A.2 B.3 C.4 D.4.56.(3分)下列图中:①线段;②正方形;③圆;④等腰梯形;⑤平行四边形是轴对称图形,但不是中心对称图形有()A.1个B.2个C.3个D.4个7.(3分)函数y=x2﹣2x+3的图象的顶点坐标是()A.(1,﹣4)B.(﹣1,2)C.(1,2)D.(0,3)8.(3分)如图,⊙O的两弦AB、CD相交于点M,AB=8cm,M是AB的中点,CM:MD=1:4,则CD=()A.12cm B.10cm C.8cm D.5cm9.(3分)圆内接四边形ABCD中,AC平分∠BAD,EF切圆于C,若∠BCD=120°,则∠BCE=()A.30°B.40°C.45°D.60°10.(3分)抛物线过点A(2,0)、B(6,0)、C(1,),平行于x轴的直线CD交抛物线于点C、D,以AB为直径的圆交直线CD于点E、F,则CE+FD的值是()A.2 B.4 C.5 D.6二、填空题(共5小题,每小题3分,满分15分)11.(3分)分解因式:x2﹣9y2+2x﹣6y=.12.(3分)函数y=的自变量x的取值范围为.13.(3分)计算:3tan30°+cot45°﹣2tan45°+2cos60°=.14.(3分)一个等腰三角形的两边长分别是2cm、5cm,则它的周长为cm.15.(3分)在矩形ABCD中,对角线AC、BD相交于点O,过点O作OE⊥BC,垂足为E,连接DE交AC于点P,过P作PF⊥BC,垂足为F,则的值是.三、解答题(共6小题,满分55分)16.(7分)计算:|1﹣|++(π﹣)0.17.(8分)解方程组:.18.(8分)在深圳“净畅宁”行动中,有一块面积为150亩的绿化工程面向全社会公开招标.现有甲、乙两工程队前来竞标,甲队计划比规定时间少4天,乙按规划时间完成.甲队比乙队每天多绿化10亩,问:规定时间是多少天?19.(10分)已知x1,x2是关于x的一元二次方程x2﹣6x+k=0的两个实数根,且x12x22﹣x1﹣x2=115.(1)求k的值;(2)求x12+x22+8的值.20.(10分)等腰梯形ABCD中,如图1,AB∥CD,AD=BC,延长AB到E,使BE=CD,连接CE.(1)求证:CE=CA;(2)上述条件下,如图2,若AF⊥CE于点F,且AF平分∠DAE,,求sin∠CAF 的值.21.(12分)直线y=﹣x+m与直线y=x+2相交于y轴上的点C,与x轴分别交于点A、B.(1)求A、B、C三点的坐标;(2)经过上述A、B、C三点作⊙E,求∠ABC的度数,点E的坐标和⊙E的半径;(3)若点P是第一象限内的一动点,且点P与圆心E在直线AC的同一侧,直线PA、PC 分别交⊙E于点M、N,设∠APC=θ,试求点M、N的距离.(可用含θ的三角函数式表示)2004年广东省深圳市中考数学试卷参考答案与试题解析一、选择题(共10小题,每小题3分,满分30分)1.(3分)(2006•芜湖)16的平方根是()A.4 B.±4 C.﹣4 D.±8【分析】根据平方根的定义,求数a的平方根,也就是求一个数x,使得x2=a,则x就是a 的一个平方根.【解答】解:∵(±4)2=16,∴16的平方根是±4.故选B.【点评】本题主要考查了平方根的定义.注意一个正数有两个平方根,它们互为相反数,0的平方根是0,负数没有平方根.2.(3分)(2004•深圳)下列等式正确的是()A.(﹣x2)3=﹣x5B.x8÷x4=x2C.x3+x3=2x3D.(xy)3=xy3【分析】根据积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘;同底数幂相除,底数不变指数相减;合并同类项,只把系数相加减,字母与字母的次数不变,对各选项计算后利用排除法求解.【解答】解:A、应为(﹣x2)3=﹣x6,故本选项错误;B、应为x8÷x4=x6,故本选项错误;C、x3+x3=2x3,正确;D、(xy)3=x3y3,故本选项错误.故选C.【点评】本题考查合并同类项,积的乘方的性质,同底数幂的除法,熟练掌握运算性质是解题的关键.3.(3分)(2004•深圳)不等式组的解集在数轴上的表示正确的是()A. B.C.D.【分析】先分别求出各不等式的解集,再求其公共解集即可.【解答】解:由(1)得x≥﹣1,由(2)得x≤3,根据“小大大小中间找”的原则可知不等式组的解集为﹣1≤x≤3.故选D.【点评】把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.求不等式组的解集应遵循“同大取较大,同小取较小,小大大小中间找,大大小小解不了”的原则.4.(3分)(2004•深圳)已知⊙O1的半径是3,⊙O2的半径是4,O1O2=8,则这两圆的位置关系是()A.相交 B.相切 C.内含 D.外离【分析】根据数量关系来判断两圆的位置关系.设两圆的半径分别为R和r,且R≥r,圆心距为d:外离,则d>R+r.外切,则d=R+r.相交,则R﹣r<d<R+r.内切,则d=R﹣r.内含,则d<R﹣r.【解答】解:∵⊙O1的半径是3,⊙O2的半径是4,O1O2=8,则3+4=7<8,∴两圆外离.故选D.【点评】本题考查了两圆的位置关系与数量之间的联系.5.(3分)(2004•深圳)学校开展为贫困地区捐书活动,以下是八名学生捐书的册数:2,2,2,3,6,5,6,7,则这组数据的中位数为()A.2 B.3 C.4 D.4.5【分析】找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数.【解答】解:题目中数据共有8个,按从小到大排列为2,2,2,3,5,6,6,7,故中位数是第4,第5两个数的平均数作为中位数,故这组数据的中位数是(3+5))=4.故选C.【点评】本题属于基础题,考查了确定一组数据的中位数的能力.要明确定义,一些学生往往对这个概念掌握不清楚,计算方法不明确而误选其它选项.注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求.如果是偶数个则找中间两位数的平均数.6.(3分)(2004•深圳)下列图中:①线段;②正方形;③圆;④等腰梯形;⑤平行四边形是轴对称图形,但不是中心对称图形有()A.1个B.2个C.3个D.4个【分析】结合线段、正方形、圆、等腰梯形、平行四边形的性质并根据轴对称图形和中心对称图形的概念即可解答.【解答】解:①,②,③既是轴对称图形又是中心对称的图形;④只是轴对称图形,但不是中心对称图形;⑤只是中心对称图形.故选A.【点评】此题考查了轴对称图形和中心对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,图形旋转180度后与原图形重合.7.(3分)(2004•深圳)函数y=x2﹣2x+3的图象的顶点坐标是()A.(1,﹣4)B.(﹣1,2)C.(1,2)D.(0,3)【分析】利用配方法化简y=x2﹣2x+3可以得到y=(x﹣1)2+2,由此即可确定顶点的坐标.【解答】解:∵y=x2﹣2x+3=x2﹣2x+1+2=(x﹣1)2+2,故顶点的坐标是(1,2).故选C.【点评】考查求抛物线的顶点坐标的方法.8.(3分)(2004•深圳)如图,⊙O的两弦AB、CD相交于点M,AB=8cm,M是AB的中点,CM:MD=1:4,则CD=()A.12cm B.10cm C.8cm D.5cm【分析】根据相交弦定理“圆内两弦相交于圆内一点,各弦被这点所分得的两线段的长的乘积相等”进行计算.【解答】解:∵CM:DM=1:4∴DM=4CM又AB=8,M是AB的中点∴MA=MB=4cm由相交弦定理得:MA•MB=MC•MD即4×4=MC•4MC解得MC=2cm∴CD=MC+MD=MC+4MC=10cm.故选B.【点评】本题主要考查相交弦定理“圆内两弦相交于圆内一点,各弦被这点所分得的两线段的长的乘积相等”的应用.9.(3分)(2004•深圳)圆内接四边形ABCD中,AC平分∠BAD,EF切圆于C,若∠BCD=120°,则∠BCE=()A.30°B.40°C.45°D.60°【分析】由弦切角定理可得:∠BCE=∠BAC;因此欲求∠BCE,必先求出∠BAC的度数.已知∠BCD=120°,由圆内接四边形的对角互补,可得出∠BAD=60°,而AC平分∠BAD,即可求出∠BAC的度数.【解答】解:∵四边形ABCD内接于⊙O,∴∠BAD+∠BCD=180°,∴∠BAD=180°﹣120°=60°,∵AC平分∠BAD,∴∠BAC=∠BAD=30°,∵EF切⊙O于C,∴∠BCE=∠BAC=30°.故选A.【点评】本题主要考查弦切角定理和圆内接四边形的性质,解题的关键是得出∠BAD=60°.10.(3分)(2004•深圳)抛物线过点A(2,0)、B(6,0)、C(1,),平行于x轴的直线CD交抛物线于点C、D,以AB为直径的圆交直线CD于点E、F,则CE+FD的值是()A.2 B.4 C.5 D.6【分析】根据题意,G为直径AB的中点,连接GE,过G点作GH⊥CD于H.知CE+FD=CD ﹣EF=CD﹣2EH,分别求出CD,EF即可.【解答】解:由题意得:D点坐标为(7,),如图,G为直径AB的中点,连接GE,过G点作GH⊥CD于H.则GH=,EG=2,则EH==1∴CE+FD=CD﹣EF=CD﹣2EH=6﹣2=4.故选B.【点评】此题首先要正确分析出各点的坐标,然后根据两点的坐标进行计算.二、填空题(共5小题,每小题3分,满分15分)11.(3分)(2004•深圳)分解因式:x2﹣9y2+2x﹣6y=(x﹣3y)(x+3y+2).【分析】当被分解的式子是四项时,应考虑运用分组分解法进行分解.本题一二项可组成平方差公式,三四项有公因式,故一二项为一组,三四项一组.【解答】解:x2﹣9y2+2x﹣6y,=(x2﹣9y2)+(2x﹣6y),=(x+3y)(x﹣3y)+2(x﹣3y),=(x﹣3y)(x+3y+2).【点评】本题考查用分组分解法进行因式分解.难点是采用两两分组还是三一分组.本题一二项可组成平方差公式,三四项有公因式,故一二项为一组,三四项一组.12.(3分)(2008•兰州)函数y=的自变量x的取值范围为x≥﹣1且x≠1.【分析】根据二次根式的性质和分式的意义,被开方数大于或等于0,分母不等于0,就可以求解.【解答】解:根据题意得:,解得:x≥﹣1且x≠1.【点评】函数自变量的范围一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数为非负数.13.(3分)(2004•深圳)计算:3tan30°+cot45°﹣2tan45°+2cos60°=.【分析】运用特殊角的三角函数值求解.【解答】解:3tan30°+cot45°﹣2tan45°+2cos60°=3×+1﹣2×1﹣2×=.【点评】本题考查特殊角三角函数值的计算,特殊角三角函数值计算在中考中经常出现,要掌握特殊角度的三角函数值.14.(3分)(2015•广元)一个等腰三角形的两边长分别是2cm、5cm,则它的周长为12 cm.【分析】本题没有明确说明已知的边长那一条是腰长,所以需要分两种情况讨论.【解答】解:分两种情况讨论①腰长为5时,三边为5、5、2,满足三角形的性质,周长=5+5+2=12cm;②腰长为2cm时,三边为5、2、2,∵2+2=4<5,∴不满足构成三角形.∴周长为12cm.故答案为:12.【点评】本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.15.(3分)(2004•深圳)在矩形ABCD中,对角线AC、BD相交于点O,过点O作OE⊥BC,垂足为E,连接DE交AC于点P,过P作PF⊥BC,垂足为F,则的值是.【分析】根据题意易证△OBE∽△DBC和△EPF∽△EDC,利用相似三角形的相似比求解.【解答】解:∵OB=OD=BD,OE⊥BC,CD⊥BC,∴△OBE∽△DBC,∴OE:CD=1:2,∵OE∥CD,∴△OEP∽△CDP,∴,∵PF∥DC,∴△EPF∽△EDC,∴,∵CE=BC,∴=.故答案为.【点评】本题考查对相似三角形性质的理解.相似三角形对应边的比相等.三、解答题(共6小题,满分55分)16.(7分)(2004•深圳)计算:|1﹣|++(π﹣)0.【分析】本题涉及零指数幂、绝对值、二次根式化简三个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.【解答】解:原式=﹣1+﹣+1=.【点评】本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握零指数幂、二次根式、绝对值等考点的运算.17.(8分)(2004•深圳)解方程组:.【分析】此题可用消元法,(1)﹣(2)把y消去再求解.【解答】解:,(1)﹣(2)得x2+3x﹣10=0,解得:x1=﹣5,x2=2,代入(2)得:y1=﹣20,y2=1,故原方程组的解为,.【点评】此题很简单,只要用(1)﹣(2)即可消去y,再解关于x的一元二次方程即可.18.(8分)(2004•深圳)在深圳“净畅宁”行动中,有一块面积为150亩的绿化工程面向全社会公开招标.现有甲、乙两工程队前来竞标,甲队计划比规定时间少4天,乙按规划时间完成.甲队比乙队每天多绿化10亩,问:规定时间是多少天?【分析】求的是时间,工作总量为150,一定是根据工作效率来列等量关系,本题的关键描述语是:甲队比乙队每天多绿化10亩.等量关系为:甲工效﹣乙工效=10.【解答】解:设规定时间为x天,则,解得x=10或x=﹣6(不合题意,舍去),经检验x=10是原方程的解.答:规定时间是10天.【点评】本题考查分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.涉及到的公式:工作总量=工作效率×工作时间.19.(10分)(2008•濮阳)已知x1,x2是关于x的一元二次方程x2﹣6x+k=0的两个实数根,且x12x22﹣x1﹣x2=115.(1)求k的值;(2)求x12+x22+8的值.【分析】(1)方程有两个实数根,必须满足△=b2﹣4ac≥0,从而求出实数k的取值范围,再利用根与系数的关系,x12x22﹣x1﹣x2=115.即x12x22﹣(x1+x2)=115,即可得到关于k 的方程,求出k的值.(2)根据(1)即可求得x1+x2与x1x2的值,而x12+x22+8=(x1+x2)2﹣2x1x2+8即可求得式子的值.【解答】解:(1)∵x1,x2是方程x2﹣6x+k=0的两个根,∴x1+x2=6,x1x2=k,∵x12x22﹣x1﹣x2=115,∴k2﹣6=115,解得k1=11,k2=﹣11,当k1=11时,△=36﹣4k=36﹣44<0,∴k1=11不合题意当k2=﹣11时,△=36﹣4k=36+44>0,∴k2=﹣11符合题意,∴k的值为﹣11;(2)∵x1+x2=6,x1x2=﹣11∴x12+x22+8=(x1+x2)2﹣2x1x2+8=36+2×11+8=66.【点评】总结:(1)一元二次方程根的情况与判别式△的关系:①△>0⇔方程有两个不相等的实数根;②△=0⇔方程有两个相等的实数根;③△<0⇔方程没有实数根.(2)根与系数的关系是:x1+x2=,x1x2=.根据根与系数的关系把x12x22﹣x1﹣x2=115转化为关于k的方程,解得k的值是解决本题的关键.20.(10分)(2004•深圳)等腰梯形ABCD中,如图1,AB∥CD,AD=BC,延长AB到E,使BE=CD,连接CE.(1)求证:CE=CA;(2)上述条件下,如图2,若AF⊥CE于点F,且AF平分∠DAE,,求sin∠CAF 的值.【分析】(1)根据等腰梯形的性质可得出AC=BD,而CD BE,因此四边形CEBD是平行四边形,CE=BD,因此可得出CE=CA;(2)要求∠CAF的正弦值,就要知道,CF和AC的比例关系.由于BD∥CE,AF⊥CE,那么AF⊥BD,而AF平分∠DAB,因此AF垂直平分BD,如果设AF,BD交于O点,那么BO=BD=AC=CE.根据CD:AE=2:5,即BE:AE=2:5,可得出AB:AE=3:5,有BO∥CE,得出BO:EF=AB:AE,也就求出了BF何CE的比例关系,便可得出CF和EC的比例关系,由于CE=AC,因此也就得出了CF和AC的比例关系即可得出∠CAF的正弦值.【解答】(1)证明:∵四边形ABCD是等腰梯形∴AC=BD,CD∥BE,∵CD=BE,∴四边形DBEC是平行四边形∴CE=BD,∴CE=CA;(2)解:∵CD=BE,且,∴=∵AF⊥EC,BD∥EC∴AF⊥BD,设垂足为O∵AF平分∠DAB∴AF垂直平分BD,即BO=BD=AC=CE∵BO∥CE∴==,即=∴EF=CE∴CF=CE=AC∴sin∠CAF==.【点评】本题主要考查了等腰梯形的性质,相似三角形的性质等知识点的应用,本题中通过AF垂直平分BD得出BO=BD,进而求出EF和CE的关系是解题的关键.21.(12分)(2004•深圳)直线y=﹣x+m与直线y=x+2相交于y轴上的点C,与x轴分别交于点A、B.(1)求A、B、C三点的坐标;(2)经过上述A、B、C三点作⊙E,求∠ABC的度数,点E的坐标和⊙E的半径;(3)若点P是第一象限内的一动点,且点P与圆心E在直线AC的同一侧,直线PA、PC 分别交⊙E于点M、N,设∠APC=θ,试求点M、N的距离.(可用含θ的三角函数式表示)【分析】(1)直线y=x+2与y轴的交点可以求出,把这点的坐标就可以求出直线y=﹣x+m的解析式,两个函数与x轴的交点就可以求出;(2)根据三角函数可以求出角的度数.根据OC、OA、OB的长度根据三角函数可以根据三角函数求出角的度数;(3)根据正弦定理就可以解决.【解答】解:(1)直线y=x+2中令x=0,解得y=2,因而C点的坐标是(0,2),把(0,2)代入直线y=﹣x+m,解得m=2,∴解析式是y=﹣x+2,令y=0,解得x=2,则A点的坐标是(2,0),在y=x+2中令y=0,解得x=2则B的坐标是(2,0);(2)根据A、B、C的坐标得到OC=2,OA=2,OB=2,根据三角函数得到∠ABC=30°.连接AE,CE,则∠AEC=60°,∴△ACE是等边三角形,边长是2,因而E的坐标是(,+1),半径是2;(3)如图所示:MN为⊙E中任一弦,它对的圆周角为∠B,当AM为直径,则∠ANM为直角,则sinB=sinA=即MN=AM•sinA①(其实就是正弦定理),这是本题的解题的理论基础.(I)当点P在⊙E外时,如图连接AN,则∠MAN=∠ANC﹣∠P=∠ABC﹣∠P=30°﹣θ由①得:MN=4sin(30°﹣θ);(II)当P在⊙E内时同理可得:MN=4sin(θ﹣30°)其它情况研究方法相同,(III)当P在⊙E上时,MN=0.【点评】本题主要考查了待定系数法求函数解析式,并且考查了三角函数的定义.。
初中数学专题与三角形有关的角典型试题

7. (江苏省第十五届初中数学竞赛初二第 1 试试题) 已知△ABC 的三个内角为 A、B、C,令 B C ,
C A A B ,则 , , 中锐角的个
数至多为( ) (A)1 (B)2 (C)3 ( D) 4 8.一个三角形的三个外角中( ) (A)至少有一个钝角 (B)至少有两个钝角 (C)至少有三个钝角 (D)可以没有钝角 9. 在 ABC 中, B, C 的平分线相交于一点 P ,设 A x , BPC y ,如果 x 每增加 1 ,那么 y 增加
图 13
1 ,求满足此条件的所有锐角三角形的度数. 4
.
27. (1998 北京市初中数学竞赛试题)
ABC 中,三个内角的度数均为整数,且 A B C , 4C 7A ,则 B
28. (1987 年宝鸡市初中数学竞赛第一试) 若三角形的三个内角 A, B, C 关系满足 A 3B, C 2 B ,则这个三角形是( (A)钝角三角形 (B)直角三角形 (C)锐角三角形但不等边 )
1 A . 2
0
图 3 中,若 E 为 ABC 两外角平分线的交点,则 BEC 90 角的外角的一半).
1 1 A 1800 A (即等于第三个 2 2 1 A . 2
E
FD
B
图 4 中,若 P 为 B 的平分线和 ABC 外角平分线的交点,则 P 图 5 中, BOC A B C . 图 6 中, 若 E 为 ABC , ADC 平分线的交点,则 E
与三角形有关的角
重要结论
A B I B C A A A P
C
D
B
C
E
B
C
图1
A
历年初中数学竞赛真题库(含答案)

历年初中数学竞赛真题库(含答案)1991年全国初中数学联合竞赛决赛试题第⼀试⼀、选择题本题共有8个⼩题,每⼩题都给出了(A )、(B )(C )、(D )四个答案结论,其中只有⼀个是正确的.请把正确结论的代表字母写在题后的圆括号内..设等式y a a x a y a a x a ---=-+-)()(在实数范围内成⽴,其中a ,x ,y 是两两不同的实数,则22223y xy x y xy x +--+的值是(A )3 ;(B )31;(C )2;(D )35.答().如图,AB ‖EF ‖CD ,已知AB =20,CD =80,BC =100,那么EF 的值是(A ) 10;(B )12;(C ) 16;(D )18.答().⽅程012=--x x 的解是(A )251±;(B )251±-;(C )251±或251±-;(D )251±-±.答().已知:)19911991(2111n n x --=(n 是⾃然数).那么nx x )1(2+-,的值是(A)11991-;(B)11991--;(C)1991)1(n -;(D)11991)1(--n .答().若M n1210099321= ,其中M为⾃然数,n 为使得等式成⽴的最⼤的⾃然数,则M(A)能被2整除,但不能被3整除;(B)能被3整除,但不能被2整除;(C)能被4整除,但不能被3整除;(D)不能被3整除,也不能被2整除.答().若a ,c ,d 是整数,b 是正整数,且满⾜c b a =+,d c b =+,a d c =+,那么 d c b a +++的最⼤值是(A)1-;(B)5-;(C)0;(D)1.答().如图,正⽅形OPQR 内接于ΔABC .已知ΔAOR 、ΔBOP 和ΔCRQ 的⾯积分别是11=S ,32=S 和13=S ,那么,正⽅形OPQR 的边长是(A)2;(B)3;(C)2 ;(D)3.答()11=S.在锐⾓ΔABC 中,1=AC ,c AB =,60=∠A,ΔABC 的外接圆半径R ≤1,则(A)21< c < 2 ;(B)0< c ≤21;答()(C )c > 2;(D )c = 2.答()⼆、填空题1.E是平⾏四边形ABCD 中BC 边的中点,AE 交对⾓线BD 于G ,如果ΔBEG 的⾯积是1,则平⾏四边形ABCD 的⾯积是.2.已知关于x 的⼀元⼆次⽅程02=++c bx ax 没有实数解.甲由于看错了⼆次项系数,误求得两根为2和4;⼄由于看错了某⼀项系数的符号,误求得两根为-1和4,那么,=+a cb 32 .3.设m ,n ,p ,q 为⾮负数,且对⼀切x >0,q pnm x x x x )1(1)1(+=-+恒成⽴,则 =++q p n m 22)2( .4.四边形ABCD 中,∠ ABC 135=,∠BCD120=,AB 6=,BC 35-=,CD = 6,则AD = .第⼆试x + y , x - y , x y , y x四个数中的三个⼜相同的数值,求出所有具有这样性质的数对(x , y ).⼆、ΔABC 中,AB <AC <BC ,D 点在BC 上,E 点在BA 的延长线上,且 BD =BE =AC ,ΔBDE 的外接圆与ΔABC 的外接圆交于F 点(如图).求证:BF =AF +CF三、将正⽅形ABCD 分割为 2n 个相等的⼩⽅格(n 是⾃然数),把相对的顶点A ,C 染成红⾊,把B ,D 染成蓝⾊,其他交点任意染成红、蓝两⾊中的⼀种颜⾊.证明:恰有三个顶点同⾊的⼩⽅格的数⽬必是偶数.120 1351992年全国初中数学联合竞赛决赛试题第⼀试⼀.选择题本题共有8个题,每⼩题都给出了(A), (B), (C), (D)四个结论,其中只有⼀个是正确的.请把正确结论的代表字母写在题后的圆括号内.1.满⾜1=+-ab b a 的⾮负整数),(b a 的个数是 (A)1; (B)2; (C)3; (D)4.2.若0x 是⼀元⼆次⽅程)0(02≠=++a c bx ax 的根,则判别式ac b 42-=?与平⽅式20)2(b ax M +=的关系是(A)?>M (B)?=M (C)?>M ; (D)不确定.3.若01132=+-x x ,则44-+x x 的个位数字是 (A)1; (B)3; (C)5; (D)7. 答( )4.在半径为1的圆中有⼀内接多边形,若它的边长皆⼤于1且⼩于2,则这个多边形的边数必为(A)7; (B)6; (C)5; (D)4. 答( )5.如图,正⽐例函数)0(>==a ax y x y 和的图像与反⽐例函数)0(>=k x ky 的图像分别相交于A 点和C 点.若AOB Rt ?和COD ?的⾯积分别为S 1和S 2,则S 1与S 2的关系是(A)21S S > (B)21S S = (C)21S S < (D)不确定答( )6.在⼀个由88?个⽅格组成的边长为8的正⽅形棋盘内放⼀个半径为4的圆,若把圆周经过的所有⼩⽅格的圆内部分的⾯积之和记为1S ,把圆周经过的所有⼩⽅格的圆内部分的⾯积之和记为2S ,则21S S 的整数部分是(A)0; (B)1; (C)2; (D)3. 答( )=∠60A ,⼜E 7.如图,在等腰梯形ABCD 中, AB //CD , AB=2CD ,是底边AB 上⼀点,且FE=FB=AC , FA=AB .则AE :EB 等于 (A)1:2 (B)1:3 (C)2:5 (D)3:10 答( )8.设9321,,,,x x x x 均为正整数,且 921x x x9x x -的最⼩值是(A)8; (B)9; (C)10; (D)11. 答( ) ⼆.填空题1.若⼀等腰三⾓形的底边上的⾼等于18cm ,腰上的中线等15cm ,则这个等腰三⾓形的⾯积等于________________.2.若0≠x ,则x x x x 44211+-++的最⼤值是__________. 3.在ABC ?中,B AC ∠∠=∠和,90的平分线相交于P 点,⼜AB PE ⊥于E 点,若3,2==AC BC ,则=?EB AE .4.若b a ,都是正实数,且0111=+--b a b a ,则=+33)()(b a a b .第⼆试⼀、设等腰三⾓形的⼀腰与底边的长分别是⽅程062=+-a x x 的两根,当这样的三⾓形只有⼀个时,求a 的取值范围.⼆、如图,在ABC ?中,D AC AB ,=是底边BC 上⼀点,E 是线段AD 上⼀点,且A CED BED ∠=∠=∠2.求证:CD BD 2=.三、某个信封上的两个邮政编码M 和N 均由0,1,2,3,5,6这六个不同数字组成,现有四个编码如下:A :320651B :105263C :612305D :316250已知编码A 、B 、C 、D 各恰有两个数字的位置与M 和N 相同.D 恰有三个数字的位置与M和N 相同.试求:M 和N.1993年全国初中数学联合竞赛决赛试题第⼀试⼀.选择题本题共有8个⼩题,每⼩题都给出了(A), (B), (C), (D)四个结论,其中只有⼀个是正确的.请把正确结论的代表字母写在题后的圆括号内.1.多项式1612+-x x 除以12-x 的余式是 (A)1; (B)-1; (C)1-x ; (D)1+x ;2.对于命题Ⅰ.内⾓相等的圆内接五边形是正五边形.Ⅱ.内⾓相等的圆内接四边形是正四边形,以下四个结论中正确的是 (A )Ⅰ,Ⅱ都对 (B )Ⅰ对,Ⅱ错 (C )Ⅰ错,Ⅱ对. (D )Ⅰ,Ⅱ都错.3.设x 是实数,11++-=x x y .下列四个结论: Ⅰ.y 没有最⼩值;Ⅱ.只有⼀个x 使y 取到最⼩值;Ⅲ.有有限多个x (不⽌⼀个)使y 取到最⼤值; Ⅳ.有⽆穷多个x 使y 取到最⼩值. 其中正确的是(A )Ⅰ (B )Ⅱ (C )Ⅲ (D )Ⅳ4.实数54321,,,,xx x x x 满⾜⽅程组=++=++=++=++=++.;;;;52154154354324321321a x x x a x x x a x x x a x x x a x x x其中54321,,,,a a a a a 是实常数,且54321a a a a a >>>>,则54321,,,,x x x x x 的⼤⼩顺序是(A)54321x x x x x >>>>; (B )53124x x x x x >>>>;(C )52413x x x x x >>>>; (D )24135x x x x x >>>>.5.不等式73)1(12+<-<-x x x 的整数解的个解 (A )等于4 (B )⼩于4 (C )⼤于5 (D )等于56.在ABC ?中,BC AO O A =∠,,是垂⼼是钝⾓, 则)cos(OCB OBC ∠+∠的值是(A)22-(B)22(C)23 (D)21-. 答( )7.锐⾓三⾓ABC 的三边是a , b , c ,它的外⼼到三边的距离分别为m , n , p ,那么m :n :p 等于(A)c b a 1:1:1; (B)c b a ::(C)C B A cos :cos :cos (D)C B A sin :sin :sin . 答( )8.13333)919294(3-+-可以化简成 (A))12(333+; (B))12(333- (C)123- (D)123+ 答( ) ⼆.填空题1. 当x 变化时,分式15632212++++x x x x 的最⼩值是___________.2.放有⼩球的1993个盒⼦从左到右排成⼀⾏,如果最左⾯的盒⾥有7个⼩球,且每四个相邻的盒⾥共有30个⼩球,那么最右⾯的盒⾥有__________个⼩球.3.若⽅程k x x =--)4)(1(22有四个⾮零实根,且它们在数轴上对应的四个点等距排列,则k =____________.4.锐⾓三⾓形ABC 中,?=∠30A .以BC 边为直径作圆,与AB , AC 分别交于D , E ,连接DE , 把三⾓形ABC 分成三⾓形ADE 与四边形BDEC ,设它们的⾯积分别为S 1, S 2,则S 1:S 2=___________.第⼆试⼀.设H 是等腰三⾓形ABC 垂⼼,在底边BC 保持不变的情况下让顶点A ⾄底边BC 的距离变⼩,这时乘积HBC ABC SS 的值变⼩,变⼤,还是不变?证明你的结论.⼆.ABC ?中, BC =5, AC =12, AB =13, 在边AB ,AC 上分别取点D ,E , 使线段DE 将ABC ?分成⾯积相等的两部分.试求这样的线段DE 的最⼩长度.三.已知⽅程0022=++=++b cx x c bx x 及分别各有两个整数根21,x x 及21,x x '',且,021>x x 021>''x x . (1)求证:;0,0,0,02121<'<'<(3)求c b ,所有可能的值.1994年全国初中数学联赛试题第⼀试(4⽉3⽇上午8:30—9:30)考⽣注意:本试共两道⼤题,满分80分.⼀、选择题(本题满分48分,每⼩题6分)本题共有8个⼩题都给出了A,B、C,D,四个结论,其中只有⼀个是正确的,请把你认为正确结论的代表字母写在题后答案中的圆括号内,每⼩题选对得6分;不选、选错或选出的代表字母超过⼀个(不论是否写在圆括号内),⼀律得0分.〔答〕( )2.设a,b,c是不全相等的任意实数,若x=a2-bc,y=b2-ca,z=c2-ab,则x,y,zA.都不⼩于0B.都不⼤于0C.⾄少有⼀个⼩0于D.⾄少有⼀个⼤于0〔答〕( )3.如图1所⽰,半圆O的直径在梯形ABCD的底边AB上,且与其余三边BC,CD,DA 相切,若BC=2,DA=3,则AB的长A.等于4B.等于5C.等于6D.不能确定〔答〕( )A.1 B.-1 C.22001D.-22001〔答〕( )5.若平⾏直线EF,MN与相交直线AB,CD相交成如图2所⽰的图形,则共得同旁内⾓A.4对B.8对C.12对D.16对〔答〕( )〔答〕( )7.设锐⾓三⾓形ABC的三条⾼AD,BE,CF相交于H。
深圳市2004年数学中考试题
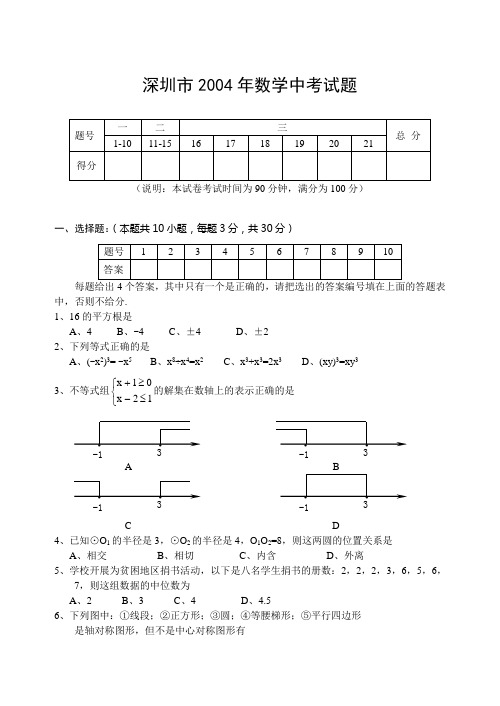
深圳市2004年数学中考试题(说明:本试卷考试时间为90分钟,满分为100分)一、选择题:(本题共10小题,每题3分,共30分)每题给出4个答案,其中只有一个是正确的,请把选出的答案编号填在上面的答题表中,否则不给分. 1、16的平方根是A 、4B 、-4C 、±4D 、±2 2、下列等式正确的是A 、(-x 2)3= -x 5B 、x 8÷x 4=x 2C 、x 3+x 3=2x 3D 、(xy)3=xy 33、不等式组⎩⎨⎧≤-≥+12x 01x 的解集在数轴上的表示正确的是A BC D4、已知⊙O 1的半径是3,⊙O 2的半径是4,O 1O 2=8,则这两圆的位置关系是 A 、相交 B 、相切 C 、内含 D 、外离5、学校开展为贫困地区捐书活动,以下是八名学生捐书的册数:2,2,2,3,6,5,6,7,则这组数据的中位数为A 、2B 、3C 、4D 、4.56、下列图中:①线段;②正方形;③圆;④等腰梯形;⑤平行四边形是轴对称图形,但不是中心对称图形有A 、1个B 、2个C 、3个D 、4个 7、函数y=x 2-2x+3的图象顶点坐标是 A 、(1,-4) B 、(-1,2) C 、(1,2) D 、(0,3)8、如图,⊙O 的两弦AB 、CD 相交于点M ,AB=8cm ,M 是AB 的中点,CM :MD=1:4,则CD=A 、12cmB 、10cmC 、8cmD 、5cm9、圆内接四边形ABCD 中,AC 平分∠BAD ,EF 切圆于C ,若∠BCD=120º,则∠BCE= A 、30º B 、40º C 、45º D 、60º(8) (9) (10)10、抛物线过点A (2,0)、B (6,0)、C (1,3),平行于x 轴的直线CD 交抛物线于点C 、D ,以AB 为直径的圆交直线CD 于点E 、F ,则CE+FD 的值是 A 、2 B 、4 C 、5 D 、6二、填空题:(共5小题,每题3分,共15分) 11、分解因式:x 2-9y 2+2x -6y=______.12、在函数式y=1x 1x -+中,自变量x 的取值范围是_______. 13、计算:3tan30º+cot45º-2tan45º+2cos60º=_______.14、等腰三角形的两边长分别为2cm 和5cm ,则它的周长为________.15、在矩形ABCD 中,对角线AC 、BD 相交于点O ,过点O 作OE ⊥BC ,垂足为E ,连结DE 交AC 于点P ,过P 作PF ⊥BC ,垂足为F ,则CBCF的值是_____.三、解答题:(本部分共6题,其中第16题7分,第17-18题各8分,第19-20题各10分,第21题12分,共55分) 16、计算:|1-2|+231++(π-2)0 (7分)17、解方程组:⎩⎨⎧=+-=+05x 3y 5y x 2 (8分)18、在深圳“净畅宁”行动中,有一块面积为150亩的绿化工程面向全社会公开招标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2004年全国初中数学联赛试题
第一试
(时间:2004年3月13日上午9:30-11:00,满分100分)
一、 选择题(每小题4分,共40分)
1.下列几何图形中,不可能既是轴对称图形又是中心对称图形的是( )
A .圆; B.正三角形; C.线段; D.矩形.
2.二次函数c bx x y ++=2的图象向左平移2个单位,再向上平移3个单位,得到函数122+-=x x y 的图象,则c b ,的值分别为( )
A .6,4; B.14,8-; C.6,6-; D.4,8--.
3.已知四边形1S 的两条对角线相等,但不垂直,顺次连结1S 各边中点得四边形2S ,顺次连结2S 各边中点得四边形3S ,以此类推,则2004S 为( )
A .是矩形但不是菱形; B. 是菱形但不是矩形;
C.既是菱形又是矩形;
D.既非矩形又非菱形.
4.α、β都是钝角,甲、乙、丙、丁四位同学计算()βα+9
1的结果依次为50°、26°、72°和90°,其中确有正确的结果,那么算得正确的是( )
A .甲; B.乙; C.丙; D.丁
5.使分式x
x z y x 42002002200119992003
2000-+-有意义的x 取值范围是( ) A .0≠x ; B.500≠≠x x 且; C.500±≠≠x x 或; D.500±≠≠x x 且
6.两个物体A 、B 所受压强分别为A P (帕)与B P (帕)(A P 、B P 为常数),它们所受压力F (牛)与受力面积S (米2)的函数关系图象分别是射线B A L L ,.如图所示,则( )
A .A P <
B P ; B.A P =B P ;
C .A P >B P ; D.A P ≤B P
7.已知a 、b 都是有理数,且b b a a ≠=,,则ab 是( ) A .负数; B.正数; C.负数或零; D.非负数.
8.若关于x 的方程
12
2-=++x a x 的解是负数,则a 的取值范围是( ) A .2-<a ; B.2->a ; C.02≠->a a 且; D.0≠a 9.有理数c b a ,,,满足:3≥a ,2-≤b ,5≥c ,且10=+-c b a ,则c b a ++3的最
大值是( )
A .1; B.2; C.3; D.5
10.在锐角△ABC 中,三个内角的度数都是质数,则这样的三角形( )
A .只有一个且为等腰三角形; B.至少有两个且都为等腰三角形;
C. 只有一个但不是等腰三角形;
D.至少有两个,其中有非等腰三角形.
二、 填空题(每小题4分,共60分)
11.2003年6月1日,举世瞩目的三峡工程正式下闸蓄水,26台机组年发电量将达到h kw ⋅08470000000. 用科学记数法应表示为 ;
12.要使分式方程3
23-=--x m x x 产生增根,则m = ; 13.在Rt △ABC 中,∠C=90°,b a ,分别是∠A 、∠B 的对边,如果3:2sin :sin =B A ,那么b a :等于 ;
14.将一个四边形的纸片一刀剪去一个角后,所得的多边形的内角之和是 ;
15.观察下列各组数:(3,4,5),(5,12,13),(7,24,25),(11,60,61)…,发现()()(),21724,21512,2134222 ÷-=÷-=÷-=若设某组数第一个数为k ,则这个组的数为(),,k ;
16.当 时,关于x 的一元二次方程()()01222=++-+-a x a x a 有实根.
17.Rt △ABC 内的点P 到三边的距离均为d ,斜边为c, 则直角三角形的面积为 ;
18.如果表示正方形ABCD 各边长的代数式如图所示,那么,阴影部分的面积是
第18题 第19题 第20题
19.在正方形ABCD 中,点E 是BC 上的一定点,且BE=5,EC=7.
点P 是BD 上的一动点,则PE+PC 的最小值是 .
20.如图,四边形ABCD 中,已知AB ∶BC ∶CD ∶DA=2∶2∶3∶1,且∠B=90°, 则∠DAB 的度数是 ;
21.()()+--2004
2002200320022002
()()+--20022003200420032003 ()()20032004200220042004--= ;
22.圆的半径为5cm ,其内接梯形的两底分别为6cm 和8cm ,则梯形的面积S= ;
23.如图所示, 是用火柴棒摆成的一序列“井”字型图案,按这种方式摆下去,当每边上A B C D 2x+3y-13x-4y+57x+8y-11B C E B A D C
摆201(即201=n )根时,需要的火柴棒的总根数是 根.
n =3n =5n =7
24.设n 为自然数,记n !n =⋅⋅⋅⋅ 321,问和数1!+2!+3!+…+2003!+2004!的个位数字是 .
25.若︒<<︒300θ,且3
1s
i n +=km θ(k 为常数,且)0k <,则m 的取值范围是 .
参考答案
一、1.B 2.C 3.B 4.B 5.D 6.A 7.C 8.B 9.B 10.A
二、11.h kw ⋅⨯10
1047.8; 12. 3 ; 13. 2:3 ; 14. 180°或360°或540° 15.2
1,2122+-k k ; 16.41-≥a 且2≠a 17.2d cd + 18.84212=⨯ 19.
13 20. 135° 21.0 22.49或7. ()()120012016=-=n f 24. 3 25. k <m<k 3161-。
