A3月考试卷

合集下载

湖南师大附中2025届高三月考数学(三)试卷及答案

大联考湖南师大附中2025届高三月考试卷(三)数学时量:120分钟满分:150分一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.集合{}0,1,2,3的真子集个数是()A .7B .8C .15D .162.“11x -<”是“240x x -<”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件3.已知角α的终边上有一点P 的坐标是)4,3(a a ,其中0a ≠,则sin2α=()A .43B .725C .2425D .2425-4.设向量a,b 满足+=-=a b a b ,则⋅a b 等于()A .B .2C .5D .85.若无论θ为何值,直线sin cos 10y x θθ⋅+⋅+=与双曲线2215x y m -=总有公共点,则m的取值范围是()A.1m ≥B .01m <≤C .05m <<,且1m ≠D .1m ≥,且5m ≠6.已知函数()2f x 的图象关于原点对称,且满足()()130f x f x ++-=,且当()2,4x ∈时,()()12log 2f x x m =--+,若()()2025112f f -=-,则m 等于()A .13B .23C .23-D .13-7.已知正三棱台111ABC A B C -所有顶点均在半径为5的半球球面上,且AB =11A B =()A .1B .4C .7D .1或78.北宋数学家沈括博学多才、善于观察.据说有一天,他走进一家酒馆,看见一层层垒起的酒坛,不禁想到:“怎么求这些酒坛的总数呢?”经过反复尝试,沈括提出对于上底有ab 个,下底有cd 个,共n 层的堆积物(如图所示),可以用公式()()()2266n nS b d a b d c c a ⎡⎤=++++-⎣⎦求出物体的总数,这就是所谓的“隙积术”,相当于求数列()()(),11,2ab a b a +++.()()()2,,11b a n b n cd ++-+-= 的和.若由小球堆成的上述垛积共7层,小球总个数为238,则该垛积最上层的小球个数为()A .2B .6C .12D .20二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.若()202422024012202412x a a x a x a x +=++++ ,则下列正确的是()A .02024a =B .20240120243a a a +++= C .012320241a a a a a -+-++= D .12320242320242024a a a a -+--=- 10.对于函数()sin cos f x x x =+和()sin cos 22g x x x ππ⎛⎫⎛⎫=--- ⎪ ⎪⎝⎭⎝⎭,下列说法中正确的有()A .()f x 与()g x 有相同的零点B .()f x 与()g x 有相同的最大值点C .()f x 与()g x 有相同的最小正周期D .()f x 与()g x 的图象有相同的对称轴11.过点()0,2P 的直线与抛物线2:4C x y =交于()()1122,,,A x y B x y 两点,抛物线C 在点A 处的切线与直线2y =-交于点N ,作NM AP ⊥交AB 于点M ,则()A .5OA OB ⋅=-B .直线MN 恒过定点C .点M 的轨迹方程是()()22110y x y -+=≠D .AB MN选择题答题卡题号1234567891011得分答案三、填空题:本题共3小题,每小题5分,共15分.12.已知复数12,z z 的模长为1,且21111z z +=,则12z z +=_____.13.在ABC 中,角,,A B C 所对的边分别为,,a b c 已知5,4a b ==,()31cos 32A B -=,则sin B =_____.14.若正实数1x 是函数()2e e x f x x x =--的一个零点,2x 是函数()g x =()()3e ln 1e x x ---的一个大于e 的零点,则()122e ex x -的值为_____.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(本小题满分13分)现有某企业计划用10年的时间进行技术革新,有两种方案:贷款利润A 方案一次性向银行贷款10万元第1年利润1万元,以后每年比前一年增加25%的利润B 方案每年初向银行贷款1万元第1年利润1万元,以后每年比前一年增加利润3000元两方案使用期都是10年,贷款10年后一次性还本付息(年末结息),若银行贷款利息均按10%的复利计算.(1)计算10年后,A 方案到期一次性需要付银行多少本息?(2)试比较A B 、两方案的优劣.(结果精确到万元,参考数据:10101.1 2.594,1.259.313≈≈)如图,四棱锥P ABCD -中,底面ABCD 为等腰梯形,22AD AB BC ==2=.点P 在底面的射影点Q 在线段AC 上.(1)在图中过A 作平面PCD 的垂线段,H 为垂足,并给出严谨的作图过程;(2)若2PA PD ==.求平面PAB 与平面PCD 所成锐二面角的余弦值.已知函数()()e sin cos ,x f x x x f x =+-'为()f x 的导数.(1)证明:当0x ≥时,()2f x '≥;(2)设()()21g x f x x =--,证明:()g x 有且仅有2个零点.在平面直角坐标系xOy 中,已知椭圆()2222:10x y C a b a b +=>>的两个焦点为12,F F P、为椭圆C 上一动点,设12F PF ∠θ=,当23πθ=时,12F PF ∆.(1)求椭圆C 的标准方程.(2)过点()0,2B 的直线l 与椭圆交于不同的两点(M N M 、在,B N 之间),若Q 为椭圆C上一点,且OQ OM ON =+,①求OBM OBNSS ∆∆的取值范围;②求四边形OMQN 的面积.飞行棋是大家熟悉的棋类游戏,玩家通过投掷骰子来决定飞机起飞与飞行的步数.当且仅当玩家投掷出6点时,飞机才能起飞.并且掷得6点的游戏者可以连续投掷骰子,直至显示点数不是6点.飞机起飞后,飞行步数即骰子向上的点数.(1)求甲玩家第一轮投掷中,投掷次数X 的均值()()1(k E X kP k ∞===∑()1lim n n k kP k ∞→=⎫⎛⎫⎪ ⎪⎝⎭⎭∑;(2)对于两个离散型随机变量,ξη,我们将其可能出现的结果作为一个有序数对,类似于离散型随机变量的分布列,我们可以用如下表格来表示这个有序数对的概率分布:(记()()()()()(1211,,mni i i j j j i j i p x p x p x y p y p y p x ξη========∑∑,)j y .)ξη1x 2x ...n X 1y ()11,p x y ()21,p x y ...()1,n p x y ()21p y 2y ()12,p x y ()22,p x y ...()2,n p x y ()22p y ...⋯⋯...⋯...my ()1,m p x y ()2,m p x y ...(),n m p x y ()2m p y ()11p x ()12p x ...()1n p x 1若已知i x ξ=,则事件{}j y η=的条件概率为{}j i P y x ηξ===∣{}{}()()1,,j i i j i i P y x p x y P x p x ηξξ====.可以发现i x ηξ=∣依然是一个随机变量,可以对其求期望{}{}()111mi j j i j i E x y P y x p x ηξηξ===⋅===∑∣∣.()1,mj i j j y p x y =∑(i )上述期望依旧是一个随机变量(ξ取值不同时,期望也不同),不妨记为{}E ηξ∣,求{}E E ηξ⎡⎤⎣⎦∣;(ii )若修改游戏规则,需连续掷出两次6点飞机才能起飞,记0ξ=表示“甲第一次未能掷出6点”,1ξ=表示“甲第一次掷出6点且第二次未能掷出6点”,2ξ=表示“甲第一次第二次均掷出6点”,η为甲首次使得飞机起飞时抛掷骰子的次数,求E η.炎德・英才大联考湖南师大附中2025届高三月考试卷(三)数学参考答案题号1234567891011答案C A C B B D A B BC ACD BC一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.C 【解析】集合{}0,1,2,3共有42115-=(个)真子集.故选C .2.A 【解析】解不等式240x x -<,得04x <<,解不等式11x -<,得02x <<,所以“11x -<”是“240x x -<”的充分不必要条件.3.C 【解析】根据三角函数的概念,2442sin cos 2tan 24tan ,sin23311tan 25y a x a αααααα======+,故选C .4.B 【解析】()()()22111911244⎡⎤⋅=+--=-=⎣⎦a b a b a b .5.B 【解析】易得原点到直线的距离1d ==,故直线为单位圆的切线,由于直线与双曲线2215x y m -=总有公共点,所以点()1,0±必在双曲线内或双曲线上,则01m <≤.6.D 【解析】依题意函数()f x 的图象关于原点对称,所以()f x 为奇函数,因为()()()133f x f x f x +=--=-,故函数()f x 的周期为4,则()()20251f f =,而()()11f f -=-,所以由()()2025112f f -=-可得()113f =,而()()13f f =-,所以()121log 323m --=,解得13m =-.7.A 【解析】上下底面所在外接圆的半径分别为123,4r r ==,过点112,,,A A O O 的截面如图:22222121534,543,1OO OO h OO OO =-==-∴=-=,故选A .8.B 【解析】由题意,得6,6c a d b =+=+,则由()()()772223866b d a b d c c a ⎡⎤++++-=⎣⎦得()()7[26212(6b b a b b a ++++++6)]()762386a a ++-=,整理得()321ab a b ++=,所以773aba b +=-<.因为,a b 为正整数,所以3ab =或6.因此有6,3a b ab +=⎧⎨=⎩或5,6.a b ab +=⎧⎨=⎩而63a b ab +=⎧⎨=⎩无整数解,因此6ab =.故选B .二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.BC 【解析】对于A :令0x =,则01a =,故A 错误;对于B :令1x =,则20240120243a a a +++= ,故B 正确;对于C :令1x =-,则012320241a a a a a -+-++= ,故C 正确;对于D ,由()202422024012202412x a a x a x a x +=++++ ,两边同时求导得()20232202312320242024212232024x a a x a x a x ⨯⨯+=++++ ,令1x =-,则12320242320244048a a a a -++-=- ,故D 错误.故选BC .10.ACD 【解析】()()32sin ,2sin 2sin 4244f x x g x x x ππππ⎛⎫⎛⎫⎛⎫=+=--=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.令()0f x =,则,4x k k ππ=-+∈Z ;令()0g x =,则3,4x k k ππ=+∈Z ,两个函数的零点是相同的,故选项A 正确.()f x 的最大值点是()2,,4k k g x ππ+∈Z 的最大值点是32,4k k ππ-+∈Z ,两个函数的最大值虽然是相同的,但最大值点是不同的,故选项B 不正确.由正弦型函数的最小正周期为2πω可知()f x 与()g x 有相同的最小正周期2π,故选项C 正确.曲线()y f x =的对称轴为,4x k k ππ=+∈Z ,曲线()y g x =的对称轴为5,4x k k ππ=+∈Z ,两个函数的图象有相同的对称轴,故选项D 正确.故选ACD.设直线AB 的方程为2y tx =+(斜率显然存在),221212,,,44x x A x B x ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭,联立22,4,y tx x y =+⎧⎨=⎩消去x 整理可得2480x tx --=,由韦达定理得12124,8x x t x x +==-,A .22121212124,84444x x y y OA OB x x y y =⋅=⋅=+=-+=- ,故A 错误;B .抛物线C 在点A 处的切线为21124x x x y ⎛⎫=+ ⎪⎝⎭,当2y =-时,11121244282222x x x x x t x x =-=-=+=-,即()2,2N t -,直线MN 的方程为()122y x t t +=--,整理得xy t=-,直线MN 恒过定点(0,0),故B 正确;C .由选项B 可得点M 在以线段OP 为直径的圆上,点O 除外,故点M 的轨迹方程是()()22110y x y -+=≠,故C 正确;D.222t MN +==,AB =则()2221412222t AB MNt +⎫==+,,m m =≥则12ABm MN m ⎛⎫=- ⎪⎝⎭,设()1,f m m m m =-≥,则()2110f m m=+>',当m ≥,()f m 单调递增,所以()min f m f==,故D 错误.故选BC .三、填空题:本题共3小题,每小题5分,共15分.12.1【解析】设()()12i ,,i ,z a b a b z c d c d =+∈=+∈R R ,因为21111z z +=,所以2122111z zz z z z +=.因为11221,1z z z z ==,所以121z z +=,所以()()i i i 1a b c d a c b d -+-=+-+=,所以1,0a c b d +=+=,所以()()12i 1z z a c b d +=+++=.13.74【解析】在ABC 中,因为a b >,所以A B >.又()31cos 32A B -=,可知A B-为锐角且()sin 32A B -=.由正弦定理,sin 5sin 4A aB b ==,于是()()()5sin sin sin sin cos cos sin 4B A A B B A B B A B B ⎡⎤==-+=-+-⎣⎦.将()cos A B -及()sin AB -的值代入可得3sin B B =,平方得2229sin 7cos 77sin B B B ==-,故7sin 4B =.14.e 【解析】依题意得,1211e e 0x x x --=,即()()12311122e e ,0,e ln 1e 0x x x x x x -=>---=,即()()3222e ln 1e ,e x x x --=>,()()()131122e e e e ln 1x x x x x ∴-==--,()()()()()()211ln 111112212e e ln 1e ,e e ln 1e e x x x x x x x x -+++⎡⎤∴-=--∴-=--⎣⎦,又22ln 1,ln 10,x x >->∴ 同构函数:()()1e e ,0x F x x x +=->,则()()312ln 1e F x F x =-=,又()()111e e e e e 1e x x x x F x x x +++=-+=-+',00,e e 1,e 10x x x >∴>=∴-> ,又()()1e 0,0,x x F x F x +>'>∴单调递增,()()()3122212222e ln 1e e ln 1,e e e ex x x x x x ---∴=-∴===.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.【解析】(1)A 方案到期时银行贷款本息为()1010110%26⨯+≈(万元).……(3分)(2)A 方案10年共获利:()()1091.2511125%125%33.31.251-+++++=≈- (万元),……(5分)到期时银行贷款本息为()1010110%25.9⨯+≈(万元),所以A 方案净收益为:33.325.97-≈(万元),……(7分)B 方案10年共获利:()()101010.31 1.3190.310123.52⨯-⨯++++⨯=⨯+= (万元),……(9分)到期时银行贷款本息为()()()()101091.11.11110%110%110%17.51.11-++++++=≈- (万元),……(11分)所以B 方案净收益为:23.517.56-≈(万元),……(12分)由比较知A 方案比B 方案更优.……(13分)16.【解析】(1)连接PQ ,有PQ ⊥平面ABCD ,所以PQ CD ⊥.在ACD 中,2222cos 54cos AC AD CD AD CD ADC ADC ∠∠=+-⋅⋅=-.同理,在ABC 中,有222cos AC ABC ∠=-.又因为180ABC ADC ∠∠+= ,所以()1cos ,0,1802ADC ADC ∠∠=∈ ,所以60ADC ∠= ,3AC =故222AC CD AD +=,即AC CD ⊥.又因为,,PQ AC Q PQ AC ⋂=⊂平面PAC ,所以CD ⊥平面PAC .CD ⊂平面PCD ,所以平面PCD ⊥平面PAC .……(5分)过A 作AH 垂直PC 于点H ,因为平面PCD ⊥平面PAC ,平面PCD ⋂平面PAC PC =,且AH ⊂平面PAC ,有AH ⊥平面PCD .……(7分)(2)依题意,22AQ PA PQ DQ =-=.故Q 为,AC BD 的交点,且2AQ ADCQ BC==.所以2222326,333AQ AC PQ PA AQ ===-.过C 作直线PQ 的平行线l ,则,,l AC CD 两两垂直,以C 为原点建立如图所示空间直角坐标系,则:()()36131,0,0,0,,0,3,0,,,03322D P A B ⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,所以()326232613261,0,0,0,,0,,,,,3333263CD CP AP BP ⎛⎛⎛===-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ .设平面PCD 的法向量为(),,x y z =m ,则()0,0,3CD x CP y ⎧⋅==⎪⎨⋅=+=⎪⎩m m取()0,=-m .同理,平面PAB的法向量)1=-n ,1cos<,3⋅>==m n m n m n ……(14分)故所求锐二面角余弦值为13.……(15分)17.【解析】(1)由()e cos sin x f x x x =++',设()e cos sin x h x x x =++,则()e sin cos x h x x x '=-+,当0x ≥时,设()()e 1,sin x p x x q x x x =--=-,()()e 10,1cos 0x p x q x x ''=-≥=-≥ ,()p x ∴和()q x 在[)0,∞+上单调递增,()()()()00,00p x p q x q ∴≥=≥=,∴当0x ≥时,e 1,sin x x x x ≥+≥,则()()()e sin cos 1sin cos sin 1cos 0x h x x x x x x x x x '=-+≥+-+=-++≥,∴函数()e cos sin x h x x x =++在[)0,∞+上单调递增,()()02h x h ∴≥=,即当0x ≥时,()2f x '≥.……(7分)(2)由已知得()e sin cos 21x g x x x x =+---.①当0x ≥时,()()()e cos sin 220,x g x x x f x g x ≥''=++-=-∴ 在[)0,∞+上单调递增,又()()010,e 20g g πππ=-<=->∴ 由零点存在定理可知,()g x 在[)0,∞+上仅有一个零点.……(10分)②当0x <时,设()()2sin cos 0e x x xm x x --=<,则()()2sin 10exx m x '-=≤,()m x ∴在(),0∞-上单调递减,()()01m x m ∴>=,()e cos sin 20,e cos sin 20x x x x g x x x '∴++-<∴=++-<,()g x ∴在(),0∞-上单调递减,又()()010,e 20g g πππ-=-<-=+> ,∴由零点存在定理可知()g x 在(),0∞-上仅有一个零点,综上所述,()g x 有且仅有2个零点.……(15分)18.【解析】(1)设()00,,P x y c 为椭圆C 的焦半距,12122F PF p S c y ∆=⋅⋅,00y b <≤ ,当0y b =时,12F PF S 最大,此时()0,P b 或()0,P b -,不妨设()0,P b ,当23πθ=时,得213OPF OPF π∠∠==,所以c =,又因为12F PF S bc ∆==,所以1,b c ==从而2,a =∴椭圆C 的标准方程为2214x y +=.……(3分)(2)由题意,直线l 的斜率显然存在.设()()1122: 2.,,,l y kx M x y N x y =+.……(4分)1112OBM S OB x x ∆∴=⋅=,同理,2OBN S x ∆=.12OBM OBN S xS x ∆∆∴= (6))联立()22222,141612044y kx k x kx x y =+⎧⇒+++=⎨+=⎩,……(8分)()()()22223164121416430,4k k k k ∴∆=-⨯⨯+=->∴>.……(9分)又121212221612,0,,1414k x x x x x x k k-+==>∴++ 同号.()()2222122121212216641421231414k x x x x k k x x x x kk-⎛⎫ ⎪++⎝⎭∴===+++.()22212122364641616,4,,42143331434x x k k x x k k ⎛⎫>∴=∈∴<++< ⎪⎛⎫+⎝⎭+ ⎪⎝⎭ .令()120x x λλ=≠,则116423λλ<++<,解得()()11,11,3,,11,333OBM OBN S S λ∆∆⎛⎫⎛⎫∈∴∈ ⎪ ⎪⎝⎭⎝⎭ .……(12分)(3)()1212,,OQ OM ON Q x x y y =+∴++.且四边形OMQN 为平行四边形.由(2)知()12121222164,41414k x x y y k x x k k-+=∴+=++=++,22164,1414kQ k k -⎛⎫∴ ⎪++⎝⎭.而Q 在椭圆C 上,2222164441414k k k -⎛⎫⎛⎫∴+⨯= ⎪ ⎪++⎝⎭⎝⎭.化简得2154k =.……(14分)∴线段161219357115224MN ==⋅+,……(15分)O到直线MN的距离d == (16))OMQN 574S MN d ∴=⋅=四边形.……(17分)19.【解析】(1)()115,1,2,3,66k P X k k -⎛⎫==⨯= ⎪⎝⎭ ,所以()()215111,1,2,3,,5126666nk n k k k P X k k kP k n =⎛⎫⋅====⨯+⨯+⨯ ⎪⎝⎭∑ ,记211112666n n S n =⨯+⨯++⨯ ,则2311111126666n n S n +=⨯+⨯++⨯ .作差得:1211111511111111661666666556616nn n n n n n S n n ++⎛⎫- ⎪⎛⎫⎛⎫⎝⎭=+++-⨯=-⨯=-+ ⎪⎪⎝⎭⎝⎭- ,所以()16111661,555566556n nn n n k n S kP k S n =⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=⋅-+==-+⎢⎥ ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦∑.故()()()116616lim lim 5565nn n n k k E X kP k kP k n ∞∞∞→→==⎡⎤⎛⎫⎛⎫⎛⎫===-+=⎢⎥ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦∑∑.……(6分)(2)(i ){}E ηξ∣所有可能的取值为:{},1,2,,i E x i n ηξ== ∣.且对应的概率{}{}()()()1,1,2,,i i i p E E x p x p x i n ηξηξξ====== ∣∣.所以{}{}()()()()()111111111,,,nnmn m i i j i j i j i j i i j i j i E E E x p x y p x y p x y p x y p x ηξηξ=====⎛⎫⎡⎤==⋅=⋅= ⎪⎣⎦ ⎪⎝⎭∑∑∑∑∑∣∣又()()()()21111111,,,nmmnmn mj i j j i j j i j j j i j j i j i j y p x y y p x y y p x y y p y E η=======⎛⎫⋅=⋅==⋅= ⎪⎝⎭∑∑∑∑∑∑∑,所以{}E E E ηξη⎡⎤=⎣⎦∣.……(12分)(ii ){}{}{}12355101,;12,;22,63636E E p E E p E p ηξηηξηη==+===+====∣∣,{}()()5513542122636363636E E E E E ηηξηηη⎡⎤==++++⨯=+⎣⎦∣,故42E η=.……(17分)。

2024学年上海川沙中学高三上学期数学月考试卷及答案(2024.09)

1川沙中学2024学年第一学期高三年级数学月考2024.09一、填空题（本大题共有12题,满分54分,第1-6题每题4分,第7-12题每题5分） 1．已知全集U R =，集合(,1)[2,)A =−∞+∞，则A =________． 2．函数()sin2f x x =的最小正周期是________．3．在等比数列{}n a 中，若公比4q =，且前3项之和等于21，则该数列的通项公式n a =________．4．参考数学竞赛决赛的15人的成绩（单位：分）依次如下：56、70、91、98、79、80、81、83、84、86、88、90、72、94、78，则15人成绩的第80百分位数是________． 5．在△ABC 中，90A ∠=︒，3AB =，4AC =，将△ABC 绕边AC 所在直线旋转一周得到几何体Γ，则Γ的侧面积为________．6．已知3nx x ⎛⎫+ ⎪⎝⎭的二项展开式的各项系数之和为256，则访二项展开式中的常数项为_____． 7．双曲线222:1y C x b−=的渐近线与直线1x =交于A ，B 两点，且4AB =，那么双曲线C 的离心率为________．8．已知△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ．若6b =，2a c =，πB 3=，则△ABC 的面积为________．9．春天是鼻炎和感冒的高发期，某人在春季里鼻炎发作的概率是45，感冒发作的概率是67，鼻炎发作且感冒发作的概率是35，则此人在鼻炎发作的条件下感冒的概率是________． 10．已知函数1()lg f x x x =−，则不等式111f x ⎛⎫−< ⎪⎝⎭的解集为________． 11．已知函数()(1)x f x x e =−，若关于x 的不等式()1f x ax <−有且仅有一个正整数解，则实数a 的取值范围是________．212．已知数列{}n a 的前n 项和为n S ，满足231(,1)n n S a n N n =−∈≥，函数()f x 定义域为R ，对任意x R ∈都有()()()111f x f x f x ++=−，若()21f =−2025()f a 的值为 .二、选择题（本大题共4题，第13、14题每题4分，第15、16题每题5分，共18分） 13．下列不等式恒成立的是（） A ．222a b ab +≤B ．222a b ab +≥− C．a b +≥ D．a b +≥−14．已知()f x 是定义在R 上的可导函数，若0(2)(2)1lim22h f h f h →+−=，则(2)f '=（）A ．1−B ．14− C ．1 D ．1415．设等比数列{}n a 的前n 项和为n S ，设甲：123a a a <<，乙：{}n S 是严格增数列，则甲是乙的（）条件．A ．充分不必要B ．必要不充分C ．充要D ．既不充分也不必要16．已知实数1x 、1y 、2x 、2y 、3x 、3y 同时满足：①11x y <，22x y <，33x y <；②112233x y x y x y +=+=+；③11332220x y x y x y +=>，则下列选项中恒成立的是（）A ．2132x x x <+B ．2132x x x >+C ．2213x x x <D ．2213x x x >三、解答题（本大题共5题，共141414181878++++=分）17.（本题满分14分.本题共2小题,第（1）小题7分,第（2）小题7分.)在直四棱柱1111ABCD A B C D −中，∥AB CD ，1AB AD ==，12D D CD ==，AB AD ⊥．（1）求证：BC ⊥平面1D DB ；（2）求点D 到平面1BCD 的距离．18.(本题满分14分.本题共2小题，第（1）小题8分,第（2）小题6分.)设函数2()f x x x a=+−，a为常数．（1）若()f x为偶函数，求a的值；（2）设0a>，()()f xg xx=，(]0,x a∈为严格减函数，求实数a的取值范围．19.(本题满分14分.本题共2小题,第（1）小题6分,第（2）小题8分.)近年来，随着智能手机的普及，网上买菜迅速进入了我们的生活。

湖南省长沙市2024-2025学年高三上学期月考(三)化学试卷含答案

2025届高三月考试卷（三）化学（答案在最后）命题人：得分：______本试题卷分选择题和非选择题两部分，共8页。

时量75分钟，满分100分。

可能用到的相对原子质量：H~1C~12N~14O~16Na~23S~32Cl~35.5Zr~91第Ⅰ卷（选择题共42分）一、选择题（本题共14小题，每小题3分，共42分，每小题只有一个选项符合题意。

）1．化学和我们的生活有十分密切的联系，下列表述不正确的是（）A.在碳素钢中加入Cr 和Ni 制得不锈钢可以增强钢的强度以及抗腐蚀能力B.改变铝制品表面氧化膜的厚度可以影响染料着色从而产生美丽的颜色C.焰色试验选择Fe 作为载体是因为铁元素受热不发生电子跃迁、不产生发射光谱D.半导体材料氮化镓是一种新型无机非金属材料2．下列化学用语表示不正确的是（）A.2，2-二甲基丁烷的结构简式：B.三氟化硼分子的空间填充模型：C.次氯酸分子的电子式： H O Cl:::D.基态溴原子的简化电子排布式：[]25Ar 4s 4p3.2024年诺贝尔化学奖表彰了三位科学家在蛋白质设计和结构预测领域作出的贡献，中国科学家颜宁在这方面也做了大量的工作，以下相关说法不正确的是（）A.蛋白质分散在水中形成的分散系可以产生丁达尔效应B.要使蛋白质晶化得到较大的蛋白质晶体需要快速结晶C.通过X 射线衍射可以得到高分辨率的蛋白质结构D.蛋白质复杂结构的形成与极性键、非极性键、氢键、范德华力等有关4．以下实验方案正确且能达到实验目的的是（）选项实验目的实验方案A 制备少量硝酸边加强热边向饱和硝酸钠溶液中滴加浓硫酸B 验证晶体的自范性将形状不规则的蔗糖块放入饱和蔗糖溶液中静置一段时间后取出C验证C 和Si 的非金属性强弱将焦炭和石英砂混合加强热（1800~2000℃），检验气体产物以证明反应发生D 测定中和热将稍过量的NaOH 固体投入装有一定量稀盐酸的烧杯中并测量其温度变化A.AB.BC.CD.D5．某化学小组在实验室尝试用氨气制备硝酸，过程如下：32NH NO NO →→→3HNO 。

湖南师范大学附属中学2022-2023学年高三上学期月考(三)数学试题

18.在△ABC中，内角A、B、C所对边分别为a、b、c，D为边BC上一点，若．
（1）证明：
①AD平分∠BAC，
② ；
（2）若，求的最大值．
19.汽车尾气排放超标是全球变暖、海平面上升的重要因素．我国近几年着重强调可持续发展，加大在新能源项目的支持力度，积极推动新能源汽车产业发展，某汽车制造企业对某地区新能源汽车的销售情况进行调查，得到下面的统计表：
年份
2017
2018
2019
2020
2021
年份代码
1
2
3
4
5
销量万辆
10
12
17
20
26
（1）统计表明销量与年份代码有较强的线性相关关系，求关于的线性回归方程，并预测该地区新能源汽车的销量最早在哪一年能突破50万辆；
（2）为了解购车车主的性别与购车种类（分为新能源汽车与传统燃油汽车）的情况，该企业心随机调查了该地区200位购车车主的购车情况作为样本其中男性车主中购置传统燃油汽车的有名，购置新能源汽车的有45名，女性车主中有20名购置传统燃油汽车．
14.已知定圆，点A是圆M所在平面内一定点，点P是圆M上的动点，若线段PA的中垂线交直线PM于点Q，则点Q的轨迹：①椭圆；②双曲线；③抛物线；④圆；⑤直线；⑥一个点．其中所有可能的结果有______个．
15.已知点O是△ABC的外心，a，b，c分别为内角A，B，C的对边，，且，则的值为________．
湖南师大附中2023届高三月考试卷（三）
数学
一､选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1.已知集合，若，则实数的取值范围为（）

高一上学期第一次月考数学试卷A3打印版

河南宏力学校高一上学期第一次月考数学试题考生注意: 1.本试卷分第Ⅰ卷（选择题）和第二卷（非选择题）两部分,共150分,考试时间120分钟. 2.请将各题答案填写在答题卡上.第Ⅰ卷（选择题共60分）一、选择题（每小题5分,共60分）1. 设集合{}10,8,6,4,2,0=A ,{}8,4=B ,则C A B =【】（A ）{}8,4 （B ）{}6,2,0 （C ）{}10,6,2,0 （D ）{}10,8,6,4,2,02. 已知集合{}{}3,1,13,2,12-=--=N m m M ,若{}3=N M ,则m 的值为【】（A ）1,4- （B ）1- （C ）1 , 4- （D ）4 3. 全集=U R ,{}03<<-=x x N ,{}1-<=x x M ,则图中阴影部分表示的集合是【】（A ）{}13-<<-x x （B ）{}03<<-x x （C ）{}01<≤-x x （D ）{}3<x x4. 设函数()⎪⎩⎪⎨⎧<-≥=0,0,x x x x x f ,若()()21=-+f a f ,则=a 【】（A ）3- （B ）3± （C ）1- （D ）1± 5. 下列各组函数是同一函数的是【】①()32x x f -=与()x x x g 2-=; ②()x x f =与()2x x g =;③()0x x f =与()01xx g =; ④()122--=x x x f 与()122--=t t t g .（A ）①② （B ）③④ （C ）①③ （D ）①④ 6. 已知函数()x f 的定义域为()1,23+-a a ,且()1+x f 为奇函数,则a 的值可以是【】（A ）2 （B ）32（C ）4 （D ）6 7. 已知定义在R 上的增函数()x f ,满足()()0=-+x f x f ,∈321,,x x x R ,且021>+x x ,032>+x x ,013>+x x ,则()()()321x f x f x f ++的值【】（A ）一定大于0 （B ）一定小于0 （C ）等于0 （D ）正负都有可能 8. 设0>a ,则函数()a x x y -=的图象的大致形状是【】（A ）（B ）（C ）（D ）9. 已知函数()x f y =在()2,0上是增函数,函数()2+=x f y 是偶函数,则下列结论中正确的是【】（A ）()⎪⎭⎫⎝⎛<⎪⎭⎫ ⎝⎛<27251f f f （B ）()⎪⎭⎫ ⎝⎛<<⎪⎭⎫⎝⎛27125f f f （C ）()12527f f f <⎪⎭⎫⎝⎛<⎪⎭⎫ ⎝⎛ （D ）()⎪⎭⎫ ⎝⎛<<⎪⎭⎫⎝⎛25127f f f 10. 已知函数()⎪⎩⎪⎨⎧>≤---=1,1,52x xa x ax x x f 是R 上的增函数,则实数a 的取值范围是【】（A ）3-≤0<a （B ）3-≤a ≤2- （C ）a ≤2- （D ）0<a11. 定义一种运算⎩⎨⎧>≤=⊗ba b ba ab a ,,,令()()t x x x x f -⊗-+=223（t 为常数）,且[]3,3-∈x ,则使函数()x f 的最大值为3的t 的集合是【】（A ）{}3,3- （B ）{}5,1- （C ）{}1,3- （D ）{}5,3- 12. 已知函数()35335+---=x x x x f ,若()()62>-+a f a f ,则a 的取值范围是【】（A ）()1,∞- （B ）()3,∞- （C ）()+∞,1 （D ）()+∞,3第Ⅱ卷非选择题（共90分）二、填空题（每小题5分,共20分） 13. 函数()211-++=x x x f 的定义域是__________. 14. 已知集合(){}(){}4,,2,=-==+=y x y x N y x y x M ,那么=N M __________.15. 已知定义在R 上的函数()322--=x x x f ,设()()()⎩⎨⎧>≤=0,0,x x f x x f x g ,若函数()t x g y -=与x 轴有且只有三个交点,则实数t 的取值范围是____________. 16. 设关于x 的不等式012<--ax ax 的解集为S ,且S S ∉∈3,2,则a 的取值范围是__________.三、解答题（共70分，解答应写出文字说明，证明过程或演算步骤） 17.（本题满分10分）已知{}{}121,42-≤≤+-=≤≤=m x m x B x x A . （1）若2=m ,求 A B A ,C R B ; （2）若∅=B A ,求m 的取值范围.18.（本题满分12分）已知函数()x mx x f +=,且()21=f . （1）判断函数()x f 的奇偶性;（2）判断函数()x f 在()+∞,1上的单调性,并用定义证明你的结论.19.（本题满分12分）已知函数()ax x x f +-=22（∈x R ）有最小值. （1）求实数a 的取值范围;（2）设()x g 为定义在R 上的奇函数,且当0<x 时,()()x f x g =,求()x g 的解析式.20.（本题满分12分）已知二次函数()12++=bx ax x f （0≠a ）和()bx a bx x g 212+-=. （1）若()x f 为偶函数,试判断()x g 的奇偶性;（2）若方程()x x g =有两个不相等的实数根,当0>a 时,判断()x f 在()1,1-上的单调性;（3）当a b 2=时,问是否存在x 的值,使满足1-≤a ≤1且0≠a 的任意实数a ,不等式()4<x f 恒成立?并说明理由.21.（本题满分12分）某工厂某种航空产品的年固定成本为250万元,每生产x 件,需另投入成本为()x C ,当年产量不足80件时,()x x x C 10312+=（万元）;当年产量不小于80件时,()14501000051-+=xx x C （万元）.每件商品售价为50万元.通过市场分析,该厂生产的商品能全部售完.（1）写出年利润()x L （万元）关于年产量x （件）的函数解析式; （2）年产量为多少件时,该厂在这一商品的生产中所获利润最大?22.（本题满分12分）已知函数()cx bax x f ++=2（∈a N *,∈b R ,c <0≤1）是定义在[]1,1-上的奇函数,()x f 的最大值为21.（1）求函数()x f 的解析式;（2）若关于x 方程()0log 2=-m x f 在⎥⎦⎤⎢⎣⎡1,21上有解,求实数m 的取值范围.。

福建省福州市高二数学下学期3月月考试卷理(含解析)

福建省福州市高二数学下学期3月月考试卷理（含解析）一.选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一个是符合题目要求的1．一个物体的运动方程为s=1﹣t+t2其中s的单位是米，t的单位是秒，那么物体在3秒末的瞬时速度是（）A．7米/秒B．6米/秒C．5米/秒D．8米/秒2．若f'（x）=3，则等于（）A．3 B．C．﹣1 D．13．若曲线y=x2+ax+b在点（1，b）处的切线方程是x﹣y+1=0，则（）A．a=1，b=2 B．a=﹣1，b=2 C．a=1，b=﹣2 D．a=﹣1，b=﹣24．设f（x）=xlnx，若f′（x0）=2，则x0=（）A．e2B．e C． D．ln25．下列积分不正确的是（）A．B．C． D．6．已知函数f（x）=x3+ax2+（a+6）x+1有极值，则a的取值范围是（）A．﹣1＜a＜2 B．﹣3＜a＜6 C．a＜﹣3或a＞6 D．a＜﹣1或a＞27．设P为曲线C：y=x2+2x+3上的点，且曲线C在点P处切线倾斜角的取值范围是，则点P横坐标的取值范围是（）A．B．[﹣1，0] C．[0，1] D．[，1]8．若函数f（x）=x3+ax﹣2在区间（1，+∞）内是增函数，则实数a的取值范围是（）A．[﹣3，+∞）B．（﹣3，+∞）C．[0，+∞）D．（0，+∞）9．设曲线在点（3，2）处的切线与直线ax+y+1=0垂直，则a=（）A．2 B．C．D．﹣210．曲线y=ln（2x﹣1）上的点到直线2x﹣y+8=0的最短距离是（）A．B．2 C．3 D．011．设f（x）、g（x）分别是定义在R上的奇函数和偶函数，当x＜0时，f′（x）g（x）+f（x）g′（x）＞0，且g（﹣3）=0，则不等式f（x）g（x）＜0的解集是（）A．（﹣3，0）∪（3，+∞）B．（﹣3，0）∪（0，3）C．（﹣∞，﹣3）∪（3，+∞）D．（﹣∞，﹣3）∪（0，3）12．已知二次函数f（x）=ax2+bx+c的导数为f′（x），f′（0）＞0，对于任意实数x，有的最小值为（）A．2 B．C．3 D．二、填空题：共4小题，每小题5分，共20分．13．函数y=x2﹣lnx的单调递减区间为．14．已知函数f（x）=f′（）sinx+cosx，则f（）= ．15．由y2=4x与直线y=2x﹣4所围成图形的面积为．16．已知函数f（x）的定义域为[﹣1，5]，部分对应值如表，f（x）的导函数y=f′（x）的图象如图示．x ﹣1 0 4 5 f（x） 1 2 2 1下列关于f（x）的命题：①函数f（x）的极大值点为0，4；②函数f（x）在[0，2]上是减函数；③如果当x∈[﹣1，t]时，f（x）的最大值是2，那么t的最大值为4；④当1＜a＜2时，函数y=f（x）﹣a有4个零点；⑤函数y=f（x）﹣a的零点个数可能为0、1、2、3、4个．其中正确命题的序号是．三、解答题：共6小题，共70分，解答写出文字说明、证明过程或演算步骤．17．已知等差数列{a n}满足a3=6，a4+a6=20（1）求通项a n；（2）设{b n﹣a n}是首项为1，公比为3的等比数列，求数列{b n}的通项公式及其前n项和T n．18．在三角形ABC中，∠A、∠B、∠C的对边分别为a、b、c，若bcosC=（2a﹣c）cosB （Ⅰ）求∠B的大小（Ⅱ）若、a+c=4，求三角形ABC的面积．19．已知椭圆=1（a＞b＞0）的一个顶点为A（0，1），离心率为，过点B（0，﹣2）及左焦点F1的直线交椭圆于C，D两点，右焦点设为F2．（1）求椭圆的方程；（2）求△CDF2的面积．20．设f（x）=ax3+bx2+cx的极小值为﹣8，其导函数y=f′（x）的图象经过点，如图所示，（1）求f（x）的解析式；（2）若对x∈[﹣3，3]都有f（x）≥m2﹣14m恒成立，求实数m的取值范围．21．已知函数f（x）=ln（ax+1）+，x≥0，其中a＞0．（Ⅰ）若f（x）在x=1处取得极值，求a的值；（Ⅱ）求f（x）的单调区间；（Ⅲ）若f（x）的最小值为1，求a的取值范围．22．已知函数，g（x）=x+lnx，其中a＞0．（1）若x=1是函数h（x）=f（x）+g（x）的极值点，求实数a的值；（2）若对任意的x1，x2∈[1，e]（e为自然对数的底数）都有f（x1）≥g（x2）成立，求实数a的取值范围．2016-2017学年福建省福州市文博中学高二（下）3月月考数学试卷（理科）参考答案与试题解析一.选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一个是符合题目要求的1．一个物体的运动方程为s=1﹣t+t2其中s的单位是米，t的单位是秒，那么物体在3秒末的瞬时速度是（）A．7米/秒B．6米/秒C．5米/秒D．8米/秒【考点】62：导数的几何意义．【分析】求导数，把t=3代入求得导数值即可．【解答】解：∵s=1﹣t+t2，∴s′=﹣1+2t，把t=3代入上式可得s′=﹣1+2×3=5由导数的意义可知物体在3秒末的瞬时速度是5米/秒，故选C2．若f'（x）=3，则等于（）A．3 B．C．﹣1 D．1【考点】6F：极限及其运算．【分析】由=﹣=﹣×f'（x0），由题意，即可求得答案．【解答】解：=﹣=﹣×f'（x0）=﹣×3=﹣1，故选C．3．若曲线y=x2+ax+b在点（1，b）处的切线方程是x﹣y+1=0，则（）A．a=1，b=2 B．a=﹣1，b=2 C．a=1，b=﹣2 D．a=﹣1，b=﹣2【考点】6H：利用导数研究曲线上某点切线方程．【分析】由y=x2+ax+b，知y′=2x+a，再由曲线y=x2+ax+b在点（1，b）处的切线方程为x ﹣y+1=0，求出a和b．【解答】解：∵y=x2+ax+b，∴y′=2x+a，∵y′|x=1=2+a，∴曲线y=x2+ax+b在点（1，b）处的切线方程为y﹣b=（2+a）（x﹣1），∵曲线y=x2+ax+b在点（1，b）处的切线方程为x﹣y+1=0，∴a=﹣1，b=2．故选B．4．设f（x）=xlnx，若f′（x0）=2，则x0=（）A．e2B．e C． D．ln2【考点】65：导数的乘法与除法法则．【分析】利用乘积的运算法则求出函数的导数，求出f'（x0）=2解方程即可．【解答】解：∵f（x）=xlnx∴∵f′（x0）=2∴lnx0+1=2∴x0=e，故选B．5．下列积分不正确的是（）A．B．C． D．【考点】68：微积分基本定理．【分析】利用微积分基本定理即可得出．【解答】解：A. = =ln3，因此正确；B．∵=2．故B不正确．==，因此正确；D. = = =．因此正确．综上可知：只有B不正确．故选B．6．已知函数f（x）=x3+ax2+（a+6）x+1有极值，则a的取值范围是（）A．﹣1＜a＜2 B．﹣3＜a＜6 C．a＜﹣3或a＞6 D．a＜﹣1或a＞2【考点】6D：利用导数研究函数的极值．【分析】求出函数的导数，利用导数有两个不相等的实数根，通过△＞0，即可求出a的范围．【解答】解：函数f（x）=x3+ax2+（a+6）x+1，所以函数f′（x）=3x2+2ax+（a+6），因为函数有极值，所以导函数有两个不相等的实数根，即△＞0，（2a）2﹣4×3×（a+6）＞0，解得：a＜﹣3或a＞6，故选：C．7．设P为曲线C：y=x2+2x+3上的点，且曲线C在点P处切线倾斜角的取值范围是，则点P横坐标的取值范围是（）A．B．[﹣1，0] C．[0，1] D．[，1]【考点】62：导数的几何意义．【分析】根据题意知，倾斜角的取值范围，可以得到曲线C在点P处斜率的取值范围，进而得到点P横坐标的取值范围．【解答】解：设点P的横坐标为x0，∵y=x2+2x+3，∴y′=2x0+2，利用导数的几何意义得2x0+2=tanα（α为点P处切线的倾斜角），又∵，∴0≤2x0+2≤1，∴．故选：A．8．若函数f（x）=x3+ax﹣2在区间（1，+∞）内是增函数，则实数a的取值范围是（）A．[﹣3，+∞）B．（﹣3，+∞）C．[0，+∞）D．（0，+∞）【考点】6A：函数的单调性与导数的关系．【分析】由已知，f′（x）=3x2≥0在[1，+∞）上恒成立，可以利用参数分离的方法求出参数a的取值范围．【解答】解：f′（x）=3x2+a，根据函数导数与函数的单调性之间的关系，f′（x）≥0在[1，+∞）上恒成立，即a≥﹣3x2，恒成立，只需a大于﹣3x2的最大值即可，而﹣3x2在[1，+∞）上的最大值为﹣3，所以a≥﹣3．即数a的取值范围是[﹣3，+∞）．故选A．9．设曲线在点（3，2）处的切线与直线ax+y+1=0垂直，则a=（）A．2 B．C．D．﹣2【考点】62：导数的几何意义．【分析】（1）求出已知函数y在点（3，2）处的斜率；（2）利用两条直线互相垂直，斜率之间的关系k1•k2=﹣1，求出未知数a．【解答】解：∵y=∴y′=﹣∵x=3∴y′=﹣即切线斜率为﹣∵切线与直线ax+y+1=0垂直∴直线ax+y+1=0的斜率为﹣a．∴﹣•（﹣a）=﹣1得a=﹣2故选D．10．曲线y=ln（2x﹣1）上的点到直线2x﹣y+8=0的最短距离是（）A．B．2 C．3 D．0【考点】6H：利用导数研究曲线上某点切线方程；3H：函数的最值及其几何意义；IT：点到直线的距离公式．【分析】在曲线y=ln（2x﹣1）上设出一点，然后求出该点处的导数值，由该导数值等于直线2x﹣y+8=0的斜率求出点的坐标，然后由点到直线的距离公式求解．【解答】解：设曲线y=ln（2x﹣1）上的一点是P（ m，n），则过P的切线必与直线2x﹣y+8=0平行．由，所以切线的斜率．解得m=1，n=ln（2﹣1）=0．即P（1，0）到直线的最短距离是d=．故选B．11．设f（x）、g（x）分别是定义在R上的奇函数和偶函数，当x＜0时，f′（x）g（x）+f（x）g′（x）＞0，且g（﹣3）=0，则不等式f（x）g（x）＜0的解集是（）A．（﹣3，0）∪（3，+∞）B．（﹣3，0）∪（0，3）C．（﹣∞，﹣3）∪（3，+∞）D．（﹣∞，﹣3）∪（0，3）【考点】6B：利用导数研究函数的单调性．【分析】先根据f’（x）g（x）+f（x）g’（x）＞0可确定[f（x）g（x）]'＞0，进而可得到f（x）g（x）在x＜0时递增，结合函数f（x）与g（x）的奇偶性可确定f（x）g（x）在x＞0时也是增函数，最后根据g（﹣3）=0可求得答案．【解答】解：设F（x）=f （x）g（x），当x＜0时，∵F′（x）=f′（x）g（x）+f （x）g′（x）＞0．∴F（x）在当x＜0时为增函数．∵F（﹣x）=f （﹣x）g （﹣x）=﹣f （x）•g （x）=﹣F（x）．故F（x）为（﹣∞，0）∪（0，+∞）上的奇函数．∴F（x）在（0，+∞）上亦为增函数．已知g（﹣3）=0，必有F（﹣3）=F（3）=0．构造如图的F（x）的图象，可知F（x）＜0的解集为x∈（﹣∞，﹣3）∪（0，3）．故选D12．已知二次函数f（x）=ax2+bx+c的导数为f′（x），f′（0）＞0，对于任意实数x，有的最小值为（）A．2 B．C．3 D．【考点】63：导数的运算；3R：函数恒成立问题；7F：基本不等式．【分析】由对于任意实数x，f（x）≥0成立求出a的范围及a，b c的关系，求出f（1）及f′（0），作比后放缩去掉c，通分后利用基本不等式求最值．【解答】解：∵f（x）≥0，知，∴c．又f′（x）=2ax+b，∴f′（0）=b＞0，f（1）=a+b+c．∴≥1+=≥1+=2．当且仅当4a2=b2时，“=”成立．故选A．二、填空题：共4小题，每小题5分，共20分．13．函数y=x2﹣lnx的单调递减区间为（0，1] ．【考点】6B：利用导数研究函数的单调性．【分析】根据题意，先求函数的定义域，进而求得其导数，即y′=x﹣=，令其导数小于等于0，可得≤0，结合函数的定义域，解可得答案．【解答】解：对于函数，易得其定义域为{x|x＞0}，y′=x﹣=，令≤0，又由x＞0，则≤0⇔x2﹣1≤0，且x＞0；解可得0＜x≤1，即函数的单调递减区间为（0，1]，故答案为（0，1]14．已知函数f（x）=f′（）sinx+cosx，则f（）= 0 ．【考点】63：导数的运算．【分析】求函数的导数，先求出f′（）的值即可得到结论．【解答】解：函数的导数为f′（x）=f′（）cosx﹣sinx，令x=，得f′（）=f′（）cos﹣sin=﹣1，则f（x）=﹣sinx+cosx，则f（）=﹣sin+cos=，故答案为：0．15．由y2=4x与直线y=2x﹣4所围成图形的面积为9 ．【考点】67：定积分．【分析】先联立方程，组成方程组，求得交点坐标，可得被积区间，再用定积分表示出曲线yy2=4x与直线y=2x﹣4所围成的封闭图形的面积，即可求得结论【解答】解：联立方程组，解得或，∴曲线y=x2与直线y=x围成的封闭图形的面积为S=（y+2﹣y2）dy=（y2+2y﹣）|=9，故答案为：916．已知函数f（x）的定义域为[﹣1，5]，部分对应值如表，f（x）的导函数y=f′（x）的图象如图示．x ﹣1 0 4 5 f（x） 1 2 2 1下列关于f（x）的命题：①函数f（x）的极大值点为0，4；②函数f（x）在[0，2]上是减函数；③如果当x∈[﹣1，t]时，f（x）的最大值是2，那么t的最大值为4；④当1＜a＜2时，函数y=f（x）﹣a有4个零点；⑤函数y=f（x）﹣a的零点个数可能为0、1、2、3、4个．其中正确命题的序号是①②⑤．【考点】6E：利用导数求闭区间上函数的最值；6D：利用导数研究函数的极值．【分析】由导数图象可知，函数的单调性，从而可得函数的极值，故可得①，②正确；因为在当x=0和x=4，函数取得极大值f（0）=2，f（4）=2，要使当x∈[﹣1，t]函数f（x）的最大值是4，当2≤t≤5，所以t的最大值为5，所以③不正确；由f（x）=a知，因为极小值f（2）未知，所以无法判断函数y=f（x）﹣a有几个零点，所以④不正确，根据函数的单调性和极值，做出函数的图象如图，即可求得结论．【解答】解：由导数图象可知，当﹣1＜x＜0或2＜x＜4时，f'（x）＞0，函数单调递增，当0＜x＜2或4＜x＜5，f'（x）＜0，函数单调递减，当x=0和x=4，函数取得极大值f（0）=2，f（4）=2，当x=2时，函数取得极小值f（2），所以①正确；②正确；因为在当x=0和x=4，函数取得极大值f（0）=2，f（4）=2，要使当x∈[﹣1，t]函数f（x）的最大值是4，当2≤t≤5，所以t的最大值为5，所以③不正确；由f（x）=a知，因为极小值f（2）未知，所以无法判断函数y=f（x）﹣a有几个零点，所以④不正确，根据函数的单调性和极值，做出函数的图象如图，（线段只代表单调性），根据题意函数的极小值不确定，分f（2）＜1或1≤f（2）＜2两种情况，由图象知，函数y=f（x）和y=a的交点个数有0，1，2，3，4等不同情形，所以⑤正确，综上正确的命题序号为①②⑤．故答案为：①②⑤．三、解答题：共6小题，共70分，解答写出文字说明、证明过程或演算步骤．17．已知等差数列{a n}满足a3=6，a4+a6=20（1）求通项a n；（2）设{b n﹣a n}是首项为1，公比为3的等比数列，求数列{b n}的通项公式及其前n项和T n．【考点】8E：数列的求和．【分析】（1）由已知条件，利用等差数列的通项公式列出方程组，求出等差数列的首项和公差，由此能求出等差数列的通项公式．（2）由a n=2n，{b n﹣a n}是首项为1，公比为3的等比数列，利用等比数列的通项公式，能求出数列{b n}的通项公式，再利用分组求和法能求出数列{b n}的前n项和T n．【解答】解：（1）∵等差数列{a n}满足a3=6，a4+a6=20，∴，解得，∴．（2）∵a n=2n，{b n﹣a n}是首项为1，公比为3的等比数列，∴，∴，∴．18．在三角形ABC中，∠A、∠B、∠C的对边分别为a、b、c，若bcosC=（2a﹣c）cosB （Ⅰ）求∠B的大小（Ⅱ）若、a+c=4，求三角形ABC的面积．【考点】HR：余弦定理；HP：正弦定理．【分析】（Ⅰ）根据正弦定理得： ===2R解出a、b、c代入到已知条件中，利用两角和的正弦函数的公式及三角形的内角和定理化简，得到cosB的值，然后利用特殊角的三角函数值求出B即可；（Ⅱ）要求三角形的面积，由三角形的面积公式S=acsinB知道就是要求ac的积及sinB，由前一问的cosA的值利用同角三角函数间的基本关系求出sinA，可根据余弦定理及、a+c=4可得到ac的值，即可求出三角形的面积．【解答】解（Ⅰ）由已知及正弦定理可得sinBcosC=2sinAcosB﹣cosBsinC∴2sinAcosB=sinBcosC+cosBsinC=sin（B+C）又在三角形ABC中，sin（B+C）=sinA≠0∴2sinAcosB=sinA，即，得（Ⅱ）∵b2=7=a2+c2﹣2accosB∴7=a2+c2﹣ac又∵（a+c）2=16=a2+c2+2ac∴ac=3∴即19．已知椭圆=1（a＞b＞0）的一个顶点为A（0，1），离心率为，过点B（0，﹣2）及左焦点F1的直线交椭圆于C，D两点，右焦点设为F2．（1）求椭圆的方程；（2）求△CDF2的面积．【考点】K4：椭圆的简单性质．【分析】（1）根据椭圆的基本概念和平方关系，建立关于a、b、c的方程，解出a=，b=c=1，从而得到椭圆的方程；（2）求出F1B直线的斜率得直线F1B的方程为y=﹣2x﹣2，与椭圆方程联解并结合根与系数的关系算出|x1﹣x2|=，结合弦长公式可得|CD|=，最后利用点到直线的距离公式求出F2到直线BF1的距离d，即可得到△CDF2的面积．【解答】解：（1）∵椭圆=1（a＞b＞0）的一个顶点为A（0，1），离心率为，∴b==1，且=，解之得a=，c=1可得椭圆的方程为；…（2）∵左焦点F1（﹣1，0），B（0，﹣2），得F1B直线的斜率为﹣2∴直线F1B的方程为y=﹣2x﹣2由，化简得9x2+16x+6=0．∵△=162﹣4×9×6=40＞0，∴直线与椭圆有两个公共点，设为C（x1，y1），D（x2，y2），则∴|CD|=|x1﹣x2|=•=•=又∵点F2到直线BF1的距离d==，∴△CDF2的面积为S=|CD|×d=×=．20．设f（x）=ax3+bx2+cx的极小值为﹣8，其导函数y=f′（x）的图象经过点，如图所示，（1）求f（x）的解析式；（2）若对x∈[﹣3，3]都有f（x）≥m2﹣14m恒成立，求实数m的取值范围．【考点】6D：利用导数研究函数的极值；36：函数解析式的求解及常用方法；3R：函数恒成立问题．【分析】（1）求出y=f'（x），因为导函数图象经过（﹣2，0）和（，0），代入即可求出a、b、c之间的关系式，再根据图象可知函数的单调性，而f（x）极小值为﹣8可得f（﹣2）=﹣8，解出即可得到a、b、c的值；（2）根据函数增减性求出函数在区间[﹣3，3]的最小值大于等于m2﹣14m，即可求出m的范围．【解答】解：（1）∵f'（x）=3ax2+2bx+c，且y=f'（x）的图象经过点（﹣2，0），，∴∴f（x）=ax3+2ax2﹣4ax，由图象可知函数y=f（x）在（﹣∞，﹣2）上单调递减，在上单调递增，在上单调递减，由f（x）极小值=f（﹣2）=a（﹣2）3+2a（﹣2）2﹣4a（﹣2）=﹣8，解得a=﹣1∴f（x）=﹣x3﹣2x2+4x（2）要使对x∈[﹣3，3]都有f（x）≥m2﹣14m恒成立，只需f（x）min≥m2﹣14m即可．由（1）可知函数y=f（x）在[﹣3，﹣2）上单调递减，在上单调递增，在上单调递减且f（﹣2）=﹣8，f（3）=﹣33﹣2×32+4×3=﹣33＜﹣8∴f（x）min=f（3）=﹣33﹣33≥m2﹣14m⇒3≤m≤11故所求的实数m的取值范围为{m|3≤m≤11}．21．已知函数f（x）=ln（ax+1）+，x≥0，其中a＞0．（Ⅰ）若f（x）在x=1处取得极值，求a的值；（Ⅱ）求f（x）的单调区间；（Ⅲ）若f（x）的最小值为1，求a的取值范围．【考点】6D：利用导数研究函数的极值；6B：利用导数研究函数的单调性；6E：利用导数求闭区间上函数的最值．【分析】（Ⅰ）对函数求导，令f′（1）=0，即可解出a值．（Ⅱ）f′（x）＞0，对a的取值范围进行讨论，分类解出单调区间．a≥2时，在区间（0，+∞）上是增函数，（Ⅲ）由（2）的结论根据单调性确定出最小值，当a≥2时，由（II）知，f（x）的最小值为f（0）=1，恒成立；当0＜a＜2时，判断知最小值小于1，此时a无解．当0＜a＜2时，（x）的单调减区间为，单调增区间为【解答】解：（Ⅰ），∵f′（x）在x=1处取得极值，f′（1）=0即 a+a﹣2=0，解得 a=1（Ⅱ），∵x≥0，a＞0，∴ax+1＞0①当a≥2时，在区间（0，+∞）上f′（x）＞0．∴f（x）的单调增区间为（0，+∞）②当0＜a＜2时，由f′（x）＞0解得由∴f（x）的单调减区间为，单调增区间为（Ⅲ）当a≥2时，由（II）知，f（x）的最小值为f（0）=1当0＜a＜2时，由（II）②知，处取得最小值，综上可知，若f（x）的最小值为1，则a的取值范围是[2，+∞）22．已知函数，g（x）=x+lnx，其中a＞0．（1）若x=1是函数h（x）=f（x）+g（x）的极值点，求实数a的值；（2）若对任意的x1，x2∈[1，e]（e为自然对数的底数）都有f（x1）≥g（x2）成立，求实数a的取值范围．【考点】6D：利用导数研究函数的极值；6B：利用导数研究函数的单调性；6E：利用导数求闭区间上函数的最值．【分析】（1）通过、x=1是函数h（x）的极值点及a＞0，可得，再检验即可；（2）通过分析已知条件等价于对任意的x1，x2∈[1，e]都有[f（x）]min≥[g（x）]max．结合当x∈[1，e]时及可知[g（x）]max=g（e）=e+1．利用，且x∈[1，e]，a＞0，分0＜a＜1、1≤a≤e、a＞e三种情况讨论即可．【解答】解：（1）∵，g（x）=x+lnx，∴，其定义域为（0，+∞），∴．∵x=1是函数h（x）的极值点，∴h′（1）=0，即3﹣a2=0．∵a＞0，∴．经检验当时，x=1是函数h（x）的极值点，∴；（2）对任意的x1，x2∈[1，e]都有f（x1）≥g（x2）成立等价于对任意的x1，x2∈[1，e]都有[f（x）]min≥[g（x）]max．当x∈[1，e]时，．∴函数g（x）=x+lnx在[1，e]上是增函数．∴[g（x）]max=g（e）=e+1．∵，且x∈[1，e]，a＞0．①当0＜a＜1且x∈[1，e]时，，∴函数在[1，e]上是增函数，∴．由1+a2≥e+1，得a≥，又0＜a＜1，∴a不合题意；②当1≤a≤e时，若1≤x＜a，则，若a＜x≤e，则．∴函数在[1，a）上是减函数，在（a，e]上是增函数．∴[f（x）]min=f（a）=2a．由2a≥e+1，得a≥，又1≤a≤e，∴≤a≤e；③当a＞e且x∈[1，e]时，，∴函数在[1，e]上是减函数．∴．由≥e+1，得a≥，又a＞e，∴a＞e；综上所述：a的取值范围为．。

新人教版六年级数学下册第三次月考试卷附答案(三篇)

新人教版六年级数学下册第三次月考试卷（附答案(三篇)目录：新人教版六年级数学下册第三次月考试卷附答案一新人教版六年级数学下册第三次月考试题及答案二新人教版六年级数学下册第三次月考试题及答案一三新人教版六年级数学下册第三次月考试卷附答案一班级：姓名：满分：100分考试时间：90分钟一、填空题。

（20分）1、小麦的出粉率是85%，3000千克小麦可磨面粉（_________）千克，要磨3400千克面粉需要小麦（________）千克。

2、一条裤子的原价是180元.现在打九折出售，现在的售价是（_____）元，比原来省了（____）元。

3、六（1）班今天出勤48人，有2人因病请假，今天六（1）班学生的出勤率是（________）。

4、一个长方体长6分米、宽5分米、高4分米，把它分成两个长方体，表面积最小增加（_____）平方分米，最多增加（_____）平方分米。

5、有一个正方形的池塘，四个角上都栽一棵树，如果每边栽7棵树，四边一共栽（______）棵树。

6、一个圆形游泳池的周长是314米，它的半径是_____，占地面积是_____．7、小芳做20道题，做对一道得5分，做错一道倒扣2分，小芳每一道题都做了，结果只得了72分，她做对了________道题，做错了________道题．8、在一幅比例尺是8∶1的精密零件图纸上,量得图纸上零件长40mm,这个零件实际长（____）cm。

9、大圆半径是小圆半径的3倍，大圆周长是小圆周长的_____倍，大圆面积是小圆面积的_____倍．10、一个三位数，既是3的倍数，又含有因数5，它百位上的数是最小的奇数，十位上的数是最小的质数，这个数是________。

二、选择题（把正确答案前面的序号填在（）里）（10分）1、表示x和y成反比例关系的式子是( )。

÷y C．x÷y=8A．y-x=8 B．x=182、用一个半圆把直径为3厘米的圆盖住，这个半圆的直径至少应是（）厘米。

2022-2023学年郴州市18中七年级数学下学期3月考试卷附答案解析

2022-2023学年郴州市18中七年级数学下学期3月考试卷一、选择题(本大题共8小题，每小题3分，满分24分)1.下列方程组中是二元一次方程组的是()A．35126x yyx-=⎧⎪⎨+=⎪⎩B.261x yxy+=⎧⎨=⎩C.13320x yx z⎧-=⎪⎨⎪+=⎩D.3723x yx y+=⎧⎪⎨+=⎪⎩2.由2x+y=1得到用x的代数式表示y的式子为()A.y=1-2xB.y=1+2x c.x=12(1-y) D.x=12(1+y)3.已是12xy=⎧⎨=⎩方程2mx-y=10的解，则m的值为()A.2B.4C.6D.104.解方程组①3759y xx y=-+=-⎧⎨⎩；②35123156x yx+=-=-⎧⎨⎩时，比较简便的方法是()A.都用代入法B.都用加减法C.①用代入法，②用加减法D.①用加减法，②用代入法5.下列计算正确的是()A.(-a)3=a3B.a2·a3=a6C.(a2)3=a6D.3a2-2a=2a6.若(x a y b)3=x6y15，则a，b的值分别为()A.2，5B.3，12C.5，2D.12，37.若单项式2x2y a+b与-13x a-b y4是同类项，则a，b的值分别为()A.a=3，b=1B.a=-3，b=1C.a=3，b=-1D.a=-3，b=-18.《九章算术》是中国古代重要的数学著作，其中“盈不足术”记载:今有共买鸡，人出九，盈十一;人出六，不足十六.问人数鸡价各几何?译文:今有人合伙买鸡，每人出九钱，会多出11钱:每人出6钱，又差16钱.问人数、买鸡的钱数各是多少?设人数为x，买鸡的钱数为y，可列方程组为()A.9x+11=y6x+16=y⎧⎨⎩B.9x-11=y6x-16=y⎧⎨⎩C.9x+11=y6x-16=y⎧⎨⎩D.9x-11=y6x+16=y⎧⎨⎩二、填空题(本大题共8小题，每小题3分，满分24分)9.计算:a3·(a3)2=.10.计算:3212⎛⎫- ⎪⎝⎭=.11.用代入消元法解二元一次方程组3-2235x yx y=+=⎧⎨⎩①②时，由①变形得y=.12.已知方程2x m+3-12y2-4n=5是二元一次方程，则m=，=.13.已知a，b满足方程组2-1228a ba b=⎧⎨+=⎩，则3a+b的值为.14.已知(y-3x+1)2+|2x+5y-12|=0，则x=，=.15.2022年第22届世界杯足球赛在卡塔尔举行，球迷小李在网上预定了小组赛和决赛两个阶段的门票共5张，总价为21200元，其中小组赛门票每张2800元，决赛门票每张6400元，若设小李预定了小组赛门票x张决赛门票y张，根据题意可列方程组为.16.根据以下对话，可以求得媛媛所买的笔的价格是，笔记本的价格是.三、解答题(本大题共10小题，17-19每小题6分，20-23每小题8分24-25每小题10分，26题12分，共82分)17.用代入法解方程组:241 x yy x+=⎧⎨=+⎩18.用加减法解方程组:237 329 x yx y+⎧⎨--⎩＝＝19.已知a3·a m·a2m+1=a25，求m的值;20.计算:-3x2y2-2xy+(xy)321.先化简，再求值:2x2y·(-2xy2)3+(2xy)3·(-xy2)2，其中x=4，y=1 4 .22.已知在等式y=kx+b中，当x=1时，y=3;当x=-1时，y=-5(1)求k、b的值(2)求当x=-12时，y的值为多少?23.某水果公司冷库收购杨梅56吨，准备加工后上市销售，该公司加工杨梅的能力是:每天可以精加工3吨或粗加工7吨，现水果公司计划用12天完成这项加工任务，则应安排几天精加工，几天粗加工?24.若规定x※y=mx+ny2，若3※2=9，2※1=1，求(7※1)※2的值.25.小英家今年1月份用水20t，交水费43元;2月份用水18t，交水费38元，该城市实行阶梯水价，14t以内按正常收费，超出部分则收较高水费.问:在限定量以内的水费每吨多少元?超出部分的水费每吨多少元?26.某校准备组织七年级学生参加夏令营，已知用3辆小客车和1辆大客车每次可运送学生105人，用1辆小客车和2辆大客车每次可运送学生110人：现有学生400人，计划租用小客车a辆，大客车b辆，一次送完，且恰好每辆车都坐满．（1）1辆小客车和1辆大客车都坐满后一次可运送多少学生？（2）请你帮学校设计出所有的租车方案．参考答案1．D 2．A 3．C4．C 5．C 6．A 7．A 8．D 9．910．−16411．3x-212．-21413．2014．1215．52800640021200x y x y ⎨⎩++⎧＝＝16．1.2元、3.6元17．12x y =⎧⎨=⎩18．13x y =-⎧⎨=⎩19．因为a 3•a m •a 2m+1=a 3+m+2m+1=a 3m+4，所以3m+4=25，所以m=720．33−322−2B 21．原式=2x 2y•（-8x 3y 6）+8x 3y 3•x 2y 4=-16x 5y 7+8x 5y 7=-8x 5y 7，当x=4，y=14时，原式=-8×45×（14）7=-12．22．（1）将x=1时，y=3；x=-1时，y=-5分别代入y=kx+b 中得：35k b k b +-+⎧⎨-⎩＝①＝②，①+②得：2b=-2，解得：b=-1，将b=-1代入①得：k=4，（2）由（1）得k=4，b=-1，则y=4x-1，当x=-12时，y=4×(−12)-1=-3．23．设应安排精加工x 天，粗加工y 天，依题意，得：123756x y x y ++⎧⎨⎩＝＝，解得：75x y ⎧⎨⎩＝＝．答：应安排精加工7天，粗加工5天．24．24.∵3※2=9，2※1=1，∴34921m n m n +⎧⎨+⎩＝＝，解得：13m n ⎩-⎧⎨＝＝，∴7※1=（-1）×7+3×12=-7+3=-4，∴（7※1）※2=（-4）※2=（-1）×（-4）+3×22=4+12=16. 25.设限定量以内的水费每吨x元，超出部分的水费每吨y元，由题意得：14201443 1418()(8)143x yx y+-+-⎧⎨⎩＝＝，解得：22.5 xy⎧⎨⎩＝＝，答：在限定量以内的水费每吨2元，超出部分的水费每吨2.5元．26.（1）设1辆小客车一次可送学生x人，1辆大客车都坐满后一次可送y名学生，由题意得：31052110 x yx y++⎧⎨⎩＝＝，解得：2045 xy⎧⎨⎩＝＝，所以x+y=65，答：1辆小客车和1辆大客车都坐满后一次可送65名学生．（2）设租小客车a辆，大客车b辆，由题意得20a+45b=400，∴a＝8094b -，∵每辆汽车恰好都坐满，∴a、b的值均为非负整数，∴a、b可取20ab⎧⎨⎩＝＝，114ab⎧⎨⎩＝＝，28ab⎧⎨⎩＝＝．∴租车方案有3种：方案一：小客车20辆，大客车0辆；方案二：小客车11辆，大客车4辆；方案三：小客车2辆，大客车8辆．。

湖南省长郡中学2023届高三月考试卷(三)化学试题附参考答案

长郡中学2023届高三月考试卷（三）化学参考答案一、选择题（本题共10小题，每小题3分，共30分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

）题号12345678910答案DBDAADBBBC3．D【解析】甲醇分子中含有电负性大、原子半径小的氧原子，溶于水时与水中的氢原子形成氢键，增加分子之间的吸引作用，导致物质相互溶解，这与氢键的形成有关，A 不符合题意；邻羟基苯甲醛会形成分子内氢健，而对烃基苯甲醛形成的是分子间氢键，增加了分子之间的作用力，导致邻烃基苯甲醛的沸点低于对烃基苯甲醛，这与氢键的形成有关，B 不符合题意；羊毛织品的主要成分是蛋白质，其中含有电负性较大的氮原子，水洗时与水分子的氢原子之间形成氢键，导致水洗后会缩小变形，这与氢键的形成有关，C 不符合题意；氟化氢分解时吸收的热量比氯化氢分解时吸收的热量多，是因为氢氟键强于氢氯键，断裂共价键消耗的能量多，则氟化氢分解时吸收的热量比氯化氢分解时吸收的热量多与氢键无关，故D 符合题意。

6．D【解析】钠元素人体血液含量已超上限，故饮食中应少食钠盐以调节人体血液内钠元素含量，A 正确；表格中胱抑素C 数据单位是，B 正确；根据题目所给表格数据，血1mg L -⋅液中钙元素最低含量为，C 正确；若血液中含葡萄糖量是12.1340mg L -⨯⋅185.2mg L -=⋅360，换算得，在合理范围（3.9～6.1）1mg L -⋅11360mmol L 2mmol L 180--⋅=⋅1mmol L -⋅之外，应是低血糖状态，D 错误。

9．B【解析】Z 是短周期元素，且能够形成离子Z ，其原子序数比W 等大，因此Z 为Na 。

根据结构示意图，8个Y 原子均形成了2个共价键，原子序数比Na 小，形成2个共价碳的只有O ，因此Y 为O ；4个W 原子均形成1个共价键，且原子序数比O 小，因此W 为H ；四种元素的原子序数总和为25，则X 的原子序数为5，为B ；B 的最外层电子数为3，一般只形成3个共价键，在此结构中，2个B 均得到1个电子（该阴离子带有2个负电荷），因此可以形成4个共价键。

安徽省青阳一中高二3月月考数学(理)试题

青阳一中2016-2017学年度高二3月份月考试卷高二数学（理科）命题人：储伟；审题施利生一、选择题 1、已知函数，那么f 的值为（）A ．9B ．C ．﹣9D ．﹣2、已知点O ，N ，P 在ABC ∆所在的平面内，且OA OB OC ==，0NA NB NC ++=，PA PB PB PC PC PA •=•=•，则点O ，N ，P依次是ABC ∆的（）A ．重心、外心、垂心B ．重心、外心、内心C ．外心、重心、垂心D ．外心、重心、内心3、如图为某几何体的三视图，则该几何体的外接球的表面积为（）A ．272π B ．27π C ．273π D ．273π4、执行如图所示的程序框图，则输出的i 值为（） A ．3 B ．4 C ．5 D ．65、已知函数()()sin 0,2f x x πωϕωϕ⎛⎫=+ ⎪⎝⎭＞＜，其图象相邻两条对称轴之间的距离为2π，且函数12f x π⎛⎫+ ⎪⎝⎭是偶函数，下列判断正确的是（）A ．函数()f x 的最小正周期为2πB ．函数()f x 在3,4ππ⎡⎤⎢⎥⎣⎦上单调递增C ．函数()f x 的图象关于直线712x π=-对称 D ．函数()f x 的图象关于点7,012π⎛⎫⎪⎝⎭对称 6、中国有个名句“运筹帷幄之中，决胜千里之外．”其中的“筹”愿意是指《孙子算经》中记载的算筹，古代是用算筹来进行计算，算筹是将几寸长的小竹棍摆在平面上进行运算，算筹的摆放形式有纵横两种形式，如图，表示一个多位数时，像阿拉伯计数一样，把各个数位的数码从左到右排列，但各位数码的筹式需要纵横相间，个位，百位，万位数用纵式表示，十位，千位，十万位用横式表示，以此类推．例如6613用算筹表示就是，则9117用算筹可表示为（）A ．B ．C ．D ．7、定义行列式运算=a 1a 4﹣a 2a 3.将函数f （x ）=的图象向左平移n （n ＞0）个单位，所得图象对应的函数为偶函数，则n 的最小值为（）. A ．B ．C ．D ．8、已知集合{}{}|12,|11A x x B x x m =-<=-<<+，若x A ∈成立的一个必要不充分条件是x B ∈，则实数m 的取值范围是（）A ．[)2,+∞B ．(],2-∞C ．()2,+∞D ．(),2-∞9、给出定义：设()f x '是函数()y f x =的导函数，()f x ''是函数()f x '的导函数，若方程()0f x ''=有实数解0x ，则称点()()00,x f x 为函数()y f x =的“拐点”，已知函数()34sin cos f x x x x =+-的拐点是()()00,M x f x ，则点M （）A ．在直线3y x =-上B ．在直线3y x =上C ．在直线4y x =-D ．在直线4y x =上10、直线3y x =与椭圆()2222:10x y C a b a b+=>>交于A B 、两点，以线段AB 为直径的圆恰好经过椭圆的右焦点，则椭圆C 的离心率为（） A．2 B．4- C．12D1 11、某产品的广告费用x 与销售額y 的统计数据如下表:根据上表可得回归方程y bx a =+中的b为9.4，据此模型预报广告费用为6万元时销售额约为（）A.63.6万元B.65.5万元C.67.7万元 D.72.0万元 12、已知函数()()2102x fx x e x =+-＜与()()2ln g x x xa =++的图象上存在关于y轴对称的点，则a 的取值范围是（）A ．⎛-∞⎝ B ．(-∞ C ．⎛ ⎝ D ．⎛⎝二．填空题 13、211dx x+=⎰⎰__________.14、不同直线 m n ，和不同平面 αβ，，给出下列命题：①n a m n m α⎫⇒⎬⊂⎭∥∥；②n m n m ββ⎫⇒⎬⊂⎭∥∥；③ m m n n αβ⊂⎫⇒⎬⊂⎭，不共面；④n m n m βα⎫⇒⎬⎭∥∥∥，写出所有假命题的序号为．15、已知直线()1:248l a x y ++=与直线()2:12l x a y +-=平行，则a 的取值为．16、设实数,x y 满足条件202400,0x y x y x y -+≥⎧⎪--≤⎨⎪≥≥⎩,若目标函数()0,0z ax by a b =+>>的最大值为12，则34a b+的最小值为_____________.三．解答17．(本题满分10分)已知ABC ∆中，c b a ,,为角,,A B C 所对的边，且(3)cos b b c A -CA CB =⋅. （Ⅰ）求A cos 的值；（Ⅱ）若ABC ∆的面积为22，并且边AB 上的中线CM 的长为217，求,b c 的长. 18、(本题满分12分)如图，在三棱锥P ABC -中，E 、F 分别为AC 、BC 的中点. (1)求证://EF 平面PAB ；(2)若平面PAC ⊥平面ABC ,且,90PA PC ABC =∠=︒,求证:BC ⊥平面PEF ．19、(本题满分12分)已知函数32()10f x x ax =-+．（1）当1a =时，求曲线()y f x =在点(2,(2))f 处的切线方程；（2）在区间[]1,2内存在实数x ，使得()0f x <成立，求实数a 的取值范围．20、(本题满分12分)在一个不透明的箱子里放有四个质地相同的小球，四个小球标的号码分别为1，1，2，3.现甲、乙两位同学依次从箱子里随机摸取一个球出来，记下号码并放回．（Ⅰ）求甲、乙两位同学所摸的球号码相同的概率；（Ⅱ）求甲所摸的球号码大于乙所摸的球号码的概率21、(本题满分12分)已知焦点在x 轴的椭圆的离心率与双曲线3322=-y x 的离心率互为倒数，且过点)23,1(. （1）求椭圆方程；（2）若直线)0(:≠+=k m kx y l 与椭圆交于不同的两点N M ,，点)0,51(P ，有NP MP =，求k的取值范围. ．22．(本题满分12分)已知函数22()en nxx x a f x --=，其中,,N R n a *∈∈e 是自然对数的底数. （1）求函数12()()()g x f x f x =-的零点；（2）若对任意,N n *∈()n f x 均有两个极值点，一个在区间(1,4)内，另一个在区间[]1,4外，求a 的取值范围；数学理科答案1-5 BCBBB 6-10 ABCBD 11-12 BB 13ln 24π+14①②③④ 15 3-1649617解：（Ⅰ）由题意得： (3)cos cos b b c A ab C -=．．．．．．．．．．．．2分由正弦定理得：sin (3sin sin )cos sin sin cos B B C A A B C -=sin 0,3sin cos sin cos sin cos sin B B A A C C A B ≠∴=+=．．．．．．．4分 1cos 3A ∴=．．．．．．．．．．．．6分（Ⅱ）由题意得：1sin 2ABC S bc A ∆==，即：6bc =．．．．．．．．．．．．8分由余弦定理得：2217144cos 322c b A c b +-==⋅，即：22425b c +=．．．．．．．．．10分联立上述两式,解得：2,3b c ==或3,42b c ==.．．．．．．．．．．．．12分 18 （1）∵,E F 分别是,AC BC 的中点，∴//EF AB . 又EF ⊄平面,PAB AB ⊂平面PAB ， ∴//EF 平面PAB .（2）在三角形PAC 中，∵,PA PC E =为AC 中点， ∴PE AC ⊥∵平面PAC ⊥平面ABC ，平面PAC ⋂平面ABC AC =， ∴PE ⊥平面ABC . ∴PE BC ⊥又//,90EF AB ABC ∠=︒， ∴EF BC ⊥，又EF PE E ⋂=， ∴BC ⊥平面PEF19 （1）当1a =时，2()32f x x x =-，(2)14f =，曲线()y f x =在点(2,(2))f 处的切线斜率'(2)8k f ==，所以曲线()y f x =在点(2,(2))f 处的切线方程为148(2)y x -=-，即820x y --=．（2）由已知得3221010x a x x x +>=+，设210()g x x x =+（12x ≤≤），320'()1g x x =-， ∵12x ≤≤，∴'()0g x <，∴()g x 在[]1,2上是减函数，min 9()(2)2g x g ==， ∴92a >，即实数a 的取值范围是9(,)2+∞．20 （1）记号码为1的小球为A 1，A 2，号码为2的小球为B ，号码为3的小球为C由题意可知，甲、乙两位同学各摸取一个小球，所有可能的结果有16个，（A 1，A 1），（A 1，A 2），（A 1，B ），（A 1，C ），（A 2，A 1），（A 2，A 2），（A 2，B ），（A 2，C ），（B ，A 1），（B ，A 2），（B ，B ），（B ，C ），（C ，A 1），（C ，A 2），（C ，B ），（C ，C ）4分（Ⅰ）用M 表示事件“甲、乙两位同学所摸的小球号码相同”，则M 包含的基本事件有：（A 1，A 1），（A 1，A 2），（A 2，A 1），（A 2，A 2），（B ，B ），（C ，C ），共有6个．所以P （M ）=388分（Ⅱ）用N 表示事件“甲所摸的球号码大于乙所摸的球号码”，则N 包含的基本事件有：（B ，A 1），（B ，A 2），（C ，A 1），（C ，A 2，），（C ，B ），共有5个．所以P （N ）=51612分 21 （1）双曲线3322=-y x ，即1322=-y x 的离心率为2131=+.由题意可得，椭圆的离心率21=e ，设椭圆方程为222222223,2,21),0(1c c a b c a a c b a b y a x =-=∴=∴=∴>>=+，∴椭圆方程为1342222=+c y c x .又点)23,1(在椭圆上，∴1,13)23(412222=∴=+c cc ，∴椭圆的方程为13422=+y x . （2）设),(),,(2211y x N y x M ，由⎪⎩⎪⎨⎧+==+m kx y y x 13422，消去y 并整理得01248)43(222=-+++m kmx x k ，∵直线m kx y +=与椭圆有两个交点，0)124)(43(4)8(222>-+-=∆m k km ，即3422+<k m ，又221438k km x x +-=+，∴MN 中点P 的坐标为)433,434(22kmk km ++-，即为NP MP =，所以P 在MN 的垂直平分线上，设MN 的垂直平分线l '方程：)51(1--=x k y ，∵P 在l '上，∴)51434(143322-+--=+k km k k m ，得k k m km k 534,035422+-==++，将上式代入①式得3425)34(2222+<+k kk ，即77,712>∴>k k 或77-<k ， ∴k 的取值范围为),77()77,(+∞--∞ . 22 （1）222122222(2)(e 1)()()()e e ex x x xx x a x x a x x a g x f x f x -------=-=-=， 44a ∆=+..．．．．．．．．．．2分① 当1a <-时，0,∆<函数()g x 有1个零点：10.x = ..．．．．．．．．．．3分 ② 当1a =-时，0,∆=函数()g x 有2个零点：120, 1.x x == ..．．．．．．．．．．4分 ③ 当0a =时，0,∆>函数()g x 有两个零点：120, 2.x x == ..．．．．．．．．．．5分 ④ 当1,0a a >-≠时，0,∆>函数()g x 有三个零点：1230,11x x x === ..．．．．．．．．．．6分（2）222(22)e (2)e 2(1)2().e e nx nx n nx nxx n x x a nx n x a n f x -----+++⋅-'== 设2()2(1)2n g x nx n x a n =-+++⋅-，()n g x 的图像是开口向下的抛物线.由题意对任意,N n *∈()0n g x =有两个不等实数根12,x x ，且()[]121,4,1,4.x x ∈∉则对任意,N n *∈(1)(4)0n n g g <,即6(1)(8)0n a n a n ⎡⎤⋅+⋅⋅--<⎢⎥⎣⎦, ..．．．．．．．．．．9分又任意,N n *∈68n -关于n 递增,681n->-, 故min 61(8),186 2.a a n-<<--<<-=所以a 的取值范围是()1,2.- ..．．．．．．．．．．12分。

A3六年级(上)11月份月考试卷

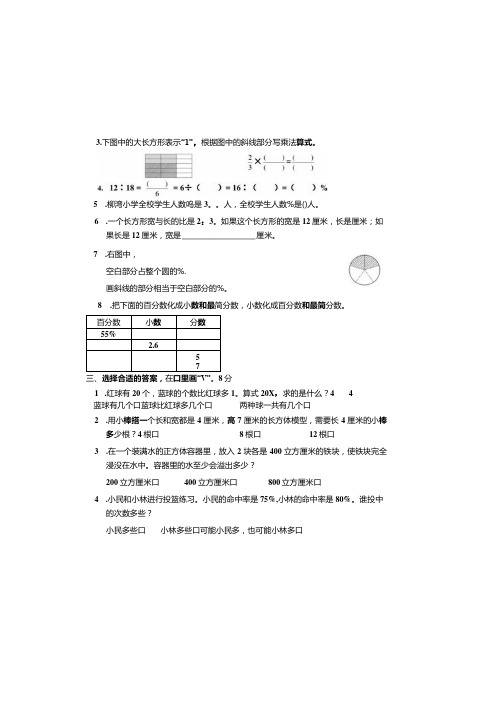
3.下图中的大长方形表示“1”，根据图中的斜线部分写乘法算式。

5.柳湾小学全校学生人数呜是3。

人，全校学生人数%是()人。

6.一个长方形宽与长的比是2：3。

如果这个长方形的宽是12厘米，长是厘米；如果长是12厘米，宽是_____________________ 厘米。

7.右图中，空白部分占整个圆的%.画斜线的部分相当于空白部分的%。

8.把下面的百分数化成小数和最简分数，小数化成百分数和最简分数。

百分数小数分数55%2.657三、选择合适的答案，在口里画“V”。

8分1.红球有20个，蓝球的个数比红球多1。

算式20X，求的是什么？4 4蓝球有几个口蓝球比红球多几个口两种球一共有几个口2.用小棒搭一个长和宽都是4厘米，高7厘米的长方体模型，需要长4厘米的小棒多少根？4根口8根口12根口3.在一个装满水的正方体容器里，放入2块各是400立方厘米的铁块，使铁块完全浸没在水中。

容器里的水至少会溢出多少？200立方厘米口400立方厘米口800立方厘米口4.小民和小林进行投篮练习。

小民的命中率是75%,小林的命中率是80%。

谁投中的次数多些？小民多些口小林多些口可能小民多，也可能小林多口六年级数学（上）11月份月考试卷一、计算。

28分1、直接写出得数（4分）-÷12= 15×-= 36÷-= 35~4 5 9 3.5一十一=-X12= •''C 一 C'一一—= —<x-= 4 8 9 28106 2、计算下面各题, 能简便计算的要简便计算（18分）∙!∙+3÷-3 103θ×4+P v×15-y 二、填空。

22分1 .用1立方厘米的小正方体摆一个棱长6厘米的正方体，需要的正方体的底面积是平方厘米。

2 .10升=立方厘米 450立方分米=立方米 9 χ 5 ^_9 χ 52 4 , 2 43、解方程（6分） 6x -4.6 = 8x÷-x=6 7 2.5x÷2= 12、李林有12。

(部编版)四年级下册语文第三次月考试卷【基础为准,含答案】

刺骨
的石顶
高高
的寒冷
高傲
的动物
八、选词填空（6 分）寻找寻觅
①那只燕子在（）安身之处。 ②他在仔细（）他丢失的铅笔盒
光亮亮光光彩光芒 1.一刹那间，太阳发出了夺目的( )，它旁边的云也有了（）。 2.太阳在黑云背后放射的( )，给黑云镶了一道发光的金边，这时候连我自己也变成( )的了。九、选择下列句子运用的描写手法。（4 分） A.景物描写 B.动作描写 C.语言描写 D.心理描写 1.她不采，总是喊:“哥，这儿有一穗!”（） 2.被风一吹，那花都往一个方向倾覆而去，露出金黄的稻草来。（） 3.青铜望着那个人，心里觉得有点儿对不住他。（） 4.他笑了笑，掉头朝那个人追了过去。（）十、按要求写句子（10 分） 1．恐龙的体表长出了羽毛。(扩句)
七、词语搭配，连线（3 分）
1．（刺骨）的寒冷 2．（高高）的石顶 3．（高傲）的动物
八、选词填空（6 分）
题号
1
2
答案
①寻觅②寻找
亮光光彩光芒光亮
九、选择（4 分）
1.C2.A3.D4B
十、按要求写句子（10 分）
1．恐龙的体表长出了美丽的羽毛。 2．我们班这次非拿到全年级第一不可! 3．这么远,箭射不到。 4．海边的一对渔民父子把琥珀挖了出来。 5．读了这个故事,我感动得流泪了。
四年级语文第三次月考试卷
一、看拼音写词语（8 分）
chóu zǐ
lú huā
fèn biàn
kuò dà
（
）（
）（
）（
）
zī tài
tàn cè
shǎn shuò
bā kāi
（
）（
）（

2019年八年级下学期英语第三次月考试卷A卷

2019年八年级下学期英语第三次月考试卷A卷一、单项选择 (共15题；共30分)1. （2分）This is easy math test. I think you can do well in test.A . an; anB . an; theC . the; anD . the; the2. （2分）—Is there _____ in today's magazine?—Yes. The mayor saw _____ "stay-home children" _____ May, 25th.A . anything special; hundreds of; onB . something special; hundred of; atC . special anything; hundreds; onD . anything special; hundreds of; in3. （2分）—Look! Somebody the lights.—Well, it wasn't me. I didn't do it.A . turns offB . is turning offC . was turning offD . has turned off4. （2分）（2015•贵州铜仁）—You won't pass the exam ________ you don't work hard. —OK, I'll do my best.A . andB . butC . ifD . so5. （2分）The boy is sad. Let's cheer him .A . downB . inC . aroundD . up6. （2分）The old woman has a bad cold. She is feeling ________ today than yesterday.A . much illB . a little badC . a little badlyD . much worse7. （2分）My brother wants to be an artist like Da Vinci in the future.A . a person who creates works of artB . a person who is very famousC . a person who makes lots of money8. （2分）— Peter is _______ than you, right?—Yes, but he is _______ runner in our class.A . heavier; bestB . heavy; the bestC . heavier; the bestD . heavy; better9. （2分）----Look at the photo I took in Jinghong, Yunnan Province.----_____ the Dai people were having! Wow! They were celebrating the Water Festival.A . What happyB . How happilyC . What funD . How a fun10. （2分）I find hard to learn English well.A . thisB . itC . thatD . they11. （2分）— I am going to Shanghai with my aunt for my holiday after the exam.— ________.A . Have a good time.B . It doesn't matter.C . You are welcome.D . Thanks a lot.12. （2分）The bus went out of control and ran into a line of people. ________, no one was badly hurt.A . UnluckilyB . FortunateC . UnfortunatelyD . Luckily13. （2分）The old farmer saw a snake _______ on the road on his way home.A . lieB . liesC . lyingD . to lie14. （2分）--- will you go to the airport ?---To meet Mr. Smith from Canada．A . Why，forB . Where，forC . What，forD . How, for15. （2分）—Will you carry the box for me, please?—Sure, ______.A . no problemB . no goodC . no ideaD . no way二、完形填空 (共1题；共10分)16. （10分）根据短文理解，从A、B、C、D四个选项中选择最佳答案填空。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

定南中学2014—2015学年上学期高二12月月考试卷（化学）可能用到的相对原子质量：H 1 C 12 O 16 Na 23 Cu 64（第I 卷选择题48分）一．选择题（每小题只有一个正确选项，共16小题，每题3分共48分）1．化学是一门以实验为基础的自然科学，化学实验在化学学习中是有极其重要作用，下列实验中所选用的仪器合理的是（）①用50mL 量筒量取5.2mL 稀硫酸 ②用分液漏斗分离苯和四氯化碳混合物 ③用托盘天平称量11.7gNaCl 晶体 ④用酸式滴定管量取23.10mL 0.2mol/L 酸性高锰酸钾溶液 ⑤用瓷坩埚灼烧各种钠的化合物 ⑥配制245mL0.20mol/LNaOH 溶液用250mL 容量瓶 A ．①②③④ B ．③④⑥ C ．③ D ．③⑤⑥2．某含钠离子的溶液中可能含有NH 4+、Fe 3+、CO 32—、I —、SO 32—。

取样，滴加足量氯水，有气泡产生；继续向溶液中加BaCl 2溶液或淀粉均无现象。

为确定该溶液的组成，还需进行的实验有（）A ．取样，滴加硫氰化钾溶液B ．取样，加氯水和CCl 4，振荡C ．取样，加足量盐酸加热，用湿润的品红试纸检验气体D ．取样，加足量的浓NaOH 溶液加热，用湿润的红色石蕊试纸检验气体3．短周期元素W 、X 、Y 、Z 的原子序数依次增大，其简单离子都能破坏水的电离平衡的是（） A ．W 2—、X + B ．X +、Y 3+ C ．Y 3+、Z 2—D ．X +、Z 2—4．一定条件下，通过下列反应可以制备特种陶瓷的原料MgO ： MgSO 4(s)+CO(g)2(g)+SO 2(g) △H>0。

该反应在恒容的密闭容器中达到平衡后，若仅改变图中横坐标x 的值，重新达到平衡后，纵坐标y 随x 变化趋势合理的是（）5．25℃时，将amol/L 一元酸HA 与bmol/L 的NaOH 等体积混合后测得溶液PH=7，则下列关系一定不正确的是（）A ．a=bB ．a>bC ．c(A —)= c(Na +) D ．c(A —)< c(Na +)6．下列各组离子在有关限定条件下的溶液中一定能大量共存的是（） A ．由水电离产生的c(H +)=10—12mol/L 的溶液中：K +、Na +、ClO —、I—B ．c(H +)=Kw mol/L 的溶液中：K +、Fe 3+、Cl —、CO 32—C ．常温下，c(H +)/c(OH —) =10—12的溶液中：K +、Na +、AlO 2—、CO 32—D ．PH=13的溶液中：AlO 2—、Cl —、HCO 3—、SO 42—7．下列说法不正确的是（）A ．将PH=4的某酸稀释10倍，测得其PH<5，则该酸为弱酸B ．相同PH 的CH 3COONa 、NaOH 和Na 2CO 3三种溶液中：c(NaOH)<c(Na 2CO 3) <c(CH 3COONa)C ．0.1mol/LNaHA 溶液PH=5，则溶液中：c(HA —) >c(H +)>c(A 2—)>c(H 2A)D ．向NH 4HSO 4溶液中滴加NaOH 溶液至中性，所得混合液中： c(Na +) >c(NH 4+)>c(SO 42—)>c(OH —)= c(H +)8．实验测得常温下0.1mol/L 某一元酸（HA ）溶液的PH 不等于1，0.1mol/L 某一元碱（BOH ）溶液里c(H +)/c(OH —)=10—12,将此两种溶液等体积混合后，所得溶液里的各种离子的物质的量浓度由大到小的排列顺序正确的是（）A ．c(A —) >c(B +)>c(H +)>c(OH —) B ．c(B +)> c(A —) >c(OH —) >c(H +)C ．c(B +)= c(A —) >c(OH —) =c(H +) D ．c(B +)> c(A —) > c(H +)>c(OH —)9．某酸性溶液中只有Na +、CH 3COO —、H +、OH —四种离子，则下列描述正确的是（）A ．该溶液可由PH=3的CH 3COOH 与PH=11的NaOH 溶液等体积混合而成B ．该溶液由等浓度、等体积的NaOH 溶液和CH 3COOH 溶液混合而成C ．加入适量NaOH ，溶液中离子浓度为c(CH 3COO —)>c(Na +)>c( OH —)>c(H +)D ．加入适量氨水，c(CH 3COO —)一定大于c(Na +)、c(NH 4+)之和10．下列关于有机化合物的说法正确的是（） A ．乙酸和乙酸乙酯可用Na 2CO 3溶液加以区别 B ．戊烷有两种同分异构体C ．乙烯、聚乙烯和苯分子中均含有碳碳双键D ．糖类、油脂和蛋白质均可发生水解 11．已知某温度下Ksp[Cu(OH)2]=2.2×10—20，Ksp[Ca(OH)2]=5.5×10—6，则下列说法正确的是（）A ．相同条件下，Cu(OH)2比Ca(OH)2更易溶于水B ．Cu(OH)2一定不能转化为Ca(OH)2C ．往相同浓度的CuCl 2和CaCl 2混合溶液中逐滴加入氨水，先产生蓝色沉淀D ．升高温度二者的Ksp 均变大12．已知酸性H 2CO 3>HCO 3—则下列反应方程式或说法正确的是()A ．相同浓度的NaHCO 3、Na 2CO 3三种溶液的PH 由小到大的顺序是：<NaHCO 3 < Na 2CO 3B+CO 2+ H 2O →3C+ NaHCO 3 2↑+ H 2OD ．溶液中有：c(Na + ) 13．某燃料电池以熔融固体Na 2O 为电解质，Pt 作电极其工作原理如图所示：则下列关于该电池的说法正确的是（）A ．通H 2一极为该电池的正极，通O 2一极为负极B ．正极反应为：O 2 +2H 2O+4e —==4OH —C ．负极反应为：H 2 + O 2—+ 2 e —== H 2OD ．原电池能将电能转化为化学能14．已知：常温下，0.01mol/L MOH 溶液的PH 为10，MOH （aq ）与H 2SO 4（aq ）反应生成1mol正盐的△H= —24. 2KJ/mol ，强酸和强碱的稀溶液的中和热为△H= —57. 3KJ/mol 则MOH 在水溶液中电离的△H 为（）A ．—69.4KJ/molB ．—45.2KJ/molC ．+69.4KJ/molD ．+45.2KJ/mol 15．工业合成氨的正反应是放热反应，下列关于N 2（g ）+ 3H 2（g ）2NH 3（g ）反应的图像中，错误的是（）A B C D16．下列关于电解池的说法正确的是（） A ．电解池是将化学能转化为电能的装置 B ．阳极发生还原反应，阴极发生氧化反应 C ．阳极可能是电极材料放电，也可能是阴离子放电 D ．电子从电源正极流出流向阳极OH ONa ONa ONa OH ONa OH O —Pt O 2PtT/K T/KT 1NH 3t/minNH 3t/min NH 3OH ONa（第II 卷非选择题52分）二、（非选题，共5大题，共52分）17.（12分）A 、B 、C 三种强电解质，它们在水中电离出的离子如下图所示：如图所示的装置中，甲、乙、丙三个烧杯分别盛放足量的A 溶液、足量的B 溶液、足量的C 溶液，电极均为石墨电极。

接通电源，经过一段时间后，测得乙中c 电极质量增加了16g 。

常温下各烧杯中溶液的PH 与电解时间t 的关系如图。

据此回答下列问题：（1）M 为电源的极（填写“正”或“负”）；电极b 上发生的电极反应为 (2)计算电极e 上生成的气体在标准状况下的体积 L(3)写出乙烧杯中发生电解反应的总反应式；（4）如果电解过程中乙烧杯溶液中的金属离子全部析出，此时电解反应（填“能”或“否”）能否继续进行，为什么；（5）此时要使丙中溶液恢复到原来的状态，操作是。

18.(6分)某学生用0.2000mol/L 的标准NaOH 溶液滴定未知浓度的盐酸，其操作为如下几步： ①用蒸馏水洗涤碱式滴定管，并立即注入NaOH 溶液至“0”刻度以上 ②固定好滴定管并使滴定管尖嘴充满液体 ③调节液面至“0”或“0”刻度以下某一刻度，并记下读数 ④移取20.00mL 等测液注入洁净的锥形瓶中，并加入3滴酚酞溶液 ⑤用标准液滴定至终点，记下滴定管液面读数。

请回答：（1）以上步骤有错误的是 (填编号)，该错误操作会导致测定结果（填“偏大”、“偏小”或“无影响”）。

（2）判断滴定终点的现象是：锥形瓶中溶液从色变为 ,且半分钟内不变色。

（3）如图是某次滴定时的滴定管中的液面，其读数为 mL 。

（4）根据下列数据：请计算待测盐酸溶液的浓度为 mol/L19.(16分)硫酸是强酸，中学阶段将硫酸在水溶液中看作完全电离。

但事实是，硫酸在水中的第一步电离是完全的，第二步电离是不完全的，其电离情况为： H 2SO 4 == H ++ HSO 4—，HSO 4—H + + SO 42—。

请回答下列相关问题：（1）Na 2SO 4溶液呈 (填“弱酸性”，“弱碱性”或“中性”)，其理由是 (用离子反应方程式表示)。

（2）H 2SO 4溶液与BaCl 2溶液反应的离子反应方程式：。

（3）若25℃时，0.1mol/L 的NaHSO 4溶液c(SO 42—)=0.29mol/L,则0.10mol/L 的H 2SO 4溶液中 c(SO 42—) 0.29mol/L(填“<”，“>”或“=”)，其理由是。

（4）若25℃时,0.10mol/LH 2SO 4溶液的PH= -lg0.11，则0.10mol/L H 2SO 4溶液中c(SO 42—)= mol/L 。

（5）在0.10mol/L 的Na 2SO 4溶液中，下列离子浓度关系正确的是（填字母） A.c(Na +)=c(SO 42—)+c(HSO 4—)+c(H 2SO 4) B.c(OH —)=c(HSO 4—)+c(H +)C.c(Na +)+c(H +)=c(OH —)+c(HSO 4—)+2c(SO 42—) D.c(Na +)=2c(SO 42—)+2c(HSO 4—)2223能量20.(8分)甲醇是一种优质燃料，可用于制作燃料电池。

（1）工业上可用下列两种反应制备甲醇。

CO （g ）+ 2H 2(g)CH 3OH(g) ΔH 1 CO 2(g) + 3H 2(g)CH 3OH(g) + H 2O(g)ΔH 2已知：2H 2(g)+ O 2（g ）=== 2H 2O(g)ΔH 3。