自动控制原理_第4章_1
自动控制原理 孟华 第4章习题解答

4-1如果单位反馈控制系统的开环传递函数1)(+=s K s G 试用解析法绘出K 从零向无穷大变化时的闭环根轨迹图,并判断下列点是否在根轨迹上: (2,j 0),(0+j 1),(3+j 2)。
解:根轨迹如习题4-1答案图所示。
(-2,+j 0)在根轨迹上;(0,+j 1), (-3, +j 2) 不在根轨迹上。
习题4-1答案图4-2设单位反馈控制系统的开环传递函数。
)12()13()(++=s s s K s G试用解析法给出开环增益K 从零增加到无穷时的闭环根轨迹图。
解: 解析法:K =0时:s=-1/2,0;K =1:s=-122;K =-∞:s=-∞,-1/3。
根轨迹如习题4-2答案图所示。
习题4-2答案图4-3 已知系统的开环传递函数)1()1()()(-+=s s s K s H s G ,试按根轨迹规则画出该系统的根轨迹图,并确定使系统处于稳定时的K 值范围。
解:分离点:;会合点: ;与虚轴交点:±j 。
稳定的K 值范围:K >1。
根轨迹如习题4-3答案图所示。
习题4-3答案图4-4已知一单位反馈系统的开环传递函数为2*)4)(1)(1()(+-+=s s s K s G (1)试粗略画出K *由0到∞的根轨迹图;(2)分析该系统的稳定性。
解:稳定性分析:系统不稳定。
根轨迹如习题4-4答案图所示。
-10-505-8-6-4-22468Root LocusReal AxisI m a g i n a r y A x i s习题4-4答案图4-5 设控制系统的开环传递函数为)164)(1()1()()(2*++-+=s s s s s K s H s G ,试绘制系统根轨迹图,并确定使系统稳定的开环增益范围。
解:渐近线:=60°,180°;=-2/3;复数极点出射角55°;分离会合点和;与虚轴交点和;使系统稳定的开环增益为 <K < (即 <K *<。
自动控制原理 第四章根轨迹

第四章根轨迹法4-1 根轨迹法的基本概念4-2 常规根轨迹的绘制法则4-3 广义根轨迹4-1 根轨迹法的基本概念一、根轨迹的概念根轨迹:系统中某个参数从零到无穷变化时,系统闭环特征根在s平面上移动的轨迹。
根指的是闭环特征根(闭环极点)。
根轨迹法是根据开环传递函数与闭环传递函数的关系,通过开环传递函数直接分析闭环特征根及系统性能的图解法。
K =0 s 1=0 s 2=-40 < K <1s 1 s 2为不等的负实根K =1s 1=-2 s 2=-21 < K < ∞s 1s2 实部均为-2由根轨迹可知:1)当K =0时,s 1=0,s 2=-1,这两点恰是开环传递函数的极点,同时也是闭环特征方程的极点.2)当0<K < 1 时,s 1,2都是负实根,随着k 的增长,s 1从s 平面的原点向左移,s 2从-1点向右移。
3) 当K = 1时, s 1,2= -2,两根重合在一起,此时系统恰好处在临界阻尼状态。
4) 1 <K <∞,s 1,2为共轭复根,它们的实部恒等于-2,虚部随着K 的增大而增大,系统此时为欠阻尼状态。
★在s平面上,用箭头标明K增大时,闭环特征根移动的方向,以数值表明某极点处的增益大小。
有了根轨迹图就可以分析系统的各种性能:(1)稳定性:根轨迹均在s的左半平面,则系统对所有K>0都是稳定的。
(2)稳态性能:如图有一个开环极点(也是闭环极点)s=0。
说明属于I型系统,阶跃作用下的稳态误差为0。
在速度信号V0t作用下,稳态误差为V0/K,在加速度信号作用下,稳态误差为∞。
(3)动态性能:过阻尼临界阻尼欠阻尼K越大,阻尼比ξ越小,超调量σ%越大。
由此可知:1、利用根轨迹可以直观的分析K的变化对系统性能的影响。
2、根据性能指标的要求可以很快确定出系统闭环特征根的位置;从而确定出可变参数的大小,便于对系统进行设计。
由以上分析知:根轨迹与系统性能之间有着密切的联系,但是,高阶方程很难求解,用直接解闭环特征根的办法来绘制根轨迹是很麻烦的。
自动控制原理课后习题第四章答案

G(s)H(s)=
Kr s(s+1)(s+3)
σ根 s=3-K+ω轨r4-3-迹+p4s132ω1-3的+~3ω32分p===s2-离+001K点.p-3r=3:KK~0θrr===012+ωω6021,o=3,=0+±1810.7o
8
jω
1.7
s1
A(s)B'系(s)统=根A'轨(s迹)B(s)
s3 p3
s=sK2±r没=j24有.8.6位×于2K.r根6=×4轨80.迹6=上7,. 舍去。
2
第四章习题课 (4-9)
4-9 已知系统的开环传递函数,(1) 试绘制出
根轨迹图。
G(s)H与(s虚)=轴s交(0点.01s+1K)(系0.统02根s+轨1迹)
jω
70.7
解: GKK(rr=s=)10H5(0s)=ωω2s1,(3=s=0+±17000K.7)r(s+50)
s1
A(s)B'(系s)统=A根'(轨s)迹B(s)
s3 p3
p2
p1
-4
-2
0
((24))ζ阻=尼03.振5s2荡+1响2应s+s的81==K-r0值0.7范+围j1.2
s=s-s10=3=.-80-56.8+50K.7r×=20=s.82-=54×-.631..1155×3.15=3.1
-2.8
450
1080
360
0σ
0σ
第四章习题课 (4-2)
4-2 已知开环传递函数,试用解析法绘制出系
统的根轨迹,并判断点(-2+j0),(0+j1),
自动控制原理第四章-根轨迹分析法

×
p4 z 2
×
p3
×
×
p 2 z1 p1
σ
规则4:根轨迹的分会点(分离点和会合点)d。 (1)定义:分会点是指根轨迹离开实轴进入复平面的点(分 离点)或由复平面进入实轴的点(汇合点),位于相邻两极点 或两零点之间。
(2)位置:大部分的分会点在实轴上,若出现在复平面内时,则 成对出现。
(3)特点:分会点对应于闭环特征方程有重根的点;根轨迹离开
(4)与虚轴的交点:
方法1:闭环特征方程为s3 + 6s2 + 8s + K*= 0 令s = jω得:-jω3 -6ω2 + j8ω + K* = 0
-6ω2 + K* = 0 即
-ω3 + 8ω= 0
K* = 48 ω= 2.8 s-1
方法2:闭环特征方程为 s3 + 6s2 + 8s + K*= 0 列劳斯表如下:
规则1:根轨迹的起点和终点。 根轨迹起始于开环极点,终止开环零点或无穷远。
m
i 1
s
zi
n
s
l 1
pl
1 K
K
K
0 s pl
s s
zi , m条 (, n
m)条
规则2: 根轨迹的条数和对称性。 n阶系统有n条根轨迹。根轨迹关于实轴对称。
规则3: 实轴上的根轨迹分布。
由实数开环零、极点将实轴分为若干段,如某段右边 开环零、极点(包括该段的端点)数之和为奇数,则该段就 是根轨迹,否则不是。如下图所示。
又因为开环传函的零极点表达式为:
m
GK (s)
G(s)H(s)
K
n
(s
自动控制原理 第四章.

s1.2 1 1 K1 1 1 2 K
第 4章
根轨迹
根轨迹的基本概念(续)
s1 0 ① K 0 s 2 2
j
2
② K 0.5 s1 s2 1 ③ K 1 s1 , 2 1 j ④ K 2.5 s1 , 2 1 j 2 p2
由于实际控制系统闭环特征方程的系数或为已知
实数,或为根轨迹增益Kg 的函数,所以当Kg 由0→∞
连续变化时,闭环特征根的变化必然也是连续的,所
以根轨迹具有连续性。 系统闭环特征方程的系数仅与系统的参数有关。
对于实际控制系统而言,这些参数都是实数。具有实
系数的闭环特征方程的根为共轭复数的形式,必然对
称于实轴。因而,根轨迹也必然பைடு நூலகம்于实轴对称。
s pi s zj
j 1
n
而 ( s z j ) ( s pi ) ( 2 K 1) ——相角方程
j 1 i 1
m
n
第 4章
根轨迹
根轨迹的基本概念(续)
若s平面上的点是闭环极点,则它与zj 、pi所组成
的相量必定满足上述两方程,而且模值方程与Kg有
第四章 根轨迹法
§4-1 根轨迹的基本概念 §4-2 绘制根轨迹的基本法则 §4-3 广义根轨迹
主要内容
1.根轨迹基本概念和根轨迹方程
2.绘制常规根轨迹的九大法则
3.参量根轨迹与零度根轨迹
第 4章
根轨迹
重点与难点
重 点
1、绘制常规根轨迹的九大法则 2、参量根轨迹与零度根轨迹 3、控制系统根轨迹法分析
§4—2 绘制根轨迹的基本法则
绘制根轨迹的基本法则(续)
自动控制原理第4章习题解——邵世凡

第四章 习题4-1 绘制具有下列开环传递函数的负反馈系统的根轨迹1、()()()()54*++=s s s K s H s G解:首先确定开环传递函数中的零极点的个数各是多少。
由开环传递函数可知 m=0,n=3,n -m=3。
即,有限零点为0个,开环极点为3个。
其中,3个开环极点的坐标分别为:p 1=0,p 2=-4,p 3=-5。
然后,在[s]平面上画出开环极点的分布情况,根据根轨迹方程的幅角条件:首先确定实轴上的闭环系统的根轨迹。
如图所示。
接着再通过所需参数的计算画出比较精确的根轨迹通过画实轴上的根轨迹图可知,有3条闭环根轨迹,分别从p 1=0,p 2=-4,p 3=-5出发奔向无穷远处的零点。
在这一过程中,从p 1=0,p 2=-4两个极点出发的根轨迹在实轴上相遇后进入复平面,因此,有必要进行分离点的坐标计算,渐进线在实轴上的坐标点和渐进线的角度计算,以及与虚轴交点的计算。
根据公式有:渐进线303054011-=----=--=∑∑==mn zp n i mj jiσ()() ,,331212ππππϕ±±=+=-+=k mn k a从p 1=0,p 2=-4两个极点出发的根轨迹在实轴上相遇后将沿着±60º进入复平面,分离点:设:()1=s N ;()()()s s s s s s s D 2095423++=++=;()0'=s N ;()201832'++=s s s D则有:()()()()()0201832''=++-=⋅-⋅s s s D s N s D s N[s ]0201832=++s s解得方程的根为s 1= -4.5275(不合题意舍去);s 2= -1.4725 得分离点坐标:d = -1.4725。
与虚轴的交点:在交点处,s=j ω,同时也是闭环系统的特征根,必然符合闭环特征方程,于是有:()020********=++--=+++*=*K j j K s s sj s ωωωω整理得: 0203=-ωω;092=-*ωK 解得01=ω;203,2±=ω;18092==*ωK 最后,根据以上数据精确地画出根轨迹。
自动控制原理第四章

K
*
s p sz
j 1 i 1 m
n
i
j
绘制根轨迹时,只需要使用相角条件。 当需要确定根轨迹上各点的值时,才使用模值条件。
• 知道了根轨迹上的点满足的基本条件, 仍实际上还是不能绘制出根轨迹。
• 要比较快捷的绘制根轨迹,需要找 出根轨迹的一些基本规律。
§4.2 绘制根轨迹的基本规则
渐近线包括两个内容:
渐近线与实轴的夹角和渐近线与实轴的交点。
规则4:渐近线与实轴的交点为
sa
pi z j
i 1 j1
n
m
nm
渐近线与实轴的夹角为
180 0 90 (2k 1)180 a nm 180 ,60 45 ,135 n m 1 nm 2 nm 3 nm 4
第四章 系统的根轨迹法
系统的性能
稳定性
动态性能
闭 环即 特闭 征环 方极 程点 的 根
开环放大倍数 开环积分环节个数
稳态误差
困
难!
困难1:系统闭环特征方程的根如何求取!
困难2:讨论或预测当系统中的某一参数发生
变化时系统闭环特征方程的根如何变 化!
参数改变,系统性能如何改变!
开环传递函数(开环零极点+开环增益)
根轨迹法的任务就是由已知的开环零极点的分布及 根轨迹增益,通过图解法找出闭环极点。 根轨迹是系统所有闭环极点的集合。
闭环极点与开环零、极点之间的关系
闭环零点=前向通道零点+反馈通道极点
闭环极点与开环零点、开环极点及 K* 均有关
开环零极点和根轨迹增益
根轨迹图
闭环极点
分析系统
4、根轨迹方程
自动控制原理第4章

p 26.6
3
自动控制理论
14
4-2 根轨迹绘制的基本法则
八、根之和 若 n-m2 ,闭环极点之和 = 开环极点之和 = 常数
p ,
i 1 i i 1 i
n
n
nm2
表明:在某些根轨迹分支(闭环极点)向左移动,而 另一些根轨迹分支(闭环极点)必须向右移动,才能 维持闭环极点之和为常数。
1 G ( s) H ( s) 0 Q( s) AP( s), P( s) 1 A 0 1 G1 ( s) H1 ( s) Q( s ) P( s ) 等效开环传递函数 G1 ( s ) H1 ( s ) A Q( s)
注意:此等效意义是在特征方程相同,或者是闭环极点相 同的前提下成立;而此时闭环零点是不同的。
180o根轨迹
( s z ) ( s p ) (2k 1)
j 1 i 1
(2k 1)180, (k 0,1,2,)
一、根轨迹的起点和终点 根轨迹起始于开环极点,终止于开环零点。
简要证明如下:
由模值条件
1 * K
(s z
j 1 n i 1
解:开环传递函数有二个极点,一个零点,此类有零点的二 阶系统的根轨迹其复数部分为一个圆,圆心在开环零点处, 半径为零点到分离点的距离。
自动控制理论 21
4-4 系统的性能分析
此系统的分离点:
d1 1.17, d1 6.83
K 2
*
j
利用幅值条件可求得两个分离 点处的根轨迹增益
j 1 j i 1 i
(k 0,1,2,)
K*
s p sz
j 1 i 1 m
n
自动控制原理PrinciplesofAutomaticControl

第4章 根轨迹法
由上述两式可见,幅值条件与k有关,而 相角条件与k无关。因此,把满足相角条件 的值代入到幅值条件中,一定能求得一个 与之相对应的k值。这就是说,相角条件是 确定s平面上的根轨迹的充分必要条件。换 言之,凡是满足相角条件的点必然也同时满 足幅值条件,反之,满足幅值条件的点未必都 能满足相角条件.
n
m
(s pl ) K (s zi ) 0
l 1
i 1
1
K
n
(s pl )
l 1
m
(s zi ) 0
i 1
当 K 时,它将蜕化成为m次方程,而m≤n。
m
(s zi ) 0
i 1
通常m < n , 还有n-m 条根轨迹终止在什么地方?
自动控制原理
第4章 根轨迹法
我们在上式中做置换,令 s 1
自动控制原理
第4章 根轨迹法
规则2 根轨迹的分支数、起点和终点
根轨迹的分支数等于开环极点数目与开环零点数目 大者。
系统的开环传递函数
G(s)H (s)
K (s z1 )(s z2 )(s zm ) (s p1 )(s p2 )(s pn )
系统的闭环传递函数
n
m
(s pl ) K(s zi ) 0
根据上式,用试探法寻求s平面上满足相角条件的点。
1) 在正实轴上任取一试验点 s1,如图4-4(a)所示,由 于 arg s1 0,arg(s1 1) 0 ,因 而该点不满足根轨迹的相角 条件。由此可知,在正实轴 上不存在系统的根轨迹。
自动控制原理
2)在(0,–1)间的实轴上
任取一试验点s2,如图4-
!绘制注意点 1)实轴、虚轴相同的刻度
精品文档-自动控制原理(第二版)(千博)-第4章

其中一条
根轨迹终止于开环零点, 即-1/τ, 另一条终止于无穷远处。
其根轨迹图如图4-5所示。
21
图 4-5 例 4-3系统的根轨迹
22
四、实轴上的根轨迹(法则四) 在坐标轴上向右看去,实轴上凡有奇数个零点和极点的区
段就是根轨迹的一部分。即实轴上根轨迹区段的右侧, 实数 零点和实数极点数目之和应为奇数。
解出s1=-0.423, s2=-1.578(舍去)。 即s1为此系统的分离点。
49
例4-6 已知D(s)=s(s+2)+K*(s+4)=0, 求闭环系统根轨迹 的分离点和会合点。
解因
所以
50
[方法一] 按式(4-10)先写出D=s(s+2), 则D′=2s+2、 N=s+4, 则N′=1, 将D、D′、N、N′代入式(4-10)中,得
(1) 渐近线的条数(分支数), 有n-m条。
25
(2) 渐近线的夹角ja。假设在无穷远处有特征根sk, 则s 平面上所有开环有限零点zi和极点pj的向量相角都相等, 即 ∠(sk-zi)=∠(sk-pj)=ja, 用它代入相角条件式(4-6), 得
26
所以渐近线的夹角为 (4-7)
当k=0时, 渐近线的夹角最小, k增大时, 夹角值重复出现, 所以独立的渐近线只有n-m条。
则有(n-m)条根轨迹终止于无穷远处。 将式(4-5)左边取极限, 得
18
例 4-3 已知单位反馈控制系统的开环传递函数为 试确定根轨迹的分支数及起点、终点。
19
解 将开环传递函数改写成 式中,
20
开环传递函数分母多项式的最高阶次n=2, 故根轨迹的分
支数为2(即有两条根轨迹)。
胡寿松自动控制原理习题解答第四章
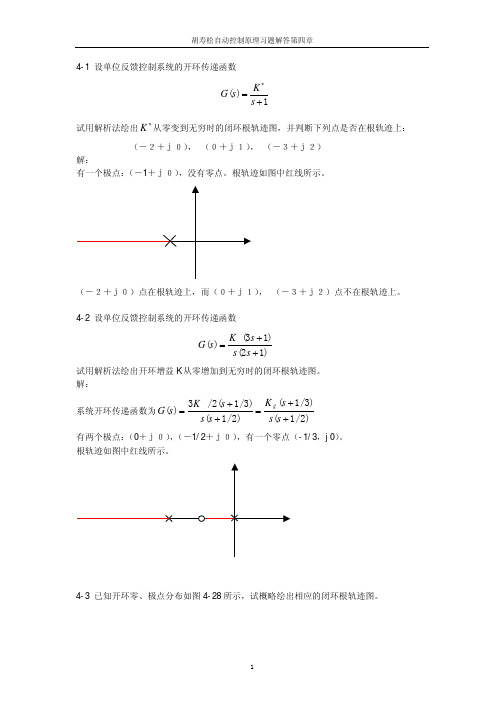
4-1 设单位反馈控制系统的开环传递函数 1)(+=∗s K s G试用解析法绘出∗K 从零变到无穷时的闭环根轨迹图,并判断下列点是否在根轨迹上: (-2+j0), (0+j1), (-3+j2) 解:有一个极点:(-1+j0),没有零点。
根轨迹如图中红线所示。
(-2+j0)点在根轨迹上,而(0+j1), (-3+j2)点不在根轨迹上。
4-2 设单位反馈控制系统的开环传递函数 )12()13()(++=s s s K s G 试用解析法绘出开环增益K 从零增加到无穷时的闭环根轨迹图。
解:系统开环传递函数为)2/1()3/1()2/1()3/1(2/3)(++=++=s s s K s s s K s g G 有两个极点:(0+j0),(-1/2+j0),有一个零点(-1/3,j0)。
根轨迹如图中红线所示。
4-3 已知开环零、极点分布如图4-28所示,试概略绘出相应的闭环根轨迹图。
图4-28 开环零、极点分布图4-4 设单位反馈控制系统开环传递函数如下,试概略绘出相应的闭环根轨迹图(要求确定分离点坐标d): (1) )15.0)(12.0()(++=s s s Ks G解:系统开环传递函数为)2)(5()2)(5(10)(++=++=s s s K s s s Ks g G 有三个极点:(0+j0),(-2+j0),(-5+j0)没有零点。
分离点坐标计算如下:051211=++++d d d 3解方程的010142=++d d 7863.31−=d ,d 88.02−=取分离点为88.0−=d根轨迹如图中红线所示。
(2) )12()1()(++=s s s K s G解:系统开环传递函数为)5.0()1()5.0()1(2/)(++=++=s s s K s s s K s g G有两个极点:(0+j0),(-0.5+j0),有一个零点(-1+j0)。
分离点坐标计算如下:115.011+=++d d d 解方程的05.022=++d d 7.11−=d ,d 29.02−=取分离点为7.11−=d ,29.02−=d 根轨迹如图中红线所示。
自控第四章

(4-7)
K 式中:
* H
为反馈通道的根轨迹增益。
* * G ( s) H ( s) K G K H
( s z ) ( s z
i 1 q i j 1 l i 1 i i 1
f
l
j
) )
(4-8)
( s p ) ( s p
j
j
K*
( s z ) ( s z
• 闭环特征方程 D(s)=1+G(s)H(s)=0 (4-11) 闭环极点就是闭环特征方程的解,也称为特征 根。 • 根轨迹方程 G(s)H(s)=-1 (4-12) 式中G(s)H(s)是系统开环传递函数,该式明确表 示出开环传递函数与闭环极点的关系。
设开环传递函数有m个零点,n个极点,并假 定n≥m,这时式(4-12)又可以写成:
最后绘制出根轨迹如图4-7所示。
图4-7
例4-3根轨迹
五、根轨迹的渐近线
渐近线与实轴正方向的夹角为
(2k 1) π a nm
渐近线与实轴相交点的坐标为
a
p z
i 1 i j 1
n
m
j
nm
例4-4 已知系统的开环传递函数
K * ( s 1) G ( s) H ( s) s ( s 4)( s 2 2 s 2)
•根轨迹法可以在已知开环零、极点时,迅速求
出开环增益(或其他参数)从零变到无穷时闭环 特征方程所有根在复平面上的分布,即根轨迹。
4-2 绘制根轨迹的基本法则 一、根轨迹的分支数
分支数=开环极点数 =开环特征方程的阶数
即为max(n,m)条。
二、根轨迹的连续性与对称性 根轨迹是连续曲线,对称于实轴
广西大学自动控制原理习题答案(本科)第4章

习题参考答案4-1已知单位反馈系统的开环传递函数为2()(0.21)K G s s s =+试求:⑴使系统增益裕度为10的K 值;⑵使系统相角裕度为30︒的K 值。
解:系统开环频率特性为2)(+=ωωωK i G (1)求10=m g 的K 值:令180ω为相角交越频率,有180arctan 0.245ω=︒,5180=ω由10)04.01(|)(|12180180180=+==K i G g m ωωω可解得K=1。
(2)求30m ϕ=︒的K 值:由定义180()180(902arctan 0.2)30m c c G i ϕωω=︒+∠=︒+-︒-=︒︒=302.0arctan c ω求得系统幅值交越频率c ω=由1)04.01(|)(|2=+=c c c Ki G ωωω85.3)04.01(2=+=c c K ωω注意:涉及相角的计算时,可以(1)逐个计算基本环节的相角,然后叠加起来。
(2)将频率特性展开为实部和虚部,然后计算相角。
计算幅值一般将各个基本环节的幅值相乘。
4-2试由幅相频率计算式()90arg tan arg tanarg tan103(5)2G i G i ωωωω∠=-︒-+-=确定最小相位系统的传递函数。
解:由相频计算式可得出传递函数的形式为(/31)()(1)(101)K s G s s s s +=++由幅频计算式(5)2G i =有2=求得10/3K ω==,所求最小相位系统的传递函数为1312(/31)()(1)(101)s G s s s s +=++4-3已知单位反馈系统开环传递函数)2)(5.1)(1()(+++=s s s Ks G 若希望系统闭环极点都具有小于-1的实部,试用Nyquist 判据确定增益K 的最大值。
解:令1u s =+,则“u 平面所有极点均处于负平面”等价于“s 平面所有闭环极点均具有小于-1的实部”,并且)1)(5.0()(++=u u u Ku G 可见)(u G 并无右半平面的开环极点,所以)(u G 的Nyquist 轨线不能包围)0,1(i -点。
朱玉华自动控制原理第4章 根轨迹复习4-1,2,3
第四章 根轨迹法
例题1,某控制系统的开环传递函数为 G(s)H (s) K 试画出实轴上的根轨迹和s→∞时的渐进线。 s(s 1)(s 4)
解:(1)在图上标出开环函数 极点p1=0,p2=-1,p3=-4
(2)在实轴上(-1,0)和(-∞,-4)区间之右的实数零、极 点数之和为奇数,故这两个区间的实轴是根轨迹。
l 1
i 1
n
(s pi )
K
i 1 m
(s zl )
l 1
考虑到 1 e j(2K 1),K 0,1,2
所以,幅值条件为:
n
(s pi )
相角条件为:
K i1 m (s zl )
l 1
m
n
(s zl ) (s pi ) (2k 1),K 0,1,2
l 1
i 1
第四章 根轨迹法
第四章 根轨迹法
课程回顾(1)
• 根轨迹:系统某一参数由 0 → ∞ 变化时,系统闭环极 点在s平面相应变化所描绘出来的轨迹 • 闭环极点 与开环零点、开环极点及 K* 均有关
• 闭环零点 = 前向通道零点 + 反馈通道极点
• 根轨迹方程 幅值条件:
相角条件:
• 根轨迹增益
第四章 根轨迹法
课程回顾(2)
按相角条件绘制根轨迹的具体方法:
(1)在复平面上标出开环极点和开环零点
G(s)H (s)
K (s z1)
(s p1)(s p2 )(s p3 )(s p4 )
(2)在复平面上任取一试验点S,画出由开环零点和开环
极点至S的矢量。
第四章 根轨迹法
(3)标出各开环 零、极点至实验 点的幅角
根据规则1)和2),根轨
自动控制原理课后答案第4章

5
的不同,系统的稳定性和动态性能不一定能同时得到满足。因此,只有当附加开环零点的位 置选配得当,才有可能使系统的稳态性能和动态性能同时得到显著改善。 ② 增加开环极点 增加开环极点后,系统阶次升高,渐近线数量增加,使得渐近线与实轴的夹角变小,从 而导致根轨迹向右弯曲,致使系统不稳定成分增加。同时,实轴上的分离点也向右移动。系 统响应减缓,过渡过程延长,调节时间增加,系统的稳定性降低。当增加的极点在[-1,0]范 围内时,越靠近虚轴的极点,其产生的阶跃响应振荡越剧烈,稳定性越差;而当增加的极点 在(-∞, -1)范围内时,越远离虚轴的极点,对根轨迹的影响越小,从而对系统的动态性能影 响越小。
式中,A(s)为开环传递函数的分母多项式,B(s)为开环传递函数的分子多项式。则分离点或 会合点坐标可用下式确定,即 A( s) B '( s ) A '( s ) B ( s ) 0 3)极值法
dK 0 ds
规则 7:根轨迹的出射角和入射角 根轨迹的出射角是指根轨迹离开开环复数极点处的切线与实轴正方向的夹角,如图 4-2 中的角 p1 ; 而根轨迹的入射角是指根轨迹进入开环复数零点处的切线与实轴正方向的夹角, 如图 4-2 中的角 z1 。
n n
n l
m
s
l 1
n
(1) n pi (1) m K z j
i 1
n
j 1
( 1)
n
s
l 1
l
(1)
nLeabharlann pi 1i
K (系统无开环零点时)
5、根轨迹与系统性能之间的关系 根轨迹可以直观地反映闭环系统特征根在[s]平面上的位置以及变化情况,所以利用根轨 迹可以很容易了解系统的稳定性和动态性能。除此之外,由于根轨迹上的任意一点都有与之对 应的开环增益值,而开环增益又与系统稳态误差有一一对应的关系,因此通过根轨迹也可以 确定出系统的稳态误差,或者根据给定系统的稳态误差要求,来确定闭环极点位置的容许范 围。由此可以看出,根轨迹与系统性能之间有着比较密切的联系。
自动控制原理 第4章

我们知道,一个闭环系统开环传递函数的分子加分母就是该 系统闭环传递函数的特征方程,这样,由已知闭环系统的开 环传递函数确定其闭环极点分布,实际上就是解决系统特征 方程的求根问题。 1948 年,伊文思( W.R.Evans )根据反馈 系统中开、闭环传递函数间的内在联系,提出了求解闭环特 征方程根的比较简易的图解方法,称之为根轨迹法。因为根 轨迹法直观形象,使用简单,所以在控制工程中获得了广泛 应用。
当 K =0.5 时,两个闭环极点均为 -1 ,闭环特征根为二 重实根,系统为临界阻尼,单位阶跃响应仍为单调上升的非 周期过程,但比上述情况稍快;
当 K >0.5 时,闭环极点为共轭复数,系统为欠阻尼振 荡,阶跃响应为衰减振荡过程,且超调量正比于 K 值。
分析表明,根轨迹与系统性能之间有着密切的联系,利 用根轨迹可以分析当系统参数增大时系统动态性能的变化趋 势。然而,对于高阶系统,用解析方法绘制系统根轨迹图显 然是不适用的,我们希望能有简便的图解方法。因为开环传 递函数相对容易得到,因此要求能够根据已知的开环传递函 数迅速绘出闭环系统的根轨迹。为此,需要研究开环零、极 点与闭环系统的根轨迹之间的关系。
第四章 控制系统的根轨迹法
4.1 根轨迹的基本概念 4.2 常规根轨迹的绘制法则 4.3 广义根轨迹 4.4 根轨迹系统性能分析 习题四
本章主要讲述根轨迹的概念、 绘制常规根轨迹的基本 法则、 广义根轨迹以及根轨迹系统性能分析等。
4. 1 根轨迹的基本概念
从第三章分析可知,一个系统可以通过找出其闭环极点 来分析系统的稳定性情况,而系统的稳态性能和动态性能又 与闭环零、极点在 s 平面上的位置密切相关。但对于高阶系 统,采用解析法求取系统的闭环特征方程根(闭环极点)通常 很困难,特别是在系统参数(如开环增益)发生变化时求根, 每变化一次都需要重新计算一次,因此解析法就显得很不 方便。
自动控制原理第4章

z2 ) p2 )
m
sm z j n1
i 1
(s zm )
(s pn )
m
(zj)
j 1
n
( pi )
i 1
自动控制原理
第四章 复域分析法-根轨迹法
如果开环零、极点的数目满足n-m 2,则 闭环特征方程为
snnp isn 1 n( p i)K *m( zj) 0
证明:系统的闭环特征方程
n
m
D(s) (spi)K* (szj)0
i1
j1
根轨迹有分离点,说明闭环特征方程有重
根。因此,
n
m
(s pi ) K* (s zj ) 0
i1
j1
d
ds
n i1
(s
pi )
K*
m j1
(s zj )
0
自动控制原理
第四章 复域分析法-根轨迹法
将上面两式相除,整理得
自动控制原理
第四章 复域分析法-根轨迹法
4.1 根轨迹的基本概念
一、根轨迹的定义
根轨迹:是指系统开环传递函数中某个参数 (如开环增益K)从零变到无穷时,闭环特征 根在s平面上移动所画出的轨迹。
常规根轨迹:当变化的参数为开环增益时 所对应的根轨迹。
广义根轨迹:当变化的参数为开环传递函 数中其它参数时所对应的根轨迹。
自动控制原理
第四章 复域分析法-根轨迹法
证明: 由根轨迹方程,得
m
(s
j 1
n
(s
zj) pi )
1 K*
i1
令K* =0,得
m
j 1 n
(s (s
zj) pi )
1 K*
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.1 引言
根轨迹法
系统的稳定性
系统的闭环极点 系统的动态性能 系统闭环特征方程的根 高阶方程情形 下求解很困难
系统参数(如开环放大倍数)的变化会引起其 变化,针对每个不同参数值都求解一遍根很麻 烦。
1
系统参数的值 一一 对应 关系
闭环极点在复 平面内的位置
如开环放 大倍数 参数连续变化
闭环极点在复平面 内画出相应的轨迹
1
根轨迹的相角条件:
G(s)H (s) s z1 s z2 s p1 s p2 2l 1
s zm s pn
l 0,1,2,
6
举例
给定开环传递函数
k ( s z1 ) G( s) H ( s) ( s p1 )( s p2 )( s p3 )( s p4 ) 开环零点:z1
Re 1 G j H j 0 1 G j H j 0 Im
所确定。
22
[例4-6]
参数
求例4-1中根轨迹与虚轴交点的坐标及相应的 的值。
k
k G( s) H ( s) s( s 1)( s 2)
的根, 其中开环传递函数为
kM ( s ) G(s) H (s) N (s)
2i 1 ,i 0,1, 2, 相邻两条根轨迹间的夹角为 l 若 l 2 ,则相邻两条根轨迹间的夹角为 。
2
附加规则
l 条根轨迹进入并离开汇合分离点时,
17
[例4-3] 求例4-1中根轨迹的汇合分离点A的坐标。
n
其中,闭环系统的特征方程为
D(s) s an1s
n
n1
a1s a0 0
25
[例4-7]
在例4-1中,给定负反馈系统的开环
传递函数为
k G( s) H ( s) s( s 1)( s 2)
当根轨迹与虚轴相交时, 已知两个闭环极点为
s1,2 j 2 , 试确定这种情况下的第三个
k G( s) H ( s) s( s 1)( s 2)
[例4-4] 求例4-3中根轨迹的汇合分离点A和B的坐标。
k ( s 2) G( s) H ( s) s( s 1)
18
7
始于开环虚数极点的根轨迹的出射角为
m n
p (2l 1) ( p1 zi ) ( p1 p j )
m
i
nm
12
5 实轴右方开环零点和开环极点数目之和为奇数的 线段是根轨迹, 实轴右方开环零点和开环极点数目之和为偶数的 线段不是根轨迹。 [例4-1] 负反馈系统的开环传递函数为
k G( s) H ( s) s( s 1)( s 2)
绘制根轨迹的大致图形。
13
Im
p3
-2
p2
-1 A 0
1 把系统的开环传递函数写成零极点形式;
2 在s平面上画出开环零点和开环极点;
3
在s平面上找出满足幅角条件的点,再把这些点 连接成根轨迹;
4
对于根轨迹上的一些必要的点,利用幅值条件
求出它们所对应的 k 值, 还可以进一步求出对应
的开环放大倍数 K 的值。
10
4.3 绘制根轨迹的基本规则
1 根轨迹的分支数等于开环零点数目与开环极点数目 中的较大者。 2 根轨迹是连续的,并且是关于实轴对称的。
开环极点:p1 , p2 , p3 , p4
Im
p2
p4
z1
p10 p3
Re
7
复平面内的试验点: s
s
2 Im p2
4
p4
1
1
规定逆时 针幅角为 正,反之 为负。 Re
z1
3 p3
p10
若成立:
G(s)H (s) 1 1 2 3 4 2l 1
则说明点 s 在根轨迹上。
3 根轨迹起始于开环极点,终止于开环零点。
11
4
若开环极点数目 n大于开环零点数目m, 则当 k 时,有
n m 条渐近线。
2l 1 nm
n
n m 条根轨迹趋向于
渐近线与实轴的夹角为
l 0,1, 2,
渐近线与实轴交点的横坐标为
p z
j 1 j i 1
, zm , pn
开环零点 开环极点
特征方程写为:
k (s z1 )(s z2 ) ( s zm ) 1 ( s p1 )( s p2 ) ( s pn )
5
根轨迹的幅值条件:
G( s) H ( s)
k s z1 s z2 s p1 s p2
s zm s pn
特征方程:
1 G( s ) H ( s ) 0 G(s) H (s) 1
此方程的根即为闭环极点。
4
开环传递函数:
k ( s z1 )( s z2 ) ( s zm ) G( s) H ( s) ( s p1 )(s p2 ) (s pn )
z1 , z2 , p1 , p2 ,
闭环极点。
求该系统临界稳定时的开环放大倍数 K 。
26
[例4-8]
给定负反馈系统的开环传递函数
K G( s) H ( s) s(0.366s 1)(0.5s 2 s 1)
绘制该系统根轨迹的大致图形。
27
Im 2
p2
1
p4
-3
-2 -1
0 p1
-1 -2
1
Re
p3
28
[例4-9]
8
然后根据根轨迹的幅值条件求取相应的参数 k 值:
由: G(s) H (s)
k s z1 s p1 s p2 s p3 s p4 s z1
1
得:
k
s p1 s p2 s p3 s p4
反过来说, 当参数 k 取该值时,闭环极点就是上述
s 点。
9
绘制根轨迹的主要步骤
给定负反馈系统的开环传递函数
G( s) H ( s)
k s( s 4)( s 2 4s 20)
绘制该系统根轨迹的大致图形。
29
p3
4 Im
10
2
2.45
p2
-4 -3 -1
1
p1
0
-1 1 Re
-2
p4
-4
30
[例4-10]
给定负反馈系统的开环传递函数
k ( s 0.4) G(s) H (s) 2 s ( s 3.6)
p1
3
rad
ห้องสมุดไป่ตู้
1
Re
14
[例4-2] 负反馈系统的开环传递函数为
k ( s 2) G( s) H ( s) s( s 1)
绘制根轨迹的大致图形。
15
Im
z1
B -2
p2
-1 A
p1
0 Re
16
6
根轨迹的汇合分离点坐标 是方程
M (s) N (s) M (s) N (s) 0
20
[例4-5] 负反馈系统的开环传递函数为 k ( s 1) G (s) H ( s) 2 s 3s 3.25 出射角 绘制该系统的根轨迹。 206.60 Im 汇合分离点
p1
1
z1
-2.12 -2
p2
-1
0 -1
Re
21
8
根轨迹与虚轴的交点坐标 及对应的参数
k 的值, 由代数方程组
绘制该系统根轨迹的大致图形。
31
Im 2 1
三重根-1.2
p3
-3.6 -3
z1
-1.6
-1 -2
p1
1 Re
-0.4 p2
32
本次课内容总结
根轨迹的基本概念
根轨迹的幅值条件 根轨迹的相角条件
绘制根轨迹的基本规则
33
伊凡思(W.R.Evans)提出根轨迹法, 以方便系统设计和调试。
2
4.2 根轨迹的基本概念
根轨迹
系统中某个参数由0变化到 时, 闭环极点在s平面内画出的轨迹。
本章首先研究
开环放大倍数从0
时,闭环极点的轨迹,
称为一般根轨迹。
3
R( s )
G ( s)
-
Y ( s)
H (s)
Y ( s) G( s) ( s) 闭环传递函数: R( s) 1 G ( s) H ( s)
23
9
根轨迹上任意一点
s
对应的参数 k 的值可由
k
s p1 s p2 s z1 s z2
s pn s zm
计算, 并由下式求出开环放大倍数。
K k
z
i 1 n j v 1
m
i
p
v 0,1, 2
j
0,I,II型系统
24
10 所有闭环极点的总和等于 an 1 , 所有闭环极点的连乘积等于 1 a0 ,
1
i 1
j 2
终止于开环虚数零点的根轨迹的入射角为
z (2l 1) ( z1 p j ) ( z1 zi )
1
n
m
j 1
i 2
l 0,1, 2,
19
注意 以上两式只给出了 p1 和 z1 的出射角和入射角, 若计算其他开环虚数零、极点处的入射、出射角, 只要将该点的编号改为1即可。 绘制根轨迹时, 横、纵坐标的单位长度必须一致。 由根轨迹关于实轴对称的原则,只要求出一个 开环虚数零、极点的入射、出射角,则与之共轭 的开环虚数零、极点的入射、出射角即可推得。
