15工商第6组叶中荣第10次作业
2020高考数学理科大一轮复习课时作业:第九章 算法初步、统计、统计案例课时作业59

课时作业59 随机抽样一、选择题1.为了解某地区的中小学生的视力情况,拟从该地区的中小学生中抽取部分学生进行调查,事先已了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异,而男女生视力情况差异不大.在下面的抽样方法中,最合理的抽样方法是( C )A .简单随机抽样B .按性别分层抽样C .按学段分层抽样D .系统抽样解析:由分层抽样的定义知,合理的抽样方法是分层抽样,要按学段分层.故选C.2.从2 018名学生中选取50名学生参加全国数学联赛,若采用以下方法选取:先用简单随机抽样法从2 018名学生中剔除18名学生,剩下的2 000名学生再按系统抽样的方法抽取,则每名学生入选的概率( C )A .不全相等B .均不相等C .都相等,且为502 018D .都相等,且为140解析:从N 个个体中抽取M 个个体,则每个个体被抽到的概率都等于M N ,故每名学生入选的概率都相等,且为502 018.3.完成下列两项调查:①从某社区125户高收入家庭、280户中等收入家庭、95户低收入家庭中选出100户,调查社会购买能力的某项指标;②从某中学的15名艺术特长生中选出3名调查学习负担情况.宜采用的抽样方法依次是(B)A.①简单随机抽样,②系统抽样B.①分层抽样,②简单随机抽样C.①系统抽样,②分层抽样D.①②都用分层抽样解析:因为社会购买能力的某项指标受到家庭收入的影响,而社区中各个家庭收入差别明显,所以①用分层抽样法;从某中学的15名艺术特长生中选出3名调查学习负担情况,个体之间差别不大,且总体和样本容量较小,所以②用简单随机抽样法.4.从编号为01,02,…,49,50的50个个体中利用下面的随机数表选取5个个体,选取方法从随机数表第1行第5列的数开始由左到右依次抽取,则选出来的第5个个体的编号为(D)C.32 D.43解析:由题意知选定的第一个数为65(第1行的第5列和第6列),按由左到右选取两位数(大于50的跳过、重复的不选取),前5个个体编号为08,12,14,07,43.故选出来的第5个个体的编号为43.故选D.5.一支田径队共有运动员98人,其中女运动员42人,用分层抽样的方法抽取一个样本,每名运动员被抽到的概率都是27,则男运动员应抽取(B)A .18人B .16人C .14人D .12人解析:∵田径队共有运动员98人,其中女运动员有42人,∴男运动员有56人,∵每名运动员被抽到的概率都是27,∴男运动员应抽取56×27=16(人).故选B.6.某初级中学领导采用系统抽样方法,从该校预备年级全体800名学生中抽50名学生做牙齿健康检查.现将800名学生从1到800进行编号,求得间隔数k =80050=16,即每16人抽取一个人.在1~16中随机抽取一个数,如果抽到的是7,则从33~48这16个数中应取的数是( B )A .40B .39C .38D .37解析:由于系统抽样是等距抽样,由题设从33~48这16个数中应取的数是7+2×16=39.应选B.7.某校高三(1)班共有48人,学号依次为1,2,3,…,48,现用系统抽样的方法抽取一个容量为6的样本,已知学号为3,11,19,35,43的同学在样本中,则还有一个同学的学号应为( A )A .27B .26C .25D .24解析:根据系统抽样的规则——“等距离”抽取,则抽取的号码差相等,易知相邻两个学号之间的差为11-3=8,所以在19与35之间还有27.8.采用系统抽样方法从1 000人中抽取50人做问卷调查,将他们随机编号1,2,…,1 000.适当分组后在第一组采用简单随机抽样的方法抽到的号码为8.若抽到的50人中,编号落入区间[1,400]的人做问卷A ,编号落入区间[401,750]的人做问卷B ,其余的人做问卷C ,则抽到的人中,做问卷C 的人数为( A )A .12B .13C .14D .15解析:根据系统抽样的特点可知,所有做问卷调查的人的编号构成首项为8,公差d =1 00050=20的等差数列{a n },∴通项公式a n =8+20(n -1)=20n -12,令751≤20n -12≤1 000,得76320≤n ≤2535,又∵n ∈N *,∴39≤n ≤50,∴做问卷C 的共有12人.二、填空题9.某商场有四类食品,食品类别和种数见下表:层抽样方法抽取样本,则抽取的植物油类与果蔬类食品种数之和为6.解析:因为总体的个数为40+10+30+20=100,所以根据分层抽样的定义可知,抽取的植物油类食品种数为10100×20=2,抽取的果蔬类食品种数为20100×20=4,所以抽取的植物油类与果蔬类食品种数之和为2+4=6.10.某市教育主管部门为了全面了解2019届高三学生的学习情况,决定对该市参加2018年高三第一次全国大联考统考(后称统考)的32所学校进行抽样调查,将参加统考的32所学校进行编号,依次为1到32,现用系统抽样的方法抽取8所学校进行调查,若抽到的最大编号为31,则最小的编号是3.解析:根据系统抽样法,将总体分成8组,组距为328=4,若抽到的最大编号为31,则最小的编号是31-4×7=3.11.某高中共有学生2 000名,已知在全校学生中随机抽取1名,抽到高三年级男生的概率是0.1,现用分层抽样的方法在全校抽取若干名学生参加社区服务,相关信息如下表:=25.解析:可得b =200,设在全校抽取n 名学生参加社区服务,则有n 2 000=10200+200.∴n =50.∴x =50-15-10=25.12.某企业三个分厂生产同一种电子产品,三个分厂产量分布如图所示.现在用分层抽样方法从三个分厂生产的产品中共抽取100件做使用寿命的测试,则第一分厂应抽取的产品件数为50.由所得样品的测试结果计算出一、二、三分厂取出的产品的使用寿命平均值分别为1 020小时、980小时、1 030小时,估计这个企业所生产的该产品的平均使用寿命为1_015小时.解析:第一分厂应抽取的产品件数为100×50%=50.该产品的平均使用寿命为1 020×0.5+980×0.2+1 030×0.3=1 015(小时).13.某工厂在12月份共生产了3 600双皮靴,在出厂前要检查这批产品的质量,决定采用分层抽样的方法进行抽取,若从一、二、三车间抽取的产品数分别为a,b,c,且a,b,c构成等差数列,则第二车间生产的产品数为(C)A.800双B.1 000双C.1 200双D.1 500双解析:因为a,b,c成等差数列,所以2b=a+c,即第二车间抽取的产品数占抽样产品总数的三分之一,根据分层抽样的性质可知,第二车间生产的产品数占12月份生产总数的三分之一,即为1 200双皮靴.14.一个总体中有100个个体,随机编号为0,1,2,…,99.依编号顺序平均分成10个小组,组号依次为1,2,3,…,10.现用系统抽样方法抽取一个容量为10的样本,如果在第一组随机抽取的号码为m,那么在第k组中抽取的号码个位数字与m+k的个位数字相同.若m =6,则在第7组中抽取的号码是(A)A.63 B.64C.65 D.66解析:若m=6,则在第7组中抽取的号码个位数字与13的个位数字相同,而第7组中的编号依次为60,61,62,63,…,69,故在第7组中抽取的号码是63.尖子生小题库——供重点班学生使用,普通班学生慎用15.已知某居民小区户主人数和户主对户型结构的满意率分别如图1和图2所示,为了解该小区户主对户型结构的满意程度,用分层抽样的方法抽取20%的户主进行调查,则样本容量和抽取的户主对四居室满意的人数分别为(A)A.100,8 B.80,20C.100,20 D.80,8解析:由题设及扇形统计图可知样本容量是100,其中对四居室满意的人数为20%×100×40%=8.故选A.16.为了解某市市民晚饭后1小时内的生活方式,调查小组设计了“阅读”“锻炼”“看电视”和“其他”四个选项,用随机抽样的方法调查了该市部分市民,并根据调查结果绘制成统计图如图所示.根据统计图所提供的信息,解答下列问题:(1)本次共调查了2_000名市民.(2)补全条形统计图.(3)该市共有480万市民,估计该市市民晚饭后1小时内“锻炼”的人数.解:(2)晚饭后选择“其他”的人数为2 000×28%=560,晚饭后选择“锻炼”的人数为2 000-800-240-560=400.将条形统计图补充完整,如图所示.(3)晚饭后选择“锻炼”的人数所占的比例为:400÷2 000=20%,该市市民晚饭后1小时内锻炼的人数为:480×20%=96(万).答:该市共有480万市民,估计该市市民晚饭后1小时内“锻炼”的人数为96万.感谢您的下载!快乐分享,知识无限!由Ruize收集整理!。
数理统计(汪荣鑫版)习题答案详细版

所以
X1 + X 2 + X3 N (0,1)
3
X1
+
X2 3
+
X3
2
χ 2 (1)
同理
X4
+
X5 3
+
X
6
2
χ 2 (1)
由于 χ2 分布的可加性,故
D X1 + X2 + X3 =1 3
1Y 3
=
X1
+
X2 3
+
X3
2
+
X4
+
X5 3
+
X6
2
可知
C=1
3
16. 解:(1)因为 ( ) Xi N 0,σ 2
题的结果可知
x = 2000 + y = 2240.444
sx2
=
s
2 y
= 197032.247
5. 解:变换
yi = 100( xi − 80)
i
1
2
3
4
5
6
7
8
9 10 11 12 13
xi 79.98 80.04 80.02 80.04 80.03 80.03 80.04 79.97 80.05 80.03 80.02 80.00 80.02
y
∫ FY4
( y) =
P {Y4
≤
y} =
P σY42
≤
y σ2
=
σ2 0
fχ2(1) ( x)dx
fχ2
(y) =
F' Y4
(y) =
y fχ2 (1) σ 2
2021-2022年高中数学第二章统计2.1.2系统抽样课后提升作业含解析新人教A版

2021-2022年高中数学第二章统计2.1.2系统抽样课后提升作业含解析新人教A版一、选择题(每小题5分,共40分)1.某市场想通过检查发票及销售记录的2%来快速估计每月的销量总额.采取如下方法:从某本发票的存根中随机抽一张,如15号,然后按顺序往后将65号,115号,165号,…抽出,发票上的销售额组成一个调查样本.这种抽取样本的方法是( )A.抽签法B.随机数法C.系统抽样法D.其他的抽样方法【解析】选C. 上述抽样方法是将发票平均分成若干组,每组50张,从第一组中抽取15号,以后各组抽取15+50n(n∈N)号,符合系统抽样的特点.2.为了解1 000名学生的学习情况,采用系统抽样的方法,从中抽取容量为40的样本,则分段的间隔为( )A.50B.40C.25D.20【解题指南】分段的间隔等于样本空间总数除以抽取容量.【解析】选C.分段的间隔为1 000÷40=25.3.(xx·菏泽高一检测)中央电视台“动画城节目”为了对本周的热心小观众给予奖励,要从已确定编号的一万名小观众中抽出十名幸运小观众.现采用系统抽样的方法抽取,每组容量为( )A.10B.100C.1 000D.10 000【解析】选C.由N=10 000,n=10,故间隔k==1 000,即每组容量为1 000.4.从2 004名学生中选取50名组成参观团,若采用下面的方法选取:先利用简单随机抽样从2 004人中剔除4人,剩下的2 000人再按系统抽样的方法进行,则每人入选的机会( )A.不会相等B.均不相等C.都相等D.无法确定【解析】选C.系统抽样为等可能抽样,每人入样的机率均为5.(xx·烟台高一检测)为了了解参加某次知识竞赛的1 252名学生的成绩,决定采用系统抽样的方法抽取一个容量为50的样本,那么从总体中应随机剔除的个体数目为( )A.2B.3C.4D.5【解析】选A.因为1 252=50×25+2,所以应随机剔除2个个体.6.(xx·广州高一检测)人们打桥牌时,将洗好的扑克牌(52张)随机确定一张为起始牌,这时,开始按次序发牌,对任何一家来说,都是从52张总体中抽取一个13张的样本.问这种抽样方法是( )A.系统抽样B.分层抽样C.简单随机抽样D.非以上三种抽样方法【解析】选A.简单随机抽样的实质是逐个地从总体中随机抽取.而这里只是随机地确定了起始牌,这时其他各张虽然是逐张发牌的,但其实各张在谁手里已被确定了,所以不是简单随机抽样,据其“等距”发牌的特点,应将其归纳为系统抽样.逐张随机抽取与随机确定一张为起始牌后逐张发牌不是一回事.本题的关键是只要抓住“等距”的特点就不难确定是属于哪类抽样.7.(xx·石家庄高一检测)某班有学生60人,现将所有学生按1,2,3,…,60随机编号,若采用系统抽样的方法抽取一个容量为5的样本(等距抽样),已知编号为4,a,28,b,52号学生在样本中,则a+b=( )A.52B.56C.45D.42【解析】选 B.因为样本容量为5,所以样本间隔为60÷5=12,因为编号为4,a,28,b,52号学生在样本中,所以a=16,b=40,所以a+b=56.【补偿训练】学校为了了解某企业1 203名职工对公司餐厅建设的意见,打算从中抽取一个容量为x的样本,已知用系统抽样且分段的间隔为30,则x=( ) A.40 B.30.1 C.30 D.12【解析】选A.了解1 203名职工对公司餐厅建设的意见,且用系统抽样,且分段间隔为30,故有30x=1 203.又1 203不能被30整除,所以先剔除3人,故有30x=1 200,x=40.8.将夏令营的600名学生编号为:001,002,…,600.采用系统抽样方法抽取一个容量为50的样本,且随机抽得的号码为003.这600名学生分住在三个营区,从001到300在第Ⅰ营区,从301到495在第Ⅱ营区,从496到600在第Ⅲ营区,三个营区被抽中的人数依次为( )A.26,16,8B.25,17,8C.25,16,9D.24,17,9【解题指南】依据题设条件,先计算出各段上学生的号码,然后再依据各营区的人数及所对应的号码即可求解.【解析】选B.依题意及系统抽样的意义可知,将这600名学生按编号依次分成50组,每组有12名学生,第k(k∈N*)组抽中的号码是3+12(k-1).令3+12(k-1)≤300得k≤,因此第Ⅰ营区被抽中的人数是25;令300<3+12(k-1)≤495得<k≤42,因此第Ⅱ营区被抽中的人数是42-25=17.从而第Ⅲ营区被抽中的人数是50-42=8.二、填空题(每小题5分,共10分)9.(xx·天水高一检测)若总体中含有1 645个个体,按0 001至1 645进行编号,采用系统抽样的方法从中抽取容量为35的样本,则编号后确定编号分为_____段,分段间隔k=_____,每段有____个个体.若第5段抽取的号码为190,则第1段应抽取的号码为________.【解析】因为N=1 645,n=35,则编号后确定编号分为35段,且k==47,则分段间隔k=47,每段有47个个体.设第1段应抽取的号码为x,则190=x+(5-1)×47,解得x=2.答案:35 47 47 210.(xx·锦州高一检测)从编号为001,002,…,800的800个产品中用系统抽样的方法抽取一个样本,已知样本中最小的两个编号分别为008,033,则样本中最大的编号应该是______.【解析】因为样本中编号最小的两个编号分别为008,033,所以样本数据组距为33-8=25,则样本容量为=32,则对应的号码数x=8+25(n-1),当n=32时,x取得最大值为x=8+25×31=783.答案:783三、解答题11.(10分)(xx·长春高一检测) 某集团有员工1 019人,其中获得过国家级表彰的有29人,其他人员990人.该集团拟组织一次出国学习,参加人员确定为:获得过国家级表彰的人员5人,其他人员30人.如何确定人选?【解析】获得过国家级表彰的人员选5人,适宜使用抽签法;其他人员选30人,适宜使用系统抽样法.(1)确定获得过国家级表彰的人员人选:①用随机方式给29人编号,号码为1,2, (29)②将这29个号码分别写在一张小纸条上,揉成小球,制成号签;③将得到的号签放入一个不透明的袋子中,搅拌均匀;④从袋子中逐个抽取5个号签,并记录上面的号码;⑤从总体中将与抽取的号签的号码相一致的个体取出,人选就确定了.(2)确定其他人员人选:第一步:将990个其他人员重新编号(分别为1,2,…,990),并分成30段,每段33人;第二步,在第一段1,2,…,33这33个编号中用简单随机抽样法抽出一个(如3)作为起始号码;第三步,将编号为3,36,69,…,960的个体抽出,人选就确定了.(1)、(2)确定的人选合在一起就是最终确定的人选.【补偿训练】一个总体中的1 000个个体编号为0,1,2,…,999,并依次将其分为10个小组,组号为0,1,2,…,9.要用系统抽样方法抽取一个容量为10的样本,规定如果在第0组随机抽取的号码为x,那么依次错位地得到后面各组的号码,即第k组中抽取的号码的后两位数为x+33k的后两位数.(1)当x=24时,写出所抽取样本的10个号码.(2)若所抽取样本的10个号码中有一个的后两位数是87,求x的取值范围.【解析】 (1)当x=24时,按规则可知所抽取样本的10个号码依次为:24,157,290,323,456,589,622,755,888,921.(2)当k=0,1,2,…,9时,33k的值依次为0,33,66,99,132,165,198,231, 264,297.又抽取样本的10个号码中有一个的后两位数是87,从而x可以为87,54, 21,88,55,22,89,56,23,90.所以x的取值范围是{21,22,23,54,55,56,87,88,89,90}.21106 5272 割37542 92A6 銦37627 92FB 鋻 @.31823 7C4F 籏23701 5C95 岕(s' 32716 7FCC 翌。
人教版高中数学必修二《第九章 统计》课后作业及答案解析

人教高中数学必修二《第九章统计》课后作业《9.1.1 简单随机抽样》课后作业基础巩固1.用简单随机抽样的方法从含有10个个体的总体中抽取一个容量为3的样本,其中某一个体a“第一次被抽到”的可能性与“第二次被抽到”的可能性分别是()A.110,110B.310,15C.15,310D.310,3102.《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为()A.0.5B.0.6C.0.7D.0.83.总体由编号01,,02,…,19,20的20个个体组成.利用下面的随机数表选取5个个体,选取方法是随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为A.08 B.07 C.02 D.014.下面抽样方法是简单随机抽样的是( )A.从平面直角坐标系中抽取5个点作为样本B.可口可乐公司从仓库中的1 000箱可乐中一次性抽取20箱进行质量检查C.某连队从200名战士中,挑选出50名最优秀的战士去参加抢险救灾活动D.从10个手机中逐个不放回地随机抽取2个进行质量检验(假设10个手机已编好) 5.为了了解某班学生的身高情况,决定从50名学生(已编号为00~49)中选取10名进行测量,利用随机数法进行抽取,得到如下4组编号,则正确的编号是()A.26,94,29,27,43,99,55,19,81,06 B.20,26,31,40,24,36,19,34,03,48C .02,38,22,41,38,24,49,44,03,11D .04,00,45,32,44,22,04,11,08,496.采用抽签法从含有3个个体的总体{}138,,中抽取一个容量为2的样本,则所有可能的样本为______.7.总体由编号为01,02,…,19,20的20个个体组成,利用下面的随机数表选取5个个体,选取方法是从随机数表第1行第5列的数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为_________.8.某单位拟从40名员工中选1人赠送电影票,可采用下面两种选法:选法一:将这40名员工按1~40进行编号,并相应地制作号码为1〜40的40个号签,把这40个号签放在一个暗箱中搅匀,最后随机地从中抽取1个号签,与这个号签编号一致的员工幸运入选;选法二:将39个白球与1个红球(球除颜色外,其他完全相同)混合放在一个暗箱中搅匀,让40名员工逐一从中摸取一个球,则摸到红球的员工幸运入选.试问:(1)这两种选法是否都是抽签法,为什么?(2)这两种选法中每名员工被选中的可能性是否相等?能力提升9.随机抽取某商场4月份5天的营业额(单位:万元)分别为3.4,2.9,3.0,3.1,2.6,则这个商场4月份的营业额大约是( )A .90万元B .450万元C .3万元D .15万元10.在容量为100的总体中用随机数表法抽取5个样本,总体编号为0001,0299,,,,给出下列几组号码:①00,01,02,03,04;②10,30,50,70,90;③49,19,46,04,67;④11,22,33,44,55.则可能成为所得样本编号的是________(填相应序号).11.选择合适的抽样方法抽样,写出抽样过程.(1)现有一批电子元件600个,从中抽取6个进行质量检测;(2)有甲厂生产的30个篮球,其中一箱21个,另一箱9个,抽取3个入样.素养达成12.某些商家为消费者提供免费塑料袋,使购物消费更加方便快捷,但是我们更应关注它对环境的潜在危害.为了解某市所有家庭每年丢弃塑料袋个数的情况,统计人员采用了科学的方法,随机抽取了200户,对他们某日丢弃塑料袋的个数进行了统计,结果如下表:(1)求当日这200户家庭平均每户丢弃塑料袋的个数;(2)假设某市现有家庭100万户,据此估计全市所有家庭每年(以365天计算)丟弃塑料袋的总数.《9.1.1 简单随机抽样》课后作业答案解析基础巩固1.用简单随机抽样的方法从含有10个个体的总体中抽取一个容量为3的样本,其中某一个体a“第一次被抽到”的可能性与“第二次被抽到”的可能性分别是()A.110,110B.310,15C.15,310D.310,310【答案】A【解析】在抽样过程中,个体a每一次被抽中的概率是相等的,因为总体容量为10,故个体a“第一次被抽到”的可能性与“第二次被抽到”的可能性均为1 10.故选A.2.《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为()A.0.5B.0.6C.0.7D.0.8【答案】C【解析】由题意得,阅读过《西游记》的学生人数为90-80+60=70,则其与该校学生人数之比为70÷100=0.7.故选C.3.总体由编号01,,02,…,19,20的20个个体组成.利用下面的随机数表选取5个个体,选取方法是随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为A.08 B.07 C.02 D.01【答案】D【解析】从第一行的第5列和第6列起由左向右读数划去大于20的数分别为:08,02,14,07,01,所以第5个个体是01,选D.4.下面抽样方法是简单随机抽样的是( )A.从平面直角坐标系中抽取5个点作为样本B.可口可乐公司从仓库中的1 000箱可乐中一次性抽取20箱进行质量检查C.某连队从200名战士中,挑选出50名最优秀的战士去参加抢险救灾活动D.从10个手机中逐个不放回地随机抽取2个进行质量检验(假设10个手机已编好) 【答案】D【解析】A中平面直角坐标系中有无数个点,这与要求总体中的个体数有限不相符,故错误;B中一次性抽取不符合简单随机抽样逐个抽取的特点,故错误;C中50名战士是最优秀的,不符合简单随机抽样的等可能性,故错误.故选D5.为了了解某班学生的身高情况,决定从50名学生(已编号为00~49)中选取10名进行测量,利用随机数法进行抽取,得到如下4组编号,则正确的编号是()A.26,94,29,27,43,99,55,19,81,06 B.20,26,31,40,24,36,19,34,03,48C.02,38,22,41,38,24,49,44,03,11 D.04,00,45,32,44,22,04,11,08,49【答案】B【解析】对于选项A :有不在00~49内的编号,故选项A 排除;选项C ,D 中都有重复的编号,故选项C 和D 排除;故选: B6.采用抽签法从含有3个个体的总体{}138,,中抽取一个容量为2的样本,则所有可能的样本为______.【答案】{}1,3,{}1,8,{}38, 【解析】从总体中任取两个个体即可组成样本,即所有可能的样本为{}1,3,{}1,8,{}38,. 故答案为:{}1,3,{}1,8,{}38, 7.总体由编号为01,02,…,19,20的20个个体组成,利用下面的随机数表选取5个个体,选取方法是从随机数表第1行第5列的数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为_________.【答案】01【解析】选取的数据依次为08,02,14,07,01,所以选出来的第5个个体的编号为018.某单位拟从40名员工中选1人赠送电影票,可采用下面两种选法:选法一:将这40名员工按1~40进行编号,并相应地制作号码为1〜40的40个号签,把这40个号签放在一个暗箱中搅匀,最后随机地从中抽取1个号签,与这个号签编号一致的员工幸运入选;选法二:将39个白球与1个红球(球除颜色外,其他完全相同)混合放在一个暗箱中搅匀,让40名员工逐一从中摸取一个球,则摸到红球的员工幸运入选.试问:(1)这两种选法是否都是抽签法,为什么?(2)这两种选法中每名员工被选中的可能性是否相等?【答案】(1)见解析;(2)这两种选法中每名员工被选中的可能性相等,均为140. 【解析】(1)选法一:满足抽签法的特征,是抽签法;选法二:不是抽签法抽签法要求所有的号签编号互不相同,而选法二中的39个白球无法相互区分(2)这两种选法中每名员工被选中的可能性相等,均为140能力提升9.随机抽取某商场4月份5天的营业额(单位:万元)分别为3.4,2.9,3.0,3.1,2.6,则这个商场4月份的营业额大约是( )A .90万元B .450万元C .3万元D .15万元 【答案】A 【解析】样本平均数为()1 3.4 2.9 3.0 3.1 2.635⨯++++=,所以这个商场4月份营业额约为3×30=90(万元)故选:A 10.在容量为100的总体中用随机数表法抽取5个样本,总体编号为0001,0299,,,,给出下列几组号码:①00,01,02,03,04;②10,30,50,70,90;③49,19,46,04,67;④11,22,33,44,55.则可能成为所得样本编号的是________(填相应序号).【答案】①②③④【解析】随机数表法是一种简单随机抽样方法,因此每一个个体都有可能被抽到,且被抽到的可能性相同,因此所列几组都可能成为所得样本的编号.答案:①②③④11.选择合适的抽样方法抽样,写出抽样过程.(1)现有一批电子元件600个,从中抽取6个进行质量检测;(2)有甲厂生产的30个篮球,其中一箱21个,另一箱9个,抽取3个入样.【答案】(1)见解析;(2)见解析【解析】(1)总体中个体数较大,用随机数法.第一步,给元件编号为1,2,3,...,99,100, (600)第二步,用随机数工具产生1~600范围内的整数随机数,把产生的随机数作为抽中的编号,使与编号对应的电子元件进入样本;第三步,依次操作,如果生成的随机数有重复,则剔除并重新产生随机数,直到样本量达到6;第四步,以上这6个号码对应的元件就是要抽取的对象.(2)总体中个体数较小,用抽签法.第一步,将30个篮球,编号为1,2, (30)第二步,将以上30个编号分别写在外观、质地等无差别的小纸条上,揉成小球状,制成号签;第三步,把号签放入一个不透明的盒子中,充分搅拌;第四步,从盒子中不放回地逐个抽取3个号签,并记录上面的号码;第五步,找出和所得号码对应的篮球.素养达成12.某些商家为消费者提供免费塑料袋,使购物消费更加方便快捷,但是我们更应关注它对环境的潜在危害.为了解某市所有家庭每年丢弃塑料袋个数的情况,统计人员采用了科学的方法,随机抽取了200户,对他们某日丢弃塑料袋的个数进行了统计,结果如下表:(1)求当日这200户家庭平均每户丢弃塑料袋的个数;(2)假设某市现有家庭100万户,据此估计全市所有家庭每年(以365天计算)丟弃塑料袋的总数.【答案】(1)3;(2)109500万个【解析】(1)()11115260365435520656003200200⨯⨯+⨯+⨯+⨯+⨯+⨯=⨯= 故当日这200户家庭平均每户丢弃塑料袋的个数为3.(2)3365100109500⨯⨯=故全市所有家庭每年丢弃塑料袋109500万个.《9.1.2 分层随机抽样》课后作业基础巩固1.从某地区中小学生中抽取部分学生,进行肺活量调查.经了解,该地区小学、初中、高中三个学段学生的肺活量有较大差异,而同一学段男女生的肺活量差异不大.在下面的抽样方法中,最合理的抽样方法是()A.抽签法 B.按性别分层随机抽样 C.按学段分层随机抽样 D.随机数法2.某实验中学共有职工150人,其中高级职称的职工15人,中级职称的职工45人,一般职员90人,现采用分层抽样抽取容量为30的样本,则抽取的高级职称、中级职称、一般职员的人数分别为()A.5、10、15 B.3、9、18 C.3、10、17 D.5、9、16A B C三个专业共有1200名学生,为了调查这些学生勤工俭学的情况,3.某学院、、拟采用分层抽样的方祛抽取一个容量为120的样本,已知该学院的A专业有380名学生,B 专业有420名学生,则在该学院的C专业应抽取的学生人数为()A.30 B.40 C.50 D.604.某单位200名职工的年龄分布情况如图所示,现要从中抽取40名职工作样本,若用分层抽样方法,则40岁以下年龄段应抽取( )A.10人B.15人C.20人D.25人5.某房地产公司为了解小区业主对户型结构——平层与复式结构的满意度,采取分层随机抽样方式对华润中央公园小区的业主进行问卷调查.20位已购买平层户型的业主满意度平均分为8,30位已购买复式户型的业主满意度平均分为9,用样本平均数估计该小区业主对户型结构满意度的平均分为()A.8.4 B.8.5 C.8.6 D.8.76.某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点.公司为了调查产品销售的情况,需从这600个销售点中抽取一个容量为100的样本,记这项调查为①;在丙地区有10个特大型销售点,要从中抽取7个销售点调查其销售收入和售后服务等情况,记这项调查为②,则完成①②这两项调查宜采用的抽样方法分别为_____.7.甲、乙两套设备生产的同类产品共4800件,采用分层抽样的方法从中抽取一个容量为80 的样本进行检测.若样本中有50件产品由甲设备生产,则乙设备生产的产品总数为________件.8.选择合适的抽样方法抽样,写出抽样过程.(1)有甲厂生产的30个篮球,其中一箱21个,另一箱9个,抽取3个;(2)有30个篮球,其中甲厂生产的有21个,乙厂生产的有9个,抽取10个.能力提升9.某校有高一学生n名,其中男生数与女生数之比为6:5,为了解学生的视力情况,现的样本,若样本中男生比女生多12人,则n=要求按分层抽样的方法抽取一个样本容量为n10()A.990 B.1320 C.1430 D.156010.我国古代数学算经十书之一的《九章算术》中有一“衰分”问题.“今有北乡八千七百五十人,西乡七千二百五十人,南乡八千三百五十人,凡三乡,发役四百八十七人.则西乡遣___________人”.11.某公司总体由1000人组成,按收入情况分成两层,第—层(高收入层)20人,第二层(低收入层)980人.从第一层随机抽取2人,调查上月收入得12000元和16000元;从第二层随机抽取8人,上月收入分别为2200元、2300元、1800元、3200元、4000元、3400元、2800元及3600元.如何来估计这月1000人的月收入?素养达成12.某单位2 000名职工,老年、中年、青年分布在管理、技术开发、营销、生产各部门中,如下表所示:(1)若要抽取40人调查身体状况,则应怎样抽样?(2)若要开一个25人的讨论单位发展与薪金调整方面的座谈会,则应怎样抽选出席人?(3)若要抽20人调查对北京9月3日阅兵情况的了解,则应怎样抽样?《9.1.2 分层随机抽样》课后作业答案解析基础巩固1.从某地区中小学生中抽取部分学生,进行肺活量调查.经了解,该地区小学、初中、高中三个学段学生的肺活量有较大差异,而同一学段男女生的肺活量差异不大.在下面的抽样方法中,最合理的抽样方法是()A.抽签法 B.按性别分层随机抽样 C.按学段分层随机抽样 D.随机数法【答案】C【解析】小学、初中、高中三个学段学生的肺活量有较大差异∴学段对统计结果影响较大同一学段男女生肺活量差异不大∴性别对统计结果无明显影响∴最合理的抽样方法是按学段分层随机抽样故选:C2.某实验中学共有职工150人,其中高级职称的职工15人,中级职称的职工45人,一般职员90人,现采用分层抽样抽取容量为30的样本,则抽取的高级职称、中级职称、一般职员的人数分别为A.5、10、15 B.3、9、18 C.3、10、17 D.5、9、16【答案】B【解析】高级职称应抽取3015=3150⨯;中级职称应抽取3045=9150⨯;一般职员应抽取3090=18150⨯.3.某学院、、A B C三个专业共有1200名学生,为了调查这些学生勤工俭学的情况,拟采用分层抽样的方祛抽取一个容量为120的样本,已知该学院的A专业有380名学生,B 专业有420名学生,则在该学院的C专业应抽取的学生人数为()A.30 B.40 C.50 D.60【答案】B【解析】C 专业的学生有1200380420400--= 由分层抽样原理,应抽取400120401200⨯=名 故选B4.某单位200名职工的年龄分布情况如图所示,现要从中抽取40名职工作样本,若用分层抽样方法,则40岁以下年龄段应抽取( )A .10人B .15人C .20人D .25人【答案】C【解析】由年龄分布情况图可得40岁以下年龄段应抽取40×50%=20人. 故选:C .5.某房地产公司为了解小区业主对户型结构——平层与复式结构的满意度,采取分层随机抽样方式对华润中央公园小区的业主进行问卷调查.20位已购买平层户型的业主满意度平均分为8,30位已购买复式户型的业主满意度平均分为9,用样本平均数估计该小区业主对户型结构满意度的平均分为( )A .8.4B .8.5C .8.6D .8.7【答案】C【解析】估计小区业主对户型结构满意度的平均分为2030898.620302030W =⨯+⨯=++.故选:C .6.某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点.公司为了调查产品销售的情况,需从这600个销售点中抽取一个容量为100的样本,记这项调查为①;在丙地区有10个特大型销售点,要从中抽取7个销售点调查其销售收入和售后服务等情况,记这项调查为②,则完成①②这两项调查宜采用的抽样方法分别为_____.【答案】分层随机抽样、简单随机抽样【解析】由调查①可知个体差异明显,故宜用分层随机抽样;调查②中个体较少,且个体没有明显差异,故宜用简单随机抽样.故答案为:分层随机抽样、简单随机抽样7.甲、乙两套设备生产的同类产品共4800件,采用分层抽样的方法从中抽取一个容量为80 的样本进行检测.若样本中有50件产品由甲设备生产,则乙设备生产的产品总数为________件.【答案】1800【解析】由题共有产品4800名,抽取样本为80,则抽取的概率为;801480060P==,再由50件产品由甲设备生产,则乙设备生产有30件,则乙设备在总体中有;30601800⨯=.8.选择合适的抽样方法抽样,写出抽样过程.(1)有甲厂生产的30个篮球,其中一箱21个,另一箱9个,抽取3个;(2)有30个篮球,其中甲厂生产的有21个,乙厂生产的有9个,抽取10个.【答案】(1)抽签法.见解析(2)分层随机抽样.见解析【解析】(1)总体容量较小,用抽签法.①将30个篮球编号,编号为00,01, (29)②将以上30个编号分别写在完全一样的小纸条上,揉成小球,制成号签;③把号签放入一个不透明的袋子中,充分搅拌;④从袋子中逐个抽取3个号签,并记录上面的号码;⑤找出和所得号码对应的篮球即可得到样本.(2)总体由差异明显的两个层次组成,需选用分层随机抽样.①确定抽取个数.因为30310=,所以甲厂生产的篮球应抽取2173=(个),乙厂生产的篮球应抽取933=(个);②用抽签法分别抽取甲厂生产的篮球7个,乙厂生产的篮球3个,这些篮球便组成了我们要抽取的样本.能力提升9.某校有高一学生n名,其中男生数与女生数之比为,为了解学生的视力情况,现要求按分层抽样的方法抽取一个样本容量为的样本,若样本中男生比女生多12人,则()A.990 B.1320 C.1430 D.1560【答案】B【解析】依题意可得,解得,故选:B 。
应用统计学课后作业答案

悉悉6641尼尼东,,京温65,85哥5华9 , 50
57
温哥华, 43
高温 低温
15
20
25
6 15.00%
6
12 30.00%
12
4 10.00%
4
13 32.50%
13
2 5.00%
2
2 5.00%
2
0 0.00%
0
0 0.00%
0
1 2.50%
1
0 0.00%
0
40 100.00%
接收 0~10 11~20 21~30 31~40 41~50 51~60 61~70 71~80 81~90 91~100 其他
3.制图制表
第(1)题
雪铁龙
1
福特
2
雪铁龙
1
大众
3
大众
3
雪铁龙
1
丰田
4
大众
3
福特
2
丰田
4
大众
3
本田
5
福特
2
福特
2
福特
2
雪铁龙
1
雪铁龙
1
福特
2
雪铁龙
1
雪铁龙
1
本田
5
雪铁龙
1
丰田
4
大众
3
福特
2
雪铁龙
1
本田
5
本田
5
福特
2
福特
2
福特
2
丰田
4
雪铁龙
1
福特
2
本田
5
雪铁龙
1
福特
2
丰田
4
福特
博学阅读书目(审题)
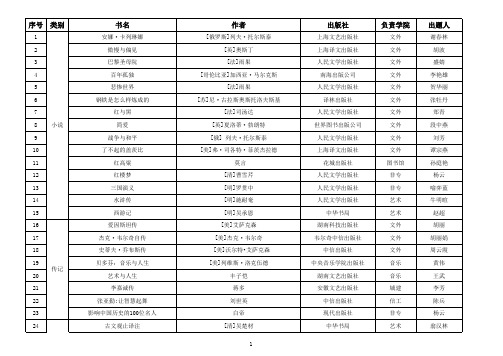
序号 类别
125 126 127 128 129 130 131 132 133 134 135 生活 136 137 138 139 礼仪 职业 成功 励志
书名
做最好的自己 左手哈佛校训,右手西点军规 当世界无法改变时改变自己 羊皮卷(经典解读版) 做事先做人 性格决定命运 人脉圈 赢得高薪1000法 求职面试一点通 决定你薪水的二十八个关键 人生不可不知的365个健康常识 小窍门 大智慧 领导致辞全书 庆典贺辞全书(未完成出题) 祝酒辞全书
路德维希·费尔巴哈与德国古典哲学的 [德]恩格斯著,中共中央马克思、列宁、恩格 终结 斯、斯大林著作编译局译 矛盾论、实践论(毛泽东选集第一卷) 毛泽东
2
序号 类别
37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 科学 文化 艺术
出版社
中华书局 中华书局 中华书局 中国青年出版社 吉林出版集团有限责任公司 上海三联书店 湖南文艺出版社 广西师范大学出版社 译林出版社 译林出版社 人民出版社 人民出版社
负责学院
非专 校办 宣传处 人事处 非专 城建 艺术 城建 文外 文外 督导室 非专
出题人
李曼 刘铭华 邓万民 向晓 向玲 辜海兵 王东昌 吕静 陆金燕 孔慧慧 武育香 曾晓辉
作者
[俄罗斯]列夫·托尔斯泰 [英]奥斯丁 [法]雨果 [哥伦比亚]加西亚·马尔克斯 [法]雨果 [苏]尼·古拉斯奥斯托洛夫斯基 [法]司汤达 [英]夏洛蒂·勃朗特 [俄] 列夫·托尔斯泰 [美]弗·司各特·菲茨杰拉德 莫言 [清]曹雪芹 [明]罗贯中 [明]施耐奄 [明]吴承恩 [美]艾萨克森 [美]杰克·韦尔奇 [美]沃尔特•艾萨克森 [美]列维斯·洛克伍德 丰子恺 蒋多 刘世英 白帝 [清]吴楚材 1
统计学导论-曾五一 肖红叶 课后习题答案

统计学导论习题参考解答第一章一、判断题1.答:错。
统计学和数学具有不同的性质特点。
数学撇开具体的对象,以最一般的形式研究数量的联系和空间形式;而统计学的数据则总是与客观的对象联系在一起。
特别是统计学中的应用统计学与各不同领域的实质性学科有着非常密切的联系,是有具体对象的方法论。
2.答:对。
3.答:错。
实质性科学研究该领域现象的本质关系和变化规律;而统计学则是为研究认识这些关系和规律提供合适的方法,特别是数量分析的方法。
4.答:对。
5.答:错。
描述统计不仅仅使用文字和图表来描述,更重要的是要利用有关统计指标反映客观事物的数量特征。
6.答:错。
有限总体全部统计成本太高,经常采用抽样调查,因此也必须使用推断技术。
7.答:错。
不少社会经济的统计问题属于无限总体。
例如要研究消费者的消费倾向,消费者不仅包括现在的消费者而且还包括未来的消费者,因而实际上是一个无限总体。
8.答:对。
二、单项选择题1. A;2. A;3.A;4. B。
三、分析问答题1.答:定类尺度的数学特征是“=”或“≠”,所以只可用来分类,民族可以区分为汉、藏、回等,但没有顺序和优劣之分,所以是定类尺度数据。
;定序尺度的数学特征是“>”或“<”,所以它不但可以分类,还可以反映各类的优劣和顺序,教育程度可划分为大学、中学和小学,属于定序尺度数据;定距尺度的主要数学特征是“+”或“-”,它不但可以排序,还可以用确切的数值反映现象在两方面的差异,人口数、信教人数、进出口总额都是定距尺度数据;定比尺度的主要数学特征是“⨯”或“÷”,它通常都是相对数或平均数,所以经济增长率是定比尺度数据。
2.答:某学生的年龄和性别,分别为20和女,是数量标志和品质标志;而全校学生资料汇总以后,发现男生1056,女生802人,其中平均年龄、男生女生之比都是质量指标,而年龄合计是数量指标。
数量指标是个绝对数指标,而质量指标是指相对指标和平均指标。
品质标志是不能用数字表示的标志,数量标志是直接可以用数字表示的标志。
概率论与数理统计第二版谢永钦课后答案

概率论与数理统计习题及答案习题一1.见教材习题参考答案.2.设A,B,C为三个事件,试用A,B,C(1)A发生,B,C都不发生;(2)A与B发生,C(3)A,B,C都发生;(4)A,B,C(5)A,B,C都不发生;(6)A,B,C(7)A,B,C至多有2个发生;(8)A,B,C至少有2个发生.【解】(1)A BC(2)AB C(3)ABC(4)A∪B∪C=AB C∪A B C∪A BC∪A BC∪A B C∪AB C∪ABC=ABC(5) ABC=A B C(6) ABC(7) A BC ∪A B C ∪AB C ∪AB C ∪A BC ∪A B C ∪ABC =ABC =A ∪B ∪C (8) AB ∪BC ∪CA =AB C ∪A B C ∪A BC ∪ABC 3..4.设A ,B 为随机事件,且P (A )=0.7,P (A -B )=0.3,求P (AB ). 【解】 P (AB )=1-P (AB )=1-[P (A )-P (A -B )] =1-[0.7-0.3]=0.65.设A ,B 是两事件,且P (A )=0.6,P (B )=0.7, (1) 在什么条件下P (AB(2) 在什么条件下P (AB【解】(1) 当AB =A 时,P (AB )取到最大值为0.6.(2) 当A ∪B =Ω时,P (AB )取到最小值为0.3.6.设A ,B ,C 为三事件,且P (A )=P (B )=1/4,P (C )=1/3且P (AB )=P (BC )=0P (AC )=1/12,求A ,B ,C 至少有一事件发生的概率.【解】 P (A ∪B ∪C )=P (A )+P (B )+P (C )-P (AB )-P (BC )-P (AC )+P (ABC )=14+14+13-112=347.52张扑克牌中任意取出13张,问有5张黑桃,3张红心,3张方块,2张梅花的概率是多少?【解】 p =5332131313131352C C C C /C 8.(1) 求五个人的生日都在星期日的概率; (2) 求五个人的生日都不在星期日的概率;(3) 求五个人的生日不都在星期日的概率. 【解】(1) 设A 1={五个人的生日都在星期日},基本事件总数为75,有利事件仅1个,故 P (A 1)=517=(17)5 (亦可用独立性求解,下同)(2) 设A 2={五个人生日都不在星期日},有利事件数为65,故P (A 2)=5567=(67)5(3) 设A 3={五个人的生日不都在星期日}P (A 3)=1-P (A 1)=1-(17)59..见教材习题参考答案.10.一批产品共N 件,其中M 件正品.从中随机地取出n 件(n <N ).试求其中恰有m 件(m ≤M )正品(记为A )的概率.(1) n 件是同时取出的; (2)n (3) n 件是有放回逐件取出的.【解】(1) P (A )=C C /C m n m nM N M N --(2) 由于是无放回逐件取出,可用排列法计算.样本点总数有P n N 种,n 次抽取中有m 次为正品的组合数为C mn 种.对于固定的一种正品与次品的抽取次序,从M 件正品中取m 件的排列数有P m M 种,从N -M 件次品中取n -m 件的排列数为P n mN M --种,故P (A )=C P P P m m n mn M N MnN-- 由于无放回逐渐抽取也可以看成一次取出,故上述概率也可写成P (A )=C C C m n mM N MnN-- 可以看出,用第二种方法简便得多.(3) 由于是有放回的抽取,每次都有N 种取法,故所有可能的取法总数为N n 种,n 次抽取中有m 次为正品的组合数为C m n 种,对于固定的一种正、次品的抽取次序,m 次取得正品,都有M 种取法,共有M m 种取法,n -m 次取得次品,每次都有N -M 种取法,共有(N -M )n -m 种取法,故()C ()/m m n m nnP A M N M N -=- 此题也可用贝努里概型,共做了n 重贝努里试验,每次取得正品的概率为MN,则取得m 件正品的概率为 ()C 1mn mmnM M P A N N -⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭11..见教材习题参考答案.12.50只铆钉随机地取来用在10个部件上,其中有3个铆钉强度太弱.每个部件用3只铆钉.若将3只强度太弱的铆钉都装在一个部件上,则这个部件强度就太弱.求发生一个部件强度太弱的概率是多少? 【解】设A ={发生一个部件强度太弱}133103501()C C /C 1960P A ==13.7个球,其中4个是白球,3个是黑球,从中一次抽取3个,计算至少有两个是白球的概率. 【解】 设A i ={恰有i 个白球}(i =2,3),显然A 2与A 3互斥.213434233377C C C 184(),()C 35C 35P A P A ====故 232322()()()35P A A P A P A =+=14.0.8和0.7,在两批种子中各随机取一粒,求:(1) 两粒都发芽的概率; (2) 至少有一粒发芽的概率; (3) 恰有一粒发芽的概率.【解】设A i ={第i 批种子中的一粒发芽},(i =1,2)(1) 1212()()()0.70.80.56P A A P A P A ==⨯= (2) 12()0.70.80.70.80.94P A A =+-⨯=(3) 2112()0.80.30.20.70.38P A A A A =⨯+⨯=15.3次正面才停止.(1) 问正好在第6次停止的概率;(2) 问正好在第6次停止的情况下,第5次也是出现正面的概率.【解】(1) 223151115()()22232p C == (2) 1342111C ()()22245/325p == 16.0.7及0.6,每人各投了3次,求二人进球数相等的概率.【解】 设A i ={甲进i 球},i =0,1,2,3,B i ={乙进i 球},i =0,1,2,3,则33312123330()(0.3)(0.4)C 0.7(0.3)C 0.6(0.4)i i i P A B ==+⨯⨯+22223333C (0.7)0.3C (0.6)0.4+(0.7)(0.6)⨯=0.32076175双不同的鞋子中任取4只,求这4只鞋子中至少有两只鞋子配成一双的概率.【解】 4111152222410C C C C C 131C 21p =-= 18.0.3,下雨的概率为0.5,既下雪又下雨的概率为0.1,求:(1) 在下雨条件下下雪的概率;(2) 这天下雨或下雪的概率. 【解】 设A ={下雨},B ={下雪}.(1) ()0.1()0.2()0.5P AB p B A P A === (2) ()()()()0.30.50.10.7p A B P A P B P AB =+-=+-=19.3个小孩,且其中一个为女孩,求至少有一个男孩的概率(小孩为男为女是等可能的). 【解】 设A ={其中一个为女孩},B ={至少有一个男孩},样本点总数为23=8,故()6/86()()7/87P AB P B A P A ===或在缩减样本空间中求,此时样本点总数为7.6()7P B A =20.5%的男人和0.25%的女人是色盲,现随机地挑选一人,此人恰为色盲,问此人是男人的概率(假设男人和女人各占人数的一半). 【解】 设A ={此人是男人},B ={此人是色盲},则由贝叶斯公式()()()()()()()()()P A P B A P AB P A B P B P A P B A P A P B A ==+0.50.05200.50.050.50.002521⨯==⨯+⨯21.9∶00~10∶00在公园会面,求一人要等另一人半小时以上的概率.题21图 题22图【解】设两人到达时刻为x,y ,则0≤x ,y ≤60.事件“一人要等另一人半小时以上”等价于|x -y |>30.如图阴影部分所示.22301604P ==22.0,1)中随机地取两个数,求:(1) 两个数之和小于65的概率; (2) 两个数之积小于14的概率.【解】 设两数为x ,y ,则0<x ,y <1. (1) x +y <65. 11441725510.68125p =-==(2) xy =<14.1111244111d d ln 242x p x y ⎛⎫=-=+⎪⎝⎭⎰⎰ 23.P (A )=0.3,P (B )=0.4,P (A B )=0.5,求P (B |A ∪B )【解】 ()()()()()()()()P AB P A P AB P B A B P A B P A P B P AB -==+- 0.70.510.70.60.54-==+-24.15个乒乓球,其中有9个新球,在第一次比赛中任意取出3个球,比赛后放回原盒中;第二次比赛同样任意取出3个球,求第二次取出的3个球均为新球的概率.【解】 设A i ={第一次取出的3个球中有i 个新球},i =0,1,2,3.B ={第二次取出的3球均为新球}由全概率公式,有3()()()i i i P B P B A P A ==∑33123213336996896796333333331515151515151515C C C C C C C C C C C C C C C C C C =∙+∙+∙+∙0.089= 25. 按以往概率论考试结果分析,努力学习的学生有90%的可能考试及格,不努力学习的学生有90%的可能考试不及格.据调查,学生中有80%的人是努力学习的,试问:(1)考试及格的学生有多大可能是不努力学习的人? (2)考试不及格的学生有多大可能是努力学习的人? 【解】设A ={被调查学生是努力学习的},则A ={被调查学生是不努力学习的}.由题意知P (A )=0.8,P (A )=0.2,又设B ={被调查学生考试及格}.由题意知P (B |A )=0.9,P (B |A )=0.9,故由贝叶斯公式知(1)()()()()()()()()()P A P B A P AB P A B P B P A P B A P A P B A ==+ 0.20.110.027020.80.90.20.137⨯===⨯+⨯即考试及格的学生中不努力学习的学生仅占2.702%(2) ()()()()()()()()()P A P B A P AB P A B P B P A P B A P A P B A ==+ 0.80.140.30770.80.10.20.913⨯===⨯+⨯即考试不及格的学生中努力学习的学生占30.77%.26. 将两信息分别编码为A 和B 传递出来,接收站收到时,A 被误收作B 的概率为0.02,而B 被误收作A 的概率为0.01.信息A 与B 传递的频繁程度为2∶1.若接收站收到的信息是A ,试问原发信息是A 的概率是多少? 【解】 设A ={原发信息是A },则={原发信息是B }C ={收到信息是A },则={收到信息是B } 由贝叶斯公式,得()()()()()()()P A P C A P A C P A P C A P A P C A =+2/30.980.994922/30.981/30.01⨯==⨯+⨯27.【解】设A i ={箱中原有i 个白球}(i =0,1,2),由题设条件知P (A i )=13,i =0,1,2.又设B ={抽出一球为白球}.由贝叶斯公式知 11112()()()()()()()i i i P B A P A P A B P A B P B P B A P A ===∑ 2/31/311/31/32/31/311/33⨯==⨯+⨯+⨯28.96%是合格品,检查产品时,一个合格品被误认为是次品的概率为0.02,一个次品被误认为是合格品的概率为0.05,求在被检查后认为是合格品产品确是合格品的概率.【解】 设A ={产品确为合格品},B ={产品被认为是合格品}由贝叶斯公式得()()()()()()()()()P A P B A P AB P A B P B P A P B A P A P B A ==+ 0.960.980.9980.960.980.040.05⨯==⨯+⨯29..统计资料表明,上述三种人在一年内发生事故的概率依次为0.05,0.15和0.30;如果“谨慎的”被保险人占20%,“一般的”占50%,“冒失的”占30%,现知某被保险人在一年内出了事故,则他是“谨慎的”的概率是多少? 【解】 设A ={该客户是“谨慎的”},B ={该客户是“一般的”},C ={该客户是“冒失的”},D ={该客户在一年内出了事故} 则由贝叶斯公式得()()(|)(|)()()(|)()(|)()(|)P AD P A P D A P A D P D P A P D A P B P D B P C P D C ==++0.20.050.0570.20.050.50.150.30.3⨯==⨯+⨯+⨯30.0.02,0.03,0.05,0.03,假定各道工序是相互独立的,求加工出来的零件的次品率.【解】设A i ={第i 道工序出次品}(i =1,2,3,4).412341()1()i i P A P A A A A ==-12341()()()()P A P A P A P A =-10.980.970.950.970.124=-⨯⨯⨯= 31.0.2,问至少必须进行多少次独立射击才能使至少击中一次的概率不小于0.9? 【解】设必须进行n 次独立射击.1(0.8)0.9n -≥即为 (0.8)0.1n ≤ 故 n ≥11 至少必须进行11次独立射击. 32.P (A |B )=P (A |B ),则A ,B 相互独立.【证】 (|)(|)P A B P A B =即()()()()P AB P AB P B P B =亦即 ()()()()P AB P B P AB P B =()[1()][()()]()P AB P B P A P AB P B -=-因此 ()()()P AB P A P B = 故A 与B 相互独立. 33.15,13,14,求将此密码破译出的概率. 【解】 设A i ={第i 人能破译}(i =1,2,3),则31231231()1()1()()()i i P A P A A A P A P A P A ==-=-42310.6534=-⨯⨯= 34.0.4,0.5,0.7,若只有一人击中,则飞机被击落的概率为0.2;若有两人击中,则飞机被击落的概率为0.6;若三人都击中,则飞机一定被击落,求:飞机被击落的概率. 【解】设A ={飞机被击落},B i ={恰有i 人击中飞机},i =0,1,2,3由全概率公式,得3()(|)()i i i P A P A B P B ==∑=(0.4×0.5×0.3+0.6×0.5×0.3+0.6×0.5×0.7)0.2+(0.4×0.5×0.3+0.4×0.5×0.7+0.6×0.5×0.7)0.6+0.4×0.5×0.7 =0.45835.25%,为试验一种新药是否有效,把它给10个病人服用,且规定若10个病人中至少有四人治好则认为这种药有效,反之则认为无效,求:(1) 虽然新药有效,且把治愈率提高到35%,但通过试验被否定的概率. (2) 新药完全无效,但通过试验被认为有效的概率. 【解】(1) 310110C(0.35)(0.65)0.5138k k k k p -===∑(2) 10102104C(0.25)(0.75)0.2241kk k k p -===∑36.6位乘客,并等可能地停于十层楼的每一层.试求下列事件的概率:(1) A =“某指定的一层有两位乘客离开”;(2) B =“没有两位及两位以上的乘客在同一层离开”; (3) C =“恰有两位乘客在同一层离开”; (4) D =“至少有两位乘客在同一层离开”.【解】 由于每位乘客均可在10层楼中的任一层离开,故所有可能结果为106种.(1) 2466C 9()10P A =,也可由6重贝努里模型:224619()C ()()1010P A =(2) 6个人在十层中任意六层离开,故6106P ()10P B =(3) 由于没有规定在哪一层离开,故可在十层中的任一层离开,有110C 种可能结果,再从六人中选二人在该层离开,有26C 种离开方式.其余4人中不能再有两人同时离开的情况,因此可包含以下三种离开方式:①4人中有3个人在同一层离开,另一人在其余8层中任一层离开,共有131948C C C 种可能结果;②4人同时离开,有19C 种可能结果;③4个人都不在同一层离开,有49P 种可能结果,故1213114610694899()C C (C C C C P )/10P C =++(4) D=B .故6106P ()1()110P D P B =-=-37. n 个朋友随机地围绕圆桌而坐,求下列事件的概率: (1) 甲、乙两人坐在一起,且乙坐在甲的左边的概率; (2) 甲、乙、丙三人坐在一起的概率;(3) 如果n 个人并排坐在长桌的一边,求上述事件的概率. 【解】 (1) 111p n =-(2) 23!(3)!,3(1)!n p n n -=>-(3) 12(1)!13!(2)!;,3!!n n p p n n n n --''===≥ 38.[0,a ]【解】 设这三段长分别为x ,y ,a -x -y .则基本事件集为由0<x <a ,0<y <a ,0<a -x -y <a 所构成的图形,有利事件集为由()()x y a x y x a x y y y a x y x+>--⎡⎢+-->⎢⎢+-->⎣ 构成的图形,即02022a x a y ax y a ⎡<<⎢⎢⎢<<⎢⎢⎢<+<⎢⎣ 如图阴影部分所示,故所求概率为14p =. 39. 某人有n 把钥匙,其中只有一把能开他的门.他逐个将它们去试开(抽样是无放回的).证明试开k 次(k =1,2,…,n )才能把门打开的概率与k 无关.【证】 11P 1,1,2,,P k n k n p k n n--===40.把一个表面涂有颜色的立方体等分为一千个小立方体,在这些小立方体中,随机地取出一个,试求它有i 面涂有颜色的概率P (A i )(i =0,1,2,3). 【解】 设A i ={小立方体有i 面涂有颜色},i =0,1,2,3.在1千个小立方体中,只有位于原立方体的角上的小立方体是三面有色的,这样的小立方体共有8个.只有位于原立方体的棱上(除去八个角外)的小立方体是两面涂色的,这样的小立方体共有12×8=96个.同理,原立方体的六个面上(除去棱)的小立方体是一面涂色的,共有8×8×6=384个.其余1000-(8+96+384)=512个内部的小立方体是无色的,故所求概率为01512384()0.512,()0.38410001000P A P A ====, 24968()0.096,()0.00810001000P A P A ====.41.对任意的随机事件A ,B ,CP (AB )+P (AC )-P (BC )≤P (A ).【证】 ()[()]()P A P A BC P AB AC ≥=()()()P AB P AC P ABC =+- ()()()P AB P AC P BC ≥+- 42.3个球随机地放入4个杯子中去,求杯中球的最大个数分别为1,2,3的概率.【解】 设i A ={杯中球的最大个数为i },i =1,2,3.将3个球随机放入4个杯子中,全部可能放法有43种,杯中球的最大个数为1时,每个杯中最多放一球,故3413C 3!3()48P A ==而杯中球的最大个数为3,即三个球全放入一个杯中,故1433C 1()416P A ==因此 213319()1()()181616P A P A P A =--=--= 或 12143323C C C 9()416P A == 43.2n 次,求出现正面次数多于反面次数的概率.【解】掷2n 次硬币,可能出现:A ={正面次数多于反面次数},B ={正面次数少于反面次数},C ={正面次数等于反面次数},A ,B ,C 两两互斥.可用对称性来解决.由于硬币是均匀的,故P (A )=P (B ).所以1()()2P C P A -=由2n 重贝努里试验中正面出现n 次的概率为211()()()22n n nn P C C =故 2211()[1C ]22n n n P A =- 44.n 次均匀硬币,求出现正面次数多于反面次数的概率.【解】设A ={出现正面次数多于反面次数},B ={出现反面次数多于正面次数},由对称性知P (A )=P (B )(1) 当n 为奇数时,正、反面次数不会相等.由P (A )+P (B )=1得P (A )=P (B )=0.5 (2) 当n 为偶数时,由上题知211()[1C ()]22nn n P A =-45.n +1次,乙掷n 次,求甲掷出正面次数多于乙掷出正面次数的概率.【解】 令甲正=甲掷出的正面次数,甲反=甲掷出的反面次数.乙正=乙掷出的正面次数,乙反=乙掷出的反面次数. 显然有>正正(甲乙)=(甲正≤乙正)=(n +1-甲反≤n -乙反) =(甲反≥1+乙反)=(甲反>乙反)由对称性知P (甲正>乙正)=P (甲反>乙反) 因此P (甲正>乙正)=1246.Sure -thing ):若P (A |C )≥P (B |C ),P (A |C )≥P (B |C ),则P (A )≥P (B ).【证】由P (A |C )≥P (B |C ),得()(),()()P AC P BC P C P C ≥即有 ()()P AC P BC ≥ 同理由 (|)(|),P A C P B C ≥ 得 ()(),P AC P BC ≥故 ()()()()()()P A P AC P AC P BC P BC P B =+≥+=47.一列火车共有n 节车厢,有k (k ≥n )个旅客上火车并随意地选择车厢.求每一节车厢内至少有一个旅客的概率.【解】 设A i ={第i 节车厢是空的},(i =1,…,n ),则121(1)1()(1)2()(1)1()(1)n k ki k ki j ki i i n P A n nP A A n n P A A A n--==-=--=-其中i 1,i 2,…,i n -1是1,2,…,n 中的任n -1个. 显然n 节车厢全空的概率是零,于是2112111122111111123111()(1)C (1)2()C (1)1()C (1)0()(1)n n nk ki ni ki j n i j nn kn i i i n i i i nn nn i ni S P A n n n S P A A n n S P A A A nS P A S S S S --=≤<≤--≤<<≤+===-=-==--==-==-+-+-∑∑∑121121C (1)C (1)(1)C (1)k kn n kn n n n nnn--=---++--故所求概率为121121()1C (1)C (1)nk i i n n i P A n n=-=--+--+111(1)C (1)n n kn n n+----48.设随机试验中,某一事件A 出现的概率为ε>0.试证明:不论ε>0如何小,只要不断地独立地重复做此试验,则A 迟早会出现的概率为1. 【证】在前n 次试验中,A 至少出现一次的概率为1(1)1()n n ε--→→∞49.袋中装有m 只正品硬币,n 只次品硬币(次品硬币的两面均印有国徽).在袋中任取一只,将它投掷r 次,已知每次都得到国徽.试问这只硬币是正品的概率是多少?【解】设A ={投掷硬币r 次都得到国徽}B ={这只硬币为正品} 由题知 (),()m nP B P B m n m n==++ 1(|),(|)12r P A B P A B == 则由贝叶斯公式知()()(|)(|)()()(|)()(|)P AB P B P A B P B A P A P B P A B P B P A B ==+ 121212r rrm m m n mnm n m n m n+==++++ 50.巴拿赫(Banach )火柴盒问题:某数学家有甲、乙两盒火柴,每盒有N 根火柴,每次用火柴时他在两盒中任取一盒并从中任取一根.试求他首次发现一盒空时另一盒恰有r 根的概率是多少?第一次用完一盒火柴时(不是发现空)而另一盒恰有r【解】以B 1、B 2记火柴取自不同两盒的事件,则有121()()2P B P B ==.(1)发现一盒已空,另一盒恰剩r 根,说明已取了2n -r 次,设n 次取自B 1盒(已空),n -r 次取自B 2盒,第2n -r +1次拿起B 1,发现已空。
(新教材)2020数学同步导学人教B第二册作业:第五章 统计与概率 课时作业 11 Word版含解析

课时作业 11一、选择题1.下面的抽样方法是简单随机抽样的是()A.在某年明信片销售活动中,规定每100万张为一个开奖组,通过随机抽取的方式确定号码的后四位为2 709的为三等奖B.某车间包装一种产品,在自动包装的传送带上,每隔30分钟抽一包产品,检验其质量是否合格C.某学校分别从行政人员、教师、后勤人员中抽取2人、14人、4人了解学校机构改革的意见D.用抽签法从10件产品中选取3件进行质量检验解析:对每个选项逐条落实简单随机抽样的特点.A、B不是简单随机抽样,因为抽取的个体间的间隔是固定的;C不是简单随机抽样,因为总体的个体有明显的层次;D是简单随机抽样.答案:D2.某工厂的质检人员对生产的100件产品,采用随机数表法抽取10件检查,对100件产品采用下面的编号方法:①1,2,3,...,100;②001,002,...,100;③00,01,02, (99)④01,02,03, (100)其中正确的序号是()A.②③④B.③④C.②③D.①②解析:根据随机数表法的步骤可知,①④编号位数不统一.答案:C3.[东营月考]从某年级的500名学生中抽取60名学生进行体重的统计分析,下列说法正确的是()A.500名学生是总体B.每个学生是个体C.抽取的60名学生的体重是一个样本D.抽取的60名学生的体重是样本容量解析:由题可知在此简单随机抽样中,总体是500名学生的体重,A错误,个体是每个学生的体重,B错误;样本容量为60,D错误.故选C.答案:C解析:在随机数表中,将处于00~29的号码选出,第一个数76不合要求,第2个63不合要求,满足要求的前4个号码为17,00,02,07.答案:17,00,02,07三、解答题8.从30架钢琴中抽取6架进行质量检查,请用抽签法确定这6架钢琴.解析:第一步,将30架钢琴编号,号码是01,02, (30)第二步,将号码分别写在一张纸条上,揉成团,制成号签;第三步,将得到的号签放入一个不透明的袋子中,并充分搅匀;第四步,从袋子中逐个抽取6个号签,并记录上面的编号;第五步,所得号码对应的6架钢琴就是要抽取的对象.9.假设要考察某公司生产的500克袋装牛奶的质量是否达标,现从800袋牛奶中抽取60袋进行检验,利用随机数表抽取样本时,先将800袋牛奶按000,001,…,799进行编号,如果从随机数表第8行第7列的数开始向右读,请你依次写出最先检测的5袋牛奶的编号________.(下面摘取了随机数表第7行至第9行)81 05 01 08 0545 57 18 24 0535 30 34 28 1488 79 90 74 39 23 40 30 97 3283 26 97 76 0202 05 16 56 9268 55 57 48 1873 05 38 52 47 18 62 33 85 7963 57 33 21 3505 32 54 70 4890 55 85 75 1828 46 82 87 09 83 40 12 56 24解析:找到第8行第7列的数开始向右读,凡不在000~799的跳过去不读,前面读过的也跳过去不读,得到的符合题意的五个数据依次为760,202,051,656,574.答案:760,202,051,656,574[尖子生题库]10.为了检验某种药品的副作用,从编号为1,2,3,...,120的服药者中用随机数法抽取10人作为样本,写出抽样过程.解析:第一步,将120名服药者重新进行编号,分别为001,002,003, (120)第二步,在随机数表(教材P103)中任选一数作为初始数,如选第9行第7列的数3;第三步,从选定的数3开始向右读,每次读取三位,凡不在001~120中的数跳过去不读,前面已经读过的也跳过去不读,依次可得到074,100,094,052,080,003,105,107,083,092;第四步,以上这10个号码所对应的服药者即是要抽取的对象.。
人教版七年级数学上册期末考试题(免费)

人教版七年级数学上册期末考试题(免费) 班级: 姓名:一、选择题(本大题共10小题,每题3分,共30分)1.已知m ,n 为常数,代数式2x 4y +mx |5-n|y +xy 化简之后为单项式,则m n 的值共有( )A .1个B .2个C .3个D .4个2.如图,在OAB 和OCD 中,,,,40OA OB OC OD OA OC AOB COD ==>∠=∠=︒,连接,AC BD 交于点M ,连接OM .下列结论:①AC BD =;②40AMB ∠=︒;③OM 平分BOC ∠;④MO 平分BMC ∠.其中正确的个数为( ).A .4B .3C .2D .13.已知x+y =﹣5,xy =3,则x 2+y 2=( )A .25B .﹣25C .19D .﹣194.将一副三角板和一张对边平行的纸条按如图摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )A .15°B .22.5°C .30°D .45°5.若x 取整数,则使分式6321x x +-的值为整数的x 值有( ) A .3个 B .4个 C .6个 D .8个6.如图,要把河中的水引到水池A 中,应在河岸B 处(AB ⊥CD )开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )A .两点之间线段最短B .点到直线的距离C .两点确定一条直线D .垂线段最短7.《增删算法统宗》记载:“有个学生资性好,一部孟子三日了,每日增添一倍多,问若每日读多少?”其大意是:有个学生天资聪慧,三天读完一部《孟子》,每天阅读的字数是前一天的两倍,问他每天各读多少个字?已知《孟子》一书共有34 685个字,设他第一天读x 个字,则下面所列方程正确的是( ).A .x +2x +4x =34 685B .x +2x +3x =34 685C .x +2x +2x =34 685D .x +12x +14x =34 685 8.如图,//DE BC ,BE 平分ABC ∠,若170∠=,则CBE ∠的度数为( )A .20B .35C .55D .709.如图,在△ABC 中,AB=AC ,∠A=30°,E 为BC 延长线上一点,∠ABC 与∠ACE 的平分线相交于点D ,则∠D 的度数为( )A .15°B .17.5°C .20°D .22.5°10.如图,在菱形ABCD 中,2,BD=6,E 是BC 边的中点,P ,M 分别是AC ,AB 上的动点,连接PE ,PM ,则PE+PM 的最小值是( )A.6 B.33 C.26 D.4.5二、填空题(本大题共6小题,每小题3分,共18分)1.81的平方根是________.2.如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB.若∠BOC=110°,则∠A=________.3.如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是________4.若关于x、y的二元一次方程组34355x y mx y-=+⎧⎨+=⎩的解满足0x y+≤,则m的取值范围是________.5.为了开展“阳光体育”活动,某班计划购买甲、乙两种体育用品(每种体育用品都购买),其中甲种体育用品每件20元,乙种体育用品每件30元,共用去150元,请你设计一下,共有________种购买方案.6.如图,两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着点B 到点C的方向平移到△DEF的位置,AB=10,DH=4,平移距离为6,则阴影部分面积是________.三、解答题(本大题共6小题,共72分)1.解下列方程(1)12225y yy-+-=-(2)()()()22431233x x x---=-+2.已知方程组3247x ymx ny-=⎧⎨+=⎩与231953mx nyy x-=⎧⎨-=⎩有相同的解,求m,n的值.3.如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.(1)求证:△ABC≌△ADE;(2)求∠FAE的度数;(3)求证:CD=2BF+DE.4.如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.(1)如果∠A=80°,求∠BPC的度数;(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A 之间的数量关系.(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.5.近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.请你根据统计图提供的信息,解答下列问题:(1)本次一共调查了多少名购买者?(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为度.(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?6.江海化工厂计划生产甲、乙两种季节性产品,在春季中,甲种产品售价50千元/件,乙种产品售价30千元/件,生产这两种产品需要A、B两种原料,生产甲产品需要A种原料4吨/件,B种原料2吨/件,生产乙产品需要A种原料3吨/件,B种原料1吨/件,每个季节该厂能获得A种原料120吨,B种原料50吨.(1)如何安排生产,才能恰好使两种原料全部用完?此时总产值是多少万元?(2)在夏季中甲种产品售价上涨10%,而乙种产品下降10%,并且要求甲种产品比乙种产品多生产25件,问如何安排甲、乙两种产品,使总产值是1375千元,A,B两种原料还剩下多少吨?参考答案一、选择题(本大题共10小题,每题3分,共30分)1、C2、B3、C4、A5、B6、D7、A8、B9、A10、C二、填空题(本大题共6小题,每小题3分,共18分)1、±32、40°3、15°4、2m ≤-5、两6、48三、解答题(本大题共6小题,共72分)1、(1)711=y (2)x=0 2、m=4,n=﹣1.3、(1)证明见解析;(2)∠FAE=135°;4、(1)130°.(2)∠Q==90°﹣12∠A ;(3)∠A 的度数是90°或60°或120°.5、(1)本次一共调查了200名购买者;(2)补全的条形统计图见解析,A 种支付方式所对应的圆心角为108;(3)使用A 和B 两种支付方式的购买者共有928名.6、(1)生产甲种产品15件,生产乙种产品20件才能恰好使两种原料全部用完,此时总产值是135万元;(2)安排生产甲种产品25件,使总产值是1375千元,A种原料还剩下20吨,B种原料正好用完,还剩下0吨.。
2019-2020学年【苏教版】六年级上册数学:第7单元-整理与复习-课时作业第2课时数的世界(二)

2019-2020学年苏教版数学精品资料
第2课时数的世界(二)
一、填空。
(1)某工厂生产200个零件,经检验有8个不合格,合格率是()。
(2)一件外套打八折出售是120元,这件外套的原价是()元。
(3)某服装厂四月份生产衬衫280件,五月份生产350件,五月份比四月份增产()%。
(4)某商场去年三月份的营业额为250万元,按规定要缴纳5%的营业税,还要按营业税的7%缴纳城市维护建设税。
该商场三月份一共要缴纳税
款()万元。
(5)一个三角形,三个内角的度数比是5∶3∶2,这是()三角形。
(6)张华把1000元存入银行,定期二年,年利率是 3.75%,到期时他应得到本金和利息()元。
二、某厂五月份生产机床160台,六月份生产200台。
六月份比五月份增产百分
之几?
三、永丰乡去年水稻的总产量是0.6万吨,比小麦多20%。
小麦的总产量是多少
万吨?
答案:一、(1)96% (2)150 (3)25 (4)13.375 (5)直角(6)1075
二、25%
三、0.5万吨。
2019-2020学年人教A版数学必修第二册课时作业配套课件:第9章 统计 9.2 课时作业43

第十八页,编辑于星期六:二十三点 二十三分。
课时综合练
第十九页,编辑于星期六:二十三点 二十三分。
一、选择题 1.下列说法正确的是( ) A.在两组数据中,平均数较大的一组极差较大 B.平均数反映数据的集中趋势,方差则反映数据波动的大小 C.方差的求法是求出各个数据与平均值的差的平方后再求和 D.在案 B
解析 设该组数据为 x1,x2,…,xn,都乘以 2 后的新数据为 2x1,2x2,…,
2xn. 由题意知-x =x1+x2+n …+xn,
则2x1+2x2+n …+2xn=2-x .
又 s=
x1--x 2+x2--x 2+…+xn--x 2, n
所以
2x1-2-x 2+2x2-2-x 2+…+2xn-2-x 2 n
第五页,编辑于星期六:二十三点 二十三分。
3.某班 40 人随机分成两组,第 1 组 15 人,第 2 组 25 人,两组学生一
次数学考试的成绩(单位:分)情况如下表:
组别
平均分
标准差
第1组
84
6
第2组
80
4
求全班学生这次数学考试的平均成绩和方差.
第六页,编辑于星期六:二十三点 二十三分。
解 由题意,知第 1 组这次数学考试的平均分-x 1=84,方差 s21=62=36, 权重 w1=4105,
第八页,编辑于星期六:二十三点 二十三分。
解 (1)-x 甲=110×(8+6+7+8+6+5+9+10+4+7)=7, -x 乙=110×(6+7+7+8+6+7+8+7+9+5)=7.
(2)由方差公式 s2=1n
n
(xi--x )2,得
i=1
s2甲=3,s2乙=1.2.
《好题》小学数学六年级下册第一单元负数测试卷(答案解析)(6)

《好题》小学数学六年级下册第一单元负数测试卷(答案解析)(6)一、选择题1.某货物检测站,物品重量记录规定10吨记为0吨,11吨记为+1吨,则下列说法错误的是()。
A. 4吨记为-4吨B. 15吨记为+5吨C. 7吨记为-3吨D. +3吨表示重量为132.下列描述正确的是()。
A. 在上图上可以找到-5、20、3.5三个数对应的点B. 上图中,直线上的数不是正数就是负数C. 在0和3之间的数只有1和23.一种饼干包装袋上标着:净重(150±5克),表示这种饼干标准的质量是150克,实际每袋最少不少于()克.A. 155B. 150C. 1454.如果规定向东走为正,那么﹣300m表示()A. 向东走300mB. 向西走300mC. 向南走300mD. 向北走300m5.在直线上,-2在-1的()边。
A. 左B. 右C. 可左也可右D. 无法确定6.如果规定前进、收入、增加为正,那么下面错误的语句是().A. -18米表示后退18米B. -42人表示增加42人C. 4万元表示支出4万元7.一种饼干的包装袋上标着:净重(150±5g)表示这种饼干标准质量是150g,实际每袋最少不小于()g。
A. 155B. 150C. 145D. 1408.如果某商店盈利800元,记作+800元,那么亏损100元,记作( )元。
A. +100B. -100C. 无法表示9.数轴上,-在-的()边。
A. 左B. 右C. 北D. 无法确定10.六年级某次考试的平均分是88分,高于平均分2 分记作+2分,低于平均8分记作()这个分数实际是()分。
A. -8分B. +8分C. -8分;80D. 96分11.丽丽从学校大门口往南走5米到达A点,记作“+5”米,接着返回往北走了8米到达B 点,B点应该记作()米。
A. +3B. +13C. -8D. -3 12.中秋节发月饼,几个小朋友平均每人得到10个月饼,小芳得到11个月饼,记为+1,那么小红得到8个记为( )。
工商导论小组作业通用模板

广告
报纸 杂志 广播 电视 户外 网络 广告 广告 广告 广告 广告 广告
2019-6-20
谢谢您的观看
营业推广
广告 人员推销 公共关系 消费品市场
13
2010年相应对策
• 第一、大力推动主营业务转型,不断提高盈利能力。 • 食品业务的工作重心是:①传统食品业务要积极推进转型,进一步加
强市场终端渠道建设,强化
2019-6-20
谢谢您的观看
7
董事会报告
• 2009 年公司主要的经营管理情况如下: • (1)食品业务生产经营情况趋于良好。营业收入相比去年同期虽下
降5.39%,但食品事业部经过
• 一年来的运作,在产品结构调整、新业务探索方面有一定进展,食品
传统业务盈利能力有所提高。零
• 售业务至2009 年末,已形成了20 家的专卖店规模,经营模式已初步
独特,质量可靠
2019-6-20
谢谢您的观看
9
市场份额
主营业务分行业、产品情况 公司依然以食品与饲料产品为主,利润增幅下降,
第二产业房地产缩水(已经暂缓放弃) 主营业务分地区情况 正在将国际市场转向国内市场的战略转换期 国内市场的比重在增加 主要供应商和客户情况 与固定客户关系稳定,前五名的采购商和销售商的 集团总额比例37.01%和37.83%
资料不足!
2019-6-20
统计教材课后全部练习答案(1)

答案2.1 (1)属于顺序数据。
(2)频数分布表如下:服务质量等级评价的频数分布服务质量等级家庭数(频率)频率%A1414B2121C3232D1818E1515合计100100(3)条形图(略)2.2 (1)频数分布表如下:(2)某管理局下属40个企分组表按销售收入分组(万元)企业数(个)频率(%)先进企业良好企业一般企业落后企业11119927.527.522.522.5合计40 100.0 2.3 频数分布表如下:某百货公司日商品销售额分组表按销售额分组(万元)频数(天)频率(%)25~30 30~35 35~40 40~45 45~5046159610.015.037.522.515.0合计40 100.0 直方图(略)。
2.4 (1)排序略。
(2)频数分布表如下:100只灯泡使用寿命非频数分布按使用寿命分组(小时)灯泡个数(只)频率(%)650~660 2 2660~670 5 5670~680 6 6680~690 14 14690~700 26 26700~710 18 18710~720 13 13720~730 10 10730~740 3 3740~750 3 3合计100 100 直方图(略)。
2.5 (1)属于数值型数据。
(2)分组结果如下:分组天数(天)-25~-20 6-20~-15 8-15~-10 10-10~-5 13-5~0 120~5 45~10 7合计60(3)直方图(略)。
2.6 (1)直方图(略)。
(2)自学考试人员年龄的分布为右偏。
(2)A 班考试成绩的分布比较集中,且平均分数较高;B 班考试成绩的分布比A 班分散,且平均成绩较A 班低。
2.82.9 (L U 。
(2)17.21=s (万元)。
2.10 (1)甲企业平均成本=19.41(元),乙企业平均成本=18.29(元);原因:尽管两个企业的单位成本相同,但单位成本较低的产品在乙企业的产量中所占比重较大,因此拉低了总平均成本。
2023-2023学年苏教版四年级上册数学暑假数学小巨人挑战卷

2023-2023学年苏教版四年级上册数学暑假数学小巨人挑战卷一、单项选择题:本题共10小题,每小题2分,共20分,在每小题给出的答案中,只有一个符合题目要求。
(共10题)第(1)题用6颗珠子在计数器上表示一个九位数,最小的数是()。
A.150000000B.100000005C.330000000D.402000000第(2)题下面各数中,读两个0的是()。
A.304066B.3400908C.30003603D.330000090第(3)题汽车车灯、手电筒等射出的光线都可以看作()。
A.直线B.射线C.线段第(4)题用一副三角板能画出的角是()。
A.70°B.75°C.80°第(5)题小丽跟妈妈学做菜,今天要做一盘炒鸡蛋,妈妈告诉她这道菜有以下几项工序:敲蛋(1分钟);搅蛋(1分钟);洗锅(2分钟);烧热锅(2分钟);烧热油(1分钟);炒蛋(4分钟)。
小丽做这道菜最少需要()分钟。
A.11B.10C.9第(6)题红星商场平均每天售出饮料580瓶,12天共售出多少瓶?竖式中箭头所指的结果表示()。
A.1天售出58瓶B.10天售出580瓶C.10天售出5800瓶D.12天售出6960瓶第(7)题我们戴的红领巾上最大的一个角是()。
A.锐角B.直角C.钝角第(8)题下面各数中,一个零也不读的数是()。
A.10101010B.11001100C.11100010D.11000011第(9)题计算器的清除键是()。
A.B.C.第(10)题王叔叔是一个跑步爱好者,如表是他四次跑步的情况。
在这四次跑步训练中,速度最快的是()。
跑步次数第一次第二次第三次第四次跑步时间45分钟1小时30分钟90分钟跑步路程6千米8500米4500米12600米A.第一次B.第二次C.第三次D.第四次二、填空题:本题共11小题,每小题3分,共33分 (共11题)第(1)题已知∠1与28°的和是一个平角,则∠1=( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
领导者如何使所在组织既能最大限度地满足个性
发展的需要,同时又能满足组织的需要
15工商叶中荣1590401045
1.组织要营造相对宽松的环境,鼓励员工提出自己的意见,提高员工的主观能动性。
由被动到主动是人性的特征之一,组织通过激励等手段提高员工的主动性,促进员工成熟个性的发展,也有利于企业的发展。
2.组织要关注员工的发展,除了物质奖励,还要让员工看到广大的发展空间。
个性发展会从只顾及当前发展为有长远打算。
组织不应该只看到员工当前的成就并给以相应的物质奖励,还应该看到员工的潜力并加以培养,给予员工广阔的发展空间。
3.组织要注意员工之间的关系,因为人的个性发展由依赖他人发展到相对独立。
组织内部关系和谐有利于员工之间相互协作,也有利于提高员工工作积极性。
