2018-2019武汉元调数学真题

合集下载

2018~2019学年度武汉市九年级元月调考数学试卷(含标准答案)

2018~2019学年度武汉市部分学校九年级调研测试数学试卷考试时间：2019年1月17日14:00~16:00 一、选择题（共10小题，每小题3分，共30分）1．将下列一元二次方程化成一般形式后，其中二次项系数是3，一次项系数是－6，常数项是1的方程是（） A ．3x 2＋1＝6xB ．3x 2－1＝6xC ．3x 2＋6x ＝1D ．3x 2－6x ＝12．下列图形中，是中心对称图形的是（）A ．B ．C ．D ．3．若将抛物线y ＝x 2先向右平移1个单位长度，再向上平移2个单位长度，就得到抛物线（）A ．y ＝(x －1)2＋2B ．y ＝(x －1)2－2C ．y ＝(x ＋1)2＋2D ．y ＝(x ＋1)2－24．投掷两枚质地均匀的骰子，骰子的六个面上分别刻有1到6的点数，则下列事件为随机事件的是（）A ．两枚骰子向上一面的点数之和大于1B ．两枚骰子向上一面的点数之和等于1C ．两枚骰子向上一面的点数之和大于12D ．两枚骰子向上一面的点数之和等于12 5．已知⊙O 的半径等于8 cm ，圆心O 到直线l 的距离为9 cm ，则直线l 与⊙O 的公共点的个数为（） A ．0B ．1C ．2D ．无法确定6．如图，“圆材埋壁”和我国古代著名数学著作《九章算术》中的问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何”用几何语言可表述为：CD 为 ⊙O 的直径，弦AB 垂直CD 于点E ，CE ＝1寸，AB ＝10寸，则直径CD 的长为（） A ．12.5寸B ．13寸C ．25寸D ．26寸第6题图第8题图第9题图7．假定鸟卵孵化后，雏鸟为雌鸟与雄鸟的概率相同．如果3枚鸟卵全部成功孵化，那么3只雏鸟中恰有2只雄鸟的概率是（） A ．61B ．83 C ．85 D ．32 8．如图，将半径为1，圆心角为120°的扇形OAB 绕点A 逆时针旋转一个角度，使点O 的对应点D 落在弧AB 上，点B 的对应点为C ，连接BC ，则图中CD 、BC 和弧BD 围成的封闭图形面积是（）A ．63π-B ．623π- C ．823π-D ．33π- 9．古希腊数学家欧几里得的《几何原本》记载，形如x 2＋ax ＝b 2的方程的图解法是：如图，画Rt △ABC ，∠ACB ＝90°，BC ＝2a ，AC ＝b ，再在斜边AB 上截取BD ＝2a，则该方程的一个正根是（） A ．AC 的长B ．BC 的长 C ．AD 的长 D ．CD 的长10．已知抛物线y ＝ax 2＋bx ＋c （a ＜0）的对称轴为x ＝－1，与x 轴的一个交点为(2，0)．若关于x 的一元二次方程ax 2＋bx ＋c ＝p （p ＞0）有整数根，则p 的值有（） A ．2个B ．3个C ．4个D ．5个二、填空题（本大题共6个小题，每小题3分，共18分）11．已知3是一元二次方程x 2＝p 的一个根，则另一根是___________12．在平面直角坐标系中，点P 的坐标是(－1，－2)，则点P 关于原点对称的点的坐标是_____ 13．一个口袋中有3个黑球和若干个白球，在不允许将球倒出来数的前提下，小刚为估计其中的白球数，采用了如下的方法：从口袋中随机摸出一球，记下颜色，然后把它放回口袋中，摇匀后再随机摸出一球，记下颜色……，不断重复上述过程，小刚共摸了100次，其中20次摸到黑球，根据上述数据，小刚可估计口袋中的白球大约有___________个14．第七届世界军人运动会将于2019年10月18日至27日在中国武汉举行，小明幸运获得了一张军运会吉祥物“兵兵”的照片．如图，该照片（中间的矩形）长29 cm ，宽为20 cm ，他想为此照片配一个四条边宽度相等的镜框（阴影部分），且镜框所占面积为照片面积的41．为求镜框的宽度，他设镜框的宽度为x cm ，依题意列方程，化成一般式为_____________第14题图第15题图第16题图15．如图是抛物线形拱桥，当拱顶离水面2 m 时，水面宽4 m ．水面下降2.5 m ，水面宽度增加___________m16．如图，正方形ABCD 的边长为4，点E 是CD 边上一点，连接AE ，过点B 作BG ⊥AE 于点G ，连接CG 并延长交AD 于点F ，则AF 的最大值是___________ 三、解答题（共8题，共72分） 17．（本题8分）解方程：x 2－3x －1＝018．（本题8分）如图，A 、B 、C 、D 是⊙O 上四点，且AD ＝CB ，求证：AB ＝CD第18题图19．（本题8分）武汉的早点种类丰富，品种繁多，某早餐店供应甲类食品有：“热干面”、 “面窝”、“生煎包”、“锅贴饺”（分别记为A ，B ，C ，D ）；乙类食品有：“米粑粑”、“烧梅”、“欢喜坨”、“发糕”（分别记为E、F、G、H），共八种美食．小李和小王同时去品尝美食，小李准备在“热干面”、“面窝”、“米粑粑”、“烧梅”（即A，B，E，F）这四种美食中选择一种，小王准备在“生煎包”、“锅贴饺”、“欢喜坨”、“发糕”（即C，D，G，H）这四种美食中选择一种，用列举法求小李和小王同时选择的美食都会是甲类食品的概率20．（本题8分）如图，在边长为1的正方形网格中，点A的坐标为(1，7)，点B的坐标为(5，5)，点C的坐标为(7，5)，点D的坐标为(5，1)(1) 将线段AB绕点B逆时针旋转，得到对应线段BE．当BE与CD第一次平行时，画出点A运动的路径，并直接写出点A运动的路径长(2) 小贝同学发现：线段AB与线段CD存在一种特殊关系，即其中一条线段绕着某点旋转一个角度可以得到另一条线段，直接写出这个旋转中心的坐标第20题图21．（本题8分）如图，在四边形ABCD中，AD∥BC，AD⊥CD，AC＝AB，⊙O为△ABC的外接圆(1) 如图1，求证：AD是⊙O的切线(2) 如图2，CD交⊙O于点E，过点A作AG⊥BE，垂足为F，交BC于点G①求证：AG＝BG②若AD＝2，CD＝3，求FG的长22．（本题10分）某商家销售一种成本为20元的商品，销售一段时间后发现，每天的销量y（件）与当天的销售单价x（元/件）满足一次函数关系，并且当x＝25时，y＝550；当x＝30时，y＝500．物价部门规定，该商品的销售单价不能超过48元/件(1) 求出y与x的函数关系式(2) 问销售单价定为多少元时，商家销售该商品每天获得的利润是8000元？(3) 直接写出商家销售该商品每天获得的最大利润23．（本题10分）如图，等边△ABC与等腰三角形△EDC有公共顶点C，其中∠EDC＝120°，2，连接BE，P为BE的中点，连接PD、ADAB＝CE＝6(1) 小亮为了研究线段AD与PD的数量关系，将图1中的△EDC绕点C旋转一个适当的角度，使CE与CA重合，如图2，请直接写出AD与PD的数量关系(2) 如图1，(1)中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由(3) 如图3，若∠ACD＝45°，求△P AD的面积24．（本题12分）如图，在平面直角坐标系中，抛物线y＝x2＋(1－m)x－m交x轴于A，B两点（点A在点B的左边），交y轴负半轴于点C(1) 如图1，m＝3①直接写出A，B，C三点的坐标②若抛物线上有一点D，∠ACD＝45°，求点D的坐标(2) 如图2，过点E(m，2)作一直线交抛物线于P，Q两点，连接AP，AQ，分别交y轴于M，N两点，求证：OM·ON是一个定值。

湖北省武汉市2018-2019学年高三四月调研测试数学理试题

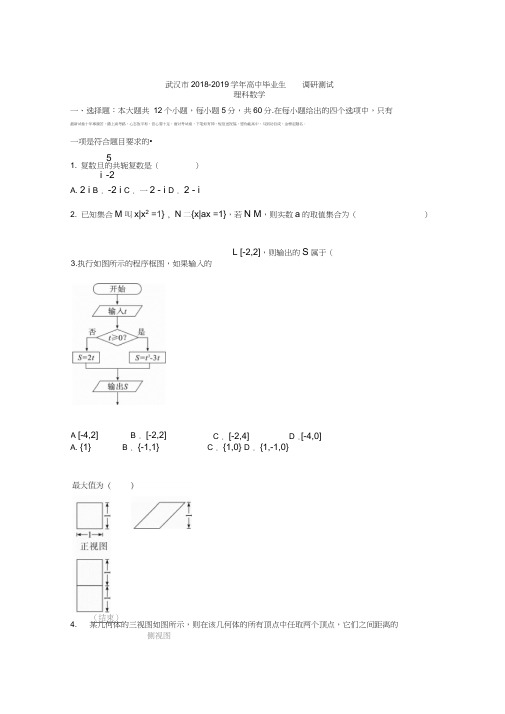
武汉市2018-2019学年高中毕业生调研测试理科数学一、选择题：本大题共 12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有最新试卷十年寒窗苦，踏上高考路，心态放平和，信心要十足，面对考试卷，下笔如有神，短信送祝福，愿你能高中，马到功自成，金榜定题名。

一项是符合题目要求的• 51. 复数旦的共轭复数是（）i -2A. 2 i B . -2 i C . 一2 - i D . 2 - i2. 已知集合M 叫x|x 2 =1} , N 二{x|ax =1}，若N M ，则实数a 的取值集合为（）A. {1}B . {-1,1}C . {1,0}D . {1,-1,0}4.某几何体的三视图如图所示，则在该几何体的所有顶点中任取两个顶点，它们之间距离的3.执行如图所示的程序框图，如果输入的L [-2,2]，则输出的S 属于（A [-4,2]B . [-2,2]C . [-2,4]D .[-4,0]（结束）侧视图俯视图A.、、3 B .、、6 C . 2\3 D . 2 6 5. 一张储蓄卡的密码共有 6位数字，每位数字都可以从 0L 9中任选一个，某人在银行自动提款机上取钱时, 忘记了密码最后「位数字，如果任意按最后位数字，不超过2次就按对的概率为（ )23C11 A.BD5105106.若实数a ,b 满足a b 1,m =叽(lOg a b), 2n = (log a b),2l = log a b ，贝U m , n ,l 的大小关系为()A. m l n B . I n m C . n I m D . I m n.既不充分也不必要条件 9.在（x 4 -1）6的展开式中，含x 5项的系数为x11.函数f （x）=2sM'xV （_0）的图象在［0,1］上恰有两个最大值点,为（）7.已知直线y 二kx 「1与双曲线x 2 _ y 2 =4的右支有两个交点，则 k 的取值范围为（）.［谆(5 .眩8.在. ABC 中，角A 、B 、C 的对应边分别为c ,条件B C A，那么条件2A.充分而不必要条件p 是条件q 成立的（.必要而不充分条件C.充要条件A. 6 .-6 .24 .-2410.若x , y满足x—1 +2 y+1 兰2，贝V M = 2x2• y2 -2x的最小值为A. -2则'-的取值范围A. ［2 二，4 二］13二25二•5 C 匚W P D2512.过点P（2, -1）作抛物线x3 =4y的两条切线，切点分别为 A , B , 于E , F两点，O为坐标原点，贝U PEF 与OAB的面积之比为（二、填空题：本大题共4小题，每小题5分，共20分.13. 已知sin： -2cos：，贝U sin : cos：二.14. 已知向量a , b , C满足a+b+2^= 0 ,且a =1 , p = 3 , |^ =2，则■I 4 4 i■> 4a b 2a c 2b c =3PA , PB分别交x轴y = f(X)-1为奇函数,f'(x) f(x)tan x 0 ,则不等式f (x) cosx的解集为16.在四面体ABCD中，AD二DB二AC二CB = 1，则四面体体积最大时，它的外接球半径R 二三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17题〜第21题为必考题，每个试题考生都必须作答.第22题〜第23题为选考题，考生根据要求作答.(一)必考题：共60分.2n17.已知正数数列｛a.｝满足：6=2 , a n - a nj 2 (n_ 2).a n — an」(1)求a2, a3 ；2 2(2)设数列｛b n｝满足0二⑻-1) 7，证明：数列｛g｝是等差数列，并求数列｛a.｝的通项18.如图，在棱长为3的正方体ABC^A1B1C1D1中，E , F分别在棱AB , CD上，且EM —平面A1EC1.AE =CF -1.(2)求直线FC1与平面A1EC1所成角的正弦值2 2X y19. 已知椭圆丨：1，过点P（1,1）作倾斜角互补的两条不同直线h , I2，设l i与椭圆4 2-交于A、B两点，12与椭圆丨交于C，D两点•（1）若P（1,1）为线段AB的中点，求直线AB的方程；AB（2）记九=―，求丸的取值范围.CD20. 在某市高中某学科竞赛中，某一个区4000名考生的参赛成绩统计如图所示•（1）求这4000名考生的竞赛平均成绩x （同一组中数据用该组区间中点作代表）；（2）由直方图可认为考生竞赛成绩z服正态分布NC,「2），其中」，二2分别取考生的平均成绩X 和考生成绩的方差s2，那么该区4000名考生成绩超过84.41分（含84.81分）的人数估计有多少人？（3）如果用该区参赛考生成绩的情况来估计全市的参赛考生的成绩情况，现从全市参赛考生中随机抽取4名考生，记成绩不超过.84.81分的考生人数为©，求P^ <3）.（精确到0.001）附：① s2=204.75，、- 204.75 =14.31 ；②Z L N（»；「2），则P（z ：：」；「）=0.6826 , P（二一2 二：：z J〔2；「）= 0.9544 ；③0.8413^0.501.21.已知函数f（x）二xe X-a（ln x x）, a R.（1）当a =e时，求f（x）的单调区间；（2）若f （x）有两个零点，求实数a的取值范围.（二）选考题：共10分.请考生在22、23题中任选一题作答，如果多做，则按所做的第一题记分•作答时请写清题号22. ［选修4-4 :坐标系与参数方程］在平面直角坐标系xOy中，以坐标原点0为极点，x轴正半轴为极轴建立极坐标系，I的极x =3cosv坐标方程为r（cos”2si nr） =10，C的参数方程为（r为参数，“ R）.y = 2si n 日（1）写出I和C的普通方程；（2）在C上求点M，使点M到I的距离最小，并求出最小值•23. ［选修4-5 :不等式选讲］已知f（x） = ax—2—x+2.（1）在a = 2时，解不等式f （x）叮；（2）若关于x的不等式-4岂f （x）岂4对x R恒成立，求实数a的取值范围.=0，武汉市2018届高中毕业生四月调研测试理科数学参考答案、选择题填空题解答题2 2 2•• a?…2 3 2( a2 - 2)，即a? ■ ■ 2a2 _— 0 .5又由a3a2 2 , a2 = 3,a3 _a22- 9 二5 ' 2( a3 - 3)，即a3 2a3 - 8 二0 .则(a* -1) - n = (an j.二…二低-1)4 -22=@2 -1)2 -122 2而b n =(a n -1) - n , 二b n =0，数列｛b n｝为等差数列4 2an " a n J = 2(an - a nJ) 2n _ 1,而a3 O 则a3 = 4.--a? =3，a^4.(2) 由已知条件可知:2 2二(an 一1) -(a n1_1)2 2二n -(n-1),1-5: BDABC 6-10: BDABD 11、12: CC13. 14. -1315. 16.17.(1)由已知a2 a1 -. 2 --a32 2…(an -■〔) n .而a n 0 ,故a n二n 1.18.解：(1)过M 作MT _ AA,于点T ,连B(T ,则AT =1.易证：.ARE 三：A1B1T，于是.ARE 二/AB J .由.A1B1T . ATB j =90；，知.AAE . ATB^90 ,••• A j E _ B1T .显然MT _ 面AA1B1B，而AE 面AA1B1B ,•- MT _ AE，又B1T Pl MT 二T ,•A1E _面MTB，• AE _ MB1 .连B1D1，则B J D J _ AG.又D<|M _ A1C1，B1D^1 D1M = D1，…A[C[—面MD[B[，•- AQ _ MB1.由RE _ MB j，AC^ MB1，A,^] A1C^A1，•B1M —面A1EC1.(2)在DQ上取一点N，使ND j =1，连接EF .易知AE/^FN .•- V A _EFS ^V N-EFS =V E_NF51 1 1S NFC 3 ( 2 3) 3 = 3.3 1 3 2对于A1EC1，AG =3 ,2，AE 二10，而EC^ <22，10 +18 + 22 1由余弦定理可知COS—EAC12 710 3丁2 V201 1 fig 3 ••• • AEG 的面积 SA 1C 1 A 1Esin .EAC 3、2 1019.2 220 2由等体积法可知 F 到平面A 1EC 1之距离h 满足1 1 36S A 1EC 1 h =V A 1 上FC ’，则 19 h = 3 , • h =3 3 219又FG =电10，设FC ’与平面AEC 1所成角为二,.匚 6厢 6 3^90 •• sin.怖 71909519.解：(1)设直线 AB 的斜率为k = tan ：•，方程为y -1 = k(x -1)，代入x 2 • 2y 2 = 4中, • x 2 2[kx -(k -1)]2 -4 =0.• (1 2k 2)x 2 -4k(k -1)x 2(k -1)2 -4 =0.判别式：-[4(k -1)k]2 -4(2k 2 1)[2(k-1)2-4] =8(3k 2 2k 1). 设 A(X i ,yJ , BXy)，则4k(k —1) X i X 222k 2 1 2 2(k —1) -4 X 1X2 ■ ■ 22k 21••• AB 中点为(1,1),1/ 、 2k(k -1) 1• 一(x , x 2) 2 1,则 k . 2 2k 2 121•直线的AB 方程为y-1 (x-1)，即x-2y ，1 = 0.(2)由(1)知 AB = .1 • k 2 x , -x 21 k2 8(3k 2 2k 1) -2k 2 十 1二、(X i X 2)2 - 4X i X 2设直线的CD方程为y -1二-k(x -1)(k = 0).同理可得c—E'耐-2k 1)2k214 3k - -2 k1令 t =3k k 小4 则 g(t) =1- t -2 g(t)在2、3] , [2、、3,■：：)分别单调递减，••• 2 一、.3 ^g(t) ：：：1 或 1 ：：： g(t)乞 2、、3.故 2 - ..3 乞■2<1 或 1 ：：2乞 2 '.3.」6 - I 26 ■、2即」[-7—5—^. 20.解：(1)由题意知:中间值 45 55 65 75 85 95 概率0.10.150.20.30.150.1• x =45 0.1 55 0.15 65 0.2 75 0.3 85 0.15 95 0.1 =70.5,• 4000名考生的竞赛平均成绩 X 为70.5分.(2)依题意z 服从正态分布 N(」,；「2)，其中亠=x =70.5，二2 二 D =204.75，丁 =14.31,• z 服从正态分布 N( J 二2) =N(70.5,14.312),而 P(」z=P(56.19 ：：： z ：： 84.81) =0.6826 ,•竞赛成绩超过84.81分的人数估计为0.1587 4000 = 634.8人” 634人. (3)全市竞赛考生成绩不超过 84.81分的概率1—0.1587 = 0.8413.而 LJ B(4,0.8413),• P (乞 3) =1 -P( =4) =^C4 0.84134 =1 - 0.501 = 0.499.AB CD3k2Lk ")•3k-2k 14k3k 2 1-2k=1 t (_：：,—2\3]U[2、：：)P(z _84.81)1 -0.68262 -0.1587.121.解：(1)定义域为：(0, •：：),f (x)在(0,1)时为减函数；在(1,：：)时为增函数(2)记 t =1 n x • x ，则 t = ln x • x 在(0, •：：)上单增，且 t R .二 f (x)二 xe x -a(ln x x)二 d -at = g(t).••• f (x)在x 0上有两个零点等价于 g(t)二at 在t R 上有两个零点.① 在a =0时，g(tHe t 在R 上单增，且g(t) 0，故g(t)无零点； ② 在 a ：：0时，g'(t)=et -a 在 R 上单增，又 g(0)=10，1 丄g(—) =e a -1 ：：：0,故g(t)在R 上只有一个零点；a③ 在a 0时，由g'(t)二et-a=0可知g(t)在t= lna 时有唯一的一个极小值g(ln a) = a(1 -In a).若 0 ：：a ：：e ， g 最小二 a(1-ln a) 0， g(t)无零点; 若a=e，g 最小=o ， g(t)只有一个零点;若 a e 时，g 最小=a(1 -1n a) ：： 0 ,而 g(0) =10，Inx由于f (x)在x e 时为减函数，可知： a e 时，e a a .x从而 g(a) =e a -a 2 - 0 , • g(x)在(0,ln a)和(In a,：：)上各有一个零点综上讨论可知：a e 时f (x)有两个零点，即所求 a 的取值范围是(ej ：：). 22.解：(1)由 I :「COST 『si n ：「T 0=0,及 x=：'cosv , y = ;?si n 「• I 的方程为x 2y -10=0.2 2由 x 二 3cos^ , y = 2S in r ，消去二得—-1.94当a = e 时, f'(x)二(1 x)(xe x e)x(2)在 C 上取点 M(3cos ,2sin ：)，则1:-—5cos("-讥)一105①3 cos 0 :其中5,sin o=- L 5当「二-o 时，d 取最小值、5989 8此时 3sin = 3cos 0, 2sin 0 = 2cos ;:0, M (,). 55 5 523.解：(1)在 a=2 时，2x —2 — x+2 兰 1. 在 x _1 时，(2x-2)—(X 2)乞 11EX ^5；在 x_-2 时，-(2x-2) • (x • 2) _1, x_3, . x 无解；11 在-2 一 x -1 时，—(2 X —^2)—'(x ，2) 一1, x ,. x_1.331综上可知：不等式 f (X )乞1的解集为{x| x 乞5}.3(2)v [x+2 —ax_2 <4恒成立，而 |x +2 — ax_2卜(1+a)x , 或 | x +2 - ax-2| 勻(1 -a)x +4 ,故只需(1+a)x|兰4恒成立，或(1—a)x+4兰4恒成立，••• a = -1 或 a =1..a 的取值为1或-1.113cos 门亠 4si n ^ -10「5。

2018~2019学年度武汉市部分学校九年级调研测试数学试卷(含答案)

2018~2019学年度武汉市部分学校九年级调研测试数学试卷考试时间：2019年1月17日14：00~16：00一、选择题（共10小题，每小题3分，共30分）1．将下列一元二次方程化成一般形式后，其中二次项系数是3，一次项系数是－6，常数项是1的方程是（）A ．3x 2＋1＝6xB ．3x 2－1＝6xC ．3x 2＋6x ＝1D ．3x 2－6x ＝12．下列图形中，是中心对称图形的是（）3．若将抛物线y ＝x 2先向右平移1个单位长度，再向上平移2个单位长度，就得到抛物线（）A ．y ＝(x －1)2＋2B ．y ＝(x －1)2－2C ．y ＝(x ＋1)2＋2D ．y ＝(x ＋1)2－24．投掷两枚质地均匀的骰子，骰子的六个面上分别刻有1到6的点数，则下列事件为随机事件的是（）A ．两枚骰子向上一面的点数之和大于1B ．两枚骰子向上一面的点数之和等于1C ．两枚骰子向上一面的点数之和大于12D ．两枚骰子向上一面的点数之和等于125．已知⊙O 的半径等于8 cm ，圆心O 到直线l 的距离为9 cm ，则直线l 与⊙O 的公共点的个数为（）A ．0B ．1C ．2D ．无法确定6．如图，“圆材埋壁”和我国古代著名数学著作《九章算术》中的问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何”用几何语言可表述为：CD 为⊙O 的直径，弦AB ⊥CD 于点E ，CE ＝1寸，AB ＝10寸，则直径CD 的长为（）A ．12．5寸B ．13寸C ．25寸D ．26寸7．假定鸟卵孵化后，雏鸟为雌鸟与雄鸟的概率相同．如果3枚鸟卵全部成功孵化，那么3只雏鸟中恰有2只雄鸟的概率是（）A ．61B ．83C ．85D ．32 8．如图，将半径为1，圆心角为120°的扇形OAB 绕点A 逆时针旋转一个角度，使点O 的对应点D 落在弧AB 上，点B 的对应点为C ，连接BC ，则图中CD 、BC 和弧BD 围成的封闭图形面积是（）A ．63π-B ．623π-C ．823π-D ．33π- 9．古希腊数学家欧几里得的《几何原本》记载，形如x 2＋ax ＝b 2的方程的图解法是：如图，画Rt △ABC ，∠ACB ＝90°，BC ＝2a ，AC ＝b ，再在斜边AB 上截取BD ＝2a ，则该方程的一个正根是（） A ．AC 的长 B ．BC 的长 C ．AD 的长 D ．CD 的长10．已知抛物线y ＝ax 2＋bx ＋c （a ＜0）的对称轴为x ＝－1，与x 轴的一个交点为(2，0)．若关于x 的一元二次方程ax 2＋bx ＋c ＝p （p ＞0）有整数根，则p 的值有（）A ．2个B ．3个C ．4个D ．5个二、填空题（本大题共6个小题，每小题3分，共18分）11．已知3是一元二次方程x 2＝p 的一个根，则另一根是___________．12．在平面直角坐标系中，点P 的坐标是(－1，－2)，则点P 关于原点对称的点的坐标是_____．13．一个口袋中有3个黑球和若干个白球，在不允许将球倒出来数的前提下，童威为估计其中的白球数，采用了如下的方法：从口袋中随机摸出一球，记下颜色，然后把它放回口袋中，摇匀后再随机摸出一球，记下颜色……，不断重复上述过程，童威共摸了100次，其中20次摸到黑球，根据上述数据，可估计口袋中的白球大约有___________个．14．第七届世界军人运动会将于2019年10月18日至27日在中国武汉矩形，小郑幸运获得了一张军运会吉祥物“兵兵”的照片．如图，该照片（中间的矩形）长29 cm 、宽为20 cm ，她想为此照片配一个四条边宽度相等的镜框（阴影部分），且镜框所占面积为照片面积的41．为求镜框的宽度，他设镜框的宽度为x cm ，依题意列方程，化成一般式为____________________．15．如图是抛物线型拱桥，当拱顶离水面2 m 时，水面宽4 m ．水面下降2．5 m ，水面宽度增加___________m ．16．如图，正方形ABCD 的边长为4，点E 是CD 边上一点，连接AE ，过点B 作BG ⊥AE 于点G ，连接CG 并延长交AD 于点F ，则AF 的最大值是___________．三、解答题（共8题，共72分）17．（本题8分）解方程：x 2－3x －1＝0．18．（本题8分）如图，A 、B 、C 、D 是⊙O 上四点，且AD ＝CB ，求证：AB ＝CD ．19．（本题8分）武汉的早点种类丰富，品种繁多，某早餐店供应甲类食品有：“热干面”、“面窝”、“生煎包”、“锅贴饺”（分别记为A 、B 、C 、D ）；乙类食品有：“米粑粑”、“烧梅”、“欢喜坨”、“发糕”（分别记为E 、F 、G 、H ），共八种美食．小童和小郑同时去品尝美食，小童准备在“热干面”、“面窝”、“米粑粑”、“烧梅”（即A 、B 、E 、F ）这四种美食中选择一种，小郑准备在“生煎包”、“锅贴饺”、“欢喜坨”、“发糕”（即C 、D 、G 、H ）这四种美食中选择一种，用列举法求小童和小郑同时选择的美食都会甲类食品的概率．20．（本题8分）如图，在边长为1的正方形网格中，A (1，7)、B (5，5)、C (7，5)、D (5，1)．(1) 将线段AB 绕点B 逆时针旋转，得到对应线段BE ．当BE 与CD 第一次平行时，画出点A 运动的路径，并直接写出点A 运动的路径长；(2) 线段AB 与线段CD 存在一种特殊关系，即其中一条线段绕着某点旋转一个角度可以得到另一条线段，直接写出这个旋转中心的坐标．21．（本题8分）如图，在四边形ABCD中，AD∥BC，AD⊥CD，AC＝AB，⊙O为△ABC的外接圆(1) 如图1，求证：AD是⊙O的切线；(2) 如图2，CD交⊙O于点E，过点A作AG⊥BE，垂足为F，交BC于点G．①求证：AG＝BG；②若AD＝2，CD＝3，求FG的长．22．（本题10分）某商家销售一种成本为20元的商品，销售一段时间后发现，每天的销量y（件）与当天的销售单价x（元/件）满足一次函数关系，并且当x＝25时，y＝550；当x＝30时，y＝500．物价部门规定，该商品的销售单价不能超过48元/件．(1) 求出y与x的函数关系式；(2) 问销售单价定为多少元时，商家销售该商品每天获得的利润是8000元？(3) 直接写出商家销售该商品每天获得的最大利润．23．（本题10分）如图，等边△ABC与等腰三角形△EDC有公共顶点C，其中∠EDC＝120°，AB＝CE ＝62，连接BE，P为BE的中点，连接PD、AD．(1) 为了研究线段AD与PD的数量关系，将图1中的△EDC绕点C旋转一个适当的角度，使CE与CA重合，如图2，请直接写出AD与PD的数量关系；(2) 如图1，(1)中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；(3) 如图3，若∠ACD＝45°，求△P AD的面积．24．（本题12分）如图，在平面直角坐标系中，抛物线y＝x2＋(1－m)x－m交x轴于A、B两点（点A在点B的左边），交y轴负半轴于点C．(1) 如图1，m＝3．①直接写出A、B、C三点的坐标；②若抛物线上有一点D，∠ACD＝45°，求点D的坐标．(2) 如图2，过点E(m，2)作一直线交抛物线于P、Q两点，连接AP、AQ，分别交y轴于M、N两点，求证：OM·ON是一个定值．。

2018-2019年武汉初三4月调考数学试卷

2018~2019学年度武汉市部分学校九年级四月调研测试数学试卷考试时间：2019年4月23日14:30~16:30一、选择题（共10小题，每小题3分，共30分）1．有理数－2的相反数是（）A．2 B．－2 C．21D．21-2．式子2-x在实数范围内有意义，则x的取值范围是（）A．x≥0 B．x≥－2 C．x≥2 D．x≤－23．下列说法：①“掷一枚质地均匀的硬币，朝上一面可能是正面”；②“从一副普通扑克牌中任意抽取一张，点数一定是3”（）A．只有①正确B．只有②正确C．①②都正确D．①②都错误4．下列四个图案中，是中心对称图形的是（）A. B. C. D.5．下列立体图形中，主视图是三角形的是（）A. B. C. D.6．《孙子算经》中有一道题，原文是：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何？”意思是：用一根绳子去量一根长木，绳子还剩余4.5尺；将绳子对折再量长木，长木还剩余1尺，问长木多少尺？如果设长木长x尺、绳长y尺，则可以列方程组是（）A．⎪⎩⎪⎨⎧=-=-1215.4xyxyB．⎪⎩⎪⎨⎧=-=-1215.4xyyxC．⎪⎩⎪⎨⎧=-=-1215.4yxyxD．⎪⎩⎪⎨⎧=-=-1215.4yxxy7．某超市为了吸引顾客，设计了一种返现促销活动：在一个不透明的箱子里放有4个相同的小球，球上分别标有“0元”、“10元”、“20元”、“30元”的字样，规定：顾客在本超市一次性消费满200元，就可以在箱子里一次性摸出两个小球，两球数字之和记为返现金额．童威刚好消费200元，则该顾客所获得返现金额不低于30元的概率是（）A．43B．32C．21D．318．若点A(x1，－3)、B(x2，－2)、C(x3，1)在反比例函数xky12+-=的图象上，则x1、x2、x3的大小关系是（）A．x1＜x2＜x3 B．x3＜x1＜x2 C．x2＜x1＜x3 D．x3＜x2＜x19．如图，等腰△ABC中，AB＝AC＝5 cm，BC＝8 cm．动点D从点C出发，沿线段CB以2 cm/s的速度向点B 运动，同时动点O 从点B 出发，沿线段BA 以1 cm /s 的速度向点A 运动，当其中一个动点停止运动时另一个动点也随时停止．设运动时间为t （s ），以点O 为圆心，OB 长为半径的⊙O 与BA 交于另一点E ，连接ED ．当直线DE 与⊙O 相切时，t 的取值是（）A ．916B ．23C ．34D ．310．我们探究得方程x ＋y ＝2的正整数解只有1组，方程x ＋y ＝3的正整数解只有2组，方程x ＋y ＝4的正整数解只有3组，……，那么方程x ＋y ＋z ＝10的正整数解得组数是（）A ．34B ．35C ．36D ．37二、填空题（本大题共6个小题，每小题3分，共18分）11．计算：9的结果是__________12．在学校举行“中国诗词大会”的比赛中，五位评委给选手小明的评分分别为：90，85，90，80，95，这组数据的众数是__________13．化简yx y x x 8164222---的结果是__________ 14．如图，D 为△ABC 中BC 边上一点，AB ＝CB ，AC ＝AD ，∠BAD ＝27°，则∠C ＝__________15．抛物线y ＝a (x －h )2＋k 经过(－1，0)，(5，0)两点，则关于的一元二次方程a (x －h ＋1)2＋k＝0的解是__________ 16．如图，在矩形ABCD 中，AB ＝6，BC ＝9，点E ,F 分别在BC ，CD 上．若BE ＝3，∠EAF ＝45°，则DF 的长是__________三、解答题（共8题，共72分）17．（本题8分）计算：3a 2·a 4＋(2a 3)2－7a 618．（本题8分）如图，AB ∥CD ，EF 分别交AB ，CD 于点G ，H ，∠BGH ，∠DHF 的平分线分别为GM ，HN ，求证：GM ∥HN19．（本题8分）为了加强学生课外阅读，开阔视野，某校开展了“书香校园，诵读经典”活动，学习随机抽查了部分学生，对他们每天的课外阅读时间进行调查，并将调查统计的结果分为四类：每天诵读时间t≤20分钟的学生记为A类，20分钟＜t≤40分钟记为B类，40分钟＜t≤60分钟记为C类，t＞60分钟记为D类，收集的数据绘制如下两幅不完整的统计图. 请根据图中提供的信息，解答下列问题：各类学生人数条形统计图各类学生人数扇形统计图(1) 这次共抽取了_________名学生进行调查统计，扇形统计图中D类所对应的扇形圆心角大小为_________(2) 将条形统计图补充完整(3) 如果该校共有2000名学生，请你估计该校C类学生约有多少人？20．（本题8分）如图，在下列10×10的网格中，横、纵坐标均为整点的数叫做格点，例如A(2，1)、B(5，4)、C(1，8)都是格点(1) 直接写出△ABC的形状(2) 要求在下图中仅用无刻度的直尺作图：将△ABC绕点A顺时针旋转角度α得到△AB1C1，α＝∠BAC，其中B，C的对应点分别为B1，C1，操作如下：第一步：找一个格点D，连接AD，使∠DAB＝∠CAB第二步：找两个格点C1，E，连接C1E交AD于B1第三步：连接AC1，则△AB1C1交即为所做出的图形请你按步骤完成作图，并直接写出D、C1、E三点的坐标21．（本题8分）如图，在等腰△ABC中，AB＝AC，AD是中线，E为边AC的中点，过B，D，E三点的⊙O交AC于另一点F，连接BF(1) 求证：BF＝BC4，求⊙O的直径(2) 若BC＝4，AD＝322．（本题10分）某公司计划购买A 、B 两种计算器共100个，要求A 种计算器数量不低于B 种的41，且不高于B 种的31．已知A 、B 两种计算器的单价分别是150元/个、100元/个，设购买A 种计算器x 个(1) 求计划购买这两种计算器所需费用y （元）与x 的函数关系式(2) 问该公司按计划购买者两种计算器有多少种方案？(3) 由于市场行情波动，实际购买时，A 种计算器单价下调了3m （m ＞0）元/个，同时B 种计算器单价上调了2m 元/个，此时童威购买这两种计算器所需最少费用为12150元，求m 的值23．（本题10分）如图，正方形ABCD 的对角线交于点O ，点E 在边BC 上，BE ＝n1BC ，AE 交OB 于点F ，过点B 作AE 的垂线BG 交OC 于点G ，连接GE(1) 求证：OF ＝OG .(2) 用含有n 的代数式表示tan ∠OBG 的值.(3) 若∠GEC ＝90°，直接写出n 的值.24．（本题12分）已知抛物线y ＝x 2＋bx ＋c 与经过点A (2，－3).(1) 如图，过点A 分别向x 轴，y 轴作垂线，垂足分别为B ，C ，得到矩形ABOC ，且抛物线经过点C.① 求抛物线的解析式.② 将抛物线向左平移m （m ＞0）个单位，分别交线段OB ，AC 于D ，E 两点．若直线DE 刚好平分矩形ABOC 的面积，求m 的值.(2) 将抛物线平移，使点A 的对应点为A 1(2－n ，3b )，其中n ≥1．若平移后的抛物线仍然经过点A ，求平移后的抛物线顶点所能达到最高点时的坐标.。

完整word版2018~2019度武汉市九年级元月调考数学试卷含标准答案

学年度武汉市部分学校九年级调研测试数学试卷2018~201914:00~16:00 日1月17考试时间：2019年分）3分，共30一、选择题（共10小题，每小题6，常数项是1 1．将下列一元二次方程化成一般形式后，其中二次项系数是3，一次项系数是－）的方程是（22221＝＋6x＝1 D．3x－6A．3x．＋1＝6x B3x3－1＝6x C．xx）2．下列图形中，是中心对称图形的是（． C D．．A B．2）个单位长度，再向上平移2个单位长度，就得到抛物线（3．若将抛物线y＝x先向右平移122222 ＝(x＋1)．x A．y＝(－B．y＝(x1)－－2 1)＋＋2 2 D y＝(x＋1)－C．y的点数，则下列事件为随机事件4．投掷两枚质地均匀的骰子，骰子的六个面上分别刻有1到6 ）的是（1 B．两枚骰子向上一面的点数之和等于A．两枚骰子向上一面的点数之和大于112 ．两枚骰子向上一面的点数之和等于C．两枚骰子向上一面的点数之和大于12 D 8 cm，圆心O到直线l的距离为9 cm，则直线O的公共点的个数l与⊙5．已知⊙O的半径等于为（）D2B ．1C．．无法确定0 A．6．如图，“圆材埋壁”和我国古代著名数学著作《九章算术》中的问题：“今有圆材，埋在壁为中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何”用几何语言可表述为：CD）的长为（＝＝于点的直径，弦⊙OAB垂直CDE，CE1寸，AB10寸，则直径CD．寸．A12.5 B13寸寸D．26 25 C．寸题图第9 第8题图6第题图枚鸟卵全部成功孵化，那么3只雏7．假定鸟卵孵化后，雏鸟为雌鸟与雄鸟的概率相同．如果3 ）鸟中恰有2只雄鸟的概率是（2351．．D C．A ．B3868OAB8．如图，将半径为1，圆心角为120°的扇形绕点A逆时针旋转一个角度，使点O的对应BD围成的封闭图形，则图中CD、BC和弧BCBD点落在弧AB上，点的对应点为C，连接）面积是（????33??．A ．B． C D．?33?82623622的方程的图解法是：如图，画b＝ax＋x．古希腊数学家欧几里得的《几何原本》记载，形如9．aa，则该方程的一个上截取BD＝，∠ACB＝90°，BC，AC＝b＝，再在斜边ABRt△ABC22 ）正根是（B．BC的长 C A．AC的长．AD的长D．CD的长2＋bx＋c（a＜0）的对称轴为xax＝－1，与x轴的一个交点为(2，0)．若关10．已知抛物线y＝2＋bx ＋c＝p（p＞0）有整数根，则p的值有（）于x的一元二次方程ax A．2个B．3个C．4个D．5个二、填空题（本大题共6个小题，每小题3分，共18分）2＝p的一个根，则另一根是是一元二次方程．已知3x___________1112．在平面直角坐标系中，点P的坐标是(－1，－2)，则点P关于原点对称的点的坐标是_____13．一个口袋中有3个黑球和若干个白球，在不允许将球倒出来数的前提下，小刚为估计其中的白球数，采用了如下的方法：从口袋中随机摸出一球，记下颜色，然后把它放回口袋中，摇匀后再随机摸出一球，记下颜色……，不断重复上述过程，小刚共摸了100次，其中20次摸到黑球，根据上述数据，小刚可估计口袋中的白球大约有___________个14．第七届世界军人运动会将于2019年10月18日至27日在中国武汉举行，小明幸运获得了一张军运会吉祥物“兵兵”的照片．如图，该照片（中间的矩形）长29 cm，宽为20 cm，他1．想为此照片配一个四条边宽度相等的镜框（阴影部分），且镜框所占面积为照片面积的4为求镜框的宽度，他设镜框的宽度为x cm，依题意列方程，化成一般式为_____________16题图第第15题图题图第1415．如图是抛物线形拱桥，当拱顶离水面2 m时，水面宽4 m．水面下降2.5 m，水面宽度增加___________m16．如图，正方形ABCD的边长为4，点E是CD边上一点，连接AE，过点B作BG⊥AE于点G，连接CG并延长交AD于点F，则AF的最大值是___________三、解答题（共8题，共72分）2－3x－1＝0 17．（本题8分）解方程：x18．（本题8分）如图，A、B、C、D是⊙O上四点，且AD＝CB，求证：AB＝CD第18题图19．（本题8分）武汉的早点种类丰富，品种繁多，某早餐店供应甲类食品有：“热干面”、“烧“米粑粑”、）；乙类食品有：D，C，B，A（分别记为“锅贴饺”“生煎包”、“面窝”、．梅”、“欢喜坨”、“发糕”（分别记为E、F、G、H），共八种美食．小李和小王同时去品尝美食，小李准备在“热干面”、“面窝”、“米粑粑”、“烧梅”（即A，B，E，F）这四种美食中选择一种，小王准备在“生煎包”、“锅贴饺”、“欢喜坨”、“发糕”（即C，D，G，H）这四种美食中选择一种，用列举法求小李和小王同时选择的美食都会是甲类食品的概率20．（本题8分）如图，在边长为1的正方形网格中，点A的坐标为(1，7)，点B的坐标为(5，5)，点C的坐标为(7，5)，点D的坐标为(5，1)(1) 将线段AB绕点B逆时针旋转，得到对应线段BE．当BE与CD第一次平行时，画出点A运动的路径，并直接写出点A运动的路径长(2) 小贝同学发现：线段AB与线段CD存在一种特殊关系，即其中一条线段绕着某点旋转一个角度可以得到另一条线段，直接写出这个旋转中心的坐标第20题图21．（本题8分）如图，在四边形ABCD中，AD∥BC，AD⊥CD，AC＝AB，⊙O为△ABC的外接圆(1) 如图1，求证：AD是⊙O的切线(2) 如图2，CD交⊙O于点E，过点A作AG⊥BE，垂足为F，交BC于点G①求证：AG＝BG②若AD＝2，CD＝3，求FG的长22．（本题10分）某商家销售一种成本为20元的商品，销售一段时间后发现，每天的销量y（件）与当天的销售单价x（元/件）满足一次函数关系，并且当x＝25时，y＝550；当x＝30时，y＝500．物价部门规定，该商品的销售单价不能超过48元/件(1) 求出y与x的函数关系式(2) 问销售单价定为多少元时，商家销售该商品每天获得的利润是8000元？(3) 直接写出商家销售该商品每天获得的最大利润，EDC＝120°ABC与等腰三角形△EDC有公共顶点C，其中∠23．（本题10分）如图，等边△26，连接BE，P为BE的中点，连接PD、AB＝CEAD＝(1) 小亮为了研究线段AD与PD的数量关系，将图1中的△EDC绕点C旋转一个适当的角度，使CE与CA重合，如图2，请直接写出AD与PD的数量关系(2) 如图1，(1)中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由(3) 如图3，若∠ACD＝45°，求△PAD的面积2＋(1－m)x－m交x轴于A，x24．（本题12分）如图，在平面直角坐标系中，抛物线y＝B两点（点A在点B的左边），交y轴负半轴于点C(1) 如图1，m＝3①直接写出A，B，C三点的坐标②若抛物线上有一点D，∠ACD＝45°，求点D的坐标(2) 如图2，过点E(m，2)作一直线交抛物线于P，Q两点，连接AP，AQ，分别交y轴于M，N两点，求证：OM·ON是一个定值。

2018~2019学年度武汉市部分学校九年级四月调研测试数学试卷真题

2018-2019学年度武汉市部分学校九年级四月调研测试数学试卷考试时间：2019年4月23日14:30~16:30一、选择题（共10小题，每小题3分，共30分）1．有理数－2的相反数是（）A ．2B ．－2C ．21D ．21- 2．式子2-x 在实数范围内有意义，则x 的取值范围是（）A ．x ≥0B ．x ≥－2C ．x ≥2D ．x ≤－23．下列说法：① “掷一枚质地均匀的硬币，朝上一面可能是正面”；② “从一副普通扑克牌中任意抽取一张，点数一定是3”（）A ．只有①正确B ．只有②正确C ．①②都正确D ．①②都错误4．下列四个图案中，是中心对称图形的是（）A ．B ．C ．D ．5．下列立体图形中，主视图是三角形的是（）A ．B ．C ．D ．6．《孙子算经》中有一道题，原文是：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何？”意思是：用一根绳子去量一根长木，绳子还剩余4.5尺；将绳子对折再量长木，长木还剩余1尺，问长木多少尺？如果设长木长x 尺、绳长y 尺，则可以列方程组是（）A ．⎪⎩⎪⎨⎧=-=-1215.4x y x yB ．⎪⎩⎪⎨⎧=-=-1215.4x y y xC ．⎪⎩⎪⎨⎧=-=-1215.4y x y xD ．⎪⎩⎪⎨⎧=-=-1215.4y x x y 7．某超市为了吸引顾客，设计了一种返现促销活动：在一个不透明的箱子里放有4个相同的小球，球上分别标有“0元”、“10元”、“20元”、“30元”的字样，规定：顾客在本超市一次性消费满200元，就可以在箱子里一次性摸出两个小球，两球数字之和记为返现金额．童威刚好消费200元，则该顾客所获得返现金额不低于30元的概率是（）A ．43B ．32C ．21D ．31 8．若点A(x 1，－3)、B(x 2，－2)、C(x 3，1)在反比例函数xk y 12+-=的图象上，则x 1、x 2、x 3的大小关系是（）A ．x 1＜x 2＜x 3B ．x 3＜x 1＜x 2C ．x 2＜x 1＜x 3D ．x 3＜x 2＜x 19．如图，等腰△ABC 中，AB ＝AC ＝5 cm ，BC ＝8 cm ．动点D 从点C 出发，沿线段CB 以2 cm/s 的速度向点B 运动，同时动点O 从点B 出发，沿线段BA 以1 cm/s 的速度向点A 运动，当其中一个动点停止运动时另一个动点也随时停止．设运动时间为t （s ），以点O 为圆心，OB 长为半径的⊙O 与BA 交于另一点E ，连接ED ．当直线DE 与⊙O 相切时，t 的取值是（）A ．916B ．23C ．34D ．310．我们探究得方程x ＋y ＝2的正整数解只有1组，方程x ＋y ＝3的正整数解只有2组，方程x ＋y ＝4的正整数解只有3组，……，那么方程x ＋y ＋z ＝10的正整数解得组数是（）A ．34B ．35C ．36D ．37二、填空题（本大题共6个小题，每小题3分，共18分）11．计算：9的结果是__________.12．在学校举行“中国诗词大会”的比赛中，五位评委给选手小明的评分分别为：90，85，90，80，95，这组数据的众数是__________.13．化简yx y x x 8164222---的结果是__________. 14．如图，D 为△ABC 中BC 边上一点，AB ＝CB ，AC ＝AD ，∠BAD ＝27°，则∠C ＝__________.15．抛物线y ＝a(x －h)2＋k 经过(－1，0)，(5，0)两点，则关于的一元二次方程a(x －h ＋1)2＋k ＝0的解是__________.16．如图，在矩形ABCD中，AB＝6，BC＝9，点E,F分别在BC，CD上．若BE＝3，∠BGH＝45°，则DF的长是__________.三、解答题（共8题，共72分）17．（本题8分）计算：3a2·a4＋(2a3)2－7a618．（本题8分）如图，AB∥CD，EF分别交AB，CD于点G，H，∠BGH，∠DHF的平分线分别为GM，HN，求证：GM∥HN19．（本题8分）为了加强学生课外阅读，开阔视野，某校开展了“书香校园，诵读经典”活动，学习随机抽查了部分学生，对他们每天的课外阅读时间进行调查，并将调查统计的结果分为四类：每天诵读时间t≤20分钟的学生记为A类，20分钟＜t≤40分钟记为B类，40分钟＜t≤60分钟记为C类，t＞60分钟记为D类，收集的数据绘制如下两幅不完整的统计图. 请根据图中提供的信息，解答下列问题：各类学生人数条形统计图各类学生人数扇形统计图（1）这次共抽取了_________名学生进行调查统计，扇形统计图中D类所对应的扇形圆心角大小为_________ （2）将条形统计图补充完整（3）如果该校共有2000名学生，请你估计该校C类学生约有多少人？20．（本题8分）如图，在下列10×10的网格中，横、纵坐标均为整点的数叫做格点，例如A(2，1)、B(5，4)、C(1，8)都是格点(1) 直接写出△ABC的形状(2) 要求在下图中仅用无刻度的直尺作图：将△ABC绕点A顺时针旋转角度α得到△AB1C1，α＝∠BAC，其中B，C的对应点分别为B1，C1，操作如下：第一步：找一个格点D，连接AD，使∠DAB＝∠CAB第二步：找两个格点C1，E，连接C1E交AD于B1第三步：连接AC1，则△AB1C1交即为所做出的图形请你按步骤完成作图，并直接写出D、C1、E三点的坐标21．（本题8分）如图，在等腰△ABC中，AB＝AC，AD是中线，E为边AC的中点，过B，D，E三点的⊙O交AC于另一点F，连接BF（1）求证：BF＝BC（2）若BC＝4，AD＝34，求⊙O的直径22．（本题10分）某公司计划购买A 、B 两种计算器共100个，要求A 种计算器数量不低于B 种的41，且不高于B 种的31．已知A 、B 两种计算器的单价分别是150元/个、100元/个，设购买A 种计算器x 个 (1) 求计划购买这两种计算器所需费用y （元）与x 的函数关系式(2) 问该公司按计划购买者两种计算器有多少种方案？(3) 由于市场行情波动，实际购买时，A 种计算器单价下调了3m （m ＞0）元/个，同时B 种计算器单价上调了2m 元/个，此时童威购买这两种计算器所需最少费用为12150元，求m 的值23．（本题10分）如图，正方形ABCD 的对角线交于点O ，点E 在边BC 上，BE ＝n1BE ，AE 交OB 于点F ，过点B 作AE 的垂线BG 交OC 于点G ，连接GE(1) 求证：OF ＝OG(2) 用含有n 的代数式表示tan ∠OBG 的值(3) 若∠GEC ＝90°，直接写出n 的值24．（本题12分）已知抛物线y＝x2＋bx＋c与x轴交于点A(2，－3)（1）如图，过点A分别向x轴，y轴作垂线，垂足分别为B，C，得到矩形ABOC，且抛物线经过点C①求抛物线的解析式②将抛物线向左平移m（m＞0）个单位，分别交线段OB，AC于D，E两点．若直线DE刚好平分矩形ABOC 的面积，求m的值（2）将抛物线平移，使点A的对应点为A1(2－n，3b)，其中n≥1．若平移后的抛物线仍然经过点A，求平移后的抛物线顶点所能达到最高点时的坐标。

2018~2019学年度武汉市九年级元月调考数学试卷(含实用标准问题详解)

2018~2019学年度市部分学校九年级调研测试数学试卷考试时间：2019年1月17日14:00~16:00 一、选择题（共10小题，每小题3分，共30分）1．将下列一元二次方程化成一般形式后，其中二次项系数是3，一次项系数是－6，常数项是1的方程是（） A ．3x 2＋1＝6xB ．3x 2－1＝6xC ．3x 2＋6x ＝1D ．3x 2－6x ＝12．下列图形中，是中心对称图形的是（）A ．B ．C ．D ．3．若将抛物线y ＝x 2先向右平移1个单位长度，再向上平移2个单位长度，就得到抛物线（）A ．y ＝(x －1)2＋2B ．y ＝(x －1)2－2C ．y ＝(x ＋1)2＋2D ．y ＝(x ＋1)2－24．投掷两枚质地均匀的骰子，骰子的六个面上分别刻有1到6的点数，则下列事件为随机事件的是（）A ．两枚骰子向上一面的点数之和大于1B ．两枚骰子向上一面的点数之和等于1C ．两枚骰子向上一面的点数之和大于12D ．两枚骰子向上一面的点数之和等于12 5．已知⊙O 的半径等于8 cm ，圆心O 到直线l 的距离为9 cm ，则直线l 与⊙O 的公共点的个数为（） A ．0B ．1C ．2D ．无法确定6．如图，“圆材埋壁”和我国古代著名数学著作《九章算术》中的问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何”用几何语言可表述为：CD 为 ⊙O 的直径，弦AB 垂直CD 于点E ，CE ＝1寸，AB ＝10寸，则直径CD 的长为（） A ．12.5寸B ．13寸C ．25寸D ．26寸第6题图第8题图第9题图7．假定鸟卵孵化后，雏鸟为雌鸟与雄鸟的概率相同．如果3枚鸟卵全部成功孵化，那么3只雏鸟中恰有2只雄鸟的概率是（） A ．61B ．83 C ．85 D ．32 8．如图，将半径为1，圆心角为120°的扇形OAB 绕点A 逆时针旋转一个角度，使点O 的对应点D 落在弧AB 上，点B 的对应点为C ，连接BC ，则图中CD 、BC 和弧BD 围成的封闭图形面积是（）A ．63π-B ．623π- C ．823π-D ．33π- 9．古希腊数学家欧几里得的《几何原本》记载，形如x 2＋ax ＝b 2的方程的图解法是：如图，画Rt △ABC ，∠ACB ＝90°，BC ＝2a ，AC ＝b ，再在斜边AB 上截取BD ＝2a，则该方程的一个正根是（） A ．AC 的长B ．BC 的长 C ．AD 的长 D ．CD 的长10．已知抛物线y ＝ax 2＋bx ＋c （a ＜0）的对称轴为x ＝－1，与x 轴的一个交点为(2，0)．若关于x 的一元二次方程ax 2＋bx ＋c ＝p （p ＞0）有整数根，则p 的值有（） A ．2个B ．3个C ．4个D ．5个二、填空题（本大题共6个小题，每小题3分，共18分）11．已知3是一元二次方程x 2＝p 的一个根，则另一根是___________12．在平面直角坐标系中，点P 的坐标是(－1，－2)，则点P 关于原点对称的点的坐标是_____ 13．一个口袋中有3个黑球和若干个白球，在不允许将球倒出来数的前提下，小刚为估计其中的白球数，采用了如下的方法：从口袋中随机摸出一球，记下颜色，然后把它放回口袋中，摇匀后再随机摸出一球，记下颜色……，不断重复上述过程，小刚共摸了100次，其中20次摸到黑球，根据上述数据，小刚可估计口袋中的白球大约有___________个14．第七届世界军人运动会将于2019年10月18日至27日在中国举行，小明幸运获得了一军运会吉祥物“兵兵”的照片．如图，该照片（中间的矩形）长29 cm ，宽为20 cm ，他想为此照片配一个四条边宽度相等的镜框（阴影部分），且镜框所占面积为照片面积的41．为求镜框的宽度，他设镜框的宽度为x cm ，依题意列方程，化成一般式为_____________第14题图第15题图第16题图15．如图是抛物线形拱桥，当拱顶离水面2 m 时，水面宽4 m ．水面下降2.5 m ，水面宽度增加___________m16．如图，形ABCD 的边长为4，点E 是CD 边上一点，连接AE ，过点B 作BG ⊥AE 于点G ，连接CG 并延长交AD 于点F ，则AF 的最大值是___________ 三、解答题（共8题，共72分） 17．（本题8分）解方程：x 2－3x －1＝018．（本题8分）如图，A 、B 、C 、D 是⊙O 上四点，且AD ＝CB ，求证：AB ＝CD第18题图19．（本题8分）的早点种类丰富，品种繁多，某早餐店供应甲类食品有：“热干面”、 “面窝”、“生煎包”、“锅贴饺”（分别记为A ，B ，C ，D ）；乙类食品有：“米粑粑”、“烧梅”、“欢喜坨”、“发糕”（分别记为E、F、G、H），共八种美食．小和小王同时去品尝美食，小准备在“热干面”、“面窝”、“米粑粑”、“烧梅”（即A，B，E，F）这四种美食中选择一种，小王准备在“生煎包”、“锅贴饺”、“欢喜坨”、“发糕”（即C，D，G，H）这四种美食中选择一种，用列举法求小和小王同时选择的美食都会是甲类食品的概率20．（本题8分）如图，在边长为1的形网格中，点A的坐标为(1，7)，点B的坐标为(5，5)，点C的坐标为(7，5)，点D的坐标为(5，1)(1) 将线段AB绕点B逆时针旋转，得到对应线段BE．当BE与CD第一次平行时，画出点A运动的路径，并直接写出点A运动的路径长(2) 小贝同学发现：线段AB与线段CD存在一种特殊关系，即其中一条线段绕着某点旋转一个角度可以得到另一条线段，直接写出这个旋转中心的坐标第20题图21．（本题8分）如图，在四边形ABCD中，AD∥BC，AD⊥CD，AC＝AB，⊙O为△ABC的外接圆(1) 如图1，求证：AD是⊙O的切线(2) 如图2，CD交⊙O于点E，过点A作AG⊥BE，垂足为F，交BC于点G①求证：AG＝BG②若AD＝2，CD＝3，求FG的长22．（本题10分）某商家销售一种成本为20元的商品，销售一段时间后发现，每天的销量y（件）与当天的销售单价x（元/件）满足一次函数关系，并且当x＝25时，y＝550；当x＝30时，y＝500．物价部门规定，该商品的销售单价不能超过48元/件(1) 求出y与x的函数关系式(2) 问销售单价定为多少元时，商家销售该商品每天获得的利润是8000元？(3) 直接写出商家销售该商品每天获得的最大利润23．（本题10分）如图，等边△ABC与等腰三角形△EDC有公共顶点C，其中∠EDC＝120°，2，连接BE，P为BE的中点，连接PD、ADAB＝CE＝6(1) 小亮为了研究线段AD与PD的数量关系，将图1中的△EDC绕点C旋转一个适当的角度，使CE与CA重合，如图2，请直接写出AD与PD的数量关系(2) 如图1，(1)中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由(3) 如图3，若∠ACD＝45°，求△P AD的面积24．（本题12分）如图，在平面直角坐标系中，抛物线y＝x2＋(1－m)x－m交x轴于A，B两点（点A在点B的左边），交y轴负半轴于点C(1) 如图1，m＝3①直接写出A，B，C三点的坐标②若抛物线上有一点D，∠ACD＝45°，求点D的坐标(2) 如图2，过点E(m，2)作一直线交抛物线于P，Q两点，连接AP，AQ，分别交y轴于M，N两点，求证：OM·ON是一个定值。

1_2018~2019学年度武汉市部分学校九年级调研测试数学试卷

2018~2019学年度武汉市部分学校九年级调研测试数学试卷一、选择题（共10小题，每小题3分，共30分）1．将下列一元二次方程化成一般形式后，其中二次项系数是3，一次项系数是－6，常数项是1的方程是（）A ．3x 2＋1＝6xB ．3x 2－1＝6xC ．3x 2＋6x ＝1D ．3x 2－6x ＝12．下列图形中，是中心对称图形的是（）3．若将抛物线y ＝x 2先向右平移1个单位长度，再向上平移2个单位长度，就得到抛物线（） A ．y ＝(x －1)2＋2B ．y ＝(x －1)2－2C ．y ＝(x ＋1)2＋2D ．y ＝(x ＋1)2－2 4．投掷两枚质地均匀的骰子，骰子的六个面上分别刻有1到6的点数，则下列事件为随机事件的是（） A ．两枚骰子向上一面的点数之和大于1 B ．两枚骰子向上一面的点数之和等于1C ．两枚骰子向上一面的点数之和大于12D ．两枚骰子向上一面的点数之和等于12 5．已知⊙O 的半径等于8 cm ，圆心O 到直线l 的距离为9 cm ，则直线l 与⊙O 的公共点的个数为（）A ．0B ．1C ．2D ．无法确定6．如图，“圆材埋壁”和我国古代著名数学著作《九章算术》中的问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何”用几何语言可表述为：CD 为⊙O 的直径，弦AB ⊥CD 于点E ，CE ＝1寸，AB ＝10寸，则直径CD 的长为（）A ．12.5寸B ．13寸C ．25寸D ．26寸7．假定鸟卵孵化后，雏鸟为雌鸟与雄鸟的概率相同．如果3枚鸟卵全部成功孵化，那么3只雏鸟中恰有2只雄鸟的概率是（）A ．61B ．83C ．85D ．32 8．如图，将半径为1，圆心角为120°的扇形OAB 绕点A 逆时针旋转一个角度，使点O 的对应点D 落在弧AB 上，点B 的对应点为C ，连接BC ，则图中CD 、BC 和弧BD 围成的封闭图形面积是（）A ．63π- B ．623π- C ．823π- D ．33π-9．古希腊数学家欧几里得的《几何原本》记载，形如x 2＋ax ＝b 2的方程的图解法是：如图，画Rt △ABC ，∠ACB ＝90°，BC ＝2a ，AC ＝b ，再在斜边AB 上截取BD ＝2a ，则该方程的一个正根是（）A ．AC 的长B ．BC 的长 C ．AD 的长 D ．CD 的长10．已知抛物线y ＝ax 2＋bx ＋c （a ＜0）的对称轴为x ＝－1，与x 轴的一个交点为(2，0)．若关于x 的一元二次方程ax 2＋bx ＋c ＝p （p ＞0）有整数根，则p 的值有（）A ．2个B ．3个C ．4个D ．5个二、填空题（本大题共6个小题，每小题3分，共18分）11．已知3是一元二次方程x 2＝p 的一个根，则另一根是___________12．在平面直角坐标系中，点P 的坐标是(－1，－2)，则点P 关于原点对称的点的坐标是_____13．一个口袋中有3个黑球和若干个白球，在不允许将球倒出来数的前提下，童威为估计其中的白球数，采用了如下的方法：从口袋中随机摸出一球，记下颜色，然后把它放回口袋中，摇匀后再随机摸出一球，记下颜色……，不断重复上述过程，童威共摸了100次，其中20次摸到黑球，根据上述数据，可估计口袋中的白球大约有___________个14．第七届世界军人运动会将于2019年10月18日至27日在中国武汉矩形，小郑幸运获得了一张军运会吉祥物“兵兵”的照片．如图，该照片（中间的矩形）长29 cm 、宽为20 cm ，她想为此照片配一个四条边宽度相等的镜框（阴影部分），且镜框所占面积为照片面积的41．为求镜框的宽度，他设镜框的宽度为x cm ，依题意列方程，化成一般式为____________________15．如图是抛物线型拱桥，当拱顶离水面2 m 时，水面宽4 m ．水面下降2.5 m ，水面宽度增加___________m16．如图，正方形ABCD 的边长为4，点E 是CD 边上一点，连接AE ，过点B 作BG ⊥AE 于点G ，连接CG 并延长交AD 于点F ，则AF 的最大值是___________三、解答题（共8题，共72分）17．（本题8分）解方程：x 2－3x －1＝018．（本题8分）如图，A 、B 、C 、D 是⊙O 上四点，且AD ＝CB ，求证：AB ＝CD19．（本题8分）武汉的早点种类丰富，品种繁多，某早餐店供应甲类食品有：“热干面”、“面窝”、“生煎包”、“锅贴饺”（分别记为A 、B 、C 、D ）；乙类食品有：“米粑粑”、“烧梅”、“欢喜坨”、“发糕”（分别记为E 、F 、G 、H ），共八种美食．小童和小郑同时去品尝美食，小童准备在“热干面”、“面窝”、“米粑粑”、“烧梅”（即A 、B 、E 、F ）这四种美食中选择一种，小郑准备在“生煎包”、“锅贴饺”、“欢喜坨”、“发糕”（即C 、D 、G 、H ）这四种美食中选择一种，用列举法求小童和小郑同时选择的美食都会甲类食品的概率20．（本题8分）如图，在边长为1的正方形网格中，A(1，7)、B(5，5)、C(7，5)、D(5，1) (1) 将线段AB绕点B逆时针旋转，得到对应线段BE．当BE与CD第一次平行时，画出点A运动的路径，并直接写出点A运动的路径长(2) 线段AB与线段CD存在一种特殊关系，即其中一条线段绕着某点旋转一个角度可以得到另一条线段，直接写出这个旋转中心的坐标21．（本题8分）如图，在四边形ABCD中，AD∥BC，AD⊥CD，AC＝AB，⊙O为△ABC的外接圆(1) 如图1，求证：AD是⊙O的切线(2) 如图2，CD交⊙O于点E，过点A作AG⊥BE，垂足为F，交BC于点G①求证：AG＝BG②若AD＝2，CD＝3，求FG的长22．（本题10分）某商家销售一种成本为20元的商品，销售一段时间后发现，每天的销量y（件）与当天的销售单价x（元/件）满足一次函数关系，并且当x＝25时，y＝550；当x＝30时，y＝500．物价部门规定，该商品的销售单价不能超过48元/件(1) 求出y与x的函数关系式(2) 问销售单价定为多少元时，商家销售该商品每天获得的利润是8000元？(3) 直接写出商家销售该商品每天获得的最大利润23．（本题10分）如图，等边△ABC与等腰三角形△EDC有公共顶点C，其中∠EDC＝120°，2，连接BE，P为BE的中点，连接PD、ADAB＝CE＝6(1) 为了研究线段AD与PD的数量关系，将图1中的△EDC绕点C旋转一个适当的角度，使CE与CA重合，如图2，请直接写出AD与PD的数量关系(2) 如图1，(1)中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由(3) 如图3，若∠ACD＝45°，求△P AD的面积24．（本题12分）如图，在平面直角坐标系中，抛物线y＝x2＋(1－m)x－m交x轴于A、B两点（点A在点B的左边），交y轴负半轴于点C(1) 如图1，m＝3①直接写出A、B、C三点的坐标②若抛物线上有一点D，∠ACD＝45°，求点D的坐标(2) 如图2，过点E(m，2)作一直线交抛物线于P、Q两点，连接AP、AQ，分别交y轴于M、N 两点，求证：OM·ON是一个定值。

2019年度武汉元调数学试卷及其规范标准答案(精校版)

2018-2019学年度武汉市部分学校九年级元月调考数学试卷一、选择题(共10小题，每小题3分，共30分) 1.下列一元二次方程化成一般形式后，其中二次项系数是3，一次项系数是-6，常数项是1的方程式是( ) A ．2316x x += B ． 2316x x -= C ． 2361x x += D ． 2361x x -= 2.下列图形中，是中心对称图形的是( )3.若将抛物线2y x =先向右平移1个单位长度，再向上平移2个单位长度，就得到抛物线( )A ．2(1)2y x =-+B ． 2(1)2y x =--C ． 2(1)2y x =++D ． 2(1)2y x =+-4.投掷两枚质地均匀的骰子，骰子的六个面上分别有刻有1和6的点数，则下列事件为随机事件的是( ) A ．两枚骰子向上一面的点数之和大于1 B ．两枚骰子向上一面的点数之和等于1 C ．两枚骰子向上一面的点数之和大于12 D ．两枚骰子向上一面的点数之和等于125.已知O e 的半径等于8cm ，圆心O 到直线l 的距离为9cm ，则直线l 与O e 的公共点的个数为( ) A ．0 B ． 1 C ． 2 D ．无法确定6.如图，“圆材埋壁” 是我国古代著名数学著作《九章算术》中的问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何.”用几何语言可表述为：CD 为O e 的直径，弦AB 垂直CD 于点E ，CE =1寸，AB =10寸，则直径CD 的长为( )A ．12.5寸B ． 13寸C ． 25寸D ． 26寸7.假定鸟卵孵化后，雏鸟为雌鸟与雄鸟的概率相同.如果3枚鸟卵全部成功孵化，那么3只雏鸟中恰有2只雄鸟的概率是( )A ．16B ．38C ．58D ．238.如图，将半径为1，圆心角为120°的扇形OAB 绕点A 逆时针旋转一个角度，使点O 的对应点D 落在»AB 上，点B 的对应点为C ，连接BC ，则图中CD ，BC 和»BD围成的封闭图形面积是( ) A6p B ．6p C ．8pD ．3p 9.古希腊数学家欧几里得的《几何原本》记载，形如22x ax b +=的方程的图解是：如图，画Rt ABC D ，∠ACB =90°，2a BC =，AC b =，再在斜边AB 上截取2aBD =.则该方程的一个正根是( )A ．AC 的长B ． BC 的长 C ． AD 的长 D ．CD 的长10.已知抛物线2(0)y ax bx c a =++<的对称轴为1x =-，与x 轴的一个交点为(2，0).若关于x 的一元一次方程2(0)ax bx c p p ++=>有整数根，则p 的值有( )D .C .B .A.CAA ．2个B ．3个C ． 4个D ．5个二、填空题(本大题共6个小题，每小题3分，共18分)11.已知3是一元二次方程2x p =的一个根，则另一个根是________.12.在平面直角坐标系中，点P 的坐标是(-1，-2)，则点P 关于原点对称的点的坐标是________.13.一个口袋中有3个黑球和若干个白球，在不允许将球倒出来的前提下，小刚为估计其中的白球数，采用了如下的方法：从口袋中随机摸出一球，记下颜色，然后把它放回口袋中，摇匀后再随机摸出一球，记下颜色，…….，不断重复上述过程，小刚共摸了100次，其中20次摸到黑球，根据上述数据，小刚可估计口袋中的白球大约有________个.14.第七届世界军人运动会将于2019年10月18日至27日在中国武汉举行.小明幸运获得了一张军运会吉祥物“兵兵”的照片，如图，该照片(中间的矩形)长29cm ，宽为20cm ，他想为此照片配一个四条边宽度相等的镜框(阴影部分)，且镜框所占面积为照片面积的14，为求镜框的宽度，他设镜框的宽度为x cm ，依题意列方程，化成一般式为________.15.如图是抛物线拱桥，当拱顶离水面2m 时，水面宽4m ，水面下降2.5m ，水面宽度增加________m .16.如图，正方形ABCD 的边长为4，点E 是CD 边上一点，连接AE ，过点B 作BG ⊥AE 于点G ，连接CG 并延长交AD 于点F ，则AF 的最大值是________.三、解答题(共8题，共72分)17.(本题8分)解方程：2310x x --=18.(本题8分)如图，A ，B ，C ，D 是⊙O 上四点，且AD =CB ，求证：AB =C D ．19.(本题8分)武汉的早点种类丰富，品种繁多.某早餐店供应甲类食品有：“热干面”、“面窝”、“生煎包”、“锅贴饺”(分别记为A ，B ，C ，D )；乙类食品有：“米粑粑”、“烧梅”、“欢喜坨”、“发糕”(分别记为E ，F ，G ，H )，共八种美食.小李和小王同时去品尝美食，小李准备在“热干面”、“面窝”、“米粑粑”、“烧梅”(即A ，B ，E ，F )这四种美食中选择一种，小王准备在“生煎包”、“锅贴饺”、“欢喜坨”、“发糕”(即C ，D ，G ，H )这四种美食中选择一种.用列举法求小李和小王同时选择的美食都是甲类食品的概率.GDA20.(本题8分)如图，在边长为1的正方形网格中，点A 的坐标为(1，7)，点B 的坐标为(5，5)，点C 的坐标为(7，5)，点D 的坐标为(5，1).(1)将线段AB 绕点B 逆时针旋转，得到对应线段BE ，当BE 与CD 第一次平行时，画出点A 运动的路径，并直接写出点A 运动的路径长；(2)小贝同学发现：线段AB 与线段CD 存在一种特殊关系，即其中一条线段绕着某点旋转一个角度可以得到另一条线段，直接写出这个旋转中心的坐标.21.(本题8分)如图，在四边形ABCD 中，AD BC P ，AD CD ⊥，AC AB =，O e 为ABC ∆的外接圆. (1)如图1，求证：AD 是O e 的切线；(2)如图2，CD 交O e 于点E ，过点A 作AG BE ⊥，垂足为F ，交BC 于点G . ①求证：AG BG =②若2AD =，3CD =，求FG 的长.图1 图222.(本题10分)某商家销售一种成本为20元的商品，销售一段时间后发现，每天的销量y (件)与当天的销售单价x (元/件)满足一次函数关系，并且当x =25时，y =550元；当x =30时，y =500.物价部门规定，该商品的销售单价不能超过48元/件. (1)求出y 与x 的函数关系式；(2)问销售单价定为多少元时，商家销售该商品每天获得的利润是8000元？ (3)直接写出商家销售该商品每天获得的最大利润.23.(本题10分)如图，等边ABC ∆与等腰EDC ∆有公共顶点C ，其中120EDC ∠=︒，AB CE ==BE ，P 为BE 的中点，连接PD AD 、.(1)小亮为了研究线段AD 与PD 的数量关系，将图1中的EDC ∆绕点C 旋转一个适当的角度，使CE 与CA 重合，如图2，请直接写出AD 与PD 的数量关系；(2)如图1，(1)中的结论是否依然成立？若成立，请给出证明，若不成立，请说明理由； (3)如图3，若45ACD ∠=︒，求PAD ∆的面积.图1图2 图3BBB24.(本题12分)如图，在平面直角坐标系中，抛物线2(1)y x m x m =+--交x 轴于A B 、两点(点A 在点B 的左边)，交y 轴负半轴于点C .(1)如图1，3m =.①直接写出A B C 、、三点的坐标；②若抛物线上有一点D ，45ACD ∠=︒，求点D 的坐标.(2)如图2，过点(2)E m ，作一直线交抛物线于P Q 、两点，连接AP AQ 、，分别交y 轴于M N 、两点，求证：OM ON ⋅是一个定值.图1图22018-2019学年度武汉市部分学校九年级元月调考数学试卷参考答案9解析：设AD 为x ，根据Rt ABC D ，222()()22x b +=+，得：222244a a x axb ++=+，22x ax b +=，所以可以求出x ，所以AD 即所求. 10解析：依图形可知二、填空题(本大题共6个小题，每小题3分，共18分) 11. -3 12.(1，2) 13. 12 14.24981450x x +-= 15. 2 16.115.解析：以抛物线的顶点为原点，建立平面直角坐标系.则A (2，-2)，B (-2，-2)∴212y x =-，令 4.5y =-，解得3x =±.∴此时水面宽度为6米，增加了2米 16.解析：∵∠AGB=90°，AB =4，∴G 在以AB 为直径的圆上运动当CF 与圆相切时，∠BCF 最大，此时AF 最大设AF =FG =x ，BC =CG=4，，则DF =4-x在Rt △FDC 中，DC 2+DF 2=FC 2，42+(4-x )2=(4+x )2，解得：x =1∴AF =1三、解答题(共8题，共72分) 17.解：∵a =1，b =-3，c =-1∴22=4(3)41(1)94130b ac ∆-=--⨯⨯-=+=＞ ∴x ==∴1x =2x =B A18.证明：∵AD =CB∴»»AD CB= ∴»»»»AD BD CB BD +=+ 即¼¼ADB CBD= ∴AB =CD19. 解：由树状图可知，小李和小王选择美食共有16种情况，且每种情况出现的可能性相等，同时都是甲类食品的情况共4种.∴P (两种都是甲类食品)=416=1420. 解：(画法如下)(2)情况一：作AD 和BC 的垂直平分线，交点即为旋转中心(6，6) 情况二：作AC 和BD 的垂直平分线，交点即为旋转中心(3，3)21(1)如图所示：连OC ，OB ，连AO 延长交BC 于点H ∵AB =AC ，∴点A 在BC 的垂直平分线上又∵OB =OC ， ∴O 在BC 的垂直平分线上∴AO 垂直平分BC ， ∴AO ⊥BC ，CH =BH ， ∴∠AHC =90° 又∵AD ∥BC ， ∴∠OAD =90°， ∴AD 为O e 的切线 (2)如图所示：①法一：由(1)可知AH ⊥BC ，∴∠HAB +∠ABH =90° ∵AG ⊥BE ，∴∠F AB +∠ABF =90° ∵AO =BO ，∴∠HAB =∠FBA ∴∠ABH =∠F AB ，∴AG =BG法二：8字倒角可得：∠F AO =∠HBO ，又∵∠OAB =∠OBA ∴∠GAB =∠GBA ，∴AG =BG ②由(1)可知四边形ADCH 为矩形. ∴AH =CD =3，CH =HB =AD =2 ∴Rt ABH ∆中 AB=在AGH ∆和BGF ∆中90AHG BFG AGH BGFAG BG ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩∴()AGH BGF AAS ∆∆≌ ∴GF GH =设GH =x ，∴AG =BG =2+x∴在Rt AGH ∆中：()22232x x +=+， 22944x x x +=++，∴54x =，∴54FG GH ==22. 解：(1)设y kx b =+将(25，550)和(30，500)代入可得： 550 =2550030k b k b +⎧⎨=+⎩ 解得：10800k b =-⎧⎨=⎩∴y 与x 的函数关系式为：10800y x =-+ (2)设利润为w 元.()()2010800w x x =--+ 21080020016000w x x x =-++- 210100016000w x x =-+-∴2800010100016000x x =-+- 即210024000x x -+= ∴()()40600x x --=解得：140x =，260x =，∵该商品的销售单价不能超过48元/件.∴x =40答：当销售单价定为40元时，商家销售该商品每天获得的利润是8000元. (3)8960元 23.(1)解：AD =2PD (2)仍然成立。

2018年度武汉市九年级元月调考数学试卷精品

2018-2018学年度武汉市九年级元月调考数学试卷2018年元月一、选择题(共2小题，每小题3分，共36分)下列各题中均有四个备选答案，其中有且只有一个正确，请在答卷上将正确答案的代号涂黑．1a的取值必须满足A．a≥3 B．a≤3 C．a≠3 D．a≠02．有两个事件，事件A：掷一次骰子，向上的一面是3；事件B：篮球队员在罚球线上投篮一次，投中．则A．只有事件S是随机事件．B．只有事件B是随机事件．C．声件A和B都是随机事件．D．事件A和B都不是随机事件．3．将一元二次方程5x2－1=4x化成一般形式后，二次项系数和一次项系数分别为A．5,－4 B．5, 4 C．5, 1 D．5x2,－4x4．如图，点C、D、D、B、A都在方格纸的格点上，若⊿AOB是由⊿COD绕点O按顺时针方向旋转而得的，则旋转的角度为A．30°B．45 ° C.90°D．135 °5．如图，小惠同学设计了一个圆半径的测量器，标有刻度的尺子OA、OB在O点钉在一起，并使它们保持垂直．在测直径时，把O点靠在圆周上，读得刻度OE=8个单位，OF=6个单位，则圆的半径为A．3个单位．B．4个单位．C．5个单位．D．6个单位．6．下列各式中计算正确的是A=B．2=C．2=D．=7．从1，－2，3三个数中随机抽取一个数，这个数是正数的概率是A．0 B．13C．23D．18．方程x2+7=8x的根的情况为A．有两个不相等的实数根．B．有两个相等的实数根．C．有一个实数根．D．没有实数根．9．为迎接“2018李娜和朋友们国际网球精英赛”，某款桑普拉斯网球包原价168元，连续两次降价a％后售价为128元．下列所列方程中正确的是A．168(1+a％)2=1 28．B．168(1--a2％)=1 28．C．168(1－2a％)=1 28．D．168(1—a％)2=128．10．如图，在以AB为直径的半圆中，有一个边长为1的内接正方形CDEF，则，以AC和BC的长为两根的一元二次方程是A．210x+=B．24205x x-+=C．24205x x+-=D．210x-=11．设12211112S=++，22112123S=++，22113134S=++…，22111(1)nSn n=+++，设nS S=+，其中n为正整数，则用含n的代数式表示S为A．211n nn--+B．221n nn++C．1(1)n n+D．21(1)nn n++12．如图，AB是半圆直径，半径OC⊥AB于点D，AD平分∠CAB交弧BC于点D，连接CD、OD. 下列结论：①A C∥OD；②CE=OE；③∠OED=∠AOD；④CD=DE. 其中正确结论的个数有A．1个．B．2个．C．3个．D．4个．二、填空题(共4小题，每小题3分，共l 2分)下列各题不需要写出解答过程，请将结果直接填写在答卷指定的位置．13= 。

武汉市部分学校2018~2019学年度九年级四月调研测试数学试卷及标准答案

武汉市部分学校2018~2019学年度九年级四月调研测试数学试卷考试时间：2019年4月23日14:30~16:30 一、选择题（共10小题，每小题3分，共30分） 1．有理数－2的相反数是（） A ．2B ．－2C ．21 D ．21-2．式子2-x 在实数范围内有意义，则x 的取值范围是（） A ．x ≥0B ．x ≥－2C ．x ≥2D ．x ≤－23．下列说法：① “掷一枚质地均匀的硬币，朝上一面可能是正面”；② “从一副普通扑克牌中任意抽取一张，点数一定是3”（） A ．只有①正确B ．只有②正确C ．①②都正确D ．①②都错误4．下列四个图案中，是中心对称图形的是（）5．下列立体图形中，主视图是三角形的是（）6．《孙子算经》中有一道题，原文是：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何？”意思是：用一根绳子去量一根长木，绳子还剩余4.5尺；将绳子对折再量长木，长木还剩余1尺，问长木多少尺？如果设长木长x 尺、绳长y 尺，则可以列方程组是（）A ．⎪⎩⎪⎨⎧=-=-1215.4x y x yB ．⎪⎩⎪⎨⎧=-=-1215.4x y y xC ．⎪⎩⎪⎨⎧=-=-1215.4y x y xD ．⎪⎩⎪⎨⎧=-=-1215.4y x x y 7．某超市为了吸引顾客，设计了一种返现促销活动：在一个不透明的箱子里放有4个相同的小球，球上分别标有“0元”、“10元”、“20元”、“30元”的字样，规定：顾客在本超市一次性消费满200元，就可以在箱子里一次性摸出两个小球，两球数字之和记为返现金额．童威刚好消费200元，则该顾客所获得返现金额不低于30元的概率是（） A ．43B ．32 C ．21 D ．31 8．若点A (x 1，－3)、B (x 2，－2)、C (x 3，1)在反比例函数xk y 12+-=的图象上，则x 1、x 2、x 3的大小关系是（）A ．x 1＜x 2＜x 3B ．x 3＜x 1＜x 2C ．x 2＜x 1＜x 3D ．x 3＜x 2＜x 1 9．如图，等腰△ABC 中，AB ＝AC ＝5 cm ，BC ＝8 cm ．动点D 从点C 出发，沿线段CB 以2 cm /s 的速度向点B 运动，同时动点O 从点B 出发，沿线段BA 以1 cm /s 的速度向点A 运动，当其中一个动点停止运动时另一个动点也随时停止．设运动时间为t （s ），以点O 为圆心，OB 长为半径的⊙O 与BA 交于另一点E ，连接ED ．当直线DE 与⊙O 相切时，t 的取值是（）A ．916B ．23C ．34D ．310．我们探究得方程x ＋y ＝2的正整数解只有1组，方程x ＋y ＝3的正整数解只有2组，方程x ＋y ＝4的正整数解只有3组，……，那么方程x ＋y ＋z ＝10的正整数解得组数是（） A ．34B ．35C ．36D ．37二、填空题（本大题共6个小题，每小题3分，共18分） 11．计算：9的结果是__________12．在学校举行“中国诗词大会”的比赛中，五位评委给选手小明的评分分别为：90，85，90，80，95，这组数据的众数是__________ 13．化简2221648x x y x y---的结果是__________14．如图，D 为△ABC 中BC 边上一点，AB ＝CB ，AC ＝AD ，∠BAD ＝27°，则∠C ＝__________15．抛物线y ＝a (x －h )2＋k 经过(－1，0)，(5，0)两点，则关于的一元二次方程a (x －h ＋1)2＋k ＝0的解是__________ 16．如图，在矩形ABCD 中，AB ＝6，BC ＝9，点E ,F 分别在BC ，CD 上．若BE ＝3，∠EAF ＝45°，则DF 的长是__________三、解答题（共8题，共72分）17．（本题8分）计算：3a 2·a 4＋(2a 3)2－7a 618．（本题8分）如图，AB ∥CD ，EF 分别交AB ，CD 于点G ，H ，∠BGH ， ∠DHF 的平分线分别为GM ，HN ，求证：GM ∥HN19．（本题8分）为了加强学生课外阅读，开阔视野，某校开展了“书香校园，诵读经典”活动，学习随机抽查了部分学生，对他们每天的课外阅读时间进行调查，并将调查统计的结果分为四类：每天诵读时间t ≤20分钟的学生记为A 类，20分钟＜t ≤40分钟记为B 类，40分钟＜t ≤60分钟记为C 类，t ＞60分钟记为D 类，收集的数据绘制如下两幅不完整的统计图. 请根据图中提供的信息，解答下列问题：各类学生人数条形统计图各类学生人数扇形统计图(1) 这次共抽取了_________名学生进行调查统计，扇形统计图中D 类所对应的扇形圆心角大小为_________ (2) 将条形统计图补充完整(3) 如果该校共有2000名学生，请你估计该校C 类学生约有多少人？20．（本题8分）如图，在下列10×10的网格中，横、纵坐标均为整点的数叫做格点，例如 A (2，1)、B (5，4)、C (1，8)都是格点(1) 直接写出△ABC 的形状(2) 要求在下图中仅用无刻度的直尺作图：将△ABC 绕点A 顺时针旋转角度α得到△AB 1C 1，α＝∠BAC ，其中B ，C 的对应点分别为B 1，C 1，操作如下：第一步：找一个格点D ，连接AD ，使∠DAB ＝∠CAB 第二步：找两个格点C 1，E ，连接C 1E 交AD 于B 1 第三步：连接AC 1，则△AB 1C 1交即为所做出的图形请你按步骤完成作图，并直接写出D 、C 1、E 三点的坐标21．（本题8分）如图，在等腰△ABC 中，AB ＝AC ，AD 是中线，E 为边AC 的中点，过B ，D ，E 三点的⊙O 交AC 于另一点F ，连接BF (1) 求证：BF ＝BC(2) 若BC ＝4，AD ＝34，求⊙O 的直径22．（本题10分）某公司计划购买A 、B 两种计算器共100个，要求A 种计算器数量不低于B 种的41，且不高于B 种的31．已知A 、B 两种计算器的单价分别是150元/个、100元/个，设购买A 种计算器x 个 (1) 求计划购买这两种计算器所需费用y （元）与x 的函数关系式 (2) 问该公司按计划购买者两种计算器有多少种方案？(3) 由于市场行情波动，实际购买时，A 种计算器单价下调了3m （m ＞0）元/个，同时B 种计算器单价上调了2m 元/个，此时购买这两种计算器所需最少费用为12150元，求m 的值23．（本题10分）如图，正方形ABCD 的对角线交于点O ，点E 在边BC 上，BE ＝n1BC ，AE 交OB 于点F ，过点B 作AE 的垂线BG 交OC 于点G ，连接GE (1) 求证：OF ＝OG(2) 用含有n 的代数式表示tan ∠OBG 的值 (3) 若∠GEC ＝90°，直接写出n 的值24．（本题12分）已知抛物线y ＝x 2＋bx ＋c 与x 轴交于点A (2，－3)(1) 如图，过点A 分别向x 轴，y 轴作垂线，垂足分别为B ，C ，得到矩形ABOC ，且抛物线经过点C ① 求抛物线的解析式② 将抛物线向左平移m （m ＞0）个单位，分别交线段OB ，AC 于D ，E 两点．若直线DE 刚好平分矩形ABOC 的面积，求m 的值(2) 将抛物线平移，使点A 的对应点为A 1(2－n ，3b )，其中n ≥1．若平移后的抛物线仍然经过点A ，求平移后的抛物线顶点所能达到最高点时的坐标。

2018-2019学年度武汉市九年级元月调考数学试卷(含答案)

2018~2019学年度武汉市九年级调研测试数学试卷考试时间：2019年1月17日14:00~16:00 一、选择题（共10小题，每小题3分，共30分）1．将下列一元二次方程化成一般形式后，其中二次项系数是3，一次项系数是－6，常数项是1的方程是（） A ．3x 2＋1＝6xB ．3x 2－1＝6xC ．3x 2＋6x ＝1D ．3x 2－6x ＝12．下列图形中，是中心对称图形的是（）A ．B ．C ．D ．3．若将抛物线y ＝x 2先向右平移1个单位长度，再向上平移2个单位长度，就得到抛物线（）A ．y ＝(x －1)2＋2B ．y ＝(x －1)2－2C ．y ＝(x ＋1)2＋2D ．y ＝(x ＋1)2－24．投掷两枚质地均匀的骰子，骰子的六个面上分别刻有1到6的点数，则下列事件为随机事件的是（）A ．两枚骰子向上一面的点数之和大于1B ．两枚骰子向上一面的点数之和等于1C ．两枚骰子向上一面的点数之和大于12D ．两枚骰子向上一面的点数之和等于12 5．已知⊙O 的半径等于8 cm ，圆心O 到直线l 的距离为9 cm ，则直线l 与⊙O 的公共点的个数为（） A ．0B ．1C ．2D ．无法确定6．如图，“圆材埋壁”和我国古代著名数学著作《九章算术》中的问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何”用几何语言可表述为：CD 为 ⊙O 的直径，弦AB 垂直CD 于点E ，CE ＝1寸，AB ＝10寸，则直径CD 的长为（） A ．12.5寸B ．13寸C ．25寸D ．26寸第6题图第8题图第9题图7．假定鸟卵孵化后，雏鸟为雌鸟与雄鸟的概率相同．如果3枚鸟卵全部成功孵化，那么3只雏鸟中恰有2只雄鸟的概率是（） A ．61B ．83 C ．85 D ．32 8．如图，将半径为1，圆心角为120°的扇形OAB 绕点A 逆时针旋转一个角度，使点O 的对应点D 落在弧AB 上，点B 的对应点为C ，连接BC ，则图中CD 、BC 和弧BD 围成的封闭图形面积是（）A ．63π-B ．623π- C ．823π-D ．33π- 9．古希腊数学家欧几里得的《几何原本》记载，形如x 2＋ax ＝b 2的方程的图解法是：如图，画Rt △ABC ，∠ACB ＝90°，BC ＝2a ，AC ＝b ，再在斜边AB 上截取BD ＝2a，则该方程的一个正根是（） A ．AC 的长B ．BC 的长 C ．AD 的长 D ．CD 的长10．已知抛物线y ＝ax 2＋bx ＋c （a ＜0）的对称轴为x ＝－1，与x 轴的一个交点为(2，0)．若关于x 的一元二次方程ax 2＋bx ＋c ＝p （p ＞0）有整数根，则p 的值有（） A ．2个B ．3个C ．4个D ．5个二、填空题（本大题共6个小题，每小题3分，共18分）11．已知3是一元二次方程x 2＝p 的一个根，则另一根是___________12．在平面直角坐标系中，点P 的坐标是(－1，－2)，则点P 关于原点对称的点的坐标是_____ 13．一个口袋中有3个黑球和若干个白球，在不允许将球倒出来数的前提下，小刚为估计其中的白球数，采用了如下的方法：从口袋中随机摸出一球，记下颜色，然后把它放回口袋中，摇匀后再随机摸出一球，记下颜色……，不断重复上述过程，小刚共摸了100次，其中20次摸到黑球，根据上述数据，小刚可估计口袋中的白球大约有___________个14．第七届世界军人运动会将于2019年10月18日至27日在中国武汉举行，小明幸运获得了一张军运会吉祥物“兵兵”的照片．如图，该照片（中间的矩形）长29 cm ，宽为20 cm ，他想为此照片配一个四条边宽度相等的镜框（阴影部分），且镜框所占面积为照片面积的41．为求镜框的宽度，他设镜框的宽度为x cm ，依题意列方程，化成一般式为_____________第14题图第15题图第16题图15．如图是抛物线形拱桥，当拱顶离水面2 m 时，水面宽4 m ．水面下降2.5 m ，水面宽度增加___________m16．如图，正方形ABCD 的边长为4，点E 是CD 边上一点，连接AE ，过点B 作BG ⊥AE 于点G ，连接CG 并延长交AD 于点F ，则AF 的最大值是___________ 三、解答题（共8题，共72分） 17．（本题8分）解方程：x 2－3x －1＝018．（本题8分）如图，A 、B 、C 、D 是⊙O 上四点，且AD ＝CB ，求证：AB ＝CD第18题图19．（本题8分）武汉的早点种类丰富，品种繁多，某早餐店供应甲类食品有：“热干面”、 “面窝”、“生煎包”、“锅贴饺”（分别记为A ，B ，C ，D ）；乙类食品有：“米粑粑”、“烧梅”、“欢喜坨”、“发糕”（分别记为E、F、G、H），共八种美食．小李和小王同时去品尝美食，小李准备在“热干面”、“面窝”、“米粑粑”、“烧梅”（即A，B，E，F）这四种美食中选择一种，小王准备在“生煎包”、“锅贴饺”、“欢喜坨”、“发糕”（即C，D，G，H）这四种美食中选择一种，用列举法求小李和小王同时选择的美食都会是甲类食品的概率20．（本题8分）如图，在边长为1的正方形网格中，点A的坐标为(1，7)，点B的坐标为(5，5)，点C的坐标为(7，5)，点D的坐标为(5，1)(1) 将线段AB绕点B逆时针旋转，得到对应线段BE．当BE与CD第一次平行时，画出点A运动的路径，并直接写出点A运动的路径长(2) 小贝同学发现：线段AB与线段CD存在一种特殊关系，即其中一条线段绕着某点旋转一个角度可以得到另一条线段，直接写出这个旋转中心的坐标第20题图21．（本题8分）如图，在四边形ABCD中，AD∥BC，AD⊥CD，AC＝AB，⊙O为△ABC的外接圆(1) 如图1，求证：AD是⊙O的切线(2) 如图2，CD交⊙O于点E，过点A作AG⊥BE，垂足为F，交BC于点G①求证：AG＝BG②若AD＝2，CD＝3，求FG的长22．（本题10分）某商家销售一种成本为20元的商品，销售一段时间后发现，每天的销量y（件）与当天的销售单价x（元/件）满足一次函数关系，并且当x＝25时，y＝550；当x＝30时，y＝500．物价部门规定，该商品的销售单价不能超过48元/件(1) 求出y与x的函数关系式(2) 问销售单价定为多少元时，商家销售该商品每天获得的利润是8000元？(3) 直接写出商家销售该商品每天获得的最大利润23．（本题10分）如图，等边△ABC与等腰三角形△EDC有公共顶点C，其中∠EDC＝120°，2，连接BE，P为BE的中点，连接PD、ADAB＝CE＝6(1) 小亮为了研究线段AD与PD的数量关系，将图1中的△EDC绕点C旋转一个适当的角度，使CE与CA重合，如图2，请直接写出AD与PD的数量关系(2) 如图1，(1)中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由(3) 如图3，若∠ACD＝45°，求△P AD的面积24．（本题12分）如图，在平面直角坐标系中，抛物线y＝x2＋(1－m)x－m交x轴于A，B两点（点A在点B的左边），交y轴负半轴于点C(1) 如图1，m＝3①直接写出A，B，C三点的坐标②若抛物线上有一点D，∠ACD＝45°，求点D的坐标(2) 如图2，过点E(m，2)作一直线交抛物线于P，Q两点，连接AP，AQ，分别交y轴于M，N两点，求证：OM·ON是一个定值。

武汉元调数学试题及答案

武汉元调数学试题及答案一、选择题（每题3分，共30分）1. 若函数f(x) = 2x^2 + 3x - 5，则f(-2)的值为：A. -15B. -13C. -11D. -9答案：C2. 已知集合A={1,2,3}，B={2,3,4}，则A∩B的元素个数为：A. 1B. 2C. 3D. 4答案：B3. 向量a=(3,2)，向量b=(-1,4)，则向量a与向量b的数量积为：A. 10B. 8C. 6D. 4答案：A4. 已知双曲线方程为x^2/9 - y^2/16 = 1，其渐近线方程为：A. y = ±(4/3)xB. y = ±(3/4)xC. y = ±(4/3)xD. y = ±(3/4)x答案：A5. 已知等差数列{an}的首项a1=1，公差d=2，则其前n项和Sn为：A. n^2B. n(n+1)C. n(n+1)/2D. n^2+n答案：D6. 已知函数f(x) = x^3 - 3x^2 + 2x，求f'(x)的表达式：A. 3x^2 - 6x + 2B. x^2 - 6x + 2C. x^3 - 6x^2 + 2xD. 3x^2 - 6x答案：A7. 已知三角形ABC中，角A=60°，边a=2，边b=√3，则边c的长度为：A. 1B. √3C. 2D. 3答案：C8. 已知圆的方程为(x-1)^2 + (y-1)^2 = 4，圆心到直线x+y-3=0的距离为：A. √2B. 2C. √5D. 3答案：A9. 已知函数f(x) = ln(x+1) - x，求f'(x)的表达式：A. 1/(x+1) - 1B. 1/(x+1) + 1C. 1/(x+1) + xD. 1/(x+1) - x答案：A10. 已知抛物线方程为y^2 = 4x，焦点F的坐标为：A. (1,0)B. (2,0)C. (0,1)D. (0,2)答案：B二、填空题（每题4分，共20分）11. 已知等比数列{bn}的首项b1=3，公比q=2，则b3的值为______。

2018-2019学年度武汉市九年级元月调考数学模拟试卷及答案

2018-2019学年度武汉市部分学校元月调考数学模拟试卷一、选择题（共10小题，每小题3分，共30分）1．方程3x2＋1＝6x的二次项系数和一次项系数分别为（）A．3和6 B．3和－6 C．3和－1 D．3和1 2．抛物线y＝(x－5)2＋6的对称轴是（）A．直线x＝－5 B．直线x＝5 C．直线x＝－6 D．直线x＝6 3．下列图形既是轴对称图形又是中心对称图形的是（）A．B．C． D4．下列事件：①在足球赛中，弱队战胜强队；②抛掷一枚硬币，落地后正面朝上；③任取两个正整数，其和大于1；④长分别为3、3、3的三条线段围成一个等腰三角形，其中确定事件的个数是（）A．1 B．2 C．3 D．45．“明天降水概率是30%”，对此消息下列说法中正确的是( ).A．明天降水的可能性较小B．明天将有30%的时间降水C．明天将有30%的地区降水D．明天肯定不降水6．如果关于x的一元二次方程mx2＋4x－1＝0没有实数根，那么m的取值范围是（）A．m＜4且m≠0 B．m＜－4 C．m＞－4且m≠0 D．m＞4 7．在⊙O 中，弦AB 的长为6，圆心O 到AB 的距离为4，OP=6，则点P 与⊙O 的位置关系是（）A．P 在⊙O 上B．P 在⊙O 外C．P 在⊙O 内D．P 与A 或B 重合8．如图所示，ABC△为O⊙的内接三角形，130AB C=∠=，°，则O⊙的内接正方形的面积为（）A．2 B．4 C．89．如图，Rt△ABC中，∠C=90°，内切圆⊙O与其三边的切点分别为D、E、F，若AB、BC、AC的长分别为c、a、b，且AE∙BE =m，a+b+c=n，则⊙O的半径r的值为( )A.n m B ．)(21n m + C ．n m 2 D ．n m -2110．如图，抛物线y ＝ax 2＋bx ＋c （c ≠0）过点(－1，0)和(0，－3)，且顶点在第四象限．设s ＝a ＋b ＋c ，则s 的取值范围是（） A ．－3＜s ＜－1 B ．－6＜s ＜0 C ．－3＜s ＜0 D ．－6＜s ＜－3二、填空题（本大题共6个小题，每小题3分，共18分） 11．点A （－2，5）关于原点的对称点B 的坐标是__________12．将抛物线 y=x2 ﹣2x+3 向左平移 2 个单位，再向上平移 1 个单位，得到的抛物线的解析式为 __________13．已知在一个不透明的口袋中有4个只有颜色不相同的球，其中1个红色球，3个黄色球．从口袋中随机取出一个球(不放回)，接着再取出一个球，则取出的两个都是黄色球的概率为__________________14．某树主干长出若干数目的支干，每个支干又长出同样数目小分支，主干、支干和小分支总数共73．若设主干长出x 个支干，则可列方程是 .15．如图，正方形ABCD 和正△AEF 都内接于⊙O ，EF 与BC 、CD 分别相交于点G 、H ，则的值是 .第15题图第16题图16. 已知⊙O 的半径为 2，A 为圆上一定点，P 为圆上一动点，以 AP 为边作等腰 Rt △APG ，P 点在圆上运动一周的过程中，OG 的最大值为___________三、解答题（共8题，共72分） 17．（本题8分）解方程：x 2－4x ＋1＝018．（本题8分）如图，⊙O中，直径CD⊥弦AB于M，AE⊥BD于E，交CD 于N，连AC（1）求证：AC＝AN；（2）若OM∶OC＝3∶5，AB＝5，求⊙O的半径；19．（本题8分）“红灯停，绿灯行”是我们在日常生活中必须遵守的交通规则，这样才能保障交通顺畅和行人安全，小刚每天从家骑自行车上学都经过三个路口，且每个路口只安装了红灯和绿灯，假如每个路口红灯和绿灯亮的时间相同，那么小刚从家随时出发去学校，回答以下问题：(1)请画树状图，列举所有可能出现的结果；(2)他遇到三次红灯的概率是多大？20．（本题8分）如图，在平面直角坐标系中，点A，B，C的坐标分别为(－1，3)，(－4，1)，(－2，1)，先将△ABC沿一确定方向平移得到△A1B1C1，点B的对应点B1的坐标是(1，2)，再将△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2，点A1的对应点为点A2.(1)画出△A1B1C1；(2)画出△A2B2C2；(3)求出在这两次变换过程中，点A经过点A1到达A2的路径总长．21．（本题8分）如图，A 是⊙O 上一点，半径OC 的延长线与过点A 的直线交于点B ，OC ＝BC ，AC ＝12OB. (1)求证：AB 是⊙O 的切线；(2)若∠ACD ＝45°，OC ＝2，求弦AD 的长．22．（本题10分）如图所示，为了改造小区环境，某小区决定要在一块一边靠墙（墙的最大可使用长度13 m ）的空地上建造一个矩形绿化带．除靠墙一边（AD ）外，用长为36 m 的栅栏围成矩形ABCD ，中间隔有一道栅栏（EF ）．设绿化带宽AB 为x m ，面积为S m 2（1）求S 与x 的函数关系式，并求出x 的取值范围（2）绿化带的面积能达到108 m 2吗？若能，请求出AB 的长度；若不能，请说明理由（3）当x 为何值时，满足条件的绿化带面积最大?23．（本题10分）23．已知正方形ABCD和正方形CGEF，且D点在CF边上，M为AE中点，连接MD、MF（1）如图1，请直接给出线段MD、MF的数量及位置关系是；（2）如图2，把正方形CGEF绕点C顺时针旋转，则（1）中的结论是否成立？若成立，请证明；若不成立，请给出你的结论并证明；（3）若将正方形CGEF绕点C顺时针旋转30°时，CF边恰好平分线段AE，请直接写出的值．24．（本题12分）已知抛物线y＝ax2－2amx＋am2＋2m＋4的顶点P在一条定直线l上．（1）直接写出直线l的解析式；（2）若存在唯一的实数m，使抛物线经过原点．①求此时的a和m的值；②抛物线的对称轴与x轴交于点A，B为抛物线上一动点，以OA、OB为边作□OACB，若点C在抛物线上，求B的坐标．（3）抛物线与直线l的另一个交点Q，若a＝1，直接写出△OPQ的面积的值或取值范围．参考答案二、填空题（共6小题，每小题3分，共18分） 11．（ 2，－5） 12．y=(x+1)2+313．1214． 1＋x ＋x 2＝7315．16．222+三、解答题（共8题，共72分） 17．解：32±=x18．解：（1）连接AC ，∵∠AED=∠AMO=90°，∴∠BDC=∠EAB=∠BAC ．∵AM ⊥OC ，∴∠AMC=∠AMN ．在△AMN 与△AMC 中，∵∠EAB=∠BAC ，AM=AM ，∠AMN=∠AMC ，∴△AMN ≌△AMC （ASA ），∴AC=AN ；（2）连接OA ，设OM=3x ，OC=5x ，∴OA=5x ，AM=4x ，∵AB=5，∴19．解：(1) 由树状图可以看出，共有8种等可能的结果，即：红红红、红红绿、红绿红、红绿绿、绿红红、绿红绿、绿绿红、绿绿绿、(2) P(三次红灯)＝1 8．20．解：(1)如图，△A1B1C1为所作．(2)如图，△A2B2C2为所作．(3)OA1＝42＋42＝42，点A经过点A1到达A2的路径总长＝52＋12＋90×42π180＝26＋22π.21．（1）证明：连接OA．∵OC=BC，AC=OB，∴OC=BC=AC=OA，∴△ACO是等边三角形，∴∠O=∠OCA=60°，又∵∠B=∠CAB，∴∠B=30°，∴∠OAB=90°．∴AB是⊙O的切线；（2）解：作AE⊥CD于点E．∵∠O=60°，∴∠D=30°．∵∠ACD=45°，AC=OC=2，∴在Rt△ACE中，CE=AE=，∵∠D=30°，∴AD=2．22．解：（1）∵四边形ABCD是矩形，∴AB=CD=EF，AD=BC，∵AB=xm，AB+BC+CD+EF=36m，∴BC=36-3x，∴绿化带的面积为：y=x•（36-3x）=﹣3x2+36x，y与x之间的函数关系式为：y=﹣3x2+36x；（2）由题意得：﹣3x 2+36x=108，解得：x 1=x 2=6，∵6能达到108 m 2．（3）∵y=﹣3x 2+36x =﹣3（x ﹣6）2+108，∵a=﹣3＜0，∴当x ＞6时，y 随x 的增大而减小，∴当y 最大，∴当x23．解：（1）线段MD 、MF 的数量及位置关系是MD=MF ，MD ⊥MF ，理由：如图1，延长DM 交EF 于点P ，∵四边形ABCD 和四边形FCGE 是正方形， ∴AD ∥EF ，∠MAD=∠MEP ．∠CFE=90°． ∴△DFP 是直角三角形． ∵M 为AE 的中点， ∴AM=EM ．在△ADM 和△EPM 中，，∴△ADM ≌△EPM （ASA ）， ∴DM=PM ，AD=PE ， ∴M 是DP 的中点．∴MF=DP=MD ， ∵AD=CD ， ∴CD=PE ， ∵FC=FE ， ∴FD=FP ，∴△DFP是等腰直角三角形，∴FM⊥DP，即FM⊥DM．故答案为：MD=MF，MD⊥MF；（2）MD=MF，MD⊥MF仍成立．证明：如图2，延长DM交CE于点N，连接FN、DF，∵CE是正方形CFEG对角线，∴∠FCN=∠CEF=45°，∵∠DCE=90°，∴∠DCF=45°，∵AD∥BC，∴∠DAM=∠NEM，在△ADM和△ENM中，，∴△ADM≌△ENM（ASA），∴EN=AD，DM=MN，∵AD=CD，∴CD=EN，在△CDF和△ENF中，，∴△CDF≌△ENF，（SAS）∴DF=NF，∴FM=DM ，FM ⊥DM ．（3）如图所示，若CF 边恰好平分线段AE ，则CF 过点M ，由（1）可得FM=DM ，FM ⊥DM ，设FM=DM=1， ∵∠DCF=30°，∴Rt △DCM 中，CM=，CD=2=CB ，∴CF=+1=CG ，∴=．24．解：(1) y=a （x-m ）2+2m+4，P （m ，2m+4），∴y=2x+4；（2）①将x=0，y=0代入，∴am 2+2m+4=0∴△=0，a=14，m=-4；②B 、C 关于对称轴对称，∴B 的横坐标为-2，y=14 （x+4）2-4，∴B （-2，-3）；（3）y=2x+4与x 轴交于点B （-2,0），交y 轴于点A （0,4），作OM ⊥AB 于M 。

武昌区(人教版)2018年元调数学试卷及答案

武昌区（人教版）2018年元调数学试卷一、认真读题、仔细计算。

（共28分）1、直接写出下面各题得数=⨯1472=⨯354125982.7÷24÷83==⨯516561＋=÷43873236.0⨯=1+12%=4136÷=4341-1÷=2、解方程。

x÷256=125125x 43x 2=－（1—40%）x=69.63、脱式计算，怎么简便怎么算。

75.0271643÷⨯524587495÷＋157415173÷⨯＋}3410152{98⨯÷（二、全面思考，谨慎填空。

（共20分）4、（）%=0.6=（）（）=12÷（）=（）：605、把0.8：21化成最简单的整数比是（），比值是（）。

6、甲商品原价1200元，按七折出售，售价是（）元；乙商品降价20%后售1600元，原价（）元。

7、在、、85530.615、60%、8%这五个数中，最大的数是（），最小的数是（）。

8、在算式76÷a(a≠0)中，当a()l 时，商大于76；当a()l 时，商等于76；当（）l 时，商小于76。

（填>、<或=）9、把一根5米长的绳子对折2次，然后沿折痕剪成若干段，每段长()米，每段的长度是这根绳子的()%。

10、在—个长5厘米，宽3厘米的长方形中画一个最大的半圆，半圆的直径是()厘米。

11、甲车从A 地到B 地要行6小时，乙车从B 地到A 地要行4小时，则甲、乙两车的最简速度比是()；如果两车同时从A、B 两地出发，相向而行，()小时相遇。

12、观察下面各图，依此规律，后面的第5个方框里有()个点，第10个方框里有()个点。

三、反复比较，合理选择。

（共20分）下列各题中均有四个备选答案，其中有且只有—个正确，请在答题卡上将正确答案的代号涂黑。

13、如果六(l)班女生人数是全班人数的115，那么这个班男生人数与女生人数的比是（）。

2018武汉元调数学试卷及答案(Word精校版)

2018武汉元调数学试卷及答案(Word精校版)第2页 / 共19页第3页 / 共19页第4页 / 共19页第5页 / 共19页是 .12.把抛物线22y x =先向下平移1个单位，再向左平移2个单位，得到的抛物线的解析式是 .13.一个不透明的口袋中有四个完全相同的小球，把它们分别标记为1，2，3，4.随机摸取一个小球然后放回，再随机摸出一个小球，两次取出的小球标号的和为5的概率是 .14.设计人体雕像时，使雕像的上部(腰以上)与下部(腰以下)的高度比，等于下部与全部(全身)的比，可以增加视觉美感，按此比例，如果雕像的高为2m ，那么上部应设计为多高？设雕像的上部高为x m ，列方程，并化成一般形式为 . 15.如图，正六边形ABCDEF 中，P 是边ED 的中点，连接AP ，则AP AB ＝ 16.在O 中，AB 所对的圆心角108AOB ∠=︒，点C 为O 上的动点，以AO ，AC 为边构造AODC ，当∠A= °时，线段BD 最长.三.解答题(共8小题，共72分)P A F EDB OA C17. (本题8分)解方程230+-=x x第6页 / 共19页第7页 / 共19页18. (本题8分)如图在O 中，半径OA 与弦BD 垂直，点C 在O 上，∠AOB=80°.(1)若点C 在优弧BD 上，求∠ACD 的大小；(2)若点C 在劣弧BD 上，直接写出∠ACD 的大小.19.(本题8分)甲，乙，丙三个盒子中分别装有除颜色以B O CO外都相同的小球，甲盒中装有两个球，分别为一个红球和一个绿球，乙盒中装有三个球，分别为两个绿球和一个红球；丙盒中装有两个球，分别为一个红球和一个绿球，从三个盒子中各随机取出一个小球.(1)请画树状图，列举所有可能的结果；(2)请直接写出事件“取出至少一个红球”的概率.第8页 / 共19页第9页 / 共19页20. (本题8分)如图，在平面直角坐标系中有点A (-4，0)，B (0，3)，P (a ，-a )三点.线段CD 与AB 关于点P 中心对称，其中A ，B 的对应点分别为C ，D ．(1)当a =-4时，①在图中画出线段CD ，保留作图痕迹；②线段CD 向下平移个单位时，四边形ABCD 为菱形；(2)当a = 时，四边形ABCD 为正方形.21. (本题8分)如图，点D 在⊙O 的直径AB 的延长线上，CD 切⊙O 于点C ，AE ⊥CD 于点E .(1)求证：AC 平分∠DAE .(2)若AB =6，BD =2，求CE 的长. x y B A O第10页 / 共19页 B C O AD22. (本题10分)投资1万元围一个矩形菜园(如图)，其中一边靠墙，另外三边选用不同材料建造.墙长24m，平行于墙的边的费用为200元/m，垂直于墙的边的费用为150元/m.设平行于墙的边长为xm.(1)设垂直于墙的一边长为y，请直接写出y与x之间的函数关系式.(2)若菜园面积为384m2，求x的值.(3)求菜园的最大面积.墙（24m2）菜园23. (本题10分)如图，点C为线段AB上一点，分别以AB，AC，CB为底作顶角为120°的等腰三角形，顶角顶点分别为D，E，F，(点E，F在AB的同侧，点D在另一侧).(1)如图1，若点C是AB的中点，则∠AED=__________；(2)如图2，若点C不是AB的中点，①求证：△DEF为等边三角形；第11页 / 共19页第12页 / 共19页②连接CD ，若∠ADC =90°，AB =3，请直接写出EF 的长.ACFAC24.(本题12分)已知抛物线22=++与x轴交于A(-1，0)，y ax x cB(3，0)两点，一次函数y=kx+b的图象l经过抛物线上的点C(m，n).(1)求抛物线的解析式；(2)若m=3，直线l与抛物线只有一个公共点，求k的值；(3)若k=-2m+2，直线l与抛物线的对称轴相交于点D，点P在对称轴上，当PD=PC时，求点P的坐标.第13页 / 共19页第14页 / 共19页2017-2018学年度武汉市部分学校九年级元月调考解析一.选择题1 2 3 4 5 6 7 8 9 10 C AD C D C D B B D9.如图：①∵∠EOF =2∠EDF ，∠EOF +∠B =180°，∴2∠EDF +∠B =180°所以①错误②∵∠EOF =2∠EDF ，∠EOF +∠B =180°，∠A +∠B +∠C =180°，∴2∠EDF =∠A +∠C 所以②正确③∵∠EDF +∠DEF =2x +y +z =90°+x ，∵∠A +∠EOD =180°，∴∠A =180°-2(y +z )=2x ， ∴2(∠EDF +∠DEF )-180°=∠A 所以③错误④∠AED +∠BFE +∠CDF =90°-x +90°-y +90°-z =270°-(x +y +z )=270°-90°=180° 所以④正确二.填空题11. 4 12.2287y x x =++ 13. 14y zzx yx DEB第15页 / 共19页14. 2-640x x += 15.13 16.27°16.延长AO 与O 交于点P ，连接DP ，如图，则 O CAO D P ∆∆≌ DP OC ∴=，即点D 的运动轨迹是以点P 为圆心，OC 长为半径的圆.如图所示，连接BP ，BP 与P 的交点记作'DBD 最大值为'BD ，此时1'272A POD APB ∠=∠=∠=三.解答题17.1113x -+1113x --18. (1)∵OA ⊥BD ， ∴AB =AD ，∴∠ACD =12∠AOB =40°(2)40°或140°19.(1)由题意可得如下树状图，由图可知共有12种等可能的情况.PD’BOAC第16页 / 共19页(2)5620.(1)如图所示 (2)2 (3)72-21.(1)证明：连OC∵CD 与⊙O 切于点C ， ∴OC ⊥DE ，∠OCD =90° ∵AE ⊥DE ， ∴∠E =90°，∴∠OCD =∠E =90°，∴OC //AE ， ∴∠1=∠2∵OC =OA ， ∴∠1=∠3， ∴∠2=∠3， ∴AC 平分∠DAE (2)解：作CH ⊥OD∵AB =6， ∴AO =OB =OC =3 ∵AC 平分∠DAE ，CH ⊥OD ，CE ⊥AE ， ∴CE =CH∵∠OCD =90°， ∴CD 22OD OC -∵OCDS ∆=12OC ·CD =12OD ·CH ， ∴CH =125， ∴CE =12522. (1)由题意可知：xyDCPBAO132H BCO A D第17页 / 共19页200x +150⨯2y =10000化简得：210033y x =-+∴y 与x 之间的函数关系式210033y x =-+(024x ＜≤) (2)210038433x x ⎛⎫-+= ⎪⎝⎭ 整理得：()22549x -= 解得：x 1=18，x 2=32 ∵024x ＜≤ ∴x =18即菜园面积为384m 2，x 的值为18. (3)设菜园的面积SS =210033x x ⎛⎫-+ ⎪⎝⎭=()2212502533x --+∵203-＜，开口向下对称轴x =25∴当024x ＜≤时，y 随x 的增大而增大. ∴当x =24时，S 的最大值为416. 所以，菜园的最大面积为416 m 2 23.(1)90°(2)①证明：延长AE 、BF 交于G ，连DG .易证四边形ADBG 为菱形，△ADG 为等边三角形，四边形EGFC 为平行四边形.可证∠DAE =∠DGF =60°，AE =CE =GF . 在△ADE 和△GDF 中.DA DG DAE DGF AE GF =⎧⎪∠=∠⎨⎪=⎩第18页 / 共19页∴△ADE ≌△GDF (SAS ) ∴DE =DF ，∠ADE =∠GDF∴∠EDF =∠EDG +∠GDF =∠EDG +∠ADE =∠ADG =60°∴△EDF 为等边三角形.②EF 2124.(1)将A (-1，0)，B (3，0)代入22y ax x c=++中得：02096a ca c=-+⎧⎨=++⎩解得：a ＝-1，c ＝3∴抛物线的解析式为223y x x =-++(2)当m ＝3时，n ＝-9+6+3=0， ∴C (3，0)，将点C 代入y ＝kx +b 中得： 0=3k +b ， ∴b =-3k ， ∴l 的解析式为y ＝kx -3k联立：2323y kx ky x x =-⎧⎨=-++⎩得：()22330x k x k +---=∵l 与抛物线只有一个交点FEBAC第19页 / 共19页∴()()224330k k ∆=----= 得：k =-4(3)当k ＝-2m +2时，y =(-2m +2)x +b 且m ≠1 将C (m ，n )代入y =(-2m +2)x +b 中得： n ＝(-2m +2)m +b ∵223n m m =-++∴23b m =+，l 的解析式为()2223y m x m =-+++ ∵D 为l 与抛物线对称轴的交点 ∴1Dx =，当x ＝1时，225y m m =-+ ∴()21,25D m m -+，()2,23C m m m -++设()1,P a ， ∵PC ＝PD ，∴22PC PD = 即()()()2222212325m m m a m m a -+-++-=-+- 解得：154a =， ∴P 的坐标为(1，154)。

湖北省武汉市部分学校2018-2019学年高一下学期期末调研测试数学试题Word版含答案.pdf

（Ⅱ）求四边形 ABCD 的面积 .
18.（本小题满分 12 分）
已知 a,b,c 均为正数且 a+b+c=1,
（Ⅰ）证明： ab
bc
ca
1
；
3
（Ⅱ）证明： a 2 b2 c 2 1． b ca
19.（本小题满分 12 分）如图，在三棱锥 P A B C中， D ，E， F分别为棱 P C， A，C A的B 中点．已知 P A A，C P 6A， BC 8 ， DF 5 ．（Ⅰ）证明：直线 PA∥平面 DEF ；（Ⅱ）证明：平面 BDE ⊥平面 ABC．
4
an 1
1
A．
4
B．5
4
C．
5
D ．2015
6.在下列中，错误的是
A ．如果一个直线上的两点在平面内，那么这条直线在此平面内
B ．过不在一条直线上的三点，有且只有一个平面
C ．如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线
D ．平行于同一个平面的两条直线平行
7.《莱因德纸草书》是世界上最古老的数学著作之一．书中有一道这样的题目：把
a0 A ． b2 4ac 0
a0 B. b2 4ac 0
a0 C． b2 4ac 0
a0 D． b2 4ac 0
1xy3
4.若实数 x, y 满足
，则 z 4x 2y 的取值范围是
1x y1
A ． 0.12
B． 2.12
C． 2.10
D． 0.10
5. 已知数列 an 中， a1
1 , an 1 1 (n 1) ，则 a2015
A ． 3 44
B． 3 44 1

2018届武昌区高三元调数学试题(理科)

（1）求椭圆 C 的方程；（2）设 F1 、 F2 分别为椭圆 C 的左、右焦点，不经过 F1 的直线 l 与椭圆 C 交于两个不同的点 A 、 B ，如果直线 AF1 、 l 、 BF1 的斜率依次成等差数列，求焦点 F2 到直线 l 的距离 d 的取值范围。
P （ K2 k ）
0.010 6.635
0.005 7.879
0.001 10.828
k
附： k
2
n(ad bc)2 (a b)(c d )(a c)(b d )
x2 y2 2 2 20. (12 分）已知椭圆 C : 2 2 1( a b 0) 经过点 P (1, 。 ) ,且离心率为 a b 2 2
5 ，求 ABC 的面积。
18.如图，三棱锥 P ABC 中，底面 ABC 是边长为 2 的正三角形， PA PC, PB 2 . （1）求证：平面 PAC 平面 ABC ；（2）若 PA PC ，求二面角 A PB C 的余弦值。
19. (12 分）通过随机询问 72 名不同性别的大学生在购买食物时是否看营养说明，得到如下列联表：性别与读营养说明列联表
1 3 1 2 2 x bx cx d 在 (0, 2) 内既有极大值又有极小值，则 c 2bc 4c 的 3 2
） B. (0, )
1 ) 16
1 4
C. (0, )
1 2
D. (0,1)
二．填空题 13.若 tan cos ，则
5
1 cos 4 __________. sin
男读营养说明不读营养说明总计 16 20 36 女 28 8 36 总计 44 28 72
（1）根据以上列联表判断，能否在犯错误的概率不超过 0.005 的前提下认为性别和是否看营养说明有关系呢？（2）从被询问的 28 名不读营养说明的大学生中，随机抽取 2 名学生，求抽到女生人数ξ的分布列和数学期望。