2018年上海市各区二模卷第25题
2018年闵行区中考数学二模试卷及答案

2018年闵行区中考数学二模试卷及答案闵行区2017学年第二学期九年级数学质量调研考试试卷注意事项:1.本试卷共25题,分为三个大题。
2.答题时,请按照要求在答题纸上作答,草稿纸和试卷上的答案无效。
3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸上写出证明或计算的主要步骤。
一、选择题(共6题,每题4分,满分24分)1.下列各式中,二次单项式是A。
x² + 1B。
xy² / 3C。
2xyD。
(-2)²2.下列运算结果正确的是A。
(a + b)² = a² + b²B。
(a - b)² = a² - b²C。
a³ * a² = a⁵D。
2a - 1 = 1 / (2a) (a ≠ 0)3.在平面直角坐标系中,反比例函数y = k / x (k ≠ 0)的图像在每个象限内,y随着x的增大而减小,那么它的图像的两个分支分别在A。
第一、三象限B。
第二、四象限C。
第一、二象限D。
第三、四象限4.有9名学生参加校民乐决赛,最终成绩各不相同,其中一名同学想要知道自己是否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的A。
平均数B。
中位数C。
众数D。
方差5.已知四边形ABCD是平行四边形,下列结论中不正确的是A。
当AB = BC时,四边形ABCD是菱形B。
当AC⊥BD时,四边形ABCD是菱形C。
当∠ABC = 90o时,四边形ABCD是矩形D。
当AC = BD时,四边形ABCD是正方形6.点A在圆O上,已知圆O的半径是4,如果点A到直线a的距离是8,那么圆O与直线a的位置关系可能是A。
相交B。
相离C。
相切或相交D。
相切或相离二、填空题(共12题,每题4分,满分48分)7.计算:-1 + 22 = 218.在实数范围内分解因式:4x² - 3 = (2x + 1)(2x - 3)9.方程2x - 1 = 1的解是 x = 110.已知关于x的方程x² - 3x - m = 0没有实数根,那么m的取值范围是 m < 9 / 411.已知直线y = kx + b(k ≠ 0)与直线y = -x平行,且截距为5,那么这条直线的解析式为 y = kx + 5已知函数f(x)=x^3-3x^2+2x+1,求其在区间[0,2]上的最大值和最小值,并确定最大值和最小值所对应的x值。
(完整版)2018上海市黄浦区2018届中考二模数学试题含答案,推荐文档

(A) y kx k ;
(B) y kx k ;
(C) y kx k ;
(D) y kx k .
4.一个民营企业 10 名员工的月平均工资如下表,则能较好反映这些员工月平均工资水平的是( )
人次
1
1
1
2
1
1
3
工资
30
3
2
1.5
1.2
2
24.(本题满 12 分)
已知抛物线 y x2 bx c 经过点 A(1,0)和 B(0,3),其顶点为 D.
(1)求此抛物线的表达式; (2)求△ABD 的面积; (3)设 P 为该抛物线上一点,且位于抛物线对称轴 右侧,作 PH⊥对称轴,垂足为 H,若△DPH 与△AOB 相 似,求点 P 的坐标.
P,则该反比例函数的解析式为
.
12.如果一次函数的图像经过第一、二、四象限,那么其函数值 y 随自变量 x 的值的增大而
.
(填“增大”或“减小”)
13.女生小琳所在班级共有 40 名学生,其中女生占 60%.现学校组织部分女生去市三女中参观,需要
从小琳所在班级的女生当中随机抽取一名女生参加,那么小琳被抽到的概率是
那么 AD∶AB=
.
三、解答题:(本大题共 7 题,满分 78 分)
19.(本题满分 10 分)
1
计算: 22 23 2
0
2018 2018 3 2 3 .
20.(本题满分 10 分)
第3页
x2 2xy y2 9
解方程组:
x
2
y2
5
.
21.(本题满分 10 分)
2
如图,AH 是△ABC 的高,D 是边 AB 上一点,CD 与 AH 交于点 E.已知 AB=AC=6,cosB= ,
上海市各区2018届中考数学二模试卷精选汇编压轴题专题(有答案)
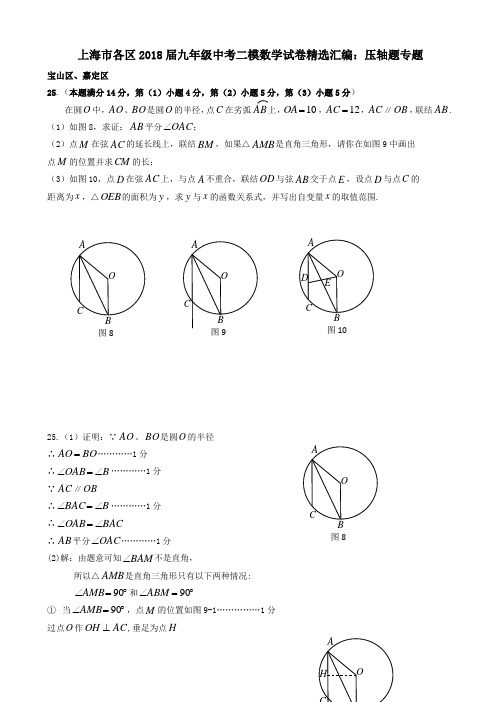
上海市各区2018届九年级中考二模数学试卷精选汇编:压轴题专题宝山区、嘉定区25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)在圆O 中,AO 、BO 是圆O 的半径,点C 在劣弧AB 上,10=OA,12=AC ,AC ∥OB ,联结AB . (1)如图8,求证:AB 平分OAC ∠;(2)点M 在弦AC 的延长线上,联结BM ,如果△AMB 是直角三角形,请你在如图9中画出 点M 的位置并求CM 的长;(3)如图10,点D 在弦AC 上,与点A 不重合,联结OD 与弦AB 交于点E ,设点D 与点C 的 距离为x ,△OEB 的面积为y ,求y 与x 的函数关系式,并写出自变量x 的取值范围.25.(1)证明:∵AO 、BO 是圆O 的半径 ∴BO AO =…………1分 ∴B OAB ∠=∠…………1分 ∵AC ∥OB∴B BAC ∠=∠…………1分 ∴BAC OAB ∠=∠∴AB 平分OAC ∠…………1分 (2)解:由题意可知BAM ∠不是直角,所以△AMB 是直角三角形只有以下两种情况:︒=∠90AMB 和︒=∠90ABM① 当︒=∠90AMB ,点M 的位置如图9-1……………1分 过点O 作AC OH ⊥,垂足为点H图8图10图8∵OH 经过圆心 ∴AC HC AH 21== ∵12=AC ∴6==HC AH 在Rt △AHO 中,222OA HO AH =+ ∵10=OA ∴8=OH∵AC ∥OB ∴︒=∠+∠180OBM AMB ∵︒=∠90AMB ∴︒=∠90OBM ∴四边形OBMH 是矩形 ∴10==HM OB∴4=-=HC HM CM ……………2分 ②当︒=∠90ABM ,点M 的位置如图9-2 由①可知58=AB ,552cos =∠CAB 在Rt △ABM 中,552cos ==∠AM AB CAB∴20=AM8=-=AC AM CM ……………2分综上所述,CM 的长为4或8.说明:只要画出一种情况点M 的位置就给1分,两个点都画正确也给1分. (3)过点O 作AB OG ⊥,垂足为点G 由(1)、(2)可知,CAB OAG ∠=∠sin sin 由(2)可得:55sin =∠CAB ∵10=OA ∴52=OG ……………1分 ∵AC ∥OB ∴ADOBAE BE =……………1分 又BE AE -=58,x AD -=12,10=OB ∴xBEBE -=-121058 ∴x BE -=22580 ……………1分∴52225802121⨯-⨯=⨯⨯=xOG BE y ∴xy -=22400……………1分自变量x 的取值范围为120<≤x ……………1分图10长宁区25.(本题满分14分,第(1)小题4分,第(2)小题4分,第(3)小题6分)在圆O 中,C 是弦AB 上的一点,联结OC 并延长,交劣弧AB 于点D ,联结AO 、BO 、AD 、BD . 已知圆O 的半径长为5 ,弦AB 的长为8.(1)如图1,当点D 是弧AB 的中点时,求CD 的长; (2)如图2,设AC =x ,y S S OBDACO=∆∆,求y 关于x 的函数解析式并写出定义域; (3)若四边形AOBD 是梯形,求AD 的长.25.(本题满分14分,第(1)小题4分,第(2)小题4分,第(3)小题6分) 解:(1)∵OD 过圆心,点D 是弧AB 的中点,AB =8, ∴OD ⊥AB ,421==AB AC (2分) 在Rt △AOC 中,︒=∠90ACO Θ,AO =5, ∴322=-=AC AO CO (1分)5=OD Θ,2=-=∴OC OD CD (1分)(2)过点O 作OH ⊥AB ,垂足为点H ,则由(1)可得AH =4,OH =3 ∵AC =x ,∴|4|-=x CH在Rt △HOC 中,︒=∠90CHO Θ,AO =5, ∴258|4|322222+-=-+=+=x x x HC HO CO , (1分)∴525882+-⋅-=⋅=⋅==∆∆∆∆∆∆x x x x OD OC BC AC S S S S S S y OBD OBC OBC ACO OBD ACO O AC DBO BA C DBAOxx x x 5402582-+-= (80<<x ) (3分)(3)①当OB //AD 时, 过点A 作AE ⊥OB 交BO 延长线于点E ,过点O 作OF ⊥AD ,垂足为点F , 则OF =AE , AE OB OH AB S ABO ⋅=⋅=∆2121Θ ∴OF OB OH AB AE ==⋅=524 在Rt △AOF 中,︒=∠90AFO Θ,AO =5, ∴5722=-=OF AO AF ∵OF 过圆心,OF ⊥AD ,∴5142==AF AD . (3分) ②当OA //BD 时, 过点B 作BM ⊥OA 交AO 延长线于点M ,过点D 作DG ⊥AO ,垂足为点G , 则由①的方法可得524==BM DG , 在Rt △GOD 中,︒=∠90DGO Θ,DO =5, ∴5722=-=DG DO GO ,518575=-=-=GO AO AG , 在Rt △GAD 中,︒=∠90DGA Θ,∴622=+=DG AG AD ( 3分)综上得6514或=AD 崇明区25.(本题满分14分,第(1)小题4分,第(2)小题4分,第(3)小题6分)如图,已知ABC △中,8AB =,10BC =,12AC =,D 是AC 边上一点,且2AB AD AC =⋅,联结BD ,点E 、F 分别是BC 、AC 上两点(点E 不与B 、C 重合),AEF C ∠=∠,AE 与BD 相交于点G . (1)求证:BD 平分ABC ∠;(2)设BE x =,CF y =,求y 与x 之间的函数关系式; (3)联结FG ,当GEF △是等腰三角形时,求BE 的长度.25.(满分14分,第(1)小题4分,第(2)小题4分,第(3)小题6分)(第25题图)A BCDGEF(备用图)ABCD(1)∵8AB =,12AC = 又∵2AB AD AC =g ∴163AD =∴16201233CD =-= ……………………………1分 ∵2AB AD AC =g ∴AD AB AB AC= 又∵BAC ∠是公共角 ∴ADB ABC △∽△ …………………………1分 ∴ABD C =∠∠,BD ADBC AB= ∴203BD =∴BD CD = ∴DBC C =∠∠ ………………………1分 ∴ABD DBC =∠∠ ∴BD 平分ABC ∠ ………………………1分 (2)过点A 作AH BC ∥交BD 的延长线于点H∵AH BC ∥ ∴16432053AD DH AH DC BD BC ==== ∵203BD CD ==,8AH = ∴163AD DH == ∴12BH = ……1分 ∵AH BC ∥ ∴AH HG BE BG = ∴812BG x BG -= ∴128xBG x =+…1分 ∵BEF C EFC =+∠∠∠ 即BEA AEF C EFC +=+∠∠∠∠ ∵AEF C =∠∠ ∴BEA EFC =∠∠ 又∵DBC C =∠∠∴BEG CFE △∽△ ……………………………………………………………1分∴BE BGCF EC= ∴12810x x x y x +=-∴228012x x y -++= …………………………………………………………1分(3)当△GEF 是等腰三角形时,存在以下三种情况:1° GE GF = 易证23GE BE EF CF == ,即23x y =,得到4BE = ………2分 2° EG EF = 易证BE CF =,即x y =,5BE =-+…………2分 3° FG FE = 易证 32GE BE EF CF == ,即32x y =3BE =-+ ………2分奉贤区25.(本题满分14分,第(1)小题满分5分,第(2)小题满分5分,第(3)小题满分4分)已知:如图9,在半径为2的扇形AOB 中,∠AOB=90°,点C 在半径OB 上,AC 的垂直平分线交OA 于点D ,交弧AB 于点E ,联结BE 、CD .(1)若C 是半径OB 中点,求∠OCD 的正弦值; (2)若E 是弧AB 的中点,求证:BC BO BE ⋅=2;(3)联结CE ,当△DCE 是以CD 为腰的等腰三角形时,求CD 的长.图9备用图ABO备用图ABO黄浦区25.(本题满分14分)如图,四边形ABCD中,∠BCD=∠D=90°,E是边AB的中点.已知AD=1,AB=2.(1)设BC=x,CD=y,求y关于x的函数关系式,并写出定义域;(2)当∠B=70°时,求∠AEC的度数;(3)当△ACE为直角三角形时,求边BC的长.25. 解:(1)过A作AH⊥BC于H,————————————————————(1分)由∠D=∠BCD=90°,得四边形ADCH为矩形.在△BAH 中,AB =2,∠BHA =90°,AH =y ,HB =1x -,所以22221y x =+-,——————————————————————(1分) 则()22303y x x x =-++<<.———————————————(2分)(2)取CD 中点T ,联结TE ,————————————————————(1分) 则TE 是梯形中位线,得ET ∥AD ,ET ⊥CD .∴∠AET =∠B =70°. ———————————————————————(1分) 又AD =AE =1,∴∠AED =∠ADE =∠DET =35°. ——————————————————(1分) 由ET 垂直平分CD ,得∠CET =∠DET =35°,————————————(1分) 所以∠AEC =70°+35°=105°. ——————————————————(1分)(3)当∠AEC =90°时,易知△CBE ≌△CAE ≌△CAD ,得∠BCE =30°, 则在△ABH 中,∠B =60°,∠AHB =90°,AB =2,得BH =1,于是BC =2. ——————————————————————(2分)当∠CAE =90°时,易知△CDA ∽△BCA ,又2224AC BC AB x =-=-,则2241174AD CAx x AC CBx -±=⇒=⇒=-(舍负)—————(2分) 易知∠ACE <90°.所以边BC 的长为2或117+.——————————————————(1分)金山区25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5 分)如图9,已知在梯形ABCD 中,AD ∥BC ,AB =DC =AD =5,3sin 5B =,P 是线段BC 上 一点,以P 为圆心,PA 为半径的⊙P 与射线AD 的另一个交点为Q ,射线PQ 与射线CD 相交于点E ,设BP =x .(1)求证△ABP ∽△ECP ;(2)如果点Q 在线段AD 上(与点A 、D 不重合),设△APQ 的面积为y ,求y 关于x 的函数关系式,并写出定义域; (3)如果△QED 与△QAP 相似,求BP 的长.25.解:(1)在⊙P 中,PA =PQ ,∴∠PAQ =∠PQA ,……………………………(1分)∵AD ∥BC ,∴∠PAQ =∠APB ,∠PQA =∠QPC ,∴∠APB =∠EPC ,……(1分) ∵梯形ABCD 中,AD ∥BC ,AB =DC ,∴∠B =∠C ,…………………………(1分) ∴△APB ∽△ECP .…………………………………………………………(1分) (2)作AM ⊥BC ,PN ⊥AD ,∵AD ∥BC ,∴AM ∥PN ,∴四边形AMPN 是平行四边形,∴AM =PN ,AN =MP .………………………………………………………(1分) 在Rt △AMB 中,∠AMB =90°,AB =5,sinB =35, ∴AM =3,BM =4,∴PN =3,PM =AN =x -4,……………………………………(1分) ∵PN ⊥AQ ,∴AN =NQ ,∴AQ = 2x -8,……………………………………(1分) ∴()1128322y AQ PN x =⋅⋅=⋅-⋅,即312y x =-,………………………(1分) 定义域是1342x <<.………………………………………………………(1分) (3)解法一:由△QED 与△QAP 相似,∠AQP =∠EQD ,①如果∠PAQ =∠DEQ ,∵△APB ∽△ECP ,∴∠PAB =∠DEQ ,又∵∠PAQ =∠APB ,∴∠PAB =∠APB ,∴BP =BA =5.………………………(2分)ABCD图9备用图②如果∠PAQ =∠EDQ ,∵∠PAQ =∠APB ,∠EDQ =∠C ,∠B =∠C ,∴∠B =∠APB ,∴ AB =AP ,∵AM ⊥BC ,∴ BM =MP =4,∴ BP =8.………(2分) 综上所述BP 的长为5或者8.………………………………………………(1分) 解法二:由△QAP 与△QED 相似,∠AQP =∠EQD , 在Rt △APN 中,AP PQ ===∵QD ∥PC ,∴EQ EPQD PC=, ∵△APB ∽△ECP ,∴AP EPPB PC=,∴AP EQ PB QD =, ①如果AQ EQ QP QD =,∴AQ AP QP PB =x=,解得5x =………………………………………………………………………(2分) ②如果AQ DQ QP QE =,∴AQ PBQP AP==解得8x =………………………………………………………………………(2分) 综上所述BP 的长为5或者8.…………………………………………………(1分)静安区25.(本题满分14分,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分4分) 如图,平行四边形ABCD 中,已知AB =6,BC =9,31cos =∠ABC .对角线AC 、BD 交于点O .动点P 在边AB 上,⊙P 经过点B ,交线段PA 于点E .设BP = x .(1) 求AC 的长;(2) 设⊙O 的半径为y ,当⊙P 与⊙O 外切时, 求y 关于x 的函数解析式,并写出定义域; (3) 如果AC 是⊙O 的直径,⊙O 经过点E , 求⊙O 与⊙P 的圆心距OP 的长.25.(本题满分14分,第(1)小题4分,第(2)小题6分,第(3)小题4分) 解:(1)作AH ⊥BC 于H ,且31cos =∠ABC ,AB =6, A 第25题图B P OC DE · 第25题备用图ABOCDDA · POE那么2316cos =⨯=∠⋅=ABC AB BH …………(2分) BC =9,HC =9-2=7,242622=-=AH , ……………………(1分) 9493222=+=+=HC AH AC ﹒ ………(1分)(2)作OI ⊥AB 于I ,联结PO , AC =BC =9,AO =4.5 ∴∠OAB =∠ABC ,∴Rt △AIO 中, 31cos cos ==∠=∠AO AI ABC IAO∴AI =1.5,IO =2322=AI ……………………(1分) ∴PI =AB -BP -AI =6-x -1.5=x -29, ……………………(1分) ∴Rt △PIO 中,41539481918)29()23(2222222+-=+-+=-+=+=x x x x x OI PI OP ……(1分) ∵⊙P 与⊙O 外切,∴y x x x OP +=+-=415392 ……………………(1分) ∴y =x x x x x x -+-=-+-153364214153922…………………………(1分) ∵动点P 在边AB 上,⊙P 经过点B ,交线段PA 于点E .∴定义域:0<x ≤3…………(1分) (3)由题意得:∵点E 在线段AP 上,⊙O 经过点E ,∴⊙O 与⊙P 相交 ∵AO 是⊙O 半径,且AO >OI ,∴交点E 存在两种不同的位置,OE =OA =29① 当E 与点A 不重合时,AE 是⊙O 的弦,OI 是弦心距,∵AI =1.5,AE =3, ∴点E 是AB 中点,321==AB BE ,23==PE BP ,3=PI , IO =23 3327)23(32222==+=+=IO PI OP ……………………(2分)② 当E 与点A 重合时,点P 是AB 中点,点O 是AC 中点,2921==BC OP ……(2分) ∴33=OP 或29. 闵行区25.(本题满分14分,其中第(1)小题4分,第(2)、(3)小题各5分)如图,已知在Rt △ABC 中,∠ACB = 90o,AC =6,BC = 8,点F 在线段AB 上,以点B 为圆心,BF 为半径的圆交BC 于点E ,射线AE 交圆B 于点D (点D 、E 不重合).(1)如果设BF = x ,EF = y ,求y 与x 之间的函数关系式,并写出它的定义域;第25题图(2)(2)如果»»2EDEF =,求ED 的长; (3)联结CD 、BD ,请判断四边形ABDC 是否为直角梯形?说明理由.25.解:(1)在Rt △ABC 中,6AC =,8BC =,90ACB ∠=o∴10AB =.……………………………………………………………(1分) 过E 作EH ⊥AB ,垂足是H , 易得:35EH x =,45BH x =,15FH x =.…………………………(1分) 在Rt △EHF 中,222223155EF EH FH x x ⎛⎫⎛⎫=+=+ ⎪ ⎪⎝⎭⎝⎭,∴(08)y x x =<<.………………………………………(1分+1分) (2)取»ED的中点P ,联结BP 交ED 于点G ∵»»2EDEF =,P 是»ED 的中点,∴»»»EP EF PD ==. ∴∠FBE =∠EBP =∠PBD .∵»»EPEF =,BP 过圆心,∴BG ⊥ED ,ED =2EG =2DG .…………(1分) 又∵∠CEA =∠DEB ,∴∠CAE =∠EBP =∠ABC .……………………………………………(1分)又∵BE 是公共边,∴BEH BEG ∆∆≌.∴35EH EG GD x ===.在Rt △CEA 中,∵AC = 6,8BC =,tan tan AC CECAE ABC BC AC∠=∠==, ∴66339tan 822CE AC CAE ⨯⨯=⋅∠===.……………………………(1分) (备用图)CBA (第25题图)CBEF DADEBACF∴9169782222BE =-=-=.……………………………………………(1分) ∴6672125525ED EG x ===⨯=.……………………………………(1分)(3)四边形ABDC 不可能为直角梯形.…………………………………(1分)①当CD ∥AB 时,如果四边形ABDC 是直角梯形, 只可能∠ABD =∠CDB = 90o. 在Rt △CBD 中,∵8BC =, ∴32cos 5CD BC BCD =⋅∠=, 24sin 5BD BC BCD BE =⋅∠==. ∴321651025CD AB ==,328153245CE BE -==; ∴CD CEAB BE≠. ∴CD 不平行于AB ,与CD ∥AB 矛盾.∴四边形ABDC 不可能为直角梯形.…………………………(2分) ②当AC ∥BD 时,如果四边形ABDC 只可能∠ACD =∠CDB = 90o. ∵AC ∥BD ,∠ACB = 90o, ∴∠ACB =∠CBD = 90o . ∴∠ABD =∠ACB +∠BCD > 90o. 与∠ACD =∠CDB = 90o矛盾.∴四边形ABDC 不可能为直角梯形.…………………………(2分)普陀区25.(本题满分14分)已知P 是O ⊙的直径BA 延长线上的一个动点,P ∠的另一边交O ⊙于点C 、D ,两点位于AB 的上方,AB =6,OP m =,1sin 3P =,如图11所示.另一个半径为6的1O ⊙经过点C 、D ,圆心距1OO n =.(1)当6m =时,求线段CD 的长;(2)设圆心1O 在直线AB 上方,试用n 的代数式表示m ;(3)△1POO 在点P 的运动过程中,是否能成为以1OO 为腰的等腰三角形,如果能,试求出此时n 的值;如果不能,请说明理由.DEBACFDC25.解:(1)过点O 作OH ⊥CD ,垂足为点H ,联结OC .在Rt △POH 中,∵1sin 3P =,6PO =,∴2OH =. ········· (1分) ∵AB =6,∴3OC =. ······················ (1分)由勾股定理得 CH = ····················· (1分)∵OH ⊥DC ,∴2CD CH == ················ (1分) (2)在Rt △POH 中,∵1sin 3P =, PO m =,∴3mOH =. ········ (1分) 在Rt △OCH 中,2293m CH ⎛⎫- ⎪⎝⎭=. ················ (1分)在Rt △1O CH 中,22363m CH n ⎛⎫-- ⎪⎝⎭=. ·············· (1分)可得 2236933m m n ⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭=,解得23812n m n -=. ········· (2分)(3)△1POO 成为等腰三角形可分以下几种情况:● 当圆心1O 、O 在弦CD 异侧时①1OP OO =,即m n =,由23812n n n-=解得9n =. ········· (1分)即圆心距等于O ⊙、1O ⊙的半径的和,就有O ⊙、1O ⊙外切不合题意舍去.(1分)②11O P OO =n =,解得23m n =,即23n 23812n n -=,解得n ·········· (1分) ● 当圆心1O 、O 在弦CD 同侧时,同理可得 28132n m n-=.∵1POO ∠是钝角,∴只能是m n =,即28132n n n-=,解得n . ·· (2分)综上所述,n .青浦区25.(本题满分14分,第(1)小题4分,第(2)小题6分,第(3)小题4分)如图9-1,已知扇形MON,∠MON=90o,点B在弧MN上移动,联结BM,作OD⊥BM,垂足为点D,C为线段OD上一点,且OC=BM,联结BC并延长交半径OM于点A,设OA= x,∠COM的正切值为y.(1)如图9-2,当AB⊥OM时,求证:AM =AC;(2)求y关于x的函数关系式,并写出定义域;(3)当△OAC为等腰三角形时,求x的值.25.解:(1)∵OD⊥BM,AB⊥OM,∴∠ODM =∠BAM=90°.··········(1分)∵∠ABM +∠M =∠DOM +∠M,∴∠ABM =∠DOM.·········(1分)∵∠OAC=∠BAM,OC =BM,∴△OAC≌△ABM,······················(1分)∴AC =AM.·························(1分)(2)过点D作DE//AB,交OM于点E.················(1分)∵OB=OM,OD⊥BM,∴BD=DM.················(1分)∵DE//AB,∴=MD MEDM AE,∴AE=EM,∵OM,∴AE=)12x.················(1分)∵DE//AB,∴2==OA OC DMOE OD OD,···················(1分)∴2=DM OAOD OE,∴=y(0<≤x·················(2分)(3)(i)当OA=OC时,∵111222===DM BM OC x,O MNDCBA图9-1ONDCBA图9-2NMO备用图在Rt △ODM中,==OD =DM y OD,1=x=x=x .(2分) (ii )当AO =AC 时,则∠AOC =∠ACO ,∵∠ACO >∠COB ,∠COB =∠AOC ,∴∠ACO >∠AOC ,∴此种情况不存在. ····················· (1分) (ⅲ)当CO =CA 时,则∠COA =∠CAO=α,∵∠CAO >∠M ,∠M =90α︒-,∴α>90α︒-,∴α>45︒,∴290α∠=>︒BOA ,∵90∠≤︒BOA ,∴此种情况不存在. ·· (1分)松江区25.(本题满分14分,第(1)小题4分,第(2)小题每个小题各5分)如图,已知Rt △ABC 中,∠ACB =90°,BC =2,AC =3,以点C 为圆心、CB 为半径的圆交AB 于点D ,过点A 作AE ∥CD ,交BC 延长线于点E.(1)求CE 的长;(2)P 是 CE 延长线上一点,直线AP 、CD 交于点Q.① 如果△ACQ ∽△CPQ ,求CP 的长;② 如果以点A 为圆心,AQ 为半径的圆与⊙C 相切,求CP 的长.25.(本题满分14分,第(1)小题4分,第(2)小题每个小题各5分) 解:(1)∵AE ∥CD∴BC DC BE AE=…………………………………1分 ∵BC=DC∴BE=AE …………………………………1分 设CE =x(第25题图)CBA DE(备用图)CBADECBA DE则AE =BE =x +2 ∵ ∠ACB =90°, ∴222AC CE AE +=即229(2)x x +=+………………………1分 ∴54x =即54CE =…………………………………1分 (2)①∵△ACQ ∽△CPQ ,∠QAC>∠P∴∠ACQ=∠P …………………………………1分 又∵AE ∥CD ∴∠ACQ=∠CAE∴∠CAE=∠P ………………………………1分 ∴△ACE ∽△PCA ,…………………………1分 ∴2AC CE CP =⋅…………………………1分 即2534CP =⋅ ∴365CP =……………………………1分 ②设CP =t ,则54PE t =- ∵∠ACB =90°,∴AP ∵AE ∥CD ∴AQ ECAP EP=……………………………1分5545454t t ==--∴AQ =1分若两圆外切,那么1AQ == 此时方程无实数解……………………………1分CBA DEPQ若两圆内切切,那么2595t AQ +== ∴21540160t t -+= 解之得2041015t ±=………………………1分又∵54t >∴2041015t +=………………………1分徐汇区25. 已知四边形ABCD 是边长为10的菱形,对角线AC 、BD 相交于点E ,过点C 作CF ∥DB 交AB 延长线于点F ,联结EF 交BC 于点H . (1)如图1,当EF BC ⊥时,求AE 的长;(2)如图2,以EF 为直径作⊙O ,⊙O 经过点C 交边CD 于点G (点C 、G 不重合),设AE 的长为x ,EH 的长为y ;① 求y 关于x 的函数关系式,并写出定义域;③ 联结EG ,当DEG ∆是以DG 为腰的等腰三角形时,求AE 的长.杨浦区25、(本题满分14分,第(1)小题4分,第(2)小题6分,第(3)小题4分)如图9,在梯形ABCD中,AD//BC,AB=DC=5,AD=1,BC=9,点P为边BC上一动点,作PH⊥DC,垂足H在边DC上,以点P为圆心PH为半径画圆,交射线PB于点E.(1)当圆P过点A时,求圆P的半径;(2)分别联结EH和EA,当△ABE△CEH时,以点B为圆心,r为半径的圆B与圆P相交,试求圆B的半径r的取值范围;(3)将劣弧沿直线EH翻折交BC于点F,试通过计算说明线段EH和EF的比值为定值,并求出此定值。
2018上海中考数学二模压轴题详解

如图1,已知平行四边形ABCD 中,AC =BC ,∠ACB =45°.将△ABC 沿着AC 翻折,点B 落在点E 处,联结DE ,那么DE AC的值为_________.图1动感体验请打开几何画板文件名“18松江18”,可以体验到,△ACH 是等腰直角三角形,DE 与AC 平行.答案 1.思路如下:如图2,设CE 与AD 交于点H .由∠ACB =45°,可知∠BCE =90°.所以△ACH 是等腰直角三角形.所以===CE CB CA CH CH CH 1=EH CH. 由△EAC ≌△BAC ≌△DCA ,可知A 、D 两点到AC 的距离相等.所以DE //AC .所以1==DE EH AC CH .图2如图1,已知抛物线y =ax 2+b x 的顶点为C (1,-1),P 是抛物线上位于第一象限内的一点,直线OP 交该抛物线于点B ,直线CP 交x 轴于点A .(1)求该抛物线的表达式;(2)如果点P 的横坐标为m ,使用m 的代数式表示线段BC 的长;(3)如果△ABP 的面积等于△ABC 的面积,求点P 的坐标.图1动感体验请打开几何画板文件名“18松江24”,拖动点P 在第一象限内的抛物线上运动,可以体验到,△ABP 与△ABC 是同高三角形,面积比等于PH 与CE 的比.思路点拨1.函数的解析式中待定两个系数,需要知道两个点的坐标.看似缺少条件,其实解析式中隐含了抛物线经过原点.2.△ABP 与△ABC 是同高三角形,面积相等时高也相等.图文解析(1)设抛物线的顶点式为y =a (x -1)2-1=ax 2-2ax +a -1.对照y =ax 2+b x ,根据常数项相等,得a -1=0.所以a =1.所以抛物线的解析式为y =(x -1)2-1=x 2-2x .(2)如图2,作PH ⊥x 轴于H ,设对称轴与x 轴交于点E ,那么E (1, 0).已知点P 的横坐标为m ,那么PH =m 2-2m . 由=BE PH OE OH ,得221-=BE m m m.所以BE =m -2. 所以BC =BE +EC =m -2+1=m -1.图2 图3(3)如图3,因为△ABP 与△ABC 是同高三角形,当它们的面积相等时,底边AP =AC . 此时PH =CE =1.所以点P 的纵坐标为1.解方程m 2-2m =1,得1=m当1=m 时,PH =m 2-2m =m (m -2)=1)=1.所以点P 的坐标是(1.考点伸展第(3)题可以从不同的角度认识△ABP 和△ABC .例如,如图3,当△ABP 与△ABC 的面积相等时,△PBC 是△ABC 面积的2倍,这两个三角形有公共底边BC ,所以高EH 是高EA 的2倍.于是得到A 是EH 的中点,进一步得到P 、C 两点的纵坐标互为相反数.再如,把BA 看作△ABP 与△ABC 的公共底边,那么P 、C 两点到直线BA 的距离相等.由于两条高是平行且相等的,这样也可以得到A 是PC 的中点.例 2018年上海市松江区中考模拟第25题如图1,已知Rt △ABC 中,∠ACB =90°,BC =2,AC =3,以点C 为圆心、CB 为半径的圆交AB 于点D ,过点A 作AE //CD ,交BC 的延长线于点E .(1)求CE 的长;(2)P 是CE 延长线上一点,直线AP 、CD 交于点Q .①如果△ACQ ∽△CPQ ,求CP 的长;②如果以点A 为圆心,AQ 为半径的圆与⊙C 相切,求CP的长.图1动感体验请打开几何画板文件名“18松江25”,拖动点P 在CE 的延长线上运动,可以体验到,⊙A 与⊙C 可以内切,不可能外切.思路点拨1.图形中A 、B 、C 、D 、E 等5个点都是确定的,因此图1中所有线段和角都是确定的.因为点P 而动的线段CP 、EP 、AP 、AQ ,都可以用CP =x 来表示.2.如果△ACQ ∽△CPQ ,那么∠P =∠ACQ =∠CAE 也是确定的.3.对于⊙A 与⊙C ,⊙C 的半径和圆心距是确定的,如果两圆相切,⊙A 的半径AQ 就是确定的.图文解析(1)如图2,由DC //AE ,得 DC BC AE BE.因为DC =BC ,所以AE =BE . 设CE =m ,那么在Rt △ACE 中,AE =BE =2+m ,AC =3.由勾股定理,得(2+m )2=32+m 2.解得CE =m =54.图2 图3(2)①如图2,在Rt △ACE 中,CE =54,AC =3,所以tan ∠CAE =512. 如图3,如果△ACQ ∽△CPQ ,那么∠ACQ =∠P .又因为∠ACQ =∠CAE ,所以∠P =∠CAE .在Rt △ACP 中,tan ∠P =AC CP =512,所以CP =125AC =365. ②对于⊙A ,r A =AQ ;对于⊙C ,r C =2;圆心距d =AC =3.当⊙A 与⊙C 内切时,AQ -2=3,此时AQ =5.当⊙A 与⊙C 外切时,AQ +2=3,此时AQ =1.如图3,在Rt △ACP 中,AC =3,设CP =x ,那么AP如图4,由DC //AE ,得555()4445==÷-=-AQ EC x AP EP x .当AQ =5545=-x 45=-x . 整理,得15x 2-40x +16=0.解得1 2.18=≈x (如图5所示),20.49=≈x (舍去).当AQ =1545=-x .所以45=-x . 整理,得9x 2+40x +200=0.此方程无实数根,所以⊙A 与⊙C 不可能外切.图4 图5考点伸展第(1)题求CE 的长,还可以这样解:如图6,设⊙C 的直径为BF ,那么∠B 是等腰三角形ABF 的底角.如图7,∠B 是等腰三角形CBD 和等腰三角形EBA 的公共底角.这三个等腰三角形两两相似. 由=BA BF BE BA ,得2134==BA BE BF .所以CE =BE -BC =1324-=54.图6 图7如果一个三角形有一条边上的高等于这条边的一半,那么我们把这个三角形叫做半高三角形.已知直角三角形ABC是半高三角形,且斜边AB=5,则它的周长等于_________.动感体验请打开几何画板文件名“18长宁17”,拖动点C在以AB为直径的半圆O上运动,可以体验到,半高三角形有两种情况,一是等腰直角三角形,二是两条直角边的比为1∶2.答案如图1,CD是Rt△ABC斜边AB上的高,CO是斜边上的中线,那么CO=12AB=52为定值.当CD=12AB时,CD与CO重合,△ABC是等腰直角三角形(如图2所示).此时△ABC的周长为5+.如图2,当AC=2BC时,设AC=2m,BC=m,由勾股定理,得5m2=52.解得m ABC的周长为5+图1 图2 图3如图1,在矩形ABCD 中,对角线BD 的长为1,点P 是线段BD 上一点,联结CP ,将△BCP 沿着直线CP 翻折,若点B 落在边AD 上的点E 处,且EP //AB ,则AB 的长等于________.图1动感体验请打开几何画板文件名“18长宁18”,拖动点A 可以改变矩形ABCD 的形状,但是对角线BD 保持不变,可以体验到,△BCP 和△ECP 关于CP 保持对称,当EP //AB 时,∠CED =∠ABD .答案 12.思路如下:已知BD =1,设AB =x ,那么AD EC =BC =AD如图2,当EP //AB 时,∠DEP =90°.根据等角的余角相等,∠CED =∠ABD . 如图3,如图4,由sin ∠CED =sin ∠ABD ,得=DC AD EC BD.1=.整理,得x 2+x -1=0.解得12-=x .图2 图3 图4如图1,在直角坐标平面内,抛物线y =ax 2+bx -3与y 轴交于点A ,与x 轴分别交于B (-1, 0)、C (3, 0)两点,点D 是抛物线的顶点.(1)求抛物线的表达式及顶点D 的坐标;(2)联结DC ,求△ACD 的面积;(3)点P 在直线DC 上,联结OP ,若以O 、P 、C为顶点的三角形与△ABC 相似,求点P 的坐标.图1动感体验请打开几何画板文件名“18长宁24”,可以体验到,△ACD 是直角三角形.拖动点P 在直线CD 上运动,可以体验到,△OCP 与△ABC 相似存在两种情况.思路点拨1.第(2)题先证明△ACD 是直角三角形,再计算面积比较方便.2.第(3)题首先要发现并证明△OCP 与△ABC 中一组相等的角,然后根据两边对应成比例分两种情况列方程.图文解析(1)因为抛物线与x 轴交于B (-1, 0)、C (3, 0)两点,所以y =a (x +1)(x -3). 对照y =ax 2+bx -3,根据常数项相等,得-3a =-3.解得a =1.所以y =(x +1)(x -3)=x 2-2x -3=(x -1)2-4.顶点为D (1,-4).(2)如图2,由A (0,-3)、C (3, 0)、D (1,-4),可得AC 2=18,AD 2=2,CD 2=20. 所以CD 2=AC 2+AD 2.所以△ACD 是直角三角形,∠CAD =90°.所以S △ACD =12⋅AC AD 3.图2 图3 图4(3)第一步,先探求∠OCD =∠BAC .如图3,由C (3, 0)、D (1,-4),可得tan ∠DCO =42=2.如图4,作BH ⊥AC 于H .由OA =OC ,得AC =C =45°.在等腰直角三角形BCH 中,BC =4,所以BH =CH =在Rt △BAH 中,AH =tan ∠BAC =BHAH =2. 所以∠OCD =∠BAC . 第二步,当点P 在射线CD 上时,∠OCP =∠BAC ,分两种情况讨论相似.如图5,作PM ⊥x 轴于M ,那么CM =5,PM =2CM .①当=CP ABCO AC 时,3CP CP 此时CM =1,PM =2.所以P (2,-2)(如图6所示).②当=CP ACCO AB 时,3CP CP . 此时CM =95,PM =185.所以OM =935-=65,P 618(,)55-(如图7所示).图5 图6 图7考点伸展第(2)题求△ACD 的面积方法多样.例如,如图8,用梯形ONDC 的面积减去直角三角形AOC 和直角三角形AND 的面积. 再如,如图9,DF 把△ACD 分割为两个三角形,DF 是公共底边,高的和等于OC . 还可以由∠OAC =∠DAN =45°,先证明直角三角形ACD ,再计算面积.图8 图9例 2018年上海市长宁区中考模拟第25题在圆O 中,C 是弦AB 上的一点,联结OC 并延长,交劣弧AB 于点D ,联结AO 、BO 、AD 、BD .已知圆O 的半径长为5,弦AB 的长为8.(1)如图1,当点D 是弧AB 的中点时,求CD 的长;(2)如图2,设AC =x ,△△ACO OBDS S =y ,求y 关于x 的函数解析式并写出定义域; (3)若四边形AOBD 是梯形,求AD 的长.图1 图2 备用图动感体验请打开几何画板文件名“18长宁25”,拖动点C 在AB 上运动,可以体验到,△AOC 与△OBC 是同高三角形,△OBD 与△OBC 也是同高三角形.还可以体验到,四边形AOBD 的两组对边各有一个时刻平行.思路点拨1.圆中已知定弦,一般先求弦心距.2.在△ACO 个△OBD 之间,找一个相关联的△OBC .3.按照对边平行,分两种情况讨论梯形AOBD .图文解析(1)如图3,当点D 是弧AB 的中点时,OD 垂直平分弦AB ,垂足为C .在Rt △OAC 中,OA =5,AC =4,所以OC =3.此时CD =OD -OC =5-3=2.图3 图4 图5(2)如图5,△ACO 和△OBD 都可以与△OBC 相关联.第一步,用x 表示OC 的长.如图4,作OH ⊥AB 于H ,那么OH =3,CH =4-x ,所以OC第二步,如图5,因为△△ACO OBC S S =AC BC =8-x x ,△△OBD OBC S S =OD OC,所以y =△△ACO OBD S S =△△△△÷ACO OBD OBC OBC S S S S=8-x x定义域是0<x <8.(3)如图6,延长BO 交圆于点E ,那么BE 是圆的直径,AE =2OH =6. 情形1,如图6,如果OA //BD ,那么∠DBA =∠BAO =∠ABO .根据相等的圆周角所对的弧相等,相等的弧所对的弦相等,此时AD =AE =6. 情形2,如图7,如果AD //BO ,那么四边形ADBE 是等腰梯形. 作AM ⊥BE 于M ,作DN ⊥BE 于N ,那么AD =MN .在Rt △AEM 中,AE =6,cos ∠E =35,所以EM =35AE =185. 此时AD =MN =BE -2EM =181025-⨯=145.图6 图7 图8考点伸展第(2)题也可以用面积公式求△ACO 的面积,用割补法求△OBD 的面积.如图8,△OBC 和△DBC 的公共底边为BC ,高OH =3,求高DG 也要先用x 表示OC 的长,再根据相似比求得DG 的长.在矩形ABCD中,AB=5,BC=12,点E是边AB上一点(不与A、B重合),以点A 为圆心,AE为半径作⊙A,如果⊙C与⊙A外切,那么⊙C的半径r的取值范围是______.动感体验请打开几何画板文件名“18崇明17”,拖动点E在AB上运动,可以体验到,⊙C的半径CF=AC-AE.答案8≤r<13.思路如下:如图2,在Rt△ABC中,AB=5,BC=12,所以AC=13.如果⊙C与⊙A外切于点F,那么⊙C的半径r=CF=AC-AE=13-AE.因为0<AE≤5,所以8≤r<13.图1如图1,△ABC 中,∠BAC =90°,AB =6,AC =8,点D 是BC 的中点,将△ABD 沿AD 翻折得到△AED ,联结CE ,那么线段CE 的长等于_________.图1动感体验请打开几何画板文件名“18崇明18”,可以体验到,A 、B 、C 、E 四点在以AB 为直径的圆D 上,四边形AEDB 是轴对称图形,可以计算得到对角线EB 的长,进而在直角三角形ECB 中得到CE 的长.答案 如图2,在Rt △ABC 中, AB =6,AC =8,所以BC =10. 在△ABD 中,DA =DB =5,AB =6,容易得到S △ABD =12. 所以S 四边形AEDB =24.再由S 四边形AEDB =12⋅AD EB =52EB =24,得EB =485. 如图3,在Rt △ECB 中,CE 2=CB 2-EB 2=224810()5-=225048()()55-=2221()(5048)5⨯-=21()9825⨯⨯=21()4945⨯⨯.所以CE =1725⨯⨯=145.图2 图3如图1,已知抛物线经过点A(0, 3)、B(4, 1)、C(3, 0).(1)求抛物线的解析式;(2)联结AC、BC、AB,求∠BAC的正切值;(3)点P是该抛物线上一点,且在第一象限内,过点P作PG⊥AP交y轴于点G,当点G在点A的上方,且△APG与△ABC相似时,求点P的坐标.图1动感体验请打开几何画板文件名“18崇明24”,拖动点P在抛物线上运动,可以体验到,△AHP 与△APG保持相似.直角三角形AHP的两条直角边的比可以为1∶3,也可以为3∶1.思路点拨1.第(1)题设抛物线的一般式列三元一次方程组比较方便.2.第(2)题先证明△ABC是直角三角形,用勾股定理的逆定理书写起来比较方便.3.第(3)题根据相似三角形的传递性,过点P作y轴的垂线段PH,转化为△AHP与△ABC相似的问题.4.根据直角边对应成比例,分两种情况讨论△AHP与△ABC相似.图文解析(1)设抛物线的解析式为y=ax2+bx+c.将A(0, 3)、B(4, 1)、C(3, 0)分别代入,得3,1641, 930.=⎧⎪++=⎨⎪++=⎩ca b ca b c解得12=a,52=-b,c=3.所以215322=-+y x x.(2)如图2,由A(0, 3)、B(4, 1)、C(3, 0),得AC2=18,BC2=2,AB2=20.所以AC2+BC2=AB2.所以△ABC是直角三角形,∠ACB=90°.所以tan∠BAC=BCAC13.图2(3)设点P 的坐标为215(,3)22-+x x x . 如图3,作PH ⊥y 轴于H ,那么△AHP ∽△APG . 如果△APG 与△ABC 相似,那么△AHP 与△ABC 也相似. 分两种情况讨论△AHP 与△ABC 相似:①如图4,当3==HA CAHP CB 时,3=HA HP . 解方程21533322-+-=x x x ,得x =11,或x =0.此时P (11, 36).②如图5,当13==HA CA HP CB 时,13=HA HP .解方程215133223-+-=x x x ,得x =173,或x =0.此时P 1726(,)33.图3 图4 图5考点伸展如果第(3)题求点G 的坐标,也需要先求点P 的坐标.如图4,HG =13HP =113,此时OG =y P +HG =11363+=1193.所以G 119(0,)3. 如图5,HG =3HP =17,此时OG =y P +HG =26173+=773.所以G 77(0,)3.例 2018年上海市崇明区中考模拟第25题如图1,已知△ABC中,AB=8,BC=10,AC=12,D是AC边上一点,且AB2=AD·AC,联结BD,点E、F分别是BC、AC上两点(点E不与B、C重合),∠AEF=∠C,AE与BD相交于点G.(1)求证:BD平分∠ABC;(2)设BE=x,CF=y,求y与x之间的函数关系式;(3)联结FG,当△GEF是等腰三角形时,求BE的长度.图1动感体验请打开几何画板文件名“18崇明25”,可以体验到,在等腰三角形ANC中,有一个“一线三等角”模型.点击屏幕左下方的按钮“第(3)题”,拖动点E在BC运动,可以体验到,△GEF的每个顶点都可以落在对边的垂直平分线上.思路点拨1.第(1)题是典型的“平分+平行”模型,过点A作BC的平行线交于BD的延长线于M,通过计算得到AM=AB.2.第(2)题如果想到了“一线三等角”,就构造一个等腰△ANC,问题迎刃而解.3.第(3)题的△GEF中,cos∠GEF是定值,设法用x表示夹∠GEF的两条边,然后分三种情况列方程.图文解析(1)由AB2=AD·AC,得26416123===ABADAC.所以1641239=÷=ADAC.所以45=ADCD.如图2,过点A作BC的平行线交BD的延长线于点M,那么45==AM ADBC CD.所以AM=45BC=8.所以AM=AB.所以∠M=∠ABM.图2 又因为∠M=MBC,所以∠ABM=∠MBC,即BD平分∠ABC.(2)第一段,如图3,作AH⊥BC于H,设BH=m,那么CH=10-m.由勾股定理,得AB2-BH2=AC2-CH2.所以82-m2=122-(10-m)2.解得m=1.因此cos ∠C =93124==CH AC . 第二段,如图3,以AH 为对称轴,构造等腰三角形ANC ,那么NB =8.第三段,如图4,由∠AEC =∠N +∠NAE ,∠AEC =∠AEF +∠CEF ,∠N =∠C = ∠AEF ,可得∠NAE =∠CEF .又因为∠N =∠C ,所以△ANE ∽△ECF . 所以=AN EC NE CF .所以12108-=+xx y. 整理,得280212+-=x x y .定义域是0<x <10.图3 图4(3)如图5,在△GEF 中,∠GEF 是定值,cos ∠GEF =cos ∠C =34. 第一步,用x 表示EG 、EF .如图6,由8==EG BE x AG AM ,得8==+EGBE xAE AM x. 所以8=+xEG AE x.如图4,由△ANE ∽△ECF ,得1012-==EFEC xAEAN . 所以1012-=xEF AE .图5 图6第二步,分三种情况讨论等腰三角形GEF . ①如图7所示,当EF =EG 时,10812-=+x x AE AE x .整理,得x 2+10x -80=0.解得5=-x .此时BE 5. ②如图8所示,当GE =GF 时,1324=EF EG .所以131028412-⨯=⨯+x xx . 整理,得x 2+16x -80=0.解得x =4,或x =-20.此时BE =4. ③如图9所示,当FE =FG 时,1324=EG EF .所以110321248-⨯=⨯+x xx. 整理,得x 2-6x -80=0.解得3=-x BE 3图7 图8 图9考点伸展第(1)题也可以这样思考:如图10,已知△ABC 的三边,由AB 2=AD ·AC ,可以求得AD 的长,也可以得到△ABD ∽△ACB .再根据对应边成比例,求得DB 的长,得到DB =DC ,得到∠DBC =∠C .经过等量代换,得到∠ABD =∠DBC .但是这个解法对第(2)、(3)题的帮助不大.图10如图1,点A、B在圆O上,弦AC与半径OB互相平分,那么∠AOC的度数为_________.图1动感体验请打开几何画板文件名“18嘉定17”,可以体验到,四边形OABC是菱形,△OAB是等边三角形.答案120°.思路如下:如图2,由弦AC与半径OB互相平分,可知四边形OABC是平行四边形.由OA=OC,得平行四边形OABC是菱形.如图3,由OA=OB=AB,得△OAB是等边三角形.于是可得∠AOC=120°.图2 图3如图1,已知△ABC 中,AB =AC =5,BC =6,点D 在边AB 上,且∠BDC =90°.如果△ACD 绕点A 顺时针旋转,使点C 与点B 重合,点D 旋转至点D 1,那么线段DD 1的长为_________.图1动感体验请打开几何画板文件名“18嘉定18”,拖动点C 1绕点A 旋转,可以体验到,△ACC 1与△ADD 1保持相似.答案4225.思路如下: 如图2,作AH ⊥BC 于H ,那么BH =CH =3.所以cos ∠B =BHAB=35. 在Rt △BCD 中,BD =BC ·cos ∠B =365⨯=185.所以AD =1855-=75.如图3,由△ADD 1∽△ACC 1,得11=AD ACDD CC . 如图4,当C 1与B 重合时,17556=DD .此时DD 1=4225.图2 图3 图4例 2018年上海市嘉定区中考模拟第24题已知平面直角坐标系中,直线y =x +m 经过点A (-4, 0)和点B (n , 3).(1)求m 、n 的值;(2)如果抛物线y =x 2+bx +c 经过点A 、B ,该抛物线的顶点为P ,求sin ∠ABP 的值;(3)设点Q 在直线y =x +m 上,且在第一象限内,直线y =x +m 与y 轴的交点为D ,如果∠AQO =∠DOB ,求点Q 的坐标.图1动感体验请打开几何画板文件名“18嘉定24”,可以体验到,△ABP 是直角三角形.点击屏幕左下方的按钮“第(3)题”,可以体验到,△BOD ∽△BQO .思路点拨1.第(2)题求sin ∠ABP 的值,可以先求tan ∠ABP 的值.如果准确描出A 、B 、P 三点的位置,答案就在图形中.2.第(3)题先根据题意画出示意图,如果能根据∠AQO =∠DOB ,发现相似三角形,那么就可以确定BQ 的长,进而求得点Q 的坐标.图文解析(1)将点A (-4, 0)代入y =x +m ,得-4+m =0.解得m =4.将点B (n , 3)代入y =x +4,得n +4=3.解得n =-1.(2)因为抛物线y =x 2+bx +c 与x 轴交于点A (-4, 0),可设y =(x +4)(x -x 2). 代入点B (-1, 3),得3=3(-1-x 2).解得x 2=-2.所以y =(x +4)(x +2)=x 2+6x +8=(x +3)2-1.顶点为P (-3,-1).如图2,由A (-4, 0)、B (-1, 3)、P (-3,-1),可知A 、B 两点间的水平距离和竖直距离都是3,A 、P 两点间的水平距离和竖直距离都是1,所以∠BAO =∠P AO=45°,AB =AP所以在Rt △ABP 中,tan ∠ABP =AP AB =13.所以sin ∠ABP 图2(3)如图3,由y =x +4,得D (0, 4).再由B (-1, 3),得BO 2=10,BD 如果∠AQO =∠DOB ,那么△BOD ∽△BQO .所以=BO BQBD BO .所以2===BO BQ BD 所以B 、Q 两点间的水平距离和竖直距离都等于5.所以Q (4, 8).图3 图4考点伸展第(3)题也可以用等角的正切值相等来解.如图4,作BF ⊥y 轴于F ,作OE ⊥AB 于E .在等腰直角三角形AOE 中,AO =4,所以OE =E (-2, 2).由于tan ∠DOB =BF OF =13,所以tan ∠AQO =OE QE =13.所以QE =3OE =. 所以Q 、E 两点间的水平距离和竖直距离都等于6.所以Q (4, 8).例 2018年上海市嘉定区中考模拟第25题在圆O中,AO、BO是圆O的半径,点C在弧AB上,OA=10,AC=12,AC//OB,联结AB.(1)如图1,求证:AB平分∠OAC;(2)点M在弦AC的延长线上,如果△AMB是直角三角形,请你在如图2中画出点M 的位置并求CM的长;(3)如图3,点D在弦AC上,与点A不重合,联结OD与弦AB交于点E,设点D 与点C的距离为x,△OEB的面积为y,求y与x的函数关系式,并写出自变量x的取值范围.图1 图2 图3动感体验请打开几何画板文件名“18嘉定25”,拖动点M在AC的延长线上运动,可以体验到,直角三角形ABM存在两种情况.拖动点D在AC上运动,可以体验到,△OEB与△OAB是同高三角形,y随x的增大而增大.思路点拨1.已知半径和弦,一般情况下先求弦心距.2.直角三角形ABM存在两种情况,∠AMB=90°和∠ABM ′=90°,两种情况的图形叠放在一起,BM就是直角三角形ABM′斜边上的高.3.第(3)题用同高三角形的面积比,运算量比较小.图文解析(1)如图4,由OA=OB,得∠OAB=∠OBA.由AC//OB,得∠CAB=∠OBA.所以∠OAB=∠CAB,AB平分∠OAC.(2)点M存在两种情况:M和M′(如图6所示).如图5,作OH⊥AC于H,那么在Rt△OAH中,OA=10,AH=6,所以OH=8.如图6,当∠AMB=90°时,AM=AH+HM=AH+OB=6+10=16.此时CM=AM-AC=16-12=4.当∠AB M ′=90°时,∠BAM=∠M ′BM.所以'81162===M M BMBM AM.所以1'42==M M BM.此时CM ′=8.图4 图5 图6(3)第一步,如图7,S △OAB =12⋅OB OH =11082⨯⨯=40. 第二步,如图8,由1012==-BE BO AE AD x ,得1022=-BE BA x . 第三步,如图9,由于△OEB 与△OAB 是同高三角形,所以1022△△==-OEB OAB S BE S BA x . 所以y =S △OEB =104022⨯-x =40022-x.定义域是0≤x <12.图7 图8 图9考点伸展第(3)题求△OEB 的面积的方法多样.例如,△ODB 的面积是定值,△OEB 与△ODB 也是等高三角形,底边OE 与OD 的比,同样根据OB 与AD 的比可以推导出来.再如,如果把EB 看作底边,那么高是定值,等腰三角形OAB 的高和底角、底边也是确定的,于是可以根据比例线段推导出EB 的长(用x 表示).如果两圆的半径之比为3∶2,当这两圆内切时圆心距为3,那么当这两圆相交时,圆心距d的取值范围是_________.动感体验请打开几何画板文件名“18金山17”,拖动圆心B向右运动,可以体验到,圆A与圆B 的位置关系依次是内切、相交和外切.答案15.思路如下:设圆A的半径为3m,圆B的半径2m.如图1,当圆A与圆B内切时,圆心距d=AB=3m-2m=3.解得m=3.如图2,当圆A与圆B外切时,圆心距d=AB=3m+2m=5m=15.如图3所示,圆A与圆B相交.图1 图2 图3如图1,Rt△ABC中,∠C=90°,AC=6,BC=8,D是AB的中点,P是直线BC上一点,把△BDP沿PD所在的直线翻折后,点B落在点Q处,如果QD⊥BC,那么点P和点B间的距离等于_________.图1动感体验请打开几何画板文件名“18金山18”,拖动点P在直线BC上运动,可以体验到,有两个时刻,直线QD与BC垂直,此时Rt△PEQ的三边比为3∶4∶5.答案52或10.思路如下:在Rt△ABC中,AC=6,BC=8,所以AB=10,sin∠B=35,tan∠B=34.如图2,设直线QD与BC交于点E,当QD⊥BC时,E为垂足.已知D为AB的中点,所以QD=BD=5.在Rt△BDE中,BD=5,所以DE=3,BE=4.在Rt△PEQ中,∠Q=∠B,QE=QD-DE=5-3=2,所以PE=34QE=32.此时PB=BE-PE=342=52.如图3,在Rt△PEQ中,QE=QD+DE=5+3=8,所以PE=34QE=6.此时PB=BE+PE=4+6=10.图2 图3如图1,平面直角坐标系中,已知抛物线y =x 2+bx +c 经过点A (1, 0)和点B (3, 0),与y 轴相交于点C ,顶点为P .(1)求这条抛物线的表达式和顶点P 的坐标;(2)点E 在抛物线的对称轴上,且EA =EC ,求点E 的坐标;(3)在(2)的条件下,记抛物线的对称轴为直线MN ,点Q 在直线MN 右侧的抛物线上,∠MEQ =∠NEB ,求点Q 的坐标.图1动感体验请打开几何画板文件名“18金山24”,可以体验到,当EA =EC 时,点E 在AC 的垂直平分线上.还可以体验到,与∠NEB 相等的∠MEQ 有两个,就是直线AE 与抛物线的两个交点,但是点A 在对称轴的左侧.思路点拨1.已知二次项系数和抛物线与x 轴的两个交点,可以直接写出交点式.2.如果EA =EC ,由两点间的距离公式,根据EA 2=EC 2列整式方程.3.已知∠MEQ =∠NEB ,构造两个直角三角形相似,用相似比求解比较简便. 图文解析(1)因为抛物线y =x 2+bx +c 与x 轴交于A (1, 0)、B (3, 0)两点,所以y =(x -1)(x -3)=x 2-4x +3=(x -2)2-1.顶点为P (2,-1).(2)如图2,由y =x 2-4x +3,得C (0, 3).设E (2, m ),已知A (1, 0).由EA 2=EC 2,得12+m 2=22+(m -3)2.解得m =2.所以点E 的坐标为(2, 2).(3)如图3,设抛物线的对称轴与x 轴交于点F .作PH ⊥MN 于H .设Q (x , x 2-4x +3),已知B (3, 0)、E (2, 2).由tan ∠HEQ =tan ∠FEB ,得=QH BF EH EF . 所以221(43)22-=-+-x x x .整理,得x 2-6x +5=0. 解得x =5,或x =1(在对称轴左侧,舍去).此时Q (5, 8).图2 图3考点伸展第(3)题求得的x 1=5,x 2=1的几何意义是什么呢?由于∠FEB 是确定的,所以∠MEQ 的大小也是确定的,位置有两个.也就是说,经过点E 的直线EQ 与抛物线有两个交点,其中一个交点就是A (1, 0).显然A 、B 两点关于抛物线的对称轴是对称的.第(2)题求得点E (2, 2)以后,通过计算可以证明,△ACE 是等腰直角三角形.常用的方法有两种,一是勾股定理的逆定理,二是相似比.方法一,由A (1, 0)、C (0, 3)、E (2, 2),可得AE 2=5,CE 2=5,AC 2=10.所以AC 2=AE 2+CE 2.所以△ACE 是直角三角形.方法二,如图2,由2==CG EF EG AF,得∠ECG =∠AEF . 由于∠ECG 与∠CEG 互余,所以∠AEF 与∠CEG 互余.于是得到∠AEC =90°.例 2018年上海市金山区中考模拟第25题如图1,已知在梯形ABCD中,AD//BC,AB=DC=AD=5,sin∠B=35,P是线段BC上一点,以P为圆心、P A为半径的圆P与射线AD的另一个交点为Q,射线PQ与射线CD 相交于点E,设BP=x.(1)求证△ABP∽△ECP;(2)如果点Q在线段AD上(与点A、D不重合),设△APQ的面积为y,求y与x的函数关系式,并写出定义域;(3)如果△QED与△QAP相似,求BP的长.图1 备用图动感体验请打开几何画板文件名“18金山25”,拖动点P在BC上运动,可以体验到,△APQ 的高是定值,就是梯形的高.还可以体验到,△QED与△QAP相似存在两种情况,每种情况下,△ABP、△ECP、△EDQ和△APQ都是等腰三角形.思路点拨1.过等腰梯形上底的两个顶点作双垂线,把所有的线段长都标记出来.2.△ABP、△ECP和△EDQ两两相似,△APQ是等腰三角形.如果这4个三角形中任何两个相似时,4个三角形都是等腰三角形.图文解析(1)如图2,因为四边形ABCD是等腰梯形,所以∠B=∠C.因为P A=PQ,所以∠1=∠2.由AD//BC,得∠1=∠3,∠2=∠4.所以∠3=∠4.所以△ABP∽△ECP.图2 图3(2)如图3,作AM⊥BC于M,作PN⊥AD于N.在Rt△ABM中,AB=5,sin∠B=35,所以AM=3,BM=4.所以AN=MP=BP-BM=x-4.由P A=PQ,PN⊥AQ,得AQ=2AN=2(x-4).所以y=S△APQ=12⋅AQ PN=12(4)42⨯-⨯x=4x-16.定义域是4<x<132.(3)按照点Q的位置分两种情况讨论△QED与△QAP相似.情形1,如图4,点Q在AD上.由于△EDQ∽△ECP∽△ABP,当△EDQ∽△APQ时,△ABP∽△APQ.因为P A=PQ,所以BP=BA=5.情形2,如图5,点Q在AD的延长线上.当△DEQ∽△APQ时,∠EDQ=∠A.所以DC//AP.所以∠3=∠C.又因为∠C=∠B,所以∠3=∠B.所以AB=AP.所以点A在BP的垂直平分线上,此时BP=2BM=8.图4 图5考点伸展第(2)题求y关于x的函数关系式,事实上,不论点Q在AD上,还是点Q在AD的延长线上,都有AQ=2AN=2MP=2(BP-BM)=2(x-4),所以关系式是一样的.这样的话,函数的定义域为4<x≤13.当x=132时,如图6所示;当x=13时,如图7所示.图6 图7在平面直角坐标系中,如果对任意一点(a, b),规定两种变换:f (a, b)=(-a,-b),g (a, b)=(b,-a),那么g [ f (1,-2)]=_________.动感体验请打开几何画板文件名“18静安17”,拖动点P(a, b)在坐标平面内运动,可以体验到,变换f (a, b)就是作点P(a, b)关于原点的对称点;变换g (a, b)分两步,先作点P(a, b)关于直线y=x的对称点Q,再作点Q关于x轴的对称点(如图1所示).答案如图2,由f (a, b)=(-a,-b),得f (1,-2)=(-1, 2).由g (a, b)=(b,-a),得g(-1, 2)=(2, 1).所以g [ f (1,-2)]=g(-1, 2)=(2, 1).图1 图2等腰△ABC 中,AB =AC ,它的外接圆⊙O 的半径为1,如果线段OB 绕点O 旋转90°后可与线段OC 重合,那么∠ABC 的余切值是_________.动感体验请打开几何画板文件名“18静安18”,可以体验到,等腰三角形ABC 与等腰直角三角形OBC 的对称轴是重合的.答案 11.思路如下:如图2,在等腰直角三角形OBC 中,OB =OC =1,所以BC设BC 的中点为H ,那么OH ⊥BC ,AH ⊥BC .所以A 、O 、H 三点共线.如图3,在Rt △ABH 中,BH ,AH =1cot ∠ABC =BH AH 1.如图3,在Rt △ABH 中,BH =2,AH =12-,所以cot ∠ABC =BH AH 1.图2 图3 图4如图1,在平面直角坐标系中,已知点B(8, 0)和点C(9,-3),抛物线y=ax2-8ax+c(a、c是常数,a≠0)经过点B、C,且与x轴的另一个交点为A,对称轴上有一点M,满足MA=MC.(1)求这条抛物线的表达式;(2)求四边形ABCM的面积;(3)如果坐标系内有一点D,满足四边形ABCD是等腰梯形,且AD//BC,求点D的坐标.图1动感体验请打开几何画板文件名“18静安24”,可以体验到,四边形ABCM是梯形.还可以体验到,如果四边形ABCD是等腰梯形,那么△ADE∽△CBF.思路点拨1.第(2)题先根据两点间的距离公式列方程求得点M的坐标,再判断四边形ABCM 的形状,然后求面积.2.第(3)题中,A、B、C三点是确定的,用一个字母n表示点D的坐标,就可以列方程了.列方程的依据可以根据腰相等,也可以根据对角线相等.图文解析(1)由y=ax2-8ax+c,可知抛物线的对称轴是直线x=4.点B(8, 0)关于直线x=4的对应点是A(0, 0).设抛物线的解析式为y=ax(x-8),代入C(9,-3),得-3=9a.解得13=-a.所以2118(8)333=--=-+y x x x x.(2)设M(4, m).由MA2=MC2,得42+m2=52+(m+3)2.解得m=-3.所以M(4,-3),MC//x轴,MC=5.所以四边形ABCM是梯形,高为3.所以S梯形ABCM=139(5+8)322⨯⨯=.图2 图3 (3)作等腰梯形ABCD的外接矩形AEHF.由B(8, 0)、C(9,-3),可得tan∠CBF=3.由∠ADE=∠DAB=∠CBF,得tan∠ADE=3.设DE =n ,AE =3n ,那么D (n ,-3n ).由DC =AB ,得DC 2=AB 2.所以(n -9)2+(3n -3)2=82.整理,得5n 2-18n +13=0.解得n =1,或n =135. 当n =1时,D(1,-3).此时DC //x 轴//AB ,四边形ABCD 是平行四边形,不合题意. 当n =135时,D 1339(,)55-.此时ABCD 是等腰梯形. 考点伸展第(3)题解等腰梯形,设好了点D 的坐标为(n ,-3n )以后,有4种列方程的方法. 上面第一种方法,由腰相等DC =AB ,根据DC 2=AB 2列方程.这个方程是一元二次方程,一个解是等腰梯形,另一个解是平行四边形.也就是说,一组对边平行,另一组对边相等的四边形是等腰梯形或平行四边形.这是因为以C 为圆心、AB 为半径的圆与直线AD 有两个交点.第二种方法,由对角线相等DB =AC ,根据DB 2=AC 2列方程.这个方程的两个解,也是等腰梯形和平行四边形.这是因为以B 为圆心、AC 为半径的圆与直线AD 有两个交点(如图4所示).第三种方法,设BC 的中点为P ,那么P 173(,)22-,根据PD 2=P A 2列方程.这个方程的两个解,一个是点A ,一个是点D .这是因为以P 为圆心、P A 为半径的圆与直线AD 有两个交点(如图5所示).第四种解法,设AD 的中点为Q ,那么Q 3(,)22-n n ,根据QB 2=QC 2列方程.这个方程是一元一次方程,有一个解.这是因为AD 的垂直平分线与BC 有且只有一个交点(如图6所示).图4 图5 图6第五种解法,设D (x , y ).由2222,,⎧=⎪⎨=⎪⎩DC AB DB AC 列方程组2222222(9)(3)8,(8)93,⎧-++=⎪⎨-+=+⎪⎩x y x y 一个解是平行四边形ABDC ,一个解是等腰梯形ABCD .例 2018年上海市静安区中考模拟第25题如图1,平行四边形ABCD 中,已知AB =6,BC =9,cos ∠ABC =13,对角线AC 、BD 交于点O ,动点P 在边AB 上,⊙P 经过点B ,交线段P A 于点E .设BP =x .(1)求AC 的长;(2)设⊙O 的半径为y ,当⊙P 与⊙O 外切时,求y 关于x 的函数解析式,并写出定义域;(3)如果AC 是⊙O 的直径,⊙O 经过点E ,求⊙O 与⊙P 的圆心距OP 的长.图1 备用图动感体验请打开几何画板文件名“18静安25”,拖动点P 在由B 向A 运动,可以体验到,⊙P 与⊙O 保持外切,直角三角形OPH 的直角边OH 是定值,斜边OP 和直角边PH 随PB 的增大而减小.思路点拨1.通过计算,可以发现平行四边形ABCD 中,△ABC 是等腰三角形.2.第(2)题和第(3)题的一般策略是,构造圆心距OP 为斜边的直角三角形. 图文解析(1)如图2,作AF ⊥BC 于F .在Rt △ABF 中,AB =6,cos ∠ABF =BF AB =13,所以BF =2.所以AF =.在Rt △ACF 中,CF =BC -BF =9-2=7,所以AC 9.图2 图3(2)如图3,作CG ⊥AB 于G ,作OH ⊥AB 于H ,那么OH =12CG . 在Rt △BCG 中,BC =9,cos ∠GBC =BG BC =13,所以BG =3.所以CG =AG =3.所以OH =12CG =AH =12AG =32.。
2018年静安区初三二模数学试卷(含详细答案)

静安区 2018学年第二学期期中教学质量调研九年级数学试卷2018.4 (满分 150分,100分钟完成)考生注意:1.本试卷含三个大题,共 25题.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、 本调研卷上答题一律无效.2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题:(本大题共 6题,每题 4分,满分 24分)[每小题只有一个正确选项,在答题纸相应题号的选项上用 2B 铅笔正确填涂]1 2 等于1. 2 (A ) 2; 2.下列二次根式里,被开方数中各因式的指数都为 1的是(A ) x 2y 2; (B ) x 2y 2; (C ) (x y )2; (D ) xy 2. (B ) 2; (C ) 2; 2 (D )2 . 2 3.关于 x 的一元二次方程 x 2 mx 1 0的根的情况是(A )有两个不相等的实数根; (C )没有实数根;(B )有两个相等的实数根;(D )不能确定. 4.一次数学作业共有 10道题目,某小组 8位学生做对题目数的情况如下表:做对题目数人数 6 1 7 1 8 2 9 3 10 1那么这 8位学生做对题目数的众数和中位数分别是(A )9和 8; (B )9和 8.5; (C )3和 2;5.在下列图形中,一定是中心对称图形,但不一定是轴对称图形的为(A )正五边形; (B )正六边形; (C )等腰梯形; (D )3和 1.(D )平行四边形. 6.已知四边形 ABCD 中,对角线 AC 与 BD 相交于点 O ,AD //BC ,下列判断中错误的是 ..(A )如果 AB =CD ,AC =BD ,那么四边形 ABCD 是矩形;(B )如果 AB //CD ,AC =BD ,那么四边形 ABCD 是矩形;(C )如果 AD =BC ,AC ⊥BD ,那么四边形 ABCD 是菱形;(D )如果 OA =OC ,AC ⊥BD ,那么四边形 ABCD 是菱形.二、填空题:(本大题共 12题,每题 4分,满分 48分)[在答题纸相应题号后的空格内直接填写答案]7.计算:2 1 20 ▲ .九年级数学 第 1页共 4页。
精品上海市各区2018届精品中考二模数学分类汇编:二次函数专题(含答案)

上海市各区2018届九年级中考二模数学试卷精选汇编:二次函数专题宝山区、嘉定区24.(本题满分12分,第(1)小题4分,第(2)小题4分,第(3)小题4分) 已知平面直角坐标系xOy (如图7),直线m x y +=的经过点)0,4(-A 和点)3,(n B . (1)求m 、n 的值;(2)如果抛物线c bx x y ++=2经过点A 、B ,该抛物线的顶点为点P ,求ABP ∠sin 的值;(3)设点Q 在直线m x y +=上,且在第一象限内,直线m x y +=与y 轴的交点为点D ,如果DOB AQO ∠=∠,求点Q 的坐标.24.解:(1) ∵直线m x y +=的经过点)0,4(-A∴04=+-m ……………………1分∴4=m ………………………………1分∵直线m x y +=的经过点)3,(n B ∴34=+n ……………………1分∴1-=n …………………………………………1分(2)由可知点B 的坐标为)3,1(-∵抛物线c bx x y ++=2经过点A 、B ∴⎩⎨⎧=+-=+-310416c b c b∴6=b , 8=c∴抛物线c bx x y ++=2的表达式为862++=x x y …………………1分∴抛物线862++=x x y 的顶点坐标为)1,3(--P ……………1分∴23=AB ,2=AP ,52=PB∴222PB BP AB =+∴︒=∠90PAB ……………………………………1分∴PB APABP =∠sin ∴1010sin =∠ABP …………………………………………1分图7(3)过点Q 作x QH ⊥轴,垂足为点H ,则QH ∥y 轴 ∵DOB AQO ∠=∠,QBO OBD ∠=∠∴△OBD ∽△QBO∴OBDBQB OB =……………1分 ∵直线4+=x y 与y 轴的交点为点D ∴点D 的坐标为)4,0(,4=OD又10=OB ,2=DB∴25=QB ,24=DQ ……………1分∵23=AB∴28=AQ ,24=DQ ∵QH ∥y 轴 ∴AQADQH OD = ∴28244=QH ∴8=QH ……………………………………1分 即点Q 的纵坐标是8又点Q 在直线4+=x y 上点Q 的坐标为)8,4(……………1分长宁区24.(本题满分12分,第(1)小题4分,第(2)小题3分,第(3)小题5分)如图在直角坐标平面内,抛物线32-+=bx ax y 与y 轴交于点A ,与x 轴分别交于点B (-1,0)、点C (3,0),点D 是抛物线的顶点.(1)求抛物线的表达式及顶点D 的坐标; (2)联结AD 、DC ,求ACD ∆的面积;(3)点P 在直线DC 上,联结OP ,若以O 、P 、C 为顶点的三角形与△ABC 相似,求点P 的坐标.24.(本题满分12分,第(1)小题4分,第(2)小题3分,第(3)小题5分) 解:(1) 点B (-1,0)、C (3,0)在抛物线32-+=bx ax y 上∴⎩⎨⎧=-+=--033903b a b a ,解得⎩⎨⎧-==21b a ( 2分)∴抛物线的表达式为322--=x x y ,顶点D 的坐标是(1,-4) ( 2分) (2)∵A (0,-3),C (3,0),D (1,-4) ∴23=AC ,52=CD ,2=AD∴222AD AC CD += ∴︒=∠90CAD ( 2分)∴.32232121=⨯⨯=⋅⋅=∆AD AC S ACD (1分) (3)∵︒=∠=∠90AOB CAD ,2==AOACBO AD , ∴△CAD ∽△AOB ,∴OAB ACD ∠=∠∵OA =OC ,︒=∠90AOC ∴︒=∠=∠45OCA OAC∴ACD OCA OAB OAC ∠+∠=∠+∠,即BCD BAC ∠=∠ ( 1分)若以O 、P 、C 为顶点的三角形与△ABC 相似 ,且△ABC 为锐角三角形 则POC ∆也为锐角三角形,点P 在第四象限由点C (3,0),D (1,-4)得直线CD 的表达式是62-=x y ,设)62,(-t t P (30<<t ) 过P 作PH ⊥OC ,垂足为点H ,则t OH =,t PH 26-=①当ABC POC ∠=∠时,由ABC POC ∠=∠tan tan 得BO AO OH PH =,∴326=-t t ,解得56=t , ∴)518,56(1-P (2分) ②当ACB POC ∠=∠时,由145tan tan tan =︒=∠=∠ACB POC 得1=OHPH ,∴126=-tt,解得2=t ,∴)2,2(2-P ( 2分) 综上得)518,56(1-P 或)2,2(2-P 崇明区24.(本题满分12分,第(1)、(2)、(3)小题满分各4分)已知抛物线经过点(0,3)A 、(4,1)B 、(3,0)C . (1)求抛物线的解析式;(2)联结AC 、BC 、AB ,求BAC ∠的正切值;(3)点P 是该抛物线上一点,且在第一象限内,过点P 作PG AP ⊥交y 轴于点G ,当点G 在点A 的上方,且APG △与ABC △相似时,求点P 的坐标.24.(本题满分12分,每小题4分)解:(1)设所求二次函数的解析式为2(0)y ax bx c a =++≠,………………………1分将A (0,3)、B (4,)、C (3,0)代入,得 1641,930,3.a b c a b c c ++=⎧⎪++=⎨⎪=⎩解得12523a b c ⎧=⎪⎪⎪=-⎨⎪=⎪⎪⎩………2分所以,这个二次函数的解析式为215322y x x =-+ ……………………………1分 (2)∵A (0,3)、B (4,)、C (3,0)∴AC =BC =AB =∴222AC BC AB +=∴90ACB =︒∠ ………………………………………………………2分∴13BC tan BAC AC ===∠ ……………………………………………2分(3)过点P 作PH y ⊥轴,垂足为H设P 215(,3)22x x x -+,则H 215(0,3)22x x -+ ∵A (0,3) ∴21522AH x x =-,PH x = ∵90ACB APG ==︒∠∠∴当△APG 与△ABC 相似时,存在以下两种可能: 1° PAG CAB =∠∠ 则13tan PAG tan CAB ==∠∠ 即13PH AH = ∴2115322x x x =- 解得11x = ………………………1分∴点P 的坐标为(11,36) ……………………………………………………1分 2° PAG ABC =∠∠ 则3tan PAG tan ABC ==∠∠ 即3PH AH = ∴231522x x x =- 解得173x = …………………………1分 ∴点P 的坐标为1744(,)39……………………………………………………1分 奉贤区24.(本题满分12分,每小题满分各4分)已知平面直角坐标系xOy (如图8),抛物线)0(3222>++-=m m mx x y 与x 轴交于点A 、B (点A 在点B 左侧),与y 轴交于点C ,顶点为D ,对称轴为直线,过点C 作直线的垂线,垂足为点E ,联结DC 、BC . (1)当点C (0,3)时,① 求这条抛物线的表达式和顶点坐标; ② 求证:∠DCE=∠BCE ;(2)当CB 平分∠DCO 时,求m 的值.黄浦区24.(本题满分12分)已知抛物线2y x bx c =++经过点A (1,0)和B (0,3),其顶点为D . (1)求此抛物线的表达式; (2)求△ABD 的面积;(3)设P 为该抛物线上一点,且位于抛物线对称轴 右侧,作PH ⊥对称轴,垂足为H ,若△DPH 与△AOB 相 似,求点P 的坐标.24. 解:(1)由题意得:013b cc=++⎧⎨=⎩,———————————————————(2分)解得:43b c =-⎧⎨=⎩,—————————————————————————(1分)所以抛物线的表达式为243y x x =-+. ——————————————(1分) (2)由(1)得D (2,﹣1),———————————————————(1分) 作DT ⊥y 轴于点T , 则△ABD 的面积=()11124131211222⨯⨯-⨯⨯-⨯+⨯=.————————(3分) (3)令P ()()2,432p p p p -+>.————————————————(1分)由△DPH 与△AOB 相似,易知∠AOB =∠PHD =90°,所以243132p p p -++=-或2431123p p p -++=-,————————————(2分) 解得:5p =或73p =,所以点P 的坐标为(5,8),78,39⎛⎫-⎪⎝⎭.————————————————(1分)金山区24.(本题满分12分,每小题4分)平面直角坐标系xOy 中(如图8),已知抛物线2y x bx c =++经过点A (1,0)和B (3,0),与y 轴相交于点C ,顶点为P .(1)求这条抛物线的表达式和顶点P 的坐标; (2)点E 在抛物线的对称轴上,且EA =EC ,求点E 的坐标;(3)在(2)的条件下,记抛物线的对称轴为直线MN ,点Q 在直线MN 右侧的抛物线 上,∠MEQ =∠NEB ,求点Q 的坐标.24.解:(1)∵二次函数2y x bx c =++的图像经过点A (1,0)和B (3,0), ∴10930b c b c ++=⎧⎨++=⎩,解得:4b =-,3c =.……………………………(2分)∴这条抛物线的表达式是243y x x =-+…………………………………(1分)顶点P 的坐标是(2,-1).………………………………………………(1分)(2)抛物线243y x x =-+的对称轴是直线2x =,设点E 的坐标是(2,m ).…(1分)根据题意得:=,解得:m=2,…(2分)∴点E 的坐标为(2,2).…………………………………………………(1分) (3)解法一:设点Q 的坐标为2(,43)t t t -+,记MN 与x 轴相交于点F .图8作QD ⊥MN ,垂足为D ,则2DQ t =-,2243241DE t t t t =-+-=-+………………………(1分) ∵∠QDE=∠BFE=90°,∠QED=∠BEF ,∴△QDE ∽△BFE ,…………………(1分)∴DQ DEBF EF =,∴224112t t t --+=, 解得11t =(不合题意,舍去),25t =.……………………………(1分) ∴5t =,点E 的坐标为(5,8).…………………………………………(1分)解法二:记MN 与x 轴相交于点F .联结AE ,延长AE 交抛物线于点Q ,∵AE=BE , EF ⊥AB ,∴∠AEF=∠NEB ,又∵∠AEF=∠MEQ ,∴∠QEM=∠NEB ,………………………………(1分)点Q 是所求的点,设点Q 的坐标为2(,43)t t t -+, 作QH ⊥x 轴,垂足为H ,则QH =243t t -+,OH =t ,AH =t -1, ∵EF ⊥x 轴,∴EF ∥QH ,∴EF AFQH AH=,∴221431t t t =-+-,………(1分) 解得11t =(不合题意,舍去),25t =.……………………………………(1分) ∴5t =,点E 的坐标为(5,8).…………………………………………(1分)静安区24.(本题满分12分,第(1)小题满分4分,第(2)小题满分4分,第(3)小题满分4分)在平面直角坐标系xOy 中,已知点B (8,0)和点C (9,3-).抛物线c ax ax y +-=82(a ,c 是常数,a ≠0)经过点B 、C ,且与x 轴的另一交点为A .对称轴上有一点M ,满足MA =MC . (1) 求这条抛物线的表达式; (2) 求四边形ABCM 的面积;(3) 如果坐标系内有一点D ,满足四边形ABCD且AD //BC ,求点D 的坐标.24.(本题满分12分,第(1)小题4分,第(2)小题4解:(1)由题意得:抛物线对称轴aax 28-=,即4=x . 点B (8,0)关于对称轴的对称点为点A (0,0)∴0=c , …………(1分)将C (9,-3)代入ax ax y 82-=,得31-=a …………………………(1分)∴抛物线的表达式:x x y 38312+-=…………………………(1分) (2)∵点M 在对称轴上,∴可设M (4,y ) 又∵MA =MC ,即22MCMA =∴2222)3(54++=+y y , 解得y =-3, ∴M (4,-3) …………………(2分) ∵MC //AB 且MC ≠AB , ∴四边形ABCM 为梯形,,AB =8,MC =5,AB 边上的高h = y M = 3 ∴2393)58(21)(21=⨯+⨯=⨯+=MH MC AB S(3) 将点B (8,0)和点C (9,﹣3)代入b kx y BC += 可得⎩⎨⎧-=+=+3908b k b k ,解得⎩⎨⎧=-=243b k 由题意得,∵AD //BC , 3-=BC k ∴3-=AD k ,x y AD 3-=…(又∵AD 过(0,0),DC =AB =8, 设D (x ,-3x ) 2228)33()9(=+-+-x x , …………………………(1分)解得11=x (不合题意,舍去), 5132=x …………………………(1分)∴5393-=-=x y ∴点D 的坐标)539,513(-.……………………(1分)闵行区24.(本题满分12分,其中每小题各4分)如图,已知在平面直角坐标系xOy 中,抛物线22y ax x c =-+与x 轴交于 点A 和点B (1,0),与y 轴相交于点C (0,3). (1)求抛物线的解析式和顶点D 的坐标;(2)求证:∠DAB=∠ACB ;(3)点Q 在抛物线上,且△ADQ 是以AD 为 底的等腰三角形,求Q 点的坐标.24.解:(1)把B (1,0)和C (0,3)代入22y ax x c =-+中,得9603a c c ++=⎧⎨=⎩,解得13a c =-⎧⎨=⎩.……………………………………(2分)∴抛物线的解析式是:223y x x =--+.……………………………(1分) ∴顶点坐标D (-1,4).……………………………………………(1分) (2)令0y =,则2230x x --+=,13x =-,21x =,∴A (-3,0)∴3OA OC ==,∴∠CAO =∠OCA .…………………………………(1分)在Rt BOC ∆中,1tan 3OB OCB OC ∠==.………………………………(1分)∵AC =,DC =AD =, ∴2220AC DC +=,220AD =;∴222AC DC AD +=,ACD ∆是直角三角形且90ACD ∠=,∴1tan 3DC DAC AC ∠==,又∵∠DAC 和∠OCB 都是锐角,∴∠DAC =∠OCB .…………………(1分) ∴DAC CAO BCO OCA ∠+∠=∠+∠,即DAB ACB ∠=∠.……………………………………………………(1分) (3)令(Q x ,)y 且满足223y x x =--+,(3A -,0),(1D -,4)∵ADQ ∆是以AD 为底的等腰三角形,∴22QD QA =,即2222(3)(1)(4)x y x y ++=++-, 化简得:220x y -+=.………………………………………………(1分) 由222023x y y x x -+=⎧⎨=--+⎩,……………………………………………………(1分)解得11x y ⎧=⎪⎪⎨⎪=⎪⎩,22x y ⎧=⎪⎪⎨⎪=⎪⎩. ∴点Q的坐标是⎝⎭,⎝⎭.…(2分) 普陀区24.(本题满分12分)如图10,在平面直角坐标系xOy 中,直线3y kx =+与x 轴、y 轴分别相交于点A 、B ,并与抛物线21742y x bx =-++的对称轴交于点()2,2C ,抛物线的顶点是点D .(1)求k 和b 的值;(2)点G 是y 轴上一点,且以点B 、C 、G 为顶点的三角形与△BCD 相似,求点G 的坐标;(3)在抛物线上是否存在点E :它关于直线AB 的对称点F 恰好在y 轴上.如果存在,直接写出点E 的坐标,如果不存在,试说明理由.24.解:(1) 由直线3y kx =+经过点()2,2C ,可得12k =-.·················································· (1分)由抛物线21742y x bx =-++的对称轴是直线2x =,可得1b =. ······················· (1分) (2) ∵直线132y x =-+与x 轴、y 轴分别相交于点A 、B ,∴点A 的坐标是()6,0,点B 的坐标是()0,3. ····················································· (2分)∵抛物线的顶点是点D ,∴点D 的坐标是92,2⎛⎫ ⎪⎝⎭.·············································· (1分) ∵点G 是y 轴上一点,∴设点G 的坐标是()0,m . ∵△BCG 与△BCD 相似,又由题意知,GBC BCD ∠=∠,∴△BCG 与△BCD 相似有两种可能情况: ·························································· (1分) ①如果BG BC CB CD =,解得1m =,∴点G 的坐标是()0,1. ···· (1分)②如果BG BC CD CB =,那么352m -=,解得12m =,∴点G 的坐标是10,2⎛⎫ ⎪⎝⎭. (1分)综上所述,符合要求的点G 有两个,其坐标分别是()0,1和10,2⎛⎫ ⎪⎝⎭.(3)点E 的坐标是91,4⎛⎫- ⎪⎝⎭或92,2⎛⎫ ⎪⎝⎭. ····································································· (2分+2分)图10xy 11 O青浦区24.(本题满分12分,第(1)、(2)、(3)小题,每小题4分)已知:如图8,在平面直角坐标系xOy 中,抛物线23y axbx =++的图像与x 轴交于点A (3,0),与y 轴交于点B ,顶点C 在直线2x =上,将抛物线沿射线AC 的方向平移,当顶点C 恰好落在y 轴上的点D 处时,点B 落在点E 处. (1)求这个抛物线的解析式;(2)求平移过程中线段BC 所扫过的面积;(3)已知点F 在x 轴上,点G 在坐标平面内,且以点C 、E 、F 、G 为顶点的四边形是矩形,求点F 的坐标. .24.解:(1)∵顶点C 在直线2x =上,∴22=-=bx a,∴4=-b a . ······················ (1分) 将A (3,0)代入23y ax bx =++,得933=0++a b , ························· (1分) 解得1=a ,4=-b . ····················································································· (1分) ∴抛物线的解析式为243=-+y x x .························································· (1分) (2)过点C 作CM ⊥x 轴,CN ⊥y 轴,垂足分别为M 、N .∵243=-+y x x =()221=--x ,∴C (2,1-).··································· (1分)∵1==CM MA ,∴∠MAC =45°,∴∠ODA =45°, ∴3==OD OA . ··························································································· (1分) ∵抛物线243=-+y x x 与y 轴交于点B ,∴B (0,3),∴6=BD . ································································································ (1分) ∵抛物线在平移的过程中,线段BC 所扫过的面积为平行四边形BCDE 的面积, ∴12262122==⨯⨯⋅=⨯=BCDEBCDSSBD CN . ································ (1分)(3)联结CE .∵四边形BCDE 是平行四边形,∴点O 是对角线CE 与BD 的交点, 即OE OC ==(i )当CE 为矩形的一边时,过点C 作1CF CE ⊥,交x 轴于点1F ,设点1F a (,0),在1Rt OCF 中,22211=OF OC CF +, 即 22(2)5a a =-+,解得 52a =,∴点152F (,0) ··········································· (1分) 同理,得点252F (-,0) ····························································································· (1分) (ii )当CE 为矩形的对角线时,以点O 为圆心,OC 长为半径画弧分别交x 轴于点3F 、4F ,可得34=OF OF OC =3F )、4F ()······· (2分) 综上所述:满足条件的点有152F (,0),252F (-,0),3F )),4F (). 松江区24.(本题满分12分,每小题各4分)如图,已知抛物线y=ax 2+bx 的顶点为C (1,1-),P 是抛物线上位于第一象限内的一点,直线OP 交该抛物线对称轴于点B ,直线CP 交x 轴于点A . (1)求该抛物线的表达式;(2)如果点P 的横坐标为m ,试用m 的代数式表示线段BC 的长; (3)如果△ABP 的面积等于△ABC 的面积,求点P 坐标.24.(本题满分12分,每小题各4分)解:(1)∵抛物线y=ax 2+bx 的顶点为C (1,1-)∴ 112a b b a +=-⎧⎪⎨-=⎪⎩…………………………………2分解得:12a b =⎧⎨=-⎩…………………………………1分∴抛物线的表达式为:y=x 2-2x ;…………………………1分 (2)∵点P 的横坐标为m ,∴P 的纵坐标为:m 2-2m ……………………………1分 令BC 与x 轴交点为M ,过点P 作PN ⊥x 轴,垂足为点N ∵P 是抛物线上位于第一象限内的一点,(第24题图)∴PN = m 2-2m ,ON =m ,O M =1由PN BMON OM =得221m m BM m -=………………………1分 ∴ BM =m -2…………………………………………………1分 ∵ 点C 的坐标为(1,1-),∴ BC= m -2+1=m -1………………………………………1分 (3)令P (t ,t 2-2t ) ………………………………………………1分 △ABP 的面积等于△ABC 的面积 ∴AC =AP过点P 作PQ ⊥BC 交BC 于点Q ∴CM =MQ =1∴t 2-2t =1 …………………………………………………1分∴1t =1t =………………………………1分∴ P 的坐标为(1)……………………………………1分徐汇区24. 如图,已知直线122y x =-+与x 轴、y 轴分别交于点B 、C ,抛物线212y x bx c =-++过点B 、C ,且与x 轴交于另一个点A .(1)求该抛物线的表达式;(2)点M 是线段BC 上一点,过点M 作直线l ∥y 轴 交该抛物线于点N ,当四边形OMNC 是平行四边形时, 求它的面积;(3)联结AC ,设点D 是该抛物线上的一点,且满足DBA CAO ∠=∠,求点D 的坐标.杨浦区24、(本题满分12分,第(1)小题4分,第(2)小题4分,第(3)小题4分)如图8,在平面直角坐标系中,抛物线于X轴交于点A、B,于y轴交于点C,直线经过点A、C,点P为抛物线上位于直线AC上方的一个动点。
2018年上海各区高三二模语文试卷汇编文言文二

放大脸脸可扫2018年上海市各区高三二模语文试卷汇编—文言文一【徐汇区】(五)阅读下文,完成第21-25题。
(13分)梁仲用默斋说王守仁[注]①仲用识高而气豪,既举进士,锐然有志天下之务。
一旦责其志曰:于呼!予乃太早。
乌有己之弗治而能治人口!”于是专心为己之学,深思其气质之偏,而病其言之易也,以“默” 名庵,过予而请其方。
予亦天下之多言人也,岂足以知默之道!然予尝自验之,气浮则多言,志轻则多言。
气浮者耀于外,志轻者放其中。
予请诵古之训而仲用自取之。
②夫默有四伪:疑而不知问,蔽而不知辩,冥然以自罔,谓之默之愚;以不言骷人者,谓之默之狡;虑人之觇其长短也,掩覆以为默,谓之默之诬;深为之情,厚为之貌,渊毒阱狠,自托于默以售其奸者,谓之默之贼。
夫是之谓四伪。
③又有八诚焉。
孔子曰:“君子耻其言而过其行。
古者言之不出,耻躬之不逮也。
”故诚知耻,而后知默。
又日:“君子欲讷于言而敏于行”,夫诚敏于行,而后欲默矣。
仁者言也讱. 非以为默而默存焉。
又曰:“默而识之”.是故必有所识也,终日不违如愚者也。
“默而成之”,是故必有所成也,退而省其私,亦足以发者也。
故善默者莫如颜子。
“暗然而日章”,默之积也。
“不言而信”,而默之道成矣。
“天何言哉?四时行焉,万物生焉。
”而默之道至矣。
非圣人其孰能与于此哉!夫是之谓八诚。
仲用盍亦知所以自取之?【注】王守仁,字伯安,别号阳明,明朝著名思想家。
其学说“阳明心学”是在继承儒家学说的基础上所发展创立,是明朝中晚期影响最大的哲学思想。
21.可填入第①段方框中的虚词是()(1分)人.也 B.者仁乎口.矣22.对第②段中“四伪”的含义理解正确的一项是()(2分)A.无知而又自我欺骗,是默之愚。
B.用不言来讨好他人,是默之狡。
C.借沉默来窥视他人,是默之诬。
D.外表沉默内心狠毒,是默之贼。
23.对第③段画线句理解准确的一项是()(2分)1放大可扫放大脸脸可扫A.仁者言语迟缓,这才能称得上是真正的沉默。
上海市各区届中考二模数学分类汇编压轴题专题含答案
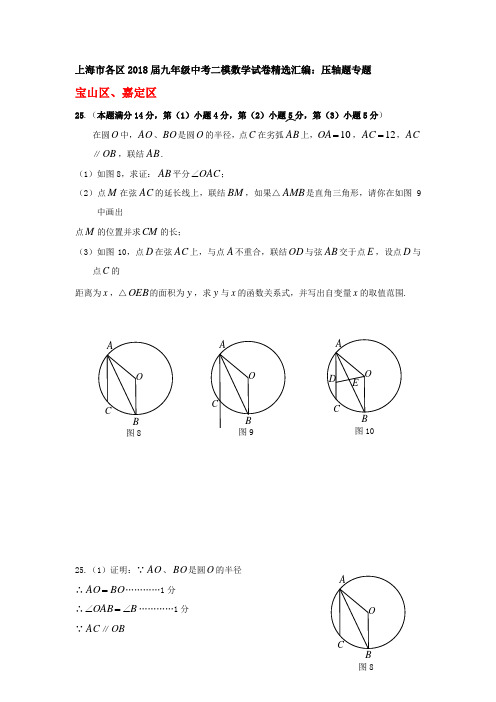
上海市各区2018届九年级中考二模数学试卷精选汇编:压轴题专题宝山区、嘉定区25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)在圆O 中,AO 、BO 是圆O 的半径,点C 在劣弧AB 上,10=OA ,12=AC ,AC ∥OB ,联结AB .(1)如图8,求证:AB 平分OAC ∠;(2)点M 在弦AC的延长线上,联结BM ,如果△AMB 是直角三角形,请你在如图9中画出点M 的位置并求CM 的长;(3)如图10,点D 在弦AC 上,与点A 不重合,联结OD 与弦AB 交于点E ,设点D 与点C 的距离为x ,△OEB 的面积为y ,求y 与x 的函数关系式,并写出自变量x 的取值范围.25.(1)证明:∵AO 、BO 是圆O 的半径 ∴BO AO =…………1分 ∴B OAB ∠=∠…………1分 ∵AC ∥OB图8图10图8∴B BAC ∠=∠…………1分 ∴BAC OAB ∠=∠∴AB 平分OAC ∠…………1分 (2)解:由题意可知BAM ∠不是直角,所以△AMB 是直角三角形只有以下两种情况:︒=∠90AMB 和︒=∠90ABM① 当︒=∠90AMB ,点M 的位置如图9-1……………1分 过点O 作AC OH ⊥,垂足为点H∵OH 经过圆心 ∴AC HC AH 21==∵12=AC ∴6==HC AH 在Rt △AHO 中,222OA HO AH =+ ∵10=OA ∴8=OH∵AC ∥OB ∴︒=∠+∠180OBM AMB ∵︒=∠90AMB ∴︒=∠90OBM ∴四边形OBMH 是矩形 ∴10==HM OB∴4=-=HC HM CM ……………2分 ②当︒=∠90ABM ,点M 的位置如图9-2由①可知58=AB ,552cos =∠CAB 在Rt △ABM 中,552cos ==∠AM AB CAB∴20=AM8=-=AC AM CM ……………2分综上所述,CM 的长为4或8.说明:只要画出一种情况点M 的位置就给1分,两个点都画正确也给1分. (3)过点O 作AB OG ⊥,垂足为点G 由(1)、(2)可知,CAB OAG ∠=∠sin sin 由(2)可得:55sin =∠CAB图10∵10=OA ∴52=OG ……………1分 ∵AC ∥OB ∴ADOBAE BE =……………1分 又BE AE -=58,x AD -=12,10=OB∴xBEBE -=-121058 ∴x BE -=22580 ……………1分∴52225802121⨯-⨯=⨯⨯=xOG BE y ∴xy -=22400……………1分自变量x 的取值范围为120<≤x ……………1分长宁区25.(本题满分14分,第(1)小题4分,第(2)小题4分,第(3)小题6分)在圆O 中,C 是弦AB 上的一点,联结OC 并延长,交劣弧AB 于点D ,联结AO 、BO 、AD 、BD . 已知圆O 的半径长为5 ,弦AB 的长为8.(1)如图1,当点D 是弧AB 的中点时,求CD 的长; (2)如图2,设AC =x ,y S S OBDACO=∆∆,求y 关于x 的函数解析式并写出定义域; (3)若四边形AOBD 是梯形,求AD 的长.25.(本题满分14分,第(1)小题4分,第(2)小题4分,第(3)小题6分) 解:(1)∵OD 过圆心,点D 是弧AB 的中点,AB =8,∴OD ⊥AB , (2分) 在Rt △AOC 中,,AO =5,∴ (1分) , (1分)(2)过点O 作OH ⊥AB ,垂足为点H ,则由(1)可得AH =4,OH =3 ∵AC =x ,∴在Rt △HOC 中,,AO =5, ∴, (1分) ∴() (3分) (3)①当OB (3分) ②当OA ABC △8AB =10BC =12AC =2AB AD AC =⋅AEF C ∠=∠ABC ∠BE x =CF y =y xGEF △8AB =12AC=2AB AD AC =g 163AD =16201233CD =-=2AB AD AC =g AD AB AB AC =BAC ∠ADB ABC △∽△ABD C =∠∠BD AD BC AB =203BD =BD CD =DBC C =∠∠ABD DBC =∠∠BD ABC ∠A AH BC ∥BD H AH BC∥16432053AD DH AH DC BD BC ====203BD CD ==8AH =163AD DH ==12BH =AH BC∥AH HGBE BG =812BG x BG-=128xBG x =+BEF C EFC=+∠∠∠BEA AEF C EFC +=+∠∠∠∠AEF C =∠∠BEA EFC=∠∠DBC C=∠∠(第25题图) A B C D G EF(备用图)AB C DBEG CFE△∽△BE BGCF EC=12810x x x y x+=-228012x x y -++=GEF GE GF=23GE BE EF CF ==23x y =4BE =EG EF =BE CF =x y =5BE =-FG FE =32GE BE EF CF ==32x y =3BE =-+BC BO BE ⋅=2知AD =1,AB =2. (1)设BC =x ,CD =y ,求y 关于x 的函数关系式,并写出定义域; (2)当∠B =70°时,求∠AEC 的度数; (3)当△ACE 为直角三角形时,求边BC 的长.25. 解:(1)过A 作AH ⊥BC 于H ,————————————————————(1分) 由∠D =∠BCD =90°,得四边形ADCH 为矩形.在△BAH 中,AB =2,∠BHA =90°,AH =y ,HB =1x -,所以22221y x =+-,——————————————————————(1分) 则()03y x =<<.———————————————(2分)(2)取CD 中点T ,联结TE ,————————————————————(1分) 则TE 是梯形中位线,得ET ∥AD ,ET ⊥CD .∴∠AET =∠B =70°. ———————————————————————(1分) 又AD =AE =1,∴∠AED =∠ADE =∠DET =35°. ——————————————————(1分) 由ET 垂直平分CD ,得∠CET =∠DET =35°,————————————(1分) 所以∠AEC =70°+35°=105°. ——————————————————(1分)(3)当∠AEC =90°时,易知△CBE ≌△CAE ≌△CAD ,得∠BCE =30°, 则在△ABH 中,∠B =60°,∠AHB =90°,AB =2,图9AB C D O E备用图ABO 备用图 AB得BH=1,于是BC=2. ——————————————————————(2分)当∠CAE=90°时,易知△CDA∽△BCA,又AC=则AD CAxAC CB=⇒=⇒=2分)易知∠ACE<90°.所以边BC的长为2或12+.——————————————————(1分)金山区25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5 分)如图9,已知在梯形ABCD中,AD∥BC,AB=DC=AD=5,3sin5B=,P是线段BC上一点,以P为圆心,PA为半径的⊙P与射线AD的另一个交点为Q,射线PQ与射线CD相交于点E,设BP=x.(1)求证△ABP∽△ECP;(2)如果点Q在线段AD上(与点A、D不重合),设△APQ的面积为y,求y关于x的函数关系式,并写出定义域;(3)如果△QED与△QAP相似,求BP的长.25.解:(1)在⊙P中,PA=PQ,∴∠PAQ =∠PQA,……………………………(1分)AB CD图9备用图∵AD ∥BC ,∴∠PAQ =∠APB ,∠PQA =∠QPC ,∴∠APB =∠EPC ,……(1分) ∵梯形ABCD 中,AD ∥BC ,AB =DC ,∴∠B =∠C ,…………………………(1分) ∴△APB ∽△ECP .…………………………………………………………(1分) (2)作AM ⊥BC ,PN ⊥AD ,∵AD ∥BC ,∴AM ∥PN ,∴四边形AMPN 是平行四边形,∴AM =PN ,AN =MP .………………………………………………………(1分) 在Rt △AMB 中,∠AMB =90°,AB =5,sinB =35, ∴AM =3,BM =4,∴PN =3,PM =AN =x -4,……………………………………(1分) ∵PN ⊥AQ ,∴AN =NQ ,∴AQ = 2x -8,……………………………………(1分)∴()1128322y AQ PN x =⋅⋅=⋅-⋅,即312y x =-,………………………(1分)定义域是1342x <<.………………………………………………………(1分)(3)解法一:由△QED 与△QAP 相似,∠AQP =∠EQD ,①如果∠PAQ =∠DEQ ,∵△APB ∽△ECP ,∴∠PAB =∠DEQ ,又∵∠PAQ =∠APB ,∴∠PAB =∠APB ,∴BP =BA =5.………………………(2分) ②如果∠PAQ =∠EDQ ,∵∠PAQ =∠APB ,∠EDQ =∠C ,∠B =∠C ,∴∠B =∠APB ,∴ AB =AP ,∵AM ⊥BC ,∴ BM =MP =4,∴ BP =8.………(2分) 综上所述BP 的长为5或者8.………………………………………………(1分) 解法二:由△QAP 与△QED 相似,∠AQP =∠EQD ,在Rt △APN 中,AP PQ ===∵QD ∥PC ,∴EQ EPQD PC=, ∵△APB ∽△ECP ,∴AP EPPB PC=,∴AP EQ PB QD =,①如果AQ EQQP QD =,∴AQ AP QP PB =x=,解得5x =………………………………………………………………………(2分) ②如果AQ DQQP QE =,∴AQ PBQP AP ==解得8x =………………………………………………………………………(2分) 综上所述BP 的长为5或者8.…………………………………………………(1分)静安区25.(本题满分14分,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分4分)如图,平行四边形ABCD 中,已知AB =6,BC =9,31cos =∠ABC .对角线AC 、BD 交于点O .动点P 在边AB 上,⊙P 经过点B ,交线段PA 于点E .设BP = x .(1) 求AC 的长;(2) 设⊙O 的半径为y ,当⊙P 与⊙O 外切时, 求y 关于x 的函数解析式,并写出定义域; (3) 如果AC 是⊙O 的直径,⊙O 经过点E , 求⊙O 与⊙P 的圆心距OP 的长.25.(本题满分14分,第(1)小题4分,第(2)小题6分,第(3)小题4分) 解:(1)作AH ⊥BC 于H ,且,AB =6, 那么…………(2分)BC =9,HC =9-2=7,, ……………………(1分) ﹒ ………(1分)(2)作OI ⊥AB 于I ,联结PO , AC =BC =9,AO = ∴∠OAB =∠ABC , ∴Rt △AIO 中,∴AI =,IO = ……………………(1分) ∴PI =AB -BP -AI ==, ……………………(1分) ∴Rt △PIO 中,A第25题图B P OC DE·第25题备用图ABOCDDA ·第25题图BP OCHE第25题图……(1分)∵⊙P 与⊙O 外切,∴ ……………………(1分) ∴= …………………………(1分)∵动点P 在边AB 上,⊙P 经过点B ,交线段PA 于点E .∴定义域:0<x ≤3…………(1分) (3)由题意得:∵点E 在线段AP 上,⊙O 经过点E ,∴⊙O 与⊙P 相交 ∵AO 是⊙O 半径,且AO >OI ,∴交点E 存在两种不同的位置,OE =OA = ① 当E 与点A 不重合时,AE 是⊙O 的弦,OI 是弦心距,∵AI =,AE =3, ∴点E 是AB 中点,,,, IO =……………………(2分)② 当E 与点A 重合时,点P 是AB 中点,点O 是AC 中点, ……(2分) ∴或.闵行区25.(本题满分14分,其中第(1)小题4分,第(2)、(3)小题各5分)如图,已知在Rt △ABC 中,∠ACB = 90o,AC =6,BC = 8,点F 在线段AB 上,以点B 为圆心,BF 为半径的圆交BC 于点E ,射线AE 交圆B 于点D (点D 、E 不重合). (1)如果设BF = x ,EF = y ,求y 与x 之间的函数关系式,并写出它的定义域; (2)如果»»2EDEF ,求ED 的长; (3)联结CD 、BD ,请判断四边形ABDC 是否为直角梯形说明理由.25.解:(1)在Rt △ABC 中,,,∴.……………………………………………………………(1分)(备用图)CBA (第25题图)CBEF DA过E作EH⊥AB,垂足是H,易得:,,.…………………………(1分)在Rt△EHF中,,∴.………………………………………(1分+1分)(2)取的中点P,联结BP交ED于点G∵,P是的中点,∴.∴∠FBE =∠EBP =∠PBD.∵,BP过圆心,∴BG⊥ED,ED =2EG =2DG.…………(1分)又∵∠CEA =∠DEB,∴∠CAE=∠EBP=∠ABC.……………………………………………(1分)又∵BE是公共边,∴.∴.在Rt△CEA中,∵AC = 6,,,∴.……………………………(1分)∴.……………………………………………(1分)∴.……………………………………(1分)(3)四边形ABDC不可能为直角梯形.…………………………………(1分)①当CD∥AB时,如果四边形ABDC是直角梯形,只可能∠ABD =∠CDB = 90o.在Rt△CBD中,∵,∴,.∴,;∴.∴CD不平行于AB,与CD∥AB矛盾.∴四边形ABDC不可能为直角梯形.…………………………(2分)②当AC∥BD时,如果四边形ABDC是直角梯形,只可能∠ACD =∠CDB = 90o.∵AC∥BD,∠ACB = 90o,∴∠ACB =∠CBD = 90o.∴∠ABD =∠ACB +∠BCD > 90o.与∠ACD =∠CDB = 90o矛盾.∴四边形ABDC不可能为直角梯形.…………………………(2分)普陀区25.(本题满分14分)已知P 是O ⊙的直径BA 延长线上的一个动点,P ∠的另一边交O ⊙于点C 、D ,两点位于AB 的上方,AB =6,OP m =,1sin 3P =,如图11所示.另一个半径为6的1O ⊙经过点C 、D ,圆心距1OO n =. (1)当6m =时,求线段的长;(2)设圆心1O 在直线AB 上方,试用n 的代数式表示m ;(3)△1POO 在点P 的运动过程中,是否能成为以1OO 为腰的等腰三角形,如果能,试求出此时n 的值;如果不能,请说明理由. 25.解:(1)过点O 作OH ⊥CD ,垂足为点H ,联结OC .在Rt △POH 中,∵1sin 3P =,6PO =,∴2OH =. ········· (1分) ∵AB =6,∴3OC =. ······················ (1分) 由勾股定理得CH = ····················· (1分)∵OH ⊥DC,∴2CD CH == ··············· (1分) (2)在Rt △POH 中,∵1sin 3P =, PO m =,∴3m OH =. ········ (1分) 在Rt △OCH 中,2293m CH ⎛⎫- ⎪⎝⎭=. ················ (1分)在Rt △1O CH 中,22363m CH n ⎛⎫-- ⎪⎝⎭=. ·············· (1分)可得 2236933m m n ⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭=,解得23812n m n -=. ········· (2分)OAB备用图PDOABC图11(3)△1POO 成为等腰三角形可分以下几种情况:● 当圆心1O 、O 在弦CD 异侧时①1OP OO =,即m n =,由23812n n n-=解得9n =. ········· (1分)即圆心距等于O ⊙、1O ⊙的半径的和,就有O ⊙、1O ⊙外切不合题意舍去.(1分) ②11O P OO =n =, 解得23m n =,即23n 23812n n-=,解得n ········· (1分) ● 当圆心1O 、O 在弦CD 同侧时,同理可得 28132n m n-=.∵1POO ∠是钝角,∴只能是m n =,即28132n n n-=,解得n . ·· (2分)综上所述,n.青浦区25.(本题满分14分,第(1)小题4分,第(2)小题6分,第(3)小题4分)如图9-1,已知扇形MON,∠MON =90o ,点B 在弧MN 上移动,联结BM ,作OD ⊥BM ,垂足为点D ,C 为线段OD 上一点,且OC =BM ,联结BC 并延长交半径OM 于点A ,设OA = x ,∠COM 的正切值为y .(1)如图9-2,当AB ⊥OM 时,求证:AM =AC ; (2)求y 关于x 的函数关系式,并写出定义域; (3)当△OAC 为等腰三角形时,求x 的值.图9-1图9-2备用图25.解:(1)∵OD ⊥BM ,AB ⊥OM ,∴∠ODM =∠BAM =90°. ·········· (1分)∵∠ABM +∠M =∠DOM +∠M ,∴∠ABM =∠DOM . ········· (1分) ∵∠OAC =∠BAM ,OC =BM ,∴△OAC ≌△ABM , ······················ (1分) ∴AC =AM . ························· (1分)(2)过点D 作DE=MD MEDMAE)12x2==OA OC DM OE OD OD 2=DM OA ODOE =y0<≤x 111222===DM BM OCx ==OD =DMyOD1=x=x =x α90α︒-α90α︒-α45︒290α∠=>︒BOA 90∠≤︒BOA (1)求CE 的长;(2)P 是 CE 延长线上一点,直线AP 、CD 交于点Q.① 如果△ACQ ∽△CPQ ,求CP 的长;② 如果以点A 为圆心,AQ 为半径的圆与⊙C 相切,求CP 的长.25.(本题满分14分,第(1)小题4分,第(2)小题每个小题各5分) 解:(1)∵AE ∥CD∴…………………………………1分 ∵BC=DC∴BE=AE …………………………………1分(第25题图)CBA DE(备用图)CBADE(第25题图)CBA DE设CE =x 则AE =BE =x +2 ∵ ∠ACB =90°, ∴即………………………1分 ∴即…………………………………1分 (2)①∵△ACQ ∽△CPQ ,∠QAC>∠P∴∠ACQ=∠P …………………………………1分 又∵AE ∥CD ∴∠ACQ=∠CAE∴∠CAE=∠P ………………………………1分 ∴△ACE ∽△PCA ,…………………………1分 ∴…………………………1分 即∴ ……………………………1分 ②设CP =t ,则 ∵∠ACB =90°, ∴ ∵AE ∥CD∴……………………………1分 即∴……………………………1分 若两圆外切,那么此时方程无实数解……………………………1分 若两圆内切切,那么 ∴21540160t t -+=CBA DEPQ解之得2015t ±=………………………1分又∵∴2015t +=………………………1分徐汇区25. 已知四边形ABCD 是边长为10的菱形,对角线AC 、BD 相交于点E ,过点C 作CF ∥DB 交AB 延长线于点F ,联结EF 交BC 于点H . (1)如图1,当EF BC ⊥时,求AE 的长;(2)如图2,以EF 为直径作⊙O ,⊙O 经过点C 交边CD 于点G (点C 、G 不重合),设AE 的长为x ,EH 的长为y ;① 求y 关于x 的函数关系式,并写出定义域;③ 联结EG ,当DEG ∆是以DG 为腰的等腰三角形时,求AE 的长.杨浦区25、(本题满分14分,第(1)小题4分,第(2)小题6分,第(3)小题4分)(1) 如图9,在梯形ABCD 中,AD 当圆P 过点A 时,求圆P 的半径;(2) 分别联结EH 和EA ,当△ABE △CEH 时,以点B 为圆心,r 为半径的圆B 与圆P 相交,试求圆B 的半径r 的取值范围;(3) 将劣弧沿直线EH 翻折交BC 于点F ,试通过计算说明线段EH 和EF 的比值为定值,并求出此定值。
2018年上海二模 化学 专题资料 白色固体题及答案
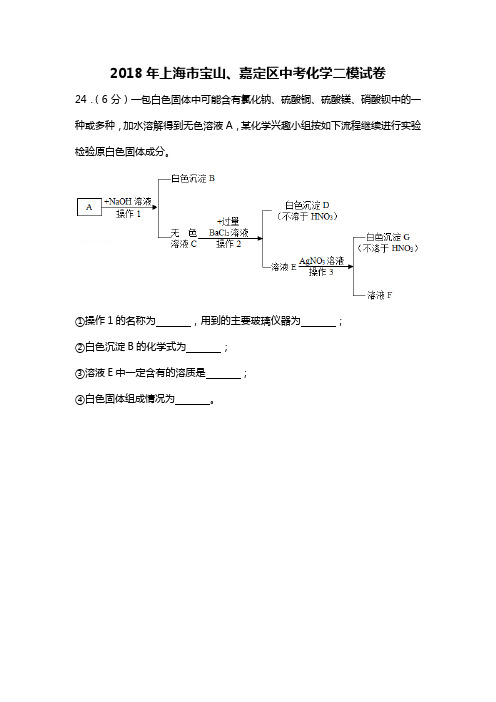
2018年上海市宝山、嘉定区中考化学二模试卷24.(6分)一包白色固体中可能含有氯化钠、硫酸铜、硫酸镁、硝酸钡中的一种或多种,加水溶解得到无色溶液A,某化学兴趣小组按如下流程继续进行实验检验原白色固体成分。
①操作1的名称为,用到的主要玻璃仪器为;②白色沉淀B的化学式为;③溶液E中一定含有的溶质是;④白色固体组成情况为。
26.(7分)一包白色粉末可能含有碳酸钙、碳酸钠、硫酸钠、氯化钠、硝酸钾中的一种或几种,为了确定其组成,进行实验,按要求进行回答:实验步骤实验过程 实验现象 结论 ① 取样,进行焰色反应,透过蓝色钴玻璃火焰呈 原粉末中含有硝酸钾②原粉末中肯定不含碳酸钙 ③有气泡产生 原粉末中肯定有④ 取步骤③试管中的溶液Ⅰ.先加入Ⅱ.再加入原粉末中肯定还有的物质是氯化钠肯定没有硫酸钠⑤反思:在步骤③中加入的稀硝酸是否一定要过量,理由是25.(9分)有一包白色固体,可能是碳酸钠、氯化钠、氢氧化钠、硝酸钡中的一种或几种,为确定成分,进行如下实验(硝酸钠溶液和硝酸钡溶液均呈中性):①白色沉淀A 是,化学方程式是。
②滤液B 中溶质一定有,可能有(任写一种情况);为确定白色固体中可能存在的物质,进一步对滤液B 进行实验,步骤如下:Ⅰ.重新取滤液B,滴加过量的试剂X;Ⅱ.向Ⅰ中的溶液滴加过量的稀硝酸;Ⅲ.向Ⅱ中的溶液滴加试剂Y。
完成填空:试剂X 是溶液(填“氯化钡”或“硝酸钡”);试剂Y 是溶液。
若(写现象及对应的步骤编号),能确定白色固体中含有氢氧化钠。
若(写现象及对应的步骤编号),能确定白色固体中含有氯化钠。
22.(5分)有一包白色固体,可能含有碳酸钠、硫酸铜、硫酸钠、氯化钠等物质中的一种或几种。
某化学兴趣小组为探究其成分做了以下实验:实验步骤实验现象分析与结论(化学方程式)1.取该固体样品溶于水澄清无色溶液一定不含有2.从步骤1中,取澄清无色溶液向其中滴入氯化钡溶液产生白色沉淀固体中一定含有再加入足量稀硝酸沉淀部分消失3.从步骤1中,取澄清无色溶液向溶液中滴加足量的硝酸钡溶液产生白色沉淀向溶液中滴加足量硝酸钡溶液的作用是。
上海市各区2018届中考数学二模试卷精选汇编:综合计算

综合计算宝山区、嘉定区21.(本题满分10分,第(1)小题5分,第(2)小题5分)如图4,在梯形ABCD 中,AD ∥BC ,︒=∠90BAD ,AD AC =. (1)如果BAC ∠︒=∠-10BCA ,求D ∠的度数; (2)若10=AC ,31cot =∠D ,求梯形ABCD 的面积.21.解:(1)∵AD ∥BC∴CAD BCA ∠=∠ …………………1分 ∵BAC ∠︒=∠-10BCA∴BAC ∠︒=∠-10CAD …………………1分 ∵︒=∠90BAD∴BAC ∠︒=∠+90CAD∴︒=∠40CAD …………………1分 ∵AD AC =∴D ACD ∠=∠ …………………1分 ∵︒=∠+∠+∠180CAD D ACD∴︒=∠70D …………………1分(2) 过点C 作AD CH ⊥,垂足为点H ,在Rt △CHD 中,31cot =∠D ∴31cot ==∠CH HD D …………………………1分 设x HD =,则x CH 3=,∵AD AC =,10=AC ∴x AH -=10 在Rt △CHA 中,222AC CHAH =+ ∴22210)3()10(=+-x x∴2=x ,0=x (舍去)∴2=HD …………1分 ∴6=HC ,8=AH ,10=AD ………………1分 ∵︒=∠=∠90CHD BAD ∴AB ∥CH∵AD ∥BC ∴四边形ABCH 是平行四边形 ∴8==AH BC ………1分 ∴梯形ABCD 的面积546)810(21)(21=⨯+=⨯+=CH BC AD S ………1分 长宁区图4DCB A图4DCBAH21.(本题满分10分,第(1)小题4分,第(2)小题6分)如图,在等腰三角形ABC 中,AB =AC ,点D 在BA 的延长线上,BC =24,135sin =∠ABC .(1)求AB 的长;(2)若AD =6.5,求DCB ∠的余切值.21.(本题满分10分,第(1)小题4分,第(2)小题6分) 解:(1)过点A 作AE ⊥BC ,垂足为点E又∵AB =AC ∴BC BE 21= ∵BC =24 ∴ BE =12 (1分)在ABE Rt ∆中,︒=∠90AEB ,135sin ==∠AB AE ABC (1分)设AE=5k,AB=13k ∵222BE AE AB += ∴1212==k BE ∴1=k , ∴55==k AE , 1313==k AB (2分) (2)过点D 作DF ⊥BC ,垂足为点F ∵AD=6.5,AB=13 ∴BD=AB+AD=19.5∵AE ⊥BC ,DF ⊥BC ∴ ︒=∠=∠90DFB AEB ∴ DF AE // ∴BDABBF BE DF AE == 又 ∵ AE =5,BE =12,AB =13, ∴18,215==BF DF (4分) ∴BF BC CF -= 即61824=-=CF (1分) 在DCF Rt ∆中,︒=∠90DFC ,542156cot ===∠DF CF DCB (1分) 崇明区21.(本题满分10分,第(1)、(2)小题满分各5分)已知圆O 的直径12AB =,点C 是圆上一点,且30ABC ∠=︒,点P 是弦BC 上一动点, 过点P 作PD OP ⊥交圆O 于点D . (1)如图1,当PD AB ∥时,求PD 的长; (2)如图2,当BP 平分OPD ∠时,求PC 的长.ADB第21题图21.(本题满分10分,每小题5分)(1)解:联结OD∵直径12AB = ∴6OB OD == ……………………………………1分∵PD OP ⊥ ∴90DPO =︒∠∵PD AB ∥ ∴180DPO POB +=︒∠∠ ∴90POB =︒∠ ……1分 又∵30ABC =︒∠,6OB =∴30OP OB tan =︒= ………………………………………………1分 ∵在Rt POD △中,222PO PD OD += ……………………………1分∴2226PD +=∴PD =……………………………………………………………1分 (2)过点O 作OH BC ⊥,垂足为H ∵OH BC ⊥∴90OHB OHP ==︒∠∠ ∵30ABC =︒∠,6OB =∴132OH OB ==,30BH OB cos =︒=……………………2分 ∵在⊙O 中,OH BC ⊥∴CH BH ==……………………………………………………1分 ∵BP 平分OPD ∠ ∴1452BPO DPO ==︒∠∠ ∴453PH OH cot =︒= ……………………………………………1分∴3PC CH PH =-=- ………………………………………1分(第21题图1)ABOP CD (第21题图2)OABDPC奉贤区21.(本题满分10分,每小题满分各5分)已知:如图6,在△ABC 中,AB =13,AC=8,135cos =∠BAC ,BD ⊥AC ,垂足为点D ,E 是BD 的中点,联结AE 并延长,交边BC 于点F . (1) 求EAD ∠的余切值; (2) 求BFCF的值. 21、(1)56; (2)58; 黄浦区21.(本题满分10分)如图,AH 是△ABC 的高,D 是边AB 上一点,CD 与AH 交于点E .已知AB =AC =6,cos B =23, AD ∶DB =1∶2.(1)求△ABC 的面积; (2)求CE ∶DE.21. 解:(1)由AB =AC =6,AH ⊥BC ,得BC =2BH .—————————————————————————(2分) 在△ABH 中,AB =6,cosB =23,∠AHB =90°, 得BH =2643⨯=,AH=2分) 则BC =8,所以△ABC 面积=182⨯=——————————————(1分) (2)过D 作BC 的平行线交AH 于点F ,———————————————(1分)由AD ∶DB =1∶2,得AD ∶AB =1∶3, 则31CE CH BH AB DE DF DF AD ====. ——————————————(4分)图6ABCD EF金山区21.(本题满分10分,每小题5分)如图5,在矩形ABCD 中,E 是BC 边上的点,AE =BC ,DF ⊥AE ,垂足为F .(1)求证:AF=BE ;(2)如果BE ∶EC=2∶1,求∠CDF 的余切值.21.解:(1)∵四边形ABCD 是矩形,∴AD =BC ,AD ∥BC ,∠B =90°,∴∠DAF=∠AEB ,……………………………………………………………………(1分) ∵AE=BC ,DF ⊥AE ,∴AD=AE ,∠ AFD=∠EBA=90°,………………………(2分) ∴△ADF ≌△EAB ,∴AF =EB ,………………………………………………………(2分)(2)设BE =2k ,EC =k ,则AD =BC =AE =3k ,AF =BE =2k ,…………………………(1分)∵∠ADC =90°,∠AFD =90°,∴∠CDF +∠ADF =90°,∠DAF +∠ADF =90°, ∴∠CDF =∠DAF …………………………………………………………………(2分) 在Rt △ADF 中,∠AFD =90°,DF=∴cot ∠CDF =cot ∠DAF=5AF DF ==.………………………………(2分) 静安区21.(本题满分10分,第(1)小题满分5分,第(2)小题满分5分)已知:如图,边长为1的正方形ABCD 中,AC 、DB 交于点H .DE 平分∠ADB ,交AC 于点E .联结BE 并延长,交边AD 于点F . (1)求证:DC =EC ; (2)求△EAF 的面积.21.(本题满分10分, 第(1)小题5分,第(2)小题5分)解:(1)∵正方形ABCD ,∴DC=BC=BA=AD , ∠BAD =∠ADC =∠DCB =∠CBA =90°AH=DH=CH=BH , AC ⊥BD ,ABCDF图5第21题图∴∠ADH =∠HDC =∠DCH =∠DAE = 45°. …………(2分) 又∵DE 平分∠AD B ∴∠ADE =∠EDH∵∠DAE +∠ADE =∠DEC , ∠EDH +∠HDC =∠EDC …………(1分) ∴∠EDC =∠DEC …………(1分) ∴DC =EC …………(1分) (2)∵正方形ABCD ,∴AD ∥BC , ∴△AFE ∽△CBE ∴2)(ECAE S S CEB AEF =∆∆ ………………………………(1分) ∵AB=BC=DC=EC =1,AC =2,∴AE =12- …………………………(1分) Rt △BHC 中, BH =22BC =22, ∴在△BEC 中,BH ⊥EC , 4222121=⨯⨯=∆BEC S ……………………(2分) ∴2)12(42-=∆AEF S , ∴4423)223(42-=-⨯=∆AEF S …………(1分) 闵行区21.(本题满分10分,其中第(1)小题4分,第(2)小题6分)已知一次函数24y x =-+的图像与x 轴、y 轴分别交于点A 、B ,以AB 为边在第一象限内作直角三角形ABC ,且∠BAC = 90o,1tan 2ABC ∠=.(1)求点C 的坐标;(2)在第一象限内有一点M (1,m ),且点M 与点C 位于直线AB 的同侧,使得ABC ABM S S ∆∆=2求点M 的坐标.21.解:(1)令0y =,则240x -+=,解得:2x =,∴点A 坐标是(2,0).令0x =,则4y =,∴点B 坐标是(0,4).………………………(1分) ∴AB ==1分) ∵90BAC ∠=,1tan 2ABC ∠=,∴AC =. 过C 点作CD ⊥x 轴于点D ,易得OBA DAC ∆∆∽.…………………(1分) ∴2AD =,1CD =,∴点C 坐标是(4,1).………………………(1分)(2)11522ABC S AB AC ∆=⋅=⨯=.………………………………(1分) ∵2ABM ABC S S ∆∆=,∴52ABM S ∆=.……………………………………(1分) ∵(1M ,)m ,∴点M 在直线1x =上;令直线1x =与线段AB 交于点E ,2ME m =-;……………………(1分) 分别过点A 、B 作直线1x =的垂线,垂足分别是点F 、G ,∴AF +BG = OA = 2;……………………………………………………(1分)∴111()222ABM BME AME S S S ME BG ME AF ME BG AF ∆∆=+=⋅+⋅=+1152222ME OA ME =⋅=⨯⨯=…………………(1分) ∴52ME =,522m -=,92m =,∴(1M ,92).……………………(1分) 普陀区21.(本题满分10分)如图7,在Rt △ABC 中,90C ∠=,点D 在边BC 上,DE ⊥AB ,点E 为垂足,7AB =,45DAB ∠=,3tan 4B =. (1)求DE 的长; (2)求CDA ∠的余弦值. 21.解:(1)∵DE ⊥AB ,∴︒=∠90DEA又∵45DAB ∠=,∴AE DE =. ················· (1分) 在Rt △DEB 中,︒=∠90DEB ,43tan =B ,∴43=BE DE . ······· (1分) 设x DE 3=,那么x AE 3=,x BE 4=.∵7AB =,∴743=+x x ,解得1=x . ··············· (2分) ∴3=DE . ··························· (1分) (2) 在Rt △ADE 中,由勾股定理,得23=AD . ··········· (1分)同理得5=BD . ························· (1分) 在Rt △ABC 中,由43tan =B ,可得54cos =B .∴528=BC . ···· (1分) ∴53=CD . ·························· (1分)ABCDE 图7∴102cos ==∠AD CD CDA . ··················· (1分)即CDA ∠青浦区21. (本题满分10分,第(1)、(2)小题,每小题5分)如图5,在Rt △ABC 中,∠C =90°,AC=3,BC =4,∠ABC 的平分线交边AC 于点D ,延长BD 至点E ,且BD=2DE ,联结AE .(1)求线段CD 的长; (2)求△ADE 的面积.21.解:(1)过点D 作DH ⊥AB ,垂足为点H . ················ (1分)∵BD 平分∠ABC ,∠C =90°,∴DH = DC =x , ························ (1分) 则AD =3-x .∵∠C =90°,AC=3,BC =4,∴AB =5. ·············· (1分) ∵sin ∠==HD BCBAC AD AB, ∴435=-x x , ························ (1分) ∴43=x . ·························· (1分) (2)1141052233=⋅=⨯⨯=ABDSAB DH . ·············· (1分) ∵BD=2DE , ∴2==ABD ADES BDSDE, ····················· (3分) ∴1015323=⨯=ADES. ···················· (1分) 松江区21.(本题满分10分, 每小题各5分) 如图,已知△ABC 中,∠B =45°,1tan 2C =, BC =6.(1)求△ABC 面积;(2)AC 的垂直平分线交AC 于点D ,交BC 于ED BA图5AB点E. 求DE 的长.21.(本题满分10分, 每小题各5分) 解:(1)过点A 作AH ⊥BC 于点H …………1分 在Rt ABC ∆中,∠B =45°设AH =x ,则BH =x ………………………………1分 在Rt AHC ∆中,1tan 2AH C HC == ∴HC=2x ………………………………………………………1分 ∵BC =6∴x+2x =6 得x =2∴AH =2…………………………………………………………1分 ∴162ABC S BC AH ∆=⋅⋅=……………………………………1分(2)由(1)得AH =2,CH =4在RtAHC ∆中,AC ==…………………2分∵DE 垂直平分AC ∴12CD AC == ED ⊥AC …………………………………………………1分 在Rt EDC ∆中,1tan 2ED C CD==……………………………1分 ∴DE = ………………………………………………1分 徐汇区21. 如图,在Rt ABC ∆中,90C ∠=︒,3AC =,4BC =,AD 平分BAC ∠交BC 于点D . (1)求tan DAB ∠;(2)若⊙O 过A 、D 两点,且点O 在边AB 上,用 尺规作图的方法确定点O 的位置并求出的⊙O 半径. (保留作图轨迹,不写作法)(第21题图)DACBE杨浦区21、(本题满分10分,第(1)小题满分3分,第(2)小题满分7分)已知,如图5,在梯形ABCD中,DC//AB, AD=BC, BD平分∠ABC,∠A=600求:(1)求∠CDB的度数(2)当AD=2时,求对角线BD的长和梯形ABCD的面积。
2018年度初三上海各区二模18-24-25

1 / 14EOBA CMHOBACDPF (2019宝山、嘉定)18.如图,点M 的坐标为(3,2),动点P 从点O 出发,沿y 轴以每秒1个单位的速度向上移动,且过点P 的直线l :y =-x +b 也随之移动,如果点M 关于l 的对称点落在坐标轴上,设点P 的移动时间为t ,那么t 的值可以是 .24.(本题满分12分,第(1)、第(2)、第(3)小题满分各4分) 如图,已知对称轴为直线1x =-的抛物线32++=bx ax y 与x 轴交于A 、B 两点,与y 轴交于C 点,其中(1,0)A . (1)求点B 的坐标及此抛物线的表达式;(2)点D 为y 轴上一点,若直线BD 和直线BC 的夹角 为15º,求线段CD 的长度;(3)设点P 为抛物线的对称轴1x =-上的一个动点, 第24题图 当BPC ∆为直角三角形时,求点P 的坐标.25.(本题满分14分,第(1)、第(2)小题满分各4分,第(3)小题满分6分)如图已知: AB 是圆O 的直径,AB=10,点C 为圆O 上异于点A 、B 的一点,点M 为弦BC 的中点.(1)如果AM 交OC 于点E ,求OE :CE 的值; (2)如果AM ⊥OC 于点E ,求∠ABC 的正弦值;(3)如果AB :BC=5:4,D 为BC 上一动点,过D 作DF ⊥OC ,交OC 于点H ,与射线BO 交于圆内点F ,请完成下列探究.探究一:设BD=x ,FO=y ,求y 关于x 的函数解析式及其定义域.探究二:如果点D 在以O 为圆心,OF 为半径的圆上,写出此时BD 的长度.2 / 14崇明18.如图4,在ABC △中,已知AB AC =,30BAC ∠=︒,将ABC △绕着点A 逆时针旋转30︒,记点C 的对应点为点D ,AD 、BC 的延长线相交于点E .如果线段DE边AB 的长为 ▲ .24.(本题满分12分,每小题满分各4分)如图8,抛物线2y x bx c =++交x 轴于点(1,0)A 和点B ,交y 轴于点(0,3)C . (1)求抛物线的解析式;(2)在抛物线上找出点P ,使PC PO =,求点P 的坐标;(3)将直线AC 沿x 轴的正方向平移,平移后的直线交y 轴于点M ,交抛物线于点N . 当四边形ACMN 为等腰梯形时,求点M 、N 的坐标.25.(本题满分14分,其中第(1)、(2)小题满分各4分,第(3)小题满分6分)如图9,在梯形ABCD 中,AD BC ∥,8AB DC ==,12BC =,3cos 5C =,点E 为AB 边上一点,且2BE =.点F 是BC 边上的一个动点(与点B 、点C 不重合),点G 在射线CD 上,且EFG B ∠=∠.设BF 的长为x ,CG 的长为y .(1)当点G 在线段DC 上时,求y 与x 之间的函数关系式,并写出自变量x 的取值范围; (2)当以点B 为圆心,BF 长为半径的⊙B 与以点C 为圆心,CG 长为半径的⊙C 相切时, 求线段BF 的长;(3)当CFG △为等腰三角形时,直接写出线段BF 的长.图8DAEB FCG图9备用图3 / 1418. 如图5,矩形ABCD ,AD =a ,将矩形ABCD 绕着顶点B 顺时针旋转,得到矩形EBGF ,顶点A 、D 、C 分别与点E 、F 、G 对应(点D 与点F 不重合).如果点D 、E 、F 在同一条直线上,那么线段DF 的长是 ▲ .(用含a 的代数式表示)24.(本题满分12分,每小题满分各4分)如图9,已知平面直角坐标系xOy ,抛物线22y ax bx =++与x 轴交于点A (-2,0)和点B (4,0) .(1)求这条抛物线的表达式和对称轴;(2)点C 在线段OB 上,过点C 作CD ⊥x 轴,垂足为点C ,交抛物线与点D ,E 是BD中点,联结CE 并延长,与y 轴交于点F . ①当D 恰好是抛物线的顶点时,求点F 的坐标; ②联结BF ,当△DBC 的面积是△BCF 面积的32时,求点C 的坐标.25.(本题满分14分,第(1)小题满分4分,第(2)小题满分5分,第(3)小题满分5分)如图10,已知△ABC ,AB ,3BC =,∠B =45°,点D 在边BC 上,联结AD , 以点A 为圆心,AD 为半径画圆,与边AC 交于点E ,点F 在圆A 上,且AF ⊥AD . (1)设BD 为x ,点D 、F 之间的距离为y ,求y 关于x 的函数解析式,并写出定义域;(2)如果E 是»DF的中点,求:BD CD 的值; (3)联结CF ,如果四边形ADCF 是梯形,求BD 的长 .图5图10图9OABxy4 / 14E 第25题图C A BD Q F P G 18.如图,在矩形ABCD 中,AB =6,点E 在边AD 上且AE =4,点F 是边BC 上的一个动点,将四边形ABFE 沿EF 翻折,A 、B 的对应点A 1、B 1与点C 在同一直线上,A 1B 1与边AD 交于点G ,如果DG =3,那么BF 的长为 ▲ .24.如图,在平面直角坐标系xOy 中,抛物线2+8y ax bx =+与x 轴相交于点A (-2,0)和点B (4,0),与y 轴相交于点C ,顶点为点P .点D (0,4)在OC 上,联结BC 、BD . (1)求抛物线的表达式并直接写出点P 的坐标;(2)点E 为第一象限内抛物线上一点,如果△COE 与△BCD 的面积相等,求点E 的坐标;(3)点Q 在抛物线对称轴上,如果△BCD ∽△CPQ ,求点Q 的坐标.25.(本题满分14分,第(1)小题5分,第(2)小题5分,第(3)小题4分)如图,AD ∥BC ,∠ABC =90°,AD =3,AB =4,点P 为射线BC 上一动点,以P 为圆心,BP 长为半径作⊙P ,交射线BC 于点Q ,联结BD 、AQ 相交于点G ,⊙P 与线段BD 、AQ 分别相交于点E 、F .(1)如果BE=FQ ,求⊙P 的半径;(2)设BP=x ,FQ=y ,求y 关于x 的函数关系式,并写出x 的取值范围; (3)联结PE 、PF ,如果四边形EGFP 是梯形,求BE 的长.C第18题图ABDE第24题图 x B O C D A y P5 / 14 BACB 1A 1 E图3D黄浦18.如图3,在ABC ∆中,90ACB ∠=︒,3sin 5B =,将ABC ∆绕顶点C 顺时针旋转,得到11A B C ∆ ,点A 、B 分别与点1A 、1B 对应,边11A B 分别交边AB 、BC 于点D 、E ,如果点E 是边11A B 的中点,那么1BDB C= ▲ .24.(本题满分12分)如图7,已知抛物线2y ax bx c=++经过原点()0,0O 、()2,0A ,直线2y x =经过抛物线的顶点B ,点C 是抛物线上一点,且位于对称轴的右侧,联结BC 、OC 、AB ,过点C 作CE ∥x 轴,分别交线段OB 、AB 于点E 、F . (1)求抛物线的表达式;(2)当BC CE =时,求证:BCE ∆∽ABO ∆; (3)当CBA BOC ∠=∠时,求点C 的坐标.25.(本题满分14分)已知四边形ABCD 中,AD ∥BC ,2ABC C ∠=∠,点E 是射线AD 上一点,点F 是射线DC 上一点,且满足BEF A ∠=∠.(1)如图8,当点E 在线段AD 上时,若AB=AD ,在线段AB 上截取AG=AE ,联结GE .求证:GE=DF ;(2)如图9,当点E 在线段AD 的延长线上时,若AB =3,AD =4,1cos 3A =,设AE x =,DF y =,求y 关于x 的函数关系式及其定义域;(3)记BE 与CD 交于点M ,在(2)的条件下,若△EMF 与△ABE 相似,求线段AE 的长.D A BCEF图9ABCE FG D图86 / 14静安18.如图4,在平面直角坐标系xOy 中,已知A(0),B (0,6),M (0,2).点Q 在直线AB 上,把△BMQ 沿着直线MQ 翻折,点B 落在点P 处,联结PQ .如果 直线PQ 与直线AB 所构成的夹角为60°,那么点P 的坐 标是 ▲ .24.在平面直角坐标系xOy 中(如图7),已知抛物线2(0)y ax bx c a =++≠经过原点,与 x 轴的另一个交点为A ,顶点为P (3-,4). (1)求这条抛物线表达式;(2)将该抛物线向右平移,平移后的新抛 物线顶点为Q ,它与y 轴交点为B ,联结PB 、 PQ .设点B 的纵坐标为m ,用含m 的代数式表示∠BPQ 的正切值;(3)联结AP ,在(2)的条件下,射线PB 平分∠APQ ,求点B 到直线AP 的距离.25.(本题满分14分,第(1)小题满分3分,第(2)小题满分6分,第(3)小题满分5分)已知:如图8,梯形ABCD 中,AD ∥BC ,AD=2,AB=BC=CD =6.动点P 在射线BA 上,以BP 为半径的⊙P 交边BC 于点E (点E 与点C 不重合), 联结PE 、PC .设BP = x ,PC = y . (1) 求证:PE ∥DC ;(2) 求y 关于x 的函数解析式,并写出定义域; (3) 联结PD ,当∠PDC =∠B 时,以D 为圆心 半径为R 的⊙D 与⊙P 相交,求R 的取值范围.图4图8A BEDP图77 / 1418.如图,在△ABC 中,AB = AC = 5,BC =D 为边AC 上一点(点D 与点A 、C 不重合).将△ABC 沿直线BD 翻折,使点A 落在点E 处,联结CE .如果CE // AB ,那么AD ︰CD = ▲ .24.(本题共3小题,每小题各4分,满分12分)已知抛物线2y x b x c =-++经过点A (1,0)、B (3,0),且与y 轴的公共点为点C . (1)求抛物线的解析式,并求出点C 的坐标; (2)求∠ACB 的正切值;(3)点E 为线段AC 上一点,过点E 作EF ⊥BC垂足为点F .如果14EF BF =,求△BCE 的面积.25.(本题共3小题,其中第(1)小题各4分,第(2)、(3)小题各5分,满分14分)如图1,点P 为∠MAN 的内部一点.过点P 分别作PB ⊥AM 、PC ⊥AN ,垂足分别为点B 、C .过点B 作BD ⊥CP ,与CP 的延长线相交于点D .BE ⊥AP ,垂足为点E . (1)求证:∠BPD =∠MAN ; (2)如果sin MAN ∠=AB =BE = BD ,求BD 的长; (3)如图2,设点Q 是线段BP 的中点.联结QC 、CE ,QC 交AP 于点F .如果 ∠MAN = 45°,且BE // QC ,求PQF CEFS S ∆∆的值.ABC(第18题图)E M(图2)A NQFPC DBMN ABCDP(图1)E(第24题图)8 / 1418.定义:如果P 是圆O 所在平面内的一点,Q 是射线OP 上一点,且线段OP 、OQ 的比 例中项等于圆O 的半径,那么我们称点P 与点Q 为这个圆的一对反演点,已知点M 、N 为 圆O 的一对反演点,且点M 、N 到圆心O 的距离分别为4和9,那么圆O 上任意一点A 到 点M 、N 的距离之比AMAN= 24. 已知抛物线213y x bx c =++经过点(3,4)M -,与x 轴相交于点(3,0)A -和点B ,与y 轴 相交于点C .(1)求这条抛物线的表达式;(2)如果P 是这条抛物线对称轴上一点,PC BC =,求点P 的坐标; (3)在第(2)小题的条件下,当点P 在x 轴上方时,求PCB ∠的正弦值.25. 已知AB 是圆O 的一条弦,P 是圆O 上的一点,过点O 作MN AP ⊥,垂足为点M ,并交射线AB 于点N ,圆O 的半径为5,8AB =. (1)当P 是优弧AB 的中点时(如图),求弦AP 的长;(2)当点N 与点B 重合时,试判断:以点O 为圆心,32为半径的圆与直线AP 的位置关系, 并说明理由;(3)当BNO BON ∠=∠,且圆N 与圆O 相切时,求圆N 的半径的长.9 / 14普陀18.如图7,AD 是△ABC 的中线,点E 在边AB 上,且DE ⊥AD ,将△BDE 绕着点D 旋转,使得点B 与点C 重合,点E 落在点F 处,联结AF 交BC 于点G ,如果52AE BE =,那么GFAB 的值等于 ▲ .24.在平面直角坐标系xOy 中,直线243y x m =-+(0)m >与x 轴、y 轴分别交于点A 、B如图11所示,点C 在线段AB 的延长线上,且2AB BC =.(1)用含字母m 的代数式表示点C 的坐标;(2)抛物线21103y x bx =-++经过点A 、C ,求此抛物线的表达式;(3)在第(2)题的条件下,位于第四象限的抛物线上,是否存在这样的点P :使2PAB OBC S S =△△,如果存在,求出点P 的坐标,如果不存在,试说明理由.25. 如图12,在Rt △ABC 中,90ACB ∠=︒,5AB =,4cos 5BAC ∠=,点O 是边AC 上一个动点(不与A 、C 重合),以点O 为圆心,AO 为半径作⊙O ,⊙O 与射线AB 交于点D ;以点C 为圆心,CD 为半径作⊙C ,设OA x =.(1)如图13,当点D 与点B 重合时,求x 的值;(2)当点D 在线段AB 上,如果⊙C 与AB 的另一个交点E 在线段AD 上时,设AE y =,试求y 与x 之间的函数解析式,并写出x 的取值范围;(3)在点O 的运动的过程中,如果⊙C 与线段AB 只有一个公共点,请直接写出x 的取值范围.图7ABCDEB图12AB COD图13AB (D )C O图11xyO AB 11青浦18.我们把满足某种条件的所有点组成的图形,叫做符合这个条件的点的轨迹.如图6,在Rt△ABC中,∠C=90°,AC=8,BC=12,动点P从点A开始沿射线AC方向以1个单位/秒的速度向点C运动,动点Q从点C开始沿射线CB方向以2个单位/秒的速度向点B 运动,P、Q两点分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,在整个运动过程中,线段PQ的中点M运动的轨迹长为▲.24.(本题满分12分,每小题满分各4分)已知:如图10,在平面直角坐标系xOy中,抛物线()经过点A(6,-3),对称轴是直线x=4,顶点为B,OA与其对称轴交于点M,M、N关于点B对称.(1)求这条抛物线的表达式和点B的坐标;(2)联结ON、AN,求△OAN的面积;(3)点Q在x轴上,且在直线x=4右侧,当∠ANQ=45°时,求点Q的坐标.25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)已知:在Rt△ABC中,∠ACB=90°,AC=1,D是AB的中点. 以CD为直径的⊙Q分别交BC、BA于点F、E,点E位于点D下方,联结EF交CD于点G.(1)如图11,如果BC=2,求DE的长;(2)如图12,设BC=x,=GDyGQ,求y关于x的函数关系式及其定义域;(3)如图13,联结CE,如果CG=CE,求BC的长.图6图10图11 图13图1218.已知Rt △ABC 中,∠ACB=90°,AC =8,BC =6.将△ABC 绕点B 旋转得到△DBE ,点A的对应点D 落在射线BC 上.直线AC 交DE 于点F ,那么CF 的长为________.24.(本题满分12分,第(1)小题3分,第(2)小题4分,第(3)小题5分)如图,抛物线24y ax x c =++过点A (6,0)、B (3,23),与y 轴交于点C .联结AB 并延长,交y 轴于点D . (1)求该抛物线的表达式;(2)求△ADC 的面积;(3)点P 在线段 AC 上,如果△OAP 和△DCA求点P 的坐标.25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)如图,已知Rt △ABC 中,∠ACB=90°,AC=24,BC=16.点O 在边BC 上,以O 为圆心,OB 为半径的弧经过点A .P 是弧AB 上的一个动点. (1)求半径OB 的长;(2)如果点P 是弧AB 的中点,联结PC ,求∠PCB 的正切值; (3)如果BA 平分∠PBC ,延长BP 、CA 交于点D ,求线段DP 的长.·(第25题图)OBC A·(备用图)OBCA18.如图,在Rt △ABC 中,∠ACB =90°,AB =6,cos B =23,先将△ACB 绕着顶点C 顺时针旋转90°,然后再将旋转后的三角形进行放大或缩小得到△A'CB'(点A'、C 、B'的对应点分别是点A 、C 、B ),联结A'A 、B'B ,如果△AA'B 和△AA'B'相似,那么A C '的长是 ▲ .24.如图,在平面直角坐标系xOy 中,抛物线214y x bx c =-++与直线132y x =-分别交于x 轴、y轴上的B 、C 两点,设该抛物线与x 轴的另一个交点为点A ,顶点为点D ,联结CD 交x 轴于点E . (1)求该抛物线的表达式及点D 的坐标; (2)求∠DCB 的正切值;(3)如果点F 在y 轴上,且∠FBC=∠DBA +∠DCB ,求点F 的坐标.25.如图,在△ABC 中,AC=BC=10,3cos 5C =,点P 是AC 边上一动点(不与点A 、C 重合),以P A 长为半径的⊙P 与边AB 的另一个交点为D ,作DE ⊥CB 于E .(1)当⊙P 与边BC 相切时,求⊙P 的半径;(2)联结BP 交DE 于点F ,设AP 的长为x ,PF 的长为y ,求y 关于x 的函数解析式,并直接写出x 的取值范围;(3)在(2)的条件下,当以PE 长为直径的⊙Q 与⊙P 相交于AC 上边的点G 时,求相交所得的公共弦的长.备用图ACEDCABPO(第18题图)18.如图,在矩形ABCD 中,过点A 的圆O 交边AB 于点E ,交边AD 于点F ,已知AD =5,AE =2,AF =4.如果以点D 为圆心,r 为半径的圆D 与圆O 有两个公共点,那么r 的取值范围是 ▲ .24.(本题满分12分,第(1)小题4分,第(2)小题4分,第(3)小题4分)已知开口向下的抛物线222y ax ax =-+与y 轴的交点为A ,顶点为B ,对称轴与x 轴的交点为C ,点A 与点D 关于对称轴对称,直线BD 与x 轴交于点M ,直线AB 与直线OD 交于点N . (1)求点D 的坐标;(2)求点M 的坐标(用含a 的代数式表示);(3)当点N 在第一象限,且∠OMB =∠ONA25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)已知圆O 的半径长为2,点A 、B 、C 为圆O 上三点,弦BC =AO ,点D 为BC 的中点. (1)如图1,联结AC 、OD ,设∠OAC =α,请用α表示∠AOD ;(2)如图2,当点B 为»AC 的中点时,求点A 、D 之间的距离; (3)如果AD 的延长线与圆O 交于点E ,以O 为圆心,AD 为半径的圆与以BC 为直径的圆相切,求弦AE 的长.D(第24题图) (第25题图)O A (图1) B CD AOBCD. (图2) A O(备用图)18.如图3,在ABC ∆中,5==AC AB ,8=BC ,将ABC ∆绕着点C 旋转, 点B A 、的对应点分别是点'A 、'B ,若点'B 恰好在线段'AA 的延长线上, 则'AA 的长等于 ▲ .交于点A ,点A 的横坐标为6,抛物线顶点为点B . (1)求这条抛物线的表达式和顶点B 的坐标;(2)过点O 作AB OP //,在直线OP 上点取一点Q ,使得OBA QAB ∠=∠,求点Q 的坐标;(3)将该抛物线向左平移)0(>m m 个单位,所得新抛物线与y 轴负半轴相交于点C 且顶点仍然在第四象限,此时点A 移动到点D 的位置,:CB25.如图7,在ABC Rt ∆中,︒=∠90ACB ,3=AC ,4=BC ,点P 在边AC 上(点P 与点A 不重合),以点P 为圆心,PA 为半径作⊙P 交边AB 于另一点D ,DP ED ⊥,交边BC 于点E .(1) 求证:DE BE =;(2) 若x BE =,y AD =,求y 关于x 的函数关系式并写出定义域;(3) 延长ED 交CA 的延长线于点F ,联结BP ,若BDP ∆与DAF ∆相似,求线段AD 的长.图3BC图6BEDBB。
2018年上海闵行区初三中考二模数学试卷及答案

闵行区2018-2018学年第二学期九年级质量调研考试 数学试卷(考试时间100分钟,满分150分)考生注意:1.本试卷含三个大题,共25题.2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答 题一律无效.3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证 明或计算的主要步骤. 一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,请选择正确选项的代号并填涂 在答题纸的相应位置上】1.如果单项式 2a (A )6; n b 2c 是六次单项式,那么 n 的值取(B )5; (C )4;(D )3.2.在下列各式中,二次根式 a 1的有理化因式是 (A ) a 1; (B ) a 1; (C ) a 1; (D ) a 1.3.下列函数中,y 随着 x 的增大而减小的是(A ) y 3x ; (B ) y 3x ; (C ) y 3 3 ;(D ) y . xx 4.一鞋店销售一种新鞋,试销期间卖出情况如下表,对于鞋店经理来说最关心哪种尺 码的鞋畅销,那么下列统计量对该经理来说最有意义的是尺码 数量(双) 22 322.5 523 1023.5 1524 824.5 325 2(A )平均数;(B )中位数; (C )众数; (D )方差.5.下列图形中,既是轴对称又是中心对称图形的是(A )正五边形;(B )等腰梯形;(C )平行四边形;(D )圆. 6.下列四个命题,其中真命题有(1)有理数乘以无理数一定是无理数;(2)顺次联结等腰梯形各边中点所得的四边形是菱形; (3)在同圆中,相等的弦所对的弧也相等;(4)如果正九边形的半径为 a ,那么边心距为 a sin 20o.(A )1个; (B )2个; (C )3个;(D )4个.二、填空题:(本大题共12题,每题4分,满分48分)7.计算: 28.在实数范围内分解因式: a9.方程2x 3 2的解是2 ▲.3 2a ▲.▲.10.不等式组34x x3 0 , x的解集是▲.11.已知关于x的方程 x2 x m 0没有实数根,那么m的取值范围是▲.212.将直线y x 1向下平移3个单位,那么所得到的直线在y轴上的截距为▲.313.如果一个四边形的两条对角线相等,那么称这个四边 A D形为“等对角线四边形”.写出一个你所学过的特殊E 的等对角线四边形的名称▲.14.如图,已知在梯形ABCD中,AD // BC,且BC = 3AD,uuur uuurr r B C 点E是边DC的中点.设AB a,AD b,那么(第14题图)uuur r r(用a、b的式子表示).AE ▲15.布袋中有大小、质地完全相同的4个小球,每个小球上分别标有数字1、2、3、4,如果从布袋中随机抽取两个小球,那么这两个小球上的数字之和为偶数的概率是▲.16.9月22日世界无车日,某校开展了“倡导绿色出行”为主题的调查,随机抽查了部分师生,将收集的数据绘制成下列不完整的两种统计图.已知随机抽查的教师人数为学生人数的一半,根据图中信息,乘私家车出行的教师人数是▲ .师生出行方式条形统计图学生出行方式扇形统计图人数24252015乘公车y%私家车15%学生教师15129105步行x%3 3 骑车25%步行乘公车骑车私家车出行方式(第16题图)17.点P为⊙O内一点,过点P的最长的弦长为10cm,最短的弦长为8cm,那么 OP cm.的长等于▲18.如图,已知在△ABC中,AB = AC,tan B 1,将△ABC翻折,使点C与点A重3 A合,折痕DE交边BC于点D,交边 AC于点E,那么 BD的值为▲.DC B C(第18题图)三、解答题:(本大题共7题,满分78分) 19.(本题满分10分)1 (cos60o 1)0132. 计算: 213 2 2 20.(本题满分10分)x 4 2 1解方程: 2x x 4 x .x21.(本题满分10分,其中每小题各5分)如图,已知在△ABC 中,∠ABC = 30º,BC = 8, Csin A 5,BD 是 AC 边上的中线.D5 求:(1)△ABC 的面积; AB(2)∠ABD 的余切值.(第21题图)22.(本题满分10分,其中每小题各5分)如图,山区某教学楼后面紧邻着一个土坡,坡面 BC 平行于地面 AD ,斜坡 AB 的坡 比为 i =1∶ 5,且 AB = 26米.为了防止山体滑坡,保障安全,学校决定对该土坡进行12 改造.经地质人员勘测,当坡角不超过 53º时,可确保山体不滑坡.C F B (1)求改造前坡顶与地面的距离 BE 的长. (2)为了消除安全隐患,学校计划将斜坡 AB 改造成 AF (如图所示),那么 BF 至少是 多少米?(结果精确到 1米)(参考数据:sin53 o0.8, cos53 0.6, o0.75).tan53 1.33, cot53o oD EA(第22题图)E23.(本题满分12分,其中每小题各6分)如图,已知在矩形 ABCD 中,过对角线 AC 的中点 O 作AC 的垂线,分别交射线 AD 和 CB 于点 E 、F ,交边 DC 于 点 G ,交边 AB 于点 H .联结 AF ,CE . GDA CB O(1)求证:四边形 AFCE 是菱形;(2)如果 OF = 2GO ,求证:GO D G GC .2HF(第23题图)24.(本题满分12分,其中每小题各4分)如图,已知在平面直角坐标系 xOy 中,抛物线 y a x 2x c 与 x 轴交于2 点 A (-1,0)和点 B ,与 y 轴相交于点 C (0,3),抛物线的对称轴为直线 l . (1)求这条抛物线的关系式,并写出其对称轴和顶点 M 的坐标; (2)如果直线 y k x b 经过 C 、M 两点,且与 x 轴交于点 D ,点 C 关于直线 l 的对称点为 N ,试证明四边形 CDAN 是平行四边形; (3)点 P 在直线 l 上,且以点 P 为圆心的 圆经过 A 、B 两点,并且与直线 CD 相切,求点 P 的坐标.y l M C D A O E B x(第24题图)25.(本题满分14分,其中第(1)小题各4分,第(2)、(3)小题各5分)如图,已知在△ABC 中,AB = AC = 6,AH ⊥BC ,垂足为点 H .点 D 在边 AB 上,且 AD = 2,联结 CD 交 AH 于点 E .(1)如图 1,如果 AE = AD ,求 AH 的长;(2)如图 2,⊙A 是以点 A 为圆心,AD 为半径的圆,交 AH 于点 F .设点 P 为边 BC 上一点,如果以点 P 为圆心,BP 为半径的圆与⊙A 外切,以点 P 为圆心,CP 为半 径的圆与⊙A 内切,求边 BC 的长;(3)如图 3,联结 DF .设 DF = x ,△ABC 的面积为 y ,求 y 关于 x 的函数解析式, 并写出自变量 x 的取值范围.A DAEDPF EBCH(第25题图1)ADF BCH(第25题图2)EBHC(第25题图3)。
上海市各区2018届中考数学二模试卷精选汇编二次函数专题

上海市各区 2018 届九年级中考二模数学试卷精选汇编:二次函数专题宝山区、嘉定区24.(本题满分 12 分,第(1)小题 4 分,第(2)小题 4 分,第(3)小题 4 分)x m A(4,0) 已知平面直角坐标系 xOy (如图 7),直线 y (1)求m 、 n 的值; 的经过点 和点 B(n ,3) . xbx c经过点 A 、B ,该抛物线的顶点为点P ,求s i n ABP 的(2)如果抛物线y 值;2 x m y x m y (3)设点Q 在直线 y 上,且在第一象限内,直线 与 轴的交点为点 D ,y如果AQ O DO B,求点Q 的坐标.Ox图 7x mA(4,0) 的经过点 24.解:(1) ∵直线 y ∴4 m 0……………………1 分 ∴ m ∵直线 y 4………………………………1 分 x m 的经过点 B(n ,3)∴ n4 3……………………1 分 ∴ n1…………………………………………1 分 (2)由可知点 B 的坐标为(1,3)xbx c ∵抛物线 y 经过点 A 、 B 2 16 4b c 0∴1 b c 3 6 c 8∴b , xbx c y x 6x 8 ∴抛物线 y ∴抛物线 y 的表达式为 …………………1 分 2 2 x6x 8 P(3,1) 的顶点坐标为 ……………1 分 2 3 2 AP 2 PB 2 5 ∴ AB ∴ AB , , BP PB 22 2PAB 90 ∴ ……………………………………1 分APABP∴s in PB 10ABP ∴s in …………………………………………1 分10x H (3)过点Q 作Q H 轴,垂足为点 ,则Q H ∥ y 轴AQ O DOB OB D QBO ∵ , ∴△OB D ∽△Q B O O B D BQ B O B∴ ……………1 分 x 4 y ∵直线 y 与 轴的交点为点 D 4∴点 D 的坐标为(0,4) ,O D 10 DB 2,又O B ∴QB 5 2 D Q 4 2 ,……………1 分3 2∵ AB ∴ A Q 8 2 D Q 4 2 , ∵Q H ∥ y 轴O D A DQ H A Q∴∴4 4 28 2Q H 8 ∴Q H ……………………………………1 分 即点Q 的纵坐标是8x 4 又点Q 在直线 y 上点Q 的坐标为(4,8) ……………1 分长宁区24.(本题满分 12 分,第(1)小题 4 分,第(2)小题 3 分,第(3)小题 5 分)ax bx 3与 y 轴交于点 A ,与 x 轴分别交于点如图在直角坐标平面内,抛物线 y 2 B (-1,0)、点 C (3,0),点 D 是抛物线的顶点. (1)求抛物线的表达式及顶点 D 的坐标; (2)联结 AD 、DC ,求AC D 的面积;(3)点 P 在直线 DC 上,联结 OP ,若以 O 、P 、C 为顶点的三角形与△ABC 相似,求点 P 的坐标.备用图第24 题图24.(本题满分 12 分,第(1)小题 4 分,第(2)小题 3 分,第(3)小题 5 分)y axbx 3 上解:(1) 点B (-1,0)、C (3,0)在抛物线 2 a b 3 09a 3b 3 0,解得 b 2a 1∴ ( 2分)( 2分)y x 2x 3 ,顶点D 的坐标是(1,-4)∴抛物线的表达式为2 AC3 2 CD 2 5 AD 2(2)∵A (0,-3),C (3,0),D (1,-4) ∴ , ,∴CD∴SAC AD2∴ CAD90 ( 2分) (1 分)22 1 2 12AC AD 3 2 2 3.ACDADBOOAB OACACAOCADAOB 90 ACD(3)∵ , 2,∴△CAD ∽△AOB ,∴ ∵OA =OC , AOC 90 OCA 45BAC ∴ OACOAB OCA ACD BCD∴ ,即 ( 1分)若以O 、P 、C 为顶点的三角形与△ABC 相似 ,且△ABC 为锐角三角形 POC 则 也为锐角三角形,点P 在第四象限(由点C (3,0),D (1,-4)得直线CD 的表达式是y 2x 6,设P(t ,2t 6) 0 t 3 )OH t PH 6 2t , 过P 作PH ⊥OC ,垂足为点H ,则PH OH AO BOPOC ABC 时,由tan POC tan ABC①当 得, 6 2t 6 5 6 183,解得 t , ∴ P ( , ) (2 分)∴t 5 51②当PO C AC B时,由 t an PO C tan ACB tan 45 1P H 得 O H1,6 2t 1,解得t 2 ,∴ P (2,2) 2 ( 2分)∴t6 18) P (2,2)综上得 P ( , 或 1 5 52 崇明区24.(本题满分 12分,第(1)、(2)、(3)小题满分各 4分)已知抛物线经过点 、 B(4,1) 、C (3, 0) . A(0, 3) (1)求抛物线的解析式;(2)联结 AC 、BC 、AB ,求BAC 的正切值;(3)点 P 是该抛物线上一点,且在第一象限内,过点P 作 交 y 轴于点 ,当点GP GAPG 在点 A 的上方,且 △AP G 与△ABC 相似时,求点 P 的坐标.yABxOC(第 24 题图)24.(本题满分 12分,每小题 4分)axbx c (a 0) 解:(1)设所求二次函数的解析式为 y 2 ,………………………1分 16a 4b c 1,3b c 0,将 A (0 ,3)、 B ( 4 ,)、C (3,0 )代入,得 9a c 3.12 a5 2 解得b………2分 c 31 5 x x 3 所以,这个二次函数的解析式为 y2 ……………………………1分2 20 3C 3 0(2)∵ A ( , )、 B ( ,)、( , )43 2 BC 22 5 , , AB∴ AC ∴ AC BC AB 22 2 ∴∠ACB90………………………………………………………2 分B CA C 2 1 ∴tan∠BA C……………………………………………2 分 3 2 3(3)过点 P 作 PH⊥y 轴,垂足为 H1 5 1 5 P (x , x x 3) H (0, x x 3) 设2 ,则 2 2 2 2 20 3∵ A ( , )1 5x x , P H x∴ A H 2 2 2 ∵∠ACB∠APG 90∴当△APG 与△ABC 相似时,存在以下两种可能: 13∠PA G ∠CAB∠ ∠ 则tan PA G tan CAB 1° P H 1 1 xx11即 ∴解得………………………1 分1 2 5 A H 3 3 x x2 2 ∴点 P 的坐标为(11,36)……………………………………………………1 分∠PA G ∠ABC 则tan ∠PA Gt an ∠AB C 32° P Hx 173 3解得 x 即∴ …………………………1 分1 2 5 A H 3xx 2 2 17 44( , ) 3 9P ∴点 的坐标为 ……………………………………………………1 分 奉贤区24.(本题满分 12 分,每小题满分各 4 分)已知平面直角坐标系 (如图 8),抛物线 y x 2mx 3m (m 0) 与 x 轴交于点xOy 2 2 yA、B(点A在点B左侧),与轴交于点C,顶点为D,对称轴y为直线,过点C作直线的垂线,垂足为点E,联结D C、BC.(1)当点C(0,3)时,①求这条抛物线的表达式和顶点坐标;②求证:∠DCE=∠BCE;(2)当CB平分∠DCO时,求的值.m黄浦区24.(本题满分12分)x bx c已知抛物线y经过点A(1,0)和B(0,3),其顶点为D.2(1)求此抛物线的表达式;(2)求△ABD的面积;(3)设P为该抛物线上一点,且位于抛物线对称轴右侧,作PH⊥对称轴,垂足为H,若△DPH与△AOB相似,求点P的坐标.01b c24.解:(1)由题意得:,———————————————————(2分)3cb 4解得:,—————————————————————————(1分)3cx 4x 3所以抛物线的表达式为y.——————————————(1分)2(2)由(1)得D(2,﹣1),———————————————————(1分)作DT⊥y轴于点T,12112则△ABD的面积=24131211.————————(3分)p 2.————————————————(1分)由△DPH与△AOB相似,易知∠AOB=∠PHD=90°,24p 3(3)令P p,p2p 4p 31p 4p 31122所以3或,————————————(2分)p 2p 2375p或解得:p,378所以点P 的坐标为(5,8),,.————————————————(1分)39金山区24.(本题满分12分,每小题4分)x bx c平面直角坐标系xOy中(如图8),已知抛物线y经过点A(1,0)和B(3,0),2与y轴相交于点C,顶点为P.(1)求这条抛物线的表达式和顶点P的坐标;(2)点E在抛物线的对称轴上,且EA=EC,求点E的坐标;(3)在(2)的条件下,记抛物线的对称轴为直线MN,点Q在直线MN右侧的抛物线上,∠MEQ=∠NEB,求点Q的坐标.图8的图像经过点A (1,0)和B(3,0),x bx c24.解:(1)∵二次函数y 2b c104c 3,∴,解得:b .……………………………(2分)93b c0x4x3∴这条抛物线的表达式是y…………………………………(1分)2顶点P 的坐标是(2,-1).………………………………………………(1分)x4x3的对称轴是直线x2,设点E的坐标是(2,m).…(1分)(2)抛物线y根据题意得:(2∴点E 的坐标为(2,2).…………………………………………………(1分)21)(m 0)(20)(m3),解得:m=2,…(2分)22224t3)(3)解法一:设点Q的坐标为(t,t,记MN与x轴相交于点F.2作QD⊥MN,垂足为D,t2DE t4t32t4t1………………………(1分)则D Q,22∵∠QDE=∠BFE=90°,∠QED=∠BEF,∴△QDE∽△BFE,…………………(1分)t2t 24t1D E∴,∴,12BF EF解得t 1(不合题意,舍去),t5.……………………………(1分)125∴t,点E的坐标为(5,8).…………………………………………(1分)解法二:记MN与x轴相交于点F.联结AE,延长AE交抛物线于点Q,∵AE=BE,EF⊥AB,∴∠AEF=∠NEB,又∵∠AEF=∠MEQ,∴∠QEM=∠NEB,………………………………(1分)4t3)点Q是所求的点,设点Q的坐标为(t,t,24t3作QH⊥x轴,垂足为H,则QH=t2,OH=t,AH=t-1,21EF AF∵EF⊥x轴,∴EF ∥QH,∴,∴,………(1分)t 24t3t1Q H A H解得t 1(不合题意,舍去),t5.……………………………………(1分)125∴t,点E的坐标为(5,8).…………………………………………(1分)静安区24.(本题满分12分,第(1)小题满分4分,第(2)小题满分4分,第(3)小题满分4 分)在平面直角坐标系xOy中,已知点B(8,0)和点C(9,3).抛物线y ax8ax c2(a,c是常数,a≠0)经过点B、C,且与x轴的另一交点为A.对称轴上有一点M ,满足yMA=MC.(1)求这条抛物线的表达式;(2)求四边形ABCM的面积;(3)如果坐标系内有一点D,满足四边形ABCD是等腰梯形,且AD//BC,求点D的坐标.O xB·C24.(本题满分12分,第(1)小题4分,第(2)小题4分,第(3)小题4分)第24题图8a2ax 4 0 解:(1)由题意得:抛物线对称轴 ,即 x . …………(1分), …………(1分) 点 B (8,0)关于对称轴的对称点为点 A (0,0)∴c 1ax8ax a 将 C (9,-3)代入 y 2 ,得 …………………………(1分) …………………………(1分)3 1 8 x x ∴抛物线的表达式: y 2 3 3(2)∵点 M 在对称轴上,∴可设 M (4,y ) MC 又∵MA =MC ,即 M A 2 2 y 5 (y 3) ∴ 42, 解得 y =-3, ∴M (4,-3) …………………(2分)2 2 2 ∵MC //AB 且 MC ≠AB , ∴四边形 ABCM 为梯形,,yAB =8,MC =5,AB 边上的高 h = y = 3 M1 1 392(AB M C) M H(8 5)3 ∴ S …………(2分)2 2 kx b (3) 将点 B (8,0)和点 C (9,﹣3)代入 y可得B CO x8k b 0 k 3 BA9k b 3,解得b 24C M3 k3 y3x…(1分)A D由题意得,∵AD //BC , k∴ , B CA D又∵AD 过(0,0),DC =AB =8,9)(3x 3) 8 设 D (x ,-3x ) (x , …………………………(1分) …………………………(1分) 2 2 2 135解得 x1(不合题意,舍去), x1239 5 13 39( , ).……………………(1分)3x ∴ y ∴点 D 的坐标 5 5 闵行区24.(本题满分 12分,其中每小题各 4分)如图,已知在平面直角坐标系 xOy 中,抛物线 y ax 2x c 与 x 轴交于 2 点 A 和点 B (1,0),与 y 轴相交于点 C (0,3).yD(1)求抛物线的解析式和顶点 D 的坐标; (2)求证:∠DAB=∠ACB ;(3)点 Q 在抛物线上,且△ADQ 是以 AD 为 底的等腰三角形,求 Q 点的坐标.24.解:(1)把 B (1,0)和 C (0,3)代入 y ax 2xc 中, 2 9 6 0 1 a c a得 ,解得 .……………………………………(2 分)c 3 c 3∴抛物线的解析式是: y x 2x 3 .……………………………(1 分) 2 ∴顶点坐标 D (-1,4).……………………………………………(1 分) (2)令 y 0 ,则 x 2x 3 0 , , ,∴A (-3,0)x 1x 3 2 1 2 ∴O A OC 3 ,∴∠CAO =∠OCA .…………………………………(1 分)1t an O CB 在 Rt B O C中, .………………………………(1 分)O C 3 ∵ A C 3 2 , D C 2 , A D 2 5 , ∴ AC DC 20 , A D 20 ;2 2 2 ∴ AC DC AD , AC D 是直角三角形且ACD 90 ,2 2 2 D C 1∴ t an DA C,A C 3 又∵∠DAC 和∠OCB 都是锐角,∴∠DAC =∠OCB .…………………(1 分) ∴ DA C CA O BC O OCA ,即 DAB ACB .……………………………………………………(1 分) (3)令Q(x , 且满足 y x 2x 3 , ,0), D(1,4)y) A( 32 ∵ AD Q 是以 AD 为底的等腰三角形,∴Q D QA ,即(x 3) y (x 1) (y 4) ,2 2 2 2 2 2 化简得: .………………………………………………(1 分) ,……………………………………………………(1 分)x 2 2y 0 x 2 2y 0由 y x 2 2x 33 413 41 x 2 x4 11 41 8 4 11 41 8 1 解得 , . ,y y 213 41 11 41 3 41 11 41 ∴点 Q 的坐标是 .…(2 分) , ,4 8 4 8普陀区24.(本题满分 12 分)如图 10,在平面直角坐标系 中,直线 与 x 轴、 轴分别相交于点 、 ,y kx 3 y A BxOy 1 7 C 2,2 并与抛物线 y x bx 的对称轴交于点 ,抛物线的顶点是点 . D2 4 2 (1)求k 和b 的值; (2)点G 是 轴上一点,且以点 、C 、G 为顶点的三角形与△BC D 相似,求点G 的坐 y B 标;(3)在抛物线上是否存在点 :它关于直线 的对称点 恰好在 轴上.如果存在,直FE AB y 接写出点 的坐标,如果不存在,试说明理由.Ex图 1024.解:C 2,2 1(1) 由直线 经过点y kx 3,可得 k. ··········· (1 分) 21 7 由抛物线 y x bx 的对称轴是直线 ,可得 . ····· (1 分) x2 b 1 2 4 2 1(2) ∵直线 y x 3与 x 轴、 轴分别相交于点 、 ,A By 2 6,0 0,3 ∴点 的坐标是 A ,点 的坐标是 B. ············ (2 分)9∵抛物线的顶点是点 ,∴点 的坐标是 2, . ·········· (1 分)D D 20,m∵点G 是 轴上一点,∴设点G 的坐标是.y ∵△BCG 与△BCD 相似,又由题意知,GB C BCD ,∴△BCG 与△ 相似有两种可能情况: ·············· (1 分) B C D 3 m5 B G B C0,1 = C B C D = = ,∴点 的坐标是 ①如果 ,那么 ,那么,解得 ,解得 . (1 分) m 1G 5 2 53 m5 B G B C m =1 1 = C D C B = 0, ②如果 ,∴点 的坐标是 G .(1 分) 5 22 2 51 和 0, 0,1综上所述,符合要求的点G 有两个,其坐标分别是.299 (3)点 的坐标是 1,或 2, .················· (2 分+2 分) E 42青浦区24.(本题满分 12 分,第(1)、(2)、(3)小题,每小题 4 分)y ax 2 b x 3 已知:如图 8,在平面直角坐标系 xOy 中,抛物线 的图像与 x 轴交于 点2上,将抛物线沿射线AC 的方向平移,当顶A (3,0),与 y 轴交于点B ,顶点C 在直线 x点 C 恰好落在 y 轴上的点 D 处时,点 B 落在点 E 处. (1)求这个抛物线的解析式;(2)求平移过程中线段 BC 所扫过的面积;(3)已知点 F 在 x 轴上,点 G 在坐标平面内,且以点 C 、E 、F 、G 为顶点的四边形是矩形, 求点 F 的坐标.yy .BBOA xOA x图 8备用图b24.解:(1)∵顶点 C 在直线 x 2上,∴ x 2a2 ,∴b 4a . ····· (1 分)y ax bx 3 9a3b 3=0,······ (1 分) 将 A (3,0)代入 ,得 2 1 b 4,解得a . ···················· (1 分) y x 4x 3 ∴抛物线的解析式为 . ············· (1 分) 2(2)过点 C 作 CM ⊥x 轴,CN ⊥y 轴,垂足分别为 M 、N .y x 4x 3 x 2 1 2 1 ∵ = ,∴C (2, ). ········ (1 分)2∵C M∴O D MA 1,∴∠MAC =45°,∴∠ODA =45°, OA 3 . ······················ (1 分)y x 4x 3 y ∵抛物线 与 轴交于点 ,∴B (0, ), B 23 ∴ B D6. ······················· (1 分) ∵抛物线在平移的过程中,线段 BC 所扫过的面积为平行四边形 BCDE 的面积,1S 2S2 BD CN 62 12 ∴ . ······· (1 分)2B C D EB C D(3)联结 CE .∵四边形 BC D E 是平行四边形,∴点O 是对角线C E 与 的交点, B D OC 5 即 OE .(i )当 CE 为矩形的一边时,过点 C 作CFCE ,交 轴于点 ,xF 11(a,0),在 Rt O C F 中,OF=O C CF 设点 F , 2 2 2 1 1 1 1 5 25(a 2) 5 a F ( ,0) 1 即 a 2 ,解得 ,∴点 ·········· (1 分)2 2 5 (- ,0) 2 同理,得点 F ······················ (1 分) 2(ii )当 CE 为矩形的对角线时,以点O 为圆心,O C 长为半径画弧分别交 轴于点 x F 、 F ,可得 O F =O FO C 5 ,得点 F ( 5,0)、 F (- 5,0)· (2 分)343 4345 5( ,0) (- ,0) ( 5,0) (- 5,0 ) , F .综上所述:满足条件的点有F , F ), F 2 2 1 2 3 4 松江区24.(本题满分 12 分,每小题各 4 分)如图,已知抛物线 y=ax +bx 的顶点为 C (1, ),P 是抛物线上位于第一象限内的一 1 2 点,直线 OP 交该抛物线对称轴于点 B ,直线 CP 交 x 轴于点 A . (1)求该抛物线的表达式;(2)如果点 P 的横坐标为 m ,试用 m 的代数式表示线段 BC 的长; (3)如果△ABP 的面积等于△ABC 的面积,求点 P 坐标.yPBOAxC24.(本题满分 12 分,每小题各 4 分)解:(1)∵抛物线 y=ax +bx 的顶点为 C (1, )1 y2 a b 1P∴ …………………………………2 分b1 2aBOAxa 1 解得:…………………………………1分2b ∴抛物线的表达式为:y=x-2x ;…………………………1分 2 (2)∵点P 的横坐标为m ,∴P 的纵坐标为:m -2m ……………………………1分 2 令BC 与x 轴交点为M ,过点P 作PN ⊥x 轴,垂足为点N ∵P 是抛物线上位于第一象限内的一点, ∴PN = m -2m ,ON =m ,O M =12 P NB Mm 2 2m B M得O N O M由 ………………………1分 m 1 ∴ BM =m -2…………………………………………………1分 ∵ 点C 的坐标为(1, ),1 ∴ BC= m -2+1=m -1………………………………………1分(3)令P (t ,t -2t ) ………………………………………………1分 2 △ABP 的面积等于△ABC 的面积 ∴AC =AP过点P 作PQ ⊥BC 交BC 于点Q ∴CM =MQ =1 ∴t -2t =1…………………………………………………1分2 t 1 2 t 1 2 ∴( 舍去)………………………………1分 ∴ P 的坐标为(1 2,1)……………………………………1分徐汇区1 1x 2 x y x b x c 24. 如图,已知直线y 与轴、 轴分别交于点B 、C ,抛物线 y2 2 2 过点B 、C ,且与x 轴交于另一个点A .(1)求该抛物线的表达式;(2)点M 是线段B C 上一点,过点M 作直线 ∥ 轴yl 交该抛物线于点N ,当四边形O M N C 是平行四边形时, 求它的面积;(3)联结AC ,设点D 是该抛物线上的一点,且满足DBA CA O ,求点D 的坐标.杨浦区24、(本题满分12分,第(1)小题4分,第(2)小题4分,第(3)小题4分)如图8,在平面直角坐标系中,抛物线于X轴交于点A、B,于y轴交于点C,直线经过点A、C,点P为抛物线上位于直线AC上方的一个动点。
2018年上海市各区二模卷第25题

页脚内容12018年上海市各区二模卷第25题1. (18徐汇)已知四边形ABCD 是边长为10的菱形,对角线AC 、BD 相交于点E ,过点C 作CF ∥DB 交AB 延长线于点F ,联结EF 交BC 于点H . (1)如图1,当EF BC ⊥时,求AE 的长;(2)如图2,以EF 为直径作⊙O ,⊙O 经过点C 交边CD 于点G (点C 、G 不重合),设AE 的长为x ,EH 的长为y ;① 求y 关于x 的函数关系式,并写出定义域;② 联结EG ,当DEG ∆是以DG 为腰的等腰三角形时,求AE 的长.2. (18杨浦)如图,在梯形ABCD 中,AD ∥BC ,5AB DC ==,1AD =,9BC =,点P 为边BC 上一动点,作PH DC ⊥,垂足H 在边DC 上,以点P 为圆心PH 为半径画圆,交射线PB 于点E . (1)当圆P 过点A 时,求圆P 的半径;(2)分别联结EH 和EA ,当ABE ∆∽CEH ∆时,以点B 为圆心,r 为半径的圆B 与圆P 相交,试求圆B 的半径r 的取值范围;(3)将劣弧¼EH沿直线EH 翻折交BC 于点F ,试通过计算说明线段EH 和EF 的比值为定值,并求出页脚内容2此定值.3. (18黄浦)如图,四边形ABCD 中,90BCD D ∠=∠=︒,E 是边AB 的中点,已知1AD =,2AB =. (1)设BC x =,CD y =,求y 关于x 的函数关系式,并写出定义域; (2)当70B ∠=︒时,求AEC ∠的度数; (3)当ACE ∆为直角三角形时,求边BC 的长.4. (18宝嘉)在圆O 中,AO 、BO 是圆O 的半径,点C 在劣弧AB 上,10OA =,12AC =,页脚内容3AC ∥OB ,联结AB .(1)如图,求证:AB 平分∠OAC ;(2)点M 在弦AC 的延长线上,联结BM ,如果△AMB 是直角三角形,请你在图中画出点M 的位置并求出CM 的长;(3)如图,点D 在弦AC 上,与点A 不重合,联结OD 与弦AB 交于点E ,设点D 与点C 的距离为x ,△OEB 的面积为y ,求y 与x 的函数关系式,并写出自变量x 的取值范围.5. (18长宁)在圆O 中,C 是弦AB 上的一点,联结OC 并延长,交劣弧AB 于点D ,联结AO 、BO 、AD 、BD ,已知圆O 的半径长为5,弦AB 的长为8. (1)如图,当点D 是弧AB 的中点时,求CD 的长;(2)如图,设AC x =,ACOOBDS y S =V V ,求y 关于x 的函数解析式并写出定义域; (3)若四边形AOBD 是梯形,求AD 的长.6. (18闵行)如图,已知在Rt△ABC中,90ACB︒∠=,6BC=,点F在线段AB上,以点B为AC=,8圆心,BF为半径的圆交BC于点E,射线AE交圆B于点D(点D、E不重合).(1)如果设BF x=,求y与x之间的函数关系式,并写出它的定义域;=,EF y(2)如果»»ED EF=,求ED的长;2(3)联结CD、BD,请判断四边形ABDC是否为直角梯形?说明理由.页脚内容47. (18奉贤)已知,如图,在半径为2的扇形AOB中,90∠=︒,点在C半径OB上,AC的垂直AOB平分线交OA于点D,交弧AB于点E,联结BE、CD.(1)若C是半径OB中点,求OCD∠的正弦值;(2)若E是弧AB的中点,求证:2=⋅;BE BO BC(3)联结CE,当DCE∆是以CD为腰的等腰三角形时,求CD的长.8. (18松江)如图,已知Rt ABCAC=,以点C为圆心,CB为半径的BC=,3∠=︒,2∆中,90ACB圆交AB于点D,过点A作AE∥CD,交BC延长线于点E.(1)求CE的长;(2)P是CE延长线上一点,直线AP、CD交于点Q.①如果ACQ∆,求CP的长;∆∽CPQ②如果以点A为圆心,AQ为半径的圆与⊙C相切,求CP的长.页脚内容59. (18普陀)已知P是⊙O的直径BA延长线上的一个动点,P∠的另一边交⊙O于点C、D,两点位于AB的上方,6AB=,OP m=,1 sin3P=,如图所示,另一个半径为6的⊙1O经过点C、D,圆心距1OO n=.(1)当6m=时,求线段CD的长;(2)设圆心1O在直线AB上方,试用n的代数式表示m;(3)1POO∆在点P的运动过程中,是否能成为以1OO为腰的等腰三角形,如果能,试求出此时n的值;如果不能,请说明理由.CBADE备用图CBADE页脚内容6页脚内容710. (18崇明)如图,已知ABC △中,8AB =,10BC =,12AC =,D 是AC 边上一点,且2AB AD AC =⋅,联结BD ,点E 、F 分别是BC 、AC 上两点(点E 不与B 、C 重合),AEF C ∠=∠,AE 与BD 相交于点G . (1)求证:BD 平分ABC ∠;(2)设BE x =,CF y =,求y 与x 之间的函数关系式; (3)联结FG ,当GEF △是等腰三角形时,求BE 的长度.11. (18青浦)如图1,已知扇形MON,∠MON =90o ,点B 在弧MN 上移动,联结BM ,作OD ⊥BM ,垂足为点D ,C 为线段OD 上一点,且OC =BM ,联结BC 并延长交半径OM 于点A ,设OA = x ,∠COM 的正切值为y .(1)如图2,当AB ⊥OM 时,求证:AM =AC ; (2)求y 关于x 的函数关系式,并写出定义域;ABCDGEF(备用图)ABCD(3)当△OAC为等腰三角形时,求x的值.12. (18金山)如图,已知在梯形ABCD中,AD∥BC,AB=DC=AD=5,3 sin5B,P是线段BC上一点,以P为圆心,PA为半径的⊙P与射线AD的另一个交点为Q,射线PQ与射线CD相交于点E,设BP=x.(1)求证△ABP∽△ECP;(2)如果点Q在线段AD上(与点A、D不重合),设△APQ的面积为y,求y关于x的函数关系式,并写出定义域;(3)如果△QED与△QAP相似,求BP的长.O MNDCBA O MNDCBANMOAB CD备用图页脚内容8页脚内容913. (18静安)如图,平行四边形ABCD 中,已知6AB =,9BC =,1cos 3ABC ∠=,对角线AC 、BD 交于点O ,动点P 在边AB 上,⊙P 经过点B ,交线段PA 于点E ,设BP x =. (1)求AC 的长;(2)设⊙O 的半径为y ,当⊙P 与⊙O 外切时,求y 关于x 的函数关系式,并写出定义域; (3)如果AC 是⊙O 的直径,⊙O 经过点E ,求⊙O 与⊙P 的圆心距OP 的长.14. (18虹口)如图,在梯形ABCD 中,AD ∥BC ,90C ∠=︒,5DC =,以CD 为半径的⊙C 与以AB 为半径的⊙B 相交于点E 、F ,联结EF 交BC 于点G .(1)设BC 与⊙C 相交于点M ,当BM AD =时,求⊙B 的半径;(2)设BC x =,EF y =,求y 关于x 的函数关系式,并写出它的定义域;页脚内容10(3)当10BC =时,点P 为平面内一点,若⊙P 与⊙C 相交于点D 、E ,且以A 、E 、P 、D 为顶点的四边形是梯形,请直接写出⊙P 的面积.(结果保留π)15.(18浦东)如图9,已知在△ABC 中,AB=AC ,21tan =B ,BC =4,点E 是在线段BA 延长线上一点,以点E 为圆心,EC 为半径的圆交射线BC 于点C 、F (点C 、F 不重合),射线EF 与射线AC 交于点P . (1)求证:AC AP AE ⋅=2;(2)当点F 在线段BC 上,设CF =x ,△PFC 的面积为y ,求y 关于x 的函数解析式及定义域;(3)当21=EF FP 时,求BE 的长.2016年度超声影像科工作总结页脚内容11。
2018年上海市宝山区、嘉定区中考二模数学试题及答案

2018年上海市宝山区、嘉定区中考二模数学试题及答案2018学年第二学期宝山嘉定区联合模拟考试数学试卷(满分150分,考试时间100分钟)同学们请注意:1.本试卷含三个大题,共25题;2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题:(本大题共6题,每题4分,满分24分) 1.2-是2的(▲)(A )相反数;(B )倒数;(C )绝对值;(D )平方根.2.不等式组≥->+125,523x x 的解在图1所示的数轴上表示为(▲)(A )(B )(C )(D )3.某运动队为了选拔“神枪手”,举行射击比赛,最后由甲、乙两名选手进入决赛,在相同条件下,两人各射靶10次,经过统计计算,甲、乙两名选手的总成绩都是99.6环,甲的方差是0. 27,乙的方差是0. 18,则下列说法中,正确的是(▲)(A )甲的成绩比乙的成绩稳定;(B )乙的成绩比甲的成绩稳定;(C )甲、乙两人成绩一样稳定;(D )无法确定谁的成绩更稳定.4.已知矩形的面积为20,则图2给出的四个图像中,能大致呈现矩形的长y 与宽x 之间的函数关系的是(▲)图 15.如果要证明平行四边形ABCD 为正方形,那么我们需要在四边形ABCD 是平行四边形的基础上,进一步证明(▲)(A )AB =AD 且AC⊥BD ;(B )AB =AD 且AC =BD ;(C )∠A =∠B 且AC =BD ;(D )AC 和BD 互相垂直平分.6.如图3,在梯形ABCD 中,AD ∥BC ,AB =6,BC=9,CD =4,DA =3,则分别以AB 、CD 为直径的⊙P 与⊙Q 的位置关系是(▲)(A )内切;(B )相交;(C )外切;(D )外离. 二、填空题:(本大题共12题,每题4分,满分48分)【请将结果直接填入答题纸的相应位置】7.计算)1(-x x 的结果是▲ .8.分式x 2-1x +1的值为零,则x 的值为▲ . 9.一元二次方程2x x =的解为▲ .10.如果关于x 的一元二次方程02)12(22=-+++-k x k x 有实数根,那么实数k 的取值范围是▲ .11.方程(x +3)2-x =0的解是▲ .12.已知反比例函数x k y 1+=的图像在第二、四象限内,那么常数k 的取值范围是▲ .13.合作交流是学习教学的重要方式之一,某校九年级六个班中,每个班合作学习小组的个数分别是:5、7、7、6、7、6,这组数据A B CD 图3 (A) (B) (C) (D)图2。
2018年上海市嘉定区中考化学二模试卷

2018年上海市嘉定区中考化学二模试卷一、单项选择题(共20分, 每题1分)1.(1.00分)空气成分中, 体积分数约占21%的是()A. 氧气B. 稀有气体C. 氮气D. 二氧化碳2. (1.00分)属于纯净物的是()A. 蒸馏水B. 可乐C. 大理石D. 稀硫酸3.(1.00分)“含氟牙膏”中的“氟”可以防止龋齿, 这里的“氟”指的是()A. 单质B. 元素C. 原子D. 分子4. (1.00分)加水能形成溶液的是()A. 食用油B. 食盐C. 面粉D. 细沙5. (1.00分)成语中体现化学变化是()A. 砸锅卖铁B. 木已成舟C. 火上浇油D. 滴水成冰6.(1.00分)镁带在空气中燃烧后的产物中有一种物质为氮化镁(Mg3N2), 其中氮元素的化合价为()A. ﹣1B. ﹣3C. +1D. +37. (1.00分)下列环境问题与物质对应不相关的是()A. 温室效应﹣﹣氮气B. 臭氧层空洞﹣﹣氟利昂(氟氯烃)C. 酸雨﹣﹣二氧化硫D. 水体富营养化﹣﹣含磷洗衣粉8. (1.00分)关于分子和原子两种微粒的叙述正确的是()A. 物质只能由分子构成B. 分子和原子都在不停运动C. 分子是保持物质性质的一种微粒D. 分子和原子在化学变化中都能够再分9.(1.00分)根据反应: 3Fe+4H2O X+4H2, 推断X的化学式为()A. FeOB. Fe2O3C. Fe3O4D. 无法确定10. (1.00分)物质用途与其性质对应错误的是()A. 石墨电极﹣﹣导电性B. 稀有气体作霓虹灯﹣﹣稳定性C. 氢气作燃料﹣﹣可燃性D. 盐酸除铁锈﹣﹣酸性11. (1.00分)物质的俗名、化学式一致的是()A. 胆矾CuSO4B. 熟石灰CaOC. 纯碱NaOHD. 水银Hg12. (1.00分)下列实验基本操作中正确的是()A.吸取液体B.倾倒液体C.过滤D.实验室制氧气13. (1.00分)有关实验现象描述错误的是()A. 木炭在空气中燃烧发红B.硫磺在空气中燃烧, 产生淡蓝色火焰C. 红磷在空气中燃烧产生白烟D.铁丝在空气中燃烧, 火星四射, 生成黑色固体14. (1.00分)如图X、Y、Z表示某些物质的pH值。
2018年上海市各区二模卷第25题

2018年上海市各区二模卷第25题1. (18徐汇)已知四边形ABCD 是边长为10的菱形,对角线AC 、BD 相交于点E ,过点C 作CF ∥DB 交AB 延长线于点F ,联结EF 交BC 于点H . (1)如图1,当EF BC ⊥时,求AE 的长;(2)如图2,以EF 为直径作⊙O ,⊙O 经过点C 交边CD 于点G (点C 、G 不重合),设AE 的长为x ,EH 的长为y ;① 求y 关于x 的函数关系式,并写出定义域;② 联结EG ,当DEG ∆是以DG 为腰的等腰三角形时,求AE 的长。
2. (18杨浦)如图,在梯形ABCD 中,AD ∥BC ,5AB DC ==,1AD =,9BC =,点P 为边BC 上一动点,作PH DC ⊥,垂足H 在边DC 上,以点P 为圆心PH 为半径画圆,交射线PB 于点E .(1)当圆P 过点A 时,求圆P 的半径;(2)分别联结EH 和EA ,当ABE ∆∽CEH ∆时,以点B 为圆心,r 为半径的圆B 与圆P 相交,试求圆B 的半径r 的取值范围;(3)将劣弧EH 沿直线EH 翻折交BC 于点F ,试通过计算说明线段EH 和EF 的比值为定值,并求出此定值.3。
(18黄浦)如图,四边形ABCD 中,90BCD D ∠=∠=︒,E 是边AB 的中点,已知1AD =,2AB =.(1)设BC x =,CD y =,求y 关于x 的函数关系式,并写出定义域; (2)当70B ∠=︒时,求AEC ∠的度数;(3)当ACE ∆为直角三角形时,求边BC 的长.4。
(18宝嘉)在圆O 中,AO 、BO 是圆O 的半径,点C 在劣弧AB 上,10OA =,12AC =, AC ∥OB ,联结AB .(1)如图,求证:AB 平分∠OAC ;(2)点M 在弦AC 的延长线上,联结BM ,如果△AMB 是直角三角形,请你在图中画出点M 的位置并求出CM 的长;(3)如图,点D 在弦AC 上,与点A 不重合,联结OD 与弦AB 交于点E ,设点D 与点C 的距离为x ,△OEB 的面积为y ,求y 与x 的函数关系式,并写出自变量x 的取值范围.5. (18长宁)在圆O 中,C 是弦AB 上的一点,联结OC 并延长,交劣弧AB 于点D ,联结AO 、BO 、AD 、BD ,已知圆O 的半径长为5,弦AB 的长为8. (1)如图,当点D 是弧AB 的中点时,求CD 的长; (2)如图,设AC x =,ACO OBDS y S=,求y 关于x 的函数解析式并写出定义域;(3)若四边形AOBD 是梯形,求AD 的长。
2018上海市黄浦区2018届中考二模数学试题含答案,推荐文档

黄浦区2018年九年级模拟考数学试卷(考试时间:100分钟 总分:150分)一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个是正确的,选择正确项的代号并填涂在答题纸的相应位置上•】2 3 1.下列实数中,介于一与一之间的是()32(A )2 ;(B3 ;(C ) 22 22;( D )72.下列方程中没有实数根的是 ( )2(A ) x x 1 0 ;(B ) 2x x 10 ;(C ) x 2 1 0 ;(D ) x 2 x 0 .3. 一个反比例函数与一个一次函数在同一坐标平面内的图像如图示,如果其中的反比例函数解析式为k y,那么该一次函数可能的解析式是()x(A ) y kx k ; (B ) y kx k ;(C ) y kx k ; (D ) y kx k .4.一个民营企业10名员工的月平均工资如下表,则能较好反映这些员工月平均工资水平的是()(工资单位:万元)(A )平均数; (B )中位数; (C )众数;(D )标准差.2018年4月uuu mu5•计算:AB BA ()uuu urn r (A) AB ;( B ) BA ;(C ) 0 ;( D ) 0 •6.下列命题中,假命题是()(A) 如果一条直线平分弦和弦所对的一条弧,那么这条直线经过圆心,并且垂直于这条弦; (B) 如果一条直线平分弦所对的两条弧,那么这条直线经过圆心,并且垂直于这条弦;(C) 如果一条直线经过圆心,并且平分弦,那么该直线平分这条弦所对的弧,并且垂直于这条弦; (D) 如果一条直线经过圆心,并且垂直弦,那么该直线平分这条弦和弦所对的弧. 二、填空题:(本大题共12题,每题4分,满分48分)17 .化简: ------ = ______ •V 2 1&因式分解:x 2 x 12 ____ .9•方程x 1 . 2x 5的解是 ________11 •已知点P 位于第三象限内,且点 P 到两坐标轴的距离分别为 2和4,若反比例函数图像经过点则该反比例函数的解析式为 _______ •12 •如果一次函数的图像经过第一、二、四象限,那么其函数值y 随自变量x 的值的增大而 ________(填“增大”或“减小”)13 •女生小琳所在班级共有 40名学生,其中女生占60%.现学校组织部分女生去市三女中参观,需要从小琳所在班级的女生当中随机抽取一名女生参加,那么小琳被抽到的概率是_____ •14 •已知平行四边形相邻两个内角相差 40 °则该平行四边形中较小内角的度数是 ____________ •10 .不等式组2x -1x 3的解集是P ,15 •半径为1的圆的内接正三角形的边长为uju r16 .如图,点D 、E 分别为△ ABC 边CA 、CB 上的点,已知DE // AB ,且DE 经过△ ABC 的重心,设CA a ,ujrr r uuir r r CB b ,贝V DE ________ .(用 a 、b 表示)的中点,则线段 MN 的长为 ________18 .如图,将矩形 ABCD 沿对角线AC 折叠,使点B 翻折到点E 处,如果DE : AC=1 : 3,那么 AD : AB=_____ .三、解答题:(本大题共7题,满分78分) 19 .(本题满分10分)1 o计算:22 23 ? J2018 2018 3 2丁3|20.(本题满分10 分)解方程组:X 2 2xy y 2 9x 2 y 2521.(本题满分10分)17 .如图,在四边形ABCD 中,ABC ADC 90 , AC 26, BD 24 , M 、N 分别是 AC 、BD(第 16 题)(第 17 题) (第 18 题)2 如图,AH是厶ABC的高,D是边AB上一点,CD与AH交于点E.已知AB=AC=6, cosB=±,3AD : DB=1 : 2.(1 )求厶ABC的面积;(2 )求CE : DE.22 .(本题满分10 分)今年1月25日,上海地区下了一场大雪•这天早上王大爷去买菜,他先去了超市,发现蔬菜普遍涨价了,青菜、花菜和大白菜这两天的价格如下表•王大爷觉得超市的菜不够新鲜,所以他又去了菜市场,他花了30元买了一些新鲜菠菜,他跟卖菜阿姨说:“你今天的菠菜比昨天涨了5元/斤。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年上海市各区二模卷第25题
1. (18徐汇)已知四边形ABCD 是边长为10的菱形,对角线AC 、BD 相交于点E ,过点C 作CF ∥DB 交AB 延长线于点F ,联结EF 交BC 于点H . (1)如图1,当EF BC ⊥时,求AE 的长;
(2)如图2,以EF 为直径作⊙O ,⊙O 经过点C 交边CD 于点G (点C 、G 不重合),设AE 的长为x ,EH 的长为y ;
① 求y 关于x 的函数关系式,并写出定义域;
② 联结EG ,当DEG ∆是以DG 为腰的等腰三角形时,求AE 的长.
!
2. (18杨浦)如图,在梯形ABCD 中,AD ∥BC ,5AB DC ==,1AD =,9BC =,点P 为边BC 上一动点,作PH DC ⊥,垂足H 在边DC 上,以点P 为圆心PH 为半径画圆,交射线PB 于点E .
(1)当圆P 过点A 时,求圆P 的半径;
(2)分别联结EH 和EA ,当ABE ∆∽CEH ∆时,以点B 为圆心,r 为半径的圆B 与圆P 相交,试求圆B 的半径r 的取值范围;
(3)将劣弧EH 沿直线EH 翻折交BC 于点F ,试通过计算说明线段EH 和EF 的比值为定值,并求出此定值.
)
3. (18黄浦)如图,四边形ABCD 中,90BCD D ∠=∠=︒,E 是边AB 的中点,
已知1AD =,2AB =.
(1)设BC x =,CD y =,求y 关于x 的函数关系式,并写出定义域; (2)当70B ∠=︒时,求AEC ∠的度数;
(3)当ACE ∆为直角三角形时,求边BC 的长.
|
4. (18宝嘉)在圆O 中,AO 、BO 是圆O 的半径,点C 在劣弧AB 上,10OA =,12AC =, AC ∥OB ,联结AB . )
(1)如图,求证:AB 平分∠OAC ;
(2)点M 在弦AC 的延长线上,联结BM ,如果△AMB 是直角三角形,请你在图中画出点M 的位置并求出CM 的长;
(3)如图,点D 在弦AC 上,与点A 不重合,联结OD 与弦AB 交于点E ,设点D 与点C 的距离为x ,△OEB 的面积为y ,求y 与x 的函数关系式,并写出自变量x 的取值范围.
{
5. (18长宁)在圆O 中,C 是弦AB 上的一点,联结OC 并延长,交劣弧AB 于点D ,联结
AO 、BO 、AD 、BD ,已知圆O 的半径长为5,弦AB 的长为8. (1)如图,当点D 是弧AB 的中点时,求CD 的长; (2)如图,设AC x =
,
ACO OBD
S y S
=,求y 关于x 的函数解析式并写出定义域;
(3)若四边形AOBD 是梯形,求AD 的长.
}
6. (18闵行)如图,已知在Rt △ABC 中,90ACB ︒∠=,6AC =,8BC =,点F 在线段AB 上,以点B 为圆心,BF 为半径的圆交BC 于点E ,射线AE 交圆B 于点D (点D 、E 不重合).
(1)如果设BF x =,EF y =,求y
与x 之间的函数关系式,并写出它的定义域; (2)如果2ED EF =,求ED 的长;
(3)联结CD 、BD ,请判断四边形ABDC 是否为直角梯形说明理由.
"
7. (18奉贤)已知,如图,在半径为2的扇形AOB 中,90AOB ∠=︒,点在C 半径OB 上,
AC 的垂直平分线交OA 于点D ,交弧AB 于点E ,联结BE 、CD .
(1)若C 是半径OB 中点,求OCD ∠的正弦值; (2)若E 是弧AB 的中点,求证:2BE BO BC =⋅;
(3)联结CE ,当DCE ∆是以CD 为腰的等腰三角形时,求CD 的长.
…
8. (18松江)如图,已知Rt ABC ∆中,90ACB ∠=︒,2BC =,3AC =,以点C 为圆心,
CB 为半径的圆交AB 于点D ,过点A 作AE ∥CD ,交BC 延长线于点E .
(1)求CE 的长;
(2)P 是CE 延长线上一点,直线AP 、CD 交于点Q . ① 如果ACQ ∆∽CPQ ∆,求CP 的长;
!
② 如果以点A 为圆心,AQ 为半径的圆与⊙C 相切,求CP 的长.
—
C
,
B
A D
E 备用图
C
B
A D
E
9. (18普陀)已知P 是⊙O 的直径BA 延长线上的一个动点,P ∠的另一边交⊙O 于点C 、
D ,两点位于AB 的上方,6AB =,OP m =,1
sin 3
P =,如图所示,另一个半径为6的
⊙1O 经过点C 、D ,圆心距1OO n =. (1)当6m =时,求线段CD 的长;
(2)设圆心1O 在直线AB 上方,试用n 的代数式表示m ;
(3)1POO ∆在点P 的运动过程中,是否能成为以1OO 为腰的等腰三角形,如果能,试求出此时n 的值;如果不能,请说明理由.
%
10. (18崇明)如图,已知ABC △中,8AB =,10BC =,12AC =,D 是AC 边上一点,且2AB AD AC =⋅,联结BD ,点E 、F 分别是BC 、AC 上两点(点E 不与B 、C 重合),AEF C ∠=∠,AE 与BD 相交于点G . (1)求证:BD 平分ABC ∠;
(2)设BE x =,CF y =,求y 与x 之间的函数关系式; (3)联结FG ,当GEF △是等腰三角形时,求BE 的长度.
)
)
A
B
备用图
P D
O
A
B
C '
A B
\
C
D
G
E
F
(备用图)
A
B
C
D
11. (18青浦)如图1,已知扇形MON
,∠MON =90,点B 在弧MN 上移动,联结BM ,作OD ⊥BM ,垂足为点D ,C 为线段OD 上一点,且OC =BM ,联结BC 并延长交半径OM 于点A ,设OA = x ,∠COM 的正切值为y . |
(1)如图2,当AB ⊥OM 时,求证:AM =AC ;
(2)求y 关于x 的函数关系式,并写出定义域; (3)当△OAC 为等腰三角形时,求x 的值.
:
12. (18金山)如图,已知在梯形ABCD 中,AD ∥BC ,AB =DC =AD =5,3
sin 5
B =
,P 是线段BC 上一点,以P
为圆心,PA 为半径的⊙P 与射线AD 的另一个交点为Q ,射线PQ 与射线CD 相交于点E ,设BP =x . :
(1)求证△ABP ∽△ECP ;
(2)如果点Q 在线段AD 上(与点A 、D 不重合),设△APQ 的面积为y ,求y 关于x 的函数关系式,并写出定义域;
(3)如果△QED 与△QAP 相似,求BP 的长.
】
O
M
N D C B
A
图1 O
N
D
C
B
A
图2
N
M
O
备用图
A
B
C
D
备用图
13. (18静安)如图,平行四边形ABCD 中,已知6AB =,9BC =,1
cos 3
ABC ∠=,对角线AC 、BD 交于点O ,动点P 在边AB 上,⊙P 经过点B ,交线段PA 于点E ,设BP x =. (1)求AC 的长;
(2)设⊙O 的半径为y ,当⊙P 与⊙O 外切时,求y 关于x 的函数关系式,并写出定义域; (3)如果AC 是⊙O 的直径,⊙O 经过点E ,求⊙O 与⊙P 的圆心距OP 的长.
~
14. (18虹口)如图,在梯形ABCD 中,AD ∥BC ,90C ∠=︒,5DC =,以CD 为半径的⊙C 与以AB 为半径的⊙B 相交于点E 、F ,联结EF 交BC 于点G . (1)设BC 与⊙C 相交于点M ,当BM AD =时,求⊙B 的半径; (2)设BC x =,EF y =,求y 关于x 的函数关系式,并写出它的定义域;
…
(3)当10BC =时,点P 为平面内一点,若⊙P 与⊙C 相交于点D 、E ,且以A 、E 、P 、
D 为顶点的四边形是梯形,请直接写出⊙P 的面积.(结果保留π)
15.(18浦东)
如图9,已知在△ABC 中,AB=AC ,2
1
tan =
B ,B
C =4,点E 是在线段BA 延长线上一点,以点E 为圆心,EC 为半径的圆交射线BC 于点C 、F (点C 、F 不重合),射线EF 与射线AC 交于点P .
(1)求证:AC AP AE ⋅=2;
(2)当点F 在线段BC 上,设CF =x ,△PFC 的面积为y ,求y 关于x 的函数解析式及定义域; (3)当2
1
=EF FP 时,求BE 的长.
备用图
图9。
