水头流量计算
水头损失计算式教学内容
0
小牲畜现有头 数
(设计大牲畜头数) (设计小牲畜头数)
(设计大牲畜)用水量 (设计小牲畜)用水量
hw(m )
L(m )
i
dj(m m)
15
(日总用水量) 57.224702 5.960906479 (日最高时用水量) m3/h
47.687252
(日平均时用 水量)
0.001656 m3/s
公式二:PVCU管
41.25976809
1.719157
(日平均时用 水量)
引水流量 m3/s 管内径 m 管长 m 比降 总损失 m 现有人数 设计人数
设计人总用 水量
0.001194 m3/s 4.3 m3/h
1.719157004 m3/h
日最高时用水 量
沿程水头损失 hi=il
25.47134316
反推管径 22.5
Q D L I=0.000875Q1.761/D4.761 hw=1.1il 人 p=p1(1+0.012)15
(管损、不可预见) (日总用水量)
0.000477544 0.042 4300
0.004451026 21.0533536581000
300 358.7805921
35.87805921
5.381708882
引水流量 (自流工程用)
内径
Q(m3/s) D(m)
管长
L(m)
比降
I=0.000915Q1.774/D4.774
总损失
hw=1.1il
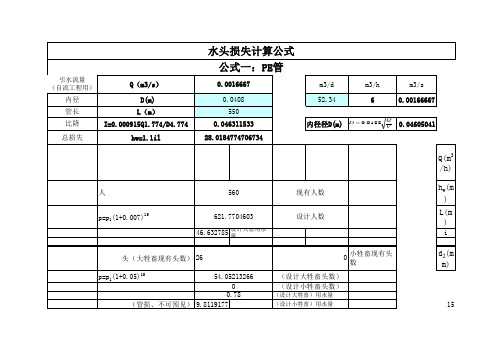
水头损失计算公式 公式一:PE管
0.0016667
0.0408 550
0.046311533 28.0184774706734
水流量计算公式

水管网流量简单算法如下:自来水供水压力为市政压力大概平均为0。
28mpa。
如果计算流量大概可以按照以下公式进行推算,仅作为推算公式,管径面积×经济流速(DN300以下管选1.2m/s、DN300以上管选1.5m/s)=流量如果需要准确数据应按照下文进行计算.水力学教学辅导第五章有压管道恒定流【教学基本要求】1、了解有压管流的基本特点,掌握管流分为长管流动和短管流动的条件。
2、掌握简单管道的水力计算和测压管水头线、总水头线的绘制,并能确定管道内的压强分布.3、了解复杂管道的特点和计算方法.【内容提要和学习指导】前面几章我们讨论了液体运动的基本理论,从这一章开始将进入工程水力学部分,就是运用水力学的基本方程(恒定总流的连续性方程、能量方程和动量方程)和水头损失的计算公式,来解决实际工程中的水力学问题。
本章理论部分内容不多,主要掌握方程的简化和解题的方法,重点掌握简单管道的水力计算。
有压管流水力计算的主要任务是:确定管路中通过的流量Q;设计管道通过的流量Q所需的作用水头H和管径d;通过绘制沿管线的测压管水头线,确定压强p沿管线的分布。
5.1 有压管道流动的基本概念(1)简单管道和复杂管道根据管道的组成情况我们把它分为简单管道和复杂管道。
直径单一没有分支而且糙率不变的管道称为简单管道;复杂管道是指由两根以上管道组成管道系统。
复杂管道又可以分为串联管道、并联管道、分叉管道、沿程泄流管和管网。
(2) 短管和长管在有压管道水力计算中,为了简化计算,常将压力管道分为短管和长管:短管是指管路中水流的流速水头和局部水头损失都不能忽略不计的管道;长管是指流速水头与局部水头损失之和远小于沿程水头损失,在计算中可以忽略的管道为,一般认为( )<(5~10)h f %可以按长管计算。
需要注意的是:长管和长管不是完全按管道的长短来区分的.将有压管道按长管计算,可以简化计算过程.但在不能判断流速水头与局部水头损失之和远小于沿程水头损失之前,按短管计算不会产生较大的误差。
水流量计算公式

水管网流量简单算法如下:自来水供水压力为市政压力大概平均为0.28mpa。
如果计算流量大概可以按照以下公式进行推算,仅作为推算公式,管径面积×经济流速(DN300以下管选1.2m/s、DN300以上管选1.5m/s)=流量如果需要准确数据应按照下文进行计算。
水力学教学辅导第五章有压管道恒定流【教学基本要求】1、了解有压管流的基本特点,掌握管流分为长管流动和短管流动的条件。
2、掌握简单管道的水力计算和测压管水头线、总水头线的绘制,并能确定管道的压强分布。
3、了解复杂管道的特点和计算方法。
【容提要和学习指导】前面几章我们讨论了液体运动的基本理论,从这一章开始将进入工程水力学部分,就是运用水力学的基本方程(恒定总流的连续性方程、能量方程和动量方程)和水头损失的计算公式,来解决实际工程中的水力学问题。
本章理论部分容不多,主要掌握方程的简化和解题的方法,重点掌握简单管道的水力计算。
有压管流水力计算的主要任务是:确定管路过的流量Q;设计管道通过的流量Q所需的作用水头H和管径d;通过绘制沿管线的测压管水头线,确定压强p沿管线的分布。
5.1 有压管道流动的基本概念(1)简单管道和复杂管道根据管道的组成情况我们把它分为简单管道和复杂管道。
直径单一没有分支而且糙率不变的管道称为简单管道;复杂管道是指由两根以上管道组成管道系统。
复杂管道又可以分为串联管道、并联管道、分叉管道、沿程泄流管和管网。
(2) 短管和长管在有压管道水力计算中,为了简化计算,常将压力管道分为短管和长管:短管是指管路中水流的流速水头和局部水头损失都不能忽略不计的管道;长管是指流速水头与局部水头损失之和远小于沿程水头损失,在计算中可以忽略的管道为,一般认为( )<(5~10)h f %可以按长管计算。
需要注意的是:长管和长管不是完全按管道的长短来区分的。
将有压管道按长管计算,可以简化计算过程。
但在不能判断流速水头与局部水头损失之和远小于沿程水头损失之前,按短管计算不会产生较大的误差。
(完整版)流量与管径、压力、流速之间关系计算公式

流量与管径、压力、流速的一般关系一般工程上计算时,水管路,压力常见为0.1--0.6MPa,水在水管中流速在1--3米/秒,常取1.5米/秒。
流量=管截面积X流速=0.002827X管内径的平方X流速(立方米/ 小时)。
其中,管内径单位:mm ,流速单位:米/秒,饱和蒸汽的公式与水相同,只是流速一般取20--40米/秒。
水头损失计算Chezy公式这里:断面水流量(m3/s)C ----- C hezy糙率系数(m1/2/s)A ----- 断面面积(m2)R ----- 水力半径(m)S 水力坡度(m/m )根据需要也可以变换为其它表示方法:DarcyWeisbach公式由于这里:h f沿程水头损失(mm3/s)Darcy-Weisbach水头损失系数(无量纲)管道长度(m)管道内径(mm)管道流速(m/s)重力加速度(m/s2)水力计算是输配水管道设计的核心,其实质就是在保证用户水量、水压安全的条件下,通过水力计算优化设计方案,选择合适的管材和确经济管径。
输配水管道水力计算包含沿程水头损失和局部水头损失,而局部水头损失一般仅为沿程水头损失的5~10% ,因此本文主要研究、探讨管道沿程水头损失的计算方法。
1.1管道常用沿程水头损失计算公式及适用条件管道沿程水头损失是水流摩阻做功消耗的能量,不同的水流流态,遵循不同的规律,计算方法也不一样。
输配水管道水流流态都处在紊流区,紊流区水流的阻力是水的粘滞力及水流速度与压强脉动的结果。
紊流又根据阻力特征划分为水力光滑区、过渡区、粗糙区。
管道沿程水头损失计算公式都有适用范围和条件,一般都以水流阻力特征区划分。
水流阻力特征区的判别方法,工程设计宜采用别式,目前国内管道经常采用的沿程水头损失水力计算公式及相应的摩阻力系数,按照水流阻力特征区划分如表沿程水头损失水力计算公式和摩阻系数13数值做为判阻力特征适用条件水力公式、摩阻系数符号意义水力光滑国叫雷诺数h:管道沿程水头损因——紊流过渡10<<500 V:平均流速d:管道内径Y水的运动粘滞系数兀沿程摩阻系数△:管道当量粗糙 度q :管道流量 Ch :海曾-威廉系数 C :谢才系数R :水力半径n :粗糙系数i :水力坡降I :管道计算长度 达西公式是管道沿程水力计算基本公式,是一个半理论半经 验的计算通式,它适用于流态的不同区间,其中摩阻系数 入可采 用柯列布鲁克公式计算,克列布鲁克公式考虑的因素多,适用范 围广泛,被认为紊流区 入的综合计算公式。
流量与管径、压力、流速之间关系计算公式

流量与管径、压力、流速之间关系计算公式-CAL-FENGHAI.-(YICAI)-Company One1流量与管径、压力、流速的一般关系一般工程上计算时,水管路,压力常见为,水在水管中流速在1--3米/秒,常取米/秒。
流量=管截面积X流速=管内径的平方X流速(立方米/小时)。
其中,管内径单位:mm ,流速单位:米/秒,饱和蒸汽的公式与水相同,只是流速一般取20--40米/秒。
水头损失计算Chezy 公式这里:Q——断面水流量(m3/s)C——Chezy糙率系数(m1/2/s)A——断面面积(m2)R——水力半径(m)S——水力坡度(m/m)根据需要也可以变换为其它表示方法:Darcy-Weisbach公式由于这里:h f——沿程水头损失(mm3/s)f ——Darcy-Weisbach水头损失系数(无量纲)l——管道长度(m)d——管道内径(mm)v ——管道流速(m/s)g ——重力加速度(m/s2)水力计算是输配水管道设计的核心,其实质就是在保证用户水量、水压安全的条件下,通过水力计算优化设计方案,选择合适的管材和确经济管径。
输配水管道水力计算包含沿程水头损失和局部水头损失,而局部水头损失一般仅为沿程水头损失的5~10%,因此本文主要研究、探讨管道沿程水头损失的计算方法。
管道常用沿程水头损失计算公式及适用条件管道沿程水头损失是水流摩阻做功消耗的能量,不同的水流流态,遵循不同的规律,计算方法也不一样。
输配水管道水流流态都处在紊流区,紊流区水流的阻力是水的粘滞力及水流速度与压强脉动的结果。
紊流又根据阻力特征划分为水力光滑区、过渡区、粗糙区。
管道沿程水头损失计算公式都有适用范围和条件,一般都以水流阻力特征区划分。
数值做为判别式,目前国内管道经常采用的沿程水头损失水力计算公式及相应的摩阻力系数,按照水流阻力特征区划分如表1。
沿程水头损失水力计算公式和摩阻系数表1阻力特征区适用条件水力公式、摩阻系数符号意义水力光滑区>10雷诺数h:管道沿程水头损失v:平均流速d:管道内径γ:水的运动粘滞系数λ:沿程摩阻系数Δ:管道当量粗糙度q:管道流量Ch:海曾-威廉系数C:谢才系数R:水力半径n:粗糙系数i:水力坡降l:管道计算长度紊流过渡区10<<500(1)(2)紊流粗糙区>500达西公式是管道沿程水力计算基本公式,是一个半理论半经验的计算通式,它适用于流态的不同区间,其中摩阻系数λ可采用柯列布鲁克公式计算,克列布鲁克公式考虑的因素多,适用范围广泛,被认为紊流区λ的综合计算公式。
流量与管径压力流速之间关系计算公式

流量与管径压力流速之间关系计算公式通常工程上计算时,水管路,压力常见为0.1--0.6MPa,水在水管中流速在1--3米/秒,常取1.5米/秒。
流量=管截面积X流速=0.002827X管内径的平方X流速(立方米/小时)。
其中,管内径单位:mm ,流速单位:米/秒,饱与蒸汽的公式与水相同,只是流速通常取20--40米/秒。
水头缺失计算Chezy 公式这里:Q ——断面水流量(m3/s)C ——Chezy糙率系数(m1/2/s)A ——断面面积(m2)R ——水力半径(m)S ——水力坡度(m/m)根据需要也能够变换为其它表示方法:Darcy-Weisbach公式由于这里:h f——沿程水头缺失(mm3/s)f ——Darcy-Weisbach水头缺失系数(无量纲)l ——管道长度(m)d ——管道内径(mm)v ——管道流速(m/s)g ——重力加速度(m/s2)水力计算是输配水管道设计的核心,事实上质就是在保证用户水量、水压安全的条件下,通过水力计算优化设计方案,选择合适的管材与确经济管径。
输配水管道水力计算包含沿程水头缺失与局部水头缺失,而局部水头缺失通常仅为沿程水头缺失的5~10%,因此本文要紧研究、探讨管道沿程水头缺失的计算方法。
1.1 管道常用沿程水头缺失计算公式及适用条件管道沿程水头缺失是水流摩阻做功消耗的能量,不一致的水流流态,遵循不一致的规律,计算方法也不一样。
输配水管道水流流态都处在紊流区,紊流区水流的阻力是水的粘滞力及水流速度与压强脉动的结果。
紊流又根据阻力特征划分为水力光滑区、过渡区、粗糙区。
管道沿程水头缺失计算公式都有适用范围与条件,通常都以水流阻力特征区划分。
水流阻力特征区的判别方法,工程设计宜使用数值做为判别式,目前国内管道经常使用的沿程水头缺失水力计算公式及相应的摩阻力系数,按照水流阻力特征区划分如表1。
沿程水头缺失水力计算公式与摩阻系数表1阻力特征区适用条件水力公式、摩阻系数符号意义水力光滑区>10雷诺数h:管道沿程水头缺失v:平均流速d:管道内径γ:水的运动粘紊流过渡区10<<500(1)(2)紊流粗糙区>500滞系数λ:沿程摩阻系数Δ:管道当量粗糙度q:管道流量Ch:海曾-威廉系数C:谢才系数R:水力半径n:粗糙系数i:水力坡降l:管道计算长度达西公式是管道沿程水力计算基本公式,是一个半理论半经验的计算通式,它适用于流态的不一致区间,其中摩阻系数λ可使用柯列布鲁克公式计算,克列布鲁克公式考虑的因素多,适用范围广泛,被认为紊流区λ的综合计算公式。
流量及管径、压力、流速之间关系计算公式

流量与管径、压力、流速的一般关系一般工程上计算时,水管路,压力常见为0.1--0.6MPa,水在水管中流速在1--3米/秒,常取1.5米/秒。
流量=管截面积X流速=0.002827X管内径的平方X流速(立方米/小时)。
其中,管内径单位:mm ,流速单位:米/秒,饱和蒸汽的公式与水相同,只是流速一般取20--40米/秒。
水头损失计算Chezy 公式这里:Q ——断面水流量(m3/s)C ——Chezy糙率系数(m1/2/s)A ——断面面积(m2)R ——水力半径(m)S ——水力坡度(m/m)根据需要也可以变换为其它表示方法:Darcy-Weisbach公式由于这里:h f——沿程水头损失(mm3/s)f ——Darcy-Weisbach水头损失系数(无量纲)l ——管道长度(m)d ——管道内径(mm)v ——管道流速(m/s)g ——重力加速度(m/s2)水力计算是输配水管道设计的核心,其实质就是在保证用户水量、水压安全的条件下,通过水力计算优化设计方案,选择合适的管材和确经济管径。
输配水管道水力计算包含沿程水头损失和局部水头损失,而局部水头损失一般仅为沿程水头损失的5~10%,因此本文主要研究、探讨管道沿程水头损失的计算方法。
1.1 管道常用沿程水头损失计算公式及适用条件管道沿程水头损失是水流摩阻做功消耗的能量,不同的水流流态,遵循不同的规律,计算方法也不一样。
输配水管道水流流态都处在紊流区,紊流区水流的阻力是水的粘滞力及水流速度与压强脉动的结果。
紊流又根据阻力特征划分为水力光滑区、过渡区、粗糙区。
管道沿程水头损失计算公式都有适用范围和条件,一般都以水流阻力特征区划分。
水流阻力特征区的判别方法,工程设计宜采用数值做为判别式,目前国内管道经常采用的沿程水头损失水力计算公式及相应的摩阻力系数,按照水流阻力特征区划分如表1。
沿程水头损失水力计算公式和摩阻系数表1达西公式是管道沿程水力计算基本公式,是一个半理论半经验的计算通式,它适用于流态的不同区间,其中摩阻系数λ可采用柯列布鲁克公式计算,克列布鲁克公式考虑的因素多,适用范围广泛,被认为紊流区λ的综合计算公式。
水电站、水利水电工程、压力管等水头压力的计算公式及参数

水电站、水利水电工程、压力管等水头压力的计算公式及参数一、工程压力单位:0.01mpa=1米水头(请参考下表)二、水电站有关装机、流量、水头经验公式电站装机容量W=集雨面积S×水头高H×0.3~0.5或W=设计流量Q×水头高H×7电站流量Q=装机容量W÷水头高H÷0.8电站引水洞径R半径=√Q÷(0.27~0.25)或R半径=√Q÷3.14÷2.7三、管径和流速计算、水头损失流量与管径、压力、流速的一般关系,一般工程上计算时,水管路,压力常见为0.1--0.6MPa,水在水管中流速在1--3米/秒,常取1.5米/秒。
流量=管截面积X流速=0.002827X管内径的平方X流速 (立方米/小时)。
其中,管内径单位:mm ,流速单位:米/秒,饱和蒸汽的公式与水相同,只是流速一般取20--40米/秒。
水头损失计算Chezy 公式Chezy这里:Q ——断面水流量(m3/s)C ——Chezy糙率系数(m1/2/s)A ——断面面积(m2)R ——水力半径(m)S ——水力坡度(m/m)根据需要也可以变换为其它表示方法:Darcy-Weisbach公式由于这里:hf ——沿程水头损失(mm3/s)f ——Darcy-Weisbach水头损失系数(无量纲)l ——管道长度(m)d ——管道内径(mm)v ——管道流速(m/s)g ——重力加速度(m/s2)水力计算是输配水管道设计的核心,其实质就是在保证用户水量、水压安全的条件下,通过水力计算优化设计方案,选择合适的管材和确经济管径。
输配水管道水力计算包含沿程水头损失和局部水头损失,而局部水头损失一般仅为沿程水头损失的5~10%,因此本文主要研究、探讨管道沿程水头损失的计算方法。
四、管道常用沿程水头损失计算公式及适用条件:管道沿程水头损失是水流摩阻做功消耗的能量,不同的水流流态,遵循不同的规律,计算方法也不一样。
流量计算公式

流量Q=[( n /4)d A2 V(1+ 入L/d+ Z )] V(2gH)
式中:Q——流量,(mA3/s); n ------- 周率;d ——管内径(m),
L 管道长度(m); g 重力加速度(m/sA2); H 管道两端水头差(m)入管道的沿程阻力系数(无单位);Z --------------------------------------- 誉道
的局部阻力系数(无单位,有多个的要累加)。
使中部的截面积变为原来的一半,其他条件都不变,这就相当于增加
了一个局部阻力系数Z,流量变为:Q =[(n /4)dA2 V(1+入L/d+ Z +Z')]V (2gH>流量比原来小了。
流量减小的程度要看增加的Z与原来沿程阻力和局部阻力的相对大小。
当管很长(L很大),管径很小,原来管道局部阻力很大时,流量变化就小。
相反当管很短(L很小),管
径很大,原来管道局部阻力很小时,流量变化就大。
定量变化必须通过定量计算确定。
流量和管径、压力、流速之间关系计算公式

流量与管径、压力、流速的一般关系一般工程上计算时,水管路,压力常见为0.1--0.6MPa,水在水管中流速在1--3米/秒,常取1.5米/秒。
流量=管截面积X流速=0.002827X管径的平方X流速(立方米/小时)。
其中,管径单位:mm ,流速单位:米/秒,饱和蒸汽的公式与水相同,只是流速一般取20--40米/秒。
水头损失计算Chezy 公式这里:Q ——断面水流量(m3/s)C ——Chezy糙率系数(m1/2/s)A ——断面面积(m2)R ——水力半径(m)S ——水力坡度(m/m)根据需要也可以变换为其它表示方法:Darcy-Weisbach公式由于这里:h f——沿程水头损失(mm3/s)f ——Darcy-Weisbach水头损失系数(无量纲)l ——管道长度(m)d ——管道径(mm)v ——管道流速(m/s)g ——重力加速度(m/s2)水力计算是输配水管道设计的核心,其实质就是在保证用户水量、水压安全的条件下,通过水力计算优化设计方案,选择合适的管材和确经济管径。
输配水管道水力计算包含沿程水头损失和局部水头损失,而局部水头损失一般仅为沿程水头损失的5~10%,因此本文主要研究、探讨管道沿程水头损失的计算方法。
1.1 管道常用沿程水头损失计算公式及适用条件管道沿程水头损失是水流摩阻做功消耗的能量,不同的水流流态,遵循不同的规律,计算方法也不一样。
输配水管道水流流态都处在紊流区,紊流区水流的阻力是水的粘滞力及水流速度与压强脉动的结果。
紊流又根据阻力特征划分为水力光滑区、过渡区、粗糙区。
管道沿程水头损失计算公式都有适用围和条件,一般都以水流阻力特征区划分。
水流阻力特征区的判别方法,工程设计宜采用数值做为判别式,目前国管道经常采用的沿程水头损失水力计算公式及相应的摩阻力系数,按照水流阻力特征区划分如表1。
沿程水头损失水力计算公式和摩阻系数表1阻力特征区适用条件水力公式、摩阻系数符号意义水力光滑区>10雷诺数h:管道沿程水头损失v:平均流速d:管道径γ:水的运动粘紊流过渡区10<<500(1)(2)紊流粗糙区>500滞系数λ:沿程摩阻系数Δ:管道当量粗糙度q:管道流量Ch:海曾-威廉系数C:谢才系数R:水力半径n:粗糙系数i:水力坡降l:管道计算长度达西公式是管道沿程水力计算基本公式,是一个半理论半经验的计算通式,它适用于流态的不同区间,其中摩阻系数λ可采用柯列布鲁克公式计算,克列布鲁克公式考虑的因素多,适用围广泛,被认为紊流区λ的综合计算公式。
堰上水头计算公式

堰上水头计算公式
堰上水头(简称S.H.),即半封闭堰,是水利水电工程水力结构物中常见的一种,它的计算是水力分析的重要环节。
堰上水头计算公式的具体内容如下:
(1)等差堰高计算:
等差堰高H=Δh/2+h0
其中Δh表示堰面距稳定水位面的高度(即堰面与上游水位高差),h0表示上游水位。
(2)等堰水头计算:
等堰水头Hf=H+H1,
其中H表示堰顶高程,H1表示堰上流量的扰动水头。
(3)堰尾水头计算:
堰尾水头Ht=H-H2,
其中H表示堰顶高程,H2表示堰尾流量的扰动水头。
这些公式只能作为参考,具体计算时依据不同情况,还需结合实际水力分析情况,使用其他公式进行计算。
- 1 -。
堰上水头计算公式

堰上水头计算公式
堰上水头计算公式是用来计算水流通过堰坝时的水头高度的公式。
在水利工程中,水头高度是一个非常重要的参数,它直接影响着水流的流速和流量。
因此,了解和计算堰上水头是水利工程设计和运行中的一个重要内容。
堰上水头计算公式的推导涉及液体静力学和动力学的知识。
在一般情况下,可以利用质量守恒定律和伯努利定律来推导堰上水头的计算公式。
根据伯努利定律,水流通过堰坝时,水头高度与水流速度和水位高度之间存在一定的关系。
具体而言,堰上水头计算公式可以表示为:
H = (V^2)/(2g) + z
其中,H表示堰上水头高度,V表示水流速度,g表示重力加速度,z表示水位高度。
这个公式告诉我们,在水流通过堰坝时,水头高度与水流速度的平方成正比,与水位高度成正比。
在实际应用中,我们可以根据堰坝的设计要求和水流条件来选择合适的计算方法和参数,从而计算出堰上水头的具体数值。
通过计算堰上水头,我们可以更好地了解水流的特性,指导工程设计和运行,确保水利工程的安全和效率。
总的来说,堰上水头计算公式是水利工程中的重要内容,它可以帮
助我们了解和分析水流的特性,指导工程设计和运行。
通过深入学习和理解堰上水头计算公式,我们可以更好地应用这些知识,提高水利工程的设计水平和管理能力。
希望大家能够认真学习和掌握堰上水头计算公式,为水利工程的发展贡献自己的力量。
