基于单神经元PID控制器的设计
单神经元PID控制
基于单神经元的PID控制1神经元单神经元作为构成神经网络的基本单位,具有自学习和自适应能力,且结构简单响应速度快。
这里将单个神经元与传统PID 控制器结合起来,一定程度上解决了传统PID 调节器不易在线实时整定参数,难以对复杂过程和时变系统参数进行有效控制等问题。
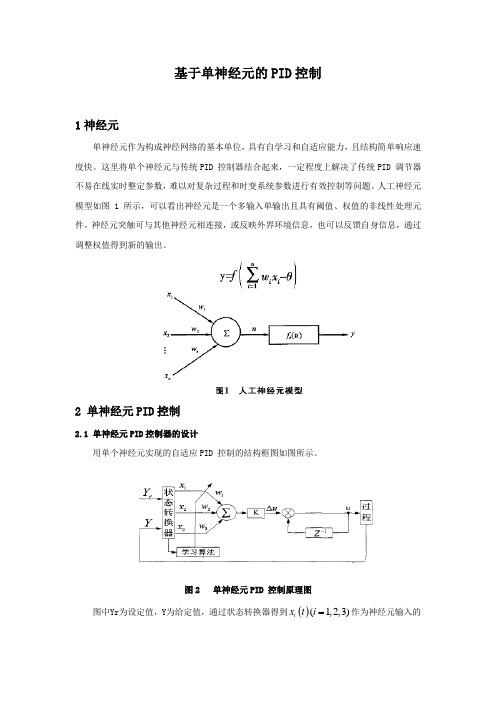
人工神经元模型如图1 所示,可以看出神经元是一个多输入单输出且具有阈值、权值的非线性处理元件。
神经元突触可与其他神经元相连接,或反映外界环境信息,也可以反馈自身信息,通过调整权值得到新的输出。
2 单神经元PID控制2.1 单神经元PID控制器的设计用单个神经元实现的自适应PID 控制的结构框图如图所示。
图2 单神经元PID 控制原理图x t i=作为神经元输入的图中Yr为设定值,Y为给定值,通过状态转换器得到()(1,2,3)i三个状态量,通过学习调节神经元权值()(1,2,3)i w t i = 最终得到输出。
神经元的输入输出关系描述为: 31i ii I w x ==∑ (2-1) ()y f I = (2-2)由PID 控制器的增量算式:[]()()(1)()[()2(1)(2)]P I D u k K e k e k K e k K e k e k e k ∆=--++--+- (2-3) 若取123()(1),(),()2(1)(2)X e k e k X e k X e k e k e k =--==--+-,则式(2-4) 变为: 123()[()(1)]()[()2(1)(2)]u k w e k e k w e k w e k e k e k ∆=--++--+- (2-4)比较式(2-3) 和(2-4) 形式完全相同,所不同的只是式(2-4) 中的系数()(1,2,3)i w t i =可以通过神经元的自学习功能来进行自适应调整,而式(2-3) 中的参数,,P I D K K K 是预先确定好且不变的。
正是由于i w 能进行自适应调整,故可大大提高控制器的鲁棒性能。
单神经元自适应PID控制器的性能优化设计

2007,43(12)1引言PID控制是最早发展起来的控制策略之一[1],因为它所设计的设计算法和控制结构都是很简单的,并且十分适用于工程应用背景,此外PID控制方案并不要求精确的受控对象的数学模型,且采用PID控制的控制效果一般是比较令人满意的,所以工业界实际应用中PID控制器是应用最广泛的一种控制策略,且都是比较成功的。
PID控制对线形非时变的且是相当低阶的控制系统,其跟踪和抗干扰能力特别强,能获得期望的特性,特别是对低阶的系统,可以达到参数最优化控制。
然而,PID控制也有局限性,当系统参数是时变的,或者系统是跟踪一个参考轨迹而不是简单的设定点变化时,控制性能严重地变坏,这是可以应用自校正控制器。
此外,当系统存在有较大的滞后时,系统的性能也会严重地变坏,必须采取特别措施[2]。
人工神经元具有自适应、自学习、并行处理及较强的容错能力。
将人工神经元用于控制过程,给控制器赋予智能,在线调整PID参数,可以预见,将使被控系统具有较强的抗干扰能力和鲁棒性。
2神经元数学模型神经元是以生物神经系统的神经细胞为基础的生物模型。
人们在对生物神经系统进行研究,以探讨人工智能的机制时,把神经元数学化,从而产生了神经元数学模型(如图1)。
神经元是一个多输入、单输出的信息处理单元,它对信息的处理是非线性的[3]。
神经元的输入输出关系为:zi=nj=1!WijXj-!i(1)yi=f(zi)(2)取其离散值后的公式为:z(k)=ni=1!Wi(k)Xi(k)-!(k)(3)yN(K)=F(z(K))(4)当取n=3,且阀值!k=0,则:z(k)=X1(K)W1(K)+X2(K)W2(K)+X3(K)W3(K)(5)3常规PID调节器PID控制器是一种线形控制器,用输出量和给定量之间的误差的时间函数的比例、积分、微分的线形组合,构成控制量u(t),称为比例积分微分控制,简称为PID控制,其算式为u(t)=Kp[e(t)+1TI"e(τ)d(τ)+TDd(e(t))dt](6)将上式进行离散化后得:单神经元自适应PID控制器的性能优化设计宋道金SONGDao-jin山东理工大学,山东,淄博255049ShandongUniversityofTechnology,Zibo,Shandong255049,ChinaE-mail:djs@sdut.edu.cnSONGDao-jin.DesignofsingleneuronadaptivePIDcontroller.ComputerEngineeringandApplications,2007,43(12):199-201.Abstract:ThesingleneuronadaptivePIDcontrollerisdiscussed,includingitsmainfeatures,suchasthecharacteristics,thecontrollaw.ArapidandapproximatemethodforcontrollingthedelicacyofthesystemisalsogiventoachievethePIDparameterself-study.Itisverifiedthatthiscontrollerhasfewadjustableparametersandexcellentrobustnessperformance,anditcanrestraintheprocesstime-delayeffectively.Keywords:singleneuron;adaptivePIDcontroller;PID摘要:研究了单神经元自适应PID摔制器性能优化问题,阐述了该摔制器的特点、控制律;给出了一种控制灵敏度的快速近似求取方法,实现了PID参数的在线自学习;使单神经元控制器具有可调参数少、易于整定、控制输出平稳、鲁棒件强的独特优点,适用于大滞后且要求平稳控制输出的工业过程。
神经元PID控制器设计及应用

神经元PID控制器设计及应用神经元PID(Proportional-Integral-Derivative)控制器是一种基于神经元模型的控制算法,结合了比例、积分和微分三个控制作用,适用于各种控制系统中。
首先,神经元PID控制器的设计主要涉及以下几个方面:1. 神经元模型:神经元模型是神经元PID控制器的基础,一般包括神经元的输入、输出和激活函数等。
常用的神经元模型有阈值神经元模型、sigmoid神经元模型等。
2. 控制算法:神经元PID控制器的核心是控制算法,其基本思想是根据控制系统的误差,通过比例、积分和微分三个作用项对输出信号进行调节。
具体来说,比例作用项是根据误差的大小进行比例放大或缩小,积分作用项是根据误差的累积进行控制,微分作用项是根据误差速率的变化进行调节。
3. 参数优化:神经元PID控制器的性能取决于其参数设置,常见的参数有比例系数KP、积分系数KI和微分系数KD。
可以通过调试参数以优化控制器的性能,主要可以采用试错法、遗传算法等方法来寻找最优参数。
4. 非线性控制:神经元PID控制器可以通过引入非线性因素来适应更复杂的控制系统。
例如,可以采用模糊PID控制器、模型预测控制器等方法来解决非线性系统的控制问题。
接下来,我们来看一下神经元PID控制器的应用。
1. 工业控制:神经元PID控制器在工业控制领域得到了广泛应用。
例如,可以用它来控制温度、压力、流量等工业过程中的变量,实现精确控制和稳定运行。
2. 机器人控制:神经元PID控制器可以用于实现机器人运动和轨迹控制。
可以根据机器人的传感器输出和预设的目标轨迹,计算出机器人的控制信号,使机器人按照预期的轨迹运动。
3. 智能交通系统:神经元PID控制器可以应用于智能交通系统中,用于交通信号灯、车辆跟随和车道保持等控制任务。
它可以根据交通系统的实时数据,自动调节信号灯的时序和车辆的速度,以实现交通流畅和安全。
4. 电力系统控制:神经元PID控制器在电力系统控制中也具有重要应用。
基于单神经元的自适应PID控制系统设计及仿真

Fe . 201 b 1
文章 编号 :0 2— 6 4 2 1 ) 1 0 5 1 0 5 3 ( 0 1 O — 0 8一o 3
基 于 单神 经 元 的 自适应 P D控 制 系统 设计 及 仿 真 I
邱 道 尹 ,张 健 ,谢 俊 明 ,孙 大 治
( . 北 水利 水 电 学 院 , 南 郑 州 4 0 1 ; . 作 黄 河 河 务 局 武 陟 第 二 黄 河 河 务局 , 南 武 陟 4 4 5 ) 1华 河 501 2 焦 河 5 9 0
使 系统 达 到 最优 或 次 优 的控 制 效 果 . I PD控 制 即 比 例、 积分 、 微分控 制是 在工 程实 际 中应 用最 为广泛 的
PD和常规 P D进行 控制 , I I 并进 行 比较.
2 单 神 经元 PD 自适 应 控 制 设 计 I
自适 应 控制 系统 主要 分 2大类 : 型 参考 自适 模
5 9
a 无 监督 H b . e b学 习规 则 : 如果 2个 神 经元 同时
对 上式 进行 拉 氏反变 换得 c ( )= 8
8
一
被 激活则 其 之 间的连 接权 值变 化 与它 们 的激励 乘 积
成 正 比.
-0 6t
oS 10 )一 o( 2 t
- t n 10 ) 6S ( 2 £. 0i
神 经元 PD 自适 应 系统结 构简单 , 较强 的鲁棒性 . I 有
系统结 构如 图 1 所示 .
图 1 单 神经 元 自适 应 P D 控 制 结 构 图 I
应 PD控 制. I 非参 数 自适 应 P D控制 不 需 要 在线 辨 I 识 被 控系统 的模 型参数 , 算法 简单 , 容易 实现在 线 控 制. 神经元 自适应 PD控 制 即 属 于非 参 数 自适 应 单 I
单神经元PID控制器设计

单神经元PID控制器设计摘要常规PID控制器具有结构简单、易于实现、鲁棒性强等优点,但实际的生产过程中,控制对象一般都具有延迟大、非线性强、干扰大的特点。
因此当工况改变时,对象的动态特性也发生改变,控制品质就会随之下降,所以采用常规PID控制器很难获得令人满意的控制效果。
神经网络具有强鲁棒性、容错性、并行处理、自学习、逼近非线性关系等特点,在解决非线性和不确定系统控制方面有很大潜力,近年来已广泛应用于工业过程控制领域。
由于单神经元模型具有自适应和自学习的能力,使得它可以作为一种很好的方法而得以应用,因此本文将单神经元模型与常规PID控制器相结合,形成了具有自适应能力的单神经元PID控制器。
本文讨论了单神经元自适应PID控制器和多变量单神经元PID控制器的结构,控制算法,并MATLAB仿真软件给出了实例仿真。
MATLAB仿真结果表明,该控制系统既保持了常规PID控制的优点,又有自学习的智能特性,因而具有良好的控制品质和较强的自适应能力。
关键词:PID控制器;数学模型;自适应控制;单神经元;MA TLAB仿真;多变量The Design of Single Neuron PID ControllerAbstractConventional PID controller is simple in structure, easy to implement, robust and other advantages. However, in the actual production process control targets have delayed the general, non-linear strong, and the heavy characteristics of the disturbance, so when the situation changes, the object of dynamic change, quality control will be declined. Therefore, the conventional PID control method is difficult to obtain satisfactory performance.Neural network has stronger robust, fault-tolerant, parallel processing, self-learning, approaching the characteristics of non-linear relationship, and uncertainty in solving nonlinear control system there is great potential, in recent years has been widely used in controlled areas. In single-neuron model is self-adaptive and self-learning ability , it can be regarded as an effective intelligent way for application ,so this article will be use single-neuron model with the conventional PID controller combine to form the adaptive capacity of a single-neuron PID controller. This paper discusses the structure and the control algorithm of the single neuron adaptive PID controller and the variable single neuron PID controller,besides,giving the simulation examples by MATLAB simulation software.The MATLAB simulation results indicated that the control system both maintained the conventional cascade PID control merit, and has from the self-learning intelligent characteristic, thus has the good control quality and the strong auto-adapted ability.Key words:PID controller;Parameters of the model;Adaptive control;Single-neuron;MATLAB simulation;multivariable目录第1章引言 (1)1.1单神经元PID控制的产生背景 (1)1.2单神经元PID控制研究现状 (1)1.3本论文的主要内容 (2)第2章神经网络理论基础 (3)2.1单神经元模型 (3)2.2神经网络的拓扑结构 (5)2.3神经网络的学习方法 (6)2.3.1神经网络学习方式 (6)2.3.2神经网络学习规则 (7)2.4感知器 (9)第3章单神经元自适应PID控制器的设计及仿真实现 (12)3.1传统PID控制 (12)3.2单神经元自适应PID控制器 (13)3.2.1自适应控制系统 (13)3.2.2控制结构 (16)3.2.3控制算法 (18)3.2.4仿真程序及分析 (19)3.3采用二次型性能指标的的单神经元自适应PID控制器 (27)第4章多变量单神经元PID控制器的设计及实现 (29)4.1二变量控制系统框图 (29)4.2控制算法 (29)4.3SIMULINK仿真 (30)第5章结论 (32)参考文献 (33)谢辞 (34)第1章引言1.1 单神经元PID控制的产生背景PID控制具有结构简单、稳定性能好、可靠性高等优点,尤其适用于不能建立精确数学模型的不确定性控制系统。
基于S7-300 PLC的单神经元PID控制器设计与实现

基于 S 7 — 3 0 0 P L C 的单神经 元 P I D控 制器 设 计 与 实现
陈 军 李 玉榕
( 福州 大学 电气 X - 程 与 自动化学 院 ,福 州 3 5 0 1 1 6 )
摘要
P I D 控制器 在被 控对 象具有 非 线性特性 或运行 环境发 生 变化 时, P I D 的 固定参数 导致控
制系 统性 能下降 。针对该 问题 ,本 文提 出在 s 7 — 3 0 0 P L C上设 计和 实现基 于 He b b学 习规则 单 神经 元P I D 控制器 。首 先根据 神经 元 的学 习能力 ,设计 了基 于 He b b学 习规 则 的单神经 元 P I D 控制器 ,
仿 真测试 表 明相对 于 P I D 控制器 ,基 于 H e b b学 习规则 的单 神经元 P I D 能够 自适应 调整控 制器 参 数 ,具有 系统 响应速度 快和 超调 量小 等优 点。最后 在 s 7 . 3 0 0 P L C上实 现 了基 于 He b b学 习规 则 的 单 神经元 P I D 控 制算 法 ,对 温度 对象进行 控 制。 实验结果 表 明,基 于 He b b学 习规则 的单神 经元 P I D算 法简 单 ,在 P L C上 易于 实现 ,有效 改善 系统性 能。 关键 词 :单神 经元 P I D; 自适 应控 制; s 7 . 3 0 0 P L C;He b b学 习规则
A b s t r a c t Wh e n c o n t r o l l e d o b j e c t l S n o n l i n e a r o r o p e r a t i n g e n v i r o n me n t c h a n g e s ,t h e i f x e d
基于单神经元PID控制器的PLC直流电机控制系统

第3卷 2
第9 期
2 1 — [0 】 00 9 1 1
务I 匐 化
实 现 自适 应 、 自组 织 功能 。权 系数 的 调 整按 有 监
督 的Heb 习规则 实现 ,不 但结构 简单 ,而且能适 b学
应 环境 变化 ,有 较强 的鲁棒 性 。采 用单 神 经元P D I 控制 器来控 制直流 电机转速 可提 高直流 电机 系统的 性能 指标 。单神经 元PD控制 系统 框 图如 图2 示 。 1 所
W U Ln — u . ig y n CHEN Ch n x a u — i
( 长江大学 电子信息学院 ,荆州 4 4 2 ) 3 0 3
摘
要: 针对传统 P 控制器 对时变及非线性系统控制能力较差的缺陷 ,利用神经 网络具有 自学习、自 I D 适 应的 能力 ,设 计 了一种 单神经 元PD控制器 ,将 其应 用于 直流 电机 控制 系统中 。本文 给出 I 了基于罗克 韦尔可编程序 控制器 S C5 0 L 0 的单神经 元PI控 制器的实 现方法 。实验结果表 明 : D
Doi1 3 6 /iis 1 0 -0 4. 0 0 3 : 9 9 .s n. 9 1 0. 0 3 21 0. 9. 0
0 引 言
目前 电 机 控 制 系统 普 遍 采 用 P D控 制 算 法 , I P D参 数 由人 工 整 定 并 固定 。 由 于 电 机 负载 、对 I 象 特 性 和 环境 变 化 等 及 非 线 性 因 素 的 影 响 ,控 制 品质 会 随 之 下 降 ,很 难 获 得 满 意 的 控 制 性 能 。单 神 经 元 P D控 制 器 是 通 过 对 加 权 系 数 的 调 整 ,实 I
基于免疫遗传算法的单神经元PID控制器设计

单神 经元 自适 应控 制 器是 通 过对 加 权 系数 的调 整 来实 现
0 引言
单神 经元 作为 构成神 经 网络 的基本单 位 , 具有 自学 习和 自 适 应 能力 , 结 构简 单 , 于 计算 ; 且 易 而传 统 的PD调 节器 也 具有 I 结 构简 单和调 整容 易等 特点 。 有 自学习 和 自适 应能 力 的神经 具 元 构成 的单神 经元 自适应P D 制器 . I控 不但 结构 简单 、 习算 法 学
3
() 3
( = 3 一 ) 田 =k u k ( ) ( 1+ D( ) ( )3 )
( = i( )y u( )e J 是 输 出 误 差 信 号 , , 分 别 )r k - otk = ( ) n j } 研, 表 示 比例 、 分 、 分 的学 习速率 。 积 微 由 以 上 公 式 可 知 。 种 单 神 经 元 应 PD控 制 ,其 权 值 W , 分 别 相 当 于 PD 制 的 I W I控
要: 传统 单神 经 元P D 制 器 中神 经元 比例 系数及 学 习速 率的初 始 值 设置 往往 依 靠 经验 。 先采 用试 凑 法再根 I控 或
据 曲线响应 加 以微 调 , 对这 一缺 点 , 出 了一 种基 于免 疫遗传 算 法的单 神经 元PD 制 器。将 比例 系数 及 学 习速 率 针 提 I控 作 为待 优化 参数 , 通过 参数 寻优 自行在 搜 索空 间 内获得全 局 最优 点。仿 真结果表 明 。 方 法 自适 应能 力更 强、 新 鲁棒性 更好, 不仅 能够保 证较 好 的控 制 效果 , 而且解 决 了传 统 方法初 始值 设置 这一 大难题 。 关 键词 : 单神 经元 ; 免疫遗 传 算法 ; 初始 值设 置 ; 参数 寻优
单神经元PID自适应控制器的设计

单神经元PID自适应控制器的设计摘要把传统的PID控制和单神经元的优点有机地结合,产生单神经元PID 自适应控制器,可以改进传统PID的控制效果。
用单神经元实现自适应PID控制器功能,对单神经元结合的控制算法进行实验仿真,证明单神经元自适应PID 控制器具有良好的鲁棒性。
关键词单神经元;自适应;鲁棒性0 引言随着科学技术的不断进步和发展,传统PID控制技术难以达到人们的精确要求。
单神经元PID自适应控制器能较好地解决这类问题而得以广泛地应用[1]。
本文设计一种具有自适应、自学习功能的单神经元PID控制器,由仿真结果研究了该控制中参数的影响性。
图1为单神经元自适应PID控制器的结构框图,其中r(k)和输出y(k)为转换器的输入,x1(k),x2(k),x3(k)为转换器输出神经元学习控制所需要的状态量。
(2-1)为性能指标,k是比例系数,且k>0。
控制信号是由神经元通过关联搜索产生的。
(2-2)式2-2中wi(k)为xi(k)加权系数。
调整加权系数可以让单神经元PID控制器实现自适应、自学习,采用不同的学习规则可以形成相应的控制算法。
2 单神经元自适应PID控制系统及MATLAB仿真2.1 单神经元自适应PID控制系统的原理利用单神经元PID的控制,我们能够实现对多个变量的控制,图2的控制系统由两个单神经元控制器组成[2]。
单神经元自适应PID控制器要实现自适应,自组织功能的功能,我们可以通过对加权系数来调整而达到这一目的,例如有监督的Hebb学习规则。
下面的公式3-1,3-2为相应的算法:(3-1)(3-2)ηP、ηI、ηD 分别代表PID控制器的比例、积分、微分学习速率,k为比例系数,k>0。
在公式3-1中,k值要在合适的范围内,过小或者过大都会产生不理想的状态。
k过小,会使系统的快速性变差;k过大,快速性好,但会导致系统不稳定。
2.2 单神经元自适应PID控制仿真程序设有耦合二变量耦合被控对象:(3-3)设采样时间T=1s,给定输入为单位阶跃输入,即:响应曲线如图3和图4所示。
单神经元自适应PID控制器实验报告
单神经元自适应PID控制器仿真实验报告一、实验目的1、熟悉单神经元PID控制器的原理。
2、通过实验进一步掌握有监督的Hebb学习规则及其算法仿真。
二、实验内容利用单神经元实现自适应PID控制器,对二阶对象和正弦对象进行控制,在MATLAB环境中进行仿真。
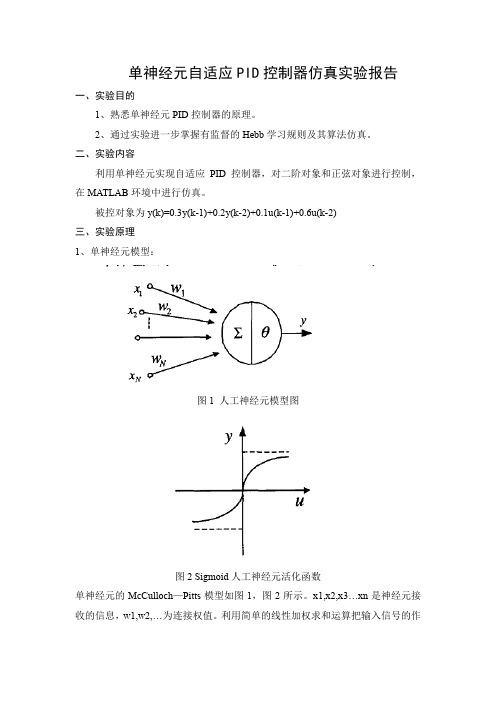
被控对象为y(k)=0.3y(k-1)+0.2y(k-2)+0.1u(k-1)+0.6u(k-2)三、实验原理1、单神经元模型:图1 人工神经元模型图图2 Sigmoid人工神经元活化函数单神经元的McCulloch—Pitts模型如图1,图2所示。
x1,x2,x3…xn是神经元接收的信息,w1,w2,…为连接权值。
利用简单的线性加权求和运算把输入信号的作用结合起来构成净输入input=∑w j x j−θ。
此作用引起神经元的状态变化,而神经元的输出v是其当前状态的激活函数。
2、神经经网络的有监督Hebb学习规则学习规则是修改神经元之间连接强度或加权系数的算法,使获得的知识结构适应周围环境的变化。
两个神经元同时处于兴奋状态或同时处理抑制状态时,它们之间的连接强度将得到加强,当一个神经元兴奋而另一个抑制时,它们之间的连接强度就应该减弱。
这一论述的数学描述被称为Hebb学习规则。
在学习过程中,网络根据实际输出与期望输出的比较,进行联接权系数的调整,将期望输出称导师信号是评价学习的标准。
这样,就得到了有监督的Hebb学习规则如果用oi表示单元i的输出,oj表示单元j的输出Wij表示单元j到单元i的连接加权系数,di表示网络期望目标输出,η为学习速率,则神经网络有监督的Hebb学习规则下式所示。
∆w ij(k)=η[di(k)−oi(k)]oi(k)oj(k)(1) 3.基于单神经元的PID控制单神经元控制系统的结构如图3所示。
图中转换器的输人为设定值r(k)和输出y(k),转换器的输出为神经元学习所需要的状态量x1,x2,x3,K为神经元的比例系数。
图3 单神经元自适应控制器结构图单神经元自适应控制器是通过对加权系数的调整来实现自适应、自组织功能的,权系数的调整是按有监督的Hebb规则实现的。
基于神经元PID控制器的远程实验系统设计

基于神经元PID控制器的远程实验系统设计李晓荣;刘志强【期刊名称】《现代电子技术》【年(卷),期】2016(039)009【摘要】Since the uncertainty of network delay in remote experiment system can impact on the experimental results,the remote experiment system based on neuron PID controller was designed. The algorithm of PID⁃NN neural network controller is studied. Its convergence and stability are analyzed. The implementation method of the system′s network communication and con⁃trol in client/server sides is given. The response contrast test for the machinery control arm was conducted in the laboratory. The experimental results show that the response overshoot,steady⁃state error and response time of the experiment system based on neuron PID controller are smaller than those of the experiment system based on common PID control method. The correctness of the algorithm was proved.%针对目前远程实验系统中网络延时的不确定对实验结果产生影响的问题,设计了基于神经元PID控制器的远程实验系统。
基于线性二次型的单神经元PID最优控制器设计及仿真

基于线性二次型的单神经元PID最优控制器设计及仿真0.前言由于传统的PID调节器算法简单、鲁棒性好及可靠性高,被广泛应用于过程控制和运动控制中,尤其适用于可建立精确数学模型的确定性系统,然而实际工业生产过程往往具有非线性、时变不确定性,难以建立精确的数学模型,应用常规的PID控制器不能达到理想的控制效果。
计算机技术和智能控制理论的发展为复杂动态不确定系统的控制提供了新的途径。
神经网络技术、模糊控制技术、遗传算法优化技术等智能控制技术发展很迅速。
将智能技术与数字PID控制结合起来,应用于工控现场,将有着广阔的发展前景。
近年来,神经网络由于具有自学习、自组织、联想记忆和并行处理等功能,因而受到了控制界的关注,在系统辨识与控制中得到了应用。
本文在自调整单神经元PID控制器中引入最优控制理论中的二次型性能指标,通过修改神经元控制器的权系数来使性能指标趋于最小,从而实现了对控制器性能的优化。
1.最优化技术及自适应PI D控制算法所谓最优控制问题,就是寻找一个控制系统的最优控制方案或最优控制规律,使系统能最优地达到预期的目标。
线性二次型最优控制系统是一类重要的最优控制系统。
这类系统得到的最优控制规律是状态变量的反馈形式,易于在工程上实现。
一般的自适应控制算法需要对过程进行辨识,然后再设计出自适应控制规律,从而限制了自适应控制算法的应用。
由Marsik和Strejc在1986年提出的无需辨识的自适应控制算法,其机理是根据过程误差的几何特性建立性能指标,这种算法无需辨识过程参数,只要在线检测过程的期望输出和实际输出,即可形成自适应控制器的控制规律。
2.基于二次型性能指标学习算法的单神经元自适应PI D控制算法单神经元自适应控制器是通过对加权系数的调整来实现自适应、自组织功能的,权系数的调整是按照有监督的Hebb学习规则实现的。
单神经元自适应控制PID控制结构如图1所示。
图 1 单神经元自适应PID 控制结构图中:rin 是给定值, yo u t 是输出值, e z rin yout ==-,这里1()x e k =;2()x e k = ;3()2(1)(2)x e k e k e k =--+-。
基于PLC的单神经元PID控制器的实现2

基于PLC的单神经元PID控制器的实现任俊杰自动化学院,北京联合大学,北京,100101,中国zdhtjunjie@摘要:考虑到复杂的控制系统非线性,纯滞后,大惯性,以及随时间变化的特点,传统的PID控制算法通常未能获得较好的控制效果。
将神经网络控制算法与传统的PID控制算法结合起来,神经元自适应PID控制能有效地提高了系统的性能。
本文设计的基于PLC的是一个单一的神经元PID控制器。
该控制系统的结构是简单的。
实现单神经元PID算法的功能块程序写在结构控制语言(SCL)。
该函数块具有常用和方便的特点。
实验结果表明,这种方法不仅高效,而且实用。
关键词:单神经元,PID,PLC,SCLI.简介由于PID控制算法简单,易于实施和良好的鲁棒性,它被广泛应用于工业过程控制系统。
但是,对于一个复杂的控制系统的非线性,纯时间延迟,大惯量和随时间变化的特性,传统的PID控制算法通常不能获得更好的控制效果。
添加先进的智能控制传统的PID控制算法,控制效果会更理想。
具有近似任意连续有界非线性函数的功能,神经网络是一种来解决非线性系统和不确定的系统有效的方式[1]。
在本文中,神经网络与传统的PID控制结合为应用PLC的神经自适应PID控制器。
他们发挥各自的优势。
与传统的PID控制相比,它具有超调小,控制高精度,抗干扰性能强的优点。
II.基于PLC的控制系统的结构单神经元PID控制器被应用到控制系统。
它具有传统PID的优点,并且还具有神经网络的优点,如并联结构,结构简单,学习和记忆功能和以及容易实现的特点[2]。
图1显示了用PLC作为控制器的单神经元PID控制系统。
图1中的虚线表示的是单个神经元PID控制器。
实际输出值y用计量装置转换为1-5V的电压信号或4-20mA的电流信号。
模拟信号连接到PLC的AI模块进行A / D转换。
用户程序中,比较了测量值y与设定值r,误差e测量和转换为三个输入信号的单神经元对应的比例,也比较了积分和差的功能。
基于单神经元PID控制器的设计

研究生课程期末论文课程名称:神经网络设计任课教师:论文题目:基于单神经元的控制系统设计姓名:学号:摘要在控制理论和技术飞跃发展的今天,PID控制由于其结构简单、稳定性能好可靠性高等优点而被广泛应用。
然而在实际的工业过程中,许多被控过程机理复杂,具有高度非线性。
这就要求在PID控制中,不仅PID参数的整定不依赖于对象数学模型,并且PID参数能在线调整,以满足实时控制的要求。
单神经元自适应PID控制将是解决这一问题的有效途径。
利用神经网络具有自学习、自组织、联想记忆和并行处理等功能和对于复杂系统控制可以达到满意效果的优势,提出了具有自学习和自适应能力的单神经元来构成单神经元自适应PID控制器的策略。
这种神经元构成的控制器不仅结构简单,且能适应环境变化,有较强的鲁棒性。
使自适应PID控制达到最优。
其仿真结果表明:该控制器与典型的PID控制器相比,系统输出能够很好地跟踪参考模型的输出显著提高了系统的动态响应能力。
关键词:自适应;PID控制;神经元第一章引言70年代以来,由于空间技术和过程控制发展的需要,特别是在微电子和计算机技术的推动下,自适应发展很快[1]。
到了80年代,建立在状态空间概念上的现代控制理论取得了很大进展,它不仅能用来解决单输入单输出控制系统的分析与设计问题,同时还能处理多输入多输出的控制系统的情况。
更为重要的是,在此期间内,线性系统,最优控制,最优估计,系统的辩识,随机控制等多个现代控制理论分支相继出现,并取得了有使用价值的成果,为自适应控制技术进一步发展提供了坚实的基础。
第二章问题描述随着工业和自动化技术的发展,自动化的应用领域日趋广泛,受控对象的复杂程度差异很大,而且控制精度的要求也参差不齐。
特别应该指出的是,对某些实际的工业受控对象来说,它们的数学模型(包括结构与参数)是很难事先提供的。
因为在实际情况中可能会出现受控对象的数学模型未知的情况和受控对象参数要发生不可知的变化的情况。
单神经元自适应控制器的设计

目录摘要 (I)Abstract (II)1 引言 ............................................................... - 1 -1.1 选题背景及意义................................................ - 1 -1.2 设计的整体安排................................................ - 1 -2 神经网络的理论基础 ................................................. -3 -2.1 单层感知器.................................................... - 3 -2.2 神经网络学习规则.............................................. - 4 -3 单神经元自适应PID控制器 .......................................... - 6 -3.1 PID控制的概述 ................................................ - 6 -3.2 神经元PID控制器.............................................. - 7 -3.3 神经元自适应PID控制器........................................ - 8 -3.4 几种典型的单神经元自适应PID控制器学习规则.................... - 9 -3.4.1无监督的Hebb学习规则.................................... - 9 -3.4.2 有监督Hebb学习规则 .................................... - 10 -3.4.3 改进的Hebb学习规则 .................................... - 11 -4 单神经元自适应PID控制器的仿真与研究 ............................. - 12 -4.1 对阶跃信号的跟踪............................................. - 12 -4.2 对外部对象发生变化时的适应性................................. - 15 -4.3 总结......................................................... - 18 -5 结束语 ............................................................ - 19 - 参考文献 ............................................................ - 20 - 致谢 .................................................... 错误!未定义书签。
PID控制器开发笔记之十三:单神经元PID控制器的实现

PID控制器开发笔记之十三:单神经元PID控制器的实现神经网络是模拟人脑思维方式的数学模型。
神经网络是智能控制的一个重要分支,人们针对控制过程提供了各种实现方式,在本节我们主要讨论一下采用单神经元实现PID控制器的方式。
1、单神经元的基本原理单神经元作为构成神经网络的基本单位,具有自学习和自适应能力,且结构简单而易于计算。
接下来我们讨论一下单神经元模型的基本原理。
1.1、单神经元模型所谓单神经元模型,是对人脑神经元进行抽象简化后得到一种称为McCulloch-Pitts模型的人工神经元,如下图所示。
根据上图所示,对于第i个神经元,x1、x2、……、xN是神经元接收到的信息,ω1、ω2、……、ωN为连接强度,又称之为权。
采用某种运算方式把输入信号的作用结合起来,得到他们总的结果,称之为“净输入”通常用neti表示。
根据所采用的运算方式的不同,净输入有不同的表示形式,比较常用的是线性加权求和,其表达式如下:其中,θi是神经元i的阈值。
而神经元i的输出yi可以表示为其当前状态的函数,这个函数我们称之为激活函数。
一般表示如下:1.2、采用的学习规则学习是神经网络的基本特征,而学习规则是实现学习过程的基本手段。
学习规则主要实现对神经元之间连接强度的修正,即修改加权值。
而学习过程可分为有监督学习和无监督学习两类。
它们的区别简单的说,就是是否引入期望输出参与学习过程,引入了则称之为有督导学习。
较为常用的学习规则有三种:1.2.1、无监督Hebb学习规则Hebb学习是一类相关学习,它的基本思想是:如果神经元同时兴奋,则它们之间的连接强度的增强与它们的激励的乘积成正比。
以Oi 表示单元i的激活值,以Oj表示单元j的激活值,以ωij表示单元j到单元i的连接强度,则Hebb学习规则可用下式表示:1.2.2、有监督Delta学习规则在Hebb学习规则中,引入教师信号,将式Oj换成网络期望目标输出dj和网络实际输出Oj之差,即为有监督Delta学习规则,即:1.2.3、有监督Hebb学习规则将无监督Hebb学习规则和有监督Delta学习规则两者结合起来,就组成有监督Hebb学习规则,即:在以上各式中,η称之为学习速度。
单神经元自适应PID控制 Hebb学习规则 matlab仿真 增量式PID 控制规律

实验一、单神经元自适应PID 控制一、实验目的1、熟悉单神经元PID 控制器的原理。
2、通过实验进一步掌握有监督的Hebb 学习规则及其算法仿真。
二、实验内容利用单神经元实现自适应PID 控制器,对如下二阶对象进行控制,在MATLAB 环境中进行仿真。
被控对象为:y(k)=0.368y(k-1)+0.26y(k-2)+0.1u(k-1)+0.632u(k-2) 三、实验原理线性神经网络是最简单的一种神经元结构,它不同于感知器,其函数是一线性函数,因此神经元的输出可以是任意值。
我们可以用它实现增量PID 控制器的功能,误差为神经元的输入,权系数为PID 控制系数,由于神经网络可以用在线学习对权系数进行实时修改,所以使得PID 控制具有了自适应功能。
PID 控制器的增量公式为一个3输入的线性神经元的计算公式为k 为神经元的比例系数,w i 为神经元权系数,x i 为神经元输入,u 为神经元的输出。
神经元的学习方法可以采用Hebb 学习规则。
有监督的Hebb 学习算法规范法处理后为3131111222333()()()()(1)()()(1)()()()()(1)()()()()(1)()()()()i i ii i i i i p d k k k u k u k k k x k k k u k e k x k k k u k e k x k k k u k e k x k ωωωωωωηωωηωωη=='==-++=++=++=+∑∑ 四、实验步骤1、编写程序实现单神经元的自适应PID 控制器,输入信号为单位阶跃信号。
单神经元控制的各参考参数为0.12,0.40,0.35,0.40p i d k ηηη====2、修改输入信号为()0.5(sin 4)r t sign t π=,进行上述试验。
3、改变被控制对象为如下几种情况,进行上述试验。
模型1:y(k)=0.368y(k-1)+0.264y(k-2)+u(k-1)+0.632u(k-2))2()(211---+-⨯+-+=∆k k k d k k P K i k e e e k e e k e k u )(332211x w x w x w k u ++=∆模型2:y(k)=0.368y(k-1)+0.264y(k-2)+gu(k-1)+0.632u(k-2)g=1+0.1*sin(0.01k)五、问题讨论神经网络学习算法的收敛速度与自适应控制效果的关系,收敛过程与学习规则中学习系数选取的关系。
基于单神经元的PID控制实现

基于单神经元的PID控制实现
介绍了一种单神经元自适应控制的方法,并提出了在线调整的方法。
该方法结构简单,便于在分散控制系统中实现。
0 引言
在工业过程控制中,PID控制是历史最悠久、生命力最强的控制方式。
这主要是因为这种控制方式具有直观、实现简单和鲁棒性能好等一系列优点。
在火电厂分散控制系统中,单输入单输出(SISO)、采用PID控制规律、简单的控制回路一般占80%以上。
但是,许多热工对象都具有大时延、大惯性的特性,使得过渡过程时间变长,调节品质变差;另外,对于高阶或多变量强耦合过程,PID的整定与控制都存在困难。
由于整定条件常常受到限制,以及对象的动态特性随着工况、环境等变化而发生变化,PID参数往往难以达到最优状态。
为此,本文提出一种单神经元自适应控制的方法。
通过大量的仿真实验表明,该方法简单易行,具有比普通PID算法好得多的控制效果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
研究生课程期末论文课程名称:神经网络设计任课教师:论文题目:基于单神经元的控制系统设计姓名:学号:摘要在控制理论和技术飞跃发展的今天,PID控制由于其结构简单、稳定性能好可靠性高等优点而被广泛应用。
然而在实际的工业过程中,许多被控过程机理复杂,具有高度非线性。
这就要求在PID控制中,不仅PID参数的整定不依赖于对象数学模型,并且PID参数能在线调整,以满足实时控制的要求。
单神经元自适应PID控制将是解决这一问题的有效途径。
利用神经网络具有自学习、自组织、联想记忆和并行处理等功能和对于复杂系统控制可以达到满意效果的优势,提出了具有自学习和自适应能力的单神经元来构成单神经元自适应PID控制器的策略。
这种神经元构成的控制器不仅结构简单,且能适应环境变化,有较强的鲁棒性。
使自适应PID控制达到最优。
其仿真结果表明:该控制器与典型的PID控制器相比,系统输出能够很好地跟踪参考模型的输出显著提高了系统的动态响应能力。
关键词:自适应;PID控制;神经元第一章引言70年代以来,由于空间技术和过程控制发展的需要,特别是在微电子和计算机技术的推动下,自适应发展很快[1]。
到了80年代,建立在状态空间概念上的现代控制理论取得了很大进展,它不仅能用来解决单输入单输出控制系统的分析与设计问题,同时还能处理多输入多输出的控制系统的情况。
更为重要的是,在此期间内,线性系统,最优控制,最优估计,系统的辩识,随机控制等多个现代控制理论分支相继出现,并取得了有使用价值的成果,为自适应控制技术进一步发展提供了坚实的基础。
第二章问题描述随着工业和自动化技术的发展,自动化的应用领域日趋广泛,受控对象的复杂程度差异很大,而且控制精度的要求也参差不齐。
特别应该指出的是,对某些实际的工业受控对象来说,它们的数学模型(包括结构与参数)是很难事先提供的。
因为在实际情况中可能会出现受控对象的数学模型未知的情况和受控对象参数要发生不可知的变化的情况。
同时在实际的工业过程中,许多被控过程机理较复杂,具有高度非线性、时变不确定性和纯滞后等特点。
在噪声、负载扰动等因素的影响下,过程参数,甚至模型结构,均会发生变化。
这就要求在PID控制中,不仅PID参数的整定不依赖于对象数学模型,并且PID参数能在线调整,以满足实时控制的要求。
第三章解决方案3.1 模型建立对于数学模型事先难以得到或事后又要发生变化的受控对象的控制问题,人们按照“仿生学”的思想,提出了一种新的控制方案——自适应控制方案。
该方案摹仿自然界中存在的“适应”过程,从而使系统具有能自动适应环境变化的能力。
如果我们把受控对象的数学模型(结构形式或和参数)或其变化事先并不知道这一特性称之为受控对象的不确定性,那么,自适应控制方案的大致思路可归纳为:系统可随时检测出本身的特性(或其变化),并在此基础上,对控制器的工作加以适当修正,以使系统内不确定性对系统性能所产生的不良影响得以减小。
自适应控制系统是一个具有一定适应能力的系统,它能够认识环境条件的变化,并自动校正控制动作,使系统达到最优或次优的控制并自动校正控制使系统达到最优或次优的控制效果。
自适应控制系统的原理框图如图3.1。
这一系统在运行过程中,根据参数输入)c和已知外部干扰(tu、对象输出)r、控制输入)(t(tn来测量对象性能指标进行比较,做出决策,然后通过适应机构来改变系统参)(t数,或者产生一个辅助的控制输入量,累加到系统上,以保证系统跟踪上给定的最优性能指标,使系统处于最优或次优的工作状态。
图3.1自适应控制系统原理框图单神经元作为构成神经网络的基本单位,具有自学习和自适应能力,而且结构简单易于计算。
而传统的PID控制器也具有结构简单、调整方便和参数整定与工程指标联系密切等特点。
若将这两者结合,则可以在一定程度上解决传统PID控制器不易在线实时整定参数、难于对一些复杂过程和参数慢时变系统进行有效控制的不足。
用神经元实现的自适应PID控制器的结构框图如图3.2所示图3.2 单神经元自适应PID控制的结构图单神经元控制系统的结构如图4.1所示。
图中转换器的输入为设定值()k r 和输出()k y ,转换器的输出为神经元学习所需要的状态量321x x x ,,,K 为神经元的比例系数。
单神经元自适应PID 控制器运用有监督Hebb 学习规则的控制算法及学习算 法为:()()()()∑=+-=31'1i i i k x k w K k u k u (3.1)()()()∑==31'/i i i ik w k w k w (3.2)()()()()()k x k u k z k w k w I 1111η+-= (3.3) ()()()()()k x k u k z k w k w P 2221η+-= (3.4) ()()()()()k x k u k z k w k w D 3331η+-= (3.5)式中 ()()k e k x =1 (3.6) ()()()12--=k e k e k x (3.7)()()()()()21223-+--=∆=k e k e k e k e k x (3.8)DP I ηηη、、分别为积分、比例、微分的学习速率,K 为神经元的比例系数,K>0,()k z 为性能指标或递进信号,对积分I 、比例P 和微分D 分别采用了不同的学习速率D P I ηηη、、,以使对不同的权系数分别进行调整。
3.2 改进的单神经元自适PID 控制器在大量的实际应用中,通过实践表明,PID 参数的在线学习修正主要与()k e 和()k e ∆有关,基于此可将单神经元自适应PID 控制算法中的加权系数学习修正部分进行改进,即将其中的()k x i 改为()()k e k e ∆+,改进后的算法如下()()()()∑=+-=311i i i k x k w K k u k u (3.9)()()()∑==31/j j j i k w k w k w (3.10)()()()()()()()k e k e k u k z k w k w I ∆++-=η111 (3.11) ()()()()()()()k e k e k u k z k w k w P ∆++-=η122 (3.12)()()()()()()()k e k e k u k z k w k w D ∆++-=η133 (3.13)式中 ()()()()()k e k z k e k e k e =--=∆,1 (4.14)采用改进后的算法后,权系数的在线修正就不完全是根据神经网络学习原理,而是参考实际经验制定的。
3.3 转换器的实现由图4.1可知,转换器的输入设定值和输出值,经过转换器后输出神经元学习控制所需要的状态控制信号,且,在SIMULINK 仿真环境中,可以通过零阶保持器来保存前一个状态,具体的状态转换器的仿真图如下所示。
3Out32Out21Out1Zero-Order Hold1Zero-Order Hold1In1图3.3 状态转换器的仿真结构图3.4常规PID 控制器与单神经元自适应PID 控制器仿真比较在工业生产过程中,考虑到大多数生产过程被控对象的普遍性和典型性,取广义对象传递函数为()2322++=S S s G 将普通PID 的响应图与采用有监督Hebb 学习规则的但神经元自适应PID 控制器的响应图做出详细的比较,以此来说明但神经元自适应PID 的优越性。
在对普通的PID 仿真中,取P k =0.8,I k =4,D k =3。
仿真波形如图4.3所示。
单神经元控制器的学习算法,用S 函数实现[10],在控制器中神经元权值的初始值分别取0.3,0.3,0.3,比例学习速率为P =680,微分学习速率D=100,积分学习速率为I=65,神经元比例系数为K=20。
第四章 实验结果由图4.3和图4.4可以看出,由传统的PID 控制器所得到的仿真波形图在一开始会出现不稳定的状态,且过渡时间较长,约需要20s 左右才能达到稳定,而采用单神经元网络自适应的PID 控制器没有超调且过渡时间进需5s 左右,由此可以看出单神经元网络自适应的PID 控制器有较强的自适应性和较高的控制精度。
图4.1 普通PID 控制器仿真结构图图4.2 单神经元自适应PID 控制器仿真结构图01020304050607080901000.20.40.60.811.21.41.6图4.3 常规PID 控制器仿真图01020304050607080901000.20.40.60.811.21.4图4.4 有监督的Hebb 学习规则阶跃跟踪曲线单神经元自适应PID 控制器学习规则可调参数的选取神经元权系数的学习确保系统的跟踪误差收敛于零。
只要跟踪误差存在,仿真过程就会使权值变化,从而使误差以最快的速度趋于零。
这样就通过关联搜索保证了系统的无静差。
只要保证学习算法的收敛性,调节系统就可以实现无静差和快速响应得控制效果。
通常学习效率对保证学习的收敛性有很大的关系,要由仿真分析来选择适当的学习效率。
单神经元自适应PID 控制器学习算法的运行效果与可调参K D P I 、、、ηηη等的选取有很大的关系。
通过大量实例仿真和实控结果,总结出以下调整规律:(1)初始加权系数()()()000321w w w 、、的选择:可以任意选取。
(2)K 值的选择:一般K 值偏大,将引起系统响应超调过大,而K 值偏小,则使过渡过程加长。
因此,可先确定一个增益K ,再根据仿真和实控结果进行调整。
(3)学习速率D P I ηηη、、的选择:由于采用了规范化学习算法,学习速率可取得较大。
选取K 使过程超调不太大,若此时过程从超调趋向平稳的时间太长,可增加D P ηη、;若超调迅速下降而低于给定值,此后又缓慢上升到稳态的时间太长,则可减少P η,增强积分项的作用。
对于大时延系统,为了减少超调,D P ηη、应选的大一些。
第五章 结论单神经元自适应PID 控制器实质上为一变系数的比例、积分、微分复合控制器,其输入与常规PID 控制器的输入类似,物理意义明确,其参数主要是通过一定的算法进行在线学习获得。
同时,神经元控制器的结构简单,计算量小,易于实现。
仿真实验和实际应用结果表明,由于神经元具有自学习特性,能够适应被控对象较大范围内的变化,具有较强的自适应能力和鲁棒性,其控制品质优于常规PID 控制器。
参考文献[1] 韩曾晋. 自适应控制[M].北京:清华大学出版社,1995.[2] 陶永华. 新型PID 控制及其应用[M].北京:机械工业出版社,2002.9. [3] 舒怀林. PID 神经元网络及其控制系统.北京:国防工业出版社,2005,1-6. [4] 周开利,康耀红.神经网络模型及其MATLAB 仿真程序应用[M].北京:清华大学出版社,2004,1-9.[5] 诸静.模糊控制原理与应用[M].北京:机械工业出版社,1998,194-179.[6] GERHARD KREISSELMEIER AND BRIAN D .ANDERSON .Robust Model Reference Adaptive Control .FELLOW , IEEE .[7] 舒前迪,李春涛,尹怡欣.单神经元自适应PID 控制器及其在电加热炉上的应用.电气传动,1995,25(1):29-32.。
