判断正比例∶
正比例和反比例判断方法(一)

正比例和反比例判断方法(一)正比例和反比例判断引言正比例和反比例是数学中常见的关系,用来描述两个变量之间的关系。
在实际生活中,我们常常需要判断两个变量之间的关系,以便进行进一步的分析和决策。
本文将详细说明正比例和反比例的判断方法,并给出示例说明。
正比例关系判断方法正比例关系是指两个变量之间的比值保持不变,即一个变量增加(或减少),另一个变量也随之增加(或减少)。
以下是正比例关系判断的方法:1.绘制散点图:将两个变量的取值绘制在坐标系中,并观察散点的分布情况。
如果散点呈现出一条直线,并且斜率大于零,则可以初步判断为正比例关系。
2.计算相关系数:利用统计学知识,可以计算两个变量之间的相关系数。
如果相关系数接近于1,则表明两个变量具有强正相关关系,可以认为是正比例关系。
3.验证比值是否保持不变:选择不同的取值,计算两个变量之间的比值,并观察比值是否保持不变。
如果比值相对稳定,则可以确定为正比例关系。
反比例关系判断方法反比例关系是指两个变量之间的乘积恒定,即一个变量增加(或减少),另一个变量随之减少(或增加)。
以下是反比例关系判断的方法:1.绘制散点图:同样的,将两个变量的取值绘制在坐标系中,并观察散点的分布情况。
如果散点呈现出一条曲线,并且通过原点,则可以初步判断为反比例关系。
2.计算乘积:计算两个变量的乘积,并观察乘积是否保持不变。
如果乘积相对稳定,则可以确定为反比例关系。
3.验证比例是否为常数:在反比例关系中,两个变量的比例应当为常数。
通过选择不同的取值,计算两个变量之间的比例,并观察比例是否保持不变。
如果比例相对稳定,则可以确定为反比例关系。
示例说明以下是几个示例,用以说明正比例和反比例的判断方法:示例 1:正比例关系变量A 变量B2 4变量A 变量B4 86 128 16根据给定的数据,我们可以通过绘制散点图观察到散点呈现一条直线,并且斜率大于零,初步判断为正比例关系。
我们还可以计算相关系数,得到相关系数接近1,进一步确认为正比例关系。
判断正比例与反比例的实例

判断正比例与反比例的实例
正比例和反比例是数学中常见的关系类型。
在实际生活中,我
们可以通过观察两个变量之间的变化关系来判断它们是正比例还是
反比例关系。
下面是一些判断正比例和反比例的实例:
判断正比例关系的实例:
1. 饼状图中的扇形大小与角度:如果在一个饼状图中,扇形的
大小与对应的角度成正比例关系,即扇形越大,对应的角度也越大,那么我们可以判断扇形的大小与角度是正比例关系。
2. 驾驶时间和行驶距离:如果我们在相同的速度下驾驶,行驶
的时间与行驶的距离应该是正比例关系。
例如,如果我们以恒定的
速度行驶,行驶一个小时可以行驶60公里,那么行驶两个小时可
以行驶120公里,行驶三个小时可以行驶180公里,可见行驶的距
离与行驶的时间成正比例关系。
判断反比例关系的实例:
1. 一个人在单位时间内所完成的工作量和工作时间:如果一个人在单位时间内完成的工作量与工作时间成反比例,即工作时间越短,完成的工作量越多,那么我们可以判断工作量和工作时间是反比例关系。
2. 人数和完成任务的时间:如果完成一个任务所需要的时间与人数成反比,即人数越多,完成任务的时间越短,那么我们可以判断人数和完成任务的时间是反比例关系。
以上是一些判断正比例与反比例关系的实例。
通过观察两个变量之间的变化规律,我们可以较容易地判断它们之间的关系类型。
正反比例判断

平行四边形的高一定,它的底和面积.
底×高=平行四边形面积 平行四边形面积÷底=高(一定) 所以平行四边形的底和面积成正比例
被除数一定,商和除数成反比例
商×除数=被除数(一定)
除数一定,商和被除数 成正比例
被除数÷商=除数(一定)
商一定,被除数和除数 成正比例
被除数÷除数=商(一定)
路程÷速度=时间(一定)
单价 总价 数量
单价一定, 总价和数量 成正比例
总价÷数量=单价(一定)
数量一定,总价与单价 成正比例
总价÷单价=数量(一定)
总价一定,单价与数量 成正比例
单价×数量=总价(一定)
长方形面积一定,长与宽
长×宽=面积(一定)
长方形长一定,面积与宽
长方形面积÷宽=长(一定)
长方形宽一定,面积与长
长方体的体积一定,它的底面积和高.
S×h=V(一定)
圆柱的体积一定,它的底面积和高.
S×h=V(一定)
圆柱的体积一定,它的底面半径和高.
r×r×h×3.14= V
一条水渠的长度一定,每天修的米 数和共需要的天数。
一条水渠的长度一定,已修的长度 和剩下的长度。
订阅《小学生学习报》的份数和钱数
从甲地到乙地,汽车行驶的速度和 所要的时间。
三角形面积一定,它的底和高 a×h÷2=S
圆的周长和半径
2π ×r= c
C÷r =2π(一定)
圆周长 6.28 12.56 18.84 25.12
半径 1 2
3
4
圆的面积和半径
2π r×r= s
S÷r = 2π r
圆面积 3.14 12.56 28.26 50.24
判断两个量是否成正比例的方法

判断两个量是否成正比例的方法判断两个量是否成正比例的方法在数学中,我们知道两个量如果成正比例,则它们的比值始终保持不变。
例如,如果两个物体的速度和距离成正比例,则它们的速度与距离的比例始终保持一致,无论它们相对于彼此的位置如何变化。
正比例关系在很多实际问题中都有着特殊的应用,因此判断两个量是否成正比例是非常重要的。
下面是一些判断两个量是否成正比例的方法:1. 画出直线图在判断两个量是否成正比例时,最常用的方法之一是绘制它们的直线图。
如果两个量成正比例关系,则它们所构成的点将会落在直线上。
更具体地说,这两个量的比率将表示为图中所画的直线的斜率。
因此,只要斜率始终保持一致,则可以判定这两个量是成正比例关系的。
2. 用一定的规律分析它们之间的关系除了绘制直线图之外,也可以通过一些规律,来分析两个量之间是否存在正比例关系。
例如,对于从固定高度落下的物体来说,它下落的时间和高度之间的关系是成正比例的。
具体来说,落下的物体从高度h开始落下到地面所需要的时间t,可以表示为t = √(2h/g),其中g是地球表面的重力加速度,它是一个常数。
因此,在这种情况下,时间和高度的比例将不会随着物体的位置而发生变化。
3. 求它们的比例常数如果两个量之间存在正比例关系,那么它们的比例关系应该是比例常数的倍数。
因此,如果想要判断两个量是否成正比例关系,则可以计算它们的比例常数。
比例常数表示为k,如果两个量成正比例,它们的比例应该始终为k。
例如,对于重力加速度和落体时间的关系,它们的比例常数k可以表示为k = √(2/g)。
如果在实验室中,我们通过观察多种高度的物体,获得它们在落下的过程中所需的时间,由此推算出它们的比例常数k,那么我们就能够证明落下的时间和物体的高度之间存在正比例关系。
4. 通过实验来证明如果不能确定两个量之间是否存在正比例关系,那么可以通过实验来证明。
例如,在这两个量之间进行若干次测量,如果它们的比例始终保持不变,则可以证明它们是成正比例的。
正比例反比例讲解

正比例反比例讲解
正比例和反比例是数学中常见的两个概念,它们描述了两个变量之间的关系。
理解这两个概念对于解决实际问题非常重要。
正比例:
当两个变量的值随着彼此的变化而同步增加或减少时,我们说它们成正比例关系。
换句话说,如果一个变量增加或减少了一定数量,另一个变量也会按相同的比例增加或减少,那么这两个变量就成正比例。
例如:
- 如果一个人的工资与工作时间成正比例,那么工作时间增加10%,工资也会增加10%。
- 如果一辆汽车的行驶距离与油箱中汽油量成正比例,那么油箱中汽油量增加20%,行驶距离也会增加20%。
数学上,如果y = kx,其中k是一个非零常数,那么y与x成正比例关系。
反比例:
当一个变量的值增加时,另一个变量的值减少,反之亦然,我们说它们成反比例关系。
也就是说,如果一个变量增加了一定数量,另一个变量会按相同的比例减少,那么这两个变量就成反比例关系。
例如:
- 如果一个人完成一项工作所需的时间与工人数量成反比例,那么工人数量增加25%,完成工作所需时间会减少25%。
- 如果一个圆的面积与半径的平方成反比例,那么半径增加10%,面积会减少19%(因为面积与半径的平方成反比)。
数学上,如果y = k/x,其中k是一个非零常数,那么y与x成反比例关系。
理解正比例和反比例关系对于解决许多实际问题非常有帮助,如计算工资、距离、面积等。
掌握这些概念有助于我们更好地分析和解决现实生活中的问题。
完整版)六年级数学正反比例

完整版)六年级数学正反比例正,反比例正比例和反比例是初中数学中的重要概念。
下面我们来整理一下相关知识点。
判断两种量是否成正比例,需要看它们是否相关联,一种量变化时,另一种量是否随之变化,以及它们的比值是否一定。
我们可以用字母x和y表示这两种量,用k表示它们的比值,正比例关系可以用y=kx表示。
判断两种量是否成反比例,同样需要看它们是否相关联,一种量变化时,另一种量是否随之变化,以及它们的乘积是否一定。
我们可以用字母x和y表示这两种量,用k表示它们的乘积,反比例关系可以用xy=k表示。
常见的正反比例题型包括圆的周长和半径、圆的面积和半径、平行四边形面积一定时的底和高等。
下面是一些典型例题:例1:某车间造纸时间和造纸总吨数的数据如下表所示。
我们可以在坐标系中描出对应的点,并根据图像的特点判断它们成正比例关系。
例2:这道题列举了多种量的情况,需要判断它们是否成比例,如果成比例,是正比例还是反比例。
例3:这道题给出了3:A = 5:B的比例关系,需要求出A与B的比例关系。
根据比例的性质,可以得出A与B成反比例关系。
2.如果3:B = A:5,则A与B成什么比例?为什么?根据题意,可以得到以下等式:3:B = A:5将等式两边乘以5,得到:15:B = A因此,A与B成15:B的比例。
这是因为等式中的比例关系是等价的,即3:B与A:5是等价的,所以它们的比例关系也是等价的。
因此,可以通过等式中的比例关系来确定A与B之间的比例关系。
举一反三:1.a和b相关联的两种量,下面哪个式子表示a和b成正比例?⑤b=7a因为当a增加时,b也会增加,且它们之间的比例关系保持不变,因此a和b成正比例。
2.x、y、z是三种相关联的量,已知x×y=z。
当(x+z)一定时,(y+z)和(y-x)成正比例。
拓展提升:1.如果ab=24,那么a和b成反比例;如果a÷b=18,那么a和b成正比例。
2.一个比例式,两个外项之和是37,差是13,两个比的比值是2.5,那么比例式为5:2.3.甲乙两人步行速度之比是7:5,甲乙分别从a、b两地同时出发,如果相向而行,0.5小时后相遇,如果他们同向而行,那么甲追上乙需要多长时间?题型一:按要求选四个数字组成各一个比例式子12的因数有1、2、3、4、6、12,选四个数字可以得到比例式1:2:3:4.举一反三:1.从36的因数有1、2、3、4、6、9、12、18、36,选四个数字可以得到比例式1:2:3:6.2.写出一个比值是24的比例式是3:1.题型五:人员调配问题一个车间有两个小组,第一个小组与第二个小组的人数比是5:3.如果第一个小组的14人到了第二个小组时,第一小组与第二小组的人数比是1:2,原来两个小组各有多少人?设第一个小组原来有5x人,第二个小组原来有3x人,则有以下等式:5x-14 : 3x+14 = 1 : 2解方程得到x=14,因此第一个小组原来有70人,第二个小组原来有42人。
正比例与反比例的判断方法

正比例与反比例的判断方法一、正比例的判断方法正比例是指两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值 (商) 一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
判断正比例的方法如下:1. 找变量:确定哪两种量是相关联的量。
2. 看定量:分析这两种相关联的量,它们之间的关系是商一定还是积一定。
3. 判断:如果商一定,就成正比例;如果积一定,就成反比例;如果商和积都不是定量,就不成比例。
举个例子,假设小明的身高和他的体重成正比例,即小明的身高每增加 1 厘米,他的体重就会增加一定的值。
假设小明的身高为 170 厘米,他的体重为 70 公斤,那么根据正比例的关系,小明的体重和身高的比值应该是 70/170,这是一个定值。
因此,我们可以得出结论,小明的身高和他的体重成正比例。
二、反比例的判断方法反比例是指两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
判断反比例的方法如下:1. 找变量:确定哪两种量是相关联的量。
2. 看定量:分析这两种相关联的量,它们之间的关系是商一定还是积一定。
3. 判断:如果积一定,就成反比例;如果商一定,就不成比例;如果商和积都不是定量,就不成比例。
举个例子,假设小明的学习时间和他的成绩成正比例,即小明的学习时间每增加 1 小时,他的成绩就会增加一定的值。
假设小明的学习时间分别为 1 小时、2 小时、3 小时,他的成绩分别为 80 分、90 分、100 分,那么根据反比例的关系,小明的学习时间和他的成绩的积应该是一个定值。
假设小明的学习时间分别为 1 小时、2 小时、3 小时,他的成绩分别为 80 分、90 分、100 分,那么根据反比例的关系,小明的学习时间和他的成绩的积应该是一个定值。
正比例和反比例判断方法

正比例和反比例判断方法
正比例和反比例是数学中基本的二元关系之一,它们可以用以下公式表示: 正比例:y = kx + b
反比例:y = 1/x + b
其中,y 表示输出,x 表示输入,k 和 b 是常数。
判断正比例和反比例的方法如下:
1. 正比例:当输出 y 与输入 x 成正比例关系时,可以使用以下公式来判断:
当 k > 0 时,y 随 x 的增大而增大,则 x 和 y 为正比例关系;
当 k < 0 时,y 随 x 的增大而减小,则 x 和 y 为正比例关系;
当 k = 0 时,y 不随 x 的增大而变化,则 x 和 y 为正比例关系。
2. 反比例:当输出 y 与输入 x 成反比例关系时,可以使用以下公式来判断:
当1/k > 0 时,y 随 x 的增大而增大,则 x 和 y 为反比例关系;
当1/k < 0 时,y 随 x 的增大而减小,则 x 和 y 为反比例关系;
当1/k = 0 时,y 不随 x 的增大而变化,则 x 和 y 为反比例关系。
在实际应用中,正比例和反比例关系常常出现在物理、化学、经济学等领域中。
例如,在物理学中,电流和电压之间的关系可以表示为正比例关系,因为电流是电压的倍数;在化学中,反应速率和反应物浓度之间的关系可以表示为正比例关系,因为反应速率是反应物浓度的倍数;在经济学中,经济增长率和人口增长率之间的关系可以表示为正比例关系,因为经济增长率是人口增长率的倍数。
判断正反比例关系

判断正反比例关系就可以用下面三步来进行:一、列乘法关系式。
正反比例必定存在乘除法关系,如是加减法关系就可直接判断不成比例。
二、划一定量。
这里需要区分一定量和常量,题意给定某个量一定我们称之为一定量,常量指具体数。
题意没有明确一定量,而乘法式子中含有常量,那么这个常量也为一定量;如果既明确了一定量,乘法式子中又有常量,那么一定量和常量可进行合并。
三、分析判断正反比例。
乘法式子中一个因数一定,则成正比例;乘法式子中积一定,则成反比例。
判断正、反比例关系的“三招”学完正、反比例这部分内容以后,很多同学感到枯燥难学,具体到判断正反比例关系的题目准确性不高。
其实只要统一正反比例思路,总结正反比例的内在联系,判断正反比例就可迎刃而解。
大家可以采用“找”、“写”、“判”这“三招”来判断正、反比例。
第一招“找”:根据题意找出两种相关联的量和一个一定的量(不变量)。
第二招“写”:根据两个相关联的量写出求定量的关系式。
第三招“判”:根据关系式进行判断,如果定量是两种相关联的量的商,则成为比例;如果定量是两种相关联量的积,则成反比例。
例如,判断下面各题中的两种量成什么比例或不成比例。
(1)长方形的面积一定,它的长和宽。
一找:两种相关联的的量是“长”和“宽”,定量是“长方形的面积”。
二写:关系式是“长×宽=面积(一定)”。
三判:长方形的面积一定,也就是长与宽的积一定。
所以,长方形的长与宽成反比例。
(2)工作效率一定,工作总量和工作时间。
一找:两种相关联的量是“工作总量”和“工作时间”,定量是“工作效率”。
二写:关系式是“工作总量÷工作时间=工作效率(一定)"。
三判:工作效率一定,也就是工作总量的与工作时间的商一定。
所以,工作总量与工作时间成正比例。
(3)有一批布,用去的米数和剩下的米数。
一找:两种相关联的量是“用去的米数”和“剩下的米数”,定量是“一批布”。
二写:关系式是“用去的米数+剩下的米数=一批布的米数(一定)”。
正比例和反比例知识点

正比例和反比例知识点一、变化的量生活中存在着大量互相依存的变量,一种量变化,另一种量也随着变化。
二、正比例1. 正比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
如果用字母x和y表示两种相关联的量,用字母k表示它们的比值(一定),正比例关系可以表示为:y/x=k(一定)。
2. 应用正比例的意义判断两种量是否成正比例:有些相关联的量,虽然也是一种量随着另一种量的变化而变化,但它们相对应的数的比值不一定,就不成正比例,如被减数与差,正方形的面积与边长等。
三、画一画正比例的图像是一条直线。
四、反比例1. 反比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
如果用字母x和y表示两种相关联的量,用k表示它们的乘积,反比例的关系式可以表示为:x·y=k(一定)。
2. 判断两个量是不是成反比例:要先想这两个量是不是相关联的量;再运用数量关系式进行判断,看这两个量的积是否一定;最后作出结论。
五、观察与探究当两个变量成反比例关系时,所绘成的图像是一条光滑曲线。
六、图形的放缩一幅图放大或缩小,只有按照相同的比来画,画的图才像。
七、比例尺1. 比例尺:图上距离与实际距离的比,叫做这幅图的比例尺。
图上距离=实际距离×比例尺实际距离=图上距离÷比例尺2. 比例尺的分类:比例尺根据实际距离是缩小还是扩大,分为缩小比例尺和放大比例尺。
根据表现形式的不同,比例尺还可分为线段比例尺和数值比例尺。
3. 比例尺的应用:已知比例尺和图上距离,求实际距离比例尺=图上距离÷实际距离图上距离=实际距离×比例尺实际距离=图上距离÷比例尺。
判断正比例与反比例专项练习题
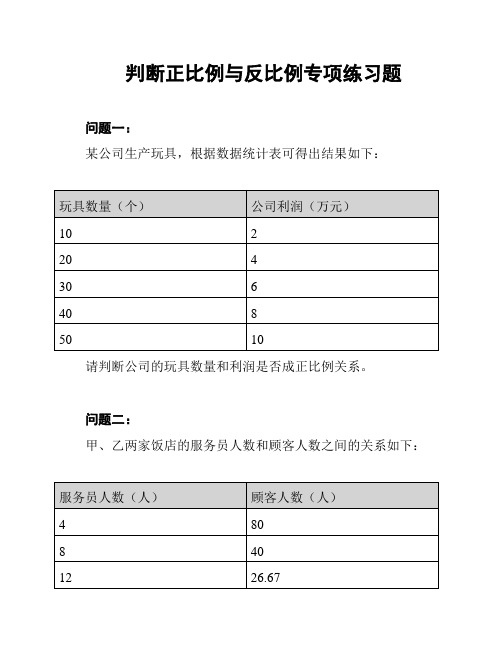
判断正比例与反比例专项练习题
问题一:
某公司生产玩具,根据数据统计表可得出结果如下:
请判断公司的玩具数量和利润是否成正比例关系。
问题二:
甲、乙两家饭店的服务员人数和顾客人数之间的关系如下:
请判断饭店的服务员人数和顾客人数是否成反比例关系。
问题三:
某池塘中的鱼的数量和水的深度之间的关系如下:
请判断池塘的水深和鱼的数量是否成反比例关系。
问题四:
某学校的学生数和书籍数的关系如下:
请判断学校的学生数和书籍数是否成反比例关系。
问题五:
某工厂织布时,织机每小时的织布米数与织物重量的关系如下:
请判断织机的织布米数和织物重量是否成正比例关系。
判断正比例的方法

判断正比例的方法引言正比例是数学中常见的一种关系,也是现实生活中广泛出现的一种情况。
在解决与正比例相关的问题时,我们需要运用一定的方法和技巧来判断是否为正比例关系。
本文将介绍判断正比例的方法,并从多个角度进行探讨。
方法一:观察法观察法是最简单直观的方法之一,通过观察给定的数据是否呈现出一定的规律或趋势来判断是否为正比例关系。
具体步骤如下: 1. 通过绘制数据的散点图来观察是否存在一条直线关系; 2. 观察数据散点图是否具有正向的趋势,即随着自变量的增大,因变量是否同步增大或减小。
如果观察到数据散点图呈现出一条直线且具有正向趋势,那么可以初步判断为正比例关系,进一步的分析可以通过其他方法来进行。
方法二:计算法计算法是一种通过计算给定数据的比值来判断是否为正比例关系的方法。
具体步骤如下: 1. 计算相邻数据对应的比值,即; 2. 观察计算得到的比值是否固定,即是否存在一个常数使得,其中和分别为自变量和因变量的取值。
如果计算得到的比值恒定不变,那么可以判断为正比例关系。
此时,该常数即为比例系数。
方法三:线性回归法线性回归法是一种通过拟合数据点到一条直线上来判断是否为正比例关系的方法。
具体步骤如下: 1. 给定一组自变量和因变量,将其绘制在坐标系中; 2. 通过线性回归分析的方法,找到一条最佳拟合直线,使其尽量穿过数据点; 3. 观察拟合直线是否具有正斜率,即从左下到右上的趋势。
如果拟合直线具有正斜率,那么可以判断为正比例关系。
此时,该直线的斜率即为比例系数。
方法四:检验法检验法是一种通过检验数据是否满足定义的正比例关系来判断的方法。
具体步骤如下: 1. 根据定义的正比例关系,列出数学模型,如; 2. 将给定的数据代入数学模型中,计算得到的预测值; 3. 比较预测值与实际值之间的差异,观察是否接近或等于零。
如果预测值与实际值之间的差异非常小,那么可以判断为正比例关系。
在此基础上,还可以计算残差来评估数据与拟合模型之间的偏差程度。
(完整版)六年级数学正反比例

正,反比例(一)知识点整理1、判断两种量是否成正比例,意识看他们是否是相关联的两种量;二是看一种量变化,另一种量是不是也随着变化;三是看它们的比值是否一定,不能省任何一步。
如果用字母x 和y 表示两种相关联的量,用k 表示他们的比值,正比例关系可以用下面的式子表示:xy=k (一定) 2、判断两种量是否成反比例,意识看他们是否是相关联的两种量;二是看一种量变化,另一种量是不是也随着变化;三是看它们的乘积是否一定,不能省任何一步。
如果用字母x 和y 表示两种相关联的量,用k 表示他们的乘积,反比例关系可以用下面的式子表示:xy=k (一定) 3、常考判断正反比例题型 (1)圆的周长和半径。
(2)圆的面积和半径。
(3)平行四边形面积一定,底和 (二)典型例题例1、某车间造纸时间和造纸总吨数如下表: 造纸时间(小时) 1 2 3 4 5 造纸总吨数20406080100根据表中的数据,在下图中描出造纸时间和造纸总吨数对应的点,再把它们按顺序连起来,并观察正比例图像的特点。
造纸总吨数2040 80 601 2 3 4 5 6 造纸时间(小时) 【结论】横轴表示时间,纵轴表示总吨数,描点时注意要看清纵轴对应的数量,描完点后,可以发现,正比例的图像成一条直线。
例2、判断下面的量是否成比例,成什么比例。
1、正方形的边长和面积。
( )2、被除数一定,除数和商。
( )3、圆的周长和半径。
( )4、运的总吨数一定,运走的和剩下的。
( )5、平行四边形面积一定,底和高。
( )6、装配一批电视机,每天装配台数和所需的天数。
( )7、每块砖的面积一定,砖的块数和铺地面积。
( ) 8、三角形面积一定,底和高。
( )9、在一定的距离内,车轮周长和它转动的圈数。
( ) 10、小明做10道数学题,做完的题和没有做的题( )11、如果a 是b 的53(a ,b ≠0),a 和b 。
( ) 12、长方体体积一定,它的体积和高( )13、平行四边形的面积和底。
怎样判断两种量是否成正比例或反比例关系?ppt

设生产零件的时间是60小时
生产每个零件所用的 1 2 3 4 5 …… 时间(小时)
生产零件的个数(个) 60 30 20 15 12 ……
对一个数进行“改写” 与求一个数的近似数有什么区别?
南京市建邺区教师进修学校 王凌
【准确数与近似数】 在计数和计算过程中,有时 能得到与实际完全相符的数,这些数叫准确数,如 某校的数学教师有15人、6×1.2=7.2等等,但在生 产、生活和计算中得到的某些数,往往只是接近于 准确数,这种数叫近似数。如“某市人口有75 万,”75万就是一个近似数。因为在统计一个城市 的人口时,由于居民的迁入和迁出,出生和死亡, 人口的数目随时都在变化,很难得出准确的人口数。 在计算圆周长的公式里,圆周率可以用3.14代入计 算,3.14也是个近似数。 可见,准确数与近似数主要区别在于是否与实际情 况完全相符。
正方形的周长和边长
正方形的周长÷边长=4(一定值) 所以正方形的周长和边长成正比例。
三角形的面积一定,它的底和高成什么比例?
因为:底×高=三角形面积×2(一定) 所以,三角形面积一定,底和高成反比例。
要关注对“两种相关联的量”的判断 例:正方体体积一定,底面积和高是否成比例?
Hale Waihona Puke 要关注对“两种相关联的量”的判断
化简算式法
如果6x=7y(x、y都不等于0),那 么x和y成什么比例?
化简算式法
如果6x=7y(x、y都不等于0),那 么x和y成什么比例?
可以根据等式的性质化简算式,得: x:y=7:6 所以x和y成正比例。
列表举例法
生产零件的时间一定,生产每个零件所用的时间 和生产零件的个数。
判断正比例反比例技巧

判断正比例反比例技巧一、引言正比例和反比例是初中数学中非常基础的知识点,但在实际应用中却非常重要。
因此,判断正比例和反比例是学习数学的基本功之一。
本文将详细介绍判断正比例和反比例的技巧。
二、正比例与反比例的定义1. 正比例:当两个量的变化方向相同时,它们之间的关系称为正比例关系。
例如,当一个物品的数量增加时,它的价格也会随之增加。
2. 反比例:当两个量的变化方向相反时,它们之间的关系称为反比例关系。
例如,当一个人跑步速度越快时,他所用的时间就会越短。
三、判断正比例与反比例1. 判断正比例:(1)对于给定的两个量x和y,在同一条件下逐渐增大或减小其中一个量,并观察另一个量是否随之增大或减小。
如果另一个量随着第一个量同步变化,则这两个量是正比例关系。
(2)可以通过计算这两个量之间的比值是否恒定来判断它们是否成正比。
即y/x是否等于某个固定值k。
2. 判断反比例:(1)对于给定的两个量x和y,在同一条件下逐渐增大或减小其中一个量,并观察另一个量是否随之减小或增大。
如果另一个量与第一个量的变化方向相反,则这两个量是反比例关系。
(2)可以通过计算这两个量之间的积是否恒定来判断它们是否成反比。
即xy是否等于某个固定值k。
四、实例分析1. 判断正比例:例如,已知一辆汽车行驶100公里需要消耗10升汽油,问行驶200公里需要消耗多少升汽油?解:根据正比例的定义,我们可以得到:100/10 = 200/x,解出x=20。
因此,行驶200公里需要消耗20升汽油。
2. 判断反比例:例如,已知5个工人可以在10天内完成一项工作,问10个工人需要多少天才能完成同样的工作?解:根据反比例的定义,我们可以得到:5×10 = 10×x,解出x=5。
因此,10个工人需要5天才能完成同样的工作。
五、总结判断正比例和反比例是初中数学中非常基础而重要的知识点。
本文从定义、判断方法和实例分析三方面详细介绍了判断正比例和反比例的技巧。
判断正比例的方法

判断正比例的方法一、前言正比例是数学中常见的概念,它指的是两个变量之间存在着一种线性关系,即当一个变量增加时,另一个变量也会按照一定比例增加。
在实际应用中,我们经常需要判断两个变量之间是否存在正比例关系。
本文将介绍几种判断正比例的方法。
二、图像法图像法是判断正比例的一种简单有效的方法。
具体步骤如下:1. 给定两个变量x和y,将它们分别作为坐标轴上的横纵坐标。
2. 将给定的数据点在坐标系中画出来。
3. 如果这些数据点在坐标系中呈现出一条直线,则说明这两个变量之间存在正比例关系。
4. 如果这些数据点不在同一条直线上,则说明这两个变量之间不存在正比例关系。
三、计算法计算法是判断正比例的另一种方法。
具体步骤如下:1. 给定两个变量x和y,并且已知它们之间存在正比例关系,即y=kx (其中k为常数)。
2. 选取任意两组数据点(x1,y1)和(x2,y2),并计算它们之间的斜率k=(y2-y1)/(x2-x1)。
3. 如果计算出来的斜率k等于常数k,则说明这两个变量之间存在正比例关系。
4. 如果计算出来的斜率k不等于常数k,则说明这两个变量之间不存在正比例关系。
四、求解方程法求解方程法是判断正比例的另一种方法。
具体步骤如下:1. 给定两个变量x和y,并且已知它们之间存在正比例关系,即y=kx (其中k为常数)。
2. 选取任意一组数据点(x,y),并代入上述公式中得到y=kx。
3. 将该公式与给定的数据点中的另外一组(x,y)代入得到另一个等式y'=kx'。
4. 将上述两个等式相除,得到y/y'=(kx)/(kx'),化简后得到x/x'=y/y',即可判断这两个变量之间是否存在正比例关系。
五、误差分析在实际应用中,由于各种因素的影响,我们很难找到完全符合正比例关系的数据点。
因此,在使用上述方法判断正比例时需要注意误差分析。
具体步骤如下:1. 对数据进行处理,例如去掉异常值或进行平滑处理等。
正比例和反比例判断方法

正比例和反比例判断方法正比例和反比例是数学中常见的关系。
在实际生活中,我们可以通过观察和分析来判断两个变量之间是否存在正比例或反比例关系。
本文将介绍如何判断正比例和反比例关系,帮助读者更好地理解和应用这些概念。
一、正比例关系的判断方法正比例关系是指两个变量之间的比例保持不变。
具体来说,当一个变量增加时,另一个变量也相应增加;当一个变量减少时,另一个变量也相应减少。
下面是判断正比例关系的方法:1. 观察变量的变化趋势:通过观察两个变量的变化趋势,可以初步判断是否存在正比例关系。
如果两个变量的变化趋势基本一致,即一增一减或一减一增,那么很可能存在正比例关系。
2. 绘制散点图:为了更直观地判断正比例关系,可以将两个变量的取值用散点图表示出来。
如果散点图呈现出一条直线,并且直线经过原点,那么可以确定存在正比例关系。
3. 计算比例系数:如果通过观察和散点图无法确定正比例关系,可以计算两个变量的比例系数。
比例系数等于一个变量的增加量与另一个变量的增加量的比值。
如果比例系数大致相等,那么可以判断存在正比例关系。
二、反比例关系的判断方法反比例关系是指两个变量之间的比例不断变化。
具体来说,当一个变量增加时,另一个变量相应减少;当一个变量减少时,另一个变量相应增加。
下面是判断反比例关系的方法:1. 观察变量的变化趋势:通过观察两个变量的变化趋势,可以初步判断是否存在反比例关系。
如果一个变量增加时,另一个变量减少,或者一个变量减少时,另一个变量增加,那么很可能存在反比例关系。
2. 绘制散点图:为了更直观地判断反比例关系,可以将两个变量的取值用散点图表示出来。
如果散点图呈现出一个倒置的双曲线形状,那么可以确定存在反比例关系。
3. 计算比例系数:如果通过观察和散点图无法确定反比例关系,可以计算两个变量的比例系数。
比例系数等于一个变量的增加量与另一个变量的减少量的比值。
如果比例系数大致相等,那么可以判断存在反比例关系。
三、正比例和反比例关系的实际应用正比例和反比例关系在实际生活中有广泛的应用。
判断正反比例的方法

判断正反比例的方法
判断正反比例的方法是一种数学基本技能,它在日常生活中也有广泛的应用。
正比例是指在两个变量之间,一个变量增加或减少,另一个变量也同样增加或减少。
反比例是指在两个变量之间,一个变量增加,另一个变量会减少,反之亦然。
以下是判断正反比例的方法:
1. 给定两个变量的数据,将它们进行简单的比较。
如果一个变量的值增加,而另一个变量的值也增加,则它们是正比例关系。
如果一个变量的值增加,而另一个变量的值减少,则它们是反比例关系。
2. 利用比例的定义,即两个变量之间的比值是否固定。
如果一个变量增加,而另一个变量的比值也增加或减少,则它们是正比例。
如果一个变量增加,而另一个变量的比值减少或增加,则它们是反比例。
3. 绘制一个图表来帮助判断正反比例关系。
如果两个变量之间存在正比例关系,则它们的图表应该呈现出一条直线。
如果两个变量之间存在反比例关系,则它们的图表应该呈现出一条反比例曲线。
除了以上的方法,还有一些其他的方法可以用来判断正反比例关系,例如利用比例的性质进行推导和证明。
不论采用哪种方法,判断正反比例关系都是数学学习的必备技能,它对于日常生活和职业发展都有重要的作用。
- 1 -。
正比例关系判断题

正比例关系判断题
嘿,朋友!咱今天来聊聊正比例关系判断题这事儿。
你说啥是正比例关系?简单来讲,就像你去买苹果,一个苹果两块钱,那买两个苹果就四块,买三个就六块,买的苹果数量越多,花的钱就越多,而且这钱增加的比例是固定的,这就是正比例关系。
那咋判断是不是正比例关系呢?咱得瞧瞧两个量之间是不是有这样的规律:一个量变大,另一个量也按照固定的比例跟着变大;一个量变小,另一个量也按同样的比例跟着变小。
这就好比你走路,步子迈得大,走的距离就远;步子迈得小,走的距离就短,而且步子大小和走的距离的变化比例是固定的。
比如说,汽车行驶的速度不变,时间越长,行驶的路程就越远。
这速度不变,时间和路程不就是正比例关系嘛!可要是速度变来变去,那就不是正比例啦,这不就跟你心情好的时候干活快,心情不好的时候干活慢,这干活的速度都不稳定,能成正比例吗?
再看个例子,给一个正方形的边长增加,它的面积也增加。
但这可不是正比例关系哟!为啥?因为边长增加的比例和面积增加的比例不一样啊。
这就好像你吃饭,吃一碗饱了点,吃两碗更饱,但饱的程度增加可不是固定的比例呀!
还有啊,做题的时候可得瞪大眼睛看清楚条件。
别一看到两个量都在变,就觉得是正比例关系。
得好好琢磨琢磨它们变化的规律是不是固定比例。
判断正比例关系就像是在迷雾中找路,稍微迷糊一点就可能走错方向。
可只要你抓住关键,也就是那固定的变化比例,就能轻松找到正确的答案。
所以说,正比例关系判断题也没那么难,只要咱用心,仔细分析,就一定能搞清楚!怎么样,是不是觉得心里有点底啦?。
六下正反比例的判断技巧

看谁最聪明
给我们的教室铺地板砖,方砖的面积和所需块 数是不是成反比例?
分析:
1、方砖的面积和所需块数是两种相关联的量。 2、方砖的面积大,所需块数多;方砖的面积小,所需块数少。
12 X
a = a×(1+25%)
即
12 X
1 = 1+25%
做一做
12、化肥厂计划生产化肥1400吨,由于改进技术5天就完
成了计划的25%,照这样计算,剩下的任务还需多少天完
成分析?:5天完成25%,25%即工作总量,效率一定,时间比等于工作
总量的比。设剩下的任务还需X天完成,则
5 X
=
25% 1-25%
反之如果一定这个量是积,那么另外两个变量就成反比 例。如:工作总量一定,工作效率和工作时间成( )比 例。因为工作总量一定,而工作总量=工作效率×工作时 间,所以工作效率和工作时间成反比例。
要注意为什么是两个“变”量?
因为这是成正、反比例的两种量必须符合的一个条 件。比如判断:圆的周长一定,圆周率和直径成反比 例。有同学认为周长一定,即“积一定”,两种相关 联的量就成反比例,而圆周率是一个固定不变的常数, 因此,上述判断是错的。要明确两种相关联的量指的 是两个“变量”,改为圆的周长和直径成正比例可以。
分析:每次所用时间相同,乙、丙速度之比等于两次所行路程之比。 设丙还差x米。则 20∶(25-x)=(100-20)∶(100-25) 解得x=6.25
11、有一个面积是12平方米的平行四边形。如果它的底增 加25%,高不变,它的面积应该是多少平方米?
