专题:比例式等积式的常见证明方法
九年级数学下册第二十七章 专题:比例式、等积式的3种证明方法

(2)EF·CG=DF·BG. 证明:在△AEF 和△ABG 中, ∠AED=∠B,∠EAF=∠BAG, ∴△A E F∽△A B G.∴BEGF =AAGF . 由(1)知△A DF ∽△A CG.∴DCGF=AAGF .
∴E F =DF .∴E F ·CG=DF ·B G.
BG CG
∴△A B F ∽△CB E .∴AB BC=ACFE .
◆类型二 等线段代换法 2.【2022 新课标·综合性】如图,AB 为⊙O 的直径, BC,CD 均为⊙O 的切线,射线 CD 交 BA 的延长线于 点 E,连接 AD,BD,OC.求证:ED·CD=OB·BE.
证明:如图,连接 DO, ∵BC,CE 为⊙O 的切线, ∴∠E DO=∠E B C=90°,B C=CD.
又∵∠E =∠E ,
∴△E OD∽△E CB . ∴EBDE =OBCD. ∴E D·B C=OD·B E . ∵OD=OB ,B C=CD,∴E D·CD=OB ·B E .
◆类型三 等比(或等积)代换法 3.如图,已知在△ABC 中,∠ACB=90°,点 D 在边 BC 上,CE⊥AB,CF⊥AD,E、F 分别是垂足,连接 E F.求证:AF ·A D=A E ·A B . 证明:∵∠A CB =90°,CF ⊥A D, ∴∠A CD=∠A F C.又∠CA D=∠FA C, ∴△A CD∽△A F C.∴A C=A D.∴A C2=A F ·A D.同理可
AF AC 证△ACE∽△ABC,∴AC=AE,即 AC2=AE·AB.
AB AC ∴A F图,在△ABC 中,点 D,E 分别在边 AB,AC 上, ∠AED=∠B,AG 分别交线段 DE,BC 于点 F,G,且 A D∶A C=DF ∶CG.求证: (1)AG 平分∠BAC; 证明:∵∠DA E +∠A E D+∠A DE =180°, ∠B A C+∠B +∠C=180°,∠A E D=∠B , ∴∠ADE=∠C.在△ADF 和△ACG 中, A D∶A C=DF ∶CG,∠A DE =∠C, ∴△ADF∽△ACG.∴∠DAF=∠CAG.∴AG 平分∠BAC.
例说证明线段比例式或等积式的方法与技巧

D
B
在这一个图形中,有两个 三 对相似,有 垂直,有____ 四 对互余的角,有_____ 三 ___ 组等积关系,它们分别是 AC2=AD· AB BC2=BD· AB
CD2=AD· BD
二 找相等的量(比、线段、等积式)替换
1等线段替换
例1 已知等腰 ABC中,AB=AC,AD BC于D, CG AB,BG分别交AD、AC于E、F, 求证:BE EF EG
D
F
C
利用等比 式代换
2.已知:如图, ∠ACB=90°,AD=DB,DE⊥AB 于D交AC于E,交BC的延长线于F,试说明: DC2=DE· DF
A
D
E
F
C
B
点,若∠A=35°, ∠C=85°,∠AED=60°,
则AD· AB= AE· AC。
A D E B C
一、三点定形法
• 注:三点定形法证明等积式的一般步骤: • 1.先把等积式转化为比例式; • 2.观察比例式的线段确定可能相似的两个 三角形; • 3.再找这两个三角形相似所需的条件.
C
A
相似三角形
——比例式、等积式的几种常见证明方法
例.弦AB和CD相交于⊙o内一点P, 求证:PA· PB=PC· PD
∴ ∠A=∠D 同理: ∠C=∠B ∴△PAC∽△PDB
O
P
⌒ ∵∠A、∠D都是CB所对的圆周角 A
D
B C
PA PC PD PB
即PA· PB=PC· PD
练习:已知D、E分别是△ABC的边AB,AC上的
2
2等比替换
例2已知梯形ABCD中,AB CD,AC、 BD交于点O,BE AD交AC的延长线 于点E,求证:OA 2 OC OE
中考 类比归纳专题:比例式、等积式的常见证明方法(含答案)

类比归纳专题:比例式、等积式的常见证明方法——直接法、间接法一网搜罗◆类型一 三点定型法:找线段对应的三角形,利用相似证明1.如图,在菱形ABCD 中,G 是BD 上一点,连接CG 并延长交BA 的延长线于点F ,交AD 于点E ,连接AG .(1)求证:AG =CG ; (2)求证:AG 2=GE ·GF .2.如图,在△ABC 中,∠ACB =90°,CD ⊥AB ,垂足为D ,E 是AC 的中点,ED 的延长线与CB 的延长线交于点F .(1)若FD =2FB ,求FDFC的值;(2)若AC =215,BC =15,求S △FDC 的值.◆类型二 利用等线段代换3.如图,在四边形ABCD 中,AB =AD ,AC 与BD 交于点E ,∠ADB =∠ACB .求证:ABAE =AC AD.◆类型三 找中间比利用等积式代换4.如图,已知CE 是Rt △ABC 斜边AB 上的高,在EC 的延长线上任取一点P ,连接AP ,作BG ⊥AP ,垂足为G ,交CE 于D ,求证:CE 2=PE ·DE .参考答案与解析1.证明:(1)∵四边形ABCD 是菱形,∴AB ∥CD ,AD =CD ,∠ADB =∠CDB ,∴∠F=∠FCD .在△ADG 与△CDG 中,⎩⎪⎨⎪⎧AD =CD ,∠ADG =∠CDG ,DG =DG ,∴△ADG ≌△CDG ,∴∠EAG =∠DCG ,AG =CG .(2)∵∠EAG =∠DCG ,∠F =∠DCG ,∴∠EAG =∠F .又∵∠AGE =∠FGA ,∴△AGE ∽△FGA ,∴AG FG =EGAG,∴AG 2=GE ·GF .2.解:(1)∵∠ACB =90°,CD ⊥AB ,∴∠A +∠ABC =∠DCB +∠ABC ,∴∠A =∠DCB .∵E 是AC 的中点,∠ADC =90°,∴ED =EA ,∴∠A =∠EDA .∵∠BDF =∠EDA ,∴∠DCB =∠BDF .又∵∠F =∠F ,∴△BDF ∽△DCF ,∴FD ∶CF =BF ∶FD =1∶2.(2)∵∠ACB =90°,CD ⊥AB ,∴∠BDC =∠ACB .∵∠ABC =∠CBD ,∴△BDC ∽△BCA ,∴BD ∶CD =BC ∶AC =15∶215=1∶2.在Rt △BAC 中,由勾股定理可得AB =53,∴S △BDC S △BCA =BC 2AB 2=15,∴S △BDC =15×12×215×15=3.∵△BDF ∽△DCF ,∴S △FBD S △FDC =⎝⎛⎭⎫BD CD 2=14,即S △BDC S △FDC =34.∵S △BDC =3,∴S △FDC =4. 3.证明:∵AB =AD ,∴∠ADB =∠ABE .∵∠ADB =∠ACB ,∴∠ABE =∠ACB .又∵∠BAE =∠CAB ,∴△ABE ∽△ACB ,∴AB AE =AC AB .又∵AB =AD ,∴AB AE =ACAD.4.证明:∵∠ACB =90°,CE ⊥AB ,∴∠ACE +∠BCE =90°,∠ACE +∠CAE =90°,∴∠CAE =∠BCE ,∴Rt △ACE ∽Rt △CBE ,∴CE BE =AECE,∴CE 2=AE ·BE .又∵BG ⊥AP ,CE ⊥AB ,∴∠DEB =∠DGP =∠PEA =90°.∵∠1=∠2,∴∠P =∠3,∴△AEP ∽△DEB ,∴PE BE =AEDE,∴PE ·DE =AE ·BE ,∴CE 2=PE ·DE .。
15.比例式、等积式的常见证明方法

语文
小魔方站作品 盗版必究
谢谢您下载使用!
更多精彩内容,微信扫描二维码获取
扫描二维码获取更多资源
附赠 中高考状元学 习方法
前
言
高考状元是一个特殊的群体,在许多 人的眼中,他们就如浩瀚宇宙里璀璨夺目 的星星那样遥不可及。但实际上他们和我 们每一个同学都一样平凡而普通,但他们 有是不平凡不普通的,他们的不平凡之处 就是在学习方面有一些独到的个性,又有 着一些共性,而这些对在校的同学尤其是 将参加高考的同学都有一定的借鉴意义。
采青 春 风
高考总分: 692分(含20分加分) 语文131分 数学145分 英语141分 文综255分 毕业学校:北京二中 报考高校: 北京大学光华管理学 院
北京市文科状元
来自北京二中,高考成绩672分,还有20 分加分。‚何旋给人最深的印象就是她 的笑声,远远的就能听见她的笑声。‛ 班主任吴京梅说,何旋是个阳光女孩。 ‚她是学校的摄影记者,非常外向,如 果加上20分的加分,她的成绩应该是 692。‛吴老师说,何旋考出好成绩的秘 诀是心态好。‚她很自信,也很有爱心。 考试结束后,她还问我怎么给边远地区
∴
∵AD⊥BC,E为直角边AC中点 ∴DE=EC ∴∠3=∠C 又∵∠3=∠2,∠1=∠C ∴∠1=∠2 而∠F是△FBD与△FDA的公共角 ∴△FBD∽△FDA
DF BD AF AD AB DF ∴ AC AF
∴
AB BD AC AD
∴AB· AF=AC· DF.
方法总结 证明线段比例式或等积式时,如果按类型一、类型二的方法仍无法证 明,可以尝试将等积式化为比例式,结合图形找到能够与比例式中的两个 比分别相等的中间比,从而证明所求证的结果成立.
C
∴∠B=∠1
比例式等积式证明的常用方法

比例式等积式证明的常用方法在数学中,我们经常会遇到需要证明等式或不等式的情况。
其中,比例式等积式是一种常见的数学问题,需要通过推理和运算来证明两个比例式或等积式之间的等式关系。
在本文中,我将介绍一些常用的方法和策略,帮助读者更好地理解和解决比例式等积式证明的问题。
一、分数乘法分数乘法是比例式等积式证明中常用的一种方法。
我们可以利用分数乘法的性质,将等式中的分数进行运算,推导出等号两边相等的关系。
例如,我们需要证明以下比例式:(3/5) × (5/7) = (4/7) × (x/3)首先,我们可以将等式右边的分数进行乘法运算:(3/5) × (5/7) = (4/7) × (x/3)(15/35) = (4x/21)接下来,我们可以通过交叉乘积的方法来求解未知数x:15 × 21 = 35 × 4x315 = 140xx = 315/140x = 9/4通过分数乘法的方法,我们成功地证明了上述比例式的成立,并求解出了未知数x的值。
二、对角线乘积对角线乘积也是比例式等积式证明中常用的一种方法。
对于一个由两个平行线段组成的类似平行四边形的图形,我们可以利用对角线的性质,将等式中的线段长度进行运算,证明两个等式或不等式之间的关系。
例如,我们需要证明以下等积式:(2x + 3) × (5x - 1) = (3x + 2) × (4x - 5)首先,我们可以将等式左边和右边的对角线进行乘积运算:(2x + 3) × (5x - 1) = (3x + 2) × (4x - 5)(10x^2 - 2x + 15x - 3) = (12x^2 - 20x + 8x - 10)接下来,我们合并同类项并化简等式:10x^2 + 13x - 3 = 12x^2 - 12x - 100 = 2x^2 - 25x - 7最后,我们可以通过求解二次方程来求解未知数x的值。
2020春九年级数学(人教)下册 类比归纳专题:比例式、等积式的常见证明方法

类比归纳专题:比例式、等积式的常见证明方法——直接法、间接法一网搜罗◆类型一 三点定型法:找线段对应的三角形,利用相似证明1.如图,在菱形ABCD 中,G 是BD 上一点,连接CG 并延长交BA 的延长线于点F ,交AD 于点E ,连接AG .(1)求证:AG =CG ;(2)求证:AG 2=GE ·GF .2.如图,在△ABC 中,∠ACB =90°,CD ⊥AB ,垂足为D ,E 是AC 的中点,ED 的延长线与CB 的延长线交于点F .(1)若FD =2FB ,求FD FC 的值; (2)若AC =215,BC =15,求S △FDC 的值.◆类型二 利用等线段代换3.如图,在四边形ABCD 中,AB =AD ,AC 与BD 交于点E ,∠ADB =∠ACB .求证:AB AE =AC AD.◆类型三 找中间比利用等积式代换4.如图,已知CE 是Rt △ABC 斜边AB 上的高,在EC 的延长线上任取一点P ,连接AP ,作BG ⊥AP ,垂足为G ,交CE 于D ,求证:CE 2=PE ·DE .参考答案与解析1.证明:(1)∵四边形ABCD 是菱形,∴AB ∥CD ,AD =CD ,∠ADB =∠CDB ,∴∠F =∠FCD .在△ADG 与△CDG 中,⎩⎪⎨⎪⎧AD =CD ,∠ADG =∠CDG ,DG =DG ,∴△ADG ≌△CDG ,∴∠EAG =∠DCG ,AG =CG .(2)∵∠EAG =∠DCG ,∠F =∠DCG ,∴∠EAG =∠F .又∵∠AGE =∠FGA ,∴△AGE ∽△FGA ,∴AG FG =EG AG ,∴AG 2=GE ·GF . 2.解:(1)∵∠ACB =90°,CD ⊥AB ,∴∠A +∠ABC =∠DCB +∠ABC ,∴∠A =∠DCB .∵E 是AC 的中点,∠ADC =90°,∴ED =EA ,∴∠A =∠EDA .∵∠BDF =∠EDA ,∴∠DCB =∠BDF .又∵∠F =∠F ,∴△BDF ∽△DCF ,∴FD ∶CF =BF ∶FD =1∶2.(2)∵∠ACB =90°,CD ⊥AB ,∴∠BDC =∠ACB .∵∠ABC =∠CBD ,∴△BDC ∽△BCA ,∴BD ∶CD =BC ∶AC =15∶215=1∶2.在Rt △BAC 中,由勾股定理可得AB =53,∴S △BDC S △BCA =BC 2AB 2=15,∴S △BDC =15×12×215×15=3.∵△BDF ∽△DCF ,∴S △FBD S △FDC =⎝⎛⎭⎫BD CD 2=14,即S △BDC S △FDC =34.∵S △BDC =3,∴S △FDC =4.3.证明:∵AB =AD ,∴∠ADB =∠ABE .∵∠ADB =∠ACB ,∴∠ABE =∠ACB .又∵∠BAE =∠CAB ,∴△ABE ∽△ACB ,∴AB AE =AC AB .又∵AB =AD ,∴AB AE =AC AD.4.证明:∵∠ACB =90°,CE ⊥AB ,∴∠ACE +∠BCE =90°,∠ACE +∠CAE =90°,∴∠CAE =∠BCE ,∴Rt △ACE ∽Rt △CBE ,∴CE BE =AE CE,∴CE 2=AE ·BE .又∵BG ⊥AP ,CE ⊥AB ,∴∠DEB =∠DGP =∠PEA =90°.∵∠1=∠2,∴∠P =∠3,∴△AEP ∽△DEB ,∴PE BE =AE DE,∴PE ·DE =AE ·BE ,∴CE 2=PE ·DE .。
123.15.比例式、等积式的常见证明方法

∴∠4=∠F 而 ∠ CPE 是 △ CPE 和
△FPC的公共角 ∴△CPE∽△FPC ∴PE∶PC=PC∶PF ∴PC2=PE·PF ∴BP2=PE·PF
∵CF∥AB
∴∠3=∠F
方法总结
运用类型一的方法证明线段的比例式或等积式时,如果相关的线段不在 某两个三角形中,则需要将其中的某条线段用与之相等的另一条线段替换, 再按类型一 的方法证明.
∴ DF BD AF AD
∴ AB DF AC AF
∴AB·AF=AC·DF.
方法总结
证明线段比例式或等积式时,如果按类型一、类型二的方法仍无法证 明,可以尝试将等积式化为比例式,结合图形找到能够与比例式中的两个 比分别相等的中间比,从而证明所求证的结果成立.
XXX X
古 X
X X X
风 设
一 岁 只 叹 伊
, 饮 罢 飞 雪 ,
负 了 青 春 举
泪 溶 了 雪 , 恰
光 ? 谁 酒 三 尺
颜 刹 那 ? 谁 饮
拾 弹 指 雪 花 ?
今 夜 无 月 亦 无
纷 纷 飘 香 。 雪
一 回 。 忆 苍 茫
前 尘 旧 梦 , 不
, 怎 敌 我 浊 酒
古 韵 清
风
中 幽 舞
梦明
国 落 月
花, 间 。
类型三:找中间比利用等积式代换
如图,在△ABC中,已知∠BAC=90 °,AD⊥BC于D,E为直角边AC的 中点,过D、E作直线交AB的延长线于F.求证:AB·AF=AC·DF.
A
1
E
B
3
2D
C
F
如图,在△ABC中,已知∠A=90°,AD⊥BC于D,E为直角边AC的中 点,过D、E作直线交AB的延长线于F.求证:AB·AF=AC·DF.
相似三角形复习——比例式、等积式的几种常见证明方法

图3 例3如图3,△ABC中,DE∥BC,BE与CD交于点O, AO与DE、BC分别交于点N、M,试说明:. 利用等
比式代 换
AN AD DE AM AB BC
AN ON AM OM
图3
ON OE DE OM OB BC
例3.如图,已知:在△ABC中,∠BAC=900, AD⊥BC,E是AC的中点,ED交AB的延长线于F
A
BDEຫໍສະໝຸດ C如上图, ∠BAC=120°, △ADE是 等边三角形,小丽发现图中有些线 段是其他两条线段的比例中项,你 知道小丽说的是哪些线段吗? 它们 分别是哪些线段的比例中项吗?
比例式得:
,由等式左边得
到△CDF,由等式右边得到△EDC,
这样只要证明这两个三角形相似就
可以得到要证的等积式了。因为
∠CDE是公共角,只需证明
∠DCE=∠F就可证明两个三角形相
似。
例2如图2,在△ABC中,AB=AC,直线DF与AB交于D,与
BC交于E,与AC的延长线交于F.图2 试说明:. DE EF
求证:
。
分 析:比例式左边AB,AC 在△ABC中,右边DF、AF在 △ADF中,这两个三角形不相 似,因此本题需经过中间比进 行代换。通过证明两套三角形 分别相似证得结论。
“双垂直”指:
“Rt△ABC中,
∠BCA=900,
CD⊥AB于D”,(如
图)在这样的条件下
有下列结论:
A
C
D
B
(1)△ADC∽△CDB∽△ACB (2)由△ADC∽△CDB得CD2=AD·BD (3)由△ADC∽△ACB得AC2=AD·AB (4)由△CDB∽△ACB得BC2=BD·AB (5)由面积得AC·BC=AB·CD (6)勾股定理 我们应熟记这些结论,并能灵活运用。
最新北师版九年级初三数学上册解题技巧专题:比例式、等积式的常见证明方法

解题技巧专题:比例式、等积式的常见证明方法——直接法、间接法一网搜罗◆类型一 找线段对应的三角形,利用相似证明1.如图,四边形ABCD 的对角线AC ,BD 交于点F ,点E 是BD 上一点,并且∠BAC=∠BDC =∠DAE.求证:AB AC =AE AD.◆类型二 利用等线段代换2.如图,在四边形ABCD 中,AB =AD ,AC 与BD 交于点E ,∠ADB =∠ACB.求证:AB AE =AC AD.3.★如图,已知AD 是△ABC 的角平分线,EF 垂直平分AD ,交BC 的延长线于E ,交AD 于F.求证:DE 2=BE·CE.◆类型三找中间比利用等积式代换4.如图,在△ABC中,点D为BC的中点,AE∥BC,ED交AB于P,交AC的延长线于Q.求证:PD·EQ=PE·DQ.解题技巧专题:比例式、等积式的常见证明方法1.证明:证法一:∵∠BAC=∠DAE,∴∠BAC+∠CAE=∠DAE+∠CAE,即∠BAE =∠CAD.∵∠BAC=∠BDC,∠BF A=∠CFD,∴180°-∠BAC-∠BF A=180°-∠BDC-∠CFD,即∠ABE=∠ACD,∴△ABE∽△ACD,∴ABAC=AE AD.证法二:∵∠BAC=∠DAE,∴∠BAC+∠CAE=∠DAE+∠CAE,即∠BAE=∠CAD.∵∠BEA=∠DAE+∠ADE,∠ADC=∠BDC+∠ADE,∠DAE=∠BDC,∴∠AEB=∠ADC.∴△ABE∽△ACD,∴ABAC=AE AD.2.证明:∵AB =AD ,∴∠ADB =∠ABE .∵∠ADB =∠ACB ,∴∠ACB =∠ABE .又∵∠CAB =∠BAE ,∴△ACB ∽△ABE ,∴AB AE =AC AB .又∵AB =AD ,∴AB AE =AC AD.3.证明:如图,连接AE .∵EF 垂直平分AD ,∴AE =DE ,∴∠DAE =∠4.∵AD 是△ABC 的角平分线,∴∠1=∠2.∵∠DAE =∠2+∠3,∠4=∠B +∠1,∴∠B =∠3.又∵∠BEA=∠AEC ,∴△BEA ∽△AEC .∴AE CE =BE AE,∴AE 2=BE ·CE ,∴DE 2=BE ·CE . 4.证明:∵AE ∥DC ,∴∠QDC =∠E ,∠QCD =∠QAE ,∴△QCD ∽△QAE ,∴DQ EQ=CD AE .∵AE ∥BD ,∴∠B =∠P AE ,∠BDP =∠AEP ,∴△BDP ∽△AEP ,∴PD PE =BD AE.∵点D 为BC 的中点,∴BD =CD ,∴PD PE =DQ EQ,即PD ·EQ =PE ·DQ .学习名言警句:1.在科学上面没有平坦的大道,只有不畏劳苦沿着陡峭山路攀登的人,才有希望到达光辉的顶点。
15.比例式、等积式的常见证明方法

典例精解
类型三:找中间比利用等积式代换
如图,在△ABC中,已知∠BAC=90 °,AD⊥BC于D,E为直角边AC 的中点,过D、E作直线交AB的延长线于F.求证:AB·AF=AC·DF.
A
1
E
B
3
2D
C
F
如图,在△ABC中,已知∠A=90°,AD⊥BC于D,E为直角边AC的 中点,过D、E作直线交AB的延长线于F.求证:AB·AF=AC·DF.
A
1
E
B
3
2D
C
F
证明:∵∠A=90°,AD⊥BC ∴∠1=∠C=90°-∠ABC 而∠BDA=∠ADC =90° ∴△ABD∽△CAD
∴ AB BD AC AD
∵AD⊥BC,E为直角边AC中点 ∴DE=EC ∴∠3=∠C 又∵∠3=∠2,∠1=∠C ∴∠1=∠2 而∠F是△FBD与△FDA的公共角 ∴△FBD∽△FDA
初中数学知识点精讲课程
比例式、等积式的常见证明方法
比例式、等积式的证明是初中几何非常常见的题型,同时也是令许多学 生头疼的一种题型,特别是在一些图形复杂、线段较多的题目中,往往令人 眼花瞭乱无从下手.
等积式的证明有没有技巧呢?其实只要我们冷静分析,我们将会发现许 多等积式的证明也是有规律可循的。
典例精解
F
∴∠CDF=∠E
A
B
∴△DCF∽△EAD E
∴ DC CF AE AD
变式题
如图,△ABC 中,∠BAC=90°,M 为 BC 的中点,DM⊥BC 交 CA 的延长
线于 D,交 AB 于 E,求证:AM2=MD·ME.
D
证明:
∴∠D=∠B=90°-∠C
∵∠BAC=90°,
相似立体模型总结2(比例式、等积式的常见证明方法)

相似立体模型总结2(比例式、等积式的常见证明方法)相似立体模型总结2 (比例式、等积式的常见证明方法)本文总结了相似立体模型中常见的比例式和等积式的证明方法。
比例式的常见证明方法1. 比例式的宽度证明要证明两个相似立体模型的宽度成比例,可以采用以下证明方法:- 首先,测量两个立体模型的宽度分别为$a$和$b$。
- 然后,利用相似三角形的性质,证明两个立体模型的相应边长之比为$\frac{a}{b}$。
2. 比例式的高度证明要证明两个相似立体模型的高度成比例,可以采用以下证明方法:- 首先,测量两个立体模型的高度分别为$h$和$k$。
- 然后,利用相似三角形的性质,证明两个立体模型的相应边长之比为$\frac{h}{k}$。
3. 比例式的长度证明要证明两个相似立体模型的长度成比例,可以采用以下证明方法:- 首先,测量两个立体模型的长度分别为$l$和$m$。
- 然后,利用相似三角形的性质,证明两个立体模型的相应边长之比为$\frac{l}{m}$。
等积式的常见证明方法1. 等积式的底面积证明要证明两个相似立体模型的底面积等积,可以采用以下证明方法:- 首先,测量两个立体模型的底面积分别为$A$和$B$。
- 然后,利用相似三角形的性质,证明两个立体模型的高度之比为$\frac{{\sqrt{A}}}{{\sqrt{B}}}$。
2. 等积式的体积证明要证明两个相似立体模型的体积等积,可以采用以下证明方法:- 首先,测量两个立体模型的体积分别为$V_1$和$V_2$。
- 然后,利用相似三角形的性质,证明两个立体模型的边长之比的立方为$\left(\frac{{V_1}}{{V_2}}\right)^{\frac{1}{3}}$。
结论以上介绍了相似立体模型中常见的比例式和等积式的证明方法,可根据具体情况选择合适的方法进行证明。
相似椭圆模型总结2(比例式、等积式的常见证明方法)

相似椭圆模型总结2(比例式、等积式的常见证明方法)比例式的常见证明方法相似椭圆模型中,比例式是常见的一种证明方法。
以下是一些常用的比例式证明方法:1. 使用比例关系:- 通过利用已知的椭圆模型的比例关系,可以推导出其他椭圆模型的比例关系。
例如,如果已知两个椭圆模型的长轴和短轴之比,就可以通过设置一个变量,用其它两个未知椭圆模型的长轴和短轴表示。
- 利用求比例的方法,可以找到已知椭圆模型和未知椭圆模型之间的比例关系。
例如,通过比较两个椭圆模型的半焦距或者直径之间的比例,可以推导出它们的其他关系。
2. 利用相似三角形:- 椭圆模型中的比例关系可以通过相似三角形来证明。
通过找到两个椭圆模型之间的相似三角形,可以得到它们的比例。
- 通过利用已知椭圆模型的角度和边长的关系,可以推导出未知椭圆模型的相似三角形,从而得到比例关系。
3. 利用已知椭圆模型的变换:- 当已知两个椭圆模型之间有某种变换关系时,可以通过这种变换关系证明它们的比例关系。
例如,如果已知一个椭圆模型是另一个椭圆模型的伸缩、平移或旋转变换,可以利用几何变换的性质来推导出它们的比例关系。
等积式的常见证明方法相似椭圆模型中,等积式也是一种常用的证明方法。
以下是一些常用的等积式证明方法:1. 利用椭圆面积公式:- 椭圆的面积可以通过一些已知参数计算得出。
利用已知椭圆模型和未知椭圆模型的面积公式,可以推导出它们的等积关系。
2. 利用轨迹与面积关系:- 椭圆模型的轨迹之间具有一定的关系,可以通过这种关系证明它们的等积关系。
例如,已知两个椭圆模型的焦点和轨迹方程相同,可以推导出它们的等积关系。
3. 利用边界条件:- 椭圆模型的边界条件也可以用于证明等积关系。
例如,已知两个椭圆模型的边界点相同,可以推导出它们的等积关系。
以上就是相似椭圆模型中比例式和等积式的常见证明方法总结。
通过运用这些方法,可以更方便地推导出相似椭圆模型之间的关系。
相似椎体模型总结2(比例式、等积式的常见证明方法)

相似椎体模型总结2(比例式、等积式的常
见证明方法)
相似椎体模型总结2(比例式、等积式的常见证明方法)
一、比例式证明方法
比例式证明方法是通过比较两个相似椎体的边长或高度之比来
证明它们相似的方法。
常见的比例式证明方法包括以下几种:
1. 比较边长:首先,我们可以比较两个相似椎体的底面边长之
比和高度之比。
如果它们的比值相等,即两个椎体的底面边长之比
等于高度之比,那么可以得出它们相似的结论。
2. 比较斜边长:有时候,我们可以通过比较两个相似椎体的斜
边长之比来证明它们相似。
如果两个椎体的斜边长之比相等,那么
可以说明它们相似。
3. 比较面积:除了边长之比,我们还可以通过比较两个相似椎
体的底面积或侧面积之比来证明它们相似。
如果它们的面积比相等,则可以推断出它们相似。
二、等积式证明方法
等积式证明方法是通过比较两个相似椎体的体积来证明它们相似的方法。
常见的等积式证明方法包括以下几种:
1. 比较体积:我们可以比较两个相似椎体的体积之比来判断它们是否相似。
如果两个椎体的体积比相等,那么可以得出它们相似的结论。
2. 比较高度:有时候,我们可以通过比较两个相似椎体的高度来判断它们是否相似。
如果两个椎体的高度相等,则可以说明它们相似。
总结:在证明相似椎体模型时,我们可以使用比例式证明方法或等积式证明方法。
比例式证明方法是通过比较边长、斜边长或面积之比来判断相似性,而等积式证明方法则是通过比较体积或高度来判断相似性。
根据具体情况选择合适的证明方法,能够简化证明过程,同时避免法律复杂性。
华师版九年级上册数学5.解题技巧专题:比例式、等积式的常见证明方法

解题技巧专题:比例式、等积式的常见证明方法——直接法、间接法—网搜罗◆类型一 找线段对应的三角形,利用相似证明 1.(虹口区模拟)如图,在△ABC 中,∠C =90°,AD 是∠CAB 的平分线,BE ⊥AE ,垂足为点E ,求证:BE 2=DE ·AE.2.如图,四边形ABCD 的对角线AC ,BD 交于点F ,点E 是BD 上一点,且∠BAC =∠BDC =∠DAE .求证:AB AC =AEAD.3.如图,在▱ABCD 中,AM ⊥BC ,AN ⊥CD ,M ,N 分别为垂足.求证:AM AB =MNAC.◆类型二 利用等线段代换证明4.如图,在四边形ABCD 中,AB =AD ,AC 与BD 交于点E ,∠ADB =∠ACB .求证:ABAE =AC AD.5.如图,已知AD 是△ABC 的角平分线,EF 垂直平分AD ,交BC 的延长线于E ,交AD 于F .求证:DE 2=BE ·CE.6.如图,在矩形ABCD 中,E 是CD 的中点,BE ⊥AC 且交AC 于F ,过F 作FG ∥AB ,交AE 于G .求证:AG 2=AF ·CF.◆类型三 找中间比利用等积式代换7.如图,在△ABC 中,点D 为BC 的中点,AE ∥BC ,ED 交AB 于P ,交AC 的延长线于Q .求证:PD ·EQ =PE ·DQ.8.★如图,CD 是Rt △ABC 斜边AB 上的高,E 为BC 的中点,ED 的延长线交CA 于F .求证:AC ·CF =BC ·DF.9.★如图,在△ABC 中,∠BAC =90°,AD ⊥BC 于D ,点E 为AC 的中点,ED 的延长线交AB 于F .求证:AB AC =DF AF.解题技巧专题:比例式、等积式的常见证明方法1.证明:∵AD 平分∠CAB ,∴∠CAD =∠BAD .∵∠C =90°,AE ⊥BE ,∴∠ADC +∠CAD =∠BDE +∠DBE .∵∠ADC =∠BDE ,∴∠CAD =∠DBE ,∴∠BAD =∠DBE ,∴Rt △ABE ∽Rt △BDE ,∴BE DE =AEBE,∴BE 2=DE ·AE .2.证明:证法一:∵∠BAC =∠DAE ,∴∠BAC +∠CAE =∠DAE +∠CAE ,即∠BAE =∠CAD .又∵∠BAC =∠BDC ,∠BF A =∠CFD ,∴180°-∠BAC -∠BF A =180°-∠BDC -∠CFD ,即∠ABE =∠ACD ,∴△ABE ∽△ACD ,∴AB AC =AEAD. 证法二:∵∠BAC =∠DAE ,∴∠BAC +∠CAE =∠DAE +∠CAE ,即∠BAE =∠CAD .又∵∠BEA =∠DAE +∠ADE ,∠ADC =∠BDC +∠ADE ,∠DAE =∠BDC ,∴∠AEB =∠ADC ,∴△ABE ∽△ACD ,∴AB AC =AEAD.3.证明:在▱ABCD 中,∠B =∠D ,AD =BC ,又∵∠AMB =∠AND =90°,∴Rt △AMB ∽Rt △AND ,∴AM AN =AB AD =ABBC.又∵AB ∥CD ,AN ⊥CD ,∴AN ⊥AB .∴∠BAM +∠MAN =∠BAM +∠B =90°,∴∠B =∠MAN ,∴△AMN ∽△BAC ,∴AM AB =MNAC.4.证明:∵AB =AD ,∴∠ADB =∠ABE .又∵∠ADB =∠ACB ,∴∠ABE =∠ACB .又∵∠BAE =∠CAB ,∴△ABE ∽△ACB ,∴AB AC =AE AB ,∴AB AE =AC AB .又∵AB =AD ,∴AB AE =ACAD .5.证明:如图,连接AE .∵EF 垂直平分AD ,∴AE =DE ,∴∠DAE =∠4.∵AD 是△ABC 的角平分线,∴∠1=∠2.∵∠DAE =∠2+∠3,∠4=∠B +∠1,∴∠B =∠3.又∵∠BEA =∠AEC ,∴△BEA ∽△AEC ,∴AE CE =BEAE,∴AE 2=BE ·CE ,∴DE 2=BE ·CE .6.证明:∵BE ⊥AC ,∴∠AFB =∠BFC =90°,∴∠ABF +∠BAF =90°.∵四边形ABCD 是矩形,∴∠ABC =90°,∴∠ABF +∠CBF =90°,∴∠BAF =∠CBF ,∴△ABF ∽△BCF ,∴BF CF =AFBF,∴BF 2=AF ·CF .∵四边形ABCD 是矩形,∴AD =BC ,∠D =∠BCE =90°.又∵点E 是CD 的中点,∴DE =CE ,∴△ADE ≌△BCE ,∴AE =BE .∵GF ∥AB ,∴AG AE =BF BE,∴AG =BF ,∴AG 2=AF ·CF .7.证明:∵AE ∥DC ,∴△QCD ∽△QAE ,∴DQ EQ =CDAE .∵AE ∥BD ,∴△BDP ∽△AEP ,∴PD PE =BD AE .∵点D 为BC 的中点,∴BD =CD ,∴PD PE =DQEQ,即PD ·EQ =PE ·DQ . 8.证明:∵CD 是Rt △ABC 斜边AB 上的高,∴∠ACB =∠ADC =∠CDB =90°,∴∠DAC +∠B =∠B +∠DCB =90°,∴∠DAC =∠DCB ,∴△ADC ∽△CDB ,∴AD CD =AC BC .∵E 为BC的中点,∴DE =CE ,∴∠EDC =∠DCE =∠DAC ,∴∠FDC =∠F AD .又∵∠F =∠F ,∴△FDC ∽△F AD ,∴CF DF =CD AD ,∴DF CF =AD DC ,∴AC BC =DFCF,∴AC ·CF =BC ·DF .9.证明:∵∠BAC =90°,AD ⊥BC ,∴∠ADB =∠CDA =90°,∠BAD +∠CAD =90°,∴∠CAD +∠C =90°,∴∠BAD =∠C ,∴△ABD ∽△CAD ,∴AB AC =BDAD .在Rt △ADC 中,∵点E 为AC 的中点,∴DE =CE ,∴∠C =∠EDC ,∴∠BAD =∠EDC .又∵∠EDC =∠FDB ,∴∠FDB =∠BAD ,即∠FDB =∠F AD .又∵∠F =∠F ,∴△DFB ∽△AFD ,∴DF AF =BD AD .∴ABAC =DF AF.。
「初中数学」证比例式或等积式的六种常用技巧

「初中数学」证比例式或等积式的六种常用技巧证比例式或等积式的题目时,若问题中无平行线或相似三角形,则需要构造平行线或相似三角形,得到成比例线段.若比例式或等积式中的线段分布在两个三角形中,可尝试证这两个三角形相似;若比例式或等积式中的线段分布不在两个三角形中,可尝试将它们转化到两个三角形中;若比例式或等积式中的线段分布在两个明显不相似的三角形中,可尝试用中间比代换.技巧一.构造平行线法1.如图,在△ABC中,D为AB的中点,DF交AC于点E,交BC 的延长线于点F,求证AE×CF=BF×EC.【分析】由AE×CF=BF×EC,变为AE/BF=EC/CF或AE/EC=BF/CF,成比例的线段明显的组不成三角形,于是寻求中间比进行代换,过C点作CM∥AB,交DF于M,如图,则BF/CF=BD/CM,AE/EC=AD/CM,而D为AB的中点,则AD=BD,∴BF/CF=AE/EC,即AE×CF=BF×EC.另,过C点作CM∥DF交AB于M,如图则AE/EC=AD/DM,又BF/CF=BD/DM,而AD=BD,∴AE/EC=BF/CF,即AE×CF=BF×EC.另,过B点作BM∥AC,交FD的延长线于M,如图则BF/CF=BM/EC,而D为AB的中点,易证AE=BM,∴BF/CF=AE/EC,即AE×CF=BF×EC,这里巧用AE等量代换了BM,得证.另,过B点作BM∥DF交AC的延长线于M,如图则BC/CF=CM/EC,∴(BC+CF)/CF=(CM+EC)/EC,即BF/CF=EM/EC,而DE是△ABM的中位线,AE=EM,∴BF/CF=AE/EC,即AE×CF=BF×EC.另,过A点作AM∥DF交BF的延长线于M,如图∵D为AB的中点,∴BF=FM,又AE/EC=FM/CF,∴AE/EC=BF/CF,即AE×CF=BF×EC.另,过A点作AM∥BC,交FD的延长线于M,如图则AM/CF=AE/EC,而D为AB的中点,易证AM=BF,∴BF/CF=AE/EC,即AE×CF=BF×EC.技巧二.构造相似三角形法2.已知△ABC的边AB上有一点D,边BC的延长线上有一点E,且AD=CE,DE交AC于点F,求证AB×DF=BC×EF.【分析】由AB×DF=BC×EF,变形为AB/BC=EF/DF,成比例的线段可构成△ABC,而EF,DF构不成三角形,可寻求中间比代换,过D作DM∥BE,交AC于M,如图则出现A型相似,△ADM∽△ABC;X型相似,△CEF∽△MDF,∴有AB/BC=AD/DM,EF/DF=CE/DM,而AD=CE,∴AB/BC=EF/DF,即AB×DF=BC×EF.另,过E点作EM∥AB,交AC的延长线于M,如图同学们自己证一下.技巧三,三点定型法3.如图,在△ABC中,∠BAC=90°,M是BC的中点,MD⊥BC,交AB于E,交CA的延长线于D,求证AM²=DM×EM.【分析】由AM²=DM×EM,化为AM/DM=EM/AM,锁定两个三角形ADM与△EAM,看是否相似,∵∠BAC=90°,M是BC的中点,∴BM=AM,∴∠B=∠BAM,而∠D,与∠B都是∠C的补角,∠B=∠D=∠EAM,∵∠AEM=∠D+∠DAE,∠DAM=∠EAM+∠DAE,∴∠AEM=∠DAM,又∠AME=∠DMA,∴△AME∽△DMA,∴AM/DM=EM/AM,即AM²=DM×EM.技巧四.等积过渡法4.如图,CE是Rt△ABC斜边上的高,在EC的延长线上任取一点P,连接AP,作BG⊥AP于点G,交CE于点D,求证CE²=DE×PE.【分析】从结论分析,成比例的线段不在三角形中,那么就要找等量代换,由BG⊥AP,DE⊥AB,∴∠AEP=∠BED=∠AGB=90°,∵∠P与∠ABG都是∠PAB的余角,∴∠P=∠ABG,∴△AEP∽△DEB,∴AE/DE=PE/BE,即AE×BE=DE×PE,又CE⊥AB,∠ACB=90°,易证△AEC∽△CEB,∴AE/CE=CE/BE,即AE×BE=CE²,∴CE²=DE×PE.技巧五.等比代换法5.如图,在△ABC中,∠BAC=90°,AD⊥BC于D,E是AC的中点,连接ED并延长,交AB的延长线于点F,求证AB/AC=DF/AF【分析】由于AD⊥BC,∠BAC=90°,∴∠ADB=∠ADC=90°,又E是AC的中点,∴DE=EC=AC/2,∴∠C=∠CDE,又∠CDE=∠FDB,∵∠BAD+∠DAC=90°,∠C+∠DAC=90°,∴∠BAD=∠C=∠FDB,又∵∠F=∠F,∴△FDB∽△FAD,∴DB/AD=DF/AF,∵∠ADB=∠ADC,∠BAD=∠C,∴△ABD∽△CAD,∴BD/AD=AB/AC,∴AB/AC=DF/AF.技巧六.等线段代换法6.在△ABC中,AB=AC,AD是BC边上的中线,CF∥AB,BF交AD于点P,交AC于点E,求证PB²=PE×PF.【分析】由结论看,PB,PE,PF三线段在同一条线上,无法找到相似三角形,考虑代换,连接PC,而AB=AC,AD是BC边上的中线,则AD垂直平分BC,∴PB=PC,∴∠PBC=∠PCB,而∠ABC=∠ACB,∴∠ABP=∠ACP,又∵CF∥AB,∴∠F=∠ABP,∴∠F=∠ACP,又∠EPC=∠FPC,∴△PEC∽△PCF,∴PC/PF=PE/PC,∴PC²=PE×PF,∵PB²=PE×PF.如图【总结】几何证明题,多种多样,证等积式等比例式,究竟用什么方法,因题而异,考虑题中的条件,灵活代换,可以是等线段代换.等比代换,等积代换等。
比例式、等积式证明的常用方法

比例式、等积式证明的常用方法一、三点定形法例1如图,在Rt^ABC中,NACB=90° , CD_LAB于D, E为AC的中点,ED的延长线交CB的延长线于点P,求证:PD2 =PB PC例2如图,在AABC中,AB _L AC , D为BC中点, DE _L BC交AC于F ,交BA延长线于E .求证:AD2 = DE DF注:三点定形法证明等积式的一般步骤:1.先把等积式转化为比例式;2.观察比例式的线段确定可能相似的两个三角形;3.再找这两个三角形相似所需的条件.二、找相等的量(比、线段、等积式)替换1、等线段替换例1 已知等腰AABC 中,AB = AC, AD _L BC 于D , CG//AB , BG 分别交AD、2 _AC 于E、F ,求证:BE =EF EGB例 2 如图,在 MBC 中,AB = AC , AD _L BC 于 D , BE _L AC 于 E , EG _L BC 于G ,L 是AF 的中点.求证:CD2=EGDL2、等比替换已知梯形 ABCD 中,AB//CD, AC 、BD 交于点O, BE// AD 交AC 的延长线于点 E,例3 求_ 2OA =OC OE.如图,在 AABC 中,AB .L AC , AD 1 BC , E 为 AC 中点, ED 延长线交AB 延长线于F .求证:AB AF =AC DFDB3、等积替换例5如图,在MBC中,AD、BF分别是BC、AC边上的高,过D作AB的垂线交AB于E ,交BF于G ,交AC延长线于H .求证:DE 2 = EG EH .例6如图,已知CE是RtAABC斜边AB上的高,在EC的延长线上取一点P,连结AP, BG_LAP 垂足为G,交CE 于D,求证:CE2 = PE DE .注:当要证明的比例式中的线段在同一条直线上时,可以用相等的比、相等的线段、相等的等积式来替换相应的量,把看似无路可走的题目盘活,从而达到“车到山前疑无路,柳暗花明又一村”的效果.三、把求证等积式、比例式转化为求证垂直、求证角、线段相等,使证明简化1 . _ 例1 已知在正方形ABCD中,E是AB的中点,F是AD上的一点,且AF=1AD,42EG -LCF ,垂足为G ,求证:EG =CG FG .四、利用相似三角形的性质例1 如图,RtAABC 中,NACB =90° , CD _L AB 于点D , /CAB 的平分AE 交CD 于点F ,交CB于点E .求证:AF CB =CD .AE .A D B注:相似三角形的对应高的比、对应中线的比、对应角平分线的比都等于相似比,我们可以利用这些性质来证明有关的等积式往往会起到事半功倍的效果!练习巩固:1.如图,点D、E分别在边AB、AC上,且/ADE =/C求证:(1) AADE s AACB ;(2) AD AB = AE AC .2.如图,MBC中,点DE在边BC上,且MDE是等边三角形,/ BAC =120〜求证:(1) AADB s ACEA ; ( 2 ) DE 2 = BD CE ; (3) AB AC = AD BC .3.如图,在平行四边形ABCD中,E为BA延长线上一点,N D =/ECA.求证:AD EC =AC EB4 .如图,AD为MBC中NBAC的平分线,EF是AD的垂直平分线.求证:FD2 = FC FB 。
级数学上册 解题技巧专题 比例式、等积式的常见证明方法(新版)北师大版.doc
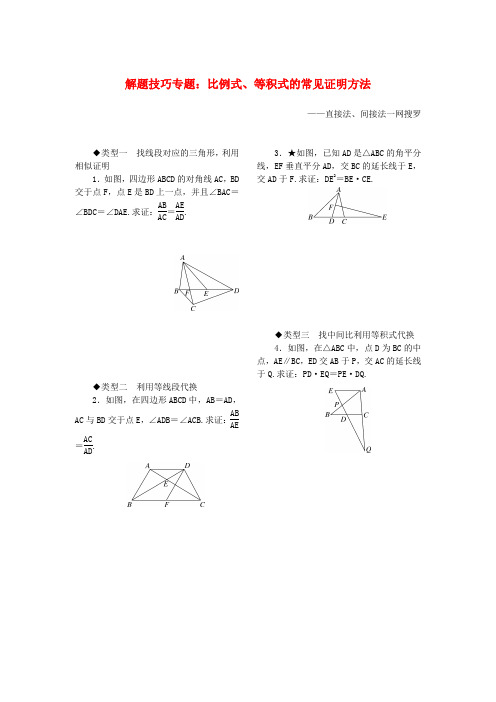
解题技巧专题:比例式、等积式的常见证明方法——直接法、间接法一网搜罗◆类型一找线段对应的三角形,利用相似证明1.如图,四边形ABCD的对角线AC,BD交于点F,点E是BD上一点,并且∠BAC=∠BDC=∠DAE.求证:ABAC=AEAD.◆类型二利用等线段代换2.如图,在四边形ABCD中,AB=AD,AC与BD交于点E ,∠ADB=∠ACB.求证:ABAE=ACAD.3.★如图,已知AD是△ABC的角平分线,EF垂直平分AD,交BC的延长线于E,交AD于F.求证:DE2=BE·CE.◆类型三找中间比利用等积式代换4.如图,在△ABC中,点D为BC的中点,AE∥BC,ED交AB于P,交AC的延长线于Q.求证:PD·EQ=PE·DQ.解题技巧专题:比例式、等积式的常见证明方法1.证明:证法一:∵∠BAC =∠DAE ,∴∠BAC +∠CAE =∠DAE +∠CAE ,即∠BAE =∠CAD .∵∠BAC =∠BDC ,∠BFA =∠CFD ,∴180°-∠BAC -∠BFA =180°-∠BDC -∠CFD ,即∠ABE =∠ACD ,∴△ABE ∽△ACD ,∴AB AC =AEAD.证法二:∵∠BAC =∠DAE ,∴∠BAC +∠CAE =∠DAE +∠CAE ,即∠BAE =∠CAD .∵∠BEA =∠DAE +∠ADE ,∠ADC =∠BDC +∠ADE ,∠DAE =∠BDC ,∴∠AEB =∠ADC .∴△ABE ∽△ACD ,∴AB AC =AE AD. 2.证明:∵AB =AD ,∴∠ADB =∠ABE .∵∠ADB =∠ACB ,∴∠ACB =∠ABE .又∵∠CAB =∠BAE ,∴△ACB ∽△ABE ,∴AB AE=AC AB .又∵AB =AD ,∴AB AE =AC AD.3.证明:如图,连接AE .∵EF 垂直平分AD ,∴AE =DE ,∴∠DAE =∠4.∵AD 是△ABC 的角平分线,∴∠1=∠2.∵∠DAE =∠2+∠3,∠4=∠B +∠1,∴∠B =∠3.又∵∠BEA =∠AEC ,∴△BEA ∽△AEC .∴AE CE=BE AE,∴AE 2=BE ·CE ,∴DE 2=BE ·CE . 4.证明:∵AE ∥DC ,∴∠QDC =∠E ,∠QCD =∠QAE ,∴△QCD ∽△QAE ,∴DQ EQ=CDAE.∵AE ∥BD ,∴∠B =∠PAE ,∠BDP =∠AEP ,∴△BDP ∽△AEP ,∴PD PE =BDAE .∵点D 为BC 的中点,∴BD =CD ,∴PD PE =DQEQ,即PD ·EQ =PE ·DQ .。
等积式、比例式的证明

等积式、比例式的证明等积式、比例式的证明是相似形一章中常见题型。
因为这种问题变化很多,同学们常常感到困难。
但是,如果我们掌握了解决这类问题的基本规律,就能找到解题的思路。
(一)遇到等积式(或比例式)时,先看是否能找到相似三角形。
等积式可根据比例的基本性质改写成比例式,在比例式各边的四个字母中如有三个不重复的字母,就可找出相似三角形。
例1、已知:如图,△ABC 中,∠ACB=900,AB 的垂直平分线交AB 于D ,交BC 延长线于F 。
求证:CD 2=DE·DF 。
分析:我们将此等积式变形改写成比例式得:CD DE DF CD ,由等式左边得到△CDF ,由等式右边得到△EDC ,这样只要证明这两个三角形相似就可以得到要证的等积式了。
因为∠CDE 是公共角,只需证明∠DCE=∠F 就可证明两个三角形相似。
证明略(请同学们证明)提示:D 为直角三角形斜边AB 的中点,所以AD=DC, 则∠DCE=∠A.(二)若由求证的等积式或比例式中找不到三角形或找到的三角形不相似,则需要进行等线段代换或等比代换。
有时还需添加适当的辅助线,构造平行线或相似三角形。
例2.如图,已知△ABC 中,AB=AC ,AD 是BC 边上的中线,CF ∥BA ,BF 交AD 于P 点,交AC 于E 点。
求证:BP 2=PE·PF 。
分析:因为BP 、PE 、PF 三条线段共线,找不到两个三角形,所以必须考虑等线段代换等其他方法,因为AB=AC ,D 是BC 中点,由等腰三角形的性质知AD 是BC 的垂直平分线,如果我们连结PC ,由线段垂直平分线的性质知PB=PC ,只需证明△PEC ∽△PCF ,问题就能解决了。
证明:连结PC在△ABC 中,∵AB=AC ,D 为BC 中点,∴AD 垂直平分BC ,∴PB=PC , ∴∠1=∠2,∵AB=AC ,∴∠ABC=∠ACB ,∴∠ABC-∠1=∠ACB-∠2,∴∠3=∠4,∵CF ∥AB ,∴∠3=∠F ,∴∠4=∠F ,又∵∠EPC=∠CPF ,∴△PCE ∽△PFC ,∴PC PF PE PC ,∴PC 2=PE·PF ,∵PC=PB , ∴PB 2=PE·PF 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题:比例式、等积式的常见证明方法
◆类型一 三点定型法:找线段对应的三角形,利用相似证明
1.如图,在菱形ABCD 中,G 是BD 上一点,连接CG 并延长交BA 的延长线于点F ,交AD 于点E ,连接AG .
(1)求证:AG =CG ; (2)求证:AG 2=GE ·GF .
2.如图,在△ABC 中,∠ACB =90°,CD ⊥AB ,垂足为D ,E 是AC 的中点,ED 的延长线与CB 的延长线交于点F .
(1)若FD =2FB ,求FD
FC
的值;
(2)若AC =215,BC =15,求S △FDC 的值.
◆类型二 利用等线段代换
3.如图,在四边形ABCD 中,AB =AD ,AC 与BD 交于点E ,∠ADB =∠ACB .求证:
AB
AE =AC AD
.
◆类型三 找中间比利用等积式代换
4.如图,已知CE 是Rt △ABC 斜边AB 上的高,在EC 的延长线上任取一点P ,连接AP ,作BG ⊥AP ,垂足为G ,交CE 于D ,求证:CE 2=PE ·DE .
参考答案与解析
1.证明:(1)∵四边形ABCD 是菱形,∴AB ∥CD ,AD =CD ,∠ADB =∠CDB ,∴∠F
=∠FCD .在△ADG 与△CDG 中,⎩⎪⎨⎪
⎧AD =CD ,∠ADG =∠CDG ,DG =DG ,∴△ADG ≌△CDG ,∴∠EAG =
∠DCG ,AG =CG .
(2)∵∠EAG =∠DCG ,∠F =∠DCG ,∴∠EAG =∠F .又∵∠AGE =∠FGA ,∴△AGE ∽△FGA ,∴AG FG =EG
AG
,∴AG 2=GE ·GF .
2.解:(1)∵∠ACB =90°,CD ⊥AB ,∴∠A +∠ABC =∠DCB +∠ABC ,∴∠A =∠DCB .∵E 是AC 的中点,∠ADC =90°,∴ED =EA ,∴∠A =∠EDA .∵∠BDF =∠EDA ,∴∠DCB =∠BDF .又∵∠F =∠F ,∴△BDF ∽△DCF ,∴FD ∶CF =BF ∶FD =1∶2.
(2)∵∠ACB =90°,CD ⊥AB ,∴∠BDC =∠ACB .∵∠ABC =∠CBD ,∴△BDC ∽△BCA ,∴BD ∶CD =BC ∶AC =15∶215=1∶2.在Rt △BAC 中,由勾股定理可得AB =53,∴S △BDC S △BCA =BC 2AB 2=15,∴S △BDC =15×12×215×15=3.∵△BDF ∽△DCF ,∴S △FBD S △FDC =⎝⎛⎭⎫BD CD 2=14,
即S △BDC S △FDC =3
4
.∵S △BDC =3,∴S △FDC =4. 3.证明:∵AB =AD ,∴∠ADB =∠ABE .∵∠ADB =∠ACB ,∴∠ABE =∠ACB .又∵∠BAE =∠CAB ,∴△ABE ∽△ACB ,∴AB AE =AC AB .又∵AB =AD ,∴AB AE =AC
AD
.
4.证明:∵∠ACB =90°,CE ⊥AB ,∴∠ACE +∠BCE =90°,∠ACE +∠CAE =90°,∴∠CAE =∠BCE ,∴Rt △ACE ∽Rt △CBE ,∴
CE BE =AE
CE
,∴CE 2=AE ·BE .又∵BG ⊥AP ,CE ⊥AB ,∴∠DEB =∠DGP =∠PEA =90°.∵∠1=∠2,∴∠P =∠3,∴△AEP ∽△DEB ,∴PE BE =AE
DE
,∴PE ·DE =AE ·BE ,∴CE 2=PE ·DE .。
