台湾2011年第一次中考数学真题及答案(台北)
2011年中考数学试题分类汇总:事件与概率

第17章 事件与概率一、选择题1. (2011广东东莞,4,3分)在一个不透明的口袋中,装有5个红球3个白球,它们除颜色外都相同,从中任意摸出一个球,摸到红球的概率为( )A .15B .13C .58D .38【答案】C2. (2011福建福州,8,4分)从1,2,-3三个数中,随机抽取两个数相乘,积是正数的概率是( )A .0B .13C .23D . 1 【答案】B3. (2011山东滨州,4,3分)四张质地、大小、背面完全相同的卡片上,正面分别画有圆、矩形、等边三角形、等腰梯形四个图案.现把它们的正面向下随机摆放在桌面上,从中任意抽出一张,则抽出的卡片正面图案是中心对称图形的概率为( ) A. 14 B. 12 C. 34D. 1 【答案】B4. (2011山东日照,8,3分)两个正四面体骰子的各面上分别标明数字1,2,3,4,如同时投掷这两个正四面体骰子,则着地的面所得的点数之和等于5的概率为( )(A ) 41 (B )163 (C )43 (D )83 【答案】A5. (2011山东泰安,16 ,3分)袋中装有编号为1,2,3的三个质地均匀、大小相同的球,从中随机取出一球记下编号后,放入袋中搅匀,再从袋中随机取出一球,两次所取球的编号相同的概率为A.19B.16C.13D.12【答案】C6. (2011 浙江湖州,6,3)下列事件中,必然事件是A .掷一枚硬币,正面朝上.B .a 是实数,l a l ≥0.C .某运动员跳高的最好成绩是20 .1米.D .从车间刚生产的产品中任意抽取一个,是次品.【答案】B7. (2011浙江衢州,1,3分)5月19日为中国旅游日,衢州推出“读万卷书,行万里路,游衢州景”的主题系列旅游惠民活动,市民王先生准备在优惠日当天上午从孔氏南宗家庙。
烂柯河、龙游石窟中随机选择一个地点;下午从江郎山、三衢石林、开化根博园中随机选择一个地点游玩.则王先生恰好上午选中孔氏南宗庙,下午选中江郎山这两个地点的概率是( ) A. 19 B. 13 C. 23 D. 29【答案】A8. (2011浙江绍兴,7,4分)在一个不透明的盒子中装有8个白球,若干个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球,它是白球的概率为23,则黄球的个数为( )A.2B.4C.12D.16【答案】B9. (2011浙江义乌,9,3分)某校安排三辆车,组织九年级学生团员去敬老院参加学雷 锋活动,其中小王与小菲都可以从这三辆车中任选一辆搭乘,则小王与小菲同车的概率为( )A .13B .19C .12D .23【答案】A10.(2011浙江省嘉兴,12,5分)从标有1到9序号的9张卡片中任意抽取一张,抽到序号是3的倍数的概率是 . A 31 B 91 C 32 D 97【答案】A 11. (2011台湾台北,3)表(一)表示某签筒中各种签的数量。
2011年中考数学试题精选汇编《矩形、菱形、正方形》

2011年中考数学试题精选汇编《矩形、菱形、正方形》一、选择题1. (2011浙江省舟山,10,3分)如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH (不重叠无缝隙).若①②③④四个平行四边形面积的和为14cm 2,四边形ABCD 面积是11cm 2,则①②③④四个平行四边形周长的总和为( )(A )48cm(B )36cm (C )24cm (D )18cm【答案】A 2. (2011山东德州8,3分)图1是一个边长为1的等边三角形和一个菱形的组合图形,菱形边长为等边三角形边长的一半,以此为基本单位,可以拼成一个形状相同但尺寸更大的图形(如图2),依此规律继续拼下去(如图3),……,则第n 个图形的周长是(A )2n (B )4n (C )12n + (D )22n +【答案】C3. (2011山东泰安,17 ,3分)如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S 1,S 2,则S 1+S 2的值为A.17B.17C.18D.19图1图2 图3……(第10题) FA B C D H E① ②③ ④ ⑤4. (2011山东泰安,19 ,3分)如图,点O是矩形ABCD的中心,E是AB上的点,沿CE 折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为A.23B. 332C. 3D.6【答案】A5. (2011浙江杭州,10,3)在矩形ABCD中,有一个菱形B F D E(点E,F分别在线段AB,CD上),记它们的面积分别为ABCD BFDES S和.现给出下列命题:()①若ABCDBFDESStan EDF∠=.②若2,DE BD EF=∙则2DF AD=.则:A.①是真命题,②是真命题 B.①是真命题,②是假命题C.①是假命题,②是真命题 D,①是假命题,②是假命题【答案】A6. (2011浙江衢州,1,3分)衢州市新农村建设推动了农村住宅旧貌变新颜,如图为一农村民居侧面截图,屋坡AF AG、分别架在墙体的点B、点C处,且AB AC=,侧面四边形BDEC为矩形,若测得100FAG∠=︒,则FBD∠=( )A. 35°B. 40°C. 55°D. 70°【答案】C7. (2011浙江温州,6,4分)如图,在矩形ABCD中,对角线AC,BD交于点O.已知∠AOB= 60°,AC=16,则图中长度为8的线段有( )A.2条B.4条C.5条D.6条8. 2011四川重庆,10,4分)如图,正方形ABCD 中,AB =6,点E 在边CD 上,且CD =3DE .将△ADE 沿AE 对折至△AFE ,延长EF 交边BC 于点G ,连结AG 、CF .下列结论:①△ABG ≌△AFG ;②BG =GC ;③AG ∥CF ;④S △FGC =3.其中正确结论的个数是( )A .1B .2C .3D .4【答案】C9. (2011浙江省嘉兴,10,4分)如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH (不重叠无缝隙).若①②③④四个平行四边形面积的和为14cm 2,四边形ABCD 面积是11cm 2,则①②③④四个平行四边形周长的总和为( )(A )48cm(B )36cm (C )24cm (D )18cm【答案】A 10.(2011台湾台北,29)如图(十二),长方形ABCD 中,E 为BC 中点,作AEC 的角平分线交AD 于F 点。
2011全国各省市中考数学试题分类汇编-—函数与一次函数(选择题及答案)

2011全国各省市中考数学试题分类汇编-—函数与一次函数(选择题及答案)一.选择题1.(2011台湾中考)1.坐标平面上,若点(3, b )在方程式923-=x y 的图形上,则b 值为何?( )(A)-1 (B) 2 (C) 3 (D) 92.(2011台湾中考)15.图(三)的坐标平面上有一正五边形ABCDE ,其中C 、D 两点坐标分别为(1,0)、(2,0) 。
若在没有滑动的情况下,将此正五边形沿着 x 轴向右滚动,则滚动过程中,下列何者会 经过点(75 , 0)?( )(A) A (B) B (C) C (D) D3.(2011台湾中考)16.已知数在线A 、B 两点坐标分别为-3、-6,若在数在线找一点C ,使得A 与C 的距离为4;找一点D ,使得B 与D 的距离为1,则下列何者不可能为C 与D 的距离?( ) (A) 0 (B) 2 (C) 4 (D) 64.(2011台湾中考)29.已知小龙、阿虎两人均在同一地点,若小龙向北直走160公尺,再向东直走80公尺后,可到神仙百货,则阿虎向西直走多少公尺后,他与神仙百货的距离为340公尺?( )(A) 100 (B) 180 (C) 220 (D) 2605.(2011台北中考)9.图(三)的坐标平面上,有一条通过点(-3,-2)的直线L 。
若四点(-2 , a )、(0 , b )、(c , 0)、(d ,-1)在L 上,则下列数值的判断,何者正确?( )(A) a =3 (B) b >-2(C) c <-3 (D) d =26.(2011台北中考)17.如图(七),坐标平面上有两直线L 、M ,其方程式分别为y =9、y =-6。
若L 上有一点P ,M 上有一点Q ,PQ 与y 轴平行,且PQ 上有一点R ,PR :RQ =1:2,则R 点与x 轴的距离为何?( )(A) 1 (B) 4 (C) 5 (D) 107.(2011台北中考)21.坐标平面上有一个线对称图形,)25,3(-A 、)211,3(-B 两点在此图形上且互为对称点。
2011年台湾第一次中考数学试题含答案word版
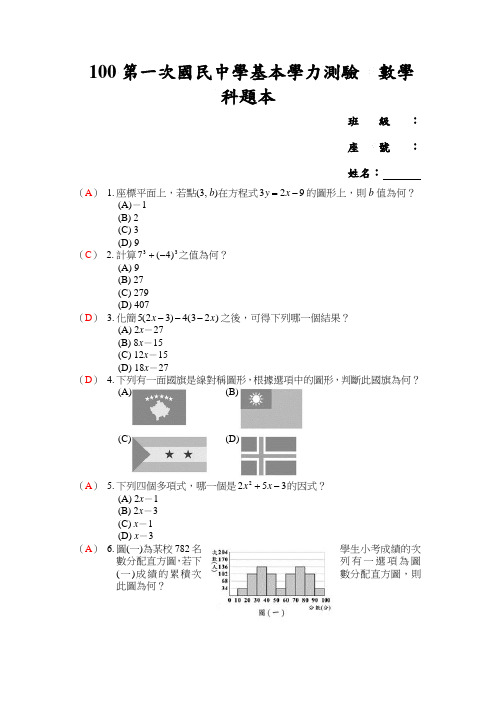
100第一次國民中學基本學力測驗 數學科題本班級: 座號:姓名:(A ) 1. 座標平面上,若點(3, b )在方程式923-=x y 的圖形上,則b 值為何?(A)-1 (B) 2 (C) 3 (D) 9(C ) 2. 計算33)4(7-+之值為何?(A) 9 (B) 27 (C) 279 (D) 407(D ) 3. 化簡)23(4)32(5x x ---之後,可得下列哪一個結果?(A) 2x -27 (B) 8x -15 (C) 12x -15 (D) 18x -27(D ) 4. 下列有一面國旗是線對稱圖形,根據選項中的圖形,判斷此國旗為何?(A) (B)(C) (D)(A ) 5. 下列四個多項式,哪一個是3522-+x x 的因式? (A) 2x -1 (B) 2x -3 (C) x -1 (D) x -3(A ) 6. 圖(一)為某校782名學生小考成績的次數分配直方圖,若下列有一選項為圖(一)成績的累積次數分配直方圖,則此圖為何?(A) (B)(C) (D)(C ) 7. 若△ABC 中,2(∠A +∠C )=3∠B ,則∠B 的外角度數為何?(A) 36 (B) 72 (C) 108 (D) 144(D ) 8. 若949)7(22+-=-bx x a x ,則b a +之值為何?(A) 18 (B) 24 (C) 39 (D) 45(B ) 9. 在早餐店裡,王伯伯買5顆饅頭,3顆包子,老闆少拿2元,只要50元。
李太太買了11顆饅頭,5顆包子,老闆以售價的九折優待,只要90元。
若饅頭每顆x 元,包子每顆y 元,則下列哪一個二元一次聯立方程式可表示題目中的數量關係?(A)⎩⎨⎧⨯=++=+9.09051125035y x y x(B)⎩⎨⎧÷=++=+9.09051125035y x y x(C)⎩⎨⎧⨯=+-=+9.09051125035y x y x(D)⎩⎨⎧÷=+-=+9.09051125035y x y x(C )10. 若(a -1):7=4:5,則10a +8之值為何?(A) 54 (B) 66 (C) 74 (D) 80(C )11. 圖(二)數線上有O 、A 、B 、C 、D 五點,根據圖中各點所表示的數,判斷18在數線上的位置會落在下列哪一線段上? (A)OA(B)AB (C)BC (D)CD(A )12. 判斷312是96的幾倍?(A) 1(B) (31)2(C) (31)6(D) (-6)2(A )13. 解不等式-51x -3>2,得其解的範圍為何?(A) x <-25 (B) x >-25 (C) x <5 (D) x >5(B )14. 計算)4(433221-⨯++之值為何?(A)-1 (B)-611 (C)-512 (D)-323(B )15. 圖(三)的座標平面上有一正五邊形ABCDE ,其中C 、D 兩點座標分別為(1,0)、(2,0) 。
一元二次方程答案

2011年全国各地中考数学试卷试题分类汇编——一元二次方程1(2011湖北荆州,9,3分)关于x的方程0)1(2)13(2=+++-axaax有两个不相等的实根1x、2x,且有axxxx-=+-12211,则a的值是A.1B.-1C.1或-1D.2【答案】B2(2011福建福州,7,4分)一元二次方程(2)0x x-=根的情况是()A.有两个不相等的实数根B.有两个相等的实数根C.只有一个实数根D.没有实数根【答案】A3(2011山东滨州,3,3分)某商品原售价289元,经过连续两次降价后售价为256元,设平均每次降价的百分率为x,则下面所列方程中正确的是( )A.()22891256x-=B.()22561289x-=C. 289(1-2x)=256D.256(1-2x)=289 【答案】A4(2011山东威海,9,3分)关于x的一元二次方程2(2)10x m x m+-++=有两个相等的实数根,则m的值是()A.0B.8C.4±D.0或8【答案】D5(2011四川南充市,6,3分)方程(x+1)(x-2)=x+1的解是()(A)2 (B)3 (C)-1,2 (D)-1,3 【答案】D6(2011台湾台北,20)若一元二次方程式)2)(1()1(++++xxxax bx+2)2(=+x的两根为0、2,则ba43+之值为何?A.2 B.5 C.7D.8【答案】B7(2011台湾台北,31)如图(十三),将长方形ABCD分割成1个灰色长方形与148个面积相等的小正方形。
根据图,若灰色长方形之长与宽的比为5:3,则AD:AB=?A.5:3 B.7:5 C.23:14 D.47:29【答案】D8(2011江西,6,3分)已知x=1是方程x2+bx-2=0的一个根,则方程的另一个根是()A.1B.2C.-2D.-1【答案】C13. (2011甘肃兰州,1,4分)下列方程中是关于x的一元二次方程的是【答案】CA.221xx+=B.20ax bx c++=C.(1)(2)1x x-+=D.223250x xy y--=9(2011山东济宁,5,3分)已知关于x 的方程x 2+bx +a =0有一个根是-a(a≠0),则a -b 的值为 A .-1 B .0 C .1 D .2 【答案】A10(2011山东潍坊,7,3分)关于x 的方程2210x kx k ++-=的根的情况描述正确的是( )A . k 为任何实数,方程都没有实数根B . k 为任何实数,方程都有两个不相等的实数根C . k 为任何实数,方程都有两个相等的实数根D. 根据 k 的取值不同,方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根三种 【答案】B11(2011四川成都,6,3分)已知关于x 的一元二次方程)0(02≠=++m k nx mx 有两个实数根,则下列关于判别式 的判断正确的是( ) (A)042<-mk n (B) 042=-mk n (C)042>-mk n (D) 042≥-mk n【答案】C12.( 2011重庆江津, 9,4分)已知关于x 的一元二次方程(a -1)x2-2x+1=0有两个不相等的实数根,则a 的取值范围是( ) A.a<2 B,a>2 C.a<2且a ≠1 D.a<-2· 【答案】C ·13. (2011江苏南通,7,3分)已知3是关于x 的方程x2-5x +c =0的一个根,则这个方程的另一个根是 -2B. 2C. 5D. 6【答案】B14(2011四川绵阳12,3)若x1,x2 (x1 <x2)是方程(x -a)(x-b) = 1(a < b)的两个根,则实数x1,x2,a,b 的大小关系为 A .x1<x2<a <b B .x1<a <x2<b C .x1<a <b <x2 D .a <x1<b <x2 【答案】B15 (2011四川凉山州,6,4分)某品牌服装原价173元,连续两次降价00x 后售价价为127元,下面所列方程中正确的是( )A .()2001731127x += B .()0017312127x -= C .()2001731127x -= D .()2001271173x +=【答案】C16. (2011湖北黄石,9,3分)设一元二次方程(x-1)(x-2)=m(m>0)的两实根分别为α,β,则α,β满足 A. 1<α<β<2 B. 1<α<2 <β C. α<1<β<2 D.α<1且β>2 【答案】D 二、填空题1. (2011山东滨州,14,4分)若x=2是关于x 的方程2250x x a --+=的一个根,则a 的值为______2(2011山东德州14,4分)若1x ,2x 是方程210x x +-=的两个根,则2212x x +=__________.【答案】33(2011甘肃兰州,19,4分)关于x的方程2()0a x m b ++=的解是x1=-2,x2=1(a ,m ,b 均为常数,a ≠0),则方程2(2)0a x m b +++=的解是 。
2011年中考数学试题及答案

2011年中考考试试卷数 学本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷第1页至第2页,第Ⅱ卷第3页至第10页.试卷满分120分,考试时间100分钟.考试结束后,将试卷和答题卡一并交回.祝各位考生考试顺利!第Ⅰ卷(选择题 共30分)注意事项:1.答第Ⅰ卷前,考生务必先将自己的姓名、准考证号,用蓝、黑色墨水的钢笔(签字笔)或圆珠笔填在“答题卡”上;用2B 铅笔将考试科目对应的信息点涂黑;在指定位置粘贴考试用条形码.2.答案答在试卷上无效,每小题选出答案后,用2B 铅笔把“答题卡”上对应题目的答案标号的信息点涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号的信息点.一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.2sin 30°的值等于( )A .1 BCD .22.在艺术字中,有些字母是中心对称图形,下面的5个字母中,是中心对称图形的有( )A .2个B .3个C .4个D .5个3.若x y ,为实数,且20x +=,则2009x y ⎛⎫ ⎪⎝⎭的值为( )A .1B .1-C .2D .2- 4.边长为a 的正六边形的内切圆的半径为( ) A .2a B .a CD .12a5.右上图是一根钢管的直观图,则它的三视图为( )A .B .C .D . 6.为参加2009年“天津市初中毕业生升学体育考试”,小刚同学进行了刻苦的练习,在投掷实心球时,测得5次投掷的成绩(单位:m )为:8,8.5,9,8.5,9.2.这组数据的众H I N A数、中位数依次是( )A .8.5,8.5B .8.5,9C .8.5,8.75D .8.64,97.在ABC △和DEF △中,22AB DE AC DF A D ==∠=∠,,,如果ABC △的周长是16,面积是12,那么DEF △的周长、面积依次为( ) A .8,3 B .8,6 C .4,3 D .4,6 8.在平面直角坐标系中,已知线段AB 的两个端点分别是()()41A B --,,1,1,将线段AB 平移后得到线段A B '',若点A '的坐标为()22-,,则点B '的坐标为( )A .()43,B .()34,C .()12--,D .()21--, 9.如图,ABC △内接于O ⊙,若28OAB ∠=°,则C ∠的大小为( )A . 28°B .56°C .60°D .62°10.在平面直角坐标系中,先将抛物线22y x x =+-关于x 轴作轴对称变换,再将所得的抛物线关于y 轴作轴对称变换,那么经两次变换后所得的新抛物线的解析式为( ) A .22y x x =--+ B .22y x x =-+- C .22y x x =-++ D .22y x x =++第(9)题2009年天津市初中毕业生学业考试试卷数 学第Ⅱ卷(非选择题 共90分)注意事项:1.答第Ⅱ卷前,考生务必将密封线内的项目和试卷第3页左上角的“座位号”填写清楚. 2. 第Ⅱ卷共8页,用蓝、黑色墨水的钢笔(签字笔)或圆珠笔直接答在试卷上.二、填空题:本大题共8小题,每小题3分,共24分,请将答案直接填在题中横线上. 11= .12.若分式22221x x x x --++的值为0,则x 的值等于 .13.我们把依次连接任意一个四边形各边中点所得的四边形叫做中点四边形.若一个四边形ABCD 的中点四边形是一个矩形,则四边形ABCD 可以是 . 14.已知一次函数的图象过点()35,与()49--,,则该函数的图象与y 轴交点的坐标为__________ _.15.某书每本定价8元,若购书不超过10本,按原价付款;若一次购书10本以上,超过10本部分打八折.设一次购书数量为本,付款金额为y 元,请填写下表:16.为了解某新品种黄瓜的生长情况,抽查了部分黄瓜株上长出的黄瓜根数,得到下面的条形图,观察该图,可知共抽查了________株黄瓜,并可估计出这个新品种黄瓜平均每株结________根黄瓜.17.如图,是由12个边长相等的正三角形镶嵌而成的平面图形,则图中的平行四边形共有_______个.18.如图,有一个边长为5的正方形纸片ABCD ,要将其剪拼成边长分别为a b ,的两个小正方形,使得2225a b +=.①a b ,的值可以是________(写出一组即可);②请你设计一种具有一般性的裁剪方法,在图中画出裁剪线,并拼接成两个小正方形,同时说明该裁剪方法具有一般性: __________________________________________ _________________________________________ _________________________________________第(17)题黄瓜根数/株第(16)题三、解答题:本大题共8小题,共66分.解答应写出文字说明、演算步骤或证明过程. 19.(本小题6分) 解不等式组5125431x x x x ->+⎧⎨-<+⎩,.20.(本小题8分)已知图中的曲线是反比例函数5m y x-=(m 为常数)图象的一支. (Ⅰ) 这个反比例函数图象的另一支在第几象限?常数m 的取值范围是什么? (Ⅱ)若该函数的图象与正比例函数2y x =的图象在第一象内限的交点为A ,过A 点作x 轴的垂线,垂足为B ,当OAB △的面积为4时,求点A 的坐标及反比例函数的解析式.21.(本小题8分)有3个完全相同的小球,把它们分别标号为1,2,3,放在一个口袋中,随机地摸出一个小球不放回,再随机地摸出一个小球.(Ⅰ)采用树形图法(或列表法)列出两次摸球出现的所有可能结果; (Ⅱ)求摸出的两个球号码之和等于5的概率.如图,已知AB 为O ⊙的直径,PA PC ,是O ⊙的切线,A C ,为切点,30BAC ∠=° (Ⅰ)求P ∠的大小;(Ⅱ)若2AB =,求PA 的长(结果保留根号).23.(本小题8分)在一次课外实践活动中,同学们要测量某公园人工湖两侧A B ,两个凉亭之间的距离.现测得30AC =m ,70BC =m ,120CAB ∠=°,请计算A B ,两个凉亭之间的距离.P CAO注意:为了使同学们更好地解答本题,我们提供了一种解题思路,你可以依照这个思路填空,并完成本题解答的全过程.如果你选用其他的解题方案,此时,不必填空,只需按照解答题的一般要求,进行解答即可.如图①,要设计一幅宽20cm ,长30cm 的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2∶3,如果要使所有彩条所占面积为原矩形图案面积的三分之一,应如何设计每个彩条的宽度?分析:由横、竖彩条的宽度比为2∶3,可设每个横彩条的宽为2x ,则每个竖彩条的宽为3x .为更好地寻找题目中的等量关系,将横、竖彩条分别集中,原问题转化为如图②的情况,得到矩形ABCD .结合以上分析完成填空:如图②,用含x 的代数式表示: AB =____________________________cm ; AD =____________________________cm ; 矩形ABCD 的面积为_____________cm 2; 列出方程并完成本题解答.图②图①已知一个直角三角形纸片OAB ,其中9024AOB OA OB ∠===°,,.如图,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边OB 交于点C ,与边AB 交于点D . (Ⅰ)若折叠后使点B 与点A 重合,求点C 的坐标;(Ⅱ)若折叠后点B 落在边OA 上的点为B ',设OB x '=,OC y =,试写出y 关于x 的函数解析式,并确定y 的取值范围; (Ⅲ)若折叠后点B 落在边OA 上的点为B ',且使B D OB '∥,求此时点C 的坐标.已知函数212y x y x bx c αβ==++,,,为方程120y y -=的两个根,点()1M T ,在函数2y 的图象上. (Ⅰ)若1132αβ==,,求函数2y 的解析式; (Ⅱ)在(Ⅰ)的条件下,若函数1y 与2y 的图象的两个交点为A B ,,当ABM △的面积为112时,求t 的值; (Ⅲ)若01αβ<<<,当01t <<时,试确定T αβ,,三者之间的大小关系,并说明理由.参考答案及评分标准评分说明:1.各题均按参考答案及评分标准评分.2.若考生的非选择题答案与参考答案不完全相同但言之有理,可酌情评分,但不得超过该题所分配的分数.一、选择题:本大题共10小题,每小题3分,共30分.1.A 2.B 3.B 4.C 5.D 6.A 7.A 8.B 9.D 10.C 二、填空题:本大题共8小题,每小题3分,共24分.1112.213.正方形(对角线互相垂直的四边形均可) 14.()01-,15.56,80,156.816.60;1317.21 18.①3,4(提示:答案不惟一);②裁剪线及拼接方法如图所示:图中的点E 可以是以BC 为直径的半圆上的任意一点(点B C ,除外).BE CE ,的长分别为两个小正方形的边长. 三、解答题:本大题共8小题,共66分 19.本小题满分6分 解:5125431x x x x ->+⎧⎨-<+⎩ ,①②由①得2x >, ························································································································ 2分由②得,52x >-···················································································································· 4分 ∴原不等式组的解集为2x >································································································ 6分 20.本小题满分8分.解:(Ⅰ)这个反比例函数图象的另一支在第三象限. ························································· 1分 因为这个反比例函数的图象分布在第一、第三象限, 所以50m ->,解得5m >. ································································································ 3分(Ⅱ)如图,由第一象限内的点A 在正比例函数2y x =的图象上,设点A 的坐标为()()00020x x x >,,则点B 的坐标为()00x ,,0014242OAB S x x =∴= △,·,解得02x =(负值舍去).∴点A 的坐标为()24,. ·········································································································· 6分 DCA E 2 31 2 3又 点A 在反比例函数5m y x-=的图象上, 542m -∴=,即58m -=. ∴反比例函数的解析式为8y x=. ··························································································· 8分 21.本小题满分8分.解(Ⅰ)法一:根据题意,可以画出如下的树形图:从树形图可以看出,摸出两球出现的所有可能结果共有6种; 法二:根据题意,可以列出下表:从上表中可以看出,摸出两球出现的所有可能结果共有6种. ············································· 4分 (Ⅱ)设两个球号码之和等于5为事件A .摸出的两个球号码之和等于5的结果有2种,它们是:()()2332,,,.()2163P A ∴==. ··················································································································· 8分 22.本小题满分8分.解(Ⅰ)PA 是O ⊙的切线,AB 为O ⊙的直径, PA AB ∴⊥.90BAP ∴∠=°.30BAC ∠= °,9060CAP BAC ∴∠=-∠=°°.················································································· 2分 又PA 、PC 切O ⊙于点A C ,. PA PC ∴=.PAC ∴△为等边三角形. 60P ∴∠=°. ··························································································································· 5分(Ⅱ)如图,连接BC , 则90ACB ∠=°.在Rt ACB △中,230AB BAC =∠=,°,AC AB ∴=·cos 2BAC ∠=cos 30°=PAC △为等边三角形, PA AC ∴=.1 2 32 13 3 1 2 第一个球 第二个球 P C B A O第二个球 第一个球 (1,3) (2,3) (1,2) (3,2)(3,1) (2,1) 3 2 1 1 2 3PA ∴=··························································································································· 8分 23.本小题满分8分解:如图,过C 点作CD 垂直于AB 交BA 的延长线于点D . ············································· 1分 在Rt CDA △中,3018018012060AC CAD CAB =∠=-∠=︒-︒=︒,°. ···················· 2分CD AC ∴=·sin 30CAD ∠=·sin 60=°AD AC =·cos 30CAD ∠=·cos 60°=15. 又在Rt CDB △中,22270BC BD BC CD == ,-,65BD ∴==. ··························································································· 7分651550AB BD AD ∴=-=-=,答:A B ,两个凉亭之间的距离为50m. ················································································ 8分24.本小题满分8分.解(Ⅰ)220630424260600x x x x ---+,,; ·································································· 3分(Ⅱ)根据题意,得2124260*********x x ⎛⎫-+=-⨯⨯ ⎪⎝⎭. ············································· 5分 整理,得2665500x x -+=.解方程,得125106x x ==,(不合题意,舍去). 则552332x x ==,. 答:每个横、竖彩条的宽度分别为53cm ,52cm. ································································· 8分25.本小题满分10分.解(Ⅰ)如图①,折叠后点B 与点A 重合, 则ACD BCD △≌△.设点C 的坐标为()()00m m >,. 则4BC OB OC m =-=-. 于是4AC BC m ==-.在Rt AOC △中,由勾股定理,得222AC OC OA =+,即()22242m m -=+,解得32m =. ∴点C 的坐标为302⎛⎫⎪⎝⎭,. ········································································································· 4分图①图②图③(Ⅱ)如图②,折叠后点B 落在OA 边上的点为B ', 则B CD BCD '△≌△. 由题设OB x OC y '==,, 则4B C BC OB OC y '==-=-,在Rt B OC '△中,由勾股定理,得222B C OC OB ''=+.()2224y y x ∴-=+,即2128y x =-+ ···················································································································· 6分 由点B '在边OA 上,有02x ≤≤,∴ 解析式2128y x =-+()02x ≤≤为所求.∴ 当02x ≤≤时,y 随x 的增大而减小,y ∴的取值范围为322y ≤≤. ······················································································· 7分(Ⅲ)如图③,折叠后点B 落在OA 边上的点为B '',且B D OB ''∥. 则OCB CB D ''''∠=∠.又CBD CB D OCB CBD ''''∠=∠∴∠=∠ ,,有CB BA ''∥. Rt Rt COB BOA ''∴△∽△. 有OB OCOA OB''=,得2OC OB ''=. ···················································································· 9分 在Rt B OC ''△中,设()00OB x x ''=>,则02OC x =. 由(Ⅱ)的结论,得2001228x x =-+,解得000808x x x =-±>∴=-+,∴点C 的坐标为()016. ····················································································· 10分 26.本小题满分10分.解(Ⅰ)212120y x y x bx c y y ==++-= ,,,()210x b x c ∴+-+=. ··································································································· 1分 将1132αβ==,分别代入()210x b x c +-+=,得 ()()22111110103322b c b c ⎛⎫⎛⎫+-⨯+=+-⨯+= ⎪ ⎪⎝⎭⎝⎭,,解得1166b c ==,. ∴函数2y 的解析式为2y 25166x x =-+. ····································································· 3分(Ⅱ)由已知,得AB =,设ABM △的高为h ,311212ABM S AB h h ∴===△·1144=.根据题意,t T -=,由21166T t t =++,得251166144t t -+-=. 当251166144t t -+=-时,解得12512t t ==;当251166144t t -+=时,解得34t t ==.t ∴的值为555121212,,. ······················································································ 6分 (Ⅲ)由已知,得222b c b c T t bt c αααβββ=++=++=++,,.()()T t t b ααα∴-=-++, ()()T t t b βββ-=-++,()()22b c b c αβααββ-=++-++,化简得()()10b αβαβ-++-=.01αβ<<< ,得0αβ-≠, 10b αβ∴++-=.有1010b b αββα+=->+=->,. 又01t <<,0t b α∴++>,0t b β++>,∴当0t a <≤时,T αβ≤≤;当t αβ<≤时,T αβ<≤;当1t β<<时,T αβ<<. ································································································· 10分。
2011年全国各地中考数学真题分类汇编

) .
D.x ≤ -2.
【答案】C 30. (2011 湖北黄石,10,3 分)已知梯形 ABCD 的四个顶点的坐标分别为 A(-1,0),B (5,0),C(2,2),D(0,2),直线 y=kx+2 将梯形分成面积相等的两部分,则 k 的值为 A. -
2 3
B. -
2 9
C. -
4 7
D. -
2 7
【答案】B 3. (2011 广东广州市,9,3 分)当实数 x 的取值使得 x-2有意义时,函数 y=4x+1 中 y 的取值范围是( ). A.y≥-7 B.y≥9 C.y>9 D.y≤9 【答案】B 4. (2011 山东滨州,6,3 分)关于一次函数 y=-x+1 的图像,下列所画正确的是( )
【答案】A 25. (2011 四川乐山 3,3 分)下列函数中,自变量 x 的取值范围为 x<1 的是 A. y 【答案】 D 26. (2011 四川乐山 8,3 分)已知一次函数 y ax b 的图象过第一、二、四象限,且与 x 轴交于点(2,0),则关于 x 的不等式 a( x 1) b 0 的解集为 A.x<-1 【答案】A B.x> -1 C. x>1 D.x<1
x 中自变量x的取值范围是( x 1
)
33. (2011贵州安顺,7,3分)函数x≠l C.x<0 D.x≥0且 x≠l 【答案】D 34. (2011 河北,5,2 分)一次函数 y=6x+1 的图象不经过( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 【答案】D 35.. (2011 浙江绍兴,9,4 分)小敏从 A 地出发向 B 地行走,同时小聪从 B 地出发向 A 地行走, 如图所示, 相交于点 P 的两条线段 l1、l2 分别表示小敏、 小聪离 B 地的距离 y (km)
2011中考数学真题解析101 与圆有关的综合题(含答案)

(2012年1月最新最细)2011全国中考真题解析120考点汇编与圆有关的综合题一、选择题1. (2011山东日照,11,4分)已知AC ⊥BC 于C ,BC=a ,CA=b ,AB=c ,下列选项中⊙O 的半径为ba ab+的是( ) A . B . C . D .考点:三角形的内切圆与内心;解一元一次方程;正方形的判定与性质;切线的性质;相似三角形的判定与性质。
专题:计算题。
分析:连接OE 、OD ,根据AC 、BC 分别切圆O 于E 、D ,得到∠OEC=∠ODC=∠C=90°,证出正方形OECD ,设圆O 的半径是r ,证△ODB ∽△AEO ,得出ODAEBD OE =,代入即可求出r=ba ab+;设圆的半径是x ,圆切AC 于E ,切BC 于D ,且AB 于F ,同样得到正方形OECD ,根据a ﹣x+b ﹣x=c ,求出x 即可;设圆切AB 于F ,圆的半径是y ,连接OF ,则△BCA ∽△OFA 得出ABAOBC OF =,代入求出y 即可.解答:解:C 、连接OE 、OD , ∵AC 、BC 分别切圆O 于E 、D , ∴∠OEC=∠ODC=∠C=90°, ∵OE=OD ,∴四边形OECD 是正方形, ∴OE=EC=CD=OD , 设圆O 的半径是r ,∵OE ∥BC ,∴∠AOE=∠B ,∵∠AEO=∠ODB , ∴△ODB ∽△AEO ,∴OD AEBD OE =, rrb r a r -=-, 解得:r=ba ab+,故本选项正确;A 、设圆的半径是x ,圆切AC 于E ,切BC 于D ,且AB 于F ,如图(1)同样得到正方形OECD ,AE=AF ,BD=BF ,则a ﹣x+b ﹣x=c ,求出x=2cb a -+,故本选项错误; B 、设圆切AB 于F ,圆的半径是y ,连接OF ,如图(2),则△BCA ∽△OFA ,∴ ABAOBC OF =,∴cy b a y -=,解得:y=b a ab+,故本选项错误; D 、求不出圆的半径等于ba ab+,故本选项错误;故选C .点评:本题主要考查对正方形的性质和判定,切线的性质,全等三角形的性质和判定,三角形的内切圆与内心,解一元一次方程等知识点的理解和掌握,能根据这些性质求出圆的半径是解此题的关键.2. (2011•台湾24,4分)如图,△ABC 的外接圆上,AB ,BC ,CA 三弧的度数比为12:13:11.自BC 上取一点D ,过D 分别作直线AC ,直线AB 的并行线,且交于E ,F 两点,则∠EDF 的度数为( )A 、55°B 、60°C 、65°D 、70°考点:圆心角、弧、弦的关系;平行线的性质。
2011年中考数学考试试题答案

1 / 12高中阶段教育学校招生统一考试数 学全卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页,第Ⅱ卷3至8页.全卷满分120分,考试时间共120分钟.答题前,请考生务必在答题卡上正确填涂自己的姓名、考号和考试科目,并将试卷密封线内的项目填写清楚;考试结束,将试卷和答题卡一并交回.第Ⅰ卷(选择题 共30分)注意事项:每小题选出的答案不能答在试卷上,须用2B 铅笔在答题卡上把对应题目....的答案标号涂黑.如需改动,用橡皮擦擦净后,再选涂其它答案.一、选择题:(本大题共10个小题,每小题3分,共30分)在每小题给出的四个选项中,只有一个选项符合题意.1. -3的绝对值是( )A. 3B. -3C.13 D. 13- 2. “中国国家馆”作为2010年上海世博会的主题场馆,充分体现了中国文化的精神与气质. 资料表明,在建设过程中使用的一种工艺,需要对中国馆的大台阶进行约5.4×107次加工. 其中5.4×107表示的数为( )A. 5 400 000B. 54 000 000C. 540 000 000D. 5 400 000 000 3. 小明调查了本班同学最喜欢的课外活动项目,并作出如图1所示的扇形统计图,则从图中可以直接看出的信息是( )A. 全班总人数B. 喜欢篮球活动的人数最多C. 喜欢各种课外活动的具体人数D. 喜欢各种课外活动的人数占本班总人数的百分比4. 顺次连接边长为2的等边三角形三边中点所得的三角形的周长为( )A. 1B. 2C. 3D. 45. 用一个平面截一个几何体,得到的截面是四边形,则这个几何体可能是( ) A. 球体 B. 圆柱 C. 圆锥 D. 三棱锥6. 若实数a 、b 满足5a b +=,2210a b ab +=-,则ab 的值是( ) A. -2B. 2图1图22 / 12C. -50D. 507. 如图2,A 为⊙O 上一点,从A 处射出的光线经圆周4次反射后到达F 处. 如果反射前后光线与半径的夹角均为50°,那么∠AOE 的度数是( )A. 30°B. 40°C. 50°D. 80°8. 为缓解考试前的紧张情绪,某校九年级举行了“猪八戒背媳妇”的趣味接力比赛. 比赛要求每位选手在50米跑道上进行折返跑,其中有50米必须“背媳妇”. 假设某同学先跑步后“背媳妇”,且该同学跑步、“背媳妇”均匀速前进,他与起点的距离为s ,所用时间为t ,则s 与t 的函数关系用图象可表示为()A. B. C. D.9. 在同一平面内,如果两个多边形(含内部)有除边界以外的公共点,则称两多边形有“公共部分”.如图3,若正方形ABCD 由9个边长为1的小正方形镶嵌而成,另有一个边长为1的正方形与这9个小正方形中的n 个有“公共部分”,则n 的最大值为( ) A. 4 B. 5 C. 6 D. 710. 如图4,已知点A 1,A 2,…,A 2011在函数2y x =位于第二象限的图象上,点B 1,B 2,…,B 2011在函数2y x =位于第一象限的图象上,点C 1,C 2,…,C 2011在y 轴的正半轴上,若四边形111OA C B 、1222C A C B ,…,2010201120112011C A C B 都是正方形,则正方形2010201120112011C A C B 的边长为( )A. 2010B. 2011C. 20102D. 20112图3图43 / 12高中阶段教育学校招生统一考试数 学第Ⅱ卷(非选择题 共90分)题号 二 三总 分总分人171819202122232425得分注意事项:本卷共6页,用黑色或蓝色钢笔或圆珠笔直接答在试卷上.请注意准确理解题意、明确题目要求,规范地表达、工整地书写解题过程或结果.二、填空题:(本大题共6个小题,每小题3分,共18分)把答案直接填在题中横线上.11. 9的平方根为____________.12. 第16届亚运会将于2010年11月12日至27日在中国广州进行,各类门票现已开始销售. 若部分项目门票的最低价和最高价如图5所示,则这六个项目门票最高价的中位数是____________ .13. 若菱形一边的垂直平分线经过这个菱形的一个顶点,则此菱形较大内角的度数为_______.14. 若关于x 的方程2220x m x m m -+-=无实数根,则实数m 的取值范围是____________.15. 如图6,已知△ABC是等腰直角三角形,CD 是斜边AB 的中线,△ADC 绕点D 旋转一定角度得到△A DC '',A D '交AC 于点E ,DC '交BC 于点F ,连接EF ,若25A E ED '=,则EF A C ''=_________ . 16. 给出下列命题:① 若方程2560x x +-=的两根分别为1x ,2x ,则121156x x +=;② 对于任意实数x 、y ,都有2233()()x y x xy y x y -++=-;③ 如果一列数3,7,11,…满足条件:“以3为第一个数,从第二个数开始每一个数与它前面相邻的数的差为4”,那么99不是这列数中的一个数;④若※表示一种运算,且1※2=1,3※2=7,4※4=8,…,按此规律,则可能有a ※b =3a -b . 其中所有正确命题的序号是__________________ .图6图54 / 12三、解答题:(本大题共9个小题,共72分)解答应写出必要的文字说明、证明过程或演算步骤.17.(本小题满分7分)化简:2162393m m m -÷+--.18.(本小题满分7分)在为迎接“世界环境日”举办的“保护环境、珍爱地球”晚会上,主持人与观众玩一个游戏:取三张完全相同、没有任何标记的卡片,分别写上“物种”、“星球”和“未来”,并将写有文字的一面朝下,随机放置在桌面上,然后依次翻开三张卡片.(1) 用列表法(或树状图)求翻开卡片后第一张是“物种”且第二张是“星球”的概率; (2) 主持人规定:若翻开的第一张卡片是“未来”,观众获胜,否则主持人获胜. 这个规定公平吗?为什么?19.(本小题满分8分)如图7,已知A 、B 、C 是数轴上异于原点O 的三个点,且O 为AB 的中点,B为AC 的中点. 若点B 对应的数是x ,点C 对应的数是2x -3x ,求x 的值.图75 / 1220.(本小题满分8分)已知关于x 的不等式组4(1)23,617x x x ax -+>⎧⎪+⎨-<⎪⎩有且只有三个整数解,求a 的取值范围.21.(本小题满分8分)如图8,已知直线l :y =kx +b 与双曲线C :my x=相交于点A (1,3)、B (32-,-2),点A 关于原点的对称点为P .(1) 求直线l 和双曲线C 对应的函数关系式; (2) 求证:点P 在双曲线C 上;(3) 找一条直线l 1,使△ABP 沿l 1翻折后,点P 能落在双曲线C 上. (指出符合要求的l 1的一个解析式即可,不需说明理由)图86 / 1222.(本小题满分8分)在军事上,常用时钟表示方位角(读数对应的时针方向),如正北为12点方向,北偏西30°为11点方向. 在一次反恐演习中,甲队员在A 处掩护,乙队员从A 处沿12点方向以40米/分的速度前进,2分钟后到达B 处. 这时,甲队员发现在自己的1点方向的C 处有恐怖分子,乙队员发现C 处位于自己的2点方向(如图9). 假设距恐怖分子100米以外为安全位置.(1) 乙队员是否处于安全位置?为什么?(2) 因情况不明,甲队员立即发出指令,要求乙队员沿原路后撤,务必于15秒内到达安全位置. 为此,乙队员至少..应用多快的速度撤离?(结果精确到个位. 参考数据:13 3.6≈0,14 3.74≈.)23.(本小题满分8分)如图10-1,已知AB 是⊙O 的直径,直线l 与⊙O 相切于点B ,直线m 垂直AB 于点C ,交⊙O 于P 、Q 两点. 连结AP ,过O 作OD ∥AP 交l 于点D ,连接AD 与m 交于点M .(1) 如图10-2,当直线m 过点O 时,求证:M 是PO 的中点;(2) 如图10-1,当直线m 不过点O 时,M 是否仍为PC 的中点?证明你的结论.图9图10-1 图10-27 / 1224.(本小题满分9分)如图11,在直角梯形ABCD 中,已知AD ∥BC ,AB =3,AD =1,BC =6,∠A =∠B =90°.设动点P 、Q 、R 在梯形的边上,始终构成以P 为直角顶点的等腰直角三角形,且△PQR 的一边与梯形ABCD 的两底边平行.(1) 当点P 在AB 边上时,在图中画出一个符合条件的△PQR (不必说明画法); (2) 当点P 在BC 边或CD 边上时,求BP 的长.图118 / 1225.(本小题满分9分)如图12,已知直线22y x =+交y 轴于点A ,交x 轴于点B ,直线l :39y x =-+交x 轴于点C .(1) 求经过A 、B 、C 三点的抛物线的函数关系式,并指出此函数的函数值随x 的增大而增大时,x 的取值范围;(2) 若点E 在(1)中的抛物线上,且四边形ABCE 是以BC 为底的梯形,求梯形ABCE 的面积; (3) 在(1)、(2)的条件下,过E 作直线EF ⊥x 轴,垂足为G ,交直线l 于F . 在抛物线上是否存在点H ,使直线l 、直线FH 和x 轴所围成的三角形的面积恰好是梯形ABCE 面积的12?若存在,求点H 的横坐标;若不存在,请说明理由.图12高中阶段教育学校招生统一考试数学试题参考答案及评分意见说明:1. 解答题中各步骤所标记分数为考生解答到这一步应得的累计分数.2. 参考答案一般只给出该题的一种解法,如果考生的解法和参考答案所给解法不同,请参照本答案及评分意见给分.3. 考生的解答可以根据具体问题合理省略非关键步骤.4. 评卷时要坚持每题评阅到底,当考生的解答在某一步出现错误、影响了后继部分时,如果该步以后的解答未改变问题的内容和难度,可视影响程度决定后面部分的给分,但不得超过后继部分应给分数的一半;如果这一步后面的解答有较严重的错误,就不给分;若是几个相对独立的得分点,其中一处错误不影响其他得分点的得分.5. 给分和扣分都以1分为基本单位.6. 正式阅卷前应进行试评,在试评中须认真研究参考答案和评分意见,不能随意拔高或降低给分标准,统一标准后须对全部试评的试卷予以复查,以免阅卷前后期评分标准宽严不同.一、选择题(每小题3分,共10个小题,满分30分):1-5. ABDCB;6-10. ABCCD.二、填空题(每小题3分,共6个小题,满分18分):11.±3;12.800元;13. 120°;14.m<0;15.57;16.①②④.(注:12、13题有无单位“元”或“°”均不扣分. ) 三、解答题(共9个小题,满分72分):17.解:原式=1633(3)(3)2mm m m-+++-····················································3分=1333m m+++···················································································5分=43m+. ··························································································7分18.(1) 解一:列表如下: ············································································································3分∴第一张是“物种”且第二张是“星球”的概率是16. ······························4分解二:树状图如下:9 / 1210 / 12···························· 3分∴ 第一张是“物种”且第二张是“星球”的概率是16. ············································(2) 这个规定不公平. ··········································································5分因为观众获胜的概率是13,主持人获胜的概率是23. ·································7分19.解:由已知,点O 是AB 的中点,点B 对应的数是x ,∴ 点A 对应的实数为-x . ····································································1分 ∵ 点B 是AC 的中点,点C 对应的数是2x -3x , ∴ (2x -3x )-x =x -(-x ). ··········································································4分 整理,得2x -6x =0,解之得 x =0,或x =6. ···············································6分 ∵ 点B 异于原点,故x =0应舍去. ∴ x 的值为6. ·····································7分 20.解:由4(1)23x x -+>得,x >2; ···························································2分由617x ax +-<得,x <a +7. ··································································5分依题意得,不等式组的解集为2<x <a +7. ··················································6分 又 ∵ 此不等式组有且只有三个整数解,故整数解只能是x =3,4,5, ∴ 5<a +7≤6,则-2<a ≤-1. ·································································8分 (注:未取等号扣1分)21. 解:(1) 将点A 、B 的坐标代入y =kx +b ,有31,32().2k b k b =⨯+⎧⎪⎨-=⨯-+⎪⎩ ·············································································2分 解得,2k =,b =1,即直线l 对应的函数关系为y =2x +1. ·····························3分将点A (1,3)(或B )的坐标代入my x =,得m =3,∴ 双曲线C 对应的函数关系为y =3x. ·····················································4分(2) ∵ P 为点A 关于原点的对称点,∴ 点P 的坐标为(-1,-3),符合双曲线C 的函数关系,故点P 在双曲线C 上. ·················································································6分(3) l 1的解析式为y =x ,或y =-x . ·····························································8分 (注:写出一个解析式即得2分.) 22.解:(1) 乙队员不安全. ······················································· 1分易求AB =80米. ∵ ∠BAC =∠C =30°,∴ BC =AB =80米<100米. ·························· 3分 ∴ 乙队员不安全.(2) 过C 点作CD ⊥AB ,垂足为D ,在AB 边上取一点B 1,使CB 1=100. ······················································································ 4分在Rt △CBD 中,∠CBD =60°,BC =80,则BD =40,CD =403. ···· 5分在Rt △1CDB 中,由勾股定理知22112013B D B C CD =-=, ·····················6分11 / 12而20134015-≈2.13米/秒, ·······························································7分 依题意,乙队员至少应以3米/秒的速度撤离. ··········································8分 (注:结果为2米/秒,本步不给分.)23.(1) 证明:连接PD ,∵ 直线m 垂直AB 于点C ,直线l 与⊙O 相切于点B ,AB 为直径,∴ ∠POA =∠DBA =90°.又∵ AP ∥OD ,∴ ∠P AO =∠DOB . ························································1分 又∵ AO =BO ,∴ △APO ≌△ODB . ·······················································2分 ∴ AP =OD ,∴ 四边形APDO 是平行四边形, ·········································3分 ∴ M 是PO 的中点. ···········································································4分(其他解法:证△APO ≌△ODB 后,据中位线定理证12OM BD =;或证△DPO ≌△DBO ,得∠DPO =∠DBO =90°,从而证四边形APDO 是平行四边形等.)(2) M 是PC 的中点. 证明如下:∵AP ∥OD ,∴ ∠P AO =∠DOB ,又 ∠PCA =∠DBO =90°,∴ △APC ∽△ODB ,∴ PC AC BD BO=.①·····················································5分 又易证△ACM ∽△ABD ,∴ AC MC AB BD=. ·················································6分 又∵ AB =2OB ,∴ 2AC MC OB BD =,∴2AC MC OB BD=.② ····································7分 由①②得,2PC MC BD BD=,∴ PC =2MC ,即M 是PC 的中点. ·························8分 24.(1) 如图.(注:答案不唯一,在图中画出符合条件的图形即可) ······················2分(2) ① 当P 在CD 边上时,由题意,PR ∥BC ,设PR =x .可证四边形PRBQ 是正方形,∴ PR =PQ =BQ =x .过D 点作DE ∥AB ,交BC 于E ,易证四边形ABED 是矩形.∴ AD =BE =1,AB =DE =3. ··········································· 3分又 PQ ∥DE ,∴△CPQ ∽△CDE ,PQ CQ DE CE=. ∴ 635x x -=, ························································ 4分 ∴ x =94,即BP =942. ············································ 5分 (注:此时,由于∠C ≠45°,因此斜边RQ 不可能平行于BC . 在答题中未考虑此问题者不扣分.) ② 当P 在BC 边上,依题意可知RQ ∥BC .过Q 作QF ⊥BC ,易证△BRP ≌△FQP ,则PB =PF . ········· 6分易证四边形BFQR 是矩形,设BP =x ,则BP =BR =QF =PF =x ,BF =RQ =2x . ·················· 7分∵ QF ∥DE ,∴ △CQF ∽△CDE ,∴ QF CF DE CE =. ······································8分12 / 12 ∴6235x x -=,∴ x =1811. ···································································9分 (注:此时,直角边不可能与两底平行. 在答题中未考虑此问题者不扣分.)25.(1) ∵ 直线AB 的解析式为22y x =+,∴ 点A 、B 的坐标分别为A (0,2),B (-1,0).又直线l 的解析式为39y x =-+,∴ 点C 的坐标为(3,0). ··························1分 由上,可设经过A 、B 、C 三点的抛物线的解析式为y =a (x +1)(x -3),将点A 的坐标代入,得 a =23-,∴ 抛物线的解析式为224233y x x =-++. ·····2分 ∴ 抛物线的对称轴为x =1.由此可知,函数值随x 的增大而增大时,x 的取值范围是x ≤1. ···················3分 (注:本步结果无等号不扣分.)(2) 过A 作AE ∥BC ,交抛物线于点E . 显然,点A 、E 关于直线x =1对称,∴ 点E 的坐标为E (2,2). ····································································4分故梯形ABCE 的面积为 S =12(2+4)×2=6. ··················································5分 (3) 假设存在符合条件的点H ,作直线FH 交x 轴于M ,由题意知,3CFM S =. 设F (m ,n ),易知m =2,将F (2,n )的坐标代入y =-3x +9中,可求出n =3,则FG =3. ························6分∴ 132CFM S FG CM ==,∴ CM =2. 由C (3,0)知,1M (5,0),2M (1,0), ·······················································7分设FM 的解析式为y =kx +b ,由1M (5,0),F (2,3)得,F 1M 的解析式为y =-x +5,则F 1M 与抛物线的交点H 满足: 25,24 2.33y x y x x =-+⎧⎪⎨=-++⎪⎩整理得,22790x x -+=, ∵ △<0,∴ 不符合题意,舍去. ······················· 8分由2M (1,0),F (2,3)得,F 2M 的解析式为y =3x -3,则F 2M 与抛物线的交点H 满足:233,24 2.33y x y x x =-⎧⎪⎨=-++⎪⎩整理得,225150x x +-=, ∴ 51454x -±=. ··············································································9分 即:H点的横坐标为51454-±.。
2011年中考数学试题分类32 圆的有关性质
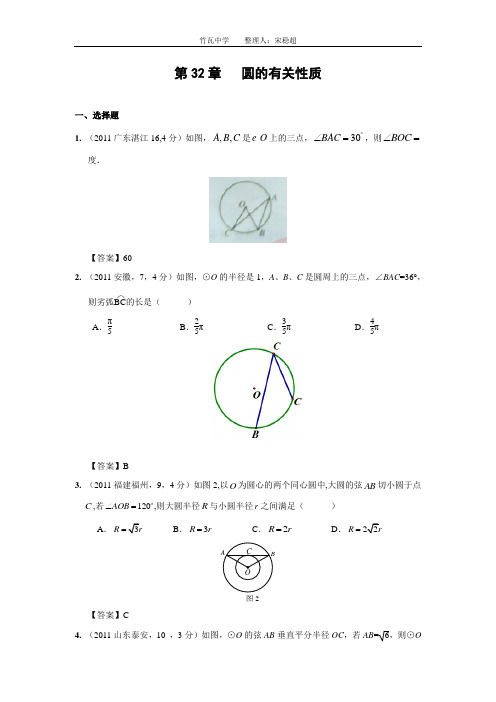
第32章 圆的有关性质一、选择题1. (2011广东湛江16,4分)如图,,,A B C 是O 上的三点,30BAC ︒∠=,则BOC ∠= 度.【答案】602. (2011安徽,7,4分)如图,⊙O 的半径是1,A 、B 、C 是圆周上的三点,∠BAC =36°,则劣弧 ⌒BC 的长是( ) A .π5B .25πC .35πD .45π【答案】B3. (2011福建福州,9,4分)如图2,以O 为圆心的两个同心圆中,大圆的弦AB 切小圆于点C ,若120AOB ∠= ,则大圆半径R 与小圆半径r 之间满足( )A.R = B .3R r =C .2R r =D.R =【答案】C4. (2011山东泰安,10 ,3分)如图,⊙O 的弦AB 垂直平分半径OC ,若AB =6,则⊙O图2的半径为()A. 2B.2 2C.22D.62【答案】A5. (2011四川南充市,9,3分)在圆柱形油槽内装有一些油。
截面如图,油面宽AB 为6分米,如果再注入一些油 后,油面AB 上升1分米,油面宽变为8分米,圆柱形油槽直径MN 为( )(A )6分米 (B )8分米 (C )10分米 (D )12分米 【答案】C6. (2011浙江衢州,1,3分)一个圆形人工湖如图所示,弦AB 是湖上的一座桥,已知桥AB 长100m ,测得圆周角45ACB ∠=︒,则这个人工湖的直径AD 为( )A.B.C.D.【答案】B7. (2011浙江绍兴,4,4分)如图,AB O 为的直径,点C 在O 上,若16C ∠=︒,则BOC ∠的度数是( )A.74︒B. 48︒C. 32︒D. 16︒【答案】C8. (2011浙江绍兴,6,4分)一条排水管的截面如图所示.已知排水管的截面圆半径10OB ,截面圆圆心O 到水面的距离OC 是6,则水面宽AB 是( )A.16B.10C.8D.6【答案】A9. (2011浙江省,5,3分)如图,小华同学设计了一个圆直径的测量器,标有刻度的尺子OA 、OB 在O 点钉在一起,并使它们保持垂直,在测直径时,把O 点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为( ) A. 12个单位 B. 10个单位 C.4个单位 D. 15个单位【答案】B10.(2011四川重庆,6,4分)如图,⊙O 是△A BC 的外接圆,∠OCB =40°则∠A 的度数等于( )A . 60°B . 50°C . 40°D . 30°【答案】B11.(2011浙江省嘉兴,6,4分)如图,半径为10的⊙O中,弦AB的长为16,则这条弦的弦心距为()(A)6 (B)8 (C)10 (D)12【答案】A12.(2011台湾台北,16)如图(六),BD为圆O的直径,直线ED为圆O的切线,A、C两点在圆上,AC平分∠BAD且交BD于F点。
2011年中考数学试题分类27 梯形

第27章 梯形一、选择题1. (2011江苏扬州,7,3分)已知下列命题:①对角线互相平分的四边形是平行四边形;②等腰梯形的对角线相等;③对角线互相垂直的四边形是菱形;④内错角相等。
其中假命题有( )A. 1个B. 2个C. 3个D. 4个 【答案】B2. (2011山东滨州,12,3分)如图,在一张△ABC 纸片中, ∠C=90°, ∠B=60°,DE 是中位线,现把纸片沿中位线DE 剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( ) A.1 B.2 C.3 D.4【答案】C3. (2011山东烟台,6,4分)如图,梯形ABCD 中,AB ∥CD ,点E 、F 、G 分别是BD 、AC 、DC 的中点.已知两底差是6,两腰和是12,则△EFG 的周长是( ) A.8 B.9 C.10 D.12【答案】B4. (2011浙江台州,7,4分)如图,在梯形ABCCD 中,AD ∥BC ,∠ABC=90º,对角线BD 、AC 相交于点O 。
下列条件中,不能判断对角线互相垂直的是( )(第6题图)ED CB A(第12题图)A.∠1=∠4B.∠1=∠3C.∠2=∠3D.OB2+OC2=BC2【答案】B5. (2011台湾台北,15)图(五)为梯形纸片ABCD,E点在BC上,且∠90DC=AEC,AD=3,BC=9,CD=8。
若以AE为折线,将C折至∠=︒=∠BE上,使得CD与AB交于F点,则BF长度为何?A.4.5 B。
5 C。
5.5 D.6【答案】B6. (2011山东潍坊,11,3分)已知直角梯形ABCD中,A D∥BC,∠BCD=90°, BC =CD=2AD , E、F分别是BC、CD边的中点,连接BF、DE交于点P,连接CP并延长交AB于点Q,连接AF,则下列结论不正确...的是()A . CP 平分∠BCD B. 四边形ABED 为平行四边形C. CQ将直角梯形ABCD 分为面积相等的两部分;D. △ABF为等腰三角形【答案】C7. (2011山东临沂,12,3分)如图,梯形ABCD中,AD∥BC,AB=CD,AD=2,BC=6,∠B=60°,则梯形ABCD的周长是()A .12B .14C .16D .18 【答案】C8. (2011四川绵阳11,3)如图,在等腰梯形站ABCD 中,AB//CD ,对角线AC 、BD 相交于O ,∠ABD =30°,AC ⊥BC , AB = 8cm,则△COD 的面积为AA. 2B. 243cmC. 2D. 223cm 【答案】A9. (2011湖北武汉市,7,3分)如图,在梯形ABCD 中,AB ∥DC ,AD =DC =CB ,若∠ABD=25°,则∠BAD 的大小是A .40°.B .45°.C .50°.D .60°.【答案】C10.(2011湖北宜昌,12,3分)如图,在梯形ABCD 中,AB∥CD,AD=BC ,点E,F,G,H 分别是AB,BC ,CD ,DA 的中点,则下列结论一定正确的是( ). A. ∠HGF = ∠GHE B. ∠GHE = ∠HEF C. ∠HEF = ∠EFG D. ∠HGF = ∠HEF【答案】D第7题图二、填空题1. (2011福建福州,13,4分)如图4,直角梯形ABCD 中,AD ∥BC ,90C ∠=o ,则A B C ∠+∠+∠= 度.【答案】2702. (2011 浙江湖州,14,4)如图,已知梯形ABCD ,AD ∥BC ,对角线AC ,BD 相交于点O ,△AOD 与△BOC 的面积之比为1:9,若AD =1,则BC 的长是 .【答案】33. (2011湖南邵阳,16,3分)如图(六)所示,在等腰梯形ABCD 中,AB ∥CD ,AD=BC ,AC ⊥BC ,∠B=60°,BC=2cm ,则上底DC 的长是_______cm 。
【史上最全】2011中考数学真题解析90_相似的基本概念(含答案)

2011全国中考真题解析120考点汇编相似基本概念一、选择题1. (2010广东,3,3分)将左下图中的箭头缩小到原来的21,得到的图形是( )考点:相似图形分析:根据相似图形的定义,结合图形,对选项一一分析,排除错误答案.解答:解:∵图中的箭头要缩小到原来的21,∴箭头的长、宽都要缩小到原来的21;选项B 箭头大小不变;选项C 箭头扩大;选项D 的长缩小、而宽没变.故选A .点评:本题主要考查了相似形的定义,联系图形,即图形的形状相同,但大小不一定相同的变换是相似变换.2. (2011,台湾省,22,5分)某校每位学生上、下学期各选择一个社团,下表为该校学生上、下学期各社团的人数比例.若该校上、下学期的学生人数不变,相较于上学期,下学期各社团的学生人数变化,下列叙述何者正确?( )A .B . D .题3图A、舞蹈社不变,溜冰社减少B、舞蹈社不变,溜冰社不变C、舞蹈社增加,溜冰社减少D、舞蹈社增加,溜冰社不变考点:比例的性质。
专题:计算题。
分析:若甲:乙:丙=a:b:c,则甲占全部的,乙占全部的,丙占全部的.解答:解:由表得知上、下学期各社团人数占全部人数的比例如下:======∴舞蹈社增加,溜冰社不变.故选D.点评:本题考查了比例的性质:两内项之积等于两外项之积.3.(2011,台湾省,33,5分)如图,梯形ABCD中,AD∥BC,E、F两点分别在AB、DC上.若AE=4,EB=6,DF=2,FC=3,且梯形AEFD与梯形EBCF相似,则AD与BC的长度比为何?()A、1:2B、2:3C、2:5D、4:9考点:相似多边形的性质。
分析:根据两个梯形相似,则对应边的比相等,即可求解.解答:解:∵梯形AEFD∽梯形EBCF,且DF:FC=2:3∴AD:EF=EF:BC=2:3⇒AD:EF:BC=4:6:9∴AD:BC=4:9.故选D.点评:本题主要考查了相似多边形的性质,正确理解性质是关键.4. (2011贵州毕节,7,3分)两个相似多边形的面积比是16:9,其中较小多边形周长为36cm,则较大多边形周长为( )A.48cm B.54cm C.56cm D.64cm考点:相似多边形的性质。
2011年中考数学试题分类26_矩形、菱形与正方形

第26章 矩形、菱形与正方形一、选择题1. (2011浙江省舟山,10,3分)如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH (不重叠无缝隙).若①②③④四个平行四边形面积的和为14cm 2,四边形ABCD 面积是11cm 2,则①②③④四个平行四边形周长的总和为( ) (A )48cm (B )36cm (C )24cm(D )18cm【答案】A2. (2011山东德州8,3分)图1是一个边长为1的等边三角形和一个菱形的组合图形,菱形边长为等边三角形边长的一半,以此为基本单位,可以拼成一个形状相同但尺寸更大的图形(如图2),依此规律继续拼下去(如图3),……,则第n 个图形的周长是(A )2n(B )4n(C )12n + (D )22n +【答案】C3. (2011山东泰安,17 ,3分)如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S 1,S 2,则S 1+S 2的值为图1图2图3……(第10题)FABCDH EG①②③④⑤A.17B.17C.18D.19 【答案】B4. (2011山东泰安,19 ,3分)如图,点O 是矩形ABCD 的中心,E 是AB 上的点,沿CE 折叠后,点B 恰好与点O 重合,若BC =3,则折痕CE 的长为 A.2 3 B.332C. 3D.6【答案】A5. (2011浙江杭州,10,3)在矩形ABCD 中,有一个菱形B F D E (点E ,F 分别在线段AB ,CD 上),记它们的面积分别 为ABCD BFDE S S 和.现给出下列命题:( )①若ABCD BFDE S S =tan EDF ∠=.②若2,DE BD EF =∙则2DF AD =. 则:A .①是真命题,②是真命题B .①是真命题,②是假命题C .①是假命题,②是真命题D ,①是假命题,②是假命题 【答案】A6. (2011浙江衢州,1,3分)衢州市新农村建设推动了农村住宅旧貌变新颜,如图为一农村民居侧面截图,屋坡AF AG 、分别架在墙体的点B 、点C 处,且AB AC =,侧面四边形BDEC 为矩形,若测得100FAG ∠=︒,则FBD ∠=( )A. 35°B. 40°C. 55°D. 70° 【答案】C7. (2011浙江温州,6,4分)如图,在矩形ABCD 中,对角线AC ,BD 交于点O .已知∠AOB = 60°,AC =16,则图中长度为8的线段有( ) A .2条B .4条C .5条D .6条【答案】D8. 2011四川重庆,10,4分)如图,正方形ABCD 中,AB =6,点E 在边CD 上,且CD =3DE .将△ADE 沿AE 对折至△AFE ,延长EF 交边BC 于点G ,连结AG 、CF .下列结论:①△ABG ≌△AFG ;②BG =GC ;③AG ∥CF ;④S △FGC =3.其中正确结论的个数是()A .1B .2C .3D .4【答案】C9. (2011浙江省嘉兴,10,4分)如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH (不重叠无缝隙).若①②③④四个平行四边形面积的和为14cm 2,四边形ABCD 面积是11cm 2,则①②③④四个平行四边形周长的总和为( ) (A )48cm (B )36cm (C )24cm(D )18cm【答案】A10.(2011台湾台北,29)如图(十二),长方形ABCD 中,E 为BC 中点,作AEC 的角平分线交AD 于F 点。
2011 台北第一次中考 数学真题与简答

2011 台北第一次中考 数学真题与简答1.图(一)数在线的O 是原点,A 、B 、C 三点所表示的数分别为a 、b 、c 。
根据图中各点的位置,下列各数的絶对值的比较何者正确?(A) |b |<|c | (B) |b |>|c | (C) |a |<|b | (D) |a |>|c | 【解题思路】:首先根据数a 、b 、c ,离开原点的位置,进行特殊值设定。
2-=a ,1=b , 3-=c ;进而得到它们的绝对值,比较大小。
【答案】:A【点评】:本题主要考察了数轴上数的特点以及有理数比较大小,运用特殊值法轻松解决此类问题。
如果利用数轴上数的特点,离原点越远绝对值越大也可以解决。
难度较小。
2. 计算(-3)3+52-(-2)2之值为何?(A) 2 (B) 5 C)-3 (D)-6【解题思路】:首先利用乘方的运算进行求值化简,进而利用有理数的加法求值。
【答案】:D【点评】:本题考察了有理数的运算顺序,以及乘方的知识。
难度较小3.表(一)表示某签筒中各种签的数量。
已知每支签被抽中的机会均相等,若自此筒中抽出一支签,则抽中红签的机率为何?(A)31 (B)21 (C)53(D)32【解题思路】:筒中共有签24只,任抽一签有24种可能,红签有16种,有16种可能,所以抽到红签的几率就是322416=【答案】:D【点评】:本题主要考察了概率的问题,难度不大。
4.计算75147-+27之值为何?(A) 53 (B) 333 (C) 311 (D) 911【解题思路】:首先把各个被开方数改写为乘积形式,并且把一部分因数写成乘方形式并进行开方。
如37334914772=⨯=⨯=,如果被开方数相同则称为同类二次根式,加减运算时,仅其系数相加减二次根式不变。
【答案】:353)357(333537=+-=+- (A )【点评】:本题主要考察了二次根式的开方和二次根式运算。
二次根式运算与合并同类项类似。
难度较小5.计算x 2(3x +8)除以x 3后,得商式和余式分别为何?(A)商式为3,余式为8x 2 (B)商式为3,余式为8(C)商式为3x +8,余式为8x 2 (D)商式为3x +8,余式为0 【解题思路】:运用整式乘法展开,使其成为323)83(x x x ÷+ 【答案】:A【点评】:本题考查了整式的除法,以及被除式、除式、商式、余数之间的关系。
【2011中考真题】台北中考试卷(有答案)
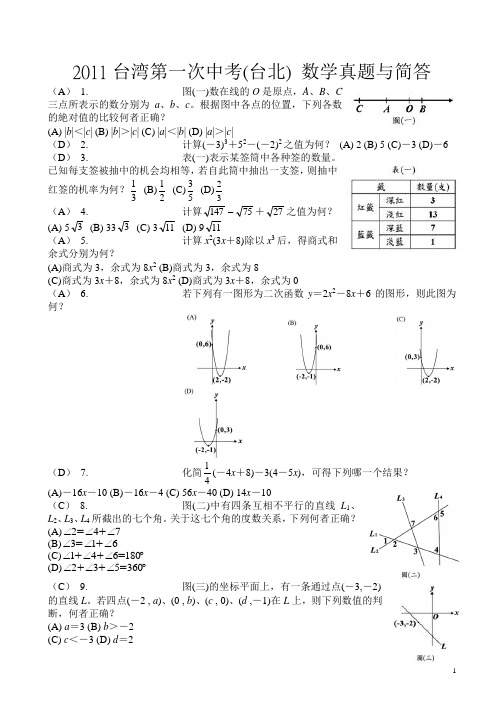
2011台湾第一次中考(台北) 数学真题与简答(A ) 1. 图(一)数在线的O 是原点,A 、B 、C三点所表示的数分别为a 、b 、c 。
根据图中各点的位置,下列各数的絶对值的比较何者正确?(A) |b |<|c | (B) |b |>|c | (C) |a |<|b | (D) |a |>|c |(D ) 2. 计算(-3)3+52-(-2)2之值为何? (A) 2 (B) 5 (C)-3 (D)-6(D ) 3. 表(一)表示某签筒中各种签的数量。
已知每支签被抽中的机会均相等,若自此筒中抽出一支签,则抽中红签的机率为何?31 (B)21 (C)53 (D)32 (A ) 4. 计算75147-+27之值为何?(A) 53 (B) 333 (C) 311 (D) 911(A ) 5. 计算x 2(3x +8)除以x 3后,得商式和余式分别为何?(A)商式为3,余式为8x 2 (B)商式为3,余式为8(C)商式为3x +8,余式为8x 2 (D)商式为3x +8,余式为0(A ) 6. 若下列有一图形为二次函数y =2x 2-8x +6的图形,则此图为何?(D ) 7. 化简41(-4x +8)-3(4-5x ),可得下列哪一个结果? (A)-16x -10 (B)-16x -4 (C) 56x -40 (D) 14x -10(C ) 8. 图(二)中有四条互相不平行的直线L 1、L 2、L 3、L 4所截出的七个角。
关于这七个角的度数关系,下列何者正确?(A)742∠∠∠+=(B)613∠∠∠+= (C)︒∠∠∠180641=++ (D)︒∠∠∠360532=++ (C ) 9. 图(三)的坐标平面上,有一条通过点(-3,-2)的直线L 。
若四点(-2 , a )、(0 , b )、(c , 0)、(d ,-1)在L 上,则下列数值的判断,何者正确?(A) a =3 (B) b >-2(C) c <-3 (D) d =2(B )10. 在1~45的45个正整数中,先将45的因子全部删除,再将剩下的整数由小到大排列,求第10个数为何?(A) 13 (B) 14 (C) 16 (D) 17(C )11. 计算45.247)6.1(÷÷--之值为何? (A)-1.1 (B)-1.8 (C)-3.2 (D)-3.9(B )12. 已知世运会、亚运会、奥运会分别于公元2009年、2010年、2012年举办。
2011年中考数学试题分类汇总单选:二次函数单选

一、选择题1. (2011山东滨州,7,3分)抛物线()223y x =+-可以由抛物线2y x =平移得到,则下列平移过程正确的是( )A.先向左平移2个单位,再向上平移3个单位B.先向左平移2个单位,再向下平移3个单位C.先向右平移2个单位,再向下平移3个单位D.先向右平移2个单位,再向上平移3个单位 【答案】B2. (2011广东广州市,5,3分)下列函数中,当x>0时y 值随x 值增大而减小的是( ). A .y = x2 B .y = x -1C . y = 34xD .y = 1x【答案】D4. (2011山东德州6,3分)已知函数))((b x a x y --=(其中a b >)的图象 如下面右图所示,则函数b ax y +=的图象可能正确的是【答案】D5. (2011山东菏泽,8,3分)如图为抛物线2y ax bx c =++的图像,A 、B 、C 为抛物线与坐标轴的交点,且OA=OC=1,则下列关系中正确的是A .a +b=-1B . a -b=-1C . b<2aD .ac<0【答案】B6. (2011山东泰安,20 ,3分)若二次函数y=ax2+bx+c 的x 与y 的部分对应值如下表:第6题图X -7 -6 -5 -4 -3 -2y -27 -13 -3 3 5 3则当x=1时,y 的值为A.5B.-3C.-13D.-27 【答案】D7. (2011山东威海,7,3分)二次函数223y x x =--的图象如图所示.当y <0时,自变量x 的取值范围是( ).A .-1<x <3B .x <-1C . x >3D .x <-1或x >3【答案】A8. (2011山东烟台,10,4分)如图,平面直角坐标系中,两条抛物线有相同的对称轴,则下列关系正确的是( )A .m =n ,k >hB .m =n ,k <hC .m >n ,k =hD .m <n ,k =h【答案】A9. (2011浙江温州,9,4分)已知二次函数的图象(0≤x≤3)如图所示.关于该函数在所给自变量取值范围内,下列说法正确的是( )A .有最小值0,有最大值3B .有最小值-1,有最大值0C .有最小值-1,有最大值3D .有最小值-1,无最大值【答案】D 10.(2011四川重庆,7,4分)已知抛物线y =ax2+bx +c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论中正确的是( )A . a>0B . b <0C . c <0D . a +b +c>0 【答案】D11. (2011台湾台北,6)若下列有一图形为二次函数y =2x2-8x +6的图形,则此图为何?【答案】A13. (2011台湾全区,28)图(十二)为坐标平面上二次函数c bx ax y ++=2的图形,且此图形通(-1 , 1)、(2 ,-1)两点.下列关于此二次函数的叙述,何者正确?A .y 的最大值小于0B .当x =0时,y 的值大于1C .当x =1时,y 的值大于1D .当x =3时,y 的值小于0 【答案】D14. (2011甘肃兰州,5,4分)抛物线221y x x =-+的顶点坐标是 A .(1,0)B .(-1,0)C .(-2,1)D .(2,-1)【答案】A15. (2011甘肃兰州,9,4分)如图所示的二次函数2y ax bx c =++的图象中,刘星同学观察得出了下面四条信息:(1)240b ac ->;(2)c>1;(3)2a -b<0;(4)a+b+c<0。
2011年中考数学真题分类汇编之第三十三章直线与圆的位置关系(附参考答案)

2011年中考数学真题分类汇编之第三十三章直线与圆的位置关系(附参考答案)第33章直线与圆的位置关系一、选择题1. (2011宁波市,11,3分)如图,⊙O1的半径为1,正方形ABCD的边长为6,点O2为正方形ABCD的中心,O1O2垂直AB与P点,O1O2=8.若将⊙O1绕点P按顺时针方向旋转360°,在旋转过程中,⊙O1与正方形ABCD的边只有一个公共点的情况一共出现A.3次B.5次C.6次D.7次【答案】B2. (2011浙江台州,10,4分)如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PB切⊙O于点B,则PB 的最小值是()A. 13B.5C. 3D.2【答案】B3. (2011浙江温州,10,4分)如图,O是正方形ABCD的对角线BD上一点,⊙O边AB,BC都相切,点E,F分别在边AD,DC上.现将△DEF沿着EF对折,折痕EF与⊙O相切,此时点D恰好落在圆心O处.若DE=2,则正方形ABCD的边长是( )A.3 B.4 C.22D.22【答案】C4. (2011浙江丽水,10,3分)如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是()A .点(0,3)B .点(2,3)C .点(5,1)D .点(6,1)【答案】C5. (2011浙江金华,10,3分)如图,在平面直角坐标系中,过格点A ,B ,C 作一圆弧,点B 与下列格点的连线中,能够与该圆弧相切的是( )A .点(0,3)B .点(2,3)C .点(5,1) D .点(6,1)【答案】C6. (2011山东日照,11,4分)已知AC ⊥BC于C ,BC =a ,CA =b ,AB =c ,下列选项中⊙O的半径为ba ab 的是( )【答案】C7. (2011湖北鄂州,13,3分)如图,AB 为⊙O的直径,PD 切⊙O 于点C ,交AB 的延长线于D ,且CO=CD ,则∠PCA=( )A .30°B .45°C .60°D .67.5°【答案】D 8. (2011 浙江湖州,9,3)如图,已知AB 是⊙O的直径,C 是AB 延长线上一点,BC =OB ,CE 是⊙O 的切线,切点为D ,过点A 作AE ⊥CE ,垂足为E ,则CD :DE 的值是A .12B .1C .2D .3【答案】C9. (2011台湾全区,33)如图(十五),AB 为圆OD AOB 第的直径,在圆O上取异于A、B的一点C,并连接BC、AC.若想在AB上取一点P,使得P与直线BC的距离等于AP长,判断下列四个作法何者正确?A.作AC的中垂线,交AB于P点B.作∠ACB的角平分线,交AB于P点C.作∠ABC的角平分线,交AC于D点,过D作直线BC的并行线,交AB于P点D.过A作圆O的切线,交直线BC于D 点,作∠ADC的角平分线,交AB于P点【答案】D10.(2011甘肃兰州,3,4分)如图,AB是⊙O 的直径,点D在AB的延长线上,DC切⊙O 于点C,若∠A=25°,则∠D等于A .20°B .30°C .40°D .50°【答案】C 11. (2011四川成都,10,3分)已知⊙O 的面积为29cm π,若点0到直线l 的距离为cm π,则直线l 与⊙O 的位置关系是C(A)相交 (B)相切 (C)相离 (D)无法确定【答案】C12. (2011重庆綦江,7,4分) 如图,PA 、PB 是⊙O的切线,切点是A 、B ,已知∠P =60°,OA=3,那么∠AOB 所对弧的长度为( )A .6лB .5лC .3лD .2л【答案】:D13. (2011湖北黄冈,13,3分)如图,AB 为A BD O C⊙O 的直径,PD 切⊙O 于点C ,交AB 的延长线于D ,且CO=CD ,则∠PCA=( )A .30°B .45°C .60°D .67.5°【答案】D 14. (2011山东东营,12,3分)如图,直线33y x =+与x 轴、y 分别相交与A 、B 两点,圆心P 的坐标为(1,0),圆P 与y 轴相切与点O 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011台湾第一次中考(台北) 数学真题与简答(A ) 1. 图(一)数在线的O 是原点,A 、B 、C 三点所表示的数分别为a 、b 、c 。
根据图中各点的位置,下列各数的絶对值的比较何者正确?(A) |b |<|c | (B) |b |>|c | (C) |a |<|b | (D) |a |>|c |(D ) 2. 计算(-3)3+52-(-2)2之值为何? (A) 2 (B) 5 (C)-3 (D)-6(D ) 3. 表(一)表示某签筒中各种签的数量。
已知每支签被抽中的机会均相等,若自此筒中抽出一支签,则抽中红签的机率为何?31 (B)21 (C)53 (D)32 (A ) 4. 计算75147-+27之值为何?(A) 53 (B) 333 (C) 311 (D) 911(A ) 5. 计算x 2(3x +8)除以x 3后,得商式和余式分别为何?(A)商式为3,余式为8x 2 (B)商式为3,余式为8(C)商式为3x +8,余式为8x 2 (D)商式为3x +8,余式为0(A ) 6. 若下列有一图形为二次函数y =2x 2-8x +6的图形,则此图为何?(D ) 7. 化简41(-4x +8)-3(4-5x ),可得下列哪一个结果?(A)-16x -10 (B)-16x -4 (C) 56x -40 (D) 14x -10(C ) 8. 图(二)中有四条互相不平行的直线L 1、L 2、L 3、L 4所截出的七个角。
关于这七个角的度数关系,下列何者正确?(A)742∠∠∠+=(B)613∠∠∠+= (C)︒∠∠∠180641=++ (D)︒∠∠∠360532=++(C ) 9. 图(三)的坐标平面上,有一条通过点(-3,-2)的直线L 。
若四点(-2 , a )、(0 , b )、(c , 0)、(d ,-1)在L 上,则下列数值的判断,何者正确?(A) a =3 (B) b >-2(C) c <-3 (D) d =2(B )10. 在1~45的45个正整数中,先将45的因子全部删除,再将剩下的整数由小到大排列,求第10个数为何?(A) 13 (B) 14 (C) 16 (D) 17(C )11. 计算45.247)6.1(÷÷--之值为何? (A)-1.1 (B)-1.8 (C)-3.2 (D)-3.9(B )12. 已知世运会、亚运会、奥运会分别于公元2009年、2010年、2012年举办。
若这三项运动会均每四年举办一次,则这三项运动会均不在下列哪一年举办?(A)公元2070年 (B)公元2071年 (C)公元2072年 (D)公元2073年(C )13. 若a :b :c =2:3:7,且a -b +3=c -2b ,则c 值为何? (A) 7 (B) 63 (C)221 (D)421 (A )14. 图(四)为某班甲、乙两组模拟考成绩的盒状图。
若甲、乙两组模拟考成绩的全距分别为a 、b ;中位数分别为c 、d ,则a 、b 、c 、d 的大小关系,下列何者正确?(A) a <b 且c >d(B) a <b 且c <d(C) a >b 且c >d(D) a >b 且c <d(B )15. 图(五)为梯形纸片ABCD ,E 点在BC 上,且︒=∠=∠=∠90D C AEC ,AD =3,BC =9,CD =8。
若以AE 为折线,将C 折至BE 上,使得CD 与AB 交于F 点,则BF 长度为何?(A) 4.5(B) 5(C) 5.5(D) 6(C )16. 如图(六),BD 为圆O 的直径,直线ED 为圆O 的切线,A 、C 两点在圆上,AC 平分∠BAD 且交BD 于F 点。
若∠ADE =︒19,则∠AFB 的度数为何?(A) 97(B) 104(C) 116(D) 142(B )17. 如图(七),坐标平面上有两直线L 、M ,其方程式分别为y =9、y=-6。
若L 上有一点P ,M 上有一点Q ,PQ 与y 轴平行,且PQ 上有一点R ,PR :RQ =1:2,则R 点与x 轴的距离为何?(A) 1(B) 4(C) 5(D) 10(A )18. 解不等式1-2x x 3297-≤,得其解的范围为何? (A)61≥x (B)61≤x (C)23≥x (D)23≤x (C )19. 若a 、b 两数满足a 567⨯3=103,a ÷103=b ,则b a ⨯之值为何? (A)9656710 (B)9356710 (C)6356710 (D)56710(B )20. 若一元二次方程式)2)(1()1(++++x x x ax bx + 2)2(=+x 的两根为0、2,则b a 43+之值为何?(A) 2 (B) 5 (C) 7 (D) 8(A )21. 坐标平面上有一个线对称图形,)25,3(-A 、)211,3(-B 两点在此图形上且互为对称点。
若此图形上有一点)9,2(--C ,则C 的对称点坐标为何?(A))1,2(- (B))23,2(-- (C))9,23(-- (D))9,8(-(B )22. 表(二)为某班成绩的次数分配表。
已知全班共有38人,且众数为50分,中位数为60分,求yx 22-之值为何?(A) 33 (B) 50 (C) 69 (D) 90(B )23. 如图(八),三边均不等长的ABC ∆,若在此三角形内找一点O ,使得OAB ∆、OBC ∆、OCA ∆的面积均相等。
判断下列作法何者正确?(A) 作中线AD ,再取AD 的中点O(B) 分别作中线AD 、BE ,再取此两中线的交点O(C) 分别作AB 、BC 的中垂线,再取此两中垂线的交点O(D) 分别作A ∠、B ∠的角平分线,再取此两角平分线的交点O(C )24. 下列四个多项式,哪一个是733+x 的倍式?(A)49332-x (B)493322+x (C)x x 7332+ (D)x x 14332+(B )25. 如图(九),圆A 、圆B 的半径分别为4、2,且AB =12。
若作一圆C 使得三圆的圆心在同一直在线,且圆C 与圆A 外切,圆C 与圆B 相交于两点,则下列何者可能是圆C 的半径长?(A) 3 (B) 4(C) 5 (D) 6(D )26. 图(十)为一ABC ∆,其中D 、E 两点分别在AB 、AC 上,且AD=31,DB =29,AE =30,EC =32。
若︒∠50=A ,则图中1∠、2∠、3∠、4∠的大小关系,下列何者正确?(A)1∠>3∠(B)2∠=4∠(C)1∠>4∠(D)2∠=3∠(D )27. 图(十一)为ABC ∆与圆O 的重迭情形,其中BC 为圆O 之直径。
若︒∠70=A ,BC =2,则图中灰色区域的面积为何? (A)π36055 (B)π360110 (C)π360125 (D)π360140(B )28. 某直角柱的两底面为全等的梯形,其四个侧面的面积依序为20平方公分、36平方公分、20平方公分、60平方公分,且此直角柱的高为4公分。
求此直角柱的体积为多少立方公分?(A) 136 (B) 192 (C) 240 (D) 544(C )29. 如图(十二),长方形ABCD 中,E 为BC 中点,作AEC ∠的角平分线交AD 于F 点。
若AB =6,AD =16,则FD 的长度为何?(A) 4(B) 5(C) 6(D) 8(D )30. 某鞋店有甲、乙两款鞋各30双,甲鞋一双200元,乙鞋一双50元。
该店促销的方式:买一双甲鞋,送一双乙鞋;只买乙鞋没有任何优惠。
若打烊后得知,此两款鞋共卖得1800元,还剩甲鞋x 双、乙鞋y 双,则依题意可列出下列哪一个方程式?(A)1800)30(50)30(200=-+-y x (B)1800)30(50)30(200=--+-y x x (C)1800)60(50)30(200=--+-y x x (D)1800])30(30[50)30(200=---+-y x x (D )31. 如图(十三),将长方形ABCD 分割成1个灰色长方形与148个面积相等的小正方形。
根据右图,若灰色长方形之长与宽的比为5:3,则AD :AB =?(A) 5:3 (B) 7:5(C) 23:14 (D) 47:29(A )32. 如图(十四),将二次函数228999931+-=x x y 的图形画在坐标平面上,判断方程式0899993122=+-x x 的两根,下列叙述何者正确?(A)两根相异,且均为正根(B)两根相异,且只有一个正根(C)两根相同,且为正根(D)两根相同,且为负根(D )33. 图(十五)为一个四边形ABCD ,其中AC 与BD 交于E 点,且两灰色区域的面积相等。
若AD =11,BC =10,则下列关系何者正确?(A)BCE DAE ∠<∠(B)BCE DAE ∠>∠ (C)BE >DE (D)BE <DE(D )34. 图(十六)表示一个时钟的钟面垂直固定于水平桌面上,其中分针上有一点A ,且当钟面显示3点30分时,分针垂直于桌面,A 点距桌面的高度为10公分。
如图(十七),若此钟面显示3点45分时,A 点距桌面的高度为16公分,则钟面显示3点50分时,A 点距桌面的高度为多少公分?(A)3322-(B)π+16(C)18(D)19。
