MATLAB实现抽样定理探讨及仿真
MATLAB实现抽样定理探讨及仿真

MATLAB实现抽样定理探讨及仿真应用 MATLAB 实现抽样定理探讨及仿真一. 课程设计的目的利用MATLAB ,仿模信号抽样与恢复系统的实际实现,探讨过抽样和欠抽样的信号以及抽样与恢复系统的性能。
二. 课程设计的原理模拟信号经过 (A/D) 变换转换为数字信号的过程称为采样,信号采样后其频谱产生了周期延拓,每隔一个采样频率 fs ,重复出现一次。
为保证采样后信号的频谱形状不失真,采样频率必须大于信号中最高频率成分的两倍,这称之为采样定理。
时域采样定理从采样信号恢复原信号必需满足两个条件: (1)必须是带限信号,其频谱函数在 > 各处为零;(对信号的要求,即只有带限信号才能适用采样定理。
)(2) 取样频率不能过低,必须 >2 (或 >2)。
(对取样频率的要求,即取样频率要足够大,)(t f )()(t t s S T δ=)(t f s 连续信号取样脉冲信号抽样信号)(ωj H )(0t f 理想低通滤波器恢复信号采得的样值要足够多,才能恢复原信号。
)如果采样频率大于或等于,即(为连续信号的有限频谱),则采样离散信号能无失真地恢复到原来的连续信号。
一个频谱在区间(-,)以外为零的频带有限信号,可唯一地由其在均匀间隔(<)上的样点值所确定。
根据时域与频域的对称性,可以由时域采样定理直接推出频域采样定理。
(a)(b)(c)图2.1抽样定理a) 等抽样频率时的抽样信号及频谱(不混叠) b) 高抽样频率时的抽样信号及频谱(不混叠)c) 低抽样频率时的抽样信号及频谱(混叠) 2.1信号采样如图1所示,给出了信号采样原理图信号采样原理图(a )由图1可见,)()()(t t f t f s T sδ⋅=,其中,冲激采样信号)(t sT δ的表达式为:∑∞-∞=-=n sT nT t t s)()(δδ其傅立叶变换为∑∞-∞=-n ss n )(ωωδω,其中ssT πω2=。
设)(ωj F ,)(ωj F s分别为)(t f ,)(t f s的傅立叶变换,由傅立叶变换的频域卷积定理,可得∑∑∞-∞=∞-∞=-=-=n ss n s s s n j F T n j F j F )]([1)(*)(21)(ωωωωδωωπω若设)(t f 是带限信号,带宽为mω, )(t f 经过采样后的频谱)(ωj F s就是将)(ωj F 在频率轴上搬移至ΛΛ,,,,,02ns ssωωω±±±处(幅度为原频谱的sT 1倍)。
MATLAB实现抽样定理探讨及仿真

MATLAB实现抽样定理探讨及仿真抽样定理,也被称为Nyquist定理或香农定理,是一种关于信号采样的基本理论。
它的核心观点是:如果对信号进行合适的采样,并且采样频率大于信号中最高频率的两倍,那么原始信号可以从采样信号中完全或几乎完全地恢复。
在MATLAB中,我们可以实现抽样定理的探讨和仿真。
下面将详细介绍如何进行这样的实现。
首先,我们可以通过使用MATLAB内置的函数来生成一个连续时间的信号。
例如,我们可以使用sinc函数生成一个带宽有限的信号,其频率范围为[-F/2, F/2],其中F是信号的最大频率。
以下是一个示例代码:```MATLABFs=100;%采样率Ts=1/Fs;%采样周期t=-1:Ts:1;%连续时间序列f_max = 10; % 信号最大频率signal = sinc(2*f_max*t); % 生成带宽有限的信号```然后,我们可以使用MATLAB的plot函数来显示生成的信号。
以下是一个示例代码:```MATLABplot(t, signal);xlabel('时间');ylabel('信号幅度');title('连续时间信号');```生成的图形将显示带宽有限的信号在连续时间域中的波形。
接下来,我们需要对信号进行离散化采样。
根据抽样定理,理想情况下,采样频率应大于信号中最高频率的两倍。
我们可以使用MATLAB的resample函数来进行采样。
以下是一个示例代码:```MATLABFs_new = 2*f_max; % 新的采样率Ts_new = 1/Fs_new; % 新的采样周期t_new = -1:Ts_new:1; % 新的时间序列signal_sampled = resample(signal, Fs_new, Fs); % 信号采样```然后,我们可以使用MATLAB的stem函数来显示采样后的信号。
以下是一个示例代码:```MATLABstem(t_new, signal_sampled);xlabel('时间');ylabel('信号幅度');title('离散时间信号');```生成的图形将显示采样后的信号在离散时间域中的序列。
应用MATLAB实现抽样定理探讨及仿真

大学2012~2013学年冬季学期本科生课程研讨报告课程名称:《通信原理B(1)》课程编号:07275128 题目: 应用MATLAB实现抽样定理探讨及仿真学生: 秀凤(组长)学号: 10123889学生: 肖勖学号: 10120787学生: 洪文琍学号: 10123043学生: 周润萍学号:学生: 航学号:评语:成 绩: 任课教师:评阅日期:应用 MATLAB 实现抽样定理探讨及仿真一. 课程设计的目的利用MATLAB ,仿模信号抽样与恢复系统的实际实现,探讨过抽样和欠抽样的信号以及抽样与恢复系统的性能。
二. 课程设计的原理模拟信号经过 (A/D) 变换转换为数字信号的过程称为采样,信号采样后其频谱产生了周期延拓,每隔一个采样频率 fs ,重复出现一次。
为保证采样后信号的频谱形状不失真,采样频率必须大于信号中最高频率成分的两倍,这称之为采样定理。
时域采样定理从采样信号恢复原信号必需满足两个条件: (1)必须是带限信号,其频谱函数在>各处为零;(对信号的要求,即只有带限信号才能适用采样定理。
) (2)取样频率不能过低,必须>2(或>2)。
(对取样频率的要求,即取样频率要足够大,采得的样值要足够多,才能恢复原信号。
)如果采样频率大于或等于,即(为连续信号的有限频谱),则采样离散信号能无失真地恢复到原来的连续信号。
一个频谱在区间(-,)以外为零的频带有限信号,可唯一地由其)(t f )()(t t s S T δ=)(t f s 连续信号取样脉冲信号抽样信号)(ωj H )(0t f 理想低通滤波器恢复信号在均匀间隔(<)上的样点值所确定。
根据时域与频域的对称性,可以由时域采样定理直接推出频域采样定理。
(a)(b)(c)图2.1抽样定理a) 等抽样频率时的抽样信号及频谱(不混叠) b) 高抽样频率时的抽样信号及频谱(不混叠) c) 低抽样频率时的抽样信号及频谱(混叠)2.1信号采样如图1所示,给出了信号采样原理图信号采样原理图(a )由图1可见,)()()(t t f t f s T s δ⋅=,其中,冲激采样信号)(t s T δ的表达式为:∑∞-∞=-=n sT nT t t s)()(δδ其傅立叶变换为∑∞-∞=-n s s n )(ωωδω,其中ss T πω2=。
MATLAB实现抽样定理探讨及仿真

应用 MATLAB 实现抽样定理探讨及仿真一. 课程设计的目的利用MATLAB ,仿模信号抽样与恢复系统的实际实现,探讨过抽样和欠抽样的信号以及抽样与恢复系统的性能。
二. 课程设计的原理模拟信号经过 (A/D) 变换转换为数字信号的过程称为采样,信号采样后其频谱产生了周期延拓,每隔一个采样频率 fs ,重复出现一次。
为保证采样后信号的频谱形状不失真,采样频率必须大于信号中最高频率成分的两倍,这称之为采样定理。
时域采样定理从采样信号恢复原信号必需满足两个条件: (1)必须是带限信号,其频谱函数在>各处为零;(对信号的要求,即只有带限信号才能适用采样定理。
)(2) 取样频率不能过低,必须>2(或>2)。
(对取样频率的要求,即取样频率要足够大,采得的样值要足够多,才能恢复原信号。
)如果采样频率大于或等于,即(为连续信号的有限频谱),则采样离散信号能无失真地恢复到原来的连续信号 。
一个频谱在区间(-,)以外为零的频带有限信号,可唯一地由其在均匀间隔(<)上的样点值所确定。
根据时域与频域的对称性,可以由时域采样定理直接推出频域采样定理。
(a))(t f )()(t t s S T δ=)(t f s 连续信号取样脉冲信号抽样信号)(ωj H )(0t f 理想低通滤波器恢复信号(b)(c)图2.1抽样定理a)等抽样频率时的抽样信号及频谱(不混叠)b)高抽样频率时的抽样信号及频谱(不混叠)c) 低抽样频率时的抽样信号及频谱(混叠)2.1信号采样如图1所示,给出了信号采样原理图信号采样原理图(a)由图1可见,)()()(ttftfsTsδ⋅=,其中,冲激采样信号)(ts Tδ的表达式为:∑∞-∞=-=nsTnTtts)()(δδ其傅立叶变换为∑∞-∞=-nssn)(ωωδω,其中ss Tπω2=。
设)(ωjF,)(ωjFs分别为)(tf,)(tfs的傅立叶变换,由傅立叶变换的频域卷积定理,可得∑∑∞-∞=∞-∞=-=-=nssnsssnjFTnjFjF)]([1)(*)(21)(ωωωωδωωπω若设)(tf是带限信号,带宽为mω,)(tf经过采样后的频谱)(ωjFs就是将)(ωjF在频率轴上搬移至,,,,,02nsssωωω±±±处(幅度为原频谱的sT1倍)。
MATLAB实现抽样定理探讨及仿真

MATLAB实现抽样定理探讨及仿真抽样定理是信号处理与通信领域中的一个重要定理,它指出在进行信号采样时,为了避免失真和信息丢失,采样频率必须至少为信号带宽的两倍。
抽样定理还提供了信号的重构方法,可以从采样信号中恢复出原始信号的全部信息。
在这篇文章中,我们将使用MATLAB对抽样定理进行探讨,并进行相关的仿真实验。
首先,我们将介绍抽样定理的基本原理。
在信号处理中,信号可以被表示为时域函数或频域函数。
在时域中,信号可以用冲激函数的线性组合来表示,而在频域中,信号可以被表示为复指数函数的线性组合。
信号的带宽是指信号中包含的频率的范围,通常用赫兹(Hz)来表示。
根据抽样定理,为了准确地恢复信号,采样频率必须至少是信号带宽的两倍。
接下来,我们将使用MATLAB对抽样定理进行仿真实验。
首先,我们将生成一个具有限带宽的信号,并对其进行采样。
然后,我们将根据抽样定理的要求重新构建信号,以验证定理的有效性。
假设我们有一个信号x(t),其频率范围为0至10赫兹,并且我们以20赫兹的采样频率对其进行采样。
我们可以使用MATLAB生成这个信号,并进行采样,代码如下所示:```matlabFs=20;%采样频率t=0:1/Fs:1-1/Fs;%1秒内的采样时刻x = sin(2*pi*10*t); % 10赫兹的正弦波信号stem(t,x);xlabel('时间(秒)');ylabel('幅度');title('原始信号');```接下来,我们将使用抽样定理的频率限制条件对信号进行重构,并绘制重构后的信号。
我们将使用插值的方法对采样信号进行重构,代码如下所示:```matlabt_recon = 0:1/(2*Fs):1-1/(2*Fs); % 重新构建信号时的采样时刻x_recon = interp1(t,x,t_recon); % 插值重构信号stem(t_recon,x_recon);xlabel('时间(秒)');ylabel('幅度');title('重构信号');```通过对原始信号和重构信号的比较,我们可以看到抽样定理的有效性。
应用MATLAB实现抽样定理探讨及仿真

上海大学2012~2013学年冬季学期本科生课程研讨报告课程名称:《通信原理B(1)》课程编号: 07275128 题目: 应用 MATLAB实现抽样定理探讨及仿真学生姓名: 李秀凤(组长)学号: 10123889 学生姓名: 肖勖学号: 10120787学生姓名: 洪文琍学号: 10123043学生姓名: 周润萍学号:学生姓名: 李航学号:评语:成绩: 任课教师: 评阅日期:应用 MATLAB 实现抽样定理探讨及仿真一. 课程设计的目的利用MATLAB ,仿模信号抽样与恢复系统的实际实现,探讨过抽样和欠抽样的信号以及抽样与恢复系统的性能。
二. 课程设计的原理模拟信号经过 (A/D) 变换转换为数字信号的过程称为采样,信号采样后其频谱产生了周期延拓,每隔一个采样频率 fs ,重复出现一次。
为保证采样后信号的频谱形状不失真,采样频率必须大于信号中最高频率成分的两倍,这称之为采样定理。
时域采样定理从采样信号恢复原信号必需满足两个条件: (1)必须是带限信号,其频谱函数在>各处为零;(对信号的要求,即只有带限信号才能适用采样定理。
)(2) 取样频率不能过低,必须>2(或>2)。
(对取样频率的要求,即取样频率要足够大,采得的样值要足够多,才能恢复原信号。
)如果采样频率大于或等于,即(为连续信号的有限频谱),则采样离散信号能无失真地恢复到原来的连续信号 。
一个频谱在区间(- ,)以外为零的频带有限信号,可唯一地由其在均匀间隔(<)上的样点值所确定。
根据时域与频域的对称性,可以由时域采样定理直接推出频域采样定理。
(a))(t f )()(t t s S T δ=)(t f s 连续信号取样脉冲信号抽样信号)(ωj H )(0t f 理想低通滤波器恢复信号(b)(c)图2.1抽样定理a) 等抽样频率时的抽样信号及频谱(不混叠) b) 高抽样频率时的抽样信号及频谱(不混叠) c) 低抽样频率时的抽样信号及频谱(混叠)2.1信号采样如图1所示,给出了信号采样原理图信号采样原理图(a )由图1可见,)()()(t t f t f s T s δ⋅=,其中,冲激采样信号)(t s T δ的表达式为:∑∞-∞=-=n sT nT t t s)()(δδ其傅立叶变换为∑∞-∞=-n s s n )(ωωδω,其中ss T πω2=。
MATLAB实现抽样定理探讨及仿真讲解

应用 MATLAB 实现抽样定理探讨及仿真一. 课程设计的目的利用MATLAB ,仿模信号抽样与恢复系统的实际实现,探讨过抽样和欠抽样的信号以及抽样与恢复系统的性能。
二. 课程设计的原理模拟信号经过 (A/D) 变换转换为数字信号的过程称为采样,信号采样后其频谱产生了周期延拓,每隔一个采样频率 fs ,重复出现一次。
为保证采样后信号的频谱形状不失真,采样频率必须大于信号中最高频率成分的两倍,这称之为采样定理。
时域采样定理从采样信号恢复原信号必需满足两个条件: (1)必须是带限信号,其频谱函数在>各处为零;(对信号的要求,即只有带限信号才能适用采样定理。
)(2) 取样频率不能过低,必须>2(或>2)。
(对取样频率的要求,即取样频率要足够大,采得的样值要足够多,才能恢复原信号。
)如果采样频率大于或等于,即(为连续信号的有限频谱),则采样离散信号能无失真地恢复到原来的连续信号 。
一个频谱在区间(-,)以外为零的频带有限信号,可唯一地由其在均匀间隔(<)上的样点值所确定。
根据时域与频域的对称性,可以由时域采样定理直接推出频域采样定理。
(a))(t f )()(t t s S T δ=)(t f s 连续信号取样脉冲信号抽样信号)(ωj H )(0t f 理想低通滤波器恢复信号(b)(c)图2.1抽样定理a)等抽样频率时的抽样信号及频谱(不混叠)b)高抽样频率时的抽样信号及频谱(不混叠)c) 低抽样频率时的抽样信号及频谱(混叠)2.1信号采样如图1所示,给出了信号采样原理图信号采样原理图(a)由图1可见,)()()(ttftfsTsδ⋅=,其中,冲激采样信号)(ts Tδ的表达式为:∑∞-∞=-=nsTnTtts)()(δδ其傅立叶变换为∑∞-∞=-nssn)(ωωδω,其中ss Tπω2=。
设)(ωjF,)(ωjFs分别为)(tf,)(tfs的傅立叶变换,由傅立叶变换的频域卷积定理,可得∑∑∞-∞=∞-∞=-=-=nssnsssnjFTnjFjF)]([1)(*)(21)(ωωωωδωωπω若设)(tf是带限信号,带宽为mω,)(t f经过采样后的频谱)(ωjFs就是将)(ωjF在频率轴上搬移至,,,,,02nsssωωω±±±处(幅度为原频谱的sT1倍)。
MATLAB实现抽样定理探讨仿真

应用MATLAB实现抽样定理探讨及仿真课程设计的目的利用MATLAB仿模信号抽样与恢复系统的实际实现,探讨过抽样和欠抽样的信号以及抽样与恢复系统的性能。
二.课程设计的原理模拟信号经过(A/D)变换转换为数字信号的过程称为采样,信号采样后其频谱产生了周期延拓,每隔一个采样频率fs,重复出现一次。
为保证采样后信号的频谱形状不失真,采样频率必须大于信号中最高频率成分的两倍,这称之为采样定理。
时域采样定理从采样信号_.. :1 i恢复原信号「[I必需满足两个条件:(1);必须是带限信号,其频谱函数在才能适用采样定理。
)叫〉2 %(或£> 2几)。
(对取样频率的要求,即取样频率要即.—id (in为连续信号GL的有限频谱),则采样离散信号''能无失真地恢复到原来的连续信号心。
一个频谱在区间(-三乙,口二)以外为零的频带有限信号Ji ,可唯一地由域采样定理直接推出频域采样定理。
f o(t)恢复信号由| > % 各处为零;(对信号的要求,即只有带限信号(2)取样频率不能过低,必须足够大,采得的样值要足够多,才能恢复原信号。
)如果采样频率—-大于或等于二)上的样点值八:所确定。
根据时域与频域的对称性,可以由时其在均匀间隔2其傅立叶变换为s ( n s ),其中s ——。
设F(j ),F s (j )分别为f(t),f s (t)的 n T s傅立叶变换,由傅立叶变换的频域卷积定理,可得1 1F s (j ) —F(j )* s (n s ) - F[j( n s )]2nI s n若设f (t)是带限信号,带宽为m, f(t)经过采样后的频谱 F s (j )就是将F(j )在频率轴1/T sA/\ A(c)b) 高抽样频率时的抽样信号及频谱 c)低抽样频率时的抽样信号及频谱(不混叠) (不混叠) (混叠)2.1信号采样如图1所示,给出了信号采样原理图相乘—:- >0)r(a )由图1可见,f s (t) f (t)Ts(t),其中,冲激采样信号Ts (t)的表达式为:(t)n(t nT s )等抽样频率时的抽样信号及频谱 a)上搬移至0, s, 2s, , ns,处(幅度为原频谱的1 T s倍)。
MATLAB实现抽样定理探讨与仿真设计
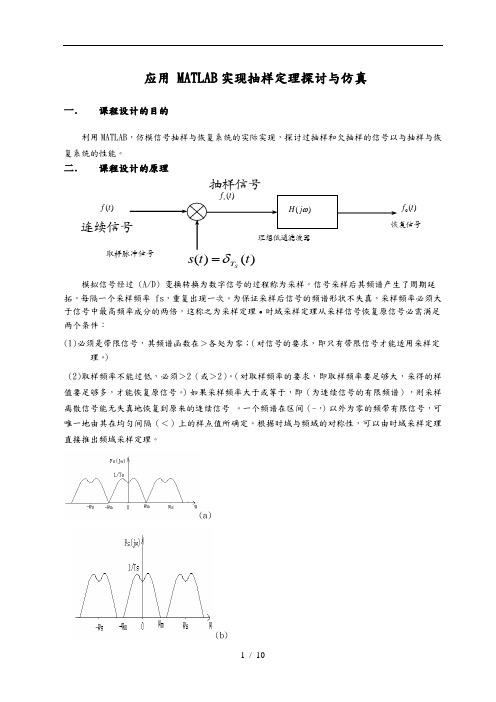
应用 MATLAB 实现抽样定理探讨与仿真一. 课程设计的目的利用MATLAB ,仿模信号抽样与恢复系统的实际实现,探讨过抽样和欠抽样的信号以与抽样与恢复系统的性能。
二. 课程设计的原理模拟信号经过 (A/D) 变换转换为数字信号的过程称为采样,信号采样后其频谱产生了周期延拓,每隔一个采样频率 fs ,重复出现一次。
为保证采样后信号的频谱形状不失真,采样频率必须大于信号中最高频率成分的两倍,这称之为采样定理。
时域采样定理从采样信号恢复原信号必需满足两个条件:(1)必须是带限信号,其频谱函数在>各处为零;(对信号的要求,即只有带限信号才能适用采样定理。
)(2)取样频率不能过低,必须>2(或>2)。
(对取样频率的要求,即取样频率要足够大,采得的样值要足够多,才能恢复原信号。
)如果采样频率大于或等于,即(为连续信号的有限频谱),则采样离散信号能无失真地恢复到原来的连续信号 。
一个频谱在区间(-,)以外为零的频带有限信号,可唯一地由其在均匀间隔(<)上的样点值所确定。
根据时域与频域的对称性,可以由时域采样定理直接推出频域采样定理。
(a)(b))(t f )()(t t s S T =)(t f s 连续信号取样脉冲信号抽样信号)(ωj H )(0t f 理想低通滤波器恢复信号(c)图2.1抽样定理a) 等抽样频率时的抽样信号与频谱(不混叠) b) 高抽样频率时的抽样信号与频谱(不混叠) c) 低抽样频率时的抽样信号与频谱(混叠)2.1信号采样如图1所示,给出了信号采样原理图 信号采样原理图(a )由图1可见,)()()(t t f t f s T s δ⋅=,其中,冲激采样信号)(t s T δ的表达式为:∑∞-∞=-=n sT nT t t s)()(δδ其傅立叶变换为∑∞-∞=-n s s n )(ωωδω,其中ss T πω2=。
设)(ωj F ,)(ωj F s 分别为)(t f ,)(t f s 的傅立叶变换,由傅立叶变换的频域卷积定理,可得∑∑∞-∞=∞-∞=-=-=n ss n s s s n j F T n j F j F )]([1)(*)(21)(ωωωωδωωπω若设)(t f 是带限信号,带宽为m ω,)(t f 经过采样后的频谱)(ωj F s 就是将)(ωj F 在频率轴上搬移至 ,,,,,02ns s s ωωω±±±处(幅度为原频谱的s T 1倍)。
应用MATLAB实现抽样定理探讨及仿真

大学2012~2013学年冬季学期本科生课程研讨报告课程名称:《通信原理B(1)》课程编号:07275128 题目: 应用MATLAB实现抽样定理探讨及仿真学生: 秀凤(组长)学号: 10123889学生: 肖勖学号: 10120787学生: 洪文琍学号: 10123043学生: 周润萍学号:学生: 航学号:评语:成 绩: 任课教师:评阅日期:应用 MATLAB 实现抽样定理探讨及仿真一. 课程设计的目的利用MATLAB ,仿模信号抽样与恢复系统的实际实现,探讨过抽样和欠抽样的信号以及抽样与恢复系统的性能。
二. 课程设计的原理模拟信号经过 (A/D) 变换转换为数字信号的过程称为采样,信号采样后其频谱产生了周期延拓,每隔一个采样频率 fs ,重复出现一次。
为保证采样后信号的频谱形状不失真,采样频率必须大于信号中最高频率成分的两倍,这称之为采样定理。
时域采样定理从采样信号恢复原信号必需满足两个条件: (1)必须是带限信号,其频谱函数在>各处为零;(对信号的要求,即只有带限信号才能适用采样定理。
)(2) 取样频率不能过低,必须>2(或>2)。
(对取样频率的要求,即取样频率要足够大,采得的样值要足够多,才能恢复原信号。
)如果采样频率大于或等于,即(为连续信号的有限频谱),则采样离散信号能无失真地恢复到原)(t f )()(t t s S T =)(t f s 连续信号取样脉冲信号抽样信号)(ωj H )(0t f 理想低通滤波器恢复信号来的连续信号 。
一个频谱在区间(- ,)以外为零的频带有限信号,可唯一地由其在均匀间隔(<)上的样点值所确定。
根据时域与频域的对称性,可以由时域采样定理直接推出频域采样定理。
(a)(b)(c)图2.1抽样定理a) 等抽样频率时的抽样信号及频谱(不混叠) b) 高抽样频率时的抽样信号及频谱(不混叠) c) 低抽样频率时的抽样信号及频谱(混叠)2.1信号采样如图1所示,给出了信号采样原理图信号采样原理图(a )由图1可见,)()()(t t f t f s T s δ⋅=,其中,冲激采样信号)(t s T δ的表达式为:∑∞-∞=-=n sT nT t t s)()(δδ其傅立叶变换为∑∞-∞=-n s s n )(ωωδω,其中ss T πω2=。
MATLAB实现抽样定理探讨及仿真

应用 MATLAB 实现抽样定理探讨及仿真一. 课程设计的目的利用MATLAB ,仿模信号抽样与恢复系统的实际实现,探讨过抽样和欠抽样的信号以及抽样与恢复系统的性能。
二. 课程设计的原理模拟信号经过 (A/D) 变换转换为数字信号的过程称为采样,信号采样后其频谱产生了周期延拓,每隔一个采样频率 fs ,重复出现一次。
为保证采样后信号的频谱形状不失真,采样频率必须大于信号中最高频率成分的两倍,这称之为采样定理。
时域采样定理从采样信号恢复原信号必需满足两个条件: (1)必须是带限信号,其频谱函数在>各处为零;(对信号的要求,即只有带限信号才能适用采样定理。
)(2) 取样频率不能过低,必须>2 (或>2)。
(对取样频率的要求,即取样频率要足够大,采得的样值要足够多,才能恢复原信号。
)如果采样频率大于或等于,即(为连续信号的有限频谱),则采样离散信号能无失真地恢复到原来的连续信号 。
一个频谱在区间(- ,)以外为零的频带有限信号,可唯一地由其在均匀间隔(<)上的样点值所确定。
根据时域与频域的对称性,可以由时域采样定理直接推出频域采样定理。
(a))(t f )()(t t s S T =)(t f s 连续信号取样脉冲信号抽样信号)(ωj H )(0t f 理想低通滤波器恢复信号(b)(c)图2.1抽样定理a) 等抽样频率时的抽样信号及频谱(不混叠) b) 高抽样频率时的抽样信号及频谱(不混叠) c) 低抽样频率时的抽样信号及频谱(混叠)2.1信号采样如图1所示,给出了信号采样原理图信号采样原理图(a )由图1可见,)()()(t t f t f s T s δ⋅=,其中,冲激采样信号)(t s T δ的表达式为:∑∞-∞=-=n sT nT t t s)()(δδ其傅立叶变换为∑∞-∞=-n s s n )(ωωδω,其中ss T πω2=。
设)(ωj F ,)(ωj F s 分别为)(t f ,)(t f s 的傅立叶变换,由傅立叶变换的频域卷积定理,可得∑∑∞-∞=∞-∞=-=-=n ss n s s s n j F T n j F j F )]([1)(*)(21)(ωωωωδωωπω若设)(t f 是带限信号,带宽为m ω, )(t f 经过采样后的频谱)(ωj F s 就是将)(ωj F 在频率轴上搬移至ΛΛ,,,,,02ns s s ωωω±±±处(幅度为原频谱的s T 1倍)。
MATLAB实现抽样定理探讨与仿真设计

应用MATLAB实现抽样定理探讨及仿真课程设计的目的利用MATLAB仿模信号抽样与恢复系统的实际实现,探讨过抽样和欠抽样的信号以及抽样与恢复系统的性能。
二. 课程设计的原理模拟信号经过(A/D)变换转换为数字信号的过程称为采样,信号采样后其频谱产生了周期延拓,每隔一个采样频率fs,重复出现一次。
为保证采样后信号的频谱形状不失真,采样频率必须大于信号中最高频率成分的两倍,这称之为采样定理。
时域采样定理从采样信号J「恢复原信号■ ■:必需满足两个条件:⑴几)必须是带限信号,其频谱函数在> 叫各处为零;(对信号的要求,即只有带限信号才能适用采样定理。
)(2)取样频率不能过低,必须q> 2 % (或J;> 2人)。
(对取样频率的要求,即取样频率要足够大,采得的样值要足够多,才能恢复原信号。
)如果采样频率二Jl' ' J-大于或等于二,即「一 Xi (I—为连续信号门的有限频谱),则采样离散信号;能无失真地恢复到原来的连续信号-'Il。
一个频谱在区间(-I],】])以外为零的频带有限信号,可唯一地由其在均匀间隔「-(]< ——)上的样点值-./J.:所确定。
根据时域与频域的对称性,可以由时□0「•Ts(t)八弋- nT s)n =^0Q0其傅立叶变换为^2五(①-n 乞),其中⑷。
设 F(j ),F s (j ■)分别为 f (t),f s (t)的 TS□0. Q0F(j A s ' • 一 n 上)二―' F[j (— n *)]T sf (t )经过采样后的频谱 F s (j 「)就是将F (j ,)在频率轴上搬移至0,一 d-」s ,…L 'ns ,…处(幅度为原频谱的1 T s 倍)。
因此,当-2'm 时,频谱不发生 混叠;而当•,s :::2 .m 时,频谱发生混叠。
傅立叶变换,由傅立叶变换的频域卷积定理, 可得(c)b) 高抽样频率时的抽样信号及频谱 c)低抽样频率时的抽样信号及频谱(不混叠) (不混叠)2.1信号采样如图1所示,给出了信号采样原理图孑相乘北)--------- A速)信号采样原理图(a )由图1可见,f s(t )f (t )七T s(t ),其中,冲激采样信号T s(t )的表达式为:F s (j )若设f (t )是带限信号,带宽为--m等抽样频率时的抽样信号及频谱 a)2.1.3信号重构设信号f(t)被采样后形成的采样信号为f s(t),信号的重构是指由f s(t)经过内插处理后,恢复出原来信号f (t)的过程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
应用 MATLAB 实现抽样定理探讨及仿真一. 课程设计的目的利用MATLAB ,仿模信号抽样与恢复系统的实际实现,探讨过抽样和欠抽样的信号以及抽样与恢复系统的性能。
二. 课程设计的原理模拟信号经过 (A/D) 变换转换为数字信号的过程称为采样,信号采样后其频谱产生了周期延拓,每隔一个采样频率 fs ,重复出现一次。
为保证采样后信号的频谱形状不失真,采样频率必须大于信号中最高频率成分的两倍,这称之为采样定理。
时域采样定理从采样信号恢复原信号必需满足两个条件: (1)必须是带限信号,其频谱函数在>各处为零;(对信号的要求,即只有带限信号才能适用采样定理。
)(2) 取样频率不能过低,必须>2(或>2)。
(对取样频率的要求,即取样频率要足够大,采得的样值要足够多,才能恢复原信号。
)如果采样频率大于或等于,即(为连续信号的有限频谱),则采样离散信号能无失真地恢复到原来的连续信号 。
一个频谱在区间(- ,)以外为零的频带有限信号,可唯一地由其在均匀间隔(<)上的样点值所确定。
根据时域与频域的对称性,可以由时域采样定理直接推出频域采样定理。
(a))(t f )()(t t s S T =)(t f s 连续信号取样脉冲信号抽样信号)(ωj H )(0t f 理想低通滤波器恢复信号(b)(c)图2.1抽样定理a) 等抽样频率时的抽样信号及频谱(不混叠) b) 高抽样频率时的抽样信号及频谱(不混叠) c) 低抽样频率时的抽样信号及频谱(混叠)2.1信号采样如图1所示,给出了信号采样原理图信号采样原理图(a )由图1可见,)()()(t t f t f s T s δ⋅=,其中,冲激采样信号)(t s T δ的表达式为:∑∞-∞=-=n sT nT t t s)()(δδ其傅立叶变换为∑∞-∞=-n s s n )(ωωδω,其中ss T πω2=。
设)(ωj F ,)(ωj F s 分别为)(t f ,)(t f s 的傅立叶变换,由傅立叶变换的频域卷积定理,可得∑∑∞-∞=∞-∞=-=-=n ss n s s s n j F T n j F j F )]([1)(*)(21)(ωωωωδωωπω若设)(t f 是带限信号,带宽为m ω, )(t f 经过采样后的频谱)(ωj F s 就是将)(ωj F 在频率轴上搬移至 ,,,,,02ns s s ωωω±±±处(幅度为原频谱的s T 1倍)。
因此,当m s ωω2≥时,频谱不发生混叠;而当m s ωω2<时,频谱发生混叠。
2.1.3信号重构设信号)(t f 被采样后形成的采样信号为)(t f s ,信号的重构是指由)(t f s 经过插处理后,恢复出原来信号)(t f 的过程。
又称为信号恢复。
若设)(t f 是带限信号,带宽为m ω,经采样后的频谱为)(ωj F s 。
设采样频率m s ωω2≥,则由式(9)知)(ωj F s 是以s ω为周期的谱线。
现选取一个频率特性⎪⎩⎪⎨⎧><=ccsT j H ωωωωω0)((其中截止频率c ω满足2sc m ωωω≤≤)的理想低通滤波器与)(ωj F s 相乘,得到的频谱即为原信号的频谱)(ωj F 。
显然,)()()(ωωωj H j F j F s =,与之对应的时域表达式为)(*)()(t f t h t f s = (10)而∑∑∞-∞=∞-∞=-=-=n s s n s s nT t nT f nT t t f t f )()()()()(δδ)()]([)(1t Sa T j H F t h ccsωπωω==- 将)(t h 及)(t f s 代入式(10)得∑∞-∞=-==n scscsccssnT t Sa nT f T t Sa T t f t f )]([)()(*)()(ωπωωπω (11) 式(11)即为用)(s nT f 求解)(t f 的表达式,是利用MATLAB 实现信号重构的基本关系式,抽样函数)(t Sa c ω在此起着插函数的作用。
三、抽样定理的仿真和探讨3.1.1 )(t Sa 的临界采样及重构图当采样频率小于一个连续的同信号最大频率的2倍,即m s ωω2=时,称为临界采样. 修改门信号宽度、采样周期等参数,重新运行程序,观察得到的采样信号时域和频域特性,以及重构信号与误差信号的变化。
程序运行结果:3.1.2 )(t Sa 的过采样及重构当采样频率大于一个连续的同信号最大频率的2倍,即m s ωω2>时,称为过采样.在不同采样频率的条件下,观察对应采样信号的时域和频域特性,以及重构信号与误差信号的变化。
程序运行结果:3.1.3 Sa(t)的欠采样及重构当采样频率小于一个连续的同信号最大频率的2倍,即m s ωω2<时,称为过采样。
利用频域滤波的方法修改实验中的部分程序,完成对采样信号的重构。
程序运行结果:误差分析:绝对误差error 已大为增加,其原因是因采样信号的频谱混叠,使得在c ωω<区域的频谱相互“干扰”所致。
四、课题研讨的小结该课程设计使我们对采样定理的一些基本公式得到了进一步巩固。
在整个实验过程中,我们查阅了很多相关知识,从这些书籍中我们受益良多。
虽然学习过采样过程和恢复过程,但是认识不深,实践能力也有所欠缺,通过这次实验对采样过程和恢复过程有了进一步掌握。
通过实验的设计使我们对采样定理和信号的重构有了深一步的掌握,也让我们在实践的过程中了解到团队合作的重要性。
虽然在实验过程中出现很多错误,但是在老师的帮助和团队成员的齐心协力下,不断的修正错误,同时也学会了MATLAB 号表示的基本方法及绘图函数的调用。
虽然刚开始我们对MATLAB 的基本使用方法没有太深刻的认识,但是该实验使我们对MATLAB 函数程序的基本结构有所了解,也提高了我们独立完成实验的能力和理论联系实际的应用能力。
通过这次课程设计,我们不仅学到了学科知识,锻炼了实践能力,更重要的是学到了学习的方法和团队合作的重要性。
我们团队分工有序,每个人都能按时完成各自的任务。
在遇到问题时,大家都能够互相理解,互相帮助,最后圆满完成课题!附录:一、)(t Sa 的临界采样及重构1.Sa(t)的临界采样及重构程序代码;wm=1; wc=wm; Ts=pi/wm; ws=2.4*pi/Ts; n=-100:100; nTs=n*Ts; f=sinc(nTs/pi);Dt=0.005;t=-20:Dt:20;fa=f*Ts*wc/pi*sinc((wc/pi)*(ones(length(nTs),1)*t-nTs'*ones(1,length(t)))); subplot(311); plot(t,fa) xlabel('t'); ylabel('fa(t)');title('sa(t)=sinc(t/pi)的原信号'); grid;t1=-20:0.5:20; f1=sinc(t1/pi); subplot(312); stem(t1,f1); xlabel('kTs'); ylabel('f(kTs)');title('sa(t)=sinc(t/pi)的临界采样信号'); grid; subplot(313); plot(t,fa) xlabel('t'); ylabel('fa(t)');title('由sa(t)=sinc(t/pi)的临界采样信号重构sa(t)'); grid;2.程序运行运行结果图与分析图3.1.1)(t Sa 的临界采样及重构图运行结果分析:为了比较由采样信号恢复后的信号与原信号的误差,可以计算出两信号的绝对误差。
当t 选取的数据越大,起止的宽度越大。
二、)(t Sa 的过采样及重构 1.Sa(t)的过采样及重构程序代码;wm=1; wc=1.1*wm;Ts=1.1*pi/wm;ws=2*pi/Ts;n=-100:100;nTs=n*Ts;f=sinc(nTs/pi);Dt=0.005;t=-10:Dt:10;fa=f*Ts*wc/pi*sinc((wc/pi)*(ones(length(nTs),1)*t-nTs'*ones(1,length(t)))); subplot(411);plot(t,fa)xlabel('t');ylabel('fa(t)');title('sa(t)=sinc(t/pi)的原信号');grid;error=abs(fa-sinc(t/pi));t1=-10:0.5:10;f1=sinc(t1/pi);subplot(412);stem(t1,f1);xlabel('kTs');ylabel('f(kTs)');title('sa(t)=sinc(t/pi)的采样信号');grid;subplot(413);plot(t,fa)xlabel('t');ylabel('fa(t)');title('由sa(t)=sinc(t/pi)的过采样信号重构sa(t)');grid;subplot(414);plot(t,error);xlabel('t');ylabel('error(t)');title('过采样信号与原信号的误差error(t)');grid;2.程序运行运行结果图与分析。
图3.1.2)(t Sa 的过采样信号、重构信号及两信号的绝对误差图运行分析:将原始信号分别修改为抽样函数Sa(t)、正弦信号sin(20*pi*t)+cos(20*pi*t)、指数信号e-2tu(t)时,在不同采样频率的条件下,可以观察到对应采样信号的时域和频域特性,以及重构信号与误差信号的变化。
三、Sa(t)的欠采样及重构 1.Sa(t)的欠采样及重构程序代码; wm=1;wc=wm; Ts=2.5 *pi/wm; ws=2*pi/Ts; n=-100:100; nTs=n*Ts; f=sinc(nTs/pi);Dt=0.005;t=-20:Dt:20;fa=f*Ts*wc/pi*sinc((wc/pi)*(ones(length(nTs),1)*t-nTs'*ones(1,length(t)))); error=abs(fa-sinc(t/pi)); subplot(411); plot(t,fa) xlabel('t'); ylabel('fa(t)');title('sa(t)=sinc(t/pi)的原信号'); grid;t1=-20:0.5:20; f1=sinc(t1/pi); subplot(412); stem(t1,f1); xlabel('kTs'); ylabel('f(kTs)');title('sa(t)=sinc(t/pi)的采样信号sa(t)'); grid; subplot(413);plot(t,fa) xlabel('t'); ylabel('fa(t)');title('由sa(t)=sinc(t/pi)的欠采样信号重构sa(t)'); grid; subplot(414); plot(t,error); xlabel('t'); ylabel('error(t)');title('欠采样信号与原信号的误差error(t)'); grid;2.程序运行运行结果图与分析图3.1.3)(t Sa 的欠采样信号、重构信号及两信号的绝对误差图。
