2019-2020年八年级期末考试试卷(二)
2019—2020学年度第二学期期末考试八年级英语试题及答案

2019~2020学年度第二学期期末考试八年级英语试题注意事项:1.本试卷考试时间为100分钟,试卷满分120分。
考试形式为闭卷。
2.本试卷中所有试题必须作答在答题纸上规定的位置,否则不给分。
3.答题前,务必将自己的学校、班级、姓名、准考证号填写在答题纸上相应位置。
听力部分(共20分)听力部分(共20小题,每小题1分, 计20分)第一部分: 听对话回答问题。
本部分共有10道小题,每小题你将听到一段对话,每段对话读两遍。
在听每段对话前,你将有5秒钟的时间阅读题目;听完后,你将有5秒钟的时间选择你认为最合适的备选答案。
1. Where would Andy like to visit for his holiday?A. B. C.2. What did Ben do last weekend?A. B. C.3. How will the boy cut the paper?A. B. C.4.What is the sign on the wall?A. B. C.5. What subject is Millie worried about?A. Math.B. English.C. PE.6. Which floor is the computer room on?A. The first floor.B. The second floor.C. The third floor.7. What will Amy and her friend plan to do?A. They will help homeless people.B. They will meet some important people.C. They will try to save money for the disabled.八年级英语试题第1页共8页8. What’s wrong with the girl?A. She’s got a toothache.B. She’s got a headache.C. She’s got a stomachache.9. What kind of book does Daniel like to read?A. Science books.B. Novels.C. Culture books.10. Why does the man need to go to the office next week?A. To take pictures for a magazine.B. To meet with his new boss.C. To go for an interview.第二部分: 听对话和独白回答问题。
汉阳区2019-2020学年度第二学期期末考试八年级物理试卷(word版含答案)

2019-2020年汉阳区八年级下学期期末物理测试题本卷中可能用到的数据:g=10N/kgρ水=1.0x103kg/m3ρ酒精=0.8x103kg/m3一.选择题(3分x18=54分)1.第七届世界军人运动会于2019年10月在武汉举行,其中羽毛球、乒乓球、男子体操和网球等4个项目首次进入世界军人运动会;关于这四项运动,下列描述错误的是()。
A. B. C. D.A.羽毛球离开球拍后能在空中飞行一段距离,是由于羽毛球具有惯性B.物理控制乒乓球的飞行路径,可以让它旋转起来,这是利用了流体压强与流速的关系C.体操运动员在手上涂防滑粉,是为了减小摩擦力D.球拍在击打网球的过程中,球拍和网球同时发生了弹性形变2.如图所示,滑板车沿水平方向运动时,下列说法正确的是()A.人和滑板车滑行的速度越快,惯性越大。
B.滑板车底部安装有滚轮,是为了增大对地面的压强。
C.滑板车的重力和地面对滑板车的支持力是一对平衡力。
D.滑行时以滑板车为参照物,景物是向后运动的。
3.如图所示,某同学将一漂浮在水面密闭的饮料罐缓缓按入水中,当饮料罐全部浸入在水中后,继续向下压一段距离,共用时t0,此过程中饮料罐所受的浮力随时间变化的图像可能是下列图中的哪一个()A. B. C. D.4.把鸡蛋浸入盛有盐水的杯中,鸡蛋沉在杯底(如图甲所示),再往杯中加盐使鸡蛋悬浮(如图乙所示),下列说法正确的是()A.鸡蛋受到的浮力:F甲<F乙B.鸡蛋排开液体的质量:m甲=m乙C.液体的密度:ρ甲=ρ乙D.液体对杯底的压强:p甲=p乙5.如图所示,潜水艇悬浮在水中时,下列说法错误的是()A.要使潜水艇下沉,应向水舱中充水B.要使潜水艇上浮,应从水舱向外排水C.潜水艇在水中受到浮力等于潜水艇总重D.潜水艇是靠改变自身重力和受到的浮力来实现浮沉的6.图甲是密度计,图乙和图丙是自制的一支简易密度计(在木棒的一端缠绕一些铜丝做成),把自制密度计先后放入盛有不同液体的两个烧杯中,下列说法正确的是()A.密度计越靠近下方的刻度,其相应的密度值越小B.自制密度计在乙杯中受到的浮力大于丙杯中受到的浮力C.乙、丙两杯中液体对密度计下表面的压强相等D.乙杯中液体的密度比丙杯中液体的密度大7.如图甲是“探究浮力的大小跟哪些因素有关”的几个实验情景。
2019—2020学年度曲阜市第二学期初二期末考试初中语文

2019—2020学年度曲阜市第二学期初二期末考试初中语文八年级语文试卷讲明:全卷总分值120分,考试时刻l20分钟。
温馨提示:友爱的同学们,当你走进语文的殿堂,色彩斑斓的世界展现在你面前,期望你捡起经历的珍宝,平复摸索,认真做答,展现自我。
祝你成功!一、积存与运用(15分)1.抄写下面的句子(2分)(书写规范漂亮可得3分)勿忘历史,珍爱和平,铸剑为犁,共同进展!2.给加点字注音。
(2分)畸.形( ) 执拗.( ) 哂.笑( ) 健脾.( )3.下表是对某中学205名学生调查的结果,请据表中资料,回答以下咨询题。
(2分)表格内容所反映的咨询题是4.我市旅行部门打算评选〝十大旅行景点〞,请你以一个市民的身份举荐一处景点,并用简洁的语言阐述举荐理由。
(2分)5.孟子的名言〝故天将降大任于斯人也,必先苦其心志,劳其筋骨,……〞正好能够用来评判«»的内容,这部名著的要紧人物有、、(2分) 6.古诗文默写。
(5分)(1)人们常用来形容老师为学生呕心沥血的诗句是:,。
(李商隐«无题»)(2)杜甫«茅屋为秋风所破歌»中诗人推己及人,心忧人民的诗句是:,_____________________。
(3)常言道〝春雨贵如油〞,韩愈在«早春呈水部张十八员外»中写春雨和春草的两句诗是:,。
(4)刘禹锡«酬乐天扬州初逢席上见赠»中包蕴人一辈子哲理,给人以鼓舞的两句诗是:,。
(5)由〝四面湖光归眼底,万家忧乐到心头〞这副对联,让人想到范仲淹«岳阳楼记»中的两句话:,。
二、古诗文阅读(16分)(一)过零丁洋文天祥辛劳遭逢起一经,干戈寥落四周星。
山河破裂风飘絮,身世浮沉雨打萍。
惶恐滩头讲惶恐,零下洋里叹零丁。
人一辈子自古谁无死? 留取丹心照汗青。
7.①此诗首联写了个人和国家的哪两件大事?(2分)②尾联是千古传诵的名句,抒发了作者如何样的思想感情?(2分)(二)(甲)假设夫日出而林霏开,云归而岩穴暝,晦明变化者,山间之朝暮也。
北京市西城区2019—2020学年度八年级第二学期期末试卷(含答案)

北京市西城区2019—2020学年度第二学期期末试卷一、基础·运用(共14分)中国人使用筷子,是一桩值得骄傲和推崇的事。
一双筷子,蕴含着中国人独特的文明气息。
初二语文组开展了“筷子的前世今生——探寻筷子文化”主题学习活动,请你完成下列任务。
1.下面是一位同学搜集的材料。
阅读材料,完成(1)-(4)题。
(共8分) 中国是筷子的发源地,中国人用筷子进餐至少有3000年的历史。
筷子在世界各受到我国影响,筷子文化也fú( )射到日本、越南、韩国和朝鲜等国家。
筷子最初叫“箸(zh ù)”或“梜(ji ā)”,到了宋代才开始有“筷子”的称呼。
古人讲究忌讳,因“箸”与“住”谐音, 【甲】 听着有“停滞不前”的意思, 【乙】 故谓不吉利之语,特别是对于行船的人更是讳言,所以古人便反其意改“住”为“快”;加之筷子多以竹子为材料,所以又在“快”字上冠以“竹”字头而名“筷”,寄寓了人们对美好生活的向往。
民以食为天��轻便灵巧的筷子被人们餐餐使用,筷子文化逐渐融化在中国人的血液里。
中央电视台曾拍过一个主题�为��筷子��的春节公益宣传片,通过八个不同地域的家庭在除夕使用筷子的故事,揭示了筷子所蕴含的丰富的传统文化和中国人特有的�r én q ín ɡ sh ì ɡù( ),令人感动。
�方寸之中有乾坤。
小小的筷子承载着中华民族几千年来深厚的文化内涵,是华夏其实/相辅相成)。
(1)根据拼音依次所填的汉字和给加点字注音全都正确的一项是(2分)A .幅射 人情世故 z àiB .辐射 人情是故 z ǎiC .辐射 人情世故 z àiD .幅射 人情是故 z ǎi(2)结合上下文,文中所应填入成语正确的一项是(2分)A.独树一帜相辅相成 B.叹为观止相辅相成C.叹为观止名副其实 D.独树一帜名副其实(3)文中方框处�依次填入标点全都正确的一�项是(2分)A.句号引号 B.冒号引号C.句号书名号 D.冒号书名号(4)下面语句是从文中第二段抽取出来的,它在文中原本的位置是(2分)不符合人们祈望兴旺发达的民族心理,【甲】【乙】2.下列有关“筷子”的表述中没有语病的一项是(2分)A.研究者们之所以认为筷子起源于中国,是因为在安阳殷墟曾出土了6支青铜箸头的原因。
河北省唐山市丰润区2019-2020学年度第二学期期末考试八年级英语试题(word版有答案)

丰润区2019-2020学年度第二学期期末考试八年级英语试卷注意事项:本试卷分卷Ⅰ和卷Ⅱ两部分,卷Ⅰ为选择题,卷Ⅱ为非选择题。
卷Ⅰ(选择题,50 分)I . 单项选择(共10小题,每小题1.5分,计15分)( )1. Once upon a time, there was old man living in a small village.A. aB. anC. theD. 不填( )2. You won ’t get good results you work hard.A. ifB. soC. unlessD. when( )3. The Yangtze River is the largest river in China. It’s 6,300 kilometers . A. high B. deepC. wideD. long ( )4. Don’t believe that man! He is trying to you.A. cheatB. trustC. checkD. shoot( )5. I saw Tim in the park. He ______ on the grass and reading a book.A. sitsB. satC. is sittingD. was sitting( )6. Our country China has a history of over five years.A. thousandB. thousandsC. thousand ofD. thousands of( )7. He has made much in French. Let ’s invite him to introduce his experience.A. spiritB. progressC. noticeD. stress( )8. It can be quite windy in the north of China, ________ in spring.A. actuallyB. suddenlyC. especiallyD. finally( )9. Because my alarm clockdidn’t ________ , I went to school late this morning.A. put offB. go offC. put upD. fix up( )10. — Sorry, I can’t help you do the housework.— ________. I’ll do it myself.A. Great ideaB. Never mind C . I’m not sure D. Excuse me阅读下面短文,掌握其大意,然后从各小题所给的四个选项中选出最佳选项。
部编人教版2019---2020学年度下学期八年级语文期末考试卷及答案(含两套题)

密学校 班级 姓名 学号密 封 线 内 不 得 答 题部编人教版2019---2020学年度下学期八年级语文期末考试卷及答案(满分:120分 时间:120分钟)第一部分(1~5题 21分)1.在下列横线上填写出相应的句子。
(每空1分,共6分) (1) , !风雨不动安如山。
(杜甫《茅屋为秋风所破歌》)(2) , ,鸣之而不能通其意。
(韩愈《马说》)(3)常建《题破山寺后禅院》中描写禅院幽静的名句是:, 。
2.给加着重号的词语注音,根据注音写出相应的词语。
(每小题1分,共4分)(1)我们拾级..( )而上,威严的穹顶也随之愈升愈高,耸入蓝天,最后仿佛独踞苍穹。
(2)置身于冰窟,远比想象的要温暖,穿着件腈纶..( )棉衣,外罩一件皮夹克,居然感觉不到冷。
(3)前往勃朗峰的途中,我们先坐火车去了马蒂尼,(y ì r ì)早晨八点多,便徒步出发。
(4)伞开得好等于安全有保障,至少保证生命 (w úy ú)。
3.依次填入下面一段文字横线处的语句,衔接最恰当的一项是( )(3分)罗丹的大理石雕像《沉思》别出心裁, , , , , , 。
罗丹曾经解释说,他是要以这个雕像集中地表现“冥想”,因而抛弃了一切与此不相关的东西。
①那忧郁而凝视的目光,紧闭的双唇 ②她那恬静、执着的沉思神情③的确令观赏者从这块石头中幻化出无数美好的想象 ④她低着头正沉浸在默默的沉思之中⑤在端庄的正方形基座上烘托着一个秀美而淳朴的女性形象⑥表露了她复杂的内心世界A .④③②①⑥⑤B .⑤④①⑥②③C .④②①⑥⑤③D .⑤②①⑥③④4.欣赏下面这幅书法作品,回答(1)~(2)题。
(每小题2分,共4分)(1)下列对这幅书法作品的赏析,不正确的一项是()A.笔画横轻竖重,撇捺出笔劲利。
B.笔力浑厚强劲,气势庄严雄浑。
C.结构阔大端正,方中见圆,具有向心力。
D.从总体上看,作品刚健而娟秀,飘逸而灵动。
(2)同样是描写洞庭湖,孟浩然《望洞庭湖赠张丞相》中的“,”却是以夸张手法描写了洞庭湖烟波浩渺、水天合一的宏伟气象。
人教部编2019-2020学年第二学期 八年级语文期末测试卷附答案解析

语文试题 第1页(共14页) 语文试题 第2页(共14页)绝密★启用前 2019-2020学年第二学期期末试卷八年级语文注意事项:1.答题前,请考生先将自己的姓名、准考证号填写清楚,并认真核对条形码上的姓名、准考证号、考室和座位号;2.必须在答题卡上答题,在草稿纸、试题卷上答题无效; 3.答题时,请考生注意各大题题号后面的答题提示; 4.请勿折叠答题卡,保持字体工整、笔迹清晰、卡面清洁; 5.答题卡上不准使用涂改液、涂改胶和贴纸。
考生注意:1.本试卷共27道小题。
2.本学科考试时量150分钟,满分150分。
一、积累与运用(共26分)1.下列各组词语中字形和加点字的注音全都正确的一项是( )(2分) A .骈.死(pi án ) 和煦 拾.级(sh è) 混然一体B .腈.纶(j īng ) 呻吟 污秽.(hu ì) 胜气凌人C .羞.愧(xi ū)砾石门楣.(m éi ) 接踵而至D .槽枥.(l ì) 迁徙哂.笑(sh ēn ) 莫衷一是2.下列加点词语运用不正确的一项是( )(2分) A .他生活底子厚实,知识渊博,写起文章来一挥而就....。
B .他是学校的长跑冠军,但与专业的短跑运动员相比,还是显得相形见绌....。
C .目前我国农村家庭普通本科毕业生失业率已高达30.5%,为了中国农村的发展,请某些用人单位摘掉有色眼镜,一视同仁....,给来自农村的学子一个公平竞争的机会! D .哥斯达黎加队从有三支世界冠军队的死亡之组脱颖而出,成为世界杯历史上的史诗级黑马,还真令人有鹤立鸡群....的感觉! 3.下列句子没有语病、表意明确的一项是( )(2分)A .随着该市博物馆的投入使用,使市民在节假日有了新的去处。
B .实践证明,能否坚持体育锻炼对提高同学们的体育成绩很有成效。
C .湘潭市文明办开展与策划“我爱莲城”的活动,得到市民很多的响应。
演达中学2019-2020学年第二学期八年级下册语文期末检测试卷【含答案】

演达中学2019—2020学年第二学期八年级语文期末检测试卷说明:1.全卷共6页,满分120分,考试时间为120分钟。
2.本试卷设有附加题,共10分,考生可答可不答;该题得分作为补偿分计入总分,但全卷最后得分不能超过120分。
3.答卷前,考生要按照要求把自己的姓名、班级、考号等信息正确填写、填涂在答题卷上。
4.答题时,选择题要用2B铅笔正确填涂在答题卡(卷)相应位置上,主观题要用黑色碳素笔按各题要求将答案写在答题卡(卷)上。
一、基础与应用(24分)1.古诗文默写。
(10分)(1)潭中鱼可百许头,口口口口口口口,日光下澈,影布石上。
(《小石潭记》)(2)口口口口,白露未晞。
所谓伊人,在水之湄。
(诗经《蒹葭》)(3)孟浩然《望洞庭湖赠张丞相》中“口口口口口,口口口口口”的诗句。
描写烟波浩渺的宏伟气象,以及汹涌澎湃的磅礴气势。
(4)口口口口口口口,口口口口口口口口口!风雨不动安如山。
(杜甫《茅屋为秋风所破歌》)(5)把陆游的《卜算子·咏梅》默写完整。
驿外断桥边,寂寞开无主。
已是黄昏独自愁,更着风和雨。
口口口口口,口口口口口。
口口口口口口口,口口口口口。
2.根据拼音写词语。
(4分)(1)最惹眼的是yì lì()在庄外临河的空地上的一座戏台,模糊在远处的月夜中。
(2)于是转入炎热的夏季,这是植物yùn yù()果实的时期。
(3)名人跟人握握手,叫píng yì jìn rén(),凡人就是巴结别人了。
(4)哈,看到了吗?如我所说吧——我可是míng fù qí shí()的车夫之王啊。
3.下列句子中加点的成语使用不.正确..的一项是( )(3分)A.当优美的旋律戛然而止....时,元宵节晚会现场出奇地寂静,人们沉浸在无尽的回味中。
B.即使是沧海桑田、海枯石烂....,最爱你的永远还是你的父母!C.面对破坏环境的行为,我们绝不能袖手旁观....。
北师大版2019-2020学年度初二数学第二学期期末考试试卷( 含答案)
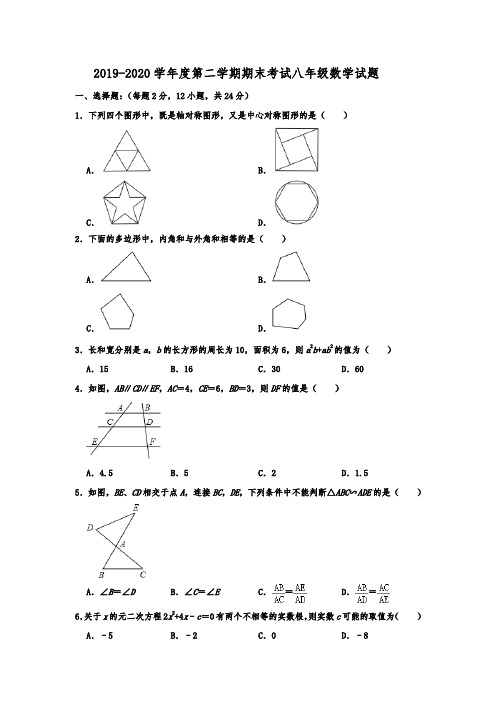
2019-2020学年度第二学期期末考试八年级数学试题一、选择题:(每题2分,12小题,共24分)1.下列四个图形中,既是轴对称图形,又是中心对称图形的是()A.B.C.D.2.下面的多边形中,内角和与外角和相等的是()A.B.C.D.3.长和宽分别是a,b的长方形的周长为10,面积为6,则a2b+ab2的值为()A.15 B.16 C.30 D.604.如图,AB∥CD∥EF,AC=4,CE=6,BD=3,则DF的值是()A.4.5 B.5 C.2 D.1.55.如图,BE、CD相交于点A,连接BC,DE,下列条件中不能判断△ABC∽ADE的是()A.∠B=∠D B.∠C=∠E C.=D.=6.关于x的元二次方程2x2+4x﹣c=0有两个不相等的实数根,则实数c可能的取值为()A.﹣5 B.﹣2 C.0 D.﹣87.某超市今年二月份的营业额为82万元,四月份的营业额比三月份的营业额多20万元,若二月份到四月份每个月的月销售额增长率都相同,若设增长率为x,根据题意可列方程()A.82(1+x)2=82(1+x)+20 B.82(1+x)2=82(1+x)C.82(1+x)2=82+20 D.82(1+x)=82+208.如图,▱ABCD中,对角线AC、BD相交于点O,OE⊥BD交AD于点E,连接BE,若▱ABCD的周长为28,则△ABE的周长为()A.28 B.24 C.21 D.149.如图,已知菱形OABC的两个顶点O(0,0),B(2,2),若将菱形绕点O以每秒45°的速度逆时针旋转,则第2019秒时,菱形两对角线交点D的横坐标为()A.B.C.1 D.﹣110.如图,菱形ABCD的对角线AC、BD相交于点O,过点C作CE⊥AD于点E,连接OE,若OB=8,S菱形ABCD=96,则OE的长为()A.2B.2C.6 D.811.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=12,点D在边BC上,点E在线段AD 上,EF⊥AC于点F,EG⊥EF交AB于点G.若EF=EG,则CD的长为()A.3.6 B.4 C.4.8 D.512.如图,四边形ABCD中,AC⊥BC,AD∥BC,BC=3,AC=4,AD=6.M是BD的中点,则CM的长为()A.B.2 C.D.3二、填空题:(每题2分,8小题,共16分)13.因式分解:m2n+2mn2+n3=.14.若分式有意义,则实数x的取值范围是.15.若关于x的分式方程=有增根,则m的值为.16.设x1,x2是一元二次方程x2﹣x﹣1=0的两根,则x1+x2+x1x2=.17.如图,菱形ABCD的对角线AC,BD交于点O,AC=4,BD=16,将△ABO沿点A到点C 的方向平移,得到△A′B′O′,当点A′与点C重合时,点A与点B′之间的距离为.18.如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长.19.如图,在Rt△ABC中,∠B=90°,AB=2,BC=3,D、E分别是AB、AC的中点,延长BC至点F,使CF=BC,连接DF、EF,则EF的长为.20.如图,边长为2的正方形ABCD中,AE平分∠DAC,AE交CD于点F,CE⊥AE,垂足为点E,EG⊥CD,垂足为点G,点H在边BC上,BH=DF,连接AH、FH,FH与AC交于点M,以下结论:①FH=2BH;②AC⊥FH;③S△ACF=1;④CE=AF;⑤EG2=FG•DG,其中正确结论的有(只填序号).三、计算题:(4小题,共18分)21.(1)化简;(m+2+)•(2)先化简,再求值;(+x+2)÷,其中|x|=222.解方程:(1)x2﹣2x﹣5=0;(2)=.四、解答题:(5小题,共42分)23.阅读下列材料:已知实数m,n满足(2m2+n2+1)(2m2+n2﹣1)=80,试求2m2+n2的值解:设2m2+n2=t,则原方程变为(t+1)(t﹣1)=80,整理得t2﹣1=80,t2=81,∴t =±9因为2m2+n2≥0,所以2m2+n2=9.上面这种方法称为“换元法”,把其中某些部分看成一个整体,并用新字母代替(即换元),则能使复杂的问题简单化.根据以上阅读材料内容,解决下列问题,并写出解答过程.已知实数x,y满足(4x2+4y2+3)(4x2+4y2﹣3)=27,求x2+y2的值.24.某书店积极响应政府“改革创新,奋发有为”的号召,举办“读书节“系列活动.活动中故事类图书的标价是典籍类图书标价的1.5倍,若顾客用540元购买图书,能单独购买故事类图书的数量恰好比单独购买典籍类图书的数量少10本.(1)求活动中典籍类图书的标价;(2)该店经理为鼓励广大读者购书,免费为购买故事类的读者赠送图1所示的精致矩形包书纸.在图1的包书纸示意图中,虚线是折痕,阴影是裁剪掉的部分,四角均为大小相同的正方形,正方形的边长为折叠进去的宽度.已知该包书纸的面积为875cm2(含阴影部分),且正好可以包好图2中的《中国故事》这本书,该书的长为21cm,宽为15cm,厚为1cm,请直接写出该包书纸包这本书时折叠进去的宽度.25.如图,在△ABC中,AB=AC,AD是BC边的中线,过点A作BC的平行线,过点B作AD 的平行线,两线交于点E.(1)求证:四边形ADBE是矩形;(2)连接DE,交AB与点O,若BC=8,AO=3,求△ABC的面积.26.如图,已知:AD为△ABC的中线,过B、C两点分别作AD所在直线的垂线段BE和CF,E、F为垂足,过点E作EG∥AB交BC于点H,连结HF并延长交AB于点P.(1)求证:DE=DF(2)若BH:HC=11:5;①求:DF:DA的值;②求证:四边形HGAP为平行四边形.27.如图,矩形ABCD中,AB=12,AD=9,E为BC上一点,且BE=4,动点F从点A出发沿射线AB方向以每秒3个单位的速度运动.连接DF,DE,EF.过点E作DF的平行线交射线AB于点H,设点F的运动时间为t(不考虑D、E、F在一条直线上的情况).(1)填空:当t=时,AF=CE,此时BH=;(2)当△BEF与△BEH相似时,求t的值;(3)当F在线段AB上时,设△DEF的面积为S,△DEF的周长为C.①求S关于t的函数关系式;②直接写出C的最小值.参考答案与试题解析一.选择题(共12小题)1.下列四个图形中,既是轴对称图形,又是中心对称图形的是()A.B.C.D.【分析】根据轴对称图形与中心对称图形的概念求解.【解答】解:A、是轴对称图形,不是中心对称图形,故此选项错误;B、不是轴对称图形,是中心对称图形,故此选项错误;C、是轴对称图形,不是中心对称图形,故此选项错误;D、既是轴对称图形,又是中心对称图形,故此选项正确.故选:D.2.下面的多边形中,内角和与外角和相等的是()A.B.C.D.【分析】根据多边形的内角和公式(n﹣2)•180°与多边形的外角和定理列式进行计算即可得解.【解答】解:设多边形的边数为n,根据题意得(n﹣2)•180°=360°,解得n=4.故选:B.3.长和宽分别是a,b的长方形的周长为10,面积为6,则a2b+ab2的值为()A.15 B.16 C.30 D.60【分析】直接利用矩形面积求法结合提取公因式法分解因式计算即可.【解答】解:∵长和宽分别是a,b的长方形的周长为10,面积为6,∴2(a+b)=10,ab=6,故a+b=5,则a2b+ab2=ab(a+b)=30.故选:C.4.如图,AB∥CD∥EF,AC=4,CE=6,BD=3,则DF的值是()A.4.5 B.5 C.2 D.1.5【分析】直接根据平行线分线段成比例定理即可得出结论.【解答】解:∵直线AB∥CD∥EF,AC=4,CE=6,BD=3,∴=,即=,解得DF=4.5.故选:A.5.如图,BE、CD相交于点A,连接BC,DE,下列条件中不能判断△ABC∽ADE的是()A.∠B=∠D B.∠C=∠E C.=D.=【分析】分别根相似三角形的判定方法,逐项判断即可.【解答】解:∵∠BAC=∠DAE,∴当∠B=∠D或∠C=∠E时,可利用两角对应相等的两个三角形相似证得△ABC∽ADE,故A、B选项可判断两三角形相似;当=时,可得=,结合∠BAC=∠DAE,则可证得△ABC∽△AED,而不能得出△ABC∽△ADE,故C不能判断△ABC∽ADE;当=时,结合∠BAC=∠DAE,可证得△ABC∽△ADE,故D能判断△ABC∽△ADE;故选:C.6.关于x的元二次方程2x2+4x﹣c=0有两个不相等的实数根,则实数c可能的取值为()A.﹣5 B.﹣2 C.0 D.﹣8【分析】利用一元二次方程根的判别式(△=b2﹣4ac)可以判断方程的根的情况,有两个不相等的实根,即△>0【解答】解:依题意,关于x的一元二次方程,有两个不相等的实数根,即△=b2﹣4ac=42+8c>0,得c>﹣2根据选项,只有C选项符合,故选:C.7.某超市今年二月份的营业额为82万元,四月份的营业额比三月份的营业额多20万元,若二月份到四月份每个月的月销售额增长率都相同,若设增长率为x,根据题意可列方程()A.82(1+x)2=82(1+x)+20 B.82(1+x)2=82(1+x)C.82(1+x)2=82+20 D.82(1+x)=82+20【分析】根据题意可以列出相应的方程,本题得以解决.【解答】解:由题意可得,82(1+x)2=82(1+x)+20,故选:A.8.如图,▱ABCD中,对角线AC、BD相交于点O,OE⊥BD交AD于点E,连接BE,若▱ABCD的周长为28,则△ABE的周长为()A.28 B.24 C.21 D.14【分析】先判断出EO是BD的中垂线,得出BE=ED,从而可得出△ABE的周长=AB+AD,再由平行四边形的周长为24,即可得出答案.【解答】解:∵四边形ABCD是平行四边形,∴OB=OD,AB=CD,AD=BC,∵平行四边形的周长为28,∴AB+AD=14∵OE⊥BD,∴OE是线段BD的中垂线,∴BE=ED,∴△ABE的周长=AB+BE+AE=AB+AD=14,故选:D.9.如图,已知菱形OABC的两个顶点O(0,0),B(2,2),若将菱形绕点O以每秒45°的速度逆时针旋转,则第2019秒时,菱形两对角线交点D的横坐标为()A.B.C.1 D.﹣1【分析】根据菱形的性质及中点的坐标公式可得点D坐标,再根据旋转的性质可得旋转后点D的坐标.【解答】解:菱形OABC的顶点O(0,0),B(2,2),得D点坐标为(,),即(1,1).∴OD=每秒旋转45°,则第2019秒时,得45°×2019,45°×2019÷360=252.375周,OD旋转了252又周,菱形的对角线交点D的坐标为(﹣,0),故选:B.10.如图,菱形ABCD的对角线AC、BD相交于点O,过点C作CE⊥AD于点E,连接OE,若OB=8,S菱形ABCD=96,则OE的长为()A.2B.2C.6 D.8【分析】由菱形的性质得出BD=16,由菱形的面积得出AC=12,再由直角三角形斜边上的中线性质即可得出结果.【解答】解:∵四边形ABCD是菱形,∴OA=OC,OB=OD=BD,BD⊥AC,∴BD=16,∵S菱形ABCD═AC×BD=96,∴AC=12,∵CE⊥AD,∴∠AEC=90°,∴OE=AC=6,故选:C.11.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=12,点D在边BC上,点E在线段AD 上,EF⊥AC于点F,EG⊥EF交AB于点G.若EF=EG,则CD的长为()A.3.6 B.4 C.4.8 D.5【分析】根据题意和三角形相似的判定和性质,可以求得CD的长,本题得以解决.【解答】解:作DH∥EG交AB于点H,则△AEG∽△ADH,∴,∵EF⊥AC,∠C=90°,∴∠EFA=∠C=90°,∴EF∥CD,∴△AEF∽△ADC,∴,∴,∵EG=EF,∴DH=CD,设DH=x,则CD=x,∵BC=12,AC=6,∴BD=12﹣x,∵EF⊥AC,EF⊥EG,DH∥EG,∴EG∥AC∥DH,∴△BDH∽△BCA,∴,即,解得,x=4,∴CD=4,故选:B.12.如图,四边形ABCD中,AC⊥BC,AD∥BC,BC=3,AC=4,AD=6.M是BD的中点,则CM的长为()A.B.2 C.D.3【分析】延长BC到E使BE=AD,则四边形ACED是平行四边形,根据三角形的中位线的性质得到CM=DE=AB,根据跟勾股定理得到AB===5,于是得到结论.【解答】解:延长BC到E使BE=AD,则四边形ACED是平行四边形,∵BC=3,AD=6,∴C是BE的中点,∵M是BD的中点,∴CM=DE=AB,∵AC⊥BC,∴AB===5,∴CM=,故选:C.二.填空题(共8小题)13.因式分解:m2n+2mn2+n3=n(m+n)2.【分析】首先提取公因式n,再利用完全平方公式分解因式得出答案.【解答】解:m2n+2mn2+n3=n(m2+2mn+n2)=n(m+n)2.故答案为:n(m+n)2.14.若分式有意义,则实数x的取值范围是x≠5 .【分析】根据分式有意义的条件可得x﹣5≠0,再解即可.【解答】解:由题意得:x﹣5≠0,解得:x≠5,故答案为:x≠5.15.若关于x的分式方程=有增根,则m的值为 3 .【分析】分式方程去分母转化为整式方程,由分式方程有增根求出x的值,代入计算即可求出m的值.【解答】解:去分母得:3x=m+3,由分式方程有增根,得到x﹣2=0,即x=2,把x=2代入方程得:6=m+3,解得:m=3,故答案为:316.设x1,x2是一元二次方程x2﹣x﹣1=0的两根,则x1+x2+x1x2=0 .【分析】直接根据根与系数的关系求解.【解答】解:∵x1、x2是方程x2﹣x﹣1=0的两根,∴x1+x2=1,x1×x2=﹣1,∴x1+x2+x1x2=1﹣1=0.故答案为:0.17.如图,菱形ABCD的对角线AC,BD交于点O,AC=4,BD=16,将△ABO沿点A到点C 的方向平移,得到△A′B′O′,当点A′与点C重合时,点A与点B′之间的距离为10 .【分析】由菱形的性质得出AC⊥BD,AO=OC=AC=2,OB=OD=BD=8,由平移的性质得出O'C=OA=2,O'B'=OB=8,∠CO'B'=90°,得出AO'=AC+O'C=6,由勾股定理即可得出答案.【解答】解:∵四边形ABCD是菱形,∴AC⊥BD,AO=OC=AC=2,OB=OD=BD=8,∵△ABO沿点A到点C的方向平移,得到△A'B'O',点A'与点C重合,∴O'C=OA=2,O'B'=OB=8,∠CO'B'=90°,∴AO'=AC+O'C=6,∴AB'===10;故答案为10.18.如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长.【分析】证出∠ACD=∠DCB=∠B,证明△ACD∽△ABC,得出=,即可得出结果.【解答】解:∵BC的垂直平分线MN交AB于点D,∴CD=BD=3,∴∠B=∠DCB,AB=AD+BD=5,∵CD平分∠ACB,∴∠ACD=∠DCB=∠B,∵∠A=∠A,∴△ACD∽△ABC,∴=,∴AC2=AD×AB=2×5=10,∴AC=.故答案为:.19.如图,在Rt△ABC中,∠B=90°,AB=2,BC=3,D、E分别是AB、AC的中点,延长BC至点F,使CF=BC,连接DF、EF,则EF的长为.【分析】连接DE,CD,根据三角形中位线的性质得到DE∥BC,DE=BC,推出四边形DCFE是平行四边形,得到EF=CD,根据勾股定理即可得到结论.【解答】解:连接DE,CD,∵D、E分别是AB、AC的中点,∴DE∥BC,DE=BC,∴DE∥CF,∵CF=BC,∴DE=CF,∴四边形DCFE是平行四边形,∴EF=CD,∵在Rt△ABC中,∠B=90°,AB=2,BC=3,∴CD===,∴EF=CD=,故答案为:.20.如图,边长为2的正方形ABCD中,AE平分∠DAC,AE交CD于点F,CE⊥AE,垂足为点E,EG⊥CD,垂足为点G,点H在边BC上,BH=DF,连接AH、FH,FH与AC交于点M,以下结论:①FH=2BH;②AC⊥FH;③S△ACF=1;④CE=AF;⑤EG2=FG•DG,其中正确结论的有①②④⑤(只填序号).【分析】①②、证明△ABH≌△ADF,得AF=AH,再得AC平分∠FAH,则AM既是中线,又是高线,得AC⊥FH,证明BH=HM=MF=FD,则FH=2BH;所以①②都正确;③可以直接求出FC的长,计算S△ACF≠1,错误;④根据正方形边长为2,分别计算CE和AF的长得结论正确;⑤利用相似先得出EG2=FG•CG,再根据同角的三角函数列式计算CG的长为1,则DG=CG,得出⑤也正确.【解答】解:①②如图1,∵四边形ABCD是正方形,∴AB=AD,∠B=∠D=90°,∠BAD=90°,∵AE平分∠DAC,∴∠FAD=∠CAF=22.5°,在△ABH和△ADF中,,∴△ABH≌△ADF(SAS),∴AH=AF,∠BAH=∠FAD=22.5°,∴∠HAC=∠FAC,∴HM=FM,AC⊥FH,∵AE平分∠DAC,∴DF=FM,∴FH=2DF=2BH,故①②正确;③在Rt△FMC中,∠FCM=45°,∴△FMC是等腰直角三角形,∵正方形的边长为2,∴AC=2,MC=DF=2﹣2,∴FC=2﹣DF=2﹣(2﹣2)=4﹣2,S△AFC=CF•AD≠1,故③不正确;④AF==2,∵△ADF∽△CEF,∴=,∴CE=,∴CE=AF,故④正确;⑤延长CE和AD交于N,如图2,∵AE⊥CE,AE平分∠CAD,∴CE=EN,∵EG∥DN,∴CG=DG,在Rt△FEC中,EG⊥FC,∴∠GEF=∠GCE,∴△EFG∽△CEG,∴=,∴EG2=FG•CG,∴EG2=FG•DG,故选项⑤正确;故答案为:①②④⑤.三、计算题:(4小题,共18分)21.(1)化简;(m+2+)•(2)先化简,再求值;(+x+2)÷,其中|x|=2【分析】(1)原式括号中两项通分并利用同分母分式的加法法则计算,约分即可得到结果;(2)原式括号中两项通分并利用同分母分式的加法法则计算,约分得到最简结果,求出x的值代入计算即可求出值.【解答】解:(1)原式=•=•=m+1;(2)原式=•=,由|x|=2,得到x=2或﹣2(舍去),当x=2时,原式=19.22.解方程:(1)x2﹣2x﹣5=0;(2)=.【分析】(1)利用公式法求解可得;(2)两边都乘以(x+1)(x﹣2)化为整式方程,解之求得x的值,继而检验即可得.【解答】解:(1)∵a=1,b=﹣2,c=﹣5,∴△=4﹣4×1×(﹣5)=24>0,则x==1±,∴;(2)两边都乘以(x+1)(x﹣2),得:x+1=4(x﹣2),解得x=3,经检验x=3是方程的解.四、解答题:(5小题,共42分)23.阅读下列材料:已知实数m,n满足(2m2+n2+1)(2m2+n2﹣1)=80,试求2m2+n2的值解:设2m2+n2=t,则原方程变为(t+1)(t﹣1)=80,整理得t2﹣1=80,t2=81,∴t =±9因为2m2+n2≥0,所以2m2+n2=9.上面这种方法称为“换元法”,把其中某些部分看成一个整体,并用新字母代替(即换元),则能使复杂的问题简单化.根据以上阅读材料内容,解决下列问题,并写出解答过程.已知实数x,y满足(4x2+4y2+3)(4x2+4y2﹣3)=27,求x2+y2的值.【分析】设t=x2+y2(t≥0),则原方程转化为(4t+3)(4t﹣3)=27,然后解该方程即可.【解答】解:设t=x2+y2(t≥0),则原方程转化为(4t+3)(4t﹣3)=27,整理,得16t2﹣9=27,所以t2=.∵t≥0,∴t=.∴x2+y2的值是.【点评】考查了换元法解一元二次方程,换元的实质是转化,关键是构造元和设元,理论依据是等量代换,目的是变换研究对象,将问题移至新对象的知识背景中去研究,从而使非标准型问题标准化、复杂问题简单化,变得容易处理.24.某书店积极响应政府“改革创新,奋发有为”的号召,举办“读书节“系列活动.活动中故事类图书的标价是典籍类图书标价的1.5倍,若顾客用540元购买图书,能单独购买故事类图书的数量恰好比单独购买典籍类图书的数量少10本.(1)求活动中典籍类图书的标价;(2)该店经理为鼓励广大读者购书,免费为购买故事类的读者赠送图1所示的精致矩形包书纸.在图1的包书纸示意图中,虚线是折痕,阴影是裁剪掉的部分,四角均为大小相同的正方形,正方形的边长为折叠进去的宽度.已知该包书纸的面积为875cm2(含阴影部分),且正好可以包好图2中的《中国故事》这本书,该书的长为21cm,宽为15cm,厚为1cm,请直接写出该包书纸包这本书时折叠进去的宽度.【分析】(1)设典籍类图书的标价为x元,根据购买两种图书的数量差是10本,列出方程并解答;(2)矩形面积=(2宽+1+2折叠进去的宽度)×(长+2折叠进去的宽度).【解答】解:(1)设典籍类图书的标价为x元,由题意,得﹣10=.解得x=18.经检验:x=18是原分式方程的解,且符合题意.答:典籍类图书的标价为18元;(2)设折叠进去的宽度为ycm,则(2y+15×2+1)(2y+21)=875,化简得y2+26y﹣56=0,∴y=2或﹣28(不合题意,舍去),答:折叠进去的宽度为2cm.【点评】此题考查了分式方程和一元二次方程的应用,(2)题结合了矩形面积的求法考查了图形的折叠问题,能够得到折叠进去的宽度和矩形纸的长、宽的关系,是解决问题的关键.25.如图,在△ABC中,AB=AC,AD是BC边的中线,过点A作BC的平行线,过点B作AD 的平行线,两线交于点E.(1)求证:四边形ADBE是矩形;(2)连接DE,交AB与点O,若BC=8,AO=3,求△ABC的面积.【分析】(1)先求出四边形ADBE是平行四边形,根据等腰三角形的性质求出∠ADB=90°,根据矩形的判定得出即可;(2)根据矩形的性质得出AB=DE=2AO=6,求出BD,根据勾股定理求出AD,根据三角形面积公式求出即可.【解答】(1)证明:∵AE∥BC,BE∥AD,∴四边形ADBE是平行四边形,∵AB=AC,AD是BC边的中线,∴AD⊥BC,即∠ADB=90°,∴四边形ADBE为矩形;(2)解:∵在矩形ADBE中,AO=3,∴AB=2AO=6,∵D是BC的中点,∴DB=BC=4,∵∠ADB=90°,∴AD===2,∴△ABC的面积=BC•AD=×8×2=8.【点评】本题考查了等腰三角形的性质和矩形的性质和判定,能求出四边形ADCE是矩形是解此题的关键.26.如图,已知:AD为△ABC的中线,过B、C两点分别作AD所在直线的垂线段BE和CF,E、F为垂足,过点E作EG∥AB交BC于点H,连结HF并延长交AB于点P.(1)求证:DE=DF(2)若BH:HC=11:5;①求:DF:DA的值;②求证:四边形HGAP为平行四边形.【分析】(1)由AAS证明△BDE≌△CDF,即可得出结论;(2)①设BH=11x,则HC=5x,BC=16x,则,DH=3x,由平行线得出△EDH∽△ADB,得出,即可得出结论;②求出=,证出FH∥AC,即PH∥AC,即可得出结论.【解答】(1)证明:∵AD为△ABC的中线,∴BD=CD,∵BE⊥AD,CF⊥AD,∴∠BED=∠CFD=90°,在△BDE和△CDF中,,∴△BDE≌△CDF(AAS),∴DE=DF;(2)①解:设BH=11x,则HC=5x,BC=16x,则,DH=3x,∵EG∥AB,∴△EDH∽△ADB,∴,∵DE=DF,∴;②证明:∵,∴,∵,∴=,∴FH∥AC,∴PH∥AC,∵EG∥AB,∴四边形HGAP为平行四边形.【点评】本题考查了平行四边形的判定、平行线的判定、全等三角形的判定与性质、相似三角形的判定与性质等知识;熟练掌握平行四边形的判定是关键.27.如图,矩形ABCD中,AB=12,AD=9,E为BC上一点,且BE=4,动点F从点A出发沿射线AB方向以每秒3个单位的速度运动.连接DF,DE,EF.过点E作DF的平行线交射线AB于点H,设点F的运动时间为t(不考虑D、E、F在一条直线上的情况).(1)填空:当t=时,AF=CE,此时BH=;(2)当△BEF与△BEH相似时,求t的值;(3)当F在线段AB上时,设△DEF的面积为S,△DEF的周长为C.①求S关于t的函数关系式;②直接写出C的最小值.【分析】(1)在Rt△ABC中,利用勾股定理可求得AB的长,即可得到AD、t的值,从而确定AE的长,由DE=AE﹣AD即可得解.(2)若△DEG与△ACB相似,要分两种情况:①AG:DE=DH:GE,②AH:EG=DH:DE,根据这些比例线段即可求得t的值.(需注意的是在求DE的表达式时,要分AD>AE和AD<AE两种情况);(3)分别表示出线段FD和线段AD的长,利用面积公式列出函数关系式即可.【解答】解:(1)∵BC=AD=9,BE=4,∴CE=9﹣4=5∵AF=CE即:3t=5,∴t=,∵EH∥DF∴△DAF∽△EBH,∴=即:=解得:BH=;当t=时,AF=CE,此时BH=;(2)由EH∥DF得∠AFD=∠BHE,又∵∠A=∠CBH=90°∴△EBH∽△DAF,∴即=∴BH=当点F在点B的左边时,即t<4时,BF=12﹣3t此时,当△BEF∽△BHE时:即42=(12﹣3t)×解得:t1=2此时,当△BEF∽△BEH时:有BF=BH,即12﹣3t=解得:t2=当点F在点B的右边时,即t>4时,BF=3t﹣12此时,当△BEF∽△BHE时:即42=(3t﹣12)×解得:t3=2+2(3)①∵EH∥DF∴△DFE的面积=△DFH的面积=FH•AD=(12﹣3t+t)×9=54﹣②如图,∵BE=4,∴CE=5,根据勾股定理得,DE=13,是定值,所以当C最小时DE+EF最小,作点E关于AB的对称点E'连接DE,此时DE+EF最小,在Rt△CDE'中,CD=12,CE'=BC+BE'=BC+BE=13,根据勾股定理得,DE'==,∴C的最小值=13+.【点评】此题考查了勾股定理、轴对称的性质、平行四边形及梯形的判定和性质、解直角三角形、相似三角形等相关知识,综合性强,是一道难度较大的压轴题.。
(人教版)2019-2020学年度八年级第二学期期末调研测试语文试卷(有答案)(加精)

2019-2020学年度第二学期期末调研测试八年级语文试卷说明:1.全卷共8页,满分120分。
考试用时120分钟。
2.答题前,请用黑色字迹的钢笔或签字笔在指定的位置写上学校、班别、姓名、座位号与试室号。
3.答非选择题必须使用黑色字迹的钢笔或签字笔,答案必须写在答题卷指定的位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液。
答选择题必须使用2B铅笔填涂。
不按以上要求作答的答案无效。
4.本试卷设有附加题,共10分。
该题得分作为补偿分计入总分,但全卷最后得分不得超过120分。
5.考试结束后只交答题卷卡。
一、基础(24分)1.根据课文默写古诗文。
(10分)(1松柏有本性。
(2。
(王勃《送杜少府之任蜀州》)(2分)(3!(4)飞来山上千寻塔,(王安石《登飞来峰》)(5(王维《终南别业》)2.根据拼音写出句子括号处应填入的词语。
(4分)(1)这对眼睛不会放过微不足道的细节,同样也能全面揭示ɡuǎnɡ mào wú yín ()的宇宙。
(2)我们不能总想着要过一种hún húnè è ()却又舒舒服服的日子。
(3)江南的雪,可是滋润měi yàn()之至了。
(4)这些闪电的影子,活像一条条火蛇,在大海里wān yán()游动,一晃就消失了。
3.下列句子加点词,使用不正确...的一项是(3分)A.在自然看来,人类上下翻飞的这片巨大空间,不过是咫尺..之间而已,就如同鲲鹏看待斥鴳一般,只是蓬蒿之间罢了。
(咫尺)B.号称千年不死的胡杨林啊,在忍受了20余年的干渴后终于..变成了干枯的“木乃伊”。
那奇形怪状的枯枝,那死后不愿倒下的身躯,似在表明胡杨在生命最后时刻的挣扎与痛苦,又像是向谁伸出求救之手!(终于)C.通过对春雁集会的日常程序的观察,人们注意到,所有的孤雁都有一种共性:它们的飞行和鸣叫很稠密..,而且声调忧郁。
2019-2020学年八年级下学期英语期末考试试卷A卷 (2)

2019-2020学年八年级下学期英语期末考试试卷A卷 (2)一、听小对话,请从A、B、C三个选项中选择最佳选项。
(每小题1分 (共5题;共5分)1. (1分)听录音,选出正确答案()A . A pig.B . A dog.C . A cat.2. (1分)How does Jim go to school?A . Take a bus.B . Take a taxi.C . Ride a bike.3. (1分)Is Tony's nose big or small?A . Big.B . Small.C . Middle.4. (1分)Why does Tina look tired?A . She didn't have breakfast.B . She didn't sleep well last night.C . She watched a cartoon late at night.5. (1分)What does Kate ask Jim to do?A . Turn down the radio.B . Turn down the TV.C . Turn down the computer.二、听较长对话,请从A、B、C三个选项中选择正确的选项,回答问题 (共2题;共10分)6. (4分)听下面一段对话,回答第小题(1)What is the woman?A . A restaurant owner.B . An interviewer.C . A cafe waitress.(2)When do people in New York usually go to restaurants?A . Between 5 and 6 p.m.B . Between 7 and 8:30 p.m.C . Between 8 and 9 p. m.(3)Which restaurants are getting popular with people in London?A . Indian restaurants.B . South American restaurants.C . Italian restaurants.7. (6分)听下面一段对话,回答问题.(1)When could he ride the bike?A . 8.B . 9.C . 10.(2)Who taught him to ride?A . His father.B . Himself.C . Jim.三、听独白,从题中所给的A、B、C三个选项中选出正确的选项,回答 (共1题;共10分)8. (10分)听下面一段独白,回答问题。
太原市2019-2020学年八年级(上)期末考试物理试题(II)卷

太原市2019-2020学年八年级(上)期末考试物理试题(II)卷姓名:________ 班级:________ 成绩:________一、单选题1 . 甲、乙、丙三个人的运动速度分别是v甲=10.8km/h、v乙=0.2km/min、v丙=2.8m/s,这三个人运动速度数值之间的关系是A.v甲>v乙>v丙B.v乙>v甲>v丙C.v丙>v甲>v乙D.v甲>v丙>v乙2 . 下列事例中,是利用声音能传递能量的是A.通过声学仪器接收到的次声波判断地震的方位B.利用超声导盲仪探测前进道路上的障碍物C.利用超声波将水变成细小的水滴,制造出超声波加湿器D.利用超声波给金属工件探伤3 . 下列情况中,物质密度不变的是()A.把纸撕成碎片B.冰熔化成水C.氧气罐中的氧气用去一部分D.把铁丝烧红4 . 如图所示,不同碗中盛不同的水,然后演奏者可以通过敲击不同的碗,可以演奏出美妙的乐曲,下列说法不正确的是()A.敲击不同的碗,音调不一样B.不同力度敲击相同的碗,音调是一样的C.若碗的材质不同,则敲击时音色将不同D.敲击时美妙的声音是通过空气振动发声的5 . 下列数据中,最接近实际情况的是A.一只成年人运动鞋的底面积约为B.健康的中学生脉搏跳动一次的时间约为5sC.教室的课桌高度约为D.一瓶500mL矿泉水的质量约为6 . 有些饭店在洗手间外安装了热风干手器,打开它就有热风吹到手上,使手上的水很快蒸发掉,使水快速蒸发的原因是A.加快了水面空气的流动并提高了水的温度B.提高了水的温度并增大了水的表面积C.加快了水面空气的流动并增大了水的表面积D.减小了水的表面积并加快了水面附近空气的流动7 . 以下的物态变化现象中,要吸热的是A.春天,冰雪消融汇成流水B.夏天,清晨草叶上出现晶莹的露珠C.秋天,早上出现缥缈的雾D.冬天,室外蔬菜上出现的霜8 . 如图图象中,反映物理量之间关系正确的是()A.汽车做匀速直线运动的图象B.铁的质量与体积的关系图象C.汽车做匀速直线运动的图象D.海波的熔化图象9 . 在探究平面镜成像特点的过程中,小明把四个模型分别面对玻璃直立在桌面上,用于研究像与物左右位置的关系,其中能够达到实验目的的是()A.B.C.D.10 . 下列光学图示中不正确的是A.平面镜成像B.光的色散C.光的反射D.光从空气射入水中11 . 在国庆70周年阅兵仪式上,空中加油飞行梯队表演空中加油的情形如图所示,下列说法中不正确的是A.加油机相对于地面是运动的B.加油机相对于受油机是静止的C.加油机与受油机是相对运动D.加油机与受油机的相对速度为零12 . 某同学用一凸透镜做实验,发现当物距为时,能在光屏上成倒立,放大的清晰的像,则以下说法正确的是()A.物距为时,能成倒立,缩小的实像B.物距为时,一定能成正立放大的虚像C.物距为时,一定能成正立放大的虚像D.物距为时,能成倒立,放大的实像二、多选题13 . 根据如表几种物质的密度判断,下列说法错误的是A.铜的密度是B.的冰质量为C.固体的密度比液体、气体的密度都大D.相同质量的水和酒精比较,水的体积大14 . 在如图所示的现象中,能用光的直线传播解释的是A.凸透镜成放大的像B.山峦水中的倒影C.墙上投出的手影D.烛焰通过小孔成像15 . 下列说法正确的是()A.物理学中,把不能导电的物体叫做绝缘体B.有经验的渔民在叉鱼时,总是向着所看到的鱼的下方叉C.物体的质量越大,该物体的密度也越大D.用手沾些冷水去拿热包子不会太烫,是因为水汽化吸热三、填空题16 . 小明同学设计的一个温度计,如图甲所示,瓶中装的是气体,瓶塞不漏气,弯管水平部分有一小段液柱.(1)将此装置放在室内,当周围的温度降低时,液柱将向________(选填“左”或“右”)移动.(2)如图乙所示是某患者测量体温时,体温计的示数图,此时患者的体温为________℃.17 . 近些年来,地震给人民群众造成了重大损失。
2019-2020学年重庆市南岸区八年级下学期期末数学试卷 (解析版)
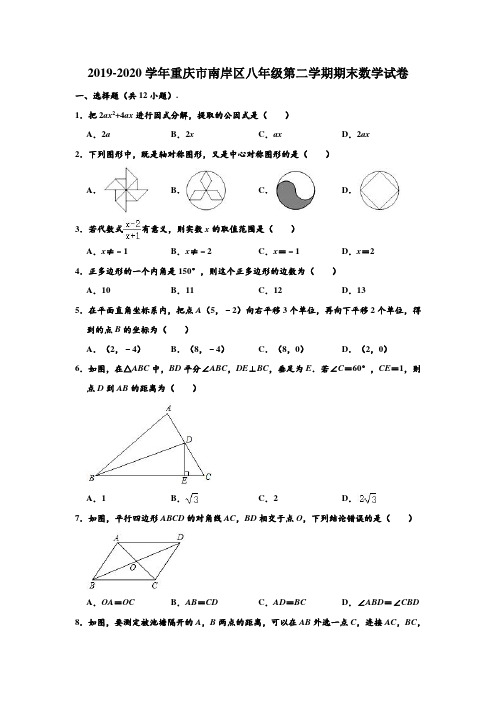
2019-2020学年重庆市南岸区八年级第二学期期末数学试卷一、选择题(共12小题).1.把2ax2+4ax进行因式分解,提取的公因式是()A.2a B.2x C.ax D.2ax2.下列图形中,既是轴对称图形,又是中心对称图形的是()A.B.C.D.3.若代数式有意义,则实数x的取值范围是()A.x≠﹣1B.x≠﹣2C.x=﹣1D.x=24.正多边形的一个内角是150°,则这个正多边形的边数为()A.10B.11C.12D.135.在平面直角坐标系内,把点A(5,﹣2)向右平移3个单位,再向下平移2个单位,得到的点B的坐标为()A.(2,﹣4)B.(8,﹣4)C.(8,0)D.(2,0)6.如图,在△ABC中,BD平分∠ABC,DE⊥BC,垂足为E.若∠C=60°,CE=1,则点D到AB的距离为()A.1B.C.2D.7.如图,平行四边形ABCD的对角线AC,BD相交于点O,下列结论错误的是()A.OA=OC B.AB=CD C.AD=BC D.∠ABD=∠CBD 8.如图,要测定被池塘隔开的A,B两点的距离,可以在AB外选一点C,连接AC,BC,并分别找出它们的中点D,E,连接ED.现测得AC=42m,BC=64m,DE=26m,则AB等于()A..42m B..52m C..56m D..64m9.如图,已知△ABC(AC<BC),用尺规在BC上确定一点P,使PA+PB=BC,则下列四种不同方法的作图中,作法正确的是()A.B.C.D.10.如图,已知直线y=ax+3与y=bx﹣3交点为P,根据图象有以下3个结论:①a>0;②b>0;③x>2是不等式ax+3>bx﹣3的解集.其中正确的个数是()A.0B.1C.2D.311.等腰三角形一腰长为5,这一腰上的高为3,则这个等腰三角形底边长为()A.B.C.或D.4或12.如图,在平面直角坐标系内,Rt△ABC的点A在第一象限,点B与点A关于原点对称,∠C=90°.AC与x轴交于点D,点E在x轴上,CD=2AD.若AD平分∠OAE,△ADE的面积为1,则△ABC的面积为()A.6B.9C.12D.15二、填空题(共6小题).13.因式分解:x2﹣10x+25=.14.计算:=.15.如图,是正在铺设的人行道上地板砖的部分,是由正六边形和四边形镶嵌而成的图形,则图中的四边形ABCD中的锐角∠BAD的度数是度.16.在抗疫情期间,准备用甲、乙两种货车将68吨的抗疫物资运往武汉某地,甲种货车的载重量为5吨,乙种货车的载重量为4吨,若安排甲、乙两种车共15辆,则甲种货车至少安排的辆数为.17.如图,规定程序运行到“判断结果是否大于100”为第一次运算,若运算进行了三次才停止,则满足条件的整数x的个数为.18.如图,在平行四边形ABCD中,对角线AC,BD交于点O,且∠ACB=45°,AE⊥BD,垂足为F,交BC于点E.若AB=AE,AO=2,则BE的长为.三、解答题:(本大题7个小题,每小题10分,共70分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形,请将解答过程书写在答题卡中对应的位置上.19.计算:(1);(2).20.解下列不等式或不等式组,并把解集在数轴上表示出来.(1);(2)21.(1)在如图所示的直角坐标系内,描出点A(1,2),B(2,2),C(2,1).并连接OA,AB,BC,CO;(2)将(1)中所画的图形向下平移四个单位,画出平移后的图形;(3)将(1)中所画的图形绕原点O逆时针旋转90°,画出旋转后的图形.22.如图,在△ABC中,点D是BC上一点,且BD=DA=AC.把边AB绕着点A顺时针旋转一定角度得到∠BAE,连接DE,交AB于点F.(1)若∠B=α,请用含α的式子表示∠C;(2)若∠CAD=∠BAE,求证:DA平分∠CDE.23.某社区的游泳馆按照顾客游泳的次数收取费用,每次的全票价为40元.在盛夏即将来临时,为吸引更多的顾客再次光顾,推出了以下两种收费方式.方式一:先交250元会员费,每次游泳按照全票价的7.5折收取费用;方式二:第一次收全票价,以后每次按照全票价的9.5折收取费用.(1)按照方式一的总费用为y1,按照方式二的总费用为y2,请分别求出y1,y2与游泳次数x的函数关系式;(2)小李把自己的学习和工作时间规划了一下,他在今年可能去该游泳馆的次数不超过40次,请为小李推荐采用哪种方式缴费合算?24.在脱贫攻坚的关键一年里,重庆市某地根据当地的高山气候,该村的村支书决定带领村民把村中余下的荒地种上甲、乙两种水果树.已知每棵甲种树苗比每棵乙种树苗贵6元,用400元购买甲种树苗的棵数与340元购买乙种树苗的棵数相同.(1)求甲、乙两种树苗每棵的价格;(2)该村计划用3610元购买100棵甲、乙两种树苗,最多能买多少棵甲种树苗?25.如图所示,在四边形ABCD中,E是BC的中点,F是线段DE上一点(不与点D重合),AB∥DE,AF∥DC.(1)如图1,当点F与E重合时,求证:四边形AFCD是平行四边形;(2)如图2,当点F不与E重合时,(1)中的结论还成立吗?请说明理由.(3)如图3,当∠BCD=90°,且CD=CE,F恰好运动到DE的中点时,直接写出AB 与DC的数量关系.四、解答题(本大题1个小题,共8分)解答时,必须给出必要的验算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡对应的位置上.26.把△ABC绕着点A逆时针旋转α,得到△ADE.(1)如图1,当点B恰好在ED的延长线上时,若α=60°,求∠ABC的度数;(2)如图2,当点C恰好在ED的延长线上时,求证:CA平分∠BCE;(3)如图3,连接CD,如果DE=DC,连接EC与AB的延长线交于点F,直接写出∠F的度数(用含α的式子表示).参考答案一、选择题:(本大题12个小题,每小题4分,共48分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的方框涂黑.1.把2ax2+4ax进行因式分解,提取的公因式是()A.2a B.2x C.ax D.2ax【分析】直接利用公因式的定义分析得出答案.解:2ax2+4ax=2ax(x+2).故选:D.2.下列图形中,既是轴对称图形,又是中心对称图形的是()A.B.C.D.【分析】根据轴对称图形与中心对称图形的概念求解.解:A、不是轴对称图形,是中心对称图形,故此选项不合题意;B、是轴对称图形,不是中心对称图形,故此选项不合题意;C、不是轴对称图形,是中心对称图形,故此选项不合题意;D、既是轴对称图形,又是中心对称图形,故此选项符合题意.故选:D.3.若代数式有意义,则实数x的取值范围是()A.x≠﹣1B.x≠﹣2C.x=﹣1D.x=2【分析】直接利用分式有意义的定义进而分析得出答案.解:代数式有意义,则x+1≠0,解得:x≠﹣1.故选:A.4.正多边形的一个内角是150°,则这个正多边形的边数为()A.10B.11C.12D.13【分析】一个正多边形的每个内角都相等,根据内角与外角互为邻补角,因而就可以求出外角的度数.根据任何多边形的外角和都是360度,利用360除以外角的度数就可以求出外角和中外角的个数,即多边形的边数.解:外角是:180°﹣150°=30°,360°÷30°=12.则这个正多边形是正十二边形.故选:C.5.在平面直角坐标系内,把点A(5,﹣2)向右平移3个单位,再向下平移2个单位,得到的点B的坐标为()A.(2,﹣4)B.(8,﹣4)C.(8,0)D.(2,0)【分析】直接利用平移中点的变化规律求解即可.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.解:原来点的横坐标是5,纵坐标是﹣2,向右平移3个单位,再向下平移2个单位得到新点的横坐标是5+3=8,纵坐标为﹣2﹣2=﹣4.则点B的坐标为(8,﹣4).故选:B.6.如图,在△ABC中,BD平分∠ABC,DE⊥BC,垂足为E.若∠C=60°,CE=1,则点D到AB的距离为()A.1B.C.2D.【分析】解直角三角形求得DE,然后根据角平分线的性质即可求得结论.解:∵DE⊥BC,∠C=60°,CE=1,∴DE=CE=,∵BD平分∠ABC,∴点D到AB和BC的距离相等,∵DE⊥BC,∴点D到AB的距离为,故选:B.7.如图,平行四边形ABCD的对角线AC,BD相交于点O,下列结论错误的是()A.OA=OC B.AB=CD C.AD=BC D.∠ABD=∠CBD 【分析】根据平行四边形的性质分别判断得出答案即可.解:A、∵平行四边形ABCD的对角线AC、BD相交于点O,∴OA=OC,故此选项不符合题意;B、∵四边形ABCD是平行四边形,∴AB=CD,故此选项不符合题意;C、∵四边形ABCD是平行四边形,∴AD=BC,故此选项不符合题意;D、当四边形ABCD是菱形时,∠ABD=∠CBD,故此选项符合题意;故选:D.8.如图,要测定被池塘隔开的A,B两点的距离,可以在AB外选一点C,连接AC,BC,并分别找出它们的中点D,E,连接ED.现测得AC=42m,BC=64m,DE=26m,则AB等于()A..42m B..52m C..56m D..64m【分析】利用三角形的中位线定理即可解决问题.解:∵CD=DA,CE=EB,∴DE是△ABC的中位线,∴DE=AB,∵DE=26m,∴AB=52m,故选:B.9.如图,已知△ABC(AC<BC),用尺规在BC上确定一点P,使PA+PB=BC,则下列四种不同方法的作图中,作法正确的是()A.B.C.D.【分析】直接利用线段垂直平分线的性质作出AC的垂直平分线进而得出答案.解:用尺规在BC上确定一点P,使PA+PB=BC,如图所示:,先做出AC的垂直平分线,即可得出AP=PC,即可得出PC+BP=PA+PB=BC.故选:B.10.如图,已知直线y=ax+3与y=bx﹣3交点为P,根据图象有以下3个结论:①a>0;③x>2是不等式ax+3>bx﹣3的解集.其中正确的个数是()A.0B.1C.2D.3【分析】根据一次函数的图象和性质可得a<0;b>0;当x<2时,直线y=ax+3在直线y=bx﹣3的上方,即x<2是不等式ax+3>bx﹣3的解集.解:由图象可知,a<0,故①错误;b>0,故②正确;当x<2是直线y=ax+3在直线y=bx﹣3的上方,即x<2是不等式ax+3>bx﹣3的解集,故③错误.故选:B.11.等腰三角形一腰长为5,这一腰上的高为3,则这个等腰三角形底边长为()A.B.C.或D.4或【分析】此题要分两种情况进行讨论:(1)当等腰三角形的顶角是钝角时,腰上的高在三角形的外部,先在Rt△ACO中由勾股定理求出AO=4,于是OB=AB+AO=9,然后在Rt△BCO中利用勾股定理即可求出BC即可;(2)当等腰三角形的顶角是锐角时,腰上的高在三角形的内部,在Rt△ACO中由勾股定理求出AD=4,于是DB=AB﹣AD=1,然后在Rt△BCD中利用勾股定理求出BC即可.解:分两种情况:(1)顶角是钝角时,如图1所示:在Rt△ACO中,由勾股定理,得AO2=AC2﹣OC2=52﹣32=16,OB=AB+AO=5+4=9,在Rt△BCO中,由勾股定理,得BC2=OB2+OC2=92+32=90,∴BC==3;(2)顶角是锐角时,如图2所示:在Rt△ACD中,由勾股定理,得AD2=AC2﹣DC2=52﹣32=16,∴AD=4,DB=AB﹣AD=5﹣4=1.在Rt△BCD中,由勾股定理,得BC2=DB2+DC2=12+32=10,∴BC=;综上可知,这个等腰三角形的底的长度为3或.故选:C.12.如图,在平面直角坐标系内,Rt△ABC的点A在第一象限,点B与点A关于原点对称,∠C=90°.AC与x轴交于点D,点E在x轴上,CD=2AD.若AD平分∠OAE,△ADE的面积为1,则△ABC的面积为()A.6B.9C.12D.15【分析】连接OC,根据直角三角形的性质可得OC=OA,进而得出∠OCD=∠OAD,根据角平分线的定义可得∠OAD=∠EAD,从而得出△ADE∽△CDO,易得ON=2EM,BC=2ON=4EM,再根据CD=2AD可得AC=3AD,所以△ABC的面积为△ADE的面积的面积的12倍.解:如图,连接OC,作EM⊥AD于M,作ON⊥AC于N,由点B与点A关于原点对称.可得OA=OB,又∵△ABC是直角三角形,∴OC=OA,所以∠OCD=∠OAD,∵AD平分∠OAE,∴得∠OAD=∠EAD,∴∠OAD=∠EAD,又∵∠ADE=∠CDO,∴△ADE∽△CDO,∵CD=2AD,∴ON=2EM,AC=3AD,∴BC=2ON=4EM,∴=.故选:C.二、填空题:(本大题6个小题,每小题4分,共24分)请将每小题的答案直接填在答题卡中对应的横线上.13.因式分解:x2﹣10x+25=(x﹣5)2.【分析】此题可直接用完全平方公式分解因式.完全平方公式:a2±2ab+b2=(a±b)2.解:x2﹣10x+25=(x﹣5)2.14.计算:=.【分析】直接利用分式的除法运算法则计算得出答案.解:=2x2y•=.故答案为:.15.如图,是正在铺设的人行道上地板砖的部分,是由正六边形和四边形镶嵌而成的图形,则图中的四边形ABCD中的锐角∠BAD的度数是60度.【分析】根据正六边形内角和定理,求出每个内角度数,然后根据邻补角求出答案.解:正六边形内角和(6﹣2)×180°=720°,所以每个内角度数720°÷6=120°,∴∠BAD=180°﹣120°=60°,故答案为60.16.在抗疫情期间,准备用甲、乙两种货车将68吨的抗疫物资运往武汉某地,甲种货车的载重量为5吨,乙种货车的载重量为4吨,若安排甲、乙两种车共15辆,则甲种货车至少安排的辆数为8.【分析】设甲种货车x辆,乙种货车(15﹣x)辆,由甲货车总的载重量+乙货车总的载重量≥68吨,列出不等式可求解.解:设甲种货车x辆,乙种货车(15﹣x)辆,由题意可得:5x+4(15﹣x)≥68,∴x≥8,答:甲种货车至少安排8辆.故答案为8.17.如图,规定程序运行到“判断结果是否大于100”为第一次运算,若运算进行了三次才停止,则满足条件的整数x的个数为7.【分析】由该运算进行了三次才停止,即可得出关于x的一元一次不等式组,解之即可得出x的取值范围,再结合x为正整数即可得出结论.解:依题意,得:,解得:4<x≤11.又∵x为整数,∴x可以为5,6,7,8,9,10,11,∴满足条件的整数x的个数为7.故答案为:7.18.如图,在平行四边形ABCD中,对角线AC,BD交于点O,且∠ACB=45°,AE⊥BD,垂足为F,交BC于点E.若AB=AE,AO=2,则BE的长为.【分析】过点A作AH⊥BC于H,过点B作BG⊥AO于点G,由平行四边形的性质求得AC,再由等腰直角三角形的性质和勾股定理求得CH,再证明BA=BO,求得OG,再由等腰直角三角形求得BC,进而得BH,再由等腰三角形的性质求得BE.解:如图,过点A作AH⊥BC于H,过点B作BG⊥AO于点G,∵四边形ABCD是平行四边形,∴AC=2AO=4,∵∠ACB=45°,AH⊥BC,∴∠ACB=∠HAC=45°,∴AH=HC,∵AH2+HC2=AC2,∴AH=HC=2,∵AB=AE,∴BH=EH,∠BAH=∠EAH,∵AE⊥BD,∵∠EAH+∠AEH=∠AEH+∠EBF=90°,∴∠EBF=∠EAH=∠BAH,∵∠BAO=∠BAH+∠CAH=∠BAH+45°,∠BOA=∠EBF+∠OCB=∠EBF+45°,∴∠BAO=∠BOA,∴BA=BO,∴OG=∴,∵OC=OA=2,∴CG=OC+OG=3,∵∠BCG=45°,∴∠CBG=∠BCG=45°,∴BG=CG=3,∴,∴,∴,故答案为:2.三、解答题:(本大题7个小题,每小题10分,共70分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形,请将解答过程书写在答题卡中对应的位置上.19.计算:(1);(2).【分析】(1)直接通分运算,进而利用分式的性质化简即可;(2)将括号里面通分运算,再利用分式的混合运算法则计算得出答案.解:(1)原式===;(2)原式====.20.解下列不等式或不等式组,并把解集在数轴上表示出来.(1);(2)【分析】(1)去分母,去括号,移项,合并同类项,系数化成1即可;(2)先求出每个不等式的解集,再求出不等式组的解集即可.解:(1)解:去分母,得3x﹣2(x﹣1)≥6,去括号,得3x﹣2x+4≥6,合并同类项,移项,得x≥2,这个不等式的解集在数轴上的表示如图所示:;(2),∵解不等式①,得x<2.解不等式②,得x≥﹣1.在同一条数轴上表示不等式①②的解集,如图所示:,∴原不等式组的解集为:﹣1≤x<2.21.(1)在如图所示的直角坐标系内,描出点A(1,2),B(2,2),C(2,1).并连接OA,AB,BC,CO;(2)将(1)中所画的图形向下平移四个单位,画出平移后的图形;(3)将(1)中所画的图形绕原点O逆时针旋转90°,画出旋转后的图形.【分析】(1)根据A,B,C三点的坐标画出四边形即可.(2)分别作出O,A,B,C的对应点O′,A′,B′,C′即可.(3)分别作出A,B,C的对应点A″,B″,C″即可.解:(1)如图,四边形OABC即为所求.(2)如图,四边形O′A′B′C′即为所求.(3)如图,四边形AA″B″C″即为所求.22.如图,在△ABC中,点D是BC上一点,且BD=DA=AC.把边AB绕着点A顺时针旋转一定角度得到∠BAE,连接DE,交AB于点F.(1)若∠B=α,请用含α的式子表示∠C;(2)若∠CAD=∠BAE,求证:DA平分∠CDE.【分析】(1)由等腰三角形的性质∠BAD=∠B=α,由外角的性质可求解;(2)由“SAS”可证△ABC≌△AED,可得∠C=∠ADE,可证∠ADE=∠ADC,可得结论.【解答】证明:(1)∵AD=BD,∠B=α,∴∠BAD=∠B=α,∴∠ADC=∠B+∠BAD=2α,∵AD=AC,∴∠C=∠ADC=2α;(2)∵∠CAD=∠BAE,∴∠CAB=∠DAE,在△ABC和△AED中,∵∴△ABC≌△AED(SAS),∴∠C=∠ADE,∵∠C=∠ADC,∴∠ADE=∠ADC,∴DA平分∠CDE.23.某社区的游泳馆按照顾客游泳的次数收取费用,每次的全票价为40元.在盛夏即将来临时,为吸引更多的顾客再次光顾,推出了以下两种收费方式.方式一:先交250元会员费,每次游泳按照全票价的7.5折收取费用;方式二:第一次收全票价,以后每次按照全票价的9.5折收取费用.(1)按照方式一的总费用为y1,按照方式二的总费用为y2,请分别求出y1,y2与游泳次数x的函数关系式;(2)小李把自己的学习和工作时间规划了一下,他在今年可能去该游泳馆的次数不超过40次,请为小李推荐采用哪种方式缴费合算?【分析】(1)根据题意列出函数关系式即可;(2)根据(1)中的函数关系式列不等式即可得到结论.解:(1)根据题意,可得y1=250+40×0.75x=30x+250;y2=40+40×0.95(x﹣1)=38x+2.(2)令y1=y2,可得30x+250=38x+2,解方程,得x=31,当0<x<31时,此时y1>y2,方式一的费用高于方式二;当x=31时,y1=y2,两种方式的费用一样;当x>31时,y1<y2,方式一的费用低于方式二.所以,从游泳的费用考虑,当游泳的次数小于31次时,选择方式二;当游泳的次数等于31次时,两种方式的费用一样,两种方式都可以选择;当去游泳的次数高于31次时,选择方式一.24.在脱贫攻坚的关键一年里,重庆市某地根据当地的高山气候,该村的村支书决定带领村民把村中余下的荒地种上甲、乙两种水果树.已知每棵甲种树苗比每棵乙种树苗贵6元,用400元购买甲种树苗的棵数与340元购买乙种树苗的棵数相同.(1)求甲、乙两种树苗每棵的价格;(2)该村计划用3610元购买100棵甲、乙两种树苗,最多能买多少棵甲种树苗?【分析】(1)根据用400元购买甲种树苗的棵数与340元购买乙种树苗的棵数相同,列出分式方程求解即可;(2)根据题意列出不等式求解即可.解:(1)设甲种树苗每棵的价格是x元,则乙种树苗每棵的价格是(x﹣6)元,根据题意,可得,解这个方程,得:x=40,经检验,x=40是原方程的根,所以x﹣6=34,答:甲种树苗每棵的价格是40元,则乙种树苗每棵的价格是34元.(2)设该村买n棵甲种树苗,买(100﹣n)棵乙种树苗,总的费用为y元,根据题意,可得y=40n+34(100﹣n),∴y=6n+3400≤3610,∴n≤35,∵n是正整数,∴n的最大值是35,答:该村用3610元最多能买35棵甲种树苗.25.如图所示,在四边形ABCD中,E是BC的中点,F是线段DE上一点(不与点D重合),AB∥DE,AF∥DC.(1)如图1,当点F与E重合时,求证:四边形AFCD是平行四边形;(2)如图2,当点F不与E重合时,(1)中的结论还成立吗?请说明理由.(3)如图3,当∠BCD=90°,且CD=CE,F恰好运动到DE的中点时,直接写出AB 与DC的数量关系.【分析】(1)由ASA证得△ABF≌△DFC,得出AF=DC,即可得出结论;(2)过点E作EG∥FA交AB于点G,易证四边形AGEF是平行四边形,得GE=AF,由ASA证得△GBE≌△DEC,得出GE=DC,推出AF=DC,又由AF∥DC,即可得出四边形AFCD是平行四边形;(3)连接AC交DE于H,由(2)得四边形AFCD是平行四边形,得出DH=FH=DF,易证△CDE是等腰直角三角形,得DE=DC,由等腰直角三角形的性质得出EF=DF,CF⊥DE,CF=DF=EF=DC,求出FH=DC,EH=DC,证明EH是△ABC的中位线,即可得出结果.【解答】(1)证明:∵AB∥DE,AF∥DC,点F与E重合,∴∠B=∠DFC,∠AFB=∠C,∵点E是BC的中点,点F与E重合,∴BF=CF,在△ABF和△DFC中,,∴△ABF≌△DFC(ASA),∴AF=DC,∵AF∥DC,∴四边形AFCD是平行四边形;(2)解:当点F不与E重合时,(1)中的结论成立;理由如下:过点E作EG∥FA交AB于点G,如图2所示:∵AB∥DE,GE∥AF,∴∠B=∠DEC,四边形AGEF是平行四边形,∴GE=AF,∵DC∥AF,∴DC∥GE,∴∠GEB=∠DCE,在△GBE和△DEC中,,∴△GBE≌△DEC(ASA),∴GE=DC,∴AF=DC,∵AF∥DC,∴四边形AFCD是平行四边形;(3)解:连接AC交DE于H,如图3所示:由(2)得:四边形AFCD是平行四边形,∴DH=FH=DF,∵∠BCD=90°,CD=CE,∴△CDE是等腰直角三角形,∴DE=DC,∵点F是DE的中点,∴EF=DF,CF⊥DE,CF=DF=EF=DC,∴FH=×DC=DC,∴EH=EF+FH=DC+DC=DC,∵AB∥DE,点E是BC的中点,∴EH是△ABC的中位线,∴AB=2EH=2×DC=DC.四、解答题(本大题1个小题,共8分)解答时,必须给出必要的验算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡对应的位置上.26.把△ABC绕着点A逆时针旋转α,得到△ADE.(1)如图1,当点B恰好在ED的延长线上时,若α=60°,求∠ABC的度数;(2)如图2,当点C恰好在ED的延长线上时,求证:CA平分∠BCE;(3)如图3,连接CD,如果DE=DC,连接EC与AB的延长线交于点F,直接写出∠F的度数(用含α的式子表示).【分析】(1)根据旋转的性质得到AD=AB,∠ABC=∠ADE.求得∠ABD=∠DAB =60°,于是得到结论;(2)根据旋转的性质得到∠E=∠ACE.等量代换得到∠ACB=∠ACE.根据角平分线的定义即可得到结论;(3)根据旋转的性质得到AE=AC,∠CAE=α,求得∠ACE=∠AEC=(180°﹣α)=90°﹣,根据全等三角形的性质得到∠EAD=∠CAD=,根据三角形的外角的性质即可得到结论.解:(1)∵α=60°,△ABC≌△ADE,∴AD=AB,∠ABC=∠ADE.∴∠ABD=∠DAB=60°.∴∠ADE=∠DAB+∠ABD=120°;(2)∵AC=AE,∠EAC=α,∴∠E=∠ACE.∵△ABC≌△ADE,∴∠ACB=∠E.∴∠ACB=∠ACE.∴CA平分∠BCE;(3)∵把△ABC绕着点A逆时针旋转α,得到△ADE,∴AE=AC,∠CAE=α,∴∠ACE=∠AEC=(180°﹣α)=90°﹣,∵DE=CD,AD=AD,∴△ADE≌△ADC(SSS),∴∠EAD=∠CAD=,∵∠BAD=∠CAE=α,∴∠BAC=,∴∠F=∠ACE﹣∠CAF=90°﹣﹣=90°﹣α.。
2019-2020学年甘肃武威第八中学第二学期期末考试八年级生物试卷(含答案)(八年级下册试卷)

武威第八中学2019-2020学年第二学期期末考试八年级生物试卷(满分60分,考试时间50分钟)一、选择题(本题共计 30 小题,每题1分,共计30分)1.马铃薯在进行无性生殖时,利用的营养器官是()A.根B.茎C.叶D.以上都可以2.在生产实践中,常利用营养器官进行繁殖的一组植物是()A.向日葵和西瓜B.桃和土豆C.花生和水稻D.萝卜和白菜3.下列不属于变态叶的是()A.仙人掌的叶B.马铃薯C.豌豆的叶卷须D.猪笼草的捕虫叶4.下列关于有性生殖的叙述,错误的是()A.有两性生殖细胞结合过程B.后代有更强的生活力C.后代变异性更强D.由植物的根、茎、叶等器官发育成的新个体5.下列说法不正确的是()A.蝌蚪用鳃呼吸,发育成蛙时,用肺呼吸B.马铃薯的生殖方式是有性生殖C.鸟卵的卵黄上的小白点是鉴定卵是否受精的依据D.要确保嫁接成功,须把接穗和砧木的形成层结合在一起6.植物组织培养技术的理论基础是()A.植物细胞的多功能性B.生殖细胞的全能性C.植物细胞的全能性D.植物细胞能分裂7.昆虫的完全变态发育过程是指()A.卵→蛹→茧B.幼虫→成虫C.卵→幼虫→蛹→成虫D.卵→蛹→成虫8.下列动物中发育为完全变态的有()①蜜蜂②蟋蟀③蚊④蝇⑤蜻蜓A.①③④B.①②C.③④D.②⑤9.两栖动物的种类和数量日益减少的原因是()①环境污染②水域面积缩减③乱捕滥杀④繁殖能力差A.①②④B.①②③C.①③④D.②③④10.两栖类动物不能脱离水成为真正陆生动物的主要原因是()A.生殖与幼体的生长都离不开水B.体温不恒定不能离开水生活C.受精过程发生在体外D.体色与陆地环境差别较大,不利于保护自己11.下列性状属于相对性状的是()A.豌豆的皱粒与圆粒B.人的身高与体重C.兔的短毛与黑毛D.猫的黑色和京巴狗的白色12.下列关于DNA的叙述中,不正确的是()A.DNA主要存在于细胞核中B.DNA和蛋白质组成了染色体C.DNA中储存有遗传信息D.DNA分子可以自由进出细胞13.双眼皮(显性)和单眼皮(隐性)是一对相对性状。
2019-2020学年安徽省六安市霍邱县八年级下学期期末数学试卷 (解析版)

2019-2020学年安徽六安市霍邱县八年级第二学期期末数学试卷一、选择题(共10小题).1.若有意义,则x的取值范围是()A.x≥2B.x≥﹣2C.x>2D.x>﹣22.下列运算正确的是()A.=﹣2B.(2)2=6C.+=D.×=3.用配方法解方程x2﹣6x﹣8=0时,配方结果正确的是()A.(x﹣3)2=17B.(x﹣3)2=14C.(x﹣6)2=44D.(x﹣3)2=1 4.如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是()A.6B.7C.8D.95.一个三角形三个内角之比为1:2:3,其所对三边之比为()A.1:2:3B.1::C.1::2D.1::3 6.如图,矩形ABCD的对角线AC=10,∠BOC=120°,则AB的长度是()A.5B.6C.8D.57.一组数据4,5,6,7,7,8的中位数和众数分别是()A.7,7B.7,6.5C.5.5,7D.6.5,78.为执行“均衡教育“政策,某区2017年投入教育经费2500万元,预计到2019年底三年累计投入1.2亿元,若每年投入教育经费的年平均增长百分率为x,则下列方程正确的是()A.2500(1+2x)=12000B.2500(1+x)2=1200C.2500+2500(1+x)+2500(1+2x)=12000D.2500+2500(1+x)+2500(1+x)2=120009.下列命题正确的是()A.一组对边相等,另一组对边平行的四边形一定是平行四边形B.对角线相等的四边形一定是矩形C.两条对角线互相垂直的四边形一定是菱形D.两条对角线相等且互相垂直平分的四边形一定是正方形10.如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=3,AF=5,则AC的长为()A.4B.4C.10D.8二、填空题(本大题共有4小题,每小题5分,共计20分)11.计算÷的结果是.12.已知x1,x2是关于x的方程x2﹣(m﹣1)x﹣m=0的两个根,且x1+x2=3,则m的值是.13.四边形具有不稳定性.如图,矩形ABCD按箭头方向变形成平行四边形A'B'C'D',变形后∠A'=30°,若矩形ABCD的面积是9,则平行四边形A'B'C'D'的面积是14.如图,Rt△ABC中,∠ACB=90°,AC=12,BC=5,延长BC至点D,连接AD,若△ABD是以AD为其中一腰的等腰三角形,则线段DC的长等于.三、解答题(本大题共有9小题,共计90分)15.计算:.16.解方程:x2﹣6x﹣4=0.17.已知:如图,E,F为▱ABCD对角线AC上的两点,且AE=CF,连接BE,DF,求证:BE=DF.18.已知关于x的方程x2+2(m﹣1)x+m2+5=0有两个不相等的实数根,化简:.19.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点都在网格交点上,请按要求完成下列各题.(1)线段AB的长为,BC的长为.(2)点D也在格点上,且以A,B,C,D为顶点的四边形是平行四边形.请在网格图中画出一个符合条件的平行四边形;(3)设(2)中你所画的平行四边形的面积为S,请通过计算说明;S=AC•BC.20.观察以下等式:第1个等式:,第2个等式:,第3个等式:,第4个等式:,…按照以上规律,解决下列问题:(1)写出第5个等式:;(2)写出你猜想的第n个等式:(用含n的等式表示),并证明其正确性.21.某校初二学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):′1号2号3号4号5号总分甲班1009811089103500乙班891009511997500经统计发现两班总数相等.此时有学生建议,可以通过考察数据中的其他信息作为参考.请你回答下列问题:(1)计算两班的优秀率;(2)求两班比赛数据的中位数;(3)计算两班比赛数据的方差哪一个小?(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班级?简述你的理由.方差的公式为.22.“疫情”期间,李晨在家制作一种工艺品,并通过网络平台进行线上销售.经过一段时间后发现:当售价是40元/件时,每天可售出该商品60件,且售价每降低1元,就会多售出3件,设该商品的售价为x元/件(20≤x≤40).(1)请用含售价x(元/件)的代数式表示每天能售出该工艺品的件数;(2)已知每件工艺品需要20元成本,每天销售该工艺品的纯利润为900元.①求该商品的售价;②为了支持“抗疫”行动,李晨决定每销售一件该工艺品便通过网络平台自动向某救助基金会捐款0.5元,求李晨每天通过销售该工艺品面捐款的数额.23.我们给出如下定义:把对角线相等的四边形叫做“对等四边形”.如图①,在四边形ABCD中,AC=BD,四边形ABCD就是“对等四边形”.(1)下列四边形中,一定是“对等四边形”的是(填序号)①平行四边形②矩形③菱形④梯形(2)如图②,在“对等四边形”ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,求证:四边形EFGH是菱形.(3)在(2)的条件下,若四边形EFGH也是“对等四边形”,且对角线长为2,求四边形ABCD的面积.参考答案一、选择题(共10小题).1.若有意义,则x的取值范围是()A.x≥2B.x≥﹣2C.x>2D.x>﹣2【分析】二次根式有意义,被开方数是非负数.解:依题意,得x﹣2≥0,解得,x≥2.故选:A.2.下列运算正确的是()A.=﹣2B.(2)2=6C.+=D.×=【分析】根据二次根式的性质以及二次根式加法,乘法及乘方运算法则计算即可.解:A:=2,故本选项错误;B:=12,故本选项错误;C:与不是同类二次根式,不能合并,故本选项错误;D:根据二次根式乘法运算的法则知本选项正确.故选:D.3.用配方法解方程x2﹣6x﹣8=0时,配方结果正确的是()A.(x﹣3)2=17B.(x﹣3)2=14C.(x﹣6)2=44D.(x﹣3)2=1【分析】方程利用完全平方公式变形即可得到结果.解:用配方法解方程x2﹣6x﹣8=0时,配方结果为(x﹣3)2=17,故选:A.4.如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是()A.6B.7C.8D.9【分析】根据多边形的内角和公式及外角的特征计算.解:多边形的外角和是360°,根据题意得:180°•(n﹣2)=3×360°解得n=8.故选:C.5.一个三角形三个内角之比为1:2:3,其所对三边之比为()A.1:2:3B.1::C.1::2D.1::3【分析】求出三角形的各个内角,利用直角三角形30度角的性质解决问题即可.解:设△ABC中,∠A:∠B:∠C=1:2:3,∵∠A+∠B+∠C=180°,∴∠A=30°,∠B=60°,∠C=90°,设BC=a,则AB=2a,AC=a,∴BC:AC:AB=1::2,故选:C.6.如图,矩形ABCD的对角线AC=10,∠BOC=120°,则AB的长度是()A.5B.6C.8D.5【分析】由矩形的性质得出OA=OB=4,证明△AOB是等边三角形,得出AB=OA即可.解:∵四边形ABCD是矩形,∴OA=AC=5,OB=OD,AC=BD=10,∴OA=OB=5,∵∠BOC=120°,∴∠AOB=60°,∴△AOB是等边三角形,∴AB=OA=5;故选:A.7.一组数据4,5,6,7,7,8的中位数和众数分别是()A.7,7B.7,6.5C.5.5,7D.6.5,7【分析】找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;众数是一组数据中出现次数最多的数据,注意众数可以不止一个.解:在这一组数据中7是出现次数最多的,故众数是7,而将这组数据从小到大的顺序排列后,处于中间位置的数是6,7,那么由中位数的定义可知,这组数据的中位数是(6+7)÷2=6.5.故选:D.8.为执行“均衡教育“政策,某区2017年投入教育经费2500万元,预计到2019年底三年累计投入1.2亿元,若每年投入教育经费的年平均增长百分率为x,则下列方程正确的是()A.2500(1+2x)=12000B.2500(1+x)2=1200C.2500+2500(1+x)+2500(1+2x)=12000D.2500+2500(1+x)+2500(1+x)2=12000【分析】设每年投入教育经费的年平均增长百分率为x,根据题意可得,2017年投入教育经费+2017年投入教育经费×(1+增长率)+2017年投入教育经费×(1+增长率)2=1.2亿元,据此列方程.解:设每年投入教育经费的年平均增长百分率为x,由题意得,2500+2500×(1+x)+2500(1+x)2=12000.故选:D.9.下列命题正确的是()A.一组对边相等,另一组对边平行的四边形一定是平行四边形B.对角线相等的四边形一定是矩形C.两条对角线互相垂直的四边形一定是菱形D.两条对角线相等且互相垂直平分的四边形一定是正方形【分析】A、一组对边相等,另一组对边平行的四边形不一定为平行四边形,例如等腰梯形满足一组对边相等,另一组对边平行,但不是平行四边形;B、对角线相等的四边形不一定为矩形,例题等腰梯形的对角线相等,但不是矩形,应改为对角线相等的平行四边形为矩形;C、对角线互相垂直的四边形不一定为菱形,例如:画出图形,如图所示,AC与BD垂直,但是显然ABCD不是菱形,应改为对角线互相垂直的平行四边形是菱形;D、两条对角线相等且互相垂直平分的四边形是正方形,根据题意画出相应的图形,如图所示,根据对角线互相平分,得到四边形为平行四边形,再由平行四边形的对角线相等,得到平行四边形为矩形,最后根据矩形的对角线互相垂直得到矩形为正方形.解:A、一组对边相等,另一组对边平行的四边形不一定是平行四边形,例如等腰梯形,一组对边平行,另一组对边相等,不是平行四边形,故本选项为假命题;B、对角线相等的四边形不一定是矩形,例如等腰梯形对角线相等,但不是矩形,故本选项为假命题;C、两条对角线互相垂直的四边形不一定是菱形,如图所示:AC⊥BD,但四边形ABCD不是菱形,本选项为假命题;D、两条对角线相等且互相垂直平分的四边形是正方形,已知:四边形ABCD,AC=BD,AC⊥BD,OA=OC,OB=OD,求证:四边形ABCD为正方形,证明:∵OA=OC,OB=OD,∴四边形为平行四边形,又AC=BD,∴四边形ABCD为矩形,∵AC⊥BD,∴四边形ABCD为正方形,则本选项为真命题,故选:D.10.如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=3,AF=5,则AC的长为()A.4B.4C.10D.8【分析】连接AE,由线段垂直平分线的性质得出OA=OC,AE=CE,证明△AOF≌△COE得出AF=CE=5,得出AE=CE=5,BC=BE+CE=8,由勾股定理求出AB==4,再由勾股定理求出AC即可.解:连接AE,如图:∵EF是AC的垂直平分线,∴OA=OC,AE=CE,∵四边形ABCD是矩形,∴∠B=90°,AD∥BC,∴∠OAF=∠OCE,在△AOF和△COE中,,∴△AOF≌△COE(ASA),∴AF=CE=5,∴AE=CE=5,BC=BE+CE=3+5=8,∴AB===4,∴AC===4;故选:A.二、填空题(本大题共有4小题,每小题5分,共计20分)11.计算÷的结果是3.【分析】根据二次根式的性质把化简,再根据二次根式的性质计算即可.解:.故答案为:312.已知x1,x2是关于x的方程x2﹣(m﹣1)x﹣m=0的两个根,且x1+x2=3,则m的值是4.【分析】根据方程的系数结合两根之和等于3,即可得出关于m的一元一次方程,解之即可得出m的值.解:∵x1,x2是关于x的方程x2﹣(m﹣1)x﹣m=0的两个根,且x1+x2=3,∴m﹣1=3,∴m=4.故答案为:4.13.四边形具有不稳定性.如图,矩形ABCD按箭头方向变形成平行四边形A'B'C'D',变形后∠A'=30°,若矩形ABCD的面积是9,则平行四边形A'B'C'D'的面积是【分析】根据30°角所对的直角边等于斜边的一半,可知平行四边形的高等于矩形的宽的一半,由于底不变,所以平行四边形A'B'C'D'的面积是矩形面积的一半.解:由题意可知,平行四边形A'B'C'D'的底边A'D'与矩形的长AD相等,平行四边形A'B'C'D'的高变为矩形的宽的一半,所以平行四边形A'B'C'D'的面积是矩形面积的一半.所以平行四边形A'B'C'D'的面积是.故答案为:.14.如图,Rt△ABC中,∠ACB=90°,AC=12,BC=5,延长BC至点D,连接AD,若△ABD是以AD为其中一腰的等腰三角形,则线段DC的长等于5或.【分析】先利用勾股定理求出AB的长,再分①AD=AB;②AD=BD两种情况进行讨论即可得出结论.解:∵Rt△ABC中,∠ACB=90°,AC=12,BC=5,∴AB===13.∵△ABD是以AD为其中一腰的等腰三角形,∴分两种情况:①当AD=AB时,∵AC⊥BD,∴DC=BC=5;②当AD=BD时,设DC=x,则AD=BD=5+x.∵Rt△ADC中,∠ACD=90°,∴DC2+AC2=AD2,即x2+122=(5+x)2,解得x=.综上所述,线段DC的长等于5或.故答案为:5或.三、解答题(本大题共有9小题,共计90分)15.计算:.【分析】首先利用乘法分配律计算乘法,然后化简,再算加减即可.解:原式=+﹣4=2+﹣4=﹣2+.16.解方程:x2﹣6x﹣4=0.【分析】此题考查了配方法解一元二次方程,解题时要注意解题步骤的准确应用,把左边配成完全平方式,右边化为常数.解:移项得x2﹣6x=4,配方得x2﹣6x+9=4+9,即(x﹣3)2=13,开方得x﹣3=±,∴x1=3+,x2=3﹣.17.已知:如图,E,F为▱ABCD对角线AC上的两点,且AE=CF,连接BE,DF,求证:BE=DF.【分析】证明△AEB≌△CFD,即可得出结论.【解答】证明:∵四边形ABCD是平行四边形,∴AB∥DC,AB=DC.∴∠BAE=∠DCF.在△AEB和△CFD中,,∴△AEB≌△CFD(SAS).∴BE=DF.18.已知关于x的方程x2+2(m﹣1)x+m2+5=0有两个不相等的实数根,化简:.【分析】首先利用根的判别式确定m的取值范围,再化简二次根式,利用绝对值的性质计算即可.解:∵x2+2(m﹣1)x+m2+5=0有两个不相等的实数根,∴△=4(m﹣1)2﹣4(m2+5)≥0,即﹣8m﹣16≥0,解得:m<﹣2,则=|1﹣m|+|m+2|=1﹣m﹣m﹣2=﹣2m﹣1.19.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点都在网格交点上,请按要求完成下列各题.(1)线段AB的长为5,BC的长为2.(2)点D也在格点上,且以A,B,C,D为顶点的四边形是平行四边形.请在网格图中画出一个符合条件的平行四边形;(3)设(2)中你所画的平行四边形的面积为S,请通过计算说明;S=AC•BC.【分析】(1)利用勾股定理计算即可.(2)根据平行四边形的判定画出图形即可.(3)利用勾股定理的逆定理证明解:(1)由题意,AB==5,BC==2,故答案为5,.(2)如图所示.(3)由勾股定理得,又∵AB=5,,∴AC2+BC2=AB2,∴∠ACB=90°,由勾股定理逆定理得△ACB为以AC和BC为直角边的直角三角形,∵,又∵所作的平行四边形的面积为△ACB面积的两倍,∴S=AC•BC.20.观察以下等式:第1个等式:,第2个等式:,第3个等式:,第4个等式:,…按照以上规律,解决下列问题:(1)写出第5个等式:5+1;(2)写出你猜想的第n个等式:(+1)(n+1﹣)=n+1(用含n的等式表示),并证明其正确性.【分析】(1)根据所给等式可得答案;(2)首先写出第n个等式,然后再利用二次根式的乘法进行计算即可.【解答】(1)解:(+1)(6﹣)=5+1,故答案为:5+1;(2)(+1)(n+1﹣)=n+1,证明:∵=∴,故答案为:(+1)(n+1﹣)=n+1.21.某校初二学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):′1号2号3号4号5号总分甲班1009811089103500乙班891009511997500经统计发现两班总数相等.此时有学生建议,可以通过考察数据中的其他信息作为参考.请你回答下列问题:(1)计算两班的优秀率;(2)求两班比赛数据的中位数;(3)计算两班比赛数据的方差哪一个小?(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班级?简述你的理由.方差的公式为.【分析】(1)优秀率等于100分以上(含100分)的人数除以总人数;(2)按大小顺序排列,中间一个数或两个数的平均数为中位数;(3)由方差的公式进行计算即可;(4)根据比赛成绩的优秀率高,中位数大,方差小,综合评定,则甲班踢毽子水平较好.解:(1)甲班的优秀率为:3÷5=0.6=60%,乙班的优秀率为:2÷5=0.4=40%;(2)甲班5名学生比赛成绩的中位数是100个乙班5名学生比赛成绩的中位数是97个;(3)甲班的平均分为,乙班的平均分为==100,甲班在这次比赛中的方差为:,乙班在这次比赛中的方差为:∴S甲2<S乙2;(4)甲班定为冠军.因为甲班5名学生的比赛成绩的优秀率比乙班高,中位数比乙班大,方差比乙班小,综合评定甲班踢毽子水平较好.22.“疫情”期间,李晨在家制作一种工艺品,并通过网络平台进行线上销售.经过一段时间后发现:当售价是40元/件时,每天可售出该商品60件,且售价每降低1元,就会多售出3件,设该商品的售价为x元/件(20≤x≤40).(1)请用含售价x(元/件)的代数式表示每天能售出该工艺品的件数;(2)已知每件工艺品需要20元成本,每天销售该工艺品的纯利润为900元.①求该商品的售价;②为了支持“抗疫”行动,李晨决定每销售一件该工艺品便通过网络平台自动向某救助基金会捐款0.5元,求李晨每天通过销售该工艺品面捐款的数额.【分析】(1)由该商品的售价结合售价每降低1元就会多售出3件,即可得出每天售出该工艺品的件数;(2)①根据总利润=每件工艺品的利润×销售数量,即可得出关于x的一元二次方程,解之取其较小值即可得出结论;②根据每天通过销售该工艺品面捐款的数额=0.5×每天销售的数量,即可得出结论.解:(1)∵该商品的售价为x元/件(20≤x≤40),且当售价是40元/件时,每天可售出该商品60件,且售价每降低1元,就会多售出3件,∴每天能售出该工艺品的件数为60+3(40﹣x)=(180﹣3x)件.(2)①依题意,得:(x﹣20)(180﹣3x)=900,整理,得:x2﹣80x+1500=0,解得:x1=30,x2=50(不合题意,舍去).答:该商品的售价为30元/件.②0.5×(180﹣3×30)=45(元).答:李晨每天通过销售该工艺品面捐款的数额为45元.23.我们给出如下定义:把对角线相等的四边形叫做“对等四边形”.如图①,在四边形ABCD中,AC=BD,四边形ABCD就是“对等四边形”.(1)下列四边形中,一定是“对等四边形”的是②(填序号)①平行四边形②矩形③菱形④梯形(2)如图②,在“对等四边形”ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,求证:四边形EFGH是菱形.(3)在(2)的条件下,若四边形EFGH也是“对等四边形”,且对角线长为2,求四边形ABCD的面积.【分析】(1)由矩形的性质可求解;(2)由三角形中位线定理可得EH=BD=FG,EF=AC=GH,由“对等四边形”的性质可得AC=BD,可得EH=FG=EF=GH,可得结论;(3)先证四边形EFGH是正方形,边长为,可得EF⊥FG,EF=FG=,由三角形中位线定理解得BD⊥AC,BD=AC=,可求解.解:(1)∵矩形的对角线相等,∴矩形一定是“对等四边形”,故答案为:②;(2)证明:连接AC、BD,∵点E,F,G,H分别为边AB,BC,CD,DA的中点,∴EH=BD=FG,EF=AC=GH,∵四边形ABCD是“对等四边形”,∴AC=BD,∴EH=FG=EF=GH,∴四边形EFGH是菱形;(3)连接EG,HF,∵四边形EFGH是菱形,∴GE与HF互相垂直平分,又∵四边形EFGH是“对等四边形”,且对角线长为2,∴GE=HF=2,∴四边形EFGH是正方形,边长为,∴EF⊥FG,EF=FG=,∵点E,F,G,H分别为边AB,BC,CD,DA的中点,∴FG∥BD,FG=BD,EF∥AC,EF=AC,∴BD⊥AC,BD=AC=,∴四边形ABCD的面积等于AC×BD=4.。
天津市部分地区2019-2020学年度第二学期期末考试八年级英语试卷(WORD版)

天津市部分区2019~2020学年度第二学期期末考试八年级英语温馨提示:使用答题卡的区, 学生作答时请将答案写在答题卡上;不使用答题卡的区, 学生作答时请将答案写在试卷上。
一、听力理解(本大题共20小题, 每小题1分, 共20分)A)在下列每小题内, 你将听到一个或两个句子并看到供选择的A、B、C三幅图画。
找出与你所听句子内容相匹配的图画。
B下面你将听到十组对话, 每组对话都有一个问题。
根据对话内容, 从每组所给的A、B、C 三个选项中找出能回答所提问题的最佳选项。
5. What did Judy's mother buy Judy?A. A new camera.B. A new hat.C. A new phone.6. What does the man think of bananas?A. Delicious.B. Not good for health.C. Awful.7. Where has Mike gone?A. To the stadium.B. To the library.C. To the dining hall.8. What has the man always wanted to do?A. To visit China.B. To fly a plane.C. To travel around the world.9. When did Toby start collecting coins?A. About three years ago.B. About four years ago.C. About five years ago.10. What's the man's hobby?A. Playing basketball.B. Collecting postcards.C. Drawing.11. Why did the girl get up early yesterday?A. To do morning exercises.B. To take the English course.C. To catch the first bus.12. How often does Molly go to the English Reading Club?A. Twice a week.B. Once a month.C. Three time!13. How long has the girl worked at the school radio station?A. For two years.B. For five years.C. For six years.14. How old was Tim when he found his first job?A. 16.B. 19.C. 22.C听下面长对话或独白。
西安市2019-2020年度八年级上学期期末考试生物试题(II)卷

西安市2019-2020年度八年级上学期期末考试生物试题(II)卷姓名:________ 班级:________ 成绩:________一、单选题1 . 尺蠖静止不动时,它的形状像树枝,这种行为属于A.生殖行为B.节律行为C.防御行为D.社会行为2 . 下列行为属于学习行为的是A.鹦鹉学舌B.蜜蜂采蜜C.蜘蛛结网D.公鸡报晓3 . 下列食品与相关细菌和真菌的对应关系错误的是A.酸奶——乳酸菌B.馒头——酵母菌C.豆腐乳——霉菌D.泡菜——醋酸菌4 . 下列关于运动系统说法,正确的是()A.人体运动系统由骨和肌肉构成B.关节软骨可起连接的作用C.骨骼肌由中间的肌键与两端的肌腹构成D.端起水喝时,肱二头肌收缩,肱三头肌舒张5 . 米勒根据模拟实验得出原始地球能形成构成生命的有机物的结论,运用的研究方法是()A.调查B.比较C.推测D.分类6 . 下列有利于生物多样性保护的是()A.严格执行海洋伏季休渔制度B.大量收集珍稀物种做标本C.随意引进外来物种D.大力开发自然保护区旅游资源7 . 两只狗为争夺一块骨头而发生争斗的行为是A.节律行为B.攻击行为C.繁殖行为D.领域行为8 . 下列有关动物行为的叙述中,描述不正确的是A.先天性行为是动物生来就有的,由体内遗传物质决定的B.学习行为的形成与遗传物质无关C.动物的社会行为,有利于动物群体的生存D.老马识途属于学习行为9 . 下列属于人体器官的是()A.消化道B.脂肪C.肾脏D.红细胞10 . 绿色植物在生物圈中的角色属于()A.生产者B.消费者C.分解者D.消费者和分解者11 . 生物的结构总是同功能相适应的,如人体运动依赖于一定的结构基础.如图表示人体部分运动器,下列有关叙述错误的是()A.关节由图乙中的⑥⑦⑨构成B.⑨内的滑液和⑩能使关节灵活C.每块完整的骨骼肌是一个器官D.产生丙图的动作时,甲图中③舒张和⑪收缩12 . 如图所示是关节结构示意图,下列有关叙述错误的是()A.结构③中的滑液能减少骨与骨之间的摩擦B.骨与骨之间通过关节等方式相连形成骨骼C.结构②的作用是提供运动的动力D.肌腱可绕过关节连在不同的骨上13 . 为诊断成年人贫血的原因,需要做骨髓穿刺抽验红细胞,抽取的部分来自骨的A.骨松质B.骨密质C.骨髓腔D.骨膜14 . 白酒酿造过程的正确顺序是:()A.制曲→发酵→糖化→蒸馏B.制曲→糖化→发酵→蒸馏C.制曲→糖化→蒸馏→发酵D.糖化→制曲→发酵→蒸馏15 . 如图为长骨结构图,下列有关说法错误的是()A.骨组织的营养物质主要依靠骨膜中的血管来供应B.人幼年时,③内的骨髓呈红色,具有造血功能C.骨折后骨能愈合,主要依赖于③骨髓D.正常情况下的成年人,有造血功能的红骨髓位于②中16 . 下列关于细菌主要特征的叙述,错误的是()A.具有成形的细胞核B.可分为球菌、杆菌、螺旋菌C.有些对人类有害D.大多数是生态系统中的分解者17 . 如图为某生物的结构示意图,下列描述错误的是()A.①是该生物的蛋白质外壳B.②是该生物的遗传物质C.该生物能通过分裂生殖D.该生物不能独立生活18 . 动物区别于植物的特征之一是可以运动,那么对于动物而言运动的意义是()①迅速改变自身的空间位置②利于寻找食物③利于躲避敌害④利于繁衍种族.A.①②③B.①③④C.②③④D.以上都是19 . 细菌、真菌在自然界中的主要作用是()A.分解无机物B.促进物质循环C.生产有机物D.导致动植物和人患病20 . 下列不属于动物本能行为的是()A.蜘蛛结网B.飞蛾扑灯C.鸟类筑巢D.导盲犬带路21 . “希臾十来往,犹恐巢中饥.辛勤三十日,母瘦雏渐肥.”(白居易)描绘的是母燕的()A.取食行为B.领域行为C.繁殖行为D.防御行为22 . 下列哪一项可以看做是一个生态系统()A.地球上所有的生物B.一片草原上所有的羊C.树林中的树D.一片森林二、填空题23 . 根据动物体内是否存在脊柱这一结构,可以将动物分为_____________动物和_____________动物两类。
2020部编版八年级下册语文《期末考试试卷》附答案解析

⑦回到家里,他和父亲,还有一大家人陷入了狂欢。父亲感动得泪水横流,不断地亲吻着他的额头:“我原本打算,你要是卖不掉,我就派人买下这件衣服。没想到你真的做到了!你真棒!我的孩子,你真的很棒……”父亲接着说道,“我只是想告诉你,一件只值一美元的旧衣服,都有办法高贵起来。何况我们这些活生生的人呢?我们有什么理由对生活丧失信心呢?我们只不过黑一点穷一点,可这又有什么关系?”就在这一刹那间,他的心中,有一轮灿烂的太阳升了起来,照亮了他的全身和眼前的世界。“连一件旧衣服都有办法高贵,我还有什么理由妄自菲薄呢!”
(二)
几千年来,劳动人民注意了草木荣枯、候鸟去来等自然现象同气候的关系,据以安排农事。杏花开了,就好像大自然在传语要赶快耕地;桃花开了,又好像在暗示要赶快种谷子。布谷鸟开始唱歌,劳动人民懂得它在唱什么:“阿公阿婆,割麦插禾。”这样看来,花香鸟语,草长莺飞,都是大自然的语言。
12. 在横线上填上恰当的词语。其字母标号依次是:____、____、____、____。
C. 修建工程浩繁复杂、修建方式难以想像 小三峡古栈道,谜语般的在大宁河上留候了千年。(谜语:此处指至今尚未破译的古栈道的修建之迷。)
D. 桥的设计完全合乎科学原理,施工技术更是巧妙绝伦。(巧妙绝伦:指建造者的创新能力很强。)
5.下列各句中,没有语病的一句是( )
A. 周汝昌先生的代表作《红楼梦新证》,被学术界誉为红学史上一部划时代的著作。
春望
国破山河在,城春草木深。感时花溅泪,恨别鸟惊心。
2019-2020年八年级下学期期末考试数学试卷(II)

2019-2020年八年级下学期期末考试数学试卷(II)一、选择题:(本大题共10小题,每题3分共计30分,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来)1.下列四个图形中,既是轴对称图形又是中心对称图形的是().A. B. C. D.2.若方程是关于的一元二次方程,则m的取值范围是()A.m≠±l B.m≥一l且m≠1 C.m≥一l D.m>一1且m≠13.已知是关于的方程的一个根,则另一个根是( )A.1 B.-1 C.-2 D.24.对抛物线y=-x2+2x-3 而言,下列结论正确的是( )A.与x轴有两个交点 B.开口向上C.与y轴的交点坐标是(0,3) D.顶点坐标是(1,-2)5.二次函数的图象与轴有交点,则的取值范围是()A. B. C.D.6. 如图,在⊙O中,直径AB垂直于弦CD,垂足为P.若PA=2,PB=8,则CD的长为()A.8 B.6 C.4 D. 27.如图,内接于圆O,,,是圆的直径,BD交AC于点E,连结DC,则等于()A.110° B.70° C.90° D.120°(第6题) (第7题)8.如图,一扇形纸扇完全打开后,外侧两竹条AB 和AC 的夹角为120°,AB 长为25cm ,贴纸部分的宽BD 为15cm ,若纸扇两面贴纸,则贴纸的面积为( ). A .cm 2B .cm 2C .cm 2D .cm 29.输入一组数据,按下列程序进行计算,输出结果如下表:分析表格中的数据,估计方程的一个正数解x 的大致范围为( ). A .20.5<x <20.6 B .20.6<x <20.7C .20.7<x <20.8D .20.8<x <20.910.在同一平面直角坐标系内,一次函数y =ax +b 与二次函数y =ax 2+8x +b 的图象可能是( )二、填空题:本大题共8小题,其中11-14题每小题3分,15-18题每小题4分,共28分.只A DBE C(第8题)静心x20.5 20.6 20.7 20.8 20.9 输出 --8.04 -2.31 3.44 9.21输入x输出+8 平方-826要求填写最后结果.11.三角形两边长分别为3和6,第三边是方程x2﹣6x+8=0的解,则此三角形周长是.12.将抛物线y=(x﹣2)2+3向右平移2个单位,再向下平移3个单位后所得抛物线的解析式为13.抛物线y=x2﹣2x﹣3与x轴的交点坐标为.14.如图,△ABC是一张三角形纸片,⊙O是它的内切圆,点D是其中的两个切点,已知AD=6cm,小明准备用剪刀沿着与⊙O相切的一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长是(第14题图) (第15题图)15.如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A 顺时针旋转到位置①可得到点,此时;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点,此时;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点,此时;…,按此规律继续旋转,直至得到点为止.则=________.16.如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,将Rt△ABC绕点A逆时针旋转45°后得到△AB′C′,点B经过的路径为,图中阴影部分面积是17.如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF长为10cm.母线OE(OF)长为10cm.在母线OF上的点A处有一块爆米花残渣,且FA=2cm,一只蚂蚁从杯口的点E处沿圆锥表面爬行到A点,则此蚂蚁爬行的最短距离为____________cm.(第16题图) (第17题图) (第18题图) 18.如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分,已知抛物线的对称轴是直线x=2,与x轴的一个交点是(﹣1,0),有下列结论:①abc<0,②4a+b=0,③抛物线与x轴的另一个交点是(5,0),④若点(﹣2,y1),(5,y2)都在抛物线上,则有y1<y2,请将正确选项的序号都填在横线上.三、解答题:本大题共7小题,共62分.解答要写出必要的文字说明、证明过程或演算步骤.19. (本题满分8分) 解方程:(1)(x﹣5)2=2(x﹣5)(2)2x(x﹣1)=3x+1.20. (本题满分8分)已知二次函数y=x2+bx+c的图象经过点(0,2)和(1,﹣1),求图象的顶点坐标和对称轴.21. (本题满分7分)如图,水平放置的圆柱形排水管的截面为⊙O,有水部分弓形的高为2,弦AB=4,求⊙O的半径.22.(本题满分11分)电动自动车已成为市民日常出行的首选工具.据某市某品牌电动自行车经销商1至3月份统计,该品牌电动自行车1月份销售150辆,3月份销售216辆.(1)求该品牌电动自行车销售量的月均增长率;(2)若该品牌电动自行车的进价为2300元,售价为2800元,则该经销商1至3月共盈利多少元?23. (本题满分6分)已知△ABC在平面直角坐标系中的位置如图所示.(1) 分别写出图中点A和点C的坐标;(2) 画出△ABC绕点A按逆时针方向旋转90°后的△AB'C';(3) 在(2)的条件下,求点C旋转到点C'所经过的路线长(结果保留π).234567yAB24、(本题满分9分)如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.(1)求证:DE是半圆⊙O的切线.(2)若∠BA C=30°,DE=2,求AD的长.25.(本题满分13分)某商店准备进一批季节性小家电,每个进价为40元,经市场预测,销售定价为50元,可售出400个;定价每增加1元,销售量将减少10个.设每个定价增加x元.(1)写出售出一个可获得的利润是多少元(用含x的代数式表示)?(2)商店若准备获得利润6000元,并且使进货量较少,则每个定价为多少元?应进货多少个?(3)商店若要获得最大利润,则每个应定价多少元?获得的最大利润是多少?-----如有帮助请下载使用,万分感谢。
2019-2020学年山东省济宁市曲阜市八年级下学期期末数学试卷 (解析版)

2019-2020学年山东济宁市曲阜市八年级第二学期期末数学试卷一、选择题(共10小题).1.要使二次根式有意义,x的值可以是()A.﹣2B.﹣3C.﹣4D.﹣52.一次函数y=2﹣x与x轴的交点为()A.(1,1)B.(0,2)C.(2,0)D.(3,0)3.在▱ABCD中、如果∠A=65°、那么∠C的度数是()A.115°B.65°C.25°D.35°4.某青年排球队l2名队员的年龄情况如下表所示:年龄1819202122人数14322则这12名队员的平均年龄是()A.18岁B.19岁C.20岁D.21岁5.以下列各组数为边长,能构成直角三角形的是()A.5,12,13B.1,2,C.,,2D.4,5,66.下列运算结果正确的是()A.=﹣3B.(﹣)2=2C.÷=2D.=±4 7.已知四边形ABCD是平行四边形,下列结论不正确的是()A.当AB=BC时,它是菱形B.当AC⊥BD时,它是菱形C.当∠ABC=90°时,它是矩形D.当AC=BD时,它是菱形8.某校举行“汉字听写比赛”,5个班级代表队的正确答题数如图.这5个正确答题数所组成的一组数据的中位数和众数分别是()A.10,15B.13,15C.13,20D.15,159.在平面直角坐标系中,一次函数y=kx+b的图象如图所示,则k和b的取值范围是()A.k>0,b>0B.k>0,b<0C.k<0,b>0D.k<0,b<0 10.已知:如图,矩形ABCD中,AB=5,BC=12,对角线AC、BD相交于点O,点P是线段AD上任意一点,且PE⊥AC于点E,PF⊥BD于点F,则PE+PF等于()A.B.C.D.二、填空题(共6小题).11.正比例函数图象经过(3,﹣6),则这个正比例函数的解析式是.12.已知:x=,y=﹣2,代数式x2﹣2xy+y2的值为.13.已知,如图,一小船以20海里/时的速度从港口A出发向东北方向航行,另一小船以15海里/时的速度同时从港口A出发向东南方向航行,离开港口1小时后,则两船相距.14.将直线y=2x﹣5向上平移2个单位,所得直线解析式为.15.如图,菱形ABCD中,对角线AC、BD相交于点O,H为AB边中点,菱形ABCD的周长为24,则OH的长等于.16.如图,正方形ABCD的边长是2,对角线AC、BD相交于点O,点E、F分别在边AD、AB上,且OE⊥OF,则四边形AFOE的面积为.三、解答题:共72分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.17.计算:×+6﹣.18.如图,每个小正方形的边长都为1(1)求四边形ABCD的周长;(2)求∠BCD的大小.19.甲、乙两名同学5次数学练习的成绩如下表:(单位:分)测试日期2月10日2月20日3月5日3月18日3月27日甲126127130133134乙130125130135130已知甲同学这5次数学练习成绩的平均数为130分,方差为10分2.(1)乙同学这5次数学练习成绩的平均数为分,方差为分2;(2)甲、乙都认为自己在这5次练习中的表现比对方更出色,请分别写出一条支持他们俩观点的理由.20.如图,在平行四边形ABCD中,E、F为对角线BD上的两点,且∠BAF=∠DCE.求证:BE=DF.21.如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x 轴相交于点B,与y轴交于点D,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.(1)求k,b的值;(2)请直接写出不等式kx+b﹣3x>0的解集;(3)M为射线CB上一点,过点M作y轴的平行线交y=3x于点N,当MN=OD时,求M点的坐标.22.“双剑合璧,天下无敌”,其意思是指两个人合在一起,取长补短,威力无比.在二次根式中也常有这种相辅相成的“对子”,如:(2+)(2﹣)=1,=3,它们的积中不含根号,我们说这两个二次根式是互为有理化因式,其中一个是另一个的有理化因式,于是,二次根式除法可以这样解:,=7+4.像这样通过分子、分母同乘一个式子把分母中的根号化去的方法,叫做分母有理化.解决下列问题:(1)将分母有理化得;+1的有理化因式是;(2)化简:=;(3)化简:……+.23.如图,矩形ABCD中,点P是线段AD上的一个动点,O为BD的中点,PO的延长线交BC于Q.(1)求证:OP=OQ;(2)若AD=8cm,AB=6cm,点P从点A出发,以1cm/s的速度向点D运动(不与D 重合).设点P运动的时间为t秒,请用t表示PD的长;并求出t为何值时,四边形PBQD是菱形?参考答案一、选择题(共10小题).1.要使二次根式有意义,x的值可以是()A.﹣2B.﹣3C.﹣4D.﹣5解:由题意得,x+2≥0,解得,x≥﹣2,故选:A.2.一次函数y=2﹣x与x轴的交点为()A.(1,1)B.(0,2)C.(2,0)D.(3,0)解:令y=0,则2﹣x=0,解得x=2,所以一次函数y=2﹣x与x轴的交点坐标是(2,0),故选:C.3.在▱ABCD中、如果∠A=65°、那么∠C的度数是()A.115°B.65°C.25°D.35°解:∵四边形ABCD是平行四边形,∴∠C=∠A=65°,故选:B.4.某青年排球队l2名队员的年龄情况如下表所示:年龄1819202122人数14322则这12名队员的平均年龄是()A.18岁B.19岁C.20岁D.21岁解:(18+4×19+3×20+2×21+2×22)÷12=(18+76+60+42+44)÷12=240÷12=20(岁).故这l2名队员的平均年龄是20岁.故选:C.5.以下列各组数为边长,能构成直角三角形的是()A.5,12,13B.1,2,C.,,2D.4,5,6解:A、52+122=132,能构成直角三角形,故选项符合题意;B、12+22≠()2,不能构成直角三角形,故选项不合题意;C、()2+22≠()2,不能构成直角三角形,故选项不合题意;D、42+52≠62,不能构成直角三角形,故选项不合题意.故选:A.6.下列运算结果正确的是()A.=﹣3B.(﹣)2=2C.÷=2D.=±4解:A、=3,故本选项不符合题意;B、(﹣)2=2,故本选项符合题意;C、÷=,故本选项不符合题意;D、=4,故本选项不符合题意;故选:B.7.已知四边形ABCD是平行四边形,下列结论不正确的是()A.当AB=BC时,它是菱形B.当AC⊥BD时,它是菱形C.当∠ABC=90°时,它是矩形D.当AC=BD时,它是菱形解:A、∵四边形ABCD是平行四边形,AB=BC,∴四边形ABCD是菱形,故正确;B、∵四边形ABCD是平行四边形,AC⊥BD,∴四边形ABCD是菱形,故正确;C、∵四边形ABCD是平行四边形,∠ABC=90°,∴四边形ABCD是矩形,故正确;D、∵四边形ABCD是平行四边形,AC=BD,四边形ABCD是矩形,故错误.故选:D.8.某校举行“汉字听写比赛”,5个班级代表队的正确答题数如图.这5个正确答题数所组成的一组数据的中位数和众数分别是()A.10,15B.13,15C.13,20D.15,15解:把这组数据从小到大排列:10、13、15、15、20,最中间的数是15,则这组数据的中位数是15;15出现了2次,出现的次数最多,则众数是15.故选:D.9.在平面直角坐标系中,一次函数y=kx+b的图象如图所示,则k和b的取值范围是()A.k>0,b>0B.k>0,b<0C.k<0,b>0D.k<0,b<0解:∵一次函数y=kx+b的图象经过一、二、四象限,∴k<0,b>0.故选:C.10.已知:如图,矩形ABCD中,AB=5,BC=12,对角线AC、BD相交于点O,点P是线段AD上任意一点,且PE⊥AC于点E,PF⊥BD于点F,则PE+PF等于()A.B.C.D.解:连接PO,∵矩形ABCD的两边AB=5,BC=12,∴S矩形ABCD=AB•BC=60,OA=OC,OB=OD,AC=BD,AC===13,∴S△AOD=S矩形ABCD=15,OA=OD=AC=,∴S△AOD=S△AOP+S△DOP=OA•PE+OD•PF=OA(PE+PF)=××(PE+PF)=15,∴PE+PF=,故选:A.二、填空题(每题3分,满分18分,将答案填在答题纸上)11.正比例函数图象经过(3,﹣6),则这个正比例函数的解析式是y=﹣2x.解:设这个正比例函数的解析式为y=kx(k≠0),∵正比例函数的图象经过点(3,﹣6),∴﹣6=3k,解得k=﹣2,∴y=﹣2x.故答案是:y=﹣2x.12.已知:x=,y=﹣2,代数式x2﹣2xy+y2的值为4.解:∵x=,y=﹣2,∴x﹣y=2,∴原式=(x﹣y)2=4,故答案为:413.已知,如图,一小船以20海里/时的速度从港口A出发向东北方向航行,另一小船以15海里/时的速度同时从港口A出发向东南方向航行,离开港口1小时后,则两船相距25海里.解:由题意得:两船的行驶方向为直角,向东北方向航行的小船行驶路程为:20×1=20(海里),向东南方向航行的小船行驶路程为:15×1=15(海里),两船的距离:=25(海里),故答案为:25海里.14.将直线y=2x﹣5向上平移2个单位,所得直线解析式为y=2x﹣3.解:由“上加下减”的原则可知,将函数y=2x﹣5向上平移,2个单位所得函数的解析式为y=2x﹣5+2,即y=2x﹣3.故答案为:y=2x﹣3.15.如图,菱形ABCD中,对角线AC、BD相交于点O,H为AB边中点,菱形ABCD的周长为24,则OH的长等于3.解:∵菱形ABCD的周长等于24,∴AB==6,∵四边形ABCD是菱形,∴AC⊥BD,∵H为AB边中点,∴在Rt△AOB中,OH为斜边上的中线,∴OH=AB=3.故答案为:3.16.如图,正方形ABCD的边长是2,对角线AC、BD相交于点O,点E、F分别在边AD、AB上,且OE⊥OF,则四边形AFOE的面积为1.解:∵四边形ABD是正方形,∴OA=OB,∠OAE=∠OBF=45°,AC⊥BD,∴∠AOB=90°,∵OE⊥OF,∴∠EOF=90°,∴∠AOE=∠BOF,在△AOE和△BOF中,,∴△AOE≌△BOF(ASA),∴△AOE的面积=△BOF的面积,∴四边形AFOE的面积=正方形ABCD的面积=×22=1;故答案为:1.三、解答题:共72分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.17.计算:×+6﹣.解:原式=+2﹣=2+2﹣=3.18.如图,每个小正方形的边长都为1(1)求四边形ABCD的周长;(2)求∠BCD的大小.解:(1)由勾股定理得:DC==,BC==2,AD==,AB==,所以四边形ABCD的周长为AB+BC+cd+ad=+2++=+3+;(2)连接BD,由勾股定理得:BD==5,∵DC=,BC=2,∴DC2+BC2=BD2,∴∠BCD=90°.19.甲、乙两名同学5次数学练习的成绩如下表:(单位:分)测试日期2月10日2月20日3月5日3月18日3月27日甲126127130133134乙130125130135130已知甲同学这5次数学练习成绩的平均数为130分,方差为10分2.(1)乙同学这5次数学练习成绩的平均数为130分,方差为10分2;(2)甲、乙都认为自己在这5次练习中的表现比对方更出色,请分别写出一条支持他们俩观点的理由.解:(1)乙的平均分=(130+125+130+135+130)=130,方差=[(130﹣130)2+(125﹣130)2+(130﹣130)2+(135﹣130)2+(130﹣130)2]=10.故答案为130,10.(2)答案不唯一,如:甲的数学成绩逐渐进步,更有潜力;乙的数学成绩在130分以上(含130分)的次数更多.20.如图,在平行四边形ABCD中,E、F为对角线BD上的两点,且∠BAF=∠DCE.求证:BE=DF.【解答】证明:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠ABF=∠CDE,在△ABF和△CDE中,∴△ABF≌△CDE(ASA),∴ED=BF,∴BD﹣CF=BD﹣DE,∴BE=DF.21.如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x 轴相交于点B,与y轴交于点D,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.(1)求k,b的值;(2)请直接写出不等式kx+b﹣3x>0的解集;(3)M为射线CB上一点,过点M作y轴的平行线交y=3x于点N,当MN=OD时,求M点的坐标.解:(1)当x=1时,y=3x=3,∴C点坐标为(1,3).直线y=kx+b经过(﹣2,6)和(1,3),则,解得:k=﹣1,b=4;(2)x<1;(3)当x=0时,y=﹣x+4=4,∴D点坐标为(0,4),∴OD=4.设点M的横坐标为m,则M(m,﹣m+4),N(m,3m),∴MN=3m﹣(﹣m+4)=4m﹣4∵MN=OD,∴4m﹣4=4,解得m=2.即M点坐标为(2,2).22.“双剑合璧,天下无敌”,其意思是指两个人合在一起,取长补短,威力无比.在二次根式中也常有这种相辅相成的“对子”,如:(2+)(2﹣)=1,=3,它们的积中不含根号,我们说这两个二次根式是互为有理化因式,其中一个是另一个的有理化因式,于是,二次根式除法可以这样解:,=7+4.像这样通过分子、分母同乘一个式子把分母中的根号化去的方法,叫做分母有理化.解决下列问题:(1)将分母有理化得;+1的有理化因式是﹣1;(2)化简:=﹣;(3)化简:……+.解:(1)==,(+1)(﹣1)=()2﹣12=2﹣1=1,即+1的有理化因式是﹣1,故答案为:,﹣1;(2)===﹣,故答案为:﹣.(3)原式=﹣1+﹣+﹣+…+﹣=﹣1=10﹣1=9.23.如图,矩形ABCD中,点P是线段AD上的一个动点,O为BD的中点,PO的延长线交BC于Q.(1)求证:OP=OQ;(2)若AD=8cm,AB=6cm,点P从点A出发,以1cm/s的速度向点D运动(不与D 重合).设点P运动的时间为t秒,请用t表示PD的长;并求出t为何值时,四边形PBQD是菱形?解:(1)∵四边形ABCD是矩形,∴AD∥BC,∴∠PDO=∠QBO,∵O为BD的中点,∴DO=BO,在△PDO和△QBO中,,∴△PDO≌△QBO(ASA),∴OP=OQ;(2)由题意知:AD=8cm,AP=tcm,∴PD=8﹣t,∵PB=PD,∴PB2=PD2,即AB2+AP2=PD2,∴62+t2=(8﹣t)2,解得t=,∴当t=时,PB=PD.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019-2020年八年级期末考试试卷(二)
一、基础知识积累与运用(共30分)
1、理解性默写(每空1分,共10分)
(1)大漠孤烟直,长河落日圆(2)白头吊古风霜里,老木苍波无限悲(3)山随平野尽,江入大荒流(4)谈笑有鸿儒,往来无白丁
(5)造化钟神秀,阴阳割昏晓
2、阅读下列语段,按照要求完成下列各题(共9分)
(1)给加点字注音并结合语境解释该词语的意思(每空1分)
风雪载.途( zaì)风雪遍地,形容气候恶劣。
暗指人生路上的挫折很多,仿佛冬天
周而复始.( shǐ)转了一圈又一圈,不断循环
(2)衰匿(3)( C )(1分)
3、综合性学习
①有关桥的故事鹊桥相会
②有关桥的诗句有关桥的诗句成语和谚语:二十四桥明月夜,玉人何处教吹箫;枯藤老树昏鸦,小桥流水人家(有错别字扣1分)
③喻桥:书本是一座桥,带着我走向知识宝藏的大门。
自信是一座桥,引导我们走向成功的彼岸
4、(D ) (2分)
5、今年4月份气温近50年最低(2分,超出规定字数扣1分)
6、②句尾加“的活动”④工作改为医院。
6、古诗鉴赏读刘禹锡的《秋词》回答下列问题(共4分)
(1)拟人积极向上(勇于进取)(2分)
(2)请选择“排”字或“引”字,说说在诗中用这一字的妙处。
(2分)
排,写出了白鹤直冲云霄的气势
引,写出了作者看到白鹤直冲云霄引发的豪迈乐观之情
7、文言文阅读读《三峡》回答下列问题(共13分)
(1)解释下面加点的字。
(每空1分,共2分)
①虽乘奔御风不以疾.也(快)②晴初霜旦.(早晨)
⑵选出加点词词义相同的一项(B )(2分)
⑶翻译下面的句子。
(4分)
(1)至于夏水襄陵,沿溯阻绝
至于夏天江水漫上丘陵的时候,下行和上行的航路都被阻断了
(2)素湍绿潭,回清倒影
雪白的急流,回旋着清波;碧绿的潭水,倒映着各种景物的影子
⑷(3分)夏:险春冬:秀秋季:凄
⑸(2分)运用侧面描写,渲染了秋天的凄清
8、课内阅读读朱自清的《背影》回答下列问题(14分)
(1)①到南京后第二日上午到下午②南京旅馆到车站③父亲④父亲坚持送我到车站
(2)因为南京的见闻与本文的中心思想关系不大,故一笔带过
(3).①言行守旧,不合时宜②衬托出父亲始终把作者看做一个还得保护的孩子(4)对往事的自责、对父亲的怀念(每点1分)
(5)要求:表述流畅1分,结合具体事例1分,抒发情感1分
9、课外阅读读《如何给地球降温》回答下列问题(10分)
⑴为了给地球降温,除特勒以外其他科学家提出哪些奇思妙想?(3分)
在地球和太阳之间万有引力互相抵消处(即拉格朗日点),安装一面直径为2000公里的半透明镜子(1分)从加强地球对太阳辐射的反射率的角度,探索给地球降温(1分)深埋二氧化碳(1分)
⑵文章主要运用了什么说明方法?(2分)
举例子、列数字
⑶不能去掉。
因为加点词语表明数据的来源,使文章语言表达更准确,更具有科学性。
(2分,只答“不能去掉”不给分)
⑷略,合理即可
10、名著阅读读《骆驼祥子》选段,回答下列问题(9分)
(1)好,“硬”字写出了祥子当时不顾一切的(反抗)心理,突出了他在暴雨中难以忍受的痛苦。
(2)文中画线的句子属于语言描写,表现了“坐车的’’的什么性格特点?试想象“坐车的”的心理活动,用一两句话描写出来。
答:性格特点:冷漠、缺乏同情心、自私;心理活动:反正你得把我平安送到。
(3)答:祥子的痛苦来自:(1) 暴雨的折磨。
(2) 坐车人的冷漠。
(每点1分)
(4)一语双关,既形象地写出了祥子当时痛苦不堪的状态,又暗示在那样的社会里祥子无法控制自己的命运。
三、写作(共40分)
等级评分标准
一类卷
1.立意明确,中心突出,材料具体生动,有真情实感。
(40—37分)
2.结构严谨,注意照应,详略得当。
3.语言得体、流畅。
二类卷
1.立意明确,中心突出,材料具体。
(37—35分)
2.结构完整,条理清楚。
3.语言规范、通顺。
三类卷
(34—30分)
1.立意明确,材料能表现中心。
2.结构基本完整,有条理。
3.语言基本通顺,有少数错别字。
四类卷
(29—15分)
1.立意不明确,材料难以表现中心。
2.结构不完整,条理不清楚。
3.语言不通顺,错别字较多。
五类卷
(14—0分)
1.没有中心,空洞无物,严重离题。
2.结构残缺,不成篇章.
3.文理不通,错别字较多。
加分
符合如下条件之一,可酌情加1—3分(加至本题满分为止):
1.立意深刻。
2.构思独特。
3.语言优美。
4.富有个性。
5.文面整洁,书写优美。
扣分1.不足600字者,每少50字扣1分。
2.错别字每3个扣1分(重复的不计),最多扣3分。
3.不能正确使用标点扣1—3分。
4.文面脏乱,字迹潦草、难以辨认者扣1—3分。
