青岛大学2016年《827信号与系统》考研专业课真题试卷
青岛大学2020年827信号与系统

信号与信息处理专业硕士入学考试大纲
考试科目代码及名称:827信号与系统
一、考试要求
掌握连续时间信号与系统分析的基本理论,掌握离散信号分析、离散时间系统设计的基本理论和方法,具备从事实际信号分析与处理工作的基本能力。
二、考试内容
(1)信号的运算和分解
(2)连续线性时不变系统的时域经典分析
(3)系统模型与系统框图
(4)单位冲激响应与卷积
(5)傅里叶变换与采样定理
(6)拉普拉斯变换与连续系统的s域分析
(7)系统函数与频率响应
(8)信号无失真传输、调制与解调
(9)离散时间系统的时域经典分析
(10)序列的z变换与离散傅里叶变换
三、试卷结构(题型分值)
1.本科目满分为150分,考试时间为180分钟。
2.题型结构
(1)选择题:占总分的16%
(2)填空题: 占总分的16%
(3)计算题:占总分的68%
四、参考书目
《信号与系统引论》,郑君里应启珩杨为理,高等教育出版社,出版时间2018-12-10。
青岛大学826电路2009-2017年考研专业课真题试卷
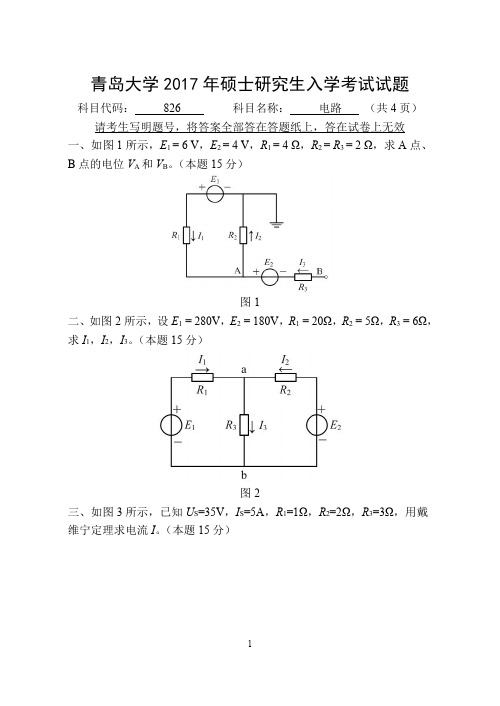
(b)
图7
八、(本大题 18 分)图 8 所示电路中
uS(t)=60sin5000t+30sin(104t+60)V, 试求电路中负载消耗的平均功率, 5
支路电流 i(t)及电流表的读数。(设 +
电流表内阻抗为 0,表计读数为有
uS(t)
−
效值)
2
+ 5V 10mH
−
0.5u 10mH
40mH
11
图6
七、(本大题 16 分)图 7(a)所示电路原已达到稳态,t=0 时开关 S 由位置 1 转换
到位置 2;电压源 uS(t)的波形如图 7(b)所示。求 t0 时的 uC(t)。
+
uS(t)
−
1 2 S(t=0)
1 2A
1H
+
0.5 uC 0.5F
−
uS(t)/V 6
0 4 t/s
(a)
++
10 u
4 3
μF
i(t) A
图8
九、(本大题 16 分)电路如图 9 所示,其中 L=0.2H,C=0.5F: 1.试以电路中的电容电压 uC、电感电流 iL 为状态变量,列写相应的状态方 程并整理成标准形式; 2.若以电感电流 iL 为输出,试判别其响应性质为振荡型?非振荡型?
+ uC −
1 C 1
L
4(t)A 1
iL
图9
十、(本大题 16 分)求图 10 中所示二端口网络的 Z 参数矩阵;当端口 2-2处接
上 R=8负载时,若 U1=18V,则 I1=?I2=?
1
+ I1 1
2
山东师范大学825信号与线性系统分析2007--2018年考研真题试卷

f (t)
** a<J]UJEJj~lf,
El:!.~%a<J*~~I~!£JEp$ H(S) 0 (22 7t)
i) (t)
+
10 IH
+
udt)
1
iL(t)
udt)
~'Q
006
-G, 1. (10 71) ~1;iiH~%;lltf!~UJFPl¥JJ;E%i'tJ§~ WN=u(k)-u(k-N), *;tt~llj$orOJm
w*Yrfjm*~
~±Wfj{j::A~~iJtiJtl!R
* * * * * * * * * * * * * * * * *"* * * * * * * * * * * * * * * * * * * * * *
lj( ali; iP<ii'Uff: 9J u (t) :gX u (k) 7:J ~M;; i*-'5 , 1, Cl 0 5}) -F YU t'iR:51hl!£ J'fi:J1'ij ~ i¥J* ~3t , ;;iJHttt 8S i1: ~~~ ~:fJ':t EEJ? £ at~ as i1: £ at ~
= 1ODcos(nk-9{fJ I'
~J ;
S 0]", (OJ t)
1[
a
m
[/3 (b)
co
61' = IO(t kT) c
(4)
?
j>?
(a)
- - ' - - - - - ' - - - - ' - - -.... CJ
青岛大学考研专业课真题——信号与系统 2007年 (附带答案及评分标准)

科目代码: 827 科目名称: 信号与系统 (共 12 页)请考生写明题号,将答案全部答在答题纸上,答在试卷上无效Ⅰ、填空题(共14题,每题3分,共42分)1.积分=-'+⎰∞∞-dt t t )1()2(2δ 。
2.如图1所示,)(t f 为原始信号,)(1t f 为变换信号,则)(1t f 的表达式为 (用)(t f 表示)。
3.若正弦序列0sin()n ω的周期10N =,则0ω的最小取值为0ω= 。
4. 给定微分方程、起始状态、激励信号分别为()2()3()d d r t r t e t dtdt+=、(0)0r -=、()()e t u t =,则(0)r += 。
5.已知)4()()()(--==n u n u n h n x ,则卷积和序列)()()(n h n x n y *=共有 个非零取值。
6.单边拉氏变换21()(2)F s s =+对应的原函数为=)(t f 。
7.图2所示因果周期矩形脉冲的拉氏变换()F s = 。
8.序列||1()2n x n ⎛⎫= ⎪⎝⎭的z 变换及其收敛域为 。
图12 0 )(t f 2t 1 3)(1t f 2t-4 -2图22TT )(t ft1T 2…科目代码: 827 科目名称: 信号与系统 (共 12 页)请考生写明题号,将答案全部答在答题纸上,答在试卷上无效9.若象函数2()(1)z F z z =-,1z <,则原序列=)(n f 。
10.调幅信号26()(100)cos(10)f t Sa t t ππ=⋅的频带宽度为 Hz 。
11.若离散线性时不变系统的单位样值响应()()2(1)3(2)(3)h n n n n n δδδδ=+---+-,则单位阶跃响应()g n 的序列波形为。
12.若某线性时不变离散时间系统的单位样值响应为)(2)1(3)(n u n u n h n n -+--=,则该系统是(因果/非因果、稳定/非稳定)系统。
青岛大学2016年硕士研究生入学考试(信号与系统)试题

科目代码:827科目名称:信号与系统(共 5页)请考生写明题号,将答案全部答在答题纸上,答在试卷上无效一、选择题(每题 3 分,共 24 分)x2(n)1.离散序列x1(n)=u(n)-u(n-2),x2(n)如32图 1所示,则卷积和序列1y(n)= x1(n)* x2(n)的最大取值发生在n 0 123()处。
图 1A. n=0B. n=1C. n=2D. n=32.以下描述系统的各方程中,x(n)为激励,y(n)为响应,则具有线性时不变特性的是()。
nA. y(n)=∑x(k)B. y(n)=2x(n)+3k =-∞C. y(n)=x(n) sin(2πn +π) D. y(n)=[x(n)]2 76∞3. 序列和∑δ(k)等于()。
k =-∞A. ∞B. u(n)C. (n+1)u(n)D. 14.已知信号 f (t)的傅里叶变换为()。
A.1⎛ω ⎫- j5ω22 F ⎪e⎝2 ⎭C.1⎛ω⎫- j5ω-22 F 2⎪e⎝⎭F(ω),则 f(2t-5)的傅里叶变换为B.1⎛ω ⎫j5ωF ⎪e22⎝ 2 ⎭D.1⎛ω ⎫j5ω-F ⎪e222⎝⎭1科目代码:827科目名称:信号与系统(共5页)请考生写明题号,将答案全部答在答题纸上,答在试卷上无效5.⎰-∞∞(e -t+ t )δ(t +2)dt =( )。
A. e-2+2B. e-2-2C. e2-2D.06.已知信号 f(t)=Sa(100t),对该信号进行抽样,其奈奎斯特抽样频率 f s 为()。
A. 25B. 50C. 100D.200Hz Hz Hz Hzππππ7. 已知某系统的单位样值响应h(n)=0.5n u(-n), 则该系统是()。
A.因果稳定B.因果不稳定 C.非因果稳定D.非因果非稳定x(n)=δ(n)-1δ(n -3)8. 已知序列8,其 z 变换收敛域为()。
A. 0<z< ∞ B.> 0 C.z≥0D. 整个z平面二、填空题(每空 3 分,共 24 分)1 .对单位冲激信号δ(t)及冲激偶函数δ'(t ),⎰-∞∞δ ( t-t0 ) f ( t ) dt=,⎰-∞∞δ'( t ) f ( t-t1 )dt=。
青岛大学826电路2017到2009九套考研真题
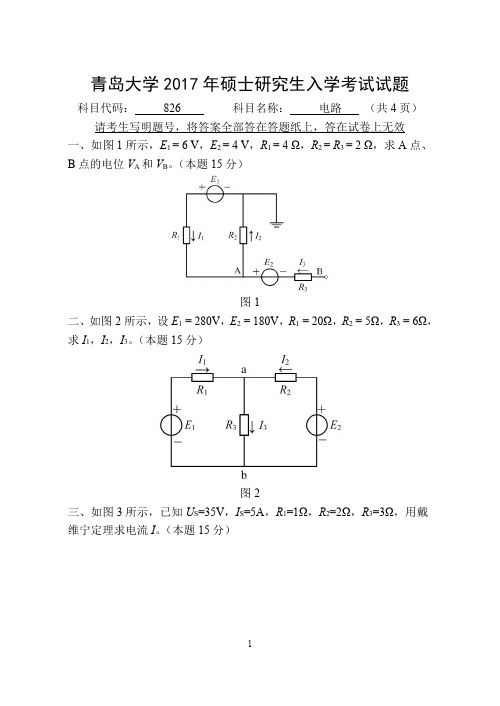
1.列写相应的基本回路矩阵 Bf(支路顺序:先连支后树支); 2.列写相应的基本割集矩阵 Qf(支路顺序:先连支后树支)。
③
2
②
1
65
3
④
①
4
图 11
3
青岛大学 2015 年硕士研究生入学考试试题
科目代码: 826 科目名称: 电路 (共 3 页) 请考生写明题号,将答案全部答在答题纸上,答在试卷上无效
+ uC −
1 C 1
L
4(t)A 1
iL
图9
十、(本大题 16 分)求图 10 中所示二端口网络的 Z 参数矩阵;当端口 2-2处接
上 R=8负载时,若 U1=18V,则 I1=?I2=?
1
+ I1 1
2
2
2 I2 +
U1
U2
4
1
2
图 10
4
2
十一、(本大题 8 分)根据图 11 所示有向图,以支路 2、4、5 为树支:
求开关 S 打开后的 iL(t),(t0)。
1:2
+
6(t)V
−
i 2 iL 2 25mH H
S (t=0)
+
4i
1 iS(t)
0.05F
−
图4
1
五、(本大题 10 分)图 5 所示电路中,L1=0.5H,L2=0.3H,M=0.2H,已知电压 表 V1 读数为 0;求电压表 V2 读数及UO 。(设电压表内阻抗无穷大,表计读 数均为有效值)
支路电流 i(t)及电流表的读数。(设 +
电流表内阻抗为 0,表计Biblioteka 数为有uS(t)−
效值)
青岛大学826电路2014--2015年考研专业课初试真题
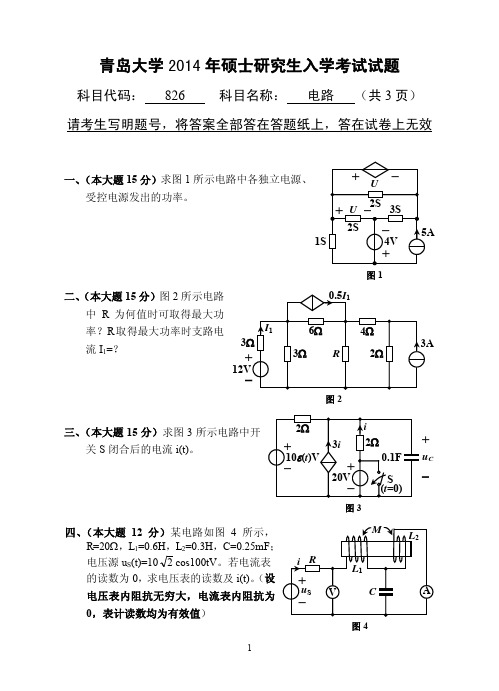
图4
1
=1000V , 五、 (本大题 16 分)某一正弦电流电路如图 5 所示,已知 U S
=100rad/s,求当可调负载阻抗 ZL 为何值时可取得最大功率 Pmax?最大功
率 Pmax=?此时电流表读数为多少?(设电流表内阻抗为 0,表计读数为有 效值) 100F iC iC 1H 5:1 A ZL
+
U1
+
N1
图 10
+
U2
N2
+
U3
1
2
3
十一、 (本大题 8 分)某电路的有向图如图 11 所示: 1.列写关联矩阵 A; 2.以支路 2、4、6 为树支,列写基本割集矩阵 Qf(支路顺序:先树支后连 支) 。 1
①
7 6
2 ② 3 5 4
③
图 11
3
青岛大学 2015 年硕士研究生入学考试试题
30
+
u
−
2 2 6
+ −
60
S (t=0) C L
8A
图2
三、 (本大题 10 分) 图 3 所示电路中 N0 为线性无源网络。当开关 S1 打开、 S2 闭合在位置 1 时,输出 uO=5V; 当开关 S1 闭合在位置 1、S2 仍闭合 在位置 1 时,输出 uO=8V;则当开 出 uO=?
uS
+ −
100
图5
六、 (本大题 15 分)图 6 所示频率 50Hz 的对 称三相电路中, 电源侧线电压为 380V, 对 A 称 Y 形负载 Z=2+j3=3.6156.31,端线 B 阻抗 Zl=1+j1。求两个功率表的读数;若 要 将 负 载 的 功 率 因 数 提 高 到 0.85 (tan=0.62 ) ,则在负载侧并联的 形电 容应为多大? C
青岛大学827固体物理2016-2017年考研专业课真题试卷

青岛大学2017年硕士研究生入学考试试题科目代码:817科目名称:固体物理(共2页)请考生写明题号,将答案全部答在答题纸上,答在试卷上无效一、简答(本题20分)1.按顺序写出下列晶体的布拉菲点阵,并写出基元中原子在晶胞中的坐标:NaCl,CsCl,Si,Na.2.共价键有什么特点?说明原子晶体的基本特征。
3.为什么晶体原胞中电子数目为奇数,相应的晶体具有金属导电性?4.什么是金属的脱出功?用你以前学过的一个实例说明脱出功的应用。
二、(本题20分)晶格常数为a 的体心立方:(1)证明密勒指数为)(hkl 的晶面族的面间距为:222hkl l k h a d ++=(2)说明密勒指数简单的晶面容易解理。
(3)若体心立方看成是等体积的硬球组成,证明其致密度π=ρ83。
三、(本题20分)惰性气体元素晶体,原子间的相互作用势⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛σ-⎪⎭⎫ ⎝⎛σε=1612r r 4)r (u ,其中σ和ε为待定常数,r 为两原子间距。
(1)说明上式中两项的物理意义;(2)证明由N 个惰性气体原子组成的晶体,总互作用势能可表示为()⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=6612122R A R A N R U σσε(3)若惰性气体元素晶体为面心立方结构,计算6A 、12A 的值(计及最近邻和次近邻原子)。
(4)证明平衡时最近邻原子间距0R 与σ之比是与晶体结构有关的常数。
四、(本题30分)用德拜模型讨论由N 个原子组成的晶体的比热问题。
(1)证明模式密度239)(ωω=ωρDN ;(2)写出晶体振动能和晶体比热的表达式;(3)讨论高低温极限下晶体比热与温度的关系。
五、(本题20分)一个有N 个自由电子的电子气系统中,能量在E E E d ~+间的电子数为()EE f E C N d d =(1)证明()23023F E N C =(2)证明绝对零度时能量在T k E B F 230-到0F E 之间的电子数()049F B E T k N N ≈'六、(本题20分)简单正交晶格在最近邻近似下,应用紧束缚法推导由原子S 态电子形成的能量表达式,并求出电子沿x k 方向的速度()x k v 表达式、画出()x k v 曲线。
武汉科技大学考研试卷及参考答案826 信号与系统-2016(B卷)

姓名: 报考专业: 准考证号码: 密封线内不要写题年攻读硕士学位研究生入学考试试题科目名称:信号与系统(□A 卷√B 卷)科目代码:姓名: 报考专业: 准考证号码: 密封线内不要写题2016年攻读硕士学位研究生入学考试试题科目名称:信号与系统(□A 卷√B 卷)科目代码:826考试时间:3小时 满分150分可使用的常用工具:□无 □计算器 √直尺 □圆规(请在使用工具前打√)注意:所有答题内容必须写在答题纸上,写在试题或草稿纸上的一律无效;考完后试题随答题纸交回。
一、选择题(共10小题,每小题4分,共40分)C AD B A B B A A D二、问答题(每题 10分,共50分)1.是线性、时不变、因果、稳定系统,理由根据定义判断。
(每个知识点2分) 2.用有限项的傅里叶级数去逼近原周期信号时所出现的一种现象,叫吉布斯现象。
特征是:(1)对于具有不连续点的函数,既使所取级数的项数无限增大,在不连续处,级数之和仍不收敛于原函数:(2)在跃变点附近的波形,总是不可避免的存在有起伏振荡,从而使跃变点附近某些点的函数值超过1而形成过冲;(3)随着级数所取项数的增多,这种起伏振荡存在的时间将缩短。
(4)随着级数所取项数的增多,其引起的过冲值则趋于约为9%的固定值。
(每个知识点2分) 3.时域样定理:为了能从采样信号中恢复原信号,必须满足两个条件: ()s f t )(t f (1)被采样的信号必须是有限频带信号,其频谱在时为零。
)(t f ||m Ω>Ω(2)采样频率或采样间隔 。
其最低允许采样频率2s m Ω≥Ω12S m mT f π≤=Ω或称为奈奎斯特采样频率,其最大允许采样间隔m s f f 2=2s m Ω=Ω称为奈奎斯特采样间隔。
12s m mT f π==Ω对带宽为40Hz 的信号进行采样,其奈奎斯特采样间隔12.5ms ,信号)(t f )21(t f 的带宽为20Hz ,其奈奎斯特采样频率为40Hz 。
上海师大《874信号与系统》考研信号与系统考研真题

上海师大《874信号与系统》考研信号与系统考研真题一、一、选择题1信号x[k]=2cos[πk/4]+sin[πk/8]-2cos[πk/2+π/6]的周期是()。
[中山大学2010研]A.8B.16C.2D.4【答案】B @@【解析】根据周期的定义T=2π/ω,cos(πk/4),sin(πk/8),cos (πk/2+π/6)的最小正周期分别为8、16、4,取最小公倍数,所以x[k]的周期为16。
2选择题序列和等于()。
[北京交通大学研]A.1B.δ[k]C.k u [k]D.(k+1)u[k]【答案】D @@【解析】由可知。
3序列和[中山大学2010研]A.4u[k]B.4C.4u[-k]D.4u[k-2]【答案】B @@【解析】由单位样值信号的定义,。
当k≠2,序列值恒为0;当k=2,序列值为4,因此4用下列差分方程描述的系统为线性系统的是()。
[西安电子科技大学研] A.y(k)+y(k-1)=2f(k)+3B.y(k)+y(k-1)y(k-2)=2f(k)C.y(k)+ky(k-2)=f(1-k)+2f(k-1)D.y(k)+2y(k-1)=2|f(k)|【答案】C @@【解析】A项,方程右边出现常数3。
B项,出现y(k-1)y(k-2)项。
D项,出现|f(k)|这些都是非线性关系。
5描述离散系统的差分方程为y(k)+y(k-1)=2f(k)+f(k-1),其中单位响应h(k)等于()。
[西安电子科技大学2013研]A.δ(k)+(-1)kε(k)B.δ(k)+ε(k)C.2δ(k)-ε(k)D.δ(k)-(-1)kε(k)【答案】A @@【解析】根据单位响应h(k)的定义,h(k)+h(k-1)=2δ(k)+δ(k-1),利用线性性质先求h(k)+h(k-1)=δ(k)时的单位响应h0(k),h0(k)=C(-1)k,h0(0)=1,因此C=1,即h0(k)=(-1)kε(k),利用线性性质得到h(k)=2h0(k)+h0(k-1)=2(-1)kε(k)+(-1)k-1ε(k-1)=2(-1)kε(k)-(-1)k[ε(k)-δ(k)]=δ(k)+(-1)kε(k)。
【青岛大学2012年考研专业课真题】信号与系统2012
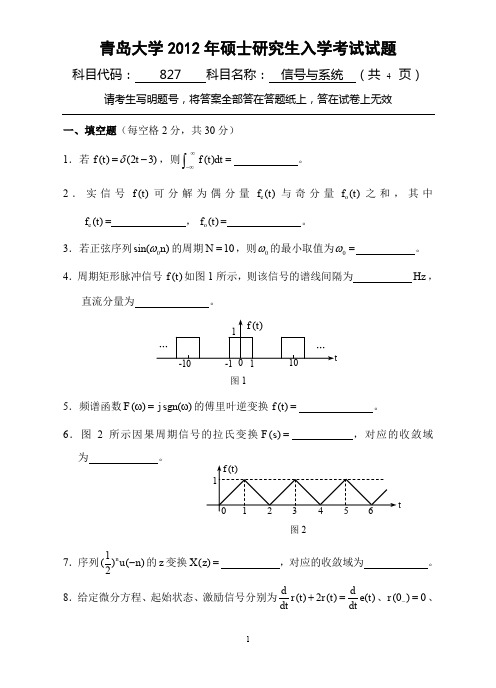
4
科目代码: 827 科目名称: 信号与系统 (共
4
页)
请考生写明题号,将答案全部答在答题纸上,答在试卷上无效
e(t ) e3t u(t ) ,则 r (0 )
。
9 .若可逆系统的单位冲激响应为 h(t ) ,其逆系统的单位冲激响应为 hI (t ) ,则
h(t ) hI (t )
。
10.图 3 所示以 f (t ) 为输入, g (t ) 为输出的对 调幅波进行相干解调的系统是 (线性/非线性) 、 的。 (时变/时不变)
f (t )
低通滤波
g (t )
cos(0t )
图3
二、 (15 分)计算图 4 所示矩形脉冲信号 h(t ) 和半波正弦脉冲信号 e(t ) 的卷积积 分 r (t ) h(t ) e(t ) ,并画出 r (t ) 的波形。
f e (t ) =
, f o (t ) =
。 。
Hz ,
3.若正弦序列 sin(0 n) 的周期 N 10 ,则 0 的最小取值为 0 4.周期矩形脉冲信号 f (t ) 如图 1 所示,则该信号的谱线间隔为 直流分量为 。
1 … -10 -1 0 1 图1 10
f (t )
…
t
5.频谱函数 F () j sgn() 的傅里叶逆变换 f (t ) 6 .图 2 所示因果周期信号的拉氏变换 F ( s) 为 。
f (t )
1 0 1 2 3
图2
。 ,对应的收敛域
4
5
6
t
1 7.序列 ( ) n u (n) 的 z 变换 X ( z ) 2
8.给定微分方程、起始状态、激励信号分别为
青岛大学信号与系统考研真题2009—2011年

(15 分)15.电路如题图 15 所示, t 0 时开关 K 处于“1”的位置而且已经达 到稳态;当 t 0 时开关 K 由“1”转向“2”。
2 K i(t) R1 1
1
+
+
4V
2V
-
-
C 1F
L 1H 4
3
R2
2
题图 15
(1)试画出开关动作后的复频域等效电路; (2)求响应电流 i(t) 在 t 0 内的表达式。
青岛大学 2009 年硕士研究生入学考试试题
科目代码: 827 科目名称: 信号与系统 (共 4 页)
请考生写明题号,将答案全部答在答题纸上,答在试卷上无效
Ⅰ、填空题(共 11 题,每空格 3 分,共 33 分)
1.对冲激偶信号 (t) , (t)dt
,
(t
t0
)
f
(t)dt
。
2.时间函数 f (t) etu(t) 的傅里叶变换 F ( )
(3) 在题图 17 所示的解调过程中,试确定 A 、1 、2 之值,使得 y(t) g(t) 。
f (t)
A
y(t )
1 1
cos(2t)
题图 17
(20 分)18.已知离散时间系统的差分方程为 y(n) 0.81y(n 2) x(n) 0.81x(n 2)
(1)求系统函数 H (z) ,画出零、极点分布图; (2)求频率响应 H (e j ) ,粗略绘出幅频响应曲线,判断系统具有何种滤波特性; (3)求系统的单位样值响应 h(n) ,画出 h(n) 的波形; (4)以使用最少数量的单位延时器为条件,画出系统的仿真框图。
u(t)
则下列说法正确的是(
)。
