绍兴市第一初级中学单元试卷
浙江绍兴市第一中学期末精选单元检测(提高,Word版 含解析)

浙江绍兴市第一中学期末精选单元检测(提高,Word 版 含解析)一、第一章 运动的描述易错题培优(难)1.一个物体做直线运动的位移—时间图象(即x t -图象)如图所示,下列说法正确的是A .物体在1s 末运动方向改变B .物体做匀速运动C .物体运动的速度大小为5m/sD .2s 末物体回到出发点【答案】BC【解析】【分析】【详解】AB .位移时间图象的斜率表示速度,根据图象可知物体一直向负方向匀速运动,故A 错误、B 正确;C .物体运动的速度大小为5m/s ,故C 正确;D .物体的出发点在5m x =的位置,2s 末在5m x =-的位置,故2s 末物体未回到出发点,故D 错误;故选BC 。
2.如图所示为某质点做直线运动时的v-t 图象图象关于图中虚线对称,则在0~t 1时间内,关于质点的运动,下列说法正确的是A .若质点能两次到达某一位置,则两次的速度都不可能为零B .若质点能三次通过某一位置,则可能三次都是加速通过该位置C .若质点能三次通过某一位置,则可能两次加速通过,一次减速通过D .若质点能两次到达某一位置,则两次到达这一位置的速度大小一定相等【答案】C【解析】【分析】【详解】AD 、分析质点运动过程可知,质点在10t 时间内能两次到达的位置有两个,分别对应质点运动速度为零的两个位置,因此A 、D 错误;BC 、如图,画出质点运动的过程图:在质点沿负方向加速运动的过程中,质点可三次通过某一位置,这时质点两次加速,一次减速;在质点沿负方向减速运动的过程中,质点可三次通过某一位置,这时质点两次减速,一次加速,故C 正确,D 错误.3.如图所示为某质点的速度-时间图象,则下列说法中正确的是( )A .在0~6s 内,质点做匀变速直线运动B .在t =12s 末,质点的加速度为-1m /s 2C .在6~10s 内,质点处于静止状态D .在4s 末,质点运动方向改变 【答案】B【解析】在0~4s 内,质点的加速度为64v a t ∆==∆ =1.5(m/s 2),在4-6s 内质点的加速度为:4-62v a t ∆==∆=-1(m/s 2),两段时间内的加速度不同,所以在0~6s 内,质点做非匀变速直线运动,故A 错误;在t=12s 末,质点的加速度为a=044v a t ∆-==∆=-1(m/s 2),故B 正确.在6s ~10s 内,质点以4m/s 的速度做匀速运动,故C 错误;在0-14s 内,质点的速度都为正,一直沿正方向运动,故在4s 末速度方向没有改变,故D 错误;故选B.点睛:本题考查学生对v-t 图象的认识,记住图象的斜率表示加速度,图象与时间轴围成的面积表示这段时间内物体通过的位移.4.甲、乙两人同时同地出发骑自行车做直线运动,前1小时内的位移—时间图象如图所示,下列表述正确的是( )A.0.2~0.5小时内,甲的加速度比乙的大B.0.2~0.5小时内,甲的速度比乙的大C.0.6~0.8小时内,甲的位移比乙的小D.0.8小时内,甲、乙骑行的路程相等【答案】B【解析】A、由图知,0.2-0.5小时内甲乙都做匀速直线运动,加速度均为零,故A错误;B、s t 图象的斜率表示速度,甲的斜率大,则甲的速度比乙的大,故B正确;C、物体的位移等于s的变化量.则知0.6-0.8小时内,甲的位移比乙的大,故C错误;D、0-0.6小时内,甲的位移比乙的大,0.6-0.8小时内,甲的位移比乙的大,所以0.8小时内,甲的路程比乙的大,故D错误.点睛:该题考查了对位移--时间图象的理解和应用,要掌握:在位移-时间图象中,图象的斜率表示质点运动的速度的大小,纵坐标的变化量表示位移.5.下列说法中正确的是()A.研究短跑运动员的起跑动作时,可将运动员看做质点B.研究汽车在上坡时有无翻倒的危险时,可将汽车看做质点C.“两岸猿声啼不住,轻舟已过万重山”是以“万重山”为参考系的D.升国旗时,观察到国旗冉冉升起,观察者是以“国旗”为参考系的【答案】C【解析】【分析】【详解】A.研究短跑运动员的起跑动作时,运动员看成质点,否则的话就没有人的动作可言了,A 错误;B.研究汽车在上坡时有无翻倒的危险时,汽车的大小和形状不能忽略,故不能看作质点,B错误;C.“两岸猿声啼不住,轻舟已过万重山“是描述轻舟相对于“万重山”在运动,是以“万重山”为参考系的,C正确;D.升国旗时,观察到国旗冉冉升起,观察者是以大地为参考系的,D错误。
浙江省绍兴市第一初级中学 九上 Unit9 单元测试

绍初九年级Unit9练习卷初三英语试题一、完型It was a Sunday and the heavy storm had lasted all night. The morning after the storm, though, was beautiful. My father realized it was a good day for 1 and invited my sister and me to go with him.On the road to the harbor(码头)we could see that the harbor wasn’t broken badly by the storm. After all,it was 2 by the arms of a bay(海湾) that had only one tiny channel(通道)to the sea. As we got on the board, we 3 two big objects on the water, not far from us.After getting 4 to them, we saw it was a mother whale with her baby. We couldn’t believe it——there have never been any whales here before. The 5 must have driven them across the ocean into the bay, in which the water was so badly polluted that 6 could survive.The little baby whale was stuck(卡住)and could not move. The mother swam under the water and came up 7 , making big whirlpools and waves. ” She’s trying to help her baby, but on the 8 side, ”my father said. Father moved our boat to the other side and pushed it softly several times, the baby turned over and swam up right beside its mum. They tried their best to 9 but missed the channel and started swimming in the wrong 10 . We hurried up to the whales and tried to 11 them towards the bay channel. Slowly, they followed us, some-times rising from the water right beside us to breathe, and to give us a 12 look with those huge eyes. As soon as they met their first part of clean water coming straight from the sea, the mum gave 13 a wave with her tail and then they swam off into the deep ocean.It felt like only a few minutes, 14 we were with those wonderful animals for almost an hour and a half. That was the simple and lasting 15 of the day. Even now, forty years later, I still look back fondly to that golden day at sea.1. A. shopping B. fishing C. hiking D. swimming2. A. protected B. held C. touched D. kept3. A. picked B. got C. noted D. noticed4. A. farther B. deeper C. closer D. friendlier5. A. rain B. clouds C. storm D. sea6. A. anything B. nothing C. everything D. something7. A. suddenly B. slowly C. carefully D. quietly8. A. wrong B. right C. one D. other9. A. run B. breathe C. jump D. escape10.A. style B. area C. direction D. water11.A. follow B. lead C. keep D. catch12.A. sad B. happy C. wonderful D. trustful13.A. them B. us C. me D. it14.A. but B. if C. while D. because15.A. job B. work C. nature D. beauty二、阅读理解Jack Johnson is one of the most popular singer-song writers in the world.He was born on May 18,1975 in Hawaii. Being the son of a famous surfer,Jack naturally has an interest in surfing. Most of his life lessons were learned in the water.At the age of 17,Jack entered the finals of the Pineline Masters-the world’s most famous surfing competition.Everyone thought Jack would become a professional surfer like his father.Unluckily,one month later,he had a deadly accident while surfing,and was seriously hurt.Life is like a revolving door.When it closes,it also opens.Jack started to practice playing the guitar and writing songs when he was staying in hospital.At first,his father thought Jack only did it for fun,but soon he was surprised at the great progress his son had made.When studying in the university,Jack didn’t stop practicing his guitar skills.He played the guitar for school parties.He wrote songs and sang for his teachers and friends.They liked his songs.His first music album Brushfire Fairytales came out in 2001.It was a great success.His second album,On and On,was much like his first one.They were filled with sweet,easy-going songs that everybody liked listening to.Later Jack had lots of concerts in and out of America.He became popular all over the world.Jack had five albums by 2010and more than 15million CDs of them were sold.His music doesn’t fit into any of the popular music styles like pop,R&B or hip-hop.It is more like folk music,which is played with a guitar and beautiful voice.When listening to his songs,you feel like lying on the beach enjoying the warm sunshine.Jack is a talent,though he himself says he is only a surfer who loves music.In his songs we can find his secret of success:Whatever happens in our lives,we have to accept it and do the best we can.1. Jack started to write songs .A, while he was staying in hospitalB: when he had concerts out of AmericaC. after his second album came outD, after he played the guitar at the school party2. What is-the secret of Jacks success?A. He was born in HawaiiB. His father was very famousC. He wrote many songs for his teachers and friends.D. He always faced difficulties bravely and tried his best.3. What's the best title of the passage?A. A Famous WriterB. A great surferC. A Guitar PlayerD. Surfing in the Music4. Which is the writer's opinion?A. When studying in the university, Jack didn't stop practicing the guitar.B. His first music album was a great success.C. He became popular all over the worldD. When listening to his songs, you feel like lying on the beach enjoying the warm sunshine三、用方框中所给词的正确形式填空1. We will never forget the of West Lake2. She cared for sick and soldiers during the war3. Abing had sad and experiences in his lifetime.4. I became a teacher because I books and children to politics.5. LiNa is a great tennis player who from Hubei, China.四、根据句意及中文完成句子1.2.3.4.5.五、语法填空六、作文针对运用微信投票越来越流行的现象,英语课上同学们就是否愿意为别人投票选举这一话题展开了讨论。
浙江省绍兴市第一初级中学八年级数学上册第一单元试卷(无答案)$825374
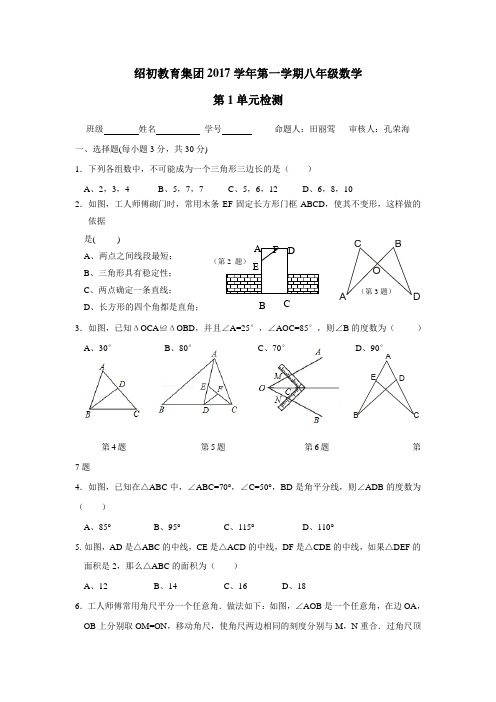
ABCDEABCDO(第3题)绍初教育集团2017学年第一学期八年级数学第1单元检测班级 姓名 学号 命题人:田丽莺 审核人:孔荣海 一、选择题(每小题3分,共30分)1.下列各组数中,不可能成为一个三角形三边长的是( ) A 、2,3,4B 、5,7,7C 、5,6,12D 、6,8,102.如图,工人师傅砌门时,常用木条EF 固定长方形门框ABCD ,使其不变形,这样做的依据 是( )A 、两点之间线段最短;B 、三角形具有稳定性;C 、两点确定一条直线;D 、长方形的四个角都是直角;3.如图,已知ΔOCA ≌ΔOBD ,并且∠A=25°,∠AOC=85°,则∠B 的度数为( ) A 、30° B 、80° C 、70° D 、90°第4题 第5题 第6题 第7题4.如图,已知在△ABC 中,∠ABC=70°,∠C=50°,BD 是角平分线,则∠ADB 的度数为( ) A 、85°B 、95°C 、115°D 、110°5. 如图,AD 是△ABC 的中线,CE 是△ACD 的中线,DF 是△CDE 的中线,如果△DEF 的 面积是2,那么△ABC 的面积为( ) A 、12B 、14C 、16D 、186.工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB 是一个任意角,在边OA ,OB 上分别取OM=ON ,移动角尺,使角尺两边相同的刻度分别与M ,N 重合.过角尺顶B C点C 的射线OC 即是∠AOB 的平分线.这种做法的依据是( )A 、边角边B 、 角边角C 、边边边D 、边边角7.如图,点D 、E 分别在AC 、AB 上,已知AB=AC ,若添加下列条件,不能说明ΔABD ≌ΔACE 的是( )A 、∠B=∠CB 、AD=AEC 、∠BDC=∠CEBD 、BD=CE8.对于命题“若a 2>b 2,则a >b”,下面四组a ,b 的值中,能说明这个命题是假命题的是( ) A 、a=3,b=2 B 、a=﹣3,b=2C 、a=3,b=﹣1D 、a=﹣1,b=39.到一个三角形三个顶点距离相等的点是这个三角形( )的交点. A 、三条内角平分线 B 、三条高 C 、三条中线 D 、三边的垂直平分线 10.如图,∠A=120°,且∠1=∠2=∠3和∠4=∠5=∠6,则∠BDE=( )A 、60°B 、70°C 、80°D 、不能确定,具体由三角形的形状确定 二、填空题(每空3分,共30分)11.在△ABC 中,若∠A -∠B=∠C ,则此三角形是________三角形;若C B A ∠=∠=∠2,由此三角形是_______三角形.(填“锐角”“直角”或“钝角”) 12.在△ABC 中,AB =7,BC =2,且三角形的周长是偶数,则AC = . 13.三角形三个外角的比为2:3:4,则最小的内角是________度.14. 小明把一副含45°,30°的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于 . .第14题 第15题 第16题15.如图,已知在△ABC 中,CD 是AB 边上的高线,BE 平分∠ABC ,交CD 于点E ,BC=5,DE=2,则△BCE 的面积等于 .16.如图,在△ABC 中, AB 的中垂线交BC 于点D ,AC 的中垂线交BC 于点E ; (1)若BC=8cm ,则△ADE 的周长为 cm. (2)若∠BAC=100°,则∠DAE= .(第17 题)(第10 题)17.如图,方格纸中△DEF 的三个顶点分别在小正方形的顶点上,像这样的三个顶点都在格点上的三角形叫格点三角形,则 图中与△DEF 全等的格点三角形还有 个. 18. 如图,△ABC 中,BC=a ,AC=b ,AB=c (b <c <a ),BC 的垂直平分线DG 交∠BAC 的角平分线AD 于点D ,DE ⊥AB 于E ,DF ⊥AC 于F ,则下列结论一定成立的是 . ①BE=CF ②CF=c ﹣b ③BE=(a ﹣b ) ④AE=(b+c ) 三、解答题19.(6分)如图,在△ABC 中, ∠BAC 是钝角,按要求完成下列作图 (要求保留作图痕迹,并写出结论):①△ABC 中∠ABC 的角平分线;(尺规作图) ②BC 边上的中线;(尺规作图) ③AB 边上的高.(作图工具不限)20.(8分) 如图,在△ABC 中,CE 是AB 边上的高,AD 平分∠BAC ,交BC 于点D ,∠ADB=100°,∠ACB=70°,求∠BAC ,∠BCE 的度数。
浙江省绍兴市第一初级中学浙教版七年级数学下册第三单元练习

a ab b 图1 图2 (第10题绍初教育集团2017学年第二学期七年级数学第三单元练习卷班级 姓名 学号 命题人:冯菊美 审核人:王颖一、选择题1、下列计算正确的是 ( )(A )3x -2x =1 (B )3x+2x=5x 2 (C) 3x ·2x=6x (D) 3x -2x=x2、如图,阴影部分的面积是( )A .xy 27B .xy 29C .xy 4D .xy 23、在下列的计算中正确的是( ) A 2x +3y =5xy ;B (a +2)(a -2)=a 2+4;C a 2•ab =a 3b ;D (x -3)2=x 2+6x +94、下列运算中结果正确的是( )A .633·x x x =;B .422523x x x =+;C .532)(x x =; D .222()x y x y +=+. 5、已知,5,3==b a x x 则=+b a x 23( )(A )52 (B )34 (C )675 (D )2256、如果(x+p)(x+1)的乘积中不含x 的项,那么p 等于( )A 1B -1C 0D -27、如果整式x 2 + mx +32 恰好是一个整式的平方,那么常数m 的值是() A 、6 B 、3 C 、±3 D 、±68、若两个数的和为3,积为—1,则这两个数的平方和为() A 、7 B 、8 C 、9 D 、119、如图,边长为a 的大正方形中一个边长为b 的小正方形,小明将图(1)的阴影部分拼成了一个矩形,如图(2)。
这一过程可以验证( )A 、a 2+b 2-2ab=(a-b)2 ;B 、a 2+b 2+2ab=(a+b)2 ;C 、2a 2-3ab+b 2=(2a-b)(a-b) ;D 、a 2-b 2=(a+b) (a-b)10、如果a ,b ,c 满足a 2+2b 2+2c 2-2ab-2bc-6c+9=0,则abc 等于( ) A.9 B.27 C.54 D.81二、填空题:11、计算:3a + 2a = ______;3a ·2a =______; a 3·a 2 =______;(—3ab 2 )2 =______12、计算:(2x + y )(2x — y )=_______;(—2a —1)2= __________;()()=-⋅-3245a a第2题图13、方程()()()()41812523=-+--+x x x x 的解是_______。
浙江省绍兴市第一初级中学八年级上学期10月月考科学试题

绍初教育集团2023学年第一学期八年级科学第1章检测卷班级________学号________姓名________ 出卷:初二科学备课组注意:本卷总分是160分,g取10N/Kg 。
一、选择题(每题3分,共计45分)1. 下列物质依次为悬浊液、乳浊液、溶液的一组是( )A. 奶、洁净的空气、澄石灰水 B 矿泉水、自来水、汽油和水的混合物C. 新鲜的血液、肥皂水、碘洒D. 钡餐的混合液体、泥浆、汽水2. 下列实验操作错误的是( )A.取用固体药品B.倾倒液体药品C. 过滤泥浆水D. 蒸发食盐水3.生活中的下列现象,不能说明气体溶解度随温度升高而减小的是( )A、烧开水时,沸腾前有气泡冒出B. 阳光充足时,盛满水的鱼缸上有小气泡C. 夏天,啤酒瓶容易爆裂D.开启啤酒瓶盖,有大量气泡选出4. 河水净化制自来水的主要步骤如下图所示,有关说法错误的是( )A. 步骤I可除去难溶性杂质B. X试剂可以是活性炭C. 步骤Ⅲ可杀菌消毒D. 步骤Ⅲ是物理变化5.“五水共治,治污为先”是我省提出改善生态环境的一项重要政策。
为防止水体污染,下列措施中不可行的是( )A. 不任意排放工业污水B. 牲畜粪便集中处理后再施用C. 生活污水经净化处理后再排放D. 禁使用农药和化肥6. 如图是我们学过的蒸馏装置,关于蒸馏实验说法不正确的是( )A. 蒸馏是我们所学的净化水的最彻底方式B. 图中冷凝水的流动方向是A→BC. 温度计应该放在蒸馏烧瓶的支管口,测气体温度D. 烧瓶中碎瓷片的作用是防止液体暴沸7. 如图所示为蒸发氯化钠溶液的过程,其中①→②→③为恒温蒸发过程,③→④为升温蒸发过程,②溶液恰好为饱和状态,分析实验过程,可以作出的正确判断是( )A. 在①→②过程中,氯化钠的质量分数保持不变B. 在②→④过程中,氯化钠的溶解度不断增大C. 在③→④过程中,求的质量分数不断增为D. 在②→④过程中,氯化钠的质量分数先不变后增大8. 以下各图是关于浮力知识的应用实例,下列说法正确的是( )A.轮船能漂浮在水面,是因为船体的体积较大B.气球内充入了二氧化碳等密度大于空气的气体,从而上浮C.若左右两图为同一支密度计,则左容器中的密度计所受浮力较大D.浸没在水中的潜水艇,若从淡水水域进入海水水域,所受的浮力会变太9.如图所示,将一小球轻轻放入装满水的溢水杯中,待(静止时台秤示数变化情况是( )A. 变大B.不变C.变小D. 先变大后不变10.‘将一个乒乓球放入倒置的饮料瓶中,然后向瓶内注入水将乒乓球浸没,如图所示,乒兵球保持静止状态则乒乓球( )A. 仍受水的浮力B. 不受水的浮力,也不受术对它的压力C. 不受水的浮力,但受水对它的压力D. 无法判断11.“生命吸管(Lifestraw)”是一种快速获取野外饮用水的吸管装置。
浙江省绍兴市第一初级中学浙教版八年级科学下册第四章《植物与土壤》测验

八下科学第四单元练习卷姓名班级学号一、选择题:1.岱庙里的千年古树,有的树心已经朽烂,变成空心洞。
可是,这样的古树还是照样枝繁叶茂。
由此推断,朽烂掉的“树心”主要是古树的()A.全部韧皮部B.部分韧皮部C.全部木质部D.部分木质部土壤浸出液2.如右图所示,土壤浸出液蒸发后的残留物是( )(A)小细砂(B)蛋白质(C)无机盐(D)金属3、世界上许多国家成立了蚯蚓养殖厂,并把蚯蚓养殖厂称为“环境净化装置”。
蚯蚓能用来净化环境的主要原因是()A.能在湿润土壤的深层生活B.身体柔软,能在垃圾中钻洞C.身体分节,运动灵活自如D.能分解枯叶、朽根等中的有机物4、“滩涂能种菜,海水能灌溉。
”这是美国著名的未来学家阿尔曼托夫勒的预言,如今在盐城沿海滩涂上已逐渐变成现实。
盐碱地上的植物能强烈的从土壤中吸收水分的主要原因是()A.根毛细胞吸胀作用大B.根毛细胞液浓度大C.根毛细胞呼吸旺盛D.叶肉细胞蒸腾作用强5.小明在探究植物根系分布与哪些因素有关时的,提出了下列假设,你认为哪个假设最不适宜()(A)植物根系分布可能与土壤结构有关(B)植物根系分布可能与光照强度有关(C)植物根系分布可能与通气状况有关(D)植物根系分布可能与地下水位高低有关6.根尖吸收水分的主要部位在()(A)根冠(B)根毛区(C)分生组织(D)侧根7.小明一连几天用妈妈清洗过咸水鱼的水浇一株花卉,不久后发现该花卉枯萎死亡其原因可能是()(A)营养过多(B)因阳光过强(C)因细胞失水而死(D)水分蒸发过多8.杭州市乔司的甘蔗是杭州的土特产之一,如果要使甘蔗丰收,平时应该多施()A.钾肥B.氮肥C.磷肥D.钙肥9.某一植物植株矮小,叶色发黄,则缺()(A)氮元素(B)磷元素(C)钾元素(D)硼元素10.有人把人行道上的树木用铁丝扎上晾衣,结果导致树木死亡,其原因是()(A)树木因缺氧而死(B)树木不能输送水和无机盐(C)树木输送有机物的功能被破坏(D)树木不能正常进行光合作用11、上壤中水分进入到植物体内,主要是由哪个器官和组织完成运输的()(A)叶,营养组织(B)茎,分生组织(C)果实,营养组织(D)根,输导组织12.小宇为了探究叶片中的输导组织功能,把芹菜叶片浸在红墨水溶液中30分钟后,用眼睛仔细观察,发现呈红色部分的是( ) (A)只有叶的边缘(B)整个叶片(C)叶脉(D)只有叶尖13.植物的根生长在土壤里,不能进行光合作用制造有机物,根不能进行光合作用的根本原因是()A.根细胞不能吸收水分B.根细胞没有叶绿体C.根细胞生活在土壤里照不到阳光D.根细胞吸收不到二氧化碳14.小明从资料中了解到,清晨割橡胶产量高,主要的理由可能是()(A)清晨植物的呼吸作用最弱,但水分最多,膨压最大(B)清晨没有进行光合作用,植物中的水分多,膨压最大(C)清晨植物的根吸收的水分最多,膨压最大(D)清晨植物蒸腾作用最弱,细胞中水分最多,膨压最大15.以下哪个结构与植物体内输送有机物密切有关()(A)导管(B)叶脉(C)根毛(D)筛管16.收割小麦的时候,甲地的农民用镰刀或机械割麦,乙地的农民则用双手把麦株连根拔起,带回到麦场脱粒,比较这两种收割方式,说法有错误的是( )(A)收割小麦时,机械操作比手工效率更高(B)割麦比拔麦更能保持土壤中的肥力(C)拔麦将会造成小麦的减产,因此割麦比拔麦好(D)拔麦可同时完成收获和灭茬两道工序,应该提倡17.中午时分,强光下植物的光合作用能力会下降,原因是( )(A)温度过高,植物生命活动下降(B)光过强,导致光合作用不能进行(C)蒸腾作用强,导致气孔关闭(D)呼吸作用过强,影响了光合作用18.小明为观察叶细胞吸收水分后的变化,在一株植物上取相同的两片叶,把甲叶片放在阳光中曝晒10分钟,乙叶片放在清水中浸泡10分钟,然后分别做成临时装片,放在显微镜下观察,可以发现其中细胞内变化最大的结构是( )(A)细胞核(B)细胞壁(C)液泡(D)叶绿体19.甲、乙两盆生长状况完全相同的菜苗,不浇水等菜苗萎蔫时,向甲盆泥土内浇足水,向乙盆的菜叶上喷水,但不浇湿土壤。
绍兴市绍兴一初一年级数学下册第四单元《100以内数的认识》单元测试卷(含答案解析)

绍兴市绍兴一初一年级数学下册第四单元《100以内数的认识》单元测试卷(含答案解析)一、选择题1.十位上的数比个位上的数小2,下面哪个数不符合要求?()A. 24B. 35C. 532.在1—100中,个位上是9的两位数有几个? ()A. 1个B. 9个C. 10个3.一个两位数,个位上是3,十位上的数字比个位上的大5,这个数是()A. 53B. 83C. 384.从23到28一共有()个数。
A. 6B. 7C. 55.一个两位数,十位上的数字是最大的一位数,个位上的数字比十位上的数字少3,这个数是( )人。
A. 69B. 93C. 966.75和80中间有()个数。
A. 5B. 4C. 67.把5个一和4个十合起来是()。
A. 45B. 54C. 98.1—100中,个位上是2的数有()个。
A. 9B. 10C. 119.用5个“ ”摆在数位上,一共可以摆出()个不同的数。
A. 5B. 6C. 710.在两位数中,整十的数一共有()个。
A. 8B. 9C. 1011.一个两位数,从右边数第一位上是5,第二位上是6,这个数是()。
A. 65B. 56C. 5512.100个一是()。
A. 10B. 100C. 1000二、填空题13.________个十和________个一合起来是________。
14.________里面有________个十和________个一,再添上1是________。
15.82是由________个十和________个一组成的,4个一和6个十合起来是________。
16.一个一个的数,与59相邻的两个数是________和________。
17.9个一和1个十是________。
18.我是5,在75这个数里面,我表示________;在53这个数里面,我表示________。
19.在50、35、54、85、30和100这几个数中,最大的数是________,个位是5的数有________;在这些数中________比50大一些,将这几个数按从大到小的顺序排列:________20.数一数,写一写。
浙江省绍兴市第一初级中学 九上 Unit9 单元测试

绍初九年级Unit9练习卷初三英语试题一、完型It was a Sunday and the heavy storm had lasted all night. The morning after the storm, though, was beautiful. My father realized it was a good day for 1 and invited my sister and me to go with him.On the road to the harbor(码头)we could see that the harbor wasn’t broken badly by the storm. After all,it was 2 by the arms of a bay(海湾) that had only one tiny channel(通道)to the sea. As we got on the board, we 3 two big objects on the water, not far from us.After getting 4 to them, we saw it was a mother whale with her baby. We couldn’t believe it ——there have never been any whales here before. The 5 must have driven them across the ocean into the bay, in which the water was so badly polluted that 6 could survive.The little baby whale was stuck(卡住)and could not move. The mother swam under the water and came up 7 , making big whirlpools and waves. ” She’s trying to help her baby, but on the 8 side, ”my father said. Father moved our boat to the other side and pushed it softly several times, the baby turned over and swam up right beside its mum. They tried their best to 9 but missed the channel and started swimming in the wrong 10 . We hurried up to the whales and tried to 11 them towards the bay channel. Slowly, they followed us, some-times rising from the water right beside us to breathe, and to give us a 12 look with those huge eyes. As soon as they met their first part of clean water coming straight from the sea, the mum gave 13 a wave with her tail and then they swam off into the deep ocean.It felt like only a few minutes, 14 we were with those wonderful animals for almost an hour and a half. That was the simple and lasting 15 of the day. Even now, forty years later, I still look back fondly to that golden day at sea.1. A. shopping B. fishing C. hiking D. swimming2. A. protected B. held C. touched D. kept3. A. picked B. got C. noted D. noticed4. A. farther B. deeper C. closer D. friendlier5. A. rain B. clouds C. storm D. sea6. A. anything B. nothing C. everything D. something7. A. suddenly B. slowly C. carefully D. quietly8. A. wrong B. right C. one D. other9. A. run B. breathe C. jump D. escape10.A. style B. area C. direction D. water11.A. follow B. lead C. keep D. catch12.A. sad B. happy C. wonderful D. trustful13.A. them B. us C. me D. it14.A. but B. if C. while D. because15.A. job B. work C. nature D. beauty二、阅读理解Jack Johnson is one of the most popular singer-song writers in the world.He was born on May 18,1975 in Hawaii. Being the son of a famous surfer,Jack naturally has an interest in surfing. Most of his life lessons were learned in the water.At the age of 17,Jack entered the finals of the Pineline Masters-the world’s most famous surfing competition.Everyone thought Jack would become a professional surfer like his father.Unluckily,one month later,he had a deadly accident while surfing,and was seriously hurt.Life is like a revolving door.When it closes,it also opens.Jack started to practice playing the guitar and writing songs when he was staying in hospital.At first,his father thought Jack only did it for fun,but soon he was surprised at the great progress his son had made.When studying in the university,Jack didn’t stop practicing his guitar skills.He played the guitar for school parties.He wrote songs and sang for his teachers and friends.They liked his songs.His first music album Brushfire Fairytales came out in 2001.It was a great success.His second album,On and On,was much like his firstone.They were filled with sweet,easy-going songs that everybody liked listening to.Later Jack had lots of concerts in and out of America.He became popular all over the world.Jack had five albums by 2010and more than 15million CDs of them were sold.His music doesn’t fit into any of the popular music styles like pop,R&B or hip-hop.It is more like folk music,which is played with a guitar and beautiful voice.When listening to his songs,you feel like lying on the beach enjoying the warm sunshine.Jack is a talent,though he himself says he is only a surfer who loves music.In his songs we can find his secret of success:Whatever happens in our lives,we have to accept it and do the best we can.1. Jack started to write songs .A, while he was staying in hospitalB: when he had concerts out of AmericaC. after his second album came outD, after he played the guitar at the school party2. What is-the secret of Jacks success?A. He was born in HawaiiB. His father was very famousC. He wrote many songs for his teachers and friends.D. He always faced difficulties bravely and tried his best.3. What's the best title of the passage?A. A Famous WriterB. A great surferC. A Guitar PlayerD. Surfing in the Music4. Which is the writer's opinion?A. When studying in the university, Jack didn't stop practicing the guitar.B. His first music album was a great success.C. He became popular all over the worldD. When listening to his songs, you feel like lying on the beach enjoying the warm sunshine三、用方框中所给词的正确形式填空1. We will never forget the of West Lake2. She cared for sick and soldiers during the war3. Abing had sad and experiences in his lifetime.4. I became a teacher because I books and children to politics.5. LiNa is a great tennis player who from Hubei, China.四、根据句意及中文完成句子1.Most young students like (电子的)books better than paper books2.Yesterday her sad looks (反映)the thought passing through her mind.3. Carmen likes cooking. In her_(空余的)time she reads books on cooking4.Mary has (掌握)the language.5.I (感觉到)a strong sadness and pain while listening to Erquan Yingyue yesterday五、语法填空prefer beautiful wound pain come六、作文针对运用微信投票越来越流行的现象,英语课上同学们就是否愿意为别人投票选举这一话题展开了讨论。
浙江省绍兴市第一初级中学浙教版七年级数学下册第三单元测试

绍初教育集团2017学年第二学期七年级数学第三单元测试卷班级 姓名 学号 命题人:冯菊美 审核人:王颖一、选择题(每小题3分,总计30分)1.计算-2x 2·(-x )3的结果是( )A .2x 5B .2x 6C .-2x 6D .-2x 52. 为了用平方差公式计算(2a -3b +1)(2a+3b -1),下列变形正确的是( ).A. [2a −(3b -1)]2B.[(2a -3b)+1][(2a -3b)-1]C.[2a -(3b -1)][2a +(3b -1)]D.[2a −(3b −1)]23.下列计算正确的是 A .-1-32a a a ÷= B .0103()= C .532)(a a = D . -21124=() 4.科学家在实验中测出某微生物约为0.0000035米,将0.0000035用科学记数法表示为( ) A ﹒3.5×10-6 B ﹒3.5×106 C ﹒3.5×10-5 D ﹒35×10-5 5.若实数a 、b 满足a+b=5,a 2+b 2=13,则ab 的值是( )A .-2B .2C .-6D .66.如图中,利用面积的等量关系验证的公式是( )A. a 2﹣b 2=(a+b )(a ﹣b )B. (a ﹣b )2=a 2﹣2ab+b 2C. (a+2b )(a ﹣b )=a 2+ab ﹣2b 2D. (a+b )2=a 2+2ab+b 27.9.已知 ,则 的值是( ) A. 5 B. 6 C. 8 D. 98.如图,长方形的长为a,宽为b,横向阴影部分为长方形,另一阴影部分为平行四边形,它们的宽都为c,则空白部分的面积是( ) 结果为2的式子是 ( )A. B.C. D9.如果a ,b ,c 满足a 2+2b 2+2c 2+2ab+2bc-16c+64=0,则(a-b)c 等于( ) A.8 B.16 C.128 D.8110.已知2225b Nab a +-是一个多项式的平方,则N 等于 ( )A 、5B 、±5C 、±10D 、10二、填空题(每小题4分,总计24分)11.计算:=__________________________)2(2=-y x 12.若5m =2,5n =3,则53m -2n +1=_______.()()=-⋅-3243a a _______ 13.(2a ﹣b )(-2a ﹣b )= ______ ._____________)2)(2(=--+y x y x 14.若x 2+y 2=4,xy=﹣2,则(x+y)2=___________.x ﹣y=_______15.若,,则的值为______. 则221x x +=_______,441x x +=________ 16.若三、解答题(总计46分)17.(4分)计算:2-+11()3--×(3-2)0-9+2017(1)-﹒18.(4分)解方程 81)9)(9()3(2)5(322=-+-+-+x x x x0152=--x x19.(4分)先化简,再求值 (2a +b )2—(a —b )(a + b )—3(a —2b )(a + 2b ),其中a =21,b = —220.(6分)已知多项式x 2+ax +b 与x 2-2x -3的乘积中不含x 3与x 2项,则a ,b 的值.21.(6分)小明与小亮在做游戏,两人各报一个整式,小明报的整式作被除式,小亮报的整式作除式,要求商式必须为2xy ﹒若小明报的是x 3y -2xy 2,小亮应报什么整式?若小亮也报x 3y -2xy 2,那么小明能报一个整式吗?说说你的理由﹒22.(6分)观察下列关于自然数的等式:22﹣9×12=-5 ①52﹣9×22=-11 ②82﹣9×32=-17 ③…根据上述规律,解决下列问题:(1)完成第四个等式:112﹣9×_______=___________.(2)根据上面的规律,写出你猜想的第n 个等式(等含n 的等式表示),并验证其正确性.23.(8分)一张如图1的长方形铁皮,四个角都剪去边长为30cm 的正方形,再将四周折起,做成一个有底无盖的铁盒如图2,铁盒底面长方形的长为4a (cm ),宽为3a (cm ),这个无盖铁盒的各个面的面积之和称为铁盒的全面积.(1)请用含a 的代数式表示图1中原长方形铁皮的面积.(2)若要在铁盒的各个面漆上某种油漆,每元钱可漆的面积为50a (cm 2),则油漆这个铁盒需要多少钱(用含a 的代数式表示)?(3)是否存在一个正整数a ,使得铁盒的全面积是底面积的正整数倍?若存在,请求出这个a 的值;若不存在,请说明理由.24.(8分)如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”﹒如:4=22-02;12=42-22;20=62-42,因此4,12,20这三个数都是神秘数.(1)28和2016这两个数是神秘数吗?为什么?(2)设两个连续偶数为2k+2和2k(其中k取非负整数),由这两个连续偶数构造的神秘数是4的奇数倍吗?为什么?(3)两个连续奇数的平方差(k取正数)是神秘数吗?为什么?。
绍兴市绍兴一初九年级数学上册第一单元《一元二次方程》测试卷(含答案解析)

一、选择题1.欧几里得在《几何原本》中,记载了用图解法解方程22x ax b +=的方法,类似地可以用折纸的方法求方程210x x +-=的一个正根,如图,裁一张边长为1的正方形的纸片ABCD ,先折出BC 的中点E ,再折出线段AE ,然后通过折叠使EB 落在线段EA 上,折出点B 的新位置F ,因而EF EB =,类似地,在AB 上折出点M 使AMAF =,表示方程210x x +-=的一个正根的线段是( )A .线段BMB .线段AMC .线段AED .线段EM 2.一面足够长的墙,用总长为30米的木栅栏(图中的虚线)围一个矩形场地ABCD ,中间用栅栏隔成同样三块,若要围成的矩形面积为54平方米,设垂直于墙的边长为x 米,则x 的值为( )A .3B .4C .3或5D .3或4.5 3.小刚在解关于x 的方程20(a 0)++=≠ax bx c 时,只抄对了1a =,4b =,解出其中一个根是1x =-.他核对时发现所抄的c 比原方程的c 值小2.则原方程的根的情况是( )A .不存在实数根B .有两个不相等的实数根C .有一个根是xD .有两个相等的实数根 4.方程()55x x x +=+的根为( )A .15=x ,25x =-B .11x =,25x =-C .0x =D .125x x ==-5.如图,在矩形ABCD 中,AB =a (a <2),BC =2.以点D 为圆心,CD 的长为半径画弧,交AD 于点E ,交BD 于点F .下列哪条线段的长度是方程2240x ax +-=的一个根( )A .线段AE 的长B .线段BF 的长C .线段BD 的长D .线段DF 的长 6.一元二次方程20x x -=的根是( )A .10x =,21x =B .11x =,21x =-C .10x =,21x =-D .121x x ==7.关于x 的方程2mx 0x +=的一个根是1-,则m 的值为( ) A .1 B .0C .1-D .1或0 8.关于x 的方程()---=2a 3x 4x 10有两个不相等的实数根,则a 的取值范围是( )A .1a ≥-且3a ≠B .1a >-且3a ≠C .1a ≥-D .1a >- 9.已知a 、b 、m 、n 为互不相等的实数,且(a +m )( a +n )=2,(b +m )( b +n )=2,则ab ﹣mn的值为( )A .4B .1C .﹣2D .﹣110.如图,BD 为矩形ABCD 的对角线,将△BCD 沿BD 翻折得到BC D '△,BC '与边AD 交于点E .若AB =x 1,BC =2x 2,DE =3,其中x 1、x 2是关于x 的方程x 2﹣4x+m =0的两个实根,则m 的值是( )A .165B .125C .3D .211.已知方程2202030x x +-=的根分别为a 和b ,则代数式2a a 2020a b ++的值为( )A .0B .2020C .1D .-2020 12.如果2是方程x²−3x+k=0的一个根,则此方程的另一根为( )A .2B .1C .−1D .−2 二、填空题13.关于x 的一元二次方程2210kx x +-=有两个不相等的实数根,则k 的取值范围是________.14.如图,要设计一幅宽20cm ,长30cm 的图案,其中有两横彩条、一竖彩条,横、竖彩条的宽度比为1:3,如果要使彩条所占面积是图案面积的19%,竖彩条的宽度为________.15.已知等腰三角形的边长是方程213360x x -+=的两个根,则这个等腰三角形的周长是______.16.等腰三角形ABC 中,8BC =,AB 、AC 的长是关于x 的方程2100x x m -+=的两根,则m 的值是___.17.已知x 1和x 2是方程2x 2-5x+1=0的两个根,则1212x x x x +的值为_____. 18.若关于x 的一元二次方程x 2+2x ﹣m 2﹣m =0(m >0),当m =1、2、3、…2020时,相应的一元二次方程的两个根分别记为α1、β1,α2、β2,…,α2020、β2020,则112220202020111111αβαβαβ++++++的值为_____.19.已知关于x 的方程x 2﹣px +q =0的两根为﹣3和﹣1,则p =_____,q =_____. 20.关于x 的一元二次方程有两个根0和3,写出这个一元二次方程的一个一般式为______.参考答案三、解答题21.已知关于x 的方程()2222x kx x k +=--,当k 取何值时,此方程(1)有两个不相等的实数根;(2)没有实数根.22.关于x 的一元二次方程()2220x k x k -++=. (1)判断方程根的情况,并说明理由.(2)若1x =是方程的一个根,求k 的值和方程的另一根.23.某地区2018年投入教育经费2000万元,2020年投入教育经费2420万元(1)求2018年至2020年该地区投入教育经费的年平均增长率;(2)按照义务教育法规定,教育经费的投入不低于国民生产总值的百分之四,结合该地区国民生产总值的增长情况,该地区到2022年需投入教育经费2900万元,如果按(1)中教育经费投入的增长率,到2022年该地区投入的教育经费是否能达到2900万元?请说明理由.24.如图,利用22米长的墙为一边,用篱笆围成一个长方形仓库ABCD ,中间用篱笆分割出两个小长方形,在与墙平行的一边要开两扇1米宽的门,总共用去篱笆34米,为了使这个长方形ABCD 的面积为96平方米,求AB 和BC 的长.25.解方程:(1)23620x x -+=(2)222(3)9x x -=-26.解下列方程(1)2210x x ++= (2)233x x【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【分析】设正方形的边长为1,AF =AM =x ,根据勾股定理即可求出答案.【详解】解:设正方形的边长为1,AF =AM =x ,则BE =EF =12,AE =x+12, 在Rt △ABE 中,∴AE 2=AB 2+BE 2,∴(x +12)2=1+(12)2, ∴x 2+x -1=0,∴AM 的长为x 2+x -1=0的一个正根,故选:B .【点睛】本题考查一元二次方程,解题的关键是根据勾股定理列出方程,本题属于中等题型. 2.D解析:D【分析】设AD 长为x 米,四边形ABCD 是矩形,根据矩形的性质,即可求得AB 的长;根据题意可得方程x (30−4x )=54,解此方程即可求得x 的值.【详解】解:设与墙头垂直的边AD 长为x 米,四边形ABCD 是矩形,∴BC =MN =PQ =x 米,∴AB =30−AD−MN−PQ−BC =30−4x (米),根据题意得:x (30−4x )=54,解得:x =3或x =4.5,∴AD 的长为3或4.5米.故选:D .【点睛】考查了一元二次方程的应用中的围墙问题,正确列出一元二次方程,并注意解要符合实际意义.3.A解析:A【分析】直接把已知数据代入进而得出c 的值,再利用根的判别式求出答案.【详解】∵小刚在解关于x 的方程20ax bx c ++=(0a ≠)时,只抄对了1a =,4b =,解出其中一个根是1x =-,∴()()21410c -+⨯-+=, 解得:3c =,∵核对时发现所抄的c 比原方程的c 值小2,故原方程中5c =,则224441540b ac =-=-⨯⨯=-<,则原方程的根的情况是不存在实数根.故选:A .【点睛】本题主要考查了根的判别式,正确利用方程的解得出c 的值是解题关键.4.B解析:B【分析】根据因式分解法解方程即可;【详解】()55x x x +=+,()()550+-+=x x x ,()()510x x +-=,11x =,25x =-;故答案选B .【点睛】本题主要考查了因式分解法解一元二次方程,准确计算是解题的关键.5.B解析:B【分析】根据勾股定理求出BF ,利用求根公式解方程,比较即可.【详解】解:∵四边形ABCD 是矩形∴CD=AB=a在Rt △BCD 中,由勾股定理得,BD =∴a ,解方程2240x ax +-=得x a =±=- ∴线段BF 的长是方程2240x ax +-=的一个根.故选:B .【点睛】本题考查的是勾股定理、一元二次方程的解法,掌握一元二次方程的求根公式、勾股定理是解题的关键.6.A解析:A【分析】方程左边分解因式后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.【详解】解:∵x 2-x=0,∴x (x-1)=0,则x=0或x-1=0,解得:x 1=0,x 2=1,故选:A .【点睛】此题考查了解一元二次方程-因式分解法,熟练掌握因式分解的方法是解本题的关键.7.A解析:A【分析】由关于x的方程x2+mx=0的一个根为-1,得出将x=-1,代入方程x2+mx=0求出m即可.【详解】解:∵-1是方程x2+mx=0的根,∴1-m=0,∴m=1,故答案为:A.【点睛】此题主要考查了一元二次方程的解,由方程的根为-1,代入方程是解决问题的关键.8.B解析:B【分析】方程有两个不相等的实数根,显然原方程应该是关于x的一元二次方程,因此得到二次项∆>即可得到答案.系数不为0即当a-3≠0时,且判别式0【详解】∵关于x的方程()32---=有两个不相等的实数根a x4x10∴a-3≠0,且2∆--⨯-⨯-=+>=(4)4(3)(1)440a aa≥-且a≠3解得:1故选B.【点睛】本题主要考查方程的解,一元二次方程的根的判别式,根据判别式,列出关于参数a的不等式,是解题的关键.9.C解析:C【分析】先把已知条件变形得到a2+(m+n) a+mn﹣2=0,b2+( m+n) b+mn﹣2=0,则可把a、b看作方程x2+( m+n) x+mn﹣2=0的两实数根,利用根与系数的关系得到ab=mn﹣2,从而得到ab﹣mn的值.【详解】解:∵(a+m)( a+n)=2,(b+m)( b+n)=2,∴a2+( m+n)a+mn﹣2=0,b2+( m+n)b+mn﹣2=0,而a、b、m、n为互不相等的实数,∴可以把a、b看作方程x2+(m+n)x+mn﹣2=0的两个实数根,∴ab=mn﹣2,∴ab﹣mn=﹣2.故选:C.本题考查一元二次方程根与系数的关系及整式的乘法,理解代数思想,把“a 、b 看作方程x 2+(m +n )x +mn ﹣2=0的两实数根”是解题关键.10.A解析:A【分析】利用根与系数的关系得到x 1+x 2=4,x 1x 2=m ,AB +12BC =4,m =AB×12BC ,再利用折叠的性质和平行线的性质得到∠EBD =∠EDB ,则EB =ED =3,所以AE =AD−DE =5−2AB ,利用勾股定理得到AB 2+(5−2AB )2=32,解得AB 或AB (舍去),则BC ,然后计算m 的值. 【详解】 ∵x 1、x 2是关于x 的方程x 2−4x +m =0的两个实根,∴x 1+x 2=4,x 1x 2=m ,即AB +12BC =4,m =AB×12BC , ∵△BCD 沿BD 翻折得到△BC′D ,BC′与边AD 交于点E ,∴∠CBD =∠EBD ,∵AD ∥BC ,∴∠CBD =∠EDB ,∴∠EBD =∠EDB ,∴EB =ED =3,在Rt △ABE 中,AE =AD−DE =BC−3=8−2AB−3=5−2AB ,∴AB 2+(5−2AB )2=32,解得AB 或AB (舍去),∴BC =8−2AB =205+,∴m =12=165. 故选:A .【点睛】本题考查了根与系数的关系:若x 1,x 2是一元二次方程ax 2+bx +c =0(a≠0)的两根时,x 1+x 2=−b a ,x 1x 2=c a.也考查了矩形的性质和折叠的性质. 11.A解析:A将a 代入方程,可得2202030a a +-=,即220302a a =-,代入要求的式子,即可得到3+ab ,而a 、b 是方程的两个根,根据韦达定理,可求出ab 的值,即可求出答案.【详解】解:∵方程2202030x x +-=的根分别为a 和b∴2202030a a +-=,即220302a a =-∴2a a 2020a b ++=32020a -+ab+2020a=3+ab∵ab=-3∴2a a 2020a b ++=32020a -+ab+2020a=3+ab=3-3=0故选:A .【点睛】本题主要考查一元二次方程的解以及韦达定理,熟练解代入方程以及观察式子特点,抵消部分式子是解决本题的关键.12.B解析:B【分析】设方程的另一个根为x 1,根据根与系数的关系可得出关于x 1的一元一次方程,解之即可得出结论.【详解】设方程的另一个根为x 1,根据题意得:2+x 1=3,∴x 1=1.故选:B .【点睛】本题考查了根与系数的关系,牢记两根之和与系数的关系是解题的关键.二、填空题13.且【分析】根据根的判别式及一元二次方程的定义解题即可【详解】∵关于x 的一元二次方程有两个不相等的实数根解得又∵该方程为一元二次方程且故答案为:且【点睛】本题主要考查根的判别式及一元二次方程的定义属于 解析:1k ->且0k ≠.【分析】根据根的判别式及一元二次方程的定义解题即可.【详解】∵关于x 的一元二次方程有两个不相等的实数根,()224241440b ac k k ∴∆=-=-⨯-=+>,解得1k >-.又∵该方程为一元二次方程,0k ∴≠,1k ∴>-且0k ≠.故答案为:1k >-且0k ≠.【点睛】本题主要考查根的判别式及一元二次方程的定义,属于基础题,掌握根的判别式及一元二次方程的定义是解题的关键.14.3cm 【分析】设横彩条的宽度是xcm 竖彩条的宽度是3xcm 根据如果要使彩条所占面积是图案面积的19可列方程求解【详解】解:设横彩条的宽度是xcm 竖彩条的宽度是3xcm 则(30-3x )(20-2x )=解析:3cm【分析】设横彩条的宽度是xcm ,竖彩条的宽度是3xcm ,根据“如果要使彩条所占面积是图案面积的19%”,可列方程求解.【详解】解:设横彩条的宽度是xcm ,竖彩条的宽度是3xcm ,则(30-3x )(20-2x )=20×30×(1-19%),解得x 1=1,x 2=19(舍去).所以3x=3.答:竖彩条的宽度是3cm .故答案为:3cm【点睛】本题考查一元二次方程的应用,解题的关键是理解题意,学会正确寻找等量关系,构建方程解决问题.15.22【分析】先利用因式分解法求出方程的两个根从而可得等腰三角形的两边长再根据等腰三角形的定义三角形的三边关系定理可得这个等腰三角形的三边长然后利用三角形的周长公式即可得【详解】因式分解得解得等腰三角 解析:22【分析】先利用因式分解法求出方程的两个根,从而可得等腰三角形的两边长,再根据等腰三角形的定义、三角形的三边关系定理可得这个等腰三角形的三边长,然后利用三角形的周长公式即可得.【详解】213360x x -+=,因式分解,得(4)(9)0x x --=,解得124,9x x ==,等腰三角形的边长是方程213360x x -+=的两个根,∴这个等腰三角形的两边长为4,9,(1)当边长为4的边为腰时,这个等腰三角形的三边长为4,4,9,此时449+<,不满足三角形的三边关系定理,舍去;(2)当边长为9的边为腰时,这个等腰三角形的三边长为4,9,9,此时499+>,满足三角形的三边关系定理,则这个等腰三角形的周长为49922++=;综上,这个等腰三角形的周长为22,故答案为:22.【点睛】本题考查了解一元二次方程、等腰三角形的定义、三角形的三边关系定理等知识点,熟练掌握一元二次方程的解法是解题关键.16.或【分析】等腰三角形ABC 中边可能是腰也可能是底应分两种情况进行讨论分别利用根与系数的关系三角形三边关系定理求得方程的两个根进而求得答案【详解】解:∵关于x 的方程∴∴∵是等腰三角形的长是关于x 的方程 解析:25或16【分析】等腰三角形ABC 中,边BC 可能是腰也可能是底,应分两种情况进行讨论,分别利用根与系数的关系、三角形三边关系定理求得方程的两个根,进而求得答案.【详解】解:∵关于x 的方程2100x x m -+=∴1a =,10b =-,c m = ∴1210b x x a +=-=,12c x x m a == ∵ABC 是等腰三角形,AB 、AC 的长是关于x 的方程2100x x m -+=的两根 ∴①当8BC =为底、两根AB 、AC 均为等腰三角形的腰时,有1210AB AC x x +=+=且AB AC =即5AB AC ==,此时等腰三角形的三边分别为5、5、8,根据三角形三边关系定理可知可以构成三角形,则1225m x x AB AC ==⋅=;②当8BC =为腰、两根AB 、AC 中一个为腰一个为底时,有122810x x x +=+=,即22x =,此时此时等腰三角形的三边分别为2、8、8,根据三角形三边关系定理可知可以构成三角形,则1216m x x AB AC ==⋅=.∴综上所述,m 的值为25或16.故答案是:25或16【点睛】本题考查了一元二次方程根与系数的关系、等腰三角形的性质、三角形三边关系定理等,熟练掌握相关知识点是解题的关键.17.5【分析】直接根据根与系数的关系求出再代入求值即可【详解】解:∵x1x2是方程2x2-5x+1=0的两个根∴x1+x2=-∴故答案为:5【点睛】本题考查了根与系数的关系:若x1x2是一元二次方程ax解析:5【分析】直接根据根与系数的关系,求出12x x +,12x x 再代入求值即可.【详解】解:∵x 1,x 2是方程2x 2-5x+1=0的两个根,∴x 1+x 2=--55-=22,121=2x x . ∴121252==512x x x x + 故答案为:5.【点睛】本题考查了根与系数的关系:若x 1,x 2是一元二次方程ax 2+bx+c=0(a≠0)的两根时,x 1+x 2=b a -,x 1x 2=c a. 18.【分析】由一元二次方程根与系数的关系解题即【详解】解:∵x2+2x ﹣m2﹣m =0m =123…2020∴由根与系数的关系得:α1+β1=﹣2α1β1=﹣1×2;α2+β2=﹣2α2β2=﹣2×3;…α 解析:40402021【分析】 由一元二次方程根与系数的关系解题,即+=-b c a a αβαβ=,. 【详解】解:∵x 2+2x ﹣m 2﹣m =0,m =1,2,3, (2020)∴由根与系数的关系得:α1+β1=﹣2,α1β1=﹣1×2;α2+β2=﹣2,α2β2=﹣2×3;…α2020+β2020=﹣2,α2020β2021=﹣2020×2021;∴原式=3320202020112211223320202020++++++++αβαβαβαβαβαβαβαβ 2222=++++12233420202021⨯⨯⨯⨯ 1111111=2(1)2233420202021⨯-+-+-++-1=2(1)2021⨯- 4040=2021 故答案为:40402021. 【点睛】 本题考查一元二次方程根与系数的关系,是重要考点,难度较易,掌握相关知识是解题关键.19.-43【分析】由根与系数的关系可得出关于p 或q 的一元一次方程解之即可得出结论【详解】解:根据题意得﹣3+(﹣1)=p ﹣3×(﹣1)=q 所以p =﹣4q =3故答案为﹣43【点睛】本题考查了根与系数的关系解析:-4 3【分析】由根与系数的关系可得出关于p 或q 的一元一次方程,解之即可得出结论.【详解】解:根据题意得﹣3+(﹣1)=p ,﹣3×(﹣1)=q ,所以p =﹣4,q =3.故答案为﹣4,3.【点睛】本题考查了根与系数的关系,根据根与系数的关系找出-3+(-1)=-p,(-3)⨯(-1)=q 是解题的关键.20.【分析】根据方程的解的定义可以得到方程【详解】解:根据题意知方程符合题意即:故答案是:【点睛】本题主要考查了一元二次方程的解的定义熟悉相关性质是解题的关键解析:230x x -=【分析】根据方程的解的定义可以得到方程-=(3)0x x .【详解】解:根据题意,知方程-=(3)0x x 符合题意,即:230x x -=.故答案是:230x x -=.【点睛】本题主要考查了一元二次方程的解的定义,熟悉相关性质是解题的关键.三、解答题21.(1)54k >; (2)54k <. 【分析】 先化方程为一般形式,它是关于x 一元二次方程,据一元二次方程判别式和根的情况列出关于k 的不等式求解.【详解】方程化为:22(21)(2)0x k x k +-+-=, ∴∆22(21)4(2)1215k k k =--⨯-=-.(1)当12150k ->,54k >时,方程有两个不相等的实数根; (2)当12150k -<,54k <时,方程没有实数根. 【点睛】此题考查一元二次方程的判别式,其关键是撑握判别式与一元二次方程根情况的关系,并据此和题意列出不等式.22.(1)有两个实数根,证明见解析;(2)1k =,2x =【分析】(1)利用根的判别式进行判断根的情况,即可得到答案;(2)把1x =代入方程,即可求出k 的值,然后解一元二次方程,即可得到另一个根.【详解】解:(1)根据题意,在一元二次方程()2220x k x k -++=中, ∵2(2)42k k ∆=+-⨯,244k k =-+,2(2)0k =-,∴对于任意的实数k ,原方程总有两个实数根.(2)∵1x =是方程2(2)20x k x k -++=的一个根.∴1(2)120k k -+⨯+=,解得:1k =,∴原方程为2320x x -+=,解得:11x =,22x =,∴原方程的另一根为22x =. 【点睛】本题考查了解一元二次方程以及根的判别式,牢记当0∆≥时方程有两个实数根是解题的关键.23.(1)10%;(2)可以,理由见解析【分析】(1)设年平均增长率是x ,列式()2200012420x +=,求出结果;(2)利用(1)中算出的增长率算出2022年的教育经费,看是否超过2900万元.【详解】解:(1)设年平均增长率是x , ()2200012420x +=1 1.1x +=±10.1x =,2 2.1x =-(舍去),答:年平均增长率是10%;(2)2022年的教育经费是()2242010.12928.2⨯+=(万元), 2928.22900>,答:教育经费可以达到2900万元.【点睛】本题考查一元二次方程的应用,解题的关键是掌握增长率问题的列式方法.24.AB=8米,BC=12米.【分析】设AB 为x 米,然后表示出BC 的长为(36-3x )米,利用矩形的面积计算方法列出方程求解即可.【详解】解:设AB 为x 米,则BC 为(36-3x )米,x (36-3x )=96,解得:x 1=4,x 2=8,当x=4时,36-3x=24>22(不合题意,舍去),当x=8时,36-3x=12.答:AB=8米,BC=12米.【点睛】本题考查了一元二次方程的应用,解题的关键是设出一边的长,并用未知数表示出另一边的长.25.(1)1x =,2x =2)x=3或x=9. 【分析】(1)根据公式法即可求出答案;(2)根据因式分解法即可求出答案.【详解】解:(1)∵3x 2-6x+2=0,∴a=3,b=-6,c=2,∴△=36-24=12,∴x ==∴1x =2x = (2)∵2(x-3)2=x 2-9,∴2(x-3)2=(x-3)(x+3),∴(x-3)[(2(x-3)-(x+3)]=0,∴(x-3)(x-9)=0∴x-3=0,x-9=0∴x=3或x=9.【点睛】本题考查解一元二次方程,解题的关键是熟练运用一元二次方程的解法,本题属于基础题型.26.(1)121x x ==-;(2)123,4x x ==.【分析】(1)利用配方法解一元二次方程即可得;(2)利用因式分解法解一元二次方程即可得.【详解】(1)2210x x ++=,2(1)0x +=,解得121x x ==-;(2)233x x ,2330x x , 3310x x ,即()()340x x --=,30x -=或40x -=,3x =或4x =,即123,4x x ==.【点睛】本题考查了解一元二次方程,主要解法包括:直接开平方法、配方法、因式分解法、公式法、换元法等,熟练掌握各解法是解题关键.。
绍兴市绍兴一初九年级数学上册第四单元《圆》测试卷(含答案解析)

一、选择题1.下列说法不正确的是( )A .不在同一直线上的三点确定一个圆B .90°的圆周角所对的弦是直径C .平分弦的直径垂直于这条弦D .等弧所对的圆周角相等2.如图,分别以AB,AC 为直径的两个半圆,其中AC 是半圆O 的一条弦,E 是弧AEC 中点,D 是半圆ADC 中点.若DE=2,AB=12,且AC˃6,则AC 长为( )A .6+2B .8+2C . 6+22D .8+22 3.如图,ABC 为O 的一个内接三角形,过点B 作O 的切线PB 与OA 的延长线交于点P .已知34ACB ∠=︒,则P ∠等于( )A .17°B .27°C .32°D .22°4.如图,一条公路的拐弯处是一段圆弧AB ,点O 是这段弧所在的圆的圆心,20cm AB =,点C 是AB 的中点,点D 是AB 的中点,且5cm CD =,则这段弯路所在圆的半径为( )A .10cmB .12.5cmC .15cmD .17cm 5.在平面直角坐标系中,以点()3,4-为圆心,半径为5作圆,则原点一定( )A .与圆相切B .在圆外C .在圆上D .在圆内6.如图,AB 圆O 的直径,弦CD AB ⊥,垂足为M ,下列结论不成立的是( )A .CM DM =B .CB BD =C .ACD ADC ∠=∠ D .OM MB = 7.如图,AB 为O 的直径,C 为O 上一点,其中6AB =,120AOC ∠=︒,P 为O 上的动点,连AP ,取AP 中点Q ,连CQ ,则线段CQ 的最大值为( )A .37B .3272+C .237+D .33722+ 8.以O 为中心点的量角器与直角三角板ABC 如图所示摆放,直角顶点B 在零刻度线所在直线DE 上,且量角器与三角板只有一个公共点P ,∠POB =40°,则∠CBD 的度数是( )A .50°B .45°C .35°D .40°9.如图,A 、B 、C 三点在O 上,D 是CB 延长线上的一点,40ABD ∠=︒,那么AOC ∠的度数为( ).A .80°B .70°C .50°D .40° 10.已知O 的半径为5,若4PO =,则点P 与O 的位置关系是( )A.点P在O内B.点P在O上C.点P在O外D.无法判断11.如图,半径为1cm的P在边长为9πcm,12πcm,15πcm的三角形外沿三遍滚动(没有滑动)一周,则圆P所扫过的面积为()cm2A.73πB.75πC.76πD.77π12.下列说法中,正确的是()A.三点确定一个圆B.在同圆或等圆中,相等的弦所对的圆周角相等C.平分弦的直径垂直于弦D.在同圆或等圆中,相等的圆心角所对的弦相等二、填空题13.如图,A、B、C是O上顺次三点,若AC、AB、BC分别是O内接正三角形、正方形、正n边形的一边,则n=______.14.如图,PA,PB是O的切线,A,B为切点,AC是O的直径,∠=︒,则PBAC35∠的度数为________.15.如图,已知点C是半圆О上一点,将弧BC沿弦BC折叠后恰好经过点,O若半圆O 的半径是2,则图中阴影部分的面积是________________________.16.如图,A ,B ,P 是半径为2的O 上的三点,45APB ∠=︒,则弦AB 的长为______.17.已知⊙O 的半径为3,圆心O 到直线l 的距离为m ,若m 满足方程290x ,则⊙O 与直线l 的位置关系是________ 18.已知圆心O 到直线l 的距离为5,⊙O 半径为r ,若直线l 与⊙O 有两个交点,则r 的值可以是________.(写出一个即可)19.如图,ABC 内接于半径为10的半圆,AB 为直径,点M 是弧AC 的中点,连结BM 交AC 于点E ,AD 平分∠CAB 交BM 于点D ,∠ADB =_____°,当点D 恰好为BM 的中点时,BM 的长为____.20.如图,⊙O 的半径为3,点A 是⊙O 外一点,OA =6,B 是⊙O 上的动点,线段AB 的中点为P ,连接 OA 、OP .则线段 OP 的最大值是______.三、解答题 21.对于平面直角坐标系xOy 中的点P 和C ,给出如下定义:如果C 的半径为r ,C 外一点P 到C 的切线长小于或等于2r ,那么点P 叫做C 的“离心点”. (1)当C 的半径为1时,①在点())12313,0,2,5,02P P P ⎛- ⎝⎭中,C 的“离心点”是_____________; ②点P(m ,n)在直线3y x =-+上,且点P 是O 的“离心点”,求点P 横坐标m 的取值范围;(2)C的圆心C在y轴上,半径为2,直线132y x=-+与x轴.y轴分别交于点A、B.如果线段AB上的所有点都是C的“离心点”,请直接写出圆心C纵坐标的取值范围.22.如图,AB、CD是O中两条互相垂直的弦,垂足为点E,且AE CE=,点F是BC的中点,延长FE交AD于点G,已知1,3,2AE BE OE===.(1)求证:AED CEB≌;(2)求证:FG AD⊥;(3)求O的半径.23.如图,O的半径为2,四边形ABCD内接于O,圆心O到AC的距离等于3.(1)求AC的长;(2)求ADC∠的度数.24.如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2,求大正方形的面积.25.如图,一条公路的转弯处是一段圆弧CD,点O是CD的圆心,E为CD上一点,OE⊥CD,垂足为F.已知CD=300m,EF=50m,求这段弯路的半径.26.如图,在平面直角坐标系xOy中,A(0,1),点P(t,0)为x轴上一动点(不与原点重合).以P为圆心,PA为半径的⊙P与x轴正半轴交于点B,连接AB,以AB为直角边在AB的右上方作等腰直角三角形ABC,且∠BAC=90°,直线BC于⊙P的另一个公共点为F,连接PF.(1)当t = 2时,点C的坐标为(,);(2)当t >0时,过点C作x轴的垂线l.①判断当点P运动时,直线l的位置是否发生变化?请说明理由;②试说明点F到直线l的距离始终等于OP的长;(3)请直接写出t为何值时,CF=2BF.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】根据确定圆的条件对A进行判断;根据垂径定理的推论对C进行判断;根据圆周角定理及其推论对B、D进行判断.【详解】解:A.不在同一直线上的三点确定一个圆,说法正确;B. 90°的圆周角所对的弦是直径,说法正确;C. 平分弦(非直径)的直径垂直于弦,所以B 选项错误;D. 等弧所对的圆周角相等,说法正确;故选:C【点睛】此题主要考查了圆的相关知识的掌握.解答此题的关键是要熟悉课本中的性质定理. 2.D解析:D【分析】连接OE ,交AC 于点F ,由勾股定理结合垂径定理求出AF 的长,即可得到结论.【详解】解:连接OE ,交AC 于点F ,∵E 为AEC 的中点,∴OE AC ⊥,F 为AC 的中点,∵12AB =∴6OE AO ==设EF x =,则6OF x =-∵F 为AC 的中点,D 为半圆ADC 的中点,∴DF AC ⊥,DF AF =∵2DE =,∴2DF x AF =+=在Rt △AOF 中,222OA OF AF =+即2226(6)(2)x x =-++, ∴122x =,222x =∴2(2)822AC x =+=+822-∵6AC > ∴822AC =+故选:D【点睛】本题考查了垂径定理,熟练掌握垂径定理,运用勾股定理求出AF 是解题的关键. 3.D解析:D连接OB,利用圆周角定理求得∠AOB,再根据切线性质证得∠OBP=90°,利用直角三角形的两锐角互余即可求解.【详解】解:连接OB,∵∠ACB=34°,∴∠AOB=2∠ACB=68°,∵PB为O的切线,∴OB⊥PB,即∠OBP=90°,∴∠P=90°﹣∠AOB=22°,故选:D.【点睛】本题考查了切线的性质、圆周角定理、直角三角形的两锐角互余,熟练掌握切线的性质和圆周角定理是解答的关键.4.B解析:B【分析】根据题意,可以推出AD=BD=10,若设半径为r,则OD=r﹣5,OA=r,结合勾股定理可推出半径r的值.【详解】解:∵OC⊥AB,AB=20,∴AD=DB=10,在Rt AOD中,OA2=OD2+AD2,设半径为r得:r2=(r﹣5)2+102,解得:r=12.5,∴这段弯路的半径为12.5,故选:B.【点睛】本题主要考查垂径定理的应用、勾股定理的应用,关键在于设出半径为r后,用r表示出OD、OA的长度.5.C【分析】设点(-3,4)为点P,原点为点O,先计算出OP的长,然后根据点与圆的位置关系的判定方法求解.【详解】解:∵设点(-3,4)为点P,原点为点O,∴OP5,而⊙P的半径为5,∴OP等于圆的半径,∴点O在⊙P上.故选:C.【点睛】本题考查了点与圆的位置关系:点的位置可以确定该点到圆心距离与半径的关系,反过来已知点到圆心距离与半径的关系可以确定该点与圆的位置关系.6.D解析:D【分析】根据垂径定理得到CM=DM,BC BD=,然后根据圆周角定理得=,AC AD∠ACD=∠ADC,而对于OM与MB的大小关系不能判断.【详解】解:∵AB是⊙O的直径,弦CD⊥AB,∴CM=DM,BC BD=,=,AC AD∴∠ACD=∠ADC.而无法比较OM,MB的大小,故选:D.【点睛】本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了圆周角定理.7.D解析:D【分析】如图,连接OQ,作CH⊥AB于H.首先证明点Q的运动轨迹为以AO为直径的⊙K,连接CK,当点Q在CK的延长线上时,CQ的值最大,利用勾股定理求出CK即可解决问题;【详解】如图,连接OQ,作CH⊥AB于H.∵AQ =QP ,∴OQ ⊥PA ,∴∠AQO =90°,∴点Q 的运动轨迹为以AO 为直径的⊙K ,连接CK ,当点Q 在CK 的延长线上时,CQ 的值最大,∵120AOC ∠=︒∴∠COH =60°在Rt △OCH 中,∵∠COH =60°,OC=12AB=3, ∴OH =12OC =32,CH 2233OC OH +=, 在Rt △CKH 中,CK 223332⎛⎫+= ⎪ ⎪⎝⎭372 ∴CQ 的最大值为33722 故选:D .【点睛】本题考查圆周角定理、轨迹、勾股定理、点与圆的位置关系等知识,解题的关键是正确寻找点Q 的运动轨迹,学会构造辅助圆解决问题,属于中考填空题中的压轴题. 8.D解析:D【分析】根据切线的性质得到∠OPB =90°,证出OP //BC ,根据平行线的性质得到∠POB =∠CBD ,于是得到结果.【详解】∵AB 是⊙O 的切线,∴∠OPB =90°,∵∠ABC =90°,∴OP //BC ,∴∠CBD =∠POB =40°,故选D .【点睛】本题考查了切线的性质,平行线的判定和性质,熟练掌握切线的判定和性质是解题的关键.9.A解析:A【分析】作弧ABC所对的圆周角∠AEC,如图,先利用邻补角计算出∠ABC=140°,再利用圆内接四边形的性质计算出∠E=40°,然后根据圆周角定理得到∠AOC的度数.【详解】解:作弧ABC所对的圆周角∠AEC,∵∠ABD=40°,∴∠ABC=180°-40°=140°,∵∠AEC+∠ABC=180°,∴∠E=40°,∴∠AOC=2∠AEC=2×40°=80°.故选:A.【点睛】本题考查了圆内接四边形对角互补,以及圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.10.A解析:A【分析】已知圆O的半径为r,点P到圆心O的距离是d,①当r>d时,点P在⊙O内,②当r=d 时,点P在⊙O上,③当r<d时,点P在⊙O外,根据以上内容判断即可.【详解】∵⊙O的半径为5,若PO=4,∴4<5,∴点P与⊙O的位置关系是点P在⊙O内,故选:A.【点睛】本题考查了点与圆的位置关系的应用,注意:已知圆O的半径为r,点P到圆心O的距离是d,①当r>d时,点P在⊙O内,②当r=d时,点P在⊙O上,③当r<d时,点P在⊙O外.11.A解析:A【分析】圆在三角形的三个角的顶点处旋转的路线是弧,通过观察可以发现圆转动时在三个角上共转动了圆心角360°,所以在三个顶点处转了一个圆的面积,在三个边上滚过的图形是以三角形边长为长,圆的直径为宽的矩形,然就分别计算,最后求和.【详解】解:根据运动特点可知三个顶点处转了一个圆的面积,在三个边上滚过的图形矩形∴圆P所扫过的面积=π+(9π+12π+15π)×2=73π故选:A【点睛】解答本题的关键是,找出圆滚动一周的图形,并将图形进行分割,拼组,化难为易,列式解答即可.12.D解析:D【分析】根据确定圆的条件、垂径定理、圆周角定理一一判断即可.【详解】解:A、任意三点确定一个圆;错误,应该的不在同一直线上的三点可以确定一个圆,不符合题意;B、在同圆或等圆中,相等的弦所对的圆周角相等或互补,错误,不符合题意;C、平分弦的直径垂直于弦,错误,此弦不是直径,不符合题意;D、在同圆或等圆中,相等的圆心角所对的弦相等,正确,符合题意;故选:D.【点睛】本题考查确定圆的条件、垂径定理、圆周角定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.二、填空题13.12【分析】如图连接OAOCOB根据角的转换求出中心角即可解决问题【详解】如图连接OAOCOB∵若ACAB分别是内接正三角形正方形的一边∴∴由题意得:∴12故答案为:12【点睛】本题考查了正多边形与解析:12【分析】即可解决问题.如图,连接OA、OC、OB,根据角的转换求出中心角BOC【详解】如图,连接OA、OC、OB.∵若AC 、AB 分别是O 内接正三角形、正方形的一边,∴120AOC ∠=︒,90AOB ∠=︒,∴30BOC AOC AOB ∠=∠-∠=︒, 由题意得:36030n︒︒=, ∴n =12,故答案为:12.【点睛】本题考查了正多边形与圆:把一个圆分成n (n 是大于2的自然数)等份,一次连接各分点所得到的多边形是这个圆的内接正多边形,这个圆叫做这个正多边形的外接圆,熟练的掌握正多边形的有关概念是解答本题的关键. 14.70°【分析】根据题意可以求得∠OAP 和∠OBP 的度数然后根据∠BAC =35°即可求得∠P 的度数【详解】解:连接OB :∵PAPB 是⊙O 的两条切线AB 是切点AC 是⊙O 的直径∴∠OAP =∠OBP =90°解析:70°【分析】根据题意可以求得∠OAP 和∠OBP 的度数,然后根据∠BAC =35°,即可求得∠P 的度数.【详解】解:连接OB :∵PA 、PB 是⊙O 的两条切线,A 、B 是切点,AC 是⊙O 的直径,∴∠OAP =∠OBP =90°,∵∠BAC =35°,OA =OB ,∴∠BAC =∠OBA =35°,∴∠PAB =∠PBA =55°,∴∠P=180°−∠PAB−∠PBA=70°,即∠P的度数是70°,故答案为:70°.【点睛】本题考查切线的性质,解答此类问题的关键是明确题意,找出所求问题需要的条件,利用切线的性质解答问题.15.【分析】过点O作OD⊥BC于E交半圆O于D点连接CD如图根据垂径定理由OD⊥BC得BE=CE再根据折叠的性质得到ED=EO则OE=OB则可根据含30度的直角三角形三边的关系得∠OBC=30°即∠AB解析:2 3π【分析】过点O作OD⊥BC于E,交半圆O于D点,连接CD,如图,根据垂径定理由OD⊥BC得BE=CE,再根据折叠的性质得到ED=EO,则OE=12OB,则可根据含30度的直角三角形三边的关系得∠OBC=30°,即∠ABC=30°则∠AOC=60°,由于OC=OB,则弓形OC的面积=弓形OB的面积,然后根据扇形的面积公式及S阴影部分=S扇形OAC即可得到阴影部分的面积.【详解】如图:过点O作OD⊥BC于E,交半圆O于D点,连接CD,∵OD⊥BC,∴BE=CE,∵半圆O沿BC所在的直线折叠,圆弧BC恰好过圆心O,∴ED=EO,∴OE=12OB,∴∠OBC=30°,即∠ABC=30°,∴∠AOC=60°;∵OC=OB,∴弓形OC的面积=弓形OB的面积,∴S阴影部分=S扇形OAC=26022 3603ππ⋅=.【点睛】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了垂定定理、圆周角定理和扇形的面积公式.16.【分析】首先连接OAOB 由圆周角定理即可求得∠AOB=90°又由OA=OB=2利用勾股定理即可求得弦AB 的长【详解】解:连接OAOB ∵∠APB=45°∴∠AOB=2∠APB=90°∵OA=OB=2∴ 解析:22【分析】首先连接OA ,OB ,由圆周角定理即可求得∠AOB=90°,又由OA=OB=2,利用勾股定理即可求得弦AB 的长.【详解】解:连接OA ,OB ,∵∠APB=45°,∴∠AOB=2∠APB=90°,∵OA=OB=2, ∴2222AB OA OB +=故答案为:2【点睛】此题考查了圆周角定理以及勾股定理.注意准确作出辅助线是解此题的关键.17.相切【分析】先解一元二次方程求出m 的值再根据圆与直线的位置关系即可得【详解】由得:是圆心O 到直线的距离又满足方程的半径为3与直线的位置关系是相切故答案为:相切【点睛】本题考查了解一元二次方程圆与直线 解析:相切 【分析】先解一元二次方程求出m 的值,再根据圆与直线的位置关系即可得.【详解】由290x 得:123,3x x ==-,m 是圆心O 到直线l 的距离,0m ∴≥,又m 满足方程290x ,3m ∴=,O 的半径为3,O ∴与直线l 的位置关系是相切,故答案为:相切.【点睛】本题考查了解一元二次方程、圆与直线的位置关系、点到直线的距离,熟练掌握圆与直线的位置关系是解题关键.18.答案不唯一如516等(满足即可)【分析】根据直线与圆的位置关系可得出圆的半径与圆心距之间的关系再取r 的值即可【详解】解:∵直线l 与⊙O 有两个交点圆心O 到直线l 的距离为5∴∴在此范围内取值即可如516 解析:答案不唯一,如5.1,6等(满足5r >即可)【分析】根据直线与圆的位置关系可得出圆的半径与圆心距之间的关系,再取r 的值即可.【详解】解:∵直线l 与⊙O 有两个交点,圆心O 到直线l 的距离为5,∴5r >∴在此范围内取值即可,如5.1,6等.【点睛】此题主要考查了直线与圆的位置关系---相交,熟知直线与圆相交满足的条件是解答此题的关键.19.【分析】(1)根据直径所对的圆周角是可得到再根据弧的中点定义同弧所对的圆周角相等角平分线定义可推导出最后有三角形的内角和定理即可求得答案;(2)在(1)的基础上结合已知条件添加辅助线连接从而构造出等解析:135【分析】(1)根据直径所对的圆周角是90︒可得到90CAB CBA ∠+∠=︒,再根据弧的中点定义、同弧所对的圆周角相等、角平分线定义可推导出45DAB DBA ∠+∠=︒,最后有三角形的内角和定理即可求得答案;(2)在(1)的基础上,结合已知条件添加辅助线“连接AM ”,从而构造出等腰Rt ADM △,利用勾股定理解Rt ABM 即可求得答案.【详解】解:(1)∵AB 是直径∴90ACB ∠=︒∴90CAB CBA ∠+∠=︒∵点M 是弧AC 的中点∴AM CM =∴CBM ABM ∠=∠∵AD 平分CAB ∠∴CAD BAD ∠=∠ ∴()1452DAB DBA CAB CBA ∠+∠=∠+∠=︒ ∴()180135ADB DAB DBA ∠=︒-∠+∠=︒.(2)连接AM ,如图:∵AB 是直径∴90AMB ∠=︒∵18045ADM ADB ∠=︒-∠=︒∴AM DM = ∵点D 为BM 的中点∴DM DB =∴2BM AM =∴设AM x =,则2BM x =∵10∴210AB =∵在Rt ABM 中,222AM BM AB +=∴22440x x +=∴122x =222x =-∴22AM =∴42BM =.【点睛】本题考查了直径所对的圆周角是90︒、弧的中点定义、同弧所对的圆周角相等、角平分线定义、三角形的内角和定理、线段的中点定义、利用勾股定理解直角三角形、解一元二次方程等知识点,通过添加辅助线构造直角三角形解决问题的关键,难度中等,属于中考常考题型.20.【分析】如图连接OB 设OA 交⊙O 于点T 连接PT 利用三角形中位线定理求出PT 根据OP≤PT+OT 可得结论【详解】如图连接OB 设OA 交⊙O 于点T 连接PT ∵OA=6OT=3∴OT=TA ∵AP=PB ∴PT=解析:92【分析】如图,连接OB ,设OA 交⊙O 于点T ,连接PT .利用三角形中位线定理求出PT ,根据OP≤PT+OT ,可得结论.【详解】如图,连接OB ,设OA 交⊙O 于点T ,连接PT .∵OA=6,OT=3,∴OT=TA ,∵AP=PB ,∴PT=12OB=32, ∵OP≤PT+OT , ∴OP≤92, 故答案为:92. 【点睛】本题考查点与圆的位置关系,三角形中位线定理等知识,解题的关键是学会添加常用辅助线,构造三角形的中位线解决问题.三、解答题21.(1)①23,P P ;②12m ≤≤;(2)圆心C 的纵坐标满足34y <≤或1515y -≤<-【分析】(1) ①分别计算123OP OP OP ,,的长,判断P 到C 的切线长是否小于或等于2r ,即可解题;②设(),3P m m -+,根据题意,当过点P 的切线长为2时,OP=5,列出相应的一元二次方程,解方程即可;(2) 分类讨论,当C 在y 轴的正半轴上时,当点C 在y 轴的负半轴上时,当圆C 与直线112y x =-+相切时,画出相应的图形,结合全等三角形的判定与性质解题. 【详解】 ①())12313,,0,2,5,022P P P ⎛- ⎝⎭1231,2,5OP OP OP ===所以点1P 不在圆上,不符合题意;因为过点2P 的切线长为2213=-=,32<所以2P 是圆的离心点因为过3P 的切线长为5122=-==所以3P 是离心点;故答案为23,P P ;②如图设(),3P m m -+当过点P 的切线长为2时,OP=5,所以22(3)5m m +-+=解得m=1或m=2观察图像得12m ≤≤(2)如图2,当C 在y 轴的正半轴上时,经过点B(1,0),A(2,0)当AC=25,点A 是离心点,此时C(0,4);观察图像知圆的纵坐标满足34y <≤,线段AB 上所有的点都是离心点;如图3,当点C 在y 轴的负半轴上时,5BC =B 是离心点,此时C(0, 125-)如图4,当圆C 与直线112y x =-+相切时,设切点为N , 如图,由题意得CNB AOB ∆≅∆5CB NB ==(0,15C ∴,观察图像得当圆C 的纵坐标满足1515y -≤<-AB 上的所有点都是离心点; 综上所述,圆C 的纵坐标满足34y <≤或1515y -≤<-【点睛】本题考查直线与圆的位置关系、切线等知识,是重要考点,难度中等,掌握相关知识是解题关键.22.(1)证明过程见解析;(2)证明过程见解析;(35【分析】(1)由圆周角定理得∠A=∠C ,由ASA 得出AED CEB ≌;(2)由直角三角形斜边上的中线性质得EF=12BC=BF ,由等腰三角形的性质得∠FEB=∠B ,由圆周角定理和对顶角相等证出∠A+∠AEG=90°,进而得出结论; (3)作OH ⊥AB 于H ,连结OB ,由垂径定理可得AH=BH=12AB=2,则EH=AH-AE=1,由勾股定理求出OH=1,5OB 的长即为O 的半径.【详解】(1)证明:由圆周角定理得∠A=∠C ,在△AED 和△CEB 中, A C AE CEAED CEB ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△AED ≌△CEB (ASA ).(2)证明:∵AB ⊥CD ,∴∠AED=∠CEB=90°,∴∠C+∠B=90°,∵点F 是BC 的中点,∴EF=12BC=BF , ∴∠FEB=∠B ,∵∠A=∠C ,∠AEG=∠FEB=∠B ,∴∠A+∠AEG=∠C +∠B =90°,∴∠AGE=90°,∴FG AD ⊥. (3)解:作OH ⊥AB 于H ,连结OB ,∵AE=1,BE=3,∴AB=AE+BE=4,∵OH ⊥AB ,∴AH=BH=12AB=2, ∴EH=AH-AE=1,∴()2222211OE EH -=-=,∴2222215BH OH ++=,即O 5【点睛】本题考查了圆周角定理、垂径定理、全等三角形的判定、直角三角形斜边上的中线的性质、勾股定理等知识.本题综合性较强,熟练掌握圆周角定理和垂径定理是解题的关键. 23.(1)2;(2)150︒【分析】(1)过点O 作OE AC ⊥于点E ,根据勾股定理求出CE ,即可得出答案;(2)连接OA ,先求出60AOC ∠=︒,根据同弧所对的圆周角是圆心角的一半得出∠B=30°,即可得出答案.【详解】(1)过点O 作OE AC ⊥于点E ,如图,则在Rt OCE 中,3OE =;2OC =,∴()2222231CE OC OE =-=-=∴22AC CE ==;(2)连接OA ,如图:∵由(1)知,在AOC △中,AC OA OC ==,∴60AOC ∠=︒,∵弧AC =弧AC ,∴1302B AOC ∠=∠=︒, ∴180********ADC B ︒︒∠=-∠=-=︒︒.【点睛】 本题考查了垂径定理,同弧所对的圆周角是圆心角的一半,掌握这些知识点是解题关键. 24.64cm 2【分析】连接OA 、OB 、OE ,证Rt △ADO ≌Rt △BCO ,推出OD=OC ,设AD=a ,则OD=12a ,由勾股定理求出5a ,求出EF=FC=4cm ,在△OFE 中由勾股定理求出a ,即可求出答案.【详解】解:连接OA 、OB 、OE ,∵四边形ABCD 是正方形,∴AD=BC ,∠ADO=∠BCO=90°,∵在Rt △ADO 和Rt △BCO 中∵OA OB AD BC =⎧⎨=⎩, ∴Rt △ADO ≌Rt △BCO ,∴OD=OC ,∵四边形ABCD 是正方形,∴AD=DC ,设AD=acm ,则OD=OC=12DC=12AD=12acm , 在△AOD 中,由勾股定理得:5acm , ∵小正方形EFCG 的面积为16cm 2,∴EF=FC=4cm ,在△OFE 中,由勾股定理得:5a)2=42+(12a+4)2, 解得:a=-4(舍去),a=8,∴正方形面积为264cm故答案为:64cm².【点睛】 本题考查了全等三角形的性质和判定,勾股定理的应用,主要考查学生运用定理进行计算的能力,用的数学思想是方程思想.25.这段弯路的半径为250米.【分析】设这段弯路的半径为R 米,可得50OFOE EF R .由垂径定理得 11300150()22CF CD m .由勾股定理可得222OC CF OF =+,解得 R 的值.【详解】解:连接OC .设这段弯路的半径为R 米则50OF OE EF ROE CD ⊥ 11300150()22CF CD m .根据勾股定理,得222OC CF OF =+即()22215050R R =+-解之,得250R =所以这段弯路的半径为250米.【点睛】本题考查了垂径定理及勾股定理的应用,熟悉相关性质是解题的关键.26.(1)1,35+2)①不变,理由见解析;②见解析;(3)43±【分析】(1)过C 作y 轴的垂线交y 轴与D 点,先根据题意求得PA 、OB 的长,然后再证明△ACD ≌△AOB ,最后根据图形即可解答;(2)①过点C 作CH ⊥y 轴,垂足为点H ,先证明△HAC ≌△OBA ,进一步得到C 点的横坐标恒为1,即可说明;②过F 作FM ⊥l 交l 与M,过点F 作FN ⊥x 轴,垂足为点N ,即∠APF =90°,再说明∠APF 、=90°,再证得△AOP ≌△PBF ,最后根据图形运用线段的和差即可解答;(3)分t >0和t <0两种情况分别求解即可【详解】解:(1)如图:过C 作y 轴的垂线交y 轴与D 点∵t=2,P (2,0),A (0,1)∴225OA OB +=∴5∵∠BAC=90°,∠CDA=90°,∴∠DAC+∠OAB=90°, ∠DAC+∠DCA=90°,∴∠OAB=∠DCA在△ACD 和△AOB 中∠OAB=∠DCA ,∠CDA=∠AOB=90°,AC=AB∴△ACD ≌△AOB (AAS )∴5∴C (1,35+); (2)①不变、理由如下:过点C 作CH ⊥y 轴,垂足为点H ,易证△HAC ≌△OBA ,得HC =OA =1,∴点C 的横坐标是定值为1,∴直线l 是过点(1,0)且垂直于x 轴的直线,直线l 的位置不发生变化;②如图:过F 作FM ⊥l 交l 与M,过点F 作FN ⊥x 轴,垂足为点N ,即∠APF =90°, ∵△ACB 为等腰直角三角形,∠CAB=90°∴∠ABC=45°∴∠APF=2∠ABC=90°同理(1)可得△AOP ≌△PBF ,∴PN =OA ,OP=FN∴ON=OP+PN=OP+OA∵直线l 为l=1∴FM=OP ;(3)∵CF=2BF∴当t >0,如图,22311MF OP BQ OB OQ t t ===-++- ∴3t=22212t t ++-,即:()3340t t -=,解得t=43 或t=0(舍去) 同理可得t <0时,可得t=-43. 综上,当t=43±时,CF=2BF .【点睛】本题属于几何综合题,主要考查了圆的性质、全等三角形的判定与性质、勾股定理、一元二次方程的解法等知识点,灵活应用所学知识成为解答本题的关键.。
浙江绍兴市第一中学期末精选单元检测(提高,Word版 含解析)

浙江绍兴市第一中学期末精选单元检测(提高,Word 版 含解析)一、第五章 抛体运动易错题培优(难)1.一小船在静水中的速度为3m/s ,它在一条河宽150m 、水流速度为4m/s 的河流中渡河,则该小船( ) A .能到达正对岸 B .渡河的时间不少于50sC .以最短时间渡河时,它渡河的位移大小为200mD .以最短位移渡河时,位移大小为150m 【答案】B 【解析】 【分析】 【详解】A .因为船在静水中的速度小于河水的流速,由平行四边形法则求合速度不可能垂直河岸,小船不可能垂直河岸正达对岸,选项A 错误;B .当船在静水中的速度垂直河岸时,渡河时间最短min 150s 50s 3d t v ===船 选项B 正确;C .船以最短时间50s 渡河时,沿水流方向的位移大小450m 200m min x v t ==⨯=水渡河位移应为水流方向的位移与垂直河岸方向位移的合位移,选项C 错误; D .因为船在静水中的速度小于河水的流速,由平行四边形法则求合速度不可能垂直河岸,小船不可能垂直河岸正达对岸。
若以最短位移渡河,情景如图根据三角形相似可知,最短位移150m 200m v s v =⨯=水船选项D 错误。
故选B 。
2.某人划船横渡一条河流,已知船在静水中的速率恒为v 1,水流速率恒为v 2,且v 1>v 2.他以最短时间方式过河用时T 1,以最短位移方式过河用时T 2.则T 1与T 2的比值为( )A .12v vB .21v vC .12212v v - D .22121v v -【答案】D 【解析】 【分析】 【详解】河水流速处处相同大小为v 2,船速大小恒为v 1,且v 1>v 2。
设河宽为d ,以最短位移过河时,所用时间为T 2,则有22122dv v T =- 以最短时间T 1过河时,有11dv T = 联立解得2212121v v T T -= 选项D 正确,ABC 错误。
绍兴市绍兴一初九年级数学上册第三单元《旋转》测试卷(含答案解析)
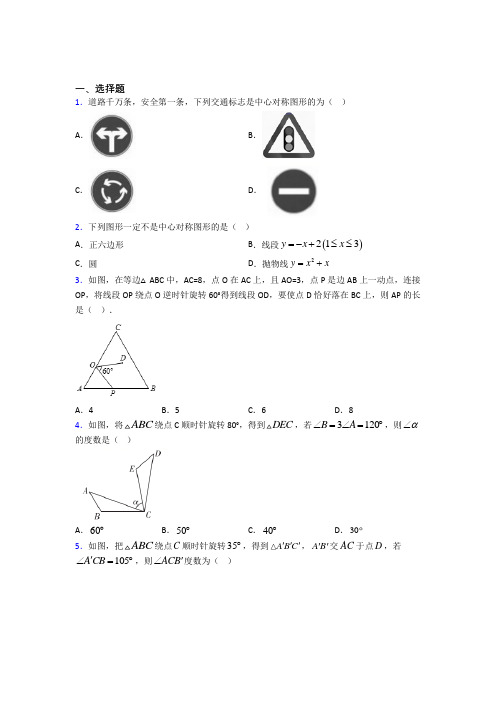
一、选择题1.道路千万条,安全第一条,下列交通标志是中心对称图形的为( )A .B .C .D .2.下列图形一定不是中心对称图形的是( )A .正六边形B .线段()213y x x =-+≤≤C .圆D .抛物线2y x x =+3.如图,在等边△ABC 中,AC=8,点O 在AC 上,且AO=3,点P 是边AB 上一动点,连接OP ,将线段OP 绕点O 逆时针旋转60°得到线段OD ,要使点D 恰好落在BC 上,则AP 的长是( ).A .4B .5C .6D .8 4.如图,将ABC 绕点C 顺时针旋转80°,得到DEC ,若3120B A ∠=∠=︒,则α∠的度数是( )A .60︒B .50︒C .40︒D .305.如图,把ABC 绕点C 顺时针旋转35︒,得到A B C ''',A B ''交AC 于点D ,若105A CB '∠=︒,则ACB '∠度数为( )A.45︒B.30C.35︒D.70︒6.下列命题的逆命题是真命题的是()A.等边三角形是等腰三角形B.若22>,则a bac bc>C.成中心对称的两个图形全等D.有两边相等的三角形是等腰三角形7.如图,将△ABC绕点C(0,-1)旋转180°得到△A′B′C,设点A的坐标为(-3,-4)则点A′的坐标为A.(3,2)B.(3,3)C.(3,4)D.(3,1)8.下列四个图案中,不是中心对称图案的是()A.B.C.D.9.如图,在正方形ABCD中,AB=3,点M在CD的边上,且DM=1,ΔAEM与ΔADM关于AM所在的直线对称,将ΔADM按顺时针方向绕点A旋转90°得到ΔABF,连接EF,则线段EF的长为()A.3 B.3C13D1510.如图,以点A为中心,把△ABC逆时针旋转120°,得到△AB'C′(点B、C的对应点分别为点B′、C′),连接BB',若AC'∥BB',则∠CAB'的度数为()A.45°B.60°C.70°D.90°11.如图,已知△ABC与△CDA关于点O成中心对称,过点O任作直线EF分别交AD,BC于点E,F,则下则结论:①点E和点F,点B和点D是关于中心O的对称点;②直线BD必经过点O;③四边形ABCD是中心对称图形;④四边形DEOC与四边形BFOA的面积必相等;⑤△AOE 与△COF成中心对称.其中正确的个数为 ( )A.2 B.3 C.4 D.512.如图①,正方形A的一个顶点与正方形B的对称中心重合,重叠部分面积是正方形A面积的12,如图②,移动正方形A的位置,使正方形B的一个顶点与正方形A的对称中心重合,则重叠部分面积是正方形B面积的()A.12B.14C.16D.18二、填空题13.如图,四边形ABCD是菱形,点O是两条对角线的交点,过点O的三条直线将菱形分成阴影和空白部分,当菱形的两条对角线长分别为12和16时,则阴影部分面积为_________.14.如图,正方形ABCD的边长为6,点E在边CD上.以点A为中心,把ADE顺时针旋转90︒至ABF的位置,若2DE=,则FC=________.15.如图,点E 在正方形ABCD 的边CB 上,将DCE 绕点D 顺时针旋转90˚到ADF 的位置,连接EF ,过点D 作EF 的垂线,垂足为点H ,于AB 交于点G ,若4AG =,3BG =,则BE 的长为___________.16.如图,已知EAD 32∠=,ADE 绕着点A 旋转50后能与ABC 重合,则BAE ∠=________度.17.如图,在△ABC 中,∠C =90°,AC =2cm ,AB =3cm ,将△ABC 绕点B 顺时针旋转60°得到△FBE ,则点E 与点C 之间的距离是_________cm .18.如图所示的美丽图案,可以看作是由一个三角形绕旋转中心旋转_____次,每次旋转_____度形成的.19.如图,把ABC ∆绕顶点C 按顺时针方向旋转得到△A B C '',当A B AC ''⊥,47A ∠=︒,128A CB ∠='︒时,B CA '∠的度数为_____.20.点()1,5A a -与点()2,5B b +-关于原点对称,则(a +b )2 020=____ . 三、解答题21.如图,在矩形ABCD 中,AB =10,AD =6.以点A 为中心,逆时针旋转矩形ABCD ,得到矩形AEFG ,点B ,C ,D 的对应点分别为点E ,F ,G .(1)如图1,当点E 落在边CD 上时,求线段CE 的长;(2)如图2,当点E 落在线段CF 上时,求证:∠EAC =∠BAC ;(3)在(2)的条件下,CD 与AE 交于点H ,求线段DH 的长.22.在Rt ACB △中,90ACB ∠=︒,AC BC =,D 为AB 上一点,连结CD ,将CD 绕C 点逆时针旋转90°至CE ,连结DE ,过C 作CF DE ⊥交AB 于F ,连结BE .(1)求证:AD BE =.(2)试探索线段AD ,BF ,DF 之间满足的等量关系,并证明你的结论. (3)若15ACD =︒∠,31CD =,求BF .(注:在直角三角形中,30°所对的直角边等于斜边的一半)23.如图,在边长为1的正方形组成的网格中,每个正方形的顶点称为格点.已知△ABC 的顶点均在格点上,建立如图所示的平面直角坐标系,△ABC 三个顶点的坐标分别为A (1,1),B (4,2),C (3,4).(1)画出△ABC关于原点对称的△A1B1C1,并直接写出△A1B1C1各顶点的坐标;(2)将线段AB绕点A顺时针旋转90 °后得到AB2,画出旋转后的图形,并直接写出点B2的坐标;(3)△A1B1C1的面积为.24.如图,△ABC为等边三角形,点P是线段AC上一动点(点P不与A,C重合),连接BP,过点A作直线BP的垂线段,垂足为点D,将线段AD绕点A逆时针旋转60︒得到线段AE,连接DE,CE.(1)求证:BD=CE;(2)延长ED交BC于点F,求证:F为BC的中点.25.如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.ABC的三个顶点A,B,C都在格点上,将ABC绕点A按顺时针方向旋转90°得到AB C''.(1)在正方形网格中,画出AB C'';(2)求线段CC'的长度.26.将边长为4的正方形ABCD与边长为5的正方形AEFG按图1位置放置,AD与AE 在同一条直线上,AB与AG在同一条直线上.将正方形ABCD绕点A逆时针旋转一周,直线EB 与直线DG 交于点P ,(1)DG 与BE 的数量关系:______;DG 与BE 的位置关系:______.(2)如图2,当点B 在线段DG 上时,求ADG 的面积.(3)连结PF ,当42PE =时,求PF 的值.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】根据中心对称图形定义可得答案.【详解】解:A 、不是中心对称图形,故此选项不合题意;B 、不是中心对称图形,故此选项不合题意;C 、不是中心对称图形,故此选项不合题意;D 、是中心对称图形,故此选项符合题意;故选:D .【点睛】本题考查了中心对称图形,关键是掌握把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形.2.D解析:D【分析】根据中心对称图形的定义即可得.【详解】A 、正六边形是中心对称图形,此项不符题意;B 、线段()213y x x =-+≤≤是中心对称图形,对称中心是点(2,0),此项不符题意;C 、圆是中心对称图形,此项不符题意;D 、抛物线2y x x =+是关于直线12x =-轴对称的,不是中心对称图形,此项符合题意;【点睛】本题考查了中心对称图形、抛物线的图象等知识点,熟练掌握概念是解题关键. 3.B解析:B【分析】连接DP ,根据题意,得OP OD =,=60DOP ∠,从而得到120AOP COD ∠+∠=;再根据等边三角形和三角形内角和性质,得120AOP OPA ∠+∠=,从而得COD OPA ∠=∠,通过全等三角形判定,即可得到答案.【详解】如图,点D 落在BC 上,连接DP∵线段OP 绕点O 逆时针旋转60°得到线段OD∴OP OD =,=60DOP ∠∴180120AOP COD DOP ∠+∠=-∠=∵等边△ABC∴180120AOP OPA A ∠+∠=-∠=∴COD OPA ∠=∠即:OP OD COD OPA A C =⎧⎪∠=∠⎨⎪∠=∠⎩∴AOP CDO △≌△∴AP OC =∵AC=8,AO=3∴5OC AC AO =-=∴5AP OC ==故选:B .【点睛】本题考查了等边三角形、全等三角形、旋转、三角形内角和的知识;解题的关键是熟练掌握等边三角形、全等三角形、旋转、三角形内角和的性质,从而完成求解.4.A解析:A根据旋转的性质找到对应点、对应角、对应线段作答.【详解】解:∵3120B A ∠=∠=︒∴120B ∠=︒,40A ∠=︒∵△ABC 绕点C 逆时针旋转80°得到△DEC ,∴∠D=∠A=40°,∠DEC=∠B=120°,∴∠DCE=180°-40°-120°=20°,∵∠DCA=80°∴∠α=∠DCA-∠DCE=80°-20°=60°.故选:A .【点睛】本题考查旋转的性质:旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.要注意旋转的三要素:①定点-旋转中心;②旋转方向;③旋转角度. 5.C解析:C【分析】先根据旋转的定义可得35BCB ACA ''∠=∠=︒,再根据角的和差即可得.【详解】由旋转的定义得:BCB '∠和ACA '∠均为旋转角,35BCB ACA ''∴∠=∠=︒,105A CB '∠=︒,35ACB BCB A A CB CA '''∠=∠-∠'∴∠-=︒,故选:C .【点睛】本题考查了旋转的定义,熟练掌握旋转的概念是解题关键.6.D解析:D【分析】先根据逆命题的定义分别写出各命题的逆命题,然后根据等腰三角形的性质、不等式的性质、中心对称的性质等进行判断.【详解】A 、逆命题为:等腰三角形是等边三角形,是假命题,故本选项错误;B 、逆命题是:如果a >b ,则ac 2>bc 2,是假命题,故本选项错误;C 、逆命题为:全等的两个图形成中心对称,是假命题,故本选项错误;D 、逆命题为:等腰三角形是有两边相等的三角形,故本选项正确;故选:D【点睛】本题考查了命题与定理的知识,解题的关键是能够正确的写出一个命题的逆命题,并熟悉课本中的性质定理.7.A解析:A【解析】试题分析:根据A 与A′关于C 点对称,设A′的坐标为(a ,b ),可知302a -+=,412b -+=-,解得a=3,b=2,因此可知A′点的坐标为(3,2). 故选A考点:中心对称8.C解析:C【分析】在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,据此进一步判断即可.【详解】A :该图形即是中心对称图形也是轴对称图形,不符合题意;B :该图形即是中心对称图形也是轴对称图形,不符合题意;C :该图形是轴对称图形,但不是中心对称图形,符合题意;D :该图形是中心对称图形,但不是轴对称图形,不符合题意;故选:C.【点睛】本题主要考查了中心对称图形的判断,熟练掌握相关概念是解题关键.9.C解析:C【分析】连接BM.证明△AFE ≌△AMB 得FE=MB ,再运用勾股定理求出BM 的长即可.【详解】连接BM ,如图,由旋转的性质得:AM=AF.∵四边形ABCD 是正方形,∴AD=AB=BC=CD ,∠BAD=∠C=90°,∵ΔAEM与ΔADM关于AM所在的直线对称,∴∠DAM=∠EAM.∵∠DAM+∠BAM=∠FAE+∠EAM=90°,∴∠BAM=∠EAF,∴△AFE≌△AMB∴FE=BM.在Rt△BCM中,BC=3,CM=CD-DM=3-1=2,∴==∴故选C.【点睛】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质.10.D解析:D【分析】先根据旋转的性质得到∠BAB′=∠CAC′=120°,AB=AB′,根据等腰三角形的性质易得∠AB′B=30°,再根据平行线的性质由AC′∥BB′得∠C′AB′=∠AB′B=30°,然后利用∠CAB′=∠CAC′-∠C′AB′进行计算.【详解】∵以点A为中心,把△ABC逆时针旋转120°,得到△AB'C′,∴∠BAB′=∠CAC′=120°,AB=AB′,∴∠AB′B=1(180°-120°)=30°,2∵AC′∥BB′,∴∠C′AB′=∠AB′B=30°,∴∠CAB′=∠CAC′-∠C′AB′=120°-30°=90°.故选:D.【点睛】此题考查旋转的性质,等腰三角形的性质,三角形内角和定理,平行线的性质,解题关键在于掌握旋转前后两图形全等,对应点到旋转中心的距离相等,对应点与旋转中心的连线段的夹角等于旋转角.11.D解析:D【分析】由于△ABC与△CDA关于点O对称,那么可得到AB=CD、AD=BC,即四边形ABCD是平行四边形,由于平行四边形是中心对称图形,且对称中心是对角线交点,可根据上述特点对各结论进行判断.【详解】△ABC 与△CDA 关于点O 对称,则AB=CD 、AD=BC ,所以四边形ABCD 是平行四边形, 因此点O 就是▱ABCD 的对称中心,则有:(1)点E 和点F ;B 和D 是关于中心O 的对称点,正确;(2)直线BD 必经过点O ,正确;(3)四边形ABCD 是中心对称图形,正确;(4)四边形DEOC 与四边形BFOA 的面积必相等,正确;(5)△AOE 与△COF 成中心对称,正确;其中正确的个数为5个,故选D .【点睛】熟练掌握平行四边形的性质和中心对称图形的性质是解决此题的关键.12.D解析:D【分析】设正方形B 的面积为S ,正方形B 对角线的交点为O ,标注字母并过点O 作边的垂线,根据正方形的性质可得OE=OM ,∠EOM=90°,再根据同角的余角相等求出∠EOF=∠MON ,然后利用“角边角”证明△OEF 和△OMN 全等,根据全等三角形的面积相等可得阴影部分的面积等于正方形B 的面积的14,再求出正方形B 的面积=2正方形A 的面积,即可得出答案.【详解】解:设正方形B 对角线的交点为O ,如图1,设正方过点O 作边的垂线,则OE =OM ,∠EOM =90°,∵∠EOF+∠EON =90°,∠MON+∠EON =90°,∴∠EOF =∠MON ,在△OEF 和△OMN 中 EOF MON OE 0MOEF OMN 90︒∠=∠⎧⎪=⎨⎪∠=∠=⎩, ∴△OEF ≌△OMN (ASA ),∴阴影部分的面积=S 四边形NOEP +S △OEF =S 四边形NOEP +S △OMN =S 四边形MOEP =14S 正方形CTKW , 即图1中阴影部分的面积=正方形B 的面积的四分之一,同理图2中阴影部分烦人面积=正方形A 的面积的四分之一,∵图①,正方形A 的一个顶点与正方形B 的对称中心重合,重叠部分面积是正方形A 面积的12, ∴正方形B 的面积=正方形A 的面积的2倍,∴图2中重叠部分面积是正方形B 面积的18, 故选D .【点睛】本题考查了正方形的性质,全等三角形的判定与性质,熟记性质并作辅助线构造出全等三角形是解题的关键.二、填空题13.48【分析】根据菱形的面积等于对角线乘积的一半求出菱形的面积再根据菱形是中心对称图形判断出阴影的面积是菱形面积的一半即可解答【详解】如图所示:∵菱形的两条对角线的长分别为12和16菱形的面积∵是菱形 解析:48 【分析】根据菱形的面积等于对角线乘积的一半求出菱形的面积,再根据菱形是中心对称图形判断出阴影的面积是菱形面积的一半即可解答.【详解】如图所示:∵菱形ABCD 的两条对角线的长分别为12和16,菱形ABCD 的面积11216962=⨯⨯=, ∵O 是菱形两条对角线的交点,菱形ABCD 是中心对称图形,∴OEG OFH ∆≅∆,四边形OMAH ≅四边形ONCG , 四边形OEDM ≅四边形OFBN ,∴阴影部分的面积11964822ABCD S ==⨯=菱形, 故答案为:48.【点睛】本题考查了菱形的性质、中心对称图形的性质、菱形的面积公式,熟知菱形的面积公式,利用菱形的性质判断出阴影的面积是菱形面积的一半是解答的关键.14.8【分析】先根据旋转的性质和正方形的性质证明CBF三点在一条直线上又知BF=DE=2可得FC的长【详解】∵四边形ABCD是正方形∴∠ABC=∠D=90°AD=AB由旋转得:∠ABF=∠D=90°BF解析:8【分析】先根据旋转的性质和正方形的性质证明C、B、F三点在一条直线上,又知BF=DE=2,可得FC的长.【详解】∵四边形ABCD是正方形,∴∠ABC=∠D=90°,AD=AB,由旋转得:∠ABF=∠D=90°,BF=DE=2,∴∠ABF+∠ABC=180°,∴C、B、F三点在一条直线上,∴CF=BC+BF=6+2=8,故答案为:8.【点睛】本题主要考查了正方形的性质、旋转变换的性质,难度适中.由旋转的性质得出BF=DE 是解答本题的关键.15.【分析】连接EG根据DG垂直平分EF即可得出EG=FG设BE=x则CE=7-x=AFFG=EG=11-x再根据Rt△BEG中BE2+BG2=EG2即可得到BE的长【详解】解:如图所示连接EG由旋转可解析:56 11【分析】连接EG,根据DG垂直平分EF,即可得出EG=FG,设BE=x,则CE=7-x=AF,FG=EG=11-x,再根据Rt△BEG中,BE2+BG2=EG2,即可得到BE的长.【详解】解:如图所示,连接EG,由旋转可知DCE≌ADF,∴DE=AF,CE=AF,∵DG⊥EF,∴H为EF的中点,∴DG垂直平分EF,∴EG=FG,设BE=x,则CE=5-x=AF,FG=EG=8-x,∵∠B=90°,∴BE2+BG2=EG2即2223(11)x x+=-解得5611 x=故答案为:56 11【点睛】本题主要考查了正方形的性质以及旋转的性质,解题时注意:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.16.【分析】根据旋转对称图形的定义解答【详解】解:∵△ADE绕着点A旋转50°后能与△ABC重合∴∠BAD=50°又∵∠EAD=32°∴∠BAE=∠BAD−∠EAD=50°−32°=18°故答案为18【解析:18【分析】根据旋转对称图形的定义解答.【详解】解:∵△ADE绕着点A旋转50°后能与△ABC重合,∴∠BAD=50°,又∵∠EAD=32°,∴∠BAE=∠BAD−∠EAD=50°−32°=18°.故答案为18.【点睛】本题考查了旋转的性质,解题的关键是根据旋转对称图形的定义解答.17.【解析】试题【解析】试题连接EC,即线段EC的长是点E与点C之间的距离,在Rt△ACB中,由勾股定理得:2222-=-=cm),AB AC325∵将△ABC绕点B顺时针旋转60°得到△FBE,∴BC=BE,∠CBE=60°,∴△BEC是等边三角形,∴518.745【详解】解:利用旋转中的三个要素(①旋转中心;②旋转方向;③旋转角度)设计图案进而判断出基本图形和旋转次数与角度故如图所示的美丽图案可以看作是由一个三角形绕旋转中心旋转次每次旋转度形成的故解析:7 45【详解】解:利用旋转中的三个要素(①旋转中心;②旋转方向;③旋转角度)设计图案,进而判断出基本图形和旋转次数与角度.故如图所示的美丽图案,可以看作是由一个三角形绕旋转中心旋转7次,每次旋转45度形成的,故答案为:7;45.19.42º【分析】根据旋转的性质可知∠A′=∠A=47°则∠A′CA=90°-47°=43°由∠BCB′=∠A′CA=43°则∠B′CA=∠A′CB-∠A′CA-∠BCB′可求【详解】根据旋转的性质可知解析:42º【分析】根据旋转的性质可知∠A′=∠A=47°,则∠A′CA=90°-47°=43°,由∠BCB′=∠A′CA=43°,则∠B′CA=∠A′CB-∠A′CA-∠BCB′可求.【详解】根据旋转的性质可知∠A′=∠A=47°,∴∠A′CA=90°-47°=43°.根据旋转的性质可知旋转角相等,即∠BCB′=∠A′CA=43°,∴∠B′CA=∠A′CB-∠A′CA-∠BCB′=128°-43°-43°=42°.故答案为:42°.【点睛】本题主要考查了旋转的性质,三角形内角和定理的应用,解决这类问题要找准旋转角、以及旋转后对应的线段和角.20.【分析】根据关于原点对称的点的横坐标与纵坐标都互为相反数求出ab的值然后相加计算即可得解【详解】∵点与点关于原点对称∴∴∴故答案为1【点睛】本题考查了关于原点对称的点的坐标关于原点的对称点横纵坐标都 解析:1【分析】根据关于原点对称的点的横坐标与纵坐标都互为相反数求出a 、b 的值,然后相加计算即可得解.【详解】∵点)A与点()2,5B b +-关于原点对称∴2=0b +∴1,2a b ==- ∴()()2 020 2 020211a b =++=- 故答案为1.【点睛】本题考查了关于原点对称的点的坐标,关于原点的对称点,横纵坐标都变成相反数. 三、解答题21.(1)2;(2)见解析;(3)165 【分析】(1)由旋转的性质知AB=AE=10,由矩形的性质得出AD=BC=6,∠BAD=∠D=90°,由勾股定理得出DE=8,即可得出答案;(2)由旋转的性质知∠AEF=∠BAD=90°,AE=AB ,证明Rt △ABC ≌Rt △AEC (HL ),即可得出结论;(3)设DH=x ,由矩形的性质得出CH=CD-DH=10-x ,∠DCA=∠BAC ,证出∠DCA=∠EAC ,得出AH=CH=10-x ,在Rt △ADH 中,由勾股定理得出方程,解方程即可得出答案.【详解】(1)解:由旋转的性质知:AB =AE =10,∵四边形ABCD 是矩形,∴AD =BC =6,∠BAD =∠D =90°,∴DE=8,∵CD =AB =10,∴CE =DC ﹣DE =10﹣8=2;(2)证明:由旋转的性质知:∠AEF =∠BAD =90°,AE =AB ,∵点E 落在线段CF 上,∴∠AEC =∠AEF =90°,在Rt △ABC 和Rt △AEC 中,AE AB AC AC =⎧⎨=⎩, ∴Rt △ABC ≌Rt △AEC (HL ),∴∠EAC =∠BAC ;(3)解:设DH =x ,在矩形ABCD 中,AB ∥CD ,AB =CD =10,∴CH =CD ﹣DH =10﹣x ,∠DCA =∠BAC ,又∵∠EAC =∠BAC ,∴∠DCA =∠EAC ,∴AH =CH =10﹣x ,在Rt △ADH 中,∵DH 2+AD 2=AH 2,∴x 2+62=(10﹣x )2,解得:x =165, ∴DH =165. 【点睛】本题是四边形综合题,考查了矩形的性质、旋转变换的性质、勾股定理、全等三角形的判定与性质、等腰三角形的判定等知识;熟练掌握旋转的性质和矩形的性质是解题的关键. 22.(1)证明见解析;(2)222AD BF DF +=,证明见解析;(3)BF =【分析】(1)将CD 绕C 点逆时针旋转90°至CE ,可得△DCE 是等腰直角三角形,再判定△ACD ≌△BCE (SAS ),即可得出AD =BE ;(2)连接FE ,根据CF 是DE 的垂直平分线,可得DF =EF ,再根据Rt △BEF 中,BE2+BF2=EF2,即可得出AD2+BF2=DF2;(3)根据∠BDE =15°=∠DEF ,可得∠BFE =30°,设BE =x,则BF =,2EF x DF ==,利用在Rt BDE △中,()2222x x +=,即可解得1x =,故可求出BF .【详解】(1)将CD 绕C 点逆时针旋转90°至CE ,可得DCE 是等腰直角三角形, 90DCE ACB ∴∠=∠=︒,DC EC =,ACD BCE ∠∠∴=,在ACD △和BCE 中,AC BC ACD BCE DC EC =⎧⎪∠=∠⎨⎪=⎩,()SAS ACD BCE ∴△≌△,AD BE ∴=.(2)222AD BF DF +=.CF DE ⊥,DCE 是等腰直角三角形,连接FE ,如图所示,CF ∴是DE 的垂直平分线,DF EF ∴=,又ACD BCE ≌,45ABC ∠=︒,45CBF A ABC ∴∠=∠=︒=∠,90EBF ∴∠=︒,∴在Rt BEF △中,222BE BF EF +=,222AD BF DF ∴+=.(3)31CD =,DCE 是等腰直角三角形,62DE ∴=15ACD ∠=︒,45A CDE ∠=∠=︒,15BDE DEF ∴∠=︒=∠,30BFE ∴∠=︒,设BE x =,则3BF x =,2EF x DF ==,∴在Rt BDE △中,()2222362x x x ++=,解得1x =, 3BF ∴=【点睛】本题主要考查了旋转的性质,勾股定理,等腰直角三角形的性质以及全等三角形的判定与性质的综合运用,解决问题的关键是作辅助线构造直角三角形,运用勾股定理进行计算求解.23.(1)图见解析;A 1(-1,-1),B 1(-4,-2),C 1(-3,-4);(2)B 2(2,-2);(3)3.5【分析】(1)先找到A 、B 、C 关于原点对称的A 1、B 1、C 1,再连线即可;(2)根据网格结构点A 、B ,找出将线段AB 绕点A 顺时针旋转90°的对应点B 2,然后连接A B 2,写出坐标即可;(3)△A 1B 1C 1的面积即为三角形ABC 的面积,利用“割补法”即可求得.【详解】解:(1)如图所示,△A 1B 1C 1即为所求:A1(-1,-1),B1(-4,-2),C1(-3,-4);(2)如图所示,A1B2即为所求:B2(2,-2);(3)S△ABC=11133232113222⨯-⨯⨯-⨯⨯-⨯⨯=3.5,∴△A1B1C1的面积= S△ABC=3.5,故填:3.5.【点睛】本题考查了坐标与图形变化−旋转与对称,熟练掌握网格结构,准确找出对应点的位置是解题的关键.24.(1)见解析;(2)见解析.【分析】(1)由等边三角形的性质和旋转的性质可得∠BAD=∠CAE ,AB=AC ,AD=AE ,即可证△BAD ≌△CAE ,可得BD=CE ;(2)过点C 作CG ∥BP ,交EF 的延长线于点G ,由等边三角形的性质和全等三角形的性质可得CG=BD ,∠BDG=∠G ,∠BFD=∠GFC ,可证△BFD ≌△CFG ,可得结论;【详解】(1)∵线段AD 绕点A 逆时针旋转60°得到线段AE ,∴△ADE 是等边三角形,在等边△ABC 和等边△ADE 中,∵ AB=AC ,AD=AE ,∠BAC=∠DAE=60°,∴∠BAD=∠CAE ,在△BAD 和△CAE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩, ∴△BAD ≌△CAE (SAS ),∴BD=CE ;(2)如图,过点C 作CG ∥BP 交DF 的延长线于点G ,∴∠G=∠BDF ,∵∠ADE=60°,∠ADB=90°,∴∠BDF=30°,∴∠G=30°,由(1)可知,BD=CE ,∠CEA=∠BDA ,∵AD ⊥BP ,∴∠BDA=90°,∴∠CEA=90°,∵∠AED=60°,∴∠CED=30°=∠G ,∴CE=CG ,∴BD=CG ,在△BDF 和△CGF 中,BDF G BFD CFG BD CG ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BDF ≌△CGF (AAS ),∴BF=FC ,即F 为BC 的中点.【点睛】本题考查了等边三角形的性质,全等三角形的判定和性质,旋转的性质,添加恰当辅助线构造全等三角形是本题的关键.25.(1)图见解析;(2)42.【分析】(1)先利用网格特点和旋转的性质画出点,C B '',再顺次连接点,,A C B ''即可得; (2)利用旋转的性质、勾股定理即可得.【详解】 (1)分以下三步:①先利用网格特点和旋转的性质画出点C ',②再利用旋转的性质可得,90B B A C BC AC CB '=∠'''=∠=︒,由此可画出点B ', ③顺次连接点,,A C B ''即可,如图中AB C ''即为所作:(2)由网格特点和旋转的性质得:4,90AC AC CAC ''==∠=︒,则2242CC AC AC ''=+=,即线段CC '的长度为42【点睛】本题考查了旋转的定义和性质、勾股定理,熟练掌握旋转的性质是解题关键.26.(1)相等;垂直;(2)4234ADG S =+△;(3)7PF =.【分析】(1)由题意可得△DAG ≌△BAE ,从而可得DG=BE ,再利用全等三角形的性质和直角三角形的知识可以得知DG ⊥BE ;(2)连结AC 交DG 于点 O ,则由勾股定理可得OG 的长度,从而得到△ADG 的面积; (3)连结GE 并旋转△PGF 至△HEF ,由勾股定理即可得到正确解答.【详解】(1)在△DAG 与△BAE 中,DA=BA ,∠DAG=∠BAE=90°,AG=AE , ∴△DAG ≌△BAE ,∴DG=BE ,∠DGA=∠BEA ,∴∠BEA+∠GDE=∠DGA+∠GDE=90°,∴∠DPE=90°,∴DG ⊥BE ;(2)如图,当B 在线段DG 上时,连结AC 交DG 于点O ,则22AO =,()2252217OG =-=,2217DG =+()122172242342ADG S =⨯+⨯=+△ (3)如图,连结GE ,以F 为中心旋转△FGP 至△FEH ,则与(1)类似有△DAG ≌△BAE ,∴∠DGA=∠BEA ,∴∠DGE+∠GEP=∠DGA+45°+∠GEP=45°+∠BEA+∠GEP=45°+45°=90°,∴∠GPE=90°,∴()()2222524232PG GE PE =-=-=,由旋转性质可知∠FEH=∠FGP,∴∠FEH+∠FEP=∠FGP+∠FEP=360°-(∠GFE+∠GPE)=360°-180°=180°,△是等腰直角三角形,∴P、E、H三点共线,且PFH∵PH=PE+EH=PE+GP==∴(2222====,PF=7.PF PH PF298,49【点睛】本题考查正方形的综合应用,灵活运用三角形全等的判定与性质、旋转的性质和勾股定理求解是解题关键.。
浙江省绍兴市第一初级中学 九上 Units1-4测试题

绍初2018学年第一学期九年级英语双休日练习Unit1-4 初三英语试题一、完型填空I was driving in my car the other day. The sun was out, the radio was playing, and I was 1 along. The song wasa 2 one and even my weak voice sounded good singing it. Then it happened however. The sweet sound of the music 3 and there came the unpleasant news. Gas prices went up again. Fans of two sports teams got into fight. I sighed(叹息)and wondered about this 4 world we live in.5 , I could take no more and turned off the6 . Silence seemed more pleasant than listening to7 else about the crazy, competitive society we live in. I slowed down as I went into a town and8 the people as I drove by. A tall man was9 an elderly lady out of a car and helping her place her walker so she could go into store. A smiling woman was 10 food onto the square while a dozen birds flew down to enjoy the food being laid out before them. A young man was walking along, carrying his 11 safely in his arms. When the daughter pulled the hat off his head, they both 12 . I laughed too as I looked at all of his 13 . The radio may have been off in my car, 14 in my heart I was still singing.In fact, this world could have more kindness and less 15 . Kindness makes us all winners in this life and our life is full of kindness, love and joy.()1.A: talking B: singing C: walking D: driving()2.A: long B: boring C: joyful D: sad()3. A: ended B: continued C: jumped D: fell()4. A: exciting B: interesting C: unusual D: crazy()5.A: Finally B: Generally C: Secretly D: Calmly()6.A: television B: radio C: gas D: lights()7.A: anything B: everything C: something D: nothing()8.A: found B: watched C: avoided D: imagined()9.A: freeing B: protecting C: helping D: keeping()10.A: collecting B: moving C: covering D: throwing()11.A: daughter B: son C: dog D: cat()12.A: stopped B: stood C: laughed D: shouted()13.A: weakness B: kindness C: loneliness D: safeness()14.A: for B: or C: and D: but ()15.A: silence B: development C: competition D: sickness二、阅读理解AWhen George Dennehy was a young boy, he never dreamed he would serve others as a motivational(励志) speaker and musician. But the armless teenager has spent the last couple of years sharing his story and encouraging others.Born with no arms in Romania, Dennehy’s condition was terrible, so his parents turned him over to an orphanage(孤儿院), and finally,Dennehy was brought up by a family in America.Early on, he says his American parents noticed his musical abilities. “When I was 8 years old, my mom decided to sigh me up for cello(大提琴) lessons and I started playing,” he says, admitting that he “didn’t really enjoy it”. His first teacher, Shalley, helped him play with his feet.“She actually learned to play the cello with her feet. She wanted to see if it was possible to do it. She made up foot exercises to do. I am really grateful for what she has done for me.” He says.At the beginning of high school, when the cello became not so cool to play, Dennehy took up playing the guitar and picked it up pretty fast.“It was necessary, though, to learn the cello first, because it’s the hardest of all to play,” he says. “The only difference in the guitar is that I’m playin g the cords(弦).” Dennehy uses a standard guitar. “ I play in the same tune as everyone else does,” he notes.Learning to play music hasn’t been an easy road. He was shy at first. But every time he got on stage to perform or play music, he could see how the audience admired him for his abilities and that gave him confidence to chase his dream.No matter what situation we’re in, anything is possible. It is so easy to give up sometimes. But we shouldn’t do that. There’s more that is meant for us.1. What can we learn about George Dennehy from the first two paragraphs?A. He doesn’t think he can serve others.B. He has encouraged others for ten years.C. His parents gave him to an American couple.D. He grew up in a Romanian orphanage.2. What is George Dennehy’s attitude toward Shalley?A. Doubtful.B. Disappointed.C. Acceptable.D. Thankful.3. How does George Dennehy think of learning the guitar?A. He thinks it difficult to learn the guitar.B. He thinks it easy to learn the guitar.C. He thinks he learned it carelessly.D. He thinks he learned it patiently.4. When did George Dennehy get confidence in running after his dream according to the passage?A. After the audience appreciated his abilities.B. When Shalley taught him to play the cello.C. After he played the guitar well in high school.D. When he shared his story and encouraged others.5. In the last paragraph, the author most wants to tell us ________.A. no pain, no gainB. little by little, one goes farC. nothing is impossibleD. the first step is always the hardestBEmpathy(同情心) lets us feel another person’s pain and drives us to help. Do any other animals feel empathy? Scientists recently found that rats(老鼠) do, too.Most people don’t like rats. In many people’s eyes, rats are only bad. But Jean Decety and his partners at the University of Chicago did an experiment. It showed that rats are kind, warm-hearted animals. They can feel each other’s pain.Scientists placed pairs of rats in plastic cages(笼子) for two weeks. During this time they got to know each other. Then they put one of the rats from each pair into a small container(容器) in the cages. The small container had a door. It was so designed as to fall to the side when the free rat touched it. Many of the trapped(困住的) rats squeaked(吱吱叫) to showIn most pairs, the free rats would become very worried about their friends. They kept trying to save their friends again and again throughout the month. Scientists put the rats’ favorite chocolate in the cages, but the rats didn’t eat it until th ey had saved their friends successfully. Scientists also found that female rats seemed to act more empathetic than male rats.“The results are the first to show that rats take action in response to another’s trouble,” Decety said. “Monkeys and chimpanzees have similar behavior. But unlike those animals, rats can be ready used in laboratory studies. They will help us to learn which parts of the brain lead to empathy and helping behavior and whether empathy is natural.”6. A person with empathy is often _____.A.kind-hearted B.clever C.active D.strong7.What does the underline word mean in Chinese? A.休息的B.睡着的C.死亡的D.受苦的8.Why didn’t the free rats eat the chocolate at first?A.Because they were full at that time.B.Because chocolate was not their favorite food.C.Because they wanted to save the trapped rats first.D.Because they were afraid that the chocolate was bad.9.What does the passage mainly tell us?A.Rats can feel other animals’ pain.B.Chocolate is rats’ favorite food.C.Female rats are more empathetic than male rats.D.Rats are empathetic and can feel each other’s pain.CEveryone knows it is very easy to cook instant(即食)noodles by putting them into the boiling water and add in those MSG(味精) packets(小包), together with other food like eggs or vegetables. However, have you ever wondered whether this is the correct way of cooking them? In order to make the noodles joined together nicely side by side it needs some form of wax coating (石蜡涂层) in order to show an attractive instant noodles in front of us. However, researches have shown that the layer (层) of wax coating on the noodles is quite harmful to our body and we should not eat it too frequently. We should have a break of 2-3 days before we start to eat another packet of instant noodles as our body needs about 3 days to clear that layer of wax coating away from our body system. Do you know the danger of having too much wax coating stored in our stomach? It will lead to CANCER if it is stored in our body system for a long period of time.There are 2 key points to take note while preparing instant noodles:1) Wash the instant noodles with warm water first, stir(搅和) it and pour away the water containing the wax coating.2) Repeat Step 1 and try to stir the noodles again to wash away the wax coating on the noodles before cooking it in a new pot of water.If you have eaten other types of noodles, you will notice that the store seller will wash the noodles in warm water first to keep the noodles from sticking together and for the case of instant noodles, the wax coating on the noodles is keeping the noodles from stickin g together. It is very important to wash away the wax coating while preparing a meal as we don’t want our body to be in danger.Hope this article will let more people have self-awareness of the hidden danger of instant noodles andthus eat safely and stay healthy.10.What do the underlined words “ too frequently” mean?A. Too much.B. very soon.C. Too often.D. Too little11. The purpose of the writer is to tell us ______.A. how the instant noodles are madeB. how to cook instant noodlesC. something about the layer of wax coating on the noodlesD. how to eat instant noodles safely and healthily12. It is true according to the passage that ______.A. the instant noodles are joined together in a mess as a piece.B. it is common to see the noodles nicely joined together.C. you can eat instant noodles as often as you like.D. too much wax coating does no harm to our health.13. Many people don't care about too much of the wax coating on the instant noodles because _____.A. they enjoy the taste of the wax coatingB. they take the wax coating for grantedC. they don't know the hidden danger at allD. their body clear it faster than other people14. The function(功能)of the wax coating in the instant noodles is to ______.A. make the noodles more delicious and tastyB. make it easier to cook for the consumersC. make the instant noodles healthier and more attractive to the consumersD. make the noodles joined in a piece and avoid them sticking (粘) together三、词汇应用(每空一词)A)用下列所给单词的适当形式填空。
016浙江省绍兴市第一初级中学人教部编版八年级语文下册第四单元检测

绍初教育集团2017学年第二学期八年级语文第四单元检测班级姓名学号命题:蒋玉英审核:韩晓丽一、语文知识积累(34分)1.根据拼音写汉字、给加点字注音、补全成语:(6分)wū( )蔑liào()望xuàn()丽暴风zhóu( )雨蛮横.()缅.怀()拙.()劣挑拨离间.()()手旁观强()夺理不修边()分()离析2.古诗文填空:(11分)(1)《题破山寺后禅院》中,与陆游的“山重水复疑无路,柳暗花明又一村”有异曲同工之妙。
(2)此地一为别,。
……挥手自兹去,。
(3),一杯一杯复一杯。
我醉欲眠卿且去,。
(4)舟从广陵去,。
,荷花镜里香。
(5),积雪浮云端。
,城中增暮寒。
(6)《大道之行》中与孟子的“老吾老以及人之老,幼吾幼以及人之幼”意相近的句子是。
3.解释加点文言词语(9分)志.怪者也()抟.扶摇而上()去以.六月息()请循.其本()不知其旨.也()学.学半()选贤与.能()不独亲.其亲()女有归.()4.下列句子中标点符号使用规范的一项是()(2分)A.“最主要的是,”他说道,“我们心中要有对弱者的同情与爱心。
”B.初夏时节,广安街头到处都摆着水果,枇杷啊、樱桃啊、桃子啊……走到哪里都闻得到诱人的香味。
C.一个人只有真正明白自己需要什么?才不会在追求理想的路上迷失方向。
D.我国南海蕴藏着丰富的海洋动力资源,如潮汐能、波能、温差能、密度差能……等。
5.下列句子中没有语病的一项是()(2分)A.在“一带一路”的推进过程中,中国将同哈萨克斯坦一道圆梦、筑梦、追梦。
B.通过哈桑的誓言“为你,千千万万遍”,使我懂得了朋友间友谊的珍贵。
C.航天员举着国旗,通过摄像机镜头送出了节日的问候。
D.共享单车具有快捷、方便、灵活,已成为广大市民出行的重要交通工具之一。
6.阅读下面从《钢铁是怎样炼成的》中节选的文字,回答相关问题。
(4分)保尔又问那女子:“您呢,女公民,您也拒绝干活吗?”但是,霎时间他愣住了,因为站在他面前的竟是她。
绍兴市第一中学七年级数学上册第一单元《有理数》基础卷(含答案解析)

一、选择题1.下列各式中,不相等的是( ) A .(﹣5)2和52 B .(﹣5)2和﹣52 C .(﹣5)3和﹣53D .|﹣5|3和|﹣53|2.下列各数中,互为相反数的是( )A .+(-2)与-2B .+(+2)与-(-2)C .-(-2)与2D .-|-2|与+(+2) 3.若21(3)0a b -++=,则b a -=( )A .-412B .-212C .-4D .14.计算4(8)(4)(1)+-÷---的结果是( )A .2B .3C .7D .435.计算112123123412542334445555555555⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-+++---+++++⋯++⋯+ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭的值( ) A .54B .27C .272D .06.如果|a |=-a ,下列成立的是( ) A .-a 一定是非负数 B .-a 一定是负数 C .|a |一定是正数D .|a |不能是07.将(-3.4)3,(-3.4)4,(-3.4)5从小到大排列正确的是( )A .(-3.4)3<(-3.4)4<(-3.4)5B .(-3.4)5<(-3.4)4<(-3.4)3C .(-3.4)5<(-3.4)3<(-3.4)4D .(-3.4)3<(-3.4)5<(-3.4)48.如果a ,b ,c 为非零有理数且a + b + c = 0,那么a b c abca b c abc+++的所有可能的值为( A .0B .1或- 1C .2或- 2D .0或- 29.如果向右走5步记为+5,那么向左走3步记为( ) A .+3B .-3C .+13D .-1310.计算-3-1的结果是( ) A .2B .-2C .4D .-411.2020年5月7日,世卫组织公布中国以外新冠确诊病例约为3504000例,把“3504000”用科学记数法表示正确的是( )A .3504×103B .3.504×106C .3.5×106D .3.504×10712.按键顺序是的算式是( ) A .(0.8+3.2)÷45= B .0.8+3.2÷45= C .(0.8+3.2)÷45= D .0.8+3.2÷45= 13.下列分数不能化成有限小数的是( )A .625 B .324C .412D .11614.有理数a ,b 在数轴上表示如图所示,则下列各式中正确的是( )A .0ab >B .b a >C .a b ->D .b a < 15.计算(-2)2018+(-2)2019等于( )A .-24037B .-2C .-22018D .22018二、填空题16.若230x y ++-= ,则x y -的值为________. 17.绝对值不大于2.1的所有整数是____,其和是____.18.33278.5 4.5 1.67--=____(精确到千分位) 19.计算:(1)(2)(3)(4)(2019)(2020)++-+++-++++-=_____.20.数轴上表示整数的点称为整点.某数轴的单位长度是1厘米,若在这个数轴上随意画出一条长为2020厘米的线段AB ,则线段AB 盖住的整点个数是______.21.阅读理解:根据乘方的意义,可得:22×23=(2×2)×(2×2×2)=25.请你试一试,完成以下题目:(1)a 3•a 4=(a•a•a )•(a•a•a•a )=__; (2)归纳、概括:a m •a n =__;(3)如果x m =4,x n =9,运用以上的结论,计算:x m+n =__. 22.若m ﹣1的相反数是3,那么﹣m =__.23.若三个互不相等的有理数,既可以表示为3,a b +,b 的形式,也可以表示为0,3ab,a 的形式,则4a b -的值________. 24.在数轴上,距离原点有2个单位的点所对应的数是________. 25.比较大小:364--_____________()6.25--. 26.某班同学用一张长为1.8×103mm ,宽为1.65×103mm 的大彩色纸板制作一些边长为3×102mm 的正方形小纸板写标题(不能拼接).则一张这样的大纸板最多能制作符合上述要求的正方形小纸板___________张.三、解答题27.计算:(﹣1)2014+15×(﹣5)+8 28.计算: (1)()222112136⎡⎤⎛⎫⎛⎫-+---÷-⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦(2)131121346⎛⎫-⨯-+ ⎪⎝⎭29.计算:(1)231+-+; (2)()3202111024⎡⎤-⨯+-÷⎣⎦. 30.计算(1)28()5(0.4)5+----; (2)1571361236⎛⎫⎛⎫-+-÷- ⎪ ⎪⎝⎭⎝⎭; (3)2336()(2)()(6)575⨯---⨯-+-⨯; (4)42019213(20.2)(2)(1)5⎡⎤---+-÷⨯---⎢⎥⎣⎦;(5)24512.5()(0.1)(2)(2)10⎡⎤÷-⨯---+-⎣⎦.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绍兴市第一初级中学七年级平行线单元测试卷
班级________姓名___________
一.选择题
1.下列说法正确的是( )
A.不相交的两条线段是平行线. B.不相交的两条直线是平行线.
C.不相交的两条射线是平行线D.在同一平面内,不相交的两条直线叫做平行线.
2.下列说法:①两直线平行,同旁内角互补;②内错角相等,两直线平行;③同位角相等,两直线平行;
④垂直于同一条直线的两条直线平行,其中是平行线的性质的是( )
A.①B.②和③C.④D.①和④
3.如图所示,AB∥CD,若∠2是∠1的2倍,则∠2等于( )
A.60°B.90°C.120°D.150°
4.如图,点D是AB上的一点,点E是AC边上的一点,且∠B=70°,∠ADE=70°,∠DEC=100°,则∠C 是( )A.70°B.80°C.100°D.110°
5.如图所示,已知AD与BC相交于点O,CD∥OE∥AB.如果∠B=40°,∠D=30°,则∠AOC的大小为( ) A.60°B.70°C.80°D.120°
6.如图,AB∥CD∥EF,BC∥AD,AC平分∠BAD,且交EF于点O,则与∠AOE相等的
角有( ) A.5个B.4个C.3个D.2个
7*.如图,AB∥CD∥EF∥GH,AE∥DG,点C在AE上,点F在DG上.设与∠α相等的角的个数为m,与∠β
8*.如图,直线MN∥PQ.点O在PQ上.射线OA⊥OB,分别交MN于点C和点D.∠BOQ=30°.若将射线OB绕点O逆时针旋转30°,则图中60°的角共有()
(A)4个(B)5个(C)6个(D)7个
9.如图,AB∥EF∥CD,∠ABC=46°,∠CEF=154°,则∠BCE等于()
A.23°B.16°C.20°D.26°
10.如图所示,直线l1∥l2,点A、B在直线l2上,点C、D在直线l1上,若△ABC的面积为S1,△ABD的面积为S2,则( )A.S1>S2B.S1=S2C.S1<S2D.不确定
A
11*. 如图3,ABCD ,AEFG ,BIHE 都是平行四边形,且E 是DC 的中点,点D 在FG 上,点C 在HI 上。
△GDA ,△DFE ,△EHC ,△BCI 的面积依次记为S 1,S 2,S 3,S 4,则( )
(A ) S 1+S 2>S 3+S 4 (B ) S 1+S 2<S 3+S 4 (C ) S 1+S 2=S 3+S 4 (D ) S 1+S 2与S 3+S 4大小关系不确定 。
二.填空题
1.如图所示,已知CD 平分∠ACB ,DE ∥AC ,∠1=30°,则∠2=______度.
2.将两张矩形纸片如图所示摆放,使其中一张矩形纸片的一个顶点恰好落在另一张矩形纸片的一条边上,则∠1+∠2=________
3.如图,已知ED ∥AC ,DF ∥AB ,有以下命题:①∠A =∠EDF ;②∠1+∠2=180°;③∠A +∠B +∠C =180°;④∠1=∠3.其中,正确的是________(填序号)
4.如图所示,AB ∥CD ,且∠BAP =α-060,∠APC =α+045,∠PCD =α-0
30,则=α________
5.如图所示的图形中的小三角形可以由△ABC 平移得到的有________个
6*.规律探究:同一平面内有直线10099321,......,,a a a a a 若...,//,433221a a a a a a ⊥⊥按此规律,1a 和100a 的位置是________
三.解答题
1.如图,已知AB ∥CD ,MG 、NH 分别平分∠BMN 与∠CNM ,试说明NH ∥MG ?
2.如图,将四边形ABCD平移到四边形EFGH的位置,根据平移后对应点所连的线段平行且相等,写出图中平行的线段和相等的线段.
3.对于同一平面内的三条直线a、b、c,给出下列五个论断:①a∥b;②b∥c;③a⊥b;④a∥c;⑤a⊥c.以其中两个论断为条件,一个论断为结论,组成真命题,试写出所有的真命题.
4.已知如图,∠ABC=∠ADC,BF、DE分别是∠ABC、∠ADC的角平分线,∠1=∠2,那么CD与AB平
行吗?写出推理过程.
5.如图所示,∠1=60°,∠2=60°,∠3=100°,要使AB∥EF,∠4应为多少度,说明理由.
6.已知,如图,BE平分∠ABD,DE平分∠CDB,且∠1与∠2互余,试判断直线AB、CD的位置关系,
请说明理由.
7.如图,AP,CP分别平分∠BAC,∠ACD,∠P=90°,设∠BAP=α.
(1)用α表示∠ACP;
(2)求证:AB∥CD;
(3)若AP∥CF,求证:FC平分∠DCE.。
