复习第七章
毛概第七章复习题

毛概第七章复习题第七章社会主义改革和对外开放一、单项选择题1.我国的改革开放是A.对原有经济体制细枝末节的修补B.对原有经济体制的自我完善和发展C.我国社会主义制度的自我完善和发展D.一个阶级推翻另一个阶级的革命2.社会主义社会的基本矛盾是A.生产关系和生产力之间的矛盾、上层建筑和经济基础之间的矛盾B.人民日益增长的物质文化需要同落后的社会生产之间的矛盾C.经济发展同人口众多、资金短缺、资源贫乏的矛盾D.无产阶级和资产阶级之间的矛盾3.改革是下列那一项的必然结果A.社会主义社会主要矛盾运动B.社会主义社会基本矛盾运动C.社会主义社会矛盾的主要方面运动D.社会主义社会矛盾的次要方面运动4.20世纪70年代中国改革在农村拉开序幕,农村改革的第一步是A.废除人民公社制度建立以家庭联产承包为主,统分结合、双层经营的新型集体所有制B.建立人民公社制度建立和以家庭联产承包为主,统分结合、双层经营的新型集体所有制C.废除人民公社制度建立以集体承包为主,统分结合、双层经营的新型集体所有制D.废除人民公社制度建立以家庭联产承包,分散经营为主的新型集体所有制5.在《南方谈话》中邓小平明确地提出了,评价和判断改革的成败与是非得失的标准是A.坚持“三个有利于”为标准B.坚持“一大二公”为标准C.坚持维护人民利益为标准D.坚持是否有利于提高国家的综合国力为标准6.我国改革的重点是A.政治体制B.完善社会主义民主政治制度C.经济体制D.教育、科技、文化、卫生体制7.1992年党的十四大明确把A.建立社会主义民主政治制度作为改革的目标B.建立社会主义市场经济体制作为经济体制改革的目标C.建立社会主义公有制制度作为改革的目标D.建立社会主义精神文明作为改革的目标8.社会主义发展的动力是A.改革B.开放C.民主D.矛盾9.发展是社会主义的A.目的B.直接动C.结果D.前提10.稳定是社会主义改革和发展的A.前提B.目的C.直接动力D.目的和直接动力11.对外开放是A.我国的基本国策B.我国的基本原则C.我国的基本路线D.我国的核心利益12.我国的对外开放格局是A.分步骤、有层次、由点到面、逐步推进、全面展开的开放格局B.全方位、多层次、宽领域的开放格局C.全方位、多层次、宽领域、有步骤的开放格局D.有计划、有步骤、由沿海到内地的开放格局13.中国正式成为WTO的成员国是A.2001年12月B.2002年12月C.2003年12月D.2004年12月(二)多项选择题1.我国的改革开放是A.建设中国特色社会主义的全新探索B.决定当代中国命运的关键抉择C.我们党和国家发展进步的活力源泉D.我国社会主义制度的自我完善和发展2.改革开放是建设中国特色社会主义的全新探索,因为改革开放A.决定当代中国命运的关键抉择B.是一个阶级推翻另一个阶级意义上的革命C.实行中华民族伟大复兴的必由之路D.没有现成的模式可以照搬3.社会主义改革与革命的不同点是A.目的和作用B.领导力量C.内容和对象D.形式和手段4.改革开放是A.发展中国、发展社会主义、发展马克思主义之路B.中国新时期最鲜明的特征C.我们党和国家发展进步的活力源泉D.经济全球化的必然结果.改革开放是5.毛泽东认为社会主义社会基本矛盾的性质和特点A.具有“又相适应又相矛盾”的特点B.是在人民根本利益一致基础上的矛盾C.是非对抗性的矛盾D.是推动社会主义社会不断前进的根本动力6.邓小平在1992年的南方谈话中明确地提出了评价和判断改革的成败与是非得失的标准,是A.是否有利于发展社会主义社会的生产力B.是否有利于构建社会主义和谐社会C.是否有利于增强社会主义国家的综合国力D.是否有利于提高人民生活水平7.发展是A.硬道理B.科学发展观的第一要义C.党执政兴国的第一要务D.中国解决所有问题的关键8.改革、发展、稳定三者的关系是A.改革是动力B.发展是目的C.发展是手段D.稳定是前提9.党在处理改革、发展、稳定关系方面积累起来的经验和主要原则A.保持改革、发展和稳定在动态中的相互协调和相互促进B.把改革的力度、发展的速度和社会可以承受的程度统一起来C.把不断改善人民生活作为处理改革发展稳定关系的重要结合点D.把坚持党的领导、人民当家作主和依法治国有机统一起来10.对外开放,下列表述正确的有A.当今的世界是开放的世界B.对外开放是充分发挥社会主义制度优越性的需要C.中国的发展离不开世界D.对外开放是我们国家的基本国策11.我国对外开放格局的特征是A.全方位B.讲平等C.多层次D.宽领域12.不断提高我国对外开放的水平,必须A.转变对外贸易增长方式,提高对外贸易效益B.切实维护国家安全C.提高对外贸易效益D.坚持“引进来”和“走出去”相结合的战略三、思考题1.如何理解改革开放是决定当代中国命运的关键抉择?答:(1)当前的改革不是我国原有经济体制细枝末节的修补,而是我国原有经济体制的根本性变革,改革是解放生产力,是一场新的革命。
最新小学数学毕业总复习——第七章解决实际问题第一课时简单应用题与一般复合应用题

题型三 【例3】学校组织同学们参加“保护地球村”资源再利用活动。 五年级一班同学把捐献的废旧报纸卖了,共得54.8元。
五年级二班共收集废旧报纸多少千克?
返回目录
精析:首先根据总价÷单价=数量来求出五年级一班捐的报纸数 量是完成本题的关键。由于废旧报纸每千克0.8元,五年级一班 卖所捐废旧报纸共得54.8元,所以五年级一班捐了(54.8÷0.8) 千克废旧报纸,又因为五年级二班捐献的报纸是五年级一班的 1.4倍,所以五年级二班捐了(54.8÷0.8×1.4)千克废旧报纸。
返回目录
典例精析及训练
题型一 【例1】一车间二组计划用21天加工1365个电风扇配件,实际每 天比计划多加工26个,实际用了多少天完成任务?
精析:从问题“实际用了多少天完成任务”出发,要解答这 个问题要知道两个条件:①一共加工的电风扇配件个数;② 实际每天加工的个数。条件①已知,而条件②未知,因此把 条件②作为问题,再去找解决它所必需的条件。
用什么方法计算,则需要认真分析题中的数量关系(已知条件和
问题的关系),然后根据四则运算的意义,以及已知的是哪两个
条件来确定。
返回目录
(2) 复合应用题:就是不能一步计算求得答案,而需要两步
或者两步以上的计算才能求得答案的应用题。
2. 解复合应用题
(1) 分析方法
①分析法:问题→条件 ②综合法:条件→问题
方法一:3.6÷(3.6÷10-0.06)-10=2(天) 方法二:3.6÷10=0.36(吨)
0.36-0.06=0.3(吨) 3.6÷0.3=12(天) 12-10=2(天) 答:这堆煤现在可以比原来多烧2天。
返回目录
三、有两堆煤,一堆560吨,另一堆286吨,一辆汽车每次能运9 吨。这辆汽车一共运多少次才能把这些煤全部运完?
中考数学 考点系统复习 第七章 作图与图形变换 微专题(七) 利用“两点之间线段最短”求最值

模型三:“两点两线”型(两个动点+两个定点) (一)利用垂直平分线的性质求四边形周长最小值 【模型分析】 点 P,Q 是∠AOB 内部的两定点,在 OA 上找点 M,在 OB 上找点 N,使得四 边形 PQNM 周长最小. 思路点拨:
8.★如图,在矩形 ABCD 中,AB=4,AD=6,AE=4,AF=2,点 G,H 分 别是边 BC,CD 上的动点,则四边形 EFGH 周长的最小值为 22 5+10+10.
【模型演变】 两定点 A,B 位于直线 l 异侧,在直线 l 上找一点 P,使得|PA-PB|值最 大. 思路点拨:将两定点异侧转化为同侧问题,同“基础模型”即可解决, 作点 B 关于直线 l 的对称点 B′,连接 AB′并延长,与直线 l 交于点 P, 点 P 即为所求.
5.★如图,在正方形 ABCD 中,AB=6,点 F 是对角线 BD 上靠近点 B 的
2.★如图,在△ABC 中,AB=AC,AB 的垂直平分线交 AB 于点 N,交 AC 于点 M,P 是直线 MN 上一动点,H 为 BC 的中点,若 AB=13,△ABC 的周 长是 36.则 PB+PH 的最小值为 112 2.
3.★如图,在矩形 ABCD 中,AB=6,AD=3,点 P 为矩形 ABCD 内一点,
【模型演变】 两定点 A,B 位于直线 l 同侧,在直线 l 上找一点 P,使得 PA+PB 值最小. 思路点拨:将两定点同侧转化为异侧问题,同“基础模型”即可解决, 作点 B 关于直线 l 的对称点 B′,连接 AB′,与直线 l 交于点 P,点 P 即 为所求.
1.如图,等边三角形 AD 边 上的动点,E 是 AB 边上一点,且 AE=2,则线段 EF+CF 的最小值为 22 3 .
1 且动点 P 满足 S△PAB=3S 矩形 ABCD,则点 P 到 A,B 两点距离之和的最小值为 22 13 .
2019届语文复习 第七章 古诗鉴赏-基于思想内容和艺术特色的鉴赏性阅读 专题三 理解必备知识,掌握

核心突破二从语言角度鉴赏-—因言得意,得意赏言诗歌是语言的艺术。
诗歌丰富的思想感情、优美的意境都是通过语言来表现的。
诗歌的语言与其他文学样式的语言相比,更加凝练、优美,更具抒情性、含蓄性、跳跃性和感染力。
古诗词语言从语音上分析,有音乐美、节奏美;从语义上分析,具体有语境表层义和特殊的深层义,有形象、情感、精练美;从语法上分析,有语序颠倒、语句跳跃、词语错位、词性活用、成分省略等,常常造成特别的艺术效果。
语言风格更是呈现出多样的变化,如热情奔放、沉郁顿挫、委婉含蓄等等。
一、炼字炼字就是根据内容和意境的需要,精心挑选最贴切、最富有表现力的字词来表情达意。
一般来说,炼字主要是锤炼诗词中的动词、形容词和虚词.1.炼动词动词往往具有凝练、形象、生动传神的特点,鉴赏古典诗词就是要反复咀嚼品味,体悟含蓄蕴藉、深刻隽永的字词。
动词具有“以最小的面积,表达最大的思想”(巴尔扎克语)的特点,同时动词在勾勒人物形象、传情达意、摹写物态方面有着独特的功能。
诗歌语言“凝练”的特点也表现在动词的运用层面。
动词具有极强的概括性,能够给鉴赏者以广阔的想象空间,如“废池乔木,犹厌言兵"(姜夔《扬州慢》),一个“厌”字,将多少“沉痛伤乱”包蕴其中。
动词,尤其是一些“多义”和“活用”的动词,是高考考查的重点。
试品味下面句子中加点词语的韵味。
乱石穿.空,惊涛拍.岸,卷.起千堆雪.(《念奴娇·赤壁怀古》)答:________________________________________________________________________答案“穿”字,化静为动,写出了乱石的陡峭、尖锐;“拍”字,运用拟人手法,点出了江流湍急的气势;“卷”字,表现了江涛冲击堤岸后形成雪花的力度。
这三个动词形象生动地描摹出赤壁山势的险要高峻和水势的汹涌澎湃,有声有色地展现了古战场雄壮的画面。
2.炼形容词诗歌是社会生活的主观化表现,少不了绘景摹状,化抽象为具体,变无形为有形,使人如闻其声,如见其人,如触其物,如临其境.这些任务,相当一部分是由形容词来承担的。
高考物理总复习 第七章 恒定电流 实验八 测量电源电动势和内电阻教案

实验八测量电源电动势和内电阻注意事项1.可选用旧电池:为了使电路的路端电压变化明显,电池的内阻宜大些,可选用已使用过一段时间的1号干电池。
2.电流不要过大,读数要快:干电池在大电流放电时,电动势E会明显下降,内阻r会明显增大。
因此,实验中不要将I调得过大,读数要快,每次读完立即断电。
3.计算法求E、r:要测出不少于6组I、U数据,且变化范围要大些,用方程组求解时,要将测出的I、U数据中,第1和第4为一组、第2和第5为一组、第3和第6为一组,分别解出E、r值,再求平均值。
4.合理选择标度:为使图线分布空间大,如图1所示,纵坐标可以不从零开始,则图线和横轴的交点不再是短路电流,电源的内阻不能用r=EI短确定,应根据r=⎪⎪⎪⎪⎪⎪ΔUΔI确定。
图1误差分析1.用图象法求E和r时作图不准确。
2.由于电流表或电压表的分压或分流存在系统误差。
本实验中测量结果是:E测<E真,r测<r真。
热点一实验原理与实验操作【例1】(2015·江苏单科,10)小明利用如图2所示的实验装置测量一干电池的电动势和内阻。
图2(1)如图2中电流表的示数为________A。
(2)调节滑动变阻器,电压表和电流表的示数记录如下:U(V) 1.45 1.36 1.27 1.16 1.06I(A)0.120.200.280.360.44由图线求得:电动势E=________V;内阻r=________Ω。
(3)实验时,小明进行了多次测量,花费了较长时间,测量期间一直保持电路闭合。
其实,从实验误差考虑,这样的操作不妥,因为___________________________ ____________________________________________________________________。
解析 (1)由实验装置图可知,电流表使用0.6 A 量程,所以读数为0.44 A ;(2)描点画图,如图所示,根据U =-Ir +E 可得电动势为E =1.60 V ;图线的斜率绝对值等于内阻r =1.22 Ω;(3)干电池长时间使用后,电动势和内阻会发生变化,导致实验误差增大。
高考数学总复习 第七章 不等式 第1节 不等式的性质与一元二次不等式教案 文(含解析)

第1节不等式的性质与一元二次不等式最新考纲 1.了解现实世界和日常生活中存在着大量的不等关系,了解不等式(组)的实际背景;2.会从实际问题的情境中抽象出一二次不等式模型;3.通过函数图像了解一元二次不等式与相应的二次函数、一元二次方程的联系;4.会解一元二次不等式,对给定的一元二次不等式,会设计求解的算法框图.知识梳理1.实数的大小顺序与运算性质的关系(1)a>b⇔a-b>0;(2)a=b⇔a-b=0;(3)a<b⇔a-b<0.2.不等式的性质(1)对称性:a>b⇔b<a;(2)传递性:a>b,b>c⇒a>c;(3)可加性:a>b⇔a+c>b+c;a>b,c>d⇒a+c>b+d;(4)可乘性:a>b,c>0⇒ac>bc;a>b,c<0⇒ac<bc;a>b>0,c >d>0⇒ac>bd;(5)可乘方:a>b>0⇒a n>b n(n∈N,n≥1);(6)可开方:a>b>0⇒n∈N,n≥2).3.三个“二次”间的关系二次函数y =ax 2+bx +c (a >0)的图像一元二次方程ax 2+bx +c =0 (a >0)的根有两相异实根x 1,x 2(x 1<x 2)有两相等实根x 1=x 2=-b2a没有实数根ax 2+bx +c >0(a >0)的解集{x |x >x 2或x <x 1}⎩⎨⎧⎭⎬⎫x |x ≠-b 2aRax 2+bx +c <0(a >0)的解集{x |x 1<x <x 2}∅∅[微点提醒]1.有关分数的性质(1)若a >b >0,m >0,则b a <b +m a +m ;b a >b -ma -m(b -m >0).(2)若ab >0,且a >b ⇔1a <1b.2.对于不等式ax 2+bx +c >0,求解时不要忘记a =0时的情形. 3.当Δ<0时,不等式ax 2+bx +c >0(a ≠0)的解集为R 还是∅,要注意区别.基 础 自 测1.判断下列结论正误(在括号内打“√”或“×”) (1)a >b ⇔ac 2>bc 2.( )(2)若不等式ax 2+bx +c <0的解集为(x 1,x 2),则必有a >0.( ) (3)若方程ax 2+bx +c =0(a <0)没有实数根,则不等式ax 2+bx +c >0(a <0)的解集为R .( )(4)不等式ax 2+bx +c ≤0在R 上恒成立的条件是a <0且Δ=b 2-4ac ≤0.( )解析 (1)由不等式的性质,ac 2>bc 2⇒a >b ;反之,c =0时,a >b ac 2>bc 2.(3)若方程ax 2+bx +c =0(a <0)没有实根,则不等式ax 2+bx +c >0(a <0)的解集为∅.(4)当a =b =0,c ≤0时,不等式ax 2+bx +c ≤0也在R 上恒成立. 答案 (1)× (2)√ (3)× (4)×2.(必修5P72思考交流改编)若a >b >0,c <d <0,则一定有( )A.a d >b cB.a d <b cC.a c >b dD.a c <b d 解析 因为c <d <0,所以0>1c >1d,两边同乘-1,得-1d>-1c>0,又a >b >0,故由不等式的性质可知-a d >-bc >0.两边同乘-1,得a d <bc. 答案 B 3.(必修5P113A1改编)已知集合A =⎩⎨⎧⎭⎬⎫x ⎪⎪⎪12x -1≤0,B ={x |x 2-x -6<0},则A ∩B =( ) A.(-2,3) B.(-2,2) C.(-2,2]D.[-2,2]解析 因为A ={x |x ≤2},B ={x |-2<x <3},所以A ∩B ={x |-2<x ≤2}=(-2,2]. 答案 C4.(2018·抚州联考)若a ,b ,c 为实数,且a <b <0,则下列命题正确的是( ) A.ac 2<bc 2B.1a <1bC.b a >a bD.a 2>ab >b 2解析 c =0时,A 项不成立; 1a -1b =b -a ab>0,选项B 错;b a -a b =b 2-a 2ab =(b +a )(b -a )ab<0,选项C 错. 由a <b <0,∴a 2>ab >b 2.D 正确. 答案 D5.(2019·河北重点八所中学模拟)不等式2x 2-x -3>0的解集为________.解析 由2x 2-x -3>0,得(x +1)(2x -3)>0, 解得x >32或x <-1.∴不等式2x 2-x -3>0的解集为⎩⎨⎧⎭⎬⎫x |x >32或x <-1.答案⎩⎨⎧⎭⎬⎫x |x >32或x <-16.(2018·汉中调研)已知函数f (x )=ax 2+ax -1,若对任意实数x ,恒有f (x )≤0,则实数a 的取值范围是______.解析 若a =0,则f (x )=-1≤0恒成立, 若a ≠0,则由题意,得⎩⎪⎨⎪⎧a <0,Δ=a 2+4a ≤0,解得-4≤a <0, 综上,得a ∈[-4,0]. 答案 [-4,0]考点一 不等式的性质多维探究角度1 比较大小及不等式性质的简单应用【例1-1】 (1)已知实数a ,b ,c 满足b +c =6-4a +3a 2,c -b =4-4a +a 2,则a ,b ,c 的大小关系是( ) A.c ≥b >a B.a >c ≥b C.c >b >aD.a >c >b(2)(一题多解)若1a <1b <0,给出下列不等式:①1a +b <1ab ;②|a |+b >0;③a -1a >b -1b;④ln a 2>ln b 2.其中正确的不等式是( )A.①④B.②③C.①③D.②④解析 (1)∵c -b =4-4a +a 2=(a -2)2≥0,∴c ≥b . 又b +c =6-4a +3a 2,∴2b =2+2a 2,∴b =a 2+1,∴b -a =a 2-a +1=⎝⎛⎭⎪⎫a -122+34>0, ∴b >a ,∴c ≥b >a .(2)法一 因为1a <1b<0,故可取a =-1,b =-2.显然|a |+b =1-2=-1<0,所以②错误;因为ln a 2=ln(-1)2=0,ln b 2=ln(-2)2=ln 4>0,所以④错误.综上所述,可排除A ,B ,D.法二 由1a <1b<0,可知b <a <0.①中,因为a +b <0,ab >0,所以1a +b <0,1ab >0.故有1a +b <1ab,即①正确; ②中,因为b <a <0,所以-b >-a >0.故-b >|a |,即|a |+b <0,故②错误;③中,因为b <a <0,又1a <1b <0,则-1a >-1b>0,所以a -1a >b -1b,故③正确;④中,因为b <a <0,根据y =x 2在(-∞,0)上为减函数,可得b 2>a 2>0,而y =ln x 在定义域(0,+∞)上为增函数,所以ln b 2>ln a 2,故④错误.由以上分析,知①③正确. 答案 (1)A (2)C角度2 利用不等式变形求范围【例1-2】 (一题多解)设f (x )=ax 2+bx ,若1≤f (-1)≤2,2≤f (1)≤4,则f (-2)的取值范围是________.解析 法一 设f (-2)=mf (-1)+nf (1)(m ,n 为待定系数),则4a -2b =m (a -b )+n (a +b ), 即4a -2b =(m +n )a +(n -m )b .于是得⎩⎪⎨⎪⎧m +n =4,n -m =-2,解得⎩⎪⎨⎪⎧m =3,n =1.∴f (-2)=3f (-1)+f (1).又∵1≤f (-1)≤2,2≤f (1)≤4. ∴5≤3f (-1)+f (1)≤10, 故5≤f (-2)≤10. 法二由⎩⎪⎨⎪⎧f (-1)=a -b ,f (1)=a +b ,得⎩⎪⎨⎪⎧a =12[f (-1)+f (1)],b =12[f (1)-f (-1)],∴f (-2)=4a -2b =3f (-1)+f (1). 又∵1≤f (-1)≤2,2≤f (1)≤4,∴5≤3f (-1)+f (1)≤10,故5≤f (-2)≤10. 法三由⎩⎪⎨⎪⎧1≤a -b ≤2,2≤a +b ≤4确定的平面区域如图阴影部分所示, 当f (-2)=4a -2b 过点A ⎝ ⎛⎭⎪⎫32,12时, 取得最小值4×32-2×12=5,当f (-2)=4a -2b 过点B (3,1)时, 取得最大值4×3-2×1=10, ∴5≤f (-2)≤10. 答案 [5,10]规律方法 1.比较两个数(式)大小的两种方法2.与充要条件相结合问题,用不等式的性质分别判断p ⇒q 和q ⇒p 是否正确,要注意特殊值法的应用.3.与命题真假判断相结合问题.解决此类问题除根据不等式的性质求解外,还经常采用特殊值验证的方法.4.在求式子的范围时,如果多次使用不等式的可加性,式子中的等号不能同时取到,会导致范围扩大.【训练1】 (1)(2019·东北三省四市模拟)设a ,b 均为实数,则“a >|b |”是“a 3>b 3”的( ) A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件(2)(2018·天一测试)已知实数a ∈(1,3),b ∈⎝ ⎛⎭⎪⎫18,14,则ab 的取值范围是________.解析 (1)a >|b |能推出a >b ,进而得a 3>b 3;当a 3>b 3时,有a >b ,但若b <a <0,则a >|b |不成立,所以“a >|b |”是“a 3>b 3”的充分不必要条件.(2)依题意可得4<1b <8,又1<a <3,所以4<ab<24.答案 (1)A (2)(4,24)考点二 一元二次不等式的解法【例2-1】 (1)(2019·河南中原名校联考)已知f (x )是定义在R 上的奇函数.当x >0时,f (x )=x 2-2x ,则不等式f (x )>x 的解集用区间表示为________.(2)已知不等式ax 2-bx -1>0的解集是{x |-12<x <-13},则不等式x 2-bx -a ≥0的解集是________.解析 (1)设x <0,则-x >0,因为f (x )是奇函数,所以f (x )=-f (-x )=-(x 2+2x ). 又f (0)=0. 于是不等式f (x )>x等价于⎩⎪⎨⎪⎧x >0,x 2-2x >x 或⎩⎪⎨⎪⎧x <0,-x 2-2x >x ,解得x >3或-3<x <0.故不等式的解集为(-3,0)∪(3,+∞).(2)由题意,知-12,-13是方程ax 2-bx -1=0的两个根,且a <0,所以⎩⎪⎨⎪⎧-12+⎝ ⎛⎭⎪⎫-13=ba,-12×⎝ ⎛⎭⎪⎫-13=-1a ,解得⎩⎪⎨⎪⎧a =-6,b =5.故不等式x 2-bx -a ≥0为x 2-5x +6≥0, 解得x ≥3或x ≤2.答案 (1)(-3,0)∪(3,+∞) (2){x |x ≥3或x ≤2} 【例2-2】 解关于x 的不等式ax 2-2≥2x -ax (a ∈R ). 解 原不等式可化为ax 2+(a -2)x -2≥0.①当a =0时,原不等式化为x +1≤0,解得x ≤-1. ②当a >0时,原不等式化为⎝⎛⎭⎪⎫x -2a (x +1)≥0,解得x ≥2a或x ≤-1.③当a <0时,原不等式化为⎝⎛⎭⎪⎫x -2a (x +1)≤0.当2a >-1,即a <-2时,解得-1≤x ≤2a;当2a =-1,即a =-2时,解得x =-1满足题意; 当2a<-1,即-2<a <0时,解得2a≤x ≤-1.综上所述,当a =0时,不等式的解集为{x |x ≤-1}; 当a >0时,不等式的解集为⎩⎨⎧⎭⎬⎫x |x ≥2a 或x ≤-1;当-2<a <0时,不等式的解集为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫2a ≤x ≤-1;当a =-2时,不等式的解集为{-1}; 当a <-2时,不等式的解集为⎩⎨⎧⎭⎬⎫x |-1≤x ≤2a .规律方法 1.解一元二次不等式的一般方法和步骤 (1)化:把不等式变形为二次项系数大于零的标准形式.(2)判:计算对应方程的判别式,根据判别式判断方程有没有实根(无实根时,不等式解集为R 或∅). (3)求:求出对应的一元二次方程的根.(4)写:利用“大于取两边,小于取中间”写出不等式的解集. 2.含有参数的不等式的求解,首先需要对二次项系数讨论,再比较(相应方程)根的大小,注意分类讨论思想的应用.【训练2】 (1)不等式x +5(x -1)2≥2的解集是( )A.⎣⎢⎡⎦⎥⎤-3,12B.⎣⎢⎡⎦⎥⎤-12,3C.⎣⎢⎡⎭⎪⎫12,1∪(1,3]D.⎣⎢⎡⎭⎪⎫-12,1∪(1,3](2)(2019·铜川一模)关于x 的不等式ax -b <0的解集是(1,+∞),则关于x 的不等式(ax +b )(x -3)>0的解集是( ) A.(-∞,-1)∪(3,+∞) B.(1,3) C.(-1,3)D.(-∞,1)∪(3,+∞)解析 (1)不等式可化为2x 2-5x -3(x -1)2≤0,即(2x +1)(x -3)(x -1)2≤0, 解得-12≤x <1或1<x ≤3.(2)关于x 的不等式ax -b <0即ax <b 的解集是(1,+∞),∴a =b <0, ∴不等式(ax +b )(x -3)>0可化为(x +1)(x -3)<0,解得-1<x <3, ∴所求不等式的解集是(-1,3). 答案 (1)D (2)C考点三 一元二次不等式恒成立问题多维探究角度1 在实数R 上恒成立【例3-1】 (2018·大庆实验中学期中)对于任意实数x ,不等式(a -2)x 2-2(a -2)x -4<0恒成立,则实数a 的取值范围是( ) A.(-∞,2) B.(-∞,2] C.(-2,2)D.(-2,2]解析 当a -2=0,即a =2时,-4<0恒成立;当a -2≠0,即a ≠2时,则有⎩⎪⎨⎪⎧a -2<0,Δ=[-2(a -2)]2-4×(a -2)×(-4)<0,解得-2<a <2.综上,实数a 的取值范围是(-2,2]. 答案 D角度2 在给定区间上恒成立【例3-2】 (一题多解)设函数f (x )=mx 2-mx -1(m ≠0),若对于x ∈[1,3],f (x )<-m +5恒成立,则m 的取值范围是________.解析 要使f (x )<-m +5在[1,3]上恒成立, 故mx 2-mx +m -6<0,则m ⎝⎛⎭⎪⎫x -122+34m -6<0在x ∈[1,3]上恒成立. 法一 令g (x )=m ⎝⎛⎭⎪⎫x -122+34m -6,x ∈[1,3]. 当m >0时,g (x )在[1,3]上是增函数, 所以g (x )max =g (3)=7m -6<0. 所以m <67,则0<m <67.当m <0时,g (x )在[1,3]上是减函数, 所以g (x )max =g (1)=m -6<0. 所以m <6,所以m <0. 综上所述,m的取值范围是⎩⎨⎧⎭⎬⎫m ⎪⎪⎪0<m <67或m <0.法二因为x 2-x +1=⎝⎛⎭⎪⎫x -122+34>0, 又因为m (x 2-x +1)-6<0,所以m <6x 2-x +1.因为函数y =6x 2-x +1=6⎝⎛⎭⎪⎫x -122+34在[1,3]上的最小值为67,所以只需m <67即可.因为m ≠0,所以m 的取值范围是⎩⎨⎧⎭⎬⎫m ⎪⎪⎪0<m <67或m <0 . 答案⎩⎨⎧⎭⎬⎫m ⎪⎪⎪0<m <67或m <0 角度3 给定参数范围的恒成立问题【例3-3】 已知a ∈[-1,1]时不等式x 2+(a -4)x +4-2a >0恒成立,则x 的取值范围为( ) A.(-∞,2)∪(3,+∞) B.(-∞,1)∪(2,+∞) C.(-∞,1)∪(3,+∞)D.(1,3)解析 把不等式的左端看成关于a 的一次函数,记f (a )=(x -2)a +x 2-4x +4,则由f (a )>0对于任意的a ∈[-1,1]恒成立, 得f (-1)=x 2-5x +6>0, 且f (1)=x 2-3x +2>0即可,解不等式组⎩⎪⎨⎪⎧x 2-5x +6>0,x 2-3x +2>0,得x <1或x >3.答案 C规律方法 1.对于一元二次不等式恒成立问题,恒大于0就是相应的二次函数的图像在给定的区间上全部在x 轴上方,恒小于0就是相应的二次函数的图像在给定的区间上全部在x 轴下方.另外常转化为求二次函数的最值或用分离参数法求最值.2.解决恒成立问题一定要搞清谁是主元,谁是参数,一般地,知道谁的范围,谁就是主元,求谁的范围,谁就是参数.【训练3】 (1)(2019·河南豫西南五校联考)已知关于x 的不等式kx 2-6kx +k +8≥0对任意x ∈R 恒成立,则k 的取值范围是( )A.[0,1]B.(0,1]C.(-∞,0)∪(1,+∞)D.(-∞,0]∪[1,+∞)(2)(2019·安庆模拟)若不等式x 2+ax +1≥0对一切x ∈⎝⎛⎦⎥⎤0,12恒成立,则a 的最小值是( ) A.0B.-2C.-52D.-3解析 (1)当k =0时,不等式kx 2-6kx +k +8≥0可化为8≥0,其恒成立,当k ≠0时,要满足关于x 的不等式kx 2-6kx +k +8≥0对任意x ∈R 恒成立,只需⎩⎪⎨⎪⎧k >0,Δ=36k 2-4k (k +8)≤0,解得0<k ≤1.综上,k 的取值范围是[0,1]. (2)由于x ∈⎝⎛⎦⎥⎤0,12,若不等式x 2+ax +1≥0恒成立,则a ≥-⎝ ⎛⎭⎪⎫x +1x ,x ∈⎝⎛⎦⎥⎤0,12时恒成立,令g (x )=x +1x ,x ∈⎝⎛⎦⎥⎤0,12,易知g (x )在⎝ ⎛⎦⎥⎤0,12上是减函数,则y =-g (x )在⎝ ⎛⎦⎥⎤0,12上是增函数.∴y =-g (x )的最大值是-⎝ ⎛⎭⎪⎫12+2=-52. 因此a ≥-52,则a 的最小值为-52.答案 (1)A (2)C [思维升华]1.比较法是不等式性质证明的理论依据,是不等式证明的主要方法之一,比较法之一作差法的主要步骤为作差——变形——判断正负.2.判断不等式是否成立,主要有利用不等式的性质和特殊值验证两种方法,特别是对于有一定条件限制的选择题,用特殊值验证的方法更简单. [易错防范]1.“三个二次”的关系是解一元二次不等式的理论基础;一般可把a <0的情况转化为a >0时的情形.2.含参数的不等式要注意选好分类标准,避免盲目讨论.基础巩固题组 (建议用时:40分钟)一、选择题1.若f (x )=3x 2-x +1,g (x )=2x 2+x -1,则f (x ),g (x )的大小关系是( ) A.f (x )=g (x ) B.f (x )>g (x )C.f (x )<g (x )D.随x 的值变化而变化解析 f (x )-g (x )=x 2-2x +2=(x -1)2+1>0⇒f (x )>g (x ). 答案 B2.(2019·北京东城区综合练习)已知x ,y ∈R ,那么“x >y ”的充要条件是( ) A.2x>2yB.lg x >lg yC.1x >1yD.x 2>y 2解析 因为2x>2y⇔x >y ,所以“2x>2y ”是“x >y ”的充要条件,A 正确;lg x >lg y ⇔x >y >0,则“lg x >lg y ”是“x >y ”的充分不必要条件,B 错误;“1x >1y”和“x 2>y 2”都是“x >y ”的既不充分也不必要条件.答案 A3.不等式|x |(1-2x )>0的解集为( )A.(-∞,0)∪⎝ ⎛⎭⎪⎫0,12B.⎝ ⎛⎭⎪⎫-∞,12C.⎝ ⎛⎭⎪⎫12,+∞D.⎝⎛⎭⎪⎫0,12解析 当x ≥0时,原不等式即为x (1-2x )>0,所以0<x <12;当x <0时,原不等式即为-x (1-2x )>0,所以x <0,综上,原不等式的解集为(-∞,0)∪⎝⎛⎭⎪⎫0,12.答案 A4.(2018·延安质检)若实数m ,n 满足m >n >0,则( ) A.-1m<-1nB.m -n <m -nC.⎝ ⎛⎭⎪⎫12m>⎝ ⎛⎭⎪⎫12nD.m 2<mn解析 取m =2,n =1,代入各选择项验证A ,C ,D 不成立.只有B 项成立(事实上2-1<2-1). 答案 B5.已知函数f (x )=⎩⎪⎨⎪⎧x ,x ≤0,ln (x +1),x >0,若f (2-x 2)>f (x ),则实数x 的取值范围是( )A.(-∞,-1)∪(2,+∞)B.(-∞,-2)∪(1,+∞)C.(-1,2)D.(-2,1)解析 易知f (x )在R 上是增函数,∵f (2-x 2)>f (x ), ∴2-x 2>x ,解得-2<x <1,则实数x 的取值范围是(-2,1). 答案 D 二、填空题6.若0<a <1,则不等式(a -x )⎝⎛⎭⎪⎫x -1a >0的解集是________.解析 原不等式可化为(x -a )⎝ ⎛⎭⎪⎫x -1a <0,由0<a <1得a <1a ,∴a <x <1a.答案⎝⎛⎭⎪⎫a ,1a7.规定记号“⊙”表示一种运算,定义a ⊙b =ab +a +b (a ,b 为正实数),若1⊙k 2<3,则k 的取值范围是________. 解析 由题意知k 2+1+k 2<3,化为(|k |+2)(|k |-1)<0,所以|k |<1, 所以-1<k <1. 答案 (-1,1)8.(2019·宜春质检)设a <0,若不等式-cos 2x +(a -1)cos x +a 2≥0对于任意的x ∈R 恒成立,则a 的取值范围是________.解析 令t =cos x ,t ∈[-1,1],则不等式f (t )=t 2-(a -1)t -a 2≤0对t ∈[-1,1]恒成立,因此⎩⎪⎨⎪⎧f (-1)≤0,f (1)≤0⇒⎩⎪⎨⎪⎧a -a 2≤0,2-a -a 2≤0,∵a <0,∴a ≤-2. 答案 (-∞,-2] 三、解答题9.已知f (x )=-3x 2+a (6-a )x +6. (1)解关于a 的不等式f (1)>0;(2)若不等式f (x )>b 的解集为(-1,3),求实数a ,b 的值. 解 (1)由题意知f (1)=-3+a (6-a )+6=-a 2+6a +3>0,即a 2-6a -3<0,解得3-23<a <3+2 3.所以不等式的解集为{a |3-23<a <3+23}. (2)∵f (x )>b 的解集为(-1,3),∴方程-3x 2+a (6-a )x +6-b =0的两根为-1,3,∴⎩⎪⎨⎪⎧(-1)+3=a (6-a )3,(-1)×3=-6-b 3,解得⎩⎪⎨⎪⎧a =3±3,b =-3.故a 的值为3±3,b 的值为-3.10.某商品每件成本价为80元,售价为100元,每天售出100件.若售价降低x 成(1成=10%),售出商品数量就增加85x 成.要求售价不能低于成本价.(1)设该商店一天的营业额为y ,试求y 与x 之间的函数关系式y =f (x ),并写出定义域;(2)若再要求该商品一天营业额至少为10 260元,求x 的取值范围. 解(1)由题意得,y =100⎝ ⎛⎭⎪⎫1-x 10·100⎝⎛⎭⎪⎫1+850x .因为售价不能低于成本价,所以100⎝ ⎛⎭⎪⎫1-x 10-80≥0,解得0≤x ≤2.所以y =f (x )=40(10-x )(25+4x ), 定义域为{x |0≤x ≤2}.(2)由题意得40(10-x )(25+4x )≥10 260, 化简得8x 2-30x +13≤0,解得12≤x ≤134.所以x的取值范围是⎣⎢⎡⎦⎥⎤12,2.能力提升题组 (建议用时:20分钟)11.已知0<a <b ,且a +b =1,则下列不等式中正确的是( )A.log 2a >0B.2a -b<12C.log 2a +log 2b <-2D.2a b +b a <12解析 由题意知0<a <1,此时log 2a <0,A 错误;由已知得0<a <1,0<b <1,所以-1<-b <0,又a <b ,所以-1<a -b <0,所以12<2a -b<1,B 错误;因为0<a <b ,所以a b +ba >2a b ·b a =2,所以2a b +b a>22=4,D 错误;由a +b =1>2ab ,得ab <14,因此log 2a +log 2b =log 2(ab )<log 214=-2,C 正确.答案 C12.(2019·保定调研)已知定义在R 上的奇函数f (x )满足:当x ≥0时,f (x )=x 3,若不等式f (-4t )>f (2m +mt 2)对任意实数t 恒成立,则实数m 的取值范围是( ) A.(-∞,-2)B.(-2,0)C.(-∞,0)∪(2,+∞)D.(-∞,-2)∪(2,+∞) 解析 因为f (x )在R 上为奇函数,且在[0,+∞)上为增函数,所以f (x )在R 上是增函数,结合题意得-4t >2m +mt 2对任意实数t 恒成立⇒mt 2+4t +2m <0对任意实数t 恒成立⇒⎩⎪⎨⎪⎧m <0,Δ=16-8m 2<0⇒m ∈(-∞,-2). 答案 A13.已知-1<x +y <4,2<x -y <3,则3x +2y 的取值范围是________.解析 设3x +2y =m (x +y )+n (x -y ),则⎩⎪⎨⎪⎧m +n =3,m -n =2,∴⎩⎪⎨⎪⎧m =52,n =12.即3x +2y =52(x +y )+12(x -y ), 又∵-1<x +y <4,2<x -y <3,∴-52<52(x +y )<10,1<12(x -y )<32, ∴-32<52(x +y )+12(x -y )<232, 即-32<3x +2y <232, ∴3x +2y 的取值范围为⎝ ⎛⎭⎪⎫-32,232. 答案 ⎝ ⎛⎭⎪⎫-32,232 14.(2019·济南质检)已知f (x )是定义在R 上的偶函数,且当x ≥0时,f (x )=e x.若对任意x ∈[a ,a +1],恒有f (x +a )≥f (2x )成立,求实数a 的取值范围.解 因为函数f (x )是偶函数,故函数图像关于y 轴对称,且在(-∞,0]上单调递减,在[0,+∞)上单调递增.所以由f (x +a )≥f (2x )可得|x +a |≥2|x |在[a ,a +1]上恒成立, 从而(x +a )2≥4x 2在[a ,a +1]上恒成立,化简得3x 2-2ax -a 2≤0在[a ,a +1]上恒成立, 设h (x )=3x 2-2ax -a 2,则有⎩⎪⎨⎪⎧h (a )=0≤0,h (a +1)=4a +3≤0,解得a ≤-34. 故实数a 的取值范围是⎝ ⎛⎦⎥⎤-∞,-34.。
复习题 第七章 内分泌与代谢性疾病病人的护理

第七章内分泌与代谢性疾病病人的护理1.人体最重要的神经内分泌器官是A.腺垂体B.神经垂体C. 下丘脑D.肾上腺皮质E.肾上腺髓质解析:下丘脑是人体最重要的神经内分泌器官,是神经系统与内分泌系统的枢纽。
答案:C 2.属于功能亢进的内分泌疾病是A.尿崩症B.糖尿病C.肢端肥大症D.呆小症E.粘液性水肿解析:神经垂体功能减退产生尿崩症;胰岛功能减退产生糖尿病;腺垂体功能亢进成年后发病肢端肥大症;甲状腺功能减退儿童期产生呆小症,成年后发病粘液性水肿。
答案:C 3.严重肥胖者摄入量,应按理想体重摄入的能量减少A.10% B.20% C.30% D.40% E.50%解析:严重肥胖者,可按理想体重所需热量减少30%或更多。
答案C 4.甲状腺功能亢进患者甲状腺激素过多的表现不包括A.低热B.心悸C.便秘D.手抖E.易激动5.下列可以鉴别甲状腺功能亢进与单纯性甲状腺肿的检查是A.甲状腺摄I131率B.血清总T3、总T4C.血清游离T4D.T3抑制试验E.促甲状腺激素释放激素兴奋试验解析:T3抑制试验口服一定剂量T3后再做摄131I率,甲亢时不受抑制,而单纯性甲状腺肿者受抑制,故此试验可作为甲亢与单纯性甲状腺肿的鉴别。
答案:D6.抗甲状腺药物的作用机制是A.对抗甲状腺激素的效应B.抑制甲状腺过氧化物酶,阻断甲状腺激素的合成C.破坏甲状腺腺泡上皮,减少甲状腺激素的合成与释放D.抑制无机碘氧化成有机碘E.破坏体内已合成的甲状腺激素7.患者肖某,女性49岁,糖尿病病史5年余,近日自感食欲减退、恶心、呕吐,常伴头痛、嗜睡、烦躁、呼吸深快,自测尿糖阳性,该患者的呼吸气味可能呈A.芳香味B.氨臭味C.大蒜味D.烂苹果味E.苦杏仁味8.直接刺激胰岛素细胞释放胰岛素的降糖药物是A.磺脲类B.双胍类C.葡萄糖苷酶抑制剂D.胰岛素激敏剂E.硫脲类9.关于1型糖尿病,叙述正确的是A.主要与环境因素有关B.多见于40岁以上的成人C.常对胰岛素发生抵抗D.易发生酮症酸中毒E.口服降糖药治疗为主10.糖尿病患者的饮食原则是A.高蛋白、高热量、高维生素B.低蛋白、高热量、高维生素C.低糖、低脂、高蛋白、高维生素D.低糖、低脂、低蛋白、高纤维E.高蛋白、高糖、高维生素、高钠低钾11.22.()甲状腺功能亢进周期性麻痹患者首要的护理措施是A.注意安全 B.卧床休息 C.执行补钾医嘱D.低糖饮食 E.避免情绪紧张12.患者,女性49岁,糖尿病病史5年余,近日自感食欲减退、恶心、呕吐,常伴头痛、嗜睡、烦躁、呼吸深快,自测尿糖阳性,该患者的呼吸气味可能呈A.芳香味 B.氨臭味 C.大蒜味 D.烂苹果味 E.苦杏仁味13.对可疑糖尿病患者最有诊断价值的检查是A.空腹血糖 B.血浆胰岛素 C.24小时尿糖测定D.口服葡萄糖耐量试验 E.糖化血红蛋白14.侏儒症的病因是A.促肾上腺皮质激素缺乏 B.甲状腺激素分泌不足 C.甲状腺激素分泌过多D.抗利尿激素分泌过多 E.生长激素释放激素缺乏15.皮质醇增多症的特征性表现为A.脊柱变形 B.多毛与座疮 C.皮肤紫纹D.向心性肥胖 E.皮肤黏膜色素沉着16.对甲状腺功能亢进面容的描述,错误的是A.面容惊愕B.表情兴奋 C.眼裂增大 D.口唇发绀 E.眼球突出17.对甲状腺功能亢进恶性突眼患者的护理,错误的是A.带深色眼镜 B.做眼球运动 C.低盐饮食,限水分D.睡眠时头低位 E.涂抗生素眼膏18.主要表现为色素沉着的内分泌紊乱是A.慢性肾上腺皮质功能减退症 B.糖尿病 C.甲状腺功能亢进症D.黏液性水肿 E.呆小症19.抗甲状腺药物最严重的不良反应是A.皮疹B.粒细胞缺乏C.消化道出血D.甲状腺危象E.肝功能受损20.糖尿病病人最基本的治疗措施是A.体育锻炼B.药物治疗C.饮食治疗D.并发症治疗E.注射胰岛素21.患者男性,55岁。
2023中考数学专题复习——第七章 四边形

2023中考专题复习——第七章四边形时间:45分钟满分:80分一、选择题(每题4分,共32分)1.下列各组条件中,不能判断一个四边形是平行四边形的是() A.两组对边分别平行的四边形B.两组对角分别相等的四边形C.两条对角线互相平分的四边形D.一组对边平行另一组对边相等的四边形2.如图,在△ABC中,∠A=90°,点M,N分别为边AB和AC的中点,若AB =2,AC=4,则MN的长度为()A.2 3 B. 3 C.2 5 D. 5(第2题)(第3题)3.如图,在▱ABCD中,连接AC,已知∠BAC=40°,∠ACB=80°,则∠BCD=()A.80°B.100°C.120°D.140°4.如图,四边形ABCD是菱形,其中A,B两点的坐标分别为A(0,3),B(4,0),则点D的坐标为()A.(0,1) B.(0,-1)C.(0,2) D.(0,-2)(第4题)(第5题)5.如图,在正方形ABCD的外侧作等边三角形CDE,连接AE,则∠DAE的度数是()A.15°B.20°C.12.5°D.10°6.如图,在矩形ABCD中,AB=4,BC=8,对角线AC,BD相交于点O,过点O作OE⊥AC交AD于点E,则DE的长是()A.3 B.5 C.2.4 D.2.5(第6题)(第7题)7.如图,在▱ABCD中,AB=BC=5,对角线BD=8,则▱ABCD的面积为() A.20 B.24 C.40 D.488.将两张全等的矩形纸片和另两张全等的正方形纸片按如图方式不重叠地放置在矩形ABCD内,其中矩形纸片和正方形纸片的周长相等.若知道图中阴影部分的面积,则一定能求出()A.正方形纸片的面积B.四边形EFGH的面积C. △BEF的面积D. △AEH的面积(第8题)(第9题)二、填空题(每题4分,共16分)9.如图是以正方形的边长为直径,在正方形内画半圆得到的图形,则此图形的对称轴有________条.10.在平面直角坐标系xOy中,已知点A(2,0),B(5,4),若四边形OABC是平行四边形,则▱OABC的周长等于________.11.如图,在Rt△ABC中,AC=3,BC=4,点D为斜边AB上一动点,DE⊥BC,DF⊥AC,垂足分别为E,F,则线段EF的最小值为________.(第11题)(第12题)12.如图,四边形ABCD是菱形,点E,F分别在边AB,AD上,且AE=DF,连接BF与DE相交于点G,已知AF=2DF,若FG =3,则GB=________.三、解答题(共32分)13.(8分)如图,在四边形ABCD中,BE⊥AC,DF⊥AC,垂足分别为E,F,且BE=DF,AF=CE.求证:四边形ABCD为平行四边形.(第13题)14.(24分)如图,已知在矩形ABCD中,点M,N分别是边AD,BC的中点,点P,Q分别是边BM,DN的中点.(1)求证:BM∥DN;(2)求证:四边形MPNQ是菱形;(3)当矩形ABCD的边AB与AD满足什么数量关系时,四边形MPNQ为正方形?请说明理由.3(第14题)答案一、1.D 2.D 3.C 4.D 5.A 6.A7.B8.C二、9.410.1411.12 512. 63点拨:如图,过点F作FP∥AB,交DE于点P,则△DFP∽△DAE.∵AF=2DF,∴FPAE=DFDA=13.∵四边形ABCD是菱形,∴AB=AD.∵AE=DF,∴BE=AF,∴BE=2AE,∴FPBE=FP2AE=16.∵FP∥AB,∴△FPG∽△BEG,∴GFGB=FPBE=16,∴GB=6GF=6 3.(第12题)三、13.证明:∵AF=CE,∴AF-EF=CE-EF,即AE=CF.∵BE⊥AC,DF⊥AC,∴∠AEB=∠CFD=90°.∵BE=DF,∴△ABE≌△CDF.∴AB=CD,∠BAE=∠DCF.∴AB∥CD.∴四边形ABCD为平行四边形.14.(1)证明:∵四边形ABCD是矩形,∴AD∥BC,AD=BC.∵点M,N分别为边AD,BC的中点,∴DM=BN,∴四边形DMBN是平行四边形.∴BM∥DN.(2)证明:由(1)可知四边形DMBN是平行四边形,∴BM=DN,BM∥DN.5∵点P,Q分别为边BM,DN的中点,∴MP=NQ.∴四边形MPNQ是平行四边形.如图,连接MN.(第14题)由(1)可知AD∥BC,AD=BC.∵点M,N分别为边AD,BC的中点,∴DM=CN,∴四边形DMNC是平行四边形.由题可知∠C=90°,∴四边形DMNC是矩形,∴∠DMN=∠C=90°.∵点Q是边DN的中点,∴MQ=NQ,∴四边形MPNQ是菱形.(3)解:当矩形ABCD的边AB与AD满足AB=12AD时,四边形MPNQ为正方形.理由:∵AB=12AD,点M是边AD的中点,∴AB=AM.易得矩形ABNM是正方形.∵P为正方形ABNM对角线BM的中点,∴∠NPM=90°.由(2)知四边形MPNQ是菱形,∴四边形MPNQ是正方形.。
中考数学考点系统复习 第七章 作图与图形变换 第三节 图形的平移、旋转、对称与位似

图④
图⑤
图⑥
(4)如图⑤,若将△ABD 绕点 A 逆时针旋转至 AB 与 AC 重合,点 D 的对应 点为 E,点 P 为 AC 的中点,连接 PE,则 PE 的最小值为 3 . (5)如图⑥,当点 D 是 BC 边上的中点时,将线段 AD 绕点 A 旋转 60°得到 AD′,连接 CD′,则 CD′=22 7或或2 2.
解:(1)如图所示,△GMH 即为所求. (2)如图所示,△MNH 即为所求. (3)45.
重难点 1:与图形的对称有关的计算
如图,在正方形纸片 ABCD 中,E 是 CD 的中点,将正方形纸片折叠,
点 B 落在线段 AE 上的点 G 处,折痕为 AF,若 AD=4 cm,则 CF 的长为 6-6-2 2 5 cm.
(2)如图③,点 D 为 BC 的中点,将△ACD 绕点 D 逆时针旋转一定角度 α(0<α<90°)得到△ECD.若 CE∥BD,则旋转角度 α=6060°°;
(3)如图④,连接 AD,将△ABD 绕点 A 逆时针旋转至△ACE 的位置,连接 DE,则旋转角度为 6060°°; ①若∠CAD=45°,则∠CAE 的度数为 1 15°5°; ②若 CD=3,则 CE 的长度为 1 1;
(3)如图③,作出△ABC 绕点 O 顺时针旋转 90°的图形△A3B3C3; 解:△A3B3C3 如图所示.
(4)如图④,以点 A 为位似中心,将△ABC 放大为原来的 2 倍,得到△A4B4C4; 解:△A4B4C4 如图所示.
(5)如图⑤,作出以 AB 为对角线的正方形 AEBF,点 E,F 也为格点,正方 形 AEBF 的面积为 10;
解:(1)线段 A1B1如图所示. (2)线段 A2B1 如图所示. (3)20.
高三复习数学:第七章不等式

学必求其心得,业必贵于专精§7。
1 不等关系与不等式的性质1.两个实数比较大小的方法(1)作差法错误!(a,b∈R);(2)作商法错误!(a∈R,b〉0).2.不等式的基本性质性质性质内容特别提醒对称性a〉b⇔b<a⇔传递性a>b,b〉c⇒a〉c⇒可加性a>b⇔a+c>b+c⇔可乘性错误!⇒ac〉bc注意c的符号错误!⇒ac〈bc学必求其心得,业必贵于专精3(1)倒数的性质①a〉b,ab〉0⇒错误!<错误!.②a〈0〈b⇒错误!<错误!。
③a>b〉0,0<c<d⇒ac〉错误!。
④0〈a〈x<b或a<x〈b<0⇒错误!〈错误!<错误!。
(2)有关分数的性质若a〉b>0,m〉0,则①错误!〈错误!;错误!>错误!(b-m〉0).②错误!〉错误!;错误!<错误!(b-m〉0).【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”)(1)a>b⇔ac2〉bc2。
( )(2)1a>错误!⇔a<b(ab≠0).( )(3)a〉b,c>d⇒ac〉bd。
( )(4)若错误!〈错误!<0,则|a|>|b|.()(5)若a3〉b3且ab<0,则错误!>错误!.()答案:(1)×(2)×(3)×(4)×(5)√1.(教材改编)下列四个结论,正确的是( )①a〉b,c〈d⇒a-c>b-d;②a>b>0,c<d<0⇒ac>bd;③a>b>0⇒错误!〉错误!;④a>b〉0⇒错误!〉错误!.A.①②B.②③C.①④D.①③答案:D2.若a<0,-1〈b<0,那么下列不等式中正确的是( )A.a<ab2<ab B.ab2〈a〈abC.a〈ab〈ab2D.ab2<ab〈a解析:选A.因为-1<b<0,所以b<0<b2<1,于是a<ab2<ab.3.若a>1>b,下列不等式中不一定成立的是()A.a-b>1-b B.a-1〉b-1C.a-1〉1-b D.1-a〉b-a解析:选C.由a>1知a-b>1-b,故A正确;由a〉b知a-1>b-1,故B正确;由1>b知1-a〉b-a,故D正确,C项错误,如当a=3,b=-3时,不成立.4.x+y<2m的一个充分不必要条件是( )A.x<m或y<m B.x<m且y〈mC.x<m且y〉m D.x〈m或y>m解析:选B。
数学(理)一轮复习 第七章 立体几何 第讲 空间向量及其运算

第6讲空间向量及其运算)1.空间向量的有关定理(1)共线向量定理:对空间任意两个向量a,b(b≠0),a∥b的充要条件是存在唯一的实数λ,使得a=λb.(2)共面向量定理:如果两个向量a,b不共线,那么向量p与向量a,b共面的充要条件是存在唯一的有序实数对(x,y),使p =x a+y b.(3)空间向量基本定理:如果三个向量a,b,c不共面,那么对空间任一向量p,存在有序实数组{x,y,z},使得p=x a+y b+z c.其中{a,b,c}叫做空间的一个基底.2.两个向量的数量积(与平面向量基本相同)(1)两向量的夹角:已知两个非零向量a,b,在空间中任取一点O,作错误!=a,错误!=b,则∠AOB叫做向量a与b的夹角,记作〈a,b〉.通常规定0≤<a,b〉≤π.若<a,b〉=错误!,则称向量a,b 互相垂直,记作a⊥b。
(2)两向量的数量积两个非零向量a,b的数量积a·b=|a||b|cos〈a,b>.(3)向量的数量积的性质①a·e=|a|cos〈a,e〉(其中e为单位向量);②a⊥b⇔a·b=0;③|a|2=a·a=a2;④|a·b|≤|a||b|。
(4)向量的数量积满足如下运算律①(λa)·b=λ(a·b);②a·b=b·a(交换律);③a·(b+c)=a·b+a·c(分配律).3.空间向量的坐标运算(1)设a=(a1,a2,a3),b=(b1,b2,b3).a+b=(a1+b1,a2+b2,a3+b3),a-b=(a1-b1,a2-b2,a3-b3),λa=(λa1,λa2,λa3),a·b=a1b1+a2b2+a3b3,a⊥b⇔a1b1+a2b2+a3b3=0,a∥b⇔a1=λb1,a2=λb2,a3=λb3(λ∈R),cos<a,b〉=错误!=错误!.(2)设A(x1,y1,z1),B(x2,y2,z2),则错误!=错误!-错误!=(x2-x1,y2-y1,z2-z1).4.直线的方向向量与平面的法向量的确定(1)直线的方向向量:l是空间一直线,A,B是直线l上任意两点,则称错误!为直线l的方向向量,与错误!平行的任意非零向量也是直线l的方向向量,显然一条直线的方向向量可以有无数个.(2)平面的法向量①定义:与平面垂直的向量,称做平面的法向量.一个平面的法向量有无数多个,任意两个都是共线向量.②确定:设a,b是平面α内两不共线向量,n为平面α的法向量,则求法向量的方程组为错误!5.空间位置关系的向量表示位置关系向量表示直线l1,l2的方向向量分别为n1,n2l1∥l2n1∥n2⇔n1=λn2 l1⊥l2n1⊥n2⇔n1·n2=0直线l的方向向量为n,平面α的法向量为m l∥αn⊥m⇔n·m=0 l⊥αn∥m⇔n=λm平面α,β的法向量分别为n,m α∥βn∥m⇔n=λm α⊥βn⊥m⇔n·m=01.辨明四个易误点(1)注意向量夹角与两直线夹角的区别.(2)共线向量定理中a∥b⇔存在唯一的实数λ∈R,使a=λb易忽视b≠0.(3)共面向量定理中,注意有序实数对(x,y)是唯一存在的.(4)向量的数量积满足交换律、分配律,但不满足结合律,即(a·b)c=a(b·c)不一定成立.2.建立空间直角坐标系的原则(1)合理利用几何体中的垂直关系,特别是面面垂直.(2)尽可能地让相关点落在坐标轴或坐标平面上.3.利用空间向量坐标运算求解问题的方法用空间向量解决立体几何中的平行或共线问题一般用向量共线定理;求两点间距离或某一线段的长度,一般用向量的模来解决;解决垂直问题一般可转化为向量的数量积为零;求异面直线所成的角,一般可转化为两向量的夹角,但要注意两种角的范围不同,最后应进行转化.1.已知a=(-2,-3,1),b=(2,0,4),c=(-4,-6,2),则下列结论正确的是( )A .a ∥c ,b ∥cB .a ∥b ,a ⊥cC .a ∥c ,a ⊥bD .以上都不对C 因为c =(-4,-6,2)=2a ,所以a ∥c 。
地理晋教版八年级下册第七章复习
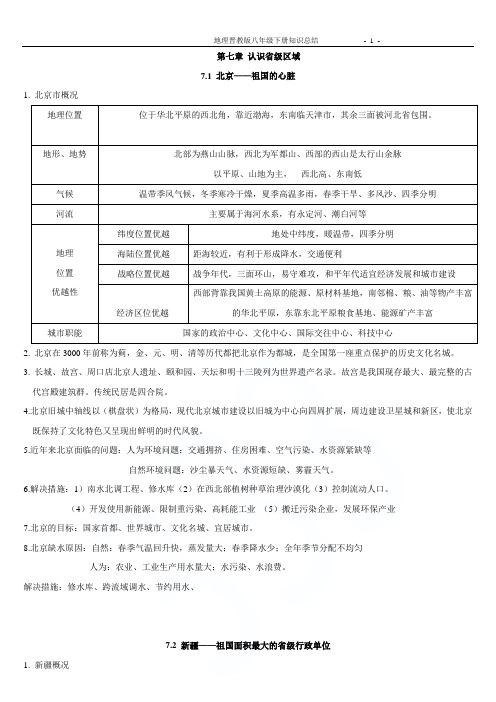
第七章认识省级区域7.1 北京——祖国的心脏1. 北京市概况2. 北京在3000年前称为蓟,金、元、明、清等历代都把北京作为都城,是全国第一座重点保护的历史文化名城。
3. 长城、故宫、周口店北京人遗址、颐和园、天坛和明十三陵列为世界遗产名录。
故宫是我国现存最大、最完整的古代宫殿建筑群。
传统民居是四合院。
4.北京旧城中轴线以(棋盘状)为格局,现代北京城市建设以旧城为中心向四周扩展,周边建设卫星城和新区,使北京既保持了文化特色又呈现出鲜明的时代风貌。
5.近年来北京面临的问题:人为环境问题:交通拥挤、住房困难、空气污染、水资源紧缺等自然环境问题:沙尘暴天气、水资源短缺、雾霾天气。
6.解决措施:1)南水北调工程、修水库(2)在西北部植树种草治理沙漠化(3)控制流动人口。
(4)开发使用新能源、限制重污染、高耗能工业(5)搬迁污染企业,发展环保产业7.北京的目标:国家首都、世界城市、文化名城、宜居城市。
8.北京缺水原因:自然:春季气温回升快,蒸发量大;春季降水少;全年季节分配不均匀人为:农业、工业生产用水量大;水污染、水浪费。
解决措施:修水库、跨流域调水、节约用水、7.2 新疆——祖国面积最大的省级行政单位1. 新疆概况加当地的财政收入和就业机会;④带动相关行业的发展。
7.3 台湾——祖国的宝岛1.台湾概况23457.4 香港和澳门——祖国的特别行政区1.香港澳门概况2.香港地理位置优势:背靠祖国内地,祖国内地联系紧密;是我国南方对外交往的门户;处于亚洲航运和国际航运的中心地位。
3.香港岛与九龙半岛之间的维多利亚港是世界上优良的天然海港之一。
4.祖国内地有丰富的自然资源和劳动力资源、市场,食品,淡水;港澳拥有雄厚的资金、技术和管理经验。
早期:“前店(港澳)、后厂(内地)”现在:优势互补,互惠互利。
5.香港经济发展的有利条件:①地理位置优越:背靠祖国大陆,南近东南亚,是沟通远东各地,与许多国家和地区有便利的海运和航空运输,居国际贸易的有利位置;②是天然良港:有天然港口优势,港阔水深;③是自由贸易港。
职高数学第七章复习

第七章 平面向量 复习卷第一节 平面向量的基本概念与其基本运算1. 向量的概念(1)定义: 既有大小又有方向的量.(2)向量的表示:用a 、b 、m 等来表示, 或用来表示(它表示以A 为始点, B 为终点的向量).(3)向量的长度(或模): 记为|a|或||.(4)0(零向量):长度为0的向量, 其方向任意, 零向量没有确定的方向.(5)e(单位向量): |e|=(6) a 的相反向量: 是指与a 长度相等且方向相反的向量, 记为(7) 相等向量(同一向量): 大小相等且方向相同的向量.2. 向量的加法运算(1)加法法则:三角形法则与平行四边形法则.(2)若干个向量相加的多边形法则A 1A 2→+A 2A 3→+A 3A 4→+A 4A 5→+…+A n -1A n = (首尾相接)(3)加法运算律: a +b =b +a (交换律) (a +b )+c =a +(b +c )(结合律) a +0=0+a =a ;a +(-a )=0; AB →+BA →=0.3. 向量的减法运算(1)减法法则(如图所示).(2)a-b=a+(-b)即-=(连接两个向量的终点, 且方向指向被减向量).(3)向量不等式 ||a|-|b||≤|a±b|≤|a|+|b|4. 实数与向量的积(数乘向量)实数λ与向量a的乘积, 叫做数乘向量, 记作λa.(1)大小: |λa|=(2)方向: λ>0, λa与方向;λ<0, λa与 a 方向;λ=0, λa=0.(3)运算律: λ(μa)=(λμ)a ; (λ+μ)a=λa+μa ;λ(a+b)=λa+λb, (λ, μ为实数)5.两个向量平行(共线)的充要条件: a∥b⇔ (a≠0, λ∈R, λ存在且唯一)练习题1. 下列说法正确的是( )A. 相等向量就是与向量长度相等的向量B. 长度相等的向量叫做相等向量C. 共线向量是指在一条直线上的向量D. 0与任一向量共线2. a的负向量是( )A. 与a方向相反的向量B. 与|a|符号相反的向量C. 与a反向且大小相等的向量D. 以上均不对3.下列关于向量的关系式中, 正确的是( )A. +=0B. -=C. +=D. -=4. -3(a-b)+4(a-b)=( )A. aB. a+bC. a-bD. 2a+b5. ++= .6. 在菱形ABCD中, 若=a, =b, 则=________, =________.7.若向量a表示“向东走6km”, 向量b表示“向北走6km”, 则向量a+b 表示________.8. 下列命题正确的是( )A. 若|a|=0, 则a=0B. 若|a|=|b|, 则a=b或a=-bC. 若a∥b, 则|a|=|b|D. 若a=0, 则-a=09.平行四边形ABCD中, =a, =b, 则=( )A. a-bB. b-aC. a+bD. -a-b10. 2(a+b)-3(2a-b)=( )A. 4a+5bB. -4a+5bC. 5a+4bD. -5a+4b11.++-++=________.12.已知=(1, 3), =(3, 9), =λ, 则λ=________.第二节平面向量的坐标表示1. 向量的坐标与其运算(1)向量的坐标在直角坐标系中, i、j分别为x, y轴正方向上的单位向量, 则i、j称为基底, 从而平面内任一向量a都可以表示成a=xi+yj, 把(x, y)叫做a的坐标, 记作a=(x, y), 其中x称为a在x轴上的坐标, y称为a在y轴上的坐标.(2)在坐标平面内, 把任一向量的始点移到坐标原点后, 向量的终点坐标即为该向量的坐标.即: 若=a, 且A(x, y), 则有a=(x, y).(3)已知A(x1, y1), B(x2, y2), 则有=(x2-x1, y2-y1).(4)向量的坐标运算若a=(x1, y1), b=(x2, y2), 则有a+b=(x1+x2, y1+y2);a-b=(x1-x2, y1-y2);λa=(λx1, λy1);a=b⇔x1=x2且y1=y2.2. a=(x1, y1), b=(x2, y2), 则a∥b⇔x1y2-x2y1=0.3. 中点坐标公式: 设A(x1, y1), B(x2, y2), A.B中点记为C(x, y), 则有x =, y=.4. 向量的长度(模)计算公式:若a=(x1, y1), 则|a|=.5.两点间距离公式:若A(x1, y1), B(x2, y2), 则||=.练习题1. 若向量a=(3, -1), b=(-1, 2), 则-3a-2b等于( )A. (7, 1)B. (-7, -1)C. (-7, 1)D. (7, -1)2. 点A(2, -1), B(-1, 3)则=( )A. 5B.C. (-3, 4)D. (3, -4)3. 已知点A(2, 3), B(4, 3), 则其中点D的坐标为( )A. (2, 1)B. (2, 2)C. (3, 3)D. (6, 6)4. 已知A(1, -1), B(1, 3), 则||=________.5. 已知a=(2, 5), b=(λ, 3), a∥b, 则λ=________.6. 已知点A(-2, 1)和B(3, -2)且=4, 则点P的坐标为________.7. 已知平面上三点A(1, 2)、B(4, 3)、C(6, 1), 若=, 则点D坐标为________.8.若平行四边形ABCD的三个顶点A(-3, 0), B(2, -2), C(5, 2), 求顶点D的坐标.第三节平面向量的内积1. 向量a与b的夹角: 把向量a与b的始点移到同一点O, 作=a, =b, 则∠AOB称为向量a、b的夹角, 记作〈a, b〉, 则〈a, b〉∈[0, π].2.向量a与b的内积: a·b=|a||b|cos〈a, b〉.3. 两向量a、b夹角的计算公式:cos〈a, b〉== .4. 向量内积的重要结论: 设a、b是两个非零向量, 则有(1)a⊥b⇔〈a, b〉=90°⇔a·b=0⇔x1x2+y1y2=0(2)a与b平行, 则a·b=±|a||b|, 且同向取正, 反向取负.特别地, a·a=a2=|a|2即|a|=.5.向量内积的坐标表示设a=(x1, y1), b=(x2, y2), 则a·b=x1x2+y1y26. 向量内积的运算律 (1)a·b=b·a (2)(λa)·b=λ(a·b)=a·(λb)(3)(a+b)·c=a·c+b·c练习题1. 若四边形ABCD中, =, 且·=0, 则四边形ABCD一定是( )A. 平行四边形B. 矩形C. 菱形D. 正方形2.已知向量a=(3, 2), b=(, 4), 则a·b=( )A. 6B. 7C. 8D. 93. 下列等式正确的为( )A. 0·a=0B. 0·a=0C. |a·b|=|a|·|b|D. a-a =04.设|a|=3, |b|=2, 且〈a, b〉=120°, 则a·b=( )A. 3B. -3C. 6D. -65.向量a=(-2, 3), b=(x, 4), 且a⊥b, 则x=( )A. 6B. -6C.D. -6. 已知a·b=3, |a|=, |b|=2, 则〈a, b〉=________.7. 已知a=(2, ), b=(0, ), 则a·(2b)=________.8. 已知a=(k, -2), b=(2k, k+1), 求k的值, 分别使: (1)a⊥b;(2)a ∥b.9. 若向量a=(4, -3), 则下列向量中与a垂直的向量是( )A. (3, -4)B. (3, 4)C. (-, )D. (, -)10.已知a=(3, -4), b=(-2, 3), 则a·(a+b)=( )A. -13B. 7C. 6D. 26。
中考物理复习课件第七章 从粒子到宇宙

从粒子到宇宙
目 1 知识精讲
录 考点清单
目
教材素材提升
录
2 江苏6年真题及拓展
思维导图
扩散现象
分子动理论的 基本观点
分子 动理论
摩擦起电 带电体 的性质 两种电荷
验电器
静电 现象
从粒子 到宇宙
返回目录
物质的 构成
宇宙探秘
第七章 从粒子到宇宙
知识精讲
返回思维导图
考点清单
一、分子动理论 1.扩散现象 (1)定义:不同的物质在相互接触时,彼此_进__入__对__方__的现象. (2)扩散现象是由分__子__无__规__则__运__动__引起的. (3)举例:酒香不怕巷子深、花香四溢、糖水变甜. 2.分子动理论的基本观点 a.常见的物质是由大量分子组成的,分子间有__空__隙___;
(八下P30WWW7-14(a))
第七章 从粒子到宇宙
返回目录
文字素材
1. (八下P25,活动改编)下列实例中,不能用来说明“分子在不停地运动” 的是( B ) A. 美味佳肴香气扑鼻 B. 扫地时灰尘飞扬 C. 用鼻子嗅气味来鉴别醋和酱油 D. 炒菜时加点盐,菜有了咸味
第七章 从粒子到宇宙
返回目录
(八上P13活动图1-12)
第七章 从粒子到宇宙
返回目录
3. 如图所示为验电器结构示意图,用带电体接触验电器的金属球. 现象:金属箔片张开. 原理:两个金属箔片带有__同__种____电荷,相互_排__斥_,且带电体带电量越 多,张开的角度就越___大_____. 【拓展】若带电体带正电,则接触时的电流方向是 __从__带__电__体__到__金__属__箔__(选填“从带电体到金属箔” 或“从金属箔到带电体”).
行政领导学期末复习(第七章:领导战略与决策)

:领导战略与决策一、单项选择题(每题2分,共18分)1.按决策问题的出现概率分类,决策可分为().选择一项:A. 程序性决策和非程序性决策B。
经验决策和科学决策C。
单目标决策和多目标决策D。
程序性决策和宏观决策正确答案是:程序性决策和非程序性决策2.按决策主体的决策方式不同分类有()。
选择一项:A. 经验决策和科学决策B。
程序性决策和非程序性决策C. 单目标决策和多目标决策D. 理性决策和有限理性决策正确答案是:经验决策和科学决策3.为决策中枢系统提供专门咨询服务的是()。
选择一项:A。
智囊系统B。
信息系统C. 执行系统D。
监督系统正确答案是:智囊系统4.不属于领导决策要素的是()。
选择一项:A。
决策者B。
决策信息C。
决策备选方案D. 决策前景正确答案是:决策前景5.不属于渐进决策模型的特点有()。
选择一项:A。
渐进主义B。
积小变大C. 稳中求变D。
最佳原则正确答案是:最佳原则6.缩小应有状态与实际状态之间的差距而制定的总体设想是()。
选择一项:A. 决策目标的确立B. 方案选择C. 发现问题D。
备选方案正确答案是:决策目标的确立7.检测决策方案实施的情况与决策目标是否相一致的方法是()。
选择一项:A。
方案修正B。
决策检查C。
决策追踪D. 慎重实施正确答案是:决策追踪8.不属于发挥专家的团体宏观智能结构效应的决策方法是()。
选择一项:A。
头脑风暴法B. 鱼缸法C。
模拟决策法D. 德尔斐法正确答案是:模拟决策法9.运用同态模型的原理进行决策的方法是()。
选择一项:A。
头脑风暴法B。
鱼缸法C. 德尔斐法D. 模拟决策法正确答案是:模拟决策法二、多项选择题(每题2分,共16分)1.战略的主要特征有().选择一项或多项:A. 后继性B。
前提性C. 稀有性D. 规律性E. 层次性正确答案是:后继性, 前提性, 稀有性,层次性2.科学预测的特征有().选择一项或多项:A。
历史感B. 现实感C. 可验证性D. 超前性E. 目标感正确答案是:历史感, 现实感, 可验证性3.决策的特征主要包括()。
中国近现代史纲要复习资料第七章

第七章为创建新中国而奋斗第一节从争取和平民主到进行自卫战1、[单选]第二次世界大战后,美国开始在资本主义世界中称雄。
2、[单选]中共中央在1945年8月25日明确提出“和平民主团结”的口号。
3、[单选]1945年10月10日,国共双方签署了《政府与中共代表会谈纪要》,又称《双十协定》。
4、[单选]1945年9月19日,中共中央针对和谈期间特殊情况,正式确定了“向北发展,向南防御”的战略方针。
5、[多选]反法西斯战争后,人民民主力量明显增长的主要表现是(1)社会主义的苏联得以较快地恢复和巩固(2)人民民主和社会主义制度在多国建立(3)民族解放运动在亚洲、非洲、拉丁美洲蓬勃兴起(4)在资本主义国家,共产党的影响显著增长,工人运动有了新的发展6、[多选]为打退国民党军队在重庆谈判期间发动的军事进攻,解放区军民进行了上党战役、邯郸战役、平绥战役、津浦战役。
7、[多选]出席1946年1月政治协商会议的党派,除国民党、共产党外,还有民主同盟、青年党。
8、[多选]1946年1月的政治协商会议通过的协议包括政府组织、国民大会、和平建国纲领、宪法草案。
9、[多选]1946年2月10日和6月23日,国民党当局先后在重庆和南京制造了较场口惨案、下关惨案。
10、[简答]毛泽东指出的必须打败蒋介石,而且能够打败他的原因。
答:(1)全面内战爆发后,中国共产党清醒地估计了国内外形势,明确而坚定地指出我们不但必须打败蒋介石,而且能够打败他。
(2)必须打败蒋介石,是因为蒋介石发动的战争,是一场院在美帝国主义指挥之下的反对中国民族独立和中国人民解放的反革命的战争。
不用革命战争反对反革命战争,中国就将变成黑暗世界,中华民族的前途就会被断送。
(3)能够打败蒋介石,是因为蒋介石军事力量的优势和美国的援助,只是暂时的现象是临时起作用的因素;而蒋介石发动的战争的反人民性质,人心的向背,则是经常起作用的因素。
人民解放战争所具有的爱国的正义的革命的性质,必然要获得全国人民的拥护。
第七章-万有引力与宇宙航行章末复习-知识点和题型总结-2023年高一物理期末高效复习专题

第七章:万有引力与宇宙航行 章末复习知识点一:开普勒行星运动定律定律 内容公式或图示开普勒第一定律所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上开普勒第二定律 对任意一个行星来说,它与太阳的连线在相等的时间内扫过相等的面积开普勒第三定律 所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等公式:a 3T 2=k ,k 是一个与行星无关的常量知识点二.万有引力定律一:内容自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小与物体的质量m 1和m 2的乘积成正比,与它们之间距离r 的二次方成反比.(2)公式 F =G m 1m 2r 2. 3.符号意义(1)G 为引力常量,其数值由英国物理学家卡文迪许测量得出,常取G =6.67×10-11N·m 2/kg 2.(2)r 为两个质点间的距离或质量均匀的两个球体的球心间的距离.二.万有引力的四个特性 特性 内容普遍性万有引力不仅存在于太阳与行星、地球与月球之间,宇宙间任何两个有质量的物体之间都存在着这种相互吸引的力相互性两个有质量的物体之间的万有引力是一对作用力和反作用力,总是满足大小相等,方向相反,作用在两个物体上宏观性地面上的一般物体之间的万有引力比较小,与其他力比较可忽略不计,但在质量巨大的天体之间或天体与其附近的物体之间,万有引力起着决定性作用特殊性两个物体之间的万有引力只与它们本身的质量和它们间的距离有关,而与它们所在空间的性质无关,也与周围是否存在其他物体无关三.万有引力的效果万有引力F =G MmR 2的效果有两个,一个是重力mg ,另一个是物体随地球自转需要的向心力F n =mrω2,如图6-2-3所示,重力是万有引力的一个分力.图6-2-31.重力与纬度的关系地面上物体的重力随纬度的升高而变大.(1)赤道上:重力和向心力在一条直线上F =F n +mg ,即G MmR 2=mrω2+mg ,所以mg =G MmR 2-mrω2.(2)地球两极处:向心力为零,所以mg =F =G MmR 2.(3)其他位置:重力是万有引力的一个分力,重力的大小mg <G MmR 2,重力的方向偏离地心.2.重力与高度的关系由于地球的自转角速度很小,故地球自转带来的影响很小,一般情况下认为在地面附近:mg =G Mm R 2,若距离地面的高度为h ,则mg =G Mm (R +h )2(R 为地球半径,g 为离地面h 高度处的重力加速度).所以距地面越高,物体的重力加速度越小,则物体所受的重力也越小.知识点三:万有引力理论的成就的应用一:天体质量与天体的密度 1.求天体质量的思路绕中心天体运动的其他天体或卫星做匀速圆周运动,做圆周运动的天体(或卫星)的向心力等于它与中心天体的万有引力,利用此关系建立方程求中心天体的质量.2.计算天体的质量下面以地球质量的计算为例,介绍几种计算天体质量的方法:(1)若已知月球绕地球做匀速圆周运动的周期为T ,半径为r ,根据万有引力等于向心力,即GM 地·m 月r 2=m 月⎝ ⎛⎭⎪⎫2πT 2r ,可求得地球质量M 地=4π2r 3GT 2.(2)若已知月球绕地球做匀速圆周运动的半径r 和月球运行的线速度v ,由于地球对月球的引力等于月球做匀速圆周运动的向心力,根据牛顿第二定律,得G M 地·m 月r 2=m 月v 2r ,解得地球的质量为M 地=r v 2G .(3)若已知月球运行的线速度v 和运行周期T ,由于地球对月球的引力等于月球做匀速圆周运动的向心力,根据牛顿第二定律,得G M 地·m 月r 2=m 月·v ·2πT G M 地·m 月r 2=m 月v 2r以上两式消去r ,解得M 地=v 3T2πG .(4)若已知地球的半径R 和地球表面的重力加速度g ,根据物体的重力近似等于地球对物体的引力,得mg =G M 地·m R 2解得地球质量为M地=R2gG.3.计算天体的密度若天体的半径为R,则天体的密度ρ=M 43πR3将M=4π2r3GT2代入上式得ρ=3πr3GT2R3.二:天体运动问题1.解决天体运动问题的基本思路一般行星或卫星的运动可看做匀速圆周运动,所需要的向心力都由中心天体对它的万有引力提供,所以研究天体时可建立基本关系式:G MmR2=ma,式中a是向心加速度.2.四个重要结论设质量为m的天体绕另一质量为M的中心天体做半径为r的匀速圆周运动(1)由G Mmr2=mv2r得v=GMr,r越大,天体的v越小.(2)由G Mmr2=mω2r得ω=GMr3,r越大,天体的ω越小.(3)由G Mmr2=m(2πT)2r得T=2πr3GM,r越大,天体的T越大.(4)由G Mmr2=ma n得a n=GMr2,r越大,天体的a n越小.以上结论可总结为“越远越慢,越远越小”.知识点四:双星问题的分析方法宇宙中往往会有相距较近、质量相当的两颗星球,它们离其他星球都较远,因此其他星球对它们的万有引力可以忽略不计.在这种情况下,它们将各自围绕它们连线上的某一固定点O做同周期的匀速圆周运动.这种结构叫做双星模型(如图6-4-1所示).双星的特点1.由于双星和该固定点O 总保持三点共线,所以在相同时间内转过的角度必然相等,即双星做匀速圆周运动的角速度必然相等,因此周期也必然相等.2.由于每颗星球的向心力都是由双星间相互作用的万有引力提供的,因此大小必然相等,即m 1ω2r 1=m 2ω2r 2,又r 1+r 2=L (L 是双星间的距离),可得r 1=m 2m 1+m 2L ,r 2=m 1m 1+m 2L ,即固定点离质量大的星球较近.知识点五:宇宙航行一:宇宙速度数值意义第一宇宙速度 7.9 km/s卫星在地球表面附近绕地球做匀速圆周运动的速度第二宇宙速度 11.2 km/s 使卫星挣脱地球引力束缚的最小地面发射速度第三宇宙速度 16.7 km/s 使卫星挣脱太阳引力束缚的最小地面发射速度1.第一宇宙速度的定义又叫环绕速度,是人造地球卫星在地面附近绕地球做匀速圆周运动所具有的速度,是人造地球卫星的最小发射速度,v =7.9 km/s.2.第一宇宙速度的计算设地球的质量为M ,卫星的质量为m ,卫星到地心的距离为r ,卫星做匀速圆周运动的线速度为v :方法一:万有引力提供向心力→G Mmr 2=m v 2r→v =GM r――→r =R =6.4×106 mM =5.98×1024 kg v =7.9 km/s方法二:重力提供向心力→mg =m v 2r →v =gr ――→r =R =6.4×106 m g =9.8 m/s 2v =7.9 km/s二:卫星各物理量分析:项目推导式关系式结论v与r的关系GMmr2=mv2r v=GMrr越大,v越小ω与r 的关系GMmr2=mrω2ω=GMr3r越大,ω越小T与r 的关系GMmr2=mr⎝⎛⎭⎪⎫2πT2T=2πr3GMr越大,T越大a与r的关系GMmr2=ma a=GMr2r越大,a越小由上表可以看出:卫星离地面高度越高,其线速度越小,角速度越小,周期越大,向心加速度越小.可以概括为“高轨低速长周期”.三.人造地球卫星的轨道人造卫星的轨道可以是椭圆轨道,也可以是圆轨道.(1)椭圆轨道:地心位于椭圆的一个焦点上.(2)圆轨道:卫星绕地球做匀速圆周运动,卫星所需的向心力由万有引力提供,由于万有引力指向地心,所以卫星的轨道圆心必然是地心,即卫星在以地心为圆心的轨道平面内绕地球做匀速圆周运动.图6-5-4总之,地球卫星的轨道平面可以与赤道平面成任意角度,但轨道平面一定过地心.当轨道平面与赤道平面重合时,称为赤道轨道;当轨道平面与赤道平面垂直时,即通过极点,称为极地轨道,如图6-5-4所示.2.地球同步卫星(1)定义:相对于地面静止的卫星,又叫静止卫星.(2)六个“一定”.①同步卫星的运行方向与地球自转方向一致.②同步卫星的运转周期与地球自转周期相同,T=24 h.③同步卫星的运行角速度等于地球自转的角速度.④同步卫星的轨道平面均在赤道平面上,即所有的同步卫星都在赤道的正上方.⑤同步卫星的高度固定不变.⑥同步卫星的环绕速度大小一定:设其运行速度为v ,由于G Mm(R +h )2=m v 2R +h,所以v =GMR +h=gR 2R +h四:卫星变轨问题的处理技巧1.当卫星绕天体做匀速圆周运动时,万有引力提供向心力,由G Mmr 2=m v 2r ,得v =GMr ,由此可见轨道半径r 越大,线速度v 越小.当由于某原因速度v突然改变时,若速度v 突然减小,则F >m v 2r ,卫星将做近心运动,轨迹为椭圆;若速度v 突然增大,则F <m v 2r ,卫星将做离心运动,轨迹变为椭圆,此时可用开普勒第三定律分析其运动.2.卫星到达椭圆轨道与圆轨道的切点时,卫星受到的万有引力相同,所以加速度也相同.[考点题型]考点题型一:开普勒行星运动定律1.(2021·河南·商丘市回民中学高一期末)人类对行星运动的研究漫长而曲折,关于开普勒行星运动定律,下列说法中正确的是( )A .牛顿发现万有引力定律后,开普勒整理牛顿的观测数据,发现了行星运动的规律B .所有行星的轨道半长轴的二次方跟公转周期的三次方的比值都相等C .开普勒行星运动定律适用于行星绕太阳运动,也适用于宇宙中其他卫星绕行星的运动D .行星环绕太阳运动时,线速度大小始终不变2.(2021·山东聊城·高一期末)2021年5月29日,上午10时30分,北斗三号全球卫星导航系统建成暨开通仪式在人民大会堂隆重举行。
理论力学第七章复习

2021/4/9
1
1.定系和动系
2.动点和牵连点 动点为研究的对象,是本章的主角。 牵连点是动点在动系上的重合点,不同瞬时,
有不同的牵连点,弄清牵连点的概念十分重要。
3.三个运动的关系 本章的主要任务就是建立这三者之间的定量关系,
从而用来解决工程实际问题(某些运动分析问题)。
2021/4/9
科氏加速度 =_________方向均须由图表示)。
2021/4/9
12
感谢您的阅读收藏,谢谢!
2021/4/9
13
5.当牵连运动为平动时,相对加速度等于相对速度对时间的
一阶导数。
2021/4/9
4
选择题: 1.在点的合成运动问题中,当牵连运动为平动时------。
① 一定会有科氏加速度
② 不一定会有科氏加速度
③ 一定没有科氏加速度
2.平行四边形机构,在图------。示瞬时,杆以角速度转动。滑块M 相对 AB 杆运动,若取M 为动点,AB 为动坐标,则该瞬时动点的牵连 速度与杆AB 间的夹角为------。
2021/4/9
9
3.已知杆OC 长
,以匀角速度 绕O 转动,若以滑块C 为
动点,AB 为动系,则当AB 杆处于铅垂位置时,动点C 的
科氏加速度 =_________,方向须由图表示。
2021/4/9
10
4.在图示平面机构中,杆AB=40cm,以匀角速度
绕 A 轴转动,
而 CD 以
绕 B 轴转动,BD=BC=30cm,图示瞬时
。
若取 AB 为动坐标,则此时 D 点的牵连速度的大小为_________,
牵连加速度的大小为_________(方向均须在图中画出)。
中考数学 考点系统复习 第七章 作图与图形变换 第一节 尺规作图

6.(2021·长春)在△ABC中,∠BAC=90°,AB≠AC.用无刻度的直尺和 圆规在BC边上找一点D,使△ACD为等腰三角形.下列作法中不正确的是
( A)
A
B
C
D
②作直线 PQ 交 AB 于点 D;
③以点 D 为圆心,AD 长为半径画弧交 PQ 于点 M,连接 AM,BM.
若 AB=2 2,则 AM 的长为
(B )
A.
B.2
C. 3
D. 2
4.(2022·衡阳)如图,在△ABC 中,分别以点 A 和点 B 为圆心,大于错误!AB 的长为半径作圆弧,两弧相交于点 M 和点 N,作直线 MN 交 CB 于点 D,连 接 AD.若 AC=8,BC=15,则△ACD 的周长为 223 3.
5.(2022·海南)如图,在△ABC 中,AB=AC,以点 B 为圆心,适当长为 半径画弧,交 BA 于点 M,交 BC 于点 N,分别以点 M,N 为圆心,大于12MN 的长为半径画弧,两弧在∠ABC 的内部相交于点 P,画射线 BP,交 AC 于 点 D,若 AD=BD,则∠A 的度数是 36
第七章 作图与图形变换 第一节 尺规作图
1.(2022·鄂尔多斯)下列尺规作图中不能得到平行线的是 ( D ) ,A) ,B) ,C) ,D)
2.如图,已知∠AOB 与∠EO′F,分别以 O,O′为圆心,以同样长为半
径画弧,分别交 OA,OB 于点 A′,B′,交 O′E,O′F 于点 E′,F′.
以 B′为圆心,以 E′F′长为半径画弧,交A′︵B′于点 H.下列结论中不
正确的是 A.∠AOB=2∠EO′F
( A)
B.∠AOB>∠EO′F
C.∠HOB=∠EO′F
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图7.1.1 线性相位FIR滤波器零点分布
第1章 时域离散信号和时域离散系统
第1章 时域离散信号和时域离散系统
第1章 时域离散信号和时域离散系统
第1章 时域离散信号和时域离散系统
第1章 时域离散信号和时域离散系统
第1章 时域离散信号和时域离散系统
•设计FIR数字滤波器可用的窗函数有哪六种?
第1章 时域离散信号和时域离散系统
复 习
1.绪论--DSP的发展和应用
2.时域离散信号和时域离散系统
3.时域离散信号和系统的频域分析 4.离散傅立叶变换DFT 5.快速付里叶变换FFT 6.时域离散系统的基本网络结构与状态变量分析法
7. IIR DF的设计(无限长脉冲响应数字滤波器的设计)
8. FIR DF 的设计(有限长单位脉冲滤波器的设计)
•什么是FIR数字滤波器中的线性相位条件? •选择窗函数的原则? •IIR与FIR设计方法的区别?
第1章 时域离散信号和时域离散系统
7.1 线性相位FIR数字滤波器的条件和特点
7.2 利用窗函数法设计FIR滤波器
7.5 IIR和FIR数字滤波器的比较
第1章 时域离散信号和时域离散系统
FIR filter概述
FIR数字滤波器的差分方程描述
y (n) ai x(n i)
对应的系统函数
第1章 时域离散信号和时域离散系统
第1章 时域离散信号和时域离散系统
3. 线性相位FIR滤波器零点分布特点
第一类和第二类线性相位的系统函数分别满足 (7.1.7)式和(7.1.10)式,综合起来用下式表示:
H ( z) z ( N 1) H ( z 1 )
(7.1.21)
零点必须是互为倒 数的共扼对。
i 0
N 1
①
H ( z ) ai z
i 0
N 1 i 0
N 1
i
因为它是一种线性时不变系统,可用卷积和形式表示
y(n) h(i) x(n i)
比较①、③得:
③
ai h(i ) H ( z ) h(i ) z i
i 0 N 1
第1章 时域离散信号和时域离散系统
