浙江省严州中学2013届高三3月阶段测试数学(理)试题 Word版含答案

合集下载

浙江省部分重点中学高三下学期3月联考数学(理)试题.pdf

第6　物态变化考纲要求备考指津1.能说出生活环境中的常见温度值。

了解体温计的工作原理。

会测量温度。

2．能区别六种物态变化，能描述六种物态变化的基本特征和条件，并能用这些知识解释生活中的相关现象。

3．能设计实验探究物态变化过程，能从实验数据和现象归纳科学结论。

由于中考注重对实验操作能力和应用知识能力的考查，因而液体温度计的使用、物态变化的实验及现象、对各种物态变化现象的解释等是中考的热点。

预计在今后的中考中涉及的内容会更加注意联系与人们生产和生活关系密切的自然现象。

题目形式活泼、新颖，数理结合，会逐渐从物态变化知识解释自然现象过渡到利用物态变化知识解决实际问题，考查学以致用的能力。

考点1　温度计 (1)温度 ①定义：温度表示物体的冷热程度。

②摄氏温度：用符号t表示，单位是摄氏度，单位符号为℃。

摄氏温度是这样规定的：在标准大气压下，把冰水混合物的温度规定为0 ℃，把沸水的温度规定为100 ℃，在0 ℃和100 ℃之间分成100等份，每一等份是摄氏温度的一个单位，叫做1摄氏度。

(2)温度计 ①原理：常用温度计是利用液体的热胀冷缩的性质制成的。

②构造：常用温度计的基本构造有：玻璃管、玻璃泡、测温液体、刻度、温标等。

③使用：估：测量前，先估计被测物体的温度；选：根据估计选择合适量程的温度计；认清温度计的量程和分度值，被测温度不能超过温度计的量程；放：测量时要将温度计的玻璃泡浸没入被测液体，不要碰到容器壁和容器底；读：待温度计的示数稳定后读数，读数时，玻璃泡要停留在被测液体中，视线必须与温度计液柱的上表面相平；记：记录测量结果后，取出温度计，测量结果包括数值和单位。

④体温计的测量范围是35～42_℃，分度值是0.1_℃；可以离开人体读数，使用前要甩几下。

⑤实验室温度计、体温计、寒暑表的异同：实验室温度计体温计寒暑表原理液体的热胀冷缩测温液体煤油、水银、酒精等水银煤油、酒精量程－20～110℃35～42 ℃－30～50 ℃分度值1_℃0.1_℃1_℃构造玻璃泡上部是均匀细管金属泡与毛细管间有一段细而弯的“缩口”玻璃泡上部是均匀细管使用方法不能离开被测物体读数，不能甩使用前要甩几下，可离开人体读数放在被测环境中直接读数，不能甩考点2　熔化和凝固 (1)熔化和凝固是两个互逆的物态变化过程：物质从固态变成液态的过程叫熔化，物质从液态变成固态的过程叫凝固。

浙江省严州中学2013届高三3月阶段测试地理试题 Word版含答案

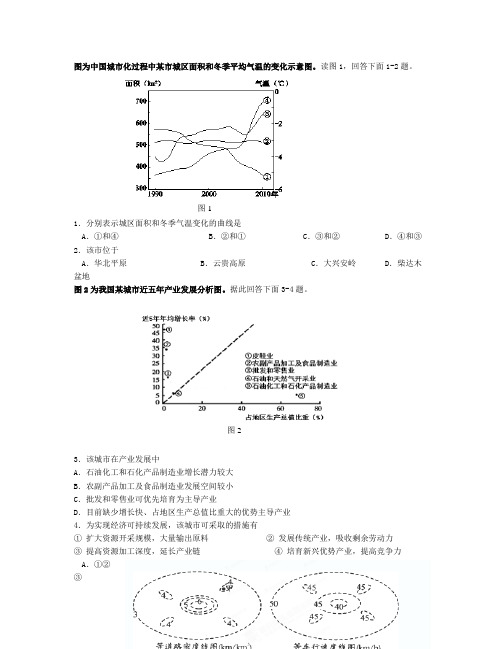
图为中国城市化过程中某市城区面积和冬季平均气温的变化示意图。

读图1，回答下面1-2题。

1．分别表示城区面积和冬季气温变化的曲线是A ．①和④B ．②和①C ．③和②D ．④和③2．该市位于A ．华北平原B ．云贵高原C ．大兴安岭D ．柴达木盆地图2为我国某城市近五年产业发展分析图。

据此回答下面3-4题。

3．该城市在产业发展中A ．石油化工和石化产品制造业增长潜力较大B ．农副产品加工及食品制造业发展空间较小C ．批发和零售业可优先培育为主导产业D ．目前缺少增长快、占地区生产总值比重大的优势主导产业4．为实现经济可持续发展，该城市可采取的措施有① 扩大资源开采规模，大量输出原料 ② 发展传统产业，吸收剩余劳动力③ 提高资源加工深度，延长产业链 ④ 培育新兴优势产业，提高竞争力A ．①②B ．③④C ．①③D ．②④道路密度指的是在一定区域内，道路网的总里程与该区域面积的比值。

平均车行速度是指某地区各种汽车的平均行车速度。

图3是某特大城市道路密度和平均车行速度等值线图。

读图完成第5题图1图 2图35．甲处不可能出现的地理事物是A ．十字路口B ．绿地C ．卫星城D ．商业区有专家提出，在京津冀地区以个别城市为主体可以构成图4所示的草原生态旅游圈、皇家遗产旅游圈、滨海度假旅游圈、红色文化旅游圈的旅游网络结构模式。

结合图文材料，回答6-7题。

6．代表草原生态旅游圈、皇家遗产旅游圈、滨海度假旅游圈、红色文化旅游圈的排序是A ．①③②④B ．①③④②C ．③①②④D ．③①④②7．一直以来，京津冀地区旅游合作收效甚微的主要瓶颈因素是A ．地形阻隔B ．交通不便C ．行政分区D ．资金不足读某山地（4°N，9°E）自然带的分布图（图5）。

读图回答8～9题。

8.该山体主要是岩浆岩构成,推测该山可能是A ．火山B ．断块山C ．背斜山D ．向斜山图4图59.该山麓的人工植被带主要种植的经济作物是A ．棉花、花生B ．可可、油棕C ．茶叶、棉花D ．亚麻、葡萄读“北半球某纬度正午太阳高度的年变化图”（图6）。

浙江省杭州市严州中学高三数学上学期第一次模拟试题理(含解析)

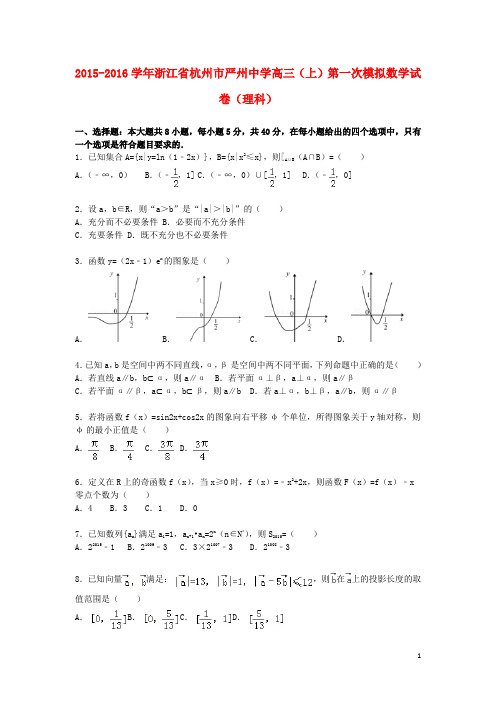
2015-2016学年浙江省杭州市严州中学高三（上）第一次模拟数学试卷（理科）一、选择题：本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一个选项是符合题目要求的．1．已知集合A={x|y=ln（1﹣2x）}，B={x|x2≤x}，则∁A∪B（A∩B）=（）A．（﹣∞，0）B．（﹣，1] C．（﹣∞，0）∪[，1] D．（﹣，0]2．设a，b∈R，则“a＞b”是“|a|＞|b|”的（）A．充分而不必要条件 B．必要而不充分条件C．充要条件 D．既不充分也不必要条件3．函数y=（2x﹣1）e x的图象是（）A．B．C．D．4．已知a，b是空间中两不同直线，α，β是空间中两不同平面，下列命题中正确的是（）A．若直线a∥b，b⊂α，则a∥αB．若平面α⊥β，a⊥α，则a∥βC．若平面α∥β，a⊂α，b⊂β，则a∥b D．若a⊥α，b⊥β，a∥b，则α∥β5．若将函数f（x）=sin2x+cos2x的图象向右平移φ个单位，所得图象关于y轴对称，则φ的最小正值是（）A．B．C．D．6．定义在R上的奇函数f（x），当x≥0时，f（x）=﹣x2+2x，则函数F（x）=f（x）﹣x零点个数为（）A．4 B．3 C．1 D．07．已知数列{a n}满足a1=1，a n+1•a n=2n（n∈N*），则S2015=（）A．22015﹣1 B．21009﹣3 C．3×21007﹣3 D．21008﹣38．已知向量满足：，则在上的投影长度的取值范围是（）A．B．C．D．二、填空题：本大题有7小题，9-12每题6分，13-15题每题4分，共36分．把答案填在答题卷的相应位置．9．若经过点P（﹣3，0）的直线l与圆M：x2+y2+4x﹣2y+3=0相切，则圆M的圆心坐标是；半径为；切线在y轴上的截距是．10．设函数f（x）=，则f（f（4））= ；若f（a）=﹣1，则a= ．11．某空间几何体的三视图（单位：cm）如图所示，则其体积是cm3，其侧视图的面积是cm2．12．设实数x，y满足，则动点P（x，y）所形成区域的面积为，z=x2+y2的取值范围是．13．点P是双曲线=1（a＞0，b＞0）上一点，F是右焦点，且△OPF是∠POF=120°的等腰三角形（O为坐标原点），则双曲线的离心率是．14．函数f（x）=sin2x+的最大值是．15．已知x＞0，y＞0，2x+y=1，若4x2+y2+﹣m＜0恒成立，则m的取值范围是．三、解答题：本大题共5小题，满分74分．解答应写出文字说明，证明过程或演算步骤．16．（15分）（2015•东阳市模拟）在△ABC中，角A，B，C所对的边分别为a，b，c，已知a，b，c成等比数列，且．（Ⅰ）求角B的大小；（Ⅱ）若b=3，求△ABC的面积最大值．17．（15分）（2015•东阳市模拟）如图，已知AB⊥平面BEC，AB∥CD，AB=BC=4，△BEC为等边三角形，（1）若平面ABE⊥平面ADE，求CD长度；（2）求直线AB与平面ADE所成角的取值范围．18．（15分）（2015•东阳市模拟）已知椭圆，离心率，且过点，（1）求椭圆方程；（2）Rt△ABC以A（0，b）为直角顶点，边AB，BC与椭圆交于B，C两点，求△ABC面积的最大值．19．（15分）（2015•东阳市模拟）函数f（x）=2ax2﹣2bx﹣a+b（a，b∈R，a＞0），g（x）=2ax﹣2b（1）若时，求f（sinθ）的最大值；（2）设a＞0时，若对任意θ∈R，都有|f（sinθ）|≤1恒成立，且g（sinθ）的最大值为2，求f（x）的表达式．20．（14分）（2015•东阳市模拟）各项为正的数列{a n}满足，，（1）取λ=a n+1，求证：数列是等比数列，并求其公比；（2）取λ=2时令，记数列{b n}的前n项和为S n，数列{b n}的前n项之积为T n，求证：对任意正整数n，2n+1T n+S n为定值．2015-2016学年浙江省杭州市严州中学高三（上）第一次模拟数学试卷（理科）参考答案与试题解析一、选择题：本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一个选项是符合题目要求的．1．已知集合A={x|y=ln（1﹣2x）}，B={x|x2≤x}，则∁A∪B（A∩B）=（）A．（﹣∞，0）B．（﹣，1] C．（﹣∞，0）∪[，1] D．（﹣，0]考点：交、并、补集的混合运算．专题：集合．分析：分别求出关于集合A、B中的x的范围，从而求出A∪B，A∩B，进而求出∁A∪B（A∩B）．解答：解：∵集合A={x|y=ln（1﹣2x）}，∴A={x|1﹣2x＞0}={x|x＜}，∵B={x|x2≤x}={x|0≤x≤1}，∴A∪B={x|x≤1}，A∩B={x|0≤x＜}，∴∁A∪B（A∩B）=（﹣∞，0）∪[，1]，故选：C．点评：本题考查了集合的交、并、补集的运算，是一道基础题．2．设a，b∈R，则“a＞b”是“|a|＞|b|”的（）A．充分而不必要条件 B．必要而不充分条件C．充要条件 D．既不充分也不必要条件考点：必要条件、充分条件与充要条件的判断．专题：简易逻辑．分析：根据充分条件和必要条件的定义进行判断即可．解答：解：若a=1，b=﹣2，满足a＞b，但|a|＞|b|不成立，若a=﹣2，b=1，满足|a|＞|b|，但a＞b不成立，即“a＞b”是“|a|＞|b|”的既不充分也不必要条件，故选：D．点评：本题主要考查充分条件和必要条件的判断，比较基础．3．函数y=（2x﹣1）e x的图象是（）A．B．C．D．考点：函数的图象．专题：函数的性质及应用．分析：先通过函数的零点排除C，D，再根据x的变化趋势和y的关系排除B，问题得以解决．解答：解：令y=（2x﹣1）e x=0，解得x=，函数有唯一的零点，故排除C，D，当x→﹣∞时，e x→0，所以y→0，故排除B，故选：A．点评：本小题主要考查函数的性质对函数图象的影响，并通过对函数的性质来判断函数的图象等问题．4．已知a，b是空间中两不同直线，α，β是空间中两不同平面，下列命题中正确的是（）A．若直线a∥b，b⊂α，则a∥αB．若平面α⊥β，a⊥α，则a∥βC．若平面α∥β，a⊂α，b⊂β，则a∥b D．若a⊥α，b⊥β，a∥b，则α∥β考点：平面与平面平行的判定．专题：空间位置关系与距离．分析：由条件利用直线和平面平行的判定定理、性质定理，直线和平面垂直的判定定理、性质定理，逐一判断各个选项是否正确，从而得出结论．解答：解：若直线a∥b，b⊂α，则a∥α或a⊂α，故A不对；若平面α⊥β，a⊥α，则a∥β或a⊂β，故B不对；若平面α∥β，a⊂α，b⊂β，则a∥b或a、b是异面直线，故C不对；根据垂直于同一条直线的两个平面平行，可得D正确，故选：D．点评：本题主要考查直线和平面的位置关系，直线和平面平行的判定定理、性质定理的应用，直线和平面垂直的判定定理、性质定理的应用，属于基础题．5．若将函数f（x）=sin2x+cos2x的图象向右平移φ个单位，所得图象关于y轴对称，则φ的最小正值是（）A．B．C．D．考点：函数y=Asin（ωx+φ）的图象变换．专题：三角函数的求值．分析：利用两角和的正弦函数对解析式进行化简，由所得到的图象关于y轴对称，根据对称轴方程求出φ的最小值．解答：解：函数f（x）=sin2x+cos2x=sin（2x+）的图象向右平移φ的单位，所得图象是函数y=sin（2x+﹣2φ），图象关于y轴对称，可得﹣2φ=kπ+，即φ=﹣，当k=﹣1时，φ的最小正值是．故选：C．点评：本题考查三角函数的图象变换，考查正弦函数图象的特点，属于基础题．6．定义在R上的奇函数f（x），当x≥0时，f（x）=﹣x2+2x，则函数F（x）=f（x）﹣x 零点个数为（）A．4 B．3 C．1 D．0考点：根的存在性及根的个数判断．专题：函数的性质及应用．分析：利用奇偶性求解f（x）解析式构造f（x）=，g（x）=x，画出图象，利用交点个数即可判断F（x）零点个数．解答：解：∵在R上的奇函数f（x），当x≥0时，f（x）=﹣x2+2x，∴当x＜0时，f（x）=﹣f（﹣x）=﹣[﹣（﹣x）2+2（﹣x）]=x2+2x，∴f（x）=，g（x）=x，根据图形可判断：f（x）=，与g（x）=x，有3个交点，即可得出函数F（x）=f（x）﹣x零点个数为3，故选：B．点评：本题考查了复杂函数的零点的判断问题，构函数转化为交点的问题求解，数形结合的思想的运用，关键是画出图象．7．已知数列{a n}满足a1=1，a n+1•a n=2n（n∈N*），则S2015=（）A．22015﹣1 B．21009﹣3 C．3×21007﹣3 D．21008﹣3考点：数列的求和．专题：等差数列与等比数列．分析：由已知得数列{a n}的奇数项是首项为1，公比为2的等比数列，偶数项是首项为2，公比为2的等比数列，由此能求出前2015项的和．解答：解：∵a1=1，a n+1•a n=2n，∴a2=2，∴当n≥2时，a n•a n﹣1=2n﹣1，∴==2，∴数列{a n}中奇数项、偶数项分别成等比数列，∴S2015=+=21009﹣3，故选：B．点评：本题考查数列的前2015项的和的求法，是中档题，解题时要认真审题，解题的关键是推导出数列{a n}的奇数项是首项为1，公比为2的等比数列，偶数项是首项为2，公比为2的等比数列．8．已知向量满足：，则在上的投影长度的取值范围是（）A．B．C．D．考点：平面向量数量积的运算．专题：平面向量及应用．分析：由=≤12可求的范围，进而可求的范围，然后由在上的投影||cosθ可求解答：解：设向量的夹角为θ∵||=13，||=1∴===≤12∴≥5∴=≥∴∵在上的投影||cosθ=cosθ故选D点评：本题主要考查了向量的数量积的性质及投影的定义的简单应用，解题的关键是弄清楚基本概念．二、填空题：本大题有7小题，9-12每题6分，13-15题每题4分，共36分．把答案填在答题卷的相应位置．9．若经过点P（﹣3，0）的直线l与圆M：x2+y2+4x﹣2y+3=0相切，则圆M的圆心坐标是（﹣2，1）；半径为；切线在y轴上的截距是﹣3 ．考点：圆的一般方程．专题：直线与圆．分析：根据圆的标准方程即可求出圆心坐标和半径，根据直线相切即可求出切线方程．解答：解：圆的标准方程为（x+2）2+（y﹣1）2=2，则圆心坐标为（﹣2，1），半径R=，设切线斜率为k，过P的切线方程为y=k（x+3），即kx﹣y+3k=0，则圆心到直线的距离d===，平方得k2+2k+1=（k+1）2=0，解得k=﹣1，此时切线方程为y=﹣x﹣3，即在y轴上的截距为﹣3，故答案为：点评：本题主要考查圆的标准方程的应用以及直线和圆相切的位置关系的应用，比较基础．10．设函数f（x）=，则f（f（4））= 5 ；若f（a）=﹣1，则a= 1或．考点：分段函数的应用；函数的值．专题：函数的性质及应用．分析：直接利用分段函数，由里及外求解函数值，通过方程求出方程的根即可．解答：解：函数f（x）=，则f（4）=﹣2×42+1=﹣31．f（f（4））=f（﹣31）=log2（1+31）=5．当a≥1时，f（a）=﹣1，可得﹣2a2+1=﹣1，解得a=1；当a＜1时，f（a）=﹣1，可得log2（1﹣a）=﹣1，解得a=；故答案为：5；1或．点评：本题考查函数的值的求法，方程的根的求解，分段函数的应用，考查计算能力．11．某空间几何体的三视图（单位：cm）如图所示，则其体积是 4 cm3，其侧视图的面积是cm2．考点：由三视图求面积、体积．专题：空间位置关系与距离．分析：判断得出该几何体是三棱锥，求解其体积：S△CBD×AB，△BCD边BD的高为，再利用直角三角形求解面积即可．解答：解：∵根据三视图得出：该几何体是三棱锥，AB=2，BC=3，DB=5，CD=4，AB⊥面BCD，BC⊥CD，∴其体积：S△CBD×AB==4，△BCD边BD的高为==侧视图的面积：×2=故答案为；4，点评：本题考查了三棱锥的三视图的运用，仔细阅读数据判断恢复直观图，关键是利用好仔细平面的位置关系求解，属于中档题．12．设实数x，y满足，则动点P（x，y）所形成区域的面积为 1 ，z=x2+y2的取值范围是[1，5] ．考点：简单线性规划．专题：不等式的解法及应用．分析：先画出满足条件的平面区域，求出A，B，C的坐标，从而求出三角形的面积，再根据z=x2+y2的几何意义，求出其范围即可．解答：解：画出满足条件的平面区域，如图示：，△ABC为平面区域的面积，∴S△ABC=×2×1=1，而z=x2+y2表示平面区域内的点到原点的距离的平方，由图象得：A或B到原点的距离最大，C到原点的距离最小，∴d最大值=5，d最小值=1，故答案为：1，[1，5]．点评：本题考察了简单的线性规划问题，考察z=x2+y2的几何意义，本题是一道中档题．13．点P是双曲线=1（a＞0，b＞0）上一点，F是右焦点，且△OPF是∠POF=120°的等腰三角形（O为坐标原点），则双曲线的离心率是+1 ．考点：双曲线的简单性质．专题：圆锥曲线的定义、性质与方程．分析：由题意可得P在双曲线的左支上，可设P在第二象限，且|OP|=|OF|=c，即有P（﹣ccos60°，csin60°），代入双曲线方程，由离心率公式，解方程即可得到结论．解答：解：由题意可得P在双曲线的左支上，可设P在第二象限，且|OP|=|OF|=c，即有P（﹣ccos60°，csin60°），即为（﹣c，c），代入双曲线方程，可得﹣=1，即为﹣=1，由e=，可得e2﹣=1，化简可得e4﹣8e2+4=0，解得e2=4±2，由e＞1，可得e=+1．故答案为：+1．点评：本题考查双曲线的方程和性质，主要方程的运用和离心率的求法，正确判断P的位置和求出P的坐标是解题的关键．14．函数f（x）=sin2x+的最大值是．考点：三角函数的最值；两角和与差的正弦函数．专题：三角函数的求值．分析：利用两角和的余弦展开，令t=cosx﹣sinx换元，转化为二次函数求最值解答．解答：解：f（x）=sin2x+=sin2x+=sin2x+=2sinxcosx+cosx﹣sinx．令t=cosx﹣sinx，则t∈[]，∴t2=1﹣2sinxcosx，2sinxcosx=1﹣t2．原函数化为y=﹣t2+t+1，t∈[]，对称轴方程为t=，∴当t=时函数有最大值为．故答案为：．点评：本题考查了两角和与差的余弦函数，考查了利用换元法求三角函数的最值，考查了二次函数最值的求法，是中档题．15．已知x＞0，y＞0，2x+y=1，若4x2+y2+﹣m＜0恒成立，则m的取值范围是．考点：函数恒成立问题．专题：综合题；函数的性质及应用．分析：4x2+y2+﹣m＜0恒成立，即m＞4x2+y2+恒成立，求出4x2+y2+的最大值，即可求得m的取值范围．解答：解：4x2+y2+﹣m＜0恒成立，即m＞4x2+y2+恒成立，∵x＞0，y＞0，2x+y=1，∴1≥2，∴0＜≤∵4x2+y2+=（2x+y）2﹣4xy+=1﹣4xy+=﹣4（﹣）2+，∴4x2+y2+的最大值为，∴．故答案为：．点评：本题考查不等式恒成立问题，考察基本不等式的运用，正确转化是关键．三、解答题：本大题共5小题，满分74分．解答应写出文字说明，证明过程或演算步骤．16．（15分）（2015•东阳市模拟）在△ABC中，角A，B，C所对的边分别为a，b，c，已知a，b，c成等比数列，且．（Ⅰ）求角B的大小；（Ⅱ）若b=3，求△ABC的面积最大值．考点：正弦定理；余弦定理．专题：解三角形．分析：（Ⅰ）由正弦定理结合已知可得sin2B=sinAsinC．又，结合sinB＞0，可求sinB的值，结合B∈（0，π），即可求得B的大小，又b2=ac，则b≤a或b≤c，即b 不是△ABC的最大边，从而可求B的值．（II）由余弦定理结合已知可得ac≤9，由三角形面积公式可得，即可求得△ABC的面积最大值．解答：解：（Ⅰ）因为a、b、c成等比数列，则b2=ac．由正弦定理得sin2B=sinAsinC．又，所以．因为sinB＞0，则．…4分因为B∈（0，π），所以B=或．又b2=ac，则b≤a或b≤c，即b不是△ABC的最大边，故．…7分（II）由余弦定理b2=a2+c2﹣2accosB得9=a2+c2﹣ac≥2ac﹣ac，得ac≤9．所以，．当a=c=3时，△ABC的面积最大值为…12分．点评：本题主要考查了正弦定理，余弦定理，三角形面积公式，基本不等式，等比数列的性质等知识的应用，综合性强，属于中档题．17．（15分）（2015•东阳市模拟）如图，已知AB⊥平面BEC，AB∥CD，AB=BC=4，△BEC为等边三角形，（1）若平面ABE⊥平面ADE，求CD长度；（2）求直线AB与平面ADE所成角的取值范围．考点：用空间向量求直线与平面的夹角；平面与平面垂直的判定．专题：综合题；空间位置关系与距离；空间角．分析：（1）设|CD|=d，取BE、AE中点O、F，连结OC、OF，以O为原点，OE、OC、OF为x，y，z轴建立坐标系，求出平面ABE的法向量、面ADE的一个法向量，利用平面ABE⊥平面ADE，求CD长度；（2）利用向量的数量积公式，求直线AB与平面ADE所成角的取值范围．解答：解：（1）设|CD|=d，取BE、AE中点O、F，连结OC、OF，以O为原点，OE、OC、OF 为x，y，z轴建立坐标系，则A（﹣2，0，4），B（﹣2，0，0），，可得平面ABE的法向量为设面ADE的一个法向量为则可得所有，所以CD长度为2．（2）由（1）可知：面ADE的一个法向量，设直线AB与面ADE所成角为θ，则，所以．点评：本题考查线面垂直，考查线面角，考查向量知识的运用，正确求出平面的法向量是关键．18．（15分）（2015•东阳市模拟）已知椭圆，离心率，且过点，（1）求椭圆方程；（2）Rt△ABC以A（0，b）为直角顶点，边AB，BC与椭圆交于B，C两点，求△ABC面积的最大值．考点：直线与圆锥曲线的综合问题．专题：直线与圆；圆锥曲线的定义、性质与方程．分析：（1）运用离心率公式和a，b，c的关系，以及点满足方程，解方程，可得a，b，进而得到椭圆方程；（2）分别设出AB，AC的方程，代入椭圆方程，求得B，C的横坐标，运用弦长公式，以及三角形的面积公式，结合基本不等式，即可得到最大值．解答：解：（1）由，即=，又a2﹣b2=c2，得a=3b，把点带入椭圆方程可得：，所以椭圆方程为：；（2）不妨设AB的方程y=kx+1，则AC的方程为．由得：（1+9k2）x2+18kx=0，k用代入，可得，从而有，于是．令，有，当且仅当，．点评：本题考查椭圆的方程和性质，主要考查椭圆的离心率和方程的运用，联立直线方程和椭圆方程，求得交点，同时考查三角形的面积公式和基本不等式的运用，属于中档题．19．（15分）（2015•东阳市模拟）函数f（x）=2ax2﹣2bx﹣a+b（a，b∈R，a＞0），g（x）=2ax﹣2b（1）若时，求f（sinθ）的最大值；（2）设a＞0时，若对任意θ∈R，都有|f（sinθ）|≤1恒成立，且g（sinθ）的最大值为2，求f（x）的表达式．考点：复合三角函数的单调性．专题：三角函数的图像与性质．分析：（1）令sinθ=t∈[0，1]，问题等价于求f（t）=2at2﹣2bt﹣a+b在t∈[0，1]的最大值，由二次函数区间的最值可得；（2）令sinθ=t∈[﹣1，1]，由恒成立和最大值可得可得二次函数的顶点坐标为（0，﹣1），进而可得ab的值，可得解析式．解答：解：（1）令sinθ=t∈[0，1]，问题等价于求f（t）=2at2﹣2bt﹣a+b在t∈[0，1]的最大值，∵a＞0，抛物线开口向上，二次函数的对称轴，由二次函数区间的最值可得（2）令sinθ=t∈[﹣1，1]，则|f（t）|≤1可推得|f（0）|≤1，|f（1）|≤1，|f（﹣1）|≤1，∵a＞0，∴g（sinθ）max=g（1）=2，而g（1）=2a﹣2b=2而f（0）=b﹣a=﹣1而t∈[﹣1，1]时，|f（t）|≤1，即﹣1≤f（t）≤1，结合f（0）=﹣1可知二次函数的顶点坐标为（0，﹣1）∴b=0，a=1，∴f（x）=2x2﹣1．点评：本题考查二次函数的性质，涉及三角换元和等价转化，属中档题．20．（14分）（2015•东阳市模拟）各项为正的数列{a n}满足，，（1）取λ=a n+1，求证：数列是等比数列，并求其公比；（2）取λ=2时令，记数列{b n}的前n项和为S n，数列{b n}的前n项之积为T n，求证：对任意正整数n，2n+1T n+S n为定值．考点：数列递推式；数列的求和．专题：等差数列与等比数列．分析：（1）把由λ=a n+1代入，整理后求解方程求得．结合a n＞0可得为常数，结论得证；（2）把λ=2代入数列递推式，得到2a n+1=a n（a n+2），变形得到，然后分别利用累积法和裂项相消法求得T n，S n，代入2n+1T n+S n证得答案．解答：证明：（1）由λ=a n+1，得，∴．两边同除可得：，解得．∵a n＞0，∴为常数，故数列是等比数列，公比为1；（2）当λ=2时，，得2a n+1=a n（a n+2），∴．∴，又，∴，故2n+1T n+S n==2为定值．点评：本题考查了数列递推式，考查了等比关系的确定，训练了累积法求数列的通项公式及裂项相消法求数列的和，是中档题．。

2013年高考数学理(浙江卷)WORD版有答案

2013年普通高等学校招生全国统一考试（浙江卷）数学（理科）选择题部分（共50分）注意事项：1．答题前，考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试卷和答题纸规定的位置上．2．每小题选出答案后，用2B 铅笔把答题纸上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

不能答在试题卷上．参考公式：如果事件A ，B 互斥，那么柱体的体积公式()()()P A B P A P B +=+ V Sh =如果事件A ，B 相互独立，那么其中S 表示柱体的底面积，h 表示柱体的高 ()()()P A B P A P B ⋅=⋅ 锥体的体积公式如果事件A 在一次试验中发生的概率是p ，那么 13V Sh = n 次独立重复试验中事件A 恰好发生k 次的概率其中S 表示锥体的底面积，h 表示锥体的高()()()1,0,1,2,,n k k k n n P k C p p k n -=-= 球的表面积公式台体的体积公式 24πS R =()1213V h S S = 球的体积公式其中12,S S 分别表示台体的上底、下底面积， 34π3V R = h 表示台体的高其中R 表示球的半径一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1，已知i 是虚数单位，则()()12i i -+-=2， A ，3i -+ B ，13i -+ C ，33i -+ D ，1i -+3，设集合{}{}22,340S x x T x x x =>-=+-≤，则()R C S T =U A ，(]2,1- B ，(],4-∞- C ，(],1-∞ D ，[)1,+∞3，已知,x y 为正实数，则A ，lg lg lg lg 222x y x y +=+ B ，()lg lg lg 222x y x y +=g C ，lg lg lg lg 222x yx y =+g D ，()lg lg lg 222xy x y =g 4，已知函数()()()cos 0,0,f x A x A R ωϕωϕ=+>>∈，则“()f x 是奇函数”是“2πϕ=”的A ，充分不必要条件B ，必要不充分条件C ，充分必要条件D ，既不充分也不必要条件5，某程序框图如图所示，若该程序运行后输出的值是95，则 A ，4a = B ，5a = C ，6a = D ，7a =6，已知,sin 2cos R ααα∈+=，则tan 2α= A ，43 B ，34 C ，34- D ，43- 7，设ABC V ，0P 是边AB 上一定点，满足014P B AB =，且对于边 AB 上任一点，恒有00PB PC P B PC ≥uu r uu u r uuu r uuu r g g ，则 A ，90ABC ∠=o B ，90BAC ∠=o C ，AB AC = D ，AC BC =8，已知e 为自然对数的底数，设函数()()()()111,2k x f x e x k =--=，则A ，当1k =时，()f x 在1x =处取到极小值B ，当1k =时，()f x 在1x =处取到极大值C ，当2k =时，()f x 在1x =处取到极小值D ，当2k =时，()f x 在1x =处取到极大值9，如图，12,F F 是椭圆221:14x C y +=与双曲线2C 的公共焦点，,A B 分别是12,C C 在第二、四象限的公共点，若四边形12AF BF 为矩形，则2C 的离心率是A B C ，32 D ，210，在空间中，过点A 作平面π的垂线，垂足为B ，记().B f A π=设,αβ是两个不同的平面，对空间任意一点P ，()()12,Q f f P Q f f P βααβ⎡⎤==⎡⎤⎣⎦⎣⎦，恒有12PQ PQ =，则A ，平面α与平面β垂直B ，平面α与平面β所成的（锐）二面角为45oC ，平面α与平面β平行D ，平面α与平面β所成的（锐）二面角为60o2013年普通高等学校招生全国统一考试（浙江卷）数学（理科）非选择题部分（共100分）注意事项：1．用黑色字迹的签字笔或钢笔将答案写在答题纸上，不能答在试题卷上．2．在答题纸上作图，可先使用2B 铅笔，确定后必须使用黑色字迹的签字笔或钢笔描黑．11，设二项式5的展开式中常数项为A ，则A = 12，某几何体的三视图（单位：cm ）如图所示，则此几何体的体积等于 3cm13，设z k x y =+，其中,x y 满足20240240x y x y x y +-≥⎧⎪-+≥⎨⎪--≤⎩，若z 的最大值为12，则实数k =14，将,,,,,A B C D E F六个字母排成一排，且,A B 均在C 的同侧，则不同的排法共有种（用数字作答）15，设F 为抛物线2:4C y x =的焦点，过点()1,0P -的直线l 交抛物线C 于,A B 两点，点Q 为线段AB 的中点，若2FQ =，则直线l 的斜率等于 16，在ABC V 中，90C ∠=o ，M 是BC 的中点。

浙江省某三县2013届高三数学上学期期中联考试题理新人教A版

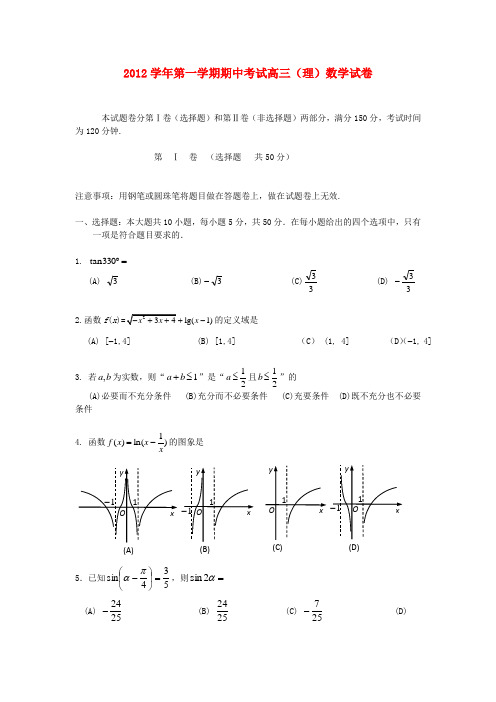
2012学年第一学期期中考试高三（理）数学试卷本试题卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分，考试时间为120分钟.第 Ⅰ 卷（选择题共50分）注意事项：用钢笔或圆珠笔将题目做在答题卷上，做在试题卷上无效.一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. =︒330tan(A) 3 (B)3- (C)33 (D) 33-2.函数f (xlg(1)x -的定义域是(A) [-1,4] (B) [1,4] （C ） (1, 4] （D ）（-1, 4]3. 若b a ,为实数，则“1≤+b a ”是“21≤a 且21≤b ”的 (A)必要而不充分条件 (B)充分而不必要条件 (C)充要条件 (D)既不充分也不必要条件4. 函数)1ln()(xx x f -=的图象是5．已知534sin =⎪⎭⎫⎝⎛-πα，则=α2sin (A) 2524-(B) 2524 (C) 257- (D)(B)(C) (D)(A)2576. 在△ABC 中，点M 满足0=++MC MB MA ，若 0=++AM m AC AB ，则实数m 的值是(A) 3 (B) 23 (C) 23- (D)3-7．等差数列{}n a 的前n 项和为n S ，且224,6a S ==，则64n nS a +的最小值是 (A) 7 (B)152(C) 8(D)1728. 若实数y x ,满足不等式组⎪⎩⎪⎨⎧≥+-≤--≤-+0033022m y x y x y x ，/且x y +/的最小值为1-，则实数m 的值是（A ）0/ （B ）1-/ （C ）1 （D ）29．函数()M f x 的定义域为R ，且定义如下：1(),()0(),M x M f x x M ∈⎧=⎨∉⎩（其中M 为非空数集且R M ⊆），在实数集R 上有两个非空真子集A 、B 满足A B =∅，则函数()1()()()1A B A B f x F x f x f x +=++的值域为(A) ∅ (B) {12} (C) {1} (D){12,1}10．将函数1y =[])20(，∈x 图像绕原点逆时针方向旋转角θ)0(αθ≤≤，得到曲线C .若对于每一个旋转角θ，曲线C 都是一个函数的图像，则α的最大值是 (A) 6π(B)4π (C)3π (D)2π第 Ⅱ 卷（非选择题共100分）注意事项：将卷Ⅱ的题目做在答题卷上，做在试题卷上无效.二、填空题：本大题共7小题，每小题4分，共28分．11.公差为1的等差数列{}n a 满足2469a a a ++=，则579a a a ++的值等于 ▲ ．12.已知a 与b 为两个不共线的单位向量，若向量a +b 与向量k a -b 垂直，则实数k = ▲ .13．在直角三角形ABC 中，，1,==⊥AC AB AC AB21=，则⋅的值等于 ▲ ． 14．函数()sin()f x A x ωϕ=+（A ，ω，ϕ是常数，0A >，0ω>）的部分图象如右图所示，则(0)f 的值是 ▲ .15.圆014222=+-++y x y x 关于直线 ),(022R b a by ax ∈=+-对称，则b a ⋅的取值范围是_ __ ▲ ____ .16.等比数列{}n a 中，120121,9a a ==，函数122012()()()()2f x x x a x a x a =---+，则曲线()y f x = 在点(0,(0))f 处的切线方程为 ___ ▲ _____ .17.函数y ＝11－x 的图象与函数2sin y x π= (24x -≤≤)的图象所有交点的横坐标之和等于 ▲ .三、解答题：本大题共5小题．共72分.解答应写出文字说明、证明过程或演算步骤.18．（本题满分14分）在ABC ∆中，角C B A ,,所对应的边分别为c b a ,,且满足sin cos b A B =．(Ⅰ)求角B 的值； (Ⅱ)若cos2A =sin C 的值．19.（本题满分14分）函数22x y -=和213y x =的图象如图所示，其中有且只有1x x =、2x 、3x 时，两函数数值相等，且1230x x x <<<，o 为坐标原点．(Ⅰ)请指出图中曲线1C 、2C 分别对应的函数； (Ⅱ)现给下列三个结论： ①当(,1)x ∈-∞-时，22x -<213x ； ②2(1,2)x ∈；③3(4,5)x ∉，请你选择两个结论判定其是否成立，并说明理由．20. (本题满分14分)已知数列}{n a ，}{n b 满足：291=a ，n n n a a 2621⋅=-+, 12+-=n n n ab (∈n N *)．(Ⅰ)证明数列}{n b 为等比数列．并求数列}{n a ，}{n b 的通项公式； (Ⅱ)记数列}{n a ，}{n b 的前n 项和分别为n n T S ,，若对任意的∈n N*都有nn n b mT S ≤，求实数m 的最小值．21．(本题满分15分) 已知二次函数)0,,,()(2≠∈++=a R c b a c bx ax x f ，0)0()2(==-f f ，)(x f 的最小值为1-．(Ⅰ)求函数)(x f 的解析式；(Ⅱ)设()()()1g x f x m f x =--+，若)(x g 在]1,1[-上是减函数，求实数m 的取值范围；22．(本题满分15分)已知定义在R 上的偶函数()f x 的最小值为1，当[0,)x ∈+∞时，()x f x ae =．（Ⅰ）求函数()f x 的解析式；（Ⅱ）求最大的整数(1)m m >，使得存在t R ∈，只要[1,]x m ∈，就有()f x t ex +≤．第19题图(注:e 为自然对数的底数)高三数学（理科）参考答案1 2 3 4 5 6 7 8 9 10 DCABDDDBCB11．18 ；12．1；13．92； 14．26；15． 1(,]4-∞； 16． 232012+=x y ；17．8 三．解答题：本大题共5小题，共72分．解答应写出文字说明、证明过程或演算步骤. 18. 在ABC ∆中，角C B A ,,所对应的边分别为c b a ,,且满足sin 3cos b A a B =． (Ⅰ)求角B 的值； (Ⅱ)若25cos2A =，求sin C 的值．解：(Ⅰ)由正弦定理BbA a sin sin =及已知条件sin 3cos b A a B =得…………………2分 B A A B cos sin 3sin sin =,………………………………………………4分又因为0sin ≠A ,所以B B cos 3sin =，即3tan =B ，……………………6分又),0(π∈B ,所以3π=B ;…………………………………………………7分(Ⅱ)因为25cos2A =，所以5312cos 2cos 2=-=A A ,………………………9分又),0(π∈A ,所以54sin =A ，由(Ⅰ)知32π=+C A ，………………………11分所以10334sin 32cos cos 32sin )32sin(sin +=-=-=A A A C πππ.…………14分 19．函数22x y -=和213y x =的图象如图所示，其中有且只有1x x =、2x 、3x 时，两函数数值相等，且1230x x x <<<，o 为坐标原点． (Ⅰ)请指出图中曲线1C 、2C 分别对应的函数； (Ⅱ)现给下列三个结论： ①当(,1)x ∈-∞-时，22x -<213x ； ②2(1,2)x ∈；③3(4,5)x ∉，请你选择两个结论判定其是否成立，并说明理由．解：（Ⅰ）1C 为213y x =，2C 为22x y -=； ………………………………………5分（Ⅱ）结论①成立，理由如下：函数22x y -=在(,1]-∞-上是增函数，∴(,1)x ∈-∞-时，2121228x ---<=. 又函数213y x =在(,1]-∞-上是减函数， ∴(,1)x ∈-∞-时，22111(1)333x >⨯-=而1183<，所以当(,1)x ∈-∞-时，22123x x -<；结论②成立，理由如下：构造函数221()23x f x x -=-，则11(1)0,(2)063f f =>=-<∴()f x 在区间(1,2)内有零点.同理()f x 在区间（5，6）内有零点，由题意∴2(1,2)x ∈ ；3(5,6)x ∈. 结论③成立，理由同② …………………………………14分 20．已知数列}{n a ，}{n b 满足：291=a ，n n n a a 2621⋅=-+, 12+-=n n n ab (∈n N *)． (Ⅰ)证明数列}{n b 为等比数列．并求数列}{n a ，}{n b 的通项公式； (Ⅱ)记数列}{n a ，}{n b 的前n 项和分别为n n T S ,，若对任意的∈n N*都有nn n b mT S ≤，求实数m 的最小值．解：（Ⅰ）由已知得 1212)2(2+++-=-n n n n a a ，……………………………2分所以n n b b 211=+，因为211=b ，所以}{n b 为等比数列. ………………………………………4分所以n n b )21(=， ……………………………………………6分进而n n n a )21(21+=+. ……………………………………………7分（Ⅱ）1211422121)2121()222(2132+--=++++++++=++n n n n n nn T S124+⋅=n ……………………………10分则nn n m 21421)124(+=+⋅≥对任意的∈n N*成立． ……………………12分所以数列}214{n +是递减数列，所以29)214(max =+n所以m 的最小值为29． ……………………………………………………14分21. 已知二次函数)0,,,()(2≠∈++=a R c b a c bx ax x f ，0)0()2(==-f f ，)(x f 的最小值为1-．(Ⅰ)求函数)(x f 的解析式；(Ⅱ)设()()()1g x f x m f x =--+，若)(x g 在]1,1[-上是减函数，求实数m 的取值范围；解: （Ⅰ）由题意设)2()(+=x ax x f ，…………………………………………3分 ∵ )(x f 的最小值为1-，∴ 0>a ，且1)1(-=-f ，∴ 1=a ，∴ x x x f 2)(2+= . ………………………………………………………6分（Ⅱ）∵ 1)1(2)1()(2++--=x m x m x g ， ………………………………8分 ① 当1=m 时，14)(+-=x x g 在[-1, 1]上是减函数，∴ 1=m 符合题意. ……………………………………………………10分② 当1≠m 时，对称轴方程为：mmx -+=11， ⅰ）当01>-m ，即 1<m 时，抛物线开口向上，由111≥-+mm ，得 m m -≥+11 ， ∴ 10<≤m ；……12分 ⅱ）当01<-m ，即 1>m 时，抛物线开口向下，由111-≤-+mm ，得 m m +-≥+11， ∴1>m . ……14分综上知，实数m 的取值范围为[)∞+,0．………………………………15分22. 已知定义在R 上的偶函数()f x 的最小值为1，当[0,)x ∈+∞时，()xf x ae =．（Ⅰ）求函数()f x 的解析式；（Ⅱ）求最大的整数(1)m m >，使得存在t R ∈，只要[1,]x m ∈，就有()f x t ex +≤．(注:e 为自然对数的底数)解：（Ⅰ）因为()xf x ae =为单调函数，故(0)1f =，得1a =, ………………2分当0x <时，0x ->，则()()3xf x f x e -=-=综上：,0(),0x x e x f x e x -⎧≥⎪=⎨<⎪⎩ ; …………………………………5分（Ⅱ）因为任意[1,]x m ∈，都有()f x t ex +≤ 故(1)f t e +≤且()f m t em +≤ 当10t +≥时，1tee +≤，从而11t +≤，10t ∴-≤≤ 当10t +<时，(1)t ee -+≤，从而(1)1t -+≤，21t ∴-≤<-综上20t -≤≤2m ≥，故0m t +> 故()f m t em +≤得：m teem +≤即存在[2,0]t ∈-，满足tm em e e≤2min {}t m eme e e-∴≥=，即30m e e m -≤ 令3()xg x e e x =-，[2,)x ∈+∞，则3'()xg x e e =- 当(2,3)x ∈时，'()0g x <，()g x 单调递减当(3,)x ∈+∞时，'()0g x >，()g x 单调递增又3(3)20g e =-<，3(2)0g e =-<，3(4)(4)0g e e =-<，32(5)(4)0g e e =-> 由此可见，方程()0g x =在区间[2,)+∞上有唯一解0(4,5)m ∈，且当0[2,]x m ∈时()0g x ≤，当0[,)x m ∈+∞时()0g x ≥m Z ∈，故max 4m =，此时2t =-. ………………………………12分下面证明：|2|(2)x f x e ex --=≤对任意[1,4]x ∈恒成立①当[1,2]x ∈时，即2xeex -≤，等价于x e xe ≤[1,2]x ∈，,1x e e x ∴≥≥，x xe e ≥②当[2,4]x ∈时，即2x e ex -≤，等价于3max {}0x e x --≤令3()x h x ex -=-，则3'()1x h x e -=-()h x ∴在(2,3)上递减，在(3,4)上递增 max max{(2),(4)}h h h ∴=而1(2)20,(4)40h h e e=-<=-< 综上所述，(2)f x ex -≤对任意[1,4]x ∈恒成立. …………………15分。

2013年浙江省高考数学试卷及答案(理科)word版

绝密★考试结束前20##普通高等学校招生全国统一考试〔##卷〕数学〔理科〕本试题卷分选择题和非选择题两部分.全卷共5页,选择题部分1至3页,非选择题部分4至5页.满分150分,考试时间120分钟.请考生按规定用笔将所有试题的答案涂、写在答题纸上.选择题部分〔共50分〕注意事项：1.答题前,考生务必将自己的##、##号用黑色字迹的签字笔或钢笔分别填写在试卷和答题纸规定的位置上.2.每小题选出答案后,用2B 铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.不能答在试题卷上. 参考公式如果事件,A B 互斥,那么如果事件,A B 相互独立,那么如果事件A 在一次试验中发生的概率为P ,那么n 次独立重复试验中事件A 恰好发生k 次的概率台体的体积公式其中1S ,2S 分别表示台体的上、下面积,h 表示台体的高柱体体积公式V Sh =其中S 表示柱体的底面积,h 表示柱体的高锥体的体积公式13V Sh =其中S 表示锥体的底面积,h 表示锥体的高球的表面积公式24S R π= 球的体积公式343V R π=其中R 表示球的半径选择题部分〔共50分〕一、选择题：本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1．已知i 是虚数单位,则(1)(2)i i -+-=< >A ．3i -+B ．13i -+C ．33i -+D ．1i -+2．设集合{|2}S x x =>-,2{|340}T x x x =+-≤,则=T S C R )( < > A ．(21]-， B ．(4]-∞-， C ．(1]-∞， D ．[1)+∞， 3．已知x ,y 为正实数,则< > A ．lg lg lg lg 222x yx y +=+ B ．lg()lg lg 222x y x y +=⋅C ．lg lg lg lg 222x yxy⋅=+ D ．lg()lg lg 222xy x y=⋅4．已知函数()cos()(0f x A x A ωϕ=+>,0ω>,)R ϕ∈,则"()f x 是奇函数〞是"2πϕ=〞的< >A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件 5．某程序框图如图所示,若该程序运行后输出的值是95,则 A ．4a = B ．5a = C ．6a = D ．7a =6．已知R α∈,sin 2cos αα+=则tan 2α=A ．43 B ．34 C ．34- D ．43- 7．设ABC ∆,0P 是边AB 上一定点,满足014P B AB =,且对于边AB 上任一点P ,恒有00PB PC P B PC ⋅≥⋅．则A ．90ABC ∠=︒B ．30BAC ∠=︒ C ．AB AC =D ．AC BC =8．已知e 为自然对数的底数,设函数()(1)(1)(12)x kf x e x k =--=，,则 A ．当1k =时,()f x 在1x =处取到极小值 B ．当1k =时,()f x 在1x =处取到极大值 C ．当2k =时,()f x 在1x =处取到极小值 D ．当2k =时,()f x 在1x =处取到极大值9．如图,1F ,2F 是椭圆221:14x C y +=与双曲线2C 的公共焦点,A ,B 分别是1C ,2C 在第二、四象限的公共点．若四边形12AF BF 为矩形,则2C 的离心率是< >〔第5题图〕ABC ．32D10．在空间中,过点A 作平面π的垂线,垂直为B ,记()B f A π=．设α,β是两个不同的平面,对空间任意一点P ,1[()]Q f f P βα=,2[()]Q f f P αβ=,恒有12PQ PQ =,则< >A ．平面α与平面β垂直B ．平面α与平面β所成的〔锐〕二面角为45︒C ．平面α与平面β平行D ．平面α与平面β所成的〔锐〕二面角为60︒非选择题部分〔共100分〕二、填空题：本大题共7小题,每小题4分,共28分.11．设二项式5的展开式中常数项为A ,则A =． 12．若某几何体的三视图〔单位：cm 〕如图所示,则此几何体的体积等于3cm ．13．设z kx y =+,其中实数x ,y 满足20240240x y x y x y +-≥⎧⎪-+≥⎨⎪--≤⎩,若z 的最大值为12,则实数k =．14．将A B C D E F ，，，，，六个字母排成一排,且A B ，均在C 的同侧,则不同的排法共有种〔用数字作答〕．15．设F 为抛物线2:4C y x =的焦点,过点(10)P -，的直线l 交抛物线C 于A ,B 两点,点Q 为线段AB 的中点．若||2FQ =,则直线l 的斜率等于．16．在ABC ∆中,90C ∠=︒,M 是BC 的中点．若1sin 3BAM ∠=,则sin BAC ∠=． 17．设1e ,2e 为单位向量,非零向量12b xe ye =+,x ,y R ∈．若1e ,2e的夹角为6π,则||||x b 的最大值等于．三、解答题：本大题共5小题,共72分,解答应写出文字说明、证明过程或演算步骤.18．〔本题满分14分〕在公差为d 的等差数列{}n a 中,已知110a =,且1a ,222a +,35a 成等比数列． 求d ,n a ；<III>若0d <,求123||||||||n a a a a ++++．19．〔本题满分14分〕设袋子中装有a 个红球,b 个黄球,c 个篮球,且规定：取出一个红球得1分,取出一个黄球得2分,取出一个篮球得3分．当331a b c ===，，时,从该袋子中任任取〔有放回,且每球取到的机会均等〕2个球,记随机变量ξ为取出此2球所得分数之和,求ξ的分布列；<II>从该袋中任取〔每球取到的机会均等〕1个球,记随机变量η为取出此球所得分数．若53E η=,59D η=,求::a b c ． 20．〔本题满分15分〕如图,在四面体A BCD -中,AD ⊥平面BCD ,BC CD ⊥,2AD =,BD =M 是AD 的中点,P 是BM 的中点,点Q 在线段AC 上,且3AQ QC =． 证明：//PQ 平面BCD ；<II>若二面角C BM D --的大小为60︒,求BDC ∠的大小．21．〔本题满分15分〕如图,点(01)P -，是椭圆22122:1x y C a b+=〔0a b >>〕的一个顶点,1C 的长轴是圆222:4C x y +=的直径．1l ,2l 是过点P 且互相垂直的两条直线,其中1l 交圆2C 于A ,B 两点,2l 交椭圆1C 于另一点D ．求椭圆1C 的方程；<II>求ABD ∆面积取最大值时直线1l 的方程． 22．〔本题满分14分〕已知a R ∈,函数32()3323f x x x ax a =-+-+．求曲线()y f x =在点(1(1))f ，处的切线方程； <II>当[02]x ∈，时,求|()|f x 的最大值．数学〔理科〕试题参考答案一、选择题：本题考查基本知识和基本运算.每小题5分,满分50分.1．B 2．C 3．D 4．B 5．A 6．C 7．D 8．C 9．D 10．A 二、填空题：本题考查基本知识和基本运算.每小题4分,满分28分. 11．-10 12．24 13．2 14．480 15．±1 16．317．2 三、解答题：本大题共5小题,共72分.18．本题主要考查等差数列、等比数列的概念,等差数列通项公式、求和公式等基础知识,同时考查运算求ABCDPQM〔第20题图〕〔第21题图〕解能力.满分14分.〔Ⅰ〕由题意得21325(21)a a a =+即2340d d --= 故1d =-或4d =所以11*n a n n N =--∈，或46*n a n n N =+∈，〔Ⅱ〕设数列{}n a 的前n 项和为n S ．因为0d <,由〔Ⅰ〕得1d =-,11n a n =--．则当11n ≤时,2123121||||||||22n n a a a a S n n ++++==-+．当12n ≥时,212311121||||||||211022n n a a a a S S n n ++++=-+=-+．综上所述,19．本题主要考查随机事件的概率和随机变量的分布列、数学期望、数学方差等概念,同时考查抽象概括、运算求解能力和应用意识.满分14分. 〔Ⅰ〕由题意得ξ取2,3,4,5,6．故331(2)664P ξ⨯===⨯, 2321(3)663P ξ⨯⨯===⨯,231225(4)6618P ξ⨯⨯+⨯===⨯,2211(5)669P ξ⨯⨯===⨯,111(6)6636P ξ⨯===⨯．所以ξ的分布列为〔Ⅱ〕由题意知η的分布列为所以235()3a b c E a b c a b c a b c η=++=++++++,222552535()(1)(2)(3)3339a b c D a b c a b c a b c η=-⋅+-⋅+-⋅=++++++．解得3a c =,2b c =,故20．本题主要考查空间点、线、面位置关系、二面角等基础知识,空间向量的应用,同时考查空间想象能力和运算求解能力.满分15分. 方法一：〔Ⅰ〕取BD 中点O ,在线段CD 上取点F ,使得3DF FC =,连结OP ,OF ,FQ 因为3AQ QC =,所以//QF AD ,且14QF AD =．因为O ,P 分别为BD ,SM 的中点,所以OP 是BDM ∆的中位线, 所以//OP DM ,且12OP DM =．又点M 是AD 的中点,所以//OP AD ,且14OP AD =．从而//OP FQ ,且OP FQ =．所以四边形OPQF 为平行四边形,故//FQ QF又PQ ⊄平面BCD ,OF ⊂平面BCD ,所以//PQ 平面BCD ．〔Ⅱ〕作CG BD ⊥于点G ,作GH BM ⊥于点H ,连结CH 因为AD ⊥平面BCD ,CG ⊂平面BCD ,所以AD CG ⊥, 又CG BD ⊥,AD BD D ⋂=,故CG ⊥平面ABD , 又BM ⊂平面ABD ,所以CG BM ⊥．又GH BM ⊥,CG GH G ⋂=,故BM ⊥平面CGH ,所以GH BM ⊥,CH BM ⊥．所以CHG ∠为二面角C BM D --的平面角,即60CHG ∠=︒．设BDC θ∠=．在Rt BCD ∆中,cos 22CD BD θθ==,cos 22sin CG CD θθθ==, 2sin 22BG BC θθ==．在Rt BDM ∆中,223sin BG DM HG BM θ⋅==．在Rt CHG ∆中,3cos tan 3sin CG CHG HG θθ∠===．所以tan 3θ=从而60θ=︒,即60BDC ∠=︒．方法二：〔Ⅰ〕如图,取BD 中点O ,以O 为原点,OD ,OP 所在射线为y ,z 轴的正半轴,建立空间直角坐标系Oxyz ．由题意知(022)A ，,(020)B ，,(020)D ，．设点C 的坐标为00(0)x y ，，,因为3AQ QC =,所以00331()442Q x y +，．因为M 是AD 的中点,故(01)M ．又P 是BM 的中点,故1(00)2P ，，．所以0033(0)44PQ x y =+，．又平面BCD 的一个法向量为(001)a =，，,故0PQ a ⋅=．又PQ ⊄平面BCD ,所以//PQ 平面BCD ．〔Ⅱ〕设()m x y z =，，为平面BMC 的一个法向量．由00(1)CM x y =-，,(01)BM =知00)00x x y y z z ⎧-++=⎪⎨+=⎪⎩, 取1y =-,得00(1y m x =-，．又平面BDM 的一个法向量为(100)n =，，,于是||1|cos<>|=2||||m n m n m n ⋅==，, 即2003y x ⎛+= ⎝⎭．〔1〕又BC CD ⊥,所以0CB CD ⋅=,故0000(0)(0)0x y x y -⋅-=，，，,即22002x y +=．〔2〕联立〔1〕,〔2〕,解得000x y =⎧⎪⎨=⎪⎩002x y ⎧=⎪⎪⎨⎪=⎪⎩．所以tan BDC ∠==．又BDC ∠是锐角,所以60BDC ∠=︒．21．本题主要考查椭圆的几何性质,直线与圆的位置关系、直线与椭圆的位置关系等基础知识,同时考查解析几何的基本思想方法和综合解题能力.满分15分. 〔Ⅰ〕由题意得12b a =⎧⎨=⎩所以椭圆1C 的方程为2214x y +=．〔Ⅱ〕设11()A x y ，,22()B x y ，,00()D x y ，．由题意知直线1l 的斜率存在,不妨设为k ,则直线1l 的方程为1y kx =-．又圆222:4C x y +=,故点O 到直线1l的距离d =所以||AB == 又12l l ⊥,故直线2l 的方程为0x ky k ++=．由22044x ky k x y ++=⎧⎨+=⎩消去y ,整理得22(4)80k x kx ++=, 故0284kx k-=+．所以||PD =设ABD ∆的面积为S ,则1||||2S AB PD =⋅=,所以3213S ==≤=当且仅当2k =±时取等号．所以直线1l的方程为12y x =±-． 22．本题主要考查导数的几何意义、导数应用等基础知识,同时考查推理论证能力,分类讨论等分析问题和解决问题的能力.〔Ⅰ〕由题意2'()363f x x x a =-+,故'(1)33f a =- 又(1)1f =,所以所求的切线方程为(33)34y a x a =--+．〔Ⅱ〕由于2'()3(1)3(1)02f x x a x =-+-≤≤，．故 当0a ≤时,有'()0f x ≤,此时()f x 在[02]，上单调递减,故{}max ()max (0)(2)33f x f f a ==-，．<ii>当1a ≥时,有'()0f x ≥,此时()f x 在[02]，上单调递增,故{}max ()max (0)(2)31f x f f a ==-，．<iii>当01a <<时,设11x =21x =则1202x x <<<,12'()3()()f x x x x x =--．由于1()12(1f x a =+-2()12(1f x a =--故12()()20f x f x +=>,12()()4(10f x f x a -=->．从而12()()f x f x >, 所以{}1max ()max (0)(2)()f x f f f x =，，．〔1〕当203a <<时,(0)(2)f f >．又21()(0)2(1(23)0f x f a a -=--=>,故1max ()()12(1f x f x a ==+- 〔2〕当213a ≤<时,(2)(2)f f =,且(2)(0)f f ≥．又21()(2)2(1(32)f x f a a -=--=,所以①当2433a ≤<时,1()(2)f x f >．故max 1()()12(1f x f x a ==+-②当413a ≤<时,1()(2)f x f ≤．故 max ()(2)31f x f a ==-．综上所述,max3303()12(1043314a a f x a a a a ⎧⎪-≤⎪⎪=+-<<⎨⎪⎪-≥⎪⎩，，。

浙江省严州中学2013届高三数学3月阶段测试试题文新人教A版

严州中学2013届高三3月阶段测试数学（文）试题选择题部分（共50分）一．选择题（本大题共10 小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的）1. 已知集合{}{}0,1,2,|2,M N x x a a M ===∈，则集合MN = ( )(A) {}0 ( B ) {}10, ( C ) {}21, ( D ) {}20, 2．若{}n a 是等差数列，则76a a <是86a a <的 ( ) (A) 充分而不必要条件 ( B ) 必要而不充分条件 ( C ) 充分必要条件 ( D ) 既不充分也不必要条件3．设复数z 的共轭复数为z ，若(2)3i z i +=-，则z z ⋅的值为 ( ) (A) 1 ( B ) 2 ( C ) 2 ( D ) 44．若向量(1,3)a =,||1b =,且()0a b b -⋅=，则与的夹角为 ( ) (A)56π ( B ) 23π ( C ) 3π ( D ) 6π5．如图所示的算法流程图中输出的最后一个数为10-，则判断框中的条件是（）(A) 5?n < ( B ) 5?n ≥ ( C ) 4?n < ( D ) 4?n ≥6．若直线l 与平面α相交，但不垂直，则有（） (A) ∀平面β，若l β⊆，都有平面β⊥平面α； ( B ) ∃平面β，若l β⊆，使得平面β⊥平面α； ( C ) ∀平面β，若l β⊆，都有平面β∥平面α； ( D )∃平面β，若l β⊆，使得平面β∥平面α． 7．若函数()sin cos f x x a x =+在区间2[,]33ππ-上单调递增，则a的值为（）( B ) ( D ) 8．设(1)y f x =-是R 上的奇函数,若()y f x =在(1,)-+∞上是增函数,且(0)1f =,则满足()1f m >-的实数m 的范围是（）(A) (2,)-+∞ ( B ) (1,)-+∞ ( C ) (2,0)- ( D ) (,0)-∞9．已知椭圆22221(0)y x a b a b+=>>的上焦点为F ，左、右顶点分别为12,B B ，下顶点为A ，直线2AB 与直线1B F 交于点P ，若22AP AB =，则椭圆的离心率为（） (A)12 ( B ) 13( C ) 14 ( D ) 23 10．已知,0,0>>b a 函数ab x b a ab x x f +--+=)4()(2是偶函数，则)(x f 的图象与y 轴交点纵坐标的最小值为（）是否开始S =1n =1n =n +1S =S +(-1)n +1n 2输出S 结束（第5题图）(A) 16 ( B ) 8 ( C ) 4 ( D ) 22非选择题部分（共100分）二．填空题(本大题共7小题，每小题4分，共28分)11，学校为了调查学生在课外读物方面的支出情况，抽出高了一个容量为n 的样本，其频率分布直方图如图所示，其中.支出在[)40,50元的同学有36人，则n 的值为． 12．已知等差数列{}n a 中,,4951π=++a a a 则 =+)sin(64a a ．13．一个几何体的三视图如图所示，则该几何体的体积为．14．．若双曲线)0(112222>=-a y a x 的一条渐近线的倾斜角为60，则=a ．15．已知向量(),a m n =，()1,1b =-，其中{},1,2,3,4,5m n ∈，则与a b 的夹角能成为直角三角形内角的概率是．16．设直线x t =与函数2()f x x =，()ln g x x =的图像分别交于点,M N ，则当MN 达到最小值时t 的值为_____________．17．已知函数()||2f x x x a x =-+-在R 上恒为增函数，则a 的取值范围是．三．解答题(本大题共5小题，共72分，解答应写出文字说明、证明过程或演算步骤) 18．（本题满分14分）已知函数21()3sin cos cos ,2f x x x x x R =--∈．（Ⅰ）求函数)(x f 的最小值和最小正周期；（Ⅱ）已知ABC ∆内角AB C 、、的对边分别为a b c 、、，且3,()0c f C ==，若向量(1,sin )m A =与(2,sin )n B =共线，求a b 、的值．19．（本题满分14分）（第13题图）（第11题图）已知等差数列{}n a 满足：37a =，5726a a +=．{}n a 的前n 项和为n S ．（Ⅰ）求n a 及n S ；（Ⅱ）令211n n b a =-（n N +∈）,求数列{}n b 的前n 项和n T ．20．（本题满分14分）如图，平面PAD ⊥平面ABCD ，四边形ABCD 是矩形，AB=1，AD=2，P 点在以AD 为直径的半圆弧上运动（不包括端点）（Ⅰ）证明：PA ⊥PC ；（Ⅱ）当二面角P ─BC ─D 达到最大值时，求直线AD 与平面PAC 所成角的正弦值． 21．（本题满分15分）设13x =-是函数32()2f x x mx mx =++-的一个极值点．（1）求函数()f x 的极值；（2）若方程()()()2f a f a f x -+=在区间],[a a -(a >0)上恰有两个不同的实根，求a 的取值范围．ABCDP严州中学2013届3月月考数学（文科）答题卷一、选择题(本大题共10小题，每小题5分，满分50分)题号 1 2 3 4 5 6 7 8 9 10 答案二、填空题：本大题共7小题，每小题4分，满分28分.11． 12． 13． 14． 15． 16． 17．班级______________ 姓名 _____________ 学号考号________________三、解答题：本大题共5小题，满分72分．解答须写出文字说明、证明过程和演算步骤．严州中学2013届3月月考数学（文科）参考答案一．选择题DCBCC BAABA二．填空题19．…… 7分（Ⅱ）由（Ⅰ）知2n+1n a =，所以b n =211n a -=21=2n+1)1-（114n(n+1)⋅=111(-)4n n+1⋅，所以n T =111111(1-+++-)4223n n+1⋅-=11(1-)=4n+1⋅n 4(n+1)． ………… 7分20．解：（Ⅰ）略 …… 6分8分 21．解：（1）∵m mx x x f ++=23)('2， ∵31-=x 是函数2)(23-++=mx mx x x f 的一个极值点， ∴031313231)31('=+=+-=-m m m f ，∴1-=m ∴2)(23---=x x x x f ，)1)(13(123)('2-+=--=x x x x x f∴)(x f 有极大值27)3(-=-f ，极小值3)1(-=f ……………6分（2）当10<<a 时，)(x f 在]31,[--a 上单调递增，在],31[a -上单调递减∵02)()(]2)()()(][2)()()([2<⎥⎦⎤⎢⎣⎡---=+---+--a f a f a f a f a f a f a f a f ∴2)()(a f a f +-在)(a f -与)(a f 之间∴方程2)()()(a f a f x f +-=在区间],[a a -上不可能有两个不同的根当1>a 时，)(x f 在]31,[--a 上单调递增，在]1,31[-上单调递减，在],1[a 上单调递增 ∴)(x f 有极小值3)1(-=f 又∵)1(322)()(2f a a f a f =-<--=+-∴方程2)()()(a f a f x f +-=在区间],[a a -上不可能有两个不同的根.当1=a 时，)(x f 在]31,1[--上单调递增，在]1,31[-上单调递减此时3)1()1(-==-f f ∴方程32)1()1()(-=+-=f f x f 有两个根为1±综上所述：1=a . …………………9分 22．解：（Ⅰ）24y x =…………7分Q-±…………8分（Ⅱ）(1,。

浙江省严州中学2013届高三自选模块3月阶段测试试题

严州中学2013届高三3月阶段测试自选模块试题题号：01语文“中国古代诗歌散文欣赏”模块（10分）阅读下面两首古诗，然后回答问题。

题金陵渡张祜金陵津渡小山楼，一宿行人自可愁。

潮落夜江斜月里，两三星火是瓜洲。

秋日赴阙题潼关①驿楼许浑红叶晚萧萧，长亭酒一瓢。

残云归太华②，疏雨过中条③。

树色随关迥，河声入海遥。

帝乡明日到，犹自梦渔樵。

【注】①潼关，在今陕西省潼关县境内，位于陕西、山西、河南三省要冲。

②太华：华山。

在今陕西省华阴县。

③中条：山名，在今山西永济县东南。

1.两首诗中的“潮落夜江斜月里，两三星火是瓜洲”和“帝乡明日到，犹自梦渔樵”分别表达了诗人怎样的情感？（4分）2.这两首诗在写作艺术方面独具匠心，请各选取一例来赏析。

（6分）题号：02“中国现代诗歌散文欣赏”模块（10分）阅读下面的散文，然后回答问题。

害怕回乡刘志坚回乡不是回家。

回家是亲切的。

记得母亲在世时，回家是那样温馨，是那样顺理成章。

一踏上故土，远远地望见屋顶上的炊烟，望见炊烟下的竹篱，竹篱后，有慈母倚门而望。

未进家门，早有乡邻，用真诚而纯朴的目光迎候你：“哇，回家来看母亲了。

”匆匆推开柴门，扑进母亲怀里，一卸世路风尘的艰辛。

母亲去世后，家就变得飘渺了。

但那是我的根，那里的陶冶过我的乡情乡音。

在那里，我懂得蒲公英是怎么飞，蚱蜢是怎么跳，画眉鸟是怎么唱，它们都在呼唤我回归。

回归是必然的。

只是先人已渺，旧居不存，算不了回家，就算回乡吧。

但回乡的路是艰难的。

当我踏上那弯曲的乡路时，山还是那座山，村还是那个村。

乡邻依旧友好，迎候你的目光也依旧真挚。

但语意里有了陌生：“啊，回来看看？”是的，回来看看。

看什么呢？流水依旧白，前山依旧青。

但自己的目光已不知往哪儿看，脚步不知往哪儿挪了。

“到乡翻似烂柯人。

”一颗系念故乡的心，顿时被悬了起来。

因为随着母亲的去世，没有了依恋的那扇柴门，也没有了那一缕炊烟。

于是无可挽回地要坠入从前，黯淡地走进童年的记忆，很悲壮地站到了昨日已远，来日无多的路口，踟蹰复踟蹰。

浙江省严州中学2013届高三3月阶段测试政治试题 Word版含答案

23．京剧是中国文化的“国粹”之一。

下列关于京剧的表述正确的是A．其基础是原流行于安徽一带的徽戏和汉族地区的汉戏B．其逐渐形成时期正是西方浪漫主义音乐流行之时C．第一次由电影来表现其唱腔魅力是谭鑫培主演的《定军山》片断D．“八亿人口八个戏”反映了京剧艺术的再次全面繁荣24.当前金融危机下民营企业融资难的问题更加凸显。

对此，中国证监会提出要积极支持有条件的民营企业通过发行股票上市融资。

企业要上市融资，应该是①公司财务必须向全社会公开②股东转让出资须征得其他股东同意③资本必须划分为等额股份④股东可以以实物、技术等形式入股A．①② B．③④ C．①③ D．②④25.党的十八大报告指出，实现发展成果由人民共享，必须深化收入分配制度改革。

为了实现收入分配公平，右图中组合正确的是A．①② B．①③C．③④ D．②④26.亚当·斯密曾在《道德情操论》中提出，人在追求物质利益的同时，不要去伤害别人，而是要帮助别人。

在当前中国，要让企业家身上也“流淌着道德的血液”，可采取的措施是①加强信用建设以规范市场秩序②用失信惩戒来替代价值引导③承担社会责任以形成内在约束④依靠媒体来监管生产经营A．①④ B．①③ C．②③ D．②④27.2012年7月4日，欧洲核子中心宣布通过实验发现了疑似上帝粒子的新亚原子粒子。

它的发现，将彻底改变现有的物理学理论体系，并进而揭开充斥在宇宙中的暗物质的神秘本质。

这从一个侧面表明了①世界的真正统一性就在于它的物质性②原有的真理常常在新的实践中被推翻③实践的最终目的是为了获取科学认识④在实践中检验和发展真理是永无止境的A．①④ B．②③ C．①③ D．②④28.2012年普利兹克建筑奖的获得者是中国建筑师王澍，他的作品中大量运用地方材料和传统工艺，用现代空间和建筑体量诠释传统文化中的空间和意境。

这说明，扎根于历史背景、具有世界性的建筑是①时尚和流行的对立统一②发展与回归的对立统一③传统和现代的对立统一④批判与否定的对立统一A．①② B．③④ C．①④ D．②③29.列宁有一句名言：“意识到自己的奴隶地位而与之作斗争的奴隶，是革命家。

浙江省考试院2013届高三测试卷数学(理)试题

大家网，全球第一学习门户！无限精彩在大家测试卷数学(理科)姓名_____________ 准考证号__________________本试题卷分选择题和非选择题两部分。

全卷共5页，选择题部分1至3页，非选择题部分4至5页。

满分150分，考试时间120分钟。

请考生按规定用笔将所有试题的答案涂、写在答题纸上。

选择题部分 (共50分)注意事项:1．答题前，考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试卷和答题纸规定的位置上。

2．每小题选出答案后，用2B 铅笔把答题纸上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

不能答在试题卷上。

一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合A ＝{y | y ＝2x ，x ∈R }，则 R A ＝A ．∅B ． (－∞，0]C ．(0，＋∞)D ．R 2．已知a ，b 是实数，则“| a ＋b |＝| a |＋| b |”是“ab ＞0”的A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件大家网，全球第一学习门户！无限精彩在大家3．若函数f(x ) (x ∈R )是奇函数，函数g(x ) (x ∈R )是偶函数，则A ．函数f [g (x )]是奇函数B ．函数g [f (x )]是奇函数C ．函数f (x )⋅g (x )是奇函数D ．函数f (x )＋g (x )是奇函数4．设函数f (x )＝x 3－4x ＋a ，0＜a ＜2．若f (x )的三个零点为x 1，x 2，x 3，且x 1＜x 2＜x 3，则A ．x 1＞－1B ．x 2＜0C ．x 2＞0D ．x 3＞25．如图，在四边形ABCD 中，AB ⊥BC ，AD ⊥DC ．若|AB |＝a ，|AD |＝b ，则AC BD ⋅＝A ．b 2－a 2B ．a 2－b 2C ．a 2＋b 2 D ．ab 6．设数列{a n }．A ．若2n a ＝4n ，n ∈N *，则{a n }为等比数列B ．若a n ⋅a n +2＝21n a +，n ∈N *，则{a n }为等比数列C ．若a m ⋅a n ＝2m +n ，m ，n ∈N *，则{a n }为等比数列D ．若a n ⋅a n +3＝a n +1⋅a n +2，n ∈N *，则{a n }为等比数列7．已知以下三视图中有三个同时表示某一个三棱锥，则不是．．该三棱锥的三视图是 ABCD8．若整数x ，y 满足不等式组 0,2100,0,x y x y y ⎧->⎪--<⎨+- 则2x ＋y 的最大值是A ．11B ．23C ．26D ．30(第6题图)侧视图正视图俯视图侧视图俯视图侧视图正视图俯视图侧视图俯视图C D大家网，全球第一学习门户！无限精彩在大家大家网，全球第一学习门户！无限精彩在大家非选择题部分 (共100分)注意事项：1．用黑色字迹的签字笔或钢笔将答案写在答题纸上，不能答在试题卷上。

浙江省严州中学高三数学3月阶段测试试题理新人教A版

严州中学2013届高三3月阶段测试数学（理）试题一．选择题（共10小题，满分50分） 1.已知条件1:01p x >+和条件:q 有意义，则p ⌝是q ⌝的 A ．充分不必要条件 B 。

必要不充分条件 C 。

充要条件 D 。

既不充分也不必要条件2.已知集合U 为实数集R ，131{|0},{|,[1,8]}U x A x C A y y x x x m+=>==∈--，则m 值是 A ．1 B 。

1- C 。

2 D 。

2-3.设01x <<则141,,11xa b x c d x x ==+==-+中最大的一个是 A ．a B 。

b C 。

c D 。

d4.等差数列{}n a 的前n 项和为n S ，若37101148,4a a a a a +-=-=，则13S 等于 A ．152 B 。

154 C 。

156 D 。

1585.一个几何体的三视图如下，若其正视图的面积等于24cm ，俯视图是正三角形，则其侧视图的面积等于A2B。

2C 。

22cm D 。

24cm6.在某次测量中得到的A 样本数据如下：82,84,84,86,86,86,88,88,88,88。

若B 样本数据恰好是A 样本数据每个都加2后所得数据，则A 、B 两样本下列数字特征对应相同的是 A ．众数 B 。

平均数 C 。

中位数 D 。

标准差7.已知6/()(2),()f x ax f x =+是()f x 导函数，若/()f x的展开式中x 的系数大于()f x 的展开式中x 的系数，则a 的取值范围是2.05A a a ><或 2.05B a << 2.5C a > 5.02D a a ><或8.直线3y x =-与抛物线24y x =交于A 、B 两点，过A 、B 两点向抛物线的准线作垂线，垂足分别为P 、Q ，则梯形APQB 的面积为A ．48B 。

56C 。

64D 。

2013年浙江省高考(理科)数学试卷及答案(Word版)

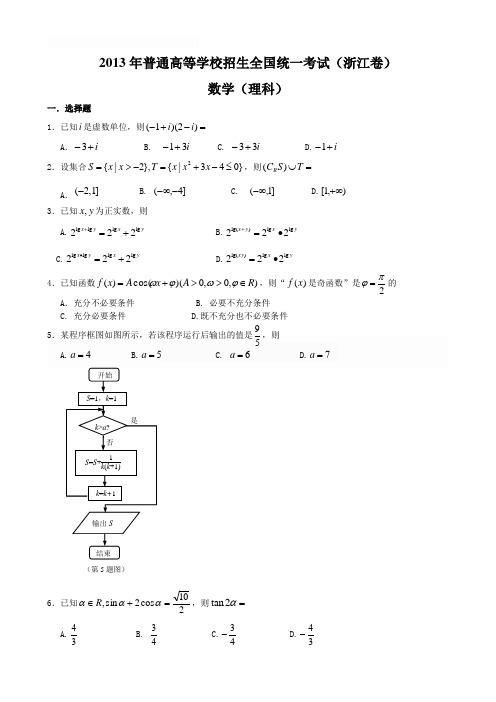
2013年普通高等学校招生全国统一考试（浙江卷）数学（理科）一．选择题1．已知i 是虚数单位，则=-+-)2)(1(i iA ．i +-3 B. i 31+- C. i 33+- D.i +-1 2．设集合}043|{},2|{2≤-+=->=x x x T x x S ，则=⋃T S C R )( A ．(2,1]- B. ]4,(--∞ C. ]1,(-∞ D.),1[+∞ 3．已知y x ,为正实数，则 A.y x yx lg lg lg lg 222+=+ B.y x y x lg lg )lg(222∙=+C.y x yx lg lg lg lg 222+=∙ D.y x xy lg lg )lg(222∙=4．已知函数),0,0)(cos()(R A x A x f ∈>>+=ϕωϕω，则“)(x f 是奇函数”是2πϕ=的A ．充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D.既不充分也不必要条件 5．某程序框图如图所示，若该程序运行后输出的值是59，则 A.4=a B.5=a C. 6=a D.7=a6．已知210cos 2sin ,=+∈αααR ，则=α2tan A.34 B. 43C.43-D.34-（第5题图）7．设0,P ABC ∆是边AB 上一定点，满足AB B P410=，且对于边AB 上任一点P ，恒有C P B P 00∙≥∙。

则A. 090=∠ABCB. 090=∠BACC. AC AB =D.BC AC = 8．已知e 为自然对数的底数，设函数)2,1()1)(1()(=--=k x e x f k x ，则A ．当1=k 时，)(x f 在1=x 处取得极小值B ．当1=k 时，)(x f 在1=x 处取得极大值C ．当2=k 时，)(x f 在1=x 处取得极小值D ．当2=k 时，)(x f 在1=x 处取得极大值9．如图，21,F F 是椭圆14:221=+y x C 与双曲线2C 的公共焦点，B A ,分别是1C ，2C 在第二、四象限的公共点。

浙江省严州中学新安江校区高三数学3月阶段测试试题理

1D ABCD 1(第6题图) 严州中学2016届高三3月阶段测试数学试卷(理科)第Ⅰ卷一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一个选项是符合题目要求的.1．平行直线l 1：3x +4y-12=0与l 2：6x +8y-15=0之间的距离为( ▲ )A ．310B ．910C ．35D ．952．命题 “∃α∈[0, +∞），sin α>α”的否定形式是( ▲ )A ．∀α∈[0, +∞），sin α≤αB ．∃α∈[0, +∞），sin α≤αC ．∀α∈(-∞,0），sin α≤αD ．∃α∈(-∞,0），sin α>α3．某几何体的三视图如图所示（单位：cm ），则该几何体的体积等于( ▲ ) cm 3A ．4+23πB ．4+32πC ．6+23πD ．6+32π4．若直线l 交抛物线C ：y 2=2px (p>0)于两不同点A ，B ，且|AB |=3p ，则线段AB 中点M 到y 轴距离的最小值为( ▲ ) A ．p2 B ． p C ．3p 2D ．2p5．已知φ是实数，f (x )=cos x ﹒cos(x +π3)，则“φ=π3”是“函数f (x )向左平移φ个单位后关于y 轴对称”的( ▲ )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件6．如图，将四边形ABCD 中△ADC 沿着AC 翻折到AD 1C ，则翻折过程中线段DB 中点M 的轨迹是( ▲ )A ．椭圆的一段B ．抛物线的一段C ．一段圆弧D ．双曲线的一段7．已知双曲线C:2222x y ab-=1(a , b >0)虚轴上的端点B (0, b )，右焦点F ，若以B 为圆心的圆与C 的一条渐近线相切于点P ，且//，(第3题图)俯视图正视图侧视图2则该双曲线的离心率为( ▲ ) A ． 5B ．2C ．1+32D ．1+528．已知非零正实数x 1, x 2, x 3依次构成公差不为零的等差数列.设函数f (x )=x α，α∈{-1, 12,2, 3}，并记M ={-1, 12, 2, 3}.下列说法正确的是( ▲ )A ．存在α∈M ，使得f (x 1) , f (x 2) , f (x 3)依次成等差数列B ．存在α∈M ，使得f (x 1), f (x 2), f (x 3)依次成等比数列C ．当α=2时，存在正数λ，使得f (x 1), f (x 2), f (x 3)- λ依次成等差数列D ．任意α∈M ，都存在正数λ>1，使得λf (x 1), f (x 2), f (x 3)依次成等比数列第Ⅱ卷二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分． 9．设集合A ={x ∈N |6x +1∈N }，B ={x |y =ln(x -1)}，则A = ▲ ，B = ▲ ，)(B C A R = ▲ . 10．设函数f (x )=A sin(2x +φ)，其中角φ的终边经过点P (-1,1)，且0<φ<π，f (π2)=-2.则φ= ▲ ，A = ▲ ，f (x )在[-π2, π2]上的单调减区间为 ▲ ．11．设a >0且a ≠1，函数f (x )=⎩⎨⎧a x +1-2,x ≤0,g (x ), x >0为奇函数，则a =▲ ，g (f (2))= ▲ ．12．如图，在直三棱柱ABC -A 1B 1C 1中，AB =BC =CC 1=2，AC =23，M 是AC 的中点，则异面直线CB 1与C 1M 所成角的余弦值为▲ .13．设实数x ,y 满足x +y -xy ≥2，则|x -2y |的最小值为 ▲ . 14．已知非零平面向量a , b , c 满足a ·c = b ·c=3，|a -b |=|c |=2，则向量a 在向量c 方向上的投影为 ▲ ，a ·b 的最小值为 ▲ .15．设f (x )=4x +1+a ·2x+b (a , b ∈R )，若对于∀x ∈[0,1]，| f (x )|≤12都成立，则=b ▲ . 三、解答题：本大题共5小题，共74分。

浙江省2013年高考数学仿真模拟试卷3(理科)

2013年数学高考模拟试卷（理科）本试卷分卷I 和卷II 两部分.考试时间120分钟.满分120分.请考生按规定用笔将所有试题的答案涂、写在答题卡上。

卷1选择题部分 (共50分)一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

(1)(原创)已知集合{}{}21,,1,M y y x x R N y y x x R ==+∈==+∈，则M N = （）(A)[1,)+∞ (B)[1,)-+∞ (C)[1,2) (D)[1,2)-(2) (原创)已知i 是虚数单位，则12i 1i+-的值为（）(A)12i 2-+ (B)3-i 2(C)-1+3i 2(D) 3＋i(3)(根据浙江省2012高考理科样卷第3题改编)如图所示某程序框图，则输出的n 的值是（）(A) 13 (B)15 (C) 16 (D)14(4)(原创)已知命题22:90,:60p x q x x -<+->，则q p ⌝⌝是的（） (A)充分不必要条件 (B)既不充分也不必要条件(C)充要条件(D)必要不充分条件(5)（原创）用a ，b ，c 表示三条不同的直线，γ表示平面，给出下列命题： ①若//,//,//;a b b c a c 则 ②若,,a b b c a c ⊥⊥⊥则； ③若//,//,a b γγ则a//b ； ④若,,//.a b a b γγ⊥⊥则其中真命题的序号是（）参考公式：如果事件A ，B 互斥，那么P (A +B )=P (A )+P (B )如果事件A ，B 相互独立，那么P (A ·B )=P (A )·P (B )如果事件A 在一次试验中发生的概率是p ,那么n 次独立重复试验中事件A 恰好发生k 次的概率P n (k )=C k n p k (1-p )n -k (k =0,1,2,…，n )台体的体积公式V=)(312211S S S S h ++其中S 1,S 2分别表示台体的上、下底面积，h 表示台体的高柱体的体积公式 Sh V = 其中S 表示柱体的底面积，h 表示柱体的高锥体的体积公式 Sh V 31= 其中S 表示锥体的底面积，h 表示锥体的高球的表面积公式 S =4πR 2 球的体积公式 3π34R V =其中R 表示球的半径开始 p ＝0，n ＝20 p=p+nP ＞100?输出n 结束 (第3题)是否n=n-1432 2 正视图侧视图俯视图（第13题）（第9题）(A) ①③ (B) ①④ (C) ②③ (D) ②④(6)原创）若实数x,y 满足不等式组⎪⎩⎪⎨⎧≥-+≤+-≤,01,032,5y x y x y 则y x z 2+=的最大值是（）(A)10 (B) 11 (C)15 (D) 14(7)(原创)若25(21)x +=24100125a a x a x a x +++，则135a a a ++的值为( )(A) 121 (B)122 (C)124 (D)120(8)（根据理科天利38套杭二中高考模拟试卷16题改编）已知六个相同的盒子里各放了一本书，其中三本是语文书，三本是数学书，现在一次打开一个盒子，直到弄清哪三个盒子里放了语文书，则打开的盒子为4个的概率为（）(A（9）(原创)如图，直角梯形ABCD 中，AD ⊥AB, AB//DC , AB=4,AD=DC=2,设点N是DC 边的中点，点M 是梯形ABCD 内或边界上的一个动点，则AM AN ⋅的最大值是( )（A ）4（B ） 6 （C ） 8 （D ）10（10）（根据宁波四中上学期期末考试理科卷第17题改编）把已知正整数n 表示为若干个正整数（至少3个，且可以相等）之和的形式，若这几个正整数可以按一定顺序构成等差数列，则称这些数为n 的一个等差分拆．将这些正整数的不同排列视为相同的分拆．如：（1，4，7）与（7，4，1）为12的相同等差分拆．问正整数36的不同等差分拆的个数是（）．（A ）20 （B ）18 （C ）19 （D ）21卷II 非选择题部分 (共100分)二、填空题: 本大题共7小题, 每小题4分, 共28分。

2013浙江理科(全word解析版)

2013浙江卷数学（理）试题答案与解析选择题部分（共50分）一、选择题：每小题5分，共50分． 1．已知i 是虚数单位，则(−1+i)(2−i)=A ．−3+iB ．−1+3iC ．−3+3iD ．−1+i2．设集合S={x|x>−2}，T={x|x 2+3x −4≤0}，则( R S)∪T=A ．(−2，1]B ．(−∞，−4]C ．(−∞，1]D ．[1，+∞) 3．已知x ，y 为正实数，则A ．2lgx+lgy =2lgx +2lgyB ．2lg(x+y)=2lgx ∙ 2lgyC ．2lgx ∙ lgy =2lgx +2lgyD ．2lg(xy)=2lgx ∙ 2lgy4．已知函数f(x)=Acos(ωx+φ)(A>0，ω>0，φ∈R )，则“f(x)是奇函数”是“φ=π2”的A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件 5．某程序框图如图所示，若该程序运行后输出的值是95，则A ．a=4B ．a=5C ．a=6D ．a=76．已知α∈R ，sin α+2cos α=102，则tan2α=A ．43B ．34C ．−34D ．−437．设△ABC ，P 0是边AB 上一定点，满足P 0B=14AB ，且对于AB 上任一点P ，恒有→PB ∙→PC ≥→P 0B ∙→P 0C ，则A ．∠ABC=90︒B ．∠BAC=90︒C ．AB=AC D8．已知e 为自然对数的底数，设函数f(x)=(e x −1)(x −1)k(k=1，2)，则A ．当k=1时，f(x)在x=1处取到极小值B ．当k=1时，f(x)在x=1处取到极大值C ．当k=2时，f(x)在x=1处取到极小值D ．当k=2时，f(x)在x=1处取到极大值9．如图，F 1，F 2是椭圆C 1：x 24+y 2=1与双曲线C 2的公共焦点，A ，B 分别是C 1，C 2在第二、四象限的公共点．若四边形AF 1BF 2为矩形，则C 2的离心率为（第5题图）A ． 2B ． 3C ．32D ．6210．在空间中，过点A 作平面π的垂线，垂足为B ，记B=f π(A)．设α，β是两个不同的平面，对空间任意一点P ，Q 1=f β[f α(P)]，Q 2=f α[f β(P)]，恒有 PQ 1= PQ 2，则 A ．平面α与平面β垂直 B ．平面α与平面β所成的（锐）二面角为45︒ C ．平面α与平面β平行 D ．平面α与平面β所成的（锐）二面角为60︒非选择题部分（共100分）二、填空题：每小题4分，共28分．11．设二项式⎝⎛⎭⎪⎪⎫x −13x 5的展开式中常数项为A ，则A= ． 12．若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积等于 cm 3． 13．设z=kx+y ，其中实数x ，y 满足⎩⎪⎨⎪⎧x+y −2≥0，x −2y+4≥0，2x −y −4≤0．若z 的最大值为12，则实数k= ．14．将A ，B ，C ，D ，E ，F 六个字母排成一排，且A ，B 均在C 的同侧，则不同的排法有种（用数字作答）．15．设F 为抛物线C ：y 2=4x 的焦点，过点F(−1，0)的直线l 交抛物线C 于A ，B 两点，点Q 为线段AB 的中点．若|FQ|=2，则直线l 的斜率等于．16．在△ABC ，∠C=90︒，M 是BC 的中点．若sin ∠BAM=13，则sin ∠BAC= ．17．设e 1，e 2为单位向量，非零向量b =x e 1+y e 2，x ，y ∈R ．若e 1，e 2的夹角为π6，则|x||b |的最大值等于．三、解答题：本大题共5小题，共72分． 18．（本小题满分14分）在公差为d 的等差数列{a n }中，已知a 1=10，且a 1，2a 2+2，5a 3成等比数列（Ⅰ）求d ，a n ；（Ⅱ）若d<0，求|a 1|+|a 2|+|a 3|+…+|a n |． 19．（本题满分14分）设袋子中装有a 个红球，b 个黄球，c 个蓝球，且规定：取出一个红球得1分，取出一个黄球得2分，取出一个蓝球得3分．（Ⅰ）当a=3，b=2，c=1时，从该袋子中任取（有放回，且每球取到的机会均等）2个球，记随机变量ξ为取出此2球所得分数之和，求ξ的分布列；（Ⅱ）从该袋子中任取（每球取到的机会均等）1个球，记随机变量η为取出此球所得分数．若 E η=53，D η=59，求a ∶b ∶c ．20．（本题满分15分）如图，在四面体A −BCD 中，AD ⊥平面BCD ，BC ⊥CD ，AD=2，BD=22．M 是AD 的中点，P 是BM 的中点，点Q 在线段AC 上，且AQ=3QC ．（Ⅰ）证明：PQ ∥平面BCD ；（Ⅱ）若二面角C −BM −D 的大小为60︒，求∠BDC 的大小．21．（本题满分15分）如图，点P(0，−1)是椭圆C 1：x 2a 2+2(a>b>0)的一个顶点，C 1的长轴是圆C 2：x 2+y 2=4l 2是过点P 且互相垂直的两条直线，其中l 1交圆C 2于两点，l 2交椭圆C 1于另一点D ．（Ⅰ）求椭圆C 1的方程；（Ⅱ）求△ABD 面积取最大值时直线l 1的方程．22．（本题满分14分）已知a ∈R ，函数f(x)=x 3−3x 2+3ax −3a+3 （Ⅰ）求曲线y=f(x)在点(1，f(1))处的切线方程；（Ⅱ）当x ∈[0，2]时，求|f(x)|的最大值．参考答案1、【答案解析】B2、【答案解析】C 因为( R S)={x|x ≤−2}，T={x|−4≤x ≤1}，所以( R S)∪T=(−∞，1].3、【答案解析】D 由指数和对数的运算法则，易知选项D 正确4、【答案解析】B 由f(x)是奇函数可知f(0)=0，即cos φ=0，解出φ=π2+k π，k ∈Z ，所以选项B 正确 5、【答案解析】A6、【答案解析】C 由(sin α+2cos α)2=⎝ ⎛⎭⎪⎫1022可得sin 2α+4cos 2α+4sin αcos α sin 2α+cos 2α=104，进一步整理可得3tan 2α−8tan α−3=0，解得tan α=3或tan α=−13，于是tan2α=2tan α1−tan 2α=−34. 7、【答案解析】D 由题意，设|→AB |=4，则|→P 0B|=1，过点C 作AB 的垂线，垂足为H ，在AB 上任取一点P ，设HP 0=a ，则由数量积的几何意义可得，→PB ∙→PC =|→PH ||→PB |=(|→PB | −(a+1))|→PB |，→P 0B ∙→P 0C =−|→P 0H ||→P 0B |=−a ，（第21题图） 0于是→PB ∙→PC ≥→P 0B ∙→P 0C 恒成立，相当于(|→PB |−(a+1))|→PB |≥−a 恒成立，整理得|→PB |2−(a+1)|→PB |+a ≥0恒成立，只需∆=(a+1)2−4a=(a −1)2≤0即可，于是a=1，因此我们得到HB=2，即H 是AB 的中点，故△ABC 是等腰三角形，所以AC=BC 8、【答案解析】C 当k=1时，方程f(x)=0有两个解，x 1=0，x 2=1，由标根法可得f(x)的大致图象，于是选项A ，B 错误；当k=2时，方程f(x)=0有三个解，x 1=0，x 2=x 3=1，其中1是二重根，由标根法可得f(x)的大致图象，易知选项C 正确。

2013年高三数学理科三月调考试题(黄冈附答案)-数学试题

2013年高三数学理科三月调考试题（黄冈附答案）-数学试题黄冈市2013年高三年级3月份质量检测数学试题（理科）第Ⅰ卷（选择题共50分）一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一个是符合题目要求的.1．复平面内，复数，则复数的共轭复数对应的点的象限A．第一象限B．第二象限C．第三象限D．第四象限2．如图所示，程序框图（算法流程图）的输出结果是A．—3 B．—2C．—1 D.03．如图2所示的韦恩图中，A、B是两非零集合，定义集合为阴影部分表示的集合，若，则为A. B.C. D.4．若设是两条不同的直线，是三个不同的平面，下列四个命题中假命题的是A.若则B.若则C.若则D.若则5．高三毕业时，甲，乙，丙等五位同学站成一排合影留念，已知甲，乙相邻，则甲丙相邻的概率为A. B. C. D.6．有以下命题：①命题“ ”的否定是：“ ”；②已知随机变量服从正态分布，则；③函数的零点在区间内；其中正确的命题的个数为A.3个B.2个C.1个D.0个7．已知A，B，C，D是函数一个周期内的图象上的四个点，如图所示，B为轴上的点，C为图像上的最低点，E为该函数图像的一个对称中心，B与D关于点E对称，在轴上的投影为，则的值为A. B. C. D.8．已知O为坐标原点，双曲线的右焦点F，以OF为直径作圆交双曲线的渐近线于异于原点的两点A、B，若，则双曲线的离心率为A.2B.3C.D.9．等差数列前项和为，已知则A. B.C. D.10．已知O是锐角三角形ⅠABC的外接圆的圆心，且若则A．B. C. D.不能确定第Ⅰ卷（非选择题共100分）二、填空题：本大题共6小题，考生共需作答5小题。

每小题5分，共25分。

请将答案填在答题卡对应题号的位置上。

答错位置，书写不清，模棱两可均不得分.（一）必考题（11－14题）11．某校共有学生1000名，其中高一年级有380人，高二年级男生有180人，已知在全校学生中制抽取1名，抽到高二年级的女生的概率为0.19，现采取分层抽样（按年级分层）在全校抽取100人，则应在高三年级抽取的人数是.12．已知则展开式中的常数项为.13．设P是不等式组表示的平面区域内的任意一点，向量，，若（为实数），则的最大值为。