七年级数学上册计算题专题训练 23题
人教版七年级数学上册《计算重难题型》专题训练-附带答案

人教版七年级数学上册《计算重难题型》专题训练-附带答案一.易错计算强化1.计算:(1)(13−52+16)×(−36);(2)(−1)2022×3−23+(−14)2÷|−125|.试题分析:(1)根据乘法分配律计算即可;(2)先算乘方再算乘除法最后算加减法即可.答案详解:解:(1)(13−52+16)×(−36)=13×(﹣36)−52×(﹣36)+16×(﹣36)=﹣12+90+(﹣6)=72;(2)(−1)2022×3−23+(−14)2÷|−125|=1×3﹣8+116÷132=1×3﹣8+116×32=3﹣8+2=﹣3.2.计算:(1)−14−(−2)3×14−16×(12−14+38).(2)−22−2×[(−3)2−3÷12 ].试题分析:(1)先算乘方再算乘法最后算加减法即可;(2)先算乘方和括号内的式子然后计算括号外的乘法最后算减法即可.答案详解:解:(1)−14−(−2)3×14−16×(12−14+38)=﹣14﹣(﹣8)×14−16×12+16×14−16×38=﹣14+2﹣8+4﹣6=﹣22;(2)−22−2×[(−3)2−3÷1 2 ]=﹣4﹣2×(9﹣3×2)=﹣4﹣2×(9﹣6)=﹣4﹣2×3=﹣4﹣6=﹣10.3.计算:(1)﹣32÷(﹣3)2+3×(﹣2)+|﹣4|;(2)[50−(79−1112+16)×(−6)2]÷(−7)2.试题分析:(1)先算乘方再算乘除法最后算加减法即可;(2)先算乘方再根据乘法分配律计算括号内的式子最后算括号外的除法.答案详解:解:(1)﹣32÷(﹣3)2+3×(﹣2)+|﹣4|=﹣9÷9+3×(﹣2)+4=﹣1+(﹣6)+4=﹣3;(2)[50−(79−1112+16)×(−6)2]÷(−7)2 =[50﹣(79−1112+16)×36]÷49=(50−79×36+1112×36−16×36)÷49 =(50﹣28+33﹣6)÷49 =49÷49 =1.4.计算:(1)(−12)﹣(﹣314)+(+234)﹣(+512);(2)﹣8+12﹣(﹣16)﹣|﹣23|; (3)42×(−23)﹣(−34)÷(﹣0•25); (4)(134−78−712)÷(−78)+(−83);试题分析:按照有理数混合运算的顺序 先乘方后乘除最后算加减 有括号的先算括号里面的 计算过程中注意正负符号的变化.答案详解:解:(1)原式=(−12)+134+114−224 =(−12)+24=0;(2)原式=(﹣8)+12+16﹣23 =﹣3;(3)原式=(﹣28)﹣3 =﹣31; (4)原式=(4224−2124−1424)×(−87)−83=(−13)−83=﹣3. 5.计算下列各题:①−14÷(−5)2×(−53)+|0.8−1|②−52−[(−2)3+(1−0.8×34)÷(−22)×(−2)].试题分析:①原式第一项被除数表示1四次幂的相反数除数表示两个﹣5的乘积再利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算最后一项利用绝对值的代数意义化简计算即可得到结果;②原式第一项表示5平方的相反数中括号中第一项表示三个﹣2的乘积第二项算计算括号中的运算再利用乘法法则计算即可得到结果.答案详解:解:①原式=﹣1÷25×(−53)+0.2=﹣1×125×(−53)+0.2=115+15=415;②原式=﹣25﹣[﹣8+(1−35)÷(﹣4)×(﹣2)]=﹣25﹣(﹣8+25×14×2)=﹣25+8−15=−17.2.二.二进制与十进制的转化6.我们常用的数是十进制数计算机程序使用的是二进制数(只有数码0和1)它们两者之间可以互相换算如将(101)2(1011)2换算成十进制数为:(101)2=1×22+0×21+1=4+0+1=5;(1011)2=1×23+0×22+1×21+1=11;两个二进制数可以相加减相加减时将对应数位上的数相加减.与十进制中的“逢十进一”、“退一还十”相类似应用“逢二进一”、“退一还二”的运算法则如:(101)2+(11)2=(1000)2;(110)2﹣(11)2=(11)2用竖式运算如右侧所示.(1)按此方式将二进制(1001)2换算成十进制数的结果是9.(2)计算:(10101)2+(111)2=(11100)2(结果仍用二进制数表示);(110010)2﹣(1111)2=35(结果用十进制数表示).试题分析:(1)根据例子可知:若二进制的数有n位那么换成十进制等于每一个数位上的数乘以2的(n﹣1)方再相加即可;(2)关于二进制之间的运算利用“逢二进一”、“退一还二”的运算法则计算即可.答案详解:解:(1)(1001)2=1×23+0×22+0×21+1=9;(2)(10101)2+(111)2=(11100)2;(110010)2﹣(1111)2=(100011)2=1×25+1×21+1=35.所以答案是:9;(11100)2;35.7.我们常用的数是十进制数计算机程序使用的是二进制数(只有数码0和1)它们两者之间可以互相换算如将(101)2(1011)2换算成十进制数应为:(101)2=1×22+0×21+1×20=4+0+1=5;(1011)2=1×23+0×22+1×21+1×20=8+0+2+1=11.按此方式将二进制(1001)2换算成十进制数和将十进制数13转化为二进制的结果分别为()A.9 (1101)2B.9 (1110)2C.17 (1101)2D.17 (1110)2试题分析:首先理解十进制的含义然后结合有理数运算法则计算出结果然后根据题意把13化成按2的整数次幂降幂排列即可求得二进制数.答案详解:解:(1001)2=1×23+0×22+0×21+1×20=9.13=8+4+1=1×23+1×22+0×21+1×20=(1101)2所以选:A.8.计算机程序使用的是二进制数(只有数码0和1)是逢2进1的计数制二进制数与常用的十进制数之间可以互相换算如将(10)2(1011)2换算成十进制数应为:(10)2=1×21+0×20=2 (1011)2=1×23+0×22+1×21+1×20=11.按此方式则(101)2+(1101)2=18.试题分析:仿照所给的方式进行求解即可.答案详解:解:(101)2+(1101)2=1×22+0×21+1×20+1×23+1×22+0×21+1×20=4+0+1+8+4+0+1=18.所以答案是:18.三.数值转化机9.按如图所示的程序运算:当输入的数据为﹣1时则输出的数据是()A.2B.4C.6D.8试题分析:把x=﹣1代入程序中计算判断结果与0的大小即可确定出输出结果.答案详解:解:把x=﹣1代入程序中得:(﹣1)2×2﹣4=2﹣4=﹣2<0把x=﹣2代入程序中得:(﹣2)2×2﹣4=8﹣4=4>0则输出的数据为4.所以选:B.10.下图是计算机计算程序若开始输入x=﹣2 则最后输出的结果是﹣17.试题分析:把﹣2按照如图中的程序计算后若<﹣5则结束若不是则把此时的结果再进行计算直到结果<﹣5为止.答案详解:解:根据题意可知(﹣2)×4﹣(﹣3)=﹣8+3=﹣5所以再把﹣5代入计算:(﹣5)×4﹣(﹣3)=﹣20+3=﹣17<﹣5即﹣17为最后结果.故本题答案为:﹣1711.按照如图所示的操作步骤若输入值为﹣3 则输出的值为55.试题分析:把﹣3代入操作步骤中计算即可确定出输出结果.答案详解:解:把﹣3代入得:(﹣3)2=9<10则有(9+2)×5=55.所以答案是:55.四.类比推理--规律类的钥匙12.观察下列各式:1 1×2+12×3=(11−12)+(12−13)=1−13=23.1 1×2+12×3+13×4=(11−12)+(12−13)+(13−14)=1−14=34.…(1)试求11×2+12×3+13×4+14×5的值.(2)试计算11×2+12×3+13×4+⋯+1n×(n+1)(n为正整数)的值.试题分析:(1)根据已知等式得到拆项规律原式变形后计算即可得到结果;(2)原式利用拆项法变形计算即可得到结果.答案详解:解:(1)原式=1−12+12−13+14−15=1−15=45;(2)原式=1−12+12−13+..+1n−1n+1=1−1n+1=n n+1.13.阅读下面的文字完成后面的问题.我们知道11×2=1−1212×3=12−1313×4=13−14那么14×5=14−1512005×2006=1 2005−1 2006.(1)用含有n的式子表示你发现的规律1n−1n+1;(2)依上述方法将计算:1 1×3+13×5+15×7+⋯+12003×2005=10022005(3)如果n k均为正整数那么1n(n+k)=1k⋅(1n−1n+k).试题分析:观察发现每一个等式的左边都是一个分数其中分子是1 分母是连续的两个正整数之积并且如果是第n个等式分母中的第一个因数就是n第二个因数是n+1;等式的右边是两个分数的差这两个分数的分子都是1 分母是连续的两个正整数并且是第n个等式被减数的分母就是n减数的分母是n+1.然后把n=4 n=2005代入即可得出第5个等式;(1)先将(1)中发现的第n个等式的规律1n(n+1)=1n−1n+1代入再计算即可;(2)先类比(1)的规律得出1n(n+2)=12(1n−1n+1)再计算即可.(3)根据(2)的规律即可得出结论.答案详解:解:∵第一个式子:11×2=1−12;第二个式子:12×3=12−13;第三个式字:13×4=13−14… ∴14×5=14−1512005×2006=12005−12006.所以答案是:14−1512005−12006;(1)由以上得出的规律可知 第n 个等式的规律 1n(n+1)=1n−1n+1;(2)原式=12(1−13+13−14⋯+12003−12005) =12(1−12005) =10022005(3)由(2)可知n k 均为正整数1k⋅(1n−1n+k).14.类比推理是一种重要的推理方法 根据两种事物在某些特征上相似 得出它们在其他特征上也可能相似的结论.阅读感知:在异分母的分数的加减法中 往往先化作同分母 然后分子相加减 例如:12−13=32×3−23×2=3−26=16我们将上述计算过程倒过来 得到16=12×3=12−13这一恒等变形过程在数学中叫做裂项.类似地 对于14×6可以用裂项的方法变形为:14×6=12(14−16).类比上述方法 解决以下问题.【类比探究】(1)猜想并写出:1n×(n+1)=1n −1n+1; 【理解运用】(2)类比裂项的方法 计算:11×2+12×3+13×4+⋯+199×100;【迁移应用】(3)探究并计算:1−1×3+1−3×5+1−5×7+1−7×9+⋯+1−2021×2023.试题分析:(1)根据题目中的例子 可以写出相应的猜想; (2)根据式子的特点 采用裂项抵消法可以解答本题; (3)将题目中的式子变形 然后裂项抵消即可解答本题. 答案详解:解:(1)1n×(n+1)=1n−1n+1所以答案是:1n−1n+1;(2)由(1)易得:(1−12)+(12−13)+(13−14)+⋯+(199−1100) =1−12+12−13+13−14+⋯+199−1100 =1−1100 =99100; (3)1−1×3+1−3×5+1−5×7+1−7×9+...+1−2021×2023=−12×(21×3+23×5+25×7+27×9+⋯+22021×2023)=−12×(1−13+13−15+15−17+17−19+⋯+12021−12023) =−12×(1−12023) =−12×20222023=−10112023. 15.“转化”是一种解决问题的常用策略 有时画图可以帮助我们找到转化的方法.例如借助图① 可以把算式1+3+5+7+9+11转化为62=36.请你观察图② 可以把算式12+14+18+116+132+164+1128转化为127128.试题分析:根据图形观察发现 把正方形看作单位“1” 即算式可以转化成1−1128 再求出答案即可.答案详解:解:12+14+18+116+132+164+1128=1−1128=127128所以答案是:127128.16.观察下列等式:第1个等式:a 1=11×2=1−12; 第2个等式:a 2=12×3=12−13; 第3个等式:a 3=13×4=13−14; 第4个等式:a 4=14×5=14−15⋯ 请解答下列问题:(1)按以上规律写出:第n 个等式a n = 1n(n+1)=1n−1n+1(n 为正整数);(2)求a 1+a 2+a 3+a 4+…+a 100的值; (3)探究计算:11×4+14×7+17×10+⋯+12020×2023.试题分析:(1)对所给的等式进行分析 不难总结出其规律; (2)利用所给的规律进行求解即可;(3)仿照所给的等式 对各项进行拆项进行 再运算即可. 答案详解:解:(1)∵第1个等式:a 1=11×2=1−12; 第2个等式:a 2=12×3=12−13; 第3个等式:a 3=13×4=13−14; 第4个等式:a 4=14×5=14−15; …∴第n 个等式:a n =1n(n+1)=1n −1n+1 所以答案是:1n(n+1)=1n−1n+1;(2)a 1+a 2+a 3+a 4+…+a 100=11×2+12×3+13×4+14×5+⋯+1100×101 =1−12+12−13+13−14+14−15+⋯+1100−1101=1−1101 =100101; (3)11×4+14×7+17×10+⋯+12020×2023 =13×(1−14+14−17+17−110+⋯+12020−12023) =13×(1−12023)=13×20222023=6742023.五.阅读类--化归思想17.阅读下列材料:计算5÷(13−14+112)解法一:原式=5÷13−5÷14+5÷112 =5×3﹣5×4+5×12=55解法二:原式=5÷(412−312+112) =5÷16=5×6=30解法三:原式的倒数=(13−14+112)÷5=(13−14+112)×15 =13×15−14×15+112×15=130∴原式=30(1)上述的三种解法中有错误的解法 你认为解法 一 是错误的(2)通过上述解题过程 请你根据解法三计算(−142)÷(16−314−23+37)试题分析:(1)根据运算律即可判断;(2)类比解法三计算可得.答案详解:解:(1)由于除法没有分配律所以解法一是错误的所以答案是:一;(2)原式的倒数=(16−314−23+37)÷(−142) =(16−314−23+37)×(﹣42) =16×(﹣42)−314×(﹣42)−23×(﹣42)+37×(﹣42) =﹣7+9+28﹣18=12∴原式=112.18.先阅读下面材料 再完成任务:【材料】下列等式:4−35=4×35+1 7−34=7×34+1 … 具有a ﹣b =ab +1的结构特征 我们把满足这一特征的一对有理数称为“共生有理数对” 记作(a b ).例如:(4 35)、(7 34)都是“共生有理数对”.【任务】(1)在两个数对(﹣2 1)、(2 13)中 “共生有理数对”是 (2 13) ; (2)请再写出一对“共生有理数对” (−12 ﹣3) ;(要求:不与题目中已有的“共生有理数对”重复)(3)若(x ﹣2)是“共生有理数对” 求x 的值;(4)若(m n )是“共生有理数对” 判断(﹣n ﹣m ) 是 “共生有理数对”.(填“是”或“不是”)试题分析:(1)读懂题意 根据新定义判断即可;(2)随意给出一个数 设另一个数为x 代入新定义 求出另一个数即可;(3)根据新定义列等式求出x的值;(4)第一对是“共生有理数对”列等式通过等式判断第二对数是否符合新定义.答案详解:解:(1)(﹣2 1)∵(﹣2)﹣1=﹣3 (﹣2)×1+1=﹣1 ﹣3=﹣1∴(﹣2 1)不是“共生有理数对”;(2 1 3)∵2−13=532×13+1=5353=53∴(2 13)是“共生有理数对”;所以答案是:(2 13);(2)设一对“共生有理数对”为(x﹣3)∴x﹣(﹣3)=﹣3x+1∴x=−1 2∴这一对“共生有理数对”为(−12﹣3)所以答案是:(−12﹣3);(3)∵(x﹣2)是“共生有理数对”∴x﹣(﹣2)=﹣2x+1∴x=−1 3;(4)∵(m n)是“共生有理数对”∴m﹣n=mn+1∴﹣n﹣(﹣m)=(﹣n)(﹣m)+1∴(﹣n﹣m)是“共生有理数对”所以答案是:是.19.阅读材料解决下列问题:【阅读材料】求n个相同因数a的积的运算叫做乘方记为a n.若10n=m(n>0 m≠1 m>0)则n叫做以10为底m的对数记作:lgm=n.如:104=10000 此时4叫做以10为底10000的对数记作:lg10000=lg104=4 (规定lg10=1).【解决问题】(1)计算:lg100=2;lg1000=3;lg100000=5;lg1020=20;(2)计算:lg10+lg100+lg1000+⋅⋅⋅+lg1010;【拓展应用】(3)由(1)知:lg100+lg1000与lg100000之间的数量关系为:lg100+lg1000=lg100000;猜想:lga+lgb=lgab(a>0 b>0).试题分析:(1)应用题目所给的计算方法进行计算即可得出答案;(2)应用题目所给的计算方法和有理数乘方法则进行计算即可得出答案;(3)应用题目所给的计算方法进行计算即可得出答案.答案详解:解:(1)根据题意可得lg100=2;lg1000=3;lg100000=5;lg1020=20;所以答案是:2 3 5 20;(2)lg10+lg100+lg1000+⋅⋅⋅+lg1010=1+2+3+……+10=55;(3)∵lg100+lg1000=2+3=5lg100000=5∴lg100+lg1000=lg100000;所以答案是:lg100+lg1000=lg100000;lga+lgb=lgab.所以答案是:lgab.20.阅读下列各式:(a•b)2=a2b2(a•b)3=a3b3(a•b)4=a4b4…回答下列三个问题:(1)验证:(2×12)100=12100×(12)100=1;(2)通过上述验证归纳得出:(a•b)n=a n b n;(abc)n=a n b n c n.(3)请应用上述性质计算:(﹣0.125)2017×22016×42015.试题分析:(1)先算括号内的乘法再算乘方;先乘方再算乘法;②根据有理数乘方的定义求出即可;③根据同底数幂的乘法计算再根据积的乘方计算即可得出答案.答案详解:解:(1)(2×12)100=1 2100×(12)100=1;②(a•b)n=a n b n(abc)n=a n b n c n③原式=(﹣0.125)2015×22015×42015×[(﹣0.125)×(﹣0.125)×2]=(﹣0.125×2×4)2015×1 32=(﹣1)2015×1 32=﹣1×1 32=−132.所以答案是:1 1;a n b n a n b n c n.。
初一上册的有理数计算题。

初一上册的有理数计算题。
初一上册的有理数计算题包括以下几种类型:
1.加法:同号的两数相加,并把绝对值相加,取相同的符号;异号且绝对值不
相等的两数相加,进行抵消后,取绝对值较大的数的符号;互为相反数的两个数相加,结果为零;任何有理数与零相加,仍得这个数。
2.减法:减去一个数相当于加上这个数的相反数。
3.乘法:两数相乘同号得正,异号得负,然后将两数的绝对值相乘,得出结果;
任何数与0相乘,结果都得0。
4.除法:除以一个不等于0的数,等于乘以这个数的倒数;两数相除,同号得
正,异号得负;0除以任何一个不等于0的数,得数都是0。
下面是一些具体的初一上册的有理数计算题示例:
1. 2 + 3 - 4 × 5 ÷ 6
2.( - 3) + ( - 2) - ( - 5)× ( - 6) ÷ ( - 12)
3.-4 + 2×(-3) -6÷0.25
4.(-5)÷[1.85-(2-1.75)×7]
5.18÷{1-[0.4+ (1-0.4)]×0.4}
6.1÷(-2/3)×7
7.-3-[4-(4-3.5×2)]×[-2+(-3)]
8.8+(-1/4)-5-(-0.25)
9.99×26
10.(3.5-7.75-4.25)÷1.1
请注意,这些题仅供参考,可以结合实际的教材内容进行选择。
初中七年级数学上册整式计算题专项练习(含答案)

整式的乘除计算训练(1)1. )2()(b a b a -++-2. (x+2)(y+3)-(x+1)(y-2)3. 22)2)(2(y y x y x ++-4. x(x -2)-(x+5)(x -5)5. ⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛--y x y x 224 6. )94)(32)(23(22x y x y y x +---7. ()()3`122122++-+a a 8. ()()()2112+--+x x x11. 22)23()23(y x y x --+ 12. 22)()(y x y x -+13. 0.125100×810014. 3022)2(21)x (4554---÷⎪⎭⎫⎝⎛--π-+⎪⎭⎫⎝⎛-÷⎪⎭⎫ ⎝⎛15. (1211200622332141)()()()-⨯+----16.999×1001 17.1992-18.298 19.2010200820092⨯-20.化简求值:)4)(12()12(2+-+-a a a ,其中2-=a 。
21. 化简求值2(2)2()()2(3)x y x y x y y x y +--++-,其中12,2x y =-=。
22. 5(x -1)(x +3)-2(x -5)(x -2) 23. (a -b )(a 2+ab +b 2)24. (3y+2)(y-4)-3(y-2)(y-3) 25. a(b-c)+b(c-a)+c(a-b)1y2)226. (-2mn2)2-4mn3(mn+1) 27. 3xy(-2x)3·(-428. (-x-2)(x+2) 29. 5×108·(3×102)30. (x-3y)(x+3y)-(x-3y)231. (a+b-c)(a-b-c)答案1. 错误!未找到引用源。
2. 错误!未找到引用源。
3. 错误!未找到引用源。
专题 有理数的混合运算计算题(50题)(解析版)-七年级数学上册

七年级上册数学《第一章有理数》专题有理数的混合运算的计算题(50题)1.(2022秋•晋安区期末)计算:(1)7﹣(﹣6)+(﹣4)×(﹣3);(2)﹣3×(﹣2)2﹣1+(−12)3.【分析】(1)根据有理数的乘法和加减法可以解答本题;(2)根据有理数的乘方、有理数的乘法和加减法可以解答本题.【解答】解:(1)7﹣(﹣6)+(﹣4)×(﹣3)=7+6+12=25;(2)﹣3×(﹣2)2﹣1+(−12)3=﹣3×4﹣1+(−18)=﹣12﹣1+(−18)=﹣1318.【点评】本题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的计算方法.2.(2022春•香坊区校级期中)计算:(1)(−23)﹣(+13)﹣|−34|﹣(−14);(2)﹣12−15×[2﹣(﹣3)2].【分析】(1)根据有理数的加减法可以解答本题;(2)根据有理数的乘法和加减法可以解答本题.【解答】解:(1)(−23)﹣(+13)﹣|−34|﹣(−14)=(−23)+(−13)−34+14=−32;(2)﹣12−15×[2﹣(﹣3)2]=﹣1−15×(﹣7)=﹣1+75=25.【点评】本题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的计算方法.3.(2023春•香坊区校级期中)计算:(1)(13−12+14)×24(2)﹣23×34−(−3)3÷9【分析】(1)根据乘法分配律简便计算即可求解.;(2)先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.【解答】解:(1)(13−12+14)×24=13×24−12×24+14×24=8﹣12+6=2;(2)﹣23×34−(−3)3÷9=﹣8×34+27÷9=﹣6+3=﹣3.【点评】考查了有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.4.(2023•西乡塘区二模)计算:6×(3−5)+(−2)2+14.【分析】先算乘方,再算乘法,然后算加减法即可.【解答】解:6×(3−5)+(−2)2+14=6×(﹣2)+4+14=﹣12+4+14=﹣734.【点评】本题考查有理数的混合运算,熟练掌握运算法则是解答本题的关键.5.(2023•南宁三模)计算:(﹣1)3+8÷22+|4﹣7|×13.【分析】先算乘方,再算乘除法,最后算加法即可.【解答】解:(﹣1)3+8÷22+|4﹣7|×13=(﹣1)+8÷4+3×13=(﹣1)+2+1=2.【点评】本题考查有理数的混合运算,熟练掌握运算法则是解答本题的关键.6.(2023•柳州三模)计算(−1)2−6÷(−2)×|−13|.【分析】先算乘方和绝对值,再算乘除,最后算加减.【解答】解:原式=1﹣(﹣3)×13=1+1=2.【点评】本题考查了有理数的混合运算,掌握有理数的运算顺序是解决本题的关键.7.(2023春•浦东新区期末)计算:﹣23+|﹣5|﹣18×(−13)2.【分析】先计算立方、绝对值和平方,再计算乘法,最后计算加减.【解答】解:﹣23+|﹣5|﹣18×(−13)2.=﹣8+5﹣18×19=﹣8+5﹣2=﹣5.【点评】此题考查了有理数的混合运算能力,关键是能准确理解运算顺序,并能进行正确地计算.8.(2023•武鸣区二模)计算:−12023+(−4)÷12−(1−32).【分析】先算括号里面的,再算乘方,除法,最后算加减即可.【解答】解:原式=﹣12023+(﹣4)÷12−(1﹣9)=﹣12023+(﹣4)÷12−(﹣8)=﹣1+(﹣4)×2+8=﹣1﹣8+8=﹣1.【点评】本题考查的是有理数的混合运算,熟知有理数混合运算的法则是解题的关键.9.(2023春•松江区期中)计算:−32−42÷|−6|+8×(−12)3.【分析】利用乘方运算、绝对值的定义和有理数的混合运算法则计算.【解答】解:−32−42÷|−6|+8×(−12)3=﹣9﹣42÷6+8×(−18)=﹣9﹣7﹣1=﹣17.【点评】本题考查了有理数的混合运算,解题的关键是掌握乘方运算、绝对值的定义和有理数的混合运算法则.10.(2022秋•万源市校级期末)﹣22+|5﹣8|+24÷(﹣3)×13.【分析】原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.【解答】解:原式=﹣4+3−83=−113.【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.11.(2022春•徐汇区校级期末)计算:−24−14×[2−(−2)2].【分析】利用有理数的混合运算法则进行计算即可.【解答】解:原式=﹣16−14×(2﹣4)=﹣16−14×(﹣2)=﹣16+12=﹣1512.【点评】本题考查有理数的混合运算,熟练掌握相关运算法则是解题的关键.12.(2023春•黄浦区期中)计算:(−1112+34)×(−42)+(−213)÷3.5【分析】原式先计算乘方运算,再计算乘除运算,最后算加减运算即可求出值.【解答】解:原式=(−1112+912)×(﹣16)−73×27=−16×(﹣16)−23=83−23=2.【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.13.(2023春•闵行区期中)计算:2×(−12)3−3×(−12)2+3×(−12)−1.【分析】先算乘方,再算乘法,最后算加减;同级运算,应按从左到右的顺序进行计算.【解答】解:原式=2×(−18)﹣3×14−32−1=−14−34−32−1=﹣312.【点评】本题考查了有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.14.(2023春•黄浦区期中)计算:(−1112−34)×(−42)+(−213)÷3.5.【分析】先算括号里面的,再算乘除,最后算加减即可.【解答】解:原式=(−1112−912)×(﹣16)+(﹣213)÷3.5=−53×(﹣16)−73×27=803−23=783=26.【点评】本题考查的是有理数的混合运算,熟知有理数混合运算的法则是解题的关键.15.(2023春•雁峰区校级期末)计算:(−3)4÷[2−(−7)]+6×(12−1).【分析】先算乘方和括号内的式子,再算括号外的乘除法,最后算加法即可.【解答】解:(−3)4÷[2−(−7)]+6×(12−1)=81÷(2+7)+6×(−12)=81÷9+(﹣3)=9+(﹣3)=6.【点评】本题考查有理数的混合运算,熟练掌握运算法则是解答本题的关键.16.(2023春•黄浦区期末)计算:(−56+34)×(−42)+(−213)÷3.5.【分析】有理数的混合运算,先算乘方,再算乘除再算加减,有括号的先算括号的,从而可求出最后结果.【解答】解:(−56+34)×(−42)+(−213)÷3.5=−10+912×(−16)+(−73)×27=−13×(−4)−23=43−23=23.【点评】本题主要考查了有理数的混合运算.本题的易错点是对于负号的计算处理.17.(2023•贺州一模)计算:﹣12023+8÷(﹣2)2﹣|﹣4|×5.【分析】按照有理数的运算法则和运算顺序进行计算即可.【解答】解:原式=﹣1+8÷4﹣4×5=﹣1+2﹣20=﹣19.【点评】本题考查了绝对值和含有乘方的有理数的混合运算,掌握相关运算法则是解题的关键.最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.18.(2023•防城港二模)计算:−14×[(−8)+2÷12]−|−3|.【分析】根据有理数的混合运算法则进行计算即可.【解答】解:原式=﹣1×(﹣8+2×2)﹣3=﹣1×(﹣8+4)﹣3=﹣1×(﹣4)﹣3=4﹣3=1.【点评】本题考查有理数的混合运算,其相关运算法则是基础且重要知识点,必须熟练掌握.19.(2023春•浦东新区期末)计算:﹣14+(1﹣0.5)×13×(﹣2)2.【分析】首先计算乘方和小括号里面的减法,然后计算乘法,最后计算加法,求出算式的值即可.【解答】解:﹣14+(1﹣0.5)×13×(﹣2)2=﹣1+12×13×4=﹣1+23=−13.【点评】此题主要考查了有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.20.(2022秋•泸县期末)计算:−23÷(−2−14)×(−13)2−3281+1.【分析】根据有理数的运算法则和顺序计算.注意同级运算中的先后顺序.【解答】解:−23÷(−2−14)×(−13)2−3281+1=−8÷(−94)×19−3281+1=−8×(−49)×19−3281+1=3281−3281+1=1.【点评】本题考查的是有理数的运算能力.注意:(1)要正确掌握运算顺序,即乘方运算(和以后学习的开方运算)叫做三级运算;乘法和除法叫做二级运算;加法和减法叫做一级运算;(2)在混合运算中要特别注意运算顺序:先三级,后二级,再一级;有括号的先算括号里面的;同级运算按从左到右的顺序.21.(2022秋•汝阳县期末)−14−(1−0.5)×(−113)×[2−(−3)2].【分析】原式先计算乘方运算以及括号中的运算,再计算乘法运算,最后算加减运算即可得到结果.【解答】解:原式=﹣1−12×(−43)×(2﹣9)=﹣1−143=−173.【点评】此题考查了有理数的混合运算,有理数的混合运算首先弄清运算顺序,先乘方,再乘除,最后算加减,有括号先算括号里边的,同级运算从左到右依次进行计算,然后利用各种运算法则计算,有时可以利用运算律来简化运算.22.(2022秋•泸县期末)计算:−23÷(−2−14)×(−13)2−3281+1.【分析】根据有理数的运算法则和顺序计算.注意同级运算中的先后顺序.【解答】解:−23÷(−2−14)×(−13)2−3281+1=−8÷(−94)×19−3281+1=−8×(−49)×19−3281+1=3281−3281+1=1.【点评】本题考查的是有理数的运算能力.注意:(1)要正确掌握运算顺序,即乘方运算(和以后学习的开方运算)叫做三级运算;乘法和除法叫做二级运算;加法和减法叫做一级运算;(2)在混合运算中要特别注意运算顺序:先三级,后二级,再一级;有括号的先算括号里面的;同级运算按从左到右的顺序.23.(2023春•吉林月考)计算:(−1)2022+|(−2)3+(−3)2|−(−14+16)×(−24).【分析】先算乘方,再算乘法,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号和绝对值,要先做括号和绝对值内的运算.注意乘法分配律的运用.【解答】解:(−1)2022+|(−2)3+(−3)2|−(−14+16)×(−24)=1+|﹣8+9|−14×24+16×24=1+1﹣6+4=0.【点评】本题考查了有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,24.(2022秋•易县期末)计算:(1)25÷23−25×(−12);(2)(﹣3)2×(12−56)+|﹣4|.【分析】(1)先把除法转化为乘法,再逆用乘法的分配律进行求解即可;(2)先算乘方,括号里的减法,绝对值,再算乘法,最后算加法即可.【解答】解:(1)25÷23−25×(−12)=25×32+25×12=25×(32+12)=25×2=50;(2)(﹣3)2×(12−56)+|﹣4|=9×(−13)+4=﹣3+4=1.【点评】本题主要考查有理数的混合运算,解答的关键是对相应的运算法则的掌握.25.(2022秋•广宗县期末)计算(1)(14−13−1)×(﹣12)(2)﹣22×14+(﹣3)3×(−827)【分析】(1)利用乘法分配律展开,再计算乘法,最后计算加减可得;(2)先计算乘方,再计算乘法,最后计算加减可得.【解答】解:(1)原式=14×(﹣12)−13×(﹣12)﹣1×(﹣12)=﹣3+4+12=13;(2)原式=﹣4×14+(﹣27)×(−827)=﹣1+8=7.【点评】本题主要考查有理数的混合运算,解题的关键是掌握有理数的混合运算顺序和运算法则.26.(2022秋•黄石港区期末)计算与化简:(1)﹣22+|﹣18﹣(﹣3)×2|÷4;(2)(14−49)×(﹣6)2+7÷(−12).【分析】(1)根据有理数的乘除法和加法可以解答本题;(2)根据乘法分配律、有理数的乘除法和加法可以解答本题.【解答】解:(1)﹣22+|﹣18﹣(﹣3)×2|÷4=﹣4+|﹣18+6|÷4=﹣4+12÷4=﹣4+3=﹣1;(2)(14−49)×(﹣6)2+7÷(−12)=(14−49)×36+7×(﹣2)=9+(﹣16)+(﹣14)=﹣21.【点评】本题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的计算方法.27.(2022秋•通川区校级期末)计算:(1)(﹣72)+37﹣(﹣22)+(﹣17)(2)﹣32×(−13)2+(34−16+38)÷(−124)【分析】(1)原式利用减法法则变形,计算即可得到结果;(2)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.【解答】解:(1)原式=﹣72+37+22﹣17=﹣89+59=﹣30;(2)原式=﹣9×19+(34−16+38)×(﹣24)=﹣1﹣18+4﹣9=﹣28+4=﹣24.【点评】此题考查了有理数的混合运算,以及乘法分配律,熟练掌握运算法则是解本题的关键.28.(2022秋•翠屏区期末)计算:(1)12×(116−13−34);(2)−22−13÷5×|1−(−4)2|.【分析】(1)根据乘法分配律计算即可;(2)先算乘方和去绝对值,然后算乘除法,最后算减法即可.【解答】解:(1)12×(116−13−34)=12×116−12×13−12×34=22﹣4﹣9=9;(2)−22−13÷5×|1−(−4)2|=﹣4−13×15×|1﹣16|=﹣4−13×15×15=﹣4﹣1=﹣5.【点评】本题考查有理数的混合运算,熟练掌握运算法则是解答本题的关键.29.(2022秋•通川区校级期末)计算:(1)(﹣72)+37﹣(﹣22)+(﹣17)(2)﹣32×(−13)2+(34−16+38)÷(−124)【分析】(1)原式利用减法法则变形,计算即可得到结果;(2)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.【解答】解:(1)原式=﹣72+37+22﹣17=﹣89+59=﹣30;(2)原式=﹣9×19+(34−16+38)×(﹣24)=﹣1﹣18+4﹣9=﹣28+4=﹣24.【点评】此题考查了有理数的混合运算,以及乘法分配律,熟练掌握运算法则是解本题的关键.30.(2022秋•和平区校级期末)计算(1)(13−18+16)×24;(2)(﹣2)4÷(﹣223)2+512×(−16)﹣0.25.【分析】(1)根据乘法分配律计算即可;(2)先算乘方,再算乘除法,最后算加减法即可.【解答】解:(1)(13−18+16)×24=13×24−18×24+16×24=8﹣3+4=9;(2)(﹣2)4÷(﹣223)2+512×(−16)﹣0.25=16÷649+112×(−16)−14=16×964+(−1112)−14=2712+(−1112)−312=1312.【点评】本题考查有理数的混合运算,熟练掌握运算法则是解答本题的关键.31.(2023•章贡区校级模拟)计算:(1)﹣12008﹣[5×(﹣2)﹣(﹣4)2÷(﹣8)];(2)(514−78−712)÷(﹣134).【分析】(1)先算乘方和括号内的式子,然后计算括号外的减法即可;(2)先把除法转化为乘法,然后根据乘法分配律计算即可.【解答】解:(1)﹣12008﹣[5×(﹣2)﹣(﹣4)2÷(﹣8)]=﹣1﹣[(﹣10)﹣16÷(﹣8)]=﹣1﹣[(﹣10)+2]=﹣1﹣(﹣8)=﹣1+8=7;(2)(514−78−712)÷(﹣134)=(214−78−712)×(−47)=214×(−47)−78×(−47)−712×(−47)=﹣3+12+13=−186+36+26=−136.【点评】本题考查有理数的混合运算,熟练掌握运算法则是解答本题的关键.32.(2023•长阳县一模)计算:(1)(12−13)×6÷|−15|;(2)(−1)2018+(−10)÷12×2−[2−(−3)3].【分析】(1)根据有理数的加减乘除混合运算法则计算即可;(2)根据有理数的加减乘除乘法混合运算法则计算即可.【解答】解:(1)(12−13)×6÷|−15|=(12−13)×6×5=(12−13)×30=12×30−13×30=15﹣10=5;(2)(−1)2018+(−10)÷12×2−[2−(−3)3]=1+(﹣10)×2×2﹣(2+27)=1﹣40﹣29=﹣68.【点评】本题考查有理数的混合运算,关键在于熟练掌握基础运算法则.33.(2022秋•定远县期中)计算:(1)−22−|0.5−1|×13×[3−(−3)2];(2)(−4.66)×49−5.34÷94+5×(23)2.【分析】(1)先计算绝对值里面的式子和中括号里面的式子,然后再计算出括号外的式子;(2)先把除法转化为乘法、然后根据有理数的乘方和乘法分配律即可解答本题.【解答】解:(1)−22−|0.5−1|×13×[3−(−3)2]=﹣4−12×13×(3﹣9)=﹣4−16×(﹣6)=﹣4+1=﹣3;(2)(−4.66)×49−5.34÷94+5×(23)2=(﹣4.66)×49−5.34×49+5×49=[(﹣4.66)﹣5.34+5]×49=﹣5×49=−209.【点评】本题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的运算法则和运算顺序.34.(2022秋•鞍山期末)计算:(1)(134−78−712)÷(−78)+(−34);(2)(﹣2)3+(﹣3)×[(﹣4)2+2]﹣(﹣3)2÷(﹣2).【分析】(1)先把除法转为乘法,再利用乘法的分配律进行运算,最后算加减即可;(2)先算乘方,再算括号里的运算,接着算乘法与除法,最后算加减即可.【解答】解:(1)(134−78−712)÷(−78)+(−34)=(74−78−712)×(−87)+(−34)=74×(−87)−78×(−87)−712×(−87)−34=﹣2+1+23−34=−1312;(2)(﹣2)3+(﹣3)×[(﹣4)2+2]﹣(﹣3)2÷(﹣2)=﹣8﹣3×(16+2)﹣9÷(﹣2)=﹣8﹣3×18﹣9×(−12)=﹣8﹣54+4.5=﹣57.5.【点评】本题主要考查有理数的混合运算,解答的关键是对相应的运算法则的掌握.35.(2022秋•正阳县期中)计算:(1)(1112−76+34−1324)×(﹣48);(2)﹣9+5×|﹣3|﹣(﹣2)2÷4;(3)﹣18+(﹣4)2÷14−(1﹣32)×(13−0.5).【分析】(1)根据乘法分配律计算即可;(2)先算乘方,再算乘除法,最后算加减法即可;(3)先算乘方和括号内的式子,然后计算括号外的乘除法,最后算加减法即可.【解答】解:(1)(1112−76+34−1324)×(﹣48)=1112×(﹣48)−76×(﹣48)+34×(﹣48)−1324×(﹣48)=﹣44+56+(﹣36)+26=2;(2)﹣9+5×|﹣3|﹣(﹣2)2÷4=﹣9+5×3﹣4÷4=﹣9+15﹣1=5;(3)﹣18+(﹣4)2÷14−(1﹣32)×(13−0.5)=﹣1+16×4﹣(1﹣9)×(−16)=﹣1+64﹣(﹣8)×(−16)=﹣1+64−43=6123.【点评】本题考查有理数的混合运算,熟练掌握运算法则是解答本题的关键,注意乘法分配律的应用.36.(2022秋•临邑县期中)计算:(1)(﹣0.5)﹣(﹣314)+2.75﹣(+712);(2)(−49)÷75×57÷(−25).(3)﹣22÷43−[22﹣(1−12×13)]×12;【分析】(1)先把减法转化为加法,然后根据加法法则计算即可;(2)先把除法转化为乘法,然后根据乘法法则计算即可;(3)先算乘方和括号内的式子,然后括号外的乘除法,最后算加减法即可.【解答】解:(1)(﹣0.5)﹣(﹣314)+2.75﹣(+712)=(−12)+314+234+(﹣712)=﹣2;(2)(−49)÷75×57÷(−25)=49×57×57×125=1;(3)﹣22÷43−[22﹣(1−12×13)]×12=﹣4×34−[4﹣(1−16)]×12=﹣3﹣(4−56)×12=﹣3﹣4×12+56×12=﹣3﹣48+10=﹣41.【点评】本题考查有理数的混合运算,熟练掌握运算法则是解答本题的关键.37.(2022秋•南票区期中)计算(1)(﹣0.8)+1.2+(﹣0.7)+(﹣2.1)+0.8+3.5;(2)(﹣5)×6×(−45)÷(﹣4);(3)﹣11×(−227)+19×(−227)+6×(−227);(4)﹣32×(﹣2)+42÷(﹣2)3﹣|﹣22|.【分析】(1)去括号,进行加减运算;(2)把除法变成乘法,再进行计算;(3)先提公因数,再计算;(4)先乘方,再乘除,最后加减运算.【解答】解:(1)(﹣0.8)+1.2+(﹣0.7)+(﹣2.1)+0.8+3.5=(﹣0.8)+0.8﹣0.7﹣2.1+1.2+3.5=0﹣2.8+4.7=1.9;(2)(﹣5)×6×(−45)÷(﹣4)=(﹣5)×6×(−45)×(−14)=﹣6;(3)﹣11×(−227)+19×(−227)+6×(−227)=(−227)×(﹣11+19+6)=(−227)×14=﹣44;(4)﹣32×(﹣2)+42÷(﹣2)3﹣|﹣22|=﹣9×(﹣2)+16÷(﹣8)﹣4=18+(﹣2)﹣4=18﹣2﹣4=12.【点评】本题考查了有理数的混合运算,解题的关键是掌握有理数的运算法则和运算顺序.38.(2022秋•库车市期中)计算:(1)(﹣53)+(+21)﹣(﹣69)﹣(+37);(2)﹣54×219+(﹣412)×29;(3)(12+56−712)×(﹣24);(4)﹣12022÷(−52)×(﹣5)2﹣|2﹣9|.【分析】(1)先去括号,再进行加减运算;(2)(3)先算乘除,再算加减;(4)先算乘方和绝对值,再算乘除,最后算加减.【解答】解:(1)(﹣53)+(+21)﹣(﹣69)﹣(+37)=﹣53+21+69﹣37=﹣53﹣37+21+69=﹣90+90=0;(2)﹣54×219+(﹣412)×29=﹣54×199+(−92)×29=﹣115;(3)(12+56−712)×(﹣24)=12×(﹣24)+56×(﹣24)−712×(﹣24)=﹣12﹣20+14=﹣32+14=﹣18;(4)﹣12022÷(−52)×(﹣5)2﹣|2﹣9|=﹣1÷(−52)×25﹣7=﹣1×(−25)×25﹣7=10﹣7=3.【点评】本题考查了有理数的混合运算,解题的关键是掌握有理数混合运算的顺序.39.(2022秋•南山区校级期中)计算:(1)(﹣12)﹣5+(﹣14)﹣(﹣39);(2)(23−112−415)×(−60);(3)−14−16×[2−(−3)2];(4)(−2)2−[(−23)+(−14)]÷112.【分析】(1)原式利用减法法则变形,计算即可得到结果;(2)原式利用乘法分配律计算计算即可得到结果;(3)原式先计算乘方运算,再计算乘法运算,最后算加减运算即可得到结果;(4)原式先计算乘方运算及括号里面的,再计算除法运算,最后算加减运算即可得到结果.【解答】解:(1)原式=﹣12﹣5﹣14+39=﹣31+39=8;(2)原式=﹣40+5+16=﹣19;(3)原式=−1−16×(2−9)=−1+76=16;(4)原式=4−(−23−14)×12=4+8+3=15.【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.40.计算:(1)4﹣(﹣28)+(﹣2);(2)(13−16)×(﹣24);(3)(﹣2)3﹣(﹣13)÷(−12);(4)﹣12﹣(1﹣0.5)÷52×15.【分析】(1)原式利用减法法则变形,计算即可求出值;(2)原式利用乘法分配律计算即可求出值;(3)原式先计算乘方运算,再计算除法运算,最后算加减运算即可求出值;(4)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可求出值.【解答】解:(1)原式=4+28﹣2=30;(2)原式=﹣8+4=﹣4;(3)原式=﹣8﹣26=﹣34;(4)原式=﹣1−12×25×15=−1−125=−1125.【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.41.计算:(1)3+(﹣6)﹣(﹣7);(2)(﹣22)×(﹣114)÷13;(3)(34−13−56)×(﹣12);(4)﹣12021﹣(−13)×(﹣22+3)+12×|3﹣1|.【分析】(1)先把减法转化为加法,然后根据有理数加法法则计算即可;(2)先算乘方、再算乘除法即可;(3)根据乘法分配律可以解答本题;(4)先算乘方和括号内的式子,再算括号外的乘法和加减法即可.【解答】解:(1)3+(﹣6)﹣(﹣7)=3+(﹣6)+7=4;(2)(﹣22)×(﹣114)÷13=(﹣4)×(−54)×3=15;(3)(34−13−56)×(﹣12)=34×(﹣12)−13×(﹣12)−56×(﹣12)=(﹣9)+4+10=5;(4)﹣12021﹣(−13)×(﹣22+3)+12×|3﹣1|=﹣1﹣(−13)×(﹣4+3)+12×2=﹣1+13×(﹣1)+1=﹣1+(−13)+1=−13.【点评】本题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的运算法则和运算顺序.42.计算:(1)(﹣5)+(﹣4)﹣(+101)﹣(﹣9);(2)−12021×[4−(−3)2]+3÷(−34);(3)(512−79+23)÷136;(4)−316×7−316×(−9)+(−196)×(−8).【分析】(1)先把减法转化为加法,然后根据有理数的加法法则计算即可;(2)先算乘方和括号内的式子,然后计算括号外的乘除法、最后算加法即可;(3)先把除法转化为乘法、然后根据乘法分配律计算即可;(4)先将带分数化为假分数,然后根据乘法分配律计算即可.【解答】解:(1)(﹣5)+(﹣4)﹣(+101)﹣(﹣9)=(﹣5)+(﹣4)+(﹣101)+9=﹣101;(2)−12021×[4−(−3)2]+3÷(−34)=﹣1×(4﹣9)+3×(−43)=﹣1×(﹣5)+(﹣4)=5+(﹣4)=1;(3)(512−79+23)÷136=(512−79+23)×36=512×36−79×36+23×36=15﹣28+24=11;(4)−316×7−316×(−9)+(−196)×(−8)=−196×7−196×(﹣9)−196×(﹣8)=−196×[7+(﹣9)+(﹣8)]=−196×(﹣10)=953.【点评】本题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的运算法则和运算顺序,注意乘法分配律的应用.43.(2022秋•西城区校级期中)计算:(1)﹣2+8﹣36﹣(﹣30);(2)﹣24÷(﹣6)×(−14);(3)(−34+56+716)×(﹣48);(4)|12−1|×(﹣1)2021﹣[1﹣(﹣6)2].【分析】(1)先把减法转化为加法,然后根据加法法则计算即可;(2)先把除法转化为乘法,然后根据乘法法则计算即可;(3)根据乘法分配律计算即可;(4)先算乘方和括号内的式子,然后算乘法,最后算减法即可.【解答】解:(1)﹣2+8﹣36﹣(﹣30)=﹣2+8+(﹣36)+30=0;(2)﹣24÷(﹣6)×(−14)=﹣24×16×14=﹣1;(3)(−34+56+716)×(﹣48)=−34×(﹣48)+56×(﹣48)+716×(﹣48)=36+(﹣40)+(﹣21)=﹣25;(4)|12−1|×(﹣1)2021﹣[1﹣(﹣6)2]=12×(﹣1)﹣(1﹣36)=−12−(﹣35)=−12+35=3412.【点评】本题考查有理数的混合运算,熟练掌握运算法则是解答本题的关键.44.计算:(1)(−58)÷143×(−165)÷(−67)(2)﹣3﹣[﹣5+(1﹣0.2×35)÷(﹣2)](3)(413−312)×(﹣2)﹣223÷(−12)(4)[50﹣(79−1112+16)×(﹣6)2]÷(﹣7)2.【分析】(1)原式从左到右依次计算即可得到结果;(2)原式先计算乘除运算,再计算加减运算即可得到结果;(3)原式先计算乘除运算,再计算加减运算即可得到结果;(4)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.【解答】解:(1)原式=−58×314×165×76=−12;(2)原式=﹣3+5+(1−325)×12=−3+5+1125=21125;(3)原式=−263+7+163=323;(4)原式=(50﹣28+33﹣6)×149=49×149=1.【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.45.计算:(1)﹣4﹣28﹣(﹣29)+(﹣24);(2)4×(﹣3)2﹣5×(﹣2)+6;(3)(−34+712−59)÷(−136);(4)﹣14﹣(1﹣0.5)÷213×[2﹣(﹣3)2].【分析】(1)先化简,再计算加减法即可求解;(2)(4)先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算;(3)将除法变为乘法,再根据乘法分配律简便计算.【解答】解:(1)﹣4﹣28﹣(﹣29)+(﹣24)=﹣4﹣28+29﹣24=﹣56+29=﹣27;(2)4×(﹣3)2﹣5×(﹣2)+6=4×9+10+6=36+10+6=52;(3)(−34+712−59)÷(−136)=(−34+712−59)×(﹣36)=34×36−712×36+59×36=27﹣21+20=26;(4)﹣14﹣(1﹣0.5)÷213×[2﹣(﹣3)2]=﹣1−12÷213×[2﹣9]=﹣1−12÷213×(﹣7)=﹣1+112=12.【点评】考查了有理数的混合运算,进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.46.(2022秋•汤阴县期中)计算:(1)−22×|−5|−6÷(12−13)×56;(2)(−56+13−34)×(−24);(3)(−1)2023×[−24×(−34)2−1];(4)24−12022×(−2)3−5.5÷415×(−815).【分析】(1)先算乘方、括号内的式子和去绝对值,然后计算括号外的乘除法,再算减法即可;(2)根据乘法分配律计算即可;(3)先算乘方和括号内的式子,再算括号外的乘法即可;(4)先算乘方,再算乘除法,最后算加减法即可.【解答】解:(1)−22×|−5|−6÷(12−13)×56=﹣4×5﹣6÷16×56=﹣20﹣6×6×56=﹣20﹣30=﹣50;(2)(−56+13−34)×(−24)=−56×(﹣24)+13×(﹣24)−34×(﹣24)=20+(﹣8)+18=30;(3)(−1)2023×[−24×(−34)2−1]=(﹣1)×(﹣16×916−1)=(﹣1)×(﹣9﹣1)=(﹣1)×(﹣10)=10;(4)24−12022×(−2)3−5.5÷415×(−815)=24﹣1×(﹣8)−112×154×(−815)=24+8+11=43.【点评】本题考查有理数的混合运算,熟练掌握运算法则和运算顺序是解答本题的关键,注意乘法分配律的应用.47.(2022秋•丰泽区校级期中)计算:(1)﹣20+(﹣14)﹣(﹣18)﹣13;(2)(−38−16+34)×(﹣24);(3)(−14)×42﹣0.25×(﹣8)×(﹣1)2017;(4)﹣22÷43−[22﹣(1−12×13)]×12.【分析】(1)先把减法转化为加法,然后根据加法法则计算即可;(2)根据乘法分配律计算即可;(3)先算乘方,再算乘法,最后算减法即可;(4)先算乘方和括号内的式子,然后计算括号外的乘除法,最后算减法即可.【解答】解:(1)﹣20+(﹣14)﹣(﹣18)﹣13=﹣20+(﹣14)+18+(﹣13)=﹣29;(2)(−38−16+34)×(﹣24)=−38×(﹣24)−16×(﹣24)+34×(﹣24)=9+4+(﹣18)=﹣5;(3)(−14)×42﹣0.25×(﹣8)×(﹣1)2017=(−14)×16−14×(﹣8)×(﹣1)=﹣4﹣2=﹣6;(4)﹣22÷43−[22﹣(1−12×13)]×12=﹣4×34−(4﹣1+16)×12=﹣3﹣(3+16)×12=﹣3﹣36﹣2=﹣41.【点评】本题考查有理数的混合运算,熟练掌握运算法则是解答本题的关键.48.计算:(1)2﹣5+4﹣(﹣7)+(﹣6)(2)(﹣2467)÷6(3)(﹣18)÷214×49÷(﹣16)(4)43−{(−3)4−[(−1)÷2.5+214×(−4)]÷(24815−27815)}.【分析】(1)原式利用减法法则变形,计算即可得到结果;(2)原式变形后,利用乘法分配律计算即可得到结果;(3)原式利用除法法则变形,约分即可得到结果;(4)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.【解答】解:(1)原式=2﹣5+4+7﹣6=2;(2)原式=(﹣24−67)×16=−4−17=−417;(3)原式=﹣18×49×49×(−116)=29;(4)原式=64﹣81+(﹣925)÷(﹣3)=64﹣81+4715=−131315.【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.49.(2023春•沈阳月考)计算:(1)3﹣(+63)﹣(﹣259)﹣(﹣41);(2)213−(+1013)+(−815)⋅(+325);(3)(−292324)×12;(4)(−24)×(1−34+16−58);(5)−32−(−2)3×(−4)÷(−14);(6)(−32+3)×[(−1)2022−(1−0.5×13)].【分析】(1)先把减法转化为加法,再根据加法法则计算即可;(2)先算乘法,再算加减法即可;(3)先变形,然后根据乘法分配律计算即可;(4)根据乘法分配律计算即可;(5)先算乘方,再算乘除法,最后算减法即可;(6)先算括号内的式子,再算括号外的乘法即可.【解答】解:(1)3﹣(+63)﹣(﹣259)﹣(﹣41)=3+(﹣63)+259+41=240;(2)213−(+1013)+(−815)⋅(+325);=213+(﹣1013)+(−415)×175=213+(﹣1013)+(−69725)=﹣8+(−69725)=−89725;(3)(−292324)×12=(﹣30+124)×12=﹣30×12+124×12=﹣360+12=﹣35912;(4)(−24)×(1−34+16−58)=﹣24×1+24×34−24×16+24×58=﹣24+18﹣4+15=5;(5)−32−(−2)3×(−4)÷(−14)=﹣9﹣(﹣8)×(﹣4)×(﹣4)=﹣9+128=119;(6)(−32+3)×[(−1)2022−(1−0.5×13)]=(﹣9+3)×[1﹣(1−16)]=(﹣6)×(1−56)=(﹣6)×16=﹣1.【点评】本题考查有理数的混合运算,熟练掌握运算法则是解答本题的关键.50.(2022秋•朝阳区校级月考)计算.(1)﹣32﹣(+11)+(﹣9)﹣(﹣16);(2)﹣9+0.8+(﹣1)+(−45)−(−10);(3)﹣212÷(−5)×(−313)÷0.75;(4)(−16−512+13)×(−72);(5)−12023+27×(−13)2−|﹣5|;(6)(−12+34)×(﹣2)3+(﹣4)2+2×12.【分析】(1)先把减法统一成加法,写成省略括号和的形式,再把负数、正数分别相加;(2)先把分数化成小数,再把和为0的放一起先加;(3)先把除法统一成乘法,再算乘法;(4)利用乘法的分配律计算比较简便;(5)先算乘方化简绝对值,再算乘法,最后算加减;(6)先算乘方,再算括号里面的,最后算乘法、加减.【解答】解:(1)﹣32﹣(+11)+(﹣9)﹣(﹣16)=﹣32﹣11﹣9+16=﹣52+16=﹣36;(2)﹣9+0.8+(﹣1)+(−45)−(−10)=﹣9+0.8﹣1﹣0.8+10=(﹣9﹣1+10)+(0.8﹣0.8)=0+0=0;(3)﹣212÷(−5)×(−313)÷0.75=−52×(−15)×(−103)÷34=−52×15×103×43=−209;(4)(−16−512+13)×(−72)=(−16)×(﹣72)−512×(﹣72)+13×(﹣72)=12+30﹣24=18;(5)−12023+27×(−13)2−|﹣5|=﹣1+27×19−5=﹣1+3﹣5=﹣3;(6)(−12+34)×(﹣2)3+(﹣4)2+2×12=(−24+34)×(﹣8)+16+2×12=14×(﹣8)+16+1=﹣2+16+1=15.【点评】本题考查了有理数的混合运算,掌握有理数的运算律、运算法则是解决本题的关键.。
初一数学上册合并同类项计算题

初一数学上册合并同类项计算题1.某学校购买了一批文具,铅笔每支x元,共买了5支;圆珠笔每支y元,共买了3支;钢笔每支z元,共买了2支。
求购买这些文具的总花费的式子,并合并同类项。
2.一个长方形的长为3a+2b,宽为a-b,求这个长方形的周长的表达式,并合并同类项。
3.小明有3x个苹果,小红有2x个苹果,小刚有x个苹果,求他们三人苹果总数的表达式,并合并同类项。
4.某仓库有5箱重量为m千克的货物,3箱重量为n千克的货物,求货物的总重量的表达式,并合并同类项。
5.一辆汽车第一小时行驶了2x千米,第二小时行驶了3x千米,第三小时行驶了x千米,求这辆汽车三小时行驶的总路程的表达式,并合并同类项。
6.三个连续的奇数,中间的奇数为2n+1,求这三个奇数的和的表达式,并合并同类项。
7.有三个单项式:-2x²,3x²,x²,求它们的和的表达式,并合并同类项。
8.一个多项式为4a³+3a²+2a,另一个多项式为-a³-2a²-a,求这两个多项式的和的表达式,并合并同类项。
9.已知A=5x²y-3xy²,B=-2x²y+4xy²,求A+B的表达式,并合并同类项。
10.某班级男生有2m人,女生有3m人,后来转走了m人,求班级现有人数的表达式,并合并同类项。
11.图书馆有文学类书籍x本,科技类书籍2x本,漫画类书籍3x本,有人借走了2x本,求图书馆剩下书籍总数的表达式,并合并同类项。
12.有三个数,第一个数为3x-1,第二个数为2x+1,第三个数为x,求这三个数的和的表达式,并合并同类项。
13.一个三角形的三条边分别为2a+3b,a-2b,3a+b,求这个三角形的周长的表达式,并合并同类项。
14.小明有4x元零花钱,花了x元买文具,又得到2x元的奖励,求他现在零花钱的表达式,并合并同类项。
15.某商店第一天盈利3x元,第二天亏损2x元,第三天盈利x元,求这三天总盈利的表达式,并合并同类项。
新人教版七年级数学上册计算题
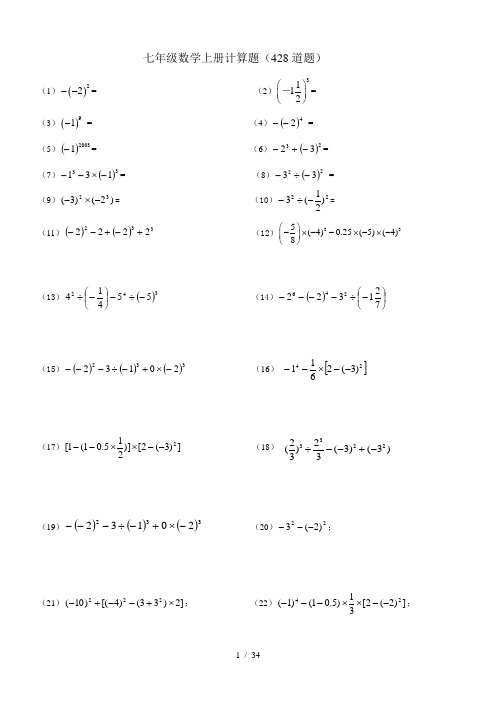
七年级数学上册计算题(428道题)(1)()22--= (2)3112⎛⎫⎪⎝⎭-=(3)()91- = (4)()42-- =(5)()20031-= (6)()2332-+-=(7)()33131-⨯--= (8)()2233-÷- =(9))2()3(32-⨯-= (10)22)21(3-÷-=(11)()()3322222+-+-- (12)235(4)0.25(5)(4)8⎛⎫-⨯--⨯-⨯- ⎪⎝⎭(13)()34255414-÷-⎪⎭⎫ ⎝⎛-÷ (14)()⎪⎭⎫ ⎝⎛-÷----721322246(15)()()()33220132-⨯+-÷--- (16) []24)3(2611--⨯--(17)])3(2[)]215.01(1[2--⨯⨯-- (18)(19)()()()33220132-⨯+-÷--- (20)22)2(3---;(21)]2)33()4[()10(222⨯+--+-; (22)])2(2[31)5.01()1(24--⨯⨯---;332222()(3)(3)33÷--+-(23)94)211(42415.0322⨯-----+-; (24)20022003)2()2(-+-;(25))2()3(]2)4[(3)2(223-÷--+-⨯--; (26)200420094)25.0(⨯-.(27)()0252423132.⨯--÷-⎛⎝ ⎫⎭⎪+⎡⎣⎢⎢⎤⎦⎥⎥ (28)()()----⨯-221410222(29)()()()-⨯÷-+-⎛⎝ ⎫⎭⎪⨯-÷-3120313312232325.. (30)()()()-⎛⎝ ⎫⎭⎪⨯-⨯-⨯-212052832.(31) (32)(56)(79)---(33)(3)(9)(8)(5)-⨯---⨯- (34)3515()26÷-+(35)5231591736342--+- (36)()()22431)4(2-+-⨯---(37)411)8()54()4()125.0(25⨯-⨯-⨯-⨯-⨯33182(4)8-÷--(38)如果0)2(12=-++b a ,求20112010()-3ab a b a a ++-()的值(39)已知|1|a +与|4|b -互为相反数,求b a 的值。
七年级数学上册计算题专项训练

七年级数学上册计算题专项训练训练一:11/(-6)/((-0.5)+1/(32/(-3-5+(1-0.2)/3)))/((-2)/(-5+2/(1-0.2/3))):这一段无法理解,删除。
x+12+2/(2+3x/3)=1:解方程,得到x=-3/2.2(2ab+3a)-3(2a-ab)/(36/24-3/4×2):化简,得到a。
48×(-36-6+12)4-6x=2x-1:化简,得到x。
训练二:32+50/22×(1/10)-1/3+50/22×(-1/5)-1:化简,得到答案。
131/6)+4-12)×(-48):化简,得到答案。
3a^2-[5a-((1/a-3)+2a^2/2)]+4:化简,得到答案。
1/(2(2/3-2/3)))-1=1:化简,得到答案。
1-(1-0.5×(1/2))×[2-(-3)^2]-34/(9/4+4/9×(-24)):化简,得到答案。
2x^2-3x^3-4x^4-1)+(1+5x^3-3x^2+4x^4):化简,得到答案。
x+4x^(-3/2)=-1.6:解方程,得到x≈-1.026.训练三:2+1/(-2)^2×(-2)-2-(-3+(-2)/2)^2/4×3:化简,得到答案。
-(-2)×(5/8)×7:化简,得到答案。
3[(4/3)a-(2/3)a^(1/3)-(2/3)]-2a:化简,得到答案。
x+1/(2(x-4/3))=2:解方程,得到x=5/3.34-2/(4-3/4×(-4))/99/(14/3-16/3):化简,得到答案。
7m^2n-5mn)-(4m^2n-5mn):化简,得到答案。
5x-1/(2(3-2x)/3)=1:解方程,得到x=5/4.训练四:5/2-((-2)^3+(1-0.8×(-1))-1)/4/(-3-2×(-4)):化简,得到答案。
(2021年整理)七年级数学上册整式计算题专项练习(含答案)

(完整版)七年级数学上册整式计算题专项练习(含答案)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整版)七年级数学上册整式计算题专项练习(含答案))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整版)七年级数学上册整式计算题专项练习(含答案)的全部内容。
(完整版)七年级数学上册整式计算题专项练习(含答案)编辑整理:张嬗雒老师尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布到文库,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是我们任然希望(完整版)七年级数学上册整式计算题专项练习(含答案) 这篇文档能够给您的工作和学习带来便利.同时我们也真诚的希望收到您的建议和反馈到下面的留言区,这将是我们进步的源泉,前进的动力.本文可编辑可修改,如果觉得对您有帮助请下载收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为〈(完整版)七年级数学上册整式计算题专项练习(含答案)> 这篇文档的全部内容。
整式的乘除计算训练(1)1. )2()(b a b a -++-2. (x+2)(y+3)-(x+1)(y —2)3。
22)2)(2(y y x y x ++- 4。
x (x -2)-(x+5)(x -5)5。
⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛--y x y x 224 6. )94)(32)(23(22x y x y y x +---7。
()()3`122122++-+a a 8. ()()()2112+--+x x x11. 22)23()23(y x y x --+ 12。
人教版初一数学上册计算题(400道题)
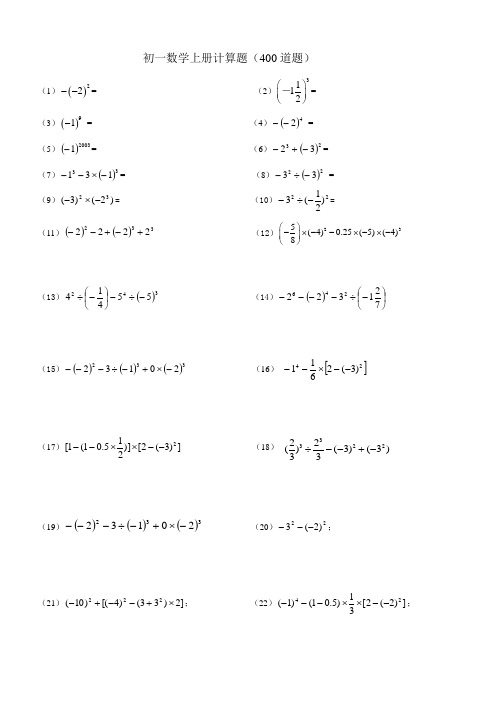
初一数学上册计算题(400道题)(1)()22--= (2)3112⎛⎫⎪⎝⎭-=(3)()91- = (4)()42-- =(5)()20031-= (6)()2332-+-=(7)()33131-⨯--= (8)()2233-÷- =(9))2()3(32-⨯-= (10)22)21(3-÷-=(11)()()3322222+-+-- (12)235(4)0.25(5)(4)8⎛⎫-⨯--⨯-⨯- ⎪⎝⎭(13)()34255414-÷-⎪⎭⎫ ⎝⎛-÷ (14)()⎪⎭⎫ ⎝⎛-÷----721322246(15)()()()33220132-⨯+-÷--- (16) []24)3(2611--⨯--(17)])3(2[)]215.01(1[2--⨯⨯-- (18)(19)()()()33220132-⨯+-÷--- (20)22)2(3---;(21)]2)33()4[()10(222⨯+--+-; (22)])2(2[31)5.01()1(24--⨯⨯---;332222()(3)(3)33÷--+-(23)94)211(42415.0322⨯-----+-; (24)20022003)2()2(-+-;(25))2()3(]2)4[(3)2(223-÷--+-⨯--; (26)200420094)25.0(⨯-.(27)()0252423132.⨯--÷-⎛⎝ ⎫⎭⎪+⎡⎣⎢⎢⎤⎦⎥⎥ (28)()()----⨯-221410222(29)()()()-⨯÷-+-⎛⎝ ⎫⎭⎪⨯-÷-3120313312232325.. (30)()()()-⎛⎝ ⎫⎭⎪⨯-⨯-⨯-212052832.(31) (32)(56)(79)---(33)(3)(9)(8)(5)-⨯---⨯- (34)3515()26÷-+(35)5231591736342--+- (36)()()22431)4(2-+-⨯---(37)411)8()54()4()125.0(25⨯-⨯-⨯-⨯-⨯33182(4)8-÷--(38)如果0)2(12=-++b a ,求20112010()-3ab a b a a ++-()的值(39)已知|1|a +与|4|b -互为相反数,求b a 的值。
七上几何计算题专项练习

七上几何计算题专项练习
本文档为七年级上学期几何计算题专项练,在这里你将能够巩固和提高你的几何计算能力。
以下是一些练题供你参考:
1. 长方形的面积计算
问题:一个长方形的长为5米,宽为3米,求其面积。
解答:
面积计算公式为:面积 = 长 ×宽
所以,该长方形的面积为 5米 × 3米 = 15平方米
2. 三角形的周长计算
问题:一个三角形的三边长分别为6厘米、8厘米和10厘米,求其周长。
解答:
周长计算公式为:周长 = 边1长 + 边2长 + 边3长
所以,该三角形的周长为 6厘米 + 8厘米 + 10厘米 = 24厘米
3. 圆的周长和面积计算
问题:一个圆的半径为2米,求其周长和面积。
解答:
圆的周长计算公式为:周长= 2πr (其中π取3.14)
所以,该圆的周长为 2 × 3.14 × 2米 = 12.56米
圆的面积计算公式为:面积= πr²
所以,该圆的面积为 3.14 × 2米 × 2米 = 12.56平方米
4. 平行四边形的面积计算
问题:一个平行四边形的底边长为8厘米,高度为5厘米,求其面积。
解答:
平行四边形的面积计算公式为:面积 = 底边长 ×高度
所以,该平行四边形的面积为 8厘米 × 5厘米 = 40平方厘米
希望以上练习题能够帮助你加深对几何计算的理解和应用。
继续努力,你会越来越擅长几何计算!。
七年级数学上册计算题专项训练

训练一 第一部分 有理数计算(要求:认真、仔细、准确率高)1、6.32.53.44.15.1+--+-2、()⎪⎭⎫⎝⎛-÷-21316 3、⎪⎭⎫⎝⎛÷⎪⎭⎫ ⎝⎛++-24161315.0 4、)7.1(5.2)4.2(5.23.75.2-⨯--⨯+⨯-5、()⎥⎦⎤⎢⎣⎡-÷⎪⎭⎫ ⎝⎛÷-+---2532.0153 6、⎪⎭⎫ ⎝⎛-÷⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛-⨯----35132211|5|7、()⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛-⨯-⨯-214124322 8、-9+5×(-6) -(-4)2÷(-8)9、()2313133.0121-÷⎪⎭⎫ ⎝⎛+⨯+- 10、321264+-=-x x 11、133221=+++xx 12、 15+(―41)―15―(―0.25)13、)32(9449)81(-÷⨯÷- 14、 —48 × )1216136141(+-- 15、()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+-⨯-85434216、(2m +2)×4m 217、(2x +y)2-(2x -y)218、(31xy)2·(-12x 2y 2)÷(-34x 3y) 19、[(3x +2y)(3x -2y)-(x +2y)(3x -2y)]÷3x20、先化简后求值:m(m -3)-(m +3)(m -3),其中m =-4.1、)3()26()2()4()14(-+++-+-++2、)15()41()26()83(++-+++-3、)2.0(3.1)9.0()7.0()8.1(-++-+++-4、)326()434()313(41-+++-+ 4、)5()]7()4[(--+--5、2.104.87.52.4+-+-6、 8+(―41)―5―(―0.25) 7、18)12()10(1130+-+---- 8、)61(41)31()412(213+---+-- 9、)]18()21(26[13-+---10、2111)43(412--+---11、)25()7()4(-⨯-⨯-12、)34(8)53(-⨯⨯-13、)1514348(43--⨯ 14、)8(45)201(-⨯⨯-15,53)8()92()4()52(8⨯-+-⨯---⨯16、)8(12)11(9-⨯-+⨯-17、)412()21()43(-÷-⨯-18、2411)25.0(6⨯-÷- 19. )21(31)32(-÷÷-20、)51(250-⨯÷-21、)3(4)2(817-⨯+-÷- 22、1)101(250322-⨯÷+ 23、911)325.0(321÷-⨯- 24、1)51(25032--⨯÷+25、])3(2[)]215.01(1[2--⨯⨯--26、)145()2(52825-⨯-÷+-27、6)3(5)3(42+-⨯--⨯28、)25.0(5)41(8----+29、)48()1214361(-⨯-+- 30、31)321()1(⨯-÷-31、)199(41212+-÷⨯32、)16(94412)81(-÷+÷-33、)]21541(43[21---- 34、)2(9449344-÷+÷-35.22)36()33(24)12581(÷-÷---⨯-36、3223121213+⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-+ 37、 (-12)÷4×(-6)÷238、 )1279543(+--÷36139、 2)5()2(10-⨯-+ 40、 (7)(5)90-⨯--÷(15)-41、 721×143÷(-9+19)42、 ()1-⎪⎭⎫⎝⎛-÷213143 、25×43―(―25)×21+25×(-41)44、(-81)÷241+94÷(-16) 45、-4÷32-(-32)×(-30)46、(-0.4)÷0.02×(-5) 47、47÷)6(3287-⨯- 48、48245834132⨯⎪⎭⎫⎝⎛+--49、|97|-÷2)4(31)5132(-⨯--50、―22+41×(-2)251、 -22 -〔-32 + (- 2)4 ÷23〕52、235(4)0.25(5)(4)8⎛⎫-⨯--⨯-⨯- ⎪⎝⎭53、 200423)1()2(161)1()21()21(-÷-⨯⎥⎦⎤⎢⎣⎡--÷--54、 100()()222---÷3)2(32-+⎪⎭⎫ ⎝⎛-÷ 55、322)43(6)12(7311-⨯⎥⎦⎤⎢⎣⎡÷-+--56、111117(113)(2)92844⨯-+⨯-57、419932(4)(1416)41313⎡⎤--⨯-÷-⎢⎥⎣⎦58、)—()—)+(—(25.0433242÷⨯59、 75)21(212)75(75211⨯-+⨯--⨯60、11)()+(2532.015[3-÷⨯----]61、12(4)4⎡⎤-|-16|-⨯-⎢⎥⎣⎦÷⎥⎦⎤⎢⎣⎡--)813(4162、 2335(2)(10.8)114⎡⎤---+-⨯÷--⎢⎥⎣⎦63、111117(113)(2)92844⨯-+⨯-64、419932(4)(1416)41313⎡⎤--⨯-÷-⎢⎥⎣⎦65、33221121(5533)22⎡⎤⎛⎫⎛⎫--÷+⨯+⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦66、2335(2)(10.8)114⎡⎤---+-⨯÷--⎢⎥⎣⎦67、(—315)÷(—16)÷(—2) 68、 –4 + 2 ×(-3) –6÷0.25 69、(—5)÷[1.85—(2—431)×7] 70、 18÷{1-[0.4+ (1-0.4)]×0.471、1÷(61-31)×6172、 –3-[4-(4-3.5×31)]×[-2+(-3) ] 73、-42+5×(-4)2-(-1)51×(-61)+(-221)÷(-241)74、20012002200336353⨯+⨯-75、()5.5-+()2.3-()5.2---4.876、21+()23-⎪⎭⎫⎝⎛-⨯2177、81)4(2833--÷-78、100()()222---÷⎪⎭⎫⎝⎛-÷3279、(-2)14×(-3)15×(-61)1480、-11312×3152-11513×41312-3×(-11513)第二部分整式的加减计算训练1、222225533y y x y y x x +-++-- 2、()()22224354ab b a abb a ---3、2(2ab +3a )-3(2a -ab )4、2a -[-4ab +(ab -2a )]-2ab 5、3a 2-[5a -(21a -3)+2a 2]+4 6、(2x 2-3x 3-4x 4-1)+(1+5x 3-3x 2+4x 4);7、3[34a -(32a -31)]-23a ; 8、(7m 2n -5mn )-(4m 2n -5mn ). 9、2213[5(3)2]42a a a a ---++ 10、)1()21(1)31(61-+-+---x x x11、{}])([22y x ----- 12、2237(43)2x x x x ⎡⎤----⎣⎦;13、22225(3)2(7)a b ab a b ab ---. 1、)4(2)3(22x x x x +++-,其中2-=x2、)(3)(3)22(22222222y y x x y x y x +++--,其中1-=x ,2=y 3、已知122-=x A ,223x B -=,求A B 2-的值。
七年级数学专题训练23 与角相关的问题(附答案)

七年级数学专题训练23 与角相关的问题阅读与思考角也是一种基本的几何图形,凡是由直线组成的图形都出现角. 角既可以看成有公共端点的两条射线组成的图形,也可以看成是一条射线绕着端点从一个位置旋转到另一个位置所成的图形.按角的大小可以分成锐角、直角和钝角. 由于直角和平角在角中显得特别重要,所以处于不同位置,但两角的和是一个直角或是一个平角的角仍然得到我们的特别关注. 两角之和为直角的,这两个角叫做互为余角;而两角之和为平角的,这两个角叫做互为补角,余角和补角的概念及其应用在几何计算和证明中都有十分重要的地位.解与角有关的问题常用到以下知识与方法: 1. 角的分类; 2. 角平分线的概念; 3. 互余、互补等数量关系角; 4. 用方程的观点来进行角的计算.例题与求解【例1】如图,在3×3的网格上标出了∠1和∠2,则12∠+∠= .21(“希望杯”邀请赛试题)解题思路:对图形进行恰当的处理,通过拼补求出12∠+∠的值.【例2】如果α∠与β∠互补,且αβ∠>∠,则下列表示β∠的余角的式子中:①90β︒-∠;②90α∠-︒;③1()2αβ∠+∠;④1()2αβ∠-∠. 其中正确的有( )A. 4个B. 3个C. 2个D. 1个(2013年浙江省衢江市数学竞赛试题)解题思路:彼此互余的角只要满足一定的数量关系即可,而与位置无关.【例3】已知80AOB ∠=︒,OC 是不在直线OA ,OB 上的任一条射线. OM ,ON 分别平分∠AOC ,∠BOC . 求∠MON 的大小.(题目中考虑的角都小于平角)B'A'O BA(湖北省武汉市武昌区调考试题)解题思路:因OC 位置不确定,故分类讨论是解本例的关键.【例4】钟表在12点钟时三针重合,经过x 分钟秒针第一次将分钟和时针所夹的锐角平分,求x 的值.(湖北省黄冈市竞赛试题)解题思路:把秒针第一次将分钟和时针所夹的锐角平分所得的两个角用x 的代数式表示,通过解方程求出x 的值.【例5】(1)现有一个19°的“模板”(如图),请你设计一种办法,只用这个“模板”和铅笔在纸上画出1°的角来.19°(2)现有一个17°的“模板”与铅笔,你能否在纸上画出一个1°的角来? (3)用一个21°的“模板”与铅笔,你能否在纸上画出一个1°的角来?对(2)(3)两问,如果能,请你简述画法步骤;如果不能,请你说明理由.(“希望杯”邀请赛试题)解题思路:若只连续使用模板,则得到的是一个19°(或17°或21°)的整数倍的角,其实,解题的关键是在于能否找到19°(或17°或21°)的一个倍数与某个特殊角的某个倍数相差1°.【例6】如图所示,O 是直线AB 上的一点,∠COD 是直角,OE 平分∠BOC . (1)如图①,若30AOC ∠=︒,求∠DOE 的度数;(2)在图①中,若AOC α∠=,直接写出∠DOE 的度数 (用含α的代数式表示);(3)将图①中的∠DOC 绕顶点O 顺时针旋转至图②的位置.① 探究∠AOC 和∠DOE 的度数之间的关系,写出你的结论,并说明理由;② 在∠AOC 的内部有一条射线OF ,满足42AOC AOF BOE AOF ∠-∠=∠+∠,试确定∠AOF 与∠DOE 的度数之间的关系,说明理由ABODCEECDOBA图 ① 图 ②(湖北省武汉市模拟试题)解题思路:(1)利用互余、互补关系易求出∠DOE 的度数;(2)先根据∠DOE 与∠COE 的互余关系列出相应的关系式,然后用∠BOC 表示出∠COE ,再根据互补角的关系用α表示出所求角的度数;(3)①可设∠BOC 为一个未知数,分别表示出∠AOC 与∠DOE ,可得相应关系;②结合①把所给等式整理为只含所求角的关系式即可.能力训练A 级1. 已知一个角的补角等于这个角余角的6倍,那么这个角等于 .(“祖冲之杯”邀请赛试题)2. 如图,45BOD ∠=︒,90AOE ∠=︒,那么不大于90°的角有 个,它们的度数之和是 .EC DOBA(“希望杯”邀请赛试题)3. 如图,150AOC BOD ∠=∠=︒,若3AOD BOC ∠=∠,则BOC ∠等于 .AB ODC4. 如图,O 是直线AB 上一点,120AOD ∠=︒,90AOC ∠=︒,OE 平分∠BOD ,则图中彼此互补的角有 对.ECDOBA(北京市“迎春杯”竞赛试题)5. 一个角的补角的117是6°,则这个角是( ) A. 68° B. 78° C. 88° D. 98°(“希望杯”邀请赛试题)6. 用一副三角板可以画出大于0°且小于176°的不同角度有( )种 A. 9 B. 10 C. 11 D. 127. 如图,若180AOB ∠=︒,∠1是锐角,则∠1的余角是( )2ABO1A.1212∠-∠B.132122∠-∠C. 1(21)2∠-∠D.1(21)3∠+∠ (甘肃省兰州市竞赛试题)8. 如图,180AOB ∠=︒,OD 是∠COB 的平分线,OE 是∠AOC 的平分线,设BOD α∠=,则与α的余角相等的角是( )αABODCEA.∠CODB.∠COEC.∠DOAD.∠COA9. 如图,已知2COB AOC ∠=∠,OD 平分∠AOB ,且19COD ∠=︒,求∠AOB 的度数.CDOBA(北京市“迎春杯”竞赛试题)10. 如图,已知∠AOB 与∠BOC 互为补角,OD 是∠AOB 的平分线,OE 在∠BOC 内,12BOE EOC ∠=∠,72DOE ∠=︒. 求∠EOC 的度数.ECDO BA11. 已知80AOB ∠=︒,OC 平分∠AOB ,60COD ∠=︒,OE 平分∠COD . 求∠AOE 的大小.EC DOB A12. 如图,已知OB ,OC ,OD 为∠AOE 内三条射线. (1)图中共有多少个角?(2)若OB ,OC ,OD 为∠AOE 四等分线,且图中所有锐角的和为400°,求∠AOE 的度数. (3)若89AOE ∠=︒,30BOD ∠=︒,求图中所有锐角的和.EC DOBAB 级1. 已知一个角的补角比这个角余角的3倍大10°,则这个角的度数是 .(浙江省杭州市竞赛试题)2. α,β,γ中有两个锐角和一个钝角,其数值已经给出,在计算1()15αβγ++的值时,有三位同学分别算出了23°,24°,25°这三个不同的结果. 其中只有一个是正确的答案,则αβγ++= .(江苏省竞赛试题)3. 如图,点O 在直线AB 上,OC ,OD ,OE ,OF 是位于AB 同一侧的射线,那么在这个图形中,不大于平角的角共有 个.F ABOD C E(五城市联赛试题)4. 如图,射线OC ,OD ,OE ,OF 分别平分∠AOB ,∠COB ,∠AOC ,∠EOC ,若24FOD ∠=︒,则AOB ∠= .F EC DOBA(2013年“希望杯”数学邀请赛试题)5. 4点钟后,从时针到分针第二次成90°角,共经过( )分钟(答案四舍五入到整数) A. 60 B. 30 C. 40 D. 33(“五羊杯”竞赛试题)6. 如图是一个3×3的正方形,则图中1239∠+∠+∠++∠的和等于( )987654321A. 270°B. 315°C. 360°D. 405°(广西省竞赛试题)7. 已知,OM ,ON ,OP 分别是∠AOB ,∠BOC ,∠AOC 的平分线,则下列各式中成立的是( )OCB APMNA.AOP MON ∠>∠B.AOP MON ∠=∠C.AOP MON ∠<∠D.以上情况都有可能 8. 如图,∠AOC 是直角,21.5COD ∠=︒,且OB ,OD 分别是∠AOC ,∠BOE 的平分线,则∠AOE 等于( )ABODCEA. 111.5°B. 138°C. 134.5°D. 178°(五城市联赛试题)9. 如图,在直线AB 上取一点O ,在AB 同侧引射线OC ,OD ,OE ,OF ,使∠COE 和∠BOE 互余,射线OF 和OD 分别平分∠COE 和∠BOE . 求证:3AOF BOD DOF ∠+∠=∠.FABODC E10. 如图,∠A 1OA 11是一个平角,322143325443A OA A OA A OA A OA A OA A OA ∠-∠=∠-∠=∠-∠==11101092A OA A OA ∠-∠=︒. 求1110A OA ∠的度数....A 5A 4A 3A 2A 10A 11A 1O(山东省竞赛试题)11. 在一个圆形时钟的表面,OA 表示秒针,OB 表示分针(O 为两针的选择中心). 若现在时间恰好是12点整,问经过多少秒后,△OAB 的面积第一次达到最大?(“CASIO 杯”全国初中数学竞赛试题)专题23 与角相关的问题例1 45°提示:如图,通过拼补得∠1+∠2=45°.例2.B提示:①(90°-∠β)+∠β=90°符合;②(∠α-90°)+∠β=∠α+∠β-90°=180°-90°=90°符合;③11(1809090 22αββββ∠+∠+∠=⨯︒+∠=︒+∠≠︒);④111()18090222αββαβ∠-∠∠=∠+∠=⨯︒=︒()+符合.故①②④能表示β∠的余角.13.∵OM、ON平分∠AOC,∠BOC,∴∠AOM=∠COM=12AOC∠,∠CON=∠BON=12BOC∠(1)如图①,若OC在∠AOB内,设∠BOC=x,则图①图② 图③ 例6 (1)20m n,2(6)0n ,且2m n 与2(6)n 互为相反数。
