3静磁场

合集下载

电动力学

英国物理学家和化学家。
最主要贡献：1831年发现了电磁感应现象。 1834年他研究电流通过溶液时产生的化学变化，提出了法拉第电解定律。这一定律为发展电结构理论开辟了道路。 1845年9月13日法拉第发现，一束平面偏振光通过磁场时发生旋转，这种现象被称为“法拉第效应”。法拉第认为光具有电磁性质，是光的电磁波理论的先驱 1852年他引进磁力线概念。他的很多成就不仅非常重要、且是带根本性的理论。

单位张量与矢量、张量的点乘
I C C I C I AB AB I AB

I : AB A B
2 B A 1.计算 A B A B 2.证明 M b a c a b c 与矢量 c 垂直,即 M c 0
林斯顿。遵照他的遗嘱，不举行任何丧礼，不筑坟墓，不立纪念碑，骨灰撒在永远对人保密的地方，为的是不使任何地方成为圣地。爱因斯坦的后半生一直从事寻找大统一理论的工作，不过这项工作没有获得成功，现在大统一理论是理论物理学研究的中心问题。爱因斯坦是耶路撒冷希伯来大学的注册商标
§2 矢量代数与张量初步
难点：公式多、数学推导较繁杂；解题难度大、
相对论概念不易理解。
二、电动力学与电磁学的联系与区别
范围
既讨论静场又讨论变化场，外加相对论。
深度
从矢量场论出发，总结电磁现象普遍规律，解题更具一般性。
方法
建立模型、求解方程、注重理论。
数学
矢量分析与场论、线性代数、数理方程、特殊函数 „
三、理论物理的特点

从零开始3D maxwell磁场仿真之边界条件

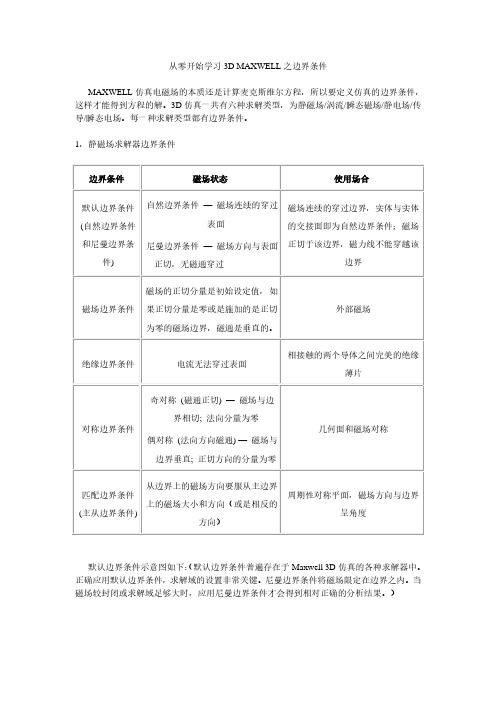
从零开始学习3D MAXWELL之边界条件MAXWELL仿真电磁场的本质还是计算麦克斯维尔方程，所以要定义仿真的边界条件，这样才能得到方程的解。

3D仿真一共有六种求解类型，为静磁场/涡流/瞬态磁场/静电场/传导/瞬态电场。

每一种求解类型都有边界条件。

1，静磁场求解器边界条件默认边界条件示意图如下：（默认边界条件普遍存在于Maxwell 3D仿真的各种求解器中。

正确应用默认边界条件，求解域的设置非常关键。

尼曼边界条件将磁场限定在边界之内。

当磁场较封闭或求解域足够大时，应用尼曼边界条件才会得到相对正确的分析结果。

）磁场边界条件：磁场边界条件指定在求解域表面：1）定义切向方向磁场强度为零的边界条件：选择要添加边界条件的面--增加切线方向磁场强度为零的磁场；2）定义正切磁场边界条件：选择要添加边界条件的面--增加正切磁场--增加X/Y方向的磁场分量值--在坐标系统中定义X/Y矢量或是使用默认值；（正切方向为零，磁场方向与表面垂直）（磁场边界条件，磁场的切向分量被指定为预定义的值，但如果该分量的值被指定为0，则其效果与Zero Tangential H Field相同，磁场与该边界垂直，适用于施加外部磁场，如地磁仿真。

）绝缘边界条件，除电流无法穿过边界以外，其他特性与Neumann边界相同，适用于2个接触导体之间完美绝缘的薄片。

(未添加绝缘边界条件)（添加绝缘边界条件后）对称边界条件：对称边界条件适合几何对称或是磁场对称的结构。

对称边界条件，奇对称（磁力线正切），磁场与边界正切，磁场法向分量为0；偶对称（磁力线垂直），磁场与边界垂直，磁场切向分量为0。

对称边界条件主要用来减少仿真时间，增加计算效率。

匹配边界条件，有主边界（Master）和从边界（Slave）两种，需要配合使用。

偶对称时，Slave边界的磁场被定义为匹配Master边界的幅值和方向。

奇对称时，Slave边界的磁场与Master边界的幅值相同，方向相反。

电动力学教学大纲

XX《电动力学》教学大纲课程编号： 3407课程名称:电动力学英文名称:学分／学时:４/64课程性质: 必修适用专业: 应用物理建议开设学期:５先修课程: 电磁学,数学物理方法,场论与复变函数开课单位：物理与光电工程学院一、课程的教学目标与任务(１）理解电磁运动的基本规律，理解电磁场基本性质；（2）获得分析和处理一些电磁基本规律问题的能力；(3)通过学习狭义相对论理论，掌握相对论的时空观及有关的基本理论；(４)为后续课程的学习和独力解决实际问题打下必要的基础。

二、课程具体内容及基本要求（一）引言（4学时）１。

基本要求了解《电动力学》的主要内容、熟悉研究对象等电磁场理论的史2.重点、难点掌握数学知识补充（矢量分析和算符运算）３。

作业及课外学习要求：课后及课本XX中的补充内容,掌握基本的矢量分析及算符运算法则（二)第一章电磁现象的普遍规律（８学时）１.基本要求第一节电荷和电场一、库仑定律(电荷连续分布带电体的电场）二、高斯定理，静电场的散度（矢量场的两个基本性质）三、静电场的旋度第二节电流和磁场一、电荷守恒定律（微分形式和积分形式)二、用毕—萨定律证明磁场旋度和散度公式第三节麦克斯韦方程组一、电磁感应定律二、位移电流三、麦克斯韦方程组四、洛伦兹力公式第四节介质的电磁性质一、极化和磁化的物理图象及描述二、极化强度的散度和磁化强度的旋度三、物质方程四、介质中的方程第五节电磁场的边值关系一、方程的积分形式二、法向分量的跃变三、切向分量的跃变第六节电磁场的能量和能流一、场和电荷系统的能量转化和守恒定律的一般形式二、电磁场能量密度和能流密度表示式三、电磁能量的传输2.重点、难点本章重点:方程及其物理根据，电磁场的边值关系，电磁场能量.难点:电磁场的矢量运算，电磁场及边值关系的物理图像。

３．作业及课外学习要求:课后题的部分内容，掌握电磁场的基本边值关系及方程.（三）第二章静电场（13学时）1.基本要求第一节静电场的标势及其微分方程一、静电场的标势二、静电势的微分方程和边值关系三、静电场的能量第二节唯一性定理一、静电问题的唯一性定理二、有导体存在时的唯一性定理第三节拉普拉斯方程分离变量法一、分离变量法二、边界条件的使用第四节电像法一、电像法的物理原理二、电像法的适用区域第五节格林函数法（选讲)一、点电荷密度二、格林函数三、格林公式和边值问题的解第六节电多极矩一、电势的多极展开二、电多极矩三、电荷体系在外电场中的能量２。

电动力学第三版_郭硕鸿_课后答案[第3章]

电动力学习题解答参考第三章静磁场1. 试用A r 表示一个沿z 方向的均匀恒定磁场0B r写出A r的两种不同表示式证明两者之差是无旋场解0B r 是沿z 方向的均匀的恒定磁场即ze B B r r =0且AB r r×∇=0在直角坐标系中zx y y z x x y z e yA x A e x A z A e z A y A A r r rr )()()(∂∂−∂∂+∂∂−∂∂+∂∂−∂∂=×∇如果用A r 在直角坐标系中表示0B r 即=∂∂−∂∂=∂∂−∂∂=∂∂−∂∂000y A x A x A z A z A y A xy zx yz 由此组方程可看出A r有多组解如解1)(,00x f y B A A A x Z y +−=== 即 xe xf y B A rr )]([0+−= 解2)(,00y g x B A A A Y z x +=== 即 ye y g x B A rr )]([0+=解1和解2之差为yx e y g x B e x f y B A r r r )]([)]([00+−+−=∆则zx y y z x x y z e y A xA e x A z A e z A y A A r r r r ])()([])()([])()([)(∂∆∂−∂∆∂+∂∆∂−∂∆∂+∂∆∂−∂∆∂=∆×∇这说明两者之差是无旋场2.均匀无穷长直圆柱形螺线管每单位长度线圈匝数为n电流强度为I 试用唯一性定理求管内外磁感应强度B解根据题意得右图取螺线管的中轴线为z 轴本题给定了空间中的电流分布故可由∫×='43dV r rJ B rr r πµ求解磁场分布又J r 在导线上所以∫×=34r r l Jd B r r r πµ1 螺线管内由于螺线管是无限长理想螺线管故由电磁学的有关知识知其内部磁内部资料料料内部资料内部电动力学习题解答参考第三章静磁场场是均匀强磁场故只须求出其中轴线上的磁感应强度即可知道管内磁场由其无限长的特性不妨取场点为零点以柱坐标计算x y x e z e a e a r r r r r ''sin 'cos −−−=ϕϕyx e ad e ad l d r r r 'cos ''sin 'ϕϕϕϕ⋅+⋅−=)''sin 'cos ()'cos ''sin '(x y x y x e z e a e a e ad e ad r l d r r r r r r r −−−×⋅+⋅−=×∴ϕϕϕϕϕϕ zy x e d a e d az e d az rrr'''sin '''cos '2ϕϕϕϕϕ+−−= 取由'''dz z z +−的以小段此段上分布有电流'nIdz ∫++−−=∴232220])'([)'''sin '''cos '('4z a e d a e d az e d az nJdz B z y x rr r r ϕϕϕϕϕπµ I n az a z d nI e nI z a dz a d z 0232023222200]1)'[()'(2])'([''4µµϕπµπ=+=⋅+=∫∫∫∞+∞−∞∞−r 2)螺线管外部:由于是无限长螺线管不妨就在xoy 平面上任取一点)0.,(ϕρP 为场点)(a >ρ 222')'sin sin ()'cos cos ('z a a x x r +−+−=−=∴ϕϕρϕϕρrr )'cos(2'222ϕϕρρ−−++=a z a ('=−=x x r r r r x e a r )'cos cos ϕϕρ−zy e z e a rr ')'sin sin (−−ϕϕρyx e ad e ad l d r r r 'cos ''sin 'ϕϕϕϕ⋅+⋅−= zy x e d a a e d az e d az r l d r r r r r ')]'cos([''sin '''cos '2ϕϕϕρϕϕϕϕ−−+−−=×∴+−+−⋅=∴∫∫∫∫∞∞−∞∞−'''sin '''''cos ''[43203200dz e r d az d dz e r d az d nI B y x rr r ϕϕϕϕϕϕπµππ]')'cos('3220∫∫∞∞−−−+z e dz r a a d rϕϕρϕπ由于磁场分布在本题中有轴对称性而螺线管内部又是匀强磁场且螺线管又是无限长故不会有磁力线穿出螺线管上述积分为0所以0=B r内部资料料料内部资料内部电动力学习题解答参考第三章静磁场3. 设有无穷长的线电流I 沿z 轴流动以z<0空间充满磁导率为µ的均匀介质z>0区域为真空试用唯一性定理求磁感应强度B 然后求出磁化电流分布解本题的定解问题为×∇=×∇=<−=∇>−=∇===010020212201211)0(,)0(,z z z A A AA z J A z J A r r r rrr rr µµµµ由本题具有轴对称性可得出两个泛定方程的特解为∫∫==rl Id x A rl Id x A rr r rr r πµπµ4)(4)(201由此可推测本题的可能解是<>=)0(,2)0(,20z er I z e r I B θθπµπµr rr 验证边界条件1)(,12021=−⋅==B B n A A z r rr r r 即题中,=⋅=θe e e n z z rr r r 且所以边界条件1满足2)(,11120102=−××∇=×∇==H H n A A z z r r rr r即µµ本题中介质分界面上无自由电流密度又θθπµπµe r I B H e rI B H r r r r r r 2222011====,012=−∴H H r r 满足边界条件0)(12=−×H H n r r r综上所述由唯一性定理可得本题有唯一解<>=)0(,2)0(,20z er I z e r I B θθπµπµr rr 在介质中MB H r r r −=0µ故在z<0的介质中22H B M r rr −=µ内部资料料料内部资料内部即θθθµππµπe r e r e r M )1(22200−=−⋅= ∴介质界面上的磁化电流密度r z M e r I e e r I n M r r r r r r )1(2)1(200−=×−=×=µµπµµπαθ总的感应电流)1()1(20200−=⋅⋅⋅−=⋅=∫∫µµϕµµππθθI e d r e r I l d M J Mr r rr 电流在z<0的空间中沿z 轴流向介质分界面4. 设x<0 半空间充满磁导率为µ的均匀介质x>0 空间为真空今有线电流I 沿z 轴流动求磁感应强度和磁化电流分布解假设本题中得磁场分布仍呈轴对称则可写作ϕπµe rI B vv 2′=其满足边界条件0)(0)(1212==−×=−⋅αvv v v v vv H H n B B n 即可得在介质中ϕµπµµe r I B H vv v 22′== 而Me r I M B H v v v v v −′=−=ϕµπµµ0022∴在x<0的介质中ϕµµµµπµe r I M vv 002−′= 则∫=ld M I Mvv 取积分路线为B A C B →→→的半圆,ϕe AB vQ ⊥ AB ∴段积分为零 002)(µµµµµ−′=I I M ϕπµe r I I B M v v 2)(0+=∴∴由ϕϕπµπµe rI B e r I I M v v v 22)(0′−==+可得02µµµµµ+=′内部资料料料内部资料内∴空间ϕπµµe rB 0+= I I M 0µµµµ+−=沿z轴5.某空间区域内有轴对称磁场在柱坐标原点附近已知)21(220ρ−−≈z C B Bz 其中B 0为常量试求该处的ρB 提示用,0=⋅∇B r 并验证所得结果满足0Hr×∇解由B v 具有轴对称性设zz e B e B B v v v +=ρρ其中 )21(220ρ−−=z c B B z 0=⋅∇B v Q 0)(1=∂∂+∂∂∴z B zB ρρρρ即02)(1=−∂∂cz B ρρρρ A cz B +=∴2ρρρ(常数) 取0=A 得ρρcz B =z e z c B e cz B vv v )]21([220ρρρ−−+=∴10,0==D j v vQ 0=×∇∴B v 即 0)(=∂∂−∂∂θρρe B z B z v2代入1式可得2式成立∴ρρcz B = c 为常数6. 两个半径为a 的同轴线圈形线圈位于L z ±=面上每个线圈上载有同方向的电流I1 求轴线上的磁感应强度2 求在中心区域产生最接近于均匀的磁场时的L 和a 的关系提示用条件022=∂∂z B z解1由毕萨定律L 处线圈在轴线上z 处产生得磁感应强度为内部资料料料内部资料内,11z z e B B = ∫∫−+==θπαπd L z a r B z 232231])([4sin 4 232220])[(121a z L Ia +−=µ同理L 处线圈在轴线上z处产生得磁感应强度为zz e B B vv 22=2322202])[(121a z L Ia B z++=µ∴轴线上得磁感应强度zz z e a z L a z L Ia e B B v v v++++−==2322232220])[(1])[(121µ 20=×∇B vQ 0)()(2=∇−⋅∇∇=×∇×∇∴B B B v v v 又0=⋅∇Bv0,0222=∂∂=∇∴z B zB v 代入1式中得62225222322212222122])[(])[()(6])[(])[()(])[(a z L a z L z L a z L a z L z L a z L +−+−−++−+−−−+−−−62225222322212222122])[(])[()(6])[(])[()(])[(a z L a z L z L a z L a z L z L a z L +−++−−++ ++++++−−0取z得)(12])(2)(2[)(22522212222122322=+++−+−+−L a L a L L a L a L 2225a L L +=∴内部资料料料内部资料内电动力学习题解答参考第三章静磁场a L 21=∴7. 半径为a 的无限长圆柱导体上有恒定电流J 均匀分布于截面上试解矢势A r的微分方程设导体的磁导率为0µ导体外的磁导率为µ解定解问题为×∇=×∇=∞<>=∇<−=∇外内内外内外内A A A A A a r A a r J A a a v v v vvv vv µµµ11)(,0)(,00202选取柱坐标系该问题具有轴对称性且解与z 无关令ze r A A v v )(内内=z e r A A vv )(外外代入定解问题得=∂∂∂∂−=∂∂∂∂0))(1))((10r r A r rr J r r A r r r 外内µ 得43212ln )(ln 41)(C r C r A C r C Jr r A +=++−=外内µ由∞<=0)(r r A 内得01=C 由外内A A v v ×∇=×∇µµ110 得 232Ja C µ−=内部资料料料内部资料内部电动力学习题解答参考第三章静磁场由aaA A 内外v v =令0==aaA A 内外v v 得 a Ja C Ja C ln 2,4124202µµ==−=∴ra a J A r a J A ln 2)(412220v v v vµµ外内8.假设存在磁单极子其磁荷为Qm它的磁场强度为304r rQ H m r r πµ=给出它的矢势的一个可能的表示式并讨论它的奇异性解rm m e rQ r r Q H v v v 2030144πµπµ== 由rm e rQ H B A v v v v 204πµ===×∇ 得=∂∂−∂∂=∂∂−∂∂=∂∂−∂∂0])([10)](sin 1[14])(sin [sin 12θφθπφθθθθφθφrr m A rA r r rA r A r r Q A A r (1)令,0==θA A r得rQ A m πθθθφ4sin )(sin =∂∂θθπθπθθφθφsin cos 144sin sin 0r Q A d rQ A mm −=∴=∴∫显然φA 满足1式∴磁单极子产生的矢势φθθπe r Q A m vv sin cos 14−=内部资料料料内部资料内部当2πθ→时φπe rQ A m v v 4→当πθ→时∞→A v故A v的表达式在πθ=具有奇异性A v不合理9. 将一磁导率为µ半径为R 0的球体放入均匀磁场0H r内求总磁感应强度B r 和诱导磁矩mr解根据题意以球心为原点建立球坐标取0H v 的方向为zev此球体在外界存在的磁场的影响下极化产生一个极化场并与外加均匀场相互作用最后达到平衡保持在一个静止的状态呈现球对称本题所满足的定解问题为−=∞<=∂∂=∂∂=>=∇<=∇∞==θϕϕϕµϕµϕϕϕϕcos )(,,,0,0000002221212121R H R R R R R R R R R m R m m m m m m m 由泛定方程和两个自然边界条件得∑∞==0)(cos 1n n n n m P R a θϕ∑∞=++−=010)(cos cos 2n nn nm P R d R H θθϕ由两个边界条件有+−−=+−=∑∑∑∑∞=+∞=−∞=+∞=0200001100100000)(cos )1(cos )(cos )(cos cos )(cos n n n nn n n n n nn n n n nn P R d n H P nR a P R d R H P R a θµθµθµθθθ得内部资料料料内部资料内≠==+−=+)1(,0223000101n d a R H d n n µµµµµµ>⋅+−+−=<+−=∴00230000000,cos 2cos ,cos 2321RR H R R R H R R R H m m θµµµµθϕθµµµϕ+==+=+−+=−∇=00011000000012323sin 23cos 231H H B H e H e H H r m v v v v vv v µµµµµµµµθµµµθµµµϕθ−⋅+−+==−⋅+−+=⋅+−−−⋅+−+=−∇=])(3[2])(3[2sin ]21[cos ]221[3050300000020230503000003300003300022R H R R R H R H H B R H R R R H R H e H R R e H R R H r m v v v v v v v vv v v v vv v µµµµµµµµµµµθµµµµθµµµµϕθ >−⋅+−+<+=∴)()(3[2)(,230305030000000000R R R H R R R H R H R R H B vv v v v vv µµµµµµµµµµ当B v在R>R 0时表达式中的第二项课看作一个磁偶极子产生的场θµµµµϕcos 20230002H RR m ⋅+−∴中可看作偶极子m v产生的势即R H R R H R R R Rm v v v v ⋅⋅+−=⋅+−=⋅⋅02300002300032cos 241µµµµθµµµµπ HR m v v300024⋅+−=∴µµµµπ10. 有一个内外半径为R 1和R 2的空心球位于均匀外磁场0H r内球的磁导率为µ求空内部资料料料内部资料内电动力学习题解答参考第三章静磁场腔内的场Br讨论0µµ>>时的磁屏蔽作用解根据题意以球心为原点取球坐标选取0H v的方向为z e v在外场0H v的作用下球壳极化产生一个附加场并与外场相互作用最后达到平衡B v的分布呈现轴对称定解问题−=∞<∂∂=∂∂∂∂=∂∂==>=∇<<=∇<=∇∞======θϕϕϕµϕµϕµϕµϕϕϕϕϕϕϕcos ,,,0,0,00000322121231223121232121321R H RR R R R R R R R R R R m R m R R m m R R m m R R m m R R m m m m m 由于物理模型为轴对称再有两个自然边界条件故三个泛定方程的解的形式为∑∞==0)(cos 1n n n n m P R a θϕ∑∞=++=01)(cos (2n n n nn n m P Rc R b θϕ∑∞=++−=010)(cos cos 3n nn nm P Rd R H θθϕ因为泛定方程的解是把产生磁场的源0H v做频谱分解而得出的分解所选取的基本函数系是其本征函数系)}(cos {θn P 在本题中源的表示是)(cos cos 100θθRP H R H −=−所以上面的解中)0(,0≠====n d c b a n n n n 故解的形式简化为θθϕθϕθϕcos cos cos )(cos 2102111321RdR H Rc R b R a mm m +−=+==内部资料料料内部资料内部电动力学习题解答参考第三章静磁场代入衔接条件得−=−−−=+−=++=2(22(32113210031110122120221212111111R c b R d H R c b a R d R H R c R b R c R b R a µµµµµ解方程组得3200312032000320001)2)(2()(2)(3)2(3R R R H R H a µµµµµµµµµµµµ++−−−++= 32003120320001)2)(2()(2)2(3R R R H b µµµµµµµµµ++−−+= 3200312031320001)2)(2()(2)(3R R R R H c µµµµµµµµµ++−−−= 320320031203132000620001)2)(2()(2)(3)2(3R H R R R R H R H d +++−−−++=µµµµµµµµµµµµ而 )3,2,1(,00=∇−==i H B i m i i ϕµµvv ze a B v v 101µ−=∴ 003212000321])()(2)2)(2()(11[HR R R R v µµµµµµµ−−++−−=当0µµ>>时1)(2)2)(2(2000≈−++µµµµµµ 01=∴B v 即球壳腔中无磁场类似于静电场中的静电屏障11. 设理想铁磁体的磁化规律为000,M M H B µµ+=rr 是恒定的与H r无关的量今将一个内部资料料料内部资料内部电动力学习题解答参考第三章静磁场理想铁磁体做成均匀磁化球0M为常值浸入磁导率为'µ的无限介质中求磁感应强度和磁化电流分布解根据题意取球心为原点做球坐标以0M v的方向为z e v本题具有球对称的磁场分布满足的定解问题为=∞<=∂∂′−∂∂=>=∇<=∇∞===0cos ,,0,021021021*******02R m R m R m m R R m m m m M R RR R R R ϕϕθµϕµϕµϕϕϕϕ ∴∑∞==0)(cos 1n n n nm P R aθϕ∑∞=+=01)(cos )(2n n n nm P R b θϕ代入衔接条件对比)(cos θn P 对应项前的系数得)1(,0≠==n b a nn µµµ+′=2001Ma 30012R M b µµµ+′=)(,cos 20001R R R M m <+′=∴θµµµϕ)(,cos 20230002R R RR M m>+′=θµµµϕ由此µµµµµµ+′′=+=<22,0000110M M H B R R v r v v ,0R R > )(3[2305030022RM R R R M R B m v r v v v −⋅+′′=∇′−=µµµµϕµ >−⋅+′′<+′′=∴)()(3[2)(,2203050300000R R R M R R R M R R R M B v r v v vv µµµµµµµµ内部资料料料内部资料内部电动力学习题解答参考第三章静磁场又0)()(0120其中αααµv v v vv v+=−×M R B B n 代入B v的表达式得ϕθµµµαe M Mvv sin 230′′12. 将上题的永磁球置入均匀外磁场0H r中结果如何解根据题意假设均匀外场0H v 的方向与0M v的方向相同定为坐标z 轴方向定解问题为−=∞<=∂∂−∂∂=>=∇<=∇∞===θϕϕθµϕµϕµϕϕϕϕcos cos ,,0,00000002022102102121R H M R RR R R R R m R m R m m R R m m m m 解得满足自然边界条件的解是)(,cos 011R R R a m <=θϕ)(,cos cos 02102R R R d R H m >+−=θθϕ代入衔接条件0013010020100012M a R d H R d R H R a µµµµ=+++−=得到 0000123µµµµ+−=H M a 3000012)(R H M d µµµµµ+−+=)(,cos 23000001R R R H M m <+−=∴θµµµµϕ内部资料料料内部资料内部电动力学习题解答参考第三章静磁场)(,cos 2)(cos 0230000002R R RR H M R H m>+−++−=θµµµµµθϕ]sin 23cos 23[000000000011θθµµµµθµµµµϕe H M e H M H r m v v v +−−+−−=−∇=∴ µµµµ+−−=0000023H M v v )(,22230002000001R R M H M H B <+++=+=v v v v v µµµµµµµµµ−+−+−−−=−∇=r m e R R H M H H v v )cos 22)(cos [(23000000022θµµµµµθϕ 350230000000)(3])sin 2)(sin (Rm R R R m H e R R H M H v v r r v v−⋅+=+−++−−θθµµµµµθ ])(3[3500202RmR R R m H H B v v r r v v v −⋅+==µµ030003000022H R R M m v vv µµµµµµµ+−++=13. 有一个均匀带电的薄导体壳其半径为R 0总电荷为Q今使球壳绕自身某一直径以角速度ω转动求球内外的磁场Br提示本题通过解m ϕ或A r的方程都可以解决也可以比较本题与5例2的电流分布得到结果解根据题意取球体自转轴为z 轴建立坐标系定解问题为=∞<=∂∂=∂∂−=∂∂−∂∂>=∇<=∇∞===0)(,4sin )(1,0,021211221000000202R m R m m m R R m m m m R R R R R Q R R R R R ϕϕϕµϕµπθωθϕθϕϕϕ其中4sin R Q πθωσ=是球壳表面自由面电流密度解得满足自然边界条件的解为内部资料料料内部资料内部)(,cos 0212R R Rb m >=θϕ代入衔接条件=+−=−024301102101R b a R Q R b R a πω解得 016R Q a πω−= πω12201R Q b =)(,cos 6001R R R R Q m <−=∴θπωϕ)(,cos 1202202R R R R Q m>=θπωϕ00016sin 6cos 61R Q e R Q e R Q H r m πωθπωθπωϕθv vv v =−=−∇=∴ωπµµvr v 001016R Q H B == ])(3[41sin 12cos 1223532032022Rm R R R m e R R Q e R R Q H r r m r v v v vv v −⋅=+=−∇=πθπωθπωϕ其中ωvv 320QR m =])(3[4350202RmR R R m H B r v v v v v −⋅==πµµ14. 电荷按体均匀分布的刚性小球其总电荷为Q 半径为R 0它以角速度ω绕自身某以直径转动求1 它的磁矩2 它的磁矩与自转动量矩之比设质量M 0是均匀分布的解1磁矩∫×=dV x J x m )(21v v v v内部资料料料内部资料内又 rR x e R == )(34)(30R R v x J ×==ωπρ∫∫×=××=∴φθθπωφθθωπφd drd R e e R Q d drd R R R R Q m r 2430230sin )(4321sin )(4321v v v v r v 又 )sin cos (cos sin y x z r e e e e e e vv v v v v φφθθθφ−−+=−=×∫∫∫−−+=∴ππφθθφφθθπω20243sin )sin cos (cos [sin 83R y x z d drd R e e e R Q m vv v v ωφθθπωππv v 5sin 8320200043300QR d drd R e R Q R z ==∫∫∫2)自转动量矩∫∫∫∫××=×=×==dV R R R M dm v R P d R L d L )(43300v v v v v v v v vωπ52sin 43sin )sin cos (cos [sin 43sin )(sin 43sin )sin (43sin )(43200203430200024302230022300223000ωφθθπωφθθφφθθπωφθθθωπφθθθωπφθθωπππππθφv v vv v v v v v v v R M d drd R R M d drd R e e e R M d drd R e R R M d drd R e e R R M d drd R e e e R R M R R y x z r r z r ==−−+=−=×−=××=∫∫∫∫∫∫∫∫∫ 0200202525M Q R M QR L m ==∴ωωv v v v15. 有一块磁矩为m r的小永磁体位于一块磁导率非常大的实物的平坦界面附近的真空中求作用在小永磁体上的力F r.内部资料料料内部资料内电动力学习题解答参考第三章静磁场解根据题意因为无穷大平面的µ很大则可推出在平面上所有的H v均和平面垂直类比于静电场构造磁矩m r 关于平面的镜像m ′r则外场为=⋅=∇−=2304cos 4r m R R m B m m e πθπϕϕµv v v)sin cos (4]sin cos 2[430330θθθθαπµθθπµe e r m e r e r m B rr e vv r v v +=−−−=∴m v∴受力为za r ee a m B m F v v vv )cos 1(643)(24022απµαθ+−=⋅∇⋅===内部资料料料内部资料内部。

电动力学-选择题填空题判断题问答题复习

《电动力学1》随教材复习题目一、章节容：第0章矢量分析第一章电磁现象的普遍规律第二章静电场第三章静磁场第四章电磁波的传播第五章电磁波的辐射二、题型1. 选择题，填空题，判断题、问答题2. 计算题（见教材例题）2018年5月第0章矢量分析一、选择题0.1设222)()()(z z y y x x r '-+'-+'-=为源点到场点的距离，r 的方向规定为从源点指向场点，则有（ B ）A. 0=∇rB. r r r ∇=C. 0=∇'rD. r r r'∇= 0.2位置矢量r 的散度等于（B ）A ．0 B.3 C.r1 D. r 0.3位置矢量r 的旋度等于（A ）A.0B.3C.r rD.3rr 0.4位置矢量大小r 的梯度等于（ C ）A.0 B .r 1 C. r r D.3rr 0.5r 1∇=？（ B ） A. 0 B.3r r - C.r r D .r 0.6⨯∇3r r =？（A ） A. 0 B .r r C.r D.r 1 0.7⋅∇3rr =？（其中r ≠0）（ A ） A.0 B.1 C.r D.r1 二、填空题0.1位置矢量r 的散度等于（ 3 ）。

0.2位置矢量r 的旋度等于（ 0 ）。

0.3位置矢量大小r r r 。

0.4无旋矢量场可以引入(标)势来处理，无源矢量场可以引入(矢)势来处理。

0.5(无旋)矢量场可以引入标势来处理，(无源)矢量场可以引入矢势来处理。

三、判断题0.1标量场的梯度必为无旋场。

（√）0.2矢量场的旋度不一定是无源场。

(×) 0.3无旋场必可表示为标量场的梯度。

(√) 0.4无源场必可表示为另一矢量的旋度。

(√)第一章电磁现象的普遍规律一、选择题1.1对于感应电场下面哪一个说确（ D ）A 感应电场的旋度为零B 感应电场散度不等于零C 感应电场为无源无旋场D 感应电场由变化磁场激发1.2从麦克斯韦方程组可知变化电场是 ( B )A 有源无旋场B 有源有旋场C 无源无旋场D 无源有旋场1.3从麦克斯韦方程组可知变化磁场是（ D） A 有源无旋场 B 有源有旋场 C 无源无旋场 D 无源有旋场。

第三章静磁场

若电流分布为体分布，。
二、磁偶极子的场与标势
由磁偶极子的势可计算出磁偶极子的场，
（其中，，）
由于
所以
如果定义为磁偶极子的磁标势。
则，
总之，一个小范围内的电流分布在远处产生的磁场的最初级近似为磁偶极近似，
矢势的最初级近似。
磁场的最初级近似。
三、小区域电流在外场中的能量
1、电流分布在外场中的相互作用能
当研究介质中的磁场时，必须考虑介质的磁化对场的影响。自由电流产生磁场，磁场作用于介质产生磁化电流，又激发磁场，场再作用于介质……也必须象静电学问题一样，求解反映场与介质相互作用的微分方程（在一定边界条件下求解）。
我们先引入静磁场的矢势，导出矢势满足的微分方程，然后再讨论磁标势及其微分方程，最后讨论磁多极展开。
球内磁场是
铁球内外的和。线总是闭合的，而线则不然。线从右半球面的正磁荷发出，止于左半球的负磁荷。在铁球内部，和反向，说明磁铁内部的和是有很大的差异。
代表磁铁内的总宏观磁场，即在物理小体积内对微观磁场的平均值，而仅为一辅助场量。
静电场
静磁场
无旋场
无源场
（由此，历史上人们错误地认为与相对应）
2、矢势的一级近似
恒定电流可以分成许多闭合电流管，我们就一个电流管计算上式。若线圈电流为，则有
由于为线圈上各点的坐标，因此（表示对带撇的变量微分）。利用全微分绕闭合回路的线积分等于零，得
因此
则
其中，是电流体系的磁偶极矩。电流分布是一个小线圈，则，是线圈的面积矢量，，为线圈法线方向单位向量，与电流方向满足右手螺旋关系。
若考虑外场变化的情况，设外场是由另一带有电流的线圈产生。

静磁场

W

1 2

(A

1 2

(
Ae
Ae ) (J J e

J e )dV

1 2
)dV
(A

Je
1 2

( A J )dV
Ae J )dV
最后一项称为相互作用能，记为
可以证明： Wi
( A J e )dV
2．矢势的形式解

A

J(
x)dV

4 V r
Ai
4
V
Ji (x)dV r
已知电流密度，可从方程直接积分求解，但一般电流分
布与磁场相互制约，因此一般情况需要求解矢量泊松方程。
3．B 的解
B

A

4
V
(
J
(x))dV r

4
V

1 r
W 1
B

HdV
1

(
A
H
)dV

1
A JdV
2
2
2
1
A JdV
2
2. 电流分布在外磁场中的相互作用能
设 Je 为外磁场电流分布，Ae为外磁场的矢
势；J 为处于外磁场 Be中的电流分布，它激
发的场的矢势为 A 。总能量：

静磁场

H 0

H

m 0

m

0

M

静磁场的主要作用

静磁场的主要作用介绍静磁场是指在不随时间变化的情况下产生的磁场。

它是由静止的电荷或电流所产生的，与静电场不同，它的作用对象是带电粒子运动中的磁性质。

静磁场在物理学、工程学和医学等领域中具有重要的作用。

本文将详细探讨静磁场的主要作用。

二级标题1：静磁场对电荷的作用三级标题1：洛伦兹力静磁场对电荷的主要作用是产生洛伦兹力。

根据洛伦兹力定律，当电荷在静磁场中运动时，它将受到一个与电荷速度和磁场强度相关的力。

洛伦兹力的方向垂直于电荷速度和磁场方向，大小由电荷量、速度和磁场强度决定。

这种力的作用使得带电粒子在磁场中做圆周运动，被广泛应用于粒子加速器、磁共振成像等领域。

三级标题2：霍尔效应静磁场对电荷的另一个重要作用是产生霍尔效应。

当电荷在静磁场中运动时，如果它们在一个导体中，将会在导体两侧产生电势差。

这是由于磁场对电荷运动的影响，导致电荷在导体中聚集或偏移。

霍尔效应被广泛应用于传感器和电子器件中，用于测量电流、磁场和导电性等参数。

三级标题3：磁场对电荷轨迹的影响静磁场还可以改变电荷的运动轨迹。

当电荷穿过静磁场时，它们将受到一个力的作用，使得它们的轨迹发生偏转。

这种现象被应用于质谱仪、电子束聚焦和粒子物理实验等领域，用于分析和控制带电粒子的运动。

二级标题2：静磁场对磁性物质的作用三级标题1：磁场对磁性物质的磁化静磁场对磁性物质的主要作用是产生磁化效应。

磁性物质在静磁场中会发生磁化，使得它们具有磁性。

磁场对磁性物质的磁化程度与磁场强度和物质的磁性特性有关。

这种现象被广泛应用于电磁铁、磁存储和磁共振等领域。

三级标题2：磁场对磁性物质的吸附和分离静磁场还可以用于吸附和分离磁性物质。

在静磁场的作用下，磁性物质会受到一个力的作用，使得它们在磁场中聚集或偏移。

这种现象被广泛应用于磁选和磁分离等领域，用于分离和提纯磁性物质。

三级标题3：磁场对磁性物质的传输和操控静磁场还可以用于磁性物质的传输和操控。

通过改变静磁场的分布和强度，可以对磁性物质进行传输和操控。

电动力学习题解答3

第三章静磁场1. 试用A 表示一个沿z 方向的均匀恒定磁场0B ，写出A 的两种不同表示式，证明二者之差为无旋场。

解：0B 是沿 z 方向的均匀恒定磁场，即 z B e B 00=，由矢势定义B A =⨯∇得0//=∂∂-∂∂z A y A y z ；0//=∂∂-∂∂x A z A z x ；0//B y A x A x y =∂∂-∂∂三个方程组成的方程组有无数多解，如：○10==z y A A ，)(0x f y B A x +-= 即：x x f y B e A )]([0+-=； ○20==z x A A ，)(0y g x B A y += 即：y y g x B e A )]([0+= 解○1与解○2之差为y x y g x B x f y B e e A )]([)]([00+-+-=∆ 则 0)//()/()/()(=∂∂-∂∂+∂∂+∂-∂=∆⨯∇z x y y x x y y A x A z A z A e e e A 这说明两者之差是无旋场2. 均匀无穷长直圆柱形螺线管，每单位长度线圈匝数为n ，电流强度I ，试用唯一性定理求管内外磁感应强度B 。

解：根据题意，取螺线管的中轴线为 z 轴。

本题给定了空间中的电流分布，故可由⎰⨯='430dV r rJ B πμ 求解磁场分布，又 J 只分布于导线上，所以⎰⨯=304r Id r l B πμ1)螺线管内部：由于螺线管是无限长理想螺线管，所以其内部磁场是均匀强磁场，故只须求出其中轴线上的磁感应强度，即可知道管内磁场。

由其无限长的特性，不z y x z a a e e e r ''sin 'cos ---=φφ， y x ad ad d e e l 'cos ''sin 'φφφφ+-= )''sin 'cos ()'cos ''sin '(z y x y x z a a ad ad d e e e e e r l ---⨯+-=⨯φφφφφφz y x d a d az d az e e e '''sin '''cos '2φφφφφ+--=取''~'dz z z +的一小段，此段上分布有电流'nIdz⎰++--=∴2/32220)'()'''sin '''cos '('4z a d a d az d az nIdz z y x e e e B φφφφφπμ ⎰⎰⎰+∞∞-+∞∞-=+=+=z z I n a z a z d nI nI z a dz a d e e 02/3202/3222200])/'(1[)/'(2)'(''4μμφπμπ2)螺线管外部：由于螺线管无限长，不妨就在过原点而垂直于轴线的平面上任取一点)0,,(φρP 为场点，其中a >ρ。

电学基础必会知识点总结

电学基础必会知识点总结一、电路理论1. 电路基本概念电路是由电流源、电阻、电感和电容等元件组成的。

其中，电流源是提供电路中电流的源泉，电阻是阻碍电流通过的元件，电感是存储电能的元件，电容是存储电荷的元件。

电路中的元件通过导线互相连接构成电路的拓扑结构。

2. 电压、电流、电阻和功率电压是电路中的电势差，是指单位电荷在电路中的两点之间所具有的电势能。

电流是电荷在电路中的流动，是单位时间内通过电路横截面的电荷量。

电阻是电路中阻碍电流通过的元件，是电压和电流的比值。

功率是描述电路中能量转换效率的物理量，是电压和电流的乘积。

3. Ohm定律Ohm定律是描述电路中电压、电流和电阻之间关系的基本定律。

它可以表示为V=IR，其中V表示电压，I表示电流，R表示电阻。

根据Ohm定律，电压和电流成正比，电压和电阻成正比，电流和电阻成反比。

4. 串联电路和并联电路在电路中，电阻、电感和电容等元件可以通过串联和并联的方式组成不同的电路结构。

串联电路是指多个元件依次连接在一起，电流只有一条路径可走；并联电路是指多个元件同时连接在一起，电流可以选择不同的路径流动。

在串联电路中，电阻和电压分别求和；在并联电路中，电阻和电流分别求和。

5. 电路的戴维南定理和诺顿定理戴维南定理和诺顿定理是描述线性电路等效变换的定理。

根据这两个定理，任意一个线性电路都可以用一个等效的电压源和电阻网络或电流源和电阻网络来代替。

这两个定理在电路分析中有着重要的应用。

6. 交流电路和直流电路交流电路和直流电路是电路中两种不同的电压类型。

交流电路中，电压随时间呈正弦变化；直流电路中，电压是恒定不变的。

交流电路和直流电路在电路分析中有着不同的特点和分析方法。

7. 电路的平衡和不平衡在电路分析中，平衡和不平衡是两种重要的电路状态。

对于线性电路，在平衡状态下，电路中的各个元件的参数不随时间变化；在不平衡状态下，电路中的各个元件的参数随时间变化。

平衡和不平衡是电路分析中需要重点关注的问题。

静磁场

∇×H =0
∇·B =0
(4)
B = µ0(H + M ) = f (H)
(5)
将(5)式带入(4)式可得：
∇ · H = −∇ · M
★将分子电流看作由一对假想磁荷组成的磁偶极子，与∇ · P = −ρp对应，假想磁荷分布为：
ρm = −µ0∇ · M
铁磁介质的磁标势方程（续）
∇ · H = ρm µ0
H · dS = 0
L
S
★ 举例：无限长直导线：H的旋度仅在r = 0点不为零，但任一绕原点的闭合曲线环量不为零；
★ 这也就是说：∇ × H是局域的，仅和当地J有关；但H并不是局域的；
★ 同理：∇ · E是局域的，仅和当地ρ有关；但E并不是局域的：∇ · E ? ⇒ E · dS = 0
★ 同理：∇ × A = B = 0 (r = 0)，但： A · dl = B · dS? = 0
L
S
★ 考虑如何选取适当的条件，解决该矛盾。
§ 2.2 关于环量积分的讨论
★ 对于任一点x ∈ L有H(x) = 0，则 H · dl = 0
L
★ 对于任一点x ∈ L有∇ × H(x) = 0，未必 H · dl = 0
L
★ 事实上应该为：对于任一点x ∈ S有∇×H(x) = 0，则 H ·dl = ∇×
+
15 8
r3a3 sin3 θ (r2 + a2)7/2
eφ
在远场条件下(r a)取第一项：
A(r, θ)
=
µ0 4π
I πa2 ez r3
×r
=
µ0 4π
m×r r3
★上式(3)相当于磁偶极子产生的矢势；

磁场的变化规律

磁场的变化规律磁场是物质产生磁效应的空间区域，它的变化规律是物理学中重要的研究对象。

本文将探讨磁场的产生和变化规律，并介绍几种常见的磁场变化方式。

一、磁场的产生磁场的主要产生方式是通过电流产生的。

当电流经过一根导线时，会形成一个环绕导线的磁场。

根据安培定律，电流越大，磁场的强度就越大；电流方向改变，磁场的方向也会相应改变。

二、磁场的变化规律1. 动态磁场当电流通过导线时，形成的磁场随着电流的变化而变化。

根据法拉第电磁感应定律，如果通过一个线圈的磁场发生变化，线圈内将产生感应电动势。

这也是电磁铁、电动机等原理的基础。

2. 静态磁场一些磁体，如永磁体和电磁铁，可以产生持久不变的磁场。

这种静态磁场的变化规律是磁场强度与距离的平方成反比。

具体来说，离磁体越近，磁场强度就越强；离磁体越远，磁场强度就越弱。

3. 磁场的翻转在某些情况下，磁场的方向会发生翻转，即从一个极性变为另一个极性。

这种翻转在地磁场中经常出现，例如地球的地磁南北极会发生位置交换。

4. 磁场的扭曲当磁场遇到某种介质时，磁场线会发生扭曲。

这种扭曲在磁材料或铁磁体附近会更加显著，因为它们对磁场具有较强的吸引力。

三、常见的磁场变化方式1. 均匀磁场均匀磁场是指在一个空间区域内，磁场强度和方向都是恒定不变的。

这种磁场常见于电磁铁或形状规则的磁体中。

在均匀磁场中，磁场线平行且间距相等。

2. 非均匀磁场与均匀磁场相反，非均匀磁场的特点是磁场强度或方向在空间区域内存在变化。

这种磁场常见于一些特殊的磁体设计中，例如磁铁的两极之间。

3. 交变磁场交变磁场是指磁场强度和方向随时间发生周期性变化的磁场。

例如，交流电在导线中产生的磁场就是交变磁场。

交变磁场的变化规律可以用正弦曲线来描述。

4. 旋转磁场旋转磁场是指磁场强度和方向绕轴线旋转的磁场。

这种磁场通常由多个电流通过的导线形成，例如交流电动机中的旋转磁场。

磁场的变化规律在各个领域都起着重要作用。

它不仅是物理学和电磁学基本理论的研究对象，也被应用于电气工程、电磁感应、磁共振成像等技术领域。

电动力学-郭硕鸿-第三版-课后题目整理

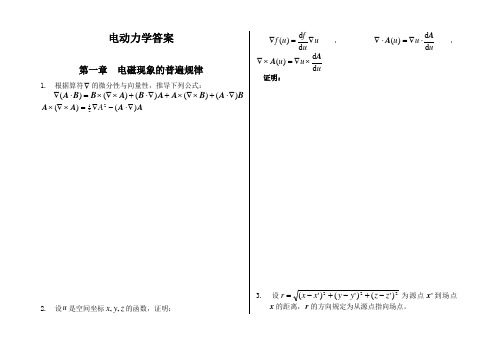
电动力学答案第一章电磁现象的普遍规律1. 根据算符∇的微分性与向量性，推导下列公式：BA B A A B A B B A )()()()()(∇⋅+⨯∇⨯+∇⋅+⨯∇⨯=⋅∇A A A A )()(221∇⋅-∇=⨯∇⨯A2. 设u 是空间坐标z y x ,,的函数，证明：u uf u f ∇=∇d d )(，uu u d d )(A A ⋅∇=⋅∇，u u u d d )(A A ⨯∇=⨯∇ 证明：3. 设222)'()'()'(z z y y x x r -+-+-=为源点'x 到场点x 的距离，r 的方向规定为从源点指向场点。

（1）证明下列结果，并体会对源变量求微商与对场变量求微商的关系：r r r /'r =-∇=∇ ； 3/)/1(')/1(r r r r -=-∇=∇ ；0)/(3=⨯∇r r ；0)/(')/(33=⋅-∇=⋅∇r r r r ， )0(≠r 。

（2）求r ⋅∇ ，r ⨯∇ ，r a )(∇⋅ ，)(r a ⋅∇ ，)]sin([0r k E ⋅⋅∇及)]sin([0r k E ⋅⨯∇ ，其中a 、k 及0E 均为常向量。

4. 应用高斯定理证明f S f ⨯=⨯∇⎰⎰SVV d d ，应用斯托克斯（Stokes ）定理证明⎰⎰=∇⨯LSϕϕl S d d5. 已知一个电荷系统的偶极矩定义为'd '),'()(V t t Vx x p ⎰=ρ，利用电荷守恒定律0=∂∂+⋅∇tρJ证明p 的变化率为：⎰=VV t t d ),'(d d x J p6. 若m 是常向量，证明除0=R 点以外，向量3/R ）（R m A ⨯=的旋度等于标量3/R R m ⋅=ϕ的梯度的负值，即ϕ-∇=⨯∇A ，其中R 为坐标原点到场点的距离，方向由原点指向场点。

7. 有一内外半径分别为1r 和2r 的空心介质球，介质的电容率为ε，使介质球内均匀带静止自由电荷f ρ，求：（1）空间各点的电场；（2）极化体电荷和极化面电荷分布。

电动力学课程教学大纲(物理学教育专业)

《电动力学》课程教学大纲（物理学教育专业）Electrodynamics(课程编号0431104)（学分 4 ，学时68）第一部份课程的性质与目的要求电动力学是高等师范院校本科物理学教育专业理论物理课程之一，是一般物理电磁学的后继课。

通过本课程的学习，不仅使学生对电磁现象的熟悉在电磁学唯象理论的基础上更深切一步，认清电磁场的本质，了解相对论的时空观，而且要学习理论物理学处置问题的方式，提高在本课程领域分析、解决实际问题的能力。

要求：学好先行课《电磁学》、《矢量分析》、《数学物理方式》。

第二部份课程内容和学时分派本大纲采纳从电磁现象的体会定律总结出麦克斯韦方程组，然后别离处置电磁场各类问题的体系，以维持电磁场理论的完整性。

要紧教学经典电动力学和狭义相对论。

共安排68学时，其中教学58学时，习题课10学时，打＊号内容能够不讲。

考虑到先行课程《矢量分析与场论》并未开设，因此安排第0章（4学时）作为预备知识，教学矢量分析与场论的基础知识。

第0章预备知识矢量分析与场论基础（4学时）一、教学内容：矢量代数梯度、散度和旋度关于散度和旋度的一些定理∇算符运算公式曲线正交坐标系二、教学要求：(1) 明白得矢量场的大体概念；（2）把握∇算符（矢量微分算符）与函数的运算；3、教学重点、难点：重点：∇算符(矢量微分算符)的运算难点：梯度、散度和旋度的明白得第一章电磁现象的普遍规律（10+2学时）一、教学内容：电荷和电场库仑定律，高斯定理，电场的散度和旋度电流和磁场电荷守恒定律，毕奥－萨伐尔定律，磁场的散度和旋度，磁场旋度和散度公式的证明麦克斯韦方程组电磁感应定律，位移电流，麦克斯韦方程组和洛仑兹力公式介质的电磁性质介质的概念，介质的极化和磁化，介质中的麦克斯韦方程组电磁场的边值关系法向分量的跃变，切向分量的跃变电磁场的能量电磁能量守恒定律的一样形式，能量密度和能流密度表示式，电磁能量的传输二、教学要求：（1）明白得描述宏观电磁场的物理量，描述宏观电磁场的麦克斯韦方程组；（2）把握真空、介质中的麦克斯韦方程组及其麦克斯韦方程组知足的边界条件；还要把握电磁场的能量、动量表达式，和能量、动量守恒定律；（3）了解描述电磁场能量密度和麦克斯韦应力张量等概念。

磁共振成像静磁场的作用

果越显著；
（3）与γ成正比：γ大的核种，宏观磁化效应M0大。
原子核的自旋与磁矩原子组成？核组成？ ➢ 电子、质子、中子有自旋特性。
1．自旋：原子核不停地绕其自身轴进行旋转（spin）(象地球高速绕自转轴旋转)。 ➢ 这种旋转与圆线圈中的电流类似，会产生磁场； ➢自旋(spin) 原子核具有磁矩的原因。
• 地球自转产生磁场
• 原子核的质子带正电荷，其自旋产生的磁场称为核磁，因而以前把磁共振成像称为核磁共振成像（NMRI）。
称为磁化强度。
• 依照量子物理学原理，原子核磁矩μN （μ）进入B0后其空间取向
发生量子化，即只能取一些确定的方向。
• μ在B0方向的投影是一些不连续的数值。 μ的不同取向，形成它与 B0相互作用能不同。μ与B0的相互作用能称为位能。在B0中μ的位
能为：
E B0 h B0 IZ / 2
• 取Z轴沿着B0方向，设μ与B0间的夹角为θ， μ的各坐标分量如图所
示。
• μZ为常数，说明μ在Z
轴上的投影是不变的。
• 质子的进动过程，Z轴代表B0磁力线方向，箭头代表某一方向的自旋质子的矢量即质子的μ ，其长短代表μ的大小。
• 质子进动的频率非常快，每秒进动的次数称“进动频率”（precession frequency）。
3．原子核的自旋角动量
• 人体有1H、13C、19F、23Na、31P等百余种元素。 • 生物组织中，1H占原子数量的2/3，1H为磁化最高的原子核，目前生物组织的磁共振成像主
要是1H成像。
1．具有较高的组织对比度和组织分辨力； 2．多方位成像； 3．多参数成像； 4．能进行形态学、功能、组织化学和生物化学方面的研究； 5．多种特殊成像； 6．以射频脉冲作为的能量源，对人体安全、无创； 7．流动测量。

磁场的矢势及其微分方程

通过曲面s的磁通量把b对任一个以回路l为边界的曲面s积分个有共同边界l的曲面则包围的区域内没有磁感应线发出也没有磁感应线终止b线连续的通过该区域因而通过曲面s的磁通量必须等于通过曲面s的磁通量
第三章静磁场
恒定电流所激发的静磁场
1
主要内容
矢势及其微分方程磁标势磁多极矩阿哈罗夫－玻姆(Aharonov-Bohm)效应超导体的电磁性质
Wi J Ae dV .
34
例1 无穷长直导线载
电流I，求磁场的矢势和磁感应强度。
35
解
得
设P点到导线的垂直距离为R,电流元Idz到P点的距离为
利用
R z
2
2
' J ( x )dV ' A( x ) r . 4
I Az 4

dz R z
2 A J
若取A满足规范条件A=0 ，得矢势的微分方程
( A 0)
20
A的每个直角分量Ai满足泊松方程
Ai J i , (i 1,2,3)
2
形式与静电场的方程相同

2

21
对比静电场的解得矢势方程的特解
' ' J ( x )dV A( x ) . r 4
的任一曲面的磁通量。只有A的环量才
有物理意义，而每点上的值没有直接的物理意义。
11
例：设有沿 Z 轴方向的均匀磁场
Bx By 0
其中B0为常量。
Bz B0 ,
12
由定义式
Ay
Ax B0 , x y Az Ay Ax Az 0 y z z x

磁场的屏蔽问题.

磁场的屏蔽问题，是一个既具有实际意义又具有理论意义的问题。

根据条件的不同，电磁场的屏蔽可分为静电屏蔽、静磁屏蔽和电磁屏蔽三种情况，这三种情况既具有质的区别，又具有内在的联系，不能混淆。

静电屏蔽在静电平衡状态下，不论是空心导体还是实心导体；不论导体本身带电多少，或者导体是否处于外电场中，必定为等势体，其内部场强为零，这是静电屏蔽的理论基础。

因为封闭导体壳内的电场具有典型意义和实际意义，我们以封闭导体壳内的电场为例对静电屏蔽作一些讨论。

（一）封闭导体壳内部电场不受壳外电荷或电场影响。

如壳内无带电体而壳外有电荷q，则静电感应使壳外壁带电（如图1）。

静电平衡时壳内无电场。

这不是说壳外电荷不在壳内产生电场，根发电场。

由于壳外壁感应出异号电荷，它们与q在壳内空间任一点激发的合场强为零。

因而导体壳内部不会受到壳外电荷q或其他电场的影响。

壳外壁的感应电荷起了自动调节作用。

如果把上述空腔导体外壳接地（图2），则外壳上感应正电荷将沿接地线流入地下。

静电平衡后空腔导体与大地等势，空腔内场强仍然为零。

如果空腔内有电荷，则空腔导体仍与地等势，导体内无电场。

这时因空腔内壁有异号感应电荷，因此空腔内有电场（图3）。

此电场由壳内电荷产生，壳外电荷对壳内电场仍无影响。

由以上讨论可知，封闭导体壳不论接地与否，内部电场不受壳外电荷影响。

（二）接地封闭导体壳外部电场不受壳内电荷的影响。

如果壳内空腔有电荷q，因为静电感应，壳内壁带有等量异号电荷，壳外壁带有等量同号电荷，壳外空间有电场存在（图4），此电场可以说是由壳内电荷q间接产生。

也可以说是由壳外感应电荷直接产生的但如果将外壳接地，则壳外电荷将消失，壳内电荷q与内壁感应电荷在壳外产生电场为零（图5）。

可见如果要使壳内电荷对壳外电场无影响，必须将外壳接地。

这与第一种情况不同。

这里还须注意：①我们说接地将消除壳外电荷，但并不是说在任何情况壳外壁都一定不带电。

假如壳外有带电体，则壳外壁仍可能带电，而不论壳内是否有电荷（图6）。

静磁场的主要作用

静磁场的主要作用一、静磁场的定义静磁场是指不随时间变化的磁场。

它由静止的电荷和电流所产生，与电荷和电流的运动速度无关。

二、静磁场的产生静磁场的产生有两种方式：一是由静止的电荷所产生的电场，当电荷运动时，会产生磁场；二是由电流所产生的磁场。

根据安培定律，电流通过导线时会形成环绕导线的磁场。

三、静磁场的特性1.磁场线：静磁场的磁力线是闭合曲线，从南极指向北极，形成环绕磁体的磁场。

2.磁感应强度：磁感应强度（B）是描述磁场强弱的物理量，单位是特斯拉（T）。

3.磁力：磁场中的物体会受到磁力的作用，磁力的大小与物体所带电流的大小和方向有关。

4.磁场的方向：磁场的方向由磁力线的方向确定，磁力线指示了磁场的方向。

5.磁场的分布：磁场的分布与磁体的形状和大小有关，磁场强度随距离的增加而减小。

1.磁力对物体的作用：静磁场中的物体会受到磁力的作用。

例如，磁铁可以吸引铁磁性物体，这是由于磁力的作用。

2.电磁感应：静磁场可以引起电磁感应现象。

当磁场发生变化时，会在电路中产生感应电动势，从而产生电流。

这是电力变压器、电动机等电器工作的基础。

3.磁场对运动带电粒子的影响：静磁场对运动带电粒子有力场和做功的作用。

例如，质子在磁场中受到洛伦兹力的作用，使得质子做圆周运动。

4.磁场的导向作用：静磁场可以导向带电粒子的运动轨迹。

利用这一特性，可以制造磁聚焦装置，如电子显微镜中的电子透镜，将电子束聚焦到一点上，提高分辨率。

5.磁场的屏蔽作用：静磁场可以被屏蔽，通过在磁场周围放置磁屏蔽材料，如铁、钴等，可以减弱或屏蔽磁场的影响。

总结：静磁场是不随时间变化的磁场，由静止的电荷和电流所产生。

它具有磁场线、磁感应强度、磁力、磁场的方向和分布等特性。

静磁场的主要作用包括磁力对物体的作用、电磁感应、磁场对运动带电粒子的影响、磁场的导向作用和磁场的屏蔽作用。

这些作用在日常生活和科学研究中都有重要应用，深入理解和研究静磁场的主要作用对于推动科学技术发展具有重要意义。

磁共振成像技术-3_真题-无答案

磁共振成像技术-3(总分100,考试时间90分钟)1. 在眼眶的MR检查中，能显示视神经全长的位置是A．横轴位和冠状位B．横轴位和斜矢状位C．冠状位和斜矢状位D．冠状位和正矢状位E．横轴位和正矢状位2. 关于空间分辨力的叙述，正确的是A．空间分辨力与FOV成正比B．空间分辨力与矩阵成反比C．空间分辨力与扫描层厚成正比D．空间分辨力与MR设备的磁场强度无关E．空间分辨力与体素大小成反比3. 关于射频脉冲的描述，正确的是A．射频脉冲的角度可以在0～180°之间，根据序列要求来选择 B．在二维傅立叶变换中，通常用选择性激发射频脉冲C．在三维傅立叶变换中，通常用选择性激发射频脉冲D．射频脉冲的宽度决定激发后的翻转角度E．射频脉冲的幅度决定激发的频率范围4. SS-EPI与MS-EPI相比较，最大优势在于A．信号强度高B．空间分辨率高C．扫描时间短D．磁敏感伪影减少E．扫描野不受限制5. 关于永磁型磁体的特点，错误的是A．无需磁场电源，电能消耗少B．磁体自重很大C．磁场强度较低D．磁场方向为水平方向E．扫描孔开放程度高6. 关于信噪比的说法，正确的是A．兴趣区内，最高信号和最低信号的差值与背景噪声的比值 B．信噪比越高越好C．信噪比与体素大小直接相关，与设备的场强大小无关D．成像的体素越大，信噪比越高；体素越小，信噪比越低 E．信噪比与射频线圈类型无关7. 被检者进行磁共振检查时，体温的变化主要是由于A．静磁场的生物效应造成的B．射频场的生物效应造成的C．层面选择梯度场的生物效应造成的D．相位编码梯度场的生物效应造成的E．频率编码梯度场的生物效应造成的8. 在二维采集时，脉冲重复期间允许采集的最多层数与哪项无关A．重复时间B．最大回波时间C．应用脂肪饱和技术D．特殊吸收率E．扫描野9. 关于垂体动态增强扫描的描述，错误的是A．垂体部位的肿瘤应常规行垂体动态增强扫描B．怀疑有垂体微腺瘤时，应行垂体动态增强扫描C．垂体动态增强扫描用半量对比剂(6～7ml)就可以D．垂体扫描时，必须用薄层(2～3mm)E．在垂体动态增强扫描图像上，正常垂体增强明显10. 关于信噪比的说法，错误的是A．TR时间延长，信噪比增加B．TE时间越长，信噪比下降C．翻转角增加，信噪比增加D．层间距与信噪比无关E．减少接收带宽，信噪比增加11. 要产生T1加权图像，应选择A．TR:2500ms、TE:100msB．TR:2500ms、TE:25msC．TR:450ms、TE:15msD．TR:450ms、TE:100msE．TR:5000ms、TE:120ms12. 腰椎矢状位扫描时，相位编码方向应选上下方向，以下解释不正确的是A．减少脑脊液的搏动伪影B．增加前后方向的空间分辨力C．可以避免前后方向的磁敏感伪影D．减少腹主动脉的搏动伪影E．减少呼吸运动带来的伪影13. 关于鼻咽部MR扫描方法的描述，不正确的是A．横轴位的定位范围为上自硬腭，下至第5颈椎下缘B．冠状位的定位方法是选正中矢状位为定位图像，定位线与喉、气管平行，覆盖整个鼻咽部C．矢状位的定位方法是选横轴位和冠状位为定位像，定位线与大脑纵裂平行D．鼻咽部的T2加权像一定要加抑脂技术E．怀疑有病变时，一定要做三个方向的增强扫描，并且都要加抑脂技术14. 要产生重T2加权图像，应选择A．TR:2500ms、TE:100msB．TR:2500ms、TE:25msC．TR:450ms、TE:15msD．TR:450ms、TE:100msE．TR:5000ms、TE:120ms15. 受检者进行磁共振检查过程中，所听到的噪音主要是由A．静磁场造成的B．射频场造成的C．梯度场造成的D．脉冲序列翻转角度不同造成的E．回波链长度造成的16. 下列操作不属于射频屏蔽的是A．磁体间的天花板和四壁及地板用铜板或不锈钢板密封安装B．操作间与磁体间的观察窗口要用铜网做屏蔽体C．所有进出磁体间的管道、电源线、信号线等，必须通过波导板或波导管D．在磁体中额外放置一个线圈，其内通以与静磁场线圈电流方向相反的电流E．磁体间的门与墙壁的磁屏蔽要密切贴合17. 关于磁场均匀度的说法，错误的是A．磁场均匀度的单位为ppmB．测量磁场均匀度时，一定要将球形空间的中心与磁体中心同心C．对于同一台设备，其磁场均匀度的大小是一个恒定的数值，与测量所用球体的大小无关D．磁场均匀度越好，图像信噪比越高E．磁场均匀度会随着周围环境的变化而变化18. 在FSE序列中，扫描时间的长短A．与TR时间成正比B．与TE时间成正比C．与TI时间成正比D．与回波链长度成正比E．与相位编码数成反比19. 脑部软化灶的MR表现是A．在T1加权像上是高信号，在T2加权像上是高信号，在DWI上是高信号B．在T1加权像上是高信号，在T2加权像上是低信号，在DWI上是高信号C．在T1加权像上是低信号，在T2加权像上是高信号，在DWI上是低信号D．在T1加权像上是低信号，在T2加权像上是高信号，在DWI上是高信号E．在T1加权像上是低信号，在T2加权像上是低信号，在DWI上是低信号20. 50 mT/m表示的意义是A．磁共振设备的梯度场线性值B．磁共振设备的梯度场强值C．磁共振设备的梯度场切换率D．磁共振设备的磁场均匀性E．磁共振设备的磁场强度21. 反转恢复脉冲序列的构成是A．小角度激发脉冲，多个180°复相脉冲B．90°激发脉冲，多个180°复相脉冲C．180°反转脉冲，90°激发脉冲，180°复相脉冲D．90°激发脉冲，一个180°复相脉冲E．多个90°脉冲，一个180°复相脉冲22. 核磁共振现象是在哪一年被发现的A．1937年B．1946年C．1952年D．1978年E．1981年23. 腰椎MR检查时，相位编码方向正确的是A．横轴位为左右方向，矢状位为前后方向，冠状位为上下方向B．横轴位为左右方向，矢状位为上下方向，冠状位为左右方向C．横轴位为前后方向，矢状位为前后方向，冠状位为上下方向D．横轴位为前后方向，矢状位为上下方向，冠状位为上下方向E．横轴位为左右方向，矢状位为前后方向，冠状位为左右方向24. 关于主磁场的说法，错误的是A．在一定范围内，主磁场强度越高，图像信噪比越高B．主磁场强度大小就是常说的静磁场的大小C．场强较高的磁共振设备，化学位移伪影较小D．磁场强度越大，设备造价越高E．提高主磁场强度的唯一途径就是采用超导磁体25. 关于梯度系统的描述，正确的是A．在梯度系统中，梯度放大器输出梯度电流，梯度电流激励梯度线圈产生梯度磁场 B．梯度放大器无需冷却装置C．梯度线圈无需冷却装置D．梯度线圈有X、Y、Z三个方向，每个方向有一个线圈形成梯度场E．梯度线圈必须浸在液氦中26. 射频线圈的作用是A．只能用来发射射频脉冲B．不能用来接收射频脉冲C．既可以发射射频脉冲，也可以用来接收射频脉冲D．进行空间定位E．维持稳定的静磁场27. “马凡综合征”扫描时，显示最好的位置是A．显示两腔心的心脏长轴位B．显示四腔心的心脏长轴位C．心脏短轴位D．主动脉弓位E．横轴位28. 关于颈部血管的描述，错误的是A．椎动脉走行于颈椎的横突孔内B．颈内动脉走行于颈椎的横突孔内C．椎基底静脉与硬膜外静脉汇合D．血管的信号在GRE序列中可以表现为高信号E．血管的信号在SE序列中可以表现为流空的低信号29. 颈部MRA检查时，自主动脉弓分出的三支大血管分别是A．椎动脉、颈内动脉、锁骨下动脉B．右颈总动脉、椎动脉、左锁骨下动脉C．右头臂干动脉、左颈总动脉、左锁骨下动脉D．右锁骨下动脉、右颈总动脉、头臂干动脉E．左颈总动脉、右颈总动脉、头臂干动脉30. 脉络膜黑色素瘤，应选择A．T1抑脂，T2不抑脂B．T1不抑脂，T2抑脂C．T1不抑脂，T2不抑脂D．T1抑脂，T2抑脂E．T1、T2抑脂不抑脂均可31. 急性期脑梗死的MR表现是A．在T1加权像上是高信号，在T2加权像上是高信号，在DWI上是高信号 B．在T1加权像上是高信号，在T2加权像上是低信号，在DWI上是高信号 C．在T1加权像上是低信号，在T2加权像上是低信号，在DWI上是低信号 D．在T1加权像上是低信号，在T2加权像上是高信号，在DWI上是高信号 E．在T1加权像上是低信号，在T2加权像上是低信号，在DWI上是低信号32. 当FOV的大小确定后，下列叙述正确的是A．矩阵数目相同时，扫描层厚越薄，空间分辨力越高B．矩阵数目相同时，扫描层厚越厚，空间分辨力越高C．扫描层厚相同时，矩阵越大，空间分辨力越低D．扫描层厚相同时，矩阵越小，空间分辨力越高E．空间分辨力的大小也就确定了33. 下列哪种疾病不适合做MR检查A．肝癌B．颈部软组织疾病C．肺部支气管扩张D．脑部疾病E．骨关节系统疾病34. 下列属于磁屏蔽操作的是A．在磁体中额外放置一个线圈，其内通以与静磁场线圈电流方向相反的电流 B．在磁体间的四壁及天花板，嵌入吸音材料板C．磁体中的失超管设计技术D．磁体间的氧气监测器E．在磁体内壁上的不同位置，放置一定形状和尺寸的专用小铁片35. 心脏扫描的轴心应选择A．与人体的长轴一致B．二尖瓣与左室心尖的连线C．三尖瓣与右室心尖的连线D．与人体长轴成30°的方向E．沿升主动脉和降主动脉的连线36. 不同组织在MRI图像上的明暗信号不同，这与什么因素无关A．组织间密度差异B．组织的T1值C．组织的T2值D．组织间质子密度差异E．组织的磁敏感性37. 延长重复时间可使A．信噪比降低B．T2权重增加C．T1权重增加D．扫描时间缩短E．允许的扫描层数减少38. 下列技术不能有效地改善化学位移伪影的是A．施加脂肪抑制技术B．改变频率编码方向C．减少频率编码方向的采样带宽D．增加频率编码方向的采样带宽E．用主磁场强度较低的设备进行扫描39. 下列不能应对卷褶伪影的是A．将扫描层面中径线较短的方向设置为相位编码方向B．相位编码方向过采样C．增大FOVD．施加空间预饱和带E．将扫描层面中径线较长的方向设置为相位编码方向40. 下列描述错误的是A．短TR短TE时，可获得T1加权图像B．长TR长TE时，可获得T2加权图像C．短TR长TE时，可获得质子密度加权图像D．长TR短TE时，可获得质子密度加权图像E．一个序列中，可同时选择两个回波时间，即双回波序列41. 关于自旋回波脉冲序列的构成，正确的是A．小角度激发脉冲，多个180°复相脉冲B．90°激发脉冲，多个180°复相脉冲C．180°反转脉冲，90°激发脉冲，180°复相脉冲D．90°激发脉冲，一个180°复相脉冲E．多个90°脉冲，一个180°复相脉冲42. 下列不属于化学位移伪影特点的是A．化学位移伪影出现在脂肪组织与其他组织交界的界面上B．随着磁场强度的升高，化学位移伪影将明显改善C．脂肪组织的信号向频率编码梯度场较低的一侧移动D．化学位移伪影既可以出现在频率编码方向上，也可以出现在相位编码方向上 E．化学位移伪影常出现在含水组织和脂肪组织交界处43. 关于磁共振设备对受检者体内铁磁性置入物的影响，错误的是A．置入物的位置发生变化B．置入物发生功能紊乱C．置入物的热效应D．置入物周围组织的灼伤E．不会有任何反应44. 绝对零度是A．0℃B．-273℃C．-173℃D．-246℃E．-146℃45. 关于卷褶伪影的说法，正确的是A．卷褶伪影是由于FOV过大造成的B．卷褶伪影在2D采集中经常出现，在3D采集中不会出现C．卷褶伪影出现在频率编码方向D．卷褶伪影出现在相位编码方向E．卷褶伪影既可以出现在相位编码方向上，也可以出现在频率编码方向上46. 关于磁场均匀度的说法，正确的是A．磁场均匀度与测量所用的球体大小成正比B．磁体的成像区域越大，其磁场均匀度越低C．磁场均匀度的单位为：mT/cm2D．磁场均匀度与成像质量无关E．在测量所用球体大小相同的情况下，ppm值越高，说明磁场均匀度越好47. 关于化学位移成像的叙述，正确的是A．在相同的磁场强度中，不同分子中的同一种的原子，其共振频率相同B．化学位移伪影可以被抑制掉C．磁场强度越大，化学位移伪影越严重D．在水脂同反相位成像中，同相位成像时，水脂信号相减；反相位时，水脂信号相加 E．STIR序列利用的就是化学位移成像技术48. 不属于HASTE序列优点的是A．仅需一次激发就可以完成采集，运动伪影明显减少B．该序列主要应用于T2加权成像C．采集方式与其他序列不同，仅采集部分相位编码行，扫描时间降低近一半D．以放射线方式填充K空间E．可用于内耳、胆道、椎管等部位的水成像检查49. 鉴别鞍区病变是出血还是脂肪时，需做哪个序列A．T1脂肪抑制序列B．T1水抑制序列C．T2脂肪抑制序列D．T2水抑制序列E．弥散加权序列50. 为观察肝脏左叶的病变，应如何设置相位编码方向A．随意设置，影响都不大B．应设置为前后方向C．应设置为左右方向D．应设置为上下方向E．应设置为下上方向51. 关于出血的MR表现，正确的是A．在T1加权像上高信号，在T2加权像上也是高信号B．在T1加权像上高信号，在T2加权像上是低信号C．在T1加权像上低信号，在T2加权像上是高信号D．在T1加权像上低信号，在T2加权像上也是低信号E．出血部位的MR信号强度与血红蛋白含氧量和红细胞的完整性有关52. 以下哪一项操作不会增加扫描时间A．增加采集次数B．增加相位编码数C．增加饱和带D．增加频率编码数E．增加重复时间53. 重复时间是指A．脉冲序列的一个周期所需要的时间B．激发脉冲与产生回波之间的时间C．在SE序列中，90°脉冲与180°脉冲之间的时间D．在SE序列中，两个180°脉冲之间的时间E．完成一个脉冲序列所需的检查时间54. 要产生质子密度加权图像，应选择A．TR:2500ms、TE:100msB．TR:2500ms、TE:25msC．TR:450ms、TE:15msD．TR:450ms、TE:100msE．TR:5000ms、TE:120ms55. 磁共振成像的空间定位依赖于A．主磁场B．梯度磁场C．射频磁场D．组织的质子密度E．组织的弛豫时间56. 在T1和T2加权像上，均呈黑色无信号的是A．脂肪组织B．肌肉组织C．骨骼D．气体E．水57. 关于运动伪影的叙述，错误的是A．运动伪影包括生理性运动伪影和自主性运动伪影B．生理性运动是无法靠外力控制的，所以，伪影也无法改善C．生理性运动伪影可以通过磁共振设备和扫描技术的进步不断地改善D．自主性运动伪影可以通过改变扫描参数，缩短扫描时间加以改善E．自主性运动伪影可以通过人为的、外加固定装置等方法加以改善58. 在T1和T2加权像上，均呈较高信号的是A．脂肪组织B．肌肉组织C．骨骼D．气体E．水59. 关于快速自旋回波序列的描述，错误的是A．90°脉冲后，多个180°复相位脉冲B．射频能量积累高于普通的SE序列C．明显缩短扫描时间，运动伪影可减少D．多个180°复相脉冲，可以产生多个回波信号，每个回波信号强度均匀一致E．回波链的长度不可以无限多60. 人体中，不可用于磁共振成像的原子核是A．氢原子核B．碳原子核C．磷原子核D．钠原子核E．钙原子核61. 为得到高信噪比的图像，应选择A．覆盖范围较大的线圈B．鸟笼式线圈C．大体线圈D．表面线圈E．根据检查部位的形状和大小来选择线圈62. 乳腺扫描时，相位编码方向正确的是A．横轴位，相位编码方向为左右B．横轴位，相位编码方向为前后C．冠状位，相位编码方向为左右D．冠状位，相位编码方向为前后E．矢状位，相位编码方向为前后63. 关于腰椎部正常解剖的描述，错误的是A．腰椎椎体的横径大于前后径B．腰椎间盘由软骨板、纤维环及髓核三部分构成C．脊髓在腰椎1～2水平移行为终丝D．随着年龄的增加，椎体骨髓腔内的脂肪成分逐渐减少E．椎管由前面的椎体、侧面的椎弓及后面的椎板、棘突组成64. 喉部的横轴位扫描定位范围在A．第2～4颈椎水平B．第2～5颈椎水平C．第3～5颈椎水平D．第3～6颈椎水平E．第5～7颈椎水平65. 关于矩阵的描述，不正确的是A．矩阵=频率编码数×相位编码数B．调整图像采集矩阵可以改变图像的信噪比C．增加相位方向编码数会增加扫描时间D．增加频率方向编码数不增加扫描时间E．当扫描野不变时，矩阵越大，图像的分辨率越低66. 关于匀场的描述，错误的是A．匀场的操作必须在励磁结束后才能进行B．主动匀场就是利用匀场线圈通以电流，产生小磁场，通过调节电流强度来提高磁场均匀性C．被动匀场就是在磁体内壁上的不同位置，放置一定形状和尺寸的专用小铁片来提高磁场均匀性D．匀场时，一般先进行主动匀场，再进行被动匀场E．匀场时，一般先进行被动匀场，再进行主动匀场67. 下列说法错误的是A．磁共振成像设备被列为甲类大型医用影像设备B．医院购买磁共振成像设备需要特别申请配置许可证C．磁共振设备要放置在严格磁屏蔽的房间内D．磁共振成像设备被列为乙类大型医用影像设备E．操作磁共振设备的工作人员应持证上岗68. 为缩短采集时间，错误的是A．减少TRB．采用并行采集技术C．减少相位编码数D．减少扫描层数E．减少TE69. 自由感应衰减信号产生于射频脉冲激励自旋质子A．之前B．之中C．之后D．任何时刻E．无法确定70. 目前，应用于临床人体成像的磁共振设备，其场强限制在A．1TB．3TC．4TD．7TE．9T71. 不是利用磁化传递技术检查的是A．MR血管成像B．骨关节检查，特别是关节软骨的显示C．MR增强检查D．扩散加权成像E．多发硬化病变的检查72. 下列哪项不是反映磁体性能的指标A．磁场强度B．磁场均匀度C．磁场稳定性D．磁体重量E．扫描孔径大小73. 关于扫描层厚的设置，不正确的是A．扫描层厚越薄，空间分辨力越高，信噪比也相应地增加 B．最薄层厚与设备的梯度场强大小相关C．应根据不同的解剖部位来设置扫描层厚D．扫描层厚过厚，易产生容积效应E．要根据病变大小来选择扫描层厚74. FISP是什么序列的缩写A．半傅立叶采集快速自旋回波序列B．稳态自由进动快速成像C．反转恢复快速梯度回波序列D．扰相位梯度回波序列E．快速梯度回波序列75. 下列哪个选项最有利于观察颅脑多发性硬化病的“垂直征”A．横轴位T1B．横轴位T2C．冠状位T1D．矢状位T1E．矢状位T276. 关于超导型磁体的说法，错误的是A．超导型磁体既适用于低场磁共振设备，也可用于高场及超高场的磁共振设备B．超导型磁体的磁共振设备，其磁场方向既可以是水平方向的，也可以是垂直方向的 C．超导型磁体的磁场均匀性很高D．超导型磁体需要液氦作为制冷剂E．超导型磁体的磁共振设备造价相当昂贵77. 关于弛豫的描述，错误的是A．外加磁场消失后，组织恢复至发生磁共振前的磁矩状态，此变化过程即为弛豫过程 B．弛豫过程分纵向弛豫和横向弛豫C．弛豫过程是能量变化的过程D．横向弛豫和纵向弛豫同时发生E．横向弛豫在先，纵向弛豫在后78. 关于化学位移成像的叙述，错误的是A．化学位移与磁场强度无关B．MRS的成像基础是化学位移C．可利用化学位移来实现压脂成像D．可利用化学位移来实现压水成像E．化学位移会导致化学位移伪影79. 关于梯度磁场的说法，错误的是A．没有梯度磁场，就无法进行空间定位，也就无法形成MR图像B．梯度磁场的大小决定了图像的最薄层厚C．梯度场切换率决定成像速度快慢D．梯度场强越高，图像的空间分辨率越高E．梯度场切换率越快，人耳听到的噪音越小80. 要产生T2加权图像，应选择A．TR:2500ms、TE:100msB．TR:2500ms、TE:25msC．TR:450ms、TE:15msD．TR:450ms、TE:100msE．TR:5000ms、TE:120ms81. 下列哪项不含脂肪抑制技术A．频率饱和法B．短时反转恢复序列C．化学位移饱和成像D．STIR序列E．FLAIR序列82. 下列哪一项不能使脂肪组织的信号下降A．化学饱和法B．频率饱和法C．短TI的反转恢复序列D．化学位移成像中的反相位成像E．自旋回波脉冲序列83. 关于MR对比剂的描述，错误的是A．MR对比剂一般无需做过敏试验B．MR对比剂非常安全，没有任何不宜使用的人群C．哺乳期妇女在用药24h后方可哺乳D．MR对比剂的用量为0.1mmol/kgE．MR对比剂的用量为0.2ml/kg84. 脑干由哪几部分组成A．延髓、脑桥、中脑B．脑桥、中脑、间脑C．延髓、中脑、间脑D．脑桥、中脑、丘脑E．中脑、间脑、丘脑85. 氢质子在3T的静磁场中，旋磁比为A．21.29MHzB．63.87MHzC．100MHzD．127.8MHzE．42.58MHz86. 关于垂体的解剖，正确的是A．垂体分为左、右两叶，左侧为腺垂体，右侧为神经垂体B．正常垂体柄的直径应≤4mmC．垂体窝两侧为海绵窦，其内有静脉窦、颈内动脉及第Ⅱ～Ⅵ对颅神经的海绵窦段 D．微腺瘤的直径＞1cmE．大腺瘤的直径＜1cm87. 回波时间是指A．一个回波与下一个回波之间的时间B．激发脉冲与下一个激发脉冲之间的时间C．激发脉冲与产生回波之间的时间D．90°脉冲与180°脉冲之间的时间E．180°脉冲与90°脉冲之间的时间88. 常导型和永磁型磁体的相同点是A．磁场方向B．需要高质量的稳定电源，且电能消耗大C．不需要液氦作为制冷剂D．磁场均匀性很高E．可制成高场强磁共振设备89. 磁共振对比剂钆喷酸葡胺(马根维显)的增强机制是A．明显延长组织的T1弛豫时间B．明显延长组织的T2弛豫时间C．明显缩短组织的T1弛豫时间D．明显缩短组织的T2弛豫时间E．改变质子密度的分布态势90. 关于正常胸段脊髓MR的影像表现，正确的是A．T1加权像上灰质信号比白质信号低B．T1加权像上灰质信号比白质信号高C．T2加权像上灰质信号比白质信号低D．脊髓灰质呈典型的蜘蛛足型E．脊髓灰质呈典型的马尾型91. 医用射频场SAR值的安全标准为A．全身平均SAR值≤0.4W/kgB．全身平均SAR值≤1.4W/kgC．全身平均SAR值≤2.4W/kgD．全身平均SAR值≤3.4W/kgE．全身平均SAR值≤4.4W/kg92. GRE序列与SE序列比较，优点有A．小角度脉冲激发可明显缩短采集时间B．脉冲能量较大，SAR值较大C．用180°复相位脉冲取代反转梯度脉冲D．可获得理想的T2加权像E．图像信噪比明显降低93. 关于反转恢复脉冲序列的描述，错误的是A．TI时间的选择，决定了磁共振图像的对比B．某组织的TI值决定于该组织的T1值，T1越长，TI值越大 C．短TI反转恢复脉冲序列常用于抑脂序列D．长TI反转恢复脉冲序列常用于抑水序列E．STIR和FLAIR序列均可以进行水抑制94. 在梯度回波序列中，为得到倾向于T2加权的图像，应选择A．翻转角为90°的射频脉冲B．翻转角为180°的射频脉冲C．翻转角为45°的射频脉冲D．翻转角为15°的射频脉冲E．翻转角为80°的射频脉冲95. 下列哪项不属于磁共振检查的优点A．多参数成像，可提供丰富的诊断信息B．无需对比剂，即可观察心脏和血管结构C．图像受外界干扰较少D．无电离辐射，可进行介入核磁治疗E．可进行功能成像，提供血流动力学方面的信息96. 考虑臂丛神经损伤时，以下不正确的是A．扫描的上下范围应包括颈4椎体上缘至胸2椎体下缘水平B．扫描的前后范围应包括椎体前缘至椎管后缘C．观察臂丛神经节前神经根时，应采用轴位扫描D．观察节后神经时，应采用冠状位扫描E．扫描序列无需加抑脂技术97. 关于K空间的描述，错误的是A．K空间是实际存在的空间，与MR信号的空间定位一一对应 B．K空间是计算机根据相位和频率的不同而给予的暂时识别定位 C．K空间中心位置的作用大于K空间周边位置的作用D．K空间的填充方式多种多样E．傅立叶变换可以解析K空间信息。

3静磁场

电动力学

从零开始3D maxwell磁场仿真之边界条件

电动力学教学大纲

电动力学 第三版_郭硕鸿_课后答案[第3章]

电动力学-选择题填空题判断题问答题复习

第三章 静磁场

静磁场

静磁场的主要作用

电动力学习题解答3

电学基础必会知识点总结

静磁场

磁场的变化规律

电动力学-郭硕鸿-第三版-课后题目整理

电动力学课程教学大纲(物理学教育专业)

磁共振成像 静磁场的作用

磁场的矢势及其微分方程

磁场的屏蔽问题.

静磁场的主要作用

磁共振成像技术-3_真题-无答案

电动力学第三版_郭硕鸿_课后答案[第3章]

第三章静磁场

磁共振成像静磁场的作用