2019-2020学年高中数学双曲线及其标准方程导学案新人教A版选修1-1.doc

合集下载

高二数学2.2.1双曲线及其标准方程学案新人教A版选修1-1

a， b， c 的关系： a＞ 0， b＞ 0， c2＝ a2＋b2．
? 思考：椭圆的标准方程和双曲线的标准方程有什么区别与联系？
答案：答案略． , ?自测自评 x2 y2
1．双曲线－＝ 1 的焦距是 ( D) 10 2
A． 3 2
B． 4 2
C． 3 3 D ． 4 3
解析： c2＝ 10＋ 2＝ 12 ，∴ c＝ 2 3，焦距 2c ＝ 4 3. x2 y2
高中数学 2.2.1 双曲线及其标准方程学案
?基础梳理
1．平面内与两个定点 F1、 F2 的距离的差的绝对值是常数 ( 小于 | F1F2| 且大于 0) 的点的轨迹叫
做双曲线，这两个定点叫做双曲线的焦点，两焦点间的距离叫做双曲线的焦距．
? 思考：在双曲线的定义中，为什么常数要大于
0 且小于 | F1F2|?
m2－ 4＜ 0，
解析：由题可知
∴－ 2＜ m＜－ 1.
m＋ 1＜ 0，
答案： ( － 2，－ 1)
c5 4．在双曲线中， a＝ 2 ，且双曲线与椭圆
4x 2＋ 9y2＝ 36 有公共焦点，求双曲线的方程．
解析：把椭圆的方程写成标准方程
x2 y2 9 ＋ 4 ＝ 1，
∴椭圆的焦点坐标是 ( ± 5， 0) ． ∵双曲线与椭圆有相同的焦点，
则由双曲线定义知 | r 1－ r 2| ＝ 2a＝ 4， ∴ ( r 1－ r 2) 2＝ r 21＋ r 22－ 2r 1r 2＝16. ①
又∵∠ F1MF2＝ 90°， ∴ r 21＋ r 22＝ | F1F2| 2＝ 4c 2＝52. ② ∴由①②得 r 1r 2＝ 18.
1 ∴ S△ F1MF2＝ 2r 1r 2＝ 9.

双曲线及其标准方程(教学设计)高二数学 (人教A版2019选择性必修第一册)

3.2.1双曲线及其标准方程教学设计本小节内容选自《普通高中数学选择性必修第一册》人教A版（2019）第二章《圆锥曲线的方程》的第二节《双曲线》。

以下是本节的课时安排：第三章圆锥曲线的方程课时内容 3.2.1双曲线及其标准方程 3.2.2双曲线的简单几何性质所在位置教材第118页教材第121页新教材内容分析双曲线是生产生活中的常见曲线，教材在用拉链画双曲线的过程中，体会双曲线的定义，感知双曲线的形状，为选择适当的坐标系，建立双曲线的标准方程、研究双曲线的几何性质做好铺垫。

通过对双曲线标准方程的讨论，使学生掌握标准方程中的a,b,c,e的几何意义及相互关系，体会坐标法研究曲线性质的基本思路与方法，感受通过代数运算研究曲线性质所具有的程序化、普适性特点。

核心素养培养通过双曲线的标准方程的推导，培养数学运算的核心素养；通过对双曲线的定义理解，培养数学抽象的核心素养。

通过双曲线的几何性质的研究，培养数学运算的核心素养；通过直线与双曲线的位置关系的判定，培养逻辑推理的核心素养。

教学主线双曲线的标准方程、几何性质学生已经学习了直线与圆的方程，已经具备了坐标法研究解析几何问题的能力。

本章学习圆锥曲线方程及几何性质，进一步提升用代数方法研究解析几何问题的方法。

1.了解双曲线的定义、几何图形和标准方程,培养数学抽象的核心素养．2.能利用双曲线的定义和待定系数法求双曲线的标准方程，培养逻辑推理的核心素养.重点：双曲线的定义及双曲线的标准方程难点：运用双曲线的定义及标准方程解决相关问题（一）新知导入双曲线也是具有广泛应用的一种圆锥曲线，如发电厂冷却塔的外形、通过声音时差测定定位等都要用到双曲线的性质。

本节我们将类比椭圆的研究方法研究双曲线的有关问题。

（二）双曲线及其标准方程知识点一双曲线的定义【探究1】取一条拉链，拉开它的一部分，在拉开的两边上各选择一点，分别固定在点F1、F2处，把笔尖放于点M，拉开闭拢拉链，笔尖经过的点可画出一条曲线，思考曲线满足什么条件？【提示】如图，曲线上的点满足条件：|MF1|－|MF2|＝常数；如果改变一下位置，使|MF2|－|MF1|＝常数，可得到另一条曲线．◆双曲线的定义F F？【思考1】双曲线的定义中，常数为2a，为什么2a12【提示】若2a＝|F1F2|，则动点的轨迹是以F1或F2为端点的射线；若2a＞|F1F2|，则动点的轨迹不存在．若a＝0，则动点的轨迹是线段F1F2的中垂线．【思考2】双曲线的定义中，为什么要加“绝对值”三个字？没有“绝对值”三个字呢？【提示】若去掉定义中的“绝对值”三个字，则动点的轨迹只能是双曲线的一支．【易错辨析】设F1、F2是双曲线的焦点，a=4,c=6,点P在双曲线上，若点P到焦点F1的距离等于9，求点P 到焦点F2的距离．【错解一】双曲线的a=4，由|PF1|－|PF2|＝8，即9－|PF2|＝8，得|PF2|＝1.【错解二】双曲线的a=4，由双曲线的定义得||PF1|－|PF2||＝8，所以|9－|PF2||＝8，所以|PF2|＝1或17.【错因】错解一是对双曲线的定义中的差的绝对值掌握不够，是概念性的错误．错解二没有验证两解是否符合题意，这里用到双曲线的一个隐含条件：双曲线的一个顶点到另一分支上的点的最小距离是2a，到一个焦点的距离是c－a，到另一个焦点的距离是a＋c，本题是2或10，|PF2|＝1小于2，不合题意．【正解】双曲线的实轴长为8，由双曲线的定义得||PF1|－|PF2||＝8，所以|9－|PF2||＝8，所以|PF2|＝1或17.因为|F1F2|＝12，当|PF2|＝1时，|PF1|＋|PF2|＝10＜|F1F2|，不符合公理“两点之间线段最短”，应舍去．所以|PF2|＝17.知识点二双曲线的标准方程【探究2】类比推导椭圆标准方程的方法，怎样推导双曲线的标准方程？【提示】(1)建系：以经过两焦点F1和F2的直线为x轴，线段F1F2的垂直平分线为y轴，建立平面直角坐标系．(2)设点：设M(x，y)是双曲线上任意一点，双曲线的焦距为2c(c>0)，那么双曲线的焦点F1，F2的坐标分别是(－c,0)，(c,0)．(3)列式：由|MF1|－|MF2|＝±2a，可得(x＋c)2＋y2－(x－c)2＋y2＝±2a.(4)化简：移项，平方后可得(c2－a2)x2－a2y2＝a2(c2－a2)．令c2－a2＝b2，得双曲线的标准方程为x2 a2－y2b2＝1(a＞0，b＞0)．◆双曲线的标准方程【思考3】怎样区分焦点在不同位置的两类双曲线的方程？它与椭圆的区分方法有何不同？【提示】椭圆由分母常数的大小判定，双曲线由各项前面的符号判定.【思考4】双曲线的标准方程与椭圆的标准方程在形式上有什么区别？a 、b 、c 之间的关系有何不同？【提示】a 、b 、c 之间的关系：椭圆是222b a c -=，双曲线是222b a c += （记忆方法：椭圆的焦点在顶点之内，所有a c <；双曲线焦点在顶点之外，所有a c >）【做一做1】双曲线x 210－y 22＝1的焦距为( )A ．32B ．4 2C ．3 3D ．43答案：D【做一做2】已知双曲线a ＝5，c ＝7，则该双曲线的标准方程为________．解析：∵a ＝5，c ＝7，∴b ＝c 2－a 2＝24＝26，当焦点在x 轴上时，双曲线方程为x 225－y 224＝1；当焦点在y 轴上时，双曲线方程为y 225－x 224＝1. 答案：x 225－y 224＝1或y 225－x 224＝1（三）典型例题1.求双曲线的标准方程例1.根据下列条件，求双曲线的标准方程．(1)经过点P (3，154)，Q (－163，5)； (2)c ＝6，经过点(－5,2)，焦点在x 轴上．[分析] 可先设出双曲线的标准方程，再构造关于a ，b 的方程组，求得a ，b ，从而求得双曲线的标准方程．注意对平方关系c 2＝a 2＋b 2的运用．[解析] (1)法一：若焦点在x 轴上，设双曲线的方程为x 2a 2－y 2b 2＝1(a >0，b >0)，由于点P (3，154)和Q (－163，5)在双曲线上，所以⎩⎨⎧9a 2－22516b 2＝1，2569a 2－25b 2＝1，解得⎩⎨⎧a 2＝－16，b 2＝－9，(舍去)．若焦点在y 轴上，设双曲线的方程为y 2a 2－x 2b 2＝1(a >0，b >0)，将P 、Q 两点坐标代入可得⎩⎨⎧22516a 2－9b 2＝1，25a 2－2569b 2＝1，解得⎩⎨⎧a 2＝9，b 2＝16，所以双曲线的标准方程为y 29－x 216＝1. 综上，双曲线的标准方程为y 29－x 216＝1.法二：设双曲线方程为x 2m ＋y 2n ＝1(mn <0)． ∵P 、Q 两点在双曲线上，∴⎩⎨⎧9m ＋22516n ＝1，2569m ＋25n ＝1，解得⎩⎨⎧m ＝－16，n ＝9.∴所求双曲线的标准方程为y 29－x 216＝1.(2)法一：依题意可设双曲线方程为x 2a 2－y 2b 2＝1(a >0，b >0)．则有⎩⎪⎨⎪⎧a 2＋b 2＝6，25a 2－4b2＝1，解得⎩⎨⎧a 2＝5，b 2＝1，求双曲线的标准方程为x 25－y 2＝1. 法二∵焦点在x 轴上，c ＝6，∴设所求双曲线方程为x 2λ－y 26－λ＝1(其中0<λ<6)．∴25λ－46－λ＝1，∴λ＝5或λ＝30(舍去)．∴所求双曲线的标准方程是x 25－y 2＝1.【类题通法】用待定系数法求双曲线标准方程的步骤(1)定位：确定双曲线的焦点位置，如果题目没有建立坐标系，一般把焦点放在x 轴上；(2)设方程：根据焦点的位置设相应的双曲线标准方程(当焦点在两个坐标轴上都有可能时，一般设为Ax 2＋By 2＝1(AB ＜0))；(3)定值：根据题目的条件确定相关的系数的方程，解出系数，代入所设方程．【巩固练习1】已知双曲线过M (1,1)，N (－2,5)两点，求双曲线的标准方程．[解析] 设双曲线的方程为Ax 2＋By 2＝1(AB <0)．∵双曲线过M (1,1)，N (－2,5)，∴⎩⎪⎨⎪⎧A ＋B ＝1，4A ＋25B ＝1，解得⎩⎨⎧A ＝87，B ＝－17，∴双曲线的标准方程为x 278－y 27＝1.2.双曲线标准方程的识别例2. (1)若曲线x 2k ＋4＋y 2k －1＝1表示双曲线，则k 的取值范围是( )A ．[－4,1)B ．(－∞，－4)∪(1，＋∞)C ．(－4,1)D ．(－∞，－4]∪[1，＋∞)(2)3<m <5是方程x 2m －5＋y 2m 2－m －6＝1表示的图形为双曲线的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分又不必要条件解析： (1)根据题意，若曲线x 2k ＋4＋y 2k －1＝1表示双曲线，则有(k ＋4)(k －1)<0，解得－4<k <1.(2)3<m <5时，m －5<0，m 2－m －6>0，方程x 2m －5＋y 2m 2－m －6＝1表示焦点在y 轴的双曲线；若方程x 2m －5＋y 2m 2－m －6＝1表示的图形为双曲线，则(m －5)(m 2－m －6)<0，所以3<m <5或m <－2，所以3<m <5是方程x 2m －5＋y 2m 2－m －6＝1表示的图形为双曲线的充分不必要条件．答案：(1)C (2)A【类题通法】将双曲线的方程化为标准方程的形式，假如双曲线的方程为x 2m ＋y 2n＝1，则当mn ＜0时，方程表示双曲线．若⎩⎪⎨⎪⎧m ＞0，n ＜0，则方程表示焦点在x 轴上的双曲线；若⎩⎪⎨⎪⎧m ＜0，n ＞0，则方程表示焦点在y 轴上的双曲线.【巩固练习2】若k >1，则关于x ，y 的方程(1－k )x 2＋y 2＝k 2－1所表示的曲线是( ) A ．焦点在x 轴上的椭圆 B ．焦点在y 轴上的椭圆 C ．焦点在y 轴上的双曲线 D ．焦点在x 轴上的双曲线解析：原方程化为y 2k 2－1－x 2k ＋1＝1，∵k >1，∴k 2－1>0，k ＋1>0.∴方程所表示的曲线为焦点在y 轴上的双曲线．答案：C3.双曲线的定义及应用例3.设双曲线x 24－y 29＝1，F 1、F 2是其两个焦点，点P 在双曲线右支上. 若∠F 1PF 2＝90°，求△F 1PF 2的面积．[分析] 用双曲线定义及余弦定理求出|PF 1|·|PF 2|. [解析] 由双曲线方程知a ＝2，b ＝3，c ＝13，设|PF 1|＝r 1，|PF 2|＝r 2(r 1>r 2)，如图所示．由双曲线定义，有r 1－r 2＝2a ＝4，两边平方得r 21＋r 22－2r 1r 2＝16. ∵∠F 1PF 2＝90°，∴r 21＋r 22＝4c 2＝4×(13)2＝52.∴2r 1r 2＝52－16＝36，∴S △F 1PF 2＝12r 1r 2＝9.【类题通法】双曲线中的焦点三角形：双曲线上的点P 与其两个焦点F 1，F 2连接而成的三角形PF 1F 2称为焦点三角形．令|PF 1|＝r 1，|PF 2|＝r 2，∠F 1PF 2＝θ，因|F 1F 2|＝2c ，所以有 (1)定义：|r 1－r 2|＝2a .(2)余弦公式：4c 2＝r 21＋r 22－2r 1r 2cos θ.(3)面积公式：S △PF 1F 2＝12r 1r 2sin θ.一般地，在△PF 1F 2中，通过以上三个等式，所求问题就会顺利解决．【巩固练习3】若F 1，F 2是双曲线x 29－y 216＝1的两个焦点，P 是双曲线上的点，且|PF 1|·|PF 2|＝32，试求△F 1PF 2的面积．[解析] 由双曲线方程x 29－y 216＝1，可知a ＝3，b ＝4，c ＝a 2＋b 2＝5.由双曲线的定义，得|PF 1|－|PF 2|＝±2a ＝±6，将此式两边平方，得|PF 1|2＋|PF 2|2－2|PF 1|·|PF 2|＝36，∴|PF 1|2＋|PF 2|2＝36＋2|PF 1|·|PF 2|＝36＋2×32＝100. 如图所示，在△F 1PF 2中，由余弦定理，得cos ∠F 1PF 2＝|PF 1|2＋|PF 2|2－|F 1F 2|22|PF 1|·|PF 2|＝100－1002|PF 1|·|PF 2|＝0，∴∠F 1PF 2＝90°，∴S △F 1PF 2＝12|PF 1|·|PF 2|＝12×32＝16.所以S △PF 1F 2＝12|PF 1||F 1F 2|·sin 120°＝12×65×2×32＝335，即△PF 1F 2的面积是35 3. 4. 与双曲线有关的轨迹问题例4.已知圆C 1：(x ＋3)2＋y 2＝1和圆C 2：(x －3)2＋y 2＝9，动圆M 同时与圆C 1及圆C 2相外切，求动圆圆心M 的轨迹方程．[解析] 如图所示，设动圆M 与圆C 1及圆C 2分别外切于点A 和B ，根据两圆外切的条件，得 |MC 1|＝|AC 1|＋|MA |，|MC 2|＝|BC 2|＋|MB |. ∵|MA |＝|MB |，∴|MC 2|－|MC 1|＝|BC 2|－|AC 1|＝3－1＝2.这表明动点M 与两定点C 2，C 1的距离的差是常数2，且2<| C 1C 2|.根据双曲线的定义，动点M 的轨迹为双曲线的左支，则2a ＝2，a ＝1，c ＝3，∴b 2＝c 2－a 2＝8.因此所求动点M 的轨迹方程为x 2－y 28＝1(x ≤1)．【类题通法】求与双曲线有关的点的轨迹问题的方法(1)列出等量关系，化简得到方程．(2)寻找几何关系，由双曲线的定义，得出对应的方程．提醒：①双曲线的焦点所在的坐标轴是x 轴还是y 轴．②检验所求的轨迹对应的是双曲线的一支还是两支．【巩固练习4】如图所示，在△ABC 中，已知|AB |＝42，且三个内角A ，B ，C 满足2sin A ＋sin C ＝2sin B ，建立适当的坐标系，求顶点C 的轨迹方程．[解析]以AB 边所在的直线为x 轴，AB 的垂直平分线为y 轴，建立平面直角坐标系，如图所示，则A (－22，0)，B (22，0)．由正弦定理，得sin A ＝|BC |2R ，sin B ＝|AC |2R ，sin C ＝|AB |2R(R 为△ABC 的外接圆半径)．∵2sin A ＋sin C ＝2sin B ，∴2|BC |＋|AB |＝2|AC |，即|AC |－|BC |＝|AB |2＝22<|AB |. 由双曲线的定义知，点C 的轨迹为双曲线的右支(除去与x 轴的交点)．由题意，设所求轨迹方程为x 2a 2－y 2b 2＝1(x >a )， ∵a ＝2，c ＝22，∴b 2＝c 2－a 2＝6.即所求轨迹方程为x 22－y 26＝1(x >2)．（四）操作演练素养提升1.平面内有两个定点F 1(－5,0)和F 2(5,0)，动点P 满足|PF 1|－|PF 2|＝6，则动点P 的轨迹方程是( ) A.x 216－y 29＝1(x ≤－4) B.x 29－y 216＝1(x ≤－3) C.x 216－y 29＝1(x ≥4) D.x 29－y 216＝1(x ≥3)解析：由已知动点P 的轨迹是以F 1，F 2为焦点的双曲线的右支，且a ＝3，c ＝5，b 2＝c 2－a 2＝16，∴所求轨迹方程为x 29－y 216＝1(x ≥3)．答案：D2.方程x 22＋m －y 22－m＝1表示双曲线，则m 的取值范围为( ) A ．－2＜m ＜2B ．m ＞0C ．m ≥0D ．|m |≥2解析：∵已知方程表示双曲线，∴(2＋m )(2－m )＞0.∴－2＜m ＜2.答案：A3.若双曲线E ：x 29－y 216＝1的左，右焦点分别为F 1，F 2，点P 在双曲线E 上，且|PF 1|＝3，则|PF 2|等于( )A ．11B ．9C ．5D ．3解析：由题意知||PF 2|－3|＝6，即|PF 2|－3＝±6，解得|PF 2|＝9或|PF 2|＝－3(舍去)．答案：B4.已知双曲线的中心在原点，两个焦点F 1，F 2分别为(5，0)和(－5，0)，点P 在双曲线上，且PF 1⊥PF 2，△PF 1F 2的面积为1，则双曲线的方程为( )A.x 22－y 23＝1B.x 23－y 22＝1C.x 24－y 2＝1 D ．x 2－y 24＝1解析：由⎩⎨⎧|PF 1|·|PF 2|＝2，|PF 1|2＋|PF 2|2＝(25)2，⇒(|PF 1|－|PF 2|)2＝16，即2a ＝4，解得a ＝2，又c ＝5，所以b ＝1，故选C.答案：C答案：1.D 2.A 3.B 4.C【设计意图】通过练习巩固本节所学知识，通过学生解决问题的能力，感悟其中蕴含的数学思想，增强学生的应用意识。

【教案】双曲线及其标准方程说课稿-高二上学期数学人教A版(2019)选择性必修第一册

3.2.1双曲线及其标准方程尊敬的各位评委：大家好！我今天说课的内容是《双曲线及其标准方程》。

下面，我将从教学内容及其解析、教学目标及其解析、教学问题诊断分析、教学支持条件分析、教学过程设计五个方面来汇报我的思考与设计。

一、教学内容及其解析1.教学内容本节课是人教A 版选择性必修第一册第三章第二节第1 课时。

其主要内容包括：双曲线的现实背景与几何情境，双曲线的几何特征与概念以及双曲线的标准方程。

2.教学内容解析本节内容是在学习直线和圆的方程以及椭圆的基础上，先类比椭圆，从几何情境中抽象出双曲线的几何特征，进而得出双曲线的概念，然后建立它的标准方程，最后再通过例题让学生进一步熟悉双曲线的定义、方程和实际应用。

本节课纵向承接椭圆和抛物线，横向为双曲线简单几何性质的探究打下了基础，起到了深化提高、承上启下的重要作用，为随后抛物线的学习提供了良好的类比价值，也为从整体上认识圆锥曲线提供了经验。

本节课的教学，继续强化了几何概念的抽象过程，充分发挥了坐标法的核心纽带作用，进一步贯彻了“先用几何眼光观察与思考、再用坐标法解决”的研究策略，促进了学生的数学抽象、直观想象、逻辑推理、数学运算等素养的发展。

基于以上分析，确定本节课的教学重点为：双曲线的几何特征，双曲线的定义以及双曲线的标准方程。

二、教学目标及其解析1.教学目标（1）能从几何情境中抽象出双曲线的几何特征，给出双曲线的定义，并能用它解决简单的问题，发展数学抽象素养。

（2）类比椭圆标准方程的建立过程，运用坐标法推导出双曲线的标准方程，并能用它解决简单的问题，进一步体会建立曲线的方程的方法，发展直观想象、数学运算等素养。

2.教学目标解析达成上述目标的标志是：（1）能通过观察利用信息技术演示绘制双曲线的过程，明确双曲线上的点满足的几何条件，明确双曲线的几何特征，形成双曲线的概念。

（2）能认识建立双曲线标准方程的过程与建立椭圆标准方程的过程是类似的。

能通过建立适当的坐标系，根据双曲线上点的几何特征，列出双曲线上点的坐标满足的方程，进而化简所列出的方程，得到双曲线的标准方程；并能用它解决简单的问题，进一步认识获得曲线的方程的方法。

人教A版高中数学选修曲线与方程教案新(1)

2.2.2双曲线及其标准方程（二）1．使学生掌握双曲线的定义，熟记双曲线的标准方程，并能初步应用；2．使学生初步会按特定条件求双曲线的标准方程；3．培养学生发散思维的能力教学重点：标准方程及其简单应用教学难点：双曲线标准方程的推导及待定系数法解二元二次方程组教学过程：一、复习引入：二、讲解范例例1判断方程13922=---k y k x 所表示的曲线。

例2 已知ABC ∆的底边BC 长为12，且底边固定，顶点A 是动点，使A C B sin 21sin sin =-，求点A 的轨迹例3点A 位于双曲线)0,0(12222>>=-b a by a x 上，21,F F 是它的两个焦点，求21F AF ∆的重心G 的轨迹方程例4．求与圆1)3(22=+-y x 及9)3(22=++y x 都外切的动圆圆心的轨迹方程课堂练习1．求焦点的坐标是（-6，0）、（6，0），并且经过点A （-5，2）的双曲线的标准方程。

2求经过点)72,3(-P 和)7,26(--Q ，焦点在y 轴上的双曲线的标准方程3．椭圆134222=+n y x 和双曲线116222=-y nx 有相同的焦点，则实数n 的值是4．已知21,F F 是双曲线191622=-y x 的焦点，PQ 是过焦点1F 的弦，且PQ 的倾斜角为600，那么PQ QF PF -+22的值为________高二数学达标作业（11/8）姓名1．椭圆134222=+n y x 和双曲线116222=-y nx 有相同的焦点，则实数n 的值是（） A 5± B 3± C 5 D 92．设21,F F 是双曲线1422=-y x 的焦点，点P 在双曲线上,且02190=∠PF F ,则点P 到x 轴的距离为( )A 1B 55C 2D 53．P 为双曲线)0,0(12222>>=-b a by a x 上一点，若F 是一个焦点，以PF 为直径的圆与圆222a y x =+的位置关系是（）A 内切B 外切C 外切或内切D 无公共点或相交4．求焦点的坐标是（-6，0）、（6，0），并且经过点A （-5，2）的双曲线的标准方程。

高中数学选修一《双曲线及其标准方程》教案与导学案和同步练习

《3.2.1双曲线及其标准方程》教案【教材分析】本节课选自《2019人教A版高中数学选择性必修第一册》第二章《直线和圆的方程》，本节课主要学习双曲线及其标准方程学生初步认识圆锥曲线是从椭圆开始的，双曲线的学习是对其研究内容的进一步深化和提高。

如果双曲线研究的透彻、清楚，那么抛物线的学习就会顺理成章。

所以说本节课的作用就是纵向承接椭圆定义和标准方程的研究，横向加深对双曲线的标准方程及简单几何性质的理解与应用。

从高考大纲要求和课程标准角度来讲，双曲线的定义、标准方程作为了解内容，在高考的考查当中以选择、填空为主。

正因如此，学生在学习过程当中对双曲线缺少应有的重视，成为了学生的一个失分点。

而且由于学生对椭圆与双曲线的区别与联系认识不够，无法做到知识与方法的迁移，在学习双曲线时极易与椭圆混淆。

在教学中要时刻注意运用类比的方法，让学生充分的类比体会椭圆与双曲线的异同点，使得椭圆与双曲线的学习能相互促进。

【教学目标与核心素养】【教学重点】：用双曲线的定义和标准方程解决简单实际问题.【教学难点】：双曲线的标准方程及其求法.【教学过程】双曲线也是具有广泛应用的一种圆锥曲线，如发电厂冷却塔的外形、通过声音时差测定定位等都要用到双曲线的性质。

类比椭圆的研究方法研究双曲线的有关问题。

我们知道，平面内与两个定点F 1，F 2的距离的和等于常数于|F 1F 2|）的点的轨迹是椭圆，一个自然的问题是：平面内与两个定点的距离的差等于常数的点的轨迹是什么？1.双曲线的定义121如图，在直线上取两个定点,，是直线上的动点。

在平面内，取定点,，以点为圆心、线段为半径作圆，在以为圆心、线段为半径作圆。

l A B P l F F F PA F PB 12如图，在＞的条件下，让两圆的交点的轨迹是什么形状？F F AB M从椭圆的情形一样，下面我们用坐标法来探讨尝试与发现中的问题，并求出双曲线的标准方程。

F(-c,0),F F(0,-c),F解：建立平面直角坐标系，使并且原点与线段的中点重合。

2019-2020学年高二数学人教A版选修1-1课件：2.2.2 双曲线的简单几何性质

1
双曲线的简单
几何性质
M 目标导航
Z 知识梳理
UBIAODAOHANG
HISHI SHULI
Z 重难聚焦
HONGNAN JVJIAO
D典例透析
IANLI TOUXI
2
【做一做 1-1】中心在原点,实轴长为 10,虚轴长为 6 的双曲线
)
的标准方程是(
2
2
A. 25 − 9 = 1
2
2
2
2
离心率
e= a ( > 1)
渐近线
F1(0,-c),F2(0,c)
c
x y
b
± =0 或y=± x
a b
a

y x
a
± =0 或y=± x
a b
b

名师点拨离心率 e= > 1, 离心率越大, =
2 -1就越大,双曲线
“张口”越大.
第四页，编辑于星期日：点十五分。
-4-
2.2.2
2
10
9
Z 知识梳理
UBIAODAOHANG
,得
HISHI SHULI
Z 重难聚焦
HONGNAN JVJIAO
D典例透析
IANLI TOUXI
题型四
2
2
=
10
9
.
设 a2=9k(k>0),
则 c2=10k,b2=c2-a2=k.
2
于是,设所求双曲线方程为 9 −
2

= 1, ①
2 2
或
UBIAODAOHANG
Z 知识梳理
HISHI SHULI
Z 重难聚焦
HONGNAN JVJIAO

高中数学双曲线及其标准方程导学案新人教A版选修1-1 学案

陕西省榆林市育才中学高中数学双曲线及其标准方程导学案新人教A 版选修1-1学习目标：1.理解双曲线的概念，掌握双曲线的定义、会用双曲线的定义解决实际问题；2.理解双曲线标准方程的推导过程及化简无理方程的常用的方法；重点、难点：理解双曲线的概念，掌握双曲线的定义；会用双曲线的定义解决实际问题.自主学习复习旧知:1. 把平面内与两个定点，的距离之和等于＿＿＿（大于）的点的轨迹叫做椭圆（ellipse ）．其中这两个定点叫做＿＿＿＿＿，两定点间的距离叫做＿＿＿＿＿＿．即当动点设为时，椭圆即为点集．2.平面内与一定点F 和一条定直线l 的距离相等的点的轨迹叫做＿＿＿定点F 不在定直线l 上)．定点F 叫做抛物线的＿＿＿，定直线l 叫做抛物线的＿＿＿.3.抛物线的＿＿＿在一次项对应的轴上，其数值是一次项系数的＿＿倍，准线方程与焦点坐标相反；反之可以逆推。

合作探究1.由教材探究过程容易得到双曲线的定义．叫做双曲线．其中这两个定点叫做双曲线的焦点，两定点间的距离叫做双曲线的焦距．即当动点设为M 时，双曲线即为点集P = 。

2.双曲线标准方程的推导过程思考：已知椭圆的图形，是怎么样建立直角坐标系的？类比求椭圆标准方程的方法自己建立直角坐标系．类比椭圆：设参量b 的意义：第一、便于写出双曲线的标准方程；第二、,,a b c 的关系有明显的几何意义．类比：写出焦点在y 轴上，中心在原点的双曲线的标准方程()222210,0y x a b b a-=>>．推导过程：3.已知双曲线两个焦点分别为()15,0F -，()25,0F ，双曲线上一点P 到1F ，2F 距离差的绝对值等于6，求双曲线的标准方程．4.已知A ，B 两地相距800m ，在A 地听到炮弹爆炸声比在B 地晚2s ，且声速为340/m s ，求炮弹爆炸点的轨迹方程．练习反馈1.求满足下列条件的双曲线的标准方程：（1）a=3,b=4,焦点在x 轴上；（2）焦点为（0，-10），（0，10），双曲线上的点到两个焦点距离之差的绝对值是16；（3）焦点为（0，-5），（0,5），经过点（2，253）。

人教版高二数学选修 2.3.1双曲线及其标准方程导学案

高二数学导学案（预习、讨论、作业）班级________ 姓名______________（选修1-1, 2-1）2.3.1双曲线及其标准方程导学案[学习目标]1.从具体情境中抽象出双曲线的模型；2.理解双曲线的概念，掌握双曲线的定义、会用双曲线的定义解决实际问题；3.理解双曲线标准方程的推导过程及化简无理方程的常用的方法；4.通过双曲线标准方程的推导过程掌握双曲线的标准方程的两种形式． [重点难点]重点：双曲线的定义。

难点：双曲线标准方程的推导过程。

[导学流程] 一. （知识链接）回顾上节课有关椭圆定义和标准方程的内容，思考回答以下问题1.椭圆的定义是什么？椭圆的标准方程是什么？2.在椭圆的标准方程22221x y a b+=中，,,a b c 有何关系？若5,3a b ==，则?c =写出符合条件的椭圆方程．3.如图2-23，把椭圆定义中的“距离的和”改为“距离的差”，点的轨迹会变化吗？已知定点12,F F 是两个按钉，MN 是一个细套管，两条细绳分别拴在按钉上且穿过套管，点M 移动时，12MF MF -是常数，这样就画出一条曲线；由21MF MF -是同一常数，可以画出另一支．二.（基础感知）（一）1. 阅读P52—P53有关双曲线的定义及标准方程内容，回答以下问题：.将椭圆定义中的“和”为定值改为“差”是定值，轨迹还是椭圆吗？2. 小组思考交流双曲线生成过程实验（P52），归纳总结重要步骤和步骤中易忽视细节；3 小组合作，类比椭圆的定义归纳双曲线定义：平面内与两定点12,F F 的距离的差的等于常数(小于12F F )的点的轨迹叫做双曲线。

两定点12,F F 叫做双曲线的，两焦点间的距离12F F 叫做双曲线的．【反思】设常数为2a ，为什么2a <12F F ？2a =12F F 时，轨迹是； 2a >12F F 时，轨迹．试试：点(1,0)A ，(1,0)B -，若1AC BC -=，则点C 的轨迹是．【思考】：类比椭圆标准方程的建立过程，应该怎样选择坐标系来建立双曲线的标准方程? （二）阅读P53有关双曲线方程推导过程的内容，回答以下问题1. 双曲线的标准方程：22222221,(0,0,)x y a b c a b a b -=>>=+（焦点在x 轴）,其焦点坐标为1(,0)F c -，2(,0)F c ．思考：若焦点在y 轴，标准方程又如何?2. 利用待定系数法求双曲线标准方程的基本步骤（重要考点）：（1）定位置：根据条件判定双曲线的焦点在x 轴上还是在y 轴上。

2019-2020学年高中数学 2-2双曲线及其标准方程学案新人教A版选修1-1.doc

2019-2020学年高中数学 2-2双曲线及其标准方程学案新人教A 版选修1-1【学习目标】1.掌握双曲线定义、标准方程；2.掌握焦点、焦距、焦点位置与方程关系；【学习重难点】学习重点：双曲线的定义及标准方程学习难点: 区分标准方程的两种不同形式【问题导学】复习1：椭圆的定义是什么？椭圆的标准方程是什么？复习2：在椭圆的标准方程12222=+b y a x 中，参数a,b,c 的几何意义及其关系有是什么？若a=5,b=3,则c=？写出符合该条件的椭圆方程。

阅读课本第24-26页的有关内容回答下列内容（作一作）取一条拉链，拉开它的一部分，在拉开的两边上各选择一点，分别固定在点21,F F 上，把笔尖放在点M 处，随着拉练逐渐拉开或者闭拢，笔尖所经过的点就画出了一条曲线，该曲线的轨迹是什么曲线？分析：（1）在上面过程中，你能说出移动的笔尖（动点）满足的几何条件吗？在这个运动过程中，什么是不变的？观察其他同学画的图形，你认为双曲线的形状与什么量有关？2、双曲线的定义是什么？与椭圆的定义有什么不同？反思：设常数为2a ，为什么 212F F a <？212F F a = 时，轨迹是， 212F F a >时，轨迹是3、类比椭圆的标准方程的推导过程，你能推倒出双曲线的标准方程吗？4、若焦点在y 轴，标准方程又如何？5、如何通过双曲线的标准方程确定焦点的位置？类比椭圆，参数a,b,c 的几何意义是什么？它们之间有什么关系？【典型例题】例1:已知双曲线两个焦点分别为)0,5(),0,5(21F F - ，双曲线上一点P 到21,F F 距离差的绝对值等于6，求双曲线的标准方程。

例2:已知A,B 两地相距800m ，在A 地听到炮弹爆炸声比B 地晚2s ，且声速为340m/s ，求炮弹爆炸点的轨迹方程。

【基础题组】1、已知点A （0，-5）、B （0,5），a PB PA 2=-，当a=3或5时，P 点的轨迹为（）A.双曲线或一条直线B.双曲线或两条直线C.双曲线的一支或一条直线D.双曲线的一支或一条射线2、双曲线2255x ky +=的一个焦点是)0,6(，那么实数k 的值为（） A. -25 B. 25 C. -1 D. 13、双曲线的两焦点分别为1(3,0)F -，2(3,0)F ，若a=2,则b=( )A. 5B. 13C.D. 4、点P 是双曲线左支上一点，12,F F 分别为双曲线的左、右焦点，双曲线的标准方程为121022=-y x ，则12PF PF -=（）A. B.- C. - D.无法确定5、若双曲线11622=+a x y 与椭圆14222++a y x 有相同的焦点，则a 的值为。

高中数学第2章2.1双曲线及其标准方程教师用书教案新人教A版选修1

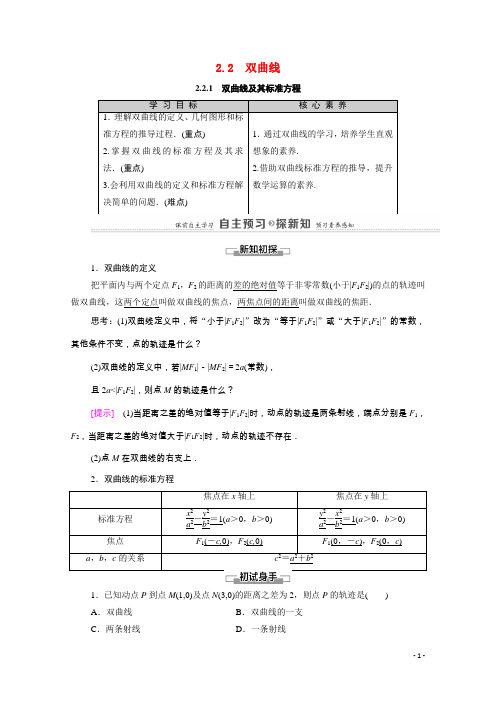
2.2 双曲线2.2.1双曲线及其标准方程学习目标核心素养1．理解双曲线的定义、几何图形和标准方程的推导过程．(重点)2.掌握双曲线的标准方程及其求法．(重点)3.会利用双曲线的定义和标准方程解决简单的问题．(难点) 1．通过双曲线的学习，培养学生直观想象的素养.2.借助双曲线标准方程的推导，提升数学运算的素养.1．双曲线的定义把平面内与两个定点F1，F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹叫做双曲线，这两个定点叫做双曲线的焦点，两焦点间的距离叫做双曲线的焦距．思考：(1)双曲线定义中，将“小于|F1F2|”改为“等于|F1F2|”或“大于|F1F2|”的常数，其他条件不变，点的轨迹是什么？(2)双曲线的定义中，若|MF1|－|MF2|＝2a(常数)，且2a<|F1F2|，则点M的轨迹是什么？[提示](1)当距离之差的绝对值等于|F1F2|时，动点的轨迹是两条射线，端点分别是F1，F2，当距离之差的绝对值大于|F1F2|时，动点的轨迹不存在．(2)点M在双曲线的右支上．2．双曲线的标准方程焦点在x轴上焦点在y轴上标准方程x2a2－y2b2＝1(a＞0，b＞0)y2a2－x2b2＝1(a＞0，b＞0)焦点F1(－c,0)，F2(c,0) F1(0，－c)，F2(0，c) a，b，c的关系c2＝a2＋b21．已知动点P到点M(1,0)及点N(3,0)的距离之差为2，则点P的轨迹是() A．双曲线B．双曲线的一支C．两条射线D．一条射线D [∵|PM |－|PN |＝2＝|MN |，∴点P 在线段MN 的延长线上，即点P 的轨迹是一条射线．] 2．双曲线x 210－y 22＝1的焦距为( )A ．32B ．42C ．33D ．43D [c 2＝10＋2＝12，所以c ＝23，从而焦距为4 3.]3．已知双曲线的a ＝5，c ＝7，则该双曲线的标准方程为( ) A ．x 225－y 224＝1B ．y 225－x 224＝1C ．x 225－y 224＝1或y 225－x 224＝1D ．x 225－y 224＝0或y 225－x 224＝0C [b 2＝c 2－a 2＝72－52＝24，故选C ．]对双曲线标准方程的理解【例1】已知曲线方程x m －1－y m 2－4＝1.(1)若方程表示双曲线，求实数m 的取值范围；(2)若方程表示焦点在y 轴上的双曲线，求实数m 的取值范围； (3)若方程表示椭圆，求实数m 的取值范围．[解] (1)依题意有(m －1)(m 2－4)>0，即(m －1)(m ＋2)(m －2)>0，解得－2<m <1或m >2.(2)依题意有⎩⎪⎨⎪⎧ m 2－4<0，m －1<0，解得－2<m <1.(3)依题意有⎩⎪⎨⎪⎧m 2－4<0，m －1>0，解得1<m <2.给出方程x 2m －y 2n ＝1，则该方程：(1)表示双曲线的条件是mn >0；(2)表示焦点在x 轴上的双曲线的条件是m >0，n >0； (3)表示焦点在y 轴上的双曲线的条件是m <0，n <0； (4)表示椭圆的条件是m >0，n <0.[跟进训练]1．(1)已知双曲线x 2a －3＋y 22－a ＝1，焦点在y 轴上，若焦距为4，则a 等于( )A ．32B ．5C ．7D ．12(2)在方程mx 2－my 2＝n 中，若mn <0，则方程所表示的曲线是( ) A ．焦点在x 轴上的椭圆 B ．焦点在x 轴上的双曲线 C ．焦点在y 轴上的双曲线D ．焦点在y 轴上的椭圆(1)D (2)C [(1)根据题意可知，双曲线的标准方程为y 22－a －x 23－a ＝1.由其焦距为4，得c ＝2，则有c 2＝2－a ＋3－a ＝4，解得a ＝12.(2)方程mx 2－my 2＝n可化为x 2n m －y 2n m＝1.由mn <0知nm <0，故方程所表示的曲线是焦点在y轴上的双曲线．]求双曲线的标准方程(1)求以椭圆x 216＋y 29＝1的短轴的两个端点为焦点，且过点A (4，－5)的双曲线的标准方程；(2)已知双曲线经过M (1,1)，N (－2,5)两点，求双曲线的标准方程．[思路点拨] 用待定系数法，根据双曲线焦点的位置设方程，根据条件确定参数．当已知双曲线的两个焦点和双曲线上某一点，也可利用双曲线的定义求解．[解] (1)法一 (待定系数法)由题意知双曲线的两焦点F 1(0，－3)，F 2(0,3)．设双曲线的标准方程为y 2a 2－x 2b 2＝1(a >0，b >0)，将点A (4，－5)代入双曲线方程得25a 2－16b2＝1，又a 2＋b 2＝9，解得a 2＝5，b 2＝4. ∴双曲线的标准方程为y 25－x 24＝1.法二 (定义法)由题意知双曲线的两个焦点分别为F 1(0，－3)，F 2(0,3)且A (4，－5)在双曲线上，则2a ＝||AF 1|－|AF 2||＝|20－80|＝25， ∴a ＝5，∴b 2＝c 2－a 2＝9－5＝4. 即双曲线的标准方程为y 25－x 24＝1.(2)法一若焦点在x 轴上，设双曲线的标准方程为x 2a 2－y 2b 2＝1(a >0，b >0)．因为M (1,1)，N (－2,5)在双曲线上，所以⎩⎪⎨⎪⎧1a 2－1b 2＝1，(－2)2a 2－52b 2＝1，解得⎩⎪⎨⎪⎧a 2＝78，b 2＝7.若焦点在y 轴上，设双曲线的标准方程为y 2a 2－x 2b2＝1(a >0，b >0)．同理有⎩⎪⎨⎪⎧1a 2－1b 2＝1，52a 2－(－2)2b 2＝1，解得⎩⎪⎨⎪⎧a 2＝－7，b 2＝－78(不合题意，舍去)．所以所求双曲线的标准方程为x 278－y 27＝1.法二设所求双曲线的方程为mx 2＋ny 2＝1(mn <0)．将点M (1,1)，N (－2,5)代入上述方程，得⎩⎪⎨⎪⎧m ＋n ＝1，4m ＋25n ＝1，解得⎩⎨⎧m ＝87，n ＝－17.所以所求双曲线的标准方程为x 278－y 27＝1.1．求双曲线标准方程的步骤(1)确定双曲线的类型，并设出标准方程； (2)求出a 2，b 2的值．2．当双曲线的焦点所在坐标轴不确定时，需分焦点在x 轴上和y 轴上两种情况讨论，特别地，当已知双曲线经过两个点时，可设双曲线方程为Ax 2＋By 2＝1(AB <0)来求解．[跟进训练]2．(1)与椭圆x 24＋y 2＝1共焦点且过点P (2,1)的双曲线方程是( )A ．x 24－y 2＝1B ．x 23－y 2＝1C ．x 22－y 2＝1D ．x 2－y 22＝1 (2)已知双曲线中心在坐标原点且一个焦点为F 1(－5，0)，点P 位于该双曲线上，线段PF 1的中点坐标为(0,2)，则该双曲线的方程是( )A ．x 24－y 2＝1B ．x 2－y 24＝1 C ．x 22－y 23＝1D ．x 23－y 22＝1(1)C (2)B [(1)设所求双曲线方程为x 2a 2－y 2b2＝1(a >0，b >0)，由题意得⎩⎪⎨⎪⎧4a 2－1b 2＝1，c 2＝a 2＋b 2＝3，解得⎩⎪⎨⎪⎧a 2＝2，b 2＝1，所以所求双曲线方程为x 22－y 2＝1.(2)由双曲线的焦点可知c ＝5，线段PF 1的中点坐标为(0,2)，所以设右焦点为F 2，则有PF 2⊥x 轴，且PF 2＝4，点P 在双曲线右支上．所以PF 1＝(25)2＋42＝36＝6，所以PF 1－PF 2＝6－4＝2＝2a ，所以a ＝1，b 2＝c 2－a 2＝4，所以双曲线的方程为x 2－y 24＝1，选B ．]双曲线定义的应用1．到两定点F 1，F 2的距离之差是常数(小于|F 1F 2|)的点的轨迹是双曲线的两支还是一支？提示：一支．2．若P 点是双曲线x 2a 2－y 2b 2＝1(a >0，b >0)上的一动点，F 1，F 2为其左、右焦点，设∠F 1PF 2＝α，则S △F 1PF 2如何用α表示？提示：S △F 1PF 2＝b 2tan α2(可借助双曲线的定义及余弦定理推导)．【例3】 (1)已知圆C 1：(x ＋3)2＋y 2＝1和圆C 2：(x －3)2＋y 2＝9，动圆M 同时与圆C 1及圆C 2相外切，则动圆圆心M 的轨迹方程为________．(2)已知F 1，F 2分别是双曲线x 29－y 216＝1的左、右焦点，若P 是双曲线左支上的点，且|PF 1|·|PF 2|＝32.试求△F 1PF 2的面积．[思路点拨] (1)由两圆外切得等量关系⇒双曲线定义⇒轨迹方程． (2)双曲线的定义及余弦定理⇒∠F 1PF 2⇒面积公式求S △F 1PF 2. (1)x 2－y 28＝1(x ≤－1) [如图，设动圆M 与圆C 1及圆C 2分别外切于点A 和B ，根据两圆外切的条件得|MC 1|－|AC 1|＝|MA |，|MC 2|－|BC 2|＝|MB |.因为|MA |＝|MB |，所以|MC 1|－|AC 1|＝|MC 2|－|BC 2|，即|MC 2|－|MC 1|＝2，这表明动点M 与两定点C 2，C 1的距离的差是常数2.根据双曲线的定义，动点M 的轨迹为双曲线的左支(点M 与C 2的距离大，与C 1的距离小)，这里a ＝1，c ＝3，则b 2＝8，∴动圆圆心M 的轨迹方程为x 2－y 28＝1(x ≤－1)．] (2)[解] 因为P 是双曲线左支上的点，所以|PF 2|－|PF 1|＝6，两边平方得|PF 1|2＋|PF 2|2－2|PF 1|·|PF 2|＝36，所以|PF 1|2＋|PF 2|2＝36＋2|PF 1|·|PF 2|＝36＋2×32＝100. 在△F 1PF 2中，由余弦定理，得cos ∠F 1PF 2＝|PF 1|2＋|PF 2|2－|F 1F 2|22|PF 1|·|PF 2|＝100－1002|PF 1|·|PF 2|＝0，所以∠F 1PF 2＝90°，所以S △F 1PF 2＝12|PF 1|·|PF 2|＝12×32＝16.把本例(2)的条件“|PF 1||PF 2|＝32”换成“∠F 1PF 2＝60°”，求S △F 1PF 2. [解] 由x 29－y 216＝1得，a ＝3，b ＝4，c ＝5.由双曲线的定义和余弦定理得|PF 2|－|PF 1|＝6， |F 1F 2|2＝|PF 1|2＋|PF 2|2－2|PF 1||PF 2|cos 60°，所以102＝(|PF 1|－|PF 2|)2＋|PF 1|·|PF 2|，所以|PF 1|·|PF 2|＝64，所以S △F 1PF 2＝12|PF 1|·|PF 2|·sin ∠F 1PF 2＝12×64×32＝16 3.1．求与双曲线有关的点的轨迹问题的方法 (1)列出等量关系，化简得到方程．(2)寻找几何关系，由双曲线的定义，得出对应的方程．提醒：①双曲线的焦点所在的坐标轴是x 轴还是y 轴． ②检验所求的轨迹对应的是双曲线的一支还是两支． 2．求双曲线中的焦点三角形△PF 1F 2面积的方法(1)①根据双曲线的定义求出||PF 1|－|PF 2||＝2a ；②利用余弦定理表示出|PF 1|、|PF 2|、|F 1F 2|之间满足的关系式；③通过配方，利用整体的思想方法求出|PF 1|·|PF 2|的值； ④利用公式S △PF 1F 2＝12×|PF 1|·|PF 2|sin ∠F 1PF 2求得面积．(2)利用公式S △PF 1F 2＝12×|F 1F 2|×|y P |求得面积．1．双曲线定义中||PF 1|－|PF 2||＝2a (2a <|F 1F 2|)不要漏了绝对值符号，当2a ＝|F 1F 2|时表示两条射线．2．在双曲线的标准方程中，a >b 不一定成立．要注意与椭圆中a ，b ，c 的区别．在椭圆中a 2＝b 2＋c 2，在双曲线中c 2＝a 2＋b 2.3．用待定系数法求双曲线的标准方程时，要先判断焦点所在的位置，设出标准方程后，由条件列出关于a ，b ，c 的方程组．如果焦点不确定要分类讨论，采用待定系数法求方程或用形如mx 2＋ny 2＝1(mn <0)的形式求解．1．判断正误(1)在双曲线标准方程中，a ，b ，c 之间的关系与椭圆中a ，b ，c 之间的关系相同． (2)点A (1,0)，B (－1,0)，若|AC |－|BC |＝2，则点C 的轨迹是双曲线． ( ) (3)在双曲线标准方程x 2a 2－y 2b 2＝1中，a ＞0，b ＞0，且a ≠b .( )[答案] (1)× (2)× (3)× 2．设双曲线x 2－y 28＝1的两个焦点分别为F 1，F 2，P 是双曲线上的一点，且|PF 1|∶|PF 2|＝3∶4，则△PF 1F 2的面积等于( )A ．10 3B ．8 3C ．8 5D ．165C [设|PF 1|＝3t ，则|PF 2|＝4t ，|PF 2|－|PF 1|＝t ＝2a ＝2，所以t ＝2，所以|PF 1|＝6，|PF 2|＝8，|F 1F 2|＝2c ＝2a 2＋b 2＝6＝|PF 1|，所以F 1到PF 2的距离为62－42＝25，所以S △PF 1F 2＝12×8×25＝8 5.]3．若双曲线E ：x 29－y 216＝1的左、右焦点分别为F 1，F 2，点P 在双曲线E 上，且|PF 1|＝3，则|PF 2|等于( )A ．11B ．9C ．5D ．3B [由题意知||PF 2|－3|＝6，即|PF 2|－3＝±6，解得|PF 2|＝9或|PF 2|＝－3(舍去)．]4．求适合下列条件的双曲线的标准方程． (1)a ＝3，c ＝4，焦点在x 轴上；(2)焦点为(0，－6)，(0,6)，经过点A (－5,6)；(3)以椭圆x 28＋y 25＝1长轴的端点为焦点，且经过点(3，10)．[解] (1)由题设知，a ＝3，c ＝4，由c 2＝a 2＋b 2，得b 2＝c 2－a 2＝42－32＝7. 因为双曲线的焦点在x 轴上，所以所求双曲线的标准方程为x 29－y 27＝1.(2)由已知得c ＝6，且焦点在y 轴上．因为点A (－5,6)在双曲线上，所以 2a ＝|(－5－0)2＋(6＋6)2－(－5－0)2＋(6－6)2|＝|13－5|＝8，则a ＝4，b 2＝c 2－a 2＝62－42＝20. 所以所求双曲线的标准方程是y 216－x 220＝1.(3)由题意得，双曲线的焦点在x 轴上，且c ＝2 2.设双曲线的标准方程为x 2a 2－y 2b 2＝1(a >0，b >0)，则有a 2＋b 2＝c 2＝8，9a 2－10b2＝1，解得a 2＝3，b 2＝5.故所求双曲线的标准方程为x 23－y 25＝1.。

2020高中数学 2.2.5双曲线及其标准方程教案新人教A版选修1-1

高中数学 2．2．5双曲线及其标准方程教案新人教A 版选修1-1（1）预习与引入过程（2）新课讲授过程（i ）由上述探究过程容易得到双曲线的定义．〖板书〗把平面内与两个定点1F ，2F 的距离的差的绝对值等于常数（小于12F F ）的点的轨迹叫做双曲线（hyperbola ）．其中这两个定点叫做双曲线的焦点，两定点间的距离叫做双曲线的焦距．即当动点设为M 时，双曲线即为点集P ={}122M MF MF a -=．（ii ）双曲线标准方程的推导过程提问：已知椭圆的图形，是怎么样建立直角坐标系的？类比求椭圆标准方程的方法由学生来建立直角坐标系．无理方程的化简过程仍是教学的难点，让学生实际掌握无理方程的两次移项、平方整理的数学活动过程．类比椭圆：设参量b 的意义：第一、便于写出双曲线的标准方程；第二、,,a b c 的关系有明显的几何意义．类比：写出焦点在y 轴上，中心在原点的双曲线的标准方程()222210,0y x a b b a-=>>．（iii ）例题讲解、引申与补充例1 已知双曲线两个焦点分别为()15,0F -，()25,0F ，双曲线上一点P 到1F ，2F 距离差的绝对值等于6，求双曲线的标准方程．分析：由双曲线的标准方程的定义及给出的条件，容易求出,,a b c ．补充：求下列动圆的圆心M 的轨迹方程：① 与⊙C ：()2222x y ++=内切，且过点()2,0A ；② 与⊙1C ：()2211x y +-=和⊙2C ：()2214x y +-=都外切；③ 与⊙1C ：()2239x y ++=外切，且与⊙2C ：()2231x y -+=内切．解题剖析：这表面上看是圆与圆相切的问题，实际上是双曲线的定义问题．具体解：设动圆M 的半径为r ．① ∵⊙C 与⊙M 内切，点A 在⊙C 外，∴2MC r =-，MA r =，因此有2MA MC -=，∴点M 的轨迹是以C 、A 为焦点的双曲线的左支，即M 的轨迹方程是()2222127y x x -=≤-； ② ∵⊙M 与⊙1C 、⊙2C 均外切，∴11MC r =+，22MC r =+，因此有211MC MC -=，∴点M 的轨迹是以2C 、1C 为焦点的双曲线的上支，∴M 的轨迹方程是22434134x y y ⎛⎫-=≥ ⎪⎝⎭； ③ ∵M e 与1C e 外切，且M e 与2C e 内切，∴13MC r =+，21MC r =-，因此124MC MC -=，∴点M 的轨迹是以1C 、2C 为焦点的双曲线的右支，∴M 的轨迹方程是()221245x y x -=≥．例 2 已知A ，B 两地相距800m ，在A 地听到炮弹爆炸声比在B 地晚2s ，且声速为340/m s ，求炮弹爆炸点的轨迹方程．分析：首先要判断轨迹的形状，由声学原理：由声速及A ，B 两地听到爆炸声的时间差，即可知A ，B 两地与爆炸点的距离差为定值．由双曲线的定义可求出炮弹爆炸点的轨迹方程．扩展：某中心接到其正东、正西、正北方向三个观察点的报告：正西、正北两个观察点同时听到了一声巨响，正东观察点听到该巨响的时间比其他两个观察点晚4s ．已知各观察点到该中心的距离都是1020m ．试确定该巨响发生的位置（假定当时声音传播的速度为340/m s ；相关点均在同一平面内）．解法剖析：因正西、正北同时听到巨响，则巨响应发生在西北方向或东南方向，以因正东比正西晚4s ，则巨响应在以这两个观察点为焦点的双曲线上．如图，以接报中心为原点O ，正东、正北方向分别为x 轴、y 轴方向，建立直角坐标系，设A 、B 、C 分别是西、东、北观察点，则()1020,0A -，()1020,0B ，()0,1020C ．设(),P x y 为巨响发生点，∵A 、C 同时听到巨响，∴OP 所在直线为y x =-……①，又因B 点比A 点晚4s 听到巨响声，∴()43401360PB PA m -=⨯=．由双曲线定义知，680a =，1020c =，∴3405b =，∴P 点在双曲线方程为222216805340x y -=⨯()680x ≤-……②．联立①、②求出P 点坐标为(6805,6805P -．即巨响在正西北方向10m 处．探究：如图，设A ，B 的坐标分别为()5,0-，()5,0．直线AM ，BM 相交于点M ，且它们的斜率之积为49，求点M 的轨迹方程，并与§2．1．例3比较，有什么发现？探究方法：若设点(),M x y ，则直线AM ，BM 的斜率就可以用含,x y 的式子表示，由于直线AM ，BM 的斜率之积是49，因此，可以求出,x y 之间的关系式，即得到点M 的轨迹方程． ◆ 情感、态度与价值观目标通过课件（a ）的展示与操作，必须让学生认同：与圆锥的轴平行的平面去截圆锥曲面所得截口曲线是一条双曲线而不是两条抛物线；必须让学生认同与体会：双曲线的定义及特殊情形当常数等于两定点间距离时，轨迹是两条射线；必须让学生认同与理解：已知几何图形建立直角坐标系的两个原则，及引入参量22b c a =-的意义，培养学生用对称的美学思维来体现数学的和谐美；让学生认同与领悟：像例1这基础题配备是必要的，但对定义的理解和使用是远远不够的，必须配备有一定灵活性、有一定的思维空间的补充题；例2是典型双曲线实例的题目，对培养学生的辩证思维方法，会用分析、联系的观点解决问题有一定的帮助，但要准确判定爆炸点，必须对此题进行扩展，培养学生归纳、联想拓展的思维能力．◆能力目标（1）想象与归纳能力：能根据课程的内容能想象日常生活中哪些是双曲线的实际例子，能用数学符号或自然语言的描述双曲线的定义，能正确且直观地绘作图形，反过来根据图形能用数学术语和数学符号表示．（2）思维能力：会把几何问题化归成代数问题来分析，反过来会把代数问题转化为几何问题来思考，培养学生的数形结合的思想方法；培养学生的会从特殊性问题引申到一般性来研究，培养学生的辩证思维能力．（3）实践能力：培养学生实际动手能力，综合利用已有的知识能力．（4）数学活动能力：培养学生观察、实验、探究、验证与交流等数学活动能力．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2019-2020学年高中数学双曲线及其标准方程导学案新人教A 版选
修1-1
学习目标：1.理解双曲线的概念，掌握双曲线的定义、会用双曲线的定义解决实际问题；
2.理解双曲线标准方程的推导过程及化简无理方程的常用的方法；
重点、难点：理解双曲线的概念，掌握双曲线的定义；
会用双曲线的定义解决实际问题.
自主学习
复习旧知:1. 把平面内与两个定点，的距离之和等于＿＿＿（大于）的点的轨迹叫做椭圆（ellipse ）．其中这两个定点叫做＿＿＿＿＿，两定点间的距离叫做＿＿＿＿＿＿．即
当动点设为时，椭圆即为点集．
2.平面内与一定点F 和一条定直线l 的距离相等的点的轨迹叫做＿＿＿定点F 不在定直线l 上)．定点F 叫做抛物线的＿＿＿，定直线l 叫做抛物线的＿＿＿.
3.抛物线的＿＿＿在一次项对应的轴上，其数值是一次项系数的＿＿倍，准线方程与焦点坐标相反；反之可以逆推。

合作探究
1.由教材探究过程容易得到双曲线的定义．叫做双曲线．其中这两个定点叫做双曲线的焦点，两定点间的距离叫做双曲线的焦距．即当动点设为M 时，双曲线即为点集P = 。

2.双曲线标准方程的推导过程
思考：已知椭圆的图形，是怎么样建立直角坐标系的？类比求椭圆标准方程的方法自己建立直角坐标系．
类比椭圆：设参量b 的意义：第一、便于写出双曲线的标准方程；第二、,,a b c 的关系有明显的几何意义．
类比：写出焦点在y 轴上，中心在原点的双曲线的标准方程()22
22
10,0y x a b b a -=>>．推导过程：
3.已知双曲线两个焦点分别为()15,0F -，()25,0F ，双曲线上一点P 到1F ，2F 距离差的绝对值等于6，求双曲线的标准方程．
4.已知A ，B 两地相距800m ，在A 地听到炮弹爆炸声比在B 地晚2s ，且声速为340/m s ，求炮弹爆炸点的轨迹方程．
练习反馈
1.求满足下列条件的双曲线的标准方程：
（1）a=3,b=4,焦点在x 轴上；
（2）焦点为（0，-10），（0，10），双曲线上的点到两个焦点距离之差的绝对值是16；
（3）焦点为（0，-5），（0,5），经过点（2，
253）。

2.证明：椭圆252x +92y =1与双曲线x 2-15y 2=15有相同的焦点。