Rossby波动原理介绍
台风螺旋雨带_涡旋Rossby波

台风螺旋雨带———涡旋Rossby波Ξ余志豪(南京大学大气科学系,南京,210093)摘 要 台风中的螺旋云雨带是由多种探测手段被观测到的现象,是为大家所共识的不争事实。
但是,对它的形成、维持的理论解释,虽有多种学说,一直以来人们都倾向于重力惯性波说。
而重力惯性波说有一个致命的弱点,即波的相速理论值为101m/s量级,它要比螺旋云雨带实测移速只有100m/s几乎大一个量级。
于是从前几年开始,人们又回到30多年前提出的涡旋2Rossby波说那里去寻找合适的解释。
经典的Rossby波是β=(d f/d y)作用的大尺度波动,而适用于台风中螺旋云雨带的涡旋———Rossby波乃是f平面(β=0)上的中尺度波动。
那末,对这两类尺度不同和成波机理不同的波动,何以均冠予Rossby波一词?本文试图从动力学等价原理上,对此作统一联系的说明。
其结果是:台风基本气流的涡度 ζ随径向(r)变化的梯度d ζd r =1r99r(r vλ),在动力学上等价于科氏参数f随纬度变化的梯度即β=d f/d y;或者说它们在绝对涡度守恒的前提下,作为波扰动的成波机理是等价的。
关键词:台风,螺旋云雨带,涡旋Rossby波。
1999年12月在苏州召开的十一届全国热带气旋科学讨论会(文集50~51页)及2001年4月在扬州召开的第五届全国动力气象学术会议,学者王玉清博士的两次报告对台风中螺旋雨带均提到了可用涡旋Rossby波来解释,但在这两次会上有教授对此质疑。
分歧的焦点是Rossby波的基本概念。
此概念在动力气象教科书中是属经典内容,给人很深印象。
然而在近代大气科学进展中,Rossby波概念已被“借用”或延伸扩展。
此Rossby波已非彼Rossby 波,但两者在成波机理方面仍有其一定的等价性。
还有一个原因,是很长一段时期来台风螺旋雨带几乎都是用重力惯性波来说明的。
这表明大气科学高等教学内容,要及时反映这些新发展,不能墨守Rossby波固有的概念,要注入新的学术含义。
地形Rossby波与定常波
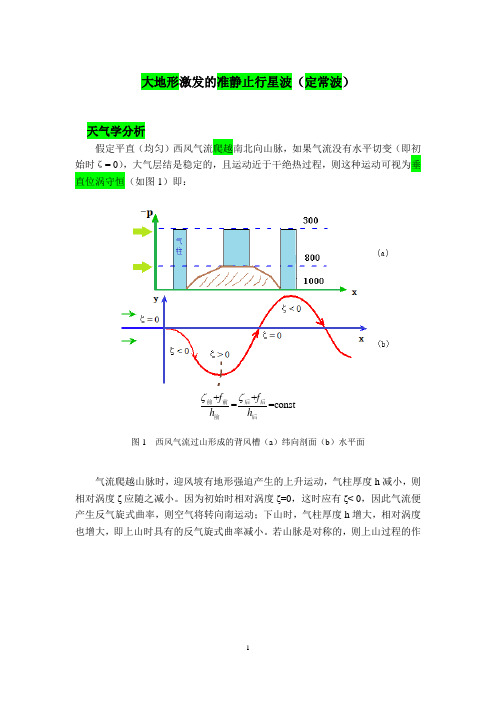
大地形激发的准静止行星波(定常波)天气学分析假定平直(均匀)西风气流爬越南北向山脉,如果气流没有水平切变(即初始时ζ= 0),大气层结是稳定的,且运动近于干绝热过程,则这种运动可视为垂直位涡守恒(如图1)即:++==constf f h h ζζ前前后后后前图1 西风气流过山形成的背风槽(a )纬向剖面(b )水平面气流爬越山脉时,迎风坡有地形强迫产生的上升运动,气柱厚度h 减小,则相对涡度ζ应随之减小。
因为初始时相对涡度ζ=0,这时应有ζ< 0,因此气流便产生反气旋式曲率,则空气将转向南运动;下山时,气柱厚度h 增大,相对涡度也增大,即上山时具有的反气旋式曲率减小。
若山脉是对称的,则上山过程的作图2 西风气流过山形成的背风槽示意图用被下山的相反作用所抵消,则在背风坡山脚,ζ恢复为零。
但是因为气流过山的全过程是反气旋路径,因此到达山脚时,气流已位于初始纬度0ϕ之南(即位于1ϕ维度),ƒ比初始时小,所以ζ必须比原来大(即下山时ζ增加的幅度大于上山时ζ减小的幅度),则在山脚变为正涡度,气流轨迹应为气旋式弯曲,即向北运动。
当气流返回到初始纬度0ϕ时,ζ应该回复到初始状态,即ζ=0.但是由于惯性作用(此时h=const .,则位涡守恒→绝对涡度守恒),气流将继续向北运动→ƒ增大→ζ减小→反气旋式弯曲,到达一定纬度2ϕ时,气流又转向南运动……(重复上述过程)。
这样,山脉背风坡形成一系列的槽脊,但是由于摩擦作用,只有第一个槽在天气图上最清楚,称为背风槽或地形槽(见图2)。
由于是气流爬越山脉时为保持位涡守恒而形成的槽,故又称为地形Rossby (罗斯贝)波。
动力学理论数学推导据图3分析:假定平直西风爬越南北向山脉,气流无水平切变(即初始时ζ= 0),大气层结稳定,运动近似于无摩擦、干绝热过程。
过山前(0x <),有一均匀西风u ,气层厚度为H ,相对涡度00ζ=; 过迎风坡山脚(=0x )后(0x >),由于存在山脉,设山脉高度为s h ,则气层厚度为s H h -,相对涡度00ζ≠。
高等大气动力学 复习重点

高等大气动力学1、自由大气:是指行星边界层以上,湍流摩擦力可忽略,空气运动不受地表摩擦影响的大气。
大致在1.5km 以上,水平气压梯度力和科氏力相平衡(准地转)。
在中、高纬度,自由大气中空气运动基本遵守地转风或梯度风法则,气流几乎与等压线平行。
D 是由于空气的内摩擦或湍流动量传输所导致的的耗散力,忽略D 就是所谓的“自由大气近似,除靠近地表面的“摩擦层”以外,对于以一天为时间单位的运动来说,使用自由大气近似大体上是可以的。
2、绝热近似:在空气运动的短期变化过程中,可以认为空气微团与外界无热量交换,这就是绝热过程。
热力学第一定律可写成热流量方程的形式:忽略dQ/dt 就是“绝热”近似,除靠近地表的“热力边界层”内、位于平流层中的臭氧层内以及有着严重的水汽相变过程的区域外,对于以一天为时间单位的运动来说,使用绝热近似大体上是可以的。
3、薄层近似:大气中90%以上的质量集中在离地表的一薄层中,其有效厚度约为几十公里,远比地球平均半径小,因此在推导球坐标系下的基本方程组时,可取r a z a =+(z 0)<<,其中a 是地球半径,z 是离地表的铅直高度。
球坐标的运动方程中,当r 处于系数时,r 用a 代替;当r 处于微商地位时,用z 代替r 。
这一近似郭晓岚称之为薄层近似。
4、标准层结近似:针对热力学量(p,ρ,θ,T )引入一个垂直方向的标准分布,亦即所谓的标准层结(气候态)。
我们据此引入标准层结近似,在运动、连续、热力学及状态方程中将这些热力学量表示成标准分布加上一个扰动量。
这样在预报、诊断等问题中只计算扰动量或其变量,而把标准分布视为已知。
好处在于降低了方程的非线性程度,易于求解,从而减少了计算误差。
()()0''0;,,,ρρρρρ<<+=t z y x z5、地球流体的基本属性⑴层结性,使之更具“弹性”。
密度和温度在垂直方向上的分布是不均匀的,这种介质的物理性质的不均匀分布,使大气具有层结的分布。
德布络依物质波原理

德布络依物质波原理
德布罗意波
1924年法国青年物理学家德布罗意在光的波粒二象性的启发下想到:自然界在许多方面都是明显地对称的,既然光具有波粒二象性,则实物粒子也应该具有波粒二象性.他假设:实物粒子也具有波动性.于是他由质能方程以及量子方程出发,推得了德布罗意波的有关公式.他发现,粒子在以v为速度运动的时候总会伴随着一个速度为c^2/v的波,这个波又因为不带任何能量与信息,所以不违反相对论.
一个实物粒子的能量为E、动量大小为p,跟它们联系的波的频率ν和波长λ的关系为
E=mc^2=hν
p=mv=h/λ
上两式称为德布罗意式.与实物粒子相联系的波称为德布罗
意波.
1927年戴维孙和革末用加速后的电子投射到晶体上进行电子衍射实验,证实了电子的波动性.同年汤姆逊做了电子衍射实验.将电子束穿过金属片(多晶膜),在感光片上产生圆环衍射图和X光通过多晶膜产生的衍射图样极其相似.这也证实了电子的波动性.
对于实物粒子波动性的解释,是1926年玻恩提出概率波的概念而得到一致公认的.至于个别粒子在何处出现,有一定的偶然性;但是大量粒子在空间何处出现的空间分布却服从一定的统计规律.
物质波的这种统计性解释把粒子的波动性和粒子性正确地联系起来了,成为量子力学的基本观点之一.。
赤道太平洋的Rossby波和Kelvin波

Sverdrup平衡的物理意义及其 适用范围
• 非常简明地刻划风应力与大洋环流之间 的关系,是物理海洋最经典的理论之一.
• 适用描述定常的运动 • 适用于远离边界层的大洋内区 • 适用于描述大尺度海洋环流 • 不能给出大洋环流的斜压结构
热带海气相互作用通常只考虑热通量和动量通量
0
ME 0 vdz
DE
ME
x 0 f
ME
w z DE
Curl z
o
f
w G
根源:风应力的不均匀性 z= 0
关键:Ekman pumping引起的 次表层垂直运动
z=-DE
在Ekman 层以
VG 下,海洋的运 动基本上是绝
热无摩擦,满
加热场关于赤道对称的解(Gill,1981)
加热场关于赤道反对称的解(Gill,1981)
正反馈(positive feedback) 与负反馈(negative feedback)
如果某种过程使得初始扰动不断增加, 就称之为正反馈过程;如果某种过程使 得初始扰动不断减弱,就称之为负反馈 过程。 0为正反馈, 0为负反馈。
数值模拟在大气和海洋科学研究中的作用
第七讲的目的
1. 什么是ENSO现象,ENSO的基本特征是什么? 2. ENSO现象的物理机制? 3. 以ENSO为例子,说明数值模拟在大气和海洋
科学研究中能起到何种作用,特别是如何看待 模式的结果和利用模式理解海气相互作的物 理过程.
பைடு நூலகம்七讲的主要内容
• 热带海洋和大气环流的平均态及 其基本的动力过程
大洋环流和海气相互作用的数值模拟
《动力气象学》课程笔记

《动力气象学》课程笔记绪论1. 动力气象学发展史1.1 重大理论发现动力气象学的早期发展主要基于对大气运动的观测和理论推测。
19世纪,科学家们开始系统地研究大气运动,并逐渐揭示了影响大气运动的一些关键因素。
这些因素包括:- 科里奥利力:由法国物理学家加斯帕尔·科里奥利首次提出,它解释了地球自转导致的风的偏转现象。
- 地转偏向力:由于地球自转,大气中的气流会相对于地面产生偏转,这个力就是地转偏向力。
- 大气压力和密度变化:大气压力和密度的变化会影响大气运动,这些变化与温度、湿度等因素有关。
1.2 数值天气预报20世纪中叶,随着计算机技术的发展,动力气象学进入了一个新的时代。
科学家们开始利用计算机来求解大气运动方程组,这种方法被称为数值天气预报。
数值天气预报的出现极大地提高了天气预报的准确性,使得气象学成为了一门更加精确的科学。
1.3 动力气象学发展新阶段近年来,动力气象学在气候变化研究中的应用变得越来越重要。
科学家们通过研究大气运动、能量转换和波动等现象,揭示了气候变化的原因和规律。
此外,动力气象学在防灾减灾、水资源管理等领域也发挥着重要作用。
2. 动力气象学的基本概念2.1 大气运动方程组大气运动方程组是描述大气运动的物理方程,包括连续性方程、动量方程和能量方程。
这些方程组基于质量守恒、牛顿第二定律和能量守恒等物理定律,为我们提供了研究大气运动的基本工具。
2.2 涡旋运动大气中的涡旋运动是天气系统和气候变化的重要因素。
涡旋运动包括环流、涡度和螺旋度等概念。
了解涡旋运动有助于我们预测天气变化和气候趋势。
2.3 准地转运动准地转运动是指大气中接近地转平衡状态的运动。
在这种状态下,大气运动主要受到地转偏向力和压力梯度力的作用。
准地转运动为我们提供了一个简化的大气运动模型,便于研究和预测天气。
2.4 大气波动大气波动是大气运动中的周期性变化,包括重力波、惯性重力波和Rossby 波等。
这些波动在天气系统和气候变化中起着关键作用,了解它们有助于我们预测天气和气候。
非均匀基本气流中的Rossby波2

∂ψ ∂t ∂ψ ∂x ∂ψ ∂y ∂ψ ∂z 1 ∂A ∂θ =( + i )ψ A ∂t ∂t 1 ∂A ∂θ =( + i )ψ A ∂x ∂x 1 ∂A ∂θ =( + i )ψ A ∂y ∂y 1 ∂A ∂θ =( + i )ψ A ∂z ∂z 1 ∂A =( − iω )ψ A ∂t 1 ∂A =( + ik )ψ A ∂x 1 ∂A =( + il )ψ A ∂y 1 ∂A =( + in)ψ A ∂z
非均匀基流中Rossby的传播 §3 非均匀基流中 的传播
1 . 球 面 Rossby 波 的 传 播 — 大 圆 理 论 1979年 Hoskins提出 提出) (1979年 Hoskins提出) 提出波列传播是为了解决气候遥相关— 提出波列传播是为了解决气候遥相关 波列遥相关
PNA型遥相关 PNA型遥相关
1 + sin ϕ x = aλ , y = a ln cos ϕ 则, dx = ad λ , dy = a dϕ cos ϕ
∂ ∂ ∂ 2ψ ′ ∂ 2ψ ′ ∂ψ ′ 方程变为, 方程变为, + u =0 M 2 + 2 + BM ∂x ∂x ∂y ∂x ∂t
d ( ∇2ψ + f ) = 0 描写的是 描写的是Rossby波,体现 β 效应 即, dt 波
1 其中, 其中,∇ = 2 a
2
1 ∂2 1 ∂ ∂ + 2 cos 2 cos ϕ ∂λ cos ϕ ∂ϕ ∂ϕ
高等大气动力学考题

高等大气动力学:1、(1)大气声波、重力外波、重力内波、惯性波和Rossby 波的物理机制各是什么?且简述一下重力外波和重力内波有何异同?(2)画图说明对导式Rossby 波;曳式Rossby 波,并说明正压Rossby 的演变及其在实际中的应用。
什么情况下?(3)波能密度(4)孤立波2、证明正压模式下准地转位涡守恒定律可以写为()()()000000=+⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂v q y v x u t β其中()ψλψψλζ2022000-∇=-=h q 3、(1)2222220220h h c t t ψψψλ∂∂-∇-∇=∂∂(2)类似的求lagrange 量或者lagrange 平均量以及频散关系。
4、已知正压模式的基本方程组 11100u u u p u v fv t x y x v v v p u v fu t x y y pg z u v w x y zρρρ∂∂∂∂++-=-∂∂∂∂∂∂∂∂+++=-∂∂∂∂∂=--∂∂∂∂++=⎧⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎩∂∂∂ 边界条件:0z =时,0w =,下界为理想刚体;z h =时,h dh w dt=,p=P=const ,上界为均质大气高度,静止时h=H=const (1) 利用静力学关系和自由面条件改写正压模式基本方程组,若以静止大气为背景,证明此时方程组可以写为20()0u fv t x v fu ty u v c tx y φφφ''∂∂'-=-∂∂''∂∂'+=-∂∂'''∂⎧⎪⎪⎪⎨∂∂++=∂∂∂⎪⎪⎪⎩,其中20gh gH gh c gh φφφ'''==+=+=+ 用上面的静态正压模式方程组(f =0f )推导Klein-Gordron 方程L =0,其中L ≡2200222h c f t∇+∂-∂ (2) 令0f φψ'=,并且设ψ是一缓变波列,ψ=a cos()θα+,kx ly t θω=+-,求方程ℒψ=0的Lagrange 量和平均Lagrange 量,并求出相应的频散关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
! (QGPV) equation is written,
dq = 0 (1) dt
with
! q"
f
+ #2$ +
f2 N2
%o&1
' 'z
( )*
%o
'$ 'z
+ ,-
.
The careful reader will notice this is the same as Pedlosky QGPV equation 6.5.21,
Vertically Propagating Rossby Waves
By: Emily Riley Submitted to: GFD II Spring, 2007
1. Introduction Vertically propagating waves have an important role in the dynamics of the
must satisfy
!
!
! 4
#" $%"t
+
u
" "x
&'(q)
+
*
"+ ) "x
=
0
(3)
where
!
q"
#
$2%" +
f
2 o
N 2&o
' 'z
( )* & o
'% 'z
"+ ,-
.
Equation (3) has separable solutions of the form,
!
#"( x, y, z, t) = $(z)ei(kx+ly%kcxt)+z / 2 H (4)
3
phenomenon of sudden stratospheric warming due to the presence of Rossby waves. Finally, section 6 concludes the paper.
2. Criteria for Vertical Propagation of Rossby Waves
where cx is the zonal phase speed. Subbing (4) into (3) gives
!
!
d2" dz 2
+
m2"
=
0
(5)
where
( ) ! m2
"
N2
f
2 o
% &'(u
# $ cx)
$
k2 + l2
(1
* )
$
4
H
2
Assuming the Rossby waves are stationary, such that cx = 0 and remembering that m2 must be positive fo!r waves to propagate vertically, we see that vertically propagating modes can only exist when the mean zonal flo!w satisfies the condition !
where " = df = constan t , to take advantage of Cartesian coordinates while still retaining
dy
!
the essential physics for the analysis. To begin, the quasi-geostrophic potential vorticity
This paper will focus on the dynamics of the extratropical vertically propagating Rossby waves. The next section will discuss quantitatively under what conditions stationary Rossby waves are able to propagate into the stratosphere. Section 3 will discuss the structure of Rossby waves in the vertical with an emphasis on how the waves propagate through the use of waveguides. Section 4 reviews the role critical levels/lines have on Rossby wave propagation. Section 5 briefly mentions the observed
safe to assume stationary Rossby waves, as their primary forcing is stationary, i.e.
except
the
vertical
! coordinate
is
defined
in
log-pressure
coordinates
as
$ z " #H ln&
%
p ps
' ) (
,
where H is a constant scale height. The waves are manifested as a small-amplitude disturbance superposed on a constant zonal-mean flow. The f!low is therefore broken
Figure 1. Seasonal mean 30 mb geopotential height (solid lines, km) and temperatures (dashed lines, °C) fields for summer (top) and winter (bottom) Northern Hemisphere seasons (After Hare, 1968)
[( ) ( )] 0 < u < "
k2 + l2
+
f
2 o
/
4Nere Uc is the Rossby critical velocity. The critical velocity says that vertical propagation of !Rossby waves can only occur in the presence of westerly winds weaker ! than a critical value that depends on the horizontal scale of the waves. Note that it is
up into a mean state and a perturbation state, such that " = " + "# and q = q + q". If the
decompositions are subbed into equation (1) and linearized the perturbation q" field
confinement of vertically propagating waves to the winter hemisphere. While their
analysis used spherical coordinates, Holton chooses to use a mid-latitude " -plane,
2
propagating extratropical waves in the southern hemisphere is most likely due to smaller difference in land-sea heating contrasts and difference in topographic forcing.
Following Holton (2004) chapter 12.3, the criteria under which Rossby waves will
propagate vertically is examined. Charney and Drazin (1961) first explained the
stratosphere. The waves interact with the stratosphere’s mean circulation, maintain the energy and momentum budget of the stratosphere, transport trace species (e.g. ozone) concentrations between the troposphere and stratosphere, and are the reason for the phenomena known as sudden stratospheric warming. The waves originate in the lower troposphere where they are forced to propagate vertically by topographic forcing or land-sea diabatic heating differences. There are two distinct regions of vertically propagating waves, the extratropics and the tropics. Quasi-stationary Rossby waves are the most significant vertically propagating mode in the extratropics, while Kelvin and mixed Rossby-gravity waves are the most prominent vertically propagating waves in the tropics (Holton, 1980). Through mechanical modeling and observations it has been found that these vertically propagating waves occur only under certain atmospheric conditions. Namely, they are most prominent in the northern hemisphere winter under weak westerly wind conditions (Charney and Drazin, 1961). Only the longest waves, i.e. wave number 1 and 2, are able to propagate beyond the troposphere into the stratosphere, as will be show quantitatively later. Figure 1 provides a remarkable example of the influence the extratropical waves have during the northern hemisphere wintertime. In the wintertime the cyclonic vortex in the 30 mb geopotential height is greatly distorted by a ridge of high pressure, the Aleutian high, which is composed of wavenumbers 1 and 2 (compare bottom wintertime picture with top summertime picture). Labitzke and van Loon (1972) found similar waves to the wave number 1 of the northern hemisphere in the southern hemisphere. The lack of prominent vertically
