余弦定理
余弦定理公式

余弦定理公式
余弦定理公式:cosA=(b²+c²-a²)/2bc,cosA=邻边比斜边。
余弦定理是描述三角形中三边长度与一个角的余弦值关系的数学定理。
运用它可解决一类已知三角形两边及夹角求第三边或者是已知三个
边求角的问题。
1余弦定理性质
对于任意三角形,任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的两倍积,若三边为a,b,c三角为A,B,C,则满足性质:
a^2=b^2+c^2-2·b·c·cosA
b^2=a^2+c^2-2·a·c·cosB
c^2=a^2+b^2-2·a·b·cosC
cosC=(a^2+b^2-c^2)/(2·a·b)
cosB=(a^2+c^2-b^2)/(2·a·c)
cosA=(c^2+b^2-a^2)/(2·b·c)
(物理力学方面的平行四边形定则以及电学方面正弦电路向量
分析也会用到)
第一余弦定理(任意三角形射影定理)
设△ABC的三边是a、b、c,它们所对的角分别是A、B、C,则有
a=b·cosC+c·cosB,b=c·cosA+a·cosC,c=a·cosB+b·cosA。
10分钟学会-余弦定理

10分钟学会-余弦定理
余弦定理是三角学中的重要定理,用于计算三角形的边长或角度。
下面是一个简单的解释:
余弦定理用于计算一个三角形的边长,基于三角形的两个边和它们夹角的余弦值之间的关系。
假设我们有一个三角形,其中边长分别为a、b和c,而夹角对应的顶点分别为A、B和C。
则余弦定理可以表示为:
c2 = a2 + b2 - 2ab * cos(C)
其中,c表示三角形的第三边长,a和b分别表示另外两条边的长度,C表示这两条边夹角的大小,cos表示夹角的余弦值。
利用余弦定理,我们可以在已知两边长度和它们夹角的情况下,计算出第三边的长度。
也可以在已知三边长度的情况下,计算出夹角的大小。
需要注意的是,余弦定理适用于任意三角形,无论是锐角三角形、直角三角形还是钝角三角形。
它为解决三角形相关问题提供了重要的数学工具。
余弦定理及推导-文档
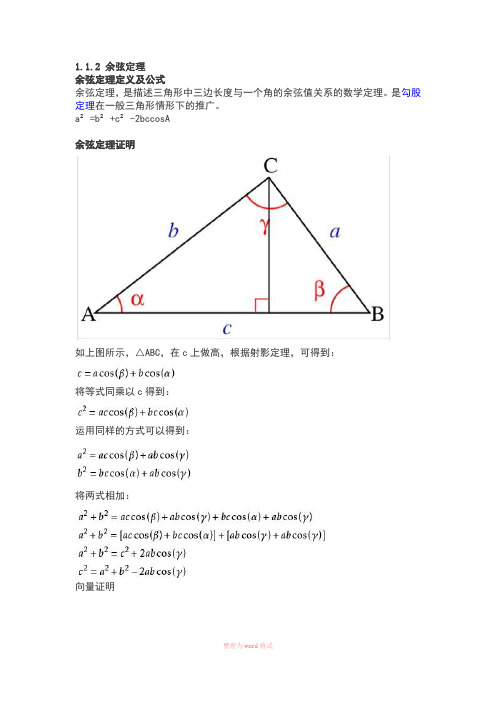
1.1.2 余弦定理
余弦定理定义及公式
余弦定理,是描述三角形中三边长度与一个角的余弦值关系的数学定理。
是勾股定理在一般三角形情形下的推广。
a²=b²+c²-2bccosA
余弦定理证明
如上图所示,△ABC,在c上做高,根据射影定理,可得到:
将等式同乘以c得到:
运用同样的方式可以得到:
将两式相加:
向量证明
正弦定理和余弦定理
正弦定理
a/sinA=b/sinB=c/sinC=2R
(1)已知三角形的两角与一边,解三角形
(2)已知三角形的两边和其中一边所对的角,解三角形
(3)运用a:b:c=sinA:sinB:sinC解决角之间的转换关系
直角三角形的一个锐角的对边与斜边的比叫做这个角的正弦。
余弦定理
是揭示三角形边角关系的重要定理,直接运用它可解决一类已知三角形两边及夹角求第三边或者是已知三个边求角的问题,若对余弦定理加以变形并适当移于其它知识,则使用起来更为方便、灵活。
直角三角形的一个锐角的邻边和斜边的比值叫这个锐角的余弦值友情提示:本资料代表个人观点,如有帮助请下载,谢谢您的浏览!。
余弦定理含义

余弦定理含义
余弦定理是在三角形中,描述了三个边和内夹角之间的关系。
它的含义可以总结如下:
在一个三角形ABC中,假设a、b、c分别表示边BC、AC和AB的长度,而角A、角B和角C分别表示对应的内夹角。
那么余弦定理的表达式如下:c^2 = a^2 + b^2 - 2ab·cos(C)。
其中的cos(C)是角C的余弦值。
余弦定理的含义是:对于任意一个三角形,如果我们知道了三个边的长度,那么可以通过余弦定理计算出对应的三个内夹角的余弦值。
反之,如果我们已知三个边的长度以及其中两个夹角的度数,也可以利用余弦定理求解第三个角的度数。
余弦定理在解决三角形相关问题时非常有用,例如计算未知边长或角度、判断三角形的形状(锐角三角形、直角三角形、钝角三角形)等。
它是解决三角学问题的重要工具之一。
三角形余弦定理公式

三角形余弦定理公式是cosA=(b²+c²-a²)/2bc,cosA=邻边比斜边。
对于任意三角形,任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。
余弦定理,欧氏平面几何学基本定理。
余弦定理是描述三角形中三边长度与一个角的余弦值关系的数学定理,是勾股定理在一般三角形情形下的推广,勾股定理是余弦定理的特例。
余弦定理是揭示三角形边角关系的重要定理。
拓展知识
判定定理,两根判别法。
若记m,c1,c2为c的两值为正根的个数,c1为c的表达式中根号前取加号的值,c2为c的表达式中根号前取减号的值。
①若m(c1,c2)=2,则有两解。
②若m(c1,c2)=1,则有一解。
③若m(c1,c2)=0,则有零解即无解。
注意:若c1等于c2且c1或c2大于0,此种情况算到第二种情况,即一解。
三角函数的余弦定理

三角函数的余弦定理三角函数的余弦定理是指在任意三角形中,三边的长度和夹角之间的关系。
它是解决三角形问题中的一个重要工具,可用于计算三边相互之间的关系,以及求解三角形的面积和角度。
余弦定理的表述如下:在一个三角形ABC中,设AB=c,BC=a,AC=b,∠ABC=A,∠BAC=B,∠CBA=C。
则余弦定理可以表示为以下公式:c² = a² + b² - 2abcosCa² = b² + c² - 2bccosAb² = a² + c² - 2accosB其中,c表示三角形的斜边,即对应于∠C的边的长度;a和b分别表示三角形的两个其他边的长度;∠A、∠B和∠C分别表示三角形的三个内角。
利用余弦定理,我们可以解决很多与三角形相关的问题。
下面我们来看几个应用实例:1. 求解第三边的长度:已知一个三角形的两边长度a和b,以及它们夹角C的度数,我们可以利用余弦定理计算出斜边c的长度。
通过代入公式c² = a² + b² - 2abcosC,即可求得c的值。
2. 求解三角形的面积:已知一个三角形的两边长度a和b,以及它们夹角C的度数,我们还可以利用余弦定理求解三角形的面积。
首先,根据公式c² = a² + b² - 2abcosC,可以求得斜边c的长度。
然后,利用海伦公式(也可根据三角形的高求解)计算出三角形的面积。
3. 求解三角形的角度:已知一个三角形的三边长度a、b和c,我们可以利用余弦定理求解三个内角的度数。
通过对公式c² = a² + b² -2abcosC进行变换,我们可以得到cosC = (a² + b² - c²) / 2ab,再利用反余弦函数,即可求出∠C的度数。
除了上述应用,余弦定理还有许多其他方面的用途,比如用于解决三角形的外心和高线的问题,或者求解两个点之间的距离等。
三角函数余弦定理公式

三角函数余弦定理公式三角函数余弦定理公式大全余弦定理对于边长为a、b、c而相应角为A、B、C的三角形,有:a^2 = b^2 + c^2 - 2bc·cosAb^2 = a^2 + c^2 - 2ac·cosBc^2 = a^2 + b^2 - 2ab·cosC也可表示为:cosC=(a^2 +b^2 -c^2)/ 2abcosB=(a^2 +c^2 -b^2)/ 2accosA=(c^2 +b^2 -a^2)/ 2bc这个定理也可以通过把三角形分为两个直角三角形来证明。
如果这个角不是两条边的夹角,那么三角形可能不是唯一的(边-边-角)。
要小心余弦定理的这种歧义情况。
延伸定理:第一余弦定理(任意三角形射影定理)设△ABC的三边是a、b、c,它们所对的角分别是A、B、C,则有a=b·cos C+c·cos B,b=c·cos A+a·cos C,c=a·cos B+b·cos A三角函数正弦定理公式正弦定理对于边长为a, b和c而相应角为A, B和C的三角形,有:sinA / a = sinB / b = sinC/c也可表示为:a/sinA=b/sinB=c/sinC=2R变形:a=2RsinA,b=2RsinB,c=2RsinC其中R是三角形的外接圆半径。
它可以通过把三角形分为两个直角三角形并使用上述正弦的定义来证明。
在这个定理中出现的公共数(sinA)/a是通过A, B和C三点的圆的直径的倒数。
正弦定理用于在一个三角形中(1)已知两个角和一个边求未知边和角(2)已知两边及其一边的对角求其他角和边的问题。
余弦定理

余弦定理一、知识梳理1.余弦定理三角形任何一边的平方等于其他两边的平方和减去这两边与它们的夹角的余弦的积的2倍.即a2=b2+c2-2bccos A,b2=c2+a2-2cacos B,c2=a2+b2-2abcos C。
.2.余弦定理的变式cos A=b2+c2-a22bc;cos B=c2+a2-b22ca;cos C=a2+b2-c22ab.想一想:已知三角形的三边,如何判断三角形的形状?提示在△ABC中,若三边a,b,c中,边a最大,则∠A最大;若a2<b2+c2,则0°<A<90°,则三角形是锐角三角形;若a2=b2+c2,则A=90°,则三角形是直角三角形,若a2>b2+c2,则90°<A<180°,则三角形是钝角三角形.名师点睛1.余弦定理(1)余弦定理是勾股定理的推广,勾股定理是余弦定理的特例.(2)余弦定理适用于任意三角形,揭示了三角形中边角间的关系.在应用余弦定理时,因为已知三边(求角)或已知两边及夹角(求第三边)时,三角形是唯一确定的,即此时的解是唯一的.(3)在余弦定理中,每一个等式中都包含四个不同的量.即三角形的三边和一边的对角这四个元素,可利用方程的思想,知三求一.2.余弦定理变形及应用(1)已知三角形的三边求角时,常用余弦定理的变形式.(2)若A为锐角,则cos A>0,即b2+c2-a2>0,即b2+c2>a2;若A为直角,则cos A=0,即b2+c2-a2=0,即b2+c2=a2;若A为钝角,则cos A<0,即b2+c2-a2<0,即b2+c2<a2.反之,也成立.(3)在解三角形时,正弦定理和余弦定理是相通的.如:已知两边和其中一边的对角,解三角形时,用正弦定理可求解,但需判别解的情况;也可用余弦定理求解.若已知a 、b 和A ,可先由余弦定理求出c ,列式为a 2=b 2+c 2-2bc ·cos A ,则关于c 的方程的解的个数对应三角形解的个数.二、典例精析题型一 余弦定理解三角形【例1】 (1)在△ABC 中,如果a ∶b ∶c =2∶6∶(3+1),求这个三角形的最小角.(2)在△ABC 中,已知a =2,b =22,∠C =15°,求角A 、B 和边c 的值. 解 (1)在三角形中,大边对大角,小边对小角,根据已知条件判断最小边应为a .∵a ∶b ∶c =2∶6∶(3+1),可设a =2k ,b =6k ,c =(3+1)k (k >0),最小角为角A ,由余弦定理得cos A =b 2+c 2-a 22bc =6k 2+(3+1)2k 2-4k 22(3+1)×6k 2=22,故∠A =45°. (2)cos 15°=cos(45°-30°)=6+24.由余弦定理知c 2=a 2+b 2-2ab cos C =4+8-22×(6+2)=8-43, ∴c =8-43=(6-2)2=6- 2.由正弦定理得a sin A =c sin C ,sin A =a sin C c =a sin 15°c =2×6-246-2=12, ∵b >a ,sin A =12,∴∠A =30°.∴∠B =180°-∠A -∠C =135°.【变式1】 在△ABC 中,设∠A 、∠B 、∠C 的对边分别为a 、b 、c ,且cos A =14.若a =4,b +c =6,且b <c ,求b 、c 的值.解 由余弦定理a 2=b 2+c 2-2bc cos A ,即a 2=(b +c )2-2bc -2bc cos A ,∴16=36-52bc ,∴bc =8.由⎩⎨⎧ b +c =6,bc =8,b <c ,可求得⎩⎨⎧b =2,c =4.. 题型二 判断三角形的形状【例2】 在△ABC 中,已知(a +b +c)(a +b -c)=3ab ,且2cos A·sin B =sin C ,试确定△ABC 的形状.解 法一 (角化边)由正弦定理,得sin C sin B =c b ,由2cos A ·sin B =sin C ,得cos A =sin C 2sin B =c 2b .又由余弦定理,得cos A =c 2+b 2-a 22bc ,∴c 2b =c 2+b 2-a 22bc,即c 2=b 2+c 2-a 2,∴a =b .又∵(a +b +c )(a +b -c )=3ab , ∴(a +b )2-c 2=3b 2,∴4b 2-c 2=3b 2,∴b =c .∴a =b =c ,∴△ABC 为等边三角形.法二 (边化角)∵∠A +∠B +∠C =180°,∴sin C =sin(A +B ).又∵2cos A ·sin B =sin C ,∴2cos A ·sin B =sin A ·cos B +cos A ·sin B ,∴sin(A -B )=0.又∵A 与B 均为△ABC 的内角,∴∠A =∠B .又由(a +b +c )(a +b -c )=3ab ,得(a +b )2-c 2=3ab ,a 2+b 2-c 2+2ab =3ab ,即a 2+b 2-c 2=ab .由余弦定理,得cos C =12,而0°<∠C <180°,∴∠C =60°.又∵∠A =∠B ,∴△ABC 为等边三角形.【变式2】 在△ABC 中,若b 2sin 2C +c 2sin 2B =2bccos Bcos C ,试判断三角形的形状.解 法一 由a sin A =b sin B =c sin C =2R ,则条件转化为4R 2·sin 2C ·sin 2B +4R 2·sin 2C ·sin 2B =8R 2·sin B ·sin C ·cos B ·cos C , 又sin B ·sin C ≠0,∴sin B ·sin C =cos B ·cos C ,即cos (B +C )=0.又0°<∠B +∠C <180°,∴∠B +∠C =90°,∴∠A =90°,故△ABC 为直角三角形.法二 将已知等式变形为b 2(1-cos 2C )+c 2(1-cos 2B )=2bc cos B cos C ,即有b 2+c 2-b 2·(a 2+b 2-c 22ab )2-c 2·(a 2+c 2-b 22ac )2=2bc ·a 2+c 2-b 22ac ·a 2+b 2-c 22ab , 即b 2+c 2=[(a 2+b 2-c 2)+(a 2+c 2-b 2)]24a 2=4a 44a 2=a 2,即b 2+c 2=a 2, ∴△ABC 为直角三角形.题型三 正、余弦定理的综合应用【例3】 在△ABC 中,BC =5,AC =3,sin C =2sin A .(1)求AB 的值;(2)求sin(2A-π4)的值.【变式3】△ABC中,a、b、c分别为角A、B、C的对边,且满足b2+c2-a2=bc,(1)求角A的值;(2)若a=3,设角B的大小为x,△ABC的周长为y,求y=f(x)的最大值.解(1)在△ABC中,由b2+c2-a2=bc及余弦定理知:cos A=b2+c2-a22bc=12,而0<A<π,∴A=π3.(2)由a=3,A=π3,及正弦定理得:bsin B=csin C=asin A=3sinπ3=2,∵B=x,C=2π3-x∴b=2sin x,c=2sin(23π-x),0<x<2π3∴y=a+b+c=3+2sin x+2sin(2π3-x)误区警示忽略三角形的隐含条件【示例】设2a+1,a,2a-1为钝角三角形的三边,求实数a的取值范围.[错解]∵2a+1,a,2a-1是三角形的三边,∴⎩⎨⎧ 2a +1>0,a >0,2a -1>0,解得a >12,∴2a +1是三边长的最大值,设其所对角为θ,∵2a +1,a,2a -1是钝角三角形的三边,∴cos θ<0,即a 2+(2a -1)2-(2a +1)22a (2a -1)=a (a -8)2a (2a -1)<0,解得12<a <8, 又∵a >12,∴a 的取值范围是12<a <8.[正解] ∵2a +1,a,2a -1是三角形的三边,∵⎩⎨⎧ 2a +1>0,a >0,2a -1>0,解得a >12,此时2a +1最大, ∴要使2a +1,a,2a -1表示三角形的三边,还需a +(2a -1)>2a +1,解得a >2. 设最长边2a +1所对的角为θ,则cos θ=a 2+(2a -1)2-(2a +1)22a (2a -1)=a (a -8)2a (2a -1)<0,解得12<a <8. ∴a 的取值范围是2<a <8.求三线段能构成钝角三角形三边的充要条件,除了要保证三边长均为正数外,还要使最大角为钝角,注意两边之和大于第三边这一隐含条件.三、课后检测1.在△ABC 中,a =7,b =43,c =13,则△ABC 的最小角为( ). A.π3 B.π6 C.π4 D.π12解析 ∵a >b >c ,∴C 为最小角,由余弦定理cos C =a 2+b 2-c 22ab =72+(43)2-(13)22×7×43=32.∴C =π6.答案 B 2.在△ABC 中,已知a =2,则b cos C +c cos B 等于( ). A .1 B. 2 C .2 D .4解析 b cos C +c cos B=b ·a 2+b 2-c 22ab +c ·c 2+a 2-b 22ac =2a 22a=a =2.答案 C 3.在△ABC 中,已知a 2=b 2+bc +c 2,则角A 为 ( ).A.π3B.π6C.2π3D.π3或2π3解析 由于b 2+c 2-a 2=-bc =2bc ·cos A∴cos A =-12,又A ∈(0,π),∴A =2π3.答案 C 4.在△ABC 中,若b =1,c =3,∠C =23π,则a = . 解析 ∵c 2=a 2+b 2-2ab cos C ,∴(3)2=a 2+12-2a ·1·cos 23π,∴a 2+a -2=0, ∴(a +2)(a -1)=0,∴a =-2(舍去)或a =1.答案 15.在△ABC 中,sin 2A 2=c -b 2c(a 、b 、c 分别为角A 、B 、C 的对边),则△ABC 的形状是 .解析 ∵sin 2A 2=1-cos A 2=c -b 2c ,∴cos A =b c =b 2+c 2-a 22bc ⇒a 2+b 2=c 2⇒△ABC 为直角三角形.答案 直角三角形6.在△ABC 中,BC =a ,AC =b ,且a ,b 是方程x 2-23x +2=0的两根,2cos(A +B )=1.(1)求角C 的度数;(2)求AB 的长;(3)求△ABC 的面积.解 (1)cos C =cos [π-(A +B )]=-cos(A +B )=-12,又∵C ∈(0,π),∴C =2π3. (2)∵a ,b 是方程x 2-23x +2=0的两根,∴⎩⎨⎧a +b =23,ab =2.∴AB 2=b 2+a 2-2ab cos 120°=(a +b )2-ab =10, ∴AB =10.(3)S △ABC =12ab sin C =12×2×sin 2π3=32.7.在△ABC 中,下列结论:①若a 2>b 2+c 2,则△ABC 为钝角三角形;②若a 2=b 2+c 2+bc ,则∠A 为60°;③若a 2+b 2>c 2,则△ABC 为锐角三角形;④若∠A ∶∠B ∶∠C =1∶2∶3,则a ∶b ∶c =1∶2∶3,其中正确的个数为( ).A .1B .2C .3D .4解析 ①cos A =b 2+c 2-a 22bc <0,∴∠A 为钝角,正确;②cos A =b 2+c 2-a 22bc =-12,∴∠A =120°,错误;③cos C =a 2+b 2-c 22ab>0,∠C 为锐角,但∠A 或∠B 不一定为锐角,错误;④∠A =30°,∠B =60°,∠C =90°,a ∶b ∶c =1∶3∶2,错误,故选A.答案 A8.在△ABC 中,已知面积S =14(a 2+b 2-c 2),则角C 的度数为 ( ). A .135° B .45° C .60° D .120°解析 ∵S =14(a 2+b 2-c 2)=12ab sin C ∴a 2+b 2-c 2=2ab sin C ,∴c 2=a 2+b 2-2ab sin C . 由余弦定理得:c 2=a 2+b 2-2ab cos C ,∴sin C =cos C ,∴C =45°答案 B9.已知△ABC 三边长分别为AB =7,BC =5,CA =6,则AB →·BC →的值为 .解析 由余弦定理可求得cos B =1935,∴AB →·BC →=|AB |·|BC |·cos(π-B )=-|AB |·|BC |·cos B =-19.答案 -1910.在△ABC 中,AB =2,AC =6,BC =1+3,AD 为边BC 上的高,则AD 的长是 .解析 ∵cos C =BC 2+AC 2-AB 22×BC ×AC =22, ∴sin C =22.∴AD =AC ·sin C = 3. 答案 311.在△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边的长,cos B =35,且AB →·BC →=-21. (1)求△ABC 的面积;(2)若a =7,求角C .解 (1)∵AB →·BC →=-21,∴BA →·BC →=21.∴BA →·BC →=|BA →|·|BC →|·cos B =ac cos B =21.∴ac =35,∵cos B =35,∴sin B =45. ∴S △ABC =12ac sin B =12×35×45=14. (2)ac =35,a =7,∴c =5.由余弦定理b 2=a 2+c 2-2ac cos B =32,∴b =4 2.∴cos C =a 2+b 2-c 22ab =49+32-252×7×42=22,又∵C ∈(0,π) ∴C =45°.12.(创新拓展)△ABC 中,内角A 、B 、C 的对边分别为a 、b 、c ,已知b 2=ac 且cos B =34. (1)求1tan A +1tan C的值;(2)设BA →·BC →=32,求a +c 的值. 解 (1)由cos B =34得sin B = 1-⎝⎛⎭⎫342=74, 由b 2=ac 及正弦定理得sin 2B =sin A sin C .于是1tan A +1tan C =cos A sin A +cos C sin C=sin C cos A +cos C sin A sin A sin C =sin (A +C )sin 2B =sin B sin 2B =1sin B =477. (2)由BA →·BC →=32得ca ·cos B =32, 由cos B =34,可得ca =2,即b 2=2. 由余弦定理b 2=a 2+c 2-2ac ·cos B , 得a 2+c 2=b 2+2ac ·cos B =5,∴(a +c )2=a 2+c 2+2ac =5+4=9, ∴a +c =3.。
余弦定理总结知识点

余弦定理总结知识点首先,我们来看一下余弦定理的数学表达式。
对于一个三角形ABC,余弦定理可以表示为:a^2 = b^2 + c^2 - 2bc * cosAb^2 = a^2 + c^2 - 2ac * cosBc^2 = a^2 + b^2 - 2ab * cosC其中,a、b、c分别表示三角形的三个边的长度,A、B、C分别表示三角形的三个内角的大小,cosA、cosB、cosC分别表示三角形的三个内角的余弦值。
通过这个数学表达式,我们可以看出余弦定理的基本思想是通过三角形中的边长和角度的关系来求解各种三角形问题。
余弦定理的优点是不仅可以用于等腰三角形和等边三角形,还可以适用于一般三角形,因此在实际应用中具有非常广泛的适用性。
余弦定理的应用场景非常广泛,比如在测量地理距离、建筑设计、航海、航空等领域都有着重要的作用。
下面我们来分别介绍一下余弦定理的几种常见应用。
1、求解三角形的边长余弦定理可以通过已知三角形的一个角和两个边长来求解第三条边的长度。
比如,已知三角形的两边长分别为3和4,并且夹角为60度,就可以通过余弦定理来求解第三条边的长度。
根据余弦定理的数学表达式,我们可以得到:c^2 = 3^2 + 4^2 - 2*3*4*cos60°= 9 + 16 - 24*0.5= 25 - 12= 13因此,第三条边的长度为√13。
2、求解三角形的角度余弦定理也可以通过已知三角形的三条边的长度来求解三角形的夹角。
比如,已知三角形的三条边长分别为3、4、5,就可以通过余弦定理来求解各个角的大小。
根据余弦定理的数学表达式,我们可以得到:cosA = (b^2 + c^2 - a^2)/(2bc)= (4^2 + 5^2 - 3^2)/(2*4*5)= (16 + 25 - 9)/40= 32/40= 0.8因此,∠A的余弦值为0.8,所以∠A的大小为cos⁻¹(0.8)≈36.87°。
余弦定理

余弦定理【知识要点】1、余弦定理:在△ABC 中2222222222cos , 2cos ,2cos a b c bc A b a c ac B c a b ab C=+-=+-=+-2、余弦定理的变形:222222222cos ,cos ,cos ,222b c a a c b a b c A B C bc ac ab+-+-+-===3、余弦定理的应用(1)已知△ABC 的两角及夹边,求第三边; (2)已知△ABC 的三边,求角. 【例题分析】1、在△ABC 中,若sin A ∶sin B ∶sin C =7∶8∶13,求∠C 。
2、在△ABC 中,求证:)cos cos (aAb Bc a b b a -=-3、已知(a 2+bc )x 2+2b 2+c 2x +1 = 0是关于x 的二次方程,其中a 、b 、c 是三角形的三边, (1)若∠A 为钝角,试判断方程根的情况; (2)若方程有两个相等的实根,求∠A 的度数.一、选择题1、在△ABC 中,若2lg sin lg cos lg sin lg =--C B A ,则△ABC 的形状是 ( )A 、直角三角形B 、等边三角形C 、不能确定D 、等腰三角形 2、在△ABC 中,若,3))((bc a c b c b a =-+++则A =( )A 、090 B 、060 C 、0135 D 、0150BACabc3、在△ABC 中,若1413cos ,8,7===C b a ,则最大角的余弦是 ( ) A 、51- B 、61- C 、71- D 、81-4.边长为5,7,8的三角形的最大角与最小角的和是( )A 、090 B 、0120 C 、0135 D 、0150 5、在△ABC 中,若=++=A c bc b a 则,222( )A 、120°B 、60°C 、45°D 、30° 6、在△ABC 中,若=+=C B C B A tan tan ,cos cos 2sin 则( )A 、4B 、2C 、3D 、347、在锐角△ABC 中,若2,3a b ==,则边长c 的取值范围是( )A 、B 、(5,23)C 、(3,13)D 、(3,28、在△ABC 中,a =,b =1,c =2,则A 等于 ( )A 、30°B 、45°C 、60°D 、75°9、在△ABC 中,a 、b 、c 分别是三内角A 、B 、C 的对边,且sin 2A -sin 2C =(sinA -sinB)sinB ,则角C 等于( )A 、π6B 、π3 C 、5π6D 、2π310、在△ABC 中,若A =60°,BC =43,AC =42,则角B 的大小为 ( )A 、30°B 、45°C 、135°D 、45°或135°11、在△ABC 中,角A 、B 、C 的对边分别是a 、b 、c ,A =π3,a =3,b =1,则c = ( ) A 、1B 、2C 、3-1D 、 312、在△ABC 中,角A 、B 、C 的对边分别是a 、b 、c ,若a =2,b =22,且三角形有两解,则角A 的取值范围是 ( )A 、⎝⎛⎭⎪⎫0,π4B 、⎝ ⎛⎭⎪⎫π4,π2C 、⎝ ⎛⎭⎪⎫π4,3π4D 、⎝ ⎛⎭⎪⎫π4,π313、在△ABC 中,角A 、B 、C 所对的边长分别为a 、b 、c.若∠C =120°,c =2a ,则 ( )A 、a >bB 、a <bC 、a =bD 、a 与b 的大小关系不能确定14、在△ABC 中,内角A 、B 、C 的对边分别是a 、b 、c ,若a 2-b 2=3bc ,sinC =23sinB ,则A = ( )A 、30°B 、60°C 、120°D 、150°15、在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,若(a 2+c 2-b 2)tanB =3ac ,则角B 的值为 ( )A 、π6B 、π3 C 、π6或5π6D 、π3或2π316、已知△ABC 中,a 、b 、c 分别为∠A 、∠B 、∠C 的对边,如果a 、b 、c 成等差数列,∠B =30°,△ABC 的面积为0.5,那么b 为 ( )A 、1+ 3B 、3+ 3C 、3+33D 、2+ 317、在△ABC 中,cos 2B2=a +c 2c(a 、b 、c 分别为角A 、B 、C 的对边),则△ABC 的形状为 ( )A 、直角三角形B 、正三角形C 、等腰三角形D 、等腰三角形或直角三角形18、在△ABC 中,tanA =12,cosB =31010,若最长边为1,则最短边的长为 ( )A 、455B 、355 C 、255D 、55二、填空题19、若在△ABC 中,060,1,ABC A b S ∆∠==则CB A cb a sin sin sin ++++=_______。
余弦定理及推导
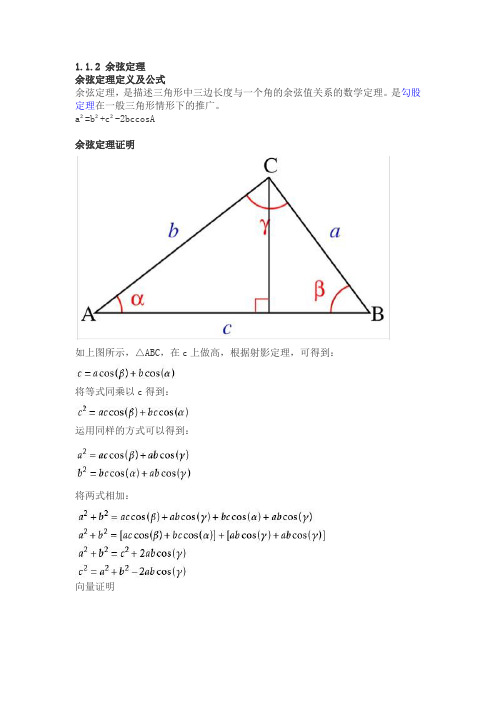
1.1.2 余弦定理
余弦定理定义及公式
余弦定理,是描述三角形中三边长度与一个角的余弦值关系的数学定理。
是勾股定理在一般三角形情形下的推广。
a²=b²+c²-2bccosA
余弦定理证明
如上图所示,△ABC,在c上做高,根据射影定理,可得到:
将等式同乘以c得到:
运用同样的方式可以得到:
将两式相加:
向量证明
正弦定理和余弦定理
正弦定理
a/sinA=b/sinB=c/sinC=2R
(1)已知三角形的两角与一边,解三角形
(2)已知三角形的两边和其中一边所对的角,解三角形
(3)运用a:b:c=sinA:sinB:sinC解决角之间的转换关系
直角三角形的一个锐角的对边与斜边的比叫做这个角的正弦。
余弦定理
是揭示三角形边角关系的重要定理,直接运用它可解决一类已知三角形两边及夹角求第三边或者是已知三个边求角的问题,若对余弦定理加以变形并适当移于其它知识,则使用起来更为方便、灵活。
直角三角形的一个锐角的邻边和斜边的比值叫这个锐角的余弦值。
正弦余弦定理公式

正弦余弦定理公式
正弦定理:设三角形的三边为a b c,他们的对角分别为a b c,外接圆半径为r,则称关系式a/sina=b/sinb=c/sinc为正弦定理。
余弦定理:设三角形的三边为a b c,他们的对角分别为a b c,则称关系式,a^2=b^2+c^2-2bc*cosa。
正弦定理:设三角形的三边为a b c,他们的对角分别为a b c,外接圆半径为r,则称关系式a/sina=b/sinb=c/sinc为正弦定理。
余弦定理:设立三角形的三边为a b c,他们的对角分别为a b c,则表示关系式
a^2=b^2+c^2-2bc*cosa
b^2=c^2+a^2-2ac*cosb
c^2=a^2+b^2-2ab*cosc。
证明:
任意三角形abc,作abc的外接圆o。
并作直径bd交⊙o于d,相连接da.
因为直径所对的圆周角是直角,所以∠dab=90度,
因为同弧所对的圆周角成正比,所以∠d等同于∠c。
所以c/sinc=c/sind=bd=2r。
相似可以证其余两个等式。
余弦定理

余弦定理余弦定理(第二余弦定理)余弦定理是揭示三角形边角关系的重要定理,直接运用它可解决一类已知三角形两边及夹角求第三边或者是已知三个边求角的问题,若对余弦定理加以变形并适当移于其他知识,则使用起来更为方便、灵活.直角三角形的一个锐角的邻边和斜边的比值叫做这个锐角的余弦值.余弦定理性质三角形中,任何一边的平方等于其他两边的平方的和减去这两边与它们的夹角的余弦的积的两倍,若三角形三边分别为a ,b ,c ,三角分别为A ,B ,C ,则满足性质:a 2=b 2+c 2-2bccosA ,b 2=c 2+ a 2-2cacosB ,c 2= a 2+b 2-2abcosC ,推论:2222cos b c a bc A +-= 2222cos c a b ca B +-= 2222cos a b c ab C +-=(物理力学方面的平行四边形定则中也会用到).第一余弦定理(任意三角形射影定理).设△ABC 的三边是a ,b ,c ,它们所对的角分别是A ,B ,C ,则有a=b·cos C+c·cos B, b=c·cos A+a·cos C, c=a·cos B+b·cos A .余弦定理证明平面向量证法∵如图,有a+b=c(平行四边形定则:两个邻边之间的对角线代表两个邻边大小).∴|c2|=(a+b)·(a+b),∴|c2|=a·a+2a·b+b·b.∴c2=a2+b2+2|a||b|cos(π-θ).(以上粗体字符表示向量)又∵cos(π-θ)=-cosθ,∴c2=a2+b2-2|a||b|cosθ,(注意:这里用到了三角函数公式)再拆开,得c2=a2+b2-2·a·b·cosC,即222 cos2+-=a b cCab同理可证其他.平面几何证法在任意△ABC中,∠C所对的边为c,∠B所对的边为b,∠A所对的边为a,作AD⊥BC.则有BD=cosB·c,AD=sinB·c,DC=BC-BD=a-cosB·c,根据勾股定理可得:AC2=AD2+DC2b2=(sinB·c)2+(a-cosB·c)2,b2=(sinB·c)2+a2-2ac·cosB+(cosB)2·c2,b2=(sin2B+cos2B)·c2-2ac·cosB+a2,b2=c2+a2-2ac·cosB,222Bcos+-=c a b作用(1)已知三角形的三条边长,可求出三个内角.(2)已知三角形的两边及夹角,可求出第三边.(3)已知三角形两边及其一边对角,可求其他的角和第三条边.(见解三角形公式,推导过程略)判定定理一(两根判别法):若记m(c1,c2)为c的值为正根的个数,c1为c的表达式中根号前取加号的值,c2为c的表达式中根号前取减号的值,①若m(c1,c2)=2,则有两解;②若m(c1,c2)=1,则有一解;③若m(c1,c2)=0,则有零解(即无解).注意:若c1等于c2且c1或c2大于0,此种情况算第二种情况,即有一解.判定定理二(角边判别法):(1)当a>bsinA时,①当b>a且cosA>0(即A为锐角)时,则有两解;②当b>a且cosA≤0(即A为直角或钝角)时,则有零解(即无解);③当b=a且cosA>0(即A为锐角)时,则有一解;④当b=a且cosA≤0(即A为直角或钝角)时,则有零解(即无解);⑤当b<a时,则有一解.(2)当a=bsinA时,①当cosA>0(即A为锐角)时,则有一解;②当cosA≤0(即A为直角或钝角)时,则有零解(即无解).(3)当a<bsinA时,则有零解(即无解),其他从余弦定理和余弦函数的性质可以看出,如果一个三角形两边的平方和等于第三边的平方,那么第三边所对的角一定是直角;如果小于第三边的平方,那么第三边所对的角是钝角;如果大于第三边的平方,那么第三边所对的角是锐角.即,利用余弦定理,可以判断三角形的形状.同时,还可以用余弦定理求三角形边长的取值范围.解三角形时,除了用到余弦定理外还常用到正弦定理.。
余弦定理

余弦定理编辑
余弦定理,是描述三角形中三边长度与一个角的余弦值关系的数学定理。
是勾股定理在一般三角形情形下的推广模式。
余玄定理
表达式
cos A=(b²+c²-a²)/2bc[1]
欧几里得
余弦定理是解三角形中的一个重要定理,可应用于以下两种需求:
当已知三角形的两边及其夹角,可由余弦定理得出已知角的对边。
当已知三角形的三边,能够由余弦定理得到三角形的三个内角。
求边
余弦定理公式可变换为以下形式所以,如果知道了三角形的两边及其夹角,可由余弦定理得出已知角的对边。
求角
余弦定理公式可变换为以下形式所以,如果已知三角形的三条边,能够由余弦定理得到三角形的三个内角。
证明编辑
三角函数证明
如上图所示,△ABC,在c上做高,根据射影定理,可得到:
将等式同乘以c得到:
使用同样的方式能够得到:
将两式相加:
向量证明
中,
,
,
:。
(经典)最全余弦定理的10种证明方法

(经典)最全余弦定理的10种证明方法——王彦文 青铜峡一中一、余弦定理余弦定理:三角形任何一边的平方等于其他两边平方的和减去这两边与他们夹角的余弦的积的两倍,即在ABC ∆中,已知AB c =,BC a =,CA b =,则有2222cos a b c bc A =+-, 2222cos b c a ca B =+-, 2222cos c a b ab C =+-.二、定理证明为了叙述的方便与统一,我们证明以下问题即可:在ABC ∆中,已知AB c =,AC b =,及角A ,求证:2222cos a b c bc A =+-. 证法一:如图1,在ABC ∆中,由CB AB AC =-可得:()()CB CB AB AC AB AC ⋅=-⋅-222AB AC AB AC =+-⋅222cos b c bc A =+-即,2222cos a b c bc A =+-.证法二:本方法要注意对A ∠进行讨论.(1)当A ∠是直角时,由22222222cos 2cos90b c bc A b c bc b c a +-=+-︒=+=知结论成立. (2)当A ∠是锐角时,如图2-1,过点C 作CD AB ⊥,交AB 于点D ,则在Rt ACD ∆中,cos AD b A =,sin CD b A =.从而,cos BD AB AD c b A =-=-.在Rt BCD ∆中,由勾股定理可得: 222BC BD CD =+22(cos )(sin )c b A b A =-+222cos c cb A b =-+图1图2-1A即,2222cos a b c bc A =+-.说明:图2-1中只对B ∠是锐角时符合,而B ∠还可以是直角或钝角.若B ∠是直角,图中的点D 就与点B 重合;若B ∠是钝角,图中的点D 就在AB 的延长线上.(3)当A ∠是钝角时,如图2-2,过点C 作CD AB ⊥,交BA 延长线于点D ,则 在Rt ACD ∆中,cos()cos AD b A b A π=-=-,sin()sin CD b A b A π=-=.从而,cos BD AB AD c b A =+=-.在Rt BCD ∆中,由勾股定理可得:222BC BD CD =+22(cos )(sin )c b A b A =-+222cos c cb A b =-+即,2222cos a b c bc A =+-.综上(1),(2),(3)可知,均有2222cos a b c bc A =+-成立. 证法三:过点A 作AD BC ⊥,交BC 于点D ,则在Rt ABD ∆中,sin BD c α=,cos ADc α=.在Rt ACD ∆中,sin CD b β=,cos ADbβ=.由cos cos()cos cos sin sin A αβαβαβ=+=-可得:2cos AD AD BD CD AD BD CDA c b c b bc-⋅=⋅-⋅= 2222AD BD CD bc -⋅=222222c BD b CD BD CD bc -+--⋅=222()2b c BD CD bc +-+=2222b c a bc+-=整理可得2222cos a b c bc A =+-. 证法四:在ABC ∆中,由正弦定理可得sin sin sin sin()a b c cA B C A B ===+. 从而有sin sin b A a B =,………………………………………………………………①sin sin()sin cos cos sin c A a A B a A B a A B =+=+. …………………………②图2-2图3将①带入②,整理可得cos cos a B c b A =-.…………………………………………③ 将①,③平方相加可得22222(cos )(sin )2cos a c b A b A b c bc A =-+=+-. 即,2222cos a b c bc A =+-.证法五:建立平面直角坐标系(如图4),则由题意可得点(0,0)A ,(,0)B c ,(cos ,sin )C b A b A ,再由两点间距离公式可得2a =22(cos )(sin )c b A b A -+222cos c cb A b =-+.即,2222cos a b c bc A =+-.证法六:在ABC ∆中,由正弦定理可得2sin a R A =,2sin b R B =,2sin c R C =. 于是,222224sin 4sin ()a R A R B C ==+222224(sin cos cos sin 2sin sin cos cos )R B C B C B C B C =++ 222224(sin sin 2sin sin 2sin sin cos cos )R B C B C B C B C =+-+ 2224(sin sin 2sin sin cos())R B C B C B C =+++ 2224(sin sin 2sin sin cos )R B C B C A =+-22(2sin )(2sin )2(2sin )(2sin )cos R B R C R B R B A =+-222cos b c bc A =+-即,结论成立.证法七:在ABC ∆中,由正弦定理可得2sin a R A =,2sin b R B =,2sin c R C =. 于是,2222cos a b c bc A =+-22222224sin 4sin 4sin 8sin sin cos R A R B R C R B C A ⇔=+-2222sin 2sin 2sin 4sin sin cos A B C B C A ⇔=+- 22sin 2cos 2cos 24sin sin cos A B C B C A ⇔=-+-222cos 22cos()cos()4sin sin cos A B C B C B C A ⇔-=-+--由于cos()cos()cos B C A A π+=-=-,因此2cos cos()cos()2sin sin cos A B C B C B C A ⇔=+-+cos cos()2sin sin A B C B C ⇔=--+cos cos cos sin sin cos()A B C B C B C ⇔=-+=-+. 这,显然成立.即,结论成立.证法八:如图5,以点C 为圆心,以CA b =为半径作C ,直线BC 与C 交于点,D E ,延长AB 交C 于F ,延长AC 交C 于G .则由作图过程知2cos AF b A =, 故2cos BF b A c =-.由相交弦定理可得:BA BF BD BE ⋅=⋅, 即,(2cos )()()c b A c b a b a ⋅-=+⋅-, 整理可得:2222cos a b c bc A =+-.证法九:如图6,过C 作CD ∥AB ,交ABC ∆的外接圆于D ,则AD BC a ==,BD AC b ==.分别过,C D 作AB 的垂线,垂足分别为,E F ,则cos AE BF b A ==,故2cos CD c b A =-.由托勒密定理可得AD BC AB CD AC BD ⋅=⋅+⋅, 即,(2cos )a a c c b A b b ⋅=⋅-+⋅.整理可得:2222cos a b c bc A =+-.证法十:由图7-1和图7-2可得2a =22(cos )(sin )c b A b A -+, 整理可得:2222cos a b c bc A =+-.c-bcosA图7-2图7-1余弦定理的证明方法还有很多,比如可以用物理方法证明、可以构造相似三角形证明、可以利用图形面积证明等.感兴趣的读者可以到图书馆或互联网中进行查询.图5GA图6。
余弦定理

课题 余弦定理1.余弦定理在三角形中任何一边的平方等于其他两边的平方的和减去这两边与它们夹角的余弦的积的两倍,即a 2=b 2+c 2-2bc cos A ,b 2=c 2+a 2-2ac cos B ,c 2=a 2+b 2-2ab cos C .2.余弦定理的推论根据余弦定理,可以得到以下推论:cos A =b 2+c 2-a 22bc ,cos B =a 2+c 2-b 22ac ,cos C =a 2+b 2-c 22ab. 3.余弦定理与勾股定理的关系在△ABC 中,由余弦定理,得c 2=a 2+b 2-2ab cos C ,若角C =90°,则cos C =0,于是c 2=a 2+b 2-2a ·b ·0=a 2+b 2,这说明勾股定理是余弦定理的特例,余弦定理是勾股定理的推广.规律:设c 是△ABC 中最大的边(或C 是△ABC 中最大的角),则a 2+b 2<c 2⇔△ABC 是钝角三角形,且角C 为钝角;a 2+b 2=c 2⇔△ABC 是直角三角形,且角C 为直角;a 2+b 2>c 2⇔△ABC 是锐角三角形,且角C 为锐角.在△ABC 中,AB =4,BC =3,B =60°,则AC 等于________. 13.边长为5、7、8的三角形中,最大角与最小角的和是________.1200在△ABC 中,sin A :sin B :sin C =3:5:7,则△ABC 是( )cA .锐角三角形B .直角三角形C .钝角三角形D .无法确定题型1 已知两边及其一角解三角形例1 △ABC 中,已知b =3,c =33,B =30°,解此三角形.解析:方法一 由余弦定理b 2=a 2+c 2-2ac cos B.得32=a 2+(33)2-2a ×33×cos 30°,∴a 2-9a +18=0,得a =3或6.当a =3时,A =30°,∴C =120°.当a =6时,由正弦定理sin A =a sin B b =6×123=1.∴A =90°,∴C =60°. 变式1:已知△ABC 中,a =1,b =1,C =120°,则边c =________. 3题型2 已知三边解三角形例2 已知△ABC 中,a ∶b ∶c =2∶6∶(3+1),求△ABC 的各内角度数.分析:由比例的性质可以引入一个字母k ,用k 表示a 、b 、c ,再由余弦定理求解各角.解析:∵a ∶b ∶c =2∶6∶(3+1),∴令a =2k ,b =6k ,c =(3+1)k.由余弦定理,有cos A =b 2+c 2-a 22bc =6k 2+(3+1)2k 2-4k 22·6k ·(3+1)k=22,∴A =45°. cos B =a 2+c 2-b 22ac =4k 2+(3+1)2k 2-6k 22×2k (3+1)k=12,∴B =60°. ∴C =180°-A -B =180°-45°-60°=75°.变式2:在△ABC 中,已知a -b =4,a +c =2b ,且最大角为120°,求三边的长.解析:由⎩⎪⎨⎪⎧a -b =4,a +c =2b 得⎩⎪⎨⎪⎧a =b +4.c =b -4. ∴a >b >c ,∴a 2=b 2+c 2-2bc cos 120°,即(b +4)2=b 2+(b -4)2-2b (b -4)×⎝⎛⎭⎫-12, 即b 2-10b =0. 解得b =0(舍去)或b =10,此时a =14,c =6.题型3 判断三角形的形状例3在△ABC 中,若b 2sin 2C +c 2sin 2B =2bc cos B cos C ,试判断△ABC 的形状.[解析] 解法一:∵b 2sin 2C +c 2sin 2B =2bc cos B cos C ,∴利用正弦定理可得 sin 2B sin 2C +sin 2C sin 2B =2sin B ·sin C ·cos B ·cos C ,∵sin B sin C ≠0,∴sin B ·sin C =cos B cos C ,∴cos(B +C )=0,∴cos A =0,∵0<A <π,∴A =π2,∴△ABC 为直角三角形. 解法二:已知等式可化为b 2-b 2cos 2C +c 2-c 2·cos 2B =2bc cos B cos C ,由余弦定理可得b 2+c 2-b 2·⎝⎛⎭⎫a 2+b 2-c 22ab 2-c 2(a 2+c 2-b 22ac )2=2bc ·a 2+b 2-c 22ab ·a 2+c 2-b 22ac ∴b 2+c 2=a 2,∴△ABC 为直角三角形.变式3: 在△ABC 中,已知c =a cos B ,b =a sin C ,判断三角形形状.解析:由余弦定理知cos B =a 2+c 2-b 22ac ,代入c =a cos B 得:c =a·a 2+c 2-b 22ac,∴c 2+b 2=a 2, ∴△ABC 是以A 为直角的直角三角形.又∵b =a sin C ,∴b =a·c a,∴b =c , ∴△ABC 也是等腰三角形.综上所述,△ABC 是等腰直角三角形.题型四:正弦、余弦定理的综合应用例4:(2013·广东东莞第五中学高二期中测试)在四边形ABCD 中,已知AD ⊥CD ,AD =10,AB =14,∠BDA =60°,∠BCD =135°,求BC 的长.[解析] 在△ABD 中,设BD =x ,由余弦定理:BA 2=BD 2+AD 2-2BD ·AD ·cos ∠BDA即142=x 2+102-2·10x ·cos60°,整理得:x 2-10x -96=0,解得x 1=16,x 2=-6(舍去),由正弦定理,得BC sin ∠CDB =BD sin ∠BCD, ∴BC =16sin135°·sin30°=8 2.变式4:如图,在△ABC 中,已知BC =15,AB AC =78,sin B =437,求BC 边上的高AD 的长. [解析] 在△ABC 中,由已知设AB =7x ,AC =8x ,由正弦定理,得7x sin C =8x sin B, ∴sin C =7x sin B 8x =78×437=32,∴C =60°(C =120°舍去,否则由8x >7x ,知B 也为钝角,不符合要求). 由余弦定理,得(7x )2=(8x )2+152-16x ×15cos60°,∴x 2-8x +15=0,∴x=3,或x=5,∴AB=21,或AB=35.在△ABD中,AD=AB sin B=437AB,∴AD=123,或AD=20 3.例5:设2a+1,a,2a-1为钝角三角形的三边,求实数a的取值范围.[正解]∵2a+1,a,2a-1为三角形的三边,∴⎩⎪⎨⎪⎧2a+1>0,a>0,2a-1>0,解得a>12,此时2a+1最大.∵2a+1,a,2a-1表示三角形的三边,还需a+(2a-1)>2a+1,解得a>2.设最长边所对角为θ,则cosθ=a2+(2a-1)2-(2a+1)22a(2a-1)=a(a-8)2a(2a-1)<0,解得12<a<8.∴a的取值范围是2<a<8.【课后巩固】1.在ABC∆中,已知Bac cos2=,试判断ABC∆的形状.2.在ABC∆中,已知cba+=2,CBA sinsinsin2=,试判断ABC∆的形状.3.如图,我炮兵阵地位于A处,两观察所分别设于C,D,已知ACD∆为边长等于a的正三角形.当目标出现于B时,测得︒=∠45CDB,︒=∠75BCD,试求炮击目标的距离AB.ACBD。
余弦定理的证明

余弦定理的证明余弦公式a^2=b^2+c^2-2bc cosA余弦定理余弦定理是揭示三角形边角关系的重要定理,直接运用它可解决两类问题:第一类是已知三角形两边及夹角,求第三边;第二类是已知三个边求角的问题,若对余弦定理加以变形并适当移于其它知识,则使用起来更为方便、灵活。
余弦定理性质对于任意三角形,任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的两倍积,若三边为a,b,c 三角为A,B,C ,则满足性质——a^2 = b^2 + c^2 - 2·b·c·c os Ab^2 = a^2 + c^2 - 2·a·c·c os Bc^2 = a^2 + b^2 - 2·a·b·cos Cc os C = (a^2 + b^2 - c^2) /(2·a·b)c os B = (a^2 + c^2 - b^2) / (2·a·c)c os A = (c^2 + b^2 - a^2) /(2·b·c)(物理力学方面的平行四边形定则以及电学方面正弦电路向量分析也会用到)第一余弦定理(任意三角形射影定理)设△ABC的三边是a、b、c,它们所对的角分别是A、B、C,则有a=b·cos C+c·cos B,b=c·cos A+a·cos C,c=a·cos B+b·cos A。
余弦定理证明平面几何证法在任意△ABC中做AD⊥BC.∠C所对的边为c,∠B所对的边为b,∠A所对的边为a则有BD=cosB*c,AD=sinB*c ,DC=BC-BD=a-cosB*c根据勾股定理可得:AC^2=AD^2+DC^2b^2=(sinB*c)^2+(a-cosB*c)^2b^2=(sinB*c)^2+a^2-2ac*cosB+(cosB)^2*c^2b^2=(sinB^2+cosB^2)*c^2-2ac*cosB+a^2b^2=c^2+a^2-2ac*cosBcosB=(c^2+a^2-b^2)/(2*a*c)作用(1)已知三角形的三条边长,可求出三个内角(2)已知三角形的两边及夹角,可求出第三边。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1一.选择题(共24小题)1.(2010•江西)E,F是等腰直角△ABC斜边AB上的三等分点,则tan∠ECF=()A.B.C.D.2.(2011•浙江)在△ABC中,角A,B,C,所对的边分别为a,b,c.若acosA=bsinB,则sinAcosA+cos2B=()A.﹣B.C.﹣1 D.13.△ABC的内角A、B、C的对边分别为a、b、c,若a、b、c成等比数列,且c=2a,则cosB=()A.B.C.D.4.(2013•淄博二模)已知△ABC中,三个内角A,B,C的对边分别为a,b,c,若△ABC的面积为S,且2S=(a+b)2﹣c2,则tanC等于()A.B.C.D.5.(2013•肇庆一模)在△ABC中,AB=3,BC=,AC=4,则△ABC的面积是()A.3B.C.3D.66.(2013•永州一模)在△ABC中,若sin2B+sin2C﹣sin2A=sinB•sinC,则cosB的取值范围为()A.(﹣,1)B.[﹣,1]C.(﹣,1)D.[﹣,1]7.(2013•天津一模)设△ABC的内角A,B,C的对边分别为a,b,c,且,则sinA=()A.B.C.D.8.(2013•韶关一模)△ABC中,角A,B,C所对边a,b,c,若a=3,C=120°,△ABC的面积S=,则c=()A.5B.6C.D.79.(2013•汕头一模)在△ABC中,内角A,B,C的对边分别是a,b,c,若,b2﹣a2=ac,则cosB=()A.B.C.D.10.(2013•南充三模)在△ABC中,角A,B,C的对边分别为a,b,c,若a2+c2﹣b2=ac,则角B的值为()A.或B.C.或D.11.(2013•泸州一模)△ABC中,AB=,AC=5,cosC=,则BC的值为()A.4B.5C.4或5 D.2或12.(2013•临沂一模)在△ABC中,角A,B,C所对的边分别为a,b,c,若,则角B为()A.B.C.D.13.(2013•丽水一模)在△ABC中,角A,B,C所对的边分别为a,b,c,若3bcosA=ccosA+acosC,则tanA的值是()A.B.C.D.14.(2013•河东区二模)在△ABC中角A、B、C的对边分别是a、b、c,若(2b﹣c)cosA=acosC,则∠A为()A.B.C.D.15.(2013•合肥二模)△ABC中,角A,B,C所对的边分别为a,b,c,若C=,3a=2c=6,则b的值为()A.B.C.﹣1 D.1+16.(2013•长春一模)直线l1与l2相交于点A,点B、C分别在直线l1与l2上,若与的夹角为60°,且,,则=()A.B.C.D.17.(2012•浙江模拟)若,,则的最大值为()A.B.2C.D.318.(2012•枣庄二模)已知△ABC中,AB=2,AC=3,BC=4,则角A,B,C中最大角的余弦值为()A.B.﹣C.D.19.(2012•贵州模拟)△ABC中,角A、B、C所对的边分别为a、b、c,且(b+4)(b﹣4)=(a+c)(a﹣c),则•=()A.﹣8 B.8C.﹣16 D.1620.(2012•贵州模拟)△ABC中,角A、B、C所对的边分别为a、b、c,且b(b﹣c)=(a+c)(a﹣c),则()A.A=60°B.C=60°C.A=120°D.C=120°21.(2012•北京模拟)在△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,且a=+1,b=2,c=,那么角C的大小是()A.30°B.45°C.60°D.120°22.(2011•郑州二模)已知△ABC中,sinA:sinB:sinC=1:1:,则此三角形的最大内角的度数是()A.60°B.90°C.120°D.135°23.(2011•宁德模拟)在△ABC中,角A,B,C所对的边分别为a,b,c.若a=1,b=2,C=120°,则的值为()A.B.C.D.24.(2011•合肥三模)在△ABC中,已知角A、B、C所对的边分别为a、b、c,且a=3,c=8,B=60°,则sinA的值是()A.B.C.D.二.填空题(共6小题)25.(2013•上海)已知△ABC的内角A、B、C所对的边分别是a、b、c,若3a2+2ab+3b2﹣3c2=0,则角C的大小是_________.26.(2013•广东)(几何证明选讲选做题)如图,在矩形ABCD中,,BC=3,BE⊥AC,垂足为E,则ED=_________.27.(2013•盐城三模)如图,在△ABC中,B=45°,D是BC边上的一点,AD=5,AC=7,DC=3,则AB的长为_________.28.(2013•盐城一模)在△ABC中,若9cos2A﹣4cos2B=5,则的值为_________.29.(2013•石家庄二模)已知△ABC中,角A、B、C所对的边长分别为a,b,c且角A,B、C成等差数列,△ABC 的面积S=,则实数k的值为_________.30.(2013•许昌三模)在△ABC中,边a,b,c所对的角分别为A,B,C,已知(b+c):(c+a):(a+b)=4:5:6,若b+c=8,则△ABC的面积是_________.一.选择题(共24小题)1.(2010•江西)E,F是等腰直角△ABC斜边AB上的三等分点,则tan∠ECF=()A.B.C.D.考点:余弦定理.专题:计算题.分析:约定AB=6,AC=BC=,先在△AEC中用余弦定理求得EC,进而在△ECF中利用余弦定理求得cosECF,进而用同角三角函数基本关系求得答案.解答:解:约定AB=6,AC=BC=,由余弦定理可知cos45°==;解得CE=CF=,再由余弦定理得cos∠ECF==,∴点评:考查三角函数的计算、解析化应用意识.2.(2011•浙江)在△ABC中,角A,B,C,所对的边分别为a,b,c.若acosA=bsinB,则sinAcosA+cos2B=()B.C.﹣1 D.1A.﹣考点:余弦定理;正弦定理.专题:计算题.分析:利用三角形中的正弦定理,将已知等式中的边用三角形的角的正弦表示,代入要求的式子,利用三角函数的平方关系求出值.解答:解:∵acosA=bsinB由正弦定理得sinAcosA=sinBsinB∴sinAcosA+cos2B=sin2B+cos2B=1故选D点评:本题考查三角形中的正弦定理、余弦定理、三角函数的平方关系.A.B.C.D.考点:余弦定理;等比数列.专题:计算题.分析:根据等比数列的性质,可得b=a,将c、b与a的关系结合余弦定理分析可得答案.解答:解:△ABC中,a、b、c成等比数列,且c=2a,则b=a,=,故选B.点评:本题考查余弦定理的运用,要牢记余弦定理的两种形式,并能熟练应用.4.(2013•淄博二模)已知△ABC中,三个内角A,B,C的对边分别为a,b,c,若△ABC的面积为S,且2S=(a+b)2﹣c2,则tanC等于()A.B.C.D.考点:余弦定理.专题:解三角形.分析:首先由三角形面积公式得到S△ABC=,再由余弦定理,结合2S=(a+b)2﹣c2,得出sinC﹣2cosC=2,然后通过(sinC﹣2cosC)2=4,求出结果即可.解答:解:△ABC中,∵S△ABC=,由余弦定理:c2=a2+b2﹣2abcosC,且2S=(a+b)2﹣c2 ,∴absinC=(a+b)2﹣(a2+b2﹣2abcosC),整理得sinC﹣2cosC=2,∴(sinC﹣2cosC)2=4.∴=4,化简可得3tan2C+4tanC=0.∵C∈(0,180°),∴tanC=﹣,故选C.点评:本题考查了余弦定理、三角形面积公式以及三角函数的化简求值,要注意角C的范围,属于中档题.5.(2013•肇庆一模)在△ABC中,AB=3,BC=,AC=4,则△ABC的面积是()A.3B.C.3D.6考点:余弦定理.专题:计算题.分析:利用余弦定理求出cosAd的值,然后求出sinA,求出三角形的面积.解答:解:由余弦定理可知coaA===.所以sinA=,故选C.点评:本题考查余弦定理与三角形的面积公式的应用,考查计算能力.6.(2013•永州一模)在△ABC中,若sin2B+sin2C﹣sin2A=sinB•sinC,则cosB的取值范围为()A.(﹣,1)B.[﹣,1]C.(﹣,1)D.[﹣,1]考点:余弦定理;正弦定理.专题:计算题;解三角形.分析:通过正弦定理以及余弦定理转化已知表达式,求出A,判断B的范围,然后求出cosB的取值范围.解答:解:因为在△ABC中,若sin2B+sin2C﹣sin2A=sinB•sinC,所以b2+c2﹣bc=a2,所以cosA=,即A=60°.B∈(0°,120°),所以cosB∈(﹣,1).故选A.点评:本题考查正弦定理与余弦定理的应用,三角形角的范围的判断,考查计算能力.7.(2013•天津一模)设△ABC的内角A,B,C的对边分别为a,b,c,且,则sinA=()A.B.C.D.考点:余弦定理;正弦定理.专题:计算题;解三角形.分析:由C为三角形的内角,及cosC的值,利用同角三角函数间的基本关系求出sinC的值,再由a与b的值,利用余弦定理列出关于c的方程,求出方程的解得到c的值,再由sinC,c及b的值,利用正弦定理即可求出sinB的值.解答:解:∵C为三角形的内角,,∴sinC==,又a=2,b=3,∴由余弦定理c2=a2+b2﹣2abcosC得:c2=4+9﹣3=10,解得:c=,又sinC=,c=,a=2,∴由正弦定理得:sinA==.故选C.点评:此题考查了同角三角函数间的基本关系,正弦、余弦定理,以及特殊角的三角函数值,熟练掌握定理及基本关系是解本题的关键.8.(2013•韶关一模)△ABC中,角A,B,C所对边a,b,c,若a=3,C=120°,△ABC的面积S=,则c=()A.5B.6C.D.7专题:解三角形.分析:利用三角形的面积公式S△=及a=3,C=120°,可得b,再利用余弦定理即可得出c.解答:解:∵△ABC的面积S==,∴ab=15,又a=3,∴b=5.∴c2=a2+b2﹣2abcosC=32+52﹣2×3×5cos120°=49,∴c=7.故选D.点评:熟练掌握三角形的面积公式和余弦定理是解题的关键.9.(2013•汕头一模)在△ABC中,内角A,B,C的对边分别是a,b,c,若,b2﹣a2=ac,则cosB=()A.B.C.D.考点:余弦定理;正弦定理.专题:计算题;解三角形.分析:根据正弦定理及得c=2a,结合余弦定理b2=a2+c2﹣2accosB算出b2=5a2+4a2cosB,再由题中边a、b 的等式化简得到b2=4a2,两式联解即可得到cosB的值.解答:解:∵,∴由正弦定理,得=2,得c=2a∵由余弦定理,得b2=a2+c2﹣2accosB,∴b2=5a2+4a2cosB∵b2﹣a2=ac,∴b2=a2+ac=4a2因此,4a2=5a2+4a2cosB,解之得cosB=故选:C点评:本题给出三角形ABC中的边角关系,求cosB的值,着重考查了运用正余弦定理解三角形和二元方程组的解法等知识,属于基础题.10.(2013•南充三模)在△ABC中,角A,B,C的对边分别为a,b,c,若a2+c2﹣b2=ac,则角B的值为()A.或B.C.或D.考点:余弦定理.专题:计算题;解三角形.分析:根据余弦定理结合题中等式,算出cosB==,结合三角形内角的范围,可得B=.解答:解:∵a2+c2﹣b2=ac∴由余弦定理,得cosB===结合B∈(0,π),可得B=故选:B11.(2013•泸州一模)△ABC中,AB=,AC=5,cosC=,则BC的值为()A.4B.5C.4或5 D.2或考点:余弦定理.专题:计算题.分析:由余弦定理可得,AB2=AC2+BC2﹣2AC•BCcosC,把已知条件代入即可求解解答:解:∵AB=,AC=5,cosC=,由余弦定理可得,AB2=AC2+BC2﹣2AC•BCcosC∴5=25+BC2﹣2×整理可得,BC2﹣9BC+20=0解可得,BC=4或BC=5故选C点评:本题主要考查了余弦定理在求解三角形中的应用及二次方程的求解,属于基础试题12.(2013•临沂一模)在△ABC中,角A,B,C所对的边分别为a,b,c,若,则角B为()A.B.C.D.考点:余弦定理;正弦定理.专题:计算题;解三角形.分析:根据正弦定理,将已知等式变形,得到,再用余弦定理算出cosB=,结合角B是三角形的内角,即可算出角B的大小.解答:解:∵△ABC中,,∴根据正弦定理,再根据余弦定理,得cosB==∵B∈(0,π),∴B=故选:A点评:本题给出△ABC中三个角的平方关系,求角B的大小,着重考查了特殊三角函数的值和利用正余弦定理解三角形等知识,属于基础题.13.(2013•丽水一模)在△ABC中,角A,B,C所对的边分别为a,b,c,若3bcosA=ccosA+acosC,则tanA的值A.B.C.D.考点:余弦定理.专题:计算题;解三角形.分析:根据余弦定理,化简可得ccosA+acosC=b,从而将等式3bcosA=ccosA+acosC化简得到cosA=>0,由同角三角函数的平方关系算出sinA=,再由商数关系即可得到tanA的值.解答:解:∵△ABC中,由余弦定理得ccosA+acosC=c×+a×=b∴根据题意,3bcosA=ccosA+acosC=b两边约去b,得3cosA=1,所以cosA=>0∴A为锐角,且sinA==因此,tanA==故选:C点评:本题给出三角形中的边角关系式,求tanA的值.着重考查了余弦定理解三角形、同角三角函数的基本有关系等知识,属于基础题.14.(2013•河东区二模)在△ABC中角A、B、C的对边分别是a、b、c,若(2b﹣c)cosA=acosC,则∠A为()A.B.C.D.考点:余弦定理.专题:计算题;解三角形.分析:已知等式利用正弦定理化简,整理后利用两角和与差的正弦函数公式及诱导公式化简,求出cosA的值,即可求出A的度数.解答:解:利用正弦定理化简已知等式得:(2sinB﹣sinC)cosA=sinAcosC,整理得:2sinBcosA=sinAcosC+cosAsinC=sin(A+C)=sinB,∵sinB≠0,∴cosA=,∵A为三角形的内角,∴∠A=.故选C点评:此题考查了正弦定理,两角和与差的正弦函数公式,以及诱导公式,熟练掌握定理及公式是解本题的关键.15.(2013•合肥二模)△ABC中,角A,B,C所对的边分别为a,b,c,若C=,3a=2c=6,则b的值为()A.B.C.﹣1 D.1+考点:余弦定理;正弦定理.专题:常规题型.解答:解:∵a=2,c=3,∠C=60°,∴根据余弦定理得:c2=a2+b2﹣2ab•cosC9=4+b2﹣2b,则b=.故选D.点评:此题考查了余弦定理,以及特殊角的三角函数值,余弦定理很好的建立了三角形的边角关系,熟练掌握余弦定理是解本题的关键.16.(2013•长春一模)直线l1与l2相交于点A,点B、C分别在直线l1与l2上,若与的夹角为60°,且,,则=()A.B.C.D.考点:余弦定理.专题:计算题;解三角形.分析:由题意,△ABC中∠A=60°,AB=2,AC=4,由余弦定理可得结论.解答:解:由题意,△ABC中∠A=60°,AB=2,AC=4,由余弦定理可知BC2=AB2+AC2﹣2AB•AC•cosA=12 ∴,故选B.点评:本题考查余弦定理的运用,考查学生的计算能力,属于基础题.17.(2012•浙江模拟)若,,则的最大值为()A.B.2C.D.3考点:余弦定理;平面向量数量积的含义与物理意义.专题:计算题;平面向量及应用.分析:根据余弦定理可得:||2=||2+||2﹣2||•||cos<>,由,,得||2=,故=||•||cos<>=,由此能求出的最大值.解答:解:根据余弦定理可得:||2=||2+||2﹣2||•||cos<>,∵,,∴1=4||2+||2﹣4||2cos<>,即1=5||2﹣4||2cos<>,||2=,=2||2cos<>=,∴当cos<>=1时,的最大值===2.故选B.点评:本题考查平面向量的数量积的含义与物理意义的应用,是基础题.解题时要认真审题,注意余弦定理的合理运用.18.(2012•枣庄二模)已知△ABC中,AB=2,AC=3,BC=4,则角A,B,C中最大角的余弦值为()A.B.C.D.﹣考点:余弦定理.专题:计算题;解三角形.分析:根据三角形大边对大角,可得∠A是最大角,结合余弦定理算出cosA的值,即得最大角的余弦之值.解答:解:∵AB=2,AC=3,BC=4,∴BC为最大边,得∠A是最大角由余弦定理,得cosA===﹣即最大角的余弦值等于﹣故选:A点评:本题给出三角形的三边之长,求最大角的余弦值,着重考查了三角形的性质和余弦定理等知识,属于基础题.19.(2012•贵州模拟)△ABC中,角A、B、C所对的边分别为a、b、c,且(b+4)(b﹣4)=(a+c)(a﹣c),则•=()A.﹣8 B.8C.﹣16 D.16考点:余弦定理;平面向量数量积的运算.专题:平面向量及应用.分析:利用余弦定理表示出cosA,将已知的等式变形后代入,表示出cosA,然后利用平面向量的数量积运算法则化简所求的式子中,将各自的值代入即可求出值.解答:解:由(b+4)(b﹣4)=(a+c)(a﹣c),整理得:b2﹣16=a2﹣c2,即b2+c2﹣a2=16,∴由余弦定理得:cosA==,则•=bccos(π﹣A)=﹣bccosA=﹣bc•=﹣8.故选A点评:此题考查了余弦定理,以及平面向量的数量积运算,熟练掌握定理及法则是解本题的关键.20.(2012•贵州模拟)△ABC中,角A、B、C所对的边分别为a、b、c,且b(b﹣c)=(a+c)(a﹣c),则()A.A=60°B.C=60°C.A=120°D.C=120°考点:余弦定理.专题:解三角形.分析:利用余弦定理表示出cosA,将已知的等式变形后代入,求出cosA的值,由A为三角形的内角,利用特殊角的三角函数值即可求出A的度数.解答:解:将b(b﹣c)=(a+c)(a﹣c)整理得:b2﹣bc=a2﹣c2,即b2+c2﹣a2=bc,∴cosA===,又A为三角形的内角,则A=60°.故选A点评:此题考查了余弦定理,以及特殊角的三角函数值,熟练掌握余弦定理是解本题的关键.21.(2012•北京模拟)在△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,且a=+1,b=2,c=,那么角C的大小是()A.30°B.45°C.60°D.120°考点:余弦定理.专题:计算题.分析:利用余弦定理求出cosC的值,然后根据角的范围求出角的度数.解答:解:根据余弦定理得cosC===∵C∈(0,π)∴∠C=30°故选A.点评:本题考查了余弦定理,解题过程中要注意在三角形中C∈(0,π),属于基础题.22.(2011•郑州二模)已知△ABC中,sinA:sinB:sinC=1:1:,则此三角形的最大内角的度数是()A.60°B.90°C.120°D.135°考点:余弦定理;正弦定理的应用.专题:计算题.分析:由正弦定理可得,可设三边长分别为k,k,k,显然三遍满足勾股定理,从而得出结论.解答:解:由正弦定理可得,可设三边长分别为k,k,k,显然三遍满足勾股定理,故此三角形的最大内角的度数是90°,故选B.点评:本题考查正弦定理,勾股定理的应用,设出三边长分别为k,k,k,是解题的关键,属于基础题.23.(2011•宁德模拟)在△ABC中,角A,B,C所对的边分别为a,b,c.若a=1,b=2,C=120°,则的值为()A.B.C.D.考点:余弦定理;正弦定理.专题:计算题.分析:由C的度数求出cosC及sinC的值,根据a,b及cosC的值,利用余弦定理列出关于c的方程,求出方程的解得出c的值,再由a,c及sinC的值,利用正弦定理列出关系式,变形后即可得出所求式子的值.解答:解:∵a=1,b=2,cosC=cos120°=﹣,∴根据余弦定理得:c2=a2+b2﹣2abcosC=1+4+2=7,∴c=,又a=1,sinC=,根据正弦定理=得:===.故选B点评:此题考查了正弦、余弦定理,以及特殊角的三角函数值,正弦、余弦定理很好的建立了三角形的边角关系,熟练掌握定理是解本题的关键.24.(2011•合肥三模)在△ABC中,已知角A、B、C所对的边分别为a、b、c,且a=3,c=8,B=60°,则sinA的值是()A.B.C.D.考点:余弦定理;正弦定理.专题:计算题.分析:在△ABC中,由余弦定理求出b的值,再由由正弦定理求出sinA的值.解答:解:在△ABC中,由余弦定理可得b2=a2+c2﹣2ac•cosB,即b2=9+64﹣48cos60°,解得b=7.再由正弦定理可得=,∴sinA=.故选D.点评:本题主要考查正弦定理、余弦定理的应用,属于基础题.二.填空题(共6小题)25.(2013•上海)已知△ABC的内角A、B、C所对的边分别是a、b、c,若3a2+2ab+3b2﹣3c2=0,则角C的大小是.考点:余弦定理.专题:解三角形.分析:把式子3a2+2ab+3b2﹣3c2=0变形为,再利用余弦定理即可得出.解答:解:∵3a2+2ab+3b2﹣3c2=0,∴,∴==.∴C=.故答案为.点评:熟练掌握余弦定理及反三角函数是解题的关键.26.(2013•广东)(几何证明选讲选做题)如图,在矩形ABCD中,,BC=3,BE⊥AC,垂足为E,则ED=.考点:余弦定理.专题:压轴题;解三角形.分析:由矩形ABCD,得到三角形ABC为直角三角形,由AB与BC的长,利用勾股定理求出AC的长,进而得到AB为AC的一半,利用直角三角形中直角边等于斜边的一半得到∠ACB=30°,且利用射影定理求出EC 的长,在三角形ECD中,利用余弦定理即可求出ED的长.解答:解:∵矩形ABCD,∴∠ABC=90°,∴在Rt△ABC中,AB=,BC=3,根据勾股定理得:AC=2,∴AB=AC,即∠ACB=30°,EC==,∴∠ECD=60°,在△ECD中,CD=AB=,EC=,根据余弦定理得:ED2=EC2+CD2﹣2EC•CDcos∠ECD=+3﹣=,则ED=.故答案为:点评:此题考查了余弦定理,勾股定理,直角三角形的性质,以及特殊角的三角函数值,熟练掌握余弦定理是解本题的关键.27.(2013•盐城三模)如图,在△ABC中,B=45°,D是BC边上的一点,AD=5,AC=7,DC=3,则AB的长为.考点:余弦定理.专题:综合题.分析:先根据余弦定理求出∠ADC的值,即可得到∠ADB的值,最后根据正弦定理可得答案.解答:解:在△ADC中,AD=5,AC=7,DC=3,由余弦定理得cos∠ADC==﹣,∴∠ADC=120°,∠ADB=60°在△ABD中,AD=5,∠B=45°,∠ADB=60°,由正弦定理得,∴AB=故答案为:.点评:本题主要考查余弦定理和正弦定理的应用,在解决问题的过程中要灵活运用正弦定理和余弦定理.属基础题.28.(2013•盐城一模)在△ABC中,若9cos2A﹣4cos2B=5,则的值为.考点:余弦定理.专题:解三角形.分析:由条件9cos2A﹣4cos2B=5 利用二倍角公式求得=,再由正弦定理可得=,从而得到答案.解答:解:在△ABC中,∵9cos2A﹣4cos2B=5,∴9(1﹣2sin2A )﹣4(1﹣2sin2B)=5,化简可得9sin2A=4sin2B,故有=.由正弦定理可得==,故答案为.点评:本题主要考查二倍角公式、正弦定理的应用,属于中档题.29.(2013•石家庄二模)已知△ABC中,角A、B、C所对的边长分别为a,b,c且角A,B、C成等差数列,△ABC 的面积S=,则实数k的值为.考点:余弦定理;等差数列的通项公式.专题:解三角形.分析:由题意求得B=,根据△ABC的面积S==ac•sinB=ac ①,而由余弦定理可得b2=a2+c2﹣ac,代入①可得=ac,由此解方程求得k的值.解答:解:△ABC中,∵角A,B、C成等差数列,∴2B=A+C,再由三角形内角和公式可得B=,A+C=.由于△ABC的面积S==ac•sinB=ac ①,而由余弦定理可得b2=a2+c2﹣2ac•cosB=a2+c2﹣ac,代入①可得=ac,解得k=,故答案为点评:本题主要考查余弦定理、三角形的面积公式,属于中档题.30.(2013•许昌三模)在△ABC中,边a,b,c所对的角分别为A,B,C,已知(b+c):(c+a):(a+b)=4:5:6,若b+c=8,则△ABC的面积是.考点:余弦定理;正弦定理.专题:计算题.分析:由题中的条件先求出a,b,c 的值,再由余弦定理求出A=120°,根据△ABC的面积是×bc•sinA运算求得结果.解答:解:∵(b+c):(c+a):(a+b)=4:5:6,若b+c=8,∴c+a=10,a+b=12,∴a=7,b=5,c=3,由余弦定理可得49=25+9﹣30cosA,∴cosA=﹣,∴A=120°,则△ABC的面积是×bcsinA=,故答案为:.点评:本题考查余弦定理的应用,根据三角函数的值求角,求三角形的面积,求出A=120°,是解题的难点.。
