二叉树的知识点总结 共19页
二叉树基本知识

{
int capacity;
int size;
int *elements;
}*tryit;
struct priorityqueue *initialize ( int maxelements )
{
struct priorityqueue *h;
(6)给定N个节点,能构成h(N)种不同的二叉树。
h(N)为卡特兰数的第N项。h(n)=C(n,2*n)/(n+1)。
4.二叉树的存储结构
(1)顺序存储方式
type node=record
Байду номын сангаасata:datatype
l,r:integer;
end;
var tr:array[1..n] of node;
(1)前序遍历
访问根;按前序遍历左子树;按前序遍历右子树
(2)中序遍历
按中序遍历左子树;访问根;按中序遍历右子树
(3)后序遍历
按后序遍历左子树;按后序遍历右子树;访问根
(4)层次遍历
即按照层次访问,通常用队列来做。访问根,访问子女,再访问子女的子女(越往后的层次越低)(两个子女的级别相同)
(2)链表存储方式,如:
type btree=^node;
node=record
data:datatye;
lchild,rchild:btree;
end;
5.普通树转换成二叉树
二叉树很象一株倒悬着的树,从树根到大分枝、小分枝、直到叶子把数据联系起来,这种数据结构就叫做树结构,简称树。树中每个分叉点称为结点,起始结点称为树根,任意两个结点间的连接关系称为树枝,结点下面不再有分枝称为树叶。结点的前趋结点称为该结点的"双亲",结点的后趋结点称为该结点的"子女"或"孩子",同一结点的"子女"之间互称"兄弟"。
二叉树知识点总结

二叉树知识点总结1. 二叉树的性质1.1 二叉树的性质一:二叉树的深度二叉树的深度是指从根节点到叶子节点的最长路径长度。
对于一个空树而言,它的深度为0;对于只有一个根节点的树而言,它的深度为1。
根据定义可知,深度为k的二叉树中,叶子节点的深度值为k。
由此可知,二叉树的深度为所有叶子节点深度的最大值。
1.2 二叉树的性质二:二叉树的高度二叉树的高度是指从根节点到叶子节点的最短路径长度。
对于一个空树而言,它的高度为0;对于只有一个根节点的树而言,它的高度为1。
由此可知,二叉树的高度总是比深度大一。
1.3 二叉树的性质三:二叉树的节点数量对于一个深度为k的二叉树而言,它最多包含2^k - 1个节点。
而对于一个拥有n个节点的二叉树而言,它的深度最多为log2(n+1)。
1.4 二叉树的性质四:满二叉树满二叉树是一种特殊类型的二叉树,它的每个节点要么是叶子节点,要么拥有两个子节点。
满二叉树的性质是:对于深度为k的满二叉树而言,它的节点数量一定是2^k - 1。
1.5 二叉树的性质五:完全二叉树完全二叉树是一种特殊类型的二叉树,它的所有叶子节点都集中在树的最低两层,并且最后一层的叶子节点从左到右依次排列。
对于一个深度为k的完全二叉树而言,它的节点数量一定在2^(k-1)和2^k之间。
2. 二叉树的遍历二叉树的遍历是指按照一定的顺序访问二叉树的所有节点。
二叉树的遍历主要包括前序遍历、中序遍历和后序遍历三种。
2.1 前序遍历(Pre-order traversal)前序遍历的顺序是:根节点 -> 左子树 -> 右子树。
对于一个二叉树而言,前序遍历的结果就是按照“根-左-右”的顺序访问所有节点。
2.2 中序遍历(In-order traversal)中序遍历的顺序是:左子树 -> 根节点 -> 右子树。
对于一个二叉树而言,中序遍历的结果就是按照“左-根-右”的顺序访问所有节点。
2.3 后序遍历(Post-order traversal)后序遍历的顺序是:左子树 -> 右子树 -> 根节点。
二叉树的复习
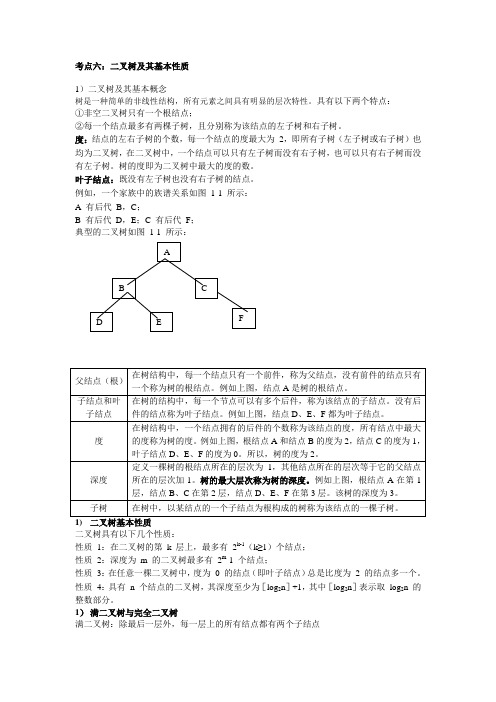
考点六:二叉树及其基本性质1)二叉树及其基本概念树是一种简单的非线性结构,所有元素之间具有明显的层次特性。
具有以下两个特点:①非空二叉树只有一个根结点;②每一个结点最多有两棵子树,且分别称为该结点的左子树和右子树。
度:结点的左右子树的个数,每一个结点的度最大为2,即所有子树(左子树或右子树)也均为二叉树,在二叉树中,一个结点可以只有左子树而没有右子树,也可以只有右子树而没有左子树。
树的度即为二叉树中最大的度的数。
叶子结点:既没有左子树也没有右子树的结点。
例如,一个家族中的族谱关系如图1-1 所示:A 有后代B,C;B 有后代D,E;C 有后代F;典型的二叉树如图1-1 所示:1)二叉树基本性质二叉树具有以下几个性质:性质1:在二叉树的第k 层上,最多有2k-1(k≥1)个结点;性质2:深度为m 的二叉树最多有2m-1 个结点;性质3:在任意一棵二叉树中,度为0 的结点(即叶子结点)总是比度为 2 的结点多一个。
性质4:具有n 个结点的二叉树,其深度至少为[log2n]+1,其中[log2n]表示取log2n 的整数部分。
1)满二叉树与完全二叉树满二叉树:除最后一层外,每一层上的所有结点都有两个子结点完全二叉树:除最后一层外,每一层上的结点数均达到最大值;在最后一层上只缺少右边的若干结点。
2)二叉树的遍历二叉树的遍历:(1) 前序遍历(DLR),首先访问根结点,然后遍历左子树,最后遍历右子树;并且,在遍历左、右子树时,仍然先访问根结点,然后遍历左子树,最后遍历右子树。
例如,对图1-1 中的二叉树进行前序遍历的结果(或称为该二叉树的前序序列)为:A,B,D,E,C,F。
(2) 中序遍历(LDR),首先遍历左子树,然后访问根结点,最后遍历右子树;并且,在遍历左、右子树时,仍然先遍历左子树,然后访问根结点,最后遍历右子树。
例如,对图1-1 中的二叉树进行中序遍历的结果(或称为该二叉树的中序序列)为:D,B,E,A,C,F。
基本二叉树知识讲解

基本二叉树知识讲解一、有关二叉树的学习性质1:二叉树上叶子结点数等于度为2的结点数加1。
性质2:二叉树的第i层上至多有2的i次方减1个结点(i>=1)。
性质3:深度为h的二叉树至多有2的h次方减1个结点。
满二叉树:在一棵二叉树中,当第i层的结点树为2的i次方减1个时,称此层的结点数是满的。
当一棵二叉树中的每一层都满时,称此树为满二叉树。
特性:除叶子结点以外的其他的结点的度皆为2,且叶子结点在同一层上。
深度为h的满二叉树中的结点数为2的h次方减1。
性质4:设含有n个结点的完全二叉树的深度为k,则k=(int)(log2n)+1,即深度k等于log2n的整数部分再加1。
二叉树的存储结构1:顺序存储结构二叉树的顺序存储结构类型定义如下:#define TREEMINSIZE 10typedef struct{BTreeDT(数据类型) *base;int spacesize;BTreeDT nullvalue;}SeqTree;2:链式存储结构(一般的二叉树主要采用链式存储结构通常有二叉链表和三叉链表两种形式)1>二叉链表存储结构二叉链表中的每个结点由data,lchild和rchild三个域组成,定义如下:typedef struct bkbtnode{BTreeDT data;struct bkbtnode *lchild;struct bkbtnode *rchild;}BTNode,*BKBTree;在二叉链表中,查找某结点的孩子很容易实现,但查找某结点的双亲不方便。
一棵喊有n个结点的二叉树采用二叉链表存储时,将有2n-(n-1)=n+1个指针域是空的。
2>三叉链表存储结构typedef struct tkbtnode{BTreeDT data;struct tkbtnode *lchild;struct tkbtnode *rchild;struct tkbtnode *parent;}TKBTNode,*TKBTree;其中,parent域存放该结点双亲的指针。
第五章二叉树

树为空
树为空
根的左右子 树都不空
二、二叉树的性质
第1层(根) 第2层 第3层
第4层
1、若层次从1开始,则第i层最多有2 i-1个结点 2、高度为h的二叉树最多有2h -1个结点 3、任何一棵二叉树,若叶子结点数为n0,度为2的结点数 为n2,则n0 = n2 + 1
5.2.2 二叉树的性质
二叉树具有下列重要性质: 性质1: 在二叉树的第i层上至多有2i-1个结点(i>=1)。
二叉树的二叉链表存储表示
Elem val(){return data;} void setVal(const Elem e){data=e;} inline BinTreeNode<Elem>* left(){return lchild;} inline BinTreeNode<Elem>* right(){return rchild;} void setLeft(BinTreeNode<Elem>* left){lchild=left;} void setRight(BinTreeNode<Elem>* right){rchild=right;} bool isLeaf()
Elem data; BinTreeNode * lchild; BinTreeNode * rchild; public:
BinTreeNode(){lchild=rchild=NULL;} BinTreeNode(Elem e,BinNodePtr*l=NULL,
BinNodePtr*r=NULL) {data=e; lchild=l; rchild=r;} ~BinTreeNode(){}
n0,度为2的结点数为n2,则n0=n2+1。
二叉树的知识点总结

引言概述:二叉树是计算机科学中一种重要的数据结构,其特点是每个节点最多有两个子节点。
在计算机科学中,二叉树被广泛应用于搜索、排序和组织数据等领域。
本文将对二叉树的知识点进行总结和详细阐述,以帮助读者更好地理解和应用二叉树。
正文内容:一、二叉树的基本概念1.二叉树的定义:二叉树是一种特殊的树结构,每个节点最多只有两个子节点。
2.二叉树的特点:每个节点最多有两个子节点,左子节点和右子节点。
3.二叉树的性质:二叉树的左子树和右子树也是二叉树,每个节点的左子树中的所有节点都小于该节点,右子树中的所有节点都大于该节点。
二、二叉树的遍历方式1.前序遍历:先访问根节点,然后递归遍历左子树和右子树。
2.中序遍历:先递归遍历左子树,然后访问根节点,最后递归遍历右子树。
3.后序遍历:先递归遍历左子树和右子树,然后访问根节点。
4.层序遍历:按层次从上到下依次访问每个节点。
三、二叉搜索树1.二叉搜索树的定义:二叉搜索树是一种特殊的二叉树,其中的节点按一定的顺序排列。
2.二叉搜索树的性质:对于任意节点,其左子树中的所有节点都小于该节点,右子树中的所有节点都大于该节点。
3.二叉搜索树的插入操作:将待插入节点与当前节点比较,根据大小关系决定是插入左子树还是右子树。
4.二叉搜索树的删除操作:删除节点时需要考虑其子节点个数,根据不同情况分为三种情况进行处理。
5.二叉搜索树的查找操作:从根节点开始,根据节点值与目标值的大小关系,逐渐向左子树或右子树遍历,直至找到目标值或到达叶子节点。
四、平衡二叉树1.平衡二叉树的定义:平衡二叉树是一种特殊的二叉搜索树,其中的节点满足平衡条件。
2.平衡二叉树的性质:对于任意节点,其左子树和右子树的高度差不超过1。
3.平衡二叉树的实现:通过旋转操作来调整树结构,使其满足平衡条件。
4.平衡二叉树的插入操作:插入节点后,通过旋转操作保持树的平衡性。
5.平衡二叉树的删除操作:删除节点后,通过旋转操作保持树的平衡性。
数据结构二叉树知识点总结

数据结构⼆叉树知识点总结术语1. 节点的度:⼀个节点含有的⼦树的个数称为该节点的度;2. 叶节点或终端节点:度为零的节点;3. ⾮终端节点或分⽀节点:度不为零的节点;4. ⽗亲节点或⽗节点:若⼀个节点含有⼦节点,则这个节点称为其⼦节点的⽗节点;5. 兄弟节点:具有相同⽗节点的节点互称为兄弟节点;6. 节点的层次:从根开始定义起,根为第1层,根的⼦节点为第2层,以此类推;7. 树的⾼度或深度:树中节点的最⼤层次;8. 堂兄弟节点:⽗节点在同⼀层的节点互为堂兄弟;9. 节点的祖先:从根到该节点所经分⽀上的所有节点;10. 孙:以某节点为根的⼦树中任⼀节点都称为该节点的⼦孙。
11. 森林:由m(m>=0)棵互不相交的树的集合称为森林;12. 满⼆叉树:⼀棵深度为k,且有2^k-1 (2的k次⽅减⼀)个节点称之为满⼆叉树13. 完全⼆叉树:完全⼆叉树是由满⼆叉树⽽引出来的。
对于深度为K的,有n个结点的⼆叉树,当且仅当其每⼀个结点都与深度为K的满⼆叉树中编号从1⾄n的结点⼀⼀对应时称之为完全⼆叉树。
叶节点只能出现在最下层和次下层,并且最下⾯⼀层的结点都集中在该层最左边的若⼲位置的⼆叉树⼆叉树的性质1.在⾮空⼆叉树中,第i层的结点总数不超过2^(i-1),i>=1;2.深度为h的⼆叉树最多有2^h-1个结点(h>=1),最少有h个结点;3.对于任意⼀棵⼆叉树,如果其叶结点数为N0,⽽度数为2的结点总数为N2,则N0=N2+1;4.具有n个结点的完全⼆叉树的深度为K =[log2n」+1(取下整数)5.有N个结点的完全⼆叉树各结点如果⽤顺序⽅式存储,则结点之间有如下关系:若I为结点编号则如果I>1,则其⽗结点的编号为I/2;6.完全⼆叉树,如果2*I<=N,则其左⼉⼦(即左⼦树的根结点)的编号为2*I;若2*I>N,则⽆左⼉⼦;如果2*I+1<=N,则其右⼉⼦的结点编号为2*I+1;若2*I+1>N,则⽆右⼉⼦。
树和二叉树知识考点整理

树和二叉树知识考点整理●树的基本概念●树的定义●n个结点的有限集●n=0代表空树●满足条件●只有一个根的结点●其余结点是互不相交的有限集,每个集合本身是一棵树,是根的子树●树是一种递归的数据结构●树的根结点没有前驱,其余结点只有一个前驱●树中所有结点可以有零个或多个后驱●基本术语●双亲、兄弟、孩子、祖先●度:孩子个数●分支结点:度大于0●叶子结点:度为0●深度:从下往上;●高度:从上往下;●有序树:从左到右是有次序的●路径和路径长度:路径是从上往下的●森林:m棵互不相交的树的集合。
●树的基本性质●结点数=所有结点度数之和+1●度为m的树中第i层上至多有m的i-1次分个结点●高度为h的m叉树至多有(m^h-1)/(m-1)个结点●具有n个结点的m叉树的最小高度为「logm(n(m-1)+1)]●二叉树的概念●定义●一种树形结构,特点是每个结点至多只有两棵子树(即二叉树中不存在度大于2的结点)并且二叉树的子树有左右之分,次序不可颠倒●二叉树与度为2的有序树区别●度为2的可以有三个结点,二叉树可以是空树●度为2的有序树的孩子左右之分是根据另一个孩子而言的;二叉树无论有没有,都要确定左右●特殊的二叉树●满二叉树●树中每一层都含有最多的结点●完全二叉树●高度为h,有n个结点的二叉树,当且仅当,每个结点都与高度为h的满二叉树中的编号一一对应●二叉排序树●用途:可用于元素的排序、搜索●左子树上所有结点的关键字均小于根结点的关键字;右子树上所有结点的关键字均大于根结点的关键字;左子树和右子树又是一棵二叉排序树●二叉树的性质●非空二叉树上的叶子结点数等于度为2的结点树加1,即n0=n2+1●非空二叉树上第k层至多有2^(k-1)个结点●高度为h的二叉树至多有2^h-1个结点●具有n个结点的完全二叉树的高度为log2(n+1)取顶或者log2n取底+1●二叉树的存储结构●顺序存储结构●只适合存储完全二叉树,数组从0开始●链式存储结构●顺序存储的空间利用率太低●至少三个指针域:数据域、左指针域、右指针域●增加了指向父结点后,变为三叉链表的存储结构●在含有n个结点的二叉链表中,含有n+1个空链域●二叉树的遍历和线索二叉树●二叉树的遍历●先序遍历●根左右●应用:求树的深度●中序遍历●左根右●后序遍历●左右根●应用:求根到某结点的路径、求两个结点的最近公共祖先等●三个遍历时间复杂度都是O(n)●递归算法和非递归算法的转换●层次遍历●需要借助队列●步骤●二叉树根结点入队,然后出队,访问出队结点,若有左子树,左子树根结点入队●遍历右子树,有右子树,右子树根结点入队。
二叉树实验知识点总结

二叉树实验知识点总结
一、二叉树的基本概念
二叉树是一种特殊的树形结构,其每个节点最多只有两个子节点。
二叉树分为满二叉树、完全二叉树和普通二叉树等类型。
二、遍历方式
1.前序遍历:先访问当前节点,再遍历左子树和右子树;
2.中序遍历:先遍历左子树,再访问当前节点,最后遍历右子树;
3.后序遍历:先遍历左子树和右子树,最后访问当前节点;
4.层次遍历:按照从上到下、从左到右的顺序依次访问每个节点。
三、常见操作
1.插入节点:在二叉搜索树中插入一个新的节点;
2.删除节点:在二叉搜索树中删除一个指定的节点;
3.查找节点:在二叉搜索树中查找一个指定的节点;
4.求深度:计算二叉搜索树的深度。
四、平衡二叉树
平衡二叉树是一种特殊的二叉搜索树,其左右子树高度差不能超过1。
常见的平衡二叉搜索包括红黑树、AVL 树等。
五、应用场景
1.数据库索引;
2.哈夫曼编码;
3.表达式求值;
4.图形处理等。
六、注意事项
1.二叉树的插入、删除和查找操作需要保证二叉树的结构不被破坏;
2.平衡二叉树的实现需要注意平衡因子的计算和旋转操作的实现;
3.在使用二叉树进行算法设计时,需要考虑遍历方式和时间复杂度等问题。
七、总结
二叉树是一种重要的数据结构,在算法设计中有广泛的应用。
掌握二叉树的基本概念、遍历方式、常见操作和应用场景,可以帮助我们更好地理解和使用这种数据结构。
同时,我们需要注意在实际应用中遵循相关规范,保证程序的正确性和效率。
数据结构树和二叉树知识点总结

数据结构树和二叉树知识点总结
1.树的概念:树是一种非线性的数据结构,由节点和边构成,每个节点只能有一个父节点,但可以有多个子节点。
2. 二叉树的概念:二叉树是一种特殊的树结构,每个节点最多只有两个子节点,一个是左子节点,一个是右子节点。
3. 二叉树的遍历:二叉树的遍历分为前序遍历、中序遍历和后序遍历三种方式。
前序遍历是先访问根节点,再访问左子树,最后访问右子树;中序遍历是先访问左子树,再访问根节点,最后访问右子树;后序遍历是先访问左子树,再访问右子树,最后访问根节点。
4. 二叉搜索树:二叉搜索树是一种特殊的二叉树,它满足左子树中所有节点的值均小于根节点的值,右子树中所有节点的值均大于根节点的值。
因此,二叉搜索树的中序遍历是一个有序序列。
5. 平衡二叉树:平衡二叉树是一种特殊的二叉搜索树,它的左子树和右子树的高度差不超过1。
平衡二叉树的插入和删除操作可以保证树的平衡性,从而提高树的查询效率。
6. 堆:堆是一种特殊的树结构,它分为最大堆和最小堆两种。
最大堆的每个节点的值都大于等于其子节点的值,最小堆的每个节点的值都小于等于其子节点的值。
堆常用于排序和优先队列。
7. Trie树:Trie树是一种特殊的树结构,它用于字符串的匹配和检索。
Trie树的每个节点代表一个字符串的前缀,从根节点到叶子节点的路径组成一个完整的字符串。
以上是数据结构树和二叉树的一些基本知识点总结,对于深入学
习数据结构和算法有很大的帮助。
计算机二级二叉树知识点

计算机二级二叉树知识点1.二叉树的定义:二叉树是一种常见的树形结构,其中每个节点最多有两个子节点,分别称为左子节点和右子节点。
二叉树的节点结构通常包括一个数据元素和指向左右子节点的指针。
2.二叉树的性质:(1)二叉树的第i层最多有2^(i-1)个节点。
(2)高度为h的二叉树最多有2^h-1个节点。
(3)对于任意一棵二叉树,如果其叶子节点数为n0,度为2的节点数为n2,则n0=n2+1(4)一棵深度为k且节点总数为n的二叉树,当且仅当其满足2^(k-1)<=n<=2^k-1时,才称为完全二叉树。
3.二叉树的分类:(1)满二叉树:除了叶子节点之外,每个节点都有两个子节点,且所有叶子节点在同一层次上。
(2)完全二叉树:最后一层之前的层都是满的,并且最后一层的节点都靠左排列。
(3)平衡二叉树:左右子树的高度差不超过1的二叉树。
(4)线索二叉树:对于每个节点,除了指向其左右子节点的指针外,还包含指向其在其中一种序列下的前驱节点和后继节点的指针。
4.二叉树的遍历方法:(1)前序遍历:先访问根节点,然后递归地遍历左子树,最后递归地遍历右子树。
(2)中序遍历:先递归地遍历左子树,然后访问根节点,最后递归地遍历右子树。
(3)后序遍历:先递归地遍历左子树,然后递归地遍历右子树,最后访问根节点。
(4)层次遍历:按照从上到下、从左到右的顺序逐层访问每个节点。
5.二叉树:二叉树(Binary Search Tree,BST)是一种特殊的二叉树,它的每个节点的值都大于其左子树中的所有节点值,小于其右子树中的所有节点值。
因此,对于一个二叉树,可以采用中序遍历的方法得到一个有序序列。
二叉树的插入操作:按照二叉树的定义,从根节点开始,将要插入的值与当前节点的值比较,如果小于当前节点的值,则向左子树递归插入,如果大于当前节点的值,则向右子树递归插入,直至找到一个空节点,然后插入新节点。
二叉树的删除操作:删除一个节点需要考虑三种情况:删除节点没有子节点、只有一个子节点、有两个子节点。
二叉树知识点总结

二叉树知识点总结二叉树是一种常见的数据结构,它由节点和边组成,每个节点最多有两个子节点。
以下是关于二叉树的知识点总结。
1. 二叉树的基本概念二叉树是一种树形结构,它由节点和边组成。
每个节点最多有两个子节点,分别称为左子节点和右子节点。
如果一个节点没有子节点,则称其为叶子节点。
二叉树可以为空。
2. 二叉树的遍历方式遍历是指按照一定顺序访问二叉树中的所有节点。
常见的遍历方式有前序遍历、中序遍历和后序遍历。
前序遍历:先访问当前节点,然后递归访问左子树和右子树。
中序遍历:先递归访问左子树,然后访问当前节点,最后递归访问右子树。
后序遍历:先递归访问左子树和右子树,最后访问当前节点。
3. 二叉搜索树二叉搜索树(Binary Search Tree)也称为有序二叉树或排序二叉树。
它是一种特殊的二叉树,在满足以下条件的情况下被称为“搜索”:对于任意节点,其左子树中的所有节点的值都小于该节点的值。
对于任意节点,其右子树中的所有节点的值都大于该节点的值。
左右子树也分别为二叉搜索树。
二叉搜索树支持快速查找、插入和删除操作。
它还有一些变种,如平衡二叉搜索树(AVL Tree)和红黑树(Red-Black Tree)等。
4. 二叉堆二叉堆是一种特殊的完全二叉树,它分为最大堆和最小堆两种类型。
最大堆满足父节点的值大于等于其子节点的值,最小堆满足父节点的值小于等于其子节点的值。
在最大堆中,根节点是整个堆中最大的元素;在最小堆中,根节点是整个堆中最小的元素。
二叉堆常用来实现优先队列(Priority Queue),即按照一定优先级顺序处理元素。
5. 二叉树常见问题5.1 判断是否为平衡二叉树平衡二叉树(Balanced Binary Tree)是指任意节点左右子树高度差不超过1的二叉搜索树。
判断一个二叉搜索树是否为平衡二叉树可以通过递归遍历每个节点,计算其左右子树的高度差。
5.2 判断是否为完全二叉树完全二叉树(Complete Binary Tree)是指除了最后一层外,其他层都是满的,并且最后一层的节点都靠左排列的二叉树。
计算机数据结构知识点梳理 二叉树的定义及其主要特征

当 n ≠ 2k , 即 n 不是2的方幂或者 n = 2k 但是一棵满二叉树,其高度为
。
当 n = 2k 但是非满二叉树,其高度为
。
②有n个结点的完全k叉树的高度为
。
性质5推广:一棵满k叉树,如果按层次顺序从1开始对全部结点编号,
①编号为p=1的结点无父结点,否则编号为p结点的父结点的编号是
(k≥2);
[题1]若一棵二叉树有126个结点,在第7层(根结点在第1层)至多有( )个结点。
A.32
B.64
C.63
D.不存在第7层
分析:根据二叉树的性质,第7层至多有64(27-1)个结点,但是题目中给出了二叉树的结点 总数126,由此来判断第7层是否可以有64个结点?
要在二叉树的第7层达到最多的结点个数,其上面6层必须是一个满二叉树,深度为6的满 二叉树有63(26-1)个结点,由此可以判断出此二叉树的第7层不可能达到64个结点,最 多是126-63=63个结点。
(2)完全二叉树:一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到 右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树 中的位置相同,则这棵二叉树称为完全二叉树。它的特点是:叶子结点只能出现在最下 层和次下层,且最下层的叶子结点集中在树的左部。
任何完全二叉树中度为1的结点只有0个或1个。
中的所有结点从1开始顺序编号,则对于任意的序号为i的结点,有:
(1)如果i>1,则序号i的结点的双亲结点的序号为 ;如果i=1,则序号为i的结点是根 结点,无双亲结点。
(2)如果2i≤n,则序号为i的结点的左孩子结点的序号为2i;如果2i>n,则序号为i的结 点无左孩子。
(3)如果2i+1≤n,则序号为i的结点的右孩子结点的序号为2i+1;如果2i+1>n,则 序号为i的结点无右孩子。
数据结构二叉树知识点总结

数据结构二叉树知识点总结二叉树是指每个节点最多有两个子节点的树结构。
它是一种重要的数据结构,在算法和程序设计中被广泛应用。
下面是对二叉树的主要知识点进行详细总结。
1.二叉树的基本概念:-树节点:树的基本单元,包含数据项(节点值)和指向其他节点的指针。
-根节点:树的第一个节点。
-叶节点(又称为终端节点):没有子节点的节点。
-子节点:一些节点的下一级节点。
-父节点:一些节点的上一级节点。
-兄弟节点:拥有同一父节点的节点。
-深度:从根节点到当前节点的路径长度。
-高度:从当前节点到最远叶节点的路径长度。
2.二叉树的分类:-严格二叉树:每个节点要么没有子节点,要么有两个子节点。
-完全二叉树:除了最后一层外,其他层的节点数都达到最大,并且最后一层的节点依次从左到右排列。
-满二叉树:每个节点要么没有子节点,要么有两个子节点,并且所有叶节点都在同一层上。
-平衡二叉树:任意节点的两棵子树的高度差不超过13.二叉树的遍历:-前序遍历:根节点->左子树->右子树。
递归实现时,先访问当前节点,然后递归遍历左子树和右子树。
-中序遍历:左子树->根节点->右子树。
递归实现时,先递归遍历左子树,然后访问当前节点,最后递归遍历右子树。
-后序遍历:左子树->右子树->根节点。
递归实现时,先递归遍历左子树,然后递归遍历右子树,最后访问当前节点。
-层序遍历:从上到下,从左到右依次访问每个节点。
使用队列实现。
4.二叉查找树(BST):-二叉查找树是一种有序的二叉树,对于树中的每个节点,其左子树的节点的值都小于当前节点的值,右子树的节点的值都大于当前节点的值。
-插入操作:从根节点开始,递归地比较要插入的值和当前节点的值,根据比较结果向左或向右移动,直到找到插入位置为止。
-查找操作:从根节点开始,递归地比较要查找的值和当前节点的值,根据比较结果向左或向右移动,直到找到目标节点或到叶节点。
-删除操作:有三种情况:-被删除节点是叶节点:直接将其删除。
二叉树知识点总结

二叉树知识点总结二叉树是数据结构中常见且重要的一种形式,它可以用于解决许多实际问题,并在算法和编程中扮演着重要的角色。
本文将对二叉树的基本概念、性质以及常见的应用进行总结。
一、基本概念和性质1. 二叉树的定义:二叉树是一种特殊的树形结构,每个节点最多有两个子节点,分别称为左子节点和右子节点。
左子节点小于等于父节点,右子节点大于等于父节点。
2. 二叉树的特点:二叉树具有递归性质,即每个子节点都可以视为一棵二叉树。
同时,二叉树的遍历方式有前序遍历、中序遍历、后序遍历和层次遍历等。
3. 二叉树的性质:a. 二叉树的第i层至多有2^(i-1)个节点;b. 深度为k的二叉树至多有2^k - 1个节点;c. 对于任意一棵二叉树,若其叶节点数为n0,度为2的节点数为n2,则n0 = n2 + 1;d. 具有n个节点的完全二叉树的深度为(log2 n) + 1。
二、二叉树的应用1. 二叉搜索树:二叉搜索树(BST)是一种特殊的二叉树,它满足左子节点小于父节点,右子节点大于父节点的条件。
BST的特性使得查找、插入和删除操作的时间复杂度为O(log n),因此在数据库、图形处理等领域经常被使用。
2. 平衡二叉树:由于BST的特性,如果数据插入的顺序不合理,可能导致树的高度过高,使得操作效率降低。
为了解决这个问题,人们提出了平衡二叉树(AVL)的概念。
AVL树通过旋转操作保持树的平衡,使得左右子树的高度差不超过1,从而保证了操作的效率。
3. 红黑树:红黑树是一种自平衡的二叉查找树,它在AVL树的基础上做了一些调整。
红黑树的特点是节点可以为红色或黑色,并且满足以下规则:根节点为黑色,叶节点为黑色且为空,红色节点的两个子节点都是黑色。
红黑树在C++标准库(STL)中的map和set等容器中得到了广泛应用。
4. 堆:堆是一种完全二叉树,它可以分为大顶堆和小顶堆。
大顶堆中,父节点的值大于或等于两个子节点的值,小顶堆则相反。
堆在排序算法中有广泛应用,如堆排序、优先队列等。
二叉树的基本概念

二叉树的基本概念一、引言二叉树是计算机科学中最基础的数据结构之一,它是由节点和边组成的树形结构,其中每个节点最多有两个子节点。
在计算机科学中,二叉树被广泛应用于搜索、排序、编译器等领域。
本文将详细介绍二叉树的基本概念。
二、定义二叉树是一种特殊的树形结构,其中每个节点最多有两个子节点。
通常将左子节点称为左子树,右子节点称为右子树。
三、基本术语1. 根节点:二叉树的顶层节点称为根节点。
2. 叶子节点:没有任何子节点的节点称为叶子节点。
3. 父节点和子节点:一个父亲可以有多个儿子,但是一个儿子只能有一个父亲。
4. 兄弟:具有相同父亲的两个或多个儿子称为兄弟。
5. 深度:从根到某个节点所经过的边数称为该节点的深度。
6. 高度:从某个节点到其所有后代中深度最大者加一(即包括该结点)称为该结点所在的二叉树的高度。
四、分类1. 满二叉树:一棵深度为k且有2^k-1个节点的二叉树称为满二叉树。
2. 完全二叉树:对于一棵深度为k的,有n个节点的二叉树,当且仅当其每一个节点都与深度为k的满二叉树中编号从1至n的节点一一对应时,称之为完全二叉树。
3. 平衡二叉树:平衡二叉树也称为AVL树,是一种自平衡的排序二叉搜索树。
它具有以下性质:左右子树高度差不超过1,并且左右子树也是平衡二叉树。
五、遍历遍历是指按照某种顺序访问每个节点。
常见的遍历方式有三种:1. 前序遍历(Pre-order):先访问当前节点,再依次遍历左子树和右子树。
2. 中序遍历(In-order):先依次遍历左子树,再访问当前节点,最后遍历右子树。
3. 后序遍历(Post-order):先依次遍历左子树和右子树,最后访问当前节点。
六、应用1. 搜索算法:在搜索算法中,二叉树被广泛应用于二分查找。
2. 排序算法:在排序算法中,二叉树被广泛应用于堆排序和快速排序。
3. 编译器:在编译器中,二叉树被广泛应用于语法分析和代码生成。
七、总结本文介绍了二叉树的基本概念、术语、分类、遍历以及应用。
二叉树常见选择题和知识点

二叉树是数据结构中的一种重要类型,常见于编程面试和计算机科学课程的考试中。
以下是一些关于二叉树的常见选择题和相关知识点:
1. 基本概念:
-什么是二叉树?
-什么是二叉搜索树(BST)?
-什么是平衡二叉树(A VL树)?
2. 二叉树遍历:
-先序遍历、中序遍历、后序遍历的定义和区别。
-给定一个二叉树的先序遍历和中序遍历结果,如何构建这棵树?
3. 二叉搜索树的性质:
-二叉搜索树的定义和性质。
-如何判断一个二叉树是否是二叉搜索树?
4. 二叉树的深度和节点计数:
-二叉树的深度是指什么?如何计算二叉树的深度?
-如何统计一个二叉树中的节点数量?
5. 平衡二叉树:
-什么是平衡二叉树?
- A VL树是如何维护平衡性的?
6. 堆和优先队列:
-什么是二叉堆?
-如何用二叉堆实现优先队列?
7. 哈夫曼树:
-什么是哈夫曼树?
-如何构建哈夫曼树?
8. 二叉树的应用:
-二叉树在数据库中的应用。
-二叉树在文件系统中的应用。
9. 二叉树的扩展:
-什么是二叉树的Morris遍历?
-什么是线索二叉树?
以上只是一些例子,实际上,关于二叉树的选择题和知识点还有很多。
在学习和准备面试时,建议对每个知识点进行深入理解,同时通过实际的编程练习加深对二叉树的掌握。
树、二叉树、哈夫曼树的知识点和考点

树、二叉树、哈夫曼树的知识点和考点嘿,朋友!咱们今天来聊聊树、二叉树还有哈夫曼树。
先来说说树吧。
你看这树,就像一个大家庭,有根节点这个大家长,然后下面有好多分支节点,就像孩子们一样。
每个节点都能有自己的“后代”,这是不是挺有意思?你想想,一个家族不断开枝散叶,越来越庞大,这不就和树的结构很像吗?二叉树呢,就像是一个有点“偏心”的家长,它每个节点最多只有两个孩子,不是左孩子就是右孩子。
这就好像你只有两只手,要么拿左边的东西,要么拿右边的东西。
二叉树在很多算法里可是大显身手呢!比如搜索、排序,都能看到它的身影。
再讲讲哈夫曼树,这可是个厉害的角色!它就像是一个精打细算的管家,总是能把资源分配得恰到好处。
比如说,要对一些字符进行编码,哈夫曼树就能通过巧妙的计算,让出现频率高的字符用短编码,出现频率低的字符用长编码,从而节省存储空间和传输时间。
这是不是很神奇?那在考试中,关于树的知识点,经常会让你画出一棵树的结构,或者问你树的深度、节点个数啥的。
这就好比让你数数一个大家庭里有多少人,关系有多复杂。
二叉树的考点呢,可能会让你进行遍历,前序、中序、后序,就像你按照不同的顺序参观一个园子,看到的景色顺序也不一样。
哈夫曼树呢,说不定会让你根据给定的字符频率来构建哈夫曼树,然后算出编码。
这就像是给你一堆东西和它们的重要程度,让你合理安排摆放位置。
总之,树、二叉树、哈夫曼树这些知识点,就像是我们生活中的小帮手,虽然有时候看起来有点复杂,但只要你用心去理解,就会发现它们其实很有趣,也很有用。
只要多做练习,多思考,考试的时候就能轻松应对,难道不是吗?所以,加油吧朋友,相信你一定能掌握好这些知识,在考试中取得好成绩!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例
75 2 4
abcd
75 6 ab
24 cd
7
11
a
56
b
24
cd
18
7 11 a
56 b
24 cd
Huffman编码 a:0 b:10 c:110 d:111
谢谢观看
谢谢!
第六章 二叉树
小组成员:林思 ,郑晓纯,唐焕新,李俊峰 何伟棋,谢智杰,吴国锵,苏晓鑫
6.1树的定义
树(tree)是n(n>=0)个结点的有限集T,n=0的树称为空树。其中:有 且仅有一个特定的结点,称为树的根(root) 当n>1时,其余结点可分为m(m>0)个互不相交的有限集T1,T2,…Tm 其中每一个集合本身又是一棵树,称为根的子树(subtree)
在线索二叉树的结点中增加两个标志域 lt :若 lt =0, lc 域指向左孩子;若 lt=1, lc域指向其前驱 rt :若 rt =0, rc 域指向右孩子;若 rt=1, rc域指向其后继
T
lt rt
0A 0
A
B
D
1B 0
0D 1
CE
1C 1
1E 1 ^
先序序列:ABCDE 先序线索二叉树
6.4 Huffman树
6.3 线索二Βιβλιοθήκη 树定义: 前驱与后继:在二叉树的先序、中序或后序遍历序列中两个相邻的结点互称 为前驱与后继。 线索:指向前驱或后继结点的指针称为线索 线索二叉树:加上线索的二叉链表表示的二叉树叫线索二叉树 线索化:对二叉树按某种遍历次序使其变为线索二叉树的过程叫线索化。 在线索二叉树的结点中增加两个标志域 lt :若 lt =0, lc 域指向左孩子;若 lt=1, lc域指向其前驱 rt :若 rt =0, rc 域指向右孩子;若 rt=1, rc域指向其后继
Huffman编码:数据通信用的二进制编码 思想:根据字符出现频率编码,使电文总长最短 编码:根据字符出现频率构造Huffman树,然后将树中结点引向其左孩子的分支标“0”, 引向其右孩子的分支标“1”;每个字符的编码即为从根到每个叶子的路径上得到的0、1序列
构造Huffman树步骤
1.根据给定的n个权值{w1,w2,……wn},构造n棵只有根结点的二叉树,令起权值为wj 2.在森林中选取两棵根结点权值最小的树作左右子树,构造一棵新的二叉树,置新二叉 树根结点权值为其左右子树根结点权值之和 3.在森林中删除这两棵树,同时将新得到的二叉树加入森林中 4.重复上述两步,直到只含一棵树为止,这棵树即哈夫曼树
树与二叉树的转换
将树转换成二叉树 加线:在兄弟之间加一连线 抹线:对每个结点,除了其左孩子外,去除其与其余孩子之间的关系 旋转:以树的根结点为轴心,将整树顺时针转45°
将二叉树转换成树 加线:若p结点是双亲结点的左孩子,则将p的右孩子,右孩子的右孩子,……
沿分支找到的所有右孩子,都与p的双亲用线连起来 抹线:抹掉原二叉树中双亲与右孩子之间的连线 调整:将结点按层次排列,形成树结构
特点: 树中至少有一个结点——根 树中各子树是互不相交的集合
树的基本术语
结点(node)——表示树中的元素,包括数据项及若干指向其子树的分支 结点的度(degree)——结点拥有的子树数 叶子(leaf)——度为0的结点 孩子(child)——结点子树的根称为该结点的孩子 双亲(parents)——孩子结点的上层结点叫该结点的~ 兄弟(sibling)——同一双亲的孩子 树的度——一棵树中最大的结点度数 结点的层次(level)——从根结点算起,根为第一层,它的孩子为第二层…… 深度(depth)——树中结点的最大层次数 森林(forest)——m(m 0)棵互不相交的树的集合
定义:带权路径长度最短的树 路径:从树中一个结点到另一个结点之间的分支构成这两个结点间的~ 路径长度:路径上的分支数 权(w):在字符使用概率不同的情况下,将字符使用概率作为二叉树中叶子结点的值 树的路径长度(l):从树根到每一个结点的路径长度之和 树的带权路径长度(wpl):树中所有带权结点的路径长度之和
A
B
C
D
先序遍历序列:A B D C 中序遍历序列:B D A C 后序遍历序列:D B C A
-
+
/
a
*
ef
b
-
c
d
先序遍历: - + a * b - c d / e f 中序遍历: a + b * c - d - e / f 后序遍历: a b c d - * + e f / 层次遍历: - + / a * e f b - c d
完全二叉树 定义:深度为k,有n个结点的二叉树当且仅当其每一个结点都与深度为k 的满二叉树中编号从1至n的结点一一对应时,称为完全二叉树。
判定
2
3
4
5
6
7
8
9
10
11
完全二叉树
12
13
14
满二叉树
二叉树的遍历
二叉树的遍历 方法 先序遍历:先访问根结点,然后分别先序遍历左子树、右子树 中序遍历:先中序遍历左子树,然后访问根结点,最后中序 遍历右子树 后序遍历:先后序遍历左、右子树,然后访问根结点 按层次遍历:从上到下、从左到右访问各结点
6.2二叉树
定义:二叉树是n(n>=0)个结点的有限集,它或为空树(n=0), 或由一个根结点和两棵分别称为左子树和右子树的互不相交 的二叉树构成
特点 每个结点至多有二棵子树(即不存在度大于2的结点) 二叉树的子树有左、右之分,且其次序不能任意颠倒
特殊的二叉树类型
满二叉树
定义:一颗深度为k且有 2 k -1个结点的二叉树称为满二叉树。
将树转换成二叉树
A
A
A
B
CD
B
CD
B
CD
E F GHI
E F G H IE F G H I
A
B
CD
E F GHI
树转换成的二叉树其右子树一定为空
B E
F
A
C D
GH I
将二叉树转换成树
B E
F
A
C D
B E
F
A
C D
B E
F
A
B
C
E
D
F
A
C D
GH
I A
GH I
GH I
GH I
B
C
D
E F GHI
