新大学物理 下册 第2版 教学课件 王祖源 张庆福 chap12_3
大学物理学第二版下册振动
-A1
x
A1
A2
o
- A2
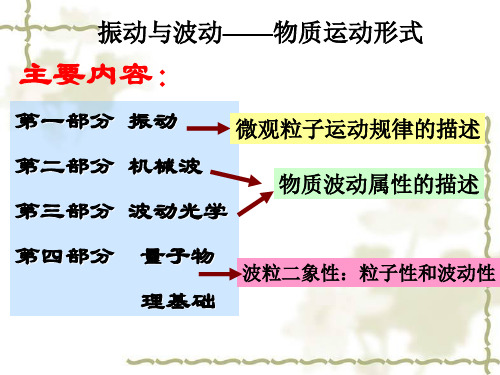
反相时振动曲线
-A1
x2 x1 t
x2 x1 t
x
A1
x2
A2
o
- A2
x1 t
-A1
x2 先于x1 到达各自同方向最大值,
x2 振动超前 x1 振动 /2 ; 或 x1 振动落后 x2 振动 /2 。
由简谐振动周期性有 x x
Acos(t ) Acos((t T ) )
0
0
Acos(t ) Acos((t T ) )
0
0
余弦函数为周期函数,周期为 2 周期的倒数称为频率
所以 T 2
把 称作角频率
T 2
1 T 2
细杆稍微偏离平衡位置( 很
小),让其摆动 D. 一质点作匀速圆周运动,它在直
径上的投影点的 运动
BCD
选项B图示
1. 周期、频率、角频率
作一次全振动的最短时间间隔称为振动的周期
由简谐振动的运动方程
记作 T
x Acos(t ) 0
A、、 0
经过一个周期,运动方程为
为一常数
x Acos((t T ) ) 0
5. 速度、加速度
x Acos(t ) 0
速度 加速度
v
dx dt
A
sin(t
0 )
a
d2x dt 2
A 2
cos(t
0 )
写成标 准形式
v
A
cos(t
0
2
)
a A 2 cos(t 0 )
大学物理学(第二版)课件:牛顿定律

d 2
(
FT
dFT
)
sin
d 2
FT FT
cos d 2
sin d 2
Ff FN
0 0
Ff
FN
O
sin d d ,cos d 1
22
2
1 2
dFT
FTd
FN
dF FTA
T
d
F FTB
T
0
FTB FTAe
FTB / FTA e
若μ=0.25
θ
FTB/FTA
π
0.46
2π 0.21
(2)牛顿第一定律指出了物体具有惯性. 物体在不受外力作用时,将保持静止状态或匀速直线运动
状态.可见,物体保持原来运动状态不变的特性,是物体固有 的,这种特性称为物体的惯性(inertia).因此牛顿第一定律又 称为惯性定律. (3)定义了一种特殊的参考系——惯性系.
一个不受力作用的物体或处于 受力平衡状态下的物体,将保持其静 止或匀速直线运动的状态不变.这样 的参考系叫惯性参考系.
* 以距源 10-15m 处强相互作用的力强度为 1
2.3 牛顿定律的应用
2.3.1 动力学问题分类 1.已知物体受力,求物体的运动状态; 2.已知物体的运动状态,求物体所受的力. 2.3.2 解题步骤(隔离体法)
• 选择研究对象(隔离物体); • 查看运动情况; • 进行受力分析(画受力图:画重力,找接触,不遗漏勿妄加) • 建立坐标系(惯性参考系),选取正方向; • 对各个隔离体列出牛顿运动方程(分量式); • 利用其他的约束条件列补充方程; • 解方程,并对结果进行分析和讨论.
力,与此同时,绳的内部各段之间也有相互的弹性力作用,这
种弹性力称为张力.
大学物理II知识点复习PPT课件

10
可编辑
2020/1/9
知识点:
库仑定律、电场力叠加原理、电场强度; 高斯定律,高斯定理应用;环路定理,电 势,电势计算,等势面和电势梯度概念。
导体静电平衡;电流密度,电动势和稳恒 电场。
电介质极化,极化强度和极化电荷,电位 移矢量,电介质中高斯定理,电容和电容 器,静电场能量。
11
可编辑
2020/1/9
热学知识点总结
4
Company Logo
2020/1/9
分子动理论重要知识点
1、热力学系统 2、理想气体的微观模型、压强和温度的统计意义 3、能量按自由度均分定理 4、麦克斯韦气体分子速率分布律
5、热学第一定律
5
可编辑
2020/1/9
与外界完全隔绝(即 与外界没有质量和 能量交换)的系统。
孤立 系统
热力学 系统
与外界没有质量交 换和但有能量交换 的系统。
封闭 系统
与外界既有质量交 换又有能量交换的 系统
开放 系统
平衡态 热力学系统的所有可 观察的宏观物理性质 不随时间变化的状态。
6
可编辑
2020/1/9
统计假设
气体分 子假设
理想气体
理想气体 宏观方程
7
可编辑
2020/1/9
统计
压强
点电荷:
均匀带电圆环 轴线上:
V 1 q
4 0 r
1
q
V 40 (R2 x2 ) 12
注意:应 用典型带 电体的电 势公式选 取相同的 零势点。
均匀带电球面: V(rR)
1
4 0
q R
V(r>R)
1
4 0
2024版大学物理PPT完整全套教学课件pptx

科里奥利力的概念
在非惯性系中,当物体相对于非 惯性系有相对运动时,会受到科 里奥利力的作用,其方向垂直于 物体相对运动方向和非惯性系的 角速度方向。
04
动量守恒定律和能量守恒 定律
动量守恒定律
定律表述
一个系统不受外力或所受合外力为零, 则系统的总动量保持不变。
适用范围
适用于宏观低速物体,也适用于微观高 速粒子;既适用于单个物体,也适用于 多个物体组成的系统。
大学物理涉及的知识面很广,包括力学、热 学、电磁学、光学、原子物理学等,因此要 拓宽知识面,掌握不同领域的知识。
02
质点运动学
质点运动的描述
01
位置矢量与位移
02
位置矢量的定义和性质
03
位移的计算方法和物理意义
质点运动的描述
加速度的定义、种类和计 算
速度的定义、种类和计算
速度与加速度
01
03 02
03
观察和实验
物理学是一门以实验为基础的自然科学, 观察和实验是物理学的基本研究方法,通 过实验可以验证物理假说和理论,发现新 的物理现象和规律。
建立理想模型
理想模型是物理学中经常采用的一种研究 方法,它忽略了次要因素,突出了主要因 素,使物理问题得到简化。
数学方法
数学是物理学的重要工具,通过数学方法 可以精确地描述物理现象和规律,推导物 理公式和定理。
03
动能定理的应用
用于解决刚体定轴转动中的功能 转换问题,如计算外力对刚体所 做的功、求解刚体的角速度等。
06
机械振动和机械波
简谐振动
简谐振动的定义和基本概 念
阐述简谐振动是物体在一定位置附近做周期性 的往返运动,介绍振幅、周期、频率等基本概 念。
大学物理

大学物理
杂 志
第6页 共36页 页 页
大学物理
第7页 共36页 页 页
大学物理
教学的时代背景
时代特征: 知识爆炸, 时代特征: 知识爆炸,科技转化为生产力的 周期越来越短。 周期越来越短。 科学 密切结合, 技术 密切结合,交叉发展 工程 对人才的要求:具有科学家头脑的工程师, 对人才的要求:具有科学家头脑的工程师, 具有工程师技术意识的科学家。 具有工程师技术意识的科学家。
大学物理
第14页 共36页 页 页
物理学具有以下特征: 物理学具有以下特征:
1) 物理学是一门理论和实验相结合的科学。 物理学是一门理论和实验相结合的科学。 2) 物理学要用“模型”回答问题。 物理学要用“模型”回答问题。 3) 物理学是一门定量的科学。 物理学是一门定量的科学。 4) 物理学的哲学基础是辨证唯物主义。 物理学的哲学基础是辨证唯物主义。
发展性
大学物理
大学: 大学: E = mc2 能量载体
F=
r2
前沿: 质量究竟是什么?是如何产生的? 前沿: 质量究竟是什么?是如何产生的? r 例如: 例如:力 F r r r 对时间积累 I = F∆t = ∆p
r r F = ma
动量定理 —— 动量守恒 对空间积累 A = FScosθ = ∆Ek 动能定理 —— 机械能守恒 力矩 M = Fd 定轴转动物体的平衡
知识、方法、 知识、方法、科学观念 1. 学习物理知识要注意整体性、发展性和迁移性 学习物理知识要注意整体性、
大学物理
整体性
注意掌握知识的结构和联系 上册教材结构和主线
对称性破缺 时空对称性 对称性 参考系等价性 无序 有序
实物世界结构层次 运动和守恒定律 相对论和时空 热力学和统计物理 多粒子 体系
大学物理学教程(第二版)下册标准答案

物理学教程下册答案9-16第九章 静 电 场9-1 电荷面密度均为+σ的两块“无限大”均匀带电的平行平板如图(A )放置,其周围空间各点电场强度E (设电场强度方向向右为正、向左为负)随位置坐标x 变化的关系曲线为图(B )中的( )题 9-1 图分析与解 “无限大”均匀带电平板激发的电场强度为02εσ,方向沿带电平板法向向外,依照电场叠加原理可以求得各区域电场强度的大小和方向.因而正确答案为(B ).9-2 下列说法正确的是( )(A )闭合曲面上各点电场强度都为零时,曲面内一定没有电荷(B )闭合曲面上各点电场强度都为零时,曲面内电荷的代数和必定为零(C )闭合曲面的电通量为零时,曲面上各点的电场强度必定为零(D )闭合曲面的电通量不为零时,曲面上任意一点的电场强度都不可能为零 分析与解 依照静电场中的高斯定理,闭合曲面上各点电场强度都为零时,曲面内电荷的代数和必定为零,但不能肯定曲面内一定没有电荷;闭合曲面的电通量为零时,表示穿入闭合曲面的电场线数等于穿出闭合曲面的电场线数或没有电场线穿过闭合曲面,不能确定曲面上各点的电场强度必定为零;同理闭合曲面的电通量不为零,也不能推断曲面上任意一点的电场强度都不可能为零,因而正确答案为(B ).9-3 下列说法正确的是( )(A) 电场强度为零的点,电势也一定为零(B) 电场强度不为零的点,电势也一定不为零(C) 电势为零的点,电场强度也一定为零(D) 电势在某一区域内为常量,则电场强度在该区域内必定为零分析与解电场强度与电势是描述电场的两个不同物理量,电场强度为零表示试验电荷在该点受到的电场力为零,电势为零表示将试验电荷从该点移到参考零电势点时,电场力作功为零.电场中一点的电势等于单位正电荷从该点沿任意路径到参考零电势点电场力所作的功;电场强度等于负电势梯度.因而正确答案为(D).*9-4在一个带负电的带电棒附近有一个电偶极子,其电偶极矩p的方向如图所示.当电偶极子被释放后,该电偶极子将( )(A) 沿逆时针方向旋转直到电偶极矩p水平指向棒尖端而停止(B) 沿逆时针方向旋转至电偶极矩p水平指向棒尖端,同时沿电场线方向朝着棒尖端移动(C) 沿逆时针方向旋转至电偶极矩p水平指向棒尖端,同时逆电场线方向朝远离棒尖端移动(D) 沿顺时针方向旋转至电偶极矩p 水平方向沿棒尖端朝外,同时沿电场线方向朝着棒尖端移动题9-4 图分析与解电偶极子在非均匀外电场中,除了受到力矩作用使得电偶极子指向电场方向外,还将受到一个指向电场强度增强方向的合力作用,因而正确答案为(B).9-5精密实验表明,电子与质子电量差值的最大范围不会超过±10-21e,而中子电量与零差值的最大范围也不会超过±10-21e,由最极端的情况考虑,一个有8个电子,8个质子和8个中子构成的氧原子所带的最大可能净电荷是多少?若将原子视作质点,试比较两个氧原子间的库仑力和万有引力的大小.分析考虑到极限情况,假设电子与质子电量差值的最大范围为2×10-21e,中子电量为10-21e,则由一个氧原子所包含的8个电子、8个质子和8个中子可求原子所带的最大可能净电荷.由库仑定律可以估算两个带电氧原子间的库仑力,并与万有引力作比较.解 一个氧原子所带的最大可能净电荷为()e q 21max 10821-⨯⨯+=二个氧原子间的库仑力与万有引力之比为1108.2π46202max <<⨯==-Gmεq F F g e 显然即使电子、质子、中子等微观粒子带电量存在差异,其差异在±10-21e 范围内时,对于像天体一类电中性物体的运动,起主要作用的还是万有引力. 9-6 1964年,盖尔曼等人提出基本粒子是由更基本的夸克构成,中子就是由一个带e 32 的上夸克和两个带e 31-的下夸克构成.若将夸克作为经典粒子处理(夸克线度约为10-20 m),中子内的两个下夸克之间相距2.60×10-15 m .求它们之间的相互作用力.解 由于夸克可视为经典点电荷,由库仑定律()r r r re r q q e e e F N 78.3π41π412202210===εε F 与径向单位矢量e r 方向相同表明它们之间为斥力.9-7 点电荷如图分布,试求P 点的电场强度.分析 依照电场叠加原理,P 点的电场强度等于各点电荷单独存在时在P 点激发电场强度的矢量和.由于电荷量为q 的一对点电荷在P 点激发的电场强度大小相等、方向相反而相互抵消,P 点的电场强度就等于电荷量为2.0q 的点电荷在该点单独激发的场强度.解 根据上述分析2020π1)2/(2π41aq a q E P εε==题 9-7 图9-8若电荷Q均匀地分布在长为L的细棒上.求证:(1) 在棒的延长线,且离棒中心为r处的电场强度为224π1LrQεE-=(2) 在棒的垂直平分线上,离棒为r处的电场强度为2204π21LrrQεE+=若棒为无限长(即L→∞),试将结果与无限长均匀带电直线的电场强度相比较.题 9-8 图分析这是计算连续分布电荷的电场强度.此时棒的长度不能忽略,因而不能将棒当作点电荷处理.但带电细棒上的电荷可看作均匀分布在一维的长直线上.如图所示,在长直线上任意取一线元d x,其电荷为d q=Q d x/L,它在点P 的电场强度为rrqεeE2dπ41d'=整个带电体在点P 的电场强度⎰=E E d接着针对具体问题来处理这个矢量积分.(1) 若点P 在棒的延长线上,带电棒上各电荷元在点P 的电场强度方向相同,⎰=L E i E d(2) 若点P 在棒的垂直平分线上,如图(a )所示,则电场强度E 沿x 轴方向的分量因对称性叠加为零,因此,点P 的电场强度就是⎰⎰==L y E E j j E d sin d α证 (1) 延长线上一点P 的电场强度⎰'=L rq E20π2d ε,利用几何关系 r ′=r -x 统一积分变量,则 ()220022204π12/12/1π4d π41L r Q εL r L r L εQ x r L x Q εE L/-L/P -=⎥⎦⎤⎢⎣⎡+--=-=⎰电场强度的方向沿x 轴.(2) 根据以上分析,中垂线上一点P 的电场强度E 的方向沿y 轴,大小为E r εq αE L d π4d sin 20⎰'= 利用几何关系 sin α=r /r ′,22x r r +=' 统一积分变量,则 ()2202/32222041π2d π41Lr r Q r x L x rQ E L/-L/+=+=⎰εε 当棒长L →∞时,若棒单位长度所带电荷λ为常量,则P 点电场强度r ελL r L Q r εE l 0220π2 /41/π21lim =+=∞→此结果与无限长带电直线周围的电场强度分布相同[图(b )].这说明只要满足r 2/L 2 <<1,带电长直细棒可视为无限长带电直线.9-9 一半径为R 的半球壳,均匀地带有电荷,电荷面密度为σ,求球心处电场强度的大小.题 9-9 图分析 这仍是一个连续带电体问题,求解的关键在于如何取电荷元.现将半球壳分割为一组平行的细圆环,如图所示,从教材第9-3节的例2可以看出,所有平行圆环在轴线上P 处的电场强度方向都相同,将所有带电圆环的电场强度积分,即可求得球心O 处的电场强度.解 将半球壳分割为一组平行细圆环,任一个圆环所带电荷元θθδδd sin π2d d 2⋅⋅==R S q ,在点O 激发的电场强度为()i E 2/3220d π41d r x q x +=ε 由于平行细圆环在点O 激发的电场强度方向相同,利用几何关系θR x cos =,θR r sin =统一积分变量,有()θθθεδθθδθεεd cos sin 2 d sin π2cos π41d π41d 02303/2220=⋅=+=R RR r x q x E 积分得 02/π004d cos sin 2εδθθθεδ⎰==E 9-10 水分子H 2O 中氧原子和氢原子的等效电荷中心如图所示,假设氧原子和氢原子等效电荷中心间距为r 0 .试计算在分子的对称轴线上,距分子较远处的电场强度.题 9-10 图分析 水分子的电荷模型等效于两个电偶极子,它们的电偶极矩大小均为00er P =,而夹角为2θ.叠加后水分子的电偶极矩大小为θcos 20er p =,方向沿对称轴线,如图所示.由于点O 到场点A 的距离x >>r 0 ,利用教材第5 -3 节中电偶极子在延长线上的电场强度302π41xp εE = 可求得电场的分布.也可由点电荷的电场强度叠加,求电场分布. 解1 水分子的电偶极矩θθcos 2cos 200er p p ==在电偶极矩延长线上30030030cos π1cos 4π412π41x θer εx θer εx p εE === 解2 在对称轴线上任取一点A ,则该点的电场强度+-+=E E E2020π42π4cos 2cos 2x εe r εθer E βE E -=-=+ 由于 θxr r x r cos 202022-+=rθr x βcos cos 0-=代入得()⎥⎥⎦⎤⎢⎢⎣⎡--+-=22/30202001cos 2cos π42x xr r x r x eE θθε 测量分子的电场时, 总有x >>r 0 , 因此, 式中()⎪⎭⎫ ⎝⎛⋅-≈⎪⎭⎫ ⎝⎛-≈-+x r x x r x xr r x θθθcos 2231cos 21cos 2032/3032/30202,将上式化简并略去微小量后,得300cos π1x θe r εE = 9-11 两条无限长平行直导线相距为r 0,均匀带有等量异号电荷,电荷线密度为λ.(1) 求两导线构成的平面上任一点的电场强度( 设该点到其中一线的垂直距离为x );(2) 求每一根导线上单位长度导线受到另一根导线上电荷作用的电场力.题 9-11 图分析 (1) 在两导线构成的平面上任一点的电场强度为两导线单独在此所激发的电场的叠加.(2) 由F =q E ,单位长度导线所受的电场力等于另一根导线在该导线处的电场强度乘以单位长度导线所带电量,即:F =λE .应该注意:式中的电场强度E 是另一根带电导线激发的电场强度,电荷自身建立的电场不会对自身电荷产生作用力.解 (1) 设点P 在导线构成的平面上,E +、E -分别表示正、负带电导线在P 点的电场强度,则有()i i E E E x r x r x r x -=⎪⎪⎭⎫ ⎝⎛-+=+=+-00000π211π2ελελ(2) 设F +、F -分别表示正、负带电导线单位长度所受的电场力,则有i E F 00π2r ελλ==-+ i E F 002π2r ελλ-=-=+- 显然有F +=F -,相互作用力大小相等,方向相反,两导线相互吸引.9-12 设匀强电场的电场强度E 与半径为R 的半球面的对称轴平行,试计算通过此半球面的电场强度通量.题 9-12 图分析 方法1:作半径为R 的平面S 与半球面S 一起可构成闭合曲面,由于闭合面内无电荷,由高斯定理∑⎰==⋅01d 0q εS S E 这表明穿过闭合曲面的净通量为零,穿入平面S ′的电场强度通量在数值上等于穿出半球面S 的电场强度通量.因而⎰⎰'⋅-=⋅=S S S E S E Φd d 方法2:由电场强度通量的定义,对半球面S 求积分,即⎰⋅=S S d s E Φ解1 由于闭合曲面内无电荷分布,根据高斯定理,有⎰⎰'⋅-=⋅=S S S E S E Φd d 依照约定取闭合曲面的外法线方向为面元d S 的方向,E R R E 22ππcos π=⋅⋅-=Φ解2 取球坐标系,电场强度矢量和面元在球坐标系中可表示为()r E e e e E ϕθθϕϕθϕsin sin cos sin cos ++=r θθR e S d d sin d 2=ER ER ER S S 2π0π02222πd sin d sin d d sin sin d ===⋅=⎰⎰⎰⎰ϕϕθθϕθϕθS E Φ9-13 地球周围的大气犹如一部大电机,由于雷雨云和大气气流的作用,在晴天区域,大气电离层总是带有大量的正电荷,云层下地球表面必然带有负电荷.晴天大气电场平均电场强度约为1m V 120-⋅,方向指向地面.试求地球表面单位面积所带的电荷(以每平方厘米的电子数表示).分析 考虑到地球表面的电场强度指向地球球心,在大气层中取与地球同心的球面为高斯面,利用高斯定理可求得高斯面内的净电荷.解 在大气层临近地球表面处取与地球表面同心的球面为高斯面,其半径E R R ≈(E R 为地球平均半径).由高斯定理∑⎰=-=⋅q εR E E 021π4d S E 地球表面电荷面密度∑--⋅⨯-=-≈=2902m C 1006.1π4/E R q E εσ单位面积额外电子数25cm 1063.6)/(-⨯=-=e n σ9-14 设在半径为R 的球体内电荷均匀分布,电荷体密度为ρ,求带电球内外的电场强度分布.分析 电荷均匀分布在球体内呈球对称,带电球激发的电场也呈球对称性.根据静电场是有源场,电场强度应该沿径向球对称分布.因此可以利用高斯定理求得均匀带电球内外的电场分布.以带电球的球心为中心作同心球面为高斯面,依照高斯定理有⎰==⋅s Q E r S E 0i 2π4d ε上式中i Q 是高斯面内的电荷量,分别求出处于带电球内外的高斯面内的电荷量,即可求得带电球内外的电场强度分布.解 依照上述分析,由高斯定理可得R r <时, 302π34π4r E r ερ= 假设球体带正电荷,电场强度方向沿径向朝外.考虑到电场强度的方向,带电球体内的电场强度为r E 03ερ= R r >时, 302π34π4R E r ερ= 考虑到电场强度沿径向朝外,带电球体外的电场强度为r e rR E 2033ερ=9-15 两个带有等量异号电荷的无限长同轴圆柱面,半径分别为R 1 和R 2 (R 2>R 1 ),单位长度上的电荷为λ.求离轴线为r 处的电场强度:(1) r <R 1 ,(2) R 1 <r <R 2 ,(3) r >R 2 .题 9-15 图分析 电荷分布在无限长同轴圆柱面上,电场强度也必定沿轴对称分布,取同轴圆柱面为高斯面,只有侧面的电场强度通量不为零,且⎰⋅=⋅rL E d π2S E ,求出不同半径高斯面内的电荷∑q .即可解得各区域电场的分布.解 作同轴圆柱面为高斯面,根据高斯定理∑=⋅0/π2εq rL Er <R 1 , 0=∑q01=ER 1 <r <R 2 , L λq =∑rελE 02π2= r >R 2, 0=∑q03=E在带电面附近,电场强度大小不连续,如图(b )所示,电场强度有一跃变 000π2π2ΔεσrL εL λr ελE === 9-16 如图所示,有三个点电荷Q 1 、Q 2 、Q 3 沿一条直线等间距分布且Q 1 =Q 3 =Q .已知其中任一点电荷所受合力均为零,求在固定Q 1 、Q 3 的情况下,将Q 2从点O 移到无穷远处外力所作的功.题 9-16 图分析 由库仑力的定义,根据Q 1 、Q 3 所受合力为零可求得Q 2 .外力作功W ′应等于电场力作功W 的负值,即W ′=-W .求电场力作功的方法有两种:(1)根据功的定义,电场力作的功为l E d 02⎰∞=Q W 其中E 是点电荷Q 1 、Q 3 产生的合电场强度.(2) 根据电场力作功与电势能差的关系,有()0202V Q V V Q W =-=∞其中V 0 是Q 1 、Q 3 在点O 产生的电势(取无穷远处为零电势).解1 由题意Q 1 所受的合力为零()02π4π420312021=+d εQ Q d εQ Q 解得 Q Q Q 414132-=-=由点电荷电场的叠加,Q 1 、Q 3 激发的电场在y 轴上任意一点的电场强度为()2/322031π2y d εQ E E E yy y +=+=将Q 2 从点O 沿y 轴移到无穷远处,(沿其他路径所作的功相同,请想一想为什么?)外力所作的功为()d εQ y y d εQ Q Q W y 022/3220002π8d π241d =+⋅⎥⎦⎤⎢⎣⎡--=⋅-='⎰⎰∞∞l E 解2 与解1相同,在任一点电荷所受合力均为零时Q Q 412-=,并由电势的叠加得Q 1 、Q 3 在点O 的电势dεQ d εQ d εQ V 003010π2π4π4=+= 将Q 2 从点O 推到无穷远处的过程中,外力作功dεQ V Q W 0202π8=-=' 比较上述两种方法,显然用功与电势能变化的关系来求解较为简洁.这是因为在许多实际问题中直接求电场分布困难较大,而求电势分布要简单得多. 9-17 已知均匀带电长直线附近的电场强度近似为r rελe E 0π2= 其中λ为电荷线密度.(1)求在r =r 1 和r =r 2 两点间的电势差;(2)在点电荷的电场中,我们曾取r →∞处的电势为零,求均匀带电长直线附近的电势时,能否这样取? 试说明.解 (1) 由于电场力作功与路径无关,若沿径向积分,则有12012ln π2d 21r r ελU r r =⋅=⎰r E (2) 不能.严格地讲,电场强度r e rελE 0π2=只适用于无限长的均匀带电直线,而此时电荷分布在无限空间,r →∞处的电势应与直线上的电势相等. 9-18 一个球形雨滴半径为0.40 mm ,带有电量1.6 pC ,它表面的电势有多大? 两个这样的雨滴相遇后合并为一个较大的雨滴,这个雨滴表面的电势又是多大?分析 取无穷远处为零电势参考点,半径为R 带电量为q 的带电球形雨滴表面电势为Rq εV 0π41= 当两个球形雨滴合并为一个较大雨滴后,半径增大为R 32,代入上式后可以求出两雨滴相遇合并后,雨滴表面的电势.解 根据已知条件球形雨滴半径R 1=0.40 mm ,带有电量q 1=1.6 pC ,可以求得带电球形雨滴表面电势V 36π411101==R q εV 当两个球形雨滴合并为一个较大雨滴后,雨滴半径1322R R =,带有电量 q 2=2q 1 ,雨滴表面电势V 5722π4113102==R q εV 9-19 电荷面密度分别为+σ和-σ的两块“无限大”均匀带电的平行平板,如图(a )放置,取坐标原点为零电势点,求空间各点的电势分布并画出电势随位置坐标x 变化的关系曲线.题 9-19 图分析 由于“无限大”均匀带电的平行平板电荷分布在“无限”空间,不能采用点电荷电势叠加的方法求电势分布:应该首先由“无限大”均匀带电平板的电场强度叠加求电场强度的分布,然后依照电势的定义式求电势分布. 解 由“无限大” 均匀带电平板的电场强度i 02εσ±,叠加求得电场强度的分布, ()()()⎪⎪⎩⎪⎪⎨⎧><<--<=a x a x a a x0 00i E εσ电势等于移动单位正电荷到零电势点电场力所作的功()a x a x εσV x<<--=⋅=⎰ d 00l E ()a x a εσV -<=⋅+⋅=⎰⎰- d d 00a-a x l E l E ()a x a V >-=⋅+⋅=⎰⎰ d d 00a a x εσl E l E 电势变化曲线如图(b )所示. 9-20 两个同心球面的半径分别为R 1 和R 2 ,各自带有电荷Q 1 和Q 2 .求:(1) 各区域电势分布,并画出分布曲线;(2) 两球面间的电势差为多少?题 9-20 图分析 通常可采用两种方法.方法(1) 由于电荷均匀分布在球面上,电场分布也具有球对称性,因此,可根据电势与电场强度的积分关系求电势.取同心球面为高斯面,借助高斯定理可求得各区域的电场强度分布,再由⎰∞⋅=p p V l E d 可求得电势分布.(2)利用电势叠加原理求电势.一个均匀带电的球面,在球面外产生的电势为rεQ V 0π4= 在球面内电场强度为零,电势处处相等,等于球面的电势RεQ V 0π4= 其中R 是球面的半径.根据上述分析,利用电势叠加原理,将两个球面在各区域产生的电势叠加,可求得电势的分布.解1 (1) 由高斯定理可求得电场分布()()()22021321201211 π4 π40R r r εQ Q R r R r εQ R r r r >+=<<=<=e E e E E 由电势⎰∞⋅=r V l E d 可求得各区域的电势分布.当r ≤R 1 时,有20210120212113211π4π4π411π40d d d 2211R εQ R εQ R εQ Q R R εQ V R R R R r +=++⎥⎦⎤⎢⎣⎡-+=⋅+⋅+⋅=⎰⎰⎰∞l E l E l E 当R 1 ≤r ≤R 2 时,有202012021201322π4π4π411π4d d 22R εQ r εQ R εQ Q R r εQ V R R r +=++⎥⎦⎤⎢⎣⎡-=⋅+⋅=⎰⎰∞l E l E当r ≥R 2 时,有rεQ Q V r 02133π4d +=⋅=⎰∞l E (2) 两个球面间的电势差⎪⎪⎭⎫ ⎝⎛-=⋅=⎰210121211π4d 21R R εQ U R R l E 解2 (1) 由各球面电势的叠加计算电势分布.若该点位于两个球面内,即r ≤R 1 ,则2021011π4π4R εQ R εQ V +=若该点位于两个球面之间,即R 1≤r ≤R 2 ,则202012π4π4R εQ r εQ V += 若该点位于两个球面之外,即r ≥R 2 ,则rεQ Q V 0213π4+=(2) 两个球面间的电势差 ()2011012112π4π42R εQ R εQ V V U R r -=-== 9-21 一半径为R 的无限长带电细棒,其内部的电荷均匀分布,电荷的体密度为ρ.现取棒表面为零电势,求空间电势分布并画出分布曲线.题 9-21 图分析 无限长均匀带电细棒电荷分布呈轴对称,其电场和电势的分布也呈轴对称.选取同轴柱面为高斯面,利用高斯定理⎰⎰=⋅V V d 1d 0ρεS E 可求得电场分布E (r ),再根据电势差的定义 ()l E d ⋅=-⎰b ab a r V V 并取棒表面为零电势(V b =0),即可得空间任意点a 的电势.解 取高度为l 、半径为r 且与带电棒同轴的圆柱面为高斯面,由高斯定理 当r ≤R 时02/ππ2ερl r rl E =⋅得 ()02εr ρr E =当r ≥R 时 02/ππ2ερl R rl E =⋅得 ()rεR ρr E 022= 取棒表面为零电势,空间电势的分布有当r ≤R 时()()22004d 2r R ερr εr ρr V R r -==⎰当r ≥R 时 ()rR εR ρr r εR ρr V Rr ln 2d 20202==⎰ 如图所示是电势V 随空间位置r 的分布曲线. 9-22 一圆盘半径R =3.00 ×10-2 m .圆盘均匀带电,电荷面密度σ=2.00×10-5 C·m -2.(1) 求轴线上的电势分布;(2) 根据电场强度与电势梯度的关系求电场分布;(3) 计算离盘心30.0 cm 处的电势和电场强度.题 9-22 图分析 将圆盘分割为一组不同半径的同心带电细圆环,利用带电细环轴线上一点的电势公式,将不同半径的带电圆环在轴线上一点的电势积分相加,即可求得带电圆盘在轴线上的电势分布,再根据电场强度与电势之间的微分关系式可求得电场强度的分布.解 (1) 如图所示,圆盘上半径为r 的带电细圆环在轴线上任一点P 激发的电势220d π2π41d x r r r σεV += 由电势叠加,轴线上任一点P 的电势的()x x R εσx r r r εσV R -+=+=⎰22002202d 2 (1) (2) 轴线上任一点的电场强度为i i E ⎥⎦⎤⎢⎣⎡+-=-=22012d d x R x εσx V (2) 电场强度方向沿x 轴方向. (3) 将场点至盘心的距离x =30.0 cm 分别代入式(1)和式(2),得V 6911=V-1m V 6075⋅=E当x >>R 时,圆盘也可以视为点电荷,其电荷为C 1065.5π82-⨯==σR q .依照点电荷电场中电势和电场强度的计算公式,有V 1695π40==xεq V 1-20m V 5649π4⋅==xεq E 由此可见,当x >>R 时,可以忽略圆盘的几何形状,而将带电的圆盘当作点电荷来处理.在本题中作这样的近似处理,E 和V 的误差分别不超过 0.3%和0.8%,这已足以满足一般的测量精度.9-23 两个很长的共轴圆柱面(R 1 =3.0×10-2m ,R 2 =0.10 m ),带有等量异号的电荷,两者的电势差为450 V.求:(1) 圆柱面单位长度上带有多少电荷?(2) r =0.05 m 处的电场强度.解 (1) 由习题9-15 的结果,可得两圆柱面之间的电场强度为 r ελE 0π2=根据电势差的定义有120212ln π2d 21R R ελU R R =⋅=⎰l E 解得 1812120m C 101.2ln /π2--⋅⨯==R R U ελ (2) 解得两圆柱面之间r =0.05m 处的电场强度10m V 475 7π2-⋅==rE ελ 9-24 轻原子核(如氢及其同位素氘、氚的原子核)结合成为较重原子核的过程,叫做核聚变.在此过程中可以释放出巨大的能量.例如四个氢原子核(质子)结合成一个氦原子核(α粒子)时,可释放出25.9MeV 的能量.即MeV 25.9e 2He H 4014211++→这类聚变反应提供了太阳发光、发热的能源.如果我们能在地球上实现核聚变,就能获得丰富廉价的能源.但是要实现核聚变难度相当大,只有在极高的温度下,使原子热运动的速度非常大,才能使原子核相碰而结合,故核聚变反应又称作热核反应.试估算:(1)一个质子(H 11)以多大的动能(以电子伏特表示)运动,才能从很远处到达与另一个质子相接触的距离? (2)平均热运动动能达到此值时,温度有多高? (质子的半径约为1.0 ×10-15 m ) 分析 作为估算,可以将质子上的电荷分布看作球对称分布,因此质子周围的电势分布为 rεe V 0π4= 将质子作为经典粒子处理,当另一质子从无穷远处以动能E k 飞向该质子时,势能增加,动能减少,如能克服库仑斥力而使两质子相碰,则质子的初始动能Re r eV E 2π41202R k 0ε=≥ 假设该氢原子核的初始动能就是氢分子热运动的平均动能,根据分子动理论知:kT E 23k = 由上述分析可估算出质子的动能和此时氢气的温度.解 (1) 两个质子相接触时势能最大,根据能量守恒eV 102.72π415202R K0⨯==≥Re r εeV E 由20k 021v m E =可估算出质子初始速率 17k 00s m 102.1/2-⋅⨯==m E v该速度已达到光速的4%.(2) 依照上述假设,质子的初始动能等于氢分子的平均动能kT E E 23k k0== 得 K 106.5329k0⨯≈=kE T 实际上在这么高的温度下,中性原子已被离解为电子和正离子,称作等离子态,高温的等离子体不能用常规的容器来约束,只能采用磁场来约束(托卡马克装置)9-25 在一次典型的闪电中,两个放电点间的电势差约为109 V,被迁移的电荷约为30 C .(1) 如果释放出来的能量都用来使0 ℃的冰融化成0 ℃的水,则可溶解多少冰? (冰的融化热L =3.34 ×105 J· kg )(2) 假设每一个家庭一年消耗的能量为3 000kW·h ,则可为多少个家庭提供一年的能量消耗?解 (1) 若闪电中释放出来的全部能量为冰所吸收,故可融化冰的质量kg 1098.8Δ4⨯===LqU L E m 即可融化约 90 吨冰. (2) 一个家庭一年消耗的能量为J 1008.1h kW 0003100⨯=⋅=E8.2Δ00===E qU E E n 一次闪电在极短的时间内释放出来的能量约可维持3个家庭一年消耗的电能.9-26 已知水分子的电偶极矩p =6.17×10-30 C· m .这个水分子在电场强度E =1.0 ×105 V · m -1的电场中所受力矩的最大值是多少?分析与解 在均匀外电场中,电偶极子所受的力矩为E p M ⨯=当电偶极子与外电场正交时,电偶极子所受的力矩取最大值.因而有m N 1017.625max ⋅⨯==-pE M9-27 电子束焊接机中的电子枪如图所示,K 为阴极,A 为阳极,阴极发射的电子在阴极和阳极电场加速下聚集成一细束,以极高的速率穿过阳极上的小孔,射到被焊接的金属上使两块金属熔化在一起.已知V 105.24AK⨯=U ,并设电子从阴极发射时的初速度为零,求:(1)电子到达被焊接金属时具有的动能;(2)电子射到金属上时的速度.分析 电子被阴极和阳极间的电场加速获得动能,获得的动能等于电子在电场中减少的势能.由电子动能与速率的关系可以求得电子射到金属上时的速度.解 (1)依照上述分析,电子到达被焊接金属时具有的动能 eV 105.24AK k ⨯==eU E(2)由于电子运动的动能远小于电子静止的能量,可以将电子当做经典粒子处理.电子射到金属上时的速度题9-27 图第十章静电场中的导体与电介质10-1将一个带正电的带电体A从远处移到一个不带电的导体B附近,则导体B的电势将()(A)升高(B)降低(C)不会发生变化(D)无法确定分析与解不带电的导体B相对无穷远处为零电势.由于带正电的带电体A 移到不带电的导体B附近时,在导体B的近端感应负电荷;在远端感应正电荷,不带电导体的电势将高于无穷远处,因而正确答案为(A).10-2将一带负电的物体M靠近一不带电的导体N,在N的左端感应出正电荷,右端感应出负电荷.若将导体N的左端接地(如图所示),则()(A)N上的负电荷入地(B)N上的正电荷入地(C)N上的所有电荷入地(D)N上所有的感应电荷入地题10-2 图分析与解导体N接地表明导体N为零电势,即与无穷远处等电势,这与导体N在哪一端接地无关.因而正确答案为(A).10-3如图所示将一个电量为q的点电荷放在一个半径为R的不带电的导体球附近,点电荷距导体球球心为d ,参见附图.设无穷远处为零电势,则在导体球球心O 点有( )(A )d εq V E 0π4,0== (B )dεq V d εq E 020π4,π4== (C )0,0==V E (D )Rεq V d εq E 020π4,π4==题 10-3 图分析与解 达到静电平衡时导体内处处各点电场强度为零.点电荷q 在导 体球表面感应等量异号的感应电荷±q′,导体球表面的感应电荷±q′在球心O 点激发的电势为零,O 点的电势等于点电荷q 在该处激发的电势.因而正确答案为(A ).10-4 根据电介质中的高斯定理,在电介质中电位移矢量沿任意一个闭合曲面的积分等于这个曲面所包围自由电荷的代数和.下列推论正确的是( )(A ) 若电位移矢量沿任意一个闭合曲面的积分等于零,曲面内一定没有自由电荷(B ) 若电位移矢量沿任意一个闭合曲面的积分等于零,曲面内电荷的代数和一定等于零(C ) 若电位移矢量沿任意一个闭合曲面的积分不等于零,曲面内一定有极化电荷(D ) 介质中的高斯定律表明电位移矢量仅仅与自由电荷的分布有关 (E ) 介质中的电位移矢量与自由电荷和极化电荷的分布有关。
大学物理电子课件.pptx

• 10、人的志向通常和他们的能力成正比例。14:16:0614:16:0614:1611/16/2020 2:16:06 PM
• 11、夫学须志也,才须学也,非学无以广才,非志无以成学。20.11.1614:16:0614:16Nov-2016-Nov-20
• 12、越是无能的人,越喜欢挑剔别人的错儿。14:16:0614:16:0614:16Monday, November 16, 2020
§6.7 耗散结构
返回
目录
第7章 气体分子动理论
§7.1 气体分子动理论的基本概念
§7.2 理想气体的压强
§7.3 温度的微观本质
§7.4 能量按自由度均分原理
§7.5 麦克斯韦速率分布定律
§7.6 玻尔兹曼分布律 §7.7 气体分子的平均自由程 §7.8 范德瓦尔斯方程
返回
目录
第8章 振动与波动
返回
上一页
目录
第1章 物质的基本性质
§1.1 物质的结构及形态 §1.2 实物的基本性质 §1.3 场与物质的相互作用 §1.4 物质的能量
返回
目录
第2章 流体力学基础
§2.1 理想流体的定常流动 §2.2 伯努利方程及其应用 §2.3 粘滞流体的定常流动 §2.4 泊肃叶定律 斯托克斯定律 §2.5 生物流体力学简介
§12.1 原子核的基本性质 §12.2 原子核的放射性衰变 §12.3 辐射生物物理基础
返回
前言
《大学物理电子教案》是作者近年来使用多媒体教学的经验总结。 该电子教案是以西北农林科技大学王国栋教授教授主编的国家十一五 规划教材《大学物理》为蓝本,章节划分与之基本对应,共12章内容; 该软件适用于农林院校理科、农科的多媒体教学, 也可作为学生课后 自学的参考软件。
2024年大学物理下课件(增加多场景)

大学物理下课件(增加多场景)大学物理下课件一、引言大学物理是高等教育中一门重要的基础课程,旨在培养学生掌握物理学的基本概念、基本原理和基本方法,提高学生的科学素养和创新能力。
本课件将重点介绍大学物理下的主要内容,包括力学、热学、电磁学、光学和现代物理等。
二、力学力学是物理学的基础,主要研究物体的运动规律和力的作用。
在大学物理下中,我们将深入学习牛顿运动定律、动量守恒定律、能量守恒定律和角动量守恒定律等基本原理,并探讨它们在实际问题中的应用。
1.牛顿运动定律:牛顿运动定律是描述物体运动状态的三个基本定律,包括惯性定律、加速度定律和作用反作用定律。
这些定律为物体的运动提供了基本的理论框架。
2.动量守恒定律:动量守恒定律是指在不受外力作用的系统中,系统的总动量保持不变。
这个定律在碰撞、爆炸等过程中有着广泛的应用。
3.能量守恒定律:能量守恒定律是指在封闭系统中,能量不能被创造或销毁,只能从一种形式转化为另一种形式。
这个定律为热力学、电磁学和光学等领域的研究提供了重要的理论基础。
4.角动量守恒定律:角动量守恒定律是指在不受外力矩作用的系统中,系统的总角动量保持不变。
这个定律在天体物理学和量子力学等领域中有着重要的应用。
三、热学热学是研究物质的热运动和热现象的学科。
在大学物理下中,我们将学习热力学的基本概念和原理,包括温度、热量、热力学第一定律和热力学第二定律等。
1.温度和热量:温度是衡量物体热状态的物理量,热量是物体与外界交换热能的量度。
温度和热量是热学中的基本概念,对于理解热现象和热力学过程至关重要。
2.热力学第一定律:热力学第一定律是能量守恒定律在热学中的应用,表明在封闭系统中,系统的内能变化等于系统与外界交换的热量与系统对外界做的功的代数和。
3.热力学第二定律:热力学第二定律是热学中的重要原理,描述了热现象中的不可逆过程。
它表明在自然过程中,热量总是从高温物体传递到低温物体,而不会自发地从低温物体传递到高温物体。
大学物理(下册)PPT模板

03
粒子的产生和湮灭
粒子可以通过相互作用产生或湮灭,这是粒子物理中重要的研究内容之
一。
宇宙射线和高能物理实验方法
宇宙射线的来源和性质
宇宙射线是来自宇宙空间的高能粒子流,其来源包括太阳、超新星遗迹、黑洞等天体。
高能物理实验方法
包括加速器实验、对撞机实验、探测器实验等,这些实验方法可以帮助我们深入了解粒子的 性质和相互作用规律。
不确定性原理的意义
不确定性原理揭示了微观世界的本质特征,即微观粒子的运动状态是不确定的、概 率性的。这一原理对量子力学的发展产生了深远影响,也是现代物理学的重要基础 之一。
04 固体物理基础
晶体结构与性质
晶体定义与分类
明确晶体概念,介绍常见晶体类型如离子晶体、 金属晶体、分子晶体等。
晶体结构描述
玻尔氢原子模型
玻尔氢原子模型
玻尔氢原子模型是指氢原子的电子只能在特定的轨道上运动, 且每个轨道上的电子具有特定的能量。当电子从一个轨道跃迁 到另一个轨道时,会吸收或发射特定频率的光子。
能量量子化
能量量子化是指氢原子的能量只能取特定的值,即能级是量子 化的。每个能级对应一个特定的电子轨道和能量值。
德布罗意波与物质波概念
能源科学
利用现代物理技术研究能源的转 换和利用过程,提高能源利用效 率并开发新能源。
环境科学
利用现代物理技术研究环境污染 的成因、监测和治理方法,为环 境保护提供科学依据。
生命科学
利用现代物理技术研究生物大分 子的结构和功能,揭示生命活动
的物理机制和规律。
THANKS
感谢观看
相位等特征量。
交流电路元件
交流电路中常用的元件包括电阻、 电感、电容等,它们在交流电路中 具有不同的阻抗特性。
《大学物理学》第二版下册习题解答

大学物理学第二版下册习题解答第一章:力学1.1 力学基本概念1.1.1 力的概念问题:什么是力?力的种类有哪些?解答:力是物体之间相互作用导致的物体运动或形变的原因。
力可以分为以下几种:•接触力:当两个物体接触时产生的力,如弹簧力、摩擦力等。
•引力:天体之间由于引力而产生的力,如地球引力、行星引力等。
•重力:地球上物体受到的引力,是一种特殊的引力。
•弹力:当物体被弹性体拉伸或压缩时,物体回复原状所产生的力。
•阻力:物体在流体中运动时受到的阻碍力,如空气阻力、水阻力等。
1.1.2 力的合成与分解问题:什么是力的合成与分解?如何进行力的合成与分解?解答:力的合成是指将多个力按照一定的规律合成为一个力的过程。
力的分解是指将一个力按照一定的规律分解为多个力的过程。
力的合成可以使用力的三角法进行。
假设有两个力F₁、F₂,其方向分别为α₁、α₂,大小分别为|F₁|、|F₂|,则合力F的大小可以通过以下公式计算:F = √(F₁² + F₂² + 2F₁F₂cos(α₁-α₂))合力F的方向则可以通过以下公式计算:tan(θ) = (F₂sin(α₁-α₂))/(F₁+F₂cos(α₁-α₂))力的分解可以使用力的正弦法和余弦法进行。
假设有一个力F,其大小为|F|,方向为α,要将该力分解为水平方向的力F x和竖直方向的力F x,可以通过以下公式计算:Fₓ = |F|cosα, Fᵧ = |F|sinα1.2 牛顿定律与惯性1.2.1 牛顿第一定律问题:什么是牛顿第一定律?牛顿第一定律适用于哪些情况?解答:牛顿第一定律,也称为惯性定律,指的是:物体在没有受到外力或受到的合外力为零时,物体保持静止或匀速直线运动的状态。
牛顿第一定律适用于只有一个物体或多个物体之间相互独立运动的情况。
当物体受到外力时,按照该定律,物体会发生运动或停止运动。
1.2.2 牛顿第二定律问题:什么是牛顿第二定律?如何计算物体所受合外力和加速度的关系?解答:牛顿第二定律指的是:物体所受合外力等于物体的质量乘以加速度。
大学物理学(下册)(第二版)(李承祖主编)PPT模板

3
费衍射光栅光谱和光
栅分辨本领
第四部分振动波动电磁波和波动光学
第21章波动光学(ⅲ)
21.1光的偏振 态偏振光的获 得
21.4偏振光的 干涉
21.2双折射现 象
*21.5人工双 折射
21.3偏振棱镜 波片圆和椭圆 偏振光的产生 和检验
问题和习题
04
o
n
e
第五部分相对论物理学中的对称性
第五部分相 对论物理学 中的对称性
01
o
n
e
前言
前言
02
o
n
e
第一版前言
第一版前言
03
o
n
e
第四部分振动波动电磁波和波动光学
第四部分振动波动 电磁波和波动光学
06
第21章波动 光学(ⅲ)
01
第16章振动
05
第20章波动 光学(ⅱ)
02
第17章机械 波
04
第19章波动 光学(ⅰ)
03
第18章电磁 波
第四部分振动波动电磁波和波动光学
01 1 7 .1 机 械波的产生 02 1 7 .2 平 面简谐波
和传播
03 1 7 .3 机 械波的能量 04 1 7 .4 惠 更斯原理波
密度和能流
的衍射、反射和折射
05 1 7 .5 波 的相干叠加 06 1 7 .6 多 普勒效应
驻波
第四部分振动波动电磁波和波动光学
第17章机械波
问题和习题
25.1对称性的概念 和描写方法
01
05
02
25.2时空 对称性和物 理量、物理 规律、物理 相互作用
04
03
*25.4动力学对称性
大学物理-电磁学-电磁感应资料讲解

E ++
a
+ ++
fe
此时电荷积累停止,
fm
ab两端形成稳定的电势差。
b
洛仑兹力是产生动生电动势的根本原因.
B
v
§12-2 动生电动势
二、动生电动势的表达式
由电动势定义:i
Ek dl
§12-1 电磁感应定律
问题的提出 产生
电流
磁场
?
电磁感应
1831年法拉第 实验
闭合回路 m 变化
产生 感应电流
§12-1 电磁感应定律
一、电磁感应现象
1、五种产生感应
电流的情况
G
磁铁与线圈相对运动时的 电磁感应现象
G
螺线管与线圈相
对运动时的电磁
感应现象
§12-1 电磁感应定律
金属棒在磁场中作切割磁
n
B
n
B
L
ε
(a) Φ > 0 ,dΦ > 0
ε < 0 , ε 与L 反向
n
L
ε
(b) Φ > 0 ,dΦ < 0
ε > 0 , ε 与L 同向
n
L
ε
B
(c) Φ < 0 ,dΦ < 0
ε > 0 , ε 与L 同向
L
ε
B
(d) Φ < 0 ,dΦ > 0
ε < 0 , ε 与L 反向
B
I
x dx
la
h
x
2 0Ihllad x x2 0Ih ln l la
线框内产生的感应电动势为:
d d Φ m t2 0I 0hln l laco ts
《大学物理2》课件-第二章
第二讲 光的粒子性_20140220 XCH
量子物理基础 - 大学物理
一个静止的电子和一能量为h0的光子碰撞后 它获得的最大能量是多少?
电子获得的能量 E mc2 m0c2 h 0 h
波长位移
0
2h m0c
sin2
2
c c 2h sin2 0 m0c 2
第二讲 光的粒子性_20140220 XCH
量子物理基础 - 大学物理
例1、在康普顿散射中,入射光的波长为0.030Å,反冲电子速 度为c×60%.求:散射光子的波长及散射角。
解:由已知,入射光的能量 的能量
,散射光子
因光子与电子碰撞时能量守恒,所以电子获得的动能 为
而由相对论:
0
hc (
0
hc)
量子物理基础 - 大学物理
1) 电子先整体吸收光子 —— 尔后放出散射光子
—— 每一步光子和电子遵循动量守恒__能量不守恒 如果在第一步过程体系都满足动量和能量守恒
Uc
h e
(
A) h
0
A h
K
h e
对比实验结果
Uc K ( 0 )Fra bibliotekA h
h 0
Ke
— 普朗克常数
逸出功 A h0 —— 电子脱离金属表面所需最小能量
第二讲 光的粒子性_20140220 XCH
10 / 51
A h0 不同的金属逸出功不同
1916年密立根实验 得出不同金属的K是相同的
h Ke h 6.56 1034 J s
量子物理基础 - 大学物理
K Uc
( 0 )
金属
钨
锌
钙
钠
大学物理学第二版下册热力学第二定律
两种表述相互沟通、完全等效!
6
二、
热力学第二定律微观意义
从微观看,任何热力学过程总包含大量分子的无序 运动状态的变化。热一律说明热运动过程中能量要 遵守的规律。热二律说明大量分子的运动的无序(分 子的位置、速度大小、方向、动能)程度变化的规律。
热功转换 微观上看:
转化为 不能
大量分子的 有序运动
大量分子的 无序运动
一切与热现象有关的实际宏观过程都是不可逆的!
可逆过程只是一种理想过程,我们所能做到的 只能是使实际过程尽量接近可逆过程。 无摩擦的准静态过程是可逆过程。
2
#1a0901015a
关于可逆过程与不可逆过程指出下列说法正确的是: A.不可逆过程是系统不能恢复到初状态的过程 B.不可逆过程是外界有变化的过程 C.不可逆过程一定找不到另一过程使系统和外界同时 复原 D.不可逆过程就是不能向反方向进行的过程
热力学概率意义:分子热运动无序性的一种量度。
系统将随着时间的变化向增大的宏观状态过渡, 最后达到为最大值的平衡状态。
18
#1a0901019a
关于热力学过程进行的方向和条件的表述中,正确的是: A.热量不能从低温物体向高温物体传递; B.功可以完全变为热量,而热量不能完全变为功;
C.不可能从单一热源吸热使之全部变为有用的功;
可逆过程
p 1 (S1)
a b
2 (S2)
O
V
表明系统由状态1变化到状态2,可通过不同的过 程来实现,其热温比的积分与过程无关,只由始、 末状态决定。
说明 (
dQ )可 逆与过程无关, 是状态的函数, 用S表示(熵) T
27
则系统沿可逆过程从状态 1 变到状态 2 时熵的增量为:
