福建省福州市八县市区一中2020届高三数学上学期期中联考试题文【含答案】
福州市八县(市、区)一中2020届高三上期中联考

福州市八县(市、区)一中2020届高三上期中联考语文试题及答案解析一、现代文阅读(36分)(一)论述类文本阅读(本题3小题,9分)阅读下面的文字,完成1-3题。
“人类命运共同体”理念是中国特色大国外交思想的重要内容。
那么,它的特色究竟“特”在哪里?我们究竟应该如何认识其思想文化本源?客观地说,世界上主要文明地区的政治文化中都有命运与共、共同体、世界主义的政治思想,例如西方基督教世界秩序及西方永久和平论、印度思想中的“不害”、伊斯兰世界的“天下一家”、中国古代的“天下大同”等观念。
总的来说,早期这些共同体观念解决的只是内部秩序问题,还没有很好地解决不同文明之间如何共生共处的问题。
其中,历史上不少共同体思想还受到二元对立世界观的局限,它们所强调构建的共同体是以一个假想或现实的敌人为目标的,这种思想很容易导致世界陷入对抗之中。
事实上,直到今天,这种思想还在影响着个别大国的外交政策,值得我们去辨别和防范。
我们倡导的“人类命运共同体”,其思想文化本源来自传统和现代两部分。
所谓传统,中国古代有丰富的中外秩序资源,在当时地理所及的范围内,形成了一套处理中外关系的思想和实践做法,这套思想和做法在今天需要创造性转化。
所谓现代,“打造人类命运共同体”还需要从马克思主义中寻找本源。
马克思主义关于社会共同体和人类解放的思想中,包含着国际主义以及很多“人类命运与共”的资源。
马克思主义政治经济学中关于世界不平等、剥削以及世界政治经济秩序根源、改造的论述等等,都是我们理解“人类命运共同体”的重要思想本源。
同时,这些思想也是“人类命运共同体”理念从学理上区别于既往及现在流行的一些共同体理论,如各种带有宗教色彩的联盟、大西洋共同体、“民主”价值观联盟等的重要依据。
以往绝大多数国际秩序思想和实践,要么服务于强者,要么用来结成一个国家联盟以反对另一个国家联盟,要么是一种宗教秩序的外在表现。
马克思主义政治经济学思想中蕴含的“人类命运共同体”理念与它们的区别在于,其并不是从排他性国家联盟的角度来狭隘地理解共同体,而是从世界范围不平等经济秩序的变革、大多数人实现自身解放从而结成联合的高度来理解共同体。
2020届福建省福州市八县(市、区)一中高三上学期期中联考语文试题

2019—2020学年度高中三年级第一学期八县(市、区)一中期中联考语文科试卷完卷时间:150分钟满分:150分一、现代文阅读(36分)(一)论述类文本阅读(本题3小题,9分)阅读下面的文字,完成1-3题。
①“人类命运共同体”理念是中国特色大国外交思想的重要内容。
那么,它的特色究竟“特”在哪里?我们究竟应该如何认识其思想文化本源?②客观地说,世界上主要文明地区的政治文化中都有命运与共、共同体、世界主义的政治思想,例如西方基督教世界秩序及西方永久和平论、印度思想中的“不害”、伊斯兰世界的“天下一家”、中国古代的“天下大同”等观念。
总的来说,早期这些共同体观念解决的只是内部秩序问题,还没有很好地解决不同文明之间如何共生共处的问题。
其中,历史上不少共同体思想还受到二元对立世界观的局限,它们所强调构建的共同体是以一个假想或现实的敌人为目标的,这种思想很容易导致世界陷入对抗之中。
事实上,直到今天,这种思想还在影响着个别大国的外交政策,值得我们去辨别和防范。
③我们倡导的“人类命运共同体”,其思想文化本源来自传统和现代两部分。
所谓传统,中国古代有丰富的中外秩序资源,在当时地理所及的范围内,形成了一套处理中外关系的思想和实践做法,这套思想和做法在今天需要创造性转化。
所谓现代,“打造人类命运共同体”还需要从马克思主义中寻找本源。
马克思主义关于社会共同体和人类解放的思想中,包含着国际主义以及很多“人类命运与共”的资源。
马克思主义政治经济学中关于世界不平等、剥削以及世界政治经济秩序根源、改造的论述等等,都是我们理解“人类命运共同体”的重要思想本源。
同时,这些思想也是“人类命运共同体”理念从学理上区别于既往及现在流行的一些共同体理论,如各种带有宗教色彩的联盟、大西洋共同体、“民主”价值观联盟等的重要依据。
④以往绝大多数国际秩序思想和实践,要么服务于强者,要么用来结成一个国家联盟以反对另一个国家联盟,要么是一种宗教秩序的外在表现。
福建省福州市八县(市)一中联考高三上学期期中数学试卷(文科) Word版含解析

2016-2017学年福建省福州市八县(市)一中联考高三(上)期中数学试卷(文科)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求,每小题选出答案后,请把答案填写在答题卡相应位置上.1.已知M={x|0<x<2},N={x|y=},则M∩N=()A.{x|0<x<2}B.{x|1≤x<2}C.{x|x>0} D.{x|x≥1}2.复数z与复数i(1﹣2i)互为共轭复数,则z=()A.﹣2+i B.﹣2﹣i C.2﹣i D.2+i3.已知命题p:∃x∈R,sinx+cosx≥,命题q:∀x∈R,x2>0,则()A.命题p∨q是假命题B.命题p∧q是真命题C.命题p∧(¬q)是假命题D.命题p∧(¬q)是真命题4.已知等差数列{a n}中,若a2=﹣1,a4=﹣5,则S5=()A.﹣7 B.﹣13 C.﹣15 D.﹣175.若a=20.5,b=ln2,c=2,则()A.a>b>c B.b>a>c C.c>a>b D.b>c>a6.函数y=4sin(ωx+φ)(ω>0,|φ|<π)部分图象如图,其中点A(,0),B(,0),则()A.ω=,φ=﹣B.ω=1,φ=﹣C.ω=,φ=﹣D.ω=1,φ=﹣7.已知函数f(x)=,则不等式f(x)<2的解集为()A.{x|2<x<8}B.{x|﹣2≤x<2}C.{x|﹣2<x<8}D.{x|x<8}8.M是△ABC所在平面内一点,,D为BC中点,则的值为()A.B.1 C.2 D.39.已知p=a+,q=﹣b2﹣2b+3(b∈R),则p,q的大小关系为()A.p≥q B.p≤q C.p>q D.p<q10.为得到函数y=cos(2x+)的图象,只需将函数y=sin2x的图象()A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度11.已知函数f(x)=|2x﹣1|,a<b<c,且f(a)>f(c)>f(b),则下列结论中,一定成立的是()A.2a+2c<2 B.2﹣a<2c C.a<0,b≥0,c>0 D.a<0,b<0,c<012.设f(x)是定义在R上的增函数,且对任意x,都有f(﹣x)+f(x)=0恒成立,如果实数x,y满足不等式f(x2﹣6x)+f(y2﹣4y+12)≤0,那么的最大值是()A.1 B.2 C. D.二、填空题:本大题共4小题,每小题5分,共20分,请把答案填在答题卡的横线上.13.已知向量=(λ+1,1),=(4,﹣2),若,则λ=.14.已知x,y满足约束条件,则z=4x﹣y的最小值为.15.已知S n为等比数列{a n}的前n项和,a n>0,S5=2,S15=14,则S10=.16.给出下列命题:①已知x∈R,则“x>1”是“x>2”的充分不必要条件;②若|+|=||﹣||,则存在实数λ,使得=λ;③命题p:“∃x∈R,e x>x+1”的否定是“∀x∈R,e x<x+1”;④方程x=sinx有且只有一个实数解;⑤函数f(x)=4cos(2x+)的一个对称中心为.其中正确命题的序号是(把你认为正确的序号都填上).三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.请在答题卡各自题目的答题区域内作答.17.已知正项数列{a n}的前n项和为S n,且S n,a n,成等差数列.(1)证明数列{a n}是等比数列;(2)若b n=log2a n+3,求数列{}的前n项和T n.18.已知向量=(sinx,cosx),=(cosx,﹣cosx),f(x)=•,(1)求f(x)的最小正周期和单调递增区间;(2)若x∈(),=,求cos2x的值.19.围建一个面积为300m2的矩形场地,要求矩形场地的一面利用旧墙(旧墙足够长,利用旧墙需维修),其他三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为75元/m,新墙的造价为150元/m,设利用的旧墙的长度为xm(x>0).(1)将总费用y元表示为xm的函数;(2)试确定x,使修建此矩形场地围墙的总费用最小,并求最小总费用.20.在△ABC中,角A,B,C的对边分别为a,b,c且满足bcosA=(2c﹣a)cosB.(1)求角B的大小;(2)若b=4=4,求a+c的值.21.等比数列{a n}的前n项和为S n,且a2=3,a5=81,等差数列{b n}的前n项和为T n,T n=n.(1)求数列{a n},{b n}的通项公式;(2)若对任意的n∈N*,≥b n恒成立,求实数k的取值范围.22.已知函数f(x)=alnx+x2(a为常数).(1)当a=﹣2时,求f(x)的单调区间;(2)当x∈(1,e]时,讨论方程f(x)=0根的个数;(3)若a>0,且对任意的x1,x2∈且x1≠x2,都有|f(x1)﹣f(x2)|<|,求实数a的取值范围.2016-2017学年福建省福州市八县(市)一中联考高三(上)期中数学试卷(文科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求,每小题选出答案后,请把答案填写在答题卡相应位置上.1.已知M={x|0<x<2},N={x|y=},则M∩N=()A.{x|0<x<2}B.{x|1≤x<2}C.{x|x>0} D.{x|x≥1}【考点】交集及其运算.【分析】先求出集合M,N,由此能求出M∩N.【解答】解:∵M={x|0<x<2},N={x|y=}={x|x≥1},∴M∩N={x|1≤x<2}.故选:B.2.复数z与复数i(1﹣2i)互为共轭复数,则z=()A.﹣2+i B.﹣2﹣i C.2﹣i D.2+i【考点】复数代数形式的乘除运算.【分析】直接由复数代数形式的乘法运算化简i(1﹣2i),再由复数z与复数i(1﹣2i)互为共轭复数,即可求出答案.【解答】解:i(1﹣2i)=i﹣2i2=2+i,∵复数z与复数i(1﹣2i)互为共轭复数,∴z=2﹣i.故选:C.3.已知命题p:∃x∈R,sinx+cosx≥,命题q:∀x∈R,x2>0,则()A.命题p∨q是假命题B.命题p∧q是真命题C.命题p∧(¬q)是假命题D.命题p∧(¬q)是真命题【考点】命题的真假判断与应用.【分析】先分析命题p,q的真假,进而根据复合命题真假判断的真值表,可得答案.【解答】解:sinx+cosx=sin(x+)∈[﹣,],故命题p:∃x∈R,sinx+cosx≥,为真命题;当x=0时,x2=0,故命题q:∀x∈R,x2>0,为假命题;故命题p∨q是真命题,命题p∧q是假命题,命题p∧(¬q)是真命题,命题p∧(¬q)是真命题,故选:D.4.已知等差数列{a n}中,若a2=﹣1,a4=﹣5,则S5=()A.﹣7 B.﹣13 C.﹣15 D.﹣17【考点】等差数列的前n项和.【分析】利用等差数列的通项公式性质及其求和公式即可得出.【解答】解:由等差数列的性质可得:S5====﹣15.故选:C.5.若a=20.5,b=ln2,c=2,则()A.a>b>c B.b>a>c C.c>a>b D.b>c>a【考点】对数值大小的比较.【分析】利用指数函数与对数函数的单调性即可得出.【解答】解:∵a=20.5>1,b=ln2∈(0,1),c=2<0,∴a>b>c.故选:A.6.函数y=4sin(ωx+φ)(ω>0,|φ|<π)部分图象如图,其中点A(,0),B(,0),则()A.ω=,φ=﹣B.ω=1,φ=﹣C.ω=,φ=﹣D.ω=1,φ=﹣【考点】正弦函数的图象.【分析】结合图象,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.【解答】解:由函数的图象可得==﹣,∴ω=.再根据五点法作图可得•+φ=0,求得φ=﹣,故选:C.7.已知函数f(x)=,则不等式f(x)<2的解集为()A.{x|2<x<8}B.{x|﹣2≤x<2}C.{x|﹣2<x<8}D.{x|x<8}【考点】其他不等式的解法.【分析】结合分段函数的各段的解析式得到不等式组分别解之.【解答】解:结合分段函数各段的解析式得到不等式组为或,解得或,所以﹣2<x<2或2≤x<8,所以原不等式的解集为{x||﹣2<x<8};故选C.8.M是△ABC所在平面内一点,,D为BC中点,则的值为()A.B.1 C.2 D.3【考点】平面向量的基本定理及其意义.【分析】由已知向量等式得到M为△ABC 的重心,由此得到所求.【解答】解:由已知M是△ABC所在平面内一点,,得到M为△ABC 的重心,则==3;故选D.9.已知p=a+,q=﹣b2﹣2b+3(b∈R),则p,q的大小关系为()A.p≥q B.p≤q C.p>q D.p<q【考点】不等式比较大小.【分析】利用基本不等式的性质、二次函数的单调性即可得出.【解答】解:∵a>2,∴p=a+=(a﹣2)++2+2=4,当且仅当a=3时取等号.q=﹣b2﹣2b+3=﹣(b+1)2+4≤4,当且仅当b=﹣1时取等号.∴p≥q.故选:A.10.为得到函数y=cos(2x+)的图象,只需将函数y=sin2x的图象()A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度【考点】函数y=Asin(ωx+φ)的图象变换.【分析】利用诱导公式、函数y=Asin(ωx+φ)的图象变换规律,得出结论.【解答】解:将函数y=sin2x的图象向左平移个单位长度,可得y=sin2(x+)=sin(2x+)=cos(2x+)的图象,故选:A.11.已知函数f(x)=|2x﹣1|,a<b<c,且f(a)>f(c)>f(b),则下列结论中,一定成立的是()A.2a+2c<2 B.2﹣a<2c C.a<0,b≥0,c>0 D.a<0,b<0,c<0【考点】不等式比较大小.【分析】根据函数在区间(﹣∞,0)上是减函数,结合题设可得D不正确;根据函数的解析式,结合举反例的方法,可得到B、C不正确;利用函数的单调性结合函数的解析式,对a<c且f(a)>f(c)加以讨论,可得A是正确的.由此不难得到正确选项.【解答】解:对于A,因为a<c,且f(a)>f(c),说明可能如下情况成立:(i)a、c位于函数的减区间(﹣∞,0),此时a<b<c<0,可得f(a)>f(b)>f(c)与题设矛盾;(ii)a、c不在函数的减区间(﹣∞,0),则必有a<0<c,所以f(a)=1﹣2a>2c﹣1=f(c),化简整理,得2a+2c<2成立.对于B,取a=0,c=3,同样f(c)=f(3)=7为最大值,与题设矛盾,故B不正确;对于C,若a<0,b≥0,c>0,可设a=﹣1,b=2,c=3,此时f(c)=f(3)=7为最大值,与题设矛盾,故C不正确;对于D,若a<0,b<0,c<0,因为a<b<c,所以a<b<c<0,而函数f(x)=|2x﹣1|在区间(﹣∞,0)上是减函数,故f(a)>f(b)>f(c),与题设矛盾,所以D不正确;综上所述,可得只有A正确故选A.12.设f(x)是定义在R上的增函数,且对任意x,都有f(﹣x)+f(x)=0恒成立,如果实数x,y满足不等式f(x2﹣6x)+f(y2﹣4y+12)≤0,那么的最大值是()A.1 B.2 C. D.【考点】奇偶性与单调性的综合.【分析】由条件利用函数的奇偶性、单调性可得(x﹣3)2+(y﹣2)2≤1,表示以(3,2)为圆心、半径等于1的圆及其内部区域.而的表示圆内的点(x,y)与点(0,2)连线的斜率,求出该圆的切线斜率,可得结论.【解答】解:∵对任意x,都有f(﹣x)+f(x)=0恒成立,即f(﹣x)=﹣f(x)恒成立,故函数f(x)为奇函数.根据f(x)是定义在R上的增函数,f(x2﹣6x)+f(y2﹣4y+12)≤0,可得f(x2﹣6x)≤﹣f(y2﹣4y+12)=f(﹣y2+4y﹣12),即x2﹣6x≤﹣y2+4y﹣12,即x2﹣6x+y2﹣4y+12≤0,即(x﹣3)2+(y﹣2)2≤1,表示以(3,2)为圆心、半径等于1的圆及其内部区域.而的表示圆内的点(x,y)与点(0,2)连线的斜率,设过点(0,2)的圆的切线的斜率为k,则切线方程为y﹣2=k(x﹣0),即kx﹣y+2=0,根据圆心(3,2)到切线的距离等于半径,可得=1,求得k=±,可得的最大值为,故选:D.二、填空题:本大题共4小题,每小题5分,共20分,请把答案填在答题卡的横线上.13.已知向量=(λ+1,1),=(4,﹣2),若,则λ=﹣3.【考点】平行向量与共线向量.【分析】由向量共线可得(﹣2)×(λ+1)﹣4×1=0,解之即可.【解答】解:∵向量=(λ+1,1),=(4,﹣2),,∴(﹣2)×(λ+1)﹣4×1=0,解得λ=﹣3.故答案为:﹣3.14.已知x,y满足约束条件,则z=4x﹣y的最小值为.【考点】简单线性规划.【分析】作出不等式组对应的平面区域,利用z的几何意义,即可得到结论.【解答】解:作出不等式组对应的平面区域如图:由z=4x﹣y得y=4x﹣z,平移直线y=4x﹣z,由图象可知当直线y=4x﹣z经过点C时,此时z最小,由,解得,即C(,),此时z=4×﹣=,故答案为:15.已知S n为等比数列{a n}的前n项和,a n>0,S5=2,S15=14,则S10=6.【考点】等比数列的前n项和.【分析】由等比数列{a n}的性质可得:S5,S10﹣S5,S15﹣S10,成等比数列,即可得出.【解答】解:由等比数列{a n}的性质可得:S5,S10﹣S5,S15﹣S10,成等比数列,∴=2•(14﹣S10),S10>0.解得S10=6.故答案为:6.16.给出下列命题:①已知x∈R,则“x>1”是“x>2”的充分不必要条件;②若|+|=||﹣||,则存在实数λ,使得=λ;③命题p:“∃x∈R,e x>x+1”的否定是“∀x∈R,e x<x+1”;④方程x=sinx有且只有一个实数解;⑤函数f(x)=4cos(2x+)的一个对称中心为.其中正确命题的序号是②④(把你认为正确的序号都填上).【考点】命题的真假判断与应用.【分析】①满足x >1的数不一定满足x >2;②由|+|=||﹣||⇒2•=|=﹣2|||,则得、反向共线; ③“>”的否定是“≤”;④在x ∈(0,)时,x >sinx ,∴函数y=x 与y=sinx 有且只有一个交点;⑤f ()=﹣1,.【解答】解:对于 ①,满足x >1的数不一定满足x >2,故错;对于②,由|+|=||﹣||⇒2•=|=﹣2|||,则得、反向共线,故正确; 对于③,“>”的否定是“≤”,故错; 对于④,在x ∈(0,)时,x >sinx ,∴函数y=x 与y=sinx 有且只有一个交点,故正确;对于⑤,f ()=﹣1,.∴不是f (x )=4cos (2x +)的一个对称中心.故错;故答案:②④.三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.请在答题卡各自题目的答题区域内作答.17.已知正项数列{a n }的前n 项和为S n ,且S n ,a n ,成等差数列. (1)证明数列{a n }是等比数列;(2)若b n =log 2a n +3,求数列{}的前n 项和T n .【考点】数列的求和.【分析】(1)由题意得2a n =S n +,易求,当n ≥2时,S n =2a n ﹣,S n ﹣1=2a n ﹣1﹣,两式相减得a n =2a n ﹣2a n ﹣1(n ≥2),由递推式可得结论;(2)由(1)可求=2n ﹣2,从而可得b n ,进而有=,利用裂项相消法可得T n ;【解答】解:(1)证明:由S n ,a n ,成等差数列,知2a n =S n +,当n=1时,有,∴,当n ≥2时,S n =2a n ﹣,S n ﹣1=2a n ﹣1﹣, 两式相减得a n =2a n ﹣2a n ﹣1(n ≥2),即a n =2a n ﹣1,由于{a n }为正项数列,∴a n ﹣1≠0,于是有=2(n ≥2),∴数列{a n }从第二项起,每一项与它前一项之比都是同一个常数2, ∴数列{a n }是以为首项,以2为公比的等比数列.(2)解:由(1)知==2n﹣2,∴b n=log2a n+3==n+1,∴==,∴T n=()+()+…+()==.18.已知向量=(sinx,cosx),=(cosx,﹣cosx),f(x)=•,(1)求f(x)的最小正周期和单调递增区间;(2)若x∈(),=,求cos2x的值.【考点】平面向量数量积的运算;正弦函数的单调性.【分析】(1)进行数量积的坐标运算,并化简即可得出,从而得出f(x)的最小正周期,而通过解,k∈Z即可得出f (x)的单调递增区间;(2)根据条件即可求得,而根据x的范围可求得的范围,进而求出的值,从而由即可求出cos2x的值.【解答】解:(1)===;∴f(x)的最小正周期为;解(k∈Z)得,,k∈Z;∴f(x)的单调递增区间为;(2)∵;∴;∵;∴;∴;∴===.19.围建一个面积为300m2的矩形场地,要求矩形场地的一面利用旧墙(旧墙足够长,利用旧墙需维修),其他三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为75元/m,新墙的造价为150元/m,设利用的旧墙的长度为xm(x>0).(1)将总费用y元表示为xm的函数;(2)试确定x,使修建此矩形场地围墙的总费用最小,并求最小总费用.【考点】函数模型的选择与应用.【分析】(1)设矩形的另一边长为am,然后列出总费用y元表示为xm的函数关系.(2)利用(1)函数的解析式,通过基本不等式求解,修建围墙的总费用的最小值.【解答】(本小题满12分)解:(1)设矩形的另一边长为am,则y=75x+150(x﹣2)+150•2a=225x+300a﹣300…由已知xa=300,得…∴…(2)∵x>0,∴…∴…当且仅当即x=20时,等号成立.…答:当x=20m时,修建围墙的总费用最小,最小总费用是8700元.…20.在△ABC中,角A,B,C的对边分别为a,b,c且满足bcosA=(2c﹣a)cosB.(1)求角B的大小;(2)若b=4=4,求a+c的值.【考点】平面向量数量积的运算.【分析】(1)由正弦定理把已知等式化边为角,利用两角和的正弦化简即可求得角B的大小;(2)由数量积为4可得ac的值,再由余弦定理整体运算求得a+c的值.【解答】解:(1)∵bcosA=(2c﹣a)cosB,由正弦定理得sinBcosA=2sinCcosB﹣sinAcosB,即sin(A+B)=2sinCcosB=sinC,∵sinC≠0,∴cosB=.又B∈(0,π),∴B=;(2)∵,∴ca•cosB=4,得ac=8.由余弦定理得b2=a2+c2﹣2accosB=a2+c2﹣ac=(a+c)2﹣3ac=(a+c)2﹣24=16.∴.21.等比数列{a n}的前n项和为S n,且a2=3,a5=81,等差数列{b n}的前n项和为T n,T n=n.(1)求数列{a n},{b n}的通项公式;(2)若对任意的n∈N*,≥b n恒成立,求实数k的取值范围.【考点】等差数列与等比数列的综合.【分析】(1)设数列{a n}的公比为q,由题意和等比数列的性质求出q,由等比数列的通项公式求出a n,由题意、数列的通项公式与前n项和的关系求出b n;(2)解法一:由(1)和等比数列的前n项和公式求出a1、S n,代入恒成立的式子化简并分离出k,令,利用列不等式组求出c n的最大值,即可求出k的范围;解法二:由(1)和等比数列的前n项和公式求出a1、S n,代入恒成立的式子化简并分离出k,令,利用作差法判断出数列{c n}的单调性,求出c n的最大值,即可求出k的范围.【解答】解:(1)设数列{a n}的公比为q,由题意得,,∴…∵T n=n,∴当n≥2时,…当n=1时,也适合上式 …综上得,…(2)解法 一:由(1)得,…由条件得,对n ∈N *恒成立,∴对∀n ∈N *恒成立 …令,设,则,解得2.5≤n ≤3.5,则n=3…∴,即…∴实数k 的取值范围是.…解法二:由(1)得,…由条件得,对n ∈N *恒成立,∴对n ∈N *恒成立…令,∵,∴当n ≤3时,c n >c n ﹣1,当n ≥4时,c n <c n ﹣1…则,即…∴实数k的取值范围是.…22.已知函数f(x)=alnx+x2(a为常数).(1)当a=﹣2时,求f(x)的单调区间;(2)当x∈(1,e]时,讨论方程f(x)=0根的个数;(3)若a>0,且对任意的x1,x2∈且x1≠x2,都有|f(x1)﹣f(x2)|<|,求实数a的取值范围.【考点】利用导数研究函数的单调性.【分析】(1)根据导数和函数的单调性的关系即可求出;(2)把原函数f(x)=alnx+x2求导,分a≥0和a<0讨论打哦函数的单调性,特别是当a <0时,求出函数f(x)在[1,e]上的最小值及端点处的函数值,然后根据最小值和F(e)的值的符号讨论在x∈[1,e]时,方程f(x)=0根的个数;(3)问题转化为等价于函数h(x)=f(x)+在时是减函数,结合函数的单调性得到a≤﹣2x2,求出a的范围即可.【解答】解:(1)当a=﹣2时,f(x)=﹣2lnx+x2,定义域为(0,+∞),∴f′(x)=﹣+2x==,当f′(x)<0,解得0<x<1,当f′(x)>0,解得x>1,∴f(x)得单调递减区间为(0,1),递增区间为(1,+∞).(2)方程f(x)=0根的个数等价于方程﹣a=根的个数.设g(x)=,∴g′(x)==,当x∈(1,)时,g′(x)<0,函数g(x)递减,当x∈(,e]时,g′(x)>0,函数g(x)递增.又g(e)=e2,g()=2e,作出y=g(x)与直线y=﹣a的图象如图,由图象知:当2e<﹣a≤e2时,即﹣e2≤a≤﹣2时,方程f(x)=0有2个相异的根;当a<﹣e2或a=﹣2e时,方程f(x)=0有1个根;当a>2e时,方程f(x)=0有0个根.(3)当a>0时,,f(x)在上是增函数,又函数y=是减函数,不妨设,则等价于,即,令h(x)=f(x)+,∴h′(x)=+2x﹣≤0恒成立,即a≤﹣2x2在时恒成立,设φ(x)=﹣2x2,∴在时是减函数.∴,又a>0,∴实数a的取值范围是(0,].2016年12月18日。
福州市八县区一中2020届高三数学(文)上学期期中联考试卷附答案解析

1 2
(
1 3
1) 5
(1 5
1) 7
...
(1 2n 1
1 2n
3)
1 2
(1 3
1 2n
) 3
1 6
……………………………10 分
18、解: (1) f (x) sin 2 x 2 sin x cos x 3cx cos x 3cos2 x ………………………………………2 分 sin 2 x cos2 x
分
-6-
所以Tn 1 3 3 5 32 7 33 ... (2n 1) 3n1
…………………8 分
3Tn 1 3 3 32 5 33 ...(2n 3) 3n1 (2n 1) 3n
相减得 2Tn 1 2(3 32 33 ... 3n1) (2n 1)3n …………………9 分 2 (2 2n) 3n
已知函数 f (x) 1 a (a R) . x
(Ⅰ) 设函数 h(x) a ln x x f (x) ,求函数 h(x)的极值; (Ⅱ) 若 g(x) a ln x x 在[1,e]上存在一点 x0,使得 g(x0 ) f (x0 ) 成立,求 a 的取值范围.
-4-
= tan 2 x 2 tan x 3 …………………………………………4 分 tan 2 x 1
= 17 …………………………………………6 分 5
(2) f (x) sin 2 x 2 sin x cos x 3cos2 x
-5-
= 2 sin(2x ) 2 …………………………………………8 分 4
福建省2020届高三数学上学期期中试题文.doc

福建省2020届高三数学上学期期中试题 文(考试时间:120分钟 总分:150分)试卷分第I 卷(选择题)和第II 卷(非选择题)两部分 第I 卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分。
每小题只有一个选项符合题意,请将正确答案填入答题卷中。
)1.已知集合{}062≤--=x x x A ,{}2>=x x B ,则( )A.)(3,2B.](3,2C.)(2,3-D.)[2,3-2.若复数z 满足5)21(=+i z ,其中i 为虚数单位,则复数z 的共轭复数=z ( ) A.i 21- B .i 21+ C .i 21+- D .i 21--3.“在()b a ,内0)(<'x f ”是“)(x f 在()b a ,内单调递减”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分又不必要条件4.已知在平面直角坐标系xoy 中,()1,2A ,()1,-m B ,若//,则=m ( )A.2B. 2-C.21 D.21- 5.设变量y x ,满足⎪⎩⎪⎨⎧≤≤--≥-+10202y y x y x ,则目标函数y x z 2+=的最小值为( )A .2B .3C .4D .56.设等差数列{}n a 的前n 项和为n S ,若352a a =,则=59S S ()A.109 B.1815 C. 59 D. 518 7.设5tan,2log ,25.05.0π===c b a ,则( )A.c a b <<B.c b a <<C.b c a <<D.c a b << 8.我们知道:在平面内,点),(00y x 到直线0=++C By Ax 的距离公式2200BA C By Ax d +++=,通过类比的方法,可求得:在空间中,点)3,4,2(到直线0222=+++z y x 的距离为( )A .3B .5 C.6 D .5518 9.中国传统扇文化有着极其深厚的底蕴. 一般情况下,折扇可看作是从一个圆面中剪下的扇形制作而成,设扇形的面积为1S ,圆面中剩余部分的面积为2S ,当1S 与2S的比值为12时,扇面看上去形状较为美观,那么此时扇形的圆心角的弧度数为( )A.π)53(+B. π)15(-C.π)15(+D.π)53(- 10.函数)62sin(2)(π-=x x f 的图像为C ,以下结论错误..的是( )A.图像C 关于直线65π=x 对称 B.图像C 关于点⎪⎭⎫⎝⎛0,127π对称 C.函数)(x f 在区间⎪⎭⎫⎝⎛-3,6ππ内是增函数D.由x y 2sin 2=图像向右平移6π个单位长度可以得到图像C11.已知直三棱柱111C B A ABC -中,︒=∠90ABC ,2,11===CC BC AB ,则异面直线1AB 与1BC 所成角的余弦值为( )A .53B .53-C .54D .54-12.已知实数b a ,满足0ln 42=--b a a ,R c ∈,则22)2()(c b c a ++-的最小值为( )A . 553B .59C .55D .51第Ⅱ卷(非选择题90分)二、填空题(本大题共4小题,每小题5分,共20分,请将正确答案填入答题卷中。
福建省福州市八县(市、区)一中2023届高三上学期期中联考化学试题附参考答案

2022~2023学年度第一学期八县(市)一中期中联考高中三年化学科试卷命题学校:连江一中命题教师:高三备课组审核教师:高三备课组考试日期:11月11 日完卷时间:75分钟满分:100分可能用到的相对原子质量:H-1 N-14 Fe-56 Na-23 C-12 O-16 Mg-24 S-32 Y-89 V-51 Cl-35.5I卷一、选择题(每题只有一个正确选项,每题3分,共42分)1. 2022年6月5日,神州十四号飞船发射成功,我国空间站建设又迈出实质性一步。
下列说法错误的是()A.“天和”核心舱中使用的氮化硼陶瓷基复合材料属于高分子化合物B.当光束通过空间站热控材料使用的纳米气凝胶时可观察到丁达尔效应C.太阳能电池帆板是载人航天工程中飞行器的动力源泉,其核心材料为硅D.航天服壳体使用的铝合金材料熔点比纯铝低2. N A为阿伏加德罗常数的值,下列说法正确的是()A. 标准状况下11.2LCO2全溶于水,溶液中的HCO3-、CO32-、H2CO3的数目之和为0.5N AB. 18g的D2O中所含质子数目和中子数目均为10N AC. 0.1mol/L KAl(SO4)2溶液中,SO42-的个数为0.2N AD. 15.6gNa2S 和Na2O2固体混合物中,阴离子数为0.2N A3.为除去某物质中所含的杂质,所选用的试剂或操作方法正确的是()序号物质杂质除杂质应选用的试剂或操作方法①MgCl2溶液AlCl3在MgCl2溶液中加过量NaOH溶液搅拌、过滤②FeSO4溶液CuSO4加入过量铁粉并过滤③CO2SO2依次通过盛有Na2CO3溶液和浓硫酸的洗气瓶④NaNO3CaCO3加稀盐酸溶解、过滤、蒸发、结晶A.② B.①② C.②③ D.①②③④4.常温下,在指定溶液中下列各组离子可能大量共存的是 ( )A.滴加KSCN显红色的溶液:NH4+、Cl-、K+、HCO3-B. K2S溶液中:SO42-、K+、Cl-、Cu2+C. 由水电离出的C(OH-)=10-12 mol/L的溶液:Al3+、H+、Cl-、Na+D. = 10-12的溶液中: Cl -、Na +、S 2O 32-、SO 42-c (OH -)c (H +)5. 下列实验装置能达到相应实验目的的是( )甲 乙 丙 丁A. 用装置甲验证Na 和水反应是否为放热反应B. 用装置乙验证SO 2的漂白性C. 用装置丙除去氯气中的少量氯化氢D. 用装置丁除去Na 2CO 3固体中少量的NaHCO 36.为防治雾霾,设计如下流程吸收工业尾气SO 2和NO ,同时获得连二亚硫酸钠(Na 2S 2O 4)和NH 4NO 3产品,以变“废”为宝。
2020届福建省福州市高三上学期期中联考数学(文)试题

2020届福建省福州市八县(市、区)一中高三上学期期中联考数学(文)试题一、单选题1.已知集合2{|560}A x x x =-+≤,{|15}B x Z x =∈<<,则A B =( )A .[2,3]B .(1,5)C .{}2,3D .{2,3,4}【答案】C【解析】解不等式简化集合A 的表示,用列举法表示集合B ,最后根据集合交集的定义求出A B .【详解】2560(2)(3)023x x x x x -+≤⇒--≤⇒≤≤,{}23A x x ∴=≤≤, 又{}{|15}2,3,4B x Z x =∈<<=,所以{}2,3A B ⋂=,故本题选C. 【点睛】本题考查了列举法表示集合、集合交集的运算,正确求解出不等式的解集是解题的关键. 2.若复数z 满足(1)3z i i +=-,则z 的共轭复数z =( ) A .23i -- B .23i -C .23i +D .23i -+【答案】D【解析】由题,先用复数的运算求得z ,再求得z 的共轭复数z . 【详解】 由题可得3123iz i i-=-=--,即z 的共轭复数23z i =-+ 故选D 【点睛】本题考查了复数的运算以及共轭复数,属于基础题. 3.已知函数是奇函数,则实数( )A .B .C .D .【答案】B【解析】根据奇函数的定义得恒成立.【详解】 依题意:恒成立,即即,,解得故选: 【点睛】本题考查了函数奇偶性的性质与判断,属基础题. 4.已知132a -=,21log 3b =,121log 3c =,则( ). A .a b c >> B .a c b >>C .c a b >>D .c b a >>【答案】C【解析】试题分析:因为13212112(0,1),log 0,log 1,33a b c -=∈==所以.b a c <<选C .【考点】比较大小5.若向量a ,b 是非零向量,则“a b a b +=-”是“a ,b 夹角为2π”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件【答案】C【解析】根据充分条件和必要条件的定义结合向量的运算进行判断即可. 【详解】2222||2||20a b a b a b ab a b ab ab +=-⇔++=+-⇔=,向量a ,b 是非零向量,0ab a b a ∴=⇔⊥⇔,b 夹角为2π ∴“a b a b +=-”是“a ,b 夹角为2π”的充要条件. 故选:C . 【点睛】本题主要考查充分条件和必要条件的判断,根据向量的运算是解决本题的关键.6.函数3222x xx y -=+在[]6,6-的图像大致为A .B .C .D .【答案】B【解析】由分子、分母的奇偶性,易于确定函数为奇函数,由(4)f 的近似值即可得出结果. 【详解】设32()22x x x y f x -==+,则332()2()()2222x x x xx x f x f x ----==-=-++,所以()f x 是奇函数,图象关于原点成中心对称,排除选项C .又34424(4)0,22f -⨯=>+排除选项D ;36626(6)722f -⨯=≈+,排除选项A ,故选B . 【点睛】本题通过判断函数的奇偶性,缩小考察范围,通过计算特殊函数值,最后做出选择.本题较易,注重了基础知识、基本计算能力的考查.7.已知定义在R 上的奇函数()y f x =满足(2)()f x f x +=-,且(1)2f =,则(2018)(2019)f f +的值为( )A .2-B .0C .2D .4【答案】A【解析】根据奇函数性质以及条件得函数周期性,再根据周期求函数值. 【详解】∵()f x 为奇函数,∴()()f x f x -=-,又()()2f x f x +=-,∴()()2f x f x +=-, ∴()()()42f x f x f x +=-+=,∴函数()f x 是周期为4的周期函数, ∴()()()()()()20182019450424504323f f f f f f +=⨯++⨯+=+, 又()()()()()200,3112f f f f f ===-=-=-,∴()()()()20182019232f f f f +=+=-.选A . 【点睛】本题考查奇函数性质、周期性质,考查基本求解能力.8.在ABC 中,AB 2=,πC 6=,则AC 的最大值为( )A .B .C .D【答案】A【解析】利用正弦定理得出ABC 的外接圆直径,并利用正弦定理化边为角,利用三角形内角和关系以及两角差正弦公式、配角公式化简,最后利用正弦函数性质可得出答案. 【详解】ABC 中,AB 2=,πC 6=,则AB2R 4sinC==,()5πAC 4sinB 4sin A 2cosA A θ6⎛⎫=+=-+=+=+ ⎪⎝⎭,其中sin θsin θ1414==由于5π0A 6<<,π0θ2<<所以4π0A θ3<+<,所以最大值为 故选A . 【点睛】本题考查正弦定理以及两角差正弦公式、配角公式,考查基本分析计算能力,属于中等题.9.已知点M 是△ABC 的边BC 的中点,点E 在边AC 上,且2EC AE =,则向量EM =()A .1123AC AB + B .1162AC AB + C .1126AC AB +D .1263AC AB +【答案】B【解析】由题意结合向量的加法法则可得:213221()3221132211.62EM EC CM AC CB AC CA AB AC AC AB AC AB =+=+=++=-+=+ 本题选择B 选项.点睛:(1)应用平面向量基本定理表示向量的实质是利用平行四边形法则或三角形法则进行向量的加、减或数乘运算.(2)用向量基本定理解决问题的一般思路是:先选择一组基底,并运用该基底将条件和结论表示成向量的形式,再通过向量的运算来解决.10.函数()()sin 02f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭,的最小正周期是π,若其图象向左平移3π个单位后得到的函数为偶函数,则函数()f x 的图象( ) A .关于点012π⎛⎫⎪⎝⎭,对称 B .关于直线12x π=对称C .关于点06π⎛⎫ ⎪⎝⎭,对称 D .关于直线6x π=对称【答案】A【解析】根据函数()f x 的最小正周期是π,求得2w =,即()()sin 2f x x ϕ=+,再根据三角函数的图象变换求得2()sin(2)3g x x πϕ=++,利用三角函数的对称性,求得6πϕ=-,得到函数()sin 26f x x π⎛⎫=- ⎪⎝⎭,再利用三角函数的性质,即可求解.【详解】由题意,函数()()sin f x x ωϕ=+的最小正周期是π,即2wππ=,解得2w =, 所以()()sin 2f x x ϕ=+, 将函数()f x 的向左平移3π个单位后得到函数2()sin[2()]sin(2)33g x x x ππϕϕ=++=++因为()g x 为偶函数,所以2(0)sin()13g πϕ=+=±,即2,32k k Z ππϕπ+=+∈, 解得,6k k Z πϕπ=-+∈,因为2πϕ<,所以6πϕ=-,所以()sin 26f x x π⎛⎫=-⎪⎝⎭,令2,6x k k Z ππ-=∈,解得,122k x k Z ππ=+∈, 令0k =,则12x π=,所以函数()f x 关于012π⎛⎫⎪⎝⎭,对称,故选A. 【点睛】本题主要考查了三角函数的图象变换,以及三角函数的图象与性质的应用,其中解答中熟练应用三角函数的图象变换求得函数的解析式,再利用三角函数的图象与性质求解是解答的关键,着重考查了推理与运算能力,属于基础题. 11.若0,0a b >>,1ab a b =++,则2+a b 的最小值为A .B .3C .3+D .7【答案】D【解析】利用等式,表示出a ,进而根据基本不等式及其性质解得最小值. 【详解】当1b =时,代入等式1a a =+不成立,因而1b ≠ 所以1ab a b -=+12111b a b b +==+-- 所以2a b +2121b b =++- ()23211b b =++--3≥+ 322≥+⨯7≥ (当a=3,b=2时取等号)即最小值为7 所以选D 【点睛】本题考查了基本不等式的简单应用,属于中档题.12.已知函数()f x 的定义域为R ,其图象关于点()1,0-中心对称,其导函数()f x ',当1x <-时,()()()()110x f x x f x '⎡⎤+++<⎣⎦,则不等式()()10xf x f ->的解集为( )A .()1,+∞B .(),1-∞-C .()1,1-D .()(),11,-∞-⋃+∞ 【答案】C【解析】由题意设()()()1g x x f x =+,则()()()()'1'g x f x x f x =++, 当1x <-时,()()()()11'0x f x x f x ⎡⎤+++<⎣⎦, ∴当1x <-时, ()()()1'0f x x f x ++>,则()g x 在(),1-∞-上递增,函数()f x 的定义域为R ,其图象关于点()1,0-中心对称, ∴函数()1f x -的图象关于点()0,0中心对称,则函数()1f x -是奇函数,令()()()()11,h x g x xf x h x =-=-∴是R 上的偶函数,且在(),0-∞递增,由偶函数的性质得:函数()h x 在()0,+∞上递减,()()10,h f =∴不等式()()10xf x f ->化为: ()()1h x h >,即1x <,解得11x -<<, ∴不等式解集是()1,1-,故选C. 【方法点睛】本题主要考察抽象函数的单调性以及函数的求导法则,属于难题.求解这类问题一定要耐心读题、读懂题,通过对问题的条件和结论进行类比、联想、抽象、概括,准确构造出符合题意的函数是解题的关键;解这类不等式的关键点也是难点就是构造合适的函数,构造函数时往往从两方面着手:①根据导函数的“形状”变换不等式“形状”;②若是选择题,可根据选项的共性归纳构造恰当的函数.本题根据方法①,联想到函数()()()1g x x f x =+,再结合条件判断出其单调性,进而得出正确结论.二、填空题13.函数()ln f x x x x =+的单调递增区间是_______. 【答案】()2,e -+∞【解析】求出函数()y f x =的定义域,并求出该函数的导数,并在定义域内解不等式()0f x '>,可得出函数()y f x =的单调递增区间.【详解】函数()ln f x x x x =+的定义域为()0,∞+,且()ln 2f x x '=+,令()0f x '>,得2x e ->.因此,函数()ln f x x x x =+的单调递增区间为()2,e -+∞,故答案为:()2,e -+∞.【点睛】本题考查利用导数求函数的单调区间,在求出导数不等式后,得出的解集应与定义域取交集可得出函数相应的单调区间,考查计算能力,属于中等题.14.等差数列{}n a 的前n 项和为n S ,若271212a a a ++=,则13S =_________. 【答案】52【解析】根据等差中项性质求出7a ,再由等差数列的前n 项公式,即可求解, 【详解】271277312,4a a a a a ++==∴=,11313713()13134522a a S a +===⨯=.故答案为:52. 【点睛】本题考查等差数列的性质、前n 项和,熟记常用结论是解题的关键,属于基础题.15.若,x y 满足约束条件250,230,50,x y x y x +-≥⎧⎪-+≥⎨⎪-≤⎩则z x y =+的最大值为__________.【答案】9【解析】作出可行域,根据目标函数的几何意义可知当5,4x y ==时,max 9z =. 【详解】不等式组表示的可行域是以(5,4),(1,2),(5,0)A B C 为顶点的三角形区域,如下图所示,目标函数z x y =+的最大值必在顶点处取得,易知当5,4x y ==时,max 9z =.【点睛】线性规划问题是高考中常考考点,主要以选择及填空的形式出现,基本题型为给出约束条件求目标函数的最值,主要结合方式有:截距型、斜率型、距离型等.16.已知函数()2242,0,0x x x x f x x e x ⎧-++≥=⎨-<⎩,若函数()()2g x f x a =+恰有两个不同的零点,则实数a 的取值范围是__________. 【答案】(]223,1e ⎧⎫--⋃⎨⎬⎩⎭【解析】分析:先根据导数研究2y ,0xx e x =-<图像,再根据()y f x =与y 2a =-图像交点情况确定实数a 的取值范围.详解:令2y ,0xx e x =-<,所以(2)0,02xy x x e x x =-+=<∴=-' 当2x <-时,240,[,0)y y e <-'∈;当20x -<<时,240,[,0)y y e>-'∈; 作()y f x =与y 2a =-图像,由图可得要使函数()()2g x f x a =+恰有两个不同的零点,需224222263 1.a a a a e e -=-≤-<∴=--<≤-或或 点睛:对于方程解的个数(或函数零点个数)问题,可利用函数的值域或最值,结合函数的单调性、草图确定其中参数范围.从图象的最高点、最低点,分析函数的最值、极值;从图象的对称性,分析函数的奇偶性;从图象的走向趋势,分析函数的单调性、周期性等.三、解答题17.n S 为等差数列{}n a 的前n 项和,已知511a =,763S =. (1)求数列{}n a 的通项公式; (2)设11n n n b a a +=,数列{}n b 的前n 项和为n T ,求证16n T <. 【答案】(1)21n a n =+;(2)证明见解析.【解析】(1)设数列{}n a 的公差为d ,将已知条件转化为1,a d 关系,即可求解; (2)根据{}n b 通项公式,用裂项相消法求出和n T ,即可证明结论. 【详解】(1)由设数列{}n a 的公差为d ,则1141172163a d a d +=⎧⎨+=⎩ 解得2d =,13a =所以{}n a 是首项为3,公差为2的等差数列, 通项公式为21n a n =+. (2)由21n a n =+111111().(21)(23)22123n n b a a n n n n +===-++++ 12n n T b b b =+++1111111()()...()235572123n n ⎡⎤=-+-++-⎢⎥++⎣⎦1111()23236n =-<+【点睛】本题考查等差数列的通项公式和前n 项公式基本量的计算,考查裂项相消法求数列和,属于基础题.18.已知函数223()sin 2sin sin()3sin ()22f x x x x x ππ=+⋅-+- (1)若1tan 2x =,求()f x 的值; (2)求函数()f x 最小正周期及单调递减区间.【答案】(1)175;(2)π,5,,88k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦. 【解析】(1)用诱导公式,化简()f x ,进而化为关于sin ,cos x x 齐次分式,化弦为切,即可求解;(2)利用三角恒等变换,将()f x 化为正弦型三角函数,运用周期公式求出周期,由正弦函数的单调递减区间结合整体代换,即可求出函数的单调递减区间.【详解】(1)22()sin 2sin cos 3cos f x x x x x =+⋅+2222sin 2sin cos 3cos sin cos x x x x x x++=+ 22tan 2tan 3tan 1x x x ++=+ 175=. (2)22()sin 2sin cos 3cos f x x x x x =+⋅+sin 2cos 22224x x x π⎛⎫=++=++ ⎪⎝⎭ ()f x 的最小正周期为22T ππ==, 由3222242k x k πππππ+≤+≤+, 解得:5,88k x k k Z ππππ+≤≤+∈ 所以()f x 的单调递减区间为5,,88k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦ 【点睛】本题考查应用诱导公式、同角间的三角函数关系求值,考查三角恒等变换以及正弦函数的性质,属于中档题.19.已知函数2()e 1(,)x f x ax bx a b =+++∈R ,曲线()y f x =在(1,(1))f 处的切线方程为(e 1)1y x =-+.(1)求实数,a b 的值;(2)求函数()y f x =在[1,2]-的最值.【答案】(1)01a b =⎧⎨=-⎩;(2)min ()2f x =,2max ()e 1f x =- 【解析】(1)()e 2x f x ax b '=++,可得到(1)e 2e 1(1)e 1ef a b f a b =++=-⎧⎨=+++='⎩,即可求出,a b的值;(2)由()1x f x e =-'可判断()f x 的单调性,从而可求出函数()y f x =在[1,2]-的最值.【详解】(1)()e 2xf x ax b '=++,则(1)e 2e 1(1)e 1e f a b f a b =++=-⎧⎨=+++='⎩,01a b =⎧∴⎨=-⎩.(2)()e 1x f x x =-+的定义域为(,)-∞+∞,()e 1x f x '=-,令()0f x '=,则0x =,∴当0x <时,()0f x '<,()f x 单调递减;当0x >时,()0f x '>,()f x 单调递增, ∴min ()(0)2f x f ==, ∵1(1)2ef -=+,2(2)e 1f =-,且(2)(1)f f >-, ∴2max ()(2)e 1f x f ==-.【点睛】本题考查了导数的几何意义,考查了函数的单调性的应用,考查了学生的计算能力,属于基础题.20.已知数列{}n a 满足11a =,121n n a S +=+,其中n S 为数列{}n a 的前n 项和. (1)求数列{}n a 的通项公式;(2)设n n b a ⎧⎫⎨⎬⎩⎭是首项为1,公差为2的等差数列,求数列{}n b 的前n 项和n T . 【答案】(1)13-=n n a ;(2)1(1)3n n T n =+-⋅.【解析】(1)1n =求出2a ,当2n ≥,由1n n n a S S -=-求出n a 递推公式,即可求解;(2)由(1)得{}n a 为等比数列,n n b a ⎧⎫⎨⎬⎩⎭是等差数列,可得{}n b 的通项为等比数列与等差数列通项的乘积,故用错位相减法求其和.【详解】(1)由11a =,121n n a S +=+,当1n =时,可得21213a a =+=.当2n ≥时,121n n a S +=+,两式相减得:12n n n a a a +=-,即13n n a a +=,且213a a =.故{}n a 是以1为首项,3为公比的等比数列.所以13-=n n a .(2)由题意12(1)21n nb n n a =+-=-, 所以1(21)3n n b n -=-⋅.所以2311335373...(21)3n n T n -=+⋅+⋅+⋅++-⋅;2313133353...(23)3(21)3n n n T n n -=⋅+⋅+⋅+-⋅+-⋅,相减得:231212(333...3)(21)3n n n T n --=+++++--2(22)3n n =-+-⋅,1(1)3n n T n =+-⋅∴.【点睛】本题考查由前n 项和求通项,要注意递推公式的起始项,考查错位相减法求数列和,属于中档题.21.如图,四边形ABCD 中90BAC ∠=︒,30ABC ∠=︒,AD CD ⊥,设ACD θ∠=.(1)若ABC ∆面积是ACD ∆面积的4倍,求θ;(2)若6ADB π∠=,求tan θ.【答案】(1)6π或3π;(2)32. 【解析】(1)将ABC ∆、ACD ∆的面积分别用,AC θ表示,结合已知,即可求解; (2)在,ABD BCD ∆∆,用正弦定理分别求出BD ,得到关于θ的关系式,化简即可求出结论.【详解】(1)设AC a =,则3AB a =,sin AD a θ=,cos CD a θ=, 由题意4ABC ACD S S ∆∆=,则1134cos sin 22a a a a θθ=⋅⋅, 所以3sin 22θ=,(0,)2πθ∈,6πθ∴=或3πθ=. (2)由正弦定理,ABD ∆中,sin sin BD AB BAD ADB =∠∠,即()3sin sin 6BD a ππθ=-① BCD ∆中,sin sin BD BC BCD CDB =∠∠,即2sin sin 33BD a ππθ=⎛⎫+ ⎪⎝⎭② ①÷②得:2sin 3sin 3πθθ⎛⎫+= ⎪⎝⎭32sin θθ=, 所以3tan θ=. 【点睛】 本题考查解三角形,涉及到直角三角形边角关系、三角恒等变换、面积公式、正弦定理等基础知识,意在考查直观想象、逻辑推理、数学计算能力,属于中档题.22.已知函数1()()a f x a R x+=∈. (1)设函数()ln ()h x a x x f x =--,求函数()h x 的极值;(2)若()ln g x a x x =-在[1,]e 上存在一点0x ,使得00()()g x f x ≥成立,求a 的取值范围.【答案】(1)当1a >-时,()h x 极大值为ln(1)2a a a +--,无极小值;当1a ≤-时,()h x 无极值;(2)211e a e +≥-或2a ≤-. 【解析】(1)求出()h x ',对a 分类讨论求出单调区间,即可求出结论;(2)()ln g x a x x =-在[1,]e 上存在一点0x ,使得00()()g x f x ≥成立,即为0)(0h x ≥,只需max ()0h x ≥,结合(1)中的结论对a 分类讨论求出min ()h x ,即可求解.【详解】(1)依题意1()ln a h x a x x x+=--,定义域为(0,)+∞, ∴22221(1)(1)[(1)]()1a a x ax a x x a h x x x x x+--++-+'=-+=-=-, ①当10a +>,即1a >-时,令()0h x '>,∵0x >,∴01x a <<+,此时,()h x 在区间(0,1)a +上单调递增,令()0h x '<,得1x a >+.此时,()h x 在区间(1,)a ++∞上单调递减.②当10a +≤,即1a ≤-时,()0h x '<恒成立,()h x 在区间(0,)+∞上单调递减.综上,当1a >-时,()h x 在1x a =+处取得极大值(1)ln(1)2h a a a a +=+--,无极小值;当1a ≤-时,()h x 在区间(0,)+∞上无极值.(2)依题意知,在[]1,e 上存在一点0x ,使得00()()g x f x ≥成立,即在[]1,e 上存在一点0x ,使得0)(0h x ≥,故函数1()ln a h x a x x x+=--在[]1,e 上,有max ()0h x ≥. 由(1)可知,①当1a e +≥,即1a e ≥-时,()h x 在[]1,e 上单调递增, ∴max 1()()0a h x h e a e e +==--≥,∴211e a e +≥-, ∵2111e e e +>--,∴211e a e +≥-. ②当011a <+≤,或1a ≤-,即0a ≤时,()h x 在[]1,e 上单调递减,∴max ()(1)110h x h a ==---≥,∴2a ≤-.③当11a e <+<,即01a e <<-时,由(2)可知,()h x 在1x a =+处取得极大值也是区间(0,)+∞上的最大值, 即max ()(1)ln(1)2[ln(1)1]2h x h a a a a a a =+=+--=+--,∵0ln(1)1a <+<,∴(1)0h a +<在[]1,e 上恒成立,此时不存在0x 使0)(0h x ≥成立.综上可得,所求a 的取值范围是211e a e +≥-或2a ≤-. 【点睛】本题考查函数和导数及其应用、不等式能成立等基础知识,考查分类讨论思想,意在考查逻辑推理与数学运算的数学核心素养,属于中档题题.。
2020-2021学年福建省福州市八县(市)一中高三(上)期中数学试卷 (解析版)

2020-2021学年福建省福州市八县(市)一中高三(上)期中数学试卷一、选择题(共8小题).1.已知集合A={x∈Z|x2﹣5x﹣6≤0},B={x|2<2x<128},则A∩B=()A.{x|1<x≤6}B.{2,3,4,5,6}C.{x|1≤x≤6}D.{﹣1,0,1,2,3,4,5,6}2.已知p:“函数y=x2+2ax+1在(1,+∞)上是增函数”,q:“a>﹣2”,则p是q的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件3.已知函数f(x)是定义在R上的偶函数,且函数f(x)在[0,+∞)上是减函数,如果f (3)=﹣1,则不等式f(x﹣1)+1≥0的解集为()A.(﹣∞,2]B.[2,+∞)C.[﹣2,4]D.[1,4]4.如图是一个正方体的展开图,则在该正方体中()A.直线AB与直线CD平行B.直线AB与直线CD相交C.直线AB与直线CD异面垂直D.直线AB与直线CD异面且所成的角为60°5.记S n为正项等比数列{a n}的前n项和,若S2=1,S4=5,则S7=()A.S7=10B.C.D.6.已知m>0,n>0,m+4n=2,则的最小值为()A.36B.16C.8D.47.已知函数f(x)=sin(ωx+φ)(ω>0,),其图象相邻两条对称轴之间的距离为,将函数y=f(x)的图象向左平移个单位后,得到的图象关于原点对称,那么函数y=f(x)的图象()A.关于点对称B.关于点对称C.关于直线对称D.关于直线对称8.已知可导函数f(x)的定义域为(﹣∞,0),其导函数f′(x)满足xf'(x)﹣2f(x)>0,则不等式f(2020+x)﹣(x+2020)2f(﹣1)<0的解集为()A.(﹣∞,﹣2021)B.(﹣2021,﹣2020)C.(﹣2021,0)D.(﹣2020,0)二、选择题(共4小题).9.已知复数z满足z(2﹣i)=i(i为虚数单位),复数z的共轭复数为,则()A.B.=﹣C.复数z的实部为﹣1D.复数z对应复平面上的点在第二象限10.已知A(2,4),B(4,1),C(9,5),D(7,8),如下四个结论正确的是()A.B.四边形ABCD为平行四边形C.与夹角的余弦值为D.11.在△ABC中,角A,B,C的对边分别是a,b,c,若,a cos B+b sin A=c,则下列结论正确的是()A.tan C=2B.C.D.△ABC的面积为612.已知直三棱柱ABC﹣A1B1C1中,AB⊥BC,AB=BC=BB1,D是AC的中点,O为A1C 的中点.点P是BC1上的动点,则下列说法正确的是()A.当点P运动到BC1中点时,直线A1P与平面A1B1C1所成的角的正切值为B.无论点P在BC1上怎么运动,都有A1P⊥OB1C.当点P运动到BC1中点时,才有A1P与OB1相交于一点,记为Q,且D.无论点P在BC1上怎么运动,直线A1P与AB所成角都不可能是30°三、填空题(共4小题).13.若cos(﹣θ)=,则sin2θ=.14.已知数列{a n}的前n项和S n=n2﹣3n﹣1,则a n=.15.在三棱锥P﹣ABC中,平面PAB垂直平面ABC,,∠BAC=120°,则三棱锥P﹣ABC外接球的表面积为.16.函数f(x)满足f(1+x)=f(1﹣x),当x>1时,,若f2(x)﹣2mf(x)+4m=0有8个不同的实数解,则实数m的取值范围是.四、解答题(本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤。
福州市八县区一中2020届高三数学(文)上学期期中联考试卷附答案解析

福州市八县区一中2020届高三上学期期中联考数学(文)试卷考试日期:11月14日 完卷时间:120分钟 满 分:150分第I 卷(选择题共60分)一、选择题:每小题各5分,共60分.在每小题给出的四个选项中,只有一项是符合题意要求的. 1. 已知集合{}0652≤+-=x xx A ,{}51<<∈=x Z x B ,则=B A I ( )A .[]3,2 B .()5,1 C .{}3,2 D .{}4,3,2 2. 若复数z 满足i i z -=+3)1(,则z 的共轭复数z =( )A .i 32--B .i 32-C .i 32+D .i 32+-3.已知函数22()log ()1f x m x =++是奇函数,则实数=m ( ) A .2- B .1- C .1 D .2 4.已知312-=a ,21log 3b =, 121log 3c =, 则( ) A . c b a >> B .b c a >> C . b a c >> D .a b c >>5.若向量,是非零向量,则“”是“,夹角为”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件6.函数xx x y -+=2223在[]6,6-的图像大致为( ) A .B .C .D .7.已知定义在R 上的奇函数)(x f y =满足)()2(x f x f -=+,且2)1(=f ,则)2019()2018(f f +的值为( )A .2-B .0C .2D .48.在ABC ∆中,2,6AB C π==,则3AC BC +的最大值为( )A .7B .37 C.47 D .27a rb r a b a b +=-r r r r a r b r2π9.已知点M 是△ABC 的边BC 的中点,点E 在边AC 上,且AE EC 2=,则向量EM u u u r=( )A .AB AC 3121+ B .AB AC 6121+ C .AB AC 2161+ D .AB AC 2361+ 10.函数(, )的最小正周期是,若其图象向左平移个单位后得到的函数为奇函数,则函数的图象( )A. 关于点对称B. 关于直线对称C. 关于点对称D. 关于直线对称11.若0>a ,0>b ,1++=b a ab ,则b a 2+的最小值为( ) A . 323+ B . 323- C . 133+ D . 7 12.已知函数的定义域为,其图象关于点中心对称,其导函数,当时, ,则不等式的解集为( )A.B. C. D.第Ⅱ卷(非选择题共90分二、填空题:每小题各5分, 共20分.把答案填在答题卡的相应位置上. 13.函数x x x x f +=ln )(的单调递增区间是 .14.等差数列{}n a 的前n 项和为n S ,若121272=++a a a ,则=13S .15.若x ,y 满足约束条件25023050x y x y x +-≥⎧⎪-+≥⎨⎪-≤⎩,则z x y =+的最大值为__________.16.已知函数2242(0)()(0)x x x x f x x e x ⎧-++≥⎪=⎨-<⎪⎩,若函数()()2g x f x a =+恰有两个不同的零点,则实数a 的取值范围是 .9. 解答题:本大题共6题,共70分.请在答题卡指定区域内作答,解答时应写出证明过程或演算步骤.17. (本小题满分10分)n S 为等差数列{}n a 的前n 项和,已知115=a ,637=S(Ⅰ)求数列{}n a 的通项公式;()()sin f x x ωϕ=+0ω>2πϕ<π3π()f x 012π⎛⎫⎪⎝⎭,12x π=06π⎛⎫⎪⎝⎭,6x π=()f x R ()1,0-()f x '1x <-()()()()110x f x x f x '⎡⎤+++<⎣⎦()()10xf x f ->()1,+∞(),1-∞-()1,1-()(),11,-∞-⋃+∞(Ⅱ)设11+=n n n a a b ,数列{}n b 的前n 项和为n T ,求证61<n T .18. (本小题满分12分) 已知函数(Ⅰ)若求的值;(Ⅱ)求函数最小正周期及单调递减区间.19. (本小题满分12分)已知函数1)(2+++=bx ax e x f x,曲线)(x f y =在点))1(,1(f 处的切线方程为1)1(+-=x e y .(Ⅰ)求实数b a ,的值;(Ⅱ)求函数)(x f y =在[]2,1-的最值.20.(本小题满分12分)已知数列{}n a 满足11=a ,121+=+n n S a ,其中n S 为数列{}n a 的前n 项和. (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)设⎭⎬⎫⎩⎨⎧n n a b 是首项为1,公差为2的等差数列,求数列{}n b 的前n 项和n T .21. (本小题满分12分)如图,四边形ABCD 中90BAC ∠=o ,30ABC ∠=o ,AD CD ⊥,设ACD θ∠=. (Ⅰ)若ABC ∆面积是ACD ∆面积的4倍,求θ; (Ⅱ)若6ADB π∠=,求tan θ.22. (本小题满分12分) 已知函数1()()af x a R x+=∈. (Ⅰ) 设函数()ln ()h x a x x f x =--,求函数h (x )的极值;(Ⅱ) 若()ln g x a x x =-在[1,e]上存在一点x 0,使得00()()g x f x ≥成立,求a 的取值范围.高中三年文科数学试卷(答案)A. 选择题:(各5分, 共60分)二. 填空题(各5分, 共20分)13.2(,)e -+∞ ;(2[,)e -+∞也正确) 14. 52; 15. 9; 16. 22(3,1]{}e --⋃ 三、解答题:共70分17、解:(1)由设数列{}n a 的公差为d ,则1141172163a d a d +=⎧⎨+=⎩ ………………………………2分解得2d =, ……………………………………3分 13a = ……………………………4分所以{}n a 是首项为3,公差为2的等差数列,通项公式为2 1.n a n =+……………………………5分(2)由21n a n =+111111().(21)(23)22123n n b a a n n n n +===-++++ ……………………7分 12n n T b b b =+++L 61)32131(21)321121(...)7151()5131(21<+-=⎥⎦⎤⎢⎣⎡+-+++-+-=n n n ……………………………10分18、解:………………………………………2分=…………………………………………4分=…………………………………………6分(2)题号 1 2 3 4 5 6 7 8 9 10 11 12 答题CDBCCBACCBDC=…………………………………………8分的最小正周期为T=…………………………………………9分由,解得…………………………………………11分所以的单调递减区间为…………………12分19、解:(1),………………………………1分则,………………………………4分.………………………………6分 (2)的定义域为,,令,则,………………………………………………8分 (1)当时,,单调递减;(2)当时,,单调递增,………………………10分,∵,,且, ∴.………………………………………………12分20、解:(1).由,,当时,可得.…………………………1分当时,,两式相减得:,即,…………………………3分且.…………………………4分故是以1为首项,3为公比的等比数列。
福建省福州市八县一中高三上学期期中联考数学(理)试题(有答案)(精选)

第一学期八县(市)一中期中联考高中 三 年 数学科(理)试卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求,每小题选出答案后,请把答案填写在答题卡相应位置上...............。
1.设集合2{3,log }P a =,{,}Q a b =,若{0}PQ =,则P Q =( )A.{3,0}B.{3,0,1}C.{3,0,2}D.{3,0,1,2} 2.已知复数131iz i+=-,则下列说法正确的是( ) A.z 的共轭复数为12i -- B.z 的虚部为2iC.5z =D.z 在复平面内对应的点在第三象限 3.函数12()log cos ()22f x x x ππ=-<<的图象大致是( )4.直线4y x =与曲线3y x =在第一象限内围成的封闭图形的面积为( )A.2B.4C.22D.24 5.下列命题中正确的是( )A.命题p :“0x R ∃∈,200210x x -+<”,则命题p ⌝:x R ∀∈,2210x x -+>B .“ln ln a b >”是“22ab>”的充要条件C.命题“若22x =,则x =x =x ≠x ≠22x ≠”D.命题p :0x R ∃∈,001ln x x -<;命题q :对x R ∀∈,总有20x>;则p q ∧是真命题6.如图,,,D C B 在地平面同一直线上,10DC m =,从,D C 两地测得A 点的仰角分别为30︒和45︒,则A 点离地面的高AB 等于( )A.10mB.C.1)mD.1)m7.已知数列{}n a 是等比数列,数列{}n b 是等差数列,若1598a a a ⋅⋅=-,2586b b b π++=,则4637cos1b b a a +-⋅的值是( )A.12 B.2 C.12- D.2-8.ABC ∆的外接圆的圆心为O ,半径为1,0OA AB AC ++=且OA AB =,则向量CA 在CB方向上的投影为( )A.12 B.12- D.9.若函数()f x 同时满足以下三个性质;①()f x 的最小正周期为π;②对任意的x R ∈,都有()()4f x f x π-=-;③()f x 在3(,)82ππ上是减函数,则()f x 的解析式可能是A.()cos()8f x x π=+B.()sin 2cos2f x x x =+C.()sin cos f x x x =D.()sin 2cos 2f x x x =-10.已知数列{}n a ,{}n b ,满足11a =且1,n n a a +是函数2()2nn f x x b x =-+的两个零点,则10b 等于( )A.64B.48C.32D.2411.已知函数)(x f 是R 上的奇函数,且满足)()2(x f x f -=+,当[0,1]x ∈时,()21xf x =-,则方程6()log (3)f x x =-在),0(+∞解的个数是( )A.6B.5C.4D.312.设函数()f x 在R 上存在导数()f x ',x R ∀∈,有2()()f x f x x -+=,在(0,)+∞上()f x x '<,若(4)()84f m f m m --≥-.则实数m 的取值范围为( )A.[2,2]-B.[2,)+∞C.[0,)+∞D.(,2][2,)-∞-+∞二、填空题 :本大题共4小题,每小题5分,共20分,请把答案填在答题卡的横线上.............。
福建省福州市八县一中高三上学期期中联考数学(文)试题(有答案)(精选)

第一学期八县(市)一中期中联考高三年数学(文科)试卷完卷时间:120分钟 满分:150分一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求,每小题选出答案后,请把答案填写在答题卡相应位置上................ 1.已知M ={|02}x x <<,N =}1|{-=x y x ,则M N =( )A .{|02}x x <<B. {|12}x x ≤< C .{|0}x x >D. {|1}x x ≥2.复数z 与复数(12)i i -互为共轭复数,则z =( ) A .2i -+B .2i --C . 2i -D . 2i +3.已知命题:,sin cos p x R x x ∃∈+≥,命题2:,0q x R x ∀∈>,则( )A .命题p q ∨是假命题B .命题p q ∧是真命题C .命题()p q ∧⌝是假命题D .命题()p q ∧⌝是真命题4.已知等差数列{}n a 中,若241,5a a =-=-,则5S =( )A .-7B .-13C .-15D .-175.若0.52a =,ln2b =,13log 2c =,则( )A .a b c >>B .b a c >>C .c a b >>D .b c a >>6.函数4sin()(0,)y x ωϕωϕπ=+>< 部分图象如图,其中点A (23π,0),B (83π,0),则( ) A .1,3πωϕ==-B .1,23πωϕ==-C. 21,3πωϕ==D .12,23πωϕ==7.已知函数213log (2),2(),2x x f x xx -<⎧⎪=⎨⎪≥⎩ ,则不等式()2f x <的解集为( )A .{28}x x <<B .{22}x x -≤<C .{28}x x -<<D .{8}xx <8.M 是ABC ∆所在平面内一点,0MA MB MC ++=,D 为BC 中点,则ABCMBCS S ∆∆的值为( )A .12B .1C .2D .3 9.已知21(2),2+3()2p a a q b b b R a =+>=--∈-,则,p q 的大小关系为( ) A .p q ≥B .p q ≤C .p q >D .p q <10.为了得到函数cos(2)3y x π=+的图象,可将函数sin 2y x =的图象( )A .向左平移56π个单位长度B .向右平移56π个单位长度 C .向左平移512π个单位长度 D .向右平移512π个单位长度 11.已知函数()21,x f x a b c =-<<,且()()()f a f c f b >> ,则下列结论中,一定成立的是( ) A .222ac +<B .22ac -<C.0,0,0a b c <≥>D . 00,0a b c <<<,12.设()f x 是定义在R 上的增函数,且对任意x ,都有()()0f x f x -+=恒成立,如果实数,x y 满足不等式22(6)(412)0f x x f y y -+-+≤,那么2y x-的最大值是( ) A. 1 B. 2C.D.二、填空题:本大题共4小题,每小题5分,共20分,请把答案填在答题卡的横线上.............. 13.已知向量(1,1),(4,2),m n λ=+=-若//m n ,则=λ .14.已知,x y 满足约束条件2024010x y x y x y +-≥⎧⎪--≤⎨⎪-+≥⎩,则4z x y =-的最小值为 .15.已知n S 为等比数列{}n a 的前n 项和,0n a >,52S =,1514S =,则10S =________.16.给出下列命题:①已知x R ∈,则“1x >”是“2x >”的充分不必要条件; ②若a b a b +=-,则存在实数λ,使得b a λ=;③命题:p “,1xx R e x ∃∈>+”的否定是“,1xx R e x ∀∈<+”;④方程sin x x =有且只有一个实数解; ⑤函数()4cos 23f x x π⎛⎫=+⎪⎝⎭的一个对称中心为,03π⎛⎫⎪⎝⎭. 其中正确命题的序号是 (把你认为正确的序号都填上).三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤. 请在答题卡各自题目的答题区域内作答.................. 17.(本小题满分10分)已知正项数列{}n a 的前n 项和为n S ,且S n 、n a 、1成等差数列. (1)证明数列{}n a 是等比数列; (2)若2log 2n n b a =+,求数列⎭⎬⎫⎩⎨⎧+11n n b b 的前n 项和为n T .18.(本小题满分12分)已知向量(3sin ,cos )a x x =,(cos ,cos )b x x =-,()f x a b = , (1)求()f x 的最小正周期和单调递增区间; (2)若75(,)126x ππ∈,54a b =-,求cos2x 的值. 19.(本小题满分12分)围建一个面积为300 m 2的矩形场地,要求矩形场地的一面利用旧墙(旧墙足够长,利用旧墙需维修),其他三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2 m 的进出口,如图所示,已知旧墙的维修费用为75元/m ,新墙的造价为150元/m ,设利用的旧墙的长度为x m(x >0).(1)将总费用y 元表示为x m 的函数;(2)试确定x ,使修建此矩形场地围墙的总费用最小,并求最小总费用. 20.(本小题满分12分)在ABC ∆中,角,,A B C 的对边分别为,,a b c 且满足cos (2)cos b A c a B =-. (1)求角B 的大小;(2)若4,4b BA BC ==,求c a +的值.21.(本小题满分12分)等比数列{}n a 的前n 项和为n S ,且253,81a a ==, 等差数列{}n b 的前n 项和为n T ,23922n T n n =-.(1)求数列{}n a ,{}n b 的通项公式;(2)若对任意的n N *∈,1()2n n S k b +≥恒成立,求实数k 的取值范围.22.(本小题满分12分)已知函数2ln )(x x a x f += (a 为常数) .(1)当2a =-时,求()f x 的单调区间;(2)当(1,]x e ∈时,讨论方程()0=x f 根的个数; (3)若0>a ,且对任意的121211,,2x x x x e ⎡⎤∈≠⎢⎥⎣⎦且,都有()()121211f x f x x x -<-,求实数a 的取值范围. 2016---2017学年度第一学期八县(市)一中期中联考高三年数学(文科)卷参考答案一、选择题(每题5分,共60分) 1-12 BCDCA BCDAC AD 二、填空题(每题5分,共20分) 13. -3 14.1215. 6 16. ②④二、解答题(17题10分,18-22每题12分,共70分) 17.(本小题满分10分)(1)证明:由题意n S 、n a 、1成等差数列,∴ 21n n a S =+………………………1分 当1n =时,1121a S =+ 1a ∴= 1 ……………………………………………………2分 当2n ≥时,1121,21,n n n n S a S a --=-=-两式相减得111222(2)02(2)nn n n n n n n a a a a a a n a n a ---=-∴=≥≠∴=≥……………4分 因此数列{}n a 是以1为首项,以2为公比的等比数列…………………………………5分(2)解:由(1)知11122n n n a a --=⋅=122log 2log 221n n n b a n -∴=+=+=+…7分()()111111212n n b b n n n n +==-++++ ………………………………………………8分12111111...()()...()23341211.......................................................................................10222(2)n n T b b b n n n n n =+++=-+-++-++=-=++则分18.(本小题满分12分)2cos 21(1)()3sin cos cos sin 222x f x x x x x a b +=-=-=解:1sin(2) (36)2x π=--分 ()f x ∴的最小正周期是π ……………………………………………………………4分222()()26263()]() (66)3k x k k Z k x k k Z f x k k k Z πππππππππππππ-≤-≤+∈-≤≤+∈∴-+∈单调递增区间为[令得的,分1sin(2)sin(2)626cos(2)63)]53(2) (744)753(,),2(,)......8.. (66) (9126624)cos 2cos[(28a b x x x x x x x ππππππππππ=-∴-∴----=-=∈∴∈∴-==+-=分分分....12分 19(本小题满分12分)解:(1)设矩形的另一边长为a m ,则75150(2)1502225300300y x x ax a =+-+⋅=+- ………………2分 由已知xa =300,得300a x= ……………………………………………4分 ∴90000225300(0)y x x x=+-> ………………………………6分 (2)∵0x >,∴900002259000x x+≥= ……………8分 ∴900002253008700y x x =+-≥………………………………………10分 当且仅当90000225x x=即20x =时,等号成立.………………………11分 答:当20x m =时,修建围墙的总费用最小,最小总费用是8700元.…12分 20(本小题满分12分) 解:(1)cos (2)cos b A c a B=-由正弦定理得sin cos 2sin cos sin cos ...............................1sin()2sin cos sin . (31)sin 0cos (52)(0,)B A C B A B A B C B C C B B π=-+==≠∴=∈∴分分分 (63)B π=分(2)4cos 48....................................................8BA BC ca B ac =∴=∴=分由余弦定理得22222222cos ()3=()2416b a c ac B a c ac a c ac a c =+-=+-=+-+-= ………………………………………………………………………………………………….………………………………11分a c ∴+=…………………………………………………………………….……………………………….12分 21(本小题满分12分) 解(1)设数列{}n a 的公比为q . 由题意352812733a q q a ===∴= ∴2212333n n n n a a q ---==⋅=……………3分 2n ≥时,2213939(1)(1)362222n n nb T T n n n n n -⎡⎤=-=-----=-⎢⎥⎣⎦…………4分1n =时,1139322b T ==-=- 也适合上式 ………………………………………5分 综上,*36()n b n n N =-∈ …………………………………………………………6分(2)解法一:11(1)13311,1132n n n n a q a S q ---====-- …………………………7分∴311()3622n k n -+≥-对n N *∈恒成立,∴6123nn k -≥对n N *∀∈恒成立 ……8分 令max 362()3n n nn c k c -=≥⋅则 由111136332.5333639 3.533n n n n n n nn n n c c n c c n n n ++----⎧≥⎪≥≥⎧⎧⎪⇒⇒⎨⎨⎨≥--≤⎩⎩⎪≥⎪⎩2.53.5,3n n ∴≤≤∴= …………………………………………………………10分∴max 31()9n c c ==,即max 22()9n k c ≥= ……………………………………………11分 ∴实数的取值范围是2[,)9+∞. ……………………………………………………12分解法二:11(1)13311,1132n n n n a q a S q ---====-- ………………………………7分∴311()3622n k n -+≥-对n N *∈恒成立,∴6123nn k -≥对n N *∈恒成立………8分 令max 362()3n n n n c k c -=≥⋅则, 111363927333n n n n n n n n c c ------+-=-= 当3n ≤时,1n n c c ->,当4n ≥时, 1n n c c -< ………………………………………10分 ∴max 31()9n c c ==,即max 22()9n k c ≥= …………………………………………11分 ∴实数的取值范围是2[,)9+∞. ……………………………………………………12分 22. (本小题满分12分)解:当2a =-时,2()2ln f x x x =-+ 定义域为(0,)+∞ …………………………1分22222(1)(1)'()2..........................................................2'()001,')(+(01)x x x f x x x x xf x x f x x f x -+-=-+==<<<>>∴∞的单调递减区间为(0,1),单调递增区间(1,)............分得得..4分(2)方程()0=x f 根的个数等价于方程xx a ln 2=-根的个数.设()x g =xxln 2, xx x xx x x x x g 222ln )1ln 2(ln 1ln 2)(-=-=' ……………………………5分当()e x ,1∈时,0)(<'x g ,函数)(x g 递减,当]e e x ,(∈时,0)(>'x g ,函数)(x g 递增. 又2)(e e g =,e e g 2)(=,作出)(x g y =与直线a y -=的图象 ……………………6分 由图象知当22e a e ≤-<时,即e a e 22-<≤-时,方程()0=x f 有2个相异的根;当2e a -< 或e a 2-=时,方程()0=xf 有1个根;当e a 2->时,方程()0=x f 有0个根. ………………………………8分(3)当0>a 时,'()20a f x x x =+>,)(x f 在11,2x e ⎡⎤∈⎢⎥⎣⎦时是增函数,不妨设12112x x e ≤≤<,则()()121211f x f x x x -<-等价于211211()()f x f x x x -<-即212111()()f x f x x x +<+,故原题等价于函数()x x f x h 1)(+=在11,2x e ⎡⎤∈⎢⎥⎣⎦时是减函数…9分 012)(2≤-+='∴x x x a x h 恒成立,即221x x a -≤在11,2x e ⎡⎤∈⎢⎥⎣⎦时恒成立………………10分21()2x x x ϕ=-在11,2x e ⎡⎤∈⎢⎥⎣⎦时是减函数 13()22a ϕ∴≤= …………………………11分 3002a a >∴的取值范围是(,] ………………………………………………………12分。
2019-2020学年福建省福州市八县(市)一中高三(上)期中数学试卷1 (含答案解析)
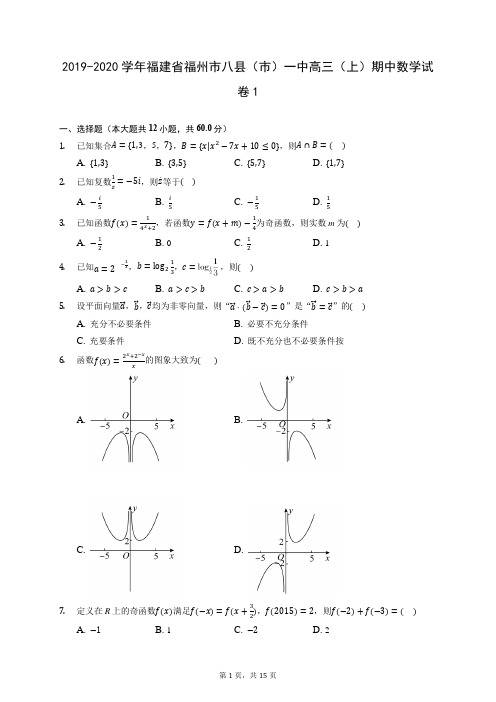
2019-2020学年福建省福州市八县(市)一中高三(上)期中数学试卷1一、选择题(本大题共12小题,共60.0分)1. 已知集合A ={1,3,5,7},B ={x|x 2−7x +10≤0},则A ∩B =( )A. {1,3}B. {3,5}C. {5,7}D. {1,7}2. 已知复数1z =−5i ,则z .等于( )A. −i5B. i5C. −15D. 153. 已知函数f(x)=14x +2,若函数y =f(x +m)−14为奇函数,则实数m 为( )A. −12B. 0C. 12D. 14. 已知a =2−13,b =log 213,c =,则( )A. a >b >cB. a >c >bC. c >a >bD. c >b >a5. 设平面向量a ⃗ ,b ⃗ ,c ⃗ 均为非零向量,则“a ⃗ ⋅(b ⃗ −c ⃗ )=0”是“b ⃗ =c ⃗ ”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件按6. 函数f(x)=2x +2−xx的图象大致为( )A.B.C.D.7. 定义在R 上的奇函数f(x)满足f(−x)=f(x +32),f(2015)=2,则f(−2)+f(−3)=( )A. −1B. 1C. −2D. 28. 在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且bcosC +ccosB =√2acosC ,则角C 为( )A. π6 B. π4 C. π3D. π29. 在△ABC 中,D 点为边BC 中点,记AB ⃗⃗⃗⃗⃗ =a ⃗ ,AC ⃗⃗⃗⃗⃗ =b ⃗ ,则AD ⃗⃗⃗⃗⃗⃗ =( ) A. 2(a ⃗ +b ⃗ )B. 2(a ⃗ −b ⃗ )C. 12(a⃗ −b ⃗ ) D. 12(a⃗ +b ⃗ ) 10. 已知函数f(x)=2sin(ωx +φ)(ω>0,0<φ<π)的最小正周期为π,若将f(x)的图象向右平移π6个单位后关于原点中心对称,则( )A. ω=2,φ=π3B. ω=2,φ=−2π3 C. ω=2,φ=π6D. ω=2,φ=2π311. 已知3a +2b =2(a >0,b >0),则ab 的最小值是( )A. 4B. 5C. 6D. 712. 已知定义在R 上的函数f(x)满足其导函数f′(x)<0在R 上恒成立,则不等式f(|x|)<f(1)的解集为( )A. (−1,1)B. (0,1)C. (1,+∞)D. (−∞,−1)∪(1,+∞)二、填空题(本大题共4小题,共20.0分)13. 已知函数f(x)=x 2−5x +2lnx ,则f(x)的单调递增区间为________14. 已知S n 为等差数列{a n }的前n 项和,且a 6+a 7=18,则S 12= ______ .(考点:数列的性质) 15. 若x ,y 满足约束条件{x −2y −2⩽0x −y +1⩾0y ⩽0,则z =3x +2y 的最大值为______.16. 已知函数f(x)={x +2,0⩽x <1,2x +12,x ⩾1,若a >b ⩾0,且f(a)=f(b),则bf(a)的取值范围是_________.三、解答题(本大题共6小题,共70.0分) 17. 在等差数列{a n }中,a 1=−8,a 2=3a 4.(1)求数列{a n }的通项公式;(2)设b n =4n(14+a n)(n ∈N ∗),T n 为数列{b n }的前n 项和,若T n =7255,求n 的值.)18.已知函数f(x)=2cos2x−cos(2x+π2)的值;(Ⅰ)求f(π8(Ⅱ)求函数f(x)的最小正周期及单调递减区间.19.已知函数f(x)=e x,g(x)=lnx.(1)求函数y=g(x)在点A(1,0)处的切线方程;(2)已知函数ℎ(x)=f(x−a)−g(x+a)(a>0)区间(0,+∞)上的最小值为1,求实数a的值.20.已知等比数列{a n}的前n项和为S n,且6S n=3n+1+a(n∈N∗).(1)求a的值及数列{a n}的通项公式;(2)若b n=(3n+1)a n,求数列{b n}的前n项和T n.21.如图所示的四边形ABCD中,已知AB⊥AD,∠ABC=120°,∠ACD=60°,AD=27,设∠ACB=θ,C点到AD的距离为h.(Ⅰ)求ℎ(用θ表示)(Ⅱ)求AB+BC的最大值.22.已知函数f(x)=xln(x+a),a∈R.(1)若f(x)不存在极值点,求a的取值范围;(2)若a≤0,证明:f(x)<e x+sin x−1.-------- 答案与解析 --------1.答案:B解析:解:B={x|2≤x≤5};∴A∩B={3,5}.故选:B.可解出集合B,然后进行交集的运算即可.考查描述法、列举法的定义,一元二次不等式的解法,交集的运算.2.答案:A解析:解:∵1z =−5i,∴z=i5,∴z.=−i5,故选:A.利用复数的运算法则、共轭复数的定义即可得出.本题考查了复数的运算法则、共轭复数的定义,考查了推理能力与计算能力,属于基础题.3.答案:C解析:本题主要考查函数奇偶性的应用以及指数方程的求解,根据g(x)=f(x+m)−14为奇函数,利用g(0)=0建立方程关系是解决本题的关键.解:设g(x)=f(x+m)−14,则g(x)的定义域为R,∵g(x)=f(x+m)−14为奇函数,∴g(0)=f(m)−14=0,即f(m)=14m+2=14,即4m+2=4,∴4m=2,解得m=12,故选:C.4.答案:C解析:【分析】本题主要考查指数函数和对数函数的性质,属于基础题.解题的关键是借助指数函数和对数函数的单调性得出a, b,c与0,1这样的特殊值的大小关系,从而得出答案. 【解答】 解: ,,,∴c >a >b , 故选C .5.答案:B解析: 【分析】根据向量的数量积关系,以及充分条件和必要条件的定义进行判断即可得到结论.本题主要考查充分条件和必要条件的判断,利用向量的数量积是解决本题的关键,比较基础. 【解答】解:若b ⃗ =c ⃗ ,则a ⃗ ⋅(b ⃗ −c ⃗ )=0成立,必要性成立,若a ⃗ ⋅(b ⃗ −c ⃗ )=0得,a ⃗ ⋅b ⃗ =a ⃗ ⋅c ⃗ ,则b ⃗ =c ⃗ 不一定成立,充分性不成立. 故“a ⃗ ⋅(b ⃗ −c ⃗ )=0”是“b ⃗ =c ⃗ ”的必要而不充分条件, 故选:B .6.答案:D解析: 【分析】本题考查函数图象,考查函数的奇偶性,属于简单题. 依题意,函数f(x)=2x +2−xx为奇函数,排除A ,C ,又x >0时,f(x)>0,排除B ,即可求得结果.【解答】解:函数f(−x)=−2x +2−xx =−f(x),得函数为奇函数,排除A ,C ,又x >0时,f(x)>0, 排除B , 故选D .7.答案:C解析:解:由f(x)为奇函数可得f(−x)=−f(x), 再由条件可得−f(x)=f(32+x),所以,f(3+x)=f[32+(32+x)]=−f(x +32)=f(x), 则函数f(x)的最小正周期是3, f(2015)=f(3×671+2)=f(2)=2, 即有f(−2)=−f(2)=−2, f(−3)=f(0)=0, 则f(−2)+f(−3)=−2. 故选C .由已知得f(3+x)=f(x),所以f(2015)=f(671×3+2)=f(2)=2.运用奇函数的性质f(0)=0,f(−2)=−f(2),即可得到结论.本题主要考查函数奇偶性和周期性的定义和性质,考查函数值的求法,属于中档题.8.答案:B解析: 【分析】此题考查了正弦定理,三角形的面积公式,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键.利用正弦定理化简已知等式,再利用两角和与差的正弦函数公式化简后,根据sin A 不为0,求出cos C 的值,即可确定出C 的度数. 【解答】解:已知等式利用正弦定理化简得:sinBcosC +sinCcosB =sin A cos C ,即sin(B +C)=sin A cos C ,变形得:sinA =sin A cos C ,∵sinA ≠0,∴cosC =,∴由C ∈(0,π),可得∠C =.故选B .9.答案:D解析:解:△ABC 中,D 点为边BC 中点,记AB ⃗⃗⃗⃗⃗ =a ⃗ ,AC ⃗⃗⃗⃗⃗ =b ⃗ ,则AD ⃗⃗⃗⃗⃗⃗ =12(AB ⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ )=12(a ⃗ +b ⃗ ), 故选:D .根据向量的加减的几何意义即可求出本题考查了向量的加减的几何意义,属于基础题10.答案:A解析:【分析】本题主要考查三角函数解析式的求解以及三角函数的性质的应用,根据条件求出函数的解析式是解决本题的关键.【解答】解:∵函数f(x)的最小正周期是π,∴T=2πω=π,解得ω=2,即f(x)=2sin(2x+φ),将其图象向右平移π6个单位后得到y=2sin[2(x−π6)+φ)]=2sin(2x−π3+φ),若此时函数关于原点对称,则−π3+φ=kπ,k∈Z即φ=π3+kπ,k∈Z∵0<φ<π,∴φ=π3,故选A.11.答案:C解析:【分析】本题考查了基本不等式的性质,考查了推理能力与计算能力,属于基础题.利用基本不等式的性质即可得出.【解答】解:∵3a +2b=2(a>0,b>0),∴2=3a +2b≥2√3a⋅2b,化为ab≥6,当且仅当a=3,b=2时取等号.∴ab的最小值是6.故选:C.12.答案:D解析:解:定义在R上的函数f(x)满足其导函数f′(x)<0在R上恒成立,可知函数f(x)是减函数,函数y=f(|x|)是偶函数,当x>0时,可得x>1,当x<0时,可得x<−1,则不等式f(|x|)<f(1)的解集为:(−∞,−1)∪(1,+∞).故选:D.利用函数的导数判断函数的单调性,结合不等式转化求解即可.本题考查函数的导数判断函数的单调性,不等式的解法,考查计算能力.13.答案:(0,12)和(2,+∞)解析: 【分析】本题考查利用导数研究函数的单调性,解决问题的关键是求导,结合导数的概念求解单调区间. 【解答】解:由题f′(x )=2x −5+2x =2x 2−5x+2x(x >0),令f′(x)>0可得{2x 2−5x +2>0x >0,∴x ∈(0,12)∪(2,+∞),故所求函数单调递增区间为(0,12)和(2,+∞), 故答案为(0,12)和(2,+∞).14.答案:108解析:解:在等差数列{a n }中,由a 6+a 7=18,得a 1+a 12=a 6+a 7=18, ∴S 12=(a 1+a 12)×122=182×12=108.故答案为:108.由已知结合等差数列的性质求得a 1+a 12,然后代入等差数列的前n 项和得答案. 本题考查等差数列的性质,考查了等差数列的前n 项和,是基础题.15.答案:6解析: 【分析】本题主要考查了线性规划,以及二元一次不等式组表示平面区域的知识,数形结合的思想方法,属于基础题.先画出线性约束条件表示的可行域,再将目标函数赋予几何意义,最后利用数形结合即可得目标函数的最值. 【解答】解:由变量x ,y 满足约束条件{x −2y −2⩽0x −y +1⩾0y ⩽0,作出可行域如图中阴影部分:,由z =3x +2y 得y =−32x +12z , 作出直线y =−32x 并平行移动结合z 的几何意义,可知当直线y =−32x +12z 经过点A 时,z 取得最大值, 由{x −2y −2=0y =0得{x =2y =0,故点A(2,0),∴z max =3×2+0=6. 故答案为6.16.答案:[54,3)解析: 【分析】画出函数f(x)={x +2,0⩽x <1,2x +12,x ⩾1,的图象,利用已知a >b ⩾0,且f(a)=f(b),可得b 、f(a)的取值范围,进而得出bf(a)的取值范围. 【解答】解:画出函数f(x)={x +2,0⩽x <1,2x +12,x ⩾1,的图象, 要使a >b ⩾0,且f(a)=f(b), 令b +2=2+12,计算得出b =12, 所以12≤b <1.则bf (a )=bf (b )=b 2+2b =(b +1)2−1. 因为12≤b <1,所以54≤bf (a )<3, 所以答案为[54,3).17.答案:解:(1)设等差数列{a n }的公差为d ,则a 2=−8+d ,a 4=−8+3d , ∵a 2=3a 4,∴−8+d =3(−8+3d),解得d =2, ∴a n =−10+2n ; (2)∵b n =4n(14+a n )=4n⋅(2n+4)=1n −1n+2,∴T n =(1−13)+(12−14)+⋯+(1n+1n+2)=1+12−1n+1−1n+2=7255,解得n =9.解析:本题主要考查了等差数列的通项公式和裂项相消法求和,属于基础题. (1)根据等差数列的通项计算即可;(2)求出数列{b n }的通项公式,根据裂项相消法即可得到结果.18.答案:解:(Ⅰ)因为f(x)=2cos 2x −cos(2x +π2)=2cos 2x +sin2x=1+cos2x +sin2x=√2sin(2x +π4)+1所以f(π8)=√2sin(π4+π4)+1=√2+1 (Ⅱ)因为f(x)=√2sin(2x +π4)+1 所以T =2π2=π又y =sinx 的单调递减区间为(2kπ+π2,2kπ+3π2),(k ∈Z)所以令2kπ+π2<2x +π4<2kπ+3π2解得kπ+π8<x <kπ+5π8所以函数f(x)的单调减区间为(kπ+π8,kπ+5π8),(k ∈Z)解析:(Ⅰ)通过二倍角公式以及两角和的正弦函数化简函数为一个角的一个三角函数的形式,然后求f(π8)的值;(Ⅱ)直接利用正弦函数的周期的求法,以及三角函数的单调性直接求函数f(x)的单调递减区间. 本题考查两角和的正弦函数与二倍角公式的应用,三角函数的周期的求法,单调区间的求法,考查计算能力.19.答案:解:(1)g ′(x)=1x ,g′(1)=1,则函数y =g(x)在点A(1,0)处的切线方程为y =x −1;……………(4分)(2)ℎ(x)=f(x −a)−g(x +a)=e x−a −ln(x +a)(a >0),ℎ′(x)=e x−a −1x+a ,∵e x−a 在区间(0,+∞)上单调递增,1x+a 在区间(0,+∞)上单调递减,存在唯一的x 0∈(0,+∞), 使得ℎ′(x 0)=e x 0−a −1x+a=0,即e x 0−a =1x 0+a(∗),……………(7分)函数ℎ′(x)=e x−a −1x+a 在(0,+∞)上单调递增,∴x ∈(0,x 0)时,ℎ′(x)<0,ℎ(x)单调递减;x ∈(x 0,+∞)时,ℎ′(x)>0,单调递增,∴ℎ(x)min =ℎ(x 0)=e x 0−a −ln(x 0+a),由(∗)式得, ∴ℎ(x)min =ℎ(x 0)=1x 0+a−ln(x 0+a),……………(9分)1x 0+a−ln(x 0+a)=1,显然x 0+a =1是方程的解,又∵y =1x −lnx 是单调减函数,方程1x 0+a−ln(x 0+a)=1有且仅有唯一的解x 0+a =1,把x 0=1−a 代入(∗)式得,e 1−2a =1,∴a =12,所求实数a 的值为12.…………………………(12分)解法2:ℎ(x)=f(x −a)−g(x +a)=e x−a −ln(x +a)(a >0),ℎ′(x)=e x−a −1x+a , ∵e x−a 在区间(0,+∞)上单调递增,1x+a 在区间(0,+∞)上单调递减,存在唯一的x 0∈(0,+∞), 使得ℎ′(x 0)=e x 0−a −1x+a=0,即e x 0−a=1x 0+a(∗),……………(7分)函数ℎ′(x)=e x−a −1x+a 在(0,+∞)上单调递增,∴x ∈(0,x 0)时,ℎ′(x)<0,ℎ(x)单调递减;x ∈(x 0,+∞)时,ℎ′(x)>0,单调递增,∴ℎ(x)min =ℎ(x 0)=e x 0−a −ln(x 0+a),由e x 0−a =1x 0+a 式得x 0−a =−ln(x 0+a),∴ℎ(x)min =ℎ(x 0)=e x 0−a −ln(x 0+a)=1x 0+a+x 0−a≥2√1x 0+a⋅(x 0+a)−2a =2−2a ,(当且仅当x 0+a =1时ℎ(x 0)=2−2a),由2−2a =1得a =12,此时x 0=12,把a =12,x 0=12代入(∗)也成立,∴实数a 的值为12.…………………………(12分)解析:(1)求出导函数,得到切线的斜率,然后求解切线方程.(2)化简函数的解析式,求出导函数,判断函数的单调性,求解函数的最小值,然后推出a 的范围即可.解法2:ℎ(x)=f(x −a)−g(x +a)=e x−a −ln(x +a)(a >0),ℎ′(x)=e x−a −1x+a ,判断函数的单调性,求解函数的最小值,利用基本不等式转化求解即可.本题考查函数的导数的应用,函数的极值以及函数的最值的求法,考查转化思想以及计算能力.20.答案:解:(1)∵6S n =3n+1+a(n ∈N ∗),∴当n =1时,6S 1=6a 1=9+a ;当n ≥2时,6a n =6(S n −S n−1)=2×3n , 即a n =3n−1, ∵{a n }为等比数列,∴a 1=1,则9+a =6,a =−3, ∴{a n }的通项公式为a n =3n−1.(2)由(1)得b n=(3n+1)3n−1,∴T n=b1+b2+⋯+b n=4×30+7×31+⋯+(3n+1)3n−1,①3T n=4×31+7×32+⋯+ (3n−2)3n−1+(3n−1)3n,②∴①−②得:−2T n=4+32+33+⋯+3n−(3n+1)3n,∴T n=(6n−1)⋅3n+14.解析:(1)直接利用已知条件求出数列的通项公式.(2)利用乘公比错位相减法求出数列的和.本题考查的知识要点:数列的通项公式的求法及应用,乘公比错位相减法在数列求和中的应用.21.答案:解:(Ⅰ)由已知得:∠ADC=360°−(90°+120°+60°+θ)=90°−θ…1分在△ACD中,ADsin∠ACD =ACsin∠ADC…3分∴AC=27cosθsin60°=18√3cosθ…4分又∠CAD=30°+θ,且0<θ<60°,∴ℎ=AC⋅sin∠CAD=18√3cosθsin(30°+θ),(0<θ<60°)…6分(Ⅱ)在△ABC中,AB=ACsinθsin120°=18sin2θ,…7分BC=ACsin(60°−θ)sin120°=36cosθsin(60°−θ)=9√3+9√3cos2θ−9sin2θ…8分∴AB+BC=9√3+9√3cos2θ+9sin2θ=9√3+18sin(2θ+60°)…10分∵0<θ<60°,…11分∴当θ=15°时,AB+BC取到最大值9√3+18…12分.解析:(Ⅰ)由已知k可求∠ADC=90°−θ,在△ACD中,由正弦定理可求AC的值,又∠CAD=30°+θ,且0<θ<60°,由ℎ=AC⋅sin∠CAD即可得解.(Ⅱ)在△ABC中,由正弦定理分别求出AB,BC,将AB+BC表示成9√3+18sin(2θ+60°),由正弦函数的图象和性质即可得解.本题主要考查了正弦定理,同角三角函数关系式,正弦函数的图象和性质的应用,解题时注意分析角的范围,属于基本知识的考查.22.答案:解:(1)f(x)的定义域为(−a,+∞),且f′(x)=ln(x+a)+xx+a,设g(x)=ln(x+a)+xx+a ,则g′(x)=1x+a+a(x+a)2=x+2a(x+a)2.[1]当−2a≤−a,即a≥0时,gˈ(x)>0,所以g(x)在(−a,+∞)上单调递增;又g(1)=ln(1+a)+11+a>0,g(e−2−a)=−1−e2a<0,即g(1)g(e−2−a)<0,所以g(x)在(−a,+∞)上恰有一个零点x0,且当x∈(−a,x0)时,fˈ(x)=g(x)<0;当x∈(x0,+∞)时,fˈ(x)=g(x)>0;所以f(x)在(−a,x0)上单调递减,在(x0,+∞)上单调递增,所以x0是f(x)的极小值点,不合题意,[2]当−2a>−a,即a<0时,令gˈ(x)=0,得x=−2a,当x∈(−a,−2a)时,gˈ(x)<0,当x∈(−2a,+∞)时,gˈ(x)>0;即g(x)在(−a,−2a)上单调递减,在(−2a,+∞)上单调递增.①当g(−a)=ln(−a)+2≥0,即a≤−e−2时,fˈ(x)=g(x)≥g(−2a)≥0恒成立,即f(x)在(−a,+∞)上单调递增,无极值点,符合题意.②当g(−2a)=ln(−a)+2<0,即−e−2<a<0时,g(1−a)=1−a>0,所以g(−2a)g(1−a)<0,所以g(x)在(−2a,+∞)上恰有一个零点x1,且当x∈(−2a,x1)时,fˈ(x)=g(x)<0;当x∈(x1,+∞)时,fˈ(x)=g(x)>0;即f(x)在(−2a,x1)上单调递减,在(x1,+∞)上单调递增,所以x1是f(x)的极小值点,不合题意.综上,a的取值范围是(−∞,−e−2];(2)因为a≤0,x>−a,所以x>0,f(x)=xln(x+a)≤xlnx,要证明f(x)<e x+sinx−1,只需证明xlnx<e x+sinx−1,当a<x≤1时,因为e x+sinx−1>0,xlnx≤0,所以xlnx<e x+sinx−1成立;当x>1时,设g(x)=e x+sinx−xlnx−1,则gˈ(x)=e x−lnx+cosx−1,−sinx,设ℎ(x)=gˈ(x),则ℎ′(x)=e x−1x因为x>1,所以ℎˈ(x)>e−1−1>0,所以ℎ(x)在[1,+∞)上单调递增,所以ℎ(x)>ℎ(1)=e+cos1−1>0,即gˈ(x)>0,所以g(x)在[1,+∞)上单调递增,所以g(x)>g(1)>=e+sin1−1>0,即xlnx<e x+sinx−1,综上,若a≤0,则f(x)<e x+sinx−1解析:本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道综合题.(1)求出函数的导数,通过讨论a的范围,根据函数的单调性求出a的范围即可.(2)设g(x)=e x+sinx−xlnx−1,根据函数的单调性证明即可.。
2019-2020学年福建省福州市八县(市、区)高一(上)期中数学试卷

2019-2020学年福建省福州市八县(市、区)高一(上)期中数学试卷一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合题目要求.)1. 设全集U ={1, 2, 3, 4, 5},集合A ={1, 2, 4},集合B ={2, 5},则(∁U A)∩B 等于( ) A.{3} B.{3, 5} C.{3, 4, 5} D.{5}2. 下列函数与函数y =x 表示同一个函数的是( ) A.y =(x 2)12B.y =lg 10xC.y =e ln xD.y =x 2⋅x −13. 利用二分法求方程log 3x =5−x 的近似解,可以取得一个区间( ) A.(0, 1) B.(1, 2) C.(2, 3) D.(3, 4)4. 函数f(x)=√x−1lg (2−x)的定义域是( ) A.(1, 2) B.[1, 2) C.(1, 2] D.[1, 2]5. 已知a =log 231.2,b =(23)−0.8,c =1.2−23,则a ,b ,c 的大小关系为( )A.a <b <cB.a <c <bC.b <c <aD.b <a <c6. 已知a >0且a ≠1,函数y =a x 与y =log a (−x)的图象可能是( )A. B. C. D.7. 有下列各式:①(√a n)n =a ;②x −34=√(1x)43;③a 34⋅a 43=a ;④√a 2+b 24=√a +b其中正确的个数是( ) A.0 B.1 C.2 D.38. 已知集合A ={x|ax −3=0},B ={x ∈N|−2≤log 12x <−1},且A ⊆B ,则实数a的所有值构成的集合是( )A.{0,1,34}B.{0,1,43}C.{1,34}D.{1,43}9. 已知f(x +1)是偶函数且在[0, +∞)上是单调递增,且满足f(2)=0,则不等式f(2x −1)≥0的解集是( ) A.(−∞, 0]∪[1, +∞) B.(−∞,12]∪[32,+∞) C.[32,+∞) D.(−∞,−32]∪[32,+∞)10. 已知函数f(x)={a −x ,x <−1(1−2a)x +3a,x ≥−1,对任意的x 1,x 2∈R(x 1≠x 2),总有f(x 1)−f(x 2)x 1−x 2>0成立,则实数a 的取值范围是( )A.(0,14]B.(0,12)C.[14,12)D.(12,1)11. 已知函数f(x)=|(12)x −2|+b 的两个零点分别为x 1,x 2(x 1<x 2),则下列结论正确的是( )A.−2<x 1<−1,x 1+x 2>−2B.−2<x 1<−1,x 1+x 2>−1C.x 1<−2,x 1+x 2>−2D.x 1<−2,x 1+x 2>−112. 若函数f(x)=lg (x 2−(2a −1)x +a 2+1)的定义域为R ,且当x >12时,f(1−x)<f(x),则实数a 的取值范围是( ) A.(−34,+∞)B.(−∞, 1)C.(−34,1]D.(12,+∞)二、填空题(本大题共4小题,每小题5分,共20分.请把答案填在答题卡相应位置.)设f(x 3)=ln x ,则f(e)=________13 .幂函数f(x)=x α的图象经过点(2,18),则函数y =log a (x −α)+2(a >0且a ≠1)的图象恒过的定点A 的坐标为________.已知函数f(x)为奇函数,当x >0时,f(x)=x 2+1x ,则当x <0时,f(x)=________.已知函数f(x)=2019x −2019−x +1,则不等式f(2x −1)+f(2x)>2的解集为________.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)计算:(1)lg 5⋅lg 20−lg 2⋅lg 50−lg 25;(2)(179)−12−(√3−1)ln 1+log 3√34+5log 153.已知集合A ={x|18<2x+1<64},B ={x|−3<x <6},C ={x|m −1≤x ≤2m +1},(m ∈R ). (1)求集合A ∪B ;(2)若C ⊆(A ∩B),求实数m 的取值范围.设函数f(x)与g(x)的定义域是{x|x ∈R 且x ≠±1},f(x)是偶函数,g(x)是奇函数,且f(x)+g(x)=x x−1.(1)求f(x)与g(x)的解析式;(2)求f(12)+f(13)+f(14)+f(2)+f(3)+f(4)的值.为响应习主席提出的“绿水青山,就是金山银山”,我省决定净化闽江上游水域的水质.省环保局于2018年年底在闽江上游水域投入一些蒲草,这些蒲草在水中的蔓延速度越来越快,2019年3月底测得蒲草覆盖面积为36m 2,2019年4月底测得蒲草覆盖面积为54m 2,蒲草覆盖面积y (单位:m 2)与月份x (单位:月)的关系有两个函数模型y =ka x (k >0, a >1)与y =mx 2+n(m >0)可供选择. (1)分别求出两个函数模型的解析式;(2)若省环保局在2018年年底投放了11m 2的蒲草,从上述两个函数模型中选择更合适的一个模型,求蒲草覆盖面积达到320m 2的最小月份? (参考数据:lg 2≈0.30,lg 3≈0.48).已知函数f(x)的定义域为R ,对任意的实数m 、n 均有f(m +n)=f(m)+f(n)−1,且当x >0时,f(x)>1.(1)用定义证明f(x)的单调性.(2)求满足不等式f(x)+f(x−2)>2的x的取值范围.已知函数f(x)=log2(4x+1)−kx是偶函数.(1)求实数k的值;(2)设函数g(x)=log(m⋅2x−2m),若方程f(x)−g(x)=0只有一个实数根,求实数2m的取值范围.参考答案与试题解析2019-2020学年福建省福州市八县(市、区)高一(上)期中数学试卷一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合题目要求.)1.【答案】D2.【答案】B3.【答案】D4.【答案】A5.【答案】B6.【答案】B7.【答案】B8.【答案】A9.【答案】B10.【答案】A11.【答案】A12.【答案】C二、填空题(本大题共4小题,每小题5分,共20分.请把答案填在答题卡相应位置.) 【答案】 13【答案】 (−2, 2) 【答案】 −x 2+1x【答案】(14, +∞) 三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 【答案】lg 5⋅lg 20−lg 2⋅lg 50−lg 25=(1−lg 2)(1+lg 2)−lg 2⋅(2−lg 2)−(2−2lg 2), =1−lg 22−2lg 2+lg 22+2lg 2−2, =−1;(179)−12−(√3−1)ln 1+log 3√34+5log 153,=(916)12−(√3−1)0+14log 33+5log 513,=34−1+14+13=13. 【答案】解:(1)A ={x|18<2x+1<64}={x|−3<x +1<6} ={x|−4<x <5}, B ={x|−3<x <6},则A ∪B ={x|−4<x <6}. (2)A ∩B ={x|−3<x <5}, 若C ⊆(A ∩B),则当C =⌀时,即m −1>2m +1得m <−2时,成立; 当C ≠⌀时,即m ≥−2时,要使C ⊆(A ∩B),则{m ≥−2,2m +1<5,m −1>−3,得{m ≥−2,m <2,m >−2,得−2<m <2.综上,m 的取值范围是{m|m <−2或−2<m <2}. 【答案】根据题意,f(x)+g(x)=xx−1,则f(−x)+g(−x)=−x−x−1=xx+1,又由f(x)是偶函数,g(x)是奇函数,则f(−x)+g(−x)=f(x)−g(x)=xx+1, 联立两式解可得:f(x)=x 2x 2−1,g(x)=xx 2−1;由(1)的结论,f(x)=x 2x 2−1,则f(1x )=1x 21x 2−1=11−x 2=−1x 2−1,则有f(x)+f(1x)=x 2x 2−1+−1x 2−1=1,则f(12)+f(13)+f(14)+f(2)+f(3)+f(4)=f(12)+f(2)+f(13)+f(3)+f(14)+f(4)=3.【答案】若选择模型y =ka x ,则{ka 3=36ka 4=54,解得a =32,k =323, 故函数模型为y =323⋅(32)x .若选择模型y =mx 2+n ,则{9m +n =3616m +n =54,解得m =187,n =907,故函数模型为y =187x 2+907.把x =0代入y =323⋅(32)x 可得y =323, 把x =0代入y =187x 2+907可得y =907,∵ |323−11|<|907−11|,故选择模型y =323⋅(32)x 更合适.令323⋅(32)x ≥320,可得(32)x ≥30,两边取对数可得x lg 32≥lg 30, 即x ≥lg 30lg 32=lg 3+1lg 3−lg 2=0.48+10.48−0.30≈8.2,故蒲草覆盖面积达到320m 2的最小月份为2019年9月.【答案】证明:∀x 1>x 2,x 1−x 2>0,所以f(x 1−x 2)>1,f(x 1)−f(x 2)=f(x 1−x 2+x 2)−f(x 2)=f(x 1−x 2)+f(x 2)−1−f(x 2)=f(x 1−x 2)−1>0,所以f(x 1)>f(x 2),所以f(x)在(−∞, +∞)上单调递增; 令m =n =0,f(0)=2f(0)−1,所以f(0)=1,因为f(x)+f(x −2)>2,所以f(x)+f(x −2)−1>1,即f(x +x −2)>f(0), 解得x >1,综上:x 的取值范围(1, +∞).【答案】解:(1)根据题意,f(x)为偶函数,则f(−x)=f(x), 则f(−1)=f(1),即log 25−k =log 2(14+1)+k ,解得:k =1. 故k 的值是1.(2)方程f(x)−g(x)=0只有一个实数根,即log 2(4x +1)−x =g(x)=log 2(m ⋅2x −2m), 亦即log 24x +12x=log 2(m ⋅2x −2m), 则m =2x +2−x 2x −2只有一个实数根,设2x −2=t ,则2x =t +2(t >−2), ∴ m =t+2+1t+2t=t 2+4t+5t 2+2t=1+2t +5t 2+2t=1+1t 2+2t 2t +5=1+42t+5+52t+5−6,令μ=2t +5,μ>1, 则m =1+4μ+5μ−6,则4m−1+6=μ+5μ,作出y =μ+5μ(μ>1)的图象如下图所示,由图象可知,4m−1+6=2√5或4m−1+6≥6, ∴ m =−√5+12或m >1.。
福建省福州市八县(市、区)一中2020届高三上学期期中联考化学试题

2019-2020学年第一学期八县(市、区)期中联考高中三年化学科试卷考试时间:8:00-9:30 完卷时间:90分钟满分:100分可能用到的相对原子质量: P—31 N—14 O—16 Cl—35.5 S—32 Al—27 Fe—56 Mn —55 K —39 Cu —64一、选择题(每题只有一个正确选项,每题2分,21小题,共42分)1.习总书记多次强调要“像对待生命一样对待生态环境”。
下列说法正确的是( )A.赤潮是海水富营养化,藻类大量繁殖,这些藻类生长消耗大量氧气,造成水体缺氧B.汽车尾气的大量排放是造成雾霾天气的人为因素之一C.用施撒熟石灰的方法可改良碱性土壤D.用明矾可消除水中Cu2+等重金属离子污染2.化学与人类生产、生活密切相关,下列说法正确的是( )A. 医用酒精、次氯酸钠等消毒液均可以将病毒氧化而达到消毒的目的B. 铁粉和生石灰均可作食品袋内的脱氧剂C. 燃料的脱硫脱氮、SO2的回收利用和NOx的催化转化都是减少酸雨产生的措施D. 高纤维食物是富含膳食纤维的食物,在人体内都可通过水解反应提供能量3.下列说法正确的是( )A.液态 HCl、固态 AgCl 均不导电,所以 HCl、AgCl 是非电解质B.NH3、CO2的水溶液均能导电,所以 NH3、CO2均是电解质C.福尔马林、水玻璃、氨水均为混合物D.金属氧化物一定是碱性氧化物4.设N A为阿伏加德罗常数,下列叙述正确的是()A.标准状况下,33.6 L氟化氢中含有氟原子的数目为1.5 N AB.阿伏加德罗常数的基准物是0.012kg的CC.1L 0.1 mol.L-1的NaHCO3 溶液中HCO3- 和CO32- 离子数之和为0.1N AD. 31克白磷含有的共价键数目为1.5 N A5.V L浓度为0.5 mol·L-1的盐酸,欲使其浓度增大1倍,采取的措施合理的是( )A. 通入标准状况下的HCl气体11.2V LB. 将溶液加热浓缩到0.5V LC. 加入10 mol.L-1的盐酸0.1V L,再稀释至1.5V LD. 加入V L 1.5 mol.L -1的盐酸混合均匀6.下列实验操作规范且能达到目的的是( )7.在硫酸工业生产中,为了有利于SO 2的转化,且能充分利用热能,采用了中间有热交换器的接触室(见右图)。
福建省福州市八县一中高三上学期期中联考数学(理)试题(有答案)

第一学期八县(市)一中期中联考高中 三 年 数学科(理)试卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求,每小题选出答案后,请把答案填写在答题卡相应位置上...............。
1.设集合2{3,log }P a =,{,}Q a b =,若{0}PQ =,则P Q =( )A.{3,0}B.{3,0,1}C.{3,0,2}D.{3,0,1,2} 2.已知复数131iz i+=-,则下列说法正确的是( ) A.z 的共轭复数为12i -- B.z 的虚部为2iC.5z =D.z 在复平面内对应的点在第三象限 3.函数12()log cos ()22f x x x ππ=-<<的图象大致是( )4.直线4y x =与曲线3y x =在第一象限内围成的封闭图形的面积为( )A.2B.4C.22D.24 5.下列命题中正确的是( )A.命题p :“0x R ∃∈,200210x x -+<”,则命题p ⌝:x R ∀∈,2210x x -+>B .“ln ln a b >”是“22ab>”的充要条件C.命题“若22x =,则x =x =的逆否命题是“若x ≠x ≠则22x ≠”D.命题p :0x R ∃∈,001ln x x -<;命题q :对x R ∀∈,总有20x>;则p q ∧是真命题6.如图,,,D C B 在地平面同一直线上,10DC m =,从,D C 两地测得A 点的仰角分别为30︒和45︒,则A 点离地面的高AB 等于( )A.10mB.C.1)mD.1)m7.已知数列{}n a 是等比数列,数列{}n b 是等差数列,若1598a a a ⋅⋅=-,2586b b b π++=,则4637cos1b b a a +-⋅的值是( )A.12 B.2 C.12- D.2-8.ABC ∆的外接圆的圆心为O ,半径为1,0OA AB AC ++=且OA AB =,则向量CA 在CB 方向上的投影为( )A.12 B.12- D.9.若函数()f x 同时满足以下三个性质;①()f x 的最小正周期为π;②对任意的x R ∈,都有()()4f x f x π-=-;③()f x 在3(,)82ππ上是减函数,则()f x 的解析式可能是A.()cos()8f x x π=+B.()sin 2cos2f x x x =+C.()sin cos f x x x =D.()sin 2cos 2f x x x =-10.已知数列{}n a ,{}n b ,满足11a =且1,n n a a +是函数2()2nn f x x b x =-+的两个零点,则10b 等于( )A.64B.48C.32D.2411.已知函数)(x f 是R 上的奇函数,且满足)()2(x f x f -=+,当[0,1]x ∈时,()21xf x =-,则方程6()log (3)f x x =-在),0(+∞解的个数是( )A.6B.5C.4D.312.设函数()f x 在R 上存在导数()f x ',x R ∀∈,有2()()f x f x x -+=,在(0,)+∞上()f x x '<,若(4)()84f m f m m --≥-.则实数m 的取值范围为( )A.[2,2]-B.[2,)+∞C.[0,)+∞D.(,2][2,)-∞-+∞二、填空题 :本大题共4小题,每小题5分,共20分,请把答案填在答题卡的横线上.............。
2020-2021学年福州市八县(市)一中高三上学期期中数学试卷(文科)(含解析)

2020-2021学年福州市八县(市)一中高三上学期期中数学试卷(文科)一、单选题(本大题共12小题,共60.0分) 1.已知集合A ={x|x 2−2x −3<0},B ={x||x|<2},则A ∩B 等于( )A. (−1,2)B. (−2,−1)C. (−2,3)D. (−1,3)2.已知i 是虚数单位,则(1+i)2的共轭复数是( )A. −2iB. −2+iC. 2iD. 1+2i3.函数是( )A. 偶函数B. 既是奇函数又是偶函数C. 奇函数D. 非奇非偶函数函数4.已知函数f(x)是函数y =log a x(a >0且a ≠1)的反函数,则函数y =f(x)+2图象恒过点的坐标为( )A. (1,0)B. (0,1)C. (1,2)D. (0,3)5.“a >2”是“一元二次方程x 2+ax +1=0有实根”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件6.已知函数f(x)在R 上为奇函数,对任意的x 1,x 2∈(0,+∞)且x 1≠x 2,总有f(x 2)−f(x 1)x 2−x 1>0且f(1)=0,则不等式f(x)−f(−x)x<0的解集为( )A. (−1,0)∪(0,1)B. (−∞,−1)∪(0,1)C. (−∞,−1)∪(1,+∞)D. (−1,0)∪(1,+∞)7.已知,且对任意,都有则的值是( )A.B.C.D.8.△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c.若B =2A ,a =1,b =,则c = ( ).A. 2B. 2C.D. 19.已知三角形ABD 的边BD 上一点M 满足AM ⃗⃗⃗⃗⃗⃗ =x AB ⃗⃗⃗⃗⃗ +y AD ⃗⃗⃗⃗⃗⃗ ,则1x +4y的最小值为( )A. 9B. 8C. 4D. 310. 函数y =Acos(ωx +φ)(A >0,ω>0,|φ|<π2)的图象如图所示,则函数y =Acos(ωx +φ)的递减区间是( )A. [2kπ+π4,2kπ+5π4],k ∈Z B. [2kπ−π4,2kπ+3π4],k ∈Z C. [kπ+π8,kπ+5π8],k ∈Z D. [kπ−π4,kπ+3π4],k ∈Z11. 下列运用基本不等式求最值,使用正确的个数是( )①已知ab ≠0,求ab +ba 的最小值;解答过程:a b+b a≥2√a b⋅ba=2;②求函数y =x 2+5√x 2+4的最小值;解答过程:可化得y =√x 2+4+1√x 2+4≥2;③设x >1,求y =x +2x−1的最小值;解答过程:y =x +2x−1≥2√2xx−1,当且仅当x =2x−1即x =2时等号成立,把x =2代入2√2x x−1得最小值为4.A. 0个B. 1个C. 2个D. 3个12. 已知函数f(x)=sinx ,f(x)的导数是( )A. 偶函数B. 奇函数C. 增函数D. 减函数二、单空题(本大题共4小题,共20.0分)13. 已知函数f(x)的定义域[−1,5],部分对应值如表,f(x)的导函数y =f′(x)的图象如图所示 x−1 0245 F(x) 1 21.5 21下列关于函数f(x)的命题; ①函数f(x)的值域为[1,2]; ②函数f(x)在[0,2]上是减函数③如果当x ∈[−1,t]时,f(x)的最大值是2,那么t 的最大值为4; ④当1<a <2时,函数y =f(x)−a 最多有4个零点. 其中正确命题的序号是______ .14. 等差数列{a n }中,a n 的前项和为S n ;若有a 1=−2014,S 20152015−S20132013=2,则S 2014= ______ . 15. 已知变量x ,y 满足{x +3≥0x −y +4≥02x +y −4≤0,则z =x +3y 的最大值为______.16. 若方程2 ax 2−1=0在(0,1)内恰有一解,则实数a 的取值范围是____________. 三、解答题(本大题共6小题,共70.0分)17. 在数列{a n }和{b n }中,已知a 1=2,a 2=6,a n+2a n =3a n+12(n ∈N ∗),b n =a n+1a n,(1)求证:数列{b n }是等比数列; (2)求数列{a n }的通项公式;(3)若P n =1log 3a n+12,S n 为数列{p n }的前n 项和,求S n .18. 已知函数f(x)=sinxcosx −sin 2x. (1)求f(x)的最小正周期;(2)设△ABC 为锐角三角形,角A 的对边长√2,角B 的对边长√3,若f(A)=0,求△ABC 的面积.19. 已知函数f(x)=lnx +ax .(1)当a >0时,求函数f(x)的单调区间;(2)若f(x)在[1,e]上的最小值为1,求实数a 的取值范围;(其中e 为自然对数的底数); (3)若f(x)<12x 在(1,+∞)上恒成立,求实数a 的取值范围.20. 各项为整数的数列{a n }的前n 项和为S n ,且满足S n =14a n2+12a n +14(n ∈N +). (1)求a n ;(2)设数列{a n +b n }的首项为1,公比为q 的等比数列,求{b n }的前n 项和S n .21. 已知△ABC 的内角A 、B 、C 所对的边分别为a 、b 、c.向量m ⃗⃗⃗ =(a,√3b),n ⃗ =(cosA,sinB)且m ⃗⃗⃗ //n ⃗ . (I)求A ;(II)若a =3,求△ABC 周长的最大值.22. 已知函数f(x)=alnx+12x2−(1+a)x(x>0),其中a为实数.(1)求函数f(x)的单调区间;(2)若函数f(x)≥0对定义域内的任意x恒成立,求实数a的取值范围;(3)证明:对任意的正整数m,n,不等式1ln(m+1)+1ln(m+2)+⋯+1ln(m+n)>nm(m+n)恒成立.【答案与解析】1.答案:A解析:解:∵A={x|x2−2x−3<0}={x|−1<x<3}=(−1,3),B={x||x|<2}=(−2,2),∴A∩B=(−1,3)∩(−2,2)=(−1,2)故选:A.先分别求出集合A和集合B,然后再求出集合A∩B.本题考查集合的性质和运算,解题时要根据实际情况,注意公式的灵活运用.2.答案:A解析:解:复数(1+i)2=2i的共轭复数为−2i.故选:A.利用复数的运算法则、共轭复数的定义即可得出.本题考查共轭复数的定义、复数的四则运算法则,考查了推理能力与计算能力,属于基础题.3.答案:C解析:试题分析:因为f(−x)=−f(x),所以选C。
福建省福州市八县(市)一中2020-2021学年高三上学期期中联考语文试题(原卷版)

福州市八县(市)一中2020-2021学年高三上学期期中联考语文试题时间:150分钟满分:150分一、现代文阅读(一)现代文阅读Ⅰ阅读下面的文字,完成下面小题。
材料一:一夜之间,官员直播“带货”风靡全国。
许多政府官员化身网红,为农副产品代言,成为老百姓眼中的“带货员”。
领导干部“直播带货”的背后,是一个包括物流、存储、包装、配送、售后服务等多个环节的产业系统。
领导干部的直播间,对接起农户与市场。
从公共管理的角度看,这更是一场政府服务的变革。
在新媒体日新月异的背景下,领导干部做工作不能只是文山会海、发号施令、签字审批、纸上来纸上去,还要走出办公室,走到田间地头,深入移动互联网世界,实实在在为老百姓干实事儿。
不可否认,领导干部“直播带货”,兴起于疫情特殊环境,有其偶然性。
但其必然性,是新技术的滚滚浪潮对基层治理理念、方式和效能产生的根本性影响。
在一些地方的实践中,也确实出现官员“直播带货”走样变形的情况。
部分领导干部将直播间当成秀场,有的地方专门发文搞摊派,有的地方“亏本赚吆喝”,搞成了形式主义。
然而,以发展的眼光来看,任何一种新兴形式在初期都有利有弊,这并不妨碍基层治理理念更新与改革的大方向。
尤其是这种嵌入移动互联网、利用新技术手段优化行政生态、提高行政效能的有益尝试,拓宽了政府与民众互动的空间和渠道,增强了老百姓对政府的信任感,值得大力探索并给以一定的容错空间。
(摘编自翟永冠、唐弢《要带货,更要带新思维》) 材料二:前不久,南昌市民万女士向南昌市市场监督管理局投诉称,自己在某电商平台直播间购买了深圳一家贸易公司销售的虾,收到后发现部分虾已经变质,“虾头都是黑的”,她在直播间向商家询问原因时,竟被污蔑为“专业差评”。
无独有偶,今年,某明星主播一场直播下来销售额超1亿元,但其中多个产品此前涉虚假宣传曾被处罚过。
中国消费者协会发布的《直播电商购物消费者满意度在线调查报告》也显示,消费者对于虚假宣传和商品来源渠道不正等乱象颇为担心。
福建省福州市八县一中高三上学期期中联考数学(理)试题(有答案)(精选)

第一学期八县(市)一中期中联考高中 三 年 数学科(理)试卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求,每小题选出答案后,请把答案填写在答题卡相应位置上...............。
1.设集合2{3,log }P a =,{,}Q a b =,若{0}PQ =,则P Q =( )A.{3,0}B.{3,0,1}C.{3,0,2}D.{3,0,1,2} 2.已知复数131iz i+=-,则下列说法正确的是( ) A.z 的共轭复数为12i -- B.z 的虚部为2iC.5z =D.z 在复平面内对应的点在第三象限 3.函数12()log cos ()22f x x x ππ=-<<的图象大致是( )4.直线4y x =与曲线3y x =在第一象限内围成的封闭图形的面积为( )A.2B.4C.22D.24 5.下列命题中正确的是( )A.命题p :“0x R ∃∈,200210x x -+<”,则命题p ⌝:x R ∀∈,2210x x -+>B .“ln ln a b >”是“22ab>”的充要条件C.命题“若22x =,则x =x =的逆否命题是“若x ≠x ≠则22x ≠”D.命题p :0x R ∃∈,001ln x x -<;命题q :对x R ∀∈,总有20x>;则p q ∧是真命题6.如图,,,D C B 在地平面同一直线上,10DC m =,从,D C 两地测得A 点的仰角分别为30︒和45︒,则A 点离地面的高AB 等于( )A.10mB.C.1)mD.1)m7.已知数列{}n a 是等比数列,数列{}n b 是等差数列,若1598a a a ⋅⋅=-,2586b b b π++=,则4637cos1b b a a +-⋅的值是( )A.12 B.2 C.12- D.2-8.ABC ∆的外接圆的圆心为O ,半径为1,0OA AB AC ++=且OA AB =,则向量CA 在CB 方向上的投影为( )A.12 B.12- D.-9.若函数()f x 同时满足以下三个性质;①()f x 的最小正周期为π;②对任意的x R ∈,都有()()4f x f x π-=-;③()f x 在3(,)82ππ上是减函数,则()f x 的解析式可能是A.()cos()8f x x π=+B.()sin 2cos2f x x x =+C.()sin cos f x x x =D.()sin 2cos 2f x x x =-10.已知数列{}n a ,{}n b ,满足11a =且1,n n a a +是函数2()2nn f x x b x =-+的两个零点,则10b 等于( )A.64B.48C.32D.2411.已知函数)(x f 是R 上的奇函数,且满足)()2(x f x f -=+,当[0,1]x ∈时,()21xf x =-,则方程6()log (3)f x x =-在),0(+∞解的个数是( )A.6B.5C.4D.312.设函数()f x 在R 上存在导数()f x ',x R ∀∈,有2()()f x f x x -+=,在(0,)+∞上()f x x '<,若(4)()84f m f m m --≥-.则实数m 的取值范围为( )A.[2,2]-B.[2,)+∞C.[0,)+∞D.(,2][2,)-∞-+∞二、填空题 :本大题共4小题,每小题5分,共20分,请把答案填在答题卡的横线上.............。
福建省福州市八县一中高三上学期期中联考数学(理)试题(有答案)(精选)

第一学期八县(市)一中期中联考高中 三 年 数学科(理)试卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求,每小题选出答案后,请把答案填写在答题卡相应位置上...............。
1.设集合2{3,log }P a =,{,}Q a b =,若{0}PQ =,则P Q =( )A.{3,0}B.{3,0,1}C.{3,0,2}D.{3,0,1,2} 2.已知复数131iz i+=-,则下列说法正确的是( ) A.z 的共轭复数为12i -- B.z 的虚部为2iC.5z =D.z 在复平面内对应的点在第三象限 3.函数12()log cos ()22f x x x ππ=-<<的图象大致是( )4.直线4y x =与曲线3y x =在第一象限内围成的封闭图形的面积为( )A.2B.4C.22D.24 5.下列命题中正确的是( )A.命题p :“0x R ∃∈,200210x x -+<”,则命题p ⌝:x R ∀∈,2210x x -+>B .“ln ln a b >”是“22ab>”的充要条件C.命题“若22x =,则x =x =的逆否命题是“若x ≠x ≠则22x ≠”D.命题p :0x R ∃∈,001ln x x -<;命题q :对x R ∀∈,总有20x>;则p q ∧是真命题6.如图,,,D C B 在地平面同一直线上,10DC m =,从,D C 两地测得A 点的仰角分别为30︒和45︒,则A 点离地面的高AB 等于( )A.10mB.C.1)mD.1)m7.已知数列{}n a 是等比数列,数列{}n b 是等差数列,若1598a a a ⋅⋅=-,2586b b b π++=,则4637cos1b b a a +-⋅的值是( )A.12 B.2 C.12- D.2-8.ABC ∆的外接圆的圆心为O ,半径为1,0OA AB AC ++=且OA AB =,则向量CA 在CB 方向上的投影为( )A.12 B.12- D.9.若函数()f x 同时满足以下三个性质;①()f x 的最小正周期为π;②对任意的x R ∈,都有()()4f x f x π-=-;③()f x 在3(,)82ππ上是减函数,则()f x 的解析式可能是A.()cos()8f x x π=+B.()sin 2cos2f x x x =+C.()sin cos f x x x =D.()sin 2cos 2f x x x =-10.已知数列{}n a ,{}n b ,满足11a =且1,n n a a +是函数2()2nn f x x b x =-+的两个零点,则10b 等于( )A.64B.48C.32D.2411.已知函数)(x f 是R 上的奇函数,且满足)()2(x f x f -=+,当[0,1]x ∈时,()21xf x =-,则方程6()log (3)f x x =-在),0(+∞解的个数是( )A.6B.5C.4D.312.设函数()f x 在R 上存在导数()f x ',x R ∀∈,有2()()f x f x x -+=,在(0,)+∞上()f x x '<,若(4)()84f m f m m --≥-.则实数m 的取值范围为( )A.[2,2]-B.[2,)+∞C.[0,)+∞D.(,2][2,)-∞-+∞二、填空题 :本大题共4小题,每小题5分,共20分,请把答案填在答题卡的横线上.............。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
此时不存在x0使h(x0)≥0成立.…………………………………………11分
综上可得,所求a的取值范围是 或a≤ . ……………………12分
7.已知定义在R上的奇函数 满足 ,且 ,则 的值为( )
A. B. C. D.
8.在 中, ,则 的最大值为( )
A. B. C. D.
9.已知点M是△ABC的边BC的中点,点E在边AC上,且 ,则向量 =( )
A. B. C. D.
10.函数 ( , )的最小正周期是 ,若其图象向左平移 个单位后得到的函数为奇函数,则函数 的图象( )
所以 . ………………………………5分
(2)由正弦定理, 中, ,即 ①
………………………………7分
中, ,即 ②
……………………………9分
①÷②得: ,化简得 ,……………11分
所以 .………………………………12分
22、解:(Ⅰ) 依题意 ,定义域为(0, +∞),
∴ , …………3分
①当a+1>0,即a> 时,令 ,∵x>0,∴0<x<1+a,
所以 ………………………………………6分
(2).由题意 ,所以 .…………7分
所以 …………………8分
相减得 …………………9分
…………………………………………………11分
…………………………………………12分
21、解:(1)设 ,则 , , ,………………………………2分 (本小题满分12分)
已知函数 .
(Ⅰ) 设函数 ,求函数h(x)的极值;
(Ⅱ)若 在[1,e]上存在一点x0,使得 成立,求a的取值范围.
2019-2020学年度第一学期八县(市)一中期中联考
高中三年文科数学试卷(答案)
一.选择题:(各5分, 共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答题
此时,h(x) 在区间(0,a+1)上单调递增,
令 ,得x>1+a.
此时,h(x)在区间(a+1,+∞)上单调递减. …………………………4分②当a+1≤0,即a≤ 时, 恒成立,h(x)在区间(0,+∞)上单调递减. ………5分
综上,当a> 时,h(x)在x=1+a处取得极大值h(1+a)= ,无极小值;
A. B. C. D.
3.已知函数 是奇函数,则实数 ( )
A. B. C. D.
4.已知 , , ,则( )
A. B. C. D.
5.若向量 , 是非零向量,则“ ”是“ , 夹角为 ”的()
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
6.函数 在 的图像大致为()
A. B. C. D.
C
D
B
C
C
B
A
C
C
B
D
C
二.填空题(各5分, 共20分)
13. ;( 也正确) 14.52;
15.9;16.
三、解答题:共70分
17、解:(1)由设数列 的公差为 ,则
………………………………2分
解得 , ……………………………………3分
……………………………4分
所以 是首项为3,公差为2的等差数列,通项公式为
当a≤ 时,h(x)在区间(0,+∞)上无极值. …………………6分
(Ⅱ)依题意知,在[1, e]上存在一点x0,使得 成立,即在[1, e]上存在一点x0,使得h(x0)≥0,
故函数 在[1, e]上,有h(x)max≥0. ………………8分
由(Ⅰ)可知,①当a+1≥e, 即a≥ 时,h(x)在[1, e]上单调递增,
∴ , ∴ ,
∵ ,∴ . ……………………9分
②当0<a+1≤1,或a≤ ,即a≤0时,h(x)在[1, e]上单调递减,
∴ ,∴a≤ . ……………………………10分
③当1<a+1<e,即0<a< 时,
由(Ⅱ)可知,h(x)在x=1+a处取得极大值也是区间(0, +∞)上的最大值,
即h(x)max=h(1+a)= ,
17. (本小题满分10分)
为等差数列 的前 项和,已知 ,
(Ⅰ)求数列 的通项公式;
(Ⅱ)设 ,数列 的前 项和为 ,求证 .
18. (本小题满分12分)
已知函数
(Ⅰ)若 求 的值;
(Ⅱ)求函数 最小正周期及单调递减区间.
19. (本小题满分12分)
已知函数 ,曲线 在点 处的切线方程为 .
(Ⅰ)求实数 的值;
13.函数 的单调递增区间是.
14.等差数列 的前 项和为 ,若 ,则 .
15.若 , 满足约束条件 ,则 的最大值为__________.
16.已知函数 ,若函数 恰有两个不同的零点,则实数 的取值范围是.
3、解答题:本大题共6题,共70分.请在答题卡指定区域内作答,解答时应写出证明过程或演算步骤.
……………………………5分
(2)由
……………………7分
……………………………10分
18、解:
………………………………………2分
= …………………………………………4分
= …………………………………………6分
(2)
= …………………………………………8分
的最小正周期为T= …………………………………………9分
(Ⅱ)求函数 在 的最值.
20.(本小题满分12分)
已知数列 满足 , ,其中 为数列 的前n项和.
(Ⅰ)求数列 的通项公式;
(Ⅱ)设 是首项为1,公差为2的等差数列,求数列 的前 项和 .
21. (本小题满分12分)
如图,四边形 中 , , ,设 .
(Ⅰ)若 面积是 面积的4倍,求 ;
(Ⅱ)若 ,求 .
福建省福州市八县(市、区)一中2020届高三数学上学期期中联考试题 文
考试日期:11月14日完卷时间:120分钟 满 分:150分
第I卷(选择题共60分)
一、选择题:每小题各5分,共60分.在每小题给出的四个选项中,只有一项是符合题意要求的.
1.已知集合 , ,则 ()
A. B. C. D.
2.若复数 满足 ,则 的共轭复数 =( )
当 时, , 单调递增,………………………10分
,∵ , ,且 ,
∴ .………………………………………………12分
20、解:(1).由 , ,当 时,可得 .…………………………1分
当 时, ,两式相减得: ,即 ,
…………………………3分
且 .…………………………4分
故 是以1为首项,3为公比的等比数列。…………………………5分
由 ,解得
…………………………………………11分
所以 的单调递减区间为 …………………12分
19、解:(1) ,………………………………1分
则 ,………………………………4分
.………………………………6分
(2) 的定义域为 , ,
令 ,则 ,………………………………………………8分
当 时, , 单调递减;
A.关于点 对称B.关于直线 对称
C.关于点 对称D.关于直线 对称
11.若 , , ,则 的最小值为()
A. B. C. D.
12.已知函数 的定义域为 ,其图象关于点 中心对称,其导函数 ,当 时, ,则不等式 的解集为( )
A. B. C. D.
第Ⅱ卷(非选择题共90分)
二、填空题:每小题各5分, 共20分.把答案填在答题卡的相应位置上.
